Đề thi thử Toán THPTQG 2019 lần 3 trường chuyên Đại học Vinh – Nghệ An

Giới thiệu đến quý thầy, cô giáo cùng toàn thể các em học sinh lớp 12 đề thi thử Toán THPTQG 2019 lần 3 trường THPT chuyên Đại học Vinh – Nghệ An

17 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

44 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
Trang 1/6 - Mã đề thi 132
TRƯỜNG ĐẠI HỌC VINH
TRƯỜNG THPT CHUYÊN
(Đề thi gồm 06 trang)
ĐỀ THI THỬ THPT QUỐC GIA NĂM 2019 – LẦN 3
Môn: TOÁN
Thời gian làm bài: 90 phút
(50 câu hỏi trắc nghiệm)
Mã đề thi
132
Họ và tên thí sinh: ..................................................................... Số báo danh: ................................
Câu 1: Cho số phức
zi2.=- +
Trong hình bên điểm biểu diễn số
phức
z
là
A.
Q.
B. M.
C. P. D. N .
Câu 2: Tất cả các nguyên hàm của hàm
fx
x
1
()
32
=
-
là
A.
23 2 .xC--+
B.
23 2 .xC-+
C.
2
32 .
3
xC-+
D.
2
32 .
3
xC--+
Câu 3: Cho hình chóp SABCD. có đáy ABCD là hình vuông cạnh
a,
SA a
và SA vuông góc với mặt
phẳng đáy. Thể tích của khối chóp
SABCD. bằng
A.
a
3
.
6
B.
a
3
.
3
C. a
3
. D.
a
3
2
.
3
Câu 4: Cho hàm số
yfx()
có đồ thị như hình bên. Hàm số đã
cho nghịch biến trên khoảng
A.

2; 0 .
B.

0; 2 .
C.

2; 3 .
D.

3; 1 .
Câu 5: Cho khối nón có độ dài đường cao bằng a2 và bán kính đáy bằng a. Thể tích của khối nón đã cho
bằng
A.
a
3
2
.
3
B.
a
3
.
3
C.
a
3
2.
D.
a
3
4
.
3
Câu 6:
Trong không gian
,Oxyz
cho hai điểm
(2; 1;3)A --
và
(0; 3; 1).B
Gọi
()a
là mặt phẳng trung trực
của
.AB Một vectơ pháp tuyến của
()a
có tọa độ là
A.
(2; 4; 1 ).-
B.
(1; 2; 1).-
C.
(1;1;2).-
D.
(1; 0; 1).
Câu 7: Cho cấp số nhân
()
n
u
có
12
1, 2.uu==-
Mệnh đề nào sau đây đúng ?
A.
2018
2019
2.u =-
B.
2019
2019
2.u =
C.
2019
2019
2.u =-
D.
2018
2019
2.u =
Câu 8:
Với
ab,
là các số thực dương bất kỳ,
2
2
log
a
b
bằng
A.
()
22
log log 2 .ab-
B.
2
1
log .
2
a
b
C.
22
log 2 log .ab-
D.
2
2log .
a
b
Câu 9: Từ các chữ số
1, 2, 3,..., 9
lập được bao nhiêu số có 3 chữ số đôi một khác nhau ?
A.
9
3. B.
3
9
.A
C.
3
9. D.
3
9
.C
Trang 2/6 - Mã đề thi 132
Câu 10: Cho hàm số
yfx()
có đồ thị như hình bên. Trên đoạn
3; 3


hàm số đã cho có mấy điểm cực trị ?
A. 4. B. 2.
C.
5.
D. 3.
Câu 11: Hình bên là đồ thị của hàm số nào dưới đây ?
A. yx
2
2. B. yx x
42
2.
C. yx x
42
2. D. yx x
2
2.
Câu 12: Trong không gian
Oxyz,
một vectơ chỉ phương của đường thẳng
xyz133
:
12 5


có tọa
độ là
A.
(1; 2; 5).
B.
(1; 2; 5).
C.
(1;3; 3).
D.
(1;3;3).
Câu 13: Trong không gian
Oxyz,
cho điểm
I(1; 2; 5)
và mặt phẳng
xyz(): 2 2 2 0.

Phương trình
mặt cầu tâm
I
và tiếp xúc với
()
là
A. xyz
222
(1)(2)(5)9. B. xyz
222
(1)(2)(5)9.
 
C. xyz
222
(1)(2)(5)3. D. xyz
222
(1)(2)(5)3.
 
Câu 14: Khi đặt
x
t3 = thì phương trình
xx11
9 3 30 0
++
--= trở thành
A.
2
3100.tt-- = B.
2
9 3 10 0.tt-- = C.
2
10 0.tt-- = D.
2
2100.tt-- =
Câu 15: Cho
fx()
và
gx()
là các hàm số liên tục bất kì trên đoạn
ab;.
Mệnh đề nào sau đây đúng ?
A.
bbb
aaa
f x g x dx f x dx g x dx() () () () .

B.

bbb
aaa
f x g x dx f x dx g x dx() () () () .

C.

bbb
aaa
fx gx dx fxdx gxdx() () () () .

D.

bbb
aaa
f x g x dx f x dx g x dx() () () () .

Câu 16:
Gọi
,mM
lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số
x
fx x() 2 cos
2
p
=+
trên đoạn
2; 2 .
éù
-
êú
ëû
Giá trị của
mM+
bằng
A.
0.
B. 2. C. 4.- D. 2.-
Câu 17: Trong không gian
Oxyz,
cho đường thẳng
xyz
d
21
:
122

và mặt phẳng
Px yz(): 2 5 0.
Tọa độ giao điểm của d với
P()
là
A.
(3; 1; 2).
B.
(2; 1; 1).
C.
(1; 3; 2).
D.
(1; 3; 2).
Câu 18: Cho hình lập phương
ABCD A B C D.

có cạnh bằng a. Diện tích xung quanh của hình trụ có hai
đáy là hai hình tròn ngoại tiếp hai hình vuông
ABCD và ABCD

bằng
A.
a
2
22 .
B.
a
2
2.
C.
a
2
.
D.
a
2
2.
Trang 3/6 - Mã đề thi 132
Câu 19: Cho hàm số
fx()
có đạo hàm
()
()
()
x
fx x x x x
2
2
() 2 2 4, .
¢
=+ - -"Î
Số điểm cực trị của
fx()
là
A. 2. B. 1. C. 4. D. 3.
Câu 20: Cho hàm số
yfx()=
có đồ thị như hình bên. Hàm
số
yfx2()=-
đồng biến trên khoảng
A.
(
)
1; 2 .
B.
(
)
2; 3 .
C.
()
1; 0 .-
D.
()
1; 1 .-
Câu 21: Cho số phức
z
thỏa mãn
262.zz i+=+
Điểm biểu diễn số phức
z
có tọa độ là
A.
()
2; 2 .-
B.
()
2; 2 .--
C.
(
)
2; 2 .
D.
()
2; 2 .-
Câu 22: Bất phương trình
()
()
xx x
2
42
log 3 log 9-> -
có bao nhiêu nghiệm nguyên ?
A. 1. B. Vô số. C. 3. D. 4.
Câu 23: Đồ thị hàm số
2
1
1
xx
y
x
++
=
-
có bao nhiêu đường tiệm cận ?
A. 2. B. 3. C. 4. D. 1.
Câu 24: Hàm số
log
a
yx=
và
log
b
yx=
có đồ thị như
hình bên. Đường thẳng
3y =
cắt hai đồ thị tại các điểm
có hoành độ là
12
,.xx
Biết rằng
21
2,xx=
giá trị
a
b
bằng
A.
1
.
3
B.
3
2.
C. 2. D. 3.
Câu 25: Hàm số
()
3
3
e
yx x=-
có bao nhiêu điểm cực trị ?
A. 2. B.
0.
C. 3. D. 1.
Câu 26:
Cho hình hộp chữ nhật
ABCD A B C D.

có
AB a AD a AC a,2, 6

. Thể tích của khối hộp
chữ nhật
ABCD A B C D.

bằng
A.
a
3
3
.
3
B.
a
3
2
.
3
C. a
3
2. D.
a
3
23 .
Câu 27: Gọi
()
D
là hình phẳng giới hạn bởi các đường
2, 0, 0
x
yyx===
và 2.x = Thể tích V của khối
tròn xoay tạo thành khi quay
()
D
xung quanh trục Ox được tính bởi công thức
A.
2
1
0
2.
x
Vdxp
+
=
ò
B.
x
Vdx
2
1
0
2.
+
=
ò
C.
2
0
4.
x
Vdx=
ò
D.
2
0
4.
x
Vdxp=
ò
Câu 28: Trong không gian
Oxyz,
cho hai đường thẳng
xyz
1
123
:
21 2


và
xyz
2
312
:.
11 4


Góc giữa hai đường thẳng
12
,
bằng
A.
0
30 . B.
0
135 . C.
0
60 . D.
0
45 .
Trang 4/6 - Mã đề thi 132
Câu 29: Gọi
zz
12
,
là các nghiệm phức của phương trình zz
2
230.-+= Mô đun của
zz
34
12
bằng
A. 81. B. 16. C.
27 3 .
D.
82.
Câu 30: Cho hình chóp tứ giác đều SABCD. có
AB a SA a2, 5.
Góc giữa hai mặt phẳng
SAB()
và
ABCD()
bằng
A.
0
60 . B.
0
45 . C.
0
30 . D.
0
75 .
Câu 31: Cho fx x x
3
() ( 1) 3 3.=- -+ Đồ thị hình bên là của
hàm số có công thức
A.
(
)
11.yfx=- + +
B.
(
)
11.yfx=- + -
C.
(
)
11.yfx=- - +
D.
(
)
11.yfx=- - -
Câu 32: Biết
()
xxx
dx a b c
xxx
3
2
43
4
cos sin cos 1
ln 2 ln 1 3 ,
cos sin cos
p
p
++
=+ + +
+
ò
với
abc,,
là các số hữu tỉ. Giá
trị của
abc bằng
A. 2.- B. 4.- C.
0.
D. 6.-
Câu 33: Hai bạn Công và Thành cùng viết ngẫu nhiên ra một số tự nhiên gồm hai chữ số phân biệt. Xác suất
để hai số được viết ra có ít nhất một chữ số chung bằng
A.
154
.
729
B.
448
.
729
C.
145
.
729
D.
281
.
729
Câu 34: Người ta xếp hai quả cầu có cùng bán kính r vào một
chiếc hộp hình trụ sao cho các quả cầu đều tiếp xúc với hai đáy,
đồng thời hai quả cầu tiếp xúc với nhau và mỗi quả cầu đều tiếp
xúc với các đường sinh của hình trụ (tham khảo hình vẽ). Biết thể
tích khối trụ là
3
120 cm ,
thể tích mỗi khối cầu bằng
A.
3
10 cm .
B.
3
40 cm .
C.
3
20 cm .
D.
3
30 cm .
Câu 35: Cho hình chóp
SABCD.
có đáy
ABCD
là hình chữ nhật, biết
AB a AD a SA a2, , 3

và
SA
vuông góc với mặt phẳng đáy. Gọi
M là trung điểm cạnh CD. Khoảng cách giữa hai đường thẳng SC và
BM bằng
A.
a33
.
4
B.
a23
.
3
C.
a3
.
2
D.
a3
.
3
Câu 36: Xét các số phức
zw,
thỏa mãn
wi z iw2, 2 .-= +=
Gọi
12
,zz
lần lượt là các số phức mà tại
đó
z
đạt giá trị nhỏ nhất và đạt giá trị lớn nhất. Mô đun
12
zz+
bằng
A.
32.
B. 3. C. 6. D.
62.
Câu 37: Cho hàm số
fx()
có bảng xét dấu đạo
hàm như hình bên. Hàm số
(
)
12yf x=-
đồng
biến trên khoảng
A.
1
;1.
2
æö
÷
ç
÷
-
ç
÷
ç
÷
ç
èø
B.
1
2; .
2
æö
÷
ç
÷
--
ç
÷
ç
÷
ç
èø
C.
3
0; .
2
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
D.
3
;3.
2
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
Trang 5/6 - Mã đề thi 132
Câu 38: Trong không gian
Oxyz,
cho hai đường thẳng
xt
dyt
zt
12
:;
13


xt
dy t
zt
2
:12
2




và mặt phẳng
Pxyz(): 2 0.
Đường thẳng vuông góc với mặt phẳng
P()
và cắt hai đường thẳng
dd,
có phương
trình là
A.
xyz312
.
111


B.
xyz111
.
114


C.
xyz211
.
111


D.
xyz114
.
222


Câu 39: Biết rằng
x
xe là một nguyên hàm của
fx()-
trên khoảng
(; ).

Gọi
Fx()
là một nguyên hàm
của
x
fxe()
¢
thỏa mãn
F(0) 1,=
giá trị của
F(1)-
bằng
A.
e5
.
2
-
B.
7
.
2
C.
5
.
2
D.
e7
.
2
-
Câu 40: Có bao nhiêu số nguyên
m
để phương trình 3
x
xme+= có 2 nghiệm phân biệt ?
A.
7.
B. 6. C.
5.
D. Vô số.
Câu 41: Hàm số
x
fx m
x
2
()
1

với m là tham số thực có nhiều nhất bao nhiêu điểm cực trị ?
A.
5.
B.
4.
C.
3.
D.
2.
Câu 42: Cho
fx()
mà đồ thị hàm số
yfx()
như
hình bên. Bất phương trình
x
fx m() sin
2

nghiệm đúng với mọi
x 1; 3



khi và chỉ khi
A.
mf(1) 1.
B.
mf(0).
C.
mf(2).
D.
mf(1) 1.
Câu 43: Có bao nhiêu số nguyên
a 2019; 2019
để phương trình

x
xa
x
11
ln 5
31

có 2
nghiệm phân biệt ?
A. 2015. B. 2014. C. 2022. D.
0.
Câu 44: Cho
fx()
mà đồ thị hàm số
yfx()
như hình bên.
Hàm số

yfx x x
2
12
đồng biến trên khoảng
A.
1; 2 .
B.

1; 0 .
C.
0; 1 .
D.

2; 1 .
Câu 45: Cho hàm số
fx()
có đạo hàm liên tục trên thỏa mãn
f (0) 3
và
fx f x x x x
2
() (2 ) 2 2, .
Tích phân xf x d x
2
0
()
bằng
A.
5
.
3
B.
4
.
3
C.
10
.
3
D.
2
.
3
Trang 6/6 - Mã đề thi 132
Câu 46: Cho khối hộp
ABCD A B C D.

có thể tích bằng
V .
Gọi
MNPQEF,,,,,
lần lượt là tâm các
hình bình hành
ABCD A B C D ABB A BCC B CDD C DAA D,,,,,.
 
Thể tích khối đa diện có các đỉnh
MPQEFN,,,,,
bằng
A.
V
.
4
B.
V
.
2
C.
V
.
6
D.
V
.
3
Câu 47: Trong không gian ,Oxyz cho đường thẳng
342
:
211
xyz
d
---
== và hai điểm
(6 ; 3 ; 2),A -
B(1; 0; 1).
Gọi D là đường thẳng đi qua
,B
vuông góc với d và thỏa mãn khoảng cách từ A đến D là
nhỏ nhất. Một véctơ chỉ phương của
D có tọa độ là
A.
(2; 1 ; 3).--
B.
(1; 1; 3).-
C.
(1; 2; 4).-
D.
(1; 1; 1).--
Câu 48: Trong không gian
Oxyz,
cho điểm
A(2; 3; 4),
đường thẳng
xyz
d
12
:
212


và mặt cầu
Sx y z
222
( ) : ( 3) ( 2) ( 1) 20.
Mặt phẳng
P()
chứa đường thẳng
d
thỏa mãn khoảng cách từ
điểm
A đến
P()
lớn nhất. Mặt cầu
S()
cắt
P()
theo đường tròn có bán kính bằng
A.
5.
B. 1. C. 4. D. 2.
Câu 49: Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên
gạch hoa hình vuông cạnh
40 (cm) như hình bên. Biết rằng người thiết kế
đã sử dụng các đường cong có phương trình
xy
24
4
và

xy
3
2
41
để tạo hoa văn cho viên gạch. Diện tích phần được tô
đậm gần nhất với giá trị nào dưới đây ?
A.
506
(cm
2
). B.
507
(cm
2
). C.
747
(cm
2
). D.
746
(cm
2
).
Câu 50: Xét các số phức
zw,
thỏa mãn
ziw i2, 2 5 1.

Giá trị nhỏ nhất của
zwz
2
4
bằng
A. 8. B. 4. C.
2293.
D.
2295.
-----------------------------------------------
----------- HẾT ----------
Câu Mã 132 Mã 209 Mã 357 Mã 485
1D A A D
2C D D D
3B A C D
4C C C A
5A B D D
6B D D C
7D B C C
8C C B A
9B D A A
10 D B D A
11 B D B B
12 A B D B
13 A A B C
14 A B A B
15 B D D C
16 D B B A
17 D A C A
18
B
D
C
D
19 D D D D
20 A D D B
21 A D A C
22 C A C C
23 B B A A
24 B D A C
25 D C C C
26 C C C C
27 D A C C
28 D C A A
29 C B D D
30 A C B B
31 A C B B
32 B A B C
33 D C B D
34 C A C A
35 D C B B
36 C B B D
37 C B C A
38 A C A B
39 B A A B
40 A A A A
41 B A C D
42 A D D D
43 A D D A
44 A D C B
45 C C B D
46 C B A B
47 B C B A
48 D B C B
49 C A D C
50 A D A A
ĐÁP ÁN MÔN TOÁN LẦN 3 - 2019
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 1
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
CHUYÊN ĐẠI HỌC VINH
ĐỀ THI THỬ THPT LẦN 3 QG NĂM 2019
MÔN: TOÁN
Thời gian làm bài: 90 phút
(không kể thời gian giao đề)
Mã Đề: 209
(Đề gồm 06 trang)
Họ và tên: .................................................................................................... SBD: ..................................................... .
Câu 1: Cho khối nón có độ dài đường cao bằng
2a
và bán kính đáy bằng
a
. Thể tích của khối
nón đã cho bằng
A.
3
2
3
a
. B.
3
4
3
a
. C.
3
3
a
. D.
3
2 a
.
Câu 2: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA a
và
SA
vuông
góc với mặt phẳng đáy. Thể tích khối chóp
.S ABCD
bằng
A.
3
6
a
. B.
3
2
3
a
. C.
3
a
. D.
3
3
a
.
Câu 3: Trong không gian
Oxyz
, một vectơ chỉ phương của đường thẳng
1 3 3
:
1 2 5
x y z
có tọa độ là
A.
1;2; 5
. B.
1;3;3
. C.
1;3; 3
. D.
1; 2; 5
.
Câu 4: Với
a
,
b
là các số thực dương bất kì,
2
2
log
a
b
bằng
A.
2
2log
a
b
. B.
2
1
log
2
a
b
. C.
2 2
log 2loga b . D.
2 2
log log 2a b
.
Câu 5: Trong không gian
Oxyz
, cho hai điểm
2; 1;3A
và
0;3;1B
. Gọi
là mặt phẳng
trung trực của
AB
. Một vectơ pháp tuyến của
có tọa độ là
A.
2;4; 1
. B.
1;2; 1
. C.
1;1;2
. D.
1;0;1
.
Câu 6: Cho cấp số nhân
n
u
có
1 2
1, 2u u . Mệnh đề nào sau đây đúng?
A.
2018
2019
2u
. B.
2019
2019
2u
. C.
2019
2019
2u
. D.
2018
2019
2u
Câu 7: Hình dưới đây là đồ thị của hàm số nào?
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
A.
2
2y x
. B.
4 2
2y x x . C.
4 2
2y x x . D.
2
2y x x .
Câu 8: Trong không gian
Oxyz
, cho điểm
1;2;5I
và mặt phẳng
: 2 2 2 0x y z
.
Phương trình mặt cầu tâm
I
và tiếp xúc với
là
A.
2 2 2
1 2 5 3x y z
. B.
2 2 2
1 2 5 3x y z
.
C.
2 2 2
1 2 5 9x y z
. D.
2 2 2
1 2 5 9x y z
.
Câu 9: Cho hàm số
y f x
có đồ thị như hình vẽ dưới đây
Trên đoạn
3;3
hàm số đã cho có mấy điểm cực trị?
A.
4
. B.
5
. C.
2
. D.
3
.
Câu 10: Cho
f x
và
g x
là các hàm số liên tục bất kì trên đoạn
;a b
. Mệnh đề nào sau đây
đúng ?
A.
d d d
b b
a
b
a a
x f x x gf x g x x x
. B.
d d d
b b
a
b
a a
x f x x gf x g x x x
.
C.
d d d
b bb
a a a
x f x x g x xf x g x
. D.
d d d
b b
a
b
a a
x f x x gf x g x x x
.
Câu 11: Cho hàm số
y f x
có đồ thị như hình vẽ bên.
Hàm số đã cho nghịch biến trên khoảng
A.
0;2
. B.
2;0
. C.
3; 1
. D.
2;3
.
Câu 12: Tất cả các nguyên hàm của hàm
1
3 2
f x
x
là
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 3
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
A. 2 3 2 x C . B.
2
3 2
3
x C
. C.
2
3 2
3
x C
. D. 2 3 2 x C .
Câu 13: Khi đặt
3
x
t
thì phương trình
1 1
9 3 30 0
x x
trở thành
A.
2
3 10 0 t t
. B.
2
9 3 10 0 t t
. C.
2
10 0 t t
. D.
2
2 1 0 t t
.
Câu 14: Từ các chữ số
1,2,3,...,9
lập được bao nhiêu số có 3 chữ số đôi một khác nhau
A.
9
3
. B.
3
9
A
. C.
3
9
. D.
3
9
C
.
Câu 15: Cho số phức
2z i
. Trong hình bên điểm biểu diễn số phức
z
là
A.
.M
B.
.Q
C.
.P
D.
.N
Câu 16: Trong không gian
Oxyz
, cho hai đường thẳng
1
1 2 3
:
2 1 2
x y z
và
2
3 1 2
:
1 1 4
x y z
. Góc giữa hai đường thẳng
1 2
, bằng
A.
0
30
. B.
0
45
. C.
0
60
. D.
0
135
.
Câu 17: Cho số phức
z
thỏa mãn
2 6 2 . z z i
Điểm biểu diễn số phức
z
có tọa độ là
A.
2; 2
. B.
2; 2
. C.
2;2
. D.
2;2
.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
2 1
:
1 2 2
x y z
d
và mặt phẳng
: 2 5 0P x y z
. Tọa độ giao điểm của
d
và
P
là
A.
2;1; 1
. B.
3; 1; 2
. C.
1;3; 2
. D.
1;3;2
Câu 19: Bất phương trình
2
4 2
log 3 log 9x x x
có bao nhiêu nghiệm nguyên?
A. vô số. B.
1
. C.
4
. D.
3
Câu 20: Hàm số
3
3
e
y x x
có bao nhiêu điểm cực trị?
A.
2
. B.
0
. C.
3
. D.
1
.
Câu 21: Gọi
D
là hình phẳng giới hạn bởi các đường 2 , 0, 0
x
y y x và
2x
. Thể tích
V
của khối tròn xoay tạo thành khi quay
D
quanh trục
Ox
được định bởi công thức
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 4
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
A.
2
1
0
2 dx
x
V
. B.
2
1
0
2 dx
x
V
. C.
2
0
4 dx
x
V
. D.
2
0
4 dx
x
V
.
Câu 22: Cho hàm số
y f x
có đồ thị như hình bên.
Hàm số
2 y f x
đồng biến trên khoảng
A.
1;2
. B.
2;3
. C.
1;0
. D.
1;1
.
Câu 23: Đồ thị hàm số
2
1
1
x x
y
x
có bao nhiêu đường tiệm cận
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 24: Hàm số log
a
y x và log
b
y x có đồ thị như hình vẽ dưới đây.
Đường thẳng
3y
cắt hai đồ thị tại các điểm có hoành độ
1
x ,
2
x . Biết rằng
2 1
2x x ,
giá trị của
a
b
bằng
A.
1
3
. B.
3
. C.
2
. D.
3
2
.
Câu 25: Cho hình hộp chữ nhật
.ABCD A B C D
có
, 2 , 6AB a AD a AC a
. Thể tích khối
hộp chữ nhật
.ABCD A B C D
bằng
A.
3
3
3
a
. B.
3
2
3
a
. C.
3
2a
. D.
3
2 3a
.
Câu 26: Cho hàm số
f x
có đạo hàm
2
2
2 2 4 , .
x
f x x x x x
Số điểm cực trị
của
f x
là
A.
2
. B.
4
. C.
3
. D.
1
.
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 5
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Câu 27: Cho hình lập phương
.ABCD A B C D
có cạnh bằng
a
. Diện tích xung quanh của hình
trụ có đáy là hai hình tròn ngoại tiếp hai hình vuông
ABCD
và
A B C D
A.
2
2 a
.
B.
2
2 a
. C.
2
a
.
D.
2
2 2 a
.
Câu 28: Gọi
1 2
,z z là các nghiệm phức của phương trình
2
2 3 0. z z
Mô đun của
3 4
1 2
.z z
bằng
A.
81
. B.
16
. C.
27 3
. D.
8 2
.
Câu 29: Gọi
m
,
M
lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số
2 cos
2
x
f x x
trên đoạn
2;2
. Giá trị của
m M
bằng
A.
2
. B.
2
. C.
0
. D.
4
.
Câu 30: Cho hình chóp đều
S.ABCD
có
2AB a
,
5SA a
. Góc giữa hai mặt phẳng
SAB
và
ABCD
bằng
A.
30
. B.
45
. C.
60
. D.
75
.
Câu 31: Hai bạn Công và Thành cùng viết ngẫu nhiên ra một số tự nhiên gồm 2 chữ số phân
biệt. Xác suất để hai số được viết ra có ít nhất một chữ số chung bằng
A.
145
729
. B.
448
729
. C.
281
729
. D.
154
729
.
Câu 32: Biết rằng
e
x
x
là một nguyên hàm của
f x
trên khoảng
;
. Gọi
F x
là một
nguyên hàm của
e
x
f x
thỏa mãn
0 1F
, giá trị của
1F
bằng
A.
7
2
. B.
5 e
2
. C.
7 e
2
. D.
5
2
.
Câu 33: Cho hình chóp
S.ABCD
có đáy là hình chữ nhật, biết
2 3AB a, AD a, SA a
và
SA
vuông góc với mặt phẳng đáy. Gọi
M
là trung điểm cạnh
CD
. Khoảng cách giữa hai
đường thẳng
SC
và
BM
bằng
A.
3 3
4
a
. B.
2 3
3
a
. C.
3
3
a
. D.
3
2
a
.
Câu 34: Cho hàm số
f x
có bảng xét dấu đạo hàm như hình bên dưới
Hàm số
1 2y f x
đồng biến trên khoảng
A.
3
0;
2
. B.
1
;1
2
. C.
1
2;
2
. D.
3
;3
2
.
Câu 35: Xét các số phức
,z w
thỏa mãn
2, 2 .w i z iw
Gọi
1 2
,z z lần lượt là các số phức mà
tại đó
z
đạt giá trị nhỏ nhất và đạt giá trị lớn nhất. Mô đun
1 2
z z
bằng
A.
3 2
. B.
3
. C.
6
. D.
6 2
.
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 6
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Câu 36: Cho
3
1 3 3f x x x
. Đồ thị hình bên là của hàm số có công thức
A.
1 1y f x
. B.
1 1y f x
. C.
1 1y f x
. D.
1 1y f x
.
Câu 37: Người ta xếp hai quả cầu có cùng bán kính
r
vào một chiếc hộp hình trụ sao cho các
quả cầu đều tiếp xúc với hai đáy, đồng thời hai quả cầu tiếp xúc với nhau và mỗi quả
cầu đề tiếp xúc với đường sinh của hình trụ ( tham khảo hình vẽ). Biết thể tích khối trụ
là
3
120 cm
, thể tích của mỗi khối cầu bằng
A.
3
10 cm
. B.
3
20 cm
. C.
3
30 cm
. D.
3
40 cm
.
Câu 38: Biết
2
3
4 3
4
cos sin cos 1
d ln 2 ln 1 3
cos sin cos
x x x
x a b c
x x x
, với
, ,a b c
là các số hữu tỉ. Giá trị
của
abc
bằng
A.
0
. B.
2
. C.
4
. D.
6
.
Câu 39: Trong không gian
,Oxyz
cho hai đường thẳng
1 2 2
: ; : 1 2
1 3 2
x t x t
d y t d y t
z t z t
và mặt
phẳng
: 2 0.P x y z
Đường thẳng vuông góc với mặt phẳng
P
và cắt cả hai
đường thẳng
,d d
có phương trình là
A.
3 1 2
1 1 1
x y z
. B.
1 1 1
1 1 4
x y z
.
C.
2 1 1
1 1 1
x y z
. D.
1 1 4
2 2 2
x y z
.
Câu 40: Có bao nhiêu số nguyên
m
để phương trình
3
x
x me
có 2 nghiệm phân biệt?
A.
7
. B.
6
. C.
5
. D. Vô số.
Câu 41: Cho
f x
mà đồ thị hàm số
y f x
như hình bên. Hàm số
2
1 2y f x x x
đồng biến trên khoảng
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 7
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
A.
1;2 .
B.
1;0 .
C.
0;1 .
D.
2; 1 .
Câu 42: Có bao nhiêu số nguyên
2019;2019a
để phương trình
1 1
ln 5 3 1
x
x a
x
có
hai nghiệm phân biệt?
A.
0
. B.
2022
. C.
2014
. D.
2015
.
Câu 43: Cho hàm số
( )f x
có đạo hàm liên tục trên
và thỏa mãn
(0) 3f
và
2
( ) (2 ) 2 2,f x f x x x x . Tích phân
2
0
( )dxf x x
bằng
A.
4
3
. B.
2
3
. C.
5
3
. D.
10
3
.
Câu 44: Hàm số
2
1
x
f x m
x
(với
m
là tham số thực) có nhiều nhất bao nhiêu điểm cực
trị?
A.
2
. B.
3
. C.
5
. D.
4
.
Câu 45: Cho hình hộp
. ' ' ' 'ABCD A B C D
có thể tích bằng
V
. Gọi
, , , , ,M N P Q E F
lần lượt là tâm
các hình bình hành
, ' ' ' ', ' ', ' ', ' ', ' '.ABCD A B C D ABB A BCC B CDD C DAA D
Thể tích khối
đa diện có các đỉnh
, , , , ,M P Q E F N
bằng
A.
4
V
. B.
2
V
. C.
6
V
. D.
3
V
.
Câu 46: Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên gạch hình vuông cạnh
40 cm
như hình bên. Biết rằng người thiết kế đã sử dụng các đường cong có phương
trình
2 2
4x y
và
3 2
4( 1)x y
để tạo hoa văn cho viên gạch. Diện tích phần được tô
đạm gần nhất với giá trị nào dưới đây?
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 8
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
A.
2
506 cm
. B.
2
747 cm
. C.
2
507 cm
. D.
2
746 cm
.
Câu 47: Xét các số phức
z
,
w
thỏa mãn
2z
,
2 5 1iw i
. Giá trị nhỏ nhất của
2
4z wz
bằng
A.
4
. B.
2 29 3
. C.
8
. D.
2 29 5
.
Câu 48: Cho
( )f x
mà đồ thị hàm số
'( )y f x
như hình vẽ bên
Bất phương trình
( ) sin
2
x
f x m
nghiệm đúng với mọi
1;3x
khi và chỉ khi
A.
(0)m f
. B.
(1) 1m f
. C.
( 1) 1m f
. D.
(2)m f
.
Câu 49: Trong không gian
Oxyz
, cho đường thẳng
3 4 2
:
2 1 1
x y z
d
và 2 điểm
6;3; 2A
,
1;0; 1B
. Gọi
là đường thẳng đi qua
B
, vuông góc với
d
và thỏa mãn khoảng cách
từ
A
đến
là nhỏ nhất. Một vectơ chỉ phương của
có tọa độ
A.
1;1; 3
. B.
1; 1; 1
. C.
1;2; 4
. D.
2; 1; 3
.
Câu 50: Trong không gian
Oxyz
, cho điểm
2; ;3;4A
, đường thẳng
1 2
:
2 1 2
x y z
d
và mặt
cầu
2 2 2
: 3 2 1 20S x y z
. Mặt phẳng
P
chứa đường thẳng
d
thỏa mãn
khoảng cách từ điểm
A
đến
P
lớn nhất. Mặt cầu
S
cắt
P
theo đường tròn có
bán kính bằng
A. 5 . B.
1
. C.
4
. D.
2
.
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 9
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
BẢNG ĐÁP ÁN
1A 2D 3A 4C 5B 6D 7B 8C 9D 10B
11D 12B 13A 14B 15D 16B 17A 18D 19D 20D
21D 22A 23B 24D 25C 26C 27A 28C 29B 30C
31C 32A 33C 34A 35C 36B 37B 38C 39A 40A
41A 42D 43D 44D 45C 46B 47C 48B 49A 50D
Câu 1: Cho khối nón có độ dài đường cao bằng
2a
và bán kính đáy bằng
a
. Thể tích của khối
nón đã cho bằng
A.
3
2
3
a
. B.
3
4
3
a
. C.
3
3
a
. D.
3
2 a
.
Lời giải
Chọn A
Thể tích khối nón:
3
2
1 2
2
3 3
a
V a a
.
Câu 2: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA a
và
SA
vuông
góc với mặt phẳng đáy. Thể tích khối chóp
.S ABCD
bằng
A.
3
6
a
. B.
3
2
3
a
. C.
3
a
. D.
3
3
a
.
Lời giải
Chọn D
a
2a
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 10
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Thể tích khối chóp
3
.
1
.
3 3
S ABCD ABCD
a
V S SA
Câu 3: Trong không gian
Oxyz
, một vectơ chỉ phương của đường thẳng
1 3 3
:
1 2 5
x y z
có tọa độ là
A.
1;2; 5
. B.
1;3;3
. C.
1;3; 3
. D.
1; 2; 5
.
Lời giải
Chọn A
Câu 4: Với
a
,
b
là các số thực dương bất kì,
2
2
log
a
b
bằng
A.
2
2log
a
b
. B.
2
1
log
2
a
b
. C.
2 2
log 2loga b . D.
2 2
log log 2a b
.
Lời giải
Chọn C
Ta có:
2
2 2 2 2 2
2
log log log log 2log
a
a b a b
b
.
Câu 5: Trong không gian
Oxyz
, cho hai điểm
2; 1;3A
và
0;3;1B
. Gọi
là mặt phẳng
trung trực của
AB
. Một vectơ pháp tuyến của
có tọa độ là
A.
2;4; 1
. B.
1;2; 1
. C.
1;1;2
. D.
1;0;1
.
Lời giải
Chọn B
Vì
là mặt phẳng trung trực của
AB
nên vectơ pháp tuyến của mặt phẳng
là :
2;4; 2 2 1; 2; 1n AB
, từ đây ta suy ra
1
1; 2; 1n
là một vectơ pháp tuyến
của
Câu 6: Cho cấp số nhân
n
u
có
1 2
1, 2u u . Mệnh đề nào sau đây đúng?
A.
2018
2019
2u
. B.
2019
2019
2u
. C.
2019
2019
2u
. D.
2018
2019
2u
C
B
A
D
S
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 11
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Lời giải
Chọn D
Cấp số nhân có
1 2
1, 2u u
2q
. Vậy:
2018
2018 2018
2019 1
2 2u u q
Câu 7: Hình dưới đây là đồ thị của hàm số nào?
A.
2
2y x
. B.
4 2
2y x x
. C.
4 2
2y x x
. D.
2
2y x x
.
Lời giải
Chọn B
Dựa vào đồ thị đã cho ta nhận thấy hàm số cần tìm chỉ có một cực trị nên đáp án C bị
loại.
Mặt khác đồ thị hàm số đã cho có tính đối xứng qua trục tung nên đáp án D bị loại.
Đồ thị hàm số đã cho đi qua hai điểm
1;0
và
1;0
nên đáp án A bị loại.
Vậy hàm số cần tìm là hàm số ở đáp án B.
Câu 8: Trong không gian
Oxyz
, cho điểm
1;2;5I
và mặt phẳng
: 2 2 2 0x y z
.
Phương trình mặt cầu tâm
I
và tiếp xúc với
là
A.
2 2 2
1 2 5 3x y z
. B.
2 2 2
1 2 5 3x y z
.
C.
2 2 2
1 2 5 9x y z
. D.
2 2 2
1 2 5 9x y z
.
Lời giải
Chọn C
Từ tọa độ tâm
1;2;5I
ta loại được hai đáp án B, D.
d
R
α( )
I
H
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 12
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Mặt khác theo bài ta có
2
2 2
1 2.2 2.5 2
, 3
1 2 2
R d I
nên đáp án A loại.
Vậy phương trình mặt cầu cần tìm có phương trình
2 2 2
1 2 5 9x y z
.
Vậy chọn C
Câu 9: Cho hàm số
y f x
có đồ thị như hình vẽ dưới đây
Trên đoạn
3;3
hàm số đã cho có mấy điểm cực trị?
A.
4
. B.
5
. C.
2
. D.
3
.
Lời giải
Chọn D
Quan sát đồ thị đã cho ta nhận thấy trên đoạn
3;3
hàm số
y f x
có ba điểm cực
trị.
Câu 10: Cho
f x
và
g x
là các hàm số liên tục bất kì trên đoạn
;a b
. Mệnh đề nào sau đây
đúng ?
A.
d d d
b b
a
b
a a
x f x x gf x g x x x
. B.
d d d
b b
a
b
a a
x f x x gf x g x x x
.
C.
d d d
b bb
a a a
x f x x g x xf x g x
. D.
d d d
b b
a
b
a a
x f x x gf x g x x x
.
Lời giải
Chọn B
Theo tính chất của tích phân ta có đáp án B là mệnh đề đúng.
Mặt khác, ta có nhận xét:
+ A sai khi
f x g x
với
;x a b
.
+ C sai khi
0.
b b
a a
f x dx g x dx
+ D sai khi
0
b
a
f x g x dx
.
Câu 11: Cho hàm số
y f x
có đồ thị như hình vẽ bên.
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 13
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Hàm số đã cho nghịch biến trên khoảng
A.
0;2
. B.
2;0
. C.
3; 1
. D.
2;3
.
Lời giải
Chọn D
Dựa vào đồ thị ta có hàm số nghịch biến trên các khoảng
1;1
và
2;3 .
Câu 12: Tất cả các nguyên hàm của hàm
1
3 2
f x
x
là
A. 2 3 2 x C . B.
2
3 2
3
x C
. C.
2
3 2
3
x C
. D. 2 3 2 x C .
Lời giải
Chọn B
Ta có
1
1
2
2
3 2
1 1 1 2
3 2 . 3 2 .
1
3 3 3
3 2
2
d d 3 2
x
x x C x Cx
x
Câu 13: Khi đặt
3
x
t
thì phương trình
1 1
9 3 30 0
x x
trở thành
A.
2
3 10 0 t t
. B.
2
9 3 10 0 t t
. C.
2
10 0 t t
. D.
2
2 1 0 t t
.
Lời giải
Chọn A
Ta có
2
1 1
9 3 30 0 9. 3 3.3 30 0
x x x x
.
Do đó khi đặt
3
x
t
ta có phương trình
2 2
9 3 30 0 3 10 0t t t t
.
Câu 14: Từ các chữ số
1,2,3,...,9
lập được bao nhiêu số có 3 chữ số đôi một khác nhau
A.
9
3
. B.
3
9
A
. C.
3
9
. D.
3
9
C
.
Lời giải
Chọn B
Gọi số cần tìm có dạng là
1 2 3 1 1 2 2 3 3 1
0, , , .a a a a a a a a a a
Mỗi bộ ba số
1 2 3
; ;a a a
là một chỉnh hợp chập 3 của 9 phần tử.
Vậy số các số cần tìm là
3
9
A
số.
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 14
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Câu 15: Cho số phức
2z i
. Trong hình bên điểm biểu diễn số phức
z
là
A.
.M
B.
.Q
C.
.P
D.
.N
Lời giải
Chọn D
Ta có
2z i
. Do đó điểm biểu diễn số phức
z
là
2; 1N
.
Câu 16: Trong không gian
Oxyz
, cho hai đường thẳng
1
1 2 3
:
2 1 2
x y z
và
2
3 1 2
:
1 1 4
x y z
. Góc giữa hai đường thẳng
1 2
, bằng
A.
0
30
. B.
0
45
. C.
0
60
. D.
0
135
.
Lời giải
Chọn B
Véc tơ chỉ phương của
1
là
1
2;1; 2u
Véc tơ chỉ phương của
2
là
2
1;1; 4u
1 2
1 2 1 2
2 2
2 2 2 2
1 2
.
2 .1 1.1 2. 4
9 2
cos , cos ,
2
3.3 2
.
2 1 2 . 1 1 4
u u
u u
u u
.
Do đó góc giữa hai đường thẳng
1
và
2
là
0
45
.
Câu 17: Cho số phức
z
thỏa mãn
2 6 2 . z z i
Điểm biểu diễn số phức
z
có tọa độ là
A.
2; 2
. B.
2; 2
. C.
2;2
. D.
2;2
.
Lời giải
Chọn A
Gọi số phức
z x yi
với
,x y
. Theo bài ra ta có
2
2 6 2 3 6 2 .
2
x
x yi x yi i x yi i
y
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 15
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Vậy điểm biểu diễn số phức
z
có tọa độ là
2; 2 .
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
2 1
:
1 2 2
x y z
d
và mặt phẳng
: 2 5 0P x y z
. Tọa độ giao điểm của
d
và
P
là
A.
2;1; 1
. B.
3; 1; 2
. C.
1;3; 2
. D.
1;3;2
Lời giải
Chọn D
Xét hệ:
2
1 2
2
2 5 0
x t
y t
z t
x y z
2 2 1 2 2 5 0t t t
1t
1;3;2A
là tọa độ giao
điểm của đường thẳng và mặt phẳng.
Câu 19: Bất phương trình
2
4 2
log 3 log 9x x x
có bao nhiêu nghiệm nguyên?
A. vô số. B.
1
. C.
4
. D.
3
Lời giải
Chọn D
Điều kiện:
2
3 0
0 3 9
9 0
x x
x x
x
Ta có:
2
4 2
log 3 log 9x x x
2
2
4 4
log 3 log 9x x x
2
2
3 9x x x
27
15 81
5
x x
.
So sánh điều kiện, ta có:
27
9
5
x
.
Vậy bất phương trình có
3
nghiệm nguyên.
Câu 20: Hàm số
3
3
e
y x x
có bao nhiêu điểm cực trị?
A.
2
. B.
0
. C.
3
. D.
1
.
Lời giải
Chọn D
Hàm số
3
3
e
y x x
có TXĐ:
3;0 3; 
1
2 3
3 3 3
e
y e x x x
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 16
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
0y
1
1
x
x
Bảng xét dấu
Vậy hàm số có
1
điểm cực trị.
Câu 21: Gọi
D
là hình phẳng giới hạn bởi các đường 2 , 0, 0
x
y y x và
2x
. Thể tích
V
của khối tròn xoay tạo thành khi quay
D
quanh trục
Ox
được định bởi công thức
A.
2
1
0
2 dx
x
V
. B.
2
1
0
2 dx
x
V
. C.
2
0
4 dx
x
V
. D.
2
0
4 dx
x
V
.
Lời giải
Chọn D
Thể tích
V
của khối tròn xoay tạo thành khi quay
D
quanh trục
Ox
được định bởi
công thức
2 2
2
0 0
d 4 d
x
V y x x
Câu 22: Cho hàm số
y f x
có đồ thị như hình bên.
Hàm số
2 y f x
đồng biến trên khoảng
A.
1;2
. B.
2;3
. C.
1;0
. D.
1;1
.
Lời giải
Chọn A
Ta có
2 2. .
y f x f x
Hàm số đồng biến
2. 0 0.f x f x
Dựa vào đồ thị hàm số ta có
0 0 2f x x
chọn đáp án A.
Câu 23: Đồ thị hàm số
2
1
1
x x
y
x
có bao nhiêu đường tiệm cận
A.
4
. B.
3
. C.
1
. D.
2
.
Lời giải
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 17
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Chọn B
Tập xác định
1\D
.
Ta có:
2
1 1
1
lim lim
1
x x
x x
y
x

;
2
1 1
1
lim lim
1
x x
x x
y
x

.
Do đó đồ thị hàm số nhận đường thẳng
1x
làm tiệm cận đứng.
Lại có:
+
2
2
2
1
1
1 1
1 1
1
lim lim lim lim 2
1
1 1
1
x x x x
x
x
x x
x
y
x x
x
   
.
Vậy đồ thị hàm số nhận đường thẳng
2y
làm tiệm cận ngang.
+
2
2
2
1
1
1 1
1 1
1
lim lim lim lim 0
1
1 1
1
x x x x
x
x
x x
x
y
x x
x
   
.
Vậy đồ thị hàm số nhận đường thẳng
0y
làm tiệm cận ngang.
Do đó đồ thị hàm số đã có 3 đường tiệm cận.
Câu 24: Hàm số log
a
y x và log
b
y x có đồ thị như hình vẽ dưới đây.
Đường thẳng
3y
cắt hai đồ thị tại các điểm có hoành độ
1
x ,
2
x . Biết rằng
2 1
2x x ,
giá trị của
a
b
bằng
A.
1
3
. B. 3 . C.
2
. D.
3
2
.
Lời giải
Chọn D
Từ đồ thị có
1
x là nghiệm của phương trình log 3
b
x nên
3
1 1
log 3
b
x x b
.
Từ đồ thị có
2
x là nghiệm của phương trình log 3
a
x nên
3
2 2
log 3
a
x x a
.
Do
2 1
2x x
3 3
2.a b
3
2
a
b
3
2
a
b
. Vậy
3
2
a
b
.
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 18
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Câu 25: Cho hình hộp chữ nhật
.ABCD A B C D
có
, 2 , 6AB a AD a AC a
. Thể tích khối
hộp chữ nhật
.ABCD A B C D
bằng
A.
3
3
3
a
. B.
3
2
3
a
. C.
3
2a
. D.
3
2 3a
.
Lời giải
Chọn C
Ta có
2 2
4 5AC a a a
,
2 2
6 5CC a a a
.
Thể tích khối hộp chữ nhật là
3
. . .2 . 2V AB AD CC a a a a
.
Câu 26: Cho hàm số
f x
có đạo hàm
2
2
2 2 4 , .
x
f x x x x x
Số điểm cực trị
của
f x
là
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Chọn C
Ta có
2
2 2
2
0
0
0 2 . 2 4 0 2 0 1
2
2 4 0
x
x
x x
x
f x x x x x x
x
.
Nhận thấy
2x
là nghiệm bội ba nên
f x
vẫn đổi dấu khi qua
2.x
Vậy hàm số đã
cho có 3 điểm cực trị.
Câu 27: Cho hình lập phương
.ABCD A B C D
có cạnh bằng
a
. Diện tích xung quanh của hình
trụ có đáy là hai hình tròn ngoại tiếp hai hình vuông
ABCD
và
A B C D
A.
2
2 a
.
B.
2
2 a
. C.
2
a
.
D.
2
2 2 a
.
Lời giải
Chọn A
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 19
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Hình trụ có
l a
, bán kính đáy bằng
2
2 2
AC a
R
.
Vậy diện tích xung quanh hình trụ bằng
2
2
2 2 2
2
xq
a
S Rl a a
.
Câu 28: Gọi
1 2
,z z là các nghiệm phức của phương trình
2
2 3 0. z z
Mô đun của
3 4
1 2
.z z
bằng
A.
81
. B.
16
. C. 27 3 . D.
8 2
.
Lời giải
Chọn C
Ta có
:
2
1,2 1 2
2 3 0 1 2 3z z z i z z
.
Do đó
3 4
3 4
3 4
1 2 1 2
. . 3 . 3 27 3z z z z
.
Câu 29: Gọi
m
,
M
lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số
2 cos
2
x
f x x
trên đoạn
2;2
. Giá trị của
m M
bằng
A.
2
. B.
2
. C.
0
. D.
4
.
Lời giải
Chọn B
2 sin
2 2
x
f x
;
Vì
sin
2 2 2 2
x
0 2 2 sin 2
2 2 2 2
x
0f x
,
2;2x
.
2 2f f x f
.
Hay ta có
2;2
min 2 5m f x f
;
2;2
max 2 3M f x f
.
Vậy
3 5 2M m
.
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 20
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Câu 30: Cho hình chóp đều
S.ABCD
có
2AB a
, 5SA a . Góc giữa hai mặt phẳng
SAB
và
ABCD
bằng
A.
30
. B.
45
. C.
60
. D.
75
.
Lời giải
Chọn C
Theo tính chất hình chóp đều
SM AB
,
MO AB
,
SAB ABCD AB
. Góc giữa
hai mặt phẳng
SAB
và
ABCD
là góc giữa hai đường thẳng
SM
và
MO
.
Vì
ABCD
là hình vuông cạnh
2a
nên
2 2AC a
2AO a
3SO a
Xét tam giác vuông
SMO
có
tan 3
SO
SMO
OM
60SMO .
Câu 31: Hai bạn Công và Thành cùng viết ngẫu nhiên ra một số tự nhiên gồm 2 chữ số phân
biệt. Xác suất để hai số được viết ra có ít nhất một chữ số chung bằng
A.
145
729
. B.
448
729
. C.
281
729
. D.
154
729
.
Lời giải
Chọn C
Cách 1: Số các số tự nhiên có hai chữ số phân biệt là
9.9 81
số.
Số phần tử của không gian mẫu là
2
81n
.
Gọi
A
là biến cố thỏa mãn bài toán.
+ Khả năng 1: Hai bạn chọn số giống nhau nên có
81
cách.
+ Khả năng 2: Hai bạn chọn số đảo ngược của nhau nên có
9.8 72
cách.
+ Khả năng 3: Hai bạn chọn số chỉ có một chữ số trùng nhau
M
O
B
A
D
C
S
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 21
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
- TH1: Trùng chữ số
0
: Công có
9
cách chọn số và Thành đều có
8
cách chọn số
nên có
9.8 72
cách.
- TH 2: Trùng chữ số
1
: Nếu Công chọn số
10
thì Thành có
16
cách chọn số có
cùng chữ số
1
. Nếu Công chọn số khác
10
, khi đó Công có
16
cách chọn số và Thành
có
15
cách chọn số có cùng chữ số
1
với Công nên có
16 16.15 16.16 256
cách.
- Các trường hợp chọn trùng chữ số
2,3,4,...9
tương tự.
Vậy
81 72 72 9.256 2529n A
.
Xác suất cần tính là
2
2529 281
81 729
n A
P A
n
.
Cách 2: Số các số tự nhiên có hai chữ số phân biệt là
9.9 81
số.
Số phần tử của không gian mẫu là
2
81n
.
Gọi
A
là biến cố thỏa mãn bài toán. Xét biến cố
A
.
- TH 1: Công chọn số có dạng
0a
nên có
9
cách. Khi đó có
25
số có ít nhất một chữ số
trùng với số
0a
nên Thành có
81 25 56
cách chọn số không có chữ số trùng với
Công. Vậy có
9.56 504
cách.
- TH 2: Công chọn số không có dạng
0a
: Có
72
cách, khi đó
32
số có ít nhất một chữ
số trùng với số của Công chọn nên Thành có
81 32 49
cách chọn số không có chữ số
nào trùng với Thành. Vậy có
72.49 3528
cách.
3528 504 4032n A
2
4032 281
1 1
81 729
P A P A
.
Câu 32: Biết rằng
e
x
x
là một nguyên hàm của
f x
trên khoảng
;
. Gọi
F x
là một
nguyên hàm của
e
x
f x
thỏa mãn
0 1F
, giá trị của
1F
bằng
A.
7
2
. B.
5 e
2
. C.
7 e
2
. D.
5
2
.
Lời giải
Chọn A
Ta có
e e e
x x x
f x x x
,
;x  
.
Do đó
e e
x x
f x x
,
;x  
.
Suy ra
e 1
x
f x x
,
;x 
.
Nên
e 1 e 2
x x
f x x x
e e 2 .e 2
x x x
f x x x
.
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 22
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Bởi vậy
2
1
2 d 2
2
F x x x x C
.
Từ đó
2
1
0 0 2 2
2
F C C
;
0 1 1F C
.
Vậy
2 2
1 1 7
2 1 1 1 2 1
2 2 2
F x x F
.
Câu 33: Cho hình chóp
S.ABCD
có đáy là hình chữ nhật, biết
2 3AB a, AD a, SA a
và
SA
vuông góc với mặt phẳng đáy. Gọi
M
là trung điểm cạnh
CD
. Khoảng cách giữa hai
đường thẳng
SC
và
BM
bằng
A.
3 3
4
a
. B.
2 3
3
a
. C.
3
3
a
. D.
3
2
a
.
Lời giải
Chọn C
Gọi
O
là tâm hình chữ nhật,
I BM AC
.
Dựng
//IN SC
N SA
,
AK BM , AH NK
K BM , H NK
.
Dễ dàng chứng minh được
AH BMN
. Khi đó:
d SC,BM d SC, BMN d C, BMN
.
Ta lại có:
2
1 1 1
3
1
2 2 2
3
CO
d C, BMN
CI
d C, BMN d A, BMN AH
AI
d A, BMN
CO CO
.
Xét tam giác vuông
ANK
:
O
S
M
N
H
A
D
C
B
I
K
3a
a
2a
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 23
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
*
2 2
2
2
2
ABM
AB.d M , AB
S
a.a
AK a
BM BM
a a
.
*
2 2 2
3 2
3 3 3
AN AI
AN AS . a a
AS AC
Suy ra:
2 2 2
2
2 2 2 3
3
2 2
AN.AK a.a a
AH
AN AK
a a
.
Vậy:
1 3
2 3
a
d SC ,BM AH
.
Cách 2:
Chọn hệ tọa độ
Oxyz
sao cho
A O
;
xB O
nên
2 ;0;0B a
,
D Oy
nên
0; ;0D a
,
S Oz
nên
0;0;3S a
2 ; ;0C a a
và
; ;0M a a
.
Ta có
2 ; ; 3SC a a a

;
; ;0BM a a

2 2 2
, 3 ;3 ;3SC BM a a a
 
và
2 ;0; 3SB a a

.
Vậy
,
, .
3
3
,
Sc BM
SC BM SB
a
d
SC BM
  
 
.
Câu 34: Cho hàm số
f x
có bảng xét dấu đạo hàm như hình bên dưới
M
C
B
A
D
S
x
y
z
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 24
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Hàm số
1 2y f x
đồng biến trên khoảng
A.
3
0;
2
. B.
1
;1
2
. C.
1
2;
2
. D.
3
;3
2
.
Lời giải
Chọn A
Ta có:
2 1 2 0y f x
1 2 0f x
Từ bảng xét dấu ta có
1 2 0f x
1 2 3
2 1 2 1
1 2 3
x
x
x
2
3
0
2
1
x
x
x
Từ đây ta suy ra hàm số đổng biến trên khoảng
3
0;
2
Câu 35: Xét các số phức
,z w
thỏa mãn
2, 2 .w i z iw
Gọi
1 2
,z z lần lượt là các số phức mà
tại đó
z
đạt giá trị nhỏ nhất và đạt giá trị lớn nhất. Mô đun
1 2
z z
bằng
A.
3 2
. B.
3
. C.
6
. D.
6 2
.
Lời giải
Chọn C
Ta có:
1
2 2z iw w z
i
1 1
2 2 2 2 1 2w i z i z
i i
3 2z
. Do đó
1 2
,z z có các điểm biểu diễn trên mặt phẳng
Oxy
thuộc đường tròn
tâm
3;0 ;I
bán kính
2R
. Vậy
1 2 1 2 1 2
1, 5 6 6.z z z z z z
Câu 36: Cho
3
1 3 3f x x x
. Đồ thị hình bên là của hàm số có công thức
A.
1 1y f x
. B.
1 1y f x
. C.
1 1y f x
. D.
1 1y f x
.
Lời giải
Chọn B
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 25
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Cách 1: Ta có
3
1 3 1f x x x
Thử điểm đối với từng đáp án
Đáp án A:
1 1y f x
1 2 1 1y f
Loại
Đáp án B:
1 1y f x
1 2 1 3y f
thoả mãn.
Đáp án C:
1 1y f x
1 0 1 3y f
Loại
Đáp án D:
1 1y f x
1 0 1 1y f
Loại
Cách 2: Từ đồ thị suy ra hàm số ứng với đồ thị trên là
3
3 1y x x .
Ta làm tường minh các hàm số cho trong các đáp án và so sánh
Đáp án A:
3
1 1 3 1y f x x x
Loại
Đáp án B:
3
1 1 3 1y f x x x
Nhận.
Câu 37: Người ta xếp hai quả cầu có cùng bán kính
r
vào một chiếc hộp hình trụ sao cho các
quả cầu đều tiếp xúc với hai đáy, đồng thời hai quả cầu tiếp xúc với nhau và mỗi quả
cầu đề tiếp xúc với đường sinh của hình trụ ( tham khảo hình vẽ). Biết thể tích khối trụ
là
3
120 cm
, thể tích của mỗi khối cầu bằng
A.
3
10 cm
. B.
3
20 cm
. C.
3
30 cm
. D.
3
40 cm
.
Lời giải
Chọn B
Chiều cao của hình trụ là
2r
.
Đường kính của hình trụ là
4r
. Suy ra bán kính của hình trụ là
2r
.
Thể tích khối trụ là
2
3
2 .2 8r r r
. Theo bài ra có
3 3 3 3 3
4
8 120 cm 15 cm 20
3
r r r
.
Vậy thể tích của mỗi khối cầu là
20
3
cm
.
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 26
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Câu 38: Biết
2
3
4 3
4
cos sin cos 1
d ln 2 ln 1 3
cos sin cos
x x x
x a b c
x x x
, với
, ,a b c
là các số hữu tỉ. Giá trị
của
abc
bằng
A.
0
. B.
2
. C.
4
. D.
6
.
Lời giải
Chọn C
Ta có:
2
3 3
2 2 4
4 3
4 4
1 tan 1
cos sin cos 1
cos cos cos
d d
cos sin cos 1 tan
x
x x x
x x x
x x
x x x x
2
2 2 2
3
4
1 tan tan 1 tan 1 tan
d
1 tan
x x x x
x
x
2
3
2
4
1 tan 1 tan
1 tan d
1 tan
x x
x x
x
2
3
2
4
1 tan
1 1 tan d
1 tan
x
x x
x
.
Đặt
1 tant x
ta được
2
d 1 tan dt x x
, đổi cận
2, 1 3
4 3
x t x t
Ta được
1 3
2
1 3 1 3
2
2 2
2
1 1
2
1 d 1 d 2ln 1 2ln 2 2ln 1 3
2
t
t
t t t t t
t t
Từ đây ta suy ra
ln2 ln 1 3 1 2ln 2 2ln 1 3a b c
.
Do đó
1, 2, 2a b c
suy ra
4.abc
Câu 39: Trong không gian
,Oxyz
cho hai đường thẳng
1 2 2
: ; : 1 2
1 3 2
x t x t
d y t d y t
z t z t
và mặt
phẳng
: 2 0.P x y z
Đường thẳng vuông góc với mặt phẳng
P
và cắt cả hai
đường thẳng
,d d
có phương trình là
A.
3 1 2
1 1 1
x y z
. B.
1 1 1
1 1 4
x y z
.
C.
2 1 1
1 1 1
x y z
. D.
1 1 4
2 2 2
x y z
.
Lời giải
Chọn A
Mặt phẳng
P
có vectơ pháp tuyến là
1;1;1 .n
Gọi
là đường thẳng cần tìm và
,A d B d
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 27
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Vì
,A d B d
nên gọi
1 2 ; ; 1 3A t t t
và
2 ; 1 2 ; 2B t t t
2 3; 2 1; 2 3 1 .AB t t t t t t
Do
P
nên
,AB n

cùng phương
2 3 2 1 2 3 1
1 1 1
t t t t t t
1; 1; 4
3 4 1
.
2 4 2 1
3; 1; 2
A
t t t
t t t
B
Đường thẳng
đi qua điểm
B
và có vectơ chỉ phương
1;1;1n
nên có phương trình
3 1 2
.
1 1 1
x y z
Câu 40: Có bao nhiêu số nguyên
m
để phương trình
3
x
x me
có 2 nghiệm phân biệt?
A.
7
. B.
6
. C.
5
. D. Vô số.
Lời giải
Chọn A
Ta có:
3 3 0
x x
x me me x
.
Đặt
3 1
x x
f x me x f x me
.
Nếu
0m
thì
0 0f x f x
có tối đa một nghiệm.
Ta xét với
0m
, khi đó
0 lnf x x m
.
Bảng biến thiên
Để phương trình
3
x
x me
có 2 nghiệm phân biệt
2
ln 2 0 0m m e
.
Từ đó suy ra
1;2;3;4;5;6;7m
.
Câu 41: Cho
f x
mà đồ thị hàm số
y f x
như hình bên. Hàm số
2
1 2y f x x x
đồng biến trên khoảng
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 28
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
A.
1;2 .
B.
1;0 .
C.
0;1 .
D.
2; 1 .
Lời giải
Chọn A
Ta có
2
1 2y f x x x
Khi đó
1 2 2y f x x
. Hàm số đồng biến khi
0y
1 2 1 0 1f x x
Đặt
1t x
thì
1
trở thành:
2 0f t t
2f t t
.
Quan sát đồ thị hàm số
y f t
và
2y t
trên cùng một hệ trục tọa độ như hình vẽ.
Khi đó ta thấy với
0;1t
thì đồ thị hàm số
y f t
luôn nằm trên đường thẳng
2y t
.
Suy ra
2 0, 0;1f t t t
. Do đó
1;2x
thì hàm số
2
1 2y f x x x
đồng
biến.
Câu 42: Có bao nhiêu số nguyên
2019;2019a
để phương trình
1 1
ln 5 3 1
x
x a
x
có
hai nghiệm phân biệt?
A.
0
. B.
2022
. C.
2014
. D.
2015
.
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 29
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Lời giải
Chọn D
Phương trình
1 1 1 1
ln 5 3 1 ln 5 3 1
x x
x a x a
x x
Đặt hàm số
1 1
( )
ln( 5) 3 1
x
f x x
x
có tập xác định
5; 4 4;0 0;D
Ta có :
2
2
1 3 ln3
'( ) 1 0
5 ln 5
3 1
x
x
f x
x x
( )f x
nghịch biến trên các khoảng của tập xác định
Các giới hạn:
5
5
1 243
lim ( ) 5 5
3 1 242
x
f x

;
4 4
lim ( ) ; lim ( )
x x
f x f x

 
0 0
lim ( ) ; lim ( )
x x
f x f x
 
;
lim ( )
x
f x


Bảng biến thiên
Phương trình
( )f x a
có hai nghiệm phân biệt khi và chỉ khi
243
5
242
a
Do
2019;2019
4;2018
aa
a
a
. Vậy có
2018 4 1 2015
giá trị của
a
.
Câu 43: Cho hàm số
( )f x
có đạo hàm liên tục trên
và thỏa mãn
(0) 3f
và
2
( ) (2 ) 2 2,f x f x x x x
. Tích phân
2
0
( )dxf x x
bằng
A.
4
3
. B.
2
3
. C.
5
3
. D.
10
3
.
Lời giải
ChọnD.
Thay
0x
ta được
(0) (2) 2 (2) 2 (0) 2 3 1f f f f
Ta có:
2 2
0 0
( )d (2 )df x x f x x
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 30
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Từ hệ thức đề ra:
2 2 2
2
0 0 0
8 4
( ) (2 ) d 2 2 d ( )d .
3 3
f x f x x x x x f x x
Áp dụng công thức tích phân từng phần, ta lại có:
2 2
2
0
0 0
4 10
( )d ( ) ( )d 2.( 1) .
3 3
xf x x xf x f x x
Câu 44: Hàm số
2
1
x
f x m
x
(với
m
là tham số thực) có nhiều nhất bao nhiêu điểm cực
trị?
A.
2
. B.
3
. C.
5
. D.
4
.
Lời giải
Chọn D
Xét hàm số
2
1
x
g x m
x
, TXĐ:
.
Ta có
2
2
2
1
1
x
g x
x
;
1
0
1
x
g x
x
.
Bảng biến thiên
Từ bảng biến thiên ta có hàm số
y g x
luôn có hai điểm cực trị.
Xét phương trình
0g x
2
2
0 0
1
x
m mx x m
x
, phương trình này có
nhiều nhất hai nghiệm.
Vậy hàm số
f x
có nhiều nhất bốn điểm cực trị.
Câu 45: Cho hình hộp
. ' ' ' 'ABCD A B C D
có thể tích bằng
V
. Gọi
, , , , ,M N P Q E F
lần lượt là tâm
các hình bình hành
, ' ' ' ', ' ', ' ', ' ', ' '.ABCD A B C D ABB A BCC B CDD C DAA D
Thể tích khối
đa diện có các đỉnh
, , , , ,M P Q E F N
bằng
A.
4
V
. B.
2
V
. C.
6
V
. D.
3
V
.
Lời giải
Chọn C
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 31
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Gọi
h
là chiều cao của hình hộp
. ' ' ' 'ABCD A B C D
.
ABCD
V h S .
Thấy hình đa diện
MPQEFN
là một bát diện nên
.
1 1 1
2. 2. . . . . . .
3 2 3
MPQEFN N PQEF PQEF PQEF
V V h S h S
Lại có:
PQEF
là hình bình hành và có
1 1
;
2 2
PQ EF AC QE PF BD
nên
1
.
2
PQEF ABCD
S S
Do đó:
1 1 1 1
. . . . . . .
3 3 2 6 6
MPQEFN PQEF ABCD ABCD
V
V h S h S h S
Câu 46: Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên gạch hình vuông cạnh
40 cm
như hình bên. Biết rằng người thiết kế đã sử dụng các đường cong có
phương trình
2 2
4x y
và
3 2
4( 1)x y
để tạo hoa văn cho viên gạch. Diện tích phần
được tô đạm gần nhất với giá trị nào dưới đây?
A.
2
506 cm
. B.
2
747 cm
. C.
2
507 cm
. D.
2
746 cm
.
Lời giải
Chọn B
Chọn hệ trục tọa độ
Oxy
như hình vẽ.
F
M
P
Q
E
N
D'
B' C'
B
A'
C
D
A
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 32
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Gọi
S
là diện tích phần tô đậm
Ta có
2 2
3
0 1
4 2 4 2 ( 1) S x dx x dx
2
2
5
3 2
1
0
8 2 16 32 16 112
1
3 5 3 5 15
x x dm
Vậy
2
2240
746,67
3
S cm
Câu 47: Xét các số phức
z
,
w
thỏa mãn
2z
,
2 5 1iw i
. Giá trị nhỏ nhất của
2
4z wz
bằng
A.
4
. B.
2 29 3
. C.
8
. D.
2 29 5
.
Lời giải
Chọn C
Cách 1:
Ta có:
2 5
2 5 1 1 5 2 1
i
iw i i w w i
i
.
Ta có:
2
2 2 2
4 2T z wz z wz z z wz z z z z z w z z w
*
Đặt
z a bi
. Suy ra:
2z z bi
. Vì
2z
nên
4 2 4b
.
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 33
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Gọi
A
,
B
lần lượt là điểm biểu diễn của
w
và
2bi
. Suy ra:
+
A
thuộc đường tròn
C
có tâm
5; 2I
, bán kính
1R
.
+
B
thuộc trục
Oy
và 4 4
B
x .
Từ
*
suy ra:
2 2 2 4 8T AB MN
(xem hình)
Dấu “
” xảy ra khi và chỉ khi
4; 2 4 2A M w i
và
0; 2 2 2 1B N bi i b
z a i
2
1 4 3a a 3z i
.
Vậy
2
4z wz
có giá trị nhỏ nhất bằng
8
.
Cách 2:
Đặt
z a bi
,
w c di
(
a
,
b
,
c
,
d
). Từ giả thiết, ta có:
2 2
2 2
4
5 2 1
a b
c d
, 2;2
6; 4 , 3; 1
a b
c d
.
Ta có:
2
2 2 2
4 2T z wz z wz z z wz z z z z z w z z w
2
2 2
2 2 2 2 2 2 2 4 8T bi c di b d c c c
(do
6; 4c
).
Dấu “
” xảy ra khi và chỉ khi
2 2
4
2 0
5 2 1
c
b d
c d
.
Suy ra một nghiệm thỏa mãn là
4
2
1
c
d
b
.
Vậy
2
4z wz
có giá trị nhỏ nhất bằng
8
.
Chú ý: Về một Lời giải SAI.
Sau khi có
2
4 2 2 2 2 2 1 2 2 2 29 5T z wz z z w z w z EF OI
.
Khi đó, đẳng thức không xảy ra, vì hệ
, 0
29 3
z w kz k
z w
vô nghiệm.
Hoặc:
2
4 4 4 2 4 2 29 3 4 2 29 5T z wz z z w z z w z w
,
cũng không có đẳng thức xảy ra. (Bạn đọc tự kiểm tra điều này).
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 34
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Câu 48: Cho
( )f x
mà đồ thị hàm số
'( )y f x
như hình vẽ bên
Bất phương trình
( ) sin
2
x
f x m
nghiệm đúng với mọi
1;3x
khi và chỉ khi
A.
(0)m f
. B.
(1) 1m f
. C.
( 1) 1m f
. D.
(2)m f
.
Lời giải
Chọn B
Xét bất phương trình
( ) sin
2
x
f x m
(1) với
1;3x
, ta có:
( ) sin ( ) sin
2 2
x x
f x m f x m
(2)
Đánh giá
( ) sin
2
x
f x
với
1;3x
+ Từ đồ thị của hàm số
'( )y f x
đã cho ta suy ra BBT của
( )f x
như sau:
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 35
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Từ BBT ta suy ra:
( ) (1), 1;3f x f x
(*)
+ Do
1;3x
nên:
3
1 3
2 2 2
x
x
Suy ra:
1 sin 1
2
x
1 sin 1
2
x
(**)
+ Từ (*) và (**) cho ta:
( ) sin (1) 1, 1;3
2
x
f x f x
. Dấu
" "
xảy ra khi
1x
Do đó: Bất phương trình
( ) sin
2
x
f x m
nghiệm đúng với mọi
1;3x
(1) 1m f
. Chọn B
Câu 49: Trong không gian
Oxyz
, cho đường thẳng
3 4 2
:
2 1 1
x y z
d
và 2 điểm
6;3; 2A
,
1;0; 1B
. Gọi
là đường thẳng đi qua
B
, vuông góc với
d
và thỏa mãn khoảng cách
từ
A
đến
là nhỏ nhất. Một vectơ chỉ phương của
có tọa độ
A.
1;1; 3
. B.
1; 1; 1
. C.
1;2; 4
. D.
2; 1; 3
.
Lời giải
Chọn A
Gọi
P
là mặt phẳng qua
B
và vuông góc với
d
nên
: 2 1 0P x y z
.
Gọi
H
là hình chiếu của
A
lên
P
, ta có:
2;1; 4H
Ta có:
P
nên
; ;d A d A P
.
Dấu đẳng thức xảy ra khi và chỉ khi
H
.
Vậy một vectơ chỉ phương của
là
1;1; 3BH

.
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 36
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Câu 50: Trong không gian
Oxyz
, cho điểm
2; ;3;4A
, đường thẳng
1 2
:
2 1 2
x y z
d
và mặt
cầu
2 2 2
: 3 2 1 20S x y z
. Mặt phẳng
P
chứa đường thẳng
d
thỏa mãn
khoảng cách từ điểm
A
đến
P
lớn nhất. Mặt cầu
S
cắt
P
theo đường tròn có
bán kính bằng
A. 5 . B.
1
. C.
4
. D.
2
.
Lời giải
Chọn D
Ta có:
d
đi qua
1; 2;0M
và có VTCP
2;1; 2
d
u
.
S
có tâm
3;2; 1I
và bán kính
2 5R
.
Ta có:
; ;d A P d A d
. Dấu “
” xảy ra khi
P
chứa
d
và vuông góc với
AK
.
Khi đó:
P
có VTPT là
,
P AKM d
n n u
.
Vì
, 6;6;3
AKM d
n u AM
9;18; 18 9 1;2; 2
P
n
.
: 1 2 2 2 0P x y z
: 2 2 3 0P x y z
.
Ta có:
; 4d d I P
.
Vậy bán kính đường tròn cần tìm:
2 2
20 16 2r R d
.
……………..HẾT…………….
NHÓM TOÁN VD – VDC ĐỀ THI THỬ THPTQG – 2018-2019
https://www.facebook.com/groups/toanvd.vdc Trang 37
NHÓM TOÁN VD – VDC
NHÓM TOÁN VD – VDC
Toàn thể ban quan trị nhóm VD-VDC xin được gửi tặng sản phẩm chuyên đại Vinh
lần 3 cho tất cả các quý thầy cô là thành viên của nhóm. Món quà nhỏ này như một
lời tri ân đến quý thầy cô đã luôn ủng hộ nhóm trong suốt thời gian qua, tất cả các dự
án đề thi thử trên nhóm lớn trong suốt mùa thi qua. Kính chúc quý thầy cô luôn có sức
khỏe và luôn tràn đầy nhiệt huyết trong nghề.
Mong thầy cô sẽ luôn ủng hộ nhóm trong những chặng đường tiếp theo. Xin chào và
hẹn gặp lại.
Dù đã cố gắng làm việc nghiêm túc nhưng chắc sẽ có những sai sót nên mong quý thầy
cô hãy thông cảm. Xin cảm ơn rất nhiều.
BAN QUẢN TRỊ NHÓM VD-VDC – 05/05/2019
| 1/44
| | Tải xuống

Có thể bạn quan tâm:

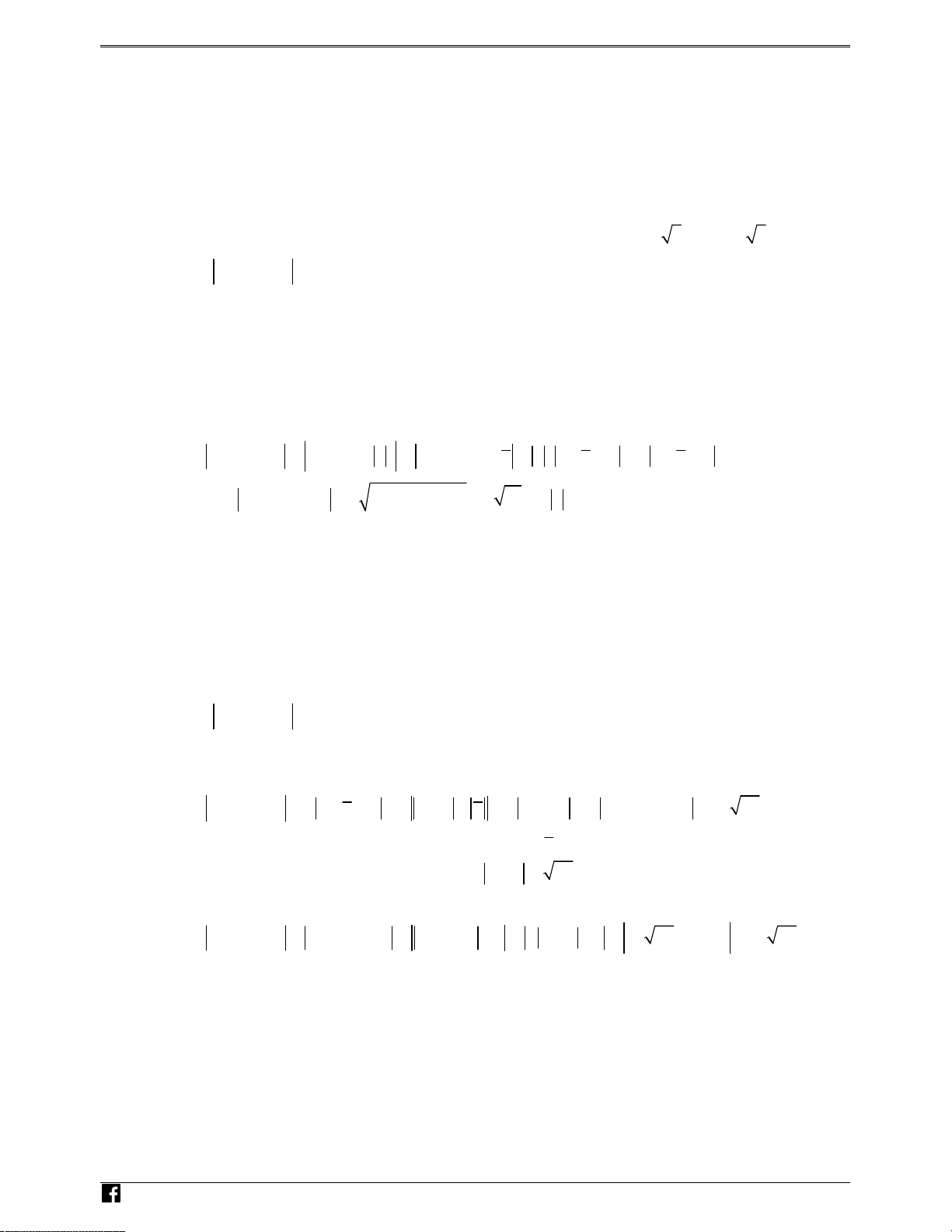
Preview text:

TRƯỜNG ĐẠI HỌC VINH
ĐỀ THI THỬ THPT QUỐC GIA NĂM 2019 – LẦN 3 TRƯỜNG THPT CHUYÊN Môn: TOÁN
Thời gian làm bài: 90 phút
(Đề thi gồm 06 trang)
(50 câu hỏi trắc nghiệm) Mã đề thi 132
Họ và tên thí sinh: ..................................................................... Số báo danh: ................................
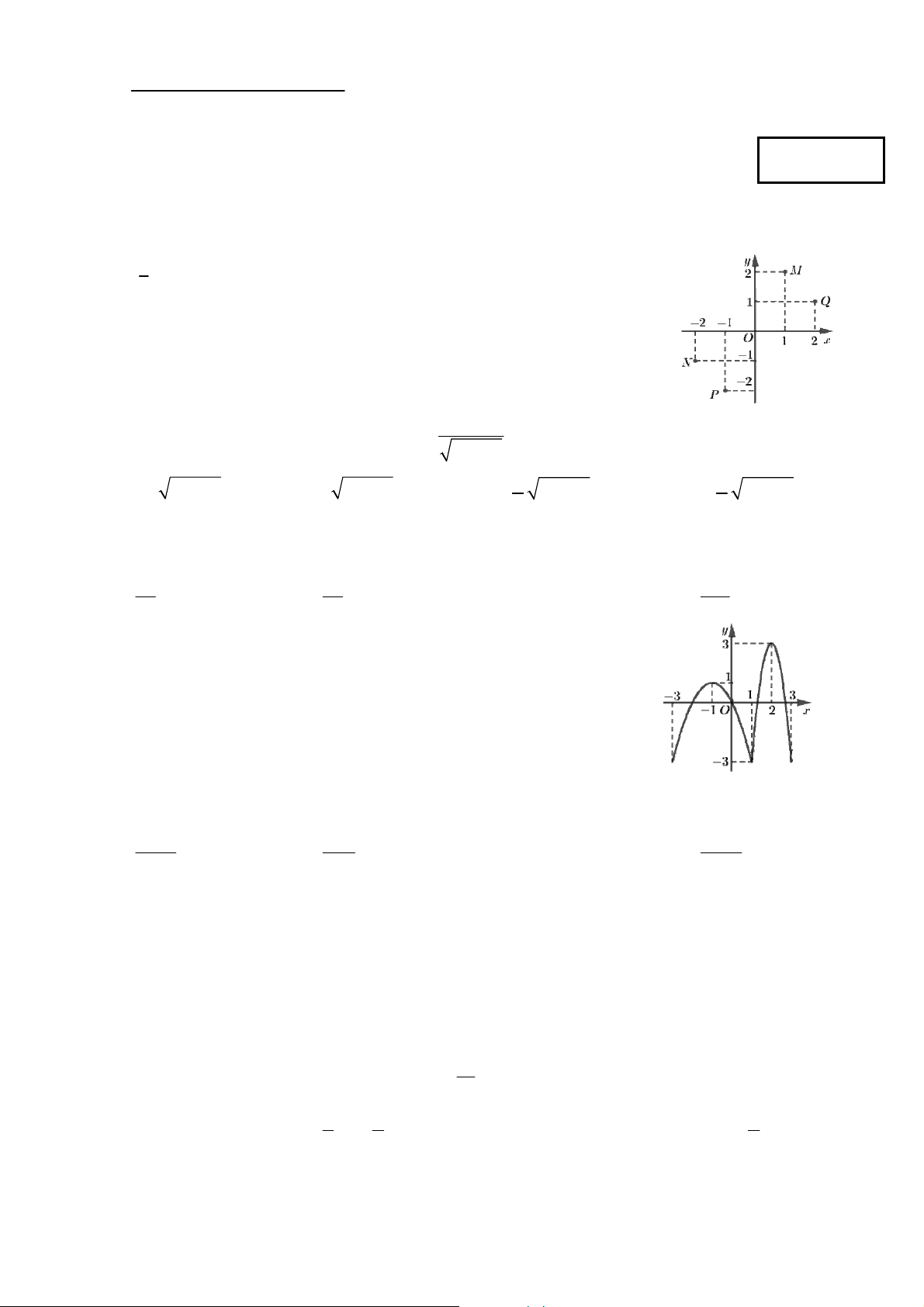
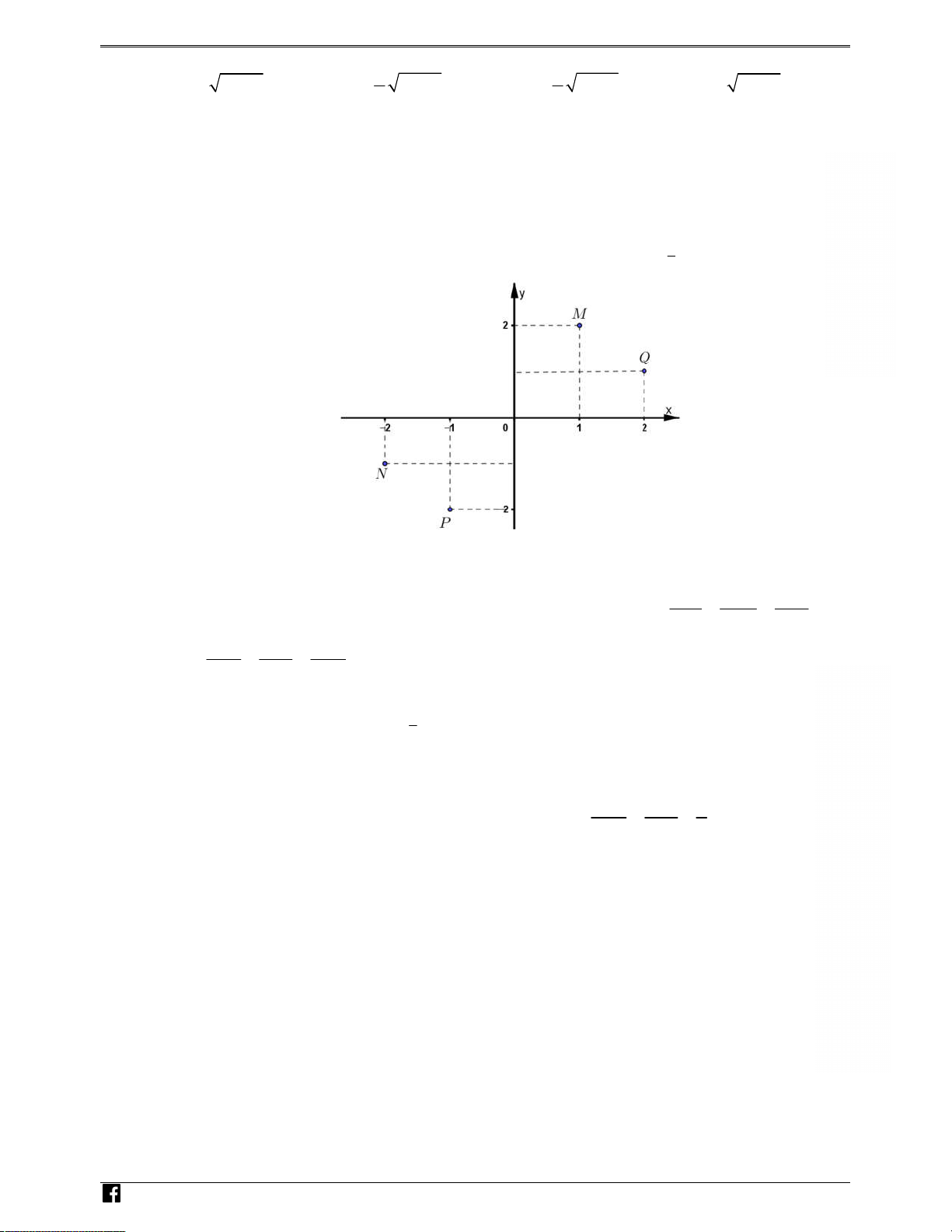
Câu 1: Cho số phức z = 2
- + i. Trong hình bên điểm biểu diễn số phức z là A. Q. B. M. C. P. D. N . 1
Câu 2: Tất cả các nguyên hàm của hàm f x ( ) = là x 3 - 2 2 2
A. -2 3x - 2 +C.
B. 2 3x - 2 +C. C. 3x - 2 + C . D. - 3x - 2 + C . 3 3
Câu 3: Cho hình chóp S A
. BCD có đáy ABCD là hình vuông cạnh a, SA a và SA vuông góc với mặt
phẳng đáy. Thể tích của khối chóp S A . BCD bằng a3 a3 a3 2 A. . B. . C. a3. D. . 6 3 3
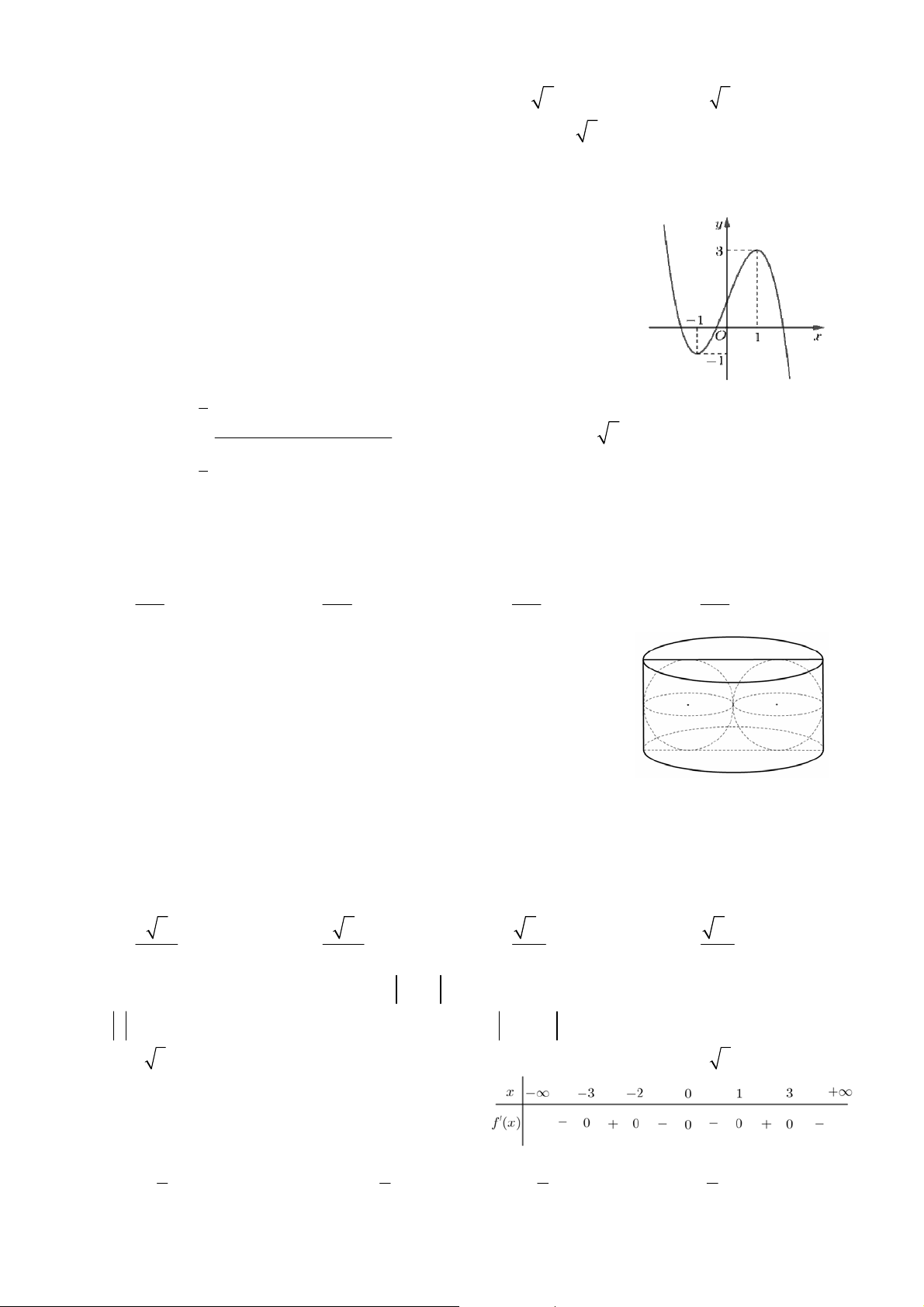
Câu 4: Cho hàm số y f x
( ) có đồ thị như hình bên. Hàm số đã
cho nghịch biến trên khoảng A. 2; 0. B. 0; 2. C. 2; 3. D. 3;  1.
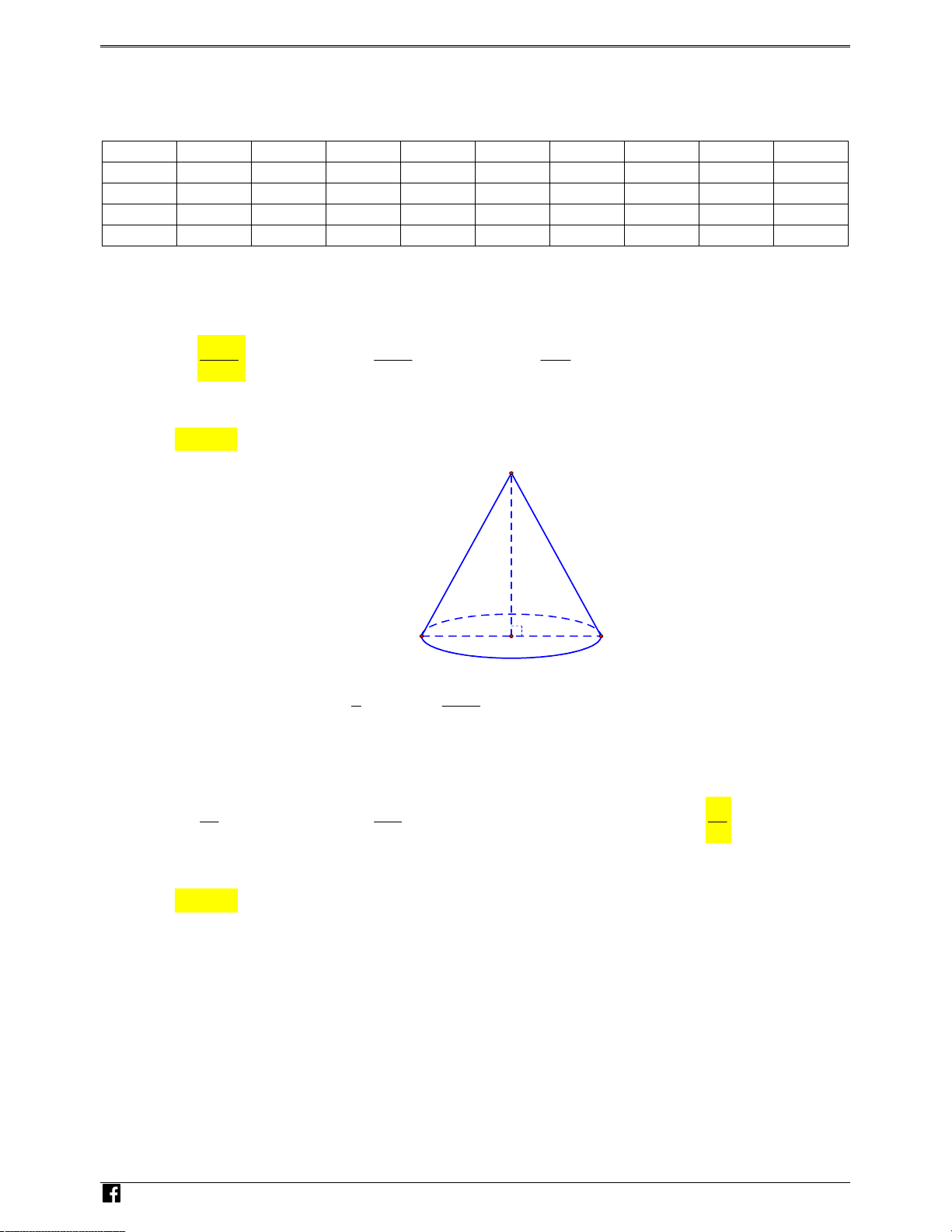
Câu 5: Cho khối nón có độ dài đường cao bằng a
2 và bán kính đáy bằng a. Thể tích của khối nón đã cho bằng a3 2 a3 a3 4 A. . B. . C. a3 2 . D. . 3 3 3
Câu 6: Trong không gian Oxyz, cho hai điểm ( A 2
- ; -1; 3) và B(0; 3; 1). Gọi (a) là mặt phẳng trung trực
của AB. Một vectơ pháp tuyến của (a) có tọa độ là A. (2; 4; - 1). B. (1; 2; - 1). C. (-1; 1; 2). D. (1; 0; 1).
Câu 7: Cho cấp số nhân (u có u = 1, u = 2
- . Mệnh đề nào sau đây đúng ? n ) 1 2 A. 2018 u = 2 - . B. 2019 u = 2 . C. 2019 u = 2 - . D. 2018 u = 2 . 2019 2019 2019 2019 a
Câu 8: Với a, b là các số thực dương bất kỳ, log bằng 2 2 b 1 a a
A. log a - log 2b . B. log .
C. log a - 2 log . b D. 2 log . 2 2 ( ) 2 2 b 2 2 2 b
Câu 9: Từ các chữ số 1, 2, 3,..., 9 lập được bao nhiêu số có 3 chữ số đôi một khác nhau ? A. 9 3 . B. 3 A . C. 3 9 . D. 3 C . 9 9
Trang 1/6 - Mã đề thi 132
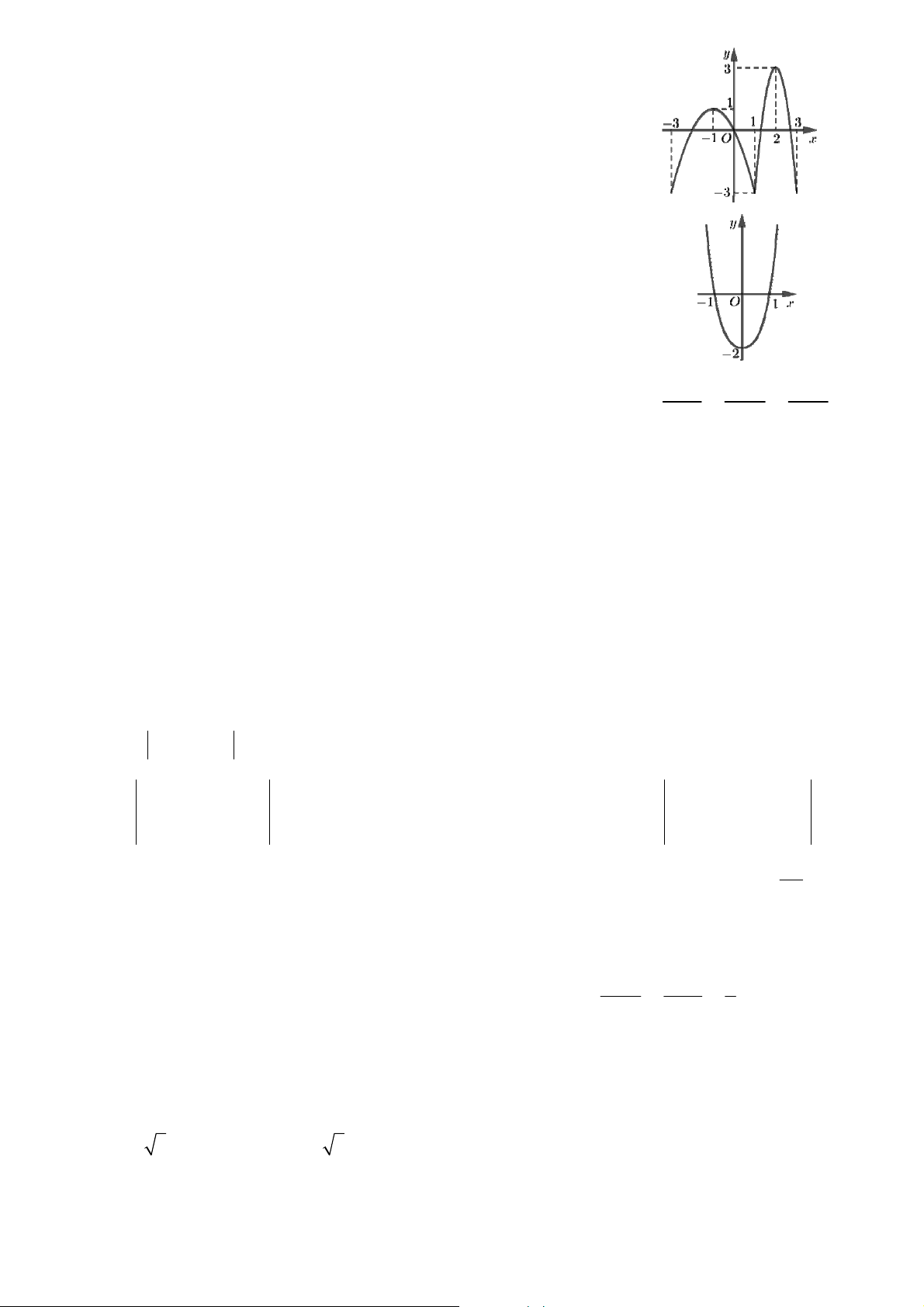
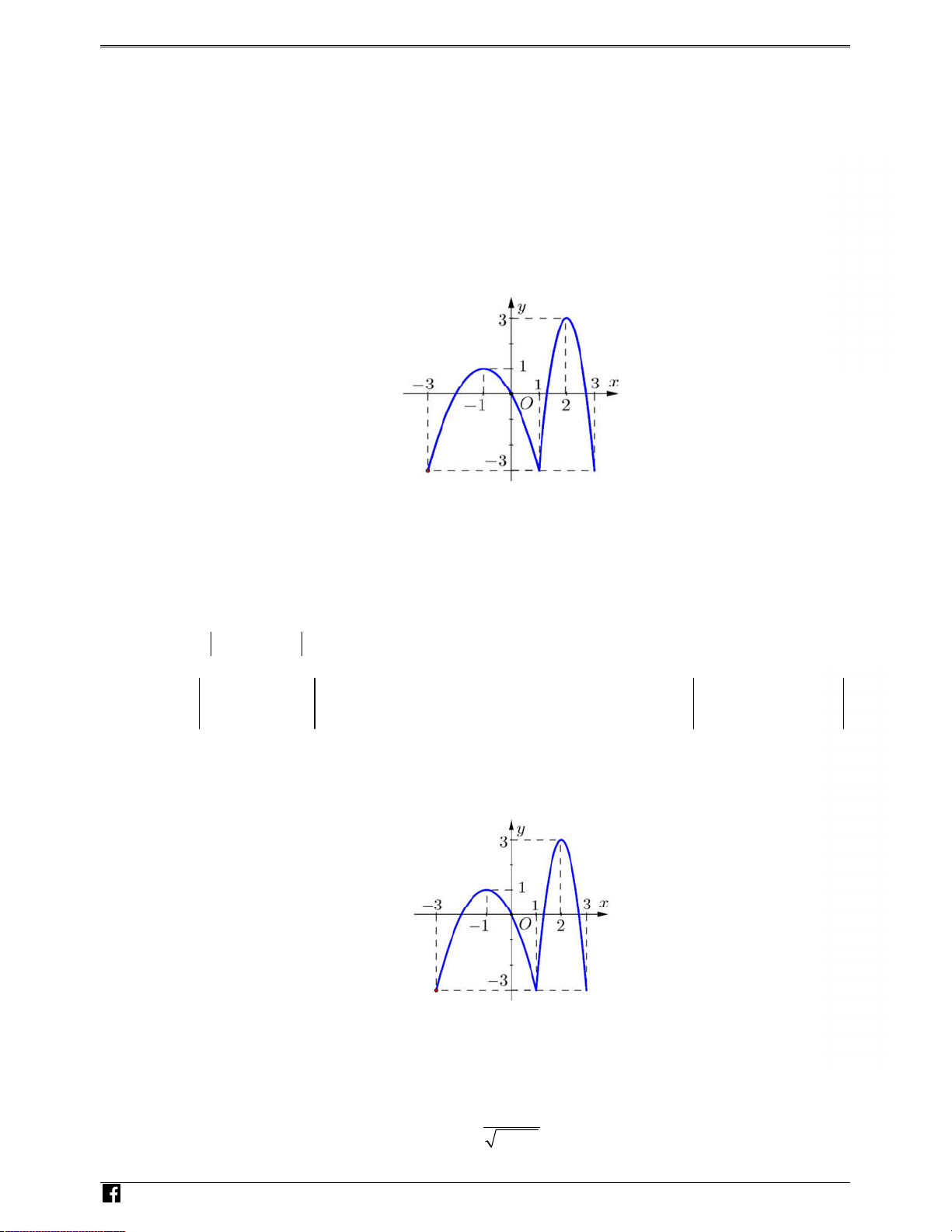
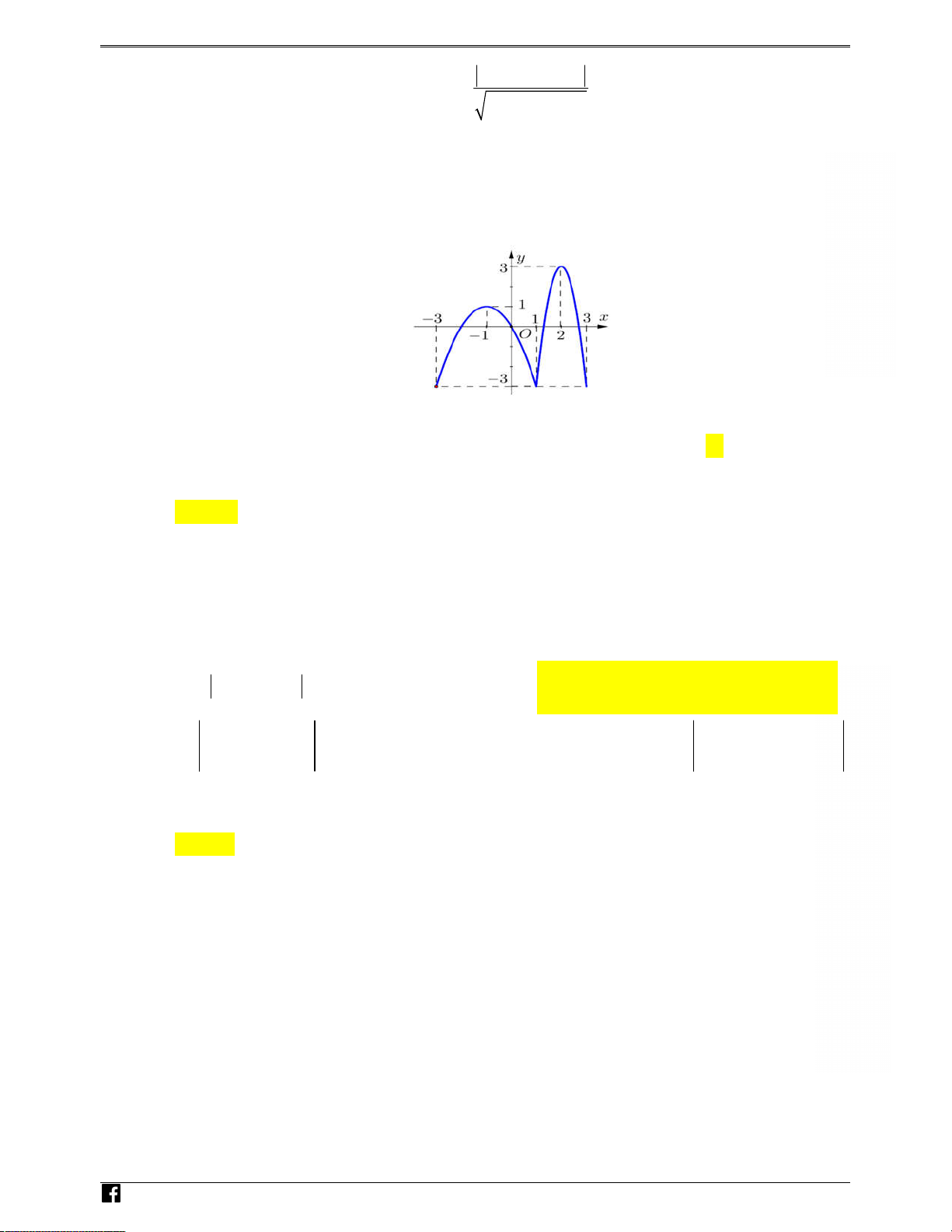
Câu 10: Cho hàm số y f x
( ) có đồ thị như hình bên. Trên đoạn 3; 3 
 hàm số đã cho có mấy điểm cực trị ? A. 4. B. 2. C. 5. D. 3.
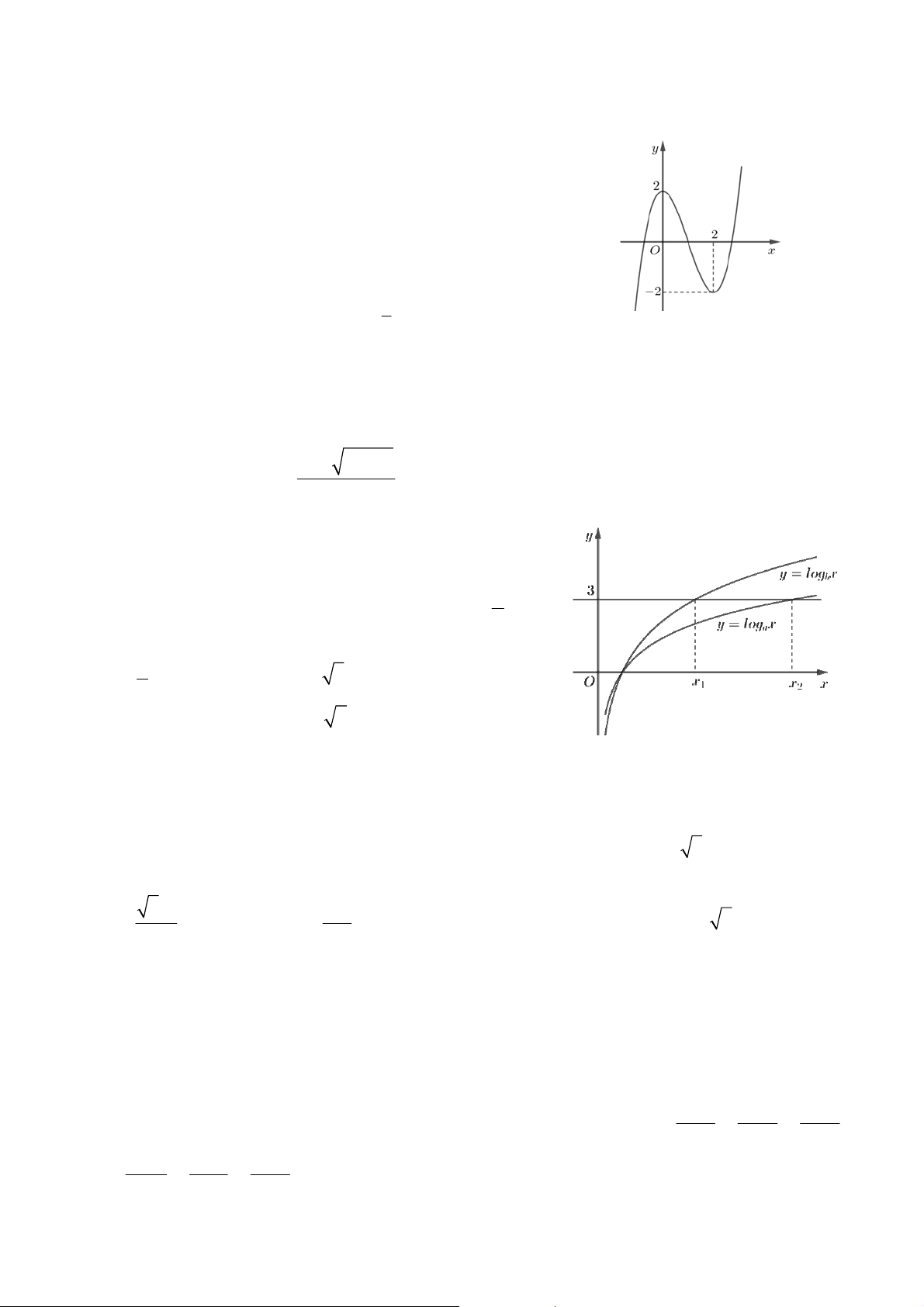
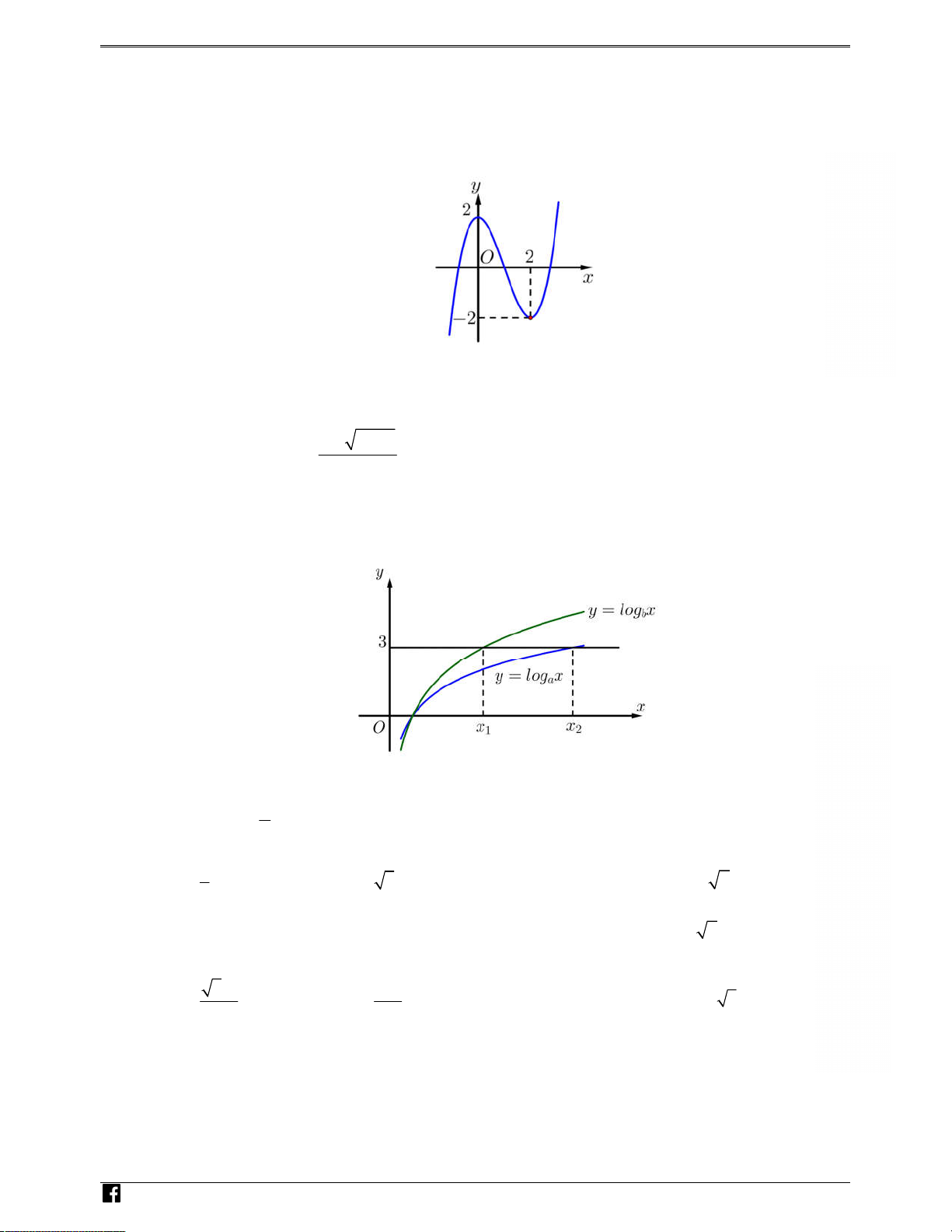
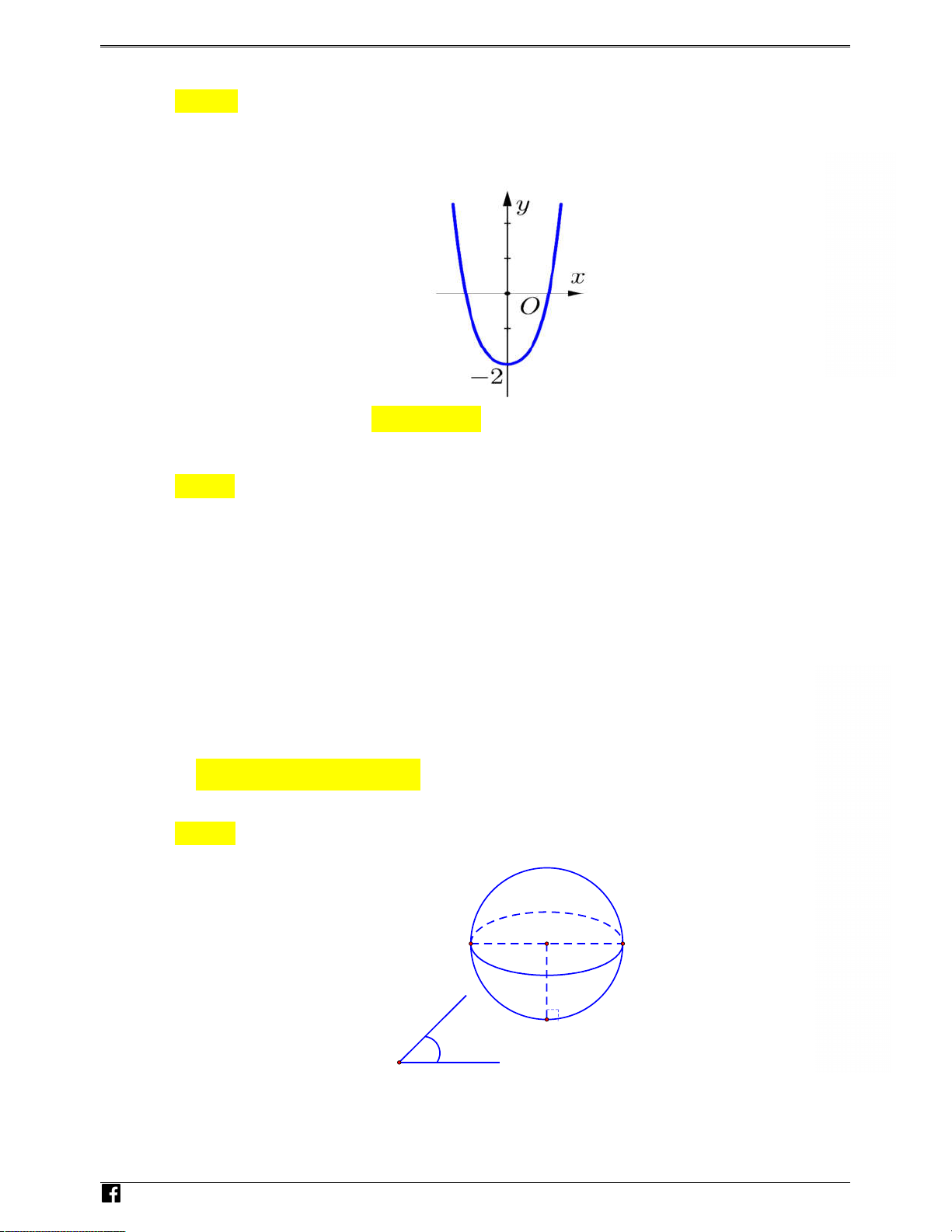
Câu 11: Hình bên là đồ thị của hàm số nào dưới đây ?
A. y x2  2.
B. y x 4  x2  2.
C. y x 4  x2  2. D. y x2  x  2. x  1 y  3 z  3
Câu 12: Trong không gian Oxyz, một vectơ chỉ phương của đường thẳng  :   có tọa 1 2 5 độ là A. (1; 2;  5). B. ( 1  ;  2;  5). C. ( 1  ; 3;  3). D. (1; 3; 3).
Câu 13: Trong không gian Oxyz, cho điểm I(1; 2; 5) và mặt phẳng () : x y 2  z
2  2  0. Phương trình
mặt cầu tâm I và tiếp xúc với () là A. x 2   y 2   z 2 ( 1) ( 2) (  5)  9. B. x 2   y 2   z 2 ( 1) ( 2) (  5)  9. C. x 2   y 2   z 2 ( 1) ( 2) (  5)  3. D. x 2   y 2   z 2 ( 1) ( 2) (  5)  3.
Câu 14: Khi đặt x
3 = t thì phương trình x 1 + x 1 9 3 + - - 30 = 0 trở thành A. 2
3t - t - 10 = 0. B. 2
9t - 3t - 10 = 0. C. 2 t - t - 10 = 0. D. 2
2t - t - 10 = 0. Câu 15: Cho f x ( ) và g x
( ) là các hàm số liên tục bất kì trên đoạn a  ; b. 
 Mệnh đề nào sau đây đúng ? b b b b b b A. f x ( )  g x ( ) dx f x ( dx )  g x ( dx ) .    B.  f x ( )  g x ( )dx f x ( dx )  g x ( dx ) .   a a a a a a b b b b b b C. f x ( )  g x ( )dx f x ( d ) x g x ( d ) x.   D. f x ( )  g x ( )dx f x ( dx )  g x ( dx ) .   a a a a a a px Câu 16: Gọi ,
m M lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số f x ( ) = x 2 + cos trên đoạn 2 é 2; 2ù - . ê + ë
úû Giá trị của m M bằng A. 0. B. 2. C. -4. D. -2. x  2 y  1 z
Câu 17: Trong không gian Oxyz, cho đường thẳng d :   và mặt phẳng 1  2 2 P ( ) : x y
2  z  5  0. Tọa độ giao điểm của d với P ( ) là A. (3;  1;  2). B. (2; 1;  1). C. (1; 3;  2). D. (1; 3; 2).
Câu 18: Cho hình lập phươngABCD A . B CD
  có cạnh bằng a. Diện tích xung quanh của hình trụ có hai
đáy là hai hình tròn ngoại tiếp hai hình vuông ABCD và AB CD   bằng A. a2 2 2 . B. a2 2 . C. a2. D. a2 2 .
Trang 2/6 - Mã đề thi 132 2
Câu 19: Cho hàm số f x ( ) có đạo hàm ¢ = ( 2 ( ) + )( - 2) ( x f x x x x 2 - 4), x " Î .
 Số điểm cực trị của f x ( ) là A. 2. B. 1. C. 4. D. 3.
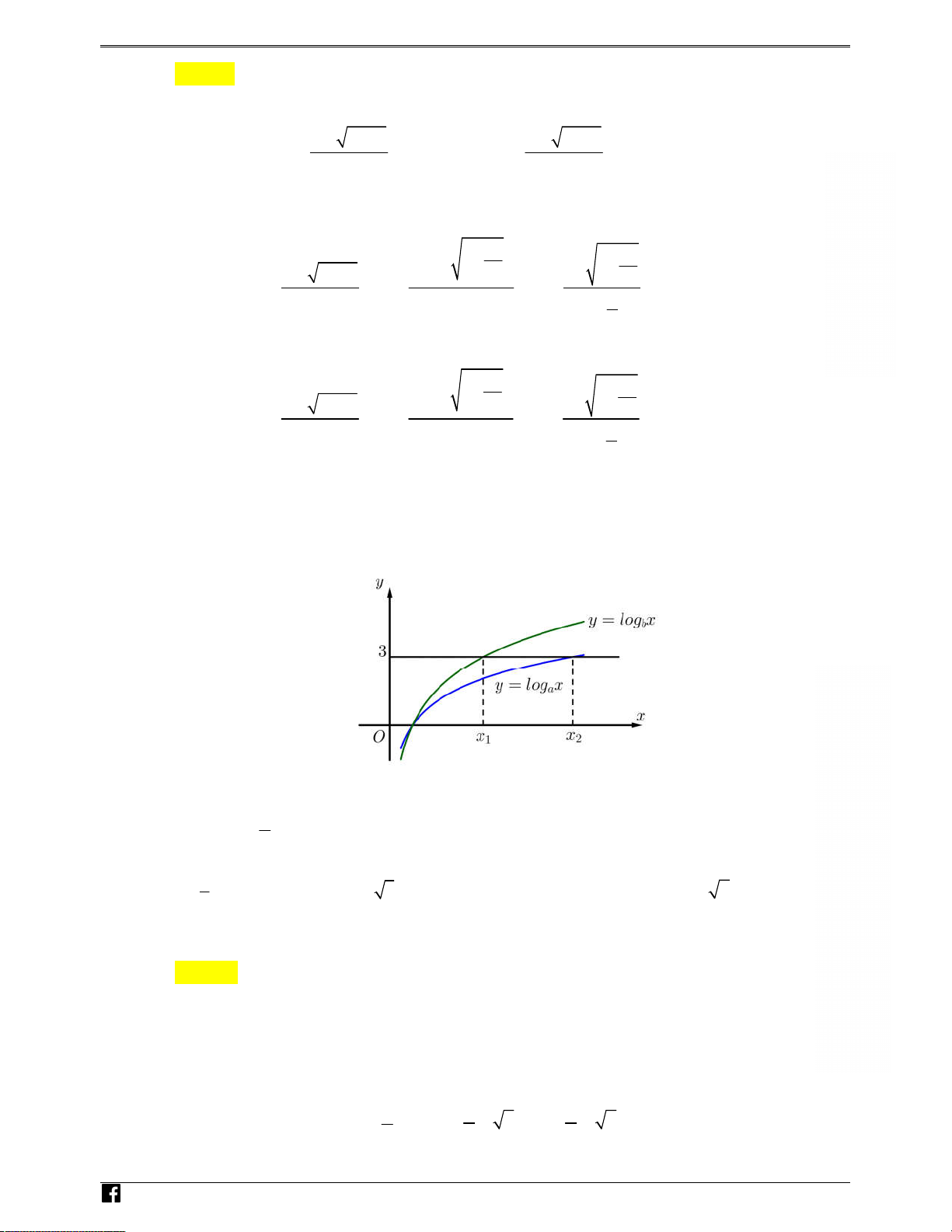
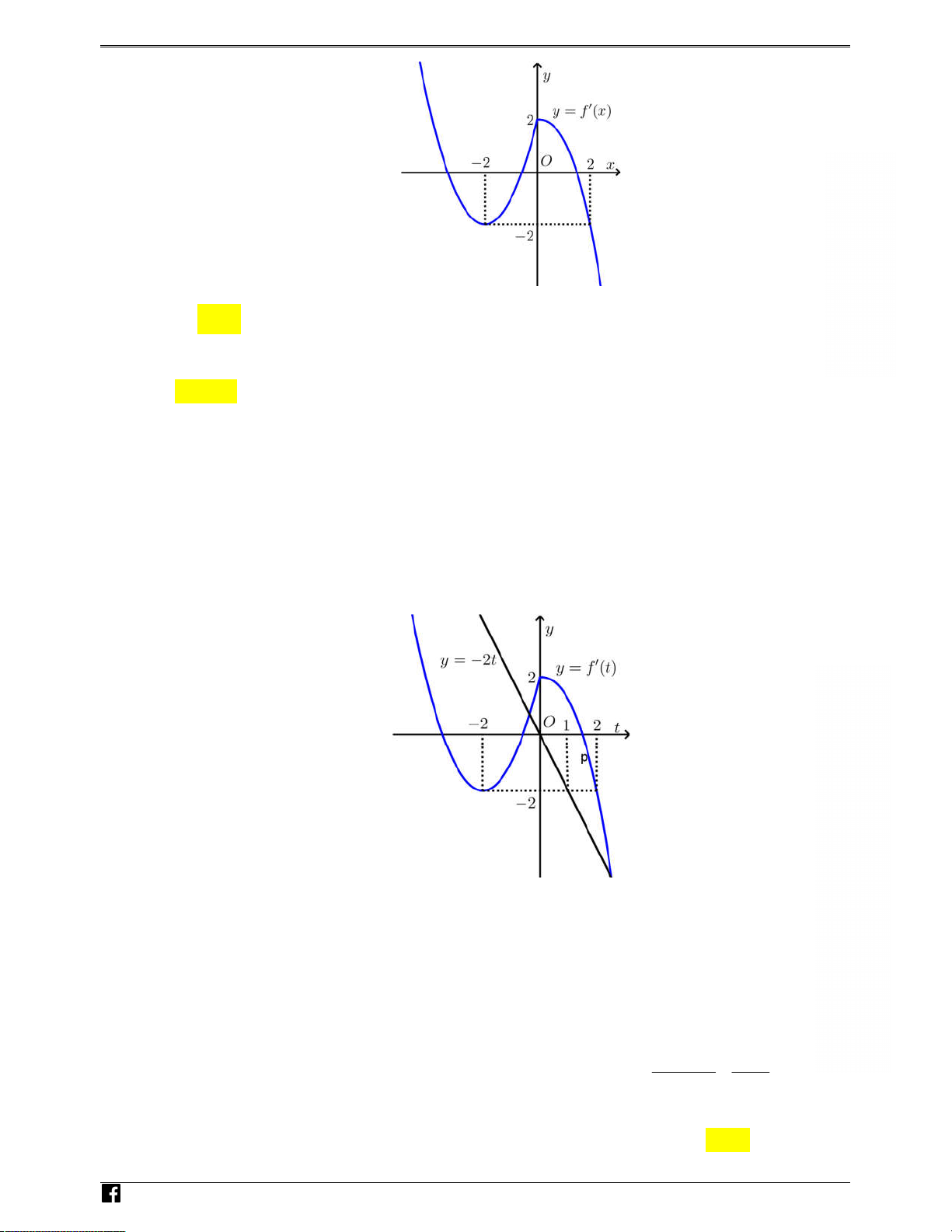
Câu 20: Cho hàm số y = f x
( ) có đồ thị như hình bên. Hàm số y = 2 - f x
( ) đồng biến trên khoảng
A. (1; 2). B. (2; ) 3 . C. (-1; ) 0 . D. (-1; ) 1 .
Câu 21: Cho số phức z thỏa mãn z + 2z = 6 + 2 .
i Điểm biểu diễn số phức z có tọa độ là A. (2;- ) 2 . B. (-2;- ) 2 . C. (2; ) 2 . D. (-2; ) 2 .
Câu 22: Bất phương trình log - 3 > log 9 -
có bao nhiêu nghiệm nguyên ? 4 (x 2 x ) 2 ( x ) A. 1. B. Vô số. C. 3. D. 4. 2 x + x + 1
Câu 23: Đồ thị hàm số y =
có bao nhiêu đường tiệm cận ? x - 1 A. 2. B. 3. C. 4. D. 1.
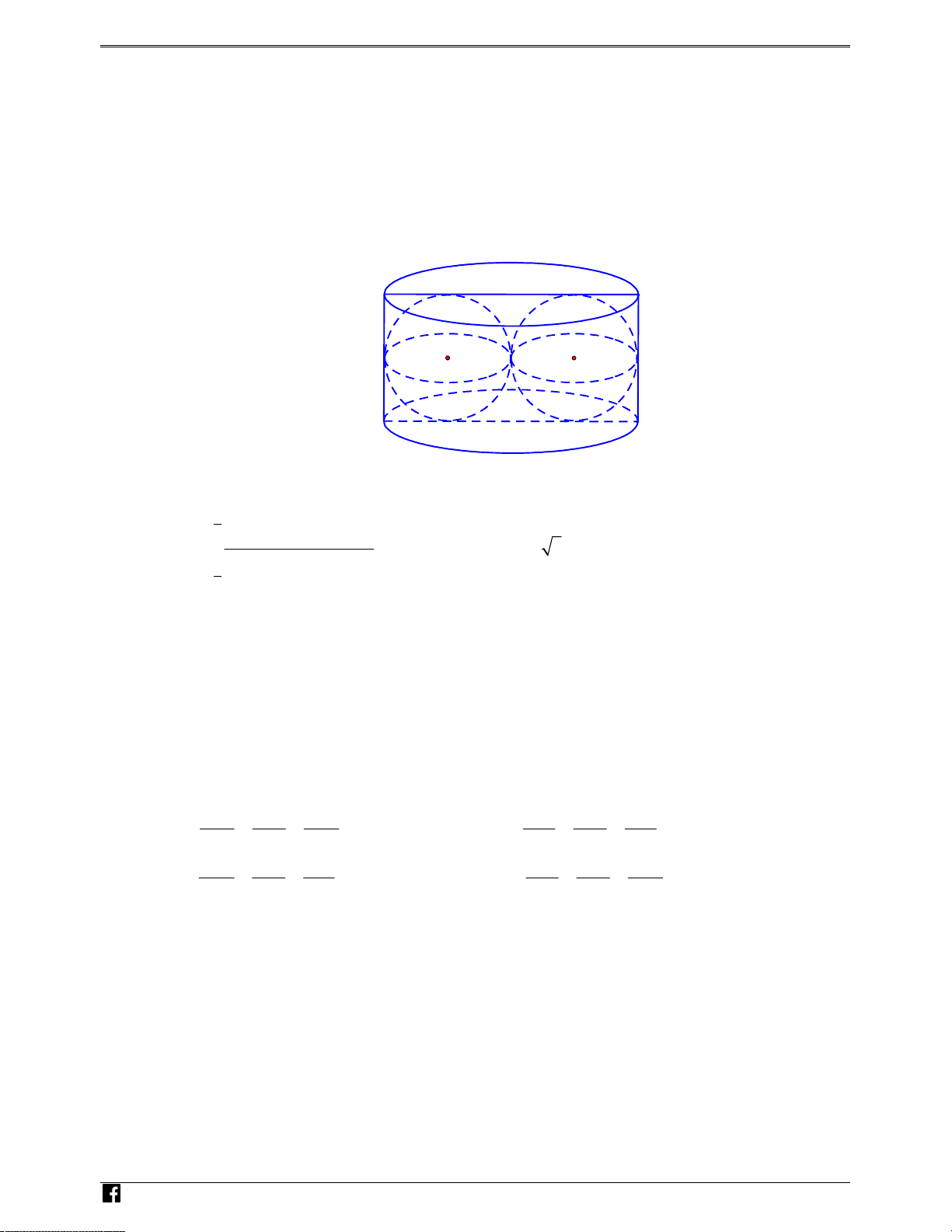
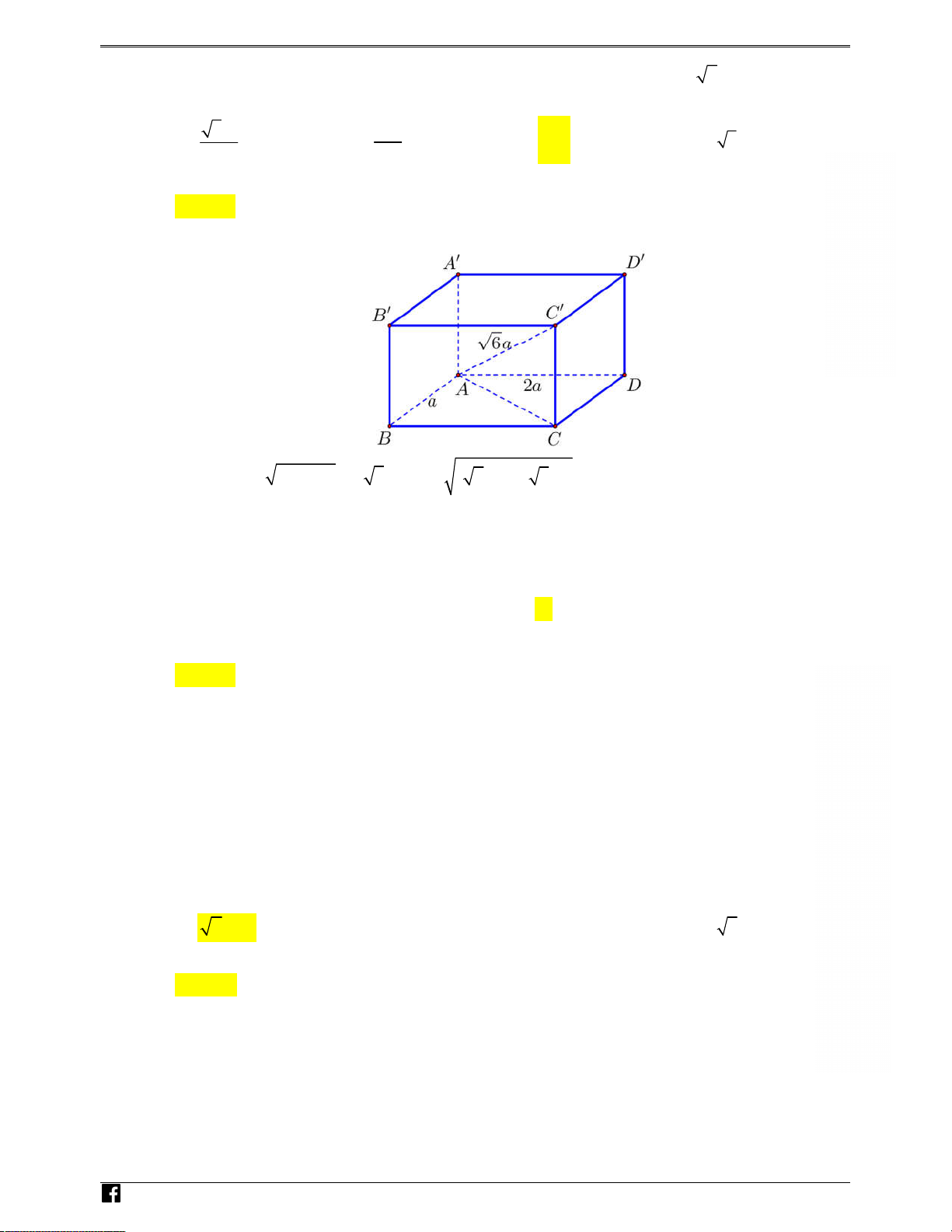
Câu 24: Hàm số y = log x và y = log x có đồ thị như a b
hình bên. Đường thẳng y = 3 cắt hai đồ thị tại các điểm a
có hoành độ là x , x . Biết rằng x = 2x , giá trị 1 2 2 1 b bằng 1 A. . B. 3 2. 3 C. 2. D. 3. e
Câu 25: Hàm số y = ( 3
x - 3x) có bao nhiêu điểm cực trị ? A. 2. B. 0. C. 3. D. 1.
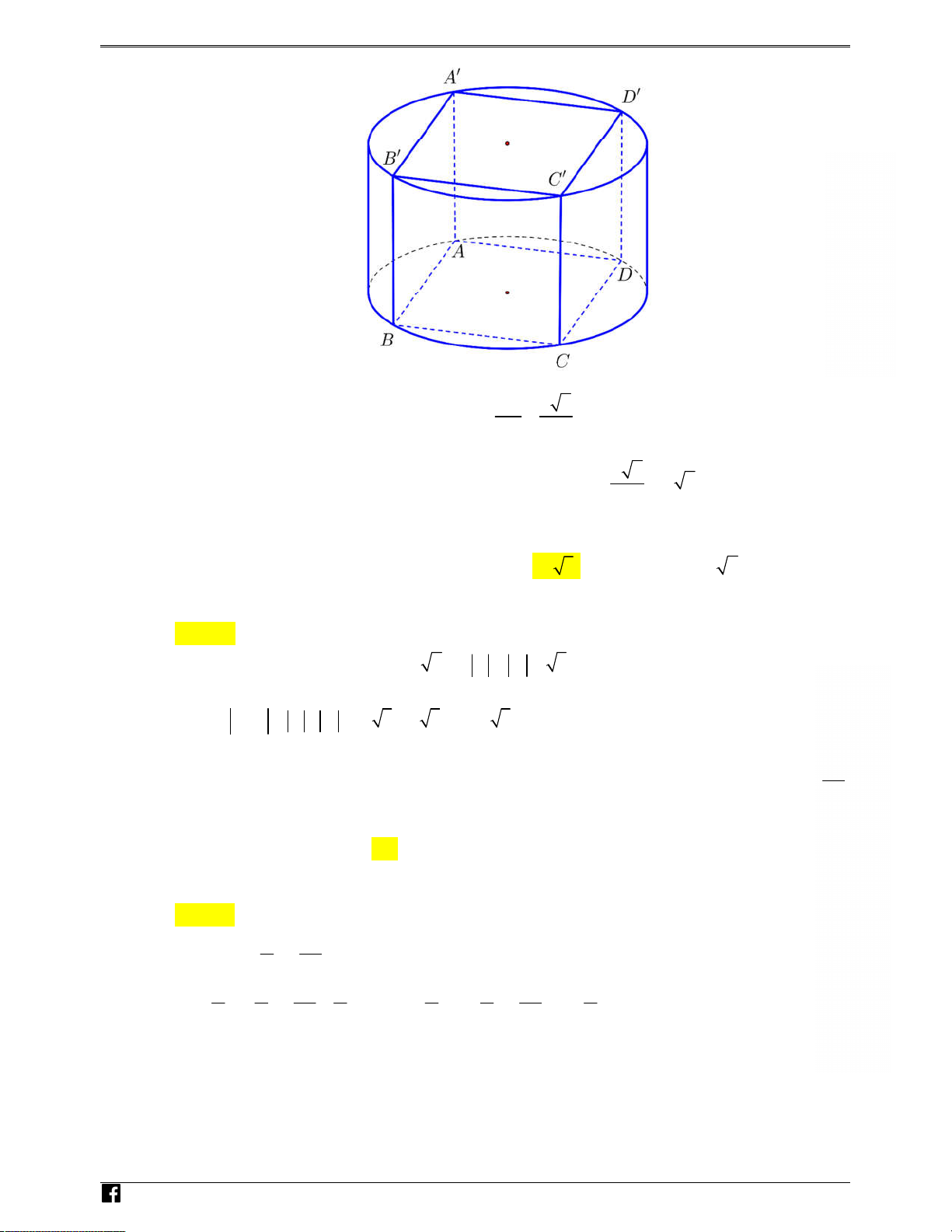
Câu 26: Cho hình hộp chữ nhật ABCD A . B CD
  có AB a, AD a 2 , AC   a
6 . Thể tích của khối hộp chữ nhật ABCD A . B CD   bằng a3 3 a3 2 A. . B. . C. a3 2 . D. a 3 2 3 . 3 3
Câu 27: Gọi (D) là hình phẳng giới hạn bởi các đường = 2x y
,y = 0,x = 0 và x = 2.Thể tích V của khối
tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính bởi công thức 2 2 2 2 A. x 1 V p 2 + = dx. ò B. x V 2 + = d 1 x. ò C. = 4x V dx. ò D. = p 4x V dx. ò 0 0 0 0 x  1 y  2 z  3
Câu 28: Trong không gian Oxyz, cho hai đường thẳng  :   và 1 2  1 2 x  3 y  1 z  2  :  
. Góc giữa hai đường thẳng  ,  bằng 2 1 1 4  1 2 A. 0 30 . B. 0 135 . C. 0 60 . D. 0 45 .
Trang 3/6 - Mã đề thi 132
Câu 29: Gọi z , z là các nghiệm phức của phương trình z2 - z
2 + 3 = 0. Mô đun của z z 3 4 bằng 1 2 1 2 A. 81. B. 16. C. 27 3. D. 8 2.
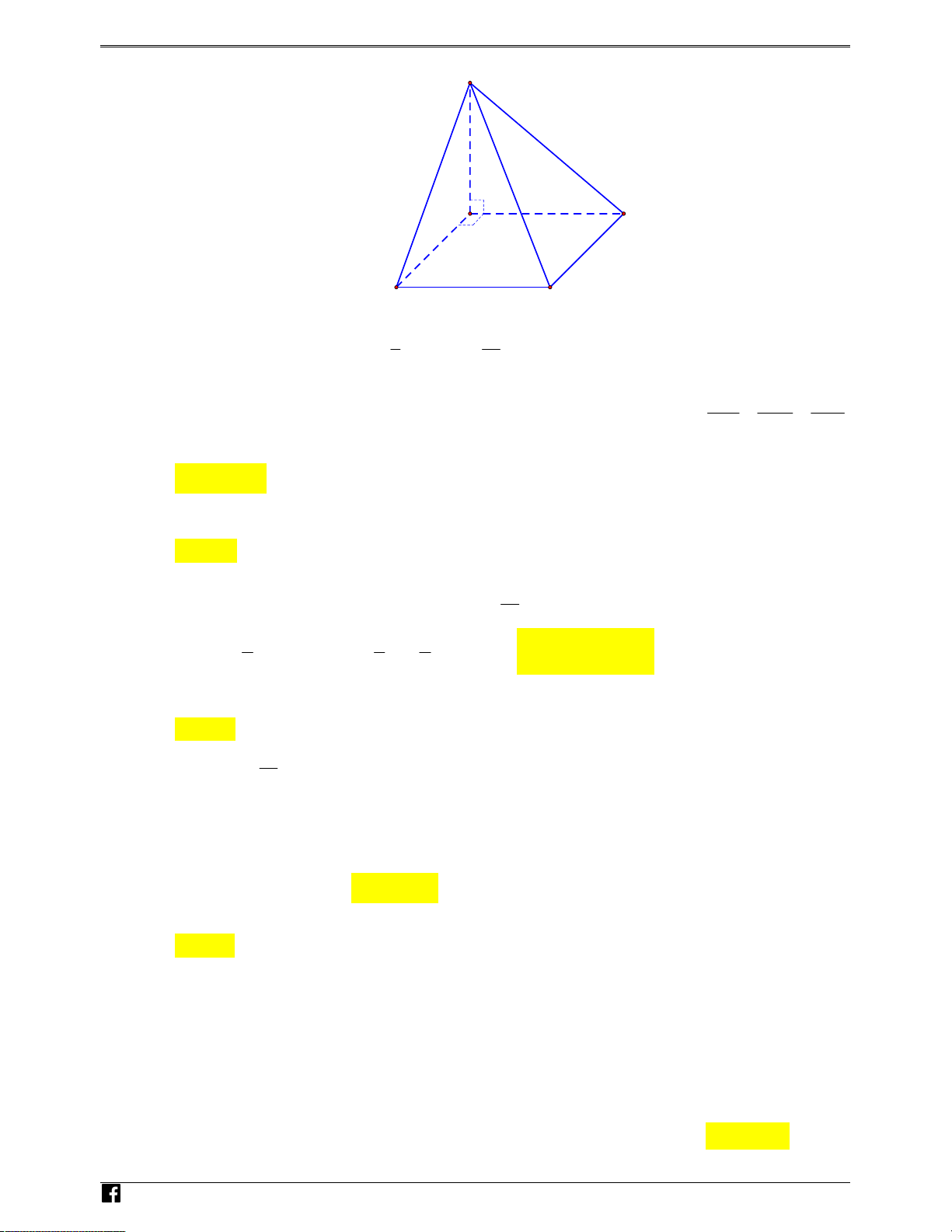
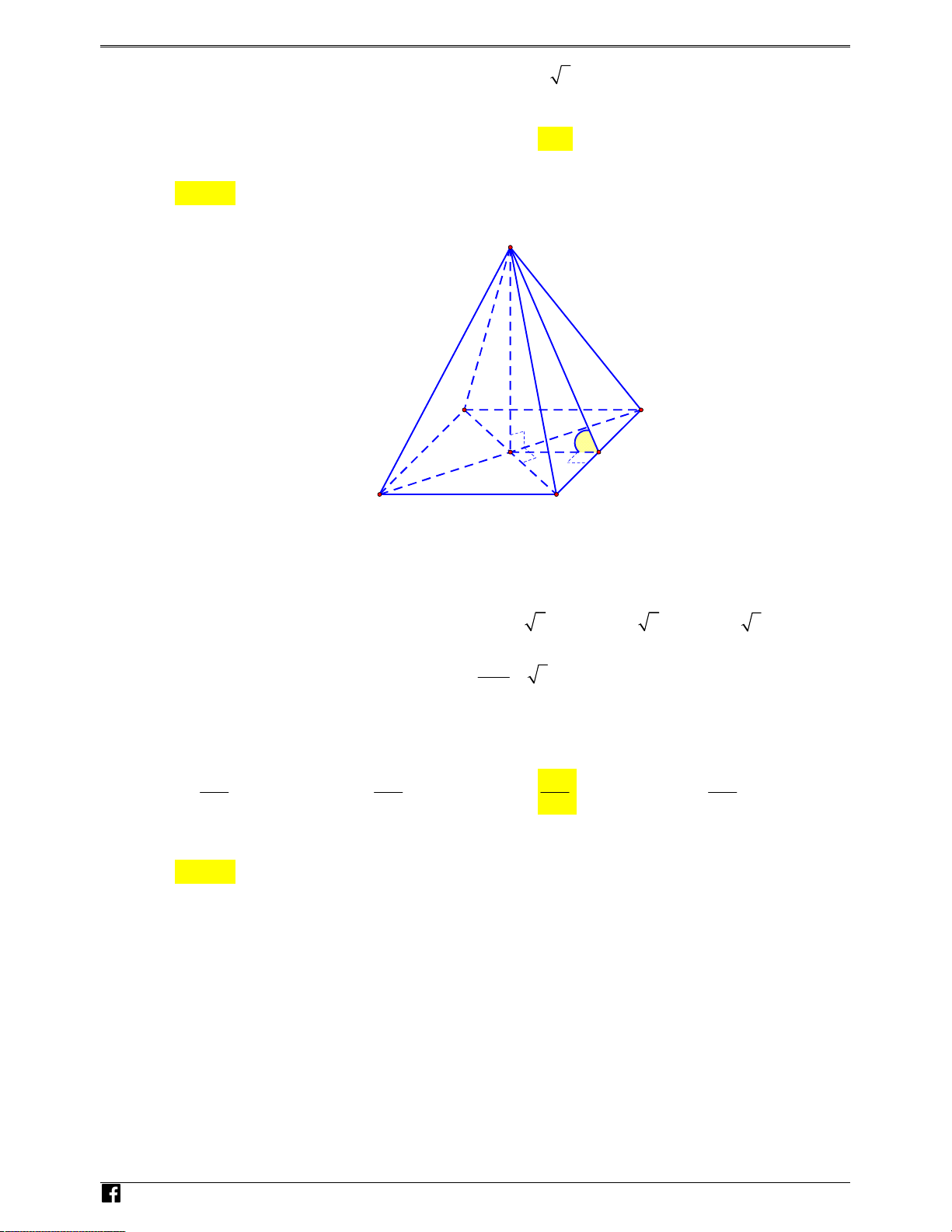
Câu 30: Cho hình chóp tứ giác đều S A
. BCD có AB a 2 ,SA a
5 . Góc giữa hai mặt phẳng SAB ( ) và AB ( CD) bằng A. 0 60 . B. 0 45 . C. 0 30 . D. 0 75 .
Câu 31: Cho f x = x 3 ( ) ( - 1) - x
3 + 3. Đồ thị hình bên là của hàm số có công thức A. y = f - (x + ) 1 + 1. B. y = f - (x + ) 1 -1. C. y = f - (x - ) 1 + 1. D. y = f - (x - ) 1 -1. p 3 2
cos x + sin x cos x + 1 Câu 32: Biết
dx = a + b ln 2 + c ln 1 + 3 , ò
với a, b, c là các số hữu tỉ. Giá 4 3 ( )
cos x + sin x cos x p 4
trị của abc bằng A. -2. B. -4. C. 0. D. -6.
Câu 33: Hai bạn Công và Thành cùng viết ngẫu nhiên ra một số tự nhiên gồm hai chữ số phân biệt. Xác suất
để hai số được viết ra có ít nhất một chữ số chung bằng 154 448 145 281 A. . B. . C. . D. . 729 729 729 729
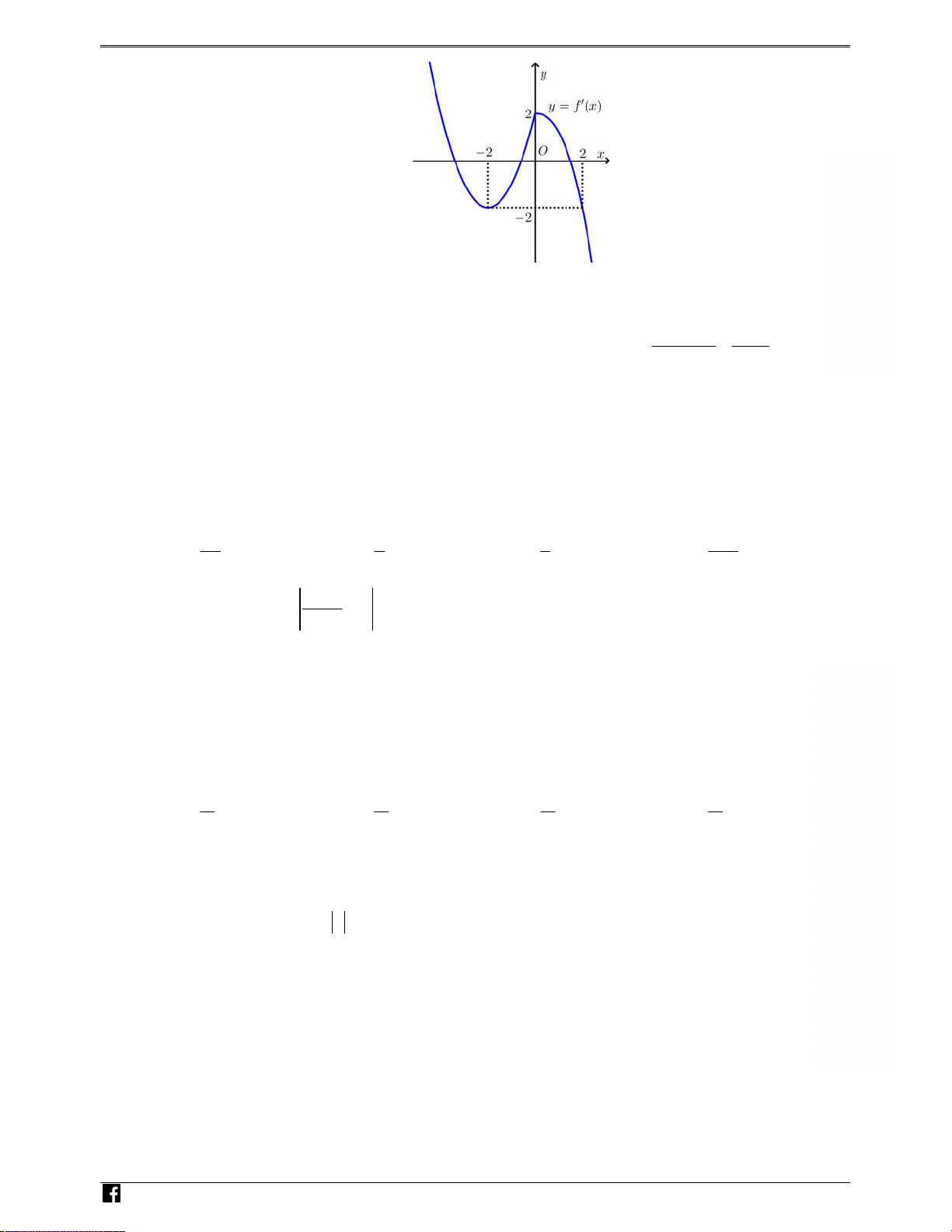
Câu 34: Người ta xếp hai quả cầu có cùng bán kính r vào một
chiếc hộp hình trụ sao cho các quả cầu đều tiếp xúc với hai đáy,
đồng thời hai quả cầu tiếp xúc với nhau và mỗi quả cầu đều tiếp
xúc với các đường sinh của hình trụ (tham khảo hình vẽ). Biết thể tích khối trụ là 3
120 cm , thể tích mỗi khối cầu bằng A. 3 10 cm . B. 3 40 cm . C. 3 20 cm . D. 3 30 cm .
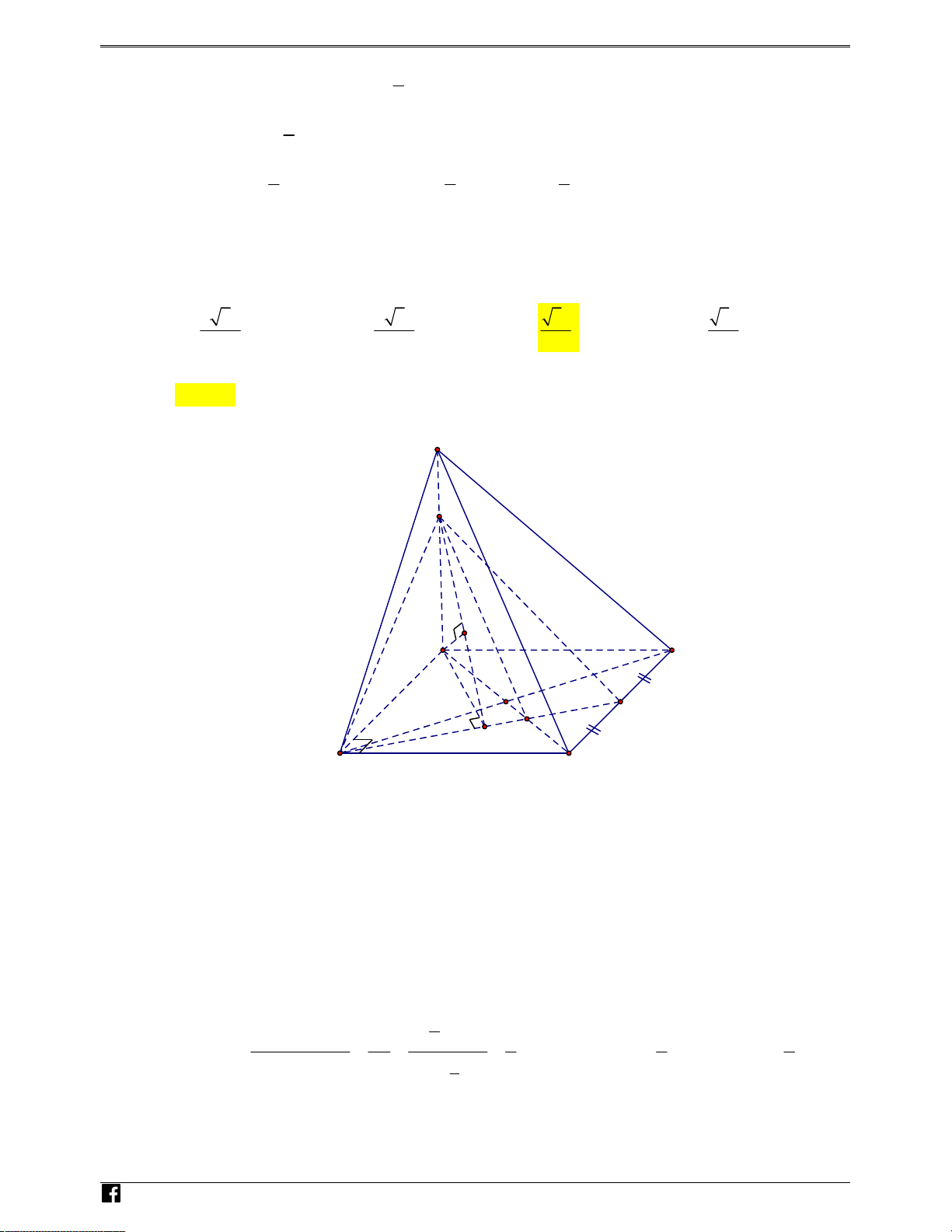
Câu 35: Cho hình chóp S A
. BCD có đáy ABCD là hình chữ nhật, biết AB a
2 , AD a, SA a 3 và SA
vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh CD. Khoảng cách giữa hai đường thẳng SC và BM bằng 3 a 3 2 a 3 a 3 a 3 A. . B. . C. . D. . 4 3 2 3
Câu 36: Xét các số phức z, w thỏa mãn w - i = 2, z + 2 = iw. Gọi z , z lần lượt là các số phức mà tại 1 2
đó z đạt giá trị nhỏ nhất và đạt giá trị lớn nhất. Mô đun z + z bằng 1 2 A. 3 2. B. 3. C. 6. D. 6 2.
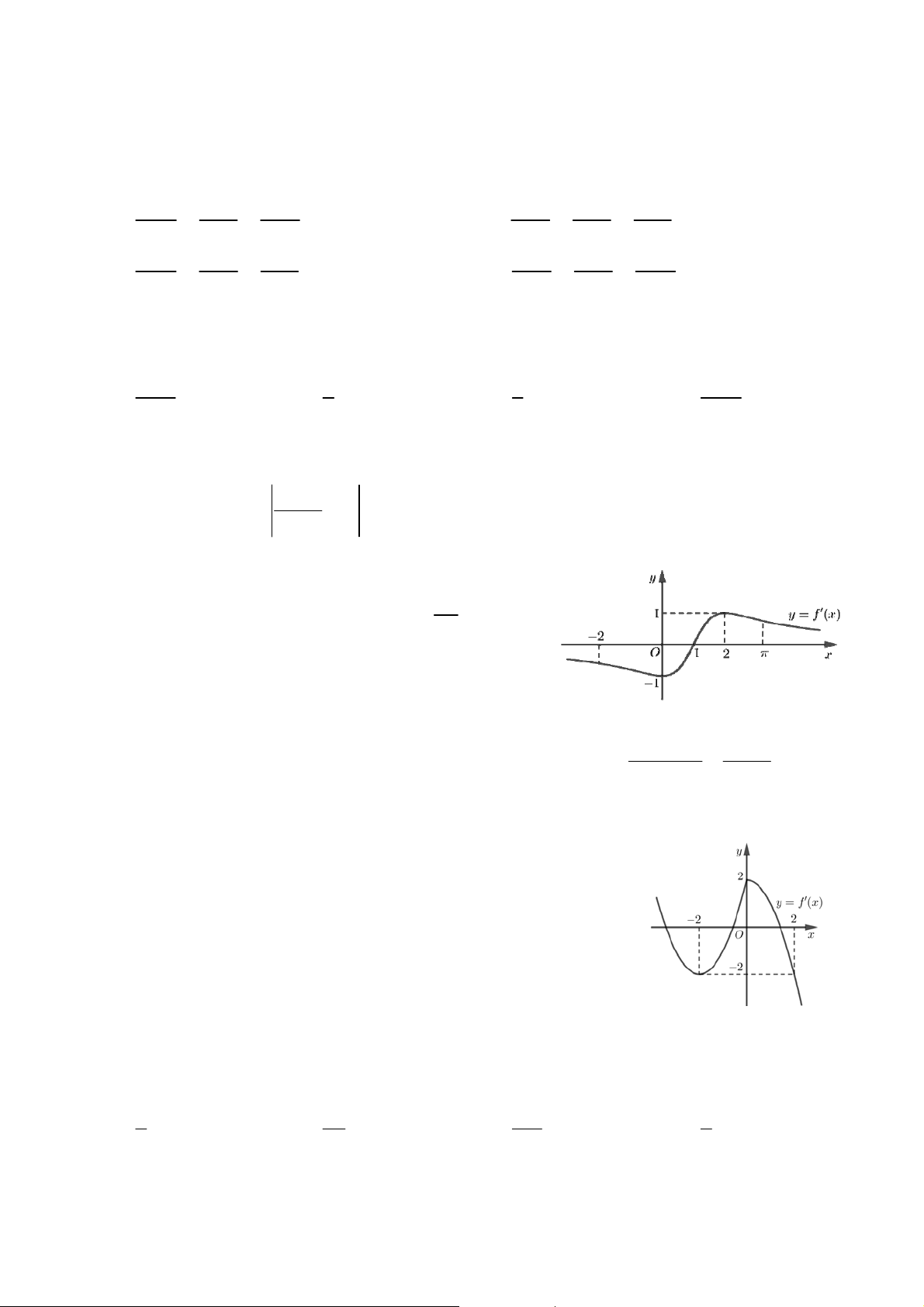
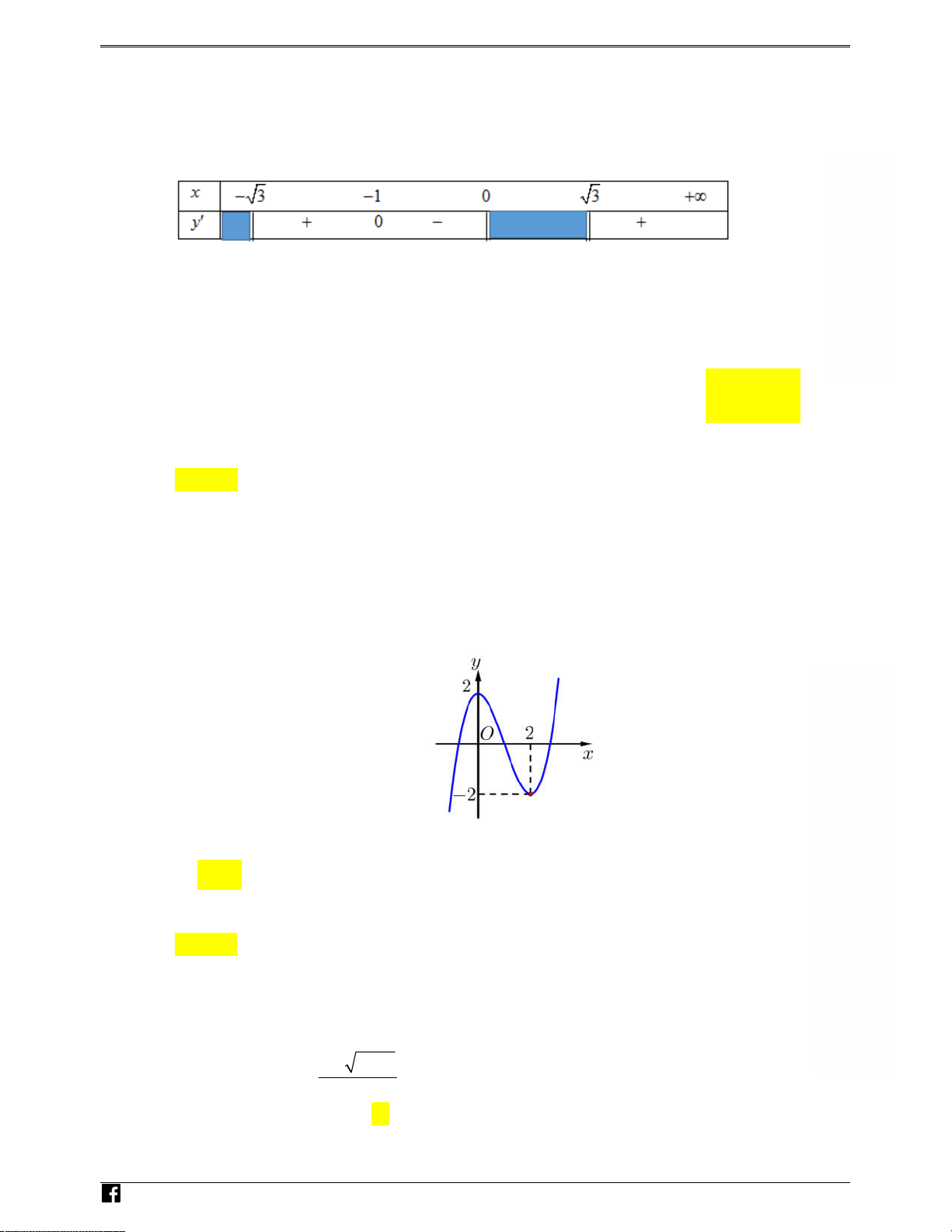
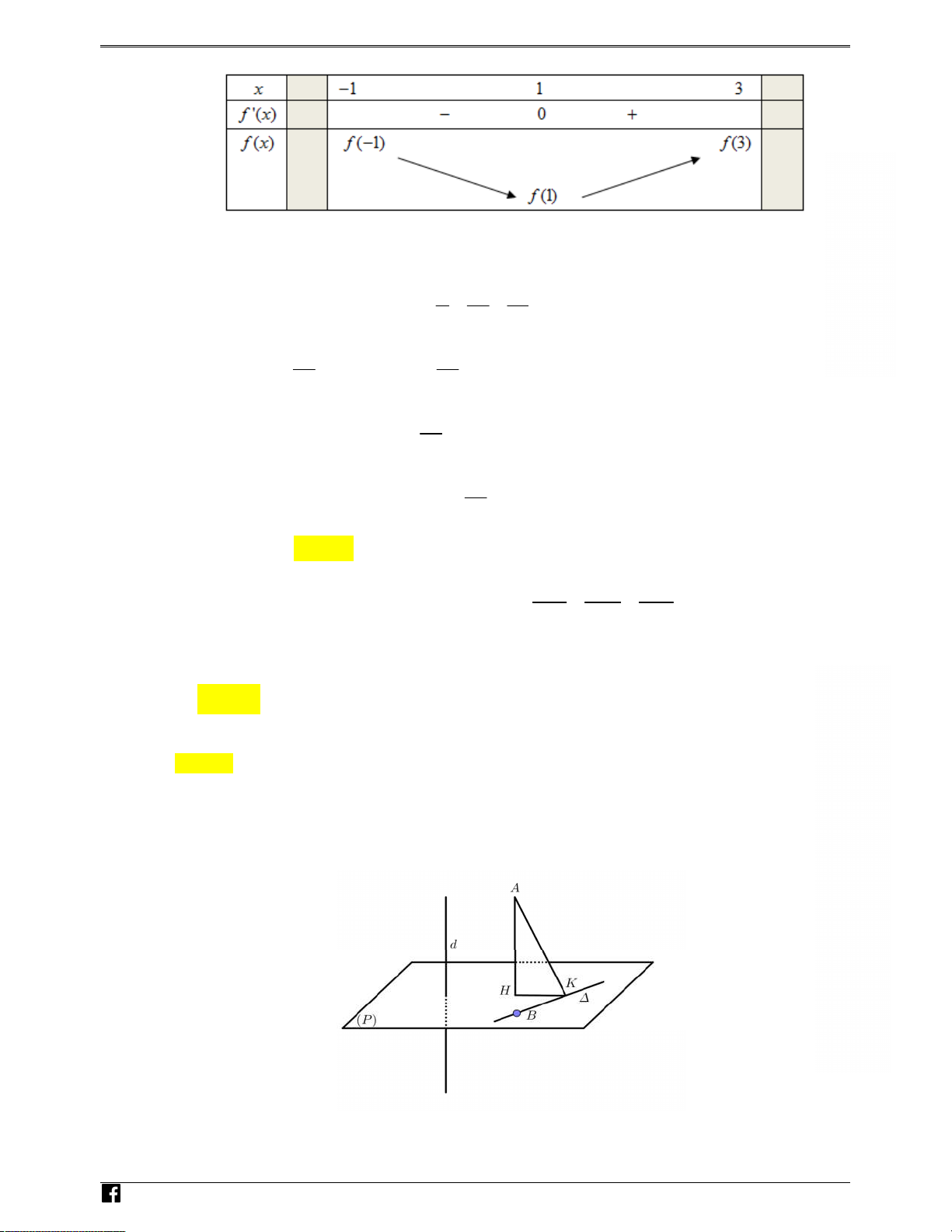
Câu 37: Cho hàm số f x
( ) có bảng xét dấu đạo
hàm như hình bên. Hàm số y = f (1- 2x) đồng biến trên khoảng æ 1 ö æ 1ö æ 3ö æ3 ö A. ç- ç ; 1÷÷. ç ÷ ç ÷ ç ÷ ç B. - ç 2; - ÷. C. 0; ç ÷. D. ç ; 3÷. çè 2 ÷÷ø çè 2÷÷ø çè 2÷÷ø çè2 ÷÷ø
Trang 4/6 - Mã đề thi 132 x   1   t 2 x   2  t  
Câu 38: Trong không gian Oxyz, cho hai đường thẳng d : y   t ; d : y   1   t 2  và mặt phẳng z   1   t 3   z   t 2   P
( ) : x y z  2  0. Đường thẳng vuông góc với mặt phẳng P
( ) và cắt hai đường thẳng d, d có phương trình là x  3 y  1 z  2 x  1 y  1 z  1 A.   . B.   . 1 1 1 1 1  4  x  2 y  1 z  1 x  1 y  1 z  4 C.   . D.   . 1 1 1 2 2 2 Câu 39: Biết rằng x
xe là một nguyên hàm của f ( x - ) trên khoảng ( ;   )  . Gọi F x ( ) là một nguyên hàm của x f ¢ x ( e
) thỏa mãn F(0) = 1, giá trị của F( 1 - ) bằng 5 - e 7 5 7 - e A. . B. . C. . D. . 2 2 2 2
Câu 40: Có bao nhiêu số nguyên m để phương trình + 3 x x
= me có 2 nghiệm phân biệt ? A. 7. B. 6. C. 5. D. Vô số. x
Câu 41: Hàm số f x ( ) 
m với m là tham số thực có nhiều nhất bao nhiêu điểm cực trị ? x2  1 A. 5. B. 4. C. 3. D. 2. Câu 42: Cho f x
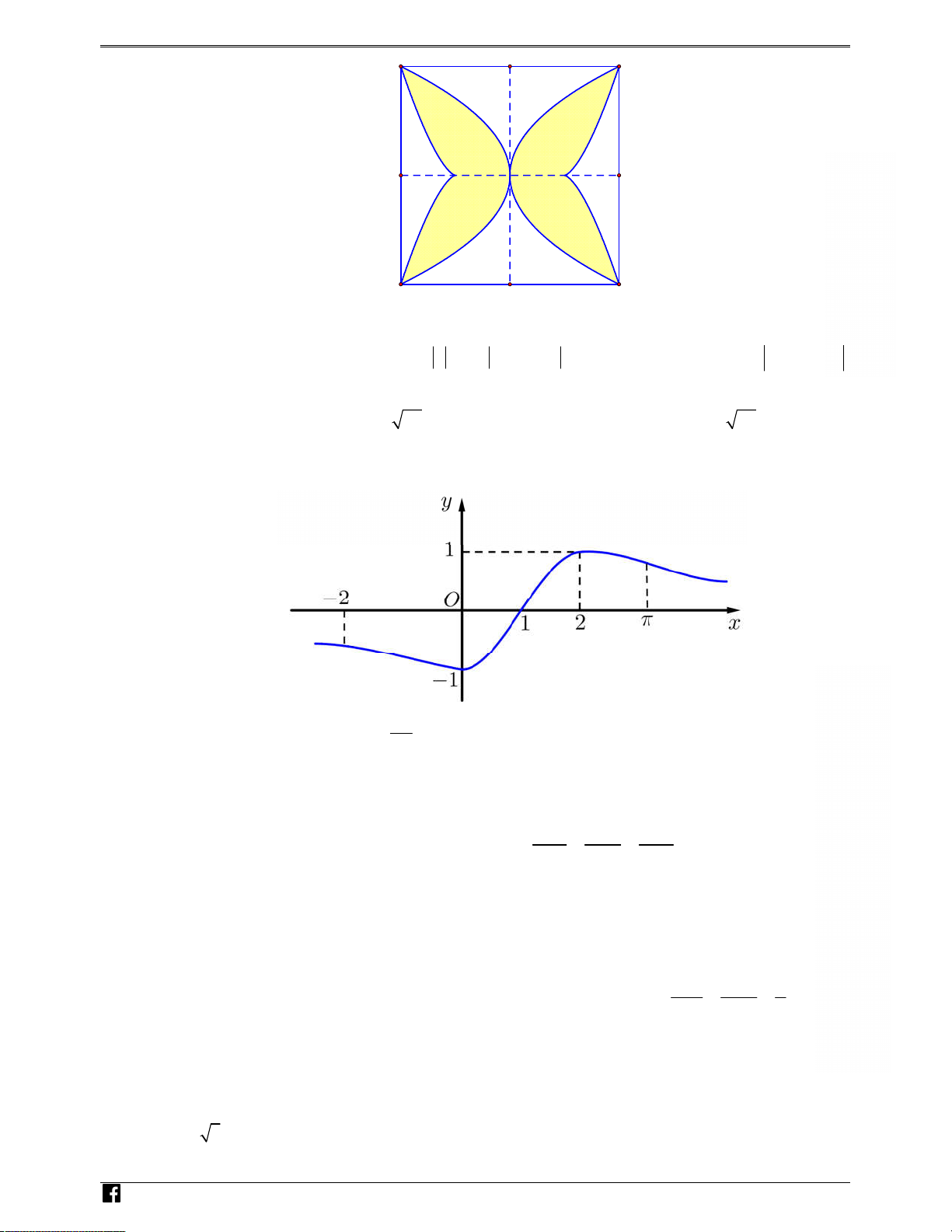
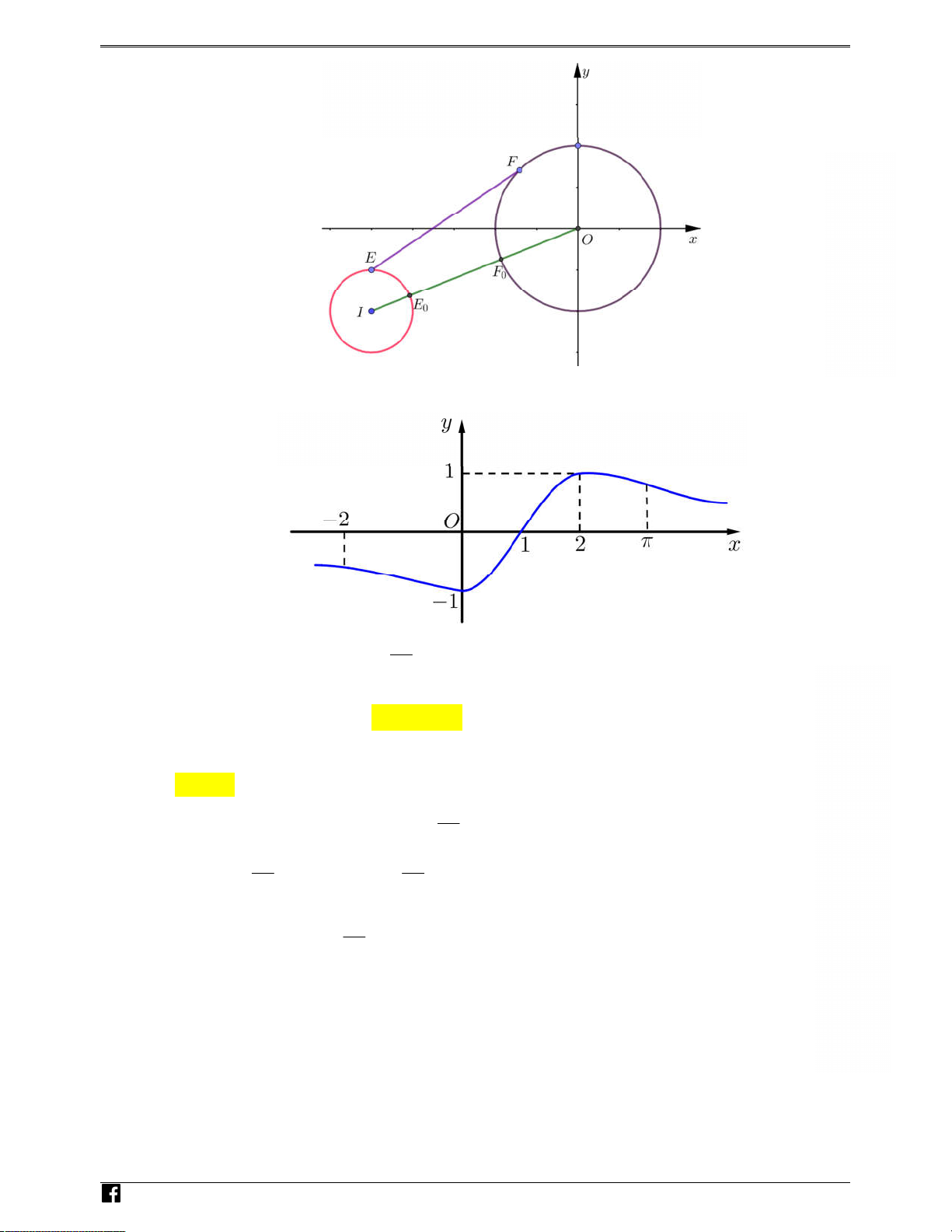
( ) mà đồ thị hàm số y f x ( ) như x
hình bên. Bất phương trình f x ( )  sin  m 2
nghiệm đúng với mọi x   1;  3   khi và chỉ khi
A. m f (1)  1.
B. m f (0).
C. m f (2).
D. m f (1)  1. 1 1
Câu 43: Có bao nhiêu số nguyên a   2019 
; 2019 để phương trình    có 2 ln x  5 x a x 3  1 nghiệm phân biệt ? A. 2015. B. 2014. C. 2022. D. 0. Câu 44: Cho f x
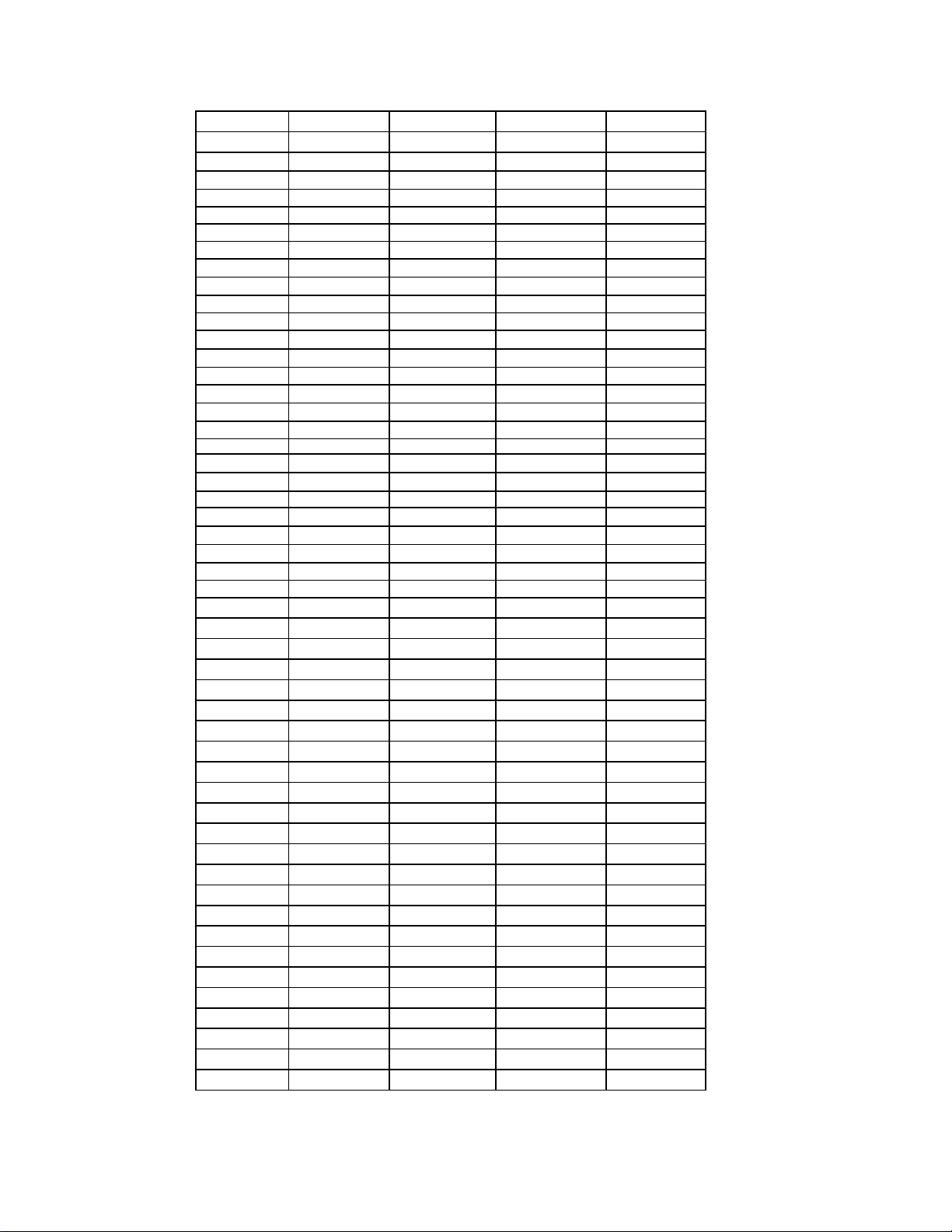
( ) mà đồ thị hàm số y f x ( ) như hình bên.
Hàm số y f x    x2 1  x
2 đồng biến trên khoảng
A. 1; 2. B.  1;  0. C. 0;  1 . D.  2;    1 .
Câu 45: Cho hàm số f x
( ) có đạo hàm liên tục trên  thỏa mãn f (0)  3 và 2 f x fx x2 ( ) (2 )  x 2  2, x   .
 Tích phân xf x ( )dx  bằng 0 5 4 10  2 A. . B. . C. . D. . 3 3 3 3
Trang 5/6 - Mã đề thi 132
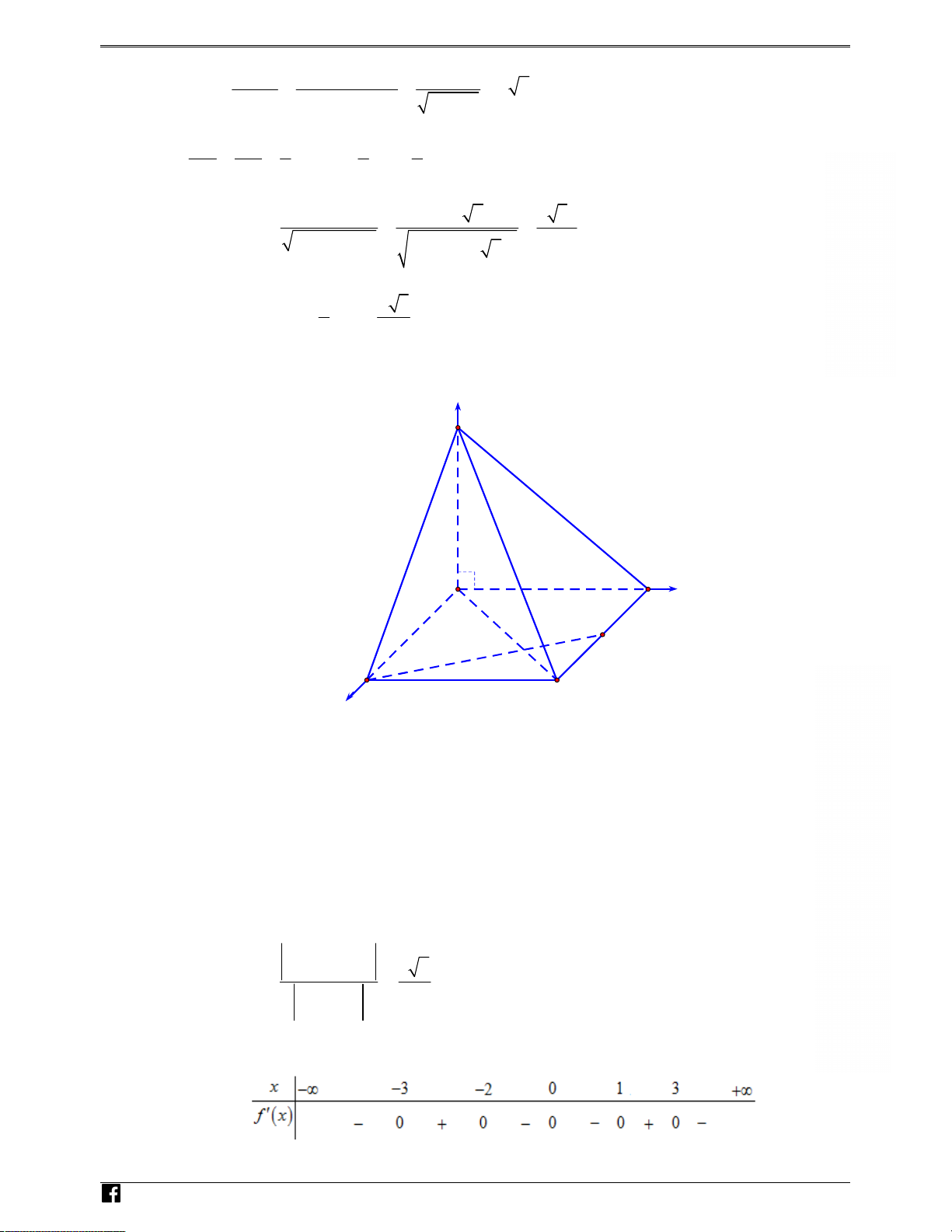
Câu 46: Cho khối hộp ABCD A . B CD
  có thể tích bằng V . Gọi M, N, P, Q, E, F lần lượt là tâm các
hình bình hành ABCD, AB CD  , ABB A  , BCC B  , CDD C
 , DAAD . Thể tích khối đa diện có các đỉnh
M, P, Q, E, F, N bằng V V V V A. . B. . C. . D. . 4 2 6 3 x - 3 y - 4 z - 2
Câu 47: Trong không gian Oxyz, cho đường thẳng d : = = và hai điểm (6 A ; 3; - 2), 2 1 1
B(1; 0;  1). Gọi D là đường thẳng đi qua B, vuông góc với d và thỏa mãn khoảng cách từ A đến D là
nhỏ nhất. Một véctơ chỉ phương của D có tọa độ là A. (2; - 1; - 3). B. (1; 1; - 3). C. (1; 2; - 4). D. (1; - 1; - 1). x  1 y  2 z
Câu 48: Trong không gian Oxyz, cho điểm A(2;  3; 4), đường thẳng d :   và mặt cầu 2 1 2 S x 2   y 2   z 2 ( ) : ( 3) ( 2)
(  1)  20. Mặt phẳng P
( ) chứa đường thẳng d thỏa mãn khoảng cách từ
điểm A đến P
( ) lớn nhất. Mặt cầu S ( ) cắt P
( ) theo đường tròn có bán kính bằng A. 5. B. 1. C. 4. D. 2.
Câu 49: Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên
gạch hoa hình vuông cạnh 40 (cm) như hình bên. Biết rằng người thiết kế
đã sử dụng các đường cong có phương trình x2 y4 4  và  3 x    y2 4 1
để tạo hoa văn cho viên gạch. Diện tích phần được tô
đậm gần nhất với giá trị nào dưới đây ? A. 506 (cm2). B. 507 (cm2). C. 747 (cm2). D. 746 (cm2).
Câu 50: Xét các số phức z, w thỏa mãn z  2, iw  2  i
5  1. Giá trị nhỏ nhất của z2  wz  4 bằng A. 8. B. 4. C. 2  29  3. D. 2  29  5.
----------------------------------------------- ----------- HẾT ----------
Trang 6/6 - Mã đề thi 132
ĐÁP ÁN MÔN TOÁN LẦN 3 - 2019 Câu Mã 132 Mã 209 Mã 357 Mã 485 1 D A A D 2 C D D D 3 B A C D 4 C C C A 5 A B D D 6 B D D C 7 D B C C 8 C C B A 9 B D A A 10 D B D A 11 B D B B 12 A B D B 13 A A B C 14 A B A B 15 B D D C 16 D B B A 17 D A C A 18 B D C D 19 D D D D 20 A D D B 21 A D A C 22 C A C C 23 B B A A 24 B D A C 25 D C C C 26 C C C C 27 D A C C 28 D C A A 29 C B D D 30 A C B B 31 A C B B 32 B A B C 33 D C B D 34 C A C A 35 D C B B 36 C B B D 37 C B C A 38 A C A B 39 B A A B 40 A A A A 41 B A C D 42 A D D D 43 A D D A 44 A D C B 45 C C B D 46 C B A B 47 B C B A 48 D B C B 49 C A D C 50 A D A A NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019
CHUYÊN ĐẠI HỌC VINH
ĐỀ THI THỬ THPT LẦN 3 QG NĂM 2019 MÔN: TOÁN
Thời gian làm bài: 90 phút
(không kể thời gian giao đề) NH Mã Đề: 209 ÓM
(Đề gồm 06 trang) TO
Họ và tên: .................................................................................................... SBD: ..................................................... . ÁN VD Câu 1:
Cho khối nón có độ dài đường cao bằng 2a và bán kính đáy bằng a . Thể tích của khối nón đã cho bằng – 3 3 3 VD 2 a 4 aa A. . B. . C. . D. 3 2 a . 3 3 3 C Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA a và SA vuông
góc với mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng 3 a 3 2a 3 a A. . B. . C. 3 a . D. . 6 3 3 x 1 y  3 z  3 Câu 3:
Trong không gian Oxyz , một vectơ chỉ phương của đường thẳng  :   1 2 5  có tọa độ là A. 1; 2; 5   . B. 1;3;3 . C.  1  ;3; 3   . D.  1  ; 2  ; 5   . a Câu 4:
Với a , b là các số thực dương bất kì, log bằng 2 2 b NH a 1 a A. 2log . B. log .
C. log a  2log b .
D. log a  log 2b . 2 2   2 2 2 2 ÓM T b 2 b Câu 5:
Trong không gian Oxyz , cho hai điểm A 2  ; 1
 ;3 và B 0;3 
;1 . Gọi   là mặt phẳng OÁ
trung trực của AB . Một vectơ pháp tuyến của   có tọa độ là N V A. 2;4;  1  . B. 1;2;  1  . C.  1  ;1; 2 . D. 1;0  ;1 . D – VD Câu 6:
Cho cấp số nhân u có u  1,u  2
 . Mệnh đề nào sau đây đúng? n  1 2 C A. 2018 u  2 . B. 2019 u  2 . C. 2019 u  2 . D. 2018 u  2 2019 2019 2019 2019 Câu 7:
Hình dưới đây là đồ thị của hàm số nào?
https://www.facebook.com/groups/toanvd.vdc Trang 1 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 A. 2 y x  2 . B. 4 2
y x x  2 . C. 4 2
y x x  2 . D. 2
y x x  2 . Câu 8:
Trong không gian Oxyz , cho điểm I 1;2;5 và mặt phẳng   : x  2y  2z  2  0 .
Phương trình mặt cầu tâm I và tiếp xúc với   là NH 2 2 2 2 2 2 ÓM A. x  
1   y  2   z  5  3 . B. x  
1   y  2   z  5  3. 2 2 2 2 2 2 TO C. x  
1   y  2   z  5  9 . D. x  
1   y  2   z  5  9 . ÁN Câu 9:
Cho hàm số y f x có đồ thị như hình vẽ dưới đây VD – VD C Trên đoạn  3  ; 
3 hàm số đã cho có mấy điểm cực trị? A. 4 . B. 5 . C. 2 . D. 3 .
Câu 10: Cho f x và g x là các hàm số liên tục bất kì trên đoạn  ;
a b . Mệnh đề nào sau đây đúng ? b b b b b b A.
f x  g x dx f x dx g x dx    .
B.  f x  g xdx f xdx g xdx   . a a a a a a NH b b b b b b ÓM T
C.  f x  g x dx f xdx g xdx  
. D.  f x  g xdx f xdx g xdx   a a a a a a OÁ . N
Câu 11: Cho hàm số y f x có đồ thị như hình vẽ bên. V D – VD C
Hàm số đã cho nghịch biến trên khoảng A. 0;2 . B.  2  ; 0 . C.  3  ;   1 . D. 2;  3 . 1
Câu 12: Tất cả các nguyên hàm của hàm f x  là 3x  2
https://www.facebook.com/groups/toanvd.vdc Trang 2 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 2 2
A. 2 3x  2  C . B.
3x  2  C . C.
3x  2  C . D. 2 
3x  2  C . 3 3
Câu 13: Khi đặt 3x t thì phương trình x 1  x 1 9 3    30  0 trở thành NH A. 2
3t t  10  0 . B. 2
9t  3t  10  0 . C. 2
t t  10  0 . D. 2
2t t 1  0 . ÓM
Câu 14: Từ các chữ số 1, 2, 3,..., 9 lập được bao nhiêu số có 3 chữ số đôi một khác nhau TO A. 9 3 . B. 3 A . C. 3 9 . D. 3 C . 9 9 ÁN
Câu 15: Cho số phức z  2  i . Trong hình bên điểm biểu diễn số phức z là VD – VD C A. M . B. . Q C. . P D. N. x 1 y  2 z  3
Câu 16: Trong không gian Oxyz , cho hai đường thẳng  :   và 1 2  1 2 x  3 y 1 z  2  :  
. Góc giữa hai đường thẳng  ,  bằng 2 1 2 NH 1 1 4  ÓM T A. 0 30 . B. 0 45 . C. 0 60 . D. 0 135 .
Câu 17: Cho số phức z thỏa mãn z  2z  6  2 .
i Điểm biểu diễn số phức z có tọa độ là OÁ A. 2; 2 . B.  2  ; 2   . C. 2; 2 . D. 2; 2 . N V x  2 y 1 z D
Câu 18: Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng – 1  2 2 VD
P : x  2y z  5  0 . Tọa độ giao điểm của d và P là C A. 2;1;  1  . B. 3; 1  ; 2   . C. 1;3; 2   . D. 1;3;2
Câu 19: Bất phương trình log  2 x  3x  log
9  x có bao nhiêu nghiệm nguyên? 4  2   A. vô số. B. 1. C. 4 . D. 3 e
Câu 20: Hàm số y   3
x  3x có bao nhiêu điểm cực trị? A. 2 . B. 0 . C. 3 . D. 1.
Câu 21: Gọi  D là hình phẳng giới hạn bởi các đường  2x y
, y  0, x  0 và x  2 . Thể tích V
của khối tròn xoay tạo thành khi quay  D quanh trục Ox được định bởi công thức
https://www.facebook.com/groups/toanvd.vdc Trang 3 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 2 2 2 2 A. x 1 V  2   dx  . B. x 1 V 2   dx  . C. 4x V  dx  . D.  4x V  dx  . 0 0 0 0
Câu 22: Cho hàm số y f x có đồ thị như hình bên. NH ÓM TO ÁN VD – VD C Hàm số y  2
f x đồng biến trên khoảng A. 1;2 . B. 2;  3 . C.  1  ;0 . D.  1  ;  1 . 2 x x 1
Câu 23: Đồ thị hàm số y
có bao nhiêu đường tiệm cận x 1 A. 4 . B. 3 . C. 1. D. 2 .
Câu 24: Hàm số y  log x và y  log x có đồ thị như hình vẽ dưới đây. a b NH ÓM T OÁ N
Đường thẳng y  3 cắt hai đồ thị tại các điểm có hoành độ x , x . Biết rằng x  2x , 1 2 2 1 V D a
giá trị của bằng – b VD 1 C A. . B. 3 . C. 2 . D. 3 2 . 3
Câu 25: Cho hình hộp chữ nhật ABC . D A BCD
  có AB a, AD  2a, AC  6a . Thể tích khối
hộp chữ nhật ABC . D A BCD   bằng 3 3a 3 2a A. . B. . C. 3 2a . D. 3 2 3a . 3 3 2
Câu 26: Cho hàm số f x có đạo hàm     2    2 2x f x x x x  4,x  .  Số điểm cực trị
của f x là A. 2 . B. 4 . C. 3 . D. 1.
https://www.facebook.com/groups/toanvd.vdc Trang 4 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019
Câu 27: Cho hình lập phương ABC . D A BCD
  có cạnh bằng a . Diện tích xung quanh của hình
trụ có đáy là hai hình tròn ngoại tiếp hai hình vuông ABCD và A BCD   A. 2 2 a . B. 2 2 a . C. 2 a . D. 2 2 2 a . NH
Câu 28: Gọi z , z là các nghiệm phức của phương trình 2
z  2z  3  0. Mô đun của 3 4 z .z bằng 1 2 1 2 ÓM TOÁ A. 81.
B. 16 . C. 27 3 . D. 8 2 .  x
Câu 29: Gọi m , M lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số f x  2x  cos N 2 VD trên đoạn  2
 ; 2 . Giá trị của m M bằng – A. 2 . B. 2  . C. 0 . D. 4  . VD C
Câu 30: Cho hình chóp đều S.ABCD có AB  2a , SA a 5 . Góc giữa hai mặt phẳng SAB và  ABCD bằng A. 30 . B. 45. C. 60 . D. 75 .
Câu 31: Hai bạn Công và Thành cùng viết ngẫu nhiên ra một số tự nhiên gồm 2 chữ số phân
biệt. Xác suất để hai số được viết ra có ít nhất một chữ số chung bằng 145 448 281 154 A. . B. . C. . D. . 729 729 729 729
Câu 32: Biết rằng ex x
là một nguyên hàm của f x trên khoảng  ;
  . Gọi F x là một
nguyên hàm của  ex f x
thỏa mãn F 0  1, giá trị của F   1 bằng 7 5  e 7  e 5 A. . B. . C. . D. . NH 2 2 2 2 ÓM TOÁ
Câu 33: Cho hình chóp S.ABCD có đáy là hình chữ nhật, biết AB  2a, AD a, SA  3a và SA
vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh CD . Khoảng cách giữa hai
đường thẳng SC và BM bằng N VD 3 3a 2 3a 3a 3a A. . B. . C. . D. . 4 3 3 2 – VD
Câu 34: Cho hàm số f x có bảng xét dấu đạo hàm như hình bên dưới C
Hàm số y f 1 2x đồng biến trên khoảng  3  1   1   3  A.  0;   . B.  ;1   . C. 2  ;   . D. ;3   .  2   2   2   2 
Câu 35: Xét các số phức z, w thỏa mãn w i  2, z  2  .
iw Gọi z , z lần lượt là các số phức mà 1 2
tại đó z đạt giá trị nhỏ nhất và đạt giá trị lớn nhất. Mô đun z z bằng 1 2 A. 3 2 . B. 3 . C. 6 . D. 6 2 .
https://www.facebook.com/groups/toanvd.vdc Trang 5 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019
Câu 36: Cho f x  x  3
1 3x  3 . Đồ thị hình bên là của hàm số có công thức
A. y   f x   1 1
 . B. y  f x  
1 1 . C. y   f x  1 1
 . D. y  f x  1 1. NH
Câu 37: Người ta xếp hai quả cầu có cùng bán kính r vào một chiếc hộp hình trụ sao cho các ÓM TOÁ
quả cầu đều tiếp xúc với hai đáy, đồng thời hai quả cầu tiếp xúc với nhau và mỗi quả
cầu đề tiếp xúc với đường sinh của hình trụ ( tham khảo hình vẽ). Biết thể tích khối trụ là 3
120 cm , thể tích của mỗi khối cầu bằng N VD – VD C A. 3 10 cm . B. 3 20 cm . C. 3 30 cm . D. 3 40 cm .  3 2
cos x  sin x cos x 1 Câu 38: Biết
dx a b ln 2  c ln 1 3 
, với a,b, c là các số hữu tỉ. Giá trị 4 3  
cos x  sin x cos x  4 của abc bằng A. 0 . B. 2  . C. 4  . D. 6  . NH x  1   2t
x  2  t   ÓM TOÁ
Câu 39: Trong không gian Oxyz, cho hai đường thẳng d :  y t
; d  :  y  1 2t và mặt z  1   3t
z  2t  
phẳng  P : x y z  2  0. Đường thẳng vuông góc với mặt phẳng  P và cắt cả hai N VD
đường thẳng d , d  có phương trình là x  3 y 1 z  2 x 1 y 1 z 1     – A. . B. . 1 1 1 1 1  4  VD x  2 y 1 z 1 x 1 y 1 z  4 C C.   . D.   . 1 1 1 2 2 2
Câu 40: Có bao nhiêu số nguyên m để phương trình  3 x x
me có 2 nghiệm phân biệt? A. 7 . B. 6 . C. 5 . D. Vô số.
Câu 41: Cho f x mà đồ thị hàm số y f  x như hình bên. Hàm số y f x   2 1  x  2x đồng biến trên khoảng
https://www.facebook.com/groups/toanvd.vdc Trang 6 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 NH ÓM TO ÁN VD A. 1;2. B.  1  ; 0. C. 0;  1 . D.  2  ;   1 . – VD 1 1
Câu 42: Có bao nhiêu số nguyên a  2
 019; 2019 để phương trình 
x a có ln x  5 3x 1 C   hai nghiệm phân biệt? A. 0 . B. 2022 . C. 2014 . D. 2015 .
Câu 43: Cho hàm số f ( )
x có đạo hàm liên tục trên  và thỏa mãn f (0)  3 và 2 2
f (x)  f (2  x)  x  2x  2, x
   . Tích phân xf (  x)dx  bằng 0 4 2 5 10 A. . B. . C. . D. . 3 3 3 3 x
Câu 44: Hàm số f x 
m (với m là tham số thực) có nhiều nhất bao nhiêu điểm cực 2 x 1 trị? NH A. 2 . B. 3 . C. 5 . D. 4 . ÓM T
Câu 45: Cho hình hộp ABC .
D A' B 'C ' D ' có thể tích bằng V . Gọi M , N, P,Q, E, F lần lượt là tâm
các hình bình hành ABCD, A' B 'C ' D ', ABB ' A', BCC ' B ',CDD 'C ', DAA' D '. Thể tích khối OÁ
đa diện có các đỉnh M , P,Q, E, F, N bằng N V V V V V D A. . B. . C. . D. . 4 2 6 3 – VD
Câu 46: Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên gạch hình vuông cạnh C
40 cm như hình bên. Biết rằng người thiết kế đã sử dụng các đường cong có phương trình 2 2 4x y và 3 2
4( x 1)  y để tạo hoa văn cho viên gạch. Diện tích phần được tô
đạm gần nhất với giá trị nào dưới đây?
https://www.facebook.com/groups/toanvd.vdc Trang 7 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 NH ÓM TO ÁN VD 2 2 2 2 A. 506 cm . B. 747 cm . C. 507 cm . D. 746 cm . –         VD
Câu 47: Xét các số phức z , w thỏa mãn z  2 , iw  2  5i  1. Giá trị nhỏ nhất của 2
z wz  4 C bằng A. 4 . B. 2 29 3 . C. 8 . D. 2 29 5 .
Câu 48: Cho f (x) mà đồ thị hàm số y f '(x) như hình vẽ bên NH ÓM T  x
Bất phương trình f (x)  sin
m nghiệm đúng với mọi x  1  ;  3 khi và chỉ khi OÁ 2 N V
A. m f (0) .
B. m f (1) 1.
C. m f (1) 1.
D. m f (2) . D – x  3 y  4 z  2 VD
Câu 49: Trong không gian Oxyz , cho đường thẳng d :  
và 2 điểm A6;3; 2   , 2 1 1 C B1;0; 
1 . Gọi  là đường thẳng đi qua B , vuông góc với d và thỏa mãn khoảng cách
từ A đến  là nhỏ nhất. Một vectơ chỉ phương của  có tọa độ A. 1;1; 3   . B. 1; 1  ;   1 . C. 1;2; 4   . D. 2; 1  ; 3   . x 1 y  2 z
Câu 50: Trong không gian Oxyz , cho điểm A2; ;
 3; 4 , đường thẳng d :   và mặt 2 1 2 2 2 2
cầu S  :  x  3   y  2   z   1
 20 . Mặt phẳng  P chứa đường thẳng d thỏa mãn
khoảng cách từ điểm A đến  P lớn nhất. Mặt cầu S  cắt  P theo đường tròn có bán kính bằng A. 5 . B. 1. C. 4 . D. 2 .
https://www.facebook.com/groups/toanvd.vdc Trang 8 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 BẢNG ĐÁP ÁN NH 1A 2D 3A 4C 5B 6D 7B 8C 9D 10B 11D 12B 13A 14B 15D 16B 17A 18D 19D 20D ÓM TOÁ 21D 22A 23B 24D 25C 26C 27A 28C 29B 30C 31C 32A 33C 34A 35C 36B 37B 38C 39A 40A 41A 42D 43D 44D 45C 46B 47C 48B 49A 50D N VD Câu 1:
Cho khối nón có độ dài đường cao bằng 2a và bán kính đáy bằng a . Thể tích của khối – nón đã cho bằng VD 3 2 a 3 4 a 3  a A. . B. . C. . D. 3 2 a . C 3 3 3 Lời giải Chọn A 2a a NH 3 ÓM TOÁ 1 2 a Thể tích khối nón: 2 V
 2a  a  . 3 3 Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA a và SA vuông N VD
góc với mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng 3 a 3 2a 3 a A. . B. . C. 3 a . D. . – 6 3 3 VD Lời giải C Chọn D
https://www.facebook.com/groups/toanvd.vdc Trang 9 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 S NH ÓM TOÁ A D N VD B C – 3 VD 1 a
Thể tích khối chóp VS .SA S . ABCD ABCD C 3 3 x 1 y  3 z  3 Câu 3:
Trong không gian Oxyz , một vectơ chỉ phương của đường thẳng  :   1 2 5  có tọa độ là A. 1;2; 5   . B. 1;3;3 . C.  1  ;3; 3   . D.  1  ; 2  ; 5   . Lời giải Chọn A a Câu 4:
Với a , b là các số thực dương bất kì, log bằng 2 2 b a 1 a A. 2log . B. log .
C. log a  2 log b .
D. log a  log 2b . 2 2   2 2 2 2 NH b 2 b Lời giải ÓM TOÁ Chọn C a Ta có: 2 log
 log a  log b  log a  2 log b . 2 2 2 2 2 2 N VD b A 2  ; 1  ;3 B 0;3;1  Câu 5:
Trong không gian Oxyz , cho hai điểm   và 
 . Gọi   là mặt phẳng – VD
trung trực của AB . Một vectơ pháp tuyến của   có tọa độ là C A. 2;4;  1  . B. 1;2;  1  . C.  1  ;1; 2 . D. 1;0;  1 . Lời giải Chọn B
Vì   là mặt phẳng trung trực của AB nên vectơ pháp tuyến của mặt phẳng   là :    n AB    
, từ đây ta suy ra n  1; 2; 1 là một vectơ pháp tuyến 1    2; 4; 2 2 1; 2;  1 của   Câu 6:
Cho cấp số nhân u có u  1,u  2
 . Mệnh đề nào sau đây đúng? n  1 2 A. 2018 u  2 . B. 2019 u  2 . C. 2019 u  2 . D. 2018 u  2 2019 2019 2019 2019
https://www.facebook.com/groups/toanvd.vdc Trang 10 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 Lời giải Chọn D
Cấp số nhân có u  1,u  2
  q  2 . Vậy: uu q  2  2 2019 1  2018 2018 2018 1 2 NH Câu 7:
Hình dưới đây là đồ thị của hàm số nào? ÓM TO ÁN VD – VD C A. 2 y x  2 . B. 4 2
y x x  2 . C. 4 2
y x x  2 . D. 2
y x x  2 . Lời giải Chọn B
Dựa vào đồ thị đã cho ta nhận thấy hàm số cần tìm chỉ có một cực trị nên đáp án C bị loại.
Mặt khác đồ thị hàm số đã cho có tính đối xứng qua trục tung nên đáp án D bị loại.
Đồ thị hàm số đã cho đi qua hai điểm  1
 ; 0 và 1;0 nên đáp án A bị loại.
Vậy hàm số cần tìm là hàm số ở đáp án B. NH Câu 8:
Trong không gian Oxyz , cho điểm I 1;2;5 và mặt phẳng   : x  2y  2z  2  0 . ÓM T
Phương trình mặt cầu tâm I và tiếp xúc với   là 2 2 2 2 2 2 A. x  
1   y  2   z  5  3 . B. x  
1   y  2   z  5  3. OÁ 2 2 2 2 2 2 N C. x  
1   y  2   z  5  9 . D. x  
1   y  2   z  5  9 . V Lời giải D – Chọn C VD C I R d H (α)
Từ tọa độ tâm I 1;2;5 ta loại được hai đáp án B, D.
https://www.facebook.com/groups/toanvd.vdc Trang 11 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 1 2.2  2.5  2
Mặt khác theo bài ta có R d I,  
 3 nên đáp án A loại. 1   2  2 2 2  2 2 2 2 NH
Vậy phương trình mặt cầu cần tìm có phương trình  x  
1   y  2   z  5  9 . ÓM Vậy chọn C TO Câu 9:
Cho hàm số y f x có đồ thị như hình vẽ dưới đây ÁN VD – VD C Trên đoạn  3  ; 
3 hàm số đã cho có mấy điểm cực trị? A. 4 . B. 5 . C. 2 . D. 3 . Lời giải Chọn D
Quan sát đồ thị đã cho ta nhận thấy trên đoạn  3  ; 
3 hàm số y f x có ba điểm cực trị.
Câu 10: Cho f x và g x là các hàm số liên tục bất kì trên đoạn  ;
a b . Mệnh đề nào sau đây đúng ? NH b b b b b b A.
f x  g x dx f x dx g x dx    .
B.  f x  g xdx f xdx g xdx   . ÓM T a a a a a a b b b b b b OÁ
C.  f x  g x dx f xdx g xdx  
. D.  f x  g xdx f xdx g xdx   a a a a a a N . V D Lời giải – VD Chọn B C
Theo tính chất của tích phân ta có đáp án B là mệnh đề đúng.
Mặt khác, ta có nhận xét:
+ A sai khi f x  g x với x  ; a b . b b
+ C sai khi f xdx g xdx  0.   a a b
+ D sai khi   f x  g xdx  0 . a
Câu 11: Cho hàm số y f x có đồ thị như hình vẽ bên.
https://www.facebook.com/groups/toanvd.vdc Trang 12 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 NH ÓM TO ÁN VD
Hàm số đã cho nghịch biến trên khoảng – 0; 2 2  ; 0 3  ; 1  2;3 A.   . B.   . C.   . D.   . VD Lời giải C Chọn D
Dựa vào đồ thị ta có hàm số nghịch biến trên các khoảng  1   ;1 và 2;3. 1
Câu 12: Tất cả các nguyên hàm của hàm f x  là 3x  2 2 2
A. 2 3x  2  C . B.
3x  2  C . C.
3x  2  C . D. 2 
3x  2  C . 3 3 Lời giải Chọn B 1 1 1 1  1 3x  22 2 2 NH Ta có dx
3x  2 d 3x  2  .  C  3x  2  C.   3x  2 3 3 1 3 ÓM T 2
Câu 13: Khi đặt 3x t thì phương trình x 1  x 1 9 3    30  0 trở thành OÁ A. 2
3t t  10  0 . B. 2
9t  3t  10  0 . C. 2
t t  10  0 . D. 2
2t t 1  0 . N Lời giải V D Chọn A – VD Ta có xx      x 2 1 1 9 3 30 0 9. 3
 3.3x  30  0 . C Do đó khi đặt 3x t  ta có phương trình 2 2
 9t  3t  30  0  3t t 10  0 .
Câu 14: Từ các chữ số 1, 2, 3,..., 9 lập được bao nhiêu số có 3 chữ số đôi một khác nhau A. 9 3 . B. 3 A . C. 3 9 . D. 3 C . 9 9 Lời giải Chọn B
Gọi số cần tìm có dạng là a a a a  0, a a , a a , a a . 1 2 3  1 1 2 2 3 3 1 
Mỗi bộ ba số a ;a ;a là một chỉnh hợp chập 3 của 9 phần tử. 1 2 3 
Vậy số các số cần tìm là 3 A số. 9
https://www.facebook.com/groups/toanvd.vdc Trang 13 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019
Câu 15: Cho số phức z  2  i . Trong hình bên điểm biểu diễn số phức z là NH ÓM TO ÁN VD – VD C A. M . B. . Q C. . P D. N. Lời giải Chọn D Ta có z  2
  i . Do đó điểm biểu diễn số phức z là N  2  ;   1 . x 1 y  2 z  3
Câu 16: Trong không gian Oxyz , cho hai đường thẳng  :   và 1 2  1 2 x  3 y 1 z  2  :  
. Góc giữa hai đường thẳng  ,  bằng 2 1 1 4  1 2 A. 0 30 . B. 0 45 . C. 0 60 . D. 0 135 . Lời giải NH ÓM T Chọn B 
Véc tơ chỉ phương của  là u  2;1; 2 1   1 OÁ  N
Véc tơ chỉ phương của  là u  1;1; 4 2   2 V D   –   u .u 1 2 2  .11.1 2. 4  9 2 VD
cos  ,   cos u ,u       . 1 2   1 2      2 2 2 2 2 2 u . u 3.3 2 2 C 1 2  2
  1  2 . 1 1   4  
Do đó góc giữa hai đường thẳng  và  là 0 45 . 1 2
Câu 17: Cho số phức z thỏa mãn z  2z  6  2 .
i Điểm biểu diễn số phức z có tọa độ là A. 2; 2 . B.  2  ; 2   . C. 2; 2 . D. 2; 2 . Lời giải Chọn A
Gọi số phức z x yi với ,
x y  . Theo bài ra ta có x  2
x yi  2 x yi  6  2i  3x yi  6  2i   . y  2  
https://www.facebook.com/groups/toanvd.vdc Trang 14 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019
Vậy điểm biểu diễn số phức z có tọa độ là 2; 2  . x  2 y 1 z
Câu 18: Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 1  2 2 NH
P : x  2y z 5  0 . Tọa độ giao điểm của d và P là ÓM TOÁ A. 2;1;  1  . B. 3; 1  ; 2   . C. 1;3; 2   . D. 1;3;2 Lời giải N Chọn D VD – x  2  t VD 
y  1 2t
 2  t  2 1 2t  2t  5  0  t   A 1;3; 2 C Xét hệ:    1   là tọa độ giao z  2t
x  2 y z  5  0 
điểm của đường thẳng và mặt phẳng.
Câu 19: Bất phương trình log  2 x  3x  log
9  x có bao nhiêu nghiệm nguyên? 4  2   A. vô số. B. 1. C. 4 . D. 3 Lời giải Chọn D 2
x  3x  0 Điều kiện: 
x  0  3  x  9 9  x  0  NH 2 ÓM TOÁ Ta có: log x  3x  log 9  x  log
x  3x  log 9  x x x    x2 2 3 9 4   4  2 2 4   2   27
 15x  81  x  . 5 N VD 27
So sánh điều kiện, ta có:  x  9 . 5 – VD
Vậy bất phương trình có 3 nghiệm nguyên. C e
Câu 20: Hàm số y   3
x  3x có bao nhiêu điểm cực trị? A. 2 . B. 0 . C. 3 . D. 1. Lời giải Chọn D e Hàm số y   3
x  3x có TXĐ:  3;0  3; 
y  ex   x xe 1 2 3 3 3 3
https://www.facebook.com/groups/toanvd.vdc Trang 15 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 x  1 y  0   x  1   Bảng xét dấu NH ÓM TO ÁN
Vậy hàm số có 1 điểm cực trị. VD x –
Câu 21: Gọi  D là hình phẳng giới hạn bởi các đường y  2 , y  0, x  0 và x  2 . Thể tích V VD
của khối tròn xoay tạo thành khi quay  D quanh trục Ox được định bởi công thức C 2 2 2 2 A. x 1 V  2   dx  . B. x 1 V 2   dx  . C. 4x V  dx  . D.  4x V  dx  . 0 0 0 0 Lời giải Chọn D
Thể tích V của khối tròn xoay tạo thành khi quay  D quanh trục Ox được định bởi 2 2 công thức 2   d   4x V y x dx   0 0
Câu 22: Cho hàm số y f x có đồ thị như hình bên. NH ÓM T OÁ N V D – Hàm số y  2
f x đồng biến trên khoảng VD C A. 1;2 . B. 2;  3 . C.  1  ;0 . D.  1  ;  1 . Lời giải Chọn A
Ta có y  2 f x 
 2. f   x. Hàm số đồng biến  2
 . f  x  0  f  x  0.
Dựa vào đồ thị hàm số ta có f  x  0  0  x  2  chọn đáp án A. 2 x x 1
Câu 23: Đồ thị hàm số y
có bao nhiêu đường tiệm cận x 1 A. 4 . B. 3 . C. 1. D. 2 . Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 16 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 Chọn B
Tập xác định D  \  1 . 2 x x 1 2 x x 1 NH Ta có: lim y  lim
  ; lim y  lim   . x 1 x 1   x 1 x 1 x 1   x 1 ÓM
Do đó đồ thị hàm số nhận đường thẳng x 1 làm tiệm cận đứng. TO Lại có: ÁN  1  1 x 1 1 2  2 1 1 2 x x x 1   x VD + lim y  lim  lim  lim  2 . x x x 1 x x 1 x 1 1 – x VD
Vậy đồ thị hàm số nhận đường thẳng y  2 làm tiệm cận ngang. C  1  1 x 1 1 2  2 1 1 2 x x 1 x +   x lim y  lim  lim  lim  0 . x x x 1 x x 1 x 1 1 x
Vậy đồ thị hàm số nhận đường thẳng y  0 làm tiệm cận ngang.
Do đó đồ thị hàm số đã có 3 đường tiệm cận.
Câu 24: Hàm số y  log x và y  log x có đồ thị như hình vẽ dưới đây. a b NH ÓM T OÁ N
Đường thẳng y  3 cắt hai đồ thị tại các điểm có hoành độ x , x . Biết rằng x  2x , 1 2 2 1 V D a –
giá trị của bằng VD b C 1 A. . B. 3 . C. 2 . D. 3 2 . 3 Lời giải Chọn D
Từ đồ thị có x là nghiệm của phương trình log x  3 nên 3
log x  3  x b . 1 b b 1 1
Từ đồ thị có x là nghiệm của phương trình log x  3 nên 3
log x  3  x a . 2 a a 2 2 3  a a a Do x  2x 3 3
a  2.b   2 3   2 . Vậy 3  2 . 2 1    b b b
https://www.facebook.com/groups/toanvd.vdc Trang 17 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019
Câu 25: Cho hình hộp chữ nhật ABC . D A BCD
  có AB a, AD  2a, AC  6a . Thể tích khối
hộp chữ nhật ABC . D A BCD   bằng 3 3a 3 2a A. . B. . C. 3 2a . D. 3 2 3a . NH 3 3 ÓM Lời giải Chọn C TO ÁN VD – VD C 2 2 Ta có 2 2
AC a  4a a 5 , CC   6a   5a  a .
Thể tích khối hộp chữ nhật là 3 V A .
B AD.CC  a.2a.a  2a . 2
Câu 26: Cho hàm số f x có đạo hàm     2    2 2x f x x x x  4,x  .  Số điểm cực trị
của f x là A. 2 . B. 4 . C. 3 . D. 1. Lời giải NH Chọn C ÓM T 2 x x  0 x  0 
Ta có f xx  
 0   x x x  22 .2  4  0   x  22 2  0  x  1  . OÁ   xx  2 2  4  0   N V
Nhận thấy x  2 là nghiệm bội ba nên f  x vẫn đổi dấu khi qua x  2. Vậy hàm số đã D –
cho có 3 điểm cực trị. VD C
Câu 27: Cho hình lập phương ABC . D A BCD
  có cạnh bằng a . Diện tích xung quanh của hình
trụ có đáy là hai hình tròn ngoại tiếp hai hình vuông ABCD và A BCD   A. 2 2 a . B. 2 2 a . C. 2  a . D. 2 2 2 a . Lời giải Chọn A
https://www.facebook.com/groups/toanvd.vdc Trang 18 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 NH ÓM TO ÁN VD – VD C AC a 2
Hình trụ có l a , bán kính đáy bằng R   . 2 2 a 2
Vậy diện tích xung quanh hình trụ bằng 2 S  2 Rl  2 a  2 a . xq 2
Câu 28: Gọi z , z là các nghiệm phức của phương trình 2
z  2z  3  0. Mô đun của 3 4 z .z bằng 1 2 1 2 A. 81.
B. 16 . C. 27 3 . D. 8 2 . Lời giải Chọn C NH Ta có : 2
z  2z  3  0  z
 1 2i z z  3 . 1,2 1 2 ÓM T 3 4 3 4 Do đó 3 4
z .z z . z  3 . 3  27 3 . 1 2 1 2     OÁ  x N
Câu 29: Gọi m , M lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số f x  2x  cos V 2 D trên đoạn  2
 ; 2 . Giá trị của m M bằng – VD A. 2 . B. 2  . C. 0 . D. 4  . C Lời giải Chọn B   x
f  x  2  sin ; 2 2    x     x  Vì    sin   0  2   2  sin  2 
f  x  0 , x   2  ; 2 . 2 2 2 2 2 2 2 2  f  2
   f x  f 2 .
Hay ta có m  min f x  f 2  5 ; M  max f x  f 2  3 . 2;2  2  ; 2
Vậy M m  3  5  2  .
https://www.facebook.com/groups/toanvd.vdc Trang 19 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019
Câu 30: Cho hình chóp đều S.ABCD có AB  2a , SA a 5 . Góc giữa hai mặt phẳng SAB và  ABCD bằng A. 30 . B. 45 . C. 60 . D. 75 . NH Lời giải ÓM TOÁ Chọn C S N VD – VD C D A M O C B
Theo tính chất hình chóp đều SM AB , MO AB , SAB  ABCD  AB . Góc giữa
hai mặt phẳng SAB và  ABCD là góc giữa hai đường thẳng SM và MO .
Vì ABCD là hình vuông cạnh 2a nên AC  2 2a AO a 2  SO a 3 NH SO
Xét tam giác vuông SMO có  tanSMO   3   SMO  60 . OM ÓM TOÁ
Câu 31: Hai bạn Công và Thành cùng viết ngẫu nhiên ra một số tự nhiên gồm 2 chữ số phân
biệt. Xác suất để hai số được viết ra có ít nhất một chữ số chung bằng N VD 145 448 281 154 A. . B. . C. . D. . 729 729 729 729 – Lời giải VD C Chọn C
Cách 1: Số các số tự nhiên có hai chữ số phân biệt là 9.9  81 số.
Số phần tử của không gian mẫu là n 2  81 .
Gọi A là biến cố thỏa mãn bài toán.
+ Khả năng 1: Hai bạn chọn số giống nhau nên có 81 cách.
+ Khả năng 2: Hai bạn chọn số đảo ngược của nhau nên có 9.8  72 cách.
+ Khả năng 3: Hai bạn chọn số chỉ có một chữ số trùng nhau
https://www.facebook.com/groups/toanvd.vdc Trang 20 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019
- TH1: Trùng chữ số 0 : Công có 9 cách chọn số và Thành đều có 8 cách chọn số nên có 9.8  72 cách.
- TH 2: Trùng chữ số 1: Nếu Công chọn số 10 thì Thành có 16 cách chọn số có NH
cùng chữ số 1. Nếu Công chọn số khác 10 , khi đó Công có 16 cách chọn số và Thành ÓM TOÁ
có 15 cách chọn số có cùng chữ số 1 với Công nên có 16 16.15 16.16  256 cách.
- Các trường hợp chọn trùng chữ số 2,3, 4,...9 tương tự. N VD
Vậy nA  81 72  72  9.256  2529. – VD n A 2529 281
Xác suất cần tính là P A    . n  81 729 C   2
Cách 2: Số các số tự nhiên có hai chữ số phân biệt là 9.9  81 số.
Số phần tử của không gian mẫu là n 2  81 .
Gọi A là biến cố thỏa mãn bài toán. Xét biến cố A .
- TH 1: Công chọn số có dạng 0
a nên có 9 cách. Khi đó có 25 số có ít nhất một chữ số trùng với số 0
a nên Thành có 81 25  56 cách chọn số không có chữ số trùng với
Công. Vậy có 9.56  504 cách.
- TH 2: Công chọn số không có dạng 0
a : Có 72 cách, khi đó 32 số có ít nhất một chữ NH
số trùng với số của Công chọn nên Thành có 81 32  49 cách chọn số không có chữ số ÓM TOÁ
nào trùng với Thành. Vậy có 72.49  3528 cách. 4032 281
n A  3528  504  4032  PA 1 PA 1  . 2 81 729 N VD
Câu 32: Biết rằng ex x
là một nguyên hàm của f x trên khoảng  ;
  . Gọi F x là một –
nguyên hàm của  ex f x
thỏa mãn F 0  1, giá trị của F   1 bằng VD 7 5  e 7  e 5 C A. . B. . C. . D. . 2 2 2 2 Lời giải Chọn A Ta có      
ex   ex  ex f x x x , x   ;   .
Do đó f x  x 
  x x e e , x   ;   .
Suy ra    ex f x 1 x , x   ;   . Nên    
 ex 1   ex f x xx  2 xx x    
f x e  e  x  2.e  x  2 .
https://www.facebook.com/groups/toanvd.vdc Trang 21 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 1
Bởi vậy F x   x  2d x   x  22  C  . 2 1
Từ đó F 0  0  22  C C  2 ; F 0 1 C  1  . 2 NH 1 2 1 2 7 ÓM TOÁ
Vậy F x   x  2 1 F   1   1   2 1  . 2 2 2
Câu 33: Cho hình chóp S.ABCD có đáy là hình chữ nhật, biết AB  2a, AD a, SA  3a và SA N
vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh CD . Khoảng cách giữa hai VD
đường thẳng SC và BM bằng – 3 3a 2 3a 3a 3a A. . B. . C. . D. . VD 4 3 3 2 C Lời giải Chọn C S N 3a H A a D NH 2a O ÓM TOÁ M I K B C N VD –
Gọi O là tâm hình chữ nhật, I BM AC . VD C
Dựng IN // SC N S
A , AK BM , AH NK K BM , H NK  .
Dễ dàng chứng minh được AH   BMN  . Khi đó:
d SC,BM   d SC,BMN   d C,BMN  . 2    CO d C , BMN CI 1 1 1 Ta lại có: 3   
d C,BMN   d A,BMN   AH .
d A,BMN  AI 1 2 2 2 CO CO 3
Xét tam giác vuông ANK :
https://www.facebook.com/groups/toanvd.vdc Trang 22 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 2S
AB.d M , AB 2a.a * ABM AK     a 2 . 2 2 BM BM a a AN AI 2 2 2 NH *    AN AS  3 . a  2a AS AC 3 3 3 ÓM AN .AK 2a.a 2 2 3a TO Suy ra: AH    . 2 2 2 2 3 AN AK ÁN
2a  a 2 VD 1 a 3 –
Vậy: d SC ,BM   AH  . 2 3 VD C Cách 2: z S A D y M NH B C ÓM T x
Chọn hệ tọa độ Oxyz sao cho A O ; B  x
O nên B2a ; 0 ; 0 , OÁ N D Oy
C2a; a;  V
nên D0 ; a ; 
0 , S Oz nên S0 ; 0 ; 3a
0 và Ma ; a ; 0. D   – VD
Ta có SC  2a ; a;3a; BM   a  ; a;0 C       SC BM     2 2 2 ,
3a ; 3a ; 3a  và SB  2a ; 0 ;3  a .  
   S
C, BM .SB   a 3 Vậy      d . Sc ,BM   3 SC, BM  
Câu 34: Cho hàm số f x có bảng xét dấu đạo hàm như hình bên dưới
https://www.facebook.com/groups/toanvd.vdc Trang 23 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019
Hàm số y f 1 2x đồng biến trên khoảng  3  1   1   3  A.  0;   . B.  ;1   . C. 2  ;    . D. ;3   .  2   2   2   2  NH Lời giải ÓM Chọn A TO Ta có: y  2
f 1 2x  0  f 1 2x  0 ÁN x  2 1   2x  3  VD  3
Từ bảng xét dấu ta có f 1 2x  0   2
  1 2x  1  0  x    2 –  1 2x  3  VD x  1   C  3 
Từ đây ta suy ra hàm số đổng biến trên khoảng 0;    2 
Câu 35: Xét các số phức z, w thỏa mãn w i  2, z  2  .
iw Gọi z , z lần lượt là các số phức mà 1 2
tại đó z đạt giá trị nhỏ nhất và đạt giá trị lớn nhất. Mô đun z z bằng 1 2 A. 3 2 . B. 3 . C. 6 . D. 6 2 . Lời giải Chọn C 1 1 1
Ta có: z  2  iw w   z  2  w i  2   z  2  i  2   z  2 1  2 i i i   NH
z  3  2 . Do đó z , z có các điểm biểu diễn trên mặt phẳng Oxy thuộc đường tròn 1 2 ÓM T
tâm I 3; 0; bán kính R  2 . Vậy z  1, z  5  z z  6  z z  6. 1 2 1 2 1 2 OÁ
Câu 36: Cho f x  x  3
1 3x  3 . Đồ thị hình bên là của hàm số có công thức N
A. y   f x   1 1
 . B. y  f x  
1 1 . C. y   f x  1 1
 . D. y  f x  1 1. VD – VD C Lời giải Chọn B
https://www.facebook.com/groups/toanvd.vdc Trang 24 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 3
Cách 1: Ta có f x  x   1 3x   1
Thử điểm đối với từng đáp án NH
Đáp án A: y   f x   1 1   y  1   f   2 1  1  Loại ÓM TOÁ
Đáp án B: y   f x   1 1  y  1   f   2 1 3  thoả mãn. N
Đáp án C: y   f x   1 1   y  1   f   0 1   3   Loại VD
Đáp án D: y   f x   1 1  y  1   f   0 1 1   Loại – VD C
Cách 2: Từ đồ thị suy ra hàm số ứng với đồ thị trên là 3
y  x  3x 1.
Ta làm tường minh các hàm số cho trong các đáp án và so sánh
Đáp án A: y   f x   3 1 1   x  3x 1   Loại
Đáp án B: y   f x   3 1 1 x
 3x 1  Nhận.
Câu 37: Người ta xếp hai quả cầu có cùng bán kính r vào một chiếc hộp hình trụ sao cho các
quả cầu đều tiếp xúc với hai đáy, đồng thời hai quả cầu tiếp xúc với nhau và mỗi quả
cầu đề tiếp xúc với đường sinh của hình trụ ( tham khảo hình vẽ). Biết thể tích khối trụ là 3
120 cm , thể tích của mỗi khối cầu bằng NH ÓM TOÁ N VD – VD A. 3 10 cm . B. 3 20 cm . C. 3 30 cm . D. 3 40 cm . C Lời giải Chọn B
Chiều cao của hình trụ là 2r .
Đường kính của hình trụ là 4r . Suy ra bán kính của hình trụ là 2r .
Thể tích khối trụ là   r 2 3 2
.2r  8 r . Theo bài ra có 4 3 3 3 3 3
8 r  120 cm   r  15 cm   r  20 . 3
Vậy thể tích của mỗi khối cầu là 20 3 cm .
https://www.facebook.com/groups/toanvd.vdc Trang 25 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019  3 2
cos x  sin x cos x 1 Câu 38: Biết
dx a b ln 2  c ln 1 3 
, với a,b, c là các số hữu tỉ. Giá trị 4 3  
cos x  sin x cos x  4 NH của abc bằng ÓM TOÁ A. 0 . B. 2  . C. 4  . D. 6  . Lời giải Chọn C N   1 tan x 1 VD 3 2 3   2 2 4
cos x  sin x cos x 1 Ta có: cos x cos x cos d x x  dx  4 3  –
cos x  sin x cos x 1 tan x   VD 4 4  C
1 tan x  tan x1 tan x 1 tan x2 2 2 2 3  dx  1 tan x  4   1 tan x   2 3 1 tan x 3 2  1 tan x     2
1 tan xdx  1   2
1 tan xdx . 1 tan x 1 tan x     4 4  
Đặt t 1 tan x ta được t   2 d
1 tan x dx , đổi cận x
t  2, x   t  1 3 4 3 Ta được 1 3   1 t 2 1 3 1 3 2 1     2   t  1  dt t 1 dt   t  2 ln t  1 2 ln 2  2 ln       1 3  t   t  2 2 2     2 NH
Từ đây ta suy ra a b ln 2  c ln 1 3 1 2ln 2  2ln1 3 . ÓM TOÁ
Do đó a  1,b  2, c  2 suy ra abc  4  . x  1   2t
x  2  t N VD  
Câu 39: Trong không gian Oxyz, cho hai đường thẳng d :  y t
; d  :  y  1 2t và mặt z  1   3t
z  2t   – VD
phẳng  P : x y z  2  0. Đường thẳng vuông góc với mặt phẳng  P và cắt cả hai C
đường thẳng d , d  có phương trình là x  3 y 1 z  2 x 1 y 1 z 1 A.   . B.   . 1 1 1 1 1  4  x  2 y 1 z 1 x 1 y 1 z  4 C.   . D.   . 1 1 1 2 2 2 Lời giải Chọn A
Mặt phẳng  P có vectơ pháp tuyến là n  1;1;  1 .
Gọi  là đường thẳng cần tìm và A    d , B    d
https://www.facebook.com/groups/toanvd.vdc Trang 26 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019
Vì A d , B d  nên gọi A 1
  2t; t; 1 3t  và B2  t ; 1 2t ;  2t 
AB  t  2t  3; 2t  t 1;  2t  3t  1. NH  
t  2t  3 2t  t 1 2
t  3t 1 ÓM TOÁ
Do    P nên AB, n cùng phương    1 1 1 3
t t  4  t   1  A  1; 1  ; 4         . N
2t  4t  2 t  1   B  3; 1;  2  VD  –
Đường thẳng  đi qua điểm B và có vectơ chỉ phương n  1;1  ;1 nên có phương trình VD x  3 y 1 z  2   . C 1 1 1
Câu 40: Có bao nhiêu số nguyên m để phương trình  3 x x
me có 2 nghiệm phân biệt? A. 7 . B. 6 . C. 5 . D. Vô số. Lời giải Chọn A Ta có: 3 x x x
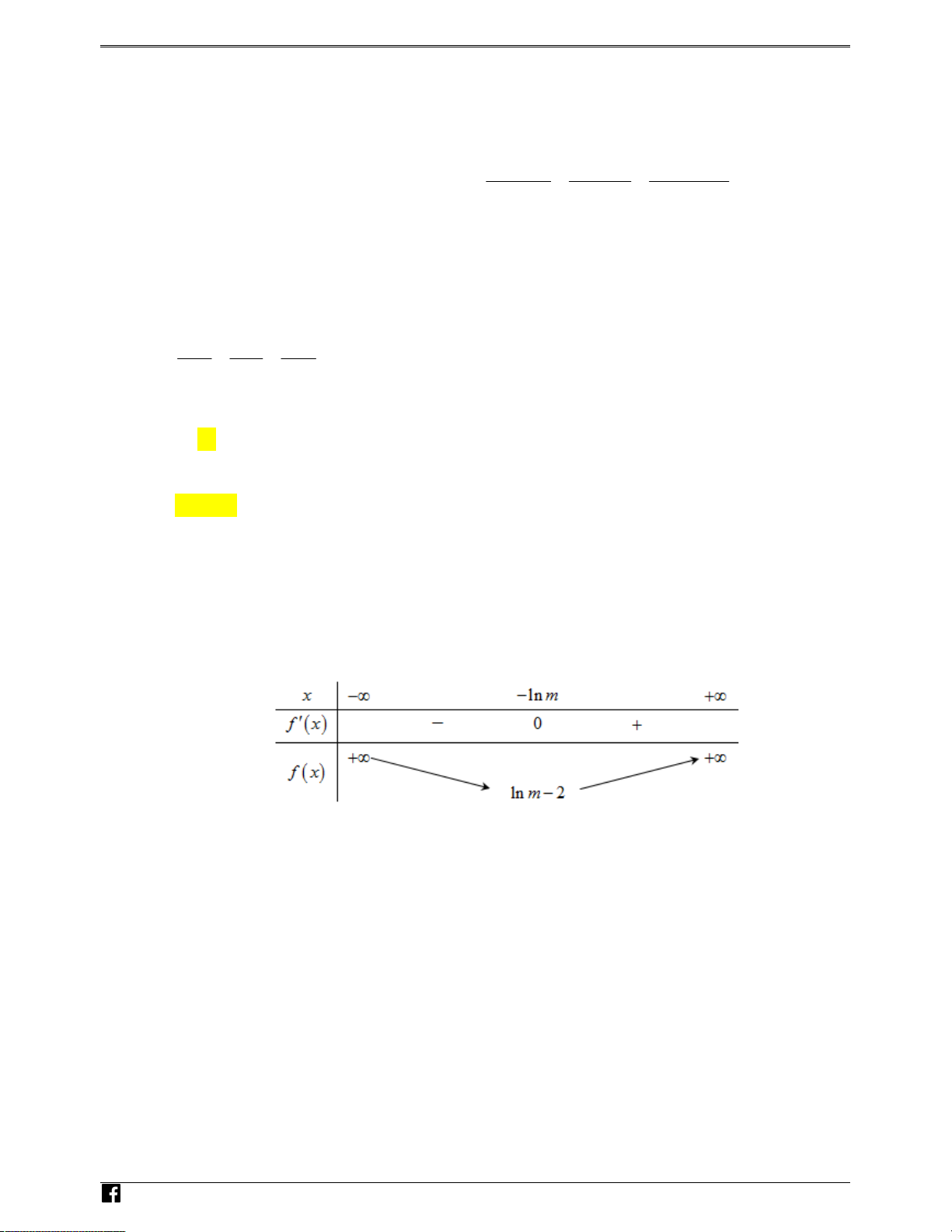
me me x 3  0 . Đặt   x    3    x f x me x f x me 1.
Nếu m  0 thì f  x  0  f x  0 có tối đa một nghiệm.
Ta xét với m  0, khi đó f  x  0  x  ln m . NH Bảng biến thiên ÓM TOÁ N VD – VD Để phương trình  3 x x
me có 2 nghiệm phân biệt 2
ln m  2  0  0  m e . C
Từ đó suy ra m1;2;3;4;5;6;  7 .
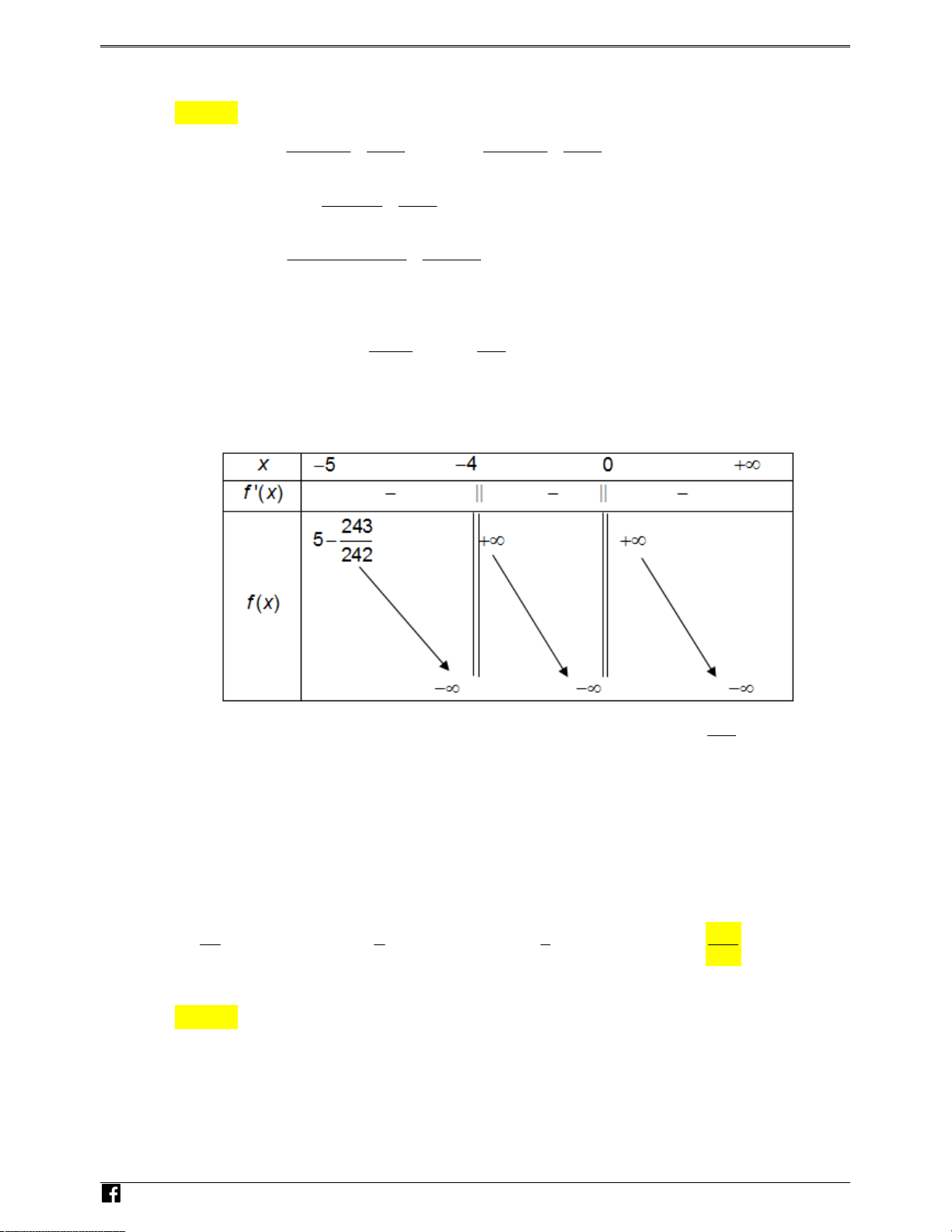
Câu 41: Cho f x mà đồ thị hàm số y f  x như hình bên. Hàm số y f x   2 1  x  2x đồng biến trên khoảng
https://www.facebook.com/groups/toanvd.vdc Trang 27 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 NH ÓM TO ÁN VD – A. 1;2. B.  1  ; 0. C. 0;  1 . D.  2  ;   1 . VD Lời giải C Chọn A
Ta có y f x   2 1  x  2x
Khi đó y  f  x  
1  2x  2 . Hàm số đồng biến khi y  0  f  x   1  2 x   1  0   1
Đặt t x 1 thì  
1 trở thành: f t  2t  0  f t   2  t .
Quan sát đồ thị hàm số y f t và y  2t trên cùng một hệ trục tọa độ như hình vẽ. NH ÓM T OÁ N V D – VD C
Khi đó ta thấy với t 0; 
1 thì đồ thị hàm số y f t luôn nằm trên đường thẳng y  2t .
Suy ra f t  2t  0, t  0;  1 . Do đó x
 1;2 thì hàm số y f x   2
1  x  2x đồng biến. 1 1
Câu 42: Có bao nhiêu số nguyên a  2
 019; 2019 để phương trình 
x a có
ln  x  5 3x 1 hai nghiệm phân biệt? A. 0 . B. 2022 . C. 2014 . D. 2015 .
https://www.facebook.com/groups/toanvd.vdc Trang 28 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 Lời giải Chọn D 1 1 1 1 NH Phương trình   x a    x a
ln  x  5 3x 1
ln  x  5 3x 1 ÓM TOÁ 1 1
Đặt hàm số f (x)  
x có tập xác định D   5  ; 4    4  ; 0 0; ln( x  5) 3x 1 1  3x ln 3
Ta có : f '(x)   1  0 N  x  5 2
ln  x  5 3x  2 1 VD
f (x) nghịch biến trên các khoảng của tập xác định – VD 1 243
Các giới hạn: lim f (x)   5  5  ; lim f (x)  ;
 lim f (x)    5    C x 5  3 1 242 x 4  x 4 
lim f (x)   ;
 lim f (x)   ; lim f (x)   x 0 x 0   x Bảng biến thiên NH ÓM TOÁ 243
Phương trình f (x)  a có hai nghiệm phân biệt khi và chỉ khi a  5  242 N VD a    a    Do   
. Vậy có 2018  4 1 2015 giá trị của a .
a  2019; 2019 a     4;2018  – VD
Câu 43: Cho hàm số f ( )
x có đạo hàm liên tục trên  và thỏa mãn f (0)  3 và 2 C 2
f (x)  f (2  x)  x  2x  2, x
   . Tích phân xf (  x)dx  bằng 0 4 2 5 10 A. . B. . C. . D. . 3 3 3 3 Lời giải ChọnD.
Thay x  0 ta được f (0) f (2)  2  f (2)  2 f (0)  23  1  2 2
Ta có: f (x)dx f (2  x)dx   0 0
https://www.facebook.com/groups/toanvd.vdc Trang 29 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 2 2 2 8 4
Từ hệ thức đề ra:  f (x)  f (2  x) dx    2
x  2x  2 dx   f (x)dx  .  3 3 0 0 0
Áp dụng công thức tích phân từng phần, ta lại có: NH 2 2 2 4 10 xf (
x)dx xf (x)  f (x)dx  2.( 1  )    .  0  ÓM TOÁ 3 3 0 0 x
Câu 44: Hàm số f x 
m (với m là tham số thực) có nhiều nhất bao nhiêu điểm cực 2 x 1 N VD trị? A. 2 . B. 3 . C. 5 . D. 4 . – VD Lời giải C Chọn D x
Xét hàm số g x   m , TXĐ:  . 2 x 1 2 1 xx  1
Ta có g x 
; g x  0   . 1 x 2 2 x  1   Bảng biến thiên NH ÓM TOÁ
Từ bảng biến thiên ta có hàm số y g x luôn có hai điểm cực trị. N VD x
Xét phương trình g x  0 2 
m  0  mx x m  0 , phương trình này có 2 x 1 – nhiều nhất hai nghiệm. VD C
Vậy hàm số f x có nhiều nhất bốn điểm cực trị.
Câu 45: Cho hình hộp ABC .
D A' B 'C ' D ' có thể tích bằng V . Gọi M , N, P,Q, E, F lần lượt là tâm
các hình bình hành ABCD, A' B 'C ' D ', ABB ' A', BCC ' B ',CDD 'C ', DAA' D '. Thể tích khối
đa diện có các đỉnh M , P,Q, E, F, N bằng V V V V A. . B. . C. . D. . 4 2 6 3 Lời giải Chọn C
https://www.facebook.com/groups/toanvd.vdc Trang 30 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 A' D' N B' C' NH ÓM TOÁ F P E N VD Q – VD D A C M B C
Gọi h là chiều cao của hình hộp ABC .
D A' B 'C ' D '  V  . h S . ABCD
Thấy hình đa diện MPQEFN là một bát diện nên 1 1 1 V  2.V  2. . . . h S  . . h S . MPQEFN N .PQEF 3 2 PQEF 3 PQEF 1 1
Lại có: PQEF là hình bình hành và có PQ EF
AC; QE PF BD nên 2 2 1 1 1 1 1 V SS . Do đó: V  . h S  . . h .S  . . h S  . PQEF 2 ABCD MPQEFN 3 PQEF 3 2 ABCD 6 ABCD 6 NH ÓM TOÁ
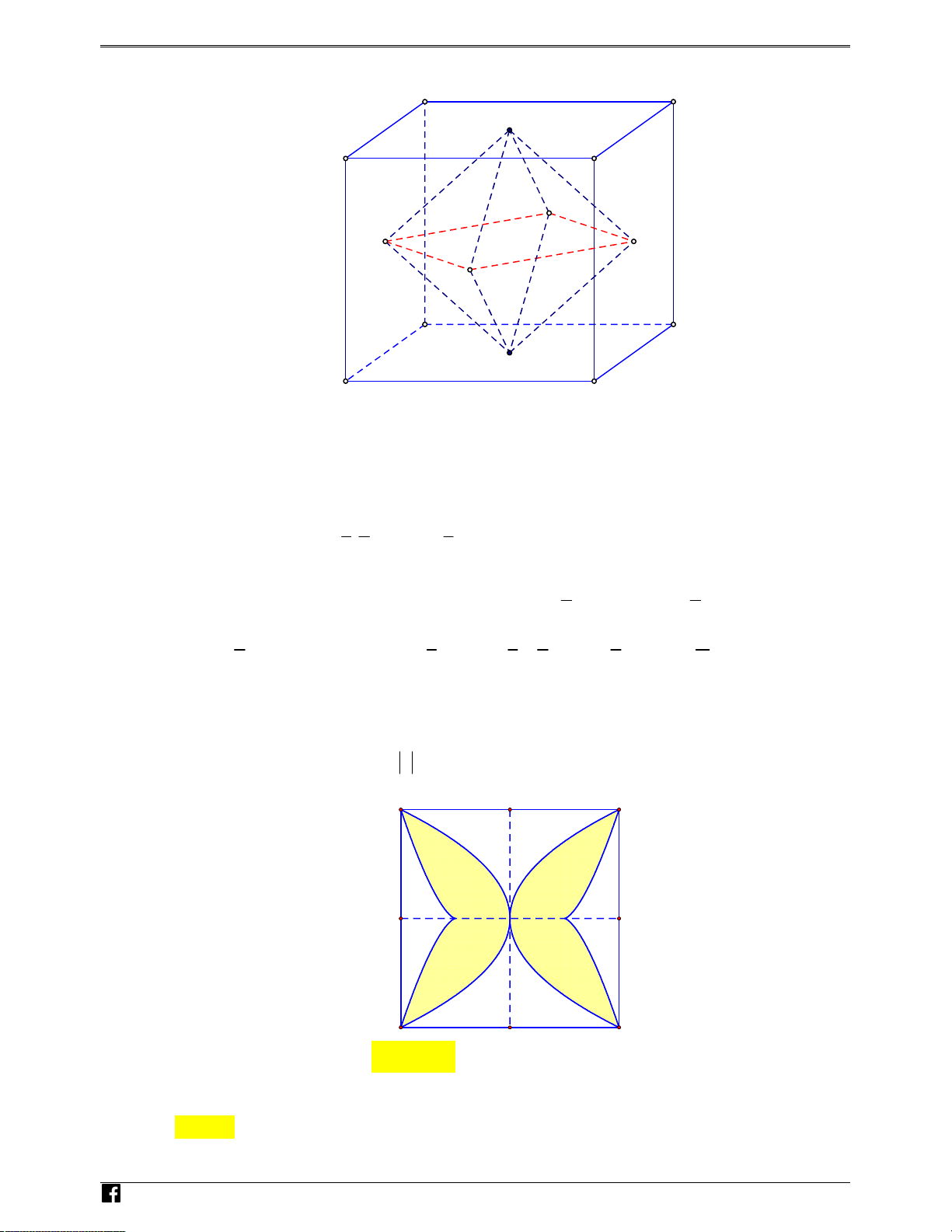
Câu 46: Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên gạch hình vuông cạnh
40 cm như hình bên. Biết rằng người thiết kế đã sử dụng các đường cong có phương trình 2 2 4x y và 3 2
4( x 1)  y để tạo hoa văn cho viên gạch. Diện tích phần N VD
được tô đạm gần nhất với giá trị nào dưới đây? – VD C A.  2 506 cm  . B.  2 747 cm  . C.  2 507 cm  . D.  2 746 cm  . Lời giải Chọn B
Chọn hệ trục tọa độ Oxy như hình vẽ.
https://www.facebook.com/groups/toanvd.vdc Trang 31 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 NH ÓM TO ÁN VD –
Gọi S là diện tích phần tô đậm VD 2 2 2 2 C  8 2  16 32 16 112 3 5 3 2 Ta có S  4
2x dx  4 2 (x 1) dx     x    x   1    dm   3  5 3 5 15 0 1 1   0 2240 Vậy S   746, 67  2 cm  3
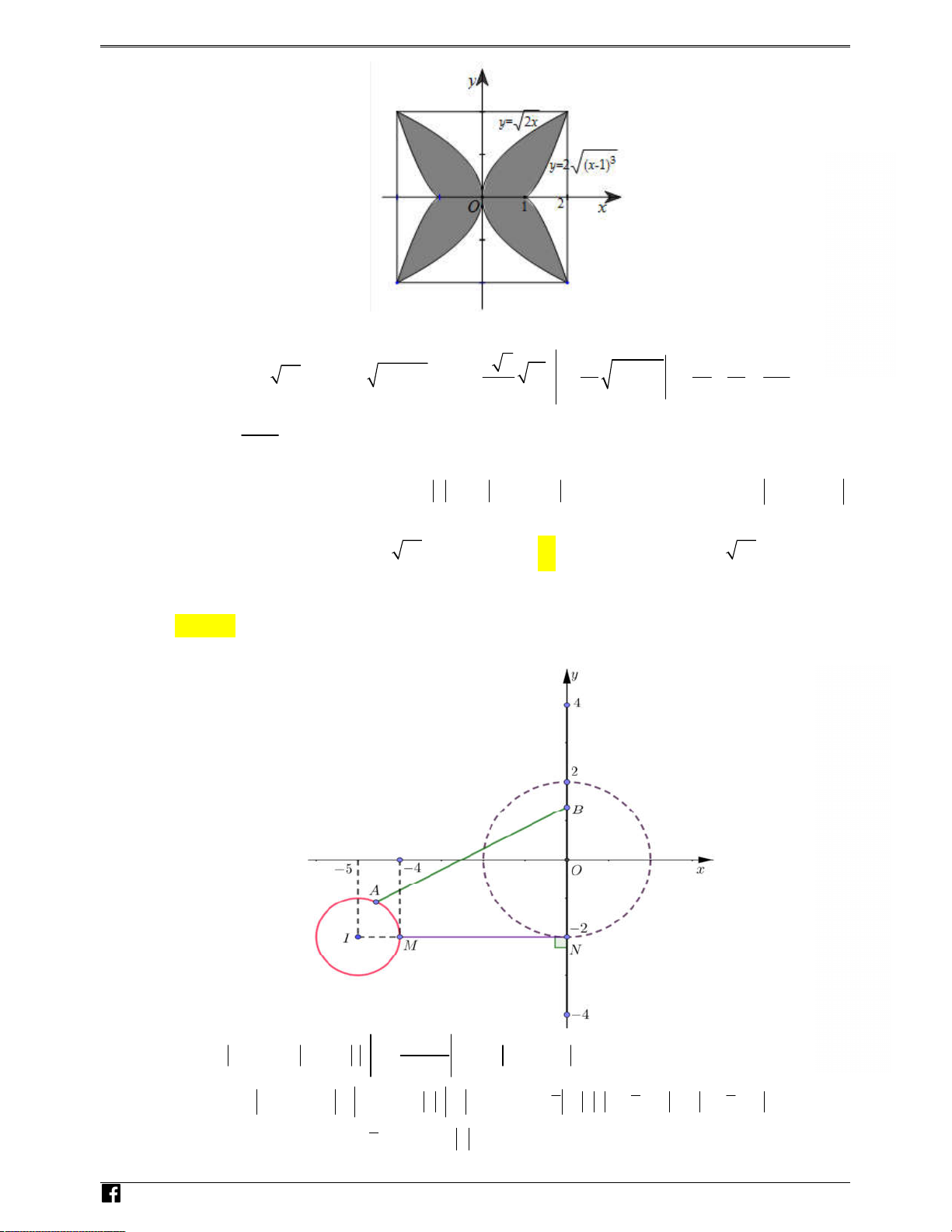
Câu 47: Xét các số phức z , w thỏa mãn z  2 , iw  2  5i  1. Giá trị nhỏ nhất của 2 z wz  4 bằng A. 4 . B. 2 29 3 . C. 8 . D. 2 29 5 . Lời giải Chọn C Cách 1: NH ÓM T OÁ N V D – VD C 2  5i
Ta có: iw  2  5i  1  i w
 1  w  5  2i  1. i Ta có: 2 2 2 2
T z wz  4  z wz z
z wz z z z z z w  2 z z w   *
Đặt z a bi . Suy ra: z z  2bi . Vì z  2 nên 4   2b  4 .
https://www.facebook.com/groups/toanvd.vdc Trang 32 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019
Gọi A , B lần lượt là điểm biểu diễn của w và 2bi . Suy ra:
+ A thuộc đường tròn C có tâm I  5  ; 2
  , bán kính R 1.
+ B thuộc trục Oy và 4  x  4 . B NH Từ  
* suy ra: T  2AB  2MN  2 4  8 (xem hình) ÓM TOÁ
Dấu “ ” xảy ra khi và chỉ khi A M  4  ; 2    w  4   2i và B N 0; 2    2bi  2
i b  1
  z a i 2
a 1  4  a   3  z   3  i . N Vậy 2
z wz  4 có giá trị nhỏ nhất bằng 8 . VD Cách 2: – VD
Đặt z a bi , w c di ( a , b , c , d  ). Từ giả thiết, ta có: 2 2  C a b  4  a, b    2  ; 2    .
c  52   d  22  1  c  6
 ; 4, d 3;    1  Ta có: 2 2 2 2
T z wz  4  z wz z
z wz z z z z z w  2 z z w T
bi  c di   b d 2 2 2 2 2 2 2
c  2 c  2 c  2  4  8 (do c  6  ; 4   ). c  4  
Dấu “ ” xảy ra khi và chỉ khi 2b d  0 . 
c  52   d  22  1  c  4  
Suy ra một nghiệm thỏa mãn là d  2 . NH b   1   ÓM TOÁ Vậy 2
z wz  4 có giá trị nhỏ nhất bằng 8 .
Chú ý: Về một Lời giải SAI. N VD Sau khi có 2
T z wz  4  2 z z w  2 z w z  2 EF  2  2 OI 1 2  2  2 29  5 . –
z w kz , k  0 VD 
Khi đó, đẳng thức không xảy ra, vì hệ  vô nghiệm. z w  29  3 C   Hoặc: 2
T z wz  4  z z w  4  z z w  4  2 z w  4  2  29  3  4  2 29  5 ,
cũng không có đẳng thức xảy ra. (Bạn đọc tự kiểm tra điều này).
https://www.facebook.com/groups/toanvd.vdc Trang 33 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 NH ÓM TO ÁN VD – VD C
Câu 48: Cho f (x) mà đồ thị hàm số y f '(x) như hình vẽ bên  x
Bất phương trình f (x)  sin
m nghiệm đúng với mọi x  1  ;  3 khi và chỉ khi NH 2 ÓM T
A. m f (0) .
B. m f (1) 1.
C. m f (1) 1.
D. m f (2) . OÁ Lời giải N Chọn B V D  x
 Xét bất phương trình f (x)  sin
m (1) với x  1  ;  3 , ta có: – 2 VD  xx f (x)  sin
m f (x)  sin  m (2) C 2 2  x
 Đánh giá f (x)  sin với x  1  ;  3 2
+ Từ đồ thị của hàm số y f '(x) đã cho ta suy ra BBT của f (x) như sau:
https://www.facebook.com/groups/toanvd.vdc Trang 34 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 NH ÓM TO ÁN
Từ BBT ta suy ra: f (x)  f (1), x   1  ;  3 (*) VD   x 3 + Do x  1  ;  3 nên: 1   x  3     – 2 2 2 VD  xx C Suy ra: 1   sin  1  1    sin  1 (**) 2 2  x
+ Từ (*) và (**) cho ta: f (x)  sin
f (1) 1, x   1  ; 
3 . Dấu "  " xảy ra khi x 1 2  x
 Do đó: Bất phương trình f (x)  sin
m nghiệm đúng với mọi x  1  ;  3 2
m f (1)  1 . Chọn B x  3 y  4 z  2
Câu 49: Trong không gian Oxyz , cho đường thẳng d :  
và 2 điểm A6;3; 2   , 2 1 1 B1;0; 
1 . Gọi  là đường thẳng đi qua B , vuông góc với d và thỏa mãn khoảng cách NH
từ A đến  là nhỏ nhất. Một vectơ chỉ phương của  có tọa độ ÓM T A. 1;1; 3   . B. 1; 1  ;   1 . C. 1;2; 4   . D. 2; 1  ; 3   . Lời giải OÁ Chọn A N
Gọi  P là mặt phẳng qua B và vuông góc với d nên  P : 2x y z 1  0 . V D
Gọi H là hình chiếu của A lên  P , ta có: H 2;1; 4 – VD
Ta có:    P nên d  ;
A    d  ; A P . C
Dấu đẳng thức xảy ra khi và chỉ khi H   . 
Vậy một vectơ chỉ phương của  là BH  1;1; 3 .
https://www.facebook.com/groups/toanvd.vdc Trang 35 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019 x 1 y  2 z
Câu 50: Trong không gian Oxyz , cho điểm A2; ;
 3; 4 , đường thẳng d :   và mặt 2 1 2 2 2 2
cầu S  :  x  3   y  2   z   1
 20 . Mặt phẳng  P chứa đường thẳng d thỏa mãn NH
khoảng cách từ điểm A đến  P lớn nhất. Mặt cầu S  cắt  P theo đường tròn có ÓM bán kính bằng A. 5 . B. 1. C. 4 . D. 2 . TO Lời giải ÁN VD Chọn D – VD C Ta có: 
d đi qua M 1; 2
 ;0 và có VTCP ud  2;1; 2 .
S  có tâm I 3;2; 
1 và bán kính R  2 5 . NH ÓM T Ta có: d  ;
A P  d  ;
A d  . Dấu “  ” xảy ra khi  P chứa d và vuông góc với AK .    OÁ
Khi đó:  P có VTPT là n    P
nAKM ,ud   . N     V Vì n    AKM
ud , AM   6
 ; 6;3  nP  9;18; 18  9 1; 2; 2 . D   – VD
  P :  x  
1  2 y  2  2z  0  P : x  2y  2z  3  0 . C
Ta có: d d I;P  4 .
Vậy bán kính đường tròn cần tìm: 2 2
r R d  20 16  2 .
……………..HẾT…………….
https://www.facebook.com/groups/toanvd.vdc Trang 36 NHÓM TOÁN VD – VDC
ĐỀ THI THỬ THPTQG – 2018-2019
Toàn thể ban quan trị nhóm VD-VDC xin được gửi tặng sản phẩm chuyên đại Vinh
lần 3 cho tất cả các quý thầy cô là thành viên của nhóm. Món quà nhỏ này như một
lời tri ân đến quý thầy cô đã luôn ủng hộ nhóm trong suốt thời gian qua, tất cả các dự NH
án đề thi thử trên nhóm lớn trong suốt mùa thi qua. Kính chúc quý thầy cô luôn có sức ÓM TOÁ
khỏe và luôn tràn đầy nhiệt huyết trong nghề.
Mong thầy cô sẽ luôn ủng hộ nhóm trong những chặng đường tiếp theo. Xin chào và
hẹn gặp lại. N VD
Dù đã cố gắng làm việc nghiêm túc nhưng chắc sẽ có những sai sót nên mong quý thầy –
cô hãy thông cảm. Xin cảm ơn rất nhiều. VD C
BAN QUẢN TRỊ NHÓM VD-VDC – 05/05/2019 NH ÓM TOÁ N VD – VD C
https://www.facebook.com/groups/toanvd.vdc Trang 37
Document Outline

  • TRƯỜNG ĐẠI HỌC VINH.pdf
    • TOÁN LẦN 3_132
    • Đáp án môn Toán lần 3 - 2019
  • TOANVD.EDU.VN-CHUYÊN-ĐẠI-HỌC-VINH-L3-HOÀN-CHỈNH.pdf