Thông tin
Hỏi đáp

Đề thi thử Toán THPTQG 2019 trường chuyên Phan Bội Châu – Nghệ An lần 2

Đề thi thử Toán THPTQG 2019 trường chuyên Phan Bội Châu – Nghệ An lần 2 có mã đề 678, đề gồm 06 trang với 50 câu hỏi và bài tập dạng trắc nghiệm khách quan

Chủ đề:

Đề thi THPTQG môn Toán năm 2023 1.2 K tài liệu

Môn:

Toán 1.8 K tài liệu

Thông tin:

32 trang 9 tháng trước

Tác giả:

Thanh Hoa

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Đề thi thử Toán THPTQG 2019 trường chuyên Phan Bội Châu – Nghệ An lần 2

35 18 lượt tải Tải xuống

HƯỚNG DẪN GIẢI CHI TIẾT

1.A

2.D

3.C

4.D

5.C

6.B

7.A

8.C

9.A

10.D

11.B

12.C

13.B

14.A

15.D

16.D

17.D

18.C

19.A

20.C

21.D

22.B

23.D

24.D

25.B

26.C

27.B

28.B

29.B

30.A

31.A

32.C

33.D

34.A

35.D

36.A

37.B

38.C

39.B

40.C

41.D

42.C

43.B

44.C

45.C

46.A

47.D

48.B

49.A

50.D

Câu 1:

Phương pháp:

- Tính công bội q, từ đó suy ra

- Sử dụng công thức

u u q





Cách giải:

Ta có:

2 2

3 1

. 18 2. 3u u q q q     

Vậy với thì

3q 

5 5

6 1

. 2.3 486u u q  

Với thì

3q  

 

6 1

. 2. 3 486u u q    

Chọn: A

Chú ý khi giải:

Nhiều HS sẽ chọn nhầm đáp án D vì đọc không kĩ đề thành cấp số “cộng”.

Nhiều em khác lại chọn nhầm B vì quên mất trường hợp

3q  

Câu 2:

Phương pháp:

Hàm số nghịch biến trên

 

ax b

y cx d

cx d



  



' 0y











 





Cách giải:

TXĐ:

 

\D m 

Ta có:

 

   

2 2

1 2 2

m m m

m m

x m x m

  

 

 

 

Để hàm số nghịch biến trên khoảng thì

 

1;

 

' 0

1 2

2 0

1 2

m m

x m



 

 

  



  







    

  



  





   



Vậy





1;2m

Chọn: D

Câu 3:

Phương pháp:

Xét phương trình hoành độ giao điểm, tìm nghiệm và tính diện tích theo công thức

   

S f x g x dx 



Cách giải:

Phương trình hoành độ giao điểm của hai đồ thị hàm số là:

2 2 2

2 1 2 4 1 3 6 0

x x x x x x





         







Dễ thấy trong khoảng nên diện tích hình phẳng cần tính là:

3 6 0x x 

 

0;2

   

2 2

2 2 2

0 0

2 2 3

2 1 2 4 1 6 3

6 3 3 4

S x x x x dx x x dx

x x dx x x

        

    

 



Chọn: C

Câu 4:

Phương pháp:

Sử dụng công thức tính đạo hàm hàm hợp và

' '

u u v v u

v v



 



 

 

 

' .ln

x x

a a a

Cách giải:

Ta có:

   

2 1 .2 .ln 2 1 1 ln 2

' '

2 2 2

x x

x x x

x x

     



 

  

 

 

Chọn: D

Câu 5:

Phương pháp:

- Cộng hai số phức theo công thức

       

' ' ' 'a bi a b i a a b b i      

- Tính mô đun số phức theo công thức

2 2

z a b 

Cách giải:

Ta có:

       

1 2

1 2 3 1 2 1 3 3 2z z i i i i          

Vậy

 

1 2

3 2 13z z    

Chọn: C

Câu 6:

Phương pháp:

Thể tích khối hộp đứng có chiều cao h và diện tích đáy S là

.V h S

Cách giải:

Giả sử là hình vuông cạnh a thì chiều cao hình hộp và

' 'ABB A

'AA a

diện tích đáy hình hộp là

ABCD

S a

Thể tích hình hộp là

2 3

'. .3 3

ABCD

V AA S a a a  

Chọn: B

Câu 7:

Phương pháp:

Biến đổi phương trình về dạng và sử dụng tương giao đồ thị tìm số nghiệm của phương

   

f x g m

trình.

Cách giải:

Ta có:

     

2 0 *

f x m f x    

Số nghiệm của phương trình (*) là số giao điểm của đồ thị hàm số và đường thẳng

 

y f x

y  

Phương trình đã cho có ba nghiệm phân biệt có ba nghiệm phân biệt

 

*

1 2

m     

Chọn: A

Câu 8:

Phương pháp:

Quan sát bảng biến thiên và lưu ý rằng hàm số có trên khoảng thì hàm số

 

y f x

 

' 0f x 

 

;a b

đồng biến trên

 

;a b

Đường thẳng là tiệm cận ngang của đồ thị hàm số nếu một trong hai điều kiện sau

y y

 

y f x

được thỏa mãn hoặc

lim

y y





lim

y y





Cách giải:

Từ BBT ta có hàm số đồng biến trên và nên A đúng

 

;1

 

2;

Hàm số có hai điểm cực trị nên B đúng

1; 2x x 

Đồ thị hàm số có 1 đường tiệm cận ngang (vì ) nên D đúng

1y  

lim 1



 

Hàm số có giá trị nhỏ nhất bằng là sai vì không tồn tại giá trị của x để

1

1y  

Chọn: C

Câu 9:

Phương pháp:

- Tìm khoảng nghịch biến của hàm số đã cho dựa vào đồ thị

- Nhận xét các đáp án (khoảng cần tìm là con của khoảng nghịch biến)

Cách giải:

Dễ thấy hàm số nghịch biến trên các khoảng và

 

; 1 

 

0;1

Mà nên hàm số cũng nghịch biến trên khoảng

 

1 2

; 0;1

2 2

 



 

 

1 2

;

2 2

 

 

 

Chọn: A

Câu 10:

Phương pháp:

Giải phương trình tìm sau đó tính toán.

1 2

,z z

Lưu ý: Với thì

 

, ,z a bi a b  

2 2

z a b 

Cách giải:

Ta có

 

2 2

1 3 1 3

2 10 0 1 9 9

1 3 1 3

z i z i

z z z i

z i z i

    

 

         

 

     

 

Khi đó

     

2 2

2 2 2

1 2

1 3 1 3 20z z        

Chọn: D

Câu 11:

Phương pháp:

- Đường thẳng có một VTCP là

0 0 0

x x y y z z

a b c

  

 

 

; ;u a b c



- Nếu là một VTCP của d thì cũng là một VTCP của d.

 

; ;u a b c



 

; ;ku ka kb kc



Cách giải:

Dễ thấy d có một VTCP là nên nó cũng nhận làm VTCP.

 

2;1;2



 

2 4;2;4

u u

 

Do đó

4; 4 8a b a b    

Chọn: B

Câu 12:

Phương pháp:

Sử dụng các công thức tổ hợp, chỉnh hợp.

Cách giải:

Với k và n là hai số nguyên dương tùy ý thỏa mãn , ta có ; ;

1k n 

k n k

n n

C C





 

n k





1 1

k k k

n n n

C C C

 



 

Nên A, B, D đúng.

Xét C: (vô lý vì )

   

! ! 1

1 0

! ! ! !

k k

n n

A C

n k k n k k

     

 

1 1

1 1 1 0

! !

k k

     

Chọn: C

Câu 13:

Phương pháp:

- Vẽ đồ thị hàm số , từ đó suy ra đồ thị hàm số và kết luận.

2 3 5y x x   

Cách giải:

Hàm số có đồ thị là parabol có hoành độ đỉnh , tung độ .

2 3 5y x x   

x 

y 

Đồ thị:

Từ đó có đồ thị hàm số như trên.

2 3 5y x x   

Dựa vào đồ thị hàm số thấy hàm số đạt cực đại tại

x 

Chọn: B

Câu 14:

Phương pháp:

Sử dụng công thức tính thể tích khối nón có bán kính đáy R và chiều cao h là

V R h





Thể tích khối cầu bán kính R và

V R





Cách giải:

Gọi H là trung điểm BC và O là trọng tâm tam giác đều ABC.

Khi đó

; 3 3 .OH r AH OH r  

Xét tam giác AHC vuông tại H có

0 0

60 tan tan 60 3

AH r

C C HC r

HC HC

        

Khi quay tam giác ABC quanh cạnh AH ta được một hình nón

có bán kính và chiều cao . Suy ra thể tích

3HC r

3AH r

khối nón thu được là

2 3

. 3

V HC AH r

 

 

Khi quay hình tròn quanh AH ta được khối cầu có diện tích là

 

;O r

V r





Vậy khi , cắt bỏ phần hình tròn và cho hình phẳng thu được quanh quanh AO thì thể tích khối tròn

 

;O r

xoay thu được là

3 3 3

4 5

3 3

n c

V V V r r r

  

    

Chọn: A

Câu 15:

Phương pháp:

Quan sát đồ thị, nhận xét dáng đồ thị, điểm đi qua, số cực trị và đối chiếu với từng đáp án.

Cách giải:

Dễ thấy đồ thị có dáng đồ thị của hàm số bậc ba có hệ số nên loại C.

0a 

Đồ thị hàm số đi qua điểm nên loại A.

 

0;1

Hàm số đạt cực trị tại các điểm nên phương trình có hai nghiệm

0, 2x x 

' 0y 

1 2

0, 2x x 

Xét đáp án B có nên loại B.

' 0 3 6 0

y x x





    



 



Đáp án D có nên D thỏa mãn.

' 0 3 6 0

y x x





    







Chọn: D

Câu 16:

Phương pháp:

Sử dụng công thức với

log log log ;log .log

a a a a a

b c b b



  

0 1; , 0a b c  

Cách giải:

Ta có:

ln ln ln 2ln ln

a b a b

 

   

 

 

Chọn: D

Câu 17:

Phương pháp:

Sử dụng công thức nguyên hàm các hàm số cơ bản và tính chất nguyên hàm.

Cách giải:

Ta có:

 

sin sin ln cos

f x dx x dx xdx x x C

x x

 

      

 

 

   

Chọn: D

Câu 18:

Phương pháp:

+ Mặt phẳng (P) có 1 VTPT là VTPT của mặt phẳng (Q).

+ với

   

 

; ;d Q P d M P

 

M Q

+ Khoảng cách từ đến mặt phẳng là

 

0 0 0

; ;M x y z

 

: 0P ax by cz d   

 

0 0 0

2 2 2

;

ax by cz d

d M P

a b c

  



 

Cách giải:

Vì nên phương trình mặt phẳng (P) có dạng

   

/ /P Q

 

2 2 0 3x y z d d     

Lấy khi đó

   

1;1;1M Q 

   

 

2 2 2

1 2.1 2.1 3

; ;

1 2 2

d d

d Q P d M P

    

  

 

Theo đề bài ta có

3 3 0

3 3 6

d d

  



 

  

 

    

 

Với đi qua nên không thỏa mãn đề bài

 

0 : 2 2 0d P x y z    

 

0;0;0O

Với (thỏa mãn)

 

6 : 2 2 6 0d P x y z      

Vậy phương trình

 

: 2 2 6 0P x y z   

Chọn: C

Câu 19:

Phương pháp:

Sử dụng phương pháp từng phần, đặt và sử dụng công thức

u x

dv e dx











udv uv vdu 

 

Cách giải:

Đặt

du dx

u x

dv e dx













 









Khi đó

2 2 2 2

2 2

1 1

2 2 2 4 2 2

x x x x

x x

xe e xe e

xe dx dx C e x C

 

       

 

 

 

Chọn: A

Câu 20:

Phương pháp:

Đặt từ đó đưa về phương trình ẩn t.

 

2 1 , 0

t t  

Giải phương trình ẩn t ta tìm được t, thay lại cách đặt để tìm x.

Lưu ý:

 

log 0 1; 0

a b x b a b     

Cách giải:

Đặt

 

2 1 , 0

t t  

Ta có

  

2 1 2 1 1 2 1

2 1

     



Ta có phương trình:

 

2 1

2 2 0 2 2 1 0

2 1

t t t TM



 

       



 





Với

 

2 1 2 1 2 1 1

t x       

Với

 

2 1 2 1 2 1 1

t x        

Vậy tích các nghiệm của phương trình là

1.1 1  

Chọn: C

Câu 21:

Phương pháp:

- Tính , tìm các nghiệm thuộc đoạn .

 

0;2

- Tính giá trị hàm số tại các điểm đó và hai đầu mút .

0, 2x x 

- So sánh các giá trị đó và kết luận.

Cách giải:

Ta có:

 

 

3 2

0 0;2

' 4 6 0 4 6 0 0;2

0;2

y x x x x x



 



          



  





Tính

   

6 13

0 1, 2 3,

2 4

y y y

 

   

 

 

Vậy giá trị lớn nhất của hàm số đạt được trong là

 

0;2

Chọn: D

Câu 22:

Phương pháp:

Đường thẳng là tiệm cận ngang của đồ thị hàm số nếu một trong hai điều kiện sau được

y y

 

y f x

thỏa mãn hoặc

lim

y y





lim

y y





Đường thẳng là tiệm cận đứng của đồ thị hàm số nếu một trong các điều kiện sau được

x x

 

y f x

thỏa mãn

0 0 0 0

lim ; lim ; lim ; lim

x x x x x x x x

y y y y

   

   

       

Cách giải:

ĐK:

 

1; 3x  

+ nên đường thẳng là một tiệm cận ngang của đồ thị

1 1

lim lim lim 0

2 3

x x x

x x

  



  

 

0y 

hàm số.

+ nên đường thẳng là một tiệm cận

  

3 3 3 3

1 1 1

lim lim lim lim

2 3 1 3 3

x x x x

x x

x x x x x

   

   

 

    

    

3x  

đứng của đồ thị hàm số.

+ nên đường thẳng không là tiệm

  

1 1 1 1

lim lim lim lim

2 3 1 3 3 4

x x x x

x x

x x x x x

   

   

 

     

    

1x 

cận đứng của đồ thị hàm số.

Vậy đồ thị hàm số đã cho có hai tiệm cận và

3x  

0y 

Chọn: B

Câu 23:

Phương pháp:

Trục Oz đi qua và có VTCP

 

0;0;0O

 

0;0;1k 



Cách giải:

Trục Oz đi qua và có VTCP nên có phương trình

 

0;0;0O

 

0;0;1k 



z t

















Chọn: D

Câu 24:

Phương pháp:

Thể tích khói chóp có chiều cao h và diện tích S là

V h S

Hình tứ diện đều có tất cả các cạnh bằng nhau nên từ thể tích ta tính được cạnh của hình tứ diện đều.

Cách giải:

Gọi tứ diện đều có AB = AC = BC = CD = x (x > 0)

Gọi M là trung điểm BC và H là trọng tâm tam giác ABC

 

;DH ABC AM BC  

Xét tam giác ABC đều cạnh x có :

3 2 3 3 3

. ;

2 3 2 3 4

ABC

x x x x

AM AH S    

Xét tam giác DAH vuông tại H có

2 2 2

3 6

3 3

x x

DH AD AH x

 

    

 

 

Thể tích khối tứ diện

2 3

1 1 6 3 2

. .

3 3 3 4 12

ABCD ABCD

x x x

V DH S  

Theo giả thiết ta có

1 2

3 12

ABCD

V a x a   

Vậy

2AB a

Chọn: D

Chú ý:

Các em có thể sử dụng luôn công thức tính thể tích khối tứ diện đều cạnh x là , từ đó tính được

V 

cạnh AB.

Câu 26:

Phương pháp:

Phương trình

   

log

f x m f x a  

Cách giải:

TXĐ:

D  

 

2 2 2

log 2 2 1 2 2 10 2 8 0

x x x x x x

 



           







Vậy tập nghiệm của phương trình là

 

2;4S  

Chọn: B

Câu 26:

Phương pháp:

Hình cầu có bán kính R thì có diện tích là S = 4 R

và thể tích là



V R





Cách giải:

Gọi bán kính hình cầu là R (R > 0)

Khi đó diện tích mặt cầu là S = 4 R

= 36 a

R = 3a





Thể tích khối cầu là

 

3 3

4 4

3 36

3 3

V R a a

  

  

Chọn: C

Câu 27:

Phương pháp:

Biến đổi P về làm xuất hiện các chú ý

3 3 3

log 5,log 6,log 22,

90 180

11 22



Sử dụng các công thức logarit của tích, thương và lũy thừa.

Cách giải:

Ta có:

 

3 3 3 3

2 2

3 3 3 3 3

3 3 3

90 180

log log log 180 log 22

11 22

log 5.6 log 22 log 5 log 6 log 22

log 5 2log 6 log 22 2

a b c

   

    

     

Chọn: B

Câu 28:

Phương pháp:

Sử dụng phương pháp đổi biến số

t x

Và tích phân không phụ thuộc vào biến

   

b b

a a

f x dx f t dt

 

Cách giải:

Xét

 

f x



Đặt

t x dt dx dx tdt

    

Đổi cận

1 1; 4 2x t x t     

Ta có

 

4 2 2

1 1 1

.2 2 2.2 4

f x

f t

dx tdt f t dt

   

  

Chọn: B

Câu 29:

Phương pháp:

Sử dụng cách giải bất phương trình

   

log 1

f x m f x a khi a   

Cách giải:

Điều kiện:

 

2 2 3 2 2

log 1 3 1 2 1 8 9

x x x x

 



          







Kết hợp với điều kiện ta được

 









Vậy tập nghiệm của bất phương trình là



 



; 3 3;   

Chọn: B

Câu 30:

Phương pháp:

Cho

     

1 1 1 2 2 2 2 1 2 1 2 1

; ; , ; ; ; ;A x y z B x y z AB x x y y z z    



Cho . Khi đó

   

; ; ; '; '; 'u x y z v x y z

 

x x

u v y y

z z







  









 

Cách giải:

Gọi

   

; ; 1; 2; 1B x y z AB x y z    



Từ giả thiết ta có

   

1 1 2

1;3;1 2 3 5 2;5;0

1 1 0

x x

AB y y B

z z

  

 

 

      

 

 

  

 



Chọn: A

Câu 31:

Phương pháp:

Mặt cầu đường kính AB có tâm là trung điểm AB và bán kính

R 

Cách giải:

Gọi I là trung điểm của AB thì

 

3;3;1I

Ta có:

     

2 2 2

5 1 4 2 1 3 6AB        

Mặt cầu đường kính AB có tâm là trung điểm AB và bán kính = 3 nên có phương trình:

R 

hay

     

2 2 2

3 3 1 3x y z     

     

2 2 2

3 3 1 9x y z     

Chọn: A

Câu 32:

Phương pháp:

+ Sử dụng cách xác định góc giữa hai mặt phẳng (P); (Q)

góc tạo bởi (P) và (Q) là góc tạo bởi hai đường thẳng a và b.

   

 

   

;

P Q d

a d a P

b Q b Q

 





  





 



+ Tính toán dựa vào định lý Pytago.

Cách giải:

Gọi I là giao điểm hai đường chéo của hình vuông ABCD . Khi đó I

là trung điểm của BD.

Xét tam giác cân tại và tam giác C BD cân tại

'A BD

' 'A A I BD 

' 'C C I BD 

Ta có góc tạo bởi và là

 

'A BD

 

'C BD

góc

' 'A IC

Gọi

Xét hình vuông ABCD có

2 ' ' 2;

AC BD x A C x DI    

Xét tam giác vuông tại A có

'AA D

2 2 2

6 10

' '

2 2

x x

A D A A AD x

 

    

 

 

Xét tam giác vuông tại I có

'A DI

2 2

10 2

' ' 2

2 2

x x

A I A D DI x

   

    

   

   

Vì

 

' ' ' ' 2A DB C DB c c c C I A I x       

Xét tam giác có nên là tam giác đều. Suy ra

' 'A IC

' ' ' ' 2A I C I A C x  

' 'A IC

' ' 60A IC 

Vậy góc tạo bởi và là góc bằng

 

'A BD

 

'C BD

' 'A IC

Chọn: C

Câu 33:

Phương pháp:

Thay vào đẳng thức bài cho, tìm a, b và kết luận.

z a bi 

Cách giải:

Có thay vào đẳng thức bài cho ta được:

z a bi z a bi    

   

' '

A BD C BD BD

A I BD

C I BD

 





 









6 6

2 2

AB x

AB x AA   

    

 

   

1 2 3 2

2 2 3 2

3 3 2

3 3

1 3

2 3

2 2

i a bi a bi i

a b a b i a bi i

a b a b i i

a b

     

       

     







 





       

 

 





 





Chọn: D

Câu 34:

Phương pháp:

+ Xác định chiều cao của hình chóp

+ Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp:

Bước 1: Xác định tâm đường tròn ngoại tiếp hình vuông ABCD

Bước 2: Xác định trục đường tròn ngoại tiếp đa giác đáy. Kẻ đường trung trực một cạnh bên giao với trục

đường tròn ở đâu đó chính là tâm mặt cầu ngoại tiếp hình chóp.

+ Tính bán kính mặt cầu ngoại tiếp hình chóp dựa vào định lý Pytago.

+ Mặt cầu có bán kính R thì có diện tích là S  4



Cách giải:

Gọi O là tâm hình vuông ABCD, gọi M , N lần lượt là trung điểm của AB; CD .

Kẻ SH MN tại H .



Ta có SN DC ; MN DC DC ( SMN ) DC SH











Mà SH MN SH (ABCD).







Vì ABCD là hình vuông cạnh a nên

;

2 2 2 2

AC a MN a

OB OC OA OD OM ON       

Vì tam giác SDC vuông cân tại S có cạnh huyền CD  a

SN 

Vì tam giác ABS đều cạnh a  SM =

Xét tam giác SNM có nên vuông tại S.

2 2 2 2 2

3 4

2 2 4

a a a

MN SN SM a a

 

 

     

 

 

SMN

Suy ra và

2 2

. .

a a

SH MN SN SM SH

   

4 4

SN a a

SN NH NM HN HO

     

Nhận thấy O là tâm đường tròn ngoại tiếp hình vuông ABCD . Kẻ tia Oy / /SH , khi đó tâm mặt cầu ngoại

tiếp hình chóp S . ABCD nằm trên đường thẳng Oy.

Trên tia OM ta lấy K sao cho OK = OA = , khi đó K (O; OA)



Trong mặt phẳng (SMN ), lấy E là trung điểm SK , kẻ EI là đường trung trực của SK (I Oy) khi đó



IK = IS = IA = IB = IC = ID nên I là tâm mặt cầu ngoại tiếp hình chóp S . ABCD và bán kính là R = IK

Kẻ SF Oy SF = OH =





;

4 4

a a

OF SH 

Gắn hệ trục Oxy với OM Ox; Oy / /SH



Đặt

 

0 0

I y IF y  

Xét tam giác vuông có

ISF

2 2 2

4 4

a a

IS IF SF y

 

    

 

 

Xét tam giác vuông có

OIK

2 2 2 2

IK OI OK y

 

   

 

 

Vì

2 2

2 2 2

0 0 0 0

3 2 3 3

4 4 2 2 4 6

a a a a a

IK IS IK IS y y y y

   

 

             

   

 

   

 

   

Suy ra bán kính mặt cầu

2 2

2 21

2 12 2 6

a a a a

R IK y

 

     

 

 

Diện tích mặt cầu ngoại tiếp hình chóp là

2 2

.21 7

4 4 .

36 3

a a

S R



 

  

Chọn: A

Câu 35:

Phương pháp:

- Trải phẳng mặt nón cắt mép SA.

- Tính góc ở tâm chắn cung AB và suy ra độ dài AC min.

Cách giải:

Độ dài cung AB là



 

 

Có . Do đó

5 10.

ASC ASC



    

2 2 2 2

min

10 5 5 5AC SA SC    

Chọn: D

Câu 36:

Phương pháp:

+ Từ giả thiết suy ra tập hợp điểm M (z) là hình vuông

+ Biến đổi để đưa P bằng với khoảng cách từ điểm I (2; 2) đến M .

+ Đánh giá để tìm max; min của P.

Cách giải:

Gọi M (x; y) là điểm biểu diễn số phức

 

;z x yi x y   

Ta có:

4z z z z   

x yi x yi x yi x yi

x y

        

  

Suy ra tập hợp điểm M là hình vuông KBCD (hình vẽ)

có các đỉnh

       

2;0 ; 0;2 ; 2;0 ; 0; 2K B C D 

Xét

       

2 2

2 2 2 2 2 2P z i x y i x y          

Nhận thấy với

     

2 2

2;2 2 2I IM x y P     

Như vậy

max max min min

;P IM P IM 

Gọi là trung điểm

 

1;1E

BK IE IK ID  

Nên và

 

max

2 2 2 2 5P ID     

   

2 2

min

1 2 1 2 2P IE     

Vậy

 

2 5 2 34;6A M m    

Chọn: A

Câu 37:

Phương pháp:

- Tìm mặt phẳng (Q) chứa d và có phương Ox .

- Đường thẳng d ' chính là giao tuyến của mặt phẳng (P) với (Q) .

Cách giải:

Gọi (Q) là mặt phẳng chứa d và có một VTCP cùng phương với Ox.

Khi đó (Q) có một VTPT

 

, 0;3; 1

n u i

 

  

 

  

Lại có nên hay cùng phương với

   

'd P Q 

 

u n















 



   

P Q

n n

 

 

 

Ta có: nên

 

1;1;1 , 0; 3;1

P Q

n n  

 

   

 

, 4; 1; 3

P Q

n n

 

  

 

 

Khi đó thì

 

673 2692;673;2019

u u   

 

2692, 673 2019a b a b      

Chọn: B

Câu 38:

Phương pháp:

Ta sử dụng mặt phẳng (P) chứa đường thẳng d thì

. 0

P d

n u 

 

Góc giữa đường thẳng và mặt phẳng (P) là thì





sin

n u







 

Từ đó tìm ra

, .b c b c

Cách giải:

Theo đề bài ta có:

 

1; ;

n b c



Đường thẳng có VTCP lần lượt là

1 2

;d d

   

1 2

2; 2; 1 ; 1;0; 1u u    

 

Vì mặt phẳng (P) đi qua nên

 

1 1

. 0 2 2 0 1

P P

n u n u b c      

   

Vì mặt phẳng (P) tạo với góc nên ta có:

 

2 2

2 2 2

sin 45

1 . 2

1 1 2 2

n u

b c

c b c b c c



  

 

          

 

Từ (1) và (2) suy ra:

2 2 0 4 4 0 2 2 . 4

b b b b c b c              

Chọn: C

Câu 39:

Phương pháp:

- Đạo hàm hàm số đến cấp 2019 (tìm công thức tổng quát).

 

f x

- Xét hàm trên khoảng và tìm điều kiện để bất phương trình

 

2019

y f x

;

12 8

 

 

 

 

 

2019

f x m

nghiệm đúng với mọi

;

12 8

 

 



 

 

Cách giải:

       

 

2 3

4 5 6 7

cos2 ; ' 2sin 2 ; '' 2 cos 2 ; ''' 2 sin 2

2 cos2 , 2 sin 2 , 2 cos 2 , 2 sin 2

f x x f x x f x x f x x

     

Do đó:

 

4 1

4 2

4 3

2 cos2

2 sin 2

2 cos2

2 sin 2

f x x









 





 









 

2019 4.504 3

2019

2 sin 2f x f x x



  

Xét hàm trên ta có:

 

2019

2 sin 2y f x x 

;

12 8

 

 

 

 

+ Trên khoảng thì và hàm

;

12 4

 

 

 

 

 

2019 2018 2019

2 ; sin 2 ;1 2 sin 2 2 ;2

6 2 2

x x x

 

   

    

   

   

đồng biến trên khoảng này.

2019

2 sin 2y x

+ Trên khoảng thì và hàm

;

4 8

 

 

 

 

4037

2019 2019

3 2

2 ; sin 2 ;1 2 sin 2 2 ;2

2 4 2

x x x

 

 

    

 

 

nghịch biến trên khoảng này.

2019

2 sin 2y x

Bảng biến thiên:



2019

2 sin 2y x

2018

2019

4037

Quan sát bảng biến thiên ta thấy, bất phương trình nghiệm đúng với mọi

 

2019

f x m

;

12 8

 

 



 

 

nếu

2018

2m 

Chọn: B

Câu 40:

Phương pháp:

Sử dụng định nghĩa xác suất trong đó là số phần tử của biến cố A và là số

 

n A

P A





 

n A

 

n 

phần tử của không gian mẫu.

Cách giải:

Gọi số tự nhiên có bốn chữ số khác nhau là , là các số tự nhiên có 1 chữ số,

abcd

, , ,a b c d

0a 

+ Có 6 cách chọn a; 6 cách chọn b; 5 cách chọn c; 4 cách chọn d có 6.6.5.4 = 720 số tự nhiên có bốn



chữ số khác nhau hay

 

720n  

Gọi A là biến cố “Số được chọn là số lớn hơn 2019 và bé hơn số 9012”

Tính :

 

n A

TH1: Nếu tùy ý khác có 1.1.4.4 = 16 số

2; 0; 3;a b c d  

; ;a b c 

TH2: Nếu tùy ý khác nhau và khác có 1.5.5.4 = 100 số

2; 0; ;a b c d 

;a b

TH3: Nếu khác nhau và khác a thì có 3.6.5.4 = 360 số

 

3;4;8 ; ; ;a b c d

TH4: Nếu thì có 1.1.5.4 = 20 số

9; 0a b 

Suy ra số

 

16 100 360 20 496n A     

Xác suất cần tìm là

 

496 31

720 45

n A

P A

  



Chọn: C

Câu 41:

Phương pháp:

- Tính và tìm nghiệm của





4 'f x

 



 

 





4 ' 0f x

 

 

 

 

- Lập bảng biến thiên của hàm số trên nửa khoảng rồi suy ra tập giá trị của m.





4y f x 



2; 3







Cách giải:

Xets hàm trên nửa khoảng ta có:





4y f x 



2; 3































2 2 2

2 2

. ' 4

' 4 ' 4 '. ' 4

' 0 . ' 4 0 4 1 0

' 4 0 3 2; 3

4 1

x f x

y f x x f x

y x f x x x

f x x

 

 

     

 

 

















           





     





 





Bảng biến thiên:

2





' 4f x







4f x

 

1

Từ đồ thị hàm số đã cho ta thấy nên để phương trình có nghiệm trong nửa

 

1 2f 





4f x m 

khoảng thì



2; 3







1 3m  

Vậy





1;3m 

Chọn: D

Chú ý khi giải:

Ở bước xét dấu lập bảng biến thiên, các em có thể lấy một giá trị bất kì của x thuộc từng khoảng cần xét

dấu, thay vào và tính toán sẽ ra kết quả, từ đó suy ra dấu của ngay.

Cụ thể: Với ta chọn thì do quan sát đồ thị hàm số ta thấy hàm số đồng biến

 

0; 3x 

1x 

 

' 3 0f 

trên khoảng . Do đó trong khoảng thì

 

1;

 

0; 3





' 4 0f x 

Câu 42:

Phương pháp:

+ Xác định điểm I sao cho . Từ đó

2 0IA IB 

  

max max min min

;P IM P IM 

+ Từ đó tìm GTLN và GTNN của IM với mặt cầu (S) tâm K bán kính R.

M 

+ Lập luận để có min

;maxIM IK R IM IK R   

Cách giải:

Gọi điểm sao cho

 

; ;I x y z

2 0IA IB 

  

   

 

2 2 4; 3; 1 3; 1; 3

2 4 3

2 3 1 5 5;5; 1

2 1 3

IA IB x y z x y z

x x

y y y I

z z

         

  









       

 

 

 

  



 

Suy ra

3; 6IA IB 

Xét

   

2 2

2 2P MA MB MI IA MI IB     

   

 

2 2 2 2

2 4 . 2 2 .

2 2.

MI MI IA IA MI MI IB IB

MI IA IB MI IA IB MI

     

     

   

  

Suy ra với

max max min min

;P IM P IM 

 

M S

Mặt cầu (S) có tâm và bán kính . Nên .

 

1;2; 1K 

3R 

5IK 

Khi đó đường thẳng IK giao với mặt cầu tại hai điểm

1 2

;M M

min 1

max 2

5 3 2

5 3 8

IM IM IK R

     







     



Do đó

2 2

min 1

2 2

max 2

2 4

8 64

P n IM

P m IM



   





   





Suy ra

64 4 60m n   

Chọn: C

Câu 43:

Phương pháp:

- Tính diện tích phần giao của hai hình tròn.

Chia làm hai hình viên phân và tính diện tích của chúng bằng cách gắn hệ trục tọa độ và sử dụng công

thức tích phân

   

S f x g x dx 



- Tính diện tích phần còn lại của sân khấu và suy ra chi phí.

Cách giải:

Đặt

' 30OH x O H x   

Ta có: vuông tại H nên

AHO

2 2 2 2

400AH OA OH x   

vuông tại H nên

'AHO

 

2 2 2

' ' 225 30AH O A O H x    

 

215

400 225 30

215 145

, '

12 12

x x x

OH O H

      

  

Khi đó

2 2

5 455

AH OA OH  

Ta tính diện tích phần giao của hai đường tròn (bằng tổng diện tích hai hình viên phân chắn bởi cung AB

và dây AB ở mỗi đường tròn)

+ Xét hình viên phân tạo bởi dây và cung AB của hình tròn tâm O bán kính 20.

Chọn hệ trục tọa độ như hình vẽ trên.

Ở đó hình viên phân tạo bở cung và dây AB giới hạn bởi nửa đường tròn

và đường thẳng

400y x 

215

y 

Phương trình hoành độ giao điểm

215 5 455

400

12 12

x x    

Do đó diện tích

 

5 455

215

400 24,96

S x dx m



 

   

 

 



+) Xét hình viên phân tạo bởi dây và cung AB của hình tròn tâm bán kính 15.

Chọn hệ trục tọa độ như hình vẽ trên. Ở đó hình viên phân tạo bởi cung

và dây AB giới hạn bởi nửa đường tròn và đường thẳng

255y x 

145

y 

Phương trình hoành độ giao điểm

145 5 455

255

12 12

x x    

Do đó diện tích

 

5 455

145

255 35,3

S x dx m



 

   

 

 



Diện tích phần giao của hai hình tròn là:

 

1 2

24,96 35,3 60,26S S S m    

Diện tích phần còn lại của hình tròn là:

   

 

2 2

' .20 60,26 .15 60,26 1842,98S m

 

    

Vậy tổng chi phí là:

1842,98 100.000 60,26 300.000 202.376.000   

Chọn: B

Câu 44:

Phương pháp:

Từ giả thiết ta biến đổi để có

 

' 0f x 

Xét hàm , tính

 

g x

   

' ; ''g x g x

Hàm số đạt cực tiểu tại thì và hoặc

0x 

 

' 0 0g 

 

'' 0 0g 

 

'' 0 0g 

Cách giải:

Với ta có

0h 

   

       

 

       

0 0 0

lim lim lim

h h h

f x h f x h

f x h f x h h h

f x h f x f x f x h

h h

f x h f x f x h f x

h h

f x h f x f x h f x

h h

  

  

  

     

    

   

   

    

   

    

Mà

 

       

0 0

' lim lim

h h

f x h f x f x h f x

f x

h h

 

 

   

 

với

     

0 ' ' 0 ' 0f x f x f x     

x 

Suy ra:

 

2019 29 4 2 2

29 100 sin 1

g x x x m m x



     

   

 

2018 28 4 2

' 2019. 29 29 100 sin 2

g x x m x m m x



      

Và

    

 

2017 27 4 2

'' 2019.2018 29 28 2 29 100 cos2

g x x m m x m m x



      

Ta thấy

 

' 0 0; 27g m  

Để hàm số đạt cực tiểu tại thì ta xét hai trường hợp hoặc

0x 

 

'' 0 0g 

 

'' 0 0g 

Xét

 

4 2

'' 0 2 29 100g m m   

TH1: Với

 

4 2

'' 0 0 29 100 0

m m

g m m









  



      









 



+ Nếu không đổi dấu qua . (loại)

   

 

2019 27 26 1992

2 1 ' 2019 27m g x x x g x x x       

0x 

+ Nếu không đổi dấu qua . (loại)

   

 

2019 31 30 1988

2 1 ' 2019 31m g x x x g x x x        

0x 

+ Nếu đổi dấu qua và

   

 

2019 24 23 1995

5 1 ' 2019 24m g x x x g x x x       

0x 

1995

2019





Nhận thấy và nên hàm số đạt cực tiểu tại .

 

' 0; 0g x x  

 

1995

' 0; ;0

2019

g x x



 

  

 

 

0x 

+ Nếu đổi dấu qua và

   

 

2019 34 23 1985

5 1 ' 2019 34m g x x x g x x x        

0x 

1985

2019





Nhận thấy và nên hàm số đạt cực tiểu tại .

 

' 0; 0g x x  

 

1985

' 0; ;0

2019

g x x



 

  

 

 

0x 

+ TH2: Với và

 

2 5

'' 0 0 4 25

5 2

g m

 



    



   



 

' 0 0; 27g m  

Nên hàm số đạt cực tiểu tại .

0x 

Vậy các giá trị nguyên của thỏa mãn đề bài là

 

27m m 

 

5; 4; 3;3;4;5m S    

Tổng các bình phương các phần tử của S là

     

2 2 2

5 4 3 3 4 5 100        

Chọn: C

Câu 45:

Phương pháp:

Thử đáp án, khoảng nào làm cho thì hàm số đã cho nghịch biến.

' 0y 

Cách giải:

Ta có:

 

' 2 ' 1 1

y f x

    



Dễ thấy

1 0,

   





Đáp án A: Xét trong khoảng thì nhưng ta chưa kết luận được dấu của

 

;1

 

1 0;x  

dẫn đến chưa nhận xét được tính nghịch biến của hàm số trong khoảng này.

 

' 1f x

Đáp án B: Xét trong khoảng thì nhưng ta chưa kết luận được dấu của

 

; 2 

 

1 3;x  

dẫn đến chưa nhận xét được tính nghịch biến của hàm số trong khoảng này.

 

' 1f x

Đáp án C: Xét trong khoảng thì và nên

 

2;0

 

1 1;3x 

 

' 1 0f x 

   

' 2 ' 1 1 0, 2;0

y f x x

        



Do đó hàm số nghịch biến trong khoảng .

 

2 1 1y f x x x    

 

2;0

Đáp án D: Xét trong khoảng thì và nhưng ta chưa kết luận được

 

3; 2 

 

1 3;4x 

 

' 1 0f x 

dấu của trong khoảng này.

Vậy chỉ có khoảng là hàm số chắc chắn nghịch biến.

 

2;0

Chọn: C

Câu 46:

Phương pháp:

+ Đặt với

 

2 3 2019

1 ...

2! 3! 2019!

x x x

g x x e      

0x 

+ Đánh giá để tìm GTLN của trên

 

' 0; 0g x x  

 

g x





0;

+ Tìm GTLN của với

 

10h x x x  

0x 

+ Từ đó tìm GTLN của trên

 

f x



+ Bất phương trình có nghiệm khi . Kết hợp với điều kiện đề bài để

 

0m f x 

 

maxm f x



tìm m.

Cách giải:

+ Đặt với . Khi đó ta có:

 

2 3 2019

1 ...

2! 3! 2019!

x x x

g x x e      

0x 

 

2 2018

2 2017

2018

2019

' 1 ...

2! 2018!

'' 1 ...

2! 2017!

.......

x x

g x x e

x x

g x x e

g x e

     

  

 

Với mọi ta có (dấu “=” xảy ra khi )

0x 

 

2019

1 0

g x e  

0x 

nghịch biến trên

 

2018

g x x e   

 

0;

 

2018 2018 2018

0 0g x g g x   

Tương tự ta có với mọi

 

' 0g x 

0x 

Suy ra





   

max 0 0f x g



 

Mặt khác xét với

   

10 25 5h x x x x     

0x 

Hàm số đạt giá trị lớn nhất (TM)

25 5x  

Suy ra

 

max 25f x





Vậy

 

max 25f x 



+ Xét phương trình có nghiệm

   

0m f x f x m   

   

max 25 5;10;15;20;25f x m m m     



Vậy có 5 giá trị m thỏa mãn đề bài.

Chọn: A

Câu 47:

Phương pháp:

- Nhận xét tính chất các véc tơ dựa vào điều kiện bài cho.

,IA IB

 

- Thay tọa độ của I vào điều kiện vừa có được ở nhận xét, từ đó tính được tọa độ của I.

Cách giải:

Ta có: nằm giữa AB.

   

; ; ,I a b c P I

 

, 2 , 2 2

5 2 1

7 3

4 2 2 0 3 0 4

5 3 5

1 2 3

d B P d A P IB IA IB IA

a a

b b b b a b c

c c

      





   











             

  

  



    









 

Chọn: D

Câu 48:

Phương pháp:

Sử dụng bài toán: Hàng tháng, một người vay (gửi) ngân hàng số tiền là a đồng với lãi suất hàng tháng là

r thì sau n tháng người ấy có tổng số tiền nợ (gửi) ngân hàng là

   

1 1 1

A r r

 

   

 

Tính số tiền anh sinh viên nợ sau 2 năm

Tính số tiền anh sinh viên trả được sau 22 tháng

Tính số tiền nợ còn lại.

Cách giải:

Trong thời gian từ tháng 01/09/2014 đến hết tháng 08/2016 là 24 tháng thì mỗi tháng anh sinh viên vay

ngân hàng 3 triệu với lãi suất 0,8%/tháng nên số tiền anh nợ ngân hàng tất cả là:

đồng.

   

3000000

1 0,8% 1 1 0,8% 79661701,06

0,8%

 

    

 

Trong thời gian từ tháng 09/2016 đến cuối tháng 06/2018 là 22 tháng thì mỗi tháng anh sinh viên trả ngân

hàng 2 triệu với lãi suất 0,8%/ tháng nên số tiền anh trả được ngân hàng là:

đồng.

   

2000000

1 0,8% 1 1 0,8% 48284037

0,8%

 

    

 

Tính đến tháng 06/2018 thì số tiền nợ ngân hàng của anh là

 

1 0,8%A 

Số tiền anh còn nợ là đồng.

 

1 2

1 46641110A A r A   

Chọn: B

Câu 49:

Phương pháp:

- Đặt

z a bi 

- Đưa bài toán về hệ phương trình ẩn và tìm điều kiện để hệ có đúng 4 nghiệm.

,a b

Chú ý: Nhận xét nghiệm của phương trình để suy ra các trường hợp có thể có của nghiệm.

Cách giải:

Đặt ta có:

z a bi 

 

2 2 2 2 2

2 2 2z z z z z a b a b a b a b           

Lại có

2 2 2

z m

a b m





 



 



Do đó bài toán trở thành tìm để hệ có đúng 4 nghiệm phân biệt

0m 

 

2 2

2 2 2

2a b a b

a b m



  





 





 

;a b

Nhận xét: Nếu hệ trên nhận một cặp số làm nghiệm thì nó cũng nhận các cặp số

 

;a b

làm nghiệm.

             

; , ; , ; , ; , ; , ; , ;a b a b a b b a b a b a b a       

Do đó để hệ có đúng bốn nghiệm phân biệt thì các nghiệm chỉ có thể thỏa mãn: Một trong hai

 

;a b

số a , b bằng 0 và số còn lại khác 0 hoặc hai số a , b thỏa mãn

0a b 

Ta chia làm hai trường hợp:

+) TH1: Nếu hệ có nghiệm thỏa mãn a = 0 hoặc b = 0 thì m = 2 (dễ dàng kiểm tra bằng cách thay a = 0

hoặc b = 0 vào hệ.

Thử lại: m = 2 thì hệ trở thành:

 

2 2

4 2 2 2 4

4 2 4 0

a b a b

a b a b a b ab

a b

ab ab



  



         



 









     







Nếu thì

0a 

b b







  









Nếu thì

0b 

a a







  









Khi đó hệ có đúng 4 nghiệm nên thỏa mãn.

       

0;2 , 0; 2 , 2;0 , 2;0 

2m 

+) TH2: Nếu hệ có nghiệm thỏa mãn thì

0a b 

2 2

2 4

2 2 2 2

a a b

a a

m m

a m

    





 

   

  

   

 



 



 



Do đó và hệ có đúng 4 nghiệm

2 2m 

       

2;2 , 2; 2 , 2; 2 , 2;2   

Vậy tập hợp các giá trị của m là

 

2;2 2

Chọn: A

Câu 50:

Phương pháp:

Đổi biến số

x t

Sử dụng phương pháp tích phân từng phần.

Cách giải:

Đặt

x t dx dt dx tdt

    

Đổi cận

0 0;x t x t

 

     

Ta có

2 sinI t tdt







Đặt

cos

sin

tdt du

t u

v t

tdt dv











 

 





Suy ra

2 2

cos .2 4 cos 2I t t t tdt J



    



Đặt

1 1

4 4

cos sin

t u dt du

tdt dv t v

 

 



 

 

 

Suy ra

0 0

4 sin 4sin 4cos 4 4 8J t t tdt t



 

       



Do đó

 

2 8 1;10







       



 



Chọn: D

Bấm Tải xuống để xem toàn bộ.

| 1/32

| | Tải xuống

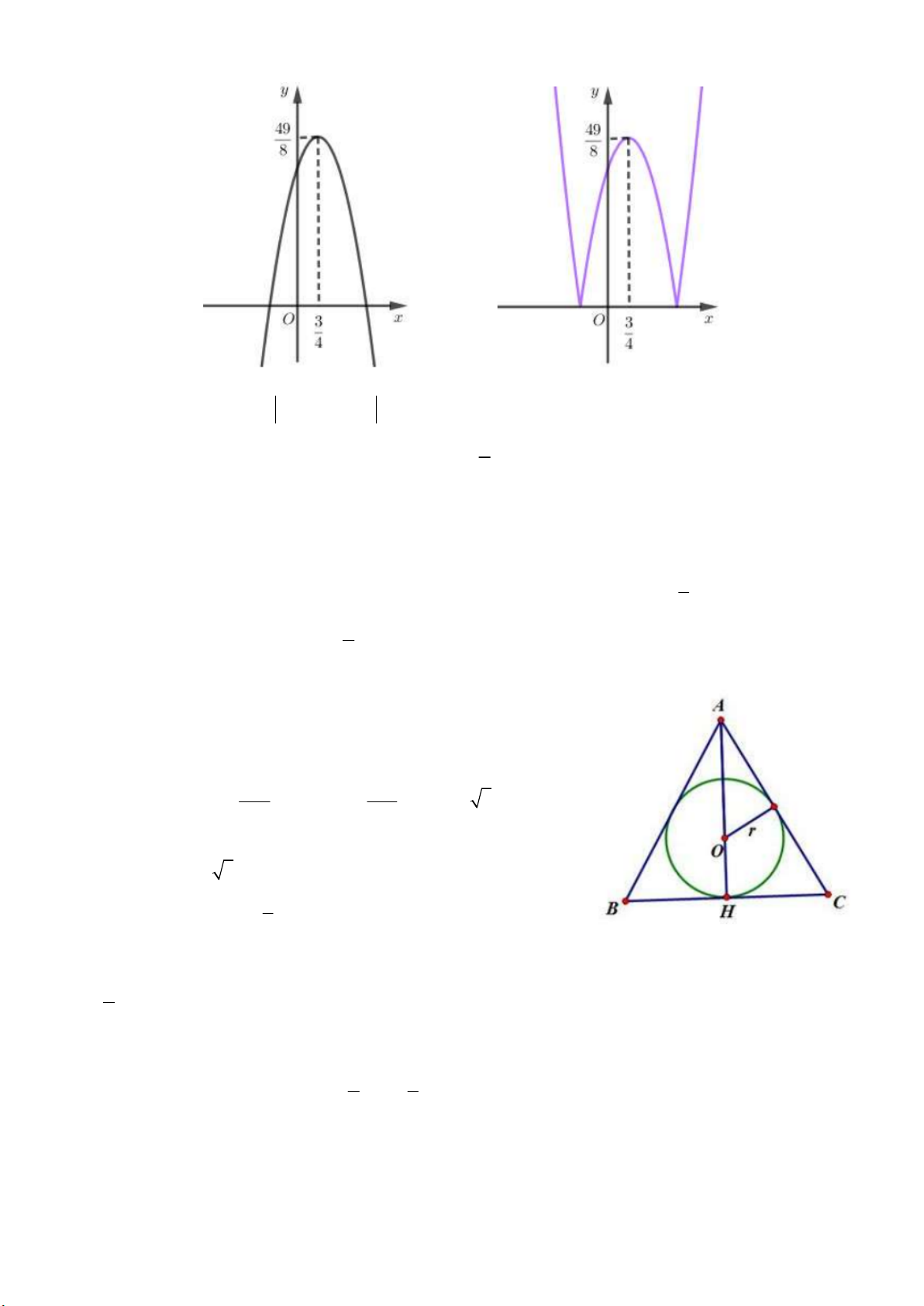
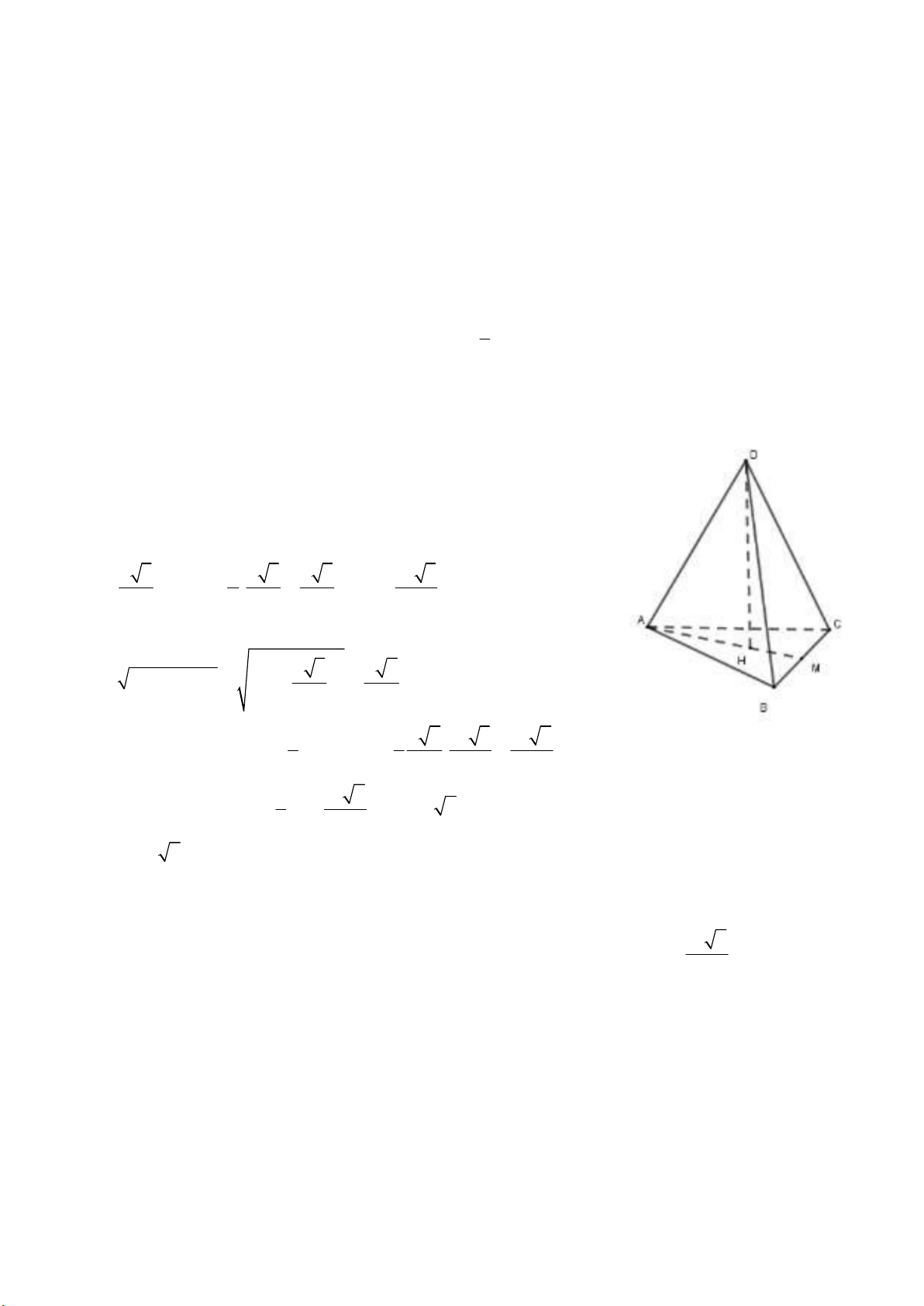
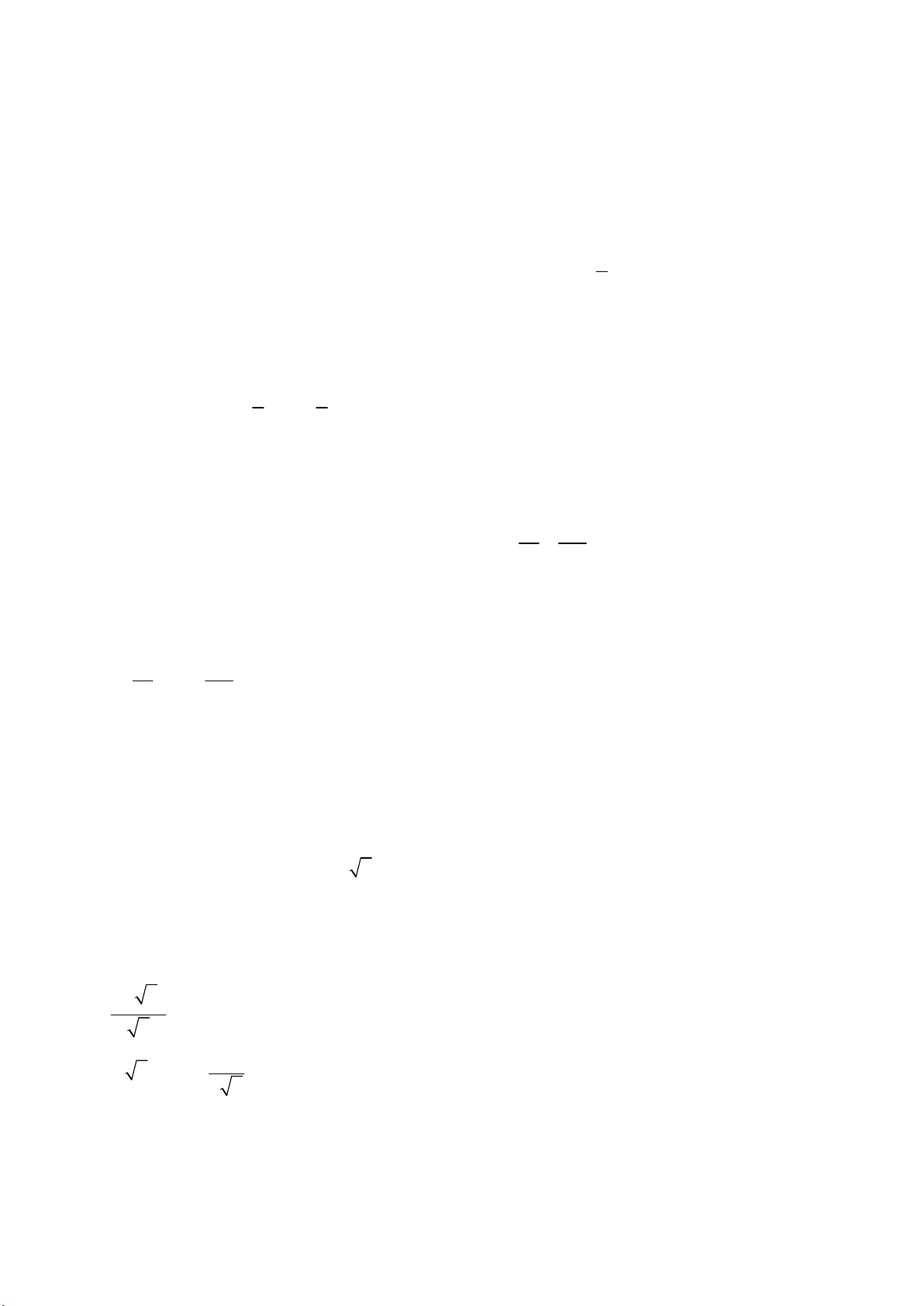
Preview text:

HƯỚNG DẪN GIẢI CHI TIẾT 1.A 2.D 3.C 4.D 5.C 6.B 7.A 8.C 9.A 10.D 11.B 12.C 13.B 14.A 15.D 16.D 17.D 18.C 19.A 20.C 21.D 22.B 23.D 24.D 25.B 26.C 27.B 28.B 29.B 30.A 31.A 32.C 33.D 34.A 35.D 36.A 37.B 38.C 39.B 40.C 41.D 42.C 43.B 44.C 45.C 46.A 47.D 48.B 49.A 50.D Câu 1: Phương pháp:
- Tính công bội q, từ đó suy ra u 6 - Sử dụng công thức n 1 u u q   n 1 Cách giải: Ta có: 2 2
u  u .q  18  2.q  q  3  3 1
Vậy với q  3 thì 5 5
u  u .q  2.3  486 6 1 Với q  3
 thì u  u .q  2. 3  5 5  4  86 6 1 Chọn: A Chú ý khi giải:
Nhiều HS sẽ chọn nhầm đáp án D vì đọc không kĩ đề thành cấp số “cộng”.
Nhiều em khác lại chọn nhầm B vì quên mất trường hợp q  3  Câu 2: Phương pháp: y '  0 ax  b  Hàm số y 
cx  d  0 nghịch biến trên K   d cx  d   K  c Cách giải:
TXĐ: D   \  m mm   2 1  2m  2 m  m  2 Ta có: y '   x  m2 x  m2
Để hàm số nghịch biến trên khoảng 1; thì 2  m  m  2 2 y '             x  m 0 2 m m 2 0 1 m 2      1  m  2       m m m 1  ;   1 1 Vậy m 1;2 Chọn: D Câu 3: 8 Phương pháp: b
Xét phương trình hoành độ giao điểm, tìm nghiệm và tính diện tích theo công thức S  f
 x gx dx a Cách giải:
Phương trình hoành độ giao điểm của hai đồ thị hàm số là: x  0 2 2 2
x  2x 1  2x  4x 1  3x  6x  0   x  2 Dễ thấy 2
3x  6x  0 trong khoảng 0;2 nên diện tích hình phẳng cần tính là: 2 2 2 2 2
S  x  2x 1 2x  4x 1 dx  6x  3x dx   0 0 2
 6x 3x dx  3x  x  2 2 2 3  4 0 0 Chọn: C Câu 4: Phương pháp:  u 
u 'v  v 'u
Sử dụng công thức tính đạo hàm hàm hợp '  và  x ' x a  a .ln a   2  v  v Cách giải: 1 x  2x
  1 x.2 .xln 2 1   x   1 ln 2 Ta có: y '  '    x  2  2  2 x 2x Chọn: D Câu 5: Phương pháp:
- Cộng hai số phức theo công thức a  bi  a' b'i  a  a'  b  b'i
- Tính mô đun số phức theo công thức 2 2
z  a  b Cách giải:
Ta có: z  z  1 i  2  3i  1 2  1 3 i  3  2i 1 2        
Vậy z  z  3  2   13 1 2  2 2 Chọn: C Câu 6: Phương pháp:
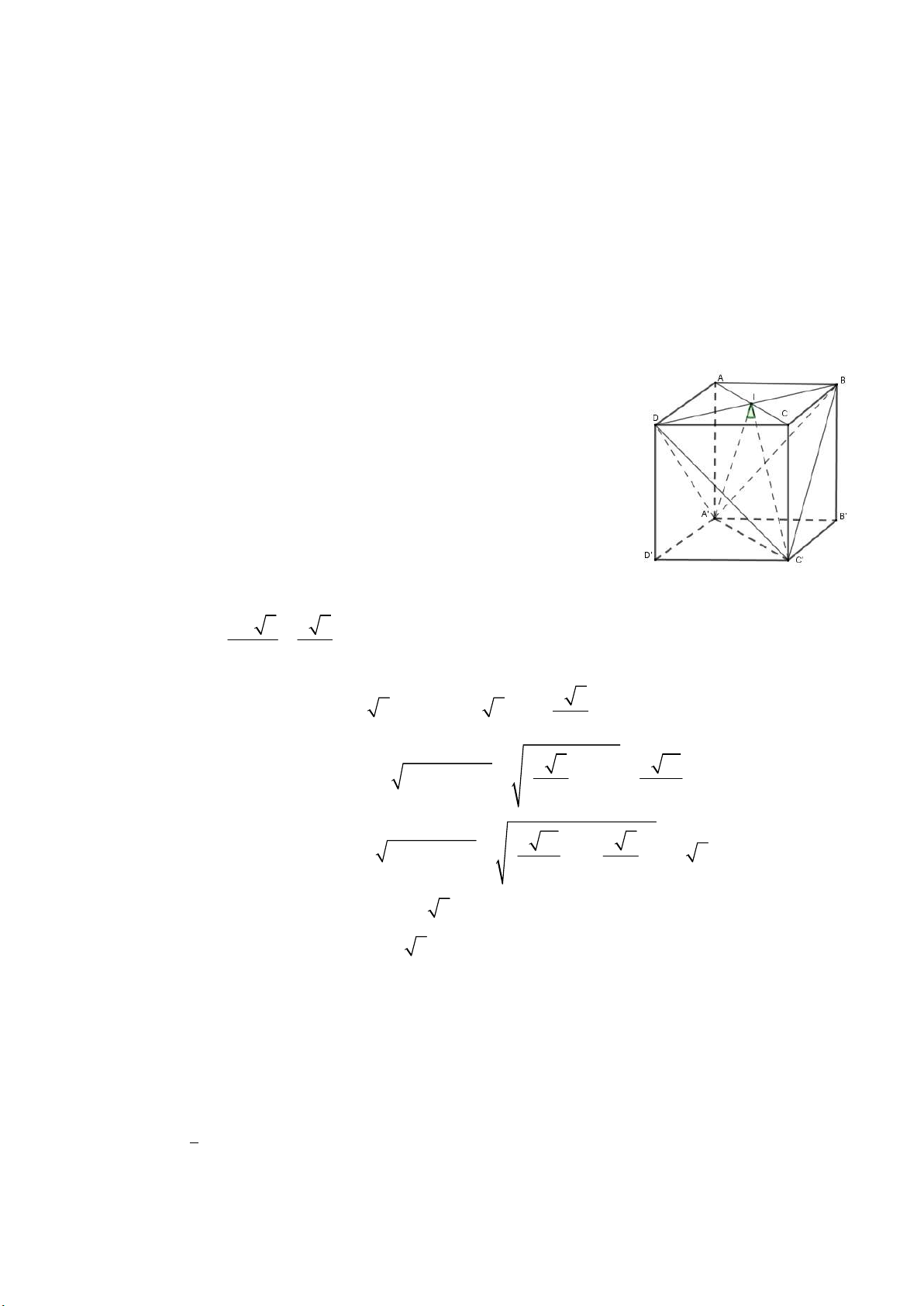
Thể tích khối hộp đứng có chiều cao h và diện tích đáy S là V  . h S Cách giải:
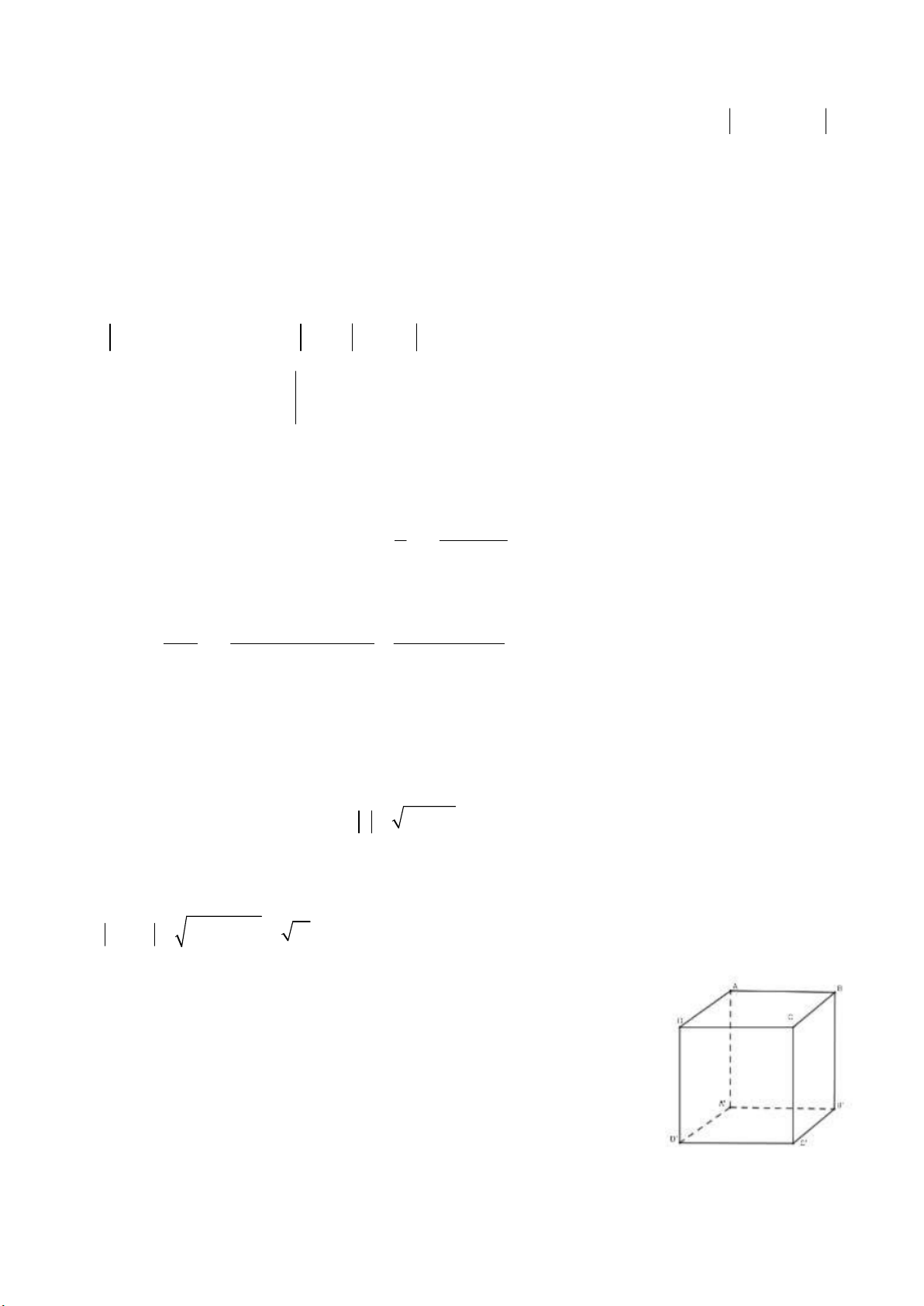
Giả sử ABB ' A' là hình vuông cạnh a thì chiều cao hình hộp AA'  a và
diện tích đáy hình hộp là 2 S  3a ABCD 9 Thể tích hình hộp là 2 3
V  AA'.S  .
a 3a  3a ABCD Chọn: B Câu 7: Phương pháp:
Biến đổi phương trình về dạng f  x  g m và sử dụng tương giao đồ thị tìm số nghiệm của phương trình. Cách giải: m
Ta có: 2 f  x  m  0  f  x   * 2 m
Số nghiệm của phương trình (*) là số giao điểm của đồ thị hàm số y  f  x và đường thẳng y   2 m
Phương trình đã cho có ba nghiệm phân biệt  * có ba nghiệm phân biệt   1  m  2  2 Chọn: A Câu 8: Phương pháp:
Quan sát bảng biến thiên và lưu ý rằng hàm số y  f  x có f ' x  0 trên khoảng  ; a b thì hàm số đồng biến trên  ; a b
Đường thẳng y  y là tiệm cận ngang của đồ thị hàm số y  f  x nếu một trong hai điều kiện sau 0
được thỏa mãn lim y  y hoặc lim y  y 0 0 x x Cách giải:
Từ BBT ta có hàm số đồng biến trên  ;  
1 và 2; nên A đúng
Hàm số có hai điểm cực trị x  1; x  2 nên B đúng
Đồ thị hàm số có 1 đường tiệm cận ngang y  1  (vì lim y  1  ) nên D đúng x
Hàm số có giá trị nhỏ nhất bằng 1
 là sai vì không tồn tại giá trị của x để y  1  Chọn: C Câu 9: Phương pháp:
- Tìm khoảng nghịch biến của hàm số đã cho dựa vào đồ thị
- Nhận xét các đáp án (khoảng cần tìm là con của khoảng nghịch biến) Cách giải:
Dễ thấy hàm số nghịch biến trên các khoảng  ;    1 và 0;  1  1 2   1 2  Mà  ;   0; 
1 nên hàm số cũng nghịch biến trên khoảng   ;  2 2      2 2   Chọn: A Câu 10: Phương pháp: 10
Giải phương trình tìm z , z sau đó tính toán. 1 2
Lưu ý: Với z  a  bi,a,b  thì 2 2
z  a  b Cách giải: z 1  3i z  1   3i
Ta có z  2z 10  0   z  2 2 2 1  9   9i    z 1 3i     z  1   3i Khi đó 2 2 z  z  1   3  1   3   20 1 2  2  2  2 2 Chọn: D Câu 11: Phương pháp: x  x y  y z  z  - Đường thẳng 0 0 0  
có một VTCP là u  ; a ; b c a b c   - Nếu u  ; a ;
b c là một VTCP của d thì ku  k ; a k ;
b kc cũng là một VTCP của d. Cách giải:   
Dễ thấy d có một VTCP là u 2;1;2
u  2u 4;2;4 d  d  nên nó cũng nhận làm VTCP.
Do đó a  4;b  4  a  b  8 Chọn: B Câu 12: Phương pháp:
Sử dụng các công thức tổ hợp, chỉnh hợp. Cách giải: n k !
Với k và n là hai số nguyên dương tùy ý thỏa mãn k  n 1, ta có k n k C C   ; A  ; n n n n  k! k k 1  k 1 C  C  C  n n n 1  Nên A, B, D đúng. n n 1 1 k k ! ! 1
Xét C: A  C   1
 0 (vô lý vì k  1  1 1   0 ) n n
n  k! k !n  k! k! k! k! Chọn: C Câu 13: Phương pháp: - Vẽ đồ thị hàm số 2 y  2
 x  3x  5 , từ đó suy ra đồ thị hàm số 2 y  2
 x  3x  5 và kết luận. Cách giải: Hàm số 2 y  2  x  3x  3
5 có đồ thị là parabol có hoành độ đỉnh x  49 , tung độ y  . 4 8 Đồ thị: 11
Từ đó có đồ thị hàm số 2 y  2
 x  3x  5 như trên. 3
Dựa vào đồ thị hàm số thấy hàm số đạt cực đại tại x  4 Chọn: B Câu 14: Phương pháp: 1
Sử dụng công thức tính thể tích khối nón có bán kính đáy R và chiều cao h là 2 V   R h 3 4
Thể tích khối cầu bán kính R và 3 V   R 3 Cách giải:
Gọi H là trung điểm BC và O là trọng tâm tam giác đều ABC.
Khi đó OH  r; AH  3OH  3r.
Xét tam giác AHC vuông tại H có AH 3r 0 0 C   60  tan C    tan 60   HC  3r HC HC
Khi quay tam giác ABC quanh cạnh AH ta được một hình nón
có bán kính HC  3r và chiều cao AH  3r . Suy ra thể tích 1 khối nón thu được là 2 3
V   HC .AH  3 r n 3 Khi quay hình tròn  ;
O r  quanh AH ta được khối cầu có diện tích là 4 3 V   r c 3 Vậy khi  ;
O r  , cắt bỏ phần hình tròn và cho hình phẳng thu được quanh quanh AO thì thể tích khối tròn 4 5 xoay thu được là 3 3 3
V  V V  3 r   r   r n c 3 3 Chọn: A Câu 15: 12 Phương pháp:
Quan sát đồ thị, nhận xét dáng đồ thị, điểm đi qua, số cực trị và đối chiếu với từng đáp án. Cách giải:
Dễ thấy đồ thị có dáng đồ thị của hàm số bậc ba có hệ số a  0 nên loại C.
Đồ thị hàm số đi qua điểm 0;  1 nên loại A.
Hàm số đạt cực trị tại các điểm x  0, x  2 nên phương trình y '  0 có hai nghiệm x  0, x  2 1 2 x  0 Xét đáp án B có 2
y '  0  3x  6x  0  nên loại B.  x  2  x  0 Đáp án D có 2
y '  0  3x  6x  0  nên D thỏa mãn.  x  2 Chọn: D Câu 16: Phương pháp: b Sử dụng công thức log  log b  log ;
c log b  .log b với 0  a  1;b,c  0 a a a a a c Cách giải: 2  a  1 Ta có: 2 ln 
  ln a  ln b  2ln a  ln b  b  2 Chọn: D Câu 17: Phương pháp:
Sử dụng công thức nguyên hàm các hàm số cơ bản và tính chất nguyên hàm. Cách giải:   dx Ta có: f  x 1 dx   sin x dx 
 sin xdx  ln x  cos x  C      x  x Chọn: D Câu 18: Phương pháp:
+ Mặt phẳng (P) có 1 VTPT là VTPT của mặt phẳng (Q).
+ d Q;P  d M ;P với M Q + Khoảng cách từ
M  x ; y ; z
P:ax by  cz  d  0 0 0 0  đến mặt phẳng là 
ax  by  cz  d d M ;P 0 0 0  2 2 2
a  b  c Cách giải:
Vì P / / Q nên phương trình mặt phẳng (P) có dạng x  2y  2z  d  0d  3   1   2.1 2.1 d 3  d Lấy M  1  ;1; 
1 Q khi đó d Q;P  d M ;P   2 2 2 1  2  2 3 13 3  d 3  d  3 d  0 Theo đề bài ta có  1   3  3 d 3     d  6 
Với d  0  P : x  2y  2z  0 đi qua O0;0;0 nên không thỏa mãn đề bài Với d  6
  P : x  2y  2z  6  0 (thỏa mãn)
Vậy phương trình P : x  2y  2z  6  0 Chọn: C Câu 19: Phương pháp: u   x
Sử dụng phương pháp từng phần, đặt 
và sử dụng công thức udv  uv  vdu   2 x dv  e dx Cách giải: du  dx u   x  Đặt 2 x    2 x e dv  e dx v   2 2 x 2 x 2 x 2 x xe e xe e x 1 x  1  Khi đó 2 2 xe dx   dx    C  e x   C     2 2 2 4 2  2  Chọn: A Câu 20: Phương pháp: x
Đặt t   2  
1 ,t  0 từ đó đưa về phương trình ẩn t.
Giải phương trình ẩn t ta tìm được t, thay lại cách đặt để tìm x. Lưu ý: x
a  b  x  log b  a  b  a 0 1; 0 Cách giải: x
Đặt t   2   1 ,t  0 Ta có      1 2 1 2 1  1 2 1  2 1 1 t  2 1 Ta có phương trình: 2
 t  2 2  0  t  2 2t 1  0   TM  t t  2 1 x
Với t  2 1   2  
1  2 1  x  1 x
Với t  2 1   2  
1  2 1  x  1 
Vậy tích các nghiệm của phương trình là 1  .1  1  Chọn: C Câu 21: Phương pháp: 14
- Tính y ' , tìm các nghiệm thuộc đoạn 0;2.
- Tính giá trị hàm số tại các điểm đó và hai đầu mút x  0, x  2 .
- So sánh các giá trị đó và kết luận. Cách giải:  x  00;2   6 Ta có: 3 y '  4
 x  6x  0  x 2
4x  6  0  x  0;2  2   6 x   0;2  2  
Tính y    y  6 13 0 1, 2  3  , y    2  4   13
Vậy giá trị lớn nhất của hàm số đạt được trong 0;2 là 4 Chọn: D Câu 22: Phương pháp:
Đường thẳng y  y là tiệm cận ngang của đồ thị hàm số y  f  x nếu một trong hai điều kiện sau được 0
thỏa mãn lim y  y hoặc lim y  y 0 0 x x
Đường thẳng x  x là tiệm cận đứng của đồ thị hàm số y  f  x nếu một trong các điều kiện sau được 0
thỏa mãn lim y   ;  lim y   ;  lim y   ;  lim y   x         0 x x 0 x x 0 x x 0 x Cách giải:
ĐK: x  1;  3 1 1  2 x 1 + lim  lim  lim x x y
 0 nên đường thẳng y  0 là một tiệm cận ngang của đồ thị 2 x
x x  2x  3 x 2 3 1  2 x x hàm số. x 1 x 1 1 + lim y  lim  lim  lim
  nên đường thẳng x  3  là một tiệm cận   2 x 3 x 3 x 3 x  2x  3   x  
1  x  3 x 3     x  3
đứng của đồ thị hàm số. x 1 x 1 1 1 + lim y  lim  lim  lim
   nên đường thẳng x  1 không là tiệm   2 x 1 x 1 x 1 x  2x  3   x  
1  x  3 x 1     x  3 4
cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có hai tiệm cận x  3  và y  0 Chọn: B Câu 23: Phương pháp: 15 
Trục Oz đi qua O0;0;0 và có VTCP k  0;0;  1 Cách giải:  x  0 
Trục Oz đi qua O0;0;0 và có VTCP k  0;0; 
1 nên có phương trình y  0 z  t  Chọn: D Câu 24: Phương pháp: 1
Thể tích khói chóp có chiều cao h và diện tích S là V  . h S 3
Hình tứ diện đều có tất cả các cạnh bằng nhau nên từ thể tích ta tính được cạnh của hình tứ diện đều. Cách giải:
Gọi tứ diện đều có AB = AC = BC = CD = x (x > 0)
Gọi M là trung điểm BC và H là trọng tâm tam giác ABC
 DH   ABC; AM  BC
Xét tam giác ABC đều cạnh x có : 2 x 3 2 x 3 x 3 x 3 AM   AH  .  ; S  2 3 2 3 ABC 4
Xét tam giác DAH vuông tại H có 2  x 3  x 6 2 2 2
DH  AD  AH  x      3  3   2 3 1 1 x 6 x 3 x 2
Thể tích khối tứ diện V  DH.S  .  ABCD 3 ABCD 3 3 4 12 3 1 x 2 Theo giả thiết ta có 3 V  a   x  a 2 ABCD 3 12
Vậy AB  a 2 Chọn: D Chú ý: 3 x 2
Các em có thể sử dụng luôn công thức tính thể tích khối tứ diện đều cạnh x là V  , từ đó tính được 12 cạnh AB. Câu 26: Phương pháp:
Phương trình log f x  m  f x  a a     m Cách giải: TXĐ: D   16 x   log 2 2
x  2x  2 2 2
 1  x  2x  2  10  x  2x  8  0   x  4
Vậy tập nghiệm của phương trình là S   2  ;  4 Chọn: B Câu 26: Phương pháp: 4
Hình cầu có bán kính R thì có diện tích là S = 4 R2 và thể tích là 3 V   R 3 Cách giải:
Gọi bán kính hình cầu là R (R > 0)
Khi đó diện tích mặt cầu là S = 4 R2 = 36 a 2  R = 3a 4 4
Thể tích khối cầu là V   R   3a3 3 3  36 a 3 3 Chọn: C Câu 27: Phương pháp: 90 180
Biến đổi P về làm xuất hiện các log 5,log 6,log 22, chú ý  3 3 3 11 22
Sử dụng các công thức logarit của tích, thương và lũy thừa. Cách giải: Ta có: 90 180 P  log  log  log 180  log 22 3 3 3 3 11 22
 log 5.6  log 22  log 5  log 6  log 22 3  2  2 3 3 3 3
 log 5  2log 6  log 22  a  2b  c 3 3 3 Chọn: B Câu 28: Phương pháp:
Sử dụng phương pháp đổi biến số t  x b b
Và tích phân không phụ thuộc vào biến f
 xdx  f  tdt a a Cách giải: 4 f  x  Xét dx  x 1 1
Đặt t  x  dt 
dx  dx  2tdt 2 x
Đổi cận x  1 t  1; x  4  t  2 17 4 f  x  2 f t 2 Ta có dx  .2tdt  2 f  
 tdt  2.2  4 x t 1 1 1 Chọn: B Câu 29: Phương pháp:
Sử dụng cách giải bất phương trình log f x  m  f x  a khi a  a     m 1 Cách giải: x  3 
Điều kiện: log x 1  3  x 1  2  x 1  8  x  9  2  2  2 3 2 2  x  3 x  3 
Kết hợp với điều kiện ta được x 3
Vậy tập nghiệm của bất phương trình là  ;    3 3; Chọn: B Câu 30: Phương pháp: 
Cho A x ; y ; z , B x ; y ; z  AB  x  x ; y  y ; z  z 1 1 1   2 2 2  2 1 2 1 2 1   x  x'    Cho u  ;
x y; z;v x'; y '; z ' . Khi đó u  v  y  y ' z  z'  Cách giải:  Gọi B ;
x y; z  AB   x 1; y  2; z   1 x 1  1 x  2   
Từ giả thiết ta có AB  1;3; 
1  y  2  3  y  5  B2;5;0 z 1 1    z  0   Chọn: A Câu 31: Phương pháp: AB
Mặt cầu đường kính AB có tâm là trung điểm AB và bán kính R  2 Cách giải:
Gọi I là trung điểm của AB thì I 3;3;  1
Ta có: AB    2    2    2 5 1 4 2 1 3  6 AB
Mặt cầu đường kính AB có tâm là trung điểm AB và bán kính R  = 3 nên có phương trình: 2
x  2  y  2 z  2 2 3 3
1  3 hay  x  2   y  2   z  2 3 3 1  9 18 Chọn: A Câu 32: Phương pháp:
+ Sử dụng cách xác định góc giữa hai mặt phẳng (P); (Q) 
 P Q  d 
a  d;a  P  góc tạo bởi (P) và (Q) là góc tạo bởi hai đường thẳng a và b.
b  Q;b   Q
+ Tính toán dựa vào định lý Pytago. Cách giải:
Gọi I là giao điểm hai đường chéo của hình vuông ABCD . Khi đó I
là trung điểm của BD.
Xét tam giác A' BD cân tại A'  A' I  BD và tam giác C BD cân tại
C '  C ' I  BD 
 A'BD C 'BD  BD  Ta có
A'I  BD góc 
tạo bởi  A'BD và C 'BD là C  'I  BD  góc A' IC ' AB 6 x 6
Gọi AB  x  AA'   2 2 x 2
Xét hình vuông ABCD có AC  BD  x 2  A'C '  x 2; DI  2 2  x 6  x 10
Xét tam giác AA' D vuông tại A có 2 2 2
A' D  A A'  AD     x   2  2   2 2
 x 10   x 2 
Xét tam giác A' DI vuông tại I có 2 2
A' I  A' D  DI        x 2  2   2      Vì A  'DB  C
 'DBc  c  c  C 'I  A'I  x 2
Xét tam giác A' IC ' có A' I  C ' I  A'C '  x 2 nên A
 'IC ' là tam giác đều. Suy ra 0 A  'IC '  60
Vậy góc tạo bởi  A'BD và C 'BD là góc A'IC ' bằng 0 60 Chọn: C Câu 33: Phương pháp:
Thay z  a  bi vào đẳng thức bài cho, tìm a, b và kết luận. Cách giải:
Có z  a  bi  z  a  bi thay vào đẳng thức bài cho ta được: 19
1ia bi 2a bi  3 2i
 a  b  a  bi  2a  2bi  3 2i
 3a  b  a  bi  3 2i  1  3    3 a a b  2 1 3    
 a  b    1  a  b  2 3 2 2 b     2 Chọn: D Câu 34: Phương pháp:
+ Xác định chiều cao của hình chóp
+ Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp:
Bước 1: Xác định tâm đường tròn ngoại tiếp hình vuông ABCD
Bước 2: Xác định trục đường tròn ngoại tiếp đa giác đáy. Kẻ đường trung trực một cạnh bên giao với trục
đường tròn ở đâu đó chính là tâm mặt cầu ngoại tiếp hình chóp.
+ Tính bán kính mặt cầu ngoại tiếp hình chóp dựa vào định lý Pytago.
+ Mặt cầu có bán kính R thì có diện tích là S  4 R2 . Cách giải:
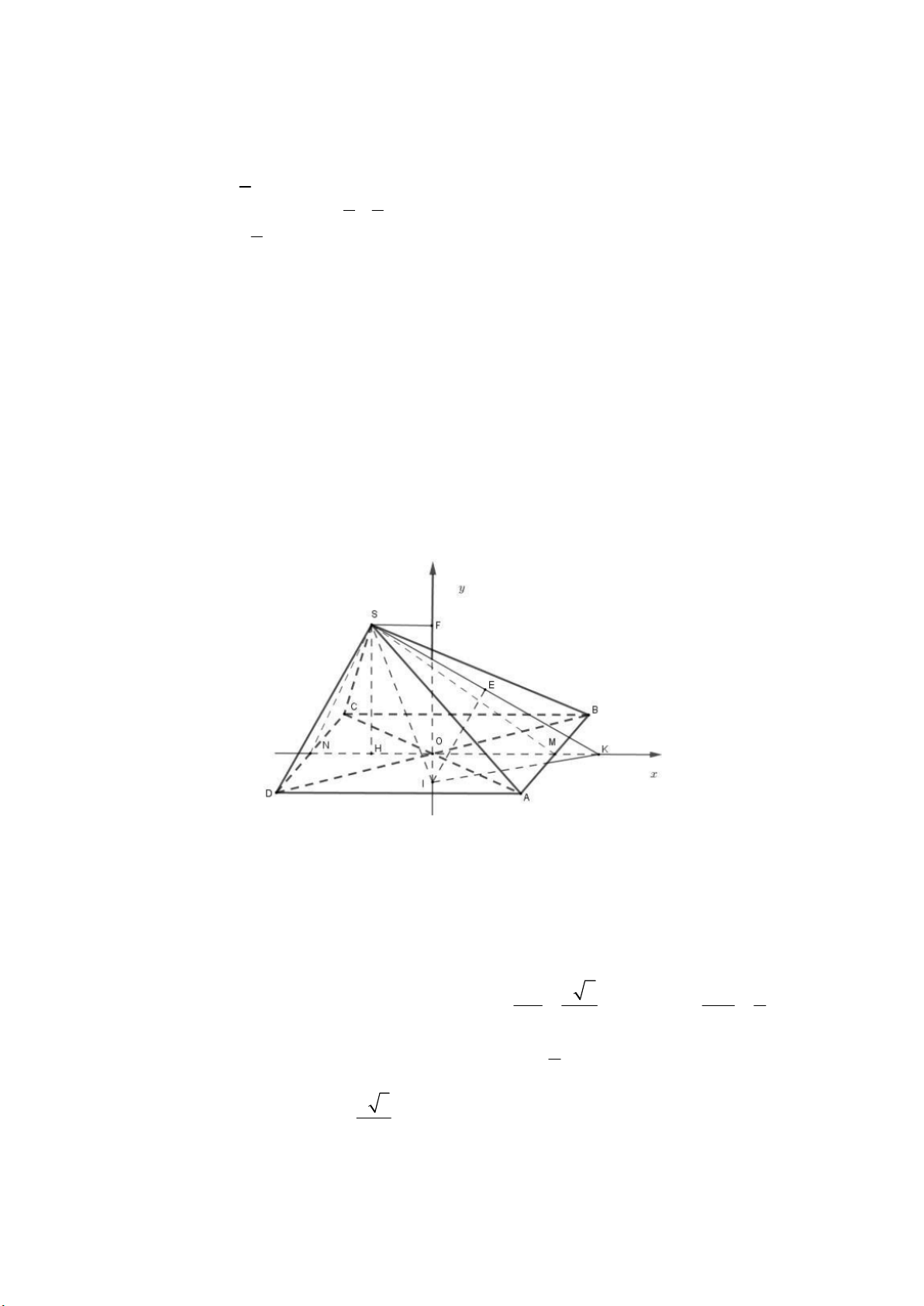
Gọi O là tâm hình vuông ABCD, gọi M , N lần lượt là trung điểm của AB; CD .
Kẻ SH  MN tại H .
Ta có SN  DC ; MN  DC  DC  ( SMN )  DC  SH
Mà SH  MN  SH  (ABCD). AC a 2 MN a
Vì ABCD là hình vuông cạnh a nên OB  OC  OA  OD   ;OM  ON   2 2 2 2 a
Vì tam giác SDC vuông cân tại S có cạnh huyền CD  a  SN  2 a 3
Vì tam giác ABS đều cạnh a  SM = 2 20 2 2  2  a  a 3 4a    Xét tam giác SNM có 2 2 2 2 2
MN  SN  SM  a         a  nên S
 MN vuông tại S.  2   2   4      a a 3 . a 3 2 SN a a Suy ra 2 2
SH.MN  SN.SM  SH   và 2
SN  NH.NM  HN    HO  a 4 MN 4 4
Nhận thấy O là tâm đường tròn ngoại tiếp hình vuông ABCD . Kẻ tia Oy / /SH , khi đó tâm mặt cầu ngoại
tiếp hình chóp S . ABCD nằm trên đường thẳng Oy. a 2
Trên tia OM ta lấy K sao cho OK = OA =
, khi đó K  (O; OA) 2
Trong mặt phẳng (SMN ), lấy E là trung điểm SK , kẻ EI là đường trung trực của SK (I  Oy) khi đó
IK = IS = IA = IB = IC = ID nên I là tâm mặt cầu ngoại tiếp hình chóp S . ABCD và bán kính là R = IK a a
Kẻ SF  Oy  3
SF = OH = ;OF  SH  4 4
Gắn hệ trục Oxy với OM  Ox; Oy / /SH a 3
Đặt I 0; y  IF   y 0  0 4 2 2  a 3   a  Xét tam giác vuông I  SF có 2 2 2
IS  IF  SF    y   0     4    4  2  a 2 
Xét tam giác vuông OIK có 2 2 2 2
IK  OI  OK  y    0  2    2 2 2 2  a 3   a   a 2  3 a a 3 Vì 2 2 2
IK  IS  IK  IS    y    y          y   y   0 0 0 0 4 4  2      2 4 6   2 2 2  a 2  a a a 21 Suy ra bán kính mặt cầu 2
R  IK  y       0  2  12 2 6   2 2 a .21 7 a
Diện tích mặt cầu ngoại tiếp hình chóp là 2
S  4 R  4.  36 3 Chọn: A Câu 35: Phương pháp:
- Trải phẳng mặt nón cắt mép SA.
- Tính góc ở tâm chắn cung AB và suy ra độ dài AC min. Cách giải: 2 R Độ dài cung AB là
  R  5 2 21 
Có 5  10. A  SC  A  SC  . Do đó 2 2 2 2 AC
 SA  SC  10  5  5 5 2 min Chọn: D Câu 36: Phương pháp:
+ Từ giả thiết suy ra tập hợp điểm M (z) là hình vuông
+ Biến đổi để đưa P bằng với khoảng cách từ điểm I (2; 2) đến M .
+ Đánh giá để tìm max; min của P. Cách giải:
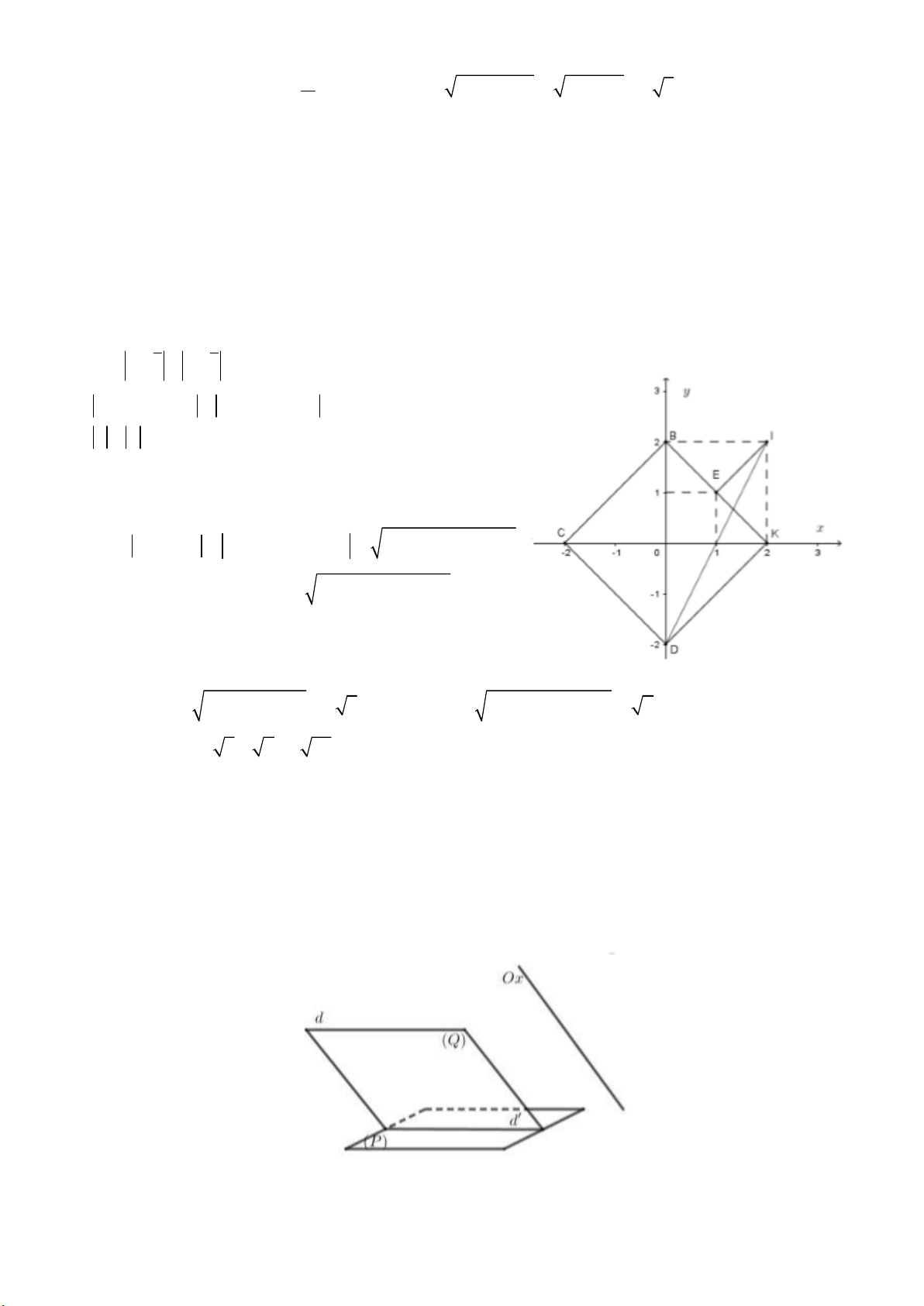
Gọi M (x; y) là điểm biểu diễn số phức z  x  yi  ; x y  
Ta có: z  z  z  z  4
 x  yi  x  yi  x  yi  x  yi  4
 x  y  2
Suy ra tập hợp điểm M là hình vuông KBCD (hình vẽ)
có các đỉnh K 2;0; B0;2;C  2  ;0; D0; 2  
Xét P  z   i   x     y  i   x  2   y  2 2 2 2 2 2 2
Nhận thấy với I 
  IM  x  2  y  2 2; 2 2 2  P Như vậy P
 IM ; P  IM max max min min Gọi E 1; 
1 là trung điểm BK  IE  IK  ID Nên P  ID  2   2  2  2 5 P  IE  1 2  1 2  2 min  2  2 max  2 2 và
Vậy A  M  m  2 5  2  34;6 Chọn: A Câu 37: Phương pháp:
- Tìm mặt phẳng (Q) chứa d và có phương Ox .
- Đường thẳng d ' chính là giao tuyến của mặt phẳng (P) với (Q) . Cách giải: 22
Gọi (Q) là mặt phẳng chứa d và có một VTCP cùng phương với Ox.   
Khi đó (Q) có một VTPT n
 u ,i   Q d 0;3; 1       u   n d      P
Lại có d '  P Q nên   hay u cùng phương với n ,n  d
 P Q u    n d  Q     Ta có: n  n  
n ,n   4; 1  ; 3  P Q  P
1;1; 1, Q 0; 3; 1 nên             Khi đó u  6  73u   2  692;673;2019 a  2
 692,b  673  a  b  2  019 d  thì Chọn: B Câu 38: Phương pháp:  
Ta sử dụng mặt phẳng (P) chứa đường thẳng d thì n .u  0 P d   n .u
Góc giữa đường thẳng  và mặt phẳng (P) là  thì sin P      n . u P  Từ đó tìm ra , b c  . b c Cách giải: 
Theo đề bài ta có: n  1; ; b c P   
Đường thẳng d ; d có VTCP lần lượt là u  2; 2  ; 1  ;u  1;0; 1  1   2   1 2    
Vì mặt phẳng (P) đi qua d nên n  u  n .u  0  2  2b  c  0 1 P 1 P 1   1
Vì mặt phẳng (P) tạo với d góc 0 45 nên ta có: 2   n .u P 2 1 c 1 0
sin 45      2 2 n . u  b  c P 1 . 2 2 2 2 b 2 2 2
 1 c  1 b  c  b  2
 c  c   2 2 2 b Từ (1) và (2) suy ra: 2 2  2b 
 0  b  4b  4  0  b  2  c  2   . b c  4  2 Chọn: C Câu 39: Phương pháp:
- Đạo hàm hàm số f  x đến cấp 2019 (tìm công thức tổng quát).     - Xét hàm 2019 y  3 f x trên khoảng ;
và tìm điều kiện để bất phương trình 2019 f x  m   12 8    3 
nghiệm đúng với mọi x  ;   12 8  Cách giải: 23
f  x  cos 2 ;
x f ' x  2  sin 2 ; x f '  x 2  2  cos 2 ; x f '' x 3  2 sin 2x 4 f x 4 5
 2 cos 2x, f x 5 6  2
 sin 2x, f x 6 7  2
 cos 2x, f x 7  2 sin 2x 4k  f x 4  2 k cos 2x  4k 1  f  x 4k 1  2   sin 2x Do đó:  4k2  f x 4k 2  2  cos 2x  4k3  f  x 4k3  2 sin 2x 2019  f x 4.5043  f x 2019  2 sin 2x     Xét hàm 2019 y  f x 2019  3 2 sin 2x trên ; ta có:   12 8           1  + Trên khoảng ; thì 2019 2x  ;  sin 2x  ;1  2 sin 2x       2018 2019 2 ; 2  và hàm   12 4   6 2   2  2019 y  2
sin 2x đồng biến trên khoảng này.   3  4037   3   2    + Trên khoảng ; thì 2019 2019 2 2x  ;  sin 2x     ;1  2 sin 2x  2 ; 2  và hàm    4 8  2 4  2        2019 y  2
sin 2x nghịch biến trên khoảng này. Bảng biến thiên:   3 x 12 4 8 2019 2 2019 y  2 sin 2x 4037 2 2 2018 2    
Quan sát bảng biến thiên ta thấy, bất phương trình 2019 f x  3
m nghiệm đúng với mọi x  ;   12 8  nếu 2018 m  2 Chọn: B Câu 40: Phương pháp: n A
Sử dụng định nghĩa xác suất P A   
trong đó n A là số phần tử của biến cố A và n là số n
phần tử của không gian mẫu. Cách giải:
Gọi số tự nhiên có bốn chữ số khác nhau là abcd , a, ,
b c, d là các số tự nhiên có 1 chữ số, a  0 24
+ Có 6 cách chọn a; 6 cách chọn b; 5 cách chọn c; 4 cách chọn d  có 6.6.5.4 = 720 số tự nhiên có bốn
chữ số khác nhau hay n  720
Gọi A là biến cố “Số được chọn là số lớn hơn 2019 và bé hơn số 9012” Tính n A:
TH1: Nếu a  2;b  0;c  3;d tùy ý khác ; a ;
b c  có 1.1.4.4 = 16 số
TH2: Nếu a  2;b  0; ;
c d tùy ý khác nhau và khác ;
a b có 1.5.5.4 = 100 số
TH3: Nếu a 3;4;  8 ; ; b ;
c d khác nhau và khác a thì có 3.6.5.4 = 360 số
TH4: Nếu a  9;b  0 thì có 1.1.5.4 = 20 số
Suy ra n A 16 100  360  20  496 số n A 496 31
Xác suất cần tìm là P A      n 720 45 Chọn: C Câu 41: Phương pháp: - Tính  f  f   2 4  x   '  0   2 4 x   ' và tìm nghiệm của  
- Lập bảng biến thiên của hàm số y  f  2
4  x  trên nửa khoảng  2; 3 
 rồi suy ra tập giá trị của m. Cách giải:
Xets hàm y  f  2
4  x  trên nửa khoảng  2; 3   ta có: x f  x y '  f   4 x    '  
 4x '.f ' 4x  . ' 2 4 2 2 2     2 4  x x  0 x   x  y '  0  . x f ' 0 0 2
4  x   0  
   x      x   f '   4  x  2 4 1 0 2  0 
x   3   2; 3    2  4  x  1  Bảng biến thiên: x  2 0 3 f  2 ' 4  x  + 0  3 f  2 4  x  f  2 1  25
Từ đồ thị hàm số đã cho ta thấy 1
  f  2 nên để phương trình f  2
4  x   m có nghiệm trong nửa khoảng  2; 3   thì 1 m3 Vậy m  1  ;  3 Chọn: D Chú ý khi giải:
Ở bước xét dấu lập bảng biến thiên, các em có thể lấy một giá trị bất kì của x thuộc từng khoảng cần xét
dấu, thay vào f ' và tính toán sẽ ra kết quả, từ đó suy ra dấu của f ' ngay.
Cụ thể: Với x 0; 3 ta chọn x 1 thì f ' 3  0 do quan sát đồ thị hàm số ta thấy hàm số đồng biến
trên khoảng 1; . Do đó trong khoảng 0; 3 thì f  2 ' 4  x   0 Câu 42: Phương pháp:   
+ Xác định điểm I sao cho 2IA  IB  0 . Từ đó P
 IM ; P  IM max max min min
+ Từ đó tìm GTLN và GTNN của IM với M  mặt cầu (S) tâm K bán kính R.
+ Lập luận để có min IM  IK  ;
R max IM  IK  R Cách giải:    Gọi điểm I  ;
x y; z sao cho 2IA  IB  0  
 2IA  IB  2x  4; y  3; z  
1   x  3; y 1; z  3
2x  4  x  3 x  5  
 2 y 3  y 1  y  5  I 5;5;  1   2 z   1  z  3 z  1   
Suy ra IA  3; IB  6
  2   2 Xét 2 2
P  2MA  MB  2MI  IA MI  IB     2 2 2 2
 2MI  4MI.IA  2IA  MI  2MI.IB  IB
   2 2 2
 MI  IA  IB  2MI 2.IA IB 2  MI Suy ra P
 IM ; P  IM với M S  max max min min
Mặt cầu (S) có tâm K 1;2; 
1 và bán kính R  3 . Nên IK  5 .
Khi đó đường thẳng IK giao với mặt cầu tại hai điểm M ; M 1 2 IM
 IM  IK  R  5  3  2 min 1   IM
 IM  IK  R  5  3  8  max 2 2 2
P  n  IM  2  4 Do đó min 1  2 2
P  m  IM  8  64  max 2
Suy ra m  n  64  4  60 26 Chọn: C Câu 43: Phương pháp:
- Tính diện tích phần giao của hai hình tròn.
Chia làm hai hình viên phân và tính diện tích của chúng bằng cách gắn hệ trục tọa độ và sử dụng công b
thức tích phân S  f
 x gx dx a
- Tính diện tích phần còn lại của sân khấu và suy ra chi phí. Cách giải:
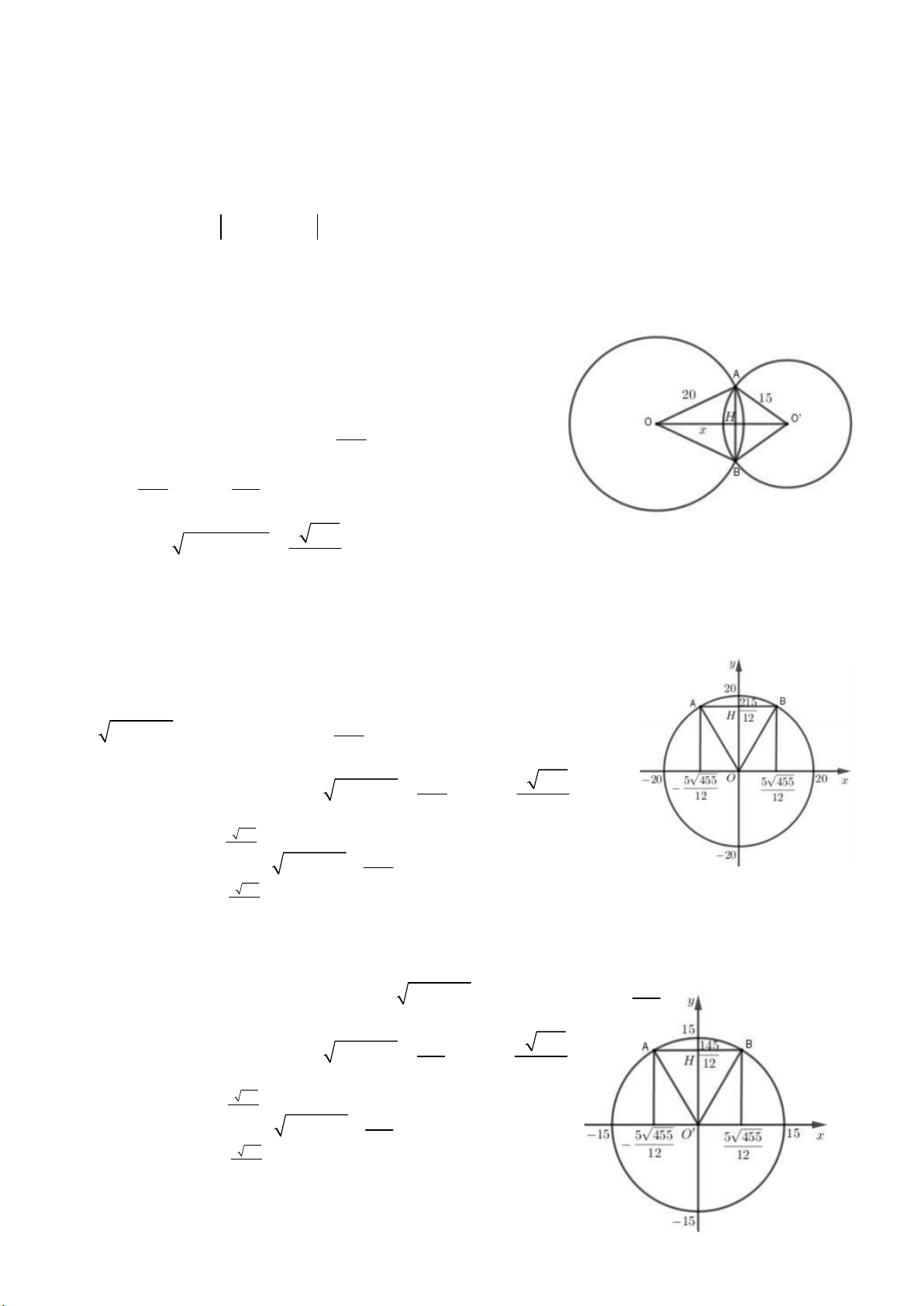
Đặt OH  x  O ' H  30  x Ta có: A
 HO vuông tại H nên 2 2 2 2
AH  OA  OH  400  x A
 HO' vuông tại H nên AH  O A  O H     x2 2 2 2 ' ' 225 30
 400  x  225  30  x2 215 2  x  12 215 145  OH  ,O ' H  12 12 5 455 Khi đó 2 2
AH  OA  OH  12
Ta tính diện tích phần giao của hai đường tròn (bằng tổng diện tích hai hình viên phân chắn bởi cung AB
và dây AB ở mỗi đường tròn)
+ Xét hình viên phân tạo bởi dây và cung AB của hình tròn tâm O bán kính 20.
Chọn hệ trục tọa độ như hình vẽ trên.
Ở đó hình viên phân tạo bở cung và dây AB giới hạn bởi nửa đường tròn 2 y  400  215
x và đường thẳng y  12 215 5 455
Phương trình hoành độ giao điểm 2 400  x   x   12 12 5 455 12  215  Do đó diện tích 2 S  400  x  dx  24,96 m 1       12  5 455  12
+) Xét hình viên phân tạo bởi dây và cung AB của hình tròn tâm O ' bán kính 15.
Chọn hệ trục tọa độ như hình vẽ trên. Ở đó hình viên phân tạo bởi cung
và dây AB giới hạn bởi nửa đường tròn 2 y  255  145
x và đường thẳng y  12 145 5 455
Phương trình hoành độ giao điểm 2 255  x   x   12 12 5 455 12  145  Do đó diện tích 2 S  255  x  dx  35,3 m 2       12  5 455  12 27
Diện tích phần giao của hai hình tròn là: S  S  S  24,96  35,3  60,26 m 1 2  
Diện tích phần còn lại của hình tròn là: S   2    2 ' .20 60,26
.15  60,26 1842,98m
Vậy tổng chi phí là: 1842,98100.000  60,26300.000  202.376.000 Chọn: B Câu 44: Phương pháp:
Từ giả thiết ta biến đổi để có f ' x  0
Xét hàm g x , tính g ' x; g '  x
Hàm số đạt cực tiểu tại x  0 thì g '0  0 và g ' 0  0 hoặc g ' 0  0 Cách giải: Với h   0 ta có   
f  x  h  f  x  h f x h f x h 2      h   h h
f  x  h  f  x  f  x  f  x  h  h   h h
f  x  h  f  x f  x  h  f  x  h    h h h
f x  h  f x
f x  h  f x  lim       h         lim lim h h 0 h 0 h 0 h h    
f x  h  f x
f x  h  f x Mà f ' x          lim  lim h 0 h 0 h    h
 0  f 'x  f 'x  0  f 'x  0 với x    Suy ra:   2019 29m g x  x  x   4 2 m  m   2 29 100 sin x 1    2018      28m g x x m x   4 2 ' 2019. 29
m  29m 100sin 2x Và   2017 
      27m g x x m m x   4 2 ' 2019.2018 29 28
2 m  29m 100cos2x
Ta thấy g '0  0; m   27
Để hàm số đạt cực tiểu tại x  0 thì ta xét hai trường hợp g ' 0  0 hoặc g ' 0  0
Xét g      4 2 ' 0
2 m  29m 100 m  2 2 m 4    m  2  TH1: Với g ' 0 4 2
 0  m  29m 100  0     2 m  25 m  5  m  5 
+ Nếu m   g x 2019 27  x
 x   g x 26  x  1992 2 1 ' 2019x
 27 không đổi dấu qua x  0 . (loại)
+ Nếu m    g x 2019 31  x
 x   g x 30  x  1988 2 1 ' 2019x  3 
1 không đổi dấu qua x  0 . (loại) 28 24
+ Nếu m   g x 2019 24  x
 x   g x 23  x  1995 5 1 ' 2019x
 24 đổi dấu qua x  0 và 1995 x   2019   Nhận thấy 24
g ' x  0; x
  0 và g 'x 1995  0; x   
;0 nên hàm số đạt cực tiểu tại x  0 .  2019   
+ Nếu m    g  x 2019 34  x
 x   g x 23  x  1985 5 1 ' 2019x
 34 đổi dấu qua x  0 và 34 1985 x   2019   Nhận thấy 34
g ' x  0; x
  0 và g 'x 1985  0; x   
;0 nên hàm số đạt cực tiểu tại x  0 .  2019    2  m  5
+ TH2: Với g ' 0 2
 0  4  m  25 
và g '0  0; m   27   5   m  2 
Nên hàm số đạt cực tiểu tại x  0 .
Vậy các giá trị nguyên của mm  27 thỏa mãn đề bài là m S   5  ; 4  ; 3  ;3;4;  5
Tổng các bình phương các phần tử của S là  2   2   2 2 2 2 5 4 3  3  4  5  100 Chọn: C Câu 45: Phương pháp:
Thử đáp án, khoảng nào làm cho y '  0 thì hàm số đã cho nghịch biến. Cách giải: x Ta có: y '  2
 f '1 x  1 2 x 1 x Dễ thấy 1  0, x    2 x 1
Đáp án A: Xét trong khoảng  ;  
1 thì 1 x 0; nhưng ta chưa kết luận được dấu của
f '1 x dẫn đến chưa nhận xét được tính nghịch biến của hàm số trong khoảng này.
Đáp án B: Xét trong khoảng  ;  2
  thì 1 x3; nhưng ta chưa kết luận được dấu của
f '1 x dẫn đến chưa nhận xét được tính nghịch biến của hàm số trong khoảng này.
Đáp án C: Xét trong khoảng  2
 ;0 thì 1 x1;3 và f '1 x  0 nên x y '  2
 f '1 x  1  0, x   2  ;0 2 x 1
Do đó hàm số y  f   x 2 2 1
 x 1  x nghịch biến trong khoảng  2  ;0 .
Đáp án D: Xét trong khoảng  3  ; 2
  thì 1 x3;4 và f '1 x  0 nhưng ta chưa kết luận được
dấu của y ' trong khoảng này. Vậy chỉ có khoảng  2
 ;0 là hàm số chắc chắn nghịch biến. 29 Chọn: C Câu 46: Phương pháp: 2 3 2019 x x x
+ Đặt g  x 1 x    ... x 
 e với x  0 2! 3! 2019!
+ Đánh giá g ' x  0; x
  0 để tìm GTLN của g x trên 0;
+ Tìm GTLN của h x 2
 x 10x với x  0
+ Từ đó tìm GTLN của f  x trên 
+ Bất phương trình m  f  x  0 có nghiệm khi m  max f  x . Kết hợp với điều kiện đề bài để  tìm m. Cách giải: 2 3 2019 x x x
+ Đặt g  x 1 x    ... x 
 e với x  0 . Khi đó ta có: 2! 3! 2019! 2 2018 x x
g ' x 1 x   ... x   e 2! 2018! 2 2017 x x
g '  x 1 x   ... x   e 2! 2017! ....... 2018 g x 1 x  x  e 2019 g x 1 x  e
Với mọi x  0 ta có 2019   1 x g x
 e  0 (dấu “=” xảy ra khi x  0 ) 2018    1 x g x
 x  e nghịch biến trên 0; 2018  g x 2018  g 0 2018  g x  0
Tương tự ta có g ' x  0 với mọi x  0
Suy ra max f  x  g 0  0 0;
Mặt khác xét h x  x  x   x  2 2 10 25 5 với x  0
Hàm số đạt giá trị lớn nhất 25  x  5  (TM)
Suy ra max f  x  25 ;0
Vậy max f  x  25 
+ Xét phương trình m  f  x  0  f  x  m có nghiệm
 max f x  m  m  25  m5;10;15;20;2  5 
Vậy có 5 giá trị m thỏa mãn đề bài. Chọn: A 30 Câu 47: Phương pháp:  
- Nhận xét tính chất các véc tơ I ,
A IB dựa vào điều kiện bài cho.
- Thay tọa độ của I vào điều kiện vừa có được ở nhận xét, từ đó tính được tọa độ của I. Cách giải: Ta có: I  ; a ;
b cP, I nằm giữa AB.  
 d B,P  2d  ,
A P  IB  2IA  IB  2  IA  7 5  21  a a a      7  3a  3      4   b  2
 2  b  0  3b  b
  0  a  b  c  4    1   c  2  3 c 5  3c 5   c   3 Chọn: D Câu 48: Phương pháp:
Sử dụng bài toán: Hàng tháng, một người vay (gửi) ngân hàng số tiền là a đồng với lãi suất hàng tháng là a
r thì sau n tháng người ấy có tổng số tiền nợ (gửi) ngân hàng là A  1 rn 1 1 r r  
Tính số tiền anh sinh viên nợ sau 2 năm
Tính số tiền anh sinh viên trả được sau 22 tháng
Tính số tiền nợ còn lại. Cách giải:
Trong thời gian từ tháng 01/09/2014 đến hết tháng 08/2016 là 24 tháng thì mỗi tháng anh sinh viên vay
ngân hàng 3 triệu với lãi suất 0,8%/tháng nên số tiền anh nợ ngân hàng tất cả là: 3000000 A 
1 0,8%24 1 1 0,8%  79661701,06 1   đồng. 0,8%  
Trong thời gian từ tháng 09/2016 đến cuối tháng 06/2018 là 22 tháng thì mỗi tháng anh sinh viên trả ngân
hàng 2 triệu với lãi suất 0,8%/ tháng nên số tiền anh trả được ngân hàng là: 2000000 A 
1 0,8%22 1 1 0,8%  48284037 1   đồng. 0,8%  
Tính đến tháng 06/2018 thì số tiền nợ ngân hàng của anh là A 1 0,8% 1  22
Số tiền anh còn nợ là A  A 1 r  A  46641110 1  22 đồng. 2 Chọn: B Câu 49: Phương pháp:
- Đặt z  a  bi
- Đưa bài toán về hệ phương trình ẩn a,b và tìm điều kiện để hệ có đúng 4 nghiệm.
Chú ý: Nhận xét nghiệm của phương trình để suy ra các trường hợp có thể có của nghiệm. Cách giải: 31
Đặt z  a  bi ta có: 2 2 2 2 2
z  z  z  z  z  2a  2b  a  b  a  b  2 a  b  m  0
Lại có z  m   2 2 2
a  b  m 2 2
a  b  2 a  b 
Do đó bài toán trở thành tìm m  0 để hệ 
có đúng 4 nghiệm phân biệt  ; a b 2 2 2
a  b  m
Nhận xét: Nếu hệ trên nhận một cặp số  ;
a b làm nghiệm thì nó cũng nhận các cặp số  ;a b  , ; a b, ; a b  , ; b a, ;
b a, ; b a, ;
b a làm nghiệm.
Do đó để hệ có đúng bốn nghiệm phân biệt  ;
a b thì các nghiệm chỉ có thể thỏa mãn: Một trong hai
số a , b bằng 0 và số còn lại khác 0 hoặc hai số a , b thỏa mãn a  b  0
Ta chia làm hai trường hợp:
+) TH1: Nếu hệ có nghiệm thỏa mãn a = 0 hoặc b = 0 thì m = 2 (dễ dàng kiểm tra bằng cách thay a = 0 hoặc b = 0 vào hệ.
Thử lại: m = 2 thì hệ trở thành: 2 2
a  b  2 a  b  
 4  2 a  b  2 2
 a  b  2  a  b  2 ab  4 2 2
a  b  4 a  0
 4  2 ab  4  ab  0  b 0 2 b   2 b Nếu a  0 thì   b  2  2 b   4 2 a  2 a Nếu b  0 thì   a  2  2 a  4
Khi đó hệ có đúng 4 nghiệm 0;2,0; 2  , 2
 ;0,2;0 nên m  2 thỏa mãn.
+) TH2: Nếu hệ có nghiệm thỏa mãn a  b  0 thì 2 2a  4 a  a  2 a  2   a  b  2          2 2 2 2a  m m  8 m  2 2 m  2 2
Do đó m  2 2 và hệ có đúng 4 nghiệm 2;2, 2  ; 2  ,2; 2  , 2  ;2
Vậy tập hợp các giá trị của m là 2;2 2 Chọn: A Câu 50: Phương pháp: 32
Đổi biến số x  t
Sử dụng phương pháp tích phân từng phần. Cách giải: 1
Đặt x  t 
dx  dt  dx  2tdt 2 x Đổi cận 2
x  0  t  0; x    t    Ta có 2
I  2t sin tdt 0 2 2t  u 4tdt  du Đặt    s
 in tdt  dv
v   cost   Suy ra 2 2
I   cost.2t
 4t costdt  2  J  0 0 4t  u 4dt  du Đặt 1 1    cos tdt  dv sin t  v  1  1   
Suy ra J  4t sin t  4sin tdt  4cost  4   4  8   0 0 0 a  2 a 1 Do đó 2
I  2  8       1  ;10 b   8  b 4 Chọn: D 33
Document Outline

[toanmath.com] - Đề thi thử Toán THPTQG 2019 trường chuyên Phan Bội Châu – Nghệ An lần 2.pdf
- [toanmath.com] - Đề thi thử Toán THPTQG 2019 trường chuyên Phan Bội Châu – Nghệ An lần 2
ACFrOgAiyE0tbHnFW2044EyKwNBEuW-f6slCD2Cz2lfYoHxdJlAjhmhIChUroBH3rr38DSgtJV4YqarikNfpPp6npXHADBWnxJSvem6SacPq4QXiivwIUMEgcCSxDrs=.pdf