Đề thi thử Toán TN THPT 2021 lần 1 trường chuyên Lê Khiết – Quảng Ngãi

Giới thiệu đến với quý thầy, cô giáo và các em học sinh đề thi thử Toán TN THPT 2021 lần 1 trường THPT chuyên Lê Khiết – Quảng Ngãi mã đề 144 gồm 07 trang với 50 câu trắc nghiệm.

Chủ đề:

Đề thi THPTQG môn Toán năm 2023 1.2 K tài liệu

Môn:

Toán 1.8 K tài liệu

Thông tin:
35 trang 10 tháng trước
Tác giả:
T
Thanh Hoa
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Đề thi thử Toán TN THPT 2021 lần 1 trường chuyên Lê Khiết – Quảng Ngãi

Giới thiệu đến với quý thầy, cô giáo và các em học sinh đề thi thử Toán TN THPT 2021 lần 1 trường THPT chuyên Lê Khiết – Quảng Ngãi mã đề 144 gồm 07 trang với 50 câu trắc nghiệm.

33 17 lượt tải Tải xuống

Chủ đề: Đề thi THPTQG môn Toán năm 2023 1.2 K tài liệu

Môn: Toán 1.8 K tài liệu

Thông tin:

35 trang 10 tháng trước

Tác giả:

Profile Thanh Hoa
Trang 1/7 - Mã đề 144
SỞ GD & ĐT QUẢNG NGÃI
TRƯỜNG THPT CHUYÊN LÊ KHIẾT
THI THỬ TỐT NGHIỆP THPT NĂM 2021 LẦN 1
NĂM HỌC 2020 - 2021
MÔN TOÁN
Thời gian làm bài : 90 Phút; (Không kể giao đề)
(Đề có 50 câu)
ĐỀ CHÍNH THỨC
(Đề có 7 trang)
Họ tên : .........................................................Số báo danh : ..............Lớp…….
Câu 1: Có bao nhiêu số tự nhiên có bốn chữ số khác nhau được tạo thành từ các chữ số
1, 2,3, 4,5,6
?
A.
6
P
. B.
4
6
C
. C.
4
A
. D.
4
6
.
Câu 2: Trong không gian
Oxyz
, cho hai điểm
( 2;3; 6)
A
và
(0;5; 2)
B
. Trung điểm của đoạn
thẳng
AB
có tọa độ là
A.
( 2;8; 4)
I
. B.
(1;1; 4)
I
. C.
( 1;4;2)
I
. D.
(2;2; 4)
I
.
Câu 3: Trong mặt phẳng tọa độ
Oxy
, điểm biểu diễn số phức
4 3
z i
có tọa độ là
A.
3;4
. B.
4;3
. C.
4; 3
. D.
3;4
.
Câu 4: Cho hàm số
3
( ) 4 2
f x x
. Trong các khẳng định sau, khẳng định nào đúng?
A.
2
( ) 12
f x dx x C
. B.
4
( ) 3 2
f x dx x x C
.
C.
4
1
( ) 2
3
f x dx x x C
. D.
4
( ) 2
f x dx x x C
.
Câu 5: Tiệm cận ngang của đồ thị hàm số
2 1
2
x
y
x
là đường thẳng :
A.
2
x
. B.
2
y
. C.
1
y
. D.
2
x
.
Câu 6: Tập nghiệm
S
của bất phương trình
2
1
5
25
x
x
là
A.
;2 .
S 
B.
;2 .
S 
C.
2; .
S

D.
1; .
S
Câu 7: Thể tích
V
của khối nón có bán kính đáy bằng
3
cm
và chiều cao bằng
4
cm
là
A.
3
12
V cm
. B.
3
36 .
V cm
C.
2
36 .
V cm
D.
2
12
V cm
.
Câu 8: Một hình lập phương có độ dài cạnh bằng
2
a
. Thể tích khối lập phương đó là
A.
3
4
a
. B.
3
a
. C.
3
8
a
. D.
3
2 2
a
.
Câu 9: Cho hàm số
( ) sin 3
f x x
. Trong các khẳng định sau, khẳng định nào đúng?
A.
1
( ) cos3
3
f x dx x C
. B.
1
( ) cos3
3
f x dx x C
.
C.
( ) 3cos3
f x dx x C
. D.
( ) 3cos3
f x dx x C
.
Câu 10: Một khối chóp có thể tích bằng
12
và diện tích đáy bằng
4
. Chiều cao của khối chóp đó
bằng
A.
3
. B.
4
9
. C.
9
. D.
1
3
.
Câu 11: Trong không gian
Oxyz
, mặt cầu
2 2 2
( ): ( 1) ( 3) 16
S x y z
có bán kính bằng
Mã đề 144
Trang 2/7 - Mã đề 144
A.
32
. B.
9
. C.
16
. D.
4
.
Câu 12: Số phức liên hợp của số phức
4 2
z i
là
A.
4 2
z i
. B.
4 2
z i
.
C.
2 4
z i
. D.
2 4
z i
.
Câu 13: Nếu
4
3
2
f x dx
và
4
5
6
f x dx
thì
5
3
f x dx
A.
12
. B.
4
. C.
8
. D.
8
.
Câu 14: Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số dưới đây?
A.
3
3 2.
y x x
B.
4 2
2 2.
y x x
C.
3 2
3 2.
y x x
D.
3 2
3 2
y x x
.
Câu 15: Cho cấp số cộng
( )
n
u
có
2
4
u
và
4
2
u
. Giá trị của
6
u
bằng
A.
6
6
u
. B.
6
0
u
. C.
6
1
u
. D.
6
1
u
.
Câu 16: Nghiệm của phương trình
3
log 2
x
là
A.
6
x
. B.
8.
x
C.
5
x
. D.
9.
x
Câu 17: Cho hàm số
y f x
có bảng biến thiên như sau :
Mệnh đề nào dưới đây đúng?
A.
min 4
y
. B.
15
C Ð
y
. C.
max 5
y
. D.
4
CT
y
.
Câu 18: Trong không gian
Oxyz
, mặt phẳng nào dưới đây không đi qua điểm
(0;1; 1)?
M
A.
4
( ): 2 15 13 0
P x y z
. B.
2
( ) : 4 2 12 10 0
P x y z
.
C.
3
( ) : 2 3 12 15 0
P x y z
. D.
1
( ): 4 2 12 17 0
P x y z
.
Câu 19: Cho hàm số
y f x
có bảng biến thiên như sau:
Trang 3/7 - Mã đề 144
Mệnh đề nào sau đây sai ?
A. Hàm số đồng biến trên khoảng
2;
.
B. Hàm số đồng biến trên khoảng
; 1

.
C. Hàm số đồng biến trên khoảng
1;

.
D. Hàm số nghịch biến trên khoảng
1;1
.
Câu 20: Tích phân
1
1
e
dx
x
bằng
A. e – 1 . B.
ln 2
e
. C. 1. D.
ln 1
e
Câu 21: Cho hai số phức
3 2
z i
và
4
w i
. Số phức
z w
bằng
A.
1
i
. B.
7
i
. C.
1 3
i
. D.
7 3
i
.
Câu 22: Cho hàm số
y f x
có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị của tham số
m
để phương trình
1
f x m
có 3 nghiệm phân biệt.
A.
1 3
m
. B.
1 4
m
. C.
2 5
m
. D.
0 4
m
.
Câu 23: Đạo hàm của hàm số
3
log 3 1
y x
trên khoảng
1
;
3
là
A.
3
.
3 1
x
B.
3
3 1 ln3
x
. C.
1
.
3 1 ln
x x
D.
3
.
1 ln3
x
Câu 24: Cho số thực
a
thỏa mãn
0 1
a
. Tính giá trị của biểu thức
3 5
2 3
15 4
. .
log
a
a a a
T
a
.
A.
8
T
. B.
11
T
.
C.
8
3
T
. D.
17
15
T
.
Câu 25: Nếu
2
1
(2 3 ( )) 4
x f x dx
thì
6
3
3
x
f dx
bằng
A.
4.
B.
1.
C.
1
3
. D.
1.
Câu 26: Gọi
,
M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
( )
1 2
x
f x
x
trên đoạn
Trang 4/7 - Mã đề 144
2;5
. Tính
3
A M m
.
A.
10
.
3
A
B.
1.
A
C.
1
A
. D.
5
.
3
A
Câu 27: Số phức
1
z
là nghiệm có phần ảo dương của phương trình bậc hai
2
2 2 0
z z
. Môđun
của số phức
1
(2 )
i z
bằng
A.
3 2.
B.
10.
C.
10.
D.
18
.
Câu 28: Cho hình chóp .
S ABCD
có đáy là hình chữ nhật với
, 5
AB a AC a
,
2
SA a
. Biết
SB BC
và
SD CD
. Thể tích của khối chóp .
S BCD
là
A.
3
.
4 .
S BCD
V a
B.
3
.
2 .
S BCD
V a
C.
3
.
2
.
3
S BCD
a
V
D.
3
.
4
.
3
S BCD
a
V
Câu 29: Cho hình chóp .
S ABC
có đáy
ABC
là tam giác vuông cân tại
A
, cạnh
AC a
, các cạnh
bên
6
2
a
SA SB SC
. Tính góc tạo bởi mặt bên
SAB
và mặt phẳng đáy
.
ABC
A.
6
. B.
4
.
C.
arctan 2
. D.
arctan2.
Câu 30: Một hình trụ có bán kính đáy bằng
a
và có thiết diện qua trục là một hình vuông. Tính diện
tích xung quanh của hình trụ.
A.
2
2
a
. B.
2
3
a
. C.
2
a
. D.
2
4
a
.
Câu 31: Cho hàm số
f x
có đạo hàm
3 2
1 2 3
f x x x x
. Hàm số đã cho có bao nhiêu điểm
cực trị?
A. 3. B. 1 C. 0. D. 2.
Câu 32: Tập nghiệm của bất phương trình
2
2
2
log (2 ) log
x x x
là
A.
1
;1 .
2
B.
(0;1).
C.
1
;1 .
2
D.
0;1
.
Câu 33: Trong không gian
Oxyz
, vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi
qua gốc tọa độ và trọng tâm tam giác
ABC
với
(0;2;1), (4; 2;1), (2;3; 4)?
A B C
A.
2
(1; 2;2)
u
B.
1
(1; 2; 1)
u
C.
3
(2;1;2)
u
D.
4
(4; 2;1)
u
Câu 34: Hàm số nào dưới đây đồng biến trên
?
A.
2
1
1
y
x
. B.
3
y x x
. C.
3 .
x
y
D.
ln .
y x
Câu 35: Cho hai số dương
a
,
b
với
1
a
. Đặt
3
log
a
M b
. Tính
M
theo
log
a
N b
.
A.
1
.
6
M N
B.
3
.
2
M N
C.
2
.
3
M N
D.
.
M N
Câu 36: Có bao nhiêu số phức
z
thỏa mãn
3
z z
?
A. 5.
B. 4.
C. 2.
D. 7.
Trang 5/7 - Mã đề 144
Câu 37: Trong không gian
Oxyz
, cho 4 điểm
1;– 2;1
A
,
0;1; 3
B
,
(1;2;3)
C
,
(2; 1;2)
D
. Phương
trình đường thẳng qua điểm
A
và vuông góc với mặt phẳng
( )
BCD
là
A.
2 3 5
1 1 4
x y z
. B.
1 2 1
1 3 4
x y z
.
C.
1 3
1 3 2
x y z
. D.
1 2 1
1 3 2
x y z
.
Câu 38: Cho tứ diện
ABCD
, gọi
M
là điểm sao cho
3 0
MA MB
. Mặt phẳng
( )
P
đi qua
M
song
song với
BC
và
AD
chia tứ diện đã cho thành 2 khối đa diện . Gọi
1
V
là thể tích của khối đa diện
chứa đỉnh
B
và
2
V
là thể tích của khối đa diện chứa đỉnh
A
. Tính tỉ số
1
2
V
V
.
A.
5
27
. B.
5
37
.
C.
5
32
. D.
1
3
.
Câu 39: Có bao nhiêu giá trị thực của tham số
m
thỏa mãn:
3 2
0
(4 2 ) 3
m
x x dx m
?
A. 2. B. 1.
C. 4. D. 3.
Câu 40: Có tất cả bao nhiêu cặp số nguyên
x
và
y
sao cho đẳng thức sau thỏa mãn?
2
101
1
2021
log 4 2 2022 20 1
y
x x
y
.
A. 1. B. 3.
C. 0. D. 2.
Câu 41: Cho hình chóp đều
.
S ABCD
có cạnh đáy bằng
a
,
AC
cắt
BD
tại
O
. Khoảng cách giữa
SA
và
CD
bằng độ dài đoạn
SO
. Tính sin của góc giữa cạnh bên và mặt phẳng đáy .
A.
3
5
B.
15
.
5
C.
10
5
D.
4
5
Câu 42: Cho hàm số
,
f x
đồ thị của hàm số
/
y f x
là đường cong như hình vẽ bên dưới. Giá
trị nhỏ nhất của hàm số
2 1 4 3
g x f x x
trên đoạn
1
1;
2
bằng
A.
2 5
f
. B.
1 1
f
. C.
1 3
f
. D.
0
f
.
Trang 6/7 - Mã đề 144
Câu 43: Trong không gian
,
Oxyz
cho tứ diện
ABCD
với
(3; 4;0) , (2;5; 4), ( 1;1;1), (3;5;3)
A B C D
. Viết
phương trình mặt cầu ngoại tiếp tứ diện đó.
A.
2 2 2
1 3 2 9
x y z
. B.
2 2 2
1 3 2 9
x y z
.
C.
2 2 2
1 3 2 9
x y z
. D.
2 2 2
1 3 2 9
x y z
.
Câu 44: Cho hình chóp .
S ABCD
có đáy là hình vuông cạnh
a
. Tam giác
SAB
đều và nằm trong
mặt phẳng vuông góc với đáy. Tính diện tích mặt cầu ngoại tiếp hình chóp đã cho.
A.
3
4
3
a
. B.
2
7
3
a
.
C.
2
7
9
a
. D.
2
4
a
.
Câu 45: Gọi A là tập tất cả các số tự nhiên có 6 chữ số khác nhau, lấy ngẫu nhiên một số từ A. Tính
xác suất để lấy được một số luôn có mặt 3 chữ số
0,1,2
và giữa 2 chữ số
0
và
1
có đúng 2 chữ số.
A.
1
15
. B.
7
162
.
C.
5
.
162
D.
7
.
405
Câu 46: Cho hàm số bậc bốn
y f x
có đồ thị
C
như hình vẽ bên. Biết hàm số
y f x
đạt
cực trị tại các điểm
1 2 3
, ,
x x x
thỏa mãn
3 1
2
x x
,
1 3 2
2
0
3
f x f x f x
và
C
nhận đường
thẳng
2
:
d x x
làm trục đối xứng. Gọi
1 2 3 4
, , ,
S S S S
là diện tích của các miền hình phẳng được đánh
dấu như hình bên.
x
y
d
S
4
S
3
S
2
S
1
x
3
x
2
x
1
O
Tỉ số
3 4
1 2
S S
S S
gần kết quả nào nhất
A.
1.62.
B.
1.68
.
C.
1.64
. D.
1.66
.
Câu 47: Cho hàm số
f x
có đạo hàm liên tục trên
, đồ thị hàm số
y f x
có đúng 4 điểm
chung với trục hoành như hình vẽ bên dưới .
Trang 7/7 - Mã đề 144
Có bao nhiêu giá trị nguyên của
m
để hàm số
3
3 2021
y f x x m
có 11 điểm cực trị?
A. 0. B. 2. C. 5. D. 1.
Câu 48: Trong không gian
Oxyz
, cho mặt phẳng
( ) : 2 0,
P x y z
đường thẳng
1 1 2
( ):
1 1 1
x y z
d
và 2 điểm
1 3
( ; 1; ), (1; 2;1)
2 2
B C
. Gọi
A
là giao điểm của
( )
d
và
( )
P
,
S
là
điểm di động trên
( )
d
(
S A
). Gọi
,
H K
lần lượt là hình chiếu của
A
trên các đường thẳng
SB
và
SC
, (
) là giao tuyến của 2 mặt phẳng
( )
AHK
và
( )
P
,
( )
M
. Giá trị nhỏ nhất của
MB MC
là
A.
14
.
2
B.
6 2 2
.
2
C.
7
.
2
D.
7
.
2
Câu 49: Có bao nhiêu số nguyên dương
m
để phương trình
1 .ln( 1)
x
e m mx
có 2 nghiệm phân
biệt trên
10;10
?
A. 2201. B. 2020. C. 2021. D. 2202.
Câu 50: Cho các số phức
1 2
,
z z
thỏa mãn
1
1 1
z i
và
2
2 4
z i
. Số phức
z
thay đổi sao
cho
1 1
1
z z i z
và
2 2
2
z z z i
là số thuần ảo. Giá trị nhỏ nhất
3 2
z i
bằng
A.
11
5
. B.
1
3
.
C. 3. D. 2.
------ HẾT ------
Cán bộ coi thi không giải thích gì thêm.
Thí sinh không được sử dụng tài liệu .
1
SỞ GD&ĐT QUẢNG NGÃI
TRƯỜNG THPT CHUYÊN LÊ KHIẾT
THI THỬ TỐT NGHIỆP THPT NĂM 2021 LẦN 1
NĂM HỌC 2020 - 2021
MÔN TOÁN
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Phần đáp án câu trắc nghiệm:
144
243
345
442
546
641
747
848
1
C
B
B
B
C
B
A
A
2
C
A
C
C
A
B
C
D
3
C
A
B
A
A
B
B
A
4
D
C
C
A
A
A
C
D
5
B
C
B
C
A
D
D
B
6
A
D
A
C
C
A
B
A
7
A
A
C
D
C
D
D
C
8
C
D
C
D
C
C
C
C
9
B
C
C
C
A
D
D
B
10
C
A
C
C
B
D
B
A
11
D
A
A
B
B
D
B
D
12
B
D
A
D
D
A
A
B
13
B
A
D
A
B
D
C
B
14
D
B
C
D
D
C
C
C
15
B
C
A
A
A
D
A
D
16
D
D
B
D
D
D
C
D
17
D
B
D
C
B
B
D
D
18
D
D
B
B
D
B
A
C
19
C
C
B
C
A
B
D
D
20
C
D
D
B
D
A
D
A
21
C
A
C
B
D
A
A
D
22
A
D
D
B
B
C
A
A
23
B
A
C
D
B
B
D
B
24
C
B
A
C
C
A
B
C
25
D
C
B
B
B
A
A
A
26
C
C
D
B
A
B
C
C
27
C
A
B
B
D
C
B
B
28
C
C
B
C
A
B
B
C
29
D
B
C
A
B
C
B
D
30
D
B
C
B
D
D
C
C
31
D
D
D
D
C
A
D
D
32
C
A
B
C
C
B
B
C
33
C
B
D
B
D
B
A
A
34
C
B
B
C
C
D
C
A
35
C
D
A
B
B
D
D
C
36
A
C
D
D
C
C
A
B
37
A
C
B
D
B
D
A
B
38
A
C
D
D
C
D
C
A
39
A
C
B
B
C
D
B
A
40
A
D
D
C
A
C
C
C
41
B
B
D
A
D
B
C
D
2
42
C
D
D
C
B
C
A
B
43
B
A
A
B
A
C
D
C
44
B
D
A
A
C
C
D
C
45
C
C
B
C
B
A
C
D
46
D
D
C
C
B
D
D
B
47
D
B
B
C
B
A
B
B
48
A
C
D
A
C
B
A
A
49
A
C
C
B
A
D
C
A
50
A
D
C
B
B
C
C
C
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 1
TRƯỜNG & THPT
---------------------------
CHUYÊN LÊ KHIẾT
QUẢNG NGÃI
MÃ ĐỀ: ......
THI THỬ TN12 LẦN 3 MÔN TOÁN
NĂM HỌC 2020 - 2021
Thời gian: 90 phút
Câu 1. Có bao nhiêu số tự nhiên có bốn chữ số khác nhau được tạo thành từ các chữ số
1,2,3, 4,5,6
?
A.
6
P
. B.
4
6
C
. C.
4
6
A
. D.
4
6
.
Câu 2. Trong không gian
Oxyz
, cho hai điểm
2;3;6A
và
0;5; 2B
. Trung điểm của đoạn thẳng
AB
có toạ độ là
A.
2;8;4I
. B.
1;1; 4I
. C.
1;4;2I
. D.
2;2; 4I
.
Câu 3. Trong mặt phẳng toạ độ
Oxy
, điểm biểu diễn số phức
4 3z i
có toạ độ là
A.
3;4
. B.
4;3
. C.
4; 3
. D.
3;4
.
Câu 4. Cho hàm số
3
4 2f x x
. Trong các khẳng định sau, khẳng định nào đúng ?
A.
2
d 12f x x x C
. B.
4
d 3 2f x x x x C
.
C.
4
1
d 2
3
f x x x x C
. D.
4
d 2f x x x x C
.
Câu 5. Tiệm cận ngang của đồ thị hàm số
2 1
2
x
y
x
là đường thẳng
A.
2x
. B.
2y
. C.
1y
. D.
2x
.
Câu 6. Tập nghiệm
S
của bất phương trình
2
1
5
25
x
x
là
A.
;2S 
. B.
;2S 
. C.
2;S 
. D.
1;S 
.
Câu 7. Thể tích
V
của khối nón có bán kính đáy bằng
3cm
và chiều cao bằng
4cm
là
A.
3
12V cm
. B.
3
36
V cm
C.
2
36V cm
. D.
2
12V cm
Câu 8. Một hình lập phương có độ dài cạnh bằng
2a
. Thể tích khối lập phương đó là
A.
3
4a
. B.
3
a
C.
3
8a
. D.
3
2 2a
Câu 9. Cho hàm số
sin 3f x x
. Trong các khẳng định sau, khẳng định nào đúng?
A.
1
cos3
3
f x dx x C
. B.
1
cos3
3
f x dx x C
.
C.
3cos3f x dx x C
. D.
cos3f x dx x C
.
Câu 10. Một khối chóp có thể tích bằng
12
và diện tích đáy bằng
4
. Chiều cao cảu khối chóp đó bằng
A.
3
. B.
4
9
. C.
9
. D.
1
3
.
Câu 11. Trong không gian
Oxyz
, mặt cầu
2 2
2
: 1 3 16S x y z
có bán kính bằng
A.
32
. B.
9
. C.
16
. D.
4
.
Câu 12. Số phức liên hợp của số phức
4 2z i
là
A.
4 2z i
. B.
4 2z i
. C.
2 4z i
. D.
2 4z i
.
Câu 13. Nếu
4
3
d 2f x x
và
4
5
d 6g x x
thì
5
3
df x x
.
A.
12
. B.
4
. C.
8
. D.
8
.
Câu 14. Đường cong trong hình vẽ bên là đồ thị hàm số nào sau đây
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 2 TÀI LIỆU ÔN THI THPT QUỐC GIA
A.
3
3 2
y x x
. B.
4 2
2 2
y x x
. C.
3 2
3 2
y x x
. D.
3 2
3 2
y x x
.
Câu 15. Cho cấp số cộng
n
u
có
2
4
u
và
4
2
u
. Giá trị của
6
u
bằng.
A.
6
6
u
. B.
6
0
u
. C.
6
1
u
. D.
6
1
u
.
Câu 16. Nghiệm của phương trình
3
log 2
x
là
A.
6
x
. B.
8
x
. C.
5
x
. D.
9
x
.
Câu 17. Cho hàm số
y f x
có bảng biến thiên như sau:
Mệnh đề nào dưới đây đúng?
A.
min 4
y
. B.
15
CD
y
. C.
max 5
y
. D.
4
CT
y
.
Câu 18. Trong không gian
Oxyz
, mặt phẳng nào dưới đây không đi qua điểm
0;1; 1
M
?
A.
4
: 2 15 13 0
P x y z
. B.
2
:4 2 12 10 0
P x y z
.
C.
3
:2 3 12 15 0
P x y z
D.
1
:4 2 12 17 0
P x y z
.
Câu 19. Cho hàm số
y f x
có bảng biến thiên như sau:
Mệnh đề nào sau đây sai?
A. Hàm số đồng biến trên khoảng
2;
. B. Hàm số đồng biến trên khoảng
; 1

.
C. Hàm số đồng biến trên khoảng
1;
. D. Hàm số nghịch biến trên khoảng
1;1
.
Câu 20. Tích phân
1
1
d
e
x
x
bằng
A.
1
e
. B.
ln 2
e
. C.
1
D.
ln 1
e
.
Câu 21. Cho hai số phức
3 2
z i
và
4
w i
. Số phức
z w
bằng
A.
1
i
. B.
7
i
. C.
1 3
i
. D.
7 3
i
.
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 3
Câu 22. Cho hàm số
( )
y f x
có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị của tham số
m
để
phương trình
1
f x m
có 3 nghiệm phân biệt.
A.
1 3
m
. B.
1 4
m
. C.
2 5
m
. D.
0 4
m
.
Câu 23. Đạo hàm của hàm số
3
log 3 1
y x
trên khoảng
1
;
3

là
A.
3
3 1
x
. B.
3
3 1 ln3
x
. C.
3
3 1 ln
x x
. D.
3
1 ln 3
x
.
Câu 24. Cho số thực
a
thỏa mãn
0 1
a
. Tính giá trị của biểu thức
5
2 3
3
15 4
. .
log
a
a a a
T
a
A.
8
T
. B.
11
T
. C.
8
3
T
. D.
17
15
T
.
Câu 25. Nếu
2
1
2 3 d 4
x f x x
thì
6
3
d
3
x
f x
bằng
A.
4
. B.
1
. C.
1
3
. D.
1
.
Câu 26. Gọi
,
M m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
1
1 2
x
f x
x
trên đoạn
2;5
. Tính
3
A M m
.
A.
10
3
A
. B.
1
A
. C.
1
A
. D.
5
3
A
.
Câu 27. Số phức
1
z
là nghiệm có phần ảo dương của phương trình bậc hai
2
2 2 0
z z
. Môđun của
số phức
1
2
i z
bằng
A.
3 2
. B.
10
. C.
10
. D.
18
.
Câu 28. Cho hình chóp .
S ABCD
có đáy là hình chữ nhật với
, 5, 2
AB a AC a SA a
. Biết
SB BC
và
SD CD
. Thể tích của khối chóp .
S BCD
là
A.
3
.
4
S BCD
V a
. B.
3
.
2
S BCD
V a
. C.
3
.
2
3
S BCD
a
V . D.
3
.
4
3
S BCD
a
V .
Câu 29. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
A
, cạnh
AC a
, các cạnh bên
6
2
a
SA SB SC
. Tính góc tạo bởi mặt bên
( )
SAB
và mặt phẳng đáy
( )
ABC
.
A.
6
. B.
4
. C.
arctan 2
. D.
arctan 2
.
Câu 30. Một hình trụ có bán kính đáy bằng
a
và có thiết diện qua trục là một hình vuông. Tính diện tích
xung quanh của hình trụ.
A.
2
2
a
. B.
2
3
a
. C.
2
a
. D.
2
4
a
.
Câu 31. Cho hàm số
( )
f x
có đạo hàm
3 2
( ) ( 1) (2 3)
f x x x x
. Hàm số đã cho có bao nhiêu điểm cực
trị?
A. 3. B. 1. C. 0. D. 2.
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 4 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 32. Tập nghiệm của bất phương trình
2
2
2
log 2 log
x x x
là
A.
1
;1
2
. B.
(0;1)
. C.
1
;1
2
. D.
0;1
.
Câu 33. Trong không gian
Ox
yz
, vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua
gốc tọa độ và trọng tâm của tam giác
ABC
với
0;2;1 , 4; 2;1 , 2;3;4
A B C
?
A.
2
1; 2;2
u
. B.
1
1; 2; 1
u
. C.
3
2;1;2
u
. D.
4
4; 2;1
u
.
Câu 34. Hàm số nào dưới đây đồng biến trên
?
A.
2
1
1
y
x
. B.
3
y x x
. C.
3
x
y
. D.
ln
y x
.
Câu 35. Cho hai số dương
,
a b
với
1
a
. Đặt
3
log
a
M b
. Tính
M
theo
log
a
N b
.
A.
1
6
M N
. B.
3
2
M N
. C.
2
3
M N
. D.
M N
.
Câu 36. Có bao nhiêu số phức
z
thỏa mãn
3
z z
?
A.
5
. B.
4
. C.
2
. D.
7
.
Câu 37. Trong không gian
Oxyz
, cho bốn điểm
1; 2;1
A
,
0;1;3
B
,
1;2;3
C
,
2; 1;2
D
. Phương
trình đường thẳng qua điểm
A
và vuông góc với mặt phẳng
BCD
là
A.
2 3 5
1 1 4
x y z
. B.
1 2 1
1 3 4
x y z
.
C.
1 3
1 3 2
x y z
. D.
1 2 1
1 3 2
x y z
.
Câu 38. Cho tứ diện
ABCD
, gọi
M
là điểm sao cho
3 0
MA MB

. Mặt phẳng
P
đi qua
M
, song
song với
BC
và
AD
chia khối tứ diện đã cho thành hai khối đa diện. Gọi
1
V
là thể tích của khối
tứ diện chứa đỉnh
B
và
2
V
là thể tích khối tứ diện chứa đỉnh
A
. Tính tỉ số
1
2
V
V
.
A.
5
27
. B.
5
37
. C.
5
32
. D.
1
3
.
Câu 39. Có bao nhiêu giá trị thực của tham số
m
thỏa mãn
3 2
0
4 2 d 3
m
x x x m
?
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 40. Có tất cả bao nhiêu cặp số nguyên
x
và
y
sao cho đẳng thức sau thỏa mãn
2
101
1
2021
log 4 2 2022 20 1.
y
x x
y
A.
1
. B.
3
. C.
0
. D.
2
.
Câu 41. Cho hình chóp đều
.
S ABCD
có cạnh đáy bằng
a
,
AC
cắt
BD
tại
O
. Khoảng cách giữa
SA
và
CD
bằng độ dài đoạn
SO
. Tính sin của góc giữa cạnh bên và mặt phẳng đáy.
A.
3
5
. B.
15
5
. C.
10
5
. D.
4
5
.
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 5
Câu 42. Cho hàm số
f x
, đồ thị của hàm số
( )
y f x
là đường cong như hình vẽ bên dưới.
Giá trị nhỏ nhất của hàm số
2 1 4 3
g x f x x
trên đoạn
1
1;
2
bằng
A.
2 5
f
. B.
1 1
f
. C.
1 3
f
. D.
0
f
.
Câu 43. Trong không gian
Oxyz
, cho tứ diện
ABCD
với
3; 4;0
A
,
2;5;4
B
,
1;1;1
C
,
3;5;3
D
.
Viết phương trình mặt cầu ngoại tiếp tứ diện đó.
A.
2 2 2
1 3 2 9
x y z
. B.
2 2 2
1 3 2 9
x y z
.
C.
2 2 2
1 3 2 9
x y z
. D.
2 2 2
1 3 2 9
x y z
.
Câu 44. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
. Tam giác
SAB
đều và nằm trong mặt
phẳng vuông góc với đáy. Tính diện tích mặt cầu ngoại tiếp hình chóp đã cho.
A.
3
4
3
a
B.
2
7
3
a
C.
2
7
9
a
D.
2
4
a
Câu 45. Gọi
A
là tập tất cả các số tự nhiên có
6
chữ số khác nhau, lấy ngẫu nhiên một số từ
A
. Tính
xác suất để lấy được một số luôn có mặt
3
chữ số
0
,
1
,
2
và giữa hai chữ số
0
và
1
có đúng
2
chữ số.
A.
1
15
. B.
7
162
. C.
5
162
. D.
7
405
.
Câu 46. Cho hàm số bậc bốn
y f x
có đồ thị
C
như hình vẽ bên. Biết hàm số
y f x
đạt cực trị
tại các điểm
1
x
,
2
x
,
3
x
thỏa mãn
3 1
2
x x
,
1 3 2
2
0
3
f x f x f x
và
C
nhận đường
thẳng
2
:
d x x
làm trục đối xứng. Gọi
1
S
,
2
S
,
3
S
,
4
S
là diện tích của các miền hình phẳng
được đánh dấu như hình bên.
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 6 TÀI LIỆU ÔN THI THPT QUỐC GIA
Tỉ số
3 4
1 2
S S
S S
gần kết quả nào nhất?
A.
1.62
. B.
1.64
. C.
1.68
. D.
1.66
.
Câu 47. Cho hàm số
( )
f x
có đạo hàm liên tục trên
, đồ thị hàm số
'( )
y f x
có đúng bốn điểm chung
với trung hoành như hình vẽ dưới.
Có bao nhiêu giá trị nguyên của
m
để hàm số
3
3 2021
y f x x m có
11
điểm cực trị.
A.
0
. B.
2
. C.
5
. D.
1
.
Câu 48. Trong không gian
,
Oxyz
cho mặt phẳng
( ) : 2 0,
P x y z
đường thẳng
1 1 2
( ) :
1 1 1
x y z
d
và hai điểm
1 3
; 1; , 1; 1;1 .
2 2
B C
Gọi
A
là giao điểm của
( )
d
và
( )
P
,
( )
S
là điểm di động trên
( ),( )
d S A
. Gọi
,
H K
lần lượt là hình chiếu vuông góc của
A
trên các đường thẳng
SB
và
SC
,
( )
là giao tuyến của hai mặt phẳng
( )
AHK
và
( ), ( )
P M
. Giá trị nhỏ nhất của
MB MC
là
A.
14
2
. B.
6 2 2
2
. C.
7
2
. D.
7
2
.
Câu 49. Có bao nhiêu số nguyên dương
m
để phương trình
1 ln 1
x
e m mx
có hai nghiệm phân biệt
trên đoạn
10;10
?
A.
2201
. B.
2020
. C.
2021
. D.
2202
.
Câu 50. Cho số các số phức
1 2
,
z z
thỏa mãn
1
1 1
z i
và
2
2 2
z i
. Số phức
z
thay đổi sao cho
1 1
1
z z i z
và
2 2
2
z z z i
là số thuần ảo. Giá trị nhỏ nhất của
3 2
z i
bằng
A.
11
5
. B.
2
. C.
2 2
. D.
13 1
.
____________________ HẾT ____________________
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 7
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C
C
C
D
B
A A
C
B
C
D
B B D
B
D
D
D
C
C
C
B B C
D
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
C
C
C
D
D
D
C
C
C
C
A
A
A
A
A
B
C
B B
C
D
D
A
A
C
LỜI GIẢI CHI TIẾT
Câu 1. Có bao nhiêu số tự nhiên có bốn chữ số khác nhau được tạo thành từ các chữ số
1,2,3, 4,5,6
?
A.
6
P
. B.
4
6
C
. C.
4
6
A
. D.
4
6
.
Lời giải
GVSB: Đồng Khoa Văn ; GVPB: Bùi Thị Bích Vân
Chọn C
Gọi số tự nhiên có 4 chữ số là
1 2 3 4
a a a a
.
Chọn 4 chữ số từ 6 chữ số đã cho và sắp xếp vào 4 vị trí từ
1
a
đến
4
a
có
4
6
A
cách.
Vậy có
4
6
A
số.
Câu 2. Trong không gian
Oxyz
, cho hai điểm
2;3;6
A
và
0;5; 2
B
. Trung điểm của đoạn thẳng
AB
có toạ độ là
A.
2;8;4
I
. B.
1;1; 4
I
. C.
1;4;2
I
. D.
2;2; 4
I
.
Lời giải
GVSB: Đồng Khoa Văn ; GVPB: Bùi Thị Bích Vân
Chọn C
Ta có trung điểm đoạn thẳng
AB
có toạ độ là
1;4;2
I
.
Câu 3. Trong mặt phẳng toạ độ
Oxy
, điểm biểu diễn số phức
4 3
z i
có toạ độ là
A.
3;4
. B.
4;3
. C.
4; 3
. D.
3;4
.
Lời giải
GVSB: Đồng Khoa Văn ; GVPB: Bùi Thị Bích Vân
Chọn C
Ta có điểm biểu diễn số phức
4 3
z i
có toạ độ là
4; 3
.
Câu 4. Cho hàm số
3
4 2
f x x
. Trong các khẳng định sau, khẳng định nào đúng ?
A.
2
d 12
f x x x C
. B.
4
d 3 2
f x x x x C
.
C.
4
1
d 2
3
f x x x x C
. D.
4
d 2
f x x x x C
.
Lời giải
GVSB: Đồng Khoa Văn ; GVPB: Bùi Thị Bích Vân
Chọn D
Ta có
3 4
d 4 2 d 2
f x x x x x x C
.
Câu 5. Tiệm cận ngang của đồ thị hàm số
2 1
2
x
y
x
là đường thẳng
A.
2
x
. B.
2
y
. C.
1
y
. D.
2
x
.
Lời giải
GVSB: Trần Ngọc; GVPB: Bùi Thị Bích Vân
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 8 TÀI LIỆU ÔN THI THPT QUỐC GIA
Chọn B
Tập xác định:
;2 2;D
 
Ta có:
2 1
lim 2
2
x
x
x

,
2 1
lim 2
2
x
x
x

.
Vậy đồ thị hàm số có đường tiệm cận ngang
2
y
.
Câu 6. Tập nghiệm
S
của bất phương trình
2
1
5
25
x
x
là
A.
;2
S 
. B.
;2
S 
. C.
2;S
. D.
1;S

.
Lời giải
GVSB: Trần Ngọc; GVPB: Bùi Thị Bích Vân
Chọn A
Ta có:
2
1
5
25
x
x
2 2
5 5
x x
2 2
x x
2
x
.
Vậy tập nghiệm
;2
S 
.
Câu 7. Thể tích
V
của khối nón có bán kính đáy bằng
3
cm
và chiều cao bằng
4
cm
là
A.
3
12
V cm
. B.
3
36
V cm
C.
2
36
V cm
. D.
2
12
V cm
Lời giải
GVSB: Trần Ngọc; GVPB: Bùi Thị Bích Vân
Chọn A
Ta có:
2 2 3
1 1
.3 .4 12
3 3
V r h cm
.
Câu 8. Một hình lập phương có độ dài cạnh bằng
2
a
. Thể tích khối lập phương đó là
A.
3
4
a
. B.
3
a
C.
3
8
a
. D.
3
2 2
a
Lời giải
GVSB: Trần Ngọc; GVPB: Bùi Thị Bích Vân
Chọn C
Ta có:
3
3
2 8
V a a
.
Câu 9. Cho hàm số
sin 3
f x x
. Trong các khẳng định sau, khẳng định nào đúng?
A.
1
cos3
3
f x dx x C
. B.
1
cos3
3
f x dx x C
.
C.
3cos3
f x dx x C
. D.
cos3
f x dx x C
.
Lời giải
GVSB: Đỗ Liên Phương; GVPB: Bùi Thị Bích Vân
Chọn B
1
sin 3 cos3
3
f x dx xdx x C
Câu 10. Một khối chóp có thể tích bằng
12
và diện tích đáy bằng
4
. Chiều cao cảu khối chóp đó bằng
A.
3
. B.
4
9
. C.
9
. D.
1
3
.
Lời giải
GVSB: Đỗ Liên Phương; GVPB: Bùi Thị Bích Vân
Chọn C
Ta có
1 3 36
. 9
3 4
V
V B h h
B
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 9
Câu 11. Trong không gian
Oxyz
, mặt cầu
2 2
2
: 1 3 16
S x y z
có bán kính bằng
A.
32
. B.
9
. C.
16
. D.
4
.
Lời giải
GVSB: Đỗ Liên Phương; GVPB: Bùi Thị Bích Vân
Chọn D
Ta có
16 4
R
Câu 12. Số phức liên hợp của số phức
4 2
z i
là
A.
4 2
z i
. B.
4 2
z i
. C.
2 4
z i
. D.
2 4
z i
.
Lời giải
GVSB: Đỗ Liên Phương; GVPB: Bùi Thị Bích Vân
Chọn B
4 2 4 2
z i z i
Câu 13. Nếu
4
3
d 2
f x x
và
4
5
d 6
g x x
thì
5
3
d
f x x
.
A.
12
. B.
4
. C.
8
. D.
8
.
Lời giải
GVSB: Hồng Hà Nguyễn; GVPB: Thanh Giang Đoàn
Chọn B
Ta có:
5
3
d
f x x
4 5
3 4
d d
f x x f x x
5 4 5 4 4
3 3 4 3 5
d d d d d 2 6 4
f x x f x x f x x f x x f x x
.
Câu 14. Đường cong trong hình vẽ bên là đồ thị hàm số nào sau đây
A.
3
3 2
y x x
. B.
4 2
2 2
y x x
. C.
3 2
3 2
y x x
. D.
3 2
3 2
y x x
.
Lời giải
GVSB: Hồng Hà Nguyễn; GVPB: Thanh Giang Đoàn
Chọn D
Từ đồ thị suy ra hàm số là bậc ba và hệ số
0
a
.
Xét
3 2 2
3 2 3 6
y x x y x x
,
2
0
0 3 6 0
2
x
y x x
x
.
Vậy
3 2
3 2
y x x
có đồ thị là hình vẽ trên.
Câu 15. Cho cấp số cộng
n
u
có
2
4
u
và
4
2
u
. Giá trị của
6
u
bằng.
A.
6
6
u
. B.
6
0
u
. C.
6
1
u
. D.
6
1
u
.
Lời giải
GVSB: Hồng Hà Nguyễn; GVPB: Thanh Giang Đoàn
Chọn B
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 10 TÀI LIỆU ÔN THI THPT QUỐC GIA
Ta có
2
4 1 2
2
2 3 2 2 2 1
2
u
u u d u d d
.
Mà
2 1 1 2
4 1 5
u u d u u d
, Suy ra
6 1
5 5 5 0
u u d
.
Câu 16. Nghiệm của phương trình
3
log 2
x
là
A.
6
x
. B.
8
x
. C.
5
x
. D.
9
x
.
Lời giải
GVSB: Hồng Hà Nguyễn; GVPB: Thanh Giang Đoàn
Chọn D
Ta có
2
3
log 2 3 9
x x
.
Câu 17. Cho hàm số
y f x
có bảng biến thiên như sau:
Mệnh đề nào dưới đây đúng?
A.
min 4
y
. B.
15
CD
y
. C.
max 5
y
. D.
4
CT
y
.
Lời giải
GVSB: Nguyễn Thuỳ Dung; GVPB: Đoàn Thanh Giang
Chọn D
Dựa vào bảng biến thiên, ta thấy
- Hàm số không có giá trị lớn nhất, giá trị nhỏ nhất.
- Hàm số có
4
CT
y
và
5
CD
y
.
Câu 18. Trong không gian
Oxyz
, mặt phẳng nào dưới đây không đi qua điểm
0;1; 1
M
?
A.
4
: 2 15 13 0
P x y z
. B.
2
:4 2 12 10 0
P x y z
.
C.
3
:2 3 12 15 0
P x y z
D.
1
:4 2 12 17 0
P x y z
.
Lời giải
GVSB: Nguyễn Thuỳ Dung; GVPB: Đoàn Thanh Giang
Chọn D
Thay toạ độ điểm
0;1; 1
M
vào phương trình
1
:4 2 12 17 0
P x y z
, ta có:
4.0 2.1 12. 1 17 3 0
.
Vậy điểm
0;1; 1
M
không nằm trong mặt phẳng
1
:4 2 12 17 0
P x y z
.
Câu 19. Cho hàm số
y f x
có bảng biến thiên như sau:
Mệnh đề nào sau đây sai?
A. Hàm số đồng biến trên khoảng
2;
.
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 11
B. Hàm số đồng biến trên khoảng
; 1

.
C. Hàm số đồng biến trên khoảng
1;
.
D. Hàm số nghịch biến trên khoảng
1;1
.
Lời giải
GVSB: Nguyễn Thuỳ Dung; GVPB: Đoàn Thanh Giang
Chọn C
Dựa vào bảng biến thiên, ta có:
- Hàm số đồng biến trên các khoảng
; 1

và
2;
.
- Hàm số nghịch biến trên khoảng
1;1
.
Vậy mệnh đề sai là: Hàm số đồng biến trên khoảng
1;
.
Câu 20. Tích phân
1
1
d
e
x
x
bằng
A.
1
e
. B.
ln 2
e
. C.
1
D.
ln 1
e
.
Lời giải
GVSB: Nguyễn Thuỳ Dung; GVPB: Đoàn Thanh Giang
Chọn C
1
1
1
d ln ln ln 1 1 0 1
e
e
x x e
x
.
Câu 21. Cho hai số phức
3 2
z i
và
4
w i
. Số phức
z w
bằng
A.
1
i
. B.
7
i
. C.
1 3
i
. D.
7 3
i
.
Lời giải
GVSB: Giang Sơn
Chọn C
Ta có
3 2 4 1 3
z w i i i
.
Câu 22. Cho hàm số
( )
y f x
có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị của tham số
m
để
phương trình
1
f x m
có 3 nghiệm phân biệt.
A.
1 3
m
. B.
1 4
m
. C.
2 5
m
. D.
0 4
m
.
Lời giải
GVSB: Giang Sơn GVPB: Ngocdiep Nguyen
Chọn A
Phương trình đưa về
1
f x m
Sử dụng tương giao giữa đường thẳng
1
y m
và đồ thị hàm số
( )
y f x
, điều kiện để phương
trình
1
f x m
có 3 nghiệm phân biệt là
0 1 4 1 3
m m
.
Câu 23. Đạo hàm của hàm số
3
log 3 1
y x
trên khoảng
1
;
3

là
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 12 TÀI LIỆU ÔN THI THPT QUỐC GIA
A.
3
3 1
x
. B.
3
3 1 ln3
x
. C.
3
3 1 ln
x x
. D.
3
1 ln 3
x
.
Lời giải
GVSB: Giang Sơn GVPB: Ngocdiep Nguyen
Chọn B
Ta có
3
3
log 3 1
(3 1)ln 3
y x y
x
.
Câu 24. Cho số thực
a
thỏa mãn
0 1
a
. Tính giá trị của biểu thức
5
2 3
3
15 4
. .
log
a
a a a
T
a
A.
8
T
. B.
11
T
. C.
8
3
T
. D.
17
15
T .
Lời giải
GVSB: Giang Sơn GVPB: Ngocdiep Nguyen
Chọn C
Ta có
1 3
2
8
5
2 3
3
3 5
3
4
15 4
15
. . 8
log log log
3
a a a
a a a a
T a
a
a
.
Câu 25. Nếu
2
1
2 3 d 4
x f x x
thì
6
3
d
3
x
f x
bằng
A.
4
. B.
1
. C.
1
3
. D.
1
.
Lời giải
GVSB: Hoàng Văn Tĩnh; GVPB: Ngocdiep Nguyen
Chọn D
Từ
2 2 2
1 1 1
2 3 d 4 2 d 3 d 4
x f x x x x f x x
2 2
1 1
1
3 3 d 4 d
3
f x x f x x
.
Đặt
1
dt= d d 3dt
3 3
x
t x x .
Đổi cận:
3 1
6 2
x t
x t
Do đó
6 2 2
3 1 1
d 3 dt 3 d 1
3
x
f x f t f x x
.
Câu 26. Gọi
,
M m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
1
1 2
x
f x
x
trên đoạn
2;5
. Tính
3
A M m
.
A.
10
3
A
. B.
1
A
. C.
1
A
. D.
5
3
A
.
Lời giải
GVSB: Hoàng Văn Tĩnh; GVPB: Ngocdiep Nguyen
Chọn C
Hàm số đã cho xác định và liên tục trên đoạn
2;5
.
Ta có
2
1
0, 2;5
2 1
f x x
x
f x
nghịch biến trên đoạn
2;5
Suy ra
2;5
1
max 2
3
M f x f
và
2;5
4
min 5
9
m f x f
.
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 13
Do đó
3 1A M m
.
Câu 27. Số phức
1
z là nghiệm có phần ảo dương của phương trình bậc hai
2
2 2 0z z
. Môđun của
số phức
1
2 i z
bằng
A.
3 2
. B.
10
. C. 10 . D.
18
.
Lời giải
GVSB: Hoàng Văn Tĩnh; GVPB: Ngocdiep Nguyen
Chọn C
1
2
2
1
2 2 0
1
z i
z z
z i
Với
1 1 1
1 2 3 2 10z i i z i i z
.
Câu 28. Cho hình chóp
.S ABCD
có đáy là hình chữ nhật với
, 5, 2AB a AC a SA a
. Biết
SB BC
và
SD CD
. Thể tích của khối chóp
.S BCD
là
A.
3
.
4
S BCD
V a
. B.
3
.
2
S BCD
V a
. C.
3
.
2
3
S BCD
a
V . D.
3
.
4
3
S BCD
a
V .
Lời giải
GVSB: Hoàng Văn Tĩnh; GVPB: Ngocdiep Nguyen
Chọn C
Ta có
BC AB
BC SAB BC SA
BC SB
(1)
CD AD
CD SAD CD SA
CD SD
(2)
Từ (1) và (2) suy ra
SA ABCD
.
Mặt khác
2 2 2 2
5 2BC AC AB a a a
.
2
1 1
. .2
2 2
BCD ABCD
S S a a a
.
Vậy
3
2
.
1 1 2
. .2 .
3 3 3
S BCD BCD
a
V SA S a a
.
Câu 29. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
A
, cạnh
AC a
, các cạnh bên
6
2
a
SA SB SC
. Tính góc tạo bởi mặt bên
( )SAB
và mặt phẳng đáy
( )ABC
.
A.
6
. B.
4
. C.
arctan 2
. D.
arctan 2
.
Lời giải
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 14 TÀI LIỆU ÔN THI THPT QUỐC GIA
GVSB: Trần Quốc Dũng; GVPB: Tuyet Trinh
Chọn D
Gọi
H
là trung điểm của
1 1
2
2 2
BC HA HB HC BC a
.
mà
6
2
a
SA SB SC
nên
SH BC
,
SHA SHB SHC
suy ra
SH ABC
.
Kẻ
, ,HI AB SAB ABC SI HI SIH
.
Ta có
1 1 1
2 2 2
HI AB AC a
(do tam giác
ABH
vuông cân tại
H
)
2 2
2 2
6 2
2 2
a a
SH SC HC a
.
Xét tam giác
SIH
vuông tại
H
, ta có
tan 2 arctan 2
1
2
SH a
SIH SIH
IH
a
.
Câu 30. Một hình trụ có bán kính đáy bằng
a
và có thiết diện qua trục là một hình vuông. Tính diện tích
xung quanh của hình trụ.
A.
2
2 a
. B.
2
3 a
. C.
2
a
. D.
2
4 a
.
Lời giải
GVSB: Trần Quốc Dũng; GVPB: Tuyet Trinh
Chọn D
Do thiết diện qua trục là một hình vuông nên
2 2l r a
.
2
2 2 . .2 4
xq
S rl a a a
.
Câu 31. Cho hàm số
( )f x
có đạo hàm
3 2
( ) ( 1) (2 3)f x x x x
. Hàm số đã cho có bao nhiêu điểm cực
trị?
A. 3. B. 1. C. 0. D. 2.
Lời giải
GVSB: Trần Quốc Dũng; GVPB: Tuyet Trinh
Chọn D
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 15
3 2
( ) ( 1) (2 3)
0
1
3
2
x
f x x x x x
x
(
3
2
x
là nghiệm kép).
Bảng xét dấu
f x
:
Vậy hàm số
( )
f x
có 2 điểm cực trị.
Câu 32. Tập nghiệm của bất phương trình
2
2
2
log 2 log
x x x
là
A.
1
;1
2
. B.
(0;1)
. C.
1
;1
2
. D.
0;1
.
Lời giải
GVSB: Trần Quốc Dũng; GVPB: Tuyet Trinh
Chọn C
Điều kiện
2
0
2 0
1
1
2
0
2
0
x
x x
x
x
x
x
.
2 2 2 2
2
2
log 2 log 2 0 0 1
x x x x x x x x x
.
So với điều kiện ta được tập nghiệm
1
;1
2
S
.
Câu 33. Trong không gian
Ox
yz
, vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua
gốc tọa độ và trọng tâm của tam giác
ABC
với
0;2;1 , 4; 2;1 , 2;3;4
A B C
?
A.
2
1; 2;2
u
. B.
1
1; 2; 1
u
. C.
3
2;1;2
u
. D.
4
4; 2;1
u
.
Lời giải
GVSB: Đinh Kiên Trung; GVPB: Tuyet Trinh
Chọn C
Trọng tâm của tam giác
ABC
là:
0 4 2 2 2 3 1 1 4
; ; 2;1;2
3 3 3
G
.
Vectơ chỉ phương của đường thẳng
OG
là:
2;1;2
OG
.
Câu 34. Hàm số nào dưới đây đồng biến trên
?
A.
2
1
1
y
x
. B.
3
y x x
. C.
3
x
y
. D.
ln
y x
.
Lời giải
GVSB: Đinh Kiên Trung; GVPB: Tuyet Trinh
Chọn C
Hàm số
3
x
y
có cơ số
3 1
a
nên hàm số
3
x
y
đồng biến trên
Câu 35. Cho hai số dương
,
a b
với
1
a
. Đặt
3
log
a
M b
. Tính
M
theo
log
a
N b
.
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 16 TÀI LIỆU ÔN THI THPT QUỐC GIA
A.
1
6
M N
. B.
3
2
M N
. C.
2
3
M N
. D.
M N
.
Lời giải
GVSB: Đinh Kiên Trung; GVPB: Tuyet Trinh
Chọn C
1
2
1
3
3
2 2
log log log
3 3
a
a
a
M b b b N
.
Câu 36. Có bao nhiêu số phức
z
thỏa mãn
3
z z
?
A.
5
. B.
4
. C.
2
. D.
7
.
Lời giải
GVSB: Đinh Kiên Trung; GVPB: Tuyet Trinh
Chọn A
Gọi số phức
z
có dạng
,z a bi a b
.
3
3 3 2 2 3
2 2
3 2
2 3
2 2
3 3
0
3 1
3
0
3
3 1.
z z a bi a bi a ab a b b i
a
a b
a ab a
b
a b b b
b a

TH1:
0 0
a b z
.
TH2:
2 2
0
0
1
3 1
a
a
b
b a
có hai số phức
z i
và
z i
.
TH3:
2 2
0
1
0
3 1
b
a
b
a b
có hai số phức
1
z
và
z
.
TH4:
2 2
2 2 2 2
2 2
3 1
4 0
3 1
a b
a b a b
b a
.
2 2
2
2 2
2 1
3 1
a b
a
b a
( vô lý).
Câu 37. Trong không gian
Oxyz
, cho bốn điểm
1; 2;1
A
,
0;1;3
B
,
1;2;3
C
,
2; 1;2
D
. Phương
trình đường thẳng qua điểm
A
và vuông góc với mặt phẳng
BCD
là
A.
2 3 5
1 1 4
x y z
. B.
1 2 1
1 3 4
x y z
.
C.
1 3
1 3 2
x y z
. D.
1 2 1
1 3 2
x y z
.
Lời giải
GVSB: Nguyễn Bảo; GVPB: Bùi Hà
Chọn A
Gọi
là đường thẳng cần tìm.
Do
BCD
nên vectơ chỉ phương của đường thẳng
trùng với vectơ pháp tuyến của mặt
phẳng
BCD
, tức là:
, 1;1; 4 1; 1;4
BCD
a n BC BD

.
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 17
Khi đó: Phương trình chính tắc của đường thẳng
là:
1 2 1
1 1 4
x y z
.
Xét điểm
2; 3;5
M
, ta thấy
M
.
Suy ra: Một phương trình chính tắc khác của đường thẳng
là
2 3 5
1 1 4
x y z
.
Câu 38. Cho tứ diện
ABCD
, gọi
M
là điểm sao cho
3 0
MA MB
. Mặt phẳng
P
đi qua
M
, song
song với
BC
và
AD
chia khối tứ diện đã cho thành hai khối đa diện. Gọi
1
V
là thể tích của khối
tứ diện chứa đỉnh
B
và
2
V
là thể tích khối tứ diện chứa đỉnh
A
. Tính tỉ số
1
2
V
V
.
A.
5
27
. B.
5
37
. C.
5
32
. D.
1
3
.
Lời giải
GVSB: Nguyễn Bảo; GVPB: Bùi Hà
Chọn A
Gọi
V
là thể tích khối chóp
ABCD
.
Trong mặt phẳng
ABC
, vẽ
//
MN BC
.
Trong mặt phẳng
ACD
, vẽ
//
NP AD
.
Trong mặt phẳng
BCD
, vẽ
//
PQ BC
.
Khi đó:
P MNPQ
.
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 18 TÀI LIỆU ÔN THI THPT QUỐC GIA
Ta có:
3
3 0
4
AM AN DP DQ
MA MB
AB AC DC DB
.
Ta có:
1 1 3
4 4 4
ABPC ABDP
CP CD V V V V
.
Xét:
9
9
64
. . 1
7 7
16
16 64
AMNP
AMNP
ABCP
BMNCP ABCP
V V
V
AM AN AP
V AB AC AP
V V V
.
Xét:
3
1
64
. . 2
15 45
16
16 64
MBQP
BMQP
BADP
AMQDP ABDP
V V
V
BM BQ BP
V BA BD BP
V V V
.
Từ
1
và
2
, ta suy ra:
1
1
2
2
5
5
32
27
27
32
V V
V
V
V V
.
Câu 39. Có bao nhiêu giá trị thực của tham số
m
thỏa mãn
3 2
0
4 2 d 3
m
x x x m
?
A.
2
. B.
1
. C.
4
. D.
3
.
Lời giải
GVSB: Nguyễn Bảo; GVPB: Bùi Hà
Chọn A
Xét:
3 2 4 2 2 4 2 2
0
0
1
4 2 d 3 3 3
1
m
m
m
x x x m x x m m m m
m
.
Suy ra: Có 2 giá trị
m
thỏa đề bài.
Câu 40. Có tất cả bao nhiêu cặp số nguyên
x
và
y
sao cho đẳng thức sau thỏa mãn
2
101
1
2021
log 4 2 2022 20 1.
y
x x
y
A.
1
. B.
3
. C.
0
. D.
2
.
Lời giải
GVSB: Vương Kenny; GVPB: Bùi Hà
Chọn A
+)
2
101
1 2 1
2021 2021
log 4 2 2022 20 1 101 log 4 2 2022 20 1
y
x x x x
y y y
1
2021
2
20 1
log 4 2 2022
101
x x
y
y
.
+) Xét hàm số
2
20 1
101
y
f y
y
,
Do
2
2 2
: 10 0 20 100 0 101 20 1
y y y y y y
nên
1
f y y
.
Suy ra
2
1 1
2021
log 4 2 2022 1 4 2 2022 2021 4 2.2 1 0 2 1 0
2 1 0 0
x x x x x x x
x
x
Với
2
2
20 1
0 1 20 100 0 10
101
y
x y y y
y
.
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 19
Vậy có 1 cặp số nguyên
,
x y
thỏa mãn yêu cầu.
Câu 41. Cho hình chóp đều
.
S ABCD
có cạnh đáy bằng
a
,
AC
cắt
BD
tại
O
. Khoảng cách giữa
SA
và
CD
bằng độ dài đoạn
SO
. Tính sin của góc giữa cạnh bên và mặt phẳng đáy.
A.
3
5
. B.
15
5
. C.
10
5
. D.
4
5
.
Lời giải
GVSB: Vương Kenny; GVPB: Bùi Hà
Chọn B
+) Ta có
//
//
AB CD
CD SAB
AB SAB
.
+)
//
; ; ; 2 ;
CD SAB
d CD SA d CD SAB d D SAB d O SAB
SA SAB
.
+) Gọi 𝐼 là trung điểm 𝐴𝐵, khi đó
SI
AB
. Kẻ
OH
SI
, khi đó
;
OH d O SAB
.
Suy ra
1 1
;
2 2
OH d CD SA SO
.
+) Tam giác 𝑆𝑂𝐼 vuông tại 𝑂, có 𝑂𝐻 là đường cao nên
2 2 2
1 1 1
OH OS OI
2 2 2 2 2
4 1 4 3 4 3
2
a
SO
SO SO a SO a
.
+) Góc giữa cạnh bên và mặt đáy bằng góc
SCO
.
2 2 2 2
3 3
3 15
2 2
sin
5
5 5
2 3
2
4 4
a a
SO SO
SCO
SC
a
OC SO a a
.
a
O
C
S
B
D
A
I
H
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 20 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 42. Cho hàm số
f x
, đồ thị của hàm số
( )
y f x
là đường cong như hình vẽ bên dưới.
Giá trị nhỏ nhất của hàm số
2 1 4 3
g x f x x
trên đoạn
1
1;
2
bằng
A.
2 5
f
. B.
1 1
f
. C.
1 3
f
. D.
0
f
.
Lời giải
GVSB: Vương Kenny; GVPB: Bùi Hà
Chọn C
+) Ta có
2 2 1 4
g x f x
.
+)
2 1 1
0 2 1 2 2 1 1
2 1 2
x
g x f x x
x
1
0
1
2
x
x
x
.
+)
1 1 1
g f
,
0 1 3
g f
;
1
2 5
2
g f
BBT:
Dựa vào BBT, hàm số
g x
đạt giá trị nhỏ nhất bằng
1 3
f
trên đoạn
1
1;
2
.
Câu 43. Trong không gian
Oxyz
, cho tứ diện
ABCD
với
3; 4;0
A
,
2;5;4
B
,
1;1;1
C
,
3;5;3
D
.
Viết phương trình mặt cầu ngoại tiếp tứ diện đó.
A.
2 2 2
1 3 2 9
x y z
. B.
2 2 2
1 3 2 9
x y z
.
C.
2 2 2
1 3 2 9
x y z
. D.
2 2 2
1 3 2 9
x y z
.
Lời giải
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 21
GVSB: Hien Nguyen ; GVPB: Nguyễn Xuân Hè
Chọn B
Gọi phương trình mặt cầu
2 2 2
: 2 2 2 0
S x y z ax by cz d
2 2 2
0
a b c d
.
Vì mặt cầu đi qua 4 điểm nên:
25 6 8 0
45 4 10 8 0
3 2 2 2 0
43 6 10 6
a b d
a b c d
a b c d
a b c d
6 8 25
4 10 8 45
2 2 2 3
6 10 6 43
a b d
a b c d
a b c d
a b c d
1
3
2
5
a
b
c
d
.
Suy ra tâm
1;3;2
I
bán kính
2 2 2
1 3 2 5 3
R
.
Vậy phương trình mặt cầu
2 2 2
1 3 2 9
x y z
.
Câu 44. Cho hình chóp .
S ABCD
có đáy là hình vuông cạnh
a
. Tam giác
SAB
đều và nằm trong mặt
phẳng vuông góc với đáy. Tính diện tích mặt cầu ngoại tiếp hình chóp đã cho.
A.
3
4
3
a
B.
2
7
3
a
C.
2
7
9
a
D.
2
4
a
Lời giải
GVSB: Hien Nguyen ; GVPB: Nguyễn Xuân Hè
Chọn B
Gọi SH là đường cao của tam giác
SAB
. Vì SAB là tam giác đều và nằm trong mặt phẳng vuông
góc với mặt đáy nên SH là đường cao của hình chóp .
S ABCD
.
Gọi O là tâm của hình vuông ABCD, từ O dựng
( )
Ox ABCD
.
Từ trọng tâm G của tam giác SAB dựng
( )
Gy SAB
.
Gọi
I Ox Gy
.
Vì
I Ox
, mà
( )
Ox ABCD
, O là tâm hình vuông ABCD nên I cách đều A, B, C, D (1).
Mặt khác G là trọng tâm của tam giác đều SAB,
I Gy
, mà
( )
Gy SAB
nên I cách đều S, A, B
(2).
Từ (1) và (2) suy ra I cách đều
, , , ,
S A B C D
. Nên I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD,
bán kính R=IB.
Vì
( )
OI ABCD
,
( )
SH ABCD
nên
/ /
OI GH
vì
G SH
(3)
Mặt khác
( )
Gy SAB
,
I Gy
mà
( )
OH SAB
(vì
,
OH AB OH SH
) nên
/ / O
GI H
(4)
Từ (3) và (4) suy ra GHOI là hình bình hành
1 1 3 3
. .
3 3 2 6
a a
OI GH SH
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 22 TÀI LIỆU ÔN THI THPT QUỐC GIA
Vì
( )
OI ABCD OI OB BOI
vuông tại B
Xét
BOI
vuông tại B ta có
2 2
2 2 2 2
3 2 7 21
6 2 12 6
a a
IB IO OB a IB a R
.
Diện tích mặt cầu là
2 2
7
4 .
3
S R a
Câu 45. Gọi
A
là tập tất cả các số tự nhiên có
6
chữ số khác nhau, lấy ngẫu nhiên một số từ
A
. Tính
xác suất để lấy được một số luôn có mặt
3
chữ số
0
,
1
,
2
và giữa hai chữ số
0
và
1
có đúng
2
chữ số.
A.
1
15
. B.
7
162
. C.
5
162
. D.
7
405
.
Lời giải
GVSB: Trần Xuân Thiện; GVPB: Nguyễn Xuân Hè
Chọn C
Số phần tử của không gian mẫu là
9.9.8.7.6.5 136080
n
.
Gọi số có
6
chữ số khác nhau có dạng
abcdef
trong đó luôn có mặt
3
chữ số
0
,
1
,
2
.
Vì giữa hai chữ số
0
và
1
có đúng
2
chữ số nên khi đó cặp số
0
và
1
có các vị trí
1, 4
,
2,5
,
3,6
.
Trường hợp 1:
0
và
1
đứng vị trí
1, 4
.
Khi đó chọn
3
số trong
7
số còn lại:
4
7
C
.
Xếp số
3
và
3
số được chọn vào
4
vị trí còn lại có
4!
cách.
Suy ra có
4
7
.4!
C
số.
Trường hợp 2:
0
và
1
đứng vị trí
2,5
.
Khi đó chọn
3
số trong
7
số còn lại:
3
7
C
.
Xếp số
3
và
3
số được chọn vào
4
vị trí còn lại có
4!
cách.
Suy ra có
3
7
2!. .4!
C
số.
Trường hợp 3:
0
và
1
đứng vị trí
3,6
.
Khi đó chọn
3
số trong
7
số còn lại:
3
7
C
.
Xếp số
3
và
3
số được chọn vào
4
vị trí còn lại có
4!
cách.
Suy ra có
3
7
.4!
C
số.
Vậy số các số thỏa mãn yêu cầu là
4 3
7 7
.4! 2.2!. .4!
n A C C
.
Vậy xác suất để lấy được số thỏa mãn là
4 3
7 7
.4! 2.2!. .4!
5
136080 162
n A
C C
P A
n
.
Câu 46. Cho hàm số bậc bốn
y f x
có đồ thị
C
như hình vẽ bên. Biết hàm số
y f x
đạt cực trị
tại các điểm
1
x
,
2
x
,
3
x
thỏa mãn
3 1
2
x x
,
1 3 2
2
0
3
f x f x f x
và
C
nhận đường
thẳng
2
:
d x x
làm trục đối xứng. Gọi
1
S
,
2
S
,
3
S
,
4
S
là diện tích của các miền hình phẳng
được đánh dấu như hình bên.
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 23
Tỉ số
3 4
1 2
S S
S S
gần kết quả nào nhất?
A.
1.62
. B.
1.64
. C.
1.68
. D.
1.66
.
Lời giải
GVSB: Trần Xuân Thiện; GVPB: Nguyễn Xuân Hè
Chọn D
Kết quả bài toán không đổi khi ta tịnh tiến đồ thị hàm số sang bên trái sao cho đường thẳng
2
:
d x x
trùng với trục tung, khi đó đồ thị
C
là đồ thị của hàm số trùng phương
y g x
có
ba điểm cực trị
1
1
x
,
2
0
x
,
3
1
x
.
Suy ra
4 2
2
y g x k x x c
với
0
k
.
Mặt khác
1 3 2
2 2 3
0 2 2 0
3 3 4
f x f x f x k c c c k
.
Suy ra
4 2
3
2
4
y g x k x x k
.
Khi đó
1
4 2
1 2
0
3 28 2 17
2 d
4 60
S S k x x x k
.
Ta lại có
1 2 3 4
0 1 .1
g g k S S S S k k
.
Suy ra
3 4
3 4
1 2
28 2 17 77 28 2 77 28 2
1.66
60 60
28 2 17
S S
S S k k k
S S
Câu 47. Cho hàm số
( )
f x
có đạo hàm liên tục trên
, đồ thị hàm số
'( )
y f x
có đúng bốn điểm chung
với trung hoành như hình vẽ dưới.
Có bao nhiêu giá trị nguyên của
m
để hàm số
3
3 2021
y f x x m
có
11
điểm cực trị.
A.
0
. B.
2
. C.
5
. D.
1
.
Lời giải
GVSB: Lê Duy; GVPB:
Chọn D
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 24 TÀI LIỆU ÔN THI THPT QUỐC GIA
+ Vì hàm số
3
3 2021
y f x x m
là hàm số chẵn nên để hàm số có 11 điểm cực trị thì
hàm số
3
( ) 3 2021 , 0
g x f x x m x
có đúng 5 điểm cực trị.
+ Ta có :
+ Sử dụng phương pháp ghép trục ta có bảng biến thiên của
3
3 , 0
y f x x x
x
0 a 1 b c d e
3
3
u x x
0 -1 -2 -1 1 2 4
( )
f u
+ Vì đồ thị hàm số
3
( ) 3 2021
g x f x x m
thu được bằng cách tịnh tiến đồ thị hàm số
3
( )
y f x x
theo vector
2021;0
v m
nên để hàm số
3
( ) 3 2021 , 0
g x f x x m x
có đúng 5 điểm cực trị thì điều kiện là
2021 0
2021 2021, (0;1) 2021
2021 0
a m
a m a a m
a m
Vậy có một giá trị của m.
Câu 48. Trong không gian
,
Oxyz
cho mặt phẳng
( ) : 2 0,
P x y z
đường thẳng
1 1 2
( ) :
1 1 1
x y z
d
và hai điểm
1 3
; 1; , 1; 1;1 .
2 2
B C
Gọi
A
là giao điểm của
( )
d
và
( )
P
,
( )
S
là điểm di động trên
( ),( )
d S A
. Gọi
,
H K
lần lượt là hình chiếu vuông góc của
A
trên các đường thẳng
SB
và
SC
,
( )
là giao tuyến của hai mặt phẳng
( )
AHK
và
( ), ( )
P M
. Giá trị nhỏ nhất của
MB MC
là
A.
14
2
. B.
6 2 2
2
. C.
7
2
. D.
7
2
.
Lời giải
GVSB: Lê Duy; GVPB:
Chọn A
+ Toạ độ của A là:
1; 1;2
A
; Vector pháp tuyến của (P) là:
( )
1;1; 1
P
n
; vector chỉ phương
của (d) là:
(d)
1;1; 1
u
nên
( ) (P)
d
và
, ( ) ( )
B C P SA ABC
+ Ta có:
2
, 2
2
AB AC
và
2 2 2
2
2 2
2 ,
2
HS SA KS SA SA
SA
HB KC
AB AC
+ Gọi
D HK BC
. Áp dụng định lý Menelaus cho tam giác SBC với K, H, D thẳng hàng, ta
có:
1
. . 1 4
4
HS KC DB DB
DB DC
HB KS DC DC
(vì D nằm ngoài BC)
1 2 5 2 1 1 1
; ; ; ; 2; 1;1
3 3 3 3 3 3 3
D AD
. Do đó giao tuyến của hai mặt phẳng
( )
AHK
và
( )
P
là đường thẳng AD có phương trình
1 2
( ): 1
2
x t
AD y t
z t
+ Ta thấy B, C nằm cùng một phía so với AD. Gọi
'
C
là điểm đối xứng của C qua AD thì
' 1;0;3
C
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 25
Vậy
14
min '
2
MB MC BC
.
Câu 49. Có bao nhiêu số nguyên dương
m
để phương trình
1 ln 1
x
e m mx
có hai nghiệm phân biệt
trên đoạn
10;10
?
A.
2201
. B.
2020
. C.
2021
. D.
2202
.
Lời giải
Chọn A
Điều kiện
1 0
mx
.
Ta có
1 ln 1
x
e m mx
1 ln 1
x
e mx mx m mx
ln 1
ln 1
mx
x
e mx e m mx
(1).
Xét hàm số
,
t
f t e mt t
.
Có
0, , 0
t
f t e m t m
. Suy ra hàm
f t
đồng biến trên
.
Từ (1) ta được
ln 1 ln 1 1
x
f x f mx x mx e mx
(2).
Ta thấy (2) luôn có một nghiệm
0 10;10
x
. Do đó ta cần tìm các giá trị của
m
để (2) có
đúng một nghiệm
0, 10;10
x x
.
Với
0
x
thì (2)
1
x
e
m
x
.
Xét hàm
1
, 10;10 \ 0
x
e
g x x
x
.
Ta có
2
1
x x
xe e
g x
x
.
Đặt
1,
x x
h x xe e x
.
Có
, 0 0
x
h x xe h x x
.
Ta thấy
lim , lim 1, 0 0
x x
h x h x h
 

.
Bảng biến thiên của hàm
h x
như sau
Từ bảng biến thiên suy ra
0, 0, 0
h x x g x x
.
Ta có
0 0
lim 1, lim 1
x x
g x g x
.
Bảng biến thiên của hàm
y g x
với
10;10 \ 0
x
như sau
x
0
h x
h x

0

1
0

ĐỀ THI THỬ: 2020-2021 NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Trang 26 TÀI LIỆU ÔN THI THPT QUỐC GIA
Từ bảng biến thiên suy ra (2) có đúng một nghiệm
0, 10;10
x x
10 10
1 1
, \ 1
10 10
e e
m
.
Do
m
nguyên dương nên
2,3,4,...,2202
m
. Vậy có
2201
giá trị của
m
thỏa mãn yêu cầu
bài toán.
Câu 50. Cho số các số phức
1 2
,
z z
thỏa mãn
1
1 1
z i
và
2
2 2
z i
. Số phức
z
thay đổi sao cho
1 1
1
z z i z
và
2 2
2
z z z i
là số thuần ảo. Giá trị nhỏ nhất của
3 2
z i
bằng
A.
11
5
. B.
2
. C.
2 2
. D.
13 1
.
Lời giải
Chọn C
Đặt
2
w 2 w 2
z i
.
Ta có
2 2 2 2 2
2 2 w
z z z i z z z i z z
là số thuần ảo
nên
2
w ,z z ki k
.
Mặt khác
2
2
4 w
w.w w 4 w
w 4
k
z z i
mà
2
w+2
z i
w w
w 2 w 2 1
4 4
k k
z i i i
.
Khi đó
w
3 2 w 1 1
4
k
P z i i
2
1 w 1 1 w 1 w 1 2 2 1 2 2 2
4 4 4 16
ki ki ki k
i i
.
Dấu bằng có chẳng hạn khi
2
2 2 2 1
z z i
và
1
z
là số phức thỏa mãn
1
1 1
z i
và
1 1
1
z z i z
là số thuần ảo.
Vậy giá trị nhỏ nhất của
3 2
z i
bằng
2 2
.
____________________ HẾT ____________________
'
y
x
y
10
0
10
1
10
1
10
e
1
10
1
10
e
| 1/35

Tài liệu khác của Toán

Preview text:

SỞ GD & ĐT QUẢNG NGÃI
THI THỬ TỐT NGHIỆP THPT NĂM 2021 LẦN 1
TRƯỜNG THPT CHUYÊN LÊ KHIẾT NĂM HỌC 2020 - 2021 MÔN TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài : 90 Phút; (Không kể giao đề) (Đề có 7 trang) (Đề có 50 câu)
Họ tên : .........................................................Số báo danh : ..............Lớp……. Mã đề 144
Câu 1: Có bao nhiêu số tự nhiên có bốn chữ số khác nhau được tạo thành từ các chữ số 1, 2,3, 4,5,6 ? A. P . B. 4 C . C. 4 A . D. 4 6 . 6 6 6
Câu 2: Trong không gian Oxyz , cho hai điểm (
A 2;3; 6) và B(0;5;  2) . Trung điểm của đoạn
thẳng AB có tọa độ là A. I (2;8; 4) . B. I (1;1;  4) . C. I (1; 4;2) . D. I (2;2;  4) .
Câu 3: Trong mặt phẳng tọa độ Oxy , điểm biểu diễn số phức z  4  3i có tọa độ là A.  3  ;4. B. 4;3. C. 4; 3  . D. 3;4. Câu 4: Cho hàm số 3
f (x)  4x  2 . Trong các khẳng định sau, khẳng định nào đúng? A. 2 f (x) dx  12x  C  . B. 4 f (x) dx  3x  2x  C  . C. 1 4 f (x) dx  x  2x  C  . D. 4 f (x) dx  x  2x  C  . 3 
Câu 5: Tiệm cận ngang của đồ thị hàm số 2x 1 y  là đường thẳng : 2  x A. x  2 . B. y  2 . C. y  1. D. x  2  .  x Câu 6: Tập nghiệm x  1  S của bất phương trình 2 5    là  25  A. S   ;   2 . B. S   ;  2. C. S  2;. D. S  1;.
Câu 7: Thể tích V của khối nón có bán kính đáy bằng 3cm và chiều cao bằng 4 cm là A. V    3 12 cm  . B. V    3 36 cm . C. V    2 36 cm . D. V    2 12 cm .
Câu 8: Một hình lập phương có độ dài cạnh bằng 2a . Thể tích khối lập phương đó là A. 3 4a . B. 3 a . C. 3 8a . D. 3 2a 2 .
Câu 9: Cho hàm số f (x)  sin 3x . Trong các khẳng định sau, khẳng định nào đúng? A. 1 f (x) dx  cos 3x  C  . B. 1 f (x) dx   cos 3x  C  . 3 3 C. f (x) dx  3cos3x  C  .
D. f (x) dx  3cos3x  C  .
Câu 10: Một khối chóp có thể tích bằng 12 và diện tích đáy bằng 4. Chiều cao của khối chóp đó bằng A. 3. B. 4 . C. 9 . D. 1 . 9 3
Câu 11: Trong không gian Oxyz , mặt cầu 2 2 2
(S) : (x 1)  y  (z  3) 16 có bán kính bằng Trang 1/7 - Mã đề 144 A. 32. B. 9. C. 16 . D. 4.
Câu 12: Số phức liên hợp của số phức z  4  2i là A. z  4   2i . B. z  4  2i . C. z  2   4i . D. z  2  4i . 4 4 5 Câu 13: Nếu f  xdx  2 và f
 xdx  6 thì f xdx  3 5 3 A. 12 . B. 4  . C. 8  . D. 8 .
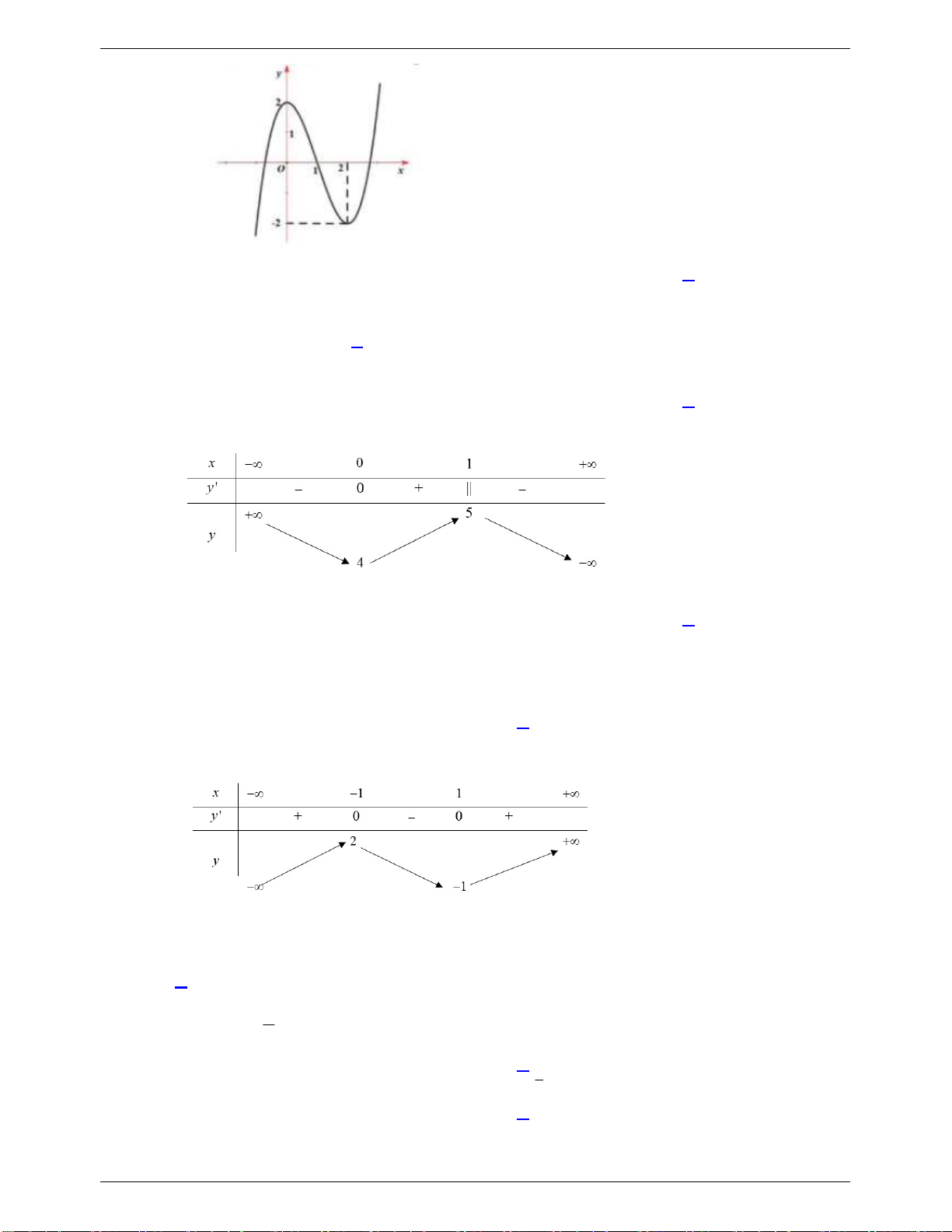
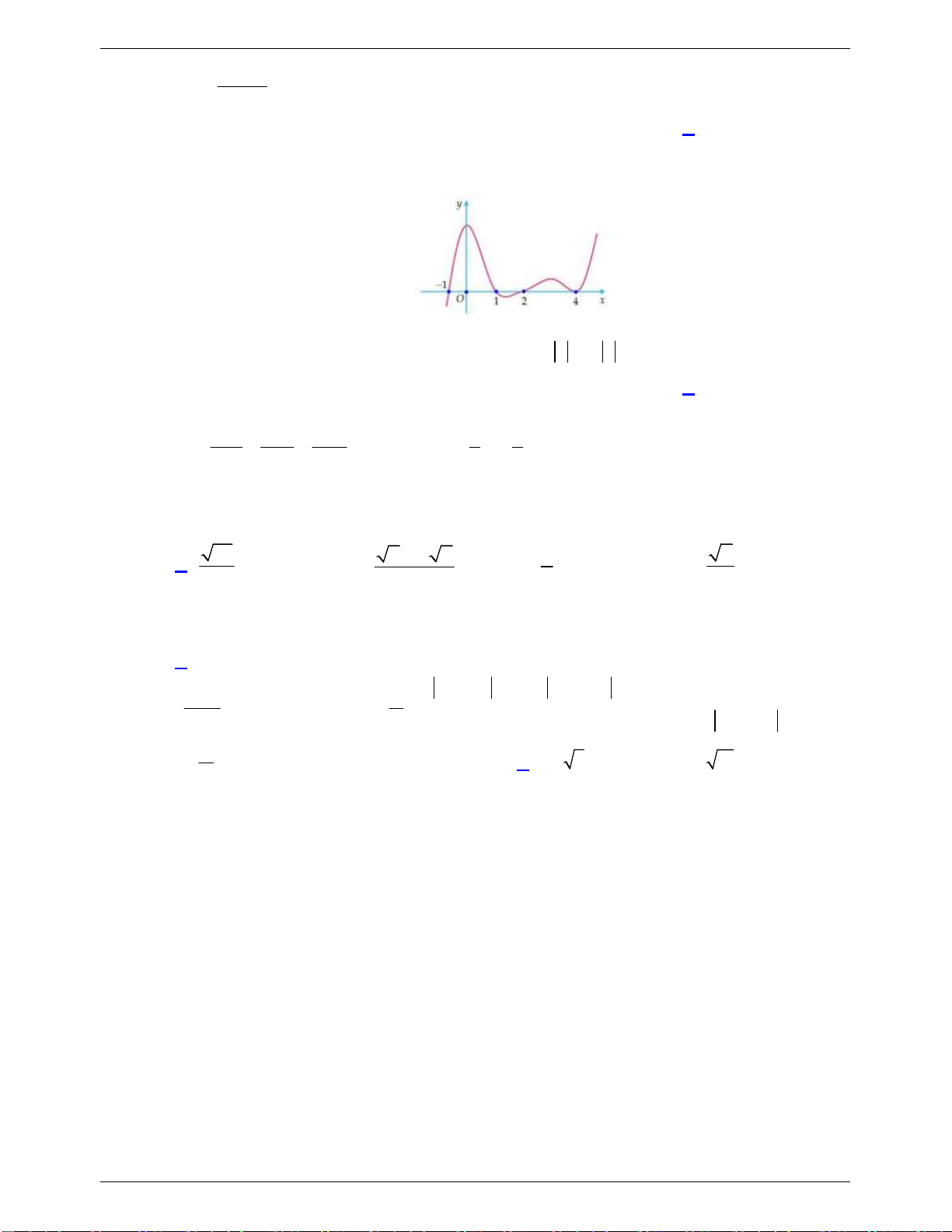
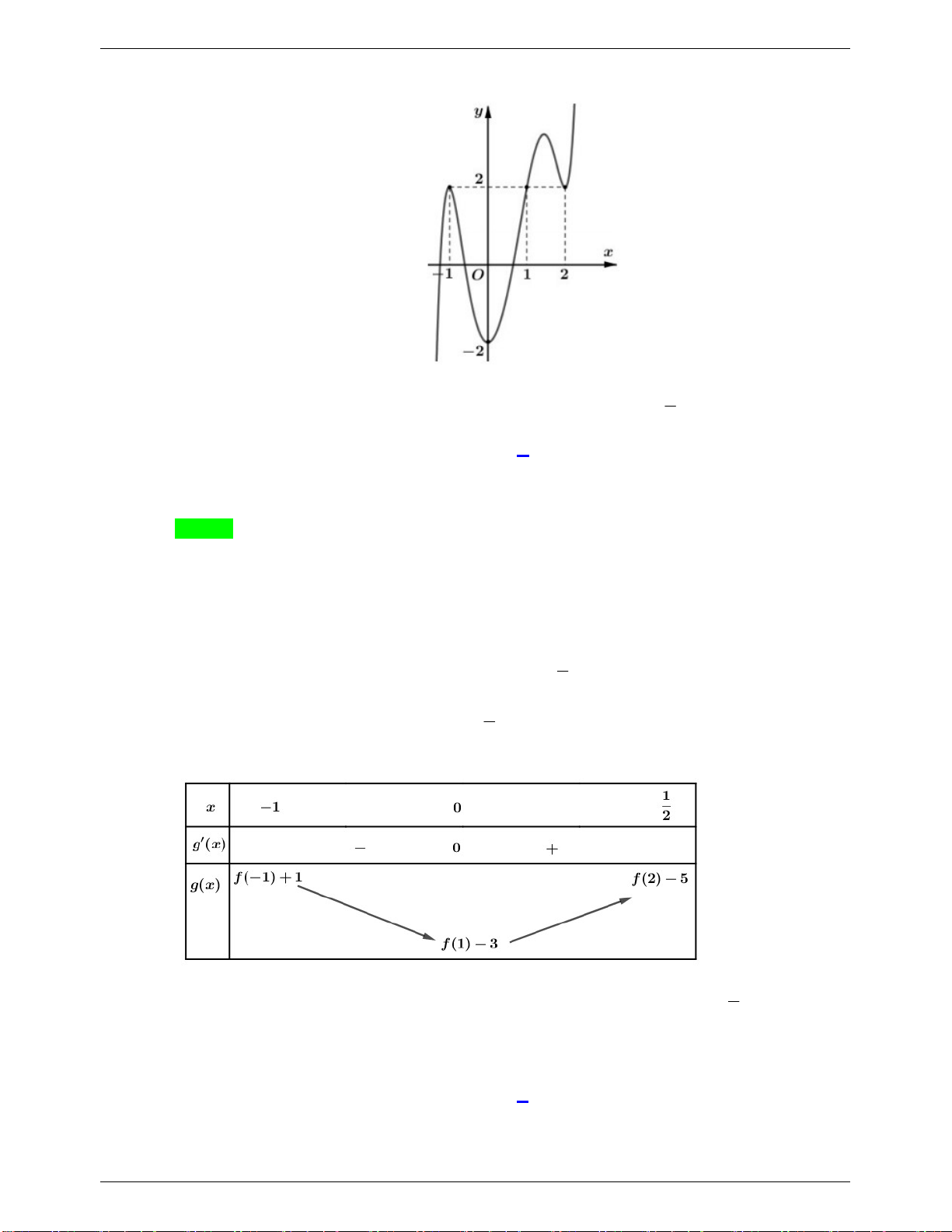
Câu 14: Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số dưới đây? A. 3 y  x 3x  2. B. 4 2 y  x  2x  2. C. 3 2 y  x  3x  2. D. 3 2 y  x  3x  2.
Câu 15: Cho cấp số cộng (u ) có u  4và u  2. Giá trị của u bằng n 2 4 6 A. u  6 . B. u  0 . C. u  1  . D. u 1. 6 6 6 6
Câu 16: Nghiệm của phương trình log3 x  2 là A. x  6 . B. x  8. C. x  5. D. x  9.
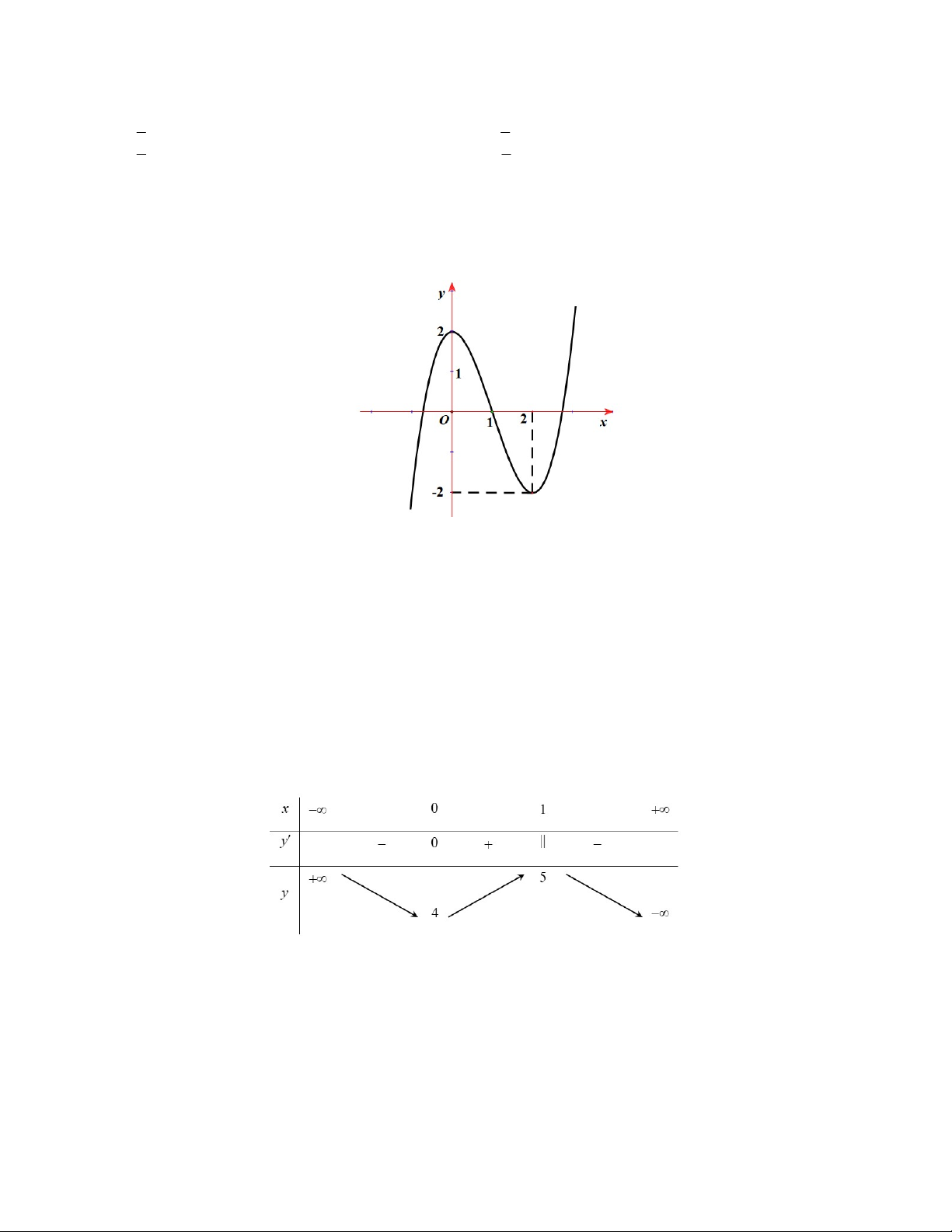
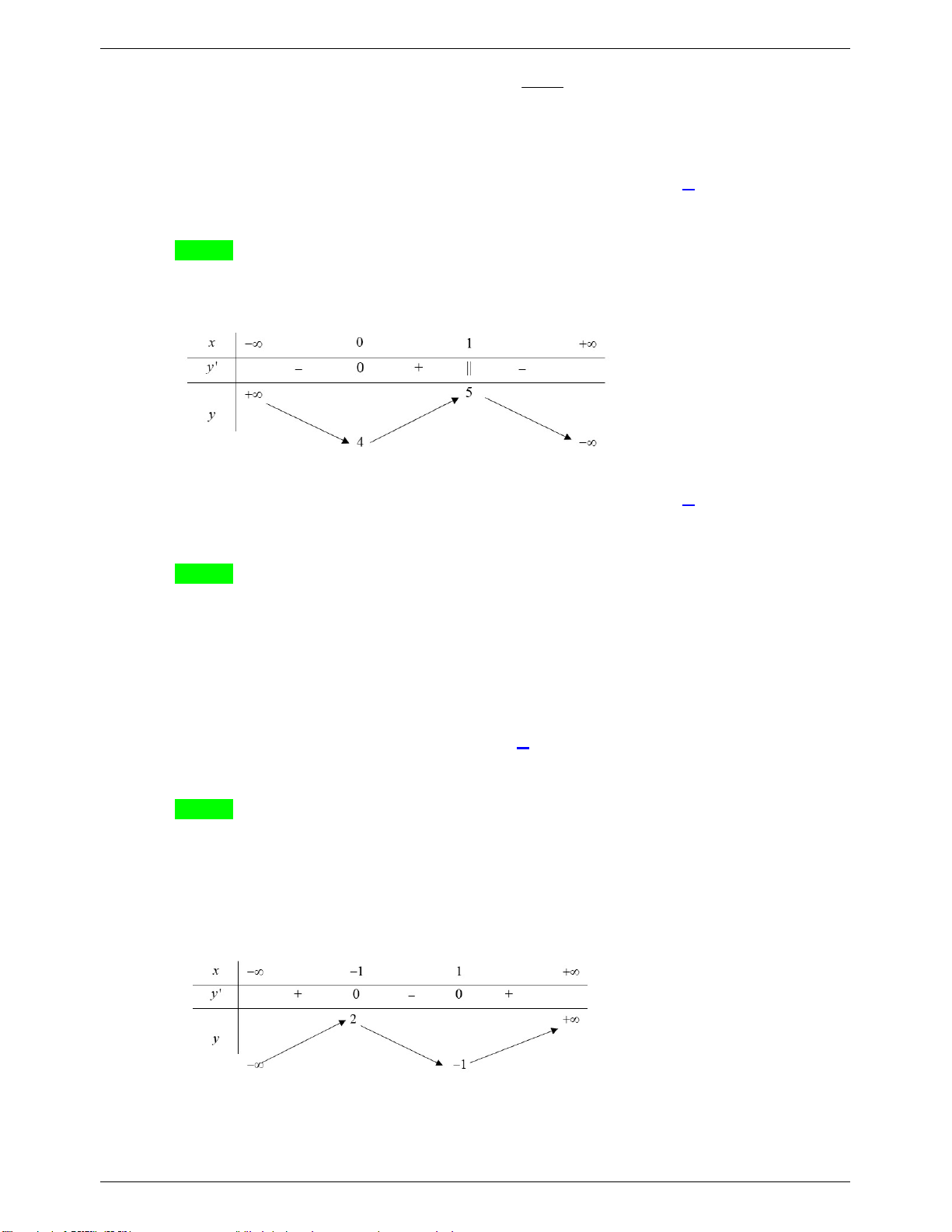
Câu 17: Cho hàm số y  f  x có bảng biến thiên như sau :
Mệnh đề nào dưới đây đúng? A. min y  4 . B. y 15 . C. max y  5 . D. y  4 .  C Ð  CT
Câu 18: Trong không gian Oxyz , mặt phẳng nào dưới đây không đi qua điểm M (0;1; 1) ?
A. (P ) : x  2y 15z 13  0 .
B. (P ) : 4x  2y 12z 10  0 . 4 2
C. (P ) : 2x 3y 12z 15  0 .
D. (P) : 4x  2y 12z 17  0 . 3 1
Câu 19: Cho hàm số y  f  x có bảng biến thiên như sau: Trang 2/7 - Mã đề 144
Mệnh đề nào sau đây sai ?
A. Hàm số đồng biến trên khoảng 2; .
B. Hàm số đồng biến trên khoảng  ;    1 .
C. Hàm số đồng biến trên khoảng  1  ;.
D. Hàm số nghịch biến trên khoảng  1  ;  1 . e Câu 20: Tích phân 1 dx  bằng x 1 A. e – 1 . B. ln 2e . C. 1. D. ln e 1
Câu 21: Cho hai số phức z  3  2i và w  4  i . Số phức z  w bằng A. 1 i . B. 7   i . C. 1 3i . D. 7   3i .
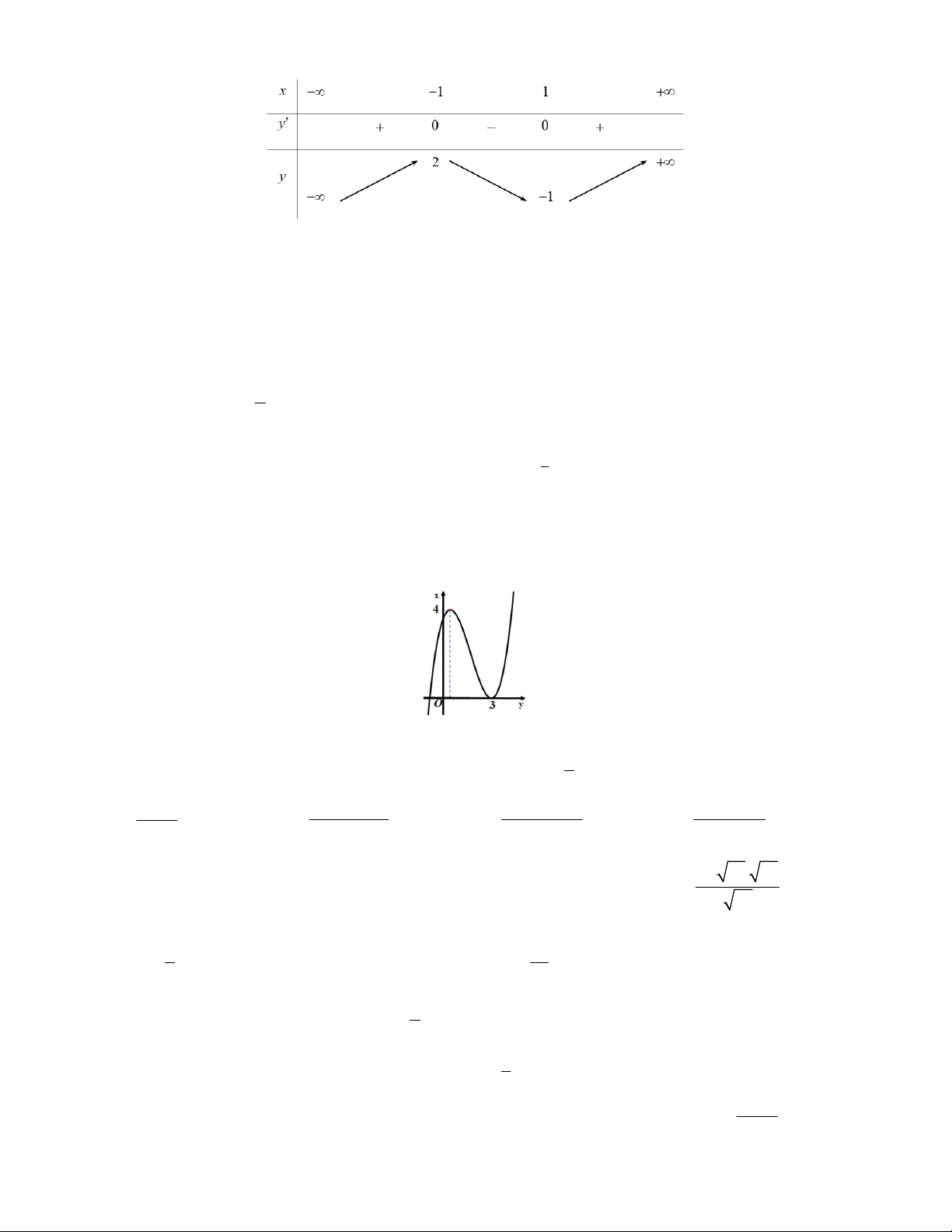
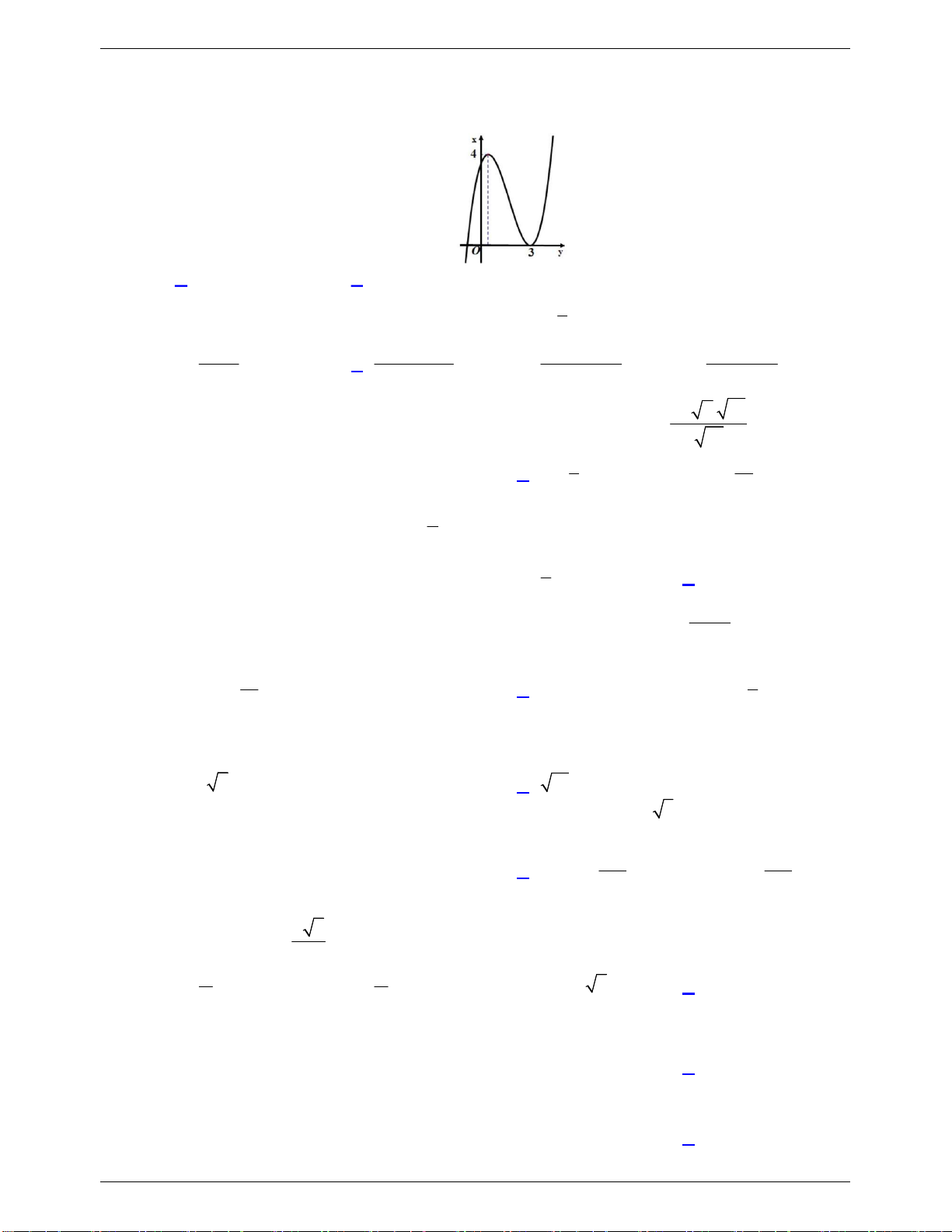
Câu 22: Cho hàm số y  f  x có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị của tham số m
để phương trình f x 1 m có 3 nghiệm phân biệt. A. 1   m  3. B. 1 m  4 . C. 2   m  5. D. 0  m  4 .  1
Câu 23: Đạo hàm của hàm số y  log 3x 1   ;  là 3   trên khoảng    3  3 1 3 A. 3 . B. . C. . D. . 3x 1 3x  1ln3 3x   1 ln x x  1ln3 2 3 5 3  a . a . a 
Câu 24: Cho số thực a thỏa mãn 0  a  1. Tính giá trị của biểu thức T  log   . a  15 4 a    A. T  8. B. T  11. C. 8 T  . D. 17 T  . 3 15 2 6 Câu 25: Nếu  x  (2x  3 f (x))dx  4  thì f dx    bằng  3  1 3 1 A. 4. B. 1. C. . D. 1  . 3  Câu 26: Gọi x
M ,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 1 f (x)  trên đoạn 1 2x Trang 3/7 - Mã đề 144
2; 5. Tính AM 3m. A. 10 A   . B. A  1  . C. A  1. D. 5 A   . 3 3
Câu 27: Số phức z là nghiệm có phần ảo dương của phương trình bậc hai 2
z  2z  2  0 . Môđun 1
của số phức (2  i)z bằng 1 A. 3 2. B. 10. C. 10. D. 18 .
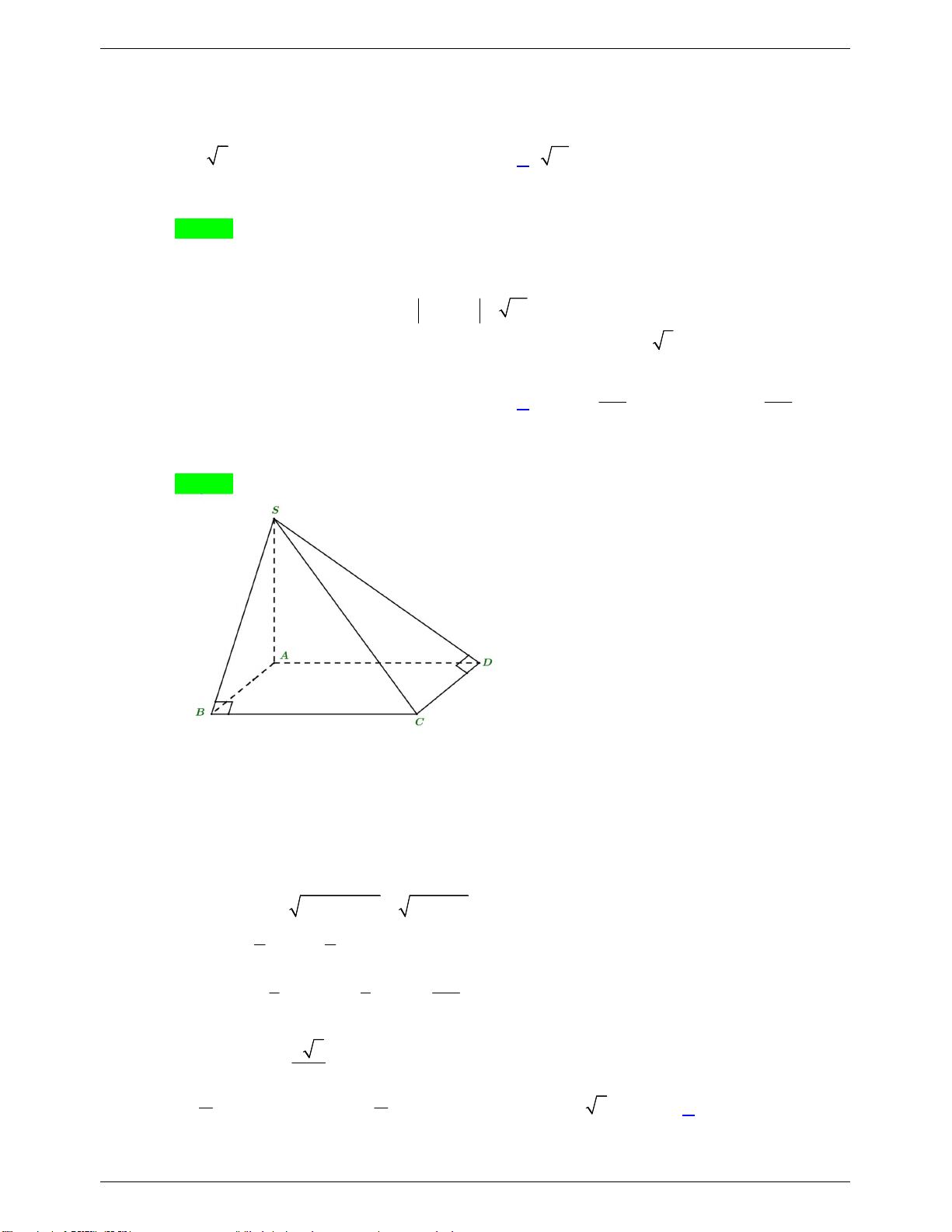
Câu 28: Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB  a, AC  a 5 , SA  2a . Biết
SB  BC và SD  CD . Thể tích của khối chóp S.BCD là A. 3 V  4a . V  2a . S .BCD B. 3 S.BCD 3 2a 3 4a C. V  . D. V  . S.BCD 3 S.BCD 3
Câu 29: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , cạnh AC  a , các cạnh bên a 6 SA  SB  SC 
. Tính góc tạo bởi mặt bên SAB và mặt phẳng đáy  ABC. 2   A. . B. . 6 4 C. arctan 2 . D. arctan 2.
Câu 30: Một hình trụ có bán kính đáy bằng a và có thiết diện qua trục là một hình vuông. Tính diện
tích xung quanh của hình trụ. A. 2 2 a . B. 2 3 a . C. 2  a . D. 2 4 a .
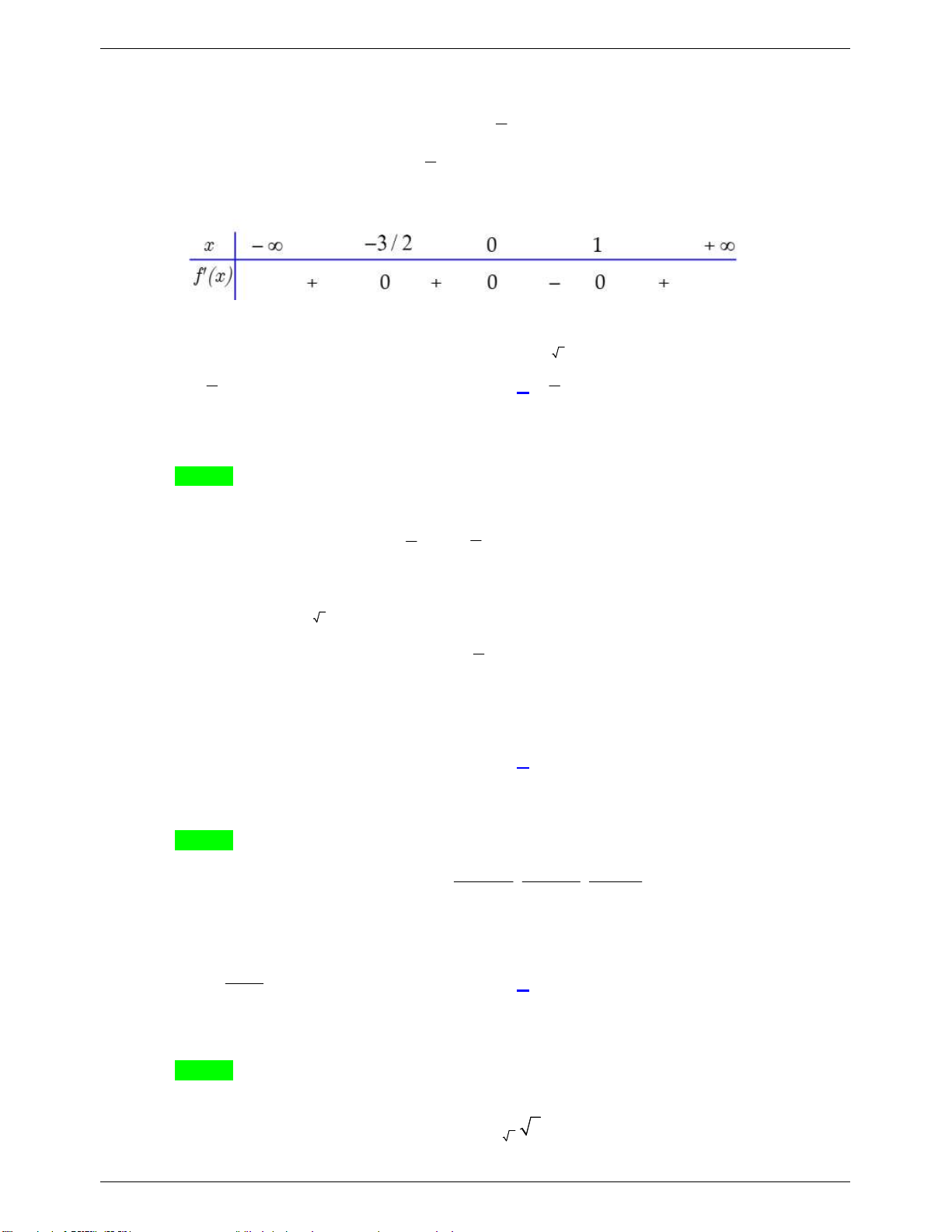
Câu 31: Cho hàm số f  x có đạo hàm f x  xx  3  x  2 1 2
3 . Hàm số đã cho có bao nhiêu điểm cực trị? A. 3. B. 1 C. 0. D. 2.
Câu 32: Tập nghiệm của bất phương trình 2 log (2x  x)  log x là 2 2 1  1 A.   ;1 .  B. (0;1). C. ;1 .  D. 0;  1 . 2    2   
Câu 33: Trong không gian Oxyz , vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi
qua gốc tọa độ và trọng tâm tam giác ABC với (
A 0; 2;1), B(4; 2;1),C(2;3; 4) ?     A. u  (1; 2  ;2) B. u  (1; 2  ; 1  ) C. u  (2;1;2) D. u  (4; 2  ;1) 2 1 3 4
Câu 34: Hàm số nào dưới đây đồng biến trên  ? A. 1 y  . B. 3 y  x  x . C. 3 .x y  D. y  ln . x 2 x 1
Câu 35: Cho hai số dương a,b với a  1. Đặt 3 M  log
b . Tính M theo N  log b . a a A. 1 M  N . B. 3 M  N. C. 2 M  N. D. M  N . 6 2 3
Câu 36: Có bao nhiêu số phức z thỏa mãn 3 z  z ? A. 5. B. 4. C. 2. D. 7. Trang 4/7 - Mã đề 144
Câu 37: Trong không gian Oxyz , cho 4 điểm A1;– 2;  1 , B0;1; 
3 ,C(1; 2;3) , D(2; 1; 2) . Phương
trình đường thẳng qua điểm A và vuông góc với mặt phẳng (BCD) là       A. x 2 y 3 z 5   . B. x 1 y 2 z 1   . 1 1 4 1 3 4      C. x y 1 z 3 x y z   . D. 1 2 1   . 1 3 2 1 3 2   
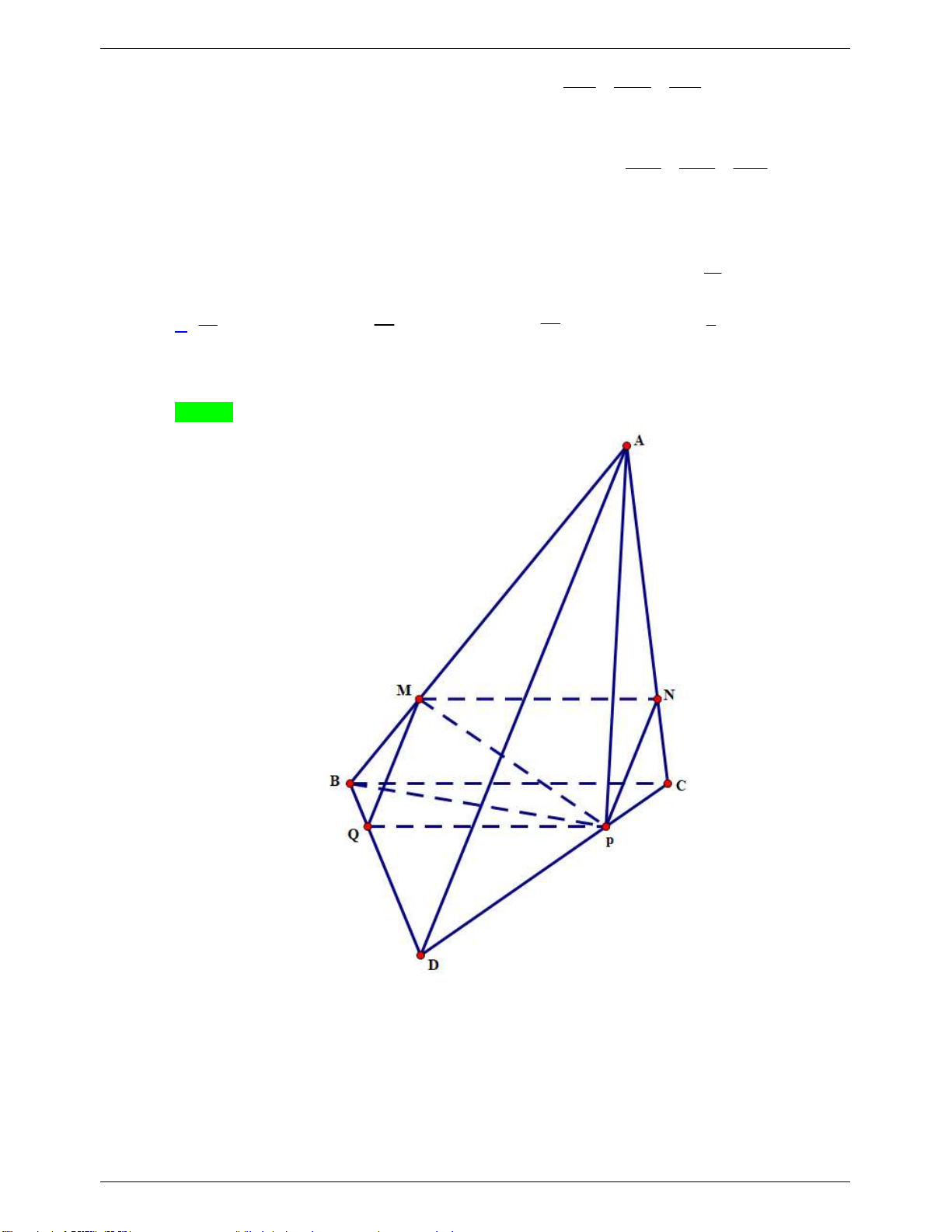
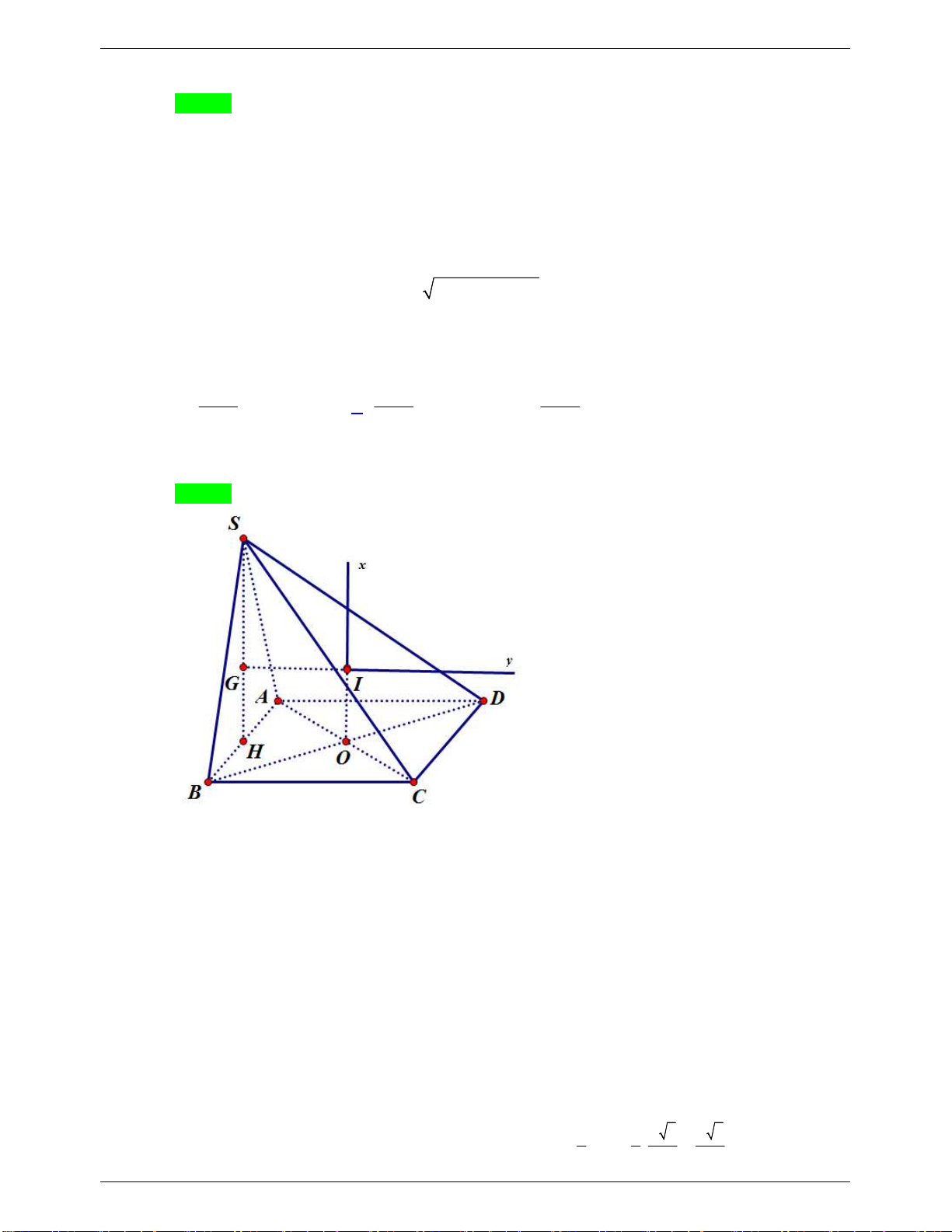
Câu 38: Cho tứ diện ABCD , gọi M là điểm sao cho MA  3MB  0 . Mặt phẳng (P) đi qua M song
song với BC và AD chia tứ diện đã cho thành 2 khối đa diện . Gọi V là thể tích của khối đa diện 1 V
chứa đỉnh B và V là thể tích của khối đa diện chứa đỉnh A . Tính tỉ số 1 . 2 V2 5 5 A. . B. . 27 37 C. 5 . D. 1 . 32 3 m
Câu 39: Có bao nhiêu giá trị thực của tham số m thỏa mãn: 3 2 (4x  2x) dx 3  m  ? 0 A. 2. B. 1. C. 4. D. 3.
Câu 40: Có tất cả bao nhiêu cặp số nguyên x và y sao cho đẳng thức sau thỏa mãn? 2 y 101 x x 1 log 4 2 2022 20y 1. 2021 A. 1. B. 3. C. 0. D. 2.
Câu 41: Cho hình chóp đều S.ABCD có cạnh đáy bằng a , AC cắt BD tại O . Khoảng cách giữa SA
và CD bằng độ dài đoạn SO . Tính sin của góc giữa cạnh bên và mặt phẳng đáy . A. 3 B. 15 . C. 10 D. 4 5 5 5 5
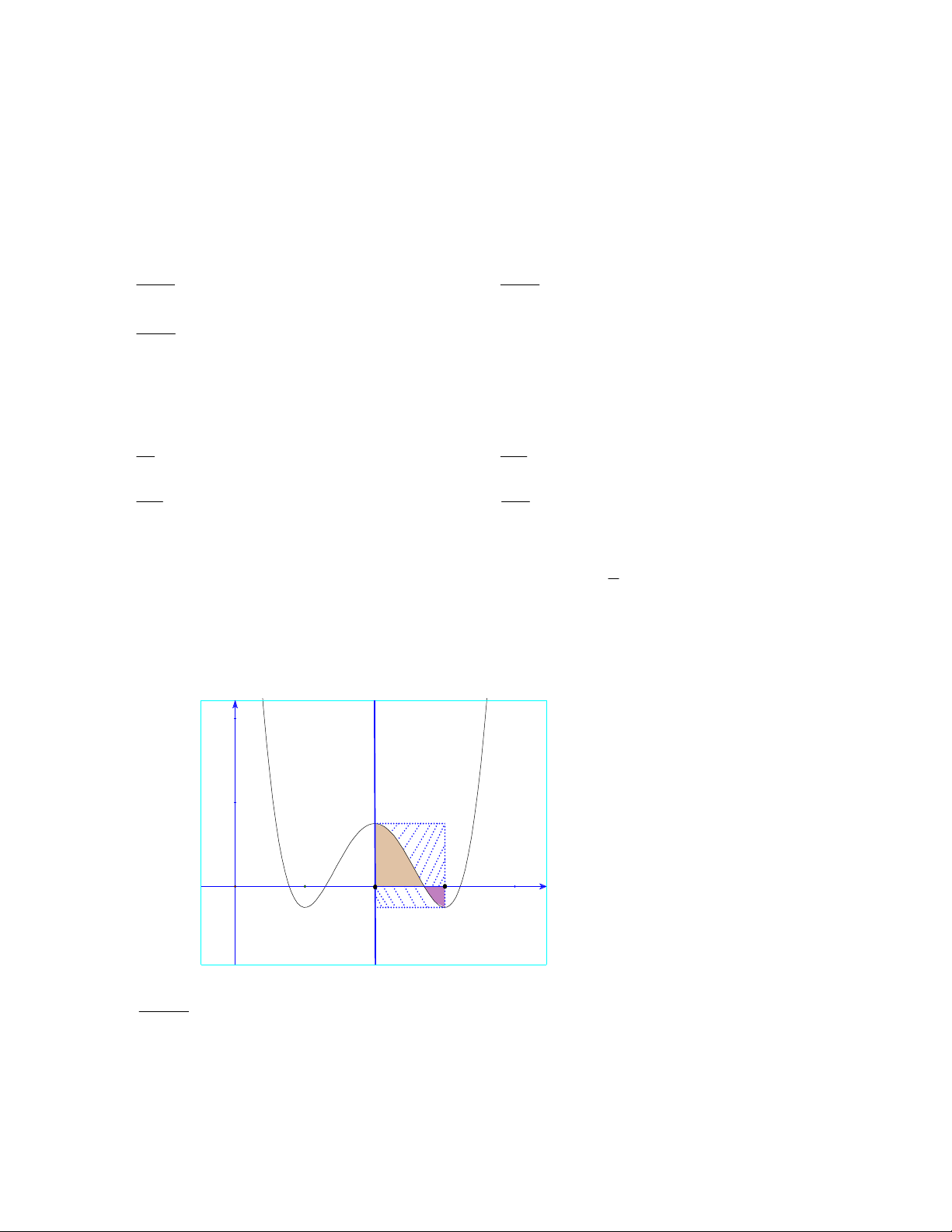
Câu 42: Cho hàm số f x, đồ thị của hàm số /
y  f  x là đường cong như hình vẽ bên dưới. Giá  1
trị nhỏ nhất của hàm số  g  x  f 2x   1  4x  3 trên đoạn 1  ;  bằng 2    A. f 2 5 . B. f   1 1. C. f   1  3. D. f 0 . Trang 5/7 - Mã đề 144
Câu 43: Trong không gian Oxyz, cho tứ diện ABCD với (
A 3; 4; 0) , B(2;5; 4) ,C(1;1;1) , D(3;5;3) . Viết
phương trình mặt cầu ngoại tiếp tứ diện đó.
A. x  2   y  2   z  2 1 3 2  9 .
B. x  2   y  2  z  2 1 3 2  9 .
C. x  2   y  2   z  2 1 3 2  9 .
D. x  2   y  2   z  2 1 3 2  9 .
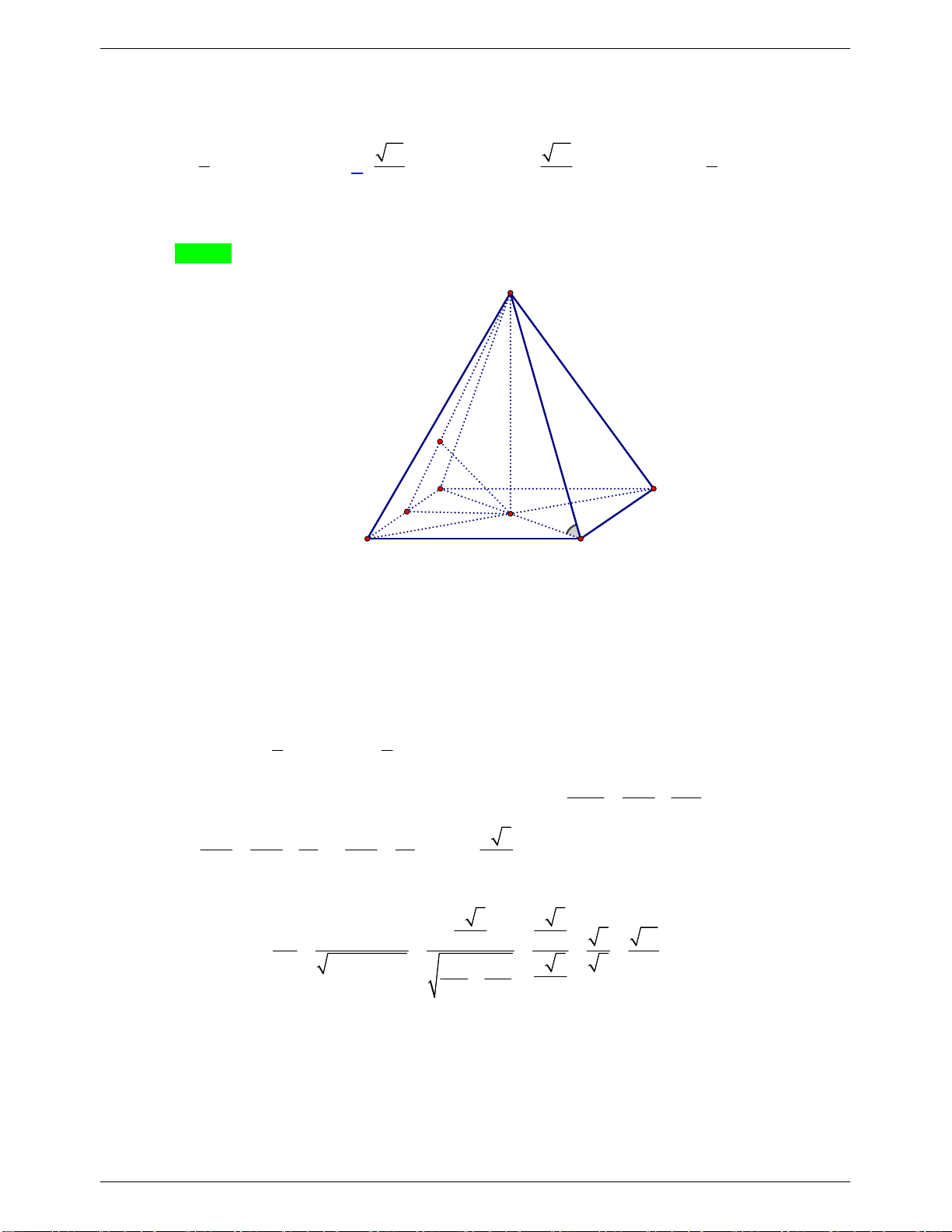
Câu 44: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Tam giác SAB đều và nằm trong
mặt phẳng vuông góc với đáy. Tính diện tích mặt cầu ngoại tiếp hình chóp đã cho. 3 4 a 2 7 a A. . B. . 3 3 2 7 a C. . D. 2 4 a . 9
Câu 45: Gọi A là tập tất cả các số tự nhiên có 6 chữ số khác nhau, lấy ngẫu nhiên một số từ A. Tính
xác suất để lấy được một số luôn có mặt 3 chữ số 0,1,2 và giữa 2 chữ số 0 và 1 có đúng 2 chữ số. A. 1 . B. 7 . 15 162 5 7 C. . D. . 162 405
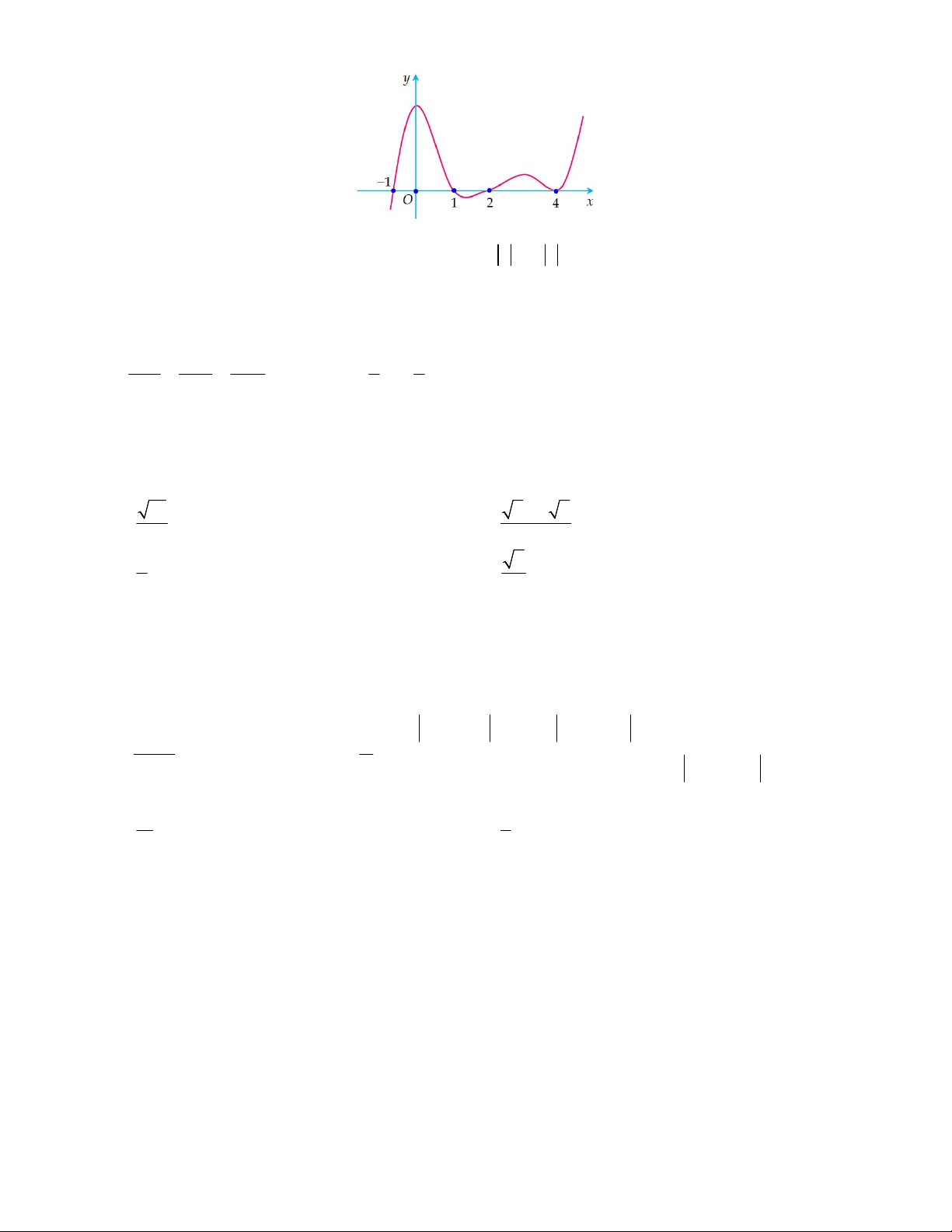
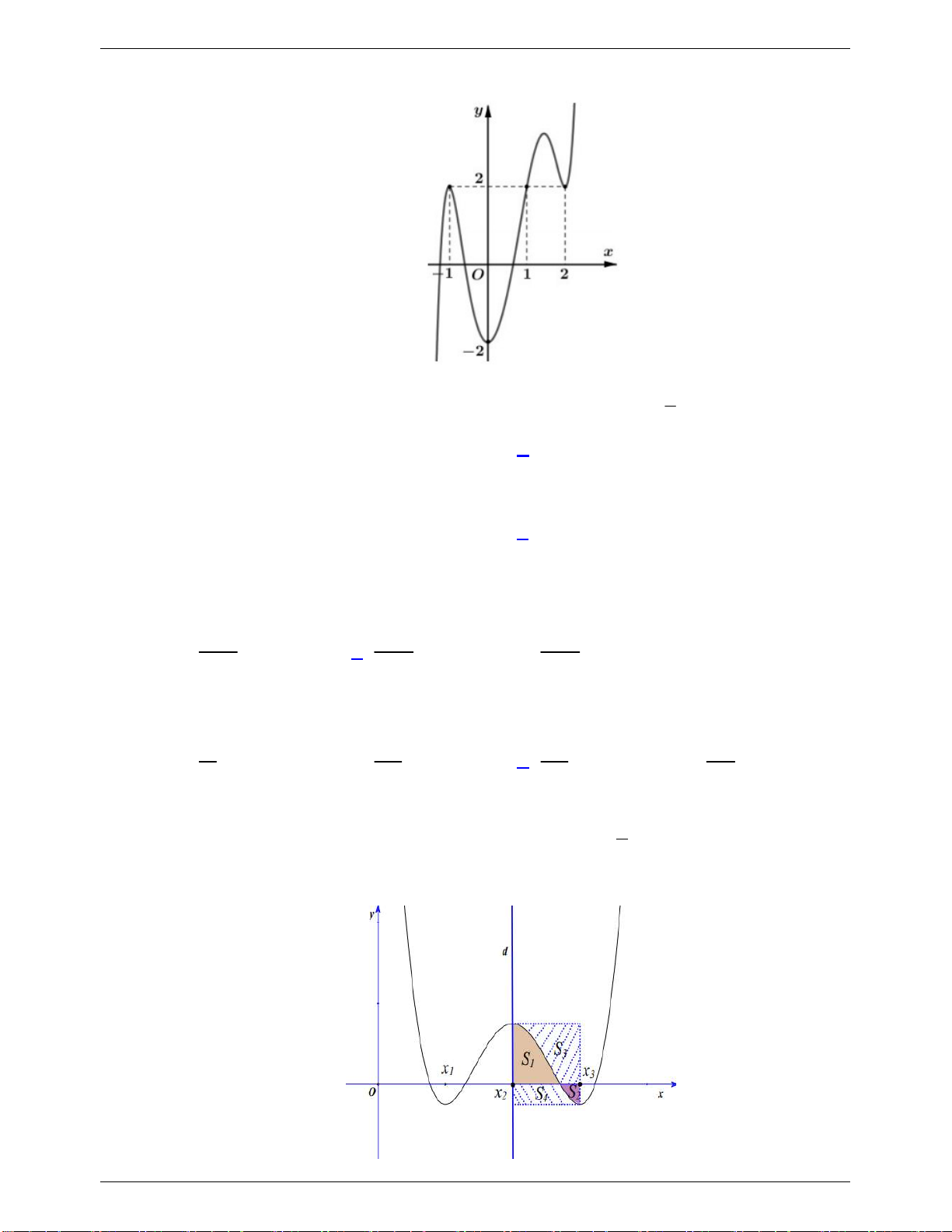
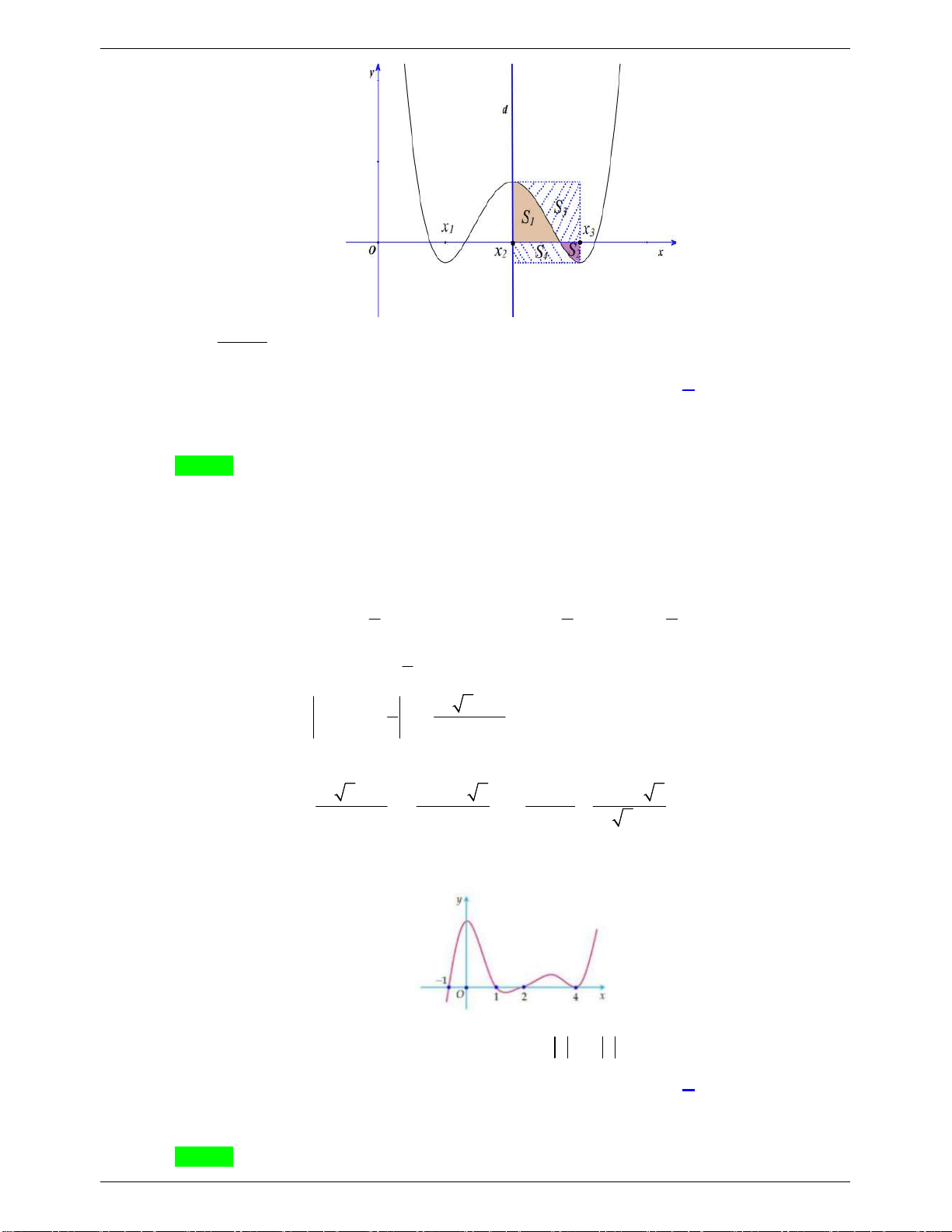
Câu 46: Cho hàm số bậc bốn y  f  x có đồ thị C  như hình vẽ bên. Biết hàm số y  f  x đạt
cực trị tại các điểm x , x , x thỏa mãn x  x  2 , f  2 x  f x 
f x  0 và C  nhận đường 1   3   2  1 2 3 3 1 3
thẳng d : x  x làm trục đối xứng. Gọi S , S , S , S là diện tích của các miền hình phẳng được đánh 2 1 2 3 4 dấu như hình bên. y d S3 S1 x1 x3 O x2 S S2 x 4 S  S Tỉ số 3
4 gần kết quả nào nhất S  S 1 2 A. 1.62. B. 1.68 . C. 1.64 . D. 1.66 .
Câu 47: Cho hàm số f  x có đạo hàm liên tục trên  , đồ thị hàm số y  f  x có đúng 4 điểm
chung với trục hoành như hình vẽ bên dưới . Trang 6/7 - Mã đề 144
Có bao nhiêu giá trị nguyên của m 3
để hàm số y  f  x  3 x  m  202  1 có 11 điểm cực trị? A. 0. B. 2. C. 5. D. 1.
Câu 48: Trong không gian Oxyz , cho mặt phẳng (P) : x  y  z  2  0, đường thẳng x 1 y 1 2  z (d) :   và 2 điểm 1 3
B( ; 1; ),C(1; 2;1) . Gọi A là giao điểm của (d) và ( ) P , S là 1 1 1 2 2
điểm di động trên (d) ( S  A). Gọi H, K lần lượt là hình chiếu của A trên các đường thẳng
SB và SC , (  ) là giao tuyến của 2 mặt phẳng (AHK) và ( )
P , M () . Giá trị nhỏ nhất của MB  MC là  A. 14 . B. 6 2 2 . 2 2 C. 7 . D. 7 . 2 2
Câu 49: Có bao nhiêu số nguyên dương m để phương trình x e 1  .
m ln(mx 1) có 2 nghiệm phân biệt trên 10;10? A. 2201. B. 2020. C. 2021. D. 2202.
Câu 50: Cho các số phức z ,z thỏa mãn z 1  i  1 và z  2  i  4 . Số phức z thay đổi sao 1 2 1 2
cho z z 1i z và z z z 2 i là số thuần ảo. Giá trị nhỏ nhất z 3 2i bằng 2  2  1 1  A. 11. B. 1 . 5 3 C. 3. D. 2. ------ HẾT ------
Cán bộ coi thi không giải thích gì thêm.
Thí sinh không được sử dụng tài liệu . Trang 7/7 - Mã đề 144 SỞ GD&ĐT QUẢNG NGÃI
THI THỬ TỐT NGHIỆP THPT NĂM 2021 LẦN 1
TRƯỜNG THPT CHUYÊN LÊ KHIẾT NĂM HỌC 2020 - 2021 MÔN TOÁN
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Phần đáp án câu trắc nghiệm: 144 243 345 442 546 641 747 848 1 C B B B C B A A 2 C A C C A B C D 3 C A B A A B B A 4 D C C A A A C D 5 B C B C A D D B 6 A D A C C A B A 7 A A C D C D D C 8 C D C D C C C C 9 B C C C A D D B 10 C A C C B D B A 11 D A A B B D B D 12 B D A D D A A B 13 B A D A B D C B 14 D B C D D C C C 15 B C A A A D A D 16 D D B D D D C D 17 D B D C B B D D 18 D D B B D B A C 19 C C B C A B D D 20 C D D B D A D A 21 C A C B D A A D 22 A D D B B C A A 23 B A C D B B D B 24 C B A C C A B C 25 D C B B B A A A 26 C C D B A B C C 27 C A B B D C B B 28 C C B C A B B C 29 D B C A B C B D 30 D B C B D D C C 31 D D D D C A D D 32 C A B C C B B C 33 C B D B D B A A 34 C B B C C D C A 35 C D A B B D D C 36 A C D D C C A B 37 A C B D B D A B 38 A C D D C D C A 39 A C B B C D B A 40 A D D C A C C C 41 B B D A D B C D 1 42 C D D C B C A B 43 B A A B A C D C 44 B D A A C C D C 45 C C B C B A C D 46 D D C C B D D B 47 D B B C B A B B 48 A C D A C B A A 49 A C C B A D C A 50 A D C B B C C C 2
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021 TRƯỜNG & THPT
THI THỬ TN12 LẦN 3 MÔN TOÁN --------------------------- NĂM HỌC 2020 - 2021 CHUYÊN LÊ KHIẾT Thời gian: 90 phút QUẢNG NGÃI MÃ ĐỀ: ......
Câu 1. Có bao nhiêu số tự nhiên có bốn chữ số khác nhau được tạo thành từ các chữ số 1, 2,3, 4,5, 6 ? A. P . B. 4 C . C. 4 A . D. 4 6 . 6 6 6
Câu 2. Trong không gian Oxyz , cho hai điểm A 2  ;3;6 và B0;5; 2
  . Trung điểm của đoạn thẳng AB có toạ độ là A. I 2;8;4 . B. I 1;1; 4   . C. I 1;4;2 . D. I 2;2;4 .
Câu 3. Trong mặt phẳng toạ độ Oxy , điểm biểu diễn số phức z  4 3i có toạ độ là A.  3  ;4. B. 4;3. C. 4; 3  . D. 3;4.
Câu 4. Cho hàm số f  x 3
 4x  2 . Trong các khẳng định sau, khẳng định nào đúng ? A. f  x 2 dx  12x  C . B. f  x 4 dx  3x  2x  C . 1 C. f  x 4 dx  x  2x  C . D. f  x 4 dx  x  2x  C . 3 2x 1
Câu 5. Tiệm cận ngang của đồ thị hàm số y  là đường thẳng 2  x A. x  2 . B. y  2  . C. y 1. D. x  2  .  x  1 x 
Câu 6. Tập nghiệm S của bất phương trình 2 5    là  25  A. S   ;  2. B. S   ;  2 . C. S  2;  . D. S  1; .
Câu 7. Thể tích V của khối nón có bán kính đáy bằng 3cm và chiều cao bằng 4cm là A. V    3 12 cm  . B. V    3 36 cm  C. V    2 36 cm  . D. V    2 12 cm 
Câu 8. Một hình lập phương có độ dài cạnh bằng 2a . Thể tích khối lập phương đó là A. 3 4a . B. 3 a C. 3 8a . D. 3 2a 2
Câu 9. Cho hàm số f  x  sin 3x . Trong các khẳng định sau, khẳng định nào đúng? A. f  x 1 dx  cos3x  C . B. f  x 1 dx   cos3x  C . 3 3 C. f
 xdx  3cos3xC . D. f
 xdx  cos3xC .
Câu 10. Một khối chóp có thể tích bằng 12 và diện tích đáy bằng 4 . Chiều cao cảu khối chóp đó bằng 4 1 A. 3 . B. . C. 9 . D. . 9 3
Câu 11. Trong không gian Oxyz , mặt cầu S   x  2  y   z  2 2 : 1
3  16 có bán kính bằng A. 32 . B. 9 . C. 16 . D. 4 .
Câu 12. Số phức liên hợp của số phức z  4  2i là A. z  4  2i . B. z  4  2i . C. z  2  4i . D. z  2  4i . 4 4 5 Câu 13. Nếu f  xdx  2 và g
 xdx  6 thì f xdx  . 3 5 3 A. 12 . B. 4 . C. 8  . D. 8 .
Câu 14. Đường cong trong hình vẽ bên là đồ thị hàm số nào sau đây
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 1 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT A. 3 y  x  3x  2 . B. 4 2 y  x  2x  2 . C. 3 2 y  x  3x  2 . D. 3 2 y  x  3x  2.
Câu 15. Cho cấp số cộng u có u  4 và u  2 . Giá trị của u bằng. n  2 4 6 A. u  6 . B. u  0 . C. u  1. D. u  1. 6 6 6 6
Câu 16. Nghiệm của phương trình log x  2 là 3 A. x  6 . B. x  8 . C. x  5 . D. x  9 .
Câu 17. Cho hàm số y  f  x có bảng biến thiên như sau:
Mệnh đề nào dưới đây đúng? A. min y  4 . B. y  15 . C. max y  5. D. y  4 . CD CT  
Câu 18. Trong không gian Oxyz , mặt phẳng nào dưới đây không đi qua điểm M  0;1;  1 ?
A. P :x  2y 15z 13  0 .
B. P :4x  2y 12z 10  0 . 2  4 
C.  P :2x  3y 12z 15  0
D. P :4x  2y 12z 17  0. 1  3 
Câu 19. Cho hàm số y  f  x có bảng biến thiên như sau:
Mệnh đề nào sau đây sai?
A. Hàm số đồng biến trên khoảng 2;  .
B. Hàm số đồng biến trên khoảng ;  1 .
C. Hàm số đồng biến trên khoảng  1  ;  .
D. Hàm số nghịch biến trên khoảng  1  ;  1 . e 1 Câu 20. Tích phân dx  bằng x 1 A. e 1. B. ln 2e . C. 1 D. ln e 1.
Câu 21. Cho hai số phức z  3  2i và w  4  i . Số phức z  w bằng A. 1 i . B. 7  i . C. 1 3i . D. 7  3i . Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
Câu 22. Cho hàm số y  f (x) có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị của tham số m để
phương trình f  x 1  m có 3 nghiệm phân biệt. A. 1  m  3 . B. 1  m  4 . C. 2  m  5 . D. 0  m  4 .  1 
Câu 23. Đạo hàm của hàm số y  log 3x 1 trên khoảng  ;  là 3      3  3 3 3 3 A. . B. . C. . D. . 3x 1 3x   1 ln 3 3x   1 ln x x  1ln3 2 3 5 3 a . a. a
Câu 24. Cho số thực a thỏa mãn 0  a  1. Tính giá trị của biểu thức T  log a 15 4 a 8 17 A. T  8. B. T  11. C. T  . D. T  . 3 15 2 6  x  Câu 25. Nếu 2x  3 f  xdx  4  thì f dx    bằng  3  1 3 1 A. 4 . B. 1. C. . D. 1  . 3 x 
Câu 26. Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f  x 1  trên đoạn 2;  5 1 2x . Tính A  M  3m . 10 5 A. A   . B. A  1  . C. A 1. D. A   . 3 3
Câu 27. Số phức z là nghiệm có phần ảo dương của phương trình bậc hai 2
z  2z  2  0 . Môđun của 1
số phức 2 i z bằng 1 A. 3 2 . B. 10. C. 10 . D. 18.
Câu 28. Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB  a, AC  a 5, SA  2a . Biết SB  BC
và SD  CD . Thể tích của khối chóp S.BCD là 3 2a 3 4a A. 3 V  4a . B. 3 V  2a . C. V  . D. V  . S .BCD S .BCD S.BCD 3 S.BCD 3
Câu 29. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , cạnh AC  a , các cạnh bên a 6 SA  SB  SC 
. Tính góc tạo bởi mặt bên (SAB) và mặt phẳng đáy (ABC) . 2   A. . B. . C. arctan 2 . D. arctan 2 . 6 4
Câu 30. Một hình trụ có bán kính đáy bằng a và có thiết diện qua trục là một hình vuông. Tính diện tích xung quanh của hình trụ. A. 2 2 a . B. 2 3 a . C. 2 a . D. 2 4 a .
Câu 31. Cho hàm số f (x) có đạo hàm 3 2 f (
 x)  x(x 1) (2x  3) . Hàm số đã cho có bao nhiêu điểm cực trị? A. 3. B. 1. C. 0. D. 2.
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 3 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Câu 32. Tập nghiệm của bất phương trình log  2 2x  x  log x là 2  2 1   1  A. ;1  . B. (0;1) . C. ;1  . D. 0;  1 . 2    2   
Câu 33. Trong không gian Oxyz , vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua
gốc tọa độ và trọng tâm của tam giác ABC với A0;2;  1 , B 4; 2  ;  1 ,C 2;3;4 ?     A. u 1; 2  ;2 . B. u 1; 2  ; 1  . C. u 2;1;2 . D. u 4; 2  ;1 . 4   3   1   2  
Câu 34. Hàm số nào dưới đây đồng biến trên  ? 1 A. y  . B. 3 y  x  x . C. 3x y  . D. y  ln x . 2 x 1
Câu 35. Cho hai số dương a,b với a  1. Đặt 3 M  log
b . Tính M theo N  log b . a a 1 3 2 A. M  N . B. M  N . C. M  N . D. M  N . 6 2 3
Câu 36. Có bao nhiêu số phức z thỏa mãn 3 z  z ? A. 5. B. 4 . C. 2 . D. 7 .
Câu 37. Trong không gian Oxyz , cho bốn điểm A1; 2; 
1 , B0;1;3 , C 1;2;3 , D2;1;2. Phương
trình đường thẳng qua điểm A và vuông góc với mặt phẳng  BCD là x  2 y  3 z  5 x 1 y  2 z 1 A.   . B.   . 1 1 4 1 3 4  x y 1 z  3 x  1 y  2 z  1 C.   . D.   . 1  3 2 1 3 2   
Câu 38. Cho tứ diện ABCD , gọi M là điểm sao cho MA  3MB  0 . Mặt phẳng P đi qua M , song
song với BC và AD chia khối tứ diện đã cho thành hai khối đa diện. Gọi V là thể tích của khối 1 V
tứ diện chứa đỉnh B và V là thể tích khối tứ diện chứa đỉnh A . Tính tỉ số 1 . 2 V2 5 5 5 1 A. . B. . C. . D. . 27 37 32 3 m
Câu 39. Có bao nhiêu giá trị thực của tham số m thỏa mãn   3 4x  2x 2 dx  3  m ? 0 A. 2 . B.1. C. 4 . D. 3 .
Câu 40. Có tất cả bao nhiêu cặp số nguyên x và y sao cho đẳng thức sau thỏa mãn y  log 4x 2x   2022 2 101 1  20y 1. 2021 A. 1. B. 3 . C. 0 . D. 2 .
Câu 41. Cho hình chóp đều S.ABCD có cạnh đáy bằng a , AC cắt BD tại O . Khoảng cách giữa SA và
CD bằng độ dài đoạn SO . Tính sin của góc giữa cạnh bên và mặt phẳng đáy. 3 15 10 4 A. . B. . C. . D. . 5 5 5 5 Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
Câu 42. Cho hàm số f  x , đồ thị của hàm số y  f (x) là đường cong như hình vẽ bên dưới.  1 
Giá trị nhỏ nhất của hàm số g  x  f 2x  
1  4x  3 trên đoạn 1;  bằng 2    A. f 2 5 . B. f   1 1. C. f   1  3. D. f 0 .
Câu 43. Trong không gian Oxyz , cho tứ diện ABCD với A3;4;0 , B 2;5;4 ,C 1;1;  1 , D 3;5;3.
Viết phương trình mặt cầu ngoại tiếp tứ diện đó.
A.  x  2   y  2   z  2 1 3 2  9 .
B.  x  2   y  2   z  2 1 3 2  9 .
C.  x  2   y  2   z  2 1 3 2  9 .
D.  x  2   y  2   z  2 1 3 2  9 .
Câu 44. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Tam giác SAB đều và nằm trong mặt
phẳng vuông góc với đáy. Tính diện tích mặt cầu ngoại tiếp hình chóp đã cho. 3 4 a 2 7 a 2 7 a A. B. C. D. 2 4 a 3 3 9
Câu 45. Gọi A là tập tất cả các số tự nhiên có 6 chữ số khác nhau, lấy ngẫu nhiên một số từ A . Tính
xác suất để lấy được một số luôn có mặt 3 chữ số 0 , 1, 2 và giữa hai chữ số 0 và 1 có đúng 2 chữ số. 1 7 5 7 A. . B. . C. . D. . 15 162 162 405
Câu 46. Cho hàm số bậc bốn y  f  x có đồ thị C  như hình vẽ bên. Biết hàm số y  f  x đạt cực trị 2
tại các điểm x , x , x thỏa mãn x  x  2 , f  x  f x  f x  0 và C  nhận đường 1   3   2  1 2 3 3 1 3
thẳng d : x  x làm trục đối xứng. Gọi S , S , S , S là diện tích của các miền hình phẳng 2 1 2 3 4
được đánh dấu như hình bên.
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 5 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT S  S Tỉ số 3
4 gần kết quả nào nhất? S  S 1 2 A. 1.62 . B. 1.64 . C. 1.68 . D. 1.66 .
Câu 47. Cho hàm số f (x) có đạo hàm liên tục trên  , đồ thị hàm số y  f '(x) có đúng bốn điểm chung
với trung hoành như hình vẽ dưới.
Có bao nhiêu giá trị nguyên của m để hàm số y  f  3
x  3 x  m  202 1 có 11 điểm cực trị. A. 0 . B. 2 . C. 5 . D. 1.
Câu 48. Trong không gian Oxyz, cho mặt phẳng (P) : x  y  z  2  0, đường thẳng x 1 y 1 2  z  1 3  (d ) :   và hai điểm B ; 1; ,C  
1;1; 1. Gọi A là giao điểm của (d) và 1 1 1  2 2 
(P) , (S) là điểm di động trên (d),(S  )
A . Gọi H , K lần lượt là hình chiếu vuông góc của A
trên các đường thẳng SB và SC , () là giao tuyến của hai mặt phẳng (AHK ) và (P), M ()
. Giá trị nhỏ nhất của MB  MC là A. 14 . B. 6  2 2 . C. 7 . D. 7 . 2 2 2 2
Câu 49. Có bao nhiêu số nguyên dương m để phương trình x e 1  mln mx  
1 có hai nghiệm phân biệt trên đoạn  1  0;10? A. 2201 . B. 2020 . C. 2021. D. 2202 .
Câu 50. Cho số các số phức z , z z 1 i 1
z  2  i  2. Số phức z 1 2 thỏa mãn 1 và 2 thay đổi sao cho
zz 1iz và zz z 2i là số thuần ảo. Giá trị nhỏ nhất của z32i bằng 2   2  1   1  11 A. . B. 2 . C. 2 2 . D. 13 1. 5
____________________ HẾT ____________________ Trang 6
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C C C D B A A C B C D B B D B D D D C C C B B C D
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
C C C D D D C C C C A A A A A B C B B C D D A A C LỜI GIẢI CHI TIẾT
Câu 1. Có bao nhiêu số tự nhiên có bốn chữ số khác nhau được tạo thành từ các chữ số 1, 2,3, 4,5, 6 ? A. P . B. 4 C . C. 4 A . D. 4 6 . 6 6 6 Lời giải
GVSB: Đồng Khoa Văn ; GVPB: Bùi Thị Bích Vân Chọn C
Gọi số tự nhiên có 4 chữ số là a a a a . 1 2 3 4
Chọn 4 chữ số từ 6 chữ số đã cho và sắp xếp vào 4 vị trí từ a đến a có 4 A cách. 1 4 6 Vậy có 4 A số. 6
Câu 2. Trong không gian Oxyz , cho hai điểm A 2  ;3;6 và B0;5; 2
  . Trung điểm của đoạn thẳng AB có toạ độ là A. I 2;8;4 . B. I 1;1;4 . C. I 1;4;2. D. I 2;2;4. Lời giải
GVSB: Đồng Khoa Văn ; GVPB: Bùi Thị Bích Vân Chọn C
Ta có trung điểm đoạn thẳng AB có toạ độ là I  1  ;4;2.
Câu 3. Trong mặt phẳng toạ độ Oxy , điểm biểu diễn số phức z  4 3i có toạ độ là A.  3  ;4. B. 4;3. C. 4; 3  . D. 3;4. Lời giải
GVSB: Đồng Khoa Văn ; GVPB: Bùi Thị Bích Vân Chọn C
Ta có điểm biểu diễn số phức z  4 3i có toạ độ là 4; 3  .
Câu 4. Cho hàm số f  x 3
 4x  2 . Trong các khẳng định sau, khẳng định nào đúng ? A. f  x 2 dx  12x  C . B. f  x 4 dx  3x  2x  C . 1 C. f  x 4 dx  x  2x  C . D. f  x 4 dx  x  2x  C . 3 Lời giải
GVSB: Đồng Khoa Văn ; GVPB: Bùi Thị Bích Vân Chọn D Ta có f
 x x   3x   4 d 4 2 dx  x  2x  C . 2x 1
Câu 5. Tiệm cận ngang của đồ thị hàm số y  là đường thẳng 2  x A. x  2 . B. y  2  . C. y 1. D. x  2  . Lời giải
GVSB: Trần Ngọc; GVPB: Bùi Thị Bích Vân
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 7 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT Chọn B
Tập xác định: D   ;  22; 2x 1 2x 1 Ta có: lim  2  , lim  2  . x 2  x x 2  x
Vậy đồ thị hàm số có đường tiệm cận ngang y  2  . x  
Câu 6. Tập nghiệm S của bất phương trình x2 1 5    là  25  A. S   ;  2. B. S   ;  2 . C. S  2; . D. S  1; . Lời giải
GVSB: Trần Ngọc; GVPB: Bùi Thị Bích Vân Chọn A x   Ta có: x2 1 5    x2 2  5
 5 x  x  2  2x  x  2.  25 
Vậy tập nghiệm S   ;  2.
Câu 7. Thể tích V của khối nón có bán kính đáy bằng 3cm và chiều cao bằng 4cm là A. V    3 12 cm  . B. V    3 36 cm  C. V    2 36 cm  . D. V    2 12 cm  Lời giải
GVSB: Trần Ngọc; GVPB: Bùi Thị Bích Vân Chọn A 1 1 Ta có: 2 2
V   r h  .3 .4  12  3 cm  . 3 3
Câu 8. Một hình lập phương có độ dài cạnh bằng 2a . Thể tích khối lập phương đó là A. 3 4a . B. 3 a C. 3 8a . D. 3 2a 2 Lời giải
GVSB: Trần Ngọc; GVPB: Bùi Thị Bích Vân Chọn C Ta có: V   a3 3 2  8a .
Câu 9. Cho hàm số f  x  sin 3x . Trong các khẳng định sau, khẳng định nào đúng? A. f  x 1 dx  cos3x  C . B. f  x 1 dx   cos3x  C . 3 3 C. f
 xdx  3cos3xC . D. f
 xdx  cos3xC . Lời giải
GVSB: Đỗ Liên Phương; GVPB: Bùi Thị Bích Vân Chọn B f  x 1
dx  sin 3xdx   cos3x  C  3
Câu 10. Một khối chóp có thể tích bằng 12 và diện tích đáy bằng 4 . Chiều cao cảu khối chóp đó bằng 4 1 A. 3 . B. . C. 9 . D. . 9 3 Lời giải
GVSB: Đỗ Liên Phương; GVPB: Bùi Thị Bích Vân Chọn C 1 3V 36 Ta có V  . B h  h    9 3 B 4 Trang 8
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
Câu 11. Trong không gian Oxyz , mặt cầu S   x  2  y   z  2 2 : 1
3  16 có bán kính bằng A. 32 . B. 9 . C. 16 . D. 4 . Lời giải
GVSB: Đỗ Liên Phương; GVPB: Bùi Thị Bích Vân Chọn D Ta có R  16  4
Câu 12. Số phức liên hợp của số phức z  4  2i là A. z  4  2i . B. z  4  2i . C. z  2   4i . D. z  2  4i . Lời giải
GVSB: Đỗ Liên Phương; GVPB: Bùi Thị Bích Vân Chọn B
z  4  2i  z  4  2i 4 4 5 Câu 13. Nếu f  xdx  2 và g
 xdx  6 thì f xdx  . 3 5 3 A. 12 . B. 4 . C. 8  . D. 8 . Lời giải
GVSB: Hồng Hà Nguyễn; GVPB: Thanh Giang Đoàn Chọn B 5 4 5 Ta có: f  xdx   f  xdx f  xdx 3 3 4 5 4 5 4 4
f xdx  f  xdx  f  xdx  f  xdx  f  xdx  2  6  4       . 3 3 4 3 5
Câu 14. Đường cong trong hình vẽ bên là đồ thị hàm số nào sau đây A. 3 y  x  3x  2 . B. 4 2 y  x  2x  2 . C. 3 2 y  x  3x  2 . D. 3 2 y  x  3x  2. Lời giải
GVSB: Hồng Hà Nguyễn; GVPB: Thanh Giang Đoàn Chọn D
Từ đồ thị suy ra hàm số là bậc ba và hệ số a  0 . x  0 Xét 3 2 2
y  x  3x  2  y  3x  6x , 2
y  0  3x  6x  0   . x  2 Vậy 3 2
y  x  3x  2 có đồ thị là hình vẽ trên.
Câu 15. Cho cấp số cộng u có u  4 và u  2 . Giá trị của u bằng. n  2 4 6 A. u  6 . B. u  0 . C. u  1. D. u  1. 6 6 6 6 Lời giải
GVSB: Hồng Hà Nguyễn; GVPB: Thanh Giang Đoàn Chọn B
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 9 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT 2  u Ta có 2
u  2  u  3d  2  u  2d  2  d   1. 4 1 2 2
Mà u  u  d  u  u  d  4 1  5 , Suy ra u  u  5d  5  5  0 . 2 1 1 2 6 1
Câu 16. Nghiệm của phương trình log x  2 là 3 A. x  6 . B. x  8 . C. x  5 . D. x  9 . Lời giải
GVSB: Hồng Hà Nguyễn; GVPB: Thanh Giang Đoàn Chọn D Ta có 2
log x  2  x  3  9 . 3
Câu 17. Cho hàm số y  f  x có bảng biến thiên như sau:
Mệnh đề nào dưới đây đúng? A. min y  4 . B. y  15 . C. max y  5. D. y  4 . CD CT   Lời giải
GVSB: Nguyễn Thuỳ Dung; GVPB: Đoàn Thanh Giang Chọn D
Dựa vào bảng biến thiên, ta thấy
- Hàm số không có giá trị lớn nhất, giá trị nhỏ nhất. - Hàm số có y  4 và y  5. CT CD
Câu 18. Trong không gian Oxyz , mặt phẳng nào dưới đây không đi qua điểm M  0;1;  1 ?
A. P :x  2y 15z 13  0 .
B. P :4x  2y 12z 10  0 . 2  4 
C.  P :2x  3y 12z 15  0
D. P :4x  2y 12z 17  0. 1  3  Lời giải
GVSB: Nguyễn Thuỳ Dung; GVPB: Đoàn Thanh Giang Chọn D
Thay toạ độ điểm M  0;1; 
1 vào phương trình P :4x  2y 12z 17  0, ta có: 1  4.0  2.112.  1 17  3  0 .
Vậy điểm M  0;1; 
1 không nằm trong mặt phẳng P :4x  2y 12z 17  0. 1 
Câu 19. Cho hàm số y  f  x có bảng biến thiên như sau:
Mệnh đề nào sau đây sai?
A. Hàm số đồng biến trên khoảng 2;  . Trang 10
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
B. Hàm số đồng biến trên khoảng ;  1 .
C. Hàm số đồng biến trên khoảng  1  ;  .
D. Hàm số nghịch biến trên khoảng  1  ;  1 . Lời giải
GVSB: Nguyễn Thuỳ Dung; GVPB: Đoàn Thanh Giang Chọn C
Dựa vào bảng biến thiên, ta có:
- Hàm số đồng biến trên các khoảng ;  1 và 2;  .
- Hàm số nghịch biến trên khoảng  1  ;  1 .
Vậy mệnh đề sai là: Hàm số đồng biến trên khoảng  1  ;  . e 1 Câu 20. Tích phân dx  bằng x 1 A. e 1. B. ln 2e . C. 1 D. ln e 1. Lời giải
GVSB: Nguyễn Thuỳ Dung; GVPB: Đoàn Thanh Giang Chọn C e 1 d  ln e x
x  ln e  ln 1  1 0  1  . 1 x 1
Câu 21. Cho hai số phức z  3  2i và w  4  i . Số phức z  w bằng A. 1 i . B. 7  i . C. 1 3i . D. 7  3i . Lời giải GVSB: Giang Sơn Chọn C
Ta có z  w  3  2i  4  i  1 3i .
Câu 22. Cho hàm số y  f (x) có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị của tham số m để
phương trình f  x 1  m có 3 nghiệm phân biệt. A. 1  m  3 . B. 1  m  4 . C. 2  m  5 . D. 0  m  4 . Lời giải
GVSB: Giang Sơn GVPB: Ngocdiep Nguyen Chọn A
Phương trình đưa về f  x  m 1
Sử dụng tương giao giữa đường thẳng y  m 1 và đồ thị hàm số y  f (x) , điều kiện để phương
trình f  x  m 1 có 3 nghiệm phân biệt là 0  m 1  4  1  m  3 .  1 
Câu 23. Đạo hàm của hàm số y  log 3x 1 trên khoảng  ;  là 3      3 
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 11 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT 3 3 3 3 A. . B. . C. . D. . 3x 1 3x   1 ln 3 3x   1 ln x x  1ln3 Lời giải
GVSB: Giang Sơn GVPB: Ngocdiep Nguyen Chọn B 3
Ta có y  log 3x 1  y  . 3   (3x 1) ln 3 2 3 5 3 a . a. a
Câu 24. Cho số thực a thỏa mãn 0  a  1. Tính giá trị của biểu thức T  log a 15 4 a 8 17 A. T  8 . B. T  11. C. T  . D. T  . 3 15 Lời giải
GVSB: Giang Sơn GVPB: Ngocdiep Nguyen Chọn C 1 3 2  2 3 5 3 8 3 5 a . a. a a 8 Ta có 3 T  log  log  log a  . a a 4 15 4 a a 3 15 a 2 6  x  Câu 25. Nếu 2x  3 f   xdx  4  thì f dx    bằng  3  1 3 1 A. 4 . B. 1. C. . D. 1  . 3 Lời giải
GVSB: Hoàng Văn Tĩnh; GVPB: Ngocdiep Nguyen Chọn D 2 2 2 2 2 1 Từ 2x  3 f  xdx  4  2 d x x  3 f  
 xdx  4  33 f xdx  4  f xdx     . 3 1 1 1 1 1 x 1
Đặt t   dt= dx  dx  3dt . 3 3 Đổi cận: x  3  t  1 x  6  t  2 6 2 2  x  Do đó f dx  3 f   tdt 3 f  xdx  1    .  3  3 1 1 x 
Câu 26. Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f  x 1  trên đoạn 2;  5 1 2x . Tính A  M  3m . 10 5 A. A   . B. A  1  . C. A 1. D. A   . 3 3 Lời giải
GVSB: Hoàng Văn Tĩnh; GVPB: Ngocdiep Nguyen Chọn C
Hàm số đã cho xác định và liên tục trên đoạn 2;  5 . 1 Ta có f x  
 0, x  2;5  f x nghịch biến trên đoạn 2;5 2   2x   1 1 4
Suy ra M  max f  x  f 2   và m  min f  x  f 5   . 2; 5 3 2; 5 9 Trang 12
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021 Do đó A  M  3m 1.
Câu 27. Số phức z là nghiệm có phần ảo dương của phương trình bậc hai 2
z  2z  2  0 . Môđun của 1
số phức 2 i z bằng 1 A. 3 2 . B. 10 . C. 10 . D. 18 . Lời giải
GVSB: Hoàng Văn Tĩnh; GVPB: Ngocdiep Nguyen Chọn C z 1 i 2 1 z  2z  2  0   z  1 i  2
Với z  1 i  2  i z  3  i  2  i z  10 . 1   1   1
Câu 28. Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB  a, AC  a 5, SA  2a . Biết SB  BC
và SD  CD . Thể tích của khối chóp S.BCD là 3 2a 3 4a A. 3 V  4a . B. 3 V  2a . C. V  . D. V  . S.BCD S.BCD S.BCD 3 S.BCD 3 Lời giải
GVSB: Hoàng Văn Tĩnh; GVPB: Ngocdiep Nguyen Chọn C Ta có BC  AB 
 BC  SAB  BC  SA (1) BC   SB C  D  AD 
 CD  SAD  CD  SA (2) CD   SD
Từ (1) và (2) suy ra SA   ABCD . Mặt khác 2 2 2 2
BC  AC  AB  5a  a  2a . 1 1 2  S  S  . . a 2a  a . BCD 2 ABCD 2 3 1 1 2a Vậy 2 V  S . A S  .2 . a a  . S.BCD 3 B  CD 3 3
Câu 29. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , cạnh AC  a , các cạnh bên a 6 SA  SB  SC 
. Tính góc tạo bởi mặt bên (SAB) và mặt phẳng đáy (ABC) . 2   A. . B. . C. arctan 2 . D. arctan 2 . 6 4 Lời giải
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 13 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
GVSB: Trần Quốc Dũng; GVPB: Tuyet Trinh Chọn D 1 1
Gọi H là trung điểm của BC  HA  HB  HC  BC  a 2 . 2 2 a 6 mà SA  SB  SC 
nên SH  BC , SHA  SHB  SHC 2 suy ra SH   ABC  .
Kẻ HI  AB  SAB, ABC     SI,HI  SIH . 1 1 1
Ta có HI  AB  AC  a (do tam giác ABH vuông cân tại H ) 2 2 2 2 2  a 6   a 2  2 2 SH  SC  HC        a  . 2   2     
Xét tam giác SIH vuông tại H , ta có SH a tan  SIH    2   SIH  arctan 2 . IH 1 a 2
Câu 30. Một hình trụ có bán kính đáy bằng a và có thiết diện qua trục là một hình vuông. Tính diện tích xung quanh của hình trụ. A. 2 2 a . B. 2 3 a . C. 2 a . D. 2 4 a . Lời giải
GVSB: Trần Quốc Dũng; GVPB: Tuyet Trinh Chọn D
Do thiết diện qua trục là một hình vuông nên l  2r  2a . 2 S  2 rl  2 . . a 2a  4 a . xq
Câu 31. Cho hàm số f (x) có đạo hàm 3 2 f (
 x)  x(x 1) (2x  3) . Hàm số đã cho có bao nhiêu điểm cực trị? A. 3. B. 1. C. 0. D. 2. Lời giải
GVSB: Trần Quốc Dũng; GVPB: Tuyet Trinh Chọn D Trang 14
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021  x  0  3 3 2 f (
 x)  x(x 1) (2x  3)  x 1 
( x   là nghiệm kép).  2 3 x    2
Bảng xét dấu f  x :
Vậy hàm số f (x) có 2 điểm cực trị.
Câu 32. Tập nghiệm của bất phương trình log  2 2x  x  log x là 2  2 1   1  A. ;1  . B. (0;1) . C. ;1  . D. 0;  1 . 2    2    Lời giải
GVSB: Trần Quốc Dũng; GVPB: Tuyet Trinh Chọn C x  0 2 2x x 0      1 1 Điều kiện     x   x  . x  0  2 2  x  0 log  2 2x  x 2 2 2
 log x  2x  x  x  x  x  0  0  x  1. 2 2  1
So với điều kiện ta được tập nghiệm S   ;1  . 2   
Câu 33. Trong không gian Oxyz , vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua
gốc tọa độ và trọng tâm của tam giác ABC với A0;2;  1 , B 4; 2  ;  1 ,C 2;3;4 ?     A. u 1; 2  ;2 . B. u 1; 2  ; 1  . C. u 2;1;2 . D. u 4; 2  ;1 . 4   3   1   2   Lời giải
GVSB: Đinh Kiên Trung; GVPB: Tuyet Trinh Chọn C
 0  4  2 2  2  3 11 4 
Trọng tâm của tam giác ABC là: G  ; ;    2;1;2 .  3 3 3  
Vectơ chỉ phương của đường thẳng OG là: OG  2;1;2 .
Câu 34. Hàm số nào dưới đây đồng biến trên  ? 1 A. y  . B. 3 y  x  x . C. 3x y  . D. y  ln x . 2 x 1 Lời giải
GVSB: Đinh Kiên Trung; GVPB: Tuyet Trinh Chọn C Hàm số 3x
y  có cơ số a  3 1 nên hàm số 3x
y  đồng biến trên 
Câu 35. Cho hai số dương a,b với a  1. Đặt 3 M  log
b . Tính M theo N  log b . a a
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 15 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT 1 3 2 A. M  N . B. M  N . C. M  N . D. M  N . 6 2 3 Lời giải
GVSB: Đinh Kiên Trung; GVPB: Tuyet Trinh Chọn C 1 2 2 3 3 M  log b  log b  log b  N . 1 a a 2 a 3 3
Câu 36. Có bao nhiêu số phức z thỏa mãn 3 z  z ? A. 5. B. 4 . C. 2 . D. 7 . Lời giải
GVSB: Đinh Kiên Trung; GVPB: Tuyet Trinh Chọn A
Gọi số phức z có dạng z  a  bi a,b .
z  z  a  bi  a  bi3 3 3 2  a  3ab   2 3 3a b  b i a  0  3 2 2 2 a 3ab  a a  3b 1     2 3 3  a b  b  b b  0  2 2 b  3a 1.
TH1: a  b  0  z  0 . a  0 a  0 TH2:   
 có hai số phức z  i và z  i . 2 2 b   3a 1 b   1  b   0 a  1  TH3:   
 có hai số phức z  1 và z  1. 2 2 a  3b 1 b   0 2 2 a  3b 1 TH4:   4 2 2 a  b  2 2  0  a  b . 2 2 b  3a 1 2 2 a  b 2   2  a  1 ( vô lý). 2 2 b  3a 1
Câu 37. Trong không gian Oxyz , cho bốn điểm A1; 2; 
1 , B0;1;3 , C 1;2;3 , D2;1;2. Phương
trình đường thẳng qua điểm A và vuông góc với mặt phẳng  BCD là x  2 y  3 z  5 x 1 y  2 z 1 A.   . B.   . 1 1 4 1 3 4  x y 1 z  3 x  1 y  2 z  1 C.   . D.   . 1  3 2 1 3 2 Lời giải
GVSB: Nguyễn Bảo; GVPB: Bùi Hà Chọn A
Gọi  là đường thẳng cần tìm.
Do   BCD nên vectơ chỉ phương của đường thẳng  trùng với vectơ pháp tuyến của mặt    
phẳng  BCD , tức là: a  n  BC, BD       .   1;1; 4 1; 1;4 BCD      Trang 16
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021 x 1 y  2 z 1
Khi đó: Phương trình chính tắc của đường thẳng  là:   . 1 1 4
Xét điểm M 2; 3;5 , ta thấy M   . x  2 y  3 z  5
Suy ra: Một phương trình chính tắc khác của đường thẳng  là   . 1 1 4   
Câu 38. Cho tứ diện ABCD , gọi M là điểm sao cho MA  3MB  0 . Mặt phẳng P đi qua M , song
song với BC và AD chia khối tứ diện đã cho thành hai khối đa diện. Gọi V là thể tích của khối 1 V
tứ diện chứa đỉnh B và V là thể tích khối tứ diện chứa đỉnh A . Tính tỉ số 1 . 2 V2 5 5 5 1 A. . B. . C. . D. . 27 37 32 3 Lời giải
GVSB: Nguyễn Bảo; GVPB: Bùi Hà Chọn A
Gọi V là thể tích khối chóp ABCD .
Trong mặt phẳng  ABC , vẽ MN //BC .
Trong mặt phẳng  ACD , vẽ NP//AD .
Trong mặt phẳng  BCD , vẽ PQ//BC .
Khi đó: P  MNPQ .
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 17 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT    AM AN DP DQ 3 Ta có: MA  3MB  0      . AB AC DC DB 4 1 1 3 Ta có: CP  CD  V  V  V  V . 4 ABPC 4 ABDP 4  9 V  V V AM AN AP 9  AMNP  Xét: AMNP 64  . .      1 . V AB AC AP 16 7 7 ABCP V   V  V BMNCP  16 ABCP 64  3 V  V V  BMQP BM BQ BP 1 MBQP  Xét: 64  . .    2 . V BA BD BP 16 15 45 BADP V   V  V AMQDP  16 ABDP 64  5 V  V  1  32 V 5 Từ   1 và 2 , ta suy ra: 1    . 27 V 27  2 V  V 2  32 m
Câu 39. Có bao nhiêu giá trị thực của tham số m thỏa mãn   3 4x  2x 2 dx  3  m ? 0 A. 2 . B.1. C. 4 . D. 3 . Lời giải
GVSB: Nguyễn Bảo; GVPB: Bùi Hà Chọn A m m  m  1 Xét:   3 4x  2x 2 dx  3  m   4 2 x  x  2 4 2 2
 3  m  m  m  3  m   . 0 0 m  1 
Suy ra: Có 2 giá trị m thỏa đề bài.
Câu 40. Có tất cả bao nhiêu cặp số nguyên x và y sao cho đẳng thức sau thỏa mãn y  log 4x 2x   2022 2 101 1  20y 1. 2021 A. 1. B. 3 . C. 0 . D. 2 . Lời giải
GVSB: Vương Kenny; GVPB: Bùi Hà Chọn A 2 y 1  01 +) log  x x 1 4 2  2022 20y 1  2y 10 1log  x x 1 4 2          2022  20y 1 2021 2021     x x 1  20y 1 log 4  2  2022  . 2021  2y 101 20y 1
+) Xét hàm số f  y  , 2 y 101 Do y y 2 2 2 :
10  0  y 20y 100  0  y 101 20y 1 nên f y1 y  . Suy ra log 4x 2x 2022 1 4x 2x     
 2022  2021  4x  2.2x 1  0  2x  2 1 1 1  0 2021  2x 1  0  x  0 20y 1 Với 2 x  0 
1 y 20y 100  0  y 10 . 2 y 101 Trang 18
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
Vậy có 1 cặp số nguyên x, y thỏa mãn yêu cầu.
Câu 41. Cho hình chóp đều S.ABCD có cạnh đáy bằng a , AC cắt BD tại O . Khoảng cách giữa SA và
CD bằng độ dài đoạn SO . Tính sin của góc giữa cạnh bên và mặt phẳng đáy. 3 15 10 4 A. . B. . C. . D. . 5 5 5 5 Lời giải
GVSB: Vương Kenny; GVPB: Bùi Hà Chọn B S H a D I A O B C AB//CD  +) Ta có   . AB   SAB CD//SAB C  D//  SAB +)   d C ;
D SA  d CD; SAB  d  ;
D SAB  2d O; SAB . SA   SAB
+) Gọi 𝐼 là trung điểm 𝐴𝐵, khi đó SI  AB . Kẻ OH  SI , khi đó OH  d O; SAB . 1 1
Suy ra OH  d CD; SA  SO . 2 2 1 1 1
+) Tam giác 𝑆𝑂𝐼 vuông tại 𝑂, có 𝑂𝐻 là đường cao nên   2 2 2 OH OS OI 4 1 4 3 4 a 3       SO  . 2 2 2 2 2 SO SO a SO a 2
+) Góc giữa cạnh bên và mặt đáy bằng góc  SCO . a 3 a 3   SO SO 3 15 2 2 sin SCO       . 2 2 2 2 SC OC  SO 2a 3a a 5 5 5  4 4 2
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 19 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Câu 42. Cho hàm số f  x , đồ thị của hàm số y  f (x) là đường cong như hình vẽ bên dưới.  1 
Giá trị nhỏ nhất của hàm số g  x  f 2x  
1  4x  3 trên đoạn 1;  bằng 2    A. f 2 5 . B. f   1 1. C. f   1  3. D. f 0 . Lời giải
GVSB: Vương Kenny; GVPB: Bùi Hà Chọn C
+) Ta có gx  2 f 2x   1  4 .  2x 1  1 x  1 
+) g x  0  f 2x   1  2     2x 1  1   x  0  . 2x 1  2   1 x   2  1  +) g   1  f  
1 1, g 0  f   1  3; g  f   25  2  BBT:  1 
Dựa vào BBT, hàm số g  x đạt giá trị nhỏ nhất bằng f   1  3 trên đoạn 1;  . 2   
Câu 43. Trong không gian Oxyz , cho tứ diện ABCD với A3;4;0 , B 2;5;4 ,C 1;1;  1 , D 3;5;3.
Viết phương trình mặt cầu ngoại tiếp tứ diện đó.
A.  x  2   y  2   z  2 1 3 2  9 .
B.  x  2   y  2   z  2 1 3 2  9 .
C.  x  2   y  2   z  2 1 3 2  9 .
D.  x  2   y  2   z  2 1 3 2  9 . Lời giải Trang 20
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
GVSB: Hien Nguyen ; GVPB: Nguyễn Xuân Hè Chọn B
Gọi phương trình mặt cầu S  2 2 2
: x  y  z  2ax  2by  2cz  d  0  2 2 2
a  b  c  d  0 .
Vì mặt cầu đi qua 4 điểm nên:
25  6a  8b  d  0 6a  8b  d  25 a  1   
45  4a 10b  8c  d  0
4a 10b  8c  d  4  5 b   3       .
3  2a  2b  2c  d  0 
2a  2b  2c  d  3  c  2  
43 6a 10b  6c  d
6a 10b  6c  d  43 d  5
Suy ra tâm I 1;3;2 bán kính 2 2 2
R  1  3  2  5  3 .
Vậy phương trình mặt cầu  x  2   y  2   z  2 1 3 2  9 .
Câu 44. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Tam giác SAB đều và nằm trong mặt
phẳng vuông góc với đáy. Tính diện tích mặt cầu ngoại tiếp hình chóp đã cho. 3 4 a 2 7 a 2 7 a A. B. C. D. 2 4 a 3 3 9 Lời giải
GVSB: Hien Nguyen ; GVPB: Nguyễn Xuân Hè Chọn B
Gọi SH là đường cao của tam giác SAB . Vì SAB là tam giác đều và nằm trong mặt phẳng vuông
góc với mặt đáy nên SH là đường cao của hình chóp S.ABCD .
Gọi O là tâm của hình vuông ABCD, từ O dựng Ox  (ABCD) .
Từ trọng tâm G của tam giác SAB dựng Gy  (SAB) . Gọi I  Ox  Gy .
Vì I  Ox , mà Ox  (ABCD) , O là tâm hình vuông ABCD nên I cách đều A, B, C, D (1).
Mặt khác G là trọng tâm của tam giác đều SAB, I Gy , mà Gy  (SAB) nên I cách đều S, A, B (2).
Từ (1) và (2) suy ra I cách đều S, ,
A B,C, D . Nên I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD, bán kính R=IB.
Vì OI  (ABCD) , SH  (ABCD) nên OI / /GH vì G  SH (3)
Mặt khác Gy  (SAB) , I Gy mà OH  (SAB) (vì OH  AB,OH  SH ) nên GI / / O H (4) 1 1 a 3 a 3
Từ (3) và (4) suy ra GHOI là hình bình hành OI  GH  SH  .  . 3 3 2 6
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 21 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT
Vì OI  ( ABCD)  OI  OB  BOI vuông tại B Xét B  OI vuông tại B ta có 2 2     2 2 2 a 3 a 2 7 2 21 IB  IO  OB        a  IB  a  R . 6 2 12 6      7 Diện tích mặt cầu là 2 2 S  4 R   a . 3
Câu 45. Gọi A là tập tất cả các số tự nhiên có 6 chữ số khác nhau, lấy ngẫu nhiên một số từ A . Tính
xác suất để lấy được một số luôn có mặt 3 chữ số 0 , 1, 2 và giữa hai chữ số 0 và 1 có đúng 2 chữ số. 1 7 5 7 A. . B. . C. . D. . 15 162 162 405 Lời giải
GVSB: Trần Xuân Thiện; GVPB: Nguyễn Xuân Hè Chọn C
 Số phần tử của không gian mẫu là n   9.9.8.7.6.5  136080 .
 Gọi số có 6 chữ số khác nhau có dạng abcdef trong đó luôn có mặt 3 chữ số 0 , 1, 2 .
Vì giữa hai chữ số 0 và 1 có đúng 2 chữ số nên khi đó cặp số 0 và 1 có các vị trí 1, 4 , 2,5 , 3, 6 .
Trường hợp 1: 0 và 1 đứng vị trí 1, 4 .
Khi đó chọn 3 số trong 7 số còn lại: 4 C . 7
Xếp số 3 và 3 số được chọn vào 4 vị trí còn lại có 4! cách. Suy ra có 4 C .4! số. 7
Trường hợp 2: 0 và 1 đứng vị trí 2,5 .
Khi đó chọn 3 số trong 7 số còn lại: 3 C . 7
Xếp số 3 và 3 số được chọn vào 4 vị trí còn lại có 4! cách. Suy ra có 3 2!.C .4! số. 7
Trường hợp 3: 0 và 1 đứng vị trí 3, 6 .
Khi đó chọn 3 số trong 7 số còn lại: 3 C . 7
Xếp số 3 và 3 số được chọn vào 4 vị trí còn lại có 4! cách. Suy ra có 3 C .4! số. 7
Vậy số các số thỏa mãn yêu cầu là n  A 4 3  C .4! 2.2!.C .4!. 7 7 4 3 n A C .4! 2.2!.C .4! 5
Vậy xác suất để lấy được số thỏa mãn là P  A   7 7    . n   136080 162
Câu 46. Cho hàm số bậc bốn y  f  x có đồ thị C  như hình vẽ bên. Biết hàm số y  f  x đạt cực trị 2
tại các điểm x , x , x thỏa mãn x  x  2 , f  x  f x  f x  0 và C  nhận đường 1   3   2  1 2 3 3 1 3
thẳng d : x  x làm trục đối xứng. Gọi S , S , S , S là diện tích của các miền hình phẳng 2 1 2 3 4
được đánh dấu như hình bên. Trang 22
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021 S  S Tỉ số 3
4 gần kết quả nào nhất? S  S 1 2 A. 1.62 . B. 1.64 . C. 1.68 . D. 1.66 . Lời giải
GVSB: Trần Xuân Thiện; GVPB: Nguyễn Xuân Hè Chọn D
 Kết quả bài toán không đổi khi ta tịnh tiến đồ thị hàm số sang bên trái sao cho đường thẳng
d : x  x trùng với trục tung, khi đó đồ thị C là đồ thị của hàm số trùng phương y  g  x có 2
ba điểm cực trị x  1, x  0 , x  1 . 1 2 3
Suy ra y  g  x  k  4 2
x  2x   c với k  0 . 2 2 3
Mặt khác f  x  f x  f x  0  2k  2c  c  0  c  k . 1   3   2  3 3 4 3
Suy ra y  g x  k  4 2 x  2x   k . 4 1  Khi đó 3 28 2 17 4 2
S  S  k x  2x  dx  k 1 2  . 4 60 0
Ta lại có g 0  g  
1  k  S  S  S  S  k.1  k . 1 2 3 4 28 2 17 77  28 2 S  S 77  28 2 Suy ra 3 4 S  S  k  k  k    1.66 3 4 60 60 S  S 28 2 17 1 2
Câu 47. Cho hàm số f (x) có đạo hàm liên tục trên  , đồ thị hàm số y  f '(x) có đúng bốn điểm chung
với trung hoành như hình vẽ dưới.
Có bao nhiêu giá trị nguyên của m để hàm số y  f  3
x  3 x  m  202 1 có 11 điểm cực trị. A. 0 . B. 2 . C. 5 . D. 1. Lời giải GVSB: Lê Duy; GVPB: Chọn D
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 23 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT + Vì hàm số y  f  3
x  3 x  m  202 1 là hàm số chẵn nên để hàm số có 11 điểm cực trị thì hàm số g x  f  3 ( ) x  3x  m  202 
1 , x  0 có đúng 5 điểm cực trị. + Ta có :
+ Sử dụng phương pháp ghép trục ta có bảng biến thiên của y  f  3 x  3x, x  0 x 0 a 1 b c d e  3 u  x  3x 0 -1 -2 -1 1 2 4 f (u)
+ Vì đồ thị hàm số g x  f  3 ( ) x  3x  m  202 
1 thu được bằng cách tịnh tiến đồ thị hàm số  3
y  f (x  x) theo vector v  m  2021;0 nên để hàm số g x  f  3 ( ) x  3x  m  202  1 , x  0 có đúng 5 điểm cực trị thì điều kiện là a  m  2021  0 
 a  2021  m  a  2021, a (0;1)  m  2  021 a  m  2021 0
Vậy có một giá trị của m.
Câu 48. Trong không gian Oxyz, cho mặt phẳng (P) : x  y  z  2  0, đường thẳng x 1 y 1 2  z  1 3  (d ) :   và hai điểm B ;1; ,C   1;1; 
1 . Gọi A là giao điểm của (d) và 1 1 1  2 2 
(P) , (S) là điểm di động trên (d),(S  )
A . Gọi H , K lần lượt là hình chiếu vuông góc của A
trên các đường thẳng SB và SC , () là giao tuyến của hai mặt phẳng (AHK ) và (P), M ()
. Giá trị nhỏ nhất của MB  MC là A. 14 . B. 6  2 2 . C. 7 . D. 7 . 2 2 2 2 Lời giải GVSB: Lê Duy; GVPB: Chọn A 
+ Toạ độ của A là: A1; 1
 ;2; Vector pháp tuyến của (P) là: n(P)  1;1;1 ; vector chỉ phương 
của (d) là: u(d)  1;1; 
1 nên (d )  (P) và B,C  (P)  SA  ( ABC) 2 2 2 2 HS SA KS SA SA + Ta có: AB  , AC  2 và 2   2SA ,   2 2 2 HB AB KC AC 2 + Gọi  
D  HK  BC . Áp dụng định lý Menelaus cho tam giác SBC với K, H, D thẳng hàng, ta HS KC DB DB 1   có: . .  1    4DB  DC (vì D nằm ngoài BC) HB KS DC DC 4  1 2  5 
  2 1 1 1  D ; ;  AD  ; ;      2; 1  ; 
1 . Do đó giao tuyến của hai mặt phẳng (AHK )  3 3 3   3 3 3  3 x 1 2t 
và (P) là đường thẳng AD có phương trình (AD) : y  1   t z  2t 
+ Ta thấy B, C nằm cùng một phía so với AD. Gọi C ' là điểm đối xứng của C qua AD thì C '1;0;3 Trang 24
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021 Vậy MB  MC 14 min  BC '  . 2
Câu 49. Có bao nhiêu số nguyên dương m để phương trình x e 1  mln mx  
1 có hai nghiệm phân biệt trên đoạn  1  0;10? A. 2201 . B. 2020 . C. 2021 . D. 2202 . Lời giải Chọn A
 Điều kiện mx 1  0 .  Ta có x e 1  mln mx   1 x
 e  mx  mx 1 mln mx   1 x lnmx  1  e  mx  e  m ln mx   1 (1). Xét hàm số   t f t  e  mt,t   . Có   t f t  e  m  0, t
  ,m  0. Suy ra hàm f t đồng biến trên  .
Từ (1) ta được    ln   1    ln   1 x f x f mx x mx  e  mx 1(2).
 Ta thấy (2) luôn có một nghiệm x  0 1
 0;10. Do đó ta cần tìm các giá trị của m để (2) có
đúng một nghiệm x  0, x  1  0;10. x e 1 Với x  0 thì (2)   m . x x e 1 Xét hàm g  x  , x  1  0;10\  0 . x x x xe  e 1 Ta có g x  . 2 x Đặt   x x
h x  xe  e 1, x  . Có   x
h x  xe , h x  0  x  0 .
Ta thấy lim h x  , lim h x 1,h0  0 . x x
Bảng biến thiên của hàm hx như sau x  0  h   x  0   1 hx 0
Từ bảng biến thiên suy ra h x  0, x
   g x  0, x   0 .
 Ta có lim g  x 1, lim g  x 1. x 0 x 0  
Bảng biến thiên của hàm y  g  x với x 1  0;10\  0 như sau
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 25 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲 BIÊN SOẠN TOÁN THPT x 10 0 10 y '   10 e 1  y 10 1 1 10 1 e  10
Từ bảng biến thiên suy ra (2) có đúng một nghiệm x  0, x  1  0;10 1  0 10 1 e e 1  m , \     1 .  10 10 
 Do m nguyên dương nên m2,3,4,...,220 
2 . Vậy có 2201 giá trị của m thỏa mãn yêu cầu bài toán.
Câu 50. Cho số các số phức z , z z 1 i 1
z  2  i  2. Số phức z 1 2 thỏa mãn 1 và 2 thay đổi sao cho
zz 1iz và zz z 2i là số thuần ảo. Giá trị nhỏ nhất của z32i bằng 2   2  1   1  11 A. . B. 2 . C. 2 2 . D. 13 1. 5 Lời giải Chọn C
 Đặt w  z  2  i  w  2 . 2 Ta có  z  z z  2  i  z  z
z  2  i  z  z w là số thuần ảo 2   2   2 2   2
nên  z  z w  ki, k  . 2    4 w k  Mặt khác 2 w.w  w  4  w   z  z  i mà z  w+2  i 2 w 4 2 w k  kw   z  w  2  i  i  w  2  1 i   . 4  4   w k 
 Khi đó P  z 3 2i  w 1 1 i    4  2  ki   ki  ki k  1 w    1i  1 w  1 i  w 1  2  2 1  2  2  2   .  4   4  4 16
 Dấu bằng có chẳng hạn khi z  z  2  2  2 1 i và z 2     1 là số phức thỏa mãn
z 1 i  1 và z  z 1i  z là số thuần ảo. 1   1  1
Vậy giá trị nhỏ nhất của z 3 2i bằng 2 2 .
____________________ HẾT ____________________ Trang 26
TÀI LIỆU ÔN THI THPT QUỐC GIA
Document Outline

  • de-thi-thu-toan-tn-thpt-2021-lan-1-truong-chuyen-le-khiet-quang-ngai
    • de-thi-thu-toan-tn-thpt-2021-lan-1-truong-chuyen-le-khiet-quang-ngai
    • Phieu-soi-dap-an
  • AAA