19 trang 56 lượt tải

Đề thi thử Toán tốt nghiệp THPT 2021 lần 1 trường Đào Duy Từ – Hà Nội

112

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi thử Toán tốt nghiệp THPT 2021 lần 1 trường THPT Đào Duy Từ, thành phố Hà Nội; đề thi có đáp án và lời giải chi tiết.

Chủ đề: Đề thi THPTQG môn Toán năm 2023 1.2 K tài liệu

Môn: Toán 2.2 K tài liệu

Tác giả:

Profile

Thanh Hoa

1 năm trước
Danh sách Quiz
/19
1
SỞ GD&ĐT HÀ NỘI
TRƯỜNG THPT ĐÀO DUY TỪ
MÃ ĐỀ THI: 209
ĐỀ THI THỬ TỐT NGHIỆP THPT - LẦN I
NĂM HỌC 2020 – 2021
MÔN TOÁN
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Câu 1: Gọi
,
M N
là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
3 1
y x x
trên
0;2 .
Khi đó
bằng
A. 3. B. 4. C. 6. D. 2.
Câu 2: Nghiệm của phương trình
2
log 3 2 2
x
là
A.
2
.
3
x
B.
2.
x
C.
1.
x
D.
4
.
3
x
Câu 3: Cho khối nón có chu vi đáy
8
và chiều cao
3.
h
Thể tích khối nón đã cho bằng?
A.
12 .
B.
4 .
C.
16 .
D.
24 .
Câu 4: Với
3
0, 1,log
a
a a a
bằng
A. 3. B.
3.
C.
1
.
3
D.
1
.
3
Câu 5: Số phức liên hợp của số phức
4 3
i
là
A.
3 4 .
i
B.
4 3 .
i
C.
3 4 .
i
D.
4 3 .
i
Câu 6: Họ các nguyên hàm của hàm số
2
2 3
f x x x
là
A.
3
2
3 .
3
x
x x C
B.
2 2 .
x C
C.
3 2
.
x x C
D.
3 2
2 3 .
x x x C
Câu 7: Đồ thị hàm số
3
6 3
x
y
x
có bao nhiêu tiệm cận đứng và tiệm cận ngang?
A. 3. B. 1. C. 2. D. 0.
Câu 8: Cho các số thực dương
, , ,
a b x y
thỏa mãn
1, 1
a b
và
1
3
.
x y
a b ab
Giá trị nhỏ nhất của biểu thức
3 4
P x y
thuộc tập hợp nào dưới đây?
A.
7;9 .
B.
11;13 .
C.
1;2 .
D.
5;7 .
Câu 9: Cho số phức
z
thỏa
2 4 8 19 .
i z z i i
Mô đun của
z
bằng
A. 5. B. 18. C.
5.
D.
13.
2
Câu 10: Tìm tất cả giá trị thực của tham số
m
sao cho khoảng
2;3
thuộc tập nghiệm của bất phương trình
2 2
5 5
log 1 log 4 1.
x x x m
A.
12;13 .
m B.
13;12 .
m C.
13; 12 .
m D.
12;13 .
m
Câu 11: Cho hàm số
f x
liên tục trên
0; .

Biết
2
1
x
là một nguyên hàm của hàm số
' ln
y f x x
và
1
2 .
ln 2
f Khi đó,
2
1
f x
dx
x
bằng
A.
7
.
4
B.
1
.
2
C.
1
.
2
D.
7
.
4
Câu 12: Trong không gian
,
Oxyz
cho mặt phẳng
: 2 1 0.
x y
Vectơ nào sau đây là một vectơ pháp
tuyến của
?
A.
1;2; 1 .
B.
1;2;0 .
C.
1; 2;0 .
D.
1;2;0 .
Câu 13: Cho số phức
z a bi
và
1
w .
2
z z
Mệnh đề nào sau đây ĐÚNG?
A.
w 2.
B.
w
là một số thực.
C.
.
w i
D.
w
là số thuần ảo.
Câu 14: Cho một khối chóp có diện tích đáy
2
6 ,
B a
chiều cao
3 .
h a
Thể tích khối chóp đã cho bằng
A.
3
6 .
a
B.
3
18 .
a
C.
3
9 .
a
D.
3
54 .
a
Câu 15: Cho tích phân:
1
1 ln
.
e
x
I dx
x
Đặt
1 ln .
u x
Khi đó
I
bằng
A.
1
2
0
2 .
I u du
B.
1
2
0
2 .
I u du
C.
0
2
1
.
2
u
I du
D.
0
2
1
.
I u du
Câu 16: Cho hàm số
y f x
có đạo hàm trên
và
4 3
' 2 3 1 2 .
f x x x x
Số điểm cực trị của
hàm số đã cho là
A. 2. B. 3. C. 1. D. 0.
Câu 17: Gọi
H
là hình phẳng giới hạn bởi đồ thị hàm số
2
5 4
y x x
và trục
.
Ox
Thể tích của khối tròn
xoay sinh ra khi quay hình
H
quanh trục
Ox
bằng:
A.
9
.
2
B.
81
.
10
C.
81
.
10
D.
9
.
2
Câu 18: Cho hàm số
.
f x
Bảng biến thiên của hàm số
'
f x
như sau:
3
Số điểm cực trị của hàm số
2
2
y f x x
là:
A. 7. B. 9. C. 3. D. 5.
Câu 19: Số giao điểm của đồ thị hàm số
4 2
4 1
y x x
và đồ thị hàm số
2
1
y x
là
A. 4. B. 3. C. 2. D. 1.
Câu 20: Hàm số
2
4
x m
y
x
đồng biến trên các khoảng
;4
 và
4;

khi
A.
2 2.
m
B.
2
.
2
m
m
C.
2
.
2
m
m
D.
2 2.
m
Câu 21: Cho hình nón
N
có đỉnh
,
S
bán kính đáy
1
r
và độ dài đường sinh
2 2.
l Mặt cầu đi qua
S
và
đường tròn đáy của
N
có bán kính bằng
A.
4 7
.
7
B.
8 7
.
7
C.
7.
D.
4
.
3
Câu 22: Tỉ lệ tăng dân số hàng năm của một quốc gia
X
là 0,2%. Năm 1998 dân số của quốc gia
X
là
125500000 người. Hỏi sau bao nhiêu năm thì dân số của quốc gia
X
là 140000000 người?
A. 54 năm. B. 6 năm. C. 55 năm. D. 5 năm.
Câu 23: Cho hàm số
1
.
1
x
y
x
Phát biểu nào sau đây đúng?
A. Hàm số đồng biến trên mỗi khoảng
;1

và
1; .

B. Hàm số đồng biến trên
;1 1; .
 
C. Hàm số đồng biến trên khoảng
;1 .

D. Hàm số đồng biến trên khoảng
1; .

Câu 24: Cho hình nón có bán kính đáy
2
r
và độ dài đường sinh
4.
l
Diện tích xung quanh của hình nón đã
cho bằng
A.
32 .
B.
8 .
C.
16 .
D.
48 .
Câu 25: Cho hàm số
y f x
có đồ thị như hình dưới. Số nghiệm thực của phương trình
1
f x
là
4
A. 3. B. 2. C. 4. D. 1.
Câu 26: Xét các số phức
z
thỏa mãn
3 2 4.
iz i
Trên mặt phẳng tọa độ
,
Oxy
tập hợp điểm biểu diễn số
phức
2 5 6
w iz i
là một đường tròn có tâm
;
I a b
, bán kính
.
R
Tính
T a b R
A. 21. B. 17. C. 5. D.
1.
Câu 27: Hàm số
3 2
3 9 7
y x x x
đạt cực đại tại
A.
3.
x
B.
1
.
3
x
x
C.
1
.
3
x
x
D.
1.
x
Câu 28: Cho đồ thị hàm số
4 2
f x ax bx c
như hình vẽ bên. Khẳng định nào sau đây là đúng
A.
2
0; 0; 0; 4 0.
a b c b ac
B.
2
0; 0; 0; 4 0.
a b c b ac
C.
2
0; 0; 0; 4 0.
a b c b ac
D.
2
0; 0; 0; 4 0.
a b c b ac
Câu 29: Trong không gian
,
Oxyz
mặt phẳng qua
3;4;1
A và song song với mặt phẳng
Oxy
có phương trình
là
A.
3 0.
x
B.
1 0.
z
C.
4 0.
y
D.
3 4 0.
x y z
Câu 30: Nghiệm của phương trình
2 3
9 81
x
là
A.
3
.
2
x
B.
1
.
2
x
C.
1
.
2
x
D.
3
.
2
x
Câu 31: Cho hàm số
f x
có đạo hàm trên đoạn
1;2 , 1 1
f
và
2 2.
f
Khi đó,
2
1
'
I f x dx
bằng
5
A.
1.
I
B.
1.
I
C.
7
.
2
I
D.
3.
I
Câu 32: Tập nghiệm của bất phương trình
2 4 1
3 3
4 4
x x
là
A.
1;2 .
B.
;5 .
 C.
5; .

D.
; 1 .

Câu 33: Số cạnh của hình bát diện đều là
A. 8. B. 12. C. 10. D. 20.
Câu 34: Thể tích của khối cầu có bán kính
3
r
là
A.
64 .
B.
48 .
C.
8 .
D.
36 .
Câu 35: Trong không gian
,
Oxyz
hình chiếu vuông góc của điểm
1;3;5
A trên mặt phẳng
Oyz
là điểm nào
sau đây?
A.
1;3;0 .
B.
1;0;5 .
C.
0;3;5 .
D.
1;0;0 .
Câu 36: Biết
2
0
2020,
f x dx
khi đó
4
0
2
x
I f dx
bằng
A. 2020. B. 1010. C.
2020.
D. 4040.
Câu 37: Cho số phức
3 4 .
z i
Tìm phần thực
a
và phần ảo
b
của số phức
.
z
A.
3, 4.
a b
B.
4, 3.
a b
C.
4, 3.
a b
D.
3, 4.
a b
Câu 38: Trong không gian
,
Oxyz
cho mặt cầu
2 2
2
: 2 1 4.
S x y z
Tâm của
S
có tọa độ là
A.
2;0;1 .
B.
2;0; 1 .
C.
2;0;1 .
D.
2;0; 1 .
Câu 39: Cho số phức
1 2
.
1
i
z
i
Trong mặt phẳng tọa độ, điểm biểu diễn số phức
z
là điểm nào dưới đây?
A.
1 3
; .
2 2
B.
1 3
; .
2 2
C.
1 3
; .
2 2
D.
1 3
; .
2 2
Câu 40: Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh bằng
2 .
a
Thể tích khối
trụ bằng
A.
3
.
a
B.
3
2
.
3
a
C.
3
.
3
a
D.
3
2 .
a
Câu 41: Đồ thị hình bên là của hàm số nào?
6
A.
3
2 .
y x x
B.
3
3 .
y x x
C.
3
3 .
y x x
D.
3
2 .
y x x
Câu 42: Trong không gian
,
Oxyz
cho điểm
1;2;5
A và mặt phẳng
: 2 1 0.
P x y z
Phương trình đường
thẳng qua
A
vuông góc với
P
là:
A.
3
2 2 .
7
x t
y t
x t
B.
1
2 2 .
5
x t
y t
z t
C.
2
2 2 .
7
x t
y t
z t
D.
1
2 2 .
5
x t
y t
z t
Câu 43: Cho tứ diện
OABC
có
, ,
OA OB OC
đôi một vuông góc và
6, .
OB OC a OA a
Thể tích khối tứ
diện đã cho bằng
A.
3
3 .
a
B.
3
2 .
a
C.
3
6 .
a
D.
3
.
a
Câu 44: Cho khối lăng trụ có diện tích đáy
8
B
và chiều cao
6.
h
Thể tích của khối lăng trụ đã cho bằng
A. 48. B. 16. C. 24. D. 14.
Câu 45: Tập xác định của hàm số
2
3
log
2
x
y
x
là
A.
3;2 .
B.
; 3 2; .
 
C.
\ 3;2 .
D.
3;2 .
Câu 46: Trong không gian
,
Oxyz
cho đường thẳng
1 2
: 1,
2 3
x y
d z
điểm nào dưới đây thuộc đường
thẳng
?
d
A.
2;3;0 .
B.
2;3;1 .
C.
1; 2; 1 .
D.
1;2;1 .
Câu 47: Trong không gian
,
Oxyz
cho điểm
4; 1;3
A và đường thẳng
1 1 3
: .
2 1 1
x y z
d
Tọa độ điểm
M
là điểm đối xứng với điểm
A
qua
d
là
7
A.
0; 1;2 .
M B.
2; 5;3 .
M C.
1;0;2 .
M D.
2; 3;5 .
M
Câu 48: Cho hàm số
y f x
liên tục trên
và có bảng biến thiên như sau:
Số nghiệm của phương trình
4 2
3 4 2
2 1 0
x x
f
là
A. 2. B. 3. C. 1. D. 5.
Câu 49: Cho các số thực
, ,
a b c
thỏa mãn
3 7 11
log 7 log 11 log 25
27, 49, 11.
a b c Giá trị của biểu thức
2 2
11
3 7
2
log 25
log 7 log 11
A a b c là
A. 129. B. 519. C. 469. D. 729.
Câu 50: Cho khối tứ diện
ABCD
có thể tích
.
V
Gọi
1 2 3 4
, , ,
G G G G
lần lượt là trọng tâm của bốn mặt của hình
tứ diện. Thể tích khối tứ diện
1 2 3 4
G G G G
bằng
A.
.
32
V
B.
.
9
V
C.
.
27
V
D.
.
12
V
--------------- HẾT --------------
8
ĐÁP ÁN
1-D 2-B 3-C 4-C 5-D 6-A 7-C 8-A 9-D 10-A
11-D 12-B 13-B 14-A 15-A 16-A 17-C 18-A 19-C 20-B
21-A 22-C 23-C 24-B 25-A 26-C 27-D 28-A 29-B 30-C
31-A 32-B 33-B 34-D 35-C 36-D 37-A 38-D 39-D 40-D
41-B 42-A 43-D 44-A 45-A 46-C 47-D 48-B 49-C 50-C
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Chọn D.
Ta có
2
' 3 3.
y x
Cho
2
1 0;2
' 0 3 3 0 .
1 0;2
x
y x
x
Ta có
0 1; 1 1; 2 3.
y y y
Vậy
3, 1 2.
M N M N
Câu 2: Chọn B.
Ta có
2
2
log 3 2 2 3 2 2 2.
x x x
Vậy nghiệm của phương trình
2
log 3 2 2
x
là
2.
x
Câu 3: Chọn C.
Gọi
r
là bán kính đáy của khối nón. Ta có:
2 8 4
r r
Thể tích của khối nón đã cho là:
2 2
1 1
.4 .3 16 .
3 3
V r h
Câu 4: Chọn C.
Với
3
1 1
0, 1,log log
3 3
a
a
a a a a
Câu 5: Chọn D.
Ta có:
4 3 4 3 .
i i
Câu 6: Chọn A.
Ta có:
3
2 2 2
2 3 2 3 3 .
3
x
f x dx x x dx x dx xdx dx x x C
9
Câu 7: Chọn C.
TXĐ:
\ 2 .
D
Ta có
3 1
lim lim
6 3 3
x x
x
y
x
 
nên đường thẳng
1
3
y
là tiệm cận ngang của đồ thị hàm số đã cho.
Mà
2 2
3
lim lim
6 3
x x
x
y
x

nên đường thẳng
2
x
là tiệm cận đứng của đồ thị hàm số đã cho.
Vậy đồ thị hàm số
3
6 3
x
y
x
có tất cả 2 đường tiệm cận, trong đó 1 đường tiệm cận ngang và 1 đường tiệm cận
đứng.
Câu 8: Chọn A.
Ta có
1
3
1 4 1
1 log log
3 3 3
.
1 1 1 1
log 1 log 1
3 3 3 log
a a
x y
b b
a
x ab b
a b ab
y ab a
b
Thay vào
,
P
ta được
4 1 1 1
3 4 3 log 4. 1
3 3 3 log
a
a
P x y b
b
16 4
log
3 3log
a
a
b
b
Vì
1, 1
a b
nên
log 0.
a
b
Áp dụng BĐT Cô-si, ta có:
16 4 16 4 16 4 3
log 2 log . .
3 3log 3 3log 3
a a
a a
P b b
b b
Dấu “=” xảy ra khi và chỉ khi
4 2 3
log log log .
3 3
a a a
b b b
Vậy giá trị nhỏ nhất của
P
bằng
16 4 3
7;9 .
3
Câu 9: Chọn D.
Gọi
, .
z a bi a b
Khi đó:
2 4 8 19 2 4 1 8 19
i z z i i i a bi a b i i
2 2 4 4 1 8 19 ,
a b a b i a b i i
nên ta có hệ phương trình
10
2 8 2 8 3
.
6 4 19 6 15 2
a b a b a
a b a b b
Vậy
13.
z
Câu 10: Chọn A.
Điều kiện xác định:
2
4 0.
x x m
Với điều kiện trên, bất phương trình tương đương với
2 2
5 1 4 .
x x x m
Để khoảng
2;3
thuộc tập nghiệm của bất phương trình thì hệ bất phương trình
2
2 2
4 0
5 1 4
x x m
x x x m
nghiệm đúng với mọi
2;3 .
x
2
2
4
4 4 5
f x x x m
g x x x m
nghiệm đúng với mọi
2;3 .
x
Xét hàm số
2
4
f x x x
trên khoảng
2;3
có
' 2 4 0, 2;3
f x x x suy ra
2 12.
f x f Do
đó
12 12
m m
Xét hàm số
2
4 4 5
g x x x
trên khoảng
2;3
có
' 8 4 0, 2;3
g x x x suy ra
2 13.
g x g
Do đó
13 13.
m m
Câu 11: Chọn D.
Vì
2
1
x
là một nguyên hàm của hàm số
' ln ,
y f x x
nên
'
2 3
1 2
' ln ' ln
f x x f x x
x x
Đặt
'
.
1
ln
u f x
du f x dx
v x
dv dx
x
Khi đó:
2 2 2
3 2
1 1 1
2 2
2 1 1
.ln ' ln 2 .ln 2 .ln 2
1 1
ln 2
f x
dx f x x f x xdx f dx
x x x
2
1 7
1 1 .
2 4
Câu 12: Chọn B.
Ta có:
1;2;0
n
là một vectơ pháp tuyến của mặt phẳng
.
Câu 13: Chọn B.
Ta có
z a bi
do đó
1 1
w
2 2
z z a bi a bi a
là một số thực.
Câu 14: Chọn A.
11
Thể tích của khối chóp
2 3
1 1
. .6 .3 6 .
3 6
V B h a a a
Câu 15: Chọn A.
Đặt
2
1 ln 1 ln
u x u x
2
dx
udu
x
(với
1 1; 0)
x u x e u
Ta có
1
2
0
2 .
I u du
Câu 16: Chọn A.
Ta có
2
' 0 3
1
2
x
f x x
x
Trong đó
1
2,
2
x x
là các nghiệm bội bậc lẻ nên hàm số
( )
y f x
có 2 điểm cực trị.
Còn
3
x
là nghiệm bội bậc chẵn nên không là điểm cực trị của hàm số
( )
y f x
.
Câu 17: Chọn C.
Xét phương trình hoành độ giao điểm của đồ thị hàm số và trục
Ox
là:
2
1
5 4 0
4
x
x x
x
Thể tích của khối tròn xoay sinh ra khi quay hình
H
quanh trục
Ox
bằng:
4
2
1
81
5 4
10
V x x dx
Vậy chọn đáp án C là đáp án đúng.
Câu 18: Chọn A.
Xét
2 2
2 ' 2 2 . ' 2
y f x x y x f x x
2
1
2
2
2
2
3
2
4
1
2 ; 1
1
' 0 2 1;0
' 2 0
2 0;1
2 1;
x
x x x
x
y x x x
f x x
x x x
x x x


12
Trường hợp 1:
2 2
1 1
2 ; 1 2 0.
x x x x x x

Ta có
1 1 1
' 1 1. 1 0, ; 1
x x x

nên phương trình vô nghiệm. Suy ra trường hợp này không có
điểm cực trị.
Trường hợp 2:
3 2
2 2
2 1;0 2 0.
x x x x x x
Ta có
2 2 2
' 1 1. 1 0, 1;0
x x x nên phương trình luôn có hai nghiệm phân biệt. Suy ra trường
hợp này có hai điểm cực trị.
Trường hợp 3:
2
3
2 0;1 .
x x x Xét thấy hệ số
a
và
c
trong phương trình luôn trái dấu nên phương trình
luôn có hai nghiệm phân biệt. Suy ra trường hợp này có hai điểm cực trị.
Trường hợp 4:
2
4
2 1; .
x x x

Xét thấy hệ số
a
và
c
trong phương trình luôn trái dấu nên phương
trình luôn có hai nghiệm phân biệt. Suy ra trường hợp này có hai điểm cực trị.
Mặt khác, các hệ số trong các phương trình ở trường hợp 2, 3, 4 vừa xét đều khác nhau hệ số
c
nên các nghiệm
của phương trình này đều khác nhau và đều khác 1.
Vậy hàm số
2
2
y f x x
có 7 điểm cực trị. Ta chọn đáp án A.
Câu 19: Chọn C.
Phương trình hoành độ giao điểm của đồ thị hàm số
4 2
4 1
y x x
và đồ thị hàm số
2
1
y x
là
4 2 2
4 1 1.
x x x
2
4 2
2
3 17
3 17
2
3 2 0 .
2
3 17
2
x
x x x
x L
Vậy số giao điểm của đồ thị hàm số
4 2
4 1
y x x
và đồ thị hàm số
2
1
y x
là 2.
Câu 20: Chọn B.
TXĐ:
;4 4; .
D
 
Ta có
2 2
2
4
' .
4
4
x m m
y y
x
x
Hàm số đồng biến trên các khoảng
;4
 và
4;

khi và chỉ khi
2
2
2
2
4
' 0 4 0 .
2
4
m
m
y m
m
x
Câu 21: Chọn A.
13
Gọi
I
là tâm của mặt cầu đi qua
S
và đường thẳng đáy của
.
N
R
là bán kính của mặt cầu cần tìm.
Theo giả thiết, ta có
2 2
7.
SO l r
Trường hợp 1.
7 .
IO SO R R
Trong tam giác vuông
,
IOB
ta có
2
2 2 2 2
4 7
7 1 .
7
IB IO OB R R R
Trường hợp 2.
7.
IO R SO R
Trong tam giác vuông
,
IOB
ta có
2
2 2 2 2
4 7
7 1 .
7
IB IO OB R R R
Câu 22: Chọn C.
Gọi
A
là dân số của quốc gia
X
năm 1998,
r
là tỷ lệ tăng dân số và
n
A
là dân số của quốc gia
X
sau
n
(năm) tính từ năm 1998.
140000000
ln
125500000
140000000 125500000. 1 0,2% 140000000 54,72.
ln 1 0,2%
n
n
A n
Vậy sau 55 năm thì dân số của quốc gia
X
là 140000000 người.
Câu 23: Chọn C.
Tập xác định
\ 1 .
D
Ta có
2
2
' 0, .
1
y x D
x
Suy ra hàm số đồng biến trên mỗi khoảng
;1

và
1; .

Câu 24: Chọn B.
Ta có
.2.4 8 .
xq
S rl
14
Câu 25: Chọn A.
Số nghiệm thực của phương trình
1
f x
là số giao điểm của đồ thị hàm số
y f x
và đường thẳng
1.
y
Vậy phương trình đã cho có 3 nghiệm phân biệt.
Câu 26: Chọn C.
Do
z z x yi
với
, .
x y
Theo đề bài:
2 5 6 2 3 2 1 2 w 1 2 2 3 2 .
w iz i iz i i i iz i
w+ 1 2 2 3 2 w+ 1 2 2 3 2 8.
i iz i i iz i
Suy ra:
2 2
2
w 1 2 8 1 2 8 1 2 8 1 2 8 .
i x yi i x y i x y
Vậy tập hợp điểm biểu diễn
w
là một đường tròn có tâm
1; 2
I
, bán kính
8
R
nên ta có:
1 2 8 5.
T a b R
Câu 27: Chọn D.
Xét
2
1
' 3 6 9 0 .
3
x
y x x
x
Ta có:
" 6 6; " 1 12 0; " 3 12 0.
y x y y
Hàm số đạt cực đại
tại điểm
1
x
và đạt cực tiểu tại điểm
3.
x
Câu 28: Chọn A.
* Từ hình vẽ suy ra
0, 0.
a c
* Xét
3 2
' 4 2 0 2 2 0.
y ax bx x ax b
Để hàm số có 3 cực trị như hình vẽ thì
;
a b
trái dấu, suy ra
0.
b
* Xét
4 2 2 2
0 0; 0
f x ax bx c at bt c t x
có một nghiệm kép theo ẩn phụ
.
t
Từ đồ thị, ta thấy
phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành chỉ có hai nghiệm
x
đối nhau
phương
trình bậc hai theo ẩn phụ
t
chỉ có một nghiệm dương
2
4 0.
b ac
Câu 29: Chọn B.
Mặt phẳng qua
3;4;1
A và song song với mặt phẳng
Oxy
có VTPT:
0;0;1
n k
Có phương trình:
0 3 0 4 1 1 0 1.
x y z z
Câu 30: Chọn C.
TXĐ:
D
Phương trình đã cho tương đương:
2 3 2
1
9 9 2 3 2 .
2
x
x x
15
Câu 31: Chọn A.
Ta có:
2
1
2
' 2 1 2 1 1.
1
I f x dx d x f f
Câu 32: Chọn B.
Bất phương trình
2 4 1 5.
x x x
Tập nghiệm của bất phương trình là
;5 .

Câu 33: Chọn B.
Câu 34: Chọn D.
Thể tích của khối cầu có bán kính
3
r
là
3 3
4 4
. .3 36 .
3 3
V r
Câu 35: Chọn C.
Hình chiếu vuông góc của điểm
; ;
M a b c
trên mặt phẳng
Oyz
là điểm
' 0; ; .
M b c
Do đó điểm cần tìm là
0;3;5 .
Câu 36: Chọn D.
Đặt
'
1
2
2 2 2
x x
t dt dx dx dx dt
Đổi cận
4 2
0 0
x t
x t
2
0
2 2.2020 4040
I f t dt
Vậy
4040.
I
Câu 37: Chọn A.
Phần thực
a
và phần ảo
b
của số phức
z
là
3, 4.
a b
Câu 38: Chọn D.
Tâm của
S
có tọa độ là
2;0; 1
Câu 39: Chọn D.
Ta có:
1 2 1
1 2 1 3 1 3
.
1 1 1 2 2 2
i i
i i
z i
i i i
Vậy trong mặt phẳng tọa độ, điểm biểu diễn số phức
z
là
1 3
; .
2 2
Câu 40: Chọn D.
16
Vì thiết diện qua trục của hình trụ là hình vuông nên 2 2
AB R a R a
và
' 2 .
h AA a
Thể tích khối trụ là
2 2 3
.2 2 .
V R h a a a
Câu 41: Chọn B.
Đồ thị hình bên là đồ thị hàm bậc 3 với hệ số
0
a
nên loại A và D. Đồ thị hàm số có hai điểm cực trị là
1;2
và
1; 2
nên
' 0 1
y x
do đó loại đáp án C và chọn đáp án B.
Câu 42: Chọn A.
Mặt phẳng
: 2 1 0
P x y z
có vectơ pháp tuyến
1; 2;1 .
n
Đường thẳng vuông góc với mp
: 2 1 0
P x y z
nhận vectơ
1; 2;1
n
hoặc vectơ
1;2; 1
u
làm
vectơ chỉ phương nên loại các đáp án B, D. Ta lại có tọa độ điểm
1;2;5
A thỏa mãn phương trình
3
2 2
7
x t
y t
z t
nên đáp án A đúng.
Câu 43: Chọn D.
Vì
, ,
OA OB OC
đôi một vuông góc nên
OA OBC
và
OBC
vuông tại
.
O
17
Nên thể tích khối chóp
OABC
là
3
1 1
. . . . 6. 6. .
6 6
V OAOB OC a a a a
Câu 44: Chọn A.
Áp dụng công thức thể tích hình trụ ta có
. 8.6.
V B h
Vậy thể tích hình trụ là
48.
V
Câu 45: Chọn A.
Hàm số
2
3
log
2
x
y
x
có điều kiện xác định:
3
0 3 2.
2
x
x
x
Vậy tập xác định
3;2 .
D
Câu 46: Chọn C.
Thay tọa độ điểm
1; 2; 1
vào đường thẳng
d
ta được:
2 2
1 1
1 1 0
2 3
(luôn đúng).
Suy ra điểm
1; 2; 1
thuộc đường thẳng
.
d
Câu 47: Chọn D.
Gọi
2 1; 1; 3
N t t t d
là hình chiếu của
A
trên
.
d
Suy ra
N
là trung điểm
.
AM
Ta có:
. 0 2 2 3 0 1.
d
AN u t t t t
Vậy
3; 2;4 .
N
Suy ra
2; 3;5 .
M
Câu 48: Chọn B.
Dựa vào bảng biến thiên, ta có
18
4 3
4 2 4 3 4 3
4 3
3 4 2
1
3 4 2 3 4 2 3 4 2
3 4 2
2
2 1 1
2 1 0 2 1 2 2
2 5
x x
x x x x x x
x x
a
f f
a
TH1:
4 3
3 4 2
2 2
x x
2
4 3 3
3 4 2 1 1 3 2 1 0 1
x x x x x x
TH2:
4 2
3 4 2
2
2
x x
a
4 3
2 2
3 4 2 log
x x a
Xét hàm số
4 3
3 4 2,
g x x x
khảo sát hàm số, ta được bảng biến thiên sau:
x

0 1

'
g x
0
0 +
g x


1
Do
2 2 2
log log 5 1
a
nên
4 3
2 2
3 4 2 log
x x a
có hai nghiệm phân biệt khác 1.
Vậy phương trình
4 3
3 4 2
2 1 0
x x
f
có 3 nghiệm phân biệt.
Câu 49: Chọn C.
Ta có
2 2
3 7 11
11
3 7
3 72 11
log 7 log 11 log 25
log 25
log 7 log 11
log 7 log 11 log 25
A a b c a b c
11
3 7 3 7 11
1
1
3 2log 25
log 7 log 11 log 7 log 11
log 25 3 2
2
2
27 49 11 3 7 11 7 11 25 469.
Câu 50: Chọn C.
Gọi
, ,
M N P
lần lượt là trung điểm của
, , .
AC AD CD
19
Ta có
1 2 3 4 1 2 4 1 2 4 1 2 4
3 1 2 4 1 2 4
1 1 1 1
, . . . , .
3 3 2 2
G G G G G G G G G G BG G G
V d G G G G S d B G G G S V
3
1 2 4 1
. . .
2 3 27 4 27
BMNP BACD
V
V V
____________________ HẾT ____________________
https://toanmath.com/

Tài liệu khác của Toán

Preview text:

SỞ GD&ĐT HÀ NỘI
ĐỀ THI THỬ TỐT NGHIỆP THPT - LẦN I TRƯỜNG THPT ĐÀO DUY TỪ NĂM HỌC 2020 – 2021 MÃ ĐỀ THI: 209 MÔN TOÁN
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Câu 1: Gọi M , N là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3
y  x  3x 1 trên 0;2. Khi đó M  N bằng A. 3. B. 4. C. 6. D. 2.
Câu 2: Nghiệm của phương trình log 3x  2  2 là 2   2 4 A. x  . B. x  2. C. x  1. D. x  . 3 3
Câu 3: Cho khối nón có chu vi đáy 8 và chiều cao h  3. Thể tích khối nón đã cho bằng? A.12. B. 4 . C.16. D. 24 .
Câu 4: Với a  0, a  1,log a bằng 3 a 1 1 A. 3. B. 3. C. . D. . 3 3
Câu 5: Số phức liên hợp của số phức 4  3i là A. 3  4 .i B. 4  3 .i C. 3  4 .i D. 4  3 .i
Câu 6: Họ các nguyên hàm của hàm số f  x 2  x  2x  3 là 3 x A. 2  x  3x  C. B. 2x  2  C. C. 3 2 x  x  C. D. 3 2 x  2x  3x  C. 3 x  3
Câu 7: Đồ thị hàm số y 
có bao nhiêu tiệm cận đứng và tiệm cận ngang? 6  3x A. 3. B. 1. C. 2. D. 0.
Câu 8: Cho các số thực dương a,b, x, y thỏa mãn a  1,b  1 và x 1  y 3 a
 b  ab. Giá trị nhỏ nhất của biểu thức
P  3x  4y thuộc tập hợp nào dưới đây? A. 7;9. B. 11;13. C. 1;2. D. 5;7.
Câu 9: Cho số phức z thỏa 2  i z  4z  i  819 .i Mô đun của z bằng A. 5. B. 18. C. 5. D. 13. 1
Câu 10: Tìm tất cả giá trị thực của tham số m sao cho khoảng 2;3 thuộc tập nghiệm của bất phương trình log  2 x   1  log  2 x  4x  m 1. 5 5  A. m  1  2;1  3 . B. m  1  3;12. C. m  1  3;12. D. m 12;1  3 . 1
Câu 11: Cho hàm số f  x liên tục trên 0;. Biết
là một nguyên hàm của hàm số y  f ' xln x và 2 x 2 f x f   1 2  . Khi đó, dx  bằng ln 2 x 1 7 1 1 7 A.  . B. . C.  . D. . 4 2 2 4
Câu 12: Trong không gian Oxyz, cho mặt phẳng   : x  2y 1  0. Vectơ nào sau đây là một vectơ pháp tuyến của  ? A. 1;2;  1 . B. 1;2;0. C. 1; 2  ;0. D. 1;2;0. 1
Câu 13: Cho số phức z  a  bi và w  z  z. Mệnh đề nào sau đây ĐÚNG? 2 A. w  2. B. w là một số thực. C. w  .i D. w là số thuần ảo.
Câu 14: Cho một khối chóp có diện tích đáy 2
B  6a , chiều cao h  3 .
a Thể tích khối chóp đã cho bằng A. 3 6a . B. 3 18a . C. 3 9a . D. 3 54a . e 1 ln x
Câu 15: Cho tích phân: I  d . x 
Đặt u  1 ln x. Khi đó I bằng x 1 1 1 0 2 u 0 A. 2 I  2 u du.  B. 2 I  2  u du.  C. I  du.  D. 2 I   u du.  2 0 0 1 1
Câu 16: Cho hàm số y  f  x có đạo hàm trên  và f  x   x  x  4   x3 ' 2 3 1 2
. Số điểm cực trị của hàm số đã cho là A. 2. B. 3. C. 1. D. 0.
Câu 17: Gọi H  là hình phẳng giới hạn bởi đồ thị hàm số 2
y  x  5x  4 và trục O .
x Thể tích của khối tròn
xoay sinh ra khi quay hình H  quanh trục Ox bằng: 9 81 81 9 A. . B. . C. . D. . 2 10 10 2
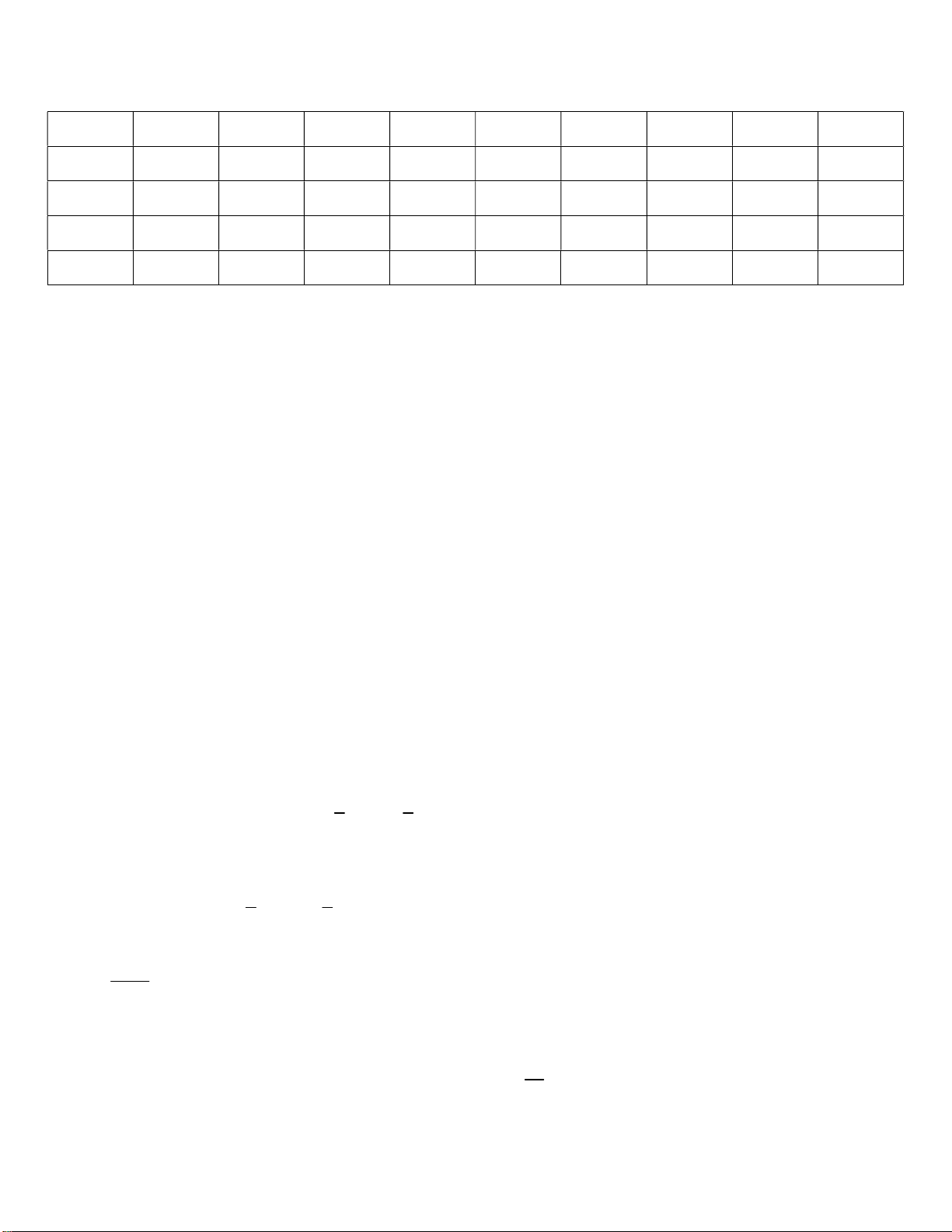
Câu 18: Cho hàm số f  x. Bảng biến thiên của hàm số f ' x như sau: 2
Số điểm cực trị của hàm số y  f  2 x  2x là: A. 7. B. 9. C. 3. D. 5.
Câu 19: Số giao điểm của đồ thị hàm số 4 2
y  x  4x 1 và đồ thị hàm số 2 y  x 1 là A. 4. B. 3. C. 2. D. 1. 2 x  m Câu 20: Hàm số y 
đồng biến trên các khoảng  ;
 4 và 4; khi x  4 m  2 m  2 A. 2  m  2. B. .  C. .  D. 2  m  2. m  2 m  2
Câu 21: Cho hình nón  N  có đỉnh S, bán kính đáy r  1 và độ dài đường sinh l  2 2. Mặt cầu đi qua S và
đường tròn đáy của  N  có bán kính bằng 4 7 8 7 4 A. . B. . C. 7. D. . 7 7 3
Câu 22: Tỉ lệ tăng dân số hàng năm của một quốc gia X là 0,2%. Năm 1998 dân số của quốc gia X là
125500000 người. Hỏi sau bao nhiêu năm thì dân số của quốc gia X là 140000000 người? A. 54 năm. B. 6 năm. C. 55 năm. D. 5 năm. x 1 Câu 23: Cho hàm số y 
. Phát biểu nào sau đây đúng? 1 x
A. Hàm số đồng biến trên mỗi khoảng  ;   1 và 1;.
B. Hàm số đồng biến trên  ;   1  1;.
C. Hàm số đồng biến trên khoảng  ;   1 .
D. Hàm số đồng biến trên khoảng 1;.
Câu 24: Cho hình nón có bán kính đáy r  2 và độ dài đường sinh l  4. Diện tích xung quanh của hình nón đã cho bằng A. 32 . B. 8 . C. 16. D. 48.
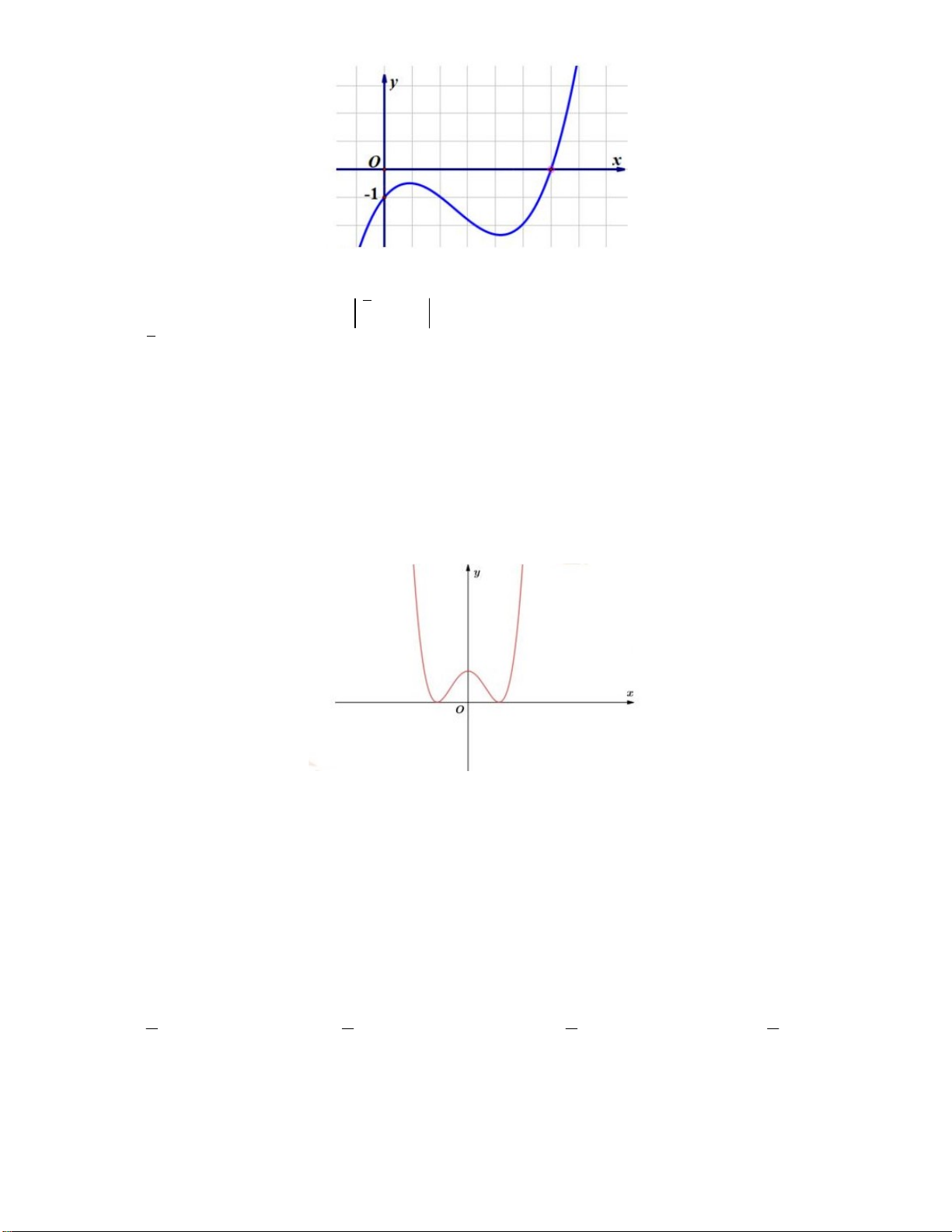
Câu 25: Cho hàm số y  f  x có đồ thị như hình dưới. Số nghiệm thực của phương trình f  x  1 là 3 A. 3. B. 2. C. 4. D. 1.
Câu 26: Xét các số phức z thỏa mãn iz  3  2i  4. Trên mặt phẳng tọa độ Oxy, tập hợp điểm biểu diễn số
phức w  2iz  5  6i là một đường tròn có tâm I  ; a b , bán kính . R Tính T  a  b  R A. 21. B. 17. C. 5. D. 1. Câu 27: Hàm số 3 2
y  x  3x  9x  7 đạt cực đại tại x  1  x  1 A. x  3. B.  . C. .  D. x  1  . x  3 x  3
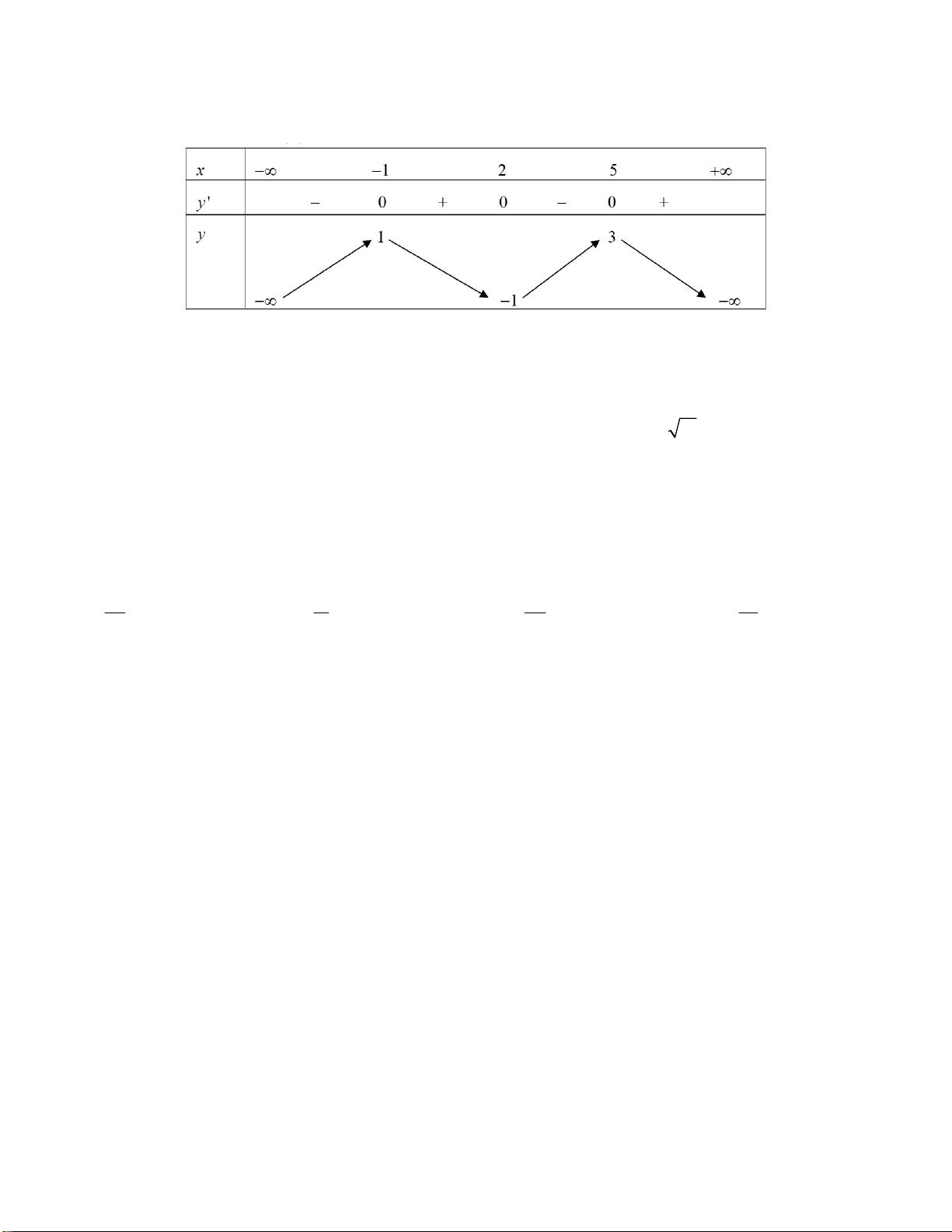
Câu 28: Cho đồ thị hàm số   4 2
f x  ax  bx  c như hình vẽ bên. Khẳng định nào sau đây là đúng A. 2
a  0;b  0;c  0;b  4ac  0. B. 2
a  0;b  0;c  0;b  4ac  0. C. 2
a  0;b  0;c  0;b  4ac  0. D. 2
a  0;b  0;c  0;b  4ac  0.
Câu 29: Trong không gian Oxyz, mặt phẳng qua A3;4; 
1 và song song với mặt phẳng Oxy có phương trình là A. x  3  0. B. z 1  0. C. y  4  0. D. 3x  4 y  z  0.
Câu 30: Nghiệm của phương trình 2x3 9  81 là 3 1 1 3 A. x   . B. x  . C. x   . D. x  . 2 2 2 2 2
Câu 31: Cho hàm số f  x có đạo hàm trên đoạn 1;2, f  
1  1 và f 2  2. Khi đó, I  f '  xdx bằng 1 4 7 A. I  1. B. I  1. C. I  . D. I  3. 2 2 x4 x 1 3 3     
Câu 32: Tập nghiệm của bất phương trình      là  4   4  A. 1;2. B.  ;  5. C.5;. D.  ;    1 .
Câu 33: Số cạnh của hình bát diện đều là A. 8. B. 12. C. 10. D. 20.
Câu 34: Thể tích của khối cầu có bán kính r  3 là A. 64. B. 48. C.8 . D. 36 .
Câu 35: Trong không gian Oxyz, hình chiếu vuông góc của điểm A1;3;5 trên mặt phẳng Oyz là điểm nào sau đây? A. 1;3;0. B. 1;0;5. C. 0;3;5. D. 1;0;0. 2 4   x  Câu 36: Biết f
 xdx  2020, khi đó I  f dx    bằng  2    0 0  A. 2020. B. 1010. C. 2020. D. 4040.
Câu 37: Cho số phức z  3  4 .i Tìm phần thực a và phần ảo b của số phức z. A. a  3,b  4. B. a  4,b  3. C. a  4,b  3. D. a  3,b  4.
Câu 38: Trong không gian Oxyz, cho mặt cầu S   x  2  y   z  2 2 : 2
1  4. Tâm của S  có tọa độ là A. 2;0;  1 . B. 2;0;  1 . C. 2;0;  1 . D. 2;0;  1 . 1 2i Câu 39: Cho số phức z 
. Trong mặt phẳng tọa độ, điểm biểu diễn số phức z là điểm nào dưới đây? 1 i  1 3   1 3   1 3   1 3  A. ;  .   B.  ;  .   C. ; .   D.  ; .    2 2   2 2   2 2   2 2 
Câu 40: Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh bằng 2 . a Thể tích khối trụ bằng 3 2 a 3  a A. 3  a . B. . C. . D. 3 2 a . 3 3
Câu 41: Đồ thị hình bên là của hàm số nào? 5 A. 3 y  x  2 . x B. 3 y  x  3 . x C. 3 y  x  3 . x D. 3 y  x  2 . x
Câu 42: Trong không gian Oxyz, cho điểm A1;2;5 và mặt phẳng P : x  2y  z 1  0. Phương trình đường
thẳng qua A vuông góc với P là: x  3 t x  1 t x  2  t x  1 t     A. y  2  2t. B. y  2  2t . C. y  2  2t. D. y  2  2t . x  7 t     z  5  t  z  7  t  z  5  t 
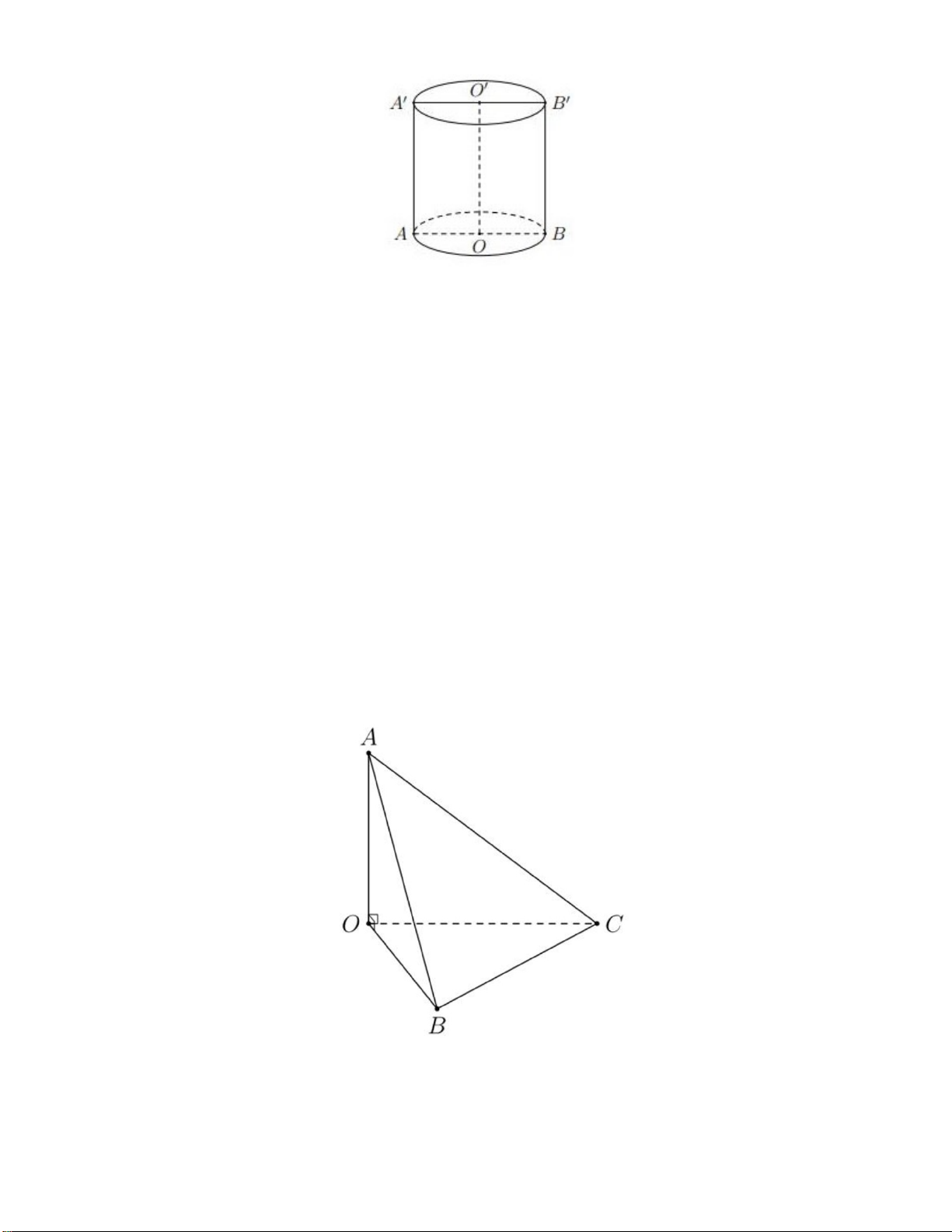
Câu 43: Cho tứ diện OABC có O ,
A OB,OC đôi một vuông góc và OB  OC  a 6,OA  . a Thể tích khối tứ diện đã cho bằng A. 3 3a . B. 3 2a . C. 3 6a . D. 3 a .
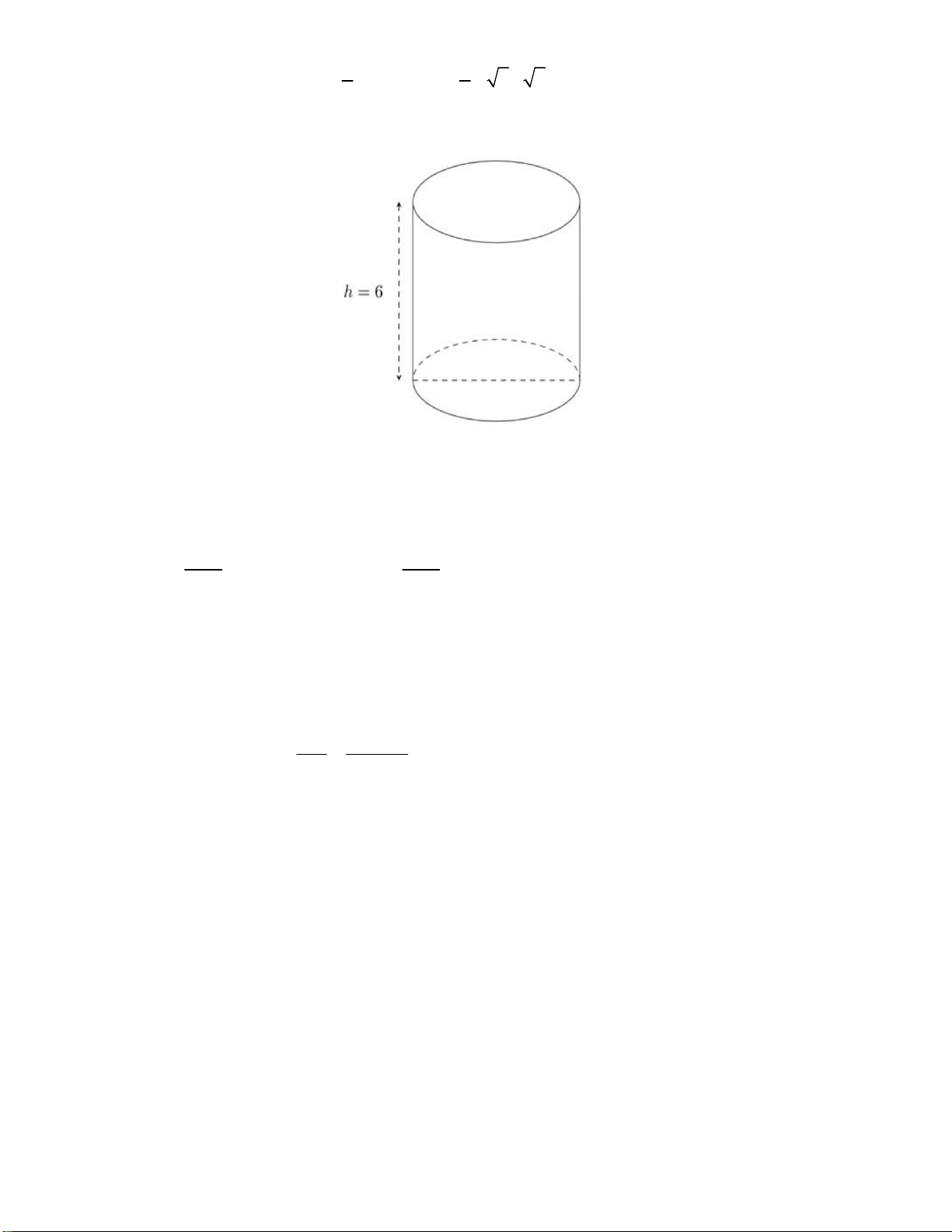
Câu 44: Cho khối lăng trụ có diện tích đáy B  8 và chiều cao h  6. Thể tích của khối lăng trụ đã cho bằng A. 48. B. 16. C. 24. D. 14. x  3
Câu 45: Tập xác định của hàm số y  log là 2 2  x A. 3;2. B.  ;
 3 2;. C.  \3;  2 . D. 3;2. x 1 y  2
Câu 46: Trong không gian Oxyz, cho đường thẳng d : 
 z 1, điểm nào dưới đây thuộc đường 2 3 thẳng d ? A. 2;3;0. B. 2;3;  1 . C. 1; 2  ;  1 . D. 1;2;  1 . x 1 y 1 z  3
Câu 47: Trong không gian Oxyz, cho điểm A4;1;3 và đường thẳng d :   . Tọa độ điểm 2 1 1
M là điểm đối xứng với điểm A qua d là 6 A. M 0;1;2. B. M 2; 5  ;3. C. M  1  ;0;2. D. M 2; 3  ;5.
Câu 48: Cho hàm số y  f  x liên tục trên  và có bảng biến thiên như sau:
Số nghiệm của phương trình f  4 2 3x 4 x 2 2 10 là A. 2. B. 3. C. 1. D. 5.
Câu 49: Cho các số thực a,b, c thỏa mãn log37 log711 lo 1 g 1 25 a  27,b  49,c
 11. Giá trị của biểu thức log 7 log 11 log 25 3 2  7 2  11 2 A  a  b  c là A. 129. B. 519. C. 469. D. 729.
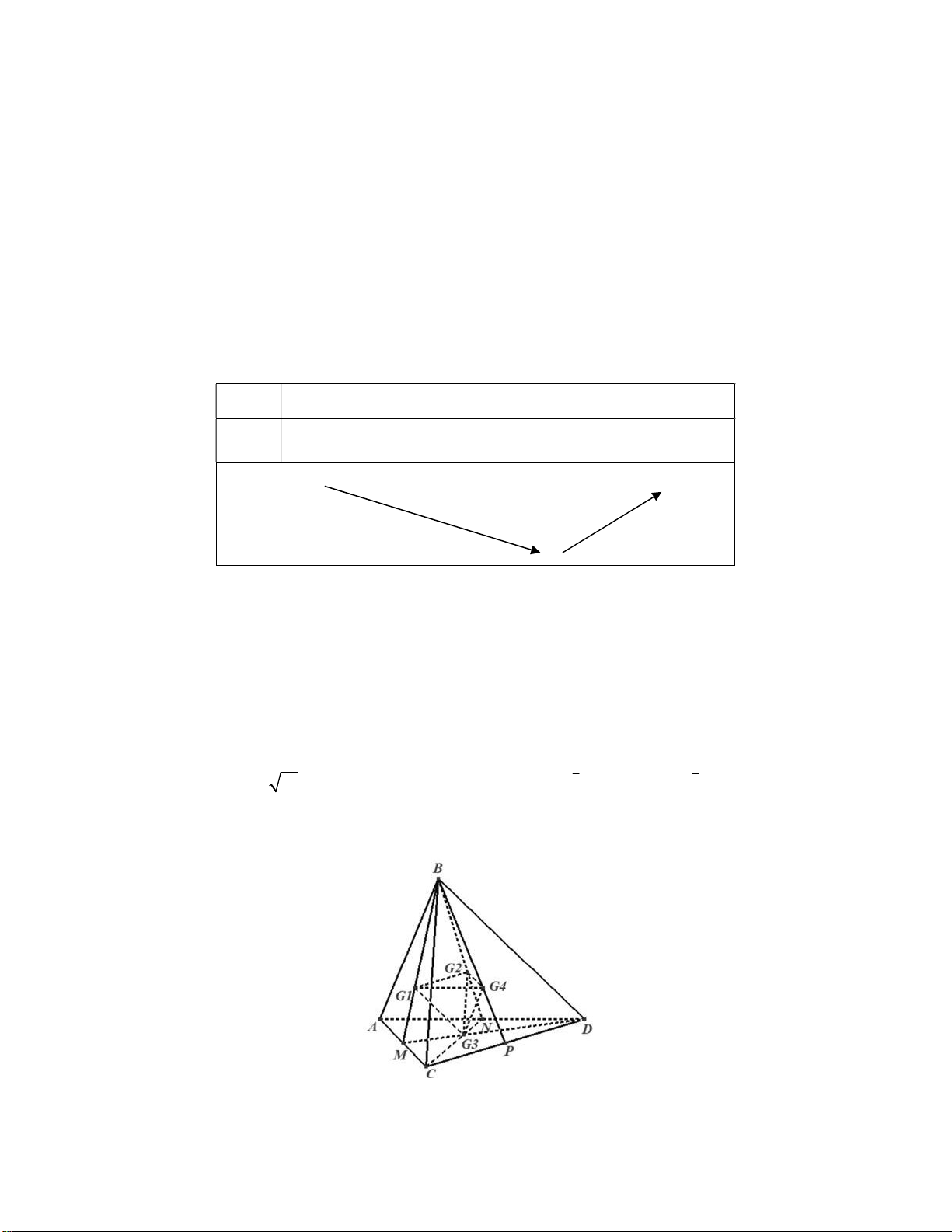
Câu 50: Cho khối tứ diện ABCD có thể tích V. Gọi G ,G ,G ,G lần lượt là trọng tâm của bốn mặt của hình 1 2 3 4
tứ diện. Thể tích khối tứ diện G G G G bằng 1 2 3 4 V V V V A. . B. . C. . D. . 32 9 27 12
--------------- HẾT -------------- 7 ĐÁP ÁN 1-D 2-B 3-C 4-C 5-D 6-A 7-C 8-A 9-D 10-A 11-D 12-B 13-B 14-A 15-A 16-A 17-C 18-A 19-C 20-B 21-A 22-C 23-C 24-B 25-A 26-C 27-D 28-A 29-B 30-C 31-A 32-B 33-B 34-D 35-C 36-D 37-A 38-D 39-D 40-D 41-B 42-A 43-D 44-A 45-A 46-C 47-D 48-B 49-C 50-C
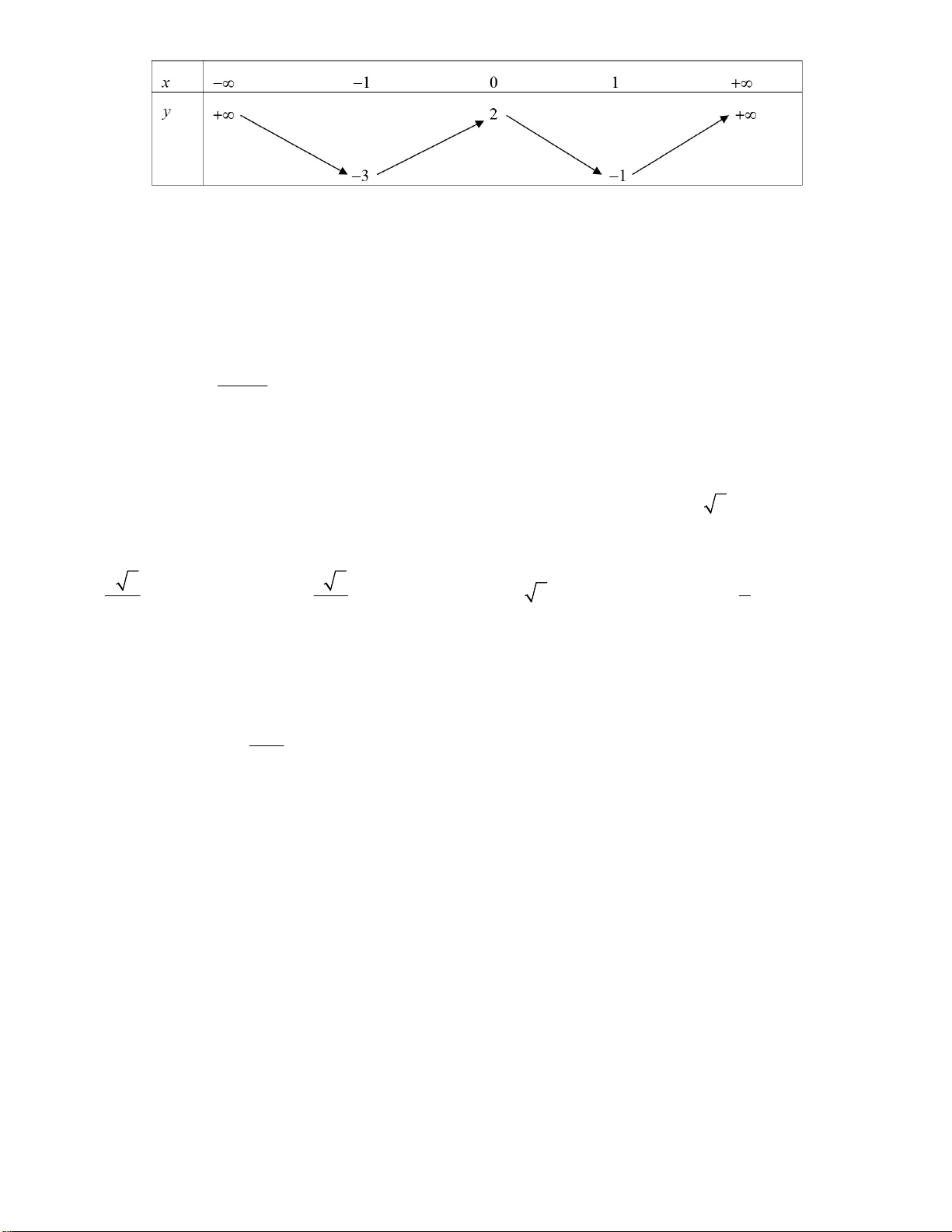
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: Chọn D. Ta có 2 y '  3x  3. x  10;2 Cho 2
y '  0  3x  3  0   x      . 1 0; 2
Ta có y 0 1; y   1  1; y 2  3.
Vậy M  3, N  1  M  N  2. Câu 2: Chọn B. Ta có log 3x  2 2
 2  3x  2  2  x  2. 2
Vậy nghiệm của phương trình log 3x  2  2 là x  2. 2   Câu 3: Chọn C.
Gọi r là bán kính đáy của khối nón. Ta có: 2 r  8  r  4 1 1
Thể tích của khối nón đã cho là: 2 2
V   r h  .4 .3  16. 3 3 Câu 4: Chọn C. 1 1
Với a  0, a  1,log a  log a  3 3 a a 3 Câu 5: Chọn D.
Ta có: 4  3i  4  3 .i Câu 6: Chọn A. x Ta có: f
 xdx  x  x   3 2 2 2 2
3 dx  x dx  2 xdx  3 dx   x  3x  C.    3 8 Câu 7: Chọn C. TXĐ: D   \  2 . x  3 1 1 Ta có lim y  lim
  nên đường thẳng y   là tiệm cận ngang của đồ thị hàm số đã cho. x x 6  3x 3 3 x  3 Mà lim y  lim
  nên đường thẳng x  2 là tiệm cận đứng của đồ thị hàm số đã cho. x 2 x 2   6  3x x  3
Vậy đồ thị hàm số y 
có tất cả 2 đường tiệm cận, trong đó 1 đường tiệm cận ngang và 1 đường tiệm cận 6  3x đứng. Câu 8: Chọn A.  1 4 1
x  1 log ab   log b  3 a 3 3 a Ta có x 1  y 3 a  b  ab   .  1 1   y  ab   a     b  b  1 1 log 1 log 1  3 3 3 log b   a  Thay vào P, ta được  4 1  1  1  P  3x  4y  3  log b  4.   1   3 3 a  3 log b  a  16  4    log b   3 a 3log b  a 
Vì a  1,b  1 nên log b  0. Áp dụng BĐT Cô-si, ta có: a 16  4  16 4 16  4 3 P   log b     2 log . b  . 3 a 3log b 3 a 3log b 3  a  a 4 2 3
Dấu “=” xảy ra khi và chỉ khi log b  log b  log b  . a 3 a a 3 16  4 3
Vậy giá trị nhỏ nhất của P bằng 7;9. 3 Câu 9: Chọn D.
Gọi z  a  bi a,b . Khi đó:
2 i z  4z i  819i  2ia bi4a b 1i  819i
 2a  b  a  2bi  4a  4b  
1 i  8 19i, nên ta có hệ phương trình 9 2a  b  8 2a  b  8  a  3      . Vậy z  13. a  6b  4  19 a  6b  15 b   2 Câu 10: Chọn A. Điều kiện xác định: 2 x  4x  m  0.
Với điều kiện trên, bất phương trình tương đương với  2 x     2 5 1 x  4x  m. 2 x  4x  m  0 
Để khoảng 2;3 thuộc tập nghiệm của bất phương trình thì hệ bất phương trình  5   2 x   1   2 x  4x  m
nghiệm đúng với mọi x 2;3.  f   x 2  x  4x  m  
nghiệm đúng với mọi x 2;3. g   x 2  4x  4x  5  m Xét hàm số f  x 2
 x  4x trên khoảng 2;3 có f 'x  2x  4  0, x
 2;3 suy ra f x  f 2 12. Do
đó 12  m  m  12 Xét hàm số g  x 2
 4x  4x  5 trên khoảng 2;3 có g 'x  8x  4  0, x
 2;3 suy ra g x  g 2 13.
Do đó 13  m  m  13. Câu 11: Chọn D. 1 '  1  2 Vì
là một nguyên hàm của hàm số y  f ' xln x, nên  f ' x ln x    f ' x ln x  2    3   2 x  x  x u   f  x  du  f 'xdx Đặt    . 1 dv  dx v  ln x  x 2 f x 2 2 2 2 1 1 2 Khi đó:
dx  f  x.ln  x  f ' xln xdx  f 2.ln 2  dx  .ln 2     3 2 x 1 x ln 2 x 1 1 1 1  1  7  1 1  .  2   2  4 Câu 12: Chọn B. 
Ta có: n  1;2;0 là một vectơ pháp tuyến của mặt phẳng  . Câu 13: Chọn B. 1 1
Ta có z  a  bi do đó w  z  z  a  bi  a  bi  a là một số thực. 2 2 Câu 14: Chọn A. 10 1 1
Thể tích của khối chóp 2 3 V  . B h  .6a .3a  6a . 3 6 Câu 15: Chọn A. Đặt 2
u  1 ln x  u  1 ln x dx   2
 udu (với x  1  u  1; x  e  u  0) x 1 Ta có 2 I  2 u du.  0 Câu 16: Chọn A.  x  2 
Ta có f ' x  0  x  3   1 x   2 1
Trong đó x  2, x  là các nghiệm bội bậc lẻ nên hàm số y  f (x) có 2 điểm cực trị. 2 Còn x  3
 là nghiệm bội bậc chẵn nên không là điểm cực trị của hàm số y  f (x) . Câu 17: Chọn C. x  1
Xét phương trình hoành độ giao điểm của đồ thị hàm số và trục Ox là: 2 x  5x  4  0   x  4
Thể tích của khối tròn xoay sinh ra khi quay hình H  quanh trục Ox bằng: 4 V    2 x  x   81 5 4 dx   10 1
Vậy chọn đáp án C là đáp án đúng. Câu 18: Chọn A. Xét y  f  2
x  x  y   x   f  2 2 ' 2 2 . ' x  2x x 1  2 x  2x  x   ;  1 1   x  1  y '  0    x  x  x   f '   2 1;0 2 x  2x 2  2    0  2 x  2x  x  0;1 3    2 x  2x  x  1;  4   11 Trường hợp 1: 2 x  2x  x  ;    2 1  x  2x  x  0. 1 1
Ta có  '  11.x 1 x  0, x    ;
 1 nên phương trình vô nghiệm. Suy ra trường hợp này không có 1  1 1   điểm cực trị. Trường hợp 2: 3 x  2x  x 1;0 2  x  2x  x  0. 2 2
Ta có  '  11.x 1 x  0, x
  1;0 nên phương trình luôn có hai nghiệm phân biệt. Suy ra trường 2  2 2  
hợp này có hai điểm cực trị. Trường hợp 3: 2
x  2x  x  0;1 . Xét thấy hệ số a và c trong phương trình luôn trái dấu nên phương trình 3  
luôn có hai nghiệm phân biệt. Suy ra trường hợp này có hai điểm cực trị. Trường hợp 4: 2
x  2x  x  1;  . Xét thấy hệ số a và c trong phương trình luôn trái dấu nên phương 4  
trình luôn có hai nghiệm phân biệt. Suy ra trường hợp này có hai điểm cực trị.
Mặt khác, các hệ số trong các phương trình ở trường hợp 2, 3, 4 vừa xét đều khác nhau hệ số c nên các nghiệm
của phương trình này đều khác nhau và đều khác 1. Vậy hàm số y  f  2
x  2x có 7 điểm cực trị. Ta chọn đáp án A. Câu 19: Chọn C.
Phương trình hoành độ giao điểm của đồ thị hàm số 4 2
y  x  4x 1 và đồ thị hàm số 2 y  x 1 là 4 2 2 x  4x 1  x 1.  3  17 2 x  2 3  17 4 2
 x  3x  2  0    x   .  3  17 2 2 x  L  2
Vậy số giao điểm của đồ thị hàm số 4 2
y  x  4x 1 và đồ thị hàm số 2 y  x 1 là 2. Câu 20: Chọn B. TXĐ: D   ;  4 4;. 2 2 x  m 4  m Ta có y   y '  . x  4 x  42
Hàm số đồng biến trên các khoảng  ;
 4 và 4; khi và chỉ khi 2 4  m m  2 2 y '   0  4  m  0  .   x  42 m  2 Câu 21: Chọn A. 12
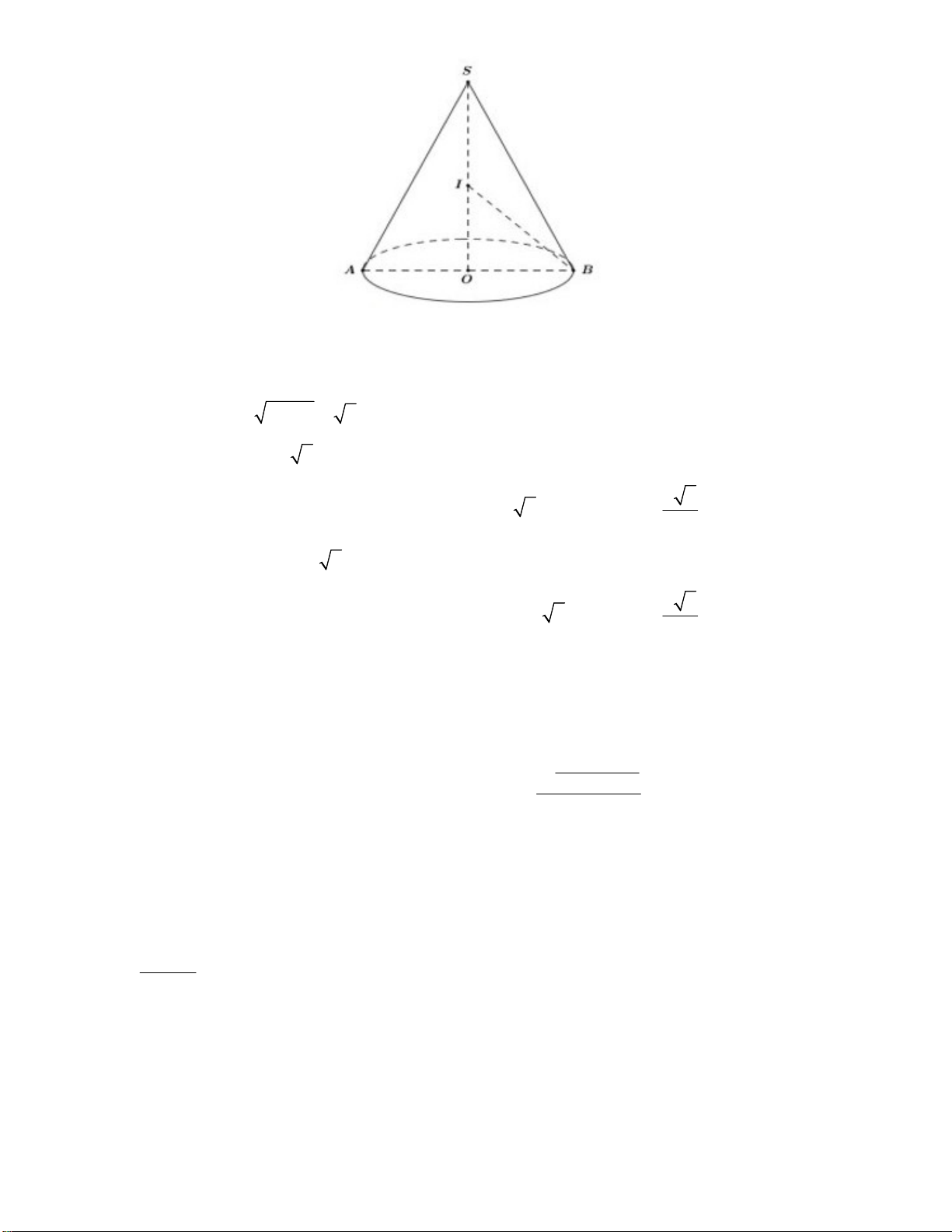
Gọi I là tâm của mặt cầu đi qua S và đường thẳng đáy của  N .
R là bán kính của mặt cầu cần tìm. Theo giả thiết, ta có 2 2 SO  l  r  7.
Trường hợp 1. IO  SO  R  7  . R
Trong tam giác vuông IOB, ta có IB  IO  OB  R    R2 2 2 2 2 4 7 7 1  R  . 7
Trường hợp 2. IO  R  SO  R  7.
Trong tam giác vuông IOB, ta có IB  IO  OB  R  R  2 2 2 2 2 4 7 7 1  R  . 7 Câu 22: Chọn C.
Gọi A là dân số của quốc gia X năm 1998, r là tỷ lệ tăng dân số và A là dân số của quốc gia X sau n n (năm) tính từ năm 1998. 140000000 ln A      n   n  n 125500000 140000000 125500000. 1 0, 2% 140000000    54,72. ln 1 0, 2%
Vậy sau 55 năm thì dân số của quốc gia X là 140000000 người. Câu 23: Chọn C.
Tập xác định D   \  1 . 2 Ta có y '   0, x   . D 1 x2
Suy ra hàm số đồng biến trên mỗi khoảng  ;   1 và 1;. Câu 24: Chọn B.
Ta có S   rl  .2.4  8. xq 13 Câu 25: Chọn A.
Số nghiệm thực của phương trình f  x  1 là số giao điểm của đồ thị hàm số y  f  x và đường thẳng y  1.
Vậy phương trình đã cho có 3 nghiệm phân biệt. Câu 26: Chọn C.
Do z    z  x  yi với x, y  . 
Theo đề bài: w  2iz  5  6i  2iz  3 2i  1 2i  w  1 2i  2iz  3 2i.
 w+1 2i  2iz  3 2i  w+1 2i  2 iz 3 2i  8. Suy ra:
   i   x  yi   i   x    y  i    x  2   y  2 2 w 1 2 8 1 2 8 1 2 8 1 2  8 .
Vậy tập hợp điểm biểu diễn w là một đường tròn có tâm I 1;2 , bán kính R  8 nên ta có: T  a  b  R  1   2  8  5. Câu 27: Chọn D. x  1 Xét 2
y '  3x  6x  9  0  . 
Ta có: y"  6x  6; y"  1  1
 2  0; y"3 12  0. Hàm số đạt cực đại x  3 tại điểm x  1
 và đạt cực tiểu tại điểm x  3. Câu 28: Chọn A.
* Từ hình vẽ suy ra a  0, c  0. * Xét 3 y  ax  bx   x  2 ' 4 2 0
2 2ax  b  0. Để hàm số có 3 cực trị như hình vẽ thì a;b trái dấu, suy ra b  0. * Xét f  x 4 2 2 2
 ax  bx  c  0  at  bt  c  0;t  x  0 có một nghiệm kép theo ẩn phụ t. Từ đồ thị, ta thấy
phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành chỉ có hai nghiệm x đối nhau  phương
trình bậc hai theo ẩn phụ t chỉ có một nghiệm dương 2    b  4ac  0. Câu 29: Chọn B.   Mặt phẳng qua A3;4; 
1 và song song với mặt phẳng Oxy có VTPT: n  k 0;0;  1
Có phương trình: 0 x  3  0 y  4 1 z   1  0  z  1. Câu 30: Chọn C. TXĐ: D  
Phương trình đã cho tương đương: 2x3 2 1 9
 9  2x  3  2  x   . 2 14 Câu 31: Chọn A. 2 2 Ta có: I  f '
 xdx  d x  f 2 f  1  211. 1 1 Câu 32: Chọn B.
Bất phương trình  2x  4  x 1  x  5.
Tập nghiệm của bất phương trình là  ;  5. Câu 33: Chọn B. Câu 34: Chọn D. 4 4
Thể tích của khối cầu có bán kính r  3 là 3 3
V   r  . .3  36 . 3 3 Câu 35: Chọn C.
Hình chiếu vuông góc của điểm M  ; a ;
b c trên mặt phẳng Oyz là điểm M '0; ;
b c. Do đó điểm cần tìm là 0;3;5. Câu 36: Chọn D. ' x  x  1 Đặt t   dt  dx  dx  dx  2dt   2  2  2 x  4  t  2 Đổi cận  x  0  t  0 2  I  2 f
 tdt  2.2020  4040 0 Vậy I  4040. Câu 37: Chọn A.
Phần thực a và phần ảo b của số phức z là a  3,b  4. Câu 38: Chọn D.
Tâm của S  có tọa độ là 2;0;  1  Câu 39: Chọn D. 1 2i
1 2i1 i 13i 1 3 Ta có: z        i  i i .i 1 1 1 2 2 2  1 3 
Vậy trong mặt phẳng tọa độ, điểm biểu diễn số phức z là  ; .    2 2  Câu 40: Chọn D. 15
Vì thiết diện qua trục của hình trụ là hình vuông nên AB  2R  2a  R  a và h  AA'  2 . a Thể tích khối trụ là 2 2 3
V   R h   a .2a  2 a . Câu 41: Chọn B.
Đồ thị hình bên là đồ thị hàm bậc 3 với hệ số a  0 nên loại A và D. Đồ thị hàm số có hai điểm cực trị là
1;2 và 1;2 nên y'  0  x  1 do đó loại đáp án C và chọn đáp án B. Câu 42: Chọn A. 
Mặt phẳng P : x  2y  z 1  0 có vectơ pháp tuyến n  1;2;  1 .  
Đường thẳng vuông góc với mp P : x  2y  z 1  0 nhận vectơ n  1;2; 
1 hoặc vectơ u  1;2;  1 làm x  3 t 
vectơ chỉ phương nên loại các đáp án B, D. Ta lại có tọa độ điểm A1;2;5 thỏa mãn phương trình y  2  2t z  7 t  nên đáp án A đúng. Câu 43: Chọn D. Vì O ,
A OB,OC đôi một vuông góc nên OA  OBC  và OBC vuông tại . O 16 1 1
Nên thể tích khối chóp OABC là 3 V  .O . A O . B OC  .a 6.a 6.a  a . 6 6 Câu 44: Chọn A.
Áp dụng công thức thể tích hình trụ ta có V  . B h  8.6.
Vậy thể tích hình trụ là V  48. Câu 45: Chọn A. x  3 x  3 Hàm số y  log
có điều kiện xác định:  0  3   x  2. 2 2  x 2  x
Vậy tập xác định D   3  ;2. Câu 46: Chọn C.
Thay tọa độ điểm 1; 2  ; 
1 vào đường thẳng d ta được: 11 2  2     1 1  0 (luôn đúng). 2 3 Suy ra điểm 1; 2  ; 
1 thuộc đường thẳng d. Câu 47: Chọn D. Gọi N 2t 1; t
 1;t  3d là hình chiếu của A trên d. Suy ra N là trung điểm AM.  
Ta có: AN.u  0  22t  3  t  t  0  t 1. d Vậy N 3;2;4. Suy ra M 2; 3  ;5. Câu 48: Chọn B.
Dựa vào bảng biến thiên, ta có 17 4 3 3x 4 x 2 2  a  1  1 1    f  4 2 3x 4 x 2 2 10 f  4 3 3x 4x 2 2  4 3 3x 4 x 2  1  2  2  4 3 3x 4 x 2 2  a  5 2  TH1: 4 3 3x 4 x 2 2  2
 x  x    x  2 4 3  3 3 4 2 1 1 3x  2x   1  0  x  1 TH2: 4 2 3 4 2 2 x x  a 2 4 3  3x  4x  2  log a 2 2 Xét hàm số g  x 4 3
 3x  4x  2, khảo sát hàm số, ta được bảng biến thiên sau: x  0 1  g ' x  0  0 + g  x   1 Do log a  log 5  1 nên 4 3
3x  4x  2  log a có hai nghiệm phân biệt khác 1. 2 2 2 2 2
Vậy phương trình f  4 3 3x 4 x 2 2
10 có 3 nghiệm phân biệt. Câu 49: Chọn C. 2 2 log 7 log 11 log 25 Ta có log 7 log 11 log 25 3   7   2   
  log37  3   log711 7   lo 1g125 A a b c a b c  11 11 1 1 log 25 3 2 11 log3 7 log711  27  49  11   log37 3   log711 7   lo 1g125 11  3 2 2 2  7 11  25  469. Câu 50: Chọn C.
Gọi M , N, P lần lượt là trung điểm của AC, AD,CD. 18 Ta có 1 1 1 1 V  d G , G G G .S  . .d B, G G G .S  V 1 G 2 G 3 G 4 G  3  1 2 4 1G 2G 4G   1 2 4 1G 2G 4G B 1 G 2 G 4 3 3 2 2 G 3 1  2  4 1 V  . V  . V  .   2  3 BMNP  27 4 BACD 27
____________________ HẾT ____________________ https://toanmath.com/ 19

Tài liệu liên quan: