














Preview text:
TRƯỜNG THPT KIM LIÊN
KỲ THI THỬ TỐT NGHIỆP THPT NĂM 2021 (LẦN I) Bài thi: TOÁN
ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề thi có 06 trang)
Họ tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 143
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 1. Tập xác định của hàm số 2021 y x là A. 0; . B. ; 0 . C. ; . D. 0; .
Câu 2. Tìm x để biểu thức x 2 2 1 có nghĩa. 1 1 1 1 A. x . B. x . C. x ; 2 . D. x . 2 2 2 2
Câu 3. Tính thể tích khối cầu có bán kính bằng 3 cm. A. 3 9 cm . B. 2 36 cm . C. 2 9 cm . D. 3 36 cm .
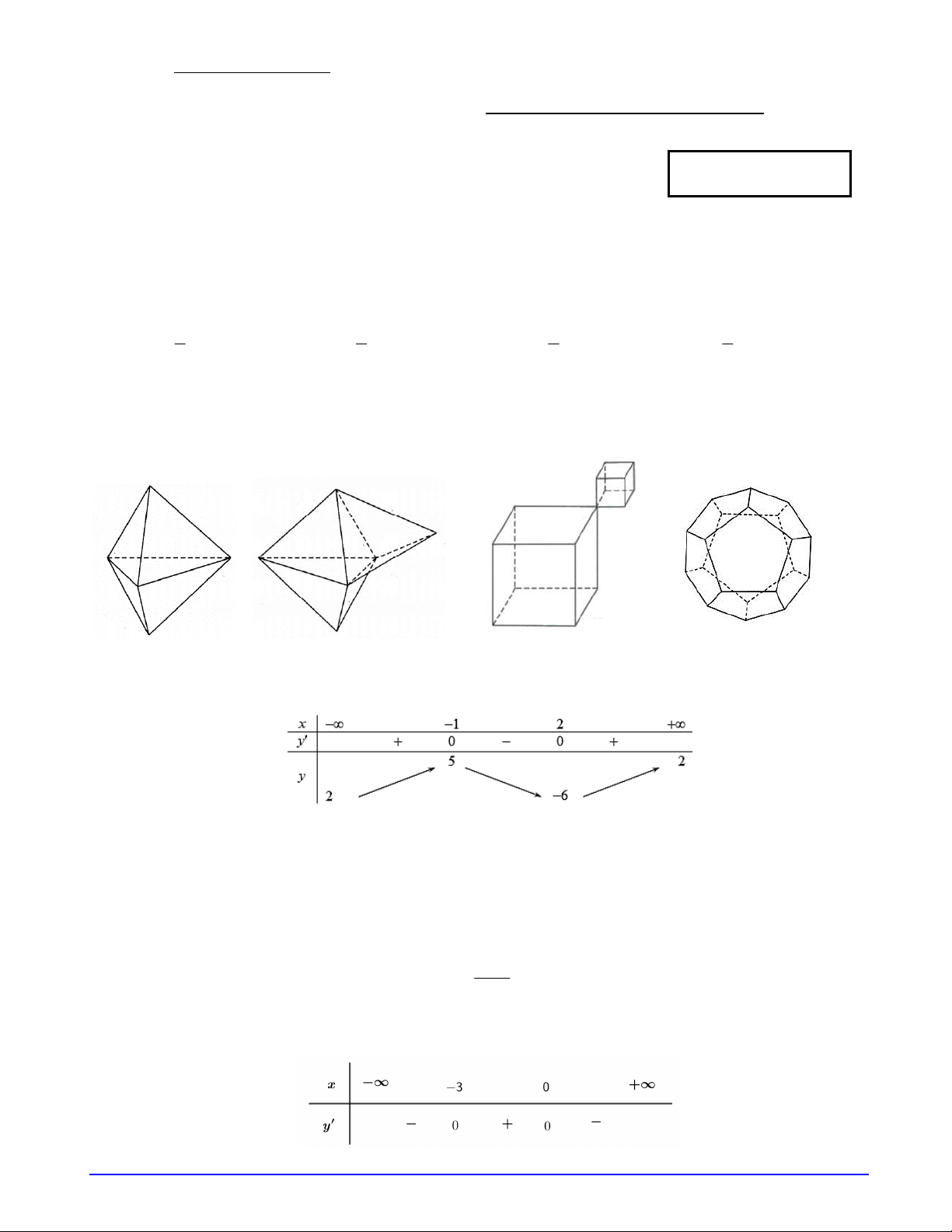
Câu 4. Hình nào dưới đây không phải là hình đa diện? Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 2. B. Hình 4. C. Hình 1. D. Hình 3.
Câu 5. Cho hàm số y f x , có bảng biến thiên như sau:
Mệnh đề nào dưới đây là đúng?
A. Hàm số không có cực đại.
B. Hàm số đạt cực tiểu tại x 2 .
C. Hàm số đạt cực tiểu tại x 6 .
D. Hàm số có bốn điểm cực trị.
Câu 6. Cho hình nón có chiều cao bằng 4a và bán kính đáy bằng 3 .
a Diện tích xung quanh của hình nón đã cho là A. 2 12 a . B. 2 36 a . C. 2 14 a . D. 2 15 a . x 1
Câu 7. Phương trình tiếp tuyến của đồ thị hàm số y
tại điểm có hoành độ bằng 1 là x 2
A. y 3x 5 .
B. y 3x 1 .
C. y 3x 5 .
D. y 3x 1.
Câu 8. Cho hàm số y f (x) có bảng xét dấu đạo hàm như sau: Trang 1/6 - Mã đề thi 143
Hàm số y f (x) đồng biến trên khoảng nào dưới đây ? A. 3 ; 0 . B. 4 ;1 . C. ; 3 .
D. 0; .
Câu 9. Trong không gian với hệ tọa độ Oxyz, cho ba vectơ a i 2 j 3k,b 3
j 4k, c i
2 j. Khẳng định
nào sau đây là đúng?
A. a 1; 2; 3 ,b 0; 3 ; 4,c 1 ; 2 ;0.
B. a 1; 2;3,b 0;3;4, c 1 ; 2 ;0.
C. a 1; 2;3,b 0; 3 ; 4, c 1 ; 2;0.
D. a 1;2; 3 ,b 3
; 4;0, c 1 ;0; 2 .
Câu 10. Một chiếc hộp có 9 thẻ được đánh số từ 1 đến 9. Có bao nhiêu cách rút được từ hộp trên 2 thẻ đều đánh số chẵn. A. 2 C . B. 2 C . C. 2 A . D. 2 A . 5 4 5 4
Câu 11. Đạo hàm của hàm số 2 4 x y là A. 2 2.4 x y ln 2 . B. 2 4 x y ln 4 . C. 2 4 . x y ln 2 . D. 2 2.4 x y ln 4 .
Câu 12. Số thực a thỏa mãn điều kiện log (log a) 0 là 3 2 1 1 A. . B. . C. 2. D. 3. 3 2
Câu 13. Diện tích toàn phần của hình trụ có chiều cao bằng h và bán kính đáy bằng r là 1
A. 2 r h r . B. 2
2 rh r . C. 2 r . h D. 2 2
r h 2 r . 3
Câu 14. Tập nghiệm của phương trình log 2
x 3x 1 là 0,25
A. 1;4 . B. 1; 4 . 32 2 3 2 2 C. 4 . D. ; . 2 2
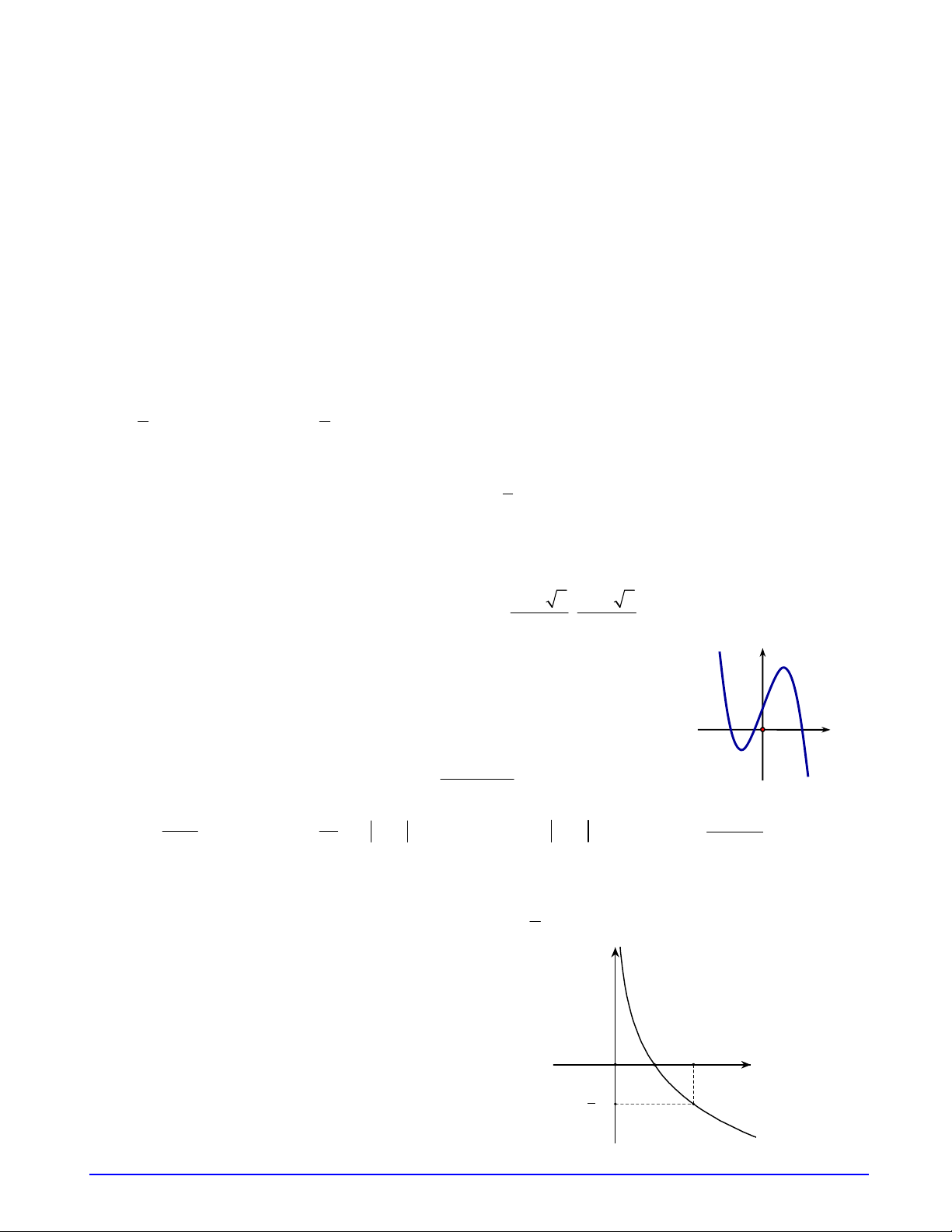
Câu 15. Đường cong trong hình bên là đồ thị của hàm số nào? y A. 3 2
y x 2x 2x 1. B. 3 2
y x 2x x 1 . 1 C. 3 2
y x 3x 3x 1. D. 3
y x 3x 1. O x 2 x 2x 1
Câu 16. Tìm họ nguyên hàm của hàm số f x . x 2 1 2 x 1 A. x C. B.
ln x 2 C. C. 2
x ln x 2 C. D. 1 C. x 2 2 x 22
Câu 17. Tìm công bội q của cấp số nhân u biết u 1 và u 4 . n 1 2 1
A. q 3 .
B. q 4 . C. q . D. q 2 . 4
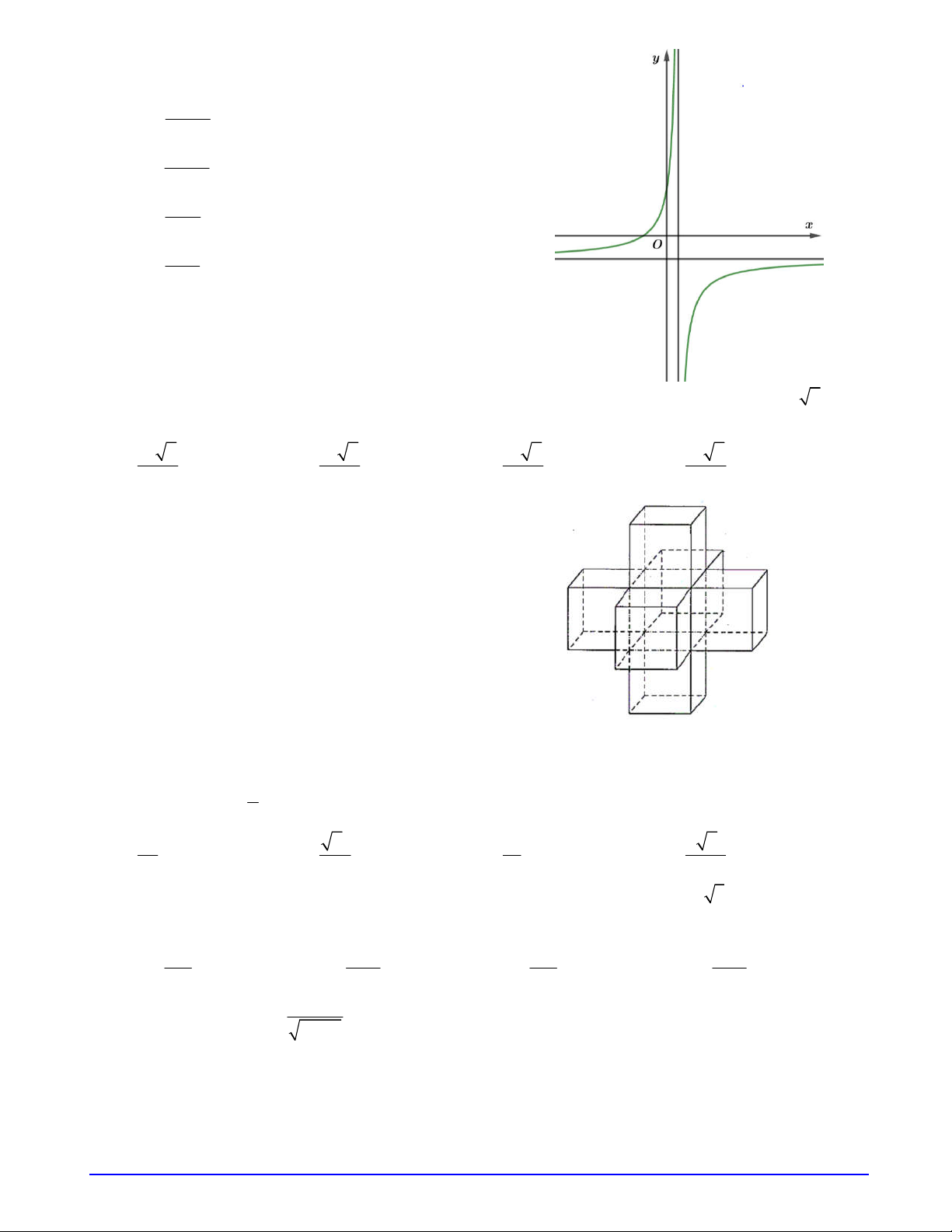
Câu 18. Đường cong trong hình bên là đồ thị của hàm số nào? y A. 2x y 5 . B. y log x . 0,5 x O 1 2
C. y log x . 2 D. 0,5x y . 1 Trang 2/6 - Mã đề thi 143
Câu 19. Trong ngày hội giao lưu văn hóa – văn nghệ, giải cầu lông đơn nữ có 12 vận động viên tham gia trong
đó có hai vận động viên Kim và Liên. Các vận động viên được chia làm hai bảng A và B, mỗi bảng gồm 6
người. Việc chia bảng được thực hiện bằng cách bốc thăm ngẫu nhiên. Tính xác suất để hai vận động viên Kim
và Liên thi đấu chung một bảng. 6 5 5 1 A. . B. . C. . D. . 11 22 11 2
Câu 20. Trong không gian cho tam giác ABC vuông cân tại A. Góc ở đỉnh của hình nón nhận được khi quay
tam giác ABC xung quanh trục AB bằng A. 0 90 . B. 0 60 . C. 0 45 . D. 0 30 .
Câu 21. Tìm tất cả các giá trị thực của tham số m để phương trình 2 2
log x log x 1 2m 1 0 có ít nhất 3 3
một nghiệm thuộc đoạn 3 1 ;3 .
A. m (0; 2) .
B. m [0; 2] .
C. m [0; 2) .
D. m (0; 2] .
Câu 22. Tìm tất cả các giá trị thực của tham số m để hàm số y mx cos x đồng biến trên .
A. m 1.
B. m 1. C. m 1 . D. m 1 . 2020
Câu 23. Cho hàm số f x có f x 2021 x x 1 x 1 x
. Hàm số đã cho có bao nhiêu điểm cực trị? A. 3. B. 0 . C. 2 . D. 1. 1 3 a 3 3 4 a a
Câu 24. Cho hàm số f a
với a 0 , a 1. Tính giá trị M f 2020 2021 . 1 a 8 3 8 1 8 a a A. 2020 M 1 2021 . B. 1010 M 2021 1 . C. 1010 M 2021 1 . D. 2019 M 2021 1 . 2 x x 1 2x 1 5 5
Câu 25. Cho bất phương trình
. Tập nghiệm của bất phương trình có dạng S a;b . Giá 7 7
trị của biểu thức A 2b a là A. 1. B. 2. C. 2 . D. 3.
Câu 26. Gọi S là tập hợp tất cả các giá trị của tham số m sao cho giá trị lớn nhất của hàm số 2
x 2mx 4m f x trên đoạn 1 ;
1 bằng 3. Tích các phần tử của S bằng x 2 1 1 3 A. . B. . C. . D. 1. 2 2 2 1
Câu 27. Hàm số f x 3 2 x x 4 3 2
có tập xác định là A. ;1
3 1;1 3 . B. 1 3 ;1 .
C. 1 3;. D. 1 3;
1 1 3; . Trang 3/6 - Mã đề thi 143
Câu 28. Đường cong trong hình bên là đồ thị của hàm số nào? 2x 2 A. y . 1 2x 2x 2 B. y . x 1 x 2 C. y . 1 x x 3 D. y . x 1
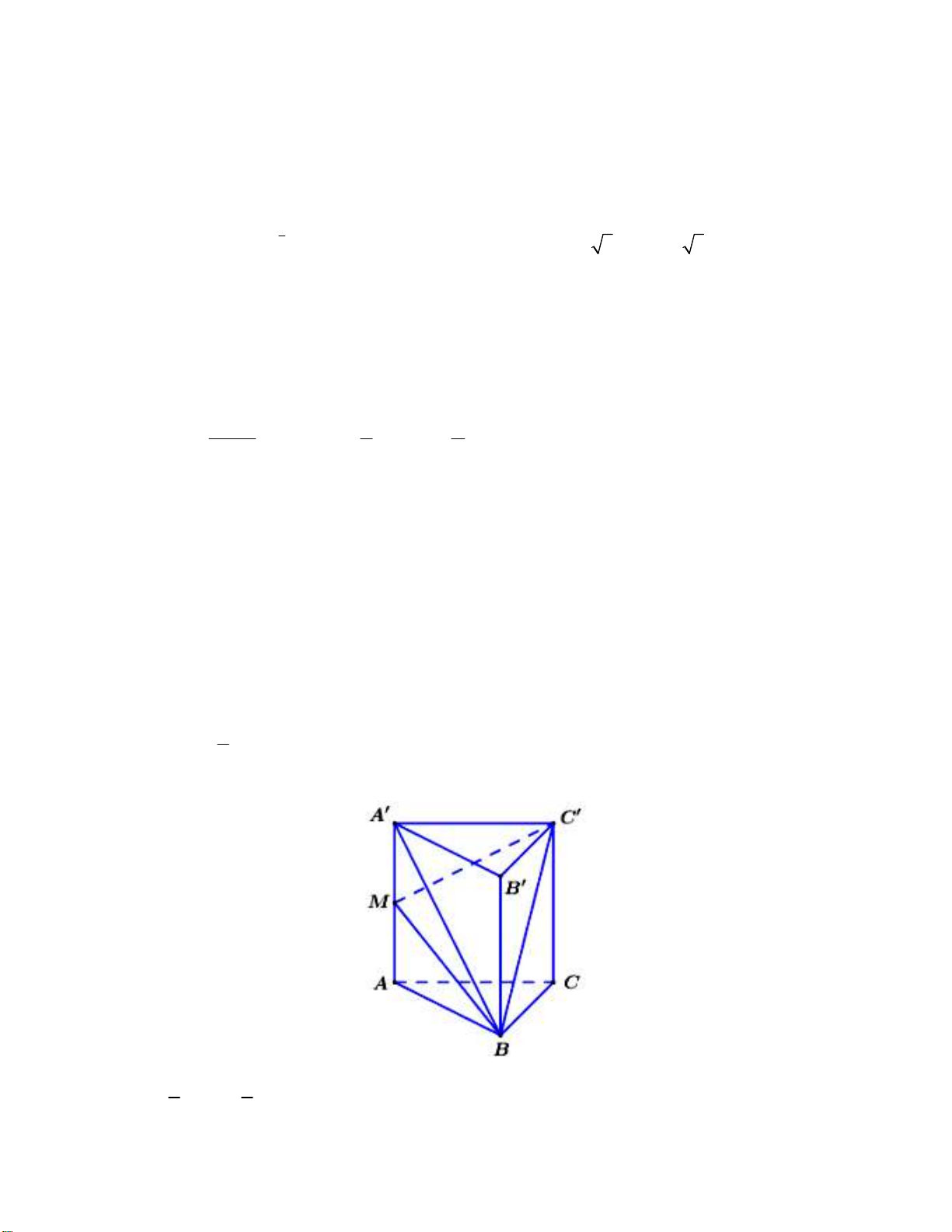
Câu 29. Cho khối lăng trụ đứng AB .
C A' B 'C ' có đáy ABC là tam giác vuông, AB AC a, AA ' a 2 . M là
trung điểm của đoạn thẳng AA’. Tính thể tích khối tứ diện MA' BC ' theo a . 3 a 2 3 a 2 3 a 2 3 a 2 A. . B. . C. . D. . 9 6 18 12
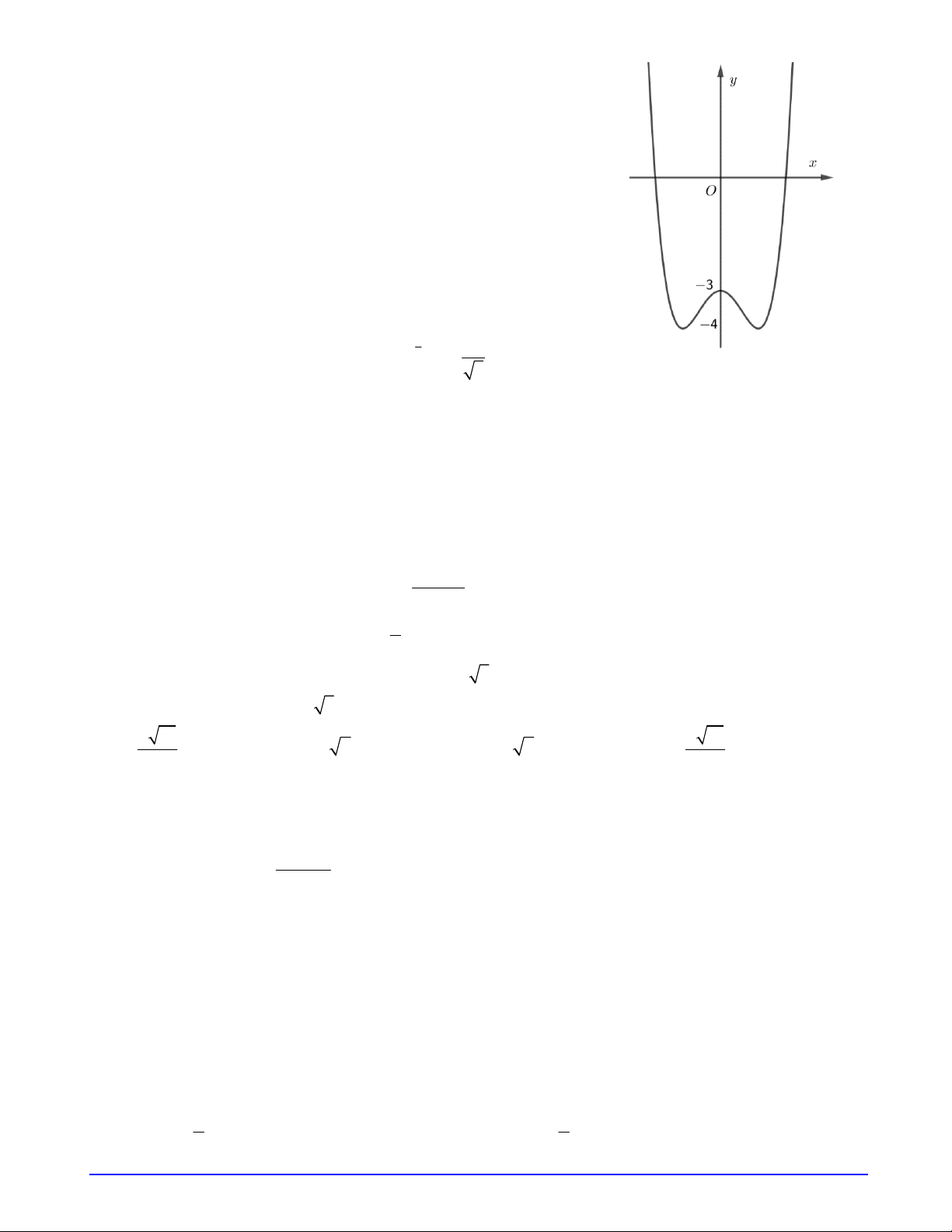
Câu 30. Khối đa diện như hình vẽ bên có bao nhiêu mặt? A. 42 mặt. B. 28 mặt. C. 30 mặt. D. 36 mặt.
Câu 31. Tính bán kính đường tròn giao tuyến của mặt cầu S ;
O r và mặt phẳng biết rằng khoảng cách từ r
tâm O đến bằng . 3 2r 6r 8r 2 2r A. . B. . C. . D. . 3 3 9 3
Câu 32. Cho các số thực dương x, a, , b c thoả mãn x a 4 log 2 log 2
2 log b 4 log c . Biểu diễn x theo
a, b, c được kết quả là 2 2a 2 4a c 2 4a 2 2a c A. x . B. x . C. x . D. x . 2 b c 2 b 2 b c 2 b x 1
Câu 33. Đồ thị hàm số y
có bao nhiêu đường tiệm cận? 2 9 x A. 2 . B. 0 . C. 1. D. 3. Trang 4/6 - Mã đề thi 143
Câu 34. Cho hàm số y f x có đồ thị là đường cong trong hình vẽ bên.
Số nghiệm của phương trình f x m 6 0 với m 3 là A. 4 . B. 2 . C. 3 . D. 1. 2 x 2 x 1
Câu 35. Tổng các nghiệm của phương trình 2 9 9. 4 0 là 3 A. 2. B. 0. C. 1. D. 4.
Câu 36. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A2; 1;
1 , B 2;1;0 và C 1;0;3 . Mệnh đề nào sau đây là đúng?
A. Ba điểm A, B,C tạo thành một tam giác có một góc bằng 0 120 .
B. Ba điểm A, B,C tạo thành một tam giác đều.
C. Ba điểm A, B,C tạo thành một tam giác vuông.
D. Ba điểm A, B,C thẳng hàng. 2 x 4x
Câu 37. Tìm giá trị nhỏ nhất của hàm số y
trên đoạn 0;3 . 2x 1 3
A. min y 0 . B. min y . C. min y 4 . D. min y 1 . 0; 3 0;3 7 0; 3 0; 3
Câu 38. Cho tam giác ABC có 0
BAC 120 , BC 2a 3 . Trên đường thẳng vuông góc với mặt phẳng (ABC)
tại A lấy điểm S sao cho SA a 3 . Tính bán kính mặt cầu ngoại tiếp tứ diện SABC theo a . a 19 a 15 A. . B. a 7. C. a 6. D. . 2 2
Câu 39. Mặt phẳng đi qua trục của khối trụ, cắt khối trụ theo thiết diện là hình vuông có cạnh bằng 6R . Thể
tích của khối trụ bằng A. 3 36 R . B. 3 18 R . C. 3 54 R . D. 3 216 R . mx 18
Câu 40. Cho hàm số y
. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số đồng biến x 2m
trên khoảng 2; . Tổng các phần tử của S bằng A. 2 . B. 3 . C. 2 . D. 5 .
Câu 41. Biết m là giá trị của tham số m để hàm số 3 2
y x 3x mx 1 có hai điểm cực trị x , x sao cho 0 1 2 2 2 x x
x x 10 . Mệnh đề nào dưới đây là đúng? 1 2 1 2 A. m 15 ; 7 .
B. m 1; 7 .
C. m 7; 1 .
D. m 7;10 . 0 0 0 0
Câu 42. Biết F x là một nguyên hàm của hàm số f (x) 2x sin x và F 0 21. Tìm F (x).
A. F x 2
x cos x 20 .
B. F x 2
x cos x 20 . 1 1
C. F x 2
x cos x 20 .
D. F x 2
x cos x 20 . 2 2 Trang 5/6 - Mã đề thi 143
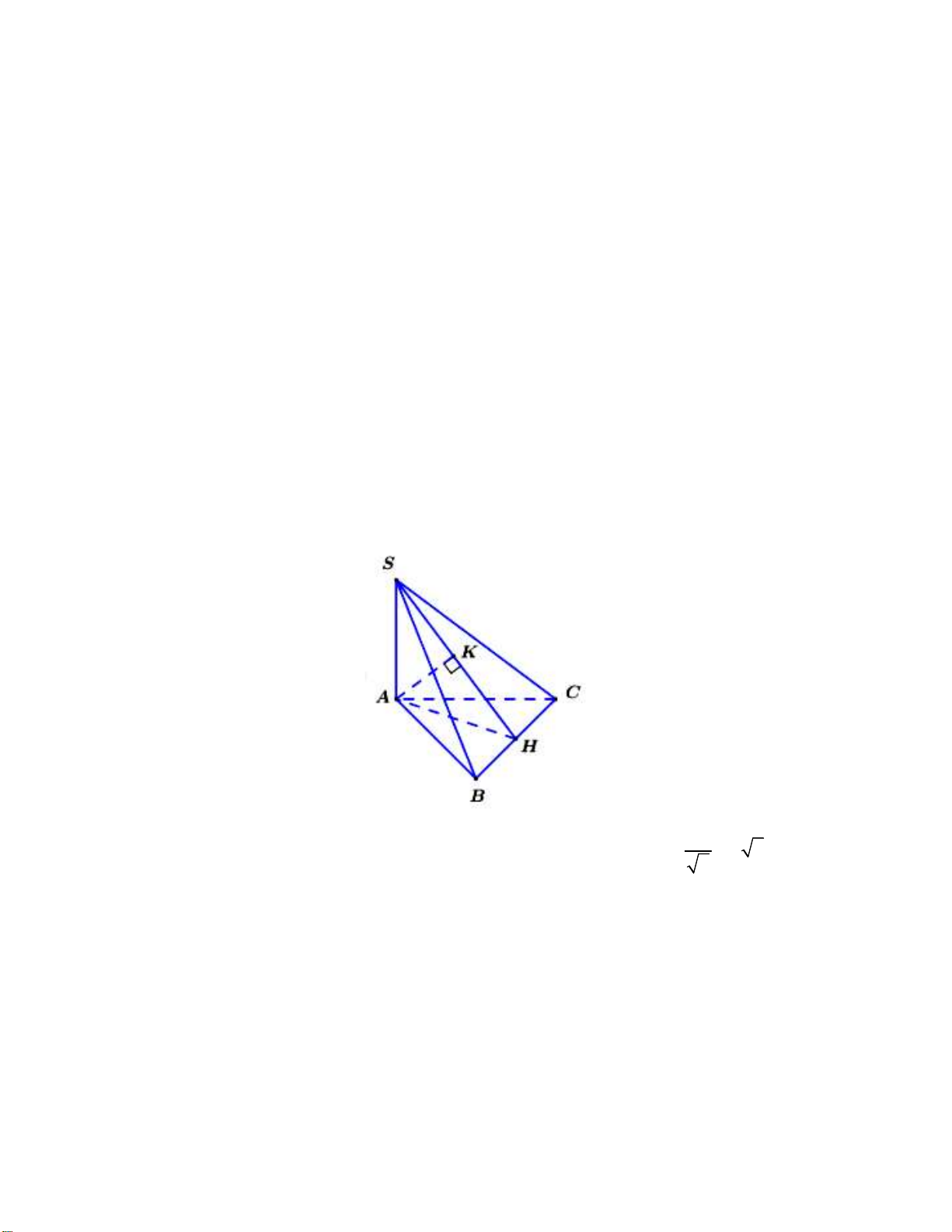
Câu 43. Cho hình chóp tam giác S.ABC có đáy là tam giác vuông tại A, SA ABC . Biết mặt bên SBC tạo với đáy một góc 0
45 và AB AC 2a . Tính theo a khoảng cách từ điểm A đến mặt phẳng (SBC). a 3 2a 3 A. . B. . a C. a 2. D. . 2 3
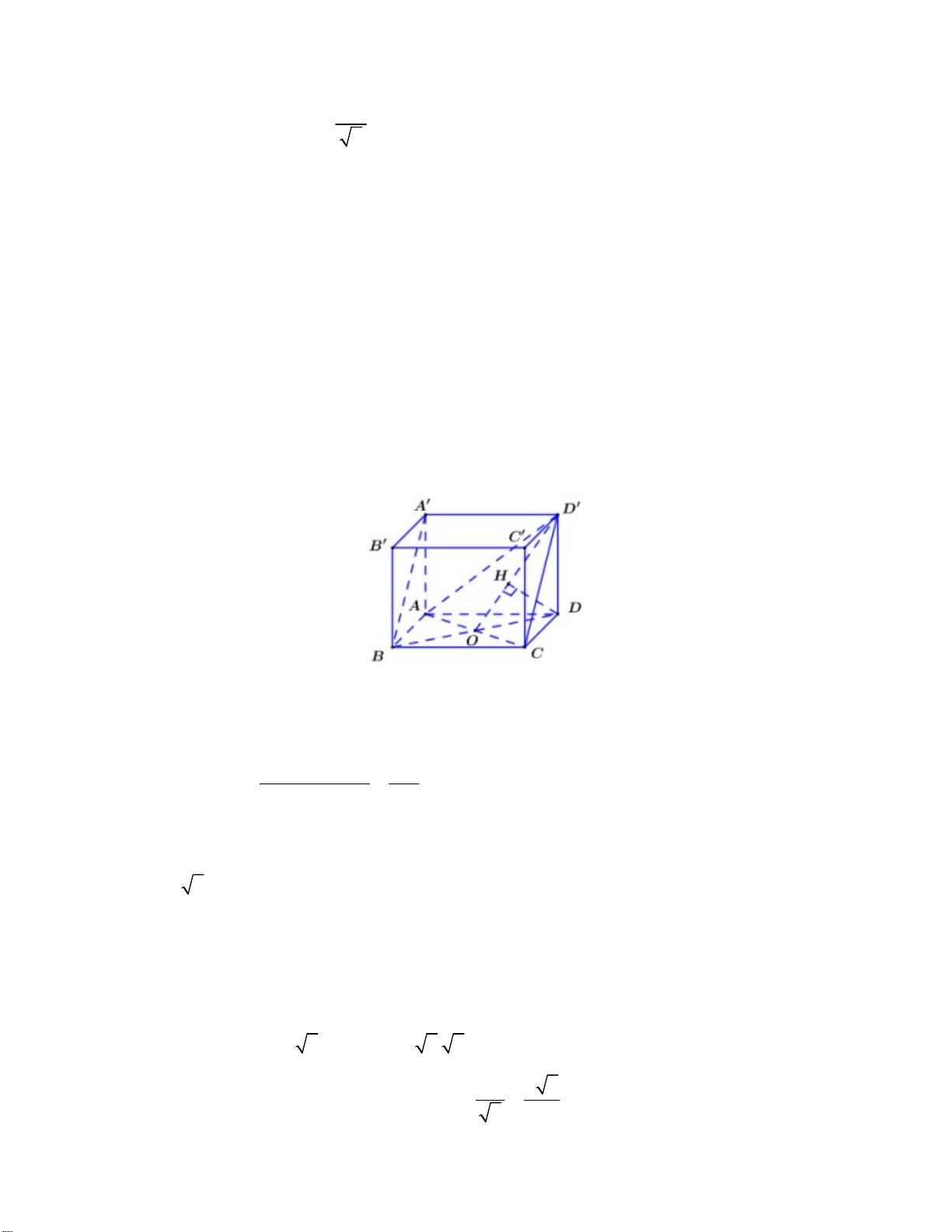
Câu 44. Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có AB AD a 2, AA' a . Tính theo a khoảng cách d
giữa hai đường thẳng A’B và AC . 2a 2 a 2 a 2 A. d . B. d . C. d .
D. d a 2 . 3 2 3
Câu 45. Dân số Việt Nam được ước tính theo công thức ni
S Ae , trong đó A là dân số của năm lấy làm
mốc tính, S là dân số sau n năm, i là tỉ lệ tăng dân số hàng năm. Biết rằng năm 2020, Việt Nam có khoảng
97, 76 triệu người và tỷ lệ tăng dân số là 1,14%. Hỏi năm 2030 Việt Nam sẽ có bao nhiêu triệu người nếu
tỉ lệ tăng dân số hàng năm không đổi (kết quả làm tròn đến hàng phần trăm)?
A. 109, 49 triệu người.
B. 109, 56 triệu người.
C. 11,80 triệu người.
D. 109, 50 triệu người.
Câu 46. Tập nghiệm của bất phương trình 9x 2 53x x 92x 1 0 là S ; a b ; c . Khi đó
a 2b c bằng A. 0. B. 4 . C. 3. D. 1.
Câu 47. Cho hai hàm số: 1 f x 3
x m 2 1 x 2
3m 4m 5 x 2021 và g x 2
m m 3 x 2
m m 2 2 5 2 4
9 x 3x 2 3
(với m là tham số).
Hỏi phương trình g f x 0 có bao nhiêu nghiệm? A. 9. B. 0 . C. 1. D. 3.
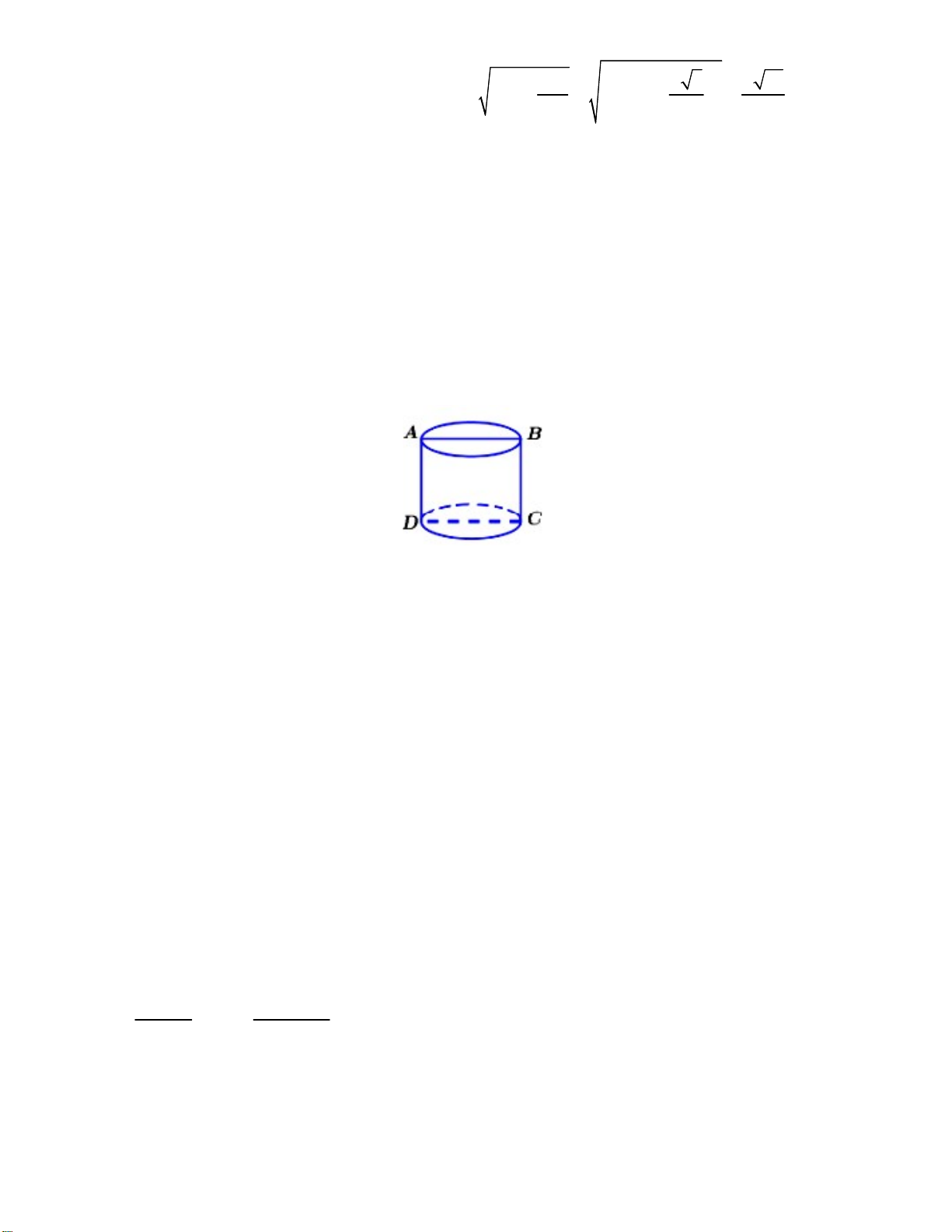
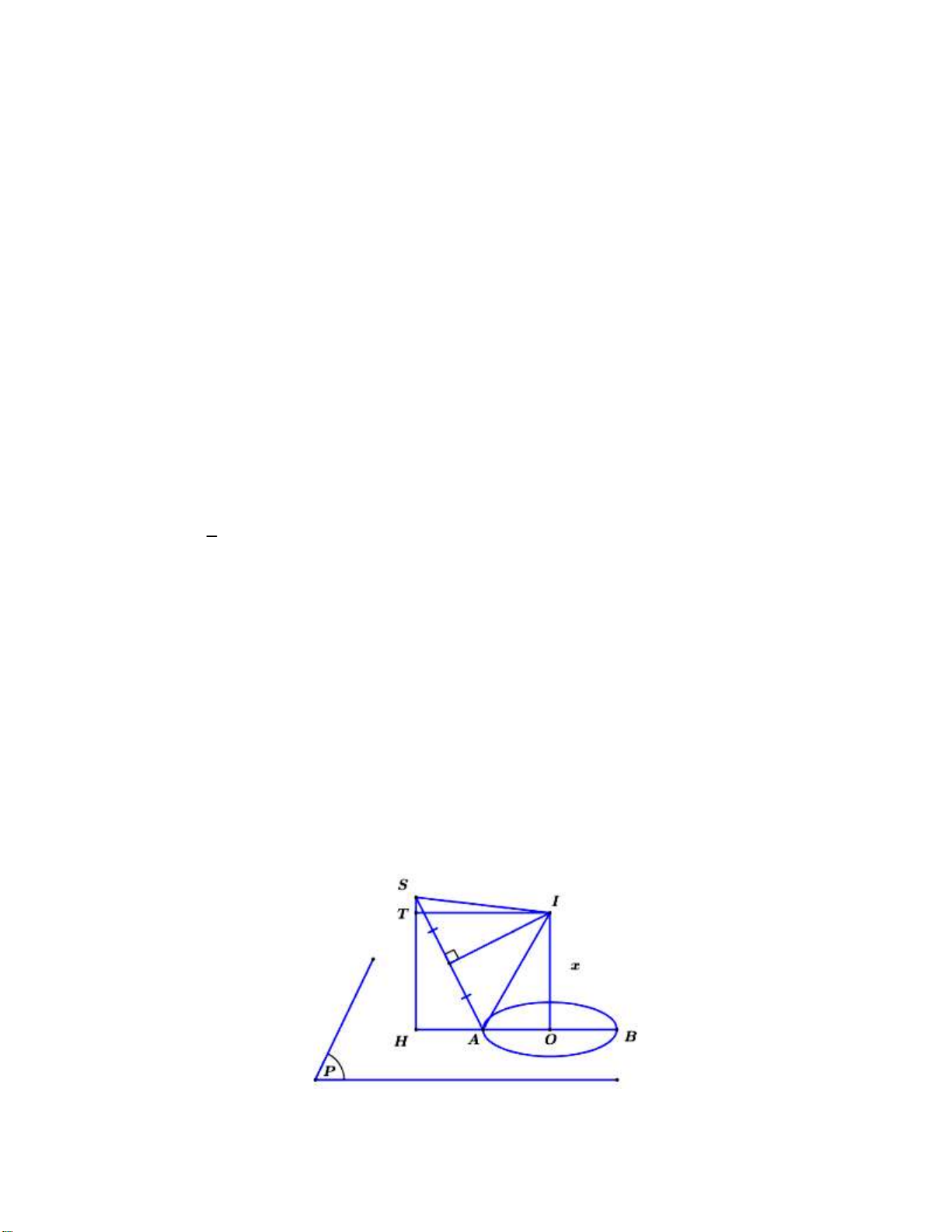
Câu 48. Trong mặt phẳng P cho đường tròn C tâm O , đường kính AB 4 . Gọi H là điểm đối xứng của
O qua A . Lấy điểm S sao cho SH P và SH 4 . Tính diện tích mặt cầu đi qua đường tròn C và điểm S . 343 65 A. 65 . B. . C. 65 . D. . 6 2
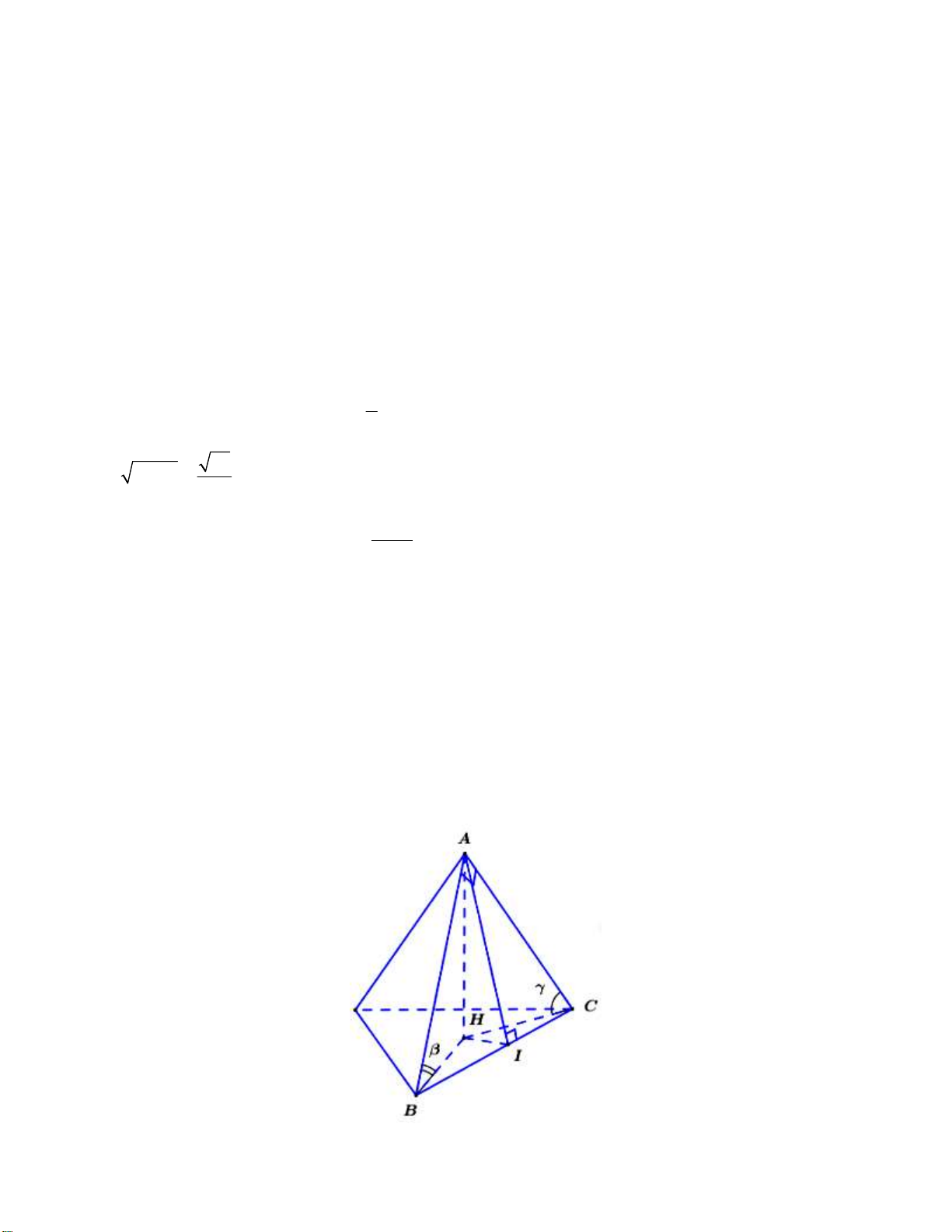
Câu 49. Cho tam giác ABC vuông tại A. Mặt phẳng P chứa BC và hợp với mặt phẳng ABC góc 0 0
0 90 . Gọi , lần lượt là góc hợp bởi hai đường thẳng AB, AC và P . Tính giá trị biểu thức 2 2 2
P cos sin sin .
A. P 0 . B. P 1 .
C. P 2 .
D. P 1 .
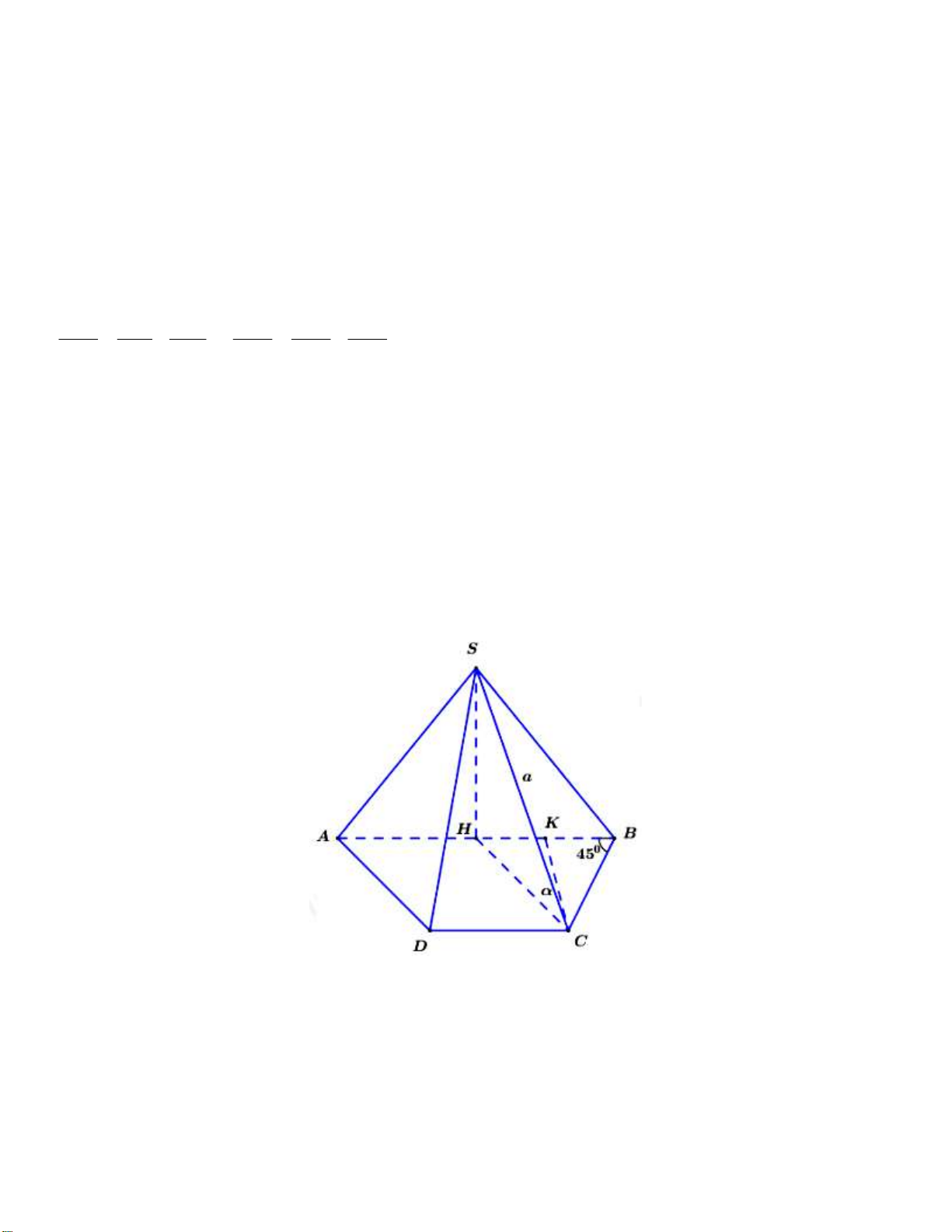
Câu 50. Cho hình chóp S.ABCD có đáy là hình thang, AB∥ CD, 0
AB 2DC, ABC 45 . Hình chiếu vuông góc
của đỉnh S trên mặt phẳng ABCD là trung điểm H của cạnh AB và SC BC, SC a . Gọi góc giữa hai mặt
phẳng SBC và ABCD là . Khi thay đổi, tìm cos để thể tích khối chóp S.ABCD có giá trị lớn nhất. 6 6 3 6
A. cos . B. cos . C. cos .
D. cos . 3 3 3 3
------------- HẾT ------------- Trang 6/6 - Mã đề thi 143
TRƯỜNG THPT KIM LIÊN
KỲ THI THỬ TỐT NGHIỆP THPT NĂM 2021 (LẦN I) Bài thi: TOÁN
ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề thi có 06 trang)
ĐÁP ÁN CÁC MÃ ĐỀ
------------------------ Mã đề [143] 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C A D D B D B A A B D C A A D B B B C A B B C B D
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
C D A D C D C A B C C D A C A C B B B B A D C D B Mã đề [295] 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D D D B A B A C A D D D C B A C B D C A A A A D C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
C C D D B B D C B C B D B A C A D A B C B D D C D Mã đề [387] 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D B A C B A B A B A C B A A D B C C C A C A A A C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
C C C A C B A A A C A B A D B C A A A D C D D B B Mã đề [415] 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B B D B D A C C D C D C A B D C B A B C A D A C D
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B C D A D B B D B A B C C C D B B B D B D A D A A BẢNG ĐÁP ÁN 1-C 2-A 3-D 4-D 5-B 6-D 7-B 8-A 9-A 10-B 11-D 12-C 13-A 14-A 15-D 16-B 17-B 18-B 19-C 20-A 21-B 22-B 23-C 24-B 25-D 26-B 27-D 28-A 29-D 30-C 31-D 32-C 33-A 34-B 35-C 36-C 37-D 38-A 39-C 40-A 41-C 42-B 43-B 44-B 45-B 46-A 47-D 48-C 49-D 50-B
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: (NB) Phương pháp: Hàm số lũy thừa n x với n
xác định với mọi .x Cách giải: Hàm số 2021 u x xác định với x . Chọn C. Câu 2: (NB) Phương pháp: Hàm số lũy thừa n x với n
xác định với mọi x 0. Cách giải: 1
Để biểu thức x 2 2
1 có nghĩa khi 2x 1 0 x . 2 Chọn A. Câu 3: (NB) Phương pháp: 4
Thể tích khối cầu bán kính R là 3 V R . 3 Cách giải: 4 Khối cầu có bán kính 3 3
3cm V r 36 cm . 3 Chọn D. Câu 4: (NB) Phương pháp:
Hình đa diện gồm một số hữu hạn đa giác phẳng thỏa mãn hai điều kiện:
a) Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung. 9
b) Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác. Cách giải:
Ta có hình số 3 không phải hình đa diện vì tồn tại những cạnh chỉ là cạnh của 1 đa giác. Chọn D. Câu 5: (NB) Phương pháp:
Dựa vào bảng biến thiên để xác định điểm cực đại của hàm số: điểm mà tại đó hàm số liên tục và đạo hàm đổi
dấu từ dương sang âm và điểm cực tiểu của hàm số: điểm mà tại đó hàm số liên tục và đạo hàm đổi dấu từ âm sang dương. Cách giải:
Dựa vào BBT ta thấy: Hàm số có 2 điểm cực trị.
Hàm số đạt cực đại bằng 5 tại x 1 .
Hàm số đạt cực tiểu bằng 6 tại x 2.
Vậy chỉ có đáp án B đúng. Chọn B. Câu 6: (TH) Phương pháp:
- Tính độ dài đường sinh 2 2 l h r .
- Áp dụng công thức tính diện tích xung quanh hình nón có đường sinh l, bán kính đáy r là S rl. xq Cách giải:
Đường sinh của hình nón bằng l h r a2 a2 2 2 4 3 5 . a
Khi đó diện tích xung quanh hình nón bằng 2 S rl .3 . a 5a 15 a . xq Chọn D. Câu 7: (NB) Phương pháp:
Phương trình tiếp tuyến của đồ thị hàm số y f x tại điểm M x ; y thuộc đồ thị hàm số là: 0 0 y f ' x x x y 0 0 0 Cách giải: TXĐ: D \ 2 . x 1 3 3 Ta có: y y ' y ' 1 3 . 2 x 2 x 2 1 10 11 Với x 1 2. 1 2
Vậy phương trình tiếp tuyến cần tìm là y 3 x 1 2 3 x 1. Chọn B. Câu 8: (NB) Phương pháp:
Dựa vào bảng xét dấu xác định các khoảng mà tại đó f ' x 0. Cách giải:
Dựa vào bảng biến thiên ta thấy hàm số đồng biến khi f ' x 0 3 x 0. Vậy hàm số y f x đồng biến trên 3;0. Chọn A. Câu 8: (NB) Phương pháp:
Dựa vào bảng xét dấu xác định các khoảng mà tại đó f ' x 0. Cách giải:
Dựa vào bảng biến thiên ta thấy hàm số đồng biến khi f ' x 0 3 x 0. Vậy hàm số y f x đồng biến trên 3;0. Chọn A. Câu 9: (NB) Phương pháp:
Sử dụng tọa độ của 1 vectơ: u ;
x y; z u xi y j zk. Cách giải: a 1;2; 3
Ta có: a i 2 j 3k,b 3 j 4k,c i 2 j b 0;3;4 c 1 ; 2 ;0 Chọn A. Câu 10: (NB) Phương pháp: Sử dụng tổ hợp. Cách giải:
Từ 1 đến 9 có 4 số chẵn là 2, 4,6,8. 11
Để rút 2 thẻ đều đánh số chẵn ta có 2 C cách 4 Chọn B. Câu 11: (TH) Phương pháp:
Áp dụng công thức tính đạo hàm của hàm mũ: u ' ' u a u a ln . a Cách giải: 2 x 2x 2 4 ' 2 '.4 .ln 4 2ln 4.4 x y y x . Chọn D. Câu 12: (NB) Phương pháp:
Giải phương trình logarit: log f x b f x a a b. Cách giải:
log log a 0 log a 1 a 2. 3 2 2 Chọn C. Câu 13: (NB) Phương pháp:
Áp dụng công thức tính diện tích toàn phần của hình trụ có chiều cao h, bán kính đáy r là 2 S 2 rh 2 r tp Cách giải:
Diện tích toàn phần của hình trụ có chiều cao h, bán kính đáy r là 2
S 2 rh 2 r 2 r h r. tp Chọn A. Câu 14: (NB) Phương pháp:
Giải phương trình logarit: log f x b f x a a b. Cách giải: log 2x 3x 2 1 1 x 3x 0, 25 0,25 x 4 2
x 3x 4 0 x 1
Vậy tập nghiệm của phương trình là 1; 4 . Chọn A. 12 Câu 15: (NB) Phương pháp:
Dựa vào hình dáng, chiều hướng của đồ thị để xác định công thức hàm số. Cách giải:
Đồ thị hàm số có chiều hướng xuống A 0 loại , A C.
Đồ thị hàm số cắt trụng tung tại điểm có tung độ bằng 1 nên loại đáp án B. Chọn D. Câu 16: (TH) Phương pháp:
- Chia tử thức cho mẫu thức. n 1 x dx n 1
- Áp dụng các công thức tính nguyên hàm: x dx C n 1, ln ax b C. n 1 ax b a Cách giải: 2 x 2x 1 1 Ta có: f x x . x 2 x 2 2 1 x f x dx x dx ln x 2 C. x 2 2 Chọn B. Câu 17: (NB) Phương pháp:
Sử dụng công thức SHTQ của cấp số nhân n 1 u u q . n 1 Cách giải: u 4 Ta có: 2 u u q q 4. 2 1 u 1 1 Chọn B. Câu 18: (NB) Phương pháp:
Dựa vào TXĐ, chiều biến thiên của đồ thị hàm số. Cách giải:
Dựa vào đồ thị ta thấy hàm số xác định trên 0; nên loại đáp án A và . D
Lại có hàm số nghịch biến trên 0; nên loại đáp án C. Chọn B. 13 Câu 19: (TH) Phương pháp:
- Tính số phần tử của không gian mẫu.
- Gọi A là biến cố: “hai vận động viên Kim và Liên thi đấu chung một bảng”, sử dụng tổ hợp chọn 4 người
còn lại vào cùng bảng đó, và tính số phần tử của biến cố A .
- Tính xác suất của biến cố. Cách giải:
Chia 12 người vào 2 bảng Số phần tử của không gian mẫu là n 6 6 C .C 924. 12 6
Gọi A là biến cố: “hai vận động viên Kim và Liên thi đấu chung một bảng”.
Số cách chọn bảng cho A và B là 2 cách.
Khi đó cần chọn thêm 4 bạn nữa là 4 C cách. 10 n A 4 2.C 420. 10
Vậy xác suất để Kim và Liên thi chung 1 bảng là P A 420 5 . 924 11 Chọn C. Câu 20: (TH) Phương pháp:
- Khi quay tam giác ABC xung quanh trục AB nhận được hình nón có chiều cao h AB, bán kính đáy r AC. r
- Góc ở đỉnh của hình nón có chiều cao h, bán kính đáy r là 2 thỏa mãn tan . h Cách giải:
Khi quay tam giác ABC xung quanh trục AB nhận được hình nón có chiều cao h AB, bán kính đáy r AC. r AC
Gọi góc ở đỉnh là 2 ta có: tan
1 (do tam giác ABC vuông cân tại A ) 0 45 . h AB
Vậy góc ở định của hình nón 0 2 90 . Chọn A. Câu 21: (TH) Phương pháp: - Đặt ẩn phụ 2
log x 1 t,t 1; 2 , đưa phương trình về dạng phương trình bậc hai ẩn t. 3 14
- Cô lập m, đưa phương trình về dạng m f t có nghiệm t 1;2. Khi đó m min f t;max f t . 1;2 1;2
- Sử dụng phương pháp hàm số để tìm min f t ;max f t. 1;2 1;2 Cách giải: Đặt 2 log x 1 t. Với 3 x 1
;3 log x 0; 3 t 1;2 . 3 3
Khi đó bài toán trở thành: Tìm m để phương trình 2 2
t t 2m 2 0 t t 2 2m* có nghiệm t 1;2. 1 Xét f t 2
t t 2 với t 1;2 ta có: f 't 2t 1 0 t 1;2. 2 Ta có f
1 0, f 2 4 min f t 0;min f t 4. 1;2 1;2
Vậy khi đó để phương trình (*) có nghiệm t 2;4 thì min f t m max f t 0 2m 4 0 m 2 1;2 1;2 Vậy m 0;2. Chọn B. Câu 22: (TH) Phương pháp:
- Để hàm số đồng biến trên thì y ' 0 x .
- Cô lập m, đưa bất phương trình về dạng m g x x
m max g x. Cách giải:
Hàm số y mx cos x đồng biến trên khi y ' m sin x 0 x m sin x x m 1. Chọn B. Câu 23: (TH) Phương pháp:
Tìm nghiệm bội lẻ của phương trình f ' x 0. 15 Cách giải: x 0nghiem boi le
Ta có: f ' x 0 x x 2020 2021 1
x 1 0 x 1nghiem boi chan . x 1 nghiem boi le
Vậy hàm số f x có 2 điểm cực trị x 0, x 1. Chọn C. Câu 24: (TH) Phương pháp: n Sử dụng công thức m n , m. n m n m a a a a a . Cách giải: 3 3 1 1 4 1 3 3 3 3 4 a a a a a a f a 1 a 3 1 8 a a 1 3 1 8 8 8 8 8 a a a a 1 a a a 1 1 1 a 1 1 a 1 a 1 2 a 1 f 2020 2021 2020 1010 2021 1 2 021 1. Chọn B. Câu 25: (TH) Phương pháp: 0 a 1 0 f x g x
Giải bất phương trình logarit: f x gx a a a 1 f
x g x 0 Cách giải: 2 x x 1 2 x 1 5 5 2 x x 1 2x 1 7 7 2
x 3x 2 0 1 x 2 a
Tập nghiệm của bất phương trình đã cho là S 1 1; 2 . b 2
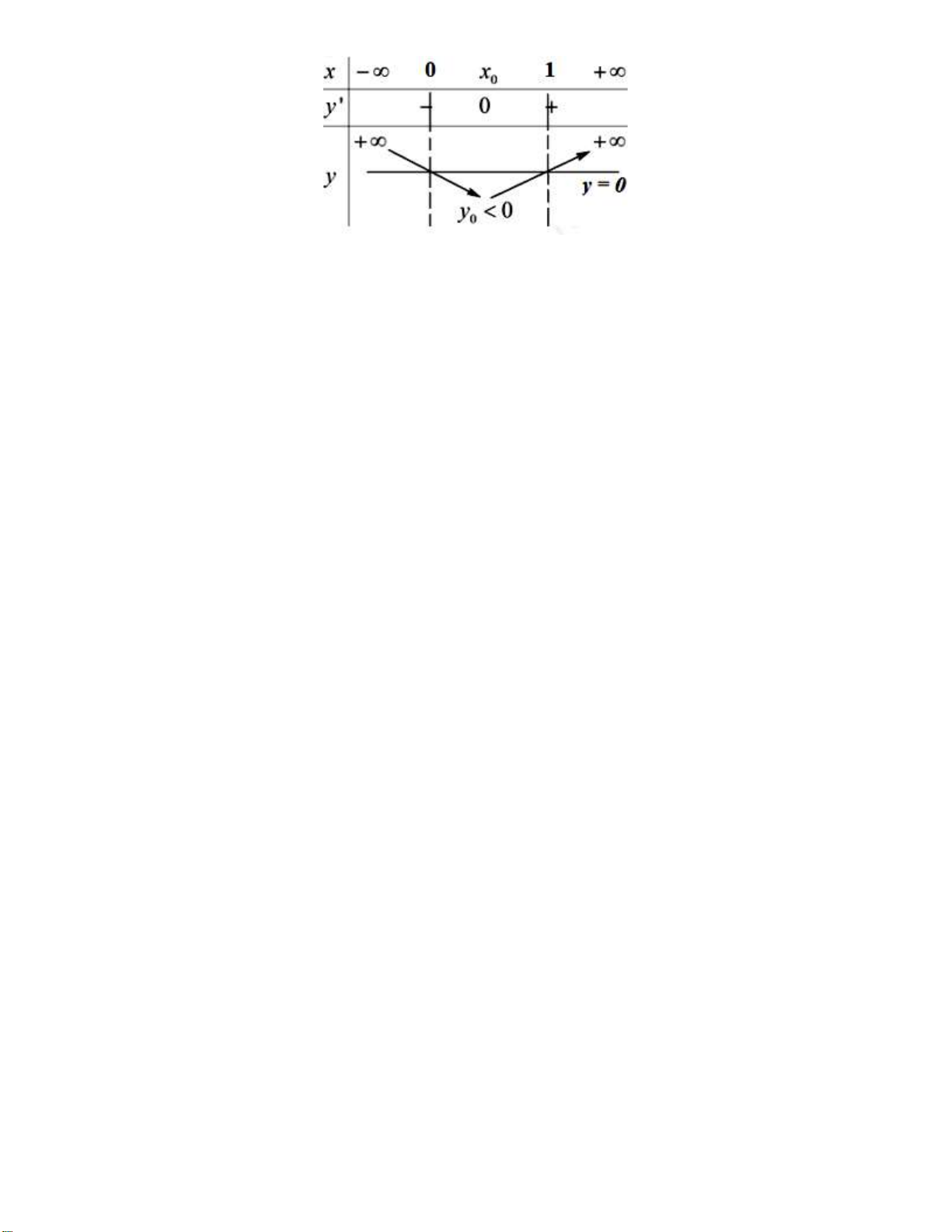
Vậy A 2b a 2.2 1 3. Chọn D. 16 Câu 26: (VD) Phương pháp: 2 x 2mx 4m
- Sử dụng phương pháp hàm số xác định GTLN, GTNN của hàm số y trên 1; 1 . x 2
- Khi đó max f x maxmax f x ; min f x . 1; 1 1 ; 1 1 ; 1
- Giải phương trình max f x 3 tìm . m 1; 1 Cách giải: 2 x 2mx 4m Xét hàm số g x ta có: x 2 2 x m x x mx m x x g ' x 2 2 2 2 4 4 x 22 x 22
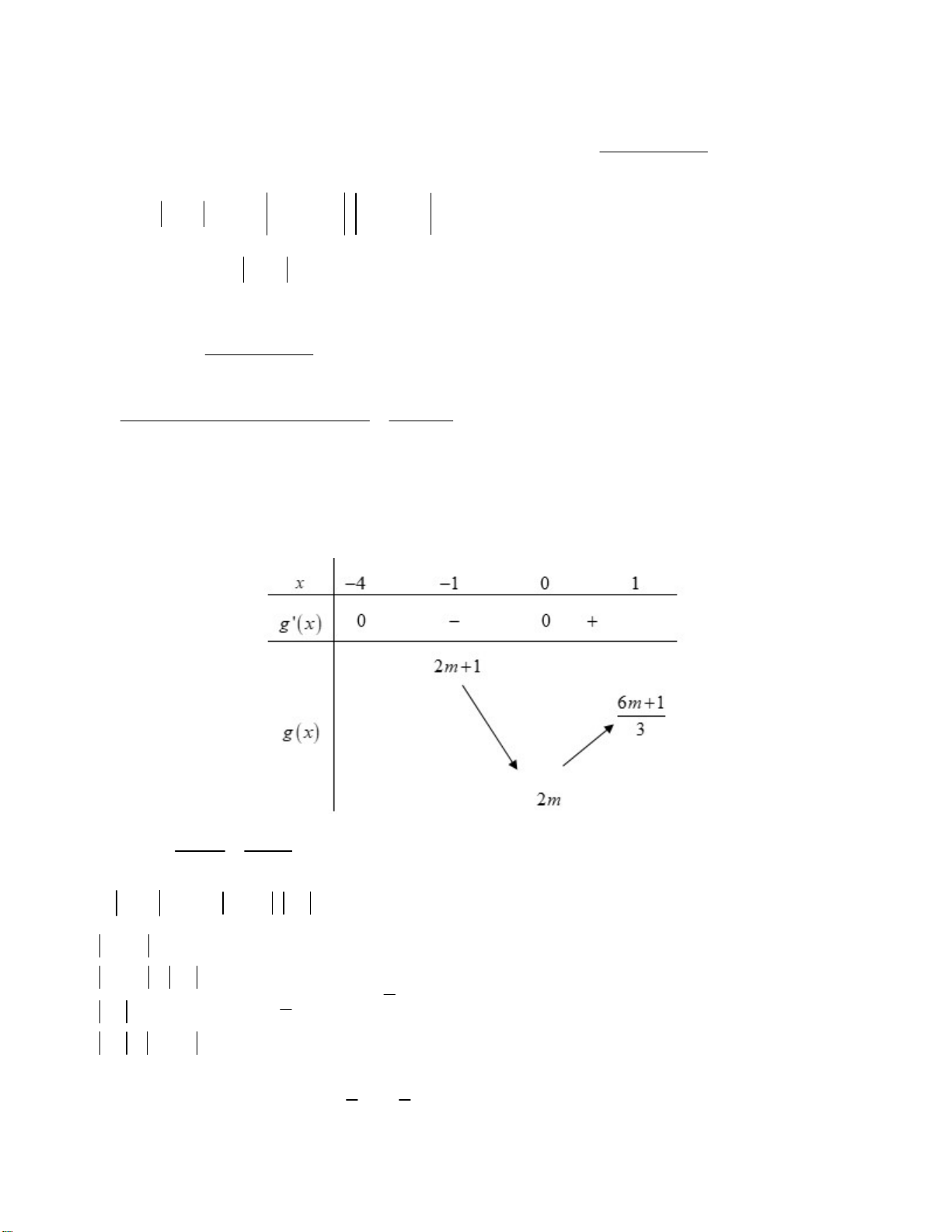
g x x x x 0 ' 0 4 0 . x 4 Bảng biến thiên: 6m 3 6m 1 Ta có: 2m 1
nên ta có: max f x 2m 1;min f x 2 . m 3 3 1; 1 1 ; 1
max f x max 2m 1 ; 2m 1; 1 2m 1 3 m 1 2m 1 2m 3 3 S 1 ; 2m 3 m 2 2 2m 2m 1 3 3
Vậy tích các phần tử của S bằng 1. . 2 2 17 Chọn B. Câu 27: (TH) Phương pháp: Hàm số lũy thừa n
y x , n xác định khi x 0. Cách giải:
Hàm số f x x x 1 3 2 4 3 2 xác định khi 3 2
x 3x 2 0 x 1 3; 1 1 3; Chọn D. Câu 28: (TH) Phương pháp:
- Dựa vào đường tiệm cận của đồ thị hàm số và giao điểm của đồ thị hàm số với trục tung. ax b a d - Đồ thị hàm số y có TCN y ,TCÐ x=- . cx d c c Cách giải:
Đồ thị hàm số có đường tiệm cận ngang nằm dưới trục hoành Loại đáp án B và D.
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ âm nên loại đáp án C. Chọn A. Câu 29: (TH) Phương pháp: - So sánh S và S , từ đó so sánh V và V . A'MB ABB ' A' C '.A'MB C '.ABB ' A' 2 - Sử dụng: V V , tính V AA'.S . C ' ABB ' A' ABC.A'B 'C ' 3 ABC.A' B 'C ' ABC Cách giải: 1 1 Ta có: S S S nên V . A'MB A'.AB ABB ' A' 2 4 C.ABB ' A' 18 2 1 Mà V V nên V V V . C.ABB ' A' ABC.A'B 'C ' 3 MA' BC ' C '.A'MB ABC.A'B 'C ' 6 2 1 a
Vì tam giác ABC vuông và có AB AC a nên ABC vuông cân tại , A suy ra S A . B AC . A BC 2 2 2 3 a a 2 V AA'.S a 2. . ABC.A'B 'C ' ABC 2 2 3 1 a 2 Vậy V V . MA' BC ' ABC.A'B 'C ' 6 12 Chọn D. Câu 30: (TH) Phương pháp:
Dựa vào khối đa diện, lập công thức tính tổng quát. Cách giải:
Khối đa diện tạo bởi 7 hình lập phương kích cỡ bằng nhau.
Nhưng chỉ 6 hình lập phương lộ măt, mỗi hình lộ 5 mặt
Vậy khối đa diện có tổng 30 mặt. Chọn C. Câu 31: (TH) Phương pháp:
Áp dụng định lý Pytago. Cách giải:
Gọi khoảng cách từ O đến là d, bán kính đường tròn giao tuyến là . R 2 r 2 2r
Áp dụng định lí Pytago ta có: 2 2 2 2 2 2
R d r R r d r . 3 3 Chọn D. Câu 32: (TH) Phương pháp: m x
- Sử dụng các công thức log m b b x y xy x y (giả sử các biểu n log ,log log log a a a a ,log log log a a a a n y thức có nghĩa).
- So sánh logarit: log x log y x y. a b 19 Cách giải: log x 2log 2a 4 log b 4log c
log x log 2a logb log c 4 2 2 4 2a2 2 4a log x log x . 2 2 b c b c Chọn C. Câu 33: (VD) Phương pháp:
Sử dụng định nghĩa đường tiệm cận của đồ thị hàm số: Cho hàm số y f x :
- Đường thẳng y y là TCN của đồ thị hàm số y f x nếu thỏa mãn một trong các điều kiện sau: 0
lim f x y hoặc lim f x y 0 0 x x
- Đường thẳng x x là TCĐ của đồ thị hàm số y f x nếu thỏa mãn một trong các điều kiện sau: 0
lim f x hoặc lim f x hoặc lim f x hoặc lim f x . x 0 x x 0 x x 0 x x 0 x Cách giải: ĐKXĐ: 2 9 x 0 3
x 3, do đó không tồn tại giới hạn của hàm số khi x , do đó đồ thị hàm số
không có tiềm cận ngang. Ta có: x 1 lim
nên x 3 là đường tiệm cận đứng của đồ thị hàm số. x 3 2 9 x x 1 lim nên x 3
là đường tiệm cận đứng của đồ thị hàm số. x 2 3 9 x x 1
Vậy đồ thị hàm số y
có 2 đường tiệm cận đứng x 3 . 2 9 x Chọn A. Câu 34: (TH) Phương pháp:
Số nghiệm của phương trình f x m là số giao điểm của đồ thị hàm số y f x và đường thẳng y m
song song với trục hoành. Cách giải:
Ta có f x m 6 0 f x m 6 3 vì m 3. 20
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y f x và đường thẳng y m 6 . Mà m 6 3
m nên đường thẳng y m 6 cắt đồ thị hàm số y f x tại 2 điểm phân biệt.
Vậy phương trình f x m 6 0 có 2 nghiệm. Chọn B. Câu 35: (VD) Phương pháp:
- Đưa về cùng cơ số 3.
- Giải phương trình bậc hai đối với hàm số mũ. Cách giải: 2x2 x 1 Ta có 2 9 9. 4 0 3 1 2x2 x 2 2 3 3 .3 4 0 x x 1 2 3 3 4 0 x x 1 3 3 4 0 x 3 3 4 0 3x 2 3 x 4.3x 3 0 3x 3 x 1 3x 1 x 0
Vậy tổng các nghiệm của phương trình đã chó là 1 0 1. Chọn C. Câu 36: (TH)
Phương pháp:
- Tính các vectơ AB, AC, BC. - Tính tích vô hướng A . B AC và kết luận. Cách giải: AB 0;2; 1 Ta có AC 1 ;1; 2 . BC 1; 1 ;3 A . B AC 0. 1 2.1 1 .2 0 ABC vuông tại . A 21 Chọn C. Câu 37: (TH) Phương pháp: Tìm TXĐ của hàm số.
- Tính y ', giải phương trình y ' 0 xác định các nghiệm x 0; 3 . i
- Tính y 0, y 3, y x . i
- Kết luận: min y miny0, y 3, y x y y y y x i , max
max 0, 3, i . 0; 3 0; 3 Cách giải: 2 x 4x Hàm số y
xác định và liên tục trên 0; 3 . 2x 1 x 4x
2x 42x 1 2 2 2 x 4x 2 2x 2x 4 Ta có y y ' 2x 1 2x 2 1 2x 2 1 x 4x
2x 42x 1 2 2 2 x 4x 2 2x 2x 4 Ta có y y ' 2x 1 2x 2 1 2x 2 1 x 20; 3 Cho 2
y ' 0 2x 2x 4 0 x . 1 0;3 3
Ta có: y 0 0, y 3 , y 1 1 . 7 Vậy min y y 1 1. 0; 3 Chọn D. Câu 38: (VD) Phương pháp:
- Sử dụng công thức giải nhanh bán kính mặt cầu ngoại tiếp chóp có cạnh bên vuông góc với đáy là 2 h 2 R R
trong đó R là bán kính đường tròn ngoại tiếp đáy, h là chiều cao của hình chóp. day 4 day a b c
- Áp dụng định lí sin trong tam giác: 2 . R sin A sin B sin C Cách giải:
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC, áp dụng định lý sin trong tam giác ABC, ta có: day BC 2a 3 2R 4a R 2 . a day 0 sin BAC sin120 day 22 2 2 SA a 3 a 19
Khi đó bán kính mặt cầu ngoại tiếp chóp S.ABC là R R a day 2 2 2 . 4 2 2 Chọn A. Câu 39: (TH) Phương pháp:
- Dựa vào giả thiết mặt phẳng đi qua trục của khối trụ, cắt khối trụ theo thiết diện là hình vuông có cạnh bằng
6R xác định chiều cao và bán kính đáy của hình trụ.
- Thể tích khối trụ có chiều cao h, bán kính đáy R là 2 V R . h Cách giải:
Mặt phẳng qua trục cắt khối trụ theo thiết diện là hình vuông cạnh 6R nên hình trụ có bán kính đáy là r 3R và chiều cao h 6 . R
Vậy thể tích khối trụ là V r h R2 2 3 . 3 .6R 54 R . Chọn C. Câu 40: (VD) Phương pháp: - Tìm TXĐ D \x . 0 y ' 0
- Để hàm số đồng biến trên a;b thì y ' 0x a;b . x ; a b 0 Cách giải: TXĐ: D \2 m . 2 mx 18 2m 18 Ta có y y ' x 2m x 2m2
Để hàm số đồng biến trên khoảng 2; thì y ' 0 x 2; 23 2 1 8 2m 0 3 m 3 3 m 3 m 2m 2; 3 1 2m 2 m 1
Mà m m2;1;0; 1 S.
Vậy tổng các phần tử của S bằng: 2 1 0 1 2. Chọn A. Câu 41: (VD) Phương pháp:
- Tìm đạo hàm của hàm số.
- Tìm điều kiện để phương trình y ' 0 có 2 nghiệm phân biệt.
- Sử dụng định lí Vi-ét. Cách giải: TXĐ: D . Ta có 3 2 2
y x 3x mx 1 y ' 3x 6x . m
Để hàm số đã cho có hai điểm cực trị x ; x thì phương trình 2
y ' 3x 6x m 0 phải có hai nghiệm phân biệt 1 2 x ; x . 1 2
' 9 3m 0 m 3. x x 2 1 2
Khi đó, áp dụng định lý Viet ta có m . x x 1 2 3 Theo bài ra ta có: 2 2 x x x x 10 1 2 1 2 x x 2 2 2 3x x 10 1 2 1 2 4 m 10 m 6 tm Vậy m 6 7 ; 1 . o Chọn C. Câu 42: (TH) Phương pháp: n 1 x
- Áp dụng các công thức tính nguyên hàm: n x dx C
n 1, sin xdx cos x C. n 1
- Sử dụng giả thiết F x 21 tìm hằng số C và suy ra F x. 24 Cách giải: Ta có F x f
xdx x x 2 2 sin dx x cos x C.
Mà F 0 211 C 21 C 20. Vậy F x 2 x cos x 20. Chọn B. Câu 43: (VD) Phương pháp:
- Gọi H là trung điểm của BC, chứng minh BC SAH .
- Trong SAH kẻ AK SH, chứng minh AK SBC d A: SBC AK.
- Xác định góc giữa SBC và ABC là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
- Tính AH. Sử dụng tính chất tam giác vuông cân hoặc hệ thức lượng trong tam giác vuông tính AK. Cách giải: AB
Gọi H là trung điểm của BC, vì ABC vuông cân tại A nên AH BC và AH a 2. 2 BC AH Ta có: BC SAH . BC SA AK SH
Trong SAH kẻ AK SH, ta có: AK SB SB
SAH AK SBC d ; A SBC AK.
SBC ABC BC
Ta có: BC SAH BC SH, khi đó ta có: SH SBC , SH BC cmt AH
ABC, AH BC cmt 25
SBC ABC SH AH 0 ; ; S HA 45 . AH
AKH vuông cân tại K AK . a 2 Vậy d ; A SBC . a Chọn B. Câu 44: (VD) Phương pháp: - Chứng minh d A' ; B AC d ; D ACD '.
- Chứng minh AC ODD ' với O AC BD, trong ODD ' kẻ OH OD '., chứng minh d ; D ACD ' OH.
- Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách. Cách giải:
Ta có CD '/ / A' B nên d A' ; B AC d A' ;
B ACD ' d B; ACD '.
Gọi O AC BD ta có O là trung điểm của B . D d B; ACD ' BO
Vì BD ACD ' O nên d 1
d B; ACD ' d D; ACD ' D ACD . ; ' DO
Trong ODD ' kẻ DH OD 'H OD '.
Vì AB AD a 2 nên là hình vuông AC BD, lại có AC DD '
AC ODD ' AC DH. DH AC Ta có
DH ACD ' d D; ACD' DH. DH OD '
Vì ABCD là hình vuông cạnh a 2 nên BD a 2. 2 2a OD . a OD a 2
OD DD ' a ODD ' vuông cân tại D DH . 2 2 26 a Vậy d A B AC 2 ' '; . 2 Chọn B. Câu 45: (TH) Phương pháp:
Thay các dữ kiện vào công thức đề bài cho. Cách giải:
Coi năm 2020 là mốc ta có A 97,76 và i 1,14%.
Từ năm 2020 đến năm 2030 là 10 năm nên n 10.
Vây dân số Việt Nam năm 2030 là: 10.0,0114 S 97,76.e 109,56 triệu người. Chọn B. Câu 46: (VDC) Phương pháp:
- Phân tích VT thành nhân tử và giải bất phương trình tích.
- Sử dụng phương pháp hàm số để tìm nghiệm của bất phương trình. Cách giải: Ta có:
9x 2 x 53x 92x 1 0
9x 9.3x 2x 1 3x 92x 1 0
3x 3x 9 2x 1 3x 9 0 3x 2x 1 3x 9 0 3x 2x 1 3x 2x 1 0 3x 9 x 2 1 3x 2x 1 3x 2x 1 0 3x 9 x 2 x x 2 2 Xét hàm số 3x y
2x 1 ta có y ' 3 ln 3 2 0 3 x log x . 3 0 ln 3 ln 3 BBT: 27 3x 2x 1 3x 2x 1 0 3x 9 x 2 1 3x 2x 1 3x 2x 1 0 3x 9 x 2 x 1 x 0 x 0 3x 2x 1 0 x 2 Dựa vào BBT ta có: x 1 . Khi đó 1 x 2 . 0 x 1 3x
2x 1 0 0 x 1 0 x 1 x 2
Suy ra tập nghiệm của bất phương trình là S 0; 1 2;.
Vậy a 0;b 1;c 2 a 2b c 0. Chọn A. Câu 47: (VDC) Phương pháp:
Xét phương trình g x 0.
Chỉ ra hàm số y f x đồng biến trên .
Suy ra số nghiệm phương trình g f x 0 Cách giải:
Xét phương trình g x 0. 28 2 m 2m 5 3 x 2 2m 4m 9 2 x 3x 2 0 2 m 2m 5 3 x 2 2m 4m 10 2 2 x x 3x 2 0 2 m 2m 5 2
x x 2 x 1 x 2 0 x 2 2 m 2m 5 2 x x 1 0 x 2
2m 2m5 2x x10 *
m 2m 5 m 2 2 1 4 0
Xét (*) vì ac 2 m 2m 5 0
nên phương trình (*) có 2 nghiệm trái dấu khác 2. 2 m 2m 5 2 2
.2 2 1 4m 8m 21 0 x 2 f x 2 1
Hay g x 0 có 3 nghiệm phân biệt x m mn 0. Do đó g f x 0 f x m2 mn 0. x n f x n 3 1 Xét hàm số f x 3 x m 2 1 x 2
3m 4m 5 x 2021 ta có: f x 2 x m 2 ' 2 1 x 3m 4m 5. 3 Ta có '
m 1 3m 4m 5 2 m 2m 4 0 m nên f 'x 0 x . f ' x 2 2 2
Suy ra hàm số f x là hàm đồng biến trên .
Do đó mỗi phương trình
1 ,2,3 có nghiệm duy nhất và các nghiệm này là khác nhau.
Vậy phương trình g x 0 có 3 nghiệm phân biệt. Chọn D. Câu 48: (VDC) Cách giải: 29
Mặt cầu S chứa đường tròn C nên tâm I của S nằm trên đường thẳng đi qua O và vuông góc với P. O I P Ta có: SH P SH / /OI.
Mà IS IA nên I nằm trên trung trực đoạn S . A
I cũng là tâm đường tròn ngoại tiếp SA . B
Kẻ IT SH tại T. Đặt OI . x
Áp dụng định lí Pytago ta có: 2 2 2 2 AI AO OI x 4.
Trong hình thang vuông IOHS và tam giác vuông SIT có:
IS IT ST OH ST x2 2 2 2 2 2 2 2 4 4 x 8x 32 Vì 2 2 7
IA IS x 4 x 8x 32 x OI 2 2 65 AI x 4 . R 2 2 R
Vậy diện tích mặt cầu S là 2 65 S 4 R 65. 4 Chọn C. Câu 49 (VDC) Phương pháp:
- Kẻ AH PH P , xác định các góc , , .
- Sử dụng hệ thức lượng trong tam giác vuông và tỉ số lượng giác của góc nhọn trong tam giác vuông tìm mối
quan hệ giữa cos ,sin ,sin . Cách giải: 30
Kẻ AH PH P ta có A ; B P A
BH ; AC;P A CH . BC HI
Kẻ HI BC I BC ta có:
BC AHI BC AI BC AH ABC P BC
AI ABC ; AI BC ABC ;P AI; HI A IH . HI P;HI BC
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có: 2 2 2 1 1 1 AH AH AH 2 2 2 2 2 2 AH AB AC AI AB AC 2 2 2
sin sin sin 2 2 2
1 cos sin sin 2 2 2
cos sin sin 1 Vậy P 1. Chọn D. Câu 50 (VDC) Cách giải: BC SC Ta có
BC SCH BC HC. BC SH
SBC ABCD BC
Khi đó ta có: SC SBC, SC BC gt
SBC; ABCD SC;HC S CH . HC ABCD,HC BC cmt 31
Xét tam giác vuông SHC ta có: SH SC.sin .
a sin, HC SC.cos . a cos HC SB cmt Ta có:
BCH vuông cân tại C HB HC. 2 a 2.cos 0 A BC 45 gt
AB 2HB 2a 2.cos và DC HB a 2.cos . 1 1
Gọi K là trung điểm của BH ta có CK HB CK AB và CK BH a 2 cos . 2 2
AB CD.CK 2a 2.cos a 2.cos 1 3 2 2 S . a 2 cos a cos . ABCD 2 2 2 2 1 1 3 2 2 1 3 V .SH.S . .
a sin. a .cos a sin ABCD 2 1 sin . 3 3 2 2 1
Đặt t sin,t 0; 1 , xét hàm số f t 3 1 t ,t 0; 1 ta có f 't 2 1 3t 0 t . 3 1 1 6 Vậy V
đạt giá trị lớn nhất khi sin cos 1 (do 0
0 90 nên cos 0). S .ABCD 3 3 3 Chọn B.
____________________ HẾT ____________________ https://toanmath.com/ 32
Document Outline
- de-thi-thu-toan-tot-nghiep-thpt-2021-lan-1-truong-thpt-kim-lien-ha-noi
- Made-143_thithulan_01_2021
- Dap-an_thi thu kim liên lan01_2021
- FSDF




