



Preview text:
SỞ GD&ĐT QUẢNG NINH
ĐỀ THI THỬ TỐT NGHIỆP THPT
TRƯỜNG THPT TRẦN NHÂN TÔNG NĂM HỌC 2020-2021 Môn: Toán
(Đề thi có 08 trang)
Thời gian làm bài 90 phút, không kể thời gian gi TSao đề
Họ và tên học sinh :..................................................... Số báo danh : ................... Mã đề 024 x + 2 P
Câu 1. Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = là x −1
A. x =1; y = 2. B. x = 1 − ; y =1.
C. x =1; y =1.
D. x = 2; y =1. -202
Câu 2. Cho khối nón có thể tích bằng 15 chiều cao h = 5 . Đường kính đáy của khối nón đã cho bằng A. 9 . B. 4 . C. 6 . D. 3 . 1
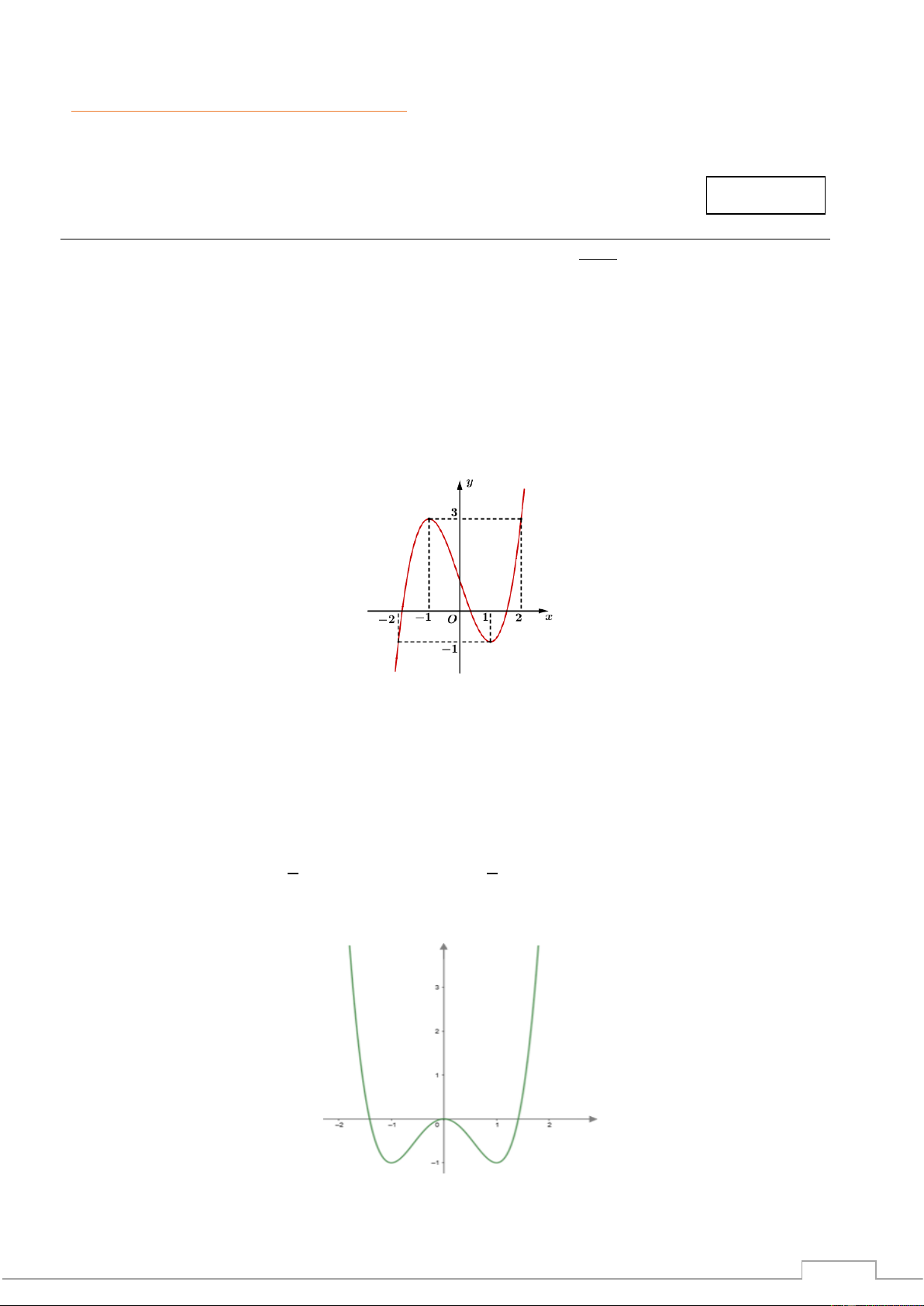
Câu 3. Cho hàm số y = f (x) có đồ thị như hình vẽ sau
Hàm số nghịch biến trên khoảng A. (−1; 2) . B. ( 1 − ;0). C. (0; 2) . D. ( 2 − ;0). TSP
Câu 4. Cho khối lăng trụ có đáy là hình vuông cạnh a và chiều cao bằng 2a . Thể tích của khối lăng trụ đã cho bằng 2 4 A. 3 2a . B. 3 a . C. 3 a . D. 3 4a . 3 3 -
Câu 5. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? 202 1 A. 3 2
y = x − 3x . B. 3 2
y = −x + 3x . C. 4 2
y = x − 2x . D. 4 2
y = −x + 2x .
GV: Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 1 1
Câu 6. Họ nguyên hàm của hàm số ( ) 2 = x f x e − là 2 x 2x e 2x e 1 2x e A.
− 2ln x + C . B. 2 2 x
e + 2ln x +C . C. + + C . D. 2 − ln x + C . 2 2 x 2 TS
Câu 7. Quay một hình vuông có chu vi là 8dm quanh một cạnh của nó ta được một khối trụ c Pó thể tích bằng A. ( 3 2 dm ) . B. ( 3 8 dm ). C. ( 2 8 dm ) . D. ( 2 2 dm ) . - x
Câu 8. Tập xác định của hàm số y = (2 − 3) là 202 A. (0; +). B. (− ; +). C. 0; + ).
D. (−; 0) .
Câu 9. Một bạn có 4 áo xanh, 3 áo trắng và 3 quần mày đen. Hỏi bạn đó có bao nhiêu cách 1 chọn
một bộ quần áo để mặc? A. 21 . B. 2 C . C. 36 . D. 10 . 10
Câu 10. Cho khối chóp có thể tích bằng 10 diện tích đáy B = 5 . Chiều cao của khối chóp đã cho bằng A. 3. B. 6. C. 2. D. 4.
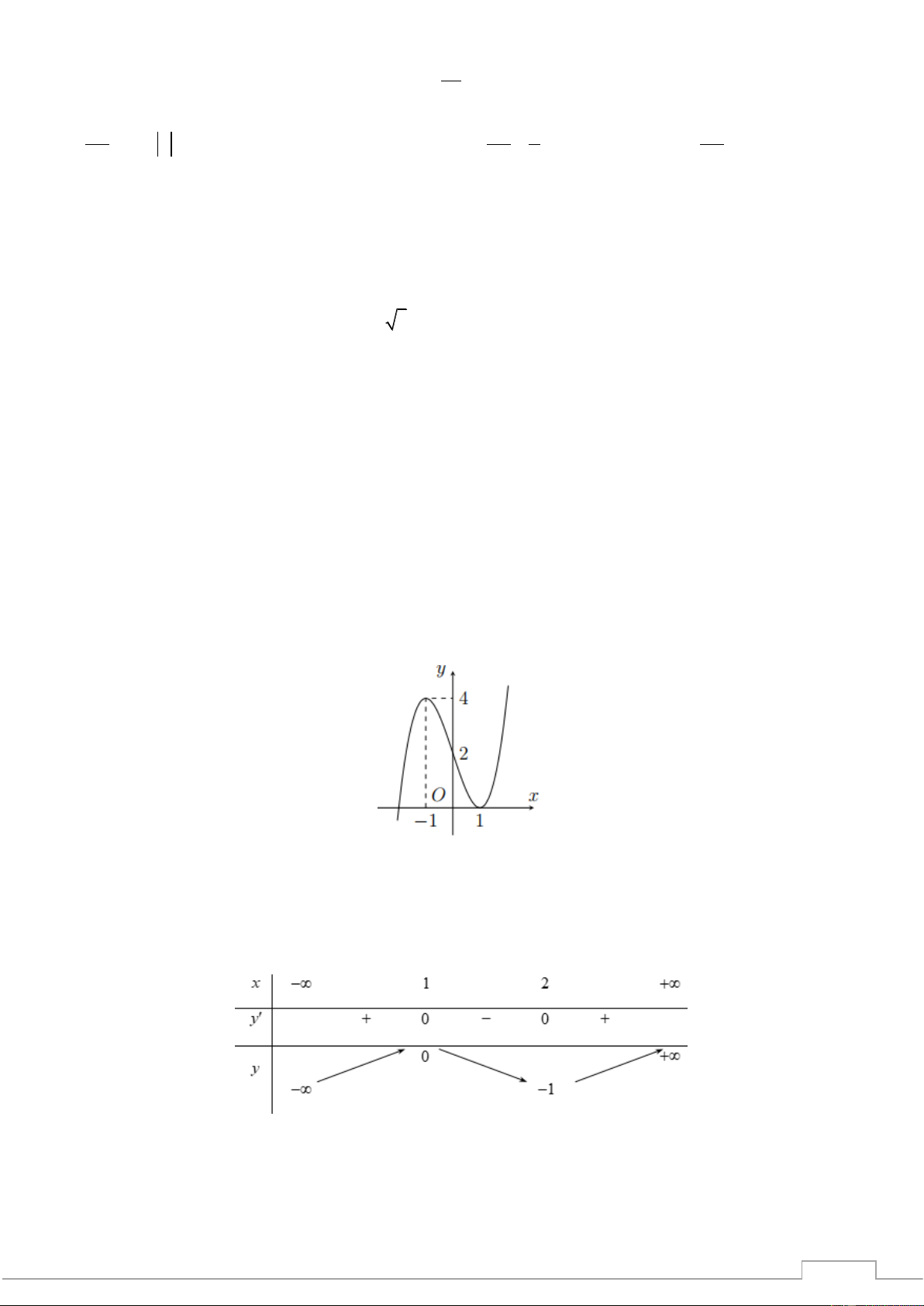
Câu 11. Đồ thị hàm số nào sau đây có dạng như đường cong bên dưới? TSP A. 3 2
y = x − 3x − 3x − 2 . B. 3 2
y = x − 3x − 3x + 2 .
y = x − x +
y = x − x − - C. 3 3 2 . D. 3 3 2 . 202
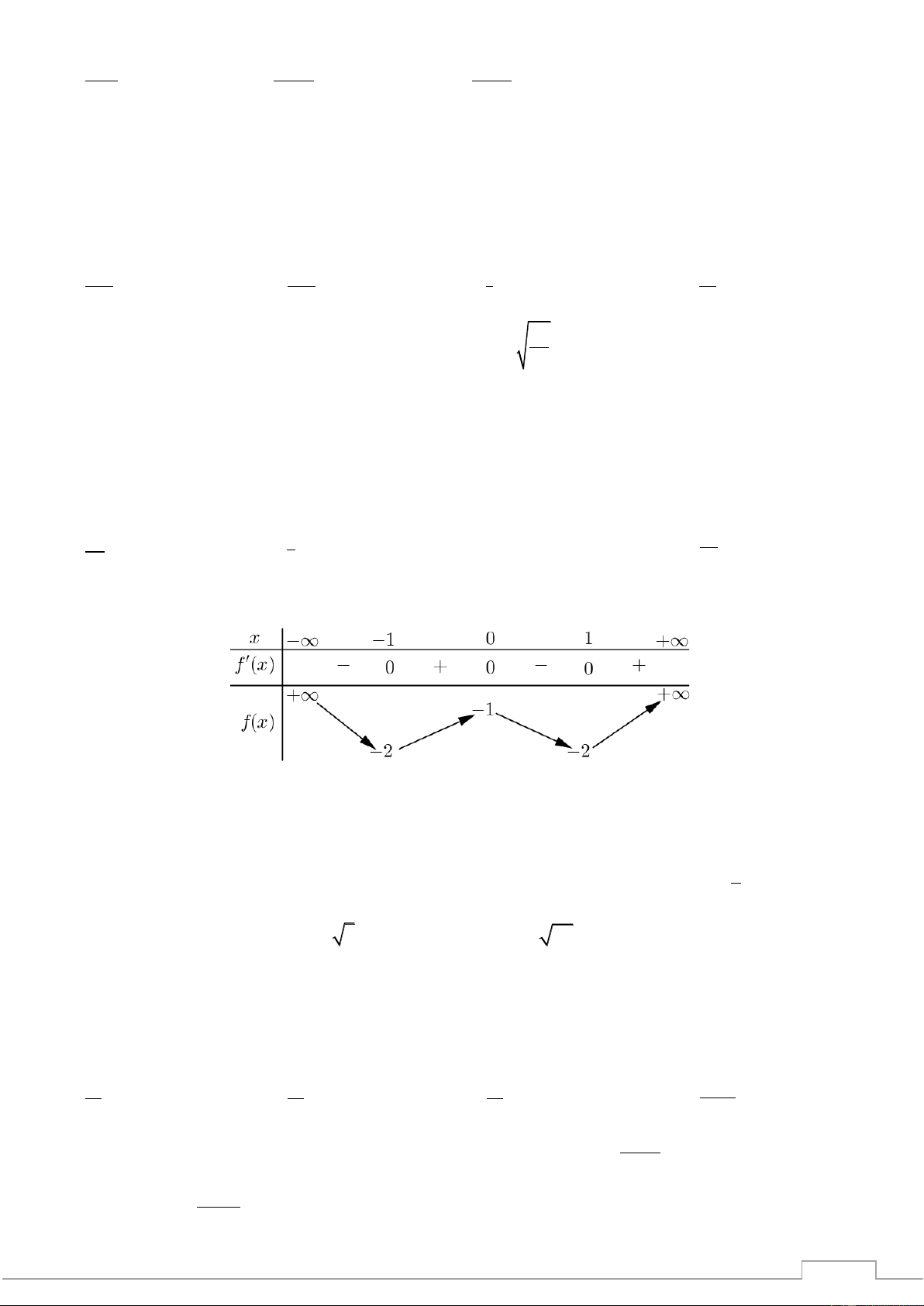
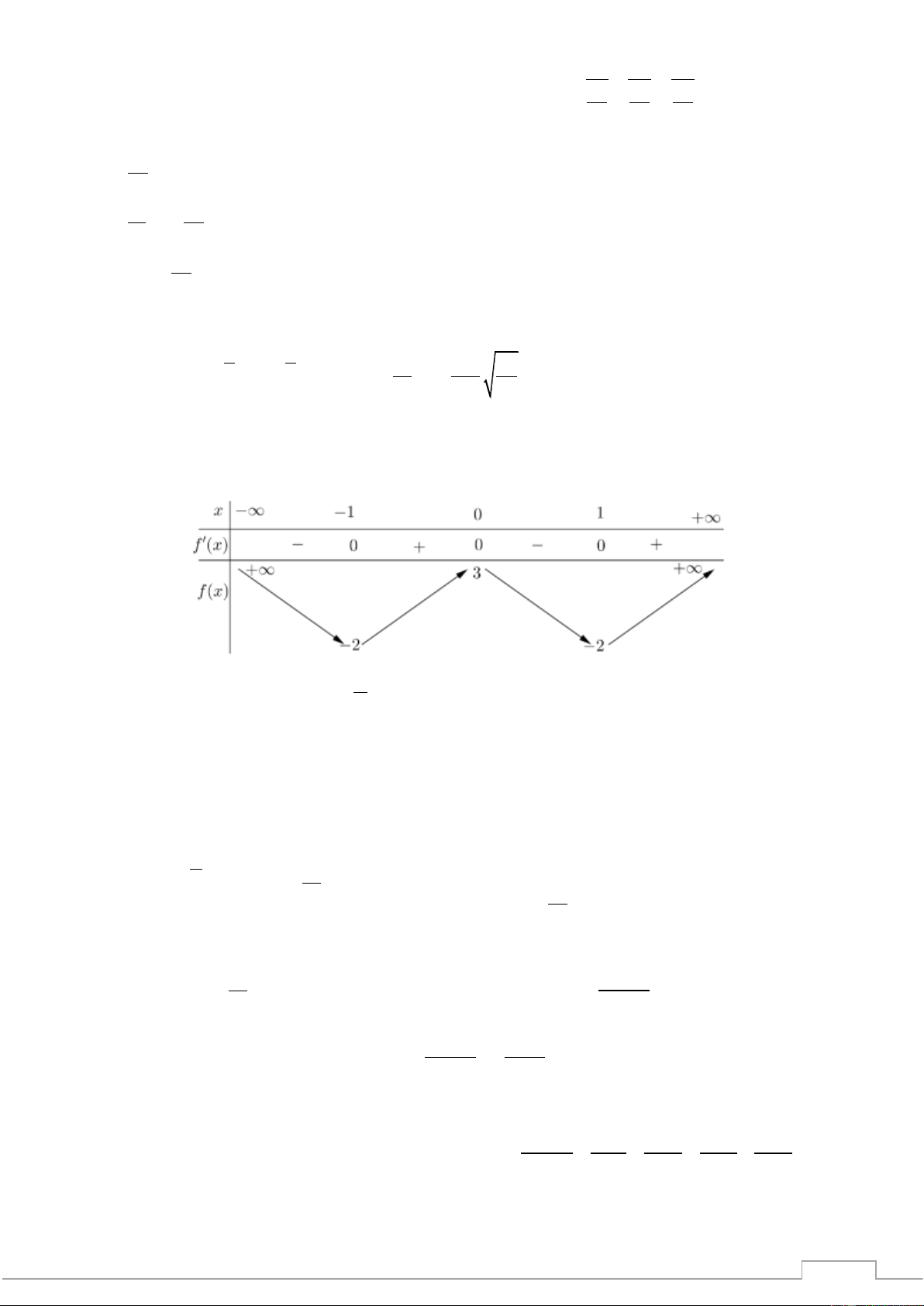
Câu 12. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ 1
Hàm số có giá trị cực tiểu bằng A. −1. B. 0 . C. 2 . D. 1.
GV: Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 2
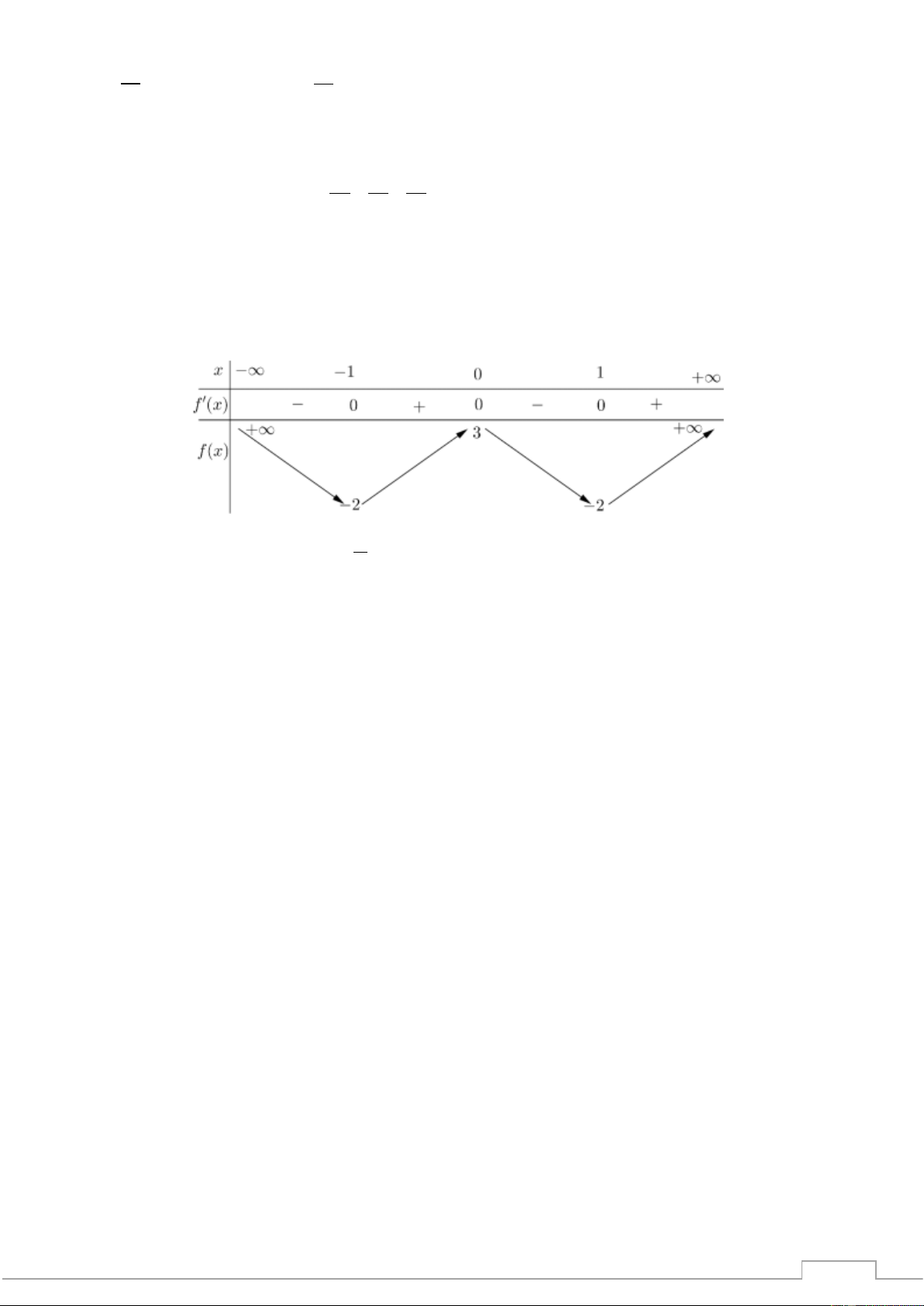
Câu 13. Cho hàm số y = f (x) có bảng biến thiên như sau: − TS P
Phát biểu nào sau đây là đúng? -
A. Hàm số nghịch biến trên (−; )
1 . B. Hàm số đồng biến trên (− ; − ) 1 . 202
C. Hàm số nghịch biến trên (− ; 0);(1;+) .
D. Hàm số đồng biến trên (0; 2) .
Câu 14. Diện tích của một mặt cầu bằng 16 . Thể tích của khối cầu bằng 1 A. 128 . B. 256 . C. 32 . D. 64 . 3 3 3 3 x−2 2021
Câu 15. Nghiệm của phương trình 2 = 4 là
A. x = 2018 .
B. x = 4038 .
C. x = 4044 .
D. x = 2023 .
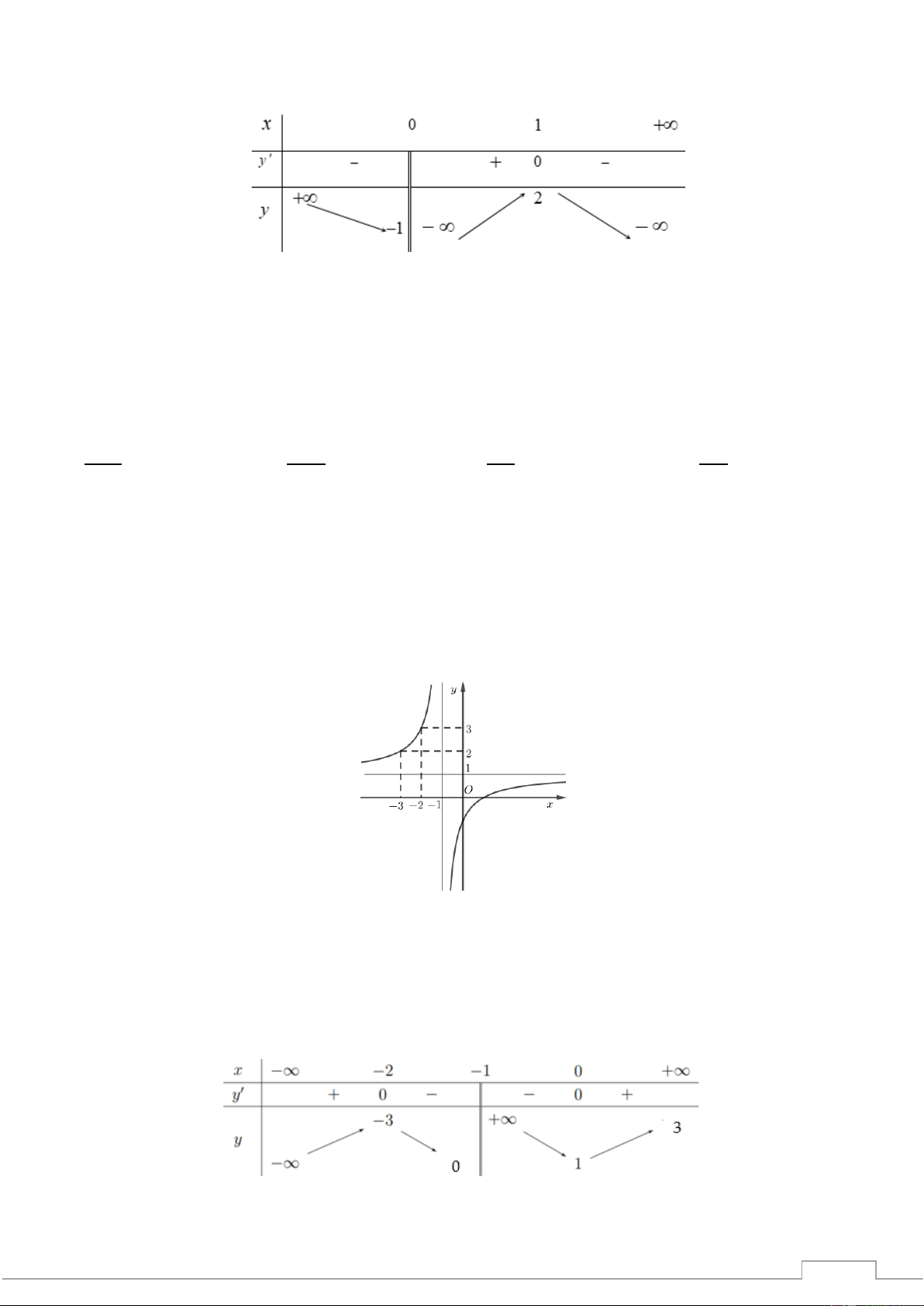
Câu 16. Cho hàm số y = f (x) là hàm phân thức bậc nhất chia bậc nhất và có đồ thị như hình vẽ
bên. Số nghiệm của phương trình f ( x) = 2021 là TSP - A. 2 . B. 1. C. 0 . D. 3 . 202
Câu 17. Cho cấp số nhân (u với u = 2 và công bội q = 3 . Tìm số hạng thứ 4 của cấp số nhân. n ) 1 A. 24 . B. 54 . C. 162 . D. 48 .
Câu 18. Cho hàm số có bảng biến thiên như sau: 1
Tổng số tiệm cận đứng và tiệm cận ngang của hàm số là
GV: Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 3 A. 3 . B. 1 . C. 0 . D. 2 .
Câu 19. Cho khối lập phương có cạnh bằng 4. Thể tích của khối lập phương đã cho bằng A. 4 . B. 12 . C. 16 . D. 64 . 2 TS
Câu 20. Tập nghiệm dương của phương trình log x − x −1 = 0 là 2 ( ) A. 1; − 2 . B. 2 . C. 1 − ; 2 . D. 1 . P
Câu 21. Diện tích xung quanh của hình trụ có độ dài đường sinh l và bán kính đáy r bằng -
A. 2 rl .
B. rl .
C. 1 rl . D. 4 rl . 202 3
Câu 22. Cho 0 a 1. Giá trị của biểu thức M = a a bằng? a ( 2 3 3log ) A. 5 . B. 3 . C. 5 . D. 7 . 2 2 1 Câu 23. Hàm số 4 2
y = ax + bx + c có đồ thị hàm số như hình vẽ dưới đây. Mệnh đề nào s au đây đúng? a b c a b c a b c a b c TSP A. 0, 0, 0 . B. 0, 0, 0 . C. 0, 0, 0 . D. 0, 0, 0 .
Câu 24. Giá trị lớn nhất của hàm số 3
y = x − 24x −10 trên đoạn 1 − 0; 4 là A. 1 − 0 + 32 2 . B. 1 − 5+ 29 3 . C. 36 . D. 35 .
Câu 25. Cho hàm số F (x) là một nguyên hàm của hàm số f (x) trên . Phát biểu nào sau đ -202ây là
sai với mọi x ? 1 A. (2 + )1d = 2 (2 + )1+ f x x F x C . B. (2 + )1d = (2 + )1+ f x x F x C . 2
C. (F(x))' = f (x). D. ( )d = ( )+
f x x F x C . 1 3 2
Câu 26. Cho hàm số y = f (x) có đạo hàm f (x) = x(x − 2) (x − 4). Số điểm cực trị của hàm
số y = f (x) là A. 1. B. 3 . C. 2 . D. 4 .
Câu 27. Thể tích khối lăng trụ đứng ABC . D A B C
D có đáy là hình vuông cạnh a và đường
GV: Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 4 chéo
A C = 2a bằng A. 3 2a . B. 3 2a . C. 3 3a . D. 3 a . 2 x x − 4
Câu 28. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = là 2 TS x − 2x − 3 A. 1. B. 4 . C. 2 . D. 3 . 4 x 2 P
Câu 29. Đồ thị hàm số y = −
+ x +1 cắt trục hoành tại mấy điểm? 2 - A. 2 . B. 4 . C. 3 . D. 0 . 202 x +
Câu 30. Họ tất cả các nguyên hàm của hàm số f (x) 2 1 = trên khoảng ( ) ;1 − là x −1 3 3 A. 2x − + C.
B. 2x + 3ln (x − ) 1 + C. C. 2x + + C .
D. 2x + 3ln (1− x) + 1 ( C x − )2 1 (x− )2 1
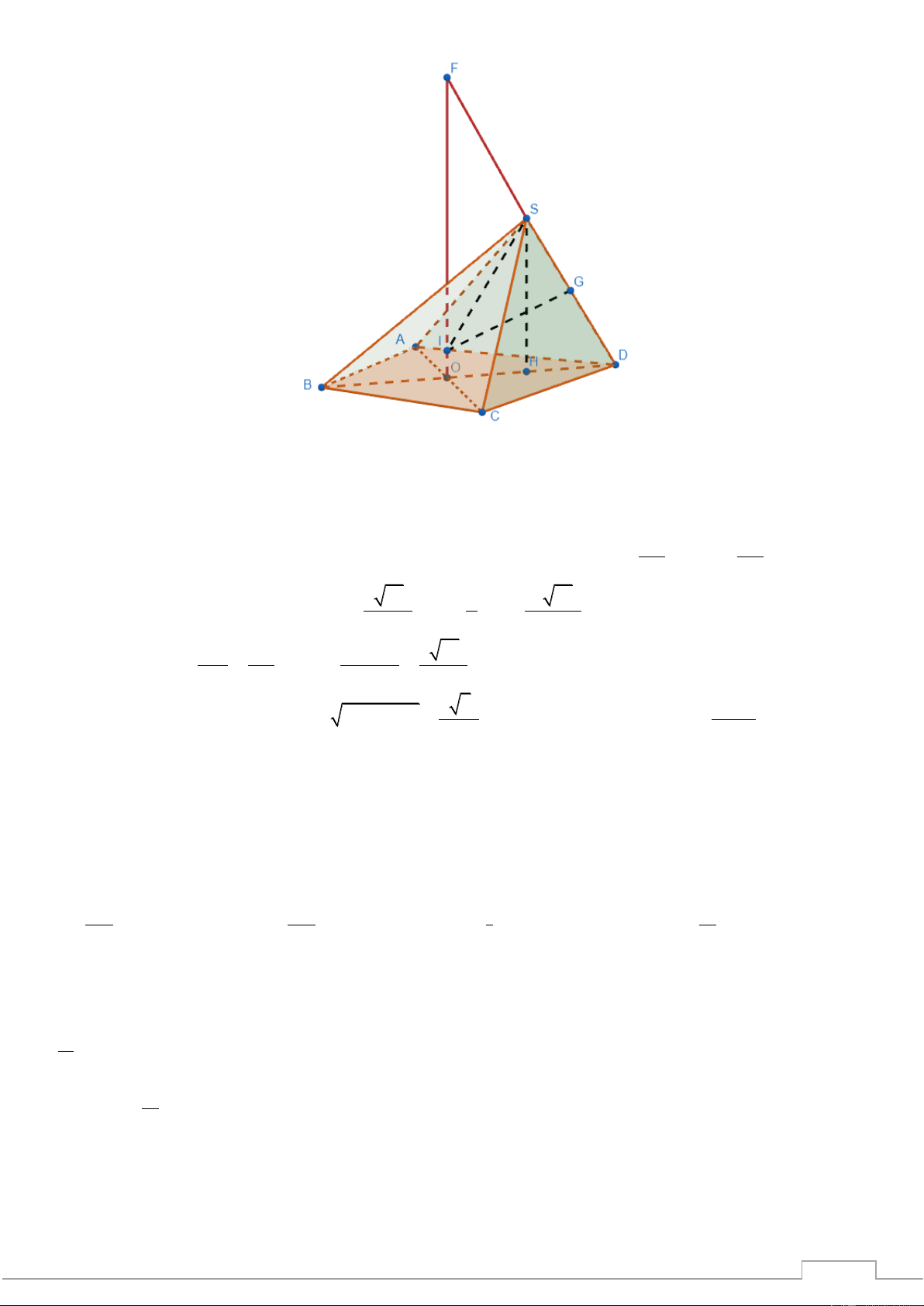
Câu 31. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Hai mặt phẳng (SAB) và (SAC)
cùngvuông góc với mặt phẳng (ABCD). Biết rằng AB = ;
a AD = a 3 và SC = 7a . Tính thể tích khối chóp S.ABCD. A. 3 3a . B. 3 a . C. 3 2a . D. 3 4a .
Câu 32. Cho hình lăng trụ tam giác đều AB . C A B
C có tất cả các canh bằng nhau. Đặt
((CAB);(BCC B)) = giá trị tan bằng A. 6 . B. 2 . C. 6 . D. 2 3 . 2 3 TSP −1 Câu 33. Cho = x I (
x , bằng cách đặt 2
t = x − 2x +3 ta đưa nguyên hàm đã cho về x − 2x + 3) d 2021 2 dạng - 1 1 1 1 A. I = d t . B. I = d t . C. I = d t . D. I = d t . 2021 2021 202 (t +3)2021 t 2t 2(t + 3)2021
Câu 34. Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a , SA = a 3 , đường thẳng SA v
ABCD . Góc giữa đường thẳng SD và mặt phẳng (SA ) B là 1uông góc với mặt phẳng ( ) A. o 30 . B. o 90 . C. o 60 . D. o 45 .
Câu 35. Tập nghiệm của bất phương trình 2
log x − 2log x + 3 0 là 3 3 A. (3; 27) .
B. (−;3) (27; +). C. (0;3) (27; +) . D. 3; 27 .
Câu 36. Họ tất cả các nguyên hàm của hàm số f (x) = 4x + sin x là
GV: Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 5 A. 2
2x − cos x +C . B. 2
x − cos x + C . C. 2
2x + cos x + C . x + x + D. 2 cos C .
Câu 37. Xét các số thực ,
a b thỏa mãn log (2 .a8b ) = log 2. Mệnh đề nào là đúng? 2 2
A. 4ab = 1.
B. 2a + 8b = 2 .
C. 2a + 6b = 1.
D. a + 3b = 2 . TS mln x + 4
Câu 38. Tập hợp tất cả các giá trị thực của tham số m để hàm số y = nghịch biến trên ln x + m
khoảng (0; e) là (a; b . Khi đó a + bbằng P A. 3 − . B. −1. C. −2 . D. 0 . 3 x −6x−4 -
Câu 39. Biết rằng phương trình 2 3 2 4 −3 .2 x x x
− 24x = 32 có nghiệm là 202 3 3
x = a − b − c,( , a ,
b c ) . Khi đó giá trị của 2abc gần với giá trị nào nhất trong các giá trị sau A. 28 . B. 24 . C. 55 . D. 50 .
Câu 40. Một người lần đầu gửi vào ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi suất 2% 1 một
quý theo hình thức lãi kép. Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng với kỳ hạn và lãi
suất như trước đó. Tổng số tiền người đó nhận được 1 năm sau khi gửi tiền gần nhất với kết quả
nào sau đây biết rằng trong suốt thời gian gửi tiền lãi suất ngân hàng không thay đổi và người đó không rút tiền ra.
A. 210 triệu đồng.
B. 212 triệu đồng.
C. 220 triệu đồng.
D. 216 triệu đồng.
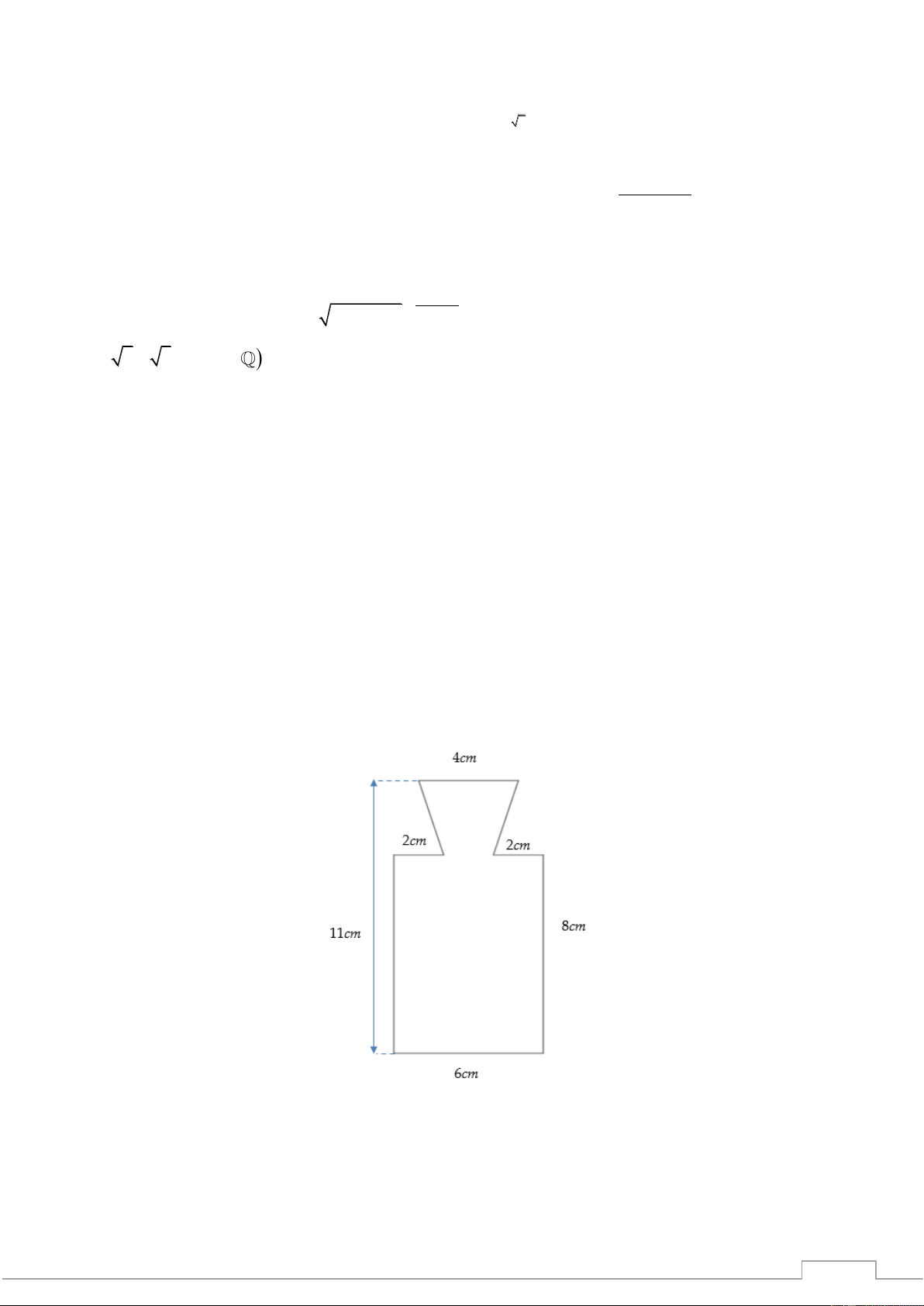
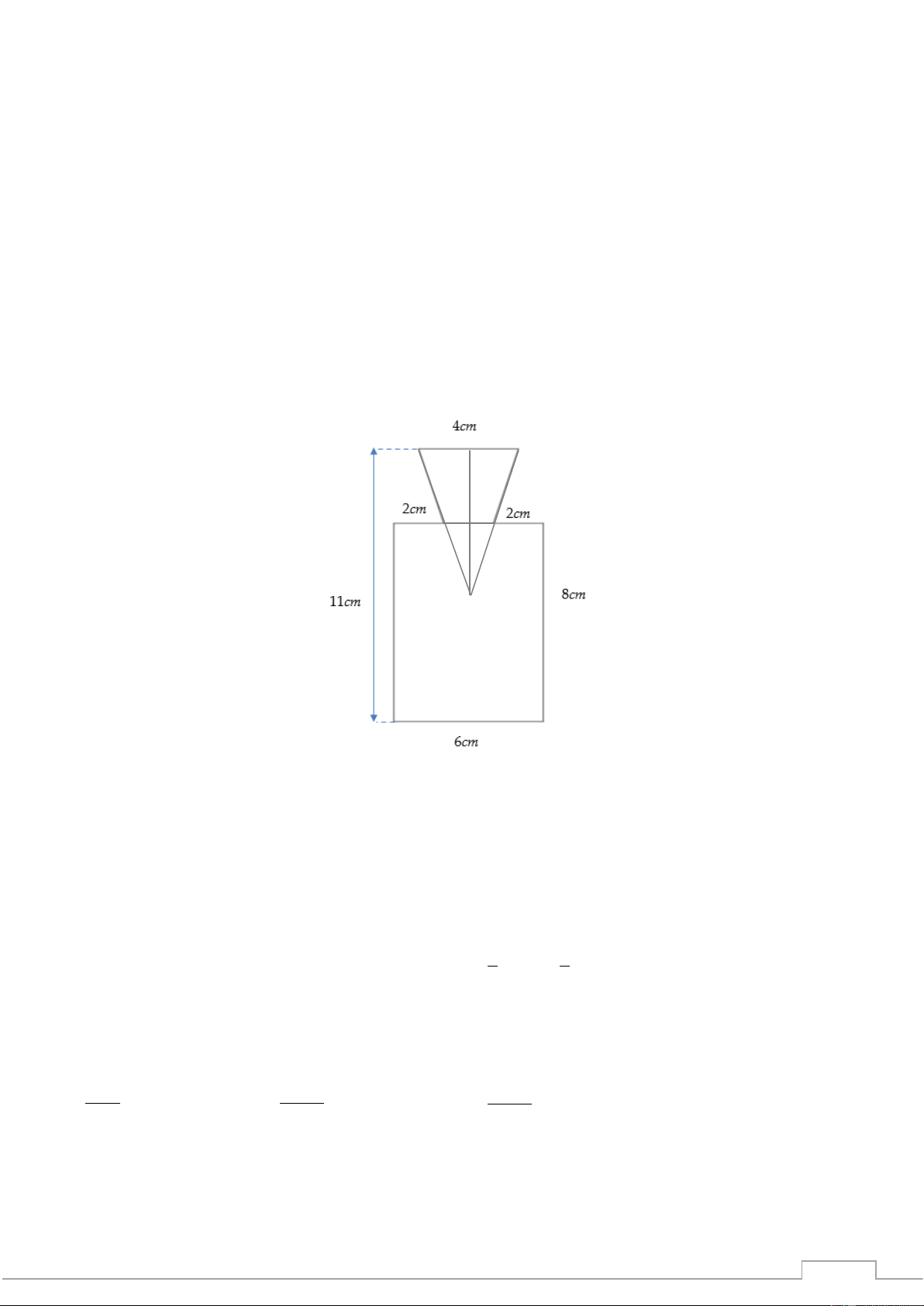
Câu 41. Một thiết bị kỹ thuật là một khối tròn xoay. Mặt cắt của khối tròn xoay đó qua trục của nó
được mô tả trong hình bên. Thể tích của thiết bị đó bằng TSP -202 1 A. 3 80cm . B. 3 312cm . C. 3 316cm . D. 3 79cm .
Câu 42. Cho hình chóp .
S ABCD có ABCD là hình chữ nhật tâm I cạnh AB = 3a, BC = 4a . Hình
chiếu của S trên mặt phẳng ( ABCD) là trung điểm ID . Biết rằng SB tạo với mặt phẳng (ABCD) một góc o
45 . Tính diện tích khối cầu ngoại tiếp khối chóp . S ABCD.
GV: Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 6 25 125 125 A. 2 a . B. 2 a . C. 2 a . D. 2 4 a . 2 4 2
Câu 43. Trong cuộc gặp mặt dặn dò trước khi lên đường tham gia kì thi HSG có 10 bạn tro TSng đội
tuyển gồm 2 bạn đến từ lớp 12A1, 3 bạn từ 12A2, 5 bạn còn lại đến từ các lớp khác nhau.Thầy giáo
xếp ngẫu nhiên các bạn kể trên ngồi vào một bàn dài mà mỗi bên có 5 ghế xếp đối diện nhau P.Tính
xác suất sao cho không có học sinh nào cùng lớp ngồi đối diện nhau. A. 73 . B. 53 . C. 5 . D. 38 . 126 126 9 63 -202 3
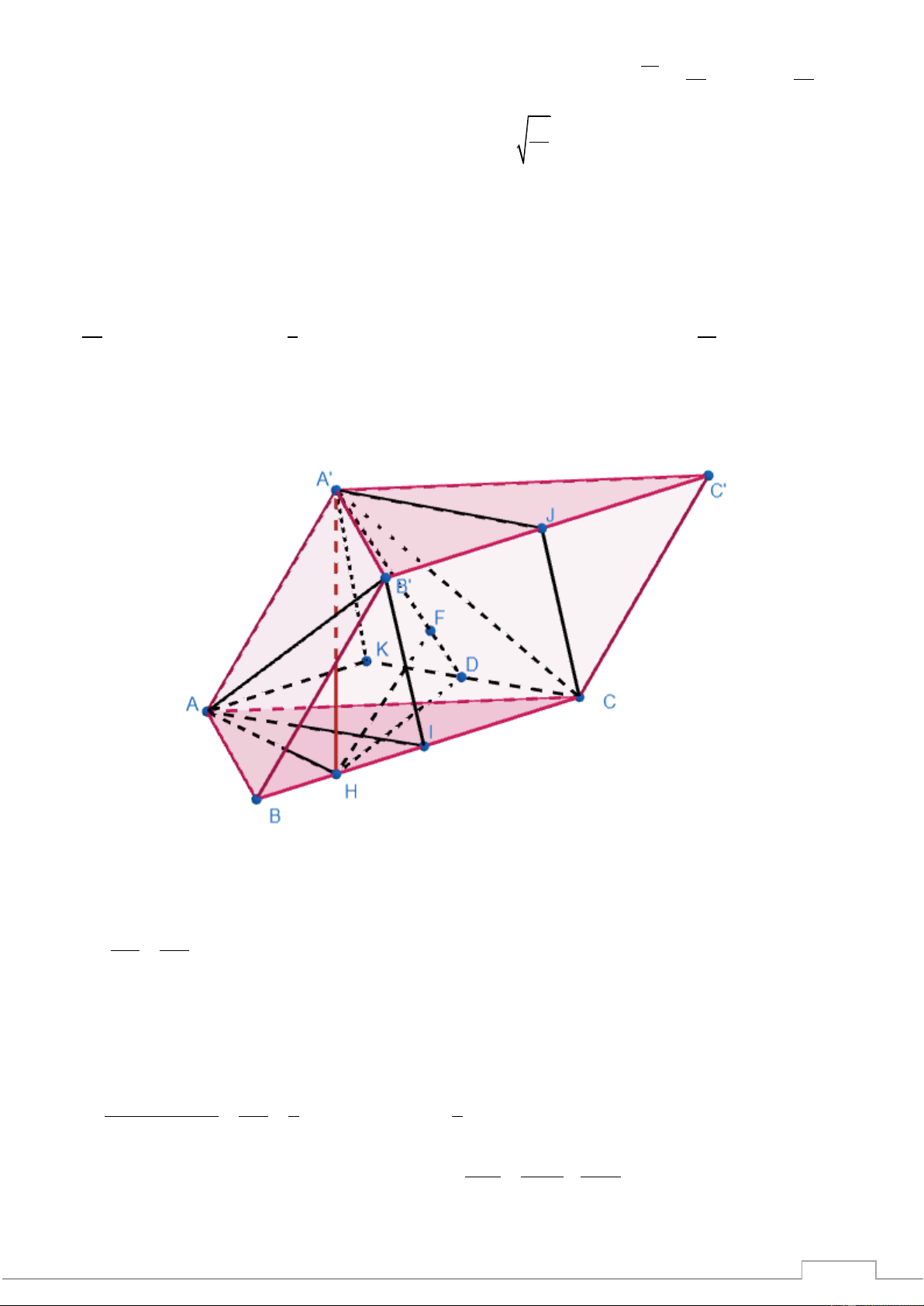
Câu 44. Cho hình lăng trụ AB . C A B C có chiều cao là 9
a . Biết rằng tam giác A BC là tam giác 35
nhọn và nằm trong mặt phẳng vuông góc với mặt đáy. Hai mặt phẳng ( AB B A );( ACC A ) 1cùng
tạo với đáy một góc bằng nhau. Góc o
BAC = 60 , AC = 3AB = 3 .
a Khoảng cách giữa hai đường thẳng AB và A C bằng 2a a 3a A. . B. . C. a . D. . 3 3 2
Câu 45. Cho hàm số f ( )
x có bảng biến thiên như sau: TSP
Có bao giá trị của tham số m để phương trình 3 f (sin x) + m = 0 có lẻ nghiệm trên đoạn − ;2 A. 4 . B. 2 . C. 1 . D. 3 . a
Câu 46. Cho các số thực a b 0 thỏa mãn 3log a = log b = log 7a − 6b . Giá trị bằng 50 2 5 ( ) b -202 A. 22 . B. 12 + 6 3 . C. 24 + 6 15 . D. 36 .
Câu 47. Cho hình chóp SABC có thể tích là V, gọi M, H, I theo thứ tự là trung điểm BC, AM
SA SB SC tại các điểm A ,
B ,C . Thể tích của khối 1,SH
một mặt phẳng qua I cắt các cạnh , ,
SA B C có giá trị lớn nhất là chóp V V V 27V A. . B. . C. . D. . 5 3 2 256 f (x)
Câu 48. Cho hàm số ( ) = ( − ) 1 x F x x
e là một nguyên hàm của hàm số
, họ tất cả các nguyên x e f (x) hàm của hàm số là 2x e
GV: Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 7 2 x 2 x A. x + x e + C B. x + + C . C. 2
x + x + C . D. ( 2 + ) x x x e + C 2 2
Câu 49. Cho các số thực dương , x , y z khi biểu thức TS xy yz zx 2 P = ( 2 2 2
log 10x + 7y +15z ) − 2log + +
+ 2(x + y + z) − 2log(xyz) đạt giá trị nhỏ nhất thì giá z x y
trị xyz gần với giá trị nào nhất trong các giá trị sau P A. 4 . B. 7 . C. 5 . D. 6 . -202
Câu 50. Cho hàm số y = f (x) là hàm số đa thức bậc bốn và có bảng biến thiên như sau: 1 1 − 3 2
Số điểm cực trị của hàm số ( ) x
g x = e ( f (x + ) 1 ) là A. 7 . B. 6 . C. 5 . D. 4 . TSP - 202 1
GV: Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 8 BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C C B A C C B B A B C A C C C B B D D B A D A A A
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 TS
C B D A D B A C A C A D A C B D B D A C C B C D D
LỜI GIẢI CÁC CÂU VẬN DỤNG-VẬN DỤNG CAO P m ln x + 4
Câu 38. Tập hợp tất cả các giá trị thực của tham số m để hàm số y = nghịch biến trên ln x + m -
khoảng (0;e) là (a;b . Khi đó a +b bằng 202 A. 3 − . B. −1. C. −2 . D. 0 . Lời giải Chọn A. Điều kiện ln 0 0 − + m x m x e 2 1 m − 4 1 Ta có y = . . 2 x + x (ln m)
Hàm số biến trên khoảng (0;e) y 0,x (0,e) 2 m −4 0 2 − m 2
− m − . − e m ( e) 2 1 0; − m e e 3 x −6x−4
Câu 39. Biết rằng phương trình 2 3 2 4 −3 .2 x x x
− 24x = 32 có nghiệm là 3 3
x = a − b − c,( , a ,
b c ) . Khi đó giá trị của 2abc gần với giá trị nào nhất trong các giá trị sau A. 28 . B. 24 . C. 55 . D. 50 . TSP Lời giải Chọn C. 3 Điều kiện x . 4 3 x −6x−4 24x 1 + 6 4x− 12 3x − 4 3x − 4 Phương trình 2 4x − 3.2 x = 8 4x − 3.( 4 2) 2 x = (4 2) x x - 2 9x +24x 16 + 3x−4 202 x− x− x − x − 4x − 3.( 3 4 3 4 4 2 )4 3 = (4 2) 4 3 2 x 4x − 3.( 4 2) = ( 4 2 ) 2 x x x t
Dễ thấy f (t) = t ( ) 2 4 . 2
đồng biến trên (0; +) nên phương trình trở thành 3x + 4 3 2 1 4x − 3 =
4x −12x − 24x −16 = 0 x 3 3 2 3
2x − 6x −12x −8 = 0 3x = (x + 2) 3 x 3 = x + 2 2 3 3 3 3 x = =1+ 3 + 9 =1− 3 − − 9 − 2abc = 54 . 3 3 −1
Câu 40. Một người lần đầu gửi vào ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi suất 2% một
quý theo hình thức lãi kép. Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng với kỳ hạn và lãi
GV: Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 9
suất như trước đó. Tổng số tiền người đó nhận được 1 năm sau khi gửi tiền gần nhất với kết quả
nào sau đây biết rằng trong suốt thời gian gửi tiền lãi suất ngân hàng không thay đổi và ngư TSời đó không rút tiền ra.
A. 210 triệu đồng.
B. 212 triệu đồng.
C. 220 triệu đồng.
D. 216 triệu đồng. Lời giải Chọn B. P
Sử dụng công thức tính lãi kép ta có số tiến sau 6 tháng là A = ( + )2 100.000.000 1 2% -
Số tiến sau 1 năm tháng là B = ( A + )( + )2 100.000.000 1 2% 212 triệu. 202
Câu 41. Một thiết bị kỹ thuật là một khối tròn xoay. Mặt cắt của khối tròn xoay đó qua trục của nó
được mô tả trong hình bên. Thể tích của thiết bị đó bằng 1 TSP A. 3 80cm . B. 3 312cm . C. 3 316cm . D. 3 79cm . Lời giải Chọn D.
Ta thấy khối tròn xoay là hợp thành của khối tru có bán kính bằng 3cm, chiều cao bằng 8cm vớ-202i
khối nón bán kính bằng 2cmchiều cao bằng 6cm. Phần chung của khối nón và khối trụ cũng là một
khối nón bán kính bằng 1cm chiều cao bằng 3cm. 1 1
Thay vào công thức tính thể tích ta được 2 2 2 3 V = 8 3 . + 3 2 . − 3 . 1 . = 79 (cm ) 3 3
Câu 42. Cho hình chóp .
S ABCD có ABCD là hình chữ nhật tâm I cạnh AB = 3a, BC = 4a . Hình
ABCD là trung điểm ID . Biết rằng SB tạo với mặt phẳng ( AB 1
chiếu của S trên mặt phẳng ( ) CD) một góc o
45 . Tính diện tích khối cầu ngoại tiếp khối chóp . S ABCD. 25 125 125 A. 2 a . B. 2 a . C. 2 a . D. 2 4 a . 2 4 2 Lời giải Chọn B.
GV: Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 10 TS P -202 1
Gọi O là giao điểm của 2 đường chéo AC và BD suy ra O chính là tâm đường tròn ngoại tiếp h ình
chữ nhật ABCD. Ké đường thẳng d qua O vuông góc với (ABCD) do d // SH nên d cắt SD tại F và
S là trung điểm DF. Mặt phẳng trung trực của SD cắt d tại I khi đó I chính là tâm mặt cầu ngoai
tiếp chóp SABCD. Gọi G là trung điểm SD ta có IG vuông góc SD. 15a 15a Giả thiết suy ra o
SBH = 45 SBH vuông cân tại B suy ra SH = BH = FO = . 4 2 5 10a 3 15 10a
Dùng đinh lý Pitago tính được FD = ; FG = FD = 2 4 8 OD IG O . D FG 5 10a Ta có tanOFD = = IG = = OF FG OF 8 5 5 125
Bán kính của mặt cầu là 2 2 = = + = a R SI IG GS
do đó diện tích mặt cầu bằng 2 a . 4 4
Câu 43. Trong cuộc gặp mặt dặn dò trước khi lên đường tham gia kì thi HSG có 10 bạn tro TSPng đội
tuyển gồm 2 bạn đến từ lớp 12A1, 3 bạn từ 12A2, 5 bạn còn lại đến từ các lớp khác nhau.Thầy giáo
xếp ngẫu nhiên các bạn kể trên ngồi vào một bàn dài mà mỗi bên có 5 ghế xếp đối diện nhau -.Tính
xác suất sao cho không có học sinh nào cùng lớp ngồi đối diện nhau. A. 73 . B. 53 . C. 5 . D. 38 . 202 126 126 9 63 Lời giải: Chọn D
Ta có không gian mẫu là n () = 10! 1
Gọi A là biến cố “ không có học sinh nào cùng lớp ngồi đối diện nhau”
A là biến cố “ có học sinh cùng lớp ngồi đối diện nhau”
A là biến cố “ học sinh A ngồi đối diện nhau”; A là biến cố “ học sinh A ngồi đối diện nhau”. 1 1 2 1 Khi đó n(
A ) = n( A + n A − n A A . 1 ) ( 2) ( 1 2 )
Xét biến cố A : Trước hết chon 1 trong 5 cặp ghế để xếp 2 hs A ngồi, đổi chỗ 2 bạn này có 2! 1 1
cách, 8 người còn lại có 8!. Theo quy tắc nhân có n ( A ) 1 = C .2!.8! 1 5
GV: Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 11 25 38
Tương tự n ( A ) 1 2
= C .A .8!; n( A A = A .2!.A .6! thay vào ta được P( A ) = P( A) = . 1 2 ) 2 2 2 5 5 3 3 63 63 3
Câu 44. Cho hình lăng trụ AB . C A B C có chiều cao là 9
a . Biết rằng tam giác A BC là tam giác 35 TS
nhọn và nằm trong mặt phẳng vuông góc với mặt đáy. Hai mặt phẳng ( AB B
A ) ,( ACC A ) BAC = , AC = AB = .
a Khoảng cách giữa hai Pcùng
tạo với đáy một góc bằng nhau. Góc o 60 3 3 -đường thẳng AB và A C bằng 2a a 3a 202 A. . B. . C. a . D. . 3 3 2 Lời giải: Chọn A 1 TSP Do tam giác A BC nhọn và (
A BC) ⊥ ( ABC) nên kẻ AH ⊥ BC AH ⊥ ( ABC) và H nằm trong AB B A ; ACC
A cùng tạo với đáy một góc bằng nhau nên H cách đ -đoạn
BC. Do hai mặt phẳng ( ) ( ) 202ều
AB và AC do đó H là chân đường phân giác trong của góc BAC . Theo tính chất đường phân giác BH AB ta có = CH = 3BH . CH AC
Gọi I, J là các trung điểm của BC,
B C suy ra ( A B I ) // (C A J ) do đó d(A
B , A'C) = d( A B I ),(C
A J)) = d(I,(C A J )) . 1
Kẻ KC = //AI KC//
A J khi đó d(I,(C
A J)) = d(I,(CK A J)) .
d (I,(CK A J )) IC 2 2 Ta có . d ( =
= d(I, CK
A J ) = d(H, CK A J ) H,(CK A J )) ( ) ( HC 3 3 1 1 1
Kẻ HD ⊥ KC, HF ⊥
A D d(H,(CK A J)) = HF và = + . 2 2 2 HF H A HD
GV: Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 12 Ta có 2 2 2 2 AB + AC BC 13a 13 2 2 2 2
BC = AB + AC − 2A .
B AC cos A = 7a BC = a 7 , 2 AI = − = AI = a . 2 4 4 2 2 2 2
AI + IC − AC 8
Xét tam giác AIC có: cos AIC = = −
. Do AICK là hình bình hành nên TS 2AI.IC 91 8 3 9 3 cos ICK = sin ICK =3
HD = HC.sin HCD = a thay vào được 91 91 4 13 P 1 1 1 1 = + =
= d(I,(CK A J )) 2 = a . 2 2 2 2 HF a HF HA HD a 3 - 202
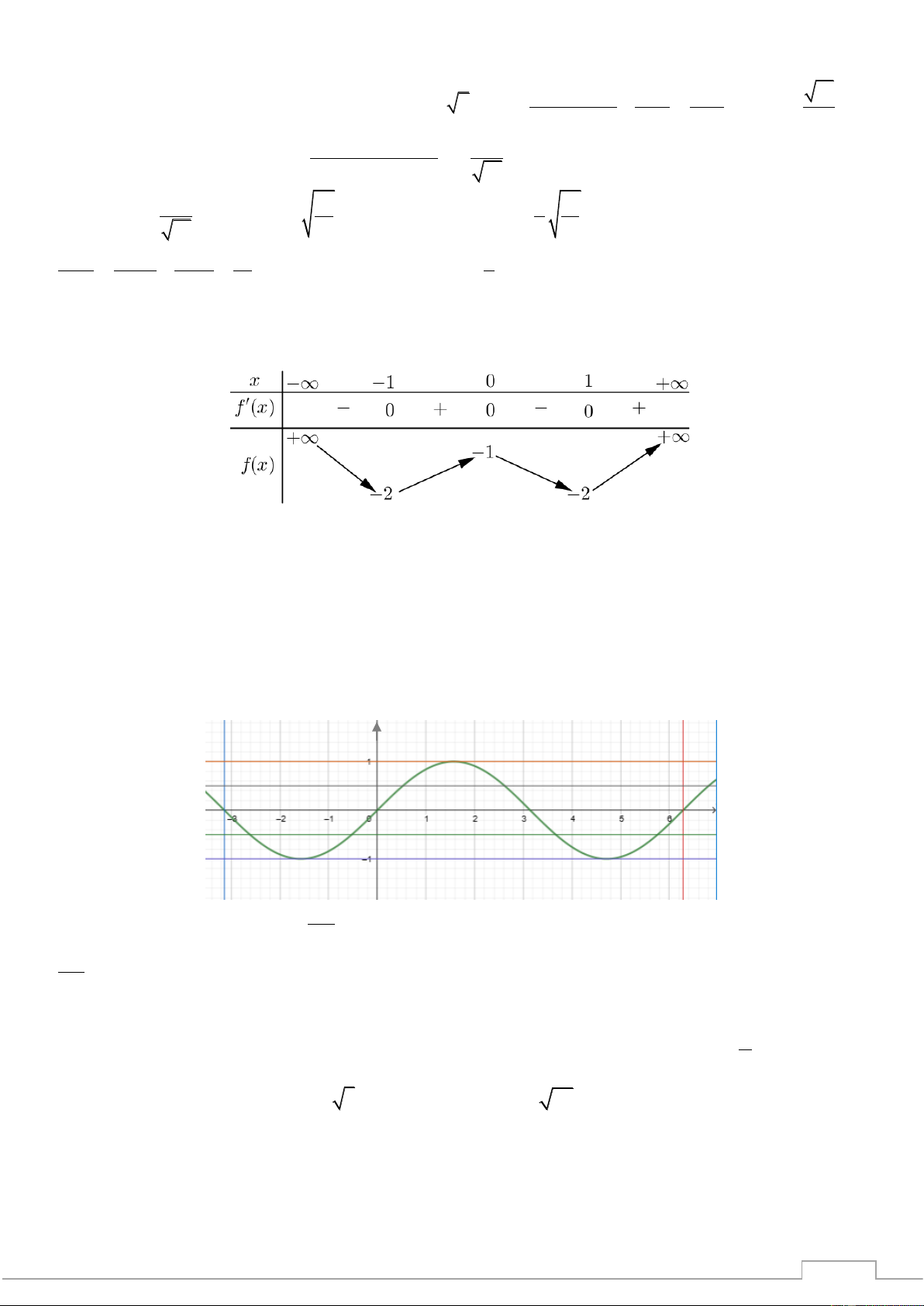
Câu 45. Cho hàm số f (x) có bảng biến thiên như sau: 1
Có bao giá trị của tham số m để phương trình 3 f (sin x) + m = 0 có lẻ nghiệm trên đoạn − ;2 . A. 4 . B. 2 . C. 1 . D. 3 . Lời giải Chọn C.
Đặt t = sin x, 1
− t 1. Xét đồ thị y = sin x trên đoạn
− ;2 (có thể dùng bảng biến thiên) TSP - −
Phương trình trở thành ( ) = m f t
(*) dựa vào bảng biến thiên của hàm f (x) ta thấy chỉ có 202 3 −m = 2
− phương trình (*) có nghiệm t = 1
suy ra phương trình đã cho có 3 nghiệm. Các trường họp 3
còn lại phương trình có chẵn nghiệm hoặc vô nghiệm. Vậy m = 6 là giá trị thỏa mãn. 1
Câu 46. Cho các số thực a b 0 thỏa mãn 3log a = log b = log 7a − 6b . Giá trị a bằng 50 2 5 ( ) b A. 22 . B. 12 + 6 3 . C. 24 + 6 15 . D. 36 . Lời giải Chọn C.
x = 50t, y = 8t
Đặt 3log x = log y = log 7x − 6y = 3t suy ra 50 2 5 ( )
7x − 6y =125 t
GV: Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 13 t t t t t t 25 125 5 7.50 − 6.8 = 125 7. − 6 = .
Đặt u = ta được 4 8 2 u =1(l) t t x 50 25 3 2
u − 7u + 6 = 0 u = 3 − 15 (l) . Do 2 = = = u = 24 + 6 15 . TS y 8 4 u = 3 + 15(t ) m
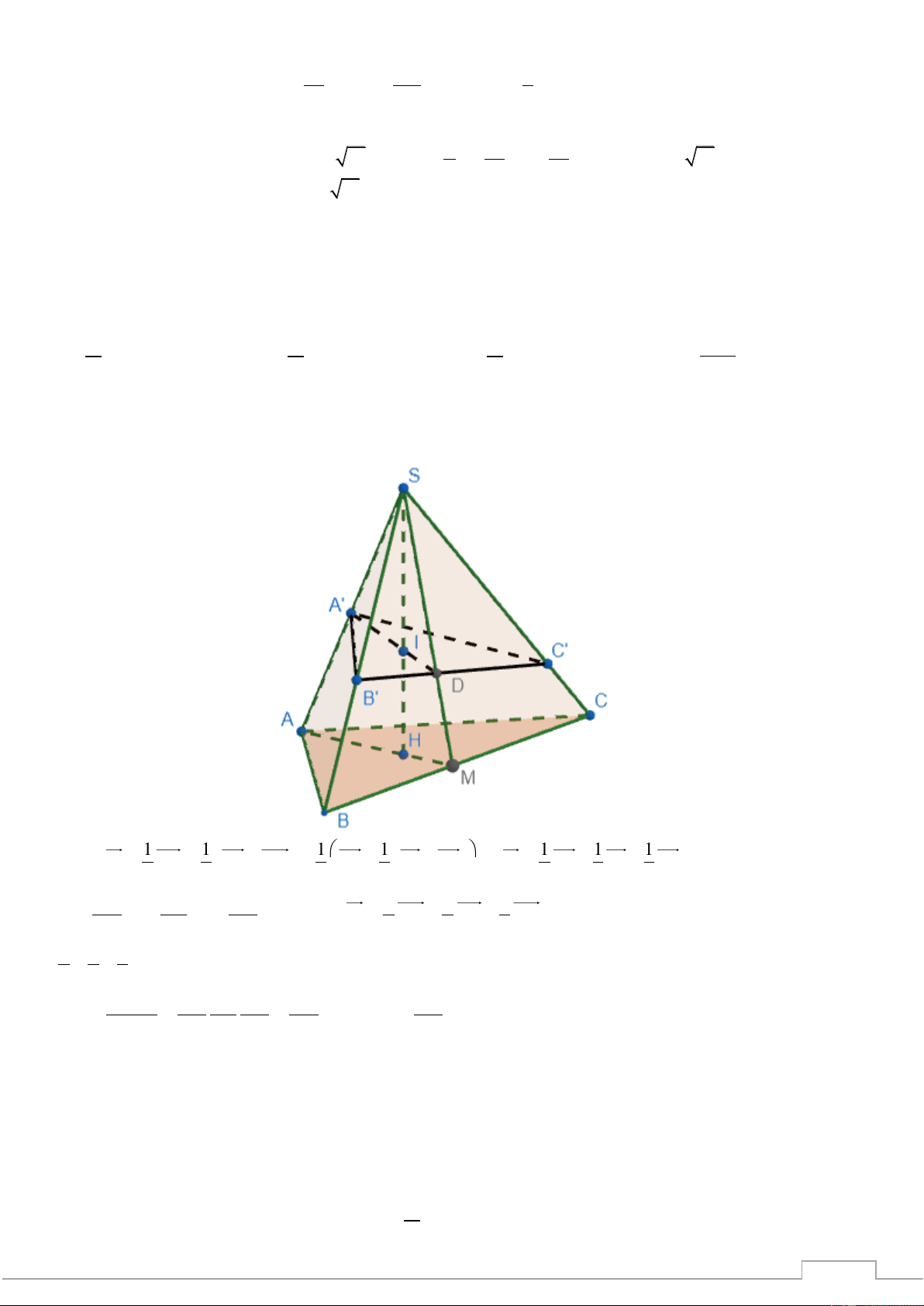
Câu 47. Cho hình chóp SABC có thể tích là V, gọi M , H , I theo thứ tự là trung điểm BC, A P
SA SB SC tại các điểm A ,
B ,C . Thể tích của khối -M,SH
một mặt phẳng qua I cắt các cạnh , ,
SA B C có giá trị lớn nhất là 202chóp V V V 27V A. . B. . C. . D. . 5 3 2 256 Lời giải Chọn B. 1 TSP 1 1 1 1 1 1 1
Ta có SI = SH = (SA + SM) =
SA + (SB + SC) SI = SA + SB + SC 2 4 4 2 4 8 8 - SA SB SC x y z Đặt = , x = , y
= z suy ra SI = S A + S
B + SC do bốn điểm I, A , B , C đồng ph 202ẳng nên S A S B SC 4 8 8
x + y + z =1 2x+ y + z = 8. 4 8 8 V SA SB SC V SA B C 1 Ta có = = V = . SA B C V SA SB SC xyz xyz SABC 1
2x + y + z = 8
Bài toán trở thành tìm giá thị nhỏ nhất của P = xyz với giải thiết .
x, y, z 1
Ta có 2x + y + z = 8 8 2x + 2 1 x 3 . Lại có ( y − ) 1 (z − )
1 0 yz y + z −1 = 7 − 2x 0 thay vào ta được
P = xyz x( − x) 2 7 2 = 2
− x + 7x = f (x) lập bảng biến thiên của f (x) trên 1;3 ta được V
f (x) 3 do đó giá trị lớn nhất của V là . SA B C 3
GV: Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 14 f (x)
Câu 48. Cho hàm số ( ) = ( − ) 1 x F x x
e là một nguyên hàm của hàm số
, họ tất cả các nguyên x e f (x) hàm của hàm số là 2x e 2 TS x 2 x A. x + x e + C B. x + + C . C. 2
x + x + C . D. ( 2 + ) x x x e + C 2 2 Lời giải P Chọn C. - 1 2 − x 202 f (x) u = u e x f (x) x d = 2 − d Xét d x đặt 2 e . Suy ra 2 d − x = x e f x e f x x x ( ) 2 + 2 − x d 2 ( ) 2x e v = f x e dv = f (x) x ( ) d f (x) x 1
Do hàm số F (x) = (x − )
1 e là một nguyên hàm của hàm số nên x e ( f x f x f (x) x − ) x e ) ( ) x ( ) = xe = f (x) 2 1 ' = x
xe thay lại ta được 2 dx = x + 2 d
x x = x + x + C . x x x e e 2 e
Câu 49. Cho các số thực dương x, y, z khi biểu thức xy yz zx 2 P = ( 2 2 2
log 10x + 7y +15z ) − 2log + +
+ 2(x + y + z) − 2log(xyz) đạt giá trị nhỏ nhất thì giá z x y
trị xyz gần với giá trị nào nhất trong các giá trị sau A. 4 . B. 7 . C. 5 . D. 6 . TSP Lời giải Chọn D. Viết lại 2 P = ( 2 2 2 x + y + z ) − ( 2 2 2 2 2 2 log 10 7 15
2 log x y + y z + z x + 2xyz (x + y + z)) 2 2 = ( 2 2 2 x + y + z ) −
(xy + yz + zx) 2 = ( 2 2 2 log 10 7 15 2 log
log 10x + 7y +15z ) − 4log (xy + yz + z 2 2 2
10x + 7y +15z m xy + yz + zx để đưa P về về một biến ta biến đổi như sau: - 2 2 2
20x +14 y + 30z 2m ( xy + yz + zx) 202x) Ta cần chỉ ra ( ) (20 + m) 2 x + (14 + m) 2 y + (30 + m) 2 z m ( 2 2 2
x + y + z + 2xy + yz + zx) x y z
(x + y + z)2 2 2 2 + + 1 1 1 1 1 20 + m 14 + m 30 + m m
Mặt khác theo bất đẳng thức SCHWARZ x y z
(x + y + z)2 2 2 2 Ta có + + 1 1 1 1 1 1 + + 20 + m 14 + m 30 + m 20 + m 14 + m 30 + m Đến đây ta 1 1 1 1
chỉ việc chọn m thỏa mãn + + =
giải ra ta chọn được m = 10 . 20 + m 14 + m 30 + m m
GV: Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 15 x y z Vậy ta được 2 2 2
10x + 7y +15z 10(xy + yz + zx) dấu bằng xảy ra khi = =
15x =12y = 20z 1 1 1 30 24 40
Ngoài ra ta cũng có thể dùng phương pháp cân bằng hệ số trong bất đẳng thức CAUCHY để chứng mi 25 2 2 x + y TSnh 4 10xy 4 15 20 2 2 x +
z 10xz cộng các vế ta được 2 2 2
10x + 7y +15z 10(xy + yz + zx) . 4 3 P 25 2 2 3y + z 10yz 3 - Từ đó ta có P
( (xy+yz+zx))−
(xy+ yz+zx) = ( (xy+ yz+zx)− )2 2 log 10 4log log 1 0 202 5 3 y = ; x z = x 15 600 10 Dấu bằng xảy ra 3 4 4 xyz = x = . 16 47 47
xy + yz + zx =10 1
Câu 50. Cho hàm số y = f (x) là hàm số đa thức bậc bốn và có bảng biến thiên như sau: 1 − 3 2
Số điểm cực trị của hàm số ( ) x
g x = e ( f (x + ) 1 ) là A. 7 . B. 6 . C. 5 . D. 4 . TSP Lời giải Chọn D. − f x + 1 = 0 1 2 ( ( ))2 1 ( ) 2 g(x) 2 x
= e ( f (x + 1))
f x + 1 + 3 f x + 1 = 0 3 ( ) ( ) 2 x -
f x + 1 + 3 f x + 1 = 0 2 3 ( ) ( ) ( ) x 202 Ta thấy ( )
1 các nghiệm của 1 là nghiệm bỗi chẵn nên qua đó g(x) không đổi dấu. 2 2
Xét phương trình (2) :
f x + 1 + 3 f x + 1 = 0 đặt t = x +1 ta đươc
f t + 3 f t = 0 3 ( ) ( ) 3 ( ) ( ) x (t − )1 1 2 f (t)
Do f (t) , f (t) không đồng thời bằng không nên + 3 = 0 * 3 −1 f (t t ) ( ) ( )
Dựa vào bảng biến thiên ta có f (t) = a(t − t t − t t − t t − t 1 ) ( 2 ) ( 3 ) ( 4 ) 2 3 3 3 3
Tính đạo hàm rồi thay vào ta được phương trình trở thành (* ) + + + + = ( ) 0 3 1 − − − − − t t t t t t t t t 1 2 3 4
GV: Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 16 2 3 3 3 3
Xét hàm số h (t) = + + + + ( ) 3 1 t − t t − t t − t t − − t t 1 2 3 4 6 − 3 − 3 − 3 − 3 − h (t) = + + + + ( . t − )4 1
(t −t )2 (t −t )2 (t −t )2 (t −t )2 1 2 3 4 TS
Ta có bảng biến thiên của h (t)
t − t t t 1 t + 1 2 3 4 P -
h '(t) − − − − − − 202 + + + + + h (t) 0 0
− − − − − 1
Từ bảng biến thiên ta thấy phương trình h (t) = 0 luôn có 4 nghiêm đơn phân biệt do đó hàm số
g (x) có 4 điểm cực trị.
==========THE END========= TSP -202 1
GV: Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 17