Đề thi thử Toán tốt nghiệp THPT 2022 lần 1 trường chuyên Biên Hòa – Hà Nam

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi thử môn Toán tốt nghiệp THPT năm học 2021 – 2022 lần 1 trường THPT chuyên Biên Hòa, tỉnh Hà Nam

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

25 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Nghiệm của phương trình là
log 4 6 1x
A. . B. . C. . D. .
9
2
x
7
4
x
4x
5x
Lời giải
Chọn C
Ta có: .
log 4 6 1 4 6 10 4x x x
Câu 2: Trong không gian cho mặt cầu . Tâm của có tọa
Oxyz
2 2 2
: ( 1) ( 2) ( 3) 4S x y z
độ là
A. . B. . C. . D. .
1; 2; 3
1; 2;3
1;2;3
1; 2; 3
Lời giải
Chọn C
Tâm của có tọa độ là .
1; 2; 3I
Câu 3: Mô đun của số phức bằng
3 2z i= -
A. . B. . C. . D. .
5
13
5
13
Lời giải
Chọn B
Ta có .
2
2
3 2 13z
Câu 4: Tìm nguyên hàm của hàm số
cos 3f x x
A. . B. .
cos3 d sin3x x x C
sin 3
cos 3 d
3
x
x x C
C. . D. .
sin 3
cos3 d
3
x
x x C
cos3 d 3sinx x x C
Lời giải
Chọn B
Ta có .
sin 3
cos 3 d
3
x
x x C
Câu 5: Cho hình chóp có , tam giác vuông tại có ,
.S ABC
( ), 3SA ABC SA a
A B C
B
2AC a
. Góc giữa đường thẳng và mặt phằng bằng
B C a
SB
( )ABC
A
C
B
S
A. . B. . C. . D. .
45
90
30
60
Lời giải
Chọn D
Vì
,
( )
SB ABC B
SB ABC SBA
SA ABC
Xét tam giác vuông tại có:
A B C
B
2 2 2 2
2AB AC BC a a a
Xét tam giác vuông tại có .
SBA
A
3
tan 3 60
SA a
SBA SBA
AB a
Vậy .
60,SB ABC SBA
Câu 6: Cho điểm phân biệt trên mặt phẳng. Hỏi có bao nhiêu véc-tơ mà điểm đầu và điểm cuối là
6
điểm đã cho
6
?
A. . B. . C. . D. .
30
15
2 1
36
Lời giải
ChọnA.
Số vectơ có điểm đầu và điểm cuối tạo từ điểm đã cho là .
6
2
6
A 30
Câu 7: Tập xác định của hàm số
D
5
9
2 ln 2y x x
A. . B. .
2; 2D
; 2 2;D
C. . D. .
2; 2D
( ; 2] [2; )
Lời giải
Chọn C
Tập xác định của hàm số là .
D
5
9
2 ln 2y x x
2; 2D
Câu 8: Cho mặt cầu có diện tích bằng . Khi đó, bán kính mặt cầu bằng
2
16 a
A. . B. . C. . D. .
2a
2
2
a
2 2a
2 a
Lời giải
Chọn D
Có .
2 2
4 16 2R a R a
Câu 9: Cho số phức thỏa mãn . Tính tích phần thực và phần ảo của
z
1 3z z i
z
A. . B. .
7
12
C. . D. .
7
12
Lời giải
Chọn B
Gọi .
z x yi
,x y
.
2 2
2 2
4
1
1 3 1 3 . 3.4 12
3
3
x
x y x
z z i x y x yi i x y
y
y
Câu 10: Diện tích xung quanh của hình nón có độ dài đường sinh và bán kính đáy bằng
l
r
A. . B. .
1
3
rl
4 r l
C. . D. .
rl
2 r l
Lời giải
Chọn C
Diện tích xung quanh của hình nón có độ dài đường sinh và bán kính đáy bằng .
l
r
rl
Câu 11: Cho hai số phức và . Số phức bằng
1
3 2z i
2
3z i
1 2
z z
A. . B. . C. . D. .
6 i
6 i
i
6 3i
Lời giải
Chọn B
Ta có
1 2
3 2 3 6z z i i i
Câu 12: Cho là một số thực dương, biểu thức viết dưới dạng lũy thừa với số mũ hữu tỷ là
a
2
3
a a
A. . B. . C. . D. .
6
7
a
7
6
a
4
3
a
5
6
a
Lời giải
Chọn B
Ta có
2 2 7
1
3 3 6
2
.a a a a a
Câu 13: Cho hàm số liên tục trên và . Giá trị của tích phân bằng
f x
6
0
d 9f x x
2
0
3 df x x
A. . B. . C. . D. .
2 7
3
18
1
Lời giải
Chọn C
Đặt .
3 3t x dt dx
2 6 6
0 0 0
1 1
3 d 3
3 3
f x x f t dt f x dx
Câu 14: Giá trị nhỏ nhất của hàm số trên đoạn là
3sin 2
sin 1
x
y
x
0;
2
A. . B. . C. . D. .
2
41
2
1
2
5
2
Lời giải
ChọnA.
Đặt .
sin , 0;1t x t
Khi đó . Suy ra hàm số đồng biến trên .
2
3 2 1
' 0
1
1
t
y y
t
t
0;1
.
0;1
(0) 2Min y y
Câu 15: Cho hình chóp tứ giác đều cạnh đáy bằng là tâm của mặt đáy. Khoảng cách
.S A B C D
2 ,a
O
giữa hai đường thẳng và bằng
SO
CD
A. . B. . C. . D. .
a
2
2
a
2a
2
a
O
A
B
D
C
S
Lời giải
ChọnA.
Vì là hình chóp tứ giác đều nên . Kẻ là trung điểm
.S A B C D
SO ABCD
OH CD H
.
CD
là đoạn vuông góc chung của và .
SO ABCD SO OH OH
SO
CD
.
1
;
2
d SO CD OH BC a
Câu 16: Chi đoàn lớp 12 Toán có 30 đoàn viên trong đó có 12 đoàn viên nam và 18 đoàn viên nữ. Tính
xác suất để khi chọn 3 đoàn viên thì có ít nhất 1 đoàn viên nữ.
A. . B. . C. . D. .
44
203
192
203
204
1015
11
203
Lời giải
Chọn B
Chọn 3 đoàn viên từ 30 đoàn viên có số cách là .
3
30
C
3
30
n C
Gọi biến cố “ Trong 3 đoàn viên được chọn có ít nhất 1 đoàn viên nữ”.
A
1 2 2 1 3
18 12 18 12 18
. .n A C C C C C
.
1 2 2 1 3
18 12 18 12 18
3
30
. .
192
203
n A
C C C C C
P A
n C
Câu 17: Trong không gian cho ba điểm , , . Khi thẳng
Oxyz
3;5; 1A
7; ;1B x
9; 2;C y
, , A B C
hàng, giá trị bằng
x y
A. . B. . C. . D. .
5
6
4
1
Lời giải
Chọn D
Ta có: ; .
6; 3; 1AC y
2;2 ; 1BC x y
Để thẳng hàng thì cùng phương với .
, , A B C
AC

BC
.
6 .2
3
3 . 2 3
2
1 . 1
AC k BC
k
k
k x x
y
y k y
.
1x y
Câu 18: Cho hình phẳng giới hạn bởi các đường . Thể tích khối tròn xoay
D
5 , 0, 2, 2
x
y y x x
tạo thành do hình phẳng quay quanh trục hoành được tính theo công thức nào dưới đây?
D
A. . B. . C. . D. .
2
2
0
2 5 d
x
V x
2
2
2
5 d
x
V x
2
2
5 d
x
V x
2
2
25 d
x
V x
Lời giải
Chọn D
Thể tích khối tròn xoay tạo thành do hình phẳng quay quanh trục hoành được tính theo công
D
thức .
2 2
2
2 2
5 d 25 d
x x
V x x
Câu 19: Tính môđun của số phức thỏa mãn
z
2 13 1i z i
A. . B. . C. . D. .
5 34
3
z
34z
34z
34
3
z
Lời giải
Chọn B
Ta có: .
2 13 1 3 5i z i z i
.
2 2
3 5 34z
Câu 20: Hàm số đạt cực tiểu tại điểm
3 2
1
3 1
3
y x x x
A. . B. . C. . D. .
3x
1x
1x
3x
Lời giải
Chọn C
Ta có: .
2
1
2 3 0
3
x
y x x
x
.
2 2y x
1 4 0
3 4 0
y
y
Vậy hàm số đã cho đạt cực tiểu tại .
1x
Câu 21: Tìm phần ảo của số phức
4 3z i
A. . B. . C. . D. .
3
3i
3
4
Lời giải
Chọn A
Phần ảo của số phức bằng .
4 3z i
3
Câu 22: Đường cong trong hình vẽ sau là đồ thị của hàm số nào dưới đây?
x
y
0
A. . B. .
3 2
3 1y x x
4 2
3 1y x x
C. . D. .
4 2
3 1y x x
3 2
3 1y x x
Lời giải
Chọn C
+) Hình vẽ là đồ thị của hàm số bậc 4 trùng phương nên loại đáp án A, D.
+) Từ đồ thị hệ suy số của nhỏ hơn loại B.
4
x
0
Câu 23: Trong không gian với hệ trục tọa độ , cho hai đường thẳng và
Oxyz
1
3 2
: 1
1 4
x t
y t
z t
. Khẳng định nào sau đây là đúng?
2
4 2 4
:
3 2 1
x y z
A. cắt . B. trùng với
1
2
1
2
C. và song song với nhau. D. và chéo nhau.
1
2
1
2
Lời giải
Chọn D
PT tham số của .
2
4 3
: 2 2
4
x a
y a a
z a
Xét hệ phương trình: ( hệ vô nghiệm).
1
7
4 3 3 2 3 2 7
23
2 2 1 2 3
7
4 1 4 4 5
4 5
a
a t a t
a t a t t
a t a t
a t
và , không cùng phương nên và chéo nhau.
1
2; 1;4u
2
3;2; 1u
1
2
Câu 24: Cho hình chóp có đáy là hình vuông cạnh , vuông góc với mặt phẳng
.S A B C D
ABC D
2 a
S A
, . Tính thể tích khối chóp
ABCD
3SA a
.S A B C D
A
B
D
C
S
A. . B. . C. . D. .
3
3a
3
12a
3
4a
3
a
Lời giải
Chọn C
Thể tích của khối chóp là: .
2
3
1 1
. 2 .3 4
3 3
ABCD
V S SA a a a
Câu 25: Trong không gian , cho mặt phẳng . Vectơ nào dưới đây là một
Oxyz
: 2 2 3 0P x y z
vectơ pháp tuyến của ?
P
A. . B. . C. . D. .
3
1; 1;3n
4
2; 1; 3n
2
2; 2; 1n
1
2;1; 3n
Lời giải
Chọn C
Một vectơ pháp tuyến của là
P
2
2; 2; 1n
Câu 26: Cho hình nón có độ dài đường sinh bằng , diện tích xung quanh bằng . Tính bán kính đáy
8
8
của hình nón đó.
R
A. . B. . C. . D. .
4R
8R
1R
2R
Lời giải
Chọn C
Diện tích xung quanh của hình nón là .
8 . . 8 1
xq
S R l R
Câu 27: Tìm tập xác định của hàm số
7
1
log
4
x
y
x
A. . B. . C. . D. .
4;1
; 1 4;
; 4 1;
1; 4
Lời giải
Chọn B
Điều kiện xác định .
1
0
1 4
4
4 0
x
x
x
x
Vậy tập xác định của hàm số là .
1; 4
Câu 28: Trong không gian , điểm nào dưới đây thuộc đường thẳng ?
Oxyz
1 2 5
:
2 3 4
x y z
d
A. . B. . C. . D. .
1;2;5N
1; 2; 5 Q
2;3;4P
1;2;5M
Lời giải
Chọn A
Nhận thấy đường thẳng đi qua điểm .
1 2 5
:
2 3 4
x y z
d
1;2;5N
Câu 29: Cho cấp số nhân có . Công bội của cấp số nhân đã cho bằng
n
u
1 2
4, 2 u u
A. . B. 2. C. 4. D. .
2
1
2
Lời giải
Chọn D
Ta có .
2
2 1
1
2 1
.
4 2
u
u u q q
u
Câu 30: Nếu và thì bằng
2
0
d 3
f x x
5
0
d 6
f x x
5
2
d
f x x
A. 18. B. 3. C. 9. D. .
3
Lời giải
Chọn B
Ta có
5 2 5 2
0 0 0
5
2 0
5
2
d d 3d d d d 6 3
f f x xx x f x x fx f x xx xf x
Câu 31: Một khối lăng trụ có diện tích đáy và có thể tích bằng thì chiều cao bằng :
4
6
A. . B. . C. . D. .
1
2
3
2
9
2
Lời giải
Chọn C
Chiều cao khối lăng trụ là:
3
2
V
h
S
Câu 32: Cho khối trụ có bán kính đáy và chiều cao . Tính thể tích khối trụ đó.
4r
3h
A. . B. . C. . D. .
48
16
32
3
8
Lời giải
ChọnA.
Thể tích khối trụ là:
2
. . 48V r h
Câu 33: Có bao nhiêu số tự nhiên có bốn chữ số khác nhau được lập từ các chữ số .
1;2;4;5;8
A. . B. . C. . D. .
10
24
5
Lời giải
ChọnA.
Số các số tự nhiên có bốn chữ số khác nhau được lập thành từ các chữ số là:
1;2;4;5;8
(số)
5.4.3.2 120
Câu 34: Hàm số nghịch biến trên khoảng nào?
3 2
3y x x
A. . B. . C. . D. .
0; 2
4;0
;0
2;
Lời giải
ChọnA.
Ta có: . Nên . Bảng biến thiên:
3 2 2
3 63 xy xx yx
0
0
2
x
y
x
Vậy hàm số nghịch biến trên khoảng .
0; 2
Câu 35: Tiệm cận đứng của đồ thị hàm số là.
3 5
2
x
y
x
A. . B. . C. . D. .
3y
2y
3x
2x
Lời giải
Chọn A
Tiệm cận đứng của đồ thị hàm số là .
3 5
2
x
y
x
2x
Câu 36: Tập nghiệm của bất phương trình là
S
1
3
log ( 3) 1x
A. . B. . C. . D. .
10
3;
3
S
10
;
3
S
3;S
10
;
3
S
Lời giải
Chọn A
.
1
3
3 0 3
10
log ( 3) 1 3
1 10
3
3
3 3
x x
x x x
x x
Câu 37: Với là số thực dương tùy ý, bằng
a
3
2
log a
A. . B. . C. . D. .
2
3log a
2
1
log
3
a
2
1
log
3
a
2
3 log a
Lời giải
Chọn A
3
2 2
3loglog aa
Câu 38: Tập xác định của hàm số là:
1
5
1y x
A. . B. . C. . D. .
0;
1;
1;
Lời giải
Chọn D
điều kiện: .
1
5
1y x
1 0 1x x
Vậy .
1;D
Câu 39: Cho hàm số là hàm đa thức và có đồ thị
như hình vẽ bên dưới. Có bao
y f x
,f x f x
nhiêu giá trị nguyên của tham số để giá trị lớn nhất của hàm số
m
trên đoạn không vượt
3
5 4 2 2
1 1
3 1 4 2022
5 2 3
x
g x f x x x m m x x
2; 3
quá .
4044
A. . B. . C. . D. .
32
30
31
2 9
Lời giải
Chọn B
Ta có
4 3 2
2
4 3 2
2 3 2 1 4
2 3 2 3 1
g x f x x x m x m x
f x x x x x mx
Xét hàm trên .
4 3 2
2 3 2 3h x x x x x
2 ; 3
.
3 2 2
1
4 6 6 2 2 1 2 2 2 0
2
h x x x x x x x x
Vì và đổi dấu qua nên .
lim
x
h x


h x
1
2
x
2;3
1 41
min
2 16
h x h
Do vậy,
.
2
4 3 2
1633 41 2311
2 3 2 3 1 0, 2;3
750 16 6000
g x f x x x x x mx x
Suy ra, hàm đồng biến trên
g x
2; 3
2
2;3
1687 381
max 3 2022 9 9 4044 14,35... 15,35...
2000 10
g x g m m m
Vậy . Có số nguyên.
14; 13;...;14;15m
30
Câu 40: Cho hình chóp tứ giác có đáy là hình vuông, mặt bên
là tam giác đều và nằm
.S A B C D
SAB
trong mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm đến mặt phẳng
bằng
A
SCD
. Thể tích của khối chóp
là
7
7
a
V
.S A B C D
A
B
D
C
S
A. . B. . C. . D. .
3
1
36
V a
3
1
3
V a
3
2
3
V a
3
18
a
V
Lời giải
Chọn D
Gọi lần lượt là trung điểm của ; là hình chiếu của lên .
,H K
,AB CD
E
H
SK
Ta có .
7
/ / / / , ,
7
a
AB CD AB SCD d A SCD d H SCD HE
Ta có vuông tại .
SH AB SH ABCD SHK
H
Đặt
3
.
2
x
AB x SH
là đường cao trong tam giác vuông nên
H E
S H K
.
2 2 2 2 2 2
1 1 1 7 1 4 3
3 3
x a
HE HS HK a x x
Vậy .
2 3
.
1 1
.S . .
3 3 2 3 18
S ABCD ABCD
a a a
V SH
Câu 41: Trong không gian , cho hai đường thẳng ;
Oxyz
1
1 2
:
1 2 1
x y z
d
2
2 1 1
:
2 1 1
x y z
d
và mặt phẳng . Tìm phương trình đường thẳng song song với mặt
: 2 5 0P x y z
d
phẳng và cắt , lần lượt tại và sao cho và điểm có hoành độ
P
1
d
2
d
A
B
29AB
A
dương
A. .B. .
1 2 2
2 4 3
x y z
2 4 3
2 4 3
x y z
C. .D. .
1 2 2
2 4 3
x y z
1 2 2
2 4 3
x y z
Lời giải
Chọn B
; .
1
1; 2 2 ; 0 1
A
A d A a a a x a
2
2 2 ; 1; 1B d B b b b
//d P
2 3;2 3; 1 1;1; 2
P
BA a b a b a b n
4 0a b
4b a
.
5 ;1 ;3BA a a
Do đó: .
29AB
2 2
5 1 9 29a a
2
2 8 6 0a a
1
3
a ktm
a tm
Suy ra: ;
2;4;3A
2;4;3BA
Vậy: (thỏa mãn)
2 4 3
:
2 4 3
x y z
d
Câu 42: Tính tổng các nghiệm nguyên thuộc đoạn của bất phương trình:
5 ;10
.
2
2 2
2 3 6 6 7 29 34
x x
x x x x
A. 54. B. 40. C. 55. D. 41.
Lời giải
Chọn B
.
2
2 2
2 3 6 6 7 29 34
x x
x x x x
2
2 2 2
2 12 24 24 7 29 34 1
x x
x x x x
Đặt ; . Suy ra: . Thay vào
2
12 24 24a x x
2
7 29 34 , 0b x x a b
2
2
5
a b
x x
1
ta được: , với là hàm số đồng biến
5
2
a b
a b
5 5
.2 .2
a b
a b
2f a f b
5
.2
t
f t t
trên khoảng .
0 ;
Vậy .
2 a b
2 2
12 24 24 7 29 34x x x x
2
2 0x x
2
1
x
x
Mà nguyên thuộc đoạn nên .
x
5 ;10
5; 4 ; 3; 2;1; 2;...;10x
Vậy tổng các nghiệm nguyên thuộc đoạn của bất phương trình đã cho là: 41.
5 ;10
Câu 43: Cho hàm số có đạo hàm là và . Tính
y f x
,
x
f x xe x
0 2022f
.
2
0
2021f x dx
A. . B. . C. . D. .
2
6
Lời giải
Chọn A
Ta có và
d d
x xx
e Cf x f x x xe x xe
0 2022f
2021
x x
x xe ef
Khi đó .
2 2
0 0
2021 d d 2
x x
f x x exe x
Câu 44: Cho hàm số và hàm số (với
4 3 2
1
2
3
f x ax x x bx
3 2
2g x cx dx x
, , ,a b c d
) là các hàm số có đồ thị như hình vẽ bên dưới. Gọi là diện tích các hình phẳng tô màu
1 2
;S S
trong hình vẽ, biết . Tính .
1
97
60
S
2
S
A. . B. . C. . D. .
143
60
133
60
153
60
163
60
Lời giải
Chọn B
Ta thấy các nghiệm của phương trình là các điểm cực trị của hàm số .
0g x
f x
4 3 2
3 2
4 4
1
2
1 1
0
3
2 2 1
4 2
0 0
a kc a c
f x ax x x
kd d
f x kg x k
k k
g x ax x x
b b
Ta có
4 3
2
1 2
1 0 2 2 2
4 4 3
x x
g a f x g x x x
Khi đó .
1 1
4 3
2
1
0 2
2
d 2
0
2 2 d
33
63
1
4
x x
S f x g x x x x x
Câu 45: Trong không gian với hệ trục tọa độ , cho mặt cầu
Oxyz
2 2 2
( ): 1 2 3 48S x y z
và đường thẳng . Điểm nằm trên đường thẳng
1 2 3
( ):
1 1
2
x y z
d
( ; ; )M a b c
( 0)a
( )d
sao cho từ kẻ được 3 tiếp tuyến đến mặt cầu thỏa mãn ,
M
, ,MA MB MC
( )S
60AMB
và . Tính .
90BMC
120CMA
Q a b c
A. . B. . C. . D. .
6 4 2Q
10 4 2Q
9 4 2Q
9 4 2Q
Lời giải
Chọn A
Mặt cầu có tâm và bán kính .
1; 2; 3I
4 3R
Gọi đường tròn là giao tuyến của mặt phẳng với mặt câu .
C
ABC
Đặt .
0MA MB MC x x
Áp dụng định lý cosin trong và , ta có:
AMB
C M A
.
2 2 2 2 2 2
2 . .cos 2 2 cos60AB MA MB MA MB AMB x x x AB x
.
2 2 2 2 2 2
2 . .cos 2 2 cos120 3 3AC MA MC MA MC AMC x x x AC x
Vì vuông tại nên: .
BMC
2 2
2BC MB MC x
Mặt khác nên vuông tại .
2 2
2 2 2 2 2
2 3 3AB BC x x x x AC
A B C
B
Gọi là trung điểm của thì là tâm của đường tròn và ba điểm thẳng
H
A C
H
C
, ,H I M
hàng.
Do nên , suy ra đều và .
120AMC
60AIC
AIC
4 3AC IA IC R
Suy ra và .
3 4 3 4x x
2 2.4 3
cos30 8
3 3
IA
IA IM IM
Điểm nên .
M d
2
2 2 2 2
1 ;2 ;3 2 2 4M t t t IM t t t t
Mà
2 2
4 3;6;3 4 2
64 4 64
4 5; 2;3 4 2
t M
IM t
t M l
Vì nên điểm cần tìm là , suy ra .
0
M
x
3;6;3 4 2M
6 4 2Q
Câu 46: Cho hình chóp có đáy là tam giác vuông cân tại , , góc
.S ABC
A B C
B
3AB B C a
và khoảng cách từ đến mặt phẳng bằng . Tính thể tích khối
90SAB SCB
A
SBC
6a
cầu ngoại tiếp hình chóp theo .
.S ABC
a
A. . B. . C. . D. .
3
108 a
3
36 a
3
6 a
2
36 a
Lời giải
Chọn B
Gọi lần lượt là trung điểm của cạnh và
,I H
SB
A C
Mặt khác, theo giả thiết ta có lần lượt là các tam giác vuông tại và
,SAB SCB
A
C
IA IB IC IS
là tâm mặt cầu ngoại tiếp hình chóp
I
.S ABC
Mặt khác: vuông tại là tâm đường tròn ngoại tiếp
A B C
B
H
A B C
IH ABC
Ta có:
;
6
2 ;
2
;
d A SBC
AC a
d H SBC
HC
d H SBC
Gọi là trung điểm của cạnh
K
BC
/ / ,HK BC HK AB AB BC
Lại có:
BC IH IH ABC BC IHK
Mặt khác: theo giao tuyến
BC SBC SBC IHK
IK
Trong , gọi tại
IH K
HP IK HP SBC
P
6
;
2
a
HP d H SBC
Xét
2
2 2 2 2
1 1 1 1 1 3 2
:
2
4
a
IHK HI
AB
HP HI HK HI
Xét . Vậy
2 2
: 3IHB IB IH HB a R
3 3
4
36
3
V R a
Câu 47: Xét hai số phức thỏa mãn và
1 2
,z z
1 1 1
2 2 2 3 3z i i z z i
2 2
1 2z i z i
. Giá trị nhỏ nhất của bằng:
1 2
z z
A. B. C. D.
7
2 6
34
5
2 2
Lời giải
Chọn D
Gọi là điểm biểu diễn cho số phức .
;M x y
1
z
Từ giả thuyết, suy ra,
1 1 1 1 1 1
2 . 2 2 3 . 3 2 2z i i z z i z i z z
2 2
2 2
2 2 1 2 2 1 4 2 5 0x y i yi x y y x x y
Tập hợp điểm biểu diễn cho số phức là parabol có phương trình .
2
z
P
2
1 5
2
2 2
y x x
Gọi là điểm biểu diễn cho số phức .
;N a b
2
z
Từ giả thuyết, suy ra
2 2 2
2
2 2
1 2 1 1 2 1 1 2z i z i a b i a b i a b a b
. Suy ra tập hợp điểm biểu diễn cho số phức là đường thẳng
2 2 4 0 2 0a b a b
2
z
có phương trình .
2 0a b
Khi đó . Điểm
1 2
z z MN
2
1 5
; 2
2 2
M P M x x x
Khoảng cách .
2
2
2
min
min
1 5
1 9
2 2
1 1 9
2 2
2 2
,
2 2
2 2 2
x x x
x x
MN d M x x
Giá trị nhỏ nhất của hàm số bằng , dấu “=” xảy ra khi .
2
1 1 9
2 2
2
x x
2 2
1x
Câu 48: Cho hàm số có đồ thị như hình vẽ. Hỏi mệnh đề nào dưới đây đúng với
2
1 2f x x x
hàm số .
2
2 . 2y x x x
A. Hàm số nghịch biến trên khoảng .
1;
B. Hàm số đồng biến trên khoảng .
1; 0
C. Hàm số nghịch biến trên khoảng .
1
;
2
D. Hàm số đồng biến trên khoảng .
1; 2
Lời giải
Chọn C
Xét hàm số
2
2
2
2 . 2 2
2 . 2
2 . 2 2
x x x khi x
y g x x x x
x x x khi x
Từ đó ta có đồ thị hàm số như sau:
g x
Từ đồ thị suy ra hàm số nghịch biến trên khoảng
g x
1
;0 ;
2
 
Do đó hàm số nghịch biến trên khoảng .
g x
1
;
2
Câu 49: Có bao nhiêu số nguyên sao cho ứng với mỗi có không quá số nguyên thỏa mãn
x
x
25 5
y
?
2
5 4
log logx y x y
A. . B. . C. . D. .
3 7
38
4 0
36
Lời giải
Chọn B
Điều kiện và . Khi đó
0x y
2
0x y
4
4
log 5
log
2 2 2
5 4
log log 5
x y
x y x y x y x y x y
4
log 5
2
x x x y x y
1
Đặt thì được viết lại là
t x y
1
4
log 5
2
x x t t
2
Với mỗi nguyên cho trước có không quá số nguyên thỏa mãn bất phương trình
x
25 5
y
1
Tương đương với bất phương trình có không quá 255 nghiệm .
2
t
Ta có hàm số đồng biến trên nên nếu thì
4
log 5
f t t t
1;
4
log 5
2
256 256 369x x
sẽ có ít nhất nghiệm nguyên .
25 6
1t
Do đó yêu cầu bài toán tương đương với (do nguyên).
2
369 18 19x x x
x
Vậy có tất cả số nguyên thỏa yêu cầu bài toán.
38
x
Câu 50: Có bao nhiêu số nguyên dương để phương trình có 2 nghiệm phức
a
2 2
3 0z a z a a
thỏa mãn ?
1 2
,z z
1 2 1 2
z z z z
A. 3. B. 4. C. 2. D. 1.
Lời giải
Chọn C
. .
2 2
3 0z a z a a
2
3 10 9a a
.
2
5 2 13 5 2 13
0 3 10 9 0
2 2
a a a
Khi đó phương trình có 2 nghiệm
2 2
1 2
3 3 10 9 3 3 10 9
,
2 2
a a a a a a
z z
.
2 2
1 2 1 2
2
2 2
3 3 10 9 3 3 10 9
0
3 3 10 9 4 4 0
1
z z z z a a a a a a
a
a a a a a
a
thỏa mãn.
1a
.(1)
2
5 2 13
2
0 3 10 9 0
5 2 13
2
a
a a
a
2 2
1 2 1 2
2
2 2
3 3 10 9 3 3 10 9
1
3 3 10 9 8 9 0
9
z z z z a i a a a i a a
a
a a a a a
a
loại vì không phải là số nguyên dương, thỏa mãn (1).
1a
9a
Vậy có 2 giá trị
| 1/25
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

HƯỚNG DẪN GIẢI CHI TIẾT Câu 1:
Nghiệm của phương trình log 4x  6  1 là 9 A. x  7 . B. x  . C. x  4 . D. x  5 . 2 4 Lời giải Chọn C
Ta có: log 4x  6  1  4x  6  10  x  4 . Câu 2:
Trong không gian Oxyz cho mặt cầu S  2 2 2
: ( x  1)  ( y  2)  ( z  3)  4 . Tâm của S  có tọa độ là
A. 1; 2; 3 . B. 1; 2;3 . C. 1;2;3. D. 1;2;3 . Lời giải Chọn C
Tâm của S  có tọa độ là I 1; 2;3 . Câu 3:
Mô đun của số phức z = 3- 2i bằng A. . 5 B. 13 . C. 5 . D. 13. Lời giải Chọn B Ta có z    2 2 3 2  13 . Câu 4:
Tìm nguyên hàm của hàm số f x   cos 3x x A. cos3 d
x x  sin3x C . B. x x   C .  sin 3 cos 3 d  3 sin 3x C. cos3 d x x    C . D. x x x C .  cos3 d 3sin  3 Lời giải Chọn B sin 3x
Ta có cos 3xdx   C .  3 Câu 5:
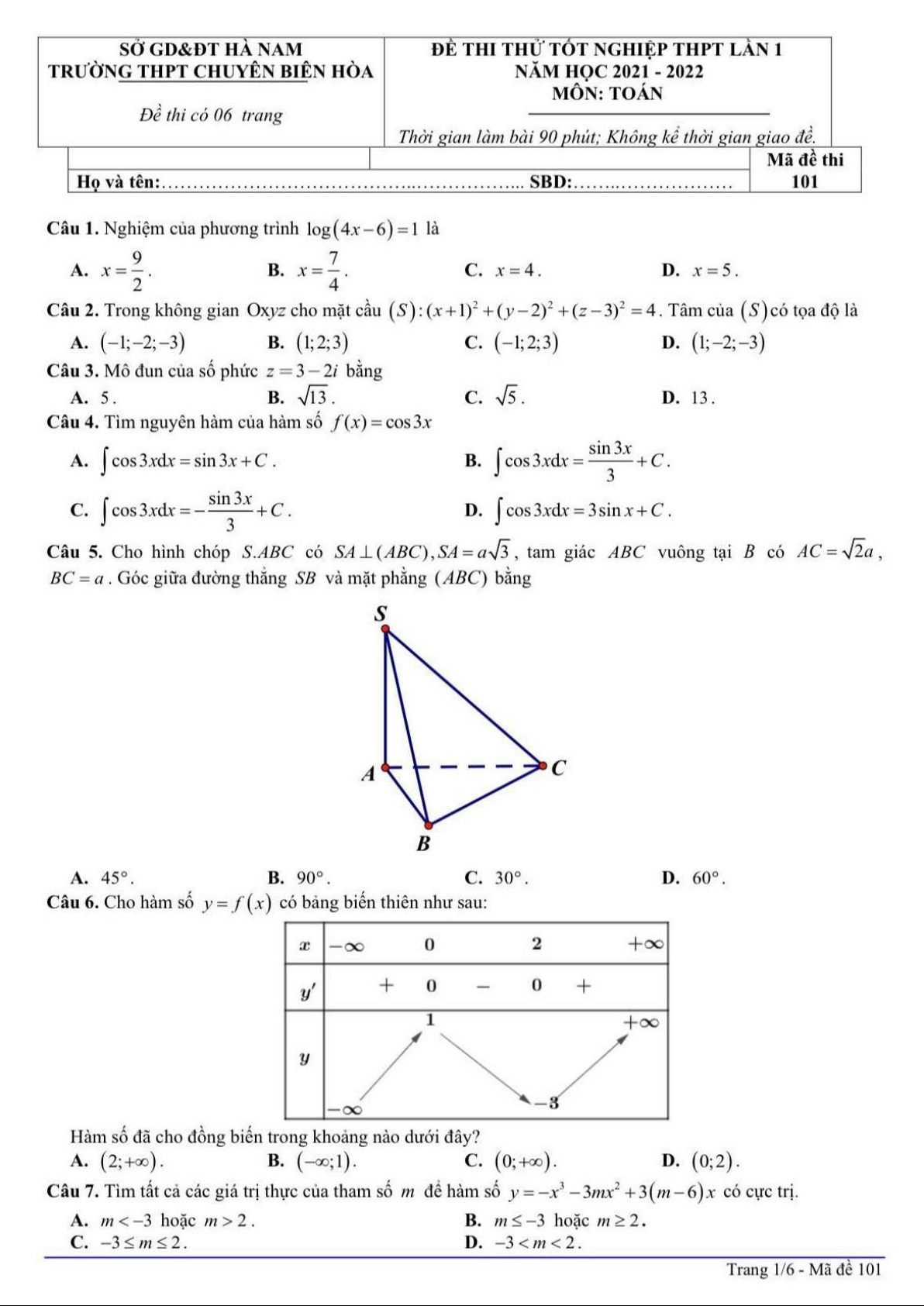
Cho hình chóp S.ABC có SA  (ABC), SA a 3 , tam giác A B C vuông tại B có AC  2a ,
B C a . Góc giữa đường thẳng SB và mặt phằng (AB ) C bằng S A C B A. 45. B. 90 . C. 30 . D. 60 . Lời giải Chọn D
SB  ABC  B Vì 
 SB, ABC   SBA
SA  (ABC)
Xét tam giác A B C vuông tại B có: 2 2 2 2 AB
AC BC  2a a a SA a 3 Xét tam giác tan  SBA    3  
SBA vuông tại A có SBA  60 . AB a
Vậy SB, ABC   SBA  60 . Câu 6:
Cho 6 điểm phân biệt trên mặt phẳng. Hỏi có bao nhiêu véc-tơ mà điểm đầu và điểm cuối là 6 điểm đã cho? A. 30. B. 15. C. 2 1 . D. 36. Lời giải ChọnA.
Số vectơ có điểm đầu và điểm cuối tạo từ 6 điểm đã cho là 2 A  30 . 6 5 Câu 7:
Tập xác định D của hàm số y    x9 2  ln  x  2
A. D  2;2 .
B. D  ; 2  2;   .
C. D  2; 2  . D. ( ;  2  ] [  2; )  . Lời giải Chọn C 5
Tập xác định D của hàm số y    x9 2
 ln  x  2 là D  2; 2  . Câu 8:
Cho mặt cầu có diện tích bằng 2
16a . Khi đó, bán kính mặt cầu bằng a 2 A. 2a . B. . C. 2 2a . D. 2 a . 2 Lời giải Chọn D Có 2 2
4R 16a R  2a. Câu 9:
Cho số phức z thỏa mãn z z  1  3i . Tính tích phần thực và phần ảo của z A. 7 . B. 12 . C.  7 . D. 12. Lời giải Chọn B
Gọi z x yi x, y  . 2 2
 x y x 1 x  4 2 2
z z  1 3i x y x yi  1 3i      . x y  3  .4  1  2 . y  3  y  3 
Câu 10: Diện tích xung quanh của hình nón có độ dài đường sinh l và bán kính đáy r bằng 1 A.  rl . B. 4 r l . 3 C.  rl . D. 2 r l . Lời giải Chọn C
Diện tích xung quanh của hình nón có độ dài đường sinh l và bán kính đáy r bằng rl .     
Câu 11: Cho hai số phức z 3 2i z 3 i z z 1 và 2 . Số phức 1 2 bằng A. 6  i . B. 6  i . C. i . D. 6  3i . Lời giải Chọn B
Ta có z z  3  2i  3  i  6  i 1 2     2
Câu 12: Cho a là một số thực dương, biểu thức 3 a
a viết dưới dạng lũy thừa với số mũ hữu tỷ là 6 7 4 5 A. 7 a . B. 6 a . C. 3 a . D. 6 a . Lời giải Chọn B 2 2 1 7 Ta có 3 3 2 6 a
a a .a a 6 2
Câu 13: Cho hàm số f x  liên tục trên  và f
 xdx  9. Giá trị của tích phân f
 3xdx bằng 0 0 A. 2 7 . B. 3 . C. 18. D. 1. Lời giải Chọn C
Đặt t  3x dt  3dx . 2 6 6 f   x 1 x f  t 1 3 d dt f
 xdx  3 3 3 0 0 0 3sin x  2 
Câu 14: Giá trị nhỏ nhất của hàm số y  trên đoạn 0; là sin x  1  2   41 1 5 A. 2 . B. . C. . D. . 2 2 2 Lời giải ChọnA.
Đặt t  sin x, t  0;1. 3t  2 1 Khi đó y   y ' 
 0 . Suy ra hàm số đồng biến trên 0;  1 . t 1 t  2 1
Min y y(0)  2 . 0; 1
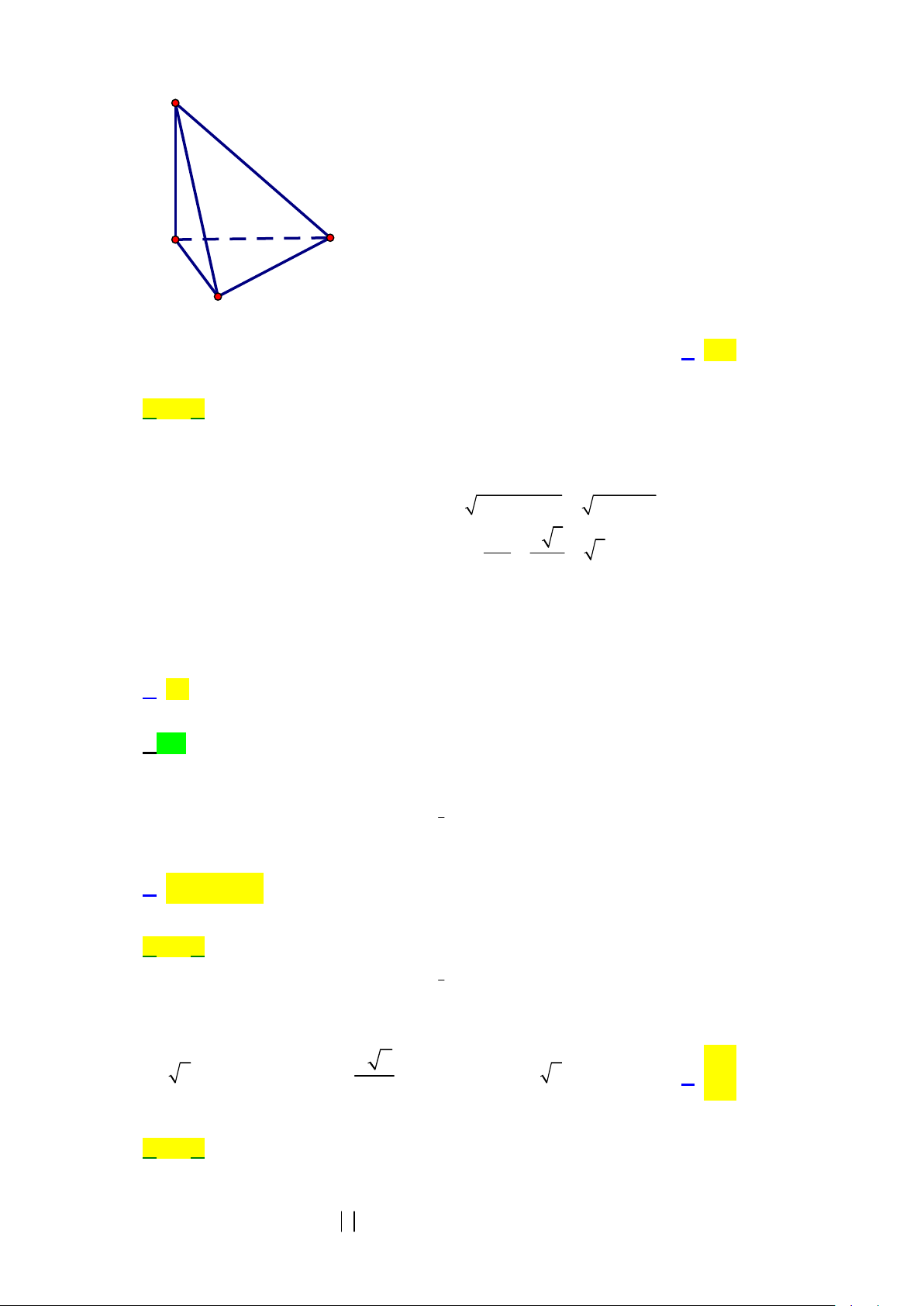
Câu 15: Cho hình chóp tứ giác đều S .A B C D cạnh đáy bằng 2 ,
a O là tâm của mặt đáy. Khoảng cách
giữa hai đường thẳng SO và CD bằng 2a a A. a . B. . C. 2a . D. . 2 2 S A D O B C Lời giải ChọnA.
Vì S .A B C D là hình chóp tứ giác đều nên SO   ABCD  . Kẻ OH CD H là trung điểm CD .
SO   ABCD   SO OH OH là đoạn vuông góc chung của SO và CD . d SO CD 1 ;
OH BC a . 2
Câu 16: Chi đoàn lớp 12 Toán có 30 đoàn viên trong đó có 12 đoàn viên nam và 18 đoàn viên nữ. Tính
xác suất để khi chọn 3 đoàn viên thì có ít nhất 1 đoàn viên nữ. 44 192 204 11 A. . B. . C. . D. . 203 203 1015 203 Lời giải Chọn B
Chọn 3 đoàn viên từ 30 đoàn viên có số cách là 3
C n  3  C . 30 30
Gọi biến cố A “ Trong 3 đoàn viên được chọn có ít nhất 1 đoàn viên nữ”.n A 1 2 2 1 3
C .C C .C C 18 12 18 12 18 1 2 2 1 3  
P AnAC .C C .C C 192 18 12 18 12 18    . n  3 C 203 30
Câu 17: Trong không gian Oxyz cho ba điểm A 3;5; 1 , B 7;  x;1 , C 9;2; y . Khi , A , B C thẳng
hàng, giá trị x y bằng A. . 5 B. 6 . C. 4 . D. . 1  Lời giải Chọn D  Ta có: AC  6; 3  ; y  1 ; BC  2;2 ; x y   1 .   Để , A ,
B C thẳng hàng thì AC cùng phương với BC.    AC k BC 6  k.2 k  3   .   3
  k.2  x  x  3   
y 1  k. y   1 y  2  
xy   . 1
Câu 18: Cho hình phẳng D giới hạn bởi các đường  5x y
, y  0, x  2
 , x  2 . Thể tích khối tròn xoay
tạo thành do hình phẳng D quay quanh trục hoành được tính theo công thức nào dưới đây? 2 2 2 2 A. 2  25 x V dx . B. 2  5 x V dx . C.  5x V dx .
D. 25x V dx .     0 2  2  2  Lời giải Chọn D
Thể tích khối tròn xoay tạo thành do hình phẳng D quay quanh trục hoành được tính theo công 2 2 2
thức   5x  d  25x V x dx .  2  2 
Câu 19: Tính môđun của số phức z thỏa mãn 2  iz 13i  1 5 34 34 A. z  . B. z  34 . C. z  34 . D. z  . 3 3 Lời giải Chọn B
Ta có: 2  iz  13i  1  z  3  5i . 2 2
z  3  5  34 . 1 Câu 20: Hàm số 3 2
y x x  3x 1 đạt cực tiểu tại điểm 3 A. x  3 . B. x  1 . C. x  1 . D. x  3 . Lời giải Chọn Cx 1 Ta có: 2
y  x  2x  3  0  .  x  3 
y  2x  2 .  y   1  4  0 y  3    4   0
Vậy hàm số đã cho đạt cực tiểu tại x  1 .
Câu 21: Tìm phần ảo của số phức z  4  3i A.  3 . B. 3i . C. . 3 D. 4 . Lời giải Chọn A
Phần ảo của số phức z  4  3i bằng  3 .
Câu 22: Đường cong trong hình vẽ sau là đồ thị của hàm số nào dưới đây? y x 0 A. 3 2
y x  3x 1. B. 4 2
y x  3x 1. C. 4 2
y  x  3x 1 . D. 3 2
y  x  3x 1. Lời giải Chọn C
+) Hình vẽ là đồ thị của hàm số bậc 4 trùng phương nên loại đáp án A, D.
+) Từ đồ thị hệ suy số của 4 x nhỏ hơn 0 loại B.x  3   2t
Câu 23: Trong không gian với hệ trục tọa độ Oxyz , cho hai đường thẳng 
 : y 1 t và 1 z  1   4tx  4 y  2 z  4  :  
. Khẳng định nào sau đây là đúng? 2 3 2 1  A.  cắt  . B.  trùng với  1 2 1 2
C.  và  song song với nhau.
D.  và  chéo nhau. 1 2 1 2 Lời giải Chọn D
x  4  3a PT tham số của 
 :  y  2  2a a   2  . z  4  a   1 a    7 4  3a  3   2t 3
a  2t  7   Xét hệ phương trình:    23  2
  2a  1 t  2a t  3  t   ( hệ vô nghiệm). 7 4 a 1 4ta 4t 5         
a  4t  5    và uu   3;2; 1   2; 1;  4 ,
không cùng phương nên  và  chéo nhau. 1 2 1 2
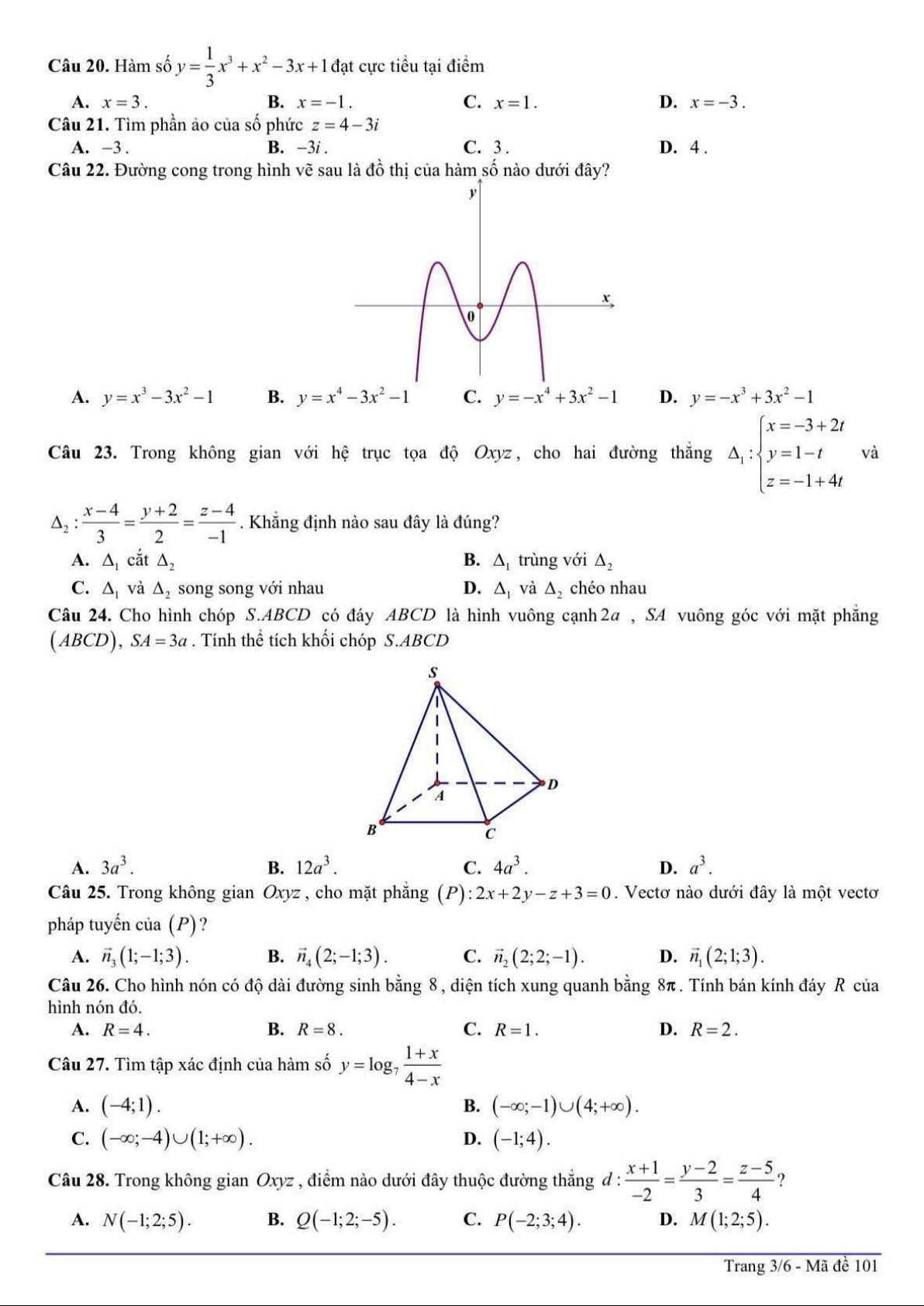
Câu 24: Cho hình chóp S .A B C D có đáy ABCD là hình vuông cạnh 2 a , SA vuông góc với mặt phẳng
ABCD, SA  3a . Tính thể tích khối chóp S.ABCD S D A B C 3 A. 3a 3 . B. 12a 3 . C. 4a 3 . D. a . Lời giải Chọn C 1 1
Thể tích của khối chóp là: V S . ABCD SA  2a2 3 .3a  4a . 3 3
Câu 25: Trong không gian Oxyz , cho mặt phẳng P  : 2x  2 y z  3  0 . Vectơ nào dưới đây là một
vectơ pháp tuyến của  P  ? A.     n 1; 1; 3 n 2; 1; 3 n 2; 2; 1 n 2;1; 3 1   2   4   3   . B. . C. . D. . Lời giải Chọn C
Một vectơ pháp tuyến của  
P  là n 2; 2; 1 2  
Câu 26: Cho hình nón có độ dài đường sinh bằng 8, diện tích xung quanh bằng 8. Tính bán kính đáy
R của hình nón đó. A. R  4 . B. R  8 . C. R  1 . D. R  2 . Lời giải Chọn C
Diện tích xung quanh của hình nón là S  8. .
R l  8R  1. xq 1  x
Câu 27: Tìm tập xác định của hàm số y  log7 4  x A. 4;1 .
B. ; 1  4;   . C. ; 4  1;   . D. 1; 4 . Lời giải Chọn B 1 x   0
Điều kiện xác định 4  x  1   x  4 . 4 x  0
Vậy tập xác định của hàm số là 1; 4 . x y z
Câu 28: Trong không gian Oxyz 1 2 5
, điểm nào dưới đây thuộc đường thẳng d :   ? 2  3 4
A. N 1;2;5 .
B. Q 1; 2; 5 .
C. P 2;3; 4 .
D. M 1;2;5. Lời giải Chọn A x 1 y  2 z  5
Nhận thấy đường thẳng d :  
đi qua điểm N 1;2;5 . 2  3 4
Câu 29: Cho cấp số nhân u u  4,u  2 n  có
. Công bội của cấp số nhân đã cho bằng 1 2 A.  1 2 . B. 2. C. 4. D. . 2 Lời giải Chọn D u 2 1 Ta có 2
u u .q q    2 1 . u 4 2 1 2 5
f xdx  3  f xdx  6 5 Câu 30: Nếu 0 và 0
thì  f xdx bằng 2 A. 18. B. 3. C. 9. D.  3 . Lời giải Chọn B 5 2 5 5 5 2
Ta có  f xdx   f xdx   f xdx   f xdx   f xdx   f xdx  63  3 0 0 2 2 0 0
Câu 31: Một khối lăng trụ có diện tích đáy 4 và có thể tích bằng 6 thì chiều cao bằng : 1 3 9 A. . B. 24 . C. . D. . 2 2 2 Lời giải Chọn C V 3
Chiều cao khối lăng trụ là: h   S 2
Câu 32: Cho khối trụ có bán kính đáy r  4 và chiều cao h  3 . Tính thể tích khối trụ đó. 32 A. 48. B. 1 6. C. . D. 8. 3 Lời giải ChọnA. Thể tích khối trụ là: 2
V .r .h  48
Câu 33: Có bao nhiêu số tự nhiên có bốn chữ số khác nhau được lập từ các chữ số 1;2;4;5;8. A. 120 . B. 10. C. 24 . D. . 5 Lời giải ChọnA.
Số các số tự nhiên có bốn chữ số khác nhau được lập thành từ các chữ số 1;2;4;5;8 là: 5.4.3.2  120 (số) Câu 34: Hàm số 3 2
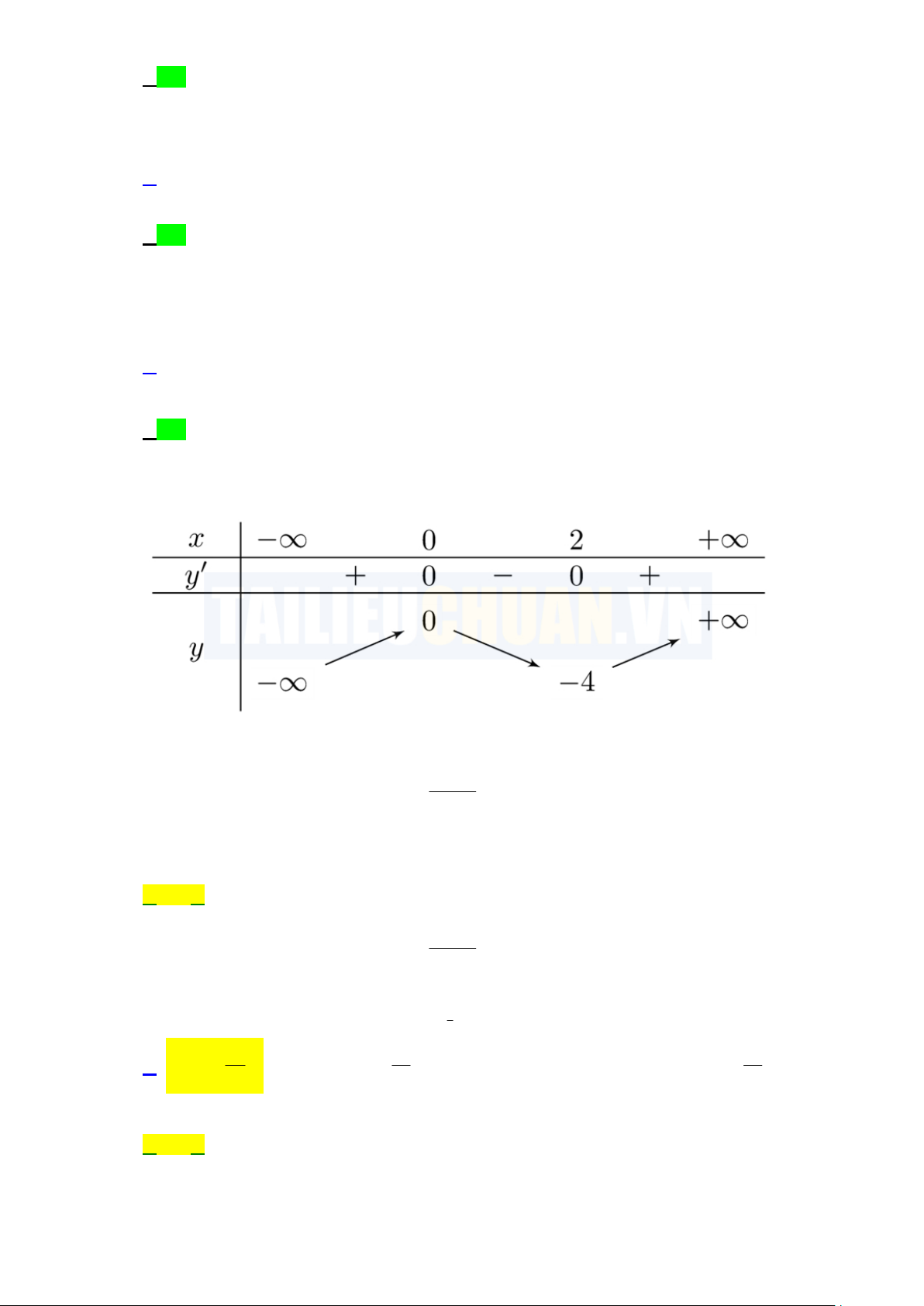
y x  3x nghịch biến trên khoảng nào? A. 0; 2 . B. 4;0 . C. ;0 . D. 2; . Lời giải ChọnA.x  0 Ta có: 3 2 2
y x  3x y  3x  6x . Nên y  0  . Bảng biến thiên:  x  2
Vậy hàm số nghịch biến trên khoảng 0; 2 . 3x  5
Câu 35: Tiệm cận đứng của đồ thị hàm số y  là. x  2 A. y  3 . B. y  2 . C. x  3 . D. x  2 . Lời giải Chọn A 3x  5
Tiệm cận đứng của đồ thị hàm số y  là x  2 . x  2
Câu 36: Tập nghiệm S của bất phương trình log (x 3) 1 1 là 3  10  10  1  0  A. S  3;   . B. S  ;  .
C. S  3;. D. S  ;   .  3   3   3  Lời giải Chọn Ax  3  0 x  3   10
log (x  3)  1   1  x  10  3  x  1 . x  3  x  3 3  3    3
Câu 37: Với a là số thực dương tùy ý, 3 log a bằng 2 1 1 A. 3log a . B.  log a . C. log a . D. 3  log a . 2 2 3 2 3 2 Lời giải Chọn A 3 log a  3log a 2 2
Câu 38: Tập xác định của hàm số y   x  15 1 là: A.  . B. 0;. C. 1;   . D. 1;   . Lời giải Chọn D
y  x  15
1 điều kiện: x  1  0  x  1 .
Vậy D  1;    .
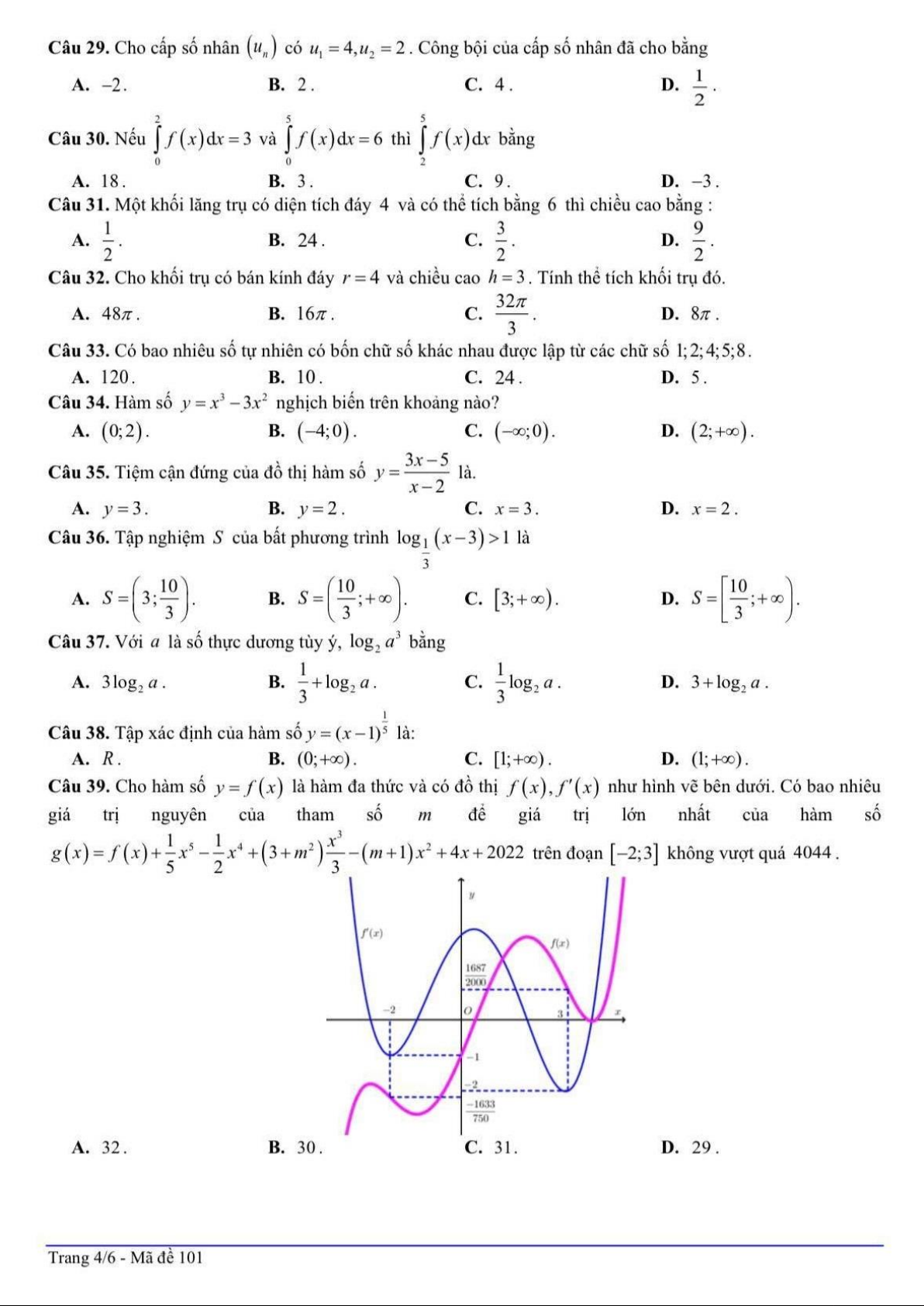
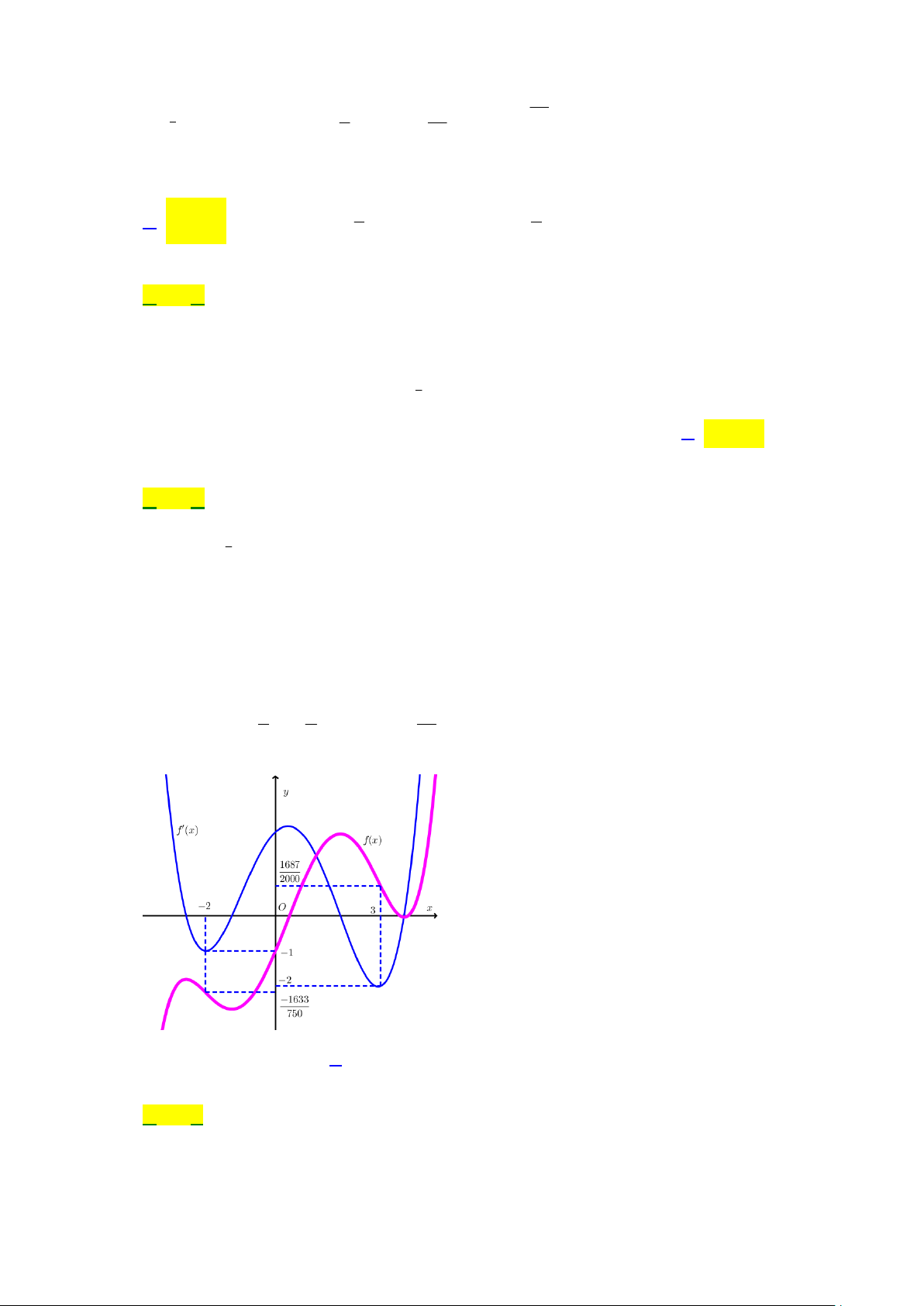
Câu 39: Cho hàm số y f x là hàm đa thức và có đồ thị f x , f  x  như hình vẽ bên dưới. Có bao
nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số 3
g x  f x 1 1 x 5 4
x x  2
3 m  m  2
1 x  4x  2022 trên đoạn 2;3 không vượt 5 2 3 quá 4044 . A. 32. B. 30. C. 31. D. 2 9 . Lời giải Chọn B Ta có
g x  f  x 4 3
x  2x  3 m 2
x  2m   1 x  4
f  x  x  2x  3x  2x  3  mx  2 4 3 2 1
Xét hàm h x 4 3 2
x  2 x  3x  2 x  3 trên 2 ;3 . h x 1 3 2
 4x  6x  6x  2  2x   1  2
2x  2x  2  0  x  . 2 1  1  41
Vì lim h x   và h x  đổi dấu qua x  nên min hx  h    . x 2  2  ;  3  2  16 Do vậy, 
g x  f  x  x  2x  3x  2x  3  mx  2 1633 41 2311 4 3 2 1     0, x   2  ;  3 . 750 16 6000 Suy ra, hàm g x  đồng biến trên 2;3
 max g x  g 3 1687 381 2  
 2022  9m  9m  4044  1
 4,35...  m  15,35...  2  ;  3 2000 10
Vậy m 14; 13;...;14;1  5 . Có 30 số nguyên.
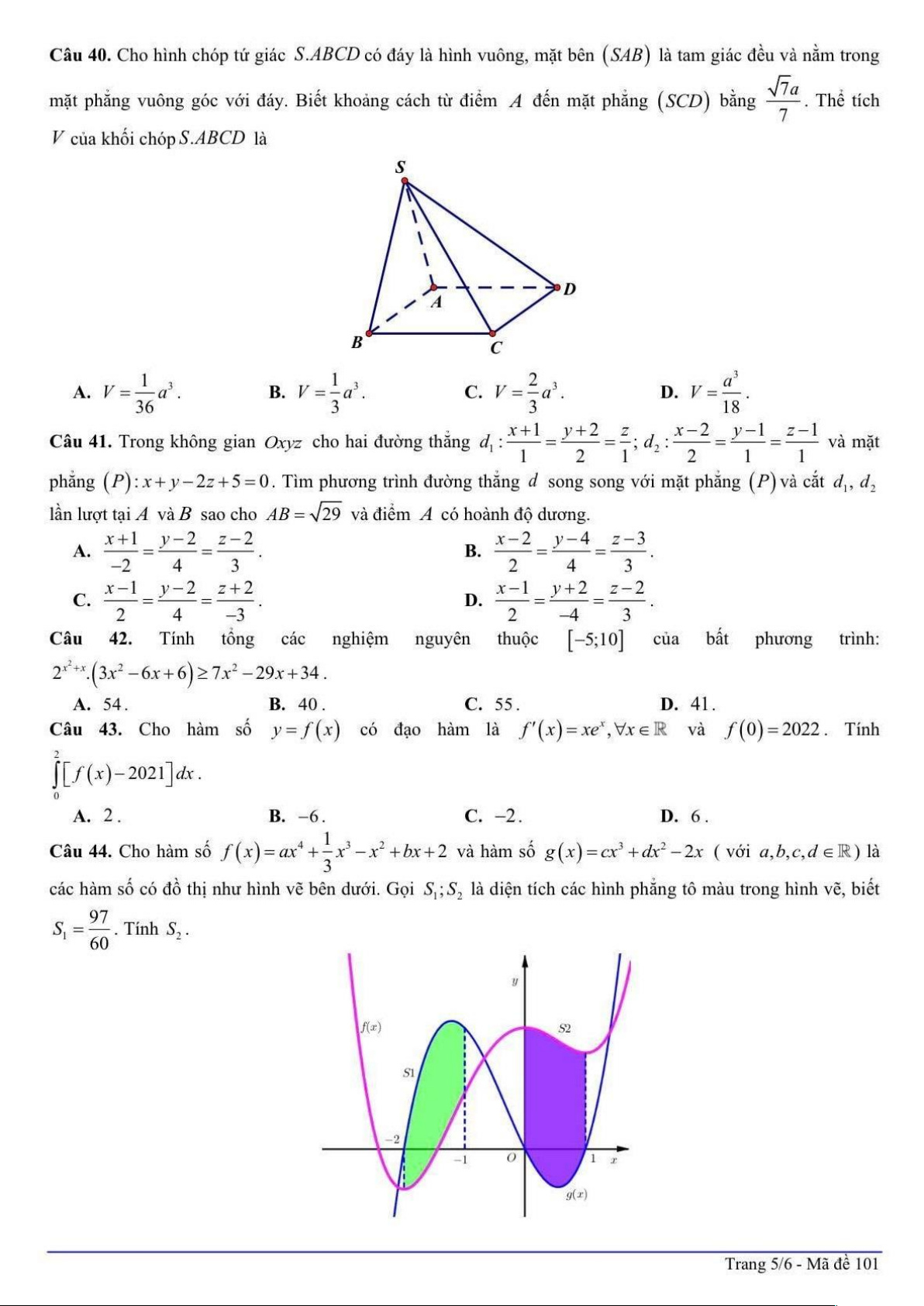
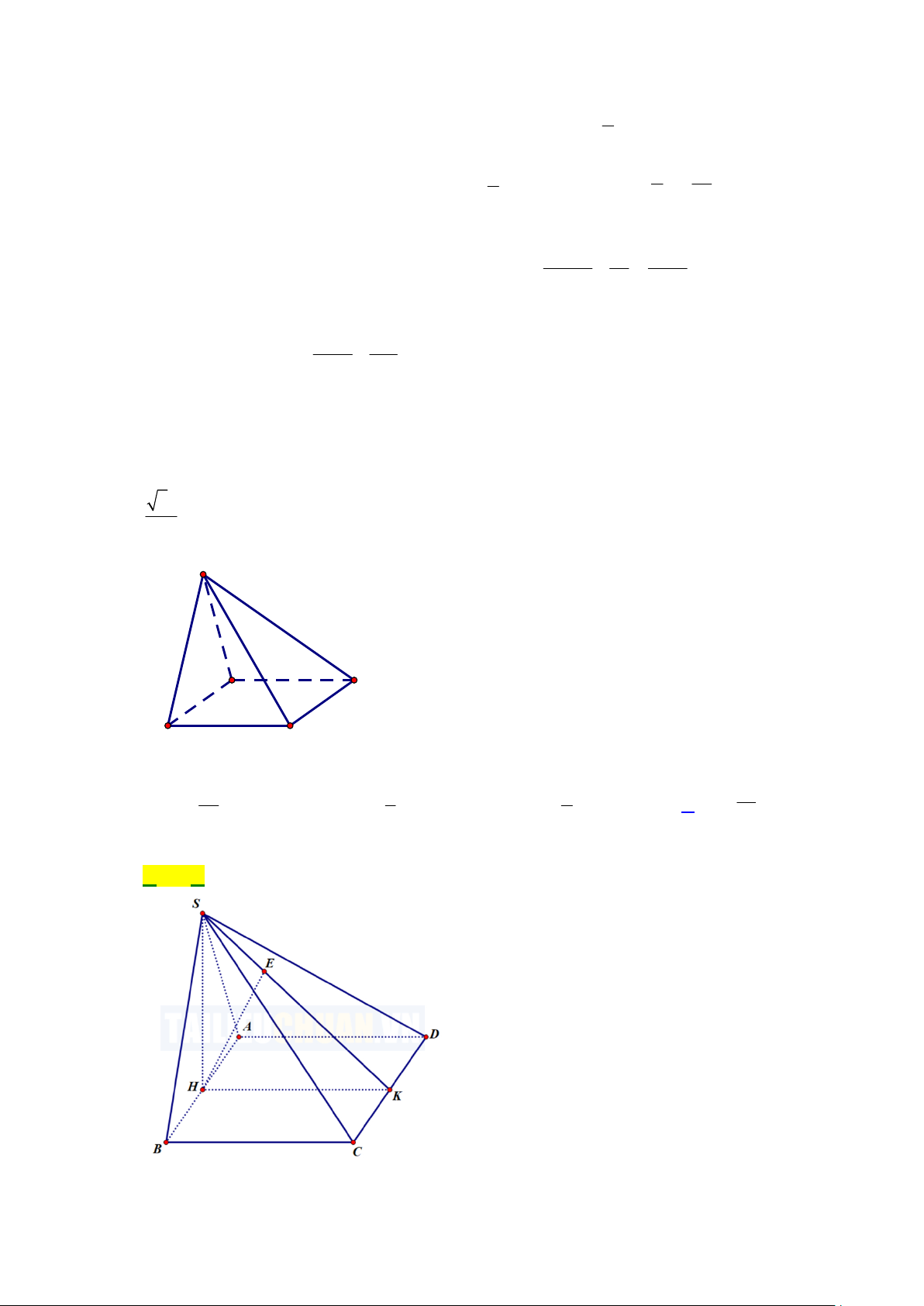
Câu 40: Cho hình chóp tứ giác S .A B C D có đáy là hình vuông, mặt bên SAB  là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm A đến mặt phẳng SCD  bằng
7a . Thể tích V của khối chópS.ABCD là 7 S D A B C 3 1 1 2 a A. 3 V a . B. 3 V a . C. 3 V a . D. V  . 36 3 3 18 Lời giải Chọn D
Gọi H , K lần lượt là trung điểm của AB,CD; E là hình chiếu của H lên SK . a
Ta có AB CD AB SCD  d A SCD  d H SCD 7 / / / / , ,  HE  . 7
Ta có SH AB SH   ABCD   SHK vuông tại H . x 3
Đặt AB x SH  . 2
H E là đường cao trong tam giác vuông S H K nên 1 1 1 7 1 4 3       x a . 2 2 2 2 2 2 HE HS HK a x 3x 3 2 3 1 1 a a a Vậy VSH.S  . .  S.ABCD ABCD . 3 3 2 3 18 x 1 y  2 z x  2 y 1 z 1
Câu 41: Trong không gian Oxyz , cho hai đường thẳng d :   ; d :   1 1 2 1 2 2 1 1
và mặt phẳng P  : x y  2z  5  0 . Tìm phương trình đường thẳng d song song với mặt
phẳng  P  và cắt d , d lần lượt tại A và B sao cho AB  29 và điểm A có hoành độ 1 2 dương x 1 y  2 z  2 x  2 y  4 z  3 A.   .B.   . 2 4 3 2 4 3 x 1 y  2 z  2 x 1 y  2 z  2 C.   .D.   . 2 4 3 2 4 3 Lời giải Chọn B
A d A a  1; 2a  2 ; a
x  0  a  1
B d B 2b  2 ; b  1; b  1 2   1    A  ; .  
d //  P   BAa  2b 3;2a b 3;a b  
1  n 1;1;2        P    a b 4 0 b a 4  B
A 5a;1a;  3 .
a 1 ktm 2 2
Do đó: AB  29  a   5 a   1 9  29 2
 2a 8a 6  0   . a  3  tm 
Suy ra: A2;4;3 ; BA2;4;  3 x  2 y  4 z  3 Vậy: d :   (thỏa mãn) 2 4 3
Câu 42: Tính tổng các nghiệm nguyên thuộc đoạn 5 ;10 của bất phương trình: 2 x x  2 x x   2 2 3 6
6  7x  29x  34 . A. 54. B. 40. C. 55. D. 41. Lời giải Chọn B 2 x x  2 x x   2 2 3 6
6  7x  29x  34 2 x x2 
 2x x  2 2 12 24
24  7x  29x  34   1 . a b Đặt 2
a 12x 24x 24; 2
b  7 x  29 x  34 a, b  0 . Suy ra: 2
x x  2  . Thay vào 1 5 ab a b t ta được: 5 2 a b 5 5  . a 2  .
b 2  f a   f b 2 , với f t 5
 .t2 là hàm số đồng biến
trên khoảng 0 ;    . x   Vậy  2 2  a  2 2
b 12x  24x  24  7x  29x 34  x x  2  2 0  .  x 1
Mà x nguyên thuộc đoạn 5 ;10 nên x 5;  4;  3; 2;1; 2;...;1  0 .
Vậy tổng các nghiệm nguyên thuộc đoạn 5 ;10 của bất phương trình đã cho là: 41.
y f x f   x x Câu 43: Cho hàm số có đạo hàm là
xe , x   f 0 và  2022 . Tính 2  f
 x2021dx .  0 A. 2 . B.  6 . C. 2 . D. 6 . Lời giải Chọn A
Ta có f x  f   xd x x xe d x x
x xe e C và 
f 0  2022  f   x x
x xe e  2021 2 2 Khi đó    2021d    x x f x x
xe e dx  2 . 0 0 1
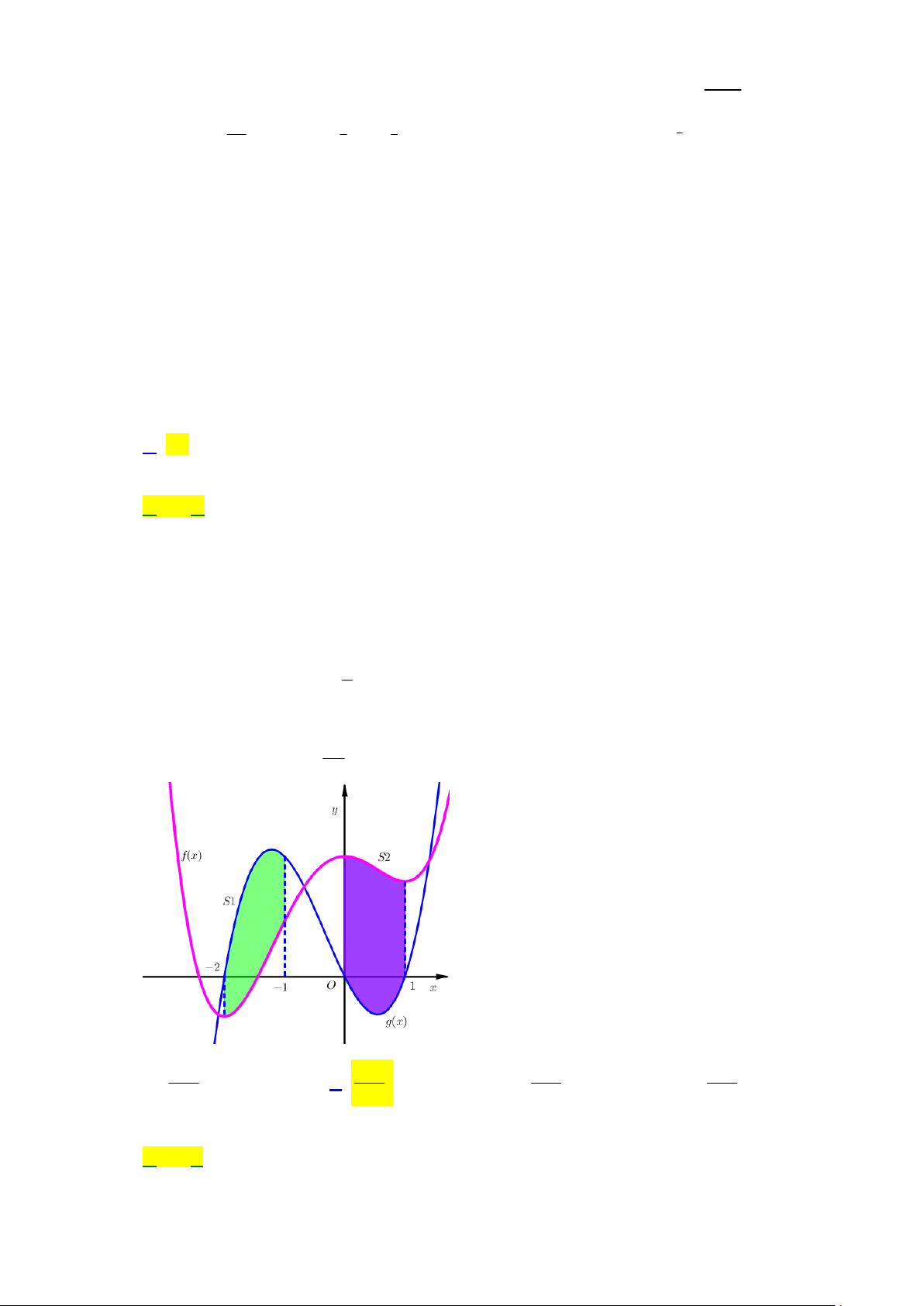
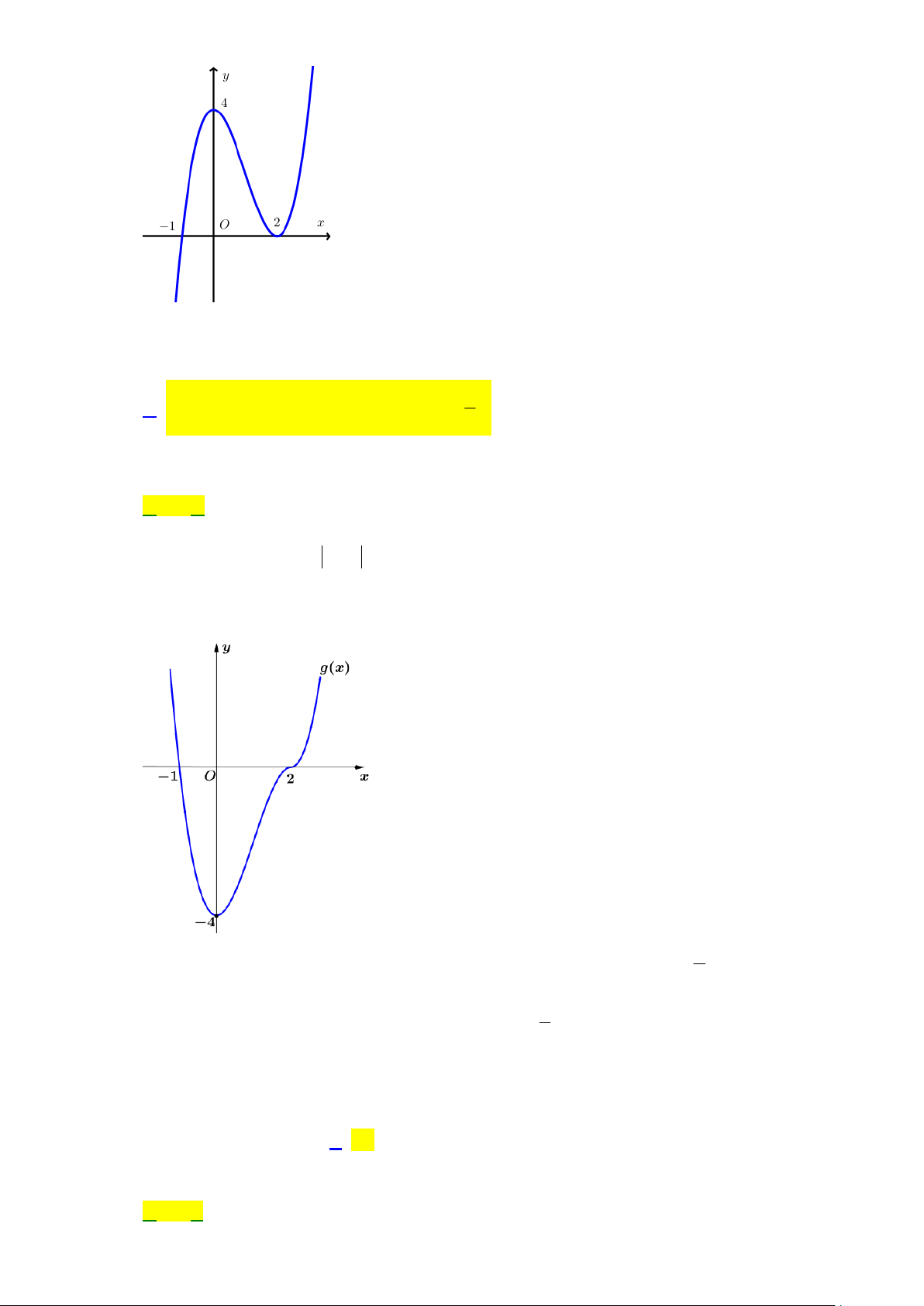
Câu 44: Cho hàm số f x 4 3 2
ax x x bx  2 và hàm số g x 3 2
cx dx  2 x (với , a , b , c d  3
) là các hàm số có đồ thị như hình vẽ bên dưới. Gọi S ; S là diện tích các hình phẳng tô màu 1 2 97
trong hình vẽ, biết S  . Tính S . 1 60 2 143 133 153 163 A. . B. . C. . D. . 60 60 60 60 Lời giải Chọn B
Ta thấy các nghiệm của phương trình g x   0 là các điểm cực trị của hàm số f x  .  4a kc 4a c    1 4 3 2         
f x  kg x kd d f x ax x x k  0 1 1   2       3 2   2  k k  1    g  x 3 2
 4ax x  2x  b  0  b  0 4 3 1 x 2x Ta có g  
1  0  a   f x  gx 2  
2x  2x  2 4 4 3 1 1 4 3   Khi đó x 2x 133
S   f x g x  dx      
 2x  2x  2 dx 1     2 .     4 3  60 0 2 2 2 2
Câu 45: Trong không gian với hệ trục tọa độ Oxyz , cho mặt cầu (S) : x  
1  y 2 z   3  48
x 1 y  2 z 3
và đường thẳng (d) :   . Điểm M( ; a ; b )
c (a  0) nằm trên đường thẳng (d) 1 1 2
sao cho từ M kẻ được 3 tiếp tuyến M , A M ,
B MC đến mặt cầu ( ) S thỏa mãn  AMB  60 ,  BMC  90 và 
CMA  120 . Tính Q a b c .
A. Q  6  4 2 .
B. Q  10  4 2 .
C. Q  9  4 2 .
D. Q  9  4 2 . Lời giải Chọn A
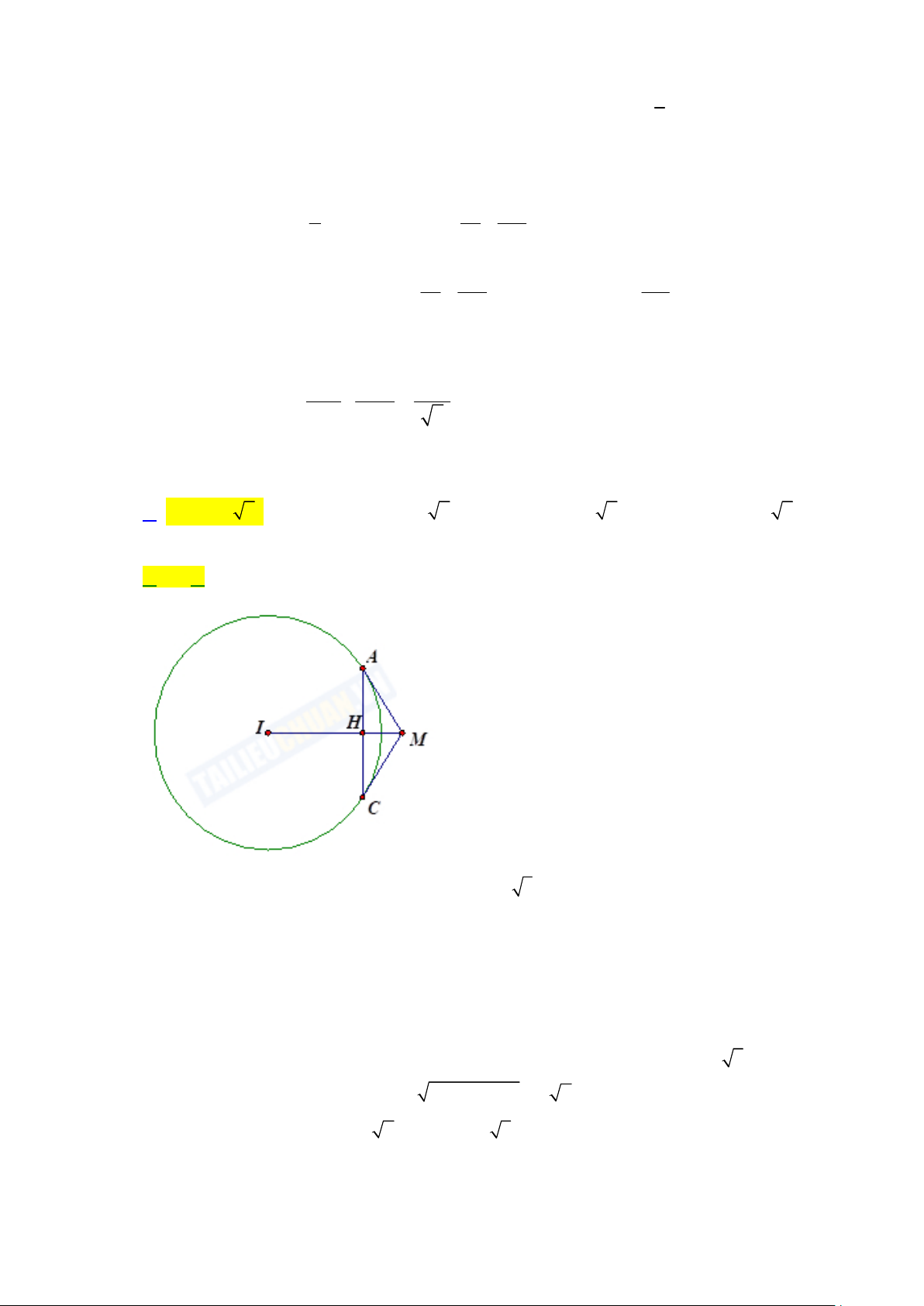
Mặt cầu S  có tâm I 1; 2;3 và bán kính R  4 3 .
Gọi đường tròn C  là giao tuyến của mặt phẳng  ABC  với mặt câu S  .
Đặt MA MB MC x x  0 .
Áp dụng định lý cosin trong AMB và CM A , ta có: 2 2 2
AB MA MB MA MB  2 2 2 2 .
.cos AMB  2x  2x cos 60  x AB x . 2 2 2
AC MA MC MA MC  2 2 2 2 .
.cos AMC  2x  2x cos120  3x AC x 3 .
Vì BMC vuông tại M nên: 2 2
BC MB MC x 2 .
Mặt khác AB BC x  x 2  x  x 2 2 2 2 2 2 2 3 3
AC nên  A B C vuông tại B .
Gọi H là trung điểm của A C thì H là tâm của đường tròn C  và ba điểm H, I,M thẳng hàng. Do  AMC  120 nên 
AIC  60 , suy ra AIC đều và AC IA IC R  4 3 . IA
Suy ra x 3  4 3  x  2 2.4 3
4 và IA IM cos30  IM    8. 3 3
Điểm M d nên M  t t t  IM t t  t2 2 2 2 2 1 ;2 ;3 2 2  4t .
t  4  M 3;6;34 2 Mà 2 2 IM 64 4t 64    
 t  4 M 
 5; 2;34 2 l
Vì x  0 nên điểm cần tìm là M 3;6;3 4 2, suy ra Q  6  4 2 . M
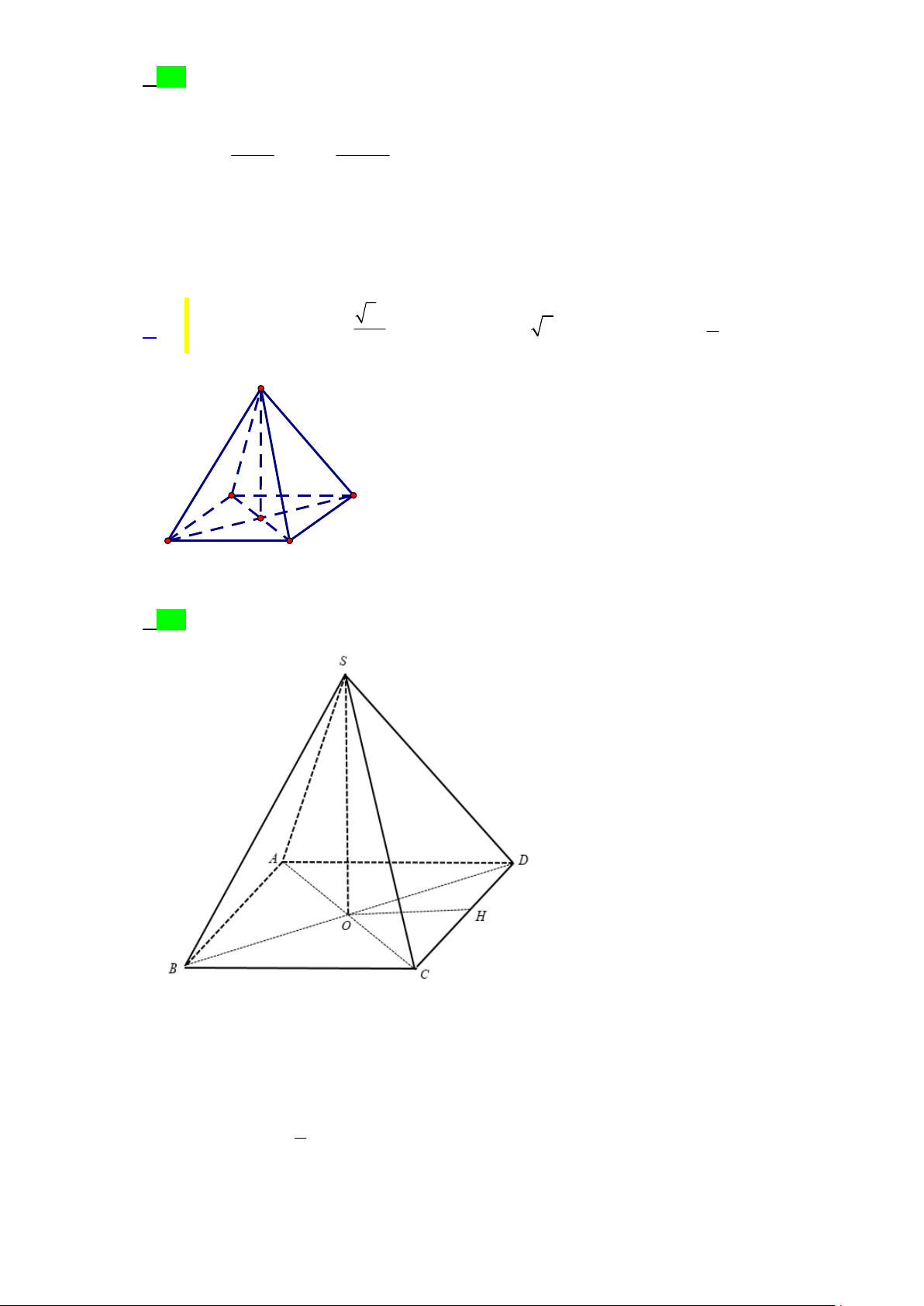
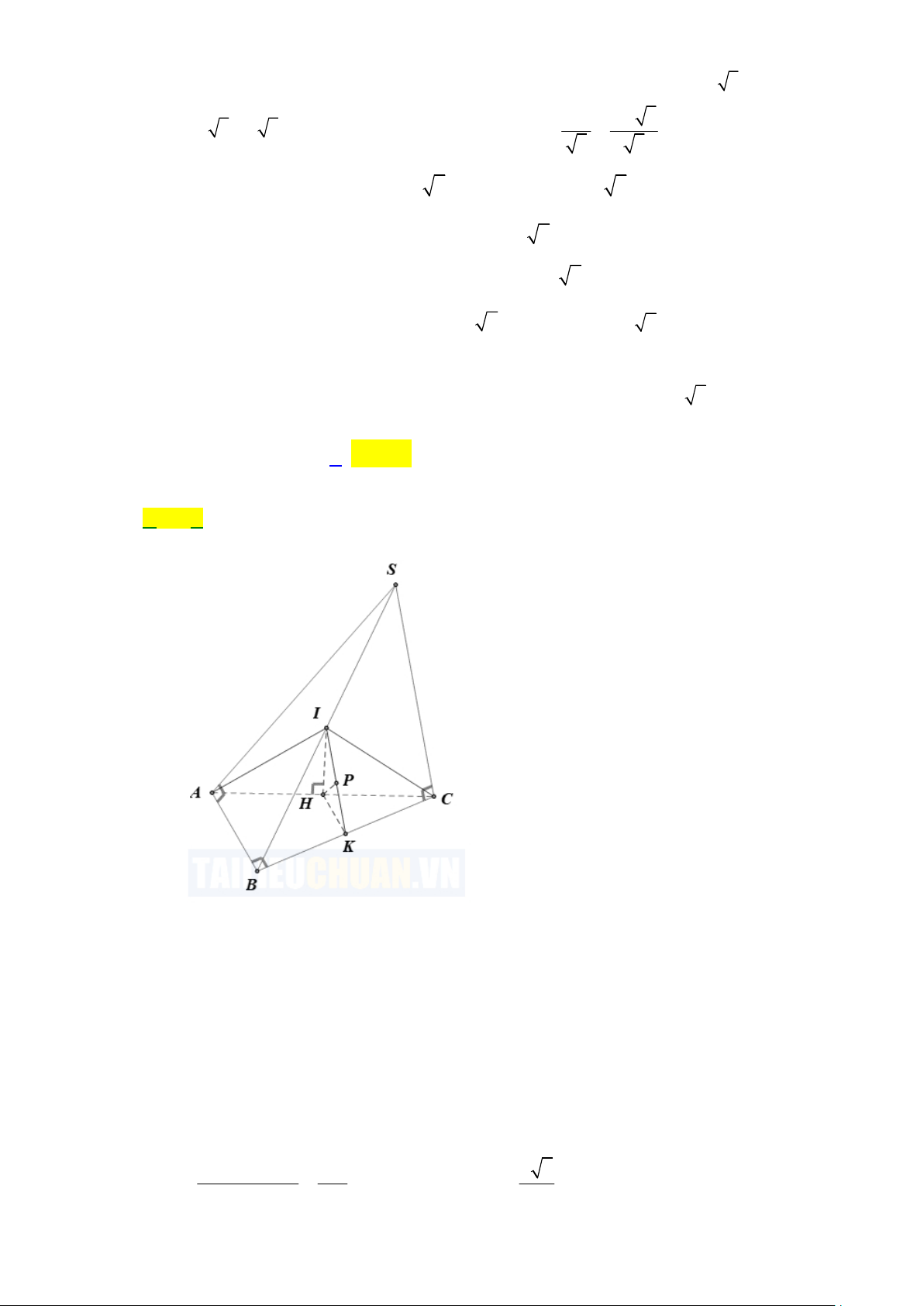
Câu 46: Cho hình chóp S.ABC có đáy A B C là tam giác vuông cân tại B , AB BC  3a , góc  SAB  
SCB  90 và khoảng cách từ A đến mặt phẳng SBC  bằng a 6 . Tính thể tích khối
cầu ngoại tiếp hình chóp S.ABC theo a . A. 3 108a . B. 3 36 a . C. 3 6 a . D. 2 36 a . Lời giải Chọn B
Gọi I,H lần lượt là trung điểm của cạnh SB và A C
Mặt khác, theo giả thiết ta có SA , B S
CB lần lượt là các tam giác vuông tại A và C
IA IB IC IS
I là tâm mặt cầu ngoại tiếp hình chóp S.ABC
Mặt khác:  A B C vuông tại B H là tâm đường tròn ngoại tiếp  A B C
IH   ABC d  ;
A SBC AC a 6 Ta có:     d  2
d H; SBC H;SBC  HC 2
Gọi K là trung điểm của cạnh BC HK BC HK / / AB, AB BC
Lại có: BC IH IH   ABC   BC  IHK
Mặt khác: BC  SBC   SBC   IHK  theo giao tuyến IK a
Trong IHK  , gọi HP IK HP  SBC  tại P HP d H SBC 6 ;  2 Xét 1 1 1 1 1 3 2aIHK :      HI  2 2 2 2 2 HP HI HK HI AB 2 4 4 Xét 2 2
IHB : IB IH HB  3a R . Vậy 3 3
V  R  36 a 3
Câu 47: Xét hai số phức z , z thỏa mãn  z  2  i 2  2 3i z z 3  i
z i z  1  2i 1    1 1  và 1 2 2 2
. Giá trị nhỏ nhất của z z bằng: 1 2 34 A. 7 B. 2 6 C. D. 2 2 5 Lời giải Chọn D
Gọi M x; y là điểm biểu diễn cho số phức z . 1 Từ giả thuyết, suy ra,
z  2  i . 2  2 3i z z . 3  i  2 z  2  i z z 1     1 1    1   1 1
 x     y  i yi  x  2   y  2 2 2 2 2 1 2 2
1  y x  4x  2y  5  0 1 5
Tập hợp điểm biểu diễn cho số phức z là parabol  P  có phương trình 2
y x  2x  . 2 2 2
Gọi N a;b  là điểm biểu diễn cho số phức z . 2 Từ giả thuyết, suy ra
z i z 1 2i a  b  
1 i  a  
1  b  2i a  b  2 1  a  2 1  b  22 2 2 2
2a  2b  4  0  a b  2  0 . Suy ra tập hợp điểm biểu diễn cho số phức z là đường thẳng 2
có phương trình a b  2  0 .  1 5 
Khi đó z z MN . Điểm M P 2  M ; x x  2x    1 2  2 2  1 2 5 1 2 9
x x  2x   2 x x  Khoảng cách 2 2 1  1 9 2 2  MNd M ,     x x  min   2 . min   2 2 2  2 2  1  1 9 
Giá trị nhỏ nhất của hàm số 2 x x  
 bằng 2 2 , dấu “=” xảy ra khi x  1 . 2  2 2 
Câu 48: Cho hàm số f x   x   x  2 1
2 có đồ thị như hình vẽ. Hỏi mệnh đề nào dưới đây đúng với
hàm số y x   2
2 . x x 2 .
A. Hàm số nghịch biến trên khoảng 1; .
B. Hàm số đồng biến trên khoảng 1; 0 .  1 
C. Hàm số nghịch biến trên khoảng  ;    .  2
D. Hàm số đồng biến trên khoảng 1; 2 . Lời giải Chọn C 2
x  2 . x x  2 khi x  2 
Xét hàm số y g x  x  2 . 2 x x  2    
 x2. 
 2x x2 khi x  2
Từ đó ta có đồ thị hàm số g x  như sau:  
Từ đồ thị suy ra hàm số g x  nghịch biến trên khoảng   1 ;0   ;      2   1 
Do đó hàm số g x  nghịch biến trên khoảng  ;    .  2
Câu 49: Có bao nhiêu số nguyên
x sao cho ứng với mỗi
x có không quá 255 số nguyên y thỏa mãn log  2
x y  log x y 5  4  ? A. 3 7 . B. 38. C. 4 0 . D. 36. Lời giải Chọn B
Điều kiện x y  0 và 2
x y  0 . Khi đó
log  2    log    2 log    2    5 x y x y x y x y
x y x y 5 4  log45 4      lo 4g5 2 x x x y
xy 1 Đặt 2 log 5
t x y thì 1 được viết lại là 4
x x tt 2 Với mỗi nguyên c x
ho trước có không quá 2 5 5 số nguyên y thỏa mãn bất phương trình 1
Tương đương với bất phương trình 2 có không quá 255 nghiệm t. Ta có hàm số   log 2 log 5 4 5 f t t
t đồng biến trên 1;   nên nếu 4 x x  256 256 369 thì
sẽ có ít nhất 2 5 6 nghiệm nguyên t  1 .
Do đó yêu cầu bài toán tương đương với 2
x x  369  1
 8 x 19 (do x nguyên).
Vậy có tất cả 38 số nguyên x thỏa yêu cầu bài toán.
Câu 50: Có bao nhiêu số nguyên dương a để phương trình 2
z  a   2
3 z a a  0 có 2 nghiệm phức
z , z thỏa mãn z z z z ? 1 2 1 2 1 2 A. 3. B. 4. C. 2. D. 1. Lời giải Chọn C 2
z  a   2
3 z a a  2 0 .   3  a 1  0a9. 5 2 13 5 2 13 2   0  3
a 10a 9  0   a  . 2 2 2 2 a  3  3
a 10a  9 a  3  3
a 10a  9
Khi đó phương trình có 2 nghiệm z  , z  1 2 2 2 2 2
z z z z  3  a  3
a 10a  9  3  a  3
a 10a  9 1 2 1 2 .  a  3  a2 0 2 2  3
a 10a  9  4a  4a  0  a 1 a  1 thỏa mãn.  5  2 13 a  2 2   0  3
a 10a  9  0   .(1)  5  2 13 a   2 2 2
z z z z  3  a i 3a 10a  9  3  a i 3a 10a  9 1 2 1 2  a   3  a2 1 2 2
 3a 10a  9  a 8a  9  0  a 9
a   1 loại vì không phải là số nguyên dương, a  9 thỏa mãn (1). Vậy có 2 giá trị
Document Outline

  • de-thi-thu-toan-tot-nghiep-thpt-2022-lan-1-truong-chuyen-bien-hoa-ha-nam
  • 65. Đề thi thử tốt nghiệp THPT năm 2021-2022 môn Toán - Chuyên Biên Hòa - Hà Nam (Lần 1) (File word có lời giải chi tiết).Image.Marked