Đề thi thử tốt nghiệp THPT 2020 môn Toán lần 1 sở GD&ĐT Hà Nội

Giới thiệu đến với các em học sinh đề thi thử tốt nghiệp THPT 2020 môn Toán lần 1 sở GD&ĐT Hà Nội gồm có 50 câu, đề thi có đáp án và lời giải chi tiết.

36 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

31 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC- $Gr oup$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 1
SỞ GD&ĐT HÀ NỘI
ĐỀ THI THỬ TỐT NGHIỆP THPTQG 2020
NĂM HỌC 2019 - 2020
MÔN TOÁN
Thời gian làm bài: 90 phút
Câu 1. Khối trụ tròn xoay có thể tích bằng và có bán kính đáy bằng 6. Đường sinh của khối trụ
bằng
A. . B. . C. . D. .
Câu 2. Trong các hàm số sau đây, hàm số nào nghịch biến trên tập ?
A. . B. . C. . D. .
Câu 3. Giá trị của tích phân bằng
A. . B. . C. . D. .
Câu 4. Đường cong ở hình bên là đồ thị của hàm số nào dưới đây?
A. . B. . C. . D. .
Câu 5. Trong không gian , cho mặt phẳng . Vectơ nào dưới đây không
phải là một vectơ pháp tuyến của mặt phẳng ?
A. . B. . C. . D. .
Câu 6. Cho số phức . Số phức liên hợp của là
A. . B. . C. . D. .
Câu 7. Trong mặt phẳng , điểm biểu diễn số phức có tọa độ là
A. . B. . C. . D. .
Câu 8. Cho các số thực dương và . Biểu thức bằng
A. . B. . C. . D. .
Câu 9. Thể tích khối lăng trụ tam giác có chiều cao bằng , cạnh đáy lần lượt bằng , , là:
144
p
4
6
12
10
!
x
y
p
=
1
3
x
y
æö
=
ç÷
èø
3
x
y =
2
0
2d
ò
xx
8
6
2
4
3
21=- + +yx x
1
1
-
=
+
x
y
x
1
1
+
=
-
x
y
x
32
1=-+yx x
Oxyz
( )
:2320200Px y z-++ =
( )
P
( )
2; 4; 6n =- -
!
( )
1; 2; 3n =- -
!
( )
1; 2; 3n =-
!
( )
2; 3 ; 2020n =-
!
53zi=+
z
53i-+
53i--
53i-
53i -
( )
Oxy
M
13zi=- -
( )
1; 3M -
( )
1; 3M --
( )
1; 3M -
,ab
1a ¹
2
log
a
ab
( )
21 log
a
b+
2log
a
b
2log
a
b+
1log
a
b+
2
3
4
5
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 2
A. . B. . C. . D. .
Câu 10. Trong các khối hình sau, khối không phải khối tròn xoay là:
A. Khối cầu. B. Khối trụ. C. Khối lăng trụ. D. Khối nón.
Câu 11. Họ tất cả các nguyên hàm của hàm số là
A. . B. .
C. . D. .
Câu 12. Trong không gian với hệ tọa độ , cho . Tọa độ của là
A. . B. . C. . D. .
Câu 13. Cho số thực dương , thỏa mãn và . Tính .
A. . B. . C. . D. .
Câu 14. Trong không gian , cho điểm và mặt phẳng . Phương
trình mặt phẳng nào dưới đây đi qua điểm và song song với .
A. . B. .
C. . D. .
Câu 15. Cho hàm số có đồ thị như hình vẽ bên.
Hàm số đã cho nghịch biến trên khoảng
A. . B. . C. . D. .
Câu 16. Đồ thị hàm số có đường tiệm cận ngang là đường thẳng nào sau đây?
A. . B. .
C. . D. .
Câu 17. Gọi là tập nghiệm của phương trình . Tổng các phần tử của bằng
8.
12.
4.
28.
( )
2
sinfx x
x
=+
cos 2lnxxC++
2
2
cosxC
x
-+
cos 2lnxxC-+ +
cos 2lnxxC-- +
Oxyz
23 5aijk=- + +
!!!!
a
!
( )
2;3;5-
( )
2;3; 5-
( )
2; 3; 5--
2
x
y
1x ¹
log 3
x
y =
3
5
log
x
Ty=
5
3
T =
9
5
T =
3
5
T =
5T =
Oxyz
( )
2; 1;3M -
( )
:2 5 1 0xyz
a
-+-=
M
( )
a
25 120xyz-+-=
25 120xyz---=
25 120xyz+--=
25 120xyz-++=
( )
yfx=
( )
0 ; 2
( )
3 ; 1--
( )
1 ; 0-
( )
1 ; 3
2
21
x
y
x
+
=
+
1x =-
2y =
1
2
y =
1
2
x
-
=
S
9 10.3 9 0
xx
-+=
S
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 3
A. . B. . C. . D. .
Câu 18. Một xe ô tô đang chuyển động đều với vận tốc thì người lái xe nhìn thấy một chướng
ngại vật nên đạp phanh tại điểm đó, ô tô chuyển động chậm dần đều với vận tốc
trong đó là thời gian (tính bằng giây) kể từ lúc đạp phanh. Quãng đường mà ô tô đi được trong
giây cuối cùng bằng
A. . B. . C. . D. .
Câu 19. Cho hàm số có đạo hàm Mệnh đề nào sau đây đúng?
A. . B. . C. . D. .
Câu 20. Cho hình vuông tâm độ dài cạnh là Đường cong là một phần parabol
đỉnh chia hình vuông thành hai hình phẳng có diện tích lần lượt là và (tham khảo hình
vẽ).
Tỉ số bằng
A. . B. . C. . D. .
Câu 21. Một cấp số nhân có số hạng thứ 3 và số hạng thứ 6 lần lượt là và . Khi đó số hạng thứ
của cấp số nhân bằng:
A. . B. . C. . D. .
Câu 22. Tìm hàm số không là nguyên hàm của hàm số .
A. . B. . C. . D. .
Câu 23. Cho hàm số xác định, liên tục trên và có bảng biến thiên như hình bên
Đồ thị hàm số cắt đường thẳng tại bao nhiêu điểm?
A. . B. . C. . D. .
1
2
10
10
3
16 /ms
( )
216vt t=- +
t
10
60m
64m
160m
96m
( )
yfx=
( )
1,fx
¢
=
.x"Î!
( ) ( )
12ff-<
( ) ( )
12ff-=
( ) ( )
12ff-³
( ) ( )
12ff->
ABCD
,O
4.cm
BOC
O
1
S
2
S
1
2
S
S
1
2
3
5
2
5
1
3
9
243-
8
2187
2187-
729
243
( )
Fx
( )
sin 2fx x=
( )
2
cosFx x=-
( )
2
sinFx x=
( )
1
cos 2
2
Fx x=-
( )
cos 2Fx x=-
( )
fx
!
x
-¥
1-
0
1
+¥
'y
+
0
-
0
+
0
-
y
3
3
-¥
1-
-¥
( )
yfx=
2y =-
0
2
1
4
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 4
Câu 24. Trong không gian cho hai điểm Phương trình mặt cầu đường
kính là
A. . B. .
C. . D. .
Câu 25. Tập nghiệm của bất phương trình là
A. . B. . C. . D. .
Câu 26. Cho hàm số liên tục trên và có bảng xét dấu của đạo hàm như hình bên.
Mệnh đề nào sau đây sai?
A. Hàm số đạt cực tiểu tại . B. Hàm số đạt cực đại tại .
C. Hàm số đạt cực đại tại . D. Hàm số đạt cực tiểu tại .
Câu 27. Cho hình hộp . Bộ 3 vectơ không đồng phẳng là:
A. . B. .
C. . D. .
Câu 28. Cho hai số phức thỏa mãn . Giá trị biểu thức bằng
A. 13. B. 25. C. 7. D. 19.
Câu 29. Trong không gian với hệ tọa độ , cho , , . Xác định tọa
độ điểm để là hình bình hành?
A. . B. . C. . D. .
Câu 30. Giá trị nhỏ nhất của hàm số trên đoạn là
A. . B. . C. . D. .
Câu 31. Cho hàm số có đạo hàm liên tục trên , thỏa mãn và . Tích
phân có giá trị là
A. . B. . C. . D. .
Câu 32. Trong không gian với hệ trục tọa độ , cho hai điểm ; . Phương trình
nào sau đây là phương trình dạng chính tắc của đường thẳng đi qua hai điểm và ?
A. . B. .
C. . D. .
Ox ,yz
( ) ( )
2; 1; 0 , 2; 5; 4 .AB--
AB
( ) ( )
22
2
2112xyz++-+=
( ) ( )
22
2
3248xy z+- ++ =
( ) ( ) ( )
222
44448xyz-+-++=
( ) ( )
22
2
3212xy z+- ++ =
( ) ( )
55
log 3 1 log 25 25xx+< -
1
;1 .
3
æö
-
ç÷
èø
6
;.
7
æö
-¥
ç÷
èø
16
;.
37
æö
-
ç÷
èø
6
;1 .
7
æö
ç÷
èø
( )
yfx=
[ ]
3; 3-
1x =
2x =
1x =-
0x =
.ABCD A B C D
¢¢¢ ¢
,,''AC BD A D
!!!" !!!" !!!!!"
,','AC AC BB
!!!" !!!!" !!! "
,',''AB BD C D
!!!" !!!!" !!!!!"
', ', 'AC B DBD
!!!!" !!!!" !!!!"
12
,zz
11 2
4, 3zz z==
22
12
Pz z=+
Oxyz
( )
2; 1; 3-M
( )
3; 2; 4-N
( )
1; 1; 2-P
Q
MNPQ
( )
2; 2; 5-Q
( )
2; 3; 5--Q
( )
0; 4;9-Q
( )
1; 3; 2-Q
2
1
-
=
+
x
y
x
[ ]
0; 3
[ ]
0;3
min 3
Î
=-
x
y
[ ]
0;3
min 2
Î
=-
x
y
[ ]
0;3
1
min
4
Î
=
x
y
[ ]
0;3
1
min
2
Î
=-
x
y
( )
yfx=
[ ]
0;1
( )
1
0
d3fx x=
ò
( )
14f =
( )
1
0
dxf x x
¢
ò
1
2
-
1
2
1
1-
Oxyz
( )
1;0;3A
( )
5;2 ; 1B -
A
B
13
52 1
xyz--
==
-
13
21 2
xyz--
==
--
311
21 2
xyz---
==
-
521
212
xyz--+
==
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 5
Câu 33. Có 3 quả bóng tennis được chứa trong một hộp hình trụ (hình vẽ bên) với chiều cao và
bán kính .
Thể tích bên trong hình trụ không bị chiếm lấy bởi các quả bóng tennis (bỏ qua độ dày của vỏ
hộp) bằng bao nhiêu?
A. . B. . C. . D. .
Câu 34. Có bao nhiêu số tự nhiên có hai chữ số khác nhau?
A. 72. B. 81. C. 90. D. 18.
Câu 35. Cho hàm số có đạo hàm Số điểm cực trị của
hàm số là
A. . B. . C. . D. .
Câu 36. Cho hàm số có đồ thị hàm số như hình vẽ bên
Hàm số đồng biến trên khoảng?
A. . B. . C. . D. .
Câu 37. Trong không gian với hệ tọa độ , cho điểm và mặt phẳng
. Mặt cầu có tâm , cắt theo một đường tròn có bán kính . Mặt cầu có phương
trình là:
A. . B. .
C. . D. .
Câu 38. Đầu tháng một người gửi ngân hàng đồng ( triệu đồng) với lãi suất gửi là
mỗi tháng theo hình thức lãi suất kép. Cuối mỗi tháng người đó đều đặn gửi vào ngân hàng số
tiền là ( triệu đồng). Hỏi sau ít nhất bao nhiêu tháng ( kể từ lúc người này ra ngân
hàng gửi tiền) thì số tiền người đó tích lũy được lớn hơn (bảy trăm triệu đồng)?
21
cm
3,5
cm
82,75
p
3
cm
87 ,25
p
3
cm
85,75
p
3
cm
87,75
p
3
cm
( )
fx
( )
( )
( ) ( )
23
2
24, .fx x xx x x
¢
=+ - - "Î!
( )
fx
2
3
1.
4
( )
yfx=
( )
yfx=
( )
2
12yfx x x=+++
( )
3; 2--
( )
3; 0-
( )
0;1
Oxyz
( )
1( 2;1 ;I
( )
:2 2 1 0Pxyz++ -=
( )
S
I
( )
P
4r =
( )
S
( ) ( ) ( )
222
21120xyz+++++=
( ) ( ) ( )
222
21118xyz-+-+-=
( ) ( ) ( )
222
21120xyz-+-+-=
( ) ( ) ( )
222
21125xyz-+-+-=
400.000.000
400
0, 6%
10.000.000
10
700.000.000
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 6
A. tháng. B. tháng. C. tháng. D. tháng.
Câu 39. Cho đồ thị hàm số như hình vẽ dưới đây:
Đồ thị của hàm số có bao nhiêu đường tiệm cận đứng?
A. . B. . C. . D. .
Câu 40. Cho hàm số có bảng xét dấu của đạo hàm như hình bên.
Hàm số nghịch biến trên khoảng
A. . B. . C. . D. .
Câu 41. Trong không gian với hệ tọa độ , cho hình hộp biết ,
, và . Tọa độ đỉnh của hình hộp là
A. . B. . C. . D. .
Câu 42. Cho hình chóp có đáy là hình vuông cạnh , là tam giác cân tại và
nằm trong mặt phẳng vuông góc với mặt phẳng . Gọi lần lượt là trung điểm của
và là trọng tâm . Biết khoảng cách từ điểm đến mặt phẳng bằng
. Thể tích của khối chóp bằng
A. . B. . C. . D. .
Câu 43. Cho hình thang biết , , , . Thể tích khối tròn
xoay tạo thành khi quay hình thang quanh trục bằng
A. . B. . C. . D. .
Câu 44. Cho lăng trụ có đáy là tam giác đều cạnh , hình chiếu vuông góc của đỉnh lên
là trung điểm của cạnh . Góc giữa đường thẳng và mặt đáy bằng . Khoảng
cách giữa và là
A. . B. . C. . D. .
22
23
25
24
32
yax bx cxd=+++
( )
( ) ( )
2
2
32
36
xx
gx
fx fx
--
=
-
5
4
3
2
( )
fx
( )
1yf x=-
( )
1; 4
( )
0; 2
( )
0;1
( )
2; 1--
Oxyz
.ABCD A B C D
¢¢¢¢
( )
1; 2;3A
( )
2;0; 1B
¢
-
( )
3;0 ; 3C -
( )
2; 4; 3D
¢
--
B
.ABCD A B C D
¢¢¢¢
( )
4; 1;1B -
( )
2; 1; 2B -
( )
4;1; 1B -
( )
0;1; 3B -
.S ABCD
2AB a=
SABD
S
( )
ABCD
,MN
,AB BC
G
SCDD
M
( )
SND
32
4
a
.G AMND
3
53
2
a
3
53
6
a
3
53
3
a
3
53
18
a
ABCD
( )
//AB CD
5AB =
3BC =
10CD =
4AD =
ABCD
( )
//AB CD
AD
128
p
84
p
112
p
90
p
.ABC A B C
¢¢¢
a
A
¢
( )
ABC
H
AB
AC
¢
60°
BB
¢
AC
¢
13
39
a
313
13
a
213
13
a
13
13
a
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 7
Câu 45. Tập xác định của hàm số là một khoảng có độ dài
với và là số nguyên dương và nguyên tố cùng nhau. Khi đó bằng:
A. . B. . C. . D. .
Câu 46. Số điểm cực đại của đồ thị hàm số bằng
A. . B. . C. . D. .
Câu 47. Cho các số thực dương , thỏa mãn và ,
, , là các số nguyên dương. Khi đó kết quả bằng
A. . B. . C. . D. .
Câu 48. Cho hàm số có đồ thị như hình vẽ bên
Giá trị nguyên lớn nhất của tham số để hàm số đồng biến trên khoảng
là
A. . B. . C. . D. .
Câu 49. Cho hàm số liên tục trên và thoả mãn .
Khi đó bằng:
A. . B. . C. . D. .
Câu 50. Một hộp đựng thẻ được đánh số từ đến . Rút ngẫu nhiên hai thẻ từ hộp nêu ở trên, tính xác
suất để tích của hai số trên hai thẻ này là số chẵn.
A. . B. . C. . D. .
…..HẾT…..
( )
14116 1
24 16
log log log log logfx x
æö
æö
æö
æö
ç÷
=
ç÷
ç÷
ç÷
ç÷
ç÷
ç÷
èø
èø
èø
èø
m
n
m
n
mn-
240-
271
241
241-
( )( )( ) ( )
123...100yx x x x=- - - -
50
99
49
100
x
y
log log log log 100xyxy+++=
log x
log y
log x
log y
xy
200
10
100
10
164
10
144
10
32
yax bx cxd=+++
m
( )
yfxm=-
( )
10 ;+¥
10-
10
9
11
( )
fx
!
( ) ( )
2
32
1,
x
xf x f x e x+-="Î!
( )
0
1
dfx x
-
ò
0
( )
31e -
( )
31 e-
3e
9
1
9
25
81
13
18
5
18
1
2
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 8
SỞ GD&ĐT HÀ NỘI
ĐÁP ÁN ĐỀ THI THỬ TỐT NGHIỆP THPTQG 2020
NĂM HỌC 2019 - 2020
MÔN TOÁN
Thời gian làm bài: 90 phút
BẢNG ĐÁP ÁN
1.A
2.B
3.D
4.C
5.D
6.C
7.B
8.C
9.B
10.C
11.C
12.B
13.D
14.A
15.C
16.C
17.B
18.D
19.A
20.A
21.B
22.D
23.B
24.D
25.C
26.D
27.D
28.A
29.C
30.B
31.C
32.C
33.C
34.B
35.B
36.D
37.C
38.B
39.A
40.D
41.A
42.D
43.B
44.B
45.D
46.C
47.C
48.C
49.B
50.B
LỜI GIẢI CHI TIẾT
Câu 1. Khối trụ tròn xoay có thể tích bằng và có bán kính đáy bằng 6. Đường sinh của khối trụ
bằng
A. . B. . C. . D. .
Lời giải
Tác giả: Bùi Thị Dung; Fb: Bui Thi Dung
Chọn A
Gọi lần lượt là chiều cao, đường sinh và bán kính đáy của khối trụ.
Ta có: .
Vậy khối trụ có độ dài đường sinh là: .
Câu 2. Trong các hàm số sau đây, hàm số nào nghịch biến trên tập ?
A. . B. . C. . D. .
Lời giải
Tác giả: Bùi Thị Dung; Fb: Bui Thi Dung
Chọn B
Hàm số mũ nghị ch biến trên tập khi và chỉ khi .
Câu 3. Giá trị của tích phân bằng
A. . B. . C. . D. .
Lời giải
Tác giả: Dương Đức Tuấn; Fb: Dương Tuấn
Chọn D
Ta có: .
Câu 4. Đường cong ở hình bên là đồ thị của hàm số nào dưới đây?
144
p
4
6
12
10
,,hl r
2
Vrh
p
=
2
144 .6 . 4hh
pp
Û= Þ=
4lh==
!
x
y
p
=
1
3
x
y
æö
=
ç÷
èø
3
x
y =
x
ya=
!
01a<<
2
0
2d
ò
xx
8
6
2
4
2
2
222
0
0
2d 2 0 4==-=
ò
xx x
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 9
A. . B. . C. . D. .
Lời giải
Tác giả: Dương Đức Tuấn; Fb: Dương Tuấn
Chọn C
Dựa vào hình vẽ suy ra đồ thị hàm số có 2 đường tiệm cận là và .
Vậy đường cong ở trên là đồ thị hàm số .
.
Câu 5. [Mức độ 1] Trong không gian , cho mặt phẳng . Vectơ nào dưới
đây không phải là một vectơ pháp tuyến của mặt phẳng ?
A. . B. . C. . D. .
Lời giải
Người làm: Nguyễn Ngọc Thảo; Fb:Nguyễn Ngọc Thảo
Chọn D
+) Mặt phẳng có một vectơ pháp tuyến là .
+) Các vectơ ở phương án A;B;C cùng phương với nên cũng là vectơ pháp tuyến của .
+) Vectơ ở phương án D không cùng phương với nên không phải là vectơ
pháp tuyến của .
Câu 6. Cho số phức . Số phức liên hợp của là
A. . B. . C. . D. .
Lời giải
Người làm: Nguyễn Ngọc Thảo; Fb:Nguyễn Ngọc Thảo
Chọn C
3
21=- + +yx x
1
1
-
=
+
x
y
x
1
1
+
=
-
x
y
x
32
1=-+yx x
1=x
1=y
1
1
+
=
-
x
y
x
Oxyz
( )
:2320200Px y z-++ =
( )
P
( )
2; 4; 6n =- -
!
( )
1; 2; 3n =- -
!
( )
1; 2; 3n =-
!
( )
2; 3 ; 2020n =-
!
( )
:2320200Px y z-++ =
( )
1; 2; 3
P
n =-
!!"
P
n
!!"
( )
P
( )
2; 3 ; 2020n =-
!
P
n
!!"
( )
P
53zi=+
z
53i-+
53i--
53i-
53i -
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 10
Số phức có số phức liên hợp là .
Vậy số phức có số phức liên hợp là .
Câu 7. Trong mặt phẳng , điểm biểu diễn số phức có tọa độ là
A. . B. . C. . D. .
Lời giải
Người làm: Nguyễn Phương Thu; Fb: Nguyễn Phương Thu
Chọn B
Điểm biểu diễn số phức là .
Câu 8. Cho các số thực dương và . Biểu thức bằng
A. . B. . C. . D. .
Lời giải
Người làm: Nguyễn Phương Thu; Fb: Nguyễn Phương Thu
Chọn C
Ta có: .
Câu 9. Thể tích khối lăng trụ tam giác có chiều cao bằng , cạnh đáy lần lượt bằng , , là:
A. . B. . C. . D.
Lời giải
Người làm:Trần Thu Hương; Fb:Trần Thu Hương
Chọn B
Khối lăng trụ tam giác có cạnh đáy lần lượt là , , .
Vậy đáy là tam giác vuông có hai cạnh góc vuông lần lượt là , .
Thể tích khối lăng trụ: .
.
Câu 10. Trong các khối hình sau, khối không phải khối tròn xoay là:
A. Khối cầu. B. Khối trụ.
C. Khối lăng trụ. D. Khối nón.
Lời giải
Ngườilàm:Trần Thu Hương; Fb: Trần Thu Hương
Chọn. C.
Khối lăng trụ không phải khối tròn xoay.
kieunga03@gmail.com; Gmail Gv phản biện vòng 2.
Câu 11. Họ tất cả các nguyên hàm của hàm số là
A. . B. .
C. . D. .
Lời giải
( )
,;zabiab=+ Î!
zabi=-
53zi=+
53zi=-
( )
Oxy
M
13zi=- -
( )
1; 3M -
( )
1; 3M --
( )
1; 3M -
M
13zi=- -
( )
1; 3M --
,ab
1a ¹
2
log
a
ab
( )
21 log
a
b+
2log
a
b
2log
a
b+
1log
a
b+
22
log log log 2 log log 2 log
aaaaa a
ab a b a b b=+= +=+
2
3
4
5
8.
12.
4.
28.
3
4
5
3
4
1
..3.4.212
2
VBh== =
( )
2
sinfx x
x
=+
cos 2lnxxC++
2
2
cosxC
x
-+
cos 2lnxxC-+ +
cos 2lnxxC-- +
A'
A
B'
B
C'
C
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 11
Tác giả: Kiều Thị Thúy, Fb: Thúy Kiều
Chọn C
.
Câu 12. Trong không gian với hệ tọa độ , cho . Tọa độ của là
A. . B. . C. . D. .
Lời giải
Tác giả: Kiều Thị Thúy, Fb: Thúy Kiều
Chọn B
Tọa độ của là .
Câu 13. Cho số thực dương , thỏa mãn và . Tính .
A. . B. . C. . D. .
Lời giải
Tác giả: Thành Đức Trung; Fb: Thành Đức Trung
Chọn D
Ta có .
Suy ra .
Vậy .
Câu 14. Trong không gian , cho điểm và mặt phẳng . Phương
trình mặt phẳng nào dưới đây đi qua điểm và song song với .
A. . B. .
C. . D. .
Lời giải
Tác giả: Thành Đức Trung; Fb: Thành Đức Trung
Chọn A
Gọi là mặt phẳng đi qua điểm và song song với .
Ta có nên có một véc-tơ pháp tuyến là .
Mặt phẳng đi qua điểm và song song với có phương trình là
.
Câu 15. Cho hàm số có đồ thị như hình vẽ bên.
2
sin d cos 2lnxx xxC
x
æö
+=-+ +
ç÷
èø
ò
Oxyz
23 5aijk=- + +
!!!!
a
!
( )
2;3;5-
( )
2;3; 5-
( )
2; 3; 5--
a
!
( )
2; 3; 5-
2
x
y
1x ¹
log 3
x
y =
3
5
log
x
Ty=
5
3
T =
9
5
T =
3
5
T =
5T =
3
log 3
x
yyx=Û =
( )
33
5
315
1
log log .15.log 5
3
x
xx
Tx x x=== =
5T =
Oxyz
( )
2; 1;3M -
( )
:2 5 1 0xyz
a
-+-=
M
( )
a
25 120xyz-+-=
25 120xyz---=
25 120xyz+--=
25 120xyz-++=
( )
P
M
( )
a
( ) ( )
//P
a
( )
P
( )
2; 5;1
P
n =-
!!"
( )
P
M
( )
a
( ) ( )
2251 3025 120xyz xyz-- ++-=Û - +-=
( )
yfx=
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 12
Hàm số đã cho nghịch biến trên khoảng
A. . B. . C. . D. .
Lời giải
Người làm: Trần Văn Đô; Fb: Tran Tran Do
Chọn C
Dựa vào đồ thị ta thấy: Hàm số nghịch biến trên các khoảng là và .
Nên hàm số cũng nghị ch biến .
Câu 16. Đồ thị hàm số có đường tiệm cận ngang là đường thẳng nào sau đây?
A. . B. .
C. . D. .
Lời giải
Người làm: Trần Văn Đô; Fb: Tran Tran Do
Chọn C
Ta có: ; .
Do đó tiệm cận ngang của đồ thị hàm số là đường thẳng .
Người làm:hoangdang.sun2018@gmail.com, người thu bài:.
Câu 17. Gọi là tập nghiệm của phương trình . Tổng các phần tử của bằng
A. . B. . C. . D. .
Lời giải
( )
0 ; 2
( )
3 ; 1--
( )
1 ; 0-
( )
1 ; 3
( )
1 ; 1-
( )
2 ; 3
( )
1 ; 0-
2
21
x
y
x
+
=
+
1x =-
2y =
1
2
y =
1
2
x
-
=
21
lim
212
x
x
x
®+¥
+
=
+
21
lim
212
x
x
x
®-¥
+
=
+
1
2
y =
S
9 10.3 9 0
xx
-+=
S
1
2
10
10
3
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 13
Người làm:Huỳnh Thị Ngọc Dung; Fb: Huỳnh Dung Ngọc Dung
Chọn B
.
Vậy tổng các phần tử của bằng .
Câu 18. Một xe ô tô đang chuyển động đều với vận tốc thì người lái xe nhìn thấy một chướng
ngại vật nên đạp phanh tại điểm đó, ô tô chuyển động chậm dần đều với vận tốc
trong đó là thời gian (tính bằng giây) kể từ lúc đạp phanh. Quãng đường mà ô tô đi được trong
giây cuối cùng bằng
A. . B. . C. . D. .
Lời giải
Người làm: Huỳnh Thị Ngọc Dung; Fb: Huỳnh Dung Ngọc Dung.
Chọn D
Lấy mốc thời gian lúc ô tô bắt đầu đạp phanh.
Khi ô tô dừng hẳn thì .
Quãng đường mà ô tô đi được trong giây cuối:
Theo đề bài: ô tô đi được 10 giây cuối cùng nên 2 giây đầu ô tô đi được: .
Vậy quãng đường ô tô đi được trong 10 giây cuối: .
Câu 19. Cho hàm số có đạo hàm Mệnh đề nào sau đây đúng?
A. . B. . C. . D. .
Lời giải
Người làm: Lương Công Sự; Fb: Lương Công Sự
Chọn A
Vì nên là hàm số đồng biến trên
.
31 0
910.390
2
39
x
xx
x
x
x
é
==
é
-+=Û Û
ê
ê
=
=
ë
ë
Þ
{ }
0,2S =
S
2
16 /ms
( )
216vt t=- +
t
10
60m
64m
160m
96m
( )
02160 8vt t t=Û-+ =Û=
8
( )
( )
( )
8
2
0
8
2 16 16 64 .
0
t dt t t m-+ =-+ =
ò
16.2 32m=
64 32 96m+=
( )
yfx=
( )
1,fx
¢
=
.x"Î!
( ) ( )
12ff-<
( ) ( )
12ff-=
( ) ( )
12ff-³
( ) ( )
12ff->
( )
10fx
¢
=>
x"Î!
( )
fx
.!
( ) ( )
12 1 2.ff-< Þ - <
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 14
Câu 20. Cho hình vuông tâm độ dài cạnh là Đường cong là một phần parabol
đỉnh chia hình vuông thành hai hình phẳng có diện tích lần lượt là và (tham khảo hình
vẽ).
Tỉ số bằng
A. . B. . C. . D. .
Lời giải
Người làm: Lương Công Sự; Fb: Lương Công Sự
Chọn A
Chọn hệ trục tọa độ với là gốc tọa độ, trục đi
qua trung điểm của và
Parabol có dạng
Vì điểm nên
Vậy
Vậy .
Câu 21. Một cấp số nhân có số hạng thứ 3 và số hạng thứ 6 lần lượt là và . Khi đó số hạng thứ
của cấp số nhân bằng:
A. . B. . C. . D. .
Lời giải
Người làm: Phạm Văn Nghiệp; Fb: Phạm Văn Nghiệp
Chọn B
Gọi là số hạng đầu, là công bội của cấp số nhân.
ABCD
,O
4.cm
BOC
O
1
S
2
S
1
2
S
S
1
2
3
5
2
5
1
3
,Oxy
O
Ox
AB
.CD
( )
2
:.Pyax=
( ) ( )
2;2CPÎ
1
24 .
2
aa=Û=
( )
2
1
:.
2
Py x=
2
2
1
2
116
2d.
23
Sxx
-
æö
=- =
ç÷
èø
ò
21
16 32
16 .
33
ABCD
SS S=-=-=
1
2
1
.
2
S
S
=
9
243-
8
2187
2187-
729
243
1
u
q
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 15
Ta có: .
Khi đó .
Câu 22. Tìm hàm số không là nguyên hàm của hàm số .
A. . B. . C. . D. .
Lời giải
Người làm: Phạm Văn Nghiệp; Fb: Phạm Văn Nghiệp
Chọn D
Vì nên không phải là một nguyên hàm của hàm số
.
Câu 23. Cho hàm số xác định, liên tục trên và có bảng biến thiên như hình bên
Đồ thị hàm số cắt đường thẳng tại bao nhiêu điểm?
A. . B. . C. . D. .
Lời giải
Người làm: Bùi Thị Nhung; Fb: Bùi Nhung
Chọn B
Vì nên đường thẳng nằm dưới đường thẳng
Từ bảng biến thiên suy ra đồ thị hàm số cắt đường thẳng tại 2 điểm phân
biệt.
Câu 24. Trong không gian cho hai điểm Phương trình mặt cầu đường
kính là
A. . B. .
C. . D. .
Lời giải
2
31
5
61
uuq
uuq
ì
=
ï
í
=
ï
î
3
6
3
243
27 3
9
u
qq
u
-
Þ= = =-Þ=-
2
86
243.9 2187uuq==- =-
( )
Fx
( )
sin 2fx x=
( )
2
cosFx x=-
( )
2
sinFx x=
( )
1
cos 2
2
Fx x=-
( )
cos 2Fx x=-
( )
cos 2 2sin 2xx
¢
-=
( )
cos 2Fx x=-
( )
sin 2fx x=
( )
fx
!
x
-¥
1-
0
1
+¥
'y
+
0
-
0
+
0
-
y
3
3
-¥
1-
-¥
( )
yfx=
2y =-
0
2
1
4
21-<-
2y =-
1.y =-
x
-¥
1-
0
1
+¥
'y
+
0
-
0
+
0
-
y
3
3
1-
2y =-
-¥
-¥
( )
yfx=
2y =-
Ox ,yz
( ) ( )
2; 1; 0 , 2; 5; 4 .AB--
AB
( ) ( )
22
2
2112xyz++-+=
( ) ( )
22
2
3248xy z+- ++ =
( ) ( ) ( )
222
44448xyz-+-++=
( ) ( )
22
2
3212xy z+- ++ =
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 16
Người làm: Bùi Thị Nhung; Fb: Bùi Nhung
Chọn D
Gọi là trung điểm của đoạn suy ra
Ta có:
Mặt cầu đường kính có tâm và bán kính có phương trình là
.
Câu 25. Tập nghiệm của bất phương trình là
A. . B. . C. . D.
Lời giải
Tác giả: Nguyễn Đắc Tuấn; Fb: Nguyễn Đắc Tuấn
Chọn C
Điều kiện:
Ta có:
Kết hợp với điều kiện ta có tập nghiệm của bất phương trình đã cho là: .
Câu 26. Cho hàm số liên tục trên và có bảng xét dấu của đạo hàm như hình bên.
Mệnh đề nào sau đây sai?
A. Hàm số đạt cực tiểu tại . B. Hàm số đạt cực đại tại .
C. Hàm số đạt cực đại tại . D. Hàm số đạt cực tiểu tại .
Lời giải
Tác giả: Nguyễn Đắc Tuấn; Fb: Nguyễn Đắc Tuấn
Chọn D
Ta có bảng biến thiên:
I
AB
( )
0; 3; 2 .I -
( )
4; 4; 4 ,AB =-
!!!"
( )
2
22
44 4 212.AB =++-=
AB
( )
0; 3; 2I -
1
12
2
RAB==
( ) ( )
22
2
3212.xy z+- ++ =
( ) ( )
55
log 3 1 log 25 25xx+< -
1
;1 .
3
æö
-
ç÷
èø
6
;.
7
æö
-¥
ç÷
èø
16
;.
37
æö
-
ç÷
èø
6
;1 .
7
æö
ç÷
èø
1
310
1
1.
3
25 25 0
3
1
x
x
x
x
x
ì
+>
>-
ì
ï
ÛÛ-<<
íí
->
î
ï
<
î
( ) ( )
55
log 3 1 log 25 25xx+< -
3 1 25 25xxÛ+<-
6
28 24 .
7
xxÛ<Û<
16
;.
37
S
æö
=-
ç÷
èø
( )
yfx=
[ ]
3; 3-
1x =
2x =
1x =-
0x =
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 17
Vậy hàm số đạt cực tiểu tại hàm số đạt cực đại tại và .
Câu 27. [Mức độ 1] Cho hình hộp . Bộ 3 vectơ không đồng phẳng là:
A. . B. .
C. . D. .
Lời giải
Người làm: Trịnh Ngọc; Fb: Ngọc Trịnh
Chọn D
3 vectơ đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.
A. có giá cùng song song với mặt phẳng .
B. có giá cùng song song với mặt phẳng .
C. có giá cùng nằm trên mặt phẳng .
Câu 28. [Mức độ 2] Cho hai số phức thỏa mãn . Giá trị biểu thức
bằng
A. 13. B. 25. C. 7. D. 19.
Lời giải
Người làm: Ngọc Trịnh; Fb: Trịnh Ngọc
Chọn A
Có ; .
Khi đó, .
Câu 29. [Mức độ 2] Trong không gian với hệ tọa độ , cho , , .
Xác định tọa độ điểm để là hình bình hành?
1;x =
1x =-
2.x =
.ABCD A B C D
¢¢¢ ¢
,,''AC BD A D
!!!" !!!" !!!!!"
,','AC AC BB
!!!" !!!!" !!! "
,',''AB BD C D
!!!" !!!!" !!!!!"
', ', 'AC B DBD
!!!!" !!!!" !!!!"
,,''AC BD A D
!!!" !!!" !!!!!"
( )
ABCD
,','AC AC BB
!!!" !!!!" !!! "
(
)
ACC A
¢¢
,',''AB BD C D
!!!" !!!!" !!!!!"
(
)
ABC D
¢¢
12
,zz
11 2
4, 3zz z==
22
12
Pz z=+
2
11 1
4zz z==
2
22
39zz=Þ =
22
12
4913.Pz z=+ =+=
Oxyz
( )
2; 1; 3-M
( )
3; 2; 4-N
( )
1; 1; 2-P
Q
MNPQ
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 18
A. . B. . C. . D. .
Lời giải
Người làm: Nguyễn Bá Long; Fb: Nguyễn Bá Long
Chọn C
là hình bình hành khi và chỉ khi .
Vậy .
Câu 30. [Mức độ 2] Giá trị nhỏ nhất của hàm số trên đoạn là
A. . B. . C. . D. .
Lời giải
Người làm: Nguyễn Bá Long; Fb: Nguyễn Bá Long
Chọn B
Hàm số liên tục trên đoạn .
Ta có .
Vậy .
Câu 31. Cho hàm số có đạo hàm liên tục trên , thỏa mãn và . Tích
phân có giá trị là
A. . B. . C. . D. .
Lời giải
Người làm: Đinh Văn Trường; Fb: Đinh Văn Trường
Chọn C
Ta có
.
( )
2; 2; 5-Q
( )
2; 3; 5--Q
( )
0; 4;9-Q
( )
1; 3; 2-Q
MNPQ
=
!!!" !!!!"
PQ NM
Û
( )
123
112
23 4
ì
-= -
ï
ï
+=--
í
ï
-=--
ï
î
Q
Q
Q
x
y
z
0
4
9
ì
=
ï
Û=-
í
ï
=
î
Q
Q
Q
x
y
z
( )
0; 4;9-Q
2
1
-
=
+
x
y
x
[ ]
0; 3
[ ]
0;3
min 3
Î
=-
x
y
[ ]
0;3
min 2
Î
=-
x
y
[ ]
0;3
1
min
4
Î
=
x
y
[ ]
0;3
1
min
2
Î
=-
x
y
2
1
-
=
+
x
y
x
[ ]
0; 3
( )
[ ]
2
3
00;3
1
¢
=>"Î
+
yx
x
[ ]
( )
0; 3
min 0 2
Î
==-
x
yy
( )
yfx=
[ ]
0;1
( )
1
0
d3fx x=
ò
( )
14f =
( )
1
0
dxf x x
¢
ò
1
2
-
1
2
1
1-
( )
1
0
dxf x x
¢
ò
( )
1
0
dxf x=
ò
( ) ( )
1
1
0
0
dxf x f x x=-
ò
( ) ( )
1
0
1dffxx=-
ò
43=-
1=
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 19
Câu 32. [Mức độ 1] Trong không gian với hệ trục tọa độ , cho hai điểm ; .
Phương trình nào sau đây là phương trình dạng chính tắc của đường thẳng đi qua hai điểm và
?
A. . B. .
C. . D. .
Lời giải
Người làm:Trịnh Thị Thu Hương; Fb:Huong Trinh
Chọn C
Một vectơ chỉ phương của đường thẳng là: .
Suy ra một vectơ chỉ phương khác của
là .
Lại có điểm thuộc đường thẳng ở phương án C vì: .
Vậy chọn C
lvnguyen51@gmail.com.
Câu 33. Có 3 quả bóng tennis được chứa trong một hộp hình trụ (hình vẽ bên) với chiều cao và
bán kính .
Thể tích bên trong hình trụ không bị chiếm lấy bởi các quả bóng tennis (bỏ qua độ dày của vỏ
hộp) bằng bao nhiêu?
A. . B. . C. . D. .
Lời giải
Người làm: Lê Văn Nguyên; Fb: Lê Văn Nguyên
Chọn C
Thể tích khối trụ là: .
Mỗi quả bóng tennis cũng có bán kính bằng nên 3 quả bóng có thể tích là:
.
Vậy thể tích cần tìm là .
Câu 34. Có bao nhiêu số tự nhiên có hai chữ số khác nhau?
A. 72. B. 81. C. 90. D. 18.
Lời giải
Oxyz
( )
1;0;3A
( )
5;2 ; 1B -
A
B
13
52 1
xyz--
==
-
13
21 2
xyz--
==
--
311
21 2
xyz---
==
-
521
212
xyz--+
==
AB
( )
4; 2; 4AB =-
!!!"
AB
( )
2;1; 2u =-
!
( )
1;0;3A
13 01 31
1
21 2
---
===-
-
21
cm
3,5
cm
82,75
p
3
cm
87 ,25
p
3
cm
85,75
p
3
cm
87,75
p
3
cm
( )
2
1
.3,5 .21 257,25V
pp
==
3
cm
3,5cm
( )
3
2
4
3. . . 3,5 171,5
3
V
pp
==
3
cm
12
257,25 171,5 85,75VVV
pp p
=- = - =
3
cm
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 20
Tác giả: Đình Khang; Fb:Đình Khang.
Chọn B
Gọi là số tự nhiên có hai chữ số khác nhau .
Ta có:
có 9 cách chọn (do ).
Ứng với mỗi cách chọn ta có 9 cách chọn (do ).
Theo quy tắc nhân ta được số tự nhiên có hai chữ số khác nhau.
Câu 35. [Mức độ 2] Cho hàm số có đạo hàm Số điểm
cực trị của hàm số là
A. . B. . C. . D. .
Lời giải
Tác giả: Đoàn Công Hoàng; Fb: Đoàn Công Hoàng
Chọn B
Xét phương trình ta có:
+ nghiệm đơn là
+ 1 nghiệm bội lẻ là
+ 1 nghiệm bội chẵn là
Vậy hàm số đạt cực trị tại các điểm
Buihuong202@gmail.com.
Câu 36. Cho hàm số có đồ thị hàm số như hình vẽ bên
Hàm số đồng biến trên khoảng?
A. . B. . C. . D. .
Lời giải
Tác giả: Bùi Thu hương; Fb: Cucai Đuong
ab
{ }
( )
,0;1;2;...;9;0ab aι
a
0a ¹
a
b
ab¹
9.9 81=
( )
fx
( )
( )
( ) ( )
23
2
24, .fx x xx x x
¢
=+ - - "Î!
( )
fx
2
3
1.
4
( )
( )
( ) ( )
23
2
240fx x xx x
¢
=+ - -=
2
0; 1.xx==-
4.x =
2.x =
( )
fx
0; 1; 4.xx x==-=
( )
yfx=
( )
yfx=
( )
2
12yfx x x=+++
( )
3; 2--
( )
3; 0-
( )
0;1
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 21
Chọn D
Đặt ( với )
Nhìn vào đồ thị nhận thấy thì hay
Khi đó .
.
Câu 37. Trong không gian với hệ tọa độ , cho điểm và mặt phẳng
. Mặt cầu có tâm , cắt theo một đường tròn có bán kính . Mặt cầu có phương
trình là:
A. . B. .
C. . D. .
Lời giải
Người làm: Nguyễn Văn Bình Facebook: Nguyễn Văn Bình
Chọn C
Ta có .
Vì mặt cầu có tâm , cắt theo một đường tròn có bán kính nên mặt cầu có
bán kính .
Vậy phương trình mặt cầu là .
Câu 38. Đầu tháng một người gửi ngân hàng đồng ( triệu đồng) với lãi suất gửi là
mỗi tháng theo hình thức lãi suất kép. Cuối mỗi tháng người đó đều đặn gửi vào ngân hàng số
tiền là ( triệu đồng). Hỏi sau ít nhất bao nhiêu tháng ( kể từ lúc người này ra ngân
hàng gửi tiền) thì số tiền người đó tích lũy được lớn hơn (bảy trăm triệu đồng)?
A. tháng. B. tháng. C. tháng. D. tháng.
Lời giải
Tác giả: Trần Lê Vĩnh Phúc; Fb: Trần Lê Vĩnh Phúc
Chọn B
( ) ( )
2
12gx f x x x=+++
( ) ( )
12 2gx f x x
¢¢
Þ=+++
( )
2ft t
¢
=+
1tx=+
02t<<
( )
2ft t
¢
>-
( )
0gx
¢
>
012x<+<
11xÞ- < <
Oxyz
( )
1( 2;1 ;I
( )
:2 2 1 0Pxyz++ -=
( )
S
I
( )
P
4r =
( )
S
( ) ( ) ( )
222
21120xyz+++++=
( ) ( ) ( )
222
21118xyz-+-+-=
( ) ( ) ( )
222
21120xyz-+-+-=
( ) ( ) ( )
222
21125xyz-+-+-=
( )
( )
22 2
2.2 1 2.1 1
2
2
;
12
I Pd
++ -
=
++
=
( )
S
I
( )
P
4r =
( )
S
( )
( )
22 22
42 25; PRrdI=+ =+=
( )
S
( ) ( ) ( )
222
21120xyz-+-+-=
400.000.000
400
0, 6%
10.000.000
10
700.000.000
22
23
25
24
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 22
Tổng quát bài toán:
Gọi là số tiền người đó gửi ban đầu.
là lãi suất mỗi tháng.
là số tiền người đó gửi vào thêm mỗi tháng.
là số tiền người đó nhận được sau tháng.
Đầu tháng 1, số tiền người đó gửi vào là .
Cuối tháng 1, .
Cuối tháng 2, .
Cuối tháng 3, .
…
Cuối tháng n,
Theo yêu cầu bài toán:
Vậy phải sau ít nhất 23 tháng thì người đó mới tích lũy được lớn hơn (bảy trăm
triệu đồng).
Câu 39. Cho đồ thị hàm số như hình vẽ dưới đây:
Đồ thị của hàm số có bao nhiêu đường tiệm cận đứng?
0
T
%r
a
n
S
n
00
ST=
( )
100 0
.% .1 %STTr aT r a=+ += + +
( ) ( )
2
211 1 0
.% .1 % .(1 %) .1 %SSSr aS r aT r a r a=+ += + += + + + +
32
30
.(1 %) .(1 %) .(1 %)ST r a r a r a=+ ++ +++
( ) ( ) ( ) ( )
( )
( )
12 1
0
0
. 1 % 1 % 1 % ... 1 % 1
1% 1
.1 % .
%
nnn
n
n
n
ST r a r r r
r
Tr a
r
--
éù
=+ ++ ++ +++ +
ëû
+-
=+ +
( )
( )
( )
( )
( )
( )
0
1 0,6%
1% 1
. 1 % . 700.000.000
%
1 0,6% 1
40. 1 0,6% 70
0,6%
1 0,6% 1,14515129
log 1,14515129 22,65
n
n
n
n
n
r
Tr a
r
n
+
+-
++ ³
+-
Û+ + ³
Û+ ³
Û³ »
700.000.000
32
yax bx cxd=+++
( )
( ) ( )
2
2
32
36
xx
gx
fx fx
--
=
-
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 23
A. . B. . C. . D. .
Lời giải
Người làm: Cao Văn Kiên; Fb: Kiên Cao Văn
Chọn A
Xét phương trình
Dựa vào đồ thị, ta có
+) Phương trình (trong đó là nghiệm đơn và là nghiệm bội
2)
, .
+) Phương trình ( đều là các nghiệm đơn)
, .
Suy ra , .
Vậy đồ thị hàm số có đường tiệm cận đứng.
uyentoa@gmail.com.
Câu 40. Cho hàm số có bảng xét dấu của đạo hàm như hình bên.
Hàm số nghịch biến trên khoảng
A. . B. . C. . D. .
Lời giải
Tác giả: Nguyễn Thị Uyên; Fb: Uyen Nguyen
Chọn D
Xét hàm số có .
Từ bảng xét dấu của ta có:
.
Suy ra hàm số nghịch biến trên các khoảng và .
Mà nên hàm số nghịch biến trên khoảng .
5
4
3
2
( ) ( )
( )
( )
2
0
360
2
fx
fx fx
fx
=
é
-=Û
ê
=
ê
ë
( )
0fx=
2
1
x
x
=-
é
Û
ê
=
ë
2x =-
1x =
( ) ( )( )
2
21fx ax xÞ=+-
( )
0a ¹
( )
2fx=
( )
( )
0
21
1
x
xm m
xn n
é
=
ê
Û= -<<-
ê
ê
=>
ë
0, ,xxmxn== =
( ) ( )( )
2fx axx m xnÞ-=--
( )
0a ¹
( )
( )( )
( ) ( )
( )( )
( )( ) ( )( )
2
2
13 2 13 2
32
321
xx xx
gx
fx fx
ax x xxmxn
-+ -+
==
-
éù
+- - -
ëû
( )
0a ¹
( )
gx
5
( )
fx
( )
1yf x=-
( )
1; 4
( )
0; 2
( )
0;1
( )
2; 1--
( )
1yf x=-
( )
1yf x
¢¢
=- -
( )
fx
¢
( )
31 2 3 12 3 4
010
11 3 1 1 3 2 0
xx x
yfx
xx x
-<- <- > -> < <
ééé
¢¢
<Û - >Û Û Û
êêê
<- < -> ->- -< <
ëëë
( )
1yf x=-
( )
3; 4
( )
2; 0-
( ) ( )
2; 1 2; 0-- Ì-
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 24
Câu 41. [Mức độ 2] Trong không gian với hệ tọa độ , cho hình hộp biết
, , và . Tọa độ đỉnh của hình hộp là
A. . B. . C. . D. .
Lời giải
Người làm: Giáp Minh Đức; Fb: Giáp Minh Đức
Chọn A
Gọi lần lượt là trung điểm của và .
Ta có , và .
Giả sử .
Theo tính chất của hình hộp ta có .
Vậy .
Câu 42. Cho hình chóp có đáy là hình vuông cạnh , là tam giác cân tại và
nằm trong mặt phẳng vuông góc với mặt phẳng . Gọi lần lượt là trung điểm của
và là trọng tâm . Biết khoảng cách từ điểm đến mặt phẳng bằng
. Thể tích của khối chóp bằng
A. . B. . C. . D. .
Oxyz
.ABCD A B C D
¢¢¢¢
( )
1; 2;3A
( )
2;0; 1B
¢
-
( )
3;0 ; 3C -
( )
2; 4; 3D
¢
--
B
.ABCD A B C D
¢¢¢¢
( )
4; 1;1B -
( )
2; 1; 2B -
( )
4;1; 1B -
( )
0;1; 3B -
,II
¢
AC
BD
¢¢
( )
2;1; 0I
( )
0;2; 2I
¢
-
( )
2;1; 2II
¢
=- -
!!"
( )
;;Babc
( )
2;;1BB a b c
¢
Þ=----
!!! "
BB II
¢¢
=
!!! " !!"
22
1
12
a
b
c
-=-
ì
ï
Û-=
í
ï
-- =-
î
4
1
1
a
b
c
=
ì
ï
Û=-
í
ï
=
î
( )
4; 1;1B -
.S ABCD
2AB a=
SABD
S
( )
ABCD
,MN
,AB BC
G
SCDD
M
( )
SND
32
4
a
.G AMND
3
53
2
a
3
53
6
a
3
53
3
a
3
53
18
a
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 25
Lời giải
Chọn A
Do là tam giác cân tại và là trung
điểm của nên ta có được . Thêm
vào đó nên chúng ta có thể suy
ra được .
Ta kẽ tại điểm và tại
điểm .
Khi đó:
. Mà
trước đó , nên ta có được .
Mặt khác:
.
Xét trong , ta có: .
Dễ thấy: . Vậy:
.
Gmail vanluu1010@gmail.com.
Câu 43. Cho hình thang biết , , , . Thể tích khối tròn
xoay tạo thành khi quay hình thang quanh trục bằng
A. . B. . C. . D. .
Lời giải
Tác giả: Bùi Văn Lưu; Fb: Bùi Văn Lưu
Chọn B
SABD
S
M
AB
SM AB^
( ) ( )
SAB ABCD^
( )
SM ABCD^
MH DN^
H
MK SH^
K
( )
MH DN
DN SHM DN MK
SM DN
^
ì
Þ^ Þ^
í
^
î
MK SH^
( ) ( )
( )
32
,
4
a
MK SDN MK d M SDN^Þ= =
( )
2
222
22
24
2
2
2
35
5
5
ABCD MBN NCD MAD
MND
a
aaa
SSSS
S
a
MH
ND
a
NC DC
DDD
D
æö
---
ç÷
---
èø
== = =
+
SMHD
222
111
3SM a
SM MK MH
=-Þ=
( )
( )
13
,
33
a
d G ABCD SM==
( )
( )
( )
22
.
113 3553
., . . . .
333 9218
G AMND AMND ABCD MBN NDC
aaaa
V d G ABCD S S S S
D
==--==
ABCD
( )
//AB CD
5AB =
3BC =
10CD =
4AD =
ABCD
( )
//AB CD
AD
128
p
84
p
112
p
90
p
G
K
A
B
C
D
H
S
M
N
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 26
Gọi là trung điểm của .
Dễ thấy tứ giác là hình bình hành vuông tại .
Gọi là giao điểm của và vuông tại .
Ta có và .
Khi quay quanh trục ta được hình nón tròn xoay có chiều cao , bán kính
đáy nên có thể tích .
Khi quay quanh trục ta được hình nón tròn xoay có chiều cao , bán kính đáy
nên có thể tích .
Vậy thể tích khối tròn xoay tạo thành khi quay hình thang quanh trục
bằng .
Câu 44. Cho lăng trụ có đáy là tam giác đều cạnh , hình chiếu vuông góc của đỉnh lên
là trung điểm của cạnh . Góc giữa đường thẳng và mặt đáy bằng . Khoảng
cách giữa và là
A. . B. . C. . D. .
Lời giải
Tác giả: Lê Quốc Đạt; Fb: Đat Le Quôc
Chọn B
E
CD
ABCE
3AE BCÞ==
DAEÞD
A
H
AD
BC
DHCÞD
H
4AH BE==
8DHÞ=
3HB =
DHCD
DH
1
8h =
1
6r =
2
111
11
.36.8 96
33
Vrh
pp p
== =
AHBD
AH
2
4h =
2
3r =
2
222
11
.9.4 12
33
Vrh
ppp
===
ABCD
( )
//AB CD
AD
12
96 12 84VV
pp p
-= - =
.ABC A B C
¢¢¢
a
A
¢
( )
ABC
H
AB
AC
¢
60°
BB
¢
AC
¢
13
39
a
313
13
a
213
13
a
13
13
a
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 27
Ta có .
.
Gọi là trung điểm của , từ kẻ
Từ kẻ .
.
Xét tam giác vuông vuông tại
.
Câu 45. Tập xác định của hàm số là một khoảng có độ dài
với và là số nguyên dương và nguyên tố cùng nhau. Khi đó bằng:
A. . B. . C. . D. .
Lời giải
Người làm: Lê Phương; Fb: lephuongtt1
Chọn D
( )
AH ABC
¢
^
( )
( )
( )
;; 60AC ABC AC HC AHC
¢¢¢
Þ==Ð=°
0
33
. tan 60 . 3
22
aa
AH HC
¢
Þ= = =
M
AC
H
13
.
24
a
HN AC HN BM^Þ = =
H
HI A N
¢
^
( )
HI A AC
¢
Þ^
( ) ( )
( )
( )
( )
( )
( )
'; ' ; ; 2 ; 2dBBAC dBB AAC dB AAC dH AAC HI
¢¢ ¢ ¢
====
AHI
¢
H
22 2
2
33
.
.313
42
.
26
33
42
aa
HN HA a
HI
HN HA
aa
¢
Þ= = =
¢
+
æö
æö
++
ç÷
ç÷
èø
èø
( )
313
;2 .
13
a
dBB AC HI
¢¢
Þ==
( )
14116 1
24 16
log log log log logfx x
æö
æö
æö
æö
ç÷
=
ç÷
ç÷
ç÷
ç÷
ç÷
ç÷
èø
èø
èø
èø
m
n
m
n
mn-
240-
271
241
241-
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 28
Hàm số xác định khi và chỉ khi
.
Suy ra tập xác định của hàm số là .
Suy ra độ dài của khoảng là .
Vậy .
Câu 46. [Mức độ 3] Số điểm cực đại của đồ thị hàm số bằng
A. . B. . C. . D. .
Lời giải
Người làm: Võ Thanh Hải; Fb: Võ Thanh Hải
Chọn C
*Ta thấy hàm số đã cho là hàm đa thức bậc 100, liên tục trên và có đúng 100 nghiệm phân
biệt ( ), nên hàm số đã cho có 99 điểm cực trị ( ), mỗi điểm
cực trị nằm giữa 2 nghiệm của phương trình . Mặt khác nên số điểm cực tiểu
nhiều hơn số điểm cực đại là một nên đồ thị hàm số đã cho có 49 điểm cực đại là .
Vậy hàm số đã cho có 49 điểm cực đại.
Câu 47. Cho các số thực dương , thỏa mãn và ,
, , là các số nguyên dương. Khi đó kết quả bằng
A. . B. . C. . D. .
Lời giải
Tác giả: Bùi Anh Dũng; Fb: Dũng Bùi
( )
14116 1
24 16
log log log log logfx x
æö
æö
æö
æö
ç÷
=
ç÷
ç÷
ç÷
ç÷
ç÷
ç÷
èø
èø
èø
èø
4 1 16 1
4 16
log log log log 0x
æö
æö
æö
>
ç÷
ç÷
ç÷
ç÷
ç÷
èø
èø
èø
116 1
416
log log log 1x
æö
æö
Û>
ç÷
ç÷
ç÷
èø
èø
16 1
16
1
0log log
4
x
æö
Û< <
ç÷
èø
1
16
1
4
1
16
log 1
log 16
x
x
>
ì
ï
ï
Û
í
ï
<
ï
î
2
1
0
16
1
16
x
x
ì
<<
ï
ï
Û
í
æö
ï
>
ç÷
ï
èø
î
11
256 16
xÛ<<
11
;
256 16
æö
ç÷
èø
11
;
256 16
æö
ç÷
èø
11 15
15, 256
16 256 256
mn-=Þ= =
241mn-=-
( )( )( ) ( )
123...100yx x x x=- - - -
50
99
49
100
!
1; 2; . . . ; 1 0 0xx x== =
12 99
;;...;xx x
0y =
®±¥
=+¥lim
x
24 98
;;...;xx x
x
y
log log log log 100xyxy+++=
log x
log y
log x
log y
xy
200
10
100
10
164
10
144
10
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 29
Chọn C
Ta có:
Vì , là các số nguyên dương nên: và là các số
nguyên dương. Do đó cần phân tích 202 thành tổng 2 số chính phương.
Cũng do 202 là số chẵn nên 2 số chính phương đó phải cùng chẵn hoặc cùng lẻ.
+) Nếu 2 số và cùng chẵn thì còn
202 không chia hết cho 4 nên không tồn tại , trong trường hợp này.
+) Nếu 2 số và cùng lẻ, suy ra chữ số tận cùng của 2 số đó là một
trong các chữ số 1, 5, hoặc 9. Vì tổng 2 chữ số tận cùng là 2 nên 2 số ,
đều có tận cùng bằng 1.
Cũng do vai trò , như nhau trong giả thiết và kết luận nên ta chỉ xét trường hợp:
. Từ đó suy ra .
Câu 48. Cho hàm số có đồ thị như hình vẽ bên
Giá trị nguyên lớn nhất của tham số để hàm số đồng biến trên khoảng
là
A. . B. . C. . D. .
Lời giải
Tác giả:Hoàng Thanh Toàn; Fb:Toàn Hoàng
Chọn C
Hàm số đồng biến trên khoảng
( ) ( )
22
log log log log 100 log 1 log 1 202xyxy x y+++=Û ++ +=
log x
log y
( )
2
log 1x +
( )
2
log 1y +
( )
2
log 1x +
( )
2
log 1y +
( ) ( )
22
log 1 log 1 4xy++ +!
x
y
( )
2
log 1x +
( )
2
log 1y +
( )
2
log 1x +
( )
2
log 1y +
x
y
( )
( )
2
2
log 1 81
log 1 121
x
y
ì
+=
ï
í
ï
+=
î
64
164
100
10
10
10
x
xy
y
ì
=
ï
Þ=
í
=
ï
î
32
yax bx cxd=+++
m
( )
yfxm=-
( )
10 ;+¥
10-
10
9
11
( )
yfxm=-
( )
10 ;+¥
( ) ( )
'' 0,10' 0,10
x
yfxm x fxm x
x
Û= - ³">Û - ³">
1
, 10
1
xm
x
xm
é-³
Û">
ê
-£-
ê
ë
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 30
.
Vậy số nguyên lớn nhất của tham số là .
Câu 49. Cho hàm số liên tục trên và thoả mãn .
Khi đó bằng:
A. . B. . C. . D. .
Lời giải
Tác giả: Quách Hồng Hiệp; Fb: Tiểu Hiệp
Chọn B
Nhân hai vế của
với ta được:
.
Lấy tích phân từ đến hai vế ta được:
Kí hiệu
Đặt ta tính được
Đặt ta tính được
Và
Nên .
Câu 50. Một hộp đựng thẻ được đánh số từ đến . Rút ngẫu nhiên hai thẻ từ hộp nêu ở trên, tính xác
suất để tích của hai số trên hai thẻ này là số chẵn.
A. . B. . C. . D. .
Lời giải
Người làm: Lê Anh Minh; Fb: Lê Anh Minh
Chọn B
.
Gọi là biến cố tích của hai số trên hai thẻ là số lẻ, ta có xác xuất cần tính là .
Nhận thấy biến cố xảy ra khi và chỉ khi rút được cả hai thẻ mang số lẻ. Trong 9 thẻ đã cho
có 5 thẻ mang số lẻ, vì thế nên .
1
, 10
1
xm
x
xm
é³+
Û">
ê
£-
ê
ë
10 1 9mmÛ³+Û£
m
9
( )
fx
!
( ) ( )
2
32
1,
x
xf x f x e x+-="Î!
( )
0
1
dfx x
-
ò
0
( )
31e -
( )
31 e-
3e
( ) ( )
2
32
1,
x
xf x f x e x+-="Î!
x
( ) ( )
2
23 2
1,
x
xf x xf x xe x+-="Î!
1-
0
( ) ( )
2
00 0
23 2
11 1
1(1)
x
xf x dx xf x dx xedx
-- -
+-=
òò ò
( ) ( )
2
00 0
23 2
11 1
;1;
x
IxfxdxKxfxdxHxedx
-- -
==-=
òò ò
3
ux=
( )
( ) ( )
000
23
111
11
33
Ixfxdx fudu fxdx
---
===
òòò
2
1ux=-
( )
( ) ( )
000
2
111
11
1
22
Kxfxdx fvdv fxdx
---
=-=- =-
òòò
( )
( )
22 2
0
00
2
1
11
111
1
222
xx x
Hxedx edx e e
-
--
== ==-
òò
( ) ( ) ( ) ( ) ( )
00 0
11 1
11 1
(1) 1 3 1
32 2
fxdx fxdx e fxdx e
-- -
Û-=-Û=-
òò ò
9
1
9
25
81
13
18
5
18
1
2
( )
2
9
nCW=
A
( )
PA
A
( )
2
5
nA C=
Sản$phẩm$của$Group$FB:$STRONG$TEAM$TOÁN$VD-VDC
Hãy$tham$gia$STRONG$TEAM$TOÁN$VD-VDC-$Group$dành$riêng$cho$GV-SV$toán!$$$$$$Trang 31
Ta có và , do đó .
…..HẾT…..
( )
( )
( )
nA
PA
n
=
W
( )
( )
1PA PA+=
( )
13
18
PA=
| 1/31
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC
SỞ GD&ĐT HÀ NỘI
ĐỀ THI THỬ TỐT NGHIỆP THPTQG 2020 NĂM HỌC 2019 - 2020 MÔN TOÁN
Thời gian làm bài: 90 phút
Câu 1. Khối trụ tròn xoay có thể tích bằng 144p và có bán kính đáy bằng 6. Đường sinh của khối trụ bằng A. 4 . B. 6 . C. 12 . D. 10 .
Câu 2. Trong các hàm số sau đây, hàm số nào nghịch biến trên tập ! ? æ 1 x ö x A. x y = p . B. y = .
C. y = 3 . D. 3x y = . ç ÷ è 3 ø 2
Câu 3. Giá trị của tích phân 2 d bằng ò x x 0 A. 8 . B. 6 . C. 2 . D. 4 .
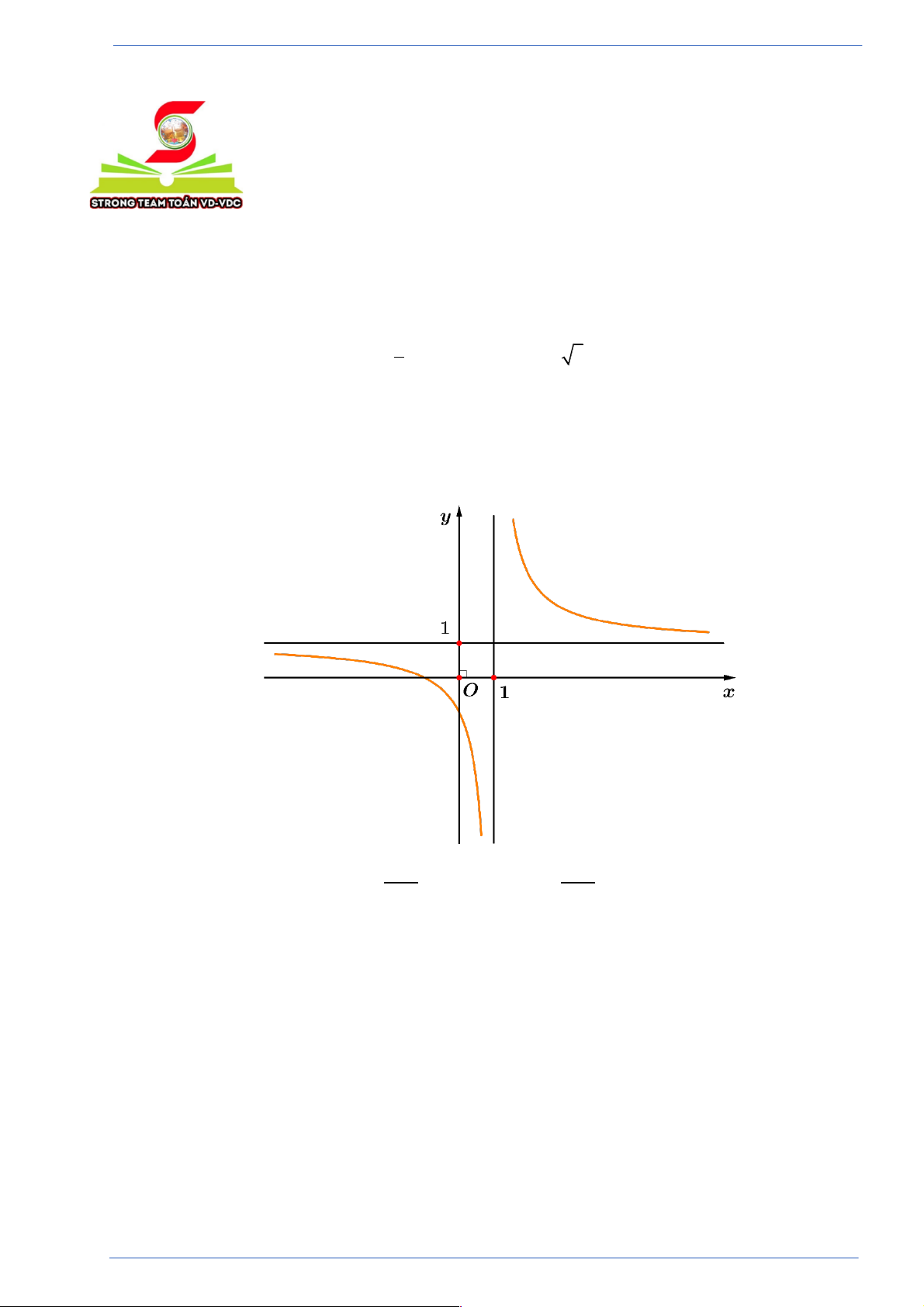
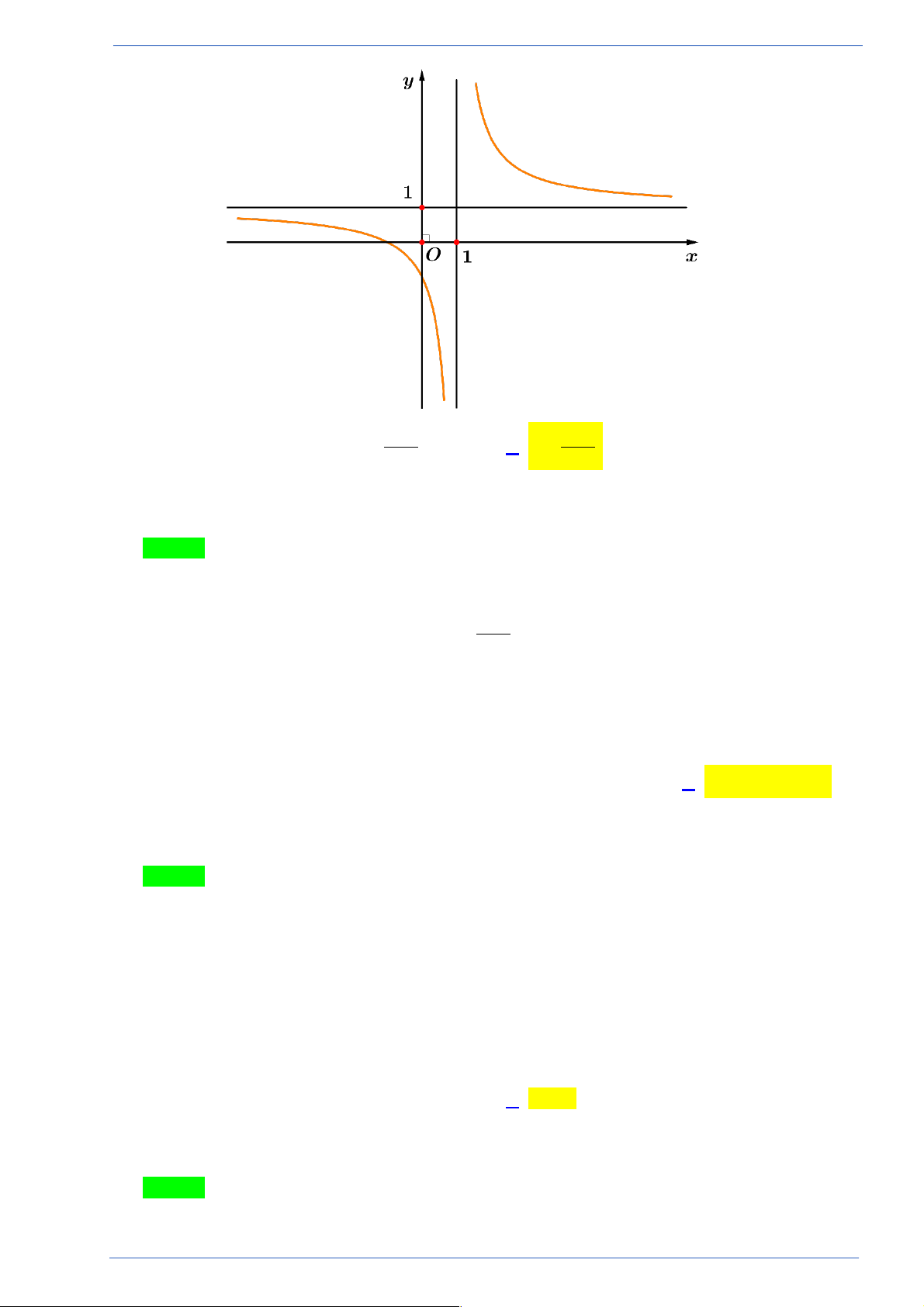
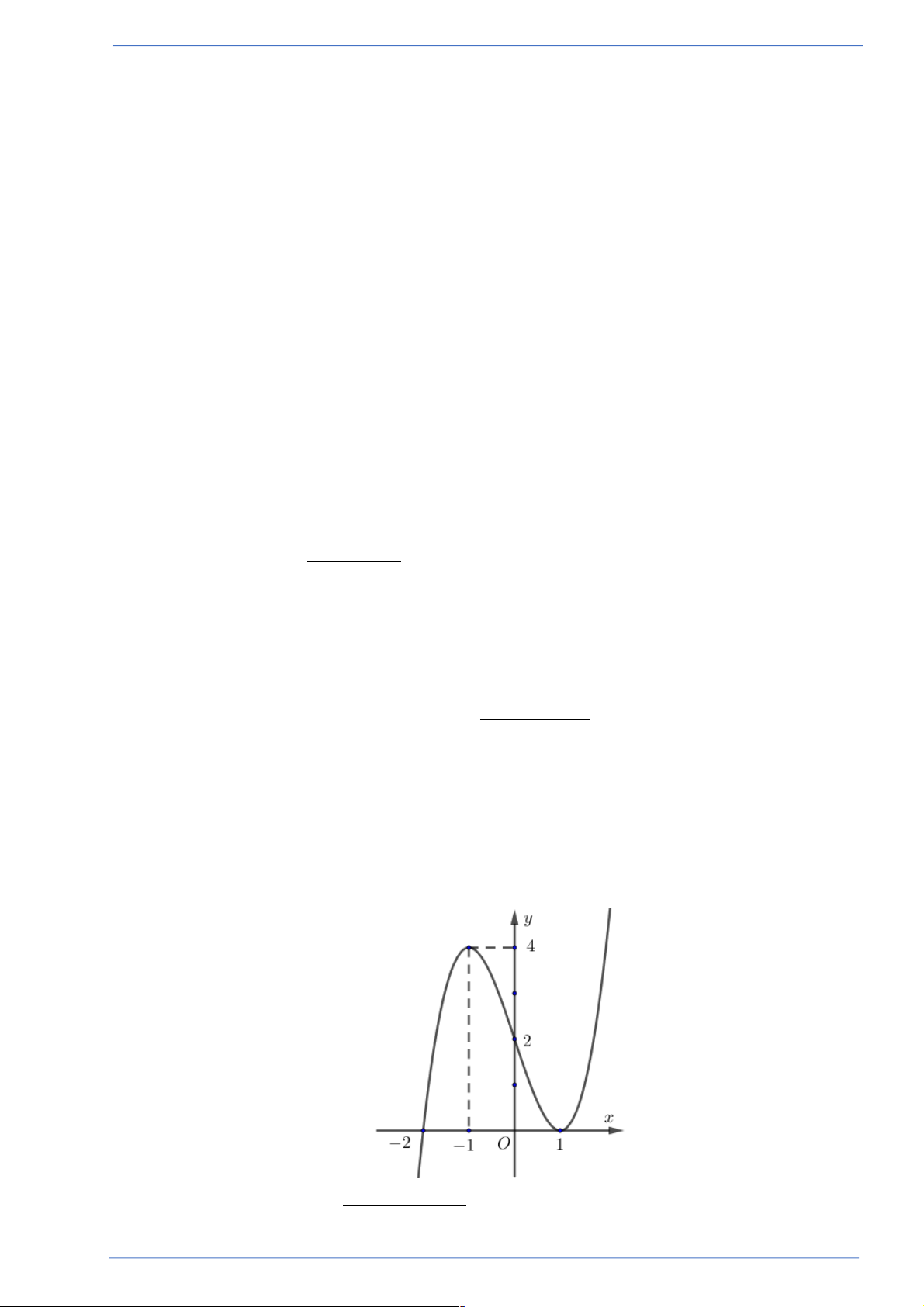
Câu 4. Đường cong ở hình bên là đồ thị của hàm số nào dưới đây? x -1 x +1 A. 3
y = -x + 2x +1. B. y = . C. y = . D. 3 2
y = x - x +1. x +1 x -1
Câu 5. Trong không gian Oxyz , cho mặt phẳng (P): x - 2y +3z + 2020 = 0. Vectơ nào dưới đây không
phải là một vectơ pháp tuyến của mặt phẳng (P)? ! ! ! ! A. n = ( 2; - 4; 6 - ). B. n = ( 1 - ;2; 3 - ). C. n = (1; 2 - ;3). D. n = ( 2; - 3;2020).
Câu 6. Cho số phức z = 5 + 3i . Số phức liên hợp của z là A. 5 - + 3i . B. 5 - - 3i . C. 5 - 3i . D. 5i - 3.
Câu 7. Trong mặt phẳng (Oxy), điểm M biểu diễn số phức z = 1
- - 3i có tọa độ là A. M (1;- ) 3 . B. M ( 1 - ;- ) 3 . C. M ( 1 - ;3). D. M (1;3).
Câu 8. Cho các số thực dương a,b và a ¹ 1. Biểu thức 2 log a b bằng a A. 2(1+ log 2log + 1+ log a b). B. . C. . D. . a b 2 loga b a b
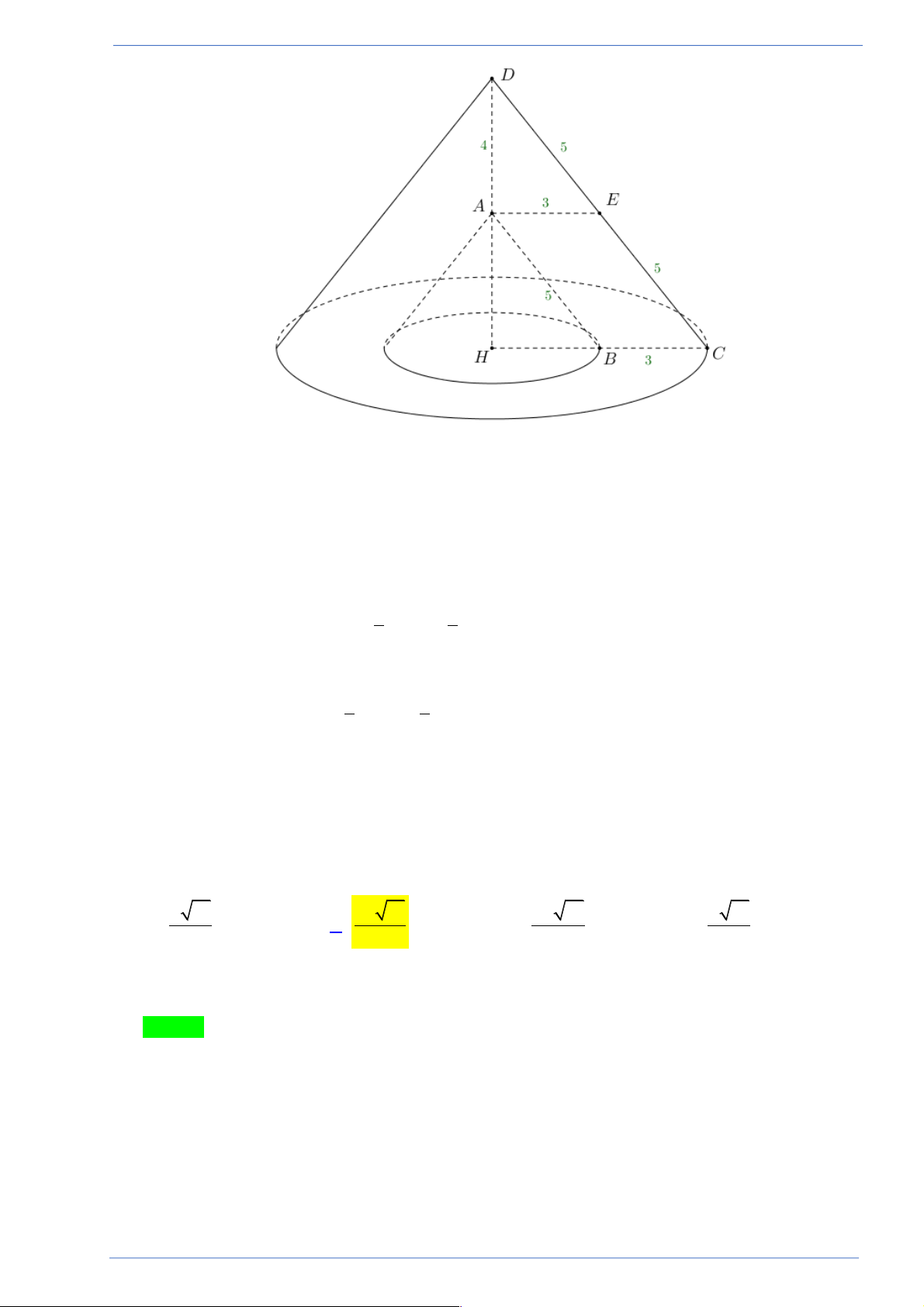
Câu 9. Thể tích khối lăng trụ tam giác có chiều cao bằng 2 , cạnh đáy lần lượt bằng 3, 4 , 5 là:
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 1
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC A. 8. . B. 12.. C. 4.. D. 28..
Câu 10. Trong các khối hình sau, khối không phải khối tròn xoay là: A. Khối cầu. B. Khối trụ. C. Khối lăng trụ. D. Khối nón.
Câu 11. Họ tất cả các nguyên hàm của hàm số f (x) 2 = sin x + là x 2
A. cosx + 2ln x + C. B. cosx - + C . 2 x
C. - cosx + 2ln x + C . D. - cosx - 2ln x + C . ! ! ! ! !
Câu 12. Trong không gian với hệ tọa độ Oxyz , cho a = 2
- i + 3 j + 5k . Tọa độ của a là A. (2;3;5). B. ( 2; - 3;5). C. (2;3;-5). D. (2;-3;-5).
Câu 13. Cho 2 số thực dương x , y thỏa mãn x ¹ 1 và log 3. Tính 5 T = log y . x y = 3 x 5 A. T = 9 . B. T = 3 . C. T = . D. T = 5. 3 5 5
Câu 14. Trong không gian Oxyz , cho điểm M (2;-1;3) và mặt phẳng (a ):2x -5y + z -1= 0. Phương
trình mặt phẳng nào dưới đây đi qua điểm M và song song với (a ).
A. 2x - 5y + z -12 = 0. B. 2x - 5y - z -12 = 0.
C. 2x + 5y - z -12 = 0. D. 2x - 5y + z +12 = 0.
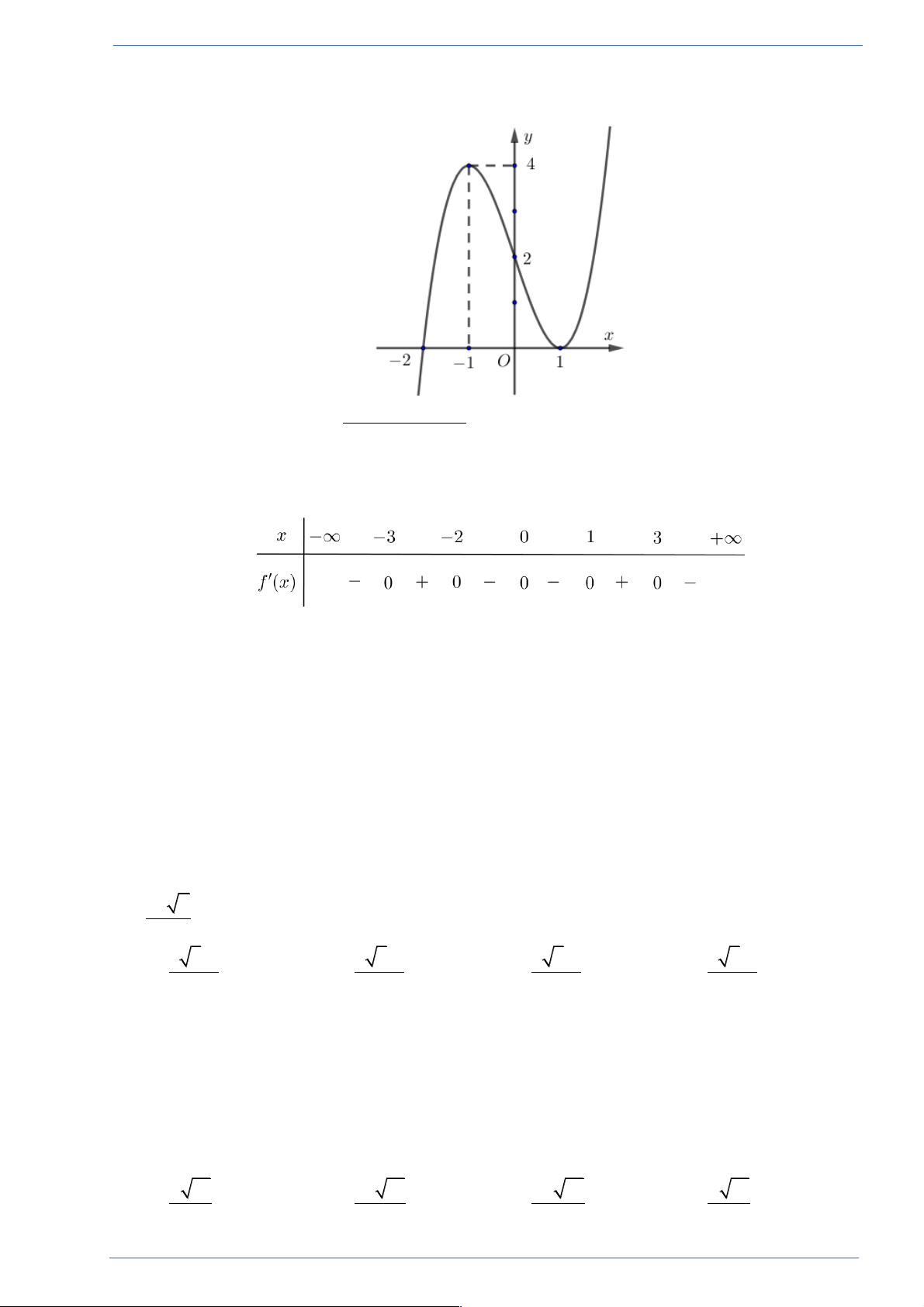
Câu 15. Cho hàm số y = f (x) có đồ thị như hình vẽ bên.
Hàm số đã cho nghịch biến trên khoảng A. (0 ; 2). B. ( 3 ; - - ) 1 . C. ( 1 - ; 0). D. (1 ; 3). x + 2
Câu 16. Đồ thị hàm số y =
có đường tiệm cận ngang là đường thẳng nào sau đây? 2x +1 A. x = 1 - . B. y = 2. 1 1 C. y = . D. x - = . 2 2
Câu 17. Gọi S là tập nghiệm của phương trình 9x 10.3x -
+ 9 = 0. Tổng các phần tử của S bằng
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 2
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC 10 A. 1. B. 2 . C. 10 . D. . 3
Câu 18. Một xe ô tô đang chuyển động đều với vận tốc 16 m / s thì người lái xe nhìn thấy một chướng
ngại vật nên đạp phanh tại điểm đó, ô tô chuyển động chậm dần đều với vận tốc v(t) = 2 - t +16
trong đó t là thời gian (tính bằng giây) kể từ lúc đạp phanh. Quãng đường mà ô tô đi được trong
10 giây cuối cùng bằng A. 60m . B. 64m . C. 160m . D. 96m .
Câu 19. Cho hàm số y = f (x) có đạo hàm f ¢(x) =1, x
" Î ! . Mệnh đề nào sau đây đúng? A. f (- ) 1 < f (2). B. f (- ) 1 = f (2). C. f (- ) 1 ³ f (2). D. f (- ) 1 > f (2).
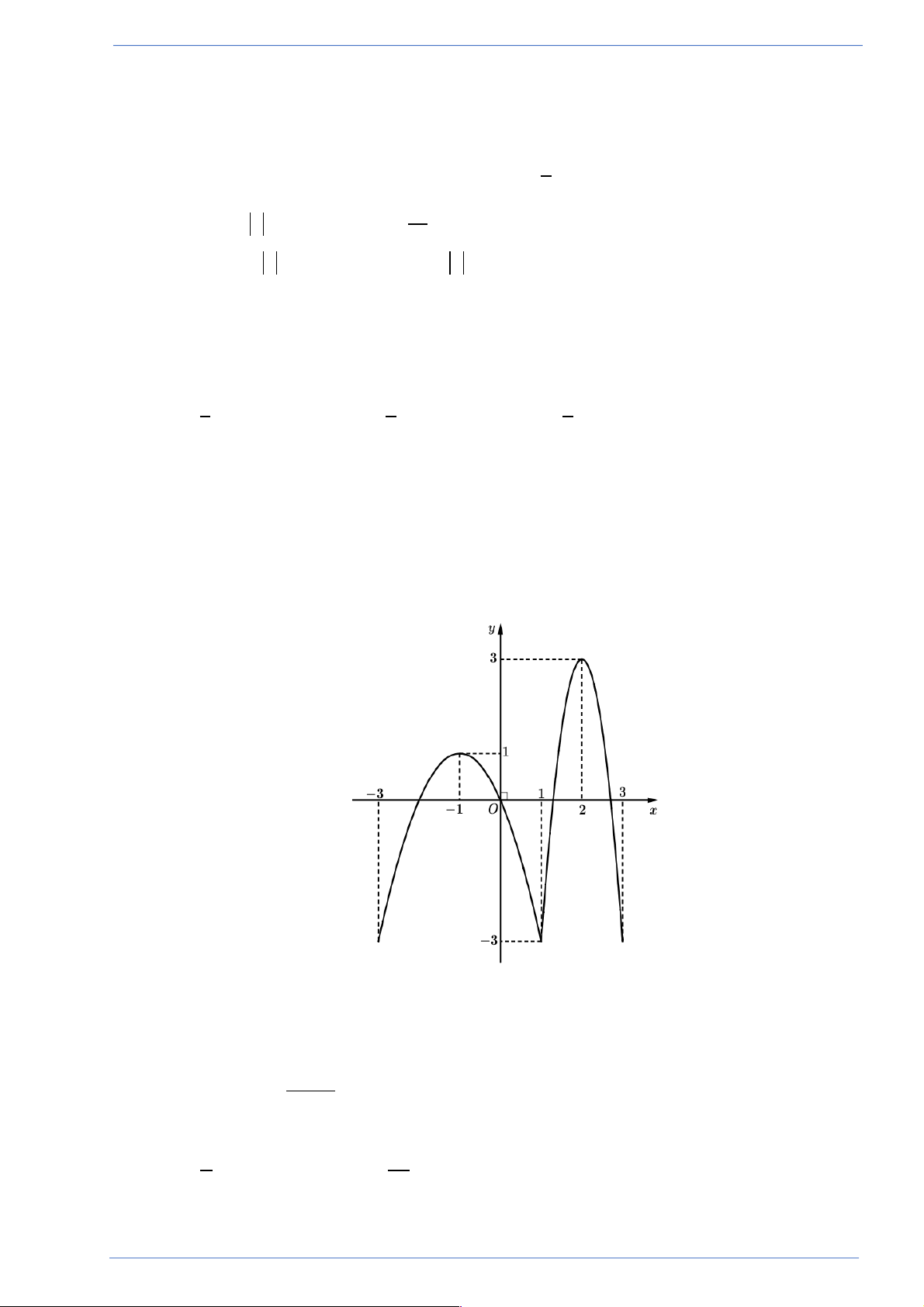
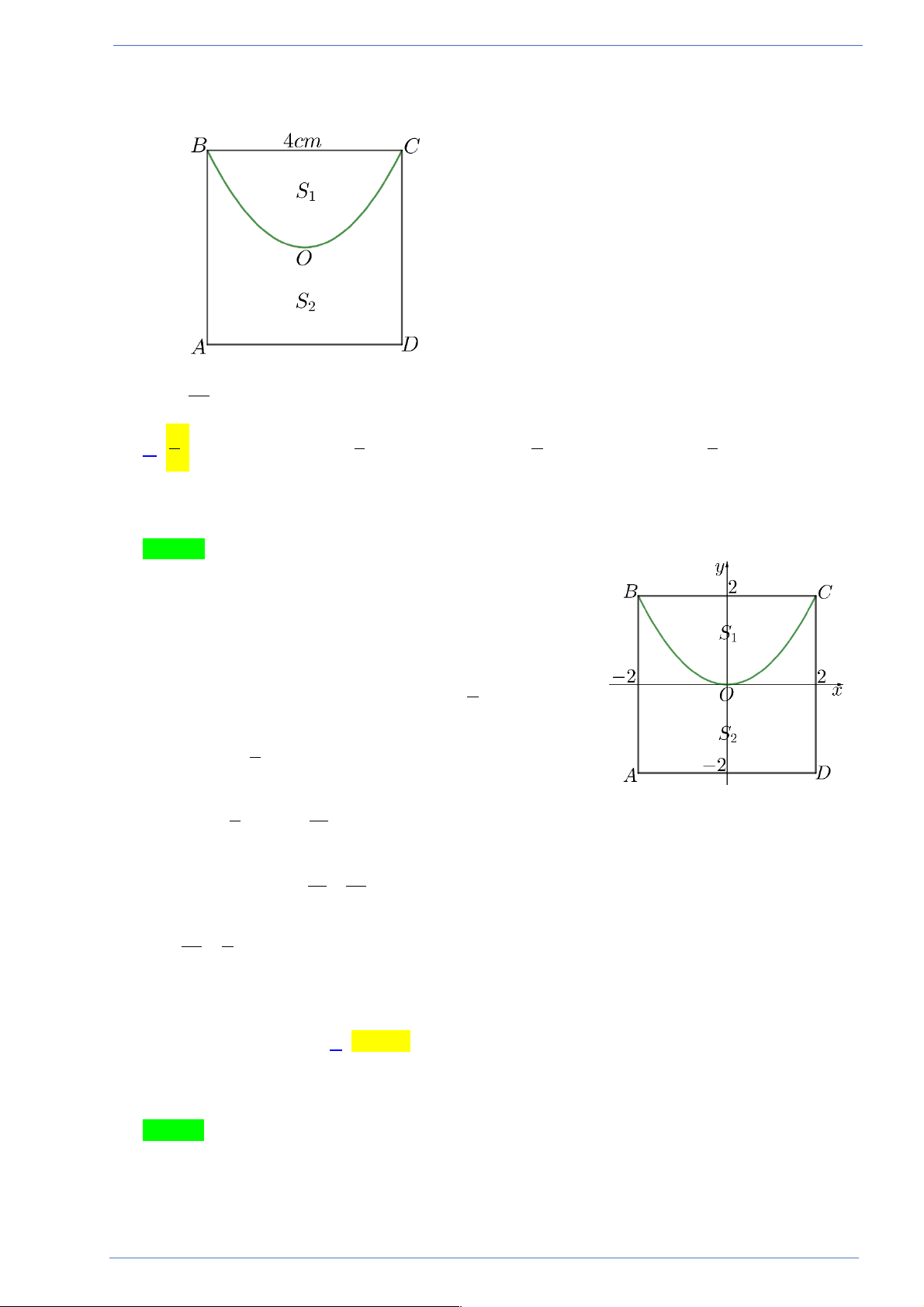
Câu 20. Cho hình vuông ABCD tâm O, độ dài cạnh là 4 .
cm Đường cong BOC là một phần parabol
đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S và S (tham khảo hình 1 2 vẽ). S Tỉ số 1 bằng S2 1 3 2 1 A. . B. . C. . D. . 2 5 5 3
Câu 21. Một cấp số nhân có số hạng thứ 3 và số hạng thứ 6 lần lượt là 9 và 243 -
. Khi đó số hạng thứ 8
của cấp số nhân bằng: A. 2187 . B. 2187 - . C. 729 . D. 243.
Câu 22. Tìm hàm số F ( x) không là nguyên hàm của hàm số f (x) = sin 2x. A. F (x) 2 = -cos x. B. F (x) 2 = sin x. C. F (x) 1
= - cos 2x. D. F (x) = -cos2x. 2
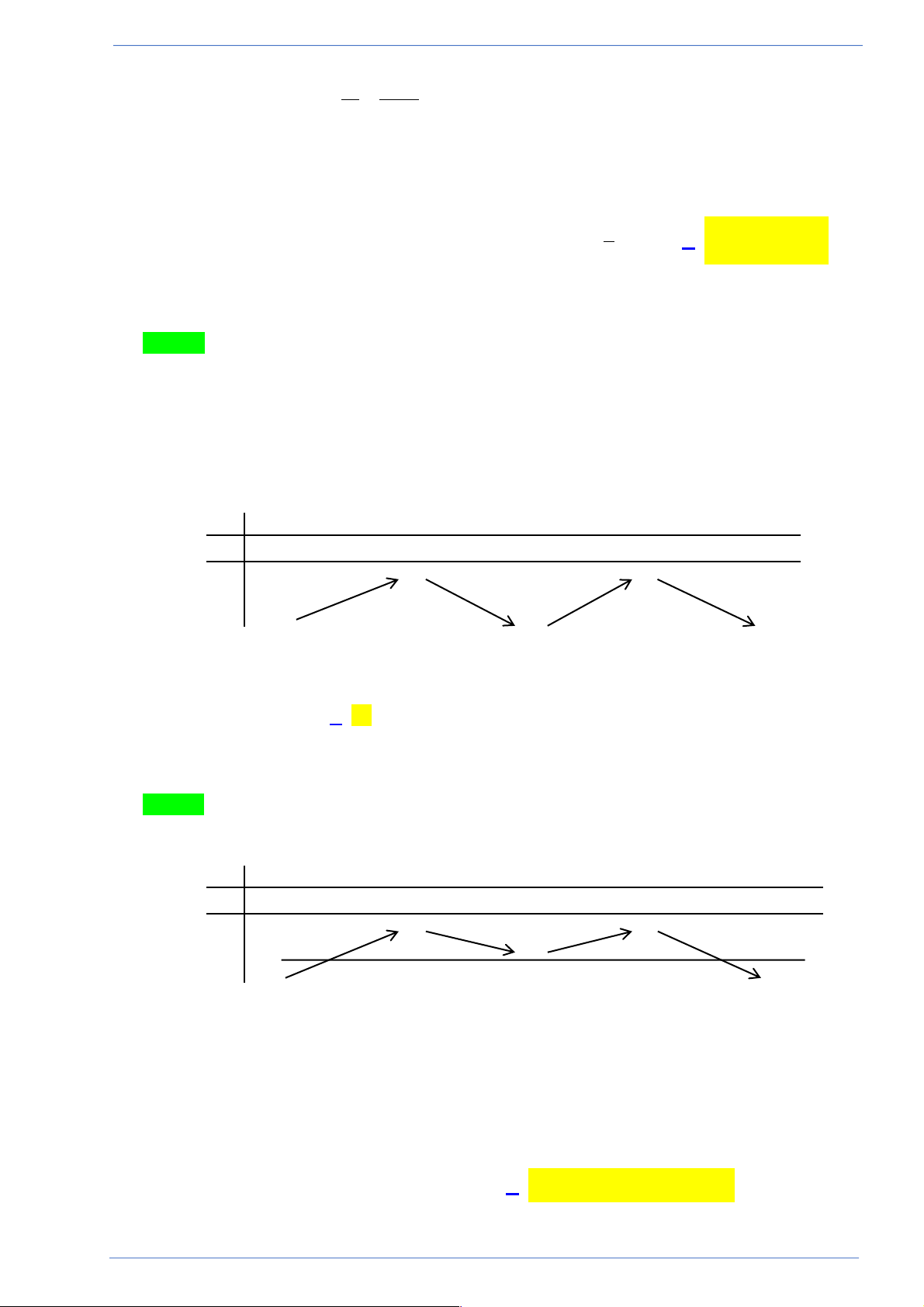
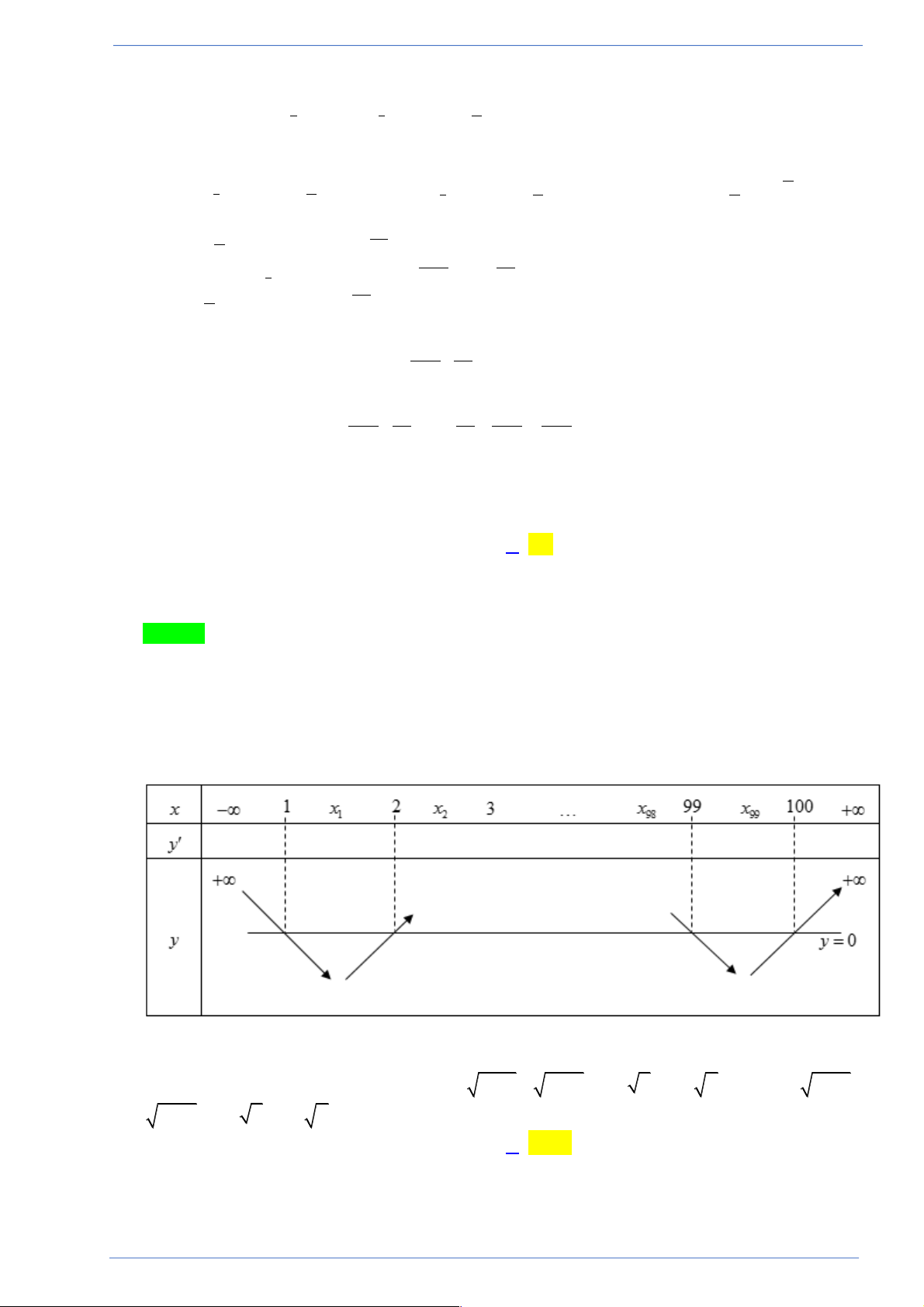
Câu 23. Cho hàm số f (x) xác định, liên tục trên ! và có bảng biến thiên như hình bên x -¥ 1 - 0 1 +¥ y ' + 0 - 0 + 0 - y 3 3 -¥ 1 - -¥
Đồ thị hàm số y = f (x) cắt đường thẳng y = -2 tại bao nhiêu điểm? A. 0 . B. 2 . C. 1. D. 4 .
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 3
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC
Câu 24. Trong không gian Oxyz, cho hai điểm A( 2;
- 1; 0), B(2; 5; -4). Phương trình mặt cầu đường kính AB là
A. (x + )2 +( y - )2 2 2 1 + z =12.
B. x + ( y - )2 +(z + )2 2 3 2 = 48.
C. (x - )2 +( y - )2 +(z + )2 4 4 4 = 48.
D. x + ( y - )2 +(z + )2 2 3 2 =12.
Câu 25. Tập nghiệm của bất phương trình log 3x +1 < log 25 - 25x 5 ( ) 5 ( ) là æ 1 ö æ 6 ö æ 1 6 ö æ 6 ö A. - ;1 .. B. ; -¥ .. C. - ; .. D. ;1 .. ç ÷ ç ÷ ç ÷ ç ÷ è 3 ø è 7 ø è 3 7 ø è 7 ø
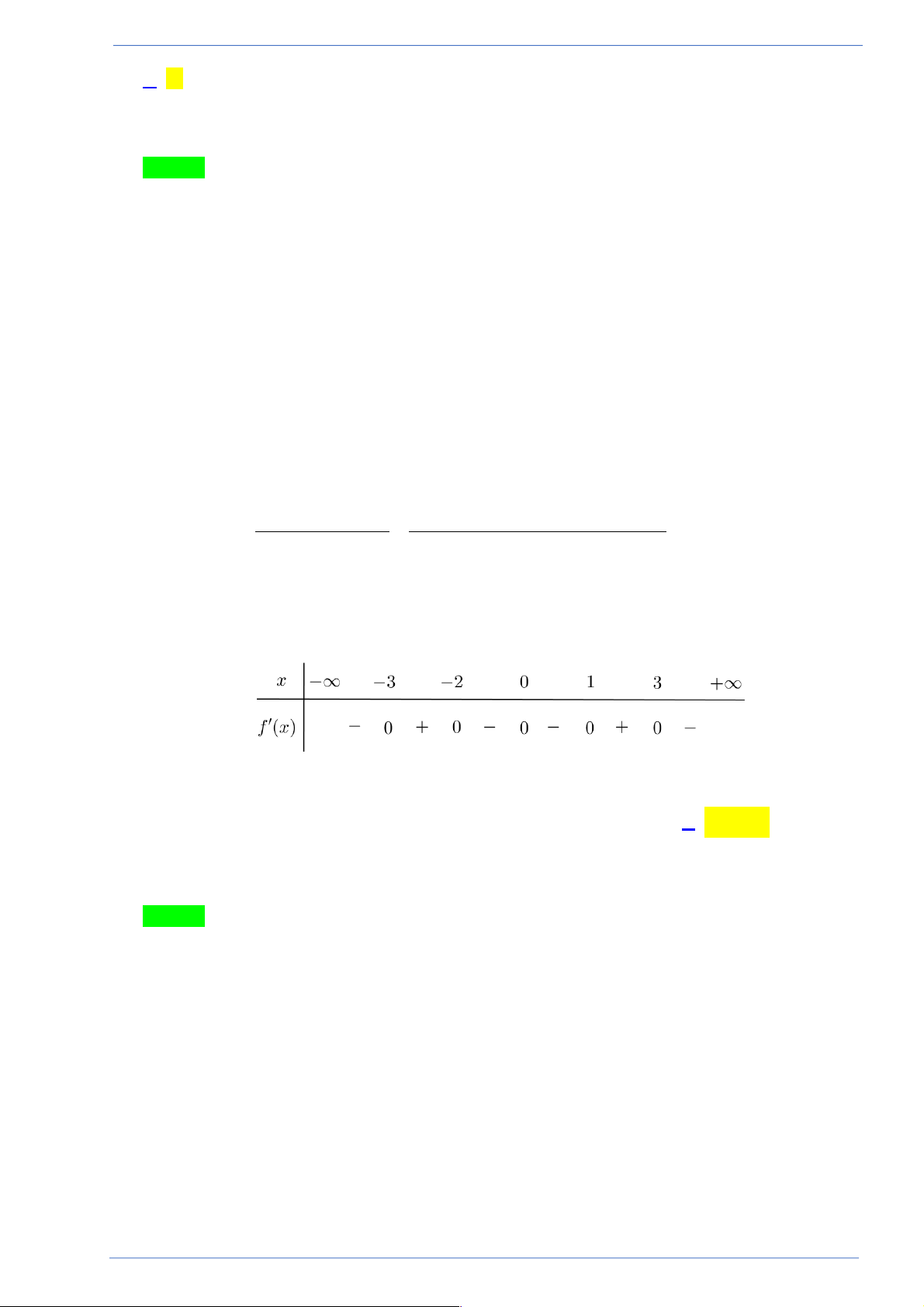
Câu 26. Cho hàm số y = f (x)liên tục trên [ 3; -
]3 và có bảng xét dấu của đạo hàm như hình bên.
Mệnh đề nào sau đây sai?
A. Hàm số đạt cực tiểu tại x = 1.
B. Hàm số đạt cực đại tại x = 2 .
C. Hàm số đạt cực đại tại x = 1 - .
D. Hàm số đạt cực tiểu tại x = 0 .
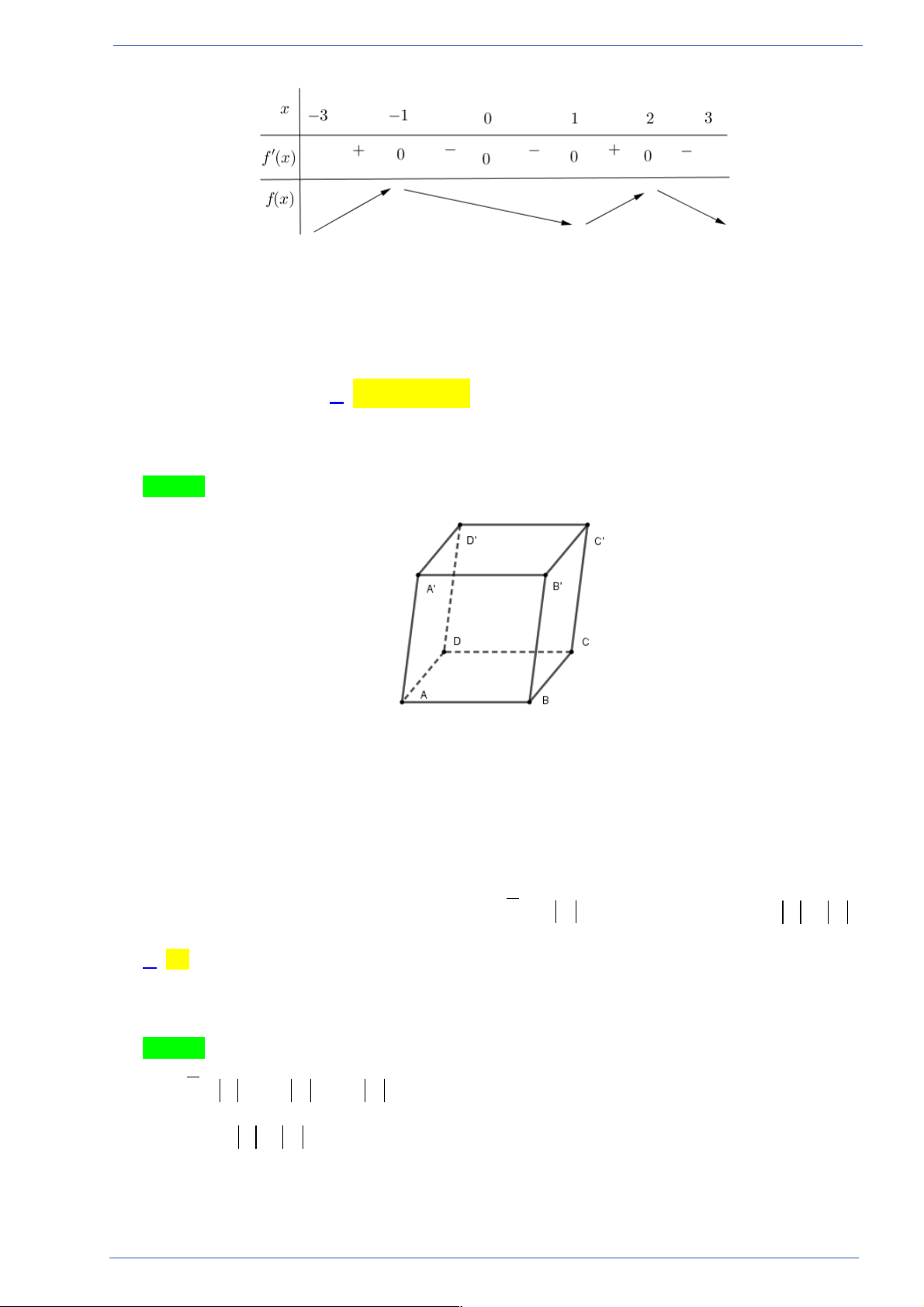
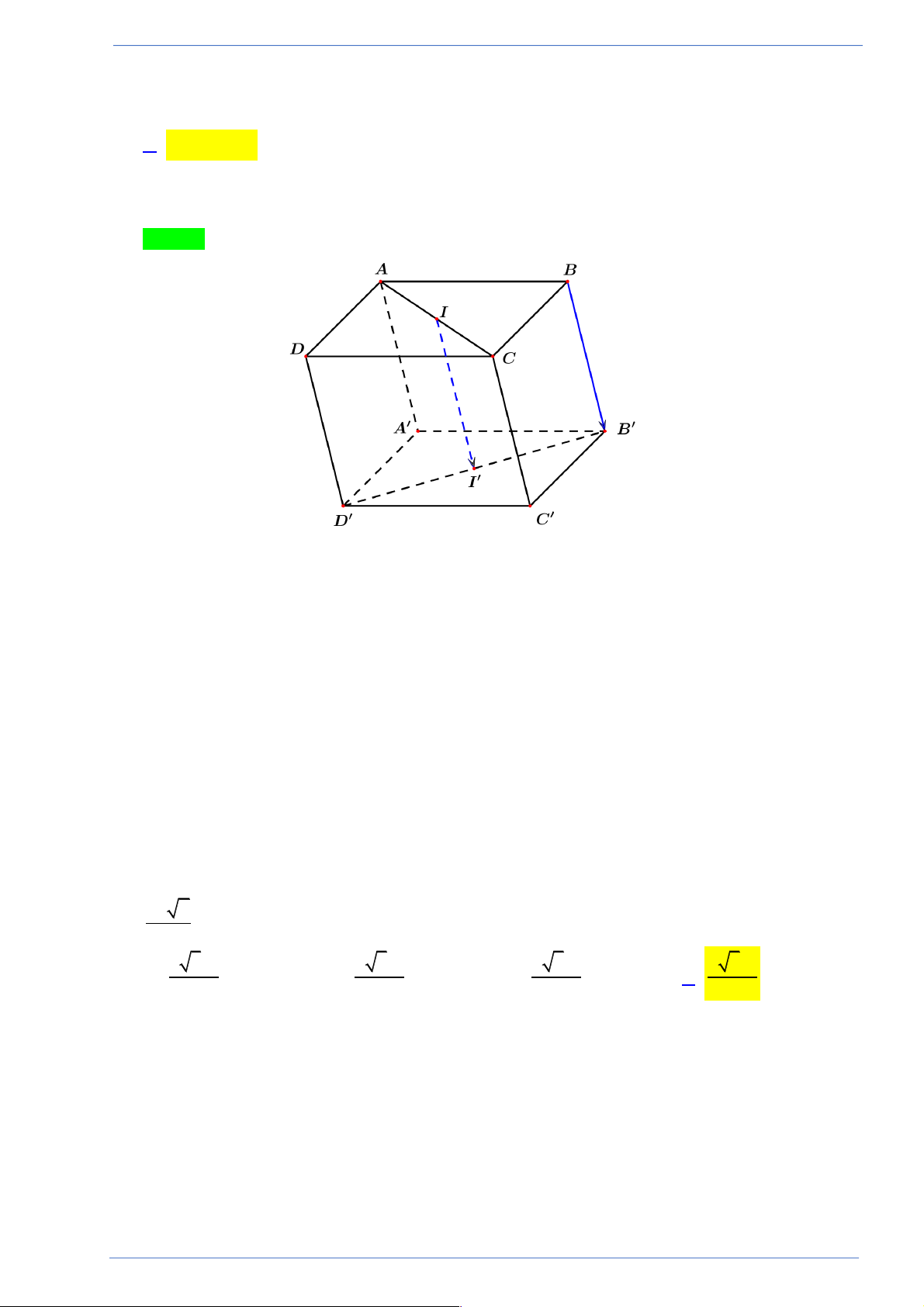
Câu 27. Cho hình hộp AB . CD A¢B C
¢ ¢D¢. Bộ 3 vectơ không đồng phẳng là: !!!" !!!" !!!!!" !!!" !!!!" !!!"
A. AC, BD, A' D '.
B. AC, AC ', BB '. !!!" !!!!" !!!!!" !!!!" !!!!" !!!!"
C. AB, BD ',C ' D '.
D. A'C, B ' D, BD '.
Câu 28. Cho hai số phức z , z thỏa mãn z z = 4, z = 3. Giá trị biểu thức 2 2
P = z + z bằng 1 2 1 1 2 1 2 A. 13. B. 25. C. 7. D. 19.
Câu 29. Trong không gian với hệ tọa độ Oxyz , cho M (2;-1;3), N (3;2;- 4), P(1;-1;2 . X ) ác định tọa
độ điểm Q để MNPQ là hình bình hành? A. Q(2;2;-5). B. Q(2;-3;-5). C. Q(0;- 4;9). D. Q(1;3;- 2). x - 2
Câu 30. Giá trị nhỏ nhất của hàm số y = trên đoạn [0; ] 3 là x +1 1 1 A. min y = -3. B. min y = -2. C. min y = . D. min y = - . x [ Î 0; ] 3 x [ Î 0; ] 3 x [ Î 0; ] 3 4 x [ Î 0; ] 3 2 1
Câu 31. Cho hàm số y = f (x) có đạo hàm liên tục trên [0 ] ;1 , thỏa mãn f
ò (x)dx = 3 và f ( )1 = 4. Tích 0 1 phân xf ¢
ò (x)dx có giá trị là 0 1 A. - 1 . B. . C. 1. D. 1 - . 2 2
Câu 32. Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm A(1;0;3); B(5;2;- ) 1 . Phương trình
nào sau đây là phương trình dạng chính tắc của đường thẳng đi qua hai điểm A và B ? x -1 y z - 3 x -1 y z - 3 A. = = . B. = = . 5 2 1 - 2 - 1 2 - x - 3 y -1 z -1 x - 5 y - 2 z +1 C. = = . D. = = . 2 1 2 - 2 1 2
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 4
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC
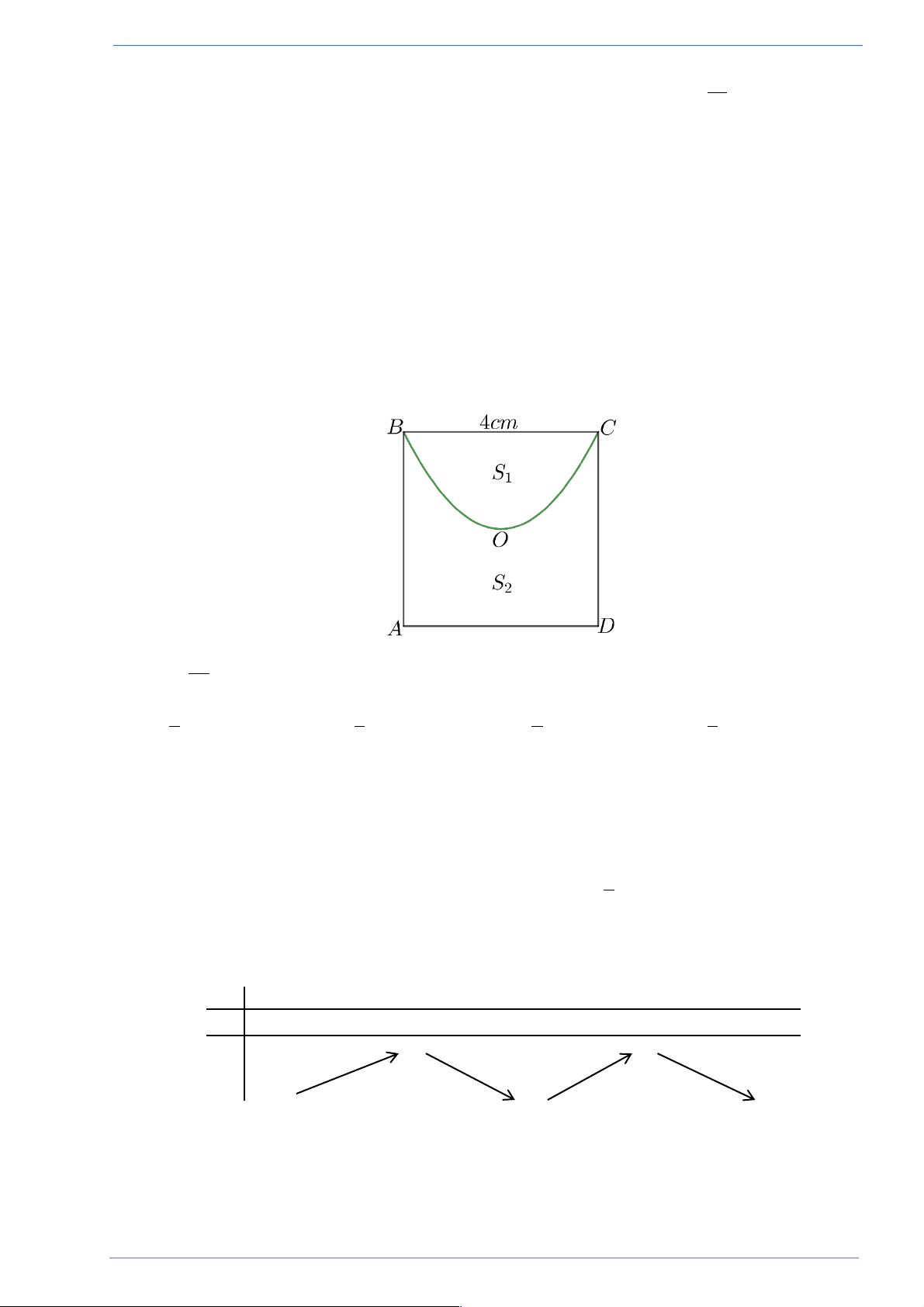
Câu 33. Có 3 quả bóng tennis được chứa trong một hộp hình trụ (hình vẽ bên) với chiều cao 21 cm và bán kính 3,5 cm .
Thể tích bên trong hình trụ không bị chiếm lấy bởi các quả bóng tennis (bỏ qua độ dày của vỏ
hộp) bằng bao nhiêu? A. 82,75p 3 cm . B. 87,25p 3 cm . C. 85,75p 3 cm . D. 87,75p 3 cm .
Câu 34. Có bao nhiêu số tự nhiên có hai chữ số khác nhau? A. 72. B. 81. C. 90. D. 18.
Câu 35. Cho hàm số f (x) có đạo hàm f ¢(x) = (x + x)(x - )2 (x - )3 2 2 4 , x
" Î! .Số điểm cực trị của
hàm số f (x) là A. 2 . B. 3 . C. 1.. D. 4 .
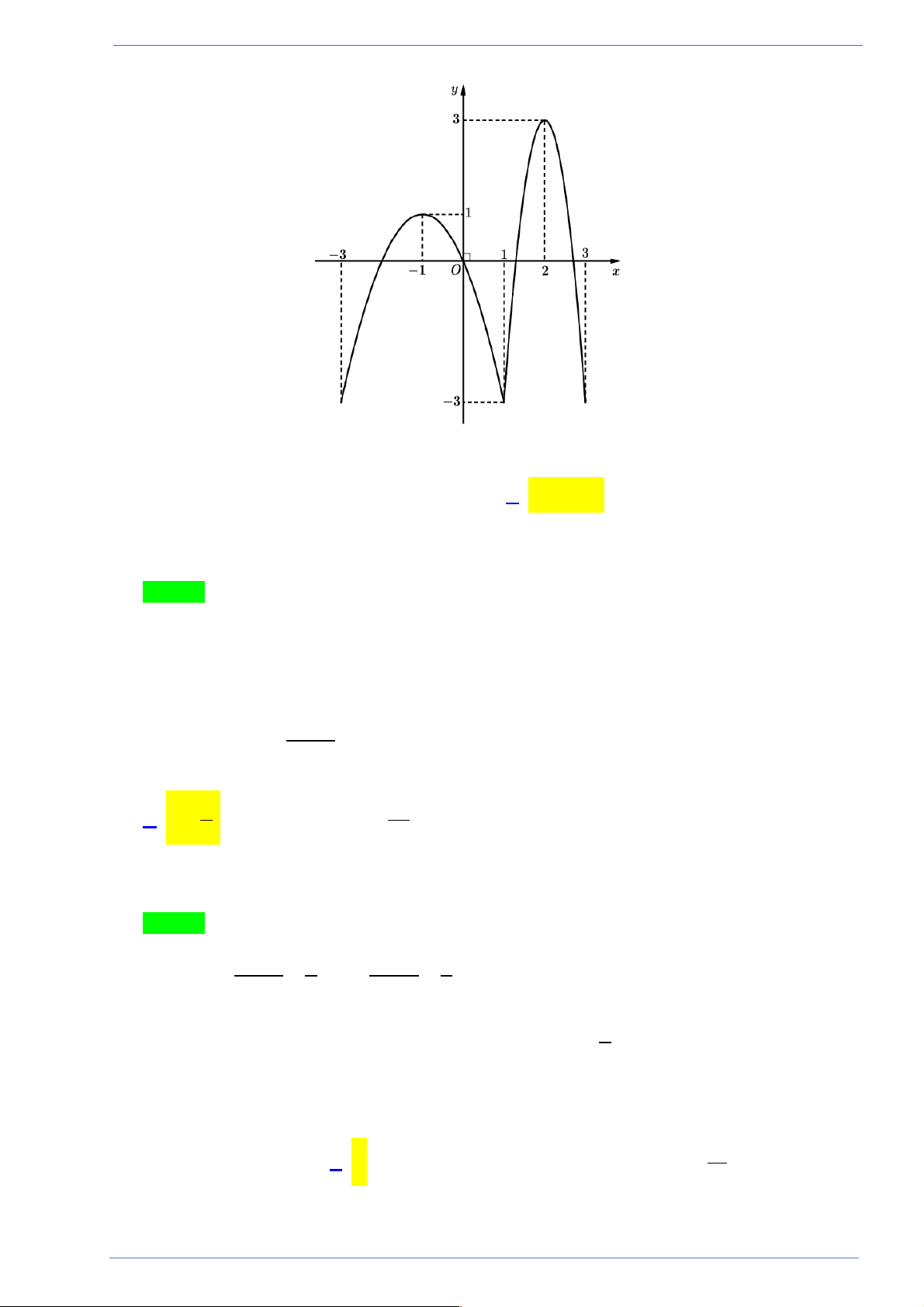
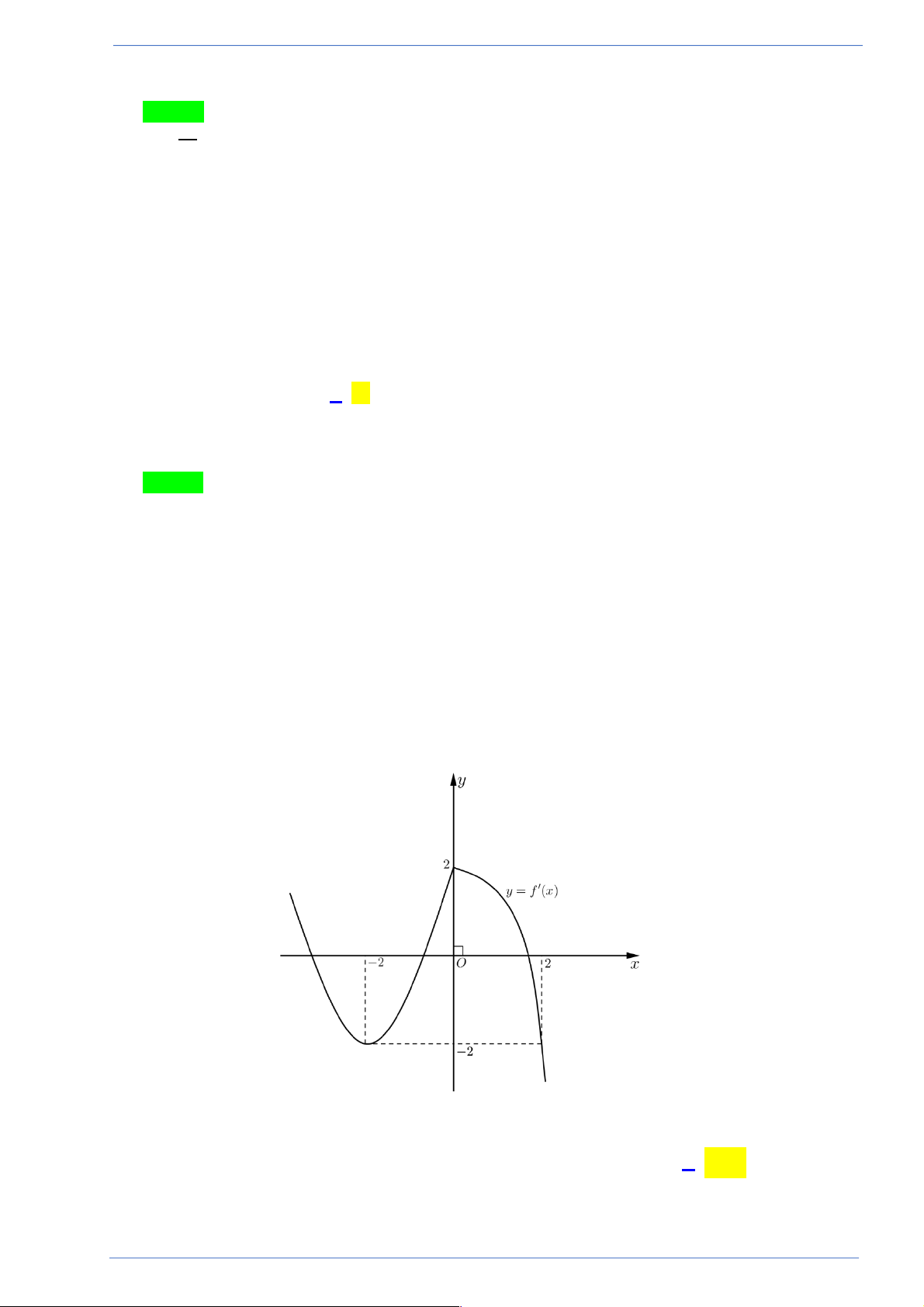
Câu 36. Cho hàm số y = f (x) có đồ thị hàm số y = f (x) như hình vẽ bên
Hàm số y = f (x + ) 2
1 + x + 2x đồng biến trên khoảng? A. ( 2; - - ) 1 . B. ( 3; - 2 - ). C. ( 3; - 0). D. (0 ) ;1 .
Câu 37. Trong không gian với hệ tọa độOxyz , cho điểm I ( ( 2;1; )
1 và mặt phẳng (P): 2x + y + 2z -1= 0
. Mặt cầu (S ) có tâm I , cắt (P) theo một đường tròn có bán kính r = 4. Mặt cầu (S ) có phương trình là:
A. (x + )2 +( y + )2 +(z + )2 2 1 1 = 20.
B. (x - )2 +( y - )2 +(z - )2 2 1 1 =1 . 8
C. (x - )2 +( y - )2 +(z - )2 2 1 1 = 20.
D. (x - )2 +( y - )2 +(z - )2 2 1 1 = 2 5 .
Câu 38. Đầu tháng một người gửi ngân hàng 400.000.000 đồng ( 400 triệu đồng) với lãi suất gửi là 0, 6%
mỗi tháng theo hình thức lãi suất kép. Cuối mỗi tháng người đó đều đặn gửi vào ngân hàng số
tiền là 10.000.000 (10 triệu đồng). Hỏi sau ít nhất bao nhiêu tháng ( kể từ lúc người này ra ngân
hàng gửi tiền) thì số tiền người đó tích lũy được lớn hơn 700.000.000 (bảy trăm triệu đồng)?
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 5
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC A. 22 tháng. B. 23 tháng. C. 25 tháng. D. 24 tháng.
Câu 39. Cho đồ thị hàm số 3 2
y = ax + bx + cx + d như hình vẽ dưới đây: 2 3x - x - 2
Đồ thị của hàm số g ( x) =
có bao nhiêu đường tiệm cận đứng? 2
3 f ( x) - 6 f ( x) A. 5. B. 4 . C. 3. D. 2 .
Câu 40. Cho hàm số f (x) có bảng xét dấu của đạo hàm như hình bên.
Hàm số y = f (1- x) nghịch biến trên khoảng A. (1;4). B. (0;2). C. (0 ) ;1 . D. ( 2; - - ) 1 .
Câu 41. Trong không gian với hệ tọa độ Oxyz , cho hình hộp ABC . D A¢B C ¢ D ¢ ¢ biết A(1;2;3), B¢(2;0;- )
1 , C (3;0;-3) và D¢( 2;
- 4;-3). Tọa độ đỉnh B của hình hộp ABC . D A¢B C ¢ D ¢ ¢ là A. B(4;-1; ) 1 . B. B(2;-1;2). C. B(4;1;- ) 1 . D. B(0;1;- ) 3 .
Câu 42. Cho hình chóp S.ABCD có đáy là hình vuông cạnh AB = 2a , SA
D B là tam giác cân tại S và
nằm trong mặt phẳng vuông góc với mặt phẳng ( ABCD). Gọi M , N lần lượt là trung điểm của
AB, BCvà G là trọng tâm SC
D D . Biết khoảng cách từ điểm M đến mặt phẳng (SND) bằng
3a 2 . Thể tích của khối chóp . G AMND bằng 4 3 5 3a 3 5 3a 3 5 3a 3 5 3a A. . B. . C. . D. . 2 6 3 18
Câu 43. Cho hình thang ABCD ( AB // CD) biết AB = 5, BC = 3, CD =10, AD = 4 . Thể tích khối tròn
xoay tạo thành khi quay hình thang ABCD ( AB //CD) quanh trục AD bằng A. 128p . B. 84p . C. 112p . D. 90p .
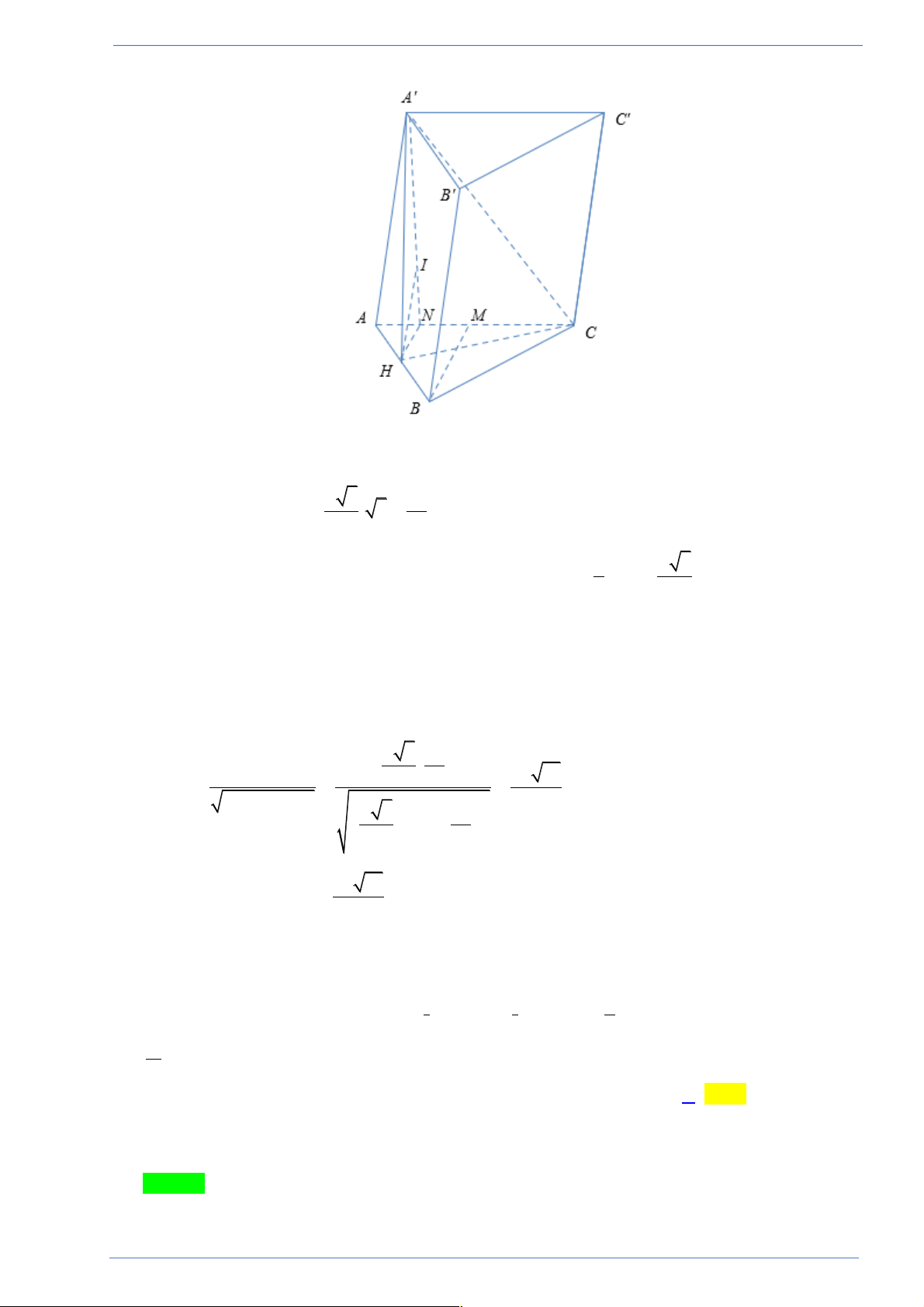
Câu 44. Cho lăng trụ ABC.A¢B C
¢ ¢có đáy là tam giác đều cạnh a , hình chiếu vuông góc của đỉnh A¢ lên
(ABC) là trung điểm H của cạnh AB . Góc giữa đường thẳng A¢Cvà mặt đáy bằng 60°. Khoảng
cách giữa BB¢ và A¢C là a 13 3a 13 2a 13 a 13 A. . B. . C. . D. . 39 13 13 13
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 6
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC æ æ æ æ öööö
Câu 45. Tập xác định của hàm số f ( x) = log çlog çlog çlog çlog x÷÷÷÷ là một khoảng có độ dài 1 4 1 16 1 ç ç ç ÷÷÷ 2 4 è è è è 16 øøøø m -
với m và n là số nguyên dương và nguyên tố cùng nhau. Khi đó m n bằng: n A. 240 - . B. 271. C. 241. D. 241 - .
Câu 46. Số điểm cực đại của đồ thị hàm số y = (x - ) 1 (x - 2)(x - )
3 ...(x -100) bằng A. 50 . B. 99 . C. 49 . D. 100 .
Câu 47. Cho các số thực dương x , y thỏa mãn log x + log y + log x + log y =100 và log x ,
log y , log x , log y là các số nguyên dương. Khi đó kết quả xy bằng A. 200 10 . B. 100 10 . C. 164 10 . D. 144 10 . Câu 48. Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ bên
Giá trị nguyên lớn nhất của tham số m để hàm số y = f ( x - m) đồng biến trên khoảng (10;+¥) là A. 10 - . B. 10. C. 9. D. 11.
Câu 49. Cho hàm số f (x) liên tục trên ! và thoả mãn ( ) + ( - ) 2 3 2 1 x xf x f x = e , x " Î! . 0 Khi đó f
ò (x)dx bằng: 1 - A. 0 . B. 3(e - ) 1 . C. 3(1-e). D. 3e .
Câu 50. Một hộp đựng 9 thẻ được đánh số từ 1 đến 9. Rút ngẫu nhiên hai thẻ từ hộp nêu ở trên, tính xác
suất để tích của hai số trên hai thẻ này là số chẵn. 25 13 5 1 A. . B. . C. . D. . 81 18 18 2 …..HẾT…..
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 7
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC
SỞ GD&ĐT HÀ NỘI
ĐÁP ÁN ĐỀ THI THỬ TỐT NGHIỆP THPTQG 2020 NĂM HỌC 2019 - 2020 MÔN TOÁN
Thời gian làm bài: 90 phút BẢNG ĐÁP ÁN 1.A 2.B 3.D 4.C 5.D 6.C 7.B 8.C 9.B 10.C 11.C 12.B 13.D 14.A 15.C 16.C 17.B 18.D 19.A 20.A 21.B 22.D 23.B 24.D 25.C 26.D 27.D 28.A 29.C 30.B 31.C 32.C 33.C 34.B 35.B 36.D 37.C 38.B 39.A 40.D 41.A 42.D 43.B 44.B 45.D 46.C 47.C 48.C 49.B 50.B
LỜI GIẢI CHI TIẾT
Câu 1. Khối trụ tròn xoay có thể tích bằng 144p và có bán kính đáy bằng 6. Đường sinh của khối trụ bằng A. 4 . B. 6 . C. 12 . D. 10 . Lời giải
Tác giả: Bùi Thị Dung; Fb: Bui Thi Dung Chọn A
Gọi h,l, r lần lượt là chiều cao, đường sinh và bán kính đáy của khối trụ. Ta có: 2 V = p r h 2
Û 144p = p.6 .h Þ h = 4.
Vậy khối trụ có độ dài đường sinh là: l = h = 4 .
Câu 2. Trong các hàm số sau đây, hàm số nào nghịch biến trên tập ! ? æ 1 x ö x A. x y = p . B. y = .
C. y = 3 . D. 3x y = . ç ÷ è 3 ø Lời giải
Tác giả: Bùi Thị Dung; Fb: Bui Thi Dung Chọn B Hàm số mũ x
y = a nghịch biến trên tập ! khi và chỉ khi 0 < a < 1. 2
Câu 3. Giá trị của tích phân 2 d bằng ò x x 0 A. 8 . B. 6 . C. 2 . D. 4 . Lời giải
Tác giả: Dương Đức Tuấn; Fb: Dương Tuấn Chọn D 2 2 Ta có: 2 2 2 2 d = = 2 - 0 = 4. ò x x x 0 0
Câu 4. Đường cong ở hình bên là đồ thị của hàm số nào dưới đây?
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 8
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC x -1 x +1 A. 3
y = -x + 2x +1. B. y = . C. y = . D. 3 2
y = x - x +1. x +1 x -1 Lời giải
Tác giả: Dương Đức Tuấn; Fb: Dương Tuấn Chọn C
Dựa vào hình vẽ suy ra đồ thị hàm số có 2 đường tiệm cận là x = 1 và y = . 1 x +1
Vậy đường cong ở trên là đồ thị hàm số y = . x -1 .
Câu 5. [Mức độ 1] Trong không gian Oxyz , cho mặt phẳng (P): x - 2y +3z + 2020 = 0. Vectơ nào dưới
đây không phải là một vectơ pháp tuyến của mặt phẳng (P)? ! ! ! ! A. n = ( 2; - 4; 6 - ). B. n = ( 1 - ;2; 3 - ). C. n = (1; 2 - ;3). D. n = ( 2; - 3;2020). Lời giải
Người làm: Nguyễn Ngọc Thảo; Fb:Nguyễn Ngọc Thảo Chọn D !!"
+) Mặt phẳng (P): x - 2y +3z + 2020 = 0 có một vectơ pháp tuyến là n = (1; 2 - ;3 P ). !!"
+) Các vectơ ở phương án A;B;C cùng phương với n nên cũng là vectơ pháp tuyến của (P). P ! !!" +) Vectơ n = ( 2;
- 3;2020) ở phương án D không cùng phương với n nên không phải là vectơ P
pháp tuyến của (P).
Câu 6. Cho số phức z = 5 + 3i . Số phức liên hợp của z là A. 5 - + 3i . B. 5 - - 3i . C. 5 - 3i . D. 5i - 3. Lời giải
Người làm: Nguyễn Ngọc Thảo; Fb:Nguyễn Ngọc Thảo Chọn C
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 9
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC
Số phức z = a + bi ,( ;
a bÎ! ) có số phức liên hợp là z = a -bi.
Vậy số phức z = 5 + 3i có số phức liên hợp là z = 5-3i.
Câu 7. Trong mặt phẳng (Oxy), điểm M biểu diễn số phức z = 1
- - 3i có tọa độ là A. M (1; 3 - ). B. M ( 1 - ;- ) 3 . C. M ( 1 - ;3). D. M (1;3). Lời giải
Người làm: Nguyễn Phương Thu; Fb: Nguyễn Phương Thu Chọn B
Điểm M biểu diễn số phức z = 1 - - 3i là M ( 1 - ;- ) 3 .
Câu 8. Cho các số thực dương a,b và a ¹ 1. Biểu thức 2 log a b bằng a A. 2(1+ log 2log + 1+ log a b). B. . C. . D. . a b 2 loga b a b Lời giải
Người làm: Nguyễn Phương Thu; Fb: Nguyễn Phương Thu Chọn C Ta có: 2 2
log a b = log a + log b = 2log a + log b = 2 + log b. a a a a a a
Câu 9. Thể tích khối lăng trụ tam giác có chiều cao bằng 2 , cạnh đáy lần lượt bằng 3, 4 , 5 là: A. 8. . B. 12.. C. 4.. D. 28. Lời giải
Người làm:Trần Thu Hương; Fb:Trần Thu Hương Chọn B A' C'
Khối lăng trụ tam giác có cạnh đáy lần lượt là 3, 4 , 5. B'
Vậy đáy là tam giác vuông có hai cạnh góc vuông lần lượt là 3 , 4 . 1
Thể tích khối lăng trụ: V = . B h = .3.4.2 = 12. 2 A C . B
Câu 10. Trong các khối hình sau, khối không phải khối tròn xoay là: A. Khối cầu. B. Khối trụ. C. Khối lăng trụ. D. Khối nón. Lời giải
Ngườilàm:Trần Thu Hương; Fb: Trần Thu Hương Chọn. C.
Khối lăng trụ không phải khối tròn xoay.
kieunga03@gmail.com; Gmail Gv phản biện vòng 2.
Câu 11. Họ tất cả các nguyên hàm của hàm số f (x) 2 = sin x + là x 2
A. cosx + 2ln x + C. B. cosx - + C . 2 x
C. - cosx + 2ln x + C . D. - cosx - 2ln x + C . Lời giải
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 10
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC
Tác giả: Kiều Thị Thúy, Fb: Thúy Kiều Chọn C æ 2 ö sinx +
dx = - cosx + 2ln x + C . òç ÷ è x ø ! ! ! ! !
Câu 12. Trong không gian với hệ tọa độ Oxyz , cho a = 2
- i + 3 j + 5k . Tọa độ của a là A. (2;3;5). B. ( 2; - 3;5). C. (2;3;-5). D. (2;-3;-5). Lời giải
Tác giả: Kiều Thị Thúy, Fb: Thúy Kiều Chọn B !
Tọa độ của a là ( 2; - 3;5).
Câu 13. Cho 2 số thực dương x , y thỏa mãn x ¹ 1 và log 3. Tính 5 T = log y . x y = 3 x 5 A. T = 9 . B. T = 3 . C. T = . D. T = 5. 3 5 5 Lời giải
Tác giả: Thành Đức Trung; Fb: Thành Đức Trung Chọn D Ta có 3 log = 3 Û = . x y y x 5 Suy ra 3 15 1 T = log = = = 3 ( x ) log 3 x .15.log x 5 . 3 x x x Vậy T = 5.
Câu 14. Trong không gian Oxyz , cho điểm M (2;-1;3) và mặt phẳng (a ):2x -5y + z -1= 0. Phương
trình mặt phẳng nào dưới đây đi qua điểm M và song song với (a ).
A. 2x - 5y + z -12 = 0. B. 2x - 5y - z -12 = 0.
C. 2x + 5y - z -12 = 0. D. 2x - 5y + z +12 = 0. Lời giải
Tác giả: Thành Đức Trung; Fb: Thành Đức Trung Chọn A
Gọi (P) là mặt phẳng đi qua điểm M và song song với (a ). !!"
Ta có (P)//(a ) nên (P) có một véc-tơ pháp tuyến là - P n = (2; 5; ) 1 .
Mặt phẳng (P) đi qua điểm M và song song với (a ) có phương trình là
2(x - 2) -5( y + )
1 + z -3 = 0 Û 2x -5y + z -12 = 0.
Câu 15. Cho hàm số y = f (x) có đồ thị như hình vẽ bên.
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 11
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC
Hàm số đã cho nghịch biến trên khoảng A. (0 ; 2). B. ( 3 ; - - ) 1 . C. ( 1 - ; 0). D. (1 ; 3). Lời giải
Người làm: Trần Văn Đô; Fb: Tran Tran Do Chọn C
Dựa vào đồ thị ta thấy: Hàm số nghịch biến trên các khoảng là ( 1 - ; ) 1 và (2 ; 3).
Nên hàm số cũng nghịch biến ( 1 - ; 0). x + 2
Câu 16. Đồ thị hàm số y =
có đường tiệm cận ngang là đường thẳng nào sau đây? 2x +1 A. x = 1 - . B. y = 2. 1 1 C. y = . D. x - = . 2 2 Lời giải
Người làm: Trần Văn Đô; Fb: Tran Tran Do Chọn C x + 2 1 x + 2 1 Ta có: lim = ; lim = .
x®+¥ 2x +1 2 x®-¥ 2x +1 2 1
Do đó tiệm cận ngang của đồ thị hàm số là đường thẳng y = . 2
Người làm:hoangdang.sun2018@gmail.com, người thu bài:.
Câu 17. Gọi S là tập nghiệm của phương trình 9x 10.3x -
+ 9 = 0. Tổng các phần tử của S bằng 10 A. 1. B. 2 . C. 10. D. . 3 Lời giải
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 12
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC
Người làm:Huỳnh Thị Ngọc Dung; Fb: Huỳnh Dung Ngọc Dung Chọn B 3x é =1 éx = 0
9x -10.3x + 9 = 0 Û ê Û . ê 3x ë = 9 ëx = 2 Þ S = {0 , } 2
Vậy tổng các phần tử của S bằng 2 .
Câu 18. Một xe ô tô đang chuyển động đều với vận tốc 16 m / s thì người lái xe nhìn thấy một chướng
ngại vật nên đạp phanh tại điểm đó, ô tô chuyển động chậm dần đều với vận tốc v(t) = 2 - t +16
trong đó t là thời gian (tính bằng giây) kể từ lúc đạp phanh. Quãng đường mà ô tô đi được trong
10 giây cuối cùng bằng A. 60m . B. 64m . C. 160m . D. 96m . Lời giải
Người làm: Huỳnh Thị Ngọc Dung; Fb: Huỳnh Dung Ngọc Dung. Chọn D
Lấy mốc thời gian lúc ô tô bắt đầu đạp phanh.
Khi ô tô dừng hẳn thì v(t) = 0 Û 2
- t +16 = 0 Û t = 8. 8 8
Quãng đường mà ô tô đi được trong 8 giây cuối: ò( 2
- t +16) dt = ( 2t
- +16t) = 64 (m). 0 0
Theo đề bài: ô tô đi được 10 giây cuối cùng nên 2 giây đầu ô tô đi được:16.2 = 32m .
Vậy quãng đường ô tô đi được trong 10 giây cuối: 64 + 32 = 96m .
Câu 19. Cho hàm số y = f (x) có đạo hàm f ¢(x) =1, x
" Î ! . Mệnh đề nào sau đây đúng? A. f (- ) 1 < f (2). B. f (- ) 1 = f (2). C. f (- ) 1 ³ f (2). D. f (- ) 1 > f (2). Lời giải
Người làm: Lương Công Sự; Fb: Lương Công Sự Chọn A
Vì f ¢(x) =1> 0 x
" Î ! nên f (x) là hàm số đồng biến trên ! . 1 - < 2 Þ f (- ) 1 < f (2)..
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 13
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC
Câu 20. Cho hình vuông ABCD tâm O, độ dài cạnh là 4 .
cm Đường cong BOC là một phần parabol
đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S và S (tham khảo hình 1 2 vẽ). S Tỉ số 1 bằng S2 1 3 2 1 A. . B. . C. . D. . 2 5 5 3 Lời giải
Người làm: Lương Công Sự; Fb: Lương Công Sự Chọn A
Chọn hệ trục tọa độ Oxy, với O là gốc tọa độ, trục Ox đi
qua trung điểm của AB và . CD Parabol có dạng (P) 2 : y = ax . 1
Vì điểm C (2 ; 2)Î(P) nên 2 = 4a Û a = . 2 1 Vậy (P) 2 : y = x . 2 2 æ 1 ö 16 2 S = 2 - x dx = . 1 ò ç ÷ è 2 ø 3 2 - 16 32 S = S - S =16 - = . 2 ABCD 1 3 3 S 1 Vậy 1 = .. S 2 2
Câu 21. Một cấp số nhân có số hạng thứ 3 và số hạng thứ 6 lần lượt là 9 và 243 -
. Khi đó số hạng thứ 8
của cấp số nhân bằng: A. 2187 . B. 2187 - . C. 729 . D. 243. Lời giải
Người làm: Phạm Văn Nghiệp; Fb: Phạm Văn Nghiệp Chọn B
Gọi u là số hạng đầu, q là công bội của cấp số nhân. 1
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 14
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC 2 u ìï = u q u 243 - Ta có: 3 1 í 3 6 Þ q = = = 27 - Þ q = 3 - . 5 u ï = u q î u 9 6 1 3 Khi đó 2
u = u q = -243.9 = 2187 - . 8 6
Câu 22. Tìm hàm số F ( x) không là nguyên hàm của hàm số f (x) = sin 2x. A. F (x) 2 = -cos x. B. F (x) 2 = sin x. C. F ( x) 1
= - cos 2x. D. F (x) = -cos2x. 2 Lời giải
Người làm: Phạm Văn Nghiệp; Fb: Phạm Văn Nghiệp Chọn D Vì ( cos2x)¢ -
= 2sin 2x nên F (x) = -cos2x không phải là một nguyên hàm của hàm số
f (x) = sin 2x.
Câu 23. Cho hàm số f (x) xác định, liên tục trên ! và có bảng biến thiên như hình bên x -¥ 1 - 0 1 +¥ y ' + 0 - 0 + 0 - y 3 3 -¥ 1 - -¥
Đồ thị hàm số y = f (x) cắt đường thẳng y = -2 tại bao nhiêu điểm? A. 0 . B. 2 . C. 1. D. 4 . Lời giải
Người làm: Bùi Thị Nhung; Fb: Bùi Nhung Chọn B Vì 2 - < 1
- nên đường thẳng y = -2 nằm dưới đường thẳng y = 1. - x -¥ 1 - 0 1 +¥ y ' + 0 - 0 + 0 - y 3 3 1 - y = -2 -¥ -¥
Từ bảng biến thiên suy ra đồ thị hàm số y = f (x) cắt đường thẳng y = -2 tại 2 điểm phân biệt.
Câu 24. Trong không gian Oxyz, cho hai điểm A( 2;
- 1; 0), B(2; 5; -4). Phương trình mặt cầu đường kính AB là
A. (x + )2 +( y - )2 2 2 1 + z =12.
B. x + ( y - )2 +(z + )2 2 3 2 = 48.
C. (x - )2 +( y - )2 +(z + )2 4 4 4 = 48.
D. x + ( y - )2 +(z + )2 2 3 2 =12. Lời giải
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 15
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC
Người làm: Bùi Thị Nhung; Fb: Bùi Nhung Chọn D
Gọi I là trung điểm của đoạn AB suy ra I (0; 3; - 2) . !!!"
Ta có: AB = (4; 4; - 4), AB = + + (- )2 2 2 4 4 4 = 2 12.
Mặt cầu đường kính AB có tâm I (0; 3; - 1
2) và bán kính R = AB = 12 có phương trình là 2
x + ( y - )2 +(z + )2 2 3 2 =12 ..
Câu 25. Tập nghiệm của bất phương trình log 3x +1 < log 25 - 25x 5 ( ) 5 ( ) là æ 1 ö æ 6 ö æ 1 6 ö æ 6 ö A. - ;1 .. B. ; -¥ .. C. - ; .. D. ;1 . ç ÷ ç ÷ ç ÷ ç ÷ è 3 ø è 7 ø è 3 7 ø è 7 ø Lời giải
Tác giả: Nguyễn Đắc Tuấn; Fb: Nguyễn Đắc Tuấn Chọn C ì 1 3 ì x +1 > 0 ïx > - 1 Điều kiện: í Û í 3 Û - < x < 1. î25 - 25x > 0 3 ïîx <1
Ta có: log 3x +1 < log 25 - 25x Û 3x +1 < 25 - 6
25x Û 28x < 24 Û x < . 5 ( ) 5 ( ) 7 æ 1 6 ö
Kết hợp với điều kiện ta có tập nghiệm của bất phương trình đã cho là: S = - ; .. ç ÷ è 3 7 ø
Câu 26. Cho hàm số y = f (x)liên tục trên [ 3; -
]3 và có bảng xét dấu của đạo hàm như hình bên.
Mệnh đề nào sau đây sai?
A. Hàm số đạt cực tiểu tại x = 1.
B. Hàm số đạt cực đại tại x = 2 .
C. Hàm số đạt cực đại tại x = 1 - .
D. Hàm số đạt cực tiểu tại x = 0 . Lời giải
Tác giả: Nguyễn Đắc Tuấn; Fb: Nguyễn Đắc Tuấn Chọn D Ta có bảng biến thiên:
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 16
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC
Vậy hàm số đạt cực tiểu tại x = 1;hàm số đạt cực đại tại x = 1 - và x = 2..
Câu 27. [Mức độ 1] Cho hình hộp AB . CD A¢B C
¢ ¢D¢. Bộ 3 vectơ không đồng phẳng là: !!!" !!!" !!!!!" !!!" !!!!" !!!"
A. AC, BD, A' D '.
B. AC, AC ', BB '. !!!" !!!!" !!!!!" !!!!" !!!!" !!!!"
C. AB, BD ',C ' D '.
D. A'C, B ' D, BD '. Lời giải
Người làm: Trịnh Ngọc; Fb: Ngọc Trịnh Chọn D
3 vectơ đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng. !!!" !!!" !!!!!"
A. AC, BD, A' D ' có giá cùng song song với mặt phẳng ( ABCD). !!!" !!!!" !!!"
B. AC, AC ', BB ' có giá cùng song song với mặt phẳng ACC¢A¢ . ( ) !!!" !!!!" !!!!!"
C. AB, BD ',C ' D ' có giá cùng nằm trên mặt phẳng ABC¢D¢ . ( )
Câu 28. [Mức độ 2] Cho hai số phức z , z thỏa mãn z z = 4, z = 3. Giá trị biểu thức 2 2 P = z + z 1 2 1 1 2 1 2 bằng A. 13. B. 25. C. 7. D. 19. Lời giải
Người làm: Ngọc Trịnh; Fb: Trịnh Ngọc Chọn A Có 2 z z = z = 4; 2 z = 3Þ z = 9. 1 1 1 2 2 Khi đó, 2 2 P = z + z = 4+9 =13.. 1 2
Câu 29. [Mức độ 2] Trong không gian với hệ tọa độ Oxyz , cho M (2;-1;3), N (3;2;- 4), P(1;-1;2).
Xác định tọa độ điểm Q để MNPQ là hình bình hành?
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 17
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC A. Q(2;2;-5). B. Q(2;-3;-5). C. Q(0;- 4;9). D. Q(1;3;- 2). Lời giải
Người làm: Nguyễn Bá Long; Fb: Nguyễn Bá Long Chọn C ìx -1= 2 -3 ìx = 0 !!!" !!!!" ï Q ï ï Q
MNPQ là hình bình hành khi và chỉ khi PQ = NM Û íy +1 = 1 - - 2 Û íy = -4. Q Q ï ï ïz - 2 = 3- î z = 9 Q ( 4 - ) î Q Vậy Q(0;- 4;9). x - 2
Câu 30. [Mức độ 2] Giá trị nhỏ nhất của hàm số y = trên đoạn [0; ] 3 là x +1 1 1 A. min y = -3. B. min y = -2. C. min y = . D. min y = - . x [ Î 0; ] 3 x [ Î 0; ] 3 x [ Î 0; ] 3 4 x [ Î 0; ] 3 2 Lời giải
Người làm: Nguyễn Bá Long; Fb: Nguyễn Bá Long Chọn B x - 2 Hàm số y =
liên tục trên đoạn [0; ] 3 . x +1 3 Ta có y¢ = > 0 "x Î 0;3 2 [ ]. (x + )1
Vậy min y = y (0) = 2 - . x [ Î 0; ] 3 1
Câu 31. Cho hàm số y = f (x) có đạo hàm liên tục trên [0 ] ;1 , thỏa mãn f
ò (x)dx = 3 và f ( )1 = 4. Tích 0 1 phân xf ¢
ò (x)dx có giá trị là 0 1 A. - 1 . B. . C. 1. D. 1 - . 2 2 Lời giải
Người làm: Đinh Văn Trường; Fb: Đinh Văn Trường Chọn C Ta có 1 1 1 xf ¢ ò (x)dx = d x f
ò (x) = xf (x)1 - f ò (x)dx 0 0 0 0 1 = f ( ) 1 - f
ò (x)dx = 4-3 =1. 0
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 18
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC
Câu 32. [Mức độ 1] Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm A(1;0;3); B(5;2;- ) 1 .
Phương trình nào sau đây là phương trình dạng chính tắc của đường thẳng đi qua hai điểm A và B ? x -1 y z - 3 x -1 y z - 3 A. = = . B. = = . 5 2 1 - 2 - 1 2 - x - 3 y -1 z -1 x - 5 y - 2 z +1 C. = = . D. = = . 2 1 2 - 2 1 2 Lời giải
Người làm:Trịnh Thị Thu Hương; Fb:Huong Trinh Chọn C !!!"
Một vectơ chỉ phương của đường thẳng AB là: AB = (4;2;- 4). !
Suy ra một vectơ chỉ phương khác của AB là u = (2;1;- 2). 1- 3 0 -1 3 -1
Lại có điểm A(1;0;3) thuộc đường thẳng ở phương án C vì: = = = - . 1 2 1 2 - Vậy chọn C
lvnguyen51@gmail.com.
Câu 33. Có 3 quả bóng tennis được chứa trong một hộp hình trụ (hình vẽ bên) với chiều cao 21 cm và bán kính 3,5 cm .
Thể tích bên trong hình trụ không bị chiếm lấy bởi các quả bóng tennis (bỏ qua độ dày của vỏ
hộp) bằng bao nhiêu? A. 82,75p 3 cm . B. 87,25p 3 cm . C. 85,75p 3 cm . D. 87,75p 3 cm . Lời giải
Người làm: Lê Văn Nguyên; Fb: Lê Văn Nguyên Chọn C
Thể tích khối trụ là: V = p. 3,5 .21 = 257,25p 3 cm 1 ( )2 .
Mỗi quả bóng tennis cũng có bán kính bằng 3,5cm nên 3 quả bóng có thể tích là: 4 V = 3. .p . 3,5 =171,5p 3 cm 2 ( )3 . 3
Vậy thể tích cần tìm là V = V -V = 257,25p -171,5p = 85,75p 3 cm . 1 2
Câu 34. Có bao nhiêu số tự nhiên có hai chữ số khác nhau? A. 72. B. 81. C. 90. D. 18. Lời giải
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 19
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC
Tác giả: Đình Khang; Fb:Đình Khang. Chọn B
Gọi ab là số tự nhiên có hai chữ số khác nhau ( , a bÎ{0;1;2;...; } 9 ;a ¹ 0 ). Ta có:
a có 9 cách chọn (do a ¹ 0 ).
Ứng với mỗi cách chọn a ta có 9 cách chọn b (do a ¹ b ).
Theo quy tắc nhân ta được 9.9 = 81 số tự nhiên có hai chữ số khác nhau.
Câu 35. [Mức độ 2] Cho hàm số f (x) có đạo hàm f ¢(x) = (x + x)(x - )2 (x - )3 2 2 4 , x " Î!. Số điểm
cực trị của hàm số f (x) là A. 2 . B. 3 . C. 1.. D. 4 . Lời giải
Tác giả: Đoàn Công Hoàng; Fb: Đoàn Công Hoàng Chọn B
Xét phương trình f ¢(x) = (x + x)(x - )2 (x - )3 2 2 4 = 0 ta có:
+ 2 nghiệm đơn là x = 0; x = 1 - .
+ 1 nghiệm bội lẻ là x = 4.
+ 1 nghiệm bội chẵn là x = 2.
Vậy hàm số f (x) đạt cực trị tại các điểm x = 0; x = 1 - ; x = 4. Buihuong202@gmail.com.
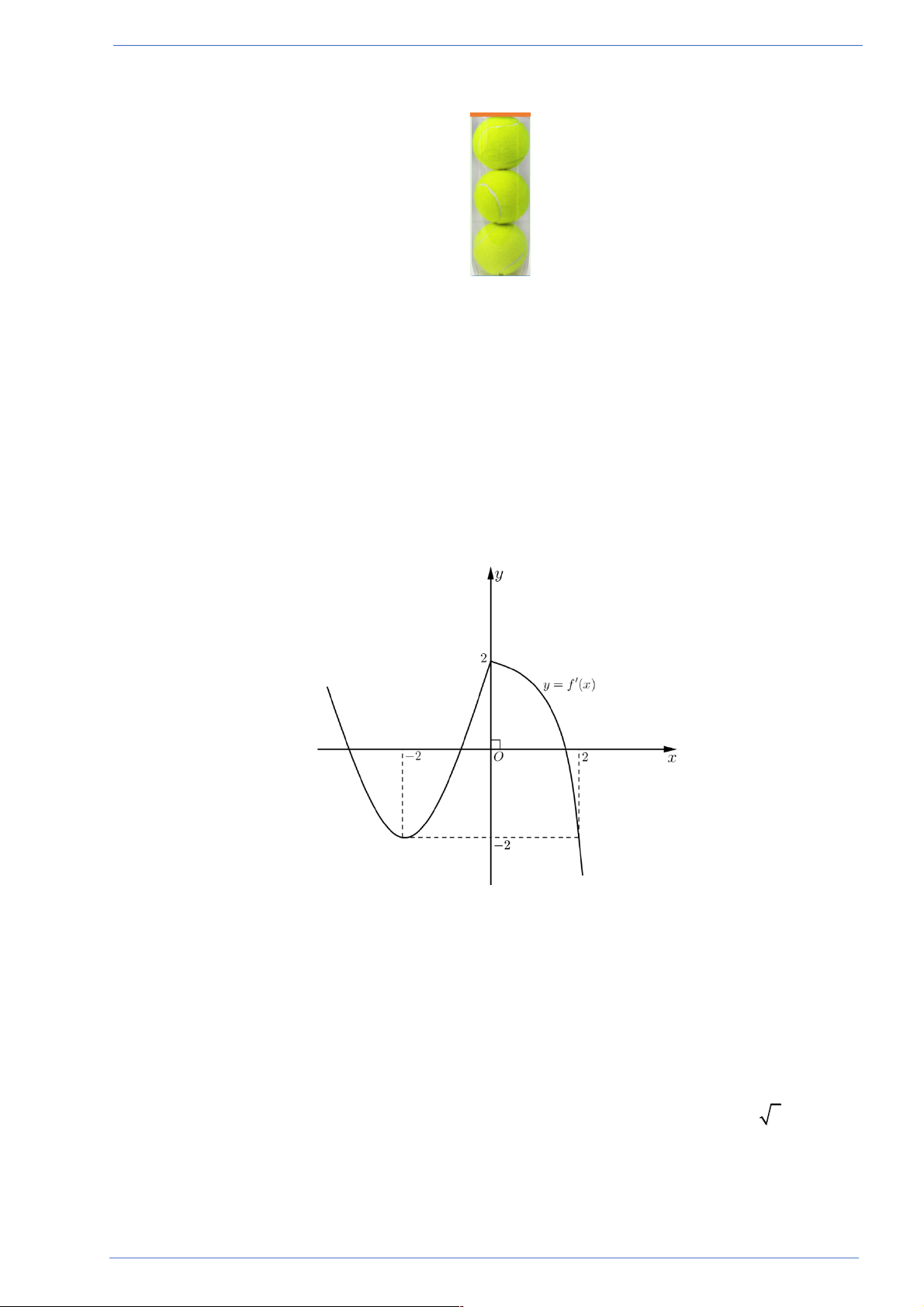
Câu 36. Cho hàm số y = f (x) có đồ thị hàm số y = f (x) như hình vẽ bên
Hàm số y = f (x + ) 2
1 + x + 2x đồng biến trên khoảng? A. ( 2; - - ) 1 . B. ( 3; - 2 - ). C. ( 3; - 0). D. (0 ) ;1 . Lời giải
Tác giả: Bùi Thu hương; Fb: Cucai Đuong
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 20
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC Chọn D
Đặt g (x) = f (x + ) 2
1 + x + 2x Þ g¢(x) = f ¢(x + )
1 + 2x + 2 = f ¢(t) + 2t ( với t = x +1)
Nhìn vào đồ thị nhận thấy 0 < t < 2 thì f ¢(t) > 2
- t hay g¢(x) > 0
Khi đó 0 < x +1 < 2 Þ 1 - < x < 1. .
Câu 37. Trong không gian với hệ tọa độOxyz , cho điểm I ( ( 2;1; )
1 và mặt phẳng (P): 2x + y + 2z -1= 0
. Mặt cầu (S ) có tâm I , cắt (P) theo một đường tròn có bán kính r = 4. Mặt cầu (S ) có phương trình là:
A. (x + )2 +( y + )2 +(z + )2 2 1 1 = 20.
B. (x - )2 +( y - )2 +(z - )2 2 1 1 =1 . 8
C. (x - )2 +( y - )2 +(z - )2 2 1 1 = 20.
D. (x - )2 +( y - )2 +(z - )2 2 1 1 = 2 5 . Lời giải
Người làm: Nguyễn Văn Bình Facebook: Nguyễn Văn Bình Chọn C 2.2 +1+ 2.1-1
Ta có d (I;(P)) = = 2. 2 2 2 2 +1 + 2
Vì mặt cầu (S ) có tâm I , cắt (P) theo một đường tròn có bán kính r = 4 nên mặt cầu (S )có bán kính 2 2
R = r + d (I;(P)) 2 2 = 4 + 2 = 2 5 .
Vậy phương trình mặt cầu (S ) là (x - )2 +( y - )2 +(z - )2 2 1 1 = 20.
Câu 38. Đầu tháng một người gửi ngân hàng 400.000.000 đồng ( 400 triệu đồng) với lãi suất gửi là 0, 6%
mỗi tháng theo hình thức lãi suất kép. Cuối mỗi tháng người đó đều đặn gửi vào ngân hàng số
tiền là 10.000.000 (10 triệu đồng). Hỏi sau ít nhất bao nhiêu tháng ( kể từ lúc người này ra ngân
hàng gửi tiền) thì số tiền người đó tích lũy được lớn hơn 700.000.000 (bảy trăm triệu đồng)? A. 22 tháng. B. 23 tháng. C. 25 tháng. D. 24 tháng. Lời giải
Tác giả: Trần Lê Vĩnh Phúc; Fb: Trần Lê Vĩnh Phúc Chọn B
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 21
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC Tổng quát bài toán:
Gọi T là số tiền người đó gửi ban đầu. 0
r% là lãi suất mỗi tháng.
a là số tiền người đó gửi vào thêm mỗi tháng.
S là số tiền người đó nhận được sau n tháng. n
Đầu tháng 1, số tiền người đó gửi vào là S = T . 0 0
Cuối tháng 1, S = T +T .r% + a = T . 1+ r% + a 1 0 0 0 ( ) .
Cuối tháng 2, S = S + S .r% + a = S .(1+ r%) 2
+ a = T .(1+ r%) + .
a 1+ r% + a 2 1 1 1 0 ( ) . Cuối tháng 3, 3 2
S = T .(1+ r%) + .( a 1+ r%) + .(
a 1+ r%) + a . 3 0 … Cuối tháng n,
S = T . + r + a + r - + + r - é + + + r + ù n (1 %)n
(1 %)n 1 (1 %)n 2 ... (1 %)1 1 0 ë û n n 1+ r% -1 = T . 1+ r% + . a 0 ( ) ( ) r% Theo yêu cầu bài toán: 1+ r% n n -1 T . 1+ r% + . a ³ 700.000.000 0 ( ) ( ) r% n Û ( + )n (1+ 0,6%) -1 40. 1 0,6% + ³ 70 0,6%
Û (1+ 0,6%)n ³1,14515129 Û n ³ log( 1,14515129 » 22,65 1+0,6%)
Vậy phải sau ít nhất 23 tháng thì người đó mới tích lũy được lớn hơn 700.000.000 (bảy trăm triệu đồng).
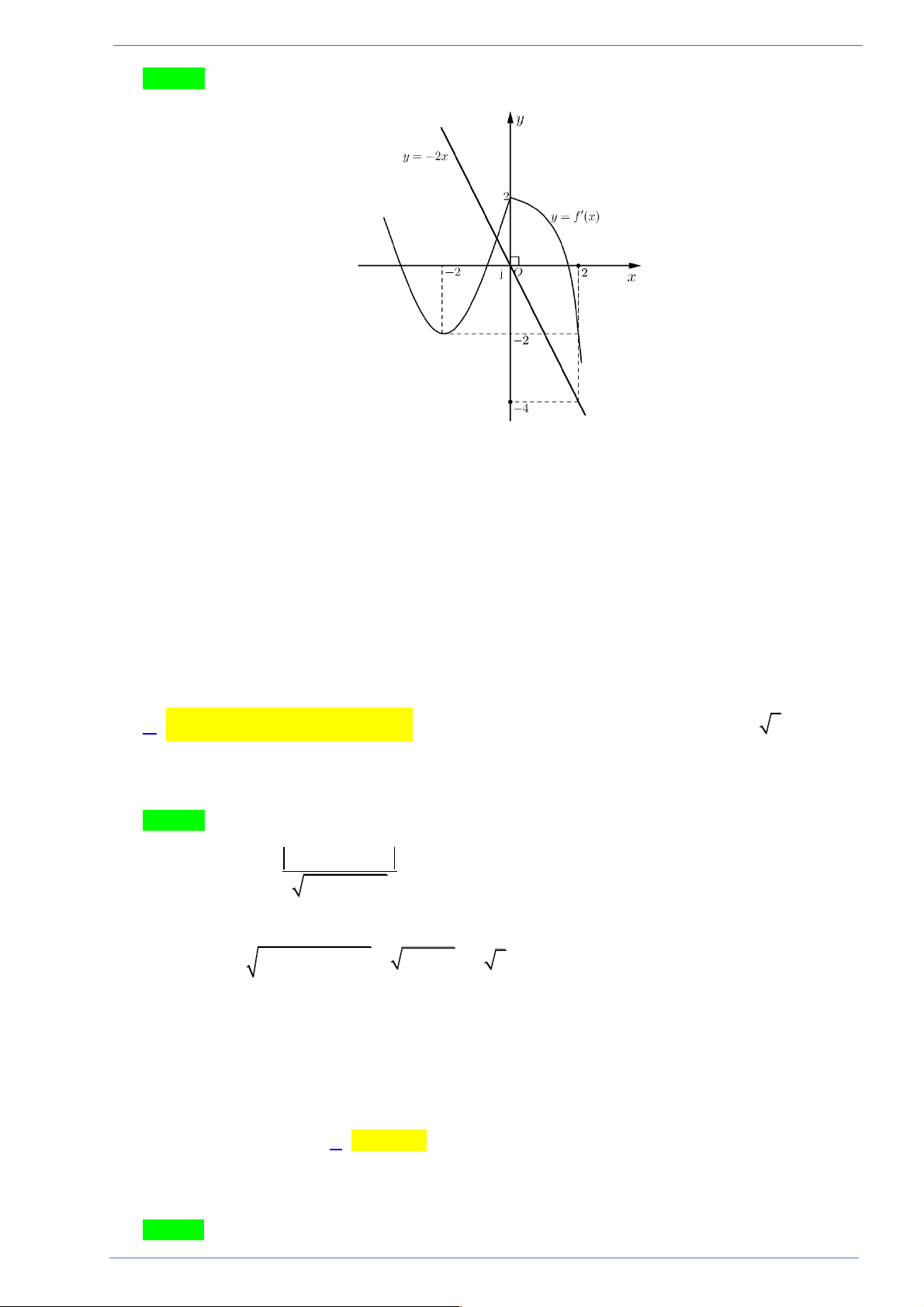
Câu 39. Cho đồ thị hàm số 3 2
y = ax + bx + cx + d như hình vẽ dưới đây: 2 3x - x - 2
Đồ thị của hàm số g ( x) =
có bao nhiêu đường tiệm cận đứng? 2
3 f ( x) - 6 f ( x)
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 22
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC A. 5. B. 4 . C. 3. D. 2 . Lời giải
Người làm: Cao Văn Kiên; Fb: Kiên Cao Văn Chọn A é f (x) = 0 Xét phương trình 2
3 f ( x) - 6 f ( x) = 0 Û ê ê f ë ( x) = 2
Dựa vào đồ thị, ta có éx = 2 -
+) Phương trình f (x) = 0 Û (trong đó x = 2
- là nghiệm đơn và x =1 là nghiệm bội ê ëx =1 2)
Þ f (x) = a(x + )(x - )2 2 1 , (a ¹ 0). éx = 0 ê
+) Phương trình f (x) = 2 Û êx = m ( 2 - < m < - ) 1 ( x = 0, x = ,
m x = n đều là các nghiệm đơn)
êx =n (n > ë )1
Þ f (x) - 2 = ax(x - m)(x - n), (a ¹ 0). x -1 3x + 2 (x - )1(3x + 2) Suy ra g ( x) ( )( ) = = , (a ¹ 0).
3 f ( x) é f
ë ( x) - 2ùû 3a ( x + 2)( x - )2 2
1 x ( x - m)(x - n)
Vậy đồ thị hàm số g (x) có 5 đường tiệm cận đứng. uyentoa@gmail.com.
Câu 40. Cho hàm số f (x) có bảng xét dấu của đạo hàm như hình bên.
Hàm số y = f (1- x) nghịch biến trên khoảng A. (1;4). B. (0;2). C. (0 ) ;1 . D. ( 2; - - ) 1 . Lời giải
Tác giả: Nguyễn Thị Uyên; Fb: Uyen Nguyen Chọn D
Xét hàm số y = f (1- x) có y¢ = - f ¢(1- x).
Từ bảng xét dấu của f ¢(x) ta có: é- < - < - é > - > é < <
y¢ < Û f ¢( - x) 3 1 x 2 3 x 1 2 3 x 4 0 1 > 0 Û Û Û . 1 ê ë 1 x 3 ê ë 1 x 1 3 ê < - < - > - > - ë 2 - < x < 0
Suy ra hàm số y = f (1- x) nghịch biến trên các khoảng (3;4) và ( 2; - 0). Mà ( 2; - - ) 1 Ì ( 2;
- 0) nên hàm số nghịch biến trên khoảng ( 2; - - ) 1 .
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 23
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC
Câu 41. [Mức độ 2] Trong không gian với hệ tọa độ Oxyz , cho hình hộp ABC . D A¢B C ¢ D ¢ ¢ biết A(1;2;3) , B¢(2;0;- )
1 , C (3;0;-3) và D¢( 2;
- 4;-3). Tọa độ đỉnh B của hình hộp ABC . D A¢B C ¢ D ¢ ¢ là A. B(4;-1; ) 1 . B. B(2;-1;2). C. B(4;1;- ) 1 . D. B(0;1;- ) 3 . Lời giải
Người làm: Giáp Minh Đức; Fb: Giáp Minh Đức Chọn A
Gọi I , I ¢ lần lượt là trung điểm của AC và B D ¢ ¢ . !!"
Ta có I (2;1;0), I¢(0;2;- 2) và II¢ = ( 2 - ;1;- 2). !!!"
Giả sử B(a;b;c) Þ BB¢ = (2 - a; -b;-1- c). ì2 - a = 2 - ìa = 4 !!!" !!" ï ï
Theo tính chất của hình hộp ta có BB¢ = II¢ Û í b - =1 Û b í = 1 - . ï 1 - - c = 2 - ï î c = 1 î Vậy B(4;-1; ) 1 .
Câu 42. Cho hình chóp S.ABCD có đáy là hình vuông cạnh AB = 2a , SA
D B là tam giác cân tại S và
nằm trong mặt phẳng vuông góc với mặt phẳng ( ABCD). Gọi M , N lần lượt là trung điểm của
AB, BCvà G là trọng tâm SC
D D . Biết khoảng cách từ điểm M đến mặt phẳng (SND) bằng
3a 2 . Thể tích của khối chóp . G AMND bằng 4 3 5 3a 3 5 3a 3 5 3a 3 5 3a A. . B. . C. . D. . 2 6 3 18
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 24
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC Lời giải S Chọn A Do SA
D B là tam giác cân tại S và M là trung
điểm của AB nên ta có được SM ^ AB . Thêm
vào đó (SAB) ^ ( ABCD) nên chúng ta có thể suy
ra được SM ^ ( ABCD). G K A
Ta kẽ MH ^ DN tại điểm H và MK ^ SH tại D điểm K . M Khi đó: B H ìMH ^ DN í
Þ DN ^ (SHM ) Þ DN ^ MK . Mà N C îSM ^ DN a
trước đó MK ^ SH , nên ta có được MK ^ (SDN ) Þ MK = d (M (SDN )) 3 2 , = . 4 2 æ ö 2 a 2 2 a - - a - a ç ÷ 2S S - S - S - S D D D D è ø a MND ( ABCD MBN NCD MAD ) 2 4 2 2 3 5 Mặt khác: MH = = = = . 2 2 ND NC + DC a 5 5 1 1 1 Xét trong SM D H , ta có: = - Þ SM = 3a. 2 2 2 SM MK MH a
Dễ thấy: d (G ( ABCD)) 1 3 , = SM = . Vậy: 3 3 1 a a a a V = d G ABCD S = S - S - S = = G AMND ( 2 2 1 3 3 5 5 3 . , . . . . . ( )) AMND ( ABCD M D BN NDC ) . 3 3 3 9 2 18
Gmail vanluu1010@gmail.com.
Câu 43. Cho hình thang ABCD ( AB //CD) biết AB = 5, BC = 3, CD =10, AD = 4 . Thể tích khối tròn
xoay tạo thành khi quay hình thang ABCD ( AB //CD) quanh trục AD bằng A. 128p . B. 84p . C. 112p . D. 90p . Lời giải
Tác giả: Bùi Văn Lưu; Fb: Bùi Văn Lưu Chọn B
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 25
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC
Gọi E là trung điểm của CD .
Dễ thấy tứ giác ABCE là hình bình hành Þ AE = BC = 3 Þ D
D AE vuông tại A .
Gọi H là giao điểm của AD và BC Þ DHC D vuông tại H .
Ta có AH = BE = 4 Þ DH = 8 và HB = 3 . Khi quay DHC D
quanh trục DH ta được hình nón tròn xoay có chiều cao h = 8, bán kính 1 1 1
đáy r = 6 nên có thể tích 2
V = p r h = p.36.8 = 96p . 1 1 1 1 3 3 Khi quay AH D
B quanh trục AH ta được hình nón tròn xoay có chiều cao h = 4, bán kính đáy 2 1 1
r = 3 nên có thể tích 2
V = p r h = p.9.4 =12p . 2 2 2 2 3 3
Vậy thể tích khối tròn xoay tạo thành khi quay hình thang ABCD ( AB //CD) quanh trục AD
bằng V -V = 96p -12p = 84p . 1 2
Câu 44. Cho lăng trụ ABC.A¢B C
¢ ¢có đáy là tam giác đều cạnh a , hình chiếu vuông góc của đỉnh A¢ lên
(ABC) là trung điểm H của cạnh AB . Góc giữa đường thẳng A¢Cvà mặt đáy bằng 60°. Khoảng
cách giữa BB¢ và A¢C là a 13 3a 13 2a 13 a 13 A. . B. . C. . D. . 39 13 13 13 Lời giải
Tác giả: Lê Quốc Đạt; Fb: Đat Le Quôc Chọn B
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 26
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC Ta có A H
¢ ^ (ABC) Þ(A C
¢ ;(ABC)) = (A C ¢ ;HC) = A Ð H ¢ C = 60°. a 3 3a 0
Þ A¢H = HC.tan 60 = . 3 = . 2 2 1 a 3
Gọi M là trung điểm của AC , từ H kẻ HN ^ AC Þ HN = BM = . 2 4
Từ H kẻ HI ^ A¢N Þ HI ^ ( A A ¢ C).
d (BB'; A'C) = d (BB¢;(A A
¢ C)) = d (B;(A A
¢ C)) = 2d (H ;(A A ¢ C)) = 2HI .
Xét tam giác vuông A¢HI vuông tại H a 3 3a . HN.HA¢ 3a 13 4 2 Þ HI = = = . 2 2 2 2 HN + HA¢ 26 æ a 3 ö æ 3a ö ç ÷ + +ç ÷ 4 è ø è 2 ø
Þ d (BB¢ A C ¢ ) 3a 13 ; = 2HI = . 13 . æ æ æ æ öööö
Câu 45. Tập xác định của hàm số f ( x) = log çlog çlog çlog çlog x÷÷÷÷ là một khoảng có độ dài 1 4 1 16 1 ç ç ç ÷÷÷ 2 4 è è è è 16 øøøø
m với m và n là số nguyên dương và nguyên tố cùng nhau. Khi đó m-n bằng: n A. 240 - . B. 271. C. 241. D. 241 - . Lời giải
Người làm: Lê Phương; Fb: lephuongtt1 Chọn D
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 27
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC æ æ æ æ öööö
Hàm số f ( x) = log çlog çlog çlog çlog x÷÷÷÷ xác định khi và chỉ khi 1 4 1 16 1 ç ç ç ÷÷÷ 2 4 è è è è 16 øøøø æ æ æ ööö æ æ öö æ ö 1
log ç log çlog çlog x÷÷÷ > 0 Û log çlog çlog x÷÷ >1Û 0 < log çlog x÷ < 4 1 16 1 ç ç ÷÷ 1 16 1 ç ÷ 16 1 4 4 è è è 16 øøø 4 è è 16 øø è 16 ø ì log x >1 ì 1 1 ï 0 < x < ï 16 ï ï 16 Û 1 1 í 1 Û í Û < x < . 2 4 ïlog x <16 ï æ 1 ö 256 16 1 x > ïî ç ÷ ï 16 î è16 ø æ 1 1 ö
Suy ra tập xác định của hàm số là ; . ç ÷ è 256 16 ø æ 1 1 ö 1 1 15
Suy ra độ dài của khoảng ; là - =
Þ m =15, n = 256. ç ÷ è 256 16 ø 16 256 256 Vậy m - n = - . 241
Câu 46. [Mức độ 3] Số điểm cực đại của đồ thị hàm số y = (x - ) 1 (x - 2)(x - )
3 ...(x -100) bằng A. 50 . B. 99 . C. 49 . D. 100 . Lời giải
Người làm: Võ Thanh Hải; Fb: Võ Thanh Hải Chọn C
*Ta thấy hàm số đã cho là hàm đa thức bậc 100, liên tục trên ! và có đúng 100 nghiệm phân
biệt ( x =1; x = 2;...; x =100), nên hàm số đã cho có 99 điểm cực trị ( x ; x ;...; x ), mỗi điểm 1 2 99
cực trị nằm giữa 2 nghiệm của phương trình y = 0. Mặt khác lim = +¥ nên số điểm cực tiểu x®±¥
nhiều hơn số điểm cực đại là một nên đồ thị hàm số đã cho có 49 điểm cực đại là x ; x ;...; x . 2 4 98
Vậy hàm số đã cho có 49 điểm cực đại.
Câu 47. Cho các số thực dương x , y thỏa mãn log x + log y + log x + log y =100 và log x ,
log y , log x , log y là các số nguyên dương. Khi đó kết quả xy bằng A. 200 10 . B. 100 10 . C. 164 10 . D. 144 10 . Lời giải
Tác giả: Bùi Anh Dũng; Fb: Dũng Bùi
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 28
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC Chọn C 2 2
Ta có: log x + log y + log x + log y =100 Û ( log x + ) 1 + ( log y + ) 1 = 202
Vì log x , log y là các số nguyên dương nên: ( x + )2 log 1 và ( y + )2 log 1 là các số
nguyên dương. Do đó cần phân tích 202 thành tổng 2 số chính phương.
Cũng do 202 là số chẵn nên 2 số chính phương đó phải cùng chẵn hoặc cùng lẻ. 2 2 +) Nếu 2 số ( x + )2 log 1 và ( y + )2 log
1 cùng chẵn thì ( log x + ) 1 + ( log y + ) 1 !4 còn
202 không chia hết cho 4 nên không tồn tại x , y trong trường hợp này. +) Nếu 2 số ( x + )2 log 1 và ( y + )2 log
1 cùng lẻ, suy ra chữ số tận cùng của 2 số đó là một
trong các chữ số 1, 5, hoặc 9. Vì tổng 2 chữ số tận cùng là 2 nên 2 số ( x + )2 log 1 , ( y + )2 log
1 đều có tận cùng bằng 1.
Cũng do vai trò x , y như nhau trong giả thiết và kết luận nên ta chỉ xét trường hợp: (ì logx + ï )2 1 = 81 64 ìïx =10 í . Từ đó suy ra 164 í Þ xy =10 . (ï 100 log y + ïîy =10 î )2 1 = 121 Câu 48. Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ bên
Giá trị nguyên lớn nhất của tham số m để hàm số y = f ( x - m) đồng biến trên khoảng (10;+¥) là A. 10 - . B. 10. C. 9. D. 11. Lời giải
Tác giả:Hoàng Thanh Toàn; Fb:Toàn Hoàng Chọn C
Hàm số y = f ( x - m) đồng biến trên khoảng (10;+¥) x Û y ' =
f '( x - m) ³ 0, x
" >10 Û f '( x - m) ³ 0, x " >10 x é x - m ³1 Û ê , x " >10 ê x - m £ 1 - ë
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 29
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC é x ³1+ m Û ê , x " >10 ê x £ m -1 ë
Û 10 ³1+ m Û m £ 9.
Vậy số nguyên lớn nhất của tham số m là 9 .
Câu 49. Cho hàm số f (x) liên tục trên ! và thoả mãn ( ) + ( - ) 2 3 2 1 x xf x f x = e , x " Î! . 0 Khi đó f
ò (x)dx bằng: 1 - A. 0 . B. 3(e - ) 1 . C. 3(1-e). D. 3e . Lời giải
Tác giả: Quách Hồng Hiệp; Fb: Tiểu Hiệp Chọn B Nhân hai vế của ( )+ ( - ) 2 3 2 1 x xf x f x = e , x " Î! với x ta được: ( )+ ( - ) 2 2 3 2 1 x x f x xf x = xe , x " Î! . 0 0 0 Lấy tích phân từ 1
- đến 0 hai vế ta được: 2 ò ( 3) + ò ( 2 - ) 2 1 x x f x dx xf x dx = xe dx (1) ò 1 - 1 - 1 - 0 0 0 Kí hiệu 2 = ò ( 3) ; = ò ( 2 - ) 2 1 ; x I x f x dx K xf x dx H = xe dx ò 1 - 1 - 1 - 0 0 0 1 1 Đặt 3
u = x ta tính được 2 I = x f ò
( 3x)dx = f
ò (u)du = f ò (x)dx 3 3 1 - 1 - 1 - 0 0 0 1 1 Đặt 2 u = x -
1 ta tính được K = xf
ò ( 2x - )1dx = - f
ò (v)dv = - f ò (x)dx 2 2 1 - 1 - 1 - 0 0 0 x 1 x 1 x 1 Và 2 2 H = xe dx = e d ò ò ( 2x) 2 = e = (1-e) 2 2 2 1 - 1 - 1 - 0 0 0 1 1 1 Nên (1) Û f (x)dx -
f (x)dx = (1- e) Û f (x)dx = 3(e - ò ò ò )1. 3 2 2 1 - 1 - 1 -
Câu 50. Một hộp đựng 9 thẻ được đánh số từ 1 đến 9 . Rút ngẫu nhiên hai thẻ từ hộp nêu ở trên, tính xác
suất để tích của hai số trên hai thẻ này là số chẵn. 25 13 5 1 A. . B. . C. . D. . 81 18 18 2 Lời giải
Người làm: Lê Anh Minh; Fb: Lê Anh Minh Chọn B n(W) 2 = C . 9
Gọi A là biến cố tích của hai số trên hai thẻ là số lẻ, ta có xác xuất cần tính là P ( A).
Nhận thấy biến cố A xảy ra khi và chỉ khi rút được cả hai thẻ mang số lẻ. Trong 9 thẻ đã cho
có 5 thẻ mang số lẻ, vì thế nên n( A) 2 = C . 5
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 30
Sản phẩm của Group FB: STRONG TEAM TOÁN VD-VDC n A Ta có P ( A) ( ) =
và P ( A) + P( A) =1, do đó P( A) 13 = . n(W) 18 …..HẾT…..
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Group dành riêng cho GV-SV toán! Trang 31