








Preview text:
SỞ GIÁO DỤC & ĐÀO TẠO HÀ NAM ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2019- 2020
TRƯỜNG THPT CHUYÊN BIÊN HÒA Môn: TOÁN
Thời gian làm bài: 90 phút (không kế thời gian phát đề)
(Đề thi gồm 50 câu trắc nghiệm) Mã đề thi 101
Họ, tên thí sinh: ..................................................................... Số báo danh: .........................
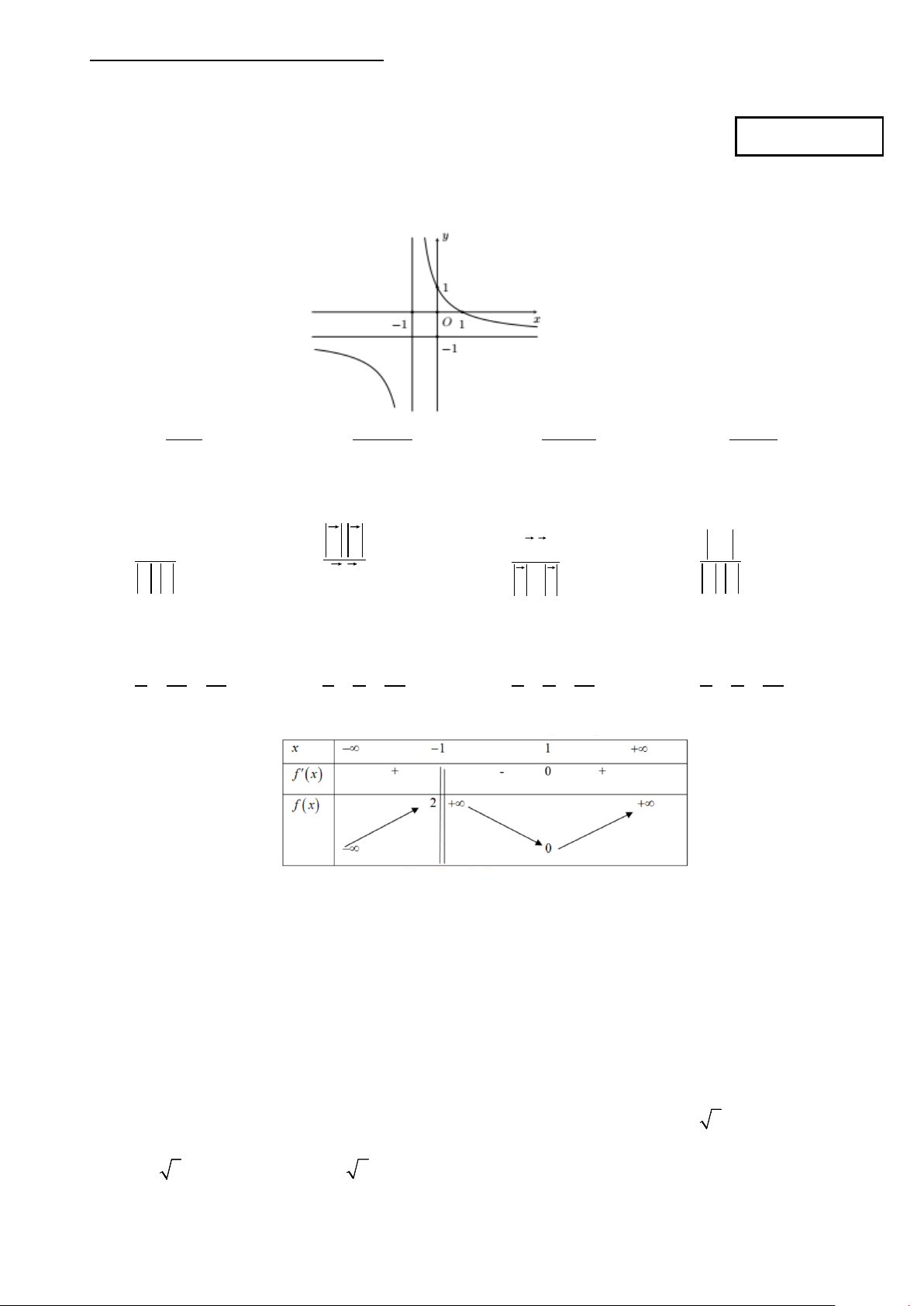
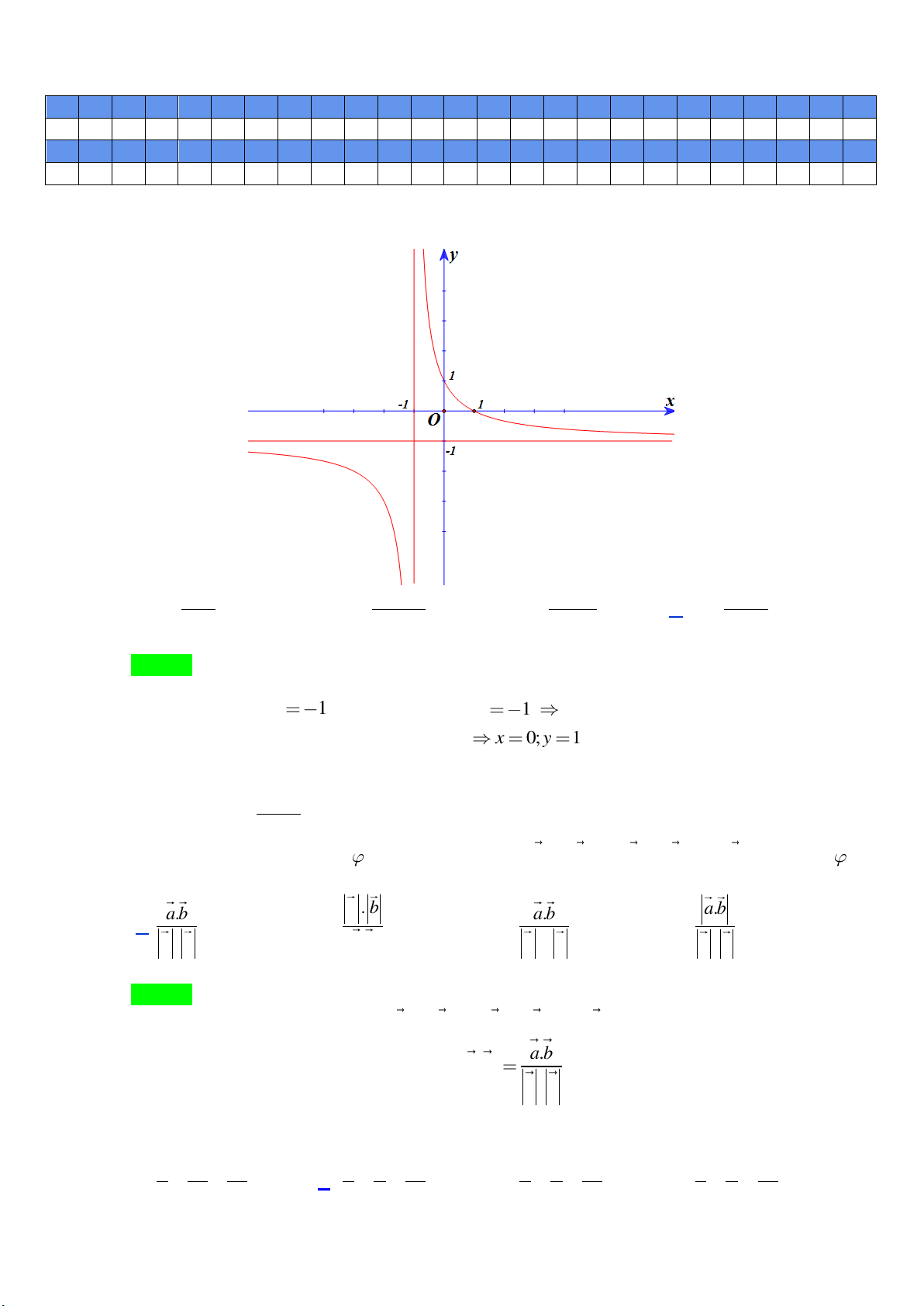
Câu 1: Hàm số nào sau đây có đồ thị như hình vẽ bên ? − − x + − x + − x + A. = x y . B. 2 1 y = . C. 2 y = . D. 1 y = . x +1 2x +1 x +1 x +1
Câu 2: Trong không gianOxyz , gọi ϕ là góc giữa hai vectơ a và b , với a và b khác 0 , khi đó cosϕ bằng a.b . a b A. . a b a b . B. . C. . . D. . a . b a b . a + b a . b
Câu 3: Trong không gian Oxyz , cho các điểm ( A 4; 3 − ;2) , B(6;1; 7 − ) ,C(2;8; 1) − . Viết phương trình
đường thẳng đi qua gốc tọa độ O và trọng tâm G của tam giác ABC . A. x y z = = . B. x y z = = . C. x y z = = . D. x y z = = . 2 1 − 1 − 2 1 1 − 2 3 1 − 4 1 3 −
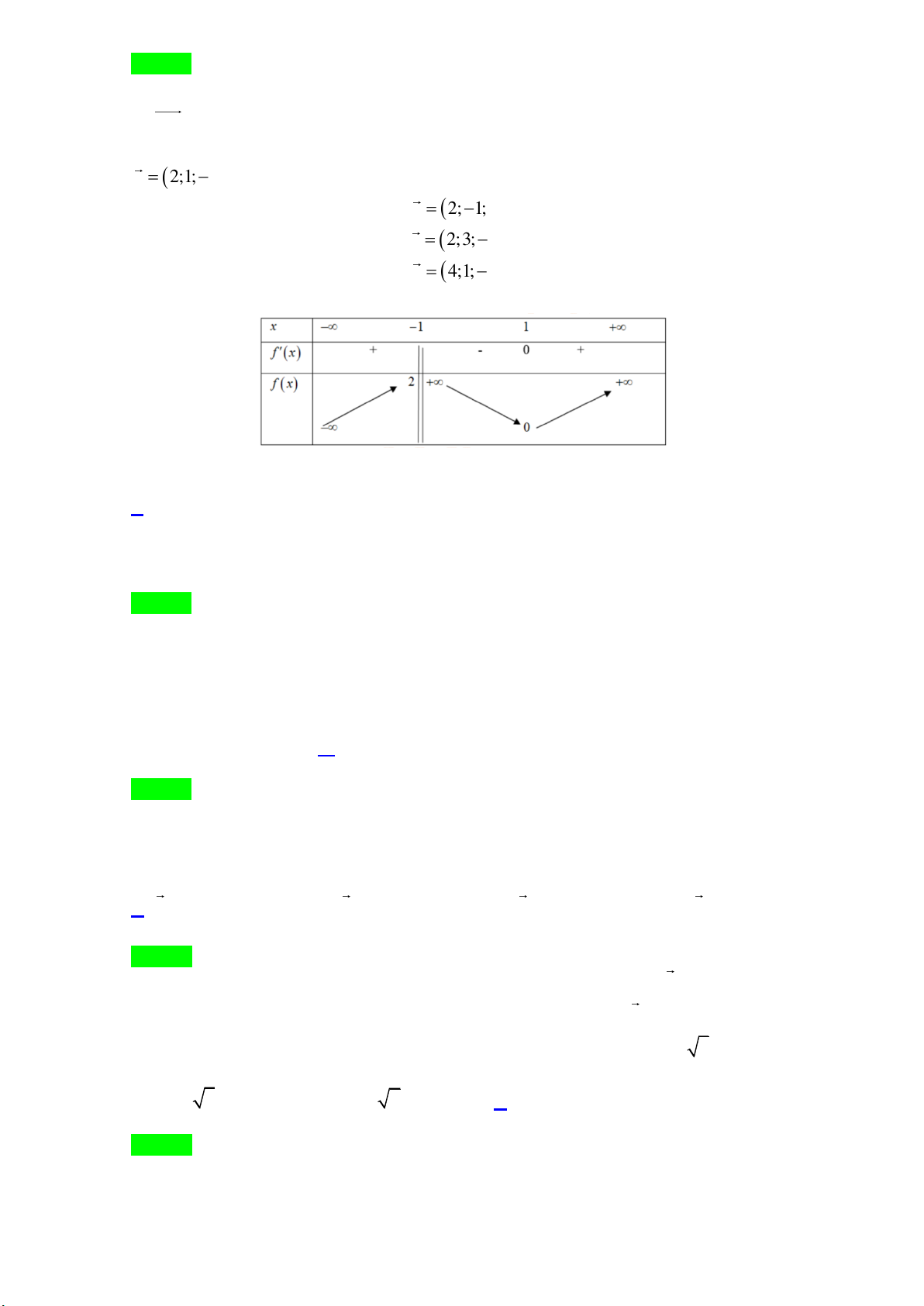
Câu 4: Cho hàm số y = f (x) có bảng biến thiên như sau:
Khẳng định nào sau đây là đúng?
A. Giá trị cực đại của hàm số y = f (x) bằng 2. B. Hàm số y = f (x) đạt cực tiểu tại x =1.
C. Hàm số y = f (x) đạt cực đại tại x = . 1 −
D. Giá trị cực tiểu của hàm số y = f (x) bằng 1.
Câu 5: Cho cấp số cộng (u có u = và công sai d = 4 . Hãy tínhu . 1 11 n ) 99 A. 401. B. 403. C. 402 . D. 404 .
Câu 6: Trong không gian Oxyz , cho mặt phẳng(P): 2x −3y + 5z −9 = 0. Vectơ nào sau đây là một vectơ
pháp tuyến của (P) ?
A. n(2;−3;5) .
B. n(2;−3;−5) . C. n(2;3;5). D. n(2;−3;9).
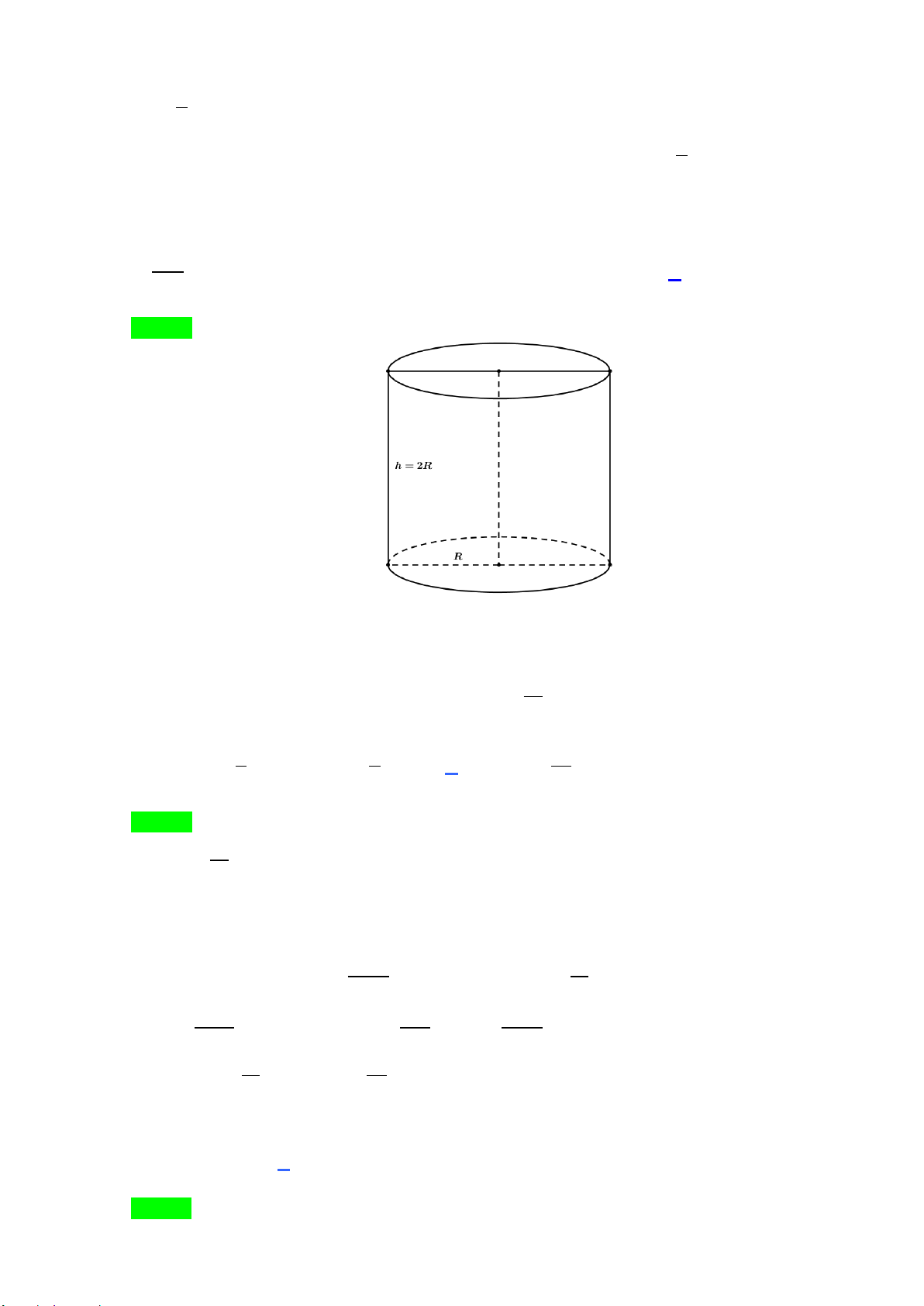
Câu 7: Trong không gian cho tam giác ABC vuông tại A , AB = a và AC = a 3 . Tính độ dài đường
sinh l của hình nón có được khi quay tam giác ABC xung quanh trục AB .
A. l = 3a .
B. l = 2a .
C. l = 2a .
D. l = a .
Câu 8: Tìm nguyên hàm của hàm số 2
f (x) = 3x + 8sin x .
Trang 1/7 - Mã đề thi 101 A. ( )d = 6 −8cos + ∫ f x x x x C . B. ( )d = 6 +8cos + ∫ f x x x x C . C. f ∫ (x) 3
dx = x −8cos x + C . D. ( ) 3 d = + 8cos + ∫ f x x x x C .
Câu 9: Cho các mệnh đề sau: 2 (I) Hàm số 2020 x y =
luôn đồng biến trên R . e (II) Hàm số α
y = x (với α là một số thực âm) luôn có một đường tiệm cận đứng và một đường tiệm cận ngang. (III) Hàm số 2
y = log x có tập xác định là ( ; 0 +∞). 2 (IV) Hàm số 1 3
y = x có đạo hàm là y'= . 3 2 . 3 x
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên? A. 2 . B. 1. C. 3. D. 4 .
Câu 10: Cho số phức z = ( − i)( + i)2 3 2 1
. Môđun của w = iz + z là A. 8 . B. 2 2 . C. 1. D. 2 .
Câu 11: Một mặt cầu có độ dài đường kính bằng 4 . Tính diện tích của mặt cầu đó? A. 128π . B. 64π . C. 64 π . D. 16π . 3
Câu 12: Đạo hàm của hàm số 3 2 3 + = x y là A. y' 2 3 . 3+ = x x .3ln 3. B. ' 3 3+ = x y .2ln 3. C. 2 3 x +2 y'= 3x 3 . . D. 2 3 3 x 1
y'= 3x .(x 3 ). 2 + +
Câu 13: Cho hai số phức z =1+ 2i và z = 2 − 3i . Phần ảo của số phức w = 3z − 2z là 1 2 1 2 A. 9. B. 12i . C. 12. D. −1.
Câu 14: Tính tổng diện tích tất cả các mặt của khối đa diện đều loại {3; } 5 có các cạnh bằng 1. A. 3 3 . B. 3 3 . C. 5 3 . D. 5 3 . 2 2
Câu 15: Gọi z ; z là hai nghiệm phức của phương trình 2
z + 2z + 4 = 0 . Khi đó 2 2 A |
= z | + | z | có giá trị 1 2 1 2 là A. .4 B. . 14 C. . 20 D. . 8
Câu 16: Cho các số thực a,b và các mệnh đề: b a b a 1. f
∫ (x)dx = − f ∫ (x)dx. 2 . 2 f
∫ (x)dx = 2 f ∫ (x)dx . a b a b 2 b b b b 3. 2 f
∫ (x)dx = f ∫ (x)dx . 4 . f
∫ (x)dx = f ∫ (u)du . a a a a
Số mệnh đề đúng trong 4 mệnh đề trên là? A. 3. B. 4 . C. 2 . D. 1.
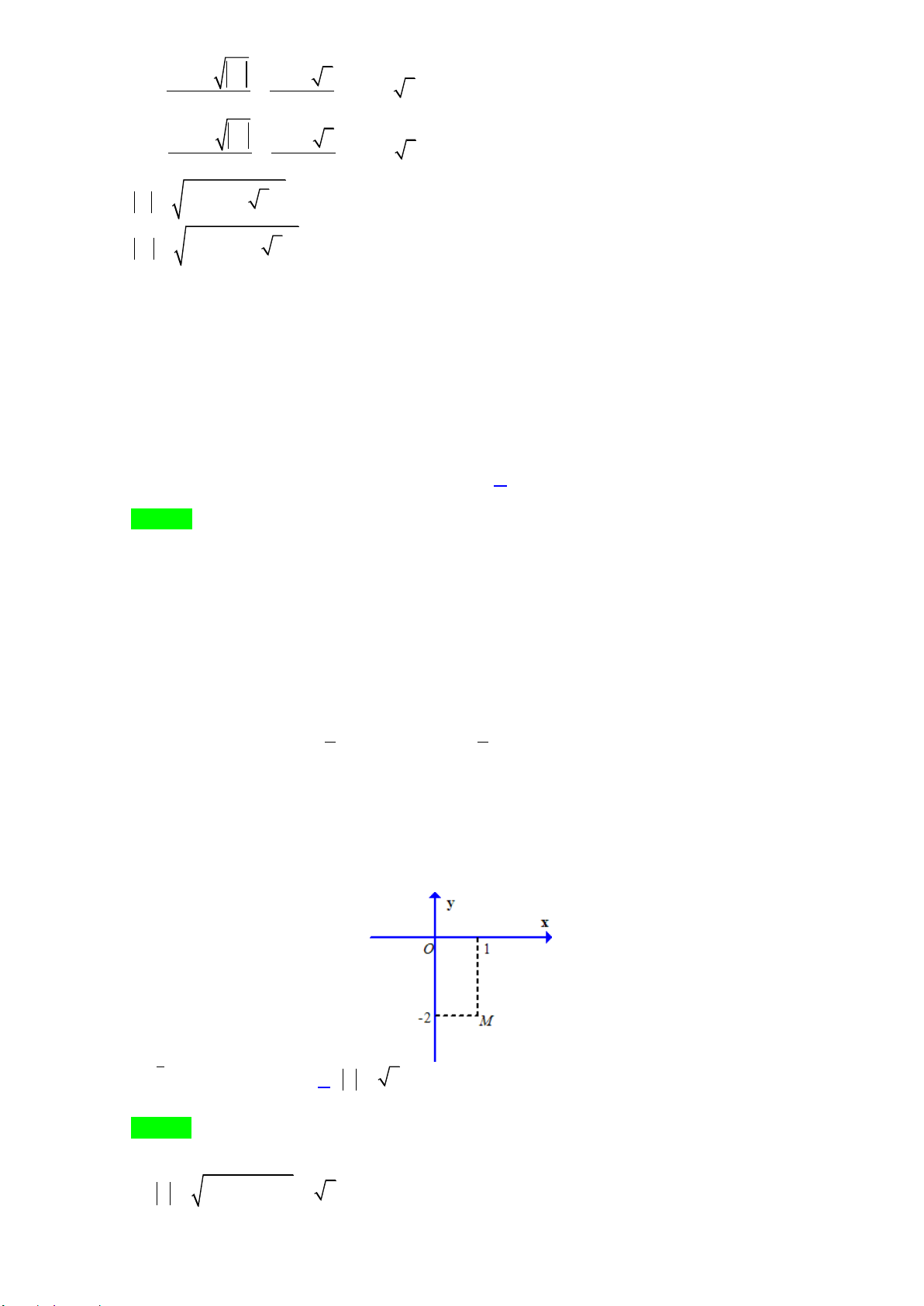
Câu 17: Trên mặt phẳng tọa độ ,điểm M trong hình vẽ bên là điểm biểu diễn số phức z . Khẳng định nào sau đây là đúng?
Trang 2/7 - Mã đề thi 101
A. z = 1− i 2 . B. z = 5
C. z = 1+ i 2 .
D. z = −2 + i .
Câu 18: Cho x,a,b là các số thực dương thỏa mãn 1 log
= 2log a − 6log b . Khi đó giá trị của x là : 7 7 49 x 3 2 A. b a
x = 2a − b 3 . B. x = . C. x = . D. 2 3 x = a b . 2 a 3 b
Câu 19: Diện tích xung quanh của hình trụ có bán kính đáy R = 2 và đường sinh l = 6bằng: A. 4π B. 8π . C. 24π D. 12π .
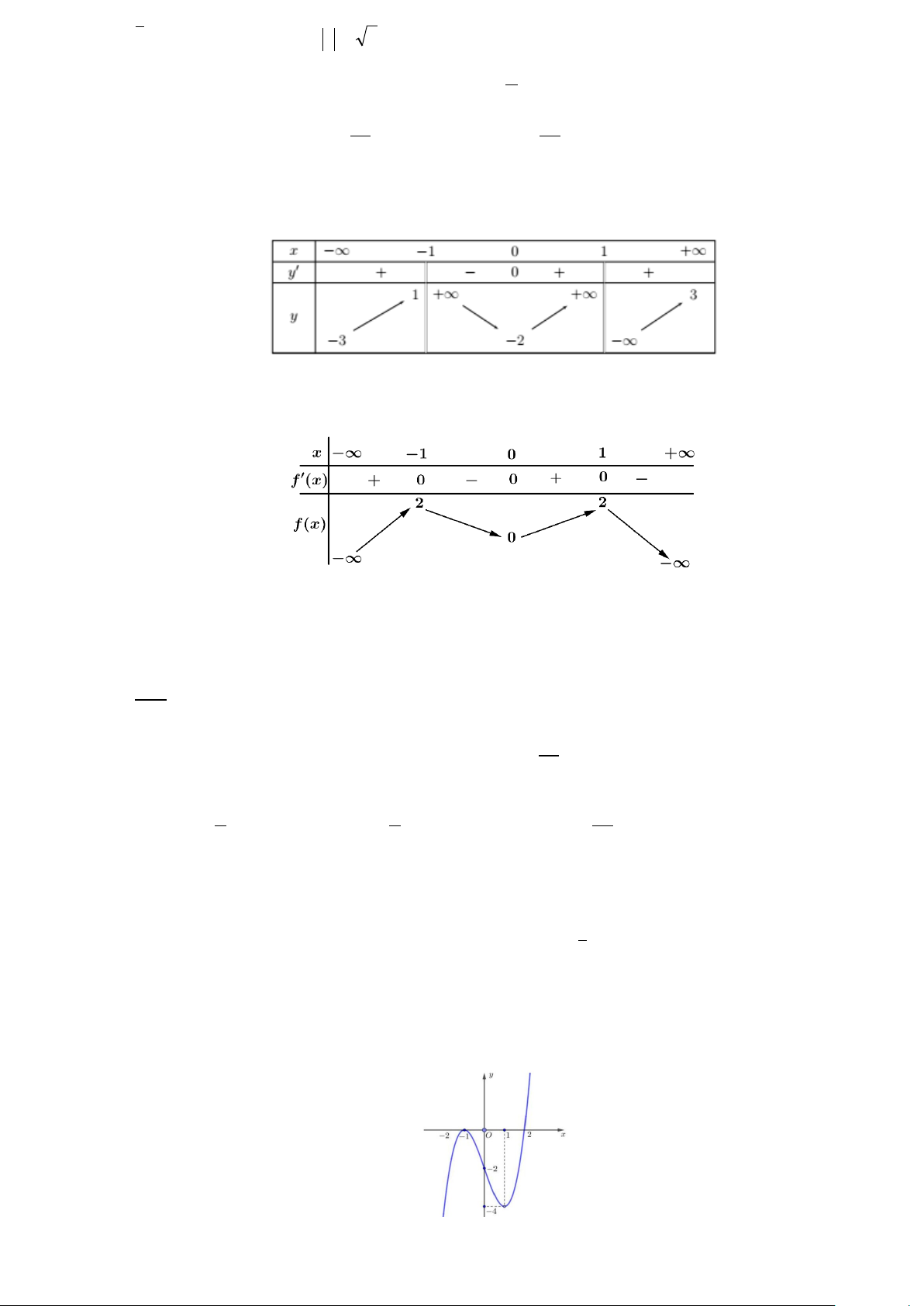
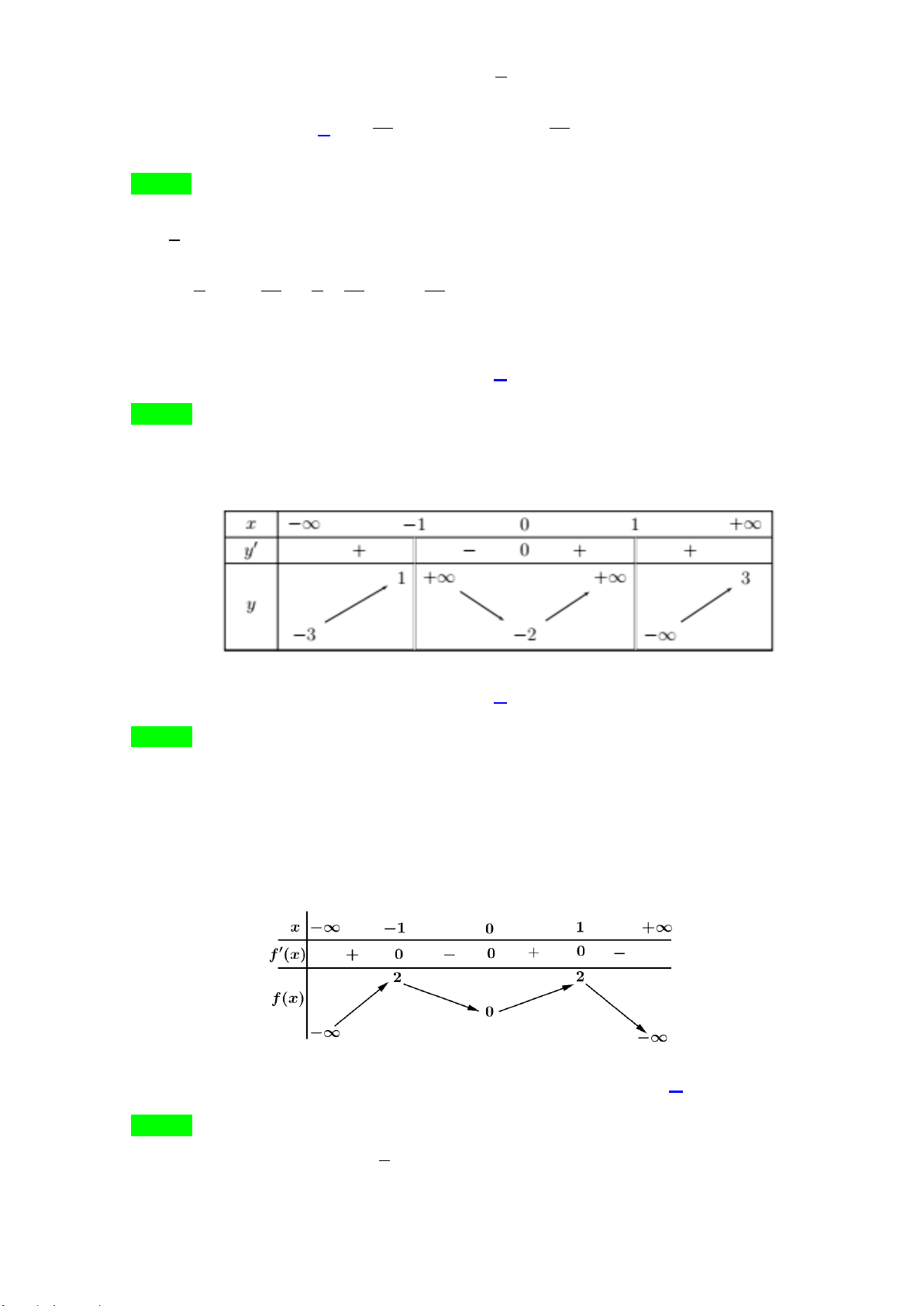
Câu 20: Cho hàm số y = f (x) có bảng biến thiên như sau:
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 2 . B. 3. C. 4 . D. 1.
Câu 21: Cho hàm số y = f (x) có bảng biến thiên như sau:
Số nghiệm của phương trình 3 f (x) + 4 = 0 là A. 4 . B. 1. C. 3. D. 2 .
Câu 22: Hình trụ có bán kính đáy bằng a và thiết diện qua trục là hình vuông, diện tích xung quanh hình trụ đó bằng 2 π A. a . B. 2 π a . C. 2 3π a . D. 2 4π a . 2 3
Câu 23: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số x 2 y =
+ 2x + 3x − 4 trên đoạn [ 4; − 0] lần lượt là 3
M và m . Giá trị của tổng M + m bằng bao nhiêu? A. 4 M + m = − . B. 4 M + m = . C. 28 M + m = − .
D. M + m = 4 − . 3 3 3
Câu 24: Trong không gian Oxyz , hình chiếu vuông góc của điểm M (5;− 6;2) lên mặt phẳng (Oxz) có tọa độ là A. (0;− 6;0) . B. (5;0;2) . C. (5;− 6;0). D. (0;− 6;2) .
Câu 25: Cho số phức z = 4 − 3i . Phần thực, phần ảo của số phức z lần lượt là A. 4;3. B. 4; 3 − . C. ; 3 4 . D. 4; − 3 .
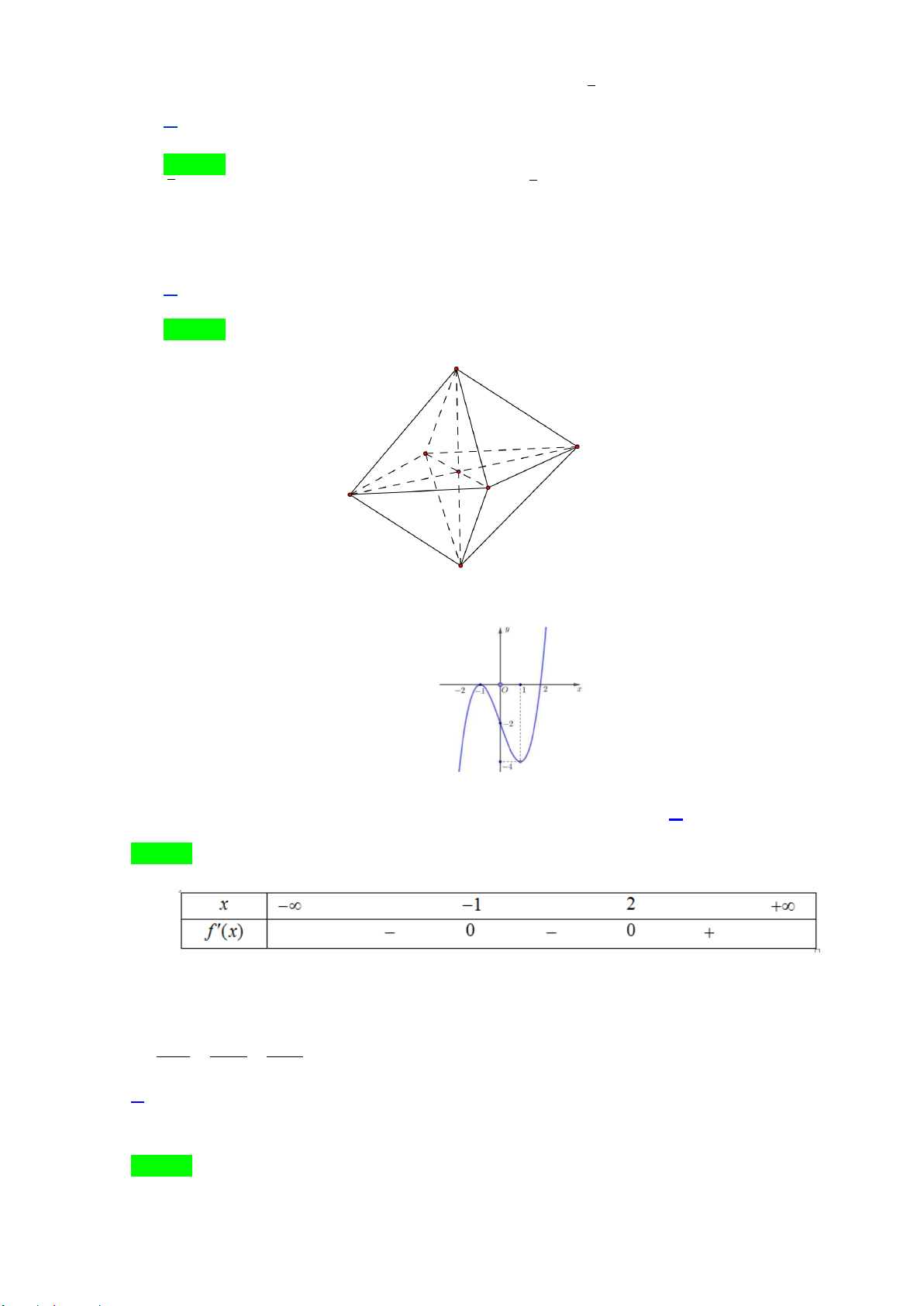
Câu 26: Khối đa diện đều loại {3; }
4 có tất cả bao nhiêu cạnh? A. 12. B. 6 . C. 14. D. 8 .
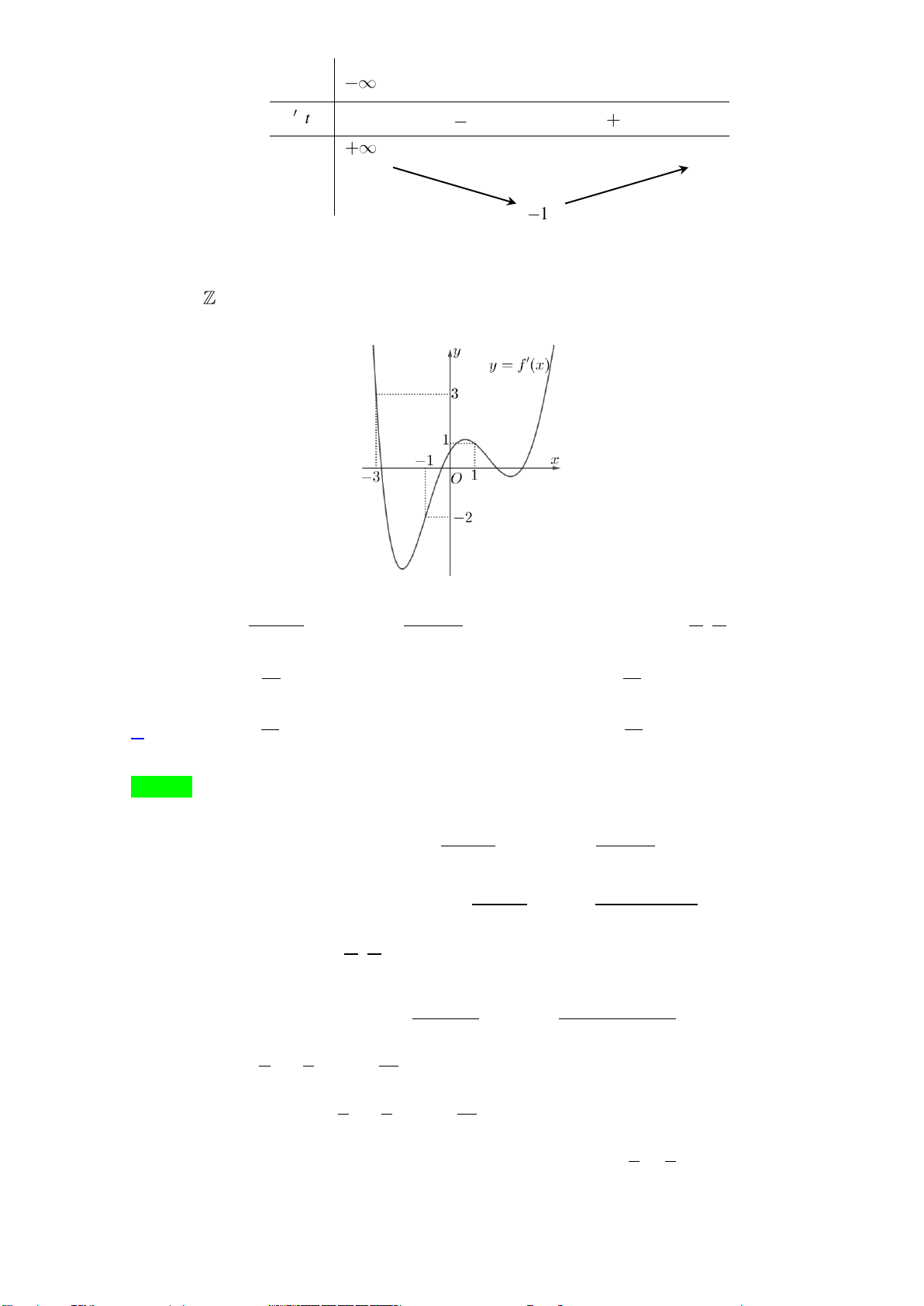
Câu 27: Cho hàm số y = f (x) có đồ thị hàm số f '(x) như hình vẽ
Trang 3/7 - Mã đề thi 101
Hàm số y = f (x) có bao nhiêu điểm cực trị? A. 3. B. 2 . C. 0 . D. 1.
Câu 28: Trong không gian với hệ trục tọa độ Oxyz , cho điểm ( A 4; 3 − ;5) và B(2; 5 − ;1).Viết phương
trình mặt phẳng (P) đi qua trung điểm I của đoạn thẳng AB và vuông góc với đường thẳng
x 1 y 5 z 9 (d + − + ) : = = . 3 2 − 13
A. 3x − 2y +13z − 56 = 0
B. 3x + 2y +13z − 56 = 0
C. 3x + 2y +13z + 56 = 0
D. 3x − 2y −13z + 56 = 0
Câu 29: Cho hàm số y = f (x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ( ) 1 ; 0 . B. (− 0 ; 1 ). C. (− ; ∞ − ) 1 . D. ( ; 0 +∞).
Câu 30: Trong không gian Oxyz cho mặt cầu (S ) có phương trình 2 2 2
x + y + z + 4x − 4y + 8z = 0 . Tìm
tọa độ tâm I và bán kính R . A. I (2; 2; − 4); R = 24 . B. I ( 2; − 2; 4 − ); R = 2 6 . C. I (2; 2; − 4); R = 2 6 . D. I ( 2; − 2; 4 − ); R = 24 . 15
Câu 31: Tìm số hạng không chứa x trong khai triển nhị thức Newtơn của ( ) 2 1 P x x = + x A. 4000 . B. 2700 . C. 3003. D. 3600.
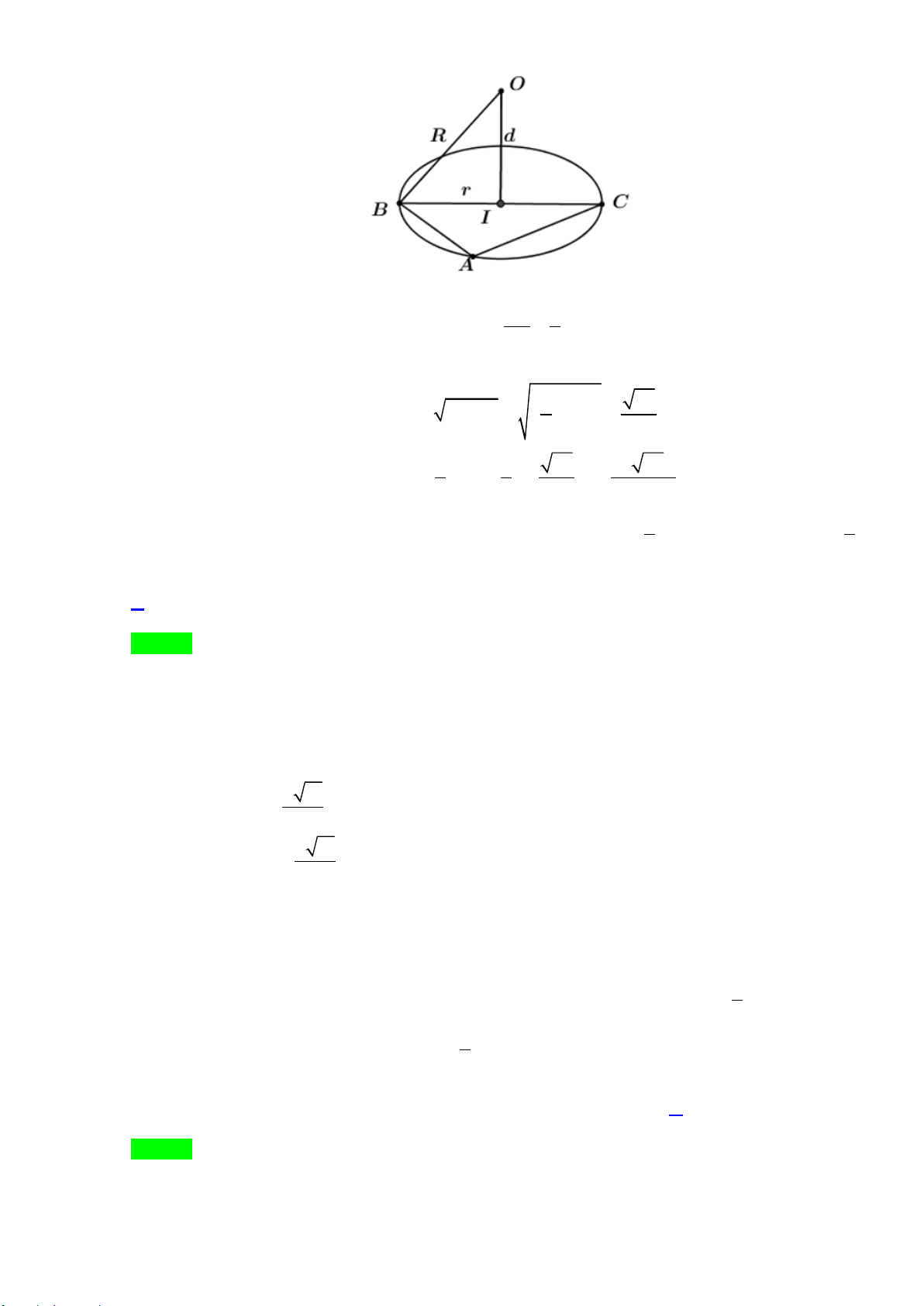
Câu 32: Cho mặt cầu (S ) tâm O và các điểm A , B , C nằm trên mặt cầu (S ) sao cho AB = 3,
AC = 4 , BC = 5 và khoảng cách từ O đến mặt phẳng ( ABC) bằng 1. Thể tích của khối cầu (S ) bằng A. 7 21π π π π . B. 4 17 . C. 29 29 . D. 20 5 . 2 3 6 3
Câu 33: Có tất cả bao nhiêu giá trị thực của tham số m để đồ thị hàm số 2 3 2
y = x − mx − ( 2 m − ) 2 2 3
1 x + có hai điểm cực trị có hoành độ x , x sao cho x x + 2 x + x =1. 1 2 ( 1 2) 3 3 1 2 A. 1. B. 0 . C. 3 . D. 2 .
Câu 34: Có bao nhiêu số tự nhiên có 4 chữ số mà tổng tất cả các chữ số của số đó bằng 7. A. 165. B. 1296. C. 343. D. 84.
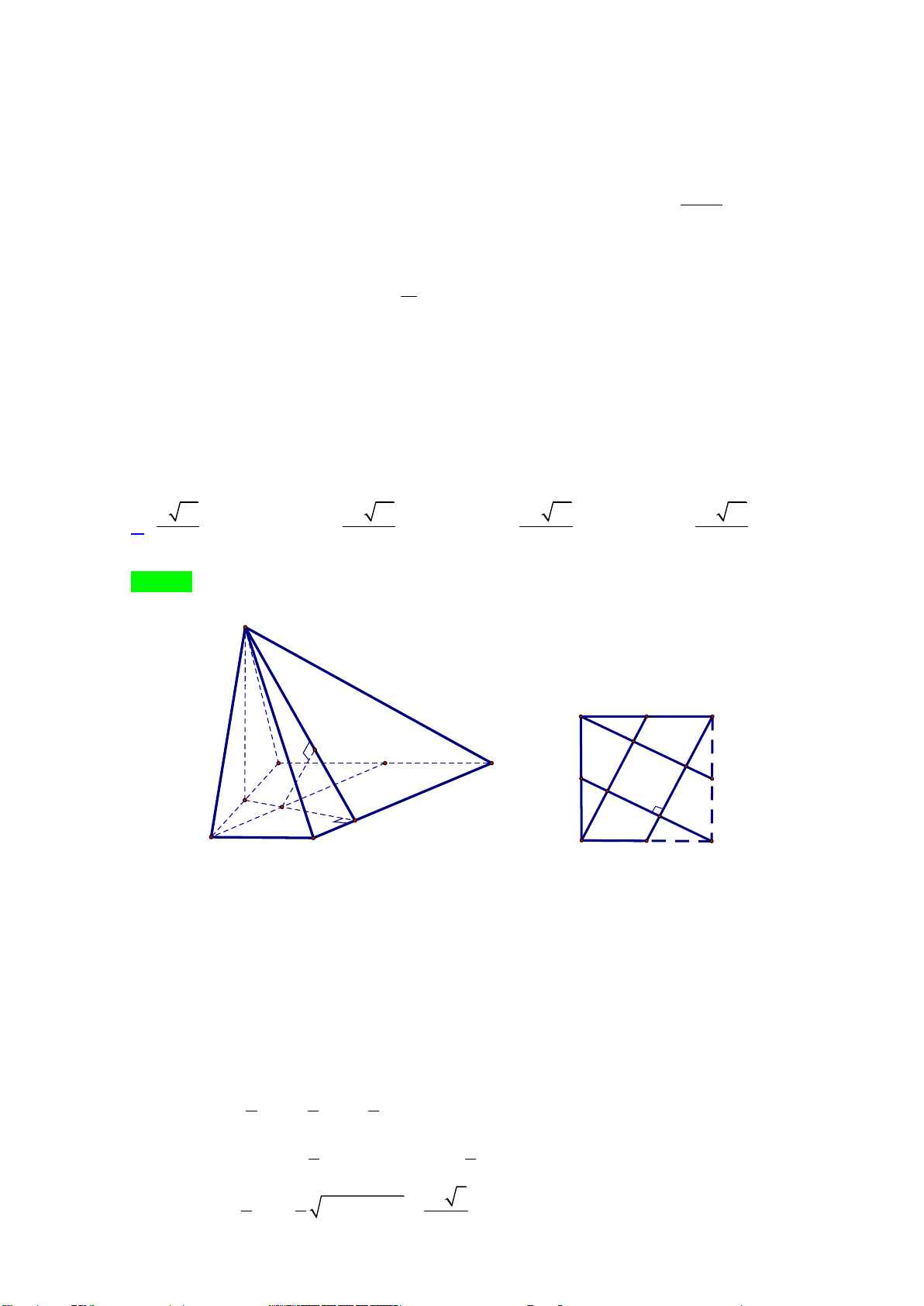
Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D AB = AD = 2a;DC = a
. Điểm I là trung điểm đoạn AD , mặt phẳng (SIB) và (SIC) cùng vuông góc với mặt phẳng ( ABCD).
Mặt phẳng (SBC) tạo với mặt phẳng ( ABCD) một góc 60°. Tính khoảng cách từ D đến(SBC) theo a . A. a 15 . B. 9a 15 . C. 2a 15 . D. 9a 15 . 5 10 5 20
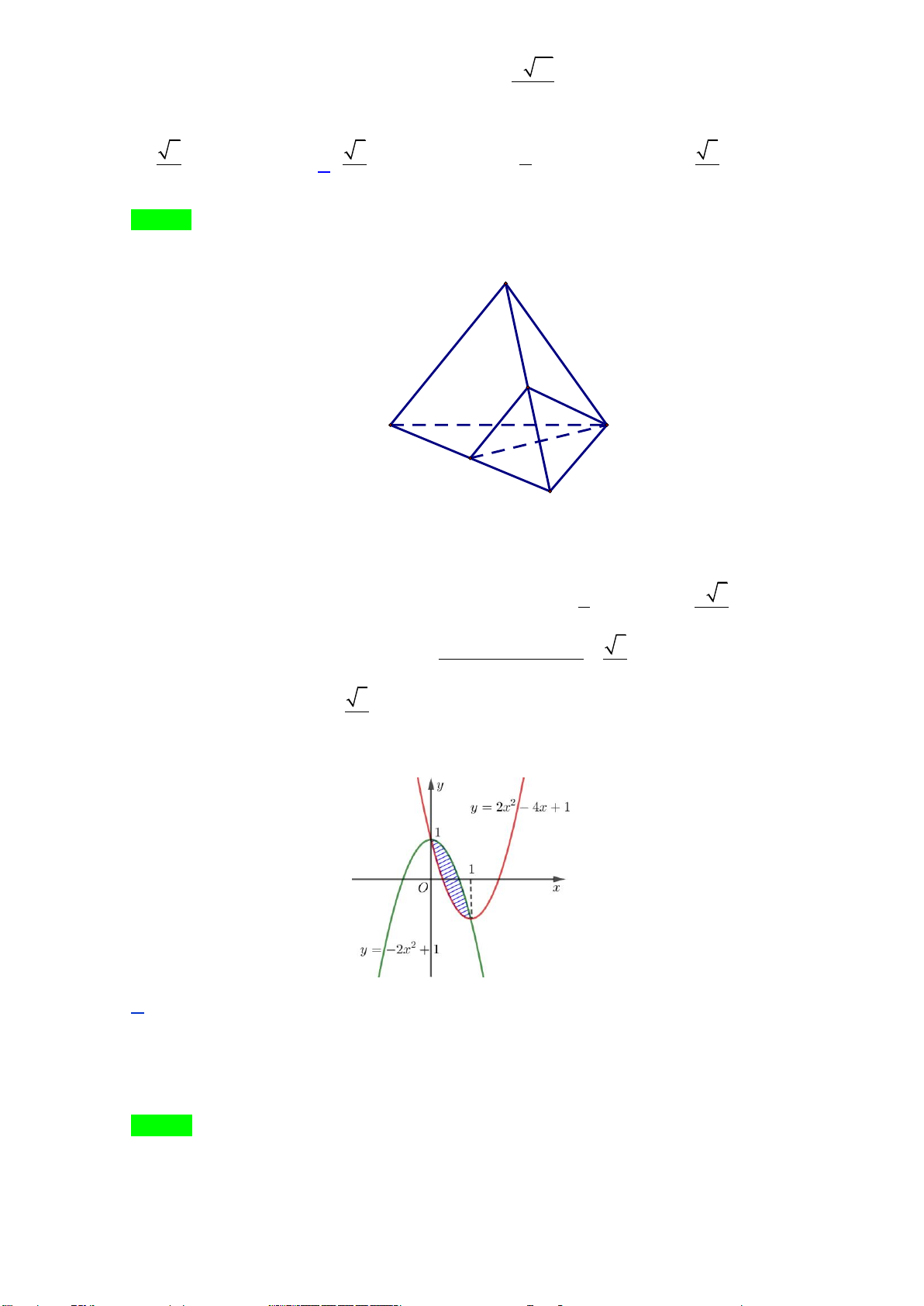
Câu 36: Cho tứ diện đều ABCD , M là trung điểm của cạnh BC . Khi đó cos( AB, DM ) bằng A. 2 . B. 3 . C. 1 . D. 3 . 2 6 2 2
Câu 37: Diện tích hình phẳng của phần tô đậm trong hình vẽ bên được tính theo công thức nào dưới đây?
Trang 4/7 - Mã đề thi 101 1 1 A. S = ∫( 2 4
− x + 4x)dx . B. S = ( 2 2x − 4x + ∫ )1dx. 0 0 1 1 C. S = ∫( 2
4x − 4x)dx . D. S = ∫ ( 2 4
− x + 4x)dx . 0 1 −
Câu 38: Bất phương trình log
x − > có tập nghiệm là 0,5 (2 ) 3 0 A. ( 3 3 − ; ∞ 2) B. ( ; 2 +∞). C. ;+∞. D. ;2 2 2
Câu 39: Phương trình log 3.2x −1 = 2x +1có tất cả bao nhiêu nghiệm thực? 2 ( ) A. 3. B. 2. C. 0. D. 1.
Câu 40: Cho phương trình 9x − (2m + 3 ).
3 x + 81 = 0 ( m là tham số thực ).Giá trị của m để phương trình
đã cho có hai nghiệm phân biệt x , x thỏa mãn 2 2
x + x = thuộc khoảng nào sau đây 1 2 1 2 10 A. ( 10 ; 5 ). B. ( 5 ; 0 ). C. ( 15 ; 10 ). D. ( ; 15 +∞).
Câu 41: Cho hàm số f (x) liên tục trên [− ;12]và thỏa mãn điều kiện f (x) = x + 2 + xf ( 2 3 − x ) 2
Tính tích phân I = ∫ f (x)dx . −1 A. 14 I = . B. 28 I = . C. 4 I = . D. I = 2 . 3 3 3 1
Câu 42: Cho hàm số f (x) liên tục trên R và thỏa mãn f ∫ (x)dx = 9 . 5 − 2
Tính tích phân f
∫ (1−3x)+9dx . 0 A. 15. B. 27 . C. 75. D. 21. − Câu 43: Cho hàm số mx y =
3 , m là tham số thực. Có tất cả bao nhiêu giá trị nguyên của m để hàm số 3x − m
đồng biến trên từng khoảng xác định? A. 5. B. 7 . C. 3. D. vô số.
------------------------------------
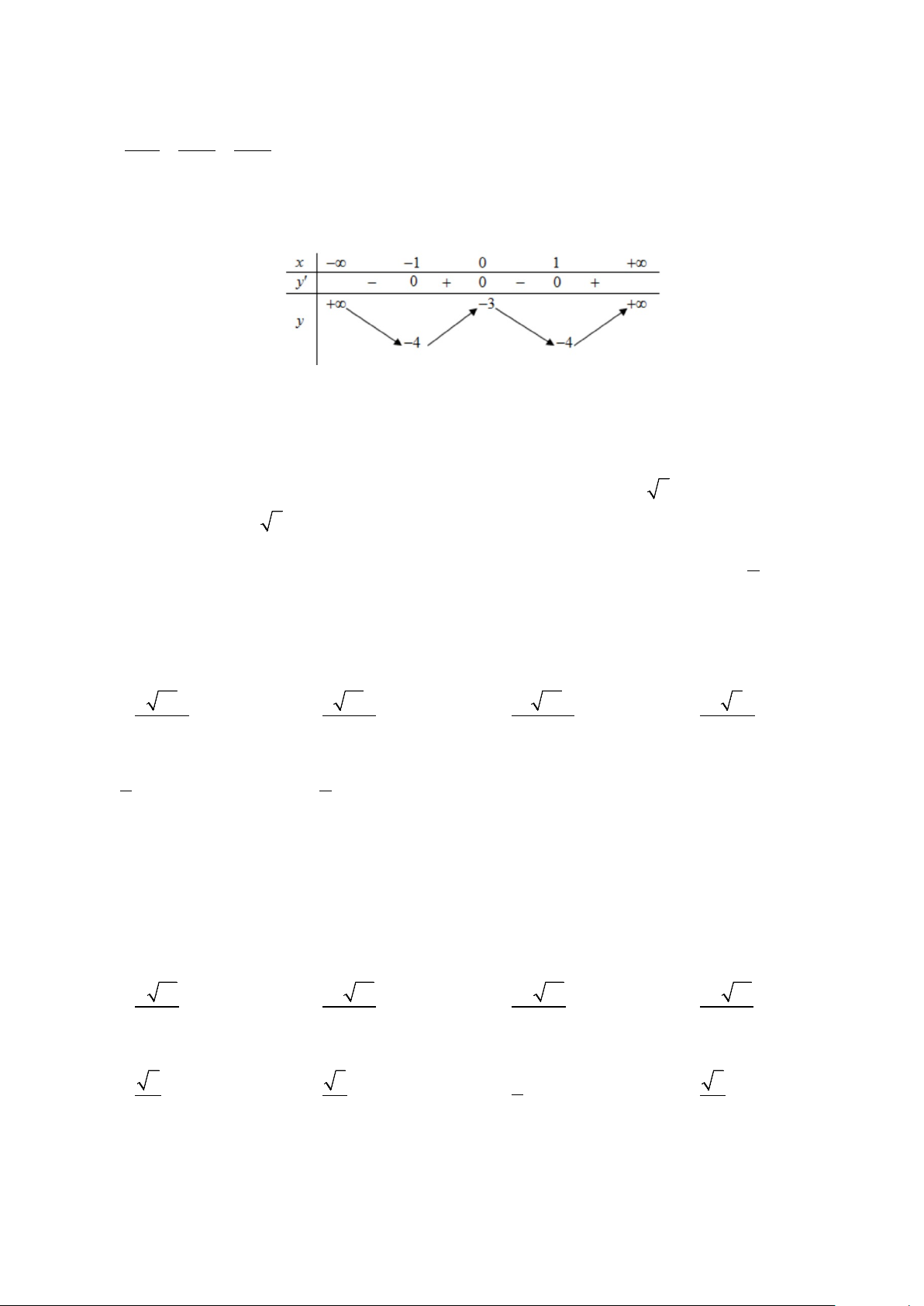
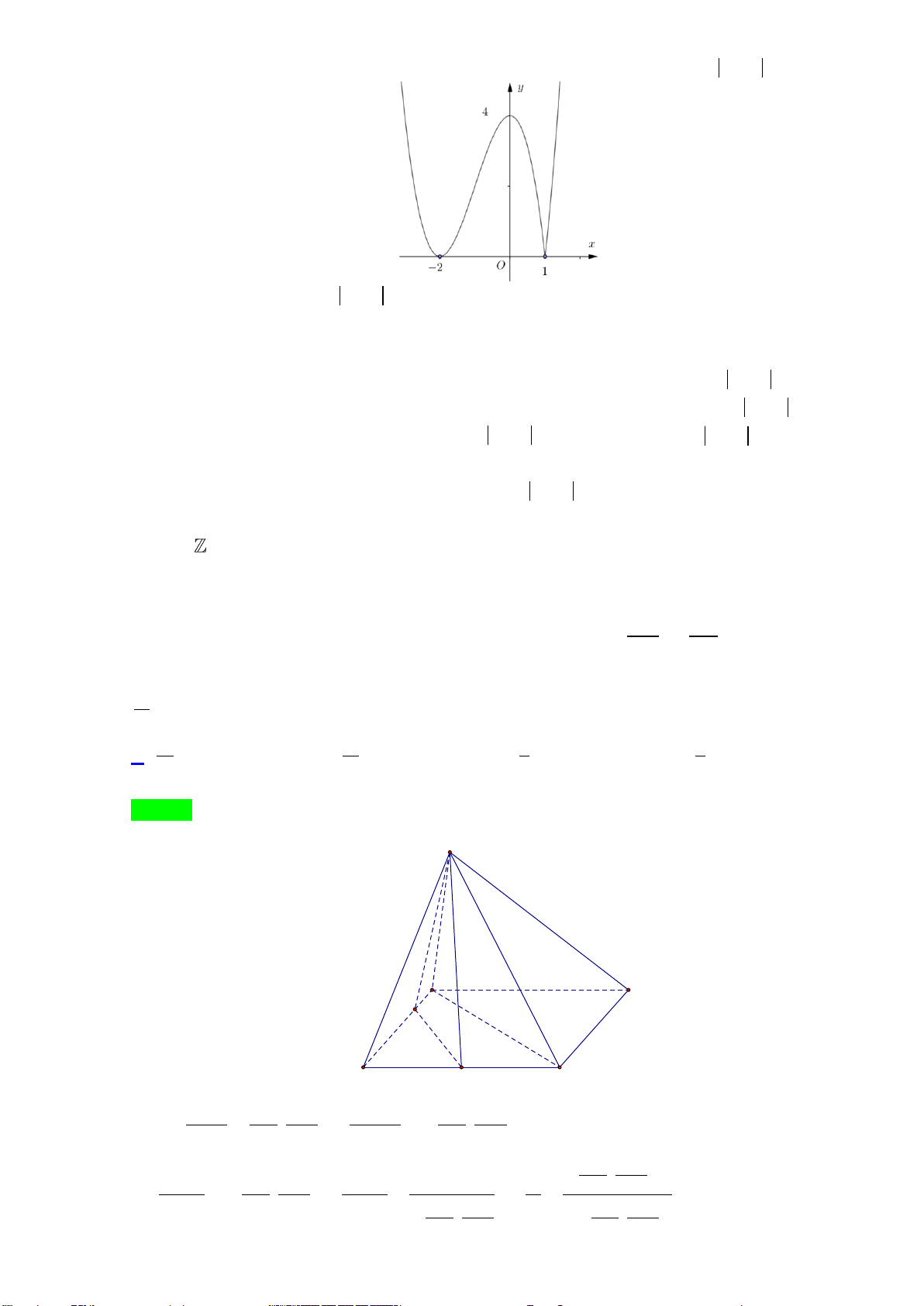
Câu 44: Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m∈[− ] 5 ;
5 sao cho phương trình log3 f x + − f x + + m − f x + + m = có 2 ( ( ) )1 log2 ( ( ) )1 (2 ) 8 log 2 1 ( ) 1 2 0 2 nghiệm x∈ (− ) 1 ; 1 . A. . 7 B. . 5 C. . 6 D. vô số.
Trang 5/7 - Mã đề thi 101
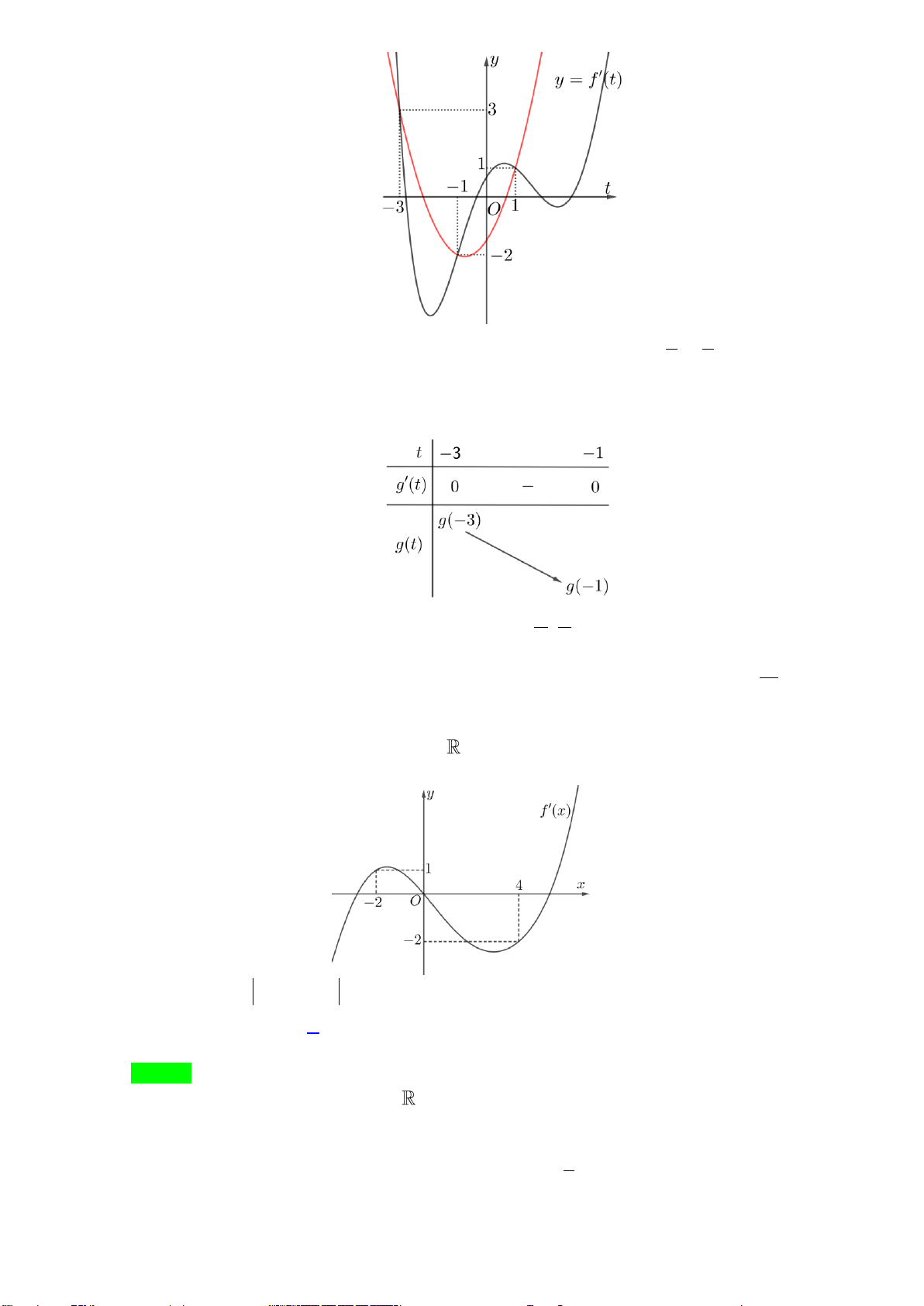
Câu 45: Cho hàm số f (x) . Hàm số y = f ′(x) có đồ thị như hình sau.
Tìm tất cả các giá trị thực của tham số
m để bất phương trình 2sin3 x 5cos2
2 f (sin x − 2) − + sin x x > m + π π nghiệm đúng với mọi x ∈− ; 3 4 2 2 A. 11 m ≤ 2 f (− ) 3 + . B. 19
m < 2 f (− ) 1 + . C. 19 m ≤ 2 f (− ) 1 + . D. 11
m < 2 f (− ) 3 + . 12 12 12 12
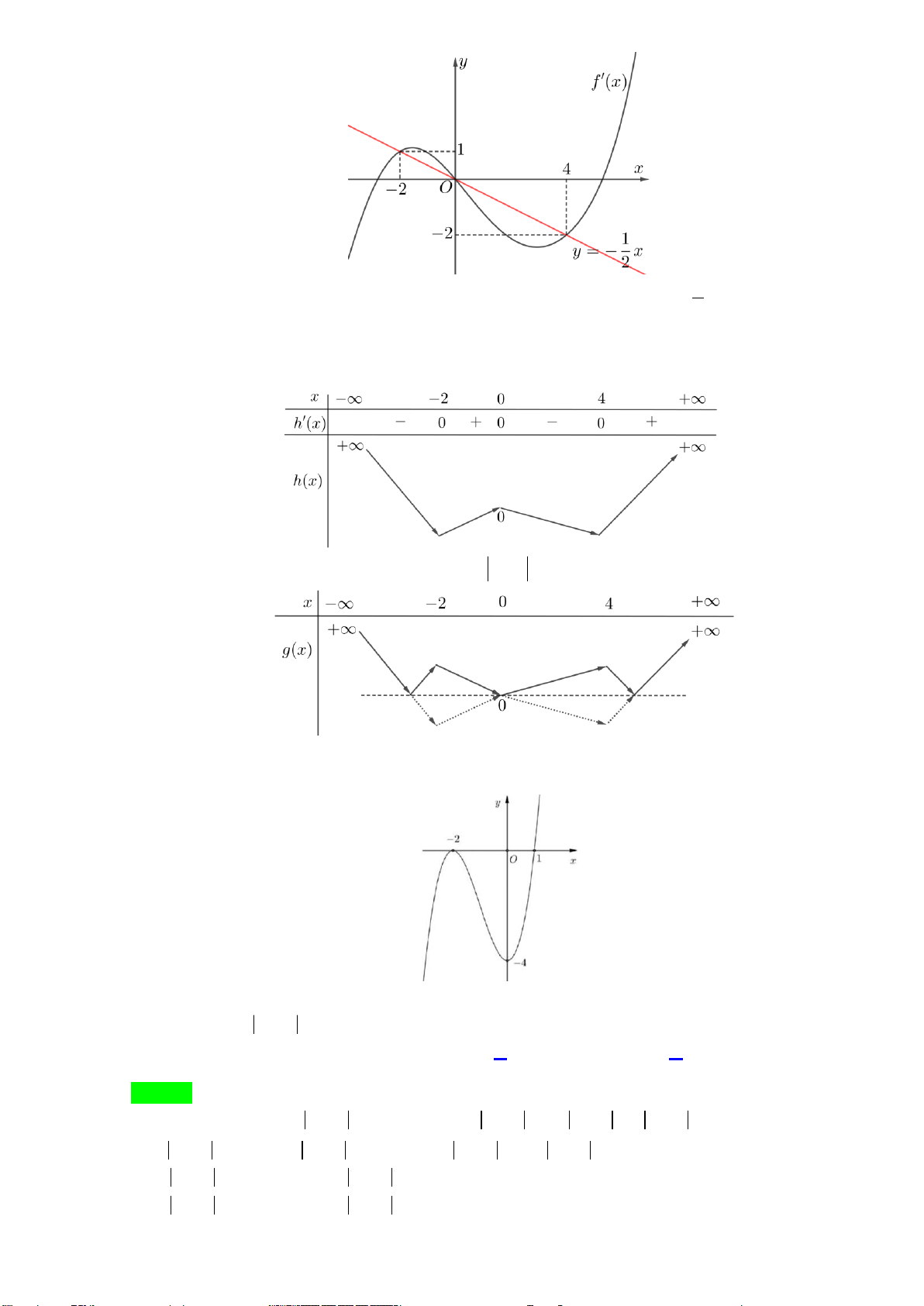
Câu 46: Cho hàm số đa thức f (x) có đạo hàm tràm trên R . Biết f ( )
0 = 0 và đồ thị hàm số y = f ′(x) như hình sau. Hàm số 2
g(x) = 4 f (x) + x đồng biến trên khoảng nào dưới đây ? A. ( ; 4 +∞). B. ( ; 0 4). C. (− ; ∞ 2 − ). D. (− 0 ; 2 ).
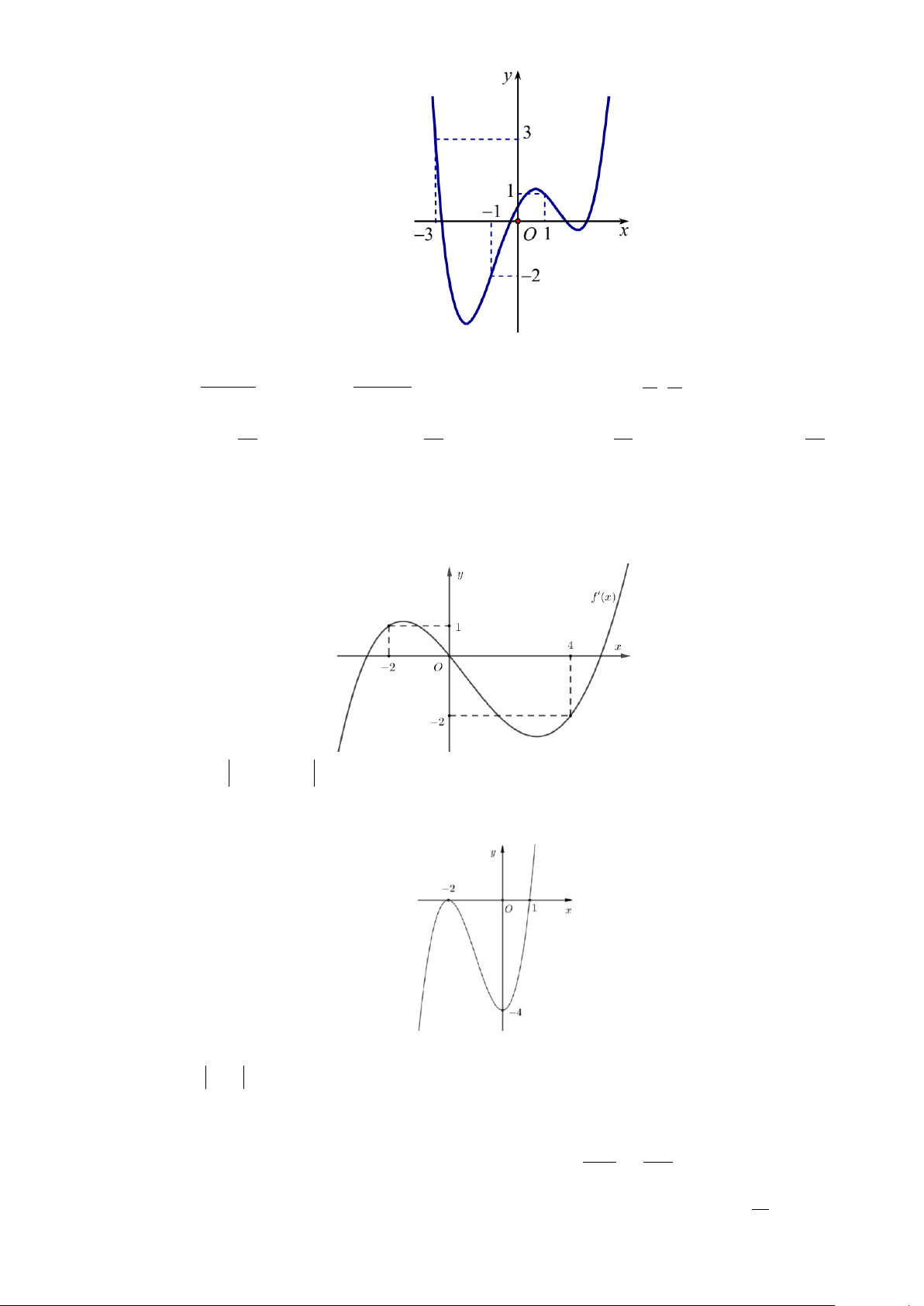
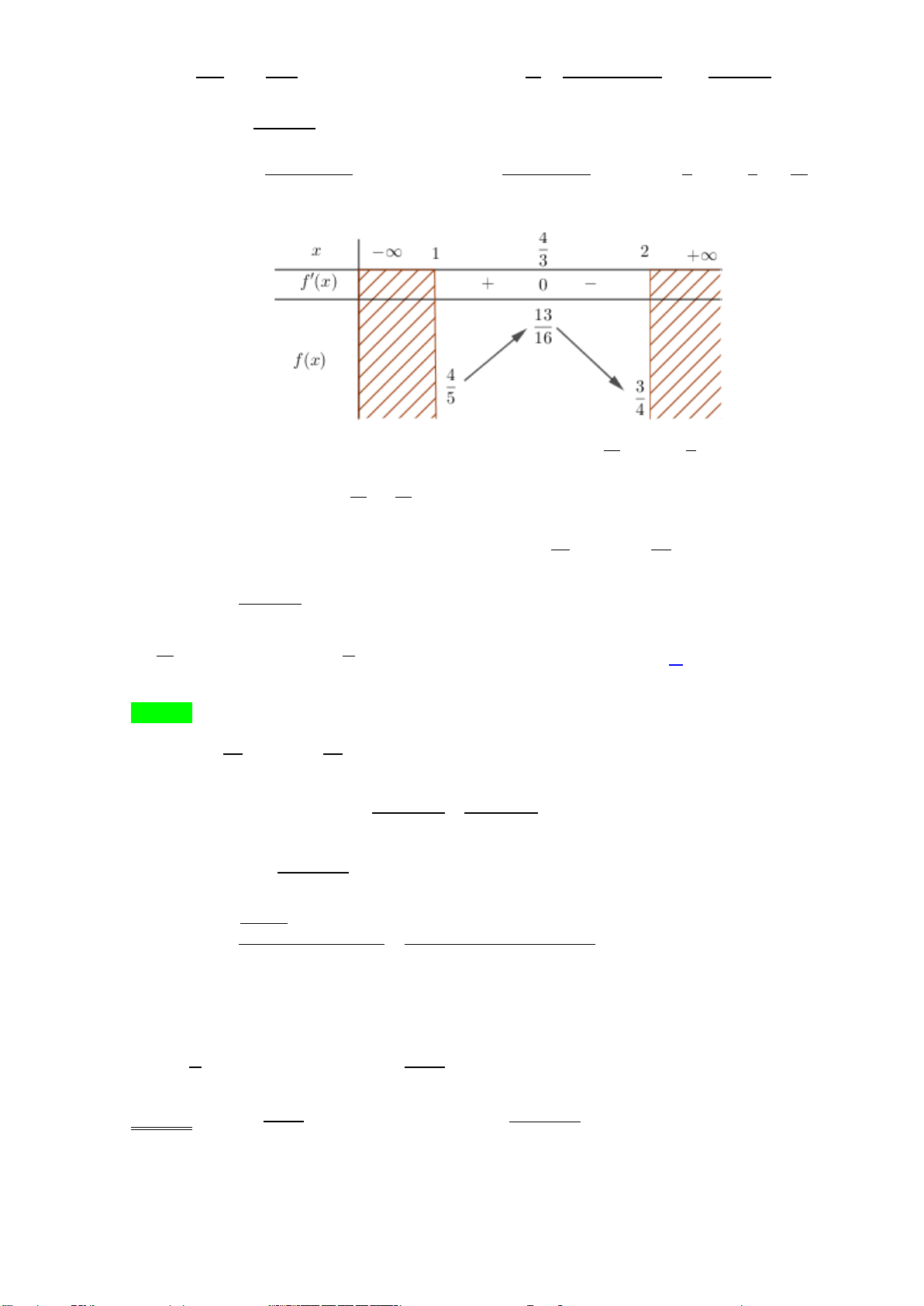
Câu 47: Cho hàm số y = f (x = ax3 )
+ bx2 + cx + d có đồ thị như hình dưới đây
Có tất cả bao nhiêu giá trị nguyên của tham số m∈(− 5 ; 5 ) để phương trình 2
f (x) − (m + )
4 f (x) + 2m + 4 = 0 có 6 nghiệm phân biệt A. 2 . B. 4 . C. 3. D. 5.
Câu 48: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Hai điểm M , N lần lượt thuộc các
đoạn thẳng AB và AD ( M và N không trùng với A ) sao cho 2 AB + 3 AD = 8 . Kí hiệu V , V lần AM AN 1
lượt là thể tích của các khối chóp S.ABCD và S.MBCDN . Tìm giá trị lớn nhất của tỉ số V1 . V
Trang 6/7 - Mã đề thi 101 A. 13 . B. 11 . C. 1 . D. 2 . 16 12 6 3 y x
Câu 49: Cho x; y là hai số thực dương thỏa mãn x x 1 y 1 ≠ y và 2 + < 2 + . 2x 2y 2 2 +
Tìm giá trị nhỏ nhất của biểu thức x 3y P = . 2 xy − y A. 13 min P = . B. 9 min P = . C. min P = − . 2 D. min P = . 6 2 2
Câu 50: Có tất cả bao nhiêu giá trị thực của tham số m∈[ 1; − ] 1 sao cho phương trình 2 2 log
x + y = log 2x + 2y − 2 có nghiệm nguyên ( ; x y)duy nhất. 2 m 1 + ( ) 2 ( ) A. 3. B. 2 . C. 1. D. 0 .
-------------------- HẾT --------------------
Trang 7/7 - Mã đề thi 101 made cauhoi dapan made cauhoi dapan 101 1 D 101 26 A 101 2 A 101 27 D 101 3 B 101 28 A 101 4 B 101 29 B 101 5 B 101 30 B 101 6 A 101 31 C 101 7 C 101 32 C 101 8 C 101 33 A 101 9 A 101 34 D 101 10 B 101 35 A 101 11 D 101 36 B 101 12 A 101 37 A 101 13 C 101 38 D 101 14 D 101 39 B 101 15 D 101 40 C 101 16 C 101 41 B 101 17 B 101 42 D 101 18 B 101 43 A 101 19 C 101 44 A 101 20 C 101 45 C 101 21 D 101 46 B 101 22 D 101 47 C 101 23 C 101 48 A 101 24 B 101 49 D 101 25 A 101 50 B BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 D A
B B B A C C A B D A C D D C B B C C D D C B A
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
A D A B B C C A D A B A D B C B D A A C B C A D B
LỜI GIẢI CHI TIẾT Câu 1.
Hàm số nào sau đây có đồ thị như hình vẽ bên ? −x 2 − x +1 −x + 2 −x +1 A. y = . B. y = . C. y = . D. y = . x +1 2x +1 x +1 x +1 Lời giải Chọn D
Dựa vào đồ thị ta thấy:
+) Tiệm cận đứng x
1 và tiệm cận ngang y 1 loại đáp án B.
+) Đồ thị cắt trục Oy tại điểm có tọa độ 0;1
x 0;y 1 nên loại đáp án A, C.
+) Đồ thị cắt trục Ox tại điểm có tọa độ 1;0 . −x +1 Vậy hàm số y = thỏa mãn. x +1 Câu 2.
Trong không gian Oxyz , gọi
là góc giữa hai vectơ a và b , với a và b khác 0 , khi đó cos bằng . a b a . b . a b . a b A. . B. . C. . D. . a . b . a b a + b a . b Lời giải Chọn A
Công thức tính góc giữa hai vectơ a và b , với a và b khác 0 : . cos( , ) a b a b a . b Câu 3.
Trong không gian Oxyz , cho các điểm ( A 4; 3 − ;2) , ( B 6;1; 7 − ) ,C(2;8; 1
− ) . Viết phương trình
đường thẳng đi qua gốc tọa độ O và trọng tâm G của tam giác ABC . x y z x y z x y z x y z A. = = . B. = = . C. = = . D. = = . 2 1 − 1 − 2 1 1 − 2 3 1 − 4 1 3 − Lời giải
Trang 8/28 – Diễn đàn giáo viên Toán Chọn B
Ta có G là trọng tâm của tam giác ABC G (4; 2; 2 − ) OG = (4;2; 2 − ) = 2(2;1;− ) 1
Đường thẳng đi qua gốc tọa độ O và trọng tâm G của tam giác ABC có một vectơ chỉ phương là u = (2;1; − ) 1 nên chọn đáp án B.
Xét đáp án A có vectơ chỉ phương là u = (2;−1;− ) 1 nên loại.
Xét đáp án C có vectơ chỉ phương là u = (2;3;− ) 1 nên loại.
Xét đáp án D có vectơ chỉ phương là u = (4;1; 3 − ) nên loại. Câu 4.
Cho hàm số y = f (x) có bảng biến thiên như sau:
Khẳng định nào sau đây là đúng?
A. Giá trị cực đại của hàm số y = f (x) bằng 2.
B. Hàm số y = f (x) đạt cực tiểu tại x =1.
C. Hàm số y = f (x) đạt cực đại tại x = . 1 − .
D. Giá trị cực tiểu của hàm số y = f (x) bằng 1. Lời giải Chọn B Từ BBT:
Hàm số y = f (x) đạt cực tiểu tại x =1 nên chọn B.
Hàm số không xác định tại x = 1
− nên đáp án A và C loại.
Giá trị cực tiểu của hàm số bằng 0 nên đáp án D loại
Câu 5. Cho cấp số cộng (u
có u = 11 và công sai d = 4 . Hãy tính u . n ) 1 99 A. 401. B. 403. C. 402. D. 404. Lời giải Chọn B
(u là cấp số cộng nên u = u +(n−1)d =11+(99−1)4 = 403 n ) 99 1
Câu 6: Trong không gian Oxyz , cho mặt phẳng ( P) : 2x − 3y + 5z − 9 = 0 . Vectơ nào sau đây là
một vectơ pháp tuyến của (P) ?
A. n (2; − 3;5) .
B. n (2; − 3; − 5) . C. n (2;3;5) .
D. n (2; − 3;9) . Lời giải Chọn A
Mặt phẳng có phương trình ax + by + cz + d = 0 có vectơ pháp tuyến là n (a ; ; b c) .
Do vậy mặt phẳng ( P) : 2x − 3y + 5z − 9 = 0 có vectơ pháp tuyến là n (2; − 3;5) . Câu 7.
Trong không gian cho tam giác ABC vuông tại A , AB = a và AC = a 3 . Tính độ dài đường
sinh l của hình nón có được khi quay tam giác ABC xung quanh trục AB .
A. l = a 3 .
B. l = a 2 .
C. l = 2a .
D. l = a . Lời giải Chọn C Trang 9/28 - WordToan
Tam giác ABC vuông tại A , có AB = a và AC = a 3 , nên khi quay tam giác ABC xung quanh
trục AB ta được hình nón có độ dài đường sinh là: 2 2 2 2 2 l = BC = AB + AC = a + 3a = 4a = 2a . Câu 8.
Tìm nguyên hàm của hàm số 2 f ( )
x = 3x + 8sin x A.
f (x)dx = 6x − 8 cos x + C . B.
f (x)dx = 6x + 8 cos x + C . C. 3
f (x)dx = x − 8 cos x + C . D. 3
f (x)dx = x + 8 cos x + C . Lời giải Chọn C Ta có f x dx = ( 2x + x) 2 3 ( ) 3 8sin
dx = 3x dx + 8sin xdx = x − 8 cos x + C .
Câu 9. Cho các mệnh đề sau: 2 x (I) Hàm số 2020 y =
luôn đồng biến trên R . e (II) Hàm số
y = x (với là một số thực âm) luôn có một đường tiệm cận đứng và một đường tiệm cận ngang. (III) Hàm số 2
y = log x có tập xác định là ( + ; 0 ). 2 (IV) Hàm số 1 3 y =
x có đạo hàm là y' = . 3 2 . 3 x
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên? A. 2 . B. 1. C. 3 . D. 4 . Lời giải Chọn A 2 2 x x 2020 2020 2020 +) Hàm số y = y = 2x ln 0 khi x 0 . e e e
Suy ra hàm số đồng biến trên (0;+) (I) là mệnh đề sai. +) Hàm số
y = x (với là một số thực âm) luôn có một đường tiệm cận đứng và một đường
tiệm cận ngang (II) là mệnh đề đúng. +) Hàm số 2
y = log x có tập xác định \
0 (III) là mệnh đề sai. 2 1 2 1 − 1 +) Hàm số 3 3 y =
x = x có đạo hàm là 3 y ' = x =
(IV) là mệnh đề đúng. 3 2 3 3. x
Vậy có 2 mệnh đề đúng.
Câu 10. Cho số phức z = ( − i)( + i)2 3 2 1
. Môđun của w = iz + z là A. 8 . B. 2 2 . C. 1. D. 2 . Lời giải Chọn B
z = ( − i)( + i)2 3 2 1
= 4 + 6i w = iz + z = i (4 + 6i) + (4 − 6i) = −2 − 2i .
w = (− )2 + (− )2 2 2 = 2 2 .
Trang 10/28 – Diễn đàn giáo viên Toán
Câu 11. Một mặt cầu có độ dài đường kính bằng 4 . Tính diện tích của mặt cầu đó? 64 A. 128 . B. 64 . C. . D. 16 . 3 Lời giải Chọn D
Bán kính mặt cầu R = 2 . Diện tích mặt cầu 2 2
S = 4 R = 4.2 =16 . 3 +
Câu 12. Đạo hàm của hàm sô 2 = 3x y là x + 3 x + A. y' 2 3 = x .3 .3ln 3. B. y' = 3 . 2 ln 3 . x + 3 x + C. 2 3 2 y'= 3x .3 . D. 2 3 1
y'= 3x .(x + 2 3 ). . Lời giải Chọn A
Áp dụng công thức ( u )' u a = a .ln . a u ' 3 3 3 + + + Ta có x 2 y = ( 3x + ) 2 x 2 2 x 3 ' 3 .ln 3. 2 ' = 3x .3 .ln 3 = x .3 .ln 3 .
Câu 13. Cho hai số phức z =1+ 2i và z = 2 − 3i . Phần ảo của số phức w = 3z − 2z là 1 2 1 2 A. 9 . B. 12i . C. 12 . D. 1 − . Lời giải Chọn C
Ta có w = 3z − 2z = 3(1+ 2i) − 2(2 − 3i) = 1 − +12i . 1 2
Vậy phần ảo của số phức w là 12 .
Câu 14. Tính tổng diện tích tất cả các mặt của khối đa diện đều loại 3; 5 có các cạnh bằng 1 . 3 3 5 3 A. 3 3 . B. . C. . D. 5 3 . 2 2 Lời giải Chọn D
Khối đa diện đều loại 3;
5 là khối 20 mặt đều (các mặt là tam giác đều và bằng nhau). 2
Diện tích của một mặt (tam giác đều) là 1 . 3 3 = . 4 4
Vậy tổng diện tích 20 mặt của khối đa diện đều loại 3 3; 5 là S = 20. = 5 3 . 4
Câu 15. Gọi z ; z là hai nghiệm phức của phương trình 2
z + 2z + 4 = 0 . Khi đó 2 2 A |
= z | + | z | có giá trị 1 2 1 2 bằng A. 4 . B. 14 . C. 20 . D. 8 . Lời giải Chọn D Phương trình 2
z + 2z + 4 = 0 . Ta có : = (b )2 ' ' − ac = −3 .
Phương trình có 2 nghiệm phức: Trang 11/28 - WordToan ' ' b − + i 1 − + i 3 z = = = 1 − + i 3 . 1 a 1 ' ' b − − i 1 − − i 3 z = = = 1 − − i 3 . 2 a 1 z = (− ) 1 + ( 3)2 2 = 2 . 1 z = (− ) 1 + (− 3)2 2 = 2 . 2 Khi đó 2 2 A |
= z | + | z | = 4 + 4 = 8. 1 2
Câu 16. Cho các số thực ,
a b và các mệnh đề: b a b a 1. f
(x)dx = − f (x)dx. 2. 2 f
(x)dx = 2 f (x)dx . a b a b 2 b b b b 3. 2 f
(x)dx = f (x)dx . 4. f
(x)dx = f (u)du. a a a a
Số mệnh đề đúng trong 4 mệnh đề trên là A.3. B. 4 . C. 2. D. 1. Lời giải Chọn C b a - Xét mệnh đề (1): f
(x)dx = − f
(x)dx. Mệnh đề này đúng theo tính chất của tích phân. a b b a -
Xét mệnh đề (2): 2 f
(x)dx = 2 f
(x)dx . Mệnh đề này sai theo tính chất của tích phân. a b 2 b b - Xét mệnh đề (3): 2 f
(x)dx = f
(x)dx . Mệnh đề này sai. a a 2 1 1 2 7 9
Phản ví dụ: ( x + ) 1 dx = ; (x + ) 1 dx = . 3 4 0 0 b b - Xét mệnh đề (4): f
(x)dx = f
(u)du. Mệnh đề này đúng theo tính chất của tích phân. a a
Vậy trong các mệnh đề trên có 2 mệnh đề đúng.
Câu 17. Trên mặt phẳng tọa độ ,điểm M trong hình vẽ bên là điểm biểu diễn số phức z . Khẳng định nào sau đây là đúng?
A. z = 1− 2i . B. z = 5 .
C. z = 1+ 2i . D. z = 2 − + i . Lời giải Chọn B
Dựa vào hình vẽ ta có điểm M (1; 2
− ) biểu diễn số phức z =1− 2i . z = ( )2 + (− )2 1 2 = 5
Trang 12/28 – Diễn đàn giáo viên Toán 1
Câu 18. Cho x , a , b là các số thực dương thỏa mãn log
= 2log a − 6log b . Khi đó giá trị của x là 7 7 49 x 3 b 2 a
A. x = 2a − 3b . B. x = . C. x = . D. 2 3
x = a b . 2 a 3 b Lời giải Chọn B Ta có: 1 2 3 log
= 2log a − 6log b = 2log a − 6log b = 2log a − 3log b = log a − log b 2 7 7 49 7 7 7 7 7 7 x 2 2 3 1 a 1 a b log = log = x = 7 7 3 3 2 x b x b a
Câu 19. Diện tích xung quanh của hình trụ có bán kính đáy R = 2 và đường sinh l = 6 bằng: A. 4 . B. 8 . C. 24 . D. 12 . Lời giải Chọn C
Diện tích xung quanh của hình trụ có bán kính đáy R = 2 và đường sinh l = 6 là: S = 2 .
R h = 2.2.6 = 24 . xq
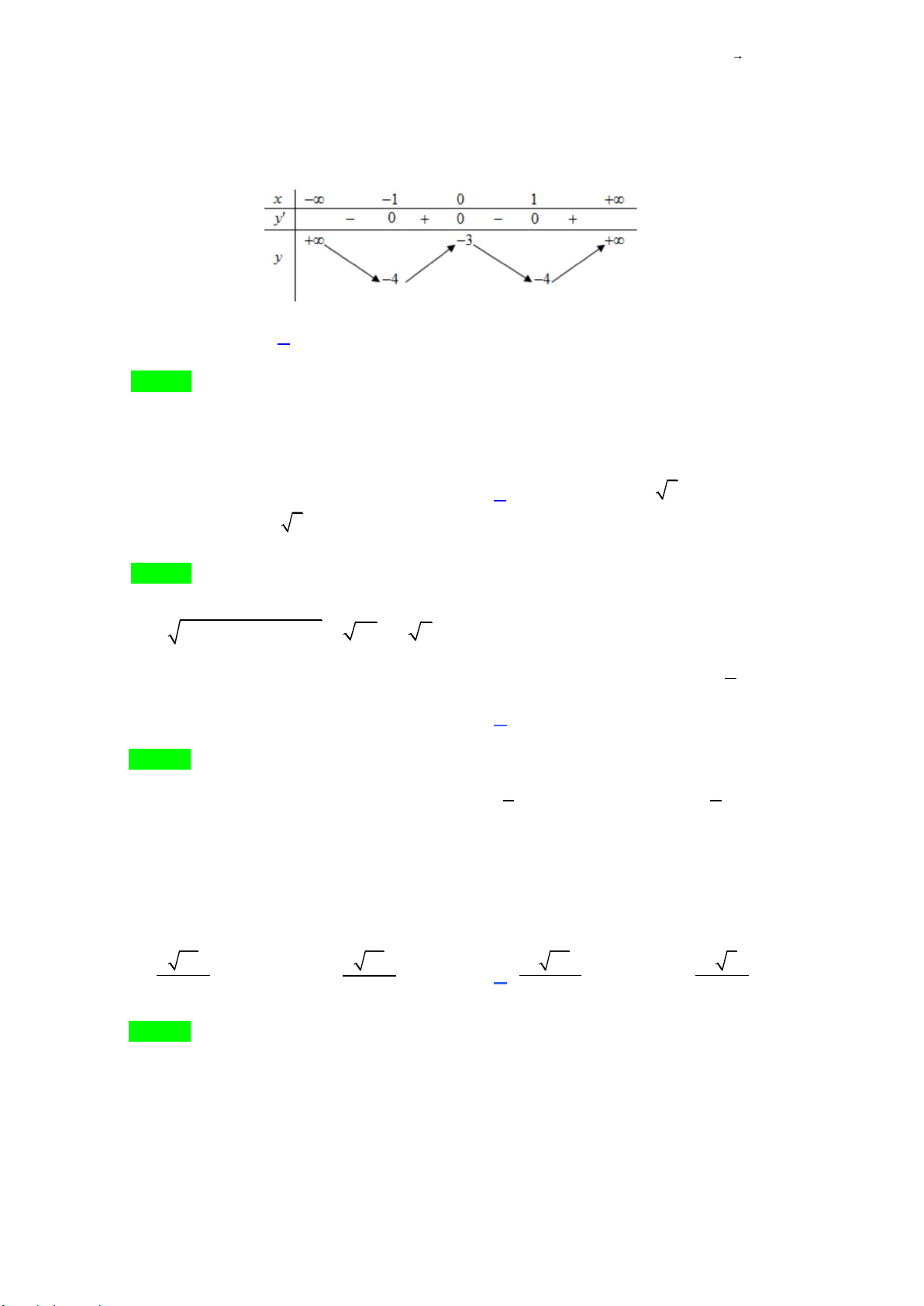
Câu 20. Cho hàm số y = f (x) có bảng biến thiên như sau:
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 2 . B. 3 . C. 4 . D. 1. Lời giải Chọn C
Dựa vào bảng biến thiên ta có:
lim f ( x) = +, lim f ( x) = −, lim f ( x) = + nên đồ thị có 2 tiệm cận đứng là x =1 và + + − x→ 1 − x 1 → x 1 → x = 1 − . lim f ( x) = 3
− , lim f (x) = 3 suy ra đồ thị có hai tiệm cận ngang là y = 3 − và y = 3. x→− x→+
Vậy đồ thị có 4 tiệm cận đứng và ngang.
Câu 21. Cho hàm số y = f (x) có bảng biến thiên như sau:
Số nghiệm của phương trình 3 f (x) + 4 = 0 là A. 4 . B.1. C. 3 . D. 2 . Lời giải Chọn D Ta có: f x + = f (x) 4 3 ( ) 4 0 = − . 3 Trang 13/28 - WordToan
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số y = f ( x) và đường thẳng 4 y = − . 3 4
Từ bảng biến thiên suy ra đồ thị hàm số y = f ( x) và đường thẳng y = − cắt nhau tại 2 điểm 3
phân biệt. Vậy phương trình đã cho có 2 nghiệm phân biệt.
Câu 22. Hình trụ có bán kính đáy bằng a và thiết diện qua trục là hình vuông, diện tích xung quanh hình trụ đó bằng 2 a A. . B. 2 a . C. 2 3 a . D. 2 4 a . 2 Lời giải Chọn D
Vì hình trụ có bán kính đáy R = a và thiết diện qua trục là hình vuông nên cạnh của thiết diện
bằng 2a . Suy ra độ dài đường sinh của hình trụ h = 2a .
Từ đó ta có diện tích xung quanh hình trụ đó bằng 2 S = 2 Rh = 2. .2 a a = 4 a . xq 3 x
Câu 23. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 y =
+ 2x + 3x − 4 trên đoạn −4;0 lần lượt là 3
M và m . Giá trị của tổng M + m bằng bao nhiêu? 4 4 28
A. M + m = − .
B. M + m = .
C. M + m = − .
D. M + m = 4 − . 3 3 3 Lời giải Chọn C 3 x Ta có 2 2 y =
+ 2x + 3x − 4 y = x + 4x + 3. 3 x = 3 − 4 − ;0 2
y = 0 x + 4x + 3 = 0 x = 1 − 4 − ;0 . 3 − Mặt khác ( 4) 16 2 y(0) = 4 − ; y( 4 − ) = + 2( 4 − ) + 3( 4 − ) − 4 = − . 3 3 3 3 ( 1 − ) 1 − 6 ( 3 − ) 2 2 y( 1 − ) = + 2( 1 − ) + 3( 1 − ) − 4 = ; y( 3 − ) = + 2( 3 − ) + 3( 3 − ) − 4 = 4 − . 3 3 3 16 28 M = 4 − ;m = − M + m = − . 3 3
Câu 24. Trong không gian Oxyz , hình chiếu vuông góc của điểm M (5; − 6; 2) lên mặt phẳng (Oxz) có tọa độ là A. (0;− 6;0) . B. (5;0;2) . C. (5;− 6;0) . D. (0;− 6;2) . Lời giải Chọn B
Mặt phẳng (Oxz) có phương trình y = 0
Trang 14/28 – Diễn đàn giáo viên Toán
Vậy hình chiếu vuông góc của điểm M (5;− 6;2) lên mặt phẳng (Oxz) có tọa độ là(5;0;2). Câu 25.
Cho số phức z = 4 −3i . Phần thực, phần ảo của số phức z lần lượt là A. 4;3. B. 4; 3 − . C. 3; 4 . D. 4 − ;3. Lời giải Chọn A
z = 4 + 3i . Nên phần thực, phần ảo của số phức z lần lượt là 4;3. Câu 26.
Khối đa diện đều loại 3;
4 có tất cả bao nhiêu cạnh? A. 12 . B. 6 . C. 14 . D. 8 . Lời giải Chọn A
Khối đa diện đều loại 3;
4 là khối bát diện đều có 12 cạnh.
Câu 27. Cho hàm số y = f (x) có đồ thị hàm số f ( x) như hình vẽ
Hàm số y = f (x) có bao nhiêu điểm cực trị? A. 3 . B. 2 . C. 0 . D. 1. Lời giải Chọn D
Dựa vào đồ thị của hàm số f '(x) ta có bảng xét dấu của f ( x) như sau:
Từ đó suy ra hàm số y = f (x) có 1 điểm cực trị.
Câu 28. Trong không gian với hệ trục tọa độ Oxyz , cho điểm ( A 4; 3 − ;5) và ( B 2; 5
− ;1).Viết phương trình mặt phẳng ( )
P đi qua trung điểm I của đoạn thẳng AB và vuông góc với đường thẳng x +1 y − 5 z + 9 d : = = . 3 2 − 13
A. 3x − 2y +13z − 56 = 0 .
B. 3x + 2y +13z − 56 = 0 .
C. 3x + 2y +13z + 56 = 0 .
D. 3x − 2y −13z + 56 = 0 Lời giải Chọn A
I là trung điểm của đoạn thẳng AB suy ra tọa độ điểm I (3; 4 − ;3) . Trang 15/28 - WordToan Mặt phẳng ( )
P vuông góc với đường thẳng d nên nhận vectơ chỉ phương u = (3; −2;13) của
đường thẳng d làm vectơ pháp tuyến. Do đó ( )
P có phương trình là
3( x − 3) − 2( y + 4) +13( z − 3) = 0 3x − 2 y +13z − 56 = 0 .
Câu 29. Cho hàm số y = f (x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ( )1 ; 0 . B. (− 0 ; 1 ). C. (− ; − ) 1 . D. ( + ; 0 ). Lời giải Chọn B
Từ bảng biến thiên ta có: Hàm số đồng biến trên khoảng (−1; 0).
Câu 30. Trong không gian Oxyz cho mặt cầu (S ) có phương trình 2 2 2
x + y + z + 4x − 4y + 8z = 0 . Tìm tọa
độ tâm I và bán kính R . A. I (2; 2 − ;4); R = 24 .
B. I (−2; 2; −4); R = 2 6 . C. I (2; 2 − ;4); R = 2 6 . D. I ( 2 − ;2; 4 − ); R = 24 . Lời giải Chọn B
Ta có: mặt cầu (S ) : 2 2 2
x + y + z + 4x − 4y + 8z = 0 . Có tâm I ( 2 − ;2; 4 − ) và bán kính 2 2 2 R = ( 2 − ) + 2 + ( 4 − ) = 24 = 2 6. 15 1
Câu 31. Tìm số hạng không chứa x trong khai triển nhị thức Newtơn của P ( x) 2 = x + x A. 4000 . B. 2700 . C. 3003 . D. 3600 . Lời giải Chọn C 15 k − Số hạng thứ ( 1 k k 1 k + )
1 trong khai triển P ( x) 2 = x +
là T = C . x . k − k = C x . k 1 + 15 ( )15 2 30 3 x 15 x T
không chứa x khi đó 30 −3k = 0 k =10 . k 1 +
Vậy số hạng không chứa x là 10 5 C = C = 3003. 15 15
Câu 32. Cho mặt cầu (S ) tâm O và các điểm A , B , C nằm trên mặt cầu (S ) sao cho AB = 3 , AC = 4 ,
BC = 5 và khoảng cách từ O đến mặt phẳng ( ABC ) bằng 1. Thể tích của khối cầu (S ) bằng 7 21 4 17 29 29 20 5 A. . B. . C. . D. . 2 3 6 3 Lời giải Chọn C
Trang 16/28 – Diễn đàn giáo viên Toán Do 2 2 2
BC = AC + AB nên ABC vuông tại A .
Vậy bán kính đường tròn ngoại tiếp BC 5 ABC là r = = . 2 2
Hình chiếu của O trên ( ABC ) trùng với tâm đường tròn ngoại tiếp ABC . 2 5 29
Khi đó bán kính khối cầu (S ) bằng 2 2 2
R = r + h = +1 = 2 2 3 4 4 29 29 29
Vậy thể tích của khối cầu (S ) bằng 3 V = R = = . 3 3 2 6 2 2
Câu 33. Có tất cả bao nhiêu giá trị thực của tham số m để đồ thị hàm số 3 2 y = x − mx − 2 ( 2 3m − ) 1 x + 3 3
có hai điểm cực trị có hoành độ x , x sao cho x x + 2 x + x = 1. 1 2 ( 1 2 ) 1 2 A. 1. B. 0 . C. 3 . D. 2 . Lời giải Chọn A Ta có : 2
y = x − mx − ( 2 m − ) = ( 2 2 ' 2 2 2 3 1
2 x − mx − 3m + ) 1 , g ( x) 2 2
= x − mx − 3m +1 ; 2 =13m − 4.
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi y ' có hai nghiệm phân biệt
g ( x) có hai nghiệm phân biệt 2 13 m 13 0 . (*) 2 13 m − 13
x + x = m x 1 2
, x là các nghiệm của g ( x) nên theo định lý Vi-ét, ta có . 1 2 2 x x = 3 − m +1 1 2 m = 0
Do đó x x + 2 x + x = 1 2 3
− m + 2m +1=1 2 3
− m + 2m = 0 . 1 2 ( 1 2 ) 2 m = 3
Đối chiếu với điều kiện (*), ta thấy chỉ 2 m =
thỏa mãn yêu cầu bài toán. 3
Câu 34. Có bao nhiêu số tự nhiên có 4 chữ số mà tổng tất cả các chữ số của số đó bằng 7? A. 165 . B. 1296 . C. 343 . D. 84 . Lời giải Chọn D
7 có thể phân tích thành 11 nhóm sau : 7 = (7+0+0+0) = (6+1+0+0) = (5+2+0+0) = (5+1+1+0) Trang 17/28 - WordToan
= (4+3+0+0) = (4+2+1+0) = (4+1+1+1)
= (3+3+1+0) = (3+2+2+0) = (3+2+1+1) = (2+2+2+1)
+) Với nhóm (7+0+0+0) viết được 1 số, đó là số: 7000.
+) Với các nhóm (6+1+0+0); (2+2+0+0) và (4+3+0+0): mỗi nhóm viết được 6 số
(chẳng hạn: với nhóm (6+1+0+0) ta có các số 6100, 6010, 6001 và hoán vị của số 6 và số 1). −
+) Với nhóm (3+3+1+0); (5+1+1+0) và (3+2+2+0): mỗi nhóm viết được 4! 3! = 9 số 2
( 3! là các số có số 0 đứng đầu, chia 2 vì có 1 số xuất hiện 2 lần).
+) Với nhóm (4+2+1+0) viết được: 4!−3!=18 số (3! là các số có số 0 đứng đầu).
+) Với nhóm (3+2+1+1) viết được: 4! = 12 số (vì xuất hiện 2 số 1). 2
+) Với các nhóm (4+1+1+1) và (2+2+2+1): mỗi nhóm viết được 4 số
(chẳng hạn: với nhóm (4+1+1+1) ta có các số: 4111; 1411; 1141; 1114).
Tổng số các số viết được là : 1+ 6.3+ 9.3+18+12 + 4.2 = 84 (số).
Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và ; D AB = AD = 2 ;
a DC = a . Điểm I là trung điểm đoạn ,
AD hai mặt phẳng ( SIB) và ( SIC )
cùng vuông góc với mặt phẳng ( ABCD) . Mặt phẳng (SBC ) tạo với mặt phẳng ( ABCD) một góc
60 . Tính khoảng cách từ D đến ( SBC ) theo a . a 15 9a 15 2a 15 9a 15 A. . B. . C. . D. . 5 10 5 20 Lời giải Chọn A S E A B H E A B U I V J I M K M K D C D C N
Theo đề ta có SI ⊥ ( ABCD).
Gọi K là hình chiếu vuông góc của I trên BC .
Suy ra: Góc giữa hai mặt phẳng ((SBC),( ABCD)) = SKI = 60
Gọi E là trung điểm của ,
AB M = IK D . E
Do BCDE là hình bình hành nên DE // (SBC )
d (D,(SBC)) = d (DE,(SBC)) = d (M ,(SBC))
Gọi H là hình chiếu vuông góc của M trên SK . Suy ra d (M ,(SCD)) = MH Dễ thấy: 1 1 1 IM = AU = KN = MK 2 2 2 1 5
IN = IM + MK + KN =
MK + MK + MK = MK 2 2 2 2 2a 5 Suy ra: 2 2 MK = IN = ID + DN = . 5 5 5
Trang 18/28 – Diễn đàn giáo viên Toán a 15
Trong tam giác MHK, ta có: MH = MK.sin 60 = 5
Câu 36: Cho tứ diện đều ABCD , M là trung điểm của cạnh BC . Khi đó cos ( AB, DM ) bằng 2 3 1 3 A. . B. . C. . D. . 2 6 2 2 Lời giải Chọn B A N B D M C
Gọi N là trung điểm của .
AC Suy ra MN // AB
Do đó: cos( AB, DM ) = cos(MN, DM ) Gọi a a 3
a là độ dài cạnh của tứ diện đều ABCD , suy ra MN = ; ND = MD = 2 2 2 2 2
MN + MD − ND 3
Trong tam giác MND ta có: cos NMD = = 2.MN.MD 6 ( AB DM ) 3 cos , = cos NMD = . 6
Câu 37. Diện tích hình phẳng của phần gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây ? 1 1 A. S = ( 2 4
− x + 4x)dx . B. S = ( 2 2x − 4x + )1dx. 0 0 1 1 C. S = ( 2
4x − 4x)dx . D. S = ( 2 4
− x + 4x)dx . 0 1 − Lời giải Chọn A
Đặt f ( x) 2
= − x + g (x) 2 2 1;
= 2x − 4x +1 .
Ta thấy trên đoạn 0;
1 đồ thị hàm số f ( x) nằm trên đồ thị hàm số g ( x) nên Trang 19/28 - WordToan 1 1 1 S = f
(x)− g(x) 2 d x = 2 − x +1− ( 2 2x − 4x + ) 1 d x = ( 2 4
− x + 4x)dx . 0 0 0
Câu 38. Bất phương trình log
2x − 3 0 có tập nghiệm là 0,5 ( ) 3 3 A. (−; 2) . B. (2; +) . C. ; + . D. ; 2 . 2 2 Lời giải Chọn D 3
Điều kiện: 2x − 3 0 x . Khi đó bất phương trình 2 log
2x − 3 0 2x − 3 1 2x 4 x 2 . 0,5 ( )
Kết hợp với điều kiện ta được tập nghiệm của bất phương trình là 3 S = ; 2 . 2
Câu 39. Phương trình log
3.2x −1 = 2x +1 có tất cả bao nhiêu nghiệm thực? 2 ( ) A. 3. B. 2. C. 0. D. 1. Lời giải Chọn B log
3.2x −1 = 2x +1 2 ( ) x 2 x 1 3.2 −1 = 2 +
3.2x −1 = 2.(2x )2 ( x )2 2. 2 − 3.2x +1 = 0 2x =1 x 1 2 = 2 x = 0 x = 1−
Tập nghiệm của phương trình là S = 1 − ;
0 . Vậy phương trình có hai nghiệm thực. Chọn B.
Câu 40. Cho phương trình 9x − (2m + 3 ). 3
x +81= 0 ( m là tham số thực). Giá trị của m để phương trình đã
cho có hai nghiệm phân biệt x , x thỏa mãn 2 2
x + x = 10 thuộc khoảng nào sau đây 1 2 1 2 A. ( 10 ; 5 ). B. ( 5 ; 0 ). C. ( ) 15 ; 10 . D. ( + ; 15 ). Lời giải Chọn C
9x − (2 + 3).3x m + 81 = 0 ( ) 1 ( x )2 3 − (2 + 3).3x m + 81 = 0 . Đặt = 3x t (t 0)
Phương trình trở thành: 2
t − (2m + 3)t + 81 = 0 (2) = ( m + )2 − = ( m + )2 2 3 4.81 2 3 − 324 Để phương trình ( )
1 có hai nghiệm phân biệt thì phương trình (2) có hai nghiệm phân biệt dương:
Trang 20/28 – Diễn đàn giáo viên Toán Điều kiện: 15 m 2m + 3 18 2 m + + − 0 ( m )2 2 3 18 3 3 2 3 324 0 m − m − 2m + 3 1 − 8 2 2 15
S 0 2m + 3 0 m 3 2m + 3 1 − 8 21 2 P 0 81 0 m − m − 2 3 2 m − 3 2 m − 2 + = + 1 t t2 2m 3
Áp dụng hệ thức Vi-ét: = 1t.t2 81 Vì x x 4 1 2 = = + = 1 t .t2 81 3 .3 3 1 x 2 x 4 Do đó: 2 2
x + x = 10 ( x + x )2 2 − = − = = 1 2 1 2 2 1 x . 2 x 10 4 2 1 x . 2 x 10 1 x . 2 x 3 x .x = 3 x =1 t = 3 Xét hệ phương trình 1 2 1 1 + = 1 t t2 30 + = = = 1 x 2 x 4 2 x 3 t 2 27 27
Nên 2m + 3 = 30 m = (TM ) 2 Vậy chọn C.
Câu 41. Cho hàm số f (x) liên tục trên −1; 2 2 = + + −
và thỏa mãn điều kiện f (x) x 2 xf (3 x ) . 2 Tích phân I = f (x)dx bằng 1 − 14 28 4 A. I = . B. I = . C. I = . D. I = 2 . 3 3 3 Lời giải Chọn B 2 2 2 2 14 Ta có I = x + 2 + xf 2 2 ( 2 3 − x ) dx = x + 2dx + xf
(3− x )dx = + xf (3− x )dx. 3 1 − 1 − 1 − 1 − 2 t Xét xf ( 2
3 − x )dx đặt 2 t = 3 − d x dt = 2 − d x x d x x = − . 2 1 − 2 1 − 2 1 1 Đổi cận khi x = 1
− t = 2; x = 2 t = 1 − . Suy ra xf ( 2
3 − x )dx = − f (t)dt = f (t)dt . 2 2 1 − 2 1 − 2 14 2 2 14 1 14 1 Khi đó I I = + xf ( 2 3 − x )dx = + f (t)dt = + f (x)dx 14 28 I = + I = . 3 3 2 3 2 3 2 3 1 − 1 − 1 − 1 2
Câu 42. Cho hàm số f ( x) liên tục trên và thỏa mãn f
(x)dx = 9 . Tích phân f
(1−3x)+9dx 5 − 0 bằng A. 15 . B. 27 . C. 75 . D. 21. Lời giải Chọn D 2 2 2 2 Ta có f
(1−3x)+9dx = f
(1−3x)dx+ 9dx = f
(1−3x)dx+18. 0 0 0 0 2 dt Xét f
(1−3x)dx , đặt t =1−3x dt = 3
− dx dx = − . 3 0 Trang 21/28 - WordToan 2 5 − 1 Đổ 1 1
i cận khi x = 0 t =1; x = 2 t = 5 − . Suy ra f
(1−3x)dx = − f (t)dt = f (t)dt . 3 3 0 1 5 − 2 1 1 Khi đó f ( − x) 1 1 1 3 + 9 dx =
f (t)dt +18 =
f (x)dx +18 = 21 . 3 3 0 5 − 5 − mx − 3
Câu 43. Cho hàm số y = 3x − , m là tham số thực. Có tất cả bao nhiêu giá trị nguyên của m để hàm số m
đồng biến trên từng khoảng xác định? A. 5 . B. 7 . C. 3 . D. vô số. Lời giải Chọn A mx − 3
Xét hàm số y = 3x − m +) TXĐ: m m D = − ; ; + 3 3 2 −m + 9
+) y = (3x−m)2
+) Để hàm số đồng biến trên từng khoảng xác định 2 m − + 9 0 3 − m 3 . Mà m
m−2;−1;0;1;
2 . Vậy có 5 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 44. Cho hàm số bậc ba y = f ( x) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m 5
− ;5 sao cho phương trình 3 log ( f ( x) + ) 2 1 − log
f x +1 + 2m − 8 log
f x +1 + 2m = 0 có nghiệm x ( 1 − ; ) 1 ? 2 2 ( ( ) ) ( ) 1 ( ) 2 A. 7 . B. 5 . C. 6 . D. vô số. Lời giải Chọn A Với x ( 1 − ; ) 1 1
− f (x) 3 0 f (x) +1 4 . Đặt t = log f x +1 t ; − 2 , x 1 − ;1 . 2 ( ( ) ) ( ) ( )
Khi đó phương trình đã cho trở thành: 3 2
t − 4t − (m − 4)t + 2m = 0 ( t = − t − 2)( 2 ; 2 2
t − 2t − m) ( ) 2 2 = 0
t − 2t − m = 0 t − 2t = m (*) 2
t − 2t − m = 0
Để phương trình đã cho có x (−1; )
1 phương trình (*) có nghiệm t ( ; − 2) .
Xét hàm số f (t ) 2
= t − 2t trên (−;2) có f (t) = 2t − 2 = 0 t =1( ; − 2).
Ta có bảng biến thiên của hàm số f (t ) 2 = t − 2t
Trang 22/28 – Diễn đàn giáo viên Toán t 1 2 f t 0 0 f t 1
Từ bảng biến thiên suy ra phương trình (*) có nghiệm t ( ;
− 2) khi và chỉ khi m 1 − . m 5 − ; 5 Mà m 1 − ;0;1;2;3;4;
5 . Vậy có 7 giá trị của m thỏa mãn yêu cầu bài toán. m
Câu 45. Cho hàm số f ( x) . Hàm số y = f ( x) có đồ thị như hình sau.
Tìm tất cả các giá trị thực của tham số m để bất phương trình f ( x − ) 3 2sin x 5cos 2x 2 sin 2 − + sin x m +
nghiệm đúng với mọi x − ; . 3 4 2 2 A. m f (− ) 11 2 3 + . B. m f (− ) 19 2 1 + . 12 12 C. m f (− ) 19 2 1 + . D. m f (− ) 11 2 3 + . 12 12 Lời giải Chọn C Ta có f ( x − ) 3 2sin x 5cos 2x 2 sin 2 − + sin x m + 3 4 5( 2 3 1− 2sin 2sin x x )
m 2 f (sin x − 2) − + sin x − 3 4
Đặt t = sin x − 2 (với x − ; thì t ( 3 − ;− )
1 , khi đó bất phương trình được viết lại thành: 2 2 5 1 − 2 + t + (t 2 2 2 )2 3
m 2 f (t ) ( ) − + (t + 2) − . 3 4 2 3 65
hay m 2 f (t ) 3 2
− t − t + 3t + (*) . 3 2 12
Xét hàm số g (t) = 2 f (t) 2 3 65 3 2
− t − t + 3t + trên đoạn −3;− 1 . 3 2 12 3 3
Ta có g(t ) = f (t ) 2 2
− 2t − 3t + 3. Do đó g(t) = 0 f (t) 2 = t + t − . 2 2 Trang 23/28 - WordToan
Dựa vào sự tương giao của đồ thị hàm số 3 3
y = f (t ) và parabol 2 y = t + t − trên đoạn −3;− 1 2 2
thì g(t ) = 0 t −3; − 1 .
Suy ra bảng biến thiên của hàm số g (t) trên đoạn −3;− 1 như sau:
Bất phương trình đã cho nghiệm đúng với mọi x − ;
khi và chỉ khi bất phương trình (*) 2 2
nghiệm đúng với mọi t ( 3 − ;− )
1 . Điều đó tương đương với m g (− ) = f (− ) 19 1 2 1 + dựa vào 12
tính liên tục của hàm số g (t) .
Câu 46. Cho hàm số đa thức f ( x) có đạo hàm trên
. Biết f (0) = 0 và đồ thị hàm số y = f ( x) như hình sau.
Hàm số g ( x) = f ( x) 2 4
+ x đồng biến trên khoảng nào dưới đây ? A. (4; +). B. (0; 4). C. (− ; 2 − ).
D. (−2;0) . Lời giải Chọn B
Xét hàm số h( x) = f ( x) 2 4 + x trên .
Vì f ( x) là hàm số đa thức nên h ( x) cũng là hàm số đa thức và h (0) = 4 f (0) = 0 .
Ta có h( x) = 4 f ( x) + 2x . Do đó h( x) = f ( x) 1 0 = − x . 2
Trang 24/28 – Diễn đàn giáo viên Toán
Dựa vào sự tương giao của đồ thị hàm số y = f ( x) và đường thẳng 1 y = − x , ta có 2
h( x) = 0 x 2 − ;0; 4
Suy ra bảng biến thiên của hàm số h ( x) như sau:
Từ đó ta có bảng biến thiên của hàm số g ( x) = h( x) như sau:
Dựa vào bảng biến thiên trên, ta thấy hàm số g ( x) đồng biến trên khoảng (0;4) . Câu 47. Cho hàm số 3 2
y = f (x) = ax + bx + cx + d có đồ thị như hình dưới đây
Có tất cả bao nhiêu giá trị nguyên của tham số m ( 5 − ;5) để phương trình 2
f (x) − (m + 4) f (x) + 2m + 4 = 0 có 6 nghiệm phân biệt A. 2 . B. 4 . C. 3 . D. 5 . Lời giải Chọn C Ta có: 2 2
f (x) − (m + 4) f (x) + 2m + 4 = 0 f (x)
− m f (x) − 4 f (x) + 2m + 4 = 0 ( f x − )2 ( ) 2
− m( f (x) − 2 ) = 0 ( f (x) − 2 )( f (x) − 2 − m ) = 0
f (x) − 2 = 0
f (x) = 2 (1)
f (x) − 2 − m = 0
f (x) = m + 2 ( 2 ) Trang 25/28 - WordToan
Dựa vào đồ thị hàm số 3 2
y = f (x) = ax + bx + cx + d ta có đồ thị hàm số y = f (x) như sau:
Dựa vào đồ thị hàm số y = f (x) suy ra phương trình (1) có 4 nghiệm phân biệt.
Suy ra phương trình đã cho có 6 nghiệm phân biệt ( 2 ) có 2 nghiệm phân biệt khác các nghiệm của phương trình (1) .
Ta có phương trình ( 2 ) là phương trình hoành độ giao điểm của hai đường y = f (x) và
y = m + 2 . Số nghiệm phương trình ( 2 ) là số giao điểm của 2 đồ thị hàm số y = f (x) và
y = m + 2 . Dựa vào hình vẽ đồ thị hàm số y = f (x) ta được phương trình f (x) = m + 2 có 2 m + 2 = 0 m = 2 −
nghiệm phân biệt khác các nghiệm của phương trình f (x) = 2 m + 2 4 m 2 m + 2 2 Do m và m ( 5 − ;5) m 2 − ;3;4.
Vậy có 3 giá trị nguyên m ( 5
− ;5) thỏa mãn điều kiện bài toán.
Câu 48. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Hai điểm M , N lần lượt thuộc các đoạn thẳng AB AD
AB và AD ( M và N không trùng với A ) sao cho 2 + 3 = 8 . Kí hiệu V , AM AN
V lần lượt là thể tích của các khối chóp S.ABCD và S.MBCDN . Tìm giá trị lớn nhất của tỉ số 1 V1 . V 13 11 1 2 A. . B. . C. . D. . 16 12 6 3 Lời giải Chọn A S D N C A M B V AD AB 2.V AD AB Ta có: SADB = . SADB = 2. . V AN AM V AN AM SANM SANM AD AB 2. . −1 V AD AB V − V 1 V 1 1 = 2. . AN AM = = V − V AN AM V AD AB V AD AB 1 2. . 2. . AN AM AN AM
Trang 26/28 – Diễn đàn giáo viên Toán V x 8 − 3x − 1 1 1 ( ) Đặ AD AB t x = 2
= 8 − 3x,(1 x 2 ) . Khi đó = = 1 + AN AM V x ( 8 − 3x ) 2 3x − 8x Đặ 1 t f ( x ) = 1 + , (1 x 2 ) 2 3x − 8x 6x − 8 6x − 8 4 4 13
Ta có: f ( x ) = −
f ( x ) = − = = = ( 0 0 x f 3x − 8x )2 2 ( x − x )2 2 3 3 16 3 8
Bảng biến thiên hàm số y = f ( x ) 13 4
Dựa vào bảng biến thiên ta được hàm số đạt giá trị lớn nhất là tại x = . 16 3 V 13
Vậy giá trị lớn nhất của tỉ số 1 là . V 16 y x x 1 y 1 Câu 49. Cho ;
x y là hai số thực dương thỏa mãn x y và 2 + 2 +
. Giá trị nhỏ nhất của 2x 2y 2 2 + biểu thức x 3y P = 2 xy − bằng y 13 9 A. . B. . C. − 2 . D. 6 . 2 2 Lời giải Chọn D y x x 1 y 1 y x Ta có 2 + 2 + (4x + ) 1 (4y + x y )1 2 2 + +
y ( + ) x ( + ) ln (4x )1 ln(4y x y )1 ln 4 1 ln 4 1 (vì , x y 0 ). x y ln (4t + ) 1
Xét hàm số f (t ) = trên khoảng (0; + ) . t
4t.ln 4 .t −ln(4t + )1 4t ln4t − + (4t + )1ln(4t + t )1 Ta có f (t ) 4 1 = = 0, t 0 2 t (4t + ) 2 1 t
f (t) luôn nghịch biến trên khoảng (0;+ ).
Lại có f ( x) f ( y) x y . 2 + Đặ x t 3 t t =
, khi đó t (1;+) P = . y t −1 2 t + 3 2 t − 2t − 3 t = 1 −
Cách 1: Xét P =
với t (1; +) , ta có P = ; P = 0 t −1 (t − )2 1 t = 3 Bảng biến thiên Trang 27/28 - WordToan
Từ bảng biến thiên, suy ra giá trị nhỏ nhất của P bằng 6 khi t = 3 hay x = 3y . 2 t + 3 4
Cách 2: Ta có P = = t −1+
+ 2 2 4 + 2 = 6 (AM – GM). t −1 t −1
Suy ra, giá trị nhỏ nhất của P bằng 6 khi t = 3 hay x = 3y .
Câu 50. Có tất cả bao nhiêu giá trị thực của tham số m 1 − ; 1 sao cho phương trình 2 2 log x + y
= log 2x + 2y − 2 có nghiệm nguyên ( ; x y ) duy nhất ? 2 m 1 + ( ) 2 ( ) A. 3 . B. 2 . C. 1. D. 0 . Lời giải Chọn B 2 2 x + y 0 Điều kiện: .
x + y −1 0 Nhận xét: Vì ,
x y có vai trò như nhau nên nếu phương trình có nghiệm ( x ; y thì ( y ; x cũng 0 0 ) 0 0 )
là một nghiệm của phương trình.
*) Điều kiện cần: Phương trình đã cho có nghiệm duy nhất x = y . 0 0
Thay vào phương trình ta được 2 log 2x = log 4x − 2 2 m 1 + ( 0 ) 2 ( 0 ) Vì x
4x − 2 1. Lại có 2
2x 4x − 2 log 4x − 2 = log 2x log 4x − 2 0 0 2 ( 0 ) 2 2 m 1 + ( 0 ) 2 ( + 0 ) 0 0 m 1 1 1 log m +1 log 2 − − log 2 x x + − m x log 1 2 4 x −2 ( ) 2 4 0 2 ( ) 4 0 2 2 4 0 0 2 2
m +1 2 m 1 mà m 1 − ; 1 m = 1 .
*) Điều kiện đủ: Với m = 1
thì phương trình đã cho trở thành = 2 2 x 1 log ( 2 2 x + y
= log 2x + 2y − 2 2 2
x + y = 2x + 2y − 2 (x − ) 1 + ( y − ) 1 = 0 2 ) 2 ( ) y =1
Suy ra phương trình đã cho có nghiệm duy nhất (1; ) 1 .
Vậy có hai giá trị m cần tìm là m = 1.
------------- HẾT -------------
Trang 28/28 – Diễn đàn giáo viên Toán
Document Outline
- de-thi-thu-tot-nghiep-thpt-2020-mon-toan-truong-chuyen-bien-hoa-ha-nam.pdf
- Chuyên Biên Hoà Hà Nam-MÃ-101-Chuẩn
- Sổ làm việc1
- Trang_tính1
- 1592713548_WT095-Chuyen Bien Hoa-Ha Nam-TNTHPT-Lan 1-2020.pdf




