










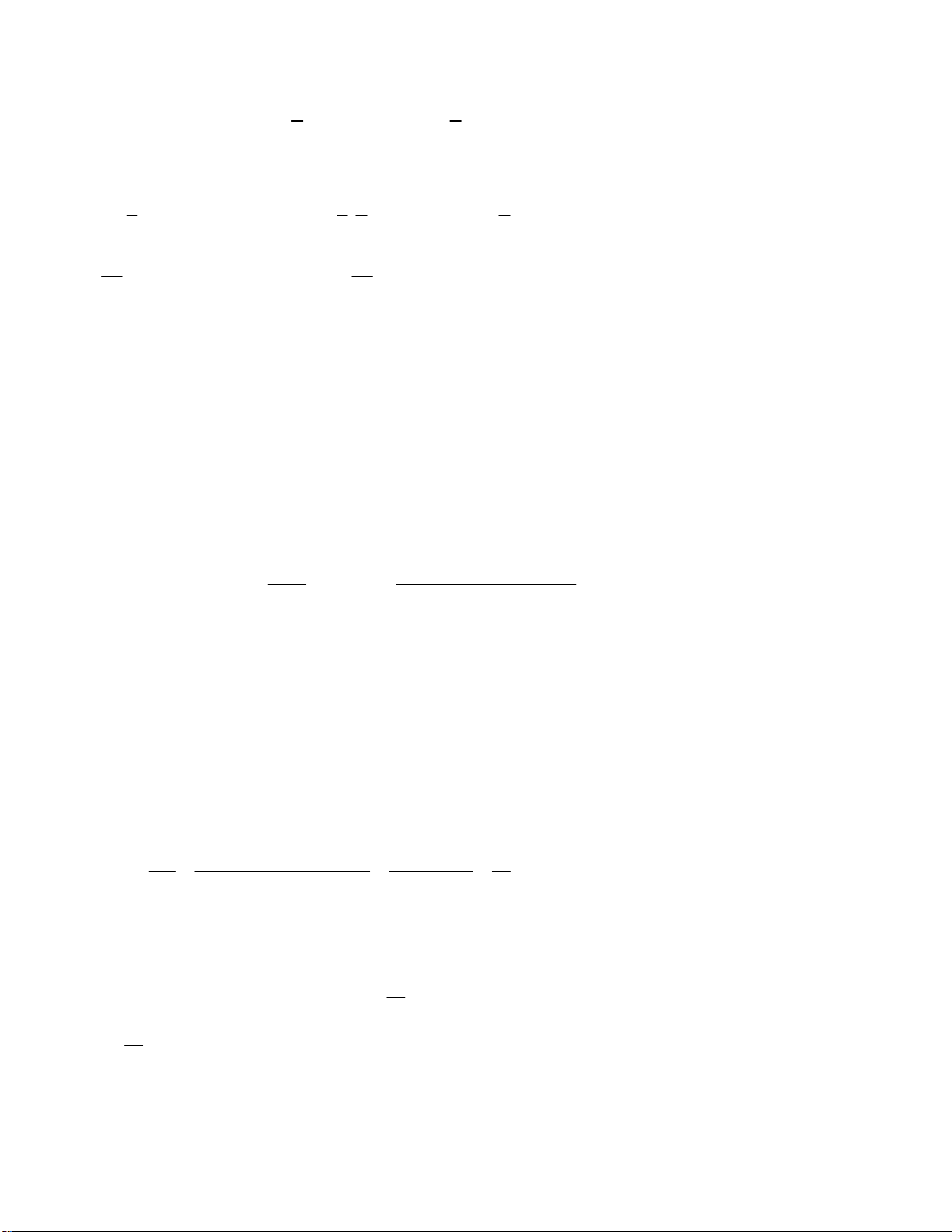
Preview text:
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: Chọn D.
Số phức liên hợp của số phức z 2
5i là z 2 5 .i Câu 2: Chọn A.
Ta có diện tích xung quanh của hình trụ bằng S 2 rl 2 .3.3 18. xq Câu 3: Chọn C. 1 1 4 x x 5 2 dx x x C. 5 2 Câu 4: Chọn A.
y ' đổi dấu khi đi qua x 2
, x 0, x 2 nên hàm số đã cho có 3 cực trị. Câu 5: Chọn D. 2 2 2 3 2 f x dx 3 dx 2 f
xdx 3 2.27 1 1 1 Câu 6: Chọn C. 1 2 1 0 x x 2 5 log 2x 1 2 x . 2 2 2x 1 2 5 2 x 2 Câu 7: Chọn B.
Số cách bốc cùng lúc 4 viên bi trong một hộp có 10 viên bi khác nhau là số tổ hợp chập 4 của 10 phần tử. Vậy số cách bốc là 4 C . 10 Câu 8: Chọn C.
Ta có z z 1 2i 2 i 3 .i 1 2 Câu 9: Chọn A. Ta có x 1 x 1 3 3
27 3 3 x 1 3 x 4. Câu 10: Chọn D.
Đồ thị trên là của hàm số dạng 4 2
y ax bx c, với a 0. Do đó chọn đáp án D. Câu 11: Chọn A. 3 3 4 r 4.3
Thể tích khối cầu là V 36. 3 3 Câu 12: Chọn B. 1 1 Ta có log b log . b 4 4 a a Câu 13: Chọn A.
Từ phương trình mặt cầu S x y 2 z 2 2 : 2
1 9, suy ra bán kính của nó là R 9 3. Câu 14: Chọn A.
ĐKXĐ: x 1 0 x 1. Tập xác định của hàm số là 1; . Câu 15: Chọn B. 2x 1 Ta có lim y lim
2. Tiệm cận ngang của đồ thị hàm số là đường thẳng y 2. x x x 1 Câu 16: Chọn D.
Thể tích khối hộp chữ nhật cần tìm là: V 2.6.7 84. Câu 17: Chọn B.
Hình chiếu vuông góc của điểm A3;5;2 trên mặt phẳng Oxy có tọa độ là 3;5;0 . Câu 18: Chọn A.
Gọi V , h lần lượt là thể tích và chiều cao của khối chóp. 3V 3.12 Khi đó: h 18. B 2
Vậy, chiều cao của khối chóp đã cho bằng 18. Câu 19: Chọn C. x 3 y 1 z 2 Vì d :
nên d có một vectơ chỉ phương là u 4;1;3. 4 1 3 Câu 20: Chọn C. Điểm M 2 ;
1 biểu diễn số phức z 2 .i
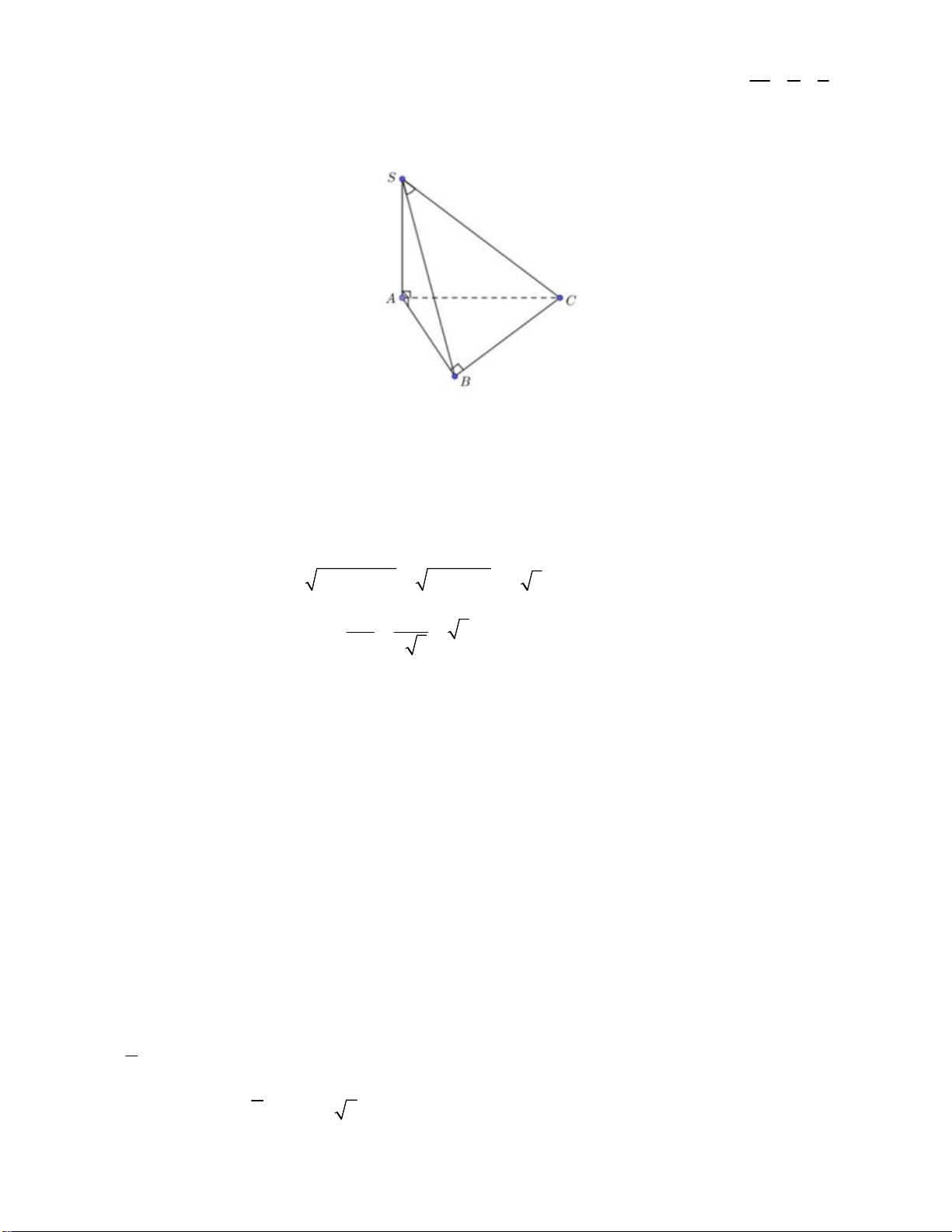
Vậy môđun của z bằng z i 2 2 2 2 1 5 . Câu 21: Chọn A. f x 2x 1 2 x 1 1 2 1 1 dx dx dx dx 2ln x 1 C 2 2 2 x 1 x 1 x 1 x 1 x 1 Câu 22: Chọn D. Ta có 2 2 u q u 2 .3 12. 3 1 Câu 23: Chọn D. 2 x y z
Mặt phẳng qua ba điểm trên ba trục tọa độ A1;0;0, B 0;2;0,C 0;0;3 có phương trình 1. 1 2 3 Câu 24: Chọn C. SA BC Ta có BC SAB AB BC
B là hình chiếu của C lên mặt SAB .
SC;SAB SC, SB BSC
Xét SAB vuông tại A có 2 2 2 2
SB AB SA a 2a a 3. BC a
Xét SBC vuông tại B có 3 tan BSC 3 SB a 3
Vậy SC SAB 0 , BSC 60 . Câu 25: Chọn B.
Từ bảng xét dấu f ' x của hàm số f x, ta thấy hàm số đổi dấu từ âm sang dương tại x 2 và x 2 nhưng
f x có tập xác định \
2 nên hàm số có 1 điểm cực tiểu. Câu 26: Chọn C.
Ta có y ' 2. f '2x
1 , hàm số nghịch biến f '2x 1 0 2x 1 3 x 2 . 1 2x 1 1 1 x 0
Vậy hàm số f 2x
1 nghịch biến trên ;
2 và 1;0 . Câu 27: Chọn B. Ta có z w i2 2. 4 2
1i 12 16i1i 4i 28
Môđun của số phức 2 z w bằng 20 2. 3 Câu 28: Chọn A. Ta có BC 2;0; 1 , BD 0; 1 ;2
Gọi n là một vec tơ pháp tuyến của mặt phẳng BCD, khi đó n BC, BD 1;4; 2 .
Đường thẳng đi qua A và vuông góc với mặt phẳng BCD có một vec tơ chỉ phương là u n 1 ; 4 ;2. x 1 t
Vậy phương trình đường thẳng cần tìm là y 4t . So sánh với các đáp án ta được phương trình đường z 2 2t x 2 t
thẳng cần tìm là y 4 4t . z 4 2t Câu 29: Chọn D.
Gọi z x yi, x, y z x y .i
Theo đề bài 3z i 2 3i z 7 16i 3x yi i 2 3ix yi 7 16i
x y x y x 3y 7 x 1 3 3 5 3 i 7 16i z 1 2 .i 3 x 5y 3 16 y 2
Vậy mô đun của số phức z là 2 2 z 1 2 5 . Câu 30: Chọn C. Do 3
F x x là một nguyên hàm của hàm số f x nên 3 I 2 f xdx
2x F x 3 3 3 2x x 2 2 1 1 1 Câu 31: Chọn C.
Dựa vào bảng biến thiên ta thấy giá trị cực tiểu của hàm số đã cho bằng 1. Câu 32: Chọn D. 4
Ta có: OA r 2 AB 4.
Tam giác SAB có: SA SB 0
, ASB 60 nên SAB đều cạnh 4. l SA SB 4.
Vậy diện tích xung quanh hình nón bằng: S rl .2.4 8. xq Câu 33: Chọn A. Theo giả thiết ' x f x e x, x nên: f x f '
xdx xe x x 1 2 dx e x C 2 1 Mà f 0 4 nên 0 2
e 0 C 4 C 3 2 x 1 Suy ra f x 2 e x 3 2 1 1 e x 1 6 13 Vậy f x 2 dx e x 3 dx 2 6 0 0 Câu 34: Chọn D.
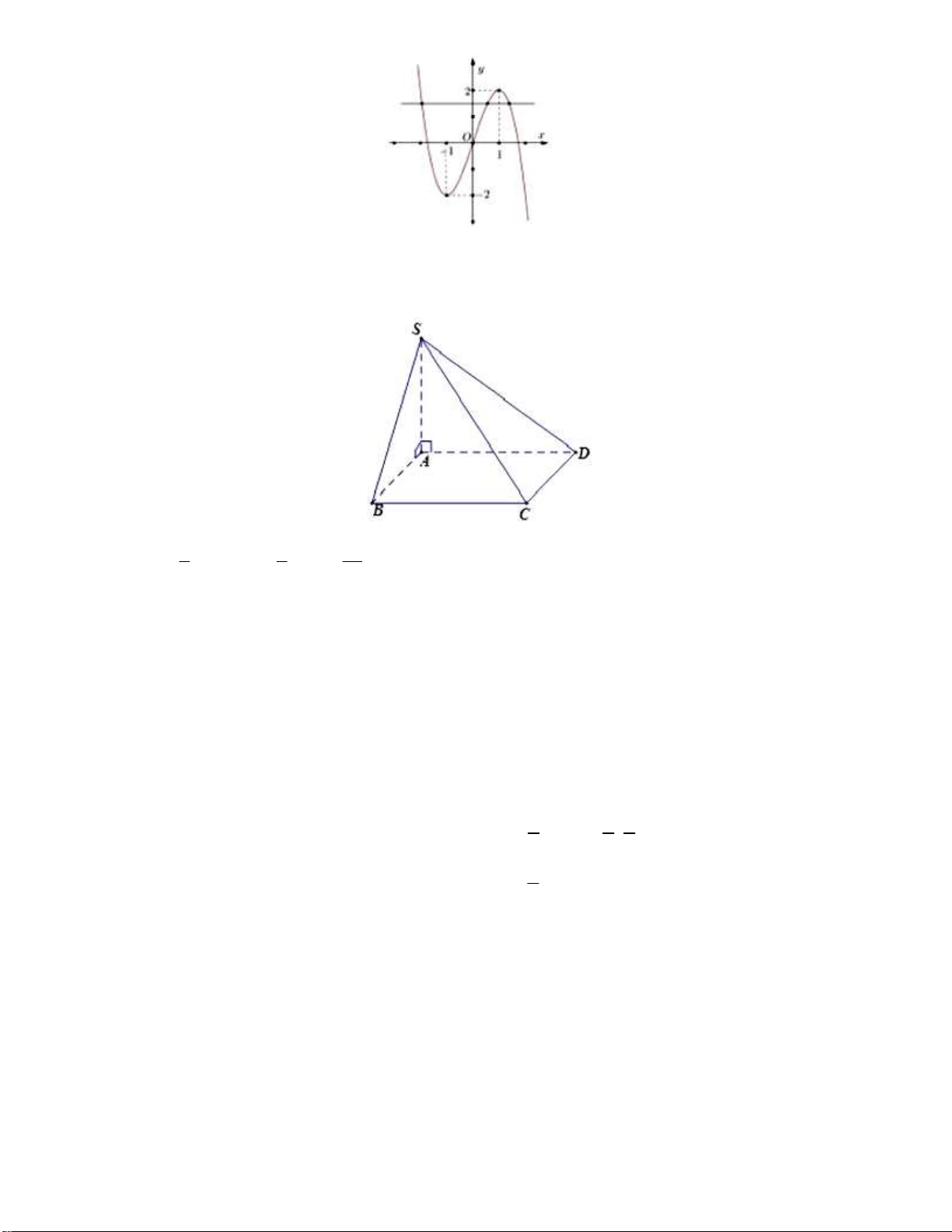
Ta có: f x f x 3 2 3 0 2 3
Do đó số nghiệm của phương trình là số giao điểm giữa đồ thị y f x và đường thẳng y . 2 5
Suy ra phương trình 2 f x 3 0 có 3 nghiệm phân biệt. Câu 35: Chọn D. 3 1 1 a Ta có: 2 V S . A S . . a a . S.ABCD 3 ABCD 3 3 Câu 36: Chọn B.
Chọn điểm I sao cho 2IA IB IC 0. Gọi I ; a ; b c suy ra: IA 1 a;1 ; b 1 c, IB ; a 1 ; b 2 c, IC 2 a; ; b 1 c. a a 0 2 1 a 2 a 0
3 3 5
Do đó: 2IA IB IC 0 21 b 1 b b 0 b I 0; ; . 4 4 4 2
1 c 2 c 1 c 0 5 c 4
2 2 2 Khi đó: 2 2 2
S 2NA NB NC 2NI IA NI IB NI IC
2 2 2 2
4NI IA IB IC 2NI 2IA IB IC 2 2 2 2
4NI IA IB IC . Do I cố định nên 2 2 2
IA IB IC không đổi. Do đó để 2 S NI NI
N là hình chiếu của I lên P. min min min 6 x t
Gọi là đường thẳng qua I và vuông góc với P 3 : y t. 4 5 z t 4 Suy ra N P. 3 5 3 1 Xét phương trình t
t t 1 0 3t 0 t . 4 4 2 2 1 5 3 38 N ; ; ON . 2 4 4 4 Câu 37: Chọn A.
Xét hàm số g x f x 2
sin x 3m trên khoảng 0; . 2 Do trên khoảng 0; ,1 f '
x 6 nên g 'x f 'xsin 2x 0, x 0; . 2 2
Như vậy hàm số y g x đồng biến trên khoảng 0; và g x g f 1 3m 2 2 2
Bất phương trình f x 2 sin x 3m,x 0;
khi và chỉ khi g x 0, x 0; . 2 2 1 Hay f 1 3m 0 m f 1 . 2 3 2 Câu 38: Chọn C.
Ta có phương trình mặt phẳng ABC là x y z 1 và 1 vectơ pháp tuyến là n 1;1;1 . 1 BC 0;1;
1 . Một vectơ pháp tuyến của P là n n , BC 2; 1 ;1 . 2 1
Suy ra phương trình mặt phẳng P là 2x y z 1 0. 1 1
Gọi H là trung điểm BC, I là tâm mặt cầu ngoại tiếp tứ diện SABC, ta có H 0; ; và IH vuông góc với 2 2 x 2t 1
mặt phẳng P. Như vậy phương trình đường thẳng IH là y t . 2 1 z t 2 7 1 1
Gọi I 2t; t; t IH , ta có 2 2 2 2 2 2 IA IB t 2 1 1 t t t2 1 1 1 1 1 1 2 1 2 t t t I ; ; . 2 2 2 2 6 3 3 3 1 1 1 2. 3. 1 3 3 3 1
Khi đó khoảng cách từ I đến mặt phẳng Q bằng d I,Q . 2 2 2 14 2 3 1 Câu 39: Chọn B. x x x 9 x 3 x Ta có 4 2 . m 6 3.9 0 3 2m 1 0. 4 2 Nhận thấy .
a c 3.1 3 0 nên nếu phương trình có hai nghiệm thì hai nghiệm đó cùng dấu. Suy ra điều kiện 2 ' m 3 0 m 3
để phương trình đã cho có nghiệm là
m 3. b 2m m 3 0 a 3 m 0
Như vậy trên đoạn 10;10 có m 1 0;9;8;7;6; 5 ; 4 ;3;
2 thỏa mãn. Hay có 9 giá trị nguyên m thỏa mãn bài toán. Câu 40: Chọn A. 3 iz Ta có w
w zw 3 iz w 3 i w z w 3 w i z . 1 z
Giả sử w a bi a,b a 2 2
b z a b 2 2 2 2 z 2 2 3 1 1 a b 2 2
6a 2 z b 9 z 0.
Vậy tập hợp các điểm biểu diễn số phức w là một đường thẳng nên 2 z 2 2 1
a b 0. Vì w 0 không thỏa
mãn bài toán, suy ra z 1. Câu 41: Chọn B.
Số phần tử của không gian mẫu: n 3 C . 100
Trong 100 số tự nhiên từ 1 đến 100 có 50 số chẵn và 50 số lẻ.
Giả sử 3 số được chọn theo thứ tự là a,b, c , ta có a c 2b, suy ra a và c có cùng tính chẵn lẻ. Ứng với mỗi
cách chọn a,c có duy nhất cách chọn . b
Do đó số cách chọn 3 số được lập cấp số cộng bằng số cách chọn 2 số cùng chẵn hoặc 2 số cùng lẻ.
Gọi A là biến cố thỏa mãn yêu cầu bài toán. Ta có n A 2 2 C C . 50 50 8 2 P A 2C50 0,015. 3 C100 Câu 42: Chọn A.
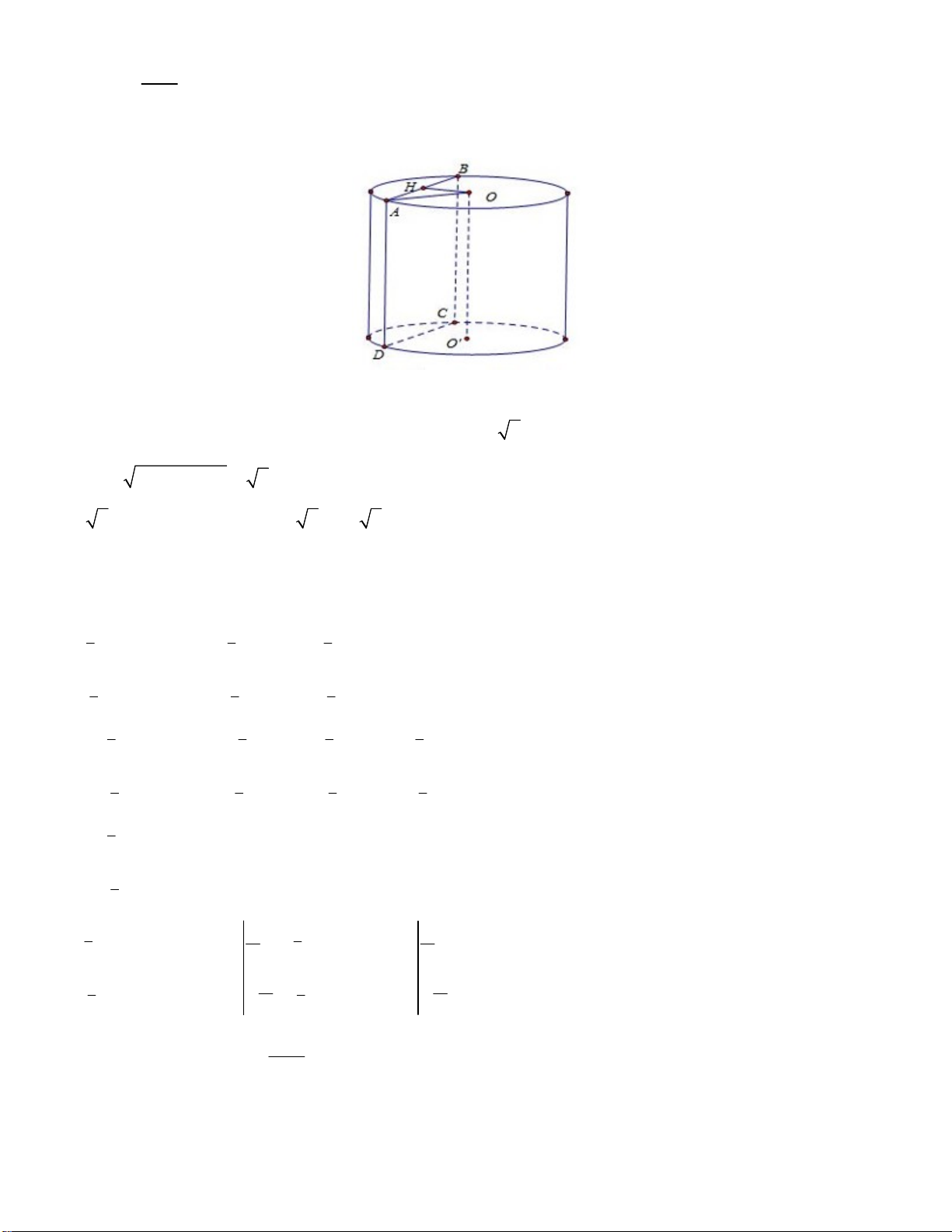
Theo giả thiết ABCD có diện tích bằng 16 AB 4.
Gọi H là trung điểm của AB OH ABCD và OH 2; AH 2 2 2 OA AH OH 6
r 6;l 4 S 2 rl 2. 6.4 8 6. xq Câu 43: Chọn C.
Từ giả thuyết: f x 2021f x x sin x, x 2 2 2 f xdx 2021 f xdx xsin xdx * 2 2 2 2 2 2 2 t x Tính: f xdx f tdt f tdt f xdx I. 2 2 2 2 2 u x du dx Tính: x sin xdx . Đặt dv sin xdx v cos x 2 2 2 2 2 x sin xdx x cos x cos xdx sin x 2 2 2 2 2 1
* I 2021.I 2 I . 1011 Câu 44: Chọn A. 9
Nhận xét: để diện tích phần phía trên trục Ox bằng diện tích phần phía dưới trục O .
x Nên đồ thị hàm số cắt trục
Ox tại ba điểm có hoành độ x , x , x lập thành cấp số cộng. 1 2 3 Nghĩa là phương trình 3 2
x 3x 4mx 2m 1 0 * có ba nghiệm x , x , x thỏa x x 2x . 1 2 3 1 3 2 1 Theo Viet: x x x 3
x 1 thế vào phương trình * ta được m . 1 2 3 2 6 3 21 x 3 1 2 4 Thử lại: với 3 2
m x 3x x 0 x 1 là một cấp số cộng. 6 3 3 3 21 x 3 1 Vậy m nhận. 6 Câu 45: Chọn C.
Gọi H là trung điểm của AB SH AB SH ABCD .
Trong ABCD , gọi K BA CD suy ra KA AH HB . a
Gọi J là trung điểm của CD suy ra HJ 2 . a 1 Ta có d ;
A SCD .d H;SCD 2
KHJ vuông cân tại H nên HD KJ, đồng thời SH KJ suy ra KJ SHD. 10 HI SD Trong SHD , dựng
HI SCD HI d H;SCD . I SD a 6 a
SH a 3, HD a 2 HI . Vậy d S SCD 1 30 ; .HI . 5 2 10 Câu 46: Chọn D. Đặt 3 t 2x 6x 2 *
Với một giá trị t 2
;6 thì phương trình * có 2 nghiệm x1;2.
Với một giá trị t 2 thì phương trình * có 1 nghiệm x 1;2.
Với một giá trị t ;
2 6; thì phương trình * không có nghiệm x 1;2. Phương trình f 3
2x 6x 2 2m 1 có 6 nghiệm phân biệt x thuộc đoạn 1;2.
Phương trình f t 2m 1 có 3 nghiệm phân biệt t 2;6. 1 3
0 2m 1 2 m . Vậy có một giá trị nguyên m 1 thỏa bài toán. 2 2 Câu 47: Chọn A.
Gọi E, F là trung điểm CD,C ' D ';G là giao điểm của C ' P và EF.
Do ME / /C ' N ME / / C ' NP d M ,C ' NP d E,C ' NP V V MCNP EC 'NP 11 Ta có: V ' V V 3V (do EG 3FG ) C 'MNP EC 'NP FC 'NP 1 3 Mà C ' D 2C ' F nên V V suy ra V ' V . FC 'NP D'C ' 2 NP ' ' 2 D C NP Lại có: 1 1 1 1 V .d P, C ' D ' N .S . d D, C ' D ' N . S D 'C ' NP C'D'N A' B 'C 'D ' 3 3 2 4 1 V
D D, A' B 'C ' D '.S A'B 'C 'D ' 24 24 3 3 V V V ' 1 Nên V ' V . . D 'C ' 2 NP 2 24 16 V 16 Câu 48: Chọn C. 2 13x 18x 13 Ta có: y ' x . 2 2 1
Giả sử đồ thị hàm số có hai điểm cực trị là A x ; y , B x ; y . Khi đó x , x là nghiệm của phương trình 1 1 2 2 1 2 2
y ' 0 13x 18x 13 0. u x u ' x .v x u x .v ' x
Mặt khác, ta có nếu f x v x f ' x
2 v x u x u x
f 'x 0 u 'x.vx u x.v'x ' 0 v x v ' x u x u x CT ' CT Có y CT v x v x CT ' CT 13x 9' 13
Áp dụng lý thuyết trên ta có hai điểm cực trị của đồ thị hàm số thuộc đường cong y . 2 x 1 ' 2x 13 13 2 1 3x 18x 13 1 1 2 13x 18x 13 Do đó: 1 1 y x 9 1 1 2x 2x 2x 2 1 1 1 13 Tương tự: y x 9 2 2 2 Nên ,
A B thuộc đường thẳng d 13 : y
x 9 hay đường thẳng đi qua hai điểm cực trị , A B là 2 d 13 : y
x 9 13x 2y 18 0 2 12 1 8 18 Vậy d O, AB . 2 2 13 2 173 Câu 49: Chọn C. 1 1
Ta có g ' x f ' x 2
x , g 'x 0 f 'x 2 x . 3 3 1
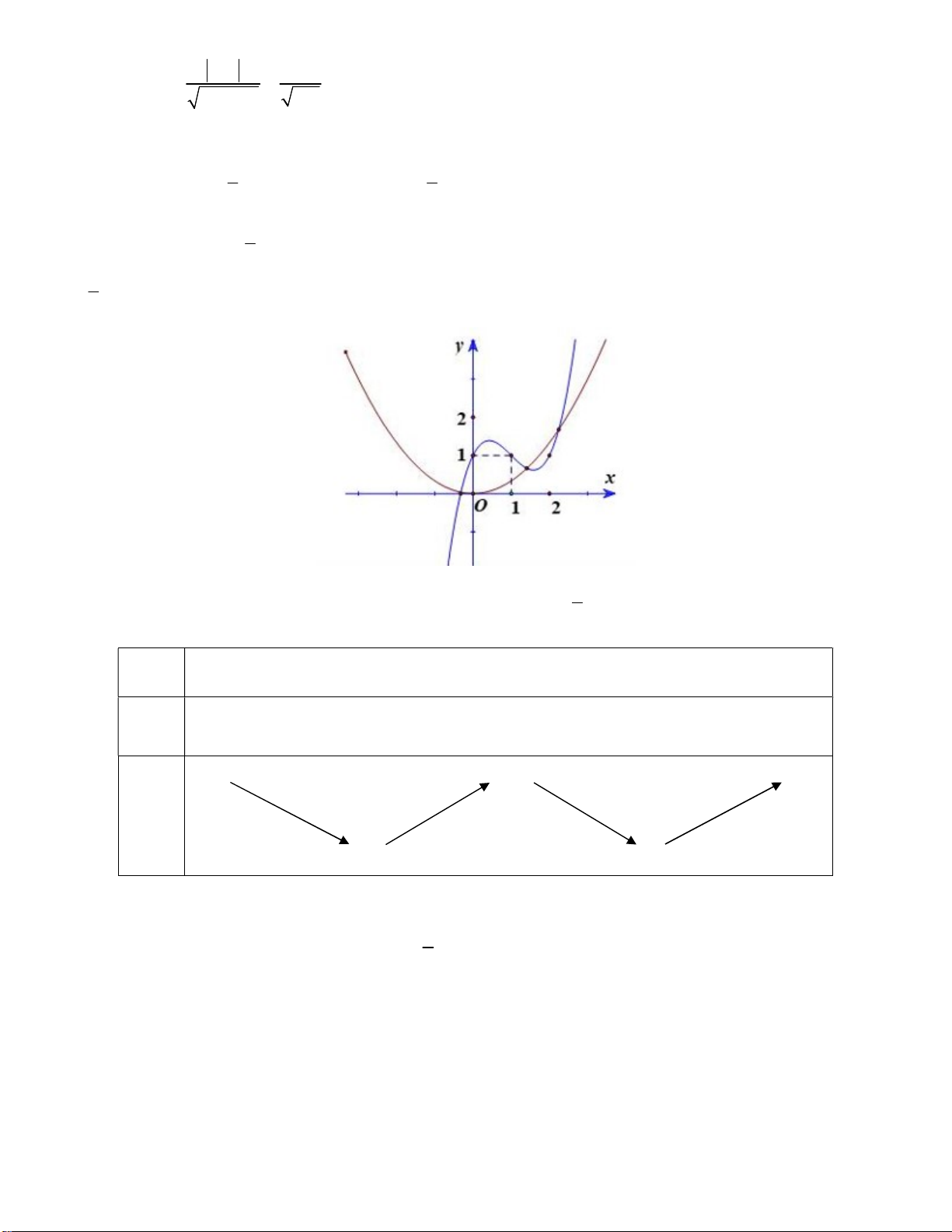
Số nghiệm của f ' x 2
x là số giao điểm của đồ thị hàm số y f 'x (như hình vẽ) và đồ thị hàm số 3 1 2 y x . 3 1
Theo hình vẽ ta có đồ thị hàm số y f ' x cắt đồ thị hàm số 2
y x tại 3 điểm phân biệt a,b, . c Lập bảng 3 biến thiên ta có x a b c g 'x 0 + 0 0 + g x CĐ CT CT 1
Vậy số điểm cực tiểu của hàm số g x f x 3 x là 2. 9 Câu 50: Chọn A.
Từ đồ thị hàm số, ta có y f x có 3 điểm cực trị là 1,0,1 nên hàm số có dạng 13 f x ax a a 2 x f x 4 2 ' 1
x x b và đồ thị hàm số f x đi qua hai điểm 0;4,1;3 nên 4 2 f x 4 2 x 2x 4 3, . x f x Điều kiện 0 suy ra m 0. 2 mx Ta có f x log
x f x mx 3
mx f x log f x .x f x f x log 2 mx 2 2 . x mx mx 2 mx
x f x x f x f x x 2 mx 2 2 log 1 . log 1 .
x mx mx do x 1 0 *
Xét hàm số g t logt t với t 0. Ta có g t 1 ' 1 0. t.ln10 f x x 2x 4 2
Từ * ta có x 1 f x x 2 4 2 2 1 mx m x 6. 2 2 x x x 2
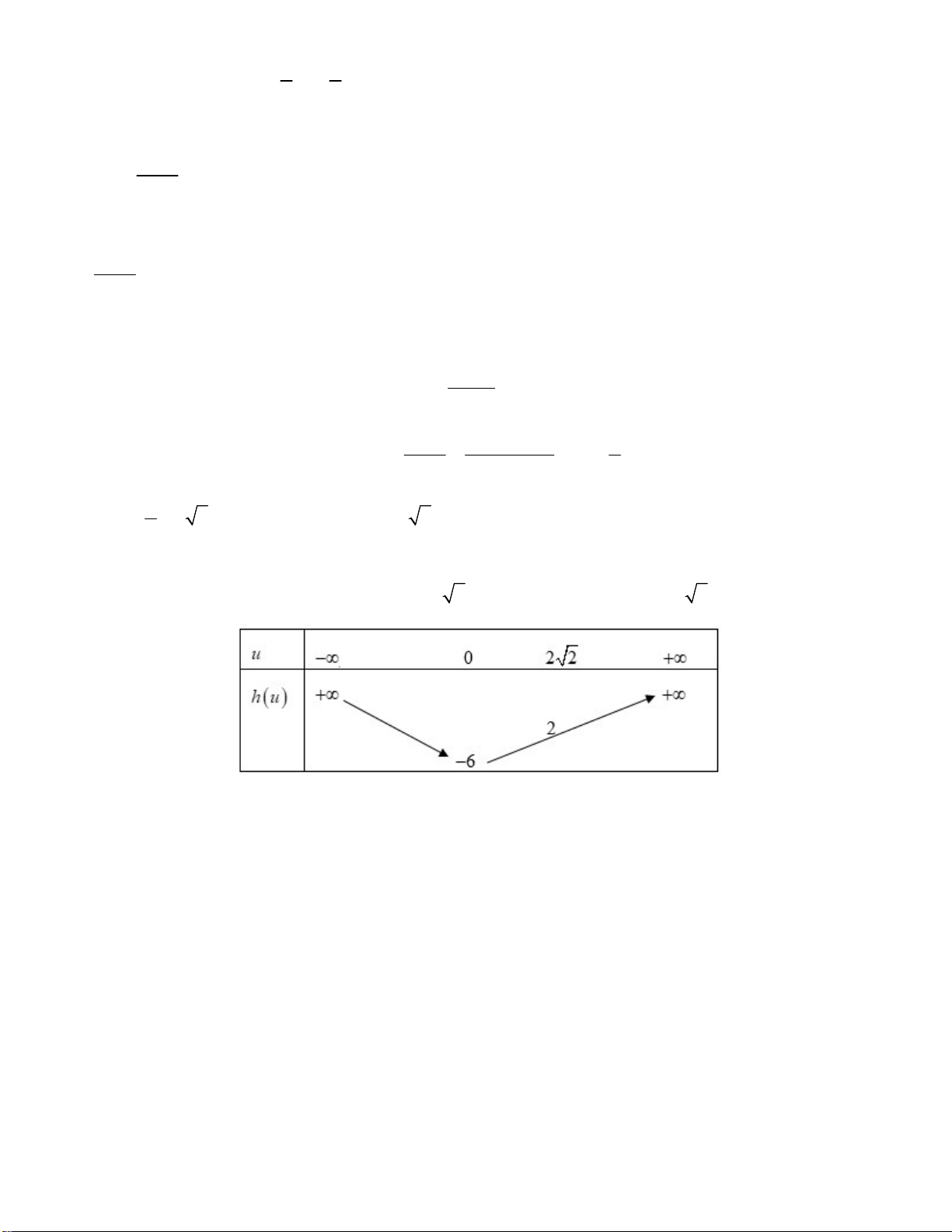
Đặt u x 2 2, khi đó 2 m u 6, u 2 2. x
Dễ thấy với mỗi giá trị của u cho ta hai giá trị của x 0, nên yêu cầu bài toán đưa về điều kiện là tìm m để phương trình 2
m u 6 có đúng một nghiệm u 2 2. Đặt hu 2 u 6 với u 2 2. Do m , m 2 021;202
1 , m 2 nên có 2019 giá trị thỏa mãn.
____________________ HẾT ____________________ https://toanmath.com/ 14
Document Outline
- de-thi-thu-tot-nghiep-thpt-2021-mon-toan-so-gddt-ha-tinh
- Hà Tĩnh - Lần 1




