


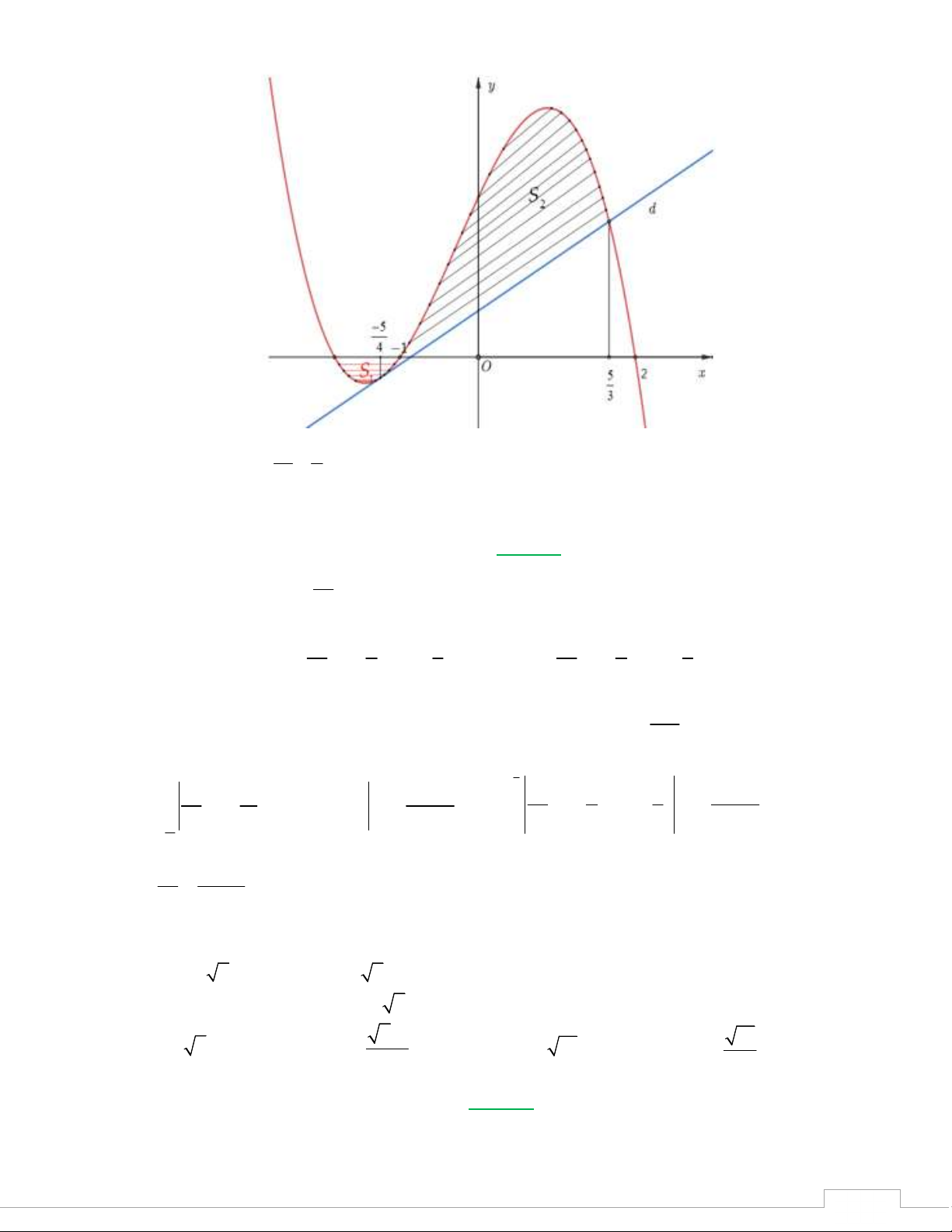
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO QUẢNG NINH KỲ THI KHẢO SÁT TỐT NGHIỆP THPT NĂM 2022
CỤM CSGD THỊ XÃ ĐÔNG TRIỀU Môn thi: TOÁN HỌC ĐỀ THI K HẢO SÁT
Thời gian làm bài: 90 phút, không kể thời gian phát đTSề
Họ, tên thí sinh: ………………………………………………
Số báo danh: …………………………………………………. P
Câu 1: Môđun của số phức z 2 2i bằng - A. 8. B. 10 . C. 10. D. 2 2 . 2
Câu 2: Trong không gian Oxyz , mặt cầu 2 2 2
(S) : (x 1) ( y 2) z 9 có bán kính bằng 0 A. 3. B. 36. C. 9. D. 6. 2
Câu 3: Điểm nào dưới đây thuộc đồ thị của hàm số 4 y x x 2 2 A. Điểm P(1; 1 ) . B. Điểm N(1; 2
) . C. Điểm M (1;0) . D. Điểm Q(1;1) .
Câu 4: Diện tích S của mặt cầu bán kính r được tính theo công thức nào dưới đây? A. 1 4 3 S r . B. 3 S 4 r . C. 2 S 4 r . D. 3 S r . 3 3 3 Câu 5: Trên khoảng
0; , họ nguyên hàm của hàm số 2 f x x là 1 1 A. 1 f x 2 dx 2x C . B. f x 2 dx x C . 2 3 1 C. f x 2 2 dx x C . D. f x 2 dx 2x C . 3 T
Câu 6: Cho hàm số f x có bảng xét dấu của đạo hàm f x như sau: SP -
Hàm số f x có bao nhiêu điểm cực trị? 20 A. 4. B. 1. C. 2. D. 3. 2
Câu 7: Tập nghiệm của bất phương trình 2x 6 là A. log 6; . B. ; 3 . C. 3; . D. ;log 6 . 2 2 2
Câu 8: Một khối chóp có thể tích bằng 60 và chiều cao bằng 10. Diện tích đáy của khối ch óp đó bằng A. 6 . B. 2. C. 150. D. 18.
Câu 9: Tập xác định của hàm số 2 y x là A. . B. \ 0 . C. 0; . D. 2;.
Th.s Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 1
Câu 10: Nghiệm của phương trình log2x 1 là A. 1 x . B. x 5 . C. x 25 D. 1 x . 5 2 T 3 2 3
Câu 11: Biết rằng f xdx 5 và f
xdx 3 khi đó giá trị f xdx bằng S 0 0 2 P A. 3. B. 2. C. 1 0. D. 7. -
Câu 12: Cho hai số phức z 3 2i và w 23i . Số phức z w bằng 2 A. 1 4i . B. 1 2i . C. 5 4i . D. 15i . 0
Câu 13: Trong không gian Oxyz , mặt phẳng P : 2x 3y 4z 1 0 có một vectơ pháp tuyến là 2 n 1 ;2; 3 . B. n 3 ;4; 1 . C. n 2; 3 ;4 . D. n 2;3;4 . 1 2 3 4 2 A.
Câu 14: Trong không gian Oxyz , cho hai vectơ A 7;3; 2 và B 2;1;
1 . Toạ độ vectơ OA 2OB là A. 3;2; 4 . B. 3;1; 4 . C. 5;2; 1 . D. 1;2; 1 .
Câu 15: Trên mặt phẳng toạ độ, điểm biểu diễn số phức 3 2i có toạ độ là A. 2;3. B. 2 ;3 . C. 3; 2 . D. 3 ; 2 .
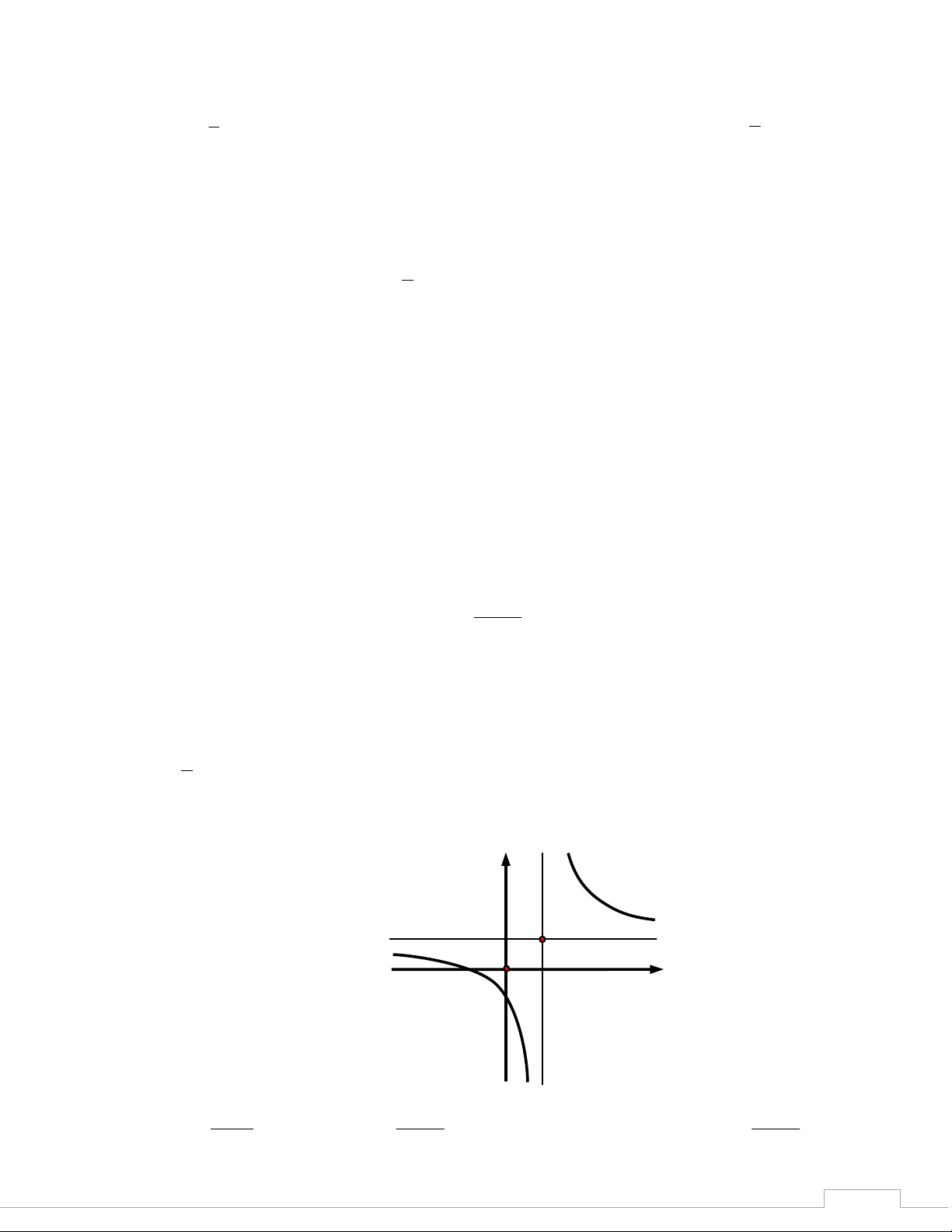
Câu 16: Tiệm cận ngang của đồ thị hàm số 2x 4 y là đường thẳng x 1 A. x 1. B. y 2 . C. y 2 . D. x 2 . 2 T
Câu 17: Với a là số thực dương tùy ý, log 81a bằng 9 1 S A. log a . B. 2log a . C. log a . D. 2 log a . 3 2 3 2 3 3 P
Câu 18: Đường cong như hình bên là đồ thị của hàm số nào sau đây? - y 2022 O x A. 3x 1 x x y . B. 2 1 y . C. 3 y x x 1 . D. 2 1 y . x 1 2x 2 2x 2
Th.s Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 2 x 1 2t Câu 19: Trong không gian
Oxyz , đường thẳng d : y 2 2t đi qua điểm nào dưới đây? z 3 3t T A. Điểm Q2;2;3.
B. Điểm N 2;2;3 . C. Điểm M 1;2;3 . D. Điểm P1;2;3 . S P
Câu 20: Với n, k là số nguyên dương và k n , công thức nào dưới đây đúng? A. n n n k ! k ! k A n!. B. A . C. A . D. k ! A . n n n n - nk! k !.n k ! k! 2
Câu 21: Cho khối lăng trụ có diện tích đáy B và chiều cao h . Thể tích V của khối lăng trụ đ 02 V Bh . B. 4 V Bh . C. V 6Bh . D. V Bh . 3 2ã cho
được tính theo công thức nào dưới đây? A. 1 3
Câu 22: Trên khoảng 0; , đạo hàm của hàm số y log x là: A. 1 y ' . B. ln10 y ' . C. 1 y ' . D. 1 y ' . log x x x x ln10
Câu 23: Cho hàm số y f (x) có bảng biến thiên như sau : T
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. 2; . B. 1 ;. C. 0;2 . D. 1 ; 1 . S
Câu 24: Cho hình trụ có bán kính đáy r và độ dài đường sinh l . Diện tích xung quanh S của hình xq P
trụ đã cho được tính theo công thức nào dưới đây? - A. S 4rl . B. S 2rl . C. S 3rl . D. S rl . xq xq xq xq 2 5 5 Câu 25: Nếu f
xdx 6 thì 3f xdx bằng 0 2 2 2 A. 6. B. 3. C. 18. D. 12. 2
Câu 26: Cho cấp số cộng u với u 3 và công sai d 4. Giá trị của u bằng n 1 3 A. 11. B. 15. C. 7. D. 10.
Câu 27: Cho hàm số f x 2cos x. Khẳng định nào dưới đây đúng? A. f
xdx 2sin xC . B. f
xdx 2xsin xC . C. f
xdx 2xsin xC . D. f xdx sin xC .
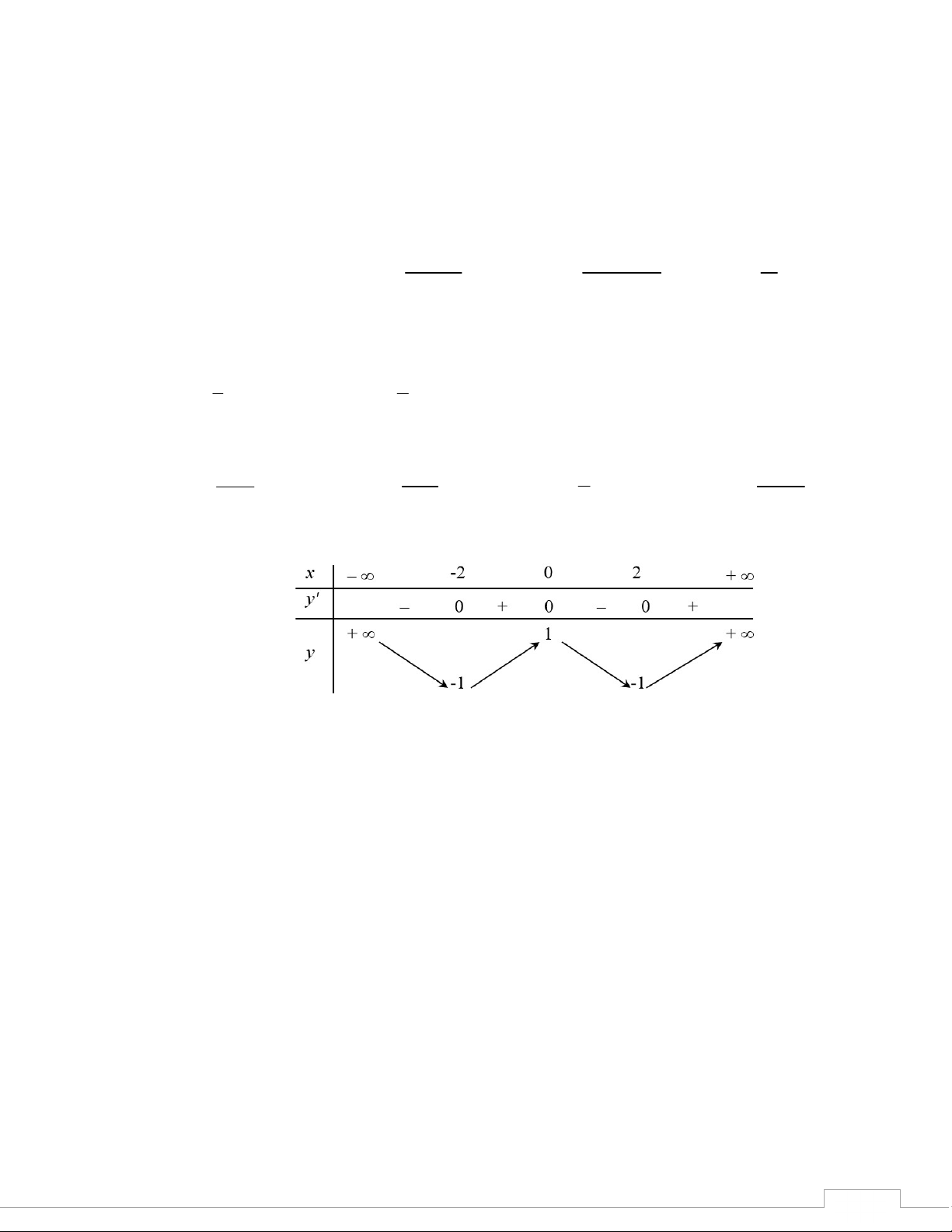
Th.s Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 3 Câu 28: Cho hàm số 4 2 y ax bx , c , a ,
b c có đồ thị là đường cong như hình bên. Giá trTị cực
tiểu của hàm số đã cho bằng? SP-20 A. 0. B. 1 . C. 3 . D. 2. 2
Câu 29: Trên đoạn 2;5, hàm số 4
y x đạt giá trị nhỏ nhất tại điểm 2 x x x x x A. 5 . B. 2 . C. 1 . D. 4 .
Câu 30: Hàm số nào dưới đây nghịch biến trên ? A. x 1 y . B. 2 x x y e . C. 3 2 y x x 4x . D. 5 3 y x 2x 2 . x 2
Câu 31: Với mọi a , b thỏa mãn log 2a 3log b 2 , khẳng định nào dưới đây đúng? 2 2 A. 2 1 a . B. 2a 3b 4 . C. a 3b 2 . D. a . 3 b 3 b
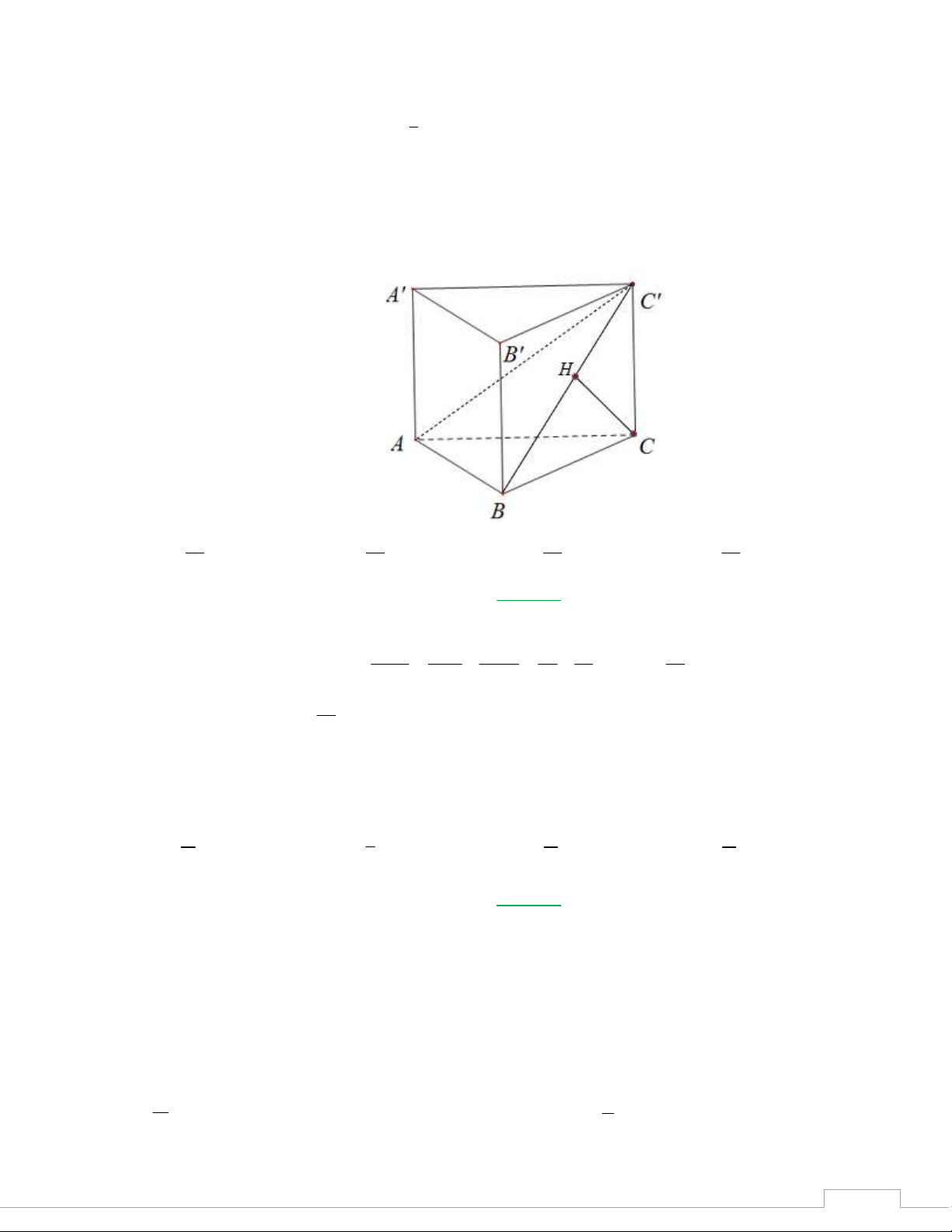
Câu 32: Cho hình lập phương ABC . D AB C D
. Góc giữa hai đường thẳng B D và AD bằng D' T C' S A' B' P D C -2 A B 0 A. 90 . B. 30 . C. 45 . D. 135. 3 2 Câu 33: Nếu 2 f
x1dx 8 2 f 1 thì f 3 bằng 1 2 A. 7 . B. 2. C. 3. D. 3 . 2 2 x 1 2t
Câu 34: Trong không gian Oxyz cho điểm M 2;5;3 và đường thẳng d :y 3t . Mặt phẳng đi z 1
qua M và vuông góc với d có phương trình là
Th.s Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 4
A. 2x y z 4 0.
B. 2x y z 6 0. C. 2x y 9 0. D. 2x y 1 0.
Câu 35: Cho số phức z thỏa mãn 1 i z 4 2 .i Phần ảo của z bằng T A. 1. B. 1 . C. 3. D. 3 . S
Câu 36: Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông cân tại B và AB 3; A P ABC là: -2A4
(tham khảo hình bên). Khoảng cách từ C đến mặt phẳng 022 A. 12 . B. 5 . C. 7 . D. 12 . 5 12 12 7 Lời giải
Gọi H là hình chiếu vuông góc của C trên BC ta chúng minh được CH ABC do 1 1 1 1 1 12
d C, ABC CH . Ta có CH . 2 2 2 2 2 CH CB CC 4 3 7 Tđó
Vây d C ABC 12 , . 7 S
Câu 37: Gọi S là tập hợp các ước tự nhiên của 31049568. Lấy 1 số thuộc S , xác suất để lấy đ P-ược 1
số không là bội của 6 bằng A. 7 . B. 2 . C. 2 . D. 5 . 9 9 7 7 2 Lời giải 0 0 a 5 2 Ta có 5 6 3
31049568 2 .3 .13 gọi 2a.3b.13c x S x
trong đó 0 b 6 . 2 0 c 3.
Do đó tập S có số phần tử là 6.7.4 n 6.7.4.
Gọi A: “Số được chọn không là bội của 6” 1 a 5
Khi đó A : “Số được chọn là bội của 6” khi đó n A 5.6.4 1 b 6
Th.s Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 5 P A 5.6.4 5
do đó P A P A 2 1 6.7.4 7 7
Câu 38: Trong không gian Oxyz , cho tam giác ABC với A1;1; 2 , B3; 2
;0và C 1;2;2. Đ T x y z x y z Sường
cao kẻ từ A của tam giác ABC có phương trình là: A. 1 1 2 . B. 1 1 2 . 1 2 2 1 1 3 P C. x 1 y 1 z 2 . D. x 1 y 1 z 2 . 1 2 2 1 1 3 -2 Lời giải 0
Gọi đường cao kẻ từ A là AH khi đó AH ABC 2 u n
BC AB AC BC 24; 24; 72 24 1; 1;3 . AH ( ABC ) AH BC 2
Vậy đường cao tam giác ABC có phương trình là: x 1 y 1 z 2 . 1 1 3
Câu 39: Có bao nhiêu số nguyên x thỏa mãn x x2 4 5.2 64 log 4x 8 0 ? 1 2 A. 15. B. 16. C. 4. D. 3 . Lời giải
Điều kiện log 4x 8 0 log 4x 8 0 x 64 . 1 2 2 log 4x 8 0 x 64 4x 5.2x 64 1 2 2 log 4x 8 0 1 x x x x2 T
2 2 20.2 64 0 2 4 5.2 64 0 x 64 x 64 x 64 S 2x 2 . 20.2x 64 0 4 2x 16 2 x 4 P
Kết hợp điều kiện ta có 4 số nguyên x thoả mãn bài toán. -
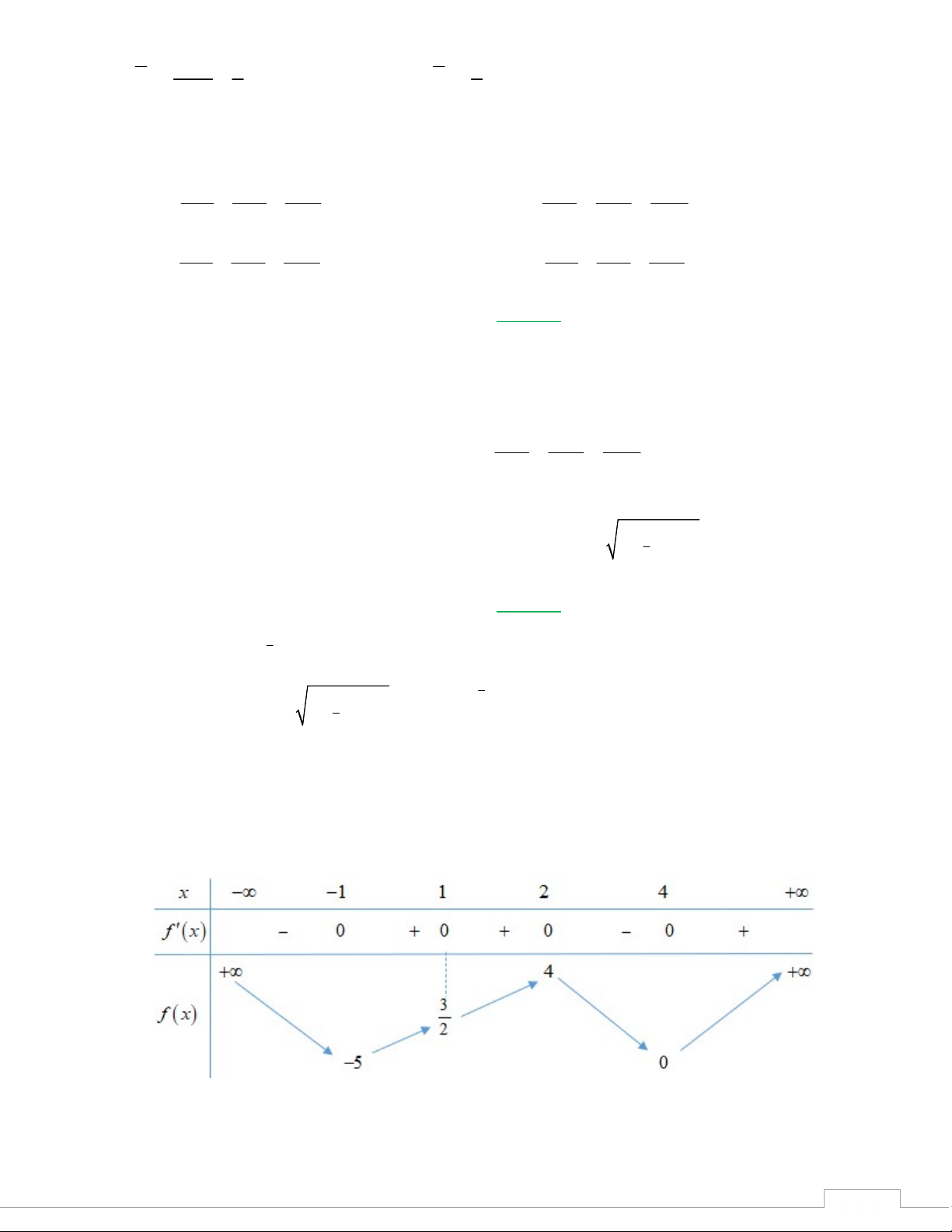
Câu 40: Cho hàm số y f x có bảng biến thiên như sau: 2022
Tập nghiệm của phương trình logx
1 .f f x 0 có số phần tử là A. 12. B. 8. C. 7. D. 13.
Th.s Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 6 Lời giải Phương trình logx
1 .f f x 0 có điều kiện x 1. Khi đó x 2 T f x 1 (Vô nghiệm) l og x 1 0 S logx 1 . f f x 0 2 nghiệm f f x f x 1 0 P f x 2 3 nghiệm f x 4
2 nghiệm, trong đó có nghiệm x -22
Vậy tập nghiệm của phương trình logx
1 .f f x 0 có 7 phần tử . 0
Câu 41. Trong tập hợp các số phức, cho phương trình 2 2
z 6z 10m m 0 ( m là tham số thực)2 z , z thỏa 2.
Tổng tất cả các giá trị của m để phương trình đó có hai nghiệm phân biệt mãn 1 2 z z z z 12 bằng 1 2 2 1 A. 6 . B. 10 . C. 20. D. 25 . Lời giải Phương trình 2 2
z 6z 10m m 0 có 2 9 10m m m 9 z z 6 Trường hợp 1: 2
9 10m m 0
. Khi đó z , z là số thực và 1 2 m 1 1 2 2 z .z 10m m 1 2
+ Nếu z .z 0 z z z z 0 không thoả mãn 1 2 1 2 2 1 + Nếu 2
z .z 0 10m m 0 0 m 10 do z z 0 z , z 0 . 1 2 1 2 1 2 T 2
z z z z 12 z z 6 10m m 6 m 5 19 ( thoả mãn). 1 2 2 1 1 2 S Trường hợp 2: 2
9 10m m 0 1 m 9 . Khi đó z , z là số phức liên hợp của nhau 1 2 P
z z z z 12 z z z 2 12 z 2 z 4 1 2 2 1 1 2 1 1 1 -2 2
z .z 4 z .z 4 10m m 4 m 5 21 ( không thoả mãn) 1 1 1 2 0
Vậy có 2 giá trị m 5 19 thoả mãn yêu cầu bài toán nên tổng tất cả các giá trị của m bằng 10.2 x y z 2
Câu 42. Trong không gian Oxyz , cho hai mặt phẳng có phương trình lần lượt là :
: 2x y 3z 3 0. Đường thẳng nằm trong đồng thời song song với mặt phẳn 30; g
và cắt trục O y đi qua điểm nào sau đây A. 2 ; 2 ; 1 . B. 2;4; 1 . C. 2 ;2; 1 . D. 2 ;1; 3 . Lời giải +Ta có : n (1;1; 1 ) ; n (2;1; 3) .
Th.s Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 7
Do () u n u ; //( ) n Suy ra:
n , n (2;1; 1) là một véctơ chỉ phương của . T
+ Do Gọi M Oy M Oy () . Suy ra M (0;3;0) . S x 2 t P
Vậy pt của là: y 3
t thay tọa độ các điểm ta thấy đường thẳng đi qua 2;4; 1 . z t - 2
Câu 43. Cho hàm số y f x có đạo hàm là f x cos x xsin , x x
. Biết Fx là nguyên0 f x F 0 F 2 F 2 thỏa mãn
, khi đó giá trị của bằng 2 2 hàm của 4 2 A. . B. 2 . C. 3. D. . 2 2 Lời giải
Giả thiết suy ra f x cosx xsin xdx sin x xsin d x x u x du dx Đặt
. Theo công thức tnguyeenm hàm từng phần suy ra dv sin d x x v cos x
f x sin x xcos x cos d x x xcos x C . 1 Lại có F x f
xdx xcosxC dx tương tự ta tìm được 1
F x xsin x cos x C x C . 1 2 T F C 1 2 0 2 1 C 2 S Do 2 F 2 . 2 1 C C 2 C 1 2 1 P - Vậy F x 2 4
xsin x cos x x 1 F 2 2 . 2 2 2 0
Câu 44. Gọi S là tập hợp tất cả các số phức z sao cho số phức 1 w
có phần ảo bằng 1 . Xét z .i| z | 4 2
các số phức z , z , z S , giá trị lớn nhất của P z . z z z . z z z . z z bằng 1 3 2 2 3 1 3 1 2 1 2 3 2 A. 6. B. 8. C. 10. D. 12. Lời giải Ta có 1 z .i| z | z .i | z | w . Đặt 2
z a b ;i a,b &i 1 . z .i| z |
z .i| z |z .i| z | 2
2 | z | i.| z | z z
Th.s Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 8 a | z | b a 1 w .i
.i giả thiết suy ra | z | 2 . 2 2 | z | 2 .
b | z | 2 | z | | z | b 2 2 | z | 2 . b | z | 2 | z |
P z . z z z . z z z . z z z z z z z z z z z z z z 1 3 2 2 3 1 3 1 2 1 2 1 2 2 3 2 3 1 3 1 3 T 2 2 2 S Sử dụng z z z z z z z z ta đươcj 1 2 1 2 1 2 1 2 P 2 2 2 2 2 2 2 2 2 2 2 2 P z z
z z z z z z z z z z z z z z z z 8 1 2 1 2 2 3 2 3 3 1 3 1 1 2 2 3 3 1 -
Trong mặt phẳng Oxy gọi A, B, C lần lượt là các điểm biểu diễn của z , z , z khi đó A, B, C thuộc 1 2 3 2
đường tròn tâm O,2 bài toán trở thành tìm giá trị lớn nhất của 0 2 2 2 P AB BC AC 8 2 + Nếu 2
A B P 2BC 8 8. Dấu bằng xảy ra khi A B C . 2
+ Nếu 3 điểm A, B, C phân biệt khi đó ABC tạo thành tam giác
Theo định lý sin ta có AB BC AC 4 do đó sin C sin A sin B A P 16 cos2 cos2B 2 2 2 sin C sin A sin B 2 8 16 sin C 1 8 2 16 2
cos C cos A B.cos A B 8 4 2 4 cos C 4cos c C os A B 8 4
2cosC cos A B2 2
8 4cos A B 12. 2cosC cos A B o 0 A B 30 T
Dấu bằng xảy ra khi và chỉ khi . cos A B o 1 C 120 S
Câu 45. Cho hàm số bậc ba f x 1 3 2
x bx cx d có đồ thị là C cắt trục hoành tại 3 phâ Pn biệt 2
trong đó 2 điểm có hoành độ hoành độ lần lượt là x 1, x 2 . Đường thẳng d tiếp t- C 2
tại điểm có hoành độ 5
x cắt đồ thị tại điểm có hành độ 5 x . Gọi S là 4 3 0uyến của đồ thị
diện tích hình phẳng giới hạn bởi phần đồ thị Cbên dưới trục hoành với trục hoàn2 1
là diện tích hình phẳng giới hạn bởi đồ thị Cvà tiếp tuyến d (như hình vẽ bên). 2h, S 2
Th.s Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 9 TSP-2022 S a
Biết rằng tỉ số 1 (phân số tối giản) khi đó 19ab bằng S b 2 A. 459 . B. 435 . C. 705. D. 775. Lời giải Giả thiết suy ra f x 1 x x
1 x 2 . Gọi phương trình tiếp tuyến d là y mx n 2 2 2 suy ra 1 5 5 f x 1 5 5 mx n x x hay f x x x mx n . 2 4 3 2 4 3 T So sánh hệ số của 2
x trong hai cách biểu diễn f x ta được 11
. Thay vào f x tính được 6 S 5 1 2 1 11 5125 3 1 5 5 28561 P S x x 1 x 2 dx , S x x dx . 1 2 6 31104 2 2 4 3 31104 11 1 6 -2 Vậy S 656 1 do đó 19a b 459. S 12005 2 02 Câu 46: Cho hình chóp .
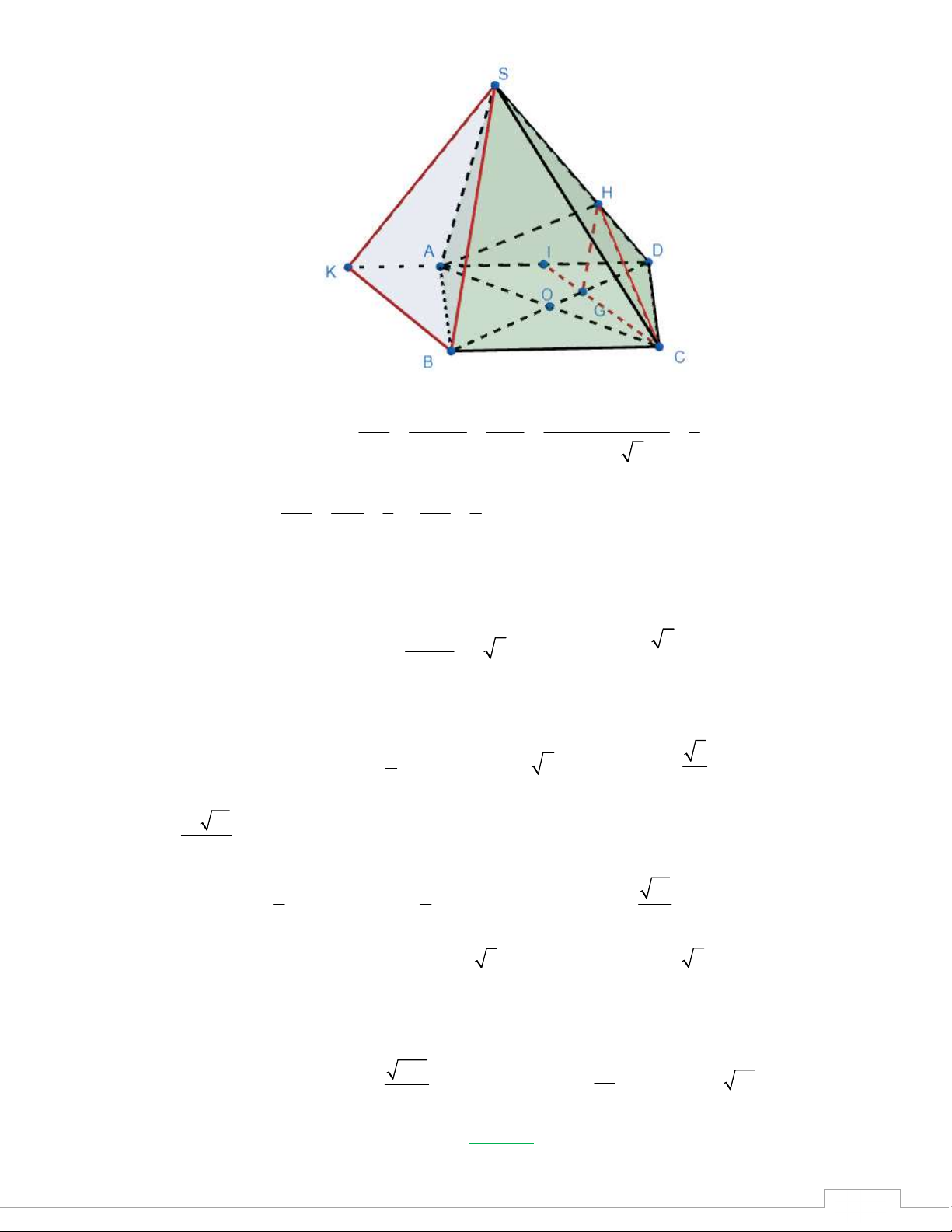
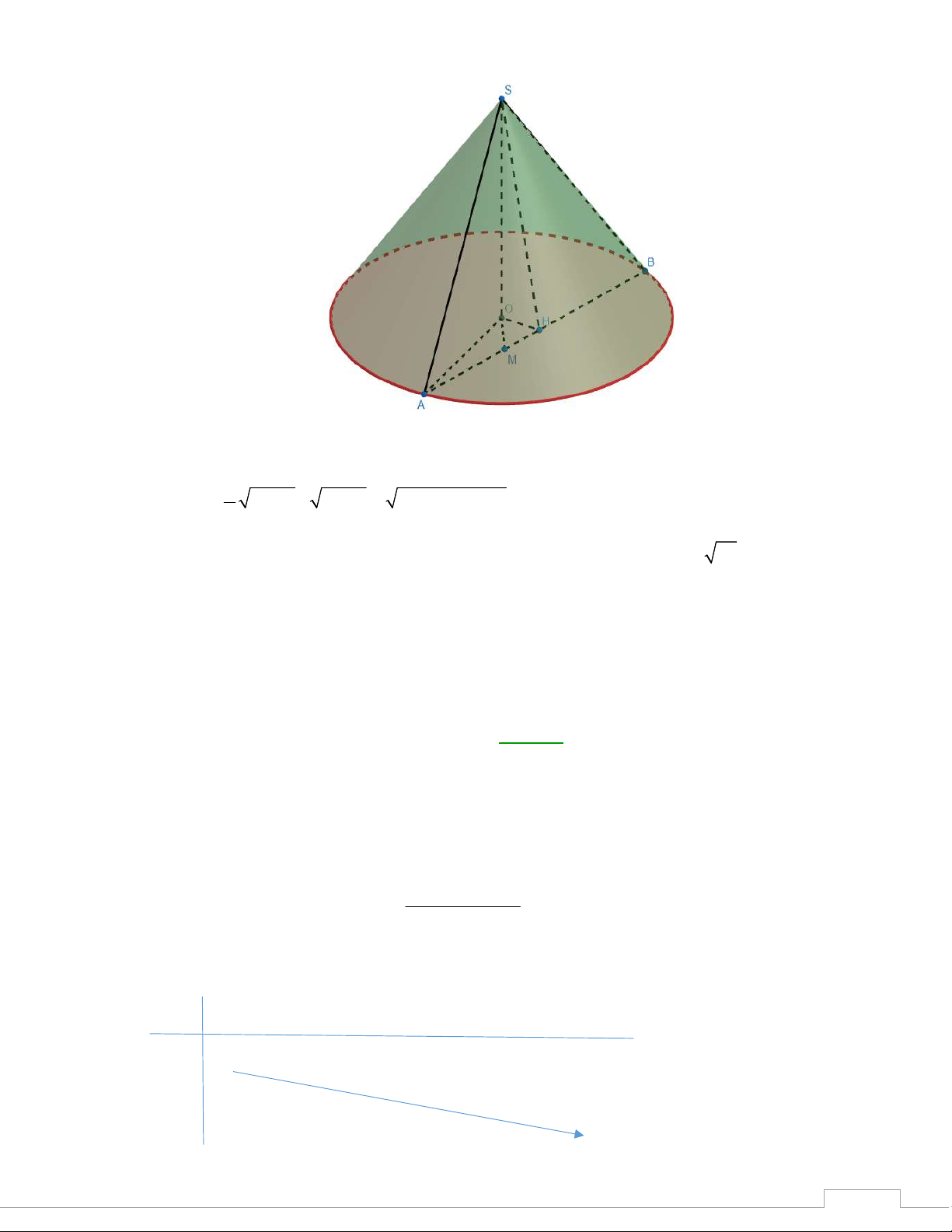
S ABCD có ABCD là hình bình hành biết rằng SAD 0 BAC 90 , SA a BC a SB
a . Gọi H là hình chiếu vuông góc của A trên SD biết kh2 cạnh 2 2 , 2 , 6 oảng
cách giữa CH và SB bằng 2a . Thể tích khối chóp . S ABCD bằng 3 A. 2a 3 10 2a . B. . C. 3 10a . D. 3 a . 3 3 Lời giải
Th.s Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 10 TSP-202 2 2 2 HD H . D SD AD 2a 1
Tam giác SAD vuông tại S nên 2 2 2 2 SD SD SD 3 2a 2 2a Kẻ DG DH 1 DF 2 HG // SB, G BD
do đó G là trọng tâm tam giác ACD và CG đi qua DB DS 3 DO 3 trung điểm I của AD.
Kẻ BK //IC, K AD HCI // SBK d CH; SB d CHI ;SBK d I;SBK . V
Do đó d I SBK d A SBK 3 ; 2 ; 2 SABK a 2 S .a 2 SBK V S SABK 6 S BK
Dễ thấy IKBC là hình bình hành và I là trung điểm AD nên A là trung điểm IK. T 1 5 S
Giả thiết suy ra SK 3a, BK CI AD a và SB 6a do đó 2 S a . 2 SBK 2 P 3 a 10 V SABK - 12 2 1 1 10 Lại có 3 S S S V V V 4V a 0 A BK I DC 4 A BCD SABK 4 SABCD SABCD SABK 3 2
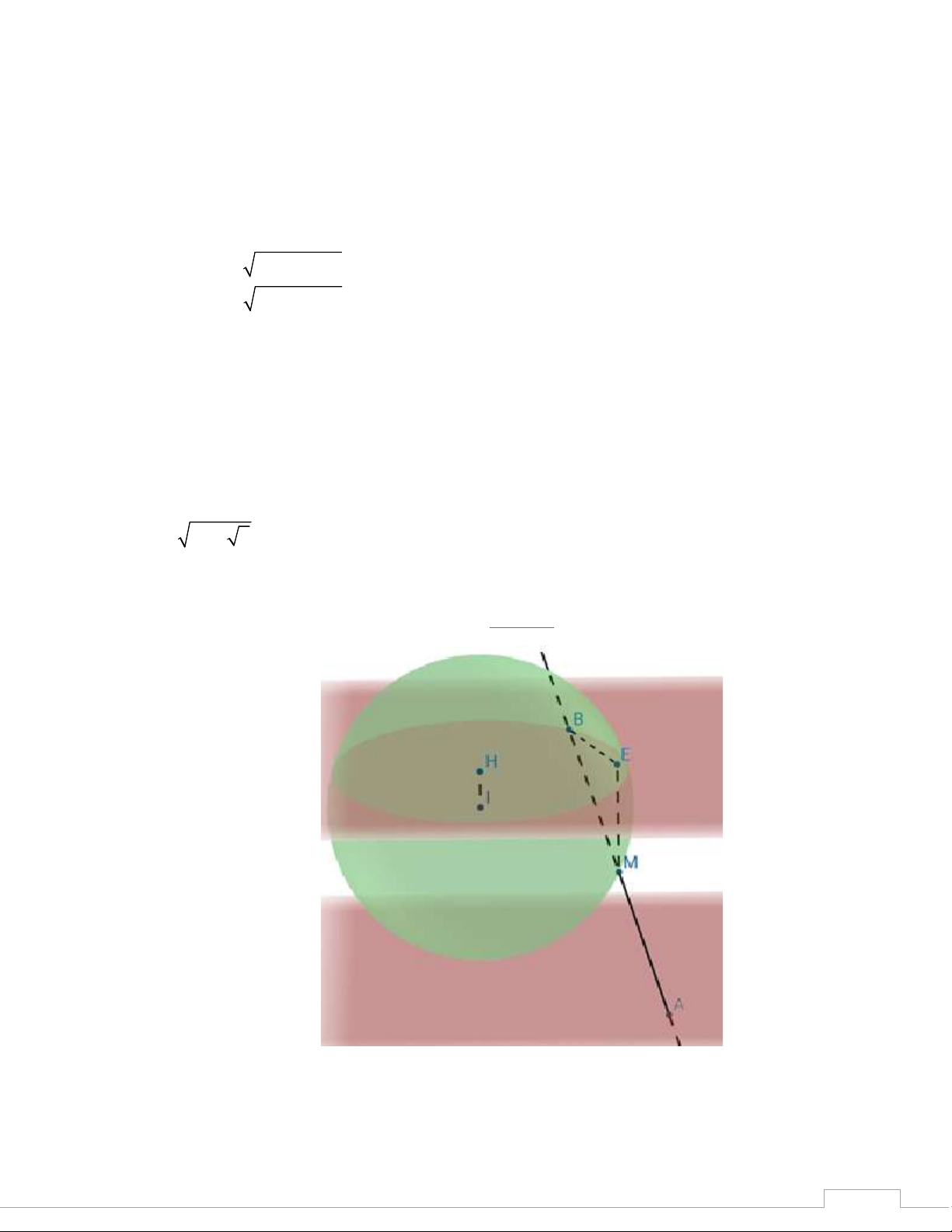
Câu 47: Cho hình nón đỉnh S có chiều cao h 5 và bán kính đáy r 2 2 . Mặt phẳng P đ2 i qua
S và điểm M nằm trong đường tròn đáy cách tâm đáy một khoảng bằng 1. Diện tích thiết
diện của hình nón cắt bởi mặt phẳng P có giá trị lớn nhất là A. 6. B. 409 . C. 13 . D. 42 . 4 2 Lời giải
Th.s Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 11 TSP-2022
Gọi thiết diện là tam giác SAB , H là trung điểm AB , O là tâm đáy đặt OH x,0 x 1 Khi đó 1 S 2 x 5.2 8 2 x 4 x 2 3x 40 SAB 2 Ta có 2 S 4 x 2
3x 40 f x dễ thấy Maxf x 42 do đóMaxS 42 . SAB SAB 0; 1
Câu 48: Có bao nhiêu số nguyên x 1
0;10 sao cho ứng với mỗi x có ít nhất 8 số nguyên y thỏa mãn 2
2 y 4x y.log 10 x y 2 70 6 65.4x y ? 2
A. 7 . B. 8 . C. 10 . D. 15 . T Lời giải S
Điều kiện 10 x y 0 y 10 x . 2 x 4 y35 P
Bất phương trình tương đương 4 log 10 x y 65 0 . 2 2 x 4 y35 -
Xét hàm số f y 4
log 10 x y 65, y ; 10 x . 2 2 2 x 4 y35 1 0 Ta có f y 4.4 ln 4 x x 10 x y 0, ;10 ln 2 2
Do đó hàm số nghịch biến trên ; 10 x . 2 x 9 x 10 x f y
Th.s Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 12 Nhận xét: f x 2 x 4 x 1 9 4
65 0,x .
Do đó y x 9 là nghiệm nguyên lớn nhất của bất phương trình đã cho . T
Do đó yêu cầu bài toán trở thành y x 2 cũng là nghiệm hay f x 2 0 S 2 4 27 4 x x log 8 65 0 2
x 4x 27 log 62 0 4 2 P x 2 15 log 62 4 - . x 2 15 log 62 2 4 0 Do x nguyên và x 1
0;10 nên x 9..... 4,8, 9 . 2
Vậy có 8 giá trị x thoả mãn bài toán. 2
Câu 49: Trong không gian Oxyz , cho mặt phẳng P : x 2y 2z 7 0 điển M 2; 1 ; 1 và m ặt cầu S 2 2 2
: x y z 4x 2y 4z 7 0 . Đường thẳng d qua M cắt P,S lần lượt tại các
điểm A, B sao cho M là trung điểm AB. Biết độ dài ngắn nhất của đoạn AB là
2 a 2 b giá trị của a b bằng A. 232 . B. 223. C. 212. D. 192 . Lời giải TSP-2022
Giả thiết suy ra mặt cầu S có tâm I 2 ; 1
;2 và bán kính R 4 . Giả thiết suy ra B thuộc
mặt phẳng Q ảnh của M qua phép đỗi xứng tâm M.
Th.s Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 13
Dễ dàng tìm được Q: x 2y 2z 11 0. Lại có BS BS Q là một đường H
bán kính r 15 . Gọi E là hình chiếu của M trên Q khi đó tìm được Ttròn tâm 7 5 8 ; ; 3 3 3 E 1; 3 ;3 . S Ta có AB BM EB EH r2 2 2 2 9 2 9
2 37 2 195 . Dấu bằng xảy ra khi H, P-
y f x là hàm đa thức có f 2 36, f 2 3
2 . Hàm số f x có 2E, B
theo thứ tự thẳng hàng. Câu 50: Cho hàm số 02bảng biến thiên như sau: 2 x
Có bao nhiêu giá trị nguyên của tham số m 5
0;50 để hàm số g x 2 1 6 f m có x 1 2x 1 5 điểm cực trị? A. 63. B. 34. C. 36. D. 62 . Lời giải Xét hàm số h x 2x 1 6 f , m 1 D \ ; 1 . T x 1 2x 1 2 S Ta có h x 2x 1 3 12 f . x 1 x 2 1 2x 2 1 P 2 x x - h x 2 1 4 1 0 f x 4 đặt 2 1 t
ta được phương trình f t 2 2 2 x 1 2x 1 x 1 t 0 Đặt u t 4
dễ dàng suy ra được bảng sau 2 t 22
Th.s Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 14 4 t 2 Do đó f t
thay lại ta được hx 0 có nghiệm duy nhất 1 x . Ta có bảng 2 t t 2 4
biến thiên của hx . TSP 36 m 36 m -2 28 m 0 2
Do hx có 1 điểm cực trị nên để hàm số hx có 5 điểm cực trị khi chỉ khi đồ thị hx cắt trục h2 3 6 m 0 oành
tại 4 điểm phân biệt do đó ta được điều kiện là 3 6 m 28. 2 8 m 0
Vậy có 63 giá trị của m.
------------------------ THE END ------------------------ T S P -2 022
Th.s Trương Đức Thịnh - THPT Trần Nhân Tông - Quảng Ninh 15




