






Preview text:
SỞ GD & ĐT HÀ TĨNH
ĐỀ THI THỬ TỐT NGHIỆP THPT
CỤM LIÊN TRƯỜNG THPT NĂM HỌC 2021 - 2022 Môn: TOÁN
ĐÁP ÁN CÁC MÃ ĐỀ Mã đề [101]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D C A A B B B C B C C A B C B C D A B A C B A B D
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
C D A D A D D B C D B A C C D B A D A C B D A A D Mã đề [102]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B D A C A B B D A A C D D C B A B A B C D A C C C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
C C D C B A A B D D D D B C B C D A A A B A D B B Mã đề [103]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D B D D D B D C B C B B B C D A C D A B C B C D C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
C A D D A C A D A A B D A C C A C B A A B A B A B Mã đề [104]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D C A C C D C A A A A D A B D C B D B C D C B D B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
D B C A C D A B C C B D B B D A A A D A A B B C B Mã đề [105]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D B C A B C B A A B A D C C A A C D A B C A D D B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
D C D C C B B A D D B A A C A C B B C B B A D D D Mã đề [106]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B A B B D D B C C A C C C D D B D A C B A D B C B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
D A C A D A B B D C D A C D B A A A A D A C B B C Mã đề [107]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C A C B A B C D A B D C A B C D D A B A B B C C C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
D C B D B A D D B B C A B A C D D A A C D A D B A Mã đề [108]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D C B D A C C D D D A A A A D A C C A A B D A B B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B B C B B C D A B A C D C A C B B A D D B C C D B
HDG MỘT SỐ CÂU VD-VDC
Câu 41. Cho hàm số y = f ( x) có đạo hàm là f ( x) = sin x − 9cos3 , x x và f = 1 . Biết 2
F ( x) là một nguyên hàm của f ( x) thỏa mãn F (0) = 2 , khi đó F ( ) bằng A. 2 − . B. 2 − 2 . C. 2 . D. 2 + 2 . Lời giải
Ta có f ( x) = f
(x)dx = (sin x −9cos3x)dx = −cosx −3sin3x +C . Do f =1 −cos − 3sin 3. + C =1 C = 2 − . 2 2 2
Nên f ( x) = − cosx − 3sin 3x − 2 .
Ta có F ( x) = (−cosx −3sin3x − 2)dx=−sin x + cos3x− 2x + C . 1
Do F (0) = 2 −sin 0 + cos(3.0) − 2.0 + C = 2 C =1. 1 1
Vậy F ( x) = −sin x + cos3x − 2x +1 F ( ) = 2 − .
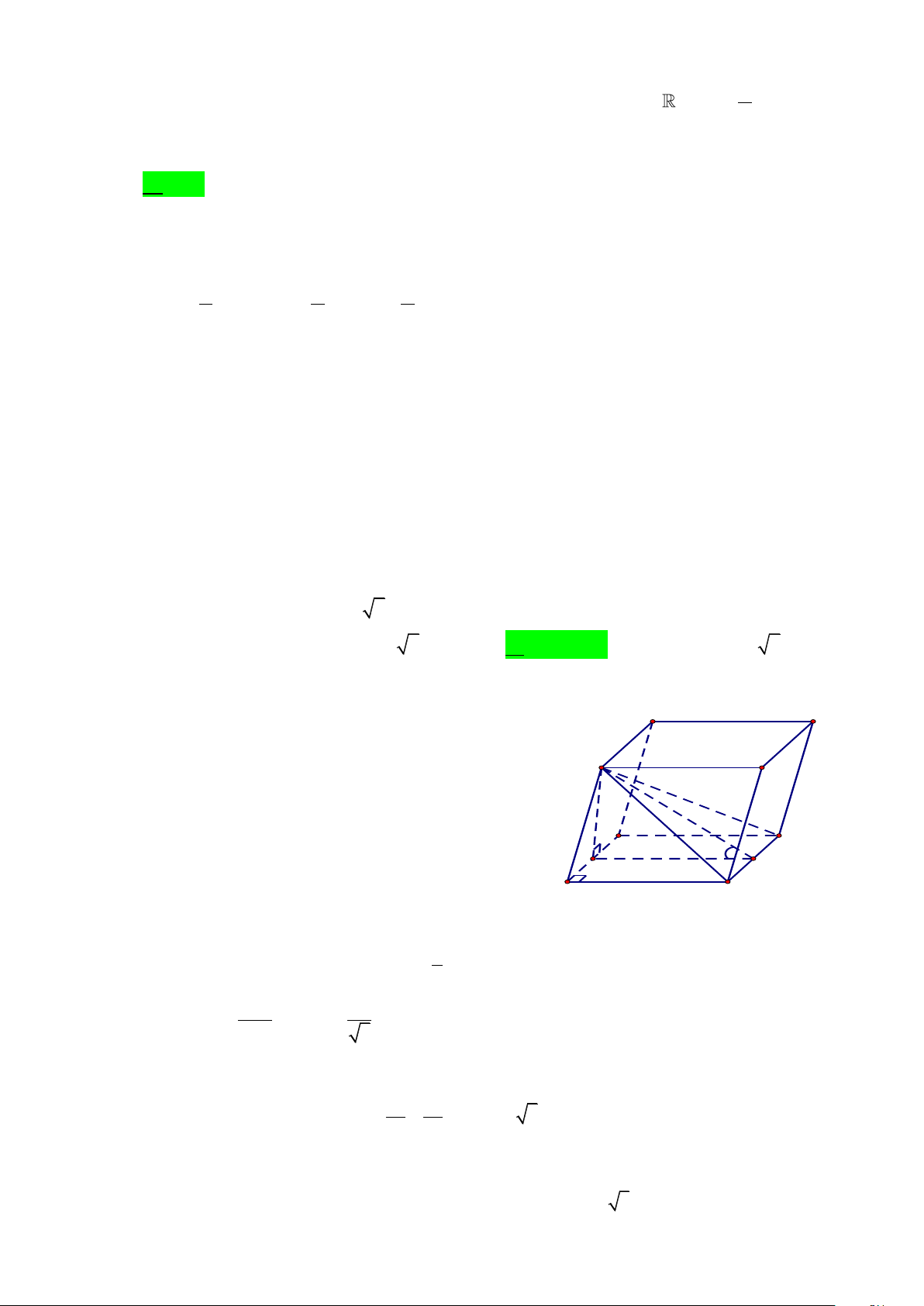
Câu 42. Cho hình lăng trụ ABC . D A B C D
có đáy là hình vuông. Hình chiếu vuông góc của
A trên mặt phẳng ( ABCD) trùng với trung điểm H của AB . Góc giữa hai mặt phẳng ( A C
D) và ( ABCD) bằng 30. Tính thể tích V của khối lăng trụ ABC . D A B C D
biết AA = a 7 . A. 3 V = 8a . B. 3 V = 4 7a . C. 3 V = 24a . D. 3 V = 12 7a . Lời giải
Gọi M là trung điểm của CD . B' C' CD ⊥ HM Ta có
CD ⊥ ( A H
M ) CD ⊥ A M CD ⊥ A H A' D' Mà ( A C
D)( ABCD) = CD và CD ⊥ HM B C
Suy ra góc giữa hai mặt phẳng ( A C D) và 30o H M
( ABCD) bằng góc giữa hai đường thẳng A D
AM và HM và bằng góc A M
H = 30 (vì tam giác AHM vuông tại H ). x
Đặt AD = x ( x 0) HM = x , AH = . 2 AH x Có tan 30 = AH = . HM 3
Trong tam giác vuông AHA có 2 2 2
A' A = A' H + AH 2 2 x x 2 7a = +
x = 2 3a = AD . 3 4 A H = 2a .
Vậy thể tích khối lăng trụ ABC . D A B C D
là V = a ( a )2 3 2 . 2 3 = 24a .
Câu 43. Trên tập hợp các số phức, xét phương trình 2 z − (m − ) 2 2
1 z + m − 3 = 0 ( m là tham số
thực).Gọi S là tập hợp giá trị của m để phương trình đó có hai nghiệm z , z thỏa 1 2
mãn z − z = 2 5 . Tính tổng các phần tử của tập S . 1 2 9 1 A. 5. B. 4. C. . D. − . 2 2 Lời giải. Xét phương trình : 2 z − (m − ) 2 2
1 z + m − 3 = 0 ( ) 1 .Ta có:
= (b)2 − ac = (m − )2 − ( 2 1
1. m − 3) = 4 − 2m . Trường hợp 1: Nếu
0 m 2 thì phương trình ( )
1 có hai nghiệm thực z , z 1 2
thỏa mãn z − z = 2 5 ( z − z )2 = 20 ( z + z )2 − 4z .z = 20 * . 1 2 1 2 1 2 1 2 ( )
z + z = 2 m −1 1 2 ( ) Theo Vi-ét ta có: thay vào (*) có 2
z .z = m − 3 1 2 ( 1 m − )2 − ( 2 4 1
4 m − 3) = 20 4 − 2m = 5 m = − (thỏa mãn). 2
Trường hợp 2: Nếu ' 0 m 2 thì phương trình ( ) 1 có hai nghiệm phức là
z = m −1 + i 2m − 4 , z = m −1 − i 2m − 4 . Ta có 2 ( ) 1 ( ) 9
z − z = 2 5 2i 2m − 4 = 2 5
2m − 4 = 5 m = (thỏa mãn). 1 2 2 1 9
Vậy S = − ; nên tổng các phần tử của S là 4. 2 2
Câu 44. Cho hai số phức z , z thỏa mãn 5 z − i = z +1+ i + 3 z −1− 3i và z + i = 5 . Giá trị lớn 1 2 1 1 1 2
nhất của biểu thức P = z + z − 2 − 4i bằng 1 2 A. 5 + 3 5 . B. 2 + 13 . C. 9 . D. 5 + 4 5 . Lời giải
Gọi z = x + y i M (x ; y ) 1 1 1 1 1 = + z x y i
N (x ; y ) 2 2 2 2 2 = z i C(0;1) 3 = − − − − z 1 i ( A 1; 1) 4 = + z 1 3i B(1;3) 5
Dễ thấy điểm C là trung điểm của AB và AB = 2 5
Theo công thức đường trung tuyến, ta có: 2 2 2 2 MA + MB AB AB 2 2 2 2 MC = −
MA + MB = 2MC + 2 4 2
Mặt khác theo bài ra ta có: 5 z − i = z +1+ i + 3 z −1− 3i 1 1 1 2 2 2 2
5MC = MA + 3MB 3 +1 . MA + MB (BĐT Bunhiakovski). 2 MC ( 2 2 MA + MB ) = ( 2 25 10 10 2MC +10) 2 2
5MC 100 MC 20 MC 2 5
P = z + z − 2 − 4i = z − i + z + i + ( 2 − − 4i 1 2 ( 1 ) ( 2 )
z − i + z + i + 2
− − 4i = 2 5 + 5+ 2 5 = 4 5 + 5. 1 2
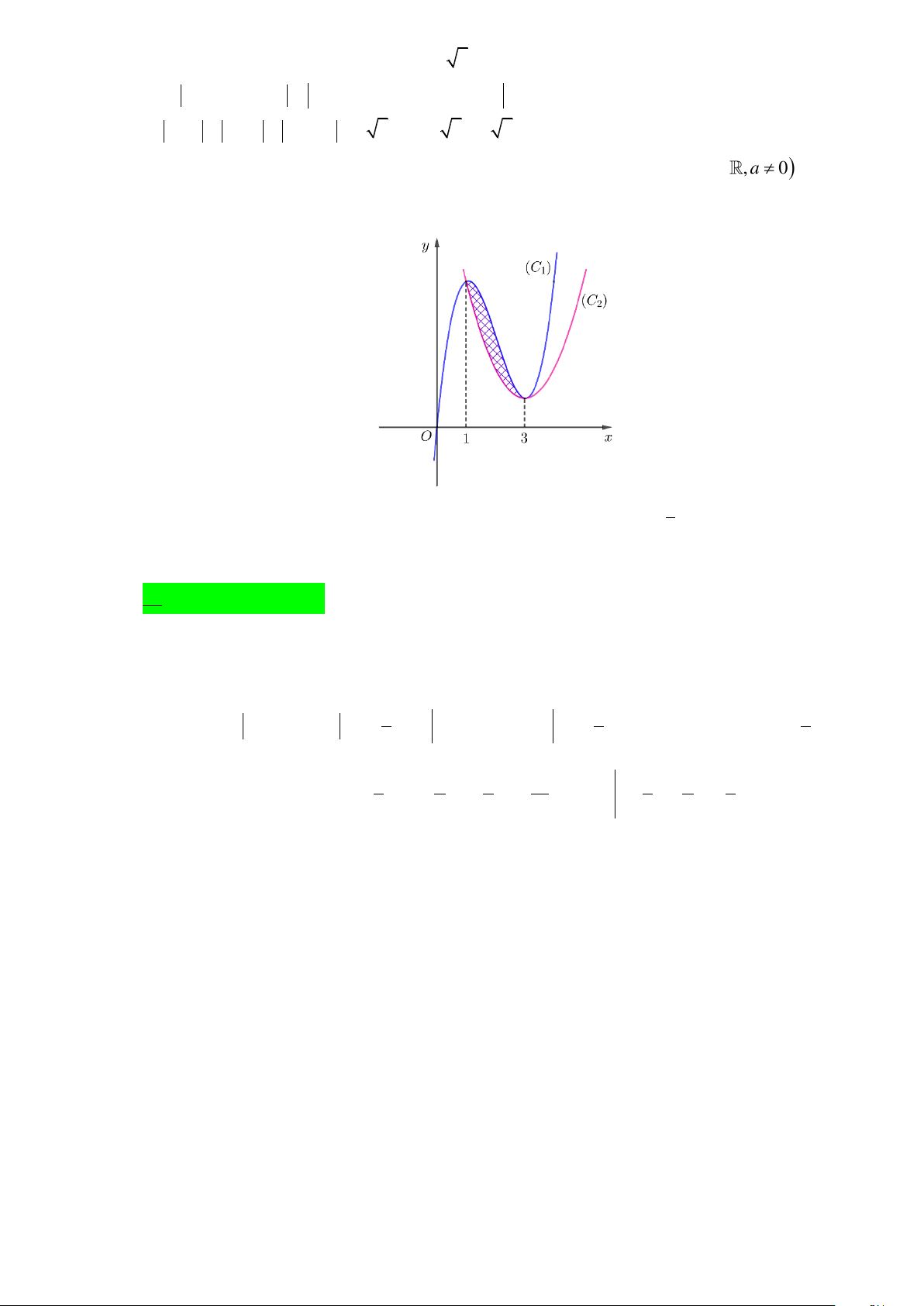
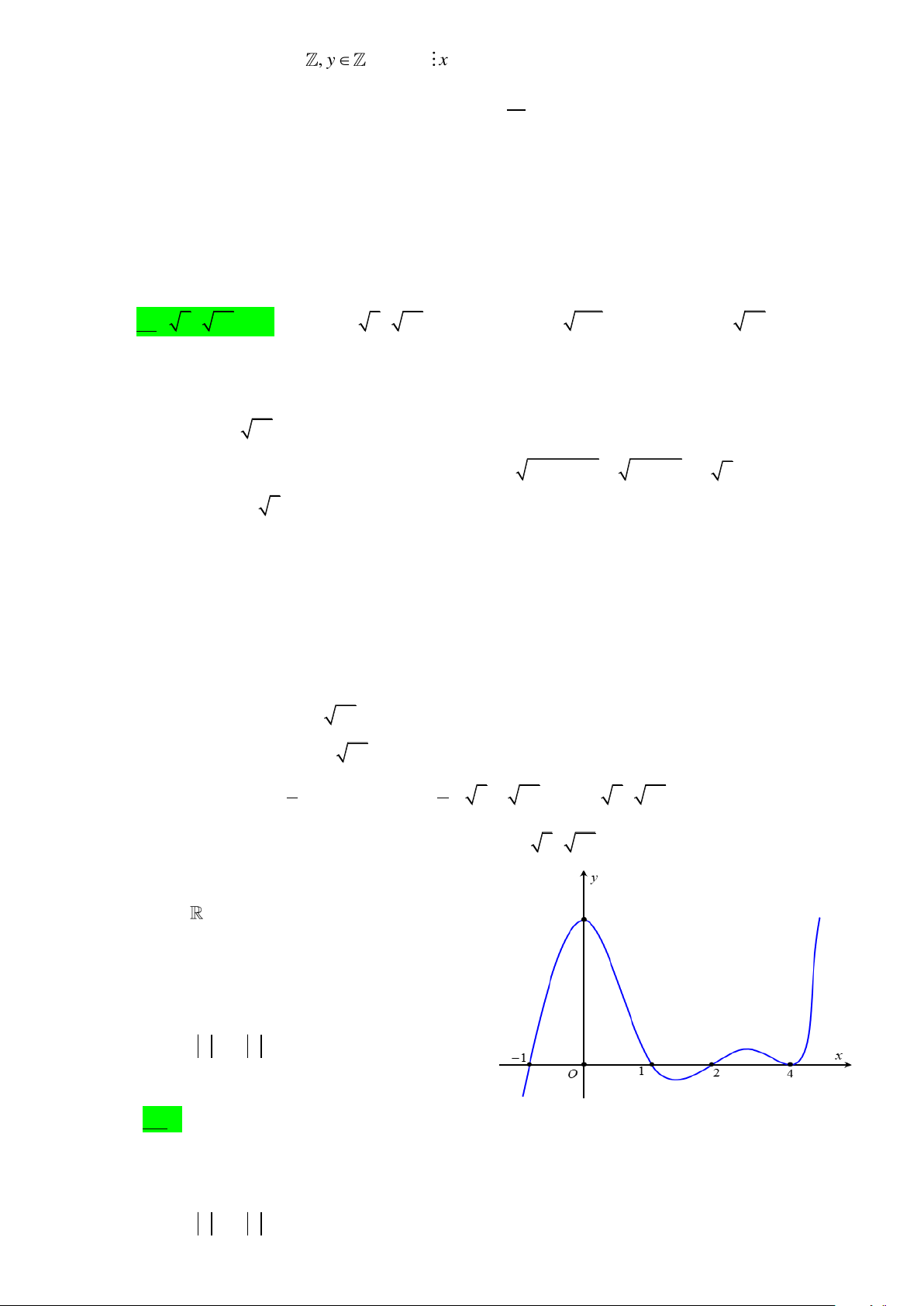
Câu 45. Cho hai hàm số ( ) 3 2
f x = ax + bx + cx + d , g ( x) 2
= ax + bx + e(a, ,
b c, d, e , a 0) có đồ
thị lần lượt là hai đường cong (C , (C ở hình vẽ bên. 2 ) 1 ) 8
Diện tích hình phẳng giới hạn bởi hai đồ thị (C , (C bằng . Tính f (2) − g (− ) 1 . 2 ) 1 ) 3
A. f (2) − g (− ) 1 = 2 − 6 .
B. f (2) − g (− ) 1 = 2 − 4 .
C. f (2) − g (− ) 1 = 2 − 8.
D. f (2) − g (− ) 1 = 3 − 0 . Lời giải
Dựa vào đồ thị, ta có f ( x) − g ( x) = a ( x − )( x − )2 1 3 và a 0 3 3 3 8 2 8 2 8 Ta có: S =
f ( x) − g ( x) dx = a ( x − )
1 ( x − 3) dx = a ( x − )
1 ( x − 3) dx = 3 3 3 1 1 1 3 a ( 8
x − 7x +15x − 9) 3 1 7 15 8 4 8 3 2 4 3 2 dx = a x − x + x − 9x
= a = a = 2 . 3 4 3 2 3 3 3 1 1
Do đó f ( x) − g ( x) = ( x − )( x − )2 2 1 3 ( 2
ax + bx + cx + d ) − (ax + bx + e) = ( x − )( x − )2 3 2 2 1 3 3
ax + (b − a) 2
x + (c − b) x + d − e = 2( 3 2
x − 7x +15x − 9)
Đồng nhất hệ số ta có a = 2 a = 2 b − a = −14 b = −12 c − b = 30 c = 18
d − e = −18 d = e −18 f (x) 3 2
= x − x + x + e − g ( x) 2 2 12 18 18;
= 2x −12x + e f (2) − g (− ) 1 = 2 − 8
Vậy f (2) − g( 1 − ) = 2 − 8 .
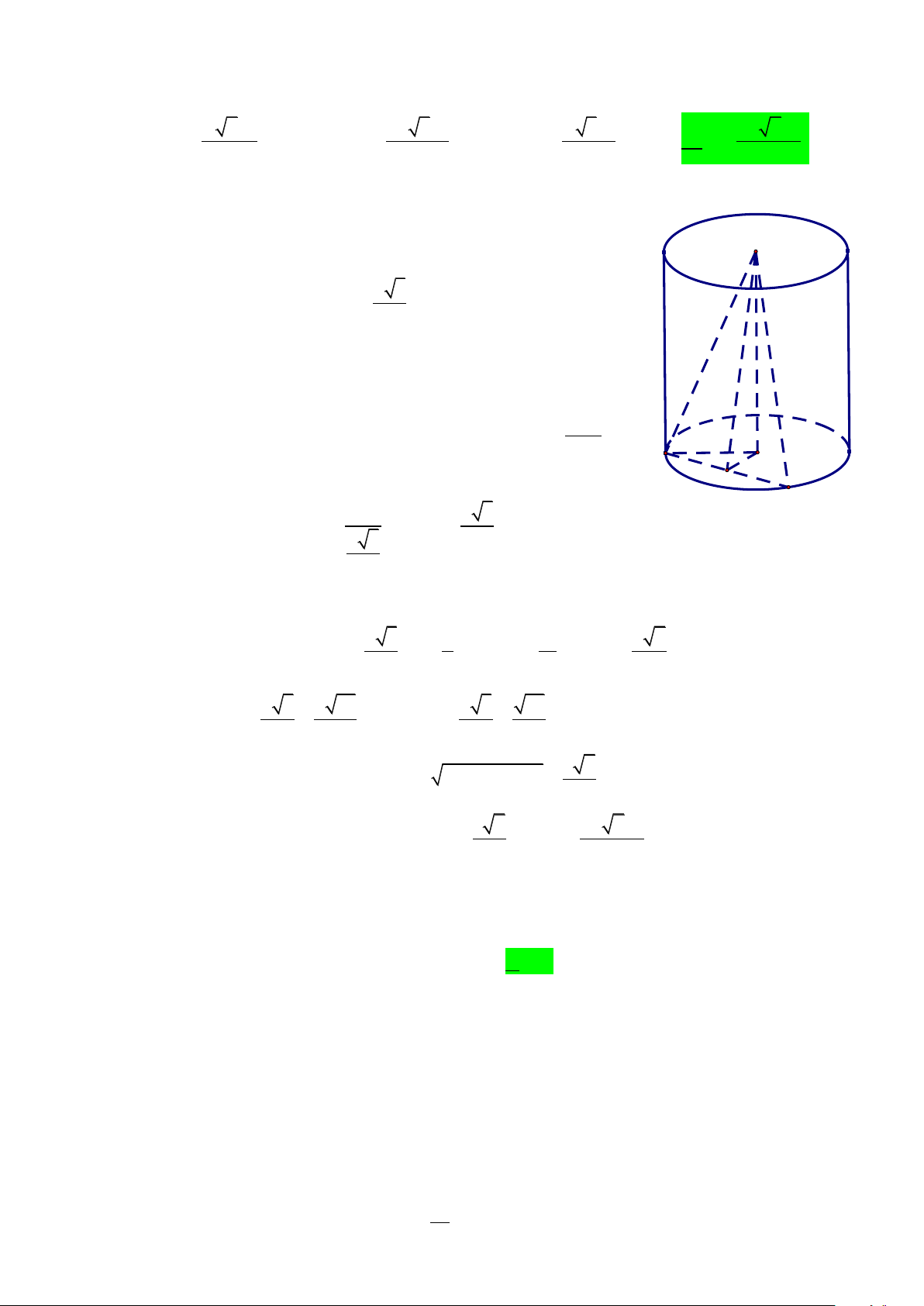
Câu 47. Cho hình trụ có hai đáy là hai hình tròn ( ;
O R) và (O ; R) . AB là một dây cung của đường tròn ( ;
O R) sao cho tam giác O A
B là tam giác đều và mặt phẳng (O AB ) tạo
với mặt phẳng chứa đường tròn ( ;
O R) một góc 60 . Tính thể tích V của khối trụ
đã cho theo R . 3 7R 3 3 5R 3 5R 3 3 7R A. V = . B. V = . C. V = . D.V = . 7 5 5 7 Lời giải
Đặt độ dài cạnh AB = x ( x 0) và M là trung điểm AB . O' Vì tam giác O A B đều nên x O A = O B = AB = 3 x O M = . 2 Vì mặt phẳng (O AB
) tạo với mặt phẳng chứa đường tròn ( ;
O R) góc 60 nên O M O = 60. OM Xét tam giác O O
M vuông tại O ta có: cosO M
O = O M . A O Suy ra M B OM x 3 cos 60 = OM = x 3 4 2
Xét tam giác OAM vuông ở M có: 2 2 2
OA = OM + AM nên 2 2
x 3 x 7 4 7 2 2 2 R = + R = x x = R 4 2 16 7 x 3 2 21 x 3 21 Do đó: O M = = R và OM = = R . Vì vậy, ta có 2 7 4 7 3 7 2 2 OO = O M − OM = R . 7 3 3 7 3 7R
Vậy thể tích khối trụ là 2 2
V = R .h = R . R V = . 7 7
Câu 48. Có bao nhiêu cặp số nguyên ( ;
x y ) thỏa mãn 0 x 2022 , y 2 và 2 + − = log − − 2x x x xy x xy x 2 ( ) ? A. 2022 . B. 12 . C. 11. D. 2023. Lời giải
Từ điều kiện 0 x 2022 , y 2, ta được xy − x = x ( y − ) 1 0.
Kết hợp điều kiện của log xy − x , ta được. 2 ( )
Đặt t = log xy − x . Khi đó ta được 2 − 2t =
− 2x 2x + . = 2t x xt x x + . x t (1) 2 ( )
Nếu x t thì 2x + . 2t x x + .
x t, với x 0 , mâu thuẫn với (1).
Tương tự x t cũng được kết quả mâu thuẫn với (1). x 2x
Từ đó: x = t xy − x = 2 y = 1+ . x
Vì 0 x 2022 , x , y nên 2x x suy ra x 0 1 2 10 2 , 2 , 2 ,..., 2 . 2x
Ứng với mỗi giá trị của x ở trên thì y = 1+
có duy nhất một giá trị tương ứng. x
Vậy có 11 cặp số nguyên thỏa yêu cầu đề bài.
Câu 49. Trong không gian với hệ tọa độ Oxyz , cho hai mặt cầu ( 2 2 S ) (
: x + 4)2 + ( y − )2 2
1 + z = 16 , (S : x + 4 + y −1 + z = 36 và điểm A(6;3;0) . Đường 2 ) ( ) ( ) 2 1
thẳng d di động nhưng luôn tiếp xúc với (S ) , đồng thời cắt (S tại hai điểm B,C . 2 ) 1
Tam giác ABC có diện tích lớn nhất là
A. 4 5.( 26 + 2) . B.8 5.( 26 + 2) . C. 4 130 . D. 8 26 . Lời giải
Mặt cầu (S , S có cùng tâm I ( 4
− ;1;0) và lần lượt có bán kính là R = 4, R = 6 . 1 ) ( 2 ) 1 2
Ta có IA = 2 26 R R , suy ra điểm A nằm ngoài (S , S . 1 ) ( 2 ) 2 1
Gọi T là hình chiếu của I trên d , ta có 2 2 2 2 TB = IB − IT = 6 − 4 = 2 5 , Suy ra BC = 4 5 .
Gọi (P) là tiếp diện của mặt cầu (S tại T , khi đó đường thẳng d qua T và nằm 1 ) trong (P) .
Gọi H là hình chiếu của A trên d .
Ta có AH AT , dấu bằng xảy ra khi d ⊥ AT .
Gọi M , N là các giao điểm của đường thẳng AI và (S với M là điểm gần A hơn. 1 )
Ta có AN = AI + R = 2 26 + 4 . 1
Mà AT AN AH 2 26 + 4 , dấu bằng xảy ra khi d ⊥ AN . 1 1 Mặt khác S
= AH.BC S
.4 5.(2 26 + 4) = 4 5.( 26 + 2). ABC 2 ABC 2
Vậy diện tích lớn nhất của tam giác ABC là 4 5.( 26 + 2) .
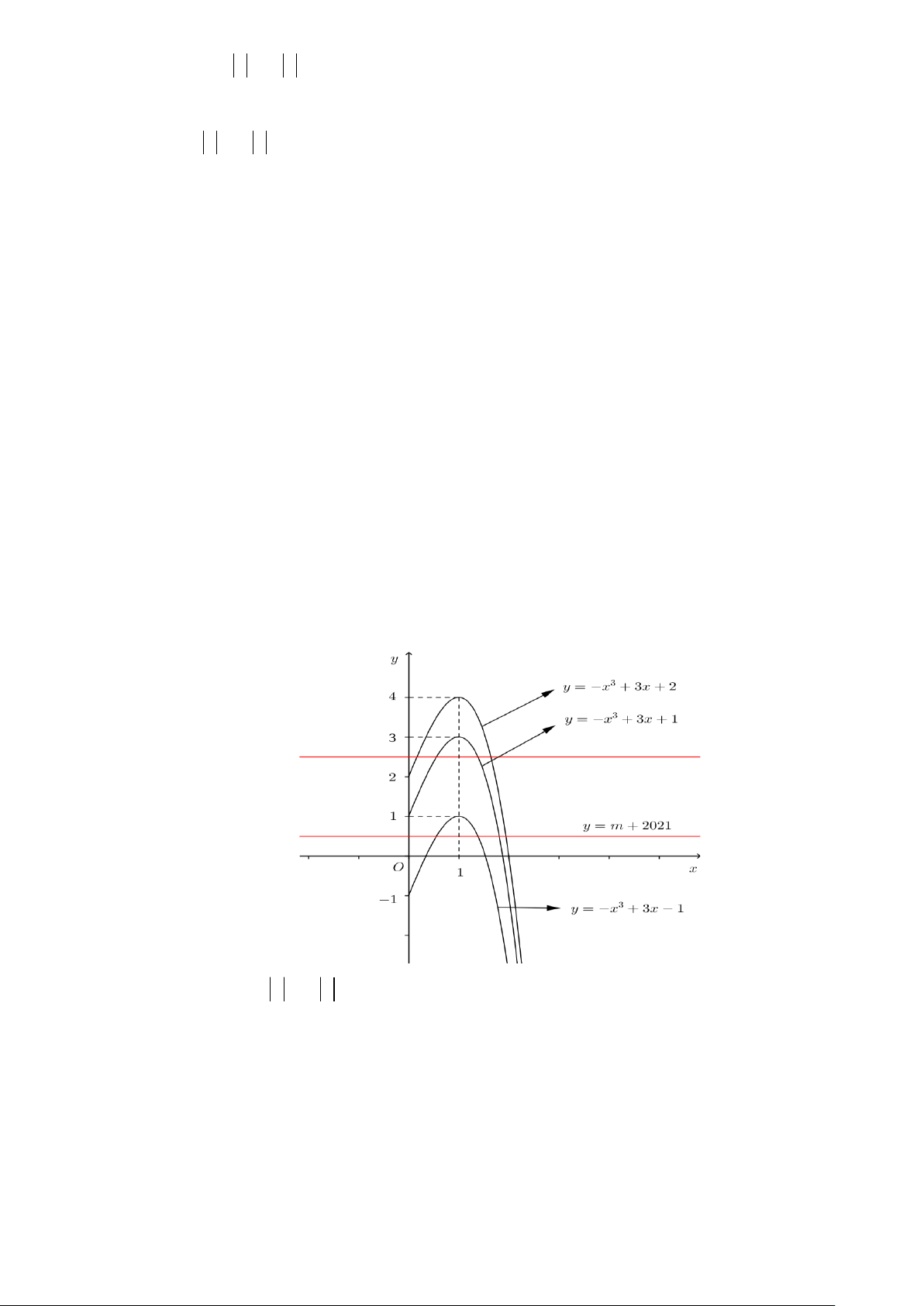
Câu 50. Cho hàm số f ( x) có đạo hàm liên tục trên
, đồ thị hàm số y = f ( x) có
đúng 4 điểm chung với trục hoành
như hình bên. Có bao nhiêu giá trị
nguyên của tham số m để hàm số y = f ( 3
x − x + m + ) 3 3 2021 + 2022m có
đúng 11 điểm cực trị? A. 1. B. 2 . C. 0 . D. 5 . Hướng dẫn giải Với mỗi tham số m thì số điểm cực trị của hàm số : y = f ( 3
x − x + m + ) 3 3 2021 + 2022m 3
và : y = f ( x −3 x + m + 202 ) 1 là như nhau.
Do đó ta chỉ cần tìm giá trị nguyên của tham số m để hàm số 3
: y = f ( x −3 x + m + 202 ) 1
có đúng 11 điểm cực trị.
Xét x 0 : Hàm số có dạng y = f ( 3
x − 3x + m + 202 ) 1
Khi đó ta có đạo hàm như sau: y = ( 2 x − ) f ( 3 3 3
x − 3x + m + 202 ) 1
Do nghiệm của phương trình 3
x − 3x + m + 2021 = 4 là các nghiệm bội chẵn của
phương trình y = 0 nên ta chỉ cần quan tâm đến các nghiệm còn lại. Tức là
x = 1 (do x 0) 2 3x − 3 = 0 3
x − 3x + m + 2021 = 1 − y = 0 f ( 3
x − 3x + m + 202 ) 1 = 0 3
x − 3x + m + 2021 = 1 3
x −3x + m + 2021= 2
x = 1 (do x 0) 3
m + 2021 = −x + 3x −1 3
m + 2021 = −x + 3x +1 3
m + 2021= −x +3x + 2 Vẽ đồ thị ba hàm số 3
y = −x + 3x −1 ; 3
y = −x + 3x +1; 3
y = −x + 3x + 2 với x 0 trên cùng một hệ trục. 3
Hàm số y = f ( x −3 x + m + 202 )
1 có đúng 11 điểm cực trị
Hàm số y = f ( 3
x − 3x + m + 202 )
1 có đúng 5 điểm cực trị dương
Phương trình f ( 3
x − 3x + m + 202 )
1 = 0 có đúng 4 nghiệm bội lẻ dương và khác 1
Đường thẳng y = m + 2021 cắt đồ thị ba hàm số 3
y = −x + 3x −1 ; 3
y = −x + 3x +1; 3
y = −x + 3x + 2 tại 4 điểm phân biệt có hoành độ dương khác 1 − + − − 1 m 2021 1 m 2022 2020
. Do điều kiện m nguyên nên m = 2021 − . 2 m + 2021 3 2 − 019 m 2 − 018
Vậy chỉ có 1 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Document Outline
- Doc1
- Đáp án môn TOÁN_Thi thử liên trường