Đề thi thử tốt nghiệp THPT 2022 môn Toán lần 2 sở GD&ĐT Hòa Bình

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi thử tốt nghiệp THPT năm 2022 môn Toán lần 2 sở Giáo dục và Đào tạo tỉnh Hòa Bình

37 19 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

33 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÒA BÌNH
ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2021 – 2022 – LẦN 1
Câu 1: Cho cấp số cộng có . Khi đó bằng
n
u
1 3
1; 5u u
2
u
A. B. C. D.
7
3
2
9
Câu 2: Cho và , khi đó bằng
3
0
5f x dx
8
3
8f x dx
A. B. C. D.
13.
3.
13.
3.
Câu 3: Hình phẳng giới hạn bởi các đường , trục hoành và hai đường thẳng
D
ln 2y x
. Diện tích hình phẳng được tính là
3
, 3
2
x x
D
A. B.
3
2
3
2
ln 2 .S x dx
3
3
2
ln 2 .S x dx
C. D.
3
3
2
ln 2 .S x dx
3
3
2
ln 2 .S x dx
Câu 4: Trong không gian , cho hai điểm . Tọa độ vectơ là
Oxyz
1;0;3 , 1;2; 2A B
AB
A. B. C. D.
2;2;1 .
2; 2; 5 .
2; 2;5 .
2;2; 5 .
Câu 5: Cho hình bát diện đều như hình bên. Số cạnh của hình bát diện đều bằng
A. B. C. D.
8.
14.
10.
12.
Câu 6: Diện tích xung quanh của hình trụ có bán kính đáy bằng và độ dài đường sinh bằng là
3
4
A. B. C. D.
21 .
42 .
24 .
48 .
Câu 7: Nghiệm của phương trình là
2 1
5 125
x-
=
A. B. C. D.
2.x = -
2.x =
1.x =
1.x = -
Câu 8: Cho hàm số có bảng biến thiên như sau
( )y f x=
Giá trị cực đại của hàm số đã cho bằng
A. B. C. D.
3.-
0.
4.
1.-
Câu 9: Hàm số nào dưới đây là một nguyên hàm của hàm số
2 1f x x
A. B. C. D.
2
.x x
2
.x x
2
2 .x x
2
2 .x x
Câu 10: Họ nguyên hàm của hàm số trên là:
1
2f x
x
0;
A. B. C. D.
2 ln .x x C
2
1
2 .C
x
ln .x C
2 ln .x x C
Câu 11: Với biểu thức bằng
0a
2
5
log
25
a
A. B. C. D.
5
2 log 1 .a
5
2 log .a
5
2 log 1 .a
5
1
log .
2
a
Câu 12: Cho . Số phức bằng
1 2
5 ; 4 3z i z i
1 2
z z z
A. . B. . C. . D. .
1 2i
1 2i
1 2i
1 2i
Câu 13: Cho hình lăng trụ có diện tích đáy và chiều cao . Thể tích khối lăng trụ đã cho
15B
6h
bằng
A. B. C. D.
30
90
45
60
Câu 14: Tập xác định của hàm số là
3
log 5y x
A. B. C. D.
;5
5;
;5
5;
Câu 15: Gọi , là hai nghiệm phức của phương trình . Giá trị của biểu thức
1
z
2
z
2
2 10 0z z
là
1 2
A z z
A. B. C. D.
10
10
2
2
Câu 16: Cho khối cầu có thể tích bằng . Bán kính khối cầu đã cho bằng
288
A. B. C. D.
6
3
4
2
Câu 17: Cho hàm số có đồ thị là đường cong trong hình bên. Giá trị nhỏ nhất của hàm số
trên đoạn bằng
2;4
A. B. C. D.
2.
3.
4.
3.
Câu 18: Với đạo hàm của hàm số bằng
0x
2022
logy x
A. B. C. D.
ln 2022
.
x
ln 2022.x
.
ln 2022
x
1
.
ln 2022x
Câu 19: Trong không gian mặt phẳng đi qua điểm nào trong các điểm
,Oxyz
:3 2 3 0P x y z
dưới đây
A. B. C. D.
1;0; 1 .
0;1; 1 .
2;3;3 .
Câu 20: Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình
2 3
1
x
y
x
A. B. C. D.
1.y
2.y
1.y
2.y
Câu 21: Số cách chọn học sinh từ nhóm có học sinh là
2
8
A. . B. . C. . D. .
2
8
2
8
A
16
2
8
C
Câu 22: Tập nghiệm của bất phương trình là
5 3
x
A. . B. . C. . D.
3
;log 5
5
;
3

5
;log 3
3
;
5

Câu 23: Cho hàm số có bảng biến thiên như sau
y g x
Hàm số đã cho đồng biến trên khoảng nào dưới đây
A. . B. . C. . D.
2;
;2
4;1
0;2
Câu 24: Cho số phức . Phần thực và phần ảo của số phức là
5 2z i
z
A. Phần thực bằng và phần ảo bằng . B. Phần thực bằng và phần ảo bằng .
5
2
5
2
C. Phần thực bằng và phần ảo bằng . D. Phần thực bằng và phần ảo bằng .
2
5
2
5
Câu 25: Đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng
4 2
2 3y x x
A. . B. . C. . D. .
0
3
1
1
Câu 26: Trong mặt phẳng , gọi , , lần lượt là các điểm biểu diễn các số phức ,
Oxy
A
B
C
1
3z i
, , là trọng tâm của tam giác . Số phức có điểm biểu diễn là
2
2 2z i
3
5z i
G
ABC
G
A. . B. . C. . D. .
1z i
1 2z i
1 2z i
2z i
Câu 27: Trong không gian , mặt phẳng đi qua ba điểm , , có
Oxyz
( )P
0;1;2A
1;3; 2B
2;1;3C
phương trình là
A. . B. .
2 5 2 9 0x y z
2 5 2 9 0x y z
C. .D. .
2 7 4 15 0x y z
7 4 15 0x y z
Câu 28: Trong không gian cho điểm và mặt phẳng Phương
,Oxyz
(2; 0; 7)M
( ) : 2 3 5 0.P x y z
trình của đường thẳng đi qua và vuông góc với có phương trình là
M
( )P
A. B. C. D.
1
2 .
2 3
x t
y t
z t
2 2
.
7 3
x t
y t
z t
3 2
1 .
2 3
x t
y t
z t
2 2
.
7 3
x t
y t
z t
Câu 29: Cho hình chóp tam giác đều có cạnh bên bằng , đường cao bằng ( tham khảo
.S ABC
2a
a
hình vẽ)
Góc giữa cạnh bên và mặt đáy bằng
A. B. C. D.
0
90 .
0
30 .
0
45
0
60
Câu 30: Hàm số nào dưới đây nghịch biến trên
?
A. B. C. D.
3
3.y x
1
.
2
x
y
x
4 2
2 .y x x
3 2
3 .y x x
Câu 31: Diện tích hình phẳng giới hạn bởi các đường là
2
, 3y x y x
A. B. . C. . D. .
9
.
2
4
3
5
2
Câu 32: Cho hình lăng trụ đứng có đáy là tam giác vuông cân tại có
.ABC A B C
ABC
B
3AB a
cạnh bên ( tham khảo hình vẽ). Khoảng cách từ điểm đến mặt phẳng là
3AA a
A
A BC
A. B. C. D.
6
.
3
a
3
.
2
a
2
.
3
a
3
.
2
a
Câu 33: Có tấm thẻ được đánh số từ đến . Chọn ngẫu nhiên thẻ. Xác suất để chọn được
10
1
10
2
2
tấm thẻ đều ghi số chẵn là
A. B. C. D.
2
.
9
1
.
4
7
.
9
1
.
2
Câu 34: Cho hàm số . Tọa độ điểm cực tiểu của đồ thị hàm số là
3 2
3 2f x x x
A. B. C. D.
2; 2
2;2
0; 2
2;0
Câu 35: Gọi lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên
,M m
4 2
2 3f x x x
đoạn . Giá trị bằng
2;1
M m
A. B. C. D.
9.
8.
1.
2.
Câu 36: Trong không gian , mặt cầu có tâm và đi qua có phương trình
Oxyz
S
1; 1;2I
1;1; 1A
là:
A. . B. .
2 2 2
2 2 4 5 0x y z x y z
2 2 2
2 2 4 11 0x y z x y z
C. . D. .
2 2 2
2 2 4 17 0x y z x y z
2 2 2
2 2 4 11 0x y z x y z
Câu 37: Cho hàm số có đồ thị như hình vẽ. Các miền và có diện tích lần lượt là 8 và 2.
A
B
Tích phân bằng:
4
1
df x x
O
x
y
A
B
1
3
4
A. 6. B. 2. C. 18. D. 10.
Câu 38: Tích các nghiệm của phương trình bằng:
2
2
log 3 7 3x x
A. . B. . C. . D. .
8
3
7
3
7
3
8
3
Câu 39: Cho tam giác vuông tại có . Thể tích khối tròn xoay sinh bởi hình tam
ABC
A
4, 2AB AC
giác khi quay quanh cạnh bằng
BC
A. . B. . C. . D. .
32 5
15
5
5
2 5
3
5
15
Câu 40: Cho hình chóp có đáy là hình thoi cạnh . Tam giác cân
.S ABCD
ABCD
0
2 , 60a ABC
SAC
tại . Góc giữa cạnh và mặt phẳng bằng . Thể tích khối chóp
, 3S SB a
SA
SBD
0
30
bằng
.S ABCD
A. . B. . C. . D. .
3
3
2
a
3
3a
3
2a
3
4a
Câu 41: Cho hàm số có đạo hàm liên tục trên đồng thời thỏa mãn
0;
2
và . Giá trị của bằng
2
2
0 0
d 3 , sin d 2
2
x
f x x x x f x
4
2
f
4
0
sin df x x x
A. . B. . C. . D. .
8 5 3
3
8 5 2
3
8 5 2
3
8 5 3
3
Câu 42: Cho hai số phức , thỏa mãn: và . Gọi , lần lượt
1
z
2
z
1 2
2z z
1 2
4 4 3 2z i z
M
m
là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức , giá trị bằng
2
1 2P z i
2 2
M m
A. . B. . C. . D. .
50
54
34
99
2
Câu 43: Cho hàm số có đồ thị như hình vẽ
Số nghiệm thuộc đoạn của phương trình là
0;5
cos 1f x
A. . B. C. . D. .
6
3
4
5
Câu 44: Số giá trị nguyên của tham số để phương trình có hai
m
2 2
2 2
1 log 10log 0m x x m
nghiệm phân biệt không nhỏ hơn là
1
A. . B. . C. . D. .
4
2
1
3
Câu 45: Biết rằng tồn tại duy nhất bộ số và là phân số tối giản sao cho
*
, ,a b c
b
c
. Giá trị của biểu thức thuộc khoảng
ln8
ln3
2
d 2ln
1
x
x
e b
x a
c
e
a b c
A. . B. . C. . D.
11;15
1;5
16;20
6;10
Câu 46: Trong không gian , cho đường thẳng và mặt phẳng
Oxyz
2 1 2
:
4 4 3
x y z
d
. Đường thẳng song song với đồng thời tạo với góc bé nhất.
( ) : 2 2 1 0P x y z
( )P
d
Biết rằng có một véc tơ chỉ phương . Giá trị biểu thức bằng
( ; ;1)u m n
2 2
T m n
A. . B. . C. . D. .
5T
2T
3T
4T
Câu 47: Biết phương trình ( là tham số thực) có hai nghiệm . Gọi
2 2
8 0 z mz m
m
1 2
,z z
, ,A B C
lần lượt là điểm biểu diễn của các số phức và . Có bao nhiêu giá trị của để
1 2
,z z
0
2z
m
đều?
ABC
A. 1. B. 3. C. 4. D. 2.
Câu 48: Trong không gian , cho đường thẳng và mặt phẳng
Oxyz
2 1
:
1 1 1
x y z
. Đường thẳng nằm trong mặt phẳng sao cho cắt đồng thời
: 2 2 6 0 P x y z
d
P
d
vuông góc với đường thẳng . Khi đó đường thẳng đi qua điểm nào trong các điểm sau
d
đây?
A. . B. . C. . D. .
2;2;0
2;2; 2
0;4;1
2;3;1
Câu 49: Cho hàm số đa thức bận bốn có đồ thị hàm số như hình vẽ:
y f x
y f x
Tổng các giá trị nguyên của để hàm số có đúng 3 điểm cực tiểu là
m
1 9y f x m
A. . B. . C. . D. .
40
34
24
30
Câu 50: Có bao nhiêu số nguyên dương , sao cho ứng với mỗi giá trị của có đúng 11 số nguyên
x
x
y
thỏa mãn bất phương trình ?
2
2 5 1 0
y y
x x
A. . B. . C. . D. .
55
34
130
88
BẢNG ĐÁP ÁN
1
2
3
4
5
6
7
8
9
1
0
1
1
1
2
1
3
1
4
1
5
1
6
1
7
1
8
1
9
2
0
2
1
2
2
2
3
2
4
2
5
B
B
C
D
D
C
B
C
B
D
C
D
B
C
C
A
D
D
C
D
D
C
A
A
B
2
6
2
7
2
8
2
9
3
0
3
1
3
2
3
3
3
4
3
5
3
6
3
7
3
8
3
9
4
0
4
1
4
2
4
3
4
4
4
5
4
6
4
7
4
8
4
9
5
0
C
C
B
B
A
B
D
A
A
A
B
A
A
A
B
D
C
D
D
D
D
D
C
D
D
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 51: Cho cấp số cộng có . Khi đó bằng
n
u
1 3
1; 5u u
2
u
A. B. C. D.
7
3
2
9
Lời giải
Chọn B
Ta có .
3 1
3 1
2 2
2
u u
u u d d
Suy ra .
2 1
1 2 3u u d
Câu 52: Cho và , khi đó bằng
3
0
5f x dx
8
3
8f x dx
A. B. C. D.
13.
3.
13.
3.
Lời giải
Chọn B
Ta có .
8 3 8
0 0 3
5 8 3f x dx f x dx f x dx
Câu 53: Hình phẳng giới hạn bởi các đường , trục hoành và hai đường thẳng
D
ln 2y x
. Diện tích hình phẳng được tính là
3
, 3
2
x x
D
A. B.
3
2
3
2
ln 2 .S x dx
3
3
2
ln 2 .S x dx
C. D.
3
3
2
ln 2 .S x dx
3
3
2
ln 2 .S x dx
Lời giải
Chọn C
3
3
2
ln 2
0
: ln 2
3
2
3
y x
y
D S x dx
x
x
Câu 54: Trong không gian , cho hai điểm . Tọa độ vectơ là
Oxyz
1;0;3 , 1;2; 2A B
AB
A. B. C. D.
2;2;1 .
2; 2; 5 .
2; 2;5 .
2;2; 5 .
Lời giải
Chọn D
1;0;3 , 1;2; 2 2;2; 5A B AB
Câu 55: Cho hình bát diện đều như hình bên. Số cạnh của hình bát diện đều bằng
A. B. C. D.
8.
14.
10.
12.
Lời giải
Chọn D
Câu 56: Diện tích xung quanh của hình trụ có bán kính đáy bằng và độ dài đường sinh bằng là
3
4
A. B. C. D.
21 .
42 .
24 .
48 .
Lời giải
Chọn C
Ta có:
2 2 .3.4 24 .
xq
S rl
Câu 57: Nghiệm của phương trình là
2 1
5 125
x-
=
A. B. C. D.
2.x = -
2.x =
1.x =
1.x = -
Lời giải
Chọn B
Ta có:
2 1 2 1 3
5 125 5 5 2 1 3 2.
x x
x x
- -
= Û = Û - = Û =
Câu 58: Cho hàm số có bảng biến thiên như sau
( )y f x=
Giá trị cực đại của hàm số đã cho bằng
A. B. C. D.
3.-
0.
4.
1.-
Lời giải
Chọn C
Dựa vào bảng biến thiên ta có giá trị cực đại của hàm số là:
4.
Câu 59: Hàm số nào dưới đây là một nguyên hàm của hàm số
2 1f x x
A. B. C. D.
2
.x x
2
.x x
2
2 .x x
2
2 .x x
Lời giải
Chọn B
Ta có:
2
d 2 1 d .f x x x x x x C
Câu 60: Họ nguyên hàm của hàm số trên là:
1
2f x
x
0;
A. B. C. D.
2 ln .x x C
2
1
2 .C
x
ln .x C
2 ln .x x C
Lời giải
Chọn D
Ta có:
1
d 2 d 2 ln .f x x x x x C
x
Câu 61: Với biểu thức bằng
0a
2
5
log
25
a
A. B. C. D.
5
2 log 1 .a
5
2 log .a
5
2 log 1 .a
5
1
log .
2
a
Lời giải
Chọn C
Ta có:
2
2 2
5 5 5 5
log log log 5 2 log 1 .
25
a
a a
Câu 62: Cho . Số phức bằng
1 2
5 ; 4 3z i z i
1 2
z z z
A. . B. . C. . D. .
1 2i
1 2i
1 2i
1 2i
Chọn D
Lời giải
Ta có:
1 2
5 4 3 1 2 .z z z i i i
Câu 63: Cho hình lăng trụ có diện tích đáy và chiều cao . Thể tích khối lăng trụ đã cho
15B
6h
bằng
A. B. C. D.
30
90
45
60
Lời giải
Chọn B
Thể tích lăng trụ đã cho là .
15.6 90V Bh
Câu 64: Tập xác định của hàm số là
3
log 5y x
A. B. C. D.
;5
5;
;5
5;
Lời giải
Chọn C
Hàm số xác định khi và chỉ khi
5 0 5x x
Vậy tập xác định .
;5D 
Câu 65: Gọi , là hai nghiệm phức của phương trình . Giá trị của biểu thức
1
z
2
z
2
2 10 0z z
là
1 2
A z z
A. B. C. D.
10
10
2
2
Lời giải
Chọn C
Áp dụng định lý Vi-ét ta có
1 2
2S z z
Vậy .
1 2
2A z z
Câu 66: Cho khối cầu có thể tích bằng . Bán kính khối cầu đã cho bằng
288
A. B. C. D.
6
3
4
2
Lời giải
Chọn A
Ta có .
3 3
4
288 216 6
3
V R R R
Câu 67: Cho hàm số có đồ thị là đường cong trong hình bên. Giá trị nhỏ nhất của hàm số
trên đoạn bằng
2;4
A. B. C. D.
2.
3.
4.
3.
Lời giải
Chọn D
Dựa vào đồ thị đã cho dễ dàng nhận thấy giá trị nhỏ nhất của hàm số trên đoạn
bằng
2;4
3.
Câu 68: Với đạo hàm của hàm số bằng
0x
2022
logy x
A. B. C. D.
ln 2022
.
x
ln 2022.x
.
ln 2022
x
1
.
ln 2022x
Lời giải
Chọn D
Xét hàm số , ta có
2022
logy x
1
' .
ln 2022
y
x
Câu 69: Trong không gian mặt phẳng đi qua điểm nào trong các điểm
,Oxyz
:3 2 3 0P x y z
dưới đây
A. B. C. D.
1;0; 1 .
0;1; 1 .
2;3;3 .
Lời giải
Chọn C
Dễ thấy điểm có tọa độ thỏa mãn phương trình mặt phẳng
0;1; 1
.P
Câu 70: Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình
2 3
1
x
y
x
A. B. C. D.
1.y
2.y
1.y
2.y
Lời giải
Chọn D
Ta có:
lim 2; lim 2.
x x
y y
 
Do đó đồ thị hàm số đã cho có tiệm cận ngang là đường thẳng
2.y
Câu 71: Số cách chọn học sinh từ nhóm có học sinh là
2
8
A. . B. . C. . D. .
2
8
2
8
A
16
2
8
C
Lời giải
Chọn D
Số cách chọn học sinh từ nhóm có học sinh là .
2
8
2
8
C
Câu 72: Tập nghiệm của bất phương trình là
5 3
x
A. . B. . C. . D.
3
;log 5
5
;
3

5
;log 3
3
;
5

Lời giải
Chọn C
Ta có . Suy ra .
5 3
x
5
log 3x
5
;log 3S 
Câu 73: Cho hàm số có bảng biến thiên như sau
y g x
Hàm số đã cho đồng biến trên khoảng nào dưới đây
A. . B. . C. . D.
2;
;2
4;1
0;2
Lời giải
Chọn A
Quan sát bảng biến thiên hàm số đã cho đồng biến trên khoảng .
2;
Câu 74: Cho số phức . Phần thực và phần ảo của số phức là
5 2z i
z
A. Phần thực bằng và phần ảo bằng . B. Phần thực bằng và phần ảo bằng .
5
2
5
2
C. Phần thực bằng và phần ảo bằng . D. Phần thực bằng và phần ảo bằng .
2
5
2
5
Lời giải
Chọn A
Ta có Phần thực bằng và phần ảo bằng
5
2
Câu 75: Đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng
4 2
2 3y x x
A. . B. . C. . D. .
0
3
1
1
Lời giải
Chọn B
Trục tung có phương trình: . Thay vào được: .
0x
0x
4 2
2 3y x x
3y
Câu 76: Trong mặt phẳng , gọi , , lần lượt là các điểm biểu diễn các số phức ,
Oxy
A
B
C
1
3z i
, , là trọng tâm của tam giác . Số phức có điểm biểu diễn là
2
2 2z i
3
5z i
G
ABC
G
A. . B. . C. . D. .
1z i
1 2z i
1 2z i
2z i
Lời giải
Chọn C
Ta có , , .
0; 3A
2; 2B
5; 1C
Gọi .
;G x y
Do là trọng tâm của tam giác nên .
G
ABC
0 2 5
1
3
3 2 1
2
3
x
y
1; 2G
Vậy là điểm biểu diễn số phức .
G
1 2z i
Câu 77: Trong không gian , mặt phẳng đi qua ba điểm , , có
Oxyz
( )P
0;1;2A
1;3; 2B
2;1;3C
phương trình là
A. . B. .
2 5 2 9 0x y z
2 5 2 9 0x y z
C. .D. .
2 7 4 15 0x y z
7 4 15 0x y z
Lời giải
Chọn C
Ta có ,
1;2; 4AB
2;0;1 , 2; 7; 4 .AC AB AC
Gọi là một véctơ pháp tuyến của mặt phẳng đi qua ba điểm .
n
P
, ,A B C
Suy ra .
2; 7; 4n
Phương trình của đi qua nhận là một véctơ pháp tuyến là
mp P
0;1;2A
n
hay .
2 0 7 1 4 2 0x y z
2 7 4 15 0x y z
Câu 78: Trong không gian cho điểm và mặt phẳng Phương
,Oxyz
(2; 0; 7)M
( ) : 2 3 5 0.P x y z
trình của đường thẳng đi qua và vuông góc với có phương trình là
M
( )P
A. B. C. D.
1
2 .
2 3
x t
y t
z t
2 2
.
7 3
x t
y t
z t
3 2
1 .
2 3
x t
y t
z t
2 2
.
7 3
x t
y t
z t
Lời giải
Chọn B
Ta có mặt phẳng
( ) : 2 3 5 0.P x y z
Mặt phẳng có véc tơ pháp tuyến là
P
2; 1;3
P
n
Gọi đường thẳng cần tìm là . Vì đường thẳng vuông góc với nên véc tơ pháp tuyến
P
của mặt phẳng là véc tơ chỉ phương của đường thẳng .
P
2; 1;3
P
u n
Vậy phương trình đường thẳng đi qua và có véc tơ chỉ phương là:
(2; 0; 7)M
2; 1;3u
2 2
.
7 3
x t
y t
z t
Câu 79: Cho hình chóp tam giác đều có cạnh bên bằng , đường cao bằng ( tham khảo
.S ABC
2a
a
hình vẽ)
Góc giữa cạnh bên và mặt đáy bằng
A. B. C. D.
0
90 .
0
30 .
0
45
0
60
Lời giải
Chọn B
Gọi là trung điểm .
F
BC
Gọi là trọng tâm tam giác .
H
ABC
là hình chiếu vuông góc của trên mặt phẳng
AH
SA
ABC
Góc giữa cạnh bên và mặt đáy bằng : .
SA
ABC
SAH
0
1
sin 30
2 2
a
SAH SAH
a
Câu 80: Hàm số nào dưới đây nghịch biến trên
?
A. B. C. D.
3
3.y x
1
.
2
x
y
x
4 2
2 .y x x
3 2
3 .y x x
Lời giải
Chọn A
Ta có:
3 2
3 3 0, , 0 0.y x y x x y x
Vậy hàm số nghịch biến trên
3
3y x
.
Câu 81: Diện tích hình phẳng giới hạn bởi các đường là
2
, 3y x y x
A. B. . C. . D. .
9
.
2
4
3
5
2
Lời giải
Chọn B
Xét phương trình: .
2
0
3
3
x
x x
x
Suy ra diện tích hình phẳng giới hạn bởi các đường là
2
, 3y x y x
3
2
0
9
3 d .
2
S x x x
Câu 82: Cho hình lăng trụ đứng có đáy là tam giác vuông cân tại có
.ABC A B C
ABC
B
3AB a
cạnh bên ( tham khảo hình vẽ). Khoảng cách từ điểm đến mặt phẳng là
3AA a
A
A BC
A. B. C. D.
6
.
3
a
3
.
2
a
2
.
3
a
3
.
2
a
Lời giải
Chọn D
Kẻ .
1AJ A B
Ta có .
2
BC AB
BC AA B BC AJ
BC AA
Từ và
1
2 AJ A BC
Vậy .
,d A A BC AJ
2 2 2 2
. 3 . 3 3
2
9 3
AA AB a a
a
AA AB a a
Câu 83: Có tấm thẻ được đánh số từ đến . Chọn ngẫu nhiên thẻ. Xác suất để chọn được
10
1
10
2
2
tấm thẻ đều ghi số chẵn là
A. B. C. D.
2
.
9
1
.
4
7
.
9
1
.
2
Lời giải
Chọn A
Số cách chọn ngẫu nhiên thẻ từ thẻ là:
2
10
2
10
C
Trong thẻ có thẻ đánh số chẵn nên số cách chọn thẻ đánh số chẵn: .
10
5
2
2
5
C
Vậy xác suất cần tính là: .
2
5
2
10
2
9
C
C
Câu 84: Cho hàm số . Tọa độ điểm cực tiểu của đồ thị hàm số là
3 2
3 2f x x x
A. B. C. D.
2; 2
2;2
0; 2
2;0
Lời giải
Chọn A
Ta có:
3 2 2
3 2 3 6f x x x f x x x
Nên: . Từ đó ta có bảng biến thiên như sau:
2
0
0 3 6 0
2
x
f x x x
x
Vậy điểm cực tiểu của đồ thị hàm số là điểm .
2; 2A
Câu 85: Gọi lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên
,M m
4 2
2 3f x x x
đoạn . Giá trị bằng
2;1
M m
A. B. C. D.
9.
8.
1.
2.
Lời giải
Chọn A
Ta có: .
4 2 3
2 3 4 4f x x x f x x x
Nên:
3
0 2;1
0 4 4 0 1 2;1
1 2;1
x
f x x x x
x
Và:
2 5, 0 3, 1 4, 1 4f f f f
Vậy: .
4, 5 9M m M m
Câu 86: Trong không gian , mặt cầu có tâm và đi qua có phương trình
Oxyz
S
1; 1;2I
1;1; 1A
là:
A. . B. .
2 2 2
2 2 4 5 0x y z x y z
2 2 2
2 2 4 11 0x y z x y z
C. . D. .
2 2 2
2 2 4 17 0x y z x y z
2 2 2
2 2 4 11 0x y z x y z
Lời giải
Chọn B
Ta có: .
2 2 2
1 1 1 1 1 2 17IA
Phương trình mặt cầu có tâm và đi qua có bán kính ,
S
1; 1;2I
1;1; 1A
17R IA
Nên ta có phương trình:
2 2 2
: 1 1 2 17S x y z
.
2 2 2
: 2 2 4 11 0S x y z x y z
Vậy phương trình mặt cầu cần tìm là .
2 2 2
: 2 2 4 11 0S x y z x y z
Câu 87: Cho hàm số có đồ thị như hình vẽ. Các miền và có diện tích lần lượt là 8 và 2.
A
B
Tích phân bằng:
4
1
df x x
O
x
y
A
B
1
3
4
A. 6. B. 2. C. 18. D. 10.
Lời giải
Chọn A
Ta có: .
4 3 4
1 1 3
d d d 8 2 6f x x f x x f x x
Vậy
4
1
d 6f x x
Câu 88: Tích các nghiệm của phương trình bằng:
2
2
log 3 7 3x x
A. . B. . C. . D. .
8
3
7
3
7
3
8
3
Lời giải
Chọn A
2
2
log 3 7 3x x
Điều kiện: .
2
7
3 7 0
3
0
x
x x
x
2 2 3
2
log 3 7 3 3 7 2x x x x
2
3 7 8 0x x
(TMĐK)
7 145
6
7 145
6
x
x
Vậy tích các nghiệm bằng .
7 145 7 145 8
.
6 6 3
Câu 89: Cho tam giác vuông tại có . Thể tích khối tròn xoay sinh bởi hình tam
ABC
A
4, 2AB AC
giác khi quay quanh cạnh bằng
BC
A. . B. . C. . D. .
32 5
15
5
5
2 5
3
5
15
Lời giải
Chọn A
Ta có .
2 2
2 5BC AB AC
Gọi là hình chiếu vuông góc của lên .
K
A
BC
Ta có .
2
2 2 2
1 1 1 1 1 5 16
16 4 16 5
AK
AK AB AC
Khi đó .
2 2 2
1 1 1 1 16 32 5
. . . . . . . .2 5
3 3 3 3 5 15
V AK BK AK CK AK BC
Câu 90: Cho hình chóp có đáy là hình thoi cạnh . Tam giác cân
.S ABCD
ABCD
0
2 , 60a ABC
SAC
tại . Góc giữa cạnh và mặt phẳng bằng . Thể tích khối chóp
, 3S SB a
SA
SBD
0
30
bằng
.S ABCD
A. . B. . C. . D. .
3
3
2
a
3
3a
3
2a
3
4a
Lời giải
Chọn B
Gọi .
O AC BD
Ta có , khi đó .
,AO BD AO SO AO SBD
0
, , 30SA SBD SA SO ASO
Khi đó , do nên là tam
0
2 .cot 30 3AC a AO a SO AO a
3SB BO a
SBO
giác đều cạnh .
3a
Vậy .
2
3
. .
3 . 3
4 4
4 . . . . 3
3 3 4
S ABCD A SBO SBO
a
V V AO S a a
Câu 91: Cho hàm số có đạo hàm liên tục trên đồng thời thỏa mãn
0;
2
và . Giá trị của bằng
2
2
0 0
d 3 , sin d 2
2
x
f x x x x f x
4
2
f
4
0
sin df x x x
A. . B. . C. . D. .
8 5 3
3
8 5 2
3
8 5 2
3
8 5 3
3
Lời giải
Chọn D
Có .
0
sin d 2
2
x
I x x f x
Đặt .
2 2
0 0
2 sin 2 2 d 2 sin 2 2 d
2
x
t I t t f t t x x f x x
Tích phân từng phần cho , ta được:
I
2
2
0
0
sin 2 2 2cos 2 2 d
2
I
x x f x x f x x
2
0
2 cos 2 1 d
2
f x f x x
2 2
2 2
0 0
4 4 sin d 4 sin d 3x f x x x f x x
Có
2 2 2
2 2 4
0 0 0
d 2 4sin d 16 sin d 3 2.3 3 0f x x xf x x x x
2
2
2
0
2 2
4sin d 0
4sin 0 4sin , 0; .
2
f x x x
f x x f x x x
Vậy .
4 4 4
3
0 0 0
sin d 4sin d 3sin sin 3 df x x x x x x x x
4
0
1 8 5 3
cos3 3cos
3 3
x x
Câu 92: Cho hai số phức , thỏa mãn: và . Gọi , lần lượt
1
z
2
z
1 2
2z z
1 2
4 4 3 2z i z
M
m
là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức , giá trị bằng
2
1 2P z i
2 2
M m
A. . B. . C. . D. .
50
54
34
99
2
Lời giải
Chọn C
Gọi lần lượt là điểm biểu diễn của ; là điểm biểu
,A B
1 2
1 2
2
2
,
z z AB
z z
z OB
4;4C
diễn của số phức .
4 4i
Có .
1 2
4 4 3 2 3 2 3 2z i z AC OB AC OB
theo thứ tự nằm trên đoạn
4 2
4 2
OB AC AB
OB BA AC OC
OC
, , ,O B A C
OC
.
Điểm biểu diễn cho số phức .
1; 2D
1 2i
.
min
2 2
2
max
5
1 2 34
29
P OD
P z i BD M m
P DN
khi trùng , trùng với .
max
(P
A
C
B
3;3N
)
Câu 93: Cho hàm số có đồ thị như hình vẽ
Số nghiệm thuộc đoạn của phương trình là
0;5
cos 1f x
A. . B. C. . D. .
6
3
4
5
Lời giải
Chọn D
Đặt: . Với mọi .
cost x
0;5 1;1x t
Khi đó, ta có .
1
2
0 1
1, 1;1
1 1;1
t
f t t
t
Ta thấy với thì phương trình có 5 nghiệm phân biệt.
0;5x
1 1
cos , 0;1x t t
Vậy số nghiệm thuộc đoạn của phương trình là 5.
0;5
cos 1f x
Câu 94: Số giá trị nguyên của tham số để phương trình có hai
m
2 2
2 2
1 log 10log 0m x x m
nghiệm phân biệt không nhỏ hơn là
1
A. . B. .C. . D. .
4
2
1
3
Lời giải
Chọn D
Điều kiện:
0x
Đặt . Phương trình trở thành: .
2 2
1 10 0 1m t t m
Để phương trình đã cho có hai nghiệm phân biệt không nhỏ hơn thì phương trình có hai
1
1
nghiệm phân biệt
3
3
1 2
2
2
25 0
0
25 0
10
0 0 0
1
0
0
0
1
m m
m m
t t S
m
m
P
m
m
Vì nguyên nên .
m
0;1;2m
Câu 95: Biết rằng tồn tại duy nhất bộ số và là phân số tối giản sao cho
*
, ,a b c
b
c
. Giá trị của biểu thức thuộc khoảng
ln8
ln3
2
d 2ln
1
x
x
e b
x a
c
e
a b c
A. . B. . C. . D.
11;15
1;5
16;20
6;10
Lời giải
Chọn B
Xét .
ln8 ln8
ln3 ln3
2
2
d d
1 1 .
x x
x
x x x
e e
e
I x x
e e e
Đặt .
2
1 1 2 d d
x x x
t e t e t t e x
Đổi cận: ; .
ln3 2x t
ln8 3x t
Khi đó
2
3 3 3
2
2 2
2
2 2 2
3 3
2 2
3
3
2
2
1 2 d
1 2
2 d 2 1 d
1 1
1
( 1) ( 1)
2 d 2 d
( 1)( 1)
1 1 1
2 2 d 2 2 ln
1 1 1
1 1 3
2 2 ln ln 2 2(ln3 ln 2) 2 2ln
2 3 2
t t t
t
I t t
t t
t t
t t
t t
t t
t
t
t t t
Suy ra .
2
3 7
2
a
b a b c
c
Câu 96: Trong không gian , cho đường thẳng và mặt phẳng
Oxyz
2 1 2
:
4 4 3
x y z
d
. Đường thẳng song song với đồng thời tạo với góc bé nhất.
( ) : 2 2 1 0P x y z
( )P
d
Biết rằng có một véc tơ chỉ phương . Giá trị biểu thức bằng
( ; ;1)u m n
2 2
T m n
A. . B. . C. . D. .
5T
2T
3T
4T
Lời giải
Chọn D
Véc tơ chỉ phương , véc tơ pháp tuyến .
: (4; 4;3)
d
d u
( ) : (2; 1;2)
P
P n
Ta có .
. 0 2 2 0 2 2
P
u n m n n m
2 2 2 2 2 2 2 2
2
2
2
2 2
. 4 4 3 4 4(2 2) 3
cos( , )
.
4 ( 4) 3 1 41 (2 2) 1
4 5
4 5
1 1 16 40 25
.
5 8 5
41 41
41 5 8 5 5 8 5
d
d
u u m n m m
d
u u
m n m m
m
m
m m
m m
m m m m
Đặt ; .
2
2
16 40 25
( )
5 8 5
m m
f m
m m
2
2
2
72 90
( )
5 8 5
m m
f m
m m
2
0
( ) 0 72 90 0
5
.
4
m
f m m m
m
Có .
2
2
5
l
16 40 25 16
5 8 5
im
m
m m
m m
®±¥
+ +
=
+ +
Ta có bảng biến thiên
Góc giữa và bé nhất khi lớn nhất. Khi đó dựa vào bảng biến thiên ta thấy
d
( )f m
. Vậy .
0 2m n= Þ =
2 2
0 4 4T m n
Cách khác:
Gọi là hình chiếu của lên , khi đó góc của và là góc của và . Mà
d
( )P
P
d
d
//( )P
nên góc và d nhỏ nhất khi .
//
Véc tơ chỉ phương , véc tơ pháp tuyến . Gọi là mặt
: (4; 4;3)
d
d u
( ) : (2; 1;2)
P
P n
( )Q
phẳng chứa và vuông góc với véc tơ pháp tuyến , là
d
( )P
, ( 5; 2;4)
Q d P
n u n
hình chiếu của lên .
d
( )P
( ) ( ) , (0; 18; 9) 2(0;2;1)
P Q
P Q u u n
.
2 2
0 4 4T m n
Câu 97: Biết phương trình ( là tham số thực) có hai nghiệm . Gọi
2 2
8 0 z mz m
m
1 2
,z z
, ,A B C
lần lượt là điểm biểu diễn của các số phức và . Có bao nhiêu giá trị của để
1 2
,z z
0
2z
m
đều?
ABC
A. 1. B. 3. C. 4. D. 2.
Lời giải
Chọn D
Để tồn tại thì phải là hai nghiệm không thuần thực của phương trình
ABC
1 2
,z z
.
2 2
8 0 z mz m
Suy ra .
2 2
32 32 32
0 5 32 0
5 5 5
m m m
Khi đó . Suy ra .
1,2
2
m i
z
; , ; , 2;0
2 2 2 2
m m
A B C
Ta có .
2
2
2 2 2 2 2
1 2 1 2 1 2
2
2
2
4 4 8 5 32 32 5
1
2 4 8 48
2 2 2
AB z z z z z z m m m AB m
m
AC BC m m
Để đều thì
ABC
2 2
1
32 5 4 8 48
2
AB AC m m m
.
2 2 2
5
2
32 5 2 12 4 2 20 0
2
m n
m m m m m
m n
Vậy có 2 giá trị của để đều.
m
ABC
Câu 98: Trong không gian , cho đường thẳng và mặt phẳng
Oxyz
2 1
:
1 1 1
x y z
. Đường thẳng nằm trong mặt phẳng sao cho cắt đồng thời
: 2 2 6 0 P x y z
d
P
d
vuông góc với đường thẳng . Khi đó đường thẳng đi qua điểm nào trong các điểm sau
d
đây?
A. . B. . C. . D. .
2;2;0
2;2; 2
0;4;1
2;3;1
Lời giải
Chọn C
Gọi
A d
A P
Tọa độ thỏa mãn hệ .
A
6
0
1 0;1; 2
2
2 1
1 1 1
2 2 0
x
x
y
A
z
z
z
y
x y
Do và nên nhận là một vectơ chỉ phương.
d P
d
1 1
. . ; 0;1;1
3 3
P
u n u
Đường thẳng đi qua nên có dạng .
0;1; 2A
0
1
2
x
y t t
z t
Nhận thấy đi qua điểm .
0;4;1
Câu 99: Cho hàm số đa thức bận bốn có đồ thị hàm số như hình vẽ:
y f x
y f x
Tổng các giá trị nguyên của để hàm số có đúng 3 điểm cực tiểu là
m
1 9y f x m
A. . B. . C. . D. .
40
34
24
30
Lời giải
Chọn D
Từ hình vẽ ta có bảng biến thiên của hàm số :
f x
Từ bảng biến thiên ta thấy được để hàm số có đúng 3 điểm cực tiểu khi
1 9y f x m
và chỉ khi .
3 9 1 6 10 6;7;8;9m m m
Câu 100: Có bao nhiêu số nguyên dương , sao cho ứng với mỗi giá trị của có đúng 11 số nguyên
x
x
y
thỏa mãn bất phương trình ?
2
2 5 1 0
y y
x x
A. . B. . C. . D. .
55
34
130
88
Lời giải
Chọn D
Đặt
2
2 5 1 0 *
y y
x x
Xét phương trình
2
2
5
2log
2 5 1 0
log 1
y y
y x
x x
y x
Với , không thỏa mãn.
1x
5
* 0 log 2y
Với thì , khi đó
2x
2 5
2log log 1x x
5 2
* log 1 2logx y x
TH1: Với ,
2;24x
5 5
2 2
log 3 log 1 2
2 2log 2log 24
x
x
2 5
2log log 1 10, 2;24x x x
Nên không tồn tại đủ 11 số nguyên thuộc Không thỏa mãn.
5 2
log 1 ;2logx x
TH2: .
5
13
7
2
2
24 124
2 log 1 3
91;92;...;124
13 2log 14
2 2
x
x
x
x
x
TH3: .
5
15
7
2
2
124 624
3 log 1 4
128;129;...;181
14 2log 15
2 2
x
x
x
x
x
TH4:
1
5
11
2 2
2
5 1 5 1
log 1 1
4 1
11 2log 12
2 8.2
n n
n n
x
n x n
n
n x n
x
Do nên Không thỏa mãn.
2
5 1 2 2 8.2 , 4
n
n n n
n
1 x
Vậy .
91;92;...;124 128;129;...;181x
| 1/33
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


SỞ GIÁO DỤC VÀ ĐÀO TẠO HÒA BÌNH
ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2021 – 2022 – LẦN 1 Câu 1:
Cho cấp số cộng u u  1;u  5 u n  có . Khi đó bằng 1 3 2 A. 7  B. 3 C. 2  D. 9  3 8 8
f xdx  5   f
 xdx 8
f xdxCâu 2: Cho 0 và 3 , khi đó 0 bằng A. 13. B. 3. C. 1  3. D. 3  . Câu 3:
Hình phẳng D giới hạn bởi các đường y  ln  x  2 , trục hoành và hai đường thẳng 3
x  , x  3 . Diện tích hình phẳng D được tính là 2 3 3 A. 2 S ln
 x 2d .x B. S  ln
 x 2d .x 3 3 2 2 3 3 C. S  ln
 x 2 d .x D. S   ln
 x 2d .x 3 3 2 2  Câu 4:
Trong không gian Oxyz , cho hai điểm A 1  ;0;3, B1;2; 2
 . Tọa độ vectơ AB là A. 2;2;  1 . B. 2; 2  ; 5  . C.  2  ; 2  ;5. D. 2;2; 5  . Câu 5:
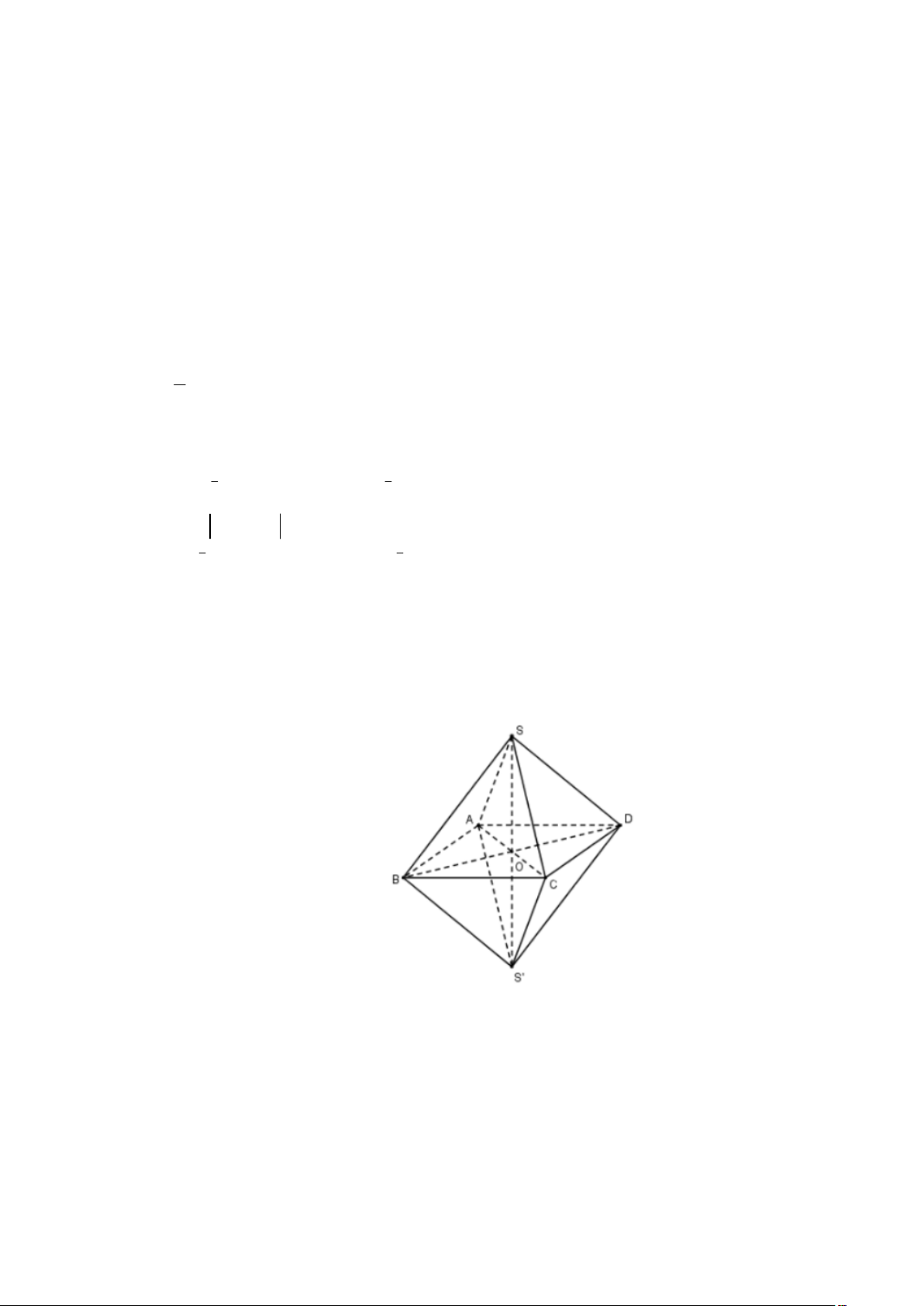
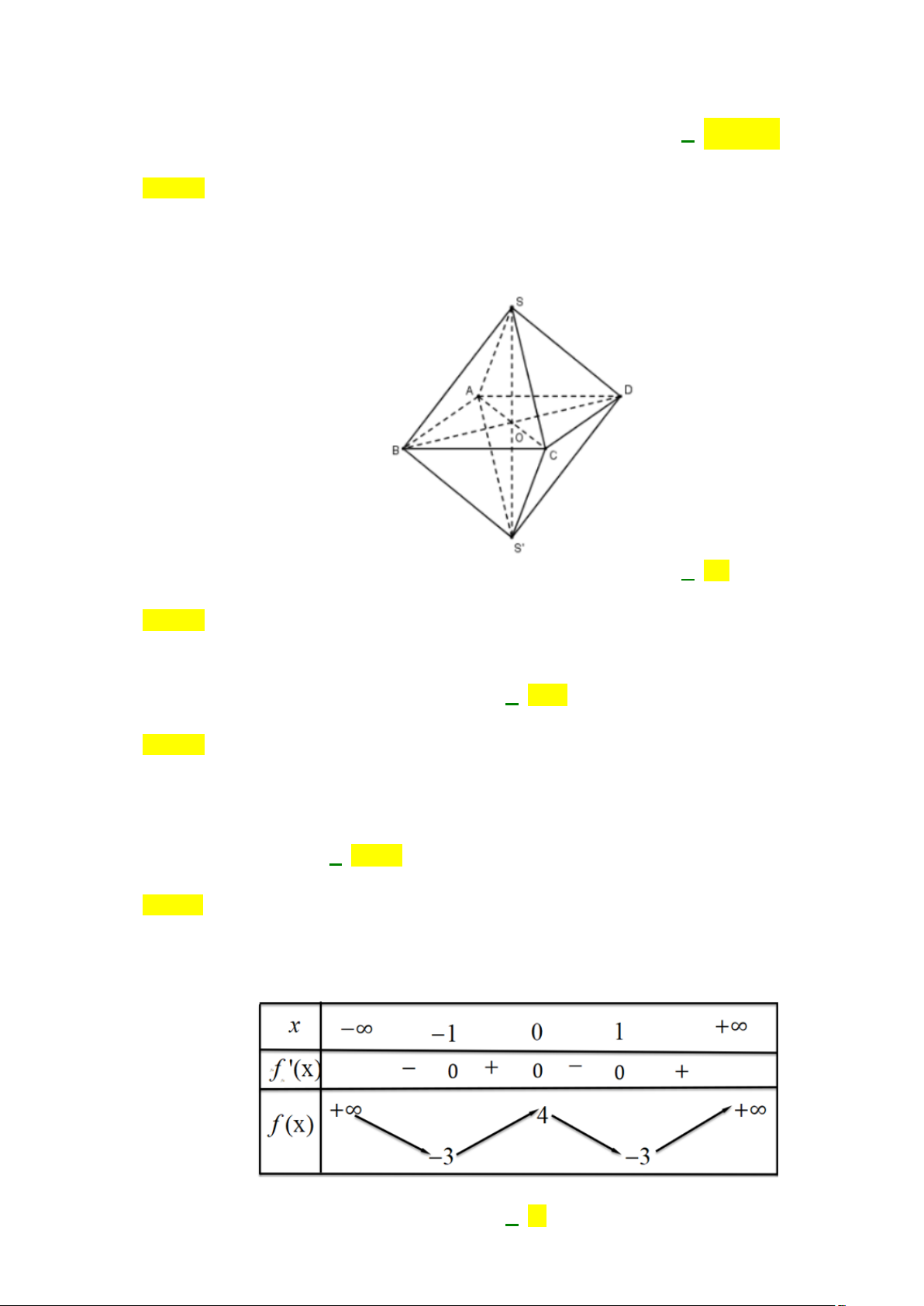
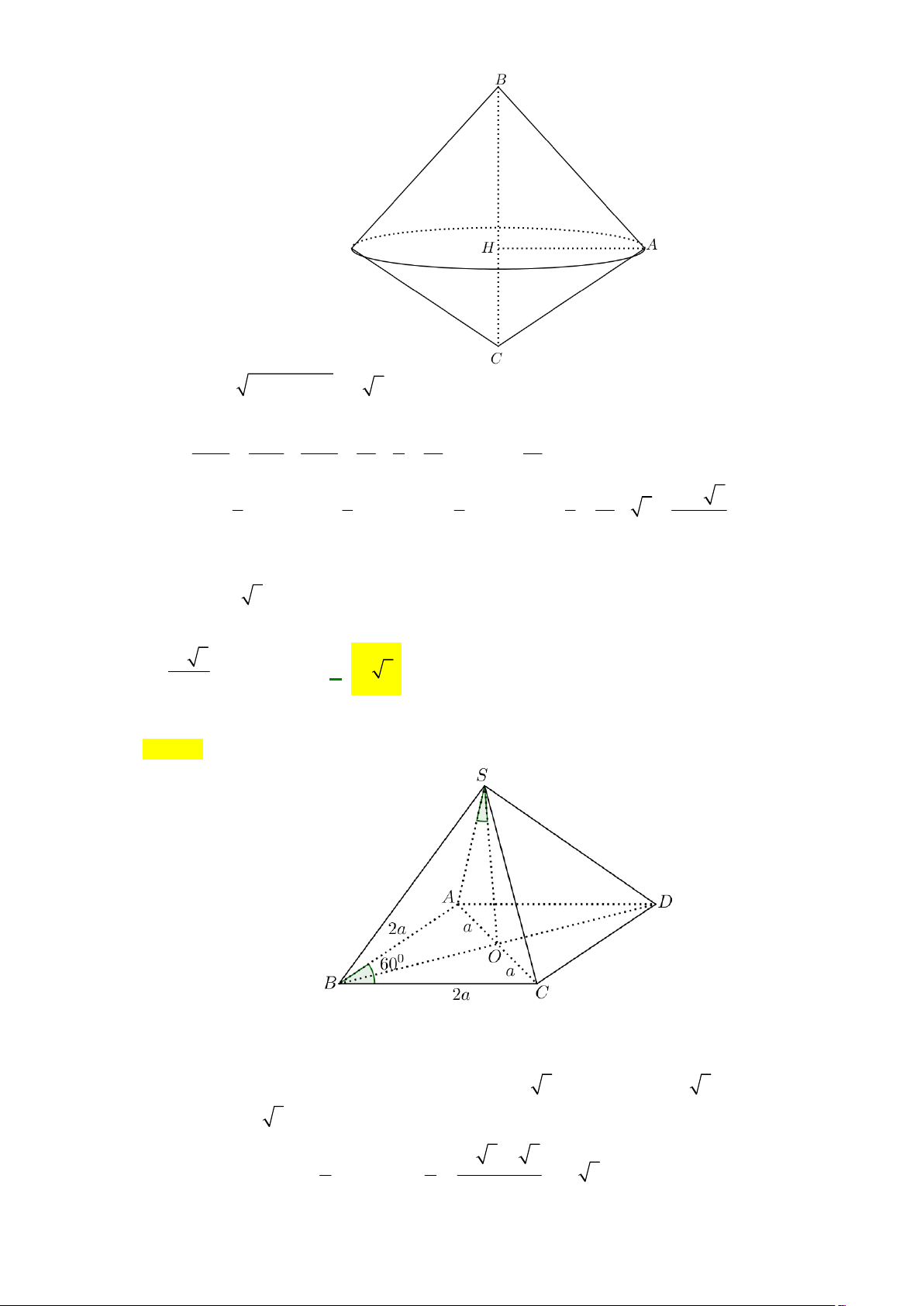
Cho hình bát diện đều như hình bên. Số cạnh của hình bát diện đều bằng A. 8. B. 14. C. 10. D. 12. Câu 6:
Diện tích xung quanh của hình trụ có bán kính đáy bằng 3 và độ dài đường sinh bằng 4 là A. 21. B. 42. C. 24. D. 48. Câu 7:
Nghiệm của phương trình 2x 1 5 - =125 là A. x = -2. B. x = 2. C. x =1. D. x = -1. Câu 8:
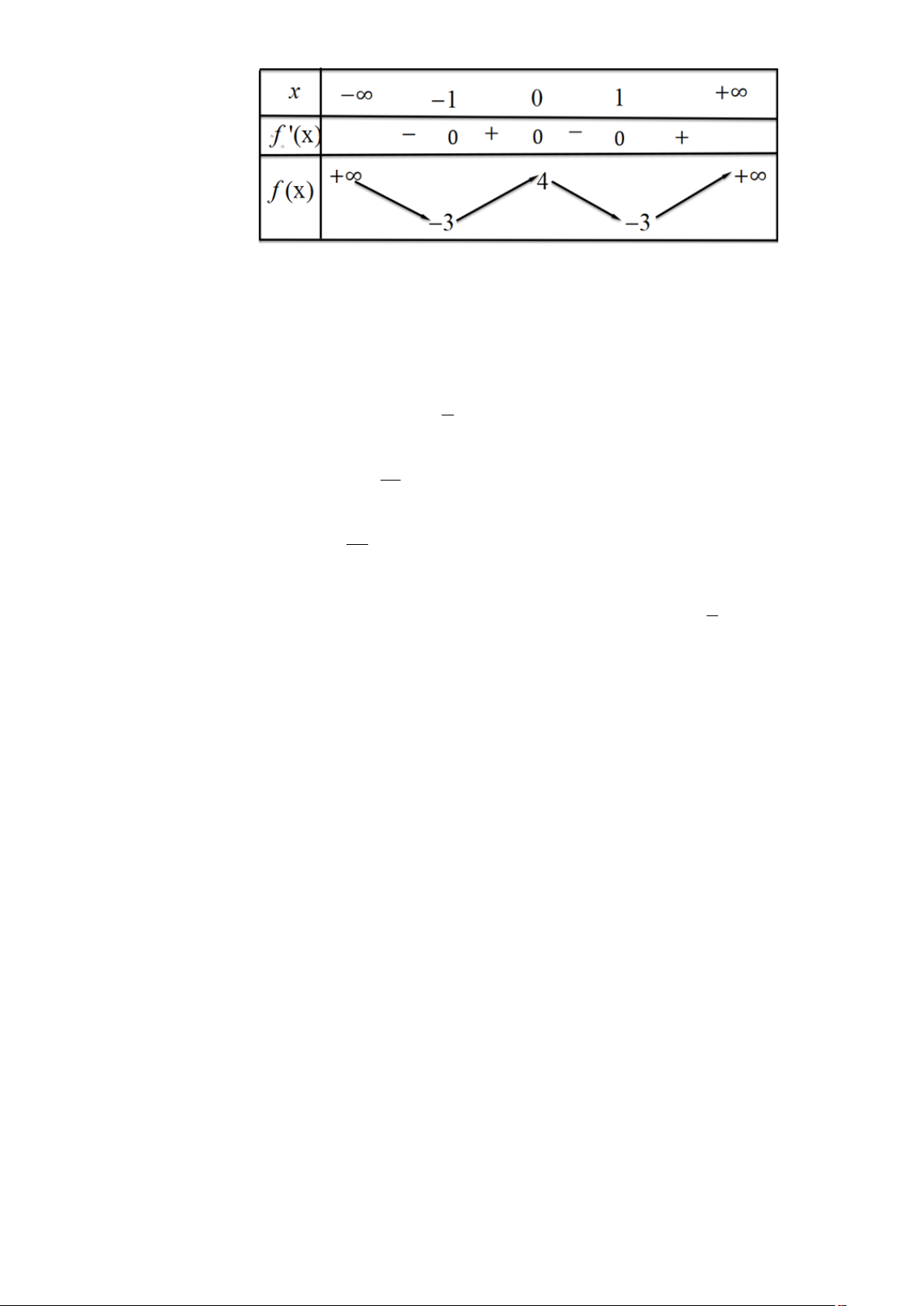
Cho hàm số y = f (x) có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng A. -3. B. 0. C. 4. D. -1. Câu 9:
Hàm số nào dưới đây là một nguyên hàm của hàm số f x  2x 1 A. 2 x x. B. 2 x  . x C. 2 x  2 . x D. 2 x  2 . x
Câu 10: Họ nguyên hàm của hàm số f x 1
 2  trên 0; là: x 1
A. 2x  ln x C. B. 2   C.
C. ln x C.
D. 2x  ln x C. 2 x 2  a
Câu 11: Với a  0 biểu thức log bằng 5   25   1
A. 2log a 1 . 2  log . a 2log a 1 . log . a 5  5  B. C. D. 5 5 2       Câu 12: Cho z 5 i; z 4 3i z z z 1 2 . Số phức 1 2 bằng A. 1   2i . B. 1 2i . C. 1   2i . D. 1 2i .
Câu 13: Cho hình lăng trụ có diện tích đáy B  15 và chiều cao h  6 . Thể tích khối lăng trụ đã cho bằng A. 30 B. 90 C. 45 D. 60
Câu 14: Tập xác định của hàm số y  log 5  x 3   là A.  ;  5 B. 5; C.  ;  5 D. 5;
Câu 15: Gọi z , z là hai nghiệm phức của phương trình 2
z  2z 10  0 . Giá trị của biểu thức 1 2
A z z là 1 2 A. 10 B. 1  0 C. 2  D. 2
Câu 16: Cho khối cầu có thể tích bằng 288. Bán kính khối cầu đã cho bằng A. 6 B. 3 C. 4 D. 2
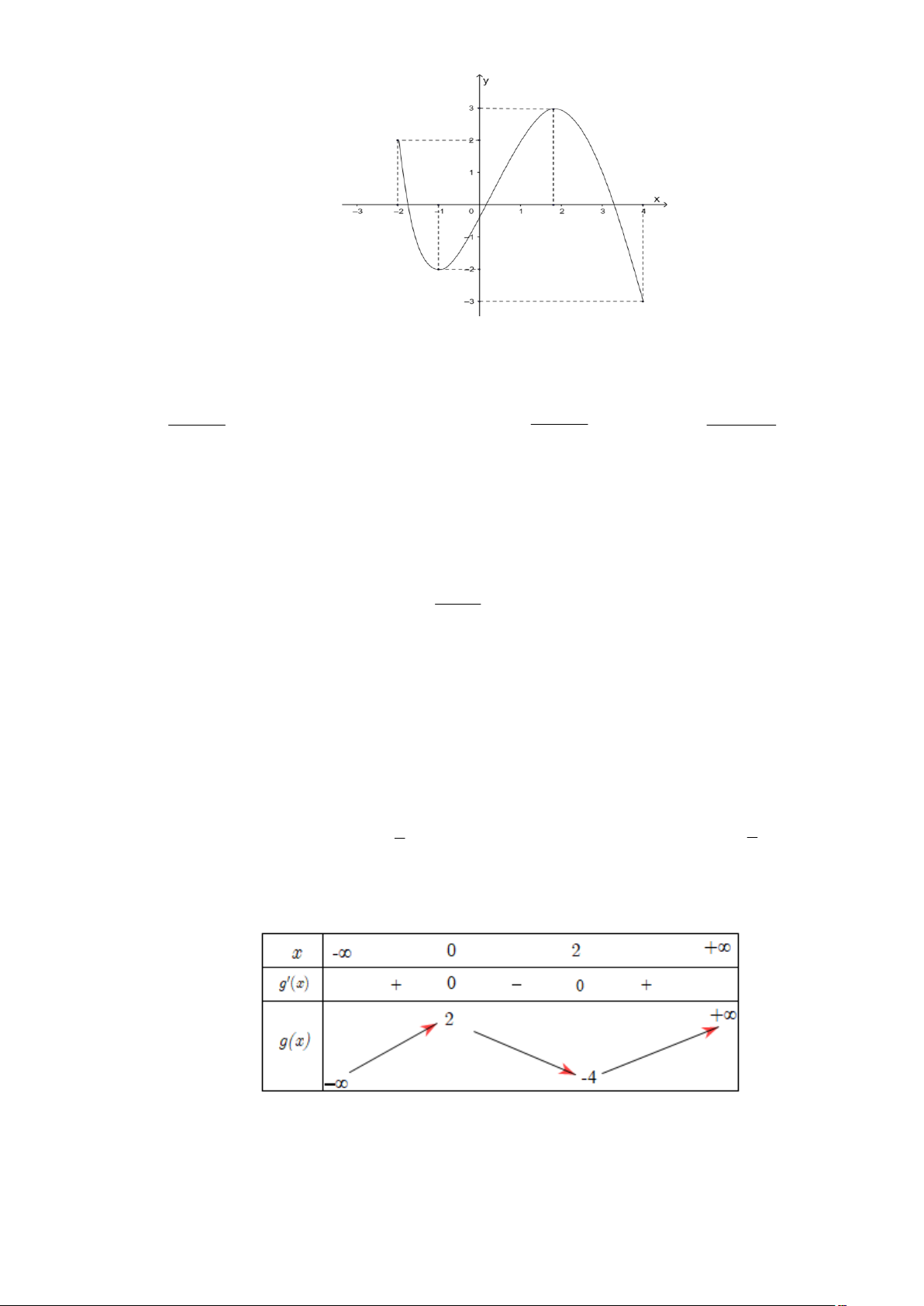
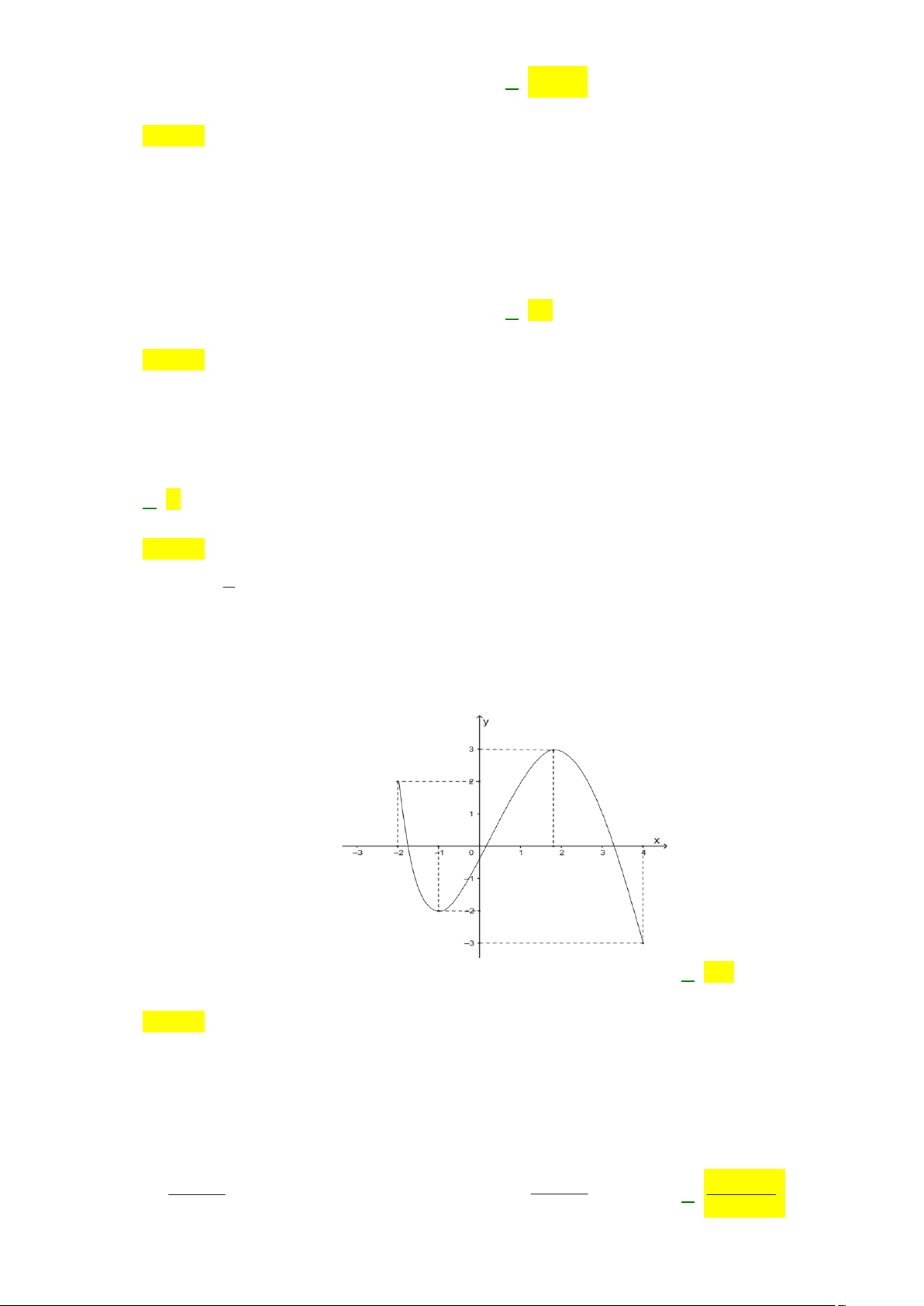
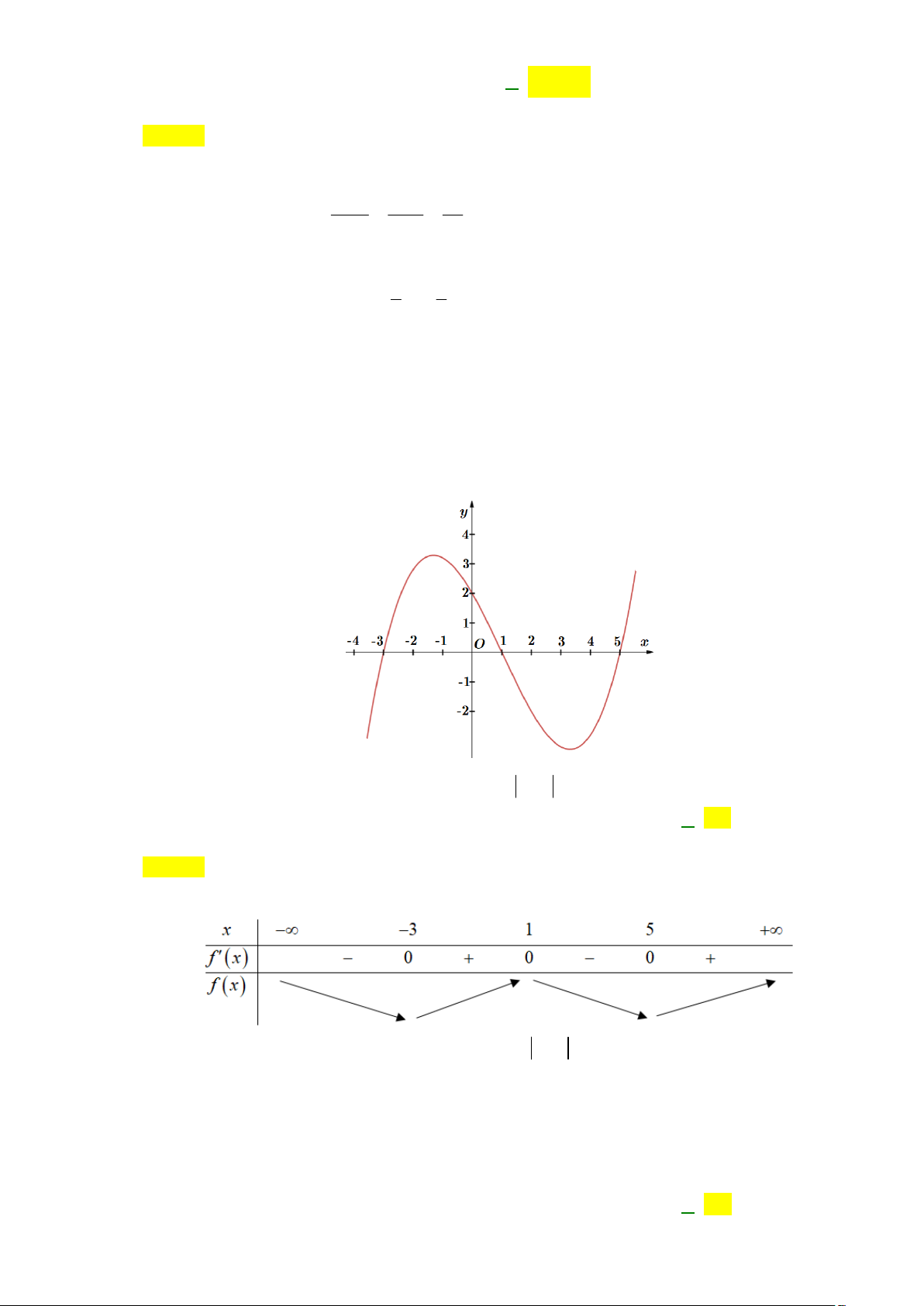
Câu 17: Cho hàm số y f x có đồ thị là đường cong trong hình bên. Giá trị nhỏ nhất của hàm số
y f x trên đoạn  2  ;4 bằng A. 2  . B. 3. C. 4. D. 3  .
Câu 18: Với x  0 đạo hàm của hàm số y  log x bằng 2022 ln 2022 x 1 A. . B. x ln 2022. C. . D. . x ln 2022 x ln 2022
Câu 19: Trong không gian Oxyz, mặt phẳng P : 3x  2y z  3  0 đi qua điểm nào trong các điểm dưới đây A. 1;0;  1 . B. 3; 3  ;2. C. 0;1;  1 . D.  2  ;3;3. 2x  3
Câu 20: Tiệm cận ngang của đồ thị hàm số y
là đường thẳng có phương trình x 1 A. y  1. B. y  2  . C. y  1  . D. y  2.
Câu 21: Số cách chọn 2 học sinh từ nhóm có 8 học sinh là A. 2 8 . B. 2 A . C. 16 . D. 2 C . 8 8
Câu 22: Tập nghiệm của bất phương trình 5x  3 là  5   A. ;log 5  ;  3 ;log 3 ; 5  3  . B. . C. . D.      3   5 
Câu 23: Cho hàm số y g x có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây A. 2;  . B. ;2 . C.  4  ;  1 . D. 0;2
Câu 24: Cho số phức z  5  2i . Phần thực và phần ảo của số phức z là
A. Phần thực bằng 5 và phần ảo bằng 2 .
B. Phần thực bằng 5 và phần ảo bằng 2  .
C. Phần thực bằng 2 và phần ảo bằng 5  .
D. Phần thực bằng 2  và phần ảo bằng 5 .
Câu 25: Đồ thị của hàm số 4 2
y x  2x  3 cắt trục tung tại điểm có tung độ bằng A. 0 . B. 3  . C. 1. D. 1  .
Câu 26: Trong mặt phẳng Oxy , gọi A , B , C lần lượt là các điểm biểu diễn các số phức z  3  i , 1
z  2  2i , z  5
  i , G là trọng tâm của tam giác ABC . Số phức có điểm biểu diễn G là 2 3 A. z  1   i .
B. z  1 2i . C. z  1   2i .
D. z  2  i .
Câu 27: Trong không gian Oxyz , mặt phẳng (P) đi qua ba điểm A0;1;2 , B 1  ;3; 2
  , C 2;1;3 có phương trình là
A. 2x  5y  2z  9  0 . B. 2x  5y  2z  9  0 .
C. 2x  7 y  4z 15  0 . D. x  7 y  4z 15  0 .
Câu 28: Trong không gian Oxyz, cho điểm M(2; 0;7) và mặt phẳng (P) : 2x y  3z  5  0. Phương
trình của đường thẳng đi qua M và vuông góc với (P) có phương trình là
x  1 t
x  2  2t
x  3  2t
x  2  2t    
A. y  2  t .
B. y  t .
C. y  1 t .
D. y  t . z  2      3t z  7   3t z  2   3t z  7   3t
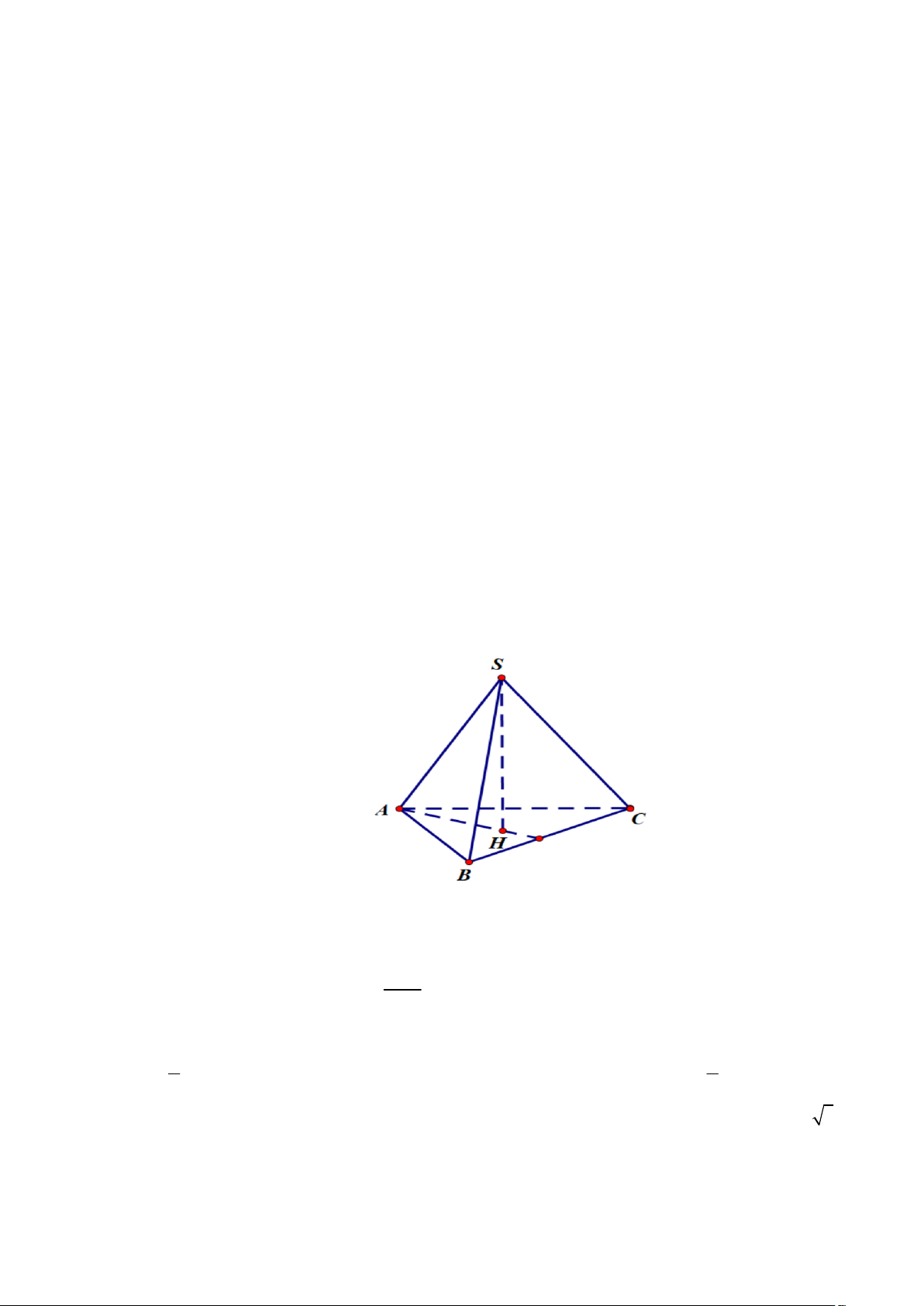
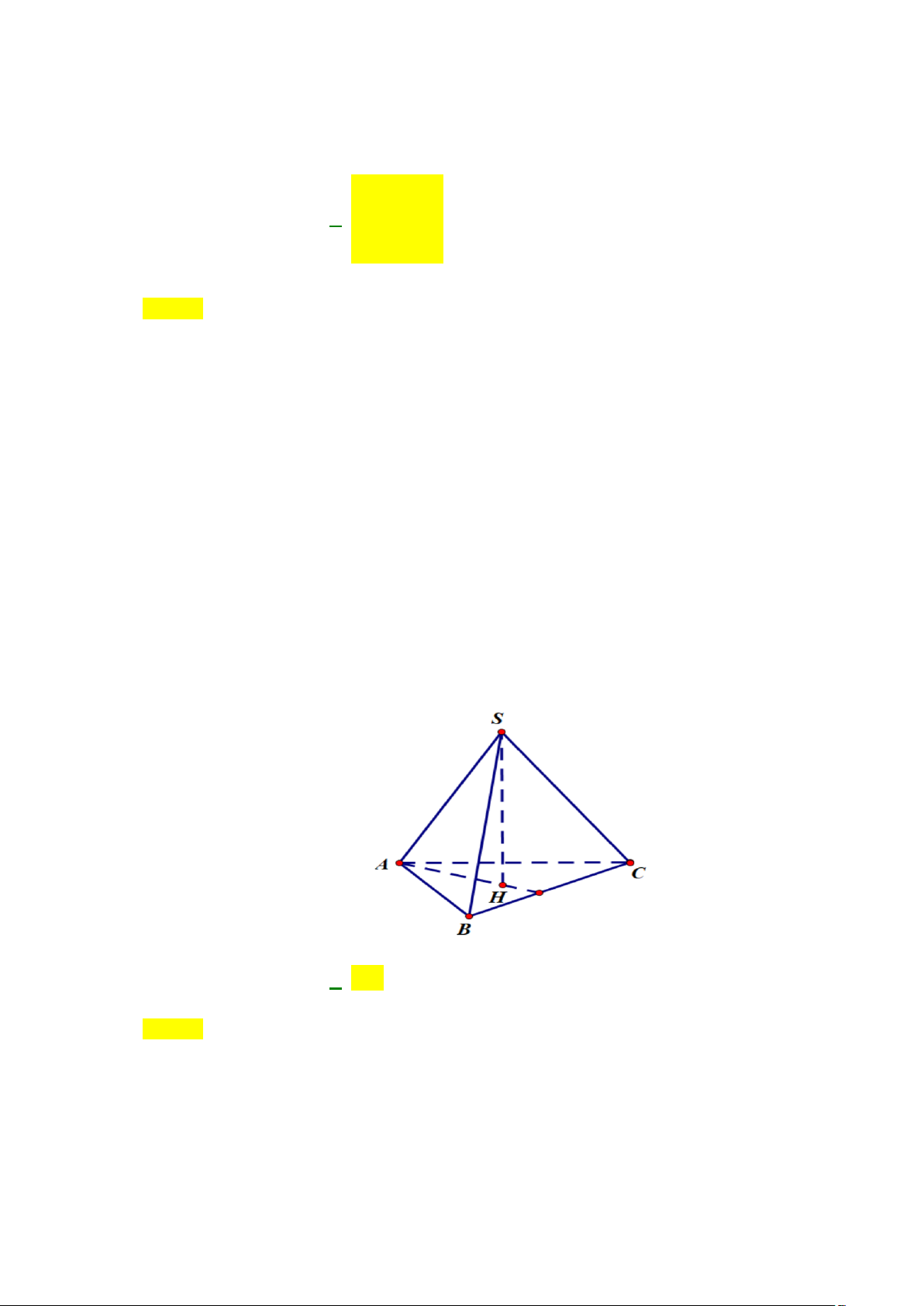
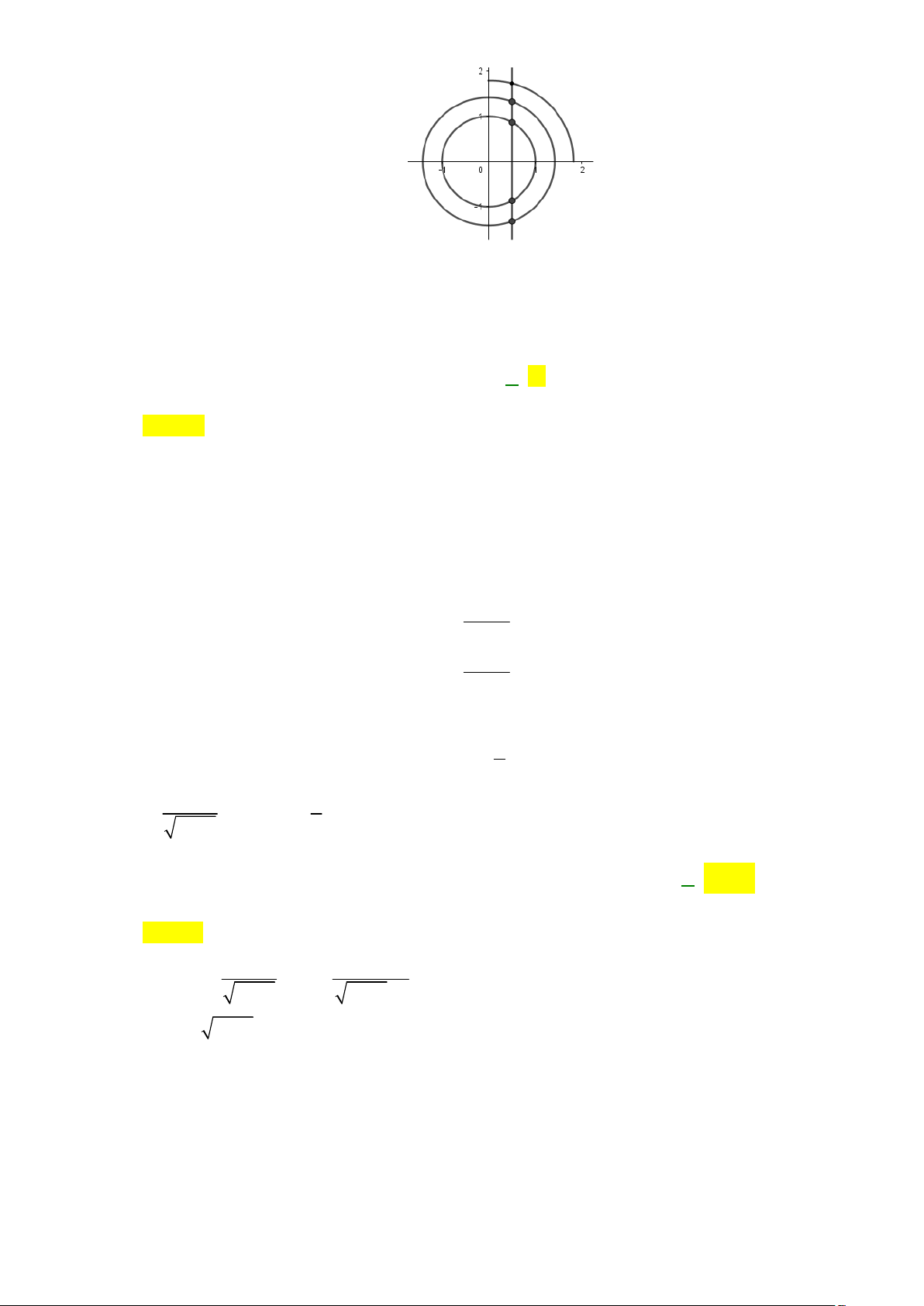
Câu 29: Cho hình chóp tam giác đều S.ABC có cạnh bên bằng 2a , đường cao bằng a ( tham khảo hình vẽ)
Góc giữa cạnh bên và mặt đáy bằng A. 0 90 . B. 0 30 . C. 0 45  D. 0 60 
Câu 30: Hàm số nào dưới đây nghịch biến trên ? x A. 3 y  x  1 3. B. y  . C. 4 2
y  x  2x . D. 3 2
y  x  3x . x  2
Câu 31: Diện tích hình phẳng giới hạn bởi các đường 2
y x , y  3x là 9 5 A. . B. 4 . C. 3 . D. . 2 2
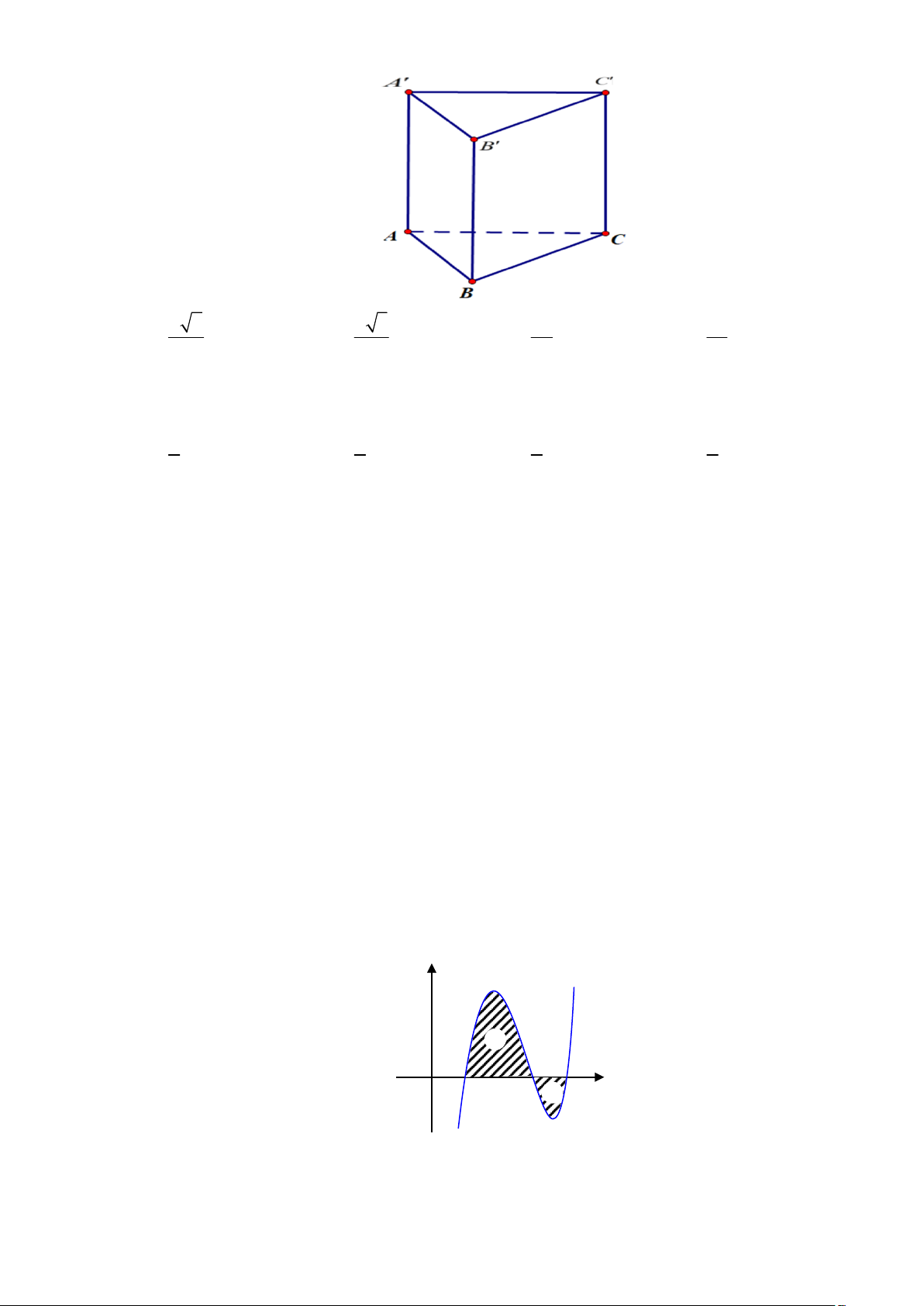
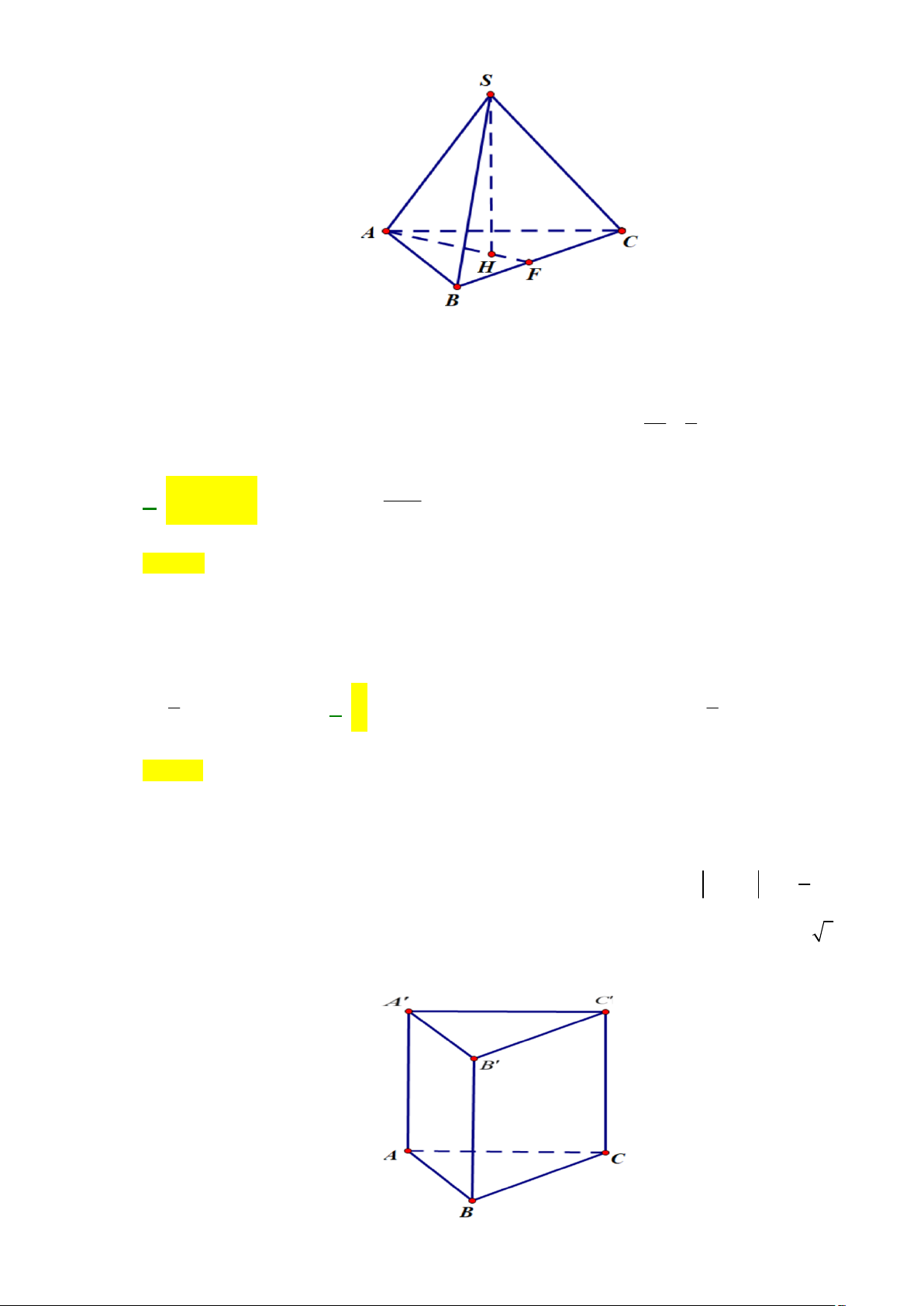
Câu 32: Cho hình lăng trụ đứng ABC.AB C
 có đáy ABC là tam giác vuông cân tại B có AB a 3
cạnh bên AA  3a ( tham khảo hình vẽ). Khoảng cách từ điểm A đến mặt phẳng  ABC là a 6 a 3 2a 3a A. . B. . C. . D. . 3 2 3 2
Câu 33: Có 10 tấm thẻ được đánh số từ 1 đến 10 . Chọn ngẫu nhiên 2 thẻ. Xác suất để chọn được 2
tấm thẻ đều ghi số chẵn là 2 1 7 1 A. . B. . C. . D. . 9 4 9 2
Câu 34: Cho hàm số f x 3 2
x  3x  2 . Tọa độ điểm cực tiểu của đồ thị hàm số là A. 2; 2   B.  2  ;2 C. 0; 2   D.  2  ;0
Câu 35: Gọi M ,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f x 4 2
 x  2x  3 trên đoạn  2  ; 
1 . Giá trị M m bằng A. 9. B. 8. C. 1  . D. 2  .
Câu 36: Trong không gian Oxyz , mặt cầu S  có tâm I  1  ; 1
 ;2 và đi qua A1;1;  1 có phương trình là: A. 2 2 2
x y z  2x  2y  4z  5  0 . B. 2 2 2
x y z  2x  2y  4z 11  0 . C. 2 2 2
x y z  2x  2y  4z 17  0 . D. 2 2 2
x y z  2x  2y  4z 11  0 .
Câu 37: Cho hàm số y f x có đồ thị như hình vẽ. Các miền A và B có diện tích lần lượt là 8 và 2. 4 Tích phân f
 xdx bằng: 1 y A 1 4 O 3 x B A. 6. B. 2. C. 18. D. 10.
Câu 38: Tích các nghiệm của phương trình log  2 3x  7x  3 2  bằng: 8 8 A.  7 . B.  7 . C. . D. . 3 3 3 3
Câu 39: Cho tam giác ABC vuông tại A có AB  4, AC  2 . Thể tích khối tròn xoay sinh bởi hình tam
giác khi quay quanh cạnh BC bằng 325 5 25 5 A. . B. . C. . D. . 15 5 3 15
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a  0
2 , ABC  60 . Tam giác SAC cân
tại S, SB a 3 . Góc giữa cạnh SA và mặt phẳng SBD bằng 0 30 . Thể tích khối chóp S.ABCD bằng 3 a 3 A. . B. 3 a 3 . C. 3 2a . D. 3 4a . 2 
Câu 41: Cho hàm số y f x có đạo hàm liên tục trên 0; đồng thời thỏa mãn  2    2 x 4 2 f
 xdx 3, sinx xf     dx  2  và f
 4 . Giá trị của f
 xsin dxx bằng      2   2  0 0 0 8  5 3 8  5 2 8  5 2 8  5 3 A. . B. . C. . D. . 3 3 3 3
Câu 42: Cho hai số phức z , z thỏa mãn: z z  2 và z  4  4i  3 2  z . Gọi M , m lần lượt 1 2 1 2 1 2
là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P z 1 2i , giá trị 2 2 M m bằng 2 99 A. 50 . B. 54 . C. 34 . D. . 2
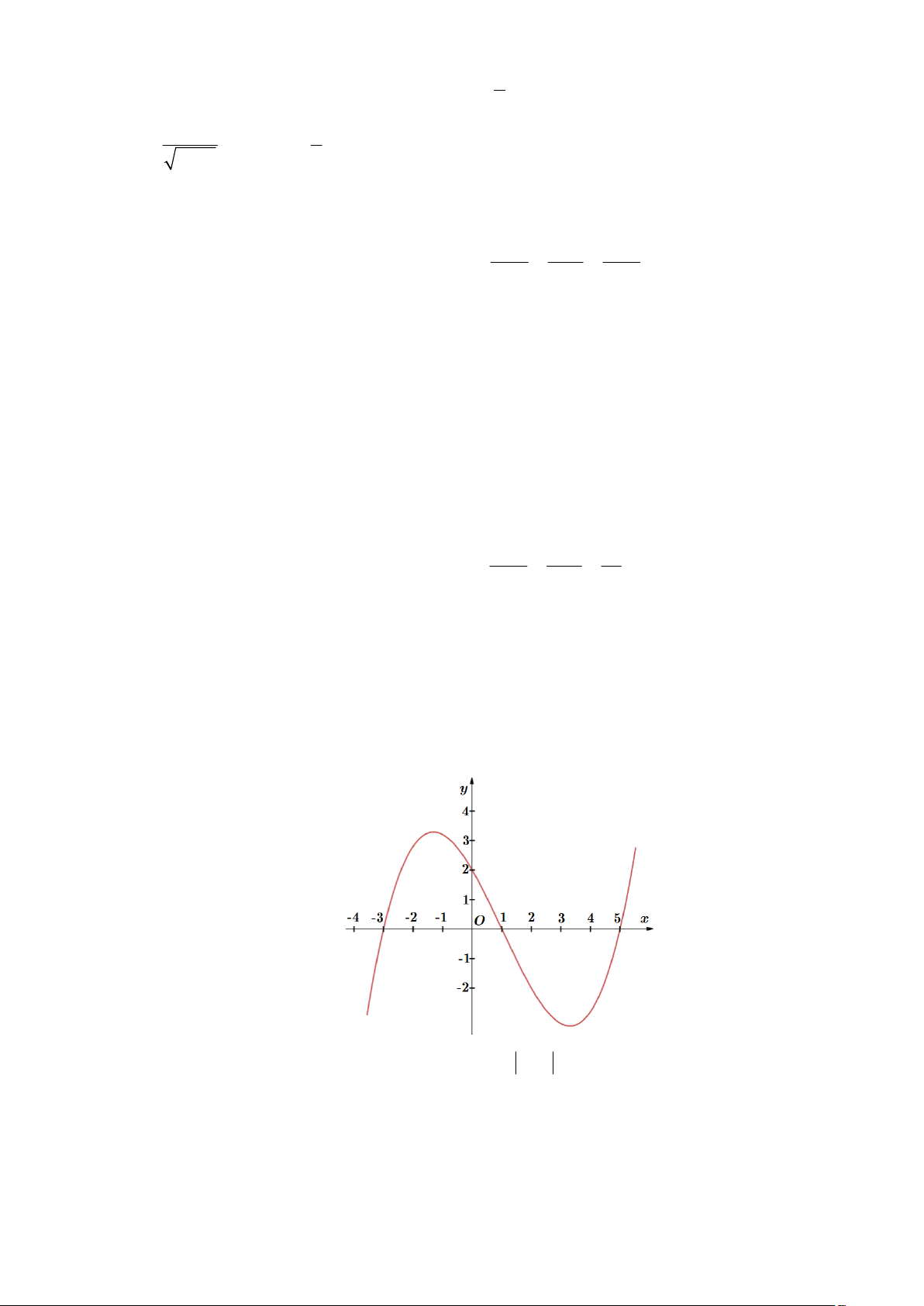
Câu 43: Cho hàm số y f x có đồ thị như hình vẽ
Số nghiệm thuộc đoạn 0;5 của phương trình f cos x 1 là A. 6 . B. 3 C. 4 . D. 5.
Câu 44: Số giá trị nguyên của tham số m để phương trình  2 m   2
1 log x 10log x m  0 có hai 2 2
nghiệm phân biệt không nhỏ hơn 1 là A. 4 . B. 2 . C. 1. D. 3.
Câu 45: Biết rằng tồn tại duy nhất bộ số * a, , b c   b
và là phân số tối giản sao cho c ln 8 x e  2 b
dx a  2ln . Giá trị của biểu thức   thuộc khoảng  a b c xe c ln 3 1 A. 11;15 . B. 1;5 . C. 16;20 . D. 6;10 x  2 y 1 z  2
Câu 46: Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 4 4  3
(P) : 2x y  2z 1  0 . Đường thẳng  song song với (P) đồng thời tạo với d góc bé nhất. 
Biết rằng  có một véc tơ chỉ phương u  ( ; m ;
n 1) . Giá trị biểu thức 2 2
T m n bằng A. T  5 . B. T  2 . C. T  3. D. T  4 .
Câu 47: Biết phương trình 2 2
z mz  8  m  0 ( m là tham số thực) có hai nghiệm z , z . Gọi , A B,C 1 2
lần lượt là điểm biểu diễn của các số phức z , z và z  2 . Có bao nhiêu giá trị của m để 1 2 0 ABC đều? A. 1. B. 3. C. 4. D. 2. x  2 y 1 z
Câu 48: Trong không gian Oxyz , cho đường thẳng  :   và mặt phẳng 1 1 1 
P: x  2y  2z  6  0 . Đường thẳng d nằm trong mặt phẳng P sao cho d cắt đồng thời
vuông góc với đường thẳng  . Khi đó đường thẳng d đi qua điểm nào trong các điểm sau đây? A.  2  ;2;0 . B. 2;2; 2   . C. 0;4;  1 . D.  2  ;3;  1 .
Câu 49: Cho hàm số đa thức bận bốn y f x có đồ thị hàm số y f  x như hình vẽ:
Tổng các giá trị nguyên của m để hàm số y f x 1  m  9 có đúng 3 điểm cực tiểu là A. 40 . B. 34 . C. 24 . D. 30.
Câu 50: Có bao nhiêu số nguyên dương x , sao cho ứng với mỗi giá trị của x có đúng 11 số nguyên y
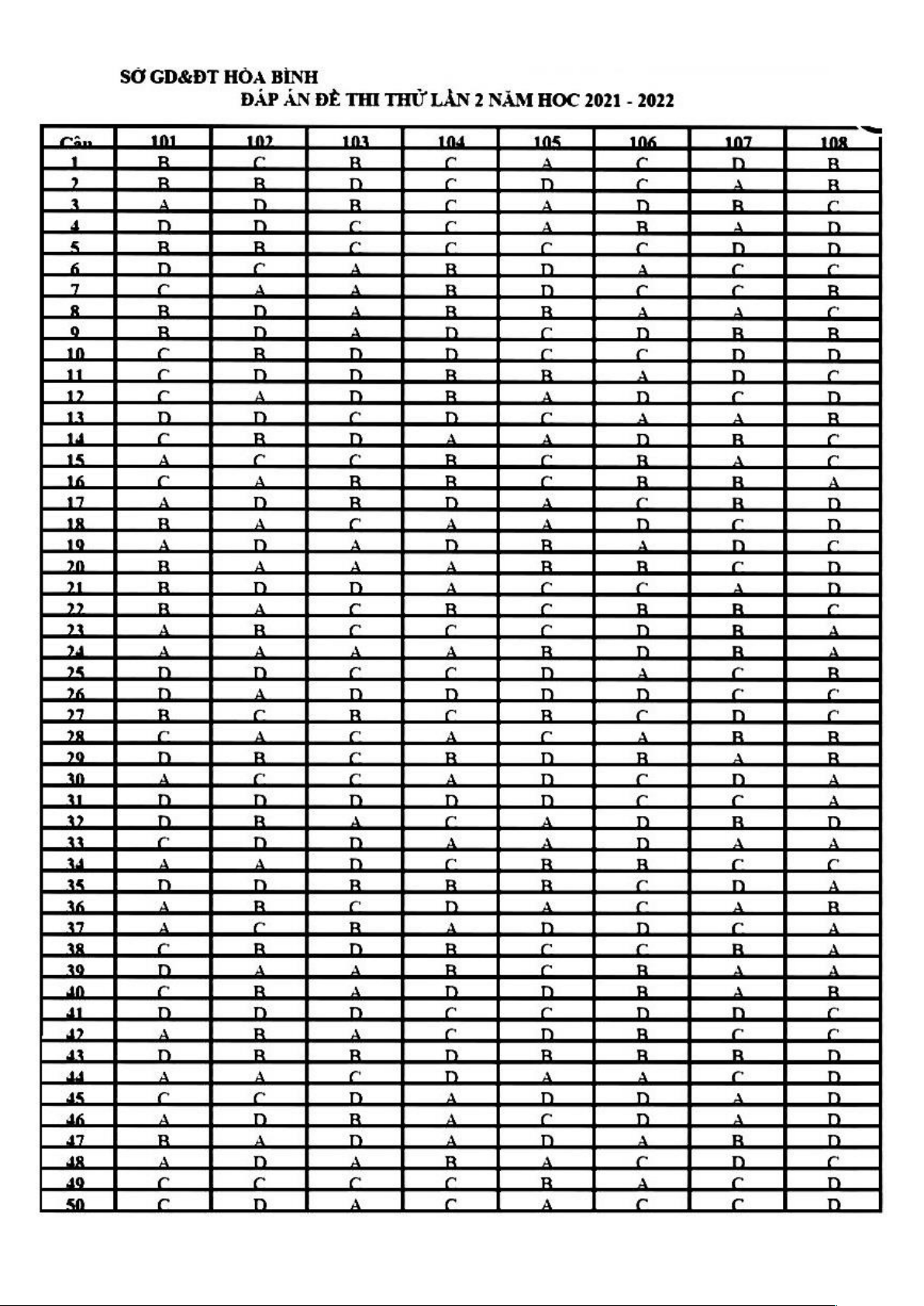
thỏa mãn bất phương trình  y 2 2  5y xx   1  0 ? A. 55 . B. 34 . C. 130 . D. 88 . BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5
B B C D D C B C B D C D B C C A D D C D D C A A B
2 2 2 2 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 5
6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0
C C B B A B D A A A B A A A B D C D D D D D C D D
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 51: Cho cấp số cộng u u  1;u  5 u n  có . Khi đó bằng 1 3 2 A. 7  B. 3 C. 2  D. 9  Lời giải Chọn B u u Ta có 3 1
u u  2d d   2 . 3 1 2
Suy ra u u d  1 2  3. 2 1 3 8 8
f xdx  5   f
 xdx 8
f xdxCâu 52: Cho 0 và 3 , khi đó 0 bằng A. 13. B. 3. C. 1  3. D. 3  . Lời giải Chọn B 8 3 8 Ta có f
 xdx f
 xdxf
 xdx  5   8  3. 0 0 3
Câu 53: Hình phẳng D giới hạn bởi các đường y  ln  x  2 , trục hoành và hai đường thẳng 3
x  , x  3 . Diện tích hình phẳng D được tính là 2 3 3 A. 2 S ln
 x 2d .x B. S  ln
 x 2d .x 3 3 2 2 3 3 C. S  ln
 x 2 d .x D. S   ln
 x 2d .x 3 3 2 2 Lời giải Chọn C
y  ln x  2 y  0 3    D :   S  ln  x2 3  dxx  3 2 2  x  3 
Câu 54: Trong không gian Oxyz , cho hai điểm A 1  ;0;3, B1;2; 2
  . Tọa độ vectơ AB là A. 2;2;  1 . B. 2; 2  ; 5  . C.  2  ; 2  ;5. D. 2;2; 5  . Lời giải Chọn D  A 1  ;0;3, B1;2; 2
   AB  2;2; 5  
Câu 55: Cho hình bát diện đều như hình bên. Số cạnh của hình bát diện đều bằng A. 8. B. 14. C. 10. D. 12. Lời giải Chọn D
Câu 56: Diện tích xung quanh của hình trụ có bán kính đáy bằng 3 và độ dài đường sinh bằng 4 là A. 21. B. 42. C. 24. D. 48. Lời giải Chọn C
Ta có: S  2 rl  2.3.4  24. xq
Câu 57: Nghiệm của phương trình 2x 1 5 - =125 là A. x = -2. B. x = 2. C. x =1. D. x = -1. Lời giải Chọn B Ta có: 2x 1 - 2 x 1 - 3 5 =125 Û 5
= 5 Û 2x-1= 3 Û x = 2.
Câu 58: Cho hàm số y = f (x) có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng A. -3. B. 0. C. 4. D. -1. Lời giải Chọn C
Dựa vào bảng biến thiên ta có giá trị cực đại của hàm số là: 4.
Câu 59: Hàm số nào dưới đây là một nguyên hàm của hàm số f x  2x 1 A. 2 x x. B. 2 x  . x C. 2 x  2 . x D. 2 x  2 . x Lời giải Chọn B Ta có: f
 xx   x   2 d 2
1 dx x x C.
Câu 60: Họ nguyên hàm của hàm số f x 1
 2  trên 0; là: x 1
A. 2x  ln x C. B. 2   C.
C. ln x C.
D. 2x  ln x C. 2 x Lời giải Chọn D   Ta có: f  x 1 dx  2 
dx  2x  ln x C.    x  2  a
Câu 61: Với a  0 biểu thức log bằng 5   25   1
A. 2log a 1 . 2  log . a 2log a 1 . log . a 5  5  B. C. D. 5 5 2 Lời giải Chọn C 2  a  Ta có: 2 2 log 
  log a  log 5  2 log a 1 . 5 5 5  5  25         Câu 62: Cho z 5 i; z 4 3i z z z 1 2 . Số phức 1 2 bằng A. 1   2i . B. 1 2i . C. 1   2i . D. 1 2i . Chọn D Lời giải
Ta có: z z z  5  i  4  3i  1 2 .i 1 2
Câu 63: Cho hình lăng trụ có diện tích đáy B  15 và chiều cao h  6 . Thể tích khối lăng trụ đã cho bằng A. 30 B. 90 C. 45 D. 60 Lời giải Chọn B
Thể tích lăng trụ đã cho là V Bh  15.6  90 .
Câu 64: Tập xác định của hàm số y  log 5  x 3   là A.  ;  5 B. 5; C.  ;  5 D. 5; Lời giải Chọn C
Hàm số xác định khi và chỉ khi 5  x  0  x  5
Vậy tập xác định D   ;  5.
Câu 65: Gọi z , z là hai nghiệm phức của phương trình 2
z  2z 10  0 . Giá trị của biểu thức 1 2
A z z là 1 2 A. 10 B. 1  0 C. 2  D. 2 Lời giải Chọn C
Áp dụng định lý Vi-ét ta có S z z  2  1 2
Vậy A z z  2  . 1 2
Câu 66: Cho khối cầu có thể tích bằng 288. Bán kính khối cầu đã cho bằng A. 6 B. 3 C. 4 D. 2 Lời giải Chọn A 4 Ta có 3 3
V  R  288R  216  R  6 . 3
Câu 67: Cho hàm số y f x có đồ thị là đường cong trong hình bên. Giá trị nhỏ nhất của hàm số
y f x trên đoạn  2  ;4 bằng A. 2  . B. 3. C. 4. D. 3  . Lời giải Chọn D
Dựa vào đồ thị đã cho dễ dàng nhận thấy giá trị nhỏ nhất của hàm số y f x trên đoạn  2  ;4 bằng 3  .
Câu 68: Với x  0 đạo hàm của hàm số y  log x bằng 2022 ln 2022 x 1 A. . B. x ln 2022. C. . D. . x ln 2022 x ln 2022 Lời giải Chọn D Xét hàm số y  1 log
x , ta có y '  . 2022 x ln 2022
Câu 69: Trong không gian Oxyz, mặt phẳng P : 3x  2y z  3  0 đi qua điểm nào trong các điểm dưới đây A. 1;0;  1 . B. 3; 3  ;2. C. 0;1;  1 . D.  2  ;3;3. Lời giải Chọn C
Dễ thấy điểm có tọa độ 0;1;  1
 thỏa mãn phương trình mặt phẳng P. 2x  3
Câu 70: Tiệm cận ngang của đồ thị hàm số y
là đường thẳng có phương trình x 1 A. y  1. B. y  2  . C. y  1  . D. y  2. Lời giải Chọn D
Ta có: lim y  2; lim y  2. x x
Do đó đồ thị hàm số đã cho có tiệm cận ngang là đường thẳng y  2.
Câu 71: Số cách chọn 2 học sinh từ nhóm có 8 học sinh là A. 2 8 . B. 2 A . C. 16 . D. 2 C . 8 8 Lời giải Chọn D
Số cách chọn 2 học sinh từ nhóm có 8 học sinh là 2 C . 8
Câu 72: Tập nghiệm của bất phương trình 5x  3 là  5   A. ;log 5  ;  3 ;log 3 ; 5  3  . B. . C. . D.      3   5  Lời giải Chọn C
Ta có 5x  3  x  log 3 . Suy ra S  ;log 3 5 . 5
Câu 73: Cho hàm số y g x có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây A. 2;  . B. ;2 . C.  4  ;  1 . D. 0;2 Lời giải Chọn A
Quan sát bảng biến thiên hàm số đã cho đồng biến trên khoảng 2;  .
Câu 74: Cho số phức z  5  2i . Phần thực và phần ảo của số phức z là
A. Phần thực bằng 5 và phần ảo bằng 2 .
B. Phần thực bằng 5 và phần ảo bằng 2  .
C. Phần thực bằng 2 và phần ảo bằng 5  .
D. Phần thực bằng 2  và phần ảo bằng 5 . Lời giải Chọn A
Ta có Phần thực bằng 5 và phần ảo bằng 2
Câu 75: Đồ thị của hàm số 4 2
y x  2x  3 cắt trục tung tại điểm có tung độ bằng A. 0 . B. 3  . C. 1. D. 1  . Lời giải Chọn B
Trục tung có phương trình: x  0 . Thay x  0 vào 4 2
y x  2x  3 được: y  3  .
Câu 76: Trong mặt phẳng Oxy , gọi A , B , C lần lượt là các điểm biểu diễn các số phức z  3  i , 1
z  2  2i , z  5
  i , G là trọng tâm của tam giác ABC . Số phức có điểm biểu diễn G là 2 3 A. z  1   i .
B. z  1 2i . C. z  1   2i .
D. z  2  i . Lời giải Chọn C
Ta có A0; 3, B 2; 2 , C  5  ;  1 . Gọi G  ; x y .  0  2  5 x   1  
Do G là trọng tâm của tam giác ABC nên 3   G  1  ; 2 . 3   2 1 y   2   3
Vậy G là điểm biểu diễn số phức z  1   2i .
Câu 77: Trong không gian Oxyz , mặt phẳng (P) đi qua ba điểm A0;1;2 , B 1  ;3; 2
  , C 2;1;3 có phương trình là
A. 2x  5y  2z  9  0 . B. 2x  5y  2z  9  0 .
C. 2x  7 y  4z 15  0 . D. x  7 y  4z 15  0 . Lời giải Chọn C     Ta có AB   1
 ;2;  4 , AC  2;0; 
1   AB, AC  2; 7; 4.   
Gọi n là một véctơ pháp tuyến của mặt phẳng P đi qua ba điểm , A B,C . 
Suy ra n  2;  7; 4 . 
Phương trình của mp P đi qua A0;1;2  nhận n là một véctơ pháp tuyến là
2 x  0  7 y  
1  4 z  2  0 hay 2x  7y  4z 15  0 .
Câu 78: Trong không gian Oxyz, cho điểm M(2; 0;7) và mặt phẳng (P) : 2x y  3z  5  0. Phương
trình của đường thẳng đi qua M và vuông góc với (P) có phương trình là
x  1 t
x  2  2t
x  3  2t
x  2  2t    
A. y  2  t .
B. y  t .
C. y  1 t .
D. y  t . z  2      3t z  7   3t z  2   3t z  7   3t Lời giải Chọn B
Ta có mặt phẳng (P) : 2x y  3z  5  0. 
 Mặt phẳng P có véc tơ pháp tuyến là n  2; 1  ;3 P   
Gọi đường thẳng cần tìm là  . Vì đường thẳng  vuông góc với P nên véc tơ pháp tuyến
của mặt phẳng P là véc tơ chỉ phương của đường thẳng  .    u n    2; 1;3 P    
Vậy phương trình đường thẳng  đi qua M(2; 0;7) và có véc tơ chỉ phương u    2; 1;3 là:
x  2  2t  y  t . z  7   3t
Câu 79: Cho hình chóp tam giác đều S.ABC có cạnh bên bằng 2a , đường cao bằng a ( tham khảo hình vẽ)
Góc giữa cạnh bên và mặt đáy bằng A. 0 90 . B. 0 30 . C. 0 45  D. 0 60  Lời giải Chọn B
Gọi F là trung điểm BC .
Gọi H là trọng tâm tam giác ABC .
AH là hình chiếu vuông góc của SA trên mặt phẳng  ABCa 1
Góc giữa cạnh bên SA và mặt đáy  ABC bằng  SAH : sin  SAH     0 SAH  30 . 2a 2
Câu 80: Hàm số nào dưới đây nghịch biến trên ? x A. 3 y  x  1 3. B. y  . C. 4 2
y  x  2x . D. 3 2
y  x  3x . x  2 Lời giải Chọn A Ta có: 3 2
y  x  3  y  3  x  0, x
  , y  0  x  0. Vậy hàm số 3
y  x  3 nghịch biến trên . 
Câu 81: Diện tích hình phẳng giới hạn bởi các đường 2
y x , y  3x là 9 5 A. . B. 4 . C. 3 . D. . 2 2 Lời giải Chọn Bx  0 Xét phương trình: 2 x  3x   . x  3 3 9
Suy ra diện tích hình phẳng giới hạn bởi các đường 2
y x , y  3x là 2
S x  3x dx  .  2 0
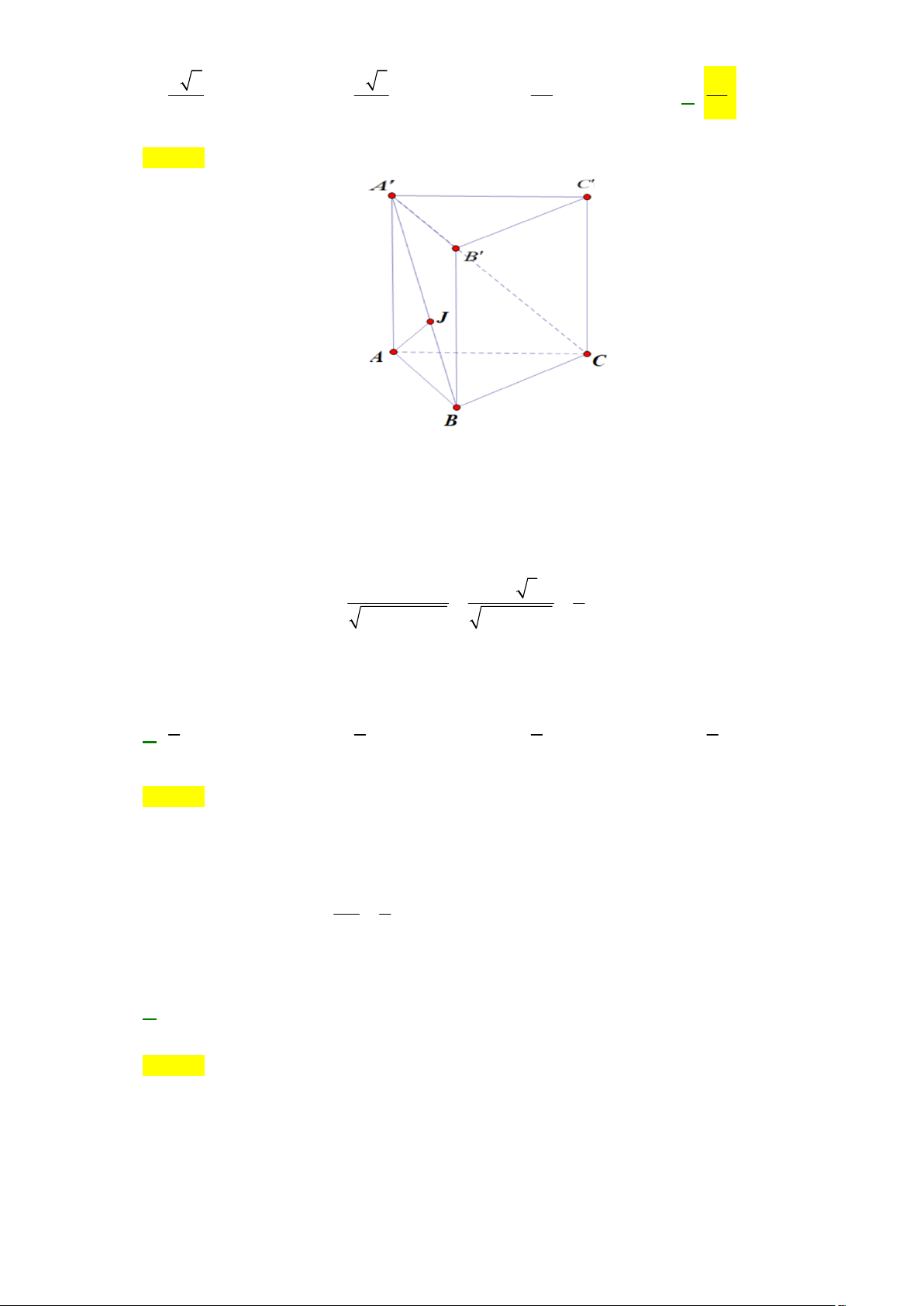
Câu 82: Cho hình lăng trụ đứng ABC.AB C
 có đáy ABC là tam giác vuông cân tại B có AB a 3
cạnh bên AA  3a ( tham khảo hình vẽ). Khoảng cách từ điểm A đến mặt phẳng  ABC là a 6 a 3 2a 3a A. . B. . C. . D. . 3 2 3 2 Lời giải Chọn D
Kẻ AJ AB   1 . BC AB Ta có 
BC   AAB  BC AJ 2. BC AA Từ  
1 và 2  AJ   ABCAA .AB 3 . a a 3 3 Vậy d  ,
A ABC  AJ    a . 2 2 2 2 AA  AB 9a  3a 2
Câu 83: Có 10 tấm thẻ được đánh số từ 1 đến 10 . Chọn ngẫu nhiên 2 thẻ. Xác suất để chọn được 2
tấm thẻ đều ghi số chẵn là 2 1 7 1 A. . B. . C. . D. . 9 4 9 2 Lời giải Chọn A
Số cách chọn ngẫu nhiên 2 thẻ từ 10 thẻ là: 2 C10
Trong 10 thẻ có 5 thẻ đánh số chẵn nên số cách chọn 2 thẻ đánh số chẵn: 2 C . 5 2 C 2
Vậy xác suất cần tính là: 5  . 2 C 9 10
Câu 84: Cho hàm số f x 3 2
x  3x  2 . Tọa độ điểm cực tiểu của đồ thị hàm số là A. 2; 2   B.  2  ;2 C. 0; 2   D.  2  ;0 Lời giải Chọn A
Ta có: f x 3 2
x x   f x 2 3 2  3x  6xx  0
Nên: f  x 2
 0  3x  6x  0 
. Từ đó ta có bảng biến thiên như sau:  x  2
Vậy điểm cực tiểu của đồ thị hàm số là điểm A2; 2   .
Câu 85: Gọi M ,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f x 4 2
 x  2x  3 trên đoạn  2  ; 
1 . Giá trị M m bằng A. 9. B. 8. C. 1  . D. 2  . Lời giải Chọn A
Ta có: f x 4 2
 x x   f x 3 2 3  4  x  4x . x  0 2  ;  1 
Nên: f  x 3  0  4
x  4x  0  x  1   2  ;  1 x 1   2  ;  1 Và: f  2    5
 , f 0  3, f   1  4, f   1  4
Vậy: M  4,m  5
  M m  9 .
Câu 86: Trong không gian Oxyz , mặt cầu S  có tâm I  1  ; 1
 ;2 và đi qua A1;1;  1 có phương trình là: A. 2 2 2
x y z  2x  2y  4z  5  0 . B. 2 2 2
x y z  2x  2y  4z 11  0 . C. 2 2 2
x y z  2x  2y  4z 17  0 . D. 2 2 2
x y z  2x  2y  4z 11  0 . Lời giải Chọn B
Ta có: IA    2    2    2 1 1 1 1 1 2  17 .
Phương trình mặt cầu S  có tâm I  1  ; 1
 ;2 và đi qua A1;1; 
1 có bán kính R IA  17 , Nên ta có phương trình:
S x  2  y  2 z  2 : 1 1 2  17  S  2 2 2
: x y z  2x  2y  4z 11  0 .
Vậy phương trình mặt cầu cần tìm là S  2 2 2
: x y z  2x  2y  4z 11  0 .
Câu 87: Cho hàm số y f x có đồ thị như hình vẽ. Các miền A và B có diện tích lần lượt là 8 và 2. 4 Tích phân f
 xdx bằng: 1 y A 1 4 O 3 x B A. 6. B. 2. C. 18. D. 10. Lời giải Chọn A 4 3 4 Ta có: f
 xdx f
 xdxf
 xdx  8 2    6 . 1 1 3 4 Vậy f
 xdx  6 1
Câu 88: Tích các nghiệm của phương trình log  2 3x  7x  3 2  bằng: 8 8 A.  7 . B.  7 . C. . D. . 3 3 3 3 Lời giải Chọn A log  2 3x  7x  3 2   7 x   Điều kiện: 2 3x 7x 0     3 .  x  0 log  2 3x  7x 2 3
 3  3x  7x  2 2 2
 3x  7x  8  0  7   145 x  6   (TMĐK)  7   145 x   6 7   145 7   145 8
Vậy tích các nghiệm bằng .   . 6 6 3
Câu 89: Cho tam giác ABC vuông tại A có AB  4, AC  2 . Thể tích khối tròn xoay sinh bởi hình tam
giác khi quay quanh cạnh BC bằng 325 5 25 5 A. . B. . C. . D. . 15 5 3 15 Lời giải Chọn A Ta có 2 2
BC AB AC  2 5 .
Gọi K là hình chiếu vuông góc của A lên BC . 1 1 1 1 1 5 16 Ta có 2       AK  . 2 2 2 AK AB AC 16 4 16 5 1 1 1 1 16 325 Khi đó 2 2 2
V .AK .BK .AK .CK .AK .BC . .2 5  . 3 3 3 3 5 15
Câu 90: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a  0
2 , ABC  60 . Tam giác SAC cân
tại S, SB a 3 . Góc giữa cạnh SA và mặt phẳng SBD bằng 0 30 . Thể tích khối chóp S.ABCD bằng 3 a 3 A. . B. 3 a 3 . C. 3 2a . D. 3 4a . 2 Lời giải Chọn B
Gọi O AC BD .
Ta có AO BD, AO SO AO  SBD , khi đó SA SBD   SA SO    0 , , ASO  30 . Khi đó 0
AC  2a AO a SO A .
O cot 30  a 3 , do SB BO a 3 nên SBO là tam
giác đều cạnh a 3 . a 32. 3 4 4 Vậy 3 V  4V  .A . O S  . . aa 3 . S.ABCD . A SBO 3 SBO 3 4 
Câu 91: Cho hàm số y f x có đạo hàm liên tục trên 0; đồng thời thỏa mãn  2    2 x 4 2 f
 xdx 3, sinx xf     dx  2  và f
 4 . Giá trị của f
 xsin dxx bằng      2   2  0 0 0 8  5 3 8  5 2 8  5 2 8  5 3 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn D x
Có I  sinx xf  dx  2  .    2  0 2 2 x
Đặt t   I  2sin 2t  2tf tdt  2sin 2x  2xf xdx . 2 0 0
Tích phân từng phần cho I , ta được: 2 I 2
 sin 2x  2xf x 2  2cos2x  2 f xdx     f  2cos2x    
1 f xdx 0 2  2  0 0 2 2 2    4
 4 sin x f  x 2 dx  4 sin x f
xdx  3 0 0 2 2 2 Có 2 f  x 2 dx  2 4sin xf  x 4 dx 16 sin d
x x  3 2.3 3 0  0 0 0 2
  f x 4sin x2 2 dx  0 0    f x 2
 4sin x  0  f x 2  4sin x, x   0; .  2    4 4 4 4  1  8  5 3 Vậy f  x 3 sin d x x  4sin d x x  
3sin xsin3xdx  cos3x3cos x  .    3  3 0 0 0 0
Câu 92: Cho hai số phức z , z thỏa mãn: z z  2 và z  4  4i  3 2  z . Gọi M , m lần lượt 1 2 1 2 1 2
là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P z 1 2i , giá trị 2 2 M m bằng 2 99 A. 50 . B. 54 . C. 34 . D. . 2 Lời giải Chọn C
 z z AB  2 Gọi ,
A B lần lượt là điểm biểu diễn của 1 2 z , z  
; C 4; 4 là điểm biểu 1 2  z OB  2 diễn của số phức 4   4i .
Có z  4  4i  3 2  z AC  3 2  OB AC OB  3 2 . 1 2 O
 B AC AB  4 2  
OB BA AC OC O, B, ,
A C theo thứ tự nằm trên đoạn OC O  C  4 2 . Điểm D  1  ; 2
  biểu diễn cho số phức 1   2i .
P OD  5 min 2 2
P z 1 2i BD  
M m  34 . 2
P DN  29  max
(P khi A trùng C , B trùng với N 3;3 ) . max
Câu 93: Cho hàm số y f x có đồ thị như hình vẽ
Số nghiệm thuộc đoạn 0;5 của phương trình f cos x 1 là A. 6 . B. 3 C. 4 . D. 5. Lời giải Chọn D
Đặt: t  cos x . Với mọi x 0;5  t  1  ;  1 . 0  t 1
Khi đó, ta có f t 1, t   1  ;  1 1   . t  1 1  ;1  2  
Ta thấy với x 0;5 thì phương trình cos x t ,t  0;1 1 1
  có 5 nghiệm phân biệt.
Vậy số nghiệm thuộc đoạn 0;5 của phương trình f cos x 1 là 5.
Câu 94: Số giá trị nguyên của tham số m để phương trình  2 m   2
1 log x 10log x m  0 có hai 2 2
nghiệm phân biệt không nhỏ hơn 1 là A. 4 . B. 2 .C. 1. D. 3. Lời giải Chọn D
Điều kiện: x  0
Đặt t  log x . Phương trình trở thành:  2 m   2
1 t 10t m  0  1. 2
Để phương trình đã cho có hai nghiệm phân biệt không nhỏ hơn 1 thì phương trình   1 có hai  3
m m  25  0   0  3   10
m m  25  0
nghiệm phân biệt t t  0  S  0    0  1 2  2 m 1   m  0 P  0   m  0  2 m 1
Vì m nguyên nên m 0;1;  2 .
Câu 95: Biết rằng tồn tại duy nhất bộ số * a, , b c   b
và là phân số tối giản sao cho c ln 8 x e  2 b
dx a  2ln . Giá trị của biểu thức   thuộc khoảng  a b c xe c ln 3 1 A. 11;15 . B. 1;5 . C. 16;20 . D. 6;10 Lời giải Chọn B ln 8 ln 8 e  2
xe  2 x x e Xét I  dx  dx .   x x x ln 3 1 e ln 3 1 e .e Đặt x 2  1  1 x   2 d x t e t e
t t e dx .
Đổi cận: x  ln 3  t  2 ; x  ln8  t  3 . Khi đó  2 3 t   3 2 3 1  2tdt t 1  2  I         t  2 dt 2 1 dt 2 t 1 t 1  t 1 2  2 2 2 2 3
3 (t 1)  (t 1)  2 dt  2 dt
 (t 1)(t 1) 2 2 3 3 1 1  t 1   2  2  dt  2  2  ln  t 1 t 1   t 1     2  2  1 1  3  2  2 ln  ln
 2  2(ln3  ln 2)  2  2ln    2 3  2 a  2  Suy ra b
  3  a b c  7 . c  2  x  2 y 1 z  2
Câu 96: Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 4 4  3
(P) : 2x y  2z 1  0 . Đường thẳng  song song với (P) đồng thời tạo với d góc bé nhất. 
Biết rằng  có một véc tơ chỉ phương u  ( ; m ;
n 1) . Giá trị biểu thức 2 2
T m n bằng A. T  5 . B. T  2 . C. T  3. D. T  4 . Lời giải Chọn D  
Véc tơ chỉ phương d : u  (4; 4
 ;3) , véc tơ pháp tuyến (P) : n  (2; 1  ;2) . d P  
Ta có u.n  0  2m n  2  0  n  2m  2 . P   u.u 4m  4n  3
4m  4(2m  2)  3 cos(, d) d      2 2 2 2 2 2 2 2 u . ud 4  ( 4
 )  3 m n 1
41 m  (2m  2) 1 4m  5 1 4m 52 2 1
16m  40m  25    . 2 2 2
41 5m  8m  5 41 5m  8m  5 41 5m  8m  5 2
16m  40m  25 2 7  2m  90m Đặt f (m)  ; f (  m)  . 2 5m  8m  5
5m 8m52 2 m  0 2 f (  m)  0  7
 2m  90m  0   5 m   .  4 2
16m + 40m + 25 16 Có lim = . 2 m®±¥ 5m +8m +5 5 Ta có bảng biến thiên
Góc giữa d và  bé nhất khi f (m) lớn nhất. Khi đó dựa vào bảng biến thiên ta thấy
m = 0 Þ n = 2 . Vậy 2 2
T m n  0  4  4 . Cách khác:
Gọi  là hình chiếu của d lên (P) , khi đó góc của P và d là góc của d và  . Mà //(P)
nên góc  và d nhỏ nhất khi // .  
Véc tơ chỉ phương d : u  (4; 4
 ;3) , véc tơ pháp tuyến (P) : n  (2; 1
 ;2) . Gọi (Q) là mặt d P   
phẳng chứa d và vuông góc với (P)  véc tơ pháp tuyến n     Q ud , nP  ( 5  ; 2  ;4) , là     
hình chiếu của d lên (P)    (P)  (Q)  u  uP , nQ  (0; 1  8; 9  )  2  (0;2;1) .   2 2
T m n  0  4  4 .
Câu 97: Biết phương trình 2 2
z mz  8  m  0 ( m là tham số thực) có hai nghiệm z , z . Gọi , A B,C 1 2
lần lượt là điểm biểu diễn của các số phức z , z và z  2 . Có bao nhiêu giá trị của m để 1 2 0 ABC đều? A. 1. B. 3. C. 4. D. 2. Lời giải Chọn D
Để tồn tại ABC thì z , z phải là hai nghiệm không thuần thực của phương trình 1 2 2 2
z mz  8  m  0 . 32 32 32 Suy ra 2 2
  0  5m  32  0  m     m  . 5 5 5   
 m    m   Khi đó  m i z . Suy ra A ; , B ;  ,C 2;0 . 1,2 2  2 2   2 2      2 2
AB z z  z z 2 2
 4z z m  4 2 8  m  2 2
 5m  32  AB  32  5m 1 2 1 2 1 2   Ta có 2 2  .  m     1 2 AC BC  2        4
m  8m  48 2  2     2    1
Để ABC đều thì 2 2
AB AC  32  5m  4
m  8m  48 2  5 m   n 2 2 2   32 5m m 2m 12 4m 2m 20 0              2 .  m  2  n
Vậy có 2 giá trị của m để ABC đều. x  2 y 1 z
Câu 98: Trong không gian Oxyz , cho đường thẳng  :   và mặt phẳng 1 1 1 
P: x  2y  2z  6  0 . Đường thẳng d nằm trong mặt phẳng P sao cho d cắt đồng thời
vuông góc với đường thẳng  . Khi đó đường thẳng d đi qua điểm nào trong các điểm sau đây? A.  2  ;2;0 . B. 2;2; 2   . C. 0;4;  1 . D.  2  ;3;  1 . Lời giải Chọn C
Gọi A d    A    P  x  2 y 1 zx  0    
Tọa độ A thỏa mãn hệ  1 1 1
  y 1  A0;1;  2 .
x  2y  2z  6  0 z  2   1  1  
Do d  P và d   nên nhận .u  .n ; u P
  0;1; 1 là một vectơ chỉ phương. 3 3  x  0 
Đường thẳng  đi qua A0;1;  2 nên  có dạng y 1 t t   .z  2    t
Nhận thấy  đi qua điểm 0;4;  1 .
Câu 99: Cho hàm số đa thức bận bốn y f x có đồ thị hàm số y f  x như hình vẽ:
Tổng các giá trị nguyên của m để hàm số y f x 1  m  9 có đúng 3 điểm cực tiểu là A. 40 . B. 34 . C. 24 . D. 30. Lời giải Chọn D
Từ hình vẽ ta có bảng biến thiên của hàm số f x :
Từ bảng biến thiên ta thấy được để hàm số y f x 1  m  9 có đúng 3 điểm cực tiểu khi và chỉ khi 3
  m  9  1  6  m  10  m 6;7;8;  9 .
Câu 100: Có bao nhiêu số nguyên dương x , sao cho ứng với mỗi giá trị của x có đúng 11 số nguyên y
thỏa mãn bất phương trình  y 2 2  5y xx   1  0 ? A. 55 . B. 34 . C. 130 . D. 88 . Lời giải Chọn D Đặt  y 2 2  5y xx   1  0 *  y  2log x
Xét phương trình  y 2
2  x 5y x   2
1  0  y  log x 1  5  
Với x  1 *  0  y  log 2, không thỏa mãn. 5
Với x  2 thì 2log x  log x 1
*  log x 1  y  2log x 5   2 5  , khi đó 2
log 3  log x 1  2 5 5  
TH1: Với x 2;24, 2  2log x  2log 24  2 2
 2log x  log x 1  10, x   2;24 2 5    
Nên không tồn tại đủ 11 số nguyên thuộc log x 1 ; 2log x  5   Không thỏa mãn. 2   24  x  124
2  log x 1  3  5   TH2:    13
x 91;92;...;12  4 . 13  2log x  14 7 2  2 2  x  2 1  24  x  624 3
  log x 1  4  5   TH3:    15
x 128;129;...;18  1 . 14  2log x  15 7 2  2  2  x  2 5n
 1  x  5n 1
n  log x 1  n 1  5   1 TH4: 
n  4   n 11 n  1
n 11  2log x n 12  2 2 2  2  x  8.2 n Do n n n 2
5 1  2 2  8.2 , n   4 nên  
1  x   Không thỏa mãn.
Vậy x 91;92;...;12  4 128;129;...;18  1 .
Document Outline

  • de-thi-thu-tot-nghiep-thpt-2022-mon-toan-lan-2-so-gddt-hoa-binh
  • 102. Đề thi thử tốt nghiệp THPT năm 2021-2022 môn Toán - SỞ HÒA BÌNH (File word có lời giải chi tiết).Image.Marked