Đề thi thử tốt nghiệp THPT năm 2020 môn Toán lần 2 sở GD&ĐT Hà Tĩnh

Đề thi thử tốt nghiệp THPT năm 2020 môn Toán lần 2 sở GD&ĐT Hà Tĩnh mã đề gốc gồm có 06 trang với 50 câu trắc nghiệm, đề thi có đáp án và lời giải chi tiết

19 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

12 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
DDD:50 Cau
Trang 1 / 1
SỞ GD&ĐT HÀ TĨNH
ĐỀ THI CHÍNH THỨC
(Đề thi gồm 04 trang – 50 câu)
KỲ THI THỬ TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2020
Bài thi: TOÁN
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Mã đề: GỐC
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 01. Cho tập hợp
{1; 2; 3; 4; 5}.A
Số tập hợp con gồm hai phần tử của tập hợp
A
là
A.
2
5
C
. B.
2
5
A
. C.
2
P
. D.
11
.
Câu 02. Cho cấp số cộng
()
n
u
với
1
3u
và công sai
4.
d
Số hạng thứ hai của cấp số đã cho bằng
A.
B.
12.
C.
10.
D.
1.
Câu 03. Tập nghiệm của phương trình
1
4 64
x
là
A.
{4}.
B.
.
C.
{3}.
D.
{5}.
Câu 04. Cho khối lăng trụ có chiều cao bằng
9,
diện tích đáy bằng
6.
Thể tích khối lăng trụ đã cho bằng
A.
54.
B.
18
C.
15.
D.
Câu 05. Tập xác định của hàm số
2
log 3yx
là
A.
3; .
B.
3; .

C.
.
D.
{3}. \
Câu 06. Cho hàm số
()y fx
liên tục trên
;ab



. Diện tích
S
của hình phẳng giới hạn bởi đồ thị của hàm số
()
y fx
, trục hoành và hai đường thẳng
,x ax b

được tính theo công thức nào sau đây?
A.
()
b
a
S f x dx
B.
() .
b
a
S f x dx
C.
2
() .
b
a
S f x dx
D.
() .
b
a
S f x dx
Câu 07. Cho khối chóp có diện tích đáy
5B
và chiều cao
6h
. Thể tích của khối chóp đã cho bằng
A.
10.
B.
30.
C.
11.
D.
15.
Câu 08. Cho hình trụ có độ dài đường sinh bằng
bán kính đáy bằng
Diện tích xung quanh của hình trụ đã
cho bằng
A.
24 .
B.
12 .
C.
36 .
D.
48 .
Câu 09. Cho khối cầu có bán kính
3.
R
Thể tích khối cầu đã cho bằng
A.
36 .
B.
4.
C.
12 .
D.
108 .
Câu 10. Cho hàm số
()y fx
có bảng biến thiên như hình vẽ. Hàm số đồng biến trên khoảng nào dưới đây?
A.
(2; ).
B.
(0; 2).
C.
(0; ).
D.
( ; 0).
Câu 11. Cho
a
là số thực dương,
1a
, khi đó
3 log 2
a
a
bằng
A.
B.
3
a
C.
6.
D.
3.a
Câu 12. Cho khối nón có chiều cao
,h
bán kính đáy
.r
Thể tích khối nón đã cho bằng
A.
2
.
3
hr
B.
2
2.
hr
C.
2
.hr
D.
2
4
.
3
hr
Câu 13. Cho hàm số
()y fx
có bảng biến thiên như hình vẽ. Giá trị cực đại của hàm số bằng
DDD:50 Cau
Trang 2 / 6
A.
B.
C.
2.
D.
1.
Câu 14. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ ?
A.
42
31yx x
. B.
42
31yx x

. C.
42
31yx x

. D.
42
31yx x
.
Câu 15. Đường tiệm cận ngang của đồ thị hàm số
3
4
x
y
x
có phương trình là
A.
3.
y
B.
4.y

C.
3.
x
D.
4.x

Câu 16. Tập nghiệm của bất phương trình
39
x
là
A.
;2 .

B.
( ;2).
C.
(2; ).
D.
2; .

Câu 17. Cho hàm số bậc ba
()y fx
có đồ thị như hình vẽ. Số nghiệm phân biệt của phương trình
() 2fx
là
A.
B.
C.
3.
D.
Câu 18. Cho
2
0
() 2f x dx
và
3
2
() 3f x dx
. Tích phân
3
0
()f x dx
bằng
A.
B.
C.
6.
D.
1.
Câu 19. Cho số phức
3 4.zi
Số phức liên hợp của số phức
z
là
A.
3 4.zi
B.
3 4.zi
C.
3 4.zi
D.
4 3.zi
Câu 20. Cho số phức
2 3.zi
Tọa độ điểm biểu diễn số phức
z
là
A.
2; 3 .
B.
2; 3 .
C.
3; 2 .
D.
2; 3 .
DDD:50 Cau
Trang 3 / 6
Câu 21. Phần ảo của số phức
5
z ii
là
A.
B.
5.i
C.
1.
D.
Câu 22. Trong không gian
,Oxyz
hình chiếu vuông góc của điểm
1; 3; 5
M
lên mặt phẳng tọa độ
Oxy
là
điểm có tọa độ
A.
1;3;0 .
B.
1; 0; 5 .
C.
0; 3; 5 .
D.
0; 0; 5 .
Câu 23. Trong không gian
,
Oxyz
cho mặt cầu
222
: 2 4 4 7 0.Sx y z x y z 
Bán kính của mặt
cầu
S
là
A.
R 4.
B.
R 16.
C.
R 2.
D.
R 2.
Câu 24. Trong không gian
,
Oxyz
cho mặt phẳng
: 2 3 4 1 0.Pxy z 
Véc tơ nào dưới đây là một véc
tơ pháp tuyến của mặt phẳng
P
?
A.
1
2; 3; 4 .n 
B.
2
2; 3; 1 .n 
C.
3
2; 3; 4 .n
D.
4
2; 4; 1 .n

Câu 25. Trong không gian
,
Oxyz
cho đường thẳng
124
:.
231
xyz

Điểm nào dưới đây thuộc
đường thẳng
?
A.
1; 2; 4 .M
B.
2; 3;1 .
N
C.
1;2;4.P 
D.
1; 2; 4 .Q
Câu 26. Cho hình chóp
.S ABC
có
SA
vuông góc với mặt phẳng
ABC
,
SA a
, tam giác
ABC
vuông
cân tại
B
và
3SC a
. Khoảng cách giữa hai đường thẳng
SA
và
BC
bằng
A.
a
. B.
2a
. C.
3a
. D.
5a
.
Câu 27. Hàm số
42
2 2019yx x
nghịch biến trên khoảng nào sau đây ?
A.
;1
. B.
1;0
. C.
1;1
. D.
;1
.
Câu 28. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
32yx x
trên đoạn
0; 2



.
Khi đó tổng
Mm
bằng
A.
4
. B.
16
. C.
2
. D.
6
.
Câu 29. Cho
,ab
là các số thực dương và
a
khác
1
, thỏa mãn
3
5
4
log 2
a
a
b


. Giá trị của biểu thức
log
a
b
bằng
A.
4
. B.
4
. C.
1
4
. D.
1
4
.
Câu 30. Số giao điểm của đồ thị hàm số
42
31yx x
với trục hoành là
A. 4. B. 3. C. 2. D. 1.
Câu 31. Tìm số nghiệm nguyên của bất phương trình
11
22
log 4 9 log 10xx
.
A.
4
. B. Vô số. C.
0
. D.
6
.
Câu 32. Trong không gian, cho tam giác
ABC
đều cạnh bằng 4. Thể tích của khối tròn xoay được tạo thành
khi quay hình tam giác
ABC
quanh cạnh
BC
là
A.
16
. B.
8
. C.
48
. D.
27
.
Câu 33. Xét
1
2020
32
0
2dxx x
, nếu đặt
2
2ux
thì
1
2020
32
0
2dxx x
bằng
DDD:50 Cau
Trang 4 / 6
A.
3
2020
2
1
2d
2
u uu
. B.
1
2020
0
2du uu
. C.
3
2020
2
2du uu
. D.
1
2020
0
1
2d
2
u uu
.
Câu 34. Diện tích phần hình phẳng gạch chéo trong hình vẽ được tính theo công thức nào dưới đây?
A.
2
2
1
2 2 4dxx x

B.
2
1
2 2d
xx

. C.
2
1
2 2dxx
. D.
2
2
1
2 2 4d
xx x

.
Câu 35. Cho hai số phức
1
2zai
và
2
1,z bi
với
,ab
. Phần ảo của số phức
12
zz
bằng
A.
2 b
. B.
2 bi
. C.
1a
. D.
2 b
.
Câu 36. Phương trình
2
2 10 0zz
có hai nghiệm là
12
,zz
. Giá trị của
12
zz
là
A.
6
. B.
3
. C.
4
. D.
2
.
Câu 37. Trong không gian
,
Oxyz
cho hai điểm
3; 1; 1 , 1; 2; 4 .
AB
Viết phương trình mặt phẳng
P
đi
qua
A
và vuông góc với đường thẳng
.AB
A.
: 2 3 3 6 0.Pxyz 
B.
: 2 3 3 16 0.Pxyz
C.
: 2 3 3 6 0.P xyz

D.
: 2 3 3 16 0.P xyz
Câu 38. Trong không gian với hệ tọa độ
Oxyz
, phương trình đường thẳng
d
đi qua điểm
1; 2; 1A
và vuông
góc với mặt phẳng
: 2 10Px yz 
là:
A.
22
:
2 42
x yz
d


. B.
121
:
1 21
xyz
d


.
C.
22
:
1 21
x yz
d


. D.
121
:
221
xyz
d


.
Câu 39. Một trường học có 25 giáo viên nam và 15 giáo viên nữ trong đó có đúng 2 cặp vợ chồng. Nhà trường
chọn ngẫu nhiên 5 người trong số 40 giáo viên đi công tác. Tính xác suất
p
của biến cố: “chọn được đúng một
cặp vợ chồng”.
A.
700
27417
p
B.
350
27417
p
C.
595
27417
p
D.
1400
27417
p
Câu 40. Cho hình chóp tứ giác đều
.S ABCD
có tất cả các cạnh đều bằng a. Gọi
M
là điểm nằm trên đoạn
SD
sao cho
2SM MD
. Giá trị tan của góc giữa đường thẳng
BM
và mặt phẳng
()ABCD
bằng:
A.
1
.
5
B.
3
.
3
C.
5
.
5
D.
1
.
3
Câu 41. Hàm số
3
2
2
3
x
y x mx
nghịch biến trên khoảng
0; 
khi và chỉ khi
A.
1; .m

B.
1; .m 
C.
0; .
m

D.
0; .
m 
DDD:50 Cau
Trang 5 / 6
Câu 42. Một trang trại nuôi gà dự tính lượng thức ăn tiêu thụ hằng ngày là không đổi và đã dữ trữ thức ăn đủ
dùng trong 60 ngày. Nhưng thực tế, kể từ ngày thứ hai trở đi lượng thức ăn tiêu thụ hàng ngày của trang
trại đã tăng thêm
2%
so với ngày trước đó. Hỏi lượng thức ăn mà trang trại đã dự trữ đủ dùng cho tối đa
là bao nhiêu ngày ?
A.
39
(ngày). B.
41
(ngày). C.
40
(ngày). D.
42
(ngày).
Câu 43. Cho hàm số
y fx
xác định trên
, có bảng biến thiên như hình vẽ. Với giá trị nào của m thì
đồ thị hàm số
2
1
()
y
fx m
có tổng số đường tiệm cận ngang và tiệm cận đứng bằng 3. Chọn đáp án đúng
A.
01m
. B.
0
m
. C.
01m
. D.
0 1.m
Câu 44. Cho hình nón có chiều cao bằng
25
. Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón theo một
thiết diện là tam giác vuông cân có diện tích bằng
18
. Thể tích của khối nón được giới hạn bởi hình nón đã cho
bằng
A.
32 5
3
. B.
32
. C.
32 5
. D.
96
.
Câu 45 . Cho
2
() 2 .
x
Fx x x e

là một nguyên hàm của
2
.
x
fxe
. Tìm họ nguyên hàm của hàm số
2x
f xe
.
A.
22
d2
xx
f xe x x e C

. B.
22
d2
xx
f xe x x e C

.
C.
22
d2
xx
f xe x x e C

. D.
22
d2
xx
f xe x x e C

.
Câu 46. Cho hàm số bậc ba
y fx
có đồ thị như hình vẽ. Số nghiệm phân biệt của phương trình
2
2 2 20
xx
ff




là
A. 2 B. 1 C. 4 D. 3
Câu 47. Gọi
S
là tập hợp tất cả các giá trị của tham số
m
sao cho hệ phương trình sau có nghiệm duy nhất.
DDD:50 Cau
Trang 6 / 6
22
22
2
2 266 2
13
22
2020 (2020 2020 ) ( 1) 3 4
2 6 11
xy xy
xy
m
xy
e x y x y me




Tổng của tất cả các phần tử thuộc tập hợp S là
A.
88.
B.
2 10 2.
C.
2 10 2.
D.
44
.
Câu 48. Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị nhỏ nhất của hàm số
3
2
3
3
36
x xm
fx
x xm


trên đoạn
0; 3



bằng
2
3
. Tổng tất cả các phần tử của
S
bằng
A.
16
. B.
12
. C.
6
. D.
2
.
Câu 49. Cho tứ khối diện đều
ABCD
có thể tích
V
. Gọi
M
là trung điểm của
,BC
N
là điểm thuộc cạnh
CD
thỏa mãn
2,CN ND
G
là trọng tâm của tam giác
ABD
. Mặt phẳng
()
MNG
chia khối tứ diện
ABCD
thành 2 khối đa diện. Gọi
1
V
là thể tích của khối đa diện chứa đỉnh
A
. Tính
1
V
V
A.
41
60
B.
31
60
C.
51
60
D.
43
60
Câu 50. Cho các số thực
,1xy
thay đổi thỏa mãn
2019 2020
log log 1xy
. Gọi
,Mm
lần lượt là giá trị lớn
nhất, giá trị nhỏ nhất của biểu thức
2020 2019
log logFxy
. Khẳng định nào sau đây đúng?
A.
22
2019
log 2020Mm
B.
22 2 2
2019 2020
log 2020 log 2019Mm
C.
2019 2020
log 2020 log 2019Mm
D.
2019
log 2020Mm
--------------- HẾT ---------------
1
Hướng dẫn các câu vận dụng, vận dụng cao
(các câu theo thứ tự của đề tham khảo)
Câu 39. Một trường học có 25 giáo viên nam và 15 giáo viên nữ trong đó có đúng 2 cặp vợ chồng. Nhà
trường chọn ngẫu nhiên 5 người trong số 40 giáo viên đi công tác. Gọi
p
là xác suất của biến cố: “chọn được
đúng một cặp vợ chồng”. Tính
p
.
A.
700
27417
p
B.
350
27417
p
C.
595
27417
p
D.
700
27417
p
Hướng dẫn
Số cách chọn 5 người bất kỳ là
5
40
C
Giả sử có 2 cặp vợ chồng là (A, B) và (C, D) trong đó A, C là chồng.
TH1: chọn cặp vợ chồng (A, B)
Cần chọn 3 người trong số 38 còn lại (trừ A, B) mà không có cặp (C, D)
- Số cách chọn 3 người bất kỳ trong 38 người là
3
38
C
- Số cách chọn 3 người trong 38 người mà có cặp (C, D) là
1
36
C
suy ra số cách chọn 3 người trong số 38 người mà không có cặp (C, D) là
3
38
C
-
1
36
C
TH2: chọn cặp vợ chồng (C, D).
Tương tự trên ta có số cách chọn là
3
38
C
-
1
36
C
Xác suất cần tính là:
31
38 36
5
40
2( )
700
27417
CC
p
C

Câu 40. Cho hình chóp tứ giác đều
.S ABCD
có tất cả các cạnh đều bằng a. Gọi
M
là điểm nằm trên đoạn
SD
sao cho
2SM MD
. Giá trị tan của góc giữa đường thẳng
BM
và mặt phẳng
()ABCD
là:
A.
3
.
3
B.
1
.
5
C.
5
.
5
D.
1
.
3
Hướng dẫn
Trong mặt phẳng
()ABCD
:
()AC BD O SO ABCD
Xét
SAO
vuông tại
O
có: .
Kẻ
MI BD
tại
I
. Suy ra:
MI SO
nên
()MI ABCD
.
Vậy góc giữa
BM
và mặt phẳng
()ABCD
là góc
MBI
.
Ta có:
12
36
a
MI SO
;
5 5 2
66
a
BI BD
.
Xét
MBI
vuông tại I ta có:
1
tan
5
MI
MBI
BI

Vậy giá trị
tan
của góc giữa
BM
và mặt phẳng
()ABCD
là
1
5
.
I
M
O
S
D
C
B
A
2
Câu 41. Hàm số
3
2
2
3
x
y x mx
nghịch biến trên khoảng
0;
khi và chỉ khi
A.
1; .m 
B.
1; .m 
C.
0; .m 
D.
0; .m 
Hướng dẫn
Hàm số nghịch biến trên khoảng
0;
khi và chỉ khi
0, 0;yx

2
2 0, 0;x x m x 
2
2 , 0;m x x x 
Xét
2
2g x x x
trên khoảng
0;
Bảng biến thiên
Dựa vào bảng biến thiên suy ra
m g x
, 0;x 
1m
Câu 42. Một trang trại nuôi gà dự tính lượng thức ăn tiêu thụ hằng ngày là không đổi và đã dữ trữ thức ăn đủ
dùng trong 60 ngày. Nhưng thực tế, kể từ ngày thứ hai trở đi lượng thức ăn tiêu thụ hàng ngày của
trang trại đã tăng thêm
2%
so với ngày trước đó. Hỏi lượng thức ăn mà trang trại đã dự trữ đủ dùng
cho tối đa là bao nhiêu ngày ?
A.
40
(ngày). B.
41
(ngày). C.
39
(ngày). D.
42
(ngày).
Hướng dẫn
Gọi
a
là lượng thức ăn cần dùng mỗi ngày theo dự kiến,
n
là số ngày thức tế hết lượng thức
ăn đã chuẩn bị.
Khi đó lượng thức ăn trang trại đã chuẩn bị là:
60a
.
Vì
n
là số ngày thực tế nên lượng thức ăn đã tiêu thụ sẽ là
31
2
.1,02 . 1,02 1. 1,02 ... . 1,02
n
a a a a
.
Ta có phương trình sau:
31
2
.1,02 . 1,02 1. 1,02 ... . 1,02 60.
n
a a a a a
21
1 1,02 1.02 ... 1.02 60.
n
aa
1 1,02
60. 1,02 2,2 39,815.
1 1,02
n
n
a a n
Vậy lượng thức ăn đủ dùng cho
39
ngày.
Câu 43. Hàm số
y f x
xác định trên có bảng biến thiên như hình vẽ sau
Với giá trị nào của m thì đồ thị hàm số
2
1
y g x
f x m

có tổng số đường tiệm cận ngang và
tiệm cận đứng bằng 3.
A.
01m
. B.
01m
. C.
01m
. D.
01m
.
Hướng dẫn
Nếu m=0, không có tiệm cận
Nếu
0m
3
Nhận xét:
lim 0;lim 0
xx
f x f x
 

, nên
11
lim ; lim
xx
g x g x
mm
 


. Suy ra đồ thị hàm số
y g x
có 1 đường tiệm cận ngang.
Suy ra đồ thị hàm số phải có 2 đường tiệm cận đứng.
Xét phương trình
22
0 *f x m f x m
TH1: nếu
0m
thì phương trình
*
vô nghiệm nên đồ thị hàm số không có tiệm cận đứng.
TH2: nếu m > 0 thì phương trình
( ) 1
*
( ) 2
f x m
f x m

Với
1
: khi
01m
thì
1
có 2 nghiệm;
1m
thì
1
có nghiệm duy nhất
Với
2
: do
0m
nên vô nghiệm.
Vậy để đồ thị hàm số có 2 tiệm cận đứng thì
0 1.m
Câu 44. Cho hình nón có chiều cao bằng
25
. Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón theo một
thiết diện là tam giác vuông cân có diện tích bằng
18
. Thể tích của khối nón được giới hạn bởi hình nón đã
cho bằng
A.
32 5
3
. B.
32
. C.
32 5
. D.
96
.
Hướng dẫn
2
18 18 6
2
SAC
SA
S SA
2
2 2 2
6 2 5 4OA SA SO
22
1 1 32 5
.4 .2 5 .
3 3 3
V OA SO
Câu 45 . Cho
2
( ) 2 .
x
F x x x e
là một nguyên hàm của
2
.
x
f x e
. Tìm họ nguyên hàm của hàm số
2x
f x e
.
A.
22
d2
xx
f x e x x e C
. B.
22
d2
xx
f x e x x e C
.
C.
22
d2
xx
f x e x x e C
. D.
22
d2
xx
f x e x x e C
.
Hướng dẫn
Cách 1. Sử dụng phương pháp từng phần
Cách 2. Sử dụng định nghĩ nguyên hàmVì
2
2
x
F x x x e
là một nguyên hàm của
2
.
x
f x e
nên ta có:
2
.
x
F x f x e
22
2 2 2
x x x
x e x x e f x e
2
42
x
xx
fx
e


Câu 46. Cho hàm số
y f x
có đồ thị như hình vẽ sau
Số nghiệm của phương trình
2
2 2 2 0
xx
ff


là
A. 5 B. 1
C. 2 D. 3
Hướng dẫn
Điều kiện:
0 2 1.
x
x
O
A
B
S
C
4
Ta có:
2
2 2 1
2 2 2 0
2 1 2
x
xx
x
f
ff
f



Quan sát đồ thị hàm số, ta thấy:
+ Đường thẳng
2y
cắt đồ thị hàm số
y f x
tại ba điểm
0 1 2
0 1 2 .x x x
Do đó
2
22
20
1 2 0;1 ( )
2 2 log log
x
x
x
a vo nghiem
b vo nghiem
c x c x c

+ Đường thẳng
1y 
cắt đồ thị hàm số
y f x
tại hai điểm
12
1; 2xx
Do đó
21
2
2 2 1 1
x
x
vo nghiem
xx

Vậy phương trình đã cho có hai nghiệm phân biệt.
Câu 47. Gọi
S
là tập hợp tất cả các giá trị của tham số
m
sao cho hệ phương trình sau có nghiệm duy nhất.
22
22
2
2 2 6 6 2
13
22
2020 (2020 2020 ) ( 1) 3 4
2 6 11
x y x y
xy
m
xy
e x y x y m e
Tổng của tất cả các phần tử thuộc tập hợp S là
A.
88.
B.
44
C.
2 10 2.
D.
44 8 10
.
Hướng dẫn
22
22
22
22
2
2 2 6 6 2
13
22
2 2 2 2 6 4
22
13
2020 (2020 2020 ) ( 1) 3 4
2 6 11
2020 2 2020 2 6 4 (1)
1 3 1 (2)
x y x y
xy
m
x y x y
xy
m
xy
e x y x y m e
x y x y
e x y m e
Ta có hàm số luôn đồng biến nên
22
22
(1) 2 2 6 4 1 3 4x y x y x y
Đặt
22
1 3 ; 0x y u u
;
(2) e 1 e 1
u m u m
u m e u m
Ta có hàm số
f(t) t 1
t
e
có giá trị nhỏ nhất bằng 0 (lập bảng biến thiên); tức là
t 1;
t
e t R
Nên
22
e 1 1 3
um
u m u m x y m
Như vậy ta tìm m để hệ bất phương trình sau có nghiệm duy nhất
22
22
1 3 4
13
xy
x y m
Với
0m
; hệ phương trình vô nghiệm.
Với
1
0
3
x
m
y


; không thỏa mãn.
Với
0m
. Gọi
12
(1;3); ( 1;3);R 2;I J R m
; hệ đã cho có nghiệm duy nhất khi
Trường hợp 1:
12
IJ 2 10 2 44 8 10R R m m
Trường hợp 2:
12
IJ 2 10 2 44 8 10R R m m
Vậy
44 8 10;44 8 10S
, suy ra tổng các phần tử thuộc tập S là 88
Câu 48. Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị nhỏ nhất của hàm số
3
2
3
3
36
x x m
fx
x x m

trên đoạn
0;3
bằng
2
3
. Tổng tất cả các phần tử của
S
bằng
A.
12
. B.
16
. C.
6
. D.
2
.
Hướng dẫn
5
Ta có
2
33
33x x m x x m
Đặt
3
30x x m t
, ta có
6
t
y
t
.
Từ giả thiết ta có
2
3 2 12 12 min 12
63
t
t t t t
t
(vì luôn tồn tại giá trị của x để t =12)
3
0;3
min 3 12 1x x m
.
Xét hàm số
3
32g x x x m
trên
0;3
, ta có:
0;3
min 2;f x m
0;3
max 18;f x m
Nếu
18
2 18 0
2
m
mm
m

, khi đó
min ( ) 0gx
. Không thỏa mãn
Nếu
2m
, suy ra
min ( ) 2g x m
. Ta có
14
2 12
10
m
m
m

, Từ điều kiện suy ra
14m
Nếu
18m 
, suy ra
min ( ) 18g x m
. Ta có
30
18 12
6
m
m
m


, Từ điều kiện suy ra
30m 
Vậy tổng các phần tử của
S
là
16
.
Câu 49. Cho tứ khối diện đều ABCD có thể tích V. Gọi M là trung điểm của BC, N là điểm thuộc cạnh CD
thỏa mãn CN=2CD, G là trọng tâm của tam giác ABD. Mặt phẳng (MNG) chia khối tứ diện ABCD
thành 2 khối đa diện. Gọi V
1
là thể tích của khối đa diện chứa đỉnh A. Tính
1
V
V
A.
41
60
B.
31
60
C.
51
60
D.
43
60
Hướng dẫn
Gọi I là giao điểm của MN và BD; P, Q lần lượt là giao điểm của IG và AD, AB.
Sử dụng định lý Talet ta có:
1
2
MK
ID BD
ID
1 1 2 1
.
2 2 3 3
PD RD RD
PA AG HG
Tương tự ta tính được
2
3
QB
QA
. Từ đó suy ra
5
8
IP
IQ
Áp dụng tỉ số thể tích ta có
.
.
.QBM
5 1 2 5 19
. . . .
8 2 3 24 24
I PDN
PDN QBM IQBM
I
V
IP ID IN
VV
V IQ IB IM
Ta tính được
..
2 19 19
5 24 60
IQMB Q IBM ABCD PDN QBM IQBM ABCD
V V V V V V
Suy ra thể tích khối đa diện chứa điểm A là
1
1
41 41
60 60
ABCD
V
VV
V
I
Q
P
N
M
G
D
C
B
A
K
N
M
C
B
D
I
R
H
G
Q
P
I
D
B
A
6
Chú ý: Có thể sử dụng định lý Menelaus để tính các tỉ số:
1
3
PD
PA
;
2
3
QB
QA
;
5
8
IP
IQ
.
Câu 50. Cho các số thực
,1xy
thay đổi thỏa mãn
2019 2020
log log 1F x y
. Gọi
,Mm
lần lượt là giá trị lớn
nhất, giá trị nhỏ nhất của biểu thức
2020 2019
log logFxy
. Khẳng định nào sau đây đúng?
A.
22
2019
log 2020Mm
B.
2 2 2 2
2019 2020
log 2020 log 2019Mm
C.
2019 2020
log 2020 log 2019Mm
D.
2019
log 2020Mm
Hướng dẫn
Đặt
2020 2019
log ; logx a y b
với
,0ab
.
Ta có
F a b
với
22
2019 2020
log 2020 log 2019 1ab
(1)
- Tìm giá trị lớn nhất: Áp dụng bất đẳng thức Bunhiacopxki ta có:
2 2 2
2019 2020 2020 2019
log 2020 log 2019 log 2019 log 2020 ( )a b a b
suy ra
2019 2020
log 2020 log 2019ab
,
dấu “=” xảy ra
22
2019 2020
2019 2020
2020 2019
log 2020 log 2019
log 2020 log 2019
log 2019 log 2020
ab
ab
Kết hợp (1) ta có
2020
2019 2020
log 2019
log 2020 log 2019
a
;
2019
2019 2020
log 2020
log 2020 log 2019
b
Do đó ta có
2019 2020
log 2020 log 2019M 
- Tìm giá trị nhỏ nhất: Ta có
22
2019 2020
1 log 2020 log 2019ab
2 2 2
2019 2019 2020
log 2020 log 2020 log 2019a b b
22
2019
log 2020ab
suy ra
2 2 2
2020 2020 2020
log 2019 ( ) log 2019 log 2019a b a b a b
, có “=” khi
2020
0; log 2019ba
Do đó ta có
2020
log 2019m
.
Vậy
22
2019
log 2020Mm
-------------------- HẾT --------------------
| 1/12
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

DDD:50 Cau
SỞ GD&ĐT HÀ TĨNH
KỲ THI THỬ TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2020 Bài thi: TOÁN
ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
(Đề thi gồm 04 trang – 50 câu) Mã đề: GỐC
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 01. Cho tập hợpA  {1;2;3;4;5}. Số tập hợp con gồm hai phần tử của tập hợp A là A. 2 C . B. 2 A . C. P . D. 11. 5 5 2
Câu 02. Cho cấp số cộng (u ) với u  3 và công sai d  4. Số hạng thứ hai của cấp số đã cho bằng n 1 A. 7. B. 12. C. 10. D. 1.
Câu 03. Tập nghiệm của phương trình x 1 4   64 là A. {4}. B. .  C. {3}. D. {5}.
Câu 04. Cho khối lăng trụ có chiều cao bằng 9, diện tích đáy bằng 6. Thể tích khối lăng trụ đã cho bằng A. 54. B. 18 C. 15. D. 5.
Câu 05. Tập xác định của hàm số y  log x  3 là 2  
A. 3;. B. 3;  .  C. .  D.  \ {3}.
Câu 06. Cho hàm số y f(x)liên tục trên a;b
  . Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số
y f (x), trục hoành và hai đường thẳng x a,x b được tính theo công thức nào sau đây? A. b b b b S f (x)dxB. S f (x)dx.  C. 2 S f (x)dx. 
D. S f (x)dx.  a a a a
Câu 07. Cho khối chóp có diện tích đáy B  5 và chiều cao h  6 . Thể tích của khối chóp đã cho bằng A. 10. B. 30. C. 11. D. 15.
Câu 08. Cho hình trụ có độ dài đường sinh bằng 4, bán kính đáy bằng 3. Diện tích xung quanh của hình trụ đã cho bằng A. 24 . B. 12 . C. 36 . D. 48 .
Câu 09. Cho khối cầu có bán kính R  3. Thể tích khối cầu đã cho bằng A. 36 . B. 4 . C. 12 . D. 108 .
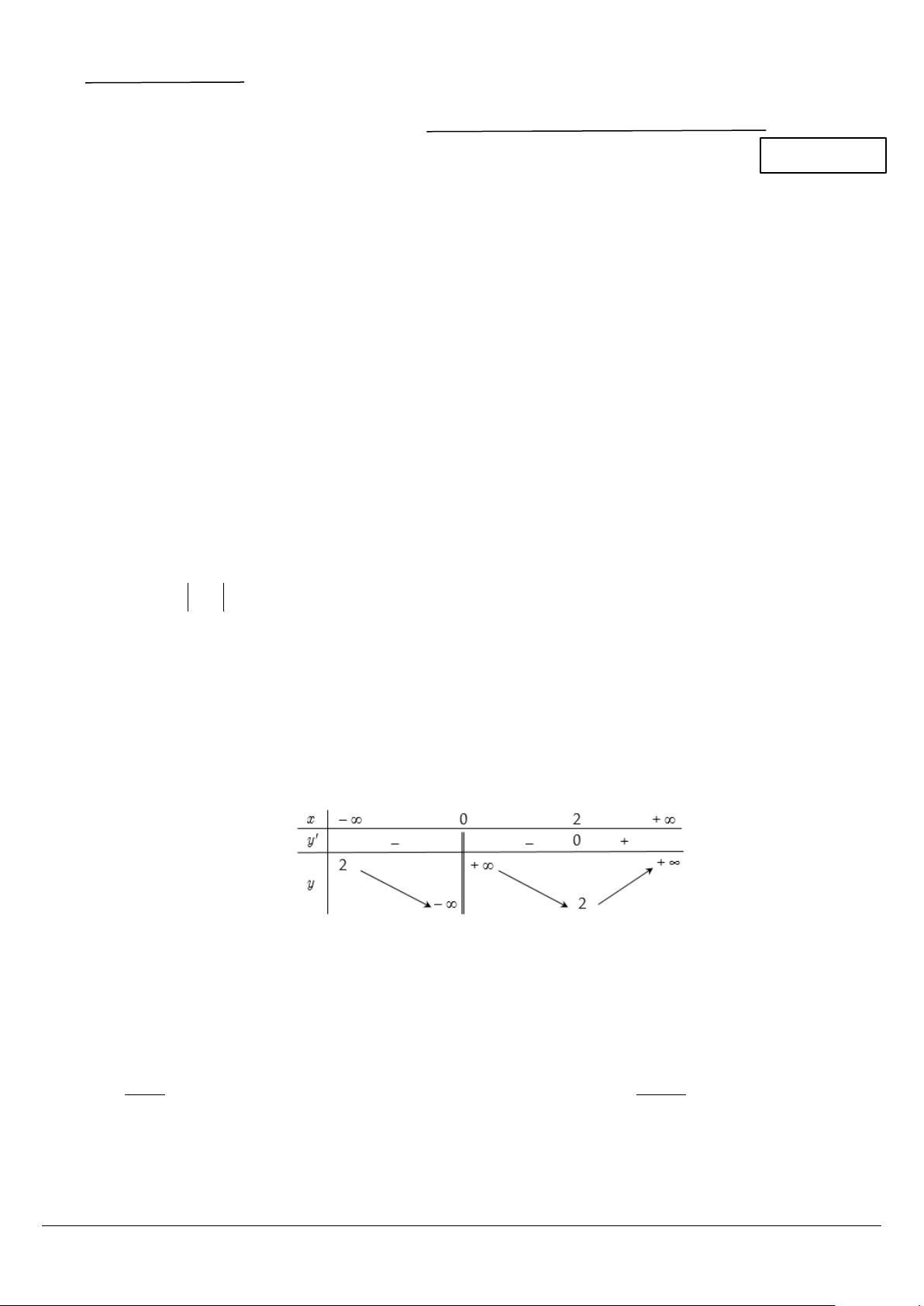
Câu 10. Cho hàm số y f(x) có bảng biến thiên như hình vẽ. Hàm số đồng biến trên khoảng nào dưới đây? A. (2; )
 . B. (0;2). C. (0; )  . D. ( ;  0).
Câu 11. Cho a là số thực dương, a  1, khi đó 3log 2 a a bằng A. 8. B. 3
a C. 6. D. 3a.
Câu 12. Cho khối nón có chiều cao h, bán kính đáy r. Thể tích khối nón đã cho bằng 2 2 A. h r 4h r . B. 2 2h r . C. 2 h r . D. . 3 3
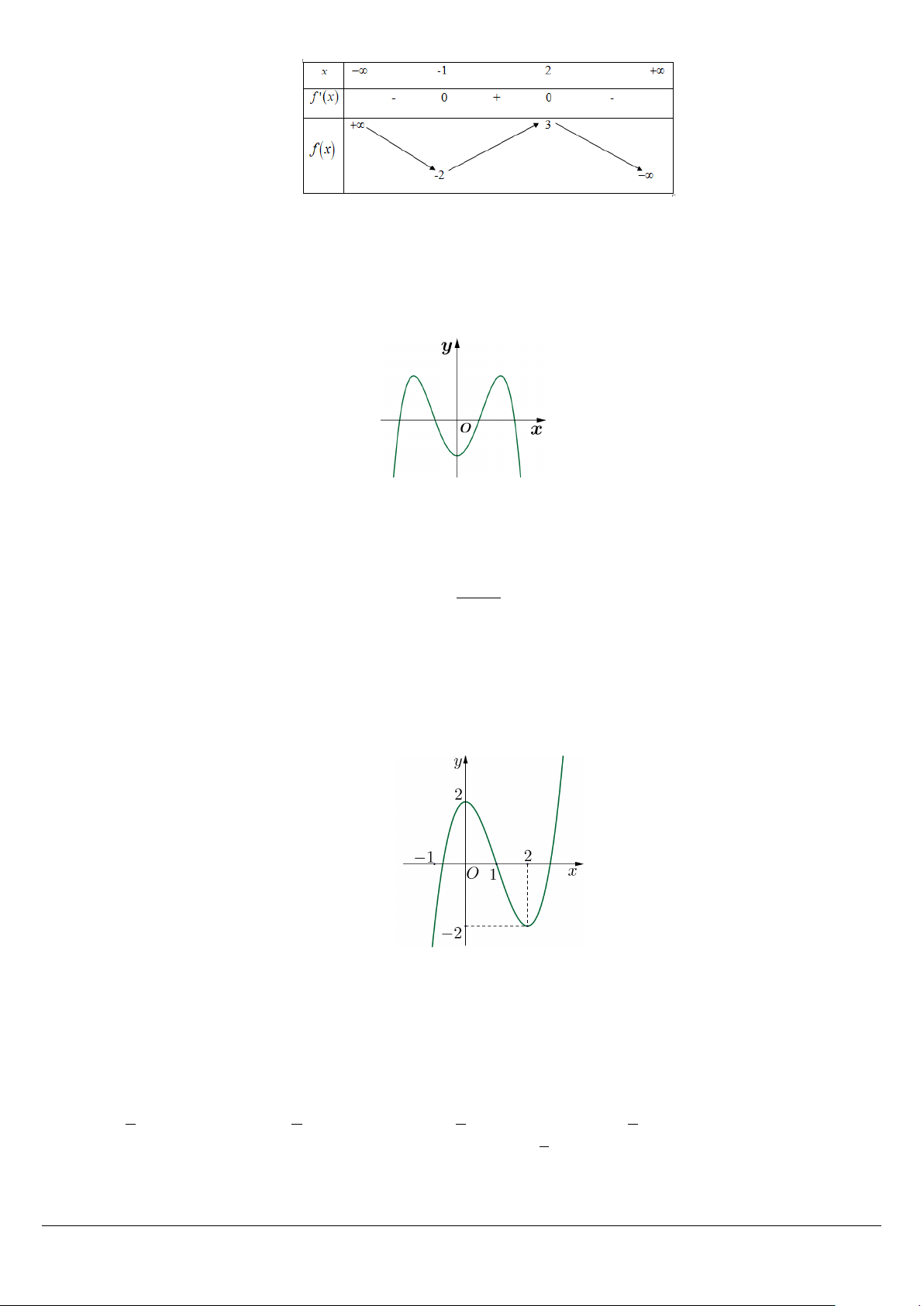
Câu 13. Cho hàm số y f(x) có bảng biến thiên như hình vẽ. Giá trị cực đại của hàm số bằng Trang 1 / 1 DDD:50 Cau A. 3. B. 2. C. 2. D. 1.
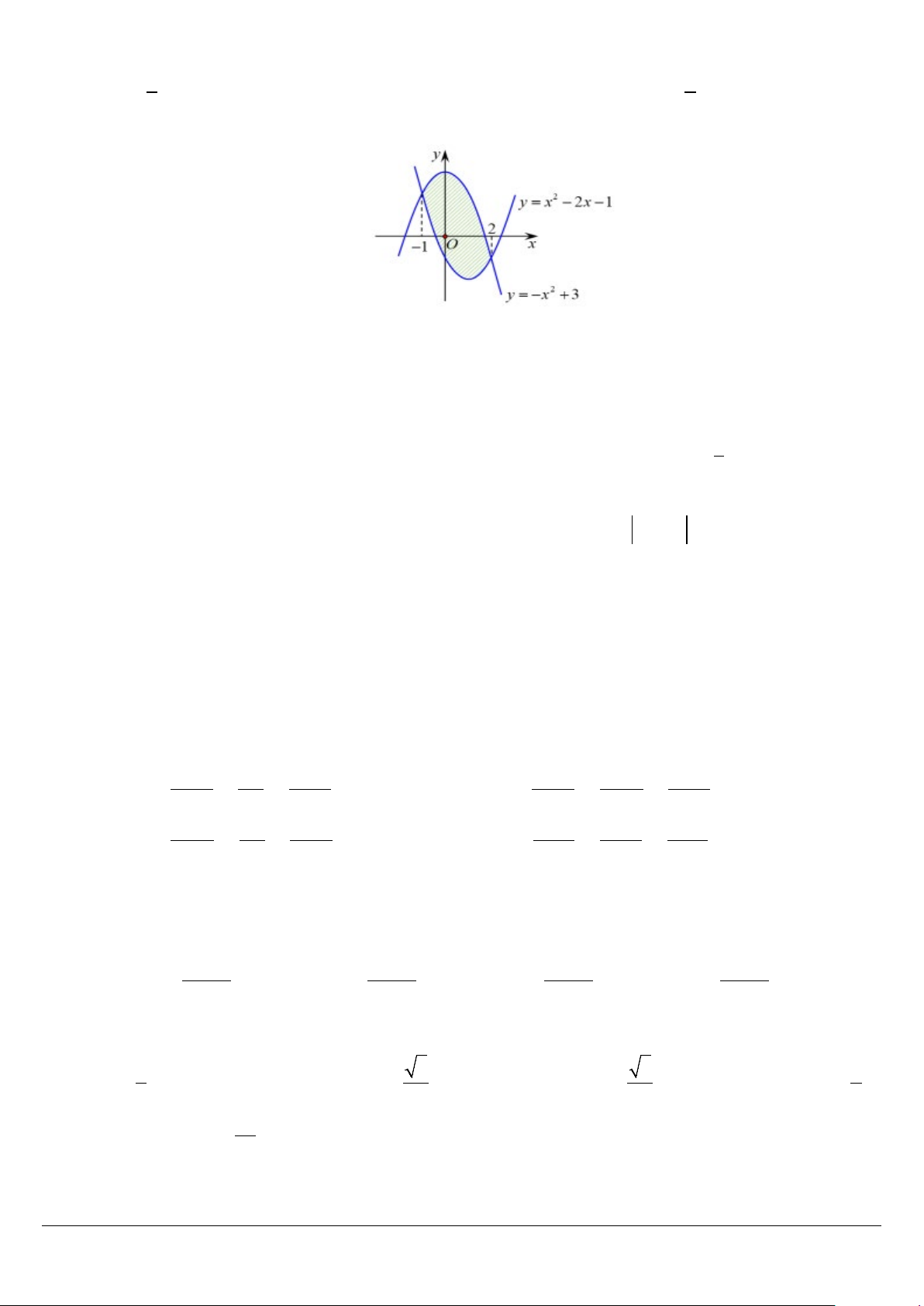
Câu 14. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ ? A. 4 2 y x
  3x  1. B. 4 2
y x  3x  1 . C. 4 2 y x
  3x  1. D. 4 2
y x  3x  1.
Câu 15. Đường tiệm cận ngang của đồ thị hàm số 3x y  có phương trình là x  4 A. y  3.
B. y  4. C. x  3. D. x  4.
Câu 16. Tập nghiệm của bất phương trình 3x  9 là A.  ;2  .   B. ( ;  2). C. (2; )  . D. 2;  . 
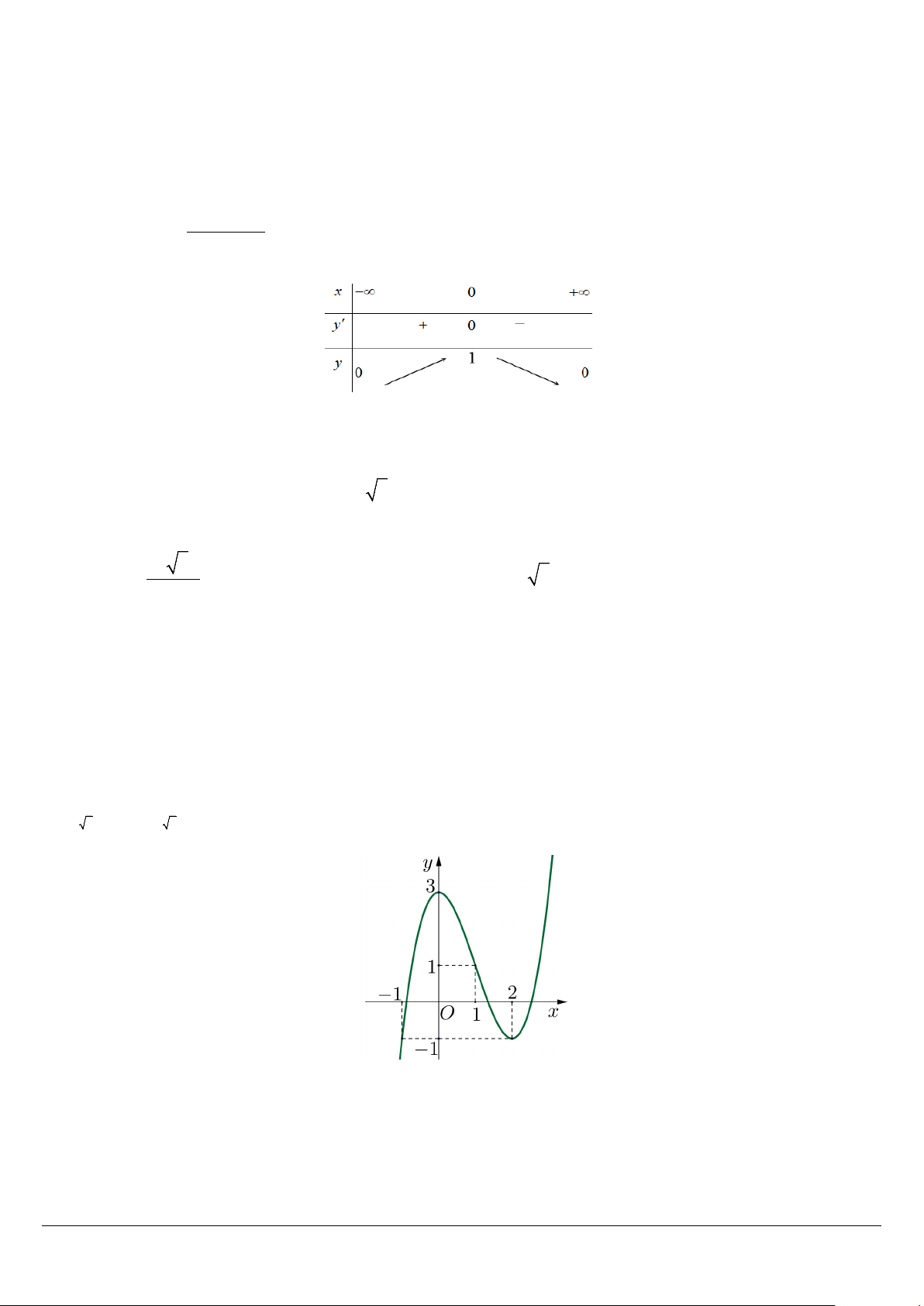
Câu 17. Cho hàm số bậc ba y f(x) có đồ thị như hình vẽ. Số nghiệm phân biệt của phương trình f(x)  2 là A. 2. B. 0. C. 3. D. 1.
Câu 18. Cho 2 f(x)dx  2 
và 3 f(x)dx  3 
. Tích phân 3 f(x)dx  bằng 0 2 0 A. 5. B. 1. C. 6. D. 1.
Câu 19. Cho số phức z  3  4i. Số phức liên hợp của số phứcz là
A. z  3  4i.
B. z  3  4i. C. z  3  4i.
D. z  4  3i.
Câu 20. Cho số phức z  2  3i. Tọa độ điểm biểu diễn số phức z là A. 2;3. B. 2;3. C. 3;2. D. 2;3. Trang 2 / 6 DDD:50 Cau
Câu 21. Phần ảo của số phức z  5 ii là A. 5. B. 5i. C. 1. D. 1.
Câu 22. Trong không gian Oxyz, hình chiếu vuông góc của điểm M 1;3;5 lên mặt phẳng tọa độ Oxy là điểm có tọa độ A. 1;3;0. B. 1;0;5. C. 0;3;5. D. 0;0;5.
Câu 23. Trong không gian Oxyz, cho mặt cầu S 2 2 2
: x y z  2x  4y  4z  7  0. Bán kính của mặt cầuS là A. R  4. B. R  16. C. R  2. D. R  2.
Câu 24. Trong không gian Oxyz, cho mặt phẳng P : 2x  3y  4z 1  0. Véc tơ nào dưới đây là một véc
tơ pháp tuyến của mặt phẳng P ? A.    
n  2;3;4 . B. n  2;3;1 . C. n  2;3;4 . D. n  2;4;1 . 4   3   2   1  
Câu 25. Trong không gian x y z
Oxyz, cho đường thẳng 1 2 4  :  
. Điểm nào dưới đây thuộc 2 3 1 đường thẳng ?
A. M 1;2;4. B. N 2;3; 
1 . C. P 1;2;4. D. Q1;2;4.
Câu 26. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng ABC , SA a , tam giác ABC vuông
cân tại B và SC a 3 . Khoảng cách giữa hai đường thẳng SA và BC bằng A. a . B. 2a . C. a 3 . D. a 5 . Câu 27. Hàm số 4 2
y x  2x  2019 nghịch biến trên khoảng nào sau đây ? A. ;  1 . B. 1;  0 . C. 1;  1 . D.   ;1 .
Câu 28. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3
y x  3x  2 trên đoạn 0;2   .
Khi đó tổng M m bằng A. 4 . B. 16 . C. 2 . D. 6. 5   Câu 29. Cho  a
a, b là các số thực dương và a khác 1, thỏa mãn log  
  2 . Giá trị của biểu thức log b 3   a 4  b  a bằng A. 4 . B. 4 . C. 1 . D. 1  . 4 4
Câu 30. Số giao điểm của đồ thị hàm số 4 2
y x  3x  1 với trục hoành là A. 4. B. 3. C. 2. D. 1.
Câu 31. Tìm số nghiệm nguyên của bất phương trình log 4x  9  log x  10 . 1   1   2 2 A. 4 . B. Vô số. C. 0 . D. 6.
Câu 32. Trong không gian, cho tam giác ABC đều cạnh bằng 4. Thể tích của khối tròn xoay được tạo thành
khi quay hình tam giác ABC quanh cạnh BC là A. 16. B. 8. C. 48. D. 27. 1 1 Câu 33. Xét 2020 x x   2020 3 2 2 dx , nếu đặt 2
u x  2 thì 3 x  2 x   2 dx bằng 0 0 Trang 3 / 6 DDD:50 Cau 3 1 3 1 A. 1   1 u  2 2020 u
du . B.  u 2 2020 u
du . C.  u 2 2020 u
du . D.  u 2 2020 u du . 2 2 2 0 2 0
Câu 34. Diện tích phần hình phẳng gạch chéo trong hình vẽ được tính theo công thức nào dưới đây? 2 2 2 2 A.   2
2x  2x  4dx B.  2x  2dx .
C.  2x 2dx . D.   2
2x  2x  4dx 1 1 1 1 .
Câu 35. Cho hai số phức z a  2i và z  1  , bi
a b   . Phần ảo của số phức z z bằng 1 2 với , 1 2
A. 2 b .
B. 2 bi .
C. a  1.
D. 2 b .
Câu 36. Phương trình 2
z  2z  10  0 có hai nghiệm là z , z . Giá trị của z z là 1 2 1 2 A. 6. B. 3 . C. 4 . D. 2 .
Câu 37. Trong không gian Oxyz, cho hai điểm A3;1; 
1 ,B 1;2;4. Viết phương trình mặt phẳng P đi
qua A và vuông góc với đường thẳng AB.
A. P : 2x  3y  3z  6  0.
B. P : 2x  3y  3z 16  0.
C. P : 2x  3y  3z  6  0.
D. P : 2x  3y  3z 16  0.
Câu 38. Trong không gian với hệ tọa độ Oxyz , phương trình đường thẳng d đi qua điểm A1;2;  1 và vuông
góc với mặt phẳng P : x  2y z 1  0 là: A. x  2 y z  2 x y z d :   . B. 1 2 1 d :   . 2 4 2 1 2 1 C. x  2 y z  2 x y z d :   . D. 1 2 1 d :   . 1 2 1 2 2 1
Câu 39. Một trường học có 25 giáo viên nam và 15 giáo viên nữ trong đó có đúng 2 cặp vợ chồng. Nhà trường
chọn ngẫu nhiên 5 người trong số 40 giáo viên đi công tác. Tính xác suất p của biến cố: “chọn được đúng một cặp vợ chồng”. A. 700 p B. 350 p C. 595 p D. 1400 p 27417 27417 27417 27417
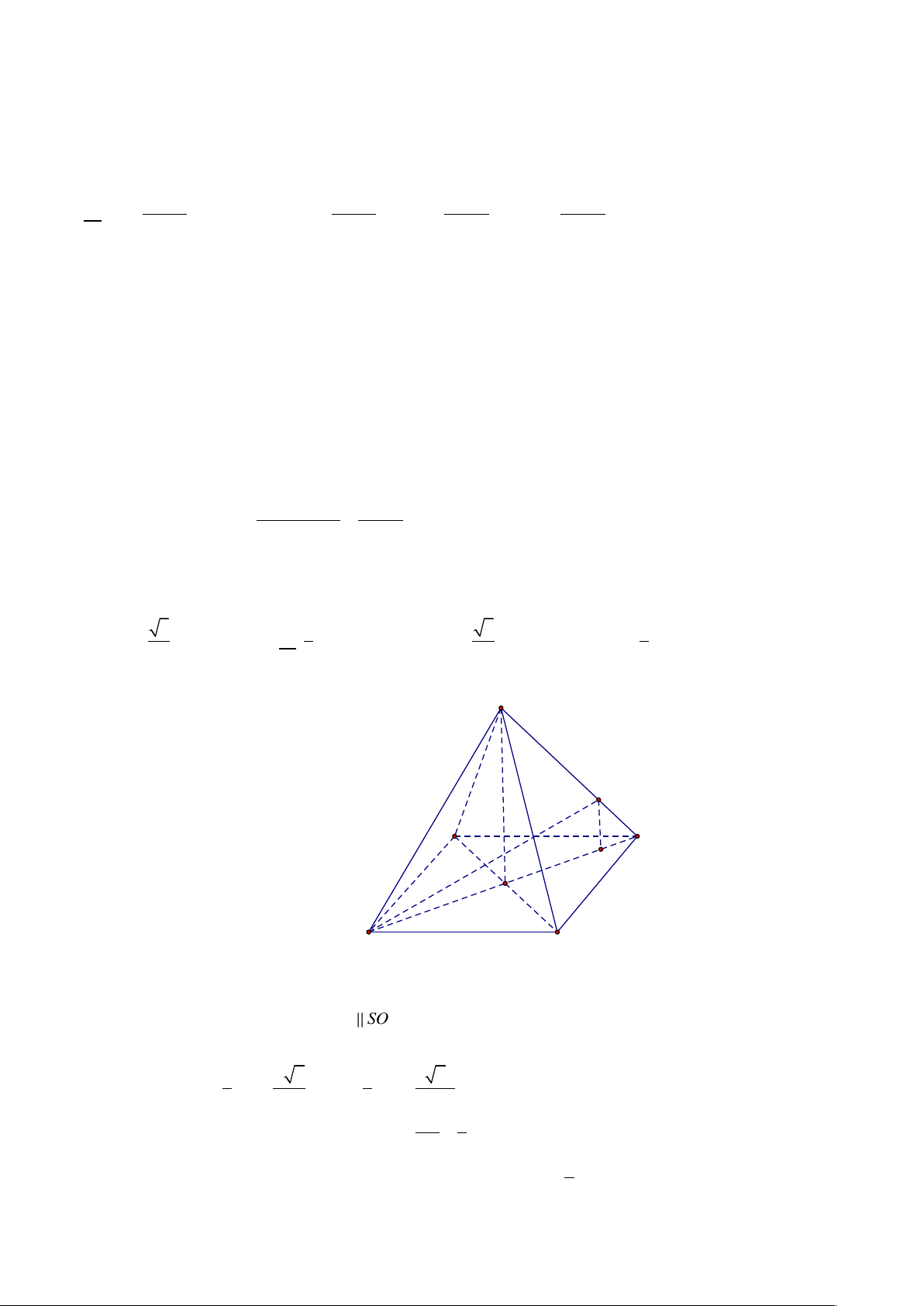
Câu 40. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Gọi M là điểm nằm trên đoạn
SD sao cho SM  2MD . Giá trị tan của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng: A. 1 . B. 3 . C. 5 . D. 1 . 5 3 5 3 3 Câu 41. Hàm số x 2 y  
x mx  2 nghịch biến trên khoảng 0; khi và chỉ khi 3 A. m 1;     . 
B. m  1;. C. m   0;  . 
D. m  0;. Trang 4 / 6 DDD:50 Cau
Câu 42. Một trang trại nuôi gà dự tính lượng thức ăn tiêu thụ hằng ngày là không đổi và đã dữ trữ thức ăn đủ
dùng trong 60 ngày. Nhưng thực tế, kể từ ngày thứ hai trở đi lượng thức ăn tiêu thụ hàng ngày của trang
trại đã tăng thêm 2% so với ngày trước đó. Hỏi lượng thức ăn mà trang trại đã dự trữ đủ dùng cho tối đa là bao nhiêu ngày ? A. 39 (ngày). B. 41 (ngày). C. 40 (ngày). D. 42 (ngày). Câu 43.
Cho hàm số y f x xác định trên  , có bảng biến thiên như hình vẽ. Với giá trị nào của m thì đồ thị hàm số 1 y
có tổng số đường tiệm cận ngang và tiệm cận đứng bằng 3. Chọn đáp án đúng 2
f (x)  m
A. 0  m  1.
B. m  0 . C. 0  m  1.
D. 0  m  1.
Câu 44. Cho hình nón có chiều cao bằng 2 5 . Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón theo một
thiết diện là tam giác vuông cân có diện tích bằng 18 . Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng A. 32 5. B. 32. C. 32 5. D. 96. 3 Câu 45 . Cho   2 ( )  2 . x F x x
x e là một nguyên hàm của   2 . x
f x e . Tìm họ nguyên hàm của hàm số   2x f x e . A.     2x   2 d 2   x f x e x x e C . B.
   2x   2 d   2 x f x e x x e C . C.
   2x   2 d    2 x f x e x x e C . D.     2x   2 d 2   x f x e x x e C .
Câu 46. Cho hàm số bậc ba y f x có đồ thị như hình vẽ. Số nghiệm phân biệt của phương trình    x  2 2    2 x f f 2  0 là   A. 2 B. 1 C. 4 D. 3
Câu 47. Gọi S là tập hợp tất cả các giá trị của tham số m sao cho hệ phương trình sau có nghiệm duy nhất. Trang 5 / 6 DDD:50 Cau  2 2 2020  (2020x y
 2020 xy )  (x  1)   y  32 2 2 6 6 2  4
 x 21 y 32 e     2 2
x y  2x  6y  11  mm e
Tổng của tất cả các phần tử thuộc tập hợp S là A. 88. B. 2 10  2. C. 2 10  2. D. 44 .
Câu 48. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị nhỏ nhất của hàm số 3  
x  3x m f x  trên đoạn 0;3  
. Tổng tất cả các phần tử của S bằng   bằng 23
x  3x m2 3  6 A. 16. B. 12 . C. 6. D. 2 .
Câu 49. Cho tứ khối diện đều ABCD có thể tích V . Gọi M là trung điểm của BC, N là điểm thuộc cạnh
CD thỏa mãn CN  2N ,
D G là trọng tâm của tam giác ABD . Mặt phẳng (MNG) chia khối tứ diện ABCD
thành 2 khối đa diện. Gọi V
V là thể tích của khối đa diện chứa đỉnh A . Tính 1 1 V A. 41 B. 31 C. 51 D. 43 60 60 60 60
Câu 50. Cho các số thực x,y  1 thay đổi thỏa mãn log x  log
y  1. Gọi M,m lần lượt là giá trị lớn 2019 2020
nhất, giá trị nhỏ nhất của biểu thức F  log x  log
y . Khẳng định nào sau đây đúng? 2020 2019 A. 2 2 M m  log 2020 B. 2 2 2 2 M m  log 2020  log 2019 2019 2019 2020
C. M m  log 2020  log 2019
D. M m  log 2020 2019 2020 2019
--------------- HẾT --------------- Trang 6 / 6
Hướng dẫn các câu vận dụng, vận dụng cao
(các câu theo thứ tự của đề tham khảo)
Câu 39. Một trường học có 25 giáo viên nam và 15 giáo viên nữ trong đó có đúng 2 cặp vợ chồng. Nhà
trường chọn ngẫu nhiên 5 người trong số 40 giáo viên đi công tác. Gọi p là xác suất của biến cố: “chọn được
đúng một cặp vợ chồng”. Tính p . 700 350 595 700 A. p B. p C. p D. p 27417 27417 27417 27417 Hướng dẫn
Số cách chọn 5 người bất kỳ là 5 C 40
Giả sử có 2 cặp vợ chồng là (A, B) và (C, D) trong đó A, C là chồng.
TH1: chọn cặp vợ chồng (A, B)
Cần chọn 3 người trong số 38 còn lại (trừ A, B) mà không có cặp (C, D)
- Số cách chọn 3 người bất kỳ trong 38 người là 3 C 38
- Số cách chọn 3 người trong 38 người mà có cặp (C, D) là 1 C 36
suy ra số cách chọn 3 người trong số 38 người mà không có cặp (C, D) là 3 C - 1 C 38 36
TH2: chọn cặp vợ chồng (C, D).
Tương tự trên ta có số cách chọn là 3 C - 1 C 38 36 3 1 2(C C ) 700 Xác suất cần tính là: 38 36 p   5 C 27417 40
Câu 40. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Gọi M là điểm nằm trên đoạn
SD sao cho SM  2MD . Giá trị tan của góc giữa đường thẳng BM và mặt phẳng ( ABCD) là: 3 1 5 1 A. . B. . C. . D. . 3 5 5 3 Hướng dẫn S M A I D O B C
Trong mặt phẳng (ABCD) : AC BD   
O SO  ( ABCD)
Xét SAO vuông tại O có: .
Kẻ MI BD tại I . Suy ra: MI SO nên MI  (ABCD) .
Vậy góc giữa BM và mặt phẳng (ABCD) là góc MBI . 1 a 2 5 5 2a
Ta có: MI SO  ; BI BD  . 3 6 6 6 MI 1 Xét M
BI vuông tại I ta có: tan MBI   BI 5 1
Vậy giá trị tan của góc giữa BM và mặt phẳng (ABCD) là . 5 1 3 x Câu 41. Hàm số 2 y  
x mx  2 nghịch biến trên khoảng 0; khi và chỉ khi 3
A. m 1;.
B. m  1;.
C. m 0;.
D. m 0;. Hướng dẫn
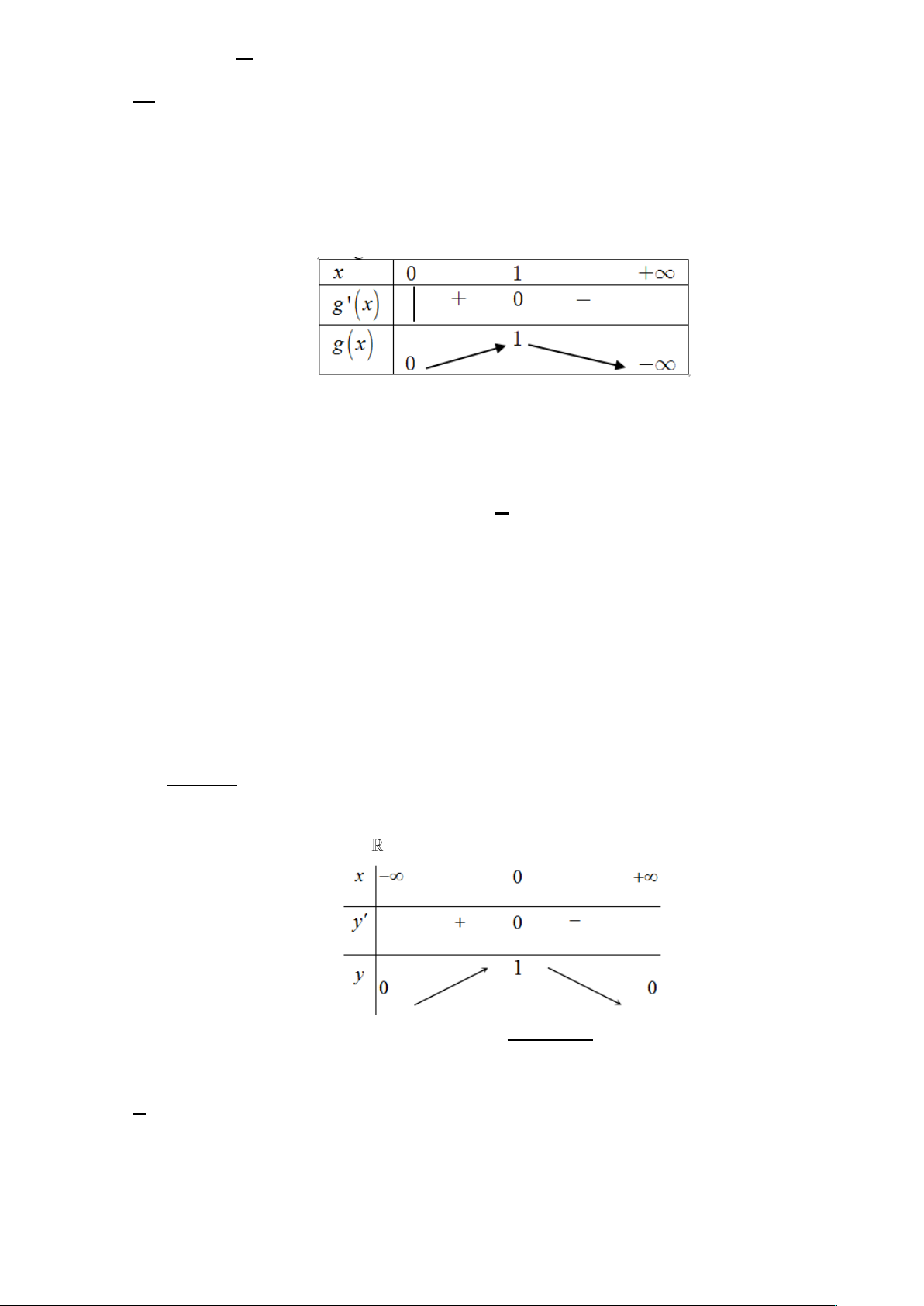
Hàm số nghịch biến trên khoảng 0; khi và chỉ khi y  0, x  0; 2
 x  2x m  0, x  0; 2
m  x  2x, x  0; Xét g x 2
 x  2x trên khoảng 0; Bảng biến thiên
Dựa vào bảng biến thiên suy ra m g x , x
 0;  m 1
Câu 42. Một trang trại nuôi gà dự tính lượng thức ăn tiêu thụ hằng ngày là không đổi và đã dữ trữ thức ăn đủ
dùng trong 60 ngày. Nhưng thực tế, kể từ ngày thứ hai trở đi lượng thức ăn tiêu thụ hàng ngày của
trang trại đã tăng thêm 2% so với ngày trước đó. Hỏi lượng thức ăn mà trang trại đã dự trữ đủ dùng
cho tối đa là bao nhiêu ngày ? A. 40 (ngày). B. 41 (ngày). C. 39 (ngày). D. 42 (ngày). Hướng dẫn
Gọi a là lượng thức ăn cần dùng mỗi ngày theo dự kiến, n là số ngày thức tế hết lượng thức ăn đã chuẩn bị.
Khi đó lượng thức ăn trang trại đã chuẩn bị là: 60a .
Vì n là số ngày thực tế nên lượng thức ăn đã tiêu thụ sẽ là  a aa
  3   a  n 1 2 .1,02 . 1,02 1. 1,02 ... . 1,02 . Ta có phương trình sau:  a aa
  3   a  n 1 2 .1,02 . 1,02 1. 1,02 ... . 1,02  60.a a 2 n 1 1 1,02 1.02 ... 1.02         60.a n 1  1,02 na
 60.a  1,02  2,2  n  39,815. 1 1, 02
Vậy lượng thức ăn đủ dùng cho 39 ngày.
Câu 43. Hàm số y f x xác định trên
có bảng biến thiên như hình vẽ sau 1
Với giá trị nào của m thì đồ thị hàm số y g x  
có tổng số đường tiệm cận ngang và
f x2  m
tiệm cận đứng bằng 3.
A. 0  m  1 .
B. 0  m  1 .
C. 0  m  1 .
D. 0  m  1 . Hướng dẫn
Nếu m=0, không có tiệm cận Nếu m  0 2 1  1 
Nhận xét: lim f x  0; lim f x  0 , nên lim g x 
; lim g x 
. Suy ra đồ thị hàm số x x x  x m  m
y g x có 1 đường tiệm cận ngang.
Suy ra đồ thị hàm số phải có 2 đường tiệm cận đứng.
Xét phương trình  f x2  m    f x2 0  m   *
TH1: nếu m  0 thì phương trình * vô nghiệm nên đồ thị hàm số không có tiệm cận đứng.
f (x)  m   1
TH2: nếu m > 0 thì phương trình *  
f (x)   m  2 Với  
1 : khi 0  m  1 thì  
1 có 2 nghiệm; m  1 thì   1 có nghiệm duy nhất
Với 2 : do m  0 nên vô nghiệm.
Vậy để đồ thị hàm số có 2 tiệm cận đứng thì 0  m  1.
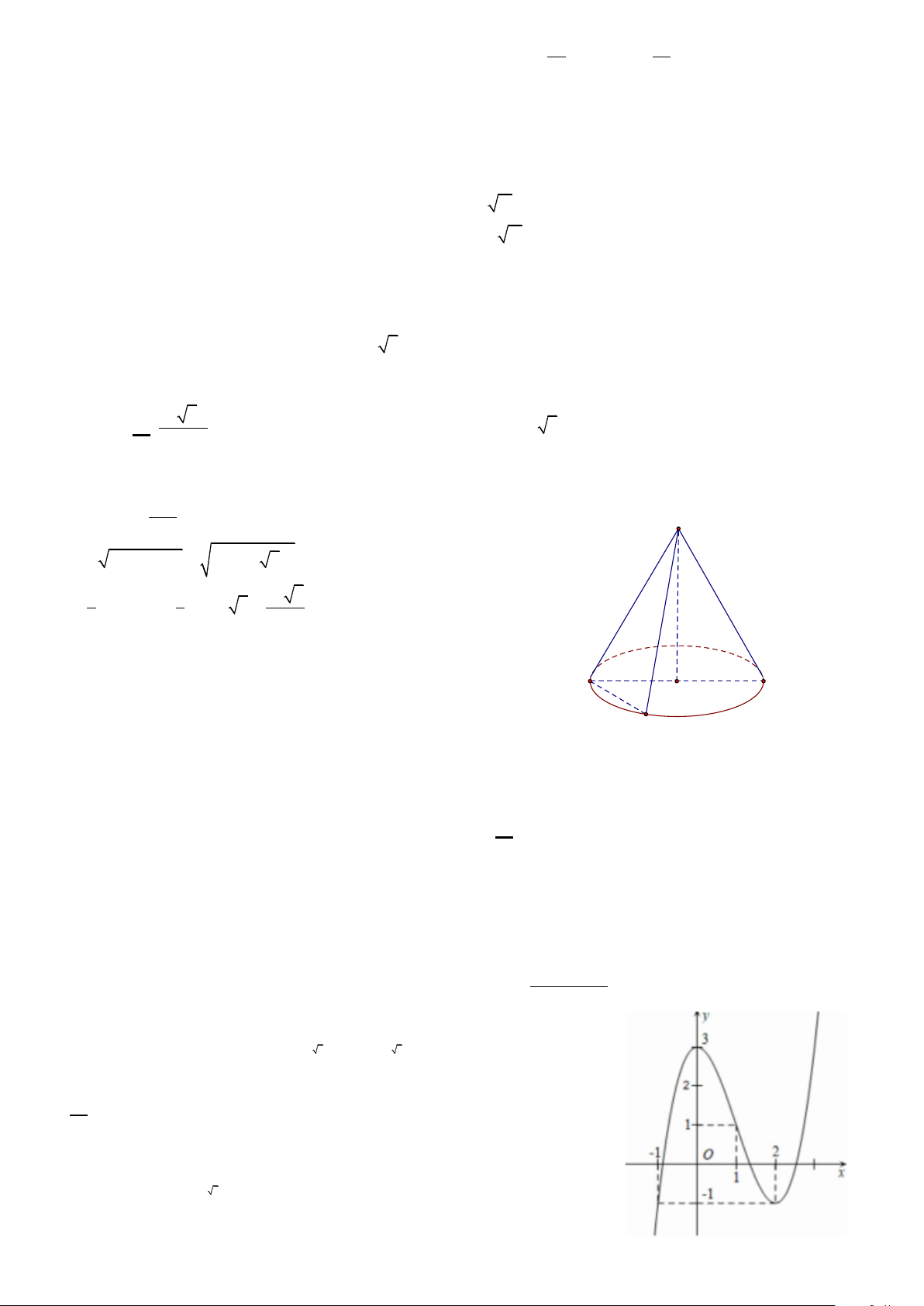
Câu 44. Cho hình nón có chiều cao bằng 2 5 . Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón theo một
thiết diện là tam giác vuông cân có diện tích bằng 18 . Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng 32 5 A. . B. 32 . C. 32 5 . D. 96 . 3 Hướng dẫn 2 SA S 18  18  SA  6 S SAC 2 OA SA SO    2 2 2 2 6 2 5  4 1 1 32 5 2 2
V   OA SO   .4 .2 5  . 3 3 3 A B O C Câu 45 . Cho   2 ( )  2 . x F x x
x e là một nguyên hàm của   2 . x
f x e . Tìm họ nguyên hàm của hàm số   2x f x e .
A.    2x   2 d 2   x f x e x x e C .
B.    2x   2 d  2 x f x e x x e C .
C.    2x   2 d   2 x f x e x x e C .
D.    2x   2 d 2   x f x e x x e C . Hướng dẫn
Cách 1. Sử dụng phương pháp từng phần
Cách 2. Sử dụng định nghĩ nguyên hàmVì
    2  2  x F x x
x e là một nguyên hàm của   2 . x f x e nên ta có:      x x  2 . x F x f x e  
  x   2   x    2 2 2 2 x x e x x e f x ef x 2 4 2  x e
Câu 46. Cho hàm số y f x có đồ thị như hình vẽ sau 2
Số nghiệm của phương trình  2 x    2 x f f 20 là A. 5 B. 1 C. 2 D. 3 Hướng dẫn Điều kiện: 0 2 x x   1. 3
f 2 x  2 1 2
Ta có:  f 2 x   f 2 x       2  0      f  2 x   1  2
Quan sát đồ thị hàm số, ta thấy:
+ Đường thẳng y  2 cắt đồ thị hàm số y f x tại ba điểm x  0  x 1 2  x . 0 1 2
2 x a  0 vo nghiem  Do đó  
1  2 x b 0;  1 (vo nghiem)  x 2
2  c  2  x  log c x  log c  2 2
+ Đường thẳng y  1
 cắt đồ thị hàm số y f x tại hai điểm x  1  ; x  2 1 2 2 x  1  vo nghiem Do đó 2  
2 x  2  x 1 x 1
Vậy phương trình đã cho có hai nghiệm phân biệt.
Câu 47. Gọi S là tập hợp tất cả các giá trị của tham số m sao cho hệ phương trình sau có nghiệm duy nhất. 2 2
2020 (2020x y  2020 xy )  (x 1)    y  32 2 2 6 6 2  4
 x 21y32 e    2 2
x y  2x  6 y  11  mm e
Tổng của tất cả các phần tử thuộc tập hợp S là A. 88. B. 44 C. 2 10  2. D. 44  8 10 . Hướng dẫn 2 2
2020 (2020x y  2020 xy )  (x 1)    y  32 2 2 6 6 2  4
 x 21y32 e    2 2
x y  2x  6 y  11  mm e 2 2 x y  2 2 2 2 x 6 y 4 2020
x y  2  2020
 2x  6y  4 (1)   
x 2  y 2 e  
x 21 y32 1 3 1 mm e (2) 2 2
Ta có hàm số luôn đồng biến nên 2 2 (1) x y 2 2x 6y 4 x 1 y 3 4 Đặt  u m u m
x  2   y  2 1 3  ; u u  0 ;(2) e u 1 m e e u m 1 Ta có hàm số f(t) t
e  t1có giá trị nhỏ nhất bằng 0 (lập bảng biến thiên); tức là te  t1; t   R
Nên um u m   u m   x  2   y  2 e 1 1 3  m   x   2
1   y  32  4
Như vậy ta tìm m để hệ bất phương trình sau có nghiệm duy nhất    x   2
1   y  32  m
Với m  0 ; hệ phương trình vô nghiệm. x  1 Với m  0   ; không thỏa mãn.  y  3
Với m  0 . Gọi I (1;3); J ( 1
 ;3);R  2; R m ; hệ đã cho có nghiệm duy nhất khi 1 2 Trường hợp 1: IJ R R 2 10 2 m m 44 8 10 1 2 Trường hợp 2: IJ R R 2 10 2 m m 44 8 10 1 2
Vậy S  44 8 10;44 8 10  , suy ra tổng các phần tử thuộc tập S là 88
Câu 48. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị nhỏ nhất của hàm số 3  
x  3x m 2 f x
trên đoạn 0;3 bằng . Tổng tất cả các phần tử của S bằng
x 3x m2 3  6 3 A. 12 . B. 16 . C. 6 . D. 2 . Hướng dẫn 4
Ta có  x x m2 3 3 3
x  3x m Đặ t t 3
x  3x m t  0 , ta có y  . t  6 t 2 Từ giả thiết ta có
  3t  2t 12  t 12  min t 12 (vì luôn tồn tại giá trị của x để t =12) t  6 3 3
 min x  3x m 12   1 . 0; 3
Xét hàm số g x 3
x  3x  2m trên 0;3 , ta có:
min f x  m  2; max f x  m 18; 0; 3 0; 3 m  
Nếu m  m   18 2 18  0  
, khi đó min g(x)  0 . Không thỏa mãn  m  2  m 14
Nếu m  2 , suy ra min g(x)  m  2 . Ta có m  2  12  
, Từ điều kiện suy ra m  14 m  10  m  30 Nếu m  18
 , suy ra min g(x)  m 18 . Ta có m 18 12  
, Từ điều kiện suy ra m  30  m  6
Vậy tổng các phần tử của S là 16 .
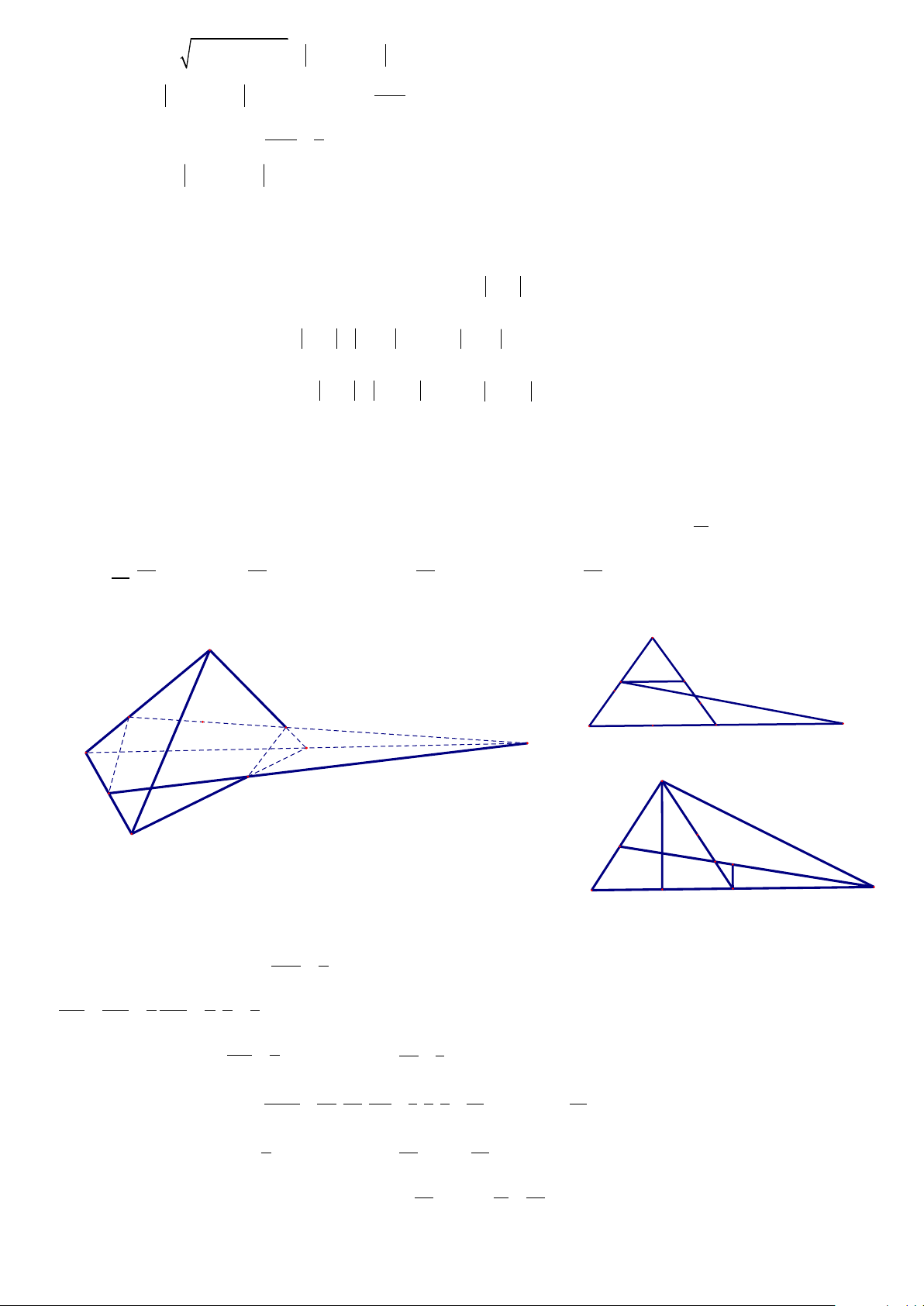
Câu 49. Cho tứ khối diện đều ABCD có thể tích V. Gọi M là trung điểm của BC, N là điểm thuộc cạnh CD
thỏa mãn CN=2CD, G là trọng tâm của tam giác ABD. Mặt phẳng (MNG) chia khối tứ diện ABCD V
thành 2 khối đa diện. Gọi V1 là thể tích của khối đa diện chứa đỉnh A. Tính 1 V 41 31 51 43 A. B. C. D. 60 60 60 60 Hướng dẫn A C K M N Q G P I D B I D B A N M Q C G P R B H I D
Gọi I là giao điểm của MN và BD; P, Q lần lượt là giao điểm của IG và AD, AB. MK 1
Sử dụng định lý Talet ta có:
  ID BD ID 2 PD RD 1 RD 1 2 1    .  PA AG 2 HG 2 3 3 Tương tự QB 2 IP ta tính được  . Từ đó suy ra 5  QA 3 IQ 8 V IP ID IN 5 1 2 5 19
Áp dụng tỉ số thể tích ta có I.PDN  . .  . .   VV PDN . V IQ IB IM 8 2 3 24 QBM 24 IQBM I . QBM Ta tính đượ 2 19 19 c VVVVVV IQMB Q.IBM ABCD PDN . 5 QBM 24 IQBM 60 ABCD 41 V 41
Suy ra thể tích khối đa diện chứa điểm A là 1 V V   1 60 ABCD V 60 5 PD 1 QB 2 IP 5
Chú ý: Có thể sử dụng định lý Menelaus để tính các tỉ số:  ;  ;  . PA 3 QA 3 IQ 8
Câu 50. Cho các số thực ,
x y 1 thay đổi thỏa mãn F  log x  log
y  1. Gọi M , m lần lượt là giá trị lớn 2019 2020
nhất, giá trị nhỏ nhất của biểu thức F  log x  log
y . Khẳng định nào sau đây đúng? 2020 2019 A. 2 2 M m  log 2020 B. 2 2 2 2 M m  log 2020  log 2019 2019 2019 2020
C. M m  log 2020  log 2019
D. M m  log 2020 2019 2020 2019 Hướng dẫn Đặt log x  ; a log
y b với a,b  0 . 2020 2019
Ta có F a b với 2 2 a log 2020  b log 2019  1 (1) 2019 2020
- Tìm giá trị lớn nhất: Áp dụng bất đẳng thức Bunhiacopxki ta có:  2 2 a log 2020  b log 2019log 2019  log 2020 2  (a  ) b 2019 2020 2020 2019
suy ra a b  log 2020  log 2019 , 2019 2020 2 2 a log 2020 b log 2019 dấu “=” xảy ra 2019 2020    alog 2020  b log 2019 2019 2020 log 2019 log 2020 2020 2019 log 2019 log 2020 Kết hợp (1) ta có 2020 a  ; 2019 b  log 2020  log 2019 log 2020  log 2019 2019 2020 2019 2020
Do đó ta có M  log 2020  log 2019 2019 2020
- Tìm giá trị nhỏ nhất: Ta có 2 2 1  a log 2020  b log 2019    2 2 a b  2 log 2020  b log 2020  log 2019   2 2 a b log 2020 2019  2019 2020  2019 2020 2019 suy ra 2 2 2 a b  log 2019  (a  ) b  log
2019  a b  log
2019 , có “=” khi b  0; a  log 2019 2020 2020 2020 2020
Do đó ta có m  log 2019 . 2020 Vậy 2 2 M m  log 2020 2019
-------------------- HẾT -------------------- 6
Document Outline

  • Sở-Hà-Tĩnh-2019-2020-lần-2-ĐỀ-GỐC
  • Sở-Hà-Tĩnh-2019-2020-lần-2-HƯỚNG-DẪN-GIẢI-VD-VDC