Đề thi thử tốt nghiệp THPT năm 2023 môn Toán sở GD&ĐT Nam Định

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi thử tốt nghiệp THPT năm học 2022 – 2023 môn Toán sở Giáo dục và Đào tạo tỉnh Nam Định

26 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

46 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
Mã đề 202 - trang 1/6
SỞ GIÁO DỤC V ĐO TẠO
NAM ĐỊNH
MÃ ĐỀ: 202
ĐỀ THI THỬ TỐT NGHIỆP LỚP 12 THPT
NĂM HC 2022 – 2023
Môn: Toán – lp 12 THPT
(Thời gian làm bài: 90 phút)
Đề thi gồm 06 trang.
Họ và tên học sinh:………………………………………
Số báo danh:………….…………………….……………
Câu 1: Gieo một đồng tiền cân đối, đồng chất ba lần. Xác suất để trong ba lần gieo có đúng hai lần
xuất hiện mặt ngửa là
A.
1
8
. B.
3
8
. C.
1
4
. D.
1
3
.
Câu 2: Có bao nhiêu cách sắp xếp 4 học sinh thành một hàng dọc?
A.
4
. B.
1
. C.
10
. D.
.
Câu 3: Trên khoảng
0; ,
đạo hàm của hàm số
e
yx
là
A.
1
.
e
y ex
B.
1
.
1
e
x
y
e
C.
1
1
.
e
yx
e
D.
ln .
e
y x x
Câu 4: Cho hàm số
y f x
liên tục trên và có bảng biến thiên như hình vẽ:
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
f x m
có bốn nghiệm phân
biệt?
A.
0.
B.
1.
C.
3.
D.
2.
Câu 5: Trên mặt phẳng tọa độ, điểm
1;1M
là điểm biểu diễn số phức nào sau đây?
A.
1zi
. B.
1zi
. C.
1zi
. D.
1zi
.
Câu 6: Cho
1
0
d2f x x
và
1
0
d5g x x
khi đó
1
0
2df x g x x


bằng
A.
3.
B.
12.
C.
8.
D.
1.
Câu 7: Đường tiệm cận đứng của đồ thị hàm số
2
1
x
y
x
là
A.
2.x
B.
1.x 
C.
1.x
D.
2.y
Câu 8: Cho hàm số
y f x
liên tục trên và có đồ thị như hình
vẽ. Khẳng định nào sau đây đúng?
A. Hàm số đạt cực đại tại
4.x
B. Giá trị cực tiểu của hàm số bằng
1.
C. Hàm số không có điểm cực trị.
D. Hàm số đạt cực tiểu tại
1.x 
ĐỀ CHNH THC
Mã đề 202 - trang 2/6
Câu 9: Trong không gian
Oxyz
, khoảng cách từ điểm
0;3; 1M
đến mặt phẳng
:2 2 2 0x y z
bằng
A.
1
. B.
1
3
. C.
3
. D.
4
3
.
Câu 10: Trong không gian
Oxyz
, đường thẳng
12
:3
2
xt
d y t
zt


có một vectơ chỉ phương là
A.
2; 1;1u
. B.
1;3;2v
. C.
1;2;3a
. D.
1; 1;1b 
.
Câu 11: Trong không gian
Oxyz
, hình chiếu của điểm
1;2; 1A
trên mặt phẳng
Oxy
là điểm nào
sau đây?
A.
1; 2;1Q 
. B.
1; 2;0P 
. C.
1;2;1M
. D.
1;2;0N
.
Câu 12: Trong không gian
Oxyz
, gọi
S
là mặt cầu có tâm
I Ox
và đi qua hai điểm
2;1; 1 ; 1;3; 2AB
. Phương trình của mặt cầu
S
là
A.
2 2 2
2 10 0x y z x
. B.
2 2 2
4 2 0x y z x
.
C.
2 2 2
2 10 0x y z x
. D.
2 2 2
4 14 0x y z x
.
Câu 13: Trong mặt phẳng toạ độ
Oxy
, biết tập hợp điểm biểu diễn của số phức
z
thỏa mãn
12z i z i
là đường thẳng
d
. Phương trình tổng quát của đường thẳng
d
là
A.
2 1 0xy
. B.
10xy
. C.
10xy
. D.
2 1 0xy
.
Câu 14: Hàm số
3
32y x x
có giá trị cực đại bằng
A.
1
. B.
4
. C.
20
. D.
0
.
Câu 15: Cho
,f x g x
là các hàm số liên tục trên . Trong các mệnh đề sau, mệnh đề nào sai?
A.
. . .f x g x dx f x dx g x dx
B.
5 5 .f x dx f x dx

C.
.f x g x dx f x dx g x dx


D.
.f x g x dx f x dx g x dx


Câu 16: Khối bát diện đều thuộc loại khối đa diện đều nào sau đây?
A.
3;5 .
B.
4;3 .
C.
3;4 .
D.
5;3 .
Câu 17: Cho khối lăng trụ đứng
. ' ' 'ABC A B C
có
, ' 2,AB AC a AA a
0
45BAC
(tham khảo hình vẽ). Tính thể tích
V
của khối lăng trụ
đã cho.
A.
3
2
4
a
. B.
3
4
a
.
C.
3
2
a
. D.
3
6
a
.
A
B
C
A'
B'
C'
Câu 18: Biết phương trình
2
22
log 2log 2 1 0xx
có hai nghiệm
12
,xx
. Giá trị của
12
.xx
bằng
A.
4.
B.
1
.
8
C.
3.
D.
1
.
2
Câu 19: Cho hàm số
y f x
có đạo hàm
3
1,f x x x x
. Hàm số
y f x
đồng biến
trên khoảng nào sau đây?
A.
1;1 .
B.
0; .
C.
0;1 .
D.
;0 .
Mã đề 202 - trang 3/6
Câu 20: Giá trị ln nhất của hàm số
5
7
x
y
x
trên đoạn
8;12
bằng
A.
15.
B.
17
.
5
C.
13.
D.
13
.
2
Câu 21: Tính diện tích
S
của hình phẳng gii hạn bởi đồ thị hàm số
2
21y x x
, trục hoành và hai
đường thẳng
1; 3xx
.
A.
37
.
3
S
B.
68
.
3
S
C.
64
.
3
S
D.
56
.
3
S
Câu 22: Cho khối nón có chiều cao bằng
a
và đường sinh bằng
. Thể tích của khối nón đã cho bằng
A.
3
3 a
. B.
3
a
. C.
3
3
3
a
. D.
3
3
a
.
Câu 23: Số phức nghịch đảo của số phức
34zi
là
A.
34
55
i
. B.
34i
. C.
34
55
i
. D.
34
25 25
i
.
Câu 24: Cho hình hộp chữ nhật
. ' ' ' 'ABCD A B C D
có
3;AB a AD a
(tham khảo hình vẽ). Góc giữa hai đường thẳng
AB
và
''AC
bằng
A.
0
60
. B.
0
45
.
C.
0
75
. D.
0
30
.
A
D
C
B
A'
D'
C'
B'
Câu 25: Cho cấp số cộng
n
u
có
1
2u
và công sai
2d 
. Giá trị của
5
u
là
A.
10
. B.
6
. C.
6
. D.
32
.
Câu 26: Cho hàm số
y f x
liên tục trên và có đồ thị
như hình vẽ.
Mệnh đề nào dưi đây đúng?
A. Hàm số nghịch biến trên
1;1 .
.
B. Hàm số nghịch biến trên
; 1 .
C. Hàm số đồng biến trên
1; . 
D. Hàm số đồng biến trên
.
Câu 27: Trong không gian
Oxyz
, gọi
là góc giữa hai mặt phẳng
: 2 2 0P x y z
và
:2 4 0Q x y z
. Tính
cos
.
A.
2
cos
3
. B.
3
cos
4
. C.
1
cos
6
. D.
1
cos
3
.
Câu 28: Tập nghiệm của bất phương trình
3 27
x
là
A.
3, .
B.
,3 .
C.
,3 .
D.
3, .
Câu 29: Tập nghiệm của bất phương trình
2
log 3 1 3x 
là
A.
3; 
. B.
1
;3
3



. C.
,3 .
D.
10
;
3




.
Câu 30: Cho số phức
12zi
, tính
z
.
A.
3z
. B.
3z
. C.
5z
. D.
5z
.
Mã đề 202 - trang 4/6
Câu 31: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
2SA a
và vuông góc vi đáy (tham khảo hình vẽ). Tính khoảng
cách giữa hai đường thẳng
BD
và
SC
.
A.
4
a
. B.
2
2
a
.
C.
2
a
. D.
2
4
a
.
A
D
C
B
S
Câu 32: Bất phương trình
2
31
9
2log (4 3) log (2 3) 2xx
có tập nghiệm là
A.
3
;
4




. B.
3
;3
4


. C.
3
;3
8



. D.
3
;3
8



.
Câu 33: Cho hình trụ có chiều cao bằng
h
và bán kính đáy bằng
r
. Diện tích xung quanh
xq
S
của hình
trụ được tính bởi công thức
A.
2
xq
S r h
. B.
1
3
xq
S rh
. C.
2
xq
S rh
. D.
xq
S rh
.
Câu 34: Vi
a
là số thực dương tùy ý,
3
81
log a
bằng
A.
3
3
log .
4
a
B.
3
1
log .
27
a
C.
3
1
log .
12
a
D.
3
4
log .
3
a
Câu 35: Cho hàm số
fx
có đạo hàm liên tục trên đoạn
1;2
,
11f
và
22f
. Tính
2
1
.I f x dx
A.
1.I
B.
1.I 
C.
3.I
D.
7
.
2
I
Câu 36: Họ tất cả các nguyên hàm của hàm số
2
2
1
( ) 3
sin
f x x
x
là
A.
3
cot .x x C
B.
2
2
6.
sin
xC
x

C.
3
tan .x x C
D.
3
cot .x x C
Câu 37: Hàm số nào dưi đây có đồ thị như hình vẽ?
A.
3
31y x x
. B.
42
2 1.y x x
C.
42
2 1.y x x
D.
3
3 1.y x x
Câu 38: Trong không gian
Oxyz
, mặt cầu
2 2 2
: 4 2 2 3 0S x y z x y z
có bán kính bằng
A.
3
. B.
9
. C.
1
. D.
6
.
Câu 39: Cho
,xy
là các số thực dương thỏa mãn
2
22
2 3 3 4
log 2 3 2 3 3.
xy x y
x x y y
x xy y

Tính giá trị ln nhất của biểu thức
1F x y
.
A.
4.
B.
3.
C.
1.
D.
2.
Câu 40: Đặt
1
2
0
(2 1) 2
d.
x
x
x e ax a
Ix
e ax
Có bao nhiêu giá trị nguyên của
a
thuộc khoảng
0;2023
để
6I
?
A.
2023.
B.
2024.
C.
1877.
D.
189.
Mã đề 202 - trang 5/6
Câu 41: Cho hàm số
4 3 2
0,y f x ax bx cx dx e a
hàm số
12y f x

có đồ thị như
hình vẽ sau:
Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
3
5g x f x x m
có ít
nhất 5 điểm cực trị?
A.
6.
B.
2.
C.
10.
D.
4.
Câu 42: Cho hàm số
y f x
có đạo hàm liên tục trên thỏa mãn
15f
và
374
1 7 35xxxf x f x x

vi mọi
x
. Tính
1
0
d.f x x
A.
.
5
6
B.
13
.
12
C.
5
6
.
D.
17
.
6
Câu 43: Xét các số phức
z
thỏa mãn
2 4 3 5 2z i z i
. Biết giá trị ln nhất của biểu thức
33P z i z i
có dạng
;,a b a b
. Giá trị của biểu thức
ab
bằng
A. 7. B. 3. C. 5. D. 9.
Câu 44: Trên tập hợp số phức, xét phương trình
22
2 1 4 3 0z m z m m
(
m
là tham số thực).
Có bao nhiêu giá trị của
m
để phương trình có hai nghiệm phân biệt
12
,zz
thỏa mãn
2
1 2 1 2
2z z m z z
?
A.
2.
B.
4.
C.
1.
D.
0
.
Câu 45: Cho hình chóp tam giác đều
.S ABC
có
AB a
, khoảng cách giữa
hai đường thẳng
SA
và
BC
bằng
6
3
a
(tham khảo hình vẽ). Thể
tích khối chóp
.S ABC
bằng
A.
3
2
2
a
. B.
3
2
6
a
.
C.
3
2
3
a
. D.
3
2
9
a
.
S
A
B
C
Câu 46: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật,
2 3 , 3AB a AD a
,
SAD
là tam giác đều và nằm trong mặt
phẳng vuông góc vi đáy (tham khảo hình vẽ). Tính thể tích khối
cầu ngoại tiếp hình chóp
.S ABCD
.
A.
3
32
3
a
. B.
3
16
3
a
.
C.
3
16 a
. D.
3
26
3
a
.
A
D
C
B
S
Mã đề 202 - trang 6/6
Câu 47: Trong không gian
Oxyz
, cho mặt phẳng
:2 3 3 0P y z
và hai đường thẳng
1
12
:
2 1 1
x y z
d


;
2
12
:1
1
xt
d y t
z

. Đường thẳng
nằm trong mặt phẳng
P
đồng thời
cắt cả hai đường thẳng
1
d
và
2
d
có phương trình là
A.
21
1 3 2
x y z

. B.
21
1 3 2
x y z

. C.
21
1 3 2
x y z

. D.
21
1 3 2
x y z

.
Câu 48: Trong không gian
Oxyz
, cho ba điểm
15;7; 11A 
,
3;1;1B
,
7; 1;5C
và đường thẳng
1 1 1
:
1 4 1
x y z
d

. Gọi
là mặt phẳng chứa
d
sao cho
A
,
B
,
C
ở cùng phía đối
vi mặt phẳng
. Gọi
1
d
,
2
d
,
3
d
lần lượt là khoảng cách từ
A
,
B
,
C
đến
. Giá trị ln
nhất của biểu thức
1 2 3
23T d d d
bằng
A.
41
. B.
82
. C.
1
41
2
. D.
2 67
.
Câu 49: Cho phương trình
2
91
3
log 1 log 1
x
x
m
(vi
m
là tham số thực). Có bao nhiêu giá trị
nguyên dương của tham số
m
để phương trình đã cho có nghiệm thực?
A.
1.
B.
3.
C. Vô số. D.
2.
Câu 50: Cho hàm số
y f x
có đạo hàm
2
2
12f x x x x
, vi
x
. Số giá trị nguyên
của tham số
m
để hàm số
32
3g x f x x m
có
8
điểm cực trị là
A.
2.
B.
3.
C.
1.
D.
4.
-----------------------------------------------
----------- HẾT ----------
Mã đề 204 - trang 1/6
SỞ GIÁO DỤC V ĐO TẠO
NAM ĐỊNH
MÃ ĐỀ: 204
ĐỀ THI THỬ TỐT NGHIỆP LỚP 12 THPT
NĂM HC 2022 – 2023
Môn: Toán – lp 12 THPT
(Thời gian làm bài: 90 phút)
Đề thi gồm 06 trang.
Họ và tên học sinh:………………………………………
Số báo danh:………….…………………….……………
Câu 1: Trong không gian
Oxyz
, khoảng cách từ điểm
0;3; 1M
đến mặt phẳng
:2 2 2 0x y z
bằng
A.
1
. B.
4
3
. C.
1
3
. D.
3
.
Câu 2: Trên khoảng
0; ,
đạo hàm của hàm số
e
yx
là
A.
1
1
.
e
yx
e
B.
1
.
e
y ex
C.
ln .
e
y x x
D.
1
.
1
e
x
y
e
Câu 3: Cho hàm số
y f x
liên tục trên và có bảng biến thiên như hình vẽ:
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
f x m
có bốn nghiệm phân
biệt?
A.
0.
B.
1.
C.
3.
D.
2.
Câu 4: Cho
1
0
d2f x x
và
1
0
d5g x x
khi đó
1
0
2df x g x x


bằng
A.
8.
B.
3.
C.
1.
D.
12.
Câu 5: Trên mặt phẳng tọa độ, điểm
1;1M
là điểm biểu diễn số phức nào sau đây?
A.
1zi
. B.
1zi
. C.
1zi
. D.
1zi
.
Câu 6: Tính diện tích
S
của hình phẳng gii hạn bởi đồ thị hàm số
2
21y x x
, trục hoành và hai
đường thẳng
1; 3xx
.
A.
37
.
3
S
B.
56
.
3
S
C.
68
.
3
S
D.
64
.
3
S
Câu 7: Cho hàm số
y f x
liên tục trên và có đồ thị
như hình vẽ.
Mệnh đề nào dưi đây đúng?
A. Hàm số nghịch biến trên
1;1 .
.
B. Hàm số nghịch biến trên
; 1 .
C. Hàm số đồng biến trên
1; . 
D. Hàm số đồng biến trên
.
ĐỀ CHNH THC
Mã đề 204 - trang 2/6
Câu 8: Cho hàm số
y f x
liên tục trên và có đồ thị như
hình vẽ. Khẳng định nào sau đây đúng?
A. Hàm số đạt cực tiểu tại
1.x 
B. Giá trị cực tiểu của hàm số bằng
1.
C. Hàm số không có điểm cực trị.
D. Hàm số đạt cực đại tại
4.x
Câu 9: Cho khối nón có chiều cao bằng
a
và đường sinh bằng
. Thể tích của khối nón đã cho bằng
A.
3
a
. B.
3
3 a
. C.
3
3
a
. D.
3
3
3
a
.
Câu 10: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
2SA a
và vuông góc vi đáy (tham khảo hình vẽ). Tính
khoảng cách giữa hai đường thẳng
BD
và
SC
.
A.
4
a
. B.
2
a
.
C.
2
4
a
. D.
2
2
a
.
A
D
C
B
S
Câu 11: Bất phương trình
2
31
9
2log (4 3) log (2 3) 2xx
có tập nghiệm là
A.
3
;
4




. B.
3
;3
4


. C.
3
;3
8



. D.
3
;3
8



.
Câu 12: Hàm số
3
32y x x
có giá trị cực đại bằng
A.
1
. B.
4
. C.
20
. D.
0
.
Câu 13: Giá trị ln nhất của hàm số
5
7
x
y
x
trên đoạn
8;12
bằng
A.
15.
B.
17
.
5
C.
13.
D.
13
.
2
Câu 14: Cho hình trụ có chiều cao bằng
h
và bán kính đáy bằng
r
. Diện tích xung quanh
xq
S
của hình
trụ được tính bởi công thức
A.
xq
S rh
. B.
2
xq
S rh
. C.
1
3
xq
S rh
. D.
2
xq
S r h
.
Câu 15: Có bao nhiêu cách sắp xếp 4 học sinh thành một hàng dọc?
A.
1
. B.
. C.
4
. D.
10
.
Câu 16: Cho khối lăng trụ đứng
. ' ' 'ABC A B C
có
, ' 2,AB AC a AA a
0
45BAC
(tham khảo hình vẽ). Tính thể tích
V
của khối lăng trụ
đã cho.
A.
3
4
a
. B.
3
2
4
a
.
C.
3
2
a
. D.
3
6
a
.
A
B
C
A'
B'
C'
Mã đề 204 - trang 3/6
Câu 17: Biết phương trình
2
22
log 2log 2 1 0xx
có hai nghiệm
12
,xx
. Giá trị của
12
.xx
bằng
A.
4.
B.
1
.
8
C.
3.
D.
1
.
2
Câu 18: Số phức nghịch đảo của số phức
34zi
là
A.
34
55
i
. B.
34
55
i
. C.
34
25 25
i
. D.
34i
.
Câu 19: Trong mặt phẳng toạ độ
Oxy
, biết tập hợp điểm biểu diễn của số phức
z
thỏa mãn
12z i z i
là đường thẳng
d
. Phương trình tổng quát của đường thẳng
d
là
A.
2 1 0xy
. B.
2 1 0xy
. C.
10xy
. D.
10xy
.
Câu 20: Cho hình hộp chữ nhật
. ' ' ' 'ABCD A B C D
có
3;AB a AD a
(tham khảo hình vẽ). Góc giữa hai đường thẳng
AB
và
''AC
bằng
A.
0
60
. B.
0
45
.
C.
0
75
. D.
0
30
.
A
D
C
B
A'
D'
C'
B'
Câu 21: Hàm số nào dưi đây có đồ thị như hình vẽ?
A.
3
31y x x
. B.
42
2 1.y x x
C.
42
2 1.y x x
D.
3
3 1.y x x
Câu 22: Cho cấp số cộng
n
u
có
1
2u
và công sai
2d 
. Giá trị của
5
u
là
A.
10
. B.
6
. C.
6
. D.
32
.
Câu 23: Cho hàm số
y f x
có đạo hàm
3
1,f x x x x
. Hàm số
y f x
đồng biến
trên khoảng nào sau đây?
A.
1;1 .
B.
;0 .
C.
0;1 .
D.
0; .
Câu 24: Tập nghiệm của bất phương trình
2
log 3 1 3x 
là
A.
3; 
. B.
1
;3
3



. C.
,3 .
D.
10
;
3




.
Câu 25: Cho
,f x g x
là các hàm số liên tục trên . Trong các mệnh đề sau, mệnh đề nào sai?
A.
5 5 .f x dx f x dx

B.
.f x g x dx f x dx g x dx


C.
. . .f x g x dx f x dx g x dx
D.
.f x g x dx f x dx g x dx


Câu 26: Đường tiệm cận đứng của đồ thị hàm số
2
1
x
y
x
là
A.
1.x
B.
2.y
C.
2.x
D.
1.x 
Câu 27: Gieo một đồng tiền cân đối, đồng chất ba lần. Xác suất để trong ba lần gieo có đúng hai lần
xuất hiện mặt ngửa là
A.
1
8
. B.
1
3
. C.
1
4
. D.
3
8
.
Mã đề 204 - trang 4/6
Câu 28: Cho số phức
12zi
, tính
z
.
A.
3z
. B.
5z
. C.
5z
. D.
3z
.
Câu 29: Tập nghiệm của bất phương trình
3 27
x
là
A.
3, .
B.
3, .
C.
,3 .
D.
,3 .
Câu 30: Vi
a
là số thực dương tùy ý,
3
81
log a
bằng
A.
3
3
log .
4
a
B.
3
1
log .
12
a
C.
3
4
log .
3
a
D.
3
1
log .
27
a
Câu 31: Trong không gian
Oxyz
, hình chiếu của điểm
1;2; 1A
trên mặt phẳng
Oxy
là điểm nào
sau đây?
A.
1; 2;0P 
. B.
1; 2;1Q 
. C.
1;2;1M
. D.
1;2;0N
.
Câu 32: Khối bát diện đều thuộc loại khối đa diện đều nào sau đây?
A.
4;3 .
B.
5;3 .
C.
3;5 .
D.
3;4 .
Câu 33: Cho hàm số
fx
có đạo hàm liên tục trên đoạn
1;2
,
11f
và
22f
. Tính
2
1
.I f x dx
A.
1.I
B.
1.I 
C.
3.I
D.
7
.
2
I
Câu 34: Trong không gian
Oxyz
, gọi
S
là mặt cầu có tâm
I Ox
và đi qua hai điểm
2;1; 1 ; 1;3; 2AB
. Phương trình của mặt cầu
S
là
A.
2 2 2
2 10 0x y z x
. B.
2 2 2
4 14 0x y z x
.
C.
2 2 2
2 10 0x y z x
. D.
2 2 2
4 2 0x y z x
.
Câu 35: Trong không gian
Oxyz
, đường thẳng
12
:3
2
xt
d y t
zt


có một vectơ chỉ phương là
A.
2; 1;1u
. B.
1; 1;1b 
. C.
1;2;3a
. D.
1;3;2v
.
Câu 36: Trong không gian
Oxyz
, mặt cầu
2 2 2
: 4 2 2 3 0S x y z x y z
có bán kính bằng
A.
3
. B.
9
. C.
1
. D.
6
.
Câu 37: Họ tất cả các nguyên hàm của hàm số
2
2
1
( ) 3
sin
f x x
x
là
A.
2
2
6.
sin
xC
x

B.
3
cot .x x C
C.
3
tan .x x C
D.
3
cot .x x C
Câu 38: Trong không gian
Oxyz
, gọi
là góc giữa hai mặt phẳng
: 2 2 0P x y z
và
:2 4 0Q x y z
. Tính
cos
.
A.
2
cos
3
. B.
3
cos
4
. C.
1
cos
6
. D.
1
cos
3
.
Câu 39: Đặt
1
2
0
(2 1) 2
d.
x
x
x e ax a
Ix
e ax
Có bao nhiêu giá trị nguyên của
a
thuộc khoảng
0;2023
để
6I
?
A.
2023.
B.
2024.
C.
1877.
D.
189.
Mã đề 204 - trang 5/6
Câu 40: Cho hàm số
y f x
có đạo hàm liên tục trên thỏa mãn
15f
và
374
1 7 35xxxf x f x x

vi mọi
x
. Tính
1
0
d.f x x
A.
.
5
6
B.
17
.
6
C.
13
.
12
D.
5
6
.
Câu 41: Trên tập hợp số phức, xét phương trình
22
2 1 4 3 0z m z m m
(
m
là tham số thực).
Có bao nhiêu giá trị của
m
để phương trình có hai nghiệm phân biệt
12
,zz
thỏa mãn
2
1 2 1 2
2z z m z z
?
A.
4.
B.
0
. C.
2.
D.
1.
Câu 42: Cho hàm số
4 3 2
0,y f x ax bx cx dx e a
hàm số
12y f x

có đồ thị như
hình vẽ sau:
Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
3
5g x f x x m
có ít
nhất 5 điểm cực trị?
A.
6.
B.
4.
C.
2.
D.
10.
Câu 43: Trong không gian
Oxyz
, cho ba điểm
15;7; 11A 
,
3;1;1B
,
7; 1;5C
và đường thẳng
1 1 1
:
1 4 1
x y z
d

. Gọi
là mặt phẳng chứa
d
sao cho
A
,
B
,
C
ở cùng phía đối
vi mặt phẳng
. Gọi
1
d
,
2
d
,
3
d
lần lượt là khoảng cách từ
A
,
B
,
C
đến
. Giá trị ln
nhất của biểu thức
1 2 3
23T d d d
bằng
A.
82
. B.
2 67
. C.
41
. D.
1
41
2
.
Câu 44: Cho hình chóp tam giác đều
.S ABC
có
AB a
, khoảng cách giữa hai
đường thẳng
SA
và
BC
bằng
6
3
a
(tham khảo hình vẽ). Thể tích khối
chóp
.S ABC
bằng
A.
3
2
2
a
. B.
3
2
6
a
.
C.
3
2
3
a
. D.
3
2
9
a
.
S
A
B
C
Câu 45: Cho phương trình
2
91
3
log 1 log 1
x
x
m
(vi
m
là tham số thực). Có bao nhiêu giá trị
nguyên dương của tham số
m
để phương trình đã cho có nghiệm thực?
A.
1.
B. Vô số. C.
3.
D.
2.
Mã đề 204 - trang 6/6
Câu 46: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật,
2 3 , 3AB a AD a
,
SAD
là tam giác đều và nằm trong mặt
phẳng vuông góc vi đáy (tham khảo hình vẽ). Tính thể tích khối
cầu ngoại tiếp hình chóp
.S ABCD
.
A.
3
16
3
a
. B.
3
16 a
.
C.
3
32
3
a
. D.
3
26
3
a
.
A
D
C
B
S
Câu 47: Cho
,xy
là các số thực dương thỏa mãn
2
22
2 3 3 4
log 2 3 2 3 3.
xy x y
x x y y
x xy y

Tính giá trị ln nhất của biểu thức
1F x y
.
A.
3.
B.
1.
C.
4.
D.
2.
Câu 48: Trong không gian
Oxyz
, cho mặt phẳng
:2 3 3 0P y z
và hai đường thẳng
1
12
:
2 1 1
x y z
d


;
2
12
:1
1
xt
d y t
z

. Đường thẳng
nằm trong mặt phẳng
P
đồng thời
cắt cả hai đường thẳng
1
d
và
2
d
có phương trình là
A.
21
1 3 2
x y z

. B.
21
1 3 2
x y z

. C.
21
1 3 2
x y z

. D.
21
1 3 2
x y z

.
Câu 49: Xét các số phức
z
thỏa mãn
2 4 3 5 2z i z i
. Biết giá trị ln nhất của biểu thức
33P z i z i
có dạng
;,a b a b
. Giá trị của biểu thức
ab
bằng
A. 3. B. 7. C. 5. D. 9.
Câu 50: Cho hàm số
y f x
có đạo hàm
2
2
12f x x x x
, vi
x
. Số giá trị nguyên của
tham số
m
để hàm số
32
3g x f x x m
có
8
điểm cực trị là
A.
2.
B.
3.
C.
1.
D.
4.
-----------------------------------------------
----------- HẾT ----------
Mã đề 206 - trang 1/6
SỞ GIÁO DỤC V ĐO TẠO
NAM ĐỊNH
MÃ ĐỀ: 206
ĐỀ THI THỬ TỐT NGHIỆP LỚP 12 THPT
NĂM HC 2022 – 2023
Môn: Toán – lp 12 THPT
(Thời gian làm bài: 90 phút)
Đề thi gồm 06 trang.
Họ và tên học sinh:………………………………………
Số báo danh:………….……………………..……………
Câu 1: Trong mặt phẳng toạ độ
Oxy
, biết tập hợp điểm biểu diễn của số phức
z
thỏa mãn
12z i z i
là đường thẳng
d
. Phương trình tổng quát của đường thẳng
d
là
A.
2 1 0xy
. B.
2 1 0xy
. C.
10xy
. D.
10xy
.
Câu 2: Cho hình hộp chữ nhật
. ' ' ' 'ABCD A B C D
có
3;AB a AD a
(tham khảo hình vẽ). Góc giữa hai đường thẳng
AB
và
''AC
bằng
A.
0
45
. B.
0
60
.
C.
0
30
. D.
0
75
.
A
D
C
B
A'
D'
C'
B'
Câu 3: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
2SA a
và vuông góc vi đáy (tham khảo hình vẽ). Tính
khoảng cách giữa hai đường thẳng
BD
và
SC
.
A.
4
a
. B.
2
a
.
C.
2
4
a
. D.
2
2
a
.
A
D
C
B
S
Câu 4: Giá trị ln nhất của hàm số
5
7
x
y
x
trên đoạn
8;12
bằng
A.
13.
B.
17
.
5
C.
13
.
2
D.
15.
Câu 5: Họ tất cả các nguyên hàm của hàm số
2
2
1
( ) 3
sin
f x x
x
là
A.
3
tan .x x C
B.
3
cot .x x C
C.
3
cot .x x C
D.
2
2
6.
sin
xC
x

Câu 6: Cho khối lăng trụ đứng
. ' ' 'ABC A B C
có
, ' 2,AB AC a AA a
0
45BAC
(tham khảo hình vẽ). Tính thể tích
V
của khối lăng trụ
đã cho.
A.
3
4
a
. B.
3
2
4
a
.
C.
3
2
a
. D.
3
6
a
.
A
B
C
A'
B'
C'
Câu 7: Tính diện tích
S
của hình phẳng gii hạn bởi đồ thị hàm số
2
21y x x
, trục hoành và hai
đường thẳng
1; 3xx
.
ĐỀ CHNH THC
Mã đề 206 - trang 2/6
A.
64
.
3
S
B.
68
.
3
S
C.
56
.
3
S
D.
37
.
3
S
Câu 8: Trên mặt phẳng tọa độ, điểm
1;1M
là điểm biểu diễn số phức nào sau đây?
A.
1zi
. B.
1zi
. C.
1zi
. D.
1zi
.
Câu 9: Cho số phức
12zi
, tính
z
.
A.
3z
. B.
5z
. C.
5z
. D.
3z
.
Câu 10: Đường tiệm cận đứng của đồ thị hàm số
2
1
x
y
x
là
A.
1.x
B.
2.y
C.
1.x 
D.
2.x
Câu 11: Trong không gian
Oxyz
, gọi
S
là mặt cầu có tâm
I Ox
và đi qua hai điểm
2;1; 1 ; 1;3; 2AB
. Phương trình của mặt cầu
S
là
A.
2 2 2
4 14 0x y z x
. B.
2 2 2
2 10 0x y z x
.
C.
2 2 2
2 10 0x y z x
. D.
2 2 2
4 2 0x y z x
.
Câu 12: Trong không gian
Oxyz
, hình chiếu của điểm
1;2; 1A
trên mặt phẳng
Oxy
là điểm nào
sau đây?
A.
1; 2;0P 
. B.
1; 2;1Q 
. C.
1;2;1M
. D.
1;2;0N
.
Câu 13: Hàm số
3
32y x x
có giá trị cực đại bằng
A.
1
. B.
4
. C.
0
. D.
20
.
Câu 14: Có bao nhiêu cách sắp xếp 4 học sinh thành một hàng dọc?
A.
1
. B.
. C.
4
. D.
10
.
Câu 15: Cho khối nón có chiều cao bằng
a
và đường sinh bằng
. Thể tích của khối nón đã cho bằng
A.
3
3
a
. B.
3
a
. C.
3
3 a
. D.
3
3
3
a
.
Câu 16: Trong không gian
Oxyz
, đường thẳng
12
:3
2
xt
d y t
zt


có một vectơ chỉ phương là
A.
2; 1;1u
. B.
1; 1;1b 
. C.
1;2;3a
. D.
1;3;2v
.
Câu 17: Số phức nghịch đảo của số phức
34zi
là
A.
34
55
i
. B.
34
55
i
. C.
34
25 25
i
. D.
34i
.
Câu 18: Hàm số nào dưi đây có đồ thị như hình vẽ?
A.
42
2 1.y x x
B.
3
31y x x
.
C.
42
2 1.y x x
D.
3
3 1.y x x
Câu 19: Cho hàm số
y f x
có đạo hàm
3
1,f x x x x
. Hàm số
y f x
đồng biến
trên khoảng nào sau đây?
A.
1;1 .
B.
;0 .
C.
0;1 .
D.
0; .
Mã đề 206 - trang 3/6
Câu 20: Trên khoảng
0; ,
đạo hàm của hàm số
e
yx
là
A.
1
1
.
e
yx
e
B.
1
.
1
e
x
y
e
C.
ln .
e
y x x
D.
1
.
e
y ex
Câu 21: Trong không gian
Oxyz
, gọi
là góc giữa hai mặt phẳng
: 2 2 0P x y z
và
:2 4 0Q x y z
. Tính
cos
.
A.
2
cos
3
. B.
3
cos
4
. C.
1
cos
6
. D.
1
cos
3
.
Câu 22: Cho
,f x g x
là các hàm số liên tục trên . Trong các mệnh đề sau, mệnh đề nào sai?
A.
5 5 .f x dx f x dx

B.
.f x g x dx f x dx g x dx


C.
. . .f x g x dx f x dx g x dx
D.
.f x g x dx f x dx g x dx


Câu 23: Cho hàm số
y f x
liên tục trên và có bảng biến thiên như hình vẽ:
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
f x m
có bốn nghiệm phân
biệt?
A.
0.
B.
3.
C.
1.
D.
2.
Câu 24: Vi
a
là số thực dương tùy ý,
3
81
log a
bằng
A.
3
3
log .
4
a
B.
3
1
log .
12
a
C.
3
4
log .
3
a
D.
3
1
log .
27
a
Câu 25: Cho
1
0
d2f x x
và
1
0
d5g x x
khi đó
1
0
2df x g x x


bằng
A.
1.
B.
8.
C.
12.
D.
3.
Câu 26: Gieo một đồng tiền cân đối, đồng chất ba lần. Xác suất để trong ba lần gieo có đúng hai lần
xuất hiện mặt ngửa là
A.
1
8
. B.
1
3
. C.
1
4
. D.
3
8
.
Câu 27: Biết phương trình
2
22
log 2log 2 1 0xx
có hai nghiệm
12
,xx
. Giá trị của
12
.xx
bằng
A.
1
.
2
B.
3.
C.
1
.
8
D.
4.
Câu 28: Tập nghiệm của bất phương trình
3 27
x
là
A.
3, .
B.
3, .
C.
,3 .
D.
,3 .
Câu 29: Cho cấp số cộng
n
u
có
1
2u
và công sai
2d 
. Giá trị của
5
u
là
A.
10
. B.
6
. C.
32
. D.
6
.
Câu 30: Tập nghiệm của bất phương trình
2
log 3 1 3x 
là
Mã đề 206 - trang 4/6
A.
,3 .
B.
1
;3
3



. C.
10
;
3




. D.
3; 
.
Câu 31: Khối bát diện đều thuộc loại khối đa diện đều nào sau đây?
A.
4;3 .
B.
5;3 .
C.
3;5 .
D.
3;4 .
Câu 32: Cho hàm số
fx
có đạo hàm liên tục trên đoạn
1;2
,
11f
và
22f
. Tính
2
1
.I f x dx
A.
1.I
B.
1.I 
C.
3.I
D.
7
.
2
I
Câu 33: Trong không gian
Oxyz
, mặt cầu
2 2 2
: 4 2 2 3 0S x y z x y z
có bán kính bằng
A.
3
. B.
9
. C.
1
. D.
6
.
Câu 34: Bất phương trình
2
31
9
2log (4 3) log (2 3) 2xx
có tập nghiệm là
A.
3
;3
4


. B.
3
;
4




. C.
3
;3
8



. D.
3
;3
8



.
Câu 35: Trong không gian
Oxyz
, khoảng cách từ điểm
0;3; 1M
đến mặt phẳng
:2 2 2 0x y z
bằng
A.
3
. B.
1
. C.
1
3
. D.
4
3
.
Câu 36: Cho hàm số
y f x
liên tục trên và
có đồ thị như hình vẽ.
Mệnh đề nào dưi đây đúng?
A. Hàm số nghịch biến trên
1;1 .
.
B. Hàm số đồng biến trên
1; . 
C. Hàm số đồng biến trên
.
D. Hàm số nghịch biến trên
; 1 .
Câu 37: Cho hình trụ có chiều cao bằng
h
và bán kính đáy bằng
r
. Diện tích xung quanh
xq
S
của hình
trụ được tính bởi công thức
A.
1
3
xq
S rh
. B.
xq
S rh
. C.
2
xq
S r h
. D.
2
xq
S rh
.
Câu 38: Cho hàm số
y f x
liên tục trên và có đồ thị như
hình vẽ. Khẳng định nào sau đây đúng?
A. Hàm số đạt cực tiểu tại
1.x 
B. Giá trị cực tiểu của hàm số bằng
1.
C. Hàm số không có điểm cực trị.
D. Hàm số đạt cực đại tại
4.x
Mã đề 206 - trang 5/6
Câu 39: Cho hình chóp tam giác đều
.S ABC
có
AB a
, khoảng cách giữa
hai đường thẳng
SA
và
BC
bằng
6
3
a
(tham khảo hình vẽ). Thể
tích khối chóp
.S ABC
bằng
A.
3
2
2
a
. B.
3
2
6
a
.
C.
3
2
3
a
. D.
3
2
9
a
.
S
A
B
C
Câu 40: Cho hàm số
4 3 2
0,y f x ax bx cx dx e a
hàm số
12y f x

có đồ thị như
hình vẽ sau:
Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
3
5g x f x x m
có ít
nhất 5 điểm cực trị?
A.
4.
B.
6.
C.
10.
D.
2.
Câu 41: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật,
2 3 , 3AB a AD a
,
SAD
là tam giác đều và nằm trong mặt
phẳng vuông góc vi đáy (tham khảo hình vẽ). Tính thể tích khối cầu
ngoại tiếp hình chóp
.S ABCD
.
A.
3
16
3
a
. B.
3
16 a
.
C.
3
32
3
a
. D.
3
26
3
a
.
A
D
C
B
S
Câu 42: Trong không gian
Oxyz
, cho ba điểm
15;7; 11A 
,
3;1;1B
,
7; 1;5C
và đường thẳng
1 1 1
:
1 4 1
x y z
d

. Gọi
là mặt phẳng chứa
d
sao cho
A
,
B
,
C
ở cùng phía đối
vi mặt phẳng
. Gọi
1
d
,
2
d
,
3
d
lần lượt là khoảng cách từ
A
,
B
,
C
đến
. Giá trị ln
nhất của biểu thức
1 2 3
23T d d d
bằng
A.
41
. B.
2 67
. C.
82
. D.
1
41
2
.
Câu 43: Xét các số phức
z
thỏa mãn
2 4 3 5 2z i z i
. Biết giá trị ln nhất của biểu thức
33P z i z i
có dạng
;,a b a b
. Giá trị của biểu thức
ab
bằng
A. 3. B. 7. C. 5. D. 9.
Mã đề 206 - trang 6/6
Câu 44: Cho hàm số
y f x
có đạo hàm liên tục trên thỏa mãn
15f
và
374
1 7 35xxxf x f x x

vi mọi
x
. Tính
1
0
d.f x x
A.
5
6
.
B.
13
.
12
C.
17
.
6
D.
.
5
6
Câu 45: Cho phương trình
2
91
3
log 1 log 1
x
x
m
(vi
m
là tham số thực). Có bao nhiêu giá trị
nguyên dương của tham số
m
để phương trình đã cho có nghiệm thực?
A.
2.
B. Vô số. C.
3.
D.
1.
Câu 46: Cho
,xy
là các số thực dương thỏa mãn
2
22
2 3 3 4
log 2 3 2 3 3.
xy x y
x x y y
x xy y

Tính giá trị ln nhất của biểu thức
1F x y
.
A.
3.
B.
1.
C.
4.
D.
2.
Câu 47: Đặt
1
2
0
(2 1) 2
d.
x
x
x e ax a
Ix
e ax
Có bao nhiêu giá trị nguyên của
a
thuộc khoảng
0;2023
để
6I
?
A.
1877.
B.
2024.
C.
2023.
D.
189.
Câu 48: Cho hàm số
y f x
có đạo hàm
2
2
12f x x x x
, vi
x
. Số giá trị nguyên của
tham số
m
để hàm số
32
3g x f x x m
có
8
điểm cực trị là
A.
2.
B.
1.
C.
3.
D.
4.
Câu 49: Trong không gian
Oxyz
, cho mặt phẳng
:2 3 3 0P y z
và hai đường thẳng
1
12
:
2 1 1
x y z
d


;
2
12
:1
1
xt
d y t
z

. Đường thẳng
nằm trong mặt phẳng
P
đồng thời
cắt cả hai đường thẳng
1
d
và
2
d
có phương trình là
A.
21
1 3 2
x y z

. B.
21
1 3 2
x y z

. C.
21
1 3 2
x y z

. D.
21
1 3 2
x y z

.
Câu 50: Trên tập hợp số phức, xét phương trình
22
2 1 4 3 0z m z m m
(
m
là tham số thực).
Có bao nhiêu giá trị của
m
để phương trình có hai nghiệm phân biệt
12
,zz
thỏa mãn
2
1 2 1 2
2z z m z z
?
A.
0
. B.
1.
C.
2.
D.
4.
-----------------------------------------------
----------- HẾT ----------
Mã đề 208 - trang 1/6
SỞ GIÁO DỤC V ĐO TẠO
NAM ĐỊNH
MÃ ĐỀ: 208
ĐỀ THI THỬ TỐT NGHIỆP LỚP 12 THPT
NĂM HC 2022 – 2023
Môn: Toán – lp 12 THPT
(Thời gian làm bài: 90 phút)
Đề thi gồm 06 trang.
Họ và tên học sinh:………………………………………
Số báo danh:………….…………………….……………
Câu 1: Trong mặt phẳng toạ độ
Oxy
, biết tập hợp điểm biểu diễn của số phức
z
thỏa mãn
12z i z i
là đường thẳng
d
. Phương trình tổng quát của đường thẳng
d
là
A.
10xy
. B.
2 1 0xy
. C.
2 1 0xy
. D.
10xy
.
Câu 2: Vi
a
là số thực dương tùy ý,
3
81
log a
bằng
A.
3
3
log .
4
a
B.
3
1
log .
12
a
C.
3
4
log .
3
a
D.
3
1
log .
27
a
Câu 3: Trong không gian
Oxyz
, gọi
S
là mặt cầu có tâm
I Ox
và đi qua hai điểm
2;1; 1 ; 1;3; 2AB
. Phương trình của mặt cầu
S
là
A.
2 2 2
4 14 0x y z x
. B.
2 2 2
2 10 0x y z x
.
C.
2 2 2
2 10 0x y z x
. D.
2 2 2
4 2 0x y z x
.
Câu 4: Cho hàm số
y f x
liên tục trên và có đồ thị
như hình vẽ.
Mệnh đề nào dưi đây đúng?
A. Hàm số nghịch biến trên
1;1 .
.
B. Hàm số đồng biến trên
1; . 
C. Hàm số đồng biến trên
.
D. Hàm số nghịch biến trên
; 1 .
Câu 5: Đường tiệm cận đứng của đồ thị hàm số
2
1
x
y
x
là
A.
2.y
B.
1.x 
C.
1.x
D.
2.x
Câu 6: Tập nghiệm của bất phương trình
3 27
x
là
A.
3, .
B.
3, .
C.
,3 .
D.
,3 .
Câu 7: Tập nghiệm của bất phương trình
2
log 3 1 3x 
là
A.
3; 
. B.
10
;
3




. C.
,3 .
D.
1
;3
3



.
Câu 8: Cho
,f x g x
là các hàm số liên tục trên . Trong các mệnh đề sau, mệnh đề nào sai?
A.
.f x g x dx f x dx g x dx


B.
.f x g x dx f x dx g x dx


C.
. . .f x g x dx f x dx g x dx
D.
5 5 .f x dx f x dx

Câu 9: Số phức nghịch đảo của số phức
34zi
là
A.
34
55
i
. B.
34
55
i
. C.
34
25 25
i
. D.
34i
.
ĐỀ CHNH THC
Mã đề 208 - trang 2/6
Câu 10: Hàm số nào dưi đây có đồ thị như hình vẽ?
A.
3
31y x x
. B.
3
3 1.y x x
C.
42
2 1.y x x
D.
42
2 1.y x x
Câu 11: Trên mặt phẳng tọa độ, điểm
1;1M
là điểm biểu diễn số phức nào sau đây?
A.
1zi
. B.
1zi
. C.
1zi
. D.
1zi
.
Câu 12: Cho khối lăng trụ đứng
. ' ' 'ABC A B C
có
, ' 2,AB AC a AA a
0
45BAC
(tham khảo hình vẽ). Tính thể tích
V
của khối lăng trụ
đã cho.
A.
3
2
4
a
. B.
3
2
a
.
C.
3
4
a
. D.
3
6
a
.
A
B
C
A'
B'
C'
Câu 13: Cho hàm số
y f x
liên tục trên và có bảng biến thiên như hình vẽ:
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
f x m
có bốn nghiệm phân
biệt?
A.
3.
B.
1.
C.
0.
D.
2.
Câu 14: Cho khối nón có chiều cao bằng
a
và đường sinh bằng
. Thể tích của khối nón đã cho bằng
A.
3
3
a
. B.
3
a
. C.
3
3 a
. D.
3
3
3
a
.
Câu 15: Cho hình hộp chữ nhật
. ' ' ' 'ABCD A B C D
có
3;AB a AD a
(tham khảo hình vẽ). Góc giữa hai đường thẳng
AB
và
''AC
bằng
A.
0
30
. B.
0
60
.
C.
0
75
. D.
0
45
.
A
D
C
B
A'
D'
C'
B'
Câu 16: Cho cấp số cộng
n
u
có
1
2u
và công sai
2d 
. Giá trị của
5
u
là
A.
10
. B.
32
. C.
6
. D.
6
.
Câu 17: Trên khoảng
0; ,
đạo hàm của hàm số
e
yx
là
A.
1
1
.
e
yx
e
B.
1
.
1
e
x
y
e
C.
ln .
e
y x x
D.
1
.
e
y ex
Mã đề 208 - trang 3/6
Câu 18: Trong không gian
Oxyz
, đường thẳng
12
:3
2
xt
d y t
zt


có một vectơ chỉ phương là
A.
1;2;3a
. B.
1;3;2v
. C.
2; 1;1u
. D.
1; 1;1b 
.
Câu 19: Có bao nhiêu cách sắp xếp 4 học sinh thành một hàng dọc?
A.
1
. B.
10
. C.
4
. D.
.
Câu 20: Trong không gian
Oxyz
, hình chiếu của điểm
1;2; 1A
trên mặt phẳng
Oxy
là điểm nào
sau đây?
A.
1; 2;0P 
. B.
1;2;0N
. C.
1; 2;1Q 
. D.
1;2;1M
.
Câu 21: Biết phương trình
2
22
log 2log 2 1 0xx
có hai nghiệm
12
,xx
. Giá trị của
12
.xx
bằng
A.
3.
B.
1
.
2
C.
1
.
8
D.
4.
Câu 22: Cho hàm số
fx
có đạo hàm liên tục trên đoạn
1;2
,
11f
và
22f
. Tính
2
1
.I f x dx
A.
1.I
B.
7
.
2
I
C.
3.I
D.
1.I 
Câu 23: Họ tất cả các nguyên hàm của hàm số
2
2
1
( ) 3
sin
f x x
x
là
A.
2
2
6.
sin
xC
x

B.
3
cot .x x C
C.
3
tan .x x C
D.
3
cot .x x C
Câu 24: Cho
1
0
d2f x x
và
1
0
d5g x x
khi đó
1
0
2df x g x x


bằng
A.
1.
B.
8.
C.
12.
D.
3.
Câu 25: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
2SA a
và vuông góc vi đáy (tham khảo hình vẽ). Tính khoảng
cách giữa hai đường thẳng
BD
và
SC
.
A.
2
a
. B.
2
2
a
.
C.
2
4
a
. D.
4
a
.
A
D
C
B
S
Câu 26: Tính diện tích
S
của hình phẳng gii hạn bởi đồ thị hàm số
2
21y x x
, trục hoành và hai
đường thẳng
1; 3xx
.
A.
56
.
3
S
B.
68
.
3
S
C.
64
.
3
S
D.
37
.
3
S
Câu 27: Cho hình trụ có chiều cao bằng
h
và bán kính đáy bằng
r
. Diện tích xung quanh
xq
S
của hình
trụ được tính bởi công thức
A.
1
3
xq
S rh
. B.
xq
S rh
. C.
2
xq
S r h
. D.
2
xq
S rh
.
Câu 28: Cho số phức
12zi
, tính
z
.
A.
3z
. B.
3z
. C.
5z
. D.
5z
.
Mã đề 208 - trang 4/6
Câu 29: Hàm số
3
32y x x
có giá trị cực đại bằng
A.
0
. B.
1
. C.
20
. D.
4
.
Câu 30: Khối bát diện đều thuộc loại khối đa diện đều nào sau đây?
A.
4;3 .
B.
5;3 .
C.
3;5 .
D.
3;4 .
Câu 31: Cho hàm số
y f x
có đạo hàm
3
1,f x x x x
. Hàm số
y f x
đồng biến
trên khoảng nào sau đây?
A.
1;1 .
B.
;0 .
C.
0; .
D.
0;1 .
Câu 32: Trong không gian
Oxyz
, mặt cầu
2 2 2
: 4 2 2 3 0S x y z x y z
có bán kính bằng
A.
3
. B.
9
. C.
1
. D.
6
.
Câu 33: Bất phương trình
2
31
9
2log (4 3) log (2 3) 2xx
có tập nghiệm là
A.
3
;3
4


. B.
3
;
4




. C.
3
;3
8



. D.
3
;3
8



.
Câu 34: Trong không gian
Oxyz
, khoảng cách từ điểm
0;3; 1M
đến mặt phẳng
:2 2 2 0x y z
bằng
A.
3
. B.
1
. C.
1
3
. D.
4
3
.
Câu 35: Giá trị ln nhất của hàm số
5
7
x
y
x
trên đoạn
8;12
bằng
A.
15.
B.
13
.
2
C.
13.
D.
17
.
5
Câu 36: Cho hàm số
y f x
liên tục trên và có đồ thị như
hình vẽ. Khẳng định nào sau đây đúng?
A. Hàm số đạt cực tiểu tại
1.x 
B. Giá trị cực tiểu của hàm số bằng
1.
C. Hàm số không có điểm cực trị.
D. Hàm số đạt cực đại tại
4.x
Câu 37: Gieo một đồng tiền cân đối, đồng chất ba lần. Xác suất để trong ba lần gieo có đúng hai lần
xuất hiện mặt ngửa là
A.
1
8
. B.
1
3
. C.
1
4
. D.
3
8
.
Câu 38: Trong không gian
Oxyz
, gọi
là góc giữa hai mặt phẳng
: 2 2 0P x y z
và
:2 4 0Q x y z
. Tính
cos
.
A.
2
cos
3
. B.
3
cos
4
. C.
1
cos
6
. D.
1
cos
3
.
Câu 39: Trong không gian
Oxyz
, cho ba điểm
15;7; 11A 
,
3;1;1B
,
7; 1;5C
và đường thẳng
1 1 1
:
1 4 1
x y z
d

. Gọi
là mặt phẳng chứa
d
sao cho
A
,
B
,
C
ở cùng phía đối
Mã đề 208 - trang 5/6
vi mặt phẳng
. Gọi
1
d
,
2
d
,
3
d
lần lượt là khoảng cách từ
A
,
B
,
C
đến
. Giá trị ln
nhất của biểu thức
1 2 3
23T d d d
bằng
A.
2 67
. B.
41
. C.
1
41
2
. D.
82
.
Câu 40: Cho phương trình
2
91
3
log 1 log 1
x
x
m
(vi
m
là tham số thực). Có bao nhiêu giá trị
nguyên dương của tham số
m
để phương trình đã cho có nghiệm thực?
A.
1.
B. Vô số. C.
3.
D.
2.
Câu 41: Trên tập hợp số phức, xét phương trình
22
2 1 4 3 0z m z m m
(
m
là tham số thực).
Có bao nhiêu giá trị của
m
để phương trình có hai nghiệm phân biệt
12
,zz
thỏa mãn
2
1 2 1 2
2z z m z z
?
A.
0
. B.
1.
C.
2.
D.
4.
Câu 42: Cho hàm số
4 3 2
0,y f x ax bx cx dx e a
hàm số
12y f x

có đồ thị như
hình vẽ sau:
Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
3
5g x f x x m
có ít
nhất 5 điểm cực trị?
A.
4.
B.
10.
C.
6.
D.
2.
Câu 43: Xét các số phức
z
thỏa mãn
2 4 3 5 2z i z i
. Biết giá trị ln nhất của biểu thức
33P z i z i
có dạng
;,a b a b
. Giá trị của biểu thức
ab
bằng
A. 7. B. 9. C. 5. D. 3.
Câu 44: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật,
2 3 , 3AB a AD a
,
SAD
là tam giác đều và nằm trong mặt
phẳng vuông góc vi đáy (tham khảo hình vẽ). Tính thể tích khối
cầu ngoại tiếp hình chóp
.S ABCD
.
A.
3
32
3
a
. B.
3
26
3
a
.
C.
3
16
3
a
. D.
3
16 a
.
A
D
C
B
S
Câu 45: Cho
,xy
là các số thực dương thỏa mãn
2
22
2 3 3 4
log 2 3 2 3 3.
xy x y
x x y y
x xy y

Tính giá trị ln nhất của biểu thức
1F x y
.
A.
2.
B.
4.
C.
3.
D.
1.
Mã đề 208 - trang 6/6
Câu 46: Cho hình chóp tam giác đều
.S ABC
có
AB a
, khoảng cách giữa
hai đường thẳng
SA
và
BC
bằng
6
3
a
(tham khảo hình vẽ). Thể
tích khối chóp
.S ABC
bằng
A.
3
2
3
a
. B.
3
2
2
a
.
C.
3
2
6
a
. D.
3
2
9
a
.
S
A
B
C
Câu 47: Cho hàm số
y f x
có đạo hàm liên tục trên thỏa mãn
15f
và
374
1 7 35xxxf x f x x

vi mọi
x
. Tính
1
0
d.f x x
A.
5
6
.
B.
17
.
6
C.
.
5
6
D.
13
.
12
Câu 48: Trong không gian
Oxyz
, cho mặt phẳng
:2 3 3 0P y z
và hai đường thẳng
1
12
:
2 1 1
x y z
d


;
2
12
:1
1
xt
d y t
z

. Đường thẳng
nằm trong mặt phẳng
P
đồng thời
cắt cả hai đường thẳng
1
d
và
2
d
có phương trình là
A.
21
1 3 2
x y z

. B.
21
1 3 2
x y z

. C.
21
1 3 2
x y z

. D.
21
1 3 2
x y z

.
Câu 49: Đặt
1
2
0
(2 1) 2
d.
x
x
x e ax a
Ix
e ax
Có bao nhiêu giá trị nguyên của
a
thuộc khoảng
0;2023
để
6I
?
A.
1877.
B.
2024.
C.
2023.
D.
189.
Câu 50: Cho hàm số
y f x
có đạo hàm
2
2
12f x x x x
, vi
x
. Số giá trị nguyên của
tham số
m
để hàm số
32
3g x f x x m
có
8
điểm cực trị là
A.
2.
B.
1.
C.
3.
D.
4.
-----------------------------------------------
----------- HẾT ----------
SỞ GIÁO DỤC V ĐO TẠO
NAM ĐỊNH
KỲ THI THỬ TỐT NGHIỆP LỚP 12 THPT
NĂM HC 2022-2023
HƯỚNG DẪN CHẤM MÔN TOÁN LỚP 12
I. TRẮC NGHIỆM (50 câu, mỗi câu 0,2 điểm)
Mã đề
Câu
202
204
206
208
1
B
A
D
A
2
D
B
C
B
3
A
D
B
C
4
D
A
A
D
5
B
D
C
B
6
C
D
C
A
7
B
B
A
A
8
D
A
C
C
9
A
A
C
C
10
A
B
C
B
11
D
B
B
C
12
A
B
D
B
13
C
C
B
D
14
B
B
B
B
15
A
B
B
A
16
C
C
A
C
17
C
A
C
D
18
A
C
D
C
19
D
C
B
D
20
C
D
D
B
21
C
D
C
D
22
B
C
C
A
23
D
B
D
D
24
D
A
B
B
25
C
C
B
A
26
B
D
D
C
27
C
D
D
D
28
D
C
A
C
29
A
A
B
D
30
D
B
D
D
31
C
D
D
B
32
B
D
A
A
33
C
A
A
A
34
C
A
A
B
35
A
A
B
C
36
A
A
D
A
37
D
B
D
D
Mã đề
Câu
202
204
206
208
38
A
C
A
C
39
B
C
B
D
40
C
B
D
D
41
B
D
C
B
42
D
C
C
D
43
B
A
A
D
44
C
B
C
A
45
B
D
A
C
46
A
C
A
C
47
A
A
A
B
48
B
D
B
A
49
D
A
A
A
50
C
C
B
B
BẢNG ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
B
D
A
D
D
B
A
A
B
B
B
C
B
B
C
A
C
C
D
D
C
B
A
C
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
D
D
C
A
B
D
D
A
A
A
A
B
C
C
D
C
C
A
B
D
C
A
D
A
C
Câu 1. Trong không gian , khoảng cách từ điểm đến mặt phẳng
Oxyz
0;3; 1M
bằng
: 2 2 2 0x y z
A. . B. . C. . D. .
1
4
3
1
3
3
Lời giải
Chọn A.
Ta có:
2
2 2
2.0 3 2. 1 2
; 1
2 1 2
d M
Câu 2. Trên khoảng , đạo hàm của hàm số là
0;
e
y x
A. B. . C. . D. .
1
1
. .
e
y x
e
1
.
e
y e x
ln
e
y x x
1
1
e
x
y
e
Lời giải
Chọn B
Ta có:
1
. .
e e
y x e x
Câu 3. Cho hàm số liên tục trên và có bảng biến thiên như hình vẽ:
y f x
Có bao nhiêu giá trị nguyên của tham số để phương trình có bốn nghiệm phân
m
f x m
biệt?
A. . B. . C. . D. .
0
1
3
2
Lời giải
Chọn D
Để phương trình có 4 nghiệm phân biệt thì suy ra có 2 giá trị nguyên
f x m
2 1m
.
1;0m
Câu 4. Cho và khi đó bằng
1
0
d 2f x x
1
0
d 5g x x
1
0
2 df x g x x
A. . B. . C. . D. .
8
3
1
12
Lời giải
Chọn A
Ta có:
1 1 1
0 0 0
2 d d 2 d 2 2.5 8f x g x x f x x g x x
Câu 5. Trên mặt phẳng tọa độ, điểm là điểm biểu diễn số phức nào sau đây?
1;1M
A. B. . C. . D. .
1 .z i
1z i
1z i
1z i
Lời giải
Chọn D.
Ta có: Điểm là điểm biểu diễn số phức
1;1M
1 .z i
Câu 6. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường
2
2 1y x x
thẳng .
1; 3x x
A. . B. . C. . D. .
37
3
S
56
3
S
68
3
S
64
3
S
Lời giải
Chọn D
Diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng
2
2 1y x x
là
1; 3x x
.
3 3
3
3
2 2 2
1
1 1
64
2 1 d 2 1 d
3 3
x
S x x x x x x x x
Câu 7. Cho hàm số liên tục trên và có đồ thị như hình vẽ
y f x
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên . B. Hàm số nghịch biến trên .
1;1
; 1
C. Hàm số đồng biến trên . D. Hàm số đồng biến trên .
1; 
Lời giải
Chọn B
Từ đồ thị hàm số ta thấy hàm số nghịch biến trên .
; 1
Câu 8. Cho hàm số liên tục trên và có đồ thị như hình vẽ
y f x
Khẳng định nào dưới đây đúng?
A. Hàm số đạt cực tiểu tại . B. Giá trị cực tiểu của hàm số bằng .
1x
1
C. Hàm số không có điểm cực trị. D. Hàm số đạt cực đại tại .
4x
Lời giải
Chọn A
Từ đồ thị hàm số ta thấy hàm số đạt cực tiểu tại .
1x
Câu 9. Cho khối nón có chiều cao bằng và đường sinh bằng . Thể tích của khối nón đã cho
a
2a
bằng
A. . B. . C. . D. .
3
a
3
3 a
3
3
a
3
3
3
a
Lời giải
Chọn A
Bán kính đường tròn đáy của hình nón bằng .
2 2
3r l h a
Thể tích của khối nón bằng .
2 3
1
3
V r h a
Câu 10. Cho hình chóp có đáy là hình vuông cạnh , và vuông góc với
.S ABCD
ABCD
a
2SA a
đáy (tham khảo hình vẽ). Tình khoảng cách giữa hai đường thẳng và
BD
SC
A. . B. . C. . D. .
4
a
2
a
2
4
a
2
2
a
Lời giải
Chọn B
Gọi là giao điểm của .
O
;AC BD
Trong mặt phẳng kẻ . Ta có
SAC
OH SC
.
BD AC SAC
BD SA SAC BD SAC BD OH
AC SA A
Từ đó nên .
OH SC
OH BD
;d SC BD OH
Ta lại có,
2 45
o
SA AC a OCH
Trong tam giác vuông có . Suy ra .
OHC
2
2
a
OC
2 2
sin .
2 2 2
a a
OH OC OCH
Vậy .
;
2
a
d SC BD
Câu 11. Bất phương trình có tập nghiệm là
2
3 1
9
2log 4 3 log 2 3 2x x
A. . B. . C. . D. .
3
;
4
3
;3
4
3
;3
8
3
;3
8
Lời giải
Chọn B
+) Điều kiện
2
3
4 3 0
3
4
3
4
2 3 0
2
x
x
x
x
x
Khi đó:
2 2
3 1 3 3
9
1
2log 4 3 log 2 3 2 log 4 3 .2log 2 3 2
2
x x x x
2 2
2
3
4 3 4 3
3
log 2 9 16 42 18 0 3.
2 3 2 3 8
x x
x x x
x x
So với điều kiện . Tập nghiệm của bất phương trình là .
3
4
x
3
;3
4
Câu 12. Hàm số có giá trị cực đại bằng
3
3 2y x x
A. . B. . C. . D. .
1
4
20
0
Lời giải
Chọn B
TXĐ . Ta có
D
2
3 3; 0 1y x y x
Suy ra giá trị cực đại của hàm số là .
4
Câu 13. Giá trị lớn nhất của hàm số trên đoạn bằng
5
7
x
y
x
8;12
A. . B. . C. . D. .
15
17
5
13
13
2
Lời giải
Chọn C
Hàm số liên tục trên đoạn . Ta có
5
7
x
y
x
8;12
2
12
0, 8;12 .
7
y x
x
Suy ra hàm số nghịch biến trên khoảng .
8;12
8;12 max 8 13y y
Câu 14. Cho hình trụ có chiều cao và bán kính đáy bằng . Diện tích xung quanh của hình trụ
h
r
xq
S
được tính bởi công thức
A. . B. . C. . D. .
xq
S rh
2
xq
S rh
1
3
xq
S rh
2
xq
S r h
Lời giải
Chọn B
Diện tích xung quanh của hình trụ là .
xq
S
2
xq
S rh
Câu 15. Có bao nhiêu cách xếp học sinh thành một hàng dọc
4
A. . B. . C. . D. .
15
24
4
10
Lời giải
Chọn B
Số cách xếp học sinh thành một hàng dọc là ( cách).
4
4! 24
Câu 16. Cho khối lăng trụ đứng có . ( tham khảo
. ' ' 'ABC A B C
0
, ' 2, 45AB AC a AA a BAC
hình vẽ). Tính thể tích của khối lằng trụ đã cho
V
A. . B. . C. . D. .
3
4
a
3
2
4
a
3
2
a
3
6
a
Lời giải
Chọn C.
Thể tích khối lăng trụ
3
1
. ' . .sin . '
2 2
ABC
a
V S AA AB AC BAC AA
Câu 17. Biết phương trình có hai nghiệm . Giá trị của bằng
2
2 2
log 2log 2 1 0x x
1 2
,x x
1 2
.x x
A. . B. . C. . D. .
4
1
8
3
1
2
Lời giải
Chọn A.
Điều kiện: .
0x
Phương trình .
2
2 2
2 2 2 2
2
1
log 1
log 2log 2 1 0 log 2log 3 0
2
log 3
8
x
x x x x
x
x
.
1 2
. 4x x
Câu 18. Số phức nghịch đảo của số phức là
3 4z i
A. . B. . C. . D. .
3 4
5 5
i
3 4
5 5
i
3 4
25 25
i
3 4i
Lời giải
Chọn C.
Ta có: .
1 1 3 4
3 4 25 25
i
z i
Câu 19. Trong mặt phẳng tọa độ , biết tập hợp điểm biểu diễn của số phức thỏa mãn
Oxy
z
là đường thẳng . Phương trình đường thẳng là
1 2z i z i
d
d
A. . B. . C. . D. .
2 1 0x y
2 1 0x y
1 0x y
1 0x y
Lời giải
Chọn C.
Gọi với . Thế vào phương trình ta được.
z x yi
,x y R
1 2z i z i
1 2 1 1 2x yi i x yi i x y i x y i
.
2 2 2
2
1 1 2 1 0x y x y x y
Câu 20. Cho hình hộp có ( tham khảo hình vẽ). Góc giữa hai
. ' ' ' 'ABCD A B C D
3,AB a AD a
đường thẳng và bằng
AB
' 'A C
A. . B. . C. . D. .
0
60
0
45
0
75
0
30
Lời giải
Chọn D.
Ta có: .
' '/ / , ' ' ,A C AC AB A C AB AC BAC
.
0
1
tan 30
3
BC
BAC BAC
AB
Câu 21. Hàm số dưới đây có đồ thị như hình vẽ?
A. . B. . C. . D. .
3
3 1y x x
4 2
2 1y x x
4 2
2 1y x x
3
3 1y x x
Lời giải
Chọn D
Câu 22. Cho cấp số cộng với công sai . Giá trị bằng
n
u
1
2u
2d
5
u
A. . B. . C. . D.
10
6
6
32
Lời giải
Chọn C
Vì là một cấp số cộng thì .
n
u
1 5 1
1 4 2 4. 2 6
n
u u n d u u d
Câu 23. Cho hàm số có đạo hàm . Hàm số đồng biến trên
f x
3
1 ,f x x x x
( )
y f x=
khoảng nào dưới đây?
A. . B. . C. . D. .
1;1
;0
0;1
0;
Lời giải
Chọn B
Ta có
0
0
1
x
f x
x
Bảng biến thiên của hàm số :
( )
y f x=
Hàm số đồng biến trên khoảng
( )
;0-¥
Câu 24. Tập nghiệm của bất phương trình .
2
log 3 1 3x
A. B. C. D.
3;
1
;3
3
;3
0;
Lời giải
Chọn A
Đkxđ:
1
3 1 0
3
x x
Bất phương trình .
3
3 1 2 3 9 3x x x
So với điều kiện , tập nghiệm của bất phương trìnhlà .
1
3
x >
( )
3;+¥
Câu 25. Cho hàm số , liên tục trên . Trong các mệnh đề sau, mệnh đề nào sau sai?
( )f x
( )g x
A. . B. .
5 ( )d 5 ( )df x x f x x
( ) ( ) ( ) ( )f x g x dx f x dx g x dx
C. . D. .
( ). ( ) d ( ) . ( )df x g x x f x dx g x x
( ) ( ) ( ) ( )f x g x dx f x dx g x dx
Lời giải
Chọn C
Câu 26. Đường tiệm cận đứng của đồ thị hàm số là.
2
1
x
y
x
A. . B. . C. . D. .
1x
2y
2x
1x
Lời giải
Chọn D.
Ta có nên đồ thị hàm số có tiệm cận đứng là .
1 1
lim ; lim
x x
y y
 
1x
Câu 27. Gieo một đồng tiền cân đối, đồng chất ba lần. Xác suất để trong ba lần gieo có đúng hai lần
xuất hiện mặt ngửa là.
A. . B. . C. . D. .
1
8
1
3
1
4
3
8
Lời giải
Chọn D.
Gieo một đồng tiền cân đối, đồng chất ba lần .
3
2 8
Biến cố A: ba lần gieo có đúng hai lần xuất hiện mặt ngửa là.
Các kết quả thuận lợi của biến cố A là: .
, , , , , , , ,N N S N S N S N N
3
3
8
A P A
Câu 28. Cho số phức . Tính .
1 2z i
z
A. . B. . C. . D. .
3z
5z
5z
3z
Lời giải
Chọn C
1 2 5z i
Câu 29. Tập nghiệm của bất phương trình là.
3 27
x
A. . B. . C. . D. .
3;
3;
;3
;3
Lời giải
Chọn A.
.
3
3 27 3 3 3 3;
x x
x x 
Câu 30. Với là số thực dương tùy ý, bằng.
a
3
81
log a
A. . B. . C. . D. .
3
3
log
4
a
3
1
log
12
a
3
4
log
3
a
3
1
log
27
a
Lời giải
Chọn B.
.
4
1
3
3
81 3 3
3
1
1
3
log log log log
4 12
a a a a
Câu 31. Trong không gian , hình chiếu của điểm trên mặt phẳng là điểm nào
Oxyz
1;2; 1A
Oxy
dưới đây?
A. . B. . C. . D. .
1; 2;0P
1; 2;1Q
1;2;1M
1;2;0N
Lời giải
Chọn D.
Câu 32. Khối bát diện đều thuộc loại bát diện đều nào sau đây?
A. . B. . C. . D. .
4;3
5;3
3;5
3;4
Lời giải
Chọn D.
Câu 33. Cho hàm số có đạo hàm liên tục trên , và . Tính
f x
1;2
1 1f
2 2f
2
1
dI f x x
A. . B. . C. . D. .
1I
1I
3I
7
2
I
Lời giải
Chọn A.
Ta có .
2
1
2
d 2 1 2 1 1
1
I f x x f x f f
Câu 34. Trong không gian , gọi là mặt cầu có tâm và đi qua hai điểm ,
Oxyz
S
I Ox
2;1; 1A
. Phương trình của mặt cầu là
1;3; 2B
S
A. . B. .
2 2 2
2 10 0x y z x
2 2 2
4 14 0x y z x
C. . D. .
2 2 2
2 10 0x y z x
2 2 2
4 2 0x y z x
Lời giải
Chọn A.
Do ,
;0;0 2 ;1; 1I Ox I x IA x
1 ;3; 2IB x
Ta có
2
2 2
2 2 2 2 2
2 1 1 1 3 2IA IB IA IB x x
, .
4 4 2 1 2 11 6 6 1 1;0;0x x x x I
11R IA
Câu 35. Trong không gian , đường thẳng có một vectơ chỉ phương là
Oxyz
1 2
: 3
2
x t
d y t
z t
A. . B. . C. . D. .
2; 1;1u
1; 1;1b
1;2;3a
1;3;2v
Câu 36. Trong không gian , mặt cầu có bán kính bằng
Oxyz
2 2 2
: 4 2 2 3 0S x y z x y z
A. . B. . C. . D. .
3
9
1
6
Lời giải
2; 1; 1; 3a b c d
.
2 2 2
4 1 1 3 3R a b c d
Câu 37. Họ tất cả các nguyên hàm của hàm số là
2
2
1
3
sin
f x x
x
A. . B. . C. . D. .
2
2
6
sin
x C
x
3
cotx x C
3
tanx x C
3
cotx x C
Lời giải
.
3
d cotf x x x x C
Câu 38. Trong không gian , gọi là góc giữa hai mặt phẳng và
Oxyz
: 2 2 0P x y z
. Tính .
:2 4 0Q x y z
cos
A. . B. . C. . D. .
2
cos
3
3
cos
4
1
cos
6
1
cos
3
Lời giải
Mặt phẳng có vectơ pháp tuyến .
P
1
1;2; 1n
Mặt phẳng có vectơ pháp tuyến .
Q
2
2; 1; 1n
Vậy .
1 2
1 2
.
2 2 1
1
cos
6
6. 6
.
n n
n n
Câu 39. Đặt . Có bao nhiêu giá trị nguyên của thuộc khoảng
2
1
0
2 1 2
d
x
x
x e ax a
I x
e ax
a
0;2023
để ?
6I
A. . B. . C. . D. .
2023
2024
1877
189
Lời giải
1 1 1
1
2
0
0 0 0
2
d 2 d d
x x
x x
x x x
x e ax e a
e a e a
I x x x x x
e ax e ax e ax
1
0
d
1
x
x
e ax
e ax
.
1
0
1 ln 1 ln
x
e ax e a
Ta có .
5 5
6 1 ln 6 ln 5 145,69I e a e a e a e a e e
Vì , nên : có giá trị nguyên.
0;2023a
a
146;147;...;2022a
1877
Câu 40. Cho hàm số có đạo hàm liên tục trên và thỏa mãn và
( )y f x
(1) 5f
với . Tính .
3 7 4
1 '( ) 5 7 3xf x f x x x x
x
1
0
( )f x dx
A. B. C. D.
5
6
13
12
5
6
17
6
Lời giải
Chọn D
.
3 7 4 2 3 8 5 2
1 '( ) 5 7 3 3 . 1 3 '( ) 3 15 21 9xf x f x x x x x f x xf x x x x x
1 1
2 3 8 5 2
0 0
3 . 1 3 '( ) 3 15 21 9x f x xf x dx x x x x dx
1 1
2 3
0 0
28
3 . 1 3 '( )
3
x f x dx xf x dx
Xét
1 0 1
2 3
0 1 0
3 . 1A x f x dx f t dt f x dx
.
1 1 1
1
0
0 0 0
'( ) . ( ) ( ) 5 ( )B xf x dx x f x f x dx f x dx
Vậy
1 1 1 1 1
2 3
0 0 0 0 0
28 17
3 . 1 3 '( ) ( ) 15 3 ( ) ( )
3 6
x f x dx xf x dx f x dx f x dx f x dx
Câu 41. Trên tập số phức, xét phương trình ( là tham số thực). Có
2 2
2 1 4 3 0z m z m m
m
bao nhiêu giá trị của để phương trình có hai nghiệm phân biệt thỏa mãn
m
1 2
,z z
2
1 2 1 2
2z z m z z
A. B. C. D.
2
4
1
0
Lời giải
Chọn C
' 2 2m
TH1: .
' 2 2 0 1m m
Phương trình có hai nghiệm là hai số thực
2 2 2
2
1 2 1 2 1 2 1 2 1 2
2 4 . 2 4 1 4 4 3 2 2( 1)z z m z z z z z z m z z m m m m m
(t/m)
5
2
m
TH2:
' 2 2 0 1m m
Phương trình có hai nghiệm là hai số phức liên hợp.
Giả sử
1 2
;z x yi z x yi
2
2
1 2 1 2
0
2 4 2 2 2
y
z z m z z y m x yi
x m
Do đó (loại) vì hai nghiệm bằng nhau.
1 2
z z m
Câu 42. Cho hàm số , hàm số có đò thị như
4 3 2
0y f x ax bx cx dx e a
' 1 2y f x
hình vẽ sau:
Có bao nhiêu giá trị nguyên dương của tham số để hàm số có ít
m
3
5g x f x x m
nhất điểm cực trị?
5
A. B. C. D.
6
4
2
10
Lời giải
Chọn C
Từ đồ thị ta có: với .
' 1 2 4 1 5f x k x x x
0k
Đặt . Suy ra:
1
1 2
2
t
t x x
.
7
1 1 1
' 4 1 5 7 3 11 0 3
2 2 2 8
11
t
t t t k
f t k t t t t
t
Ta có: có tập xác định là
3 2 2
5 5 5g x f x x m f x x m f x x m
nên ta có: . Do đó hàm
D
0 0
2
2
5 5
x D x D
g x f x x m f x x m g x
là hàm chẵn nên đồ thị đối xứng nhau qua trục tung, suy ra số điểm cực trị hàm
g x
g x
có dạng trong đó là số điểm cực trị có hoành độ dương của đồ thị hàm số
2 1m
m
.
3
5y f x x m
Theo giả thiết ta có: . Vậy yêu cầu bài toán tương đương với: “ Tìm để
2 1 5 2m m
m
hàm số có ít nhất hai điểm cực trị có hoành độ dương”.
3
5y f x x m
Xét hàm với .
3
5y f x x m
0;x 
Ta có:
có ít nhất hai nghiệm dương.
2 3 3
3 3
3 3
3 3
' 3 5 ' 5 0 ' 5 0
5 7 5 7
5 3 5 3
5 11 5 11
y x f x x m f x x m
x x m m x x
x x m m x x
x x m m x x
Ta lập bảng biến thiên cả ba hàm trên cùng một bảng ta có:
Để có ít nhất hai nghiệm dương thì . Mà .
3m
1;2m m
Vậy có hai giá trị nguyên dương của tham số thỏa mãn yêu cầu bài toán.
m
Câu 43. Trong không gian , cho ba điểm và đường thẳng
Oxyz
15;7; 11 , 3;1;1 , 7; 1;5A B C
. Gọi là mặt phẳng chứa sao cho ở cùng phía đối
1 1 1
:
1 4 1
x y z
d
d
, ,A B C
với mặt phẳng . Gọi lần lượt là khoảng cách từ đến . Giá trị lớn
1 2 3
, ,d d d
, ,A B C
nhất của biểu thức bằng
1 2 3
2 3T d d d
A. . B. . C. . D. .
82
2 67
41
41
2
Lời giải
Chọn A
Gọi lần lượt là trung điểm của . Từ đó suy ra
,M N
,AB BC
9;4; 5 , 2;0;3M N
và .
1 2
;
2
M
d d d
2 3
;
2
N
d d d
, với là trọng tâm .
1 2 3 3
; ; ;
2 3 2 2 2 6
M N G
T d d d d d d d
0;1;1G
MNC
Đường thẳng qua điểm , VTCP
d
1; 1; 1M
1;4;1u
; 6;1;2GM u
Vậy: khi là hình chiếu lên
max
;
;
6 ;
6max 6 6 82
G d
d G
GM u
T GK d
u
K
G
d
.
Câu 44. Cho hình chóp tam giác đều có , khoảng cách giữa hai đường thẳng và
.S ABC
AB a
SA
bằng (tham khảo hình vẽ).
BC
6
3
a
Thể tích khối chóp bằng
.S ABC
A. B. C. D.
3
2
.
2
a
3
2
.
6
a
3
2
.
3
a
3
2
.
9
a
Lời giải
Chọn B
Gọi là trung điểm và là tâm đường tròn ngoại tiếp .
M
BC
O
ABC SO ABC
Kẻ . Kẻ .
6
3
a
MK SA MK
2 2 6
3 9
a
OH SA OH MK
đều cạnh và .
ABC
2 3 3
.
3 2 3
a a
a OA
2
3
4
ABC
a
S
Ta có: .
2 2
. 2 6
3
OH OA a
SO
OA OH
Vậy thể tích khối chóp là .
.S ABC
3
1 2
.
3 6
ABC
a
V SO S
Câu 45. Cho phương trình ( với là tham số thực). Có bao nhiêu giá trị
2
9 1
3
log 1 log 1
x
x
m
m
nguyên dương của tham số để phương trình đã cho có nghiệm thực?
m
A. . B. Vô số. C. . D. .
1
3
2
Lời giải
Chọn D
Xét nguyên dương nên ta có điều kiện phương trình . Khi đó
m
0x
.
2
9 1 3 3 3
3
3 3
log 1 log 1 log 1 log log 1
1 3
log log
1 3
3 1
x
x x x m
m
x
x m
x m x
x m x
Xét hàm số .
2
1
' 0, 0
1
1
x
y y x
x
x
Bảng biến thiên
Để phương trình có nghiệm thì .
0 1 0 3 1,2
3
m
m
m m

Câu 46. Cho hình chóp có đáy là hình chữ nhật, là tam giác
.S ABCD
2 3 , 3 ,AB a AD a SAD
đều và nằm trong mặt phẳng vuông góc với đáy (tham khảo hình vẽ). Tính thể tích khối cầu
ngoại tiếp chóp .
.S ABCD
A. . B. . C. . D. .
3
16
3
a
3
16 a
3
32
3
a
3
26
3
a
Lời giải
Chọn C
Ta có theo giao tuyến là . Gọi là trung điểm của
SAD ABCD
AD
M
.
,AD SM AD SM ABCD
Xét đường thẳng qua : là trục của hình chữ nhật .
d
, / /O AC BD O SM
d
ABCD
Ta có , là trọng tâm tam giác .
,OM AD OM SM OM SAD
G
SAD
Xét đường thẳng qua : là trục của tam giác . Khi đó thì là
'd
, / /G MO
d
SAD
'd d I
I
tâm mặt cầu ngoại tiếp hình chóp .
.S ABCD
Ta có .
2 2
R ID IO OD
Với , .
1 1 3 1 3
. . . . 3
3 3 2 3 2 2
a
IO GM SM AD a
2 2
1 1 15
2 2 2
a
OD BD AB AD
Suy ra .
3
3
4 32
2
3 3
a
R a V R
Câu 47. Cho , là các số thực dương thỏa mãn
x
y
( ) ( )
2
2 2
2 3 3 4
log 2 3 2 3 3
xy x y
x x y y
x xy y
+ + +
= - + - -
+ +
. Tính giá trị lớn nhất của biểu thức .
1F x y= + -
A. . B. . C. . D. .
3
1
4
2
Lời giải
Chọn A
Ta có
( ) ( )
( ) ( )
( ) ( )
2
2 2
2 2 2 2
2 2
2 3 3 4
log 2 3 2 3 3
log 2 3 3 4 2 3 3 4 log 2 2 2 2 2 2 .
xy x y
x x y y
x xy y
xy x y xy x y x xy y x xy y
+ + +
= - + - -
+ +
Û + + + + + + + = + + + + +
Đặt , ta có suy ra hàm số đồng biến trên
( )
2
logf t t t= +
( )
1
1 0, 0
ln 2
f t t
t
¢
= + > " >
( )
f t
.
( )
0;+¥
Do đó
( )
( )
( ) ( ) ( )
2
2 2
2 2
2 3 3 4 2 2 2
2 3 3 4 2 2 2
3
2 2 0. *
2
f xy x y f x xy y
x
x y xy x y
y x y x xy y
+ + + =
+
Û + - - + -
+ +
= + +
=
Û + +
Mặt khác . Thay vào , ta được
1
1
1
y F x
F x y
x y F
ì
= + -
ï
ï
= + - Þ
í
ï
+ = +
ï
î
( )
*
( ) ( ) ( )
( ) ( ) ( ) ( )
2
2
2
3
1 2 1 1 2 0
2
3
2 2 1 1 1 2 0. **
2
F x F x F
x F x F F
+ - + - - + - =
Û - + + + - + - =
Tồn tại khi .
x
2
6 0 2 3F F F
¢
D = - + + ³ Û - £ £
Dấu đẳng thức xảy ra
2
3
2.
x
F
y
ì
=
ï
ï
= Þ
í
ï
=
ï
î
Vậy giá trị lớn nhất của biểu thức là tại và .
1F x y= + -
3
2x =
2y =
Câu 48. Trong không gian , cho mặt phẳng và hai đường thẳng
Oxyz
( )
:2 3 3 0P y z- - =
; . Đường thẳng nằm trong mặt phẳng đồng
1
1 2
:
2 1 1
x y z
d
- +
= =
-
2
1 2
: 1
1
x t
d y t
z
ì
= - +
ï
ï
ï
ï
= +
í
ï
ï
=
ï
ï
î
D
( )
P
thời cắt cả hai đường thẳng và có phương trình là
1
d
2
d
A. . B. .
2 1
1 3 2
x y z+ -
= =
-
2 1
1 3 2
x y z- +
= =
-
C. . D. .
2 1
1 3 2
x y z+ -
= =
2 1
1 3 2
x y z- +
= =
Lời giải
Chọn D
Ta có . Gọi .
1
2
: 1
2
x a
d y a
z a
ì
=
ï
ï
ï
ï
= -
í
ï
ï
= - +
ï
ï
î
( )
1 1
A d P d=DÇ = Ç
Suy ra suy ra .
( ) ( )
2 1 3 2 3 0 1a a a- - - + - = Û =
( )
2;0; 1A -
Ta có . Gọi .
2
1 2
: 1
1
x t
d y t
z
ì
= - +
ï
ï
ï
ï
= +
í
ï
ï
=
ï
ï
î
( )
2 2
B d P d=DÇ = Ç
Suy ra suy ra .
( )
2 1 3 1 3 0 2t t+ - × - = Û =
( )
3;3;1B
Khi đó suy ra .
( )
1;3;2AB =

2 1
:
1 3 2
x y z
AB
- +
= =
Câu 49. Xét các số phức thỏa mãn . Biết giá trị lớn nhất của biểu thức
z
2 4 3 5 2z i z i
có dạng . Giá trị của biểu thức bằng
3 3P z i z i
; ,a b a b
a b
A. . B. . C. . D. .
3
7
5
9
Lời giải
Chọn A
Gọi có điểm biểu diễn trên mặt phẳng tọa độ là
; ,z x yi x y
M
Gọi
2;4 , 3; 1 5 2A B AB
Ta có:
2 4 3 5 2
5 2
z i z i
MA MB AB
Vậy nằm trên đoạn thẳng
M
: 2 0AB x y
;2 , 2;3M x x x
Gọi
2 2 2
2
0; 1 , 3;3 3 ; 3 1I J MI x x MJ x x
2 2
3 3 2 6 9 2 4 10P z i z i MI MJ x x x x f x
Sử dụng CASIO ta được:
2;3
max 2 29 26 29; 26f x f a b
Câu 50. Cho hàm số có đạo hàm , . Số giá trị nguyên của
y f x
2
2
1 2f x x x x
x
tham số để hàm số có 8 điểm cực trị là
m
3 2
3g x f x x m
A. . B. . C. . D.
2
3
1
4
Lời giải
Chọn C
Ta có:
2 3 2 3 2
3 6 3 3 2 3g x x x f x x m x x f x x m
3 2
3 2
3 2
3 2
3 2
3 2
0
0
2
0
2
0 2 3 0
3 1
3 2
3 0
3 2 2
3 1
x
x
x
x
x
g x x x x m
x x m
x x m
f x x m
x x m
x x m L
Xét
3 2 2
3 3 6h x x x h x x x
0
0
2
x
h x
x
Để hàm số có 8 điểm cực trị thì phương trình phải có tổng 6 nghiệm phân biệt
g x
1 , 2
khác và . Từ bảng biến thiên ta có:
0
2
h x
4 0 0 4
2 4 3
4 2 0 2 6
m m
m m
m m
| 1/46
| | Tải xuống

Có thể bạn quan tâm:

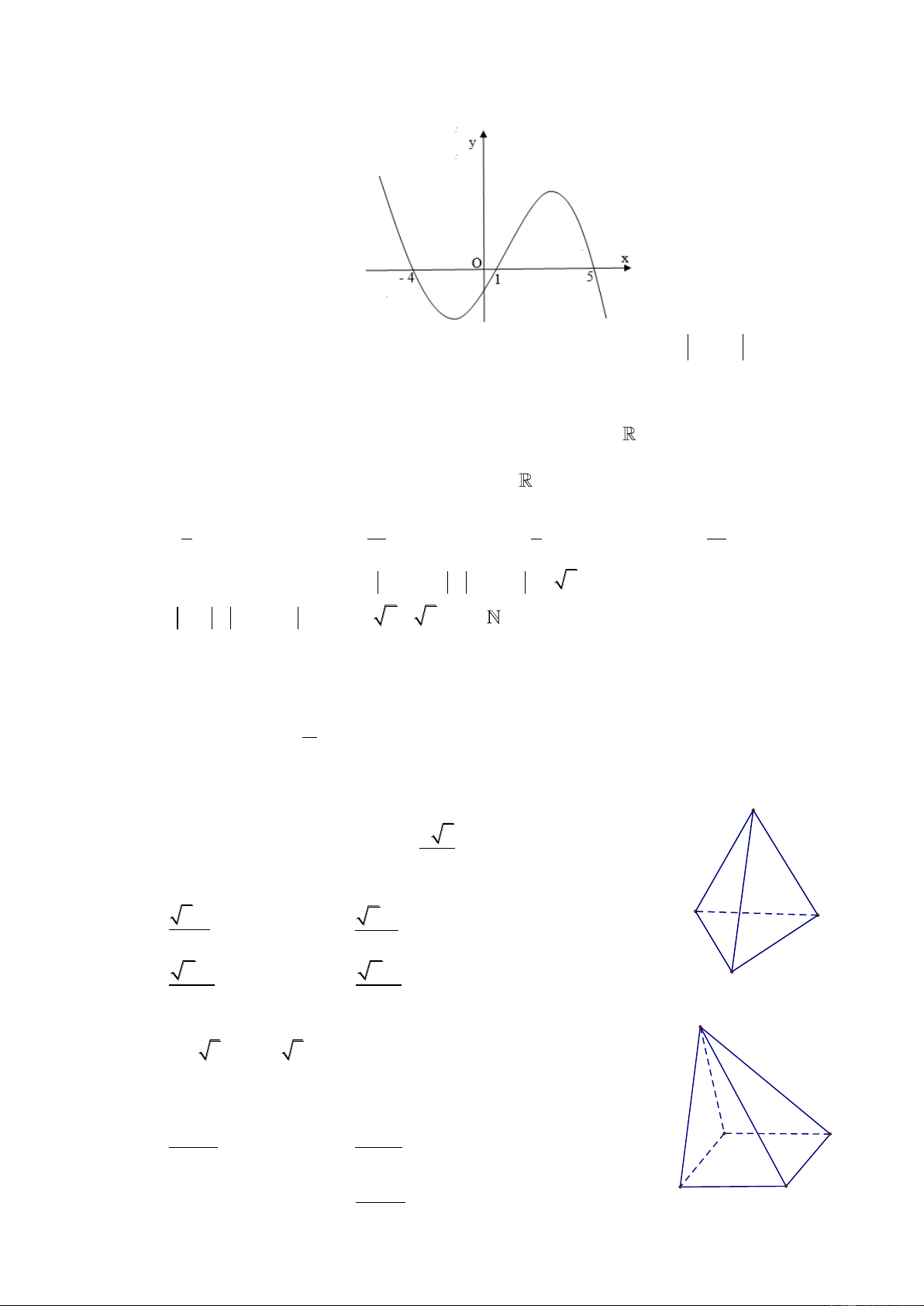
Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ TỐT NGHIỆP LỚP 12 THPT NAM ĐỊNH
NĂM HỌC 2022 – 2023
Môn: Toán – lớp 12 THPT ĐỀ CHÍNH THỨC
(Thời gian làm bài: 90 phút) MÃ ĐỀ: 202
Đề thi gồm 06 trang.
Họ và tên học sinh:………………………………………
Số báo danh:………….…………………….…………… Câu 1:
Gieo một đồng tiền cân đối, đồng chất ba lần. Xác suất để trong ba lần gieo có đúng hai lần
xuất hiện mặt ngửa là 1 3 1 1 A. . B. . C. . D. . 8 8 4 3 Câu 2:
Có bao nhiêu cách sắp xếp 4 học sinh thành một hàng dọc? A. 4 . B. 1. C. 10 . D. 24 . Câu 3:
Trên khoảng 0; , đạo hàm của hàm số e y x là e 1 x  1 A. e 1 y ex    . B. y  . C. e 1 y x    . D. e y  x ln . x e 1 e Câu 4:
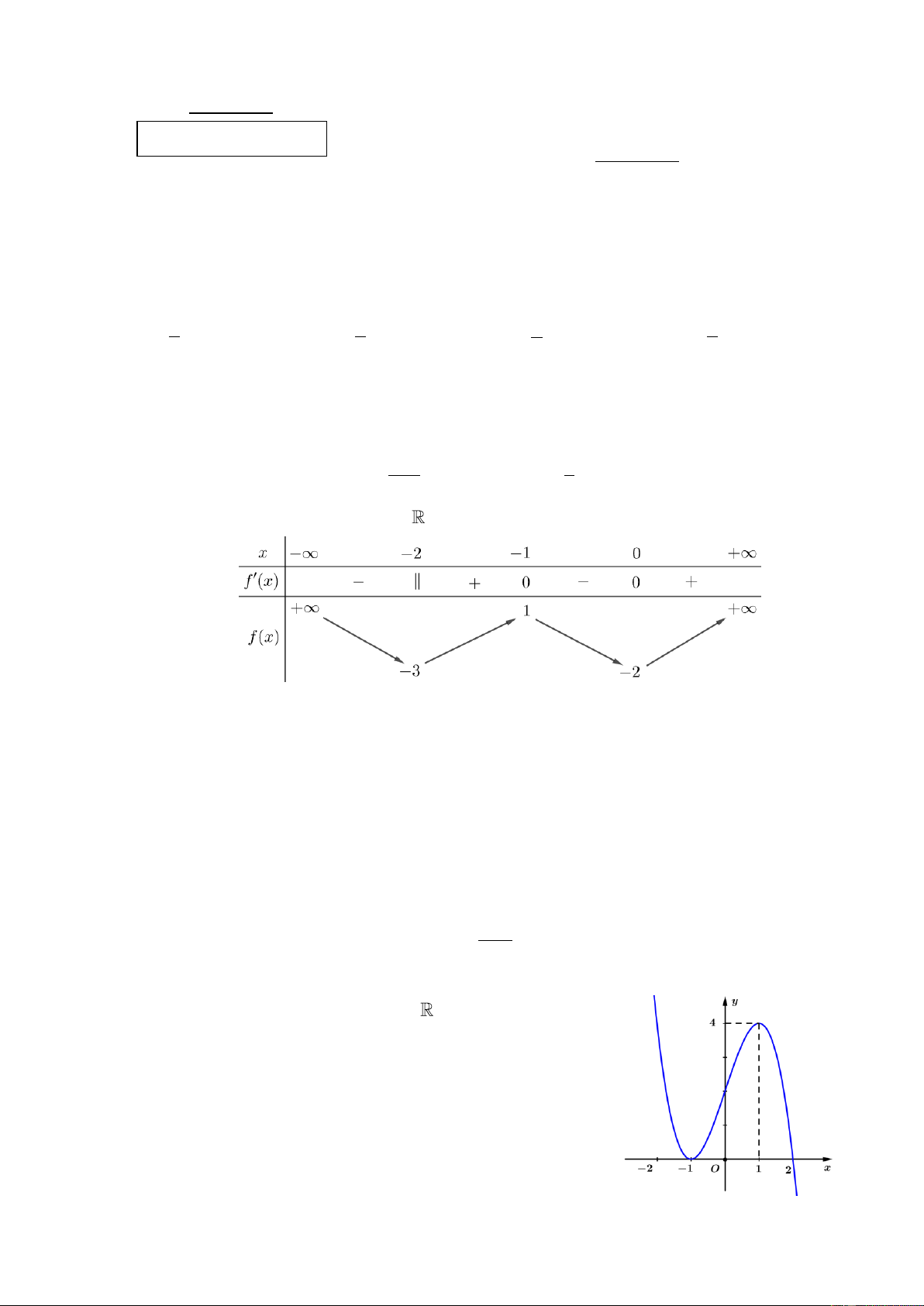
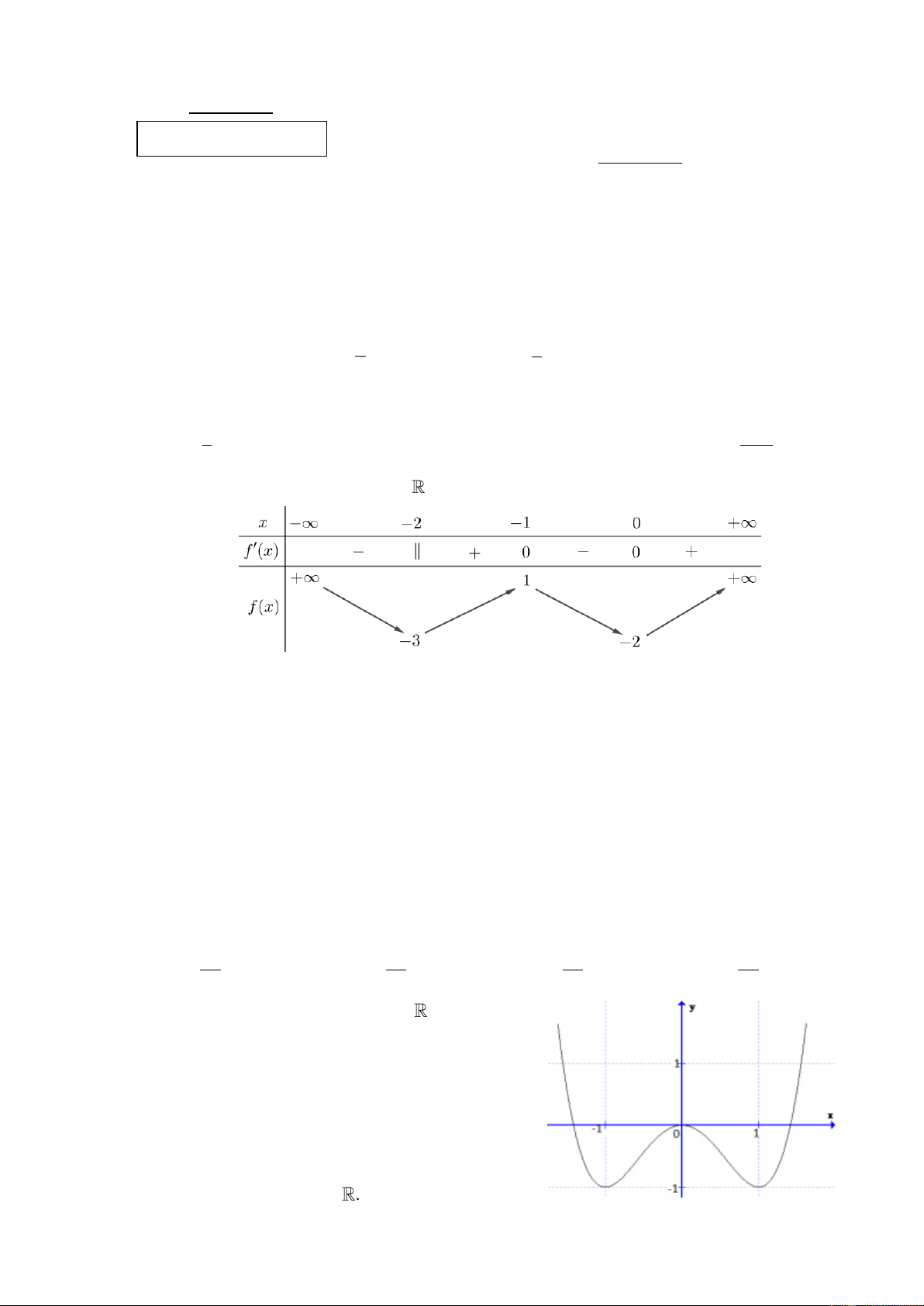
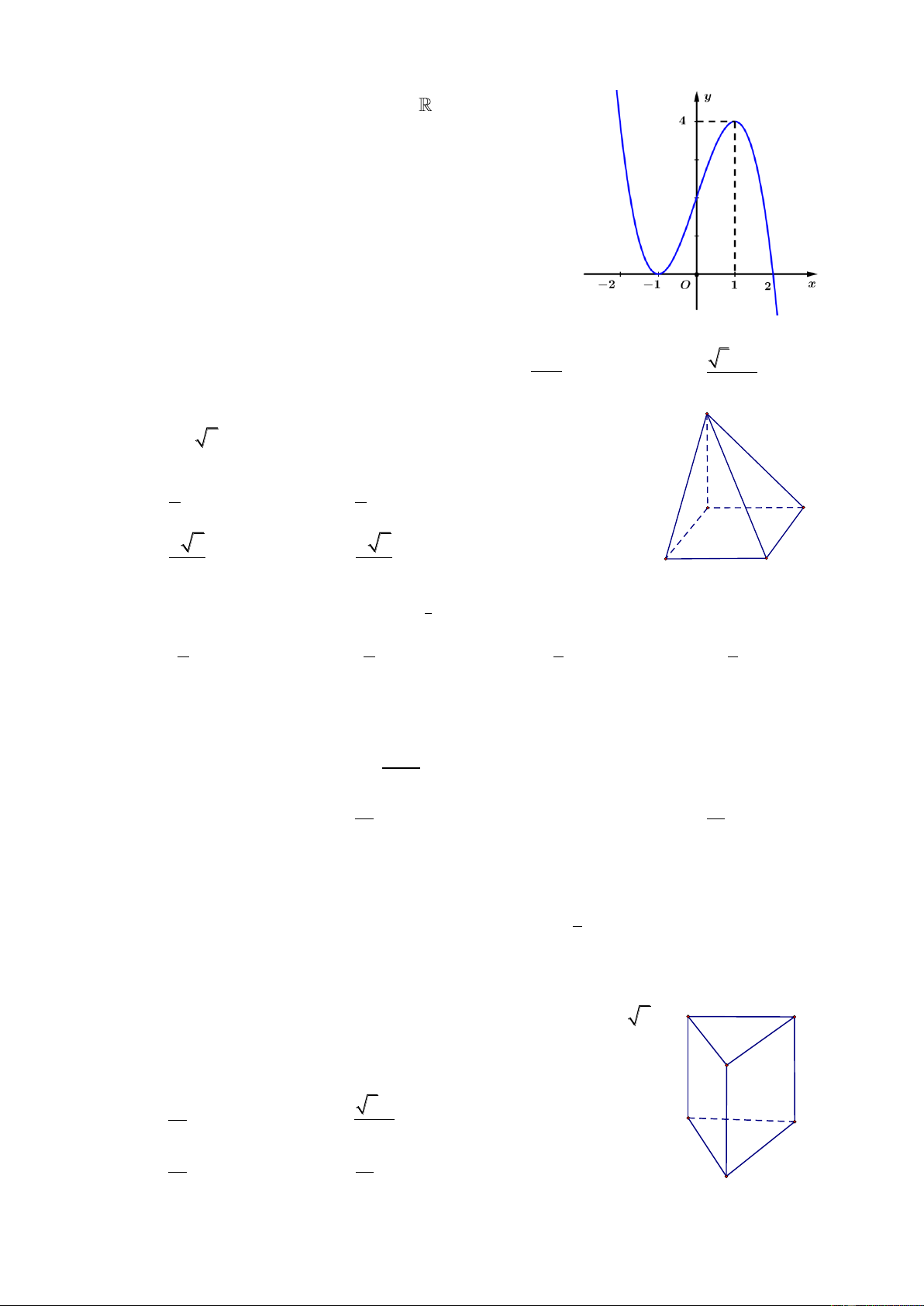
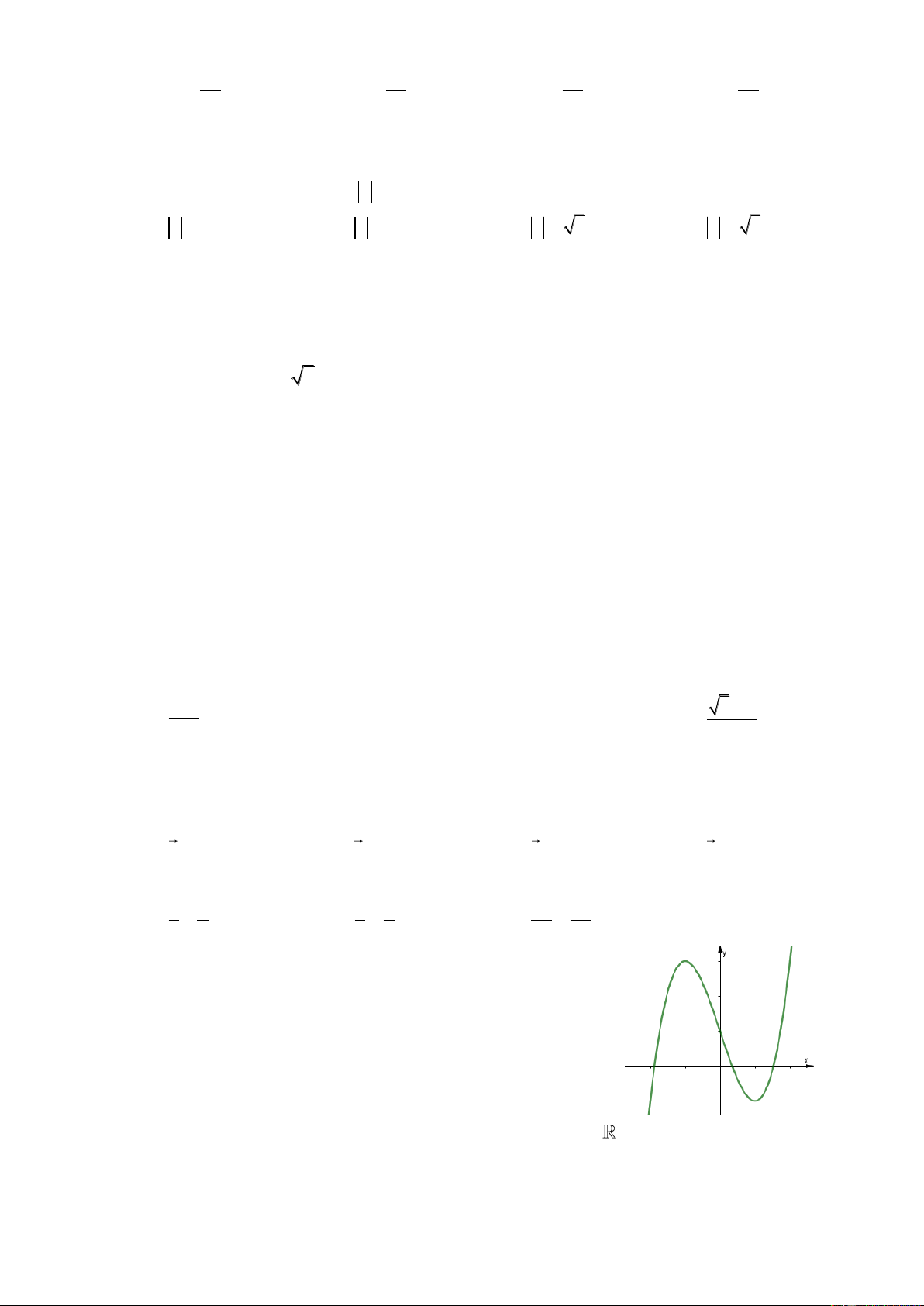
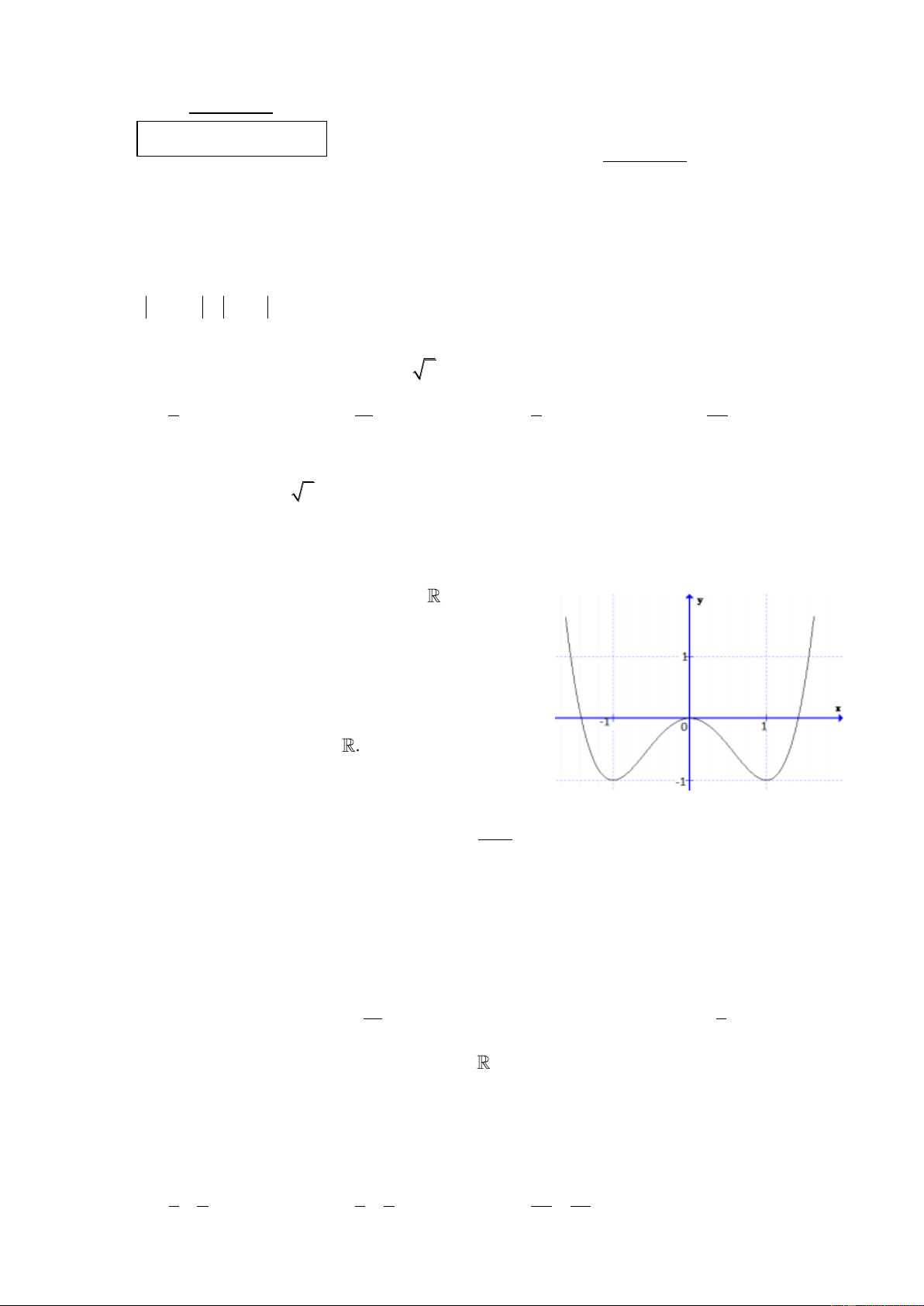
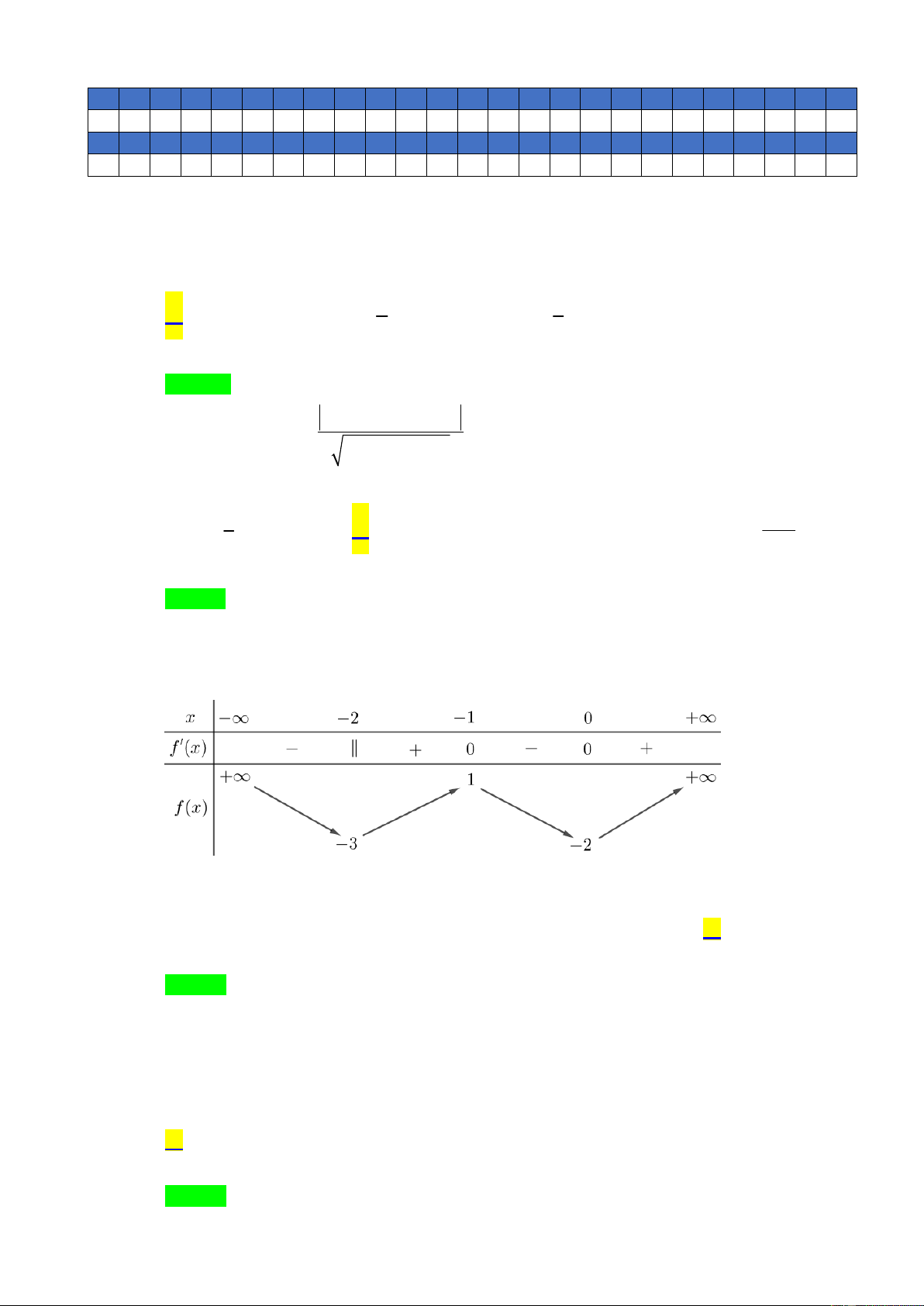
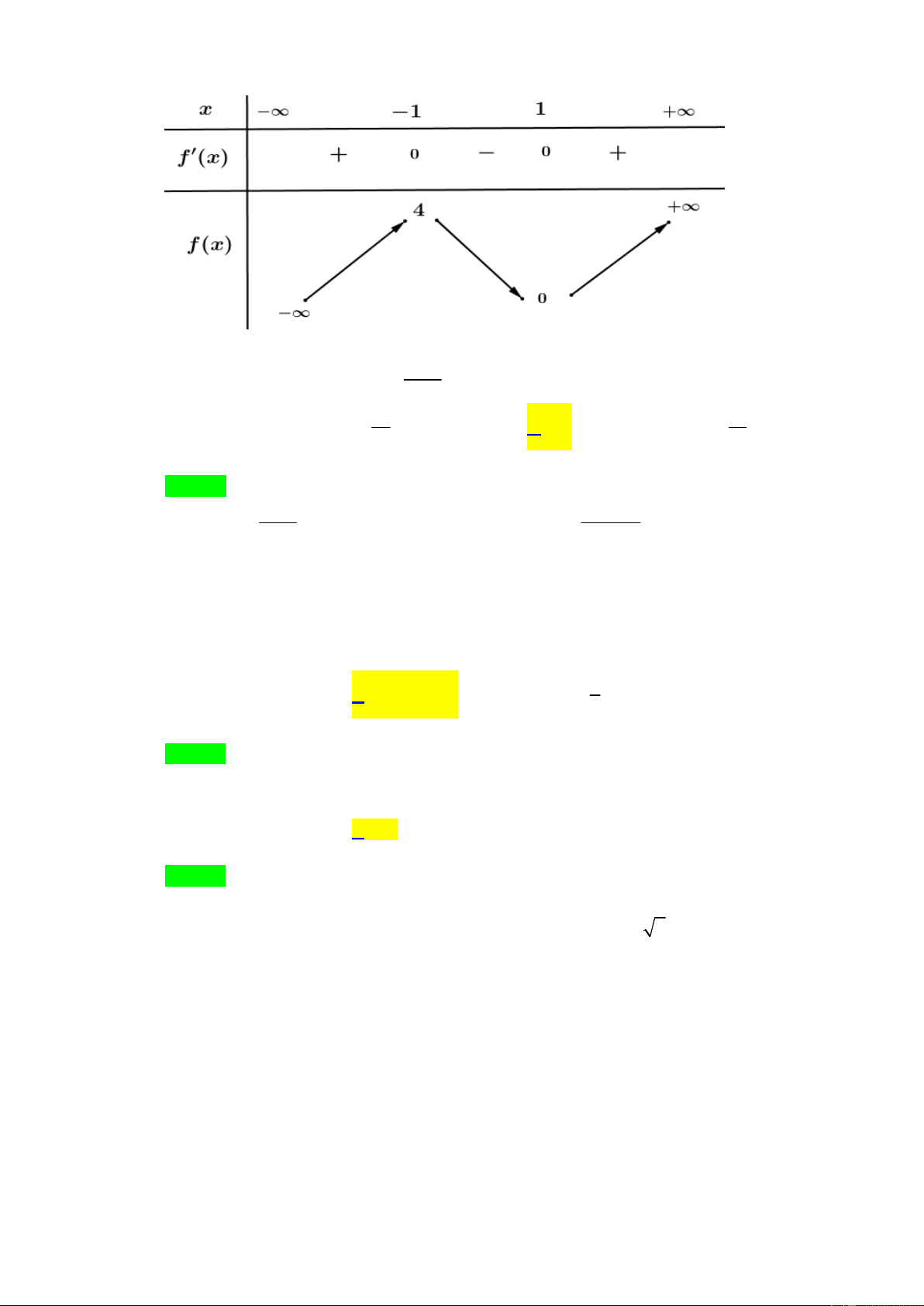
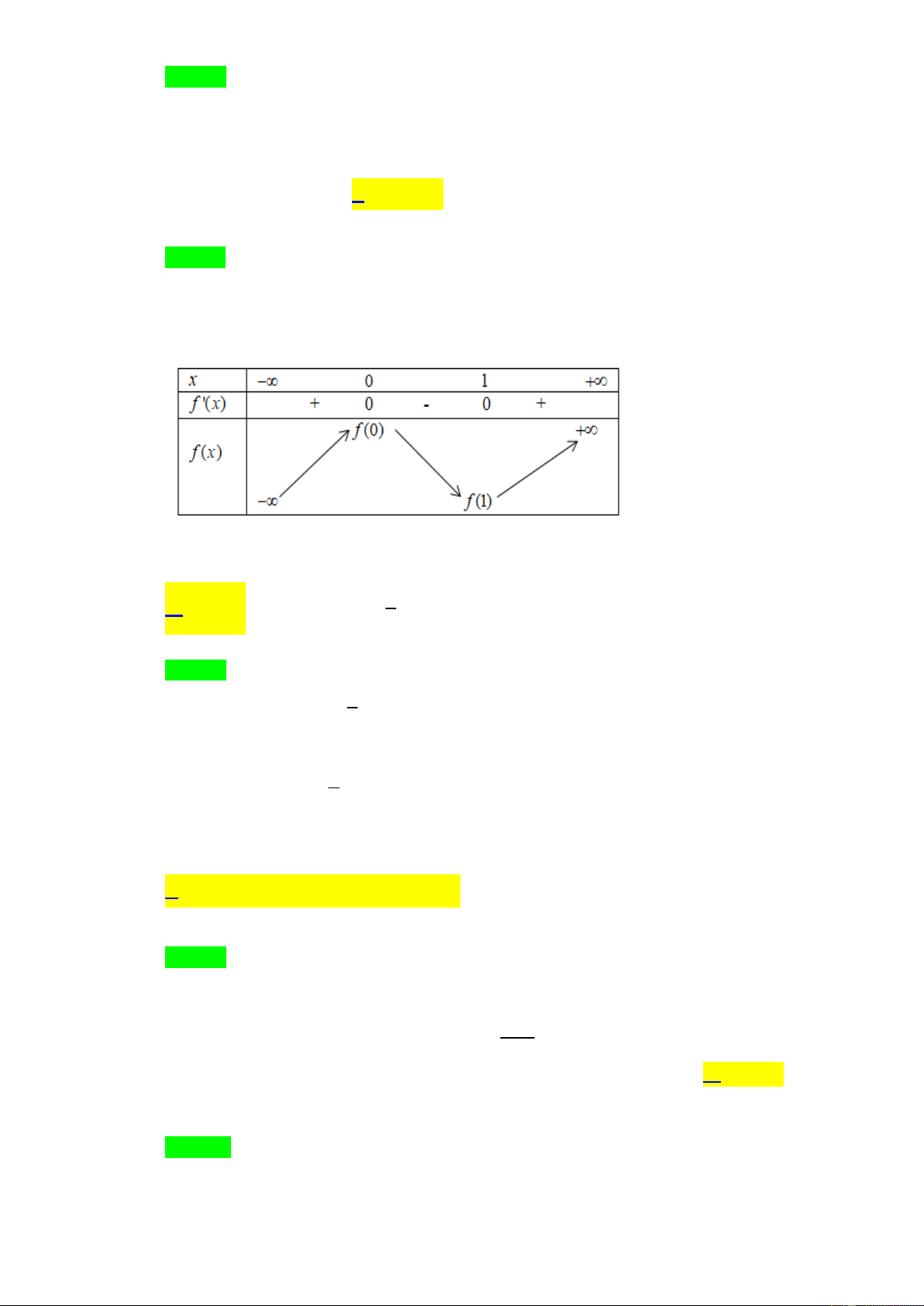
Cho hàm số y f x liên tục trên
và có bảng biến thiên như hình vẽ:
Có bao nhiêu giá trị nguyên của tham số m để phương trình f x  m có bốn nghiệm phân biệt? A. 0. B. 1. C. 3. D. 2. Câu 5:
Trên mặt phẳng tọa độ, điểm M  1  ; 
1 là điểm biểu diễn số phức nào sau đây?
A. z  1 i . B. z  1   i .
C. z  1 i . D. z  1  i . 1 1 1 Câu 6: Cho f
 xdx  2 và g
 xdx  5 khi đó  f
 x2gxdx  bằng 0 0 0 A. 3.  B. 12. C. 8.  D. 1. x Câu 7:
Đường tiệm cận đứng của đồ thị hàm số 2 y x  là 1 A. x  2. B. x  1.  C. x  1. D. y  2. Câu 8:
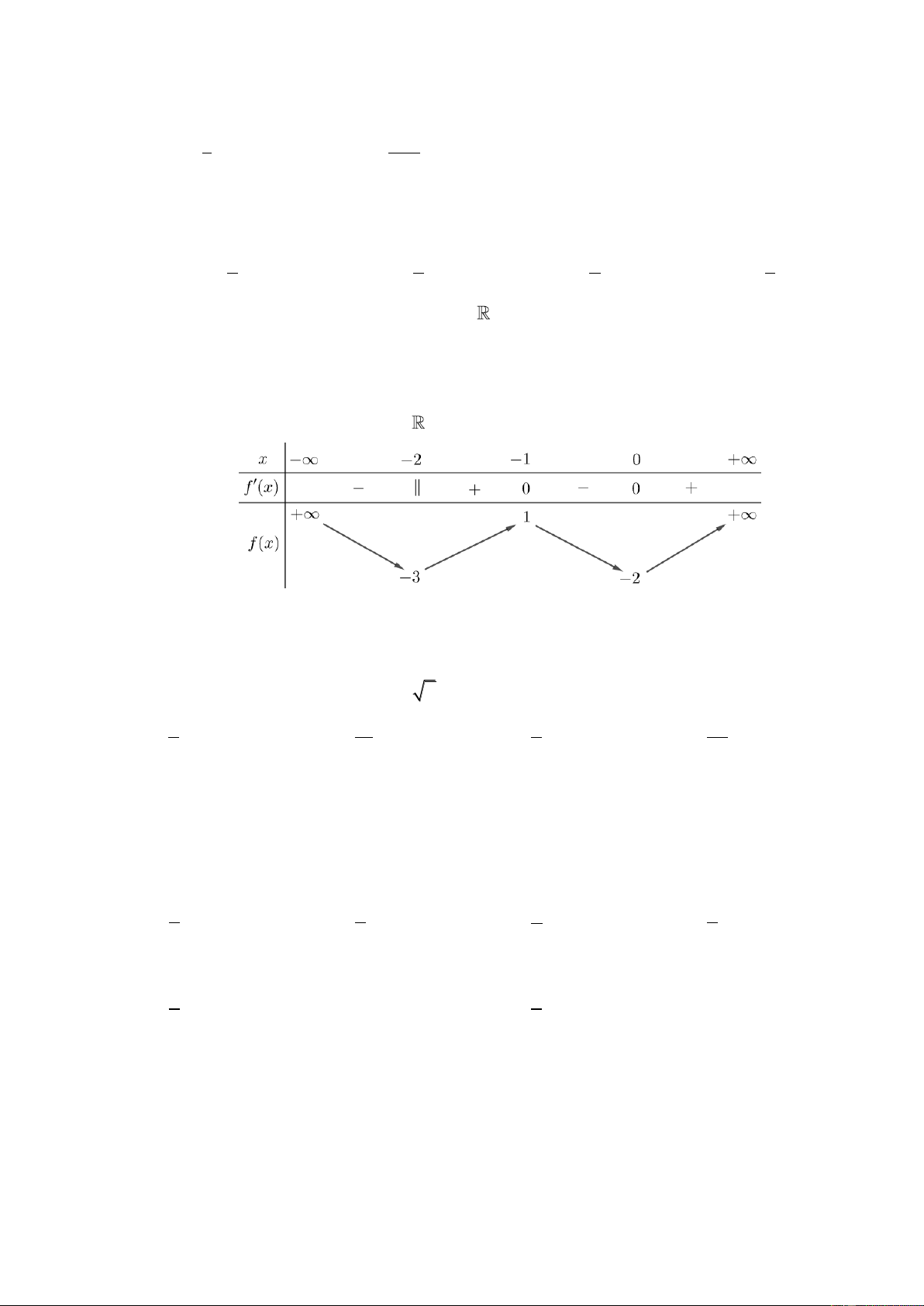
Cho hàm số y f x liên tục trên
và có đồ thị như hình
vẽ. Khẳng định nào sau đây đúng?
A. Hàm số đạt cực đại tại x  4.
B. Giá trị cực tiểu của hàm số bằng 1. 
C. Hàm số không có điểm cực trị.
D. Hàm số đạt cực tiểu tại x  1. 
Mã đề 202 - trang 1/6 Câu 9: Trong không gian
Oxyz , khoảng cách từ điểm M 0;3;  1 đến mặt phẳng
:2xy 2z 2  0 bằng 1 4 A. 1. B. . C. 3 . D. . 3 3 x  1   2t
Câu 10: Trong không gian Oxyz , đường thẳng d :  y  3  t
có một vectơ chỉ phương là z  2tA. u 2; 1  ;  1 . B. v  1  ;3;2. C. a  1  ;2;3. D. b  1  ; 1  ;  1 .
Câu 11: Trong không gian Oxyz , hình chiếu của điểm A1;2;  
1 trên mặt phẳng Oxy là điểm nào sau đây? A. Q  1  ; 2  ;  1 . B. P  1  ; 2  ;0 . C. M 1;2;  1 .
D. N 1;2;0 .
Câu 12: Trong không gian Oxyz , gọi S  là mặt cầu có tâm I Ox và đi qua hai điểm A2;1;  1 ; B  1
 ;3; 2 . Phương trình của mặt cầu S là A. 2 2 2
x y z  2x 10  0 . B. 2 2 2
x y z  4x  2  0 . C. 2 2 2
x y z  2x 10  0 . D. 2 2 2
x y z  4x 14  0 .
Câu 13: Trong mặt phẳng toạ độ Oxy , biết tập hợp điểm biểu diễn của số phức z thỏa mãn
z 1 i z  2i là đường thẳng d . Phương trình tổng quát của đường thẳng d là
A. 2x y 1  0 .
B. x y 1  0 .
C. x y 1  0 .
D. x  2y 1  0 . Câu 14: Hàm số 3
y x  3x  2 có giá trị cực đại bằng A. 1  . B. 4 . C. 20 . D. 0 .
Câu 15: Cho f x, g x là các hàm số liên tục trên
. Trong các mệnh đề sau, mệnh đề nào sai? A. f
 x.gxdx f
 xd .x g
 xd .x B. 5 f
 xdx 5 f
 xd .x C. f
 x gxdx f
 xdxg
 xd .x D. f
 x gxdx f
 xdxg
 xd .x
Câu 16: Khối bát diện đều thuộc loại khối đa diện đều nào sau đây? A. 3;  5 . B. 4;  3 . C. 3;  4 . D. 5;  3 .
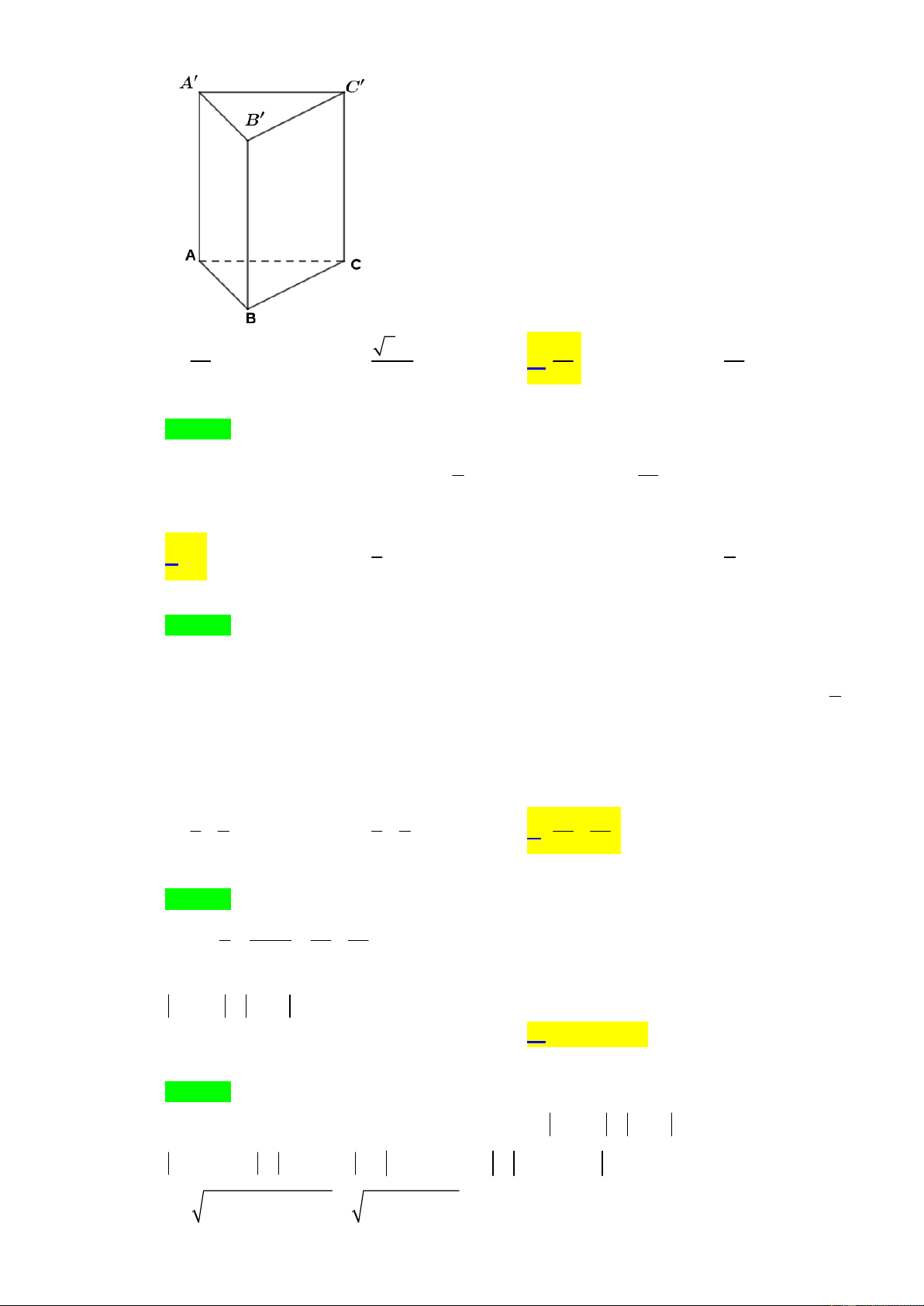
Câu 17: Cho khối lăng trụ đứng AB .
C A' B 'C ' có AB AC  , a AA'  a 2, A' C' 0
BAC  45 (tham khảo hình vẽ). Tính thể tích V của khối lăng trụ đã cho. B' 3 2a 3 a A. . B. . A C 4 4 3 a 3 a C. . D. . 2 6 B
Câu 18: Biết phương trình 2 log x  2log
2x 1  0 có hai nghiệm x , x . Giá trị của x .x bằng 2 2   1 2 1 2 1 1 A. 4. B. . C. 3.  D. . 8 2
Câu 19: Cho hàm số y f x có đạo hàm f  x  xx   3 1 , x
  . Hàm số y f x đồng biến
trên khoảng nào sau đây? A.  1  ;  1 . B. 0;  . C. 0  ;1 . D. ;0.
Mã đề 202 - trang 2/6 x
Câu 20: Giá trị lớn nhất của hàm số 5 y
trên đoạn 8;12 bằng x  7 17 13 A. 15. B. . C. 13. D. . 5 2
Câu 21: Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y x  2x 1, trục hoành và hai
đường thẳng x  1  ; x  3 . 37 68 64 56 A. S  . B. S  . C. S  . D. S  . 3 3 3 3
Câu 22: Cho khối nón có chiều cao bằng a và đường sinh bằng 2a . Thể tích của khối nón đã cho bằng 3 3 a 3  a A. 3 3 a . B. 3  a . C. . D. . 3 3
Câu 23: Số phức nghịch đảo của số phức z  3  4i là 3 4 3 4 3 4 A. i . B. 3  4i . C. i . D. i . 5 5 5 5 25 25 A' B'
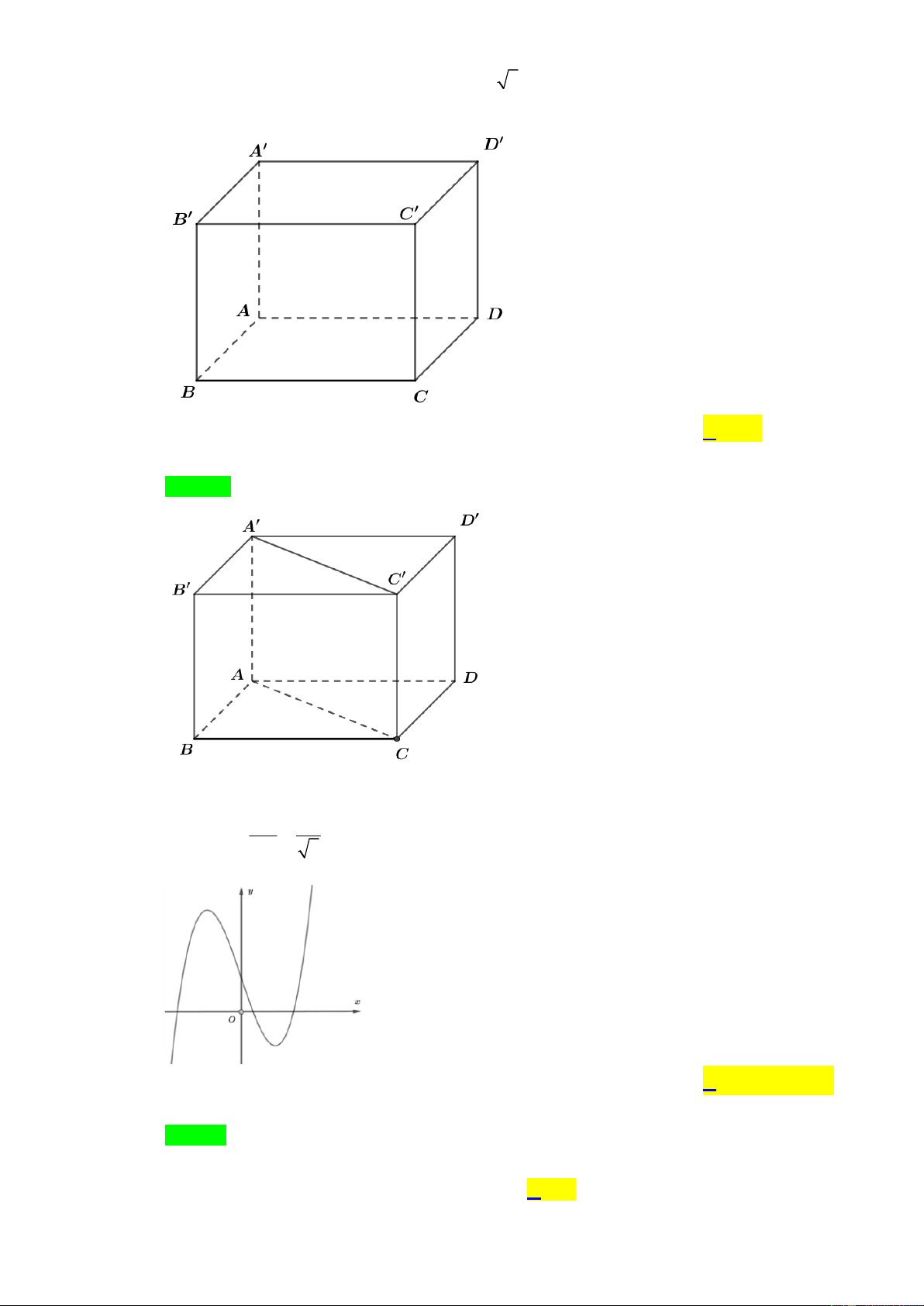
Câu 24: Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có AB a 3; AD a
(tham khảo hình vẽ). Góc giữa hai đường thẳng AB và A'C ' C' D' bằng A. 0 60 . B. 0 45 . A B C. 0 75 . D. 0 30 . D C
Câu 25: Cho cấp số cộng u có u  2 và công sai d  2
 . Giá trị của u là n  1 5 A. 10 . B. 6 . C. 6  . D. 32 .
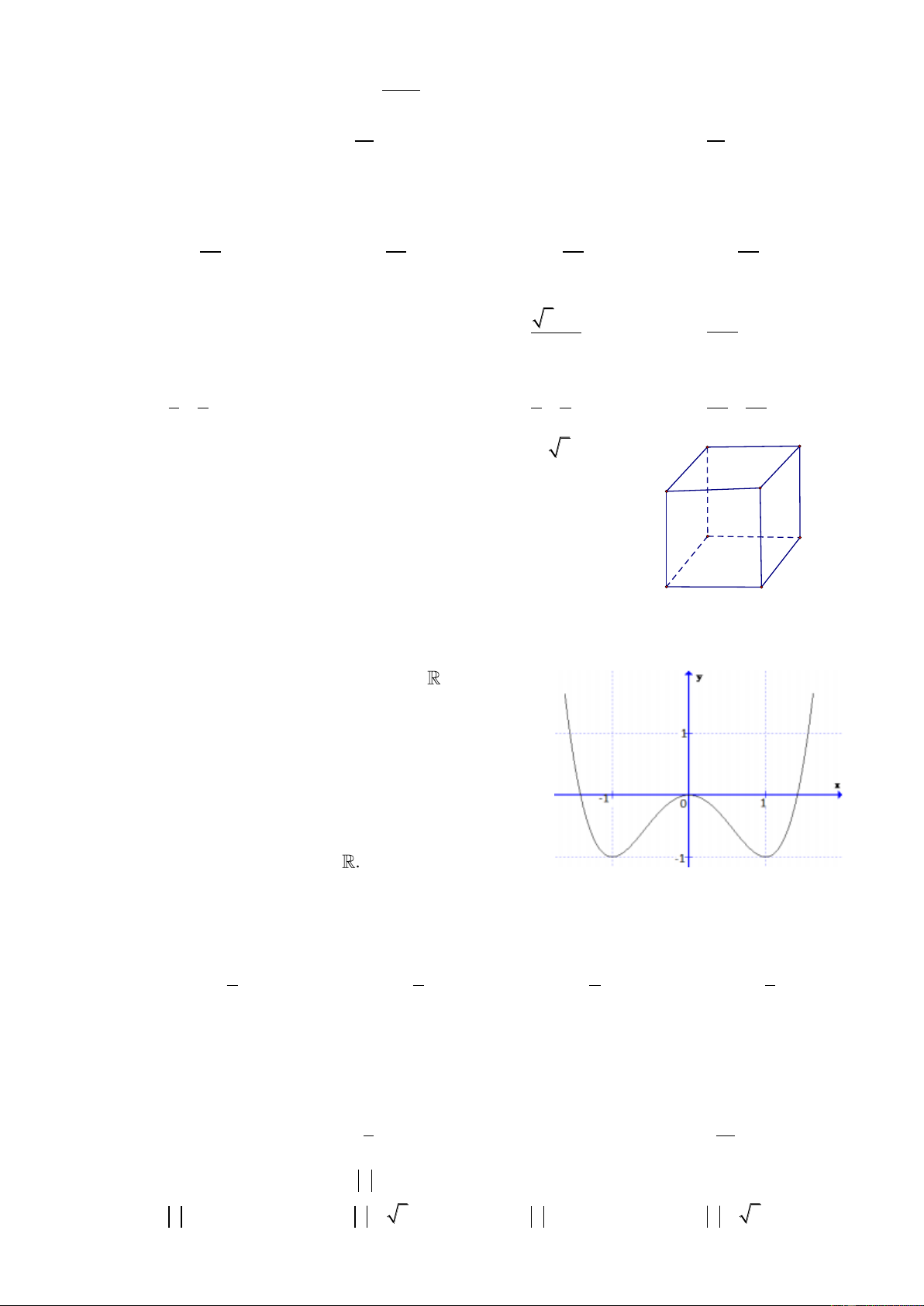
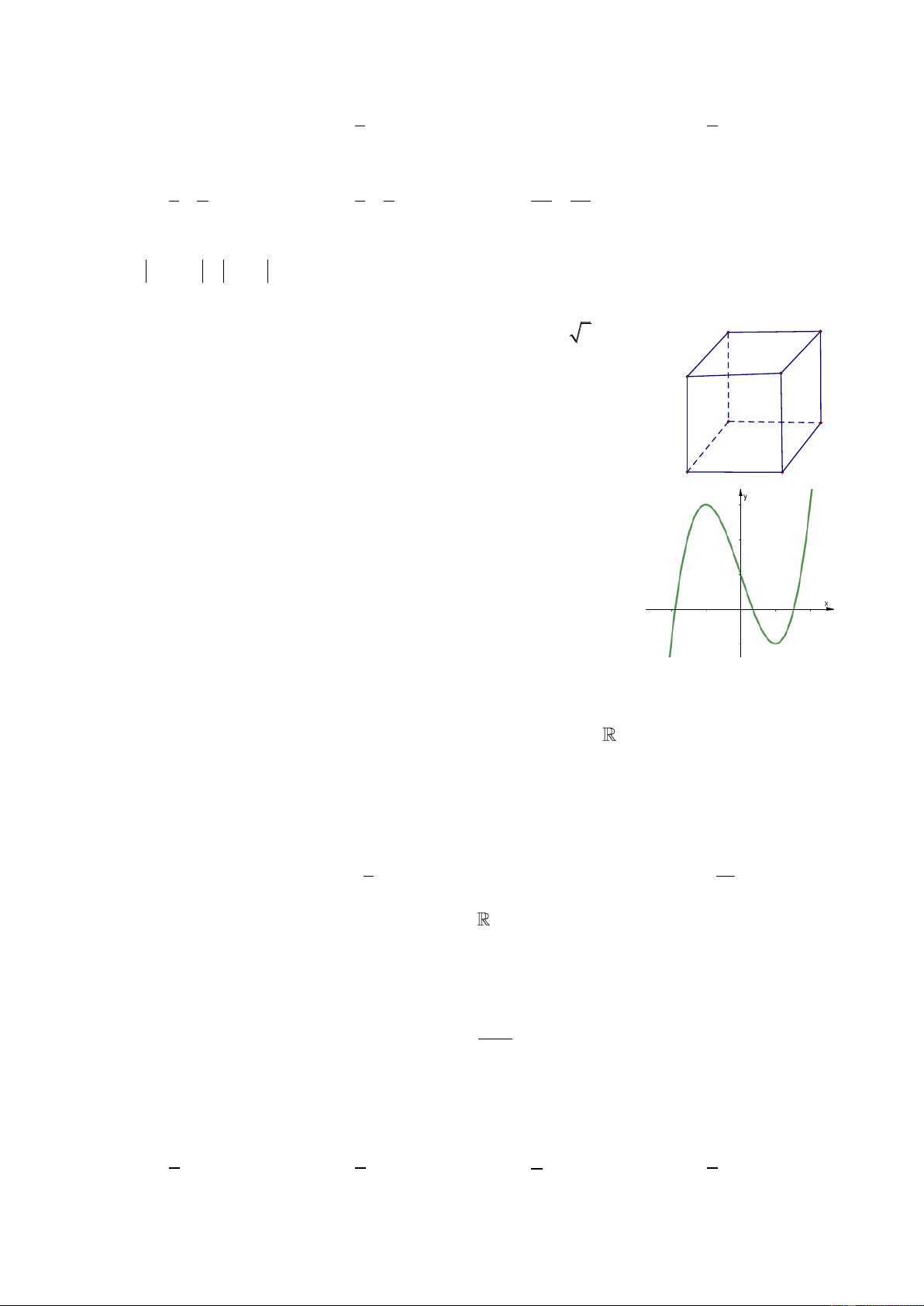
Câu 26: Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ.
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên  1  ;  1 . .
B. Hàm số nghịch biến trên  ;    1 .
C. Hàm số đồng biến trên  1  ;.
D. Hàm số đồng biến trên .
Câu 27: Trong không gian Oxyz , gọi  là góc giữa hai mặt phẳng P : x  2y z  2  0 và
Q:2x y z 4  0. Tính cos . 2 3 1 1 A. cos  . B. cos  . C. cos  . D. cos  . 3 4 6 3
Câu 28: Tập nghiệm của bất phương trình 3x  27 là A. 3, . B.  ,  3. C.  ,   3 . D. 3, .
Câu 29: Tập nghiệm của bất phương trình log 3x 1  3 là 2    1  10  A. 3;  . B. ;3   . C.  ,  3. D. ;    .  3   3 
Câu 30: Cho số phức z  1 2i , tính z . A. z  3 . B. z  3 . C. z  5 . D. z  5 .
Mã đề 202 - trang 3/6
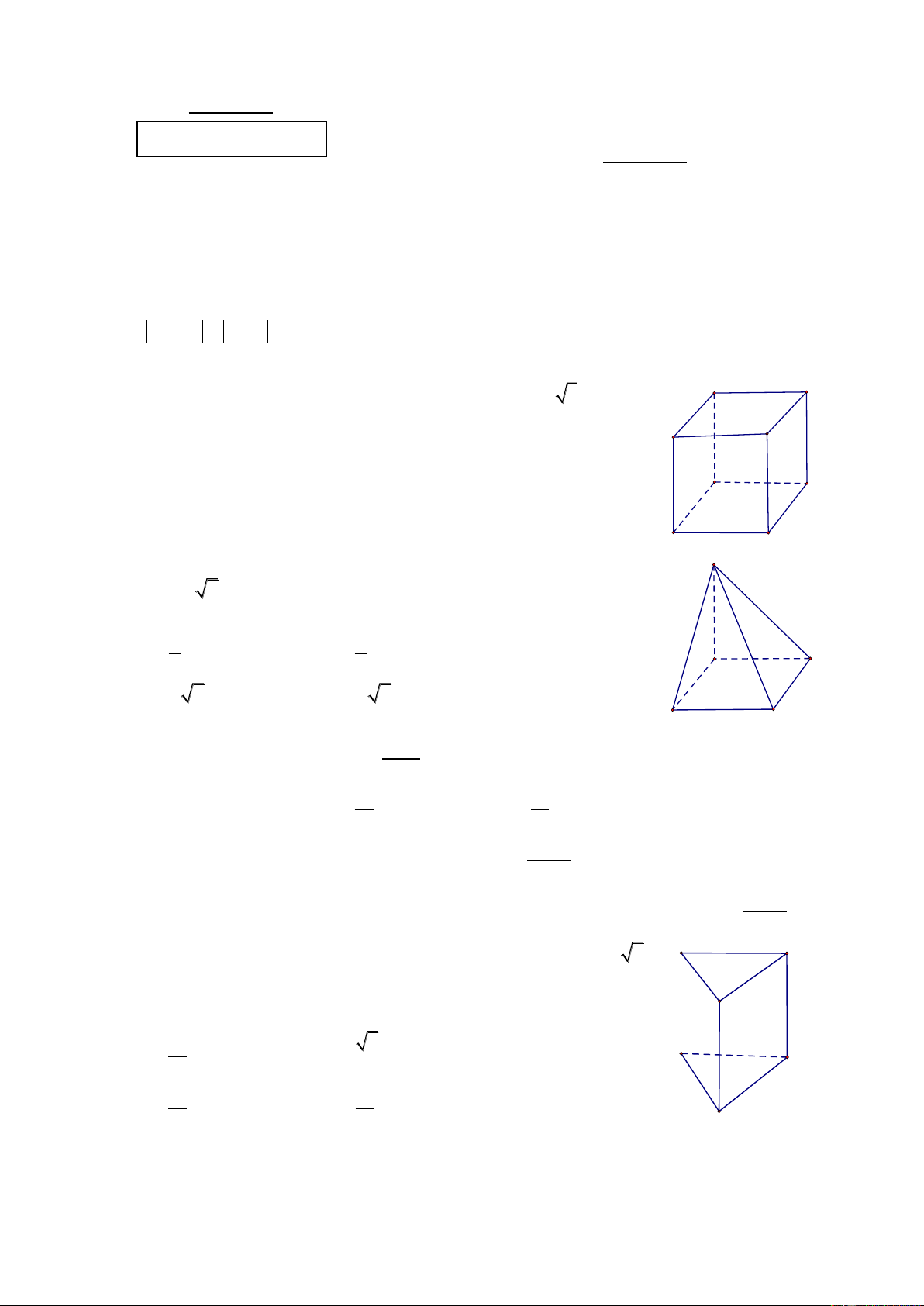
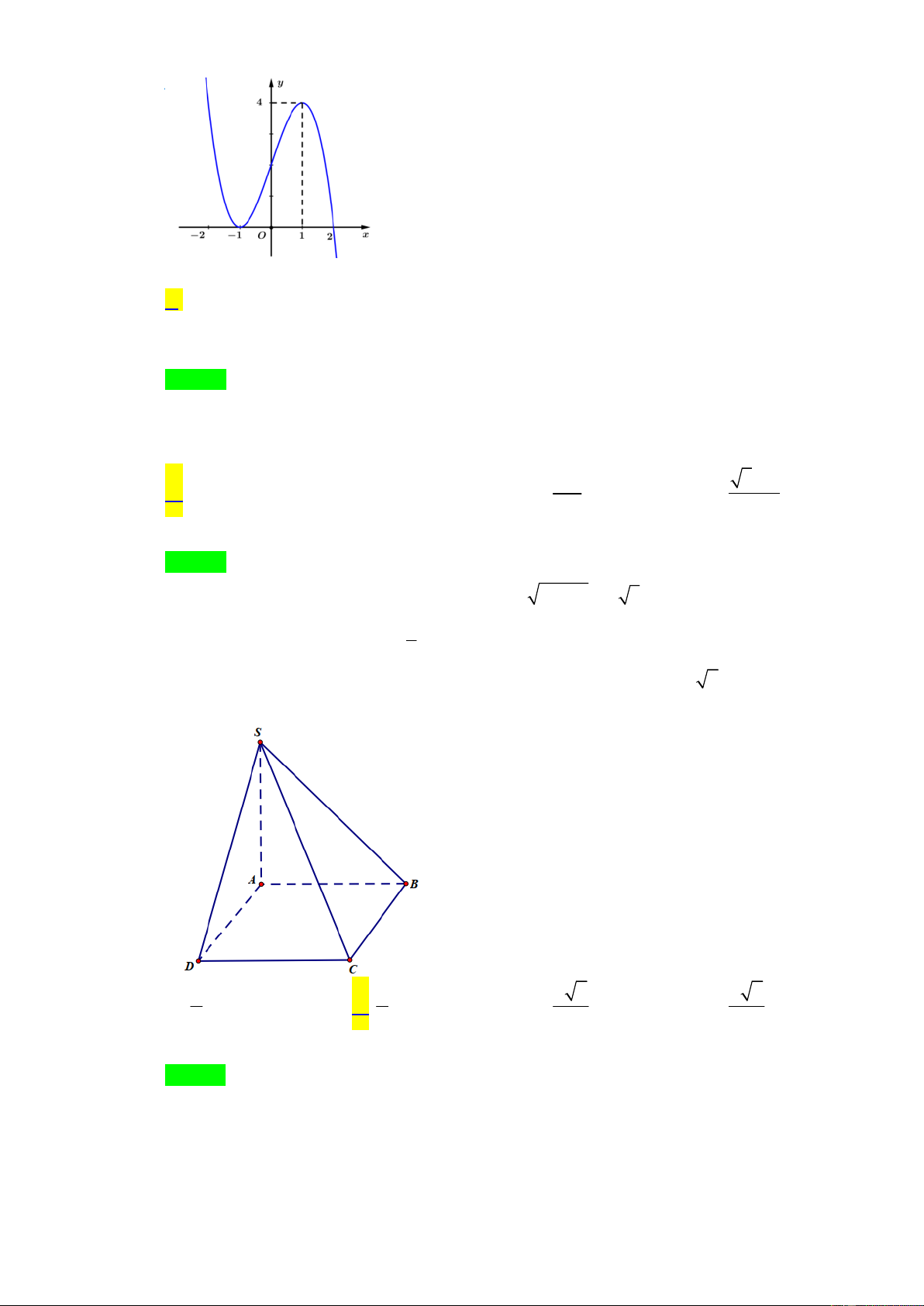
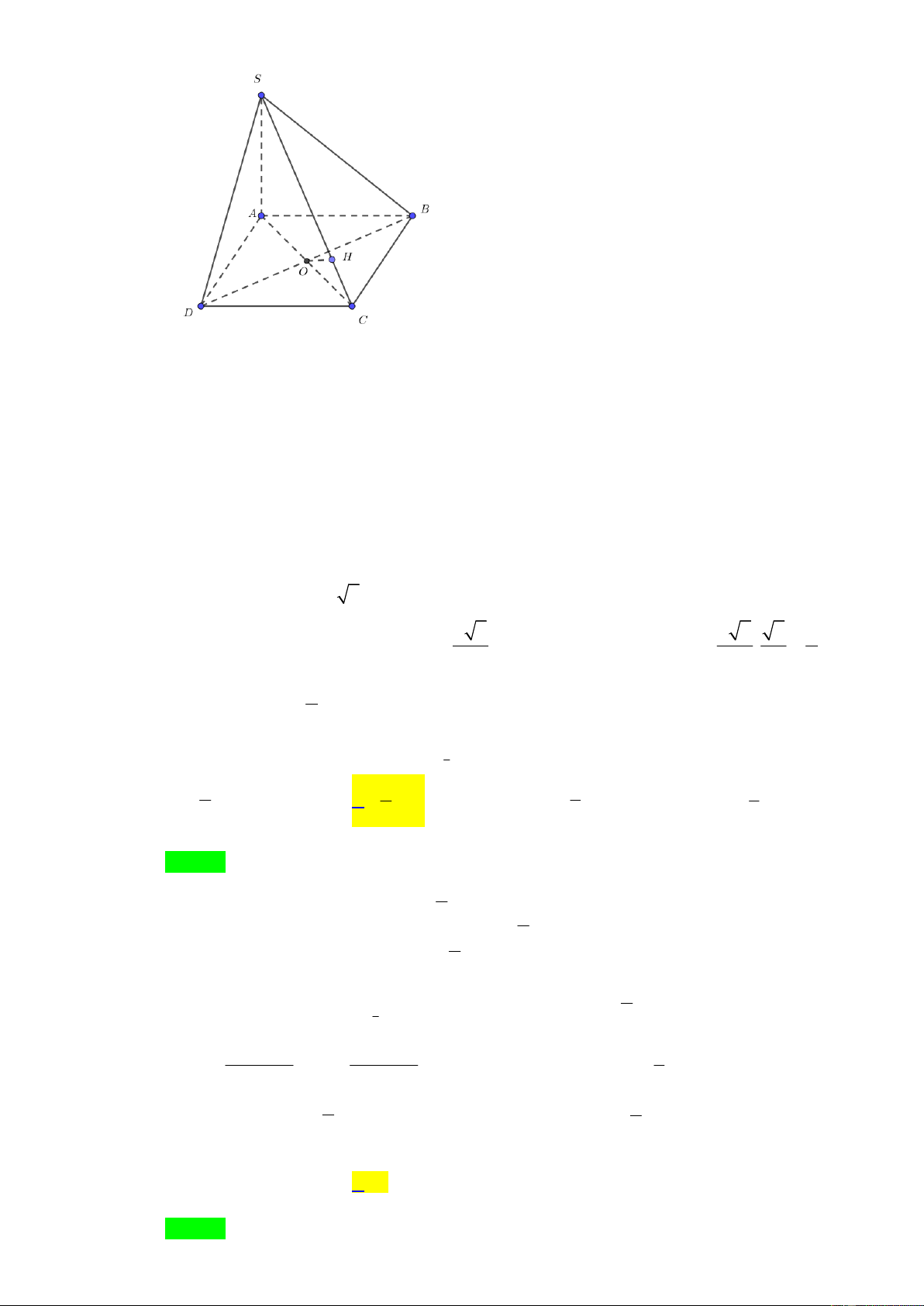
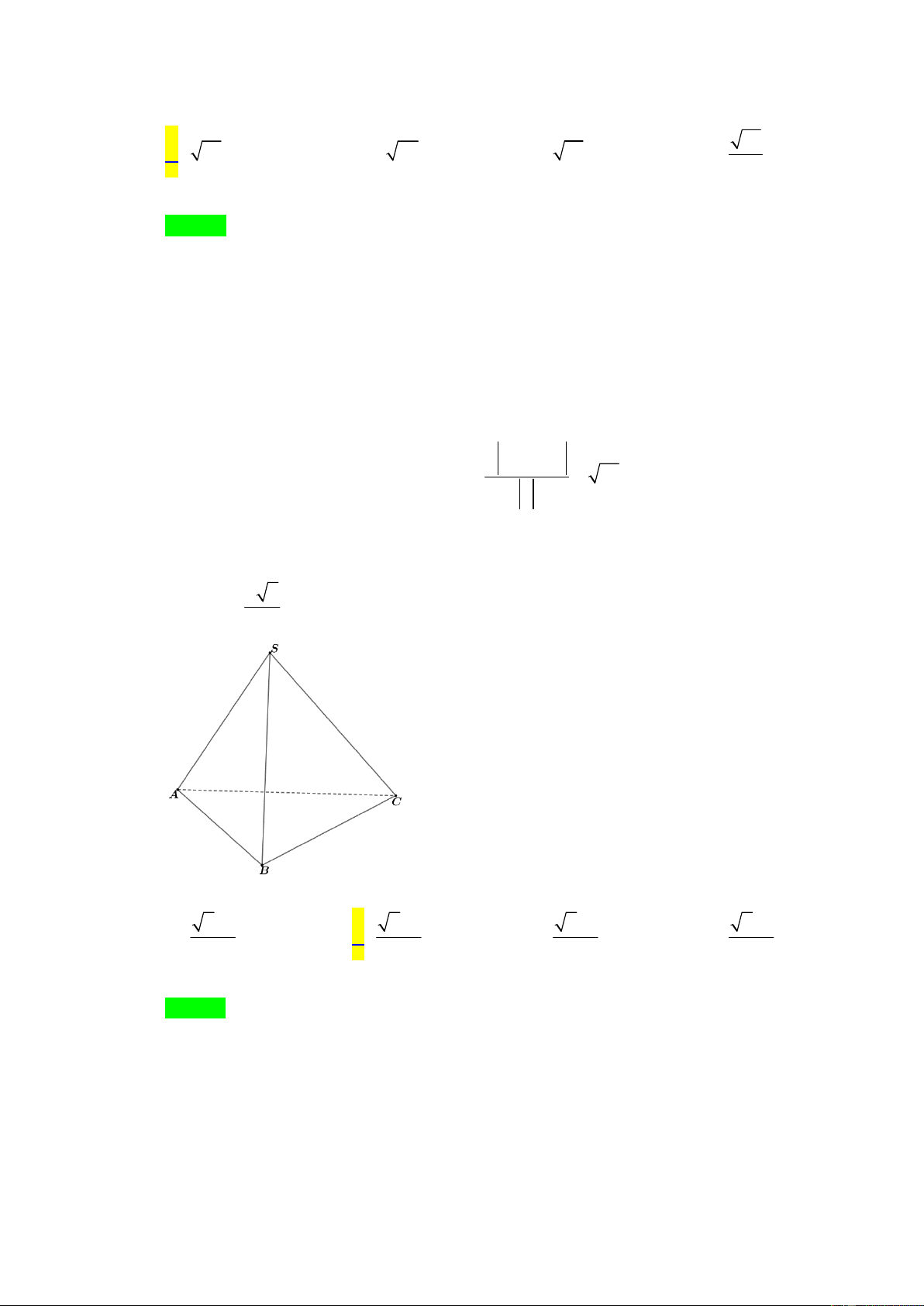
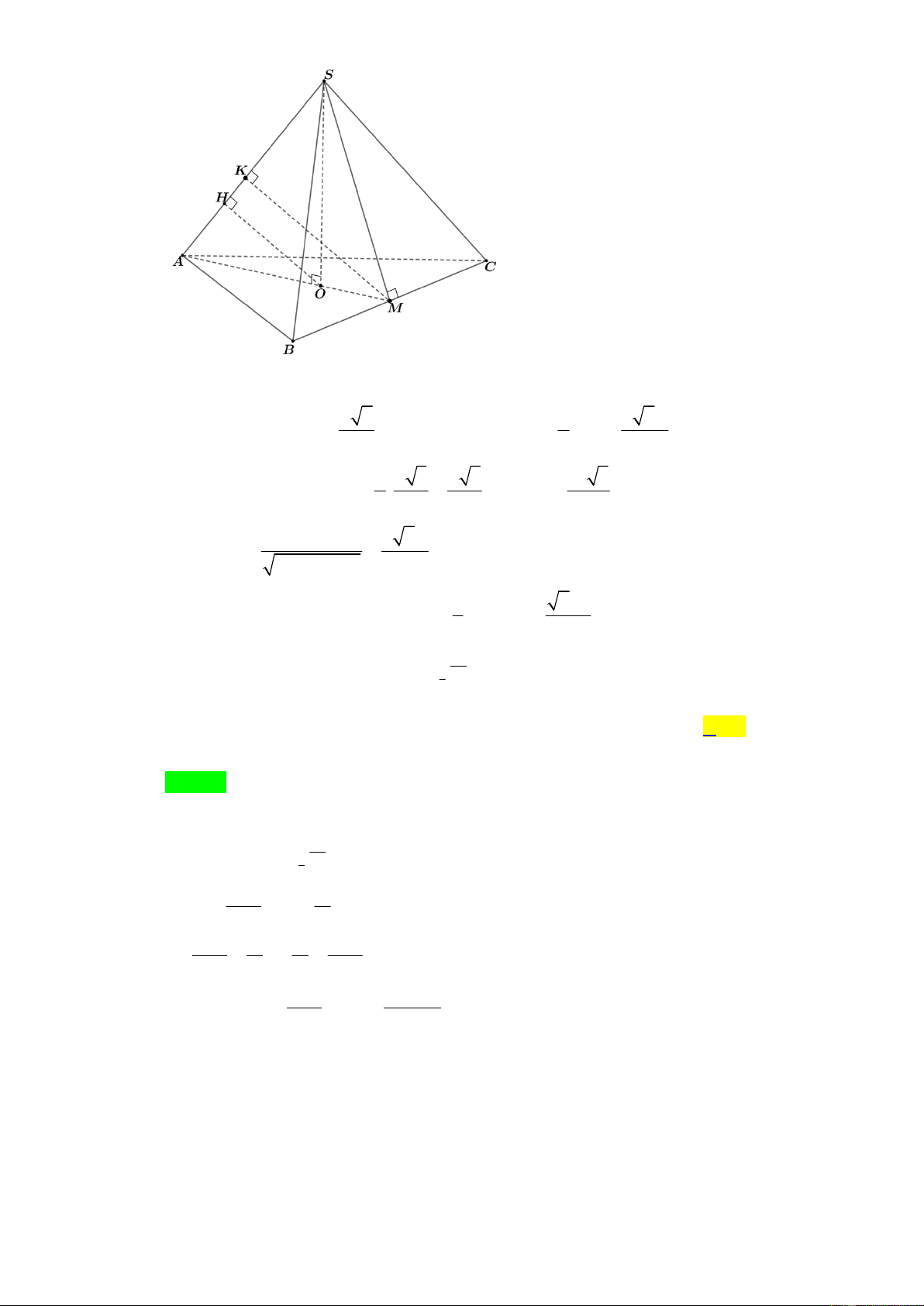
Câu 31: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , S
SA a 2 và vuông góc với đáy (tham khảo hình vẽ). Tính khoảng
cách giữa hai đường thẳng BD và SC . a a 2 A. . B. . A B 4 2 a a 2 C. . D. . D C 2 4
Câu 32: Bất phương trình 2
2 log (4x  3)  log (2x  3)  2 có tập nghiệm là 3 1 9  3   3   3   3  A. ;   . B. ;3  . C.  ;3   . D.  ;3 .     4   4   8   8 
Câu 33: Cho hình trụ có chiều cao bằng h và bán kính đáy bằng r . Diện tích xung quanh S của hình xq
trụ được tính bởi công thức 1 A. 2 S  r h .
B. S   rh . C. S  2rh . D. S  rh . xq xq xq xq 3
Câu 34: Với a là số thực dương tùy ý, 3 log a bằng 81 3 1 1 4 A. log . a B. log . a C. log . a D. log . a 3 4 3 27 3 12 3 3
Câu 35: Cho hàm số f x có đạo hàm liên tục trên đoạn 1; 2, f  
1  1 và f 2  2 . Tính 2 I f
 xd .x 1 7 A. I  1. B. I  1.  C. I  3. D. I  . 2 1
Câu 36: Họ tất cả các nguyên hàm của hàm số 2
f (x)  3x  là 2 sin x 2 A. 3
x  cot x  . C B. 6x   C. C. 3
x  tan x  . C D. 3
x  cot x  . C 2 sin x
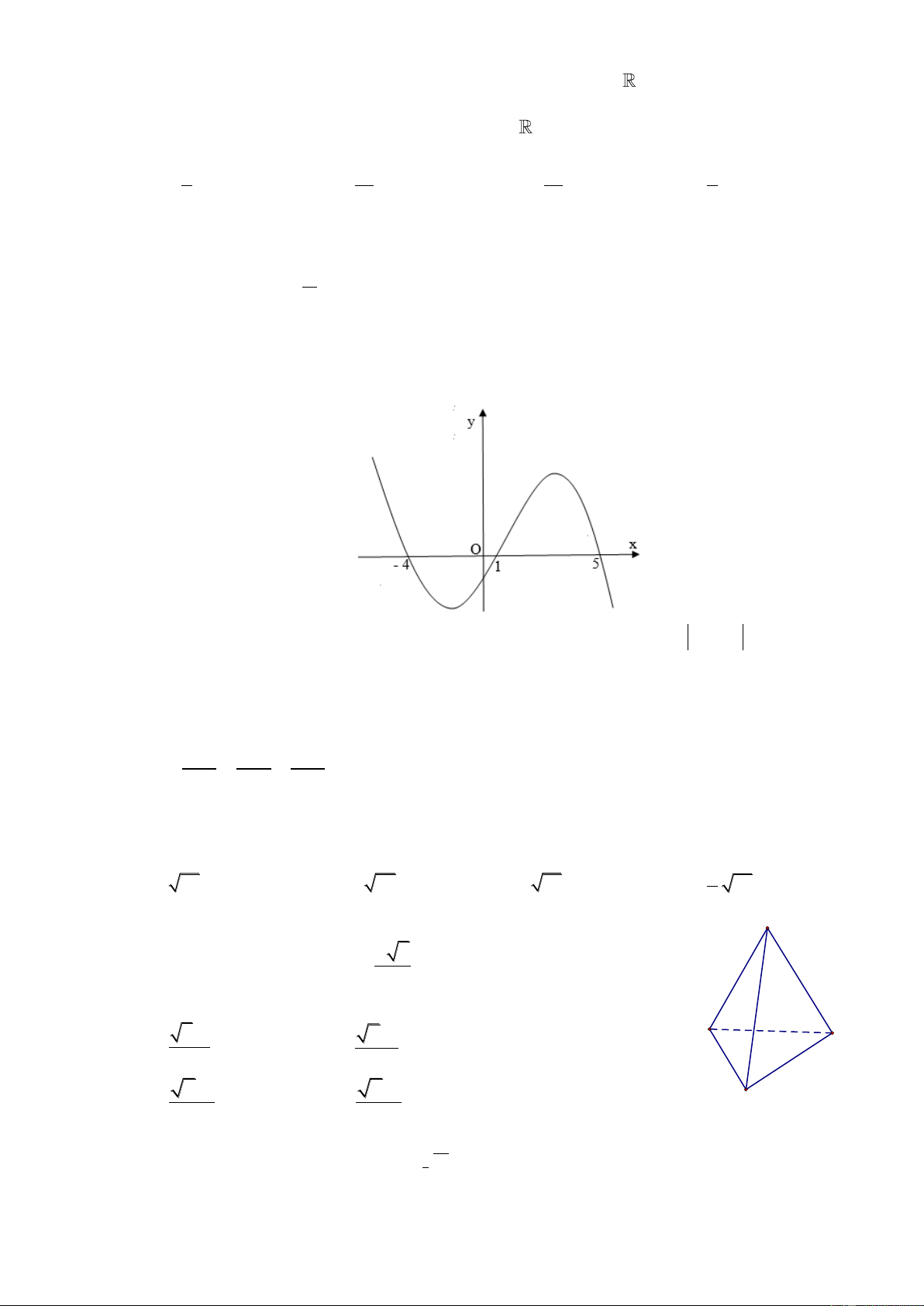
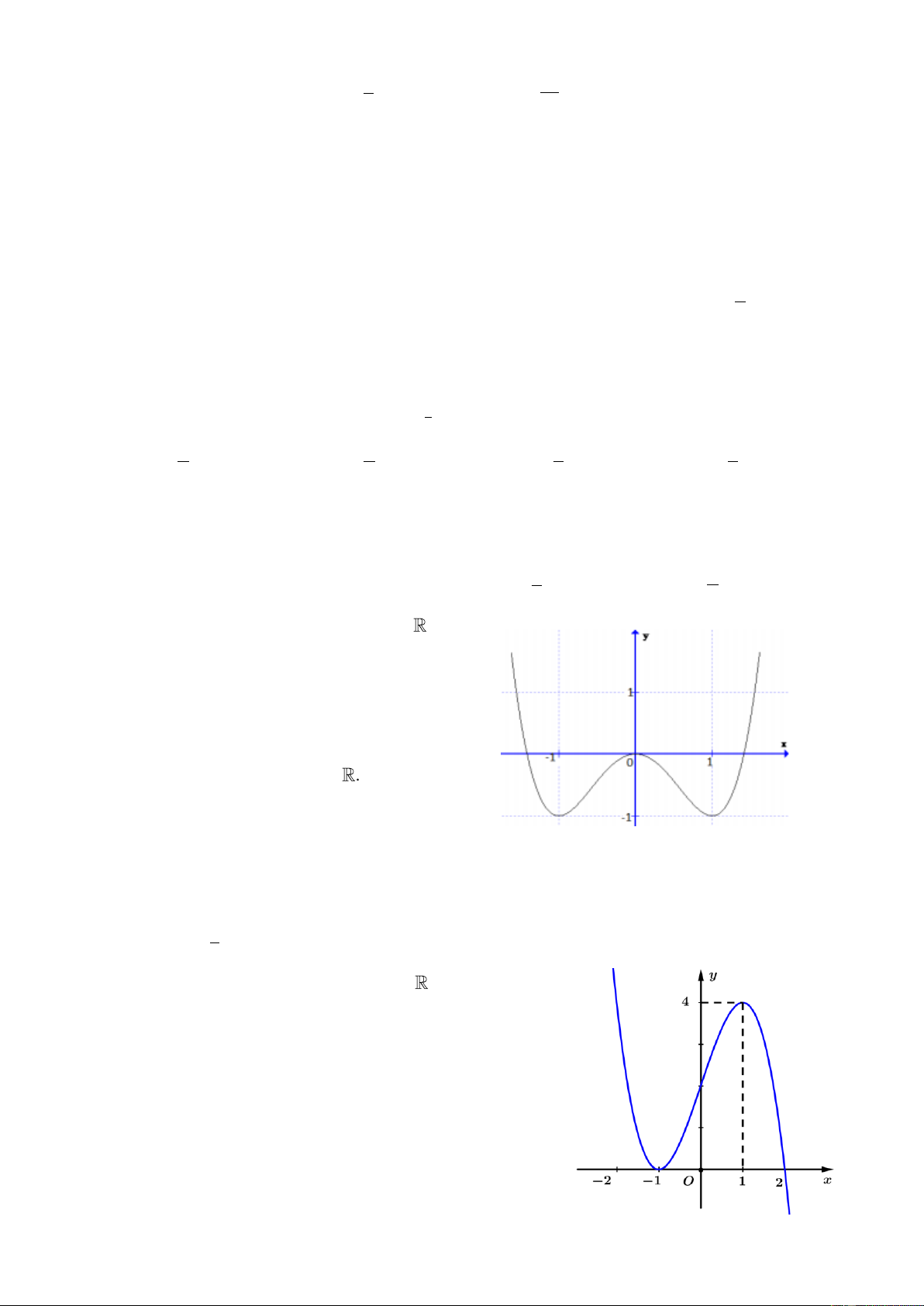
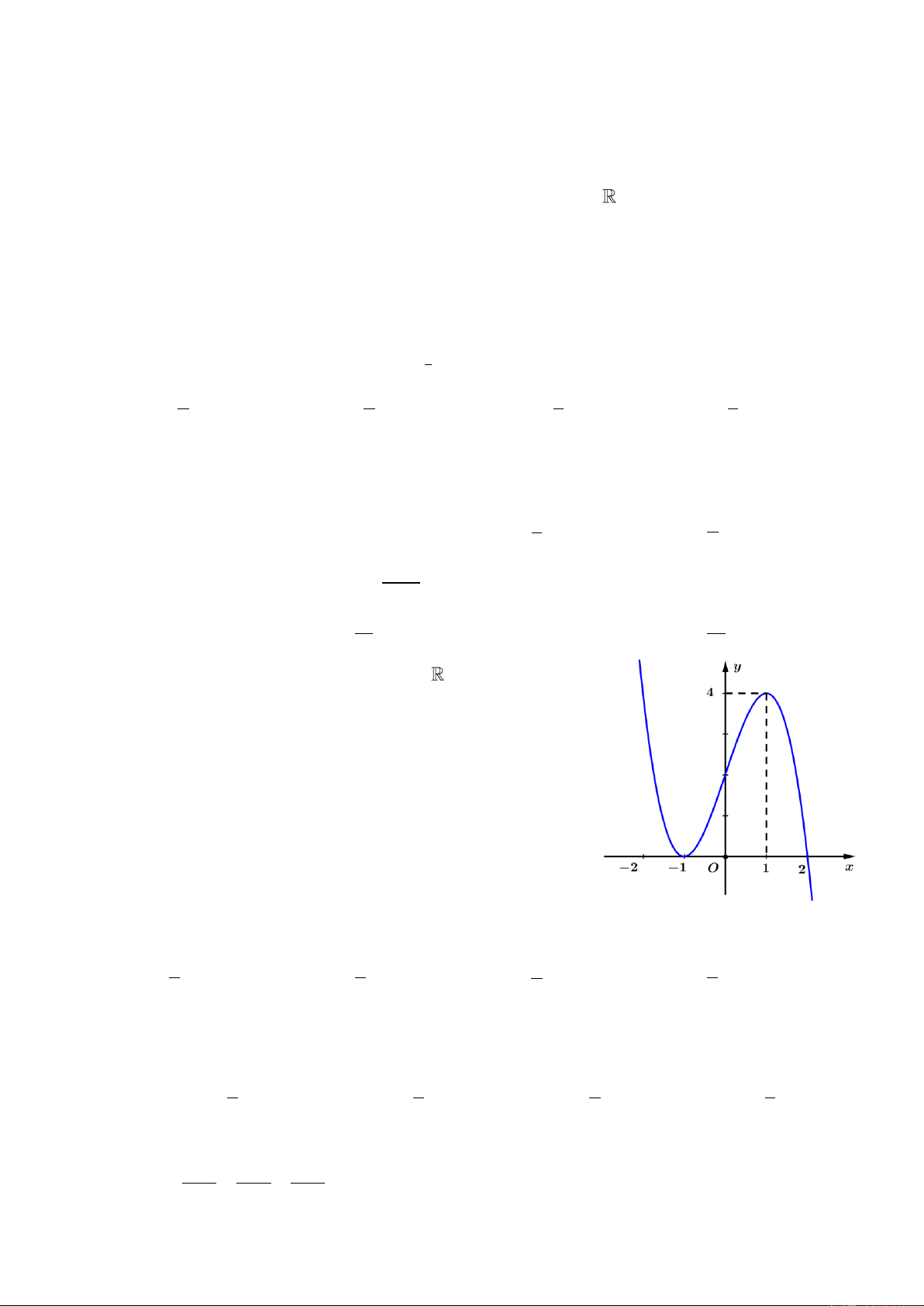
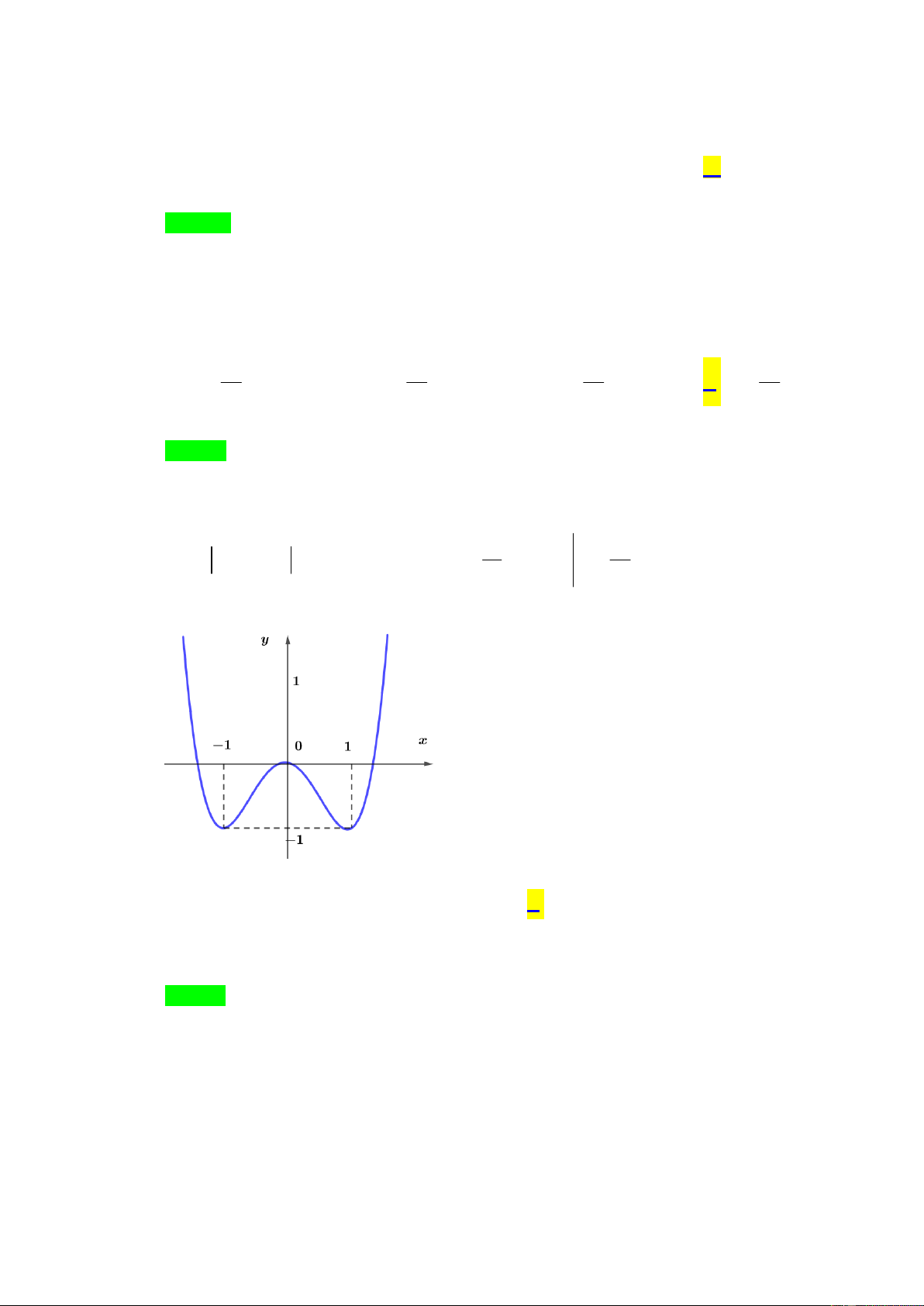
Câu 37: Hàm số nào dưới đây có đồ thị như hình vẽ? 3 4 2
A. y  x  3x 1.
B. y x  2x 1. 4 2 3
C. y  x  2x 1.
D. y x  3x 1.
Câu 38: Trong không gian Oxyz , mặt cầu S  2 2 2
: x y z  4x  2y  2z  3  0 có bán kính bằng A. 3 . B. 9 . C. 1. D. 6 .
2xy  3x  3y  4 Câu 39: Cho ,
x y là các số thực dương thỏa mãn log
x 2x  3  y 2y  3  3. 2 2 2     x xy y
Tính giá trị lớn nhất của biểu thức F x y 1. A. 4. B. 3. C. 1. D. 2. 1 x 2
(2x 1)e  2ax a
Câu 40: Đặt I  d . x
Có bao nhiêu giá trị nguyên của a thuộc khoảng 0;2023 để x e ax 0 I  6 ? A. 2023. B. 2024. C. 1877. D. 189.
Mã đề 202 - trang 4/6
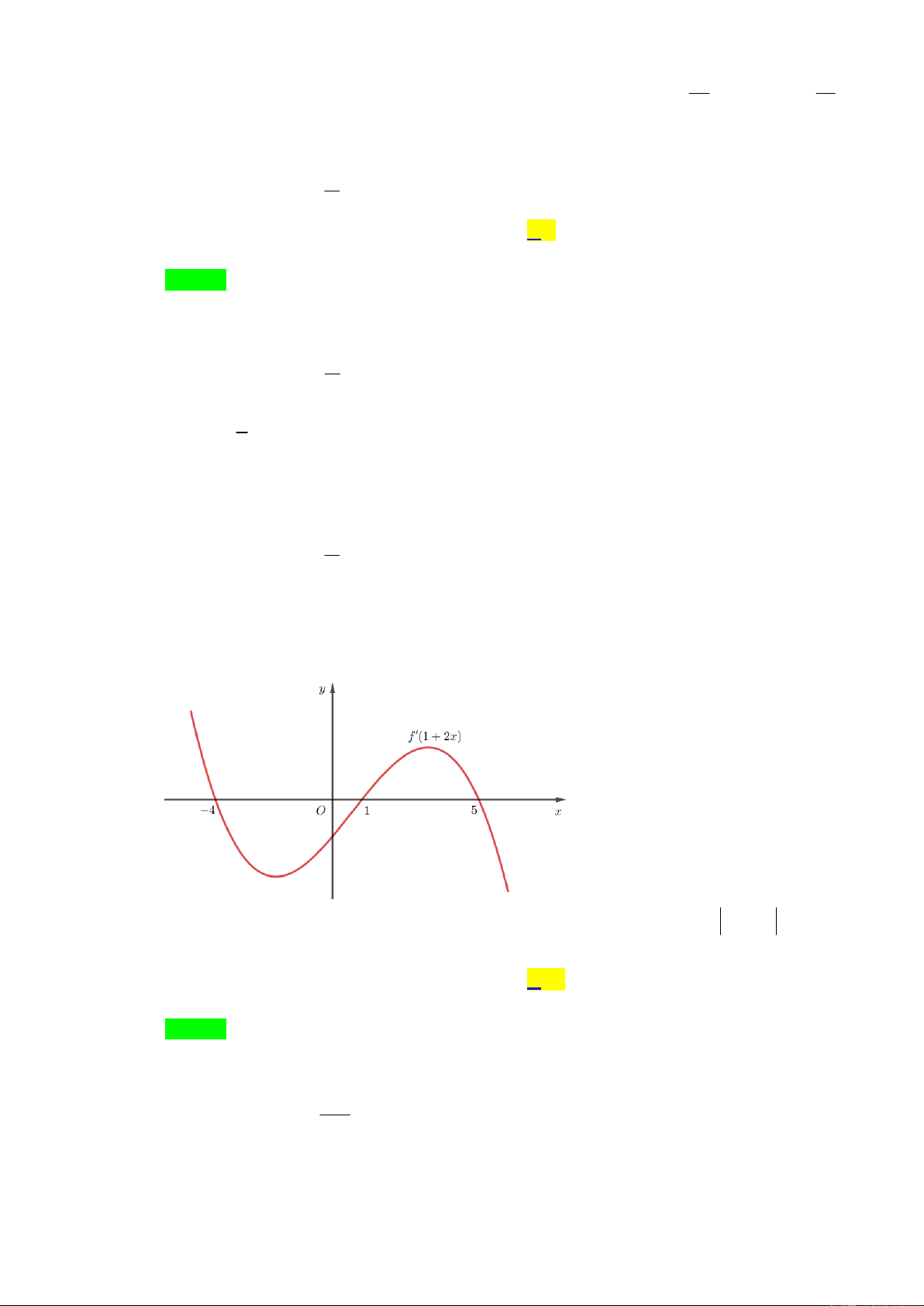
Câu 41: Cho hàm số y f x 4 3 2
ax bx cx dx e a  0, hàm số y f 1 2x có đồ thị như hình vẽ sau:
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g x  f  3
x  5x m có ít nhất 5 điểm cực trị? A. 6. B. 2. C. 10. D. 4. Câu 42: Cho hàm số
y f x có đạo hàm liên tục trên thỏa mãn f   1  5 và 1 xf  3
x  f x 7 4 1
x 5x  7x  3 với mọi x . Tính f xd .x  0 5 13 5 17 A.  . B.  . C. . D. . 6 12 6 6
Câu 43: Xét các số phức z thỏa mãn z  2  4i z  3  i  5 2 . Biết giá trị lớn nhất của biểu thức
P z i z  3  3i có dạng a b; , a b
. Giá trị của biểu thức a b bằng A. 7. B. 3. C. 5. D. 9.
Câu 44: Trên tập hợp số phức, xét phương trình 2
z  m   2 2
1 z m  4m  3  0 ( m là tham số thực).
Có bao nhiêu giá trị của m để phương trình có hai nghiệm phân biệt z , z thỏa mãn 1 2
z z 2  2m z z ? 1 2 1 2 A. 2. B. 4. C. 1. D. 0 .
Câu 45: Cho hình chóp tam giác đều S.ABC có AB a , khoảng cách giữa S hai đường thẳng a
SA và BC bằng
6 (tham khảo hình vẽ). Thể 3
tích khối chóp S.ABC bằng 3 2a 3 2a A C A. . B. . 2 6 3 2a 3 2a C. . D. . B 3 9
Câu 46: Cho hình chóp
S.ABCD có đáy là hình chữ nhật, S AB  2 3 ,
a AD  3a , SAD là tam giác đều và nằm trong mặt
phẳng vuông góc với đáy (tham khảo hình vẽ). Tính thể tích khối
cầu ngoại tiếp hình chóp S.ABCD . 3 32 a 3 16 a A B A. . B. . 3 3 3 26 a D C C. 3 16 a . D. . 3
Mã đề 202 - trang 5/6
Câu 47: Trong không gian Oxyz , cho mặt phẳng P : 2y  3z  3  0 và hai đường thẳng x  1   2t x y 1 z  2  d :  
; d :  y  1 t
. Đường thẳng  nằm trong mặt phẳng P đồng thời 1 2 2 1  1 z 1 
cắt cả hai đường thẳng d và d có phương trình là 1 2 x  2 y z 1 x  2 y z 1 x  2 y z 1 x  2 y z 1 A.   . B.   . C.   . D.   . 1 3 2 1 3  2 1 3 2 1 3  2
Câu 48: Trong không gian Oxyz , cho ba điểm A 1  5;7; 1   1 , B  3  ;1;  1 , C 7; 1
 ;5 và đường thẳng     d x 1 y 1 z 1 :  
. Gọi   là mặt phẳng chứa d  sao cho A , B , C ở cùng phía đối 1  4 1
với mặt phẳng   . Gọi d , d , d lần lượt là khoảng cách từ A , B , C đến   . Giá trị lớn 1 2 3
nhất của biểu thức T d  2d  3d bằng 1 2 3 1 A. 41 . B. 82 . C. 41 . D. 2 67 . 2 x
Câu 49: Cho phương trình log  x  2 1  log
1 (với m là tham số thực). Có bao nhiêu giá trị 9 1 m 3
nguyên dương của tham số m để phương trình đã cho có nghiệm thực? A. 1. B. 3. C. Vô số. D. 2. 2
Câu 50: Cho hàm số y f x có đạo hàm f  x   x    2 1
x  2x , với x
  . Số giá trị nguyên
của tham số m để hàm số g x  f  3 2
x  3x m có 8 điểm cực trị là A. 2. B. 3. C. 1. D. 4.
----------------------------------------------- ----------- HẾT ----------
Mã đề 202 - trang 6/6
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ TỐT NGHIỆP LỚP 12 THPT NAM ĐỊNH
NĂM HỌC 2022 – 2023
Môn: Toán – lớp 12 THPT ĐỀ CHÍNH THỨC
(Thời gian làm bài: 90 phút) MÃ ĐỀ: 204
Đề thi gồm 06 trang.
Họ và tên học sinh:………………………………………
Số báo danh:………….…………………….…………… Câu 1: Trong không gian
Oxyz , khoảng cách từ điểm M 0;3;  1 đến mặt phẳng
:2xy 2z 2  0 bằng 4 1 A. 1. B. . C. . D. 3 . 3 3 Câu 2:
Trên khoảng 0; , đạo hàm của hàm số e y x là  1 e 1 x A. e 1 y x    . B. e 1 y ex    . C. e y  x ln . x D. y  . e e 1 Câu 3:
Cho hàm số y f x liên tục trên
và có bảng biến thiên như hình vẽ:
Có bao nhiêu giá trị nguyên của tham số m để phương trình f x  m có bốn nghiệm phân biệt? A. 0. B. 1. C. 3. D. 2. 1 1 1 Câu 4: Cho f
 xdx  2 và g
 xdx  5 khi đó  f
 x2gxdx  bằng 0 0 0 A. 8.  B. 3.  C. 1. D. 12. Câu 5:
Trên mặt phẳng tọa độ, điểm M  1  ; 
1 là điểm biểu diễn số phức nào sau đây?
A. z  1 i . B. z  1  i .
C. z  1 i . D. z  1   i . Câu 6:
Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y x  2x 1, trục hoành và hai
đường thẳng x  1  ; x  3 . 37 56 68 64 A. S  . B. S  . C. S  . D. S  . 3 3 3 3 Câu 7:
Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ.
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên  1  ;  1 . .
B. Hàm số nghịch biến trên  ;    1 .
C. Hàm số đồng biến trên  1  ;.
D. Hàm số đồng biến trên .
Mã đề 204 - trang 1/6 Câu 8:
Cho hàm số y f x liên tục trên và có đồ thị như
hình vẽ. Khẳng định nào sau đây đúng?
A. Hàm số đạt cực tiểu tại x  1. 
B. Giá trị cực tiểu của hàm số bằng 1. 
C. Hàm số không có điểm cực trị.
D. Hàm số đạt cực đại tại x  4. Câu 9:
Cho khối nón có chiều cao bằng a và đường sinh bằng 2a . Thể tích của khối nón đã cho bằng 3  a 3 3 a A. 3  a . B. 3 3 a . C. . D. . 3 3
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , S
SA a 2 và vuông góc với đáy (tham khảo hình vẽ). Tính
khoảng cách giữa hai đường thẳng BD và SC . a a A. . B. . A B 4 2 a 2 a 2 C. . D. . D 4 2 C
Câu 11: Bất phương trình 2
2 log (4x  3)  log (2x  3)  2 có tập nghiệm là 3 1 9  3   3   3   3  A. ;   . B. ;3  . C.  ;3   . D.  ;3 .     4   4   8   8  Câu 12: Hàm số 3
y x  3x  2 có giá trị cực đại bằng A. 1  . B. 4 . C. 20 . D. 0 . x
Câu 13: Giá trị lớn nhất của hàm số 5 y
trên đoạn 8;12 bằng x  7 17 13 A. 15. B. . C. 13. D. . 5 2
Câu 14: Cho hình trụ có chiều cao bằng h và bán kính đáy bằng r . Diện tích xung quanh S của hình xq
trụ được tính bởi công thức 1 A. S  rh . B. S  2rh . C. S   rh . D. 2 S  r h . xq xq xq xq 3
Câu 15: Có bao nhiêu cách sắp xếp 4 học sinh thành một hàng dọc? A. 1. B. 24 . C. 4 . D. 10 .
Câu 16: Cho khối lăng trụ đứng AB .
C A' B 'C ' có AB AC  , a AA'  a 2, A' C' 0
BAC  45 (tham khảo hình vẽ). Tính thể tích V của khối lăng trụ đã cho. B' 3 a 3 2a A. . B. . A C 4 4 3 a 3 a C. . D. . 2 6 B
Mã đề 204 - trang 2/6
Câu 17: Biết phương trình 2 log x  2log
2x 1  0 có hai nghiệm x , x . Giá trị của x .x bằng 2 2   1 2 1 2 1 1 A. 4. B. . C. 3.  D. . 8 2
Câu 18: Số phức nghịch đảo của số phức z  3  4i là 3 4 3 4 3 4 A. i . B. i . C. i . D. 3  4i . 5 5 5 5 25 25
Câu 19: Trong mặt phẳng toạ độ Oxy , biết tập hợp điểm biểu diễn của số phức z thỏa mãn
z 1 i z  2i là đường thẳng d . Phương trình tổng quát của đường thẳng d là
A. 2x y 1  0 .
B. x  2y 1  0 .
C. x y 1  0 .
D. x y 1  0 . A' B'
Câu 20: Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có AB a 3; AD a
(tham khảo hình vẽ). Góc giữa hai đường thẳng AB và A'C ' bằng C' D' A. 0 60 . B. 0 45 . C. 0 75 . D. 0 30 . A B D C
Câu 21: Hàm số nào dưới đây có đồ thị như hình vẽ? 3 4 2
A. y  x  3x 1.
B. y x  2x 1. 4 2 3
C. y  x  2x 1.
D. y x  3x 1.
Câu 22: Cho cấp số cộng u có u  2 và công sai d  2
 . Giá trị của u là n  1 5 A. 10 . B. 6 . C. 6  . D. 32 .
Câu 23: Cho hàm số y f x có đạo hàm f  x  xx   3 1 , x
  . Hàm số y f x đồng biến
trên khoảng nào sau đây? A.  1  ;  1 . B. ;0. C. 0  ;1 . D. 0;  .
Câu 24: Tập nghiệm của bất phương trình log 3x 1  3 là 2    1  10  A. 3;  . B. ;3   . C.  ,  3. D. ;    .  3   3 
Câu 25: Cho f x, g x là các hàm số liên tục trên
. Trong các mệnh đề sau, mệnh đề nào sai? A. 5 f
 xdx 5 f
 xd .x B. f
 x gxdx f
 xdxg
 xd .x C. f
 x.gxdx f
 xd .x g
 xd .x D. f
 x gxdx f
 xdxg
 xd .x x
Câu 26: Đường tiệm cận đứng của đồ thị hàm số 2 y x  là 1 A. x  1. B. y  2. C. x  2. D. x  1. 
Câu 27: Gieo một đồng tiền cân đối, đồng chất ba lần. Xác suất để trong ba lần gieo có đúng hai lần
xuất hiện mặt ngửa là 1 1 1 3 A. . B. . C. . D. . 8 3 4 8
Mã đề 204 - trang 3/6
Câu 28: Cho số phức z  1 2i , tính z . A. z  3 . B. z  5 . C. z  5 . D. z  3 .
Câu 29: Tập nghiệm của bất phương trình 3x  27 là A. 3, . B. 3, . C.  ,   3 . D.  ,  3.
Câu 30: Với a là số thực dương tùy ý, 3 log a bằng 81 3 1 4 1 A. log . a B. log . a C. log . a D. log . a 3 4 3 12 3 3 3 27
Câu 31: Trong không gian Oxyz , hình chiếu của điểm A1;2;  
1 trên mặt phẳng Oxy là điểm nào sau đây? A. P  1  ; 2  ;0. B. Q  1  ; 2  ;  1 . C. M 1;2;  1 .
D. N 1;2;0 .
Câu 32: Khối bát diện đều thuộc loại khối đa diện đều nào sau đây? A. 4;  3 . B. 5;  3 . C. 3;  5 . D. 3;  4 .
Câu 33: Cho hàm số f x có đạo hàm liên tục trên đoạn 1; 2, f  
1  1 và f 2  2 . Tính 2 I f
 xd .x 1 7 A. I  1. B. I  1.  C. I  3. D. I  . 2
Câu 34: Trong không gian Oxyz , gọi S  là mặt cầu có tâm I Ox và đi qua hai điểm A2;1;  1 ; B  1
 ;3; 2 . Phương trình của mặt cầu S là A. 2 2 2
x y z  2x 10  0 . B. 2 2 2
x y z  4x 14  0 . C. 2 2 2
x y z  2x 10  0 . D. 2 2 2
x y z  4x  2  0 . x  1   2t
Câu 35: Trong không gian Oxyz , đường thẳng d :  y  3  t
có một vectơ chỉ phương là z  2tA. u 2; 1  ;  1 . B. b  1  ; 1  ;  1 . C. a  1  ;2;3. D. v  1  ;3;2.
Câu 36: Trong không gian Oxyz , mặt cầu S  2 2 2
: x y z  4x  2y  2z  3  0 có bán kính bằng A. 3 . B. 9 . C. 1. D. 6 . 1
Câu 37: Họ tất cả các nguyên hàm của hàm số 2
f (x)  3x  là 2 sin x 2 A. 6x   C. B. 3
x  cot x  . C C. 3
x  tan x  . C D. 3
x  cot x  . C 2 sin x
Câu 38: Trong không gian Oxyz , gọi  là góc giữa hai mặt phẳng P : x  2y z  2  0 và
Q:2x y z 4  0. Tính cos . 2 3 1 1 A. cos  . B. cos  . C. cos  . D. cos  . 3 4 6 3 1 x 2
(2x 1)e  2ax a
Câu 39: Đặt I  d . x
Có bao nhiêu giá trị nguyên của a thuộc khoảng 0;2023 để x e ax 0 I  6 ? A. 2023. B. 2024. C. 1877. D. 189.
Mã đề 204 - trang 4/6 Câu 40: Cho hàm số
y f x có đạo hàm liên tục trên thỏa mãn f   1  5 và 1 xf  3
x  f x 7 4 1
x 5x  7x  3 với mọi x . Tính f xd .x  0 5 17 13 5 A.  . B. . C.  . D. . 6 6 12 6
Câu 41: Trên tập hợp số phức, xét phương trình 2
z  m   2 2
1 z m  4m  3  0 ( m là tham số thực).
Có bao nhiêu giá trị của m để phương trình có hai nghiệm phân biệt z , z thỏa mãn 1 2
z z 2  2m z z ? 1 2 1 2 A. 4. B. 0 . C. 2. D. 1.
Câu 42: Cho hàm số y f x 4 3 2
ax bx cx dx e a  0, hàm số y f 1 2x có đồ thị như hình vẽ sau:
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g x  f  3
x  5x m có ít nhất 5 điểm cực trị? A. 6. B. 4. C. 2. D. 10.
Câu 43: Trong không gian Oxyz , cho ba điểm A 1  5;7; 1   1 , B  3  ;1;  1 , C 7; 1
 ;5 và đường thẳng     d x 1 y 1 z 1 :  
. Gọi   là mặt phẳng chứa d  sao cho A , B , C ở cùng phía đối 1  4 1
với mặt phẳng   . Gọi d , d , d lần lượt là khoảng cách từ A , B , C đến   . Giá trị lớn 1 2 3
nhất của biểu thức T d  2d  3d bằng 1 2 3 1 A. 82 . B. 2 67 . C. 41 . D. 41 . 2
Câu 44: Cho hình chóp tam giác đều S.ABC có AB a , khoảng cách giữa hai S đường thẳng a
SA và BC bằng
6 (tham khảo hình vẽ). Thể tích khối 3
chóp S.ABC bằng 3 2a 3 2a A C A. . B. . 2 6 3 2a 3 2a C. . D. . B 3 9 x
Câu 45: Cho phương trình log  x  2 1  log
1 (với m là tham số thực). Có bao nhiêu giá trị 9 1 m 3
nguyên dương của tham số m để phương trình đã cho có nghiệm thực? A. 1. B. Vô số. C. 3. D. 2.
Mã đề 204 - trang 5/6
Câu 46: Cho hình chóp
S.ABCD có đáy là hình chữ nhật, S AB  2 3 ,
a AD  3a , SAD là tam giác đều và nằm trong mặt
phẳng vuông góc với đáy (tham khảo hình vẽ). Tính thể tích khối
cầu ngoại tiếp hình chóp S.ABCD . 3 16 a A A. . B. 3 16 a . B 3 3 32 a 3 26 a C. . D. . D C 3 3
2xy  3x  3y  4 Câu 47: Cho ,
x y là các số thực dương thỏa mãn log
x 2x  3  y 2y  3  3. 2 2 2    
x xy y
Tính giá trị lớn nhất của biểu thức F x y 1. A. 3. B. 1. C. 4. D. 2.
Câu 48: Trong không gian Oxyz , cho mặt phẳng P : 2y  3z  3  0 và hai đường thẳng x  1   2t x y 1 z  2  d :  
; d :  y  1 t
. Đường thẳng  nằm trong mặt phẳng P đồng thời 1 2 1  1 2 z 1 
cắt cả hai đường thẳng d và d có phương trình là 1 2 x  2 y z 1 x  2 y z 1 x  2 y z 1 x  2 y z 1 A.   . B.   . C.   . D.   . 1 3  2 1 3  2 1 3 2 1 3 2
Câu 49: Xét các số phức z thỏa mãn z  2  4i z  3  i  5 2 . Biết giá trị lớn nhất của biểu thức
P z i z  3  3i có dạng a b; , a b
. Giá trị của biểu thức a b bằng A. 3. B. 7. C. 5. D. 9. 2
Câu 50: Cho hàm số y f x có đạo hàm f  x   x    2 1
x  2x , với x
  . Số giá trị nguyên của
tham số m để hàm số g x  f  3 2
x  3x m có 8 điểm cực trị là A. 2. B. 3. C. 1. D. 4.
----------------------------------------------- ----------- HẾT ----------
Mã đề 204 - trang 6/6
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ TỐT NGHIỆP LỚP 12 THPT NAM ĐỊNH
NĂM HỌC 2022 – 2023
Môn: Toán – lớp 12 THPT ĐỀ CHÍNH THỨC
(Thời gian làm bài: 90 phút) MÃ ĐỀ: 206
Đề thi gồm 06 trang.
Họ và tên học sinh:………………………………………
Số báo danh:………….……………………..…………… Câu 1:
Trong mặt phẳng toạ độ Oxy , biết tập hợp điểm biểu diễn của số phức z thỏa mãn
z 1 i z  2i là đường thẳng d . Phương trình tổng quát của đường thẳng d là
A. 2x y 1  0 .
B. x  2y 1  0 .
C. x y 1  0 .
D. x y 1  0 . A' B' Câu 2:
Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có AB a 3; AD a
(tham khảo hình vẽ). Góc giữa hai đường thẳng AB và A'C ' C' D' bằng A. 0 45 . B. 0 60 . A B C. 0 30 . D. 0 75 . D C Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , S
SA a 2 và vuông góc với đáy (tham khảo hình vẽ). Tính
khoảng cách giữa hai đường thẳng BD và SC . a a A. . B. . A B 4 2 a 2 a 2 C. . D. . D 4 2 C x Câu 4:
Giá trị lớn nhất của hàm số 5 y
trên đoạn 8;12 bằng x  7 17 13 A. 13. B. . C. . D. 15. 5 2 1 Câu 5:
Họ tất cả các nguyên hàm của hàm số 2
f (x)  3x  là 2 sin x 2 A. 3
x  tan x  . C B. 3
x  cot x  . C C. 3
x  cot x  . C D. 6x   C. 2 sin x Câu 6:
Cho khối lăng trụ đứng AB .
C A' B 'C ' có AB AC  , a AA'  a 2, A' C' 0
BAC  45 (tham khảo hình vẽ). Tính thể tích V của khối lăng trụ đã cho. B' 3 a 3 2a A. . B. . A C 4 4 3 a 3 a C. . D. . 2 6 B Câu 7:
Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y x  2x 1, trục hoành và hai
đường thẳng x  1  ; x  3 .
Mã đề 206 - trang 1/6 64 68 56 37 A. S  . B. S  . C. S  . D. S  . 3 3 3 3 Câu 8:
Trên mặt phẳng tọa độ, điểm M  1  ; 
1 là điểm biểu diễn số phức nào sau đây?
A. z  1 i .
B. z  1 i . C. z  1   i . D. z  1  i . Câu 9:
Cho số phức z 1 2i , tính z . A. z  3 . B. z  5 . C. z  5 . D. z  3 . x
Câu 10: Đường tiệm cận đứng của đồ thị hàm số 2 y  là x 1 A. x  1. B. y  2. C. x  1.  D. x  2.
Câu 11: Trong không gian Oxyz , gọi S  là mặt cầu có tâm I Ox và đi qua hai điểm A2;1;  1 ; B  1
 ;3; 2 . Phương trình của mặt cầu S là A. 2 2 2
x y z  4x 14  0 . B. 2 2 2
x y z  2x 10  0 . C. 2 2 2
x y z  2x 10  0 . D. 2 2 2
x y z  4x  2  0 .
Câu 12: Trong không gian Oxyz , hình chiếu của điểm A1;2;  
1 trên mặt phẳng Oxy là điểm nào sau đây? A. P  1  ; 2  ;0. B. Q  1  ; 2  ;  1 . C. M 1;2;  1 .
D. N 1;2;0 . Câu 13: Hàm số 3
y x  3x  2 có giá trị cực đại bằng A. 1  . B. 4 . C. 0 . D. 20 .
Câu 14: Có bao nhiêu cách sắp xếp 4 học sinh thành một hàng dọc? A. 1. B. 24 . C. 4 . D. 10 .
Câu 15: Cho khối nón có chiều cao bằng a và đường sinh bằng 2a . Thể tích của khối nón đã cho bằng 3  a 3 3 a A. . B. 3  a . C. 3 3 a . D. . 3 3 x  1   2t
Câu 16: Trong không gian Oxyz , đường thẳng d :  y  3  t
có một vectơ chỉ phương là z  2tA. u 2; 1  ;  1 . B. b  1  ; 1  ;  1 . C. a  1  ;2;3. D. v  1  ;3;2.
Câu 17: Số phức nghịch đảo của số phức z  3  4i là 3 4 3 4 3 4 A. i . B. i . C. i . D. 3  4i . 5 5 5 5 25 25
Câu 18: Hàm số nào dưới đây có đồ thị như hình vẽ? 4 2 3
A. y  x  2x 1.
B. y  x  3x 1. 4 2 3
C. y x  2x 1.
D. y x  3x 1.
Câu 19: Cho hàm số y f x có đạo hàm f  x  xx   3 1 , x
  . Hàm số y f x đồng biến
trên khoảng nào sau đây? A.  1  ;  1 . B. ;0. C. 0  ;1 . D. 0;  .
Mã đề 206 - trang 2/6
Câu 20: Trên khoảng 0;  , đạo hàm của hàm số e y x là  1 e 1 x A. e 1 y x    . B. y  . C. e y  x ln . x D. e 1 y ex    . e e 1
Câu 21: Trong không gian Oxyz , gọi  là góc giữa hai mặt phẳng P : x  2y z  2  0 và
Q:2x y z 4  0. Tính cos . 2 3 1 1 A. cos  . B. cos  . C. cos  . D. cos  . 3 4 6 3
Câu 22: Cho f x, g x là các hàm số liên tục trên
. Trong các mệnh đề sau, mệnh đề nào sai? A. 5 f
 xdx 5 f
 xd .x B. f
 x gxdx f
 xdxg
 xd .x C. f
 x.gxdx f
 xd .x g
 xd .x D. f
 x gxdx f
 xdxg
 xd .x
Câu 23: Cho hàm số y f x liên tục trên
và có bảng biến thiên như hình vẽ:
Có bao nhiêu giá trị nguyên của tham số m để phương trình f x  m có bốn nghiệm phân biệt? A. 0. B. 3. C. 1. D. 2.
Câu 24: Với a là số thực dương tùy ý, 3 log a bằng 81 3 1 4 1 A. log . a B. log . a C. log . a D. log . a 3 4 3 12 3 3 3 27 1 1 1 Câu 25: Cho f
 xdx  2 và g
 xdx  5 khi đó  f
 x2gxdx  bằng 0 0 0 A. 1. B. 8.  C. 12. D. 3. 
Câu 26: Gieo một đồng tiền cân đối, đồng chất ba lần. Xác suất để trong ba lần gieo có đúng hai lần
xuất hiện mặt ngửa là 1 1 1 3 A. . B. . C. . D. . 8 3 4 8
Câu 27: Biết phương trình 2 log x  2log
2x 1  0 có hai nghiệm x , x . Giá trị của x .x bằng 2 2   1 2 1 2 1 1 A. . B. 3.  C. . D. 4. 2 8
Câu 28: Tập nghiệm của bất phương trình 3x  27 là A. 3, . B. 3, . C.  ,   3 . D.  ,  3.
Câu 29: Cho cấp số cộng u có u  2 và công sai d  2
 . Giá trị của u là n  1 5 A. 10 . B. 6  . C. 32 . D. 6 .
Câu 30: Tập nghiệm của bất phương trình log 3x 1  3 là 2  
Mã đề 206 - trang 3/6  1  10  A.  ,  3. B. ;3   . C. ;    . D. 3;  .  3   3 
Câu 31: Khối bát diện đều thuộc loại khối đa diện đều nào sau đây? A. 4;  3 . B. 5;  3 . C. 3;  5 . D. 3;  4 .
Câu 32: Cho hàm số f x có đạo hàm liên tục trên đoạn 1; 2, f  
1  1 và f 2  2 . Tính 2 I f
 xd .x 1 7 A. I  1. B. I  1.  C. I  3. D. I  . 2
Câu 33: Trong không gian Oxyz , mặt cầu S  2 2 2
: x y z  4x  2y  2z  3  0 có bán kính bằng A. 3 . B. 9 . C. 1. D. 6 .
Câu 34: Bất phương trình 2
2 log (4x  3)  log (2x  3)  2 có tập nghiệm là 3 1 9  3   3   3   3  A. ;3   . B. ;   . C.  ;3   . D.  ;3 .    4   4   8   8 
Câu 35: Trong không gian
Oxyz , khoảng cách từ điểm M 0;3;  1 đến mặt phẳng
:2xy 2z 2  0 bằng 1 4 A. 3 . B. 1. C. . D. . 3 3
Câu 36: Cho hàm số y f x liên tục trên và
có đồ thị như hình vẽ.
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên  1  ;  1 . .
B. Hàm số đồng biến trên  1  ;.
C. Hàm số đồng biến trên .
D. Hàm số nghịch biến trên  ;    1 .
Câu 37: Cho hình trụ có chiều cao bằng h và bán kính đáy bằng r . Diện tích xung quanh S của hình xq
trụ được tính bởi công thức 1 A. S   rh . B. S  rh . C. 2 S  r h . D. S  2rh . xq xq xq xq 3
Câu 38: Cho hàm số y f x liên tục trên và có đồ thị như
hình vẽ. Khẳng định nào sau đây đúng?
A. Hàm số đạt cực tiểu tại x  1. 
B. Giá trị cực tiểu của hàm số bằng 1. 
C. Hàm số không có điểm cực trị.
D. Hàm số đạt cực đại tại x  4.
Mã đề 206 - trang 4/6
Câu 39: Cho hình chóp tam giác đều S.ABC có AB a , khoảng cách giữa S hai đường thẳng a
SA và BC bằng
6 (tham khảo hình vẽ). Thể 3
tích khối chóp S.ABC bằng 3 A 2a 3 2a C A. . B. . 2 6 3 2a 3 2a B C. . D. . 3 9
Câu 40: Cho hàm số y f x 4 3 2
ax bx cx dx e a  0, hàm số y f 1 2x có đồ thị như hình vẽ sau:
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g x  f  3
x  5x m có ít nhất 5 điểm cực trị? A. 4. B. 6. C. 10. D. 2. Câu 41: Cho hình chóp S.ABCD
có đáy là hình chữ nhật, S AB  2 3 ,
a AD  3a , SAD là tam giác đều và nằm trong mặt
phẳng vuông góc với đáy (tham khảo hình vẽ). Tính thể tích khối cầu
ngoại tiếp hình chóp S.ABCD . 3 16 a A B A. . B. 3 16 a . 3 3 32 a 3 26 a D C C. . D. . 3 3
Câu 42: Trong không gian Oxyz , cho ba điểm A 1  5;7; 1   1 , B  3  ;1;  1 , C 7; 1
 ;5 và đường thẳng     d x 1 y 1 z 1 :  
. Gọi   là mặt phẳng chứa d  sao cho A , B , C ở cùng phía đối 1  4 1
với mặt phẳng   . Gọi d , d , d lần lượt là khoảng cách từ A , B , C đến   . Giá trị lớn 1 2 3
nhất của biểu thức T d  2d  3d bằng 1 2 3 1 A. 41 . B. 2 67 . C. 82 . D. 41 . 2
Câu 43: Xét các số phức z thỏa mãn z  2  4i z  3  i  5 2 . Biết giá trị lớn nhất của biểu thức
P z i z  3  3i có dạng a b; , a b
. Giá trị của biểu thức a b bằng A. 3. B. 7. C. 5. D. 9.
Mã đề 206 - trang 5/6 Câu 44: Cho hàm số
y f x có đạo hàm liên tục trên thỏa mãn f   1  5 và 1 xf  3
x  f x 7 4 1
x 5x  7x  3 với mọi x . Tính f xd .x  0 5 13 17 5 A. . B.  . C. . D.  . 6 12 6 6 x
Câu 45: Cho phương trình log  x  2 1  log
1 (với m là tham số thực). Có bao nhiêu giá trị 9 1 m 3
nguyên dương của tham số m để phương trình đã cho có nghiệm thực? A. 2. B. Vô số. C. 3. D. 1.
2xy  3x  3y  4 Câu 46: Cho ,
x y là các số thực dương thỏa mãn log
x 2x  3  y 2y  3  3. 2 2 2    
x xy y
Tính giá trị lớn nhất của biểu thức F x y 1. A. 3. B. 1. C. 4. D. 2. 1 x 2
(2x 1)e  2ax a
Câu 47: Đặt I  d . x
Có bao nhiêu giá trị nguyên của a thuộc khoảng 0;2023 để x e ax 0 I  6 ? A. 1877. B. 2024. C. 2023. D. 189. 2
Câu 48: Cho hàm số y f x có đạo hàm f  x   x    2 1
x  2x , với x
  . Số giá trị nguyên của
tham số m để hàm số g x  f  3 2
x  3x m có 8 điểm cực trị là A. 2. B. 1. C. 3. D. 4.
Câu 49: Trong không gian Oxyz , cho mặt phẳng  P : 2y  3z  3  0 và hai đường thẳng x  1   2t x y 1 z  2  d :  
; d :  y  1 t
. Đường thẳng  nằm trong mặt phẳng P đồng thời 1 2 1  1 2 z 1 
cắt cả hai đường thẳng d và d có phương trình là 1 2 x  2 y z 1 x  2 y z 1 x  2 y z 1 x  2 y z 1 A.   . B.   . C.   . D.   . 1 3 2 1 3 2 1 3  2 1 3  2
Câu 50: Trên tập hợp số phức, xét phương trình 2
z  m   2 2
1 z m  4m  3  0 ( m là tham số thực).
Có bao nhiêu giá trị của m để phương trình có hai nghiệm phân biệt z , z thỏa mãn 1 2
z z 2  2m z z ? 1 2 1 2 A. 0 . B. 1. C. 2. D. 4.
----------------------------------------------- ----------- HẾT ----------
Mã đề 206 - trang 6/6
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ TỐT NGHIỆP LỚP 12 THPT NAM ĐỊNH
NĂM HỌC 2022 – 2023
Môn: Toán – lớp 12 THPT ĐỀ CHÍNH THỨC
(Thời gian làm bài: 90 phút) MÃ ĐỀ: 208
Đề thi gồm 06 trang.
Họ và tên học sinh:………………………………………
Số báo danh:………….…………………….…………… Câu 1:
Trong mặt phẳng toạ độ Oxy , biết tập hợp điểm biểu diễn của số phức z thỏa mãn
z 1 i z  2i là đường thẳng d . Phương trình tổng quát của đường thẳng d là
A. x y 1  0 .
B. x  2y 1  0 .
C. 2x y 1  0 .
D. x y 1  0 . Câu 2:
Với a là số thực dương tùy ý, 3 log a bằng 81 3 1 4 1 A. log . a B. log . a C. log . a D. log . a 3 4 3 12 3 3 3 27 Câu 3:
Trong không gian Oxyz , gọi S  là mặt cầu có tâm I Ox và đi qua hai điểm A2;1;  1 ; B  1
 ;3; 2 . Phương trình của mặt cầu S là A. 2 2 2
x y z  4x 14  0 . B. 2 2 2
x y z  2x 10  0 . C. 2 2 2
x y z  2x 10  0 . D. 2 2 2
x y z  4x  2  0 . Câu 4:
Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ.
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên  1  ;  1 . .
B. Hàm số đồng biến trên  1  ;.
C. Hàm số đồng biến trên .
D. Hàm số nghịch biến trên  ;    1 . x Câu 5:
Đường tiệm cận đứng của đồ thị hàm số 2 y x  là 1 A. y  2. B. x  1.  C. x  1. D. x  2. Câu 6:
Tập nghiệm của bất phương trình 3x  27 là A. 3, . B. 3, . C.  ,   3 . D.  ,  3. Câu 7:
Tập nghiệm của bất phương trình log 3x 1  3 là 2   10   1  A. 3;  . B. ;    . C.  ,  3. D. ;3   .  3   3  Câu 8:
Cho f x, g x là các hàm số liên tục trên
. Trong các mệnh đề sau, mệnh đề nào sai? A. f
 x gxdx f
 xdxg
 xd .x B. f
 x gxdx f
 xdxg
 xd .x C. f
 x.gxdx f
 xd .x g
 xd .x D. 5 f
 xdx 5 f
 xd .x Câu 9:
Số phức nghịch đảo của số phức z  3 4i là 3 4 3 4 3 4 A. i . B. i . C. i . D. 3  4i . 5 5 5 5 25 25
Mã đề 208 - trang 1/6
Câu 10: Hàm số nào dưới đây có đồ thị như hình vẽ? 3 3
A. y  x  3x 1.
B. y x  3x 1. 4 2 4 2
C. y x  2x 1.
D. y  x  2x 1.
Câu 11: Trên mặt phẳng tọa độ, điểm M  1  ; 
1 là điểm biểu diễn số phức nào sau đây?
A. z  1 i . B. z  1  i . C. z  1   i .
D. z  1 i .
Câu 12: Cho khối lăng trụ đứng AB .
C A' B 'C ' có AB AC  , a AA'  a 2, A' C' 0
BAC  45 (tham khảo hình vẽ). Tính thể tích V của khối lăng trụ đã cho. B' 3 2a 3 a A. . B. . 4 2 A C 3 a 3 a C. . D. . 4 6 B
Câu 13: Cho hàm số y f x liên tục trên
và có bảng biến thiên như hình vẽ:
Có bao nhiêu giá trị nguyên của tham số m để phương trình f x  m có bốn nghiệm phân biệt? A. 3. B. 1. C. 0. D. 2.
Câu 14: Cho khối nón có chiều cao bằng a và đường sinh bằng 2a . Thể tích của khối nón đã cho bằng 3  a 3 3 a A. . B. 3  a . C. 3 3 a . D. . 3 3 A' B'
Câu 15: Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có AB a 3; AD a
(tham khảo hình vẽ). Góc giữa hai đường thẳng AB và A'C ' bằng C' D' A. 0 30 . B. 0 60 . C. 0 75 . D. 0 45 . A B D C
Câu 16: Cho cấp số cộng u có u  2 và công sai d  2
 . Giá trị của u là n  1 5 A. 10 . B. 32 . C. 6  . D. 6 .
Câu 17: Trên khoảng 0;  , đạo hàm của hàm số e y x là  1 e 1 x A. e 1 y x    . B. y  . e y  x x D. e 1 y ex    . e e C. ln . 1
Mã đề 208 - trang 2/6 x  1   2t
Câu 18: Trong không gian Oxyz , đường thẳng d :  y  3  t
có một vectơ chỉ phương là z  2tA. a  1  ;2;3. B. v  1  ;3;2. C. u 2; 1  ;  1 . D. b  1  ; 1  ;  1 .
Câu 19: Có bao nhiêu cách sắp xếp 4 học sinh thành một hàng dọc? A. 1. B. 10 . C. 4 . D. 24 .
Câu 20: Trong không gian Oxyz , hình chiếu của điểm A1;2;  
1 trên mặt phẳng Oxy là điểm nào sau đây? A. P  1  ; 2  ;0.
B. N 1;2;0 . C. Q  1  ; 2  ;  1 . D. M 1;2;  1 .
Câu 21: Biết phương trình 2 log x  2log
2x 1  0 có hai nghiệm x , x . Giá trị của x .x bằng 2 2   1 2 1 2 1 1 A. 3.  B. . C. . D. 4. 2 8
Câu 22: Cho hàm số f x có đạo hàm liên tục trên đoạn 1; 2, f  
1  1 và f 2  2 . Tính 2 I f
 xd .x 1 7 A. I  1. B. I  . C. I  3. D. I  1.  2 1
Câu 23: Họ tất cả các nguyên hàm của hàm số 2
f (x)  3x  là 2 sin x 2 A. 6x   C. B. 3
x  cot x  . C C. 3
x  tan x  . C D. 3
x  cot x  . C 2 sin x 1 1 1 Câu 24: Cho f
 xdx  2 và g
 xdx  5 khi đó  f
 x2gxdx  bằng 0 0 0 A. 1. B. 8.  C. 12. D. 3. 
Câu 25: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , S
SA a 2 và vuông góc với đáy (tham khảo hình vẽ). Tính khoảng
cách giữa hai đường thẳng BD và SC . a a 2 A. . B. . A B 2 2 a 2 a C. . D. . D C 4 4
Câu 26: Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y x  2x 1, trục hoành và hai
đường thẳng x  1  ; x  3 . 56 68 64 37 A. S  . B. S  . C. S  . D. S  . 3 3 3 3
Câu 27: Cho hình trụ có chiều cao bằng h và bán kính đáy bằng r . Diện tích xung quanh S của hình xq
trụ được tính bởi công thức 1 A. S   rh . B. S  rh . C. 2 S  r h . D. S  2rh . xq xq xq xq 3
Câu 28: Cho số phức z  1 2i , tính z . A. z  3 . B. z  3 . C. z  5 . D. z  5 .
Mã đề 208 - trang 3/6 Câu 29: Hàm số 3
y x  3x  2 có giá trị cực đại bằng A. 0 . B. 1  . C. 20 . D. 4 .
Câu 30: Khối bát diện đều thuộc loại khối đa diện đều nào sau đây? A. 4;  3 . B. 5;  3 . C. 3;  5 . D. 3;  4 .
Câu 31: Cho hàm số y f x có đạo hàm f  x  xx   3 1 , x
  . Hàm số y f x đồng biến
trên khoảng nào sau đây? A.  1  ;  1 . B. ;0. C. 0;  . D. 0  ;1 .
Câu 32: Trong không gian Oxyz , mặt cầu S  2 2 2
: x y z  4x  2y  2z  3  0 có bán kính bằng A. 3 . B. 9 . C. 1. D. 6 .
Câu 33: Bất phương trình 2
2 log (4x  3)  log (2x  3)  2 có tập nghiệm là 3 1 9  3   3   3   3  A. ;3   . B. ;   . C.  ;3   . D.  ;3 .    4   4   8   8 
Câu 34: Trong không gian
Oxyz , khoảng cách từ điểm M 0;3;  1 đến mặt phẳng
:2xy 2z 2  0 bằng 1 4 A. 3 . B. 1. C. . D. . 3 3 x
Câu 35: Giá trị lớn nhất của hàm số 5 y
trên đoạn 8;12 bằng x  7 13 17 A. 15. B. . C. 13. D. . 2 5
Câu 36: Cho hàm số y f x liên tục trên và có đồ thị như
hình vẽ. Khẳng định nào sau đây đúng?
A. Hàm số đạt cực tiểu tại x  1. 
B. Giá trị cực tiểu của hàm số bằng 1. 
C. Hàm số không có điểm cực trị.
D. Hàm số đạt cực đại tại x  4.
Câu 37: Gieo một đồng tiền cân đối, đồng chất ba lần. Xác suất để trong ba lần gieo có đúng hai lần
xuất hiện mặt ngửa là 1 1 1 3 A. . B. . C. . D. . 8 3 4 8
Câu 38: Trong không gian Oxyz , gọi  là góc giữa hai mặt phẳng P : x  2y z  2  0 và
Q:2x y z 4  0. Tính cos . 2 3 1 1 A. cos  . B. cos  . C. cos  . D. cos  . 3 4 6 3
Câu 39: Trong không gian Oxyz , cho ba điểm A 1  5;7; 1   1 , B  3  ;1;  1 , C 7; 1
 ;5 và đường thẳng     d x 1 y 1 z 1 :  
. Gọi   là mặt phẳng chứa d  sao cho A , B , C ở cùng phía đối 1  4 1
Mã đề 208 - trang 4/6
với mặt phẳng   . Gọi d , d , d lần lượt là khoảng cách từ A , B , C đến   . Giá trị lớn 1 2 3
nhất của biểu thức T d  2d  3d bằng 1 2 3 1 A. 2 67 . B. 41 . C. 41 . D. 82 . 2 x
Câu 40: Cho phương trình log  x  2 1  log
1 (với m là tham số thực). Có bao nhiêu giá trị 9 1 m 3
nguyên dương của tham số m để phương trình đã cho có nghiệm thực? A. 1. B. Vô số. C. 3. D. 2.
Câu 41: Trên tập hợp số phức, xét phương trình 2
z  m   2 2
1 z m  4m  3  0 ( m là tham số thực).
Có bao nhiêu giá trị của m để phương trình có hai nghiệm phân biệt z , z thỏa mãn 1 2
z z 2  2m z z ? 1 2 1 2 A. 0 . B. 1. C. 2. D. 4.
Câu 42: Cho hàm số y f x 4 3 2
ax bx cx dx e a  0, hàm số y f 1 2x có đồ thị như hình vẽ sau:
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g x  f  3
x  5x m có ít nhất 5 điểm cực trị? A. 4. B. 10. C. 6. D. 2.
Câu 43: Xét các số phức z thỏa mãn z  2  4i z  3  i  5 2 . Biết giá trị lớn nhất của biểu thức
P z i z  3  3i có dạng a b; , a b
. Giá trị của biểu thức a b bằng A. 7. B. 9. C. 5. D. 3.
Câu 44: Cho hình chóp
S.ABCD có đáy là hình chữ nhật, S AB  2 3 ,
a AD  3a , SAD là tam giác đều và nằm trong mặt
phẳng vuông góc với đáy (tham khảo hình vẽ). Tính thể tích khối
cầu ngoại tiếp hình chóp S.ABCD . 3 32 a 3 26 a A B A. . B. . 3 3 3 16 a C. . D. 3 16 a . D C 3
2xy  3x  3y  4 Câu 45: Cho ,
x y là các số thực dương thỏa mãn log
x 2x  3  y 2y  3  3. 2 2 2     x xy y
Tính giá trị lớn nhất của biểu thức F x y 1. A. 2. B. 4. C. 3. D. 1.
Mã đề 208 - trang 5/6
Câu 46: Cho hình chóp tam giác đều S.ABC có AB a , khoảng cách giữa S hai đường thẳng a
SA và BC bằng
6 (tham khảo hình vẽ). Thể 3
tích khối chóp S.ABC bằng 3 A 2a 3 2a C A. . B. . 3 2 3 2a 3 2a C. . D. . B 6 9 Câu 47: Cho hàm số
y f x có đạo hàm liên tục trên thỏa mãn f   1  5 và 1 xf  3
x  f x 7 4 1
x 5x  7x  3 với mọi x . Tính f xd .x  0 5 17 5 13 A. . B. . C.  . D.  . 6 6 6 12
Câu 48: Trong không gian Oxyz , cho mặt phẳng P : 2y  3z  3  0 và hai đường thẳng x  1   2t x y 1 z  2  d :  
; d :  y  1 t
. Đường thẳng  nằm trong mặt phẳng P đồng thời 1 2 2 1  1 z 1 
cắt cả hai đường thẳng d và d có phương trình là 1 2 x  2 y z 1 x  2 y z 1 x  2 y z 1 x  2 y z 1 A.   . B.   . C.   . D.   . 1 3 2 1 3 2 1 3  2 1 3  2 1 x 2
(2x 1)e  2ax a
Câu 49: Đặt I  d . x
Có bao nhiêu giá trị nguyên của a thuộc khoảng 0;2023 để x e ax 0 I  6 ? A. 1877. B. 2024. C. 2023. D. 189. 2
Câu 50: Cho hàm số y f x có đạo hàm f  x   x    2 1
x  2x , với x
  . Số giá trị nguyên của
tham số m để hàm số g x  f  3 2
x  3x m có 8 điểm cực trị là A. 2. B. 1. C. 3. D. 4.
----------------------------------------------- ----------- HẾT ----------
Mã đề 208 - trang 6/6
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI THỬ TỐT NGHIỆP LỚP 12 THPT NAM ĐỊNH NĂM HỌC 2022-2023
HƯỚNG DẪN CHẤM MÔN TOÁN LỚP 12
I. TRẮC NGHIỆM (50 câu, mỗi câu 0,2 điểm) Mã đề Câu 202 204 206 208 1 B A D A 2 D B C B 3 A D B C 4 D A A D 5 B D C B 6 C D C A 7 B B A A 8 D A C C 9 A A C C 10 A B C B 11 D B B C 12 A B D B 13 C C B D 14 B B B B 15 A B B A 16 C C A C 17 C A C D 18 A C D C 19 D C B D 20 C D D B 21 C D C D 22 B C C A 23 D B D D 24 D A B B 25 C C B A 26 B D D C 27 C D D D 28 D C A C 29 A A B D 30 D B D D 31 C D D B 32 B D A A 33 C A A A 34 C A A B 35 A A B C 36 A A D A 37 D B D D Mã đề Câu 202 204 206 208 38 A C A C 39 B C B D 40 C B D D 41 B D C B 42 D C C D 43 B A A D 44 C B C A 45 B D A C 46 A C A C 47 A A A B 48 B D B A 49 D A A A 50 C C B B BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A B D A D D B A A B B B C B B C A C C D D C B A C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
D D C A B D D A A A A B C C D C C A B D C A D A C Câu 1.
Trong không gian Oxyz , khoảng cách từ điểm M 0;3;  1 đến mặt phẳng
:2x y  2z  2  0 bằng 4 1 A. 1. B. . C. . D. 3 . 3 3 Lời giải Chọn A. 2.0  3  2. 1   2
Ta có: d M ;     1 2 1   2  2 2 2 Câu 2.
Trên khoảng 0;, đạo hàm của hàm số e y x là 1 e 1 x A. e 1 y .x    . B. 1 . e y e x    . C. e
y  x ln x . D. y  . e e 1 Lời giải Chọn B
Ta có: y   e x  e 1  . e x  . Câu 3.
Cho hàm số y f x liên tục trên  và có bảng biến thiên như hình vẽ:
Có bao nhiêu giá trị nguyên của tham số m để phương trình f x  m có bốn nghiệm phân biệt? A. 0 . B. 1. C. 3 . D. 2 . Lời giải Chọn D
Để phương trình f x  m có 4 nghiệm phân biệt thì 2
  m 1 suy ra có 2 giá trị nguyên m  1  ;  0 . 1 1 1 f
 xdx  2 g
 xdx  5  f
 x2g xdxCâu 4. Cho 0 và 0 khi đó 0 bằng A. 8  . B. 3  . C. 1. D. 12 . Lời giải Chọn A 1 1 1 Ta có:  f
 x2gxdx f
 xdx2 g
 xdx  22.5  8  0 0 0 Câu 5.
Trên mặt phẳng tọa độ, điểm M  1  ; 
1 là điểm biểu diễn số phức nào sau đây?
A. z  1 .i B. z  1   i .
C. z  1 i . D. z  1   i . Lời giải Chọn D. Ta có: Điểm M  1  ; 
1 là điểm biểu diễn số phức z  1   .i Câu 6.
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y x  2x 1, trục hoành và hai đường thẳng x  1  ; x  3. 37 A. S  56 . B. S  68 . C. S  64 . D. S  . 3 3 3 3 Lời giải Chọn D
Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y x  2x 1, trục hoành và hai đường thẳng x  1  ; x  3 là 3 3  x  64 2 S
x  2x 1 dx  
  2x  2x  3 3 2 1 dx  
x x   . 3 3 1  1    1  Câu 7.
Cho hàm số y f x liên tục trên  và có đồ thị như hình vẽ
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên  1  ;  1 .
B. Hàm số nghịch biến trên  ;    1 .
C. Hàm số đồng biến trên  1  ; .
D. Hàm số đồng biến trên  . Lời giải Chọn B
Từ đồ thị hàm số ta thấy hàm số nghịch biến trên  ;    1 . Câu 8.
Cho hàm số y f x liên tục trên  và có đồ thị như hình vẽ
Khẳng định nào dưới đây đúng?
A. Hàm số đạt cực tiểu tại x  1  .
B. Giá trị cực tiểu của hàm số bằng 1  .
C. Hàm số không có điểm cực trị.
D. Hàm số đạt cực đại tại x  4 . Lời giải Chọn A
Từ đồ thị hàm số ta thấy hàm số đạt cực tiểu tại x  1  . Câu 9.
Cho khối nón có chiều cao bằng a và đường sinh bằng 2a . Thể tích của khối nón đã cho bằng 3 a  3 3 aA. 3 a  . B. 3 3 a  . C. . D. . 3 3 Lời giải Chọn A
Bán kính đường tròn đáy của hình nón bằng 2 2
r l h a 3 . 1
Thể tích của khối nón bằng 2 3 V rh a  . 3
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA a 2 và vuông góc với
đáy (tham khảo hình vẽ). Tình khoảng cách giữa hai đường thẳng BD và SC a a a 2 a 2 A. . B. . C. . D. . 4 2 4 2 Lời giải Chọn B
Gọi O là giao điểm của AC; BD .
Trong mặt phẳng SAC kẻ OH SC . Ta có
BD AC  SAC 
BD SA  SAC  BD  SAC  BD OH . AC SA     A OH SC Từ đó 
nên d SC; BD  OH . OH BD Ta lại có,   2    45o SA AC a OCH a 2 a a
Trong tam giác vuông OHC có OC
. Suy ra OH OC  2 2 sin OCH  .  . 2 2 2 2 a
Vậy d SC; BD  . 2
Câu 11. Bất phương trình 2log 4x  3  log 2x  3  2 3   1  2 có tập nghiệm là 9  3   3  3   3 A.   ;   . B. ;3 . C.  ;3 . D.  ;3 .      4   4     8   8    Lời giải Chọn B  3 4 3 0 x x       4 3 +) Điều kiện     x    2x  3  2  0 3 4 x    2 1
Khi đó: 2log 4x  3  log 2x  32  2  log 4x  32  .2log 2x  3  2 3 1 3 3   2 9 4x 32 4x 32 3 2  log  2 
 9  16x  42x 18  0    x  3. 3 2x  3 2x  3 8 3 So với điều kiện   x  3
. Tập nghiệm của bất phương trình là ;3 . 4  4    Câu 12. Hàm số 3
y x  3x  2 có giá trị cực đại bằng A. 1  . B. 4 . C. 20 . D. 0 . Lời giải Chọn B
TXĐ D   . Ta có 2
y  3x  3; y  0  x  1 
Suy ra giá trị cực đại của hàm số là 4 . x  5
Câu 13. Giá trị lớn nhất của hàm số y
trên đoạn 8;12 bằng x  7 17 13 A. 15 . B. . C.13 . D. . 5 2 Lời giải Chọn C x  5 1  2 Hàm số y
liên tục trên đoạn 8;12 . Ta có y   0, x   8;12 . 2   x  7 x 7
Suy ra hàm số nghịch biến trên khoảng 8;12  max y y 8 13 . 8;12
Câu 14. Cho hình trụ có chiều cao h và bán kính đáy bằng r . Diện tích xung quanh S của hình trụ xq
được tính bởi công thức
A. S  rh . B. S  1 2 rh .
C. S  rh . D. 2 S  r h . xq xq xq 3 xq Lời giải Chọn B
Diện tích xung quanh S của hình trụ là S  2 rh . xq xq
Câu 15. Có bao nhiêu cách xếp 4 học sinh thành một hàng dọc A. 15 . B. 24 . C. 4 . D. 10 . Lời giải Chọn B
Số cách xếp 4 học sinh thành một hàng dọc là 4!  24 ( cách).
Câu 16. Cho khối lăng trụ đứng ABC.A' B 'C ' có AB AC a AA a  0 , '
2, BAC  45 . ( tham khảo
hình vẽ). Tính thể tích V của khối lằng trụ đã cho 3 a 3 2a 3 a 3 a A. . B. . C. . D. . 4 4 2 6 Lời giải Chọn C. a
Thể tích khối lăng trụ V S AA AB AC  3 1 . ' . .sin BAC.AA'  ABC 2 2
Câu 17. Biết phương trình 2
log x  2log 2x 1  0 x , x x .x 2 2   có hai nghiệm . Giá trị của bằng 1 2 1 2 1 A. 4 . B. . C. 3  1 . D. . 8 2 Lời giải Chọn A.
Điều kiện: x  0 .  1 log  1  x  Phương trình 2 log x 2log 2x 1 0 log x 2log x 3 0           2 2   2 2  2 . 2 2 log x  3   2 x  8  x .x  4 . 1 2
Câu 18. Số phức nghịch đảo của số phức z  3  4i là 3 4 A.  3 4 i . B.  3 4 i . C.i . D. 3  4i . 5 5 5 5 25 25 Lời giải Chọn C. 1 1 3 4 Ta có:    i . z 3  4i 25 25
Câu 19. Trong mặt phẳng tọa độ Oxy , biết tập hợp điểm biểu diễn của số phức z thỏa mãn
z 1 i z  2i là đường thẳng d . Phương trình đường thẳng d là
A. 2x y 1  0 .
B. x  2y 1  0 .
C. x y 1  0 .
D. x y 1  0 . Lời giải Chọn C.
Gọi z x yi với x, y R . Thế vào phương trình z 1 i z  2i ta được.
x yi 1 i x yi  2i x 1  y  
1 i x   y  2i
 x  2   y  2 2 1
1  x   y  22  x y 1  0.
Câu 20. Cho hình hộp ABC .
D A' B 'C ' D ' có AB a 3, AD a ( tham khảo hình vẽ). Góc giữa hai
đường thẳng AB và A'C ' bằng A. 0 60 . B. 0 45 . C. 0 75 . D. 0 30 . Lời giải Chọn D.
Ta có: A'C '/ / AC   AB, A'C '   AB, AC   BAC .  BC 1 tan BAC     0 BAC  30 . AB 3
Câu 21. Hàm số dưới đây có đồ thị như hình vẽ? A. 3
y  x  3x 1. B. 4 2
y x  2x 1. C. 4 2
y  x  2x 1. D. 3
y x  3x 1. Lời giải Chọn D
Câu 22. Cho cấp số cộng u u  2 d  2  u n  với công sai . Giá trị bằng 1 5 A. 10 . B. 6 . C. 6  . D. 32 Lời giải Chọn C Vì u
u u n 1 d u u  4d  2  4. 2   6  n 1   5 1  
n  là một cấp số cộng thì .
Câu 23. Cho hàm số f x có đạo hàm f  x  xx  3 1 , x
   . Hàm số y = f (x)đồng biến trên khoảng nào dưới đây? A.  1  ;  1 . B.  ;  0 . C. 0;  1 . D. 0; . Lời giải Chọn B x
Ta có f  x 0  0  x 1
Bảng biến thiên của hàm số y = f (x):
Hàm số đồng biến trên khoảng (- ; ¥ 0)
Câu 24. Tập nghiệm của bất phương trình log 3x 1  3 2   .  1  A. 3; B. ;3 C.  ;  3 D.   0;  3  Lời giải Chọn A 1
Đkxđ: 3x 1  0  x  3 Bất phương trình 3
 3x 1  2  3x  9  x  3. 1
So với điều kiện x > , tập nghiệm của bất phương trìnhlà (3;+¥). 3
Câu 25. Cho hàm số f (x) , g(x) liên tục trên  . Trong các mệnh đề sau, mệnh đề nào sau sai?
A. 5 f (x)dx  5 f (x)dx . B.
f (x)  g(x) dx f (x)dx g(x)dx .      
C.  f (x).g(x)dx f (x)d .x g(x)dx. D.
f (x)  g(x) dx f (x)dx g(x)dx .       Lời giải Chọn C 2x
Câu 26. Đường tiệm cận đứng của đồ thị hàm số y  là. x 1 A. x  1. B. y  2 . C. x  2 . D. x  1  . Lời giải Chọn D. Ta có lim y   ;
 lim y   nên đồ thị hàm số có tiệm cận đứng là x  1  . x   1  x   1     
Câu 27. Gieo một đồng tiền cân đối, đồng chất ba lần. Xác suất để trong ba lần gieo có đúng hai lần
xuất hiện mặt ngửa là. 1 1 1 3 A. . B. . C. . D. . 8 3 4 8 Lời giải Chọn D.
Gieo một đồng tiền cân đối, đồng chất ba lần 3    2  8 .
Biến cố A: ba lần gieo có đúng hai lần xuất hiện mặt ngửa là.
Các kết quả thuận lợi của biến cố A là:  N, N, S , N, S, N ,S, N, N  .
A   PA 3 3  8
Câu 28. Cho số phức z  1 2i . Tính z . A. z  3 . B. z  5 . C. z  5 . D. z  3 . Lời giải Chọn C
z  1 2i  5
Câu 29. Tập nghiệm của bất phương trình 3x  27 là. A. 3; . B. 3; . C.  ;   3 . D.  ;  3 . Lời giải Chọn A. x x 3
3  27  3  3  x  3  x 3; .
Câu 30. Với a là số thực dương tùy ý, 3 log a bằng. 81 3 1 4 1 A. log a . B. log a . C. log a . D. log a . 3 4 3 12 3 3 3 27 Lời giải Chọn B. 1 1 1 3 3  3 log a log a  log a  log a 4 81   . 3 3 3 4 12
Câu 31. Trong không gian Oxyz , hình chiếu của điểm A1;2; 
1 trên mặt phẳng Oxy là điểm nào dưới đây? A. P  1  ; 2  ;0 . B. Q  1  ; 2  ;  1 . C. M 1;2;  1 .
D. N 1;2;0 . Lời giải Chọn D.
Câu 32. Khối bát diện đều thuộc loại bát diện đều nào sau đây? A. 4;  3 . B. 5;  3 . C. 3;  5 . D. 3;  4 . Lời giải Chọn D. f x
1;2 f  1 1 f 2  2 2 Câu 33. Cho hàm số
có đạo hàm liên tục trên , và
. Tính I f   xdx 1 7 A. I  1. B. I  1  . C. I  3 . D. I  . 2 Lời giải Chọn A. 2 2
Ta có I f
 xdx f x  f 2 f  1  211. 1 1
Câu 34. Trong không gian Oxyz , gọi S  là mặt cầu có tâm I Ox và đi qua hai điểm A2;1;  1 , B  1
 ;3; 2  . Phương trình của mặt cầu S là A. 2 2 2
x y z  2x 10  0 . B. 2 2 2
x y z  4x 14  0 . C. 2 2 2
x y z  2x 10  0 . D. 2 2 2
x y z  4x  2  0 . Lời giải Chọn A.  
Do I Ox I  ;
x 0;0  IA  2  ; x 1;   1 , IB   1   ; x 3; 2 
Ta có IA IB IA IB    x      x    2 2 2 2 2 2 2 2 2 1 1 1 3 2
 4  4x  2  1 2x 11  6x  6   x  1   I  1
 ;0;0 , R IA  11 . x  1   2t
Câu 35. Trong không gian Oxyz , đường thẳng d : y  3 t có một vectơ chỉ phương là z  2t      A. u  2; 1  ;  1 . B. b   1  ; 1  ;  1 . C. a   1  ;2;3 . D. v   1  ;3;2 .
Câu 36. Trong không gian Oxyz , mặt cầu S  2 2 2
: x y z  4x  2y  2z  3  0 có bán kính bằng A. 3 . B. 9 . C. 1. D. 6 . Lời giải a  2;b  1  ;c  1  ;d  3  2 2 2
R a b c d  4 11 3  3 . 1
Câu 37. Họ tất cả các nguyên hàm của hàm số f x 2  3x  là 2 sin x 2 A. 6x   C . B. 3
x  cot x C . C. 3
x  tan x C . D. 3
x  cot x C . 2 sin x Lời giải f  x 3
dx x  cot x C .
Câu 38. Trong không gian Oxyz , gọi là góc giữa hai mặt phẳng P :x  2y z  2  0 và
Q:2x y z  4  0. Tính cos. 2 A. cos 3 . B. cos 1 . C. cos 1 . D. cos . 3 4 6 3 Lời giải 
Mặt phẳng P có vectơ pháp tuyến n  1;2;1 1   . 
Mặt phẳng Q có vectơ pháp tuyến n  2;1;1 2   .   n .n 2  2 1 1 Vậy 1 2
cos     . n . n 6. 6 6 1 2
1 2x   x 2
1 e  2ax a
Câu 39. Đặt I
dx . Có bao nhiêu giá trị nguyên của thuộc khoảng 0; 2023  a   x e ax 0 để I  6 ? A. 2023. B. 2024 . C. 1877 . D. 189 . Lời giải 1 2x x
e axx 1 x 1 xe ae a  1 d  x e ax 1 e a 2 I  dx  2x    dx   x  dx  1  x x 0 x e axe ax e ax x e ax 0 0 0 0 1  1 ln x
e ax  1 ln e a . 0
Ta có I    e a   e a 5 5 6 1 ln 6 ln
 5  e a e a e e 145,69 .
Vì a 0;2023, a  nên a 146;147;...;202 
2 : có 1877 giá trị nguyên.
Câu 40. Cho hàm số y f (x) có đạo hàm liên tục trên  và thỏa mãn f (1)  5 và 1 xf  3  x  7 4 1
f '(x)  x  5x  7x  3 với x
   . Tính f (x)dx . 0 5 5 17 A.  13 B. C. D. 6 12 6 6 Lời giải Chọn D xf  3  x  7 4 2
f x x x x    x f  3  x  8 5 2 1 '( ) 5 7 3 3 . 1
 3xf '(x)  3
x 15x  21x  9x . 1  3
x . f 1 x  3xf '(x) 1 2 3 dx   8 5 2 3
x 15x  21x  9xdx 0 0 1 3
x . f 1 x  1 28 2
3 dx  3 xf '(x)dx     3 0 0 1 0 1 Xét 2 A  3  x . f   3
1 x dx f
 tdt   f  xdx 0 1 0 1 1 1 1
B xf '(x)dx  .
x f (x)  f (x)dx  5  f (x)dx .    0 0 0 0 1 1 1 1 1 28 17 Vậy 2 3  x . f  3
1 x dx  3 xf '(x)dx   f (x)dx 15  3 f (x)dx  
f (x)dx       3 6 0 0 0 0 0
Câu 41. Trên tập số phức, xét phương trình 2
z  m   2 2
1 z m  4m  3  0 ( m là tham số thực). Có
bao nhiêu giá trị của m để phương trình có hai nghiệm phân biệt z , z thỏa mãn 1 2
z z 2  2m z z 1 2 1 2 A. 2 B. 4 C.1 D. 0 Lời giải Chọn C  '  2  m  2 TH1:  '  2
m  2  0  m  1  .
Phương trình có hai nghiệm là hai số thực
z z 2  2m z z  z z 2  4z .z  2m z z  4m  2 1  4 2
m  4m  3  2m  2(m 1) 1 2 1 2 1 2 1 2 1 2  5  m   (t/m) 2 TH2:  '  2
m  2  0  m  1 
Phương trình có hai nghiệm là hai số phức liên hợp.
Giả sử z x yi; z x yi 1 2    z z 2 y 0 2
 2m z z  4
y  2m  2x  2yi  1 2 1 2  x m
Do đó z z m (loại) vì hai nghiệm bằng nhau. 1 2
Câu 42. Cho hàm số y f x 4 3 2
ax bx cx dx e a  0, hàm số y f '1 2x có đò thị như hình vẽ sau:
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g x  f  3
x  5x m có ít nhất 5 điểm cực trị? A. 6 B. 4 C. 2 D. 10 Lời giải Chọn C
Từ đồ thị ta có: f '1 2x  k x  4 x  
1  x  5 với k  0 . t 1
Đặt t  1 2x x  . Suy ra: 2 t  7          t t 1 t 1 t 1 k f ' k 4 1 5    
t 7t 3t 1  1 0            t  3 . 2 2 2 8      t 11 
Ta có: g x  f  3
x x m  f   2
x   x m  f x  2 5 5
x  5  m có tập xác định là  x
  D  x D 0 0 
D   nên ta có:  2 . Do đó hàm g
 x  f
x  x  m f x  2 5
x  5  m  g x
g x là hàm chẵn nên đồ thị đối xứng nhau qua trục tung, suy ra số điểm cực trị hàm g x
có dạng 2m  
1 trong đó m là số điểm cực trị có hoành độ dương của đồ thị hàm số y f  3
x  5x m .
Theo giả thiết ta có: 2m 1  5  m  2 . Vậy yêu cầu bài toán tương đương với: “ Tìm m để
hàm số y f  3
x  5x m có ít nhất hai điểm cực trị có hoành độ dương”.
Xét hàm y f  3
x  5x m với x0; . Ta có: y '   2
3x  5 f ' 3
x  5x m  0  f ' 3
x  5x m  0 3 3
x  5x m  7 
m  x  5x  7
có ít nhất hai nghiệm dương.   3 3
x  5x m  3  m  x  5x  3    3  3
x  5x m  11
m  x  5x 11  
Ta lập bảng biến thiên cả ba hàm trên cùng một bảng ta có:
Để có ít nhất hai nghiệm dương thì m  3 . Mà m
  m  1;  2 .
Vậy có hai giá trị nguyên dương của tham số m thỏa mãn yêu cầu bài toán.
Câu 43. Trong không gian Oxyz , cho ba điểm A 1  5;7;1  1 , B  3  ;1; 
1 ,C 7;1;5 và đường thẳng    
d x 1 y 1 z 1 :  
. Gọi  là mặt phẳng chứa d  sao cho ,
A B,C ở cùng phía đối 1  4 1
với mặt phẳng  . Gọi d , d , d lần lượt là khoảng cách từ ,
A B,C đến  . Giá trị lớn 1 2 3
nhất của biểu thức T d  2d  3d bằng 1 2 3 41 A. 82 . B. 2 67 . C. 41 . D. . 2 Lời giải Chọn A
Gọi M , N lần lượt là trung điểm của AB, BC M  9
 ;4; 5, N 2;0;3 . Từ đó suy ra
d d  2d
và d d  2d . 1 2
M ; 2 3
N;
T d  2d  3d  2d  2d  2d  6d , với G 0;1;  1 là trọng tâm MNC . 1 2 3
M ;
N; 3
G;   
Đường thẳng d  qua điểm M 1;1;  1 , VTCP u   1  ;4; 
1  GM ;u  6;1;2     6 GM ;u   Vậy: T  6 max  6GK  6d  
 82 khi K là hình chiếu G lên d  max
d G; G;du .
Câu 44. Cho hình chóp tam giác đều S.ABC có AB a , khoảng cách giữa hai đường thẳng SA và a 6 BC bằng (tham khảo hình vẽ). 3
Thể tích khối chóp S.ABC bằng 3 2 a 3 2 a 3 2 a 3 2 a A. . B. . C. . D. . 2 6 3 9 Lời giải Chọn B
Gọi M là trung điểm BC và O là tâm đường tròn ngoại tiếp A
BC SO   ABC. a 6 a
Kẻ MK SA MK  2 2 6
. Kẻ OH SA OH MK  . 3 3 9 a a 2 a 3 A  2 3 3
BC đều cạnh a OA  .  và S  . 3 2 3 ABC 4 OH.OA 2 6 a Ta có: SO   . 2 2 OA OH 3 3 1 2 a
Vậy thể tích khối chóp S.ABC là V S . O S  . 3 ABC 6 x
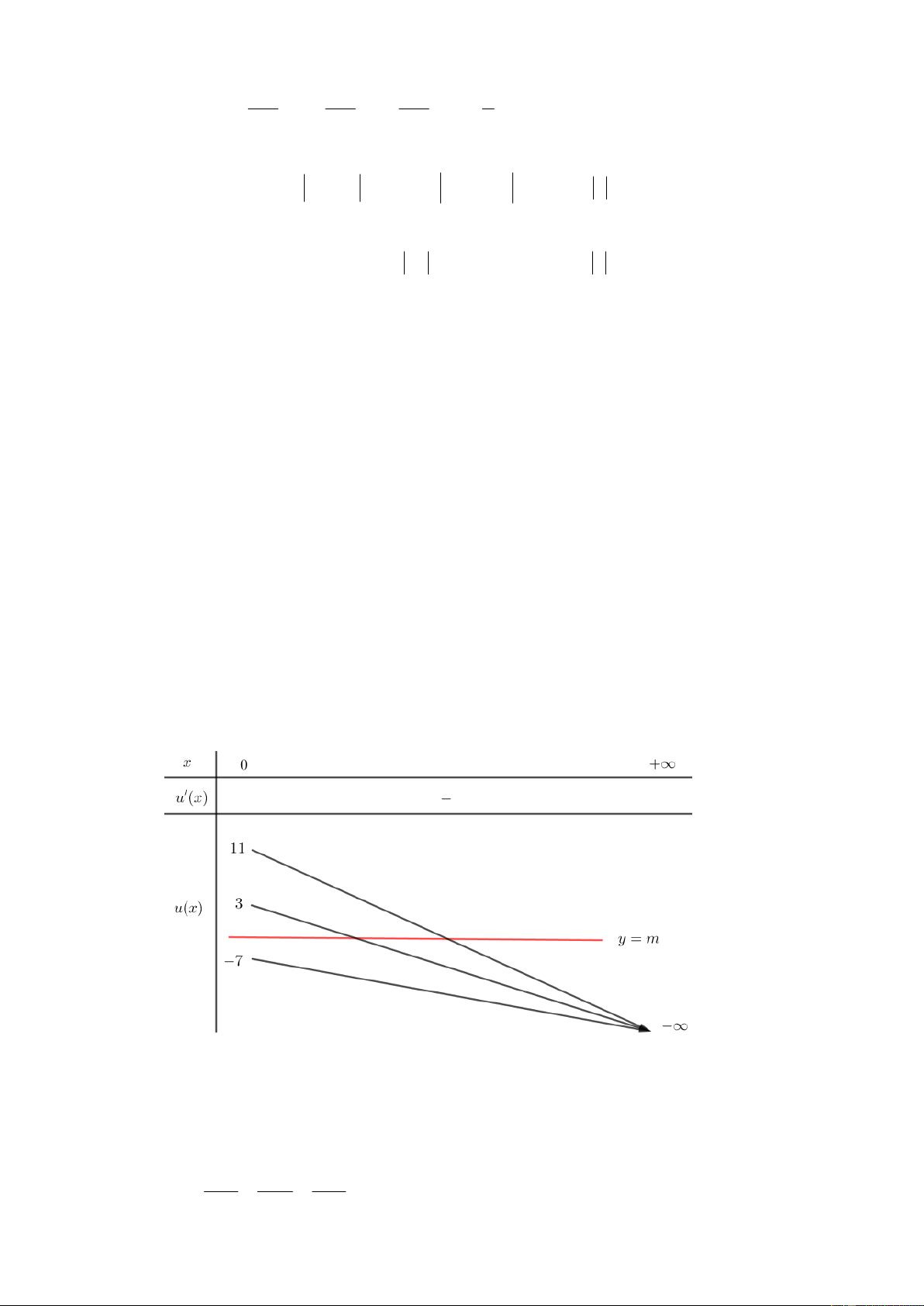
Câu 45. Cho phương trình log x 1  log  1 m 9  2 ( với
là tham số thực). Có bao nhiêu giá trị 1 m 3
nguyên dương của tham số m để phương trình đã cho có nghiệm thực? A. 1. B. Vô số. C. 3 . D. 2 . Lời giải Chọn D
Xét m nguyên dương nên ta có điều kiện phương trình x  0 . Khi đó x log  x  2 1  log
 1  log x 1  log x  log m  1 9 1 3   3 3 m 3 x 1 3  log  log . 3 3 x m x 1 3 m x     x m 3 x 1 x 1 Xét hàm số y   y '   0, x   0 . x 1 x  2 1 Bảng biến thiên m
Để phương trình có nghiệm thì 0 1 0 m 3 m        
m1,  2 . 3
Câu 46. Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB  2 3a, AD  3a, SAD là tam giác
đều và nằm trong mặt phẳng vuông góc với đáy (tham khảo hình vẽ). Tính thể tích khối cầu
ngoại tiếp chóp S.ABCD . 3 3 32 a 3 A. 16 a . B. 3 16 a . C. . D. 26 a . 3 3 3 Lời giải Chọn C
Ta có SAD   ABCD theo giao tuyến là AD . Gọi M là trung điểm của
AD, SM AD SM   ABCD .
Xét đường thẳng d qua O AC BD O, / / SM : d là trục của hình chữ nhật ABCD .
Ta có OM AD,OM SM OM  SAD , G là trọng tâm tam giác SAD .
Xét đường thẳng d ' qua G, / / MO : d là trục của tam giác SAD . Khi đó d d '  I thì I là
tâm mặt cầu ngoại tiếp hình chóp S.ABCD . Ta có 2 2
R ID IO OD . 1 1 3 1 3 a 1 1 15a
Với IO GM SM  . .AD  . . 3a  , 2 2 OD BD AB AD  . 3 3 2 3 2 2 2 2 2 3 4 32 a Suy ra 3
R  2a V  R  . 3 3
2xy +3x +3y + 4
Câu 47. Cho x , y là các số thực dương thỏa mãn log
= x 2x-3 + y 2y-3 -3 2 2 2 ( ) ( )
x + xy + y
. Tính giá trị lớn nhất của biểu thức F = x + y -1. A. 3 . B. 1. C. 4 . D. 2 . Lời giải Chọn A Ta có
2xy +3x +3y + 4 log
= x 2x-3 + y 2y-3 -3 2 2 2 ( ) ( )
x + xy + y
Û log (2xy +3x+3y +4)+(2xy +3x+3y +4)= log ( 2 2
2x + 2xy + 2y )+( 2 2
2x + 2xy + 2y . 2 2 )
Đặt f (t)= log t +t , ta có f ¢(t) 1 =
+1> 0,"t > 0 suy ra hàm số f (t) đồng biến trên 2 t ln 2 (0;+¥). Do đó
f (2xy +3x +3y + 4)= f ( 2 2
2x + 2xy + 2y ) 2 2
Û 2xy +3x +3y +4 = 2x +2xy +2y Û (x+ y)2 3
-2xy- (x+ y)-2 = 0. ( )* 2
ìïy = F +1-x Mặt khác F x y 1 ï = + - Þ . Thay vào ( ) * , ta được íïx ï + y = F +1 î
(F + )2 - x(F + -x) 3 1 2 1 - (F + ) 1 -2 = 0 2 Û 2x -2(F + ) 1 x +(F + )2 3 2 1 - (F + ) 1 -2 = 0. (* ) * 2 Tồn tại x khi 2
D¢ =-F + F +6 ³ 0 Û -2 £ F £3 . ìïx = 2
Dấu đẳng thức xảy ra F 3 ï = Þíïyï=2. î
Vậy giá trị lớn nhất của biểu thức F = x + y -1 là 3 tại x = 2 và y = 2 .
Câu 48. Trong không gian Oxyz , cho mặt phẳng (P): 2y-3z-3= 0 và hai đường thẳng ìïx =-1+2t x y -1 z + 2 ïï d : = = ; d : y í =1+t D (P) 2 . Đường thẳng nằm trong mặt phẳng đồng 1 2 -1 1 ïïïz=1 ïî
thời cắt cả hai đường thẳng d và d có phương trình là 1 2 x + 2 y z -1 x -2 y z +1 A. = = . B. = = . 1 -3 2 1 -3 2 x + 2 y z -1 x - y z + C. = = 2 1 . D. = = . 1 3 2 1 3 2 Lời giải Chọn D ìïx = 2a ï Ta có d :ïy
í =1-a . Gọi A=DÇd = P Çd 1 ( ) . 1 ï 1 ïïz =-2+a ïî Suy ra 2(1-a)- ( 3 2
- +a)-3=0 Û a =1 suy ra ( A 2;0;- ) 1 . ìïx =-1+2t ïï Ta có d : y í =1+t
B =DÇd = P Çd 2 ( ) 2 . Gọi . ïï 2 ïz =1 ïî Suy ra 2(1+t)-3 1
× -3=0 Ût = 2 suy ra B(3;3; )1.  x -2 y z +1
Khi đó AB =(1;3;2) suy ra AB : = = . 1 3 2
Câu 49. Xét các số phức z thỏa mãn z  2  4i z  3  i  5 2 . Biết giá trị lớn nhất của biểu thức
P z i z  3  3i có dạng a b;a,b   . Giá trị của biểu thức a b bằng A. 3 . B. 7 . C. 5 . D. 9 . Lời giải Chọn A
Gọi z x yi; x, y   có điểm biểu diễn trên mặt phẳng tọa độ là M Gọi A 2
 ;4, B3;  1  AB  5 2 Ta có:
z  2  4i z  3  i  5 2
MA MB  5 2  AB
Vậy M nằm trên đoạn thẳng AB : x y  2  0  M  ;
x 2  x, x  2  ;  3
Gọi I    J
  MI x x  2 MJ  x  2 x  2 2 0; 1 , 3;3 3 ; 3 1 2 2
P z i z  3  3i MI MJ  2x  6x  9  2x  4x 10  f x
Sử dụng CASIO ta được: max f x  f  2
   29  26  a  29;b  26  2  ;  3
Câu 50. Cho hàm số y f x có đạo hàm f  x   x  2  2 1
x  2x, x
   . Số giá trị nguyên của
tham số m để hàm số g x  f  3 2
x  3x m có 8 điểm cực trị là A. 2. B. 3 . C. 1. D. 4 Lời giải Chọn C
Ta có: g x   2
x xf  3 2
x x m  xx   f  3 2 3 6 3 3 2
x  3x m x  0  x  0 x  0 x  2    x  2 g x  3 2  0  x  2
x  3x m  0   3 2 
x 3x  m    f    1 3 2
x  3x m 3 2  0
x  3x m  2  3 2 
x  3x  m  2  2 3 2
x  3x m  1  L Xét hx 3 2
x x hx 2 3  3x  6x   h xx 0  0  x  2
Để hàm số g x có 8 điểm cực trị thì phương trình  
1 ,2 phải có tổng 6 nghiệm phân biệt
khác 0 và 2 . Từ bảng biến thiên hx ta có:  4   m  0 0  m  4   
 2  m  4  m  3  4
  m  2  0 2  m  6
Document Outline

  • de-thi-thu-tot-nghiep-thpt-nam-2023-mon-toan-so-gddt-nam-dinh
    • 1. Mã đề 202
    • 2. Mã đề 204
    • 3. Mã đề 206
    • 4. Mã đề 208
    • 5. Đáp án và hướng dẫn chấm
  • 110. ĐỀ THI THỬ TN THPT 2023 - MÔN TOÁN - SỞ GIÁO DỤC NAM ĐỊNH (Bản word có giải).Image.Marked