26 trang 32 lượt tải

Đề thi thử tốt nghiệp THPT năm 2023 môn Toán sở GD&ĐT Quảng Bình

63

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi thử tốt nghiệp THPT năm 2023 môn Toán sở Giáo dục và Đào tạo tỉnh Quảng Bình

Chủ đề: Đề thi THPTQG môn Toán năm 2023 1.2 K tài liệu

Môn: Toán 2.2 K tài liệu

Tác giả:

Profile

Thanh Hoa

1 năm trước
Danh sách Quiz
/26
Trang 1/5 Mã đề 001
SỞ GD&ĐT QUẢNG BÌNH
ĐỀ THI CHÍNH THỨC
(Đề thi có 05 trang)
KỲ THI THỬ TỐT NGHIỆP THPT NĂM 2023
Bài thi: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Họ, tên thí sinh:…………………………………………..
Số báo danh:………………………………………………
Câu 1. Số phức đối của số phức
12
zi
= −
là
A.
12zi
′
=−−
. B.
12zi
′
= +
. C.
12zi
′
=−+
. D.
2
zi
′
=−+
.
Câu 2. Hàm số nào sau đây đồng biến trên
?
A.
1
5
x
y

=


. B.
3
2
x
y

=


. C.
1
10
x
y

=


. D.
.
Câu 3. Tập xác định của hàm số
4
7
( ) ( 3)y fx x= = −
là
A.
. B.
{
}
3\
. C.
(3; )+∞
. D.
(0; )+∞
.
Câu 4. Tập nghiệm của bất phương trình
log 2x ≥
là
A.
(
)
10; +∞
. B.
( )
0; +∞
. C.
[
)
100;
+∞
. D.
.
Câu 5. Cho cấp số nhân
( )
n
u
với
1
81u =
và
2
27u =
. Công bội của cấp số nhân
( )
n
u
là
A.
1
3
q = −
. B.
1
3
q =
. C.
3q =
. D.
3
q = −
.
Câu 6. Mặt phẳng nào sau đây song song với mặt phẳng
( )
α
có phương trình
2 20
xy z++ +=
?
A.
(
)
: 2 20Qxy z+− −=
. B.
(
)
: 2 10Rxy z+ − +=
.
C.
( )
: 2 10Sxy z+ + −=
. D.
( )
: 2 20Pxy z−+ −=
.
Câu 7. Đồ thị hàm số
1
1
−
=
+
x
y
x
cắt trục
Oy
tại điểm có tọa độ là
A.
( )
0;1
. B.
( )
1; 0
. C.
( )
0; 1−
. D.
( )
1;1
.
Câu 8. Cho hàm số
( )
y fx=
có đạo hàm
( )
fx
′
liên tục trên
[ ]
0;1
và thỏa mãn
( ) ( )
0 1, 1 3ff=−=
. Tính
( )
1
0
dI fxx
′
=
∫
.
A.
( )
1
0
d2fxx
′
=
∫
. B.
( )
1
0
d4fxx
′
= −
∫
. C.
( )
1
0
d2fxx
′
= −
∫
. D.
( )
1
0
d4fxx
′
=
∫
.
Câu 9. Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào trong các hàm số dưới
đây?
A.
41
2
x
y
x
−+
=
−
. B.
42
42
y xx=−+
.
C.
42
42yx x= −
. D.
32
42y xx=−−
.
Câu 10. Trong không gian Oxyz, phương trình mặt cầu có tâm
( )
1;0;0I
và bán kính bằng
2
là
A.
( )
2
22
12x yz− ++=
. B.
( )
2
22
12x yz+ ++=
.
C.
( )
2
22
14x yz−++=
. D.
( )
2
22
14x yz+ ++=
.
Mã đề thi: 001
Trang 2/5 Mã đề 001
Câu 11. Trong không gian Oxyz, cho điểm
(1;2;2)A
và mặt phẳng
( ): 2 2 4 0xyz
α
+ − −=
.
Khoảng cách
d
từ điểm
A
đến mặt phẳng
()
α
là
A.
1
3
d =
. B.
1d =
. C.
13
3
d
=
. D.
3d =
.
Câu 12. Số phức
z
thỏa mãn điều kiện
( )
3 53 0
iz i− −+ =
là
A.
92
.
55
zi=−+
B.
92
.
55
zi= −
C.
92
.
55
zi=−−
D.
67
.
55
zi=−−
Câu 13. Khối chóp có diện tích đáy bằng
2
a
và chiều cao bằng
2a
, thể tích của khối chóp đã
cho bằng
A.
3
3
a
. B.
3
a
. C.
3
2a
. D.
3
2
3
a
.
Câu 14. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
,A
3, 2.AB a AC a= =
Cạnh
bên
SA
vuông góc với đáy,
Thể tích của khối chóp
.S ABC
là
A.
3
45a
. B.
3
45
3
a
V =
. C.
3
4Va
=
. D.
3
12Va=
.
Câu 15. Cho mặt cầu có bán kính
5
r =
. Diện tích của mặt cầu đã cho bằng
A.
100
3
π
. B.
100
π
. C.
25
π
. D.
500
3
π
.
Câu 16. Cho số phức
20 - 21zi=
. Môđun của số phức
z
bằng
A.
20z
=
. B.
841
z
=
. C.
. D.
29z =
.
Câu 17. Cho khối trụ có bán kính đáy
4r
và chiều cao
2h
. Thể tích khối trụ đó là
A.
8π
. B.
32π
. C.
16π
. D.
32
3
π
.
Câu 18. Trong không gian với hệ toạ độ
Oxyz
một vectơ chỉ phương của đường thẳng
( )
d
:
1 32
235
xy z−−−
= =
là
A.
( )
2;3;5
u =
. B.
( )
1; 3; 2
u =
. C.
( )
1; 3; 2
u = −
. D.
( )
2; 3; 5u = −
.
Câu 19. Cho hàm số
( )
y fx=
có bảng biến thiên:
Số điểm cực trị của hàm số đã cho là
A.
3.
B.
4.
C.
1.
D.
2.
Câu 20. Tiệm cận đứng của đồ thị hàm số
21
1
x
y
x
+
=
−
là:
A.
1x =
. B.
1y = −
. C.
1
2
x = −
. D.
2y =
.
Câu 21. Tập nghiệm của bất phương trình
1
2
99
x
x
+
≤
là
A.
[
)
1; +∞
. B.
. C.
(
]
;1−∞
. D.
.
Câu 22. Có bao nhiêu cách xếp chỗ ngồi cho bốn bạn học sinh vào bốn chiếc ghế kê thành một
hàng ngang?
A.
24
. B.
4
. C.
12
. D.
8
.
Trang 3/5 Mã đề 001
Câu 23. Họ nguyên hàm của hàm số
( )
35
2
x
fx
x
+
=
+
là:
A.
3 ln 2xx C− ++
. B.
3 ln 2xx C+ ++
.
C.
3 4 ln 2x xC− ++
. D.
3 4ln 2x xC+ ++
.
Câu 24. Cho hàm số
( )
y fx=
liên tục trên đoạn
[ ]
5;12−
và thỏa mãn
( )
12
5
d7
fx x
−
=
∫
,
( )
6
2
d3fx x=
∫
. Giá trị của biểu thức
(
)
( )
2 12
56
ddP fx x fx x
−
= +
∫∫
là
A.
4P =
. B.
10P =
. C.
3P =
. D.
2
P
=
.
Câu 25. Cho hàm số
(
)
2
3 sin cos 2 .fx x x x=+−
Nguyên hàm
(
)
Fx
của hàm số
( )
fx
thỏa mãn
( )
02F =
là
A.
( )
3
1
cos sin 2 2.
2
Fx x x x=−− +
B.
( )
3
1
cos sin 2 3.
2
Fx x x x
=−− +
C.
( )
3
1
cos sin 2 3.
2
Fx x x x=−− −
D.
( )
3
1
cos sin 2 2.
2
Fx x x x=−− −
Câu 26. Tất cả các khoảng đồng biến của hàm số
32
1
2 31
3
yxxx
= − ++
là
A.
( )
;1−∞
và
( )
3; +∞
. B.
( )
1; 3
. C.
(
)
;3
−∞ −
và
( )
1;− +∞
. D.
( )
3; +∞
.
Câu 27. Điểm cực tiểu của đồ thị hàm số
42
45yx x

là
A.
0x
. B.
0; 5
. C.
. D.
2; 1
.
Câu 28. Cho
,,abc
là các số thực dương khác
1
thỏa mãn
log 6, log 3
ac
bb= =
. Khi đó
log
a
c
bằng
A.
2
. B.
9
. C.
1
2
. D.
18
.
Câu 29. Diện tích
S
của hình phẳng giới hạn bởi các đường
32
4 31yx x x=− +−
và
21yx=−+
là:
A.
3S
=
. B.
2S =
. C.
1
12
S =
. D.
1
2
S =
.
Câu 30. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
B
. Cạnh bên
SA
vuông góc
với mặt phẳng đáy. Gọi
I
là trung điểm của
BC
. Góc giữa mặt phẳng
(
)
SBC
và mặt phẳng
( )
ABC
là
A.
SIA
. B.
SBA
. C.
SCA
. D.
ASB
.
Câu 31. Số giao điểm của đường cong
32
21yx x x= − +−
và đường thẳng
12
yx= −
là
A.
3
. B.
0
. C.
1
. D.
2
.
Câu 32. Cho hàm số
( )
y fx=
có đạo hàm
( )
( )
( )
2
1 2,fx x x x
′
= + − ∀∈
. Mệnh đề nào dưới
đây đúng?
A. Hàm số nghịch biến trên khoảng
( )
2; +∞
.
B. Hàm số đồng biến trên khoảng
( )
;−∞ +∞
.
C. Hàm số đồng biến trên khoảng
( )
1; 2−
.
D. Hàm số nghịch biến trên khoảng
( )
;2−∞
.
Câu 33. Chọn ngẫu nhiên hai số tự nhiên bé hơn 10. Xác suất để hai số được chọn có tổng chia
hết cho 2 là:
A.
5
9
. B.
4
45
. C.
11
45
. D.
4
9
.
Trang 4/5 Mã đề 001
Câu 34. Cho phương trình
4
log 3.2 1 1
x
x 
có hai nghiệm
12
,xx
. Tổng
12
xx
là:
A. 2. B.
2
log 6 4 2
. C.
2
log 12
. D. 12.
Câu 35. Cho số phức z thỏa mãn
12zi z i− = −+
. Tập hợp các điểm biểu diễn của số phức
( )
21w iz
=−+
là một đường thẳng có phương trình
A.
7 90xy+ +=
. B.
7 90xy+ −=
. C.
7 90xy− −=
. D.
7 90xy
− +=
.
Câu 36. Trong không gian
Oxyz
, cho tam giác
ABC
với
( )
1; 4; 3A −−
,
(
)
1; 0; 2B
,
( )
3;4;2.C −−
Phương trình đường trung tuyến
AM
của tam giác
ABC
là:
A.
22
1 21
xyz
−+
= =
−
. B.
143
3 63
xy z−+−
= =
−
.
C.
143
363
xy z−−−
= =
. D.
22
1 21
xyz
+−
= =
−
.
Câu 37. Trong không gian
Oxyz
, cho điểm
( )
1; 2; 3A −−
. Hình chiếu của điểm
A
lên mặt
phẳng
()Oxy
có tọa độ là
A.
(1; 2; 0 ) .
−
B.
( 1; 2; 0).−
C.
( )
1; 0; 3−−
. D.
( )
1; 0; 3
.
Câu 38. Cho khối chóp
.S ABCD
có đáy
ABCD
là hình vuông,
( )
SA ABCD⊥
và
SA a=
, góc giữa đường thẳng
SC
và mặt phẳng
( )
ABCD
bằng
30°
(tham
khảo hình vẽ). Tính khoảng cách giữa đường thẳng
AD
và mặt phẳng
()SBC
.
A.
2
a
. B.
6
a
. C.
15
5
a
. D.
3
6
a
.
Câu 39. Có bao nhiêu số nguyên dương
a
thỏa mãn
33
63
log ( ) logaa a
+>
?
A.
3
6.
B.
6
3.
C.
6
3 1.−
D.
3
6 1.−
Câu 40. Cho hàm số
()fx
liên tục trên
. Gọi
(), ()Fx Gx
là hai nguyên hàm của
()fx
trên
thỏa mãn
(10) (1) 11
FG+=
và
(0) (10) 1
FG+=−
. Khi đó,
4
0
cos 2 . (sin 2 )xf xdx
π
∫
bằng
A.
5
. B.
10.
C.
12.
D.
6.
Câu 41. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
53
18
2023
53
y x x mx= − −+
có
bốn điểm cực trị?
A.
17
. B.
10.
C.
16.
D.
15.
Câu 42. Cho số thực
0a >
và các số phức
z
thỏa mãn
| 6 8| .z ia+− =
Gọi
,Mm
lần lượt là giá
trị lớn nhất và giá trị nhỏ nhất của
||z
. Có bao nhiêu số nguyên
a
để
3Mm<
?
A.
4
. B. Vô số. C.
3.
D.
12.
Câu 43. Cho khối lăng trụ đứng
.ABC A B C
′′′
có đáy là tam giác cân tại
, .A BC a=
Mặt phẳng
( )
A BC
′
tạo với đáy góc
0
60
và tam giác
A BC
′
có diện tích bằng
2
6.a
Thể tích của khối lăng
trụ đã cho bằng
A.
3
64 3a
. B.
3
23a
. C.
3
9a
. D.
3
18 3 .a
S
A
B
C
D
Trang 5/5 Mã đề 001
Câu 44. Cho hàm số
( )
y fx=
liên tục trên khoảng
( )
0; +∞
và
( )
0fx≠
với mọi
0
x >
, biết
rằng
( ) ( ) ( )
2
21fx x f x
′
= +
và
(
)
1
1
2
f
= −
. Diện tích hình phẳng giới hạn bởi các đường
( ), 1,
y fx x x e
= = =
bằng
A.
2
1 ln
1e
+
+
. B.
1
1 ln
2
e +
−+
. C.
1
1 ln
1e
−
+
. D.
1
1 ln
2
e +
+
.
Câu 45: Trên tập hợp các số phức, xét phương trình
22
2 20z mz m m+ ++=
(
m
là tham số
thực). Tích của tất cả các giá trị thực của
m
để phương trình đó có 2 nghiệm phân biệt
12
,
zz
thỏa mãn
12
| | 2| |zz=
là
A.
0.
B.
18.−
C.
2.
D.
4.
Câu 46: Trong không gian
,Oxyz
cho mặt phẳng
()
α
vuông góc với mặt phẳng
(
)
: 3 2 20
Px y z
+ − +=
và chứa đường thẳng
114
:
2 11
xyz
d
−+−
= =
−
. Khoảng cách từ điểm
( )
1;2; 1A −
đến mặt phẳng
()
α
bằng
A.
83
3
. B.
43
3
. C.
24 3
3
. D.
83
.
Câu 47: Có bao nhiêu cặp số nguyên dương
(; )xy
sao cho ứng với mỗi giá trị nguyên dương
của
y
có không quá
15
giá trị nguyên dương của
x
thỏa mãn
2 2 22 2 2
5 3 53
log (3 36 ) log ( 12 ) log ( ) log ( 16 12 ) 1?
x xy y x y xy x xy y++++< ++++
A.
40
. B.
36
. C.
21
. D.
33
.
Câu 48. Cho khối nón tròn xoay có đường cao h = 20cm, bán kính đáy r = 25cm. Mặt phẳng
(P) đi qua đỉnh của khối nón và cách tâm O của đáy khối nón một khoảng bằng 12cm. Khi đó
diện tích thiết diện của khối nón cắt bởi mặt phẳng (P) bằng
A.
2
500cm
. B.
2
475cm
. C.
2
450cm
. D.
2
550cm
.
Câu 49. Trong không gian
Oxyz
, cho mặt cầu
( )
2 22
: 6 4 2 11 0Sx y z x y z++−− −−=
và điểm
( )
0; 2;1M
−
. Gọi
1
d
,
2
d
,
3
d
là ba đường thẳng thay đổi không đồng phẳng cùng đi qua điểm
M
và lần lượt cắt mặt cầu
( )
S
tại điểm thứ hai là
A
,
B
,
C
. Thể tích của tứ diện
MABC
đạt
giá trị lớn nhất bằng
A.
50 3
9
. B.
1000 3
27
. C.
100 3
9
. D.
500 3
27
.
Câu 50. Cho hàm số bậc bốn
y fx
có
3
2
2
f



và
1 0.f
Biết hàm
số
y fx
có đồ thị như hình vẽ bên. Hàm số
2
1
28
xx
gx f



đồng
biến trên khoảng nào trong các khoảng dưới đây?
A.
;4
. B.
5; 
. C.
2; 4
. D.
3; 1
.
…………….HẾT……………
SỞ GIÁO DỤC VÀ ĐÀO TẠO QUẢNG BÌNH
ĐỀ THI THỬ TỐT NGHIỆP THPT – NĂM HỌC 2022 – 2023
Câu 1. Số phức liên hợp của số phức là
1 2 z i
A. . B. . C. . D. .
2 z i
1 2 z i
1 2 z i
1 2 z i
Câu 2. Tập xác định của hàm số là
5
log 2 y x
A. . B. . C. . D. .
2;
2;
;2
Câu 3. Hàm số nào sau đây đồng biến trên ?
A. . B. . C. . D. .
x
y x
3
y x
2
y x
3
2
y x
Câu 4. Tập nghiệm của bất phương trình là
log 3x
A. . B. . C. . D. .
10;
0;
1000;
;10
Câu 5. Công bội của cấp số nhân với và là
q
n
u
1
1u
2
4u
A. . B. . C. . D. .
3q
4q
1
4
q
2 q
Câu 6. Trong không gian cho hai mặt phẳng và ,
Oxyz
: 2 3 1 0
x y z
: 2 4 6 1 0
x y z
khi đó:
A. . B. . C. . D.
cắt .
//
Câu 7. Tọa độ giao điểm của đồ thị hàm số với trục hoành là
2 3
2
x
y
x
A. . B. . C. . D. .
3
;0
2
2;0
0; 2
3
0;
2
Câu 8. Cho hàm số có liên tục trên và . Giá trị của tích phân
( )y f x
'( )f x
0;1
(1) (0) 2 f f
bằng
1
0
'( )d
I f x x
A. . B. . C. . D. .
1 I
1I
2I
0I
Câu 9. Đồ thị của hàm số nào sau đây có dạng như hình vẽ bên?
A. . B. . C. . D. .
4 2
2 y x x
3 2
3 1 y x x
3
3 y x x
3
3 y x x
Câu 10. Trong hệ tọa độ , mặt cầu tâm và bán kính bằng có phương trình là
Oxyz
(2;0;0)I
3
A. . B. .
2
2 2
2 3 x y z
2
2 2
2 9 x y z
C. . D. .
2
2 2
2 9 x y z
2
2 2
2 3 x y z
Câu 11. Trong không gian , cho điểm và mặt phẳng . Khoảng
Oxyz
2; 1;3M
: 2 2 1 0 P x y z
cách điểm đến mặt phẳng bằng
M
P
A. . B. . C. . D. .
2
5
3
3
10
3
Câu 12. Số phức thỏa mãn là
z
1 2 8 3 2 z i i i
A. . B. . C. . D. .
6 17 i
6 17
5 5
i
2 21
5 5
i
12 5 i
Câu 13. Thể tích của khối chóp có diện tích đáy bằng và chiều cao bằng là
3
4
A. . B. . C. . D. .
12
4
36
8
Câu 14. Cho khối chóp có vuông góc với mặt đáy, và . Thể
.S ABC
SA
4, 6, 10 SA AB BC
8CA
tích khối chóp đã cho bằng
A. . B. . C. . D. .
24
32
40
192
Câu 15. Cho mặt cầu có bán kính . Diện tích mặt cầu đã cho bằng
5r
A. . B. . C. . D. .
100
3
25
500
3
100
Câu 16. Môđun của số phức bằng
1 2 z i
A. . B. . C. . D. .
1
5
3
5
Câu 17. Cho khối trụ có bán kính đáy và chiều cao . Thể tích của khối trụ đã cho bằng
5r
3h
A. . B. . C. . D. .
75
30
25
5
Câu 18. Trong không gian với hệ trục tọa độ , cho đường thẳng . Một véctơ
Oxyz
4 8
: 6 11 ,
3 2
x t
d y t t
z t
chỉ phương của là
d
A. . B. . C. . D. .
4; 6; 3
u
8; 6; 3
u
8; 11; 2
u
8; 6; 2
u
Câu 19. Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực đại của hàm số là
y f x
y f x
O
x
y
A. . B. . C. . D. .
1
2
3
0
Câu 20. Đường tiệm cận ngang của đồ thị hàm số là
3 4
1
x
y
x
A. . B. . C. . D. .
1y
1x
3y
3x
Câu 21. Tập nghiệm của bất phương trình là
3
1
2
8
x
A. . B. . C. . D. .
8; S
6; S
0; S
6; S
Câu 22. Số cách xếp 5 học sinh thành một hàng dọc là
A. . B. . C. . D. .
25
120
1
5
Câu 23. Họ nguyên hàm của hàm số
5 9
2
x
f x
x
A. . B. . C. . D. .
5 ln 2 x x C
5 ln 2 x x C
5 4ln 2 x x C
5 4ln 2 x x C
Câu 24. Cho hàm số liên tục trên đoạn và thỏa mãn , .
y f x
6;11
11
6
d 8
f x x
6
2
d 3
f x x
Giá trị của biểu thức bằng
2 11
6 6
d d
P f x x f x x
A. . B. . C. . D. .
4P
11P
5P
2P
Câu 25. Cho hàm số . Nguyên hàm của hàm số thỏa mãn
2
3 sin cos 2 f x x x x
F x
f x
là
0 2F
A. . B. .
3
1
cos sin 2 2
2
F x x x x
3
1
cos sin 2 3
2
F x x x x
C. . D. .
3
1
cos sin 2 3
2
F x x x x
3
1
cos sin 2 2
2
F x x x x
Câu 26. Hàm số nghịch biến trên khoảng
3 2
6 1 y x x
A. . B. . C. . D. .
;1
1;5
0;4
1; 
Câu 27. Giá trị cực tiểu của hàm số là
4 2
4 3 y x x
A. . B. . C. . D. .
0
CT
y
1
CT
y
3
CT
y
2
CT
y
Câu 28. Cho , giá trị của bằng
log 2;log 3
a a
b c
2
log
a
Q b c
A. . B. . C. . D. .
7Q
4Q
10Q
12Q
Câu 29. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số và hai đường thẳng
3 2
11 6, 6 y x x y x
là
0, 2 x x
A. . B. . C. . D. .
2S
2
5
S
5S
5
2
S
Câu 30. Cho hình lập phương có lần lượt là tâm của hình vuông và
.
ABCD A B C D
,
O O
ABCD
. Góc giữa hai mặt phẳng và là
A B C D
A BD
ABCD
A. . B. . C. . D. .
AOA
OA A
A DA
A OC
Câu 31. Số giao điểm của đồ thị hàm số và đường thẳng là
3
3 3 y x x
y x
A.
.
B.
.
C.
.
D.
.
1
2
3
0
Câu 32. Cho hàm số liên tục trên và có đạo hàm . Hàm số
y f x
1 3
f x x x
y f x
đồng biến trên khoảng nào trong các khoảng dưới đây?
A.
.
B.
.
C.
.
D.
.
1;0
;0
3;
; 1
Câu 33. Chọn ngẫu nhiên hai số tự nhiên bé hơn . Xác suất để hai số được chọn có tổng không chia
10
hết cho là
2
A.
.
B.
.
C.
.
D.
.
5
9
4
45
11
45
4
9
Câu 34. Phương trình có hai nghiệm thực , . Giá trị của bằng
2
log 5 2 2
x
x
1
x
2
x
1 2 1 2
. P x x x x
A. 11. B.
9. C.
3. D.
2.
Câu 35. Cho số phức thỏa mãn . Tập hợp các điểm biểu diễn của số phức
z
3 z i z i
1 2 1 w i z
là đường thẳng có phương trình
A. . B.
. C.
. D.
.
2 7 0 x y
2 7 0 x y
2 7 0 x y
2 7 0 x y
Câu 36. Trong không gian , cho tam giác với Phương
Oxyz
ABC
2;4;2 , 1;0;2 , 3; 4; 2 . A B C
trình đường trung tuyến của tam giác là
AM
ABC
A. . B. .
2 2
2 3 1
x y z
2 4 2
4 6 2
x y z
C. . D. .
1 4 3
3 6 3
x y z
2 2
1 2 1
x y z
Câu 37. Trong không gian , cho điểm . Hình chiếu của điểm lên mặt phẳng
Oxyz
1;2; 3 A
A
Oyz
có tọa độ là
A. . B. . C. . D. .
1; 2;0
0;2; 3
1;0; 3
1;0;3
Câu 38. Cho khối chóp có đáy là hình vuông, và , góc giữa
.S ABCD
ABCD
SA ABCD
SA a
đường thẳng và mặt phẳng bằng (tham khảo hình vẽ). Tính khoảng cách giữa
SC
ABCD
30
đường thẳng và mặt phẳng .
AD
SBC
A. . B. . C. . D. .
2
a
6
a
15
5
a
3
6
a
Câu 39. Có bao nhiêu số nguyên dương thỏa mãn ?
a
3 3
6 3
log log a a a
A. . B. . C. . D. .
3
6
6
3
6
3 1
3
6 1
Câu 40. Cho hàm số liên tục trên . Gọi là hai nguyên hàm của trên thỏa
( )f x
( ), ( )F x G x
( )f x
mãn và . Khi đó, bằng
(10) (1) 11 F G
(0) (10) 1 F G
4
0
cos2 . (sin 2 )
x f x dx
A. . B. . C. . D. .
5
10
12
6
Câu 41. Có bao nhiêu giá trị nguyên của tham số để hàm số có bốn điểm
m
5 3
1 8
2023
5 3
y x x mx
cực trị?
A. . B. . C. . D. .
17
10
16
15
Câu 42. Cho số thực và các số phức thỏa mãn Gọi lần lượt là giá trị lớn
0a
z
| 6 8 | . z i a
,M m
nhất và giá trị nhỏ nhất của . Có bao nhiêu số nguyên để ?
| |z
a
3M m
A. . B. Vô số. C. . D. .
4
3
12
Câu 43. Cho khối lăng trụ đứng , có đáy là tam giác cân tại Mặt phẳng
' ' '
ABC.A B C
, .A BC a
'
(A BC)
tạo với đáy góc và tam giác có diện tích . Thể tích của khối lăng trụ đã cho bằng
0
60
'
A BC
2
6a
A. . B. . C. . D. .
3
64 3 .a
3
2 3 .a
3
9 .a
3
18 3 .a
Câu 44. Cho hàm số liên tục trên và . Biết rằng và
( )f x
(0; )
( ) 0, 0 f x x
' 2
( ) (2 1) ( ) f x x f x
Diện tích của hình phẳng giới hạn bởi các đường bằng
1
(1) .
2
f
2
( ), 1, e y f x x x
A. . B. . C. . D. .
2
2
2 ln
1
e
2
2
2 ln
1
e
2
1
1 ln
1
e
1
1 ln
2
e
Câu 45. Trên tập hợp số phức, xét phương trình ( là tham số thực). Tích của
2 2
2 2 0 z mz m m
m
tất cả các giá trị thực của để phương trình có hai nghiệm phân biệt thỏa mãn
m
1 2
,z z
1 2
2z z
là
A. . B. . C. . D. .
0
18
2
4
Câu 46. Trong không gian cho mặt phẳng vuông góc với mặt phẳng
,Oxyz
: 3 2 2 0 P x y z
và chứa đường thẳng . Khoảng cách từ điểm đến mặt phẳng
1 1 4
:
2 1 1
x y z
d
1; 2; 1 A
bằng
A. . B. . C. . D. .
8 3
3
4 3
3
24 3
3
8 3
Câu 47. Có bao nhiêu cặp số nguyên dương sao cho ứng với mổi giá trị nguyên dương của có
( , )x y
y
không quá 15 giá trị nguyên dương của thỏa mãn
x
2 2 2 2 2 2
5 3 5 3
log 3 36 log 12 log ( ) log 16 12 1? x xy y x y xy x xy y
A. 40. B. 36. C. 21. D. 33.
Câu 48. Cho khối nón tròn xoay có đường cao , bán kính đáy . Mặt phẳng đi
= 20 cmh
25 cmr
( )P
qua đỉnh của khối nón và cách tâm của đáy khối nón một khoảng bằng . Khi đó diện
O
12 cm
tích thiết điện của khổi nón cắt bởi mặt phằng bằng:
( )P
A. . B. . C. . D. .
2
500 cm
2
475 cm
2
450 cm
2
550 cm
Câu 49. Trong không gian , cho mặt cầu và điểm
Oxyz
2 2 2
( ) : 6 4 2 11 0 S x y z x y z
. Gọi là ba đường thẳng thay đổi không đồng phẳng cùng đi qua điểm
(0; 2;1)M
1 2 3
, ,d d d
và lần lượt cắt mặt cầu tại điểm thứ hai là . Thể tích của tứ diện
(0; 2;1)M
(S)
, ,A B C
MABC
đạt giá trị lớn nhất bằng
A. . B. . C. . D. .
50 3
9
1000 3
27
100 3
9
500 3
27
Câu 50. Cho hàm số bậc bốn có và . Biết hàm số có đồ thị
y f x
3
2
2
f
1 0f
y f x
như hình vẽ bên. Hàm số đồng biến trên khoảng nào dưới đây?
2
1
2 8
x x
g x f
A. . B. . C. . D. .
; 4
5;
2;4
3; 1
HẾT
BẢNG ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
A
B
C
B
A
A
C
D
C
D
B
B
B
D
D
A
C
B
C
D
B
A
C
B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
C
B
A
D
A
C
A
A
D
A
A
B
C
C
D
D
B
D
A
D
A
B
A
B
C
HƯỚNG DẪN GIẢI
Câu 1. Số phức liên hợp của số phức là
1 2 z i
A. . B. . C. . D. .
2 z i
1 2 z i
1 2 z i
1 2 z i
Lời giải
Chọn D
Số phức liên hợp của số phức là .
1 2 z i
1 2 z i
Câu 2. Tập xác định của hàm số là
5
log 2 y x
A. . B. . C. . D. .
2;
2;
;2
Lời giải
Chọn A
Điều kiện .
2 0 2 x x
Tập xác định của hàm số là .
5
log 2 y x
2;
Câu 3. Hàm số nào sau đây đồng biến trên ?
A. . B. . C. . D. .
x
y x
3
y x
2
y x
3
2
y x
Lời giải
Chọn B
Xét hàm số , ta có nên hàm số đồng biến trên .
3
y x
2
3 0,
y x x
3
y x
Câu 4. Tập nghiệm của bất phương trình là
log 3x
A. . B. . C. . D. .
10;
0;
1000;
;10
Lời giải
Chọn C
Ta có .
log 3 1000 x x
Tập nghiệm của bất phương trình là .
log 3x
1000;
Câu 5. Công bội của cấp số nhân với và là
q
n
u
1
1u
2
4u
A. . B. . C. . D. .
3q
4q
1
4
q
2 q
Lời giải
Chọn B
Công bội của cấp số nhân là .
q
n
u
2
1
4
u
q
u
Câu 6. Trong không gian cho hai mặt phẳng và ,
Oxyz
: 2 3 1 0
x y z
: 2 4 6 1 0
x y z
khi đó:
A. . B. . C. . D.
cắt .
/ /
Lời giải
Chọn A
Vectơ pháp tuyến ;
1; 2;3
n
2; 4;6
n
Ta có:
2
( 1;0;0)
n n
M M
Chứng tỏ .
/ /
Câu 7. Tọa độ giao điểm của đồ thị hàm số với trục hoành là
2 3
2
x
y
x
A. . B. . C. . D. .
3
;0
2
2;0
0; 2
3
0;
2
Lời giải
Chọn A
Cho
2 3 3
0 0 2 3 0
2 2
x
y x x
x
Tọa độ giao điểm của thị hàm số với trục hoảnh là .
2 3
2
x
y
x
3
;0
2
Câu 8. Cho hàm số có liên tục trên và . Giá trị của tích phân
( )y f x
'( )f x
0;1
(1) (0) 2 f f
bằng
1
0
'( )d
I f x x
A. . B. . C. . D. .
1 I
1I
2I
0I
Lời giải
Chọn C
.
1
0
1
'( )d ( ) (1) (0) 2
0
I f x x f x f f
Câu 9. Đồ thị của hàm số nào sau đây có dạng như hình vẽ bên?
A. . B. . C. . D. .
4 2
2 y x x
3 2
3 1 y x x
3
3 y x x
3
3 y x x
Lời giải
Chọn D.
Câu 10. Trong hệ tọa độ , mặt cầu tâm và bán kính bằng có phương trình là
Oxyz
(2;0;0)I
3
A. . B. .
2
2 2
2 3 x y z
2
2 2
2 9 x y z
C. . D. .
2
2 2
2 9 x y z
2
2 2
2 3 x y z
Lời giải
Chọn C
Mặt cầu tâm và bán kính bằng có phương trình là:
(2;0;0)I
3
.
2
2 2
2 9 x y z
Câu 11. Trong không gian , cho điểm và mặt phẳng . Khoảng
Oxyz
2; 1;3M
: 2 2 1 0 P x y z
cách điểm đến mặt phẳng bằng
M
P
A. . B. . C. . D. .
2
5
3
3
10
3
Lời giải
Chọn D
.
2
2 2
2.2 2. 1 3 1
10
,
3
2 2 1
d M P
Câu 12. Số phức thỏa mãn là
z
1 2 8 3 2 z i i i
A. . B. . C. . D. .
6 17 i
6 17
5 5
i
2 21
5 5
i
12 5 i
Lời giải
Chọn B
.
2 8 3 6 17
1 2 8 3 2
1 2 5 5
i i
z i i i z z i
i
Câu 13. Thể tích của khối chóp có diện tích đáy bằng và chiều cao bằng là
3
4
A. . B. . C. . D. .
12
4
36
8
Lời giải
Chọn B
.
1 1
. .3.4 4
3 3
V B h
Câu 14. Cho khối chóp có vuông góc với mặt đáy, và . Thể
.S ABC
SA
4, 6, 10 SA AB BC
8CA
tích khối chóp đã cho bằng
A. . B. . C. . D. .
24
32
40
192
Lời giải
Chọn B
Vì thỏa nên vuông tại .
ABC
2 2 2
BC AB AC
A
Khi đó, thể tích khối chóp đã cho bằng .
1 1 1
. . . .6.8.4 32
3 3 2
ABC
V S SA
Câu 15. Cho mặt cầu có bán kính . Diện tích mặt cầu đã cho bằng
5r
A. . B. . C. . D. .
100
3
25
500
3
100
Lời giải
Chọn D
Diện tích mặt cầu đã cho bằng .
2
4 100
S r
Câu 16. Môđun của số phức bằng
1 2 z i
A. . B. . C. . D. .
1
5
3
5
Lời giải
Chọn D
Ta có .
2
2
1 2 5 z
Câu 17. Cho khối trụ có bán kính đáy và chiều cao . Thể tích của khối trụ đã cho bằng
5r
3h
A. . B. . C. . D. .
75
30
25
5
Lời giải
Chọn A
Thể tích của khối trụ đã cho là .
2 2
.5 .3 75
V r h
Câu 18. Trong không gian với hệ trục tọa độ , cho đường thẳng . Một véctơ
Oxyz
4 8
: 6 11 ,
3 2
x t
d y t t
z t
chỉ phương của là
d
A. . B. . C. . D. .
4; 6; 3
u
8; 6; 3
u
8; 11; 2
u
8; 6; 2
u
Lời giải
Chọn C
Một véctơ chỉ phương của là .
d
8; 11; 2
u
Câu 19. Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực đại của hàm số là
y f x
y f x
O
x
y
A. . B. . C. . D. .
1
2
3
0
Lời giải
Chọn B
Từ đồ thị đã cho ta suy ra hàm số có hai điểm cực đại.
y f x
Câu 20. Đường tiệm cận ngang của đồ thị hàm số là
3 4
1
x
y
x
A. . B. . C. . D. .
1y
1x
3y
3x
Lời giải
Chọn C
Ta có .
3 4
lim lim 3
1
 
x x
x
y
x
Do đó đồ thị hàm số đã cho có một đường tiệm cận ngang là .
3y
Câu 21. Tập nghiệm của bất phương trình là
3
1
2
8
x
A. . B. . C. . D. .
8; S
6; S
0; S
6; S
Lời giải
Chọn D
Ta có: .
3 3 3
1
2 2 2 3 3 6 6; .
8
x x
x x x
Câu 22. Số cách xếp 5 học sinh thành một hàng dọc là
A. . B. . C. . D. .
25
120
1
5
Lời giải
Chọn B
Số cách xếp 5 học sinh thành một hàng dọc là: .
5! 120.
Câu 23. Họ nguyên hàm của hàm số
5 9
2
x
f x
x
A. . B. . C. . D. .
5 ln 2 x x C
5 ln 2 x x C
5 4ln 2 x x C
5 4ln 2 x x C
Lời giải
Chọn A
Ta có: .
5 2 1
5 9 1
d d d 5 d 5 ln 2
2 2 2
x
x
f x x x x x x x C
x x x
Câu 24. Cho hàm số liên tục trên đoạn và thỏa mãn , .
y f x
6;11
11
6
d 8
f x x
6
2
d 3
f x x
Giá trị của biểu thức bằng
2 11
6 6
d d
P f x x f x x
A. . B. . C. . D. .
4P
11P
5P
2P
Lời giải
Chọn C
Ta có:
11 2 6 11 2 11
6 6 2 6 6 6
d 8 d d d 8 d 3 d 8
f x x f x x f x x f x x f x x f x x
.
2 11
6 6
d d 5 5
f x x f x x P
Câu 25. Cho hàm số . Nguyên hàm của hàm số thỏa mãn
2
3 sin cos 2 f x x x x
F x
f x
là
0 2F
A. . B. .
3
1
cos sin 2 2
2
F x x x x
3
1
cos sin 2 3
2
F x x x x
C. . D. .
3
1
cos sin 2 3
2
F x x x x
3
1
cos sin 2 2
2
F x x x x
Lời giải
Chọn B
Ta có:
2 3
1
3 sin cos 2 d cos sin 2 .
2
F x x x x x x x x C
.
3 3
1 1
0 2 0 1 .0 2 3 cos sin 2 3.
2 2
F C C F x x x x
Câu 26. Hàm số nghịch biến trên khoảng
3 2
6 1 y x x
A. . B. . C. . D. .
;1
1;5
0;4
1; 
Lời giải
Chọn C
Tập xác định: .
D
Ta có . Giải .
2
3 12
y x x
2
0 3 12 0 0;4
y x x x
Hàm số nghịch biến trên khoảng .
3 2
6 1 y x x
0;4
Câu 27. Giá trị cực tiểu của hàm số là
4 2
4 3 y x x
A. . B. . C. . D. .
0
CT
y
1
CT
y
3
CT
y
2
CT
y
Lời giải
Chọn B
Tập xác định: .
D
Ta có . Giải .
3
4 8
y x x
3
0
0 4 8 0
2
x
y x x
x
Bảng biến thiên:
Giá trị cực tiểu của hàm số là .
4 2
4 3 y x x
1
CT
y
Câu 28. Cho , giá trị của bằng
log 2;log 3
a a
b c
2
log
a
Q b c
A. . B. . C. . D. .
7Q
4Q
10Q
12Q
Lời giải
Chọn A
Ta có .
2 2
log log log 2log log 2.2 3 7
a a a a a
Q b c b c b c
Câu 29. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số và hai đường thẳng
3 2
11 6, 6 y x x y x
là
0, 2 x x
A. . B. . C. . D. .
2S
2
5
S
5S
5
2
S
Lời giải
Chọn D
Giải phương trình: .
3 2 3 2
1
11 6 6 6 11 6 0 2
3
x
x x x x x x x
x
Ta có .
2 1 2
3 2 3 2 3 2
0 0 1
5
6 11 6 d 6 11 6 d 6 11 6 d
2
S x x x x x x x x x x x x
Câu 30. Cho hình lập phương có lần lượt là tâm của hình vuông và
.
ABCD A B C D
,
O O
ABCD
. Góc giữa hai mặt phẳng và là
A B C D
A BD
ABCD
A. . B. . C. . D. .
AOA
OA A
A DA
A OC
Lời giải
Chọn A
Ta có .
BD AO
BD A AO BD A O
BD AA
Ta có .
' , , ,
,
A BD ABCD BD
A O BD A O A BD A BD ABCD A O AO AOA
AO BD AO ABCD
Câu 31. Số giao điểm của đồ thị hàm số và đường thẳng là
3
3 3 y x x
y x
A.
.
B.
.
C.
.
D.
.
1
2
3
0
Lời giải
Chọn C
Phương trình hoành độ giao điểm: .
3 3
1
1 13
3 3 4 3 0
2
1 13
2
x
x x x x x x
x
Vậy số giao điểm đồ thị hàm số và đường thẳng là .
3
3 3 y x x
y x
3
Câu 32. Cho hàm số liên tục trên và có đạo hàm . Hàm số
y f x
1 3
f x x x
y f x
đồng biến trên khoảng nào trong các khoảng dưới đây?
A.
.
B.
.
C.
.
D.
.
1;0
;0
3;
; 1
Lời giải
Chọn A
Ta có .
1
0 1 3 0
3
x
f x x x
x
Bảng biến thiên
Từ bảng biến thiên ta có hàm số đồng biến trên khoảng .
y f x
1;3
Vậy hàm số đồng biến trên khoảng .
y f x
1;0
Câu 33. Chọn ngẫu nhiên hai số tự nhiên bé hơn . Xác suất để hai số được chọn có tổng không chia
10
hết cho là
2
A.
.
B.
.
C.
.
D.
.
5
9
4
45
11
45
4
9
Lời giải
Chọn A
Có tất cả số tự nhiên bé hơn .
10
10
Chọn ngẫu nhiên số tự nhiên từ số, số phần tử của không gian mẫu là .
2
10
2
10
45 n C
Để hai số được chọn có tổng không chia hết cho thì hai số đó phải gồm một số lẻ và một số
2
chẵn.
Số cách chọn là .
5.5 25
Vậy xác suất cần tìm là .
25 5
45 9
P
Câu 34. Phương trình có hai nghiệm thực , . Giá trị của bằng
2
log 5 2 2
x
x
1
x
2
x
1 2 1 2
. P x x x x
A. 11. B. 9. C. 3. D. 2.
Lời giải
Chọn D
Điều kiện .
2
5 2 0 2 5 log 5
x x
x
Ta có .
2 2
2
4
log 5 2 2 5 2 2 5 2 2 5.2 4 0
2
x x x x x x
x
x
Đặt , phương trình trở thành .
2 0
x
t t
2
1
5 4 0
4
t
t t tm
t
Với .
1 2 1 0
x
t x
Với .
4 2 4 2
x
t x
Vậy .
1 2 1 2
. 0 2 0.2 2 P x x x x
Câu 35. Cho số phức thỏa mãn . Tập hợp các điểm biểu diễn của số phức
z
3 z i z i
1 2 1 w i z
là đường thẳng có phương trình
A. . B. . C. . D. .
2 7 0 x y
2 7 0 x y
2 7 0 x y
2 7 0 x y
Lời giải
Chọn A
Ta có .
1
1 2 1
1 2
w
w i z z
i
Từ đó
1 1
3 3 1 1 2 1 1 2 3
1 2 1 2
w w
z i z i i i w i i w i i
i i
.
1 7 3 w i w i
Đặt . Suy ra
2
; , ; 1 w x yi x y i
1 7 3 1 1 7 3 w i w i x y i x y i
2 2 2 2
1 1 7 3 x y x y
2 2 2 2
2 1 2 1 14 49 6 9 x x y y x x y y
.
16 8 56 0 2 7 0 x y x y
Câu 36. Trong không gian , cho tam giác với Phương
Oxyz
ABC
2;4;2 , 1;0;2 , 3; 4; 2 . A B C
trình đường trung tuyến của tam giác là
AM
ABC
A. . B. .
2 2
2 3 1
x y z
2 4 2
4 6 2
x y z
C. . D. .
1 4 3
3 6 3
x y z
2 2
1 2 1
x y z
Lời giải
Chọn A
Trung điểm của là .
BC
2; 2;0M
VTCP của đường thẳng là
AM
4; 6; 2 .
AM
Phương trình chính tắc của có dạng: .
AM
2 2
2 3 1
x y z
Câu 37. Trong không gian , cho điểm . Hình chiếu của điểm lên mặt phẳng
Oxyz
1;2; 3 A
A
Oyz
có tọa độ là
A. . B. . C. . D. .
1; 2;0
0;2; 3
1;0; 3
1;0;3
Lời giải
Chọn B
Hình chiếu của điểm lên mặt phẳng có tọa độ là .
A
Oyz
0;2; 3
Câu 38. Cho khối chóp có đáy là hình vuông, và , góc giữa
.S ABCD
ABCD
SA ABCD
SA a
đường thẳng và mặt phẳng bằng (tham khảo hình vẽ). Tính khoảng cách giữa
SC
ABCD
30
đường thẳng và mặt phẳng .
AD
SBC
A. . B. . C. . D. .
2
a
6
a
15
5
a
3
6
a
Lời giải
Chọn C
Ta có
, 30 .
SC ABCD SCA
Vì
/ / / / , , . AD BC AD SBC d AD SBC d A SBC
Dựng . Dễ dàng chứng mình
AH SB
.AH SBC
Suy ra
2 2
, .
SA AB
d A SBC AH
SA AB
Ta có
6
3 .
2
a
AC a AB
Suy ra .
15
5
a
AH
Câu 39. Có bao nhiêu số nguyên dương thỏa mãn ?
a
3 3
6 3
log log a a a
A. . B. . C. . D. .
3
6
6
3
6
3 1
3
6 1
Lời giải
Chọn C
Đặt , do
6
t a
0 0. a t
Bất phương trình trở thành:
3 2 2 3 2 2
6 3 6 3
log log log log 0. t t t t t t
Xét hàm số:
3 2 2
6 3
log log , 0. f t t t t t
Khi đó,
2
2
3 2
3 2 2
' 0, 0.
ln3
ln 6
t t t
f t t
t
t t
Suy ra hàm số luôn nghịch biến với mọi
f t
0t
Suy ra là nghiệm duy nhất của phương trình
3t
0.f t
Yêu cầu bài toán
(do hàm số luôn nghịch biến với mọi ).
0 3 0 3 f t f t f t
f t
0t
Suy ra . Vì a nguyên dương nên có số nguyên dương thỏa yêu cầu bài
6
6
3 3 a a
6
3 1
a
toán.
Câu 40. Cho hàm số liên tục trên . Gọi là hai nguyên hàm của trên thỏa
( )f x
( ), ( )F x G x
( )f x
mãn và . Khi đó, bằng
(10) (1) 11 F G
(0) (10) 1 F G
4
0
cos2 . (sin 2 )
x f x dx
A. . B. . C. . D. .
5
10
12
6
Lời giải
Chọn D
Vì là hai nguyên hàm của nên ta có
( ), ( )F x G x
( )f x
( ) ( ) F x G x C
Theo đề
(10) (1) 11 (10) (1) 11
1 0 12
(0) (10) 1 (0) (10) 1
F G G C G
G G
F G G C G
Xét .
4
0
cos2 . (sin 2 )
I x f x dx
Đặt , đổi cận .
1
sin 2 d cos2 d
2
t x t x x
0 0
1
4
x t
x t
Khi đó .
1
1
0
0
1 1 1
( ) 1 0 6.
2 2 2
I f t dt G t G G
Câu 41. Có bao nhiêu giá trị nguyên của tham số để hàm số có bốn điểm
m
5 3
1 8
2023
5 3
y x x mx
cực trị?
A. . B. . C. . D. .
17
10
16
15
Lời giải
Chọn D
Ta có ; (1).
4 2
8
y x x m
4 2
0 8
y x x m
Ycbt có bốn nghiệm phân biệt.
1
Xét hàm số , có . .
4 2
8 g x x x
3
4 16
g x x x
3
0
0 4 16 0
2
x
g x x x
x
Bảng biến thiên.
Từ đây ta có , vậy có giá trị nguyên của tham số thỏa mãn.
16 0 m
15
m
Câu 42. Cho số thực và các số phức thỏa mãn Gọi lần lượt là giá trị lớn
0a
z
| 6 8 | . z i a
,M m
nhất và giá trị nhỏ nhất của . Có bao nhiêu số nguyên để ?
| |z
a
3M m
A. . B. Vô số. C. . D. .
4
3
12
Lời giải
Chọn B
Ta có , khi đó tập hợp điểm biểu diễn của số phức là đường tròn tâm
| 6 8 | z i a
z
6;8 ,I
bán kính , với .
R a
10OI
Giá trị lớn nhất của là .
| |z
10 M OI a a
TH1: .
10a
Khi đó giá trị nhỏ nhất của là .
| |z
10 m OI a a
Để .
3 10 3 10 5 M m a a a
TH này có giá trị của thỏa mãn, .
4
a
1, 2,3,4a
TH2: .
10a
Khi đó giá trị nhỏ nhất của là .
| |z
10 m a OI a
Để .
3 10 3 10 20 M m a a a
TH này có vô số giá trị của thỏa mãn, .
a
/ 20 a a
KL: Vậy có vô số giá trị nguyên của thỏa mãn yêu cầu bài toán.
a
Câu 43. Cho khối lăng trụ đứng , có đáy là tam giác cân tại Mặt phẳng
' ' '
ABC.A B C
, .A BC a
'
(A BC)
tạo với đáy góc và tam giác có diện tích . Thể tích của khối lăng trụ đã cho bằng
0
60
'
A BC
2
6a
A. . B. . C. . D. .
3
64 3 .a
3
2 3 .a
3
9 .a
3
18 3 .a
Lời giải
Chọn D
Gọi H là trung điểm của
'
BC AH BC A H BC
Mặt phẳng tạo với đáy góc nên
'
(A BC)
0
60
' 0
60AHA
'
' '
1
. 12
2
A BC
S A H BC A H a
' ' 0 ' 0
.sin 60 6 3; .cos60 6 . AA A H a AH A H a
Thể tích khối lăng trụ là: .
3
1
. . . 18 3
2
ABC
V S AA AH BC AA a
Câu 44. Cho hàm số liên tục trên và . Biết rằng và
( )f x
(0; )
( ) 0, 0 f x x
' 2
( ) (2 1) ( ) f x x f x
Diện tích của hình phẳng giới hạn bởi các đường bằng
1
(1) .
2
f
2
( ), 1, e y f x x x
A. . B. . C. . D. .
2
2
2 ln
1
e
2
2
2 ln
1
e
2
1
1 ln
1
e
1
1 ln
2
e
Lời giải
Chọn A
Từ giả thiết:
'
'
' 2
2
( ) 1
( ) (2 1) ( ) 2 1 2 1
( ) ( )
f x
f x x f x x x
f x f x
Do đó:
2
1
( 2 1)
( )
x dx x x C
f x
Mà nên . Vậy
1
(1)
2
f
0C
2
1
( ) .
f x
x x
Diện tích của hình phẳng giới hạn bởi các đường là
2
( ), 1, e y f x x x
.
2
2 2
1
1 2
d 2 ln
1
e
S x
x x e
Câu 45. Trên tập hợp số phức, xét phương trình ( là tham số thực). Tích của
2 2
2 2 0 z mz m m
m
tất cả các giá trị thực của để phương trình có hai nghiệm phân biệt thỏa mãn
m
1 2
,z z
1 2
2z z
là
A. . B. . C. . D. .
0
18
2
4
Lời giải
Chọn D
Ta có .
' 2 m
TH1:
' 0 0 m
Phương trình có hai nghiệm phân biệt là hai số thực.
1 2
1 2
1 2
2
2
2
z z
z z
z z
Theo viet có .
2
1 2 1 2
2 ; . 2 z z m z z m m
Nếu
2 2 2
1 2 2 1 1 2
0
2 2 ; 4 . 8 2 9 2 0
2
9
m
z z z m z m z z m m m m m
m
Do .
2
0
9
m m
Nếu
2 2 2
1 2 2 1 1 2
0
2 4 8 1
2 ; . 2 2 0
18
3 3 9 9
m
m m
z z z z z z m m m m m
m
Do .
0 18 m m
TH2:
' 0 0 m
Phương trình có hai nghiệm là hai số phức liên hợp nên .
1 2
z z
.
1 2 1 1
2 0 0 z z z z
Thay vào phương trình ta được ( loại).
2
2 0 0; 2 m m m m
Vậy .
2
.( 18) 4
9
Câu 46. Trong không gian cho mặt phẳng vuông góc với mặt phẳng
,Oxyz
: 3 2 2 0 P x y z
và chứa đường thẳng . Khoảng cách từ điểm đến mặt phẳng
1 1 4
:
2 1 1
x y z
d
1; 2; 1 A
bằng
A. . B. . C. . D. .
8 3
3
4 3
3
24 3
3
8 3
Lời giải
Chọn A
.
( )
1;3; 2 , 2; 1;1 ; 1; 5; 7
P d P d
n u n n u
Điểm .
(1; 1;4)
M d M
Phương trình mặt phẳng là .
1 1 5 1 7 4 0 5 7 22 0 x y z x y z
.
8 3
;
3
d A
Câu 47. Có bao nhiêu cặp số nguyên dương sao cho ứng với mổi giá trị nguyên dương của có
( , )x y
y
không quá 15 giá trị nguyên dương của thỏa mãn
x
2 2 2 2 2 2
5 3 5 3
log 3 36 log 12 log ( ) log 16 12 1? x xy y x y xy x xy y
A. 40. B. 36. C. 21. D. 33.
Lời giải
Chọn B
2 2 2 2 2 2
5 3 5 3
log 3 36 log 12 log ( ) log 16 12 1 x xy y x y xy x xy y
2 2 2 2
5 3
2 2
3 36 3 48 36
log log
12
x xy y x xy y
xy x y
5 3
12 48
log 3 1 log 3
12
x y
x y
y x
y x
Đặt . Ta được .
12
0
x y
a
y x
5 3
48
log (3 1) log 3 0
a
a
Xét
5 3
48
( ) log (3 1) log 3 ,
f a
a
a
(0, ). a
2
48
3
( ) 0, 0.
48
(3 1)ln5
3 ln 3
a
f a a
a
a
đồng biến trên
( ) f a
(0 )
Mà . Khi đó ta có
(8) 0 ( ) 0 8 f f a a
2 2 2 2
12 8 12 8 8 12 0 ( 2 )( 6 ) 0
x y
x y xy x xy y x y x y
y x
2 6 . y x y
Để mỗi giá trị của có không quá 15 giá trị nguyên dương của thì điều kiện là
y
x
*
(6 1) (2 1) 1 15 4, 1 4. y y y y N y
Với có 3 cặp
1 2;6 y x
; .x y
Với có 7 cặp
2 4;12 y x
; .x y
Với có 11 cặp
3 6;18 y x
; .x y
Với có 15 cặp
4 8;24 y x
; .x y
Vậy có 36 cặp thỏa yêu cầu bài toán.
;x y
Câu 48. Cho khối nón tròn xoay có đường cao , bán kính đáy . Mặt phẳng đi
= 20 cmh
25 cmr
( )P
qua đỉnh của khối nón và cách tâm của đáy khối nón một khoảng bằng . Khi đó diện
O
12 cm
tích thiết điện của khổi nón cắt bởi mặt phằng bằng:
( )P
A. . B. . C. . D. .
2
500 cm
2
475 cm
2
450 cm
2
550 cm
Lời giải
Chọn A
Gọi là đình của khối nón. Mặt phẳng đi qua đỉnh cắt khối nón theo hai đường sinh bằng
S
(P)
S
nhau là nên ta có thiết diện là tam giác cân .
SA SB
SAB
Gọi I là trung điêm của đoạn , ta có . Từ tâm của đáy ta kẻ tại , ta
AB
OI AB
O
OH SI
H
có và do đó theo giả thiết ta có . Xét tam giác vuông SOI
( )OH SAB
12 cmOH
2 2 2 2 2
1 1 1 1 1
ta có: 15( cm).
21 20
OI
OI OH OS
Mặt khác, xét tam giác vuông SOI ta còn có:
. .OS OI SI OH
. 20.15
25( cm).
12
OS OI
SI
OH
Gọi là diện tích của thiết diện tam giác . Ta có: , trong đó
t
S
SAB
1
.
2
t
S AB SI
. Vì nên và .
2AB AI
2 2 2 2 2 2
25 15 20 AI OA OI
20 cmAI
40 cmAB
Vậy thiết diện có diện tích là: .
SAB
2
1
40 25 500 cm
2
t
S
Câu 49. Trong không gian , cho mặt cầu và điểm
Oxyz
2 2 2
( ) : 6 4 2 11 0 S x y z x y z
. Gọi là ba đường thẳng thay đổi không đồng phẳng cùng đi qua điểm
(0; 2;1)M
1 2 3
, ,d d d
và lần lượt cắt mặt cầu tại điểm thứ hai là . Thể tích của tứ diện
(0; 2;1)M
(S)
, ,A B C
MABC
đạt giá trị lớn nhất bằng
A. . B. . C. . D. .
50 3
9
1000 3
27
100 3
9
500 3
27
Lời giải
Chọn B
Mặt cầu có tâm bán kính
2 2 2
( ) : 6 4 2 11 0 S x y z x y z
(3;2;1)
5R
Mặt phẳng chứa ba điểm cắt mặt cầu ta được một hình tròn tâm I.
, ,A B C
(S)
Thể tích của tứ diện đạt giá trị lớn nhất khi thể tích hình nón đỉnh có đáy là hình tròn
MABC
M
tâm I lớn nhất.
Gọi lần lượt là chiều cao và bán kính đáy hình nón
,h r
Ta có:
2 2 2
2 2 2
10 10
2 2
l r h
R S h r h r h h
h h
Thể tích hình nón là:
2 2
2
1 1
. . .(10h ).
3 3
1 20 10 2
' .(20h 3 ) 0
3 3 3
V r h h h
V h h r
Xét đường tròn đi qua 3 điểm :
, ,A B C
Diện tích tam giác ABC lớn nhất khi tam giác ABC đều
.
50 1 1000 3
. .
3 27
3
ABC MABC ABC
S MaxV h S
Câu 50. Cho hàm số bậc bốn có và . Biết hàm số có đồ thị
y f x
3
2
2
f
1 0f
y f x
như hình vẽ bên. Hàm số đồng biến trên khoảng nào dưới đây?
2
1
2 8
x x
g x f
A. . B. . C. . D. .
; 4
5;
2;4
3; 1
Lời giải
Chọn C
Ta đặt
2
1
1 1
2 8 2 2 4
x x x x
h x f h x f
1
0 1 0 1 , 1
2 2 4 2 2
x x x x
h x f f
Đặt
1 2 2
2
3 0
1 1 1 4
1 4
x
t x t
t x
f t t t x
t x
Ta có BBT
Vậy hàm số đồng biến trên khoảng .
g x
2;4
HẾT

Tài liệu khác của Toán

Preview text:

SỞ GD&ĐT QUẢNG BÌNH
KỲ THI THỬ TỐT NGHIỆP THPT NĂM 2023 Bài thi: TOÁN
ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề thi có 05 trang)
Họ, tên thí sinh:…………………………………………..
Số báo danh:……………………………………………… Mã đề thi: 001
Câu 1. Số phức đối của số phức z =1− 2i là A. z′ = 1 − − 2i .
B. z′ =1+ 2i . C. z′ = 1 − + 2i . D. z′ = 2 − + i .
Câu 2. Hàm số nào sau đây đồng biến trên  ? x x x x A. 1 y   =  . B. 3 y   = . C. 1 y   = . D. 1 y   = . 5           2  10   2  4
Câu 3. Tập xác định của hàm số 7
y = f (x) = (x −3) là A.  . B.  \{ } 3 . C. (3;+∞) . D. (0;+∞) .
Câu 4. Tập nghiệm của bất phương trình log x ≥ 2 là A. (10;+∞). B. (0;+∞). C. [100;+∞) . D. ( ; −∞ 10).
Câu 5. Cho cấp số nhân (u u = 81 u = 27 u n ) với 1 và 2
. Công bội của cấp số nhân ( n ) là A. 1 q = − . B. 1 q = .
C. q = 3. D. q = 3 − . 3 3
Câu 6. Mặt phẳng nào sau đây song song với mặt phẳng (α ) có phương trình
x + y + 2z + 2 = 0 ?
A. (Q): x + y − 2z − 2 = 0.
B. (R): x + y − 2z +1= 0.
C. (S): x + y + 2z −1= 0 .
D. (P): x − y + 2z − 2 = 0 .
Câu 7. Đồ thị hàm số 1− = x y cắt trục Oy x +1
tại điểm có tọa độ là A. (0; ) 1 . B. (1;0) . C. (0;− ) 1 . D. (1; ) 1 .
Câu 8. Cho hàm số y = f (x) có đạo hàm f ′(x) liên tục trên [0; ] 1 và thỏa mãn 1 f (0) = 1, − f ( )
1 = 3 . Tính I = f ′
∫ (x)dx. 0 1 1 1 1 A. f ′
∫ (x)dx = 2 .
B. f ′(x)dx = 4 − ∫
. C. f ′(x)dx = 2 − ∫ . D. f ′ ∫ (x)dx = 4 . 0 0 0 0
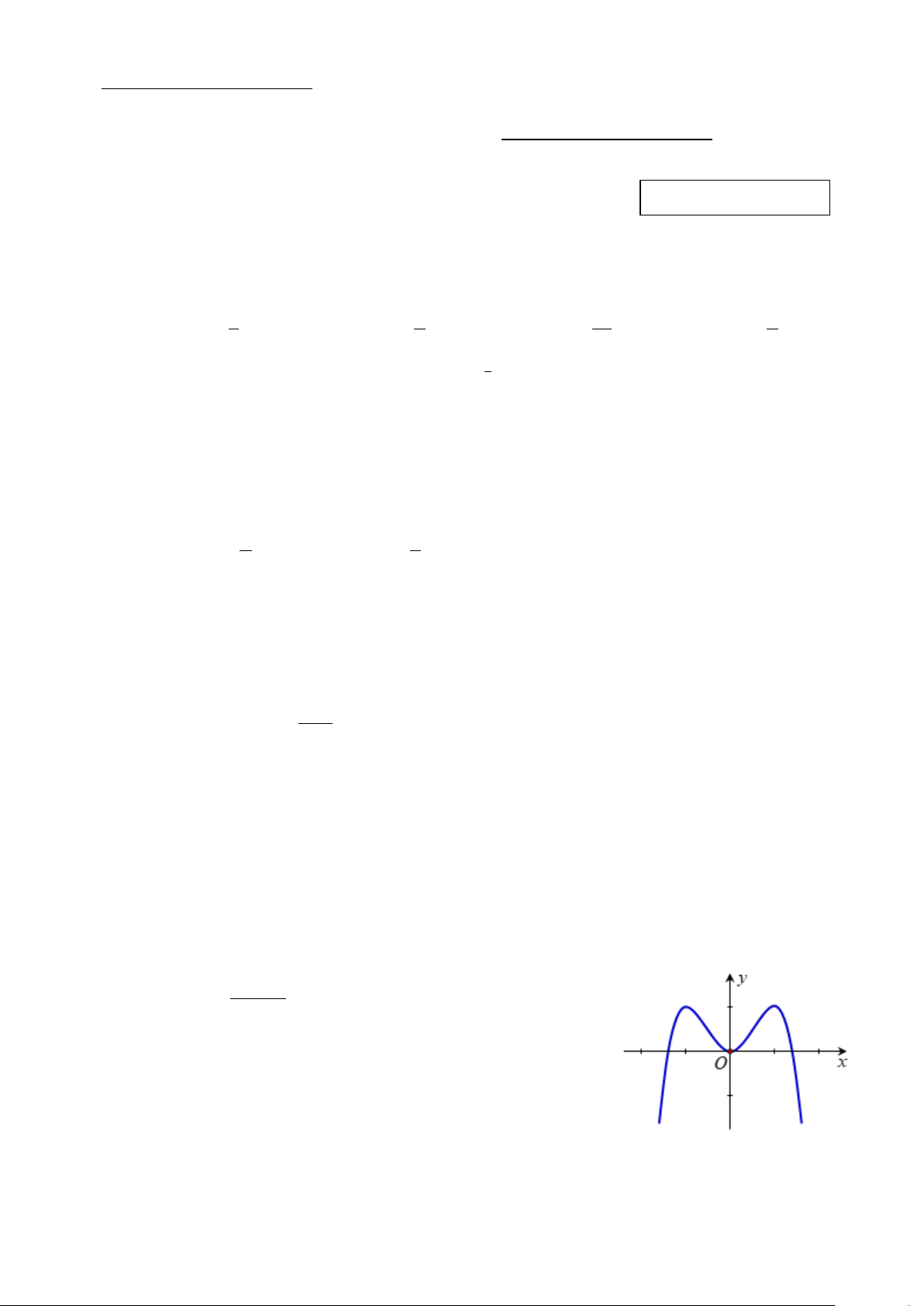
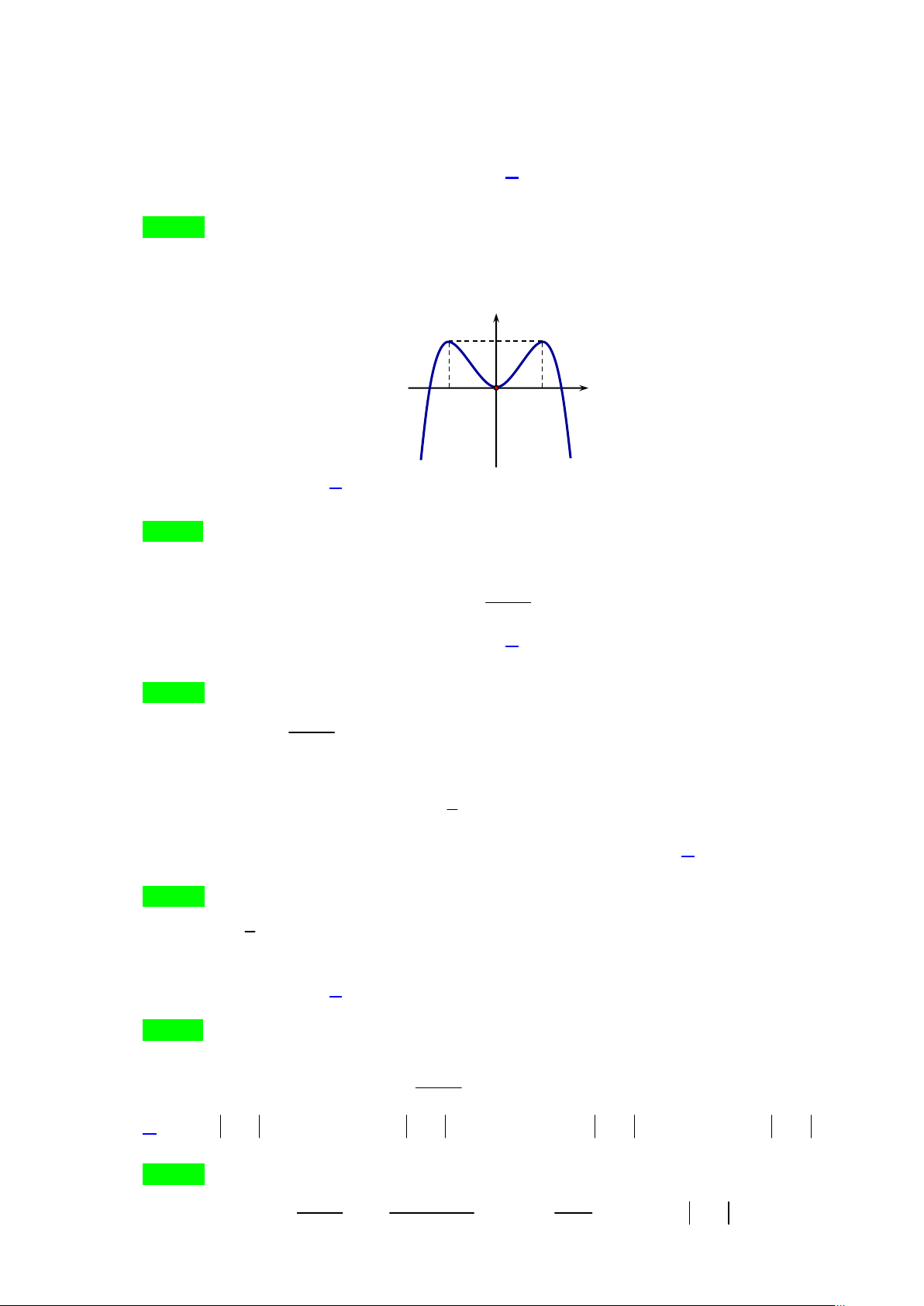
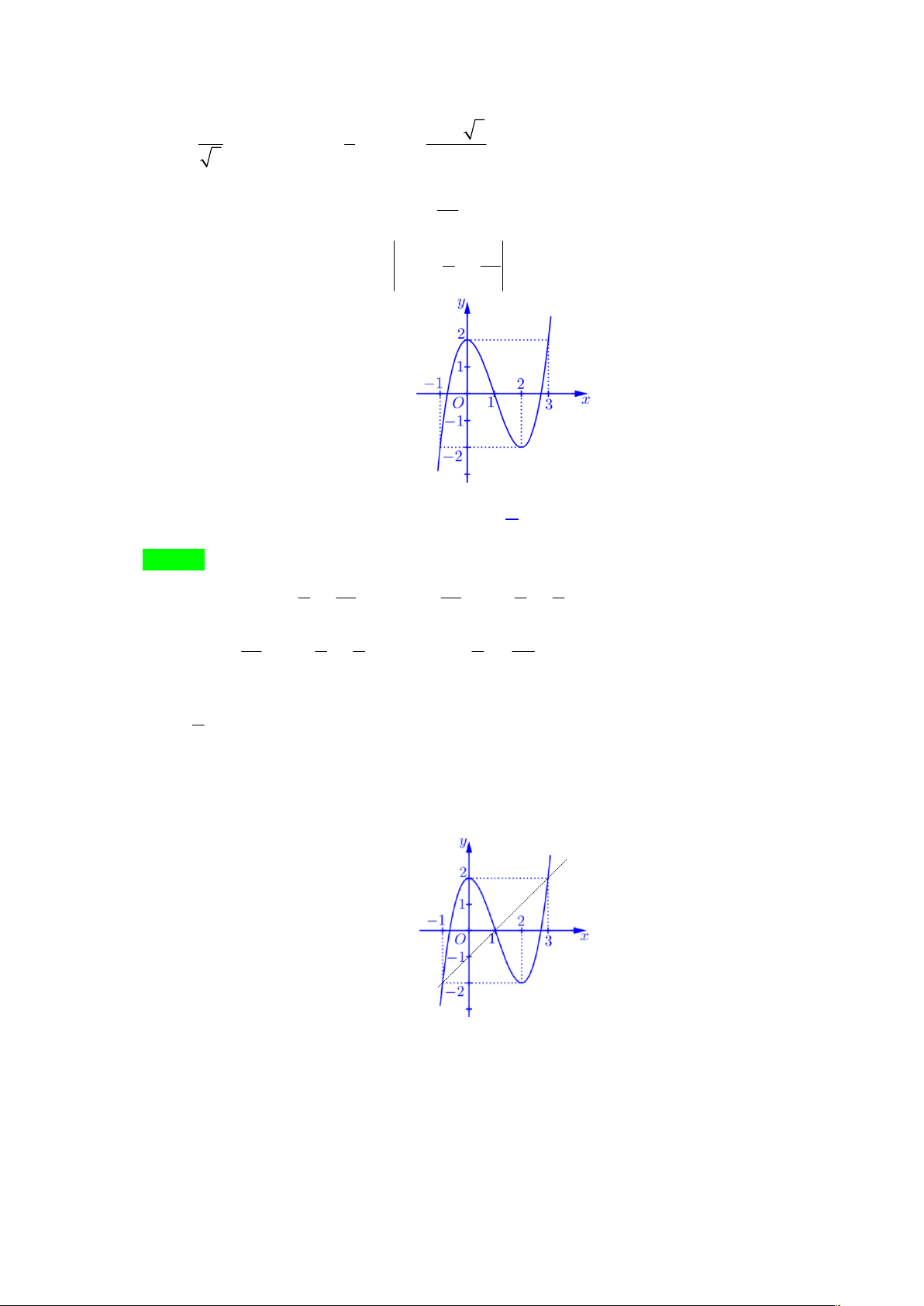
Câu 9. Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào trong các hàm số dưới đây? 4 − x +1 A. y =
y = − x + x x . B. 4 2 4 2 . − 2 C. 4 2
y = 4x − 2x . D. 3 2 y = 4 − x − 2x .
Câu 10. Trong không gian Oxyz, phương trình mặt cầu có tâm I (1;0;0) và bán kính bằng 2 là A. (x − )2 2 2
1 + y + z = 2 . B. (x + )2 2 2 1 + y + z = 2. C. (x − )2 2 2
1 + y + z = 4 . D. (x + )2 2 2 1 + y + z = 4.
Trang 1/5 Mã đề 001
Câu 11. Trong không gian Oxyz, cho điểm (
A 1;2;2) và mặt phẳng (α ) : x + 2y − 2z − 4 = 0 .
Khoảng cách d từ điểm A đến mặt phẳng (α) là A. 1 d = . B. d =1. C. 13 d = . D. d = 3. 3 3
Câu 12. Số phức z thỏa mãn điều kiện (i −3) z −5+ 3i = 0 là A. 9 2 z = − + .i B. 9 2
z = − .i C. 9 2 z = − − .i D. 6 7 z = − − .i 5 5 5 5 5 5 5 5
Câu 13. Khối chóp có diện tích đáy bằng 2
a và chiều cao bằng 2a , thể tích của khối chóp đã cho bằng 3 a 3 2a A. . B. 3 a . C. 3 2a . D. . 3 3
Câu 14. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại ,
A AB = 3a, AC = 2 . a Cạnh
bên SA vuông góc với đáy, SA = 4 .
a Thể tích của khối chóp S.ABC là 3 A. 3 4a 5 . B. 4a 5 V = . C. 3 V = 4a . D. 3 V = 12a . 3
Câu 15. Cho mặt cầu có bán kính r = 5 . Diện tích của mặt cầu đã cho bằng 100π 500π A. 3 . B. 100π . C. 25π . D. 3 .
Câu 16. Cho số phức z = 20i - 21. Môđun của số phức z bằng
A. z = 20.
B. z = 841.
C. z = 29 . D. z = 29.
Câu 17. Cho khối trụ có bán kính đáy r  4 và chiều cao h  2 . Thể tích khối trụ đó là A.8π . B.32π. C. 16π. D. 32π . 3
Câu 18. Trong không gian với hệ toạ độ Oxyz một vectơ chỉ phương của đường thẳng
(d ): x −1 y −3 2− z = = là 2 3 5    
A. u = (2;3;5).
B. u = (1;3;2) .
C. u = (1;3;− 2).
D. u = (2;3;−5) .
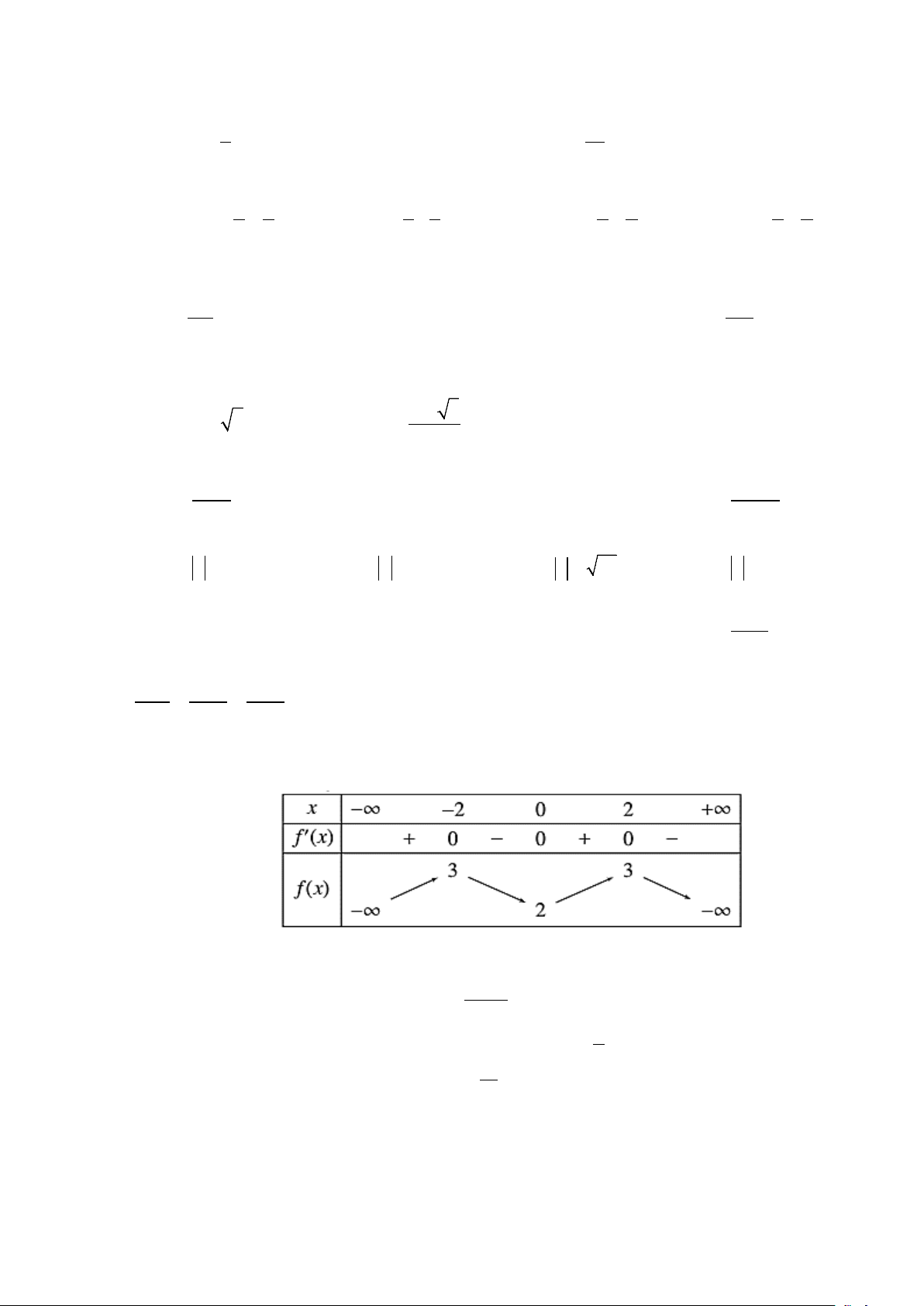
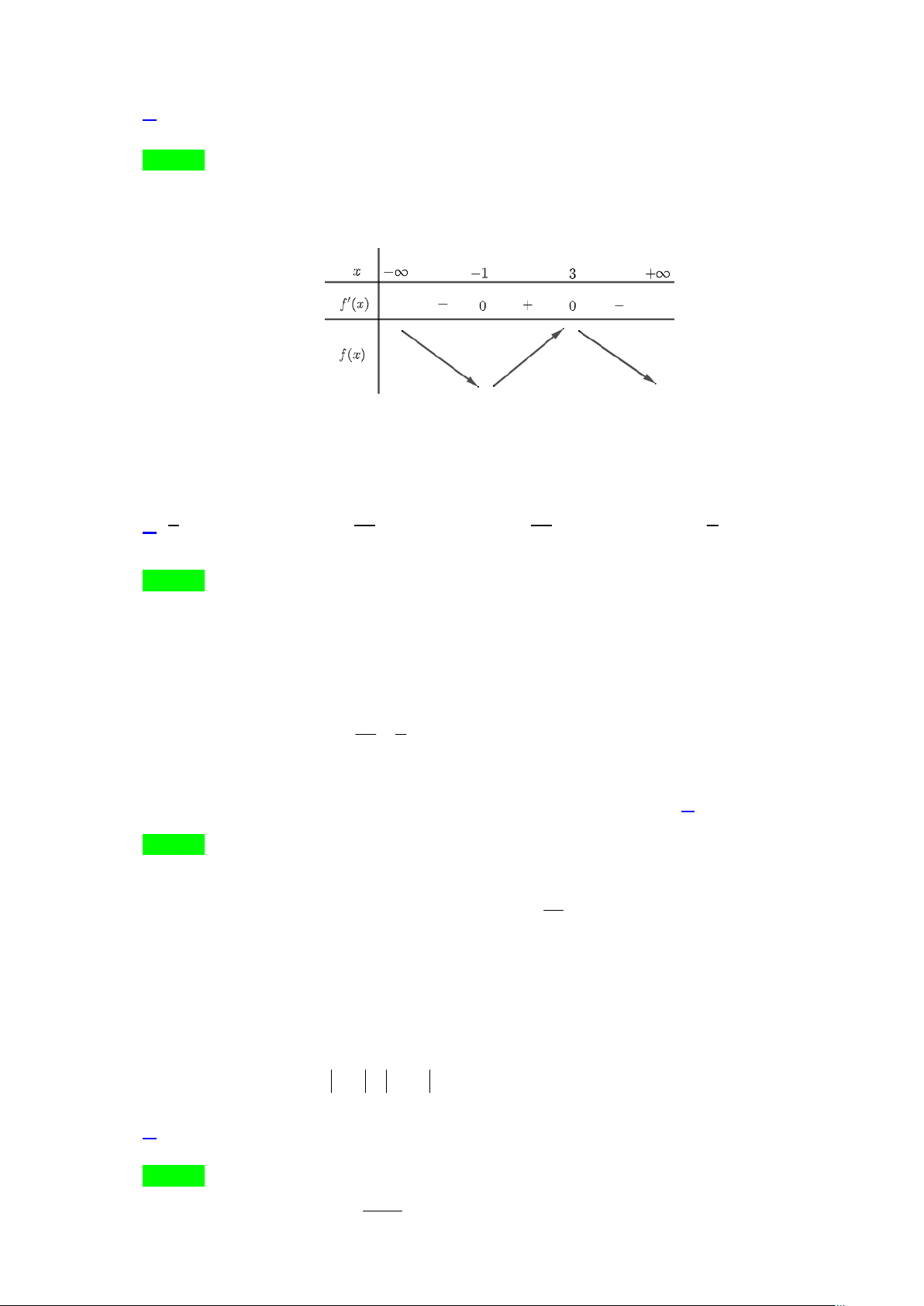
Câu 19. Cho hàm số y = f (x) có bảng biến thiên:
Số điểm cực trị của hàm số đã cho là A. 3. B. 4. C. 1. D. 2.
Câu 20. Tiệm cận đứng của đồ thị hàm số 2x +1 y = là: x −1 A. x =1. B. y = 1 − . C. 1 x = − . D. y = 2 . 2 x 1 +
Câu 21. Tập nghiệm của bất phương trình x 2 9 ≤ 9 là A.[1;+∞) . B.  . C. ( ] ;1 −∞ . D. ( ; −∞ − ] 1 .
Câu 22. Có bao nhiêu cách xếp chỗ ngồi cho bốn bạn học sinh vào bốn chiếc ghế kê thành một hàng ngang? A. 24 . B. 4. C. 12. D. 8.
Trang 2/5 Mã đề 001
Câu 23. Họ nguyên hàm của hàm số f (x) 3x +5 = là: x + 2
A. 3x − ln x + 2 + C .
B. 3x + ln x + 2 + C .
C. 3x − 4ln x + 2 + C .
D. 3x + 4ln x + 2 + C . 12
Câu 24. Cho hàm số y = f (x) liên tục trên đoạn [ 5;
− 12] và thỏa mãn f ∫ (x)dx =7 , 5 − 6 2 12 f (x)dx 3 = ∫
. Giá trị của biểu thức P = f
∫ (x)dx+ f
∫ (x)dx là 2 5 − 6
A. P = 4 .
B. P =10.
C. P = 3. D. P = 2 .
Câu 25. Cho hàm số f (x) 2
= 3x + sin x − cos2 .x Nguyên hàm F (x) của hàm số f (x) thỏa mãn F (0) = 2 là A. F (x) 3 1
= x − cos x − sin 2x + 2. B. F (x) 3 1
= x − cos x − sin 2x + 3. 2 2 C. F (x) 3 1
= x − cos x − sin 2x − 3. D. F (x) 3 1
= x − cos x − sin 2x − 2. 2 2
Câu 26. Tất cả các khoảng đồng biến của hàm số 1 3 2
y = x − 2x + 3x +1 là 3 A. ( ) ;1
−∞ và (3;+ ∞) . B. (1;3) . C. ( ; −∞ − 3) và ( 1;
− + ∞) . D. (3;+ ∞) .
Câu 27. Điểm cực tiểu của đồ thị hàm số 4 2
y  x  4x 5 là
A. x  0 . B. 0;  5 .
C. x  2 . D.  2; 1.
Câu 28. Cho a ,b,c là các số thực dương khác 1 thỏa mãn log b =
b = . Khi đó log c bằng a 6, logc 3 a A. 2. B. 9. C. 1 . D. 18. 2
Câu 29. Diện tích S của hình phẳng giới hạn bởi các đường 3 2
y = x − 4x + 3x −1 và y = 2 − x +1 là:
A. S = 3.
B. S = 2. C. 1 S = . D. 1 S = . 12 2
Câu 30. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B . Cạnh bên SA vuông góc
với mặt phẳng đáy. Gọi I là trung điểm của BC . Góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) là A. SIA . B. SBA. C. SCA. D. ASB .
Câu 31. Số giao điểm của đường cong 3 2
y = x − 2x + x −1 và đường thẳng y = 1− 2x là A. 3. B. 0. C. 1. D. 2.
Câu 32. Cho hàm số y = f (x) có đạo hàm f ′(x) = ( 2x + ) 1 (x − 2), x
∀ ∈  . Mệnh đề nào dưới
đây đúng? A. Hàm số nghịch biến trên khoảng (2;+∞).
B. Hàm số đồng biến trên khoảng ( ; −∞ +∞) .
C. Hàm số đồng biến trên khoảng ( 1; − 2) .
D. Hàm số nghịch biến trên khoảng ( ;2 −∞ ) .
Câu 33. Chọn ngẫu nhiên hai số tự nhiên bé hơn 10. Xác suất để hai số được chọn có tổng chia hết cho 2 là: A. 5. B. 4 . C. 11 . D. 4 . 9 45 45 9
Trang 3/5 Mã đề 001
Câu 34. Cho phương trình log x x , x x x 4 3.2  
1  x1 có hai nghiệm 1 2 . Tổng 1 2 là: A. 2. B. log . log 12. 2 6 4 2 C. 2 D. 12.
Câu 35. Cho số phức z thỏa mãn z −i = z −1+ 2i . Tập hợp các điểm biểu diễn của số phức
w = (2−i) z +1 là một đường thẳng có phương trình
A. x + 7y + 9 = 0 .
B. x + 7y − 9 = 0 . C. x − 7y − 9 = 0 .
D. x − 7y + 9 = 0 .
Câu 36. Trong không gian Oxyz , cho tam giác ABC với A( 1;
− 4;− 3) , B(1;0;2) , C (3;− 4;− 2).
Phương trình đường trung tuyến AM của tam giác ABC là:
A. x − 2 y + 2 z − + − = = .
B. x 1 y 4 z 3 = = . 1 2 − 1 3 6 − 3
C. x −1 y − 4 z −3 + − = = .
D. x 2 y 2 z = = . 3 6 3 1 2 − 1
Câu 37. Trong không gian Oxyz , cho điểm A( 1;
− 2;− 3) . Hình chiếu của điểm A lên mặt
phẳng (Oxy) có tọa độ là A.(1; 2 − ;0). B. ( 1; − 2;0). C. ( 1; − 0;− 3) . D. (1;0;3).
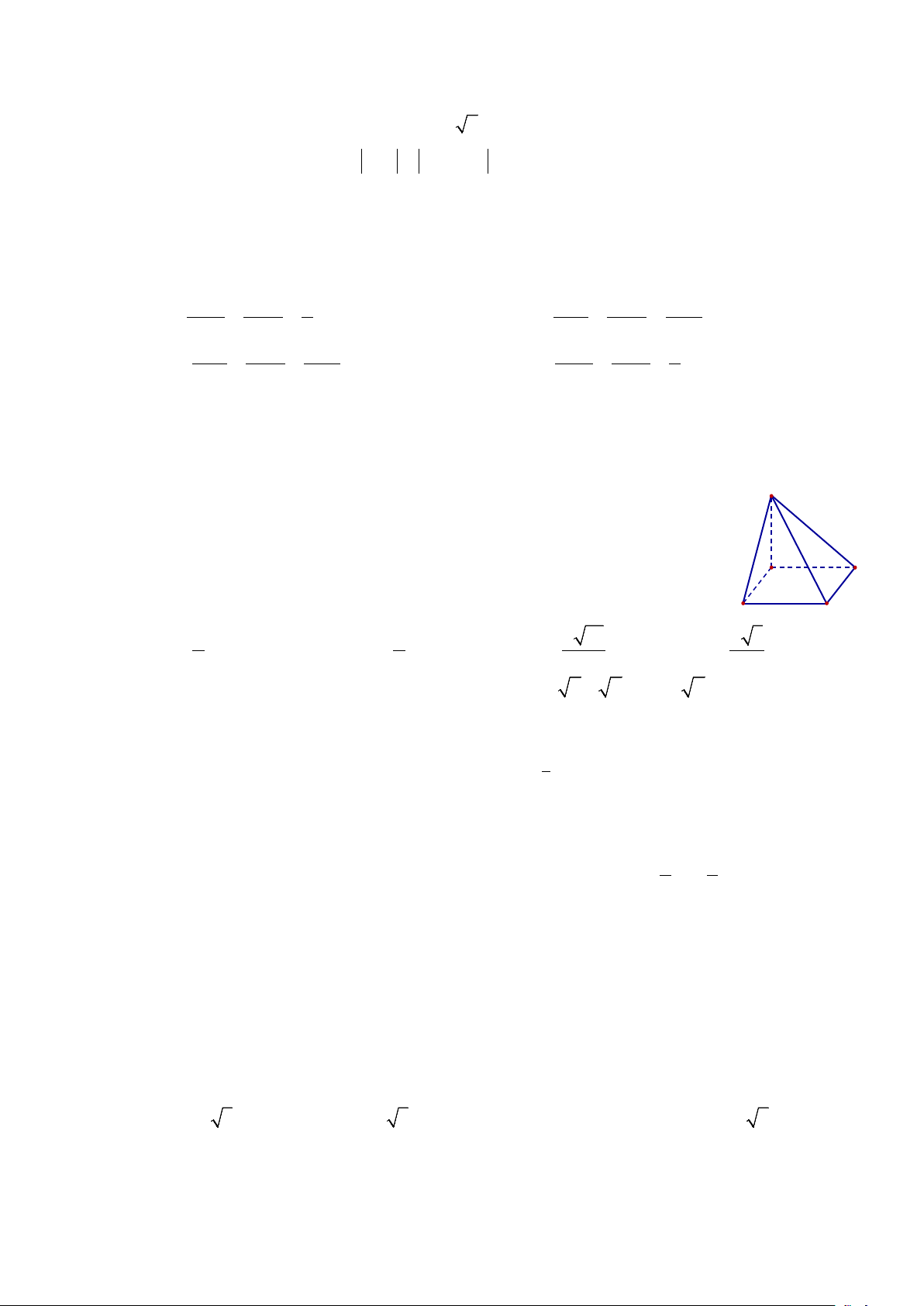
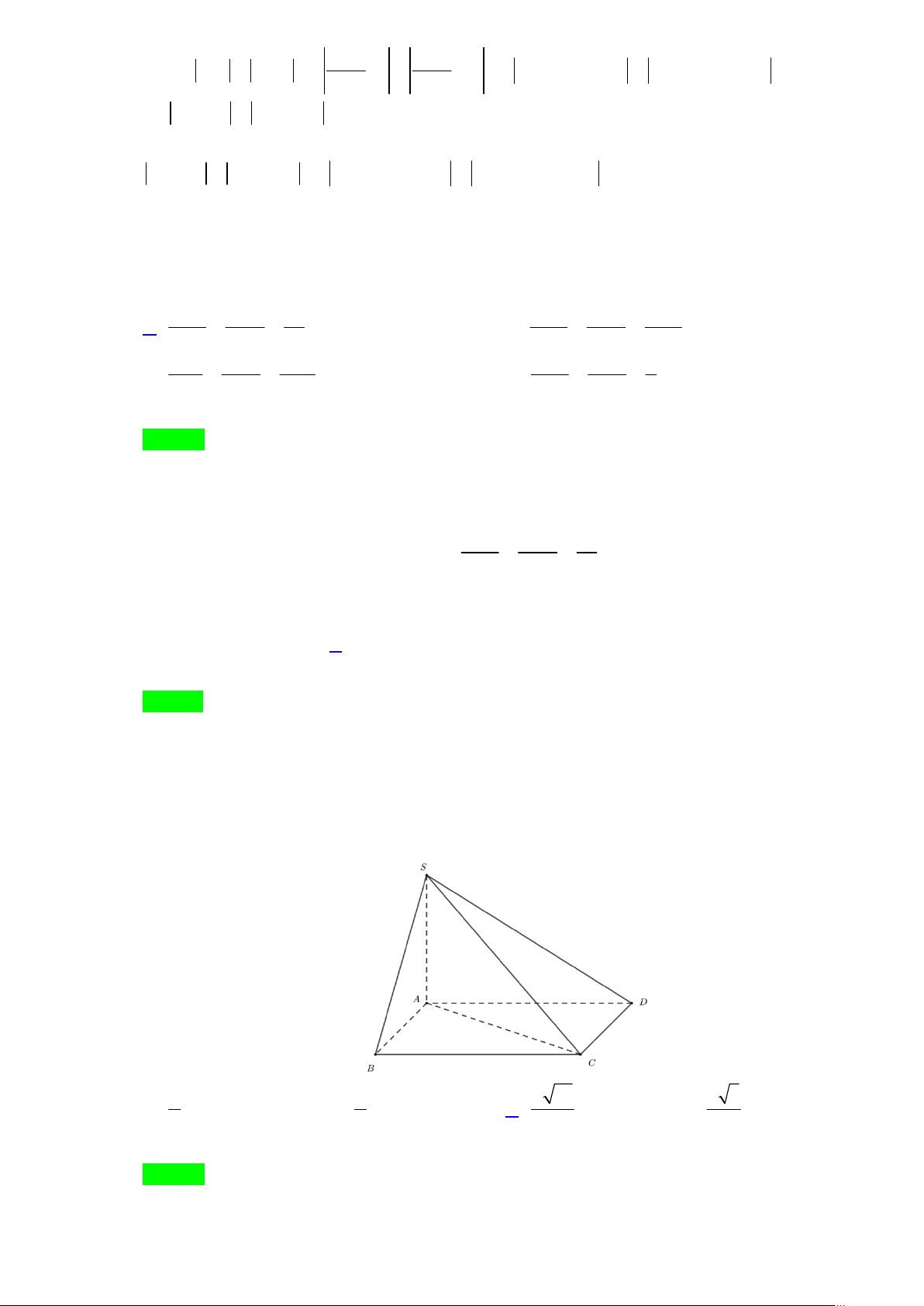
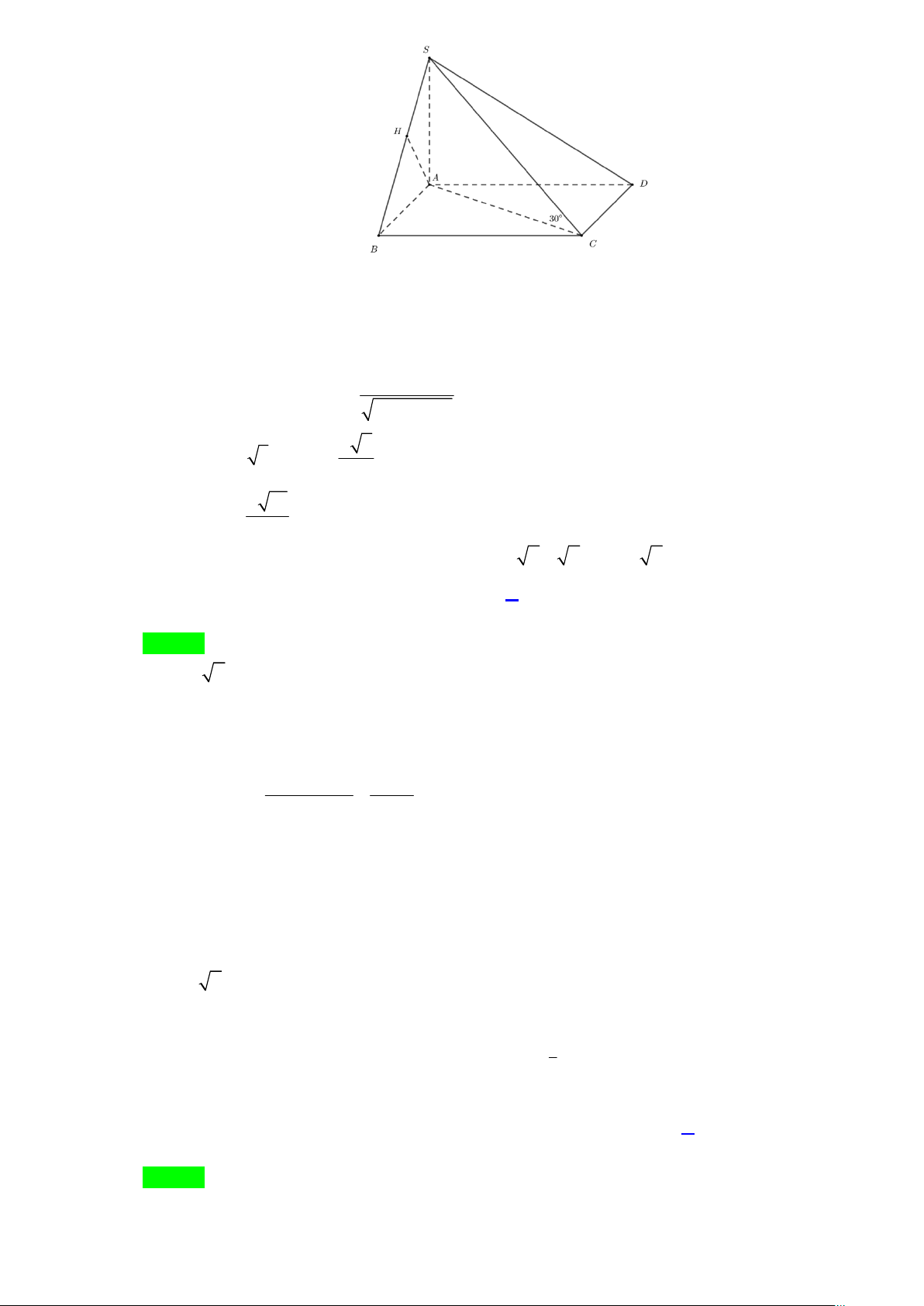
Câu 38. Cho khối chóp S.ABCD có đáy ABCD là hình vuông, SA ⊥ ( ABCD) S
và SA = a , góc giữa đường thẳng SC và mặt phẳng ( ABCD) bằng 30° (tham
khảo hình vẽ). Tính khoảng cách giữa đường thẳng AD và mặt phẳng (SBC) A . D B C
A. a . B. a . C. a 15 . D. a 3 . 2 6 5 6
Câu 39. Có bao nhiêu số nguyên dương a thỏa mãn 3 3
log ( a + a) > log a ? 6 3 A. 3 6 . B. 6 3 . C. 6 3 −1. D. 3 6 −1.
Câu 40. Cho hàm số f (x) liên tục trên  . Gọi F(x),G(x) là hai nguyên hàm của f (x) trên  π 4
thỏa mãn F(10) + G(1) =11và F(0) + G(10) = 1 − . Khi đó, cos 2 .
x f (sin 2x)dx ∫ bằng 0
A. 5. B. 10. C. 12. D. 6.
Câu 41. Có bao nhiêu giá trị nguyên của tham số m để hàm số 1 5 8 3
y = x − x − mx + 2023 có 5 3 bốn điểm cực trị? A. 17 . B. 10. C. 16. D. 15.
Câu 42. Cho số thực a > 0 và các số phức z thỏa mãn | z + 6 −8i |= .a Gọi M,m lần lượt là giá
trị lớn nhất và giá trị nhỏ nhất của | z |. Có bao nhiêu số nguyên a để M < 3m ?
A. 4 . B. Vô số. C. 3. D. 12.
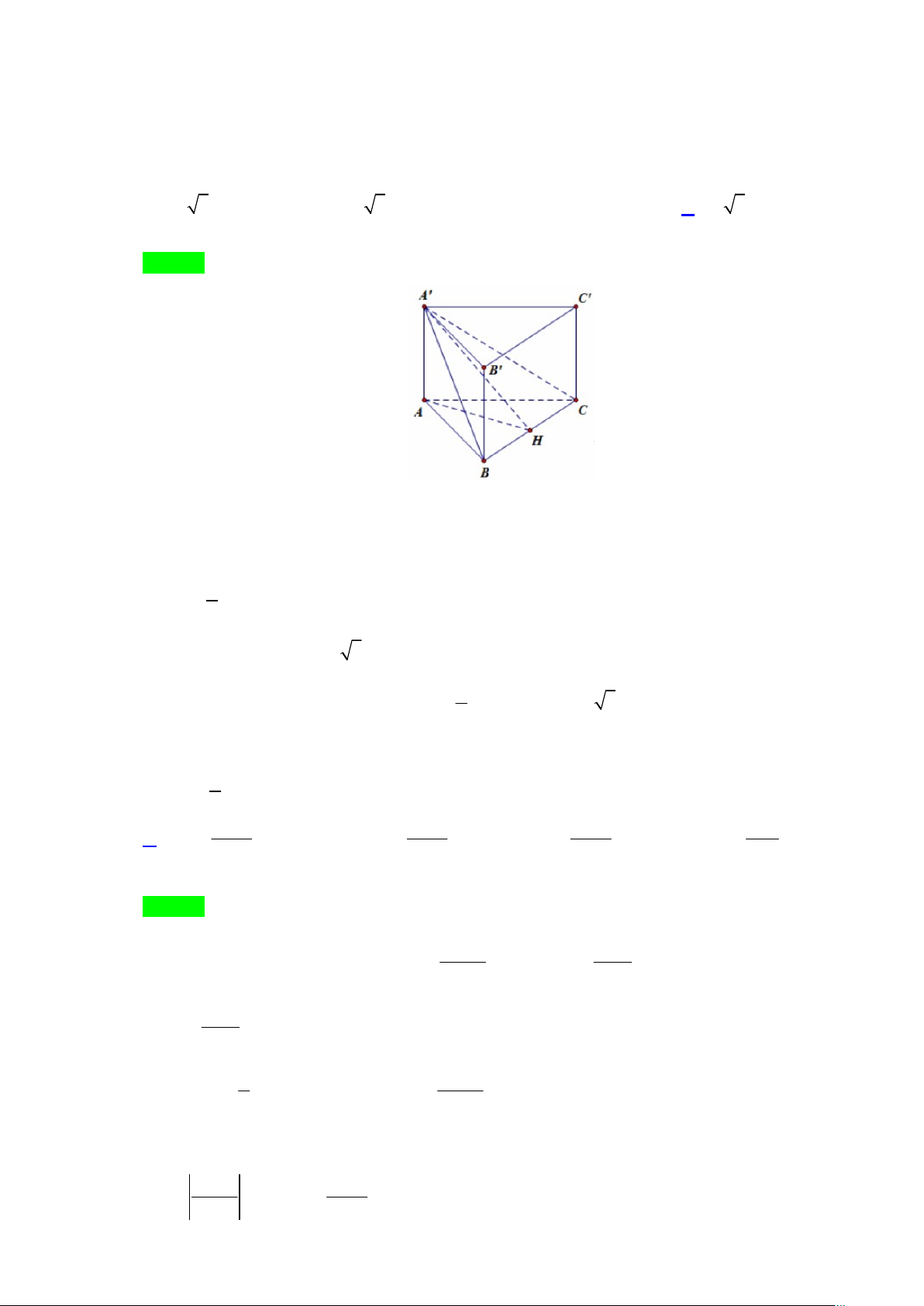
Câu 43. Cho khối lăng trụ đứng ABC.A′B C
′ ′ có đáy là tam giác cân tại , A BC = . a Mặt phẳng
( A′BC) tạo với đáy góc 0
60 và tam giác A′BC có diện tích bằng 2
6a . Thể tích của khối lăng trụ đã cho bằng A. 3 64 3a . B. 3 2 3a . C. 3 9a . D. 3 18 3a .
Trang 4/5 Mã đề 001
Câu 44. Cho hàm số y = f (x) liên tục trên khoảng (0;+∞) và f (x) ≠ 0 với mọi x > 0 , biết
rằng f ′(x) = ( x + ) 2
2 1 f (x) và f ( ) 1
1 = − . Diện tích hình phẳng giới hạn bởi các đường 2
y = f (x), x =1, x = e bằng A. 2 1+ ln . B. e +1 1 − + ln . C. 1 1− ln . D. e +1 1+ ln . e +1 2 e +1 2
Câu 45: Trên tập hợp các số phức, xét phương trình 2 2
z + 2mz + m + 2m = 0 ( m là tham số
thực). Tích của tất cả các giá trị thực của m để phương trình đó có 2 nghiệm phân biệt z , z 1 2
thỏa mãn | z |= 2 | z | là 1 2 A. 0. B. 18. − C. 2. D. 4.
Câu 46: Trong không gian Oxyz, cho mặt phẳng (α) vuông góc với mặt phẳng (P): x + 3y − 2z + 2 = 0
và chứa đường thẳng x −1 y +1 z − 4 d : = =
. Khoảng cách từ điểm A(1;2;− )
1 đến mặt phẳng (α) bằng 2 1 − 1
A. 8 3 . B. 4 3 .
C. 24 3 . D. 8 3 . 3 3 3
Câu 47: Có bao nhiêu cặp số nguyên dương ( ;x y) sao cho ứng với mỗi giá trị nguyên dương
của y có không quá 15 giá trị nguyên dương của x thỏa mãn 2 2 2 2 2 2
log (3x + xy + 36y ) + log (x +12y ) < log (xy) + log (x +16xy +12y ) +1? 5 3 5 3 A. 40 . B. 36. C. 21. D. 33.
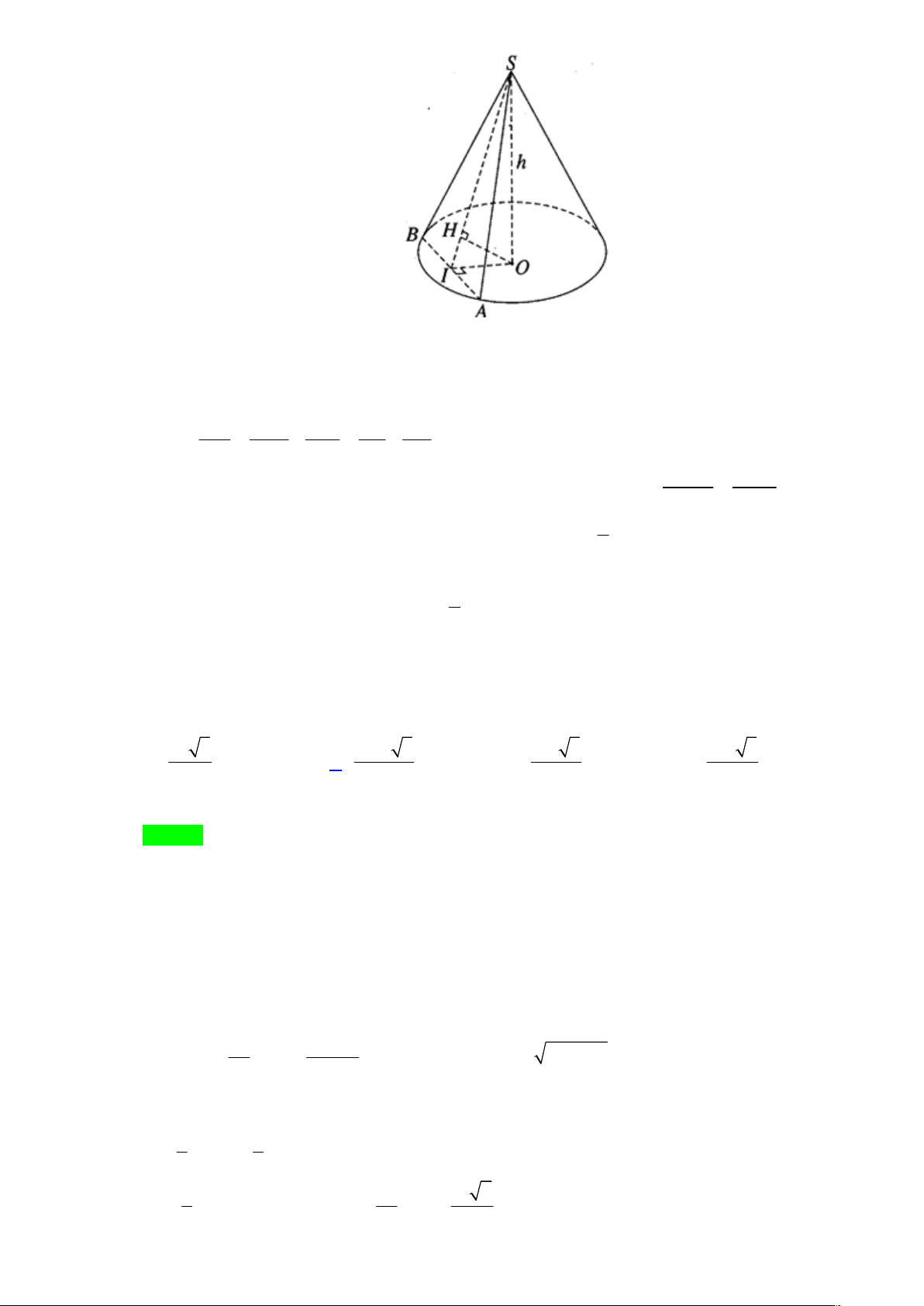
Câu 48. Cho khối nón tròn xoay có đường cao h = 20cm, bán kính đáy r = 25cm. Mặt phẳng
(P) đi qua đỉnh của khối nón và cách tâm O của đáy khối nón một khoảng bằng 12cm. Khi đó
diện tích thiết diện của khối nón cắt bởi mặt phẳng (P) bằng A. 2 500cm . B. 2 475cm . C. 2 450cm . D. 2 550cm .
Câu 49. Trong không gian Oxyz , cho mặt cầu (S) 2 2 2
:x + y + z − 6x − 4y − 2z −11= 0 và điểm M (0;− 2; )
1 . Gọi d , d , d là ba đường thẳng thay đổi không đồng phẳng cùng đi qua điểm 1 2 3
M và lần lượt cắt mặt cầu (S ) tại điểm thứ hai là A , B , C . Thể tích của tứ diện MABC đạt
giá trị lớn nhất bằng A. 50 3 . B.1000 3 . C. 100 3 . D. 500 3 . 9 27 9 27  
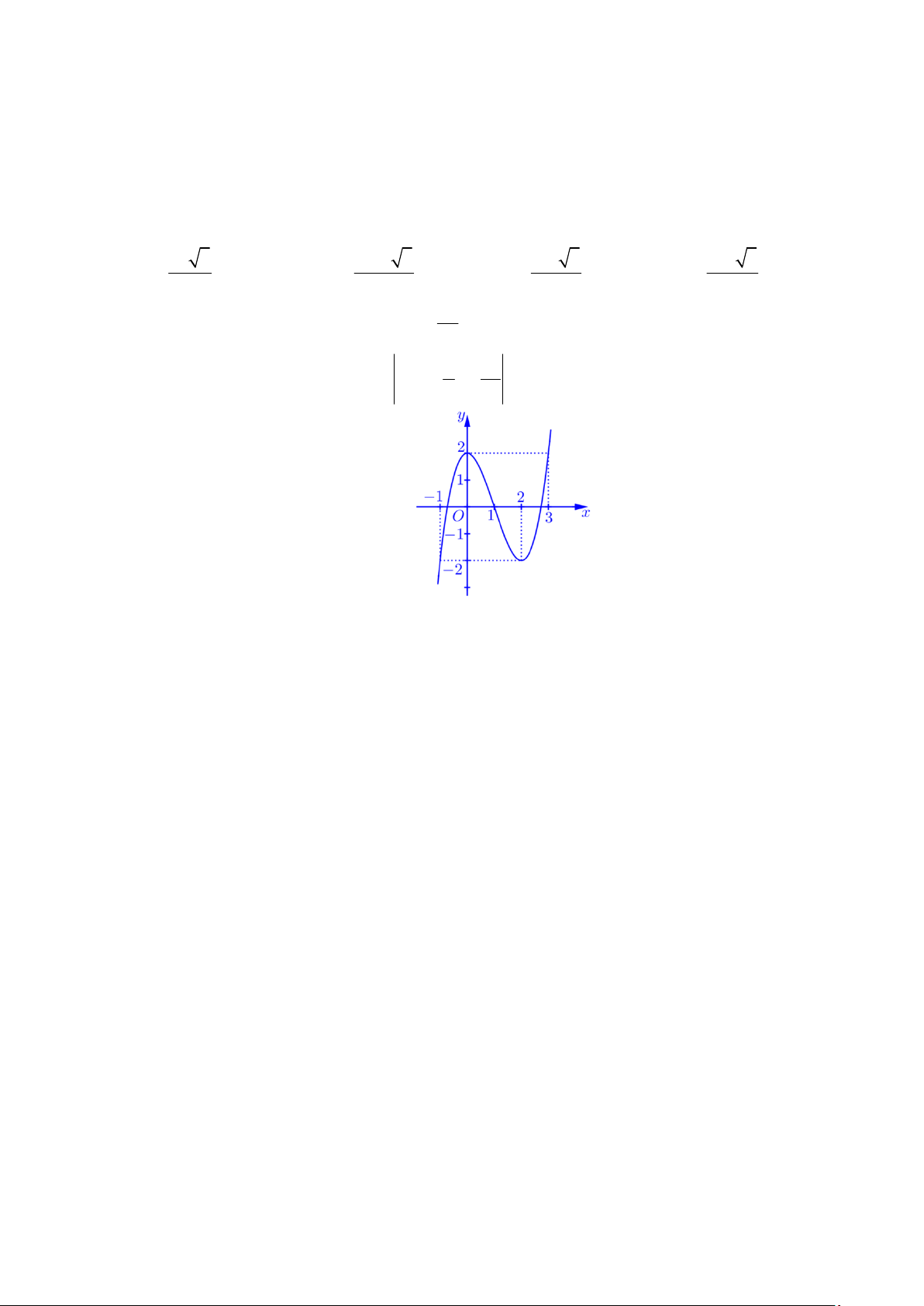
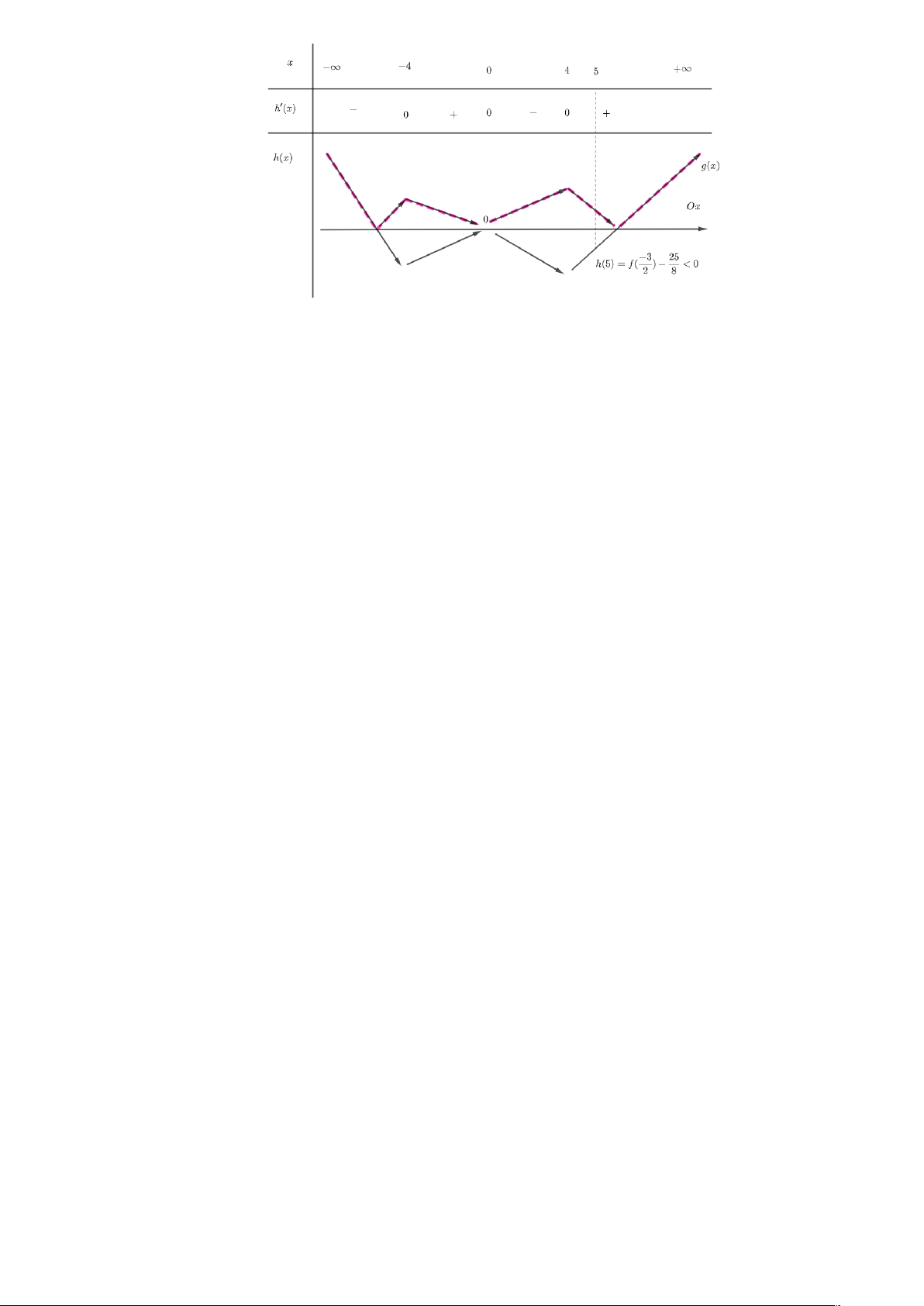
Câu 50. Cho hàm số bậc bốn y f x có 3 f       2  và f   1  0. Biết hàm  2   số x   x
y f x có đồ thị như hình vẽ bên. Hàm số g x 2  f 1      đồng  2 8
biến trên khoảng nào trong các khoảng dưới đây? A.  ;  4.
B. 5;. C. 2;4. D. 3;  1 .
…………….HẾT……………
Trang 5/5 Mã đề 001
SỞ GIÁO DỤC VÀ ĐÀO TẠO QUẢNG BÌNH
ĐỀ THI THỬ TỐT NGHIỆP THPT – NĂM HỌC 2022 – 2023 Câu 1.
Số phức liên hợp của số phức z  1 2i là
A. z  2  i . B. z  1   2i . C. z  1   2i .
D. z  1 2i . Câu 2.
Tập xác định của hàm số y  log x  2 5   là A. 2; . B. 2; . C.  . D.  ;  2 . Câu 3.
Hàm số nào sau đây đồng biến trên  ? 3 A.x y x . B. 3 y x . C. 2 y x . D. 2 y x . Câu 4.
Tập nghiệm của bất phương trình log x  3 là A. 10;  . B. 0;  . C. 1000;  . D. ;10 . Câu 5.
Công bội q của cấp số nhân u u  1 u  4 n  với và là 1 2 1 A. q  3. B. q  4 . C. q  . D. q  2  . 4 Câu 6.
Trong không gian Oxyz cho hai mặt phẳng  : x  2y  3z 1  0 và  : 2x  4y  6z 1  0 , khi đó:
A.  //  .
B.    .
C.    .
D.  cắt . 2x  3 Câu 7.
Tọa độ giao điểm của đồ thị hàm số y  với trục hoành là x  2  3   3  A.  ;0 . B.  2  ;0 . C. 0; 2   . D. 0; .      2   2  Câu 8.
Cho hàm số y f (x) có f '(x) liên tục trên 0; 
1 và f (1)  f (0)  2 . Giá trị của tích phân 1
I f '(x)dx bằng 0 A. I  1  . B. I  1. C. I  2 . D. I  0 . Câu 9.
Đồ thị của hàm số nào sau đây có dạng như hình vẽ bên? A. 4 2
y x  2x . B. 3 2
y x  3x 1. C. 3
y  3x x . D. 3
y x  3x .
Câu 10. Trong hệ tọa độ Oxyz , mặt cầu tâm I (2;0;0) và bán kính bằng 3 có phương trình là
A. x  2 2 2
2  y z  3.
B. x  2 2 2
2  y z  9 .
C. x  2 2 2
2  y z  9 .
D. x  2 2 2
2  y z  3.
Câu 11. Trong không gian Oxyz , cho điểm M 2; 1
 ;3 và mặt phẳng P : 2x  2y z 1  0 . Khoảng
cách điểm M đến mặt phẳng P bằng 5 10 A. 2 . B. . C. 3 . D. . 3 3
Câu 12. Số phức z thỏa mãn z 1 2i 8  3i  2i là 6 17 2 21 A. 6 17i . B.i . C.i . D. 1  2  5i . 5 5 5 5
Câu 13. Thể tích của khối chóp có diện tích đáy bằng 3 và chiều cao bằng 4 là A. 12 . B. 4 . C. 36 . D. 8 .
Câu 14. Cho khối chóp S.ABC có SA vuông góc với mặt đáy, SA  4, AB  6, BC  10 và CA  8 . Thể
tích khối chóp đã cho bằng A. 24 . B. 32 . C. 40 . D. 192 .
Câu 15. Cho mặt cầu có bán kính r  5 . Diện tích mặt cầu đã cho bằng 100 A. . B. 25 500 . C. . D. 100. 3 3
Câu 16. Môđun của số phức z  1   2i bằng A. 1. B. 5 . C. 3 . D. 5 .
Câu 17. Cho khối trụ có bán kính đáy r  5 và chiều cao h  3 . Thể tích của khối trụ đã cho bằng A. 75. B. 30. C. 25. D. 5.
x  4  8t
Câu 18. Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d : y  6
 11t , t   . Một véctơ z  3 2  t
chỉ phương của d là     A. u  4; 6  ; 3 . B. u  8; 6  ; 3 .
C. u  8; 11; 2 . D. u  8; 6  ; 2 .
Câu 19. Cho hàm số y f x có đồ thị như hình vẽ bên. Số điểm cực đại của hàm số y f x là y O x A. 1. B. 2 . C. 3 . D. 0 . 3x  4
Câu 20. Đường tiệm cận ngang của đồ thị hàm số y  là x 1 A. y  1. B. x  1. C. y  3 . D. x  3 . x 1
Câu 21. Tập nghiệm của bất phương trình 3 2  là 8 A. S   8  ;  . B. S   6  ;  .
C. S  0;  . D. S   6  ;  .
Câu 22. Số cách xếp 5 học sinh thành một hàng dọc là A. 25 . B. 120 . C. 1. D. 5 . x
Câu 23. Họ nguyên hàm của hàm số f x 5 9  x2
A. 5x  ln x  2  C .
B. 5x  ln x  2  C .
C. 5x  4ln x  2  C . D. 5x  4ln x  2  C . 11 6
Câu 24. Cho hàm số y f x liên tục trên đoạn  6  ;1 
1 và thỏa mãn  f xdx  8,  f xdx  3. 6  2 2 11
Giá trị của biểu thức P
f xdx  
f xdx bằng 6  6 A. P  4 . B. P  11 . C. P  5 . D. P  2 .
Câu 25. Cho hàm số f x 2
 3x  sin x  cos 2x . Nguyên hàm F x của hàm số f x thỏa mãn F 0  2 là 1 1
A. F x 3
x  cos x  sin 2x  2 .
B. F x 3
x  cos x  sin 2x  3 . 2 2 1 1
C. F x 3
x  cos x  sin 2x  3.
D. F x 3
x  cos x  sin 2x  2 . 2 2 Câu 26. Hàm số 3 2
y x  6x 1 nghịch biến trên khoảng A.  ;   1 . B. 1;5 . C. 0;4 . D.  1  ; .
Câu 27. Giá trị cực tiểu của hàm số 4 2
y x  4x  3 là A. y  0 . B. y  1  . C. y  3 . D. y  2 . CT CT CT CT
Câu 28. Cho log b  2;log c  3 , giá trị của Q b c a  2 log  bằng a a A. Q  7 . B. Q  4 . C. Q  10 . D. Q  12 .
Câu 29. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số 3 2
y x 11x  6, y  6x và hai đường thẳng
x  0, x  2 là 2 5 A. S  2 . B. S  . C. S  5. D. S  . 5 2
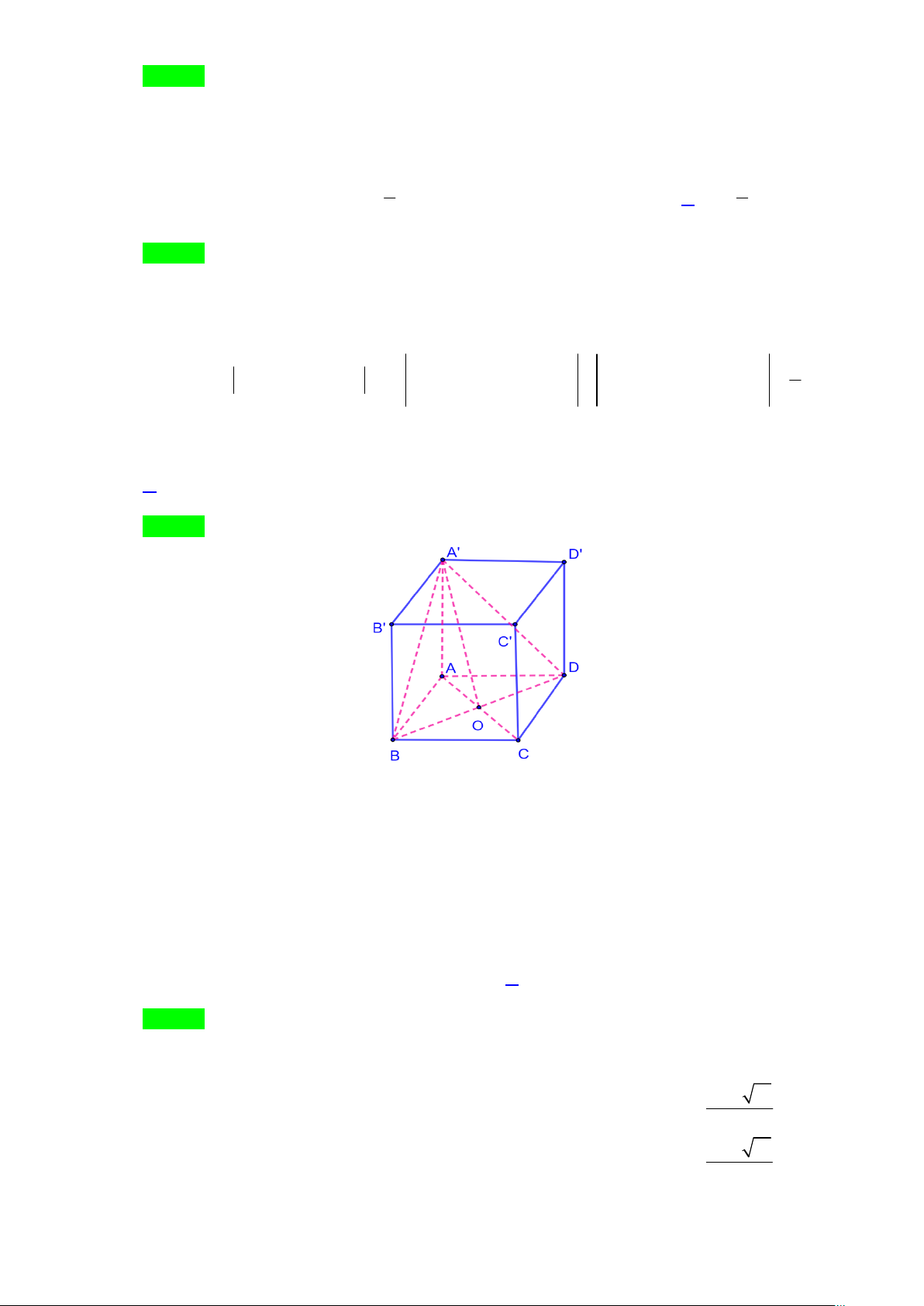
Câu 30. Cho hình lập phương ABC . D
A BCD có O,O lần lượt là tâm của hình vuông ABCD và 
A BCD . Góc giữa hai mặt phẳng  
A BD và  ABCD là A. AO A . B.O A A . C.   A DA . D.   A OC .
Câu 31. Số giao điểm của đồ thị hàm số 3
y x  3x  3 và đường thẳng y x là A. 1. B. 2 . C. 3 . D. 0 .
Câu 32. Cho hàm số y f x liên tục trên  và có đạo hàm f  x   x  
1 3 x . Hàm số y f x
đồng biến trên khoảng nào trong các khoảng dưới đây? A.  1  ;0 ;0 3;  ;  . B. . C. . D. 1 .
Câu 33. Chọn ngẫu nhiên hai số tự nhiên bé hơn 10 . Xác suất để hai số được chọn có tổng không chia hết cho 2 là 5 4 11 4 A. . B. . C. . D. . 9 45 45 9
Câu 34. Phương trình log 5  2x  2  x x x
P x x x .x 2  
có hai nghiệm thực , . Giá trị của bằng 1 2 1 2 1 2 A. 11. B. 9. C. 3. D. 2.
Câu 35. Cho số phức z thỏa mãn z i z  3i . Tập hợp các điểm biểu diễn của số phức w  1 2iz 1
là đường thẳng có phương trình
A. 2x y  7  0 .
B. 2x y  7  0 .
C. x  2y  7  0 .
D. x  2y  7  0 .
Câu 36. Trong không gian Oxyz , cho tam giác ABC với A 2
 ;4;2, B1;0;2, C 3; 4  ; 2  . Phương
trình đường trung tuyến AM của tam giác ABC là x  2 y  2 z x  2 y  4 z  2 A.   . B.   . 2 3  1  4 6  2  x 1 y  4 z  3 x  2 y  2 z C.   . D.   . 3 6 3 1 2  1
Câu 37. Trong không gian Oxyz , cho điểm A 1  ;2; 3
  . Hình chiếu của điểm A lên mặt phẳng Oyz có tọa độ là A. 1; 2  ;0 . B. 0;2; 3   . C.  1  ;0; 3   . D. 1;0;3 .
Câu 38. Cho khối chóp S.ABCD có đáy ABCD là hình vuông, SA   ABCD và SA a , góc giữa
đường thẳng SC và mặt phẳng  ABCD bằng 30 (tham khảo hình vẽ). Tính khoảng cách giữa
đường thẳng AD và mặt phẳng SBC . a a a 15 a 3 A. . B. . C. . D. . 2 6 5 6
Câu 39. Có bao nhiêu số nguyên dương a thỏa mãn log a a  log a 6  3  3 ? 3 A. 3 6 . B. 6 3 . C. 6 3 1. D. 3 6 1.
Câu 40. Cho hàm số f (x) liên tục trên  . Gọi F(x),G(x) là hai nguyên hàm của f (x) trên  thỏa 4
mãn F(10)  G(1)  1
 1 và F(0)  G(10)  1. Khi đó, cos 2 . (sin 2 ) bằng  x f x dx 0 A. 5 . B. 10 . C. 1  2 . D. 6  . 1 8
Câu 41. Có bao nhiêu giá trị nguyên của tham số m để hàm số 5 3
y x x mx  2023 có bốn điểm 5 3 cực trị? A. 17 . B. 10 . C. 16 . D. 15 .
Câu 42. Cho số thực a  0 và các số phức z thỏa mãn | z  6  8i | .
a Gọi M , m lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của | z |. Có bao nhiêu số nguyên a để M  3m ? A. 4 . B. Vô số. C. 3 . D. 12 .
Câu 43. Cho khối lăng trụ đứng ' ' '
ABC.A B C , có đáy là tam giác cân tại , A BC  . a Mặt phẳng ' (A BC) tạo với đáy góc 0 60 và tam giác ' A BC có diện tích 2
6a . Thể tích của khối lăng trụ đã cho bằng A. 3 64 3a .. B. 3 2 3a .. C. 3 9a .. D. 3 18 3a . .
Câu 44. Cho hàm số f (x) liên tục trên (0; ) và f (x)  0,x  0 . Biết rằng ' 2
f (x)  (2x 1) f (x) và 1
f (1)   . Diện tích của hình phẳng giới hạn bởi các đường 2
y f (x), x  1, x  e bằng 2 2 2 1 1 A. 2  ln . B. 2   ln . C. 1 ln . D. 1 e ln . 2 e 1 2 e 1 2 e 1 2
Câu 45. Trên tập hợp số phức, xét phương trình 2 2
z  2mz m  2m  0 ( m là tham số thực). Tích của
tất cả các giá trị thực của m để phương trình có hai nghiệm phân biệt z , z thỏa mãn z  2 z 1 2 1 2 là A. 0 . B. 1  8 . C. 2 . D. 4 .
Câu 46. Trong không gian Oxyz, cho mặt phẳng  vuông góc với mặt phẳng P : x  3y  2z  2  0 x 1 y 1 z  4
và chứa đường thẳng d :  
. Khoảng cách từ điểm A1; 2  ;  1 đến mặt phẳng 2 1  1  bằng 8 3 4 3 24 3 A. . B. . C. . D. 8 3 . 3 3 3
Câu 47. Có bao nhiêu cặp số nguyên dương (x, y) sao cho ứng với mổi giá trị nguyên dương của y có
không quá 15 giá trị nguyên dương của x thỏa mãn log  2 2
3x xy  36y   log  2 2
x 12y   log (xy)  log  2 2
x 16xy 12y 1? 5 3 5 3  A. 40. B. 36. C. 21. D. 33.
Câu 48. Cho khối nón tròn xoay có đường cao h = 20 cm , bán kính đáy r  25 cm . Mặt phẳng (P) đi
qua đỉnh của khối nón và cách tâm O của đáy khối nón một khoảng bằng 12 cm . Khi đó diện
tích thiết điện của khổi nón cắt bởi mặt phằng (P) bằng: A. 2 500 cm . B. 2 475 cm . C. 2 450 cm . D. 2 550 cm .
Câu 49. Trong không gian Oxyz , cho mặt cầu 2 2 2
(S) : x y z  6x  4y  2z 11  0 và điểm M (0; 2
 ;1) . Gọi d , d , d là ba đường thẳng thay đổi không đồng phẳng cùng đi qua điểm 1 2 3 M (0; 2
 ;1) và lần lượt cắt mặt cầu (S) tại điểm thứ hai là ,
A B,C . Thể tích của tứ diện MABC
đạt giá trị lớn nhất bằng 50 3 1000 3 100 3 500 3 A. . B. . C. . D. . 9 27 9 27  3  
Câu 50. Cho hàm số bậc bốn y f x có f  2 và f  
1  0 . Biết hàm số y f  x có đồ thị    2  2  x x
như hình vẽ bên. Hàm số g x  f 1 
đồng biến trên khoảng nào dưới đây?    2  8 A.  ;  4   . B. 5; . C. 2;4 . D.  3  ;  1 .  HẾTBẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D A B C B A A C D C D B B B D D A C B C D B A C B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
C B A D A C A A D A A B C C D D B D A D A B A B C HƯỚNG DẪN GIẢI Câu 1.
Số phức liên hợp của số phức z  1 2i là
A. z  2  i . B. z  1   2i . C. z  1   2i .
D. z  1 2i . Lời giải Chọn D
Số phức liên hợp của số phức z  1 2i là z  1 2i . Câu 2.
Tập xác định của hàm số y  log x  2 5   là A. 2; . B. 2; . C.  . D.  ;  2 . Lời giải Chọn A
Điều kiện x  2  0  x  2 .
Tập xác định của hàm số y  log x  2 2; 5   là . Câu 3.
Hàm số nào sau đây đồng biến trên  ? 3 A. x y x . B. 3 y x . C. 2 y x . D. 2 y x . Lời giải Chọn B Xét hàm số 3
y x , ta có 2
y  3x  0,x   nên hàm số 3
y x đồng biến trên  . Câu 4.
Tập nghiệm của bất phương trình log x  3 là A. 10;  . B. 0;  . C. 1000;  . D. ;10 . Lời giải Chọn C
Ta có log x  3  x  1000 .
Tập nghiệm của bất phương trình log x  3 là 1000;  . Câu 5.
Công bội q của cấp số nhân u u  1 u  4 n  với và là 1 2 1 A. q  3. B. q  4 . C. q  . D. q  2  . 4 Lời giải Chọn B u
Công bội q của cấp số nhân u 2 q   4 n  là . u1 Câu 6.
Trong không gian Oxyz cho hai mặt phẳng  : x  2y  3z 1  0 và  : 2x  4y  6z 1  0 , khi đó:
A.  / /  .
B.    .
C.    .
D.  cắt . Lời giải Chọn A  
Vectơ pháp tuyến n  1; 2  ;3 n  2; 4  ;6  ;   n  2n Ta có:  M ( 1  ;0;0) 
  M 
Chứng tỏ  / /  . 2x  3 Câu 7.
Tọa độ giao điểm của đồ thị hàm số y  với trục hoành là x  2  3   3  A.  ;0 . B.  2  ;0 . C. 0; 2   . D. 0; .      2   2  Lời giải Chọn A 2x  3 3 Cho y  0 
 0  2x  3  0  x   x  2 2 2x  3  3 
Tọa độ giao điểm của thị hàm số y
với trục hoảnh là  ;0 .   x  2  2  Câu 8.
Cho hàm số y f (x) có f '(x) liên tục trên 0; 
1 và f (1)  f (0)  2 . Giá trị của tích phân 1
I f '(x)dx bằng 0 A. I  1  . B. I  1. C. I  2 . D. I  0 . Lời giải Chọn C 1 1
I f '(x)dx f (x)  f (1)  f (0)  2 .  0 0 Câu 9.
Đồ thị của hàm số nào sau đây có dạng như hình vẽ bên? A. 4 2
y x  2x . B. 3 2
y x  3x 1. C. 3
y  3x x . D. 3
y x  3x . Lời giải Chọn D.
Câu 10. Trong hệ tọa độ Oxyz , mặt cầu tâm I (2;0;0) và bán kính bằng 3 có phương trình là
A. x  2 2 2
2  y z  3.
B. x  2 2 2
2  y z  9 .
C. x  2 2 2
2  y z  9 .
D. x  2 2 2
2  y z  3. Lời giải Chọn C
Mặt cầu tâm I (2;0;0) và bán kính bằng 3 có phương trình là: x  2 2 2
2  y z  9 .
Câu 11. Trong không gian Oxyz , cho điểm M 2; 1
 ;3 và mặt phẳng P : 2x  2y z 1  0 . Khoảng
cách điểm M đến mặt phẳng P bằng 5 10 A. 2 . B. . C. 3 . D. . 3 3 Lời giải Chọn D
d M P 2.2  2.  1  3 1 10 ,    .    2 2 2 3 2 2 1
Câu 12. Số phức z thỏa mãn z 1 2i 8  3i  2i là 6 17 2 21 A. 6 17i . B. i . C. i . D. 1  2  5i . 5 5 5 5 Lời giải Chọn B z   i 2i  8  3i 6 17
1 2  8  3i  2i z   z   i . 1 2i 5 5
Câu 13. Thể tích của khối chóp có diện tích đáy bằng 3 và chiều cao bằng 4 là A. 12 . B. 4 . C. 36 . D. 8 . Lời giải Chọn B 1 1 V  . B h  .3.4  4 . 3 3
Câu 14. Cho khối chóp S.ABC có SA vuông góc với mặt đáy, SA  4, AB  6, BC  10 và CA  8 . Thể
tích khối chóp đã cho bằng A. 24 . B. 32 . C. 40 . D. 192 . Lời giải Chọn B Vì ABC thỏa 2 2 2
BC AB AC nên vuông tại A . 1 1 1
Khi đó, thể tích khối chóp đã cho bằng V  .S
.SA  . .6.8.4  32 . 3 ABC 3 2
Câu 15. Cho mặt cầu có bán kính r  5 . Diện tích mặt cầu đã cho bằng 100 A. . B. 25 500 . C. . D. 100. 3 3 Lời giải Chọn D
Diện tích mặt cầu đã cho bằng 2
S  4 r  100.
Câu 16. Môđun của số phức z  1   2i bằng A. 1. B. 5 . C. 3 . D. 5 . Lời giải Chọn D
Ta có z   2 2 1  2  5 .
Câu 17. Cho khối trụ có bán kính đáy r  5 và chiều cao h  3 . Thể tích của khối trụ đã cho bằng A. 75. B. 30. C. 25. D. 5. Lời giải Chọn A
Thể tích của khối trụ đã cho là 2 2
V  r h .5 .3  75.
x  4  8t
Câu 18. Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d : y  6
 11t , t   . Một véctơ z  3 2  t
chỉ phương của d là     A. u  4; 6  ; 3 . B. u  8; 6  ; 3 .
C. u  8; 11; 2 . D. u  8; 6  ; 2 . Lời giải Chọn C
Một véctơ chỉ phương của d là u  8; 11; 2 .
Câu 19. Cho hàm số y f x có đồ thị như hình vẽ bên. Số điểm cực đại của hàm số y f x là y O x A. 1. B. 2 . C. 3 . D. 0 . Lời giải Chọn B
Từ đồ thị đã cho ta suy ra hàm số y f x có hai điểm cực đại. 3x  4
Câu 20. Đường tiệm cận ngang của đồ thị hàm số y  là x 1 A. y  1. B. x  1. C. y  3 . D. x  3 . Lời giải Chọn C 3x  4 Ta có lim y  lim  3. x
x x 1
Do đó đồ thị hàm số đã cho có một đường tiệm cận ngang là y  3 . x 1
Câu 21. Tập nghiệm của bất phương trình 3 2  là 8 A. S   8  ;  . B. S   6  ;  .
C. S  0;  . D. S   6  ;  . Lời giải Chọn D x 1 Ta có: 3 x3 3 2 2 2     x  3  3   x  6   x  6  ; .. 8
Câu 22. Số cách xếp 5 học sinh thành một hàng dọc là A. 25 . B. 120 . C. 1. D. 5 . Lời giải Chọn B
Số cách xếp 5 học sinh thành một hàng dọc là: 5!  120.. x
Câu 23. Họ nguyên hàm của hàm số f x 5 9  x2
A. 5x  ln x  2  C .
B. 5x  ln x  2  C .
C. 5x  4ln x  2  C . D. 5x  4ln x  2  C . Lời giải Chọn A 5x  9 5 x  2 1  1 
Ta có:  f x   dx  dx  dx  5 
dx  5x  ln x  2  C .     x  2 x  2  x  2  11 6
Câu 24. Cho hàm số y f x liên tục trên đoạn  6  ;1 
1 và thỏa mãn  f xdx  8,  f xdx  3. 6  2 2 11
Giá trị của biểu thức P
f xdx  
f xdx bằng 6  6 A. P  4 . B. P  11 . C. P  5 . D. P  2 . Lời giải Chọn C 11 2 6 11 2 11
Ta có:  f xdx  8   f xdx   f xdx   f xdx  8   f xdx 3  f xdx  8 6  6  2 6 6  6 2 11
  f xdx   f xdx  5  P  5. 6  6
Câu 25. Cho hàm số f x 2
 3x  sin x  cos 2x . Nguyên hàm F x của hàm số f x thỏa mãn F 0  2 là 1 1
A. F x 3
x  cos x  sin 2x  2 .
B. F x 3
x  cos x  sin 2x  3 . 2 2 1 1
C. F x 3
x  cos x  sin 2x  3.
D. F x 3
x  cos x  sin 2x  2 . 2 2 Lời giải Chọn B 1
Ta có: F x   2
3x  sin x  cos 2x 3
dx x  cos x  sin 2x C. 2 F 0 1 1 3
 2  0 1 .0  C  2  C  3  F x 3
x  cos x  sin 2x  3. . 2 2 Câu 26. Hàm số 3 2
y x  6x 1 nghịch biến trên khoảng A.  ;   1 . B. 1;5 . C. 0;4 . D.  1  ; . Lời giải Chọn C
Tập xác định: D   . Ta có 2
y  3x 12x . Giải 2
y  0  3x 12x  0  x 0;4 . Hàm số 3 2
y x  6x 1 nghịch biến trên khoảng 0;4 .
Câu 27. Giá trị cực tiểu của hàm số 4 2
y x  4x  3 là A. y  0 . B. y  1  . C. y  3 . D. y  2 . CT CT CT CT Lời giải Chọn B
Tập xác định: D   . x  0 Ta có 3
y  4x  8x . Giải 3
y  0  4x  8x  0   . x   2 Bảng biến thiên:
Giá trị cực tiểu của hàm số 4 2
y x  4x  3 là y  1  . CT
Câu 28. Cho log b  2;log c  3 , giá trị của Q b c a  2 log  bằng a a A. Q  7 . B. Q  4 . C. Q  10 . D. Q  12 . Lời giải Chọn A Ta có Q b c b c b c a  2  2 log  log  log  2log  log  2.2  3  7 . a a a a
Câu 29. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số 3 2
y x 11x  6, y  6x và hai đường thẳng
x  0, x  2 là 2 5 A. S  2 . B. S  . C. S  5. D. S  . 5 2 Lời giải Chọn Dx 1 Giải phương trình: 3 2 3 2 x 11x 6 6x x 6x 11x 6 0           x  2 .  x  3  2 1 2 5 Ta có 3 2
S x  6x 11x  6 dx    3 2
x  6x 11x  6dx   3 2
x  6x 11x  6dx  . 2 0 0 1
Câu 30. Cho hình lập phương ABC . D
A BCD có O,O lần lượt là tâm của hình vuông ABCD và 
A BCD . Góc giữa hai mặt phẳng  
A BD và  ABCD là A. AO A . B. O A A . C.   A DA . D.   A OC . Lời giải Chọn ABD AO Ta có   BD   
A AO  BD   A O . BD A A   
A BD  ABCD  BD
Ta có A'O BD,  A O    A BD   
A BD, ABCD
   AO, AO    AO A .
AO BD, AO    ABCD
Câu 31. Số giao điểm của đồ thị hàm số 3
y x  3x  3 và đường thẳng y x là A. 1. B. 2 . C. 3 . D. 0 . Lời giải Chọn C  x 1   1   13
Phương trình hoành độ giao điểm: 3 3
x  3x  3  x x  4x  3  0  x  .  2   1   13 x   2
Vậy số giao điểm đồ thị hàm số 3
y x  3x  3 và đường thẳng y x là 3 .
Câu 32. Cho hàm số y f x liên tục trên  và có đạo hàm f  x   x  
1 3 x . Hàm số y f x
đồng biến trên khoảng nào trong các khoảng dưới đây? A.  1  ;0 ;0 3;  ;  . B. . C. . D. 1 . Lời giải Chọn Ax  
Ta có f  x    x    x 1 0 1 3  0  .  x  3 Bảng biến thiên
Từ bảng biến thiên ta có hàm số y f x đồng biến trên khoảng  1  ;3.
Vậy hàm số y f x đồng biến trên khoảng  1  ;0 .
Câu 33. Chọn ngẫu nhiên hai số tự nhiên bé hơn 10 . Xác suất để hai số được chọn có tổng không chia hết cho 2 là 5 4 11 4 A. . B. . C. . D. . 9 45 45 9 Lời giải Chọn A
Có tất cả 10 số tự nhiên bé hơn 10 .
Chọn ngẫu nhiên 2 số tự nhiên từ 10 số, số phần tử của không gian mẫu là n 2  C  45 . 10
Để hai số được chọn có tổng không chia hết cho 2 thì hai số đó phải gồm một số lẻ và một số chẵn.
Số cách chọn là 5.5  25 . 25 5
Vậy xác suất cần tìm là P   . 45 9
Câu 34. Phương trình log 5  2x  2  x x x
P x x x .x 2  
có hai nghiệm thực , . Giá trị của bằng 1 2 1 2 1 2 A. 11. B. 9. C. 3. D. 2. Lời giải Chọn D
Điều kiện 5  2x  0  2x  5  x  log 5 . 2 x xx x 4
Ta có log 5  2  2  x  5  2  2  5  2 
 2 x  5.2x  4  0 2   2 2 . 2xt  1 Đặt  2x t
t  0 , phương trình trở thành 2t 5t  4  0   tm . t  4 Với  1 2x t  1  x  0 . Với  4  2x t  4  x  2 .
Vậy P x x x .x  0  2  0.2  2 . 1 2 1 2
Câu 35. Cho số phức z thỏa mãn z i z  3i . Tập hợp các điểm biểu diễn của số phức w  1 2iz 1
là đường thẳng có phương trình
A. 2x y  7  0 .
B. 2x y  7  0 .
C. x  2y  7  0 .
D. x  2y  7  0 . Lời giải Chọn A w
Ta có w    i 1
1 2 z 1  z  . 1 2i w 1 w 1
Từ đó z i z  3i   i
 3i w 1 1 2ii w 1 1 2i3i 1 2i 1 2i
w 1 i w  7  3i . Đặt 2
w x yi ; x, y  ;i  1  . Suy ra
w 1 i w  7  3i   x   1   y  
1 i   x  7   y  3i
 x  2   y  2  x  2   y  2 1 1 7 3 2 2 2 2
x  2x 1 y  2y 1  x 14x  49  y  6y  9
 16x  8y  56  0  2x y  7  0 .
Câu 36. Trong không gian Oxyz , cho tam giác ABC với A 2
 ;4;2, B1;0;2, C 3; 4  ; 2  . Phương
trình đường trung tuyến AM của tam giác ABC là x  2 y  2 z x  2 y  4 z  2 A.   . B.   . 2 3  1  4 6  2  x 1 y  4 z  3 x  2 y  2 z C.   . D.   . 3 6 3 1 2  1 Lời giải Chọn A
Trung điểm của BC là M 2; 2  ;0 . 
VTCP của đường thẳng AM là AM  4; 6  ; 2  . x  2 y  2 z
Phương trình chính tắc của AM có dạng:   . 2 3  1 
Câu 37. Trong không gian Oxyz , cho điểm A 1  ;2; 3
  . Hình chiếu của điểm A lên mặt phẳng Oyz có tọa độ là A. 1; 2  ;0 . B. 0;2; 3   . C.  1  ;0; 3   . D. 1;0;3 . Lời giải Chọn B
Hình chiếu của điểm A lên mặt phẳng Oyz có tọa độ là 0;2; 3   .
Câu 38. Cho khối chóp S.ABCD có đáy ABCD là hình vuông, SA   ABCD và SA a , góc giữa
đường thẳng SC và mặt phẳng  ABCD bằng 30 (tham khảo hình vẽ). Tính khoảng cách giữa
đường thẳng AD và mặt phẳng SBC . a a a 15 a 3 A. . B. . C. . D. . 2 6 5 6 Lời giải Chọn C
Ta có SC, ABCD  SCA 30 .  
Vì AD / /BC AD / / SBC  d AD,SBC  d  , A SBC.
Dựng AH SB . Dễ dàng chứng mình AH  SBC. SAAB Suy ra d  ,
A SBC  AH  . 2 2 SA AB 6 Ta có  3   a AC a AB . 2 15 Suy ra  a AH . 5
Câu 39. Có bao nhiêu số nguyên dương a thỏa mãn log a a  log a 6  3  3 ? 3 A. 3 6 . B. 6 3 . C. 6 3 1. D. 3 6 1. Lời giải Chọn C Đặt 6
t a , do a  0  t  0.
Bất phương trình trở thành: log  3 2 t t  2
 log t  log  3 2 t t  2  log t  0. 6 3 6 3
Xét hàm số: f t  log  3 2 t t  2
 log t , t  0. 6 3 2 3t  2t 2t
Khi đó, f 't     0, t  0. 3 2 t t  2 ln 6 t ln 3
Suy ra hàm số f t luôn nghịch biến với mọi t  0
Suy ra t  3 là nghiệm duy nhất của phương trình f t  0. Yêu cầu bài toán
f t  0  f t  f 3  0  t  3 (do hàm số f t luôn nghịch biến với mọi t  0 ). Suy ra 6 6
a  3  a  3 . Vì a nguyên dương nên có 6
3 1 số nguyên dương a thỏa yêu cầu bài toán.
Câu 40. Cho hàm số f (x) liên tục trên  . Gọi F(x),G(x) là hai nguyên hàm của f (x) trên  thỏa 4
mãn F(10)  G(1)  1
 1 và F(0)  G(10)  1. Khi đó, cos 2 . (sin 2 ) bằng  x f x dx 0 A. 5 . B. 10 . C. 1  2 . D. 6  . Lời giải Chọn D
Vì F(x),G(x) là hai nguyên hàm của f (x) nên ta có F(x)  G(x)  C
F(10)  G(1)  1  1
G(10)  C G(1)  1  1 Theo đề     G   1  G 0  1  2
F(0)  G(10)  1
G(0)  C G(10)  1 4 Xét I  cos 2 .
x f (sin 2x)dx . 0
x  0  t  0 1 
Đặt t  sin 2x  dt  cos2 d x x , đổi cận  . 2 x   t  1  4 1 1 1 1 1 Khi đó I
f (t)dt   
G t    G  
1  G 0  6  ..  0 2 2 2 0 1 8
Câu 41. Có bao nhiêu giá trị nguyên của tham số m để hàm số 5 3
y x x mx  2023 có bốn điểm 5 3 cực trị? A. 17 . B. 10 . C. 16 . D. 15 . Lời giải Chọn D Ta có 4 2
y  x  8x m ; 4 2
y  0  x  8x m (1). Ycbt   
1 có bốn nghiệm phân biệt. x  0
Xét hàm số g x 4 2
x 8x , có gx 3
 4x 16x . gx 3
 0  4x 16x  0  .  x  2  Bảng biến thiên. Từ đây ta có 1
 6  m  0 , vậy có 15 giá trị nguyên của tham số m thỏa mãn.
Câu 42. Cho số thực a  0 và các số phức z thỏa mãn | z  6  8i | .
a Gọi M , m lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của | z |. Có bao nhiêu số nguyên a để M  3m ? A. 4 . B. Vô số. C. 3 . D. 12 . Lời giải Chọn B
Ta có | z  6  8i | a , khi đó tập hợp điểm biểu diễn của số phức z là đường tròn tâm I  6  ;8,
bán kính R a , với OI  10 .
Giá trị lớn nhất của | z | là M OI a  10  a . TH1: a  10 .
Khi đó giá trị nhỏ nhất của | z | là m OI a  10  a .
Để M  3m  10  a  310  a  a  5 .
TH này có 4 giá trị của a thỏa mãn, a 1,2,3,  4 . TH2: a  10 .
Khi đó giá trị nhỏ nhất của | z | là m a OI a 10 .
Để M  3m  10  a  3a 10  a  20 .
TH này có vô số giá trị của a thỏa mãn, a  / a  2  0 .
KL: Vậy có vô số giá trị nguyên của a thỏa mãn yêu cầu bài toán.
Câu 43. Cho khối lăng trụ đứng ' ' '
ABC.A B C , có đáy là tam giác cân tại , A BC  . a Mặt phẳng ' (A BC) tạo với đáy góc 0 60 và tam giác ' A BC có diện tích 2
6a . Thể tích của khối lăng trụ đã cho bằng A. 3 64 3a .. B. 3 2 3a .. C. 3 9a .. D. 3 18 3a . . Lời giải Chọn D
Gọi H là trung điểm của '
BC AH BC A H BC Mặt phẳng ' (A BC) tạo với đáy góc 0 60 nên ' 0 AHA  60 1 ' ' S
A H.BC A H  12a ' A BC 2 ' ' 0 ' 0
AA A H.sin 60  6a 3; AH A H.cos 60  6 . a 1
Thể tích khối lăng trụ là: 3 V S .A
A AH.BC.A A  18 3a . ABC 2
Câu 44. Cho hàm số f (x) liên tục trên (0; ) và f (x)  0,x  0 . Biết rằng ' 2
f (x)  (2x 1) f (x) và 1
f (1)   . Diện tích của hình phẳng giới hạn bởi các đường 2
y f (x), x  1, x  e bằng 2 2 2 1 1 A. 2  ln . B. 2   ln . C. 1 ln . D. 1 e ln . 2 e 1 2 e 1 2 e 1 2 Lời giải Chọn A ' ' f (x)  1  Từ giả thiết: ' 2
f (x)  (2x 1) f (x)    2  x 1   2  x 1 2   f (x)  f (x)  1 Do đó: 2  ( 2  1)      x dx x x C f (x) 1 1
Mà f (1)   nên C  0 . Vậy f (x)  . 2 2 x x
Diện tích của hình phẳng giới hạn bởi các đường 2
y f (x), x  1, x  e là 2 e 1 2 S  d x  2  ln .  2 2 x x 1 e 1
Câu 45. Trên tập hợp số phức, xét phương trình 2 2
z  2mz m  2m  0 ( m là tham số thực). Tích của
tất cả các giá trị thực của m để phương trình có hai nghiệm phân biệt z , z thỏa mãn z  2 z 1 2 1 2 là A. 0 . B. 1  8 . C. 2 . D. 4 . Lời giải Chọn D Ta có  '  2  m .
TH1:  '  0  m  0
Phương trình có hai nghiệm phân biệt là hai số thực. z  2  z 1 2 z  2 z  1 2  z  2  z 1 2 Theo viet có 2 z z  2  ;
m z .z m  2m . 1 2 1 2  m  0 Nếu 2 2 2 z 2z z 2 ; m z 4m z .z 8m m 2m 9m 2m 0                 1 2 2 1 1 2 2  m   9 2
Do m  0  m   . 9 2  m 4  m 8 1  m  0 Nếu 2 2 2
z  2z z  ; z
z .z m m  2m m  2m  0  1 2 2 1 1 2 3 3 9 9  m  1  8
Do m  0  m  1  8 .
TH2:  '  0  m  0
Phương trình có hai nghiệm là hai số phức liên hợp nên z z . 1 2
z  2 z z  0  z  0 . 1 2 1 1
Thay vào phương trình ta được 2
m  2m  0  m  0; m  2  ( loại). 2  Vậy .( 1  8)  4 . 9
Câu 46. Trong không gian Oxyz, cho mặt phẳng  vuông góc với mặt phẳng P : x  3y  2z  2  0 x 1 y 1 z  4
và chứa đường thẳng d :  
. Khoảng cách từ điểm A1; 2  ;  1 đến mặt phẳng 2 1  1  bằng 8 3 4 3 24 3 A. . B. . C. . D. 8 3 . 3 3 3 Lời giải Chọn A  n u n n u P      1;3; 2  , d 2; 1  ;  1    ;   1; 5  ; 7  (P) d   .     Điểm M (1; 1
 ;4) d M  .
Phương trình mặt phẳng  là 1 x   1  5 y  
1  7 z  4  0  x  5y  7z  22  0 .
d A  8 3 ;  . 3
Câu 47. Có bao nhiêu cặp số nguyên dương (x, y) sao cho ứng với mổi giá trị nguyên dương của y có
không quá 15 giá trị nguyên dương của x thỏa mãn log  2 2
3x xy  36y   log  2 2
x 12y   log (xy)  log  2 2
x 16xy 12y 1? 5 3 5 3  A. 40. B. 36. C. 21. D. 33. Lời giải Chọn B log  2 2
3x xy  36y   log  2 2
x 12y   log (xy)  log  2 2
x 16xy 12y 1 5 3 5 3  2 2 2 2
3x xy  36y
3x  48xy  36  y log  log 5 3 2 2 xy x 12y  
  x 12y    48   log 3  1     log 3   5 3   y x    x y 12     y x x 12y  48  Đặt a  
 0 . Ta được log (3a 1)  log 3   0 .   y x 5 3  a   48 
Xét f (a)  log (3a 1)  log 3  , a  (0, ). 5 3    a  48 2  3  ( )   a f a  0,a  0. (3a 1) ln 5  48  3  ln 3    a
f (a) đồng biến trên (0  )
Mà f (8)  0  f (a)  0  a  8 . Khi đó ta có x y 2 2 2 2
12  8  x 12y  8xy x  8xy 12y  0  (x  2y)(x  6y)  0  2y x  6 . y y x
Để mỗi giá trị của y có không quá 15 giá trị nguyên dương của x thì điều kiện là *
(6y 1)  (2y 1) 1  15  y  4, y N  1  y  4.
Với y  1 x 2;6  có 3 cặp  ; x y.
Với y  2  x 4;12  có 7 cặp  ; x y.
Với y  3  x 6;18  có 11 cặp  ; x y.
Với y  4  x 8;24  có 15 cặp  ; x y. Vậy có 36 cặp  ;
x y thỏa yêu cầu bài toán.
Câu 48. Cho khối nón tròn xoay có đường cao h = 20 cm , bán kính đáy r  25 cm . Mặt phẳng (P) đi
qua đỉnh của khối nón và cách tâm O của đáy khối nón một khoảng bằng 12 cm . Khi đó diện
tích thiết điện của khổi nón cắt bởi mặt phằng (P) bằng: A. 2 500 cm . B. 2 475 cm . C. 2 450 cm . D. 2 550 cm . Lời giải Chọn A
Gọi S là đình của khối nón. Mặt phẳng (P) đi qua đỉnh S cắt khối nón theo hai đường sinh bằng
nhau là SA SB nên ta có thiết diện là tam giác cân SAB .
Gọi I là trung điêm của đoạn AB , ta có OI AB . Từ tâm O của đáy ta kẻ OH SI tại H , ta
có OH  (SAB) và do đó theo giả thiết ta có OH  12 cm . Xét tam giác vuông SOI 1 1 1 1 1 ta có:      OI  15( cm). 2 2 2 2 2 OI OH OS 2 1 20 OS.OI 20.15
Mặt khác, xét tam giác vuông SOI ta còn có: OS.OI SI.OH SI    25( cm). OH 12 1
Gọi S là diện tích của thiết diện tam giác SAB . Ta có: S A . B SI , trong đó t t 2
AB  2AI . Vì 2 2 2 2 2 2
AI OA OI  25 15  20 nên AI  20 cm và AB  40 cm . 1
Vậy thiết diện SAB có diện tích là: S   40 25  500 t  2 cm  . 2
Câu 49. Trong không gian Oxyz , cho mặt cầu 2 2 2
(S) : x y z  6x  4y  2z 11  0 và điểm M (0; 2
 ;1) . Gọi d , d , d là ba đường thẳng thay đổi không đồng phẳng cùng đi qua điểm 1 2 3 M (0; 2
 ;1) và lần lượt cắt mặt cầu (S) tại điểm thứ hai là ,
A B,C . Thể tích của tứ diện MABC
đạt giá trị lớn nhất bằng 50 3 1000 3 100 3 500 3 A. . B. . C. . D. . 9 27 9 27 Lời giải Chọn B Mặt cầu 2 2 2
(S) : x y z  6x  4y  2z 11  0 có tâm (3; 2;1) bán kính R  5
Mặt phẳng chứa ba điểm ,
A B,C cắt mặt cầu (S) ta được một hình tròn tâm I.
Thể tích của tứ diện MABC đạt giá trị lớn nhất khi thể tích hình nón đỉnh M có đáy là hình tròn tâm I lớn nhất. Gọi ,
h r lần lượt là chiều cao và bán kính đáy hình nón 2 2 2 l r h Ta có: 2 2 2 R   S
10h r h r  10h h 2h 2h Thể tích hình nón là: 1 1 2 2
V .r .h .(10 h h ).h 3 3 1 20 10 2 2
V '  .(20 h 3h )  0  h   r  3 3 3
Xét đường tròn đi qua 3 điểm , A B,C :
Diện tích tam giác ABC lớn nhất khi tam giác ABC đều 50 1 1000 3 S   MaxV  . . h S  . ABC 3 MABC 3 ABC 27  3  
Câu 50. Cho hàm số bậc bốn y f x có f  2 và f  
1  0 . Biết hàm số y f  x có đồ thị    2  2  x x
như hình vẽ bên. Hàm số g x  f 1 
đồng biến trên khoảng nào dưới đây?    2  8 A.  ;  4   . B. 5; . C. 2;4 . D.  3  ;  1 . Lời giải Chọn C 2  x x 1   x x
Ta đặt hx  f 1    h x  f  1       2  8 2  2  4   1   x xx    x h x 0  f  1
  0  f  1  ,      1 2  2  4  2  2 Đặt  x
t 1  x  2  2t 2 t  3 x  0  
1  f t  t 1   t  1    x  4    t  1  x  4   Ta có BBT
Vậy hàm số g x đồng biến trên khoảng 2;4 .  HẾT
Document Outline

  • de-thi-thu-tot-nghiep-thpt-nam-2023-mon-toan-so-gddt-quang-binh
  • 91. ĐỀ THI THỬ TN THPT 2023 - MÔN TOÁN - THPT SỞ QUẢNG BÌNH L2 (Bản word kèm giải).Image.Marked

Tài liệu liên quan: