Đề thi thử tốt nghiệp THPTQG 2021 môn Toán trường THPT chuyên Hà Tĩnh

Giới thiệu đến với quý thầy, cô giáo và các bạn học sinh đề thi thử tốt nghiệp THPTQG 2021 môn Toán trường THPT chuyên Hà Tĩnh mã đề 001 gồm 06 trang với 50 câu trắc nghiệm

Chủ đề:

Đề thi THPTQG môn Toán năm 2023 1.2 K tài liệu

Môn:

Toán 1.8 K tài liệu

Thông tin:
33 trang 10 tháng trước
Tác giả:
T
Thanh Hoa
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Đề thi thử tốt nghiệp THPTQG 2021 môn Toán trường THPT chuyên Hà Tĩnh

Giới thiệu đến với quý thầy, cô giáo và các bạn học sinh đề thi thử tốt nghiệp THPTQG 2021 môn Toán trường THPT chuyên Hà Tĩnh mã đề 001 gồm 06 trang với 50 câu trắc nghiệm

29 15 lượt tải Tải xuống

Chủ đề: Đề thi THPTQG môn Toán năm 2023 1.2 K tài liệu

Môn: Toán 1.8 K tài liệu

Thông tin:

33 trang 10 tháng trước

Tác giả:

Profile Thanh Hoa
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 1
TRƯỜNG & THPT
---------------------------
CHUYÊN HÀ TĨNH
MÃ ĐỀ: ......
THI THỬ TN12 LẦN 1 MÔN TOÁN
NĂM HỌC 2020 - 2021
Thời gian: 90 phút
Câu 1. Đạo hàm của hàm số
.3
x
yx=
là
A.
' 3 .ln 3
x
y =
. B.
' (1 ln 3).3
x
yx= +
. C.
' (1 ).3
x
yx
= +
. D.
'3
x
y =
.
Câu 2. Cho hàm số
có bảng biến thiên như hình vẽ bên.
Hàm số đã cho đạt cực đại tại
A.
2x =
. B.
0x
=
. C.
1x =
. D.
1x = −
.
Câu 3. Từ các chữ số
0;1; 2;3; 4;5
lập được bao nhiêu số tự nhiên có
5
chữ số phân biệt?
A.
720
. B.
120
. C.
96
. D.
600
.
Câu 4. Tích phân
( )
3
2
3
d 3, , .x x a b ab=+∈
∫
Khi đó
2ab−
bằng
A.
10
. B.
7
. C.
8
. D.
11
.
Câu 5. Tập xác định của hàm số
( ) (
)
2
log 3 1
y xx
π
= −+−
A.
( )
{ }
;3 \ 1−∞
. B.
( )
;1−∞
. C.
( )
3; +∞
. D.
(
)
1; 3
.
Câu 6. Cho hình lập phương
.ABCD A B C D
′′′′
có đường chéo
3
AC a
′
=
. Thể tích khối lập phương đó
bằng
A.
3
a
. B.
3
33a
. C.
3
4a
. D.
3
2a
.
Câu 7. Cho số phức
35zi= −
. Phần ảo của
z
A.
i
. B.
5−
. C.
3
. D.
5
.
Câu 8. Cho hàm số
( )
fx
có đạo hàm
( )
(
)
( )
2
2f x xx x x
′
=−−
.Số điểm cực trị của hàm số đã cho là
A.
2
. B.
3
. C.
4
. D.
1
.
Câu 9. Với
a
là số thực dương tùy ý,
bằng
A.
2
a
. B.
a
. C.
2
a
. D.
2
a
.
Câu 10. Cho hàm số
( )
fx
có bảng biến thiên như hình vẽ bên
Hàm số đã cho đồng biến trên khoảng nào dưới đây
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 󰱃 BIÊN SOẠN TOÁN THPT
Trang 2 TÀI LIỆU ÔN THI THPT QUỐC GIA
A.
(
)
1;2
. B.
( )
2;+∞
. C.
( )
2;2−
. D.
( )
;1−∞
.
Câu 11. Nếu
( )
3
1
d1fx x
−
= −
∫
và
( )
1
1
d2
fx x
−
= −
∫
thì
( )
3
1
2dfx x
∫
bằng
A.
6−
. B.
2−
. C.
2
. D.
0
.
Câu 12. Cho số phức
23
zi
= −
. Điểm
M
biểu diễn số phức
( )
w 12 3iz i
=−+
có tọa độ là
A.
( )
8;2
. B.
( )
1;8
. C.
( )
8; 1−
. D.
( )
2;8
.
Câu 13. Cho hàm số bậc hai
( )
y fx=
có đồ thị trong hình bên. Số nghiệm của phương trình
( )
2 50fx−=
là
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 14. Tập nghiệm của bất phương trình
( )
1
4
log 1 1x − >−
là
A.
5
;
4

+∞


. B.
5
1;
4



. C.
(
)
;2
−∞
. D.
(
)
1; 5
.
Câu 15. Cho số phức
z
thỏa mãn
( )
13 5 7iz i− +=
. Mệnh đề nào sau đây đúng?
A.
13 4
55
zi= +
. B.
13 4
55
zi= −
. C.
13 4
55
zi=−+
. D.
13 4
55
zi=−−
.
Câu 16. Cho khối nón có bán kính đáy bằng
a
và chiều cao bằng
3a
. Diện tích xung quanh của khối
nón đã cho bằng
A.
2
2
a
π
. B.
2
4 a
π
. C.
2
8 a
π
. D.
2
2 a
π
.
Câu 17. Cho cấp số cộng có số hạng đầu bằng
2
, công sai bằng
4
. Số hạng thứ
3
của cấp số cộng đó
bằng
A.
10
. B.
12
. C.
6
. D.
8
.
Câu 18. Cho hình bát diện đều cạnh
a
. Thể tích khối bát diện đều này là
A.
3
2
3
a
. B.
3
3
3
a
. C.
3
2
4
a
. D.
3
6
3
a
.
Câu 19. Cho hàm số
( )
sin 2021fx x= +
. Trong các khẳng định sau khẳng định nào đúng?
A.
( )
d cos 2021fxx x xC=−+ +
∫
. B.
( )
d cos 2021fxx x xC=++
∫
.
C.
( )
d cosfxx xC= +
∫
. D.
( )
d cosfxx xC=−+
∫
.
Câu 20. Tiệm cận đứng của đồ thị hàm số
21
1
x
y
x
+
=
−
là đường thẳng
A.
1y =
. B.
2x =
. C.
1x =
. D.
2
x = −
.
Câu 21. Thể tích của khối cầu có đường kính bằng
2a
là
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 3
A.
3
8
3
a
π
. B.
3
4 a
π
. C.
3
4
3
a
π
. D.
3
2 a
π
.
Câu 22. Hàm số
( )
2
ln 4yx= −
đồng biến trên khoảng
A.
(
)
2; 2
−
. B.
( )
;2
−∞
. C.
( )
0; 2
. D.
( )
2; 0−
.
Câu 23. Cho hàm số
(
)
31
x
fx e
−+
=
. Trong các khẳng định sau, khẳng định nào đúng?
A.
( )
31
d3
x
fx x e C
−+
=−+
∫
. B.
( )
31
d
x
fx x e C
−+
= +
∫
.
C.
(
)
31
1
d
3
x
fx x e C
−+
=−+
∫
. D.
( )
31
1
d
3
x
fx x e C
−+
= +
∫
.
Câu 24. Đồ thị hàm số nào dưới đây có dạng như đường cong hình bên?
A.
32
3yx x=−+
. B.
42
3yx x= −
. C.
32
3yx x
= −
. D.
42
3yx x
=−+
.
Câu 25. Trong không gian
Oxyz
, cho ba điểm
(
) (
)
( )
1;1; 2 , 3; 1; 0 , 1; 1; 1
AB C
−
. Trọng tâm của tam giác
ABC
có tọa độ là
A.
( )
2;1;1
. B.
( )
3; 3; 3
. C.
( )
1;1; 1
. D.
(
)
6; 2; 2
.
Câu 26. Cho đồ thị hàm số
42
y ax bx c=++
có điểm cực đại
(
)
0; 3A −
và điểm cực tiểu
( )
1; 5B −−
.
Tính giá trị của
23Pa b c=++
.
A.
3P =
. B.
5P = −
. C.
9P = −
. D.
15P = −
.
Câu 27. Trong không gian
Oxyz
, đường thẳng đi qua hai điểm
(
)
3;1; 0A
và
(
)
1;1;1B −
có phương
trình là
A.
74
1
1
xt
y
zt
= −
=
=−+
. B.
14
1
1
xt
y
zt
=−+
=
= +
. C.
34
1
xt
yt
zt
= −
=
= +
. D.
34
1
xt
yt
zt
= −
= +
=
.
Câu 28. Một học sinh tô ngẫu nhiên
5
câu trắc nghiệm (mỗi câu có
4
phương án lựa chọn, trong đó chỉ
có
1
phương án đúng). Xác suất để học sinh đó tô sai cả
5
câu bằng
A.
15
1024
. B.
3
4
. C.
243
1024
. D.
1
1024
.
Câu 29. Trong không gian
Oxyz
, cho hai điểm
( )
1;1; 2A
và
( )
3;1; 0B
. Mặt cầu đường kính
AB
có
phương trình là
A.
( )
( ) ( )
2 22
2 1 18x yz− +− +− =
. B.
( ) ( ) ( )
2 22
2 1 12x yz− +− +− =
.
C.
( ) ( ) ( )
22 2
1 1 28xyz−+−+− =
. D.
( ) ( )
22
2
31 2x yz− +− +=
.
Câu 30. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
, cạnh bên
SA
vuông
góc với mặt đáy và
2SA a=
,
222AD AB BC a= = =
. Côsin của góc giữa
2
mặt phẳng
( )
SAD
và
( )
SCD
bằng
A.
3
.
2
B.
3
.
2
C.
2
.
2
D.
1
.
2
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 󰱃 BIÊN SOẠN TOÁN THPT
Trang 4 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 31. Nếu
( )
5
3
2 d3
fx x=
∫
thì
( )
2
1
2 1dfx x
+
∫
A.
3
.
2
B.
3.
C.
6.
D.
3
.
4
Câu 32. Trong không gian
Oxyz
, cho hai điểm
( )
1;2;1M −
và
( )
3;0; 1N −
. Mặt phẳng trung trực của
MN
có phương trình là
A.
4 2 2 1 0.xyz− − +=
B.
2 1 0.xyz− + ++=
C.
2 0.xy+−=
D.
2 7 0.xyz− +++=
Câu 33. Tìm tất cả các giá trị thực của tham số
m
để phương trình
2
12
220
x
m
+
−=
có nghiệm.
A.
1
1
m
m
≥
≤−
. B.
0
m >
. C.
( )
;0−∞
. D.
( )
0;1
.
Câu 34. Cho hàm số
( )
( )
23
22
x2
3
m mx
y m mx m
−
= + − ++
. Có bao nhiêu giá trị nguyên của
m
để
hàm số đồng biến trên
?
A.
3
. B.
5
. C.
1
. D.
2
.
Câu 35. Trong không gian
Oxyz
, đường thẳng nào dưới đây đi qua điểm
( )
1; 2; 1M −
?
A.
1
121
:
2 13
xy z
d
−−+
= =
−
. B.
3
1 21
:
2 31
xy z
d
−+−
= =
−
.
C.
3
1 21
:
213
xy z
d
++−
= =
. D.
3
1 21
:
23 1
xy z
d
−++
= =
−
.
Câu 36. Trong không gian
Oxyz
, mặt cầu
( ) ( ) ( )
22
2
: 1 24
Sx y z+− ++ =
có tọa độ tâm
I
là
A.
(
)
0;1; 2I
−
. B.
( )
0;1; 2I
. C.
( )
0; 1; 2
I −
. D.
(
)
1;1; 2I −
.
Câu 37. Cho lăng trụ
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
, góc giữa hai mặt phẳng
( )
ABC
′′′
và
( )
BCC B
′′
bằng
60°
, hình chiếu của
B
′
lên mặt phẳng
( )
ABC
trùng với trọng tâm tam giác
ABC
. Khoảng cách giữa hai đường thẳng
AA
′
và
BC
′
bằng
A.
3
4
a
. B.
2
a
. C.
3
4
a
. D.
4
a
.
Câu 38. Cho hai số phức
1
z
,
2
z
là các nghiệm của phương trình
2
4 13 0zz++=
. Khi đó môđun của số
phức
( )
1 2 12
w z z i zz=++
bằng
A.
13 5
. B.
195
. C.
185
. D.
13
.
Câu 39. Một gia đình muốn làm cánh cổng (như hình vẽ). Phần phía trên cổng có hình dạng là một
parabol với
2,5mIH =
, phần phía dưới là một hình chữ nhật kích thước cạnh là
4mAD =
,
6mAB =
. Giả sử giá để làm phần cổng được tô màu là
( )
2
1.000.0 0 đ0 /m
và giá để làm phần
cổng phía trên là
( )
2
1.200.0 0 đ0 /m
. Số tiền gia đình đó phải trả là
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 5
A.
24.400.000
đ
. B.
36.000.000đ
. C.
38.000.000đ
. D.
38.800.000đ
.
Câu 40. Có bao nhiêu giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2xm
y
xm
−−
=
−
trên đoạn
[ ]
0;4
bằng
1
2
?
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 41. Cho hàm số
( )
fx
có đạo hàm trên
thỏa mãn
( )
23f =
,
( )
4
1
d2
fx
x
x
=
∫
,
( )
2
0
d3xf x x
′
=
∫
.
Tính
( )
1
0
dfx x
∫
.
A.
5
. B.
1
. C.
2
. D.
3
.
Câu 42. Cho số phức
z x yi= +
(
;xy∈
) thỏa mãn
( )
21z iz i
+ += +
và
3z >
. Giá trị của biểu thức
23S xy= −
là
A.
6−
. B.
3−
. C.
6
. D.
3
.
Câu 43. Cho hình chóp
.
S ABC
có
SA
vuông góc với mặt đáy,
2 2 3,
SA BC a AC a
= = =
và
120BAC
°
=
. Hình chiếu vuông góc của
A
lên các cạnh
SB
và
SC
lần lượt là
M
và
N
. Thể
tích của khối đa diện
AMNCB
bằng
A.
3
24
169
a
. B.
3
25
338
a
. C.
3
25
169
a
. D.
3
12
169
a
.
Câu 44. Trong không gian
Oxyz
, cho hai đường thẳng
1
11
:
1 12
xyz
d
−+
= =
−
và
2
1
:
121
xy z
d
−
= =
.
Đường thẳng
d
đi qua
( )
1; 0; 1A
lần lượt cắt
12
,dd
tại
B
và
C
. Độ dài
BC
bằng
A.
. B.
33
2
. C.
53
2
. D.
76
2
.
Câu 45. Có bao nhiêu giá trị nguyên dương của tham số
m
để bất phương trình
2
33
log 3log 2
0
2
x
xx
m
−+
<
−
có không quá 3 nghiệm nguyên dương?
A.
127
. B.
128
. C.
63
. D.
64
.
Câu 46. Trong không gian
Oxyz
, cho mặt cầu
( )
S
:
( ) ( )
22
2
11 4x yz− ++ +=
và hai điểm
( )
1;1;1
A −
;
( )
2; 2;1B −
. Điểm
M
di chuyển trên mặt cầu
( )
S
. Giá trị lớn nhất của
23MA MB−
đạt được
là:
A.
65
. B.
67
. C.
69
. D.
61
.
Câu 47. Có bao nhiêu giá trị thực của tham số
m
để bất phương trình sau có nghiệm duy nhất?
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 󰱃 BIÊN SOẠN TOÁN THPT
Trang 6 TÀI LIỆU ÔN THI THPT QUỐC GIA
(
)
( )
22
15
log 5 1 .log 6 log 3 0
m
m
x mx x mx
+++ +++ ≥
.
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 48. Cho hình
( )
H
giới hạn bởi đồ thị hàm số bậc hai (nét mảnh) và đồ thị hàm số bậc ba (nét đậm)
như hình vẽ. Thể tích khối tròn xoay khi quay hình
(
)
H
quanh trục
Ox
là:
A.
1024
35
π
. B.
4096
35
. C.
5017
35
π
. D.
4096
35
π
.
Câu 49. Cho số phức
z
thay đổi thỏa mãn
32zi+=
. Giá trị lớn nhất của biểu thức
11 3
Sz z z i
=−++++
là
A.
4
3
. B.
16
3
. C.
2
3
. D.
8
3
.
Câu 50. Cho hàm số
32
( 2) (2 13) 2y x m x m xm= − + − + −−
có đồ thị
( ),
m
C
đường thẳng
:8d y mx m= ++
và điểm
( )
1; 4 .I
Tính tổng tất cả các giá trị của tham số
,m
biết rằng đường
thẳng
d
cắt đồ thị
()
m
C
tại ba điểm phân biệt
,,ABC
với
A
có hoành độ bằng
2−
và tam giác
IBC
cân tại
.I
A.
12−
. B.
6
−
. C.
4−
. D.
10−
.
____________________ HẾT ____________________
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 7
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT
BẢNG ĐÁP ÁN
1.B
2.B
3.D
4.D
5.D
6.A
7.B
8.A
9.C
10.A
11.C
12.A
13.B
14.D
15.C
16.D
17.A
18.A
19.A
20.C
21.C
22.D
23.C
24.B
25.C
26.D
27.A
28.C
29.B
30.D
31.D
32.B
33.A
34.D
35.B
36.A
37.A
38.C
39.B
40.D
41.C
42.A
43.B
44.A
45.C
46.B
47.B
48.C
49.D
50.B
LỜI GIẢI CHI TIẾT
Câu 1. Đạo hàm của hàm số
.3
x
yx=
là
A.
' 3 .ln 3
x
y =
. B.
' (1 ln 3).3
x
yx= +
. C.
' (1 ).3
x
yx= +
. D.
'3
x
y =
.
GVSB: Lương Công Hảo; GVPB: Phạm Hiền
Lời giải
Chọn B
Có
( )
( )
( )
( )
' .3 .3 3 . 3 3 .ln 3. 1 ln 3 .3
x x x xx x
yx x x x x
′′
′
==+=+ =+
.
Câu 2. Cho hàm số
có bảng biến thiên như hình vẽ bên.
Hàm số đã cho đạt cực đại tại
A.
2x =
. B.
0x
=
. C.
1x =
. D.
1x
= −
.
GVSB: Lương Công Hảo; GVPB: Phạm Hiền
Lời giải
Chọn B
Qua BBT có
'y
đổi dấu từ
+
sang
−
khi đi qua
0x =
. Suy ra hàm số đạt cực đại tại
0x =
.
Câu 3. Từ các chữ số
0;1; 2; 3; 4;5
lập được bao nhiêu số tự nhiên có
5
chữ số phân biệt?
A.
720
. B.
120
. C.
96
. D.
600
.
GVSB: Lương Công Hảo; GVPB: Phạm Hiền
Lời giải
Chọn D
Số các số có
5
chữ số phân biệt lấy từ bộ
{
}
0;1; 2; 3; 4; 5
là
54
65
600.AA−=
Câu 4. Tích phân
( )
3
2
3
d 3, , .x x a b ab=+∈
∫
Khi đó
2ab−
bằng
A.
10
. B.
7
. C.
8
. D.
11
.
Lời giải
GVSB: Thu Ha Cao; GVPB: Phạm Hiền
Chọn D
( )
( )
3
3
3
3
23
3
3
1
d 3 3 93
33
x
xx==−=−
∫
.
9, 1 2 11a b ab⇒ = =−⇒ − =
.
Câu 5. Tập xác định của hàm số
( ) ( )
2
log 3 1y xx
π
= −+−
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 󰱃 BIÊN SOẠN TOÁN THPT
Trang 8 TÀI LIỆU ÔN THI THPT QUỐC GIA
A.
(
) {
}
;3 \ 1−∞
. B.
( )
;1−∞
. C.
( )
3; +∞
. D.
( )
1; 3
.
Lời giải
GVSB: Thu Ha Cao; GVPB: Phạm Hiền
Chọn D
Hàm số xác định khi
30 3
13
10 1
xx
x
xx
−> <

⇔ ⇔< <

−> >

.
Câu 6. Cho hình lập phương
.ABCD A B C D
′′′′
có đường chéo
3AC a
′
=
. Thể tích khối lập phương đó
bằng
A.
3
a
. B.
3
33a
. C.
3
4a
. D.
3
2a
.
Lời giải
GVSB: Thu Ha Cao; GVPB: Phạm Hiền
Chọn A
Hình lập phương cạnh
a
có đường chéo bằng
3a
.
Do đó hình lập phương đã cho có cạnh là
a
. Thể tích tích khối lập phương đó bằng
3
a
.
Câu 7. Cho số phức
35zi= −
. Phần ảo của
z
A.
i
. B.
5−
. C.
3
. D.
5
.
Lời giải
GVSB: Thu Ha Cao; GVPB: Phạm Hiền
Chọn B
Phần ảo của số phức
35zi= −
là
5
−
.
Câu 8. Cho hàm số
(
)
fx
có đạo hàm
( )
( )
( )
2
'2f x xx x x=−−
.Số điểm cực trị của hàm số đã cho là
A.
2
. B.
3
. C.
4
. D.
1
.
Lời giải
GVSB: Trần Thị Hòa; GVPB: Nguyễn Hiền Lương
Chọn A
Ta có
( )
(
)
( ) ( )( )
22
' 2 12f x xx x x x x x= − −= − −
.
( )
fx
′
đổi dấu 2 lần.Vậy hàm số
( )
fx
có 2 điểm cực trị.
Câu 9. Với
a
là số thực dương tùy ý,
bằng
A.
2
a
. B.
a
. C.
2
a
. D.
2
a
.
Lời giải
GVSB: Trần Thị Hòa; GVPB: Nguyễn Hiền Lương
Chọn C
Ta có
( )
( )
2
22
2
log
log log
22
42 2
a
aa
a= = =
.
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 9
Câu 10. Cho hàm số
( )
fx
có bảng biến thiên như hình vẽ bên
Hàm số đã cho đồng biến trên khoảng nào dưới đây
A.
(
)
1;2
. B.
(
)
2;
+∞
. C.
( )
2;2−
. D.
(
)
;1
−∞
.
Lời giải
GVSB: Trần Thị Hòa; GVPB: Nguyễn Hiền Lương
Chọn A
Từ BBT của hàm số ta thấy hàm số đồng biến trên khoảng
( )
1;2
.
Câu 11. Nếu
( )
3
1
d1fx x
−
= −
∫
và
( )
1
1
d2fx x
−
= −
∫
thì
( )
3
1
2d
fx x
∫
bằng
A.
6−
. B.
2−
. C.
2
. D.
0
.
Lời giải
GVSB: ThienMinh Nguyễn; GVPB:Nguyễn Hiền Lương
Chọn C
Ta có:
( ) ( ) ( )
3 13
1 11
d ddfx x fx x fx x
−−
= +
∫∫∫
.
Suy ra
( ) ( ) ( )
3 31
1 11
d d d 121fx x fx x fx x
−−
= − =−+ =
∫∫∫
.
Nên
( ) ( )
33
11
2 d 2 d 2.1 2fx x fx x= = =
∫∫
.
Câu 12. Cho số phức
23zi
= −
. Điểm
M
biểu diễn số phức
( )
w 12 3iz i=−+
có tọa độ là
A.
( )
8;2
. B.
( )
1;8
. C.
( )
8; 1−
. D.
( )
2;8
.
Lời giải
GVSB: ThienMinh Nguyễn; GVPB: Nguyễn Hiền Lương
Chọn A
( )
w 12 3iz i=−+
( )( )
w 12 23 3 82i ii i⇔=− + +=+
.
Nên điểm biểu diễn số phức
w
là điểm có tọa độ
( )
8;2
.
Câu 13. Cho hàm số bậc hai
( )
y fx=
có đồ thị trong hình bên. Số nghiệm của phương trình
( )
2 50
fx−=
là
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 󰱃 BIÊN SOẠN TOÁN THPT
Trang 10 TÀI LIỆU ÔN THI THPT QUỐC GIA
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
GVSB: ThienMinh Nguyễn; GVPB: Nguyễn Hiền Lương
Chọn B
Ta có:
( )
2 50fx−=
⇔
( )
5
2
fx=
. Số nghiệm của phương trình là số giao điểm của đồ thị hàm
số
( )
y fx=
và đường thẳng
5
2
y =
.Dựa vào đồ thị ta thấy đường thẳng
5
2
y =
cắt đồ thị hàm
số
( )
y fx=
tại 3 điểm nên số nghiệm của phương trình
( )
2 50fx−=
là 3.
Câu 14. Tập nghiệm của bất phương trình
( )
1
4
log 1 1x − >−
là
A.
5
;
4

+∞


. B.
5
1;
4



. C.
( )
;2−∞
. D.
( )
1; 5
.
Lời giải
GVSB: Bùi Hoàng Nguyên; GVPB: Nguyễn Hiền Lương
Chọn D
Ta có: BPT
( )
1
4
log 1 1x − >−
1
1
01 1 5
4
xx
−

⇔ < −< ⇔< <


.
Vậy tập nghiệm
( )
1; 5S
=
.
Câu 15. Cho số phức
z
thỏa mãn
(
)
13 5 7iz i− +=
. Mệnh đề nào sau đây đúng?
A.
13 4
55
zi
= +
. B.
13 4
55
zi= −
. C.
13 4
55
zi
=−+
. D.
13 4
55
zi=−−
.
Lời giải
GVSB: Bùi Hoàng Nguyên; GVPB: Nguyễn Hiền Lương
Chọn C
Ta có:
( )
5 7 13 4
13 5 7
13 5 5
i
iz i z i
i
−+
− += ⇔= =− −
−
Suy ra
13 4
55
zi=−+
.
Câu 16. Cho khối nón có bán kính đáy bằng
a
và chiều cao bằng
3a
. Diện tích xung quanh của khối
nón đã cho bằng
A.
2
2
a
π
. B.
2
4 a
π
. C.
2
8 a
π
. D.
2
2 a
π
.
Lời giải
GVSB: Bùi Hoàng Nguyên; GVPB: Nguyễn Hiền Lương
Chọn D
O
S
A
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 11
Theo đề, ta có:
,3AOaSOa
= =
Suy ra, đường sinh
22
2l SA SO AO a== +=
Vậy diện tích xung quanh của hình nón là
2
.2
xq
S rl AO S A a
ππ π
= = =
.
Câu 17. Cho cấp số cộng có số hạng đầu bằng
2
, công sai bằng
4
. Số hạng thứ
3
của cấp số cộng đó
bằng
A.
10
. B.
12
. C.
6
. D.
8
.
Lời giải
GVSB: Anh Tuấn;GVPB:
Chọn A
Ta có số hạng thứ
3
của cấp số cộng là
31
2 2 2.4 10uu d=+=+=
.
Câu 18. Cho hình bát diện đều cạnh
a
. Thể tích khối bát diện đều này là
A.
3
2
3
a
. B.
3
3
3
a
. C.
3
2
4
a
. D.
3
6
3
a
.
Lời giải
GVSB: Anh Tuấn;GVPB:
Chọn A
Gọi
V
là thể tích khối bát diện đều cạnh
a
. Ta có
.
2
S ABCD
VV=
.
Do tứ giác
ABCD
là hình vuông nên
2
22
2
a
AC BD BC a OA== = ⇒=
.
Ta có
( )
2
22 2
22
42
aa
SO ABCD SO OA SO SA OA a⊥ ⇒⊥⇒= − = − =
.
Mà
3
22 2
.
1 12 2
. ..
3 32 6
ABCD S ABCD ABCD
aa
S AB a V SO S a==⇒= = =
.
Vậy
33
22
2.
63
aa
V = =
.
Câu 19. Cho hàm số
( )
sin 2021fx x= +
. Trong các khẳng định sau khẳng định nào đúng?
A.
( )
d cos 2021fxx x xC=−+ +
∫
. B.
( )
d cos 2021fxx x xC=++
∫
.
C.
( )
d cosfxx xC= +
∫
. D.
(
)
d cosfxx xC=−+
∫
.
Lời giải
O
D
B
A
C
S
S'
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 󰱃 BIÊN SOẠN TOÁN THPT
Trang 12 TÀI LIỆU ÔN THI THPT QUỐC GIA
GVSB: Anh Tuấn;GVPB:
Chọn A
Ta có
( ) ( )
d sin 2021 d cos 2021fxx x x x xC= + =−+ +
∫∫
.
Câu 20. Tiệm cận đứng của đồ thị hàm số
21
1
x
y
x
+
=
−
là đường thẳng
A.
1
y =
. B.
2
x =
. C.
1x =
. D.
2x = −
.
Lời giải
GVSB: Trần Ngọc; GVPB:
Chọn C
Ta có
1
21
lim
1
x
x
x
−
→
+
= −∞
−
;
1
21
lim
1
x
x
x
+
→
+
= +∞
−
.
Vậy đồ thị hàm số có đường tiện cận đứng là
1x =
.
Câu 21. Thể tích của khối cầu có đường kính bằng
2a
là
A.
3
8
3
a
π
. B.
3
4 a
π
. C.
3
4
3
a
π
. D.
3
2 a
π
.
Lời giải
GVSB: Trần Ngọc; GVPB:
Chọn C
Ta có bán kính mặt cầu
Ra=
, suy ra
33
44
33
VR a
ππ
= =
.
Câu 22. Hàm số
( )
2
ln 4yx= −
đồng biến trên khoảng
A.
( )
2; 2−
. B.
( )
;2−∞
. C.
(
)
0; 2
. D.
( )
2; 0−
.
Lời giải
GVSB: Trần Ngọc; GVPB:
Chọn D
Tập xác định
( )
2; 2D
= −
.
Ta có
2
2
4
x
y
x
−
′
=
−
.
Trên
D
ta có
2
40x−>
nên hàm số đồng biến khi
0y
′
≥
( )( )
2
0
22
x
xx
−
⇔≥
−+
0x⇔≤
.
Vậy hàm số đã cho đồng biến trên khoảng
( )
2; 0−
.
Câu 23. Cho hàm số
( )
31x
fx e
−+
=
. Trong các khẳng định sau, khẳng định nào đúng?
A.
( )
31
d3
x
fx x e C
−+
=−+
∫
. B.
( )
31
d
x
fx x e C
−+
= +
∫
.
C.
( )
31
1
d
3
x
fx x e C
−+
=−+
∫
. D.
( )
31
1
d
3
x
fx x e C
−+
= +
∫
.
Lời giải
GVSB: Thúy Bình Đinh; GVPB: Don Lee
Chọn C
Ta có
(
)
31 31
1
dd
3
xx
fx x e x e C
−+ −+
= =−+
∫∫
.
Câu 24. Đồ thị hàm số nào dưới đây có dạng như đường cong hình bên?
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 13
A.
32
3yx x=−+
. B.
42
3yx x= −
. C.
32
3yx x= −
. D.
42
3yx x=−+
.
Lời giải
GVSB: Thúy Bình Đinh; GVPB: Don Lee
Chọn B
Đường cong hình bên là đồ thị hàm số
42
y ax bx c=++
với
0a >
.
Câu 25. Trong không gian
Oxyz
, cho ba điểm
( ) (
)
( )
1;1; 2 , 3; 1; 0 , 1; 1; 1AB C−
. Trọng tâm của tam giác
ABC
có tọa độ là
A.
( )
2;1;1
. B.
( )
3; 3; 3
. C.
( )
1;1; 1
. D.
( )
6; 2; 2
.
Lời giải
GVSB: Thúy Bình Đinh; GVPB: Don Lee
Chọn C
Trọng tâm
G
của tam giác
ABC
có tọa độ là
1
3
1
3
1
3
ABC
G
ABC
G
ABC
G
xxx
x
yyy
y
zzz
z
++
= =
++
= =
++
= =
.
Vậy
( )
1;1; 1G
.
Câu 26. Cho đồ thị hàm số
42
y ax bx c=++
có điểm cực đại
( )
0; 3A −
và điểm cực tiểu
( )
1; 5B −−
.
Tính giá trị của
23Pa b c=++
.
A.
3P =
. B.
5P = −
. C.
9P = −
. D.
15P = −
.
Lời giải
GVSB: Thúy Bình Đinh; GVPB: Don Lee
Chọn D
Đồ thị hàm số đi qua điểm
( )
0; 3A
−
và
( )
( )
21
3
1; 5
5
3.
ab
c
B
abc
c
+=−
= −
−− ⇒ ⇒

++=−
= −
42 3
42y ax bx c y ax bx
′
= + +⇒ = +
.
Đồ thị hàm số có điểm cực tiểu
( )
1; 5B −−
(
)
4 2 0. 2ab⇒− − =
Từ (1) và (2) suy ra
22
4 2 0 4.
ab a
ab b
+=− =

⇔

−− = =−

Với
42 3 2
2
4 2 4 3 8 8 24 8
3
a
b yx x y x xy x
c
=
′ ′′
=−⇒ = − −⇒ = − ⇒ = −
= −
.
0
0
1.
x
y
x
=
′
= ⇔
= ±
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 󰱃 BIÊN SOẠN TOÁN THPT
Trang 14 TÀI LIỆU ÔN THI THPT QUỐC GIA
( )
0 80y
′′
=−< ⇒
( )
0; 3A
−
là điểm cực đại.
( )
1 16 0
y
′′
−= >⇒
( )
1; 5B −−
là điểm cực tiểu.
Vậy
2
4 2 3 15
3
a
b Pa b c
c
=
=−⇒ = + + =−
= −
.
Câu 27. Trong không gian
Oxyz
, đường thẳng đi qua hai điểm
(
)
3;1; 0
A
và
( )
1;1;1B
−
có phương
trình là
A.
74
1
1
xt
y
zt
= −
=
=−+
. B.
14
1
1
xt
y
zt
=−+
=
= +
. C.
34
1
xt
yt
zt
= −
=
= +
. D.
34
1
xt
yt
zt
= −
= +
=
.
Lời giải
GVSB: Phạm Thái; GVPB: Nguyễn Minh Đức
Chọn A
Đường thẳng
AB
có vecto chỉ phương
(
)
4;0;1AB
= −

Do đó
14
:1
1
xt
AB y
zt
=−−
=
= +
Suy ra đường thẳng
AB
cũng đi qua
( )
7; 1; 1C −
Vậy
74
:1
1
xt
AB y
zt
= −
=
=−+
.
Câu 28. Một học sinh tô ngẫu nhiên
5
câu trắc nghiệm (mỗi câu có
4
phương án lựa chọn, trong đó chỉ
có
1
phương án đúng). Xác suất để học sinh đó tô sai cả
5
câu bằng
A.
15
1024
. B.
3
4
. C.
243
1024
. D.
1
1024
.
Lời giải
GVSB: Phạm Thái; GVPB: Nguyễn Minh Đức
Chọn C
Xác suất tô sai
1
câu là
3
4
Vậy xác suất để học sinh đó tô sai cả
5
câu là:
5
3 243
4 1024

=


.
Câu 29. Trong không gian
Oxyz
, cho hai điểm
( )
1;1; 2A
và
( )
3;1; 0
B
. Mặt cầu đường kính
AB
có
phương trình là
A.
( ) ( ) ( )
2 22
2 1 18x yz− +− +− =
. B.
( ) ( ) ( )
2 22
2 1 12x yz− +− +− =
.
C.
( ) ( ) ( )
22 2
1 1 28xyz−+−+− =
. D.
( ) ( )
22
2
31 2x yz− +− +=
.
Lời giải
GVSB: Phạm Thái; GVPB: Nguyễn Minh Đức
Chọn B
Ta có
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 15
Mặt cầu có tâm
(
)
2;1;1
I
.
Mặt cầu có bán kính
2R AI= =
Vậy mặt cầu có phương trình:
( )
(
)
(
)
2 22
2 1 12x yz
− +− +− =
.
Câu 30. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
, cạnh bên
SA
vuông
góc với mặt đáy và
2SA a=
,
222AD AB BC a
= = =
. Côsin của góc giữa
2
mặt phẳng
( )
SAD
và
( )
SCD
bằng
A.
3
.
2
B.
3
.
2
C.
2
.
2
D.
1
.
2
Lời giải
GVSB: Nguyễn Thắng; GVPB: Nguyễn Minh Đức
Chọn D
Gọi
M
là trung điểm
AD
thì
ABCM
là hình vuông nên
CM AD⊥
suy ra
( )
CM SAD⊥
.
Kẻ
( )
MH SD H SD
⊥∈
thì
( )
SD CMH⊥
.
Ta có
( ) (
)
( )
SAD SCD SD
SD CMH
∩=
⊥
nên góc giữa
( )
SAD
và
( )
SCD
là góc
MHC
.
Trong
SAD∆
thì
23
tan sin
23
SA
SDA SDA
AD
==⇒=
Trong
MHD
∆
vuông tại
H
thì
3
sin .
3
MH a
SDA MH
MD
=⇒=
Trong
MHC
∆
vuông tại
M
thì
2
2 22
3 23
33
aa
HC MC MH a

= +=+ =



3
1
3
cos
2
23
3
a
MH
MHC
HC
a
= = =
.
Câu 31. Nếu
(
)
5
3
2 d3fx x=
∫
thì
( )
2
1
2 1dfx x+
∫
A.
3
.
2
B.
3.
C.
6.
D.
3
.
4
Lời giải
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 󰱃 BIÊN SOẠN TOÁN THPT
Trang 16 TÀI LIỆU ÔN THI THPT QUỐC GIA
GVSB: Nguyễn Thắng; GVPB: Nguyễn Minh Đức
Chọn D
Ta có
( ) ( ) ( )
( )
22 5
11 3
1 1 13 3
21d 21d21 d . .
2 2 22 4
fx x fx x fxx+ = + += = =
∫∫ ∫
Câu 32. Trong không gian
Oxyz
, cho hai điểm
(
)
1;2;1M
−
và
(
)
3;0; 1N
−
. Mặt phẳng trung trực của
MN
có phương trình là
A.
4 2 2 1 0.
xyz− − +=
B.
2 1 0.xyz− + ++=
C.
2 0.xy+−=
D.
2 7 0.xyz− +++=
Lời giải
GVSB: Nguyễn Thắng; GVPB: Nguyễn Minh Đức
Chọn B
Gọi
( )
1;1;0I
là trung điểm
MN
.
Ta có
( ) ( )
4; 2; 2 2 2; 1; 1MN = − − = −−

.
Mặt phẳng trung trực của
MN
đi qua
I
và nhận vectơ
( )
2;1;1n = −
làm VTPT nên có phương
trình là
( ) ( ) ( )
2 11 11 0 0xyz− −+ −+ − = ⇔
2 10xyz− + ++=
.
Câu 33. Tìm tất cả các giá trị thực của tham số
m
để phương trình
2
12
220
x
m
+
−=
có nghiệm.
A.
1
1
m
m
≥
≤−
. B.
0
m >
. C.
( )
;0
−∞
. D.
( )
0;1
.
Lời giải
GVSB: Giang Sơn GVPB: Phạm Thanh Liêm
Chọn A
Phương trình đưa về
2
12
22
x
m
+
=
.
Nhận xét
2
1
22
x +
≥
, điều kiện có nghiệm là
22
1
22 1
1
m
mm
m
≥
≥ ⇔ ≥⇔
≤−
.
Câu 34. Cho hàm số
( )
( )
23
22
2
3
m mx
y m m x mx
−
= + − ++
. Có bao nhiêu giá trị nguyên của
m
để
hàm số đồng biến trên
?
A.
3
. B.
5
. C.
1
. D.
2
.
Lời giải
GVSB: Giang Sơn GVPB: Phạm Thanh Liêm
Chọn D
Xét
2
02
0
12
my
mm
m yx
=⇒=
−=⇔
=⇒=+
, chọn
1m =
.
Xét
2
0mm−>
.
Hàm số đồng biến trên
khi
( ) ( )
2
2 22
3a 0 0b c mm mmm− ≤⇔ − − − ≤
( )( )
( )( )
22 2
0
2 0 1 20
12
m
m mm m mm m
m
=
⇔ − − ≤⇔ − − ≤⇔
≤≤
.
Như vậy
12m≤≤
dẫn đến 2 giá trị nguyên
m
cần tìm.
Câu 35. Trong không gian
Oxyz
, đường thẳng nào dưới đây đi qua điểm
( )
1; 2; 1M
−
?
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 17
A.
1
121
:
2 13
xy z
d
−−+
= =
−
. B.
3
1 21
:
2 31
xy z
d
−+−
= =
−
.
C.
3
1 21
:
213
xy z
d
++−
= =
. D.
3
1 21
:
23 1
xy z
d
−++
= =
−
.
Lời giải
GVSB: Giang Sơn GVPB: Phạm Thanh Liêm
Chọn B
Thử trực tiếp ta có
3
1 21
:
2 31
xy z
d
−+−
= =
−
đi qua
( )
1; 2; 1
M
−
.
Câu 36. Trong không gian
Oxyz
, mặt cầu
(
) (
)
( )
22
2
: 1 24
Sx y z+− ++ =
có tọa độ tâm
I
là
A.
( )
0;1; 2I −
. B.
( )
0;1; 2I
. C.
( )
0; 1; 2I −
. D.
( )
1;1; 2I −
.
Lời giải
GVSB: Trần Xuân Thiện; GVPB: Phạm Thanh Liêm
Chọn A
Mặt cầu
(
)
( )
(
)
22
2
: 1 24
Sx y z+− ++ =
có tâm
( )
0;1; 2I −
.
Câu 37. Cho lăng trụ
.
ABC A B C
′′′
có đáy là tam giác đều cạnh
a
, góc giữa hai mặt phẳng
( )
ABC
′′′
và
( )
BCC B
′′
bằng
60
°
, hình chiếu của
B
′
lên mặt phẳng
( )
ABC
trùng với trọng tâm tam giác
ABC
. Khoảng cách giữa hai đường thẳng
AA
′
và
BC
′
bằng
A.
3
4
a
. B.
2
a
. C.
3
4
a
. D.
4
a
.
Lời giải
GVSB: Vũ Viên; GVPB: Phạm Thanh Liêm
Chọn A
Gọi
G
là trọng tâm tam giác
ABC
và
M
là trung điểm của
BC
.
Từ giả thiết ta có
( )
B G ABC
′
⊥
.
Ta có
( ) ( )
( )
( ) ( )
( )
, , 60A B C BCC B ABC BCC B B MG
α
′′′ ′′ ′′ ′
= = = = °
.
Vì
( )
//AA BCC B
′ ′′
nên
( ) ( )
( )
( )
( )
( )
( )
, , , 3. ,d AA B C d AA BCC B d A BCC B d G BCC B
′ ′ ′ ′′ ′′ ′′
= = =
.
Gọi
K
là hình chiếu của
G
lên mặt phẳng
(
)
BCC B
′′
.
Ta có
1 13 3
.
3 32 6
aa
GM AM= = =
.
( )
( )
,d G BCC B GK
′′
⇒=
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 󰱃 BIÊN SOẠN TOÁN THPT
Trang 18 TÀI LIỆU ÔN THI THPT QUỐC GIA
Xét tam giác vuông
33
: sin 60 .
624
GK a a
GMK GK
GM
°= ⇒ = =
.
( )
3
, 3.
4
a
d AA B C GK
′′
⇒==
.
Câu 38. Cho hai số phức
1
z
,
2
z
là các nghiệm của phương trình
2
4 13 0zz
++=
. Khi đó môđun của số
phức
( )
1 2 12
w z z i zz
=++
bằng
A.
13 5
. B.
195
. C.
185
. D.
13
.
Lời giải
GVSB: Vũ Viên; GVPB: Phạm Thanh Liêm
Chọn C
Gọi
1
z
,
2
z
là các nghiệm của phương trình
2
4 13 0zz++=
. Áp dụng định lí Viet ta có:
12
12
4
13
zz
zz
+=−
=
(
)
1 2 12
4 13w z z i zz i⇒ = + + =−+
.
22
4 13 185
w⇒= + =
.
Câu 39. Một gia đình muốn làm cánh cổng (như hình vẽ). Phần phía trên cổng có hình dạng là một
parabol với
2,5mIH =
, phần phía dưới là một hình chữ nhật kích thước cạnh là
4mAD =
,
6mAB =
. Giả sử giá để làm phần cổng được tô màu là
( )
2
1.000.0 0 đ0 /m
và giá để làm phần
cổng phía trên là
(
)
2
1.200.0 0 đ0 /m
. Số tiền gia đình đó phải trả là
A.
24.400.000
đ
. B.
36.000.000
đ
. C.
38.000.000
đ
. D.
38.800.000
đ
.
Lời giải
GVSB: Vũ Viên; GVPB: Phạm Thanh Liêm
Chọn B
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 19
Xét hệ trục tọa độ như hình vẽ: Gốc tọa độ
O
trùng điểm
H
,
A
và
B
thuộc trục
Ox
,
H
thuộc trục
Oy
.
Khi đó
( )
0; 0
H
,
( )
0; 2, 5I
,
( )
3; 0B
,
( )
3; 0
A −
.
Gọi parabol cần tìm có dạng
( )
2
:P y ax bx c= ++
.
Do
A
,
B
,
I
thuộc
( )
P
nên ta có hệ
5
93 0
18
93 0 0
2,5 5
2
a
a bc
a bc b
c
c
= −
− +=
+ +=⇔ =


=
=
.
Do đó parabol là
( )
2
55
:
18 2
Py x=−+
.
Diện tích phần phía trên cổng có hình dạng là một parabol là
3
3
3
2
3
3
55 5 5
d . 10
18 2 18 3 2
x
xx x
−
−


−+ =− + =




∫
.
Giá tiền để làm phần cổng phía trên là
10x1.200.000 12.000.000=
.
Diện tích phần phía dưới là một hình chữ nhật là
4.6 24
=
.
Giá tiền để làm phần cổng được tô màu là
24x1.000.000 24.000.000=
.
Số tiền gia đình đó phải trả là
12.000.000 24.000.000 36.000.000+=
.
Câu 40. Có bao nhiêu giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2xm
y
xm
−−
=
−
trên đoạn
[ ]
0;4
bằng
1
2
?
A.
0
. B.
2
. C.
3
. D.
1
.
Lời giải
GVSB: Nguyễn Việt Dũng; GVPB: Giao Nguyen
Chọn D
Hàm số
2
2xm
y
xm
−−
=
−
.
Tập xác định:
{ }
\Dm=
.
Ta có:
( )
2
2
2mm
y
xm
−+
′
=
−
.
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 󰱃 BIÊN SOẠN TOÁN THPT
Trang 20 TÀI LIỆU ÔN THI THPT QUỐC GIA
Vì
2
2
17
20
24
mm m

−+= − +>


với
m∀
0
y
′
⇒>
với
m∀
⇒
Hàm số đồng biến trong từng khoảng xác định với
m∀
.
Do đó, giá trị lớn nhất của hàm số
2
2xm
y
xm
−−
=
−
trên đoạn
[
]
0;4
bằng
1
2
[
]
( )
0;4
1
4
2
m
y
∉
⇔
=
[ ]
2
0;4
4 21
22
m
m
m
∉
⇔
−−
=
−
[ ]
2
0;4
42 2
m
mm
∉
⇔
−=−
[ ]
2
0;4
2 60
m
mm
∉
⇔
+ −=
[ ]
0;4
3
2
2
m
m
m
∉
⇔
=
= −
2m⇔=−
.
Vậy có
1
giá trị của tham số
m
thỏa mãn yêu cầu của bài toán.
Câu 41. Cho hàm số
( )
fx
có đạo hàm trên
thỏa mãn
( )
23f =
,
( )
4
1
d2
fx
x
x
=
∫
,
( )
2
0
d3
xf x x
′
=
∫
.
Tính
( )
1
0
dfx x
∫
.
A.
5
. B.
1
. C.
2
. D.
3
.
Lời giải
GVSB: Nguyễn Việt Dũng; GVPB: Giao Nguyen
Chọn C
•
Gọi
( )
4
1
d
fx
Ax
x
=
∫
.
Đặt
xt=
d
d
2
x
t
x
⇒=
d 2dx xt⇒=
.
11xt
=⇒=
;
42xt= ⇒=
( )
( )
22
11
.2 d
2d
f t xt
A ft t
x
⇒= =
∫∫
.
Mà
2A =
( )
2
1
d1fx x⇒=
∫
.
•
Gọi
( )
2
0
dB xf x x
′
=
∫
.
Ta có:
( ) ( )
( )
( )
( ) ( ) ( )
22 2 2
2
0
00 0 0
d d d 22 dB xf x x x fx xfx fx x f fx x
′
= = =−=−
∫∫ ∫ ∫
.
Mà
( )
23f =
và
3B =
( )
2
0
6 d3fx x⇒− =
∫
( )
2
0
d3fx x⇒=
∫
.
Vậy
( ) ( ) ( )
1 22
0 01
d d d 31 2
fx x fx x fx x= − =−=
∫∫∫
.
Câu 42. Cho số phức
z x yi= +
(
;xy∈
) thỏa mãn
( )
21z iz i+ += +
và
3z >
. Giá trị của biểu thức
23S xy= −
là
A.
6−
. B.
3−
. C.
6
. D.
3
.
Lời giải
GVSB: Nguyễn Việt Dũng; GVPB: Giao Nguyen
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 21
Chọn A
Số phức
z x yi= +
(
;xy
∈
)
22
z xy
⇒= +
.
Ta có:
( )
21
z iz i
+ += +
2x yi i z z i⇔ + + += +
(
)
21
x y i z zi
⇔++ + = +
2
1
xz
yz
+ =
⇔
+=
( ) ( )
22
2
1
21
yx
x xx
= +
⇔
+ =++
2
1
2 30
yx
xx
= +
⇔
− −=
1
0
3
4
x
y
x
y
=−
=
⇔
=
=
.
Mà
22
3
z xy= +>
3
4
x
y
=
⇒
=
2 3 2.3 3.4 6S xy⇒= − = − =−
.
Câu 43. Cho hình chóp
.S ABC
có
SA
vuông góc với mặt đáy,
2 2 3,SA BC a AC a= = =
và
120BAC
°
=
. Hình chiếu vuông góc của
A
lên các cạnh
SB
và
SC
lần lượt là
M
và
N
. Thể
tích của khối đa diện
AMNCB
bằng
A.
3
24
169
a
. B.
3
25
338
a
. C.
3
25
169
a
. D.
3
12
169
a
.
Lời giải
GVSB: Quách Đăng Thăng; GVPB: Giao Nguyen
Chọn B
Xét tam giác
ABC
, theo định lý Cô sin ta có
222
2 . .cosBC AB AC AB AC A=+−
2 22 0
3 2 . .cos120a AB a AB a⇔ = +−
22 2
3 20
2
AB a
a AB AB a
AB a
=
⇔ = +− =⇔
= −
.
Suy ra
AB a=
.
Vì
( )
SA AB
SA ABC
SA AC
⊥
⊥⇒
⊥
và
AB AC a= =
,
SA
chung nên
SAB SAC∆=∆
.
Hình chiếu vuông góc của
A
lên các cạnh
SB
và
SC
lần lượt là
M
và
N
nên
AM AN=
và
//MN BC
, suy ra
SM SN
SB SC
=
.
Ta có
22
13SB SA AB a= +=
và
2
2
22
. 12
.
13
SA SM SB SM
SA SM SB
SB SB SB
= ⇒= ⇔=
.
120
0
2a
3
a
3
a
A
C
B
S
M
N
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 󰱃 BIÊN SOẠN TOÁN THPT
Trang 22 TÀI LIỆU ÔN THI THPT QUỐC GIA
Do đó
2
.
.
144
..
169
S AMN
S ABC
V
SA SM SN SM
V SA SB SC SB

= = =


..
144
169
S AMN S ABC
VV⇒=
.
Lại có
..
S ABC S AMN AMNCB
VVV
= +
.. . . .
144 25
169 169
AMNCB S ABC S AMN S ABC S ABC S ABC
V VV V V V⇒ =−=− =
.
Mà
3
0
.
1 11 1 1
. . . . . . .sin .2 3. . . .sin120
3 32 3 2 2
S ABC ABC
a
V SA S SA AB AC BAC a a a
∆
= = = =
.
Vậy
3
.
25 25
169 338
AMNCB S ABC
a
VV
= =
.
Câu 44. Trong không gian
Oxyz
, cho hai đường thẳng
1
11
:
1 12
xyz
d
−+
= =
−
và
2
1
:
121
xy z
d
−
= =
.
Đường thẳng
d
đi qua
( )
1; 0; 1A
lần lượt cắt
12
,
dd
tại
B
và
C
. Độ dài
BC
bằng
A.
. B.
33
2
. C.
53
2
. D.
76
2
.
Lời giải
GVSB: Quách Đăng Thăng; GVPB:
Chọn A
Ta có phương trình tham số của
12
,dd
là
1
1
:1
2
xt
dy t
zt
= +
=−−
=
và
2
: 12
xs
dy s
zs
=
= +
=
.
Vì
( )
11
1 ; 1 ;2
d d B Bd B t tt∩ = ⇒ ∈ ⇒ + −−
và
( )
22
;1 2 ;d d C C d C s ss∩ =⇒∈ ⇒ +
.
Suy ra
( )
( )
; 1 ; 2 1 , 1;1 2 ; 1t tt A
AB C s ss
−− − = − +=
−


.
Do
,,
ABC
thẳng hàng nên
0:k AB k AC∃≠ =
 
( )
( )
( )
1
1 12
21 1
t ks
tk s
t ks
= −
⇒ −− = +
−= −
( )
( )
1
1 12
21
t ks
tk s
tt
= −
⇔ −−= +
−=
(
)
( )
1
11
12 2
t
ks
ks
=
⇔ −=
+=−
1
1
22
t
ks k
ks k
=
⇔ −=
+=−
1
1
3
4
3
t
ks
k
=
⇔=−
= −
1
1
4
4
3
t
s
k
=
⇔=
= −
.
Do đó
( )
131
2; 2; 2 , ; ;
424
BC

−


76
4
BC⇒=
.
Câu 45. Có bao nhiêu giá trị nguyên dương của tham số
m
để bất phương trình
2
33
log 3log 2
0
2
x
xx
m
−+
<
−
có không quá 3 nghiệm nguyên dương?
A.
127
. B.
128
. C.
63
. D.
64
.
Lời giải
GVSB: Quách Đăng Thăng; GVPB:
Chọn C
Điều kiện
0
20
x
x
m
>
−>
21
x
mm⇒> ⇒>
.
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 23
Ta có
2
33
log 3log 2
0
2
x
xx
m
−+
<
−
2
33
log 3log 2 0
0
20
x
x
x
m
x
⇔
−
>
−
+<
>
( )( )
33
log 1 log 2 0
0
20
x
x
m
xx
⇔
−
>
−
−<
>
3
1 log
0
20
2
x
x
m
x
>
−>
⇔
<
<
2
39
0
x
x
m
x
⇔
<
>
<
>
2
39
x
x
m
<
⇔
<
>
(I).
Để bất phương trình có không quá 3 nghiệm nguyên dương khi và chỉ bất phương trình
2
x
m >
có không quá 3 nghiệm nguyên dương
( )
3; 9
x ∈
.
Xét hàm số
( )
2
x
y fx= =
với
( )
3; 9x ∈
có
(
)
2 .ln 2 0,
x
fx x
′
= >∀
.
Bảng biến thiên
Từ bảng biến thiên suy ra
64m ≤
.
Mà
1m >
và
m
nguyên dương nên
{ }
2;3; 4;...;64m∈
.
Vậy có 63 giá trị nguyên dương của tham số
m
thoả mãn.
Câu 46. Trong không gian
Oxyz
, cho mặt cầu
( )
S
:
( ) ( )
22
2
11 4x yz− ++ +=
và hai điểm
( )
1;1;1A −
;
(
)
2; 2;1
B −
. Điểm
M
di chuyển trên mặt cầu
( )
S
. Giá trị lớn nhất của
23MA MB
−
đạt được
là:
A.
65
. B.
67
. C.
69
. D.
61
.
Lời giải
GVSB: Bùi Thanh Sơn; GVPB:
Chọn B
Mặt cầu
(
)
S
có tâm
( )
1; 1; 0I −
, bán kính
2R =
.
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 󰱃 BIÊN SOẠN TOÁN THPT
Trang 24 TÀI LIỆU ÔN THI THPT QUỐC GIA
Ta có:
3IA =
;
3
IB
=
.
Gọi
( )
E AI S=
; điểm
F
xác định bởi
2
3
IF IE
=
 
⇒
4
3
IF =
⇒
4
9
IF IA=
 
⇒
1 14
;;
9 99
F

−


.
Dễ thấy
MAI FMI∆∆
⇒
3
2
MA IA
MF IM
= =
⇒
23MA MF=
.
Ta có:
2 3 3 3 67
MA MB MF MB BF
− = −≤ =
.
Vậy
min 2 3 67MA MB−=
khi
( )
M BF S
=
sao cho
F
nằm giữa
B
và
M
.
Câu 47. Có bao nhiêu giá trị thực của tham số
m
để bất phương trình sau có nghiệm duy nhất?
(
)
( )
22
15
log 5 1 .log 6 log 3 0
m
m
x mx x mx+++ +++ ≥
.
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
GVSB: Bùi Thanh Sơn; GVPB:
Chọn B
ĐK:
01m<≠
.
Bất phương trình đã cho có nghiệm duy nhất thì suy ra phương trình
(
)
(
)
22
15
log 5 1 .log 6 log 3 0
m
m
x mx x mx+++ +++ =
( )
1
có nghiệm duy nhất.
ĐK cần: Dễ thấy nếu
0
x
là nghiệm của
( )
1
thì
0
mx−−
cũng là nghiệm của
( )
1
⇒
00
x mx
=−−
⇒
0
2
m
x = −
là nghiệm của
( )
1
.
⇒
22
15
log 5 1 .log 6 log 3 0
44
m
m
mm


−+ − + =





⇔
22
5
log 5 1 .log 6 log 3
44
mm
mm


−+ − =





⇔
22
35
log 5 1 .log 6 1
44
mm


−+ − =





(
)
2
Xét hàm số
( ) ( )
( )
2
35
log 1 .log 1ft t t=++
trên
[
)
0;+∞
( )
( )
( )
( )
( )
[
)
2
53
2
12
.log 1 .log 1 0 0;
1 ln 3
1 ln 5
t
ft t t t
t
t
′
= + + + > ∀ ∈ +∞
+
+
⇒
Hàm số
đồng biến trên
[
)
0;+∞
Mà
( )
21f =
Do đó
( )
2
⇔
( )
2
51
4
m
ff

−=



⇔
2
51
4
m
−=
⇔
2m =
.
ĐK đủ: Thử lại thấy với
2m =
thì bất phương trình đã cho có nghiệm duy nhất
1
x = −
.
Vậy có một giá trị
m
thỏa mãn yêu cầu bài toán.
Câu 48. Cho hình
( )
H
giới hạn bởi đồ thị hàm số bậc hai (nét mảnh) và đồ thị hàm số bậc ba (nét đậm)
như hình vẽ. Thể tích khối tròn xoay khi quay hình
( )
H
quanh trục
Ox
là:
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 25
A.
1024
35
π
. B.
4096
35
. C.
5017
35
π
. D.
4096
35
π
.
Lời giải
GVSB: Bùi Thanh Sơn; GVPB:
Chọn C
Từ đồ thị suy ra hàm số bậc hai là
2
yx=
và hàm số bậc ba là
32
3yx x= −
.
Xét các phương trình:
•
23 2
3xx x= −
⇔
( )
2
40
xx−=
⇔
0
4
x
x
=
=
•
2
0x =
⇔
0x =
•
32
30xx−=
⇔
( )
2
30xx−=
⇔
0
3
x
x
=
=
Vậy thể tích khối tròn xoay khi quay hình
( )
H
quanh trục
Ox
là:
( ) ( )
2 44
22
32 4 32
0 23
5017
3d d 3d
35
V xxx xx xxx
π
π ππ
=− + −− =
∫ ∫∫
.
ĐỀ THI THỬ: 2020-2021 NHÓM WORD 󰱃 BIÊN SOẠN TOÁN THPT
Trang 26 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 49. Cho số phức
z
thay đổi thỏa mãn
32zi+=
. Giá trị lớn nhất của biểu thức
11 3Sz z z i=−++++
là
A.
4
3
. B.
16
3
. C.
2
3
. D.
8
3
.
Lời giải
GVSB: Lê Duy Hiền; GVPB: Lê Hồng Vân
Chọn D
+ Gọi M là điểm biểu diễn của
z
thì M thuộc đường tròn
()C
có tâm
1
0;
3
I



, bán kính
2
3
R =
+ Gọi
(1; 0 ) , ( 1; 0) , ( 0; 3 )
AB C−−
. Ta thấy
,, ()
ABC C∈
và tam giác
ABC
đều.
+ Không mất tính tổng quát giả sử M thuộc cung nhỏ
AB
. Lấy
D
thuộc đoạn
MC
sao cho
MD MA=
. Ta có
0
60AMD ABC MAD= = ⇒∆
đều
ABM ACD MB DC⇒∆ =∆ ⇒ =
+ Do đó :
2S MA MB MC MC=++ =
lớn nhất khi MC lớn nhất hay MC là đường kính.
Vậy
8
max 4
3
SR= =
Câu 50. Cho hàm số
32
( 2) (2 13) 2y x m x m xm
= − + − + −−
có đồ thị
( ),
m
C
đường thẳng
:8d y mx m= ++
và điểm
( )
1; 4 .
I
Tính tổng tất cả các giá trị của tham số
,m
biết rằng đường
thẳng
d
cắt đồ thị
()
m
C
tại ba điểm phân biệt
,,
ABC
với
A
có hoành độ bằng
2−
và tam giác
IBC
cân tại
.I
A.
12−
. B.
6−
. C.
4−
. D.
10−
.
Lời giải
GVSB: Lê Duy Hiền; GVPB :Lê Hồng Vân:
Chọn B
+ Phương trình hoành độ giao điểm của
d
và
()
m
C
là:
3
2
( 2) (3 13) 2 10 0 1
5
x
x m x m xm x
xm
= −
−+ − + − −=⇔ =−
= +
x
y
D
I
C
B
A
M
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 27
+ Để đường thẳng
d
cắt đồ thị
()
m
C
tại ba điểm phân biệt
,,ABC
thì
7
6
m
m
≠−
≠−
+ Giả sử
2
( 1;8), ( 5; 6 8)B Cm m m− + ++
. Để tam giác
IBC
cân tại
I
thì
2 2 22 2
2
20 ( 4) ( 6 4) 6( )
23
m
IB IC m m m m l
m
= −
= ⇔=+ + ++ ⇔ =−
=−±
Vậy có ba giá trị của m thỏa mãn nên tổng các giá trị của m bằng
6−
.
____________________ HẾT ____________________
| 1/33

Tài liệu khác của Toán

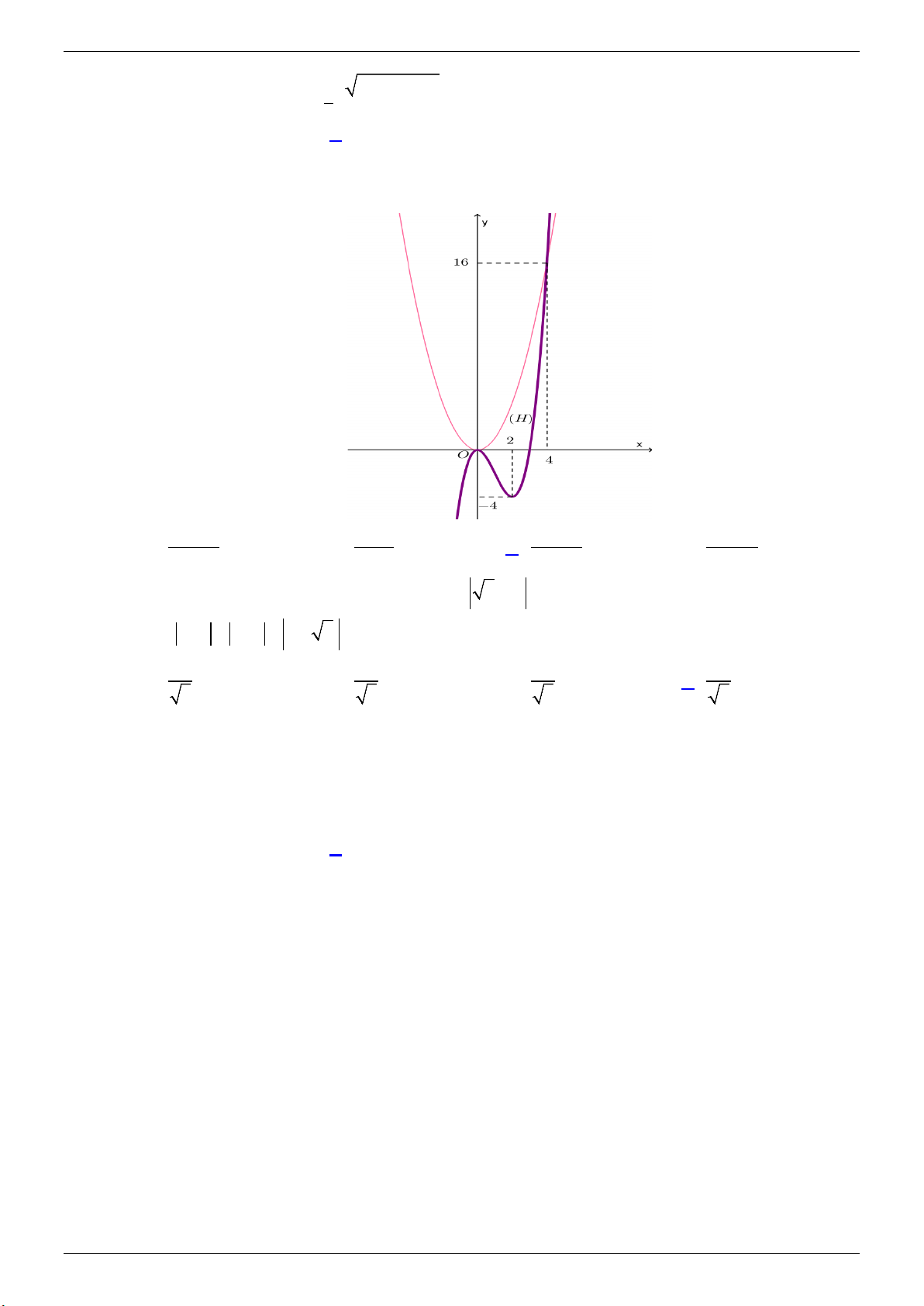
Preview text:

NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021 TRƯỜNG & THPT
THI THỬ TN12 LẦN 1 MÔN TOÁN
--------------------------- NĂM HỌC 2020 - 2021 CHUYÊN HÀ TĨNH Thời gian: 90 phút MÃ ĐỀ: ......
Câu 1. Đạo hàm của hàm số = .3x y x là A. ' 3x y = .ln 3.
B. ' = (1+ ln 3).3x y x
. C. ' = (1+ ).3x y x . D. ' 3x y = .
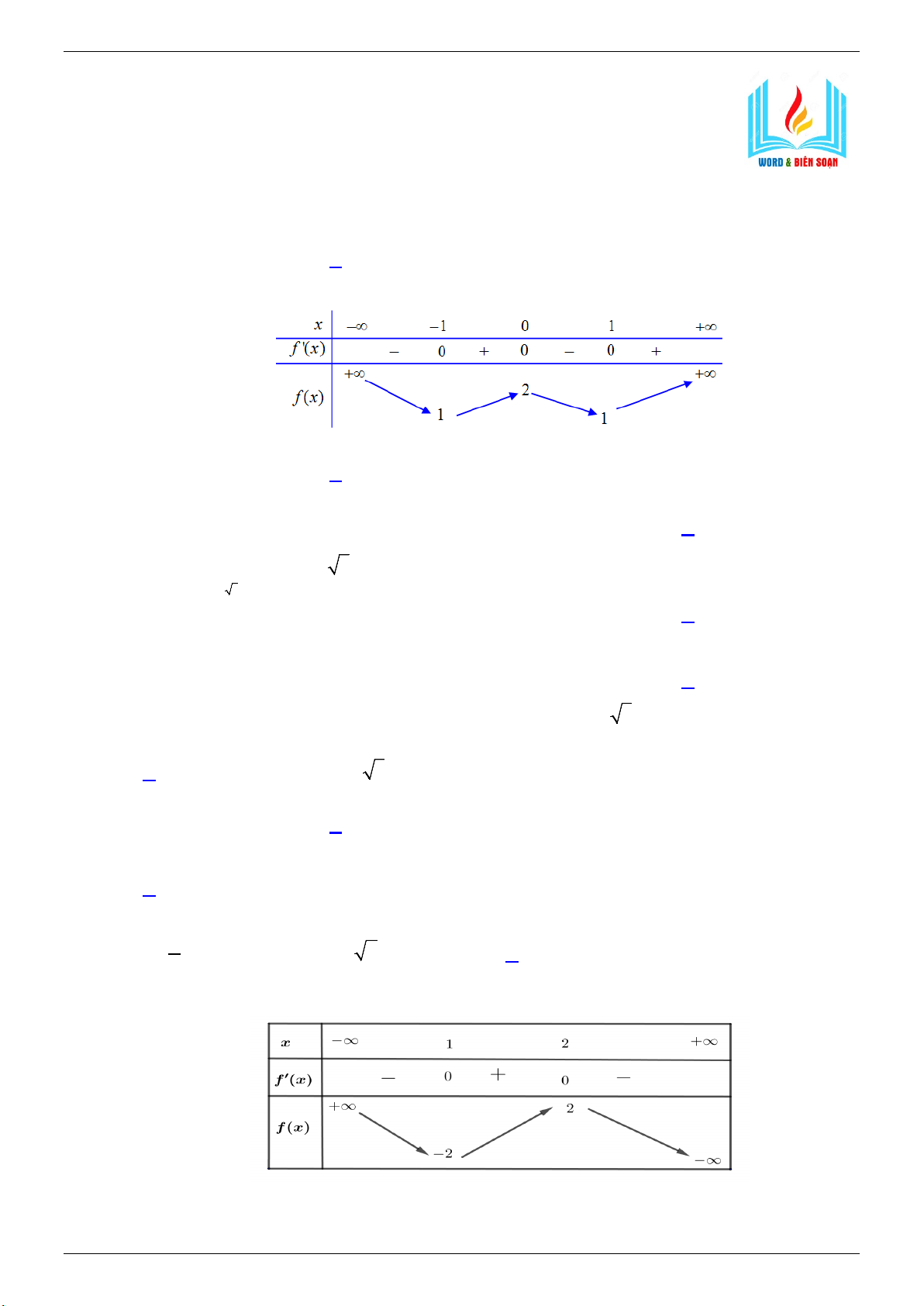
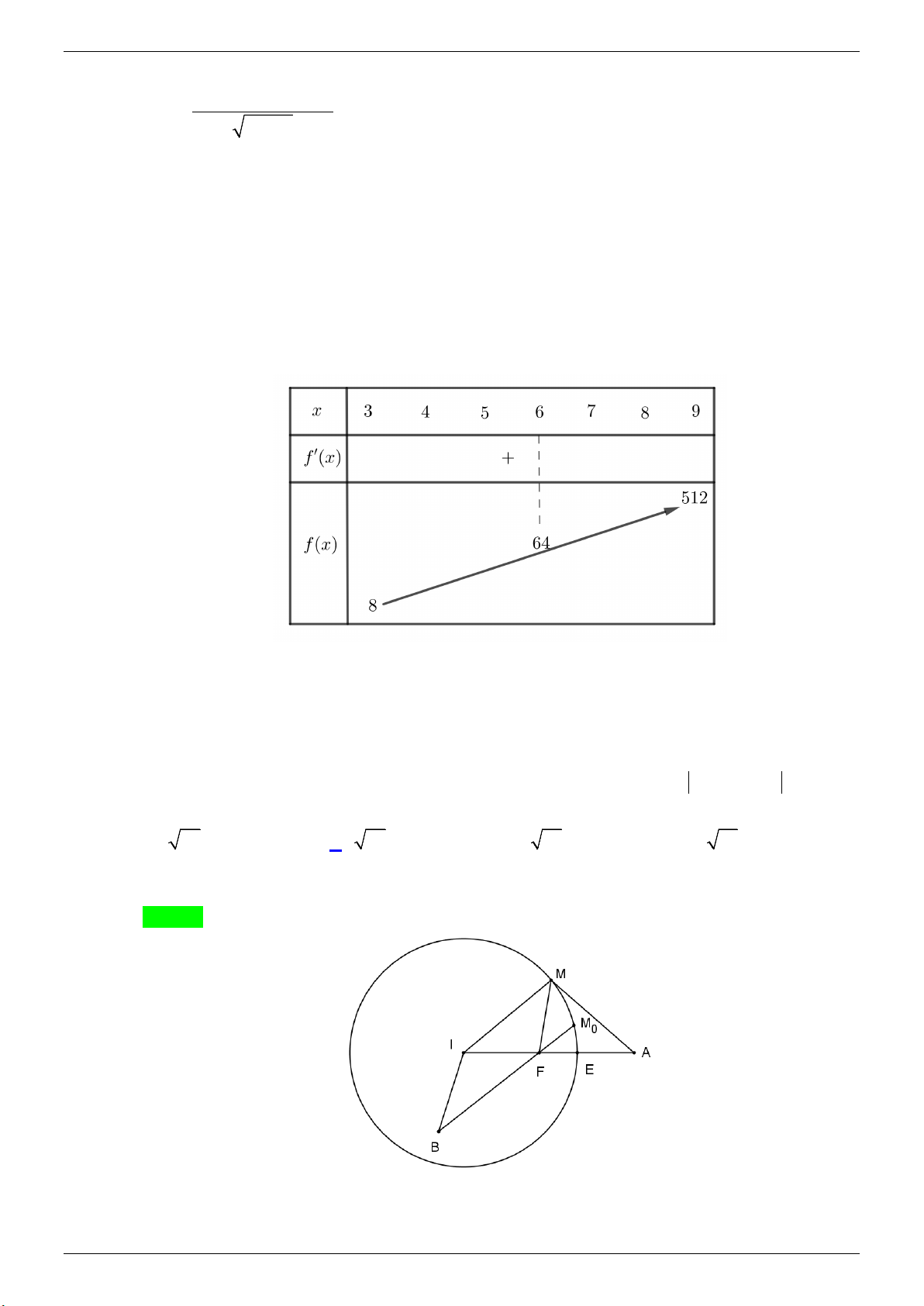
Câu 2. Cho hàm số f (x) có bảng biến thiên như hình vẽ bên.
Hàm số đã cho đạt cực đại tại A. x = 2 . B. x = 0 . C. x =1. D. x = 1 − .
Câu 3. Từ các chữ số 0;1;2;3;4;5 lập được bao nhiêu số tự nhiên có 5 chữ số phân biệt? A. 720 . B. 120. C. 96. D. 600 . 3 Câu 4. Tích phân 2
x dx = a + b 3,(a,b∈ ∫
). Khi đó a − 2b bằng 3 A. 10. B. 7 . C. 8 . D. 11.
Câu 5. Tập xác định của hàm số y log 3 x x 1 π = − + − 2 ( ) ( ) A. ( ; −∞ 3) \{ } 1 . B. ( ) ;1 −∞ . C. (3;+∞) . D. (1;3).
Câu 6. Cho hình lập phương ABC . D A′B C ′ D
′ ′ có đường chéo AC′ = a 3 . Thể tích khối lập phương đó bằng A. 3 a . B. 3 3 3a . C. 3 4a . D. 3 2a .
Câu 7. Cho số phức z = 3−5i . Phần ảo của z A. i . B. 5 − . C. 3. D. 5.
Câu 8. Cho hàm số f (x) có đạo hàm f ′(x) = x( 2
x − x)(x − 2) .Số điểm cực trị của hàm số đã cho là A. 2 . B. 3. C. 4 . D. 1.
Câu 9. Với a là số thực dương tùy ý, log2 4 a bằng A. a . B. a . C. 2 a . D. 2a . 2
Câu 10. Cho hàm số f (x) có bảng biến thiên như hình vẽ bên
Hàm số đã cho đồng biến trên khoảng nào dưới đây
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 1 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲🙲 BIÊN SOẠN TOÁN THPT A. (1;2). B. (2;+ ∞) . C. ( 2; − 2) . D. (−∞ ) ;1 . 3 1 3
Câu 11. Nếu f (x)dx = 1 − ∫
và f (x)dx = 2 − ∫
thì 2 f (x)dx ∫ bằng 1 − 1 − 1 A. 6 − . B. 2 − . C. 2 . D. 0 .
Câu 12. Cho số phức z = 2 −3i . Điểm M biểu diễn số phức w = (1− 2i) z + 3i có tọa độ là A. (8;2) . B. (1;8) . C. (8;− ) 1 . D. (2;8) .
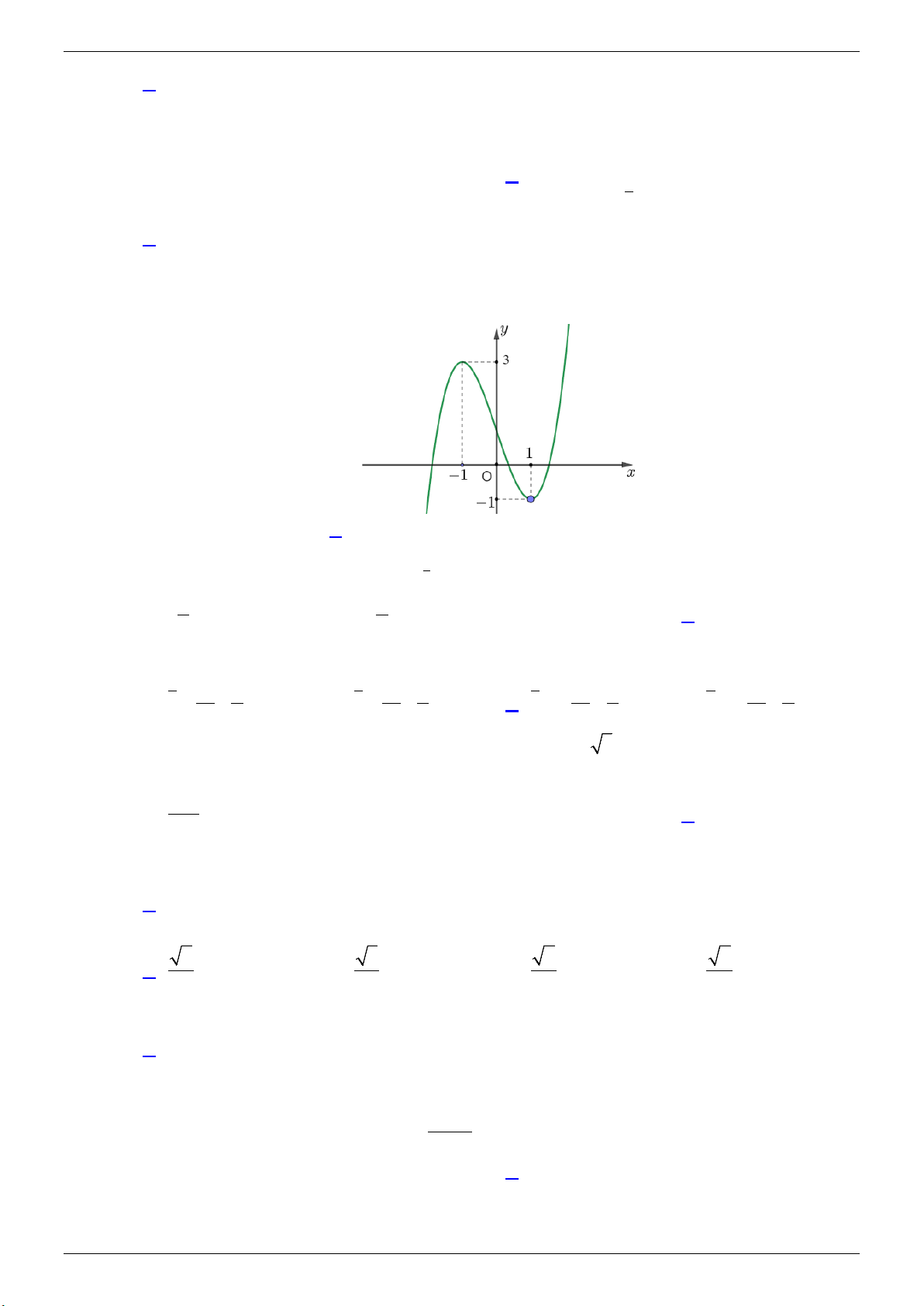
Câu 13. Cho hàm số bậc hai y = f (x) có đồ thị trong hình bên. Số nghiệm của phương trình
2 f (x) − 5 = 0 là A. 2 . B. 3. C. 1. D. 0 .
Câu 14. Tập nghiệm của bất phương trình log x −1 > 1 − là 1 ( ) 4 A.  5 ;  +∞    . B. 5 1; . C. ( ;2 −∞ ) . D. (1;5). 4      4 
Câu 15. Cho số phức z thỏa mãn (1−3i) z + 5 = 7i . Mệnh đề nào sau đây đúng? A. 13 4 z = + i . B. 13 4 z = − i . C. 13 4 z = − + i . D. 13 4
z = − − i . 5 5 5 5 5 5 5 5
Câu 16. Cho khối nón có bán kính đáy bằng a và chiều cao bằng a 3 . Diện tích xung quanh của khối nón đã cho bằng 2 π A. a . B. 2 4π a . C. 2 8π a . D. 2 2π a . 2
Câu 17. Cho cấp số cộng có số hạng đầu bằng 2 , công sai bằng 4 . Số hạng thứ 3 của cấp số cộng đó bằng A. 10. B. 12. C. 6 . D. 8 .
Câu 18. Cho hình bát diện đều cạnh a . Thể tích khối bát diện đều này là A. 2 3 a . B. 3 3 a . C. 2 3 a . D. 6 3 a . 3 3 4 3
Câu 19. Cho hàm số f (x) = sin x + 2021. Trong các khẳng định sau khẳng định nào đúng? A. f
∫ (x)dx = −cos x+2021x+C . B. f
∫ (x)dx = cos x+2021x+C . C. f
∫ (x)dx = cos x+C . D. f
∫ (x)dx = −cos x+C . +
Câu 20. Tiệm cận đứng của đồ thị hàm số 2x 1 y = là đường thẳng x −1 A. y =1. B. x = 2 . C. x =1. D. x = 2 − .
Câu 21. Thể tích của khối cầu có đường kính bằng 2a là Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021 A. 8 3 π a . B. 3 4π a . C. 4 3 π a . D. 3 2π a . 3 3
Câu 22. Hàm số y = ( 2
ln 4 − x ) đồng biến trên khoảng A. ( 2; − 2) . B. ( ;2 −∞ ) . C. (0;2) . D. ( 2; − 0) .
Câu 23. Cho hàm số f (x) 3x 1 e− + =
. Trong các khẳng định sau, khẳng định nào đúng? A. ∫ ( ) 3 − 1 d 3 x f x x e + = − + C . B. ∫ ( ) 3 − 1 d x f x x e + = + C . C. f ∫ (x) 1 3−x 1 dx e + = − + C . D. f ∫ (x) 1 3−x 1 dx e + = + C . 3 3
Câu 24. Đồ thị hàm số nào dưới đây có dạng như đường cong hình bên? A. 3 2
y = −x + 3x . B. 4 2
y = x − 3x . C. 3 2
y = x − 3x . D. 4 2
y = −x + 3x .
Câu 25. Trong không gian Oxyz , cho ba điểm A(1;1;2), B( 3;1;0), C ( 1; − 1; )
1 . Trọng tâm của tam giác
ABC có tọa độ là A. (2;1 ) ;1 . B. (3;3;3). C. (1;1; ) 1 . D. (6;2;2).
Câu 26. Cho đồ thị hàm số 4 2
y = ax + bx + c có điểm cực đại A(0; 3
− ) và điểm cực tiểu B( 1; − 5 − ) .
Tính giá trị của P = a + 2b + 3c . A. P = 3. B. P = 5 − . C. P = 9 − . D. P = 15 − .
Câu 27. Trong không gian Oxyz , đường thẳng đi qua hai điểm A(3;1;0) và B( 1; − 1; ) 1 có phương trình là x = 7 − 4tx = 1 − + 4tx = 3 − 4tx = 3 − 4t A.     y = 1 . B. y =1 .
C. y = t .
D. y =1+ t . z = 1 − +     t z =1+  t z =1+  t z =  t
Câu 28. Một học sinh tô ngẫu nhiên 5 câu trắc nghiệm (mỗi câu có 4 phương án lựa chọn, trong đó chỉ
có 1 phương án đúng). Xác suất để học sinh đó tô sai cả 5 câu bằng A. 15 . B. 3 . C. 243 . D. 1 . 1024 4 1024 1024
Câu 29. Trong không gian Oxyz , cho hai điểm A(1;1;2) và B(3;1;0) . Mặt cầu đường kính AB có phương trình là
A. (x − )2 + ( y − )2 + (z − )2 2 1 1 = 8.
B. (x − )2 + ( y − )2 + (z − )2 2 1 1 = 2 .
C. (x − )2 + ( y − )2 + (z − )2 1 1 2 = 8.
D. (x − )2 + ( y − )2 2 3 1 + z = 2 .
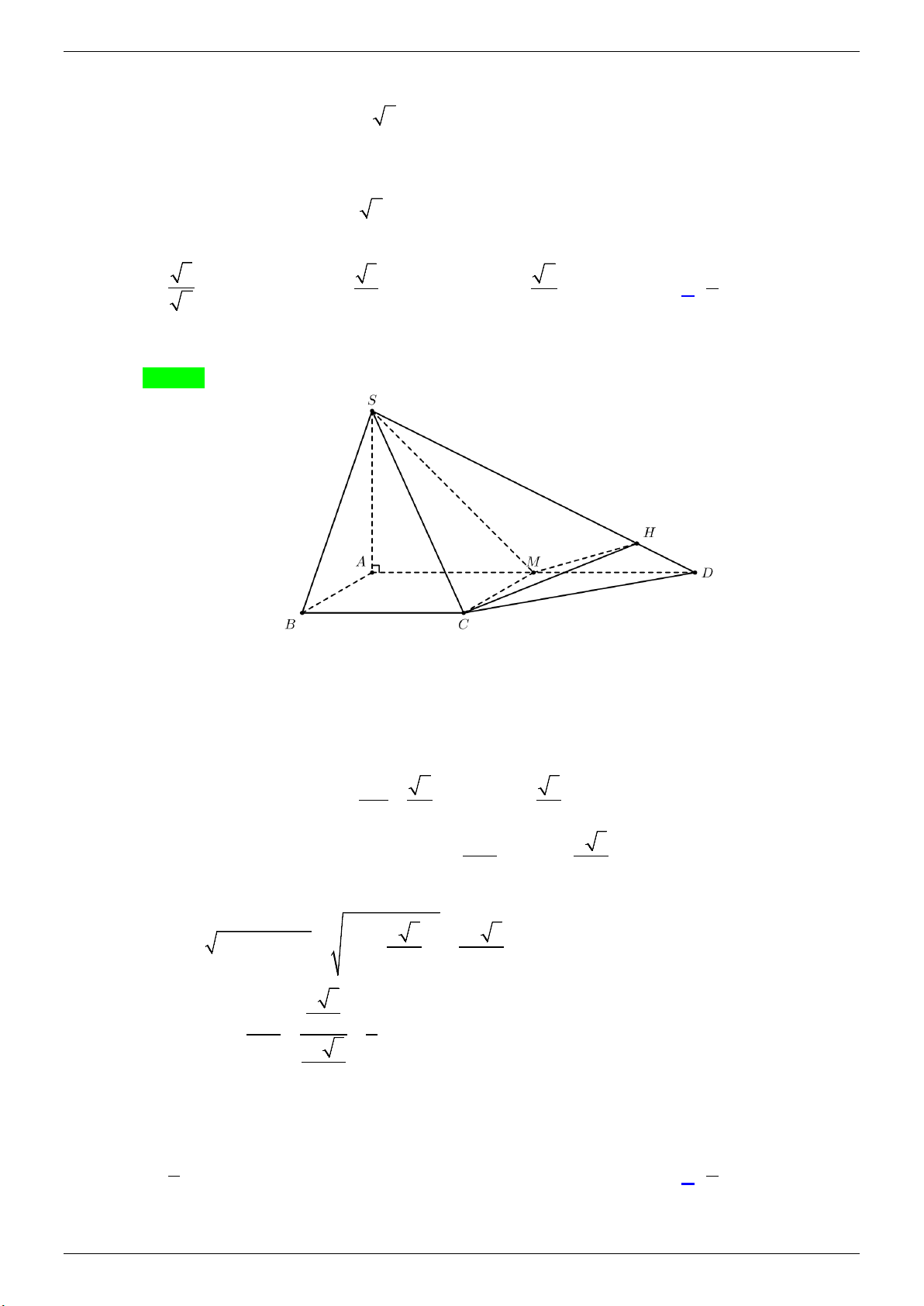
Câu 30. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B , cạnh bên SA vuông
góc với mặt đáy và SA = a 2 , AD = 2AB = 2BC = 2a . Côsin của góc giữa 2 mặt phẳng
(SAD) và (SCD) bằng A. 3 . B. 3 . C. 2 . D. 1 . 2 2 2 2
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 3 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲🙲 BIÊN SOẠN TOÁN THPT 5 2
Câu 31. Nếu 2 f
∫ (x)dx = 3 thì f (2x+ ∫ )1dx 3 1 A. 3 . B. 3. C. 6. D. 3 . 2 4
Câu 32. Trong không gian Oxyz , cho hai điểm M ( 1; − 2; ) 1 và N (3;0;− )
1 . Mặt phẳng trung trực của
MN có phương trình là
A. 4x − 2y − 2z +1 = 0. B. 2
− x + y + z +1 = 0. C. x + y − 2 = 0. D. 2
− x + y + z + 7 = 0.
Câu 33. Tìm tất cả các giá trị thực của tham số m để phương trình 2x 1+ 2 2
− 2m = 0 có nghiệm. m ≥1 A.  . B. m > 0. C. ( ;0 −∞ ). D. (0; ) 1 . m ≤ 1 − ( 2 m − m) 3 x
Câu 34. Cho hàm số y = + ( 2 m − m) 2 x + x
m + 2 . Có bao nhiêu giá trị nguyên của m để 3
hàm số đồng biến trên  ? A. 3. B. 5. C. 1. D. 2 .
Câu 35. Trong không gian Oxyz , đường thẳng nào dưới đây đi qua điểm M (1; 2 − ; ) 1 ? A.
x 1 y 2 z 1 d − − + : = = . B.
x 1 y 2 z 1 d − + − : = = . 1 2 1 − 3 3 2 3 − 1 C.
x 1 y 2 z 1 d + + − : = = . D.
x 1 y 2 z 1 d − + + : = = . 3 2 1 3 3 2 3 1 −
Câu 36. Trong không gian Oxyz , mặt cầu (S ) 2 : x + ( y − )2
1 + (z + 2)2 = 4 có tọa độ tâm I là
A. I (0;1;− 2) . B. I (0;1;2).
C. I (0;−1;2) .
D. I (1;1;− 2) .
Câu 37. Cho lăng trụ ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a , góc giữa hai mặt phẳng ( A′B C ′ ′) và
(BCC B′′) bằng 60°, hình chiếu của B′ lên mặt phẳng ( ABC) trùng với trọng tâm tam giác
ABC . Khoảng cách giữa hai đường thẳng AA′ và B C ′ bằng A. 3a . B. a . C. a 3 . D. a . 4 2 4 4
Câu 38. Cho hai số phức z , z là các nghiệm của phương trình 2
z + 4z +13 = 0 . Khi đó môđun của số 1 2
phức w = (z + z i + z z bằng 1 2 ) 1 2 A. 13 5 . B. 195 . C. 185 . D. 13.
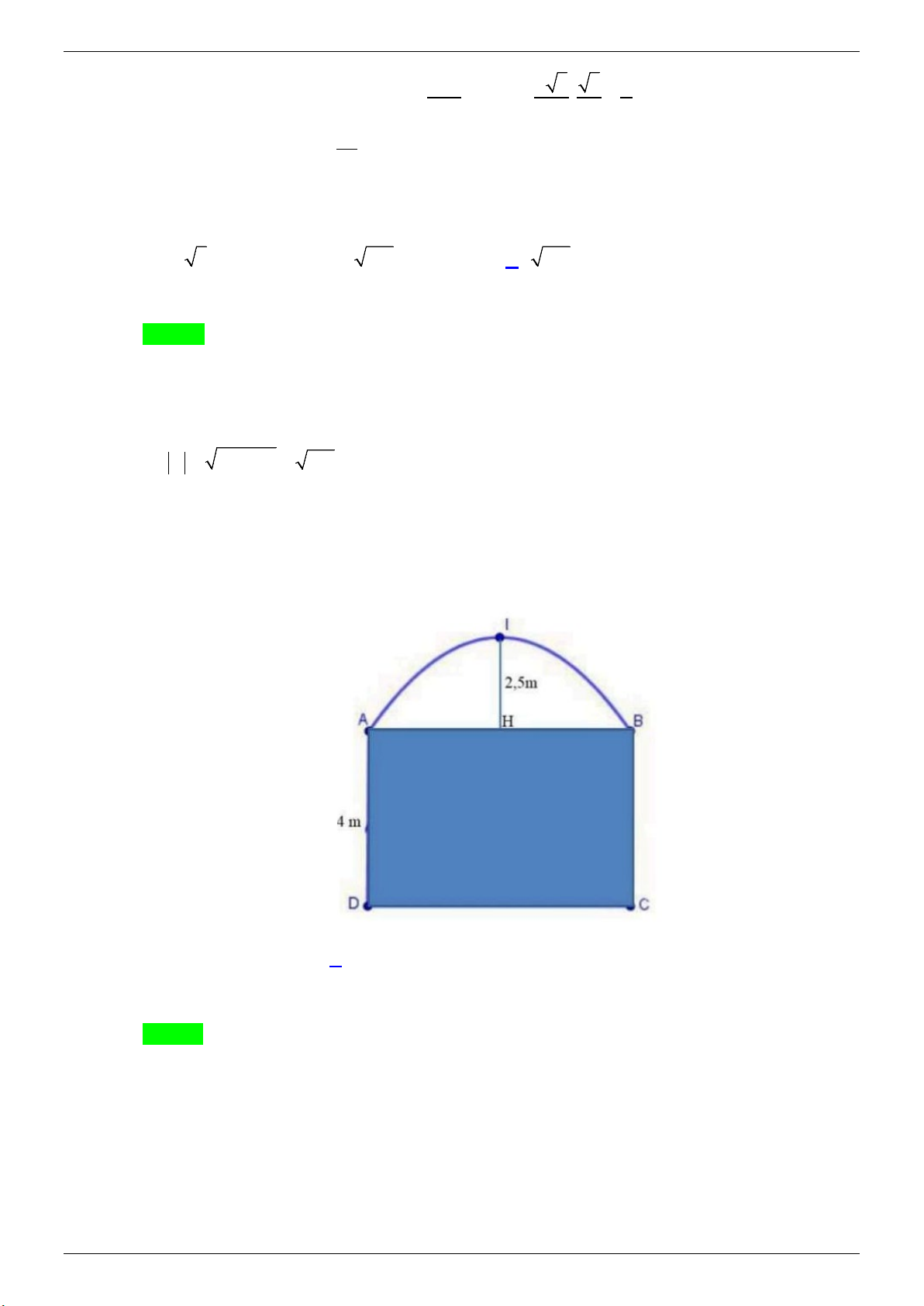
Câu 39. Một gia đình muốn làm cánh cổng (như hình vẽ). Phần phía trên cổng có hình dạng là một
parabol với IH = 2,5m , phần phía dưới là một hình chữ nhật kích thước cạnh là AD = 4m ,
AB = 6m . Giả sử giá để làm phần cổng được tô màu là 0 ( 2
1.000.0 0 đ/m ) và giá để làm phần cổng phía trên là 0 ( 2
1.200.0 0 đ/m ) . Số tiền gia đình đó phải trả là Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021 A. 24.400.000đ . B. 36.000.000đ . C. 38.000.000đ . D. 38.800.000đ . 2 − −
Câu 40. Có bao nhiêu giá trị của tham số x m
m để giá trị lớn nhất của hàm số 2 y = trên đoạn x − m [0;4] bằng 1 ? 2 A. 0 . B. 2 . C. 3. D. 1. 4 f ( x ) 2
Câu 41. Cho hàm số f (x) có đạo hàm trên  thỏa mãn f (2) = 3, dx = 2 ∫ , xf ′ ∫ (x)dx = 3. 1 x 0 1
Tính f (x)dx ∫ . 0 A. 5. B. 1. C. 2 . D. 3.
Câu 42. Cho số phức z = x + yi ( x; y ∈ ) thỏa mãn z + 2 + i = z (1+ i) và z > 3 . Giá trị của biểu thức
S = 2x − 3y là A. 6 − . B. 3 − . C. 6 . D. 3.
Câu 43. Cho hình chóp S.ABC có SA vuông góc với mặt đáy, SA = 2BC = 2a 3, AC = a và  BAC 120° =
. Hình chiếu vuông góc của A lên các cạnh SB và SC lần lượt là M và N . Thể
tích của khối đa diện AMNCB bằng A. 24 3 a . B. 25 3 a . C. 25 3 a . D. 12 3 a . 169 338 169 169
Câu 44. Trong không gian Oxyz , cho hai đường thẳng x 1 y 1 : z d − + = = và x y 1 : z d − = = . 1 1 1 − 2 2 1 2 1
Đường thẳng d đi qua A(1;0; )
1 lần lượt cắt d ,d tại B và C . Độ dài BC bằng 1 2 A. 7 6 . B. 3 3 . C. 5 3 . D. 7 6 . 4 2 2 2 2
log x − 3log x + 2
Câu 45. Có bao nhiêu giá trị nguyên dương của tham số m để bất phương trình 3 3 < 0 m − 2x
có không quá 3 nghiệm nguyên dương? A. 127 . B. 128. C. 63. D. 64 .
Câu 46. Trong không gian Oxyz , cho mặt cầu (S ): (x − )2 + ( y + )2 2 1
1 + z = 4 và hai điểm A( 1; − 1; ) 1 ; B(2;− 2; )
1 . Điểm M di chuyển trên mặt cầu (S ) . Giá trị lớn nhất của 2MA − 3MB đạt được là: A. 65 . B. 67 . C. 69 . D. 61 .
Câu 47. Có bao nhiêu giá trị thực của tham số m để bất phương trình sau có nghiệm duy nhất?
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 5 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲🙲 BIÊN SOẠN TOÁN THPT
log ( 2x + mx +5 + )1.log ( 2x + mx +6 +log ≥ . m 3 0 1 5 ) m A. 4 . B. 1. C. 2 . D. 3.
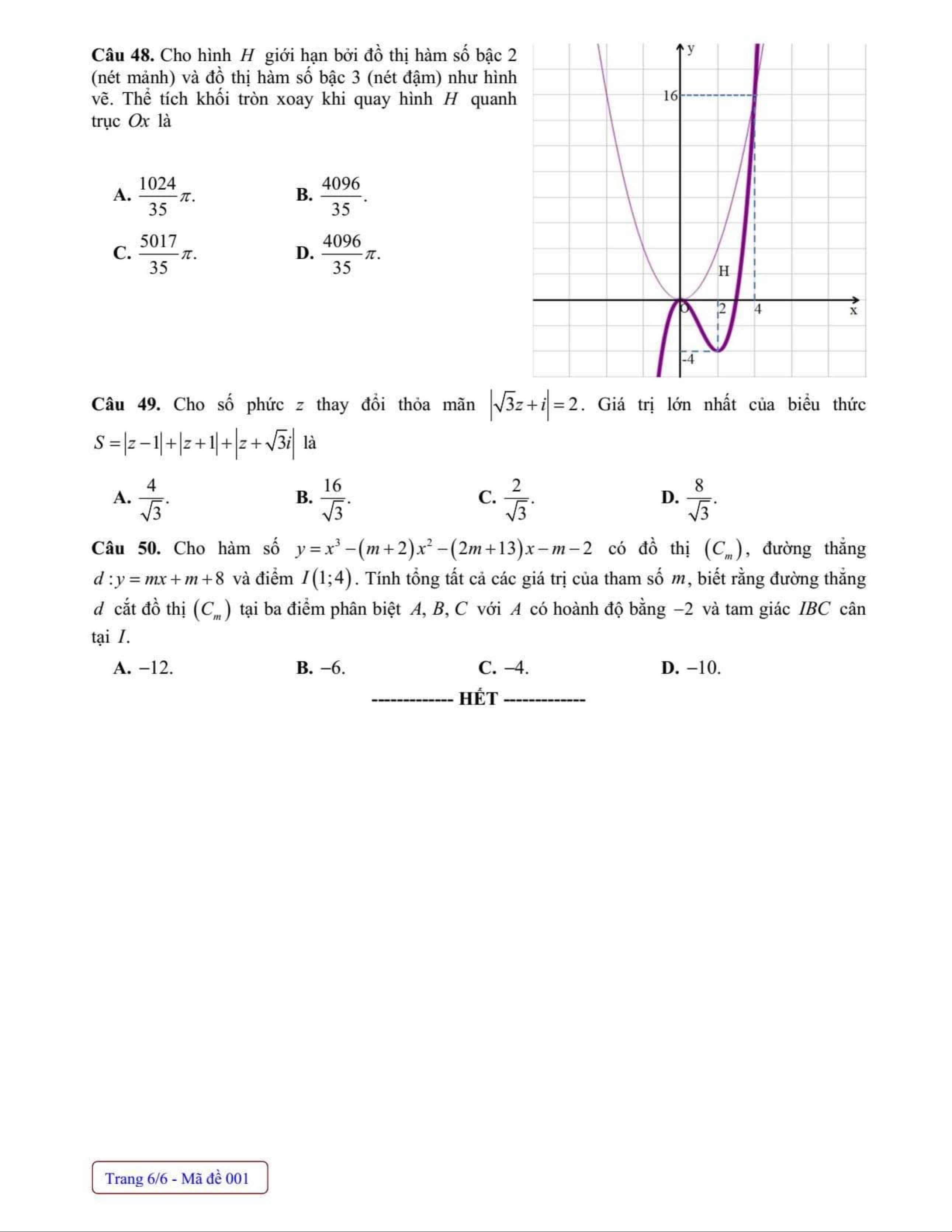
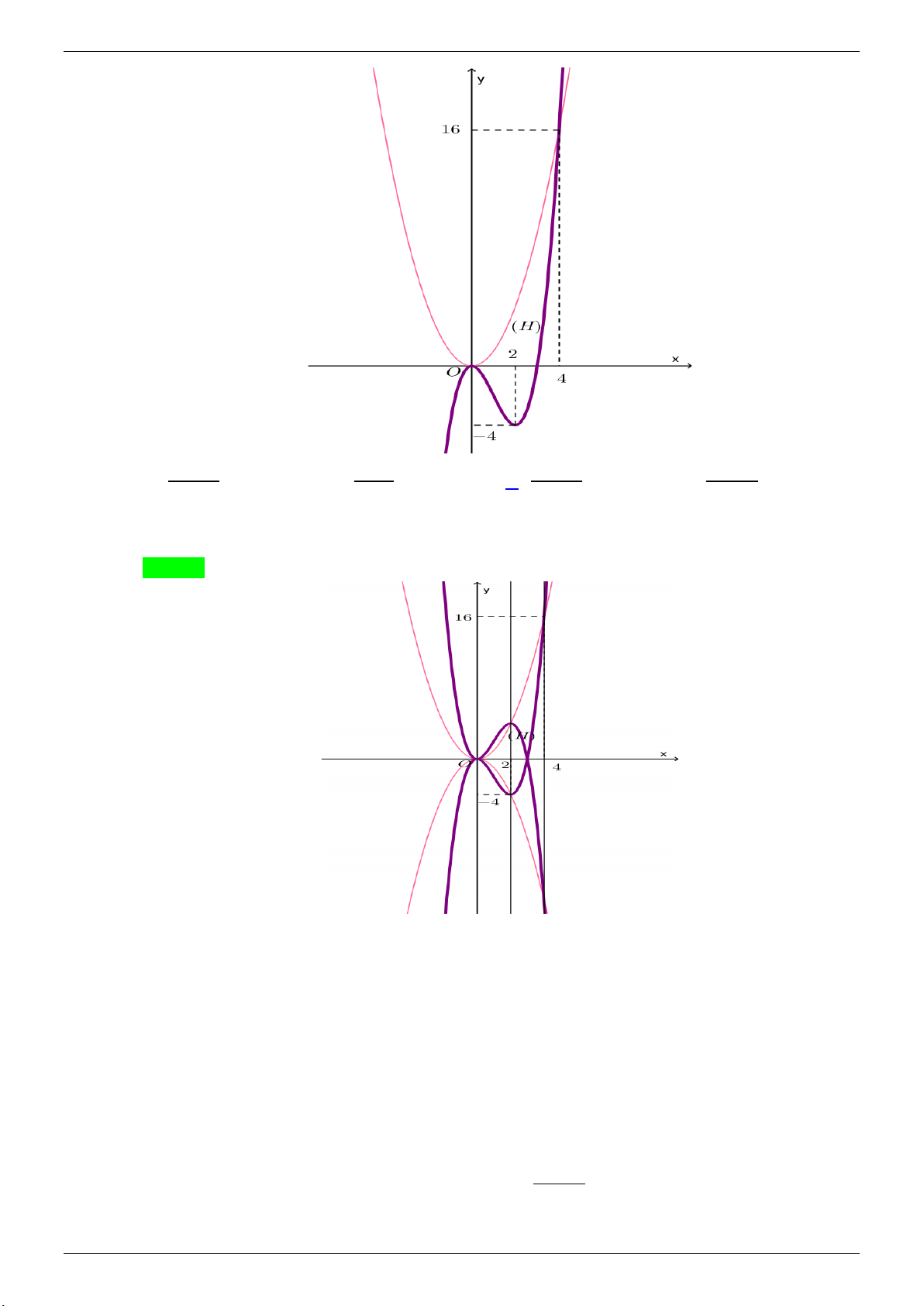
Câu 48. Cho hình (H ) giới hạn bởi đồ thị hàm số bậc hai (nét mảnh) và đồ thị hàm số bậc ba (nét đậm)
như hình vẽ. Thể tích khối tròn xoay khi quay hình (H ) quanh trục Ox là: π π π A. 1024 . B. 4096 . C. 5017 . D. 4096 . 35 35 35 35
Câu 49. Cho số phức z thay đổi thỏa mãn
3z + i = 2 . Giá trị lớn nhất của biểu thức
S = z −1 + z +1 + z + 3i là A. 4 . B. 16 . C. 2 . D. 8 . 3 3 3 3 Câu 50. Cho hàm số 3 2
y = x − (m + 2)x − (2m +13)x − m − 2 có đồ thị (C đường thẳng m ),
d : y = mx + m + 8 và điểm I (1;4). Tính tổng tất cả các giá trị của tham số ,
m biết rằng đường
thẳng d cắt đồ thị (C tại ba điểm phân biệt , A B,C với m )
A có hoành độ bằng 2 − và tam giác
IBC cân tại I. A. 12 − . B. 6 − . C. 4 − . D. 10 − .
____________________ HẾT ____________________ Trang 6
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT BẢNG ĐÁP ÁN 1.B 2.B 3.D 4.D 5.D 6.A 7.B 8.A 9.C 10.A 11.C 12.A 13.B 14.D 15.C 16.D 17.A 18.A 19.A 20.C 21.C 22.D 23.C 24.B 25.C 26.D 27.A 28.C 29.B 30.D 31.D 32.B 33.A 34.D 35.B 36.A 37.A 38.C 39.B 40.D 41.C 42.A 43.B 44.A 45.C 46.B 47.B 48.C 49.D 50.B
LỜI GIẢI CHI TIẾT
Câu 1. Đạo hàm của hàm số = .3x y x là A. ' 3x y = .ln 3.
B. ' = (1+ ln 3).3x y x
. C. ' = (1+ ).3x y x . D. ' 3x y = .
GVSB: Lương Công Hảo; GVPB: Phạm Hiền Lời giải Chọn B
 Có ' ( .3x )′ ( )′ = =
.3x + (3x )′. = 3x + 3x.ln3. = (1+ ln3).3x y x x x x x .
Câu 2. Cho hàm số f (x) có bảng biến thiên như hình vẽ bên.
Hàm số đã cho đạt cực đại tại A. x = 2 . B. x = 0 . C. x =1. D. x = 1 − .
GVSB: Lương Công Hảo; GVPB: Phạm Hiền Lời giải Chọn B
 Qua BBT có y ' đổi dấu từ + sang − khi đi qua x = 0 . Suy ra hàm số đạt cực đại tại x = 0 .
Câu 3. Từ các chữ số 0;1;2;3;4;5 lập được bao nhiêu số tự nhiên có 5 chữ số phân biệt? A. 720 . B. 120. C. 96. D. 600 .
GVSB: Lương Công Hảo; GVPB: Phạm Hiền Lời giải Chọn D
 Số các số có 5 chữ số phân biệt lấy từ bộ {0;1;2;3;4; } 5 là 5 4 A − A = 600. 6 5 3 Câu 4. Tích phân 2
x dx = a + b 3,(a,b∈ ∫
). Khi đó a − 2b bằng 3 A. 10. B. 7 . C. 8 . D. 11.
Lời giải GVSB: Thu Ha Cao; GVPB: Phạm Hiền Chọn D 3 3 3 x 1 x dx = = ∫ (3 −( 3)3 2 3 )=9− 3. 3 3 3 3 ⇒ a = 9,b = 1
− ⇒ a − 2b =11.
Câu 5. Tập xác định của hàm số y log 3 x x 1 π = − + − 2 ( ) ( )
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 7 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲🙲 BIÊN SOẠN TOÁN THPT A. ( ; −∞ 3) \{ } 1 . B. ( ) ;1 −∞ . C. (3;+∞) . D. (1;3).
Lời giải GVSB: Thu Ha Cao; GVPB: Phạm Hiền Chọn D 3  − x > 0 x < 3 Hàm số xác định khi  ⇔  ⇔ 1< x < 3. x −1 > 0 x >1
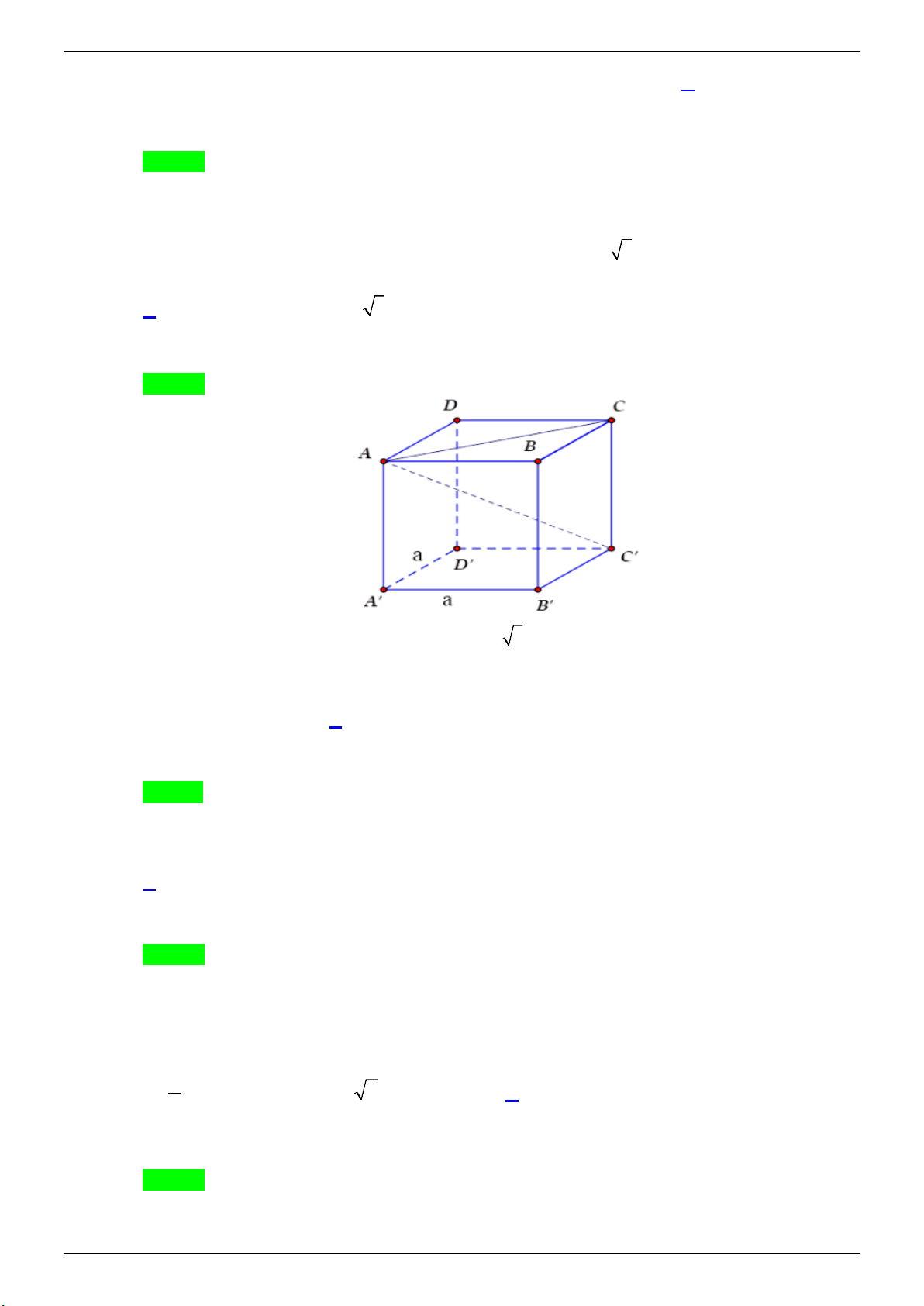
Câu 6. Cho hình lập phương ABC . D A′B C ′ D
′ ′ có đường chéo AC′ = a 3 . Thể tích khối lập phương đó bằng A. 3 a . B. 3 3 3a . C. 3 4a . D. 3 2a .
Lời giải GVSB: Thu Ha Cao; GVPB: Phạm Hiền Chọn A
Hình lập phương cạnh a có đường chéo bằng a 3 .
Do đó hình lập phương đã cho có cạnh là a . Thể tích tích khối lập phương đó bằng 3 a .
Câu 7. Cho số phức z = 3−5i . Phần ảo của z A. i . B. 5 − . C. 3. D. 5.
Lời giải GVSB: Thu Ha Cao; GVPB: Phạm Hiền Chọn B
Phần ảo của số phức z = 3− 5i là 5 − .
Câu 8. Cho hàm số f (x) có đạo hàm f (x) = x( 2 '
x − x)(x − 2).Số điểm cực trị của hàm số đã cho là A. 2 . B. 3. C. 4 . D. 1. Lời giải
GVSB: Trần Thị Hòa; GVPB: Nguyễn Hiền Lương Chọn A
Ta có f (x) = x( 2
x − x)(x − ) 2 ' 2 = x (x − ) 1 (x − 2) .
f ′(x) đổi dấu 2 lần.Vậy hàm số f (x) có 2 điểm cực trị.
Câu 9. Với a là số thực dương tùy ý, log2 4 a bằng A. a . B. a . C. 2 a . D. 2a . 2 Lời giải
GVSB: Trần Thị Hòa; GVPB: Nguyễn Hiền Lương Chọn C
Ta có log a = ( 2 )log2a 2 2 = ( log2a ) 2 4 2 2 = a . Trang 8
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
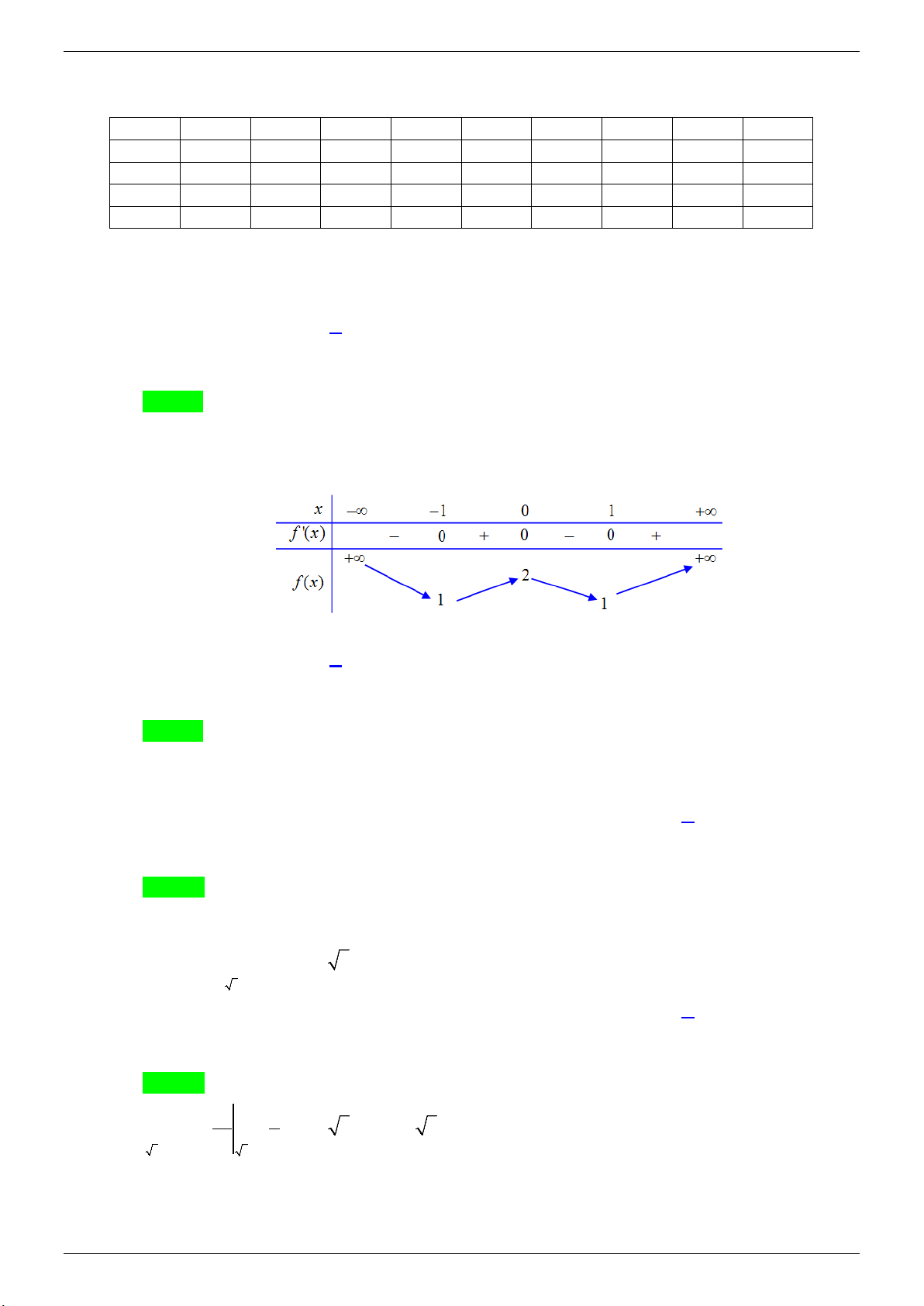
Câu 10. Cho hàm số f (x) có bảng biến thiên như hình vẽ bên
Hàm số đã cho đồng biến trên khoảng nào dưới đây A. (1;2). B. (2;+ ∞) . C. ( 2; − 2) . D. (−∞ ) ;1 . Lời giải
GVSB: Trần Thị Hòa; GVPB: Nguyễn Hiền Lương Chọn A
Từ BBT của hàm số ta thấy hàm số đồng biến trên khoảng (1;2). 3 1 3
Câu 11. Nếu f (x)dx = 1 − ∫
và f (x)dx = 2 − ∫
thì 2 f (x)dx ∫ bằng 1 − 1 − 1 A. 6 − . B. 2 − . C. 2 . D. 0 . Lời giải
GVSB: ThienMinh Nguyễn; GVPB:Nguyễn Hiền Lương Chọn C 3 1 3 Ta có: f
∫ (x)dx = f
∫ (x)dx+ f ∫ (x)dx. 1 − 1 − 1 3 3 1 Suy ra f
∫ (x)dx = f
∫ (x)dx− f ∫ (x)dx = 1 − + 2 =1. 1 1 − 1 − 3 3 Nên 2 f
∫ (x)dx = 2 f
∫ (x)dx = 2.1= 2. 1 1
Câu 12. Cho số phức z = 2 −3i . Điểm M biểu diễn số phức w = (1− 2i) z + 3i có tọa độ là A. (8;2) . B. (1;8) . C. (8;− ) 1 . D. (2;8) . Lời giải
GVSB: ThienMinh Nguyễn; GVPB: Nguyễn Hiền Lương Chọn A
w = (1− 2i) z + 3i ⇔ w = (1− 2i)(2 + 3i) + 3i = 8 + 2i .
Nên điểm biểu diễn số phức w là điểm có tọa độ (8;2) .
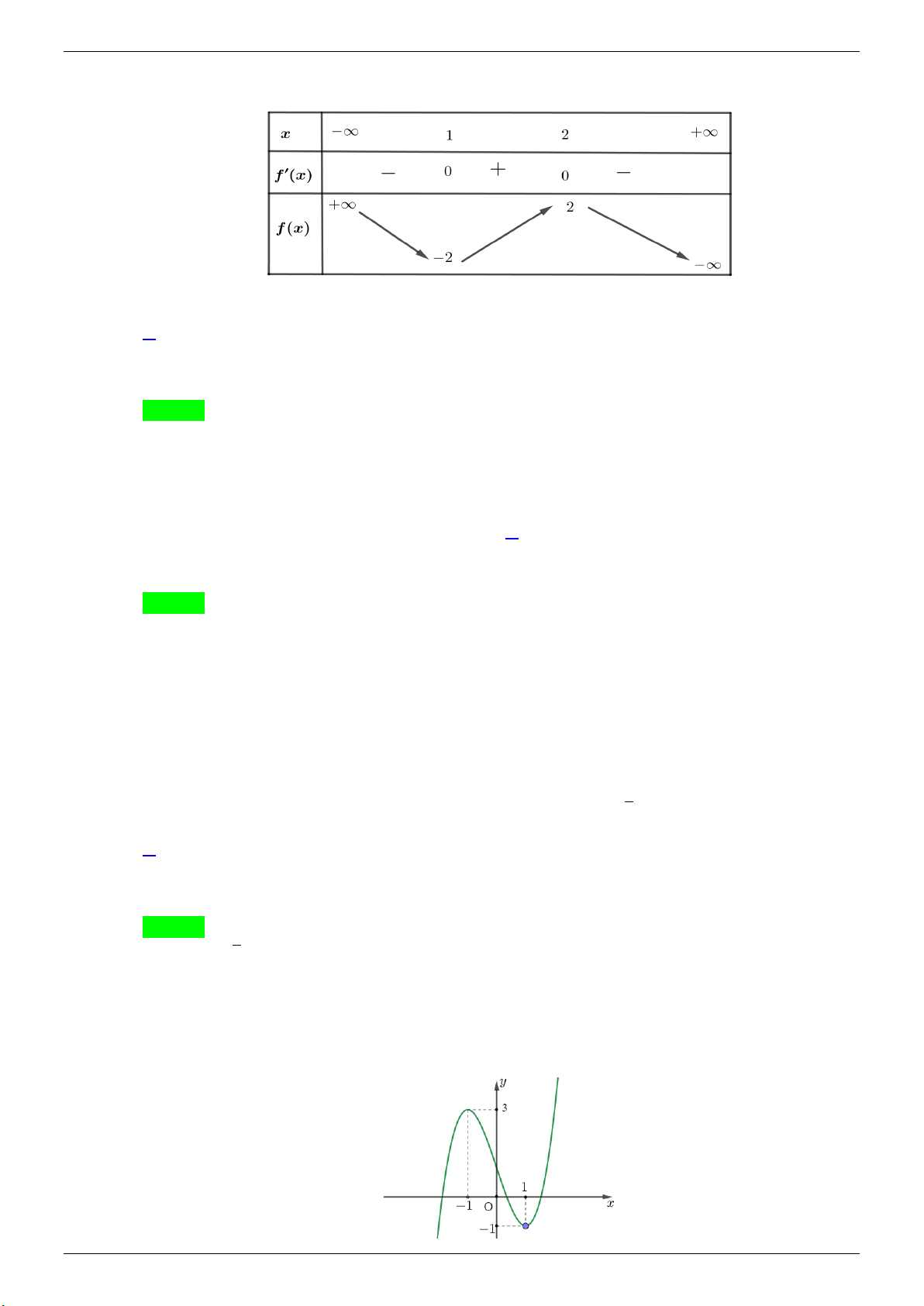
Câu 13. Cho hàm số bậc hai y = f (x) có đồ thị trong hình bên. Số nghiệm của phương trình
2 f (x) − 5 = 0 là
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 9 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲🙲 BIÊN SOẠN TOÁN THPT A. 2 . B. 3. C. 1. D. 0 . Lời giải
GVSB: ThienMinh Nguyễn; GVPB: Nguyễn Hiền Lương Chọn B
Ta có: 2 f (x) − 5 = 0 ⇔ f (x) 5
= . Số nghiệm của phương trình là số giao điểm của đồ thị hàm 2
số y = f (x) và đường thẳng 5
y = .Dựa vào đồ thị ta thấy đường thẳng 5
y = cắt đồ thị hàm 2 2
số y = f (x) tại 3 điểm nên số nghiệm của phương trình 2 f (x) − 5 = 0 là 3.
Câu 14. Tập nghiệm của bất phương trình log x −1 > 1 − là 1 ( ) 4 A.  5 ;  +∞    . B. 5 1; . C. ( ;2 −∞ ) . D. (1;5). 4      4  Lời giải
GVSB: Bùi Hoàng Nguyên; GVPB: Nguyễn Hiền Lương Chọn D 1 −
Ta có: BPT log x −1 > 1 −  1 0 x 1  ⇔ < − < ⇔ 1< x <   5. 1 ( )  4 4 
Vậy tập nghiệm S = (1;5) .
Câu 15. Cho số phức z thỏa mãn (1−3i) z + 5 = 7i . Mệnh đề nào sau đây đúng? A. 13 4 z = + i . B. 13 4 z = − i . C. 13 4 z = − + i . D. 13 4
z = − − i . 5 5 5 5 5 5 5 5 Lời giải
GVSB: Bùi Hoàng Nguyên; GVPB: Nguyễn Hiền Lương Chọn C − + Ta có: ( − i) 5 7i 13 4
1 3 z + 5 = 7i ⇔ z = = − − i 1− 3i 5 5 Suy ra 13 4 z = − + i . 5 5
Câu 16. Cho khối nón có bán kính đáy bằng a và chiều cao bằng a 3 . Diện tích xung quanh của khối nón đã cho bằng 2 π A. a . B. 2 4π a . C. 2 8π a . D. 2 2π a . 2 Lời giải
GVSB: Bùi Hoàng Nguyên; GVPB: Nguyễn Hiền Lương Chọn D S A O Trang 10
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
Theo đề, ta có: AO = a, SO = a 3 Suy ra, đường sinh 2 2
l = SA = SO + AO = 2a
Vậy diện tích xung quanh của hình nón là 2
S = π rl = π AO SA = a π . xq . 2
Câu 17. Cho cấp số cộng có số hạng đầu bằng 2 , công sai bằng 4 . Số hạng thứ 3 của cấp số cộng đó bằng A. 10. B. 12. C. 6 . D. 8 . Lời giải
GVSB: Anh Tuấn;GVPB: Chọn A
Ta có số hạng thứ 3 của cấp số cộng là u = u + 2d = 2 + 2.4 =10 . 3 1
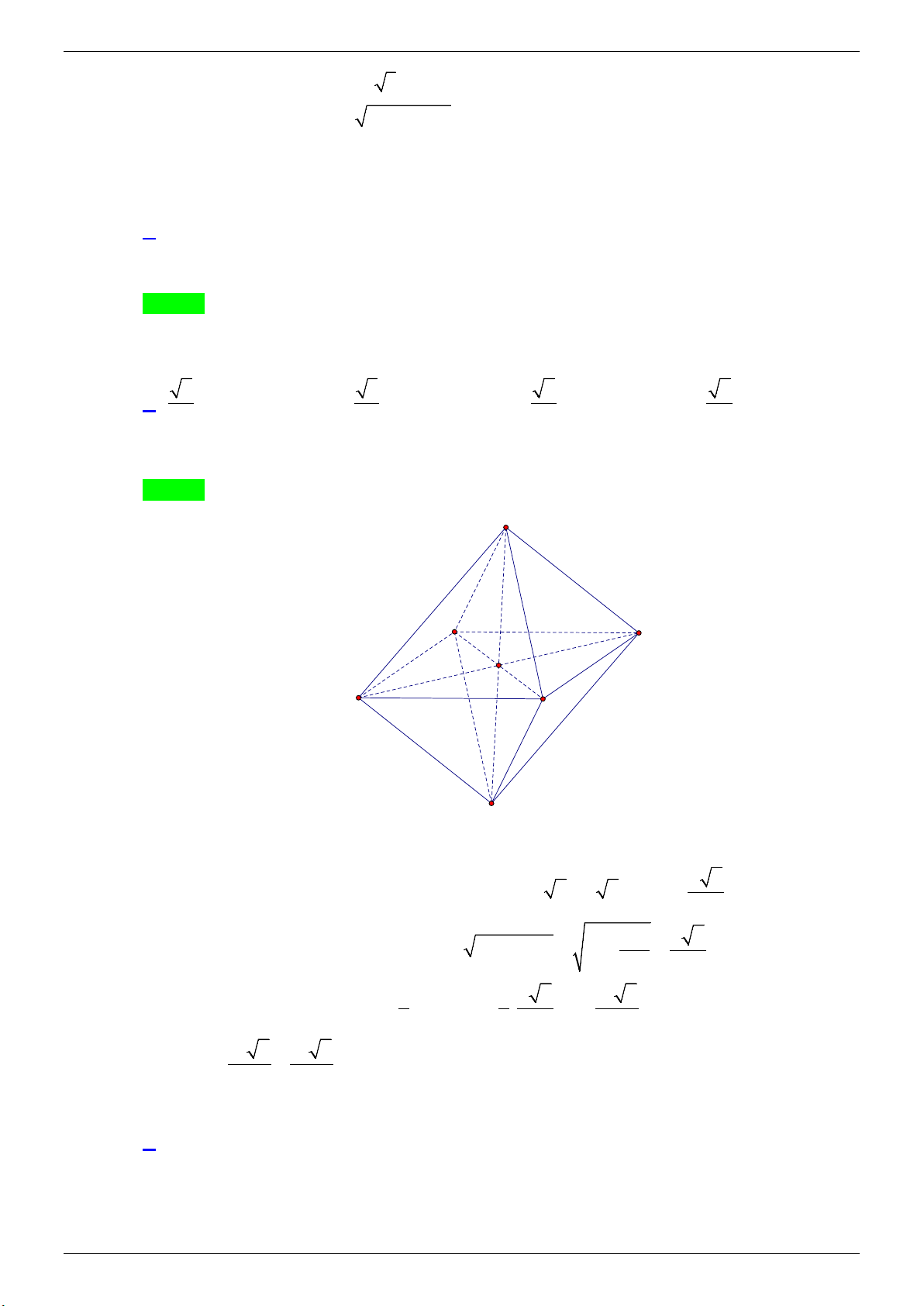
Câu 18. Cho hình bát diện đều cạnh a . Thể tích khối bát diện đều này là A. 2 3 a . B. 3 3 a . C. 2 3 a . D. 6 3 a . 3 3 4 3 Lời giải
GVSB: Anh Tuấn;GVPB: Chọn A S C D O B A S'
Gọi V là thể tích khối bát diện đều cạnh a . Ta có V = 2V . S.ABCD
Do tứ giác ABCD là hình vuông nên a 2
AC = BD = BC 2 = a 2 ⇒ OA = . 2 2 a a
Ta có SO ⊥ ( ABCD) 2 2 2 2 2
⇒ SO ⊥ OA ⇒ SO = SA − OA = a − = . 4 2 3 Mà 2 2 1 1 a 2 2 a 2 S
= AB = a ⇒ V = SO S = a = . ABCD S ABCD . ABCD . . . 3 3 2 6 3 3 Vậy a 2 a 2 V = 2. = . 6 3
Câu 19. Cho hàm số f (x) = sin x + 2021. Trong các khẳng định sau khẳng định nào đúng? A. f
∫ (x)dx = −cos x+2021x+C . B. f
∫ (x)dx = cos x+2021x+C . C. f
∫ (x)dx = cos x+C . D. f
∫ (x)dx = −cos x+C . Lời giải
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 11 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲🙲 BIÊN SOẠN TOÁN THPT
GVSB: Anh Tuấn;GVPB: Chọn A Ta có f
∫ (x)dx = ∫(sin x+ )
2021 dx = −cos x + 2021x + C . +
Câu 20. Tiệm cận đứng của đồ thị hàm số 2x 1 y = là đường thẳng x −1 A. y =1. B. x = 2 . C. x =1. D. x = 2 − . Lời giải
GVSB: Trần Ngọc; GVPB: Chọn C + + Ta có 2x 1 lim = −∞ ; 2x 1 lim = +∞ . x 1− → x −1 x 1+ → x −1
Vậy đồ thị hàm số có đường tiện cận đứng là x =1.
Câu 21. Thể tích của khối cầu có đường kính bằng 2a là A. 8 3 π a . B. 3 4π a . C. 4 3 π a . D. 3 2π a . 3 3 Lời giải
GVSB: Trần Ngọc; GVPB: Chọn C
Ta có bán kính mặt cầu R = a , suy ra 4 3 4 3
V = π R = π a . 3 3
Câu 22. Hàm số y = ( 2
ln 4 − x ) đồng biến trên khoảng A. ( 2; − 2) . B. ( ;2 −∞ ) . C. (0;2) . D. ( 2; − 0) . Lời giải
GVSB: Trần Ngọc; GVPB: Chọn D
Tập xác định D = ( 2; − 2) . − Ta có 2x y′ = . 2 4 − x − Trên x D ta có 2
4 − x > 0 nên hàm số đồng biến khi y′ ≥ 0 2 ⇔ ( ≥ ⇔ x ≤ 0 . − x)( + x) 0 2 2
Vậy hàm số đã cho đồng biến trên khoảng ( 2; − 0) .
Câu 23. Cho hàm số f (x) 3x 1 e− + =
. Trong các khẳng định sau, khẳng định nào đúng? A. ∫ ( ) 3 − 1 d 3 x f x x e + = − + C . B. ∫ ( ) 3 − 1 d x f x x e + = + C . C. f ∫ (x) 1 3−x 1 dx e + = − + C . D. f ∫ (x) 1 3−x 1 dx e + = + C . 3 3
Lời giải GVSB: Thúy Bình Đinh; GVPB: Don Lee Chọn C Ta có f ∫ (x) 3 − x 1 + 1 3−x 1 dx e dx e + = = − + C ∫ . 3
Câu 24. Đồ thị hàm số nào dưới đây có dạng như đường cong hình bên? Trang 12
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021 A. 3 2
y = −x + 3x . B. 4 2
y = x − 3x . C. 3 2
y = x − 3x . D. 4 2
y = −x + 3x .
Lời giải GVSB: Thúy Bình Đinh; GVPB: Don Lee Chọn B
Đường cong hình bên là đồ thị hàm số 4 2
y = ax + bx + c với a > 0 .
Câu 25. Trong không gian Oxyz , cho ba điểm A(1;1;2), B( 3;1;0), C ( 1; − 1; )
1 . Trọng tâm của tam giác
ABC có tọa độ là A. (2;1 ) ;1 . B. (3;3;3). C. (1;1; ) 1 . D. (6;2;2).
Lời giải GVSB: Thúy Bình Đinh; GVPB: Don Lee Chọn C x + x + x A B C x = =  G 1 3   + +
Trọng tâm G của tam giác ABC có tọa độ là y y y A B Cy = = . G 1 3   z + z + z A B C z = =  G 1  3 Vậy G (1;1; ) 1 .
Câu 26. Cho đồ thị hàm số 4 2
y = ax + bx + c có điểm cực đại A(0; 3
− ) và điểm cực tiểu B( 1; − 5 − ) .
Tính giá trị của P = a + 2b + 3c . A. P = 3. B. P = 5 − . C. P = 9 − . D. P = 15 − .
Lời giải GVSB: Thúy Bình Đinh; GVPB: Don Lee Chọn D c = 3 − a + b = 2 − 1
Đồ thị hàm số đi qua điểm A(0; 3 − ) và B( 1; − 5 − ) ( ) ⇒  ⇒ a b c 5  + + = − c = 3. − 4 2 3
y = ax + bx + c ⇒ y′ = 4ax + 2bx .
Đồ thị hàm số có điểm cực tiểu B( 1; − 5 − ) ⇒ 4
− a − 2b = 0. (2) a + b = 2 − a = 2 Từ (1) và (2) suy ra  ⇔  4a 2b 0 b  − − =  = 4. − a = 2 Với  4 2 3 2 b  = 4
− ⇒ y = 2x − 4x − 3 ⇒ y′ = 8x −8x ⇒ y′′ = 24x −8. c = 3 −  x = 0 y′ = 0 ⇔  x = 1. ±
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 13 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲🙲 BIÊN SOẠN TOÁN THPT y′′(0) = 8 − < 0 ⇒ A(0; 3
− ) là điểm cực đại. y′′(− ) 1 =16 > 0 ⇒ B( 1; − 5
− ) là điểm cực tiểu. a = 2 Vậy b   = 4
− ⇒ P = a + 2b + 3c = 15 − . c = 3 − 
Câu 27. Trong không gian Oxyz , đường thẳng đi qua hai điểm A(3;1;0) và B( 1; − 1; ) 1 có phương trình là x = 7 − 4tx = 1 − + 4tx = 3 − 4tx = 3 − 4t A.     y = 1 . B. y =1 .
C. y = t .
D. y =1+ t . z = 1 − +     t z =1+  t z =1+  t z =  t Lời giải
GVSB: Phạm Thái; GVPB: Nguyễn Minh Đức Chọn A 
Đường thẳng AB có vecto chỉ phương AB = ( 4; − 0; ) 1 x = 1 − − 4t
Do đó AB : y =1 z =1+  t
Suy ra đường thẳng AB cũng đi qua C (7;1;− ) 1 x = 7 − 4t
Vậy AB : y =1 . z = 1 − +  t
Câu 28. Một học sinh tô ngẫu nhiên 5 câu trắc nghiệm (mỗi câu có 4 phương án lựa chọn, trong đó chỉ
có 1 phương án đúng). Xác suất để học sinh đó tô sai cả 5 câu bằng A. 15 . B. 3 . C. 243 . D. 1 . 1024 4 1024 1024 Lời giải
GVSB: Phạm Thái; GVPB: Nguyễn Minh Đức Chọn C
Xác suất tô sai 1 câu là 3 4 5
Vậy xác suất để học sinh đó tô sai cả 5 câu là:  3  243 =  . 4    1024
Câu 29. Trong không gian Oxyz , cho hai điểm A(1;1;2) và B(3;1;0) . Mặt cầu đường kính AB có phương trình là
A. (x − )2 + ( y − )2 + (z − )2 2 1 1 = 8.
B. (x − )2 + ( y − )2 + (z − )2 2 1 1 = 2 .
C. (x − )2 + ( y − )2 + (z − )2 1 1 2 = 8.
D. (x − )2 + ( y − )2 2 3 1 + z = 2 . Lời giải
GVSB: Phạm Thái; GVPB: Nguyễn Minh Đức Chọn B Ta có Trang 14
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
Mặt cầu có tâm I (2;1 ) ;1 .
Mặt cầu có bán kính R = AI = 2
Vậy mặt cầu có phương trình: (x − )2 + ( y − )2 + (z − )2 2 1 1 = 2 .
Câu 30. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B , cạnh bên SA vuông
góc với mặt đáy và SA = a 2 , AD = 2AB = 2BC = 2a . Côsin của góc giữa 2 mặt phẳng
(SAD) và (SCD) bằng A. 3 . B. 3 . C. 2 . D. 1 . 2 2 2 2 Lời giải
GVSB: Nguyễn Thắng; GVPB: Nguyễn Minh Đức Chọn D
Gọi M là trung điểm AD thì ABCM là hình vuông nên CM ⊥ AD suy ra CM ⊥ (SAD).
Kẻ MH ⊥ SD (H ∈ SD) thì SD ⊥ (CMH ). (
 SAD)∩(SCD) = SD Ta có 
nên góc giữa (SAD) và (SCD) là góc  MHC . SD ⊥  (CMH ) Trong S ∆ AD thì  SA 2 = = ⇒  3 tan SDA sin SDA = AD 2 3 Trong MH ∆
D vuông tại H thì  MH a 3 sin SDA = ⇒ MH = . MD 3 Trong MH ∆
C vuông tại M thì 2   2 2 2 a 3 2a 3
HC = MC + MH = a +   =  3  3   a 3  MH 3 1  cos MHC = = = . HC 2a 3 2 3 5 2
Câu 31. Nếu 2 f
∫ (x)dx = 3 thì f (2x+ ∫ )1dx 3 1 A. 3 . B. 3. C. 6. D. 3 . 2 4 Lời giải
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 15 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲🙲 BIÊN SOẠN TOÁN THPT
GVSB: Nguyễn Thắng; GVPB: Nguyễn Minh Đức Chọn D 2 2 5 Ta có f ∫ ( x+ ) 1 x = f
∫ ( x+ ) ( x+ ) 1 = f ∫ (x) 1 3 3 2 1 d 2 1 d 2 1 dx = . = . 2 2 2 2 4 1 1 3
Câu 32. Trong không gian Oxyz , cho hai điểm M ( 1; − 2; ) 1 và N (3;0;− )
1 . Mặt phẳng trung trực của
MN có phương trình là
A. 4x − 2y − 2z +1 = 0. B. 2
− x + y + z +1 = 0.
C. x + y − 2 = 0. D. 2
− x + y + z + 7 = 0. Lời giải
GVSB: Nguyễn Thắng; GVPB: Nguyễn Minh Đức Chọn B
Gọi I (1;1;0) là trung điểm MN . 
Ta có MN = (4;− 2;− 2) = 2(2;−1;− ) 1 . 
Mặt phẳng trung trực của MN đi qua I và nhận vectơ n = ( 2 − ;1 )
;1 làm VTPT nên có phương trình là 2 − (x − ) 1 +1( y − ) 1 +1(z − 0) = 0 ⇔ 2
− x + y + z +1 = 0 .
Câu 33. Tìm tất cả các giá trị thực của tham số m để phương trình 2x 1+ 2 2
− 2m = 0 có nghiệm. m ≥1 A.  . B. m > 0. C. ( ;0 −∞ ). D. (0; ) 1 . m ≤ 1 − Lời giải
GVSB: Giang Sơn GVPB: Phạm Thanh Liêm Chọn A
Phương trình đưa về 2x 1+ 2 2 = 2m . m ≥1 Nhận xét 2x 1
2 + ≥ 2 , điều kiện có nghiệm là 2 2
2m ≥ 2 ⇔ m ≥1 ⇔  . m ≤ 1 − ( 2 m − m) 3 x
Câu 34. Cho hàm số y = + ( 2 m − m) 2
x + mx + 2 . Có bao nhiêu giá trị nguyên của m để 3
hàm số đồng biến trên  ? A. 3. B. 5. C. 1. D. 2 . Lời giải
GVSB: Giang Sơn GVPB: Phạm Thanh Liêm Chọn D
m = 0 ⇒ y = 2 Xét 2
m − m = 0 ⇔  , chọn m =1.
m =1⇒ y = x + 2 Xét 2
m − m > 0 .
Hàm số đồng biến trên 2  khi 2
b − c ≤ ⇔ ( 2
m − m) − m( 2 3a 0 m − m) ≤ 0 ⇔ ( m = 0 2 m − m)( 2 m − 2m) 2
≤ 0 ⇔ m (m − ) 1 (m − 2) ≤ 0 ⇔ . 1   ≤ m ≤ 2
Như vậy 1≤ m ≤ 2 dẫn đến 2 giá trị nguyên m cần tìm.
Câu 35. Trong không gian Oxyz , đường thẳng nào dưới đây đi qua điểm M (1; 2 − ; ) 1 ? Trang 16
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021 A.
x 1 y 2 z 1 d − − + : = = . B.
x 1 y 2 z 1 d − + − : = = . 1 2 1 − 3 3 2 3 − 1 C.
x 1 y 2 z 1 d + + − : = = . D.
x 1 y 2 z 1 d − + + : = = . 3 2 1 3 3 2 3 1 − Lời giải
GVSB: Giang Sơn GVPB: Phạm Thanh Liêm Chọn B Thử trực tiếp ta có
x 1 y 2 z 1 d − + − : = = đi qua M (1; 2 − ; ) 1 . 3 2 3 − 1
Câu 36. Trong không gian Oxyz , mặt cầu (S ) 2 : x + ( y − )2
1 + (z + 2)2 = 4 có tọa độ tâm I là
A. I (0;1;− 2) . B. I (0;1;2).
C. I (0;−1;2) .
D. I (1;1;− 2) . Lời giải
GVSB: Trần Xuân Thiện; GVPB: Phạm Thanh Liêm Chọn A
 Mặt cầu (S ) 2 : x + ( y − )2
1 + (z + 2)2 = 4 có tâm I (0;1;− 2) .
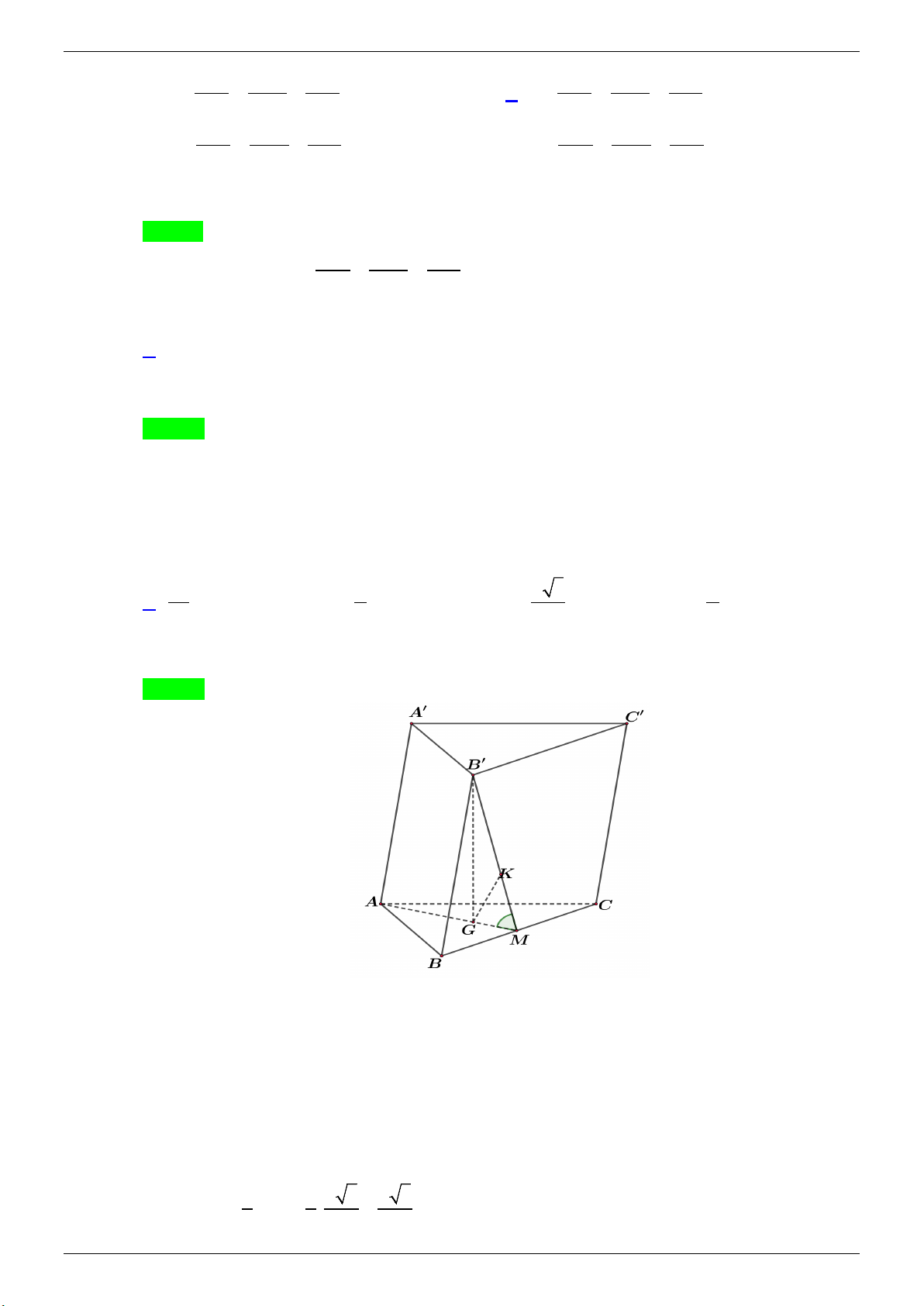
Câu 37. Cho lăng trụ ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a , góc giữa hai mặt phẳng ( A′B C ′ ′) và
(BCC B′′) bằng 60°, hình chiếu của B′ lên mặt phẳng ( ABC) trùng với trọng tâm tam giác
ABC . Khoảng cách giữa hai đường thẳng AA′ và B C ′ bằng A. 3a . B. a . C. a 3 . D. a . 4 2 4 4 Lời giải
GVSB: Vũ Viên; GVPB: Phạm Thanh Liêm Chọn A
Gọi G là trọng tâm tam giác ABC và M là trung điểm của BC .
Từ giả thiết ta có B G ′ ⊥ ( ABC) .
Ta có α = (( A′B C ′ ′) (BCC B
′ ′)) = (( ABC) (BCC B ′ ′)) =  , , B M ′ G = 60°.
Vì AA′// (BCC B ′ ′)
nên d ( AA ,′ B C
′ ) = d ( AA ,′(BCC B ′ ′)) = d ( , A (BCC B
′ ′)) = 3.d (G,(BCC B ′ ′)) .
Gọi K là hình chiếu của G lên mặt phẳng (BCC B
′ ′) ⇒ d (G,(BCC B ′ ′)) = GK . Ta có 1 1 a 3 a 3 GM = AM = . = . 3 3 2 6
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 17 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲🙲 BIÊN SOẠN TOÁN THPT Xét tam giác vuông GK a 3 3 : sin 60° = ⇒ = . a GMK GK = . GM 6 2 4 ⇒ ( ′ ′ ) 3 , = 3. a d AA B C GK = . 4
Câu 38. Cho hai số phức z , z là các nghiệm của phương trình 2
z + 4z +13 = 0 . Khi đó môđun của số 1 2
phức w = (z + z i + z z bằng 1 2 ) 1 2 A. 13 5 . B. 195 . C. 185 . D. 13. Lời giải
GVSB: Vũ Viên; GVPB: Phạm Thanh Liêm Chọn C
Gọi z , z là các nghiệm của phương trình 2
z + 4z +13 = 0 . Áp dụng định lí Viet ta có: 1 2 z + z = 4 − 1 2 
⇒ w = (z + z i + z z = 4 − i +13. 1 2 ) z z =  13 1 2 1 2 2 2 ⇒ w = 4 +13 = 185 .
Câu 39. Một gia đình muốn làm cánh cổng (như hình vẽ). Phần phía trên cổng có hình dạng là một
parabol với IH = 2,5m , phần phía dưới là một hình chữ nhật kích thước cạnh là AD = 4m ,
AB = 6m . Giả sử giá để làm phần cổng được tô màu là 0 ( 2
1.000.0 0 đ/m ) và giá để làm phần cổng phía trên là 0 ( 2
1.200.0 0 đ/m ) . Số tiền gia đình đó phải trả là A. 24.400.000đ . B. 36.000.000đ . C. 38.000.000đ . D. 38.800.000đ . Lời giải
GVSB: Vũ Viên; GVPB: Phạm Thanh Liêm Chọn B Trang 18
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021
Xét hệ trục tọa độ như hình vẽ: Gốc tọa độ O trùng điểm H , A và B thuộc trục Ox , H thuộc trục Oy .
Khi đó H (0;0) , I (0;2,5) , B(3;0) , A( 3 − ;0) .
Gọi parabol cần tìm có dạng (P) 2
: y = ax + bx + c .  5 9  − 3 + = 0 a a b c = −  18  
Do A , B , I thuộc (P) nên ta có hệ 9
a + 3b + c = 0 ⇔ b  = 0 . c 2,5  =  5 c =  2 Do đó parabol là (P) 5 2 5 : y = − x + . 18 2
Diện tích phần phía trên cổng có hình dạng là một parabol là 3 3 3  5    2 5 5 x 5 − ∫ 
x + dx = − . + x =10 . −  18 2   18 3 2 3  3−
Giá tiền để làm phần cổng phía trên là 10x1.200.000 =12.000.000 .
Diện tích phần phía dưới là một hình chữ nhật là 4.6 = 24 .
Giá tiền để làm phần cổng được tô màu là 24x1.000.000 = 24.000.000 .
Số tiền gia đình đó phải trả là 12.000.000 + 24.000.000 = 36.000.000 . 2 − −
Câu 40. Có bao nhiêu giá trị của tham số x m
m để giá trị lớn nhất của hàm số 2 y = trên đoạn x − m [0;4] bằng 1 ? 2 A. 0 . B. 2 . C. 3. D. 1. Lời giải
GVSB: Nguyễn Việt Dũng; GVPB: Giao Nguyen Chọn D 2 − − Hàm số x m 2 y = . x − m
Tập xác định: D =  \{ } m . 2 Ta có: m − m + 2 y′ = . (x − m)2
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 19 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲🙲 BIÊN SOẠN TOÁN THPT 2 Vì 2  1  7
m − m + 2 = m − + >   0 với m
∀ ⇒ y′ > 0 với m ∀  2  4
⇒ Hàm số đồng biến trong từng khoảng xác định với m ∀ . m∉[0;4] 2 − −
Do đó, giá trị lớn nhất của hàm số x m 2 y = trên đoạn [  0;4] bằng 1 ⇔ x  − m 2 y ( ) 1 4 =  2 m∉[0;4] m∉[0;4]   m∉[0;4] m∉[0;4] ⇔  3 2
4 − m − 2 1 ⇔  ⇔  ⇔  m = ⇔ m = 2 − .  = 2
4 − 2m = m − 2 2
2m + m − 6 = 0   2  m − 2 2  m = 2 −
Vậy có 1 giá trị của tham số m thỏa mãn yêu cầu của bài toán. 4 f ( x ) 2
Câu 41. Cho hàm số f (x) có đạo hàm trên  thỏa mãn f (2) = 3, dx = 2 ∫ , xf ′ ∫ (x)dx = 3. 1 x 0 1
Tính f (x)dx ∫ . 0 A. 5. B. 1. C. 2 . D. 3. Lời giải
GVSB: Nguyễn Việt Dũng; GVPB: Giao Nguyen Chọn C 4 f ( x ) • Gọi A = dx ∫ . 1 x Đặt x = t dx ⇒
= dt ⇒ dx = 2 xdt . 2 x 2 f (t) 2 .2 xdt
x =1⇒ t =1; x = 4 ⇒ t = 2 ⇒ A = = 2 f ∫ ∫ (t)dt . 1 x 1 2 Mà A = 2 ⇒ f ∫ (x)dx =1. 1 2
• Gọi B = xf ′ ∫ (x)dx. 0 2 2 2 2
Ta có: B = xf ′ ∫ (x)dx = d x
∫ ( f (x)) = xf (x) 2 − f
∫ (x)dx = 2 f (2)− f ∫ (x)dx. 0 0 0 0 0 2 2
Mà f (2) = 3 và B = 3 ⇒ 6 − f
∫ (x)dx = 3 ⇒ f ∫ (x)dx = 3. 0 0 1 2 2 Vậy f
∫ (x)dx = f
∫ (x)dx− f
∫ (x)dx = 3−1= 2 . 0 0 1
Câu 42. Cho số phức z = x + yi ( x; y ∈ ) thỏa mãn z + 2 + i = z (1+ i) và z > 3 . Giá trị của biểu thức
S = 2x − 3y là A. 6 − . B. 3 − . C. 6 . D. 3. Lời giải
GVSB: Nguyễn Việt Dũng; GVPB: Giao Nguyen Trang 20
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021 Chọn A
Số phức z = x + yi ( x; y ∈ ) 2 2
⇒ z = x + y .
Ta có: z + 2 + i = z (1+ i) ⇔ x + yi + 2 + i = z + z i ⇔ x + 2 + ( y + )
1 i = z + z i x = 1 − x + 2 =   zy = x +1 y = x +1 y = 0 ⇔   ⇔  ⇔  ⇔ . y +1 = z 2 2 2 2   (  x + 2  ) = x +(x + )1
x − 2x − 3 = 0 x = 3  y = 4 x = 3 Mà 2 2
z = x + y > 3 ⇒ 
⇒ S = 2x − 3y = 2.3− 3.4 = 6 − . y = 4
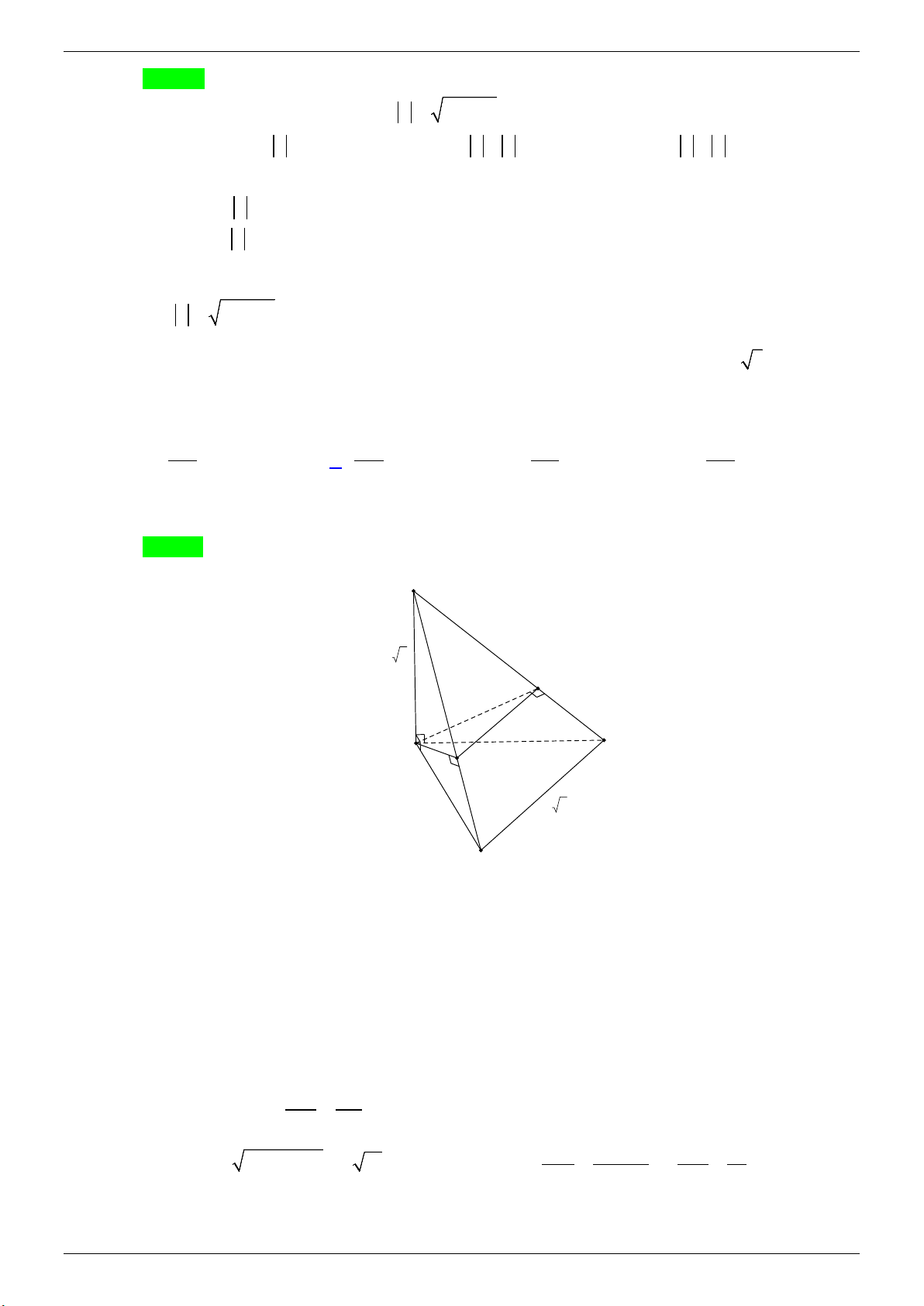
Câu 43. Cho hình chóp S.ABC có SA vuông góc với mặt đáy, SA = 2BC = 2a 3, AC = a và  BAC 120° =
. Hình chiếu vuông góc của A lên các cạnh SB và SC lần lượt là M và N . Thể
tích của khối đa diện AMNCB bằng A. 24 3 a . B. 25 3 a . C. 25 3 a . D. 12 3 a . 169 338 169 169 Lời giải
GVSB: Quách Đăng Thăng; GVPB: Giao Nguyen Chọn B S 2a 3 N a A C 1200 M a 3 B
Xét tam giác ABC , theo định lý Cô sin ta có 2 2 2
BC = AB + AC − 2A . B AC.cos A AB = a 2 2 2 0
⇔ 3a = AB + a − 2A . B . a cos120 2 2 2
⇔ 3a = AB + AB − 2a = 0 ⇔  . AB = 2 − a Suy ra AB = a .  ⊥ Vì ⊥ ( ) SA AB SA ABC ⇒ 
và AB = AC = a , SA chung nên S ∆ AB = S ∆ AC . SA ⊥ AC
Hình chiếu vuông góc của A lên các cạnh SB và SC lần lượt là M và N nên AM = AN và
MN / /BC , suy ra SM SN = . SB SC 2 Ta có 2 2 SB SA SM.SB SM 12
= SA + AB = a 13 và 2
SA = SM.SB ⇒ = ⇔ = . 2 2 SB SB SB 13
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 21 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲🙲 BIÊN SOẠN TOÁN THPT 2 Do đó V SA SM SN SM 144 S AMN  144 . = . . = = ⇒ V = V . V
SA SB SC  SB S.AMN S. 169 ABC S ABC  169 . Lại có V = V +V 144 25 ⇒ V = V −V = V − V = V . S.ABC S.AMN AMNCB AMNCB S.ABC S.AMN S.ABC S.ABC S. 169 169 ABC Mà 1 1 1 = =  3 1 1 0 a V SA S = = . ∆ SA AB AC BAC a a a S ABC . . ABC . . . . .sin .2 3. . . .sin120 . 3 3 2 3 2 2 3 Vậy 25 25a V = V = . AMNCB S. 169 ABC 338
Câu 44. Trong không gian Oxyz , cho hai đường thẳng x 1 y 1 : z d − + = = và x y 1 : z d − = = . 1 1 1 − 2 2 1 2 1
Đường thẳng d đi qua A(1;0; )
1 lần lượt cắt d ,d tại B và C . Độ dài BC bằng 1 2 A. 7 6 . B. 3 3 . C. 5 3 . D. 7 6 . 4 2 2 2 Lời giải
GVSB: Quách Đăng Thăng; GVPB: Chọn A x = 1+ tx = s
Ta có phương trình tham số của d ,d là d  
y = − − t và d y = + s . 1 2 : 1 : 1 2 1 2 z =   2t z =  s
Vì d ∩ d = B ⇒ B ∈d ⇒ B 1+ t; 1
− − t;2t và d ∩ d = C ⇒ C ∈ d ⇒ C s;1+ 2s;s . 2 2 ( ) 1 1 ( )  
Suy ra AB = (t; 1
− − t;2t − )
1 , AC = (s −1;1+ 2s;s − ) 1 . t  = k (s − ) 1 t  = k (s − ) 1     Do ,
A B,C thẳng hàng nên k
∃ ≠ 0 : AB = k AC ⇒  1
− − t = k (1+ 2s) ⇔  1
− − t = k (1+ 2s)
2t −1= k(s−   ) 1 2t −1 = t      t  =1 t =1 t =1 t  = 1     1  1 ⇔  k (s − ) 1 =1
⇔ ks − k =1
⇔ ks = − ⇔ s = .  3 4 k (1+ 2s) = 2 −     2ks + k = 2 −   4 k = −  4  k = −  3  3 Do đó B( ) 1 3 1 2; 2;2 ,C  ; ;  − 7 6  ⇒ BC = . 4 2 4    4 2
log x − 3log x + 2
Câu 45. Có bao nhiêu giá trị nguyên dương của tham số m để bất phương trình 3 3 < 0 m − 2x
có không quá 3 nghiệm nguyên dương? A. 127 . B. 128. C. 63. D. 64 . Lời giải
GVSB: Quách Đăng Thăng; GVPB: Chọn C x > 0 Điều kiện  ⇒ > 2x m ⇒ m >1.
m − 2x > 0 Trang 22
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021 x > 0 x > 0 2
log x − 3log x + 2 Ta có 3 3 < 0 
⇔ m − 2x > 0
⇔ m − 2x > 0 m − 2x  2 
log x − 3log x + 2 < 0
(log x −1 log x − 2 < 0  3 )( 3 ) 3 3 x > 0 x > 0  m > 2x ⇔ 
m − 2x > 0
⇔ m > 2x ⇔  (I). 3  < x < 9 1
 < log x < 2   3 < x < 9 3 
Để bất phương trình có không quá 3 nghiệm nguyên dương khi và chỉ bất phương trình 2x m >
có không quá 3 nghiệm nguyên dương x ∈(3;9) .
Xét hàm số = ( ) = 2x y f x
với x ∈(3;9) có ′( ) = 2x f x .ln 2 > 0, x ∀ . Bảng biến thiên
Từ bảng biến thiên suy ra m ≤ 64 .
Mà m >1 và m nguyên dương nên m∈{2;3;4;...; } 64 .
Vậy có 63 giá trị nguyên dương của tham số m thoả mãn.
Câu 46. Trong không gian Oxyz , cho mặt cầu (S ): (x − )2 + ( y + )2 2 1
1 + z = 4 và hai điểm A( 1; − 1; ) 1 ; B(2;− 2; )
1 . Điểm M di chuyển trên mặt cầu (S ) . Giá trị lớn nhất của 2MA − 3MB đạt được là: A. 65 . B. 67 . C. 69 . D. 61 . Lời giải
GVSB: Bùi Thanh Sơn; GVPB: Chọn B
Mặt cầu (S ) có tâm I (1;−1;0), bán kính R = 2 .
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 23 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲🙲 BIÊN SOẠN TOÁN THPT
Ta có: IA = 3; IB = 3 .    
Gọi E = AI (S ) ; điểm F xác định bởi 2 IF = IE ⇒ 4 IF = ⇒ 4 IF = IA ⇒ 1 1 4 F  ; ;  − . 3 3 9 9 9 9    Dễ thấy MA MA IA ∆ I F ∆ MI ⇒ 3 =
= ⇒ 2MA = 3MF . MF IM 2
Ta có: 2MA − 3MB = 3 MF − MB ≤ 3BF = 67 .
Vậy min 2MA − 3MB = 67 khi M = BF (S ) sao cho F nằm giữa B và M .
Câu 47. Có bao nhiêu giá trị thực của tham số m để bất phương trình sau có nghiệm duy nhất?
log ( 2x + mx +5 + )1.log ( 2x + mx +6 +log ≥ . m 3 0 1 5 ) m A. 4 . B. 1. C. 2 . D. 3. Lời giải
GVSB: Bùi Thanh Sơn; GVPB: Chọn B
ĐK: 0 < m ≠ 1.
Bất phương trình đã cho có nghiệm duy nhất thì suy ra phương trình
log ( 2x + mx +5 + )1.log ( 2x + mx +6 +log = ( )1 có nghiệm duy nhất. m 3 0 1 5 ) m
ĐK cần: Dễ thấy nếu x là nghiệm của ( )
−m − x cũng là nghiệm của ( ) 0 1 thì 0 1
⇒ x = −m − x ⇒ m
x = − là nghiệm của ( ) 0 0 1 . 0 2  2  2   ⇒ log  5 m − +1.log 6 m −  + log 3 = 0 1 5  4     4 m m   2  2    2  2   ⇔ log m m m m  − +   −  = ⇔ log  5 − +1.log 6 −  = 1 (2) m 5 1 .log 6 logm 3 5  4  3 5      4  4    4 
Xét hàm số f (t) = log (t + )
1 .log ( 2t +1 trên [0;+ ∞) 3 5 ) ′( ) 1 = ( 2 2 .log +1 t f t t +
.log t +1 > 0 t ∀ ∈ 0;+ ∞ 5 ) (t + ) 1 ln 3 ( 2t + ) 3 ( ) [ ) 1 ln 5
⇒ Hàm số f (t) đồng biến trên [0;+ ∞) Mà f (2) =1  2  2 m Do đó ( m 2) ⇔ f  5 −  = f ( ) 1 ⇔ − = ⇔  5 1 m = 2 . 4    4
ĐK đủ: Thử lại thấy với m = 2 thì bất phương trình đã cho có nghiệm duy nhất x = 1 − .
Vậy có một giá trị m thỏa mãn yêu cầu bài toán.
Câu 48. Cho hình (H ) giới hạn bởi đồ thị hàm số bậc hai (nét mảnh) và đồ thị hàm số bậc ba (nét đậm)
như hình vẽ. Thể tích khối tròn xoay khi quay hình (H ) quanh trục Ox là: Trang 24
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021 π π π A. 1024 . B. 4096 . C. 5017 . D. 4096 . 35 35 35 35 Lời giải
GVSB: Bùi Thanh Sơn; GVPB: Chọn C
Từ đồ thị suy ra hàm số bậc hai là 2
y = x và hàm số bậc ba là 3 2
y = x − 3x . Xét các phương trình: x = 0 • 2 3 2
x = x − 3x ⇔ 2
x (x − 4) = 0 ⇔  x = 4 • 2 x = 0 ⇔ x = 0 x = 0 • 3 2
x − 3x = 0 ⇔ 2
x (x − 3) = 0 ⇔  x = 3
Vậy thể tích khối tròn xoay khi quay hình (H ) quanh trục Ox là: 2 π
V = π (x − x ) 4 4
2 x +π x x −π (x − x )2 3 2 4 3 2 5017 3 d d 3 dx = ∫ ∫ ∫ . 35 0 2 3
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 25 ĐỀ THI THỬ: 2020-2021
NHÓM WORD 🙲🙲 BIÊN SOẠN TOÁN THPT
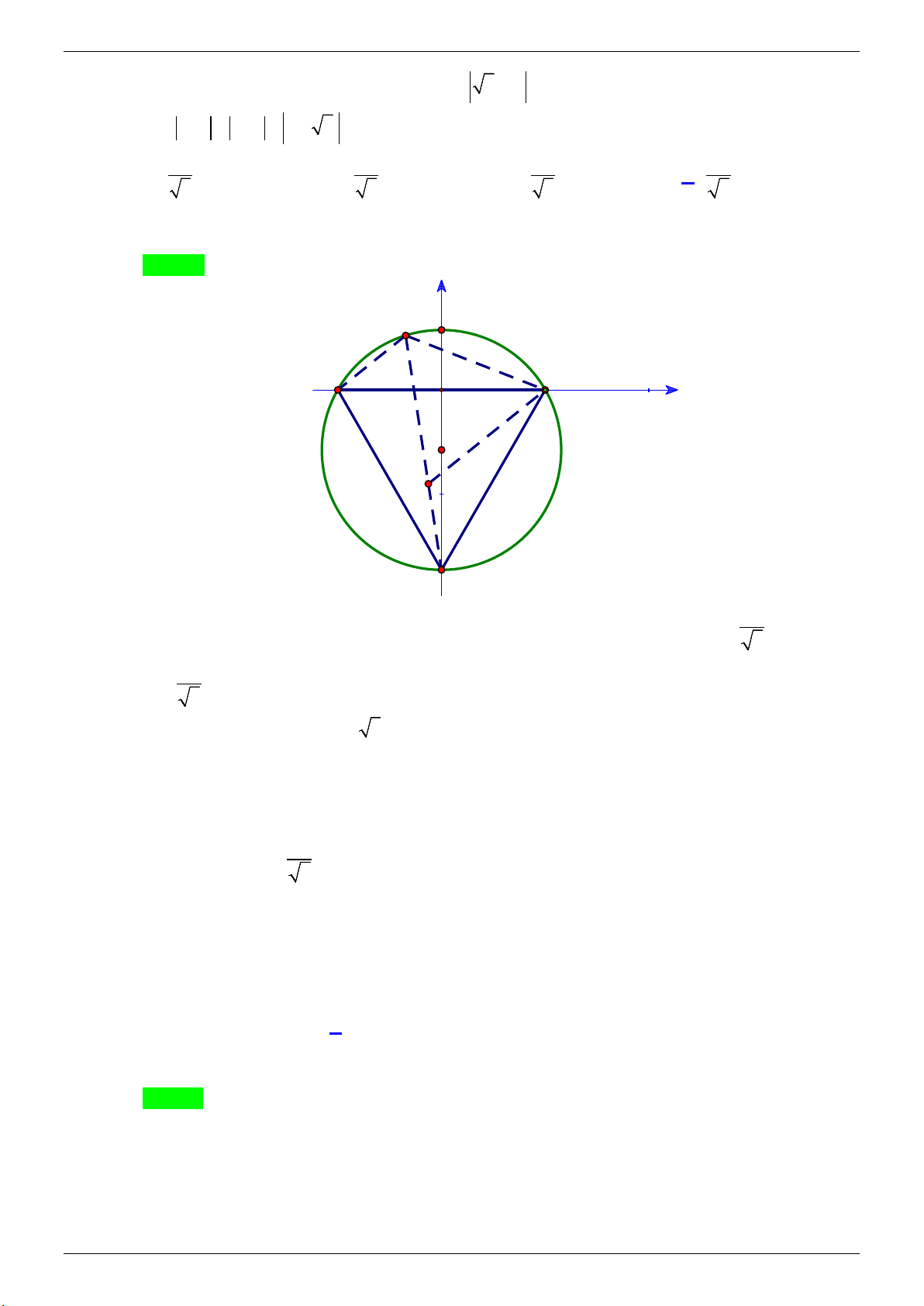
Câu 49. Cho số phức z thay đổi thỏa mãn
3z + i = 2 . Giá trị lớn nhất của biểu thức
S = z −1 + z +1 + z + 3i là A. 4 . B. 16 . C. 2 . D. 8 . 3 3 3 3 Lời giải
GVSB: Lê Duy Hiền; GVPB: Lê Hồng Vân Chọn D y M B A x I D C 1 
+ Gọi M là điểm biểu diễn của z thì M thuộc đường tròn (C)có tâm I 0; , bán kính 3    2 R = 3 + Gọi ( A 1;0), B( 1;
− 0),C(0;− 3) . Ta thấy ,
A B,C ∈(C) và tam giác ABC đều.
+ Không mất tính tổng quát giả sử M thuộc cung nhỏ 
AB . Lấy D thuộc đoạn MC sao cho
MD = MA. Ta có  =  0
AMD ABC = 60 ⇒ M
∆ AD đều ⇒ A ∆ BM = A
∆ CD ⇒ MB = DC
+ Do đó : S = MA + MB + MC = 2MC lớn nhất khi MC lớn nhất hay MC là đường kính. Vậy 8 max S = 4R = 3 Câu 50. Cho hàm số 3 2
y = x − (m + 2)x − (2m +13)x − m − 2 có đồ thị (C đường thẳng m ),
d : y = mx + m + 8 và điểm I (1;4). Tính tổng tất cả các giá trị của tham số ,
m biết rằng đường
thẳng d cắt đồ thị (C tại ba điểm phân biệt , A B,C với m )
A có hoành độ bằng 2 − và tam giác
IBC cân tại I. A. 12 − . B. 6 − . C. 4 − . D. 10 − . Lời giải
GVSB: Lê Duy Hiền; GVPB :Lê Hồng Vân: Chọn B + Phương trình hoành độ giao điểm của d và (Cm) là: x = 2 − 3
x (m 2)x (3m 13)x 2m 10 0  − + − + − − = ⇔ x = 1 −  x = m +  5 Trang 26
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN ĐỀ THI THỬ: 2020-2021 m ≠ 7 −
+ Để đường thẳng d cắt đồ thị (C tại ba điểm phân biệt , A B,C thì m )  m ≠ 6 − + Giả sử 2 B( 1
− ;8),C(m + 5;m + 6m + 8) . Để tam giác IBC cân tại I m = 2 −  thì 2 2 2 2 2
IB = IC ⇔ 20 = (m + 4) + (m + 6m + 4) ⇔ m = 6 −  (l)  m = 2 − ± 3
Vậy có ba giá trị của m thỏa mãn nên tổng các giá trị của m bằng 6 − .
____________________ HẾT ____________________
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 27
Document Outline

  • de-thi-thu-tot-nghiep-thptqg-2021-mon-toan-truong-thpt-chuyen-ha-tinh
    • 186056012_3929238367169667_759677945388621657_n
    • 185402251_3929238377169666_2562717599994455458_n
    • 185782598_3929238380502999_4327015426150371683_n
    • 186382594_3929238517169652_8280418226203688617_n
    • 184675885_3929238563836314_2679376180182141787_n
    • 183439205_3929238553836315_1449534797785941369_n
  • NW459-ĐỀ-THI-THỬ-TN12-LẦN-1-THPT-CHUYÊN-HÀ-TĨNH-2020-2021-GV