Thầuvà Lê Minh Trí - 0327.030.253
Lũyhiện thi THPT Quốc Gia
THẦCó LÊ MINH TRÍ KỲ THI HỌC KỲ 1 ĐỀ THI THỬ VÌ THẾ 9
Bài này: ĐẾNMỘT
( Đề thi có N trang )
Thời gian làm bài: 90 phút (không kể thời gian phát đề).
Họ, tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Vì thế báo danh sách: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 1. Cho hình chặt S. AB CD có SA ⊥ ( ABCD ) , ABCD là hình vuông cạnh bằng 2 v à SA = một . Tnghiêm
tích V của khối cnhảy lò cò S. AB CĐ . 3 2 a . A. V = B . V Lời giải. = 2a3.C.V = 43 a 3 . Diện tích hình vuông 2 2 ABCD là SAB = ( 2a ) = 4a . S CD 1 1 3 S . 4
Thể tích khối cnhảy lò cò S. AB CD là V =· SA = 2 3 ABCD · 4 · 3 a a a = MỘT B 3 Đ C Chọn đáp MỘT D 3
Câu 2. Giăm bông Vì thế f ( x ) = 2 x + 4 có đạo giăm bông là 3 .
A.f ′ ( x ) = 2 x + 4 ln2. B . f 2 3 trong 2 3 . x + 4 C.f ′ ( x )
= 3 · 2 x + 4 ln2. D.f ′ ( x ) = Lời giải. trong 2 ′ Áp áp dụng công thức ′ ( u ) = u · u lnMột ′ ′ 3 3
TMột có f ( x ) = ( 3 x + 4 )
· 2 x + 4 ln2 = 3 · 2 x + 4 ln2 . Chọn đáp MỘT C
Câu 3. Cho các Vì thế thực a , b cân bằng người đàn ông log0 log0
. Khẳng định nào sau đãvà đúng khôn , 2 a > , 2 b
A. b > a > 1. B .
a > b > 1. C . a > b > 0. D. b Lời giải.
Vì logarit x với 0 < a < 1 là giăm bông nghịch biến nên từ log0 log0 , 2 a >
, 2 b ⇔ b > a > 0 . a Chọn đáp MỘT D x
nghịch biến trên khoảng nào dưới đãbạn?
Câu 4. Giăm bông Vì thế + 1 y = A. ( − ∞ ; + ∞ ) . x − 1 B. ( − ∞ ; 2 ) . C . ( 1;2 ) . D . ( − + 1; ∞ ) . Lời giải. Tâp xác định D = R \{ 1 } . − < ( ) ′ TMột có 2 y = 2 0 , ∀ x∈
D . LÀM đó giăm bông Vì thế nghịch biến trên khoảng 1; 2 . ( x − 1 )
220 Xô Viết Nghệ Tĩnh, phường 21, quận Bình Thanh Tvang lên 1
Thầuvà Lê Minh Trí - 0327.030.253
Lũyhiện thi THPT Quốc Gia Chọn đáp MỘT C
Câu 5. Cho hình chặt S. AB CD có đávà ABCD là hình chữ ngày, AB = một , BC = 2 một , đường thẳng SA vuôn
ggiày với mặt Giày (ABCD ) và SA = 3 giờ . Thể tích của khối cnhảy lò cò S. AB CD bằng A. 3. 3 a B . 2 a 3. C . Lời giải. 2 TMột có S SAB
= AB · BC = 2 a . đĩa CD 1 1 S · · · 3 VMộtvà · a 2 a 3 a = 2 a . V = SA = ABCD 3
S. AB đĩa CD 3 MỘT D C B Chọn đáp MỘT B
Câu 6. Thể tích của khối lăng trụ có chiều cao bằng h vMột định danh tích đávà bằng B là 1 1 1 Bh.D.V Bh A.V Bh.B.V Bh.C.V = = . = = Lời giải. 2 3 6
Áp áp dụng công thức thể tích của khối lăng hình trụ. Chọn đáp MỘT D
Câu 7. Cho hình mũ ( N ) có chiều cao h , bán kính đávà R vMột độ dài đường sinh là l. Công thức tính diện
tích xung quanh S của (N) là A. 1 S = πRl. B. S = π π Rl.
C. S = 4 R2.
D. S = 2πRh. 3 Lời giải.
Công thức tính diện tích xung quanh S của (N) là S = πRl. Chọn đáp án A □ Câu 8. Hàm số x3 y =
− 3x2 + 5x − 2 nghịch biến trên khoảng 3 A. (1;6). B. (5;+∞). C. (−∞;1). D. (2;3). Lời giải.
Tập xác định D = R. Đạo hàm y′ = x2 −6x +5.
Ta có y′ < 0 ⇔ x2 −6x +5 < 0 ⇔ 1 < x < 5.
Suy ra hàm số đã cho nghịch biến trên khoảng (1;5) nên hàm số nghịch biến trên khoảng (2;3). Chọn đáp án D □
Câu 9. Tính diện tích S của mặt cầu có đường kính bằng 2a.
A. S = 2πa2.
B. S = 4πa2.
C. S = πa2.
D. S = 16πa2.
220 Xô Viết Nghệ Tĩnh, phường 21, quận Bình Thạnh Trang 2
Thầy Lê Minh Trí - 0327.030.253
Luyện thi THPT Quốc Gia Lời giải.
Mặt cầu có đường kính bằng 2a nên có bán kính R = a.
Vậy diện tích mặt cầu là S = 4πR2 = 4πa2. Chọn đáp án B □
Câu 10. Chiều cao của khối chóp có diện tích đáy bằng B và thể tích bằng V là A. V 6V 3V 2V h = . B. h = . C. h = . D. h = . B B B B Lời giải. Ta có 1 3V
V = hB ⇒ h = . 3 B Chọn đáp án C □
Câu 11. Cho khối trụ (T) có chiều cao và đường kính đáy cùng bằng 2a. Tính diện tích toàn phần S tp của (T ).
A. S tp = 5πa2.
B. S tp = 3πa2.
C. S tp = 4πa2.
D. S tp = 6πa2. Lời giải.
Ta có Stp = Sxq + 2Sđáy = 4πa2 + 2πa2 = 6πa2. Chọn đáp án D □
Câu 12. Cho hàm số y = f (x) có đồ thị như đường cong hình bên. Phương trình f (x) = 2 có bao nhiêu nghiệm? y 2 1 x O A. 1. B. 3. C. 2. D. 4. Lời giải.
Số nghiệm phương trình f (x) = 2 là số giao điểm của đồ thị hàm số y = f (x) và đường thẳng y = 2.
Dựa vào đồ thị suy ra phương trình f (x) = 2 có 4 nghiệm phân biệt. Chọn đáp án D □
Câu 13. Cho hình trụ có chiều cao bằng 2a, bán kính đáy bằng a. Tính diện tích xung quanh của hình trụ. A. 2πa2. B. πa2. C. 2a2. D. 4πa2.
220 Xô Viết Nghệ Tĩnh, phường 21, quận Bình Thạnh Trang 3
Thầy Lê Minh Trí - 0327.030.253
Luyện thi THPT Quốc Gia Lời giải.
Diện tích xung quanh của hình trụ bằng
Sxq = 2πrh = 2πa · 2a = 4πa2. Chọn đáp án D □
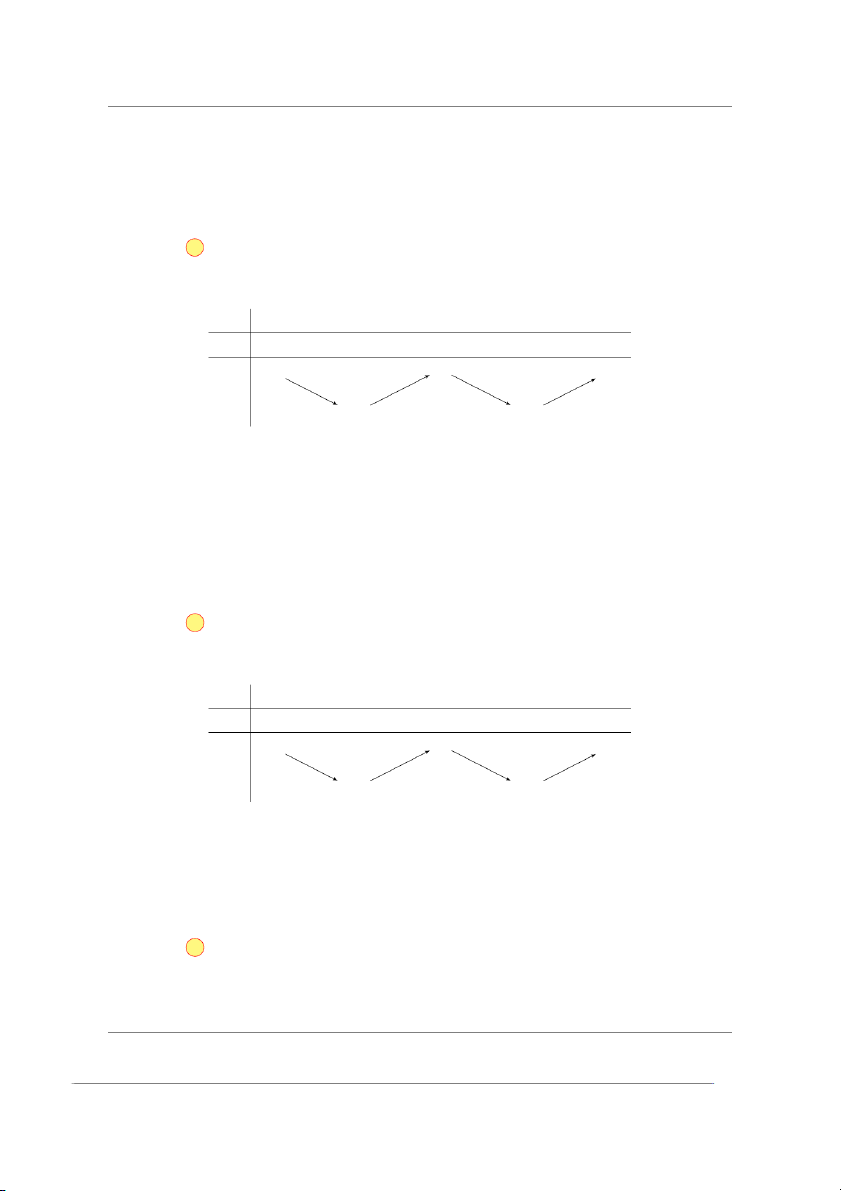
Câu 14. Cho hàm số y = f (x) có bảng biến thiên như sau x −∞ −1 0 1 +∞ f ′(x) − 0 + 0 − 0 + +∞ 3 +∞ f (x) −2 −2
Mệnh đề nào dưới đây là sai?
A. Điểm cực đại của đồ thị hàm số là x = 0.
B. Hàm số có ba điểm cực trị.
C. Hàm số có hai điểm cực tiểu.
D. Hàm số có giá trị cực đại bằng 3. Lời giải.
Dựa vào bảng biến thiên, hàm số đã cho có ba cực trị. Có hai điểm cực tiểu là (−1;−2) và (1;2), một điểm cực đại (0;3). Chọn đáp án A □
Câu 15. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên sau: x −∞ −1 0 1 +∞ f ′(x) − 0 + 0 − 0 + +∞ 1 +∞ f (x) −4 −4
Tìm m để phương trình f (x) = m + 1 có bốn nghiệm phân biệt.
A. −5 < m < 0.
B. −4 ⩽ m ⩽ 1.
C. −4 < m < 1.
D. −5 ⩽ m ⩽ 0. Lời giải.
Để phương trình có bốn nghiệm phân biệt thì −4 < m+1 < 1 ⇔ −5 < m < 0. Chọn đáp án A □
Câu 16. Cho hàm số y = f (x) có tập xác định (−∞;2] và có bảng biến thiên như hình vẽ bên. Mệnh đề nào
sau đây sai về hàm số đã cho?
220 Xô Viết Nghệ Tĩnh, phường 21, quận Bình Thạnh Trang 4
Thầy Lê Minh Trí - 0327.030.253
Luyện thi THPT Quốc Gia x −∞ −1 0 1 2 2 2 f (x) −∞ −1 1
A. Giá trị cực tiểu bằng −1.
B. Hàm số có 2 điểm cực đại.
C. Giá trị cực đại bằng 2.
D. Hàm số có 2 điểm cực tiểu. Lời giải.
Cho hàm số y = f (x) có tập xác định (−∞;2] và từ bảng biến thiên ta suy ra hàm số chỉ có một điểm cực
tiểu. Do đó mệnh đề “Hàm số có 2 điểm cực tiểu” sai. Chọn đáp án D □
Câu 17. Với a là số thực dương bất kỳ, mệnh đề nào dưới đây đúng? A. 1 1 ln 3a = 3 ln a.
B. ln3a = lna.
C. lna3 = 3lna.
D. lna3 = lna. 3 3 Lời giải.
Vì a > 0 nên lna3 = 3lna. Chọn đáp án C □
Câu 18. Số giao điểm của đường cong y = x3 −2x2 +2x+1 và đường thẳng y = 1−x là A. 2. B. 0. C. 1. D. 3. Lời giải.
Xét phương trình hoành độ giao điểm
x3 − 2x2 + 2x + 1 = 1 − x ⇔ x3 − 2x2 + 3x = 0 ⇔ x(x2 − 2x + 3) = 0 ⇔ x = 0. Chọn đáp án C □
Câu 19. Trong các hàm số dưới đây, hàm số nào đồng biến trên tập R?
A. y = 21−3x. B. y = log 1 2 (x + )2. C. y = log 1 2(x − ). D. y = log 1 2 (2x + ). Lời giải. Ta xét 1. y = log 2
2 ( x + 1) xác định trên R và có cơ số a = 2 > 1 nên hàm số đồng biến trên R.
2. y = log2 (x+1)2 xác định trên R\ {−1} và có cơ số a = 2 > 1 nên hàm số đồng biến trên (−∞;−1) và (−1;+∞).
3. y = 21−3x xác định trên R và có y′ = −3·21−3x < 0 nên hàm số nghịch biến trên R.
4. y = log2(x−1) xác định trên (1;+∞) và có cơ số a = 2 > 1 nên hàm số đồng biến trên (1;+∞).
220 Xô Viết Nghệ Tĩnh, phường 21, quận Bình Thạnh Trang 5
Thầy Lê Minh Trí - 0327.030.253
Luyện thi THPT Quốc Gia Chọn đáp án D □
Câu 20. Hệ số góc tiếp tuyến của đồ thị hàm số y = log tại điểm có hoành độ bằng 3 x x = 2 A. 1 . B. 2ln3. C. ln3. D. 1 . ln 3 2 ln 3 Lời giải.
Hệ số góc tiếp tuyến của đồ thị hàm số 1 y = log tại điểm có hoành độ . 3 x
x = 2 bằng y′(2) = 2ln3 Chọn đáp án D □
Câu 21. Cho hàm số y = f (x) liên tục trên (−∞;1) và (1;+∞) có bảng biến thiên như sau x −∞ −1 1 +∞ f ′(x) − 0 + + 1 +∞ −1 f (x) √2 −∞
Số nghiệm thực của phương trình 2 f (x) −1 = 0 là A. 4. B. 1. C. 2. D. 3. Lời giải. 1
2 f (x) − 1 = 0 ⇔ f (x) = . 2
Dựa vào bảng biến thiên ta có phương trình đã cho có 2 nghiệm. Chọn đáp án C □
Câu 22. Tập nghiệm của phương trình log log 2 là 3(x2 − x) = 3(2x − ) A. S = {1;2}.
B. S = {−2;−1}. C. S = {2}. D. S = {−1}. Lời giải.  x > 1     2x − 2 > 0   log log 3(x2 − x) = 3(2x − 2) ⇔ ⇔ x = 1 ⇔ x = 2.
x2 − x = 2x − 2       x = 2
Vậy tập nghiệm của phương trình đã cho là S = {2}. Chọn đáp án C □
Câu 23. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = a, AD = 2BC = 2a,
SA ⊥ (ABCD) và cạnh SD tạo với đáy một góc 60◦. Tính thể tích khối chóp S.ABCD. √ A. a3 . B. a3 3. C. √ √ 2a3 3. D. a3 3. 2 3 Lời giải.
220 Xô Viết Nghệ Tĩnh, phường 21, quận Bình Thạnh Trang 6
Thầy Lê Minh Trí - 0327.030.253
Luyện thi THPT Quốc Gia
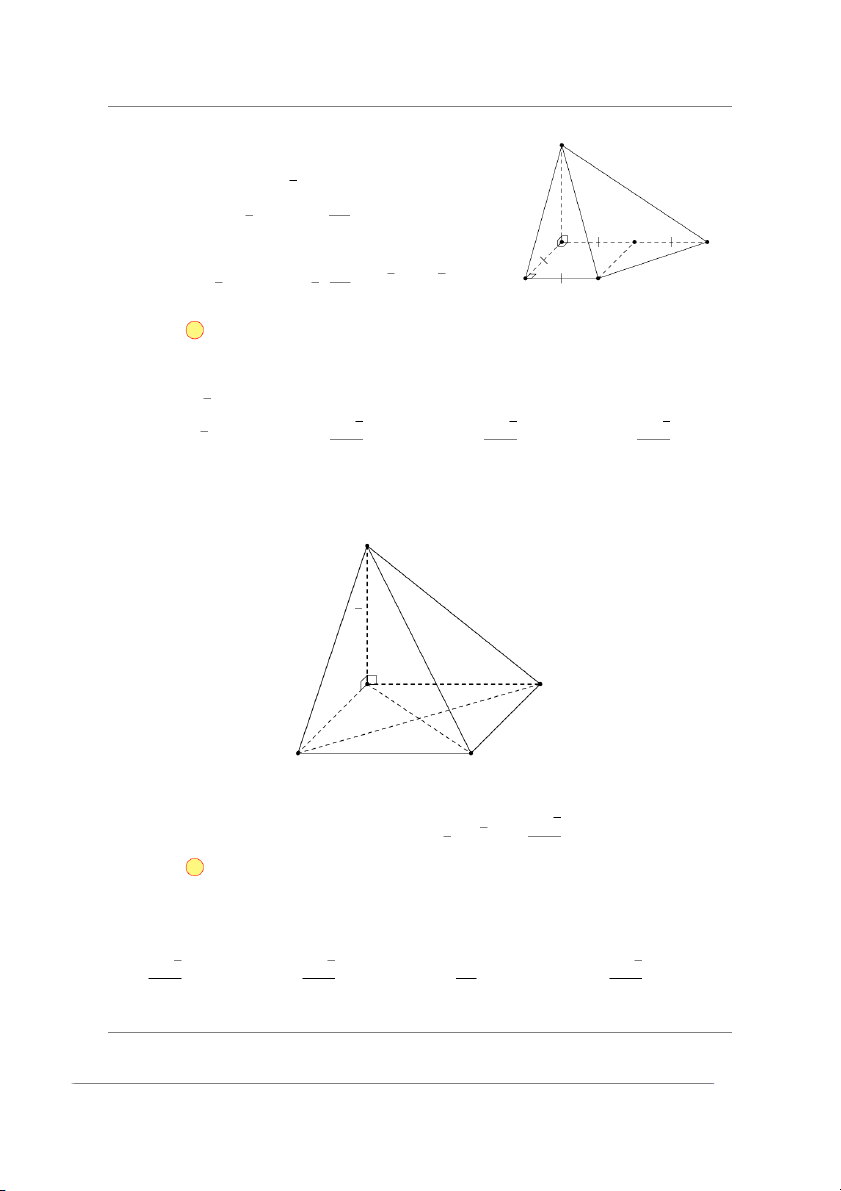
Do SA ⊥ (ABCD) nên S
(SD, (ABCD)) = (SD, AD) = ‘ SDA = 60◦. Suy ra √
SA = AD tan 60◦ = 2a 3. Diện tích đáy 1 3a2
SABCD = (a + 2a)a = . 2 2
Vậy thể tích khối chóp S.ABCD là A D 1 1 3a2 √ √ V 3 B S.ABCD =
· SABCD · SA = · · 2a 3 = a 3. 3 3 2 C Chọn đáp án D □
Câu 24. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và √
SA = a 2. Tính thể tích V của khối chóp S.ABCD. √ √ √ A. √ a3 2 a3 2 a3 2 V = a3 2. B. V = . C. V = . D. V = . 6 4 3 Lời giải. S √ a 2 A D B C √ √ Diện tích đáy 1 a3 2 S .
ABCD = a2. Suy ra thể tích khối chóp V = · a 2 · a2 = 3 3 Chọn đáp án D □
Câu 25. Cho lăng trụ tam giác đều ABC.A′B′C′ có cạnh đáy bằng a, góc giữa mặt phẳng (A′BC) và mặt
phẳng (ABC) bằng 45◦. Tính thể tích của khối lăng trụ ABC.A′B′C′. √ √ √ A. a3 3. B. a3 3. C. 3a3 . D. a3 3. 2 8 8 4 Lời giải.
220 Xô Viết Nghệ Tĩnh, phường 21, quận Bình Thạnh Trang 7
Thầy Lê Minh Trí - 0327.030.253
Luyện thi THPT Quốc Gia
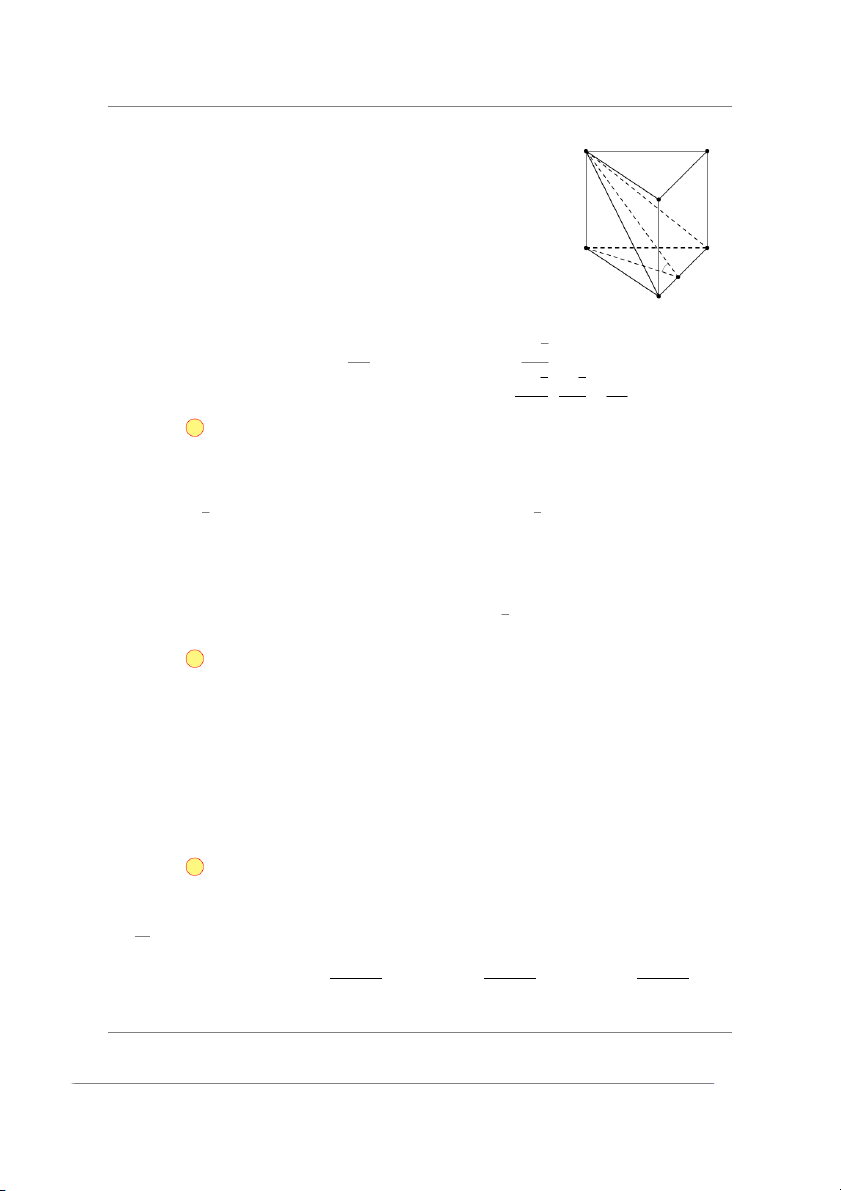
Trong tam giác đều ABC, gọi M là trung điểm của BC suy ra A′ C′ BC ⊥ AM. BC ⊥ AA′ Ta có  B′
⇒ BC ⊥ (AA′M) ⇒ BC ⊥ A′M. BC ⊥ AM 
(ABC) ∩ (A′BC) = BC  A ◦ C   Khi đó, ta có  45
BC ⊥ AM; AM ⊂ (ABC) M     ′ ′ ′
BC ⊥ A M; A M ⊂ (A BC) B
⇒ [(ABC),(A′BC)] = (AM,A′M) = ’ AMA′ = 45◦. √ Xét AA′ a 3
△AMA′ vuông tại A, có tan ’ AMA′ =
⇒ AA′ = AM · tan45◦ = . AM 2 √ √
Thể tích của khối lăng trụ a2 3 a 3 3a3
ABC.A′B′C′ là V .
ABC.A′B′C′ = S△ABC · AA′ = · = 4 2 8 Chọn đáp án C □
Câu 26. Tìm m để hàm số y = mx3 −2mx2 +3x−1 có cực đại và cực tiểu. A. 9 9 0 < m < . B. m < 2.
C. m < 0 ∨m > . D. m > 2. 4 4 Lời giải.
Ta thấy m = 0 hàm số suy biến thành y = 3x −1 không có cực trị. m = 0
Hàm số có cực đại và cực tiểu  9 ⇔
⇔ m < 0 ∨ m > . 4
4m2 − 9m > 0 Chọn đáp án C □
Câu 27. Thiết diện qua trục của hình trụ là một hình vuông có cạnh bằng 2a. Khi đó thể tích của khối trụ là A. 4πa3. B. πa3. C. 8πa3. D. 2πa3. Lời giải.
Chiều cao hình trụ là 2a, bán kính đáy hình trụ là a ⇒ thể tích khối trụ là V = πr2h = 2πa3. Chọn đáp án D □
Câu 28. Cho hình chóp S.ABC có SA,SB,SC đôi một vuông góc với nhau và SA = 3a, SB = 4a và AC = √
3a 17. Tính theo a thể tích V của khối cầu đi qua các đỉnh của hình chóp S.ABC. A. 8788πa3 2197πa3 2197πa3 V = 8788πa3. B. V = . C. V = . D. V = . 3 2 6 Lời giải.
220 Xô Viết Nghệ Tĩnh, phường 21, quận Bình Thạnh Trang 8
Thầy Lê Minh Trí - 0327.030.253
Luyện thi THPT Quốc Gia
Gọi E là trung điểm của AB. C
Qua E kẻ đường thẳng d vuông góc với mặt phẳng (SAB).
Gọi F là trung điểm của SC. Trong mp(SA,d) kẻ đường trung trực của
SC cắt d tại G thì G là tâm mặt cầu ngoại tiếp hình chóp S.ABC. F √ Ta có G AB =
SA2 + SB2 = p(3a)2 + (4a)2 = 5a, suy ra AB 5a SE = = . 2 2 √ » Và √ S B SC = AC2 − SA2 =
(3a 17)2 − (3a)2 = 12a, suy ra SC E SF = = 6a. 2 A
Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là Å ã2 p 5a 13a R = GS = SF 2 + SE2 = + (6a)2 = . 2 2 Å ã3 Do đó, 4 4 13a 2197πa3 V = πR3 = π = . 3 3 2 6 Chọn đáp án D □
Câu 29. Đồ thị hàm số y = x3 − 3x2 − 9x + 1 có hai điểm cực trị A, B. Điểm nào dưới đây thuộc đường thẳng AB? A. Q(−1;10). B. P(1;0). C. M(0;−1). D. N(1;−10). Lời giải.  x = −1
Ta có y′ = 3x2 −6x −9,∀x ∈ R; y′ = 0 ⇔  x = 3.
Khi đó, đồ thị hàm số có hai điểm cực trị là A(−1;6) và B(3;−26).
Ta có phương trình đường thẳng y − 6 AB là x + 1 =
. Đường thẳng này đi qua điểm N(1;−10). 4 −32 Chọn đáp án D □ Câu 30. Thể tích √
V của khối hộp chữ nhật ABCD.A′B′C′D′ biết AB = a, AD = 2a, AC′ = a 14 là √ A. √ a3 14 V = 6a3.
B. V = a3 5. C. V = .
D. V = 2a3. 3 Lời giải.
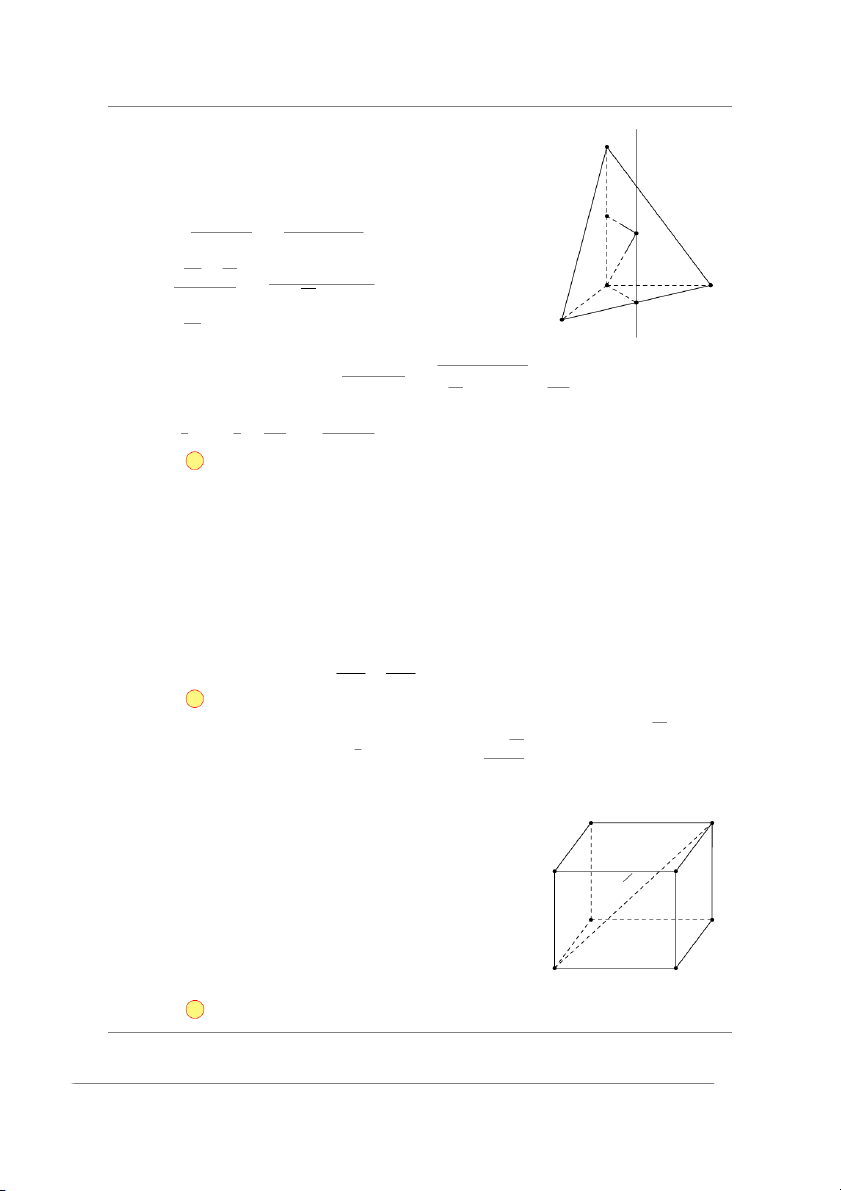
Ta có AC′2 = AA′2 + AB2 + AD2 C′ D′
⇒ 14a2 = AA′2 + a2 + 4a2 ⇒ AA′ = 3a.
Thể tích khối hộp chữ nhật là A′ B′ √ 14 a
V = AB · AD · AA′ = a · 2a · 3a = 6a3. D C 2a A a B Chọn đáp án A □
220 Xô Viết Nghệ Tĩnh, phường 21, quận Bình Thạnh Trang 9
Thầy Lê Minh Trí - 0327.030.253
Luyện thi THPT Quốc Gia
Câu 31. Tìm tập xác định D của hàm số y = x2π−3. A. D = R\ {0}. B. D = (0;+∞). C. D = R. D. D = [0;+∞). Lời giải.
Hàm số y = x2π−3 có điều kiện xác định là x > 0.
Vậy tập xác định D = (0;+∞). Chọn đáp án B □
Câu 32. Cho hàm số y = x4 −2mx2 +3m−2 (với m là tham số). Có bao nhiêu giá trị của tham số m để đồ
thị hàm số có ba điểm cực trị đều nằm trên các trục tọa độ? A. 2. B. 0. C. 3. D. 1. Lời giải.
Ta có y = x4 −2mx2 +3m−2 ⇒ y′ = 4x3 −4mx.  x = 0
Khi đó y′ = 0 ⇔  √ x = ± m. Với √
m > 0 thì đồ thị hàm số có 3 điểm cực trị và các điểm cực trị là A(0; 3m − 2), B( m; −m2 + 3m − 2) và √
C(− m; −m2 + 3m − 2).
Điểm A đã nằm trên trục tung, vậy để các điểm cực trị đều nằm trên các trục tọa độ thì hai điểm B và C phải m = 2
nằm trên trục hoành, suy ra −m2 +3m−2 = 0 ⇔  m = 1.
Vậy có 2 giá trị của tham số m thỏa mãn yêu cầu bài toán. Chọn đáp án A □
Câu 33. Cho hình chóp √
S.ABCD có đáy ABCD là hình vuông cạnh a. Biết SA ⊥ (ABCD) và SA = a 3.
Tính thể tích của khối chóp S.ABCD. √ √ √ A. a3 3. B. a3 . C. 3 a3 3. D. a3 . 3 4 12 Lời giải.
Thể tích khối chóp S.ABCD là S √ 1 1 √ a3 3 V =
· SABCD · SA = · a2 · a 3 = . 3 3 3 A B D C Chọn đáp án A □
Câu 34. Cho hàm số y = log . Mệnh đề nào sau đây ? 5 x sai
A. Hàm số nghịch biến trên tập xác định.
B. Tập xác định của hàm số là (0;+∞).
220 Xô Viết Nghệ Tĩnh, phường 21, quận Bình Thạnh Trang 10