





































Preview text:
NHÓM TOÁN VD – VDC MÃ ĐỀ 101
BỘ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Bài thi: TOÁN
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
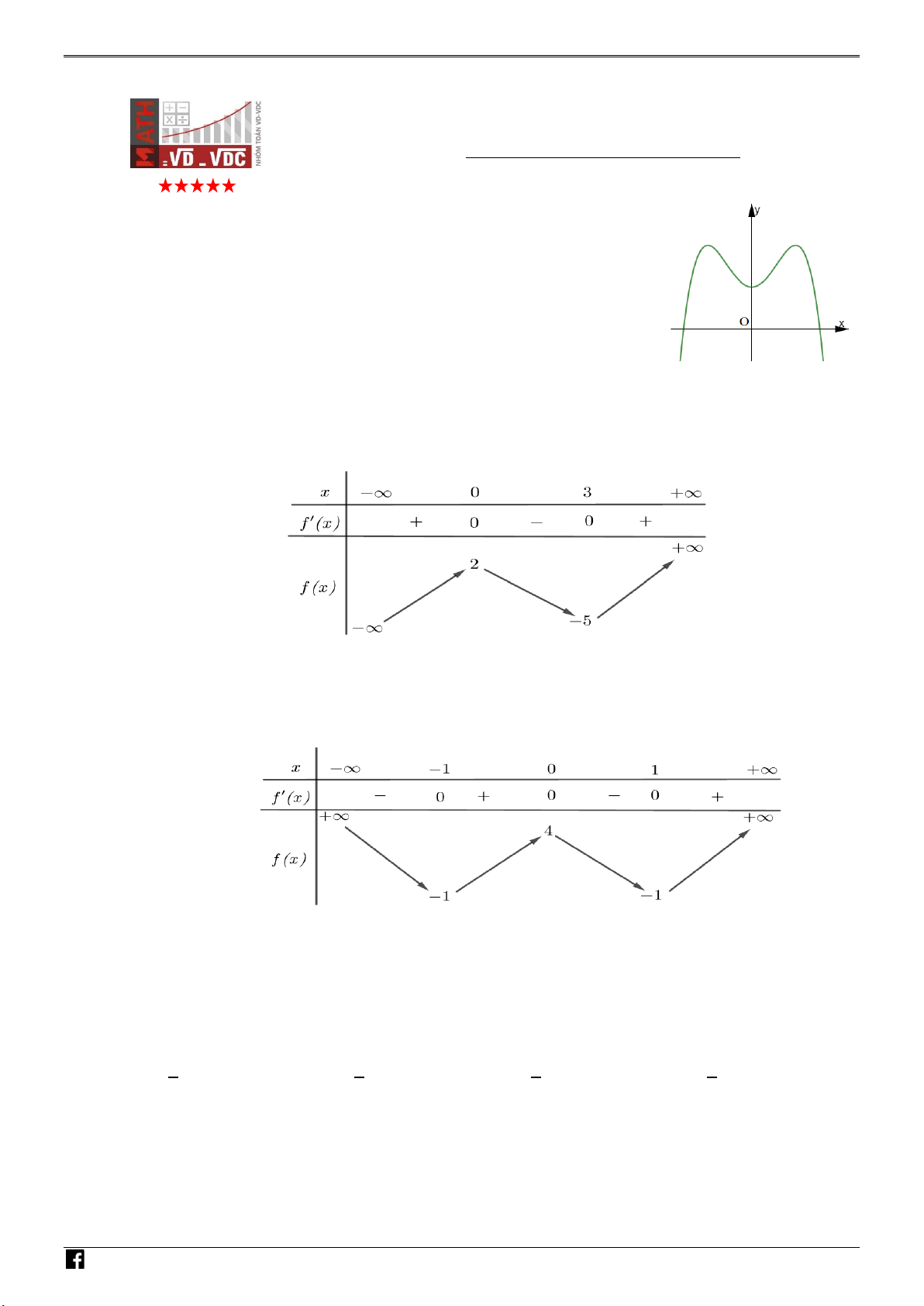
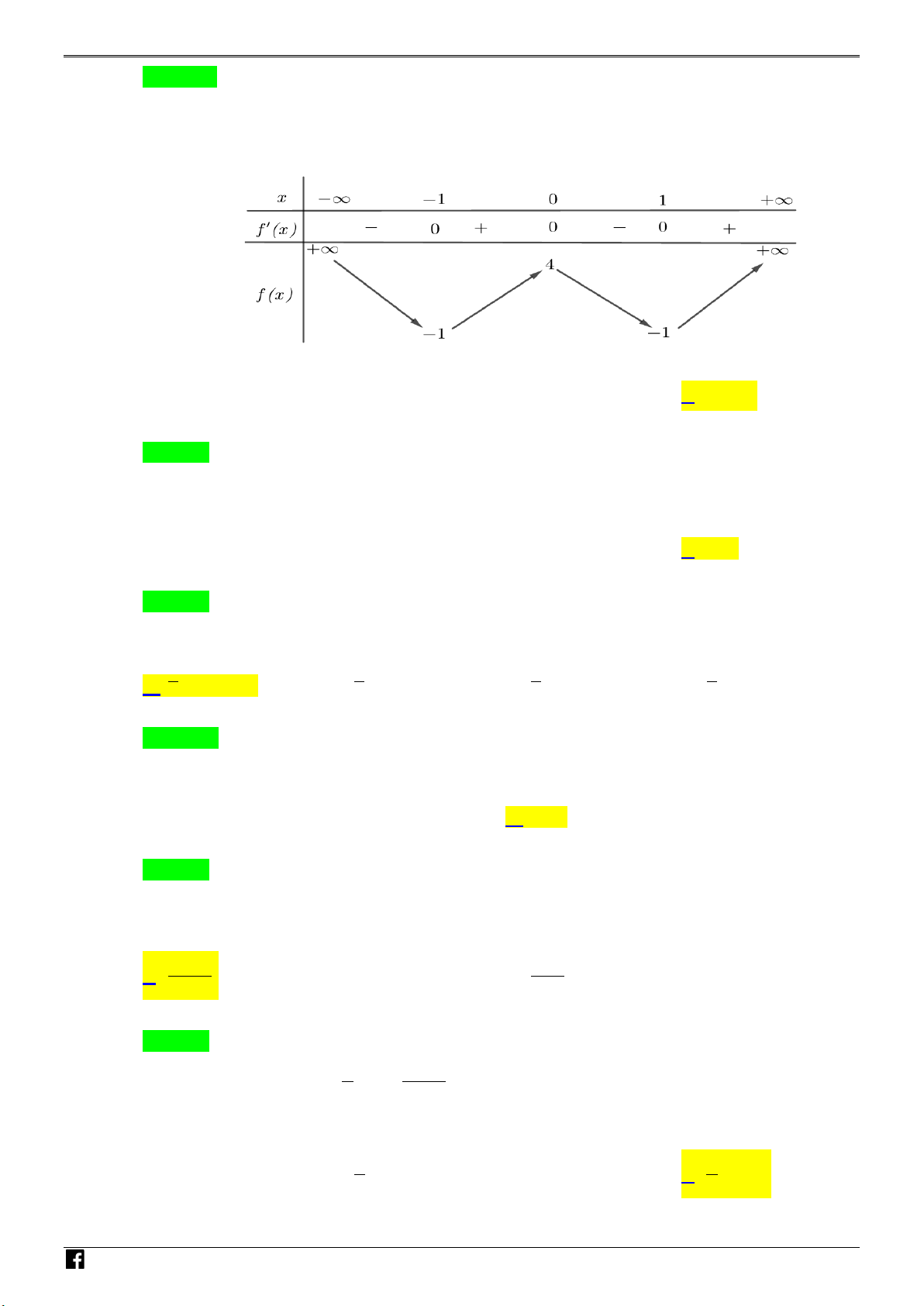
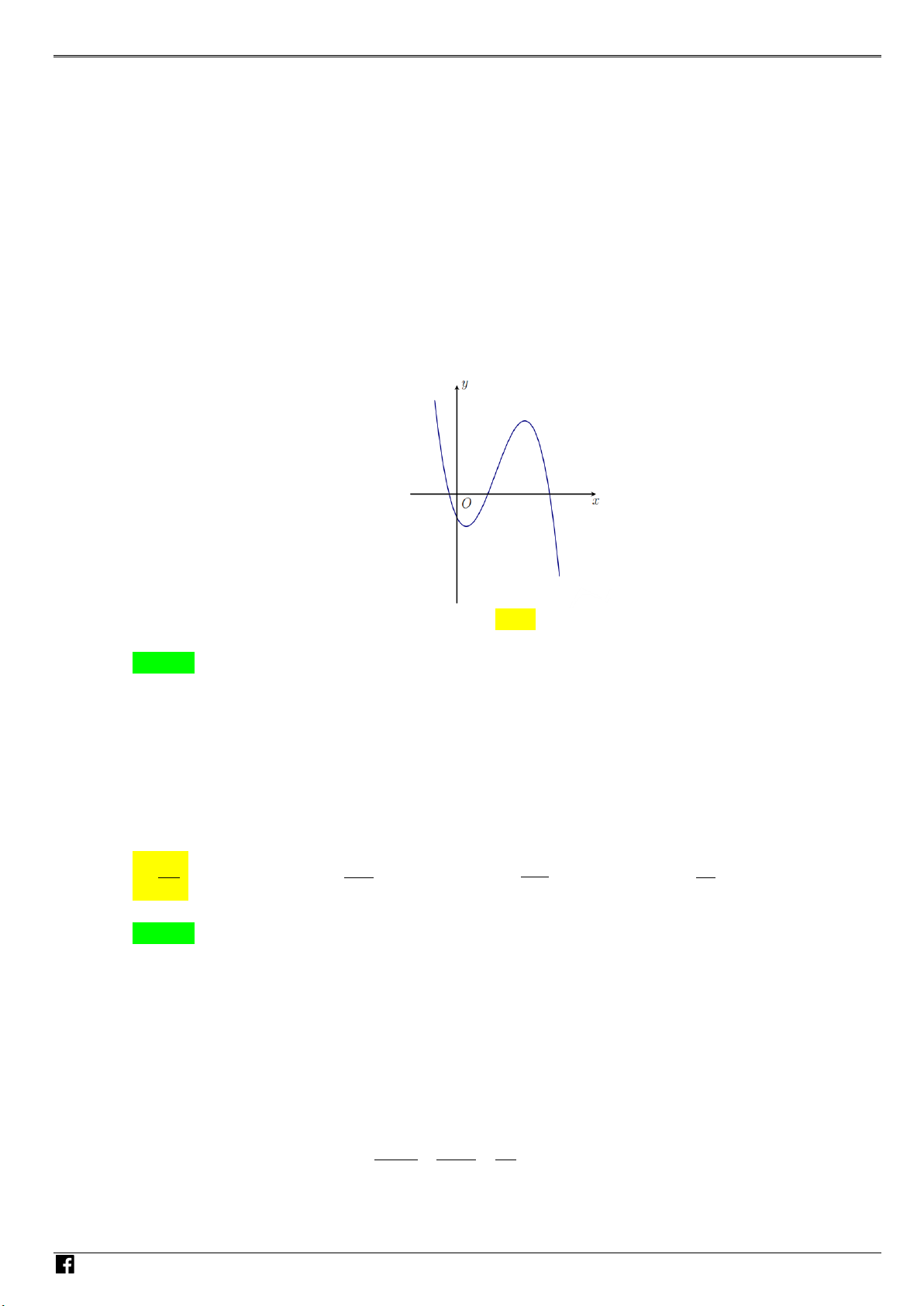
Câu 1: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên ? A. 3 2
y = x − 3x +1 . B. 3 2
y = −x + 3x +1. C. 4 2
y = −x + 2x +1. D. 4 2
y = x − 2x +1 . N H Ó M x−
Câu 2: Nghiệm của phương trình 1 3 = 9 là TO A. x = 2 − . B. x = 3 . C. x = 2 . D. x = 3 − . ÁN
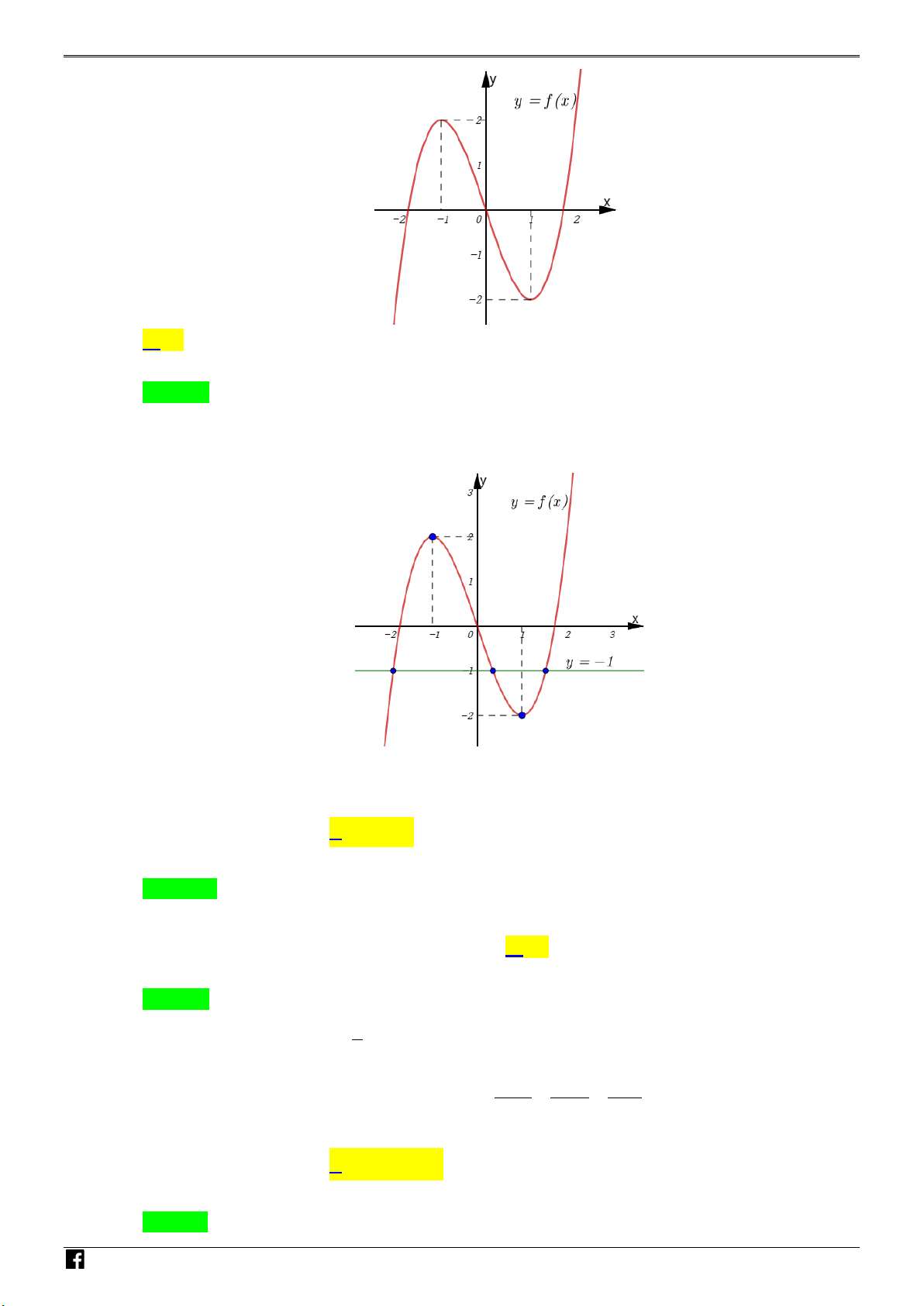
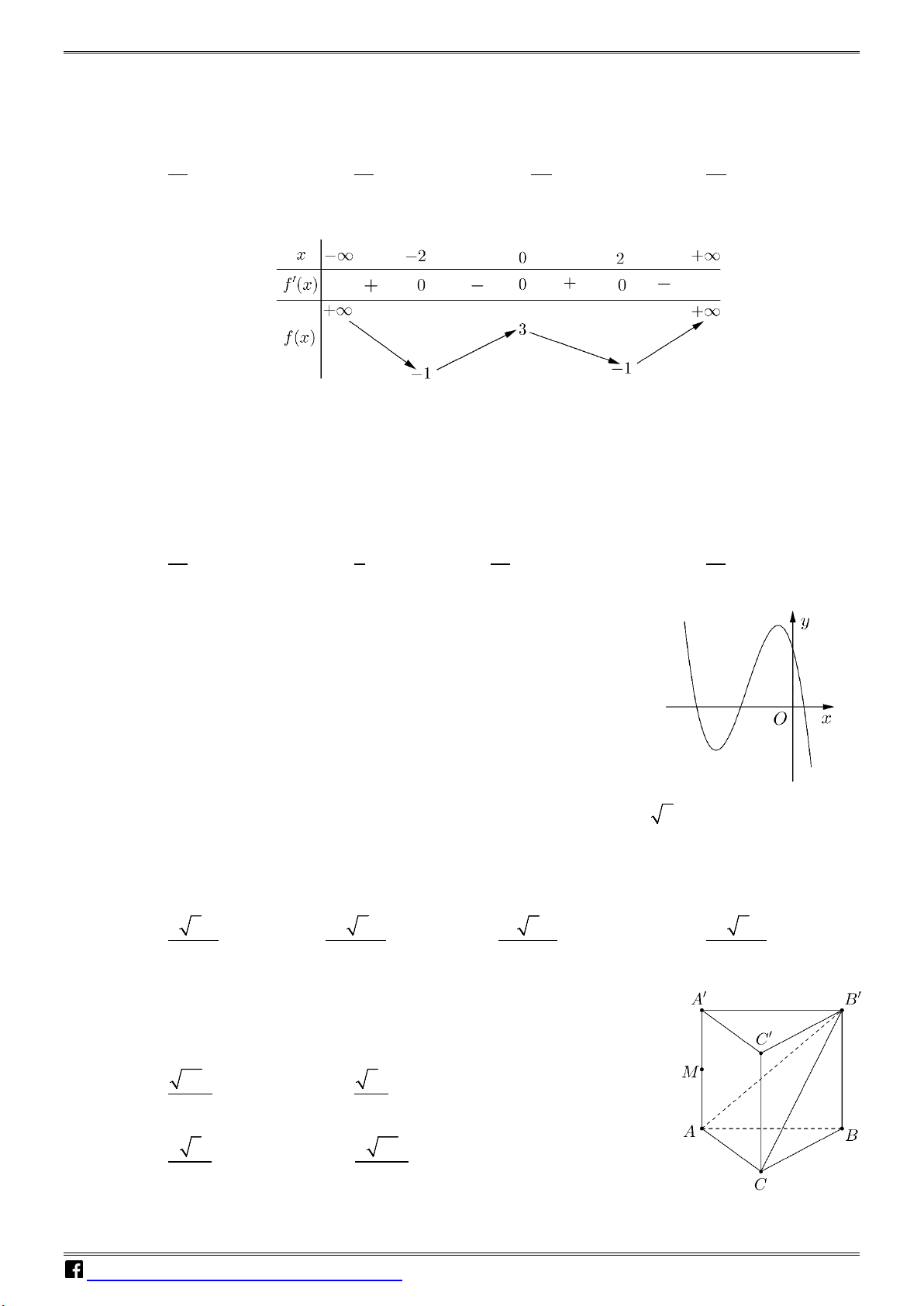
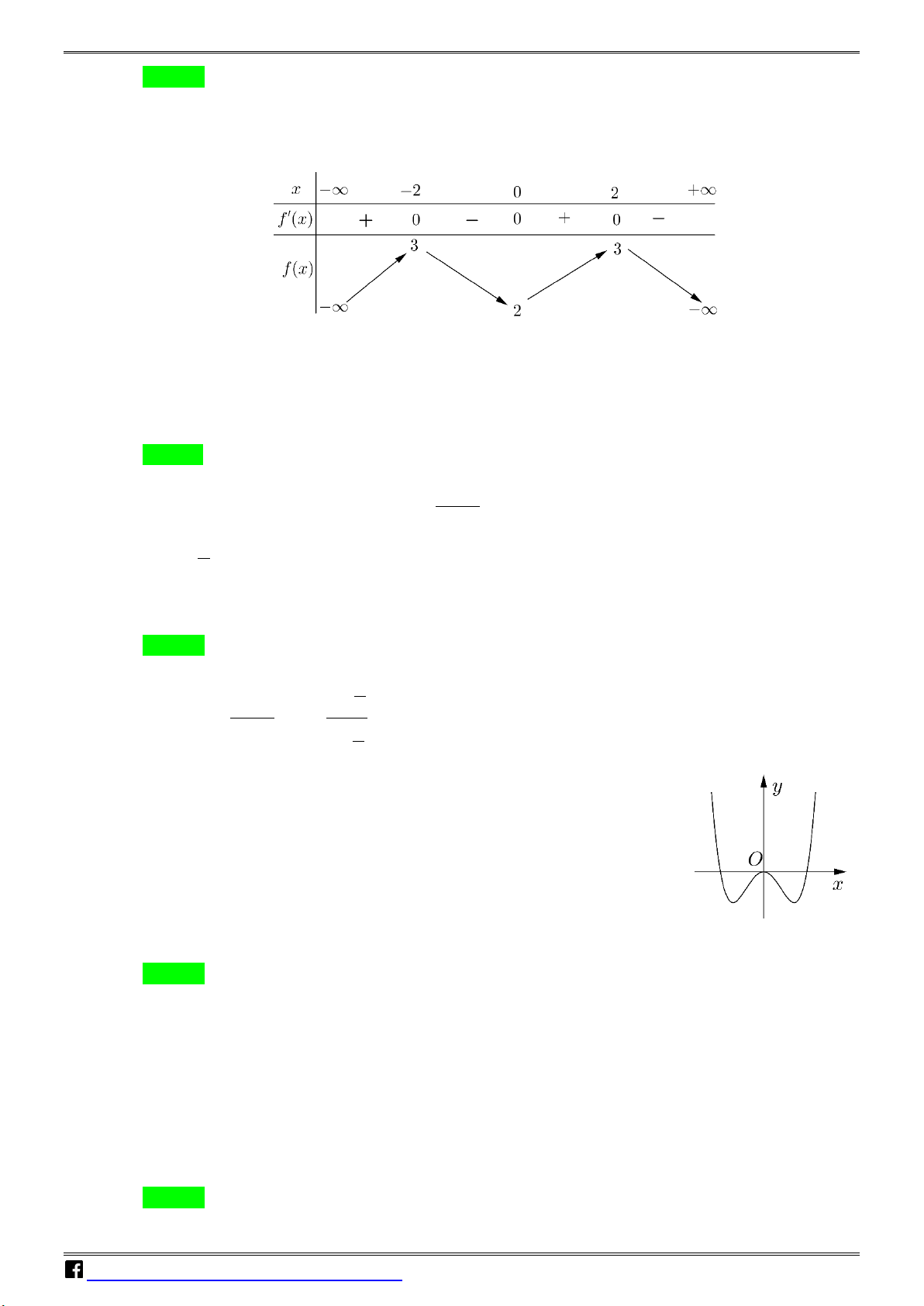
Câu 3: Cho hàm f (x) có bảng biến thiên như sau: VD – VDC
Giá trị cực tiểu của hàm số đã cho bằng A. 3. B. 5 − . C. 0 . D. 2 .
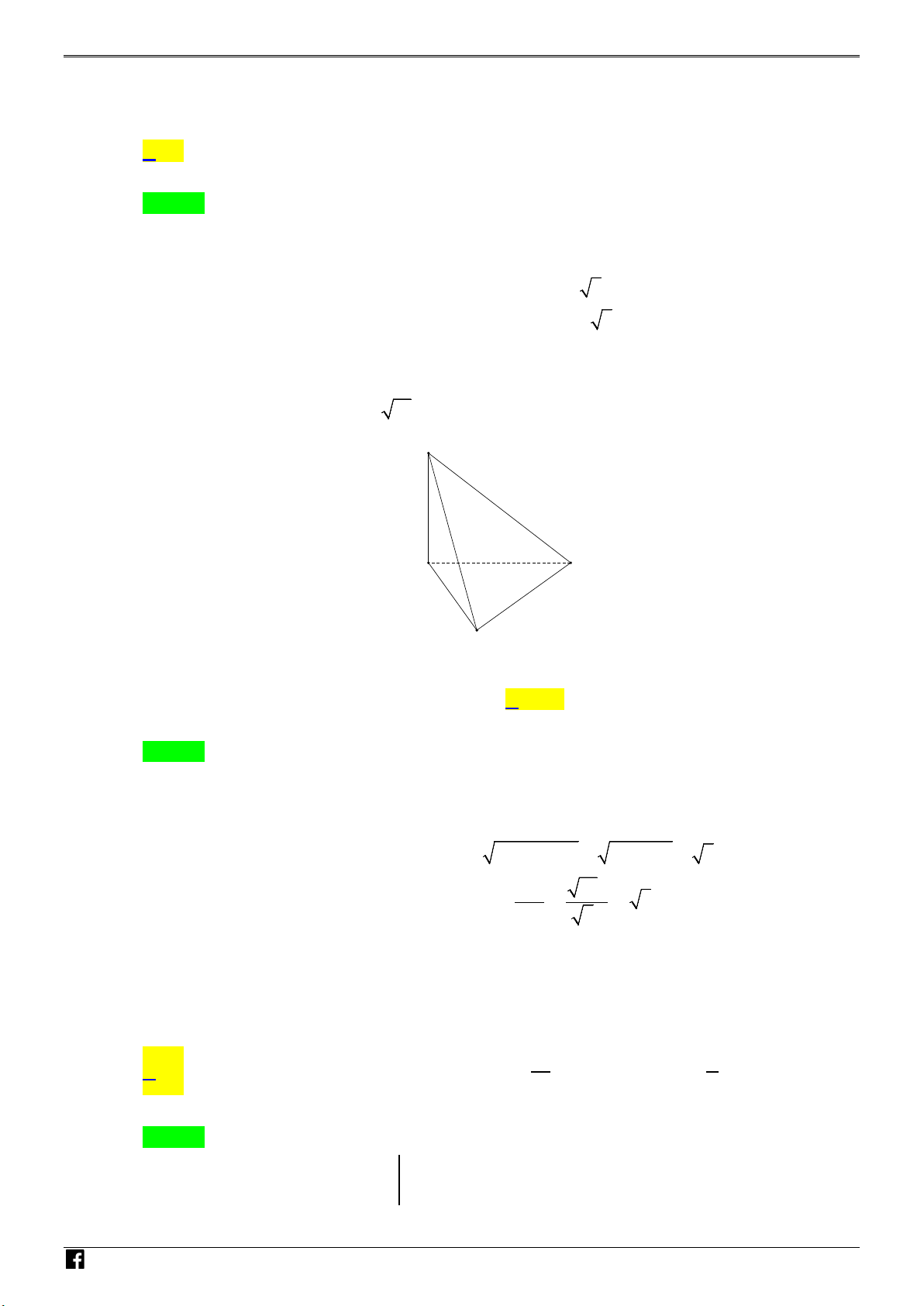
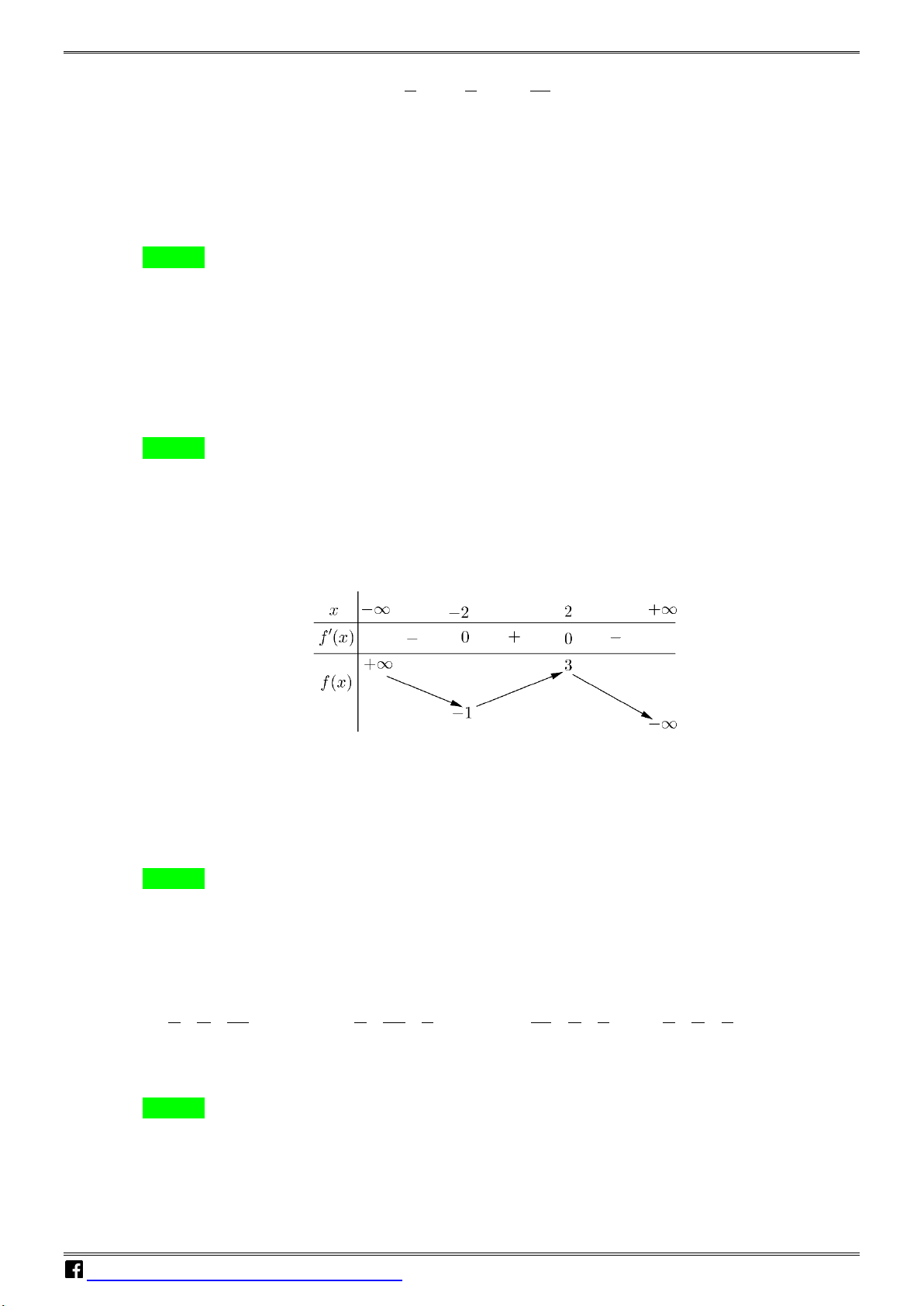
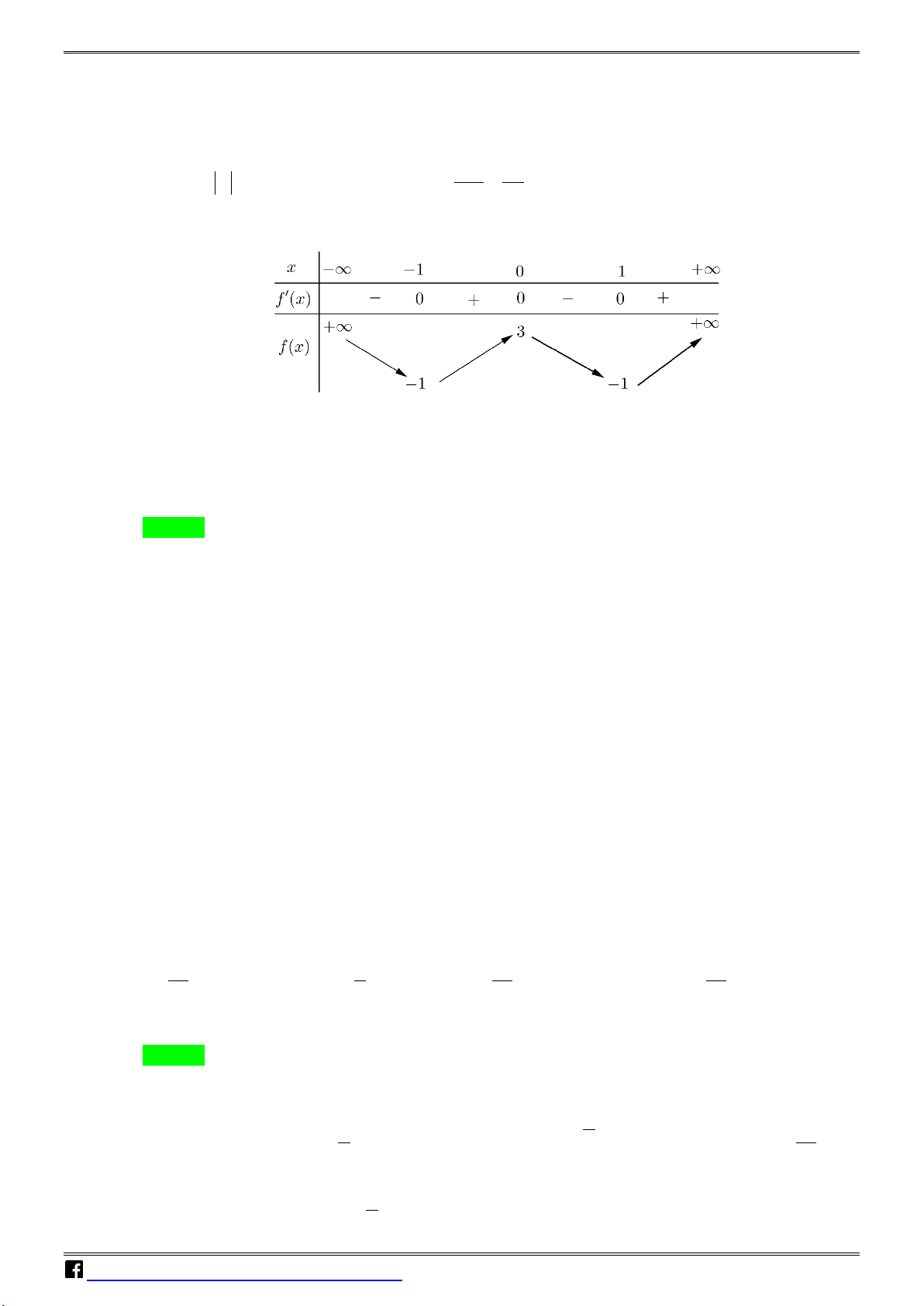
Câu 4: Cho hàm số f (x) có bảng biến thiên như sau: N H Ó M T
Hàm số đã cho đồng biến trên khoảng nào dưới đây ? O Á A. ( ; −∞ − ) 1 . B. (0; ) 1 . C. ( 1; − ) 1 . D. ( 1; − 0) N VD
Câu 5: Cho khối hộp chữ nhật có 3 kích thước 3;4;5. Thể tích của khối hộp đã cho bằng – A. 10 . B. 20 . C. 12 . D. 60 . VD
Câu 6: Số phức liên hợp của số phức z = 3 − + 5i là C A. z = 3 − − 5i .
B. z = 3+ 5i . C. z = 3 − + 5i .
D. z = 3−5i .
Câu 7: Cho hình trụ có bán kính đáy r = 8 và độ dài đường sinh l = 3 . Diện tích xung quanh của hình trụ đã cho bằng A. 24π . B. 192π . C. 48π . D. 64π .
Câu 8: Cho khối cầu có bán kính r = 4 . Thể tích của khối cầu đã cho bằng
https://www.facebook.com/groups/toanvd.vdc Trang 1 NHÓM TOÁN VD – VDC MÃ ĐỀ 101 π π A. 256 . B. 64π . C. 64 . D. 256π . 3 3
Câu 9: Với a,b là các số thực dương tùy ý và a ≠1, log b bằng 5 a A. 5log b . B. 1 + log b . C. 5 + log b . D. 1 log b . a 5 a a 5 a
Câu 10: Trong không gian Oxyz, cho mặt cầu (S ) 2 2
: x + y + (z + 2)2 = 9. Bán kính của (S) bằng A. 6 . B. 18. C. 9. D. 3. +
Câu 11: Tiệm cận ngang của đồ thị hàm số 4x 1 y = là N x −1 H Ó M A. 1 y = . B. y = 4 . C. y =1. D. y = 1 − . 4 TO
Câu 12: Cho khối nón có bán kính đáy r = 5 và chiều cao h = 2 . Thể tích khối nón đã cho bằng ÁN π π V A. 10 . B. 10π . C. 50 . D. 50π . D 3 3 –
Câu 13: Nghiệm của phương trình log x −1 = 2 là 3 ( ) VDC A. x = 8. B. x = 9 . C. x = 7 . D. x =10 . Câu 14: 2 x dx ∫ bằng A. 2x 1 + C . B. 3 x + C . C. 3 x + C . D. 3 3x + C 3
Câu 15: Có bao nhiêu cách xếp 6 học sinh thành một hàng dọc ? A. 36. B. 720 . C. 6 . D. 1.
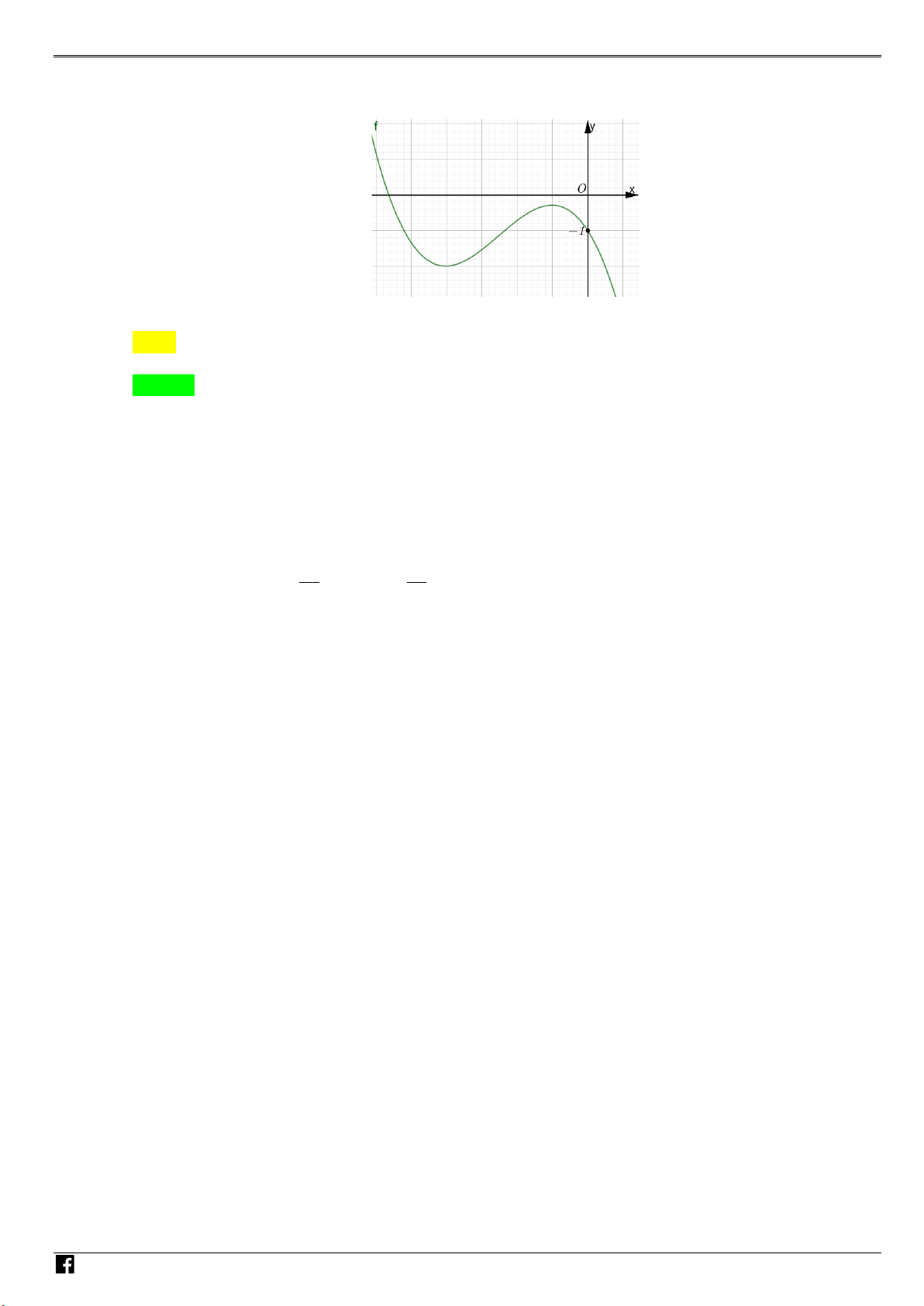
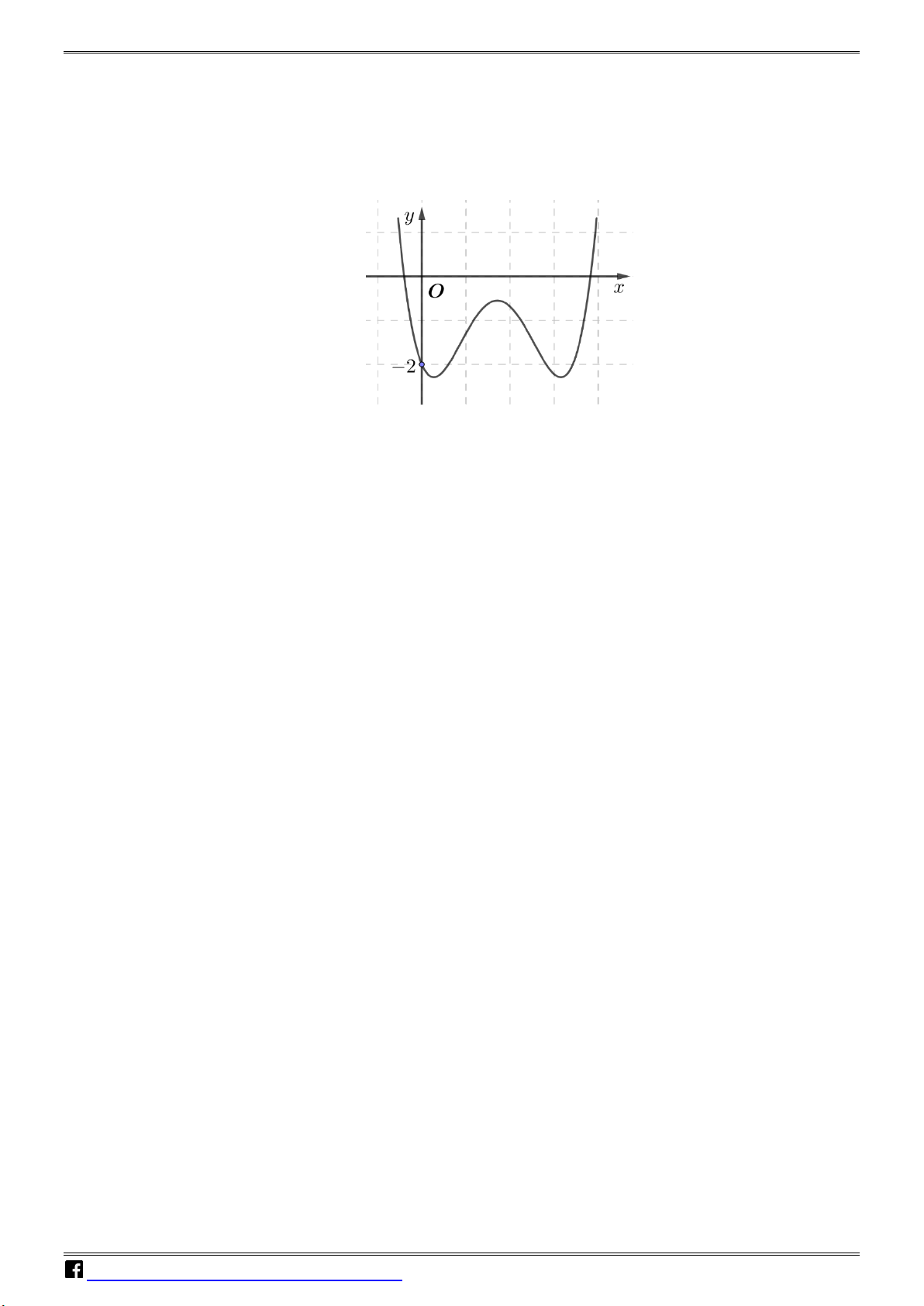
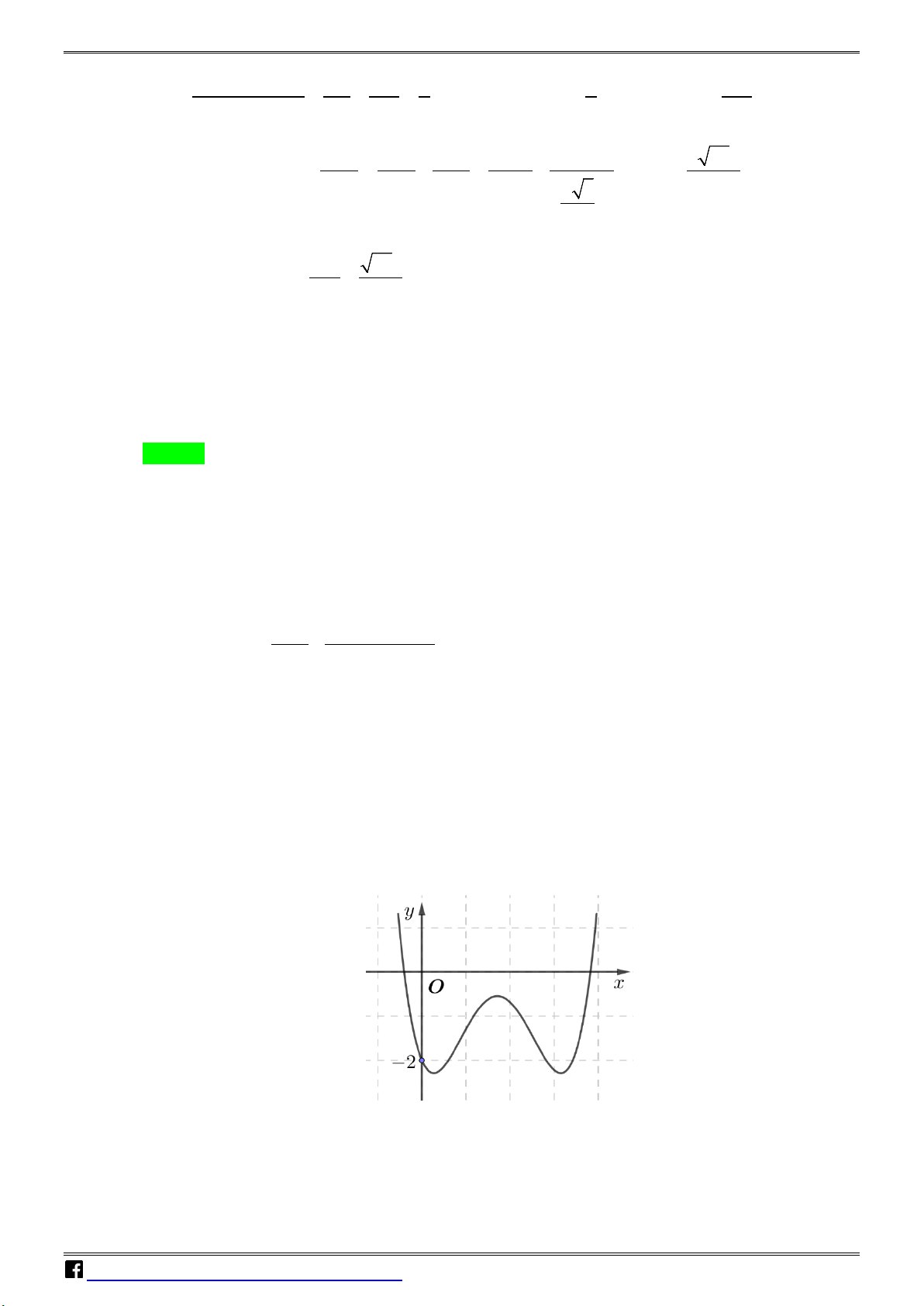
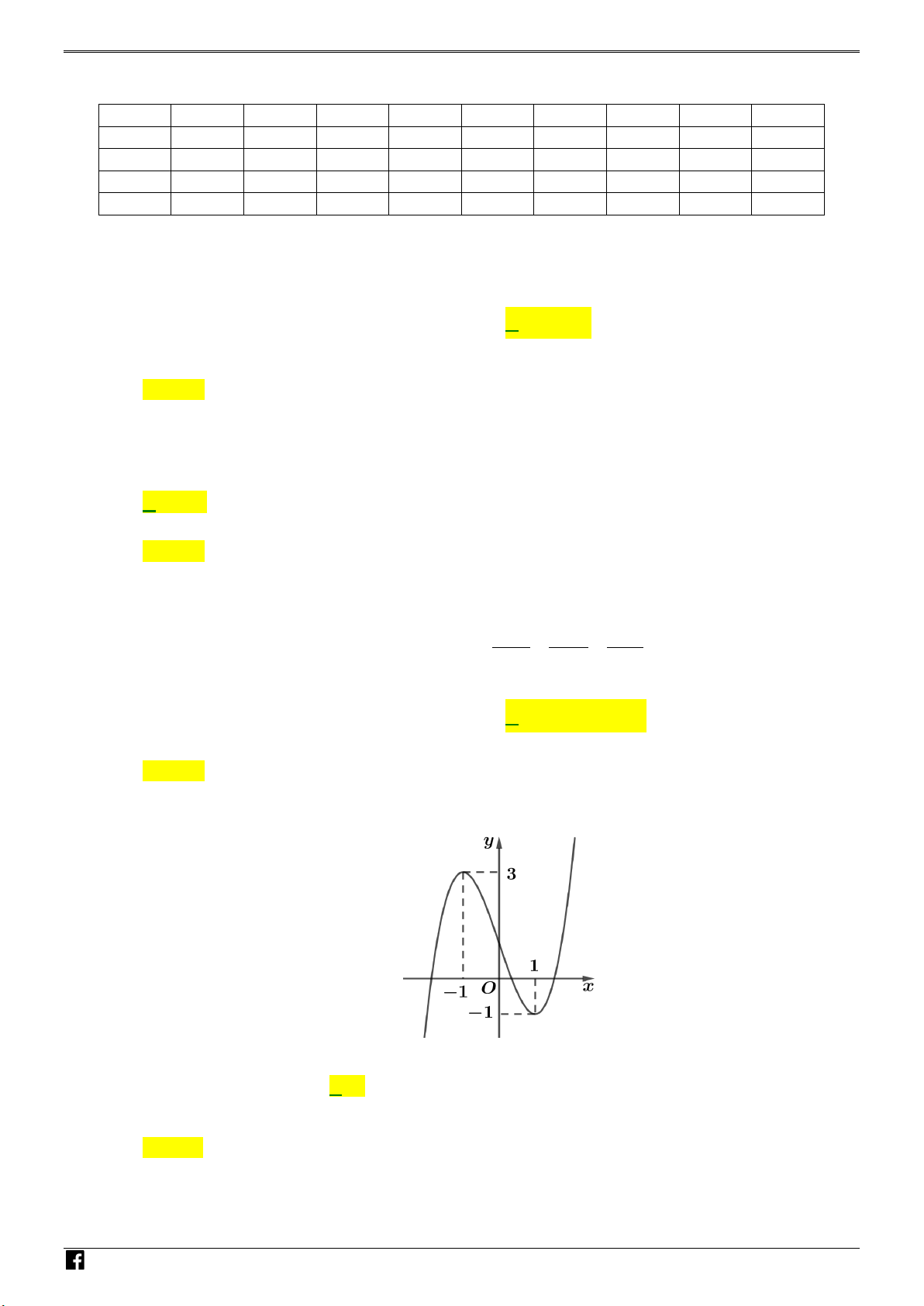
Câu 16: Cho hàm số bậc ba y = f (x) có đồ thị là đường cong trong hình
bên. Số nghiệm thực của phương trình f (x) = 1 − là A. 3. B. 1. C. 0 . D. 2 . N H Ó M
Câu 17: Trong không gian Oxyz, hình chiếu vuông góc của điểm A(3;2; )
1 trên trục Ox có tọa độ là TOÁ A. (0;2; ) 1 . B. (3;0;0). C. (0;0; ) 1 . D. (0;2;0) . N V
Câu 18: Cho khối chóp có diện tích đáy B = 6 và chiều cao h = 2 . Thể tích của khối chóp đã cho bằng D – A. 6 . B. 3. C. 4 . D. 12. VD x − y − z + C
Câu 19: Trong không gian Oxyz, cho đường thẳng 3 4 1 d : = =
. Vectơ nào dưới đây là một 2 5 − 3
vectơ chỉ phương của d ? A. u = 2;4; 1 − . B. u = 2; 5; − 3 .
C. u = 2;5;3 .
D. u = 3;4;1 . 4 ( ) 3 ( ) 1 ( ) 2 ( )
Câu 20: Trong không gian Oxyz, cho ba điểm A(3;0;0) , B(0;1;0) và C (0;0; 2
− ) . Mặt phẳng ( ABC) có phương trình là
https://www.facebook.com/groups/toanvd.vdc Trang 2 NHÓM TOÁN VD – VDC MÃ ĐỀ 101 A. x y z + + = 1. B. x y z + + = 1. C. x y z + + = 1. D. x y z + + = 1. 3 1 − 2 3 1 2 − 3 1 2 3 − 1 2
Câu 21: Cho cấp số nhân (u với u = 3 và công bội q = 2 . Giá trị của u bằng n ) 1 2 A. 8 . B. 9. C. 6 . D. 3 . 2
Câu 22: Cho hai số phức z = 3− 2i và z = 2 + i . Số phức z + z bằng 1 2 1 2 A. 5 + i . B. 5 − + i . C. 5 − i . D. 5 − − i . 3 3
Câu 23: Biết f (x)dx = 3 ∫
. Giá trị của 2 f (x)dx ∫ bằng N 1 1 H Ó A. 5. B. 9. C. 6 . D. 3 . M 2 TO
Câu 24: Trên mặt phẳng tọa độ, biết M ( 3 − )
;1 là điểm biểu diễn số phức z. Phần thực của z bằng ÁN A. 1. B. 3 − . C. 1 − . D. 3. VD
Câu 25: Tập xác định của hàm số y = log x là 5 – V A. [0;+ ∞) . B. (−∞;0) . C. (0;+ ∞) . D. (−∞;+ ∞). D C
Câu 26: Số giao điểm của đồ thị hàm số 3 2
y = x + 3x và đồ thị hàm số 2
y = 3x + 3x là A. 3. B. 1. C. 2 . D. 0 .
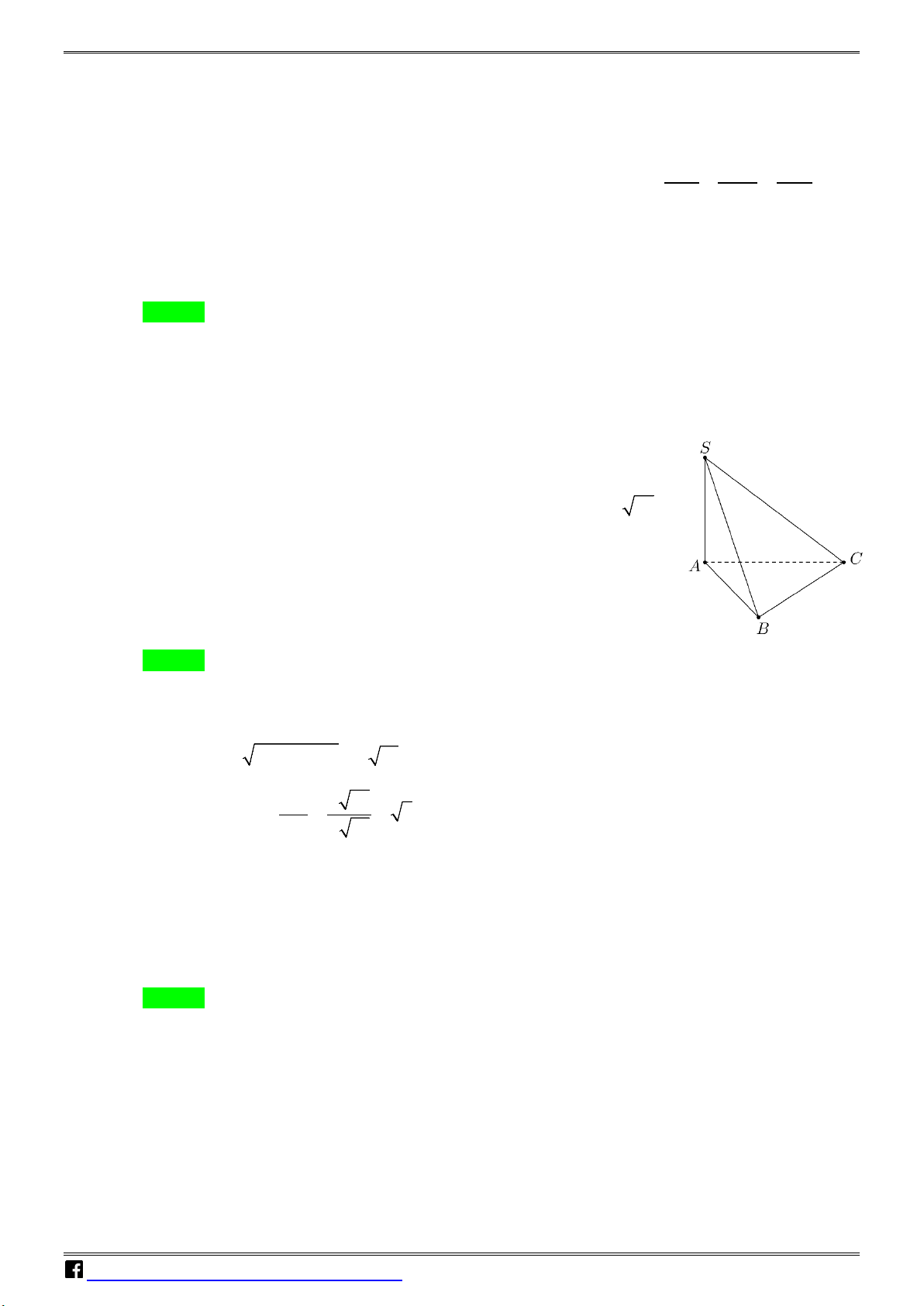
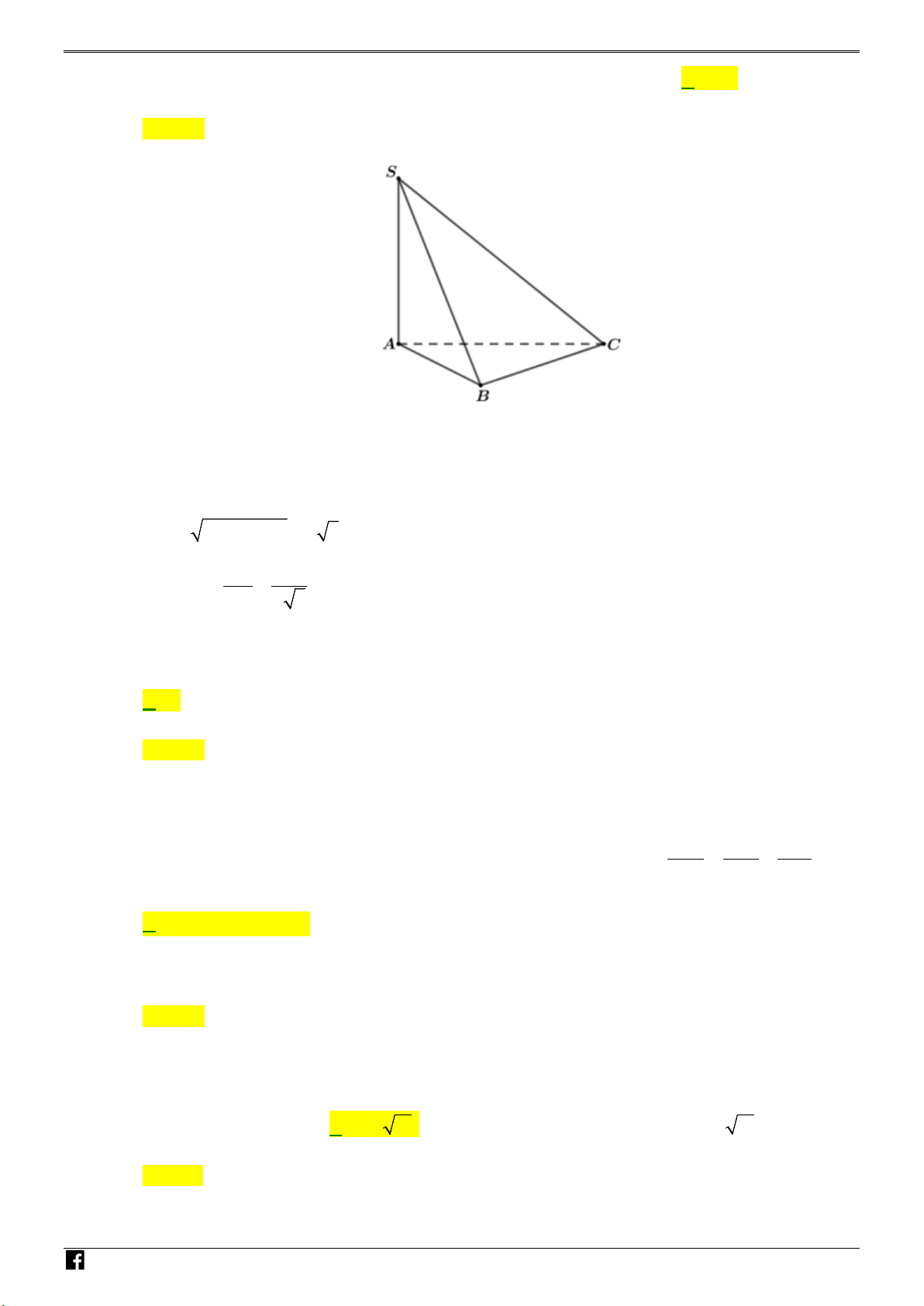
Câu 27: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , S
AB = a, BC = 2a; SA vuông góc với mặt phẳng đáy và SA = 15a
(tham khảo hình bên). Góc giữa đường thẳng SC và mặt phẳng đáy bằng A. 45°. B. 30° . C A C. 60°. D. 90° . B 2 N Câu 28: Biết 2
F(x) = x là một nguyên hàm của hàm số f (x) trên . Giá trị của ∫[2+ f (x)]dx bằng H 1 Ó M A. 5. B. 3. C. 13 . D. 7 . T 3 3 O Á
Câu 29: Diện tích hình phẳng giới hạn bởi hai đường 2
y = x − 4 và y = 2x − 4 bằng N V π D A. 36. B. 4 . C. 4 . D. 36π . – 3 3 VD − + −
Câu 30: Trong không gian x y z Oxyz,
M 2;− 2;3 và đường thẳng d : 1 2 3 = = . Mặt C cho điểm ( ) 3 2 1 −
phẳng đi qua điểm M và vuông góc với đường thẳng d có phương trình là
A. 3x + 2y − z +1 = 0 .
B. 2x − 2y + 3z −17 = 0 .
C. 3x + 2y − z −1 = 0 .
D. 2x − 2y + 3z +17 = 0 .
Câu 31: Gọi z là nghiệm phức có phần ảo dương của phương trình 2
z + 6z +13 = 0 . Trên mặt phẳng 0
tọa độ, điểm biểu diễn số phức 1− z là 0
https://www.facebook.com/groups/toanvd.vdc Trang 3 NHÓM TOÁN VD – VDC MÃ ĐỀ 101 A. N ( 2; − 2) . B. M (4;2). C. P(4;− 2) . D. Q(2;− 2).
Câu 32: Trong không gian Oxyz, cho ba điểm A(1;0; )
1 , B(1;1;0) và C (3;4;− ) 1 . Đường thẳng đi
qua A và song song với BC có phương trình là
A. x −1 y z −1 + + − − + + = = .
B. x 1 y z 1 = =
. C. x 1 y z 1 = =
. D. x 1 y z 1 = = . 4 5 1 − 2 3 1 − 2 3 1 − 4 5 1 −
Câu 33: Cho hàm số f (x) liên tục trên và có bảng xét dấu của f (′x) như sau: N H Ó
Số điểm cực đại của hàm số đã cho là M A. 4 . B. 1. C. 2 . D. 3. TO
Câu 34: Tập nghiệm của bất phương trình 2x 13 3 − < 27 là ÁN − −∞ A. (4;+ ∞) . B. ( 4;4) . C. ( ;4) . D. (0;4). VD
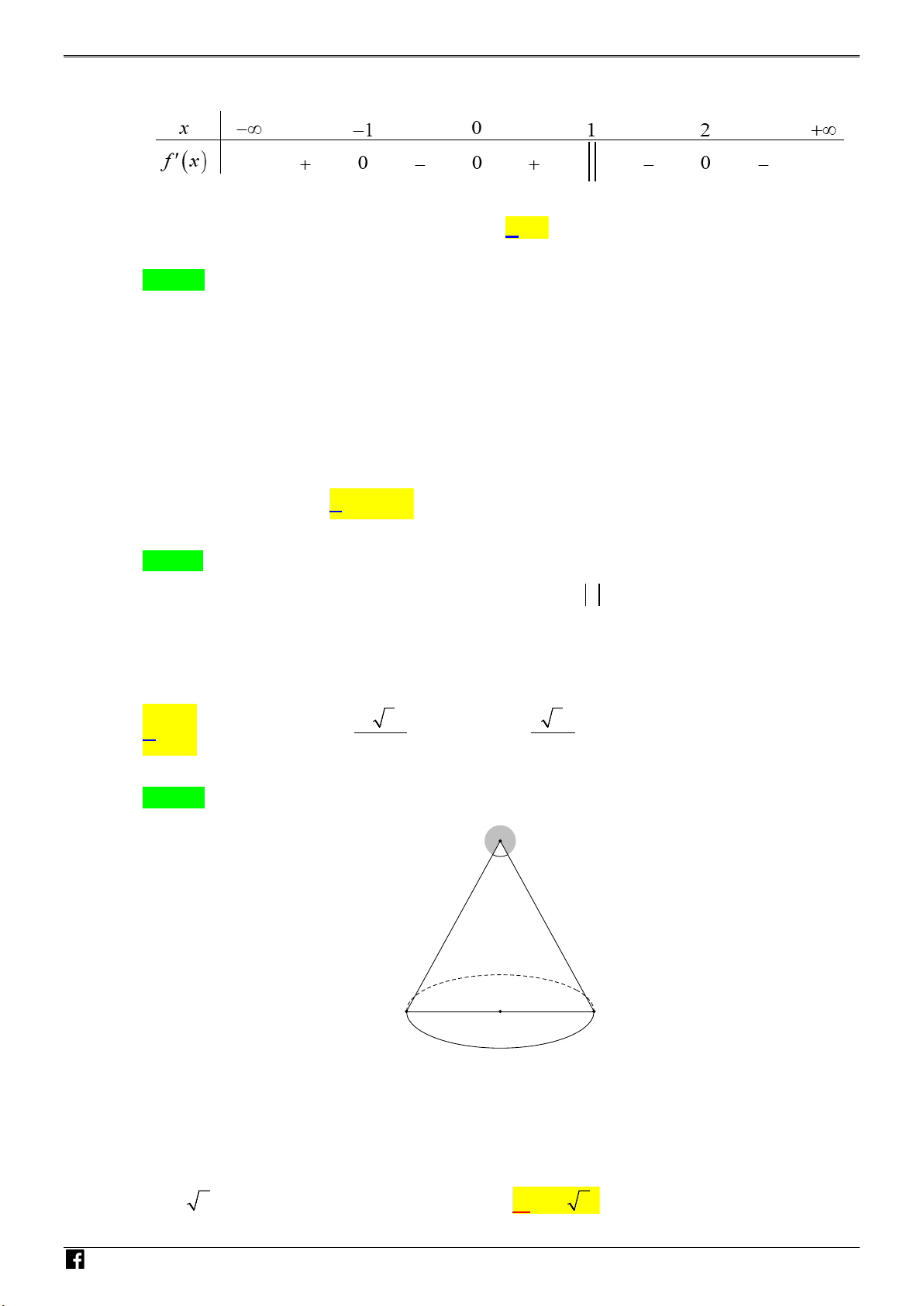
Câu 35: Cho hình nón có bán kính đáy bằng 2 và góc ở đỉnh bằng 60°. Diện tích xung quanh của hình – V nón đã cho bằng D C π π A. 8π . B. 16 3 . C. 8 3 . D. 16π . 3 3
Câu 36: Giá trị nhỏ nhất của hàm số 3
f (x) = x − 24x trên đoạn [2;19] bằng A. 32 2 . B. 40 − . C. 32 − 2 . D. 45 − .
Câu 1: Cho hai số phức z =1+ 2i và w = 3+ i . Môđun của số phức z.w bằng A. 5 2 . B. 26 . C. 26 . D.50. 2
Câu 2: Cho a và b là hai số thực dương thỏa mãn log2(a b) 3 4
= 3a . Giá trị của 2 ab bằng A. 3. B. 6 . C. 12. D. 2 .
Câu 3: Cho hàm số ( ) x f x =
. Họ tất cả các nguyên hàm của hàm số g (x) = (x + )
1 . f ′(x) là 2 x + 2 N 2 x + 2x − 2 x − 2 2 x + x + 2 x + 2 H A. + C . B. + C . C. + C . D. + C . Ó 2 2 x + 2 2 x + 2 2 x + 2 2 2 x + 2 M T x + = O
Câu 40: Tập hợp tất cả các giá trị thực của tham số m để hàm số 4 y
đồng biến trên khoảng x + m ÁN (−∞;−7) là VD A. [4;7) . B. (4;7]. C. (4;7) . D. (4;+ ∞) . – VD
Câu 41: Trong năm 2019, diện tích rừng trồng mới của tỉnh A là 600 ha . Giả sử diện tích rừng trồng C
mới của tỉnh A mỗi năm tiếp theo đều tăng 6% so với diện tích rừng trồng mới của năm liền
trước. Kể từ sau năm 2019, năm nào dưới đây là năm đầu tiên tỉnh A có diện tích rừng trồng
mới trong năm đó đạt trên 1000 ha ? A. Năm 2028. B. Năm 2047. C. Năm 2027. D. Năm 2046.
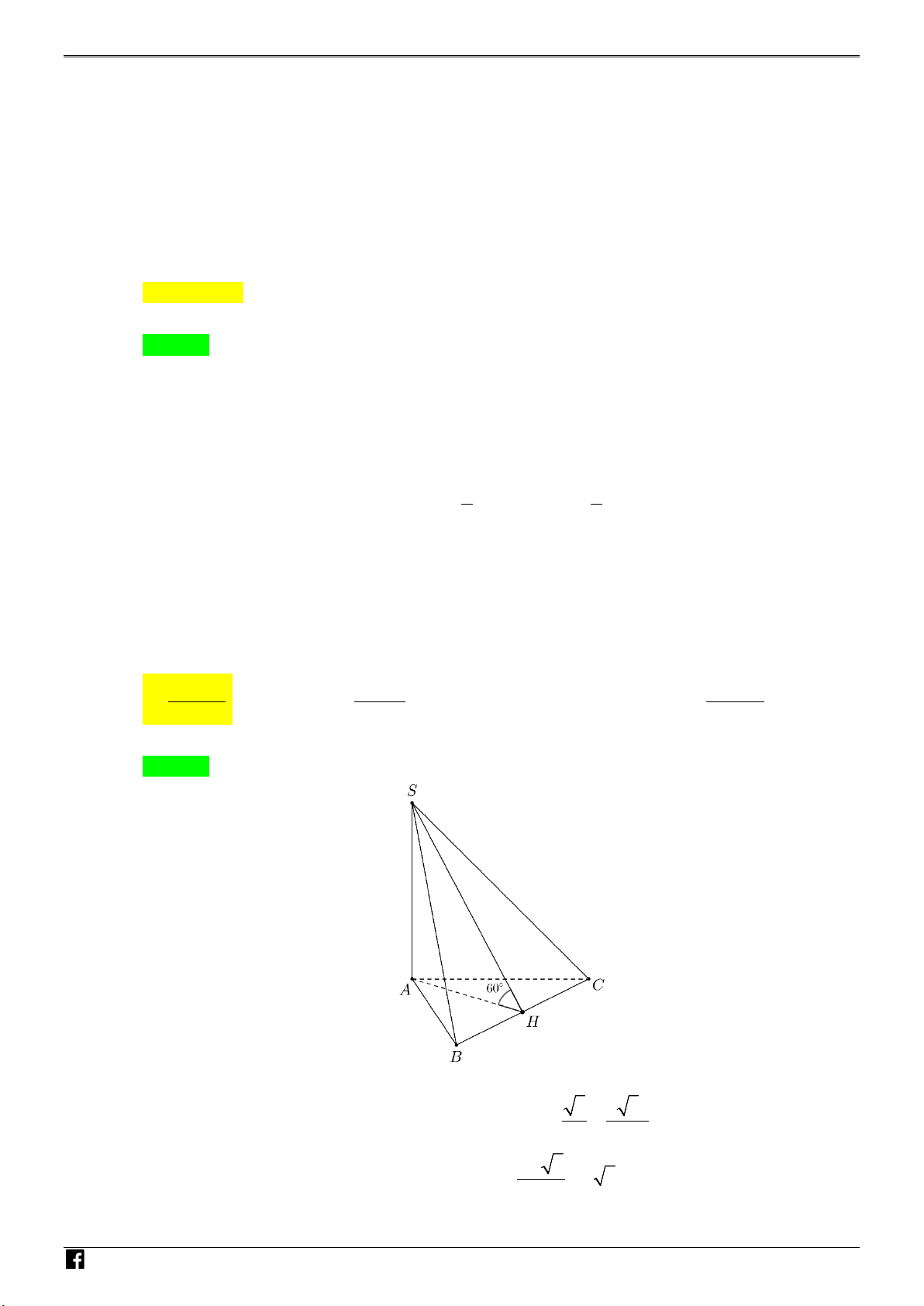
Câu 42: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 4a , SA vuông góc với mặt phẳng đáy, góc
giữa mặt phẳng (SBC) và mặt phẳng đáy bằng 60°. Diện tích của mặt cầu ngoại tiếp hình chóp S.ABC bằng
https://www.facebook.com/groups/toanvd.vdc Trang 4 NHÓM TOÁN VD – VDC MÃ ĐỀ 101 2 2 2 A. 172πa . B. 76π a . C. 2 84πa . D. 172πa 3 3 9
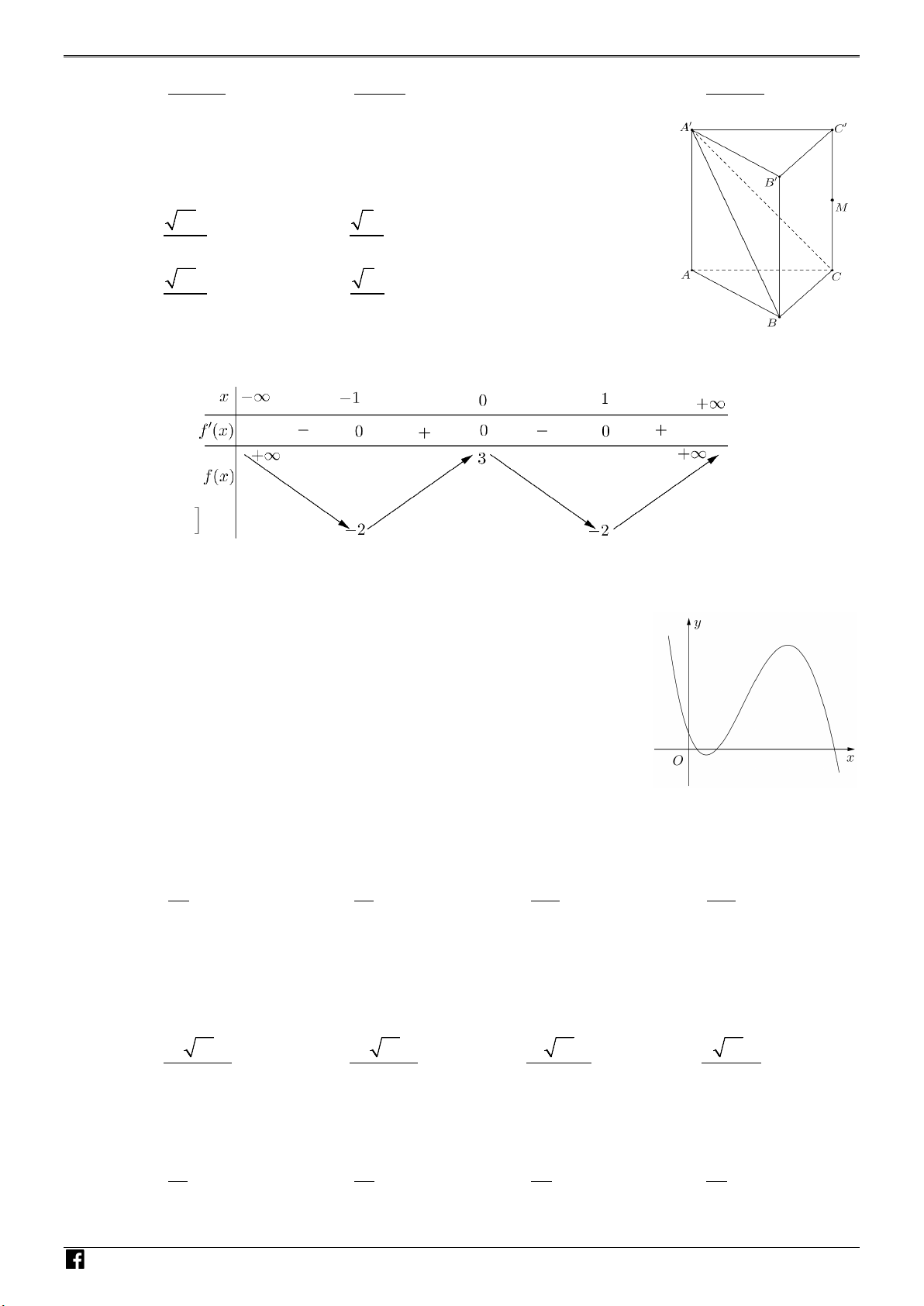
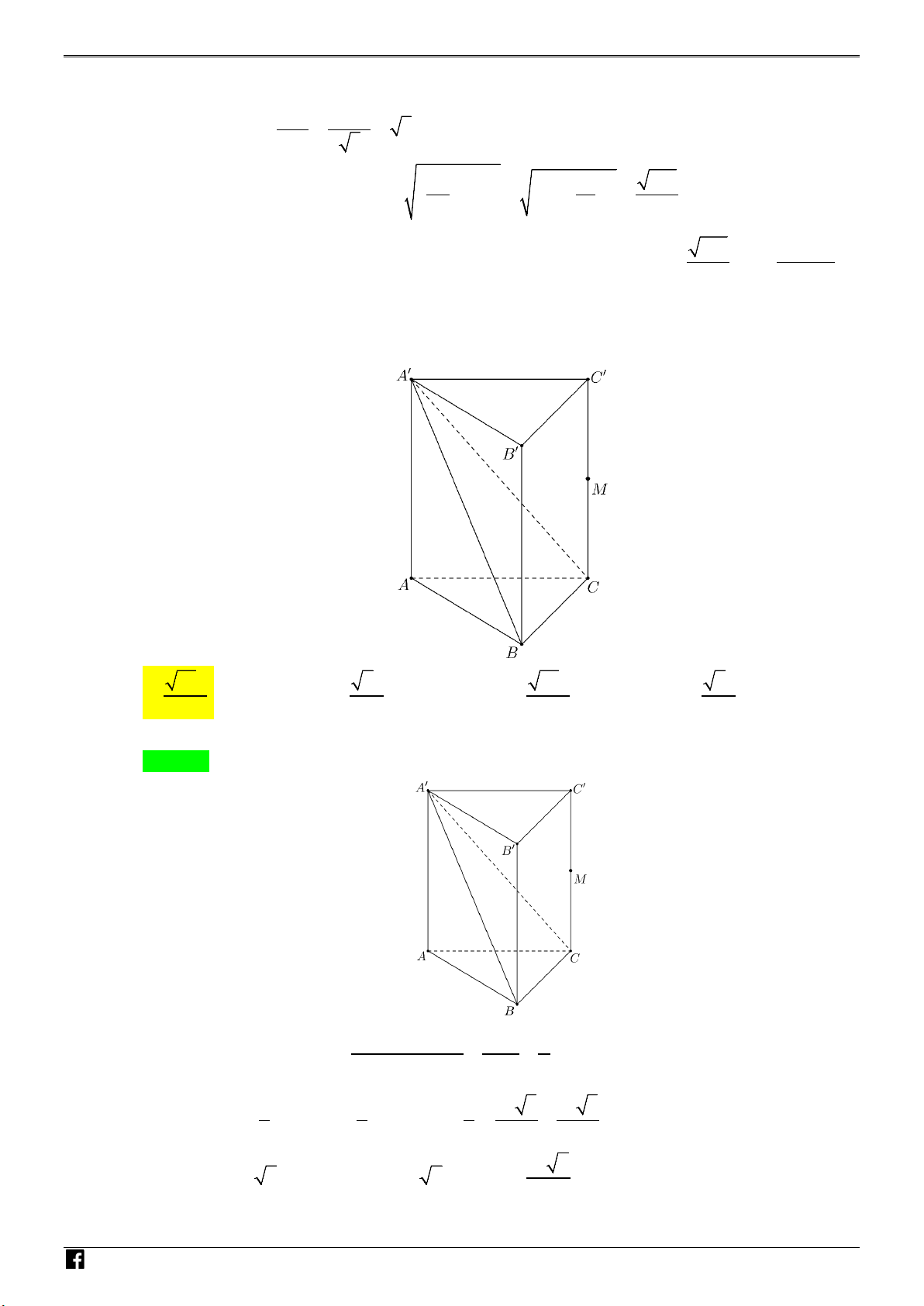
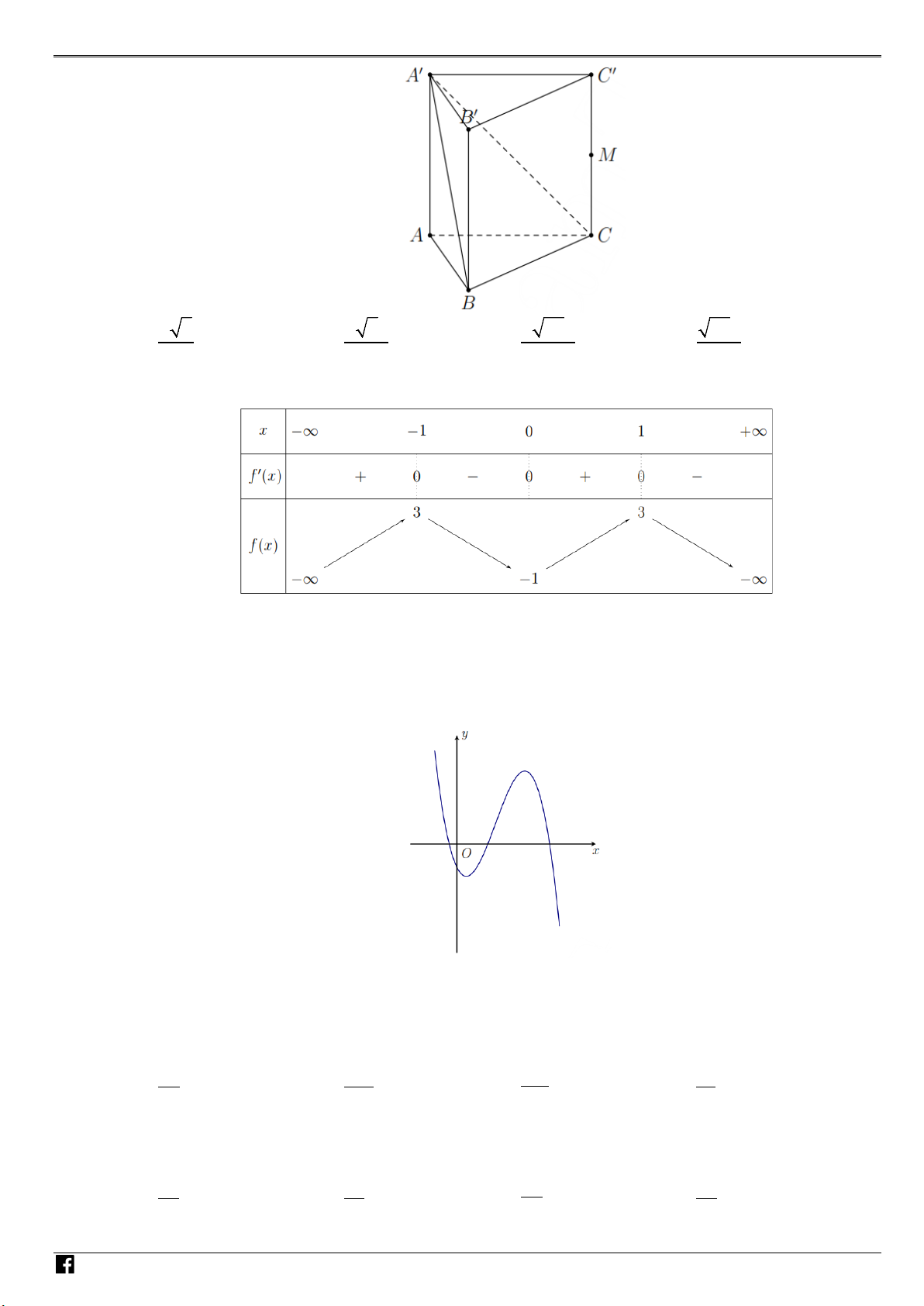
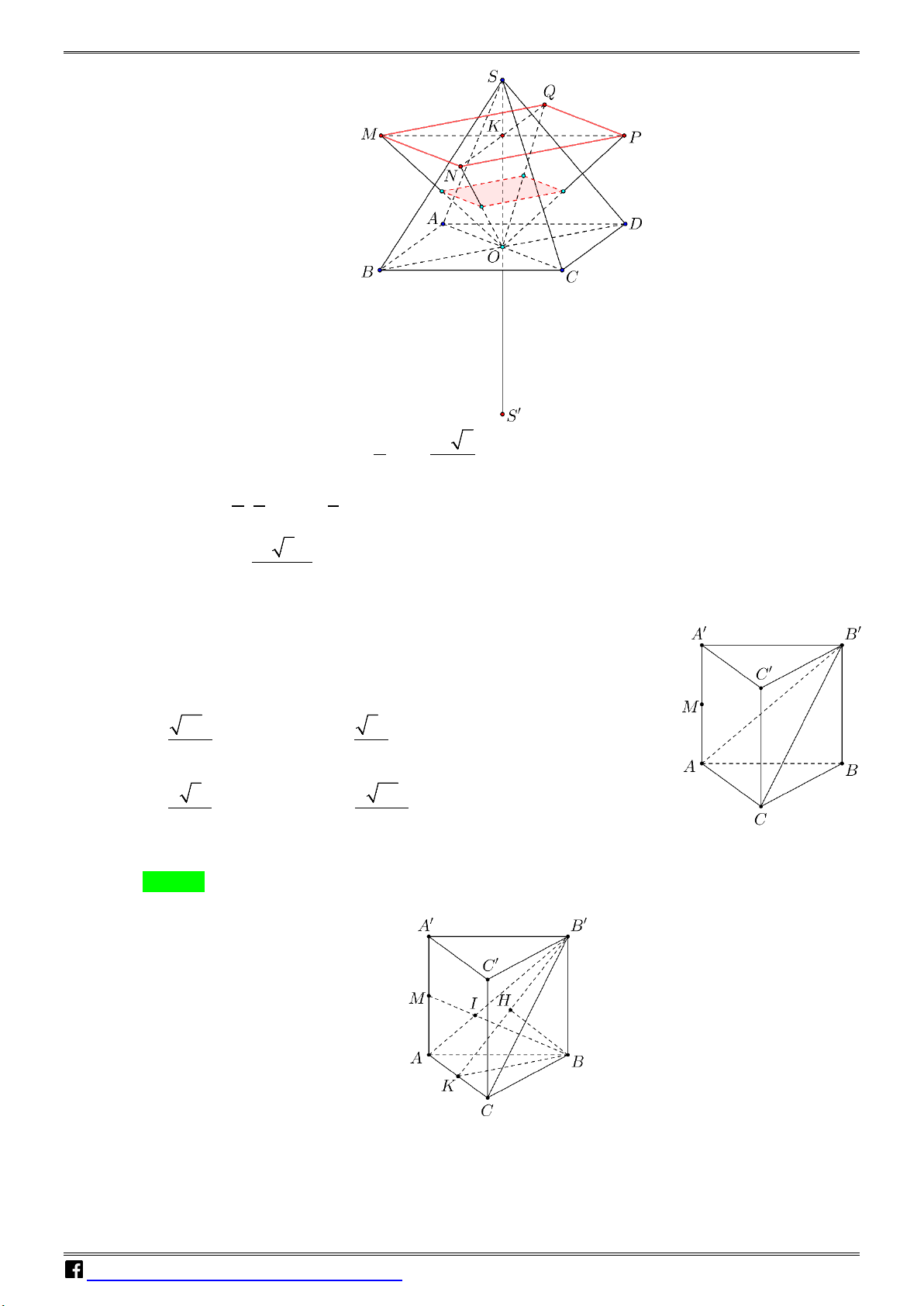
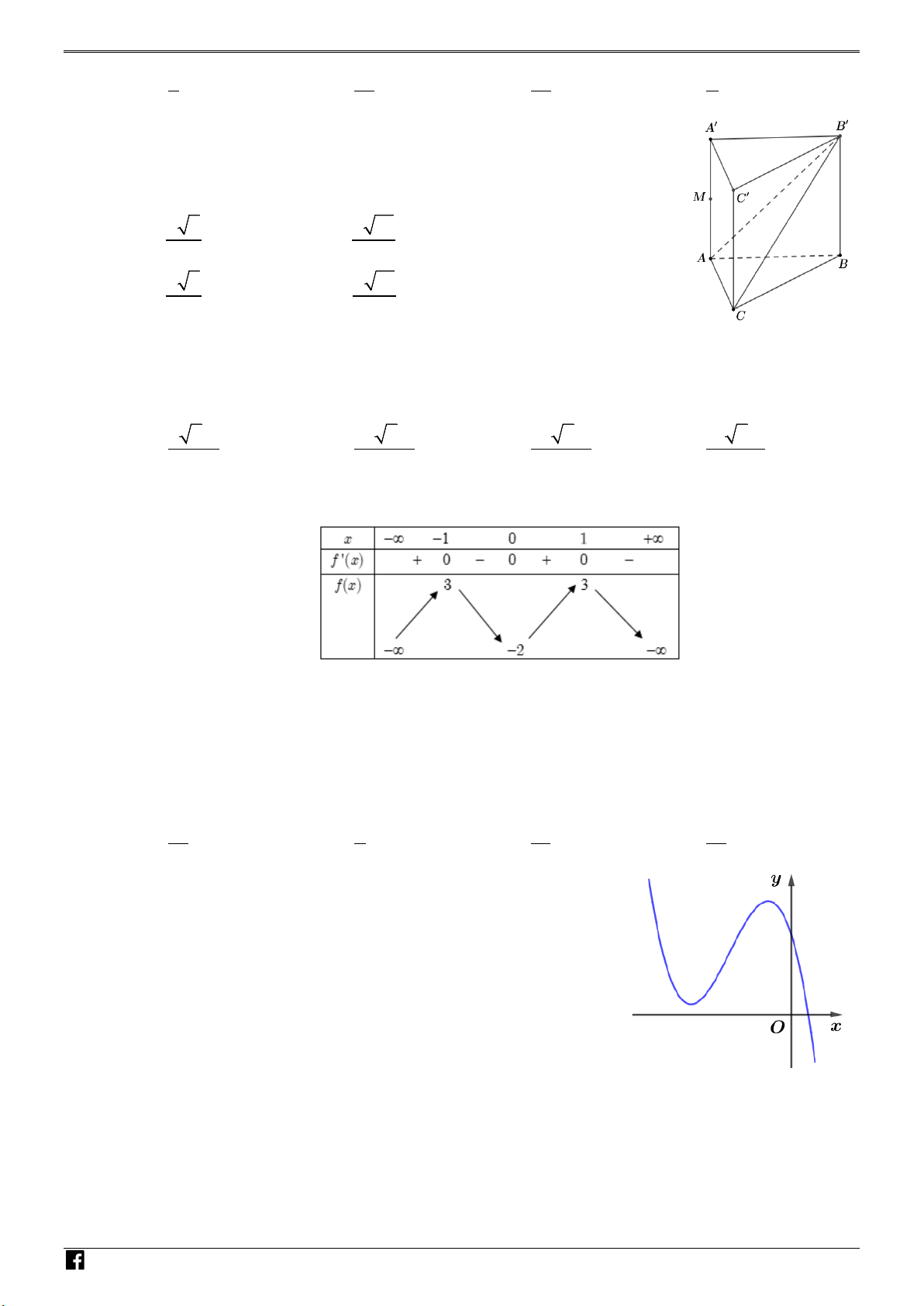
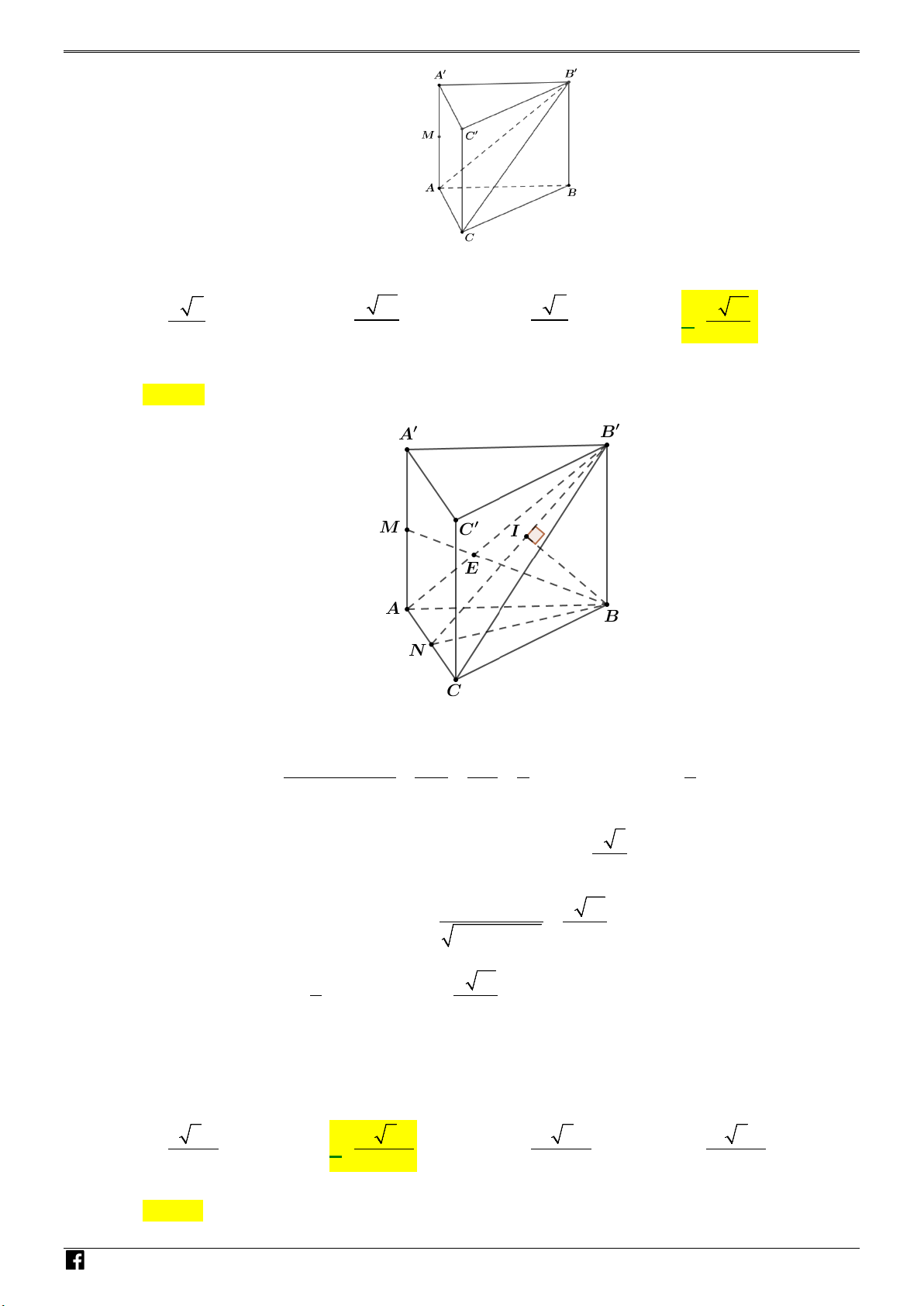
Câu 43: Cho hình lăng trụ đứng ABC.A′B C
′ ′ có tất cả các cạnh bằng a .
Gọi M là trung điểm của CC′ (tham khảo hình bên). Khoảng cách
từ M đến mặt phẳng ( A′BC) bằng A. 21a . B. 2a . 14 2 C. 21a . D. 2a . 7 4 N H Ó
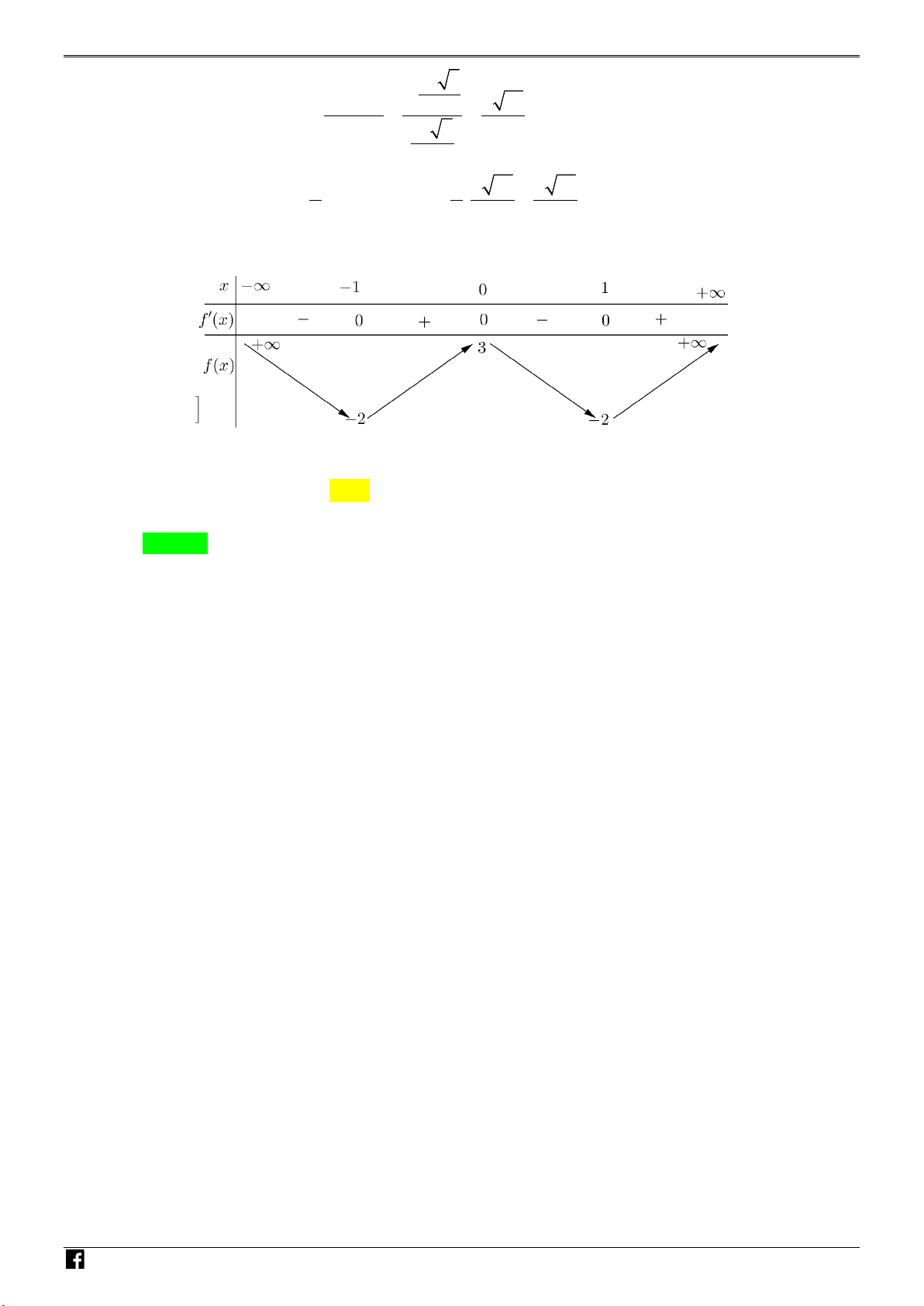
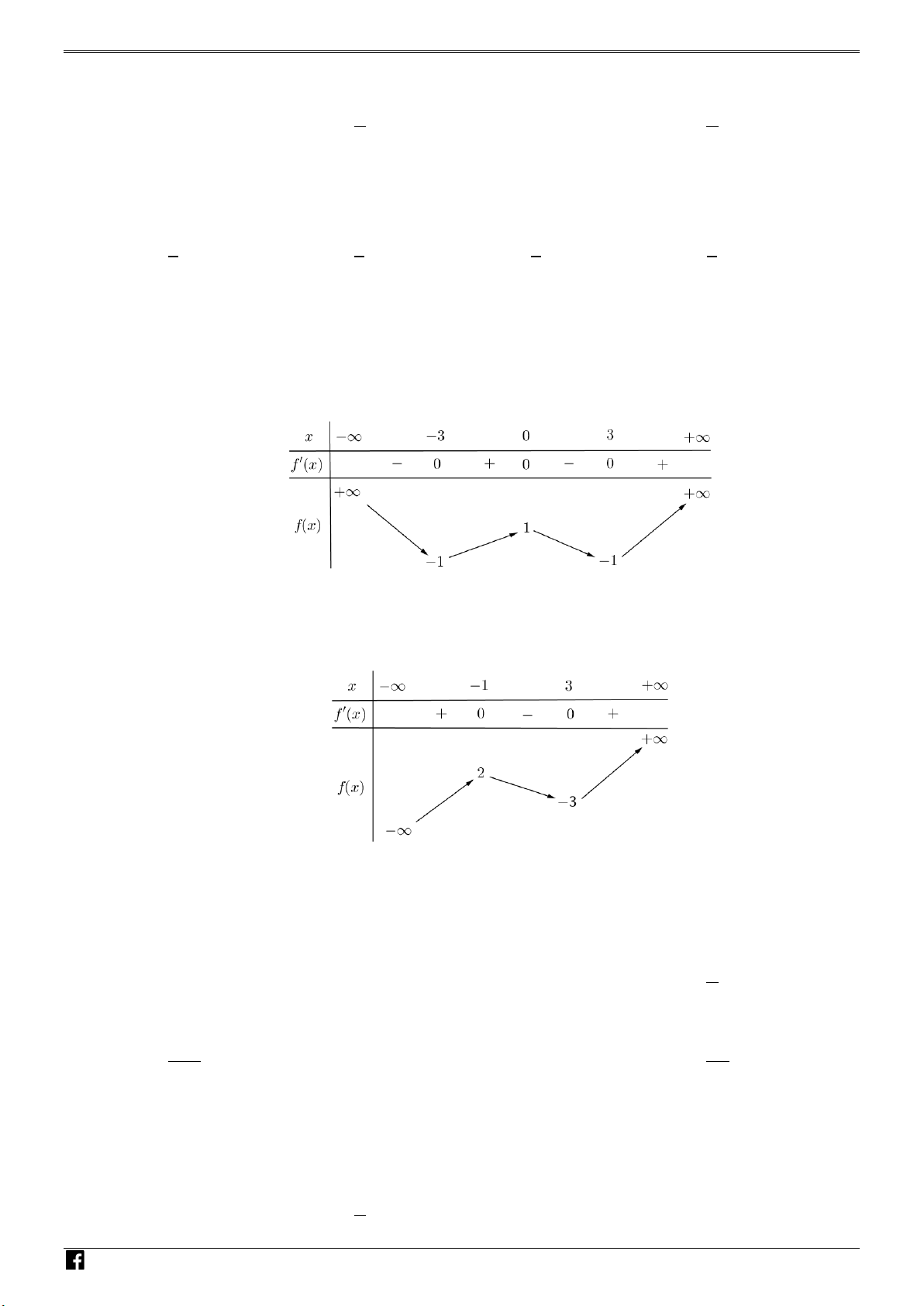
Câu 44: Cho hàm số bậc bốn f (x) có bảng biến thiên như sau: M TOÁN VD – VDC
Số điểm cực trị của hàm số g (x) = x f (x + ) 2 4 1 là A. 11. B. 9. C. 7 . D. 5. Câu 45: Cho hàm số 3 2
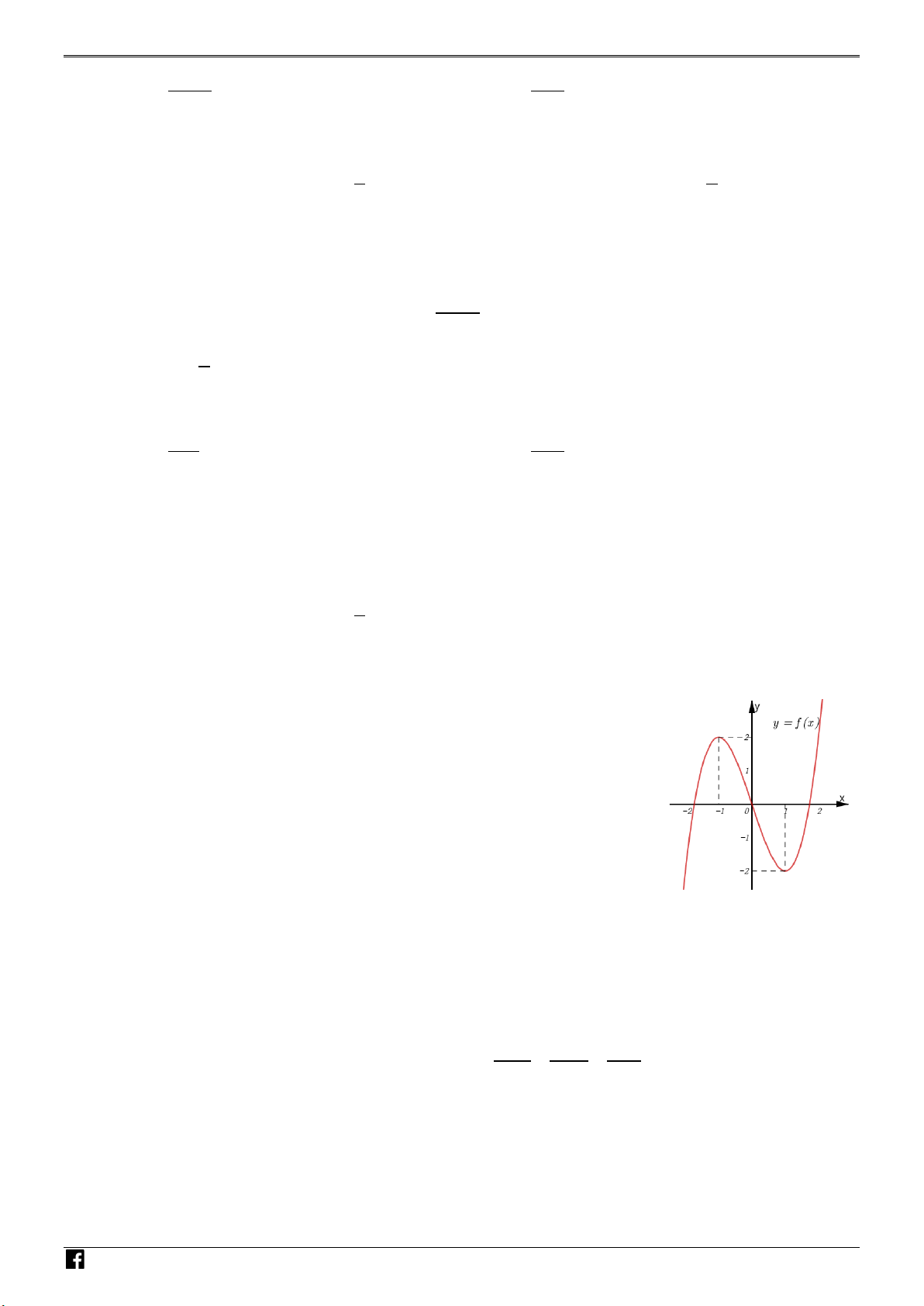
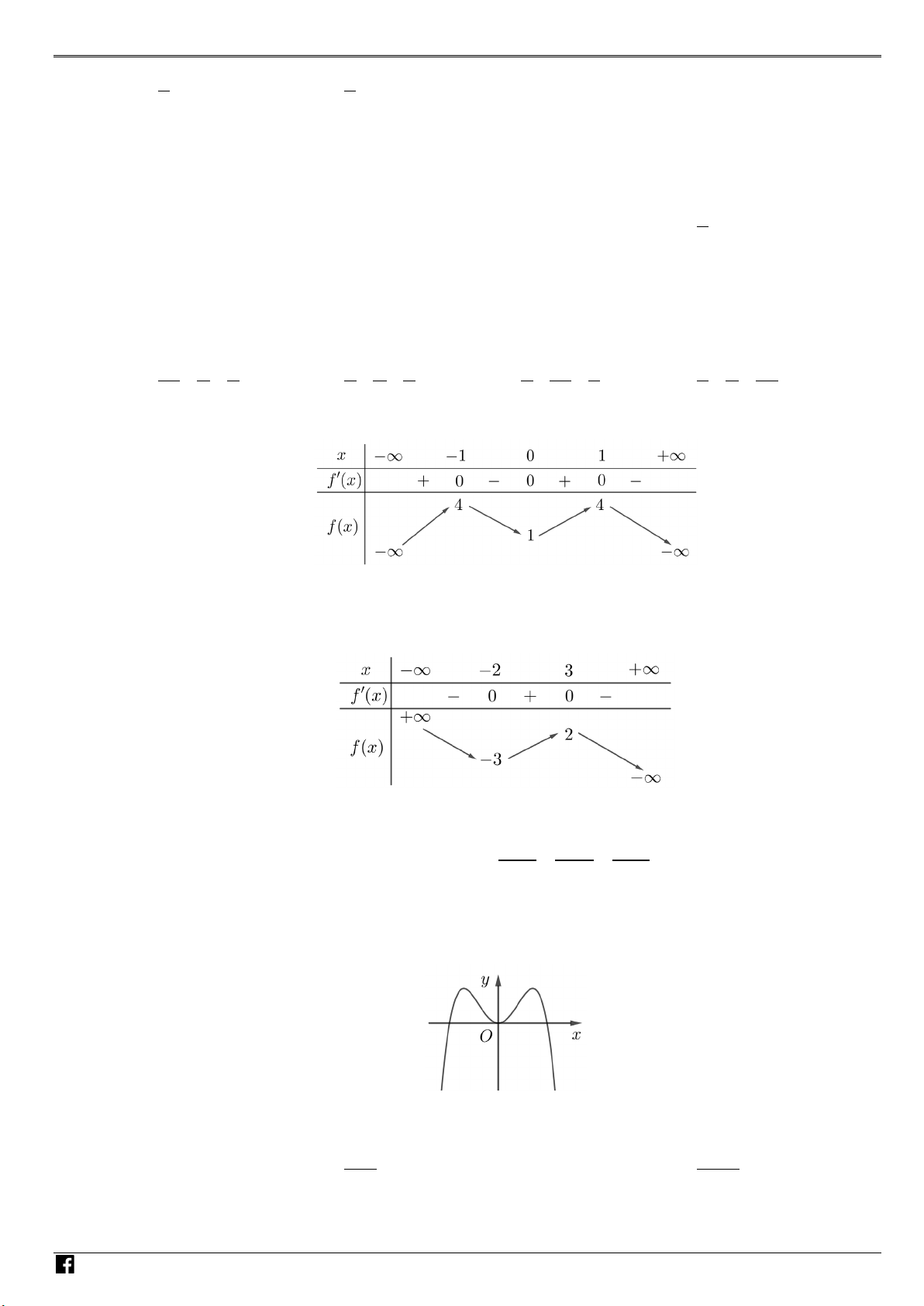
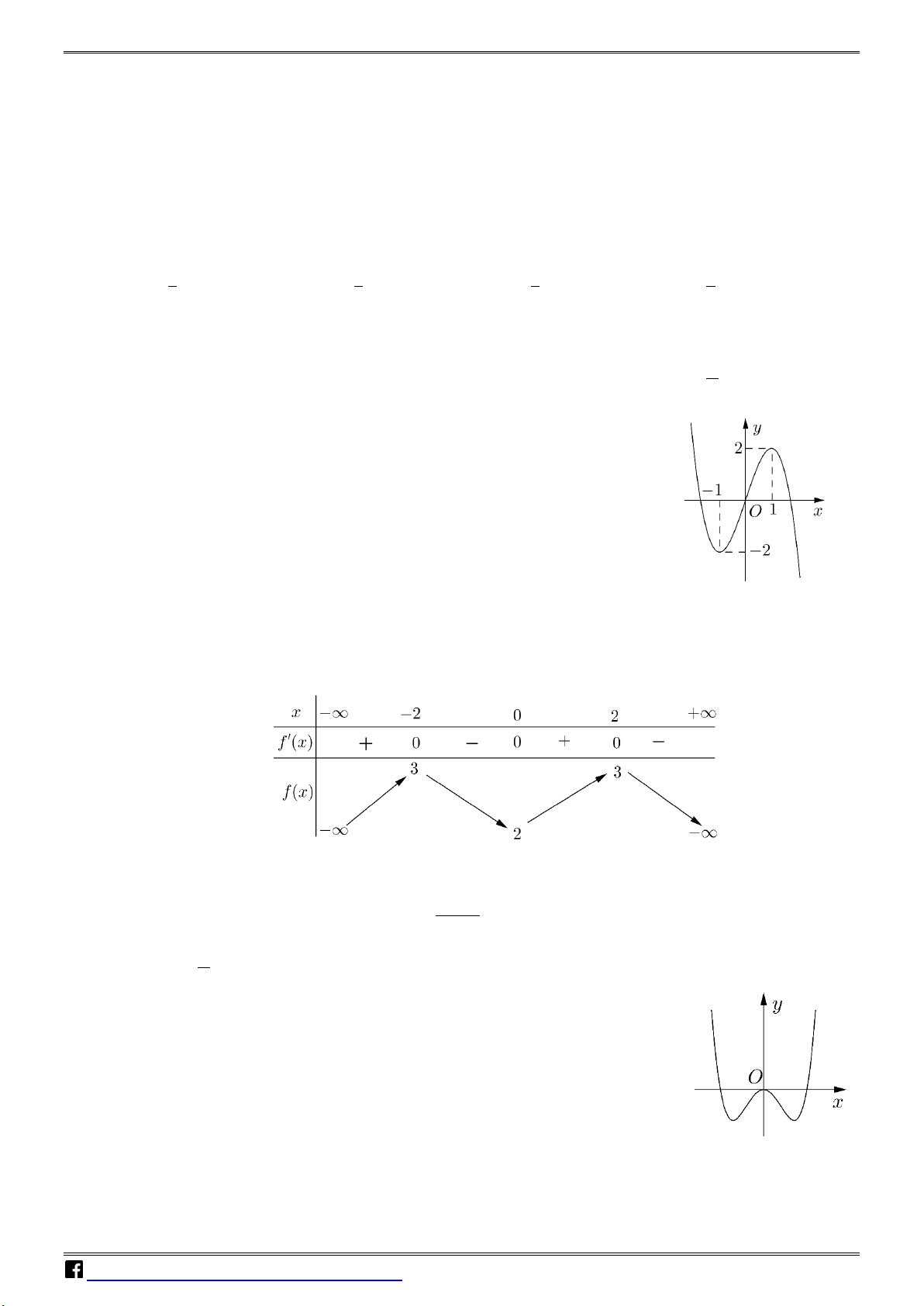
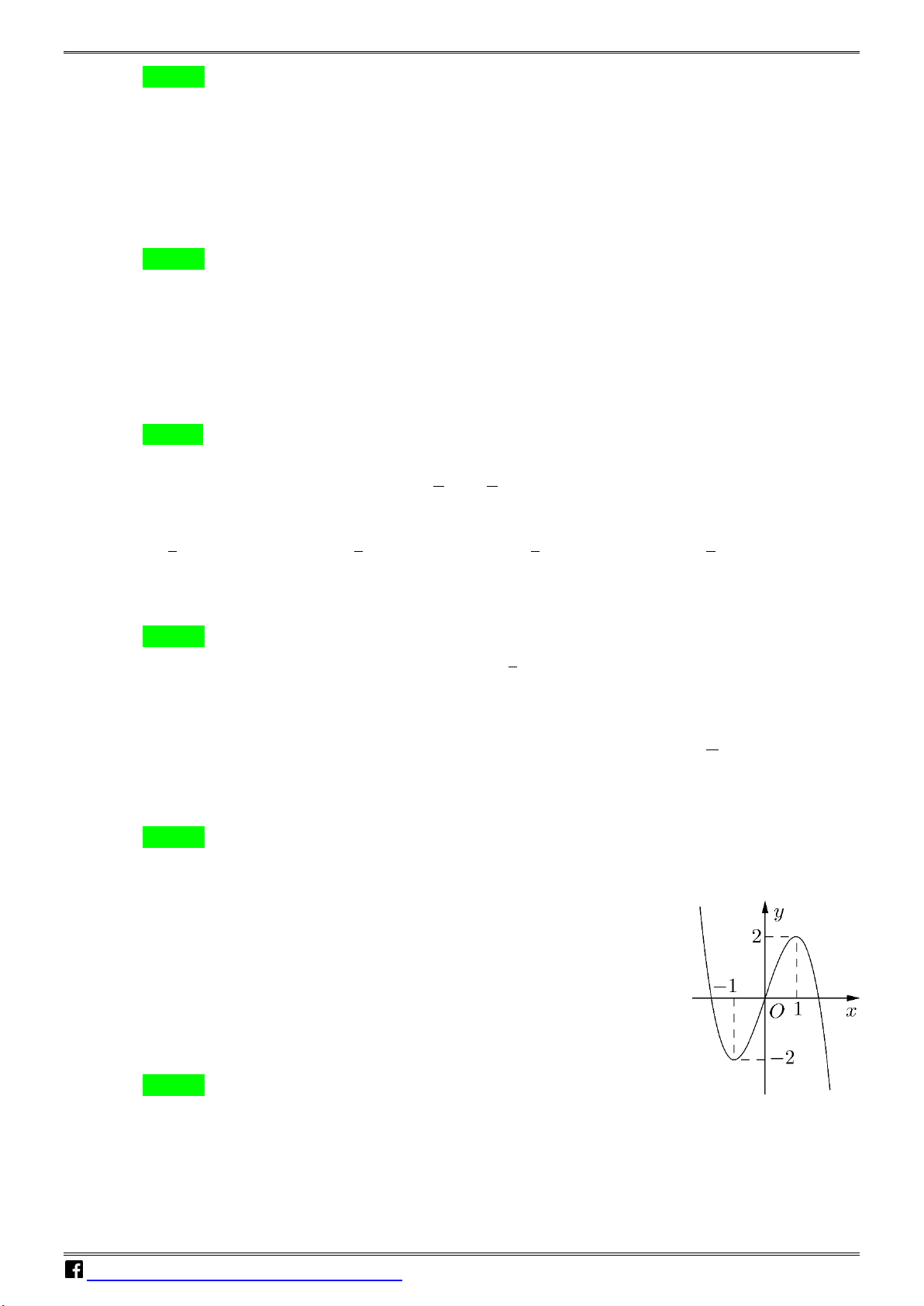
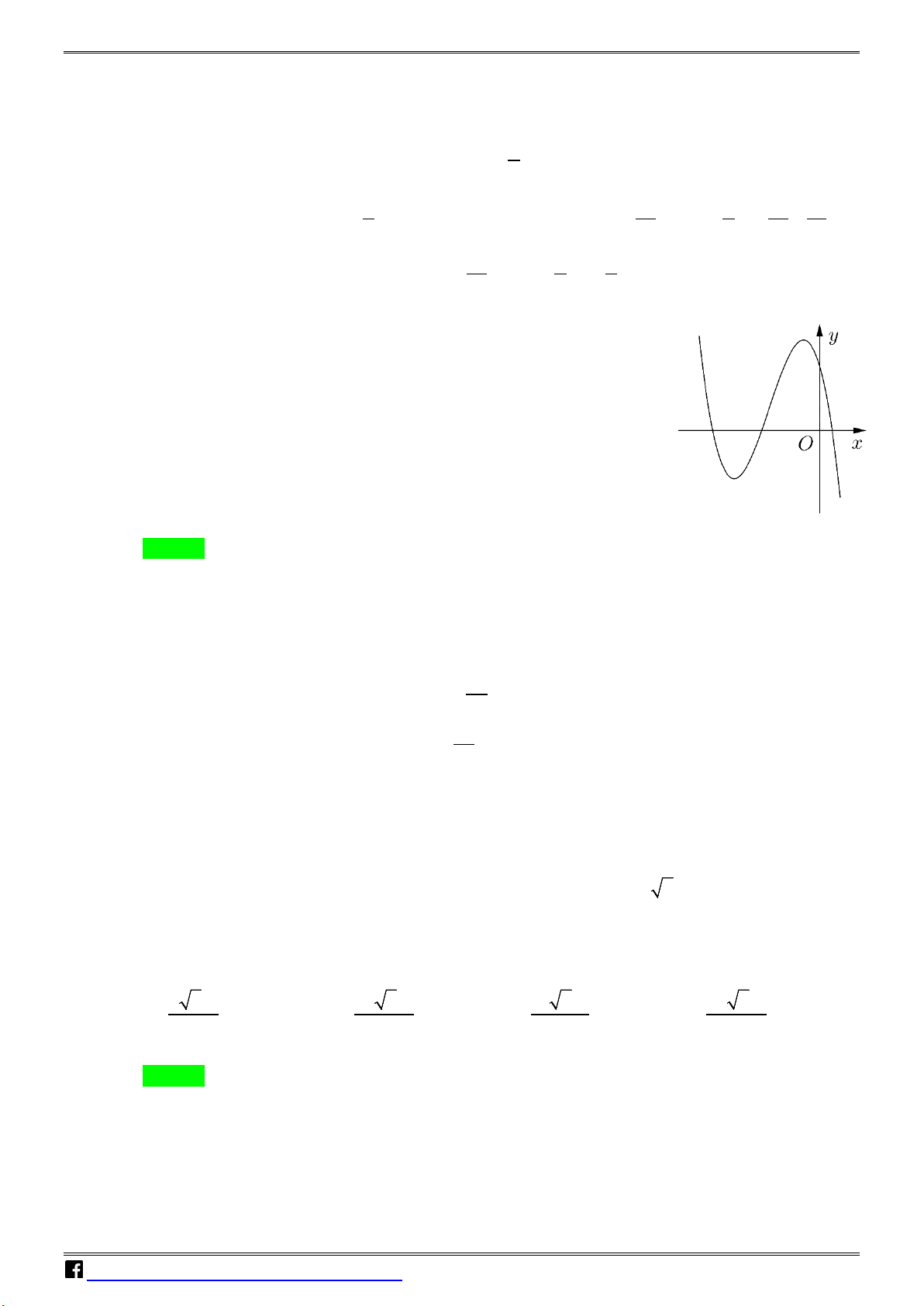
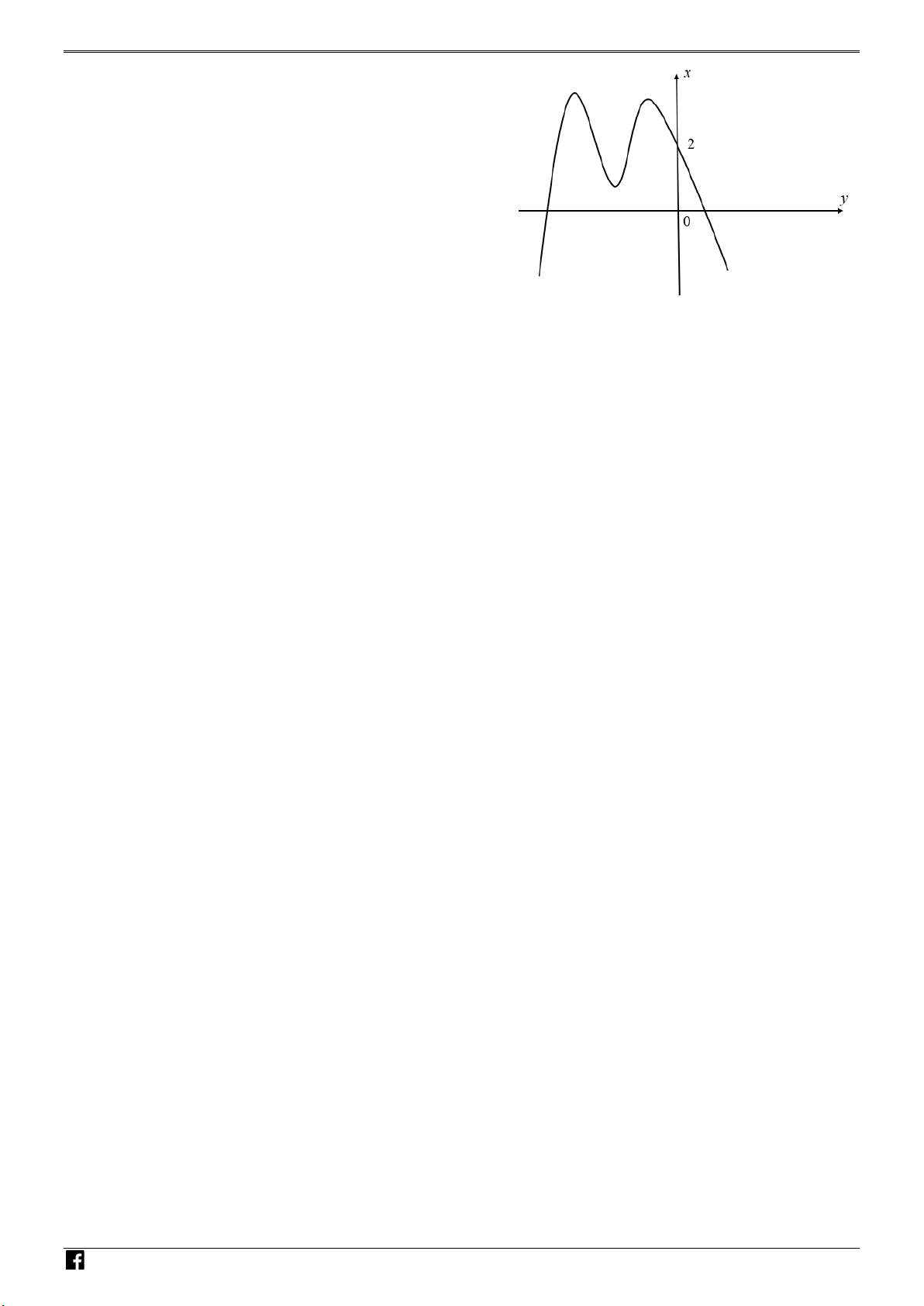
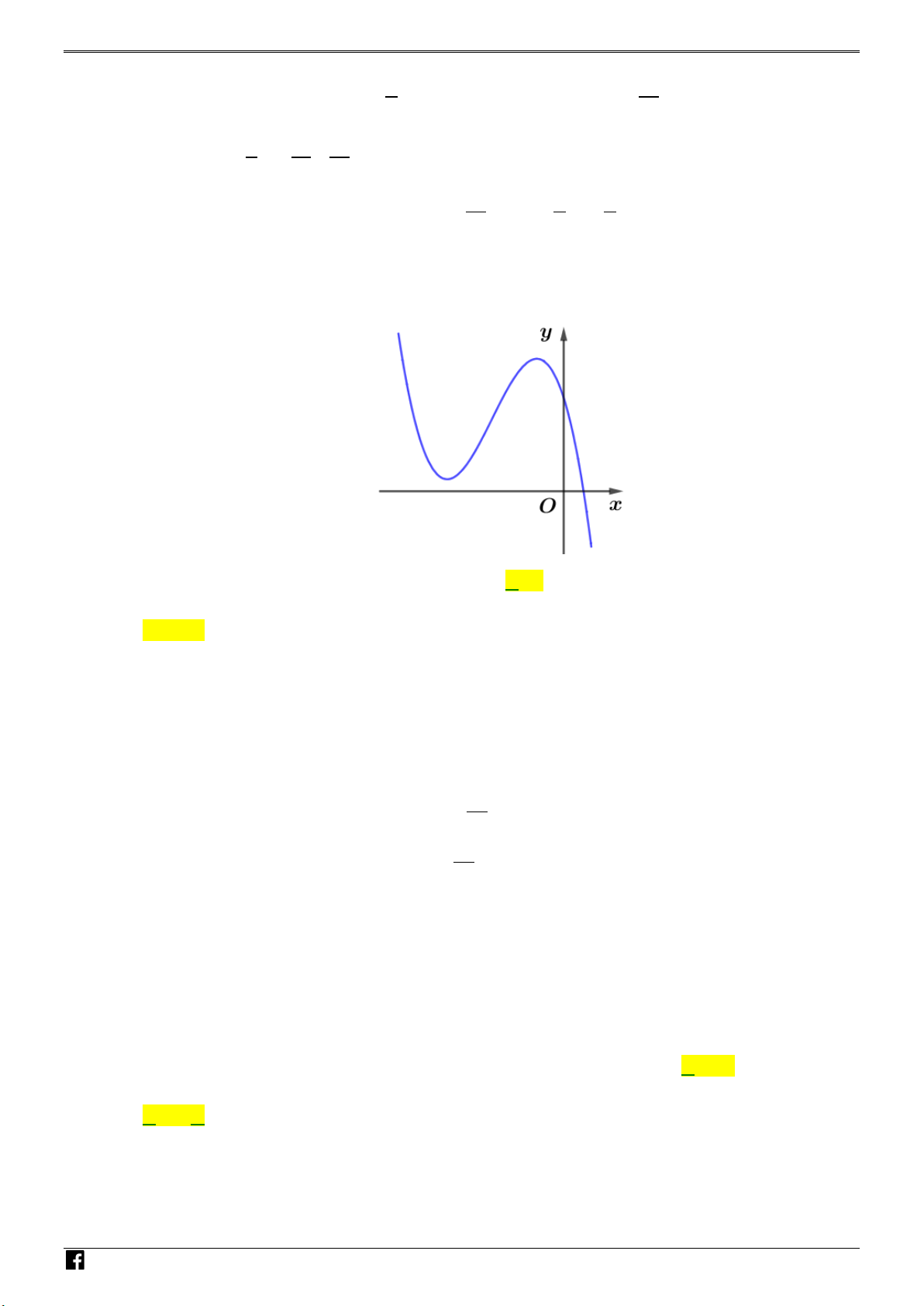
y = ax + bx + cx + d a,b,c,d có đồ thị là
đường cong trong hình bên. Có bao nhiêu số dương trong các số
a , b , c , d ? A. 4 . B. 1. C. 2 . D. 3.
Câu 46: Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số đôi một khác nhau và các chữ số thuộc tập {1,2,3,4,5,6,7,8, }
9 . Chọn ngẫu nhiên một số thuộc S , xác suất để số đó không có hai chữ số N
liên tiếp nào cùng chẵn bằng H Ó M A. 25 . B. 5 . C. 65 . D. 55 . 42 21 126 126 TO
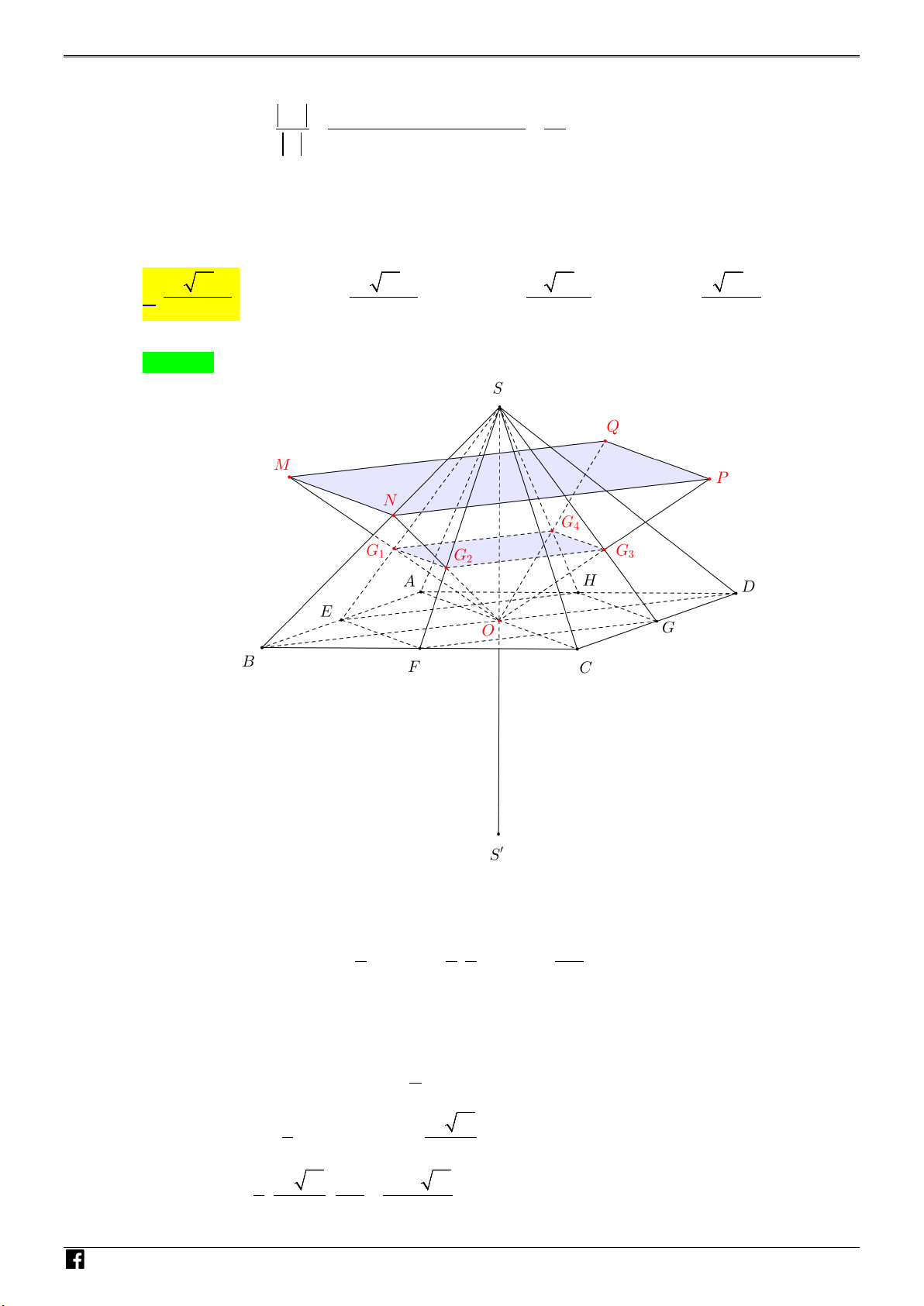
Câu 47: Cho hình chóp đều S.ABCD có cạnh đáy bằng a , cạnh bên bằng 2a và O là tâm của đáy. ÁN
Gọi M , N , P , Q lần lượt là các điểm đối xứng với O qua trọng tâm của các tam giác SAB , VD
SBC , SCD , SDA và S ' là điểm đối xứng với S qua O . Thể tích của khối chóp S '.MNPQ – bằng VD 3 20 14a 3 40 14a 3 10 14a 3 2 14a C A. . B. . C. . D. . 81 81 81 9
Câu 48: Xét các số thực không âm x và y thỏa mãn x y 1 2x .4 y + − +
≥ 3. Giá trị nhỏ nhất của biểu thức 2 2
P = x + y + 4x + 6y bằng A. 33 . B. 65 . C. 49 . D. 57 . 4 8 8 8
https://www.facebook.com/groups/toanvd.vdc Trang 5 NHÓM TOÁN VD – VDC MÃ ĐỀ 101
Câu 49: Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 728 số nguyên y thỏa mãn log ( 2
x + y ≥ log (x + y) ? 4 ) 3 A. 59. B. 58. C. 116. D. 115.
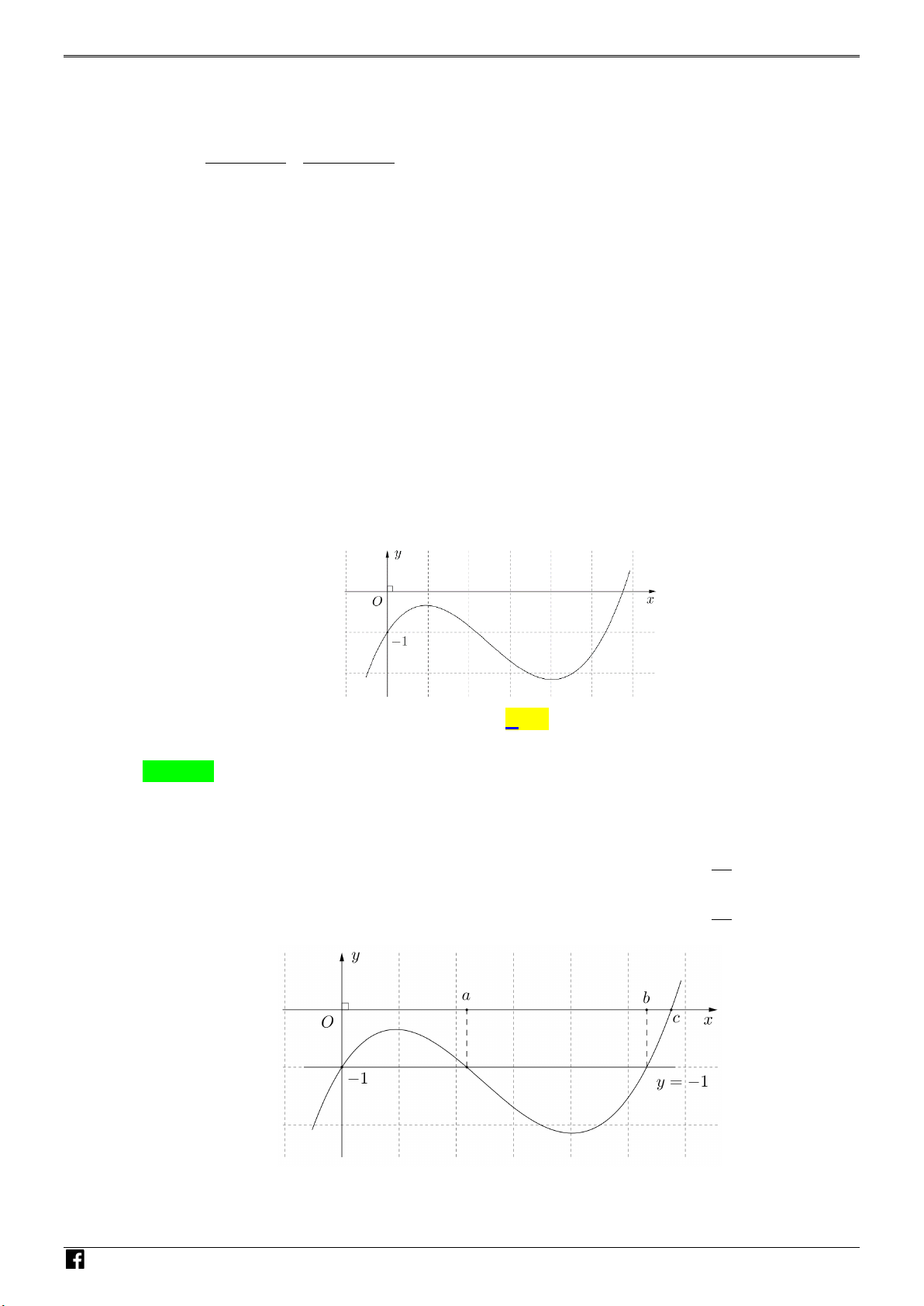
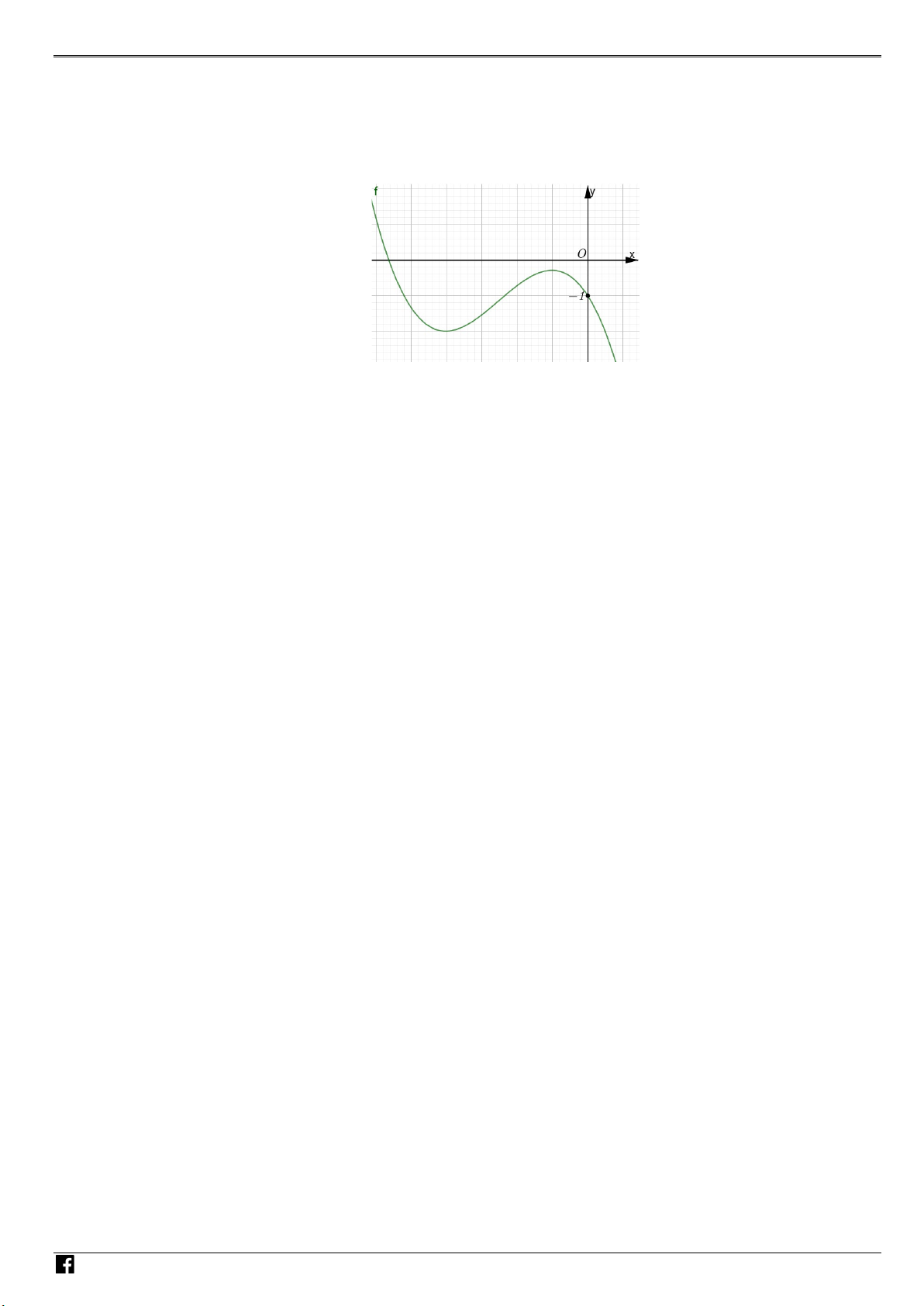
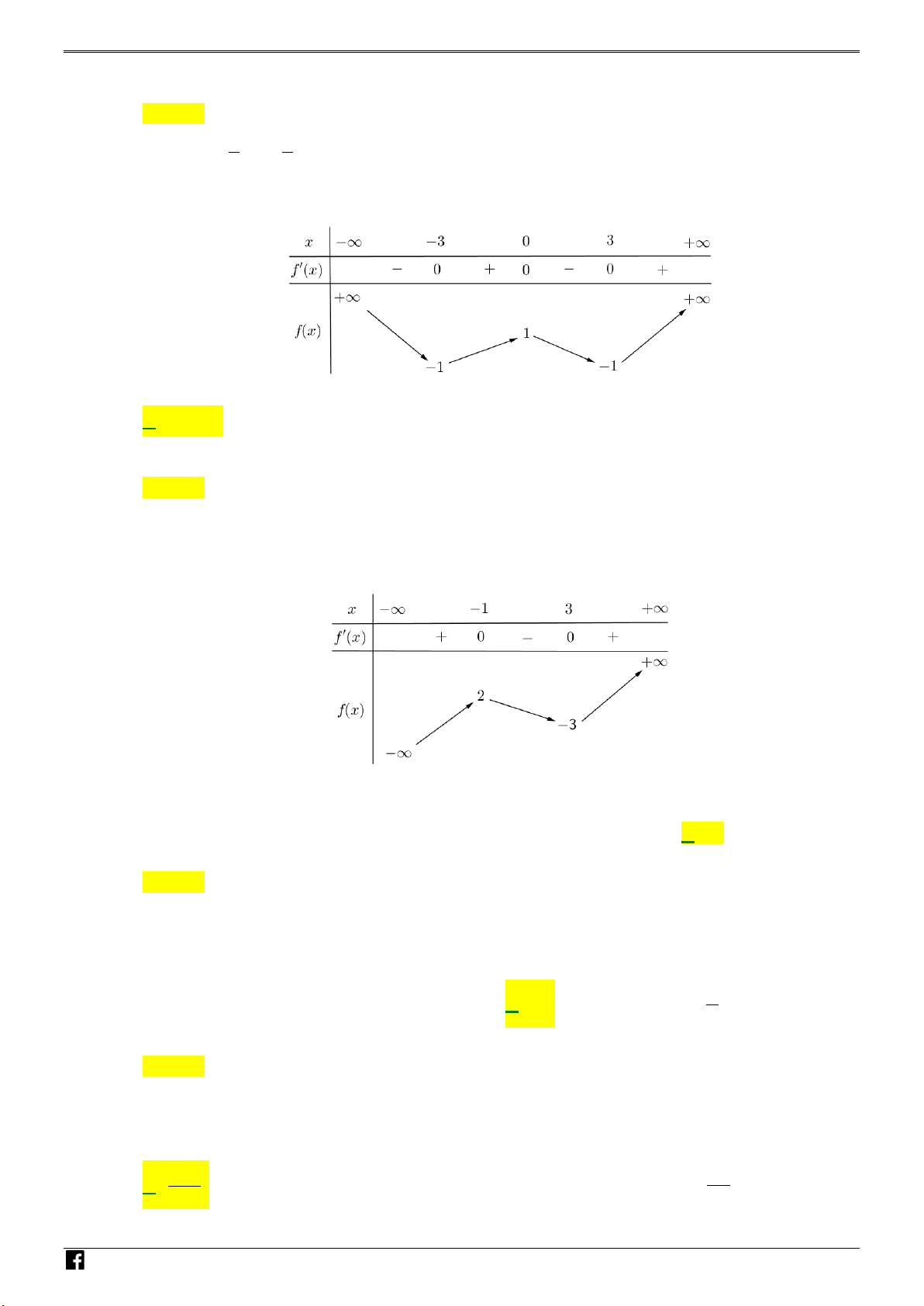
Câu 50: Cho hàm số bậc ba y = f (x) có đồ thị là đường
cong trong hình bên. Số nghiệm thực phân biệt
của phương trình f ( 3
x f (x)) +1 = 0 là A. 8 . B. 5. C. 6 . D. 4 . N H Ó
-------------------- HẾT -------------------- M TOÁN VD – VDC N H Ó M TOÁN VD – VDC
https://www.facebook.com/groups/toanvd.vdc Trang 6 NHÓM TOÁN VD – VDC MÃ ĐỀ 101
BẢNG ĐÁP ÁN – MÃ ĐỀ 101
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C B B D D A C A D D B C D B B A B C B B C C C B C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
A C A B A C C C B A C A A B B A A A B C A A B C C HƯỚNG DẪN GIẢI N
Câu 1: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? H Ó M TOÁN VD – VDC A. 3 2
y = x − 3x +1 . B. 3 2
y = −x + 3x +1. C. 4 2
y = −x + 2x +1. D. 4 2
y = x − 2x +1 . Lời giải Chọn C .
Từ hình có đây là hình dạng của đồ thị hàm bậc 4.
lim f (x) = lim f (x) = −∞ ⇒ a < 0 x→−∞ x→+∞
Câu 2: Nghiệm của phương trình x 1 3 − = 9 là: A. x = 2 − . B. x = 3 . C. x = 2 . D. x = 3 − . Lời giải N Chọn B . H Ó x 1
3 − = 9 ⇔ x −1 = log 9 ⇔ x −1 = 2 ⇔ x = 3 3 M T
Câu 3: Cho hàm f (x) có bảng biến thiên như sau: O ÁN VD – VDC
Giá trị cực tiểu của hàm số đã cho bằng A. 3. B. 5 − . C. 0 . D. 2 . Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 7 NHÓM TOÁN VD – VDC MÃ ĐỀ 101 Chọn B .
Từ BBT ta có hàm số đạt giá trị cực tiểu f (3) = 5 − tại x = 3
Câu 4: Cho hàm số f (x) có bảng biến thiên như sau: N H Ó M
Hàm số đã cho đồng biến trên khoảng nào dưới đây? T A. ( ; −∞ − ) 1 . B. (0; ) 1 . C. ( 1; − ) 1 . D. ( 1; − 0) O Á Lời giải N V Chọn D. D
Hàm số đã cho đồng biến trên khoảng ( 1; − 0) và (1;+∞) – VD
Câu 5: Cho khối hộp chữ nhật có 3 kích thước 3;4;5. Thể tích của khối hộp đã cho bằng? C A. 10 . B. 20 . C. 12 . D. 60 . Lời giải Chọn D.
Thể tích của khối hộp đã cho bằng V = 3.4.5 = 60
Câu 6: Số phức liên hợp của số phức z = 3 − + 5i là: A. z = 3 − − 5i .
B. z = 3+ 5i . C. z = 3 − + 5i .
D. z = 3−5i . Lời giải Chọn A .
Câu 7: Cho hình trụ có bán kính đáy R = 8 và độ dài đường sinh l = 3 . Diện tích xung quanh của hình trụ đã cho bằng: A. 24π . B. 192π . C. 48π . D. 64π . Lời giải N H Chọn C. Ó M
Diện tích xung quanh của hình trụ S = π rl = π xq 2 48 TO
Câu 8: Cho khối cầu có bán kính r = 4. Thể tích của khối cầu đã cho bằng: ÁN π π A. 256 . B. 64π . C. 64 . D. 256π . V 3 3 D – Lời giải VD Chọn A. C 4 256π
Thể tích của khối cầu 3 V = π r = 3 3
Câu 9: Với a,b là các số thực dương tùy ý và a ≠1, log b bằng: 5 a A. 5log b . B. 1 + log b . C. 5 + log b . D. 1 log b . a 5 a a 5 a Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 8 NHÓM TOÁN VD – VDC MÃ ĐỀ 101 Chọn D.
Câu 10: Trong không gian Oxyz , cho mặt cầu (S ) 2 2
: x + y + (z + 2)2 = 9. Bán kính của (S) bằng A. 6 . B. 18. C. 9. D. 3. Lời giải Chọn D. +
Câu 11: Tiệm cận ngang của đồ thị hàm số 4x 1 y = là x −1 A. 1 y = . B. y = 4 . C. y =1. D. y = 1 − . 4 N H Lời giải Ó Chọn B. M T = = = O Tiệm cận ngang 4 lim y lim y 4 x→+∞ x→−∞ 1 ÁN
Câu 12: Cho khối nón có bán kính đáy r = 5 và chiều cao h = 2 . Thể tích khối nón đã cho bằng: VD π π – A. 10 . B. 10π . C. 50 . D. 50π . V 3 3 D C Lời giải Chọn C. π Thể tích khối nón 1 2 50 V = π r h = 3 3
Câu 13: Nghiệm của phương trình log x −1 = 2 là 3 ( ) A. x = 8. B. x = 9 . C. x = 7 . D. x =10 . Lời giải Chọn D. TXĐ: D = (1;+∞) log (x − ) 2
1 = 2 ⇔ x −1 = 3 ⇔ x =10 3 Câu 14: 2 x dx ∫ bằng N H 1 Ó
A. 2x + C . B. 3 x + C . C. 3 x + C . D. 3 3x + C M 3 T Lời giải O Á Chọn B. N V
Câu 15: Có bao nhiêu cách xếp 6 học sinh thành một hàng dọc? D A. 36. B. 720 . C. 6 . D. 1. – V Lời giải D C Chọn B.
Có 6!= 720 cách xếp 6 học sinh thành một hàng dọc
Câu 16: Cho hàm số bậc ba y = f (x) có đồ thị là đường cong trong hình bên. Số nghiệm thực của
phương trình f (x) = 1 − là:
https://www.facebook.com/groups/toanvd.vdc Trang 9 NHÓM TOÁN VD – VDC MÃ ĐỀ 101 N H A. 3. B. 1. C. 0 . D. 2 . Ó M Lời giải T Chọn A. O Á
Số nghiệm thực của phương trình f (x) = 1
− chính là số giao điểm của đồ thị hàm số N − V
y = f (x) và đường thẳng y = 1. D – VDC
Từ hình vẽ suy ra 3 nghiệm.
Câu 17: Trong không gian Oxyz , hình chiếu vuông góc của điểm A(3;2; )
1 trên trục Ox có tọa độ là: A. (0;2; ) 1 . B. (3;0;0). C. (0;0; ) 1 . D. (0;2;0) . N H Lời giải Ó Chọn B . M T
Câu 18: Cho khối chóp có diện tích đáy B = 6 và chiều cao h = 2 . Thể tích của khối chóp đã cho bằng: OÁ A. 6 . B. 3. C. 4 . D. 12. N Lời giải VD Chọn C. – V
Thể tích của khối chóp 1
V = Bh = 4 D 3 C − − +
Câu 19: Trong không gian Oxyz , cho đường thẳng
x 3 y 4 z 1 d : = =
. Vecto nào dưới đây là một 2 5 − 3
vecto chỉ phương của d ? A. u 2;4; 1 − . B. u 2; 5; − 3 . C. u 2;5;3 . D. u 3;4;1 . 4 ( ) 3 ( ) 1 ( ) 2 ( ) Lời giải Chọn B.
https://www.facebook.com/groups/toanvd.vdc Trang 10 NHÓM TOÁN VD – VDC MÃ ĐỀ 101
Câu 20: Trong không gian Oxyz , cho ba điểm A(3;0;0) , B(0;1;0) và C (0;0; 2
− ) . Mặt phẳng ( ABC) có phương trình là: A. x y z + + = 1. B. x y z + + = 1. 3 1 − 2 3 1 2 − C. x y z + + = 1. D. x y z + + = 1. 3 1 2 3 − 1 2 Lời giải Chọn B. ( ): x y z ABC + + = 1 hay ( ): x y z ABC + + = 1 . a b c 3 1 2 − N H Ó
Câu 21: Cho cấp số nhân (u với u = 3 và công bội
. Giá trị của u bằng n ) q = 2 1 2 M T A. 8 . B. 9. C. 6 . D. 3 . O 2 ÁN Lời giải VD Chọn C –
Ta có: u = u .q = 3.2 = 6 . 2 1 VD Câu 22:
z = 3− 2i và z = 2 + i . Số phức z + z bằng C Cho hai số phức 1 2 1 2 A. 5 + i . B. 5 − + i . C. 5 − i . D. 5 − − i . Lời giải Chọn C
Ta có: z + z = 3− 2i + 2 + i = 5 − i . 1 2 3 3
Câu 23: Biết f
∫ (x)dx = 3. Giá trị của 2 f (x)dx ∫ bằng 1 1 A. 5. B. 9. C. 6 . D. 3 . 2 Lời giải Chọn C 3 3 N Ta có: 2 f
∫ (x)dx = 2 f
∫ (x)dx = 2.3 = 6. H 1 1 Ó M
Câu 24: Trên mặt phẳng tọa độ, biết M ( 3 − )
;1 là điểm biểu diễn số phức z . Phần thực của z bằng TO A. 1. B. 3 − . C. 1 − . D. 3. ÁN Lời giải VD Chọn B – Điểm M ( 3 − )
;1 là điểm biểu diễn số phức = − + . z , suy ra z 3 i VD
Vậy phần thực của z bằng 3 − . C
Câu 25: Tập xác định của hàm số y = log x là 5 A. [0;+ ∞) . B. (−∞;0) . C. (0;+ ∞) . D. (−∞;+ ∞). Lời giải Chọn C
Điều kiện: x > 0 .
https://www.facebook.com/groups/toanvd.vdc Trang 11 NHÓM TOÁN VD – VDC MÃ ĐỀ 101
Tập xác định: D = (0;+ ∞) .
Câu 26: Số giao điểm của đồ thị hàm số 3 2
y = x + 3x và đồ thị hàm số 2
y = 3x + 3x là A. 3. B. 1. C. 2 . D. 0 . Lời giải Chọn A
Phương trình hoành độ giao điểm của hai đồ thị đã cho là: x = 0 3 2 2 3
x + 3x = 3x + 3x ⇔ x − 3x = 0 ⇔ x( 2
x − 3) = 0 ⇔ x = 3 . N x = − 3 H Ó
Hai đồ thị đã cho cắt nhau tại 3 điểm. M
Câu 27: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB = a , BC = 2a , SA vuông TO
góc với mặt phẳng đáy và SA = 15a (tham khảo hình bên). ÁN S VD – VDC C A B
Góc giữa đường thẳng SC và mặt phẳng đáy bằng A. 45°. B. 30° . C. 60°. D. 90° . Lời giải Chọn C
Do SA vuông góc với mặt phẳng đáy nên AC là hình chiếu vuông góc của SC lên mặt phẳng
đáy. Từ đó suy ra: SC ABC SC AC ; ; SCA . N
Trong tam giác ABC vuông tại B có: 2 2 2 2
AC = AB + BC = a + 4a = 5a . H Ó SA a M
Trong tam giác SAC vuông tại A có: 15 tan SCA 3 SCA 60. AC T 5a O Á
Vậy SC ;ABC 60. N VD 2 = + – Câu 28: Biết ( ) 2 F x
x là một nguyên hàm của hàm số f (x) trên . Giá trị của 2 f ∫ (x) dx bằng V 1 D C . . A. 5. B. 3. C. 13 D. 7 3 3 Lời giải Chọn A 2 2 Ta có: 2 + f ∫ (x)dx = ( 2
2x + x ) = 8−3 = 5 1 1
https://www.facebook.com/groups/toanvd.vdc Trang 12 NHÓM TOÁN VD – VDC MÃ ĐỀ 101
Câu 29: Diện tích hình phẳng giới hạn bởi hai đường 2
y = x − 4 và y = 2x − 4 bằng π A. 36. B. 4 . C. 4 . D. 36π . 3 3 Lời giải Chọn B
Phương trình hoành độ giao điểm của hai đồ thị đã cho là: x = 0 2 2
x − 4 = 2x − 4 ⇔ x − 2x = 0 ⇔ . x = 2
Diện tích hình phẳng giới hạn bởi hai đồ thị đã cho là: N 2 2 2 3 x 2 H
S = ∫ ( 2x − )−( x − ) 2
x = x − x x = ∫ ∫( 2 x − x ) 2 4 4 2 4 d 2 d 2
dx = x − = . Ó 3 0 3 M 0 0 0 T x − y + z − O
Câu 30: Trong không gian Oxyz , cho điểm M (2;− 2;3) và đường thẳng d : 1 2 3 = = . Mặt Á 3 2 1 − N
phẳng đi qua điểm M và vuông góc với đường thẳng d có phương trình là VD
A. 3x + 2y − z +1 = 0 .
B. 2x − 2y + 3z −17 = 0 . – V
C. 3x + 2y − z −1 = 0 .
D. 2x − 2y + 3z +17 = 0 . D C Lời giải Chọn A
Gọi (P) là mặt phẳng đi qua M và vuông góc với đường thẳng d .
Ta có: n = u =
− là một véc tơ pháp tuyến của mặt phẳng (P) . P d (3;2; )1
Phương trình mặt phẳng (P) là: 3(x − 2) + 2( y + 2) −1(z −3) = 0 ⇔ 3x + 2y − z +1 = 0 .
Câu 31: Gọi z là nghiệm phức có phần ảo dương của phương trình 2
z + 6z +13 = 0 . Trên mặt phẳng 0
tọa độ, điểm biểu diễn số phức 1− z là 0 A. N ( 2; − 2) . B. M (4;2). C. P(4;− 2) . D. Q(2;− 2). Lời giải Chọn C N z = 3 − + 2i H Ta có: 2
z + 6z +13 = 0 ⇔ . z = 3 − − 2i Ó M
Do z là nghiệm phức có phần ảo dương của phương trình đã cho nên z = 3 − + 2i . 0 0 TO
Từ đó suy ra điểm biểu diễn số phức 1− z = 4 − 2i là điểm P(4;− 2) . Á 0 N V
Câu 32: Trong không gian Oxyz , cho ba điểm A(1;0; )
1 , B(1;1;0) và C (3;4;− ) 1 . Đường thẳng đi D qua –
A và song song với BC có phương trình là V x − y z − x + y z + x − y z − x + y z + D A. 1 1 = = . B. 1 1 = = . C. 1 1 = = . D. 1 1 = = . C 4 5 1 − 2 3 1 − 2 3 1 − 4 5 1 − Lời giải Chọn C
Đường thẳng d đi qua A và song song với BC nhận BC = (2;3;− ) 1 làm một véc tơ chỉ phương.
Phương trình của đường thẳng d : x −1 y z −1 = = . 2 3 1 −
https://www.facebook.com/groups/toanvd.vdc Trang 13 NHÓM TOÁN VD – VDC MÃ ĐỀ 101
Câu 33: Cho hàm số f (x) liên tục trên và có bảng xét dấu của f ′(x) như sau:
Số điểm cực đại của hàm số đã cho là A. 4 . B. 1. C. 2 . D. 3. Lời giải Chọn C
Do hàm số f (x) liên tục trên , f ′(− ) 1 = 0 , N H f ′( )
1 không xác định nhưng do hàm số liên tục trên nên tồn tại f 1 Ó M
và f ′(x) đổi dấu từ "+" sang "−" khi đi qua các điểm x = 1
− , x =1 nên hàm số đã cho đạt TO
cực đại tại 2 điểm này. ÁN
Vậy số điểm cực đại của hàm số đã cho là 2. VD
Câu 34: Tập nghiệm của bất phương trình 2x 13 3 − < 27 là – V A. (4;+ ∞) . B. ( 4; − 4) . C. (−∞;4) . D. (0;4). D C Lời giải Chọn B Ta có: 2 2 x 13 − x 13 − 3 2 2 3 < 27 ⇔ 3
< 3 ⇔ x −13 < 3 ⇔ x <16 ⇔ x < 4 ⇔ 4 − < x < 4.
Vậy tập nghiệm của bất phương trình đã cho là S = ( 4; − 4).
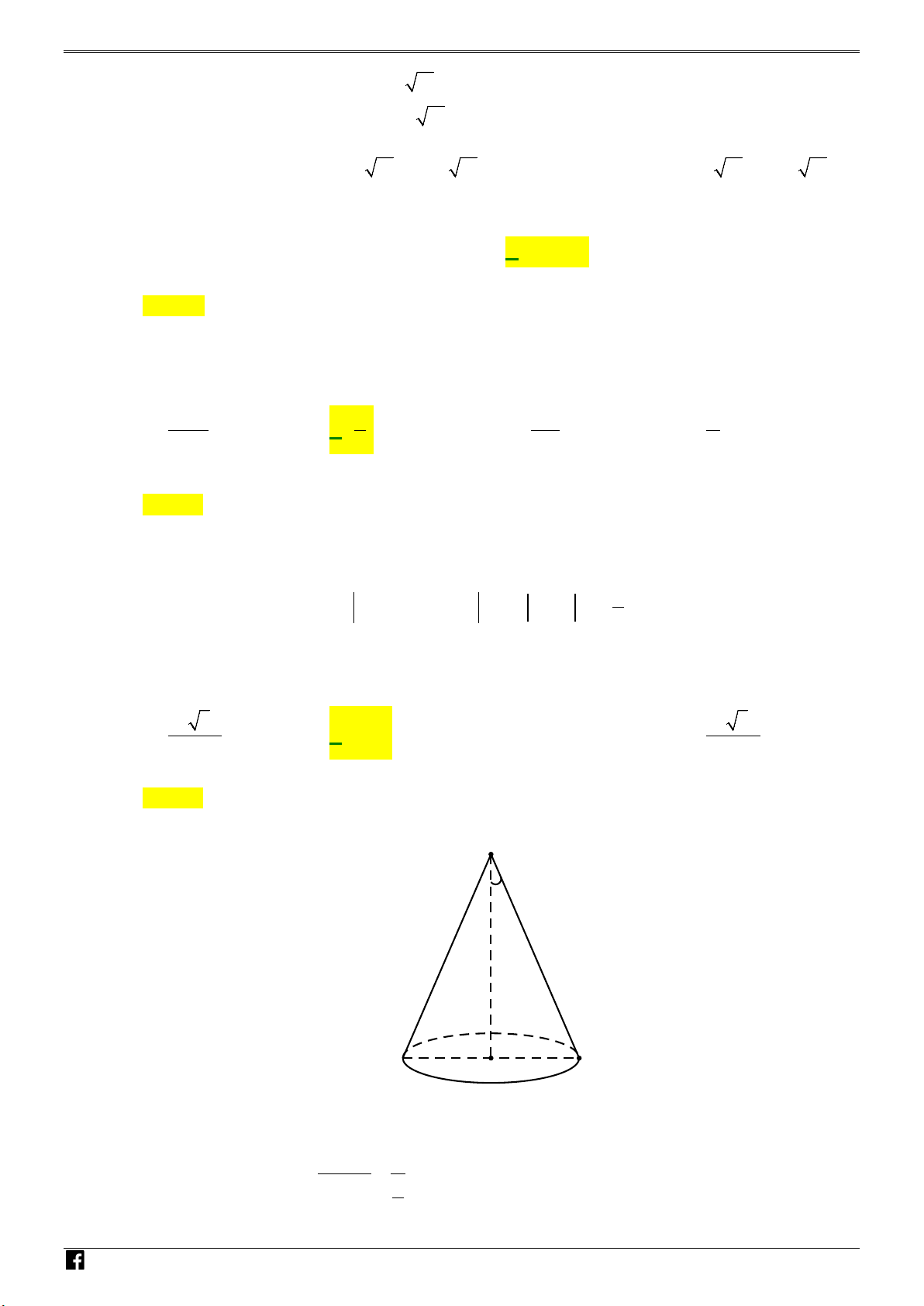
Câu 35: Cho hình nón có bán kính đáy bằng 2 và góc ở đỉnh bằng 60°. Diện tích xung quanh của hình nón đã cho bằng A. 8π . B. 16 3π . C. 8 3π . D. 16π . 3 3 Lời giải Chọn A S N H 60° Ó M TOÁN VD – A B VDC
Gọi S là đỉnh của hình nón và AB là một đường kính của đáy.
Theo bài ra, ta có tam giác SAB là tam giác đều ⇒ l = SA = AB = 2r = 4.
Vậy diện tích xung quanh của hình nón đã cho là S = π rl = π . xq 8
Câu 36: Giá trị nhỏ nhất của hàm số f (x) 3
= x − 24x trên đoạn [2;19] bằng A. 32 2 . B. 40 − . C. 32 − 2 . D. 45 − .
https://www.facebook.com/groups/toanvd.vdc Trang 14 NHÓM TOÁN VD – VDC MÃ ĐỀ 101 Lời giải Chọn C. x = 2 2 ∈[2;19] Ta có f ′(x) 2 = 3x − 24 = 0 ⇔ . x = 2 − 2 ∉ [2;19] f ( ) 3 2 = 2 − 24.2 = 40 − ; f ( )=( )3 2 2 2 2 − 24.2 2 = 32 − 2 ; f ( ) 3
19 =19 − 24.19 = 6403 .
Vậy giá trị nhỏ nhất của hàm số f (x) 3
= x − 24x trên đoạn [2;19] bằng 32 − 2 .
Câu 37: Cho hai số phức z =1+ 2i và w = 3+ i . Môđun của số phức z.w bằng N A. 5 2 . B. 26 . C. 26 . D.50. H Ó Lời giải M T Chọn A. O Á Ta có 2 2
z.w = z . w = z . w = 1+ 2 . 3 +1 = 5 2. N V 2 D
Câu 38: Cho a và b là hai số thực dương thỏa mãn log2(a b) 3 4
= 3a . Giá trị của 2 ab bằng – V A. 3. B. 6 . C. 12. D. 2 . D C Lời giải Chọn A. 2 2 2 Ta có log a b log a b 2 2 ( ) 3 2 ( ) 3 = a ⇔ = a ⇔ ( 2 a b) 3 4 2 3 2 4 3 2 3
= 3a ⇔ a b = 3a ⇔ ab = 3.
Câu 39: Cho hàm số ( ) x f x =
. Họ tất cả các nguyên hàm của hàm số g (x) = (x + )
1 . f ′(x) là 2 x + 2 2 2
A. x + 2x − 2 − + + + + C . B. x 2 x x 2 + C . C. + C .
D. x 2 + C . 2 2 x + 2 2 x + 2 2 x + 2 2 2 x + 2 Lời giải Chọn B. 2 x + ′ x N
Tính g (x) = ∫(x + )1f ′(x)dx = (x + )1 f (x)− ∫(x + )1 f (x)dx = − f ∫ (x)dx 2 H x + 2 Ó 2 + 2 + − M x x x = − dx ∫ x x 2 x 2 = − x + 2 + C = + C. 2 2 2 2 T x + 2 x + 2 x + 2 x + 2 O Á x + N
Câu 40: Tập hợp tất cả các giá trị thực của tham số m để hàm số 4 y =
đồng biến trên khoảng V x + m D (−∞;−7) là – VD A. [4;7) . B. (4;7]. C. (4;7) . D. (4;+ ∞) . C Lời giải Chọn B
Tập xác định: D \ m . Ta có: m − 4 y′ = . (x + m)2
https://www.facebook.com/groups/toanvd.vdc Trang 15 NHÓM TOÁN VD – VDC MÃ ĐỀ 101
Hàm số đã cho đồng biến trên khoảng (−∞;− 7) ⇔ y′ > 0 , x ∀ ∈(−∞;− 7) m − 4 > 0 m > 4 m > 4 ⇔ ⇔ ⇔ ⇔ 4 < m ≤ 7 . −m∉ (−∞;−7) −m ≥ 7 − m ≤ 7
Câu 41: Trong năm 2019, diện tích rừng trồng mới của tỉnh A là 600 ha . Giả sử diện tích rừng trồng
mới của tỉnh A mỗi năm tiếp theo đều tăng 6% so với diện tích rừng trồng mới của năm liền
trước. Kể từ sau năm 2019, năm nào dưới đây là năm đầu tiên tỉnh A có diện tích rừng trồng
mới trong năm đó đạt trên 1000 ha ? A. Năm 2028. B. Năm 2047. C. Năm 2027. D. Năm 2046. N Lời giải H Chọn A. Ó M
Diện tích rừng trồng mới của năm 2019 +1 là ( + )1 600 1 6% . TO
Diện tích rừng trồng mới của năm 2019 + 2 là ( + )2 600 1 6% . ÁN n V
Diện tích rừng trồng mới của năm 2019 + n là 600(1+ 6%) . D – n n 5 5 V
Ta có 600(1+ 6%) >1000 ⇔ (1+ 6%) > ⇔ n > log( ≈ + 8,76 1 6%) D 3 3 C
Như vậy kể từ năm 2019 thì năm 2028 là năm đầu tiên diện tích rừng trồng mới đạt trên 1000 ha .
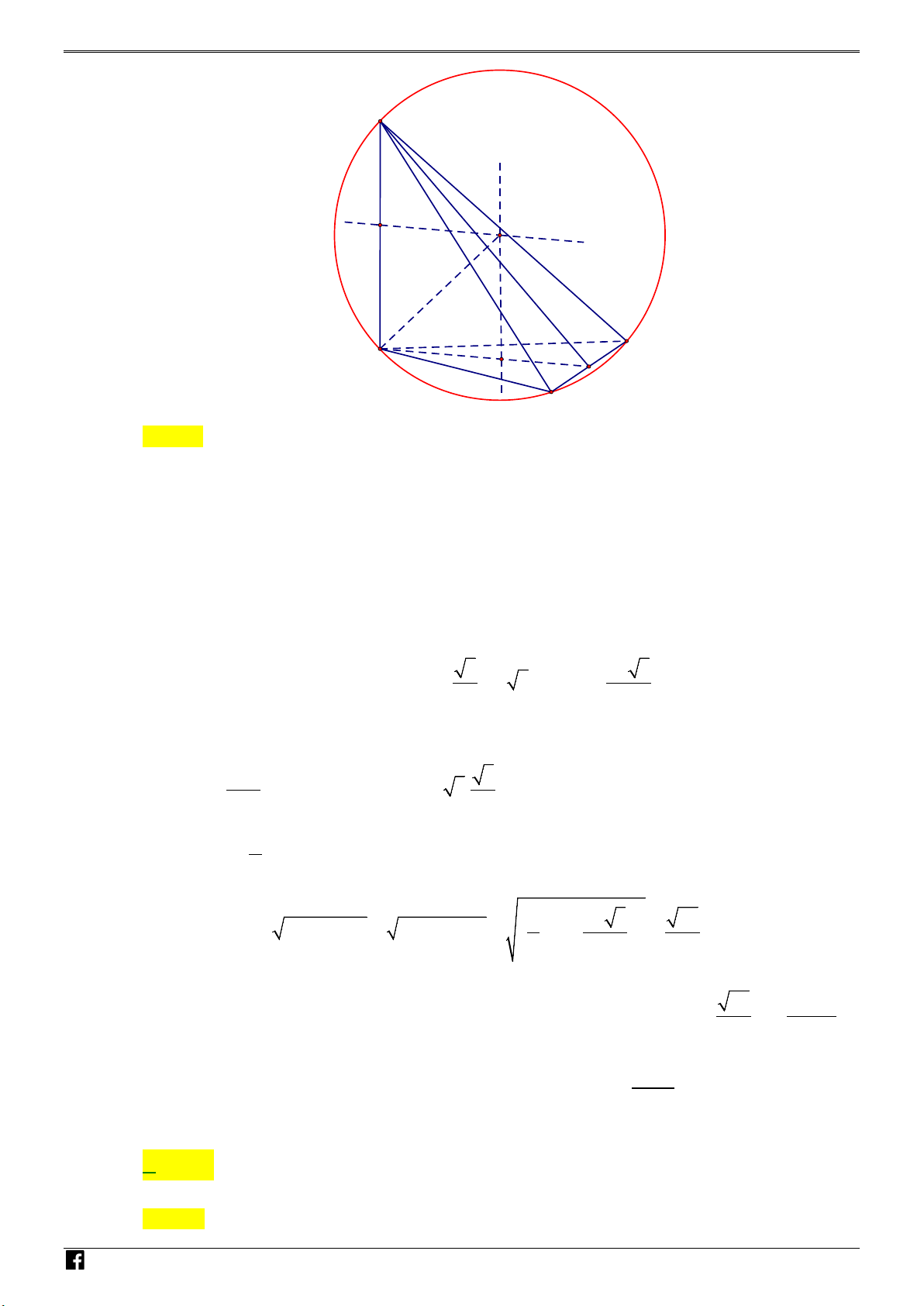
Câu 42: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 4a , SA vuông góc với mặt phẳng đáy, góc
giữa mặt phẳng (SBC) và mặt phẳng đáy bằng 60°. Diện tích của mặt cầu ngoại tiếp hình chóp S.ABC bằng 2 2 2 A. 172πa π π . B. 76 a . C. 2 84πa . D. 172 a 3 3 9 Lời giải Chọn A. N H Ó M TOÁN VD – VDC
Ta có tâm của đáy cũng là giao điểm ba đường cao (ba đường trung tuyến) của tam giác đều a
ABC nên bán kính đường tròn ngoại tiếp đáy là 3 4 3 r = 4 . a = . 3 3
Đường cao AH của tam giác đều a ABC là 4 . 3 AH = = 2 3a . 2
https://www.facebook.com/groups/toanvd.vdc Trang 16 NHÓM TOÁN VD – VDC MÃ ĐỀ 101
Góc giữa mặt phẳng (SBC) và mặt phẳng đáy bằng 60° suy ra SHA = 60°. Suy ra tan SA SA SHA = =
= 3 ⇒ SA = 6a . AH 2 3a 2
Bán kính mặt cầu ngoại tiếp SA 2 2 16 2 129 R = + r = a + a = a . mc 9 2 3 3 2 2
Diện tích mặt cầu ngoại tiếp của hình chóp π a S.ABC là 2 129 172
S = π R = π a = . mc 4 4 3 3
Câu 43: Cho hình lăng trụ đứng ABC.A′B C
′ ′ có tất cả các cạnh bằng a . Gọi M là trung điểm của CC′ NH
(tham khảo hình bên). Khoảng cách từ M đến mặt phẳng ( A′BC) bằng Ó M TOÁN VD – VDC A. 21a . B. 2a . C. 21a . D. 2a . 14 2 7 4 Lời giải Chọn A. N H Ó M TOÁN VD – V
d (M ,( A′BC)) ′ D C M 1 C M
′ ∩( A′BC) = C , suy ra = = . C
d (C ,′( A′BC)) C C ′ 2 2 3 Ta có 1 1 1 a 3 a 3 V = = ′ = = ′ ′ V ′ ′ ′ C C S . ∆ a C A BC ABC A B C . . ABC . . . . 3 3 3 4 12 2 Lại có a 7
A′B = a 2 , CB = a , A′C = a 2 ⇒ S = . A′BC 4
https://www.facebook.com/groups/toanvd.vdc Trang 17 NHÓM TOÁN VD – VDC MÃ ĐỀ 101 3 a 3 3.
Suy ra d (C ,′( A′BC)) 3V ′ ′ a C A BC 12 21 . = = = . 2 S A∆′BC a 7 7 4
Vậy d (M ( A′BC)) 1
= d (C′ ( A′BC)) 1 a 21 a 21 , , = . = . 2 2 7 14
Câu 44: Cho hàm số bậc bốn f (x) có bảng biến thiên như sau: N H Ó M TOÁN V
Số điểm cực trị của hàm số g (x) = x f (x + ) 2 4 1 là D – A. 11. B. 9. C. 7 . D. 5. VD Lời giải C Chọn B.
Ta chọn hàm f (x) 4 2
= 5x −10x + 3 . Đạo hàm
g′(x) = x f (x + ) 2 3 4
+ x f (x + ) f ′(x + ) 3 4 1 2 1 1 = 2x f (x + ) 1 2 f (x + ) 1 + xf ′(x + ) 1 . x = 0 3 2x f (x + ) 1 = 0
Ta có g′(x) = 0 ⇔
⇔ f (x + ) = . f
(x + )+ xf ′(x + ) 1 0 2 1 1 = 0 2 f
(x + )1+ xf ′(x + )1 = 0 x +1 ≈1, 278 x +1≈ 0,606 +) f (x + ) 1 = 0 (*) ⇔ (x + )4 5 1 −10(x + )
1 + 3 = 0 ⇔ x+1≈ 0−,606 N x +1 ≈ 1 − ,278 H Ó
⇒ Phương trình có bốn nghiệm phân biệt khác 0 . M t=x 1 + T
+) f (x + ) + xf ′(x + ) = ⇒ ( 4 2
t − t + ) + (t − )( 3 2 1 1 0 2 5 10 3
1 20t − 20t) = 0 O ÁN t ≈ 1,199 V D t ≈ 0,731 4 3 2 ⇔ − − + + = ⇔
30t 20t 40t 20t 6 0 – t ≈ 0 − ,218 V D t ≈ 1 − ,045 C
⇒ Phương trình có bốn nghiệm phân biệt khác 0 và khác các nghiệm của phương trình (*) .
Vậy số điểm cực trị của hàm số g (x) là 9. Câu 45: Cho hàm số 3 2
y = ax + bx + cx + d (a,b,c,d ∈) có đồ thị là đường cong trong hình bên. Có
bao nhiêu số dương trong các số a , b , c , d ?
https://www.facebook.com/groups/toanvd.vdc Trang 18 NHÓM TOÁN VD – VDC MÃ ĐỀ 101 A. 4 . B. 1. C. 2 . D. 3. Lời giải N Chọn C. H Ó
Ta có lim y = +∞ ⇒ a < 0 . M x→+∞ T
Gọi x , x là hoành độ hai điểm cực trị của hàm số suy ra x , x nghiệm phương trình 1 2 1 2 O Á 2
y′ = 3ax + 2bx + c = 0 nên theo định lý Viet: N V 2b b D
+) Tổng hai nghiệm x + x = −
> 0 ⇒ < 0 ⇒ b > 0. 1 2 3a a – V c D
+) Tích hai nghiệm x x = > 0 ⇒ c < 0 . 1 2 C 3a
Lại có đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên d > 0 .
Vậy có 2 số dương trong các số a , b , c , d .
Câu 46: Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số đôi một khác nhau và các chữ số thuộc tập {1,2,3,4,5,6,7,8, }
9 . Chọn ngẫu nhiên một số thuộc S , xác suất để số đó không có hai chữ số
liên tiếp nào cùng chẵn bằng A. 25 . B. 5 . C. 65 . D. 55 . 42 21 126 126 Lời giải Chọn A Có 4
A cách tạo ra số có 4 chữ số phân biệt từ X = {1,2,3,4,5,6,7,8, }. 9 9 4 ⇒ S = A = 3024. N 9 H ⇒ Ω = . Ó 3024 M
Gọi biến cố A:”chọn ngẫu nhiên một số thuộc S , xác suất để số đó không có hai chữ số liên TO tiếp nào cùng chẵn”. ÁN
Nhận thấy không thể có 3 chữ số chẵn hoặc 4 chữ số chẵn vì lúc đó luôn tồn tại hai chữ số V
chẵn nằm cạnh nhau. D
Trường hợp 1: Cả 4 chữ số đều lẻ. – V
Chọn 4 số lẻ từ X và xếp thứ tự có 4 A số. 5 D C
Trường hợp 2: Có 3 chữ số lẻ, 1 chữ số chẵn.
Chọn 3 chữ số lẻ, 1 chữ số chẵn từ X và xếp thứ tự có 3 1 C .C .4! số. 5 4
Trường hợp 3: Có 2 chữ số chẵn, 2 chữ số lẻ.
Chọn 2 chữ số lẻ, 2 chữ số chẵn từ X có 2 2 C .C cách. 5 4
Xếp thứ tự 2 chữ số lẻ có 2! cách.
Hai chữ số lẻ tạo thành 3 khoảng trống, xếp hai chữ số chẵn vào 3 khoảng trống và sắp thứ tự có 3! cách.
https://www.facebook.com/groups/toanvd.vdc Trang 19 NHÓM TOÁN VD – VDC MÃ ĐỀ 101
⇒ trường hợp này có 2 2 C .C .2!.3! số. 5 4 4 3 1 2 2
ΩA A + C .C .4!+ C .C .2!.3! 25 Vậy P( A) 5 5 4 5 4 = = = . Ω 3024 42
Câu 47: Cho hình chóp đều S.ABCD có cạnh đáy bằng a , cạnh bên bằng 2a và O là tâm của đáy.
Gọi M , N , P , Q lần lượt là các điểm đối xứng với O qua trọng tâm của các tam giác SAB ,
SBC , SCD , SDA và S ' là điểm đối xứng với S qua O . Thể tích của khối chóp S '.MNPQ bằng 3 3 3 3 A. 20 14a . B. 40 14a . C.10 14a . D. 2 14a . 81 81 81 9 N H Lời giải Ó Chọn A. M TOÁN VD – VDC N H Ó
Gọi G ,G ,G ,G lần lượt là trọng tâm SA ∆ B, SB ∆ C, SC ∆ D, SD ∆ A . 1 2 3 4 M
E, F,G, H lần lượt là trung điểm của các cạnh AB, BC,CD, DA . TO 2 Á 4 4 1 8a N Ta có S = S = S = EG HF = . MNPQ
4 GG G G 4. EFGH 4. . . 1 2 3 4 9 9 2 9 VD
d (S ,′(MNPQ)) = d (S ,′( ABCD)) + d (O,(MNPQ)) – V
= d (S,( ABCD)) + 2d (O,(G G G G 1 2 3 4 )) D C 2
= d (S,( ABCD)) + d (S,( ABCD)) 3 5
= d (S ( ABCD)) 5a 14 , = 3 6 2 3 Vậy 1 5a 14 8a 20a 14 V = ⋅ ⋅ = . S .′MNPQ 3 6 9 81
https://www.facebook.com/groups/toanvd.vdc Trang 20 NHÓM TOÁN VD – VDC MÃ ĐỀ 101
Câu 48: Xét các số thực không âm x và y thỏa mãn x y 1 2x .4 y + − +
≥ 3. Giá trị nhỏ nhất của biểu thức 2 2
P = x + y + 4x + 6y bằng A. 33 . B. 65 . C. 49 . D. 57 . 4 8 8 8 Lời giải Chọn B. Cách 1:
Nhận xét: Giá trị của x, y thỏa mãn phương trình x+ y 1 2x y 4 − + ⋅ = 3( )
1 sẽ làm cho biểu thức P
nhỏ nhất. Đặt a = x + y , từ ( ) 1 ta được phương trình N H a 1 − 2 3 4 + .a − 2 − = 0 . Ó y y M T Nhận thấy a 1 − 2 3 = + − −
là hàm số đồng biến theo biến O y 4 .a 2
a , nên phương trình trên có y y ÁN V nghiệm duy nhất 3 3
a = ⇒ x + y = . D 2 2 – 2 1 1 65 65 V
Ta viết lại biểu thức P = (x + y) + 4(x + y) + 2 y − − = . Vậy P = . D 4 8 8 min 8 C Cách 2:
Với mọi x, y không âm ta có 3 3 1 x+ y− 3 3 x+ y x y − + − 2 2 2x + .4 y ≥ 3 ⇔ x + .4 y
≥ ⇔ x + y − + . y 4 −1 ≥ 0 (1) 2 2 3 Nếu 3
x + y − < 0 thì 3 x+ y−2 x + y − + . y 4 −1 < 0 + .y( 0 4 − ) 1 = 0 (vô lí) 2 2 Vậy 3 x + y ≥ . 2
Áp dụng bất đẳng thức Bunhyakovski ta được 2 2
P = x + y + 4x + 6y = (x + 3)2 + ( y + 2)2 −13 N 2 1 2 1 3 65 H
≥ (x + y + 5) −13 ≥ + 5 −13 = Ó 2 2 2 8 M 5 T 3 y = O x + y = 4 Á
Đẳng thức xảy ra khi 2 ⇔ . N 1 + = + x 3 y 2 x = V D 4 – V Vậy 65 min P = . D 8 C
Câu 49: Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 728 số nguyên y thỏa mãn log ( 2
x + y ≥ log (x + y) ? 4 ) 3 A. 59. B. 58. C. 116. D. 115. Lời giải Chọn C.
Với mọi x∈ ta có 2 x ≥ x .
https://www.facebook.com/groups/toanvd.vdc Trang 21 NHÓM TOÁN VD – VDC MÃ ĐỀ 101
Xét hàm số f (y) = log (x + y) − log ( 2 x + y . 3 4 ) Tập xác định D = (− ; x +∞) (do 2
y > −x ⇒ y > −x ). 1 1 f '(y) = − ≥ x ∀ ∈ D (do 2
x + y ≥ x + y > 0 , ln 4 > ln 3) (x + y)ln 3 ( 0, 2 x + y)ln 4
⇒ f tăng trên D .
Ta có f (−x +1) = log (x − x +1) − log ( 2
x − x +1 ≤ 0 . 3 4 )
Có không quá 728 số nguyên y thỏa mãn f ( y) ≤ 0 2 N
⇔ f (−x + 729) > 0 ⇔ log 729 − log x − x + 729 > 0 3 4 ( ) H Ó 2 6
⇔ x − x + 729 − 4 < 0 ⇔ 2
x − x − 3367 < 0 M ⇔ 57 − ,5 ≤ x ≤ 58,5 TO − − Á
Mà x∈ nên x∈{ 57, 56,..., } 58 . N V Vậy có 58 − ( 57
− ) +1 =116 số nguyên x thỏa. D –
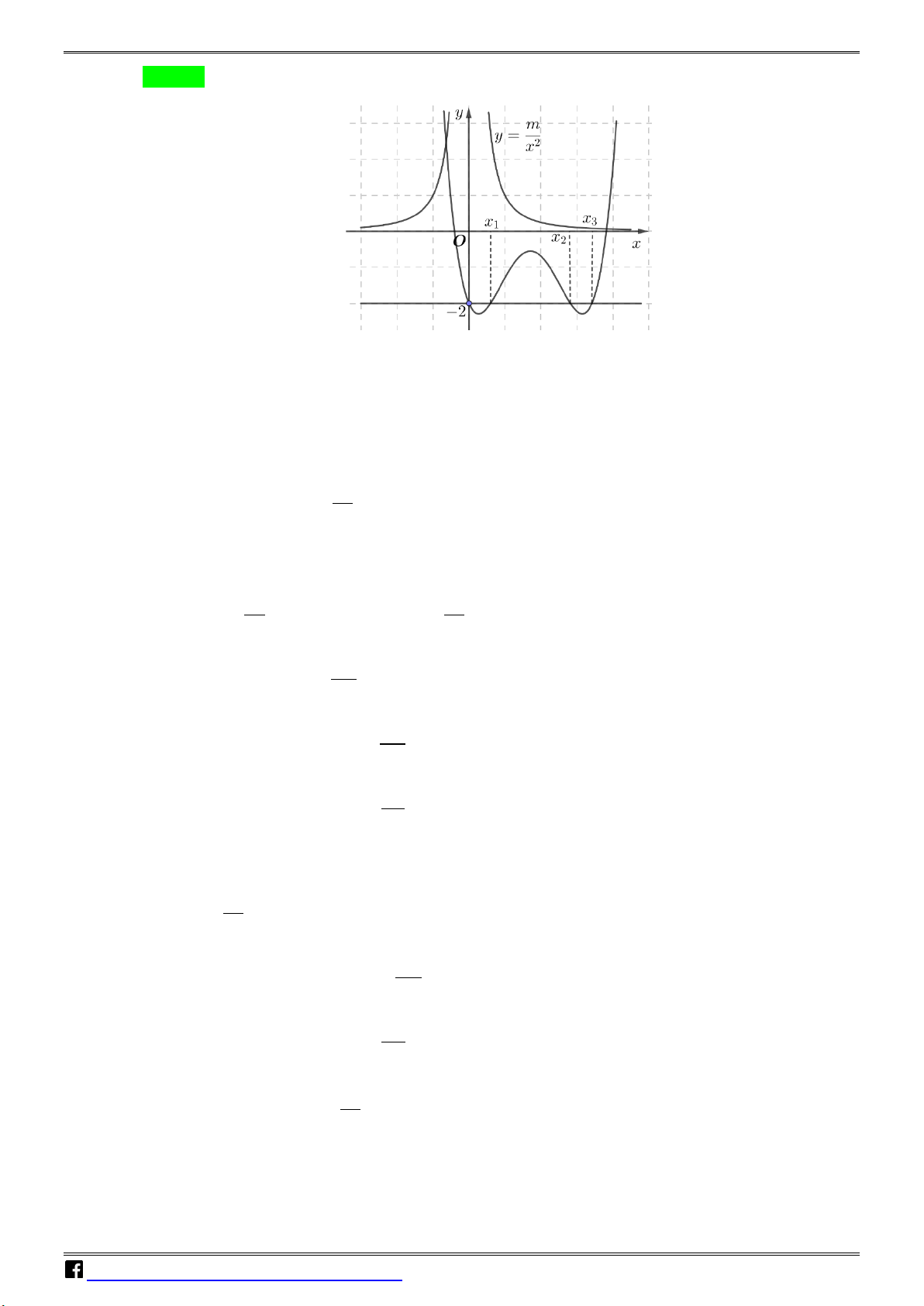
Câu 50: Cho hàm số bậc ba y = f (x) có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt V 3 D
của phương trình f (x f (x)) +1 = 0 là C A. 8 . B. 5. C. 6 . D. 4 . Lời giải Chọn C. x = 0 3 f (x) = = 0 x f (x) 0 N 3 3 3 a H
f (x f (x)) +1 = 0 ⇔ f (x f (x)) = 1
− ⇔ x f (x) = a > 0 ⇔ f (x) = (do x ≠ 0) 3 Ó 3 x = > M
x f (x) b 0 b T f (x) = (do x ≠ 0) 3 O x ÁN VD – VDC •
f (x) = 0 có một nghiệm dương x = c .
https://www.facebook.com/groups/toanvd.vdc Trang 22 NHÓM TOÁN VD – VDC MÃ ĐỀ 101
• Xét phương trình ( ) k f x =
với x ≠ 0, k > 0 . 3 x Đặt ( ) = ( ) k g x f x − . 3 x 3 (′ ) = '( ) k g x f x + . 4 x 3 Với k
x > c , nhìn hình ta ta thấy f (′x) > 0 ⇒ g (′x) = f (′x) + > 0 4 x
⇒ g(x) = 0 có tối đa một nghiệm.
g(c) < 0 N Mặt khác
và g(x) liên tục trên ( ; c +∞) H lim g(x) = +∞ x→+∞ Ó M
⇒ g(x) = 0 có duy nhất nghiệm trên ( ; c +∞) . TO
Với 0 < x < c thì ( ) < 0 k f x <
⇒ g(x) = 0 vô nghiệm. Á 3 x N V 3k D
Với x < 0 , nhìn hình ta ta thấy f (′x) > 0 ⇒ g (′x) = f (′x) + > 0 4 x – V
⇒ g(x) = 0 có tối đa một nghiệm. D C
lim g(x) > 0 − Mặt khác x 0 →
và g(x) liên tục trên ( ;0 −∞ ).
lim g(x) = −∞ x→−∞
⇒ g(x) = 0 có duy nhất nghiệm trên ( ;0 −∞ ).
Tóm lại g(x) = 0 có đúng hai nghiệm trên \{ } 0 .
Suy ra hai phương trình ( ) a f x = , ( ) b f x =
có 4 nghiệm phân biệt khác 0 và khác c . 3 x 3 x
Vậy phương trình f ( 3
x f (x)) +1 = 0 có đúng 6 nghiệm.
-------------------- HẾT -------------------- N H Ó M TOÁN VD – VDC
https://www.facebook.com/groups/toanvd.vdc Trang 23 NHÓM TOÁN VD – VDC MÃ ĐỀ 102
BỘ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Bài thi: TOÁN
Thời gian làm bài: 90 phút (không kể thời gian phát đề) 5 5 Câu 1: Biết f
∫ (x)dx = 4. Giá trị của 3f (x)dx ∫ bằng 1 1 A. 7 . B. 4 . C. 64 . D. 12. 3
Câu 2: Trong không gian Oxyz , hình chiếu vuông góc của điểm A(1;2;5) trên trục Ox có tọa độ là N H A. (0;2;0) . B. (0;0;5) . C. (1;0;0) . D. (0;2;5) . Ó M
Câu 3: Cho hình trụ có bán kính đáy r = 4 và độ dài đường sinh l = 3 . Diện tích xung quanh của hình trụ T đã cho bằng O Á A. 48π . B. 12π . C. 16π . D. 24π . N M 1;
− 3 là điểm biểu diễn số phức z . Phần thực của z bằng V
Câu 4: Trên mặt phẳng tọa độ, biết ( ) D A. 3. B. 1 − . C. 3 − . D. 1. – V
Câu 5: Cho cấp số nhân (u với u = 2 và công bội q = 3. Giá trị của u bằng n ) 1 2 D C A. 6 . B. 9. C. 8 . D. 2 . 3
Câu 6: Cho hai số phức z = 3+ 2i và z = 2 − i . Số phức z + z bằng 1 2 1 2 A. 5 − i . B. 5 + i . C. 5 − − i . D. 5 − + i .
Câu 7: Trong không gian Oxyz , cho mặt cầu (S ) 2 x + ( y − )2 2 :
2 + z = 9 . Bán kính của (S ) bằng A. 6 . B. 18. C. 3. D. 9.
Câu 8: Nghiệm của phương trình log x −1 = 3 là 2 ( ) A. x =10 . B. x = 8. C. x = 9 . D. x = 7 .
Câu 9: Tiệm cận ngang của đồ thị hàm số 5x +1 y = là x −1 A. y =1. B. 1 y = . C. y = 1 − . D. y = 5. 5 N
Câu 10: Cho khối nón có bán kính đáy r = 4 và chiều cao h = 2 . Thể tích của khối nón đã cho bằng H Ó π π A. 8 . B. 8π . C. 32 . D. 32π . M 3 3 TO
Câu 11: Cho hàm số bậc ba y = f (x) có đồ thị là đường cong trong hình bên. Số nghiệm thực của phươ Áng N
trình f (x) =1 là VD – VDC A. 0 . B. 3. C. 1. D. 2 .
Câu 12: Với a , b là các số thực dương tùy ý và a ≠1, log b bằng 2 a
https://www.facebook.com/groups/toanvd.vdc Trang 1 NHÓM TOÁN VD – VDC MÃ ĐỀ 102 A. 1 + log b . B. 1 log b . C. 2 + log b. D. 2log b . 2 a 2 a a a
Câu 13: Nghiệm của phương trình x−2 3 = 9 là A. x = 3 − . B. x = 3. C. x = 4 . D. x = 4 − .
Câu 14: Họ nguyên hàm của hàm số ( ) 3 f x = x là A. 4 4x + C . B. 2 3x + C . C. 4 x + C . D. 1 4 x + C . 4
Câu 15: Cho khối chóp có diện tích đáy B = 3 và chiều cao h = 2 . Thể tích khối chóp đã cho bằng A. 6 . B. 12. C. 2 . D. 3.
Câu 16: Trong không gian Oxyz , cho ba điểm A( 2;
− 0;0), B(0;3;0) và C (0;0;4) . Mặt phẳng ( ABC) có NH phương trình là Ó M A. x y z + + =1. B. x y z + + =1. C. x y z + + = 1. D. x y z + + =1. T 2 − 3 4 2 3 4 2 3 − 4 2 3 4 − O Á
Câu 17: Cho hàm số f (x) có bảng biến thiên như sau. N VD – VDC
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (1;+∞). B. ( 1; − ) 1 . C. (0; ) 1 . D. ( 1; − 0) .
Câu 18: Cho hàm số f (x) có bảng biến thiên như sau.
Giá trị cực đại của hàm số đã cho bằng A. 3. B. 2 . C. 2 − . D. 3 − . x − y + z − N
Câu 19: Trong không gian Oxyz , cho đường thẳng 2 5 2 d : = =
. Vectơ nào dưới đây là m Hột 3 4 1 − Ó
vectơ chỉ phương của d ? M u = 3;4; 1 − . u = 2; 5; − 2 . u = 2;5; 2 − . u = 3;4;1 . T A. B. C. D. 3 ( ) 3 ( ) 1 ( ) 2 ( ) O Á
Câu 20: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? N VD – VDC A. 4 2
y = −x + 2x . B. 3
y = −x + 3x . C. 4 2
y = x − 2x . D. 3
y = x − 3x .
Câu 21: Cho khối cầu có bán kính r = 4. Thể tích của khối cầu đã cho bằng π π A. 64π . B. 64 . C. 256π . D. 256 . 3 3
Câu 22: Có bao nhiêu cách xếp 7 học sinh thành một hàng dọc?
https://www.facebook.com/groups/toanvd.vdc Trang 2 NHÓM TOÁN VD – VDC MÃ ĐỀ 102 A. 7 . B. 5040. C. 1. D. 49 .
Câu 23: Cho khối hộp hình chữ nhật có ba kích thước 2; 4; 6 . Thể tích của khối hộp đã cho bằng A. 16. B. 12. C. 48 . D. 8 .
Câu 24: Số phức liên hợp của số phức z = 2 − + 5i là
A. z = 2 − 5i .
B. z = 2 + 5i . C. z = 2 − + 5i . D. z = 2 − − 5i .
Câu 25: Tập xác định của hàm số y = log x là 6 A. [0;+∞) . B. (0;+∞). C. ( ;0 −∞ ). D. ( ; −∞ +∞) .
Câu 26: Giá trị nhỏ nhất của hàm số f (x) 3
= x − 21x trên đoạn [2;19] bằng A. 36 − . B. 14 − 7 . C. 14 7 . D. 34 − . N
Câu 27: Cho hình chóp S.ABC có đáy là tam giác vuông tại B , AB = 3a, BC = 3a, SA vuông góc vớ HÓi
mặt phẳng đáy và SA = 2a (tham khảo hình vẽ). M S TOÁN VD – A C VDC B
Góc giữa đường thẳng SC và mặt phẳng đáy bằng A. 60 . B. 0 45 . C. 0 30 . D. 0 90 .
Câu 28: Cho hàm f (x) liên tục trên và có bảng xét dấu f ′(x) như sau:
Số điểm cực tiểu của hàm số là A. 1. B. 2 . C. 3. D. 4 .
Câu 29: Trong không gian − +
Oxyz cho điểm M (1;1; 2 x y z − ) và đường thẳng 1 2 d : = = . Mặt phẳng đi 1 2 3 −
qua M và vuông góc với d có phương trình là N H
A. x + 2y −3z −9 = 0. B. x + y − 2z − 6 = 0 . Ó
C. x + 2y −3z + 9 = 0 . D. x + y − 2z + 6 = 0. M log (ab) T
Câu 30: Cho a và b là các số thực dương thỏa mãn 2 4
= 3a . Giá trị của 2 ab bằng O A. 3. B. 6 . C. 2 . D. 12. ÁN
Câu 31: Cho hai số phức z = 2 + 2i
= + . Mô đun của số phức zw và w 2 i VD A. 40 . B. 8. C. 2 2 . D. 2 10 . – V
Câu 32: Diện tích hình phẳng giới hạn bởi hai đường 2
y = x −1 và y = x −1 D π π C A. . B. 13 . C. 13 . D. 1 . 6 6 6 6
Câu 33: Số giao điểm của đồ thị hàm số 3 2
y x x và đồ thị hàm số 2
y x 5x là A. 2 . B. 3. C. 1. D. 0 . 2 Câu 34: Biết ( ) 3
F x = x là một nguyên hàm của hàm số f (x) trên . Giá trị của ∫(2+ f (x))dx bằng 1
https://www.facebook.com/groups/toanvd.vdc Trang 3 NHÓM TOÁN VD – VDC MÃ ĐỀ 102 A. 23 . B. 7 . C. 9. D. 15 . 4 4
Câu 35: Trong không gian Oxyz , cho ba điểm A(1;2;3), B(1;1; )
1 ,C (3;4;0) . Đường thẳng đi qua A và
song song với BC có phương trình là
A. x +1 y + 2 z + 3 − − − = =
. B. x 1 y 2 z 3 = = . 4 5 1 4 5 1
C. x −1 y − 2 z − 3 + + + = =
. D. x 1 y 2 z 3 = = . 2 3 1 − 2 3 1 −
Câu 36: Cho hình nón có bán kính bằng 5 và góc ở đỉnh bằng 60°. Diện tích xung quanh của hình nón đã cho bằng N π π H A. 50π . B. 100 3 . C. 50 3 . D. 100π . Ó 3 3 M x − T
Câu 37: Tập nghiệm của bất phương trình 2 23 3 < 9 là O A. ( 5; − 5) . B. ( ; −∞ 5) . C. (5;+∞) . D. (0;5). ÁN V Câu 38: Gọi z − + = . Trên mặt phẳng tọa
0 là nghiệm phức có phần ảo dương của phương trình 2 z 6z 13 0 D
độ, điểm biểu diễn số phức 1− z là – 0 V A. M ( 2; − 2). B. Q(4; 2 − ) . C. N (4;2) . D. P( 2; − 2 − ) . D C +
Câu 39: Tập hợp tất cả các giá trị thực của tham số m để hàm số x 5 y = đồng biến trên khoảng x + m ( ; −∞ 8 − ) là A. (5;+∞) . B. (5;8]. C. [5;8) . D. (5;8) .
Câu 40: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 4a , SA vuông góc với mặt phẳng đáy, góc giữa
mặt phẳng (SBC) và mặt phẳng đáy bằng 30° . Diện tích mặt cầu ngoại tiếp hình chóp S.ABC bằng 2 π 2 π 2 π A. 2 172 76 76 52π a a a a . B. . C. . D. . 3 9 3
Câu 41: Cho hàm số ( ) x f x =
. Họ tất cả các nguyên hàm của hàm số g (x) = (x + )
1 f ′(x) là x2 + 3 2 + 2 − 3 + 3 2 2 + + 3 − 3 N A. x x + C . B. x + C . C. x x + C . D. x + C . H 2 x2 + 3 2 x2 + 3 x2 + 3 x2 + 3 Ó M
Câu 42: Trong năm 2019, diện tích rừng trồng mới của tỉnh A là 1000 ha. Giả sử diện tích rừng trồng mớ Ti
của tỉnh A mỗi năm tiếp theo đều tăng 6% so với diện tích rừng trồng mới của năm liền trước. K Oể
từ sau năm 2019, năm nào dưới đây là năm đầu tiên tỉnh A có diện tích rừng trồng mới trong nă ÁNm đó đạt trên 1400 ha. V A. 2043. B. 2025. C. 2024 . D. 2042. D –
Câu 43: Cho hình chóp đều S.ABCD có cạnh đáy bằng a , cạnh bên bằng a 3 và O là tâm của đáy. G Vọi
M , N, P,Q lần lượt là các điểm đối xứng với O qua trọng tâm của các tam gi DCác
SAB, SBC, SCD, SDA và S′ là điểm đối xứng với S qua O . Thể tích của khối chóp S .′MNPQ bằ ng A. a3 40 10 . B. a3 10 10 . C. a3 20 10 . D. a3 2 10 . 81 81 81 9
Câu 44: Cho lăng trụ đứng ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh a và AA′ = 2a . Gọi M là trung
điểm của CC′ (tham khảo hình bên). Khoảng cách từ M đến mặt phẳng ( A′BC) bằng
https://www.facebook.com/groups/toanvd.vdc Trang 4 NHÓM TOÁN VD – VDC MÃ ĐỀ 102 N 2 5 2 57 57 H A. a 5 . B. a . C. a . D. a . Ó 5 5 19 19 M
Câu 45: Cho hàm số bậc bốn f (x) có bảng biến thiên như sau: TOÁN VD – VDC
Số điểm cực trị của hàm số g (x) = x f (x − ) 1 4 2 là A. 7 . B. 8 . C. 5. D. 9 .
Câu 46: Cho hàm số y = ax3 + bx2 + cx + d (a,b,c,d ∈ ) có đồ thị là đường cong trong hình bên. Có bao
nhiêu số dương trong các hệ số a,b,c,d ? N H Ó M TOÁN A. 4 . B. 3. C. 1. D. 2 . VD
Câu 47: Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số đôi một khác nhau và các chữ số thuộc tập hợ –p {1, 2, 3, 4, 5, 6, 7, 8, }
9 . Chọn ngẫu nhiên một số thuộc S , xác suất để số đó không có hai chữ s Vố D
liên tiếp nào cùng lẻ bằng C 31 A. 17 . B. 41 . C. . D. 5 . 42 126 126 21
Câu 48: Xét các số thực không âm x và y thỏa mãn x y 1 2x .4 y + − +
≥ 3 . Giá trị nhỏ nhất của biểu thức 2 2
P = x + y + 6x + 4y bằng 49 A. 65 . B. 33 . C. . D. 57 . 8 4 8 8
https://www.facebook.com/groups/toanvd.vdc Trang 5 NHÓM TOÁN VD – VDC MÃ ĐỀ 102
Câu 49: Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 242 số nguyên y thỏa mãn log ( 2
x + y ≥ log x + y ? 4 ) 3 ( ) A. 55. B. 28 . C. 29 . D. 56.
Câu 50: Cho hàm số f (x) có đồ thị là đường cong như hình vẽ bên dưới. N H Ó M
Số nghiệm thực phân biệt của phương trình f ( 3
x f (x)) +1= 0 là TO A. 6 . B. 4 . C. 5. D. 8. ÁN V
-------------------- HẾT -------------------- D – VDC N H Ó M TOÁN VD – VDC
https://www.facebook.com/groups/toanvd.vdc Trang 6 NHÓM TOÁN VD – VDC MÃ ĐỀ 102
BẢNG ĐÁP ÁN - MÃ ĐỀ 102 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D C D B A B C C D C B B C D C A C B A A D B C D B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B C B A A A D D C C A A D B D D B B D C C A A D A ĐÁP ÁN CHI TIẾT 5 5 Câu 1: Biết f
∫ (x)dx = 4. Giá trị của 3f (x)dx ∫ bằng 1 1 A. 7 . B. 4 . C. 64 . D. 12. 3 N H Lời giải Ó Chọn D M 5 5 T Ta có 3 f
∫ (x)dx = 3 f
∫ (x)dx = 3.4 =12. O 1 1 ÁN
Câu 2: Trong không gian Oxyz , hình chiếu vuông góc của điểm A(1;2;5) trên trục Ox có tọa độ là VD A. (0;2;0) . B. (0;0;5) . C. (1;0;0) . D. (0;2;5) . – Lời giải VD Chọn C C
Hình chiếu vuông góc của điểm A(1;2;5) trên trục Ox có tọa độ là (1;0;0) .
Câu 3: Cho hình trụ có bán kính đáy r = 4 và độ dài đường sinh l = 3. Diện tích xung quanh của hình trụ đã cho bằng A. 48π . B. 12π . C. 16π . D. 24π . Lời giải Chọn D
Diện tích xung quanh của hình trụ đã cho là S = 2π rl = 2π.4.3 = 24π .
Câu 4: Trên mặt phẳng tọa độ, biết M ( 1;
− 3) là điểm biểu diễn số phức z . Phần thực của z bằng A. 3. B. 1 − . C. 3 − . D. 1. Lời giải Chọn B Ta có M ( 1;
− 3) là điểm biểu diễn số phức z ⇒ z = 1 − + 3i .
Vậy phần thực của z bằng 1 − .
Câu 5: Cho cấp số nhân (u với u = 2 và công bội q = 3. Giá trị của u bằng n ) N 1 2 H Ó A. 6 . B. 9. C. 8 . D. 2 . M 3 T Lời giải O Chọn A ÁN
Ta có u = u q = 2.3 = 6 . 2 1 V
= + và = − . Số phức + bằng D
Câu 6: Cho hai số phức z 3 2i z 2 i z z 1 2 1 2 – A. 5 − i . B. 5 + i . C. 5 − − i . D. 5 − + i . V Lời giải D C Chọn B
Ta có z + z = 3+ 2i + 2 − i = 5 + i . 1 2
Câu 7: Trong không gian Oxyz , cho mặt cầu (S ) 2 x + ( y − )2 2 :
2 + z = 9 . Bán kính của (S ) bằng A. 6 . B. 18. C. 3. D. 9. Lời giải Chọn C
Bán kính của (S ) là R = 9 = 3 .
https://www.facebook.com/groups/toanvd.vdc Trang 7 NHÓM TOÁN VD – VDC MÃ ĐỀ 102
Câu 8: Nghiệm của phương trình log x −1 = 3 là 2 ( ) A. x =10 . B. x = 8. C. x = 9 . D. x = 7 . Lời giải Chọn C x −1 > 0 x >1
Ta có log x −1 = 3 ⇔ ⇔ ⇔ x = 9 . 2 ( ) 3 x −1 = 2 x = 9
Câu 9: Tiệm cận ngang của đồ thị hàm số 5x +1 y = là x −1 A. y =1. B. 1 y = . C. y = 1 − . D. y = 5. 5 N Lời giải H Ó Chọn D M 5x +1 lim y = lim = 5 T x→+∞ x→+∞ x −1 O Ta có
⇒ y = 5 là tiệm cận ngang của đồ thị hàm số. Á 5x +1 N lim y = lim = 5 x→−∞ x→−∞ − V x 1 D
Câu 10: Cho khối nón có bán kính đáy r = 4 và chiều cao h = 2 . Thể tích của khối nón đã cho bằng – π π V A. 8 . B. 8π . C. 32 . D. 32π . D 3 3 C Lời giải Chọn C π
Thể tích của khối nón đã cho là 1 2 1 2 32
V = π r h = π.4 .2 = . 3 3 3
Câu 11: Cho hàm số bậc ba y = f (x) có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương
trình f (x) =1 là N H Ó A. 0 . B. 3. C. 1. D. 2 . M Lời giải T Chọn B O Á
Ta thấy đường thẳng y =1 cắt đồ thị hàm số y = f (x) tại 3 điểm phân biệt nên phương trình N V
f (x) =1 có 3 nghiệm. D Câu 12:
a ≠ , log b bằng –
Với a , b là các số thực dương tùy ý và 1 2 a VD A. 1 + log b . B. 1 log b . C. 2 + log b. D. 2log b . C 2 a 2 a a a Lời giải Chọn B Ta có 1 log b = log b . 2 a 2 a
Câu 13: Nghiệm của phương trình x−2 3 = 9 là A. x = 3 − . B. x = 3. C. x = 4 . D. x = 4 − .
https://www.facebook.com/groups/toanvd.vdc Trang 8 NHÓM TOÁN VD – VDC MÃ ĐỀ 102 Lời giải Chọn C Ta có x−2
3 = 9 ⇔ x − 2 = 2 ⇔ x = 4 .
Câu 14: Họ nguyên hàm của hàm số ( ) 3 f x = x là A. 4 4x + C . B. 2 3x + C . C. 4 x + C . D. 1 4 x + C . 4 Lời giải Chọn D 4 Ta có 3d x x x = + C ∫ . 4 N
Câu 15: Cho khối chóp có diện tích đáy B = 3 và chiều cao h = 2 . Thể tích khối chóp đã cho bằng H A. 6 . B. 12. C. 2 . D. 3. Ó Lời giải M Chọn C TO
Thể tích khối chóp đã cho là 1 1
V = Bh = .3.2 = 2 . ÁN 3 3 VD A 2;
− 0;0 , B 0;3;0 và C 0;0;4 . Mặt phẳng có
Câu 16: Trong không gian Oxyz , cho ba điểm ( ) ( ) ( ) ( ABC) – V phương trình là D x y z x y z x y z x y z C A. + + =1. B. + + =1. C. + + = 1. D. + + =1. 2 − 3 4 2 3 4 2 3 − 4 2 3 4 − Lời giải Chọn A
Mặt phẳng ( ABC) có phương trình là x y z + + =1. 2 − 3 4
Câu 17: Cho hàm số f (x) có bảng biến thiên như sau.
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (1;+∞). B. ( 1; − ) 1 . C. (0; ) 1 . D. ( 1; − 0) . N H Lời giải Ó Chọn C M
Dựa vào bảng biến thiên, ta thấy hàm số đã cho đồng biến trên các khoảng ( ; −∞ − ) 1 và (0; ) 1 . TOÁ
Câu 18: Cho hàm số f (x) có bảng biến thiên như sau. N VD – VDC
Giá trị cực đại của hàm số đã cho bằng A. 3. B. 2 . C. 2 − . D. 3 − . Lời giải Chọn B
Dựa vào bảng biến thiên, ta thấy giá trị cực đại của hàm số đã cho là y = . CĐ 2
https://www.facebook.com/groups/toanvd.vdc Trang 9 NHÓM TOÁN VD – VDC MÃ ĐỀ 102
Câu 19: Trong không gian − + −
Oxyz , cho đường thẳng
x 2 y 5 z 2 d : = =
. Vectơ nào dưới đây là một 3 4 1 −
vectơ chỉ phương của d ? A. u = 3;4; 1 − . B. u = 2; 5; − 2 . C. u = 2;5; 2 − . D. u = 3;4;1 . 3 ( ) 3 ( ) 1 ( ) 2 ( ) Lời giải Chọn A Đường thẳng
x − 2 y + 5 z − 2 d : = =
có một vectơ chỉ phương là u = 3;4; 1 − . 2 ( ) 3 4 1 −
Câu 20: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? N H Ó M TOÁN VD A. 4 2
y = −x + 2x . B. 3
y = −x + 3x . C. 4 2
y = x − 2x . D. 3
y = x − 3x . – Lời giải V Chọn A D C
Đường cong trong hình là đồ thị hàm trùng phương 4 2
y = ax + bx + c (a ≠ 0) có hệ số a < 0 .
Câu 21: Cho khối cầu có bán kính r = 4. Thể tích của khối cầu đã cho bằng π π A. 64π . B. 64 . C. 256π . D. 256 . 3 3 Lời giải Chọn D π
Thể tích của khối cầu đã cho bằng 4 3 4 3 256
V = π R = π.4 = . 3 3 3
Câu 22: Có bao nhiêu cách xếp 7 học sinh thành một hàng dọc? A. 7 . B. 5040. C. 1. D. 49 . Lời giải Chọn B
Xếp 7 học sinh thành một hàng dọc có 7!= 5040 cách.
Câu 23: Cho khối hộp hình chữ nhật có ba kích thước 2; 4; 6 . Thể tích của khối hộp đã cho bằng N A. 16. B. 12. C. 48 . D. 8 . H Ó Lời giải M Chọn C T
Thể tích của khối hộp đã cho bằng 2.4.6 = 48. O
Câu 24: Số phức liên hợp của số phức z = 2 − + 5i là ÁN
A. z = 2 − 5i .
B. z = 2 + 5i . C. z = 2 − + 5i . D. z = 2 − − 5i . V Lời giải D Chọn D –
Số phức liên hợp của số phức z = 2
− + 5i là z = 2 − − 5i . VD
Câu 25: Tập xác định của hàm số y = log x là C 6 A. [0;+∞) . B. (0;+∞). C. ( ;0 −∞ ). D. ( ; −∞ +∞) . Lời giải Chọn B
Điều kiện: x > 0.
Vậy tập xác định của hàm số đã cho là D = (0;+∞).
Câu 26: Giá trị nhỏ nhất của hàm số f (x) 3
= x − 21x trên đoạn [2;19] bằng
https://www.facebook.com/groups/toanvd.vdc Trang 10 NHÓM TOÁN VD – VDC MÃ ĐỀ 102 A. 36 − . B. 14 − 7 . C. 14 7 . D. 34 − . Lời giải Chọn B x = − 7 ∉ 2;19 2 [ ]
Trên đoạn [2;19], ta có: y′ = 3x − 21⇒ y′ = 0 ⇔ . x = 7 ∈ [2;19] Ta có: y(2) = 34 − ; y ( 7) = 14 −
7; y (19) = 6460 . Vậy m = 14 − 7 .
Câu 27: Cho hình chóp S.ABC có đáy là tam giác vuông tại B , AB = 3a, BC = 3a, SA vuông góc với
mặt phẳng đáy và SA = 2a (tham khảo hình vẽ). S N H Ó M TO A C ÁN VD – B VD
Góc giữa đường thẳng SC và mặt phẳng đáy bằng C A. 60 . B. 0 45 . C. 0 30 . D. 0 90 . Lời giải Chọn C
Ta có: SC ABC ; SCA SA 2a 3 0 tan SCA SCA 30 . AC
a a2 2 3 3 3
Vậy SC ABC o ; 30 .
Câu 28: Cho hàm f (x) liên tục trên và có bảng xét dấu f ′(x) như sau: N
Số điểm cực tiểu của hàm số là H Ó A. 1. B. 2 . C. 3. D. 4 . M Lời giải T Chọn B O
Ta thấy f ′(x)
− sang (+) khi qua các điểm x = 1; − x =1 Á đổi dấu 2 lần từ ( )
nên hàm số có 2 điể N m cực tiểu. VD Câu 29: M x y z − . Mặt phẳng
Trong không gian Oxyz cho điểm (1;1; 2) d − + = = – và đường thẳng 1 2 : đi 1 2 3 − VD
qua M và vuông góc với d có phương trình là C
A. x + 2y −3z −9 = 0. B. x + y − 2z − 6 = 0 .
C. x + 2y − 3z + 9 = 0 . D. x + y − 2z + 6 = 0. Lời giải Chọn A
Mặt phẳng đi qua M (1;1; 2
− ) và vuông góc với d nhận véc tơ n(1;2; 3)
− làm véc tơ pháp tuyến nên
có phương trình: x −1+ 2(y −1) − 3(z + 2) = 0 ⇔ x + 2y − 3z − 9 = 0
Câu 30: Cho a và b là các số thực dương thỏa mãn log2(ab) 4
= 3a . Giá trị của 2 ab bằng
https://www.facebook.com/groups/toanvd.vdc Trang 11 NHÓM TOÁN VD – VDC MÃ ĐỀ 102 A. 3. B. 6 . C. 2 . D. 12. Lời giải Chọn A
Từ giả thiết ta có : log2(ab) 4 = 3a
⇔ log (ab).log 4 = log (3a) 2 2 2
⇔ 2(log a + log b) = log a + log 3 2 2 2 2
⇔ log a + 2log b = log 3 2 2 2 2 ⇔ log (ab ) = log 3 2 2 2 ⇔ ab = 3
Câu 31: Cho hai số phức z = 2+ 2i và w = 2+i. Mô đun của số phức zw N H A. 40 . B. 8. C. 2 2 . D. 2 10 . Ó Lời giải M Chọn D TO
zw = (2 + 2i)(2 − i) = 6 + 2i = 2 10 ÁN
Câu 32: Diện tích hình phẳng giới hạn bởi hai đường 2
y = x −1 và y = x −1 VD π π A. . B. 13 . C. 13 . D. 1 . – 6 6 6 6 VD Lời giải C Chọn D x = 0
Phương trình hoành độ giao điểm hai đường là: 2 2
x −1 = x −1 ⇔ x − x = 0 ⇔ . x =1 1
Diện tích hình phẳng giới hạn bởi hai đường là 2 1
x − x dx = ∫ . 6 0
Câu 33: Số giao điểm của đồ thị hàm số 3 2
y x x và đồ thị hàm số 2
y x 5x là A. 2 . B. 3. C. 1. D. 0 . Lời giải Chọn B
Số giao điểm của đồ thị hàm số 3 2
y x x và đồ thị hàm số 2
y x 5x chính là số nghiệm x 0 thực của phương trình 3 2 2 3
x x x 5x x 5x 0 . x 5 2 N H Câu 34: Biết ( ) 3
F x = x là một nguyên hàm của hàm số f (x) trên . Giá trị của ∫(2+ f (x))dx bằng Ó 1 M . . T A. 23 B. 7 . C. 9. D. 15 O 4 4 Á Lời giải N Chọn C V 2 2 2 D 2 2 2 2 3
Ta có ∫(2+ f (x))dx = 2dx + f (x)dx = 2x + F(x) = 2x + x = 9 – ∫ ∫ 1 1 1 1 V 1 1 1 D
Câu 35: Trong không gian Oxyz , cho ba điểm A(1;2;3), B(1;1; )
1 ,C (3;4;0) . Đường thẳng đi qua A C và
song song với BC có phương trình là
A. x +1 y + 2 z + 3 − − − = =
. B. x 1 y 2 z 3 = = . 4 5 1 4 5 1
C. x −1 y − 2 z − 3 + + + = =
. D. x 1 y 2 z 3 = = . 2 3 1 − 2 3 1 −Lời giải Chọn C
https://www.facebook.com/groups/toanvd.vdc Trang 12 NHÓM TOÁN VD – VDC MÃ ĐỀ 102 Ta có BC = (2;3;− )
1 , đường thẳng song song nên có vec tơ chỉ phương cùng phương với BC = (2;3;− ) 1 .
Do vậy đường thẳng đi qua A và song song với BC có phương trình là
x −1 y − 2 z − 3 = = 2 3 1 −
Câu 36: Cho hình nón có bán kính bằng 5 và góc ở đỉnh bằng 60°. Diện tích xung quanh của hình nón đã cho bằng A. 50π . B. 100 3π . C. 50 3π . D. 100π . 3 3 Lời giải N Chọn A H Ó
Ta có độ dài đường sinh là r 5 l = = = 10 . M α sin 30° sin T 2 O Á
Diện tích xung quanh S = π rl = π . xq 50 N x − V
Câu 37: Tập nghiệm của bất phương trình 2 23 3 < 9 D là 5; − 5 ; −∞ 5 5;+∞ 0;5 – A. ( ). B. ( ). C. ( ). D. ( ). V Lời giải D C Chọn A Ta có 2x−23 2 2 3
< 9 ⇔ x − 23 < 2 ⇔ x < 25 ⇔ 5 − < x < 5 .
Vậy nghiệm của bất phương trình 2x−23 3 < 9 là ( 5; − 5) . Câu 38: Gọi z − + = . Trên mặt phẳng tọa
0 là nghiệm phức có phần ảo dương của phương trình 2 z 6z 13 0
độ, điểm biểu diễn số phức 1− z là 0 A. M ( 2; − 2). B. Q(4; 2 − ) . C. N (4;2) . D. P( 2; − 2 − ) . Lời giải Chọn D
z = 3+ 2i(TM ) Ta có 2
z − 6z +13 = 0 ⇔ . z = 3 − 2i (L)
Suy ra 1− z =1− 3+ 2i = 2
− − 2i . Điểm biểu diễn số phức 1− z là P( 2; − 2 − ) . 0 ( ) 0 x + N
Câu 39: Tập hợp tất cả các giá trị thực của tham số m để hàm số 5 y =
đồng biến trên khoản Hg x + m Ó ( ; −∞ 8 − ) M là T A. (5;+∞) . B. (5;8]. C. [5;8) . D. (5;8) . O Á Lời giải N Chọn B VD
Điều kiện x ≠ −m . – m − 5 Ta có y′ = VD (x + m)2 C Để hàm số x + 5 y =
đồng biến trên khoảng ( ; −∞ 8 − ) x + m thì y′ > 0 m − 5 > 0 ⇒ ⇒ < ≤ . −m∉ (−∞ − ) 5 m 8 ; 8 −m ≥ 8 −
https://www.facebook.com/groups/toanvd.vdc Trang 13 NHÓM TOÁN VD – VDC MÃ ĐỀ 102
Câu 40: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 4a , SA vuông góc với mặt phẳng đáy, góc giữa
mặt phẳng (SBC) và mặt phẳng đáy bằng 30° . Diện tích mặt cầu ngoại tiếp hình chóp S.ABC bằng 2 π 2 π 2 π A. 2 172 76 76 52π a a a a . B. . C. . D. . 3 9 3 Lời giải Chọn D d S N H Ó P I M TOÁN A C VD G N M – VD B C Gọi
M , N, P lần lượt là trung điểm của BC, AB, SA
Gọi G là trọng tâm tam giác đồng thời là tâm đường tròn ngoại tiếp tam giác ABC .
Qua G ta dựng đường thẳng d vuông góc mặt đáy.
Kẻ đường trung trực SA cắt đường thẳng d tại I , khi đó I là tâm mặt cầu ngoại tiếp khối chóp S.ABC .
Ta có ((SBC),( ABC)) = SMA = 30°, 3 3
⇒ SA = AM.tan 30° = 4 . a . = 2a SA ⇒ AP = = a 2 3 2 2 2 3 4a 3 4a 3 AG = AM = .4 . a = ⇒ PI = AG = 3 3 2 3 3 2
Xét tam giác API vuông tại P có 2 2 2 4a 3 a 57
AI = AP + PI = a + = . 3 3 N H Bán kính a 57 R = AI = . Ó 3 M 2 π a T Diện tích mặt cầu 2 76 S = 4π R = O 3 ÁN
Câu 41: Cho hàm số ( ) x f x =
. Họ tất cả các nguyên hàm của hàm số g (x) = (x + )
1 f ′(x) là V 2 D x + 3 2 2 – + 2 − 3 + 3 2 + + 3 − 3 V A. x x + C . B. x + C . C. x x + C . D. x + C . 2 2 2 2 D 2 x + 3 2 x + 3 x + 3 x + 3 C Lời giải Chọn D
Ta có ∫(x + ) f ′(x) x = (x + ) f (x) x x − 3 1 d 1 − dx = + C ∫ . 2 2 x + 3 x + 3
Câu 42: Trong năm 2019, diện tích rừng trồng mới của tỉnh A là 1000 ha. Giả sử diện tích rừng trồng mới
của tỉnh A mỗi năm tiếp theo đều tăng 6% so với diện tích rừng trồng mới của năm liền trước. Kể
https://www.facebook.com/groups/toanvd.vdc Trang 14 NHÓM TOÁN VD – VDC MÃ ĐỀ 102
từ sau năm 2019, năm nào dưới đây là năm đầu tiên tỉnh A có diện tích rừng trồng mới trong năm đó đạt trên 1400 ha. A. 2043. B. 2025. C. 2024 . D. 2042. Lời giải Chọn B
Ta có sau n năm thì diện tích rừng trồng mới của tỉnh A là: 1000.(1 0.06)n +
Khi đó, 1000.(1+ 0.06)n >1400 ⇒ 1. n
06 > 1.4 ⇒ n > 5.774 .
Vậy vào năm 2025 thì diện tích rừng trong mới trong năm đó đạt trên 1400 ha.
Câu 43: Cho hình chóp đều S.ABCD có cạnh đáy bằng a , cạnh bên bằng a 3 và O là tâm của đáy. Gọi
M , N, P,Q lần lượt là các điểm đối xứng với O qua trọng tâm của các tam giác N
SAB, SBC, SCD, SDA và S′ là điểm đối xứng với S qua O . Thể tích của khối chóp S .′MNPQ bằng HÓM A. a3 40 10 . B. a3 10 10 . C. a3 20 10 . D. a3 2 10 . 81 81 81 9 TO Lời giải Á Chọn B N VD S – M VDC Q N P G1 G2 G4 G3 B A O a D C N H Ó M T S' O Á Ta gọi G
lần lượt là trọng tâm của tam giác SAB, SBC, SCD, SDA thì
1, G2 , G3 , G N 4 V 5 5 5 D
d (S ,′(MNPQ)) = d (O,(MNPQ)) ⇒V = = ′ V V S MNPQ O MNPQ .8 . . O. 1 G 2 G 3 G 4 G 2 2 2 – 3 V 2
20 1 a 10 2 10 10a D = 10V = V = a = . S G G G G 10. S ABCD . . . . 1 2 3 4 . C 27 27 3 2 81
Câu 44: Cho lăng trụ đứng ABC.A′B C
′ ′ có đáy ABC là tam giác đều cạnh a và AA′ = 2a . Gọi M là trung
điểm của CC′ (tham khảo hình bên). Khoảng cách từ M đến mặt phẳng ( A′BC) bằng
https://www.facebook.com/groups/toanvd.vdc Trang 15 NHÓM TOÁN VD – VDC MÃ ĐỀ 102 N 2 5 2 57 57 H A. a 5 . B. a . C. a . D. a . Ó 5 5 19 19 M Lời giải T Chọn D O ′ Á
Gọi H, K lần lượt là hình chiếu của A lên BC và A H . N VD – VDC K H
Ta có d (M ( A′BC)) 1
= d (C′ ( A′BC)) 1
= d ( A ( A′BC)) 1 , , , = AK . 2 2 2 ′ Mà a 3 AH =
; AA′ = 2a nên AH.AA 2a 57 AK = = . 2 2 2 AH + AA′ 19
Vậy d (M ( A′BC)) a 57 ; = . 19 N
Câu 45: Cho hàm số bậc bốn f (x) có bảng biến thiên như sau: H Ó M TOÁN VD – VDC 4
Số điểm cực trị của hàm số g (x) = x2 f (x − ) 1 là A. 7 . B. 8 . C. 5. D. 9 . Lời giải Chọn C
Ta có g′(x) = x f (x − ) 4
+ x f ′(x − ) f (x − ) 3
= x f (x − ) 3 2 2 . 1 4 1 1 2 . 1
( f ( x − )
1 + 2xf ′(x − ) 1 )
https://www.facebook.com/groups/toanvd.vdc Trang 16 NHÓM TOÁN VD – VDC MÃ ĐỀ 102 x = 0
Vậy g′(x) = 0 ⇒ f (x − ) 1 = 0 ( ) 1
f (x− )1+2xf ′(x− )1 = 0 (2) Phương trình ( ) 1 có 4 nghiệm phân biệt
Phương trình (2) có f (x − ) 1 = 2
− xf ′(x − ) 1 ⇒ f (x) = 2 − (x + ) 1 f ′(x)
Từ bảng biến thiên suy ra hàm f (x) là bậc bốn trùng phương nên ta có
f (x) = − x4 + x2 3 6
−1 thay vào f (x) = 2 − (x + )
1 f ′(x) vô nghiệm
Vậy hàm g (x) có 5 điểm cực trị. N
Câu 46: Cho hàm số y = ax3 + bx2 + cx + d (a,b,c,d ∈ ) có đồ thị là đường cong trong hình bên. Có bao HÓ
nhiêu số dương trong các hệ số a,b,c,d ? M TOÁN VD – VDC A. 4 . B. 3. C. 1. D. 2 . Lời giải Chọn C
Ta có lim f (x) = −∞ ⇒ a < 0 x→+∞
Đồ thị hàm số có hai điểm cực trị nằm cùng phía của trục tung nên ac > 0 ⇒ c < 0
Đồ thị hàm số có điểm uốn nằm bên phải trục tung nên ab < 0 ⇒ b > 0
Đồ thị hàm số cắt trục tung ở dưới trục hoành ⇒ d < 0
Câu 47: Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số đôi một khác nhau và các chữ số thuộc tập hợp {1, 2, 3, 4, 5, 6, 7, 8, }
9 . Chọn ngẫu nhiên một số thuộc S , xác suất để số đó không có hai chữ số
liên tiếp nào cùng lẻ bằng N 31 H A. 17 . B. 41 . C. . D. 5 . Ó 42 126 126 21 M Lời giải T Chọn A O Á
Số các phần tử của S là 4 A = 3024 . 9 N V
Chọn ngẫu nhiên một số từ tập S có 3024 (cách chọn). Suy ra n(Ω) = 3024. D
Gọi biến cố A: “ Chọn được số không có hai chữ số liên tiếp nào cùng lẻ”. – V
Trường hợp 1: Số được chọn có 4 chữ số chẵn, có 4!= 24 (số). D
Trường hợp 2: Số được chọn có = (số). C
1 chữ số lẻ và 3 chữ số chẵn, có 5.4.4! 480
Trường hợp 3: Số được chọn có 2 chữ số lẻ và 2 chữ số chẵn, có 2 2
3.A .A = 720 (số). 5 4
Do đó, n( A) = 24 + 480 + 720 =1224 . n A
Vậy xác suất cần tìm là P( A) ( ) 1224 17 = = = . n(Ω) 3024 42
https://www.facebook.com/groups/toanvd.vdc Trang 17 NHÓM TOÁN VD – VDC MÃ ĐỀ 102
Câu 48: Xét các số thực không âm x và y thỏa mãn x y 1 2x .4 y + − +
≥ 3 . Giá trị nhỏ nhất của biểu thức 2 2
P = x + y + 6x + 4y bằng 49 A. 65 . B. 33 . C. . D. 57 . 8 4 8 8 Lời giải Chọn A Ta có x+ y 1 − 2x+2 y−2 2x + .4 y ≥ 3 ⇔ .2 y ≥ 3− 2x 2 y ( ) 3 2 2 .2 3 2 .2 x y x − ⇔ ≥ − (*) Hàm số ( ) = .2t f t
t đồng biến trên , nên từ (*) ta suy ra 2y ≥ 3− 2x ⇔ 2x + 2y −3 ≥ 0 ( ) 1 Ta thấy ( )
1 bất phương trình bậc nhất có miền nghiệm là nửa mặt phẳng có bờ là đường thẳng N
d : 2x + 2y − 3 = 0 (phần không chứa gốc tọa độ O ), kể cả các điểm thuộc đường thẳng d . H Ó 2 2 2 2 M
Xét biểu thức P = x + y + 6x + 4y ⇔ (x + 3) + ( y + 2) = P +13 (2) T
Để P tồn tại thì ta phải có P +13 ≥ 0 ⇔ P ≥ 13 − . O Á
Trường hợp 1: Nếu P = 13 − thì x = 3 − ; y = 2 − không thỏa ( )
1 . Do đó, trường hợp này không thể N V xảy ra. D
Trường hợp 2: Với P > 13
− , ta thấy (2) là đường tròn (C) có tâm I ( 3 − ; 2 − ) và bán kí – nh V R = P +13 . D C
Để d và (C) có điểm chung thì d (I d ) 13 65 ; ≤ R ⇔
≤ P +13 ⇔ P ≥ . 2 2 8 Vậy 65 min P = 8
Câu 49: Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 242 số nguyên y thỏa mãn log ( 2
x + y ≥ log x + y ? 4 ) 3 ( ) A. 55. B. 28 . C. 29 . D. 56. Lời giải Chọn D 2 x + y > 0 Điều kiện: . x + y > 0 2
x + y ≥ 4t 2
x − x ≥ 4t − 3t (*) Đặt + = , ta có ⇔ . N log x y t 3 ( ) t t H x + y = 3
y = 3 − x Ó t t M
Nhận xét rằng hàm số f (t) = 4 −3 đồng biến trên khoảng (0;+∞) và f (t) > 0 với mọi t > 0 T
Gọi n∈ thỏa n n 2
4 − 3 = x − x , khi đó (*) ⇔ t ≤ n O Á t n N
Từ đó, ta có −x < y = 3 − x ≤ 3 − x . n V
Mặt khác, vì có không quá 242 số nguyên y thỏa mãn đề bài nên 3 ≤ 242 ⇔ n ≤ log 242 . D 3 – Từ đó, suy ra 2 log3 242 x − x ≤ 4 − 242 ⇔ 27, − 4 ≤ x ≤ 28,4 . VD
Mà x∈ nên x∈{ 27, − − 26, ..., 27, } 28 . C
Vậy có 56 giá trị nguyên của x thỏa yêu cầu đề bài.
https://www.facebook.com/groups/toanvd.vdc Trang 18 NHÓM TOÁN VD – VDC MÃ ĐỀ 102
Câu 50: Cho hàm số f (x) có đồ thị là đường cong như hình vẽ bên dưới.
Số nghiệm thực phân biệt của phương trình f ( 3
x f (x)) +1= 0 là N H A. 6 . B. 4 . C. 5. D. 8. Ó M Lời giải Chọn A TO 3
x f (x) = a∈( 6; − 5 − ) ( ) 1 Á N
Dựa vào đồ thị, ta thấy f ( 3 x f (x) 3 3 +1 = 0 ⇔ f x f x = 1
− ⇔ x f (x) = b∈( 3 − ; 2 − ) (2) ) ( ( )) VD 3 x f ( x) = 0 (3) – V x = 0 x = 0 D
+ Phương trình (3) tương đương ⇔ . C f (x) = 0 x = x , 6
− < x < a < 5 − 1 ( 1 ) + Các hàm số ( ) a g x = và ( ) b h x =
đồng biến trên các khoảng ( ;0
−∞ ) và (0;+∞), và nhận xét 3 x 3 x
rằng x = 0 không phải là nghiệm của phương trình ( ) 1 nên:
f (x) = g (x) ( ) 1 ⇔ . f
( x) = h( x)
lim f (x) = ;
+∞ lim f (x) = 1 − x→−∞ x→0− + Trên khoảng ( ;0
−∞ ), ta có lim g (x) = lim h(x) = 0
nên các phương trình f (x) = g (x) x→−∞ x→−∞
lim g ( x) = lim h( x) = +∞ x→0− x→0−
và f (x) = h(x) có nghiệm duy nhất. N = −∞ = − H lim f (x) ; lim f (x) 1 x→+∞ x→0+ Ó M
+ Trên khoảng (0;+∞), ta có lim g (x) = lim h(x) = 0
nên các phương trình f (x) = g (x) x→+∞ x→+∞ T O
lim g ( x) = lim h( x) = −∞ + + → → Á x 0 x 0 N
và f (x) = h(x) có nghiệm duy nhất. VD
Do đó, phương trình f ( 3
x f (x)) +1= 0 có 6 nghiệm phân biệt. – VD
-------------------- HẾT -------------------- C
https://www.facebook.com/groups/toanvd.vdc Trang 19 NHÓM TOÁN VD – VDC MÃ ĐỀ 103
BỘ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Bài thi: TOÁN
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Câu 1. Cho hình trụ có bán kính đáy r = 5 và độ dài đường sinh l = 3 . Diện tích xung quanh của hình trụ đã cho bằng A. 15π B. 25π . C. 30π . D. 75π . N
Câu 2. Cho khối nón có bán kính r = 2 chiều cao h = 5. Thể tích của khối nón đã cho bằng H π π Ó A. 20 . B. 20π . C. 10 . D. 10π . M 3 3 T 2 3 O Á Câu 3. Biết f
∫ (x)dx = 2. Giá trị của 3f (x)dx ∫ bằng N 1 1 VD A. 5. B. 6 . C. 2 . D. 8 . – 3 VD − + + C
Câu 4. Trong không gian Oxyz , cho đường thẳng
x 3 y 1 z 2 d : = =
. Vecto nào dưới đây là một 4 2 − 3
vecto chỉ phương của d A. u = 3; 1 − ; 2 − .
B. u = 4;2;3 . C. u = 4; 2; − 3 .
D. u = 3;1;2 . 1 ( ) 2 ( ) 4 ( ) 3 ( )
Câu 5. Cho khối cầu có bán kính r = 2. Thể tích của khối cầu đã cho bằng π π A. 16π . B. 32 . C. 32π . D. 8 . 3 3
Câu 6. Trong không gian Oxyz , hình chiếu vuông góc của điểm A(3;5;2) trên trục Ox có tọa độ là A. (0;5;2) . B. (0;5;0) . C. (3;0;0). D. (0;0;2) .
Câu 7. Nghiệm của phương trình log x − 2 = 3 là: 2 ( )
A. x = 6 . B. x = 8. C. x =11.
D. x =10 .
Câu 8. Cho hàm số f (x) có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 2 . B. 2 − . C. 3. D. 1 − .
Câu 9. Trong không gian Oxyz , cho 3 điểm A( 1
− ;0;0), B(0;2;0) và C (0;0;3). Mặt phẳng ( ABC) có phương trình là A. x y z + + =1. B. x y z + + =1. C. x y z + + =1.D x y z + + =1. 1 2 3 − 1 2 − 3 1 − 2 3 1 2 3
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 1 NHÓM TOÁN VD – VDC MÃ ĐỀ 103
Câu 10. Nghiệm của phương trình x 1 3 + = 9 là A. x =1.
B. x = 2 . C. x = 2 − . D. x = 1 − .
Câu 11. Cho khối hộp chữ nhật có ba kích thước 2;6;7 . Thể tích của khối hộp đã cho bằng A. 28 . B. 14. C. 15. D. 84 .
Câu 12. Cho khối chóp có diện tích B = 2 và chiều cao h = 3. Thể tích của khốp chóp bằng A. 12. B. 2 . C. 3. D. 6 .
Câu 13. Số phức liên hợp của số phức z = 2 −5i là
A. z = 2 + 5i . B. z = 2 − + 5i .
C. z = 2 −5i . D. z = 2 − − 5i . N H
Câu 14. Cho cấp số nhân (u với u = 3 và công bội q = 4 . Giá trị của u bằng n ) 1 2 Ó M A. 64 . B. 81. C. 12. D. 3 . T 4 O ÁN
Câu 15. Cho hàm số bậc ba y = f (x) có đồ thị là đường cong trong hình bên. VD
Số nghiệm thực của phương trình f (x) =1 là – A. 1. B. 0 . VD C. 2 . D. 3. C
Câu 16. Cho hai số phức z =1− 2i và z = 2 + i . Số phức z + z bằng 1 2 1 2 A. 3+ i B. 3 − − i C. 3−i D. 3 − + i
Câu 17. Cho hàm số f (x) có bảng biến thiên như sau A. ( 2; − 2) B. (0;2) C. ( 2; − 0) D. (2;+∞) . Câu 18. +
Tiệm cận ngang của đồ thị hàm số 2x 1 y = là x −1 A. 1 y = B. y = 1 − C. y =1 D. y = 2 2
Câu 19. Đồ thị của hàm số nào dưới đây có dạng như đường cong như hình bên A. 4 2
y = −x + 2x B. 3 2
y = x − 3x C. 4 2
y = x − 2x D. 3 2
y = −x + 3x
Câu 20. Trong không gian Oxyz , cho mặt cầu 2 2 2
(S) : x + y + (z −1) =16 . Bán kính của (S) là A. 32 B. 8 C. 4 D. 16
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 2 NHÓM TOÁN VD – VDC MÃ ĐỀ 103
Câu 21. Trong mặt phẳng tọa độ, biết điểm M ( 2
− ;1) là điểm biểu diễn số phức z . Phần thực của z bằng A. 2 − B. 2 C. 1 D. 1 −
Câu 22. Tập xác định của hàm số y = log x là 3 A. (− ; ∞ 0) B. (0;+∞) C. (− ; ∞ +∞) D. [0;+∞)
Câu 23. Có bao nhiêu cách xếp 5 học sinh thành một hàng dọc? A. 1 B. 25 C. 5 D. 120
Câu 24. Với a,b là các số thực dương tùy ý và a ≠1, log b bằng 3 a N H
A. 3+ log b
B. 3log b C. 1 + log b D. 1 log b a a a a Ó 3 3 M T Câu 25. 4 x dx O ∫ bằng ÁN A. 1 5 x + C B. 3 4x + C C. 5 x + C D. 5 5x + C V 5 D – 3 V Câu 26. Biết 3
F(x) = x là một nguyên hàm của hàm số f (x) trên . Giá trị của (1+ f (x))dx D ∫ bằng 1 C A. 20. B. 22. C. 26. D. 28.
Câu 27. Cho hình nón có bán kính bằng 3 và góc ở đỉnh bằng 0
60 . Diện tích xung quanh của hình nón đã cho bằng A. 18π . B. 36π . C. 6 3π . D. 12 3π .
Câu 28. Diện tích hình phẳng giới hạn bởi hai đường 2
y = x − 2 và y = 3x − 2 bằng π π A. 9 . B. 9 . C. 125 . D. 125 . 2 2 6 6
Câu 29. Tập nghiệm của bất phương trình 2x−7 2 < 4 là A. ( 3 − ;3) . B. (0;3). C. (− ; ∞ 3) . D. (3;+∞) .
Câu 30. Cho a và b là hai số thực dương thỏa mãn log3(ab) 9
= 4a . Giá trị của 2 ab bằng A. 3. B. 6. C. 2 D. 4 Câu 31. − + −
Trong không gian Oxyz , cho điểm M (2; 1; − 2) và đường thẳng
x 1 y 2 z 3 d : = = . Mặt 2 3 1
phẳng đi qua điểm qua M và vuông góc với d có phương trình là
A. 2x + 3y + z − 3 = 0.
B. 2x − y + 2z − 9 = 0.
C. 2x + 3y + z + 3 = 0.
D. 2x − y + 2z + 9 = 0.
Câu 32. Cho hình chóp S.ABC và có đáy ABC là tam giác vuông tại
B, AB = a, BC = 3 ;
a SA vuông góc với mặt phẳng đáy và SA = 30a
(tham khảo hình bên). Góc giữa đường thẳng SC và mặt đáy bằng A. 45°. B. 90°. C. 60°. D. 30°.
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 3 NHÓM TOÁN VD – VDC MÃ ĐỀ 103
Câu 33. Cho z là nghiệm phức có phần ảo dương của phương trình 2
z + 4z +13 = 0 . Trên mặt phẳng 0
tọa độ, điểm biểu diễn của số phức 1− z là 0 A. P( 1; − 3 − ). B. M ( 1; − 3). C. N(3; 3 − ). D. Q(3;3).
Câu 34. Trong không gian Oxyz , cho ba điểm (
A 1;2;0), B(1;1;2) và C(2;3;1) . Đường thẳng đi qua A
và song song với BC có phương trình là
A. x −1 y − 2 z − − + + + + = =
. B. x 1 y 2 z =
= . C. x 1 y 2 z =
= . D. x 1 y 2 z = = . 1 2 1 − 3 4 3 3 4 3 1 2 1 −
Câu 35. Giá trị nhỏ nhất của hàm số 3
f (x) = x − 30x trên đoạn [2;19] bằng N H A. 20 10. B. 63. − C. 20 − 10. D. 52. − Ó M
Câu 36. Cho hàm số f (x) liên tục trên và có bảng xét dấu của f (′x) như sau TOÁN VD
Số điểm cực tiểu của hàm số đã cho là – V A. 2. B. 4. C. 3. D. 1. D C
Câu 37. Cho hai số phức z = 4 + 2i và w =1+ i . Môđun của số phức z.w bằng A. 2 2. B. 8. C. 2 10. D. 40.
Câu 38. Số giao điểm của đồ thị hàm số 3 2
y = x + x và đồ thị hàm số 2
y = x + 5x A. 3. B. 0 . C. 1. D. 2.
Câu 39. Trong năm 2019 , diện tích rừng trồng mới của tỉnh A là 900 ha. Giả sử diện tích rừng trồng
mới của tỉnh A mỗi năm tiếp theo đều tăng 6% so với diện tích rừng trồng mới của năm liền
trước. Kể từ sau năm 2019, năm nào dưới đây là năm đầu tiên của tỉnh A có diện tích rừng
trồng mới trong năm đó đạt trên 1700 ha? A. Năm 2029. B. Năm 2051. C. Năm 2030. D. Năm 2050.
Câu 40. Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a , SA vuông góc với mặt phẳng đáy, góc
giữa mặt (SBC) và mặt phẳng đáy là 60o . Diện tích của mặt cầu ngoại tiếp hình chóp S.ABC bằng 2 2 2 A. 43π a π π .
B. 19 a .
C. 43 a . D. 2 21πa . 3 3 9 +
Câu 41. Tập hợp tất cả các giá trị thực của tham số m để hàm số x 2 y =
đồng biến trên khoảng x + m ( ; −∞ 5) − A. (2;5]. B. [2;5) . C. (2;+∞) . D. (2;5) .
Câu 42. Cho hàm số ( ) x f x =
. Họ tất cả các nguyên hàm của hàm số g(x) = (x +1) f '(x) 2 x +1 2 + 2 −
A. x + 2x −1 x 1 + + x 1 + C . B.
+ C . C. 2x x 1 +C . D. + C . 2 2 x +1 2 x +1 2 x +1 2 x +1
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 4 NHÓM TOÁN VD – VDC MÃ ĐỀ 103
Câu 43. Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số đôi một khác nhau và các chữ số thuộc tập hợp {1,2,3,4,5,6, }
7 . Chọn ngẫu nhiên một số thuộc S , xác suất để số đó không có hai chữ số
liên tiếp nào cùng chẵn bằng A. 9 . B. 16 . C. 22 . D. 19 . 35 35 35 35
Câu 44. Cho hàm số bậc bốn f (x) có bảng biên thiên như sau: N H Ó M TO
Số điểm cực trị của hàm số 4 2
g(x) = x [f (x −1)] là ÁN V A. 7 . B. 5. C. 9. D. 11. D – x y
Câu 45. Xét các số thực không âm x và y thỏa mãn 1 2x .4 y + − +
≥ 3 . Giá trị nhỏ nhất của biểu thức VD 2 2
P = x + y + 2x + 4y bằng C A. 33 . B. 9 . C. 21 . D. 41 . 8 8 4 8 Câu 46. Cho hàm số 3 2
y = ax + bx + cx + d (a, ,
b c,d ∈ ) có đồ thị là
đường cong trong hình bên. Có bao nhiêu số dương trong các số
a,b,c,d ? A. 4 . B. 2 . C. 1. D. 3.
Câu 47. Cho hình chóp đều S.ABCD có cạnh đáy bằng a , cạnh bên bằng 2a và O là tâm của đáy.
Gọi M , N, P,Q lần lượt là các điểm đối xứng với O qua trọng tâm của các tam giác
SAB, SBC, SCD, SDA và S′ là điểm đối xứng với S qua O . Thể tích khối chóp S .′MNPQ bằng. 3 3 3 3 A. 2 6a . B. 40 6a . C. 10 6a . D. 20 6a . 9 81 81 81
Câu 48. Cho hình lăng trụ đứng ABC.A′B C
′ ′ có đáy ABC là tam giác đều
cạnh a và A′A = 2a . Gọi M là trung điểm của A′A (tham khảo hình
vẽ bên). Khoảng cách từ M đến mặt phẳng ( AB C ′ ) bằng A. 57a . B. 5a . 19 5 C. 2 5a . D. 2 57a . 5 19
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 5 NHÓM TOÁN VD – VDC MÃ ĐỀ 103
Câu 49. Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 127 số nguyên y thỏa mãn log ( 2
x + y ≥ log x + y ? 3 ) 2 ( ) A. 89 . B. 46 . C. 45 . D. 90.
Câu 50. Cho hàm số bậc bốn y = f (x) có đồ thị là đường cong trong hình vẽ bên. N H Ó M TOÁN
Số nghiệm thực phân biệt của phương trình f ( 2
x f (x)) + 2 = 0 là VD – A. 8 . B. 12. C. 6 . D. 9. VDC
-------------------- HẾT --------------------
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 6 NHÓM TOÁN VD – VDC MÃ ĐỀ 103
LỜI GIẢI CHI TIẾT
Câu 1. Cho hình trụ có bán kính đáy r = 5 và độ dài đường sinh l = 3 . Diện tích xung quanh của hình trụ đã cho bằng A. 15π B. 25π . C. 30π . D. 75π . Lời giải Chọn C
Áp dụng công thức diện tích xung quanh hình trụ ta được: S = π rl = π . xq 2 30
Câu 2. Cho khối nón có bán kính r = 2 chiều cao h = 5. Thể tích của khối nón đã cho bằng N H π π Ó A. 20 . B. 20π . C. 10 . D. 10π . 3 3 M T Lời giải O ÁN Chọn A VD 2 2 π r h π.2 .5 20π –
Áp dụng công thức thể tích khối nón ta được: V = = = . V 3 3 3 D C 2 3 Câu 3. Biết f
∫ (x)dx = 2. Giá trị của 3f (x)dx ∫ bằng 1 1 A. 5. B. 6 . C. 2 . D. 8 . 3 Lời giải Chọn B 2 2 Ta có : 3 f
∫ (x)dx = 3 f
∫ (x)dx = 3.2 = 6 . 1 1 Câu 4. − + +
Trong không gian Oxyz , cho đường thẳng
x 3 y 1 z 2 d : = =
. Vecto nào dưới đây là một 4 2 − 3
vecto chỉ phương của d A. u = 3; 1 − ; 2 − .
B. u = 4;2;3 . C. u = 4; 2; − 3 .
D. u = 3;1;2 . 1 ( ) 2 ( ) 4 ( ) 3 ( ) Lời giải Chọn C
Một vectơ chỉ phương của đường thẳng d là u 4; 2; − 3 . 2 ( )
Câu 5. Cho khối cầu có bán kính r = 2. Thể tích của khối cầu đã cho bằng π π A. 16π . B. 32 . C. 32π . D. 8 . 3 3 Lời giải Chọn B
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 7 NHÓM TOÁN VD – VDC MÃ ĐỀ 103
Thể tích của khối cầu đã cho : 4 3 4 3 32
V = π r = π.2 = π . 3 3 3
Câu 6. Trong không gian Oxyz , hình chiếu vuông góc của điểm A(3;5;2) trên trục Ox có tọa độ là A. (0;5;2) . B. (0;5;0) . C. (3;0;0). D. (0;0;2) . Lời giải Chọn C
Hình chiếu vuông góc của điểm A(3;5;2) trên trục Ox có tọa độ là (3;0;0). N H
Câu 7. Nghiệm của phương trình log x − 2 = 3 là: 2 ( ) Ó M
A. x = 6 . B. x = 8. C. x =11.
D. x =10 . TO Lời giải ÁN V Chọn D D –
Điều kiện: x − 2 > 0 ⇔ x > 2 . VD
log x − 2 = 3 ⇔ x − 2 = 8 ⇔ x =10 (thỏa). 2 ( ) C
Vậy phương trình có nghiệm x =10 .
Câu 8. Cho hàm số f (x) có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 2 . B. 2 − . C. 3. D. 1 − . Lời giải Chọn D
Gía trị cực tiểu của hàm số đã cho bằng 1 − .
Câu 9. Trong không gian Oxyz , cho 3 điểm A( 1
− ;0;0), B(0;2;0) và C (0;0;3). Mặt phẳng ( ABC) có phương trình là A. x y z + + =1. B. x y z + + =1. C. x y z + + =1. D x y z + + =1. 1 2 3 − 1 2 − 3 1 − 2 3 1 2 3 Lời giải Chọn C
Câu 10. Nghiệm của phương trình x 1 3 + = 9 là A. x =1.
B. x = 2 . C. x = 2 − . D. x = 1 − . Lời giải
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 8 NHÓM TOÁN VD – VDC MÃ ĐỀ 103 Chọn A Ta có: x 1+ x 1 + 2
3 = 9 ⇔ 3 = 3 ⇔ x +1 = 2 ⇔ x =1.
Câu 11. Cho khối hộp chữ nhật có ba kích thước 2;6;7 . Thể tích của khối hộp đã cho bằng A. 28 . B. 14. C. 15. D. 84 . Lời giải Chọn D
Thể tích của khối hộp đã cho là: V = 2.6.7 = 84 . N H
Câu 12. Cho khối chóp có diện tích B = 2 và chiều cao h = 3. Thể tích của khốp chóp bằng Ó M A. 12. B. 2 . C. 3. D. 6 . T Lời giải O ÁN Chọn B VD –
Thể tích của khối chóp đã cho là: 1 1
V = Bh = .2.3 = 2 . V 3 3 D C
Câu 13. Số phức liên hợp của số phức z = 2 −5i là
A. z = 2 + 5i . B. z = 2 − + 5i .
C. z = 2 −5i . D. z = 2 − − 5i . Lời giải Chọn A
Ta có số phức liên hợp của số phức z = 2 − 5i là z = 2 + 5i .
Câu 14. Cho cấp số nhân (u với u = 3 và công bội q = 4 . Giá trị của u bằng n ) 1 2 A. 64 . B. 81. C. 12. D. 3 . 4 Lời giải Chọn C
Ta có u = u .q = 3.4 =12. 2 1
Câu 15. Cho hàm số bậc ba y = f (x) có đồ thị là đường cong trong hình bên.
Số nghiệm thực của phương trình f (x) =1 là A. 1. B. 0 . C. 2 . D. 3. Lời giải Chọn D
Từ đồ thị hàm số ta có số nghiệm thực của phương trình f (x) =1 là 3.
Câu 16. Cho hai số phức z =1− 2i và z = 2 + i . Số phức z + z bằng 1 2 1 2 A. 3+ i B. 3 − − i C. 3−i D. 3 − + i Lời giải
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 9 NHÓM TOÁN VD – VDC MÃ ĐỀ 103 Chọn C
Tacó: z + z =1− 2i + 2 + i = 3− i . 1 2
Câu 17. Cho hàm số f (x) có bảng biến thiên như sau: N H Ó
Hàm số đã chođồng biến trên khoảng nào dưới đây M A. ( 2; − 2) B. (0;2) C. ( 2; − 0) D. (2;+∞) . TOÁ Lời giải N V Chọn B D – x + V
Câu 18. Tiệm cận ngang của đồ thị hàm số 2 1 y = là: D x −1 C A. 1 y = . B. y = 1 − . C. y =1. D. y = 2 . 2 Lời giải Chọn D 1 2 + Ta có 2x +1 lim = lim
x = 2. Suy ra đồ thị hàm số có tiệmcận ngang là y = 2. x→±∞ x −1 x→±∞ 1 1− x
Câu 19. Đồ thị của hàm số nào dưới đây có dạng như đường cong như hình bên A. 4 2
y = −x + 2x . B. 3 2
y = x − 3x . C. 4 2
y = x − 2x . D. 3 2
y = −x + 3x . Lời giải Chọn C
Dựa vào hình dạng đồ thị Đồ thị của hàm trùng phương 4 2
y ax bx c (a 0)
Dựa vào nhánh bên phải của đồ thị có hướng đi lên a 0 .
Câu 20. Trong không gian Oxyz , cho mặt cầu 2 2 2
(S) : x + y + (z −1) =16 . Bán kính của (S) là: A. 32 B. 8 C. 4 D. 16 Lời giải Chọn C
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 10 NHÓM TOÁN VD – VDC MÃ ĐỀ 103
Từ phương trình mặt cầu 2 2 2
(S) : x y (z 1) 16 Bán kính R 16 4
Câu 21. Trong mặt phẳng tọa độ, biết điểm M ( 2
− ;1) là điểm biểu diễn số phức z . Phần thực của z bằng: A. 2 − B. 2 C. 1 D. 1 − Lời giải Chọn A N
Điểm M (2;1) là điểm biểu diễn số phức z z 2i H Ó M
Vậy phần thực của z là 2 TO
Câu 22. Tập xác định của hàm số y = log x là 3 ÁN A. (− ; ∞ 0) B. (0;+∞) C. (− ; ∞ +∞) D. [0;+∞) VD Lời giải – V Chọn B. D
Điều kiện xác định: x > 0 . C
Câu 23. Có bao nhiêu cách xếp 5 học sinh thành một hàng dọc? A. 1 B. 25 C. 5 D. 120 Lời giải Chọn D
Số cách xếp 5 học sinh thành một hàng dọc là số hoán vị của 5 phần tử, có: 5!=120 (cách).
Câu 24. Với a,b là các số thực dương tùy ý và a ≠1, log b bằng 3 a A. 3+ log b B. 3log b C. 1 + log b D. 1 log b a a 3 a 3 a Lời giải Chọn D Ta có: 1 log b = log . b 3 a 3 a Câu 25. 4 x dx ∫ bằng A. 1 5 x + C B. 3 4x + C C. 5 x + C D. 5 5x + C 5 Lời giải Chọn A 4 x dx ∫ 1 5 = x + C . 5
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 11 NHÓM TOÁN VD – VDC MÃ ĐỀ 103 3 Câu 26. Biết 3
F(x) = x là một nguyên hàm của hàm số f (x) trên . Giá trị của (1+ f (x))dx ∫ bằng 1 A. 20. B. 22. C. 26. D. 28. Lời giải Chọn D 3 3 3
Ta có ∫[1+ f (x)]dx =[x + F(x)] 3
= x + x ) = 30 − 2 = 28 . 1 1 1 N
Câu 27. Cho hình nón có bán kính bằng 3 và góc ở đỉnh bằng 0
60 . Diện tích xung quanh của hình nón H Ó đã cho bằng M A. 18π . B. 36π . C. 6 3π . D. 12 3π . TOÁ Lời giải N V Chọn A D –
Gọi l là đường sinh, r là bán kính đáy ta có r = 3. VDC
Gọi α là góc ở đỉnh. Ta có r r 3 α = ⇒ = = = . sin l 6 0 l sinα sin 30
Vậy diện tích xung quanh S = π rl = π.3.6 =18π .
Câu 28. Diện tích hình phẳng giới hạn bởi hai đường 2
y = x − 2 và y = 3x − 2 bằng π π A. 9 . B. 9 . C. 125 . D. 125 . 2 2 6 6 Lời giải Chọn A
Xét phương trình hoành độ giao điểm, ta có: x 0. 2
x 2 3x2 x3. 3
Như vậy, diện tích hình phẳng được gới hạn bằng 9 2 x
2 3x2 dx . 2 0
Câu 29. Tập nghiệm của bất phương trình 2x−7 2 < 4 là A. ( 3 − ;3) . B. (0;3). C. (− ; ∞ 3) . D. (3;+∞) . Lời giải Chọn A Ta có : 2x 7 2 4 2 x 7 2 2 2 2 x 7 2 2
x 9 x 3; 3 .
Câu 30. Cho a và b là hai số thực dương thỏa mãn log3(ab) 9
= 4a . Giá trị của 2 ab bằng A. 3. B. 6. C. 2 D. 4 Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 12 NHÓM TOÁN VD – VDC MÃ ĐỀ 103 Ta có : log3ab 9
4a 2log ab log 4a log 2 2 a b log 4a 2 2 a b 4a 3 3 3 3 2 ab 4 . Câu 31. − + −
Trong không gian Oxyz , cho điểm M (2; 1; − 2) và đường thẳng
x 1 y 2 z 3 d : = = . Mặt 2 3 1
phẳng đi qua điểm qua M và vuông góc với d có phương trình là
A. 2x + 3y + z − 3 = 0. B. 2x − y + 2z − 9 = 0. C. 2x + 3y + z + 3 = 0. D. 2x − y + 2z + 9 = 0. Lời giải Chọn A N H
Đường thẳng d có một vecto chỉ phương là u = (2;3; ) 1 Ó M
Mặt phẳng (P) vuông góc với d nên nhận u làm vecto pháp tuyến TO
Phương trình mặt phẳng cần tìm là: ÁN
2(x − 2) + 3( y + )
1 +1(z − 2) = 0 ⇔ 2x + 3y + z − 3 = 0 . VD
Câu 32. Cho hình chóp S.ABC và có đáy ABC là tam giác vuông tại – V
B, AB = a, BC = 3 ;
a SA vuông góc với mặt phẳng đáy và SA = 30a D C
(tham khảo hình bên). Góc giữa đường thẳng SC và mặt đáy bằng A. 45°. B. 90°. C. 60°. D. 30°. Lời giải Chọn C
Do AC là hình chiếu vuông góc của SC trên mặt phẳng ( ABC) nên (SC ( ABC)) = , SCA Ta có: 2 2
AC = AB + BC = a 10 Khi đó SA a 30 = = = ⇒ 0 tan SCA 3 SCA = 60 . AC a 10
Câu 33. Cho z là nghiệm phức có phần ảo dương của phương trình 2
z + 4z +13 = 0 . Trên mặt phẳng 0
tọa độ, điểm biểu diễn của số phức 1− z là 0 A. P( 1; − 3 − ). B. M ( 1; − 3). C. N(3; 3 − ). D. Q(3;3). Lời giải Chọn C z = 2 − + 3i Ta có 2
z + 4z +13 = 0 ⇔
. Do z có phần ảo dương nên suy ra z = 2 − + 3i z = 2 − − 3i 0 0 Khi đó 1− z =1− 2
− + 3i = 3− 3i . Vậy điểm biểu diễn số phức 1− z là N (3; 3 − ) 0 ( ) 0
Câu 34. Trong không gian Oxyz , cho ba điểm (
A 1;2;0), B(1;1;2) và C(2;3;1) . Đường thẳng đi qua A
và song song với BC có phương trình là
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 13 NHÓM TOÁN VD – VDC MÃ ĐỀ 103
A. x −1 y − 2 z − − + + + + = =
. B. x 1 y 2 z =
= . C. x 1 y 2 z =
= . D. x 1 y 2 z = = . 1 2 1 − 3 4 3 3 4 3 1 2 1 − Lời giải Chọn A
Gọi d là phương trình đường thẳng qua A(1;2;0) và song song với BC . − − Ta có x 1 y 2 BC z = (1;2;− ) 1 ⇒ d : = = . 1 2 1 −
Câu 35. Giá trị nhỏ nhất của hàm số 3
f (x) = x − 30x trên đoạn [2;19] bằng N H Ó A. 20 10. B. 63. − C. 20 − 10. D. 52. − M T Lời giải O Chọn C ÁN V x = 10 (n) 2 2 D
Ta có f ′(x) = 3x −30 ⇒ f ′(x) = 0 ⇔ 3x −30 = 0 ⇔ . – x = − 10 (l) VDC Khi đó f (2) = 52 − ; f ( 10) = 20 − 10 và f (19) = 6289.
Vậy min f (x) = f = − . ∈ ( 10) 20 10 x [2;19]
Câu 36. Cho hàm số f (x) liên tục trên và có bảng xét dấu của f (′x) như sau:
Số điểm cực tiểu của hàm số đã cho là A. 2. B. 4. C. 3. D. 1. Lời giải Chọn A
Câu 37. Cho hai số phức z = 4 + 2i và w =1+ i . Môđun của số phức z.w bằng A. 2 2. B. 8. C. 2 10. D. 40. Lời giải Chọn C
Ta có: z.w = (4 + 2i)(1−i) = 6 − 2 .i Suy ra z.w = 40 = 2 10.
Câu 38. Số giao điểm của đồ thị hàm số 3 2
y = x + x và đồ thị hàm số 2
y = x + 5x A. 3. B. 0 . C. 1. D. 2. Lời giải Chọn A x = 0
Phương trình hoành độ giao điểm: 3 2 2 3
x + x = x + 5x ⇔ x − 5x = 0 ⇔ . x = ± 5
Vậy số giao điểm của 2 đồ thị là 3.
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 14 NHÓM TOÁN VD – VDC MÃ ĐỀ 103
Câu 39. Trong năm 2019 , diện tích rừng trồng mới của tỉnh A là 900 ha. Giả sử diện tích rừng trồng
mới của tỉnh A mỗi năm tiếp theo đều tăng 6% so với diện tích rừng trồng mới của năm liền
trước. Kể từ sau năm 2019, năm nào dưới đây là năm đầu tiên của tỉnh A có diện tích rừng
trồng mới trong năm đó đạt trên 1700 ha? A. Năm 2029. B. Năm 2051. C. Năm 2030. D. Năm 2050. Lời giải Chọn C.
Trong năm 2019, diện tích rừng trồng mới của tỉnh A là A = 900 ha.
Trong năm 2020, diện tích rừng trồng mới của tỉnh A là A = A + 6%A = A 1+ 6% ha. 1 ( ) N H
Trong năm 2021, diện tích rừng trồng mới của tỉnh A là Ó M A = A + A = A + = A + + = A + ha. 6% (1 6%) (1 6%)(1 6%) (1 6%)2 2 1 1 1 TO
Trong năm 2022, diện tích rừng trồng mới của tỉnh A là ÁN 2 3 V
A = A + 6%A = A 1+ 6% = A 1+ 6% 1+ 6% = A 1+ 6% ha. 3 2 2 2 ( ) ( ) ( ) ( ) D – … V n D Trong năm 2019 + ,
n diện tích rừng trồng mới của tỉnh A là A = A ha. n (1+ 6%) C
Khi đó, diện tích rừng trồng mới đạt trên 1700 ha khi A > ⇔ A n ( + )n n n 17 1700
1 6% >1700 ⇔ 900.1,06 >1700 ⇔ 1,06 > 9 17 ⇔ n > log ≈10,9 ⇒ n =11. 1,06 min 9
Vậy năm 2030 là năm đầu tiên của tỉnh A có diện tích rừng trồng mới trong năm đó đạt trên 1700 ha.
Câu 40. Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a , SA vuông góc với mặt phẳng đáy, góc
giữa mặt (SBC) và mặt phẳng đáy là 60o . Diện tích của mặt cầu ngoại tiếp hình chóp S.ABC bằng 2 2 2 A. 43πa π π .
B. 19 a .
C. 43 a . D. 2 21π a . 3 3 9 Lời giải Chọn A .
Gọi I, J lần lượt là trung điểm của BC, SA . Ta có (SBC) ( ABC) ( )= , SIA = 60 .°, SA 3a
⇒ SA = AI.tan 60° = 3a ⇒ KG = = 2 2
Gọi G trọng tâm tam giác đồng thời là tâm đường tròn ngoại tiếp tam giác ABC .
Qua G ta dựng đường thẳng ∆ ⊥ ( ABC).
Dựng trung trực SA cắt đường thẳng ∆ tại K , khi đó KS = KA = KB = KC nên K là tâm mặt
cầu ngoại tiếp khối chóp S.ABC . 2 Ta có π a 2 2 43
R = KA = KG + AG = . a .Diện tích mặt cầu 2 43 S = 4π R = ⋅ 12 3
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 15 NHÓM TOÁN VD – VDC MÃ ĐỀ 103 +
Câu 41. Tập hợp tất cả các giá trị thực của tham số m để hàm số x 2 y =
đồng biến trên khoảng x + m ( ; −∞ 5) − A. (2;5]. B. [2;5) . C. (2;+∞) . D. (2;5) . Lời giải Chọn A
Tập xác định: D = \{− } m . Ta có: m − 2 y ' = 2 (x + m) N H y ' > 0 x ∀ ∈( ; −∞ 5) − m − 2 > 0 Ó
Hàm số đồng biến trên khoảng ( ; −∞ 5) − ⇔ ⇔ ⇔ 2 < m ≤ 5 . M −m∉( ; −∞ 5) − −m ≥ 5 − TO x Á
Câu 42. Cho hàm số f (x) =
. Họ tất cả các nguyên hàm của hàm số g(x) = (x +1) f '(x) N 2 x +1 V 2 2 D x + 2x −1 x +1 2x + x +1 x −1 A. + C . B. + C . C. + C . D. + C . – 2 2 2 2 2 x +1 x +1 x +1 x +1 VDC Lời giải Chọn D u = x +1 du = dx
Xét g(x)dx = (x +1) f '(x)dx ∫ ∫ . Đặt ⇔
dv f '(x)dx =
v = f (x) Vậy +
g(x)dx = (x +1) f (x) − f (x)dx ∫ ∫ (x 1) ⇒ ( ) x x g x dx = − dx ∫ ∫ 2 2 x +1 x +1 (x +1)x 2 2 2
x + x − x −1
⇒ g(x)dx = − x +1 + C ∫
⇒ g(x)dx = + C ∫ 2 x +1 2 x +1 x −1
⇒ g(x)dx = + C. ∫ 2 x +1
Câu 43. Gọi S là tập hợp tất cả các số tự nhiên có bốn chữ số đôi một khác nhau và các chữ số thuộc tập hợp {1;2;3;4;5;6; }
7 . Chọn ngẫu nhiên một số thuộc S , xác suất để số đó không có hai chữ
số liên tiếp nào cùng chẵn bằng A. 9 . B. 16 . C. 22 . D. 19 . 35 35 35 35 Lời giải Chọn C Không gian mẫu 4 Ω = A = 840. 7
Gọi biến cố A thỏa mãn yêu cầu bài toán. Có các trường hợp sau:
TH1: 4 chữ số đều lẻ: 4! số.
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 16 NHÓM TOÁN VD – VDC MÃ ĐỀ 103
TH2: 3 chữ số lẻ, 1 chữ số chẵn: 3 1 C .C .4! số. 4 3
TH3: 2 chữ số lẻ, 2 chữ số chẵn: 2 2 2
C .C .2!.A số. 4 3 3
Như vậy A = 528. Vậy xác suất P( A) 528 22 = = . 840 35
Câu 44. Cho hàm số bậc bốn f (x) có bảng biên thiên như sau: N H Ó M TOÁ
Số điểm cực trị của hàm số 4 2
g(x) = x [f (x −1)] là N VD A. 7 . B. 5. C. 9. D. 11. – V Lời giải D C Chọn C Ta có : 4 2 2
f (x) = 4x −8x + 3 ⇒ f (′x) =16x(x −1) Ta có 3
g (′x) = 2x . f (x −1).[2 f (x −1) + .
x f (′x −1)] 3 x = 0 (1) g (x) 0 ′
= ⇔ f (x −1) = 0 (2)
2 f (x −1) + .x f (′x −1) = 0 (3)
Phương trình (1) có x = 0 (nghiệm bội ba).
Phương trình (2) có cùng số nghiệm với phương trình f (x) = 0 nên (2) có 4 nghiệm đơn.
Phương trình (3) có cùng số nghiệm với phương trình : 4 2 2
2 f (x) + (x +1). f (′x) = 0 ⇔ 2(4x −8x + 3) +16x(x +1)(x −1) = 0 4 3 2
⇔ 24x +16x − 32x −16x + 6 = 0 có 4 nghiệm phân biệt.
Dễ thấy 9 nghiệm trên phân biệt nên hàm số g(x) = 0 có tất cả 9 điểm cực trị.
Câu 45. Xét các số thực không âm x và y thỏa mãn x y 1 2x .4 y + − +
≥ 3 . Giá trị nhỏ nhất của biểu thức 2 2
P = x + y + 2x + 4y bằng A. 33 . B. 9 . C. 21 . D. 41 . 8 8 4 8 Lời giải Chọn D Ta có x+ y 1 − + ≥ ⇔ ( − ) −x y 1 − 2 + ≥ ⇔ y ≥ ( − ) 3−2 2 .4 3 2 3 .4 .4 0 2 .2 3 2 2 x x y x y y x (1) 3 x ≥ Xét TH: 3
3− 2x ≤ 0 ⇔ x ≥ . (1) đúng với mọi giá trị 2 2 21
2 ⇒ P = x + y + 2x + 4y ≥ (2) 2 4 y ≥ 0 Xét TH: 3
3− 2x > 0 ⇔ 0 ≤ x < . 2
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 17 NHÓM TOÁN VD – VDC MÃ ĐỀ 103
Xét hàm số ( ) = .2t f t
t với t ≥ 0
⇒ ′( ) = 2t + .2t f t
t .ln 2 > 0 với mọi t ≥ 0
(1) ⇔ f (2y) ≥ f (3− 2x) 3
⇔ 2y ≥ 3− 2x ⇔ y ≥ − x . Khi đó: 2 2 2 2 2 2 3 P x y x y x x = + + + ≥ + − + 5 41 41 x + ( − x) 2 33 2 4 2
2 3 2 = 2x − 5x + = 2 x − + ≥ (3) 2 4 4 8 8
So sánh (2) và (3) ta thấy GTNN của P là 41 khi 5 1 x = , y = . 8 4 4 N Câu 46. Cho hàm số 3 2
y = ax + bx + cx + d (a, ,
b c,d ∈) có đồ thị là đường H Ó
cong trong hình bên. Có bao nhiêu số dương trong các số a,b,c,d ? M T A. 4 . B. 2 . O C. 1. D. 3. ÁN VD – VD Lời giải C Chọn C Ta có 2
y′ = 3ax + 2bx + c . Dựa vào đồ thị ta thấy a < 0 2 b − 9ac > 0 ∆′ > y′ 0 2b b < 0
Hàm số có 2 cực trị âm nên S < 0 ⇔ − < 0 ⇒ ⇒ 3a c < 0 P > 0 c > 0 3a
Đồ thị cắt trục Oy tại điểm (0;d ) nên d > 0 .
Vậy có đúng một số dương trong các số a,b,c,d
Câu 47. Cho hình chóp đều S.ABCD có cạnh đáy bằng a , cạnh bên bằng 2a và O là tâm của đáy.
Gọi M , N, P,Q lần lượt là các điểm đối xứng với O qua trọng tâm của các tam giác
SAB, SBC, SCD, SDA và S′ là điểm đối xứng với S qua O . Thể tích khối chóp S .′MNPQ bằng. 3 3 3 3 A. 2 6a . B. 40 6a . C. 10 6a . D. 20 6a . 9 81 81 81 Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 18 NHÓM TOÁN VD – VDC MÃ ĐỀ 103 N H Ó M TOÁN a V Ta có: 2 5 6 S K ′ = S O
′ + OK = SO + SO = ⋅ D 3 6 – 1 4 8 2 V , S = ⋅ ⋅ S = a MNPQ 4 ABCD . D 2 9 9 C 3 20 6a Vậy: V = ⋅ S .′MNPQ 81
Câu 48. Cho hình lăng trụ đứng ABC.A′B C
′ ′ có đáy ABC là tam giác đều
cạnh a và A′A = 2a . Gọi M là trung điểm của A′A (tham khảo hình
vẽ bên). Khoảng cách từ M đến mặt phẳng ( AB C ′ ) bằng A. 57a . B. 5a . 19 5 C. 2 5a . D. 2 57a . 5 19 Lời giải Chọn A
Gọi I = BM ∩ AB′ và K là trung điểm AC .
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 19 NHÓM TOÁN VD – VDC MÃ ĐỀ 103
d (M ,( AB C ′ )) Ta có MI MA 1 1 BH = = = ⇒ ′ = ′ = . d (
d (M , AB C )
d (B, AB C ) B,( AB C ′ )) ( ) ( ) BI BB′ 2 2 2 Xét tam giác 1 1 1 1 1 2 57 BB K ′ có a = + = + ⇒ BH = . 2 2 2 BH B B ′ BK (2a)2 2 19 a 3 2 Vậy ( ( )) BH 57 , a d M AB C ′ = = 2 19 N
Câu 49. Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 127 số nguyên y thỏa mãn HÓ log ( 2
x + y ≥ log x + y ? 3 ) 2 ( ) M T A. 89 . B. 46 . C. 45 . D. 90. O Á Lời giải N V Chọn D D – 2
Ta có log x + y ≥ log x + y 1 3 ( ) 2 ( )( ) VDC
Đặt t = x + y ∈* (do x, y ∈, x + y > 0 ) (1) ⇔ log ( 2
x − x + t) ≥ log t ⇔ g(t) = log t − log ( 2
x − x + t ≤ 0 2 3 2 2 3 ) ( ) Đạo hàm 1 1 g (′t) = −
> với mọi y . Do đó g (t) đồng biến trên [1;+∞) t ln 2 ( 0 2
x − x + t)ln3
Vì mỗi x nguyên có không quá 127 giá trị t ∈* nên ta có
g(128) > 0 ⇔ log 128 − log ( 2
x − x +128 > 0 2 3 ) 2 7
⇔ x − x +128 < 3 ⇔ 44 − ,8 ≤ x ≤ 45,8
Như vậy có 90 giá trị thỏa yêu cầu bài toán
Câu 50. Cho hàm số bậc bốn y = f (x) có đồ thị là đường cong trong hình vẽ bên.
Số nghiệm thực phân biệt của phương trình f ( 2
x f (x)) + 2 = 0 là A. 8 . B. 12. C. 6 . D. 9. Lời giải
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 20 NHÓM TOÁN VD – VDC MÃ ĐỀ 103 Chọn D N H Ó 2 = M x f (x) 0 2 T
x f (x) = a 1 2 O
f (x f (x)) ( ) + 2 = 0 ⇔
với 0 < a < b < c . 2 Á
x f (x) = b(2) N 2
x f (x) = c (3) VD – m V
Xét phương trình f (x) = 1 m > 0 . 2 ( ) ( ) D x C
Gọi α, β là hoành độ giao điểm của (C) : y = f (x) và Ox ; α < 0 < β .
(1) ⇔ f (x) m −
= 0. Đặt g(x) f (x) m = − 2 x 2 x Đạo hàm 2 (′ ) = (′ ) m g x f x + . 3 x Trường hợp 1: 2
< α; (′ ) < 0; m x f x
< 0 ⇒ g (′x) < 0 3 x Ta có lim ( ) = +∞, ( ) m g x g α = −
< 0. Phương trình g (x) = 0 có một nghiệm thuộc ( ; −∞ α ) . 2 x→−∞ α
Trường hợp 2: α < x < β m f (x) < 0,
> 0 suy ra g(x) < 0 x ∀ ∈(α, β ) . 2 x Trường hợp 3: 2 > β; (′ ) > 0; m x f x
> 0 ⇒ g (′x) > 0 3 x Ta có lim ( ) = +∞, ( ) m g x g β = −
< 0 . Phương trình g (x) = 0 có một nghiệm thuộc (β;+∞) . 2 x→−∞ β
Vậy phương trình ( ) m f x = có hai nghiệm m ∀ > 0. 2 x Ta có: 2
x f (x) = 0 ⇔ x = 0 ∨ f (x) = 0: có ba nghiệm. Vậy phương trình ( ) 1 có 9 nghiệm.
-------------------- HẾT --------------------
https://www.facebook.com/groups/toanvd.vdc - Kết nối đam mê - Nâng tầm tri thức Trang 21 NHÓM TOÁN VD – VDC MÃ ĐỀ 104
BỘ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG 2020 Bài thi: TOÁN
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Câu 1: Tập xác định của hàm số y = log x là 4 A. ( ; −∞ 0). B. [0;+∞) . C. (0;+∞). D. ( ; −∞ +∞) .
Câu 2: Cho hình trụ có bán kính đáy r = 7 và độ dài đường sinh l = 3. Diện tích xung quanh của hình N trụ đã cho bằng H Ó A. 42π . B. 147π . C. 49π . D. 21π . M x − y + z − T
Câu 3: Trong không gian Oxyz, cho đường thẳng 4 2 3 d : = =
. Vectơ nào dưới đây là một O 3 1 − 2 − ÁN
vectơ chỉ phương của d ? V D A. u = 4; 2; − 3 . B. u = 4;2; 3 − . C. u = 3; 1 − ; 2 − . D. u = 3;1;2 . 1 ( ) 3 ( ) 4 ( ) 2 ( ) – V
Câu 4: Cho hàm số bậc ba y = f (x) có đồ thị là đường cong trong hình bên. D C
Số nghiệm thực của phương trình f (x) = 2 là A. 0 . B. 3. C. 1. D. 2 . 3 3
Câu 5: Biết f (x)dx = 6. ∫
Giá trị của 2 f (x)dx ∫ bằng 2 2 A. 36. B. 3. C. 12. D. 8 .
Câu 6: Tiệm cận ngang của đồ thị hàm số 3x +1 y = là x −1 A. 1 y = . B. y = 3. C. y = 1 − . D. y =1. N 3 H Ó
Câu 7: Trong không gian Oxyz, hình chiếu vuông góc của điểm (
A 8;1;2) trên trục Ox có tọa độ là M A. (0;1;0) . B. (8;0;0). C. (0;1;2) . D. (0;0;2) . TOÁ
Câu 8: Nghiệm của phương trình x+2 3 = 27 là N V A. x = 2 − . B. x = 1 − . C. x = 2 . D. x =1. D –
Câu 9: Cho khối nón có bán kính đáy r = 2 và chiều cao h = 4 . Thể tích của khối nón đã cho bằng V π π D A. 8π . B. 8 . C. 16 . D. 16π . C 3 3
Câu 10: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2
y = x − 2x +1. B. 3 2
y = −x + 3x +1. C. 3 2
y = x − 3x +1. D. 4 2
y = −x + 2x +1.
https://www.facebook.com/groups/toanvd.vdc Trang 1 NHÓM TOÁN VD – VDC MÃ ĐỀ 104
Câu 11: Với a,b là hai số thực dương tùy ý và a ≠ 1, log b bằng 4 a A. 4 + log b. B. 1 log b . C. 4log b . D. 1 + log b . a 4 a a 4 a
Câu 12: Trong không gian Oxyz, cho mặt cầu (S ) 2 2
: x + y + (z − 2)2 =16 . Bán kính của (S ) bằng A. 4 . B. 32. C. 16. D. 8 .
Câu 13: Số phức liên hợp của số phức z = 3− 5i là A. z = 3 − − 5i .
B. z = 3+ 5i . C. z = 3 − + 5i .
D. z = 3− 5i .
Câu 14: Cho khối hộp chữ nhật có ba kích thước 2;3;7. Thể tích của khối hộp đã cho bằng N A. 7 . B. 42 . C. 12. D. 14. H
Câu 15: Cho khối chóp có diện tích đáy B = 3 và chiều cao h = 8. Thể tích của khối chóp đã cho bằng Ó M A. 24 . B. 12. C. 8 . D. 6 . T
Câu 16: Cho hàm số f (x) có bảng biến thiên như sau: O ÁN VD – VDC
Hàm số đã cho đồng biến trên khoảng nào dưới đây ? A. ( 3 − ;0) . B. ( 3 − ;3) . C. (0;3). D. (− ; ∞ 3 − ) .
Câu 17: Cho hàm số f (x) có bảng biến thiên như sau: N H
Giá trị cực đại của hàm số đã cho bằng Ó M A. 3. B. 3 − . C. 1 − . D. 2 . T
Câu 18: Cho cấp số nhân (u với u = 4 và công bội q = 3. Giá trị của u bằng n ) O 1 2 ÁN A. 64 . B. 81. C. 12. D. 4 . VD 3 –
Câu 19: Cho khối cầu có bán kính r = 2 . Thể tích của khối cầu bằng VD A. 32π . B. π 16π . C. 32π . D. 8 . C 3 3
Câu 20: Trên mặt phẳng tọa độ, biết M ( 1;
− 2) là điểm biểu diễn của số phức z. Phần thực của z bằng A. 1. B. 2 . C. 2 − . D. 1 − . Câu 21: 5 x dx ∫ bằng A. 4 5x + C . B. 1 6 x + C . C. 6 x + C . D. 6 6x + C . 6
https://www.facebook.com/groups/toanvd.vdc Trang 2 NHÓM TOÁN VD – VDC MÃ ĐỀ 104
Câu 22: Nghiệm của phương trình log x − 2 = 2 là 3 ( ) A. x =11. B. x =10 . C. x = 7 . D. x = 8.
Câu 23: Trong không gian Oxyz, cho ba điểm A(2;0;0) , B(0; 1;
− 0), C (0;0;3). Mặt phẳng ( ABC) có phương trình là A. x y z + + =1. B. x y z + + = 1. C. x y z + + = 1. D. x y z + + =1. 2 − 1 3 2 1 3 − 2 1 3 2 1 − 3
Câu 24: Có bao nhiêu cách xếp 8 học sinh thành một hàng dọc ? A. 8 . B. 1. C. 40320 . D. 64 . N
Câu 25: Cho hai số phức z =1− 3i và z = 3+ i . Số phức z + z bằng 1 2 1 2 H Ó A. 4 − 2i . B. 4 − + 2i . C. 4 + 2i . D. 4 − − 2i . M
Câu 26: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , TO
AB = a, BC = 2a; SA vuông góc với mặt phẳng đáy và SA = a (tham ÁN
khảo hình bên). Góc giữa đường thẳng SC và mặt phẳng đáy bằng VD A. 0 90 . B. 0 45 . – V C. 0 60 . D. 0 30 . D C 2 log3 a b 3
Câu 27: Cho hai số a và b là hai số thực dương thỏa mãn ( ) 9
= 4a . Giá trị của 2 ab bằng A. 4 . B. 2 . C. 3. D. 6 .
Câu 28: Trong không gian gian − + −
Oxyz, cho điểm M (3; 2 − ;2) và đường thẳng
x 3 y 1 z 1 d : = = . 1 2 2 −
Mặt phẳng đi qua M và vuông góc với d có phương trình là
A. x + 2y − 2z + 5 = 0 .
B. 3x − 2y + 2z −17 = 0 .
C. 3x − 2y + 2z +17 = 0 .
D. x + 2y − 2z − 5 = 0 .
Câu 29: Giá trị nhỏ nhất của hàm số 3
f (x) = x − 33x trên đoạn [2;19] bằng A. 72 − . B. 22 − 11. C. 58 − . D. 22 11 .
Câu 30: Tập nghiệm của bất phương trình 2x 1 2 − < 8 là N A. (0;2) . B. ( ;2 −∞ ) . C. ( 2; − 2) . D. (2;+∞) . H Ó M
Câu 31: Diện tích hình phẳng giới hạn bởi hai đường 2
y = x − 3 và y = x − 3 bằng T π π O A. 125 . B. 1 . C. 125 . D. . Á 6 6 6 6 N V
Câu 32: Cho hình nón có bán kính đáy bằng 4 và góc ở đỉnh bằng o
60 . Diện tích xung quanh của hình D – nón đã cho bằng VD A. 64 3π . B. π 32π . C. 64π . D. 32 3 . C 3 3
Câu 33: Gọi z là nghiệm phức có phần ảo dương của phương trình 2
z − 4z +13 = 0 . Trên mặt phẳng 0
tọa độ, điểm biểu diễn của số phức 1− z là 0 A. M (3; 3 − ). B. P( 1; − 3) . C. Q(1;3) D. N ( 1; − 3 − ).
Câu 34: Cho hàm số f (x) liên tục trên R có bảng xét dấu f (′x) như sau:
https://www.facebook.com/groups/toanvd.vdc Trang 3 NHÓM TOÁN VD – VDC MÃ ĐỀ 104
Số điểm cực đại của hàm số đã cho là A. 3. B. 1. C. 2. D. 4.
Câu 35: Trong không gian Oxyz, cho ba điểm A(1;1;0), B(1;0; )
1 ,C (3;1;0) . Đường thẳng đi qua A và
song song với BC có phương trình là
A. x +1 y +1 z + + − − − − = =
. B. x 1 y 1 z =
= . C. x 1 y 1 z = =
. D. x 1 y 1 z = = . 2 1 1 − 4 1 1 2 1 1 − 4 1 1 N H
Câu 36: Cho hai số phức z =1+ 3i và w =1+ i . Môđun của số phức z.w bằng Ó M A. 2 5 . B. 2 2 . C. 20 . D. 8 . TO
Câu 37: Số giao điểm của đồ thị hàm số 2
y = −x + 3x và đồ thị hàm số 3 2
y = x − x là ÁN A. 1. B. 0 . C. 2 . D. 3 V 3 D Câu 38: Biết 2
F(x) = x là một nguyên hàm của hàm số f (x) trên
1+ f (x) dx bằng – . Giá trị của ∫[ ] V 1 D C A. 10. B. 8 . C. 26 . D. 32 . 3 3
Câu 39: Cho hàm số ( ) x f x =
. Họ tất cả các nguyên hàm của hàm số g (x) = (x + ) 1 f ′(x) là 2 x + 4 2 2 A. x + 4 − + − + + + C .
B. x 4 + C .
C. x 2x 4 + C . D. 2x x 4 +C . 2 2 x + 4 2 x + 4 2 2 x + 4 2 x + 4
Câu 40: Trong năm 2019 , diện tích rừng trồng mới của tỉnh A là 800 ha. Giả sử diện tích rừng trồng
mới của tỉnh A mỗi năm tiếp theo đều tăng 6% so với diện tích rừng trồng mới của năm liền
trước. Kể từ sau năm 2019, năm nào dưới đây là năm đầu tiên tỉnh A có diện tích rừng trồng
mới trong năm đó đạt trên 1400 ha ? ? A. Năm 2029 . B. Năm 2028 . C. Năm 2048 . D. Năm 2049 . N
Câu 41: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a , SA vuông góc với mặt phẳng đáy, góc HÓ
giữa mặt phẳng (SBC) và mặt phẳng đáy bằng 0
30 . Diện tích của mặt cầu ngoại tiếp hình M
chóp S.ABC bằng TO 2 43π a 2 19π a 2 19π a Á A. . B. . C. . D. 2 13π a . N 3 3 9 VD x + –
Câu 42: Tập hợp tất cả các giá trị thực của tham số m để hàm số 3 y =
đồng biến trên khoảng + V x m D −∞ − C ( ; 6) là A. (3;6] . B. (3;6). C. (3;+∞) . D. [3;6) .
Câu 43: Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số đôi một khác nhau và các chữ số thuộc tập hợp {1;2;3;4;5;6; }
7 . Chọn ngẫu nhiên một số thuộc S , xác suất để số đó không có hai chữ số
liên tiếp nào cùng lẻ bằng
https://www.facebook.com/groups/toanvd.vdc Trang 4 NHÓM TOÁN VD – VDC MÃ ĐỀ 104 A. 1 . B. 13 . C. 9 . D. 2 . 5 35 35 7
Câu 44: Cho hình lăng trụ đứng ABC.A′B C
′ ′ có tất cả các cạnh bằng a . Gọi
M là trung điểm của AA′ (tham khảo hình vẽ). Khoảng cách từ M
đến mặt phẳng ( AB C ′ ) bằng A. a 2 . B. a 21 . 4 7 C. a 2 . D. a 21 . 2 14 N H
Câu 45: Cho hình chóp đều S.ABCD có tất cả các cạnh bằng a và O là tâm của đáy. Gọi M , N, P,Q Ó M
lần lượt là các điểm đối xứng với O qua trọng tâm của các tam giác SAB, SBC, SCD, SDA và T
S′ là điểm đối xứng với S qua O . Thể tích khối chóp S MN ′ PQ bằng O Á 3 3 3 3 N 2 2a . 20 2a 40 2a . 10 2a . A. B. . C. D. V 9 81 81 81 D –
Câu 46: Cho hàm số bậc bốn f (x) có bảng biến thiên như sau VDC
Số điểm cực trị của hàm số g x = x [ f x + ]4 2 ( ) ( 1) là A. 7 . B. 8 . C. 9. D. 5.
Câu 47: Xét các số thực không âm x và y thỏa mãn x y 1 2x .4 y + − +
≥ 3 . Giá trị nhỏ nhất của biểu thức 2 2
P = x + y + 4x + 2y bằng A. 33 . B. 9 . C. 21 . D. 41 . N 8 8 4 8 H Ó Câu 48: Cho hàm số 3 2
y = ax + bx + cx + d (a,b,c,d ∈) có đồ thị là M T
đường cong trong hình bên. Có bao nhiêu số dương trong các O
số a, b, c, d ? ÁN A. 4 . B. 2 . VD C. 1. D. 3. – VD C
Câu 49: Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 255 số nguyên y thỏa mãn log ( 2
x + y ≥ log x + y ? 3 ) 2 ( ) A. 80 . B. 79 . C. 157 . D. 158.
https://www.facebook.com/groups/toanvd.vdc Trang 5 NHÓM TOÁN VD – VDC MÃ ĐỀ 104
Câu 50: Cho hàm số y = f (x) có đồ thị là đường
cong trong hình vẽ bên. Số nghiệm thực của phương trình f ( 2 x f (x)) = 2 là A. 6. B. 12. C. 8. D. 9. N
-------------------- HẾT -------------------- H Ó M TOÁN VD – VDC N H Ó M TOÁN VD – VDC
https://www.facebook.com/groups/toanvd.vdc Trang 6 NHÓM TOÁN VD – VDC MÃ ĐỀ 104 BẢNG ĐÁP ÁN 1.C 2.A 3.C 4.B 5.C 6.B 7.B 8.D 9.C 10.A 11.B 12.A 13.B 14.B 15.C 16.A 17.D 18.C 19.A 20.D 21.B 22.A 23.D 24.C 25.A 26.D 27.A 28.A 29.B 30.C 31.B 32.B 33.D 34.C 35.C 36.A 37.D 38.A 39.B 40.A 41.B 42.A 43.B 44.D 45.B 46.C 47.D 48.C 49.D 50.D
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Tập xác định của hàm số y = log x là 4 −∞ N A. ( ;0) . B. [0;+∞) . C. (0;+∞). D. ( ; −∞ +∞) . H Ó Lời giải M Chọn C TO
Điều kiện x > 0 . ÁN
Câu 2: Cho hình trụ có bán r = 7 và độ dài đường sinh l = 3 . Diện tích xung quanh của hình trụ đã VD cho bằng – A. 42π . B. 147π . C. 49π . D. 21π . VD Lời giải C Chọn A
S = π rl = π . xq 2 42
Câu 3: Trong không gian Oxyz , cho đường thẳng
x − 4 y + 2 z − 3 d : = =
. Vectơ nào dưới đây là một 3 1 − 2 −
vectơ chỉ phương của d ? A. u = 4; 2; − 3 . B. u = 4;2; 3 − . C. u = 3; 1 − ; 2 − . D. u = 3;1;2 . 1 ( ) 3 ( ) 4 ( ) 2 ( ) Lời giải Chọn C
Câu 4: Cho hàm số bậc ba y = f (x) có đồ thị là đường cong trong hình vẽ bên. N H Ó M TOÁN VD – VD
Số nghiệm thực của phương trình f (x) = 2 là: C A. 0 . B. 3. C. 1. D. 2 . Lời giải Chọn B
Ta có số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f (x) với đường thẳng y = 2.
https://www.facebook.com/groups/toanvd.vdc Trang 7 NHÓM TOÁN VD – VDC MÃ ĐỀ 104
Dựa vào đồ thị ta có phương trình có ba nghiệm phân biệt. 3 3 Câu 5: Biết f
∫ (x)dx = 6. Giá trị của 2 f (x)dx ∫ bằng. 2 2 A. 36. B. 3. C. 12. D. 8 . Lời giải Chọn C 3 3 Ta có : 2 f
∫ (x)dx = 2 f ∫ (x)dx =12.. 2 2 N x + H
Câu 6: Tiệm cận ngang của đồ thị hàm số 3 1 y = là: Ó x −1 M T A. 1 y = . B. y = 3. C. y = 1 − . D. y =1. O 3 ÁN Lời giải V Chọn B D – + + x x V Ta có : 3 1 lim y = lim = 3 và 3 1 lim y = lim
= 3 nên y = 3 là tiệm cận ngang của đồ D x→+∞ x→+∞ x −1 x→−∞
x→−∞ x −1 C thị hàm số.
Câu 7: Trong không gian Oxyz , hình chiếu vuông góc của điểm (
A 8;1;2) trên trục Ox có tọa độ là A. (0;1;0) . B. (8;0;0) . C. (0;1;2) . D. (0;0;2) . Lời giải Chọn B
Hình chiếu vuông góc của điểm (
A 8;1;2) trên trục Ox là (8;0;0) .
Câu 8: Nghiệm của phương trình x+2 3 = 27 là A. x = 2 − . B. x = 1 − . C. x = 2 . D. x =1. Lời giải N Chọn D H Ta có x+2 x+2 3
3 = 27 ⇔ 3 = 3 ⇔ x + 2 = 3 ⇔ x =1. Ó M
Câu 9: Cho khối nón có bán kính đáy r = 2 và chiều cao h = 4 . Thể tích của khối nón đã cho bằng TO π π Á A. 8π . B. 8 . C. 16 . D. 16π . N 3 3 VD Lời giải – V Chọn C D C 1 1 16π Ta có 2 2
V = .r .π.h = .2 .π.4 = . 3 3 3
Câu 10: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
https://www.facebook.com/groups/toanvd.vdc Trang 8 NHÓM TOÁN VD – VDC MÃ ĐỀ 104 A. 4 2
y = x − 2x +1. B. 3 2
y = −x + 3x +1. C. 3 2
y = x − 3x +1. D. 4 2
y = −x + 2x +1. N Lời giải H Ó Chọn A M
Dựa vào hình vẽ, ta thấy đồ thị hàm số có ba điểm cực trị nên loại các đáp án B và C. TO Mặt khác, ta thấy ( 4 2 lim x − 2x + ) 1 = +∞ nên chọn đáp án A. Á x→+∞ N VD
Câu 11: Với a,b là hai số thực dương tùy ý và a ≠ 1, log b bằng 4 a – V A. 4 + log b . B. 1 log b . C. 4 + log b. D. 1 + log b . D a 4 a a 4 a C Lời giải Chọn B Ta có 1 log b = log b . 4 a 4 a
Câu 12: Trong không gian Oxyz, cho mặt cầu (S ) 2 2
: x + y + (z − 2)2 =16 . Bán kính của mặt cầu (S ) bằng A. 4 . B. 32. C. 16. D. 8 . Lời giải Chọn A
Bán kính của mặt cầu (S ) 2 2
: x + y + (z − 2)2 =16 là R = 16 = 4 . N H
Câu 13: Số phức liên hợp của số phức z = 3−5i là Ó M A. z = 3 − − 5i .
B. z = 3+ 5i . C. z = 3 − + 5i .
D. z = 3− 5i . T Lời giải O ÁN Chọn B VD
Ta có: z = 3− 5i ⇒ z = 3+ 5i . – V
Câu 14: Cho khối hộp chữ nhật có ba kích thước 2 ; 3; 7 . Thể tích của khối hộp đã cho bằng D C A. 7 . B. 42 . C. 12. D. 14. Lời giải Chọn B
Ta có: V = 2.3.7 = 42 .
Câu 15: Cho khối chóp có diện tích đáy B = 3 và chiều cao h = 8. Thể tích của khối chóp đã cho bằng A. 24 . B. 12. C. 8 . D. 6 .
https://www.facebook.com/groups/toanvd.vdc Trang 9 NHÓM TOÁN VD – VDC MÃ ĐỀ 104 Lời giải Chọn C Ta có: 1 1
V = Bh = .3.8 = 8. 3 3
Câu 16: Cho hàm số f (x) có bảng biến thiên như sau: N H Ó M
Hàm số đã cho đồng biến trên khoảng nào dưới đây? TO A. ( 3 − ;0) . B. ( 3 − ;3) . C. (0;3). D. (− ; ∞ 3 − ) . ÁN Lời giải VD – Chọn A V
Hàm số đã cho đồng biến trên khoảng − và 3;+∞ . D ( 3;0) ( ) C
Câu 17: Cho hàm số f (x) có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng A. 3. B. 3 − . C. 1 − . D. 2 . N Lời giải H Ó Chọn D M
Giá trị cực đại của hàm số đã cho bằng 2. TOÁ
Câu 18: Cho cấp số nhân (u với u = 4 và công bội q = 3. Giá trị của u bằng n ) N 1 2 VD A. 64 . B. 81. C. 12. D. 4 . – 3 V Lời giải D C Chọn C
u = u .q = 4.3 =12. 2 1
Câu 19: Cho khối cầu có bán kính r = 2. Thể tích của khối cầu bằng π A. 32π . B. 16π . C. 32π . D. 8 . 3 3 Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 10 NHÓM TOÁN VD – VDC MÃ ĐỀ 104 Chọn A Ta có: 4 3 4 3 32
V = π r = π 2 = π 3 3 3
Câu 20: Trên mặt phẳng tọa độ, biết M ( 1;
− 2) là điểm biểu diễn của số phức z. Phần thực của z bằng A. 1. B. 2 . C. 2 − . D. 1 − . Lời giải Chọn D Câu 21: 5 x dx ∫ bằng 1 N A. 4 5x + C . B. 6 x + C . C. 6 x + C . D. 6 6x + C . H 6 Ó Lời giải M T Chọn B O Á
Câu 22: Nghiệm của phương trình log x − 2 = 2 là 3 ( ) N V A. x = 11. B. x = 10. C. x = 7 . D. 8 . D – Lời giải VD Chọn A C
Điều kiện: x > 2
Phương trình tương đương với 2
x − 2 = 3 ⇔ x = 11
Câu 23: Trong không gian Oxyz , cho ba điểm A(2;0;0) , B(0; 1;
− 0), C (0;0;3). Mặt phẳng ( ABC) có phương trình là A. x y z + + = 1. B. x y z + + = 1. C. x y z + + = 1. D. x y z + + = 1. 2 − 1 3 2 1 3 − 2 1 3 2 1 − 3 Lời giải Chọn D
Phương trình mặt phẳng qua ba điểm A(a;0;0) , B(0; ;
b 0) , C (0;0;c) (với abc ≠ 0) có dạng x y z + + = 1 a b c N H Ó
Câu 24: Có bao nhiêu cách xếp 8 học sinh thành một hàng dọc? M A. 8. B. 1. C. 40320 . D. 64 . T Lời giải O ÁN Chọn C V = D
Số cách xếp 8 học sinh thành một hàng dọc là 8! 40320 (cách) – V
Câu 25: Cho hai số phức z =1− 3i và z = 3+ i . Số phức z + z bằng. 1 2 1 2 D C A. 4 − 2i . B. 4 − + 2i . C. 4 + 2i . D. 4 − − 2i . Lời giải Chọn A
Ta có: z + z =1− 3i + 3+ i = 4 − 2i . 1 2
Câu 26: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB = a ; BC = a 2 ; SA vuông
góc với mặt phẳng đáy và SA = a . Góc giữa đường thẳng SC và đáy bằng
https://www.facebook.com/groups/toanvd.vdc Trang 11 NHÓM TOÁN VD – VDC MÃ ĐỀ 104 A. 0 90 . B. 0 45 . C. 0 60 . D. 0 30 . Lời giải Chọn D N H Ó M TOÁN
Ta có : Góc SC và đáy là góc SCA. VD –
Xét tam giác SCA vuông tại A có: VD 2 2 C
AC = AB + BC = a 3 SA a = = ⇒ 0 tan SCA SCA = 30 . AC a 3 2
Câu 27: Cho hai số a và b là hai số thực dương thỏa mãn log3(a b) 3 9
= 4a . Giá trị của biểu thức 2 ab bằng A. 4 . B. 2 . C. 3. D. 6 . Lời giải Chọn A 2 Ta có : log ( 2ab) log 3 ( 2ab 2 3 3 ) 3 = a ⇔ = a ⇔ ( 2 a b) 3 2 9 4 3 4
= 4a ⇔ ab = 4 . x − y + z − N
Câu 28: Trong gian gian Oxyz, cho điểm M (3; 2 − ;2) và đường thẳng 3 1 1 d : = = . Mặt H 1 2 2 − Ó
phẳng đi qua M và vuông góc với d có phương trình là M + − + = − + − = T
A. x 2y 2z 5 0 . B. 3x 2y 2z 17 0 . O
C. 3x − 2y + 2z +17 = 0 . D. x + 2y − 2z − 5 = 0 . ÁN Lời giải VD Chọn A – V
Mặt phẳng nhận vectơ nhận (1;2; 2
− ) là vecto pháp tuyến và đáp án cần chọn là A. D C
Câu 29: Giá trị nhỏ nhất của hàm số f (x) 3
= x − 33x trên đoạn [2;19] bằng A. 72 − . B. 22 − 11. C. 58 − . D. 22 11 . Lời giải Chọn B
https://www.facebook.com/groups/toanvd.vdc Trang 12 NHÓM TOÁN VD – VDC MÃ ĐỀ 104 x = 11∈[2;19] Ta có f ′(x) 2 = 3x − 33 = 0 ⇔ . x = − 11∉ [2;19]
Khi đó ta có f (2) = 58 − , f ( 11) = 22 −
11 , f (19) = 6232. Vậy f = f 11 = 22 − 11 . min ( )
Câu 30: Tập nghiệm của bất phương trình 2x 1 2 − < 8 là A. (0;2) . B. ( ;2 −∞ ) . C. ( 2; − 2) . D. (2;+∞) . Lời giải Chọn C N H Từ phương trình ta có 2 x −1< 3 ⇔ 2 − < x < 2 . Ó M
Câu 31: Diện tích hình phẳng giới hạn bởi hai đường 2
y = x −3 và y = x −3 bằng TO π π Á A. 125 . B. 1 . C. 125 . D. . N 6 6 6 6 VD Lời giải – V Chọn B D x = C 0
x − 3 = x − 3 ⇔ x − x = 0 ⇔
Ta có Phương trình hoành độ giao điểm: 2 2 . x =1 1 1
Diện tích hình phẳng: S = ( 2
x − ) −(x − ) 2 1 3
3 dx = x − xdx = ∫ ∫ . 6 0 0
Câu 32: Cho hình nón có bán kính đáy bằng 4 và góc ở đỉnh bằng 0
60 . Diện tích xung quanh của hình nón đã cho bằng π π A. 64 3 . B. 32π . C. 64π . D. 32 3 . 3 3 Lời giải Chọn B S N H Ó 300 M TOÁ l N VD – VDC r O B
Ta có Góc ở đỉnh bằng 0 ⇒ 0 60 OSB = 30 . r 4
Độ dài đường sinh: l = = = 8 . 0 sin 30 1 2
https://www.facebook.com/groups/toanvd.vdc Trang 13 NHÓM TOÁN VD – VDC MÃ ĐỀ 104
Diện tích xung quanh hình nón: S = π rl = π.4.8 = . xq 32π Câu 33: Gọi z z − z + =
0 là nghiệm phức có phần ảo dương của phương trình 2 4 13 0 . Trên mặt phẳng
tọa độ, điểm biểu diễn của số phức 1− z0 là A. M (3; 3 − ). B. P( 1; − 3) . C. Q(1;3) D. N ( 1; − 3 − ). Lời giải Chọn D Ta có 2
z − 4z +13 = 0 ⇔ z = 2 ± 3i . Vậy z = 2 + 3i ⇒1− z = 1 − − 3i 0 0 . N
Điểm biểu diễn của 1− z N − −
0 trên mặt phẳng tọa độ là: ( 1; 3). H Ó M
Câu 34: Cho hàm số f (x) liên tục trên R có bảng xét dấu f '(x) TOÁN VD –
Số điểm cực đại của hàm số đã cho là: VD A. 3. B. 1. C. 2. D. 4. C Lời giải Chọn C
Ta có: f '(x) = 0 , f '(x) không xác định tại x = 2
− ; x =1; x = 2, x = 3. Nhưng có 2 giá trị x = 2;
− x = 2 mà qua đó f '(x) đổi dấu từ dương sang âm nên hàm số đã cho có 2 điểm cực đại.
Câu 35: Trong không gian Oxyz , cho ba điểm A(1;1;0), B(1;0; )
1 ,C (3;1;0) . Đường thẳng đi qua A và
song song với BC có phương trình là:
A. x +1 y +1 z + + = = .
B. z 1 y 1 z = = . 2 1 1 4 1 1
C. x −1 y −1 z − − = =
. D. x 1 y 1 z = = . 2 1 1 − 4 1 1 N H Lời giải Ó Chọn C M T − O
Đường thẳng đi qua A(1;1;0), song song với BC nên nhận BC = (2;1; )
1 là véc tơ chỉ phương ÁN x − y − z
do đó có phương trình là: 1 1 = = . V 2 1 1 − D –
Câu 36: Cho hai số phức z =1+ 3i và w =1+ i . Môđun của số phức z.w bằng VDC A. 2 5 . B. 2 2 . C. 20 . D. 8 . Lời giải Chọn A
Ta có: w =1+ i ⇒ w =1− i
z.w = (1+ 3i)(1−i) = 4 + 2i Từ đây ta suy ra: 2 2
z.w = 4 + 2 = 2 5 .
https://www.facebook.com/groups/toanvd.vdc Trang 14 NHÓM TOÁN VD – VDC MÃ ĐỀ 104
Câu 37: Số giao điểm của đồ thị hàm số 2
y = −x + 3x và đồ thị hàm số 3 2
y = x − x là A. 1. B. 0 . C. 2 . D. 3 Lời giải Chọn D
Phương trình hoành độ giao điểm của hai đồ thị là x = 0 3 2 2 3
x − x = −x + 3x ⇔ x − 3x = 0 ⇔ . x = ± 3 3 Câu 38: Biết ( ) 2
F x = x là một nguyên hàm của hàm số f (x) trên . Giá trị của ∫[1+ f (x)]dx bằng N 1 H Ó A. 10. B. 8. C. 26 . D. 32 . M 3 3 T Lời giải O ÁN Chọn A V 3 3 3 D
Ta có ∫[1+ f (x)]dx = (x + F (x)) 2 = x + x = 12 − 2 =10. ( ) – 1 1 1 VDC x
Câu 39: Cho hàm số f (x) =
. Họ tất cả các nguyên hàm của hàm số g (x) = (x + ) 1 f ′(x) là 2 x + 4 2 2 A. x + 4 − + − + + + C .
B. x 4 + C .
C. x 2x 4 + C . D. 2x x 4 +C . 2 2 x + 4 2 x + 4 2 2 x + 4 2 x + 4 Lời giải Chọn B ′ 2
x .′ x + 4 − ( 2x + 4) .x Ta có: ( ) x f x = ⇒ f ′(x) = 2 x + 4 2 x + 4 2 2 2 x x + 4 + 4 − . − x x x ⇒ f ′(x) 2 2 x + 4 x + 4 4 = = = 2 2 3 N x + 4 x + 4 ( 2x +4) H Ó M
Suy ra: g (x) = (x + )
1 f ′(x) = .x f ′(x) + f ′(x) TO g
∫ (x)dx = .xf ′
∫ (x)+ f ′(x)dx = .xf ′
∫ (x)dx+ f ′ ∫ (x)dx ÁN 4x = + ′ V dx f x dx ∫ 3 ∫ D 2 x + 4 ( ) ( ) – VD Xét: 4x I = dx C ∫ ( x +4)3 2 Đặt 2
t = x + 4 ⇒ dt = 2xdx 1 3 − − 2 Suy ra: 2dt 2dt t 4 − 4 − 2 I = ∫ ( = = = + = + = + ∫ ∫ t ) 2 t dt 2 C C C 3 3 1 1 1 1 2 t 2 x + − 4 t 2
https://www.facebook.com/groups/toanvd.vdc Trang 15 NHÓM TOÁN VD – VDC MÃ ĐỀ 104 và: J = f ′
∫ (x)dx = f (x)+C2 Vậy: g ∫ (x) 4 − x x − 4 dx = + + C = + C . 2 2 2 x + 4 x + 4 x + 4
Cách 2: g (x) = (x + ) 1 f ′(x)
⇒ g (x)dx = (x + ∫ ∫
)1 f ′(x)dx u = x +1 du = dx Đặt: ⇒ dv = f (x)dx ′ v = f (x) x +1 x x N Suy ra: g
∫ (x)dx = (x+ )1 f (x)− f ∫ (x) ( ) dx = − dx ∫ 2 2 H x + 4 x + 4 Ó 2 M 2 x + x d (x + 4) 2 x + x 2 x − 4 = − = − x + 4 + C = + C . T ∫ 2 2 2 2 O x + 4 2 x + 4 x + 4 x + 4 ÁN
Câu 40: Trong năm 2019 , diện tích rừng trồng mới của tỉnh A là 800ha . Giả sử diện tích rừng trồng VD
mới của tỉnh A mỗi năm tiếp theo đều tăng 6% so với diện tích rừng trồng mới của năm liền –
trước. Kể từ sau năm 2019 , năm nào dưới đây là năm đầu tiên tỉnh A có diện tích rừng trồng VD
mới trong năm đó đạt trên 1400ha ? C A. Năm 2029 . B. Năm 2028 . C. Năm 2048 . D. Năm 2049 . Lời giải Chọn A
Trong năm 2019 , diện tích rừng trồng mới của tỉnh A là 800ha . Giả sử diện tích rừng trồng
mới của tỉnh A mỗi năm tiếp theo đều tăng 6% so với diện tích rừng trồng mới của năm liền
trước nên sau n (năm) diện tích rừng trồng mới của tỉnh A là 800.(1 6%)n + với n∈ . Ta có ( + )n n 7 7
800. 1 6% ≥1400 ⇔ 1,06 ≥ ⇔ n ≥ log ≈ 9,60402 . 1,06 4 4
Vì n∈ nên giá trị nhỏ nhất thỏa mãn là n =10 .
Vậy: kể từ sau năm 2019 , năm đầu tiên tỉnh A có diện tích rừng trồng mới trong năm đó đạt
trên 1400ha là năm 2029 . N
Câu 41: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a , SA vuông góc với mặt phẳng đáy, góc HÓ
giữa mặt phẳng (SBC) và mặt phẳng đáy bằng 0
30 . Diện tích của mặt cầu ngoại tiếp hình chóp M S.ABC bằng TO 2 43π a 2 19π a 2 19π a Á A. . B. . C. . D. 2 13π a . N 3 3 9 V Lời giải D – VDC
https://www.facebook.com/groups/toanvd.vdc Trang 16 NHÓM TOÁN VD – VDC MÃ ĐỀ 104 S d' N d I R N H C A Ó M G M T B O ÁN Chọn B V
Gọi M là trung điểm của đoạn BC . D –
N là trung điểm của đoạn SA. V
G là trọng tâm A ∆ BC . D C
Gọi d′ là đường thẳng đi qua trọng tâm G của A
∆ BC và vuông góc với mặt phẳng đáy.
d là đường trung trực của đoạn thẳng SA.
Từ đó suy ra tâm I của mặt cầu ngoại tiếp hình chóp S.ABC là giao điểm của hai đường thẳng d và d′ .
Suy ra: bán kính mặt cầu R = AI . Ta có: A
∆ BC đều cạnh 2a 3 ⇒ AM = 2 . a = a 3 và 2a 3 AG = . 2 3
Góc giữa mặt phẳng (SBC) và mặt phẳng đáy là góc 0 SMA = 30 SA 0 3 tan SMA =
⇒ SA = AM.tan 30 = a 3. = a . AM 3 a N Suy ra: AN = . H 2 Ó M 2 2 a a T Do đó: 2 2 2 2 2 3 57
R = AI = AN + NI = AN + AG = + = O 2 3 6 ÁN V 2 2 D 2 57 19π a
Vậy diện tích của mặt cầu ngoại tiếp hình chóp S.ABC là: S = 4π.R = 4π. = . – 6 3 V D C x +
Câu 42: Tập hợp tất cả các giá trị thực của tham số m để hàm số 3 y =
đồng biến trên khoảng x + m ( ; −∞ 6 − ) là A. (3;6] . B. (3;6). C. (3;+∞) . D. [3;6) . Lời giải Chọn A
https://www.facebook.com/groups/toanvd.vdc Trang 17 NHÓM TOÁN VD – VDC MÃ ĐỀ 104
Hàm số xác định khi: x + m ≠ 0 ⇔ x ≠ −m . x + 3 m − 3 y = ⇒ y′ = x + m (x + m)2
y′ > 0, x ∀ ∈( ; −∞ 6 − )
Hàm số đồng biến trên khoảng ( ; −∞ 6
− ) khi và chỉ khi: −m∉ ( ; −∞ 6 − ) m −3 > 0 m > 3 m > 3 ⇔ ⇔ ⇔ ⇔ < ≤ . −m∈ [− +∞) 3 m 6 6; −m ≥ 6 − m ≤ 6 N H Vậy: m∈(3;6] . Ó M T
Câu 43: Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số đôi một khác nhau và các chữ số thuộc tập O hợp {1;2;3;4;5;6; }
7 . Chọn ngẫu nhiên một số thuộc S , xác suất để số đó không có hai chữ số ÁN
liên tiếp nào cùng lẻ bằng VD – A. 1 . B. 13 . C. 9 . D. 2 . V 5 35 35 7 D Lời giải C Chọn B
Số phần tử không gian mẫu là n(Ω) 4 = A . 7
Để chọn được số thỏa mãn bài toán, ta có các trường hợp:
+ Trường hợp số được chọn có đúng 1 chữ số lẻ:
Chọn chữ số lẻ trong 4 số lẻ: có 4 cách.
Xếp các chữ số lấy được có 4! cách.
Trường hợp này có 4 ⋅4! = 96 cách.
+ Trường hợp số được chọn có 2 chữ số lẻ và 2 chữ số chẵn. N H
Lấy ra 2 chữ số lẻ và 2 chữ số chẵn có 2 2 C ⋅C cách. 4 3 Ó M
Xếp các chữ số chẵn có 2 cách, tiếp theo xếp 2 chữ số lẻ vào 3 vị trí ngăn cách bởi các số TO chẵn có 2 A cách. 3 ÁN V
Suy ra trường hợp này có 2 2 2
C ⋅C ⋅2⋅ A = 216 cách. D 4 3 3 – + = V
Số kết quả thuận lợi cho biến cố 96 216 312 D C 312 13
Xác suất của biến cố P = = . 4 A 35 7
Câu 44: Cho hình lăng trụ đứng ABC.A′B C
′ ′ có tất cả các cạnh bằng a . Gọi M là trung điểm của AA′ (tham khảo hình vẽ).
https://www.facebook.com/groups/toanvd.vdc Trang 18 NHÓM TOÁN VD – VDC MÃ ĐỀ 104
Khoảng cách từ M đến mặt phẳng ( AB C ′ ) bằng A. a 2 . B. a 21 . C. a 2 . D. a 21 . N 4 7 2 14 H Ó Lời giải M T Chọn D O ÁN VD – VDC Trong ( ABB A
′ ′) , gọi E là giao điểm của BM và AB′. Khi đó hai tam giác EAM và EB B ′
d (M ,( AB C ′ )) đồng dạng. Do đó EM MA 1 1 = = = ⇒ ′ = ⋅ ′ . d (
d (M , AB C )
d (B, AB C ) B,( AB C ′ )) ( ) ( ) EB BB′ 2 2 ⊥ a ′ = N
Từ B kẻ BN AC thì N là trung điểm của AC và 3 BN = , BB a . H 2 Ó M BB′⋅ BN a 21 Kẻ BI ⊥ B N
′ thì d (B,( AB C ′ )) = BI = = . T 2 2 BB′ + BN 7 O ÁN 1 a 21 V
Vậy d (M,( AB C
′ )) = ⋅d (B,( AB C ′ )) = . D 2 14 – V
S ABCD có tất cả các cạnh bằng a và O là tâm của đáy. Gọi D
Câu 45: Cho hình chóp đều .
M , N, P,Q C
lần lượt là các điểm đối xứng với O qua trọng tâm của các tam giác SAB, SBC, SCD, SDA và
S′ là điểm đối xứng với S qua O . Thể tích khối chóp S MN ′ PQ bằng 3 3 3 3 A. 2 2a .
B. 20 2a . C. 40 2a . D. 10 2a . 9 81 81 81 Lời giải Chọn B
https://www.facebook.com/groups/toanvd.vdc Trang 19 NHÓM TOÁN VD – VDC MÃ ĐỀ 104 S Q I M P N K G A D O B C N H Ó M S' TOÁ a N Ta có 2 SO = V 2 D –
Gọi G, K lần lượt là trọng tâm của tam giác SAB và tam giác SCD . VDC = = = Suy ra 4 MP 2GK a , tương tự 4 NQ a . 3 3 8 2 ⇒ S = a . MNPQ 9
Ta có (MNPQ) // ( ABCD)
d (M ( ABCD)) = d (G ( ABCD)) 2 a 2 , 2 , = SO = . 3 3
⇒ d ((MNPQ) ( ABCD)) a 2 , = 3 a a N
⇒ d (S′ (MNPQ)) 2 5 2 , = S O ′ + = H 3 6 Ó M 2 3 1 5a 2 8a 20 2a T ⇒ V = = . S MN ′ PQ . . O 3 6 9 81 ÁN
Câu 46: Cho hàm số bậc bốn f (x) có bảng biến thiên như sau VD – VDC
Số điểm cực trị của hàm số g x = x [ f x + ]4 2 ( ) ( 1)
https://www.facebook.com/groups/toanvd.vdc Trang 20 NHÓM TOÁN VD – VDC MÃ ĐỀ 104 A. 7 . B. 8 . C. 9. D. 5. Lời giải Chọn C
g x = x[ f x + ]4 + x [ f x + ]3 f x + = x[ f x + ]3 2 '( ) 2 ( 1) 4 ( 1) . '( 1) 2
( 1) .[ f (x +1) + 2 .x f '(x +1)]
g '(x) = 0 ta được + TH1: x = 0 x = a < 2 − N x = b∈( 2 − ; 1) − H
+ TH2: f (x 1) 0 + = ⇔ Ó x = c∈( 1; − 0) M x = d > 0 TOÁ
+ TH3: f (x +1) + 2 .x f '(x +1) = 0 . N VD
Từ bảng biến thiên ta có hàm số thỏa mãn là 4 2 f (x) = 5
− x +10x − 2 – VD
⇒ f (x +1) + 2 .
x f '(x +1) = 0 ⇔ h(x) = f (x +1) + 2(x +1). f '(x +1) − 2 f '(x +1) = 0 C
Với t = x +1 ta có: 4 2 3 3 h(t) = 5
− t +10t − 2 + 2t( 20
− t + 20t) − 2( 20 − t + 20t) = 0 ⇔ 4 3 2 45
− t + 40t + 50t − 40t − 2 = 0
Lập bảng biến thiên ta suy ra có 4 nghiệm t ⇒ 4 nghiệm x Vậy có 9 cực trị.
Câu 47: Xét các số thực không âm x và y thỏa mãn x+ y 1 2x .4 − + y
≥ 3 . Giá trị nhỏ nhất của biểu thức 2 2
P = x + y + 4x + 2y bằng A. 33 . B. 9 . C. 21 . D. 41 . 8 8 4 8 Lời giải N H Chọn D Ó x+ y 1 − − x y 1 − 2 y 3−2x M Ta có 2x + .4 y
≥ 3 ⇔ (2x − 3).4 + .4 y ≥ 0 ⇔ 2 .2 y ≥ (3− 2x)2 (1) T 3 O x ≥ 33 Á Xét TH 3
3− 2x ≤ 0 ⇔ x ≥ . (1) đúng với mọi giá trị 2 2
2 ⇒ P = x + y + 4x + 2y ≥ (2) N 2 4 y ≥ V 0 D – Xét TH 3
3− 2x > 0 ⇔ 0 ≤ x < . V 2 D t C
Xét hàm số f (t) = t.2 với t ≥ 0
⇒ ′( ) = 2t + .2t f t
t .ln 2 > 0 với mọi t ≥ 0
(1) ⇔ f (2y) ≥ f (3− 2x)
⇔ 2y ≥ 3− 2x 3 ⇔ y ≥ − x 2
https://www.facebook.com/groups/toanvd.vdc Trang 21 NHÓM TOÁN VD – VDC MÃ ĐỀ 104 2 2 2 2 3
⇒ P = x + y + x + y ≥ x + − x + x + ( − x) 2 21 4 2 4 3 2 = 2x − x + 2 4 2 1 41 41 ⇒ P = 2 x − + ≥ (3) 4 8 8
So sánh (2) và (3) ta thấy GTNN của P là 41 khi 1 5 x = , y = 8 4 4 Câu 48: Cho hàm số 3 2
y = ax + bx + cx + d (a, ,
b c,d ∈) có đồ thị là đường cong trong hình bên. Có
bao nhiêu số dương trong các số a, b, c, d ? N H Ó M TOÁN VD – VDC A. 4 . B. 2 . C. 1. D. 3. Lời giải Chọn C Ta có: 2
y′ = 3ax + 2bx + c
Dựa vào đồ thị ta thấy a < 0 2
b − 9ac > 0 ∆′ > y′ 0 2b b < 0
Hàm số có 2 cực trị âm nên S < 0 ⇔ − < 0 ⇒ 3 a c < 0 P > 0 c N > 0 H 3a Ó M
Đồ thị cắt trục Oy tại điểm (0;d ) nên d > 0 TOÁ
Vậy có đúng 1 số dương trong các số a, b, c, d . N VD
Câu 49: Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 255 số nguyên y thỏa mãn – 2
log x + y ≥ log x + y ? 3 ( ) 2 ( ) VDC A. 80 . B. 79 . C. 157 . D. 158 Lời giải Chọn D Ta có: log ( 2
x + y ≥ log x + y 2 log 2 log 3 2( ) 3 x y x y + ⇔ + ≥
⇔ x + y ≥ (x + y) 2 ( ) 1 3 ) 2 ( )
Đk: x + y ≥1 ( do x, y ∈, x + y > 0)
Đặt t = x + y ≥1, nên từ ( ) 2 log2 3
1 ⇒ x − x ≥ t − t (2)
https://www.facebook.com/groups/toanvd.vdc Trang 22 NHÓM TOÁN VD – VDC MÃ ĐỀ 104 Để ( )
1 không có quá 255 nghiệm nguyên y khi và chỉ khi bất phương trình (2) có không quá
255 nghiệm nguyên dương t .
Đặt M = f (255) với ( ) log23 f t = t − t .
Vì f là hàm đồng biến trên [1,+∞) nên (2) ⇔ 1 − ≤ ≤ ( 2 1 t f x − x) khi 2 x − x ≥ 0 .
Vậy (2) có không quá 255 nghiệm nguyên 1 f − ⇔
( 2x − x) ≤ 255 2
⇔ x − x ≤ 255 ⇔ 78
− ≤ x ≤ 79 (x∈) .
Vậy có 158 số nguyên x thỏa mãn yêu cầu bài toán.
Câu 50: Cho hàm số y = f (x) có đồ thị là đường cong trong hình vẽ bên. N H Ó M TOÁN VD – VDC
Số nghiệm thực của phương trình f ( 2 x f (x)) = 2là: A. 6. B. 12. C. 8. D. 9. Lời giải Chọn D 2 x f (x) = 0 2
x f ( x) = a < 0 Ta có: f ( 2
x f (x)) = 2 ⇒ . 2
x f (x) = b < 0 2 x f (x) = c < 0 x = 0 N Xét phương trình: 2 x f (x) = 0 ⇔
mà f (x) = 0 có hai nghiệm 2
⇒ x . f (x) = 0 có ba H f (x) = 0 Ó M nghiệm. T 2 O
Xét phương trình: x f (x) = a < 0 ÁN a Do 2
x ≥ 0; x = 0 không là nghiệm của phương trình⇒ f (x) = < 0 V 2 D x – a 2 − a = ⇒ ′ = V Xét g (x) g x 2 ( ) 3 D x x C Bảng biến thiên:
https://www.facebook.com/groups/toanvd.vdc Trang 23 NHÓM TOÁN VD – VDC MÃ ĐỀ 104
Từ bảng biến thiên với f (x) < 0 ⇒ ( ) a f x = có 2 nghiệm. 2 x Tương tự: 2
x f (x) = b và 2
x f (x) = c ( ,
b c < 0) mỗi phương trình cũng có hai nghiệm. N H Ó
Vậy số nghiệm của phương trình f ( 2
x f (x)) = 2 là 9 nghiệm. M TO
-------------------- HẾT -------------------- ÁN VD – VDC N H Ó M TOÁN VD – VDC
https://www.facebook.com/groups/toanvd.vdc Trang 24
Document Outline
- Pages from Dap an cac mon TN
- dap-an-va-loi-giai-chi-tiet-de-thi-tot-nghiep-thpt-nam-2020-mon-toan
- Binder1
- Mã 101_Nhom toan VD-VDC_De TN 2020
- Mã 102_Nhom toan VD-VDC_De TN 2020
- Mã 103_Nhom toan VD-VDC_De TN 2020
- Mã 104_Nhom toan VD-VDC_De TN 2020
- Binder1




