Đề thi và đáp án môn Toán khối A năm 2012

BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH ĐẠI HỌC NĂM 2012
Môn: TOÁN; Khối A và khối A1 ĐỀ CHÍNH THỨC
Thời gian làm bài: 180 phút, không kể thời gian phát đề
I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7,0 điểm)
Câu 1 (2,0 điểm). Cho hàm số 4 2 2
y = x − 2(m +1)x + m (1), với m là tham số thực.
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = 0.
b) Tìm m để đồ thị của hàm số (1) có ba điểm cực trị tạo thành ba đỉnh của một tam giác vuông.
Câu 2 (1,0 điểm). Giải phương trình 3 sin 2x + cos 2x = 2cos x −1. 3 2 3 2
⎧x − 3x − 9x + 22 = y + 3y − 9y ⎪
Câu 3 (1,0 điểm). Giải hệ phương trình ⎨ (x, y ∈ \). 2 2 1
⎪x + y − x + y = ⎩ 2 3 1+ ln(x +1)
Câu 4 (1,0 điểm). Tính tích phân I = d . x ∫ 2 x 1
Câu 5 (1,0 điểm). Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S
trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA = 2H .
B Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng o
60 . Tính thể tích của khối chóp S.ABC và tính khoảng cách giữa hai đường thẳng SA và BC theo a.
Câu 6 (1,0 điểm). Cho các số thực x, y, z thỏa mãn điều kiện x + y + z = 0. Tìm giá trị nhỏ nhất của biểu thức | x− y| | y−z| | z−x| 2 2 2 P = 3 + 3 + 3
− 6x + 6y + 6z .
II. PHẦN RIÊNG (3,0 điểm): Thí sinh chỉ được làm một trong hai phần riêng (phần A hoặc phần B)
A. Theo chương trình Chuẩn
Câu 7.a (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD. Gọi M là trung điểm 11 1
của cạnh BC, N là điểm trên cạnh CD sao cho CN = 2 .
ND Giả sử M ( ; ) và đường thẳng AN có 2 2
phương trình 2x − y − 3 = 0. Tìm tọa độ điểm A. x +1 y z − 2
Câu 8.a (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : = = và 1 2 1
điểm I (0;0;3). Viết phương trình mặt cầu (S) có tâm I và cắt d tại hai điểm A, B sao cho tam giác IAB vuông tại I.
Câu 9.a (1,0 điểm). Cho n là số nguyên dương thỏa mãn 1 5 n C − 3 n = n
C . Tìm số hạng chứa 5 x trong khai 2 n nx 1
triển nhị thức Niu-tơn của ( − ) , x≠0. 14 x
B. Theo chương trình Nâng cao
Câu 7.b (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn 2 2
(C): x + y = 8. Viết phương
trình chính tắc của elip (E), biết rằng (E) có độ dài trục lớn bằng 8 và (E) cắt (C) tại bốn điểm tạo thành
bốn đỉnh của một hình vuông. x +1 y z − 2
Câu 8.b (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : = = , mặt 2 1 1
phẳng (P): x + y − 2z + 5 = 0 và điểm (1
A ; −1; 2). Viết phương trình đường thẳng ∆ cắt d và (P) lần lượt
tại M và N sao cho A là trung điểm của đoạn thẳng MN. 5(z + i)
Câu 9.b (1,0 điểm). Cho số phức z thỏa mãn
= 2 − i. Tính môđun của số phức 2
w =1+ z + z . z +1
---------- HẾT ----------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:....................................................................; Số báo danh: ..............................................
BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN – THANG ĐIỂM
⎯⎯⎯⎯⎯⎯⎯⎯
ĐỀ THI TUYỂN SINH ĐẠI HỌC NĂM 2012 ĐỀ CHÍNH THỨC
Môn: TOÁN; Khối A và khối A1
(Đáp án – thang điểm gồm 04 trang) Câu Đáp án Điểm 1
a) (1,0 điểm)
(2,0 điểm) Khi m = 0, ta có: 4 2
y = x − 2x .
• Tập xác định: D = . \ 0,25 • Sự biến thiên: − Chiều biến thiên: 3 y ' = 4x − 4 ;
x y ' = 0 ⇔ x = 0 hoặc x = ±1.
Các khoảng nghịch biến: ( ; −∞ 1 − ) à
v (0; 1); các khoảng đồng biến: ( 1 − ; 0) và (1;+∞).
− Cực trị: Hàm số đạt cực tiểu tại x = 1, ± yCT = 1;
− đạt cực đại tại x = 0, yCĐ =0. 0,25
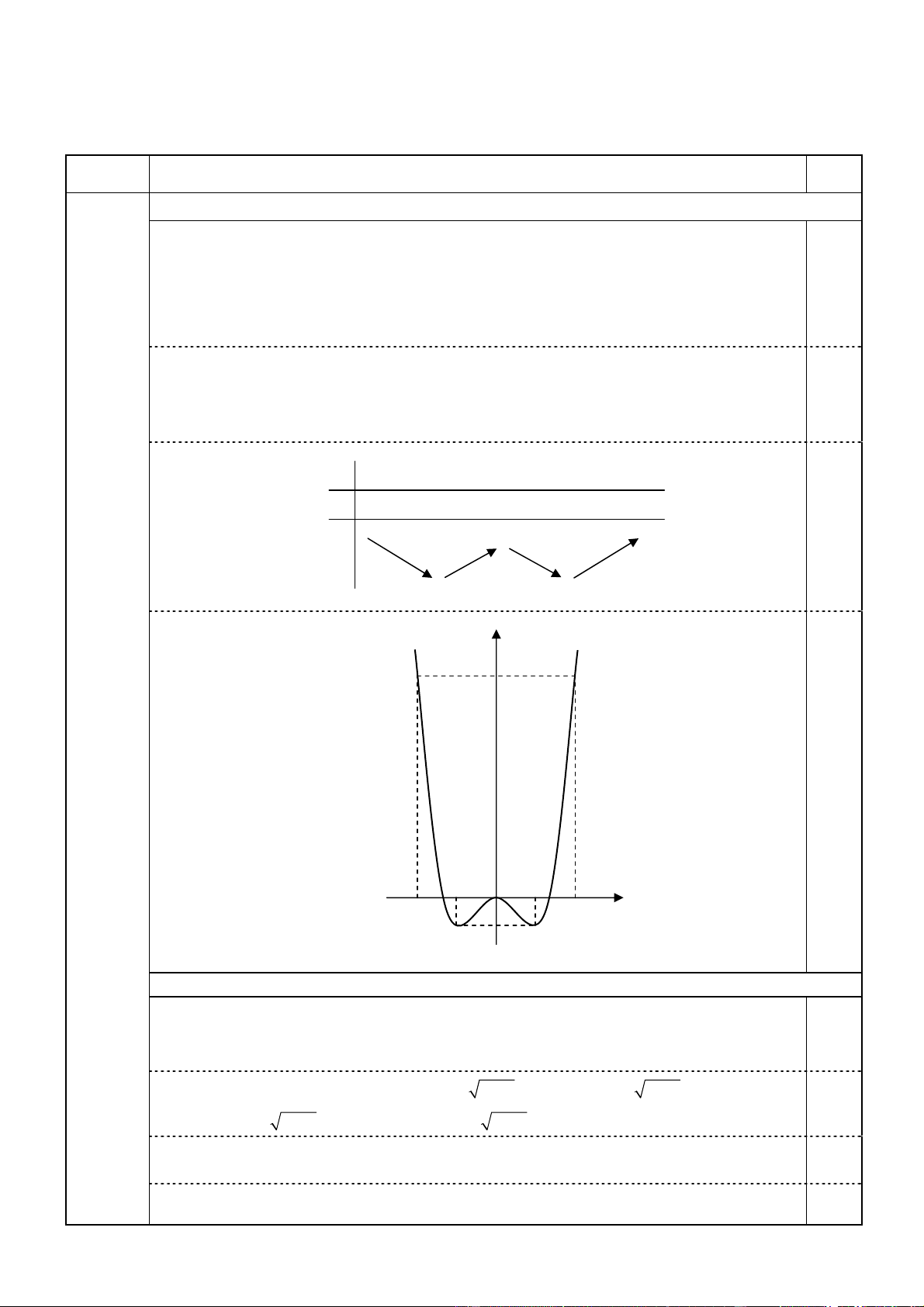
− Giới hạn: lim y = lim y = + . ∞ x →−∞ x → + ∞ − Bảng biến thiên:
x −∞ –1 0 1 + ∞ y ' – 0 + 0 – 0 + +∞ +∞ 0,25 0 y –1 –1 • Đồ thị: y 8 0,25 –1 O 1 –2 2 x – 1
b) (1,0 điểm) Ta có 3 2
y ' = 4x − 4(m + 1)x = 4x(x − m − 1). 0,25
Đồ thị hàm số có 3 điểm cực trị khi và chỉ khi m +1 > 0 ⇔ m > −1 (*).
Các điểm cực trị của đồ thị là 2 (0
A ; m ), B(− m + 1; − 2m −1) và C( m + 1; − 2m −1). JJJG JJJG 0,25 Suy ra: 2
AB = (− m + 1; − (m + 1) ) và 2
AC = ( m + 1; − (m + 1) ). JJJG JJJG
Ta có AB = AC nên tam giác ABC vuông khi và chỉ khi . AB AC = 0 0,25 ⇔ 4
(m +1) − (m +1) = 0. Kết hợp (*), ta được giá trị m cần tìm là m = 0. 0,25 Trang 1/4 Câu Đáp án Điểm 2
Phương trình đã cho tương đương với ( 3 sin x + cos x −1)cos x = 0. 0,25
(1,0 điểm) π
• cos x = 0 ⇔ x = + π k (k ∈ ]). 0,25 2 • π π
3 sin x + cos x −1 = 0 ⇔ cos(x − ) = cos 0,25 3 3 ⇔ 2π
x = k 2π hoặc x =
+ k2π (k ∈]). 3 0,25 π 2π
Vậy nghiệm của phương trình đã cho là x = + π
k , x = k 2π và x =
+ k 2π (k ∈]). 2 3 3 3 3 (
⎧ x −1) −12(x −1) = (y +1) −12(y +1) (1) ⎪
(1,0 điểm) Hệ đã cho tương đương với: (⎨ 1 0,25 ⎪ x − ⎩ )2 +( 1 y + )2 =1. (2) 2 2 1 1 1 3 Từ (2), suy ra 1
− ≤ x − ≤ 1 và 1 − ≤ y + ≤ 1⇔ 3 1
− ≤ x −1 ≤ và − ≤ y +1 ≤ . 2 2 2 2 2 2 0,25 3 3 Xét hàm số 3 ⎡ ⎤
f (t) = t −12t trên − ; ⎢ = − < ⎣ f t t
, suy ra f(t) nghịch biến. 2 2⎥⎦ , ta có 2 '( ) 3( 4) 0
Do đó (1) ⇔ x – 1 = y + 1 ⇔ y = x – 2 (3). 2 2 1 3 1 3 0,25
Thay vào (2), ta được (x − ) + (x − ) =1 ⇔ 2
4x − 8x + 3 = 0 ⇔ x = hoặc x = . 2 2 2 2 1 3 3 1
Thay vào (3), ta được nghiệm của hệ là ( ;
x y) = ( ; − ) hoặc ( ; x y) = ( ; − ). 0,25 2 2 2 2 4 dx d 1 Đặt x
u = 1 + ln(x + 1) và dv = , suy ra du = và v = − . 0,25 2
(1,0 điểm) x x + 1 x 3 3 1+ ln(x +1) dx I = − + ∫ 0,25 x + 1 x(x 1) 1 3 3 2 + ln 2 + = + ∫(1 1 − ) 2 ln2 x dx = + ln 0,25 3 x x + 1 3 x + 1 1 1 2 2 = + ln3 − ln 2. 0,25 3 3 5 Ta có n
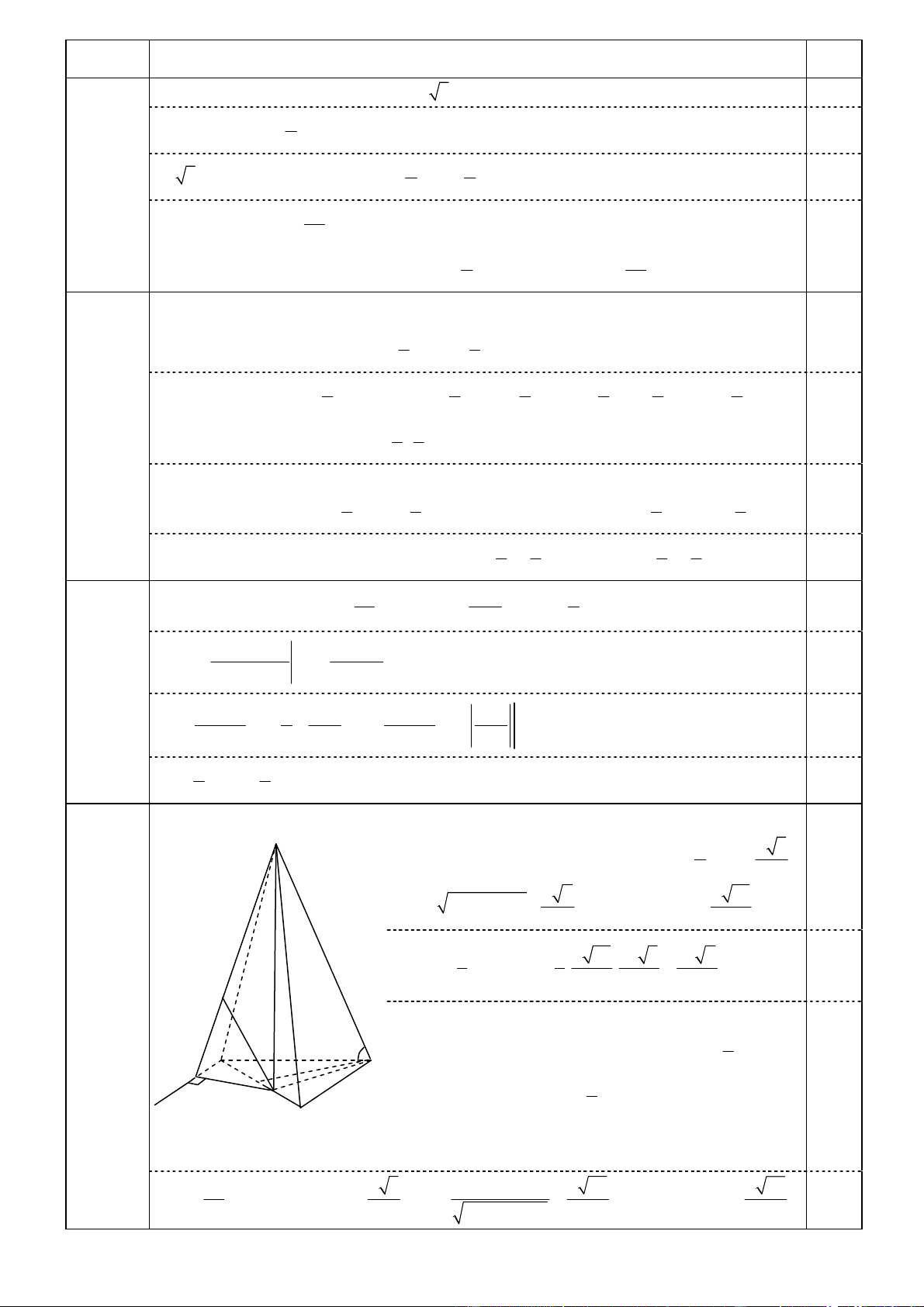
SCH là góc giữa SC và (ABC), suy ra n o SCH = 60 .
(1,0 điểm) S a 3 Gọi a
D là trung điểm của cạnh AB. Ta có: HD = , CD = , 6 2 0,25 2 2 a 7 a
HC = HD +CD = , o 21 SH = HC.tan60 = . 3 3 2 3 1 1 a 21 a 3 a 7 V = .SH.S = . . = . 0,25 S . ABC 3 ∆ABC 3 3 4 12 K
Kẻ Ax//BC. Gọi N và K lần lượt là hình chiếu vuông góc 3
của H trên Ax và SN. Ta có BC//(SAN) và BA = HA nên A 2 N D C x 3 0,25 d (S ,
A BC) = d (B, (SAN )) =
d (H , (SAN )). H 2 B
Ta cũng có Ax ⊥ (SHN ) nên Ax ⊥ HK. Do đó
HK ⊥ (SAN ). Suy ra d (H , (SAN )) = HK. 2a o a 3 SH .HN a 42 a 42 AH =
, HN = AH sin 60 = , HK = = . Vậy d (S , A BC) = . 0,25 3 3 2 2 12 SH + HN 8 Trang 2/4 Câu Đáp án Điểm 6
Ta chứng minh 3t ≥ t +1, t ∀ ≥ 0 (*).
(1,0 điểm) Xét hàm ( ) = 3t f t
− t −1, có '( ) = 3t f t ln 3 −1 > 0, t
∀ ≥ 0 và f (0) = 0 , suy ra (*) đúng. 0,25
Áp dụng (*), ta có |x−y| | y−z| | z−x| 3 +3 +3
≥3+| x− y|+| y−z|+|z−x|.
Áp dụng bất đẳng thức | a | + | b | ≥ | a + b | , ta có: 2 2 2 2
(| x− y|+| y−z|+|z− x|) =| x− y| +| y− z| + | z− x| +|x− y|(| y− z|+| z− x|)+| y− z|(| z− x|+| x− y|) 0,25
+ z−x x− y + y−z ≥ ( 2 2 2 | |(| | | |)
2 | x− y| + | y− z| + | z− x| ).
Do đó x− y + y−z + z−x ≥ ( 2 2 2
x− y + y− z + z− x ) 2 2 2 | | | | | | 2 | | | | |
| = 6x +6y +6z −2( x+ y+z)2 . 0,25 Mà 2 2 2
x+ y+ z =0, suy ra | x− y|+| y− z|+| z− x| ≥
6x +6y +6z . Suy ra | x−y| | y−z| | z−x| 2 2 2 P =3 +3 +3
− 6x +6y +6z ≥3. 0,25
Khi x = y = z = 0 thì dấu bằng xảy ra. Vậy giá trị nhỏ nhất của P bằng 3. 7.a
Gọi H là giao điểm của AN và BD. Kẻ đường thẳng qua H
(1,0 điểm)
và song song với AB, cắt AD và BC lần lượt tại P và Q.
Đặt HP = x. Suy ra PD = x, AP = 3x và HQ = 3x. A 0,25 B
Ta có QC = x, nên MQ = x. Do đó ∆AHP = ∆HMQ, suy ra AH ⊥ HM .
Hơn nữa, ta cũng có AH = HM . M 0,25
Do đó AM = 2MH = 2d (M ,(AN )) = 3 10 . H 2 P Q
A∈AN, suy ra A(t; 2t – 3). C D 3 10 2 2 11 7 45 0,25 N MA =
⇔ (t − ) +(2t − ) = 2 2 2 2 ⇔ 2 t − t
5 + 4 = 0 ⇔ t = 1 hoặc t = 4. 0,25 Vậy: ( A 1; 1 − ) hoặc ( A 4;5). JJG 8.a
Véc tơ chỉ phương của d là a = (1; 2; 1). Gọi H là trung điểm của AB, suy ra IH ⊥ AB.
(1,0 điểm) JJJG 0,25
Ta có H ∈d nên tọa độ H có dạng H (t 1
− ; 2t;t +2)⇒ IH =(t 1 − ; 2t;t 1 − ). JJJG JJG JJJG 2 2 2
IH ⊥ AB ⇔ IH . a = 0 ⇔ t −1 + 4t + t −1 = 1 0 ⇔ t =
⇒ IH = (− ; ; − ). 0,25 3 3 3 3 2 6
Tam giác IAH vuông cân tại H, suy ra bán kính mặt cầu (S) là R = IA = 2IH = . 0,25 3
Do đó phương trình mặt cầu cần tìm là 2 2 2 8
(S): x + y + (z − 3) = . 0,25 3 9.a −1
n(n −1)(n − 2)
(1,0 điểm) 5 n C = 3 ⇔ 5n = 0,25 n Cn 6
⇔ n = 7 (vì n nguyên dương). 0,25 n 7 7 2 2 7 2 −k k 7 ⎛ nx 1 ⎞ ⎛ x 1 ⎞ ⎛ ⎞ − k x 1 ( 1)k k Khi đó C − k ⎜ − ⎟ =⎜ − ⎟ = ∑ 7 C ⎜ ⎟ (− ) 7 14 3 = x . ∑ 0,25 7 ⎝ 14 x ⎠ ⎝ 2 x ⎠ ⎝ 2 −k ⎠ x k =0 k = 0 2 Số hạng chứa 5
x tương ứng với 14 − 3k = 5 ⇔ k = 3 . 3 3 ( 1 − ) .C 35 0,25
Do đó số hạng cần tìm là 7 5 5 x =− x . 4 2 16 Trang 3/4 Câu Đáp án Điểm 7.b 2 2
(1,0 điểm)
Phương trình chính tắc của ( x y E) có dạng: + =1, 2 2 a b 0,25 y
với a >b>0 và 2a = 8. Suy ra a = 4.
Do (E) và (C) cùng nhận Ox và Oy làm trục đối xứng và A 2
các giao điểm là các đỉnh của một hình vuông nên (E) và 0,25
(C) có một giao điểm với tọa độ dạng (
A t; t), t > 0. O 2 x
A∈(C) ⇔ t2 + t2 = 8, suy ra t = 2. 0,25 4 4 (2
A ; 2) ∈ (E) ⇔ + =1 ⇔ 2 16 b = . 2 16 b 3 2 2 0,25
Phương trình chính tắc của ( x y E) là + =1. 16 16 3 8.b
M thuộc d, suy ra tọa độ của M có dạng M(2t – 1; t; t + 2). 0,25
(1,0 điểm)
MN nhận A là trung điểm, suy ra N(3 – 2t; – 2 – t; 2 – t). 0,25
N∈(P) ⇔ 3 − 2t − 2 − t − 2(2 − t) + 5 = 0 ⇔ t = 2, suy ra M(3; 2; 4). 0,25 x −1 y +1 − Đường thẳng ∆ đi qua z 2
A và M có phương trình ∆ : = = . 0,25 2 3 2 9.b Đặt
z = a + bi (a,b ∈ \), z ≠ 1. −
(1,0 điểm) 5(z + i) 0,25 Ta có
= 2 − i ⇔ (3a − b − 2) + (a − 7b + 6)i = 0 z +1
⎧3a − b − 2 = 0 ⎧a = 1 ⇔ ⎨ ⇔ ⎨ 0,25 a − 7b + 6 = ⎩ 0 b = 1. ⎩ Do đó 2 2 z 1
= + .i Suy ra w=1+ z + z =1+1+i+(1+i) = 2+3 .i 0,25
Vậy w = 2+3i = 13. 0,25
------------- HẾT ------------- Trang 4/4