lOMoARcPSD|50713028 ĐỀ TỰ LUYỆN
KỲ THI TRUNG HỌC PHỔ THÔNG QUỐC GIA NĂM 2023 Bài thi: TOÁN SỐ 12
Thời gian làm bài: 90 phút, không kể thời gian phát ề (Đề thi có 5 trang)
Họ và tên thí sinh:………………………………………….........
Số iện thoại:……………………………………………………..
Câu 1: Nguyên hàm sin2 dx x bằng: A. cos2x C . B. cos2x C . C. cos2x C . D. cos2x C .
Câu 2: Điểm nào dưới ây không thuộc ồ thị của hàm số y x3 3x2 2 A. Điểm P(1;2). B. Điểm N(0; 2) . C. Điểm M( 1 ;2). D. Điểm Q( 1 ;0) .
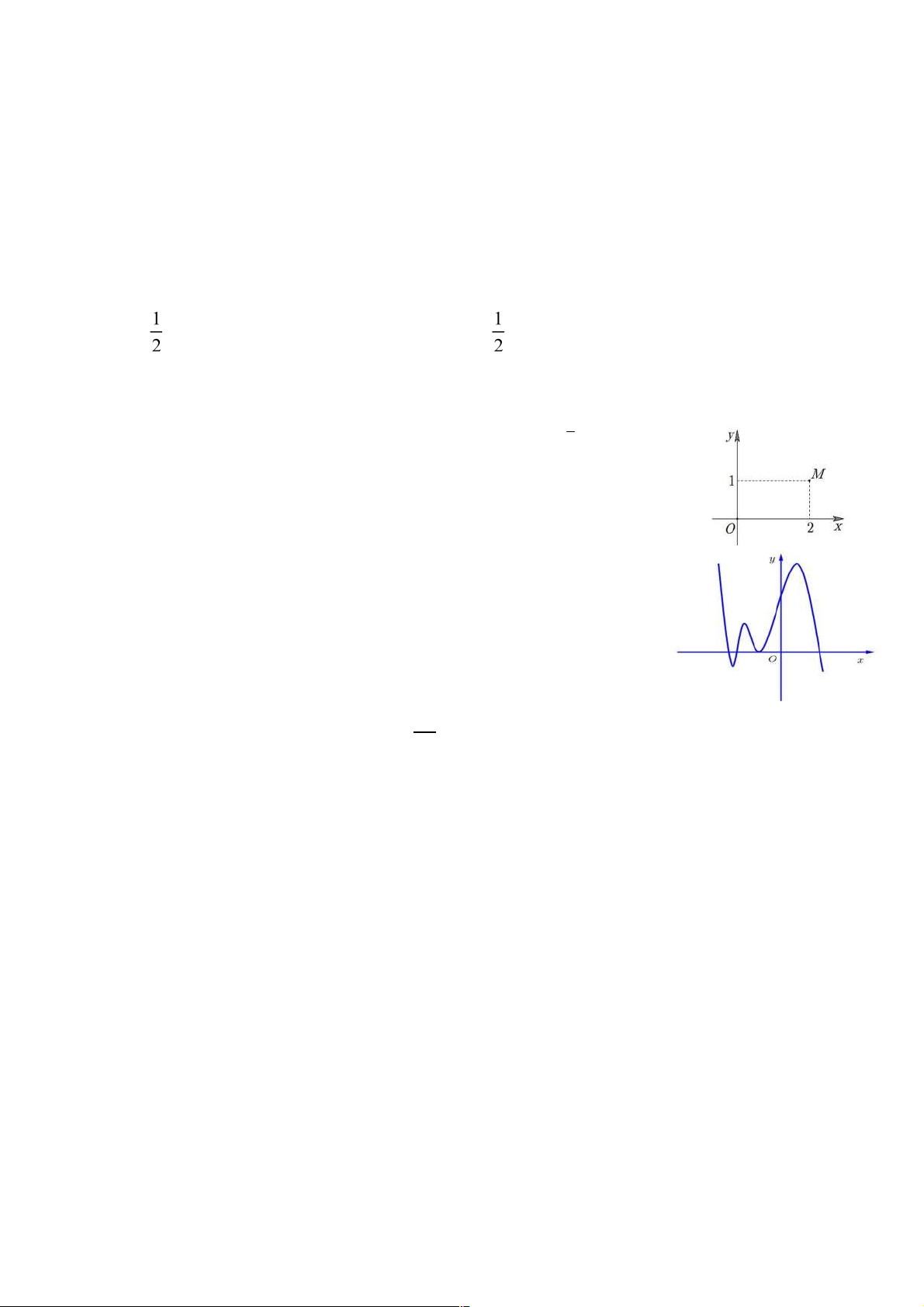
Câu 3: Trong hình vẽ bên, iểm M biểu diễn số phức z . Số phức z là: A. 1 2 i . B. 2 i . C. 1 2 i . D. 2 i .
Câu 4: Cho hàm số y f x xác ịnh trên và có ồ thị hàm số y f x là
ường cong ở hình bên. Hỏi hàm số y f x có bao nhiêu iểm cực trị? A. 6 . B. 5 . C. 4. D. 3 .
Câu 5: Số {ệm cận ứng của ồ thị hàm số y x 5 6x 22 bằng: x 3 2x A. 2 B. 1 C. 3 D. 0 6 2
Câu 6: Cho f x dx 12 . Tính I f 3x dx 0 0 A. I 6 B. I 36 C. I 4 D. I 5
Câu 7: Cho mặt phẳng :2x 3y 4z 1 0. Khi ó, một véctơ pháp tuyến của ? A. n 2;3;1 . B. n 2;3; 4 . C. n 2; 3;4 . D. n 2;3;4 .
Câu 8: Có bao nhiêu số có năm chữ số khác nhau ược tạo thành từ các chữ số 1,2,3,4,5,6 ? A. A 5 5 6 . B. P6 . C. C6 . D. P5 . lOMoARcPSD|50713028
Câu 9: Cho hàm số y f x có ồ thị như hình bên.
Giá trị cực ại của hàm số là A. y 2. B. y 1. C. y 3. D. y 1.
Câu 10: Hãy chọn cấp số nhân trong các dãy số ược cho sau ây: A. u 1 n 41n 1. B. un n2 C. un 4n 2 . D. u nn 2 4
Câu 11: Trong hình vẽ bên, iểm M biểu diễn số phức z . Khi ó số phức w 2z là A. w 4 2i . B. w 4 2i . C. w 4 2i . D. w 4 2i.
Câu 12: Tìm tập xác ịnh D của hàm số y x2 1 12 . A. D \ 1 . B. D \ 1 . C. D 1,1 . D. D ;1 1; .
Câu 13: Trong không gian với hệ toạ ộ Oxyz, cho ường thẳng d : x 1 y z 5 và mặt phẳng 1 3 1
P :3x 3y 2z 6 0. Mệnh ề nào dưới ây úng?
A. d cắt và không vuông góc với P B. d vuông góc với P C. d song song với P D. d nằm trong P
Câu 14: Bán kính R của khối cầu có thể •ch V 32 a3 là: 3 A. R 2a . B. R 2 2a . C. 2a . D. 3 7a .
Câu 15: Giải bất phương trình 34 x2 4 1 ta ược tập nghiệm T . Tìm T . A. T 2;2 . B. T 2; . C. T ; 2 . D. T ; 2 2;
Câu 16: Đường cong trong hình dưới là ồ thị của hàm số nào sau ây? A. y x 1 x 1 . B. y . C. y x4 2x2 1. D. y x3 3x 2. x 1 x 1 lOMoARcPSD|50713028 x 2 y 1 z 3
Câu 17: Trong không gian Oxyz , cho ường thẳng d :
. Vectơ nào dưới ây là một 1 2 1
vectơ chỉ phương của d ?
A. u 4 (1;2; 3). B. u 3 ( 1;2;1). C. u 1 (2;1; 3). D. u 2 (2;1;1)
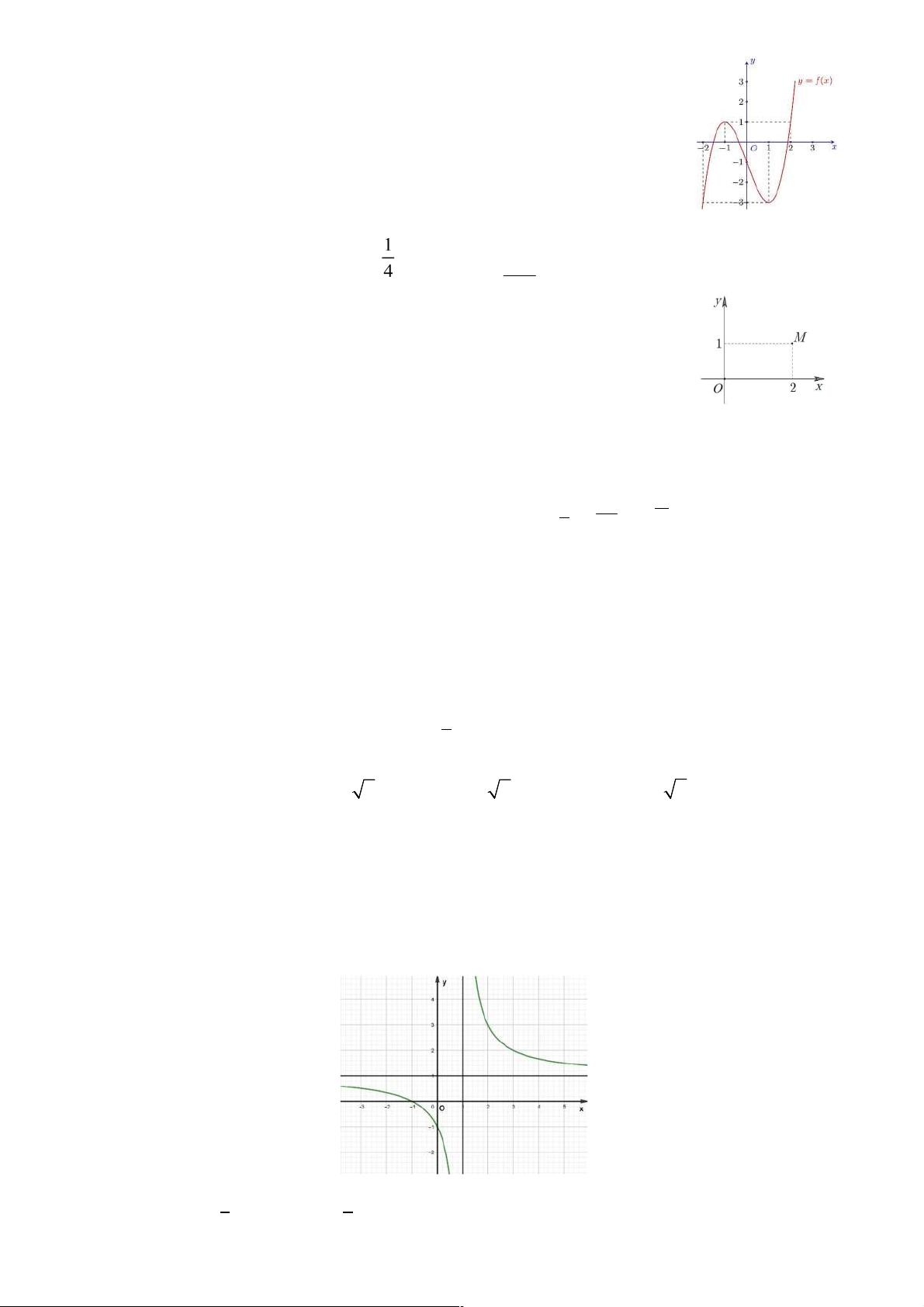
. Câu 18: Cho hàm số y ax4 bx3 cx2 dx e a 0 . Biết rằng hàm
số f x có ạo hàm là f ' x và hàm số y f ' x có ồ thị như
hình vẽ dưới. Hàm số nghịch biến trên A.Khoảng , 2 B.Khoảng 0,1 C.Khoảng 1,1 D.Khoảng 1,
Câu 19: Tính ạo hàm của hàm số y 17 x A. y 17 x ln17. B. y x.17 x 1. C. y 17 x. D. y 17 x ln17.
Câu 20: Cho hình lăng trụ ứng có diện •ch áy là 3a2 . Độ dài cạnh bên là a 2 . Khi ó thể •ch của khối lăng trụ là: A. 6a3 . B. 3a3. C. 2a3. D. . 3
Câu 21: Cho cấp số cộng un với số hạng ầu u1 1 và công sai d 3. Hỏi số 34 là số hạng thứ mấy? A. 12 B. 9 C. 11 D. 10
Câu 22: Cho hình chóp S ABC. có áy là tam giác ều cạnh bằng a, cạnh bên SB vuông góc với mặt phẳng
ABC , SB 2a . Tính thể •ch khối chóp S ABC. . a3 a3 3 3a3 a3 3 A. . B. . C. . D. . 4 6 4 2
Câu 23: Trong không gian với hệ tọa ộ Oxyz cho a 2i 3 j k , b 2; 3; 7 . Tìm tọa ộ của x 2a 3b A. x 2; 1;19 B. x 2; 3;19 C. x 2; 3;19 D. x 2;1;19
Câu 24: Bạn Minh ngồi trên máy bay i du lịch thế giới và vận tốc chuyển ộng của máy bay là v t 3t2
5 (m/s). Tính quãng ường máy bay i ược từ giây thứ 4 ến giây thứ 10. A. 246 m . B. 252 m . C. 1134 m . D. 966 m .
Câu 25: Trong không gian Oxyz , cho iểm M 1; 2; 3 và mặt phẳng P :2x y 3z 1 0. Phương
trình của ường thẳng i qua M và vuông góc với P là lOMoARcPSD|50713028 x 1 2t x 1 2t x 2 t x 1 2t A. y 2 t . B. y 2 t . C. y 1 2t . D. y 2 t . z 3 3t z 3 3t z 3 3t z 3 3t
Câu 26: Trên oạn 3;2 , hàm số f x x4 10x2 1 ạt giá trị nhỏ nhất tại iểm A. x 0 . B. x 3. C. x 2 . D. x 5 .
Câu 27: Hình lăng trụ tứ giác ều có bao nhiêu mặt phẳng ối xứng? A. 3. B. 5. C. 6. D. 4.
Câu 28: Cho a và b là hai số thực dương thỏa mãn 9log (3 ab) 4a . Giá trị của ab2 bằng A. 3. B. 6. C. 2 D. 4
Câu 29: Tổng phần thực và phần ảo của số phức z thoả mãn iz 1 i z 2i bằng A. 6 B. 2 C. 2 D. 6
Câu 30: Cho hình chóp S ABC. có SA ABC , SA a 3 và ABC vuông tại B có cạnh BC a , AC a 5 .
Tính theo akhoảng cách từ A ến SBC . 2a 21 a 21a 15 A. . B. . C. a 3 D. . 7 73
Câu 31: Cho hàm số y f x biết f 0 và f x xex2 với mọi x . Khi ó 1 xf x dx bằng 0 A. e 1. B. e 1. C. e 1. D. e 1. 4 4 2 2
Câu 32: Cho hai số thực x và y thỏa mãn 3x yi
4 2i 5x 2i với ilà ơn vị ảo. Giá trị của biểu thức T 2x y bằng A. 2. B. 8. C. 6. D. 4.
Câu 33: Cho hình trụ có bán kính áy bằng a, chu vi của thiết diện qua trục bằng 16a . Thể •ch của khối trụ ã cho bằng A. 5 a3. B. 2 a3. C. 4 a3. D. 6 a3.
Câu 34: Cho hàm số y f x liên tục trên 1;4 và thỏa mãn 12 f x dx 12 , 34 f x dx .
Tính giá trị biểu thức I 14 f x dx 23 f x dx . A. I . B. I . C. I . D. I . lOMoARcPSD|50713028
Câu 35: Cho hình hộp chữ nhật ABCD ABC D. , biết áy ABCD là hình vuông. Tính góc giữa AC và BD . A. 90 . B. 30 . C. 60 . D. 45 .
Câu 36: Biết f 2x dx sin2 x ln x C . Tìm nguyên hàm f x dx ? A. f x dx sin2 x ln x C . B. f x dx 2sin2 2x 2ln x C . 2 C. f x dx 2sin2 x 2ln x C . D. f x dx 2sin2 x 2lnx C . 2
Câu 37: Trong không gian Oxyz , cho hai
ường thẳng chéo nhau d1 : x 2 y 6 z 2 và 2 2 1
d2 : x 4 y 1 z 2 . Phương trình mặt phẳng P chứa d1 và P song song với ường thẳng d2 là 1 3 2 A. P : x 5y 8z 16 0. B. P : x 5y 8z 16 0. C. P : x 4y 6z 12 0. D. P :2x y 6 0.
Câu 38: Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số ôi một khác nhau và các chữ số thuộc tập hợp
1, 2, 3, 4, 5, 6, 7, 8, 9 . Chọn ngẫu nhiên một số thuộc S , xác suất ể số ó không có hai chữ số liên {ếp nào cùng lẻ bằng A. . B. . C. . D. .
Câu 39: Một khối nón có chiều cao bằng 12 , ặt trên áy một hình trụ ( các áy của
chúng nằm trên cùng một mặt phẳng, như hình vẽ bên dưới), biết ường kính áy khối
nón bằng bán kính áy hình trụ. Hình trụ ược ổ nước vào cho ến ộ cao bằng 12. Độ cao
của nước khi ã lấy khối nón ra ngoài hình trụ bằng A. 8. B. 11. C. 10. D. 6.
Câu 40: Nhằm tạo môi trường xanh, sạch, ẹp và thân thiện. Đoàn trường THPT Hồ Nghinh ã phát ộng
phong trào trồng hoa toàn bộ khuôn viên ường vào trường. Sau một ngày thực hiện ã trồng ược một phần
diện •ch. Nếu {ếp tục với {ến ộ như vậy thì dự kiến sau úng 15 ngày nữa sẽ hoàn thành. Nhưng thấy công
việc có ý nghĩa nên mỗi ngày số lượng oàn viên tham gia ông hơn vì vậy từ ngày thứ hai mỗi ngày diện •ch
trồng tăng lên 3% so với ngày kế trước. Hỏi công việc sẽ hoàn thành vào ngày bao nhiêu?
Biết rằng ngày 26 / 03 là ngày bắt ầu thực hiện và làm liên tục. A. 09 / 04 . B. 08 / 04 . C. 07 / 04. D. 06 / 04.
Câu 41: Tập nghiệm của bất phương trình (32x 9)(3x ) 3x 1 1
0 chứa bao nhiêu số nguyên ? lOMoARcPSD|50713028 A. 2. B. 3. C. 4. D. 5.
Câu 42: Cho hàm số f x liên tục trên và có ồ thị như hình vẽ.
Hỏi hàm số g x f f x có bao nhiêu iểm cực trị A. 8. B. 10. C. 7. D. 9.
Câu 43: Cho hàm số f x có f 0
và f x sin3 .cos 2 ,x 2 x x . Biết F x là nguyên hàm
của f x thỏa mãn F 0 0 , khi ó F 2 bằng A. . B. . C. . D. .
Câu 44: Cho hình chóp S ABC.
có áy ABC là tam giác vuông cân tại B , AB BC 3a 2 , SAB SCB 90o .
Biết khoảng cách từ A ến mặt phẳng SBC bằng 2a 3 . Tính thể •ch mặt cầu ngoại {ếp hình chóp S ABC. A.72 2 a3 B. 18 2 a3 C. 72 18 a3 D. 54 2 a3
Câu 45: Trên tập hợp các số phức, xét phương trình z2 4az b2 2 0, (a b, là các tham số thực). Có bao
nhiêu cặp số thực a b; sao cho phương trình ó có hai nghiệm z z1 2, thỏa mãn z1 2iz2 3 3i? A. 4. B. 1. C. 2. D. 3.
Câu 46: Trong không gian với hệ toạ ộ Oxyz , cho ường thẳng d : x 2 y 1 z và mặt cầu 2 3 1
S : x 2 2 y 1 2 z 1 2 6 . Hai mặt phẳng P , Q chứa d và {ếp xúc với S . Gọi
A B, là {ếp iểm và I là tâm của mặt cầu S . Giá trị cos AIB bằng A. . B. . C. . D. .
Câu 47: Cho các hàm số y f x ;y f f x
;y f x 2 2x 1 có ồ thị lần lượt là C1 ; C2 ; C3 .
Đường thẳng x 2 cắt C1 ; C2 ; C3 lần lượt tại A B C, , . Biết phương trình {ếp tuyến của C1 tại
A và của C2 tại B lần lượt là y 2x 3 và y 8x 5. Phương trình {ếp tuyến của C3 tại C là A. y 8x 9. B. y 12x 3. C. y 24x 27 . D. y 4x 1.
Câu 48: Cho 2 số phức z w, phân biệt thỏa mãn z w 4 và z i
w i là số thực. Giá trị nhỏ nhất của z w bằng lOMoARcPSD|50713028 A. 2 3 . B. 2 14 . C. 2 15 . D. 8. Câu 49: Cho hàm số f x
nhận giá trị dương và có ạo hàm liên tục trên 0;3 và thoả mãn f 0 3, f 3 8 và 3 f 0 f x
x 12 dx 43 . Giá trị của f 2 bằng A. . B. . C. . D. .
Câu 50: Có bao nhiêu số nguyên m 2;2022 ể tồn tại hai cặp số thực x y; thoả mãn x2 y3 m và log2 xlog3 y 1? A. 2019 . B. 2004 . C. 2006 . D. 2005 .