



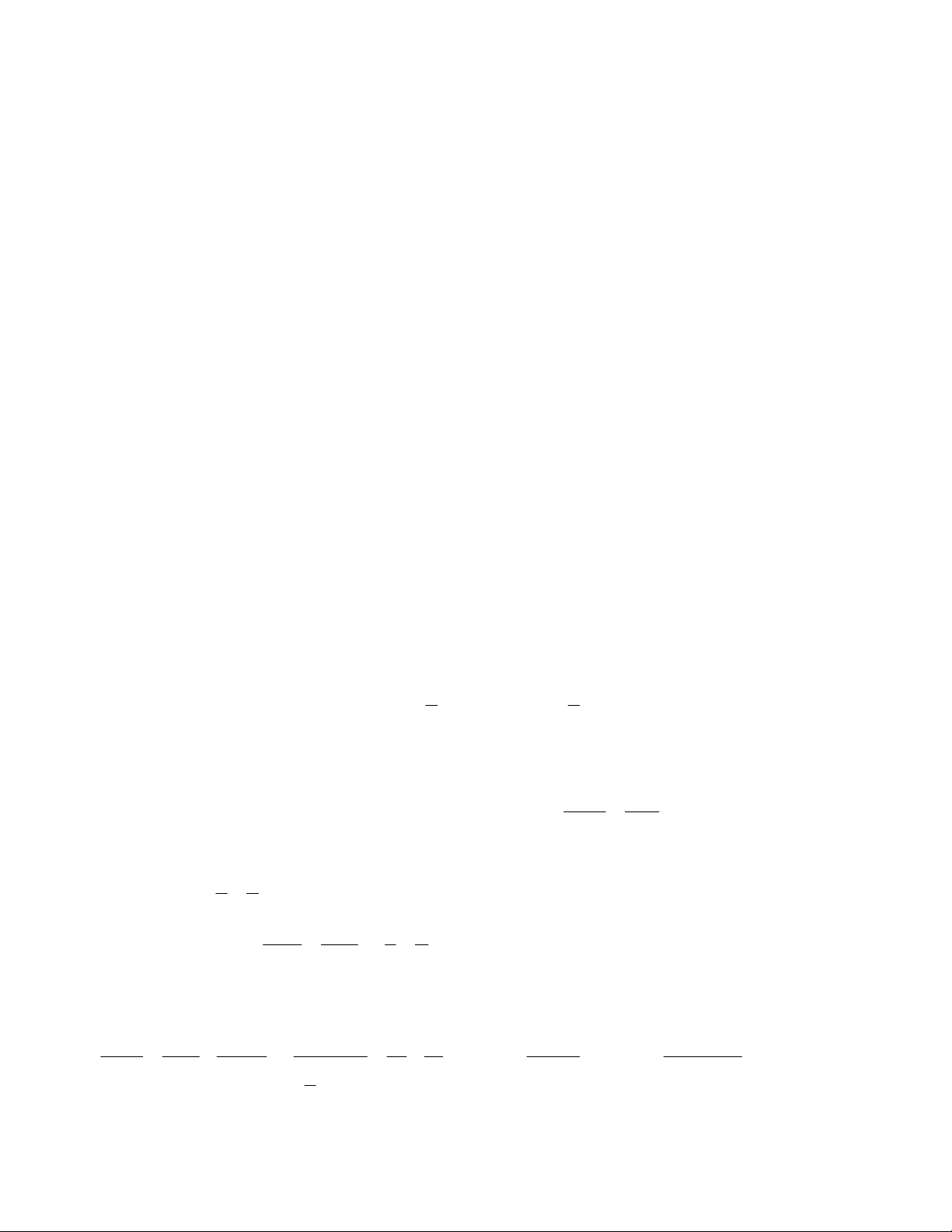




Preview text:
Định lý bốn điểm và ứng dụng giải một số bài toán hình học phẳng
Nguyễn Hữu Tâm – THPT chuyên Lê Quý Đôn Bình Định
Trong Hình học phẳng, bài toán về quan hệ vuông góc giữa hai đường thẳng có ảnh hưởng sâu
sắc và liên quan đến nhiều kết quả rất quan trọng và thú vị. Nhiều bài toán sau khi phân tích có thể quy
về việc chứng minh sự vuông góc giữa hai đường thẳng.
Có rất nhiều cách để chứng minh hai đường thẳng vuông góc nhau. Tuy nhiên, đứng trước một
bài toán hay một kết quả cần chứng minh của Hình học phẳng, khó khăn rất lớn đối với học sinh là lựa
chọn công cụ hay hướng tiếp cận bài toán đó.
Trong quá trình tham gia dạy lớp chuyên và bồi dưỡng đội tuyển học sinh giỏi các cấp, đặc biệt là
đội tuyển tỉnh thi quốc gia (phần Hình học phẳng) tôi nhận thấy có một cách để tiếp cận những bài toán
chứng minh hai đường thẳng vuông góc tương đối hiệu quả. Đó là sử dụng một mở rộng của định lý
Pytago (Pythagoras) mà ta gọi là “Định lý bốn điểm”.
1. Định lý bốn điểm
1.1. Định lý. Cho bốn điểm A, B, C, D phân biệt trong mặt phẳng. Khi đó AB vuông góc với CD khi và chỉ khi 2 2 2 2
AC − AD = BC − BD . Chứng minh
Cách 1. (Dùng tích vô hướng) Ta có 2 2 2 2
AC − AD = BC − BD 2 2 2 2
⇔ AC − AD = BC − BD
⇔ DC ( AC + AD) = DC (BC + BD)
⇔ DC ( AC + CB + AD + DB) = 0 ⇔ A .
B DC = 0 ⇔ AB ⊥ CD
Cách 2. (Dùng định lý Pytago). Gọi H, K lần lượt là hình chiếu của A, B lên đường thẳng CD.
Nếu AB vuông góc với CD thì H = K nên theo định lý Pytago ta có 2 2 2 2 2 2
AC − AD = HC − HD = BC − BD . Ngược lại, nếu 2 2 2 2
AC − AD = BC − BD = a thì ta có 2 +
a = AC − AD = HC − HD = HC − (CD ± HC )2 a CD 2 2 2 2 2 ⇒ HC = ∓ 2CD 2 a + CD
Đổi vai trò H cho K ta cũng có KC = ∓
. Do đó HC = KC. 2CD
Lại đổi vai trò C bởi D ta cũng chứng minh được HD = KD. Như vậy H trùng K, suy ra AB vuông góc với CD. 1
1.2. Nhận xét.
1/ Khi B trùng C thì ta có AB vuông góc với BD khi và chỉ khi 2 2 2
AB + BD = AD . Ta gặp lại định lý Pytago.
2/ Định lý được phát biểu dạng điều kiện cần và đủ nên ta có thể vận dụng hai chiều. Ngoài
ra, điều kiện vuông góc được biểu thị dạng hiệu hai bình phương nên có thể lợi dụng tính chất
bình phương vô hướng của vectơ và phương tích của một điểm đối với một đường tròn.
3/ Theo cách chứng minh thứ nhất thì ta đã dùng công cụ tích vô hướng, còn theo cách
chứng minh thứ hai thì ta chỉ cần dùng đến định lý Pytago. Vì vậy với đối tượng là học sinh
THCS, các em cũng có thể vận dụng kết quả của định lý trên để chứng minh hai đường thẳng vuông góc.
2. Ứng dụng định lý bốn điểm giải một số bài toán Hình học phẳng
2.1. Một số bài toán về chứng minh hai đường thẳng vuông góc
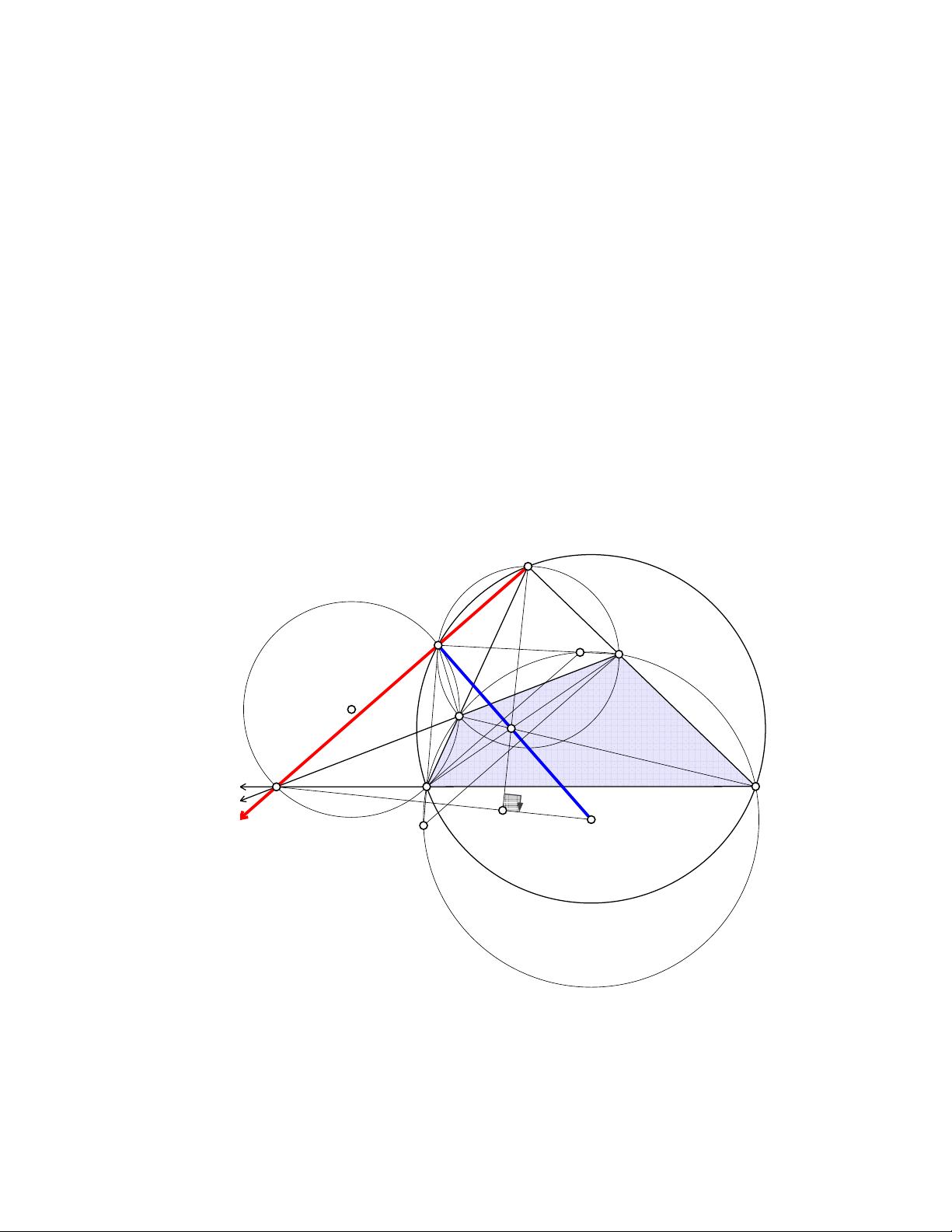
Bài toán 1. (IMO 1985). Cho tam giác ABC, một đường tròn tâm O đi qua A, C và cắt lại các cạnh
BA, BC tại K, N. Giả sử các đường tròn (BKN) và (ABC) cắt nhau tại hai điểm B và M, chứng
minh rằng BM vuông góc với MO. B M' C' M K N S m C A P B' K' O
Lời giải 1. (Dùng phép đối xứng trục)
Gọi m là đường thẳng qua O và vuông góc với BM, ta cần chứng minh M thuộc m. Xét phép đối
xứng trục m, biến C, K thành C', K'. Khi đó CC', KK' cùng vuông góc với m. Do đó CC', KK', BM song song nhau. Ta có
KC 'C = KAC = BNK = BMK 2
suy ra C', K, M thẳng hàng. Lại có 0
C 'CK ' = CC ' K = CAK = CAB = 180 − BMC = C 'CM
suy ra C, K', M thẳng hàng.
Do đó các đường thẳng C'K, CK' giao nhau tại M.
Vì C'K và CK' đối xứng nhau qua m nên M thuộc m.
Lời giải 2. (Dùng phép nghịch đảo)
Gọi S, P, M' lần lượt là giao điểm của các cặp đường thẳng (KC, AN), (KN, AC), (SO, BP). Khi đó
theo kết quả của bài toán Brocard, ta có O là trực tâm tam giác BSP. Ta cần chứng minh M' = M.
Xét phép nghịch đảo f(O, R), khi đó P biến thành B', A biến thành A và C biến thành C. Do đó
theo tính chất của phép nghịch đảo, đường thẳng AC không đi qua cực O nên biến thành đường
tròn đi qua O. Như vậy các điểm O, A, B', C đồng viên. Từ đó suy ra
PA.PC = PB'.PO = PM'.PB
suy ra M' thuộc đường tròn (ABC). Do đó
PK.PN = PA.PC = PM'.PB
suy ra M' thuộc đường tròn (BKN). Từ đó M' = M.
Lời giải 3. (Dùng biến đổi góc) B K M R N S T L C A P O 3
Giả sử tam giác ABC nhọn (trường hợp tam giác ABC tù giải tương tự). Gọi T và R lần lượt là tâm
các đường tròn (ABC) và (KBN) tương ứng. Vì
BNK = BAC nên hai tam giác BNK và BAC đồng dạng. Ta lại có 0
CBR = ABT = 90 − ACB
Suy ra BR vuông góc với AC do đó BR // OT.
Tương tự, BT vuông góc với KN suy ra BT // OR. Do đó BROT là hình bình hành.
Gọi L là điểm đối xứng với B qua R thì RLOT cũng là hình bình hành và vì TR vuông góc với BM
nên ta có OL vuông góc với BM. Mặt khác LM cũng vuông góc với BM nên suy ra O, L, M thẳng
hàng, do vậy OM vuông góc với BM.
Lời giải 4. (Dùng định lý bốn điểm)
Vì các đường thẳng BM, NK và CA là trục đẳng phương của các cặp của ba đường tròn nên chúng
đồng quy tại một điểm P. Do các tứ giác MNKB và KNCA nội tiếp nên ta có
PMN = BKN = NCA
Suy ra tứ giác MNCP nội tiếp, do đó ta có 2 2
BM .BP = BN.BC = OB − r 2 2
PM .PB = PN.PK = OP − r Suy ra 2 2 2 2
OB − OP = BP(BM − MP) = (BM + MP)(BM − MP) = MB − MP
Vậy, OM vuông góc với PB, suy ra đpcm.
Nhận xét. 1/ Bài toán này có nhiều cách tiếp cận khác nhau, mỗi cách có một thế mạnh riêng. Ở
lời giải 1, ta dùng tính chất của phép đối xứng trục, kiến thức lớp 11. Trong lời giải 2 ta đã dùng
đến phép nghịch dảo, một công cụ tương đối mạnh và chỉ được học ở các lớp chuyên. Còn ở các
lời giải 3 và lời giải 4 chúng ta dùng ít kiến thức hơn. Lời giải 3 tuy thuần túy về hình học nhưng
phải xét trường hợp (nếu không thì phải dùng góc định hướng giữa hai đường thẳng) và phải vẽ
thêm đường phụ. Với lời giải 4, ta không cần vẽ đường phụ mà chỉ dùng kiến thức của phương
tích, trục đẳng phương để tính toán rồi dùng định lý bốn điểm để suy ra đpcm, hướng tiếp cận này
tương đối nhẹ nhàng và tường minh.
2/ Từ các lời giải ở trên ta rút ra được một tính chất khá thú vị đó là các điểm O, L, S, M thẳng hàng.
Bài toán 2. Cho tam giác ABC cân tại A, điểm P nằm trên tia BC; các điểm X, Y lần lượt nằm trên
tia BA và AC sao cho PX // AC và PY // AB. Gọi AT là đường kính của đường tròn ngoại tiếp tam
giác ABC. Chứng minh rằng PT vuông góc với XY.
Lời giải 1. (Dùng tích vô hướng) Ta có 4 PC PB T . P XY = .TB + .TC ( XA + AY ) BC BC = PC.T . B AY + P . B TC.XA = PC.T .
B AY cos (TB, AY ) + P .
B TC.XAcos (TC, XA) X A O C P B T Y
Mà cos (TB, AY ) = −cos(TC, XA),TB = TC nên ta cần chứng minh PC.AY = PB.XA.
Thật vậy, ta có tam giác CYP đồng dạng với CAB đồng dạng với PXB nên suy ra CY PX =
⇒ CY.PB = PX .CP (*) CP PB
Mặt khác PX // AC, suy ra BX = PX và PY // AB,
suy ra CY = PY = XA. Ta cũng có PX = AY nên từ (*) suy ra PC.AY = PB.XA. Từ đó ta có T .
P XY = 0 . Vậy TP vuông góc với XY.
Lời giải 2. (Dùng định lý bốn điểm)
Theo tính chất góc nội tiếp nửa đường tròn, ta có: 2 2 2
AB ⊥ BT ⇔ TX = BX + BT ) 1 ( 2 2 2 2 2
AC ⊥ CT ⇔ TY = TC + CY = BT + CY (2) Từ (1) và (2) suy ra 2 2 2 2
TX − TY = BX − CY ) 3 (
Mặt khác, PX // AC, suy ra BX = PX (4)
Và PY // AB, suy ra: CY = PY (5)
Thế (4), (5) vào (3), ta được: TX 2 − TY 2 = PX 2 − PY 2 ⇔ TP ⊥ XY (đpcm). 5
Nhận xét. Rõ ràng việc biến đổi góc là cách tiếp cận rất khó khăn ở bài toán này, do đó chúng ta
nghĩ đến công cụ tích vô hướng hoặc dùng định lý bốn điểm để tấn công. So sánh hai lời giải trên,
ta thấy rất rõ ràng cách tiếp cận bằng định lý bốn điểm trong trường hợp này là giản dị và nhẹ nhàng hơn rất nhiều.
Bài toán 3 (2001- China) Cho tam giác ABC nhọn, O là tâm đường tròn ngoại tiếp tam giác và ba
đường cao AD, BE, CF gặp nhau tại H. Gọi M, N lần lượt là giao điểm của ED với AB và FD với
AC. Chứng minh rằng OB ⊥ DF ,OC ⊥ DE và OH ⊥ MN .
Lời giải 1. (Dùng tính chất đường đẳng giác, trục đẳng phương và đường thẳng Euler)
Theo giả thiết, ta có DF đối song với AC. Mặt khác BE vuông góc với AC, còn BO và BE đẳng giác trong góc
ABC nên BO vuông góc với DF. Tương tự, CO vuông góc với DE. Ta còn phải
chứng minh OH ⊥ MN
Ta có MA.MB = ME.MD nên M thuộc trục đẳng phương của hai đường tròn (ABC) và (DEF).
Tương tự ta cũng có N thuộc trục đẳng phương của hai đường tròn này. Suy ra MN vuông góc với
đoạn nối tâm OO’ (với O’ là tâm đường tròn (DEF). Mà O, O’ và H cùng thuộc đường thẳng
Euler của tam giác ABC nên suy ra OH vuông góc với MN. N A E F H O' O B D C M
Lời giải 2. (Dùng định lý bốn điểm)
Theo giả thiết ta có tứ giác ACDF nội tiếp, do đó 0 0
BAC = BDF ⇒ OBC = 90 − BAC = 90 − BDF 6 Suy ra 0
OBC + BDF = 90 .
Vậy, OB ⊥ DF
Chứng minh hoàn toàn tương tự, ta cũng có OC ⊥ DE
Ta còn chứng minh OH ⊥ MN Ta có: 2 2 2 2
MA ⊥ CH ⇔ MC − MH = AC − AH ) 1 ( 2 2 2 2
NA ⊥ BH ⇔ NB − NH = AB − AH (2) 2 2 2 2
DA ⊥ BC ⇔ DB − DC = AB − AC ) 3 ( 2 2 2 2
BO ⊥ DF ≡ ND ⇔ BN − BD = ON − OD (4) 2 2 2 2
CO ⊥ DE ≡ MD ⇔ CM − CD = OM − OD ) 5 (
Lấy (1) - (2) + (3) +(4) - (5) vế theo vế, ta được:
HN 2 − HM 2 = ON 2 − OM 2 ⇔ OH ⊥ MN (đpcm). Nhận xét
1/ Lời giải 1 có vẻ ngắn gọn, tuy nhiên ta đã dùng một số kết quả đã biết về đường thẳng Euler,
đường đẳng giác và trục đẳng phương. Còn lời giải 2 ta chỉ thuần túy sử dụng hai chiều của định
lý bốn điểm để giải, một cách tiếp cận khá bình dị.
2/ Nếu gọi giao điểm của BC và EF là P thì theo định lý Desargues ta có P, M, N thẳng hàng. Như
vậy vai trò của M, N, P trong bài toán là như nhau.
Bài toán 4. (1995-USSR) Cho tứ giác lồi ABCD thỏa điều kiện AB = AD và 0
ABC = CDA = 90 .
Điểm F và E nằm trên đường thẳng BC và CD tương ứng sao cho DF vuông góc với AE. Chứng
minh rằng AF vuông góc với BE. A D X E P B F C
Lời giải 1 (Dùng biến đổi góc và tam giác đồng dạng)
Gọi X là giao điểm của AE và DF và P là giao điểm của AF với BE, ta có 2 2
AX .AE = AD = AB 7
Do đó tam giác AEB đồng dạng tam giác ABX suy ra ABX = AEB mà
ABX = AFX nên suy ra
AFX = AEB ⇒ PFX = XEP
Vậy, tứ giác XPEF nội tiếp suy ra đpcm.
Lời giải 2. (Dùng định lý bốn điểm)
Áp dụng định lý bốn điểm và từ giả thiết, ta có: 2 2 2 2
AE ⊥ DF ⇔ AD − AF = ED − EF ) 1 ( 2 2 2
AB ⊥ BF ⇔ AB − AF = −BF (2) 2 2 2
AD ⊥ DE ⇔ AD − AE = −DE ) 3 (
Lấy (1) - (2) + (3) ta được theo vế (với chú ý AD = AB) ta được
AB2 − AE2 = FB2 − FE2 ⇔ AF ⊥ BE (đpcm)
Nhận xét. Lời giải 1 thuần túy biến đổi góc nhưng phải viện đến điểm phụ là P và X. Lời giải 2
chỉ đơn thuần tính toán và áp dụng định lý bốn điểm.
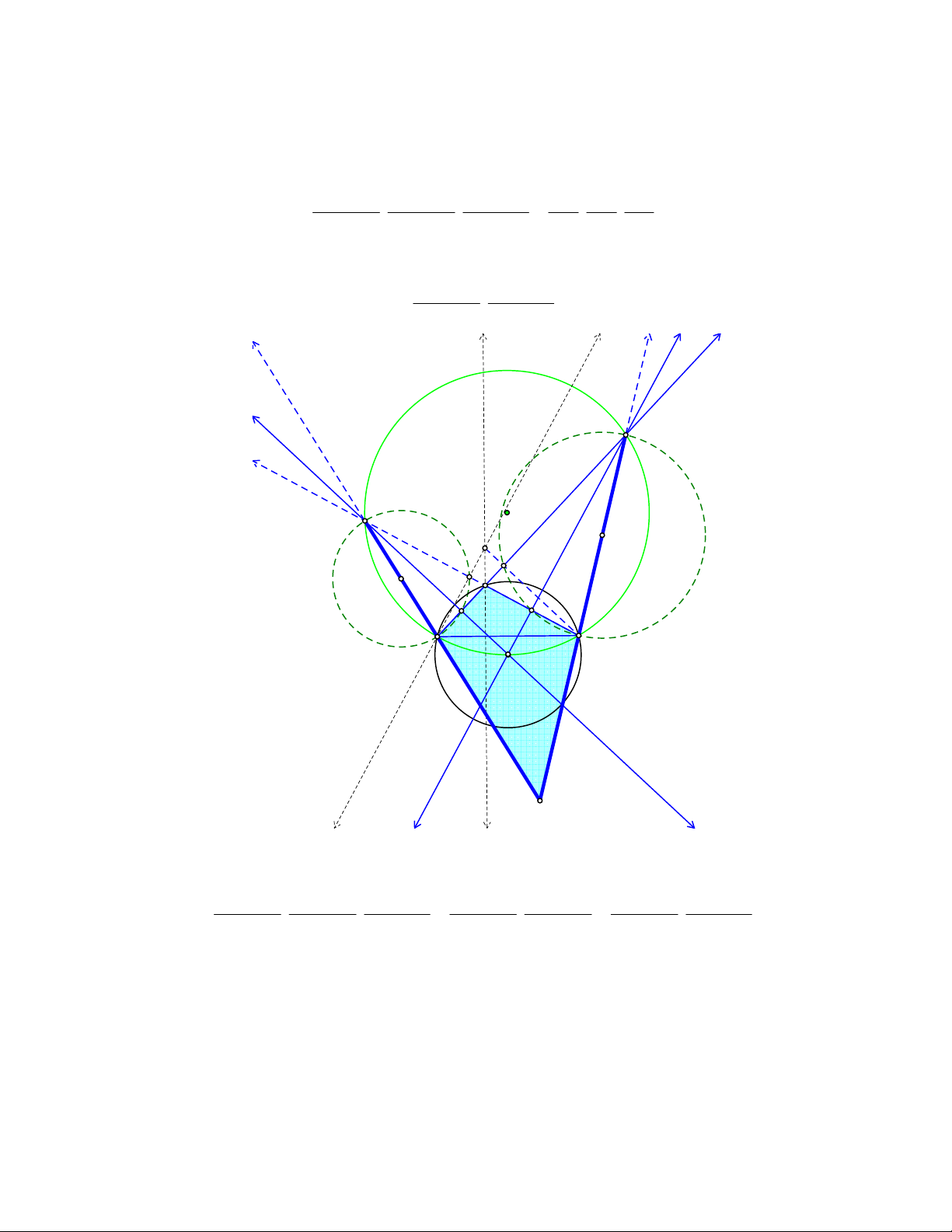
Bài toán 5. Cho tứ giác ABCD nội tiếp đường tròn tâm (O) đồng thời lại ngoại tiếp một đường
tròn khác (O’), có các tiếp điểm N, P, Q, M lần lượt với các cạnh AB, BC, CD, DA của tứ giác đã
cho. Chứng minh rằng MP ⊥ NQ . E A N R M O D B O' Q T P C F
Lời giải 1. (Dùng phép nghịch đảo) 8
Xét phép nghịch đảo đối với đường tròn (O’), các điểm A, B, C, D lần lượt biến thành các trung
điểm H, K, E, L của các đoạn MN, NP, PQ, QM. Tứ giác HKEL là hình bình hành vì HK và EL
lần lượt là đường trung bình của các tam giác NMP và QMP. Mặt khác vì các đỉnh A, B, C, D
cùng thuộc đường tròn (O) (không qua cực nghịch đảo) nên ảnh của chúng qua phép nghịch đảo
cũng thuộc một đường tròn. Do đó HKEL là hình bình hành nội tiếp nên nó là một hình chữ nhật.
Từ đó suy ra HL vuông góc với HQ, do vậy suy ra MP vuông góc với NQ.
Lời giải 2. (Dùng góc định hướng giữa hai đường thẳng)
Gọi E, F lần lượt là giao của AB và CD, AD và BC. Gọi giao điểm của FO’ với AB, CD lần lượt là R và T.
Ta có EO’, FO’ là các đường phân giác của các góc
AED, AFB . Dễ thấy NQ vuông góc với EO’
và MP vuông góc với FO’. Như vậy ta chỉ cần chứng minh EO’ vuông góc với FO’.
Thật vậy, theo tính chất góc ngoài của tam giác ta có
(RT , RE) = (RF , F ) A + (F , A R )
A = (FC, FT ) + (CT , CF ) = (TC,TF ) = (TE,TR) (modπ )
Suy ra tam giác ERT cân tại E, do đó EI vuông góc với RT hay EI vuông góc với FI. Vậy khẳng
định của bài toán đã được chứng minh.
Lời giải 3. (Dùng định lý bốn điểm)
Gọi O’A ∩ MN = H và O’C ∩ PQ = E. Ta có tứ giác ABCD nội tiếp đường tròn (O) nên 0
A + C = 180 . Tứ giác ABCD lại ngoại tiếp đường tròn (O’) nên theo tính chất hai tiếp tuyến cắt nhau, ta có: 1 1 O ' AM = A ; O 'CQ = C 2 2 0
⇒ O ' AM + O 'CQ = 90 ⇒ O ' AM = CO 'Q ∆ MA ∼ C ∆ QO
(g g) O'M MA O ' ' . ⇒ = CQ QO '
Đặt MA = AN = x ; BN = BP = y ; CP = CQ = z ; DQ = DM = t ; O’M = O’Q = r. r x Khi đó ta có : 2
= ⇒ r = x ⋅ z Tương tự ta cũng có : z r O ' N NB r y 2 O ∆ ' NB ∼ D ∆ MO ' ⇒ = ⇒ =
⇒ r = y ⋅t . Suy ra : 2
r = x ⋅ z = y ⋅t DM MO ' t r
Do AM và AN là hai tiếp tuyến của đường tròn (O’) nên ta có O’A ⊥ MN tại M và H là trung
điểm của MN. Áp dụng hệ thức lượng vào ∆O ' MA vuông tại M , có đường cao MH được : 2 2 2 1 1 1 1 1 1 4x r 4x x ⋅ z 2 2 ( ) = + ⇒ = + ⇒ MN = ⇒ MN = 2 2 2 2 2 2 2 2 2 MH MA O ' M 1 x r x + r
x + ( x ⋅ z) MN 2 9 2 4x ⋅ z
(do r2 = x.z ) . Suy ra : 2 MN = . x + z 2 2 2 4xz 4 y t 4 yt
Hoàn toàn tương tự, ta cũng có : 2 2 2 PQ = ; NP = ; MQ = x + z y + t y + t Suy ra B N A H K M O O' L D P E Q C 2 2 4x z 4xz 4xz x + z 2 2 ( ) 2 MN + PQ = + = = 4xz = 4r x + z x + z x + z
(do r 2= x.z = y.t ) 2 2 4 y t 4 yt 4 yt y + t 2 2 ( ) 2 NP + MQ = + = = 4yt = 4r y + t y + t y + t
Như vậy tứ giác ABCD có 2 2 2 2
MN + PQ = NP + MQ . Vậy, MP ⊥ NQ.
Nhận xét. Đây là một tính chất hình học rất đẹp của tứ giác lưỡng tiếp.
- Lời giải 1 đã dùng đến phép nghịch đảo, đây là công cụ mạnh nên lời giải rất gọn gàng và đẹp mắt.
- Lời giải 2 dùng biến đổi góc, đây cũng là một lời giải đẹp, kinh điển, thuần túy hình học.
- Lời giải 3 sau khi đặt MA = AN = x ; BN = BP = y; CP = CQ = z; DQ = DM = t; O’M = O’Q = r, 10
dùng định lý bốn điểm tính toán và cũng đưa đến kết quả. Tuy việc tính toán hơi cồng kềnh nhưng
hướng đi rõ ràng, trong khi đó hai lời giải trên tuy gọn gàng và đẹp mắt nhưng không dễ gì ai cũng nghĩ đến.
Tương tự như vậy, ta xét tiếp bài toán sau, dù biến đổi và tính toán hơi phức tạp nhưng hướng đi cũng rất rõ ràng.
2.2. Một số bài toán chứng minh song song, đồng quy, thẳng hàng
Nhiều bài toán chứng minh quan hệ song song, đồng quy hoặc thẳng hàng có thể đưa về
việc chứng minh hai đường thẳng vuông góc. Do vậy chúng ta cũng có thể vận dụng định lý bốn
điểm để tiếp cận những dạng toán như vậy.
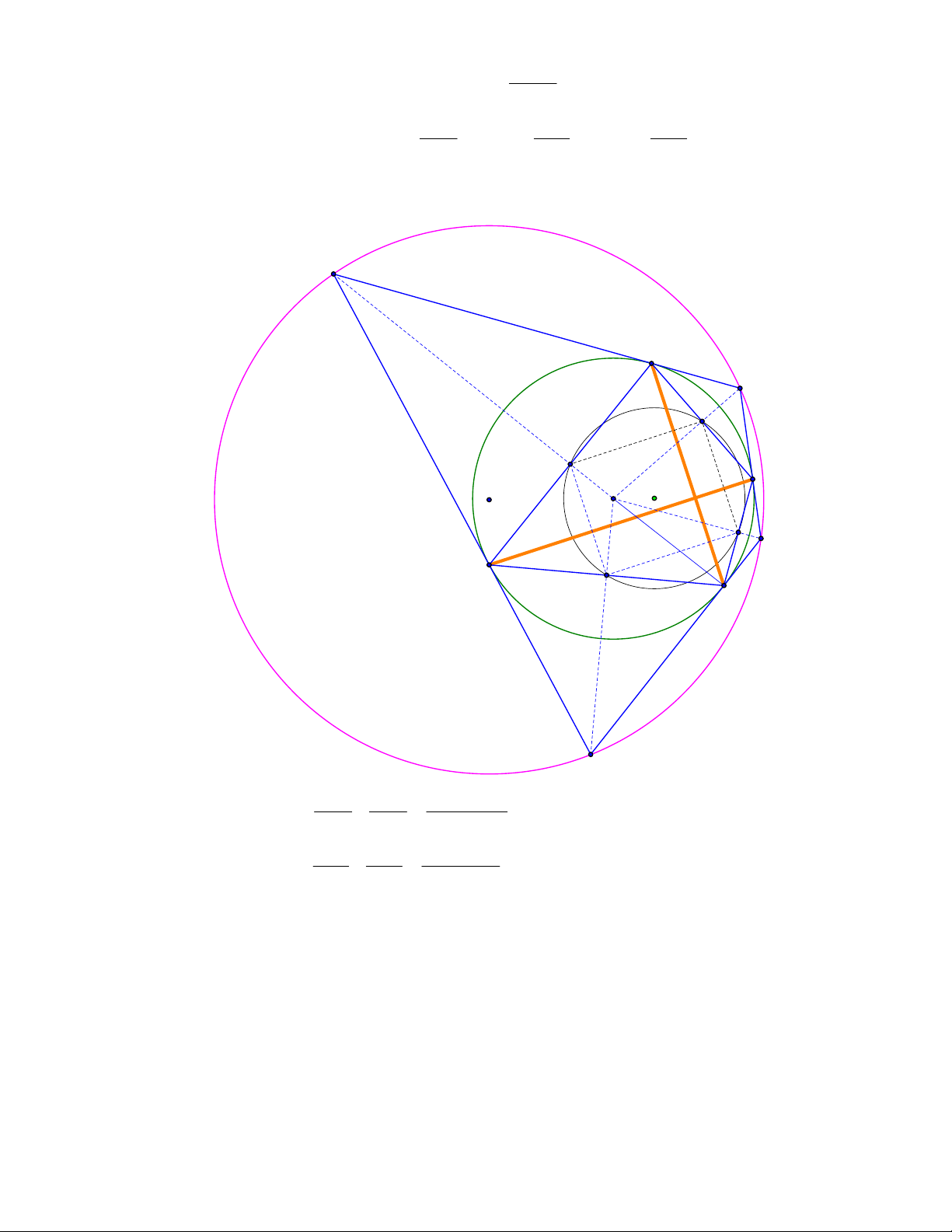
Bài toán 6. Cho tam giác ABC và các điểm B’, C’ thuộc BC (khác B, C). Các điểm E, F theo thứ
tự thuộc AC, AB sao cho BE // B ' A;CF // C ' A. X là giao điểm thứ hai của đường tròn ngoại tiếp các
tam giác ABC, AB’C’. Chứng minh rằng AX // EF.
Lời giải 1. (Chứng minh hai góc đồng vị bằng nhau)
Gọi K, L theo thứ tự là giao điểm thứ hai của AE, AF và (AB’C’). F E A X F' E' O' K O L B C B' C'
Vì A, B’, C’, L, K đồng viên và BF // B ' A;CE // C ' A nên
BL = BL.BA CA = BB'.BC' CA = BB' BC' CA = EA BA CA = AE . . . . . . . CK CK.CA BA CC '.CB ' BA CB ' CC ' BA CA FA BA AF 11 Dễ thấy X ∆ LB ∼ X ∆ KC (g − g) BL XL Do đó = . CK XK AE XL Vậy, = . AF XK Kết hợp với
EAF = LAK = LXK, suy ra ∆AEF ∼ ∆XLK. Do đó XAL = XKL = EFA.
Điều đó có nghĩa là AX // EF.
Lời giải 2. (Dùng phương tích, độ dài đại số)
Ta cần có một bổ đề.
Bổ đề. Cho hai đường tròn (O1), (O2), trục đẳng phương ∆. M là điểm bất kì và H là hình chiếu
vuông góc của M trên ∆. Khi đó P − P = 2O O .HM. M /(O ) M /(O ) 1 2 1 2
Trở lại giải bài toán 2.
Gọi (O), (O’) là đường tròn ngoại tiếp các tam giác ABC, AB’C’; E’, F’ theo thứ tự là hình chiếu
của E, F trên AX; K, L theo thứ tự là giao điểm thứ hai của AE, AF và (AB’C’) . Vì AX là trục
đẳng phương của (O), (O’) nên, theo bổ đề trên, P − P E /(O') E /(O) 2O ' O.E ' E E ' E = = 1 ( ). P − P 2O ' O.F ' F F ' F F /(O') F /(O) Mặt khác CC '.CB ' EA. EA EK EC P - P E /(O ') E /(O) EA.EK EA.EC ( − − ) = = EA.CK CA P - P FA.FL FA.FB FA FL FB FA.BL BB '.BC ' F /(O') F /(O) ( ) = = − − FA. BA
= EA BA CC ' CB ' = BB ' BC ' CC ' CB ' . . . . . . = 1 (2). CA FA BB ' BC ' CB ' CC ' BB ' BC '
Từ (1) và (2) suy ra E ' E = F ' F.
Điều đó có nghĩa là AX // EF.
Lời giải 3 (Dùng định lý bốn điểm)
Theo giả thiết thì AX là trục đẳng phương của hai đường tròn (O) và (O’), do đó AX ⊥ O ' O . Ta cần
chứng minh FE cũng vuông góc với OO’. Ta có 2 2 OE − OF = ( 2 2 OE − R ) − ( 2 2
OE − R ) = E . A EC − F . A FB 2 2
O ' E − O ' F = ( 2 2
O ' E − R ' ) − ( 2 2
O ' E − R ' ) = E . A EK − F . A FL Cần chứng minh 2 2 2 2
OE − OF = O ' E − O ' F ⇔ EA( EC − EK ) = FA( FB − FL) KC FA ⇔ E . A KC = F . A LB ⇔ = (1) LB EA 12 KC XK AF
Mặt khác hai tam giác XKC và XLB đồng dạng nên suy ra = = (2) LB XL AE
Nhận xét. - Lời giải 1 chủ yếu sử dụng tam giác đồng dạng và định lý Thales để tính toán và đưa
đến chứng minh hai góc đồng vị bằng nhau. Đây là lời giải chỉ sử dụng kiến thức THCS và rất kinh điển.
- Lời giải 2 sử dụng một kết quả quen thuộc về phương tích và dùng độ dài đại số để tính toán.
Tuy có dùng đến kiến thức lớp 10 nhưng lời giải này có tính tổng quát cho mọi trường hợp và áp
dụng được khi mở rộng bài toán.
- Lời giải 3 sử dụng định lý bốn điểm, hướng giải quyết rất rõ ràng và rất dễ áp dụng.
Bài toán 7. (APMO 2010). Tam giác ABC nội tiếp đường tròn (O) và có trực tâm H, (HAB) cắt
AC tại N và (HAC) cắt AB tại M. Chứng minh tâm đường tròn (HMN) thuộc HO.
Lời giải 1. (Dùng phép đồng dạng và định lý Thales) U V A N M N' Q O' M' P S O R H B C
Dễ chứng minh được HMM'B và HNN'C là những hình thoi đồng dạng. Gọi O' là tâm (HMN) và
gọi P, Q là hình chiếu của O' lên HM, HN thì P, Q là trung điểm HM, HN. Xét phép đồng dạng f 13
biến HMM'B thành HNN'C, khi đó biến HM thành HN và BM' thành CN', do đó biến P thành Q và
R thành S (R, S là hình chiếu của O lên HM, HN). HP HQ Do đó ta có = HR HS
Gọi X, Y là giao của HO' với trung trực BM', CN' thì ta có
RX // PO' và SY // QO' nên HX HR HS HY = = = HO ' HP HQ HO '
Suy ra X = Y do vậy X, Y là giao của trung trực BM' và CN' nên phải trùng O. Vậy H, O, O' thẳng hàng.
Lời giải 2. (Dùng định lý bốn điểm kết hợp với phương tích và trục đẳng phương)
HM cắt AC tại U và HN cắt AB tại V, ta có UA.UC = UH.UM nên U thuộc trục đẳng phương của
(O) và (HMN). Tương tự, V cũng thuộc trục đẳng phương của (O) và (HMN).
Suy ra OO' vuông góc với UV. Ta cần chứng minh OH vuông góc với UV. Ta có
ANV = ABH = ACH = AMU
nên suy ra MNUV nội tiêp suy ra
HM .HU = HN.HV Do đó 2 2 OU − OV = ( 2 2 OU − R ) − ( 2 2
OV − R ) = UM .UH −VN.VH
= UH (UH + HM ) −VH (VH + HN ) 2 2 = HU − HV
Vậy OH vuông góc với UV, từ đó suy ra đpcm.
Nhận xét. Việc phát hiện hai hình thoi HMM'B và HNN'C đồng dạng gợi cho ta hướng tiếp cận
bài toán bằng cách dùng phép đồng dạng. Tuy nhiên nếu phát hiện ra U, V có cùng phương tích
với hai đường tròn (O) và (HMN) thì bài toán quy về việc chứng minh OH vuông góc với UV, do
đó một cách rất tự nhiên, ta nghỉ đến phương tích và định lý bốn điểm.
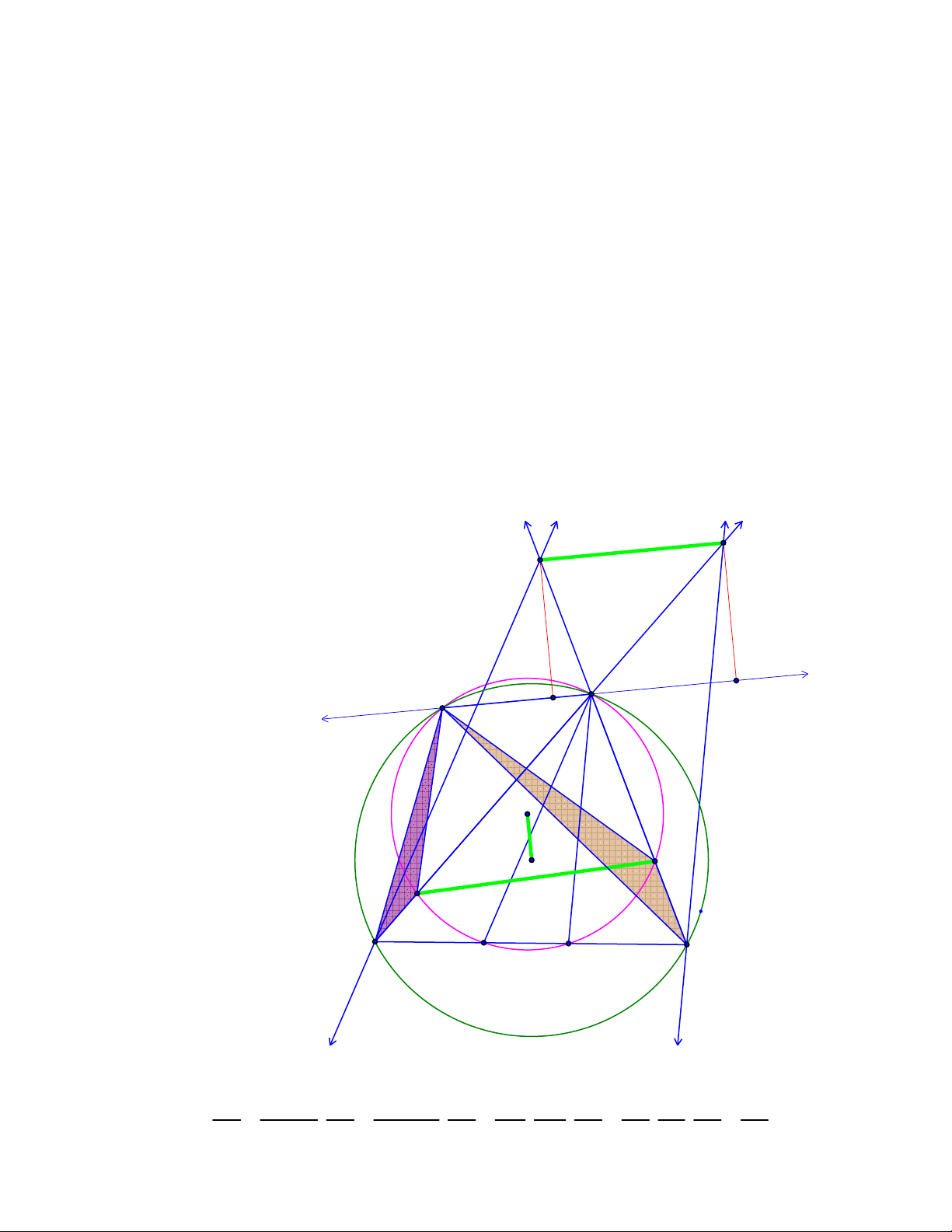
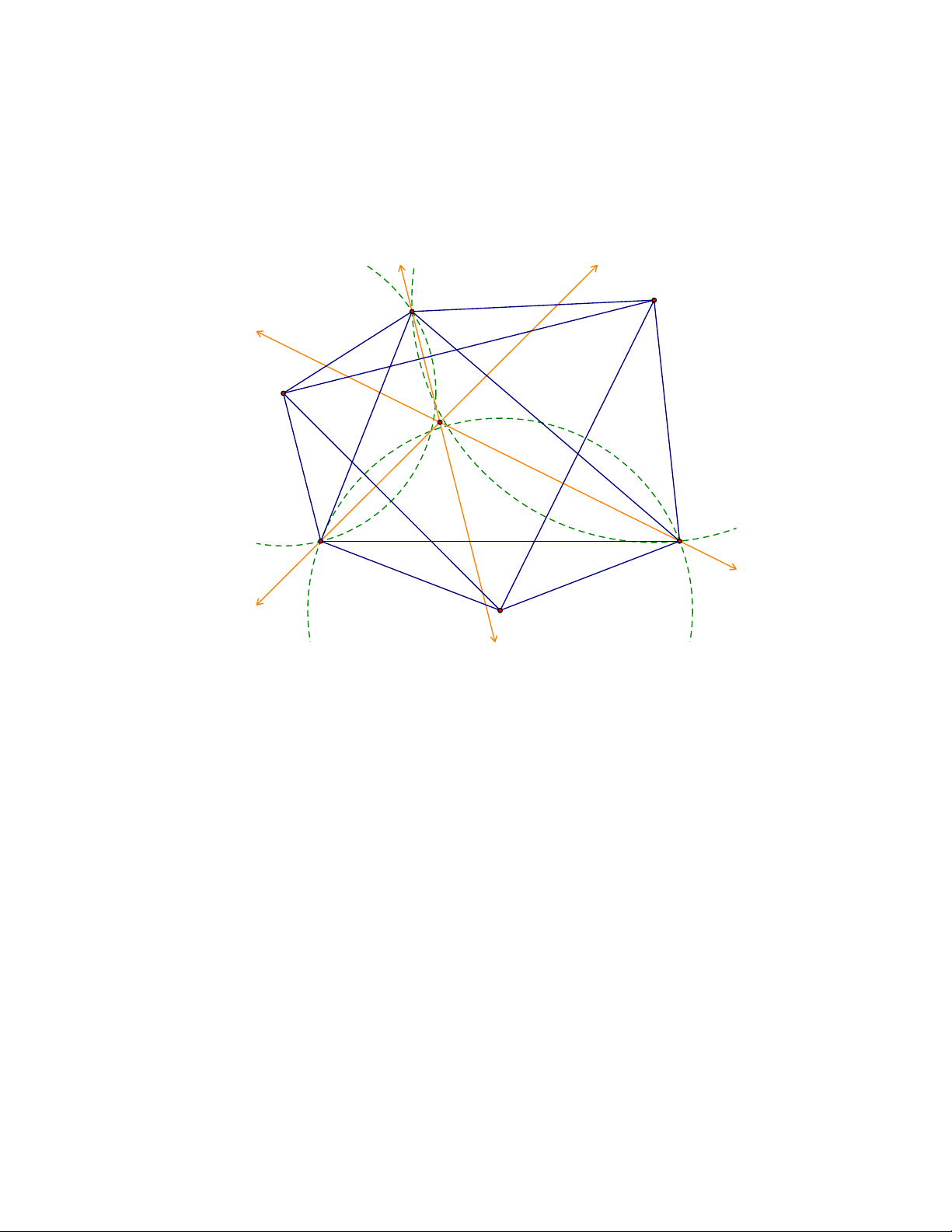
Bài toán 8. Cho tứ giác ABCD có 0
DAB = ABC = BCD > 90 . Chứng minh rằng đường thẳng Euler của A
∆ BC đi qua D.
Lời giải 1 (Dùng biến đổi góc và định lý Ceva-sin) Đặt BAC = ,
A ABC = B, ACB = C . Khi đó do B > 900 nên B nằm trong tam giác AHC (H là trực tâm
tam giác ABC). Gọi O là tâm đường tròn ngoại tiếp tam giác ABC. Khi đó ta có 0
ACO = CAO = HCB = HAB = B − 90
(do H, O là 2 điểm đẳng giác trong tam giác ABC)(1)
Suy ra O nằm ngoài tam giác AHC Ta có 14
HAO = A + HAB + OAC = A + ( 0 2 B − 90 )
= B − C = BCD − C = ACD Tương tự, 0
HCO = CAD = B − ,
A HAD = HCD = 2B − 90
Theo định lý Sin, ta lại có
sin AHD sin HCD sin CAD AD HD CD . . = . . = 1
sin HAD sin CHD sin ACD HD CD AD Mà HAD = HCD nên sin AHD sin CAD . = 1 sin CHD sin ACD N M J H C1 B1 I B N1 M1 A C O D Từ đó ta có
sin AHD sin HCO sin CAO sin AHD sin HCO sin AHD sin CAD . . = . = . = 1
sin CHD sin ACO sin HAO sin CHD sin HAO sin CHD sin ACD
Theo định lý Ceva sin cho tam giác AHC ta có CO, AO, DH đồng quy. Vậy, H, O, D thẳng hàng.
Lời giải 2. (Dùng định lý bốn điểm)
Gọi DA ∩ CB = M, AB ∩ DC = N. Các đường cao MM1, NN1 của các tam giác AMB và BNC cắt nhau tại O. Do
DAB = ABC = BCD nên các tam giác AMB , BNC là các tam giác cân tại M và N. Do đó OM và
ON lần lượt là các đường trung trực của AB và BC. Từ đó suy ra O là tâm đường tròn ngoại tiếp 15 A
∆ BC . Gọi H là trực tâm của tam giác A ∆ BC . Vì 0
ABC > 90 nên H nằm ngoài A
∆ BC vµ ta cã HA
⊥ BC t¹i B vµ HC ⊥ AB t¹i C . 1 1
Như vậy, các tứ giác sau nội tiếp được: AM1B1M, AB1C1C, CN1C1N và MACN. Gọi I , J lần lượt là
trung điểm của MA và CN. Khi đó I , J lần lượt là tâm các đường tròn ngoại tiếp tứ giác AM1B1M
và CN1C1N. Do đó ta có 2 2
HB ⋅ HA = HI − IA và 2 2
OM ⋅OM = OI − IA 1 1 2 2
HC ⋅ HC = HJ − JC và 2 2
ON ⋅ON = OJ − JC 1 1
HC ⋅ HC = HB ⋅ HA 1 1 Suy ra 2 2 2 2 2 2 2 2
HI − IA = HJ − JC ⇒ HI − HJ = IA − JC (1) Tương tự, 2 2 2 2 2 2 2 2
OM ⋅OM = ON ⋅ ON ⇒ OI − IA = OJ − JC ⇒ OI − OJ = IA − JC 1 1 Từ đó suy ra 2 2 2 2 2 2 2 2
HI − HJ = OI − OJ ⇒ HI + OJ = OI + HJ .
Theo định lý 4 điểm thì OH ⊥ IJ (2)
Mặt khác, do tứ giác MACN nội tiếp được nên DA.DM = DC.DN
⇒ ( DI – IA ).( DI + IA ) = ( DJ – JC ).( DJ – JC ) 2 2 2 2 2 2 2 2
⇒ DI − IA = DJ − JC ⇒ DI − DJ = IA − JC (3) Từ (1) và (3) suy ra 2 2 2 2 2 2 2 2
HI − HJ = DI − DJ ⇒ HI + DJ = DI + HJ
Theo định lý 4 điểm thì DH ⊥ IJ (4). Từ (2) và (4) suy ra H, O, D thẳng hàng.
Do đó đường thẳng Euler của tam giác ABC đi qua D.
Nhận xét. Đây là một bài toán khó, vì giả thiết bài toán rất đơn giản và cũng rất khó khai thác.
Ở lời giải 1 ta đưa bài toán chứng minh ba điểm thẳng hàng về chứng minh ba đường thẳng đồng
quy, do đó ta sử dụng định lý Ceva-sin để công phá, từ đó đòi hỏi chúng ta phải biến đổi góc. Còn
ở lời giải 2, để chứng minh H, O, D thẳng hàng ta đưa về hai bài toán chứng minh vuông góc, đó
là chứng minh OH và DH cùng vuông góc với IJ, việc phát hiện ra các tứ giác nội tiếp AM1B1M,
AB1C1C, CN1C1N và MACN là rất quan trọng, vì nó gợi ý cho ta có thể sử dụng phương tích và
định lý bốn điểm để công phá bài toán.
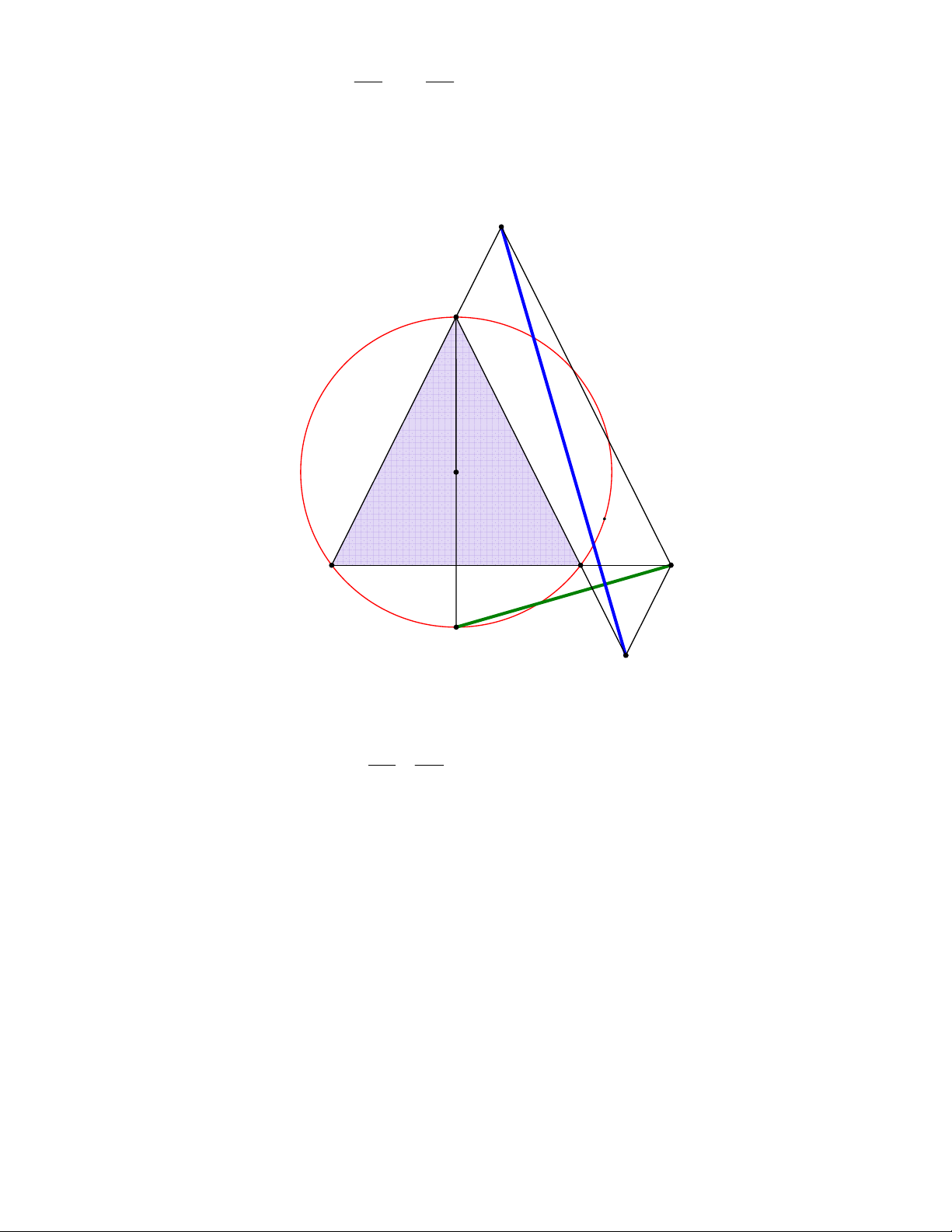
Bài toán 9. (1997-USA) Cho tam giác ABC và dựng các tam giác cân BCD, CAE và ABF nằm bên
ngoài tam giác ABC với BC, CA và AB là các cạnh đáy. Chứng minh rằng các đường thẳng qua A,
B, C tương ứng vuông góc với EF, FD, DE thì đồng quy.
Lời giải 1. (Dùng tính chất của trục đẳng phương)
Xét các đường tròn có tâm là D, E, F và có bán kính lần lượt là DB, EC, FA. Khi đó đường thẳng
qua A và vuông góc với EF là trục đẳng phương của hai đường tròn (E, EC) và (F, FA), đường
thẳng qua B và vuông góc với FD là trục đẳng phương của hai đường tròn (D, DB) và (F, FA),
đường thẳng qua C và vuông góc với ED là trục đẳng phương của hai đường tròn (D, DB) và (E,
EC). Mà ba đường tròn này có tâm không thẳng hàng nên ba đường thẳng trên đồng quy tại tâm
đẳng phương của ba đường tròn. 16
Lời giải 2. (Dùng định lý Carnot)
Theo giả thiết ta có AE = CE, AF = BF, BD = CD . Do đó ta có ( 2 2 AE − AF ) + ( 2 2 BF − BD ) + ( 2 2 CD − CE ) = ( 2 2 AE − CE ) + ( 2 2 BF − AF ) + ( 2 2 CD − BD ) = 0
Áp dụng định lý Carnot cho tam giác DEF với các điểm A, B, C ta có các đường thẳng qua A, B, C
tương ứng vuông góc với EF, FD, DE thì đồng quy. E A F P B C D
Lời giải 3. (Dùng định lý bốn điểm)
Để chứng minh FE, FD, ED đồng qui, ta gọi P là giao điểm của đường thẳng qua B vuông góc với
FD với đường thẳng qua C vuông góc với DE, ta cần chứng minh PA vuông góc với FE.
Áp dụng định lý bốn điểm và sử dụng tích chất các tam giác cân, ta có: 2 2 2 2 2 2
PB ⊥ FD ⇔ PF − PD = BF − BD = AF − CD ) 1 ( 2 2 2 2 2 2
PC ⊥ DE ⇔ PD − PE = CD − CE = CD − AE (2)
Từ (1) và (2) suy ra: PF 2 − PE 2 = AF 2 − AE 2 ⇔ PA ⊥ FE (đpcm).
Nhận xét. Bài toán có nội dung rất đơn giản nhưng ý tưởng rất hay, những dữ kiện của nó có thể
dễ dàng gợi cho ta hướng tiếp cận bằng định lý bốn điểm hoặc định lý Canort. Tuy vậy nhưng lời
giải bằng cách sử dụng phương tích, trục đẳng phương cũng khá bất ngờ và độc đáo.
2.3. Một số bài toán về chứng minh điểm thuộc đường thẳng cố định hoặc đường
thẳng luôn đi qua điểm cố định
Về bản chất, bài toán chứng minh điểm thuộc đường thẳng cố định chính là chứng minh
tính thẳng hàng của các điểm mà ở đó đường thẳng chứa các điểm đó (giá của hàng điểm) có tính 17
cố định khi một số yếu tố thay đổi. Tương tự, bài toán chứng minh đường thẳng qua điểm cố định
chính là bài toán về sự đồng quy mà điểm đồng quy (tâm của chùm đường thẳng) có tính cố định
khi một số yếu tố khác thay đổi). Vì vậy, với dạng toán này chúng ta cũng có thể đưa về việc
chứng minh quan hệ vuông góc bằng cách vận dụng định lý bốn điểm như đã nêu trên.
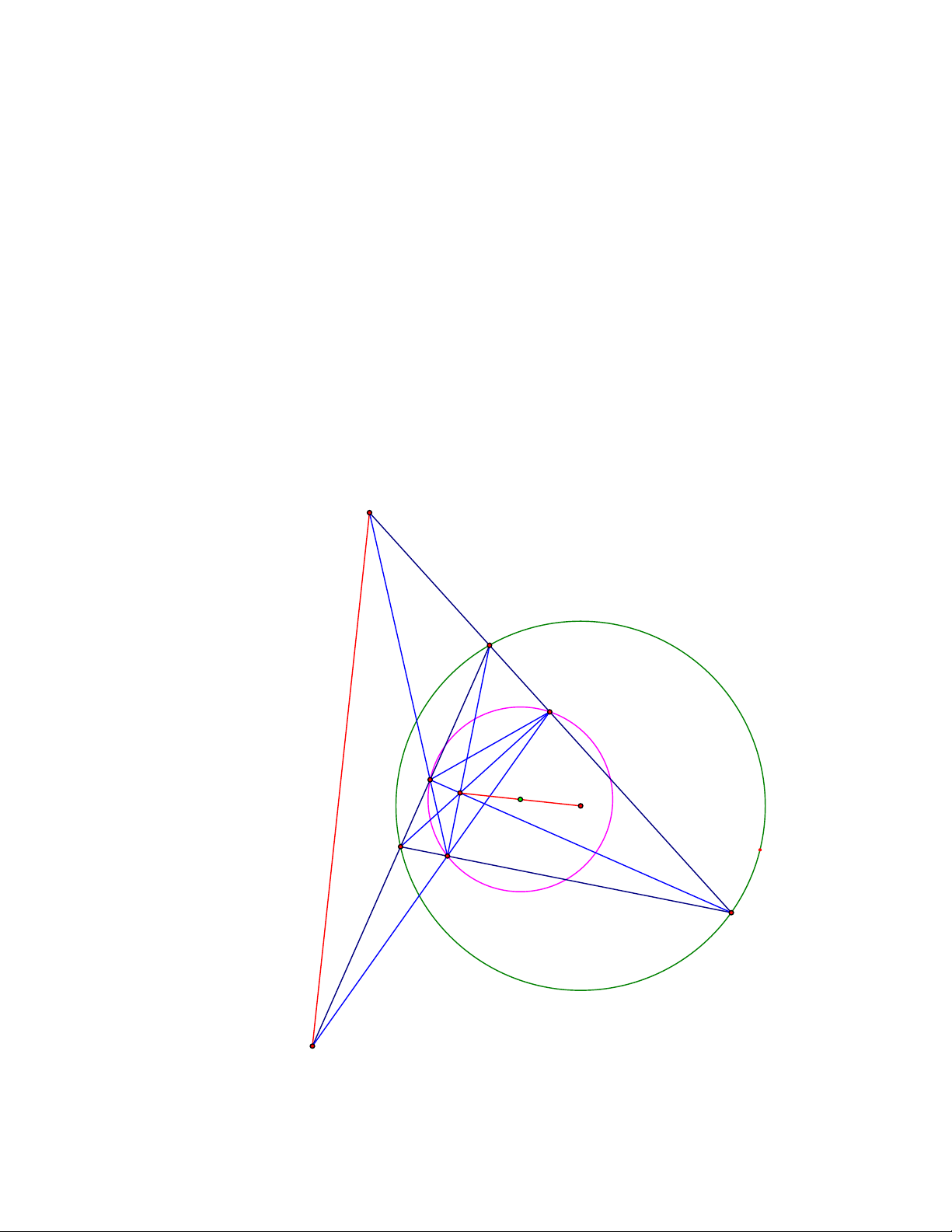
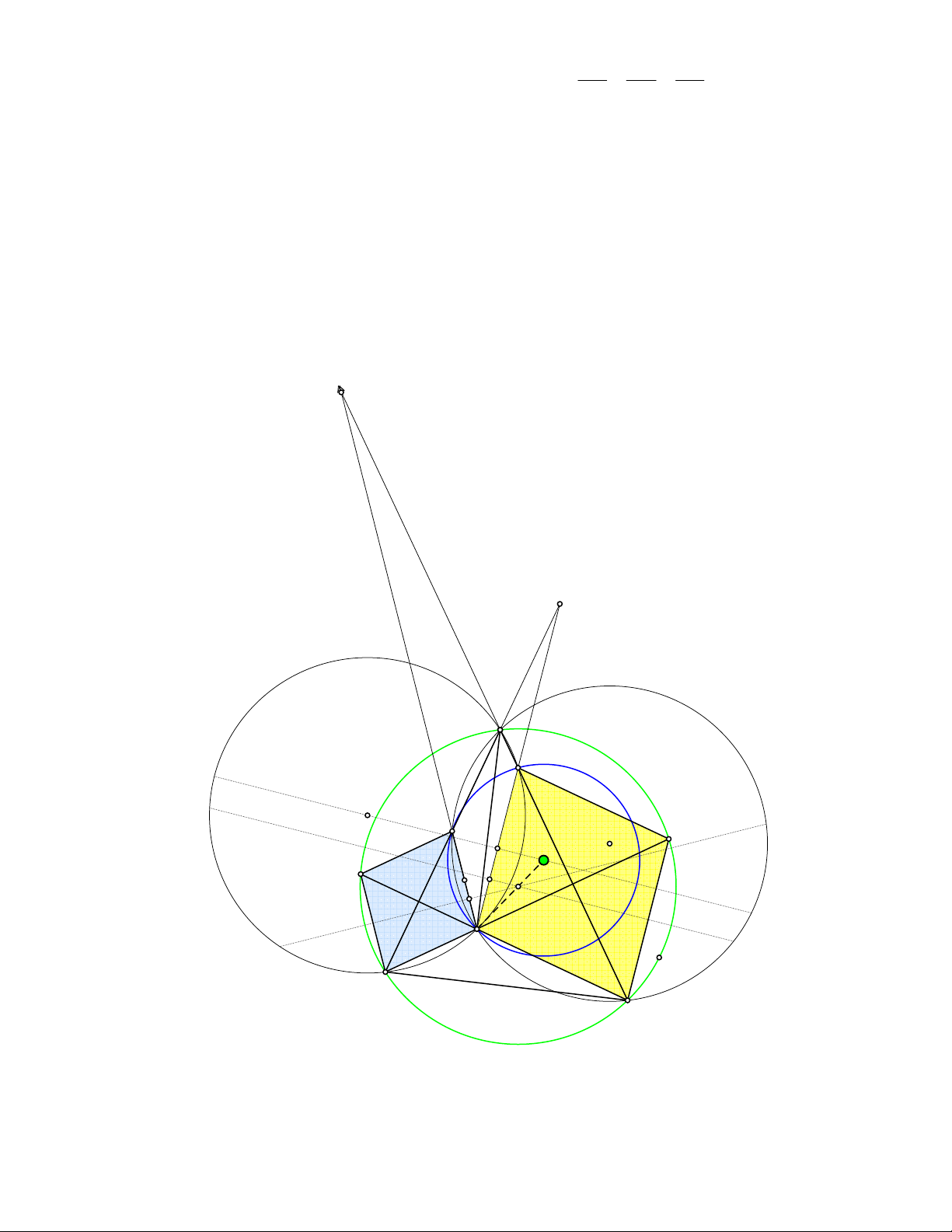
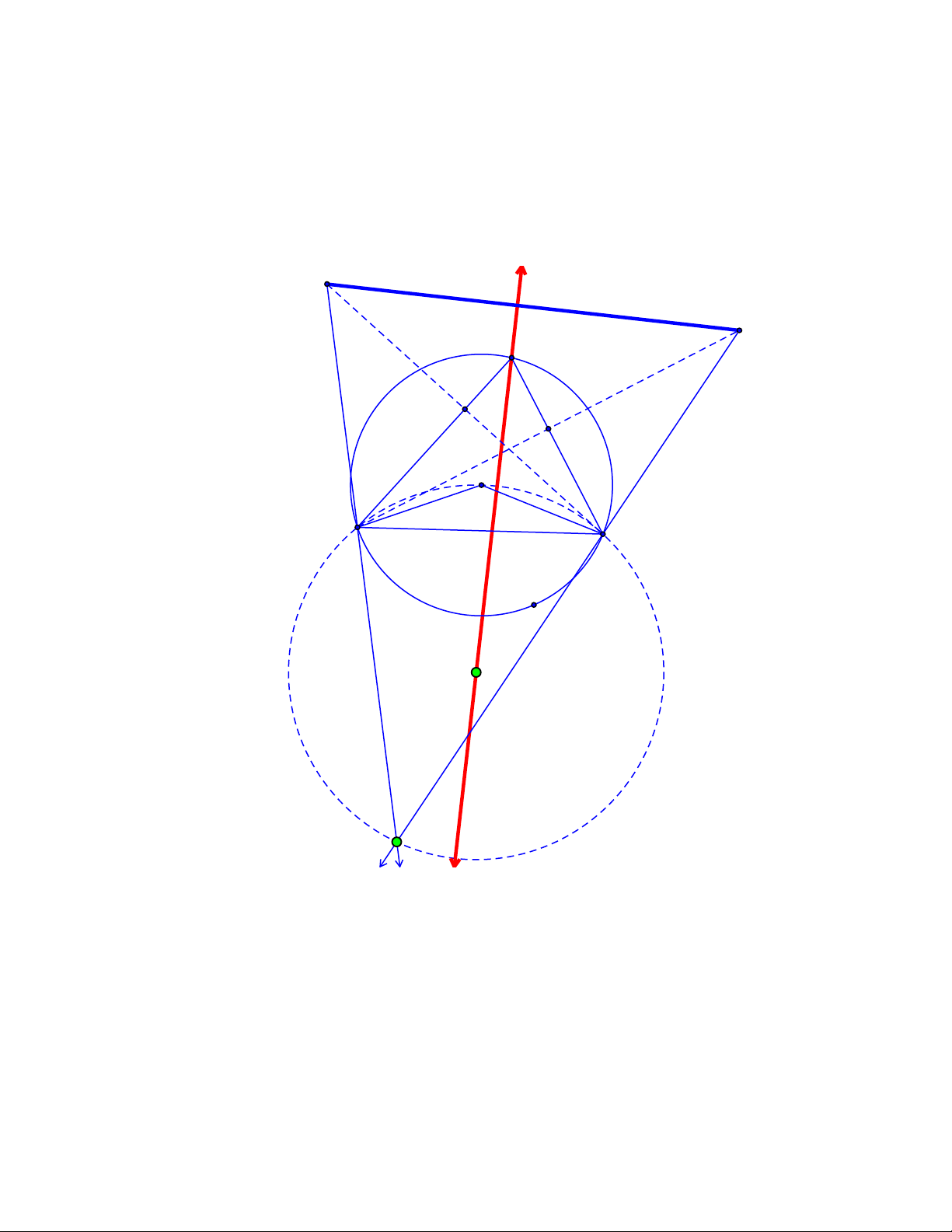
Bài toán 10. Cho hai điểm B, C cố định trên đường tròn tâm O và A là một điểm thay đổi trên (O)
khác B và C. Gọi B’ là điểm đối xứng với B qua AC và C’ là điểm đối xứng với C qua AB. Chứng
minh rằng đường thẳng qua A và vuông góc với B’C’ luôn đi qua một điểm cố định. C' B' A E D O B C X F
Lời giải 1. (Dùng tích vô hướng)
Do D, E lần lượt là trung điểm BB’, CC’ nên ' ' = 2 − , AX = + OX B C DE BC AO Do đó
B 'C '.AX = (2DE − BC)( + OX AO ) = 2A . O DE − A . O BC + 2OX. − OX DE .BC
Mà OX vuông góc với BC và AO vuông góc với DE nên ta có 18 ' '.AX = . + 2OX B C OA BC .DE = O . A BC.cos (O ,
A BC ) + 2OX.DE.cos(OX , DE) = O . A BC.cos (O ,
A DE ) + (DE, BC) + 2OX .DE.cos (OX , BC) +
(BC,DE) 2 BC π 2 π = BC cos + (DE,BC) + cos − (DE,BC) = 0 2sin A 2 2sin BOC 2
Lời giải 2. (Dùng định lý bốn điểm)
Gọi F là giao điểm của BC’ và B’C, ta có 0
BFC = 180 − CBF − BCF 0 0
= 180 − (180 − 2ABC) 0 − (180 − 2ACB) 0
= 2ABC + 2ACB −180 Mà
BOC = 2BAC nên từ đây suy ra tứ giác BOCF nội tiếp. 2 2 B X − C X = ( 2 2
B X − R ) − ( 2 2 ' ' '
C ' X − R )
= B 'C.B ' F − C ' .
B C ' F = B 'C ( B 'C + CF ) − C ' B (C ' B + BF )
= BC (CF − BF )
Dễ thấy A là tâm đường tròn bàng tiếp góc F của tam giác BCF nên
B’A2 – C’A2 = AB2 – AC2 = BC(CF – BF). Như vậy ta có 2 2 2 2
B ' X − C ' X = B ' A − C ' A . Từ đó suy ra AX vuông góc với B’C’.
Nhận xét. 1/ Việc dự đoán điểm cố định là tâm X của đường tròn (OBC) không quá khó, bài toán
quy về việc chứng minh AX vuông góc với B’C’. Tuy nhiên với bài toán này, việc biến đổi góc
gặp nhiều khó khăn, vì vậy cách tốt nhất để tiếp cận bài toán là dùng công cụ tích vô hướng hoặc
định lý bốn điểm. Việc phát hiện tứ giác BOCF nội tiếp và A là tâm bàng tiếp góc F của tam giác
BCF là điểm then chốt giúp ta tiếp cận bài toán bằng định lý bốn điểm và thu được lời giải đơn
giản hơn lời giải 1 rất nhiều.
2/ Nếu gọi Y, Z lần lượt là tâm các đường tròn, (OCA), (OAB) thì AX, BY, CZ đồng quy tại một
điểm gọi là điểm Kosnita của tam giác ABC. Kết quả của bài toán trên là một trong rất nhiều tính
chất đẹp của điểm Kosnita của tam giác.
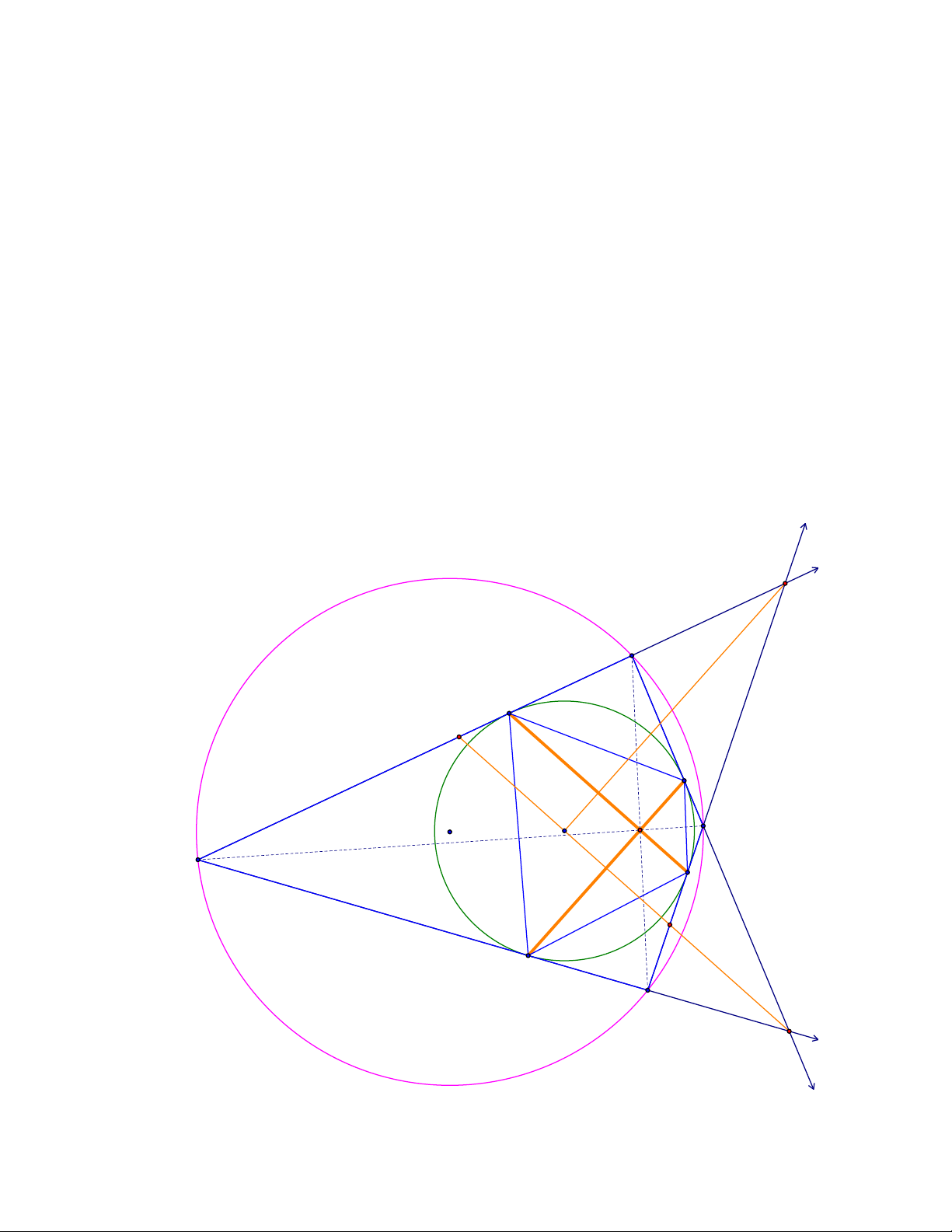
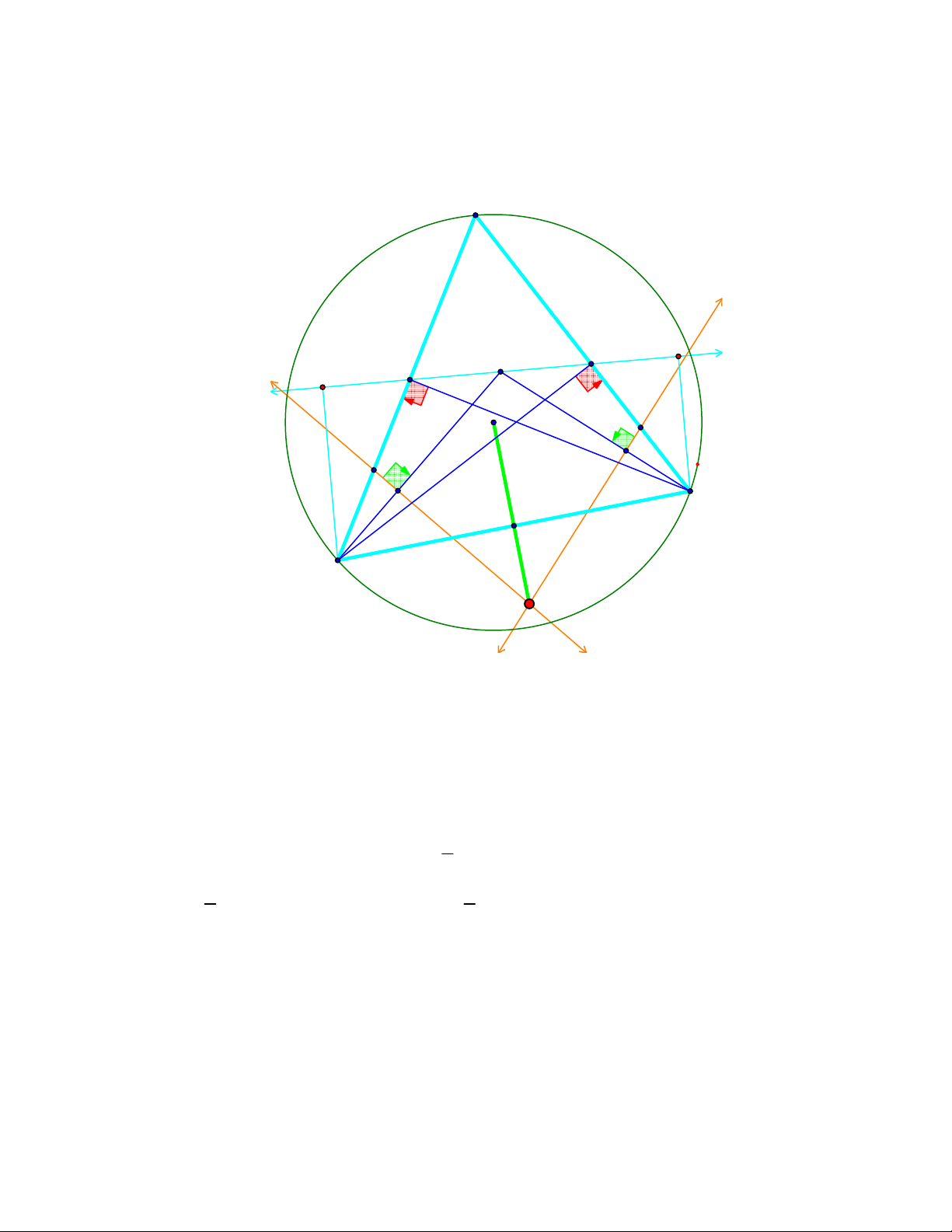
Bài toán 11. Trên đường tròn (O) cố định lấy hai điểm B, C cố định và lấy điểm A thay đổi khác
B, C vẽ các đường cao BE, CF. Gọi M, S, N lần lượt là trung điểm của BF, FE, EC. Đường thẳng
qua M và vuông góc với BS cắt đường thẳng qua N và vuông góc với CS tại K. Chứng minh K
luôn chạy trên một đường thẳng cố định khi A thay đổi.
Lời giải 1. (Dùng tính chất trục đẳng phương và định lý Canort)
Gọi T là trung điểm BC và B’, C’ lần lượt là hình chiếu của B, C lên E, F. Dễ thấy B, C, E, F cùng
thuộc đường tròn đường kính BC, tâm T. Vì TS vuông góc với EF nên S là trung điểm B’C’, do đó
ta có SE.SC’ = SF.SB’ (*) 19
Ngoài ra ta cũng có AF.AB = AE.AC nên kết hợp với (*) ta suy ra AS là trục đẳng phương của
hai đường tròn (BF) và (CE). Suy ra AS vuông góc với MN. Xét hai tam giác SBC và TMN. Vì các
đường thẳng qua B, C, S lần lượt vuông góc với TM, TN, MN đồng quy tại A nên các đường
thẳng qua M, N, T và lần lượt vuông góc với BS, CS, BC cũng đồng quy tại K.
Vậy, K luôn nằm trên trung trực của BC. A C' S E B' F N O M T C B K
Lời giải 2. (Dùng định lý 4 điểm)
Vì MK vuông góc với BS và NK vuông góc vơi CS nên theo định lý bốn điểm ta có 2 2 2 2
BK − SK = BM − SM 2 2 2 2
CK − SK = CN − SN Suy ra 1 2 2 BK − CK = ( 2 2
BM − SM ) − ( 2 2
CN − SN ) = ( 2 2
BF − BE ) − ( 2 2 CE − CF ) 4 1 = ( 1 2 2 BF + CF ) − ( 2 2 BE + CE ) = ( 2 2 BC − BC ) = 0 4 4
Do đó K luôn cách đều B và C. Vậy K luôn nằm trên trung trực của đoạn BC.
Nhận xét. Bằng phương pháp giới hạn (cho A tiến đến điểm chính giữa cung BC) ta có thể dự
đoán đường thẳng cố định là trung trực của BC.
Trong lời giải 1, điều quan trọng là phát hiện ra AS là trục đẳng phương của hai đường tròn (BF)
và (CE), từ đó mới có ý tưởng dùng định lý Carnot thuận và đảo cho các tam giác SBC và TMN.
Còn ở lời giải 2, vì MK vuông góc với BS và NK vuông góc vơi CS nên dùng định lý bốn điểm ta
có thể dễ dàng chứng minh K cách đều B và C, từ đó suy ra K thuộc trung trực của BC. 20



