BÀI GIẢNG
ĐỒ HOẠ KỸ THUẬT Phần I Hình họa Chương 1 Mở đầu
Cơ sở của biểu diễn
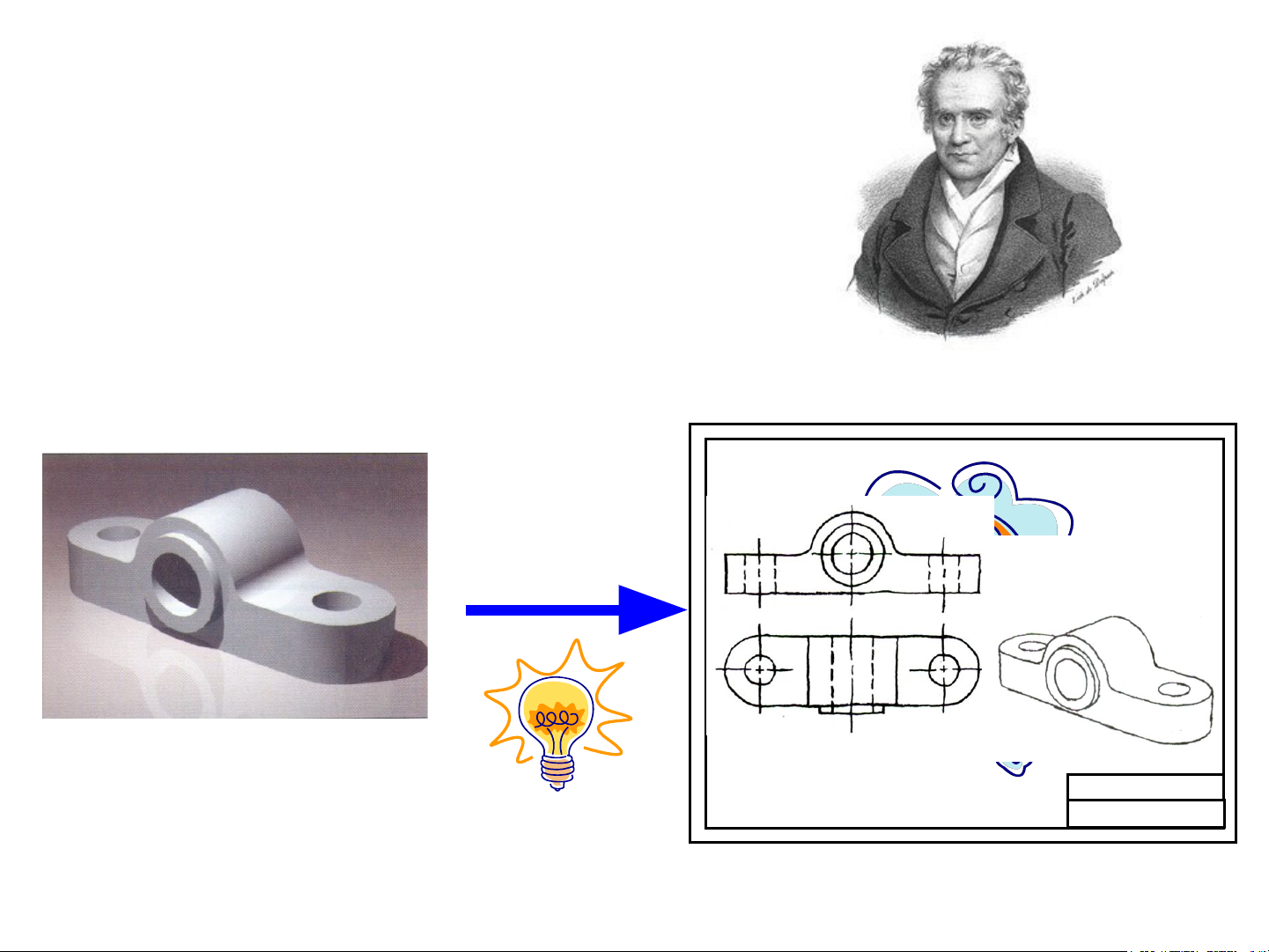
Trong kỹ thuật, bản vẽ kỹ thuật( trên giấy)
được sử dụng trong sản xuất và trao đổi thông
tin giữa các nhà thiết kế.
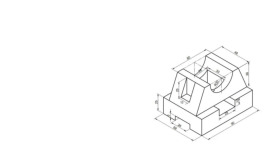
Bản vẽ kỹ thuật là một mặt phẳng 2 chiều còn
hầu hết vật thể đều là các vật thể 3 chiều.
Vậy làm sao để biểu diễn các đối tượng 3
chiều lên mặt phẳng 2 chiều? Gaspard Monge Hình họa
1.1- Đối tượng môn học
- Nghiên cứu các phương pháp biểu diễn các hình không gian trên một mặt phẳng
- Nghiên cứu các phương pháp giải các bài toán không gian trên một mặt phẳng 1.2- Các phép chiếu S
1- Phép chiếu xuyên tâm
a) Xây dựng phép chiếu
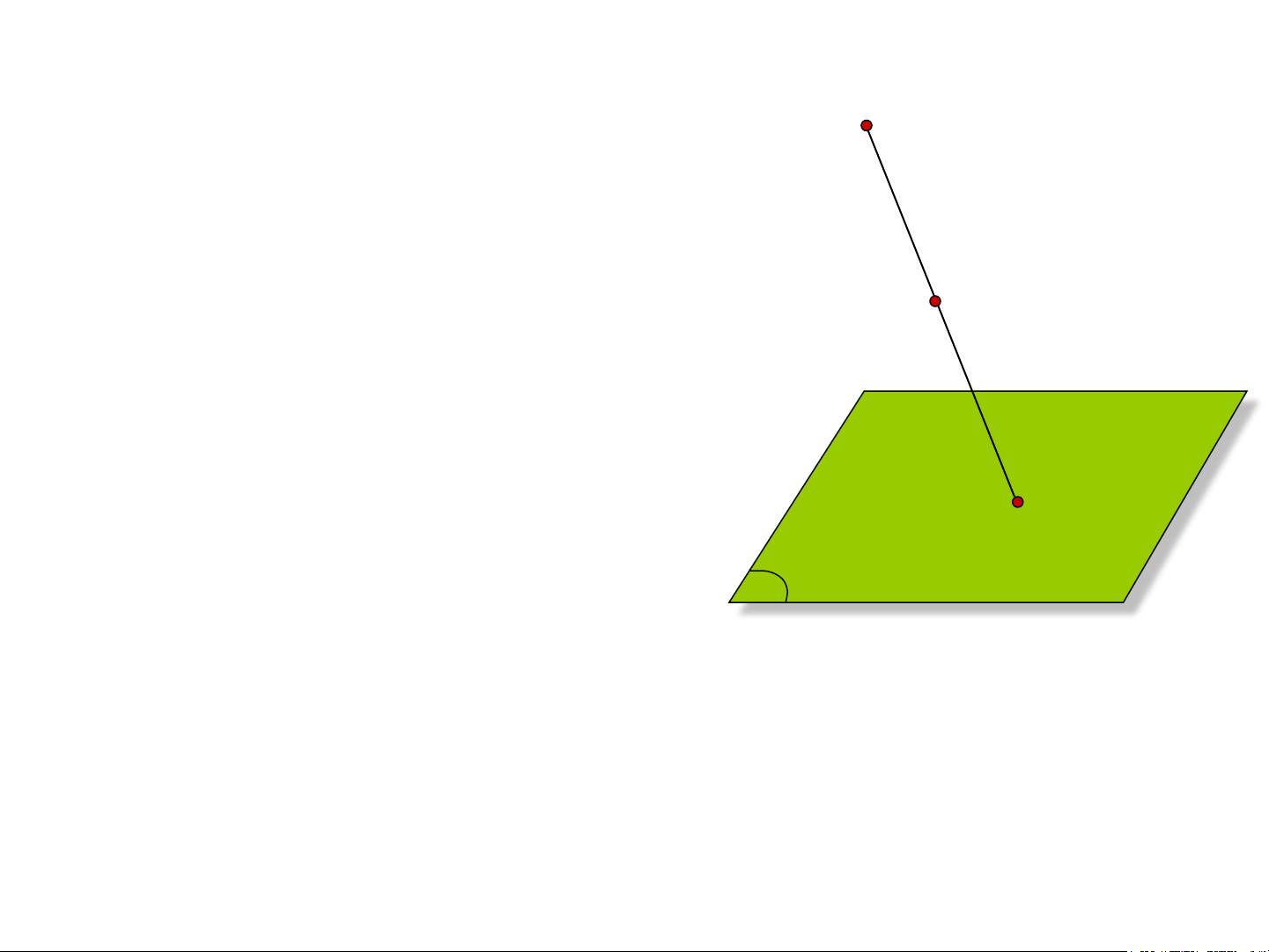
- Cho mặt phẳng Π, một điểm S không thuộc A
Π và một điểm A bất kỳ.
- Gọi A’ là giao của đường thẳng SA với mặt phẳng Π.
*Ta có các định nghĩa sau:
+ Mặt phẳng Π gọi là mặt phẳng hình chiếu A’
+ Điểm S gọi là tâm chiếu
+ Điểm A’ gọi là hình chiếu xuyên tâm của П
điểm A lên mặt phẳng hình chiếu Π
+ Đường thẳng SA gọi là tia chiếu của điểm A
Hình 0.1 Xây dựng phép chiếu xuyên tâm
b) Tính chất phép chiếu П C’ C S A’ C A S E F’ B B B’ A D D’ F D C’=D’ E’ A’ B’ T’ b) П
Hình 0.2a,b Tính chất phép chiếu xuyên tâm a)
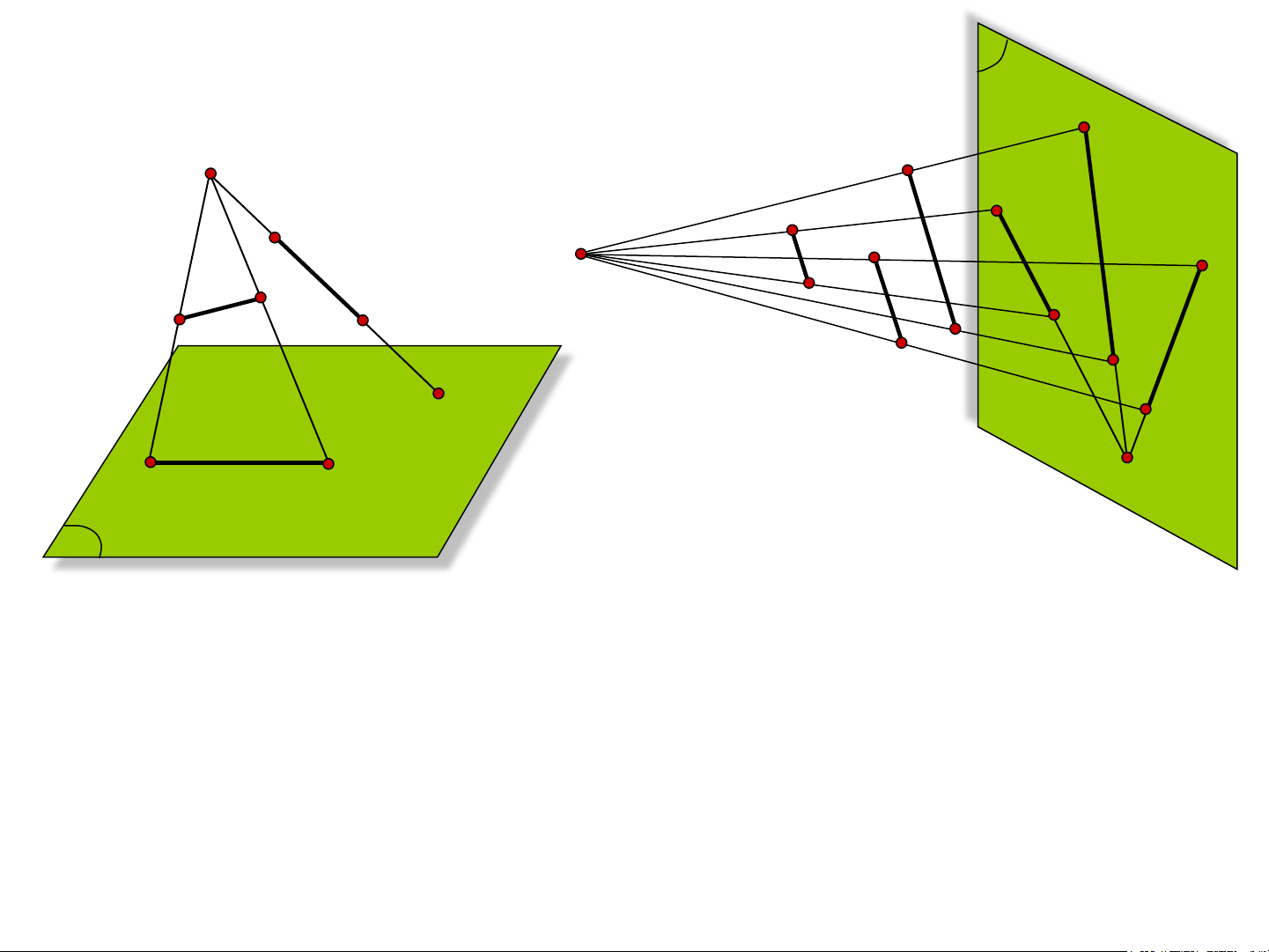
- Nếu AB là đoạn thẳng không đi qua tâm chiếu S thì hình chiếu xuyên tâm của nó
là một đoạn thẳng A’B’.
- Nếu CD là đường thẳng đi qua tâm chiếu S thì C’=D’.(Hình chiếu suy biến) (Hình 0.2.a)
- Hình chiếu xuyên tâm của các đường thẳng song song nói chung là các đường đồng quy. (Hình 0.2.b) 2- Phép chiếu song song
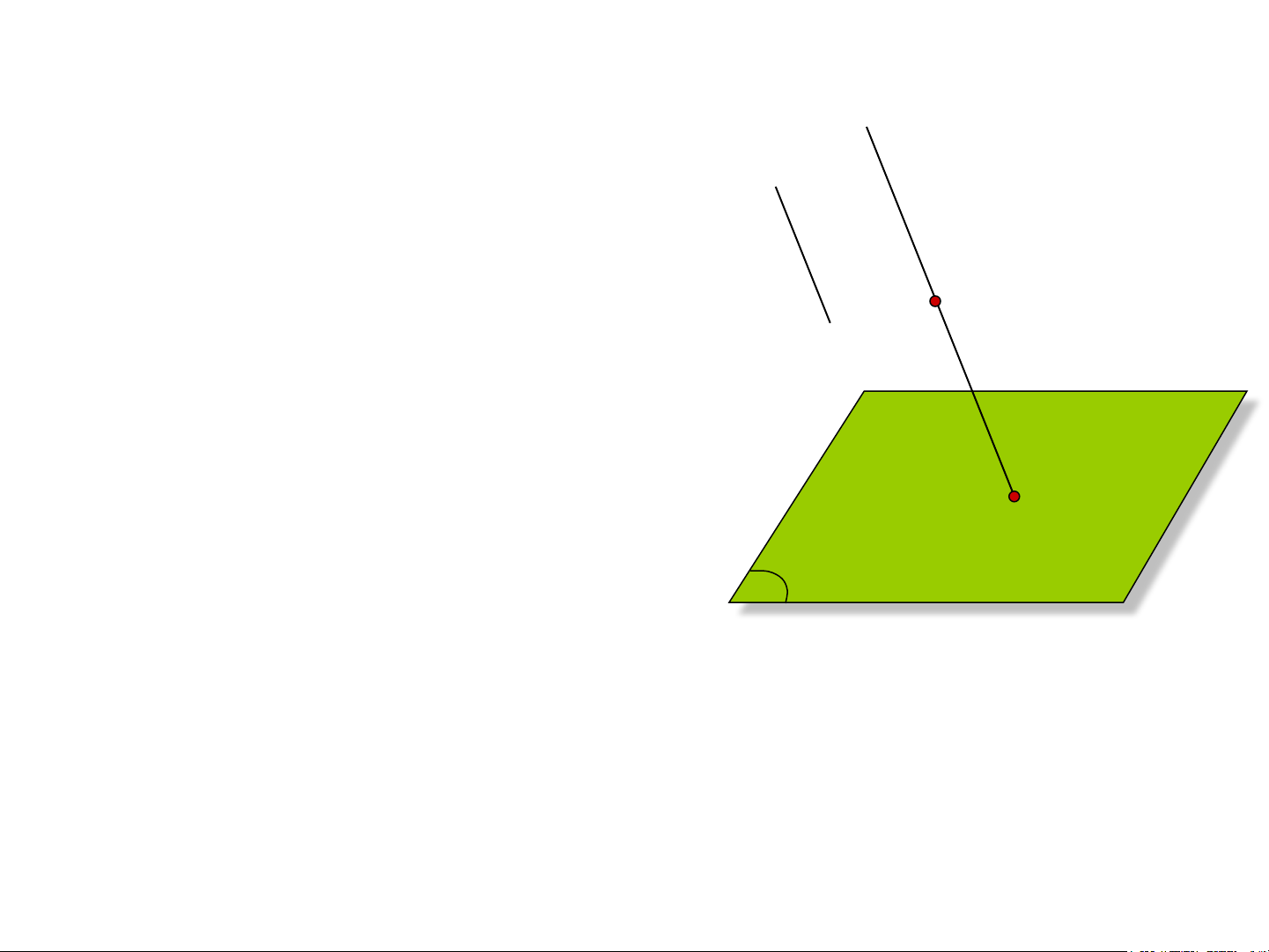
a) Xây dựng phép chiếu a
- Cho mặt phẳng Π, một đường thẳng s
không song song mặt phẳng Π và một s
điểm A bất kỳ trong không gian. A
- Qua A kẻ đường thẳng a//s . A’ là giao
của đường thẳng a với mặt phẳng Π.
* Ta có các định nghĩa sau:
+ Mặt phẳng Π gọi là mặt phẳng hình chiếu A’
+ Đường thẳng s gọi là phương chiếu П
+ Điểm A’ gọi là hình chiếu song song
của điểm A lên mặt phẳng hình chiếu Π theo phương chiếu s
Hình 0.3 Xây dựng phép
+ Đường thẳng a gọi là tia chiếu của chiếu xuyên tâm điểm A
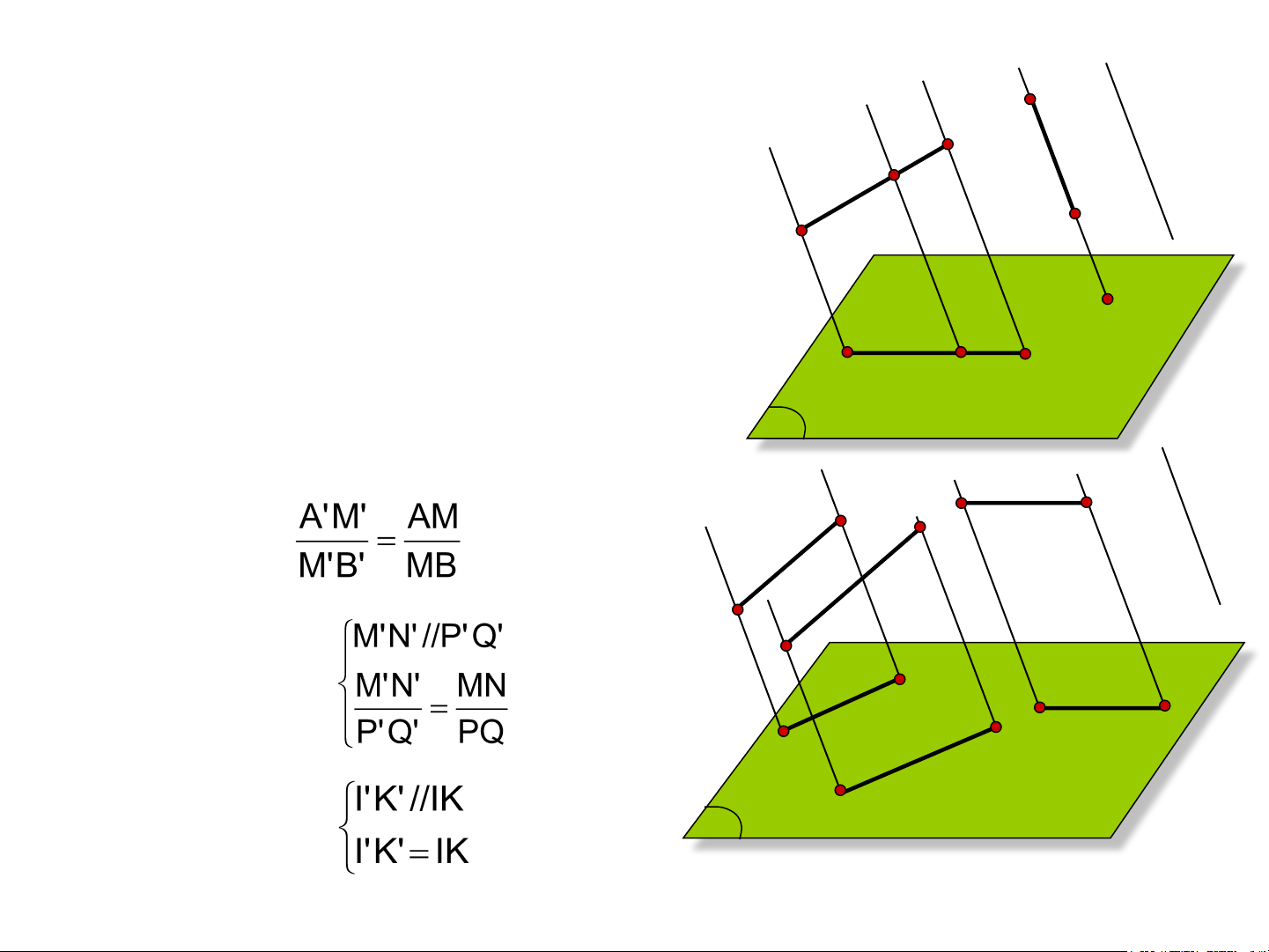
b) Tính chất phép chiếu C
- Nếu đường thẳng AB không song song a) s B M
với phương chiếu s thì hình chiếu song song D
của nó là đường thẳng A’B’ A
- Nếu CD song song với phương chiếu s C’=D’
thì hình chiếu song song của nó là một điểm C’=D’ A’ B’ M’
- Nếu M thuộc đoạn AB thì M’ thuộc A’B’ П
+ Tỷ số đơn của 3 điểm không đổi: b) I K N Q s - Nếu MN//QP thì: M P N’ M’ I’ K’ - Nếu IK// Π thì: Q’ П P’
Hình 0.4a,b Tính chất phép chiếu song song a
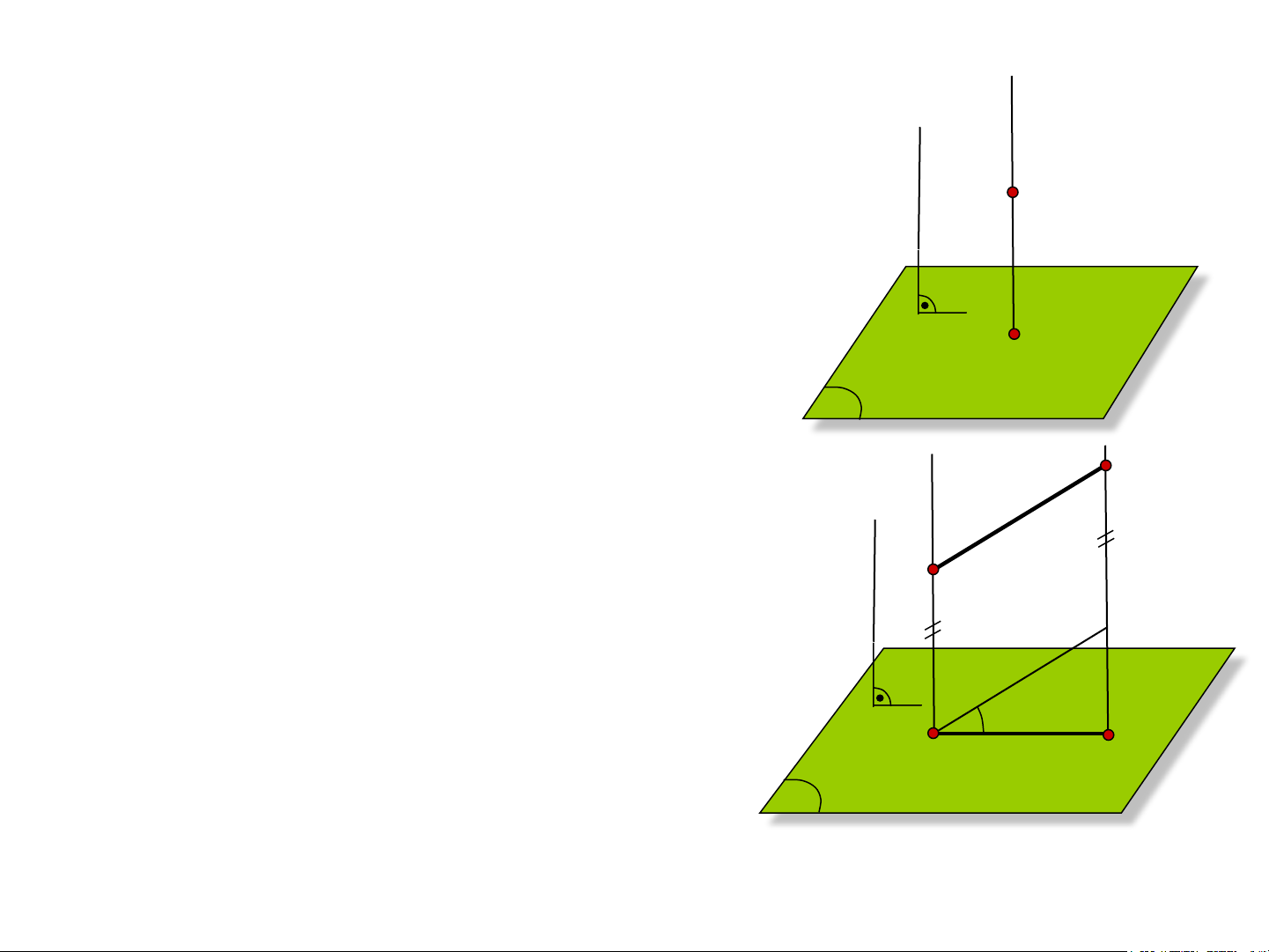
3- Phép chiếu vuông góc a)
- Phép chiếu vuông góc trường hợp đặc s A
biệt của phép chiếu song song khi phương
chiếu vuông góc với mặt phẳng hình chiếu.
- Phép chiếu vuông góc có đầy đủ tính A’
chất của phép chiếu song song, ngoài ra П
có thêm các tính chất sau:
+ Chỉ có một phương chiếu s duy nhất b) B
+ Giả sử AB tạo với П một góc φ thì: A’B’=AB.cosφ s A’B’ ≤ AB A
- Sau đây là những ứng dụng của phép
chiếu vuông góc mà ta gọi là phương
pháp hình chiếu thẳng góc φ A’ B’ П
Hình 0.5a,b. Phép chiếu vuông góc Chương 2
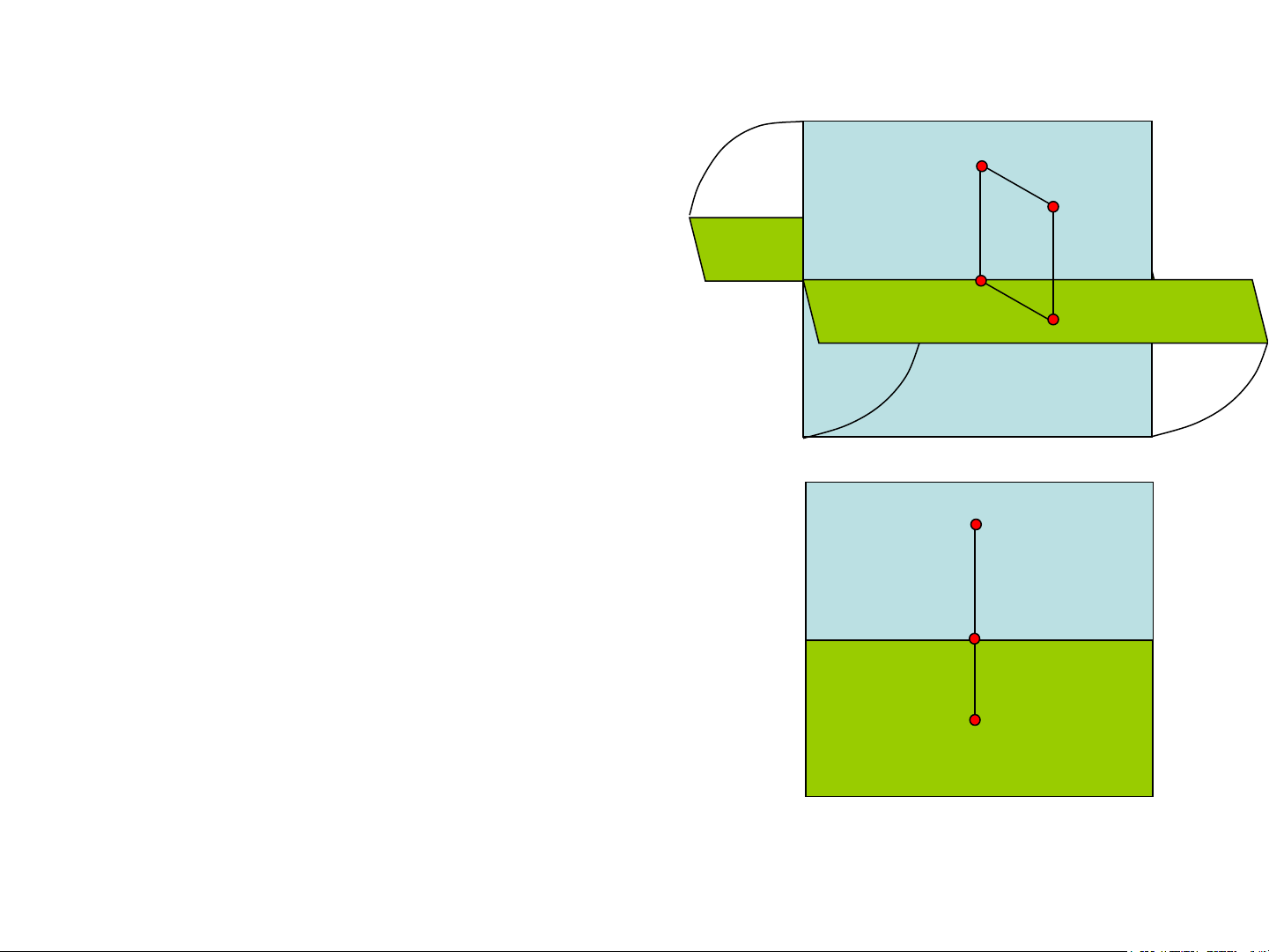
Biểu diễn, liên thuộc 2.1 – Điểm a)
2.1.1 Đồ thức của một điểm Π
a) Hệ thống hai mặt phẳng hình chiếu 1 A1
- Trong không gian lấy hai mặt phẳng A vuông góc nhau П và П . x A 1 2 x
- Mặt phẳng П có vị trí thẳng đứng. 1 Π A 2 2
- Mặt phẳng П có vị trí nằm ngang. 2
- Gọi x là giao điểm của П và П 1 2 (x = П ∩П ) 1 2 b)
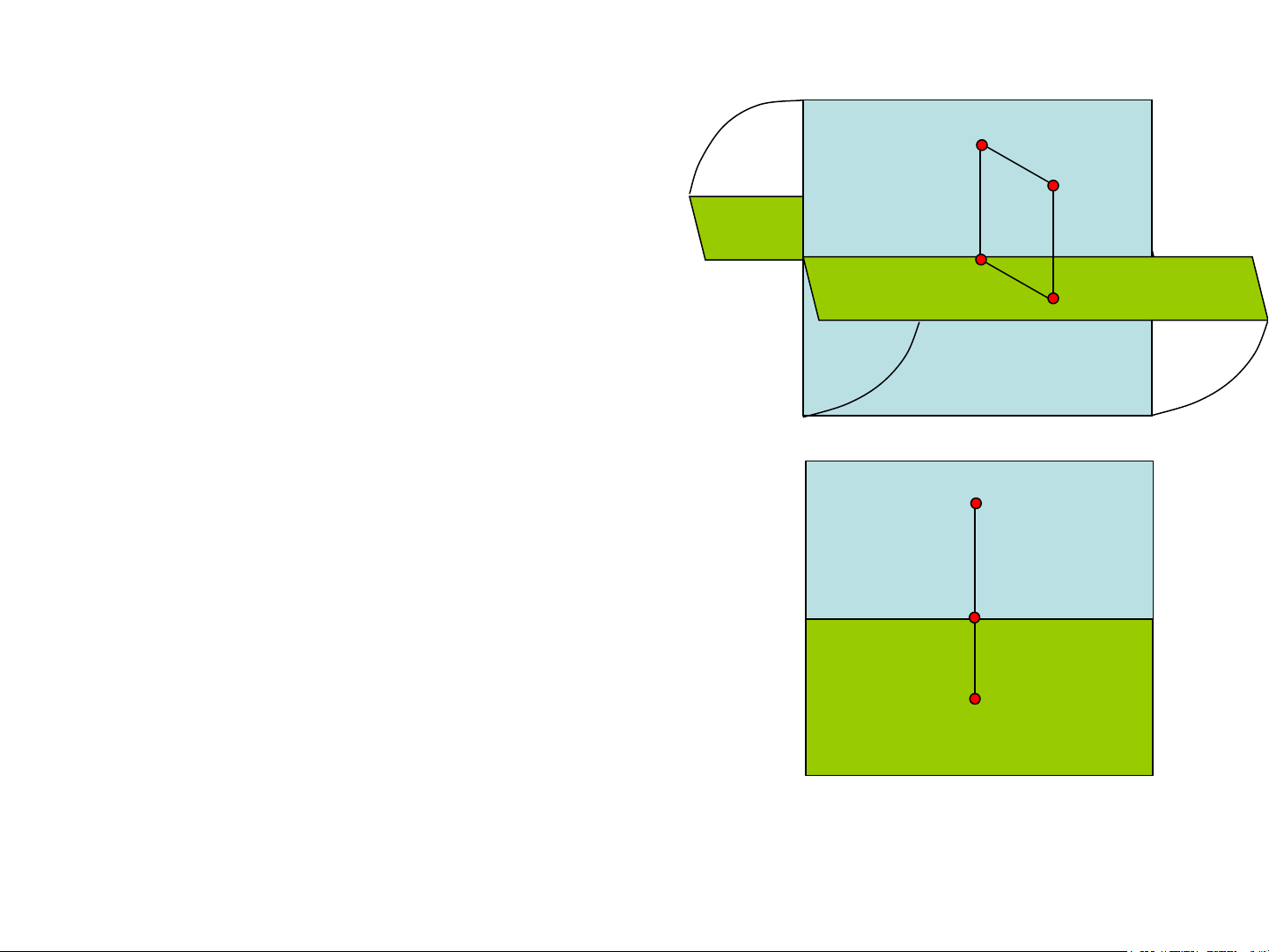
- Chiếu vuông góc điểm A lên mặt phẳng Π
П và П ta nhận được các hình chiếu A và A 1 A A 1 2 1 2 1
- Cố định mặt phẳng П , quay mặt phẳng 1
П quanh đường thẳng x theo chiều quay x 2 Ax
được chỉ ra trên Hình 1.1.a cho đến khi П 2
trùng vớiП . Ta nhận được đồ thức của điểm 1 A
A trong hệ hai mặt phẳng hình chiếu (Hình 1.1.b) 2 Π2
Hình 1.1a,b. Xây dựng đồ thức của một điểm
trên hệ thống hai mặt phẳng hình chiếu a)
* Các định nghĩa và tính chất Π1 A
- Mặt phẳng П : mặt phẳng hình chiếu đứng 1 1 A
- Mặt phẳng П : mặt phẳng hình chiếu bằng 2
- Đường thẳng x : trục hình chiếu x Ax
- A : hình chiếu đứng của điểm A 1 Π A 2 2
- A : hình chiếu bằng của điểm A 2
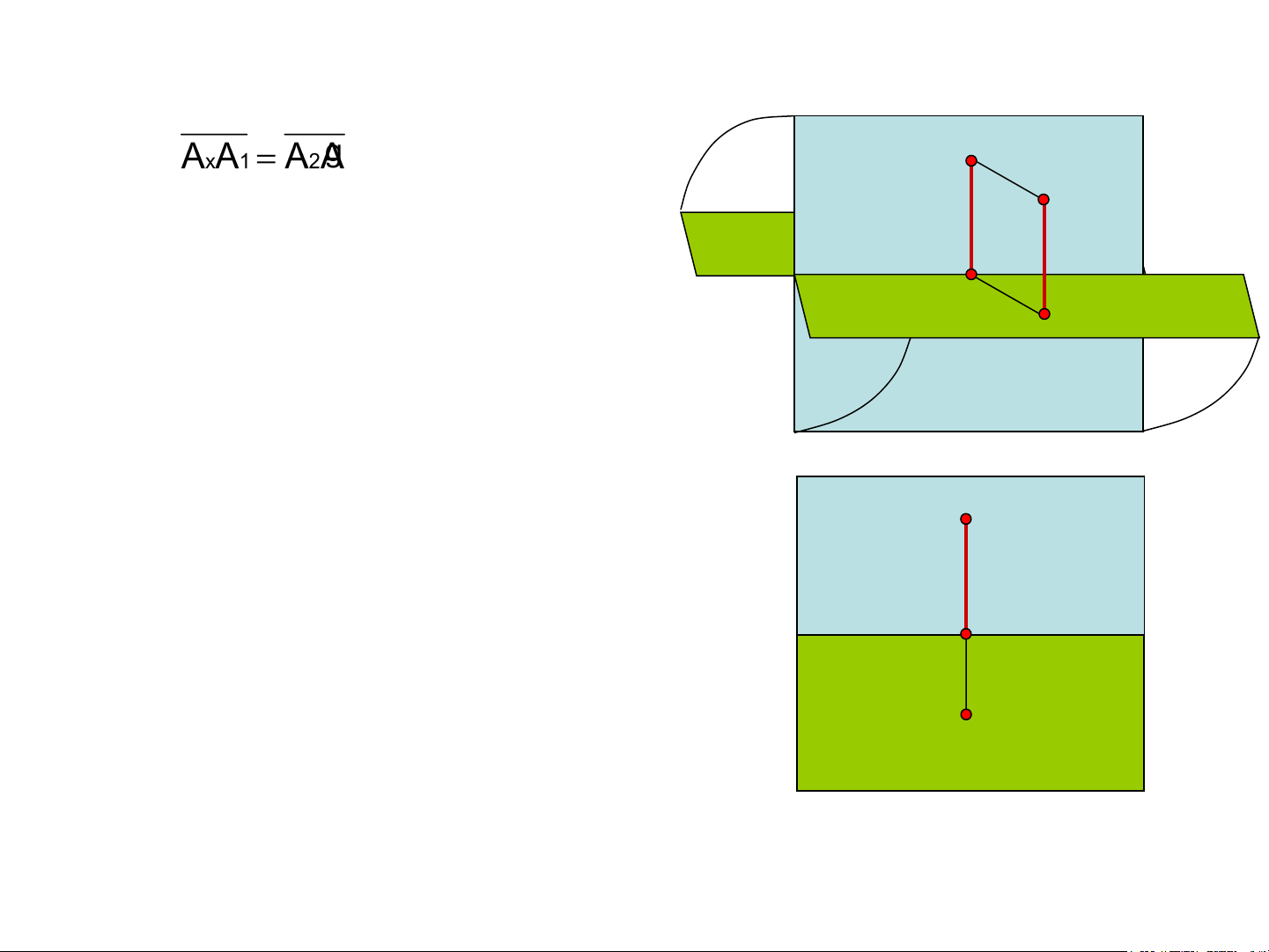
- Gọi A là giao của trục x và mặt phẳng x (AA A ) 1 2
- Trên đồ thức, A ,A , A cùng nằm trên một b) 1 x 2 Π
đường thẳng vuông góc với trục x gọi là 1 A A 1
đường dóng thẳng đứng. x Ax A2 Π2
Hình 1.1a,b. Xây dựng đồ thức của
một điểm trên hệ thống hai mặt phẳng hình chiếu
* Độ cao của một điểm a) - Ta có:
gọi là độ cao của điểm A Π1 A1 - Quy ước: A
+ Độ cao dương : khi điểm A nằm x Ax phía trên П2
+ Độ cao âm: khi điểm A nằm phía Π A 2 2 dưới П . 2
- Dấu hiệu nhận biết trên đồ thức:
+ Độ cao dương: A nằm phía trên trục x 1 b)
+ Độ cao âm: A nằm phía dưới trục x Π1 1 A A 1 x Ax A2 Π2
Hình 1.1a,b. Xây dựng đồ thức của một điểm
trên hệ thống hai mặt phẳng hình chiếu
* Độ xa của một điểm a) Π1 A - Ta có:
gọi là độ xa của điểm A 1 A - Quy ước:
+ Độ xa dương : khi điểm A nằm x Ax phía trước П1 Π A 2 2
+ Độ xa âm: khi điểm A nằm phía sau П . 1
- Dấu hiệu nhận biết trên đồ thức:
+ Độ xa dương: A nằm phía dưới b) 2 trục x A1
+ Độ xa âm: A nằm phía trên trục x 2 x Ax
*Chú ý: Với một điểm A trong không gian
có đồ thức là một cặp hình chiếu A , A . 1 2 A
Ngược lại cho đồ thức A A , ta có thể 2 1 2
xây dựng lại điểm A duy nhất trong Π2
không gian. Như vậy đồ thức của một
Hình 1.1a,b. Xây dựng đồ thức của
điểm A có tính phản chuyển
một điểm trên hệ thống hai mặt phẳng hình chiếu
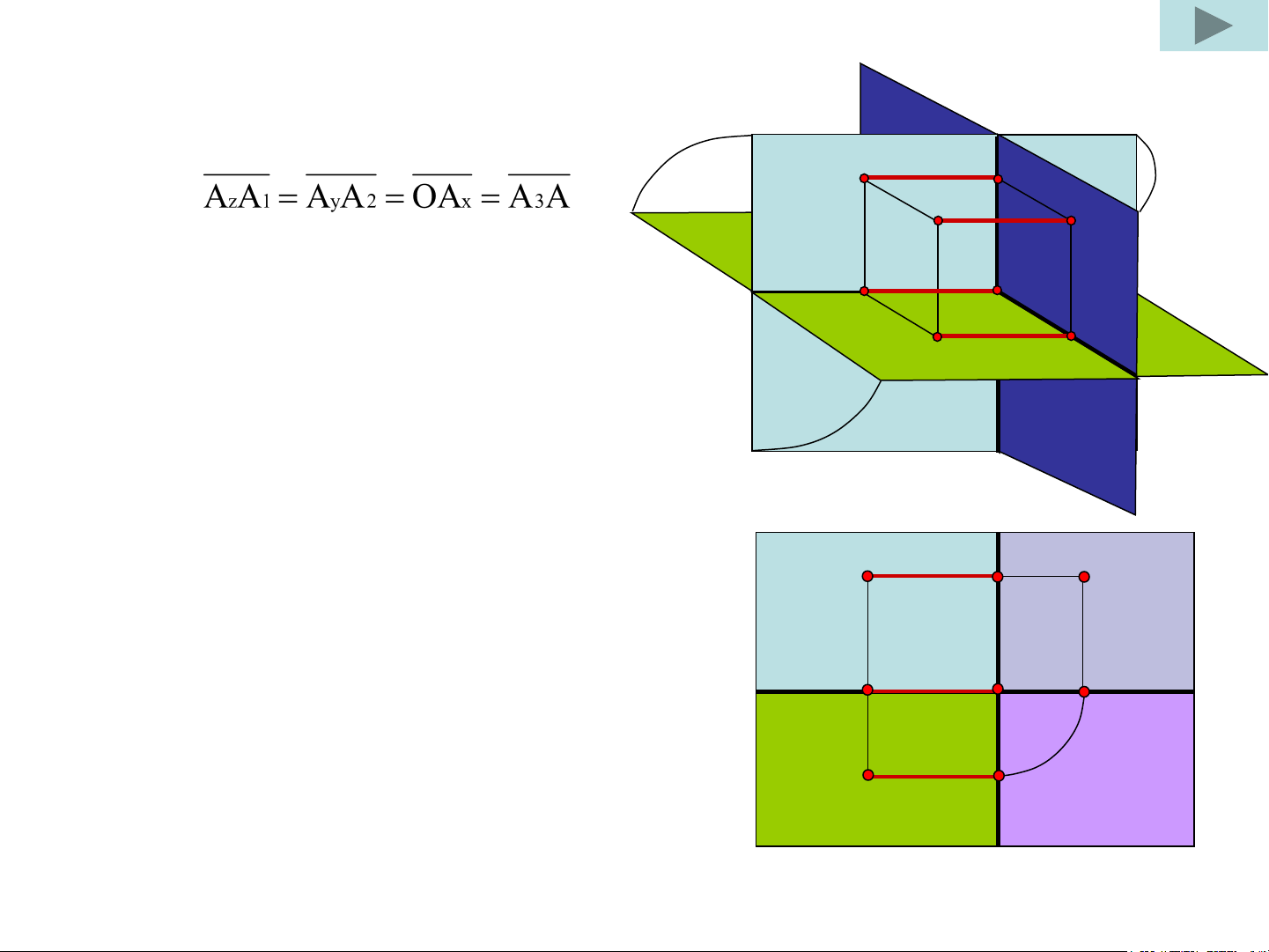
b) Hệ thống ba mặt phẳng hình chiếu a)
- Trong không gian, lấy ba mặt phẳng z
П П ,П vuông góc với nhau từng đôi một. Π1 A A 1’ 2 3 1 z
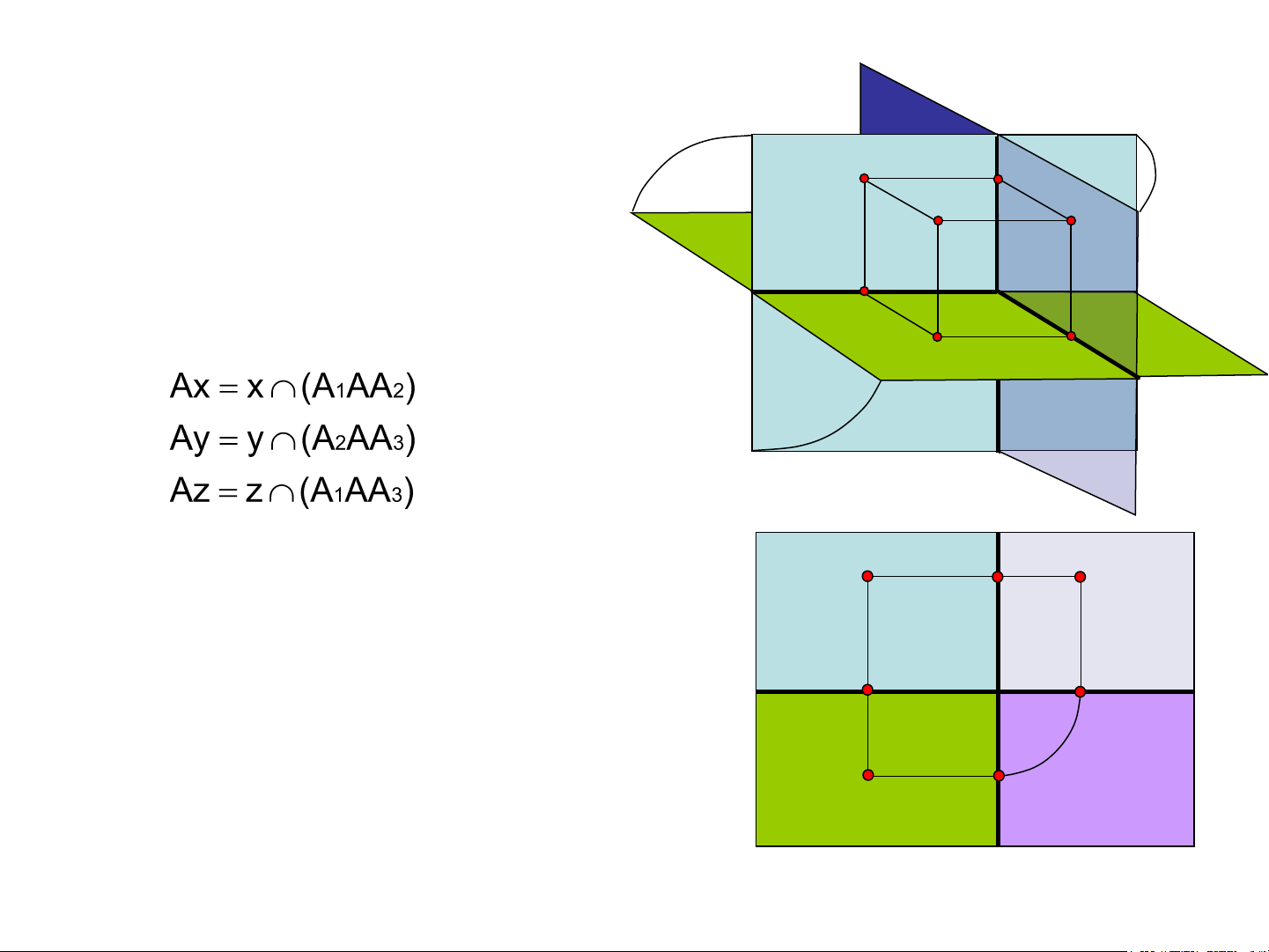
+ Gọi x là giao điểm của П và П (y = П ∩П ) A 1 2 1 2 A 3
+ Gọi y là giao điểm của П và П (y = П ∩П ) 2 3 2 3 x Ax O
+ Gọi z là giao điểm của П và П (z = П ∩П ) A 1 3 1 3 y A A 2 y Π 2 2
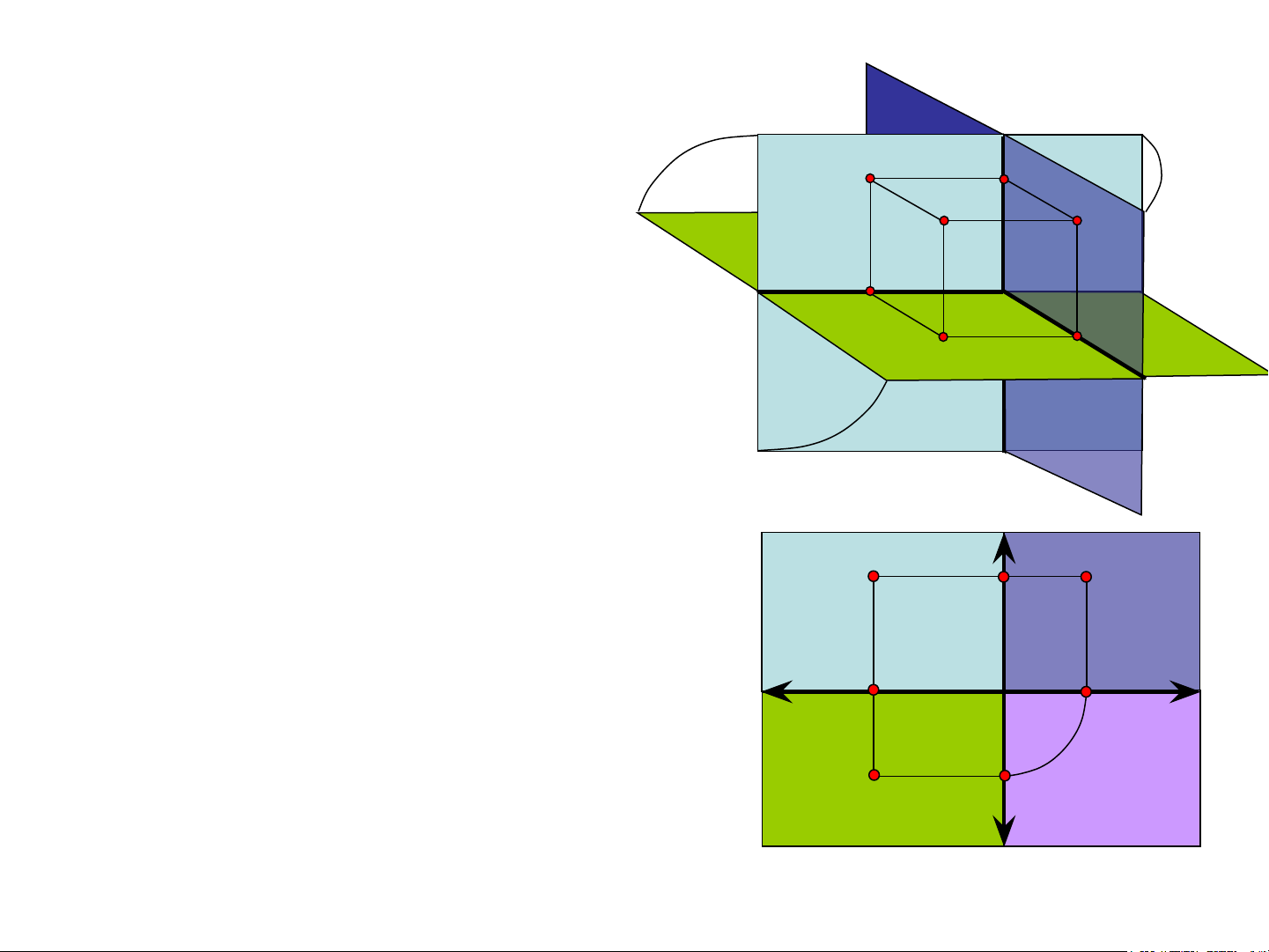
- Chiếu vuông góc điểm A lên mặt phẳng
П , П và П ta nhận được các hình chiếu A , 1 2 3 1 A và A 2 3 Π3 b) z
- Cố định mặt phẳng П , quay mặt phẳng Π A A Π 1 1 1 A 3 3
П quanh đường thẳng x, quay mặt phẳng П A 2 3 z
quanh trục z theo chiều quay được chỉ ra trên
Hình 1.2.a cho đến khi П trùng với П ,П trùng x A O A 2 1 3 x y
với П . Ta nhận được đồ thức của điểm A trong y 1
hệ hai mặt phẳng hình chiếu (Hình 1.2.b) Ay A2 Π2 y
Hình 1.2a,b. Xây dựng đồ thức của một điểm
trên hệ thống ba mặt phẳng hình chiếu
b) Các định nghĩa và tính chất a)
Bổ xung thêm các định nghĩa z Π1 A A và tính chất sau: 1 z
- Mặt phẳng П : mặt phẳng hình chiếu cạnh A3 3 A
- Đường thẳng x, y, z : trục hình chiếu x Ax O A
- A : hình chiếu cạnh của điểm A y 3 A A y - Gọi 2 Π 2 2 Π3 - Trên đồ thức: b) z Π A A Π 1 1 3 3
+ A , A , A cùng nằm trên một đường A A 1 x 2 z
thẳng vuông góc với trục x gọi là đường dóng thẳng đứng x A A x O y y
+ A , A , A cùng nằm trên một đường 1 z 3 A
thẳng song song với trục x gọi là đường y A dóng nằm ngang. 2 Π2 y
Hình 1.2a,b. Xây dựng đồ thức của một điểm
trên hệ thống ba mặt phẳng hình chiếu
b) Các định nghĩa và tính chất (tiếp theo) a)
* Độ xa cạnh của một điểm z Π1 A A - Ta có: 1 z A A
gọi là độ xa cạnh của điểm A 3 - Quy ước: x Ax O
+ Độ xa cạnh dương : khi điểm A nằm A A y 2 y phía bên trái П Π A2 3 2
+ Độ xa cạnh âm: khi điểm A nằm phía bên phải П . 3 Π
- Dấu hiệu nhận biết trên đồ thức: 3
+ Độ xa cạnh dương: A nằm phía bên b) z A 3 Π A Π 1 1 A 3 3 phải trục x Az
+ Độ xa cạnh âm: A nằm phía bên trái 3 trục x x A A x O y y Ay A2 Π2 y
Hình 1.2a,b. Xây dựng đồ thức của một điểm
trên hệ thống ba mặt phẳng hình chiếu
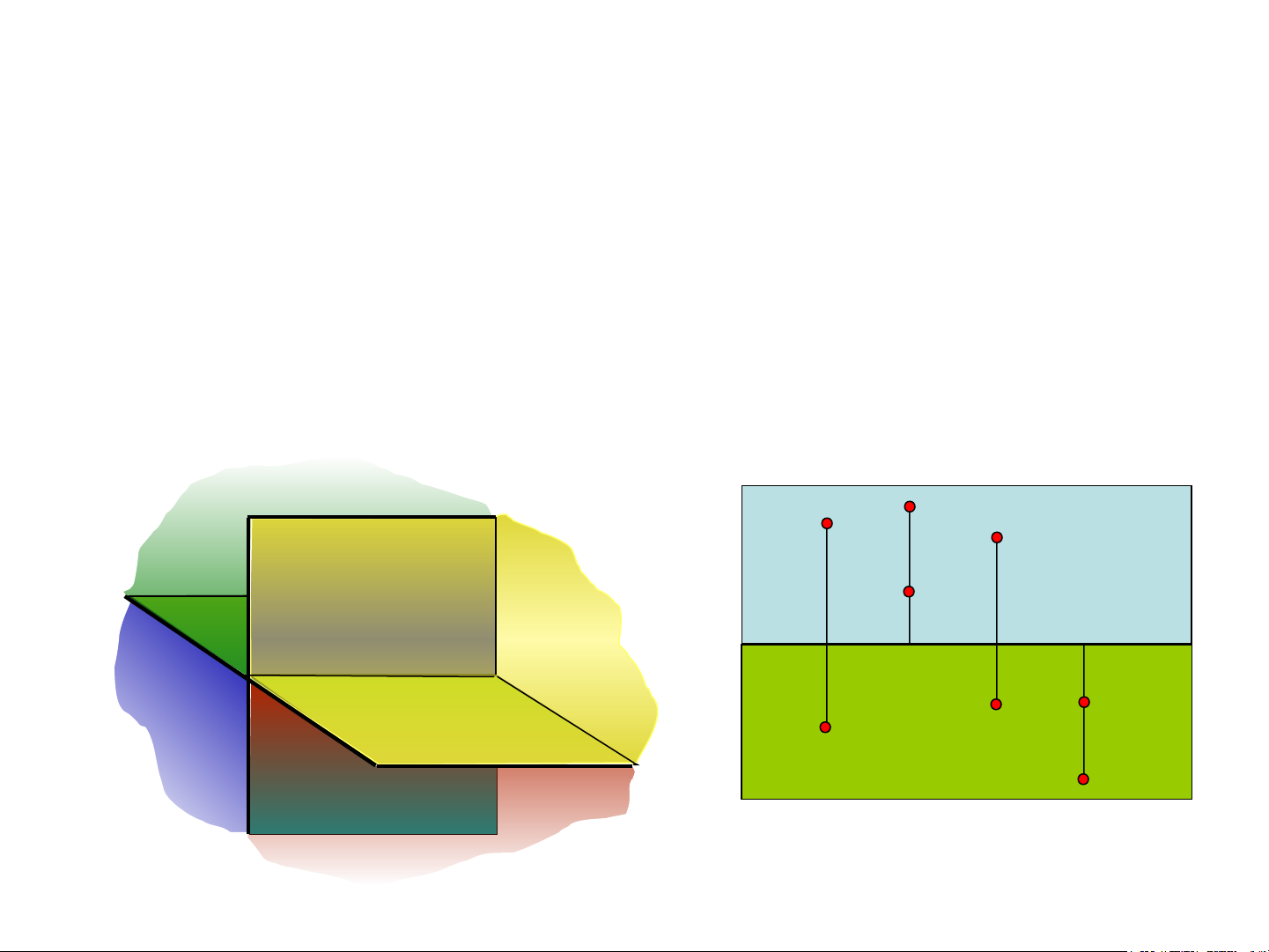
2.1.2 Một số định nghĩa khác 2.1.2.1– Góc phần tư
- Hai mặt phẳng hình chiếu П , П vuông góc với nhau chia không gian thành bốn 1 2
phần, mỗi phần được gọi là một góc phần tư.
+ Phần không gian phía trước П , trên П được gọi là góc phần tư thứ nhất. (I) 1 2
+ Phần không gian phía sau П , trên П được gọi là góc phần tư thứ hai. (II) 1 2
+ Phần không gian phía sau П , dưới П được gọi là góc phần tư thứ ba. (III) 1 2
+ Phần không gian phía trước П , dưới П được gọi là góc phần tư thứ tư. (IV) 1 2
Ví dụ: Tự cho đồ thức của các điểm A, B, C, D lần lượt thuộc các góc phần tư I, II, III, IV Π B1 Π 1 A ( II ) 1 1 C2 ( I ) B2 x ( III ) C A D A 1 1 2 Π 2 2 Π D2 2 ( IV )
Hình 1.5. Các điểm A,B,C,D thuộc
Hình 1.4. Góc phần tư I, II, III, IV
các góc phần tư I, II, III, IV
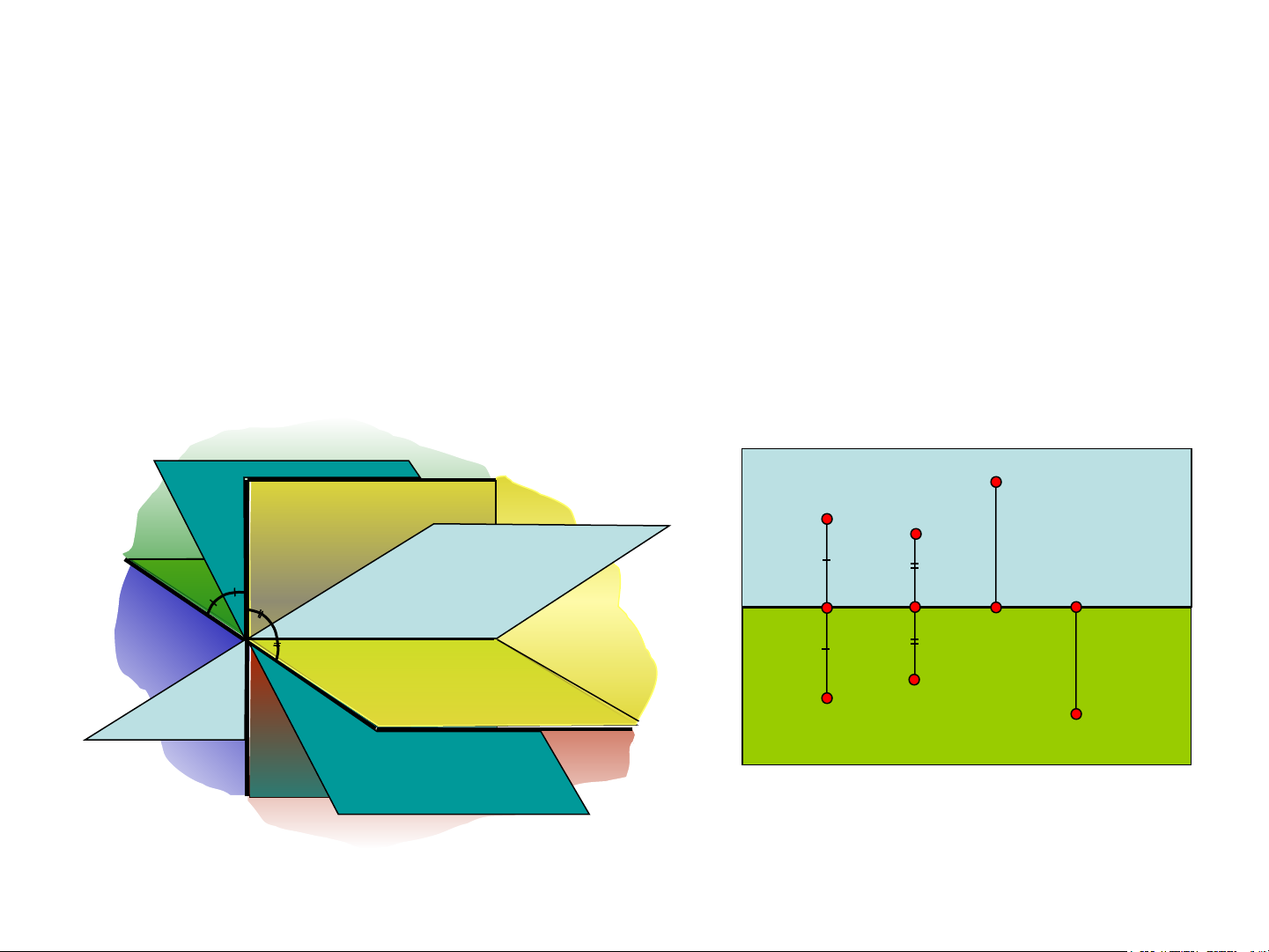
2.1.2.2 – Mặt phẳng phân giác
- Có hai mặt phẳng phân giác
+ Mặt phẳng đi qua trục x chia góc nhị diện phần tư (I) và góc phần tư (III) thành
các phần bằng nhau gọi là mặt phẳng phân giác I. (Pg1)
+ Mặt phẳng đi qua trục x chia góc nhị diện phần tư (II) và góc phần tư (IV) thành
các phần bằng nhau gọi là mặt phẳng phân giác II.(Pg2)
Ví dụ: Vẽ đồ thức của các điểm A, B thuộc mặt phẳng phân giác I; C, D thuộc mặt phẳng
phân giác II, A thuộc góc phần tư (I), B thuộc (III), C thuộc (II), D thuộc (IV) Π C =C 1 Π 1 2 A 1 ( II ) 1 B (Pg1) 2 x A B C D x x x x x ( III ) ( I ) A A B 2 Π 2 1 D =D 2 1 2 Π ( IV ) 2 (Pg2)
Hình 1.7. Đồ thức các điểm A,B,C,D thuộc
Hình 1.6. Mặt phẳng phân giác I và II
mặt phẳng phân giác (P1) và (P2)