Đồ thị có hướng Trần Vĩnh Đức Ngày 24 tháng 7 năm 2018 1 / 34 Tài liệu tham khảo
▶ Eric Lehman, F Thomson Leighton & Albert R Meyer,
Mathematics for Computer Science, 2013 (Miễn phí)
▶ Ngô Đắc Tân, Lý thuyết Tổ hợp và Đồ thị, NXB ĐHQG Hà Nội, 2004.
▶ Douglas B. West. Introduction to Graph Theory. 2nd Edition, 2000. 2 / 34 Nội dung Định nghĩa và ví dụ Đồ thị thi đấu Định nghĩa
Một đồ thị có hướng là một cặp có thứ tự G = (V, E), ở đây V là
một tập, còn E là một tập con của tích đề các V × V, tức E là
một quan hệ hai ngôi trên V.
▶ Các phần tử của V thường được gọi là các đỉnh.
▶ Các phần của E gọi là các cung.
▶ Cụ thể hơn, nếu (a, b) ∈ E thì (a, b) được gọi là cung của G
với đỉnh đầu là a và đỉnh cuối là b,
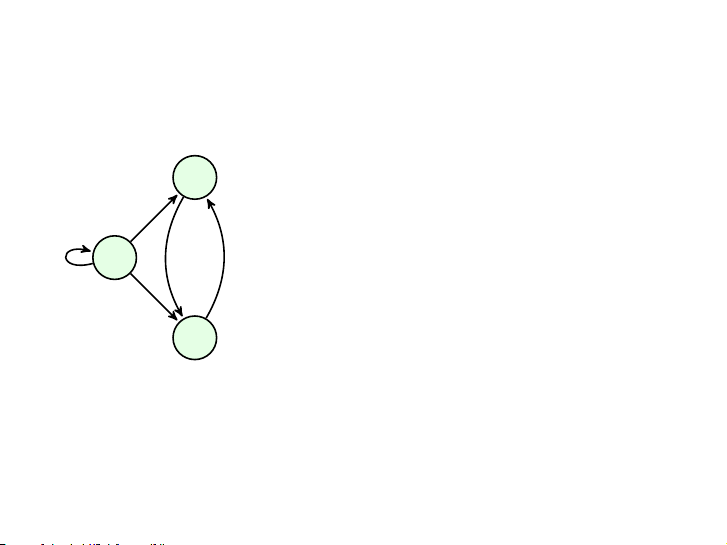
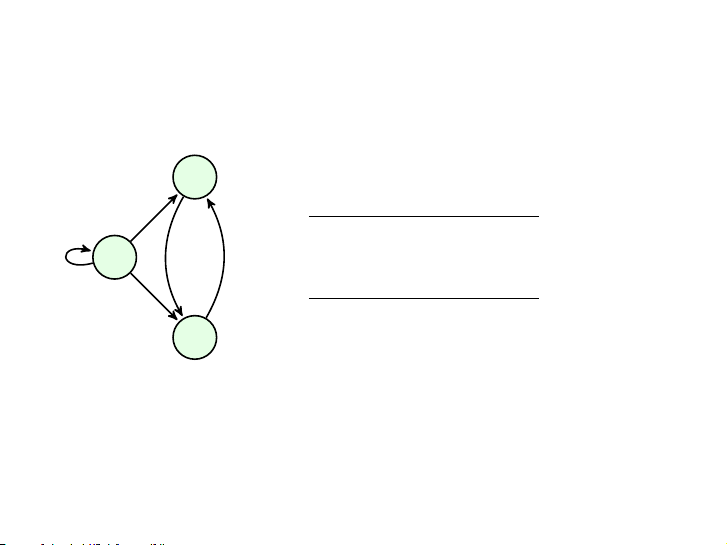
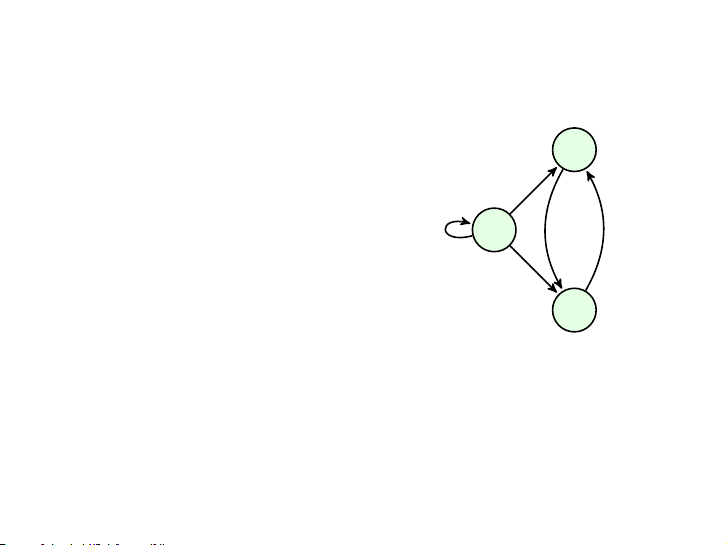
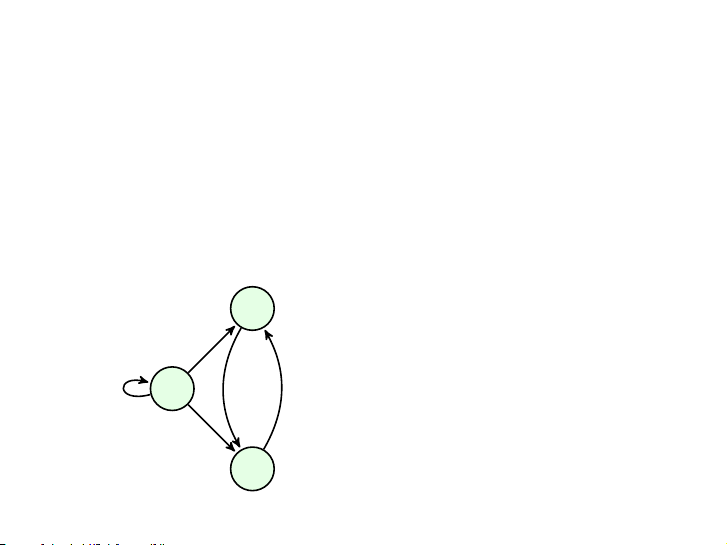
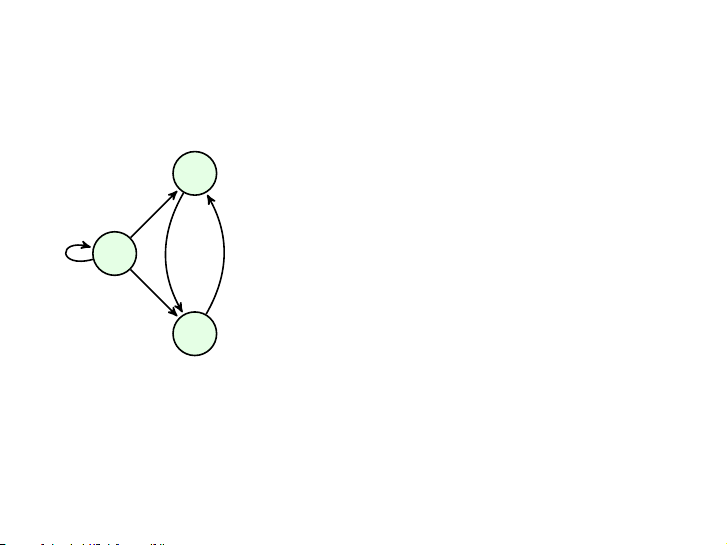
▶ và ta viết a → b 4 / 34 Đồ thị có hướng v
Đồ thị có hướng G = 2 (V, E): V = {v v
1, v2, v3} 1
E = {v1 → v1, v1 → v2, v1 → v3,
v2 → v3, v3 → v2} v3 5 / 34 Bậc vào & bậc ra v2 Đỉnh indeg outdeg v1 1 3 v1 v2 2 1 v3 2 1 5 5 v3 6 / 34 v2 Mệnh đề ∑ ∑ v1 indeg(v) = outdeg(v) = |E| v∈V v∈V v3 7 / 34
Hành trình có hướng và đường đi có hướng Hành trình Hành trình đơn Đường đi Lặp cạnh 3 7 7 Lặp đỉnh 3 3 7 8 / 34 Định nghĩa
Xét G = (V, E) là đồ thị có hướng với V = {v1, v2, . . . , vn}.
Ma trận kề A = (aij) của G định nghĩa bởi {1 nếu v a i → vj ij = 0 ngược lại. Ví dụ v2   1 1 1 v1 A = 0 0 1 0 1 0 v3 9 / 34 Định lý
Xét G = (V, E) là đồ thị có hướng với n đỉnh
V = {v1, v2, . . . , vn}.
và A = (aij) là ma trận kề của G. Xét (p(k)
ij ) là số hành trình có
hướng từ vi tới vj. Khi đó
Ak = (p(k) ij ). 10 / 34 Ví dụ v2   1 1 1 A = 0 0 1 v 0 1 0 1     1 2 2 1 3 3 A2 = 0 1 0 A3 = 0 0 1 v3 0 0 1 0 1 0 11 / 34 Chứng minh
▶ Bằng quy nạp theo độ dài hành trình.
▶ Ta ký hiệu a(k) là phần tử ở hàng i cột j của ma trận Ak. ij ▶ Ta đặt
P(k) := ∀i, j a(k) ij = p(k) ij
▶ Bước cơ sở: k = 1. 3 Tại sao? 12 / 34
Chứng minh: Bước quy nạp
▶ Giả sử P(k) 3
▶ Hành trình độ dài k + 1 từ vi đến vj có thể tách thành v k i ; vh → vj ▶ với v k
i ; vh là một hành trình độ dài k từ vi tới vh
▶ và h : vh → vj là một cạnh trong G. 13 / 34
Chứng minh: Bước quy nạp (tiếp) ∑ n ∑ p(k+1) p(k) p(k) · a ij = ih = ih hj h: vh→vj h=1 n ∑ = a(k) · a ih hj (giả thiết quy nạp) h=1 = a(k+1) (quy tắc nhân ma trận) ij 3 14 / 34 Định nghĩa
Một đồ thị có hướng G = (V, E) là liên thông mạnh nếu với mọi
u, v ∈ V, tồn tại một đường đi có hướng từ u tới v trong G. 15 / 34 Định nghĩa
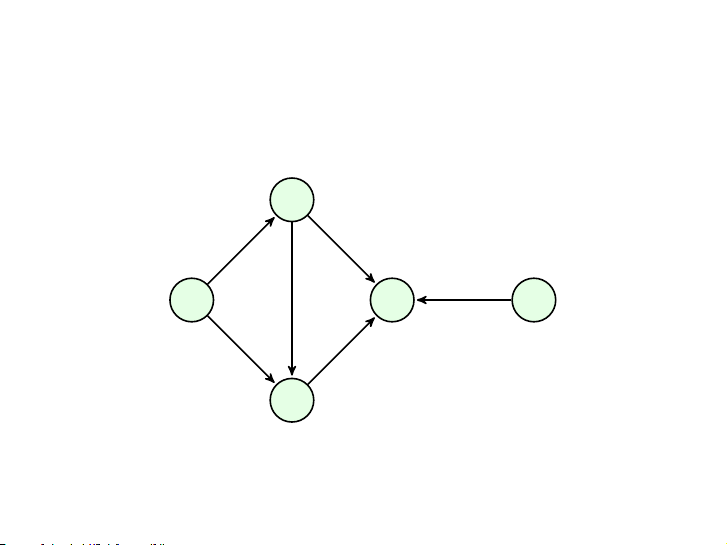
Một đồ thị có hướng được là phi chu trình (DAG) nếu nó không
chứa chu trình có hướng. v2 v1 v4 v5 v3 16 / 34 Nội dung Định nghĩa và ví dụ Đồ thị thi đấu Định nghĩa
▶ Một đồ thị định hướng của một đồ thị (vô hướng)
G = (V, E) là một đồ thị có hướng thu được từ G bằng cách chọn một hướng
x → y hoặc y → x
cho mỗi cạnh xy ∈ E.
▶ Đồ thị thi đấu là một đồ thị định hướng của một đồ thị đầy đủ nào đó. 18 / 34 Ví dụ
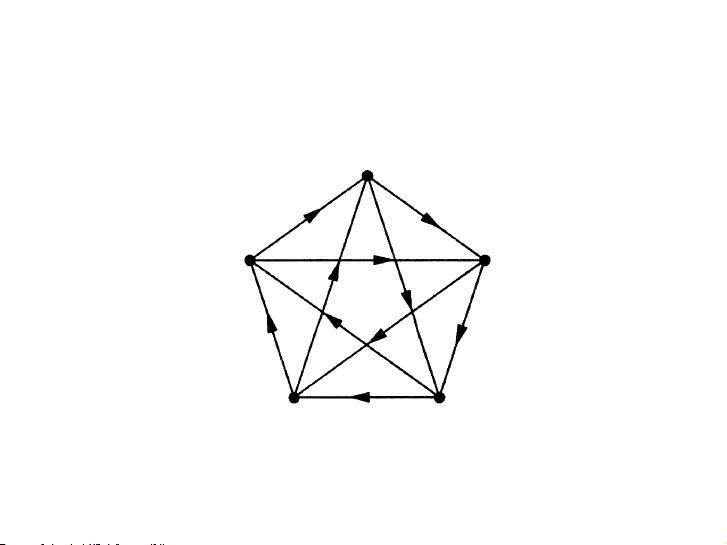
▶ Đồ thị định hướng của đồ thị đầy đủ cho phép mô hình hóa
các giải đấu thể thao kiểu “round-robin”.
▶ Giải đấu gồm n đội và mỗi đội thi đấu với tất cả các đội khác.
▶ Với mỗi cặp u, v, ta có cạnh u → v nếu u thắng v.
▶ Cuối giải ta có một đồ thị định hướng của Kn.
▶ “Điểm số” của mỗi đội chính là bậc ra của đội đó, là số lần thắng. 19 / 34 Đội nào vô địch? 20 / 34