[ĐVĐ] - Đề 40 câu ăn chắc 1-8 điểm số 06 - Còn 08 ngày - Tài liệu tham khảo | Đại học Hoa Sen

[ĐVĐ] - Đề 40 câu ăn chắc 1-8 điểm số 06 - Còn 08 ngày - Tài liệu tham khảo | Đại học Hoa Sen và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả

3 2 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Nguyên lý Kế toán (KT 204DV02)

Trường: Đại học Hoa Sen

Thông tin:

5 trang 11 giờ trước

Tác giả:

Profile Kim Oanh
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầ ỗy Đ Văn Đức – http://facebook.com/dovanduc2020 1
Câu 1. Phầ ả ủn o c a s c ố phứ 𝑧 𝑧 = 22𝑖𝑖 − 1 là
A.
A.
A.
A. A.
1.−
B.
B.
B.
B. B.
1.
C.
C.
C.
C. C.
22.−
D.
D.
D.
D. D.
22.
Câu 2.
Cho hàm số 𝑦 𝑦 = 𝑎𝑎𝑥𝑥 𝑏𝑏𝑥𝑥
4
+
2
+ 𝑐𝑐 có đồ thị như hình vẽ. Điể ự ạ ủ ồm c c đ i c a đ thị hàm số đã cho có tọ
độ là
A.
A.
A.
A.A.
( )
1; 4 .−
B.
B.
B.
B. B.
( )
1; 4 .− −
C.
C.
C.
C. C.
( )
0; 3 .−
D.
D.
D.
D. D.
Câu 3.
Nếu blog
𝑎 𝑎
𝑏 𝑏 = 2 thì giá trị 𝑃 𝑃 = log
𝑎𝑎
(𝑎𝑎
2
𝑏𝑏) ằng
A.
A.
A.
A. A.
6.P =
B.
B.
B.
B. B.
5.P =
C.
C.
C.
C. C.
2.P =
D.
D.
D.
D. D.
4.P =
Câu 4. Cho hàm số 𝑦 𝑦 = 𝑓𝑓(𝑥𝑥) liên tục trên
[ ]
; .a b
Diện tích hình phẳng giới h i đạn bở ồ thị hàm số 𝑦 𝑦 = 𝑓𝑓
(
𝑥𝑥
)
,
trục hoành và hai đường thẳng được tính theo công thứ𝑥 𝑥 = 𝑎𝑎, 𝑥 𝑥 = 𝑏𝑏 c
A.
A.
A.
A. A.
( )
d .
b
a
S f x x
=
∫
B.
B.
B.
B. B.
( )
d .
a
b
S f x x
=
∫
C.
C.
C.
C. C.
( )
d .
b
a
S f x x
=
∫
D.
D.
D.
D. D.
( )
d .
a
b
S f x x
= −
∫
Câu 5. Cho m t phặ ẳng (𝑃𝑃) c u ắt mặt cầ 𝑆𝑆
(
𝐼𝐼; 𝑅𝑅
)
. Gọi 𝑑𝑑 là khoảng cách từ 𝐼𝐼 đến
( )
𝑃𝑃 . Khẳng định nào dưới đ
đúng?
A.
A.
A.
A. A.
.d R<
B.
B.
B.
B. B.
.d R>
C.
C.
C.
C. C.
.d R=
D.
D.
D.
D. D.
2 .
d R=
Câu 6. Tiệm cận ngang củ ồ ốa đ thị hàm s
3 1
5 1
x
y
x
+
=
−
là đường thẳng có phương trình
A.
A.
A.
A. A.
1
.
5
y =
B.
B.
B.
B. B.
3
.
5
y = −
C.
C.
C.
C. C.
1
.
5
y = −
D.
D.
D.
D. D.
3
.
5
y =
Câu 7. Trong không gian góc giữ ụ𝑂𝑂𝑥𝑥𝑦𝑦𝑧𝑧, a tr c 𝑂𝑂𝑦𝑦 và mp(𝑂𝑂𝑥𝑥𝑧𝑧) bằng
A.
A.
A.
A. A.
120 .°
B.
B.
B.
B. B.
90 .
°
C.
C.
C.
C. C.
60 .°
D.
D.
D.
D. D.
45 .°
Câu 8. Tập nghiệm của bất phương trình log
(
𝑥𝑥 − 3
)
< 1 là
A.
A.
A.
A. A.
( )
3;4 .
B.
B.
B.
B. B.
( )
;13 .−∞
C.
C.
C.
C. C.
( )
3;13 .
D.
D.
D.
D. D.
( )
13; .+ ∞
Câu 9. Cho s ph ố ức 𝑧𝑧 thỏa mãn
2.z =
Giá trị
z
b ằng
A.
A.
A.
A. A.
2.−
B.
B.
B.
B. B.
0.
C.
C.
C.
C. C.
4.
D.
D.
D.
D. D.
2.
CHU
CHU
CHU
CHUCHU
Ỗ
Ỗ
Ỗ
ỖỖ
I
I
I
I I
-
-
-
- -
THI TH
THI TH
THI TH
THI THTHI TH
Ử
Ử
Ử
ỬỬ
-
-
-
--
8
8
8
8 8
40
40
40
40 40
CÂU Ă
CÂU Ă
CÂU Ă
CÂU ĂCÂU Ă
N CH
N CH
N CH
N CHN CH
Ắ
Ắ
Ắ
ẮẮ
C 1
C 1
C 1
C 1C 1
BU
BU
BU
BUBU
Ổ
Ổ
Ổ
ỔỔ
I 0
I 0
I 0
I 0I 0
6 -
6 -
6 -
6 - 6 -
2K6
2K6
2K6
2K62K6
CÒN
CÒN
CÒN
CÒN CÒN
08
08
08
0808
NGÀY
NGÀY
NGÀY
NGÀYNGÀY
_________________________________________________________________________________________________________________________________________________________________________________________________________________
2 ầ ỗ Th y Đ Văn Đức – http://facebook.com/dovanduc2020
Câu 10. Trong không gian
,Oxyz
m t phặ ẳng
( )
: 2 2 1 0P x y z+ − + =
có một vecto pháp tuyến là
A.
A.
A.
A. A.
( )
1
1;2; 2 .
n = −
B.
B.
B.
B. B.
( )
4
1; 2;2 .n = −
C.
C.
C.
C. C.
( )
3
2;1; 2 .n = −
D.
D.
D.
D. D.
( )
2
1;2;2 .n =
Câu 11. Với
x
c u thlà số thực dương tùy ý, giá trị ủa biể ức
( ) ( )
ln 10 ln 5x x−
b ằng
A.
A.
A.
A. A.
( )
ln 5 .x
B.
B.
B.
B. B.
2.
C.
C.
C.
C. C.
( )
( )
ln 10
.
ln 5
x
x
D.
D.
D.
D. D.
ln 2.
Câu 12. Trên mặ ẳng tọ ộ, điểm biểu diễ ố ọ ột ph a đ n s phức 𝑧 𝑧 = −3𝑖𝑖 có t a đ là
A.
A.
A.
A. A.
( )
3;0 .−
B.
B.
B.
B. B.
( )
3;1 .−
C.
C.
C.
C. C.
( )
1; 3 .−
D.
D.
D.
D. D.
( )
0; 3 .
−
Câu 13. Cho hàm s ố
( )
y f x=
. có bảng biến thiên như hình vẽ
x
−∞
1−
1
+∞
( )
f x
+∞
2−
2
−∞
Số nghiệm của phương trình
( )
2 0f x + =
là
A.
A.
A.
A. A.
1.
B.
B.
B.
B. B.
2.
C.
C.
C.
C. C.
3.
D.
D.
D.
D. D.
4.
Câu 14. Họ nguyên hàm của hàm số
( )
2
e
x
f x x= +
là
A.
A.
A.
A.A.
2
1
e .
2 2
x
x
C
+ +
B.
B.
B.
B. B.
2
2
1
e .
2 2
x
x
C+ +
C.
C.
C.
C. C.
2
2 1
1
e .
2 1 2
x
x
C
x
+
+ +
+
D.
D.
D.
D. D.
2
2e 1 .
x
C+ +
Câu 15. Tập xác định của hàm số
2
log
y x
=
là
A.
A.
A.
A. A.
.
B.
B.
B.
B. B.
( )
0; .+ ∞
C.
C.
C.
C. C.
( )
;0 .−∞
D.
D.
D.
D. D.
{ }
\ 0 .
Câu 16. Cho kh tích kh ối nón tròn xoay có chiều cao bằng 𝑎𝑎 và bán kính đáy bằng 𝑎𝑎
√
2 thì thể ối nón bằng
A.
A.
A.
A. A.
3
2 .a
π
B.
B.
B.
B. B.
3
6.a
π
C.
C.
C.
C. C.
3
3.a
π
D.
D.
D.
D. D.
3
2
.
3
a
π
Câu 17. Trong không gian
,Oxyz
cho mặt cầu
( )
S
có tâm
( )
0;0; 3
I −
và đi qua điểm
( )
4;0;0 .M
Phương
trình của mặ ầt c u
( )
S
là
A.
A.
A.
A.A.
( )
2
2 2
3 25.
x y z+ + + =
B.
B.
B.
B. B.
( )
2
2 2
3 5.x y z+ + + =
C.
C.
C.
C. C.
( )
2
2 2
3 5.x y z+ + − =
D.
D.
D.
D. D.
( )
2
2 2
3 25.x y z+ + − =
Câu 18. Trên khoảng
( )
0; ,+ ∞
o hàm c đạ ủa hàm số
e
y x=
là
A.
A.
A.
A. A.
( )
e 1
e 1 .
x
−
−
B.
B.
B.
B. B.
e 1
e .
x
−
C.
C.
C.
C. C.
e 1
.
e 1
x
+
+
D.
D.
D.
D. D.
e 1
.y x
−
=
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầ ỗy Đ Văn Đức – http://facebook.com/dovanduc2020 3
Câu 19. Nếu
( )
4
0
d 8f x x =
∫
thì
( )
4
0
1
4 d
2
f x x
−
∫
b ằng
A.
A.
A.
A. A.
4.
B.
B.
B.
B. B.
6.−
C.
C.
C.
C. C.
8.
D.
D.
D.
D. D.
12.−
Câu 20. Cho m a kh ột hình trụ có chiều cao bằng 2 và bán kính đáy bằng 3. Thể tích củ ố ụi tr đã cho bằng
A.
A.
A.
A. A.
18 .
π
B.
B.
B.
B. B.
9 .
π
C.
C.
C.
C. C.
15 .
π
D.
D.
D.
D. D.
6 .
π
Câu 21. Cho khối chóp có diện tích đáy bằng
2
12cm
và chiều cao
6
cm. Th a khể ủ tích c ối chóp đã cho bằng
A.
A.
A.
A. A.
3
28cm .
B.
B.
B.
B. B.
3
24cm .
C.
C.
C.
C. C.
3
26cm .
D.
D.
D.
D. D.
3
22cm .
Câu 22. Tìm điều kiệ ủ ốn c a tham s
b
để hàm số
4 2
y x bx c= + +
có 3 điểm cực trị?
A.
A.
A.
A. A.
0.b =
B.
B.
B.
B. B.
0.
b ≠
C.
C.
C.
C. C.
0.b <
D.
D.
D.
D. D.
0.b >
Câu 23. Gọi
,M N
l phtrong hình vẽ ần lượ ểm biểu diễt là các đi n các số ức
1 2
, .z z
Giá trị
1 2
z z+
b ằng
A.
A.
A.
A. A.
5 2 .i− +
B.
B.
B.
B. B.
1 2 .i−
C.
C.
C.
C. C.
5 2 .i−
D.
D.
D.
D. D.
1 2 .i
+
Câu 24. Thể tích kh ối chóp 𝑆𝑆. 𝐴𝐴𝐴𝐴𝐴𝐴 có
( )
, 2SA ABC SA BC⊥ = =
và
ABC
∆
vuông cân tại
A
là
A.
A.
A.
A. A.
2.
B.
B.
B.
B. B.
4
.
3
C.
C.
C.
C. C.
1.
D.
D.
D.
D. D.
2
.
3
Câu 25. Trong không gian vớ ọ ội hệ t a đ
,Oxyz
cho đường thẳng
1 1
: .
1 2 2
x y z− −
∆ = =
−
Điểm nào dưới đây
không thuộc
?∆
A.
A.
A.
A. A.
( )
2; 2;3 .E −
B.
B.
B.
B. B.
( )
3; 4; 5 .
F −
C.
C.
C.
C. C.
( )
0;2;1 .M
D.
D.
D.
D. D.
( )
1;0;1 .N
Câu 26. Khoảng nào sau đây là khoảng đồng biế ủ ốn c a hàm s
( )
2222 ?f x x= −
A.
A.
A.
A. A.
( )
1;1 .−
B.
B.
B.
B. B.
( )
1;2222 .
C.
C.
C.
C. C.
( )
2222; .+ ∞
D.
D.
D.
D. D.
( )
; 1 .−∞ −
Câu 27. Cho hình chóp là hình vuông cạ ằng ạnh bên và𝑆𝑆. 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 có đáy 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 nh b 𝑎𝑎, c 𝑆𝑆𝐴𝐴 = 2𝑎𝑎
với mặ ẳng đáy. Gọt ph i 𝑂𝑂 là tâm của hình vuông ối chóp 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴. Thể tích kh 𝑆𝑆. 𝑂𝑂𝐴𝐴𝐴𝐴 là
A.
A.
A.
A. A.
3
1
.
6
V a=
B.
B.
B.
B. B.
3
2
.
3
V a=
C.
C.
C.
C. C.
3
1
.
2
V a=
D.
D.
D.
D. D.
3
1
.
8
V a=
Câu 28. Cho s phố ức
2 3 .z i= −
S phố ức
2
2
z
w
z i
−
=
+
có ph n th ầ ực bằng
A.
A.
A.
A. A.
15.−
B.
B.
B.
B. B.
15
.
29
−
C.
C.
C.
C. C.
15.
D.
D.
D.
D. D.
15
.
29
_________________________________________________________________________________________________________________________________________________________________________________________________________________
4 – Thầ ỗy Đ Văn Đức http://facebook.com/dovanduc2020
Câu 29. Tìm t ịất cả các giá tr thực củ ốa tham s
m
để hàm số
( )
3 2
2 1 2y x x m x= − + − − +
nghịch biến trên
khoảng
( )
; .−∞ + ∞
A.
A.
A.
A. A.
7
.
3
m >
B.
B.
B.
B. B.
7
.
3
m ≤
C.
C.
C.
C. C.
7
.
3
m ≥
D.
D.
D.
D. D.
1
.
3
m ≥
Câu 30. Hàm số
( )
y f x
=
có đồ thị như hình vẽ có thể là đồ thị của hàm số nào trong
các hàm số sau:
A.
A.
A.
A. A.
e .
x
y =
B.
B.
B.
B. B.
1.y x
= −
C.
C.
C.
C. C.
1
e
log .y x
−
=
D.
D.
D.
D. D.
ln .y x
=
Câu 31. Tính thể tích khối tròn xoay thu được khi quay hình phẳng giới h i hai đưạn bở ờng
2
2
y x x
= − +
và
0y =
quanh trục
Ox
b ằng
A.
A.
A.
A. A.
16
.
15
V =
B.
B.
B.
B. B.
8
.
3
V
π
=
C.
C.
C.
C. C.
8
.
3
V =
D.
D.
D.
D. D.
16
.
15
V
π
=
Câu 32.
Số nghiệm của phương trình
(
𝑥𝑥
2
− 2 3𝑥𝑥 −
)
. log
2
𝑥 𝑥 = 0 là
A.
A.
A.
A. A.
2.
B.
B.
B.
B. B.
0.
C.
C.
C.
C. C.
3.
D.
D.
D.
D. D.
1.
Câu 33. Cho hàm s ố
( )
f x
thỏa mãn
( )
3
2 3 .f x x x= −
S c ố điểm cực trị ủa hàm số
( )
f x
là
A.
A.
A.
A. A.
0.
B.
B.
B.
B. B.
1.
C.
C.
C.
C. C.
2.
D.
D.
D.
D. D.
3.
Câu 34. Cho hàm s ố
( )
f x
liên tục trên
,
có
( )
2
0
d 4.f x x
π
=
∫
Khi đó
( )
4
0
2 sin df x x x
π
−
∫
b ằng
A.
A.
A.
A. A.
2
2 .
2
−
B.
B.
B.
B. B.
2
1 .
2
+
C.
C.
C.
C. C.
2
3 .
2
−
D.
D.
D.
D. D.
2
2 .
2
+
Câu 35. Trong không gian cho ba điể𝑂𝑂𝑥𝑥𝑦𝑦𝑧𝑧, m 𝐴𝐴
(
1; 0; −2
)
, 𝐴𝐴
(
1; 1; 1 0; 1; 2
)
, 𝐴𝐴
(
−
)
. Biết rằng mặ ẳngt ph
qua 3 điể có phương trình
m 𝐴𝐴, 𝐴𝐴, 𝐴𝐴 7𝑥 𝑥 + 𝑏𝑏𝑦𝑦 + 𝑐𝑐𝑧𝑧 + 𝑑 𝑑 = 0. Giá trị b𝑏𝑏
2
+ 𝑐𝑐
2
+ 𝑑𝑑
2
ằng
A.
A.
A.
A. A.
84.
B.
B.
B.
B. B.
49.
C.
C.
C.
C. C.
26.
D.
D.
D.
D. D.
35.
Câu 36. Cho hàm số
( )
f x
có
( ) ( )( )
1 1f x x x m
′
= + − +
.x
∀ ∈
Điều kiện cần và đủ để ố hàm s đồng biến
trên
( )
2; + ∞
là
A.
A.
A.
A. A.
2.m ≤
B.
B.
B.
B. B.
3.m ≤
C.
C.
C.
C. C.
3.m ≥
D.
D.
D.
D. D.
2.m ≥
Câu 37. Cho hình chóp đều
.S ABCD
có chiều cao bằng
,a
2
AC a=
(tham khảo
hình bên). Tính khoảng cách giữa hai đường thẳng
AB
và
.SC
A.
A.
A.
A. A.
3
.
3
a
B.
B.
B.
B. B.
2 .a
C.
C.
C.
C. C.
2 3
.
3
a
D.
D.
D.
D. D.
2
.
2
a
_________________________________________________________________________________________________________________________________________________________________________________________________________________
Thầ ỗy Đ Văn Đức – http://facebook.com/dovanduc2020 5
Câu 38.
Cho s p hố ph T c tức 𝑧𝑧 thỏa mãn
|
𝑧𝑧 − 𝑎𝑎 𝑧𝑧 −
2
|
+
|
4𝑎𝑎
|
= 5 (𝑎𝑎 ∈ ℝ). ất cả các giá trị ủa 𝑎𝑎 để ậ ợp điểm
biểu diễ ố ộn s phức 𝑧𝑧 là m t elip là:
A.
A.
A.
A. A.
1 5.a− < <
B.
B.
B.
B. B.
1 5.a− ≤ ≤
C.
C.
C.
C. C.
5
.
1
a
a
>
< −
D.
D.
D.
D. D.
5
.
1
a
a
≥
≤ −
Câu 39. Cho hàm s ố 𝑦 𝑦 = 𝑓𝑓
(
𝑥𝑥
)
. Hàm số 𝑦 𝑦 = 𝑓𝑓′(𝑥𝑥) có bảng biến thiên như hình sau:
x
−∞
2−
3
+∞
( )
f x
′
−∞
4
0
+∞
Bất phương trình
( )
1xf x mx> +
có nghiệm đúng với mọi
[
)
1; 22x ∈
khi và chỉ khi
A.
A.
A.
A. A.
( )
1
22 .
22
m f
≥ −
B.
B.
B.
B. B.
( )
1
22 .
22
m f> −
C.
C.
C.
C. C.
( )
1 1.m f
≤ −
D.
D.
D.
D. D.
( )
1 1.m f
< −
Câu 40. Gọi
1
S
và
2
S
lần lượ ện tích các hình phẳng giớt là di i hạn bởi
( ) ( )
2
: 0P y x k k= + >
và đường thẳng
: 2d y x
=
. N u như hình vẽ ế
1 2
S S=
thì
k
b ằng
A.
A.
A.
A. A.
2
.
5
B.
B.
B.
B. B.
7
.
9
C.
C.
C.
C. C.
3
.
2
D.
D.
D.
D. D.
3
.
4
--- Hết ---
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CH C U H ỖI I - TH T I H I T H T Ử 40 4 0 CÂ C U Â Ă U N C N H C ẮC C 1 - 1 8 BU B ỔI I 0 6 - 2K 2 6 K CÒ C N Ò 08 0 8 NG N À G Y À Y Câu 1. Phầ ả
n o của số phức 𝑧 𝑧 = 22𝑖𝑖 − 1 là A. A . 1 − . B. B .1. C. C . 2 − 2. D. D . 22.
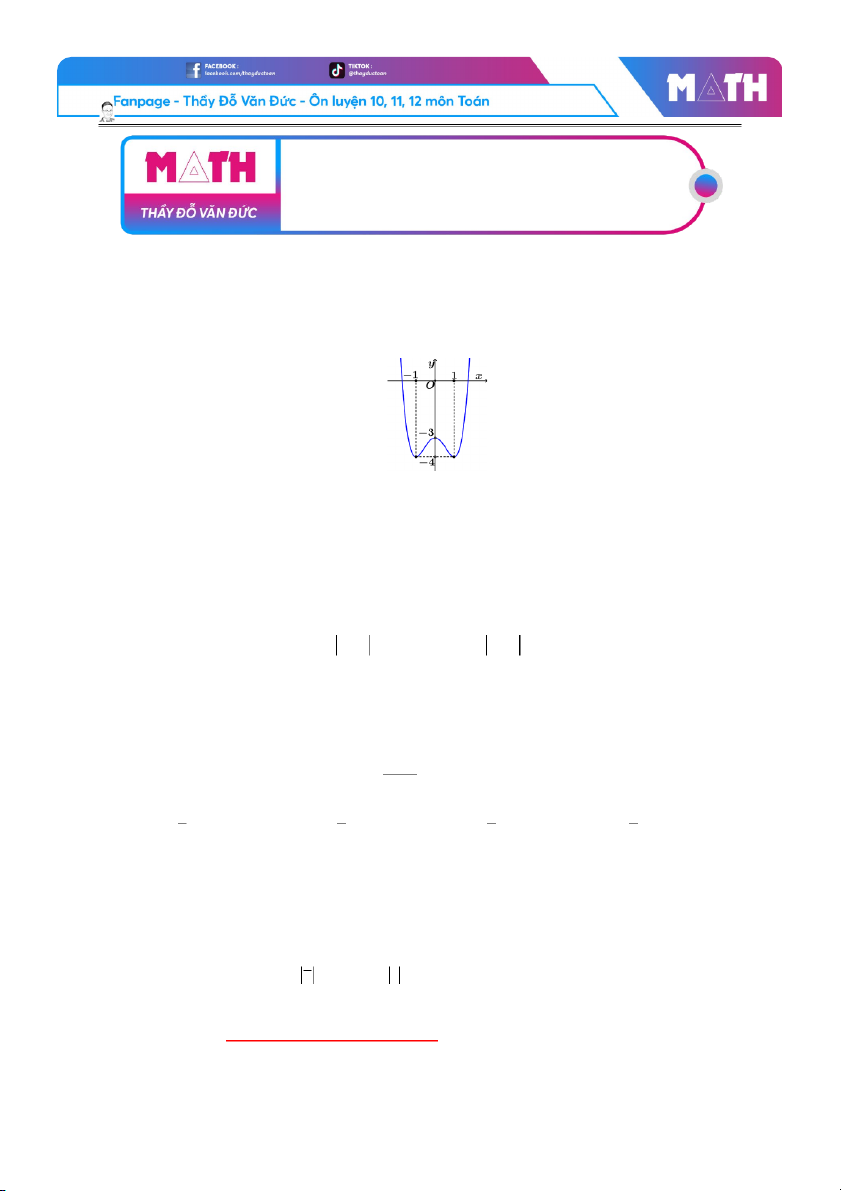
Câu 2. Cho hàm số 𝑦 𝑦 = 𝑎𝑎𝑥𝑥4 + 𝑏𝑏𝑥𝑥2 + 𝑐𝑐 có đ
ồ thị như hình vẽ. Điểm cực đại ủ c a ồ
đ thị hàm số đã cho có tọ độ là A. A (1; − 4). B. B . ( 1 − ; − 4). C. C . (0; − 3). D. D . (−3;0).
Câu 3. Nếu log𝑎 𝑎 𝑏 𝑏 = 2 thì giá trị 𝑃 𝑃 = log𝑎𝑎(𝑎𝑎2𝑏𝑏) bằng A. A . P = 6. B. B . P = 5. C. C . P = 2. D. D . P = 4.
Câu 4. Cho hàm số 𝑦 𝑦 = 𝑓𝑓(𝑥𝑥) liên tục t[rê a n ;
b ].Diện tích hình phẳng giới hạn bởi đồ thị hàm số 𝑦 𝑦 = 𝑓𝑓(𝑥𝑥) ,
trục hoành và hai đường thẳng 𝑥 𝑥 = 𝑎𝑎, 𝑥 𝑥 = 𝑏𝑏 được tính theo công thứ c b a b a A. A . S = f (x )dx. ∫ B. B . S = f ( x) d . x ∫ C. C . S = f ( x) d . x ∫ D.
D . S = − f ( x)d . x ∫ a b a b
Câu 5. Cho mặt phẳng (𝑃𝑃) cắt mặt cầu 𝑆𝑆(𝐼𝐼; 𝑅𝑅). Gọi 𝑑𝑑 là khoảng cách từ 𝐼𝐼 đến (𝑃𝑃). Khẳng định nào dưới đ đúng? A. A . d < . R B. B . d > . R C. C . d = . R D. D . d = 2R. 3x +1
Câu 6. Tiệm cận ngang của ồ đ thị hàm ố s y =
là đường thẳng có phương trình 5x −1 1 3 1 3 A. A . y = . B. B . y = − . C. C . y = − . D. D . y = . 5 5 5 5
Câu 7. Trong không gian 𝑂𝑂𝑥𝑥𝑦𝑦𝑧𝑧, góc giữ a t ụ
r c 𝑂𝑂𝑦𝑦 và mp(𝑂𝑂𝑥𝑥𝑧𝑧) bằng A. A .120 . ° B. B . 90°. C. C . 60 . ° D. D . 45 . °
Câu 8. Tập nghiệm của bất phương trình log(𝑥𝑥 − 3) < 1 là A. A . (3; 4). B. B . (− ; ∞ 13). C. C . (3;13 ). D. D . (13; + ∞ ).
Câu 9. Cho số phức 𝑧𝑧 thỏa mãn z = 2. Giá trị z bằng A. A . 2 − . B. B . 0. C. C . 4. D. D . 2.
_________________________________________________________________________________________________________________________________________________________________________________________________________________ Thầy ỗ
Đ Văn Đức – http://facebook.com/dovanduc2020 1
Câu 10. Trong không gian Oxyz, mặt phẳng ( P) : x + 2y − 2z +1 = 0 có một vect o pháp tuyến là     A. A . n = 1; 2; − 2 . B. B . n = 1; − 2; 2 . C. C . n = 2;1; − 2 . D. D .n = 1; 2; 2 . 2 ( ) 3 ( ) 4 ( ) 1 ( )
Câu 11. Với x là s
ố thực dương tùy ý, giá trị của biểu thức ln(10x) − ln( 5x) bằng ln (10x ) A. A . ln( 5 ) x . B. B .2. C. C . ( D. D . ln 2. x) . ln 5
Câu 12. Trên mặt phẳng tọa ộ, điểm biểu diễ đ
n số phức 𝑧 𝑧 = −3𝑖𝑖 có ọ t a ộ đ là A. A . ( 3 − ;0). B. B . ( 3 − ;1). C. C . (1; − 3). D. D . (0; −3). Câu 13. Cho hàm s
ố y = f ( x) có b .
ảng biến thiên như hình vẽ x −∞ 1 − 1 +∞ +∞ 2 f (x ) 2 − −∞
Số nghiệm của phương trình f (x ) + 2 = 0 là A. A .1. B. B . 2. C. C . 3. D. D . 4.
Câu 14. Họ nguyên hàm của hàm s ố ( ) 2 = e x f x + x là 2 1 x 2 1 2 1 + x A. A e x + + . C B. B . 2 e x x + + . C C. C . 2x 1 e + + C. D. D . 2 2e x +1+ C. 2 2 2 2 2x + 1 2
Câu 15. Tập xác định của hàm số y = log x là 2 A. A . .  B. B . (0;+ ∞ ). C. C . (−∞;0 ). D. D . \ {0}.
Câu 16. Cho khối nón tròn xoay có chiều cao bằng 𝑎𝑎 và bán kính đáy bằng 𝑎𝑎√2 thì thể tích kh ối nón bằng 2 A. A . 3 2πa . B. B . 3 a π 6. C. C . 3 πa 3. D. D . 3 πa . 3
Câu 17. Trong không gian Oxyz, cho mặt cầu (S ) có tâm I (0;0; −3) và đi qua điểm M (4;0;0). Phương
trình của mặt cầu (S ) là A.
A x + y + (z + )2 2 2 3 = 25. B.
B .x + y + (z + )2 2 2 3 = 5. C.
C .x + y + (z − )2 2 2 3 = 5. D.
D . x + y + ( z − )2 2 2 3 = 25.
Câu 18. Trên khoảng (0; + ∞ ), đạo hàm của hàm s ố e y = x là e 1 x + A. A . ( ) e 1 e 1 x − − . B. B . e 1 ex − . C. C . . D. D . e 1 y x − = . e + 1
_________________________________________________________________________________________________________________________________________________________________________________________________________________ 2 T ầ h y ỗ
Đ Văn Đức – http://facebook.com/dovanduc2020 4 4  1  Câu 19. Nếu f
∫ ( )x dx = 8 thì f ∫ (x ) −4 dx   bằng  2  0 0 A. A . 4. B. B . 6 − . C. C . 8. D. D . 1 − 2.
Câu 20. Cho một hình trụ có chiều cao bằng 2 và bán kính đáy bằng 3. Thể tích c a kh ủ ối tr ụ đã cho bằng A. A .18π. B. B . 9π . C. C .15π. D. D . 6π .
Câu 21. Cho khối chóp có diện tích đáy bằng 2
12cm và chiều cao 6 cm. Thể tích c a
ủ khối chóp đã cho bằng A. A . 3 28 cm . B. B . 3 24 cm . C. C . 3 26 cm . D. D . 3 22 cm .
Câu 22. Tìm điều kiện của tham ố s b để hàm s ố 4 2
y = x + bx + c có 3 điểm cực trị? A. A . b = 0. B. B . b ≠ 0. C. C . b < 0. D. D .b > 0.
Câu 23. Gọi M , N trong hình vẽ lần lượt là các đ ểm biểu diễ i n các s ph ố
ức z , z . Giá trị z + z bằng 1 2 1 2 A. A . 5 − + 2 .i B. B .1− 2 . i C. C . 5 − 2 . i D. D .1+ 2 . i
Câu 24. Thể tích khối chóp 𝑆𝑆. 𝐴𝐴𝐴𝐴𝐴𝐴 S Acó
⊥ ( ABC), SA = BC = 2 và A
∆ BC vuông cân tại A là 4 2 A. A . 2. B. B . . C. C . 1. D. D . . 3 3 x − y z −
Câu 25. Trong không gian với hệ tọa ộ
đ Oxyz, cho đường thẳng 1 1 ∆ : = = . Điểm nào dưới đây 1 −2 2 không thuộc ∆ ? A. A . E( 2; − 2; ) 3 . B. B . F (3; − 4;5). C. C .M (0;2; ) 1 . D. D . N (1;0;1).
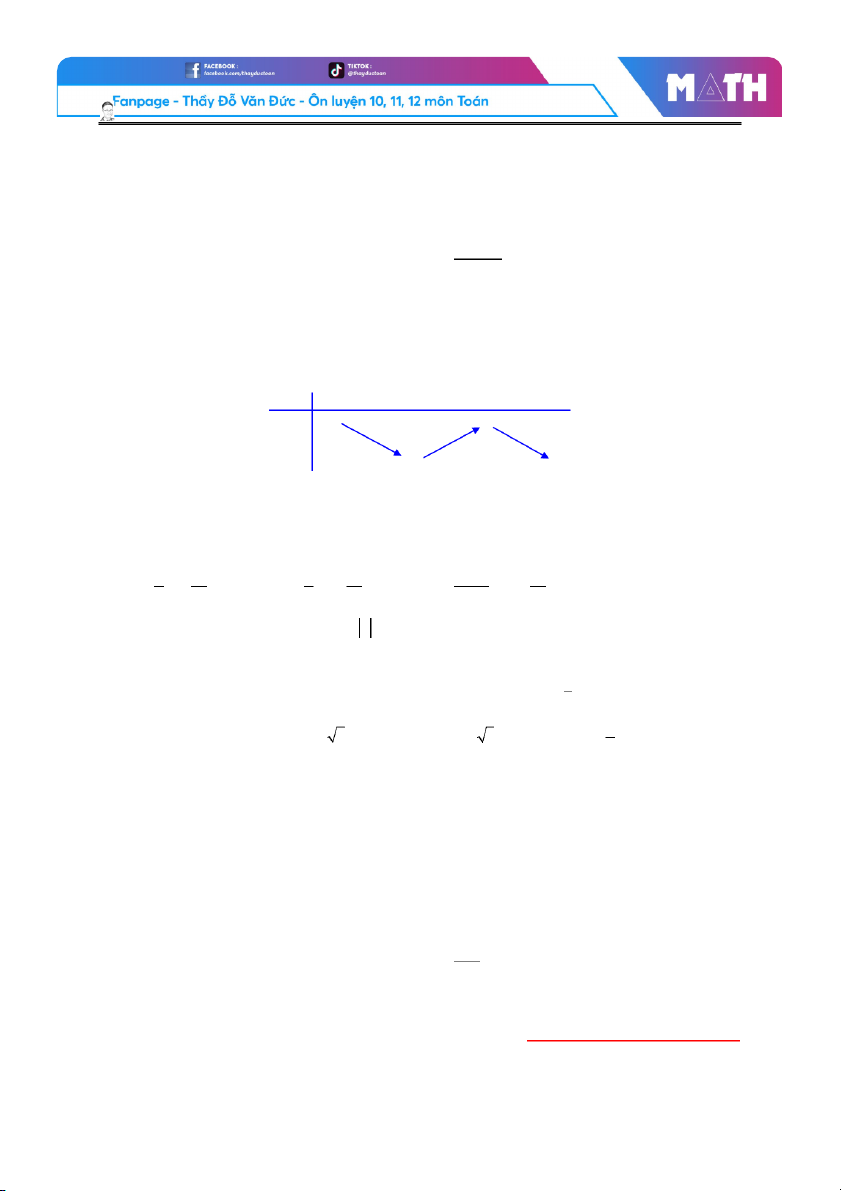
Câu 26. Khoảng nào sau đây là khoảng đồng biến của hàm ố
s f ( x) = 2222 − x ? A. A . (−1;1). B. B .(1; 2222). C. C . (2222; + ∞ ). D. D . (−∞; −1).
Câu 27. Cho hình chóp 𝑆𝑆. 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 có đáy 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 là hình vuông cạnh bằng 𝑎𝑎, cạnh bên 𝑆𝑆𝐴𝐴 = 2𝑎𝑎 và
với mặt phẳng đáy. Gọi 𝑂𝑂 là tâm của hình vuông 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴. Thể tích khối chóp 𝑆𝑆. 𝑂𝑂𝐴𝐴𝐴𝐴 là 1 2 1 1 A. A . 3 V = a . B. B . 3 V = a . C. C . 3 V = a . D. D . 3 V = a . 6 3 2 8 z − 2
Câu 28. Cho số phức z = 2 − 3 .i S ph ố ức w = có phần thực bằng z + 2i 15 15 A. A . 1 − 5. B. B . − . C. C . 15. D. D . . 29 29
_________________________________________________________________________________________________________________________________________________________________________________________________________________ Thầy ỗ
Đ Văn Đức – http://facebook.com/dovanduc2020 3
Câu 29. Tìm tất cả các giá t ị r thực của tham ố s m để hàm số 3 2
y = −x + 2x − (m − )
1 x + 2 nghịch biến trên khoảng (−∞; + ∞ ). 7 7 7 1 A. A . m > . B. B . m ≤ . C. C . m ≥ . D. D . m ≥ . 3 3 3 3
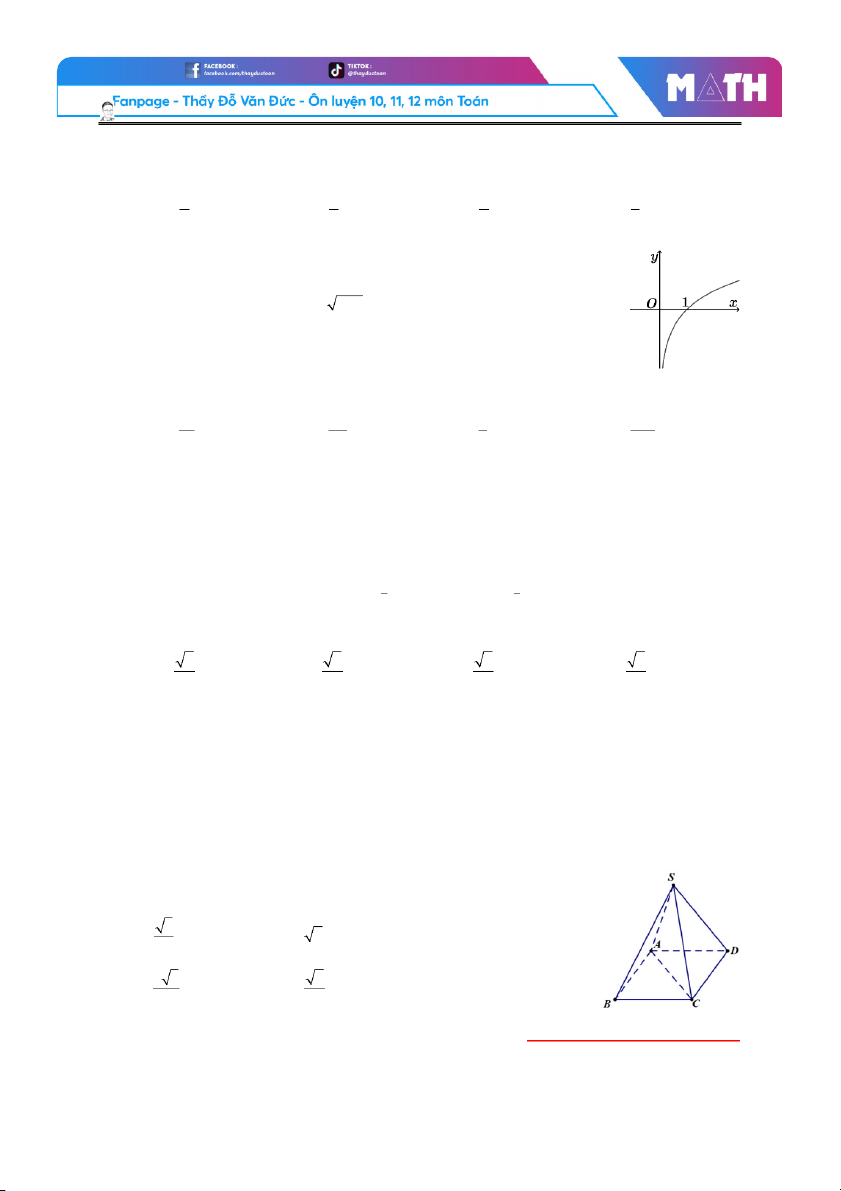
Câu 30. Hàm số y = f ( x) có đ
ồ thị như hình vẽ có thể là đồ thị của hàm s ố nào trong các hàm số sau: A. A . ex y = . B. B . y = x −1. C. C . y = log D. D . y = ln . x − . x 1 e
Câu 31. Tính thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường 2
y = − x + 2x và y = 0 quanh trục Ox bằng 16 8π 8 16π A. A .V = . B. B .V = . C. C .V = . D. D .V = . 15 3 3 15
Câu 32. Số nghiệm của phương trình (𝑥𝑥2 − 2𝑥𝑥 − 3). log2 𝑥 𝑥 = 0 là A. A . 2. B. B . 0. C. C . 3. D. D .1. Câu 33. Cho hàm s
ố f ( x) thỏa mãn f ( ) 3 2x = x − 3 . x S
ố điểm cực trị của hàm s ố f ( x) là A. A . 0. B. B .1. C. C . 2. D. D . 3. π π 2 4 Câu 34. Cho hàm s
ố f ( x) liên tục trên , có f
∫ ( )x dx= 4. Khi đó  f
∫ (2x)− sin xdx  bằng 0 0 2 2 2 2 A. A . 2 − . B. B .1 + . C. C . 3− . D. D . 2 + . 2 2 2 2
Câu 35. Trong không gian 𝑂𝑂𝑥𝑥𝑦𝑦𝑧𝑧, cho ba điểm 𝐴𝐴(1; 0; −2), 𝐴𝐴(1; 1; 1), 𝐴𝐴(0; −1; 2). Biết rằng mặt phẳng
qua 3 điểm 𝐴𝐴, 𝐴𝐴, 𝐴𝐴 có phương trình
7𝑥 𝑥 + 𝑏𝑏𝑦𝑦 + 𝑐𝑐𝑧𝑧 + 𝑑 𝑑 = 0. Giá trị 𝑏𝑏2 + 𝑐𝑐2 + 𝑑𝑑2 bằng A. A . 84. B. B . 49. C. C . 26. D. D . 35.
Câu 36. Cho hàm số f ( x) có f ′( x) = ( x + ) 1 ( x − m + ) 1 x ∀ ∈ .
 Điều kiện cần và đủ để hàm ố s đồng biến trên (2;+ ∞ ) là A. A .m ≤ 2. B. B . m ≤ 3. C. C . m ≥ 3. D. D . m ≥ 2.
Câu 37. Cho hình chóp đều S.ABCD có chiều cao bằng a, AC = 2a (tham khảo
hình bên). Tính khoảng cách giữa hai đường thẳng AB và SC. 3 A. A . . a B. B . 2 . a 3 2 3 2 C. C . . a D. D . . a 3 2
_________________________________________________________________________________________________________________________________________________________________________________________________________________ 4 Thầy Đ
ỗ Văn Đức – http://facebook.com/dovanduc2020
Câu 38. Cho số phức 𝑧𝑧 thỏa mãn |𝑧𝑧 − 𝑎𝑎2| + |𝑧𝑧 − 4𝑎𝑎| = 5 (𝑎𝑎 ∈ ℝ). Tất cả các giá trị của 𝑎𝑎 để tập hợp điểm
biểu diễn số phức 𝑧𝑧 là ộ m t elip là: a  > 5 a  ≥ 5 A.
A . −1 < a < 5. B. B . −1 ≤ a ≤ 5. C. C . .  D. D . .  a < 1 −  a ≤ −1  Câu 39. Cho hàm s
ố 𝑦 𝑦 = 𝑓𝑓(𝑥𝑥) .Hàm s
ố 𝑦 𝑦 = 𝑓𝑓′(𝑥𝑥
) có bảng biến thiên như hình sau: x −∞ 2 − 3 +∞ 4 +∞ f ′ ( x) −∞ 0
Bất phương trình xf ( x) > mx +1 có nghiệm đúng với mọi x ∈[1; 22 ) khi và chỉ khi A. A . m ≥ f ( ) 1 22 − . B. B . m > f ( ) 1 22 − . C. C . m ≤ f ( ) 1 − 1. D. D . m < f ( ) 1 − 1. 22 22
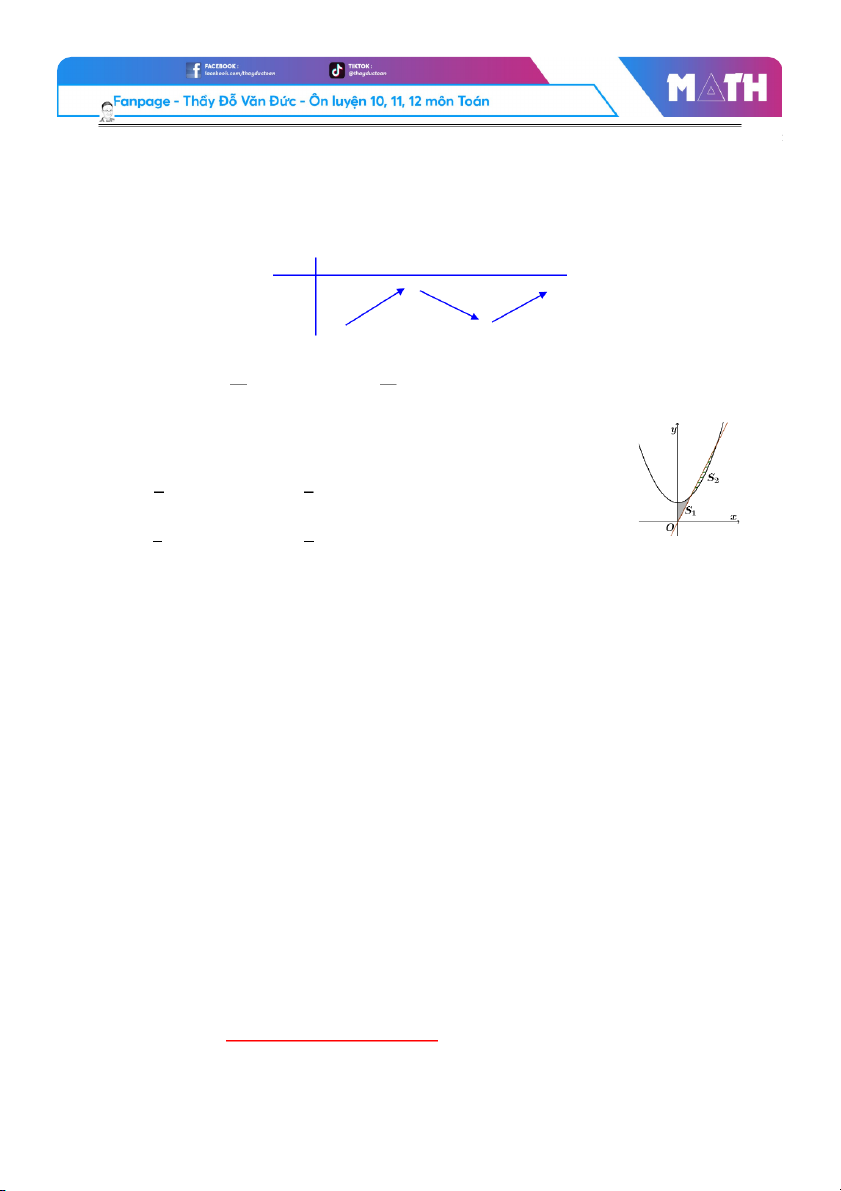
Câu 40. Gọi S và S lần lượt là diện tích các hình phẳng giới hạn bởi 1 2 (P) 2
: y = x + k (k > 0) và đường thẳng d : y = 2x . N như hình vẽ
ếu S = S thì k bằng 1 2 2 7 A. A . . B. B . . 5 9 3 3 C. C . . D. D . . 2 4 --- Hết ---
_________________________________________________________________________________________________________________________________________________________________________________________________________________ Thầy ỗ
Đ Văn Đức – http://facebook.com/dovanduc2020 5