Khởi động

Bài học trước cho em tháy việc tìm kiếm trên một dãy đã sắp xếp nhanh hơn với việc tìm kiếm tuần tự. Vì vậy bài toán tìm kiếm liên quan mật thiết đến bài toán sắp xếp. Bài toán sắp xếp cơ bản có dạng như sau:

Cho dãy A gồm n phần tử:

A[0], A[1],…., A[n-1] (1)

Cần sắp xếp dãy A theo thứ tự tăng dần:

A[0] ≤ A[1] ≤ ... ≤ A[n-1] (2)

Em hãy trình bày ý tưởng của mình để giải bài toán sắp xếp với dãy có bốn phần tử.

Bài làm

Em có thể thực hiện như sau:

- Duyệt qua từng phần tử của dãy từ đầu đến cuối.

- So sánh hai phần tử liền kề, nếu phần tử sau lớn hơn phần tử trước thì hoán đổi chúng.

- Tiếp tục duyệt qua các phần tử còn lại cho đến khi không còn phần tử nào cần hoán đổi.

- Lặp lại quá trình trên cho đến khi toàn bộ dãy được sắp xếp.

Hoặc:

-Duyệt qua từng phần tử của dãy từ đầu đến cuối.

-Lưu giá trị của phần tử hiện tại vào biến tạm thời.

-So sánh phần tử hiện tại với các phần tử bên trái, nếu phần tử nào lớn hơn phần tử hiện tại thì dời chúng sang phải một vị trí.

-Chèn giá trị của phần tử hiện tại vào vị trí đúng sau khi dời các phần tử.

-Tăng vị trí phần tử hiện tại lên 1 và lặp lại quá trình trên cho đến khi toàn bộ dãy được sắp xếp.

1. Thuật toán sắp xếp chèn

Hoạt động 1: Quan sát sơ đồ mô phỏng, trao đổi, thảo luận về ý tưởng chính của thuật toán sắp xếp chèn.

Bài làm

Ý tưởng của thuật toán sắp xếp chèn là thực hiện vòng lặp duyệt từ phần tử thứ hai đến cuối dãy. Sau mỗi bước lặp phần tử tương ứng sẽ được chèn vào vị trí đúng của dãy con đã sắp xếp là các phần tử phía trước vị trí đang duyệt.

Câu hỏi 1: Mô phỏng chi tiết các bước lặp sắp xếp chèn dãy A = [5, 0, 4, 2, 3]

Bài làm

Câu hỏi 2: Nếu dãy ban đầu đã được sắp xếp thì thuật toán sắp xếp chèn sẽ thực hiện như thế nào?

Bài làm

Nếu dãy ban đầu đã được sắp xếp, thì thuật toán sắp xếp chèn sẽ không thực hiện thay đổi nào trên dãy vì mỗi phần tử trong dãy đã đứng đúng vị trí của nó. Cụ thể, các bước của thuật toán sẽ được thực hiện như sau:

Xác định phần tử đầu tiên trong dãy là phần tử thứ 2 (i = 1), không cần thực hiện bất kỳ thay đổi nào vì phần tử này đã đứng đúng vị trí của nó trong dãy đã được sắp xếp.

Kiểm tra phần tử thứ 3 (i = 2) so với các phần tử trước nó trong dãy. Nếu phần tử này đã đứng đúng vị trí, không cần thực hiện thay đổi nào.

Tiếp tục kiểm tra và so sánh từng phần tử còn lại trong dãy với các phần tử trước nó. Nếu phần tử đang xét đã đứng đúng vị trí, không cần thực hiện thay đổi nào.

Sau khi kiểm tra hết các phần tử trong dãy, thuật toán kết thúc mà không có bất kỳ thay đổi nào được thực hiện trên dãy ban đầu, vì dãy đã được sắp xếp.

2. Thuật toán sắp xếp chọn

Hoạt động 2: Quan sát sơ đồ mô phỏng, trao đổi thảo luận về ý tưởng chính của thuật toán sắp xếp chọn.

Bài làm

Thuật toán sắp xếp chọn thực hiện một vòng lặp với chỉ số i chạy từ 0 (phần tử đầu tiên) đến n-2 (phần tử gần cuối). Tại mỗi bước lặp, chọn phần tử nhỏ nhất nằm trong dãy A[i], A[i+1],…,A[n-1] và đổi chỗ phần tử này với A[i].

Câu hỏi 1: Thực hiện mô phỏng sắp xếp theo thuật toán sắp xếp chọn dãy sau: 4, 5, 2, 1, 3.

Bài làm

Câu hỏi 2: Theo thuật toán sắp xếp chọn, sau mỗi bước thứ i thì các phần tử A[0]. A[1]..... A[i] đã được sắp xếp đúng. Đúng hay sai?

Bài làm

Đúng. Theo thuật toán sắp xếp chọn (Selection Sort), sau mỗi bước thứ i, phần tử nhỏ nhất (hoặc lớn nhất, tùy thuật toán sắp xếp chọn làm việc với phần tử nhỏ nhất hoặc lớn nhất) trong đoạn từ A[0] đến A[i] sẽ được đưa về vị trí đúng của nó trong mảng. Nghĩa là sau mỗi bước thứ i, các phần tử A[0], A[1], ..., A[i] đã được sắp xếp đúng thứ tự so với nhau. Các phần tử A[i+1], A[i+2], ..., A[n-1] (n là số phần tử trong mảng) vẫn chưa được sắp xếp đúng thứ tự. Quá trình này tiếp tục cho đến khi tất cả các phần tử trong mảng được sắp xếp đúng thứ tự.

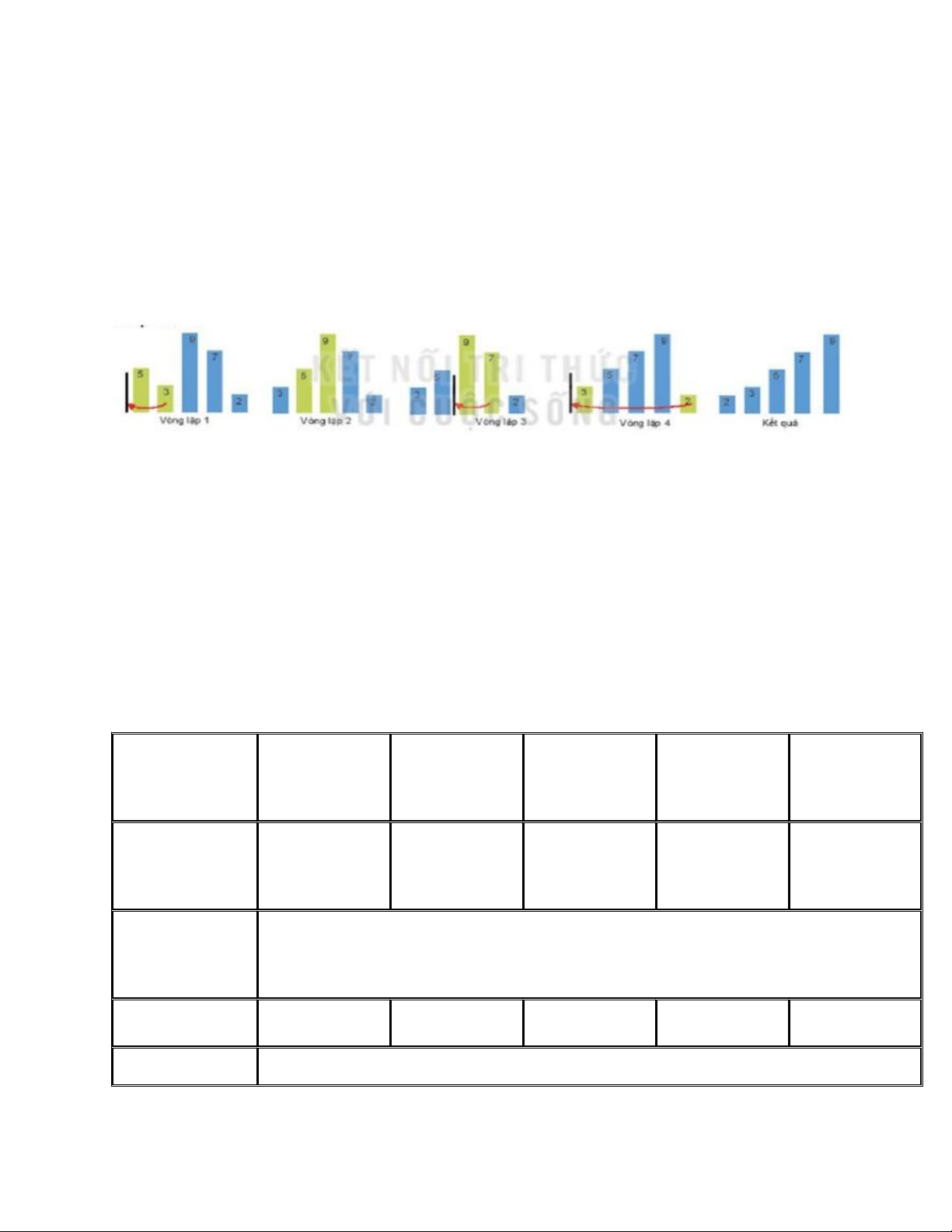
3. Thuật toán sắp xếp nổi bọt

Hoạt động 3: Cùng trao đổi, thảo luận về các ý tưởng của thuật toán sắp xếp nổi bọt.

Bài làm

Thuật toán sắp xếp nổi bọt thực hiện nhiều vòng lặp, kiểm tra hai phần tử cạnh nhau, nếu chúng chưa sắp xếp đúng thì đổi chỗ.

Câu hỏi 1: Mô tả các bước thuật toán sắp xếp nổi bọt của dãy A = [4, 3, 1, 2]

Bài làm

Câu hỏi 2: Khi nào thì các mũi tên ở tất cả các bước trong sơ đồ mô phỏng thuật toán sắp xếp nổi bọt đều có màu đỏ?

Bài làm

Thuật toán sắp xếp nổi bọt hoạt động bằng cách so sánh các phần tử kế tiếp trong danh sách và hoán đổi chúng nếu chúng không được sắp xếp theo thứ tự. Quá trình lặp sẽ tiếp tục cho đến khi tất cả các phần tử đều được sắp xếp. Vì vậy khi màu của tất cả các mũi tên đều đỏ trong sơ đồ mô phỏng thì có nghĩa là không còn phần tử nào được sắp xếp theo thứ tự tăng dần hoặc giảm dần và không cần thực hiện bất kỳ hoán đổi nào nữa.

Luyện tập và vận dụng

Luyện tập

Câu hỏi 1: Cho dãy A= [5, 8, 1, 0, 10, 4, 3]. Viết các chương trình sắp xếp dãy A theo thứ tự tăng dần theo các thuật toán sắp xếp chèn, sắp xếp chọn và sắp xếp nổi bọt.

Câu hỏi 2: Viết chương trình nhập một dãy số từ bàn phím, các số cách nhau bởi dấu cách, thực hiện sắp xếp dãy đã nhập theo một trong các thuật toán sắp xếp rồi in kết quả ra màn hình.

Vận dụng

Câu hỏi 1: Viết lại các thuật toán sắp xếp trong bài theo thứ tự giảm dần.

Câu hỏi 2: Nêu ý nghĩa thực tế của các thuật toán sắp xếp đã học, chẳng hạn sắp xếp các học Sinh trong lớp theo chiều cao tăng dần.

--------------------------------