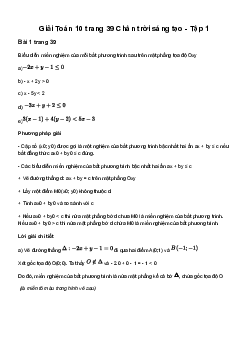

Preview text:
Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn
Hoạt động Toán 10 trang 29, 30 Chân trời sáng tạo Hoạt động 1
Bạn Nam để dành được 700 nghìn đồng. Trong một đợt ủng hộ các bạn học sinh ở vùng bị bão
lụt, Nam đã ủng hộ x tờ tiền loại 20 nghìn đồng, y tờ tiền loại 50 nghìn đồng từ tiền để dành của mình.
a) Biểu diễn tổng số tiền bạn Nam đã ủng hộ theo x và y.
b) Giải thích tại sao ta lại có bất đẳng thức 20x + 50y ≤ 700 Gợi ý đáp án a) Theo bài ra ta có:
Nam đã ủng hộ x tờ tiền loại 20 nghìn đồng
=> Số tiền loại 20 nghìn đồng Nam ủng hộ là: 20x (nghìn đồng)
Nam đã ủng hộ y tờ tiền loại 50 nghìn đồng
=> Số tiền loại 5 nghìn đồng Nam ủng hộ là: 50y (nghìn đồng)
=> Tổng số tiền Nam đã ủng hộ là 20x + 50y.
b) Do số tiền để dành của Nam là 700 nghìn đồng
=> Số tiền quyên góp của Nam không quá 700 nghìn đồng
Hay nói cách khác là: 20x + 50y ≤ 700 Hoạt động 2
Trường hợp nào sau đây thỏa mãn tình huống nêu trong hoạt động khám phá 1.
Trường hợp 1: Nam ủng hộ 2 tờ tiền có mệnh giá 20 nghìn và 3 tờ tiền có mệnh giá 50 nghìn đồng.
Trường hợp 2: Nam ủng hộ 15 tờ tiền có mệnh giá 20 nghìn đồng và 10 tờ tiền có mệnh giá 50 nghìn đồng. Gợi ý đáp án
Theo hoạt động khám phá 1: Số tiền Nam ủng hộ là 20x + 50y (nghìn đồng), số tiền này không
vượt quá 700 nghìn đồng, vậy nên ta có bất phương trình 20x + 50y ≤ 700.
=> 20x + 50y – 700 ≤ 0 với x là số tờ tiền có mệnh giá 20 nghìn đồng và y là số tờ tiền có mệnh giá 50 nghìn đồng.
Vì thế để kiểm tra các trường hợp trên có thỏa mãn hay không thì ta phải kiểm tra xem số tờ
tiền 20 nghìn đồng và 50 nghìn đồng tương ứng với các cặp (x; y) có thỏa mãn bất phương
trình 20x + 50y – 700 ≤ 0 hay không.
Trường hợp 1: Nam ủng hộ 2 tờ tiền có mệnh giá 20 nghìn đồng và 3 tờ tiền có mệnh giá 50
nghìn đồng. Khi đó ta có: x = 2; y = 3.
Vì 20 . 2 + 50 . 3 – 700 = - 510 < 0 nên x = 2; y = 3 thỏa mãn bất phương trình trên.
Trường hợp 2: Nam ủng hộ 15 tờ tiền có mệnh giá 20 nghìn đồng và 10 tờ tiền có mệnh giá 50
nghìn đồng. Khi đó x = 15; y = 10.
Ta có: 20 . 15 + 50 . 10 – 700 = 100 > 0
=> x = 15; y = 10 không thỏa mãn bất phương trình trên.
Vậy trường hợp 1 thỏa mãn tình huống trong hoạt động khám phá 1.
Giải Toán 10 trang 32 Chân trời sáng tạo - Tập 1 Bài 1 trang 32
Cho bất phương trình bậc nhất hai ẩn x - 2y + 6 > 0
a) (0;0) có phải là một nghiệm của bất phương trình đã cho không?
b) Chỉ ra ba cặp số (x;y) là nghiệm của bất phương trình đã cho.
c) Biểu diễn miền nghiệm của các bất phương trình đã cho trên mặt phẳng tọa độ Oxy Gợi ý đáp án
a) Vì 0 - 2.0 + 6 = 6 > 0 nên (0;0) là một nghiệm của bất phương trình đã cho.
b) Vì 0 - 2.1 + 6 = 4 > 0 nên (0;1) là một nghiệm của bất phương trình đã cho.
Vì 1 - 2.0 + 6 = 7 > 0 nên (1;0) là một nghiệm của bất phương trình đã cho.
Vì 1 - 2.1 + 6 = 5 > 0 nên (1;1) là một nghiệm của bất phương trình đã cho.
c) Vẽ đường thẳng :x - 2y + 6 = 0 đi qua hai điểm A(0;3) và
Xét gốc tọa độ O(0;0). Ta thấy và 0 - 2.0 + 6 = 6 > 0
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ , chứa gốc tọa độ O Bài 2 trang 32
Biểu diễn miền nghiệm của các bất phương trình sau trên mặt phẳng tọa độ Oxy: a) - x + y + 2 > 0 Gợi ý đáp án a) Vẽ đường thẳng
đi qua hai điểm A(2;0) và
Xét gốc tọa độ O(0;0). Ta thấy và - 0 + 0 + 2 = 2 > 0
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ , chứa gốc tọa độ O
(miền không gạch chéo trên hình)
b) Vẽ đường thẳng :y + 2 = 0 đi qua hai điểm A(0; - 2) và
Xét gốc tọa độ O(0;0). Ta thấy và 0 + 2 = 2 > 0
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ , chứa gốc tọa độ O
(miền không gạch chéo trên hình) c) Vẽ đường thẳng
đi qua hai điểm A(2;0) và
Xét gốc tọa độ O(0;0). Ta thấy và - 0 + 2 = 2 > 0
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ , không chứa gốc tọa độ O
(miền không gạch chéo trên hình) Bài 3 trang 32
Biểu diễn miền nghiệm của các bất phương trình sau trên mặt phẳng tọa độ Oxy:
a) - x + 2 + 2(y - 2) < 2(1 - x)
b) 3(x - 1) + 4(y - 2) < 5x - 3 Gợi ý đáp án a) Ta có:
Vẽ đường thẳng :2y + x - 4 = 0 đi qua hai điểm A(2;1) và
Xét gốc tọa độ O(0;0). Ta thấy và 2.0 + 0 - 4 = - 4 < 0
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ , chứa gốc tọa độ O
(miền không gạch chéo trên hình) b) Ta có: Vẽ đường thẳng
đi qua hai điểm A(0;2) và
Xét gốc tọa độ O(0;0). Ta thấy và 2.0 - 0 - 4 = - 4 < 0
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ , chứa gốc tọa độ O
(miền không gạch chéo trên hình) Bài 4 trang 32
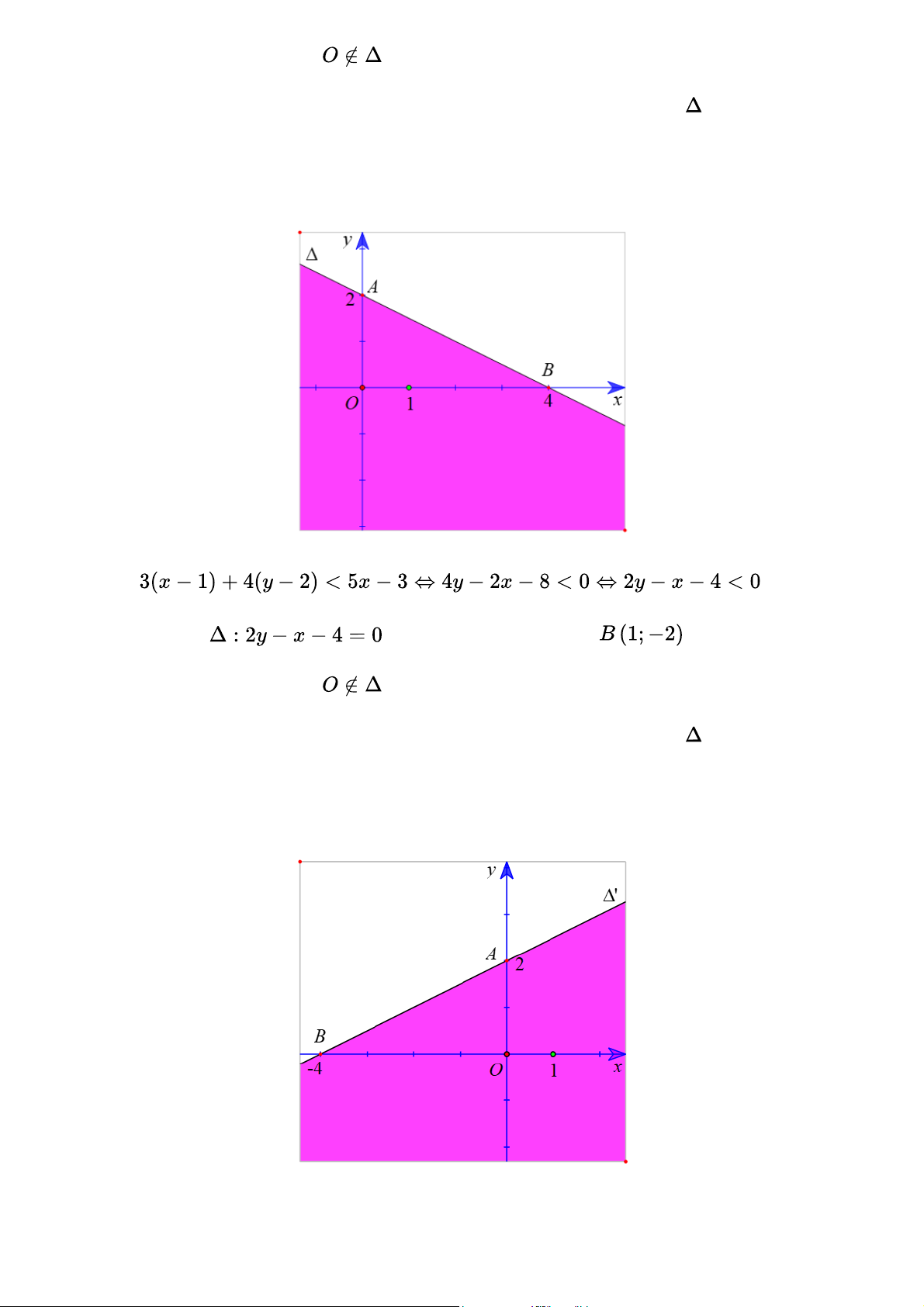
Bạn Cúc muốn pha hai loại nước cam. Để pha một lít nước cam loại I cần 30 g bột cam, còn
một lít nước cam loại II cần 20 g bột cam. Gọi x và y lần lượt là số lít nước cam loại I và II pha
chế được. Biết rằng Cúc chỉ có thể dùng không quá 100 gam bột cam. Hãy lập các bất phương
trình mô tả lít nước cam loại I và II mà bạn Cúc có thể pha chế được và biểu diễn miền nghiệm
của các bất phương trình đó trên cùng một mặt phẳng tọa độ Oxy. Gợi ý đáp án
Để pha x lít nước cam loại I cần 30x g bột cam,
Để pha y lít nước cam loại II cần 20y g bột cam,
Vì Cúc chỉ có thể dùng không quá 100 gam bột cam nên ta có bất phương trình
Vẽ đường thẳng :3x + 2y - 10 = 0 đi qua hai điểm A(0;5) và
Xét gốc tọa độ O(0;0). Ta thấy
và 3.0 + 2.0 - 10 = - 10 < 0
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ , chứa gốc tọa độ O
(miền không gạch chéo trên hình) Bài 5 trang 32
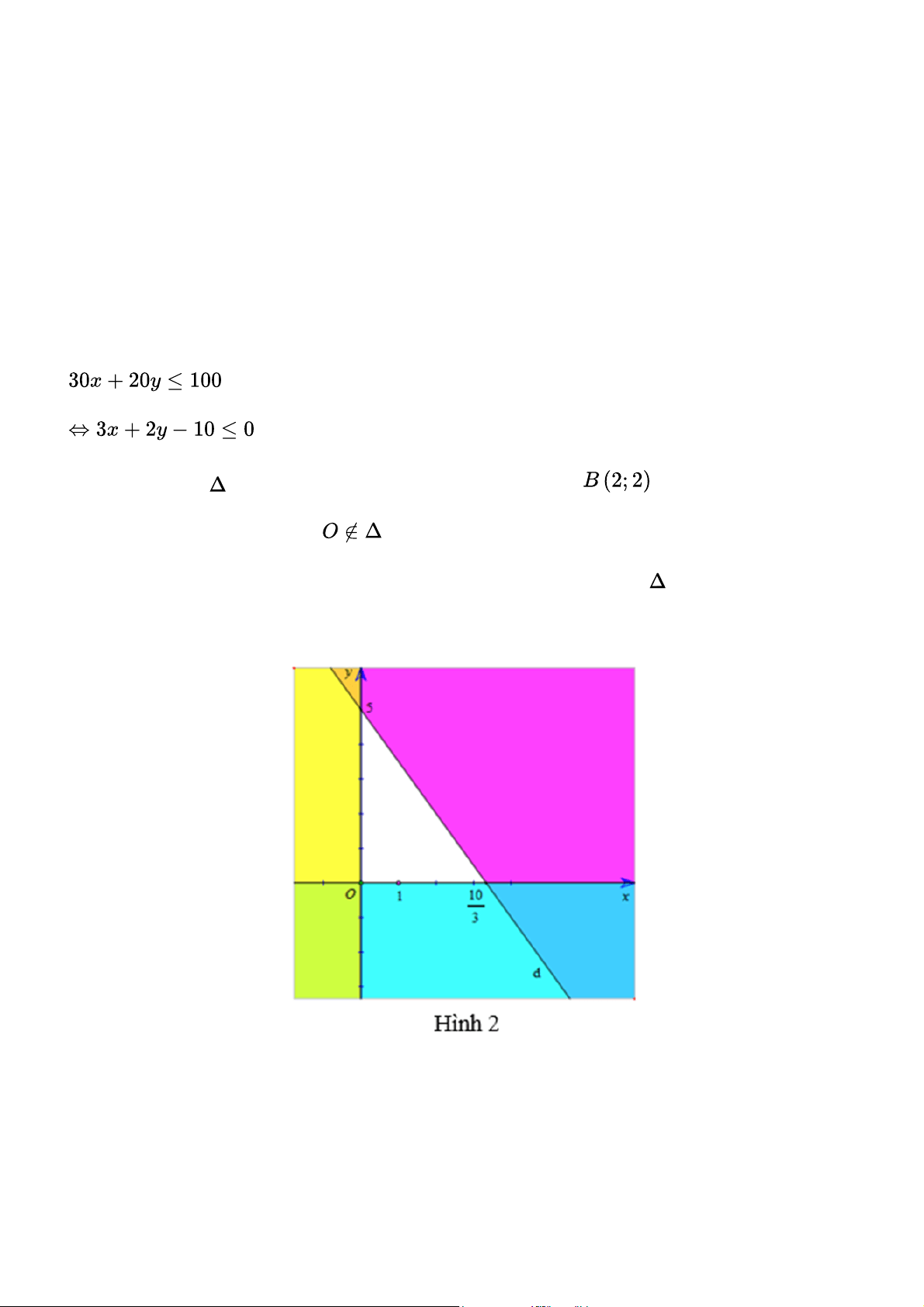
Miền không gạch chéo (không kể bờ d) trong mỗi hình dưới đây là miền nghiệm của bất phương trình nào? Gợi ý đáp án
Gọi phương trình đường thẳng d:ax + by + c = 0
a) Từ hình a) ta thấy d đi qua hai điểm A(0;2) và B( - 5;0) Chọn a = 2
b = - 5;c = 10 và d:2x - 5y + 10 = 0
Điểm O (0;0) thuộc miền nghiệm và 2.0 - 5.0 + 10 = 10 > 0
Vậy bất phương trình cần tìm là 2x - 5y + 10 > 0
b) Từ hình b) ta thấy d đi qua hai điểm A(0;2) và B(3;0) Chọn a = 2
b = 3;c = - 6 và d:2x + 3y - 6 = 0
Điểm O (0;0) không thuộc miền nghiệm và 2.0 + 3.0 - 6 = - 6 < 0
Vậy bất phương trình cần tìm là 2x + 3y - 6 > 0