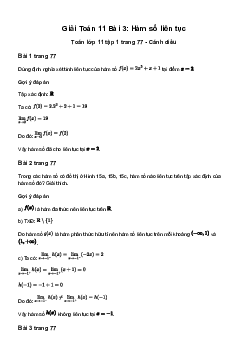
Preview text:
Giải Toán 11 Bài 2: Giới hạn của hàm số
Toán lớp 11 tập 1 trang 72- Cánh diều Bài tập 1 trang 72
Sử dụng định nghĩa, tìm các giới hạn sau: a) ; b) . Gợi ý đáp án a)
b) Giả sử ( ) là dãy số bất kì, thỏa mãn và , ta có: Do đó: . Bài tập 2 trang 72 Biết rằng hàm số thỏa mãn và
. Trong trường hợp này có tồn tại giới hạn hay không? Giải thích. Gợi ý đáp án Ta có:
Vậy không tồn tại giới hạn . Bài tập 3 trang 72 Tính các giới hạn sau: a) ; b) ; c) . Gợi ý đáp án a) ; b) ; c) . Bài tập 4 trang 72 Tính các giới hạn sau: a) ; b) ; c) ; d) ; e) ; g) . Gợi ý đáp án a) ; b) ; c) ; d) ; e) ; g) . Bài tập 5 trang 72
Một công ty sản xuất máy tính đã xác định được rằng, trung bình một nhân viên có thể lắp ráp được
bộ phận mỗi ngày sau ngày đào tạo. Tính và cho biết ý nghĩa của kết quả. Gợi ý đáp án
Vậy khi số ngày đào tạo càng nhiều thì số bộ phận mà trung bình một nhân viên có thể lắp ráp
được tiến dần đến 50. Bài tập 6 trang 72
Chi phí (đơn vị: nghìn đồng) để sản xuất sản phẩm của một công ty được xác định bởi hàm số: . a) Tính chi phí trung bình
để sản xuất một sản phẩm. b) Tính
và cho biết ý nghĩa của kết quả. Gợi ý đáp án a) b) Ta có:
Vậy khi số sản phẩm càng lớn thì chi phí trung bình để sản xuất một sản phẩm tiến dần đến 105 (nghìn đồng).