Giải VBT môn Toán 3 - Bài 18: Hình tam giác, hình tứ giác. Hình chữ nhật, hình vuông | Kết nối tri thức

V B Ở ÀI T P Ậ TOÁN L P Ớ 3 K T Ế N I T Ố RI TH C Ứ
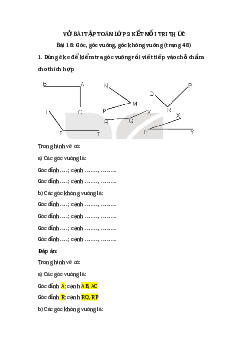
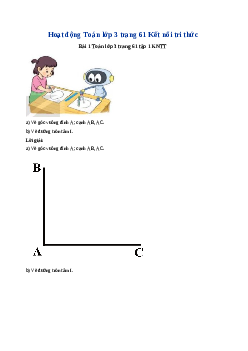
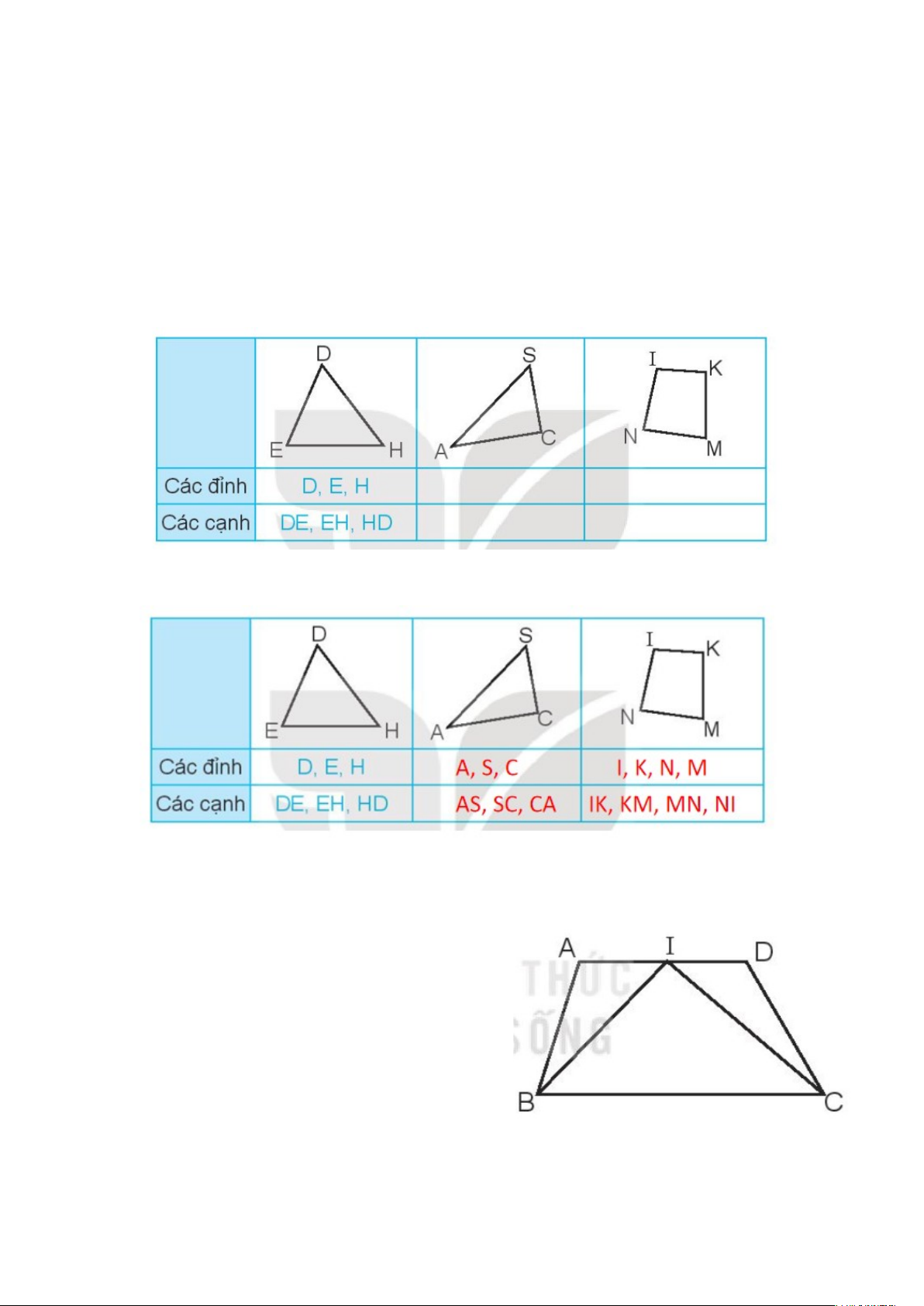
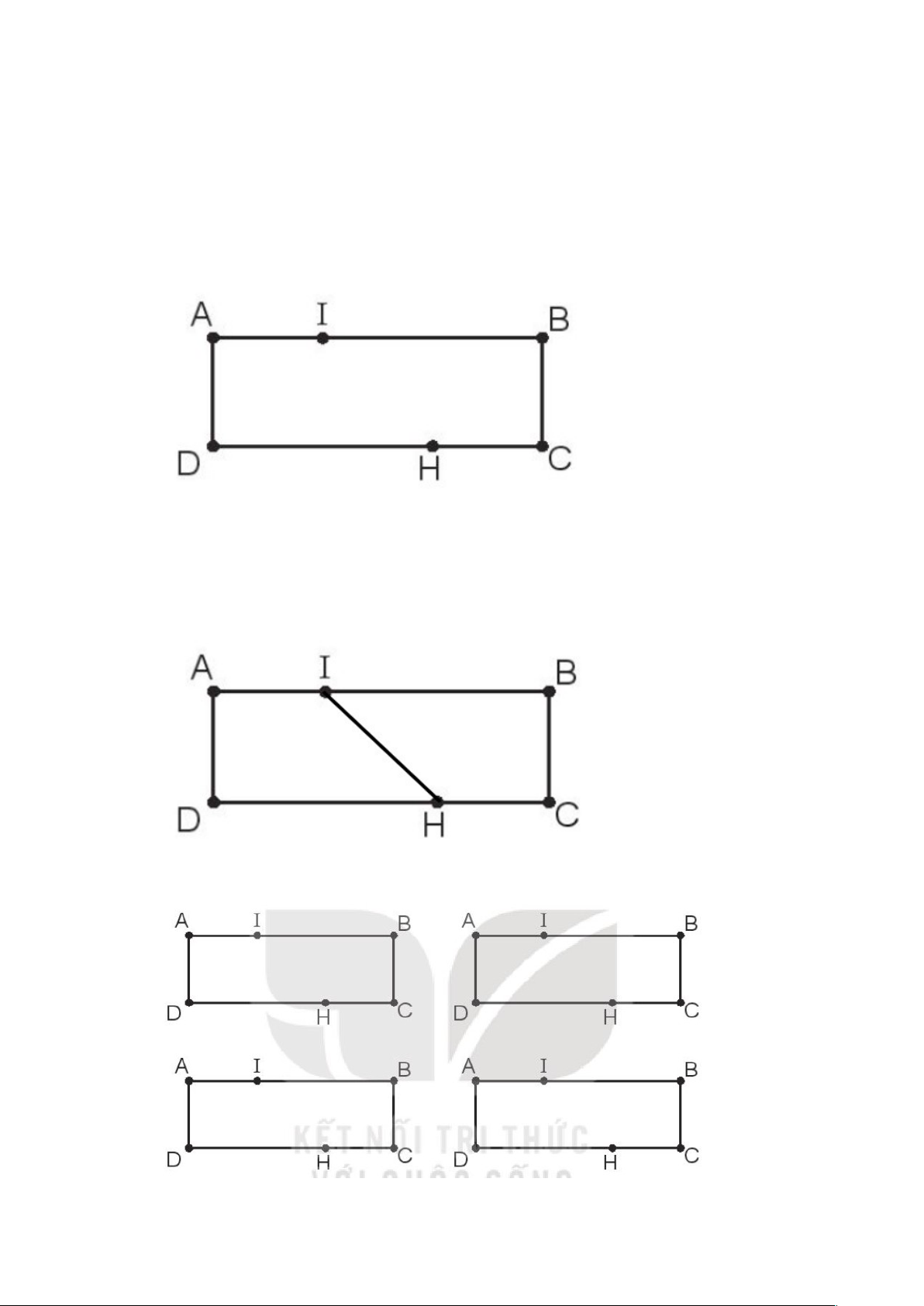
Bài 19: Hình tam giác, hình t g ứ iác. Hình ch n ữ h t ậ , hình vuông (trang 49,50,51,52,53) Ti t ế 1 (trang 49, 50) 1. Vi t ế tên các đ n ỉ h và các c n ạ h c a m ủ i h ỗ ình (theo m u ẫ ). Đáp án: 2. Vi t ế ti p ế vào ch ỗ ch m ấ cho thích h p ợ . Trong hình vẽ bên có: a) Các hình tam giác là:
…………………………………….
….………………………………… b) Các hình t g ứ iác là:
……………………………………
….………………………………… Đáp án:
a) Các hình tam giác là: AIB, IDC, IBC b)Các hình t g ứ iác là: BAIC, CDIB, ABCD 3. Qua b n ố đ n ỉ h c a h ủ
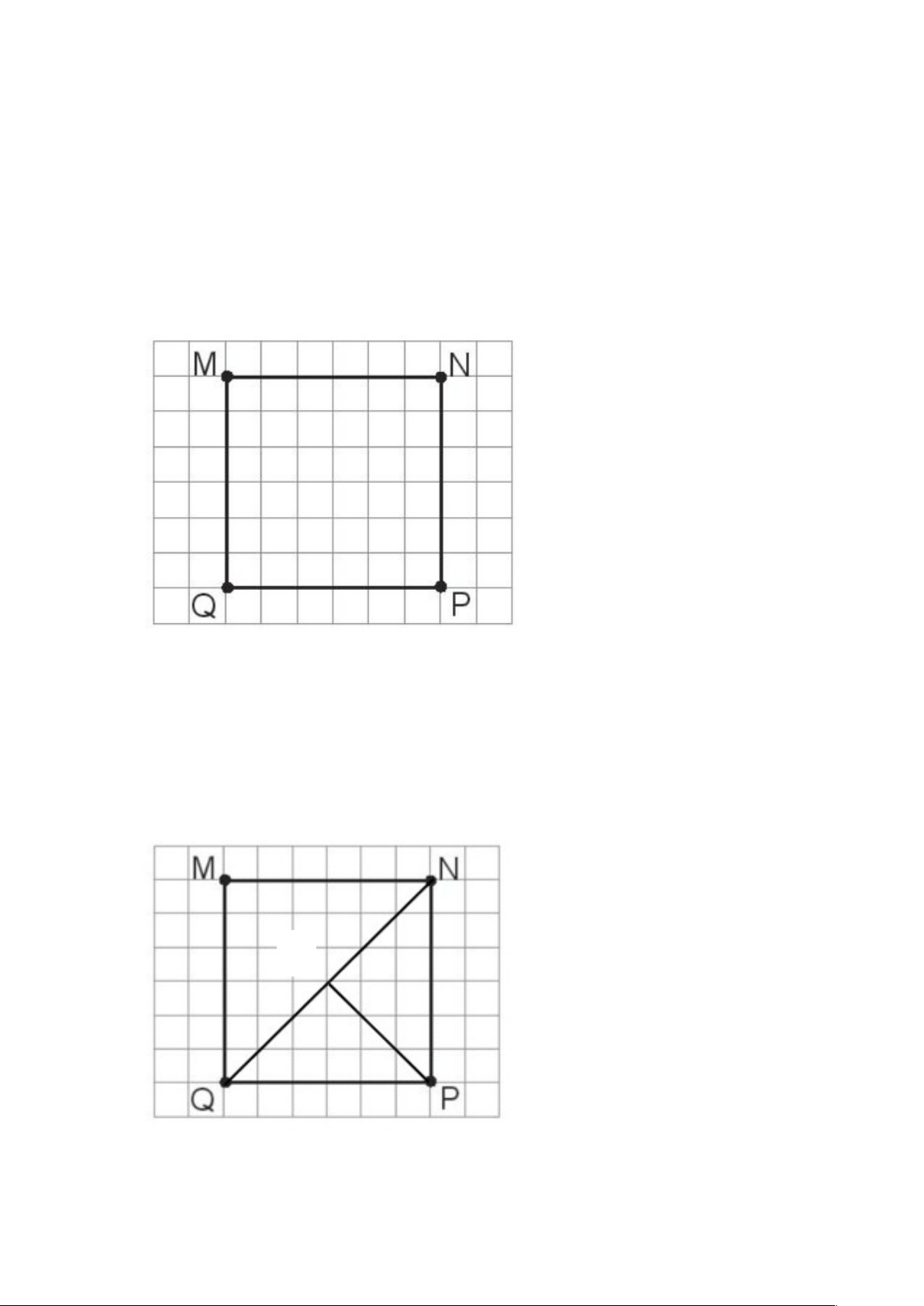
ình vuôn MNPQ, hãy vẽ các đo n ạ th n ẳ g đ ể
chia hình vuông đó thành 4 hình tam giác. Đáp án: Ta nối đ n ỉ h Q v i ớ đ n ỉ h N, t đ ừ n ỉ h P ta vẽ m t ộ đư n ờ g th n ẳ g t i Q ớ N và đư n ờ g th n ẳ g đó c t ắ QN t i ạ H
Ta có 4 hình tam giác là: MNQ, QNP, QHP, PHN H 4. Mảnh vư n
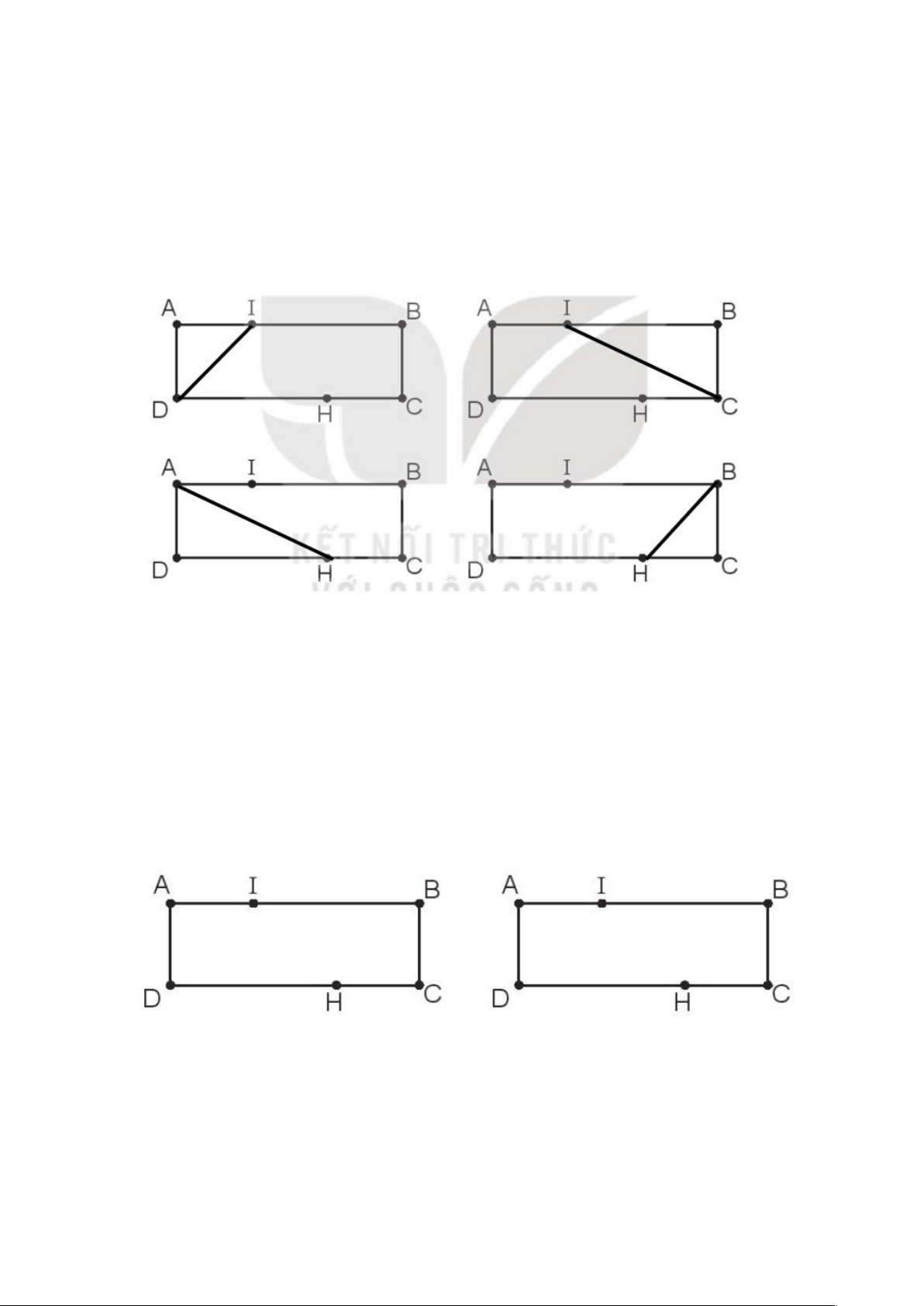
ờ nhà cô Lan có d n ạ g hình ch n ữ h t ậ ABCD. Em hãy n i c ố ác đi m ể đã đánh d u ấ (nh h ư ình vẽ) đ ể giúp cô Lan chia m n ả h vư n ờ đó theo m i y ỗ êu c u ầ dư i ớ đây.
a) Chia thành 2 hình t ứ giác. Đáp án: Nối I v i H ớ Ta có 2 hình t ứ giác: AIHD, IHCB
b) Chia thành 1 hình tam giác và 1 hình t giá ứ c (tìm 4 cách làm) Đáp án: Nối I v i D ớ , ta có: Nối I v i C ớ , ta có Tam giác: AID Tam giác: IBC T g ứ iác: IDCB T g ứ iác: AICD Nối A v i H ớ , ta có: Nối B v i H ớ , ta có: Tam giác: AHD Tam giác: HBC T g ứ iác: AHCB T g ứ iác: ABHD
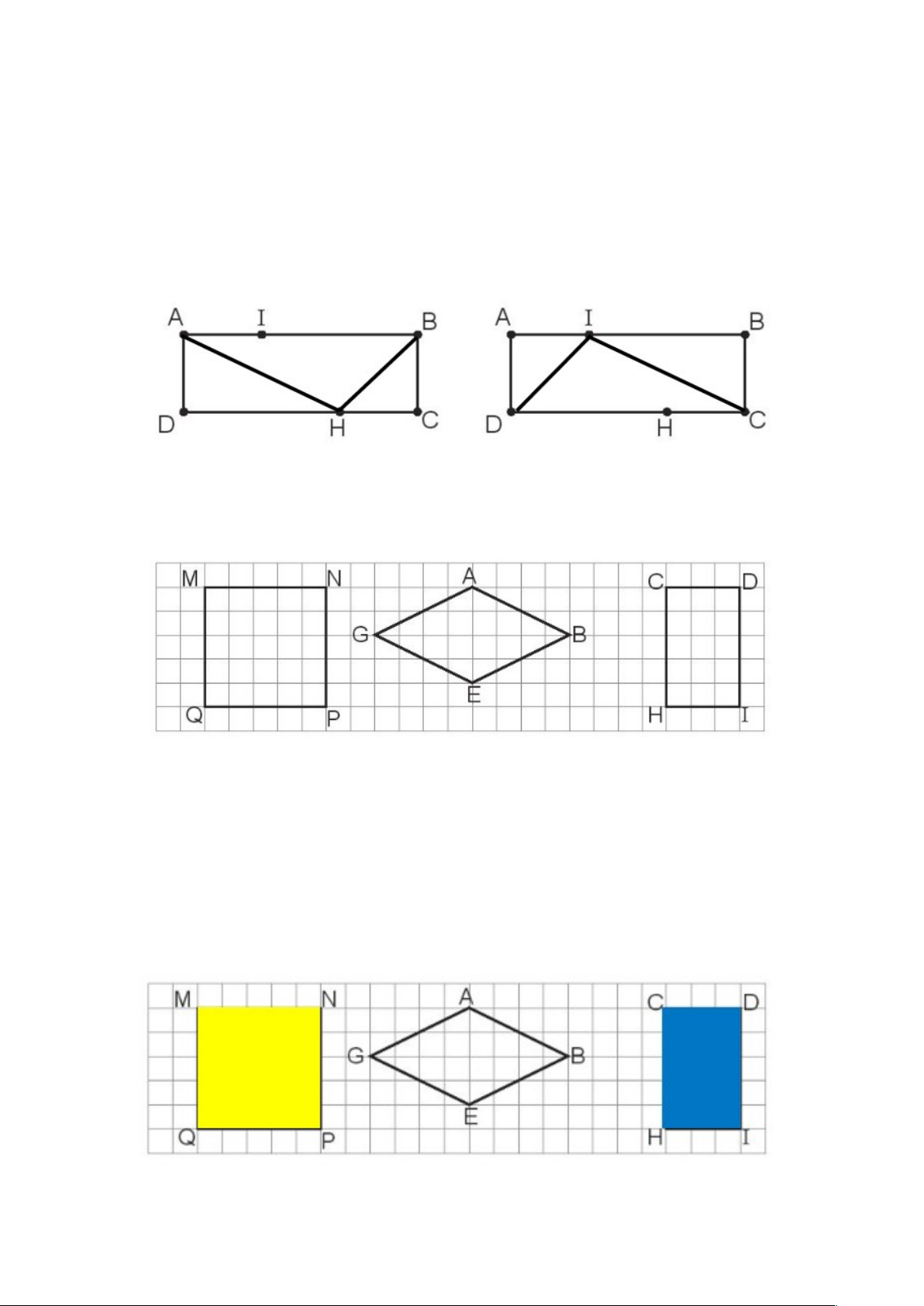
c) Chia thành 3 hình tam giác (tìm 2 cách làm) Đáp án: Nối A v i H ớ , B v i H ớ , ta có: Nối D v i I ớ , C v i I ớ , ta có: 3 tam giác: AHD, AHB, BHC 3 tam giác: ADI, DIC, ICB Ti t ế 2 (trang 51, 52
1. a) Tô màu vàng vào hình vuông, màu xanh vào hình ch n ữ h t ậ . Đáp án:
- Hình vuông MNPQ có 4 góc vuông: M, N, P, Q và 4 c n ạ h b n ằ g nhau: MN = NP= PQ = QM. - Hình ch n ữ h t
ậ CDIH có 4 góc vuông: C, D, I, H và c n ạ h CD = c n ạ h HI, c n ạ h CH = c n ạ h DI. b) Khoanh vào ch đ ữ t ặ trư c ớ câu tr l ả i đ ờ úng.
Trong hình vẽ có m y ấ hình ch ữ nh t ậ ?
A. 1 hình B. 2 hình C. 3 hình D. 4 hình Đáp án:
Trong hình vẽ có 2 hình ch ữ nh t ậ - Hình ch n ữ h t
ậ ABCD có 4 góc vuông và 2 c n ạ h ng n ắ b n ằ g nhau, 2 c n ạ h dài b n ằ g nhau. - Hình ch n ữ h t
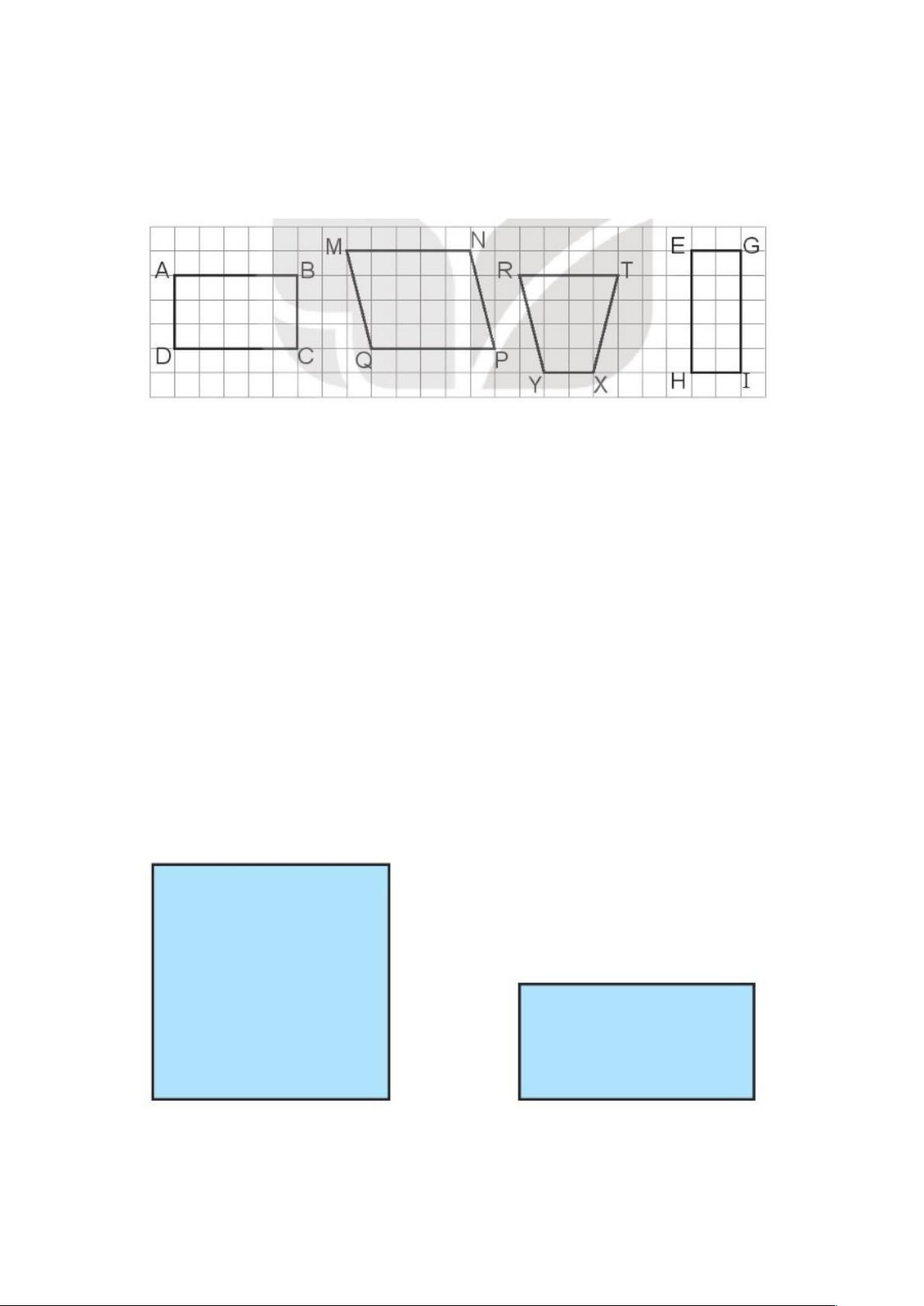
ậ EGIH có 4 góc vuông và 2 c n ạ h ng n ắ b n ằ g nhau, 2 c n ạ h dài b n ằ g nhau. 2. Đ, S?
Cho hình vuông và hình ch n ữ h t ậ nh s ư au: Dùng thư c ớ có v c
ạ h chia xăng - ti - mét đ đ ể o đ d ộ ài các đo n ạ th n ẳ g trong hình, ta có: a) Hình vuông có c n ạ h 5 cm. b) Hình ch n ữ h t ậ có chi u ề r n ộ g 4 cm. c) Hình ch n ữ h t ậ có chi u ề dài 2 cm. Đáp án: a) Hình vuông có c n ạ h 5 cm. Đ b) Hình chữ nh t ậ có chi u ề r n ộ g 4 cm. S c) Hình ch n ữ h t ậ có chi u ề dài 2 cm. S 3. Hãy đo đ d ộ ài các đ v ồ t ậ dư i đ ớ ây b n ằ g gang tay ho c ặ s i t ả ay của em r i v ồ i t ế s t ố hích h p ợ vào ch c ỗ h m ấ . a) B n ả g l p e ớ m có chi u ề dài kho n ả g ……… s i ả tay. b) B n ả g l p e ớ m có chi u ề dài kho n ả g ………. gang tay. c) Bàn h c ọ c a ủ em có chi u ề dài kho n ả g …………. gang tay. d) Bàn h c ọ c a ủ em có chi u ề r n ộ g kho n ả g ………. gang tay. (H c ọ sinh tự th c ự hành đo các đ v ồ t ậ và vi t ế vào ch c ỗ h m ấ sao cho thích h p) ợ 4. Vi t ế s t ố hích h p ợ vào ch ỗ ch m ấ . M i ỗ viên g c
ạ h hoa trang trí có c n ạ h 5dm. M t ộ hình ch n ữ h t ậ đư c ợ ghép b i 6 v ở iên g c ạ h hoa nh h ư ình vẽ. a) Chi u ề dài c a ủ hình ch n ữ h t ậ đó là……. dm b) Chi u ề r n ộ g c a ủ hình ch n ữ h t ậ đó là…….dm Đáp án: a) Chi u ề dài c a ủ hình ch n ữ h t
ậ đó là: 15dm (5 x 3 = 15) b) Chi u ề r n ộ g c a ủ hình ch n ữ h t
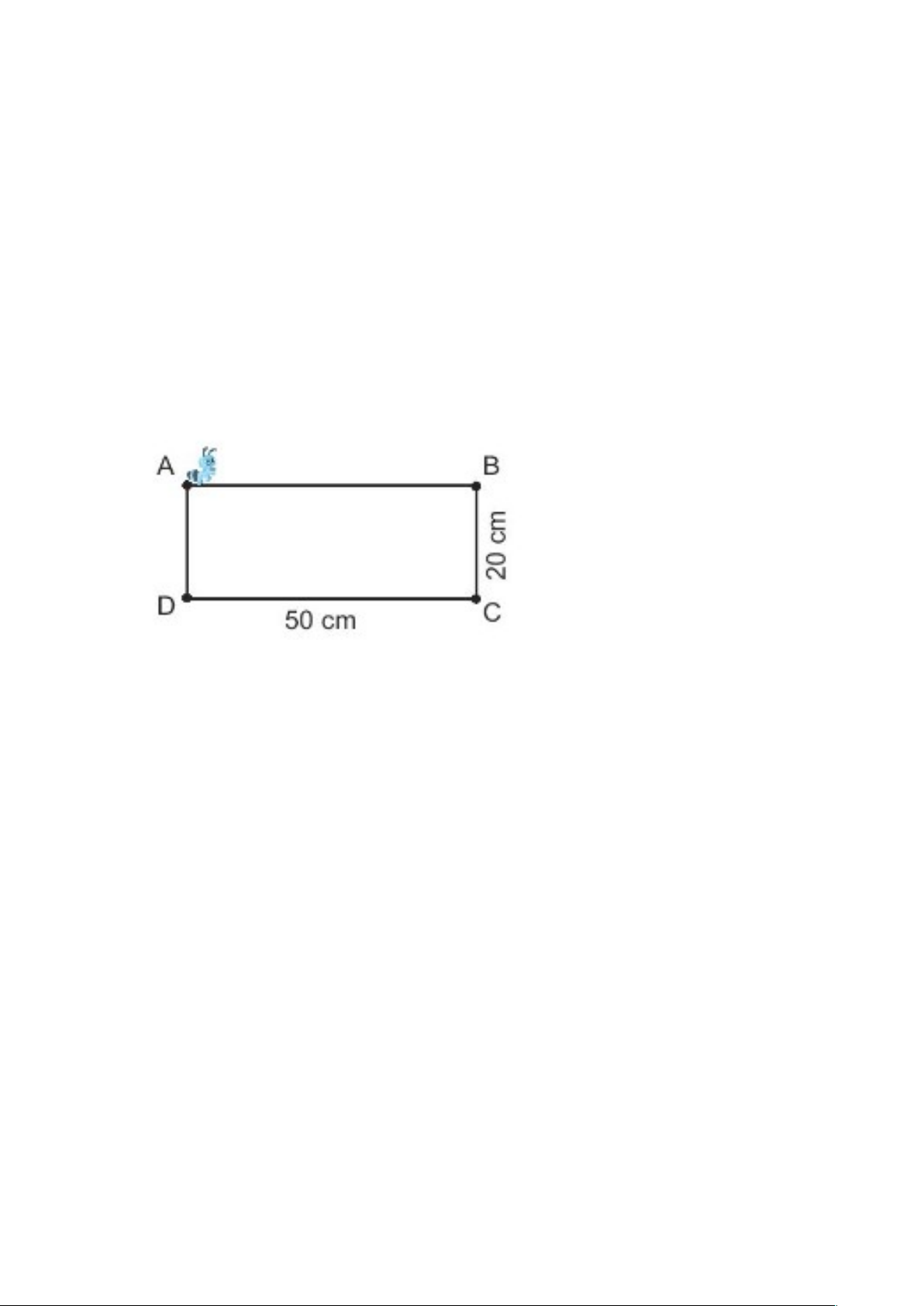
ậ đó là: 10dm (5 x 2 = 10) Ti t ế 3 (trang 52, 53) 1. Vi t ế s t ố hích h p ợ vào ch ỗ ch m ấ . Cho ABCD là hình ch n ữ h t
ậ có BC = 20cm, CD = 50cm. M t ộ con ki n ế đang ở đi m ể A (nh ư hình vẽ). a) N u ế con ki n ế mu n ố bò đ n ế đi m ể B theo c n ạ h AB thì ph i ả bò m t ộ đo n ạ đư n ờ g dài …. cm. b) N u ế con ki n ế mu n ố bò đ n ế đi m ể D theo c n ạ h AD thì ph i ả bò m t ộ đo n ạ đư n ờ g dài …. cm c) N u ế con ki n ế mu n ố bò đ n ế đi m ể C theo đư n ờ g g p ấ khúc ABC thì ph i ả bò m t ộ đo n ạ đư n ờ g dài ….cm. Đáp án: Vì hình ABCD là hình ch n ữ h t
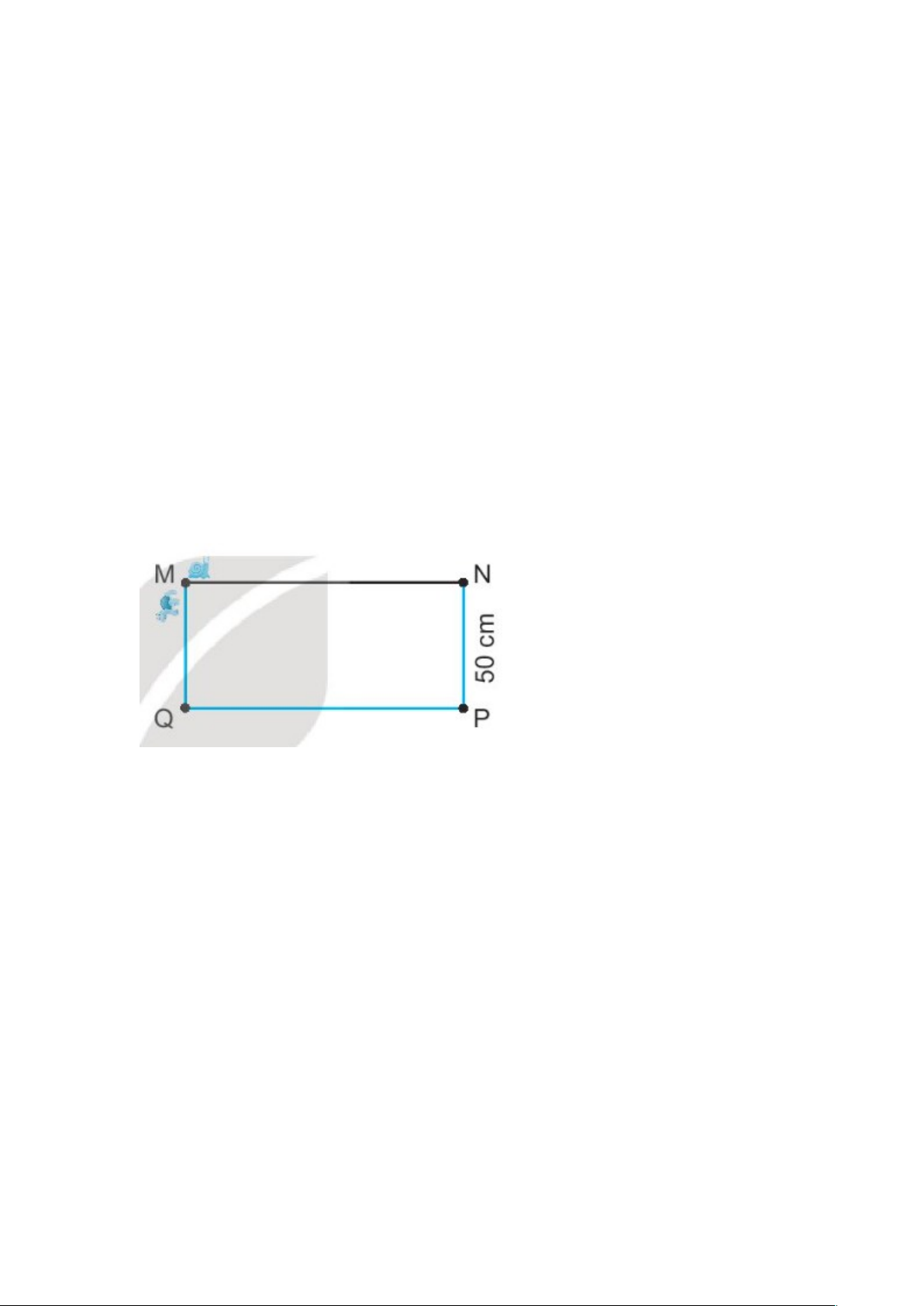
ậ có BC = AD = 20cm, AB = CD = 50cm a) Đo n ạ th n ẳ g AB dài 50cm N u ế con ki n ế mu n ố bò đ n ế đi m ể B theo c n ạ h AB thì ph i b ả ò m t ộ đo n ạ đư n ờ g dài 50cm. b) Đo n ạ th n ẳ g AD dài 20cm N u ế con ki n ế mu n ố bò đ n ế đi m ể D theo c n ạ h AD thì ph i ả bò m t ộ đo n ạ đư n ờ g dài 20cm. c) Độ dài đư n ờ g g p k ấ húc ABC là: 50 + 20 = 50cm N u ế con ki n ế mu n ố bò đ n ế đi m ể C theo đư n ờ g g p ấ khúc ABC thì ph i ả bò m t ộ đo n ạ đư n ờ g dài 70cm. 2. Vi t ế s t ố hích h p ợ vào ch ỗ ch m ấ . Rùa và c Ố sên thi ch y ạ . Hai b n ạ cùng xu t ấ phát t đ ừ i m ể M ch y ạ đ n ế đích đi m ể N nh n ư g theo hai đư g ờ khác nhau. c Ố sên ch y ạ đ n ế đích theo c n ạ h MN, còn Rùa ch y ạ đ n ế đích theo đư n ờ g g p k ấ húc MQPN. Bi t ế r n ằ g MNPQ là hình ch n ữ h t ậ có NP = 50cm. Đo n ạ đư n ờ g Rùa ch y ạ dài h n ơ đo n ạ đư n ờ g c Ố sên ch y ạ là …….cm. Đáp án: Vì MNPQ là hình ch n ữ h t
ậ , nên MN = QP, MQ = NP = 50cm. Đo n ạ đư n ờ g c Ố sên ch y ạ là đo n ạ th n ẳ g MN. Đo n ạ đư n ờ g Rùa ch y ạ là:
MQ + QP + PN = MQ + MN + NP (do QP = MN) = 50 + MN + 50 Đo n ạ đư n ờ g Rùa ch y ạ dài h n ơ đo n ạ đư n ờ g c Ố sên ch y ạ là: 50 + 50 = 100(cm) Đáp số: 100cm Đo n ạ đư n ờ g Rùa ch y ạ dài h n ơ đo n ạ đư n ờ g c Ố sên ch y ạ là 100cm. 3. Khoanh vào ch đ ữ t ặ trư c ớ câu tr l ả i đ ờ ùng. a) V i s ớ ố lư n
ợ g các que tính gi n ố g nhau nào dư i ớ đây thì x p ế đư c ợ m t
ộ hình vuông (không th a q ừ ue tính nào)?
A. 6 que tính B. 7 que tính C. 8 que tính Đáp án:
Đáp án đúng là C. 8 que tính. Vì hình vuông có 4 c n ạ h b n ằ g nhau nên s q ố ue tính x p t ế hành hình vuông ph i là ả m t ộ s c ố hia h t ế cho 4. Ta có 8 : 4 = 2 V y ậ 8 que tính thì x p ế đư c ợ m t ộ hình vuông v i m ớ i c ỗ n ạ h là 2 que tính. b) V i s ớ l ố ư n
ợ g các que tính gi n
ố g nhau nào dư i đ ớ ây thì không thể x p ế đư c ợ m t ộ hình ch n ữ h t ậ (không th a q ừ ue tính nào)?
A. 6 que tính B. 7 que tính C. 10 que tính Đáp án:
Đáp án đúng là đáp án B. 7 que tính. Vì hình ch n ữ h t ậ có 2 c n ạ h dài b n ằ g nhau, 2 c n ạ h ng n ắ b n ằ g nhau nên s q ố ue tính x p t ế hành hình ch n ữ h t ậ ph i là ả m m t ộ s c ố hia h t ế cho 2. Ta có 7 không chia h t ế cho 2. V y ậ 7 que tính không th x ể p đ ế ư c ợ m t ộ hình ch n ữ h t ậ .