Giải Vở bài tập Toán lớp 5 bài 120 Luyện tập chung chương 3

Giải Vở bài tập Toán lớp 5 bài 120 Luyện tập chung chương 3
1. Lý thuyết tính thể tích toán lớp 5
1.1. Thể tích hình hộp chữ nhật là gì?
Hình hộp chữ nhật, một loại hình học không gian hay còn gọi là khối lập
phương, đặc trưng bởi việc có 6 mặt, và tất cả các mặt này đều là hình chữ
nhật. Trong hình hộp chữ nhật, có 2 mặt không có cạnh chung với nhau,
chúng thường được gọi là 2 mặt đối diện và thường được xem như là các
mặt đáy của hình hộp chữ nhật, còn lại là các mặt bên.
Thể tích của hình hộp chữ nhật, đơn giản là không gian mà hình này chiếm,
được tính bằng cách nhân chiều cao của nó với diện tích của mặt đáy.
Ngoài ra, có một số tính chất quan trọng về hình hộp chữ nhật mà chúng ta cần ghi nhớ:
- Hình hộp chữ nhật có tổng cộng 12 cạnh, 8 đỉnh và 6 mặt.
- Hai đường chéo của hình hộp chữ nhật có 2 đầu mút là 2 đỉnh đối diện và
chúng gặp nhau tại 1 điểm.
- Diện tích của 2 mặt đối diện trong hình hộp chữ nhật luôn bằng nhau.
- Chu vi của 2 mặt đối diện trong hình hộp chữ nhật cũng luôn bằng nhau.
1.2. Công thức tính thể tích hình hộp chữ nhật toán lớp 5
Để tính thể tích của một hình hộp chữ nhật, ta thực hiện phép nhân giữa
chiều dài, chiều rộng và chiều cao của hình. Chú ý rằng, tất cả các đơn vị đo
phải được sử dụng cùng một đơn vị.
Công thức tính thể tích hình hộp chữ nhật được biểu diễn như sau: V = a x b x c
Trong công thức này:
- V đại diện cho thể tích của hình hộp chữ nhật.
- a là chiều dài của hình hộp chữ nhật.
- b là chiều rộng của hình hộp chữ nhật.
- c là chiều cao của hình hộp chữ nhật.
1.3. Hướng dẫn cách tính thể tích hình hộp chữ nhật chi tiết
Để giải bài tập về thể tích của hình hộp chữ nhật trong môn toán lớp 5, ta có
thể tuân theo các bước dưới đây để thực hiện một cách chính xác:
Bước 1: Đầu tiên, ta cần xác định chiều dài của hình hộp chữ nhật đã cho.
Chiều dài là phần cạnh dài nhất của mặt phẳng hình chữ nhật, nằm phía dưới
hoặc phía trên của hình hộp chữ nhật. Ví dụ, giả sử bài toán cho chiều dài
của hình hộp chữ nhật là 5 cm.
Bước 2: Tiếp theo, ta xác định chiều rộng của hình hộp chữ nhật. Chiều rộng
là phần cạnh ngắn nhất của mặt phẳng hình chữ nhật, nằm bên dưới hoặc
trên của hình hộp. Ví dụ, giả sử chiều rộng của hình hộp chữ nhật là 4 cm.
Bước 3: Sau đó, ta cần xác định chiều cao của hình hộp chữ nhật. Chiều cao
chính là cạnh đứng của hình, cũng như là cạnh nâng hình chữ nhật lên thành
khối 3 chiều. Ví dụ, cho chiều cao của hình hộp chữ nhật là 3 cm.
Bước 4: Bây giờ, ta thực hiện tính thể tích của hình hộp chữ nhật đã cho. Để
tính thể tích, ta sử dụng công thức Thể tích (V) = chiều dài (l) * chiều rộng (w)
* chiều cao (h), có thể viết ngắn gọn là V = lwh. Tương đương, ta nhân các
đơn vị chiều dài, chiều rộng và chiều cao với nhau. Với ví dụ trên, thể tích của
hình hộp chữ nhật sẽ là: V = 5 (cm) * 4 (cm) * 3 (cm) = 60 (cm³).
Bước 5: Cuối cùng, ta ghi kết quả đáp số với đơn vị khối tương ứng. Khi
thực hiện tính toán thể tích trong không gian 3 chiều, dù đơn vị trong bài toán
là gì (mét, centimet, decimet…), chúng ta phải đưa ra kết quả thể tích với đơn vị khối tương ứng.
2. Giải Vở bài tập Toán lớp 5 bài 120 Luyện tập chung chương 3
Vở bài tập toán lớp 5 tập 2 bài 120 Câu 1
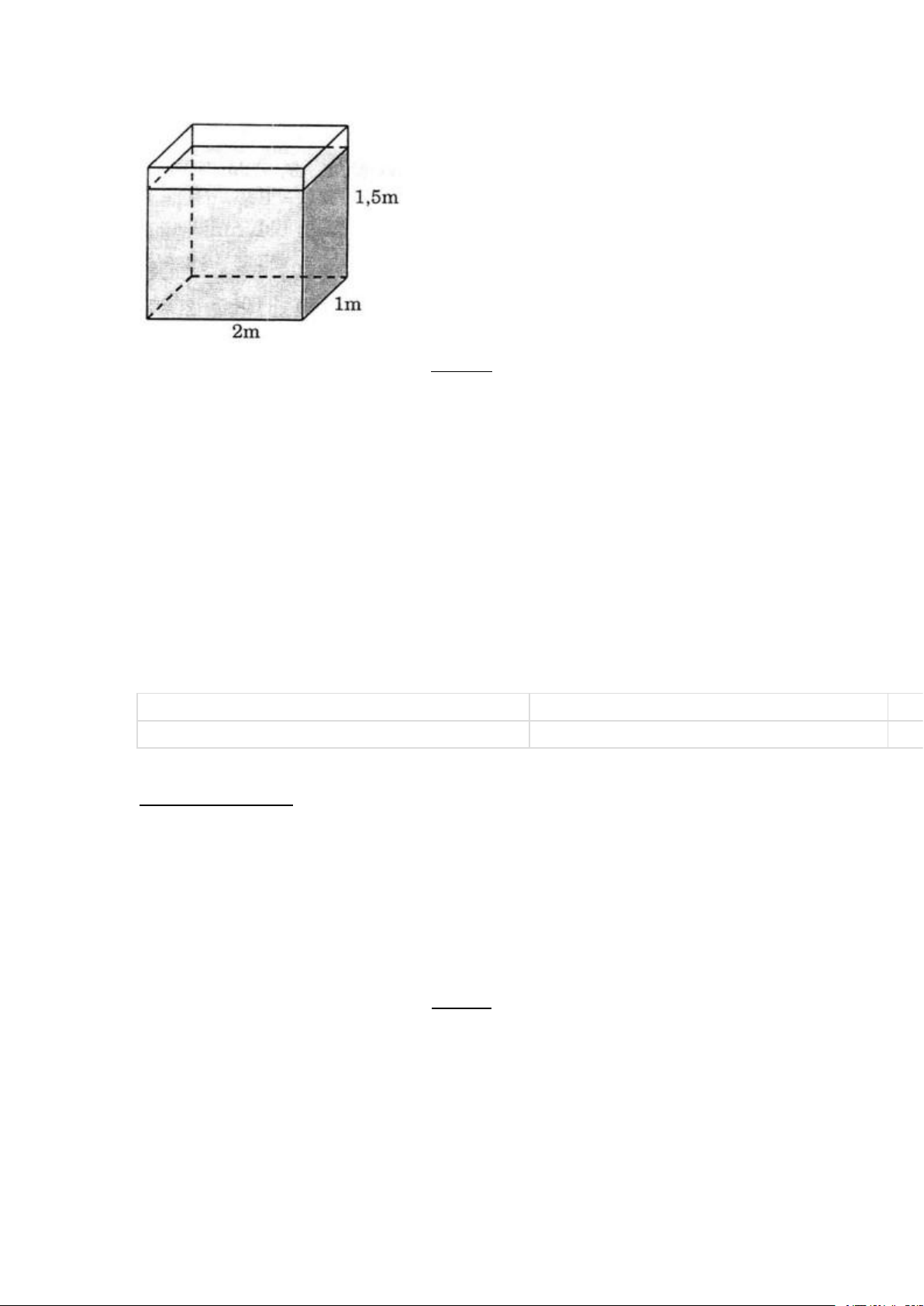
Một hồ nước hình hộp chữ nhật có kích thước bên trong là: chiều dài 2 mét,
chiều rộng 1,5 mét và chiều cao 1 mét. Mức nước trong hồ cao bằng 4/5
chiều cao của hồ. Bài toán yêu cầu tính thể tích nước trong hồ bằng đơn vị lít. (Chú ý: 1 dm³ = 1 lít) Phương pháp giải:
- Để tính thể tích, ta sử dụng công thức: Thể tích = chiều dài × chiều rộng ×
chiều cao (cùng đơn vị đo).
- Với bài toán này, mức nước trong hồ cao bằng 4/5 chiều cao của hồ. Điều
này có nghĩa là chỉ có 1/5 phần dưới của hồ chứa nước. Bài giải
Thể tích trong lòng bể là: 2 ⨯ 1 ⨯ 1,5 = 3 (m3)
3 m³ tương đương với 3000 dm³ hoặc 3000 lít. Vì vậy, thể tích nước trong hồ là 3000 lít.
Bởi vì mức nước trong hồ chỉ chiếm 4/5 tổng thể tích của hồ, chúng ta sẽ tính
số lít nước trong hồ bằng cách nhân với 4/5: 3000 x 4/5 = 2400l
Vậy, số lít nước trong hồ là 2400 lít.
Vở bài tập toán lớp 5 tập 2 bài 120 Câu 2
Cho một hình lập phương có cạnh 0,5m. Tính rồi viết kết quả vào ô trống: Diện tích xung quanh
Diện tích toàn phần Thể tích Phương pháp giải:
Để giải bài toán này, chúng ta sẽ sử dụng các công thức sau:
Diện tích bề mặt của hình lập phương = Diện tích một mặt × Số mặt bên =
Cạnh × Cạnh × Số mặt bên.
Diện tích toàn phần của hình lập phương = Diện tích một mặt × Tổng số mặt
= Cạnh × Cạnh × Tổng số mặt.
Thể tích của hình lập phương = Cạnh × Cạnh × Cạnh. Đáp án
Diện tích xung quanh của hình lập phương là:
Sxq = 0,5 ⨯ 0,5 ⨯ 4 = 1 (m2)
Diện tích toàn phần của hình lập phương là:
Stp = 0,5 ⨯ 0,5 ⨯ 6 = 1,5 (m2)
Thể tích của hình lập phương là:
V = 0,5 ⨯ 0,5 ⨯ 0,5 = 0,125 (m3) Diện tích xung quanh
Diện tích toàn phần Thể tích 1m2 1,5m2 0,125m2
Vở bài tập toán lớp 5 tập 2 bài 120 Câu 3​
a. Viết số đo thích hợp vào ô trống:
Hình hộp chữ nhật (1) (2) Chiều dài 2m 1m Chiều rộng 1m 0,5m Chiều cao 0,4m 0,2m Thể tích
b. Viết số thích hợp vào chỗ chấm:
Chiều dài hình (1) gấp …. lần chiều dài hình (2)
Chiều rộng hình (1) gấp …. lần chiều rộng hình (2)
Chiều cao hình (1) gấp …. lần chiều cao hình (2)
Thể tích hình (1) gấp …. lần thể tích hình (2) Phương pháp giải:
Chúng ta sử dụng công thức tính thể tích: Thể tích = Chiều dài × Chiều rộng
× Chiều cao (phải có cùng đơn vị đo).
Sau đó, từ kết quả tính toán trong bảng, chúng ta có thể so sánh chiều dài,
chiều rộng, chiều cao và thể tích của hai hình hộp chữ nhật (1) và (2). Đáp án
Hình hộp chữ nhật (1) (2) Chiều dài 2m 1m Chiều rộng 1m 0,5m Chiều cao 0,4m 0,2m Thể tích 0,8m3 0,1m3
b. Chiều dài hình (1) gấp 2 lần chiều dài hình (2)
Chiều rộng hình (1) gấp 2 lần chiều rộng hình (2)
Chiều cao hình (1) gấp 2 lần chiều cao hình (2)
Thể tích hình (1) gấp 8 lần thể tích hình (2) 3. Bài tập tự luyện
Bài 1: Tính thể tích của hình hộp chữ nhật theo các kích thước sau:
a) Chiều dài 6,5m; chiều rộng 4m; chiều cao 4,5m
b) Chiều dài 25cm, chiều rộng 2dm, chiều cao 3dm
Bài 2: Tính thể tích của hình lập phương có cạnh lần lượt là 7dm, 4,3cm, 2,4m.
Bài 3: Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lập phương có cạnh 3,5cm.
Bài 4: Tính thể tích của một hình hộp chữ nhật có chiều dài 8cm, chiều rộng
5cm, chiều cao 5cm, sau đó tính thể tích của một hình lập phương có cạnh
bằng trung bình cộng của 3 kích thước hình hộp chữ nhật trên.
Bài 5: Tính thể tích của khối gỗ hình hộp chữ nhật ban đầu có chiều dài 1,2m,
chiều rộng 1m, chiều cao 50cm, sau khi cắt đi một phần là hình lập phương có cạnh 30cm.
Bài 6: Biết tỉ số thể tích của hai hình lập phương là 3:4, và thể tích của hình
lập phương bé là 60 cm³, hãy tính thể tích của hình lập phương lớn.
Bài 7: Tính thể tích của một hình hộp chữ nhật có diện tích xung quanh bằng
448 cm², chiều cao 8cm, và chiều dài hơn chiều rộng 4cm.
Bài 8: Tính thể tích của một hình lập phương khi biết diện tích toàn phần của nó là 294 cm².
Bài 9: Tính thể tích của hòn Non Bộ sau khi thả vào một bể cá hình hộp chữ
nhật có chiều dài 1,2m, chiều rộng 0,4m, chiều cao 0,6m, và mực nước trong
bể tăng từ 35cm lên 47cm.
Bài 10: Cho một bể cá hình hộp chữ nhật bằng kính với chiều dài 80cm,
chiều rộng 50cm, và chiều cao 45cm. Tính:
a) Diện tích bề mặt kính của bể cá.
b) Mực nước trong bể cá sau khi cho vào một hòn đá có thể tích 10dm³.
Document Outline

• Giải Vở bài tập Toán lớp 5 bài 120 Luyện tập chung
  • 1. Lý thuyết tính thể tích toán lớp 5
    • 1.1. Thể tích hình hộp chữ nhật là gì?
    • 1.2. Công thức tính thể tích hình hộp chữ nhật toá
    • 1.3. Hướng dẫn cách tính thể tích hình hộp chữ nhậ
  • 2. Giải Vở bài tập Toán lớp 5 bài 120 Luyện tập ch
  • 3. Bài tập tự luyện