Giao điểm là gì? Tính chất giao điểm và Cách vẽ giao điểm
Trong thực tế, ta bắt gặp rất nhiều hình ảnh về giao điểm. Vậy giao điểm là gì? Trong bài viết này, Luật
Minh Khuê sẽ trình bày một số kiến thức trọng tâm như khái niệm và cách xác định giao điểm của hai
đường thẳng, cùng với đó là các dạng bài tập hay và ví dụ để từ đó cung cấp những thông tin bổ ích cho quý bạn đọc
Mục lục bài viết
1. Giao điểm là gì?
• Trong hình học, một giao điểm là một điểm cùng thuộc về hai, hoặc nhiều hơn, đoạn thẳng,
tia, hoặc đường thẳng, đường cong, mặt phẳng, hoặc các bề mặt hoặc các hình khối khác
nhau. Giao điểm là điểm giao nhau của hai đường thẳng
• Giống như là hai đường thẳng cắt nhau tại O • O: Giao điểm
• Tương tự, giao tuyến là đường thẳng hoặc đường cong cùng thuộc về hai hoặc nhiều hơn,
đường thẳng, đường cong hoặc mặt phẳng, bề mặt hoặc các hình khối khác nhau.
• Trong hình học Ơclít, hai đường thẳng khác nhau, có một giao điểm hoặc không có giao điểm
nào nếu chúng song song với nhau.
• Việc xác định giao điểm trong hình học phẳng là một bài toán đại số tuyến tính, tìm nghiệm
cho hệ phương trình tuyến tính. Trong hình học phức tạp hơn, việc xác định giao điểm hoặc
giao tuyến tương ứng với tìm nghiệm của hệ phương trình phi tuyến, có thể được thực hiện
bằng phương pháp số, ví dụ dùng vòng lặp Newton. Ví dụ, việc tìm các giao điểm giữa một
đường thẳng với một đường conic (đường tròn, elíp, parabon,...) hoặc với một mặt bậc hai
(mặt cầu, mặt trụ, hypeboloit,...) dẫn đến việc giải quyết hệ phương trình bậc hai.
2. Các dạng toán về giao điểm của 2 đường thẳng
2.1 Dạng 1: Bài toán tìm giao điểm của 2 đường thẳng
*Phương pháp giải: Muốn tìm giao điểm của hai đường thẳng, ta xác định một điểm chung duy nhất
của hai đường thẳng đó, khi đó điểm chung tìm được chính là giao điểm mà ta cần tìm.
Bài tập vận dụng
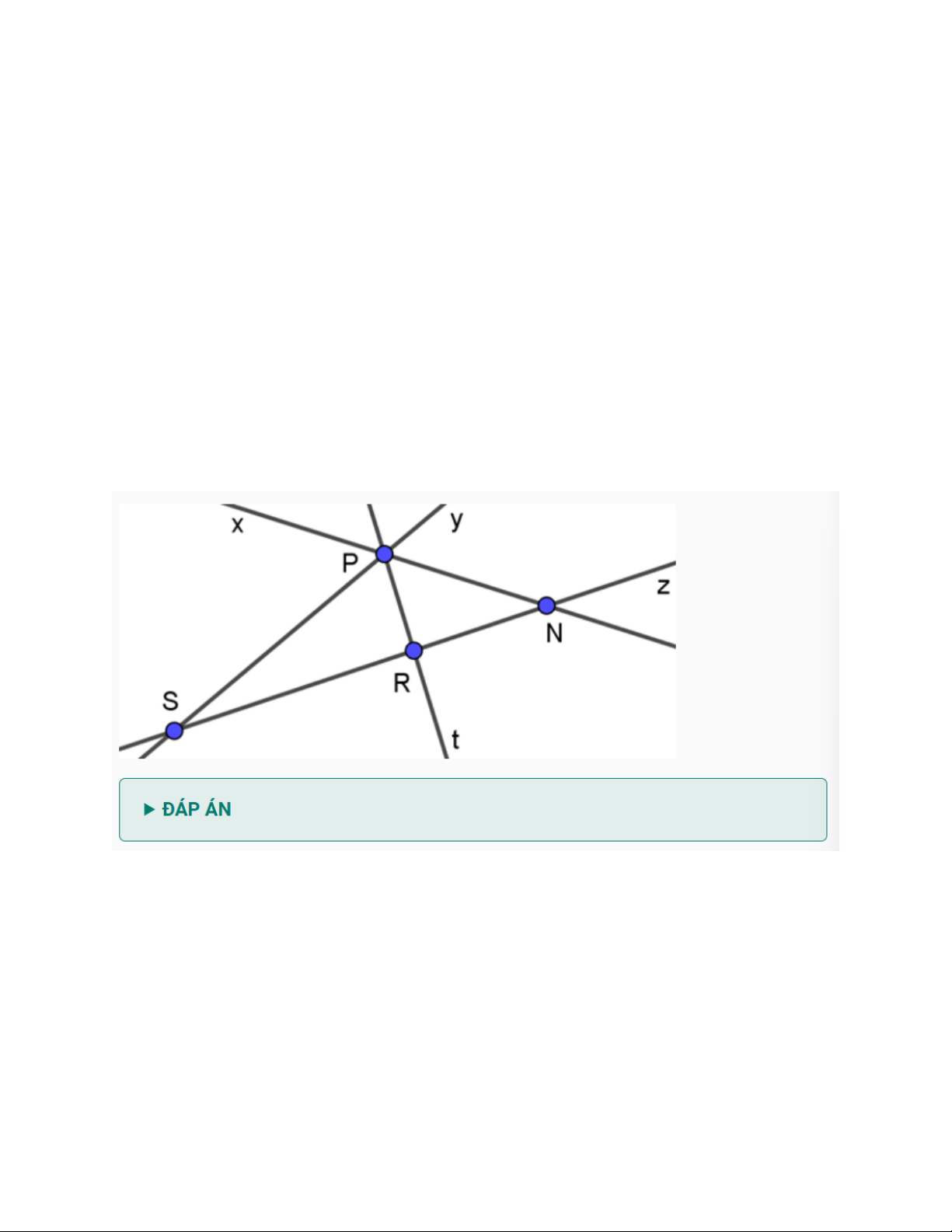
Em hãy quan sát hình vẽ dưới đây và chỉ ra các giao điểm của các cặp đường thẳng cắt nhau đó.
2.2 Dạng 2: Bài tập tính số giao điểm
Ví dụ 1: Cho n (n>1) đường thẳng, biết hai đường thẳng bất kỳ nào trong n đường thẳng đó luôn cắt
nhau tại một điểm và không có ba đường thẳng nào cùng có một điểm chung. Hãy tính số giao điểm của chúng.
*Phương pháp giải:
• Ta chọn ra 1 đường thẳng trong n đường thẳng đã cho, khi đó đường thẳng này sẽ cắt n-1
đường thẳng còn lại và số giao điểm được tạo ra là: n-1 (giao điểm);
• Vì có n đường thẳng nên số giao điểm được tạo ra là: n * (n-1) (giao điểm);
• Số giao điểm bị lặp lại 2 lần nên số giao điểm thực tế là: n * (n-1) : 2 (giao điểm).
Đáp số: Số giao điểm cần tính là n * (n-1) : 2 giao điểm.
Ví dụ 2: Cho 10 đường thẳng, biết hai đường thẳng bất kỳ nào trong 10 đường thẳng đó luôn cắt nhau
tại một điểm và không có ba đường thẳng nào cùng có một điểm chung. Hãy tính số giao điểm của chúng
Phương pháp giải
• Ta chọn ra 1 đường thẳng trong 10 đường thẳng đã cho, khi đó đường thẳng này sữ cắt 9
đường thẳng còn lại và số giao điểm được tạo ra là: 9 (giao điểm);
• Vì có 10 đường thẳng nên số giao điểm được tạo ra là: 10 * 9 = 90 (giao điểm);
• Số giao điểm bị lặp lại 2 lần nên số giao điểm thực tế là: 90 : 2 = 45 (giao điểm).
Đáp số : Số giao điểm cần tính là 45 giao điểm.
Bài tập vận dụng:
Cho 32 đường thẳng, biết hai đường thẳng bất kỳ nào trong 32 đường thẳng đó luôn cắt nhau tại một
điểm và không có ba đường thẳng nào cùng có một điểm chung. Hãy tính số giao điểm của chúng.
3. Bài tập có liên quan đến giao điểm của hai đường thẳng
Bài tập 1: Cho ba điểm S, Q, T không thẳng hàng. Em hãy vẽ các đường thẳng SQ, ST và QT và cho biết
ba điểm S, Q, T lần lượt là giao điểm của cặp đường thẳng nào?
Hướng dẫn giải:
• Điểm S là giao điểm của đường thẳng SQ và đường thẳng ST;
• Điểm Q là giao điểm của đường thẳng SQ và đường thẳng QT;
• Điểm T là giao điểm của đường thẳng ST và đường thẳng QT.
Bài tập 2: Cho 218 đường thẳng, biết hai đường thẳng bất kỳ nào trong 218 đường thẳng đó luôn cắt
nhau tại một điểm và không có ba đường thẳng nào cùng có một điểm chung. Hãy tính số giao điểm của chúng.
Hướng dẫn giải:
• Ta chọn ra 1 đường thẳng trong 218 đường thẳng đã cho, khi đó đường thẳng này sẽ cắt 217
đường thẳng còn lại và số giao điểm được tạo ra là 217 (giao điểm);
• Vì có 218 đường thẳng nên số giao điểm được tạo ra là: 218 * 217 = 47306 (giao điểm);
• Số giao điểm bị lặp lại 2 lần nên số giao điểm thực tế là: 47306 : 2 = 23653 (giao điểm).
Đáp số: Số giao điểm cần tính là 23653 giao điểm
4. Cách tìm giao điểm của đường thẳng, mặt phẳng
- Tìm giao điểm của đường thẳng và mặt phẳng là tìm các điểm chung của đường thẳng và mặt phẳng.
- Trường hợp ta tìm giao điểm của a với một đường thẳng b nào đó nằm trong (P).
Trường hợp không thấy đường thẳng b, ta thực hiện theo các bước sau:
• Tìm một mặt phẳng (Q) chứa a.
• Tìm giao tuyến b của (P) và (Q).
• Gọi: A = a giao b thì: A = a giao (P)
Lưu ý: Hai đường thẳng cắt nhau thuộc một mặt phẳng.
5. Đường trung tuyến
5.1 Khái niệm đường trung tuyến của tam giác
Đường trung tuyến của một tam giác được định nghĩa là đoạn thẳng nối từ một đỉnh của tam giác đến
trung điểm của cạnh đối diện. Chính vì vật, với mỗi tam giác bất kỳ, chúng ta sẽ có được 3 đường
trung tuyến tới từ 3 đỉnh.
Ví dụ: Giả sử tam giác ABC có điểm E là trung điểm của cạnh BC. Nối E với A ta được đường trung
tuyến AE ứng với cạnh BC hoặc ứng với đỉnh A. Nếu trung điểm của 2 cạnh AC và AB còn lại lần lượt là
F và L thì ta có được 2 đường trung tuyến BF và CL.
5.2 Tính chất ba đường trung tuyến của tam giác
Mỗi loại đường trong một tam giác đều thể hiện sự đặc trưng riêng biệt của mình thông qua những
tính chất. Đương nhiên, đường trung tuyến cũng không phải là trường hợp ngoại lệ.
Chúng ta có định lý về tính chất ba đường trung tuyến của tam giác như sau: 3 đường trung tuyến của
tam giác cùng đi qua 1 điểm. Điểm này cách các đỉnh của tam giác một đoạn bằng 2/3 độ dài của chính
các đường trung tuyến đi qua đỉnh đó. Giao điểm này được gọi là trọng tâm.
Ví dụ: Tam giác ABC có trung điểm của 3 cạnh: AB, AC, BC lần lượt là E, F, L. 3 đường trung tuyến CE,
BF và AL cắt nhau tại 1 điểm đặt tên là G. G chính là trọng tâm của tam giác ABC. Trong đó: EG/EC = FG/FB = IG/IB = 2/3.
6. Đường trung trực
6.1 Khái niệm đường trung trực của tam giác
Trong một tam giác, đường trung trực của mỗi cạnh gọi là đường trung trực của tam giác đó
Chẳng hạn như trong tam giác ABC: a là đường trung trực ứng với cạnh BC, b là đường trung trực ứng
với cạnh AC và c là đường trung trực ứng với cạnh AB.
• Trong mỗi tam giác đều có ba đường trung trực
• Tính chất của đường trung trực: Trong một tam giác cân, đường trung trực của cạnh đáy đồng
thời là đường trung tuyến ứng với cạnh này
6.2 Tính chất ba đường trung trực của tam giác
Tính chất ba đường trung trực của tam giác cụ thể như sau:
• Bất kỳ tam giác nào cũng được sở hữu 3 đường trung trực, tính chất chung của 3 đường này
như sau: Cùng đi qua một điểm, điểm này cách đều ba đỉnh của tam giác đó.
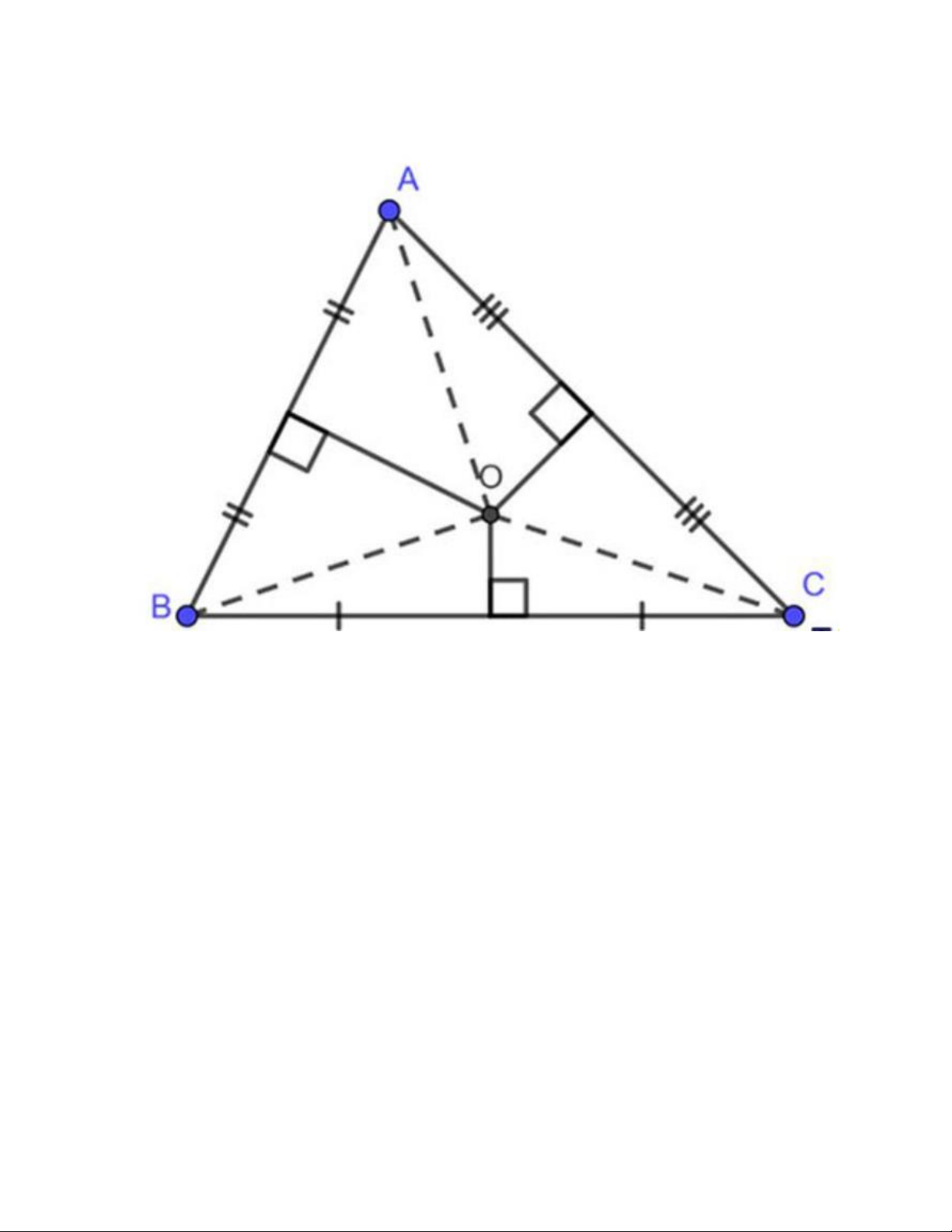
Chẳng hạn như: O là giao điểm ba đường trung trực của tam giác ABC, suy ra ta có OA = OB = OC
Lưu ý: nếu một đường tròn lấy giao điểm của 3 đường trung trực làm tâm và đi qua 3 đỉnh của tam
giác thì đường tròn đó được gọi là đường tròn ngoại tiếp tam giác.
Chẳng hạn như: O là giao điểm của 3 đường trung trực tam giác ACB và một đường tròn tâm O đi qua
ba đỉnh A, B, C thì đường tròn đó là đường tròn ngoại tiếp tam giác ABC.