lOMoARcPSD| 41967345 KIẾ N TRÚC MÁY TÍNH
Gi ả ng viên: ThS. Phan Thanh Toàn 1 v1.0014102207 1 lOMoARcPSD| 41967345 BÀI 1 KIẾNTRÚCC Ơ BẢN CỦAM ÁY VIT ÍNH
Gi ả ng viên: ThS. Phan Thanh Toàn 2 v1.0014102207 lOMoARcPSD| 41967345 MỤC TIÊU BÀI HỌC 3 v1.0014102207 lOMoARcPSD| 41967345
CÁC KIẾN THỨC CẦN CÓ 4 v1.0014102207 lOMoARcPSD| 41967345 HƯỚNG DẪN HỌC 5 v1.0014102207 lOMoARcPSD| 41967345 CẤU TRÚC NỘI DUNG 6 v1.0014102207 lOMoARcPSD| 41967345
1.1. MÁY TÍNH VÀ CÁC THÀNH PHẦN CƠ BẢN 1.1.1
. M ộ t s ố khái ni ệ m 1.1.2 . S ơ ồ kh ố i và
c ơ b ả n và phân lo ạ i nguyên t ắ c thông tin máy tính
tín hi ệ u trong máy tính
1.1.3 . Các thi ế t b ị ngo ạ i vi c ơ b ả n 7 v1.0014102207 lOMoARcPSD| 41967345
1.1.1. MỘT SỐ KHÁI NIỆM CƠ BẢN VÀ PHÂN LOẠI MÁY TÍNH ộng logic. 8 v1.0014102207 lOMoARcPSD| 41967345
1.1.2. SƠ ĐỒ KHỐI VÀ NGUYÊN TẮC THÔNG TIN TÍN HIỆU TRONG MÁY TÍNH
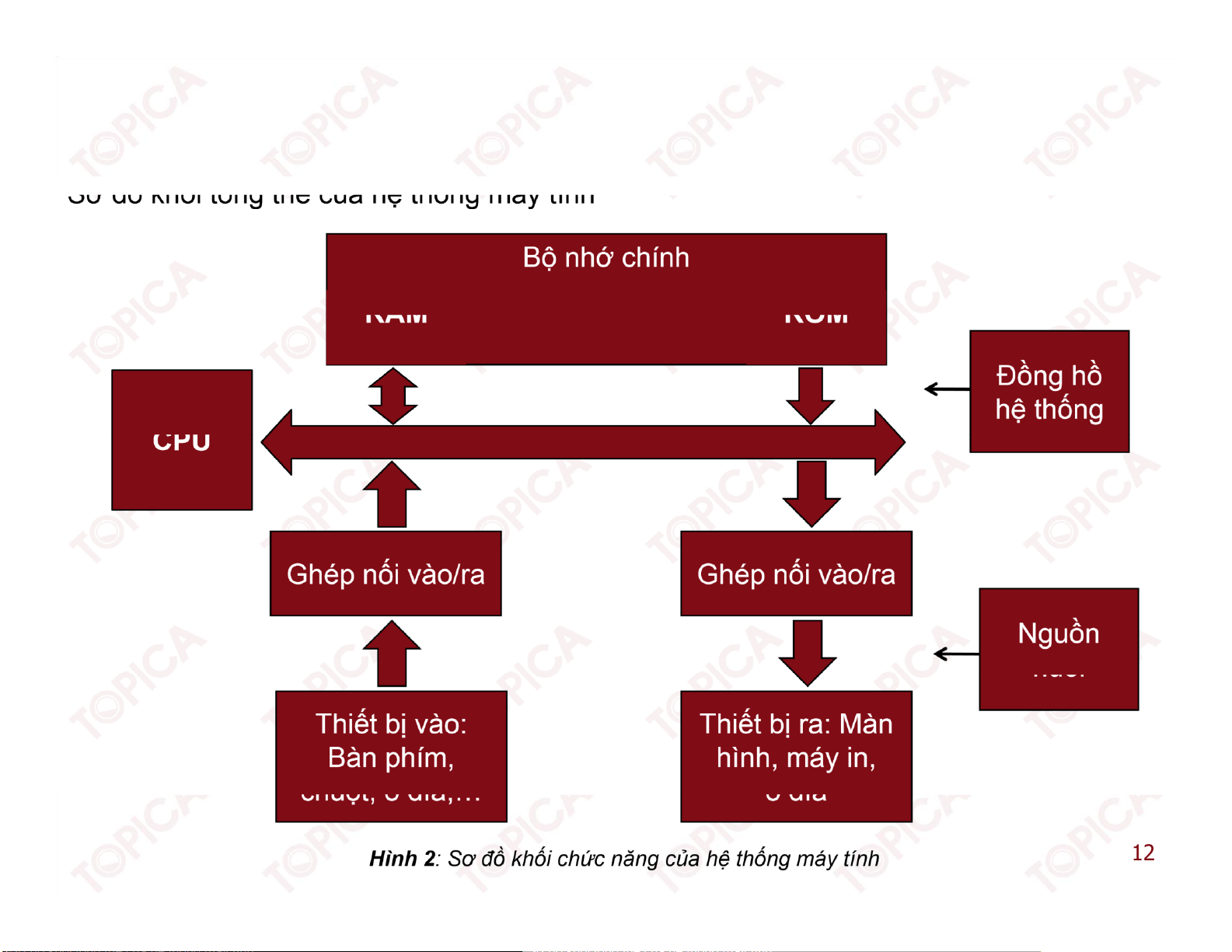
Sơ ồ khối của máy tính: 9 v1.0014102207 lOMoARcPSD| 41967345
1.1.2. SƠ ĐỒ KHỐI VÀ NGUYÊN TẮC THÔNG TIN TÍN HIỆ (tiếp theo) 1. Màn hình 10 v1.0014102207 lOMoARcPSD| 41967345
1.1.2. SƠ ĐỒ KHỐI VÀ NGUYÊN TẮC THÔNG TIN TÍN HIỆU TRONG MÁY TÍNH (tiếp theo) U TRONG MÁY TÍNH 11 v1.0014102207 lOMoARcPSD| 41967345
1.1.2. SƠ ĐỒ KHỐI VÀ NGUYÊN TẮC THÔNG TIN TÍN HIỆ (tiếp theo) 12 v1.0014102207 lOMoARcPSD| 41967345
1.1.2. SƠ ĐỒ KHỐI VÀ NGUYÊN TẮC THÔNG TIN TÍN HIỆU TRONG MÁY TÍNH (tiếp theo) 13 v1.0014102207 lOMoARcPSD| 41967345
1.1.2. SƠ ĐỒ KHỐI VÀ NGUYÊN TẮC THÔNG TIN TÍN HIỆU TRONG MÁY TÍNH (tiếp theo) 14 v1.0014102207 lOMoARcPSD| 41967345
1.1.2. SƠ ĐỒ KHỐI VÀ NGUYÊN TẮC THÔNG TIN TÍN HIỆU TRONG MÁY TÍNH (tiếp theo) ngoại vi. 15 v1.0014102207 lOMoARcPSD| 41967345
1.1.2. SƠ ĐỒ KHỐI VÀ NGUYÊN TẮC THÔNG TIN TÍN HIỆU TRONG MÁY TÍNH (tiếp theo) 16 v1.0014102207 lOMoARcPSD| 41967345
1.1.2. SƠ ĐỒ KHỐI VÀ NGUYÊN TẮC THÔNG TIN TÍN HIỆU TRONG MÁY TÍNH (tiếp theo)
Hình 3: CPU sử dụng bus ể trao ổi thông tin với thiết bị 2 17 v1.0014102207 lOMoARcPSD| 41967345
1.1.2. SƠ ĐỒ KHỐI VÀ NGUYÊN TẮC THÔNG TIN TÍN HIỆU TRONG MÁY TÍNH (tiếp theo)
Các linh kiện trên bảng mạch chính (mainboard) 18 v1.0014102207 lOMoARcPSD| 41967345
1.1.2. SƠ ĐỒ KHỐI VÀ NGUYÊN TẮC THÔNG TIN TÍN HIỆU TRONG MÁY TÍNH (tiếp theo) 19 v1.0014102207 lOMoARcPSD| 41967345
1.1.3. THIẾT BỊ NGOẠI VI CƠ BẢN lOMoARcPSD| 41967345
1.2. CÁC PHÉP TÍNH SỐ TRONG MÁY TÍNH 1.2.1 . Các h ệ ế m 1.2.2 . Mã hóa ký t ự 1.2.3 . Các mã phát 1 . .2.4 Bi ể u di ễ n hi ệ n và s ử a l ỗ i s ố nguyên 1.2 . .6 Các phé p tính 1 . 2 . 5 . S ố c ó d ấ u s ố h ọ c v ớ i s ố ch ấ m ộ ng nh ị phân 21 v1.0014102207 lOMoARcPSD| 41967345
1.2.1. CÁC HỆ ĐẾM Hệ ếm 10 (thập phân) lOMoARcPSD| 41967345
1.2.1. CÁC HỆ ĐẾM (tiếp theo) 23 v1.0014102207 lOMoARcPSD| 41967345
Hệ ếm 2 (nhị phân) lOMoARcPSD| 41967345
1.2.2. MÃ HÓA KÍ TỰ 25 v1.0014102207 lOMoARcPSD| 41967345 ặc biệt. lOMoARcPSD| 41967345
1.2.3. CÁC MÃ PHÁT HIỆN VÀ SỬA L ỖI
Khi truyền tín hiệu giữa các thành phần trong hệ thống có thể tín hiệu bị ảnh hưởng bởi nhiễu, thiết bị,…
Cần có các phương pháp phát hiện và sửa các lỗi.
Phương pháp thông dụng là sử dụng các mã phát hiện và sửa lỗi.
Phát hiện lỗi với bit chẵn lẻ (parity)
 Truyền một dãy bit sẽ thêm một bit gọi là bit chẵn lẻ;
 Bit parity chẵn (lẻ) là bit thêm vào ể làm cho số lượng bit 1 trở thành số chẵn (lẻ).
Ví dụ: Sử dụng parity chẵn
Dãy bit cần truyền là: 0110 1000 thì bit cần thêm là 1;
Dãy bit cần truyền là: 0110 1001 thì bit cần thêm là 0. 27 v1.0014102207 lOMoARcPSD| 41967345
1.2.3. CÁC MÃ PHÁT HIỆN VÀ SỬA LỖI (tiếp theo)
 Phát hiện lỗi: Bên thu khi nhận ược dãy bit sẽ dựa vào bit chẵn lẻ ể phát hiện lỗi. p theo) 28 v1.0014102207 lOMoARcPSD| 41967345
1.2.3. CÁC MÃ PHÁT HIỆN VÀ SỬA LỖI (tiế
Phát hiện lỗi với bit chẵn lẻ cho khối dữ liệu (parity) 29 v1.0014102207 lOMoARcPSD| 41967345
1.2.3. CÁC MÃ PHÁT HIỆN VÀ SỬA LỖI (tiếp theo)
 Truy ề nm ộ tkh ố icácbit.
 S ử d ụ ng2lo ạ ibitki ể mtrach ẵ nl ẻ : bitch ẵ nl ẻ theochi ề ud ọ c(VRC)vàbitch ẵ n
l ẻ theo chi ề u ngang ( LRC ) .  Víd ụ Bit t ừ 1 t ừ 2 t ừ 3 t ừ 4 t ừ 5 t ừ 6 t ừ 7 LRC D 0 1 1 0 0 0 1 1 0 D 1 0 0 1 0 1 1 0 1 D 1 1 0 1 1 0 1 1 2 D 3 0 0 1 0 1 1 1 0 (VRC )
B ả ng 1 : S ử d ụ ng bit ch ẵ n -l ẻ ch ẵ n cho kh ố i d ữ li ệ u 30 v1.0014102207 lOMoARcPSD| 41967345
1.2.3. CÁC MÃ PHÁT HIỆN VÀ SỬA LỖI (tiế
Phát hiện lỗi bằng mã dư thừa CRC (Cyclic Redundancy Check) 31 v1.0014102207 lOMoARcPSD| 41967345
1.2.3. CÁC MÃ PHÁT HIỆN VÀ SỬA LỖI (tiếp theo) 32 v1.0014102207 lOMoARcPSD| 41967345
1.2.3. CÁC MÃ PHÁT HIỆN VÀ SỬA LỖI (tiếp theo) 33 v1.0014102207 lOMoARcPSD| 41967345
1.2.3. CÁC MÃ PHÁT HIỆN VÀ SỬA LỖI (tiếp theo) 34 v1.0014102207 lOMoARcPSD| 41967345 ỂU DIỄN SỐ 1.2.4. BI
NGUYÊN KHÔNG DẤU VÀ CÓ DẤU
Một số nhị phân n bit sẽ biểu diễn ược 2n số nguyên không dấu có giá trị 0 – 2n -1.
Ví dụ: Sử dụng 1 byte = 8 bit có thể biểu diễn ược các số nguyên từ 0 – 255.
Để biểu diễn số nguyên có dấu ta sử dụng bit tận cùng bên trái làm bit dấu:
bit = 0 biểu diễn số dương; bit = 1 biểu diễn số âm.
Với n bit có thể biểu diễn các số có dấu từ -(2n-1 ) ến +(2n-1 -1). Số bù 1
 Số bù 1 của một số nhị phân là một số nhị phân mà khi cộng với số nhị phân ã
cho thì tất cả các bit ều bằng 1.
 Tìm số bù 1: số bù 1 của một số ược sinh ra bằng cách ảo các bit 0 thành 1 và bit 1 thành 0.
Ví dụ: số 1011 có số bù 1 là: 0100 Số bù 2
 Số bù 2 của một số bằng số bù 1 của số ó và cộng thêm với 1. Ví dụ:
số 1011 có số bù 2 là: 0101 35 v1.0014102207 lOMoARcPSD| 41967345
1.2.3. CÁC MÃ PHÁT HIỆN VÀ SỬA LỖI (tiếp theo)
 A – B = A + (-B): Phép trừ ược thực hiện thông qua phép cộng. Để thực
hiện AB ta lấy A cộng với số bù 2 của B (Vì số bù 2 của B là –B). 36 v1.0014102207 lOMoARcPSD| 41967345 ỂU DIỄN SỐ 1.2.5. BI
CÓ DẤU CHẤM ĐỘNG 37 v1.0014102207 lOMoARcPSD| 41967345
1.2.6. CÁC PHÉP TOÁN TRONG HỆ ĐẾM NHỊ Mỗi số dấu chấm e 38 v1.0014102207 lOMoARcPSD| 41967345 ỂU DIỄN SỐ 1.2.5. BI
CÓ DẤU CHẤM ĐỘNG 39 v1.0014102207 lOMoARcPSD| 41967345
1.2.6. CÁC PHÉP TOÁN TRONG HỆ ĐẾM NHỊ PHÂN Phé p c n ộ g  C ộ ng2bitnh ị phân A B A+B 0 0 0 0 1 1 1 0 1 1 1 10
 C ộ ng2s ố nh ị phânkhôngd ấ u
Th ự c hi ệ n c ộ ng t ừ ng bit t ừ ph ả i qua trái .
Víd ụ : 11 (3) 11.011 (3.375) 110 (6) 10.110 (2.750) 1001 (9) 110.001 (6.125) 40 v1.0014102207 lOMoARcPSD| 41967345
1.2.6. CÁC PHÉP TOÁN TRONG HỆ ĐẾM NHỊ PHÂN (tiế p theo) 41 v1.0014102207 lOMoARcPSD| 41967345
1.2.6. CÁC PHÉP TOÁN TRONG HỆ ĐẾM NHỊ PHÂN (tiếp theo) Phé p tr ừ  Tr ừ 2 bitnh ị phân A B A-B 0 0 0 0 1 1 Nh ớ 1 cho bit cao h ơ n 1 0 1 1 1 0
 Tr ừ 2 s ố nh ị phânkhôngd ấ u
Th ự c hi ệ n tr ừ t ừ ng bit t ừ ph ả i qua trái
Víd ụ : 1011 (11) 0101 (5) 0110 (6) 42 v1.0014102207 lOMoARcPSD| 41967345
1.2.6. CÁC PHÉP TOÁN TRONG HỆ ĐẾM NHỊ PHÂN (tiếp theo) Phép chia Chia2s ố nh ị phân Th ự chi ệ n:Chia2s
ố nh ị phân ượ cth ự chi ệ nbìnhth ườ ngnh ư chia2s ố th ậ p phân .
Víd ụ : 10011111:1100 43 v1.0014102207 lOMoARcPSD| 41967345
1.2.6. CÁC PHÉP TOÁN TRONG HỆ ĐẾM NHỊ PHÂN (tiếp theo) Bi
ể udi ễ ns ố cód ấ u: Đ ể bi ể udi ễ ns ố nh ị hân p cód ấ u , tas ử d n ụ g m tbit ộ ở t ncù ậ n g bêntráilàmbitd
ấ u,th ườ ngqui ướ cbitd ấ u=0làs
ố d ươ ng,bitd ấ u=1làs ố âm.
Cácbitcònl ạ ilàbitgiátr ị .
Ví d ụ : 0110100=+52 1110100=-52 Bit d ấ u Bit d ấ u
Cáchbi ể udi ễ nnàyd ẫ n ế ncó2giátr ị 0(Vì+0=-0).
Đồ ngth ờ icáchbi ể udi ễ nnày
th ườ ngd ẫ n ế nsaisótkhith ự chi ệ nphéptoán.
Víd ụ : 01000 (+8) 01000 (+8) + 10010 (- 2 ) + 01010 (+10) 11010 (-10) 10010 (-2) 44 v1.0014102207 lOMoARcPSD| 41967345
1.2.6. CÁC PHÉP TOÁN TRONG HỆ ĐẾM NHỊ PHÂN (tiếp theo) Số bù 1 và số bù 2
 Số bù 1 của một số nhị phân là một số nhị phân mà khi cộng với số nhị phân ã
cho thì tất cả các bit ều bằng 1.
Tìm số bù 1 của một số ta ảo tất cả các bit 0 thành 1 và 1 thành 0.
Ví dụ: Số nhị phân: 1101 sẽ có số bù 1 là: 0010 -12 110100 -9 110111 -21 1101011 45 v1.0014102207 lOMoARcPSD| 41967345
1.2.6. CÁC PHÉP TOÁN TRONG HỆ ĐẾM NHỊ PHÂN (tiếp theo)
 Số bù 2: Số bù 2 của một số nhị Bỏ qua bit số 6 (26) 101011
phân bằng số bù 1 của số ó cộng
với 1. Ví dụ: Số nhị phân 1101 sẽ có số bù 2 là: 0011
Cộng trừ 2 số có dấu dùng số bù 2
A + B: Cộng 2 số nhị phân có dấu tiến hành cộng bình thường như cộng 2 số nhị
phân không dấu, kể cả bit dấu. Lưu ý bit có trong số 2n bị loại khỏi kết quả.
Ví dụ 1: 001100 + 001001
Ví dụ 2: 110100 + 1101011 12 001100 9 001001 21 010101 46 v1.0014102207 lOMoARcPSD| 41967345
1.2.6. CÁC PHÉP TOÁN TRONG HỆ ĐẾM NHỊ PHÂN (tiếp theo) Tr
ừ 2 s ố cód ấ udùn g s ố bù2 A–B=A+(-B):Phéptr
ừ ượ cth ự chi ệ nthôngquaphépc
ộ ng. Để th ự chi ệ nA-B
tal ấ yAc ộ ngv ớ is ố bù2c ủ aB(Vìs ố bù2c ủ aBlà–B).
Ví d ụ 1 : 10 – 5 = 10 + ( - 5 ) 10 1010 10=1010 -5 1011 5=0101 S ố bù1c ủ a5là:1010 5 10101 S ố bù2c ủ a5là:1011 Lo ạ i b ỏ bit 1 0101
V ậ y ta có 10 – 5 = 1010 + 1011 5 10 47 v1.0014102207 lOMoARcPSD| 41967345
1.3. CÁC MẠCH ĐIỆN TỬ SỐ TRONG MÁY TÍNH 48 v1.0014102207 lOMoARcPSD| 41967345
1.3.1. ĐẠI SỐ LOGIC A B Z A B Z 0 0 0 0 0 0 0 1 0 0 1 1 1 0 0 1 0 1 1 1 1 1 1 1 49 v1.0014102207 lOMoARcPSD| 41967345
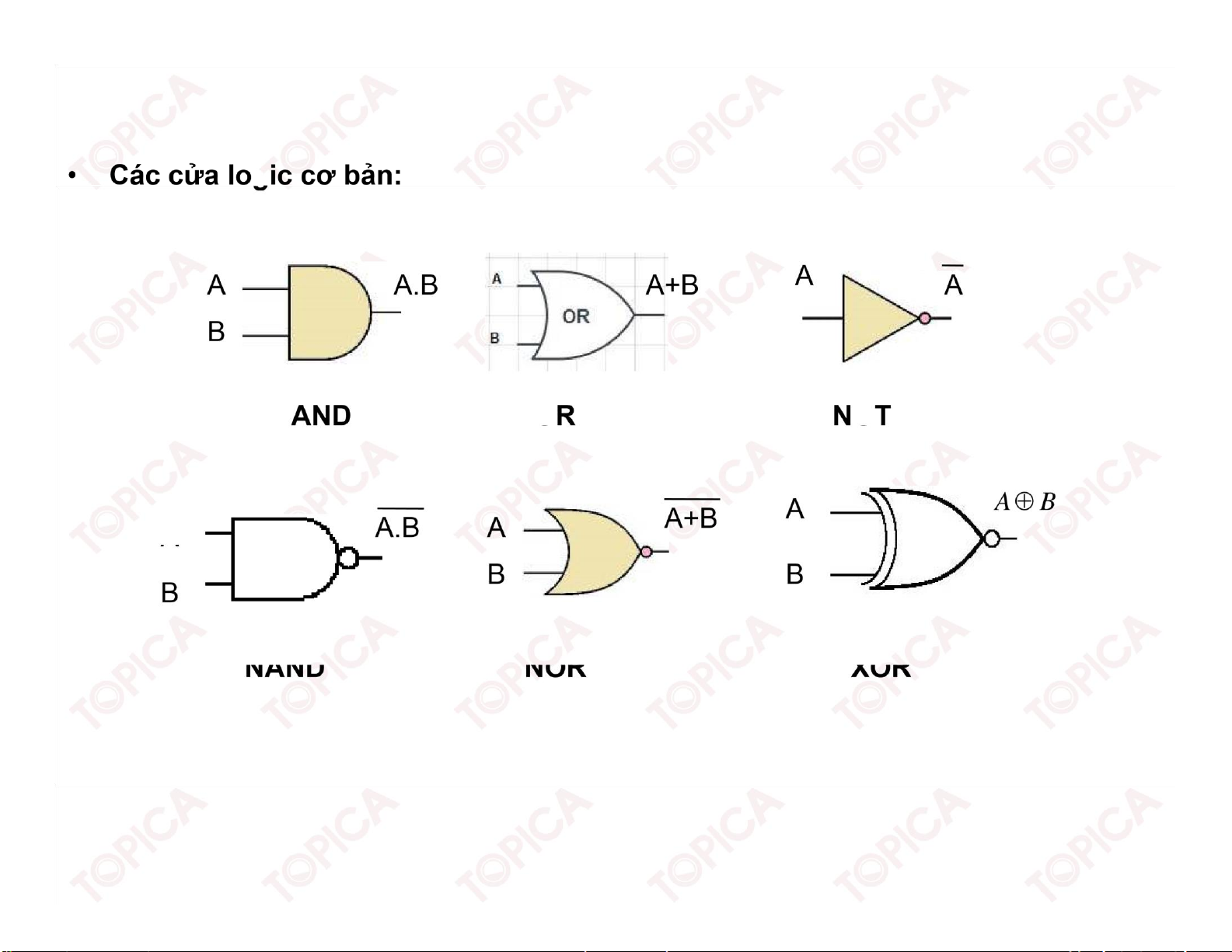
Hàm logic là hàm có một hoặc nhiều biến, mỗi biến chỉ nhận một trong hai giá trị là Hàm AND Hàm OR HàmNAND: ZAB . HàmNOR: ZAB HàmXOR: ZAB 50 v1.0014102207 lOMoARcPSD| 41967345
1.3.1. ĐẠI SỐ LOGIC (tiếp theo) 51 v1.0014102207 lOMoARcPSD| 41967345
1.3.2. CÁC MẠCH ĐIỆN TỬ LOGIC 52 v1.0014102207 lOMoARcPSD| 41967345
1.3.3. MẠCH SỐ HỌ 53 v1.0014102207 lOMoARcPSD| 41967345
1.3.3. MẠCH SỐ HỌ
C VÀ LOGIC (ALU) (tiếp theo) Chọn:
Số liệu có mức tích cực cao S3 M 1= S2
M 0= Các phép toán số học các S1 phép S0 C =1 N (không nh ớ ) toán CN =0 (Có nhớ) logic 0000 F=A F=A F=A-1 0001 F=A+B F=A+B F=(A+B)+1 0010 F=A.B F=(A+B)+1 F=A+B 0011 F=0 F=-1 F=0 54 v1.0014102207 lOMoARcPSD| 41967345
1.3.3. MẠCH SỐ HỌ 0100 F=A.B F=A+A.B F=A+A.B+1 0101 F=B F=(A+B)+A.B F=(A+B)+A.B+1 F=A-B-1 0110 F=A B F=A-B 0111 F=A.B F=A.B-1 F=A.B
Nguyên tắc hoạt ộng của mạch ALU 55 v1.0014102207 lOMoARcPSD| 41967345
1.3.3. MẠCH SỐ HỌ Chọn:
Số liệu có mức tích cực cao S3 S2 M=1 các S1 S0 phép toán
M=0 Các phép toán s ố h ọ c logic CN =1 (không nhớ) CN =0 (Có nhớ) 1000 F=A+B F=A+A.B F=A+A.B+1 1001 F=A B F=A+B F=A+B+1 F=(A+B)+A.B 1010 F=B F=(A+B)+A.B+1 56 v1.0014102207 lOMoARcPSD| 41967345
1.3.3. MẠCH SỐ HỌ 1011 F=A.B F=A.B-1 F=A.B 1100 F=1 F=A+A* F=A+B+1 1101 F=A+B F=(A+B)+A+1 F=(A+B)+A 1110 F=A+B F=(A+B)+A F=(A+B)+A+1 1111 F=A F=A-1 F=A
C VÀ LOGIC (ALU) (tiếp theo) 57 v1.0014102207 lOMoARcPSD| 41967345
TÓM LƯỢC CUỐI BÀI 58 v1.0014102207