










































































Preview text:
LỜI NÓI ĐẦU
Môn học kỹ thuật thủy khí nhằm trang bị cho sinh viên những kiến thức cơ bản về lý
thuyết của chất lỏng và chất khí cũng như kỹ thuật tính toán, thiết kế và mô phỏng một hệ
thống truyền động thủy khí.
Giáo trình này được chia làm 4 chương, trình bày từ những khái niệm cơ bản về thủy khí
đến các hệ truyền động thủy khí và cuối cùng là mô phỏng một hệ thống thực tế.
Giáo trình là tài liệu dùng cho sinh viên ngành Cơ khí, Tự động hóa, Thủy điện, nhiệt
điện và quản lý năng lượng của các trường. Nó cũng là tài liệu tham khảo bổ ích cho sinh
viên, kỹ sư và các cán bộ kỹ thuật muốn tìm hiểu về các khái niệm thủy khí và các hệ thống
thủy khí cơ bản ngày nay
Đây là lần xuất bản đầu tiên, chắc chắn cuốn sách này còn có những thiều sót. Chúng
tôi xin trân trọng cảm ơn và mong nhận được ý kiến đóng góp của bạn đọc để lần tái bản
sau cuốn sách này được hoàn thiện hơn.
Mọi ý kiến phản hồi xin gửi về địa chỉ:
Khoa Công nghệ Cơ khí - Đại học Điện lực
235 Hoàng Quốc Việt, Từ liêm, Hà nội Điện thoại: 04-2-2185580 Email: cnck@epu.edu.vn Tác giả MỤC LỤC
Lòi nói đầu .......................................................................................................... 1
Mục lục ................................................................................................................ 2
Chương 1. Tính chất vật lý cơ bản ..................................................................... 5
1.1.Các thông số trạng thái .................................................................................... 5
1.1.1 Thể tích riêng. ........................................................................................ 6
1.1.2. Áp suất. ................................................................................................ 6
1.1.3. Nhiệt độ. ............................................................................................... 7
1.1.4. Nội năng ............................................................................................... 7
1.1.5. Năng lượng đẩy (thế năng áp suất) ........................................................ 8
1.1.6. Entanpi ................................................................................................. 8
1.1.7. Entropi. ................................................................................................. 9
1.1.8. Execgi và Anecgi. ................................................................................. 9
1. 2. Phương trình trạng thái của chất khí. ............................................................ 9
1.2.1. Đối với khí lý tưởng .............................................................................. 9
1.2.2. Đối với khí thực .................................................................................... 10
1.3. Biến thiên thể tích môi chất ............................................................................ 10
1.3.1. Tính thay đổi thể tích do áp lực ............................................................. 10
1.3.2. Tính thay đổi thể tích do nhiệt độ .......................................................... 12
1..4. Sức căng mặt ngoài và hiện tượng mao dẫn ................................................... 12
1.5. Tính nhớt ....................................................................................................... 13
1.6. Tính bốc hơi và độ hoà tan của chất khí trong chất nước ................................ 14
1.7. Sự trao đổi nhiệt lượng và khối lượng ............................................................ 15
1.8. Lực tác dụng lên môi chất ............................................................................. 15
1.9. Tĩnh học chất khí ........................................................................................... 16
1.9.1. Chất khí nén được ................................................................................ 16
1.9.2. Khí quyển ............................................................................................. 17
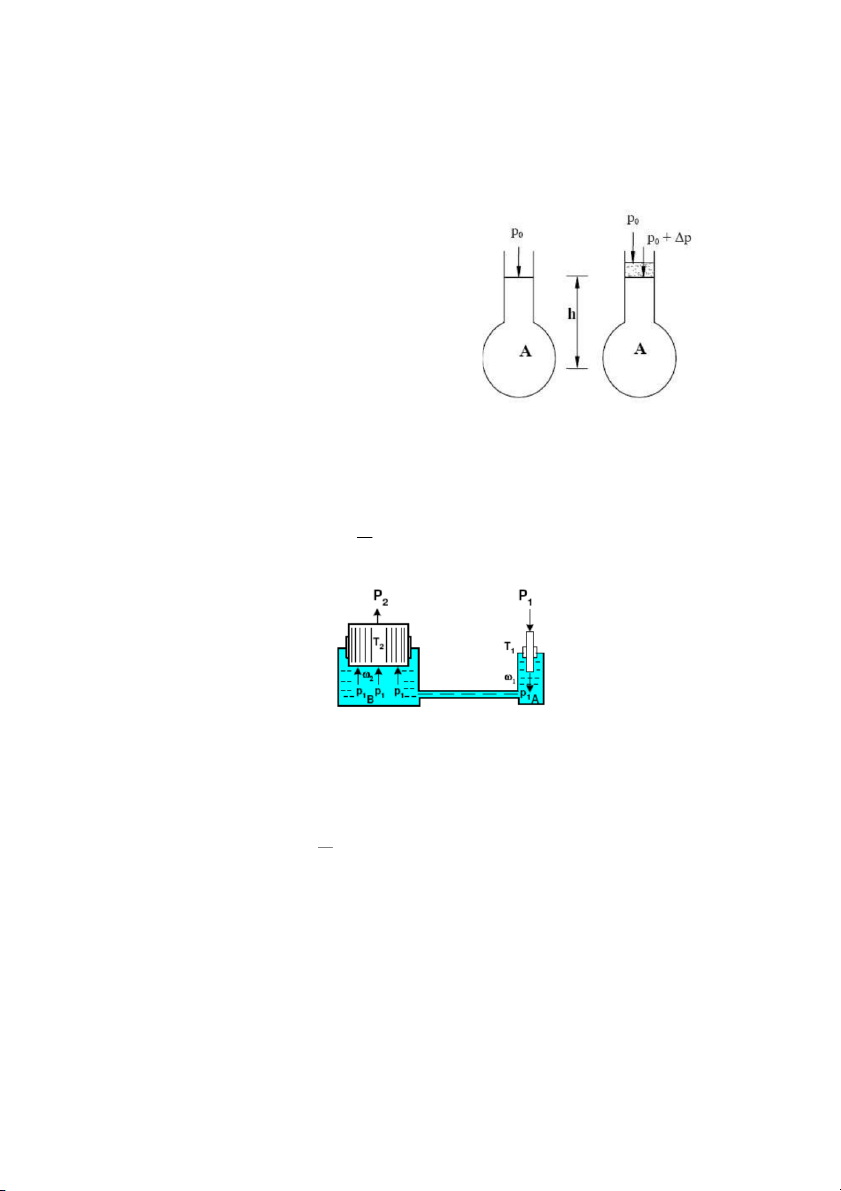
1.9.3. Khí cầu ................................................................................................. 19
Câu hỏi và bài tập chương 1 .................................................................................. 20
Chương 2. Tĩnh học chất lưu ............................................................................ 21
2.1. Khái niệm áp suất thuỷ tĩnh - áp lực ............................................................... 21
2.2. Các tính chất của áp suất thuỷ tĩnh ................................................................. 21
2.2.1. Tính chất 1 (phương và chiều). ............................................................. 21 2
2.2.2. Tính chất 2 (trị số). ............................................................................... 21
2.3. Phương trình vi phân của chất lỏng đứng cân bằng......................................... 22
2.4. Sự cân bằng của chất lỏng trọng lực ............................................................... 25
2.4. 1. Định luật bình thông nhau .................................................................... 25
2.4.2. Định luật pascal .................................................................................... 26
2.4.3. Biểu diễn áp suất bằng cột chất lỏng ..................................................... 27
2.5. Ý nghĩa hình học và năng lượng của phương trình cơ bản của thủy tĩnh ......... 28
2.5.1. Ý nghĩa hình học ................................................................................... 28
2.5.2. Ý nghĩa năng lượng .............................................................................. 28
2.6. Biểu đồ áp lực ................................................................................................ 29
2.7. Áp lực chất lỏng lên thành phẳng có hình dạng bất kỳ .................................... 30
2.7. 1. Trị số của áp lực .................................................................................. 31
2.7.2..Xác định phương, chiều của áp lực thuỷ tĩnh P ..................................... 32
2.7.3. Xác định điểm đặt của áp lực thuỷ tĩnh P .............................................. 32
2.8. Áp lưc chất lỏng lên thành phẳng hình chữ nhật có đáy đặt nằm ngang .......... 34
2.8.1. Xác định trị số của p ............................................................................. 34
2.8.2. Điểm đặt của áp lực. ............................................................................. 34
2.9. Áp lực của chất lỏng lên thàng cong. .............................................................. 37
Câu hỏi và bài tập chương 2 .................................................................................. 41
Chương 3. Động lực học chất lưu ....................................................................... 46
3.1. Khái niệm cơ bản ........................................................................................... 46
3.2. Các định nghĩa. .............................................................................................. 47
3.2.1. Quỹ đạo ................................................................................................ 47
3.2.2. Đường dòng .......................................................................................... 47
3.2.3. Dòng nguyên tố và dòng chảy ............................................................... 47
3.2.4. Những yếu tố thuỷ lực của dòng chảy ................................................... 48
3.2.5. Phân loại dòng chảy. ............................................................................. 49
3.3. Phương trình liên tục của dòng chảy ổn định .................................................. 50
3.4. Phương trình Becnuli của dòng nguyên tố chảy ổn định ................................. 51
3.4.1. Đối với chất lỏng lý tưởng .................................................................... 51
3.4.2. Phương trình Becbuli của dòng nguyên tố chất lỏng thực chảy ổn định . 53
3.4.3.Ý nghĩa phương trình Becnuli viết cho dòng nguyên tố chảy ổn định..... 53
3.4.4. Độ dốc thuỷ lực và độ dốc đo áp của dòng nguyên tố............................ 55 3
3.5. Phương trình becnuli của toàn dòng chất lỏng thực chảy ổn định ................... 56
3.5.1. Dòng chảy đổi dần ................................................................................ 56
3.5.2. Phương trình Becnuli của toàn dòng chất lỏng thực chảy ổn định ......... 57
3.6. Phương trình động lượng của toàn dòng chảy ổn định .................................... 60
3.6.1. Tính độ biến thiên động lượng của đoạn dòng ....................................... 60
3.6.2. Tính xung lượng của các ngoại lực. ...................................................... 62
3.6.3. Ý nghĩa vật lý của hệ số o. .................................................................. 62
3.7. Ứng dụng của phương trình Becnuli. .............................................................. 63
3.7.1. Ống Pitot .............................................................................................. 63
3.7.2. Ống Venturi .......................................................................................... 63
Câu hỏi và bài tập chương 3 .................................................................................. 67
Chương 4. Tính toán, thiết kế hệ thống thủy khí .............................................. 69
4.1. tổn thất cột nước ............................................................................................ 69
4.1.1. Các dạng tổn thất năng lượng. ............................................................... 69
4.1.2. Hai trạng thái chuyển động của chất lỏng. ............................................. 69
4.1.3. Tổn thất cột nước dọc đường ................................................................ 71
4.1.4. Tổn thất cục bộ ..................................................................................... 74
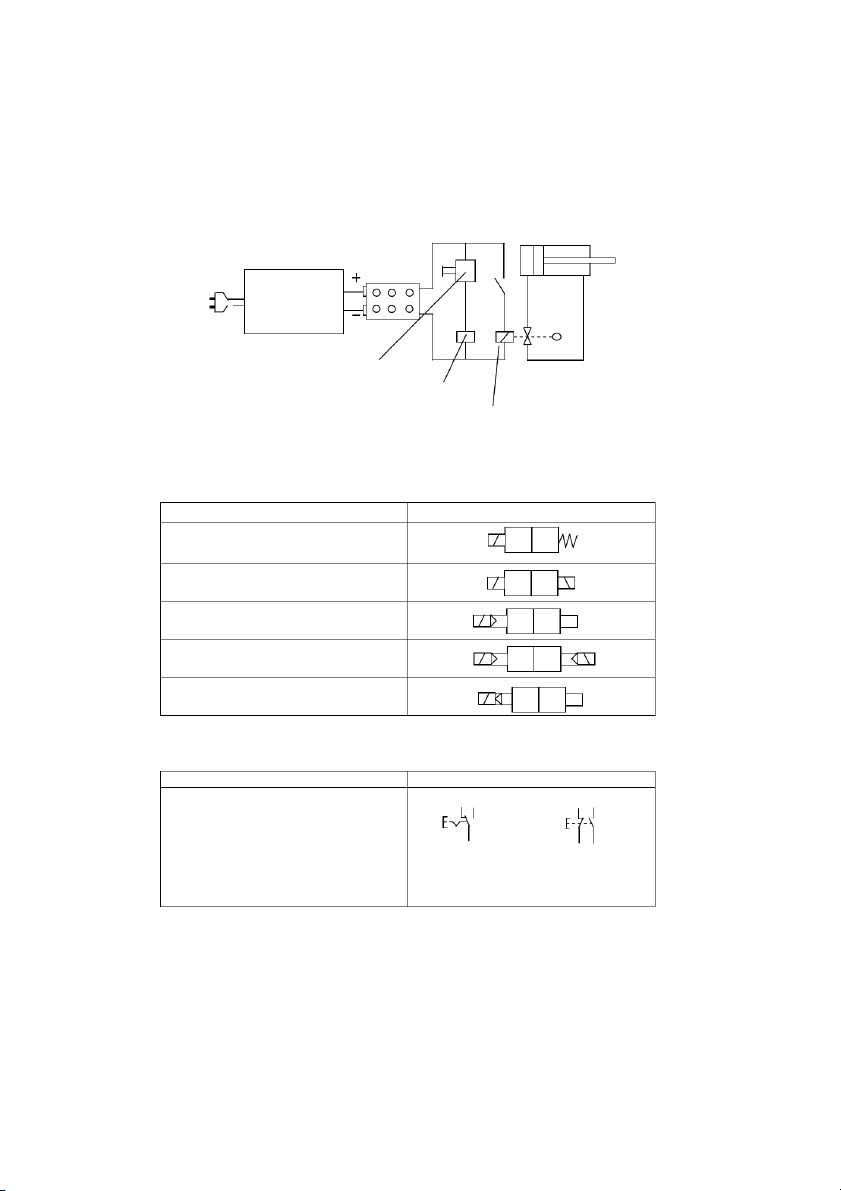
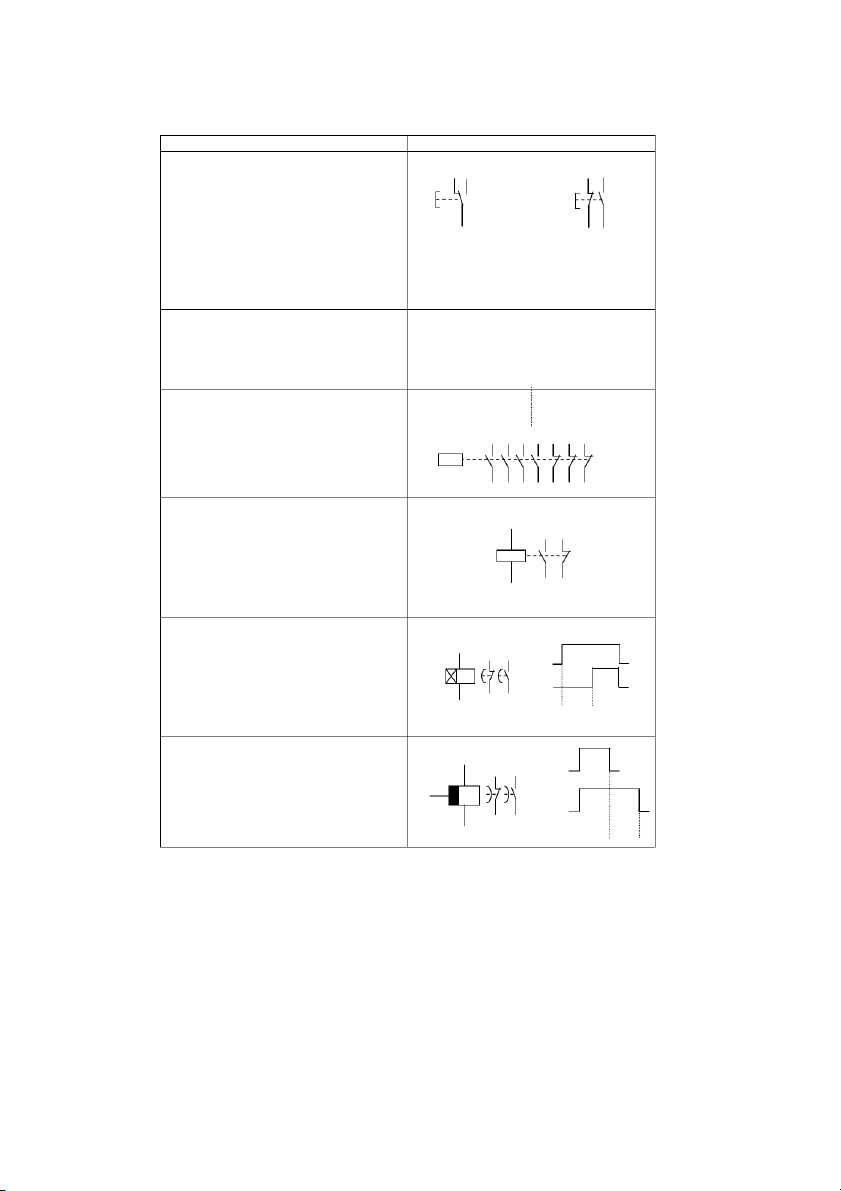
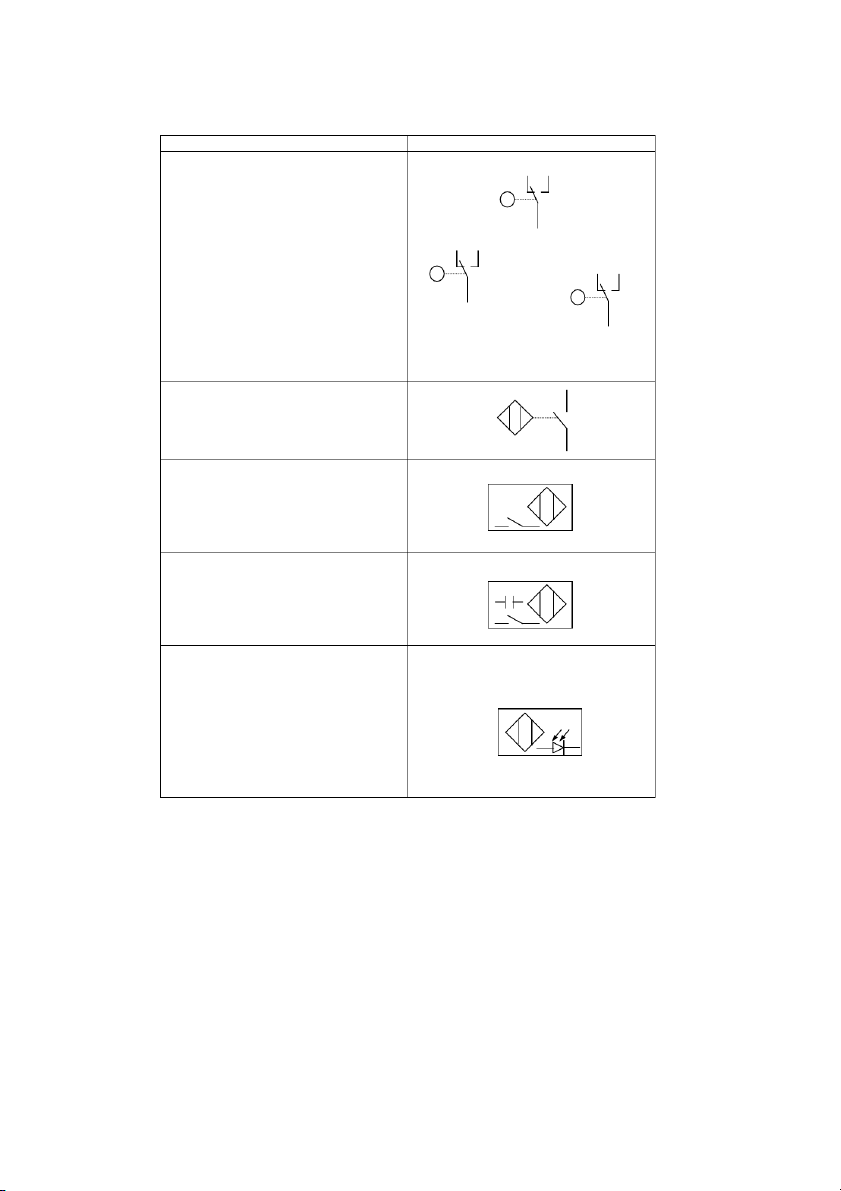
4.2. Hệ thống điều khiển thủy khí ......................................................................... 78
4.2.1. Nguyên lý cơ bản .................................................................................. 78
4.2.2. Các phần tử điện – thủy khí ................................................................. 79
4.2.3. Ứng dụng PLC trong điều khiển ........................................................... 82
4.3. Mô hình hóa ................................................................................................... 86
4.3.1. Phần mềm FluidSIM ............................................................................. 86
4.3.2. Phần mềm kết nối PLC thủy khí............................................................ 90
4.3.3. Các phần mềm khác .............................................................................. 90
Bài tập chương 4 ................................................................................................... 94
Tài liệu tham khảo .............................................................................................. 95 4 Chương 1.
TÍNH CHẤT VẬT LÝ CƠ BẢN
Đối tượng nghiên cứu của môn học là chất lỏng và chất khí. Chất lỏng ở đây hiểu
theo nghĩa rộng, bao gồm chất lỏng ở thể nước - Chất lỏng không nén được ( Khối lượng
riêng ρ không thay đổi) và chất lỏng ở thể khí - Chất lỏng nén được ( Khối lượng riêng thay
đổi ρ ≠ const ). Để tiện cho việc nghiên cứu, cũng như theo sự phát triển của khoa học,
người ta chia chất lỏng thành chất lỏng lý tưởng hay là chất lỏng không nhớt và chất lỏng
thực, còn gọi là chất lỏng nhớt (độ nhớt μ ≠ 0). Chất lỏng tuân theo quy luật về lực nhớt của
Niu-Tơn là chất lỏng Niu-Tơn. Còn những chất lỏng không tuân theo quy luật này người ta
gọi là chất lỏng phi Niu-Tơn, như dầu thô chẳng hạn. Thuỷ khí động lực nghiên cứu các quy
luật cân bằng và chuyển động của chất lỏng. Thông thường trong giáo trình, người ta chia thành ba phần: -
Tĩnh học chất lỏng: nghiên cứu các điều kiện cân bằng của chất lỏng ở trạnh thái tĩnh. -
Động học chất lỏng: nghiên cứu chuyển động của chất lỏng theo thời gian,
không kể đến nguyên nhân gây ra chuyển động. -
Động lực học chất lỏng: nghiên cứu chuyển động của chất lỏng và tác dụng
tương hỗ của nó với vật rắn.
1.1. CÁC THÔNG SỐ TRẠNG THÁI.
Các chất được cấu tạo từ phân tử. Đó là những phần tử nhỏ bé nhất. Giữa chúng có lực
tương tác tác dụng. Giữa các phân tử có khoảng cách. Nếu khoảng cách này nhỏ hơn 3.10-
10 m thì các phân tử đẩy nhau, còn nếu nó lớn hơn 3.10-10 m thì chúng hút nhau. Nhưng nếu
khoảng cách đó lớn hơn 15.10-10 m thì lực tương tác giữa các phân tử rất nhỏ, các phân tử
được coi là không tương tác nhau nữa. Các phân tử chuyêen động không ngừng. Theo
thuyết động năng thì vân tốc của chúng phụ thuộc vào nhiệt độ của vật thể. Tuỳ theo sự so
sánh giữa lực liên kết và động năng của phân tử do chuyển động nhiệt vật chất được phân ra
ba loại chất rắn, chất lỏng và chất khí.
Các phân tử chất lỏng chuyển động quanh vị trí cân bằng, đồng thời các vị trí cân bằng
này lại di chuyển, nên chất lỏng có hình dạng theo vật chứa và không thể chống lại sự biến
dạng về hình dáng. Do còn bị ảnh hưởng đáng kể lực tương tác giữa các phân tử nên chất
nước không chịu nén, không chịu cắt và chịu kéo. Tuỳ theo nhiệt độ và áp suất của môi
trườngng chất lỏng có tính chất như chất rắn hay chất khí. Đói với chất khí lực liên kết giữa
các phân tử nhỏ hơn động năng chuyển động do nhiệt. Các phân tử chuyển động hỗn loạn,
tự do. Vì thế chất khí không có thể tích và hình dáng nhất định. Các phân tử khí có khả năng
điền đầy thể tích mà nó có mặt. Khi có sự thay đổi áp suất, nhiệt độ thì thể tích chất khí thay
đổi lớn. Tuy nhiên trong điều kiện áp suất nhiệt độ khí trời và vận tốc dòng khí nhỏ thì vẫn
có thể coi chất khí là chất lỏng không nén được. Nghĩa là có thể áp dụng các qui luật của
chất lỏng cho chất khí. Chất lỏng và chất khí được coi là đồng tính đẳng hướng
Thông số trạng thái là các đại lượng vật lý xác định trạng thái của môi chất ở một thời
điểm nào đó. Như vậy thông số trạng thái chỉ phụ thuộc vào trạng thái của môi chất mà
không phụ thuộc vào quá trình. Người ta chia các thông số trạng thái ra làm hai loại: Thông
sô cơ bản và thông số phụ thuộc. Các thông số cơ bản là các thông số có thể đo được (như 5
nhiệt độ, áp suất, thể tích riêng). Còn các thông số phụ thuộc thì không đo được trực tiếp mà
phải xác đinh thông qua các thông số cơ bản. 1.1.1. Thể tích riêng:
Là thể tích của một đơn vị khối lượng được ký hiệu bằng v và được xác định theo biểu thức: V v ; 3 m G kg (1-1)
Trong đó: V: Thể tích của vật (m3)
G: Khối lượng của vật (kg)
Đại lượng nghịch đảo của thể tích riêng là khối lượng riêng được ký hiệu bằng : 1 G ; kg (1-2a) v V 3 m Tỷ khối γ = ρ.g (N/m3) (1-2b)
Bảng 1.1. Khối lượng riêng nước theo nhiệt độ t0(C) 0 4 10 30 60 80 100 ρ (kg/m3) 999,9 1000 999,7 995,7 983,3 971,8 958,4
Khối lượng riêng của một số chất lỏng thường gặp :
Nước biển : 1030 kg/m3, Thủy ngân : 13546 kg/m3, Grixerin : 1260 kg/m3, Dầu : 800 kg/m3. 1.1.2. Áp suất:
Áp suất của một chất khí hay chất lỏng là lực tác dụng của các phần tử chất khí hay chất
lỏng đó trên 1 đơn vị diện tích thành bình, theo phương pháp tuyến với thành bình. Áp suất
(ký hiệu là p) được xác định theo biểu thức: F p ; N (1-3) S 2 m
Trong đó: F: là lực tác dụng lên thanh bình của các phần tử chất khí hoặc lỏng do
chuyển động hỗn loạn của chúng gây nên (N)
S: Diện tích thành bình (m2)
Đơn vị đo áp suất là Pascal (P N a) : 1P 1
. Ngoài ra còn có các đơn vị đo áp suất a 2 m
khác như bar, atmotphe (at), cột thủy ngân (mmHg); cột nước (mH2O); Psi. Quan hệ của các đơn vị như sau:
1 at = 0,98 bar = 735,5 mmHg = 10 mH2O = 1 kG/cm2 1 bar = 750 mmHg = 105 N ; 1 Psi = 6895 N 2 m 2 m
Bảng 1.2. Bảng chuyển đổi đơn vị đo áp suất Đơn vị Pa (N/m2) bar at (kG/cm2) atm torr (mm Hg) Pa 1 10 1,01972.10-5 0,98692.10-5 7,5006.10-3 6 bar 105 1 1,01972 0,98692 7,5006.102 at 0.98066.105 0,98066 1 0.96784 7,3556.102 atm 1.01325.105 1,01325 1.03332 1 7.60.102 torr 1.3332.102 1,3332.10-3 1,3995.10-3 1,31579.10-3 1
Có các loại áp suất sau đây:
- Áp suất tuyệt đối (p): Đó là áp suất thật của chất khí và nó là một thông số trạng thái.
- Áp suất dư (pd): Nếu gọi po là áp suất tuyệt đối của khí quyển thì phần áp suất của môi
chất lơn hơn áp suất khí quyển gọi là áp suất dư. Vậy ta có:
p p p hoặc p p p ; (1-4) d o o d
- Áp suất chân không (pck) (hay còn gọi là độ chân không) là phần áp suất nhỏ hơn áp
suất khí quyển. Vậy ta có:
p p p hoặc p p p ; (1-5) ck o o ck
Để đo áp suất tuyệt đối của khí quyển người ta dùng barômét. Đo áp suất dư bằng
manômét và đo áp suất chân không bằng chân không kế.
Tất cả dụng cụ đo trên được gọi chung là Áp kế: Áp kế banômét, áp kế manômét, áp kế chân không. 1.1.3. Nhiệt độ:
Là mức đo trạng thái nhiệt ( nóng, lạnh) của vật. Nhiệt độ của vật được đo bằng nhiệt kế.
Tùy theo thang nhiệt độ mà có các nhiệt kế khác nhau. Thông thường, nhiều nước trên thế
giới sử dụng loại nhiệt kế bách phân để xác định nhiệt độ bách phân (ký hiệu là oC) và nhiệt
kế Kelvin để xác định nhiệt độ tuyệt đối. (ký hiệu oK)
Nếu gọi t và T tương ứng là nhiệt độ bách phân và nhiệt độ tuyệt đối, ta có quan hệ: T = 273,15 + t 273 + t; (1-6)
Ngoài ra ở một số nước (chủ yếu là Tây Âu) còn dùng thang nhiệt độ Farenheit (ký hiệu
oF), thang nhiệt độ Rankine (ký hiệu là oR). Nếu gọi tF, tR tương ứng là giá trị nhiệt đọ đo
theo thang Farenheit và Rankine ta có quan hệ: 5 5 t (t 32);T t ; (1-7) F R 9 9
hoặc: t 1,8T 492 1,8t 460 t ; (1-8) R F 1.1.4. Nội năng:
Nội năng được ký hiệu là U (J) hoặc u ( J
) là toàn bộ các dạng năng lượng bên trong kg
của vật bao gồm nội nhiệt năng và dạng năng lượng khác (như hóa năng, năng lượng
nguyên tử…). Trong nhiệt động kỹ thuật không xét đến năng lượng phản ứng nên nội năng
được hiểu là nội nhiệt năng (do chuyển động hỗn loạn các nguyên tử, phân tử tạo thành).
Nội năng bao gồm nội động năng và nội thế năng. Nội động năng phụ thuộc vào nhiệt độ (vì
nhiệt độ khác nhau chuyển động hỗn loạn của các phân tử, nguyên tử khác nhau). Nội thế
năng phụ thuộc vào thể tích riêng (thể tích riêng khác nhau thì khoảng cách các phân tử 7
khác nhau nên lực tác động tương hỗ giữa chúng sẽ khác nhau). Như vậy ta dễ dàng rút ra
nhận xét là: Nội năng khí thực phụ thuộc cả nhiệt độ và thể tích riêng, còn nội năng khí lí
tưởng chỉ phụ thuộc vào nhiệt độ. Do đó, đối với khí lý tưởng ta luôn có quan hệ: du = Cv d T và u C T ; (1-9) v
Ở đây: Cv là nhiệt dung riêng khối lượng đẳng tích.
1.1.5. Năng lượng đẩy (thế năng áp suất):
Năng lượng đẩy (hay còn gọi là thế năng áp suất) được ký hiệu bằng D(J) hoặc d( J ). kg
Nó là năng lượng giúp do môi chất chuyển động ngoài tác động của động năng và thế năng
bên ngoài. Người ta đã chứng minh được quan hệ: D = p.V; và d = p.v; (1-10)
hoặc viết dưới dạng vi phân:
d(D) = d(pv); và d(d) = d(pv) ; (1-11)
Chú ý rằng: Năng lượng đẩy chỉ có trong hệ hở. 1.1.6. Entanpi
Entanpi được ký hiệu I (J) hoặc i( J kg ). Trong tính toán nhiệt động thường gặp tổng hai
số hạng u và pv (hoặc U và pV) và người ta gọi tổng đó là Entanpi. Do đó i u pv; ü ý (1-12) I U pV;þ
hoặc viết dưới dạng vi phân di = du + d(pv);
Entanpi là một thông số trạng thái có cả trong hệ kín và hệ hở.
Đối với hệ hở ta có thể viết: di = du + d(d);ü i u d; ý (1-13) I U D; þ
Entanpi của khí thực phụ thuộc vào hai trong ba thông số cơ bản p, v, T còn Entanpi của
khí lí tưởng chỉ phụ thuộc vào nhiệt độ
Do vậy đối với khí lí tưởng ta có: di = CP dT; i C T ; (1-14) P
Ở đây CP: là nhiệt dung riêng khối lượng đẳng áp. 1.1.7. Entropi: 8
Entropi được ký hiệu bằng S(J) hoặc s ( J ) kg
Trong nhiệt động kỹ thuật người ta đã chứng minh được rằng: vi phân nhiệt lượng (dq)
chia cho nhiệt độ tuyệt đối (T) của vật khi trao đổi nhiệt là một vi phân toàn phần của hàm
trạng thái nào đó và được gọi là Entropi (viết dưới dạng vi phân), mặc dầu nhiệt lượng
không phải là hàm trạng thái nên vi phân nhiệt lượng (dq) không phải là vi phân toàn phần.
Ta có biểu thực định nghĩa Entropi như sau: dq ds = ; (1-15) T 1.1.8. Execgi và Anecgi:
Execgi được ký hiệu là E (J) hoặc e ( J
) là năng lượng có thể biến đổi hoàn toàn kg
thành công trong quá trình thuận nghịch. Còn Anecgi được ký hiệu là A (J) hoặc a ( J kg ) là
năng lượng không thể biến đổi thành công trong quá trình thuận nghịch. Vậy thì ta có: q e a; J ( )ü kg (1-16) Q E A; ý (J) þ
1. 2. PHƯƠNG TRÌNH TRẠNG THÁI CỦA CHẤT KHÍ.
1.2.1. Đối với khí lý tưởng
Ở phổ thông ta đã được học biểu thức định luật Bôi-mariôt: pv = const khi T = const và v
biểu thức định luật Gayluxăc
= const khi p = const. Vì vậy ta có thể tổng quát hóa để có T
phương trình trạng thái:
Áp dụng cho 1kg khí lí tưởng pv = RT; J (1-17) kg Áp dụng cho G kg thì pV = GRT; J (1-18)
Trong đó R là hằng số chất khí ( J o ) kg K
Nhân hai về của (1-17) với khối lượng kilomol ( kg kmol ) và khi biết rằng v. v ;
R. R , ta có phương trình trạng thái viết cho 1kmol chất khí là pv R .T ; J kmol (1-19) và do đó pV M.R .T ; J (1-20)
Trong đó V v .M là thể tích chất khí (m3)
v : thể tích của 1kmol chất khí ( 3 m kmol ) 9 M: số kilomol chất khí
R : Hằng số phổ biến của khí lí tưởng ( J ) o kmol K Từ (1-19) ta có p.v R ; J (1-21) T o kmol K
Thay giá trị đã biết ở điều kiện tiêu chuẩn vào (1-21): 760 p = 760mmHg = 2 N m 750 3 m v 22,414 kmol T = 273,15oK Ta tìm được o R 8314(J kmol K) (1-22a)
và do đó hằng số chất khí R sẽ là: R 8314 R ; ( o J kg K ) (1-22b)
1.2.2. Đối với khí thực
Cho đến nay lý thuyết cũng như thực nghiệm chưa tìm được một phương trình trạng thái
nào áp dụng cho mọi khí thực, mà chỉ có thể tìm ra một phương trình trạng thái áp dụng cho
một hoặc vài chất khí ở một phạm vi nhất định của áp suất và nhiệt độ.
Ví dụ phương trình Van-der Walls sử dụng cho các chất khí ở áp suất nhỏ và thể tích lớn có dạng: a (p )(v b) RT ; (1-23) 2 v
Trong đó: a, b là các hệ số thực nghiệm phụ
thuộc vào tứng chất khí
1.3. BIẾN THIÊN THỂ TÍCH MÔI CHẤT p dV
1.3.1. Tính thay đổi thể tích do áp lực V dp + p
- Khi áp suất tăng từ P lên P+dP thì thể tích vật thể V - dV giảm từ V xuống V - dV.
- Tính nén của chất lỏng được đặc trưng bằng hệ số co
thể tích β , để biểu thị sự giảm tương đối của thể tích P
Hình 1.1. Biến thiên thể tích
chất lỏng V ứng với sự tăng áp suất P lên một đơn vị áp suất. 1 dV (1-24) p V dp 10
- Thực nghiệm chứng tỏ: Trong phạm vi áp suất thay đổi từ 1 đến 500 at và nhiệt độ từ 0 0 2
đến 20 C thì β p = 0,00005 (cm /kG) ≈ 0. Như vậy trong thủy lực chất lỏng coi như không nén được.
- Đại lượng nghich đảo của của hệ số co thể tích gọi là mô đun đàn hồi K. 1 K (1-25) p
Nếu áp suất chất lỏng không làm giảm đi quá một nửa so với thể tích ban đầu của
chất lỏng thì K không thay đổi và nó có ý nghĩa như mô đun đàn hồi của chất rắn. Tính nén
của chất lỏng phụ thuộc vào áp suất và nhiệt độ. Nhưng sự thay đổi này không đáng kể.
Trong quá trình nén chất lỏng thì khối lượng của nó không thay đổi nên chúng ta có thể viết. m =ρ.V = const.
Lấy đạo hàm biểu thức này ta có : ρdV + Vdρ = 0 Hay dV d (1-26) V
Kết hợp với công thức tính mô đun đàn hồi ta có đối với chất lỏng K dp (1-27) d
Đơn vị tính là bình phương của đơn vị vận tốc, vì vậy ta có thể viết K dp a (1-28) d
Theo Vật lý thì a gọi là vận tốc truyền âm trong chất lỏng và cũng là vận tốc truyền
sóng áp suất ; trong nước a = 1414,2m/s ; trong chất lỏng không nén được a → ∞.
Đối với chất khí quá trình nén khí xảy ra rất nhanh chúng ta có thể coi là quá trình
đoạn nhiệt và vận tốc truyền âm được tính theo công thức p a n.R T . n (1-29) Trong đó:
n là chỉ số đoạn nhiệt,
R là hằng số chất khí.
Nếu cho G trọng lượng phân tử chất khí thì : RT a n (1-30) G
1.3.2. Tính thay đổi thể tích do nhiệt độ 11
- Khi thay đổi nhiệt độ dùng hệ số co giãn vì nhiệt β để biểu thị sự biến đổi của thể tích chất t, o
lỏng V ứng với sự tăng nhiệt độ t lên 1 C. 1 dV (1-31) p V dt 0
- Thí nghiệm cho thấy: Trong điều kiện áp suất bằng áp suất khí trời Pa thì: o 0
Khi t = 4 C đến 10 C thì β = 0,00014. t o 0
t = 10 C đến 20 C thì β = 0,00015. t
Như vậy:Trong thủy lực chất lỏng coi như không co giãn dưới tác dụng của nhiệt độ.
Tóm lại: Trong thủy lực, chất lỏng thường được coi là có tính chất không thay đổi
thể tích mặc dù có sự thay đổi về áp lực hoặc nhiệt độ tức βt ≈0, βp ≈0
1..4. SỨC CĂNG MẶT NGOÀI VÀ HIỆN TƯỢNG MAO DẪN
Tính chất này của chất lỏng thể hiện rõ ở những bề mặt giửa chất lỏng này với chất
lỏng khác (giữa nước với thành rắn, ...) mà giữa chúng không thực hiện phản ứng hoá học.
Ở các mặt tiếp xúc này chất lỏng tạo ra một màng mỏng bao quanh bề mặt chất lỏng.
Nguyên nhân xuất hiện sức căng bề mặt là lực hút giữa các phân tử. Các phân tử lỏng ở
trong chất lỏng chiu tác dụng mọi phía như nhau. Còn ở các phân tử trên bề mặt tiếp xúc
hoặc ở lớp ngoài có bề dày nhỏ hơn 10-9 m thì các lực tác dụng lên chúng không bằng nhau.
Các phân tử này chịu tác dụng một lực tổng hơp hướng vào trong chất lỏng và tạo nên một
màng mỏng trên bề mặt tiếp xúc gọi là sức căng bề mặt (hình 1-2a). Hệ số sức căng bề mặt
(ký hiệu C) là lực tác dụng lên một đơn vị độ dài bề mặt thẳng góc với độ dài và nằm trong
bề mặt của chất lỏng (hình 1-2b)
Dựa vào tính chất sức căng bề mặt của chất lỏng để khảo sát các vấn đề sau:
- Sức bề mặt giữa các lớp chất lỏng với nhau.
- Hiện tượng dính ướt. a b
Hình 1.2. Sức căng mặt ngoài
- Hiện tượng mao dẫn : Khi chất lỏng ở trong ống có đường kính nhỏ (gọi là ống mao dẫn)
nếu lực dính ướt (Fr) lớn hơn lực kéo các phần tử lỏng (Fc) thì chất lỏng dâng lên trong ống
cao hơn mực nước bên ngoài. Độ cao này gọi là độ cao mao dẫn (chất lỏng là nước). Còn 12
nếu như Fc>Fr thì chất lỏng trong ống tụt xuống so với mực chất lỏng bên ngoài. Hiện
tượng này gọi là hạ mao dẫn (chất lỏng là thuỷ ngân).
Hình 1.3. Hiện tượng mao dẫn
Độ cao mao dẫn được tính từ điều kiện cân bằng giữa trọng lượng cột chất lỏng và lực căng bề mặt: .d.c d 2 h . ..g (1-32) 4 c 4 Nên: h (1-33) g . d .
Công thức này thường dùng để tính hệ số sức căng bề mặt. Để tránh hiện tượng mao
dẫn trong các dụng cụ đo bằng chất lỏng (đo áp suất, nhiệt độ ) phải chọn đường kính ống đo lớn hơn 10 mm. 1.5. TÍNH NHỚT
Tính nhớt là đặc tính rất quan trọng của chất lỏng, vì nó là nguyên nhân gây ra sự tổn
thất năng lượng khi chất lỏng chuyển động. Mọi chất lỏng thực đều có tính nhớt.
Khi các lớp chất lỏng chuyển động, do vận tốc của các lớp khác nhau nên giữa chúng
nảy sinh ra tác dụng lôi đi kéo lại, tức là xuất hiện sức ma sát làm chuyển biến một bộ phận
cơ năng của chất lỏng thành nhiệt năng mất đi không lấy lại đợc. Sức ma sát này gọi là ma
sát trong (nội ma sát) của chất lỏng chuyển động.
Tính chất nảy sinh ra sức ma sát trong giữa các lớp chất lỏng chuyển động gọi là tính
nhớt của chất lỏng. Định luật ma sát trong do Niutơn đa ra năm 1686 đợc thể hiện nh sau: du F S (1-34) dy
Trong đó: F- Lực ma sát giữa hai lớp chất lỏng; S - Diện tích tiếp xúc giữa hai lớp chất lỏng;
m - Hệ số nhớt động lực của chất lỏng, phụ thuộc vào lọai chất lỏng và nhiệt độ;
u = f(y) - Quy luật phân bố vận tốc điểm theo phương y;
du - Gradien vận tốc theo phương y. dy 13
Gọi t là ứng suất tiếp tại mặt tiếp xúc giữa hai lớp chất lỏng thì t đợc tính nh sau: F du (1-35) S dy
Công thức (1-34) và (1-35) dùng cho dòng chảy tầng của chất lỏng.
Tính nhớt của chất lỏng đợc biểu thị bởi hai hệ số: 1 Ns
1 Hệ số nhớt động lực m có đơn vị là Ns/m2 hoặc kg/ms; đơn vị ứng với gọi là 2 10 m Poazơ (P).
2 Hệ số động học nhớt n có đơn vị là m2/s.
Mối liên hệ giữa các hệ số m và n như sau:
; trong đó: r - khối lượng đơn vị.
Những hệ số m và n phụ thuộc vào loại chất lỏng và nhiệt độ, trị số của nó có trong các bảng tra Thuỷ lực
Khi nghiên cứu chất lỏng ở trạng thái đứng yên thì không cần phân biệt chất lỏng thực
với chất lỏng lý tưởng. Nhưng khi nghiên cứu chất lỏng chuyển động thì từ chất lỏng lý
tưởng sang chất lỏng thực phải bổ sung thêm ảnh hưởng của lực ma sát trong.
Hình 1.4. Quy luật phân bố theo tính nhớt
- Loại chất lỏng tuân theo định luật ma sát trong của Newton gọi là chất lỏng thực
hoặc chất lỏng Newton. Môn thủy lực nghiên cứu chất lỏng này.
- Các loại chất lỏng như sơn, hồ không tuân theo định luật ma sát trong gọi là chất lỏng phi Newton.
- Chất lỏng lý tưởng là chất lỏng tưởng tượng không có tính nhớt.
1.6. TÍNH BỐC HƠI VÀ ĐỘ HOÀ TAN CỦA CHẤT KHÍ TRONG CHẤT NƯỚC
Bốc hơi là đặc trưng của chất lỏng thành hạt, nó phụ thuộc vào loại chất lỏng và áp
suất, nhiệt độ ... của môi trường xung quanh. Lượng khí hoà tan trong một đơn vị thể tích
chất lỏng (chất nước) phụ thuộc vào các chấ, nước khác nhau và áp suất của môi trường: VK p2 k (1-36) Vn p1 14 Trong đó:
Vn , VK - thể tích nước và thể tích của khí hoà tan trong điều kiện thường
k - hệ số hoà tan (độ hoà tan).
p1, p2 - áp suất của nước trước và sau khi đã hoà tan.
Độ hoà tan k ở 200C của dầu xăng: 0,127 , dầu biến thế: 0,083. Trong trường hợp áp suất
thấp, chất khí hoà tan bị tách ra khỏi chất lỏng rất mạnh, chất lỏng bị bốc hơi nhiều "sôi"
lên, sẽ gây hiện tượng xâm thực (khí thực) làm hư hỏng các hệ thống thuỷ lực, máy thuỷ lực.
1.7. SỰ TRAO ĐỔI NHIỆT LƯỢNG VÀ KHỐI LƯỢNG
Quá trình trao đổi động lượng chỉ xảy ra khi có chuyển động, còn quá trình trao đổi
nhiệt và khối lượng thì không chỉ xảy ra trong môi trường động mà cả trạng thái tĩnh nữa.
Nhiệt lượng truyền qua một đơn vị diện tích trong một đơn vị thời gian tỷ lệ với
gradien nhiệt độ, còn khối lượng chất lỏng khuếch tán truyền qua một đơn vị diện tích trong
một đơn vị thời gian tỷ lệ với gradien nồng độ của chất lỏng đó trong dòng chất lỏng, tức là
sự truyền nhiệt trong chất lỏng tuân theo định luật Furie: dT q (1-37) dn
Sự truyền khối lượng tuân theo định luật Fích dc m D (1-38) dn Trong đó:
q, m - nhiệt lượng và khối lượng truyền qua một đơn vị diện tích trong một đơn vị thời gian.
c T, - Nhiệt độ và nồng độ của vật chất.
λ, D - Hệ số dẫn nhiệt và hệ số khuếch tán.
Tính chất này cũng khá quan trọng trong khi nghiên cứu về thuỷ khí động lực học và khí động lực học.
1.8. LỰC TÁC DỤNG LÊN MÔI CHẤT
Tất cả các lực tác dụng lên chất lỏng đều có thể phân ra làm hai loại là lực khối và
lực mặt. Lực khối tỷ lệ với thể tích chất lỏng (còn gọi là lực thể tích). Lực khối gồm có
trọng lượng, lực quán tính,... . Nó được biểu diễn bằng biểu thức. F R dV (1-39) R .. . (V ) Trong đó:
V là thể tích hữu hạn của chất lỏng chịu tác dụng bởi lực khối,
ρ là khối lượng riêng của chất lỏng,
R là gia tốc khối (hay lực khối đơn vị).
Nếu chất lỏng chỉ chịu tác dụng bởi trọng lực thì gia tốc khối là gia tốc trọng trường.
Nếu chất lỏng chuyển động với gia tốc thì gia tốc lực khối gồm gia tốc trọng trường và gia
tốc quán tính của chuyển động. 15
Lực mặt tỷ lệ với diện tích bề mặt chất lỏng. Lực mặt gồm các lực nhu lực áp, lực ma
sát. Lực mặt được tính theo công thức: F p dS (1-40) p . (S )
Trong đó p là lực mặt tính trên một đơn vị dịên tích. Nếu Fp thẳng góc với mặt chất
lỏng thì p là áp suất. Nếu Fp tác dụng theo phưong tiếp tuyến với mặt S thì p là ứng suất tiếp. Ví dụ 1.1. 3 0 2
a. Tìm sự thay đổi thể tích của 1m nước ở nhiệt độ 27 C khi áp suất gia tăng 21KG/cm . 0 3 2
(Cho K ở 27 c là 22,90.10 kG/cm )
b. Theo những số liệu thực nghiệm sau đây, xác định mô đun đàn hồi thể tích của nước. 2 3 2 3
Với 35 kG/cm thể tích là 30 dm và với 250 kG/cm thể tích là 29,70 dm Giải: 4 7 -4 3
a. Ta có : dV = - Vdp/ K = - 1. 21 .10 / 22,9. 10 = - 9,15.10 m
b. Mô đun đàn hồi thể tích của nước là : 3 4 3 7 2
K = -Vdp / dV = -30.10 .(250-35). 10 / (29,70-30).10 = 21,5. 10 kG/m Ví dụ 1.2.
Tính ứng suất tiếp tại mặt trong của một ống dẫn nhiên liệu. Cho biết:
Hệ số nhớt động học γ = 7,25x10-5 (m2)
Khối lượng thể tích (mật độ):ρ = 932 kg/m Gradien vận tốc: du 4 dn Bài giải:
Hệ số nhớt động lực của nhiên liệu: 5 2 2 , 7 25 1 x 0 9 x 32 7 , 6 6 1 x 0 N / m
Ứng suất tiếp tại mặt trong của ống: du 2 2 . , 6 76 1 x 0 x4 , 0 27 N / m dn 1.9. TĨNH HỌC CHẤT KHÍ
Đối với lưu chất nén được ta khảo sát một số trường hợp sau đây:
1.9.1. Chất khí nén được
Khảo sát quá trình đẳng nhiệt ta có được phương trình xác định thể tích khối khí là: V V [1 ( p p )] 0 0 0 1 1 Hay là: [1 ( p p )] (1-41) 0 0 0
Trong đó : 0 chỉ trạng thái đã xác định 16
hệ số giãn nở đẳng nhiệt 0
Chọn trục z’ theo phương thẳng đứng hướng xuống ta có phương trình vi phân: d gdz
Thay (1-41) vào phương trình trên, sau khi tích phân ta có: 1 2
p p ( p p ) 0 0 0 0 gz 2 Hay là: 0 (p p ) 1 ( p p ) gz 0 0 0 2
Vì 0 ( p p ) quá nhỏ so với 1 nên ta có thể viết 0 2 0 p p gz ' 1 gz ' (1-42) 0 0 0 2 1.9.2. Khí quyển
Khảo sát phương trình trạng thái của không khí: p h 29,3T RT (1-43) T
Ở nhiệt độ 00C ta có chiều cao tương ứng h0 = 7989m ≈ 8000m T
Ở nhiệt độ T0 K: h h (1-44) T 0 273
Chọn trục z hướng lên từ mặt đất ta có phương trình vi phân: dp gdz
Kết hợp với biểu thức (1-43) - (1-44) ta suy ra: dp 273 dz dz dz . ( dz - tính bằng m) (1-45) p T h h 8.000 0 T
Dưới đây khảo sát các biểu thức xác định áp suất và khối lượng riêng theo chiều cao trong một số trường hợp.
-Trường hợp đẳng nhiệt:
Tích phân phương trình (1-45) với chú ý: T=Tm=const ta được: p 273 z z z z 0 0 ln . p T h h z0 m 0 Tm 17 Hay là : 273 z z0 p p exp . z z 0 T h m 0 z z0 p exp (1-46) 0 z h Tm
Tương tự (1-46) ta có biểu thức xác định khối lượng riêng : 273 z z 0 exp . z 0 z T h m 0 z z 0 (1-47) z exp 0 h Tm
-Trường hợp nhiệt độ thay đổi tuyến tính : T T 1 B (z z ) (1-48) z z 0 0 B - hằng số
Thay (1-48) vào (1-45) với chú ý : Tz0 h h 29,3T T 0 z z 0 0 273 273 1 K h BT BT 0 z0 z0 p
Ta có : ln z K ln 1 B(z z ) 0 p 0z K Hay là : T p p 1 B( K z (1-49) z z z z0 ) pz 0 0 T 0z
Từ phương trình trạng thái suy ra công thức tương tự : K T B z z (1-50) z z 1 ( ) K z 1 0 1 0 0 z T 0z
Thông thường đối với bài toán trong khí quyển ta chọn gia tốc trọng trường g không đổi,
trọng lượng riêng không khí trong điều kiện tiêu chuẩn là 1,293 kg/m3, còn trọng lượng
riêng của không khí ở áp suất 760 mmHg ở nhiệt độ 150C ( hay 2880K) ở độ cao bằng không là 1,225 kg/m3.
Khi 0< z < 11.000 m, nhiệt độ thay đổi tuyến tính theo công thức :
tz=15 – 0,0065 z ; ( z – m, tz – 0C) Hay là :
T= 288 ( 1- 22,6.10-6z) ; ( z-m, T- 0K) 18
Khi z> 11 000 m ta có t= - 56,5 0C ; ( T= 216,50 K)
Từ độ cao 300 km nhiệt độ T 15000K 1.9.3. Khí cầu
Gọi G- Trọng lượng khí cầu (kể cả trọng lượng khí trong khí cầu) ; V- thể tích khí cầu ;
γ- trọng lượng riêng của không khí
γ’- trọng lượng riêng của khí trong khí cầu. Ta sẽ có biểu thức xác định lực đẩy
F V G V (V ' G ) V (1 ) G z z 2 z 0 0 z Trong đó : '
- tỉ trọng chất khí ;
G0 trọng lượng của khí cầu không kể khí bên trong.
Tại vị trí khí cầu đạt độ cao cực đại zM ta có FZ=0 ; nghĩa là : G Vg (1 ) 0 z M
Khảo sát môi trường khí quyển đẳng nhiệt, kết hợp với biểu thức (1-48) ta có : 273 z z M 0 G V z z ( )exp . 0 0 T 8000 zM , z0 tính bằng m. T V (1 Hay là : z 0 z z 8000 .2,3lg (1-51) M 0 273 G 0 19
Câu hỏi và bài tập chương 1 Câu hỏi:
Câu 1.1. Tính chất của sự trao đổi nhiệt và khối lượng trong chất lỏng.
Câu 1.2. Phân biệt giữa khối lượng riêng và trọng lượng riêng.
Câu 1.3. Tính nén được và giãn nở vì nhiệt là gì? cách xác định?
Câu 1.4. Tính bốc hơi và độ hoà tan và cách xác định ?
Câu 1.5. Sức căng bề mặt là gì? cách xác định ?
Câu 1.6. Tính nhớt (nguyên nhân và cách xác định).
Câu 1.7. Khái niệm về chất lỏng thực, chất lỏng lý tưởng. Tại sao lại phải dùng khái niệm
về chất lỏng thực, chất lỏng lý tưởng? Bài tập
Bài 1.1: Ống dẫn nước có đường kính trong d=500mm và dài l=1000m chứa đầy nước ở o
trạng thái tĩnh dưới áp suất p =4 at và nhiệt độ t =5 C. Bỏ qua sự biến dạng và nén, giãn nở 0 o 0
của thành ống. Xác định áp suất trong ống khi nhiệt độ nước trong ống tăng lên t =15 C, 1
biết hệ số giãn nở do nhiệt độ của nước βt =0,000014 và hệ số nén βp = 1/21000 cm2/kG
Bài 1.2: Đem thí nghiệm thủy lực một ống có đường kính d=400mm, chiều dài l=2000mm, -10
áp suất nước trong ống tăng lên 45 at, sau giảm xuống còn 40 at. Cho biết βp =5,1.10 2
m /N. Bỏ qua sự biến dạng của vỏ ống. Hỏi thể tích nước rỉ ra ngoài là bao nhiêu?
Bài 1.3. Tính lượng nước cần thiết mà bơm phải cung cấp để thử thủy lực đường ống.
Đường kính ống d=350 mm ; ống dài l=50 m ; áp suất thử p=5.106 Pa (áp suất dư) ; mô đun
đàn hồi của nước K=2.109 Pa.
Bài 1.4: Xác định lực ma sát tại mặt trong của một ống dẫn dầu có đường kính trong
d=80mm, chiều dài l=10m, nếu lưu tốc trên mặt cắt ngang của ống thay đổi theo qui luật: u 2
=25y - 312 y , trong đó y là khoảng cách tính từ mặt trong của ống (0 ≤ y ≤ d/2). Hệ số nhớt 2
động lực của dầu μ =0,0599 N.s/m .
+ Lưu tốc lớn nhất của dầu trong ống là bao nhiêu?
+ Vẽ biểu đồ chỉ rõ qui luật phân bố lưu tốc trong ống theo mặt cắt ngang ống
Bài 1.5: Hệ thống sưởi (nồi hơi, lò sưởi và đường ống) của một căn nhà có dung tích V =
0,4 m3 nước. Cần bổ xung bao nhiêu nước vào hệ thống khi nước được đun từ 200 C đến 900C.
Bài 1.6. Để đảm bảo tích định kỳ thể tích nước bổ sung khi nhiệt độ thay đổi, người ta nối
vào điểm trên của hệ thống sưởi bằng nước một bình chứa mở rộng hở. Xác định thể tích
nhỏ nhất của bình chứa mở rộng để nó không bị cạn. Độ dao động cho phép của nhiệt độ
nước trong thời gian ngừng làm việc của lò sưởi là Δt = 250C. Thể tích nước trong hệ thống là V=0,55 m3. Lấy 6 0 1 600 1 x t 0 C 20 Chương 2 TĨNH HỌC CHẤT LƯU
Trong chương này chúng ta nghiên cứu điều kiện cân bằng của chất lỏng ở trạng thái
tĩnh, qui luật phân bố áp suất và tính lực chất lỏng tác dụng lên vật tiếp xúc hay ngập trong
chất lỏng. Trong tĩnh học chất lỏng chúng ta có thể coi chất lỏng như chất lỏng lý tưởng vì
ảnh hưởng tính nhớt không thể hiện.. Đồng thời, cũng nghiên cứu và tìm hiểu về tĩnh học chất khí.
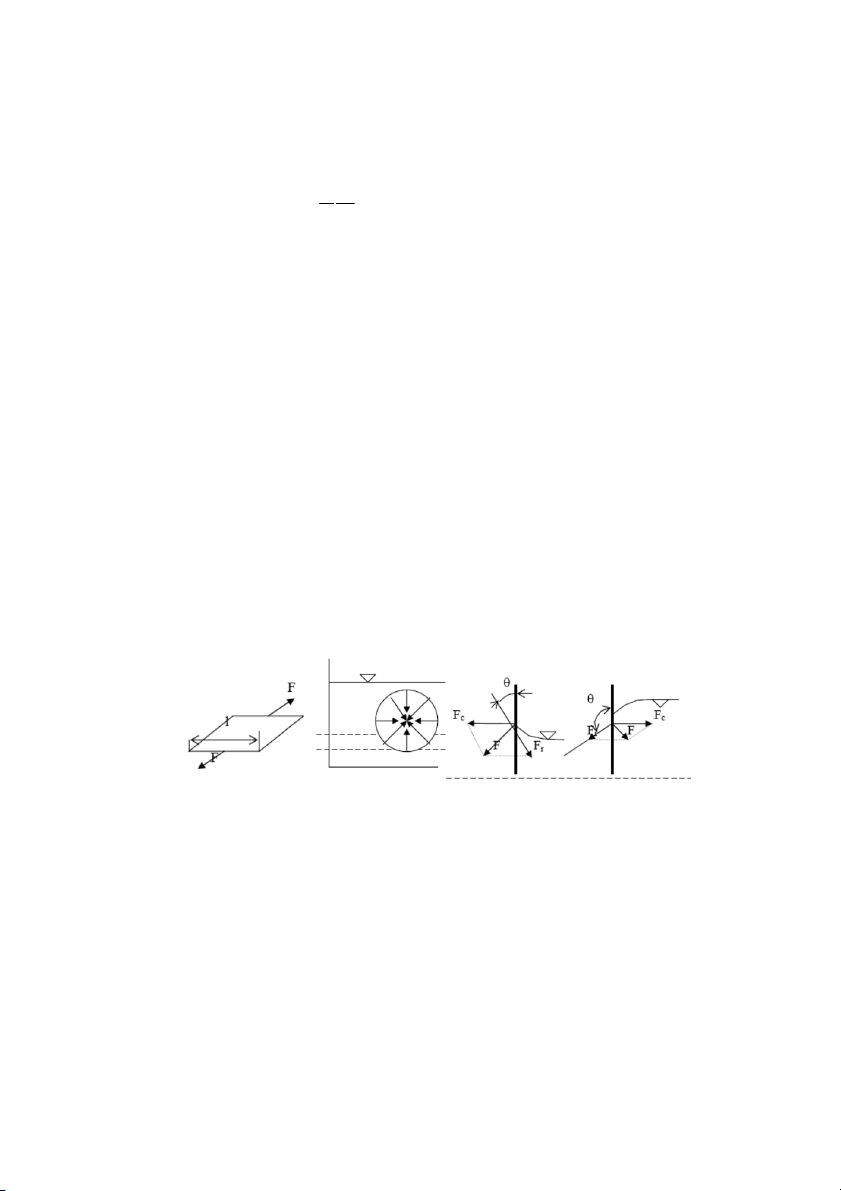
2.1. KHÁI NIỆM ÁP SUẤT THUỶ TĨNH - ÁP LỰC
- Khối chất lỏng V đang cân bằng
- Giả sử cắt bỏ phần trên, ta phải tác dụng vào mặt cắt đó bằng
một hệ lực tương đương thì phần dưới mới cân bằng như cũ.
- Trên tiết diện cắt quanh điểm 0 ta lấy một diện tích ω, gọi P là
lực của phần trên tác dụng lên ω.
Hình 2.1. Xác định áp suất
Áp suất thuỷ tĩnh l những ứng suất gây ra bởi các lực khối và lực bề mặt. Ta hãy xét một
thể tích chất lỏng giới hạn bởi diện tích Ω (Hình 2 -1). Tưởng tượng cắt khối chất lỏng bằng
mặt phẳng AB, chất lỏng phần I tác dụng lên phần II qua diện tích mặt cắt ω. Bỏ I mà vẫn
giữ II ở trạng thái cân bằng thì phải thay tác dụng I lên II bằng lực P gọi l áp suất thuỷ tĩnh
tác dụng lên mặt ω. áp suất trung bình P p (2-1) tb dP p lim Áp suất tại điểm M : M d
; Đơn vị đo áp suất như trong chương 1 d 0
2.2. CÁC TÍNH CHẤT CỦA ÁP SUẤT THUỶ TĨNH
2.2.1. Tính chất 1 (phương và chiều):
Áp suất thủy tĩnh tác dụng thẳng góc với diện tích chịu lực và hướng vào diện tích ấy.
2.2.2. Tính chất 2 (trị số):
- Không phụ thuộc vào hướng đặt của diện tích chịu lực..
- Áp suất thuỷ tĩnh chỉ phụ thuộc vào vị trí của điểm O nghĩa là p = f (x, y, z).
Biểu thức: px = py = pz = pn (2-2)
Có thể chứng minh bằng cách xét khối chất lỏng tứ diện có các cạnh dx, dy, dz, vô 21
cùng bé. Chứng minh biểu thức (2-2) khi dx, dy, dz 0 Ta cũng nhận thấy áp suất thuỷ
tĩnh tại một điểm chỉ phụ thuộc v o vị trí của nó: p = f (x, y , z)
Hình 2.2. Biểu diễn theo các phương vuông
Hình 2.3. Biểu diễn theo mọi phương bằng góc nhau Ví dụ 2.1.
Xác định phương, chiều của áp suất thủy tĩnh tại
điểm A trong hình vẽ 2-4 . Ví dụ:
Xác định phương, chiều của áp suất thủy tĩnh tại
điểm A trong hình vẽ sau đây
- Hướng của lực tại A: p A(1) Vuông góc với mặt
(1) tại A và pA(2) Vuông góc với mặt (2) tại A
hướng vào. Về trịc số pA
Hình 2.4. Xác định áp suất tại cùng một (1) = pA(2) điểm A
2.3. PHƯƠNG TRÌNH VI PHÂN CỦA CHẤT LỎNG ĐỨNG CÂN BẰNG
Trong môi trường chất lỏng đứng cân bằng lấy ra một khối chất lỏng hình hộp chữ nhật
vô cùng nhỏ, có các cạnh là x , y , z
, trọng tâm tại M (hình 2-5). Các lực tác dụng vào khối
chất lỏng hình hộp này bao gồm:
1 Lực khối lượng: Gọi F là lực khối lượng đơn vị thì lực khối lượng tác dụng lên toàn hình hộp là: F.M= F . v = . F . . x y z
Hình chiếu của lực khối lên trục Ox: Fx = x y z
2 Lực mặt: Khối hộp có 6 mặt nên có 6 lực mặt.
Xét một khối hình hộp chất lỏng vô cùng bé đứng cân bằng có các cạnh δx, δy, δz.
Tâm M(x, y, z) chịu tác động áp suất p(x, y, z). Hệ tọa độ như hình vẽ. 22
Hình 2.5. Các thành phần của phương trình vi phân
Điều kiện cân bằng: Tổng hình chiếu lên các trục của lực mặt và lực thể tích tác dụng lên khối phải bằng không.
Bằng khai triển Taylor, bỏ qua vi phân bậc cao, lấy số hạng thứ nhất
Khi đó: Áp suất tại trọng tâm mặt trái là: p x p . (2-3) x 2
Áp suất tại trọng tâm mặt phải là: p x p . (2-4) x 2
Lực thể tích tác dụng lên một đơn vị khối lượng chất lỏng theo phương Ox là F . x
Theo điều kiện cân bằng ta có : - Xét theo phương x : p x p x ( p . ). y . z (p . ) y . z .Fx. x . y . z 0 x 2 x 2 p x . . 2 . .yz . F .x .x .yz 0 x 2 p . .Fx 0 x 1 p Hay Fx 0 (2-5) x
- Tương tự theo phương y và z ta có hệ sau: 23 1 p Fx 0 x 1 p Fy 0 (2-6) y 1 p Fz 0 z Hay 1 F gradp 0 (2-7)
Đây là hệ phương trình vi phân cơ bản của chất lỏng đứng cân bằng hay hệ phương trình Euler.
Phương trình này biểu thị sự phụ thuộc của áp suất thủy tĩnh theo tọa độ: p= p(x,y,z)
Áp dụng đối với trường hợp F = P (Trọng lực)
Khi lực thể tích tác dụng vào chất lỏng chỉ là trọng lực thì chất lỏng được gọi là chất lỏng
trọng lực. Trong hệ tọa độ vuông góc mà trục Oz đặt theo phương thẳng đứng hướng lên
trên, thì đối với lực thể tích F tác dụng lực một đơn vị khối lượng của chất lỏng trọng lực, ta c: F = 0; F = 0; F = - g x y z - Khi Fx = 0 Từ phương trình 1 p p Fx 0 ta có
0 hay p không phụ thuộc vào x x x
Tương tự khi Fy = 0 thì p không phụ thuộc vào y 1 p
- Đối với Fz = -g ta có g 0 hay p g .. z tính tích phân ta có z p g.. z C (2-8)
Cần xác định hằng số C
Theo hình vẽ 2.6. tại mặt thoáng z = z0 thì p = p0 thay vào ta có C = p0
p0 + g.ρ.z0 thay vào phương trình (2-8) ta có z0
p = p0 + g.ρ.(z0 – z) = p0 + γ.h (2-9) h
Phương trình (2-9) là phương trình cơ bản của thủy tĩnh p z
Kết luận: Áp suất thuỷ tĩnh tại một điểm có độ sâu h bất kỳ trong
chất lỏng sẽ bằng áp suất tại mặt thoáng cộng với tích của trọng
lượng đơn vị của chất lỏng đó với độ sâu h. p p0 Hình 2-6 z z (2-10) 0 const
Phương trình (2-10) là phương trình cơ bản thuỷ tĩnh dạng 2.
Từ (2-9) ta thấy : Ứng với một giá trị h ta có một giá trị p, tức áp suất tại những điểm cùng
nằm trên mặt phẳng vuông góc với z sẽ bằng nhau hay chúng đều nằm trên mặt đẳng áp. 24
* Tính chất của mặt đẳng áp
- Mặt đẳng áp là mặt có áp suất bằng nhau.
- Mặt đẳng áp của chất lỏng trọng lực là những mặt song song và thẳng góc với trục oz. Nói
cách khác chúng là những mặt phẳng nằm ngang. * Nhận xét:
- Những điểm cùng độ sâu thì áp suất sẽ bằng nhau đối với cùng một loại chất lỏng.
- Những điểm ở sâu hơn thì áp suất thuỷ tĩnh sẽ lớn hơn và ngược lại. Ví dụ 2.2
Trong hình vẽ 2-7 sau ba điểm A, B, C có cùng độ
sâu h cùng áp suất mặt thoáng như nhau thuộc ba
hình thì có áp suất bằng nhau (trong trường hợp lộ
ra khí trời áp suất mặt thoáng p bằng p = 0 a 2
98100N/m - áp suất khí trời). Hình 2-7 Ví dụ 2.3
Tìm áp suất tại một điểm ở đáy bể đựng nước sâu 4m. Biết trọng lượng đơn vị của 3 2
nước γ = 9810N/m , áp suất tại mặt thoáng p = p = 98100N/m . 0 a Giải:
Áp suất tại điểm ở đáy bể có chiều sâu 4m là: 2 2
p = p + γh = 98100 + 9810x4 = 137340N/m = 14000kG/m 0
2.4. SỰ CÂN BẰNG CỦA CHẤT LỎNG TRỌNG LỰC
2.4. 1. Định luật bình thông nhau:
Nếu hai bình thông nhau đựng chất lỏng khác
nhau có áp suất mặt thoáng bằng nhau, độ cao của
chất lỏng mỗi bình tính từ mặt phân chia hai chất
lỏng đến mặt thoáng sẽ tỉ lệ nghịch với trọng lượng
đơn vị của chất lỏng. Tức là h 2 1 (2-12) h 1 2 Chứng minh:
Hình 2-8. Nguyên tắc bình thông nhau
Vì p = p (Tính chất mặt đẳng áp) 1 2 h Suy ra:
p .h p .h nên .h .h hay 2 1 (2-13) 0 1 1 0 2 2 1 1 2 2 h 1 2 25
Nhận xét: Nếu chất lỏng chứa ở bình thông nhau cùng một loại (γ1 =γ2) thì mặt tự do
của chất lỏng ở hai bình cùng trên một độ cao tức là h = h 1 2 2.4.2. Định luật pascal
Áp suất tại điểm A nào đó là: p = p + γh I 0
Nếu ta tăng áp suất tại mặt thoáng lên Δp thì áp suất
tại điểm A đó sẽ là: p = (p + Δp) + γh II 0
Vậy tại A áp suất tăng: p - p = Δp, như vậy: II I
“Độ biến thiên của áp suất thủy tĩnh trên mặt
giới hạn của một thể tích chất lỏng cho trước được
truyền đi nguyên vẹn đến mọi điểm của thể tích chất lỏng đó”.
Nhiều máy móc đã được chế tạo theo định
luật Pascal như: Máy ép thủy lực, máy kích, máy
tích năng, các bộ phận truyền động v.v...
Hình 2-9. Định luật pascal
Xét một ứng dụng máy ép thủy lực:
Máy gồm hai xy lanh có diện tích khác nhau thông với nhau, chứa cùng một chất
lỏng và có pittông di chuyển. Pittông nhỏ gắn vào đòn bẩy, khi một lực F nhỏ tác dụng lên
đòn bẩy, thì lực tác dụng lên pittông nhỏ sẽ tăng lên và bằng P và áp suất tại xylanh nhỏ 1 P bằng: 1 p (2-14) 1 1
Hình 2-10. Nguyên tắc kích thủy khí
Trong đó ω là diện tích xylanh nhỏ. 1
Theo định luật Pascal, áp suất p này sẽ truyền tới mọi điểm trong môi chất lỏng, do đó sẽ 1
truyền lên mặt piton lớnω , như vậy, tổng áp lực P tác dụng lên pittông ω 2 2 2 P1 P p (2-15) 2 1 2 2 1
Trong đó: ω - diện tích mặt pittông lớn 2 26
Nếu coi ω , p là không đổi, khi muốn tăng P thì phải tăng ω 1 1 2 2
Từ quan hệ (2-15) ta sử dụng để thiết kế các bộ kích thủy lực hay khí nén thường dùng
trong thực tế (trên hình 2-10). Các bộ này còn gọi là bộ trợ lực hay khuyếc đại.
2.4.3. Biểu diễn áp suất bằng cột chất lỏng
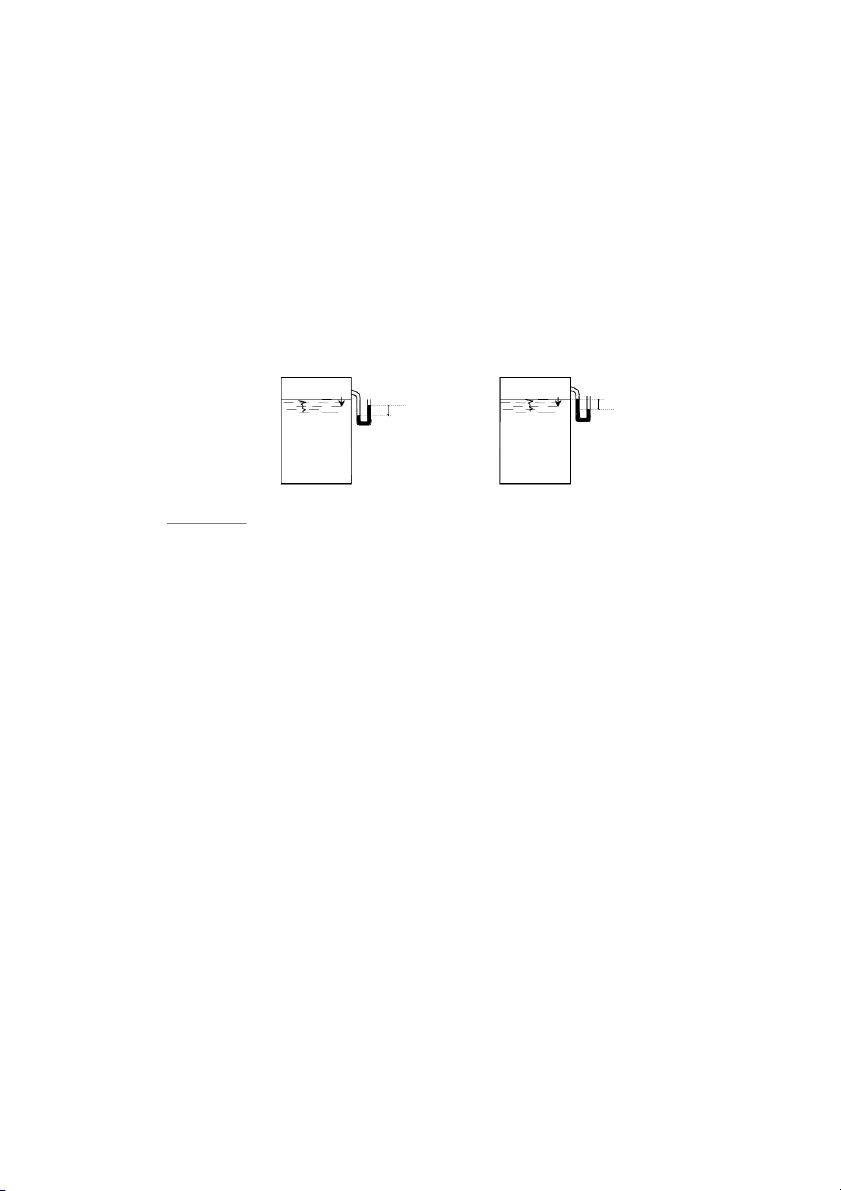
- Áp suất tại một điểm có thể đo bằng chiều cao cột chất lỏng (nước, thuỷ ngân,
rượu...) kể từ điểm đang xét đến mặt thoáng chất lỏng đó.
a. Áp suất tuyệt đối (hay áp suất toàn phần) pt: p p h (2-16) t 0
áp suất tuyệt đối luôn dương.
b. Áp suất dư pd: Là phần lớn hơn của áp suất tuyệt đối so với áp suất khí quyển pd p p p (2-17) d t a
Nếu mặt thoáng của chất lỏng tiếp xúc với không khí thì p p . 0 a Khi đó: p (2- 18) d h
c. Áp suất chân không pCK: Là phần áp suất còn thiếu để áp suất tuyệt đối bằng áp suất khí quyển p p p p (2-19) CK a t d
Nh vậy áp suất chân không có dấu ngược với áp suất d p p ck d
Chú ý: Trong điều kiện bình thường, áp suất khí quyển p = 1at = 98100 N/m2 , tương a p 98100 đương với cột nước h a 10m cột nước. 0 9810 H 2
Có thể dùng chiều cao cột nước để đo pt, pd, pCK.
Hình 2-11. Biểu diễn các dạng đo áp
- Ống kín ± : hút hết không khí
h : cột nước biểu thị áp suất tuyệt đối tại A. t
- Ống hở ²: hở ra khí trời
h : cột nước biểu thị áp suất dư tại A d 27
- Ống hở →: mức nước trong ống thấp hơn điểm A.
h : cột nước biểu thị áp suất chân không tại điểm A ck
Ví dụ 2.4: Xác định áp suất tại mặt thoáng p , áp suất tuyệt đối và áp suất dư thuỷ tĩnh tại A 0
của bình đựng nước như hình vẽ 2-12.
Giải: - Ống đo áp hở ra khí trời, đó là ống đo áp suất dư.
- Chênh lệch 1m là do chênh lệch giữa áp suất mặt với áp suất khí trời 2
p = p + γh = 98100 + 9810.1 = 109710 (N/m ) 0 a 2
p = p + γh = 98100 + 9810.3 = 127530 (N/m ) tA a 2
p = p - p = 127530-98100 = 29430 (N/m ) dA tA a Hình 2-12
2.5. Ý NGHĨA HÌNH HỌC VÀ NĂNG LƯỢNG CỦA PHƯƠNG TRÌNH CƠ BẢN CỦA THỦY TĨNH 2.5.1. Ý nghĩa hình học
Trong phương trình cơ bản của thuỷ tĩnh (2-10) z + p = const
z là độ cao hình học hay cột nước vị trí;
p là độ cao áp suất hay cột nước đo áp;
z + p = H là cột nước thuỷ tĩnh.
Trong một môi trường chất lỏng trọng lực đứng cân bằng, cột nước thuỷ tĩnh đối với
mọi điểm của nó là một hằng số: p z + = H = Const (2-20)
2.5.2. Ý nghĩa năng lượng
Phương trình (2-10) viết cho một đơn vị trọng lượng chất lỏng nên: z là vị năng đơn vị; p là áp năng đơn vị p z+
là thế năng đơn vị. (H hoặc E) 28
Vì vậy, thế năng đơn vị của một khối chất lỏng đứng cân bằng là một hằng số đối với
bất kỳ vị trí nào trong khối chất lỏng đó.
Hình 2-13. Biểu diễn ý nghĩa của phương trình cơ bản
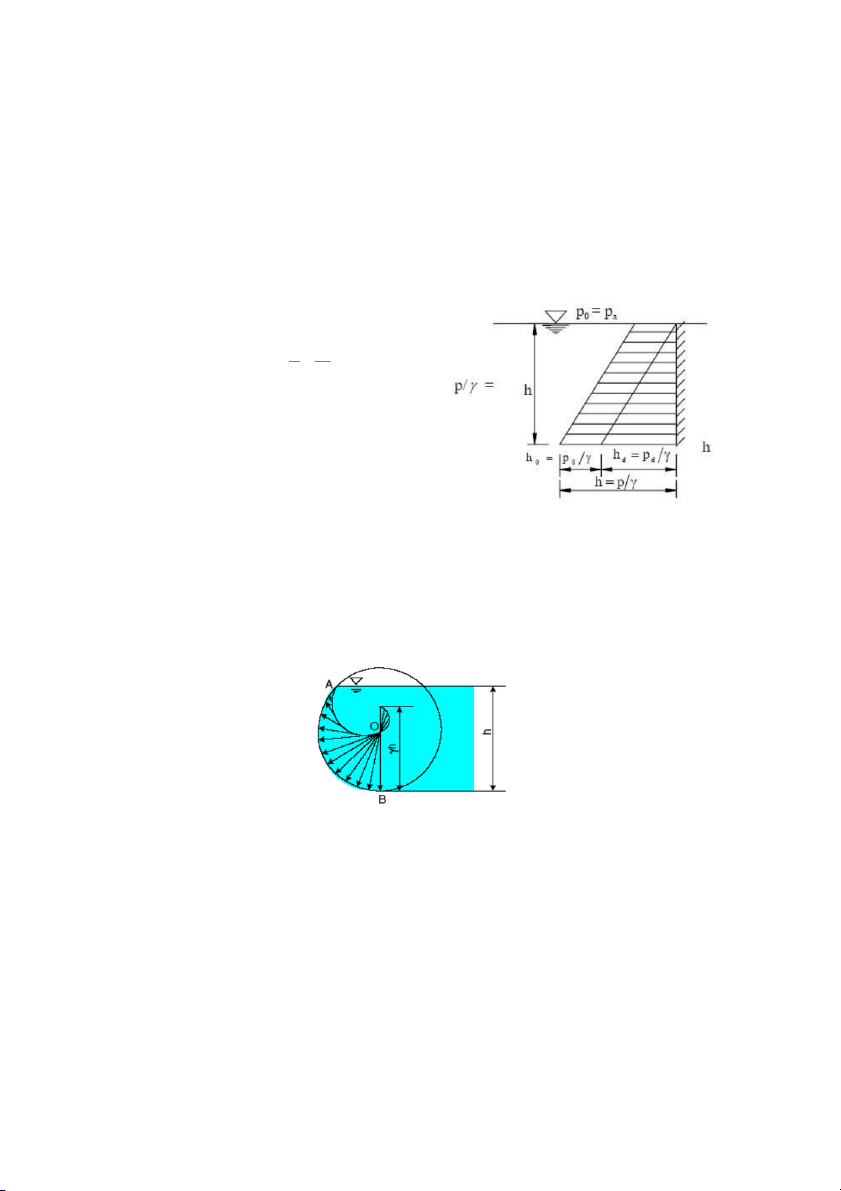
Vậy: Thế năng đơn vị của chất lỏng đứng cân bằng là một hằng số đối với mọi điểm trong chất lỏng 2.6. BIỂU ĐỒ ÁP LỰC
Phương trình cơ bản của thủy tĩnh học chứng tỏ rằng đối với một chất lỏng trọng lực
nhất định, trong điều kiện áp suất tại mặt tự do p cho trước, áp suất p là hàm số bậc nhất o của độ sâu h.
Hình 2-14a. Biểu đồ áp lực
Như vậy trong hệ tọa độ (p, h), phương trình (2-10) được biểu diễn bằng một đường
thẳng. Để giản đơn việc trình bày ta giả thiết p = p khi đó p = γh. o a d
Ta chọn hệ trục tọa độ có trục h thẳng đứng hướng xuống dưới và trục p đặt nằm ngang. Sự
biểu diễn bằng đồ thị hàm số trong hệ tọa độ nói trên gọi là đồ phân bố áp suất thủy tĩnh
theo đường thẳng đứng tức là theo những điểm trên đường thẳng đứng đó 29
Trước tiên ta xét đến đường biểu diễn áp suất dư p = γh theo đường thẳng đứng; d
đường biểu diễn này là một đường thẳng, do đó chỉ cần xác định hai điểm là vẽ được.
Với h = 0 (ở mặt tự do), ta có: p = 0 nên O(0, 0) d
Ta được hai điểm O và A’ , tam giác OAA’ chính là đồ phân bố áp suất dư.
Dùng đồ phân bố áp suất dư, ta có thể xác định áp suất dư p tại một điểm có độ sâu h bất kỳ.
Muốn có đồ phân bố áp suất tuyệt đối ta chỉ cần tịnh tiến đường OA’ theo phương
thẳng góc với Oh một đoạn p và được đường O’A’’. Đồ phân bố áp suất tuyệt đối là hình o
thang vuông góc OO’A’’A.
1. Ta có thể thay trục nằm ngang p bằng trục p p 0 h (2-21)
Khi đó cả hai trục đều là đơn vị độ dài,
áp suất lúc đó có thể biểu thị độ dài cột nước.
Trong thực tiễn, ta cũng thường vẽ biểu đồ
phân bố với tọa độ như vậy để tính áp lực. Đồ
phân bố với tọa độ như thế gọi là biểu đồ áp lực.
2. Do tính chất áp suất tại một điểm phải
thẳng góc với mặt chịu áp lực tại điểm đó,
Hình 2-14b. Phân bố áp lực
nên đồ phân bố áp suất cũng như đồ áp lực
đối với một đường thẳng bao giờ cũng là một tam giác vuông hoặc hình thang vuông. Trong
trường hợp vẽ biểu đồ áp lực trên đường thẳng nghiêng hoặc đường thẳng gãy cũng không
gì khó khăn vì trong trường hợp này đồ áp lực cũng là tam giác vuông hoặc hình thang vuông.
3. Còn vẽ đồ phân bố áp suất trên đường cong ta phải biểu diễn bằng đồ thị hình 2-15 trị số
áp suất tại từng điểm theo phương trình cơ bản rồi nối lại thành đường cong của đồ phân bố
Hình 2-15. Phân bố áp lực trên mặt trụ tròn nằm ngang 30
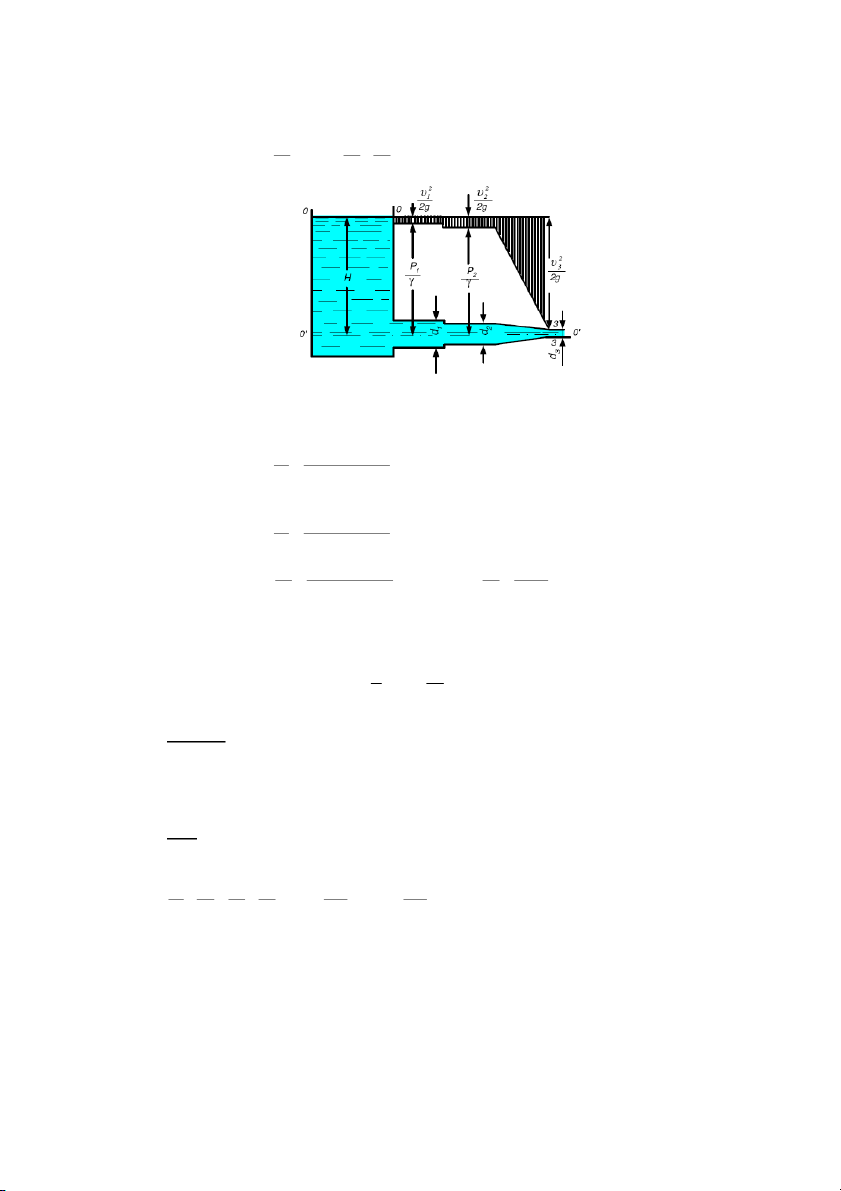
2.7. ÁP LỰC CHẤT LỎNG LÊN THÀNH PHẲNG CÓ HÌNH DẠNG BẤT KỲ.
Trường hợp thành rắn là mặt phẳng, thì áp suất tác dụng lên thành rắn đều song song
với nhau, do đó chúng có một hợp lực hay còn gọi là áp lực tổng hợp P duy nhất. Ta nghiên
cứu trị số của P, điểm đặt và xác định phương chiều của lực
2.7. 1. Trị số của áp lực
Xét một thành phẳng AB hình dạng bất kỳ, có diện tích ω, được đặt nghiêng một góc α
so với phương nằm ngang, áp suất trên mặt thoáng là p0. Hệ trục toạ độ được chọn như hình 2-16.
Trên mặt phẳng ω lấy một vi phân diện tích dω xung quanh một điểm I bất kỳ có toạ độ
(y, z), độ ngập sâu là h, áp suất tại I là p. Áp lực thuỷ tĩnh tác dụng lên vi phân diện tích dω đợc xác định như sau: dP = p.dω = (p0 + gh)d ω
Áp lực P tác dụng lên toàn bộ diện tích mặt phẳng ω là:
P dp (p h d ) 0 p d sin 0 z d .
Từ hình 2-16 có thể thấy rằng: h = z.sina Như vậy P p d si n (2-22) 0 z d p si n 0 z d Tích phân z
d S chính là mômen tĩnh của diện tích ω đối với trục Oy. Gọi z y 0 C là
khoảng cách từ trọng tâm C của diện tích ω đến trục Oy. Theo cơ học lý thuyết có thể viết: Soy = zC ω
Gọi hc là độ ngập sâu của trọng tâm C, thì hc = zCsina hc Do đó S oy sin
Biểu thức (2-22) có thể viết lại thành P=(p0 + γhC)ω (2-23)
Trong (2-23), thành phần (p0 + γhC)ω là áp suất tại trọng tâm C của diện tích phẳng ω đang xét.
Khi p0 là p0t thì Pt = (pot + γhC) gọi là áp lực tuyệt đối. Khi p0 là p0d thì:
Pd = (pod +γhc)ω - gọi là áp lực dư.
Nh vậy: áp lực của chất lỏng tác dụng lên một diện tích phẳng bất kỳ bằng tích số của
áp suất tại trọng tâm diện tích phẳng đó nhân với diện tích ấy.
Nếu áp suất trên mặt thoáng bằng áp suất khí quyển: p0 = pa, nghĩa là pod = 0 thì áp
lực tác dụng lên mặt phẳng AB có thể viết dưới dạng sau: Pd = γ hCω (2-24)
Biểu thức (2-24) dùng để tính áp lực dư tác dụng lên tấm phẳng AB có diện tích ω, khi pd = 0. 31
Trong thực tiễn kỹ thuật, nhiều khi mặt phẳng đang xét chịu áp lực thuỷ tĩnh từ một
phía, còn phía kia lại tiếp xúc với không khí và chịu tác dụng của áp lực không khí. Trong
trường hợp đó mặt phẳng chỉ chịu tác dụng của áp lực dư mà thôi vì áp lực không khí truyền
từ mặt thoáng đến mặt phẳng đã cân bằng với áp lực không khí tác dụng vào phía khô của mặt phẳng. p0 O ▼ α h dP h C A y hD P n z C D I dω C z C zD B y yD D z ω n Hình 2-16 Trường hợp riêng:
Áp lực chất lỏng tác dụng lên đáy bình đặt nằm ngang P = γ .h.ω (vì h = h là độ sâu c
nước trong bình) - không phụ thuộc vào hình dạng của bình.
Hình 2-17. Các dạng bình khác nhau
2.7.2..Xác định phương, chiều của áp lực thuỷ tĩnh P
Theo tính chất của áp suất thuỷ tĩnh, áp lực và áp suất phải hướng vào diện tích chịu
lực (là mặt phẳng AB) và vuông góc với diện tích ấy.
2.7.3. Xác định điểm đặt của áp lực thuỷ tĩnh P
Điểm đặt của áp lực gọi là áp tâm. Tuỳ theo từng trường hợp áp lực tuyệt đối hay áp
lực dư mà áp tâm gọi là áp tâm tuyệt đối hay áp tâm dư. Cách xác định vị trí của áp tâm
trong cả hai trường hợp đều tương tự nhau.
Dới đây chỉ nêu phơng pháp xác định điểm đặt của áp lực dư, khi áp suất trên mặt
thoáng bằng áp suất khí quyển (p0t = pa), nghĩa là pod = 0 32
Gọi điểm D(zD,yD) là điểm đặt của áp lực dư (hình 2-16), cần tìm các toạ độ của điểm D là zD và yD a. Xác định zD
Mô men của áp lực dư Pd đối với trục Oy bằng M = Pd zD = ghC ω zD (2-25)
Áp lực dư của chất lỏng tác dụng lên vi phân diện tích dω sẽ là: dPd=gh dω
Tổng số mômen đối với trục Oy của các áp lực dư lên các vi phân diện tích thuộc ω là M = zdp 2 sin (2-26) du
zhd z d
Trong đó: độ ngập sâu của điểm I là h = zsina.
Theo định luật cân bằng mômen đối với trục Oy thì: Mômen của áp lực dư Pd bằng
tổng số mômen của các áp lực thành phần. Như vậy: h z 2 sin (2-27) C D z d
Theo cơ học lý thuyết thì: z2
d I là mômen quán tính của diện tích ω đối với trục y Oy và I 2
Y = IC + ωzC ; với I C là mô men quán tính của diện tích ω đối với trục n-n song song
với Oy và đi qua trọng tâm C của diện tích phẳng ω.Thay các kết quả này vào biểu thức (2-
27), sau đó thu gọn lại sẽ được: sin I I 2 . y y I z I z C C C D = z (2-28) h z z C z C C C C
Như vậy, tâm áp lực D bao giờ cũng đặt sâu hơn trọng tâm C của mặt phẳng AB. b. Xác định yD
Tương tự như xác định zD , viết phương trình mômen cho trục oz M P y ydP du D du hcy D yPdud hyd Trong đó: h = z.sina Như vậy sin.z sin C y D zy d zyd y (2-29) D z C
Tuy nhiên, trong thực tế thường gặp trường hợp diện tích phẳng ω có hình dạng đối
xứng và trục đối xứng song song với 0z. Khi đó điểm D nằm trên trục đối xứng này và chỉ
cần xác định giá trị zD theo công thức (2-29) là đủ. 33
2.8. ÁP LƯC CHẤT LỎNG LÊN THÀNH PHẲNG HÌNH CHỮ NHẬT CÓ ĐÁY ĐẶT NẰM NGANG
2.8.1. Xác định trị số của p Trong sơ đồ này: A : có độ sâu h 1 B : có độ sâu h 2
AB nghiêng góc α so với mặt nằm ngang
Hình chữ nhật có các cạnh b x h Ta chỉ tính áp lực dư Trị số của P
Hình 2-18. Áp lực lên hình chữ nhật p .h c . h h . b h Vì vậy: p 1 2 b . h . (2-30) 2 h h 1 2 h c 2 h h Nhận xét: Giá trị 1 2 h
. Chính là diện tích đồ phân bố áp suất thủy tĩnh - tức bằng diện 2
tích hình thang AA’BB’, ký hiệu Ω. Vậy: P = γ.Ω .b
Trong trường hợp hình chữ nhật có cạnh đặt nằm ngang:
Áp lực dư bằng tích số của diện tích đồ phân bố ấp suất thủy tĩnh nhân với trọng
lượng riêng và chiều rộng của hình chữ nhật.
2.8.2. Điểm đặt của áp lực.
Đi qua trọng tâm thể tích tạo bởi đồ phân bố áp suất thủy tĩnh và hình chữ nhật chịu
lực. Trên hình vẽ 2-18 ta thấy đi qua trọng tâm của đồ phân bố áp suất và có hướng vuông góc với AB. Ví dụ 2.5:
Xác định áp suất tại mặt thoáng của chất lỏng trong bình chứa kín trong 2 trường hợp
sau (hình 2-19a và 2-19b), biết rằng chất lỏng trong áp kế là thuỷ ngân có trọng lượng riêng
Hg 136,và trọng lượng riêng của nước trong bình là = 9810 N/m3, độ chênh mực 2 H 0 H 0 2
thuỷ ngân trong áp kế là 20cm (khi tính toán bỏ qua tác dụng của không khí trong bình). Giải
Cả 2 trường hợp trên áp suất tại điểm B bằng áp suất khí quyển : pB = pa
Trường hợp 1: (hình 2-19a) 34
Trên áp kế, kẻ một mặt đẳng áp nằm ngang AC đi qua điểm A (mặt thuỷ ngân tiếp
xúc với không khí trong áp kế) và điểm C trong thuỷ ngân.
Như vậy, áp suất tại điểm A bằng áp suất mặt thoáng trong bình kín p0dư vì bỏ qua tác dụng của không khí: p01 = pA (*)
Trên mặt đẳng áp vừa vẽ có: pA = pC
Trong khi đó pC = pa + z Hg
Thay vào (*) ta được : p 01t = pa + (áp suất p Hg z
01t là áp suất tuyệt đối)
Hay áp suất dư trên mặt thoáng chất lỏng trong bình là: p 01 dư = z Hg Thay số vào được p 2
0dư = 13,69.8100,2 = 26.683,2 N/m . p p A ▼ 01 ▼ 02 B z A z C B C Hình 2-19a Hình 2-19b
Trường hợp 2: (hình 2-19b)
Tương tự như trên, kẻ một mặt đẳng áp nằm ngang BC đi qua điểm B (mặt thuỷ ngân
tiếp xúc với không khí ngoài trời) và điểm C trong thuỷ ngân.
Trên mặt đẳng áp có: pB = pC = pa
Trên áp kế còn có: pC = pA + Hg z
Áp suất tại mặt thoáng của chất lỏng trong bình : p02 = pA Như vậy: p02 = pB - = p Hg z a - H z g
Trong trường hợp này áp suất tại mặt thoáng của chất lỏng trong bình nhỏ hơn áp
suất khí quyển, tức là trên mặt thoáng của chất lỏng trong bình có áp suất chân không, trị số bằng: pCK = z Hg Thay số vào được p 2
CK = 13,69,8100,2 = 26.683,2 N/m .
Lưu ý: Hai trường hợp vừa xét trên, trường hợp 1 mặt thoáng của chất lỏng trong bình kín
có áp suất dư ( hình 2-19a), rõ ràng rằng áp suất trong bình p 0dư lớn hơn áp suất không khí
ngoài bình pa, cho nên đã đẩy cột thuỷ ngân của áp kế lệch lên, làm cho mực thuỷ ngân
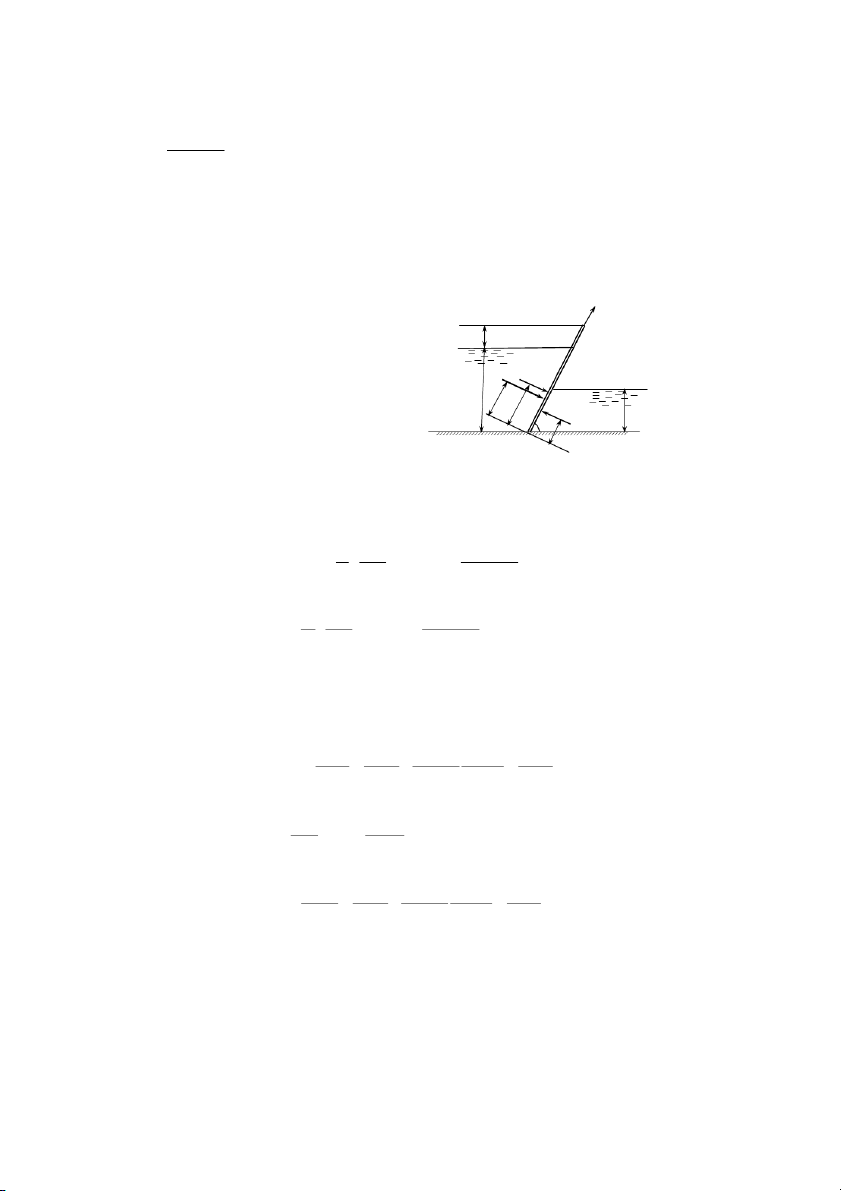
phía ngoài (tiếp xúc với khí trời) cao hơn mực thuỷ ngân phía trong (tiếp xúc với không khí trong bình).
Trường hợp 2 (hình 2-19b) thì hoàn toàn ngược lại mực thuỷ ngân phía ngoài (tiếp
xúc với khí trời) thấp hơn phía trong. Trong bình xuất hiện áp suất chân không. 35 Ví dụ 2.6.
Một tấm phẳng hình chữ nhật, có đáy nằm ngang, rộng b = 8m, được đặt nghiêng một góc
θ=700 so với mặt nằm ngang. Độ sâu mực nước thượng lưu h1 = 3m, độ sâu hạ lưu h 2 = 2m,
khoảng cách từ mực nước thượng lưu tới mép trên tấm phẳng là a = 1m (hình 2-20)
1. Xác định trị số của áp lực dư tác dụng lên tấm phẳng.
2. Xác định vị trí điểm đặt của áp lực tổng hợp tác dụng lên tấm phẳng.
3. Xác định lực nâng ban đầu T để nâng được tấm phẳng, biết tấm phẳng dày t =
0,1m; trọng lượng riêng của tấm phẳng ρ = 1300 kg/m3; hệ số ma sát của bản lề f = 0,4. Giải T
1. Xác định áp lực thuỷ tĩnh dư tác dụng A lên tấm phẳng a ▼ M
Áp lực thuỷ tĩnh dư tác dụng lên tấm
phẳng được xác định theo công thức: h1 P1 D1 N ▼ ℓ P = γ.ω.h P D c D2 ℓ h 1 2 P Trong đó: h θ 2
c – Là khoảng cách từ mặt
thoáng đến trọng tâm của phần B ℓ2
ngập sâu trong nước của tấm Hình 2-20 phẳng.
ω - Là diện tích phần ngập trong nước của tấm phẳng
Như vậy áp lực thuỷ tĩnh dư tác dụng lên tấm phẳng bởi nước thượng lưu (mặt BM): h h 2 P 3 1 1 1 = b = 9 8 . 10 8 375 8 . 25 N 2 sin 2 sin 700
Áp lực thuỷ tĩnh dư tác dụng lên tấm phẳng bởi nước hạ lưu (mặt BN): 2 P h h 2 2 2 2 = b 9810 8 = 167.033,3 N 0 2 sin 2 sin 70
Áp lực thuỷ tĩnh dư tổng hợp tác dụng lên tấm phẳng được xác định bởi công thức:
P = P1 - P2 = 375.825 – 167.033,3 = 208.791,7 N
2. Xác định vị trí điểm đặt của áp lực thuỷ tĩnh
+ Khoảng cách từ điểm đặt của áp lực P1 đến điểm M ở thượng lưu là: 3 I h bh h 01 1 1 2sin2 2 1 Z Z 1 , 2 3 m 1 D 1 C ZC b h 1 1 2sin 12sin 3 . 2 3sin 1
Khoảng cách từ điểm đặt của áp lực P1 đến điểm B (cuối tấm phẳng) là: h 3 ℓ 1 1 = Z 13 , 2 063 , 1 m sin D1 sin 70 0
+ Khoảng cách từ điểm đặt của áp lực P2 đến điểm N ở hạ lưu là: 3 I h bh h 02 2 2 2sin 2 2 2 Z m D Z 2 C 2 , 1 42 Z C 2sin bh 2 2 12sin3 2 3sin 2 36
Khoảng cách từ điểm đặt của áp lực P2 đến điểm B (cuối tấm phẳng) là: h 2 ℓ 2 2 = Z 42 , 1 708 , 0 m sin D 2 sin 700
+ Mômen của các lực P1, P2, và P đối với điểm B là: MB = Pℓ = P1ℓ1 - P2ℓ2 P P 1 1 2 2 375 8 . 25 0 , 1 63 167 033 3 , 7 , 0 08 ℓ = 3 , 1 5 m P 208 791 7 ,
Như vậy điểm đặt của áp lực dư tổng hợp cách điểm B (cuối tấm phẳng) một đoạn là: ℓ = 1,35m
3. Xác định lực nâng ban đầu T để nâng được tấm phẳng
T G sin P G co s f
Trong đó: G là trọng lượng tấm phẳng; h a 4 1 G g bt 1300 9 81 , 8 1 , 0 , 428 . 43 67 N sin sin 70 0
Vậy Lực T ban đầu để nâng tấm phẳng là T = 135673.87 N = 135,67 KN
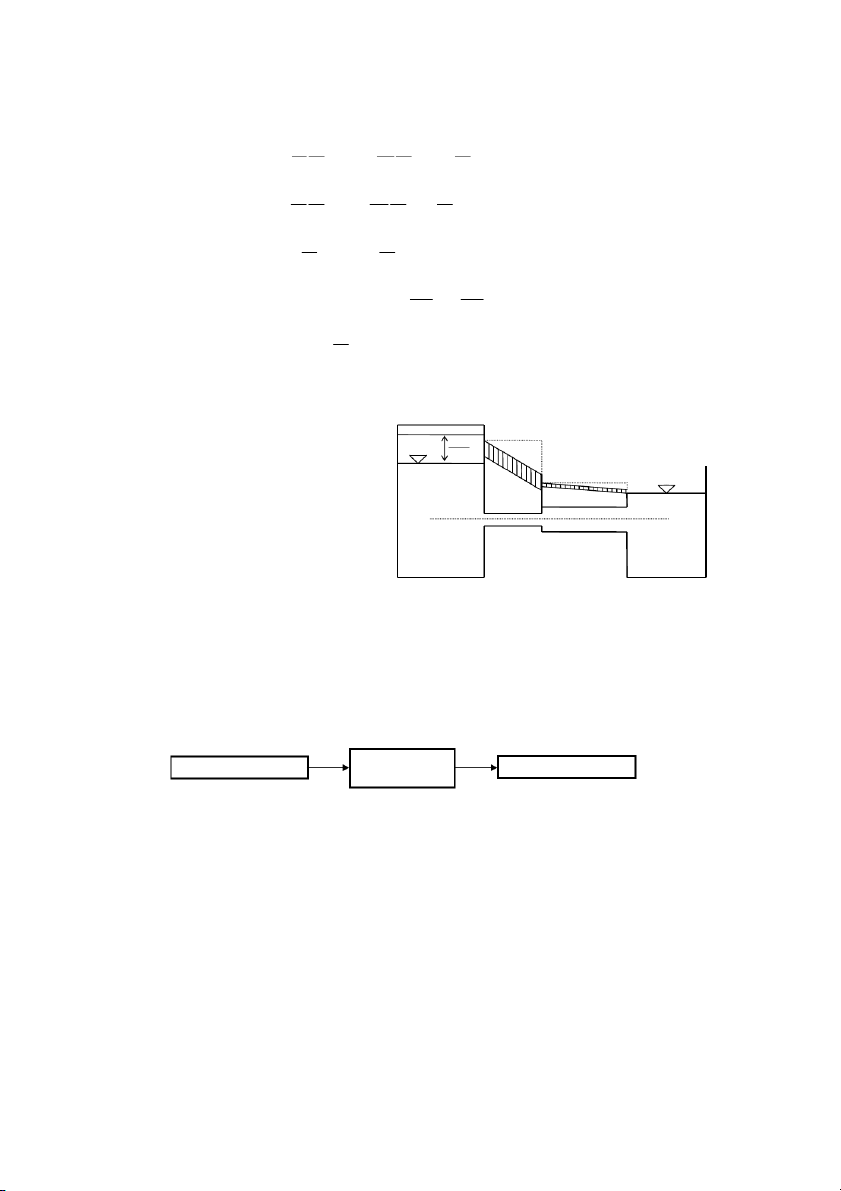
2.9. ÁP LỰC CỦA CHẤT LỎNG LÊN THÀNG CONG.
Nói chung nếu thành cong có hình dạng bất kỳ, thì những áp lực nguyên tố không hợp
lại thành một áp lực tổng hợp duy nhất.
Giới hạn trường hợp xét:
- Thành cong hình trụ tròn có đường sinh đặt nằm ngang.
- Để đơn giản nhưng không làm mất tính tổng quát, ta chỉ xét áp lực dư: tức trường hợp: p = p 0 a O x
Xét khối lăng trụ ABCDEFGH G H
chứa đầy chất lỏng, mặt trụ ABCD có
đường sinh ℓ đặt nằm ngang (hình 2- ℓ Ω
21). Mặt trụ này chịu tác dụng của áp Z D
lực thủy tĩnh do chất lỏng gây ra. Vì ℓ C
mặt thoáng của chất lỏng tiếp xúc với y F E ℓ
không khí nên mặt trụ ABCD sẽ chiụ d ω
tác dụng của áp lực dư. Chọn hệ trục h
toạ độ 0xyz có mặt x0y trùng với mặt A
thoáng của chất lỏng, trục 0y song
song với đường sinh ℓ của mặt trụ. z B
Trục Oz đặt thẳng đứng. Hình 2-21
Vì p0 = pa cho nên ở đây chỉ xét
đến áp lực thuỷ tĩnh dư Pd. Áp lực dư này được xác định bởi ba thành phần chiếu lên ba trục toạ độ 2 2 2 P P P P d X Y Z (2-31) 37
Trong đó: PX, PY, PZ - hình chiếu của Pd lên các trục Ox, Oy và Oz; PY = 0 vì trục Oy
song song với đường sinh của mặt trụ nên Pd vuông góc với Oy. Như vậy áp lực thuỷ tĩnh
trong trờng hợp này đợc xác định bằng công thức: 2 2 P P P d X Z (2-32)
Trên mặt trụ ABCD lấy một vi phân diện F dω E
tích dω đặt ở độ sâu h bất kỳ. Vì diện tích dω ▼ z
rất nhỏ và dài theo đường sinh nên dω được
coi là phẳng. Do đó áp lực nguyên tố tác dụng Pz
vào vi phân diện tích dω là: dP = gh dω hCx O
Áp lực này được phân tích ra làm 2 dPd dPz A thành phần: dP M
X nằm ngang và dPZ thẳng đứng β
(hình 2-22), và các giá trị đó bằng: Px C x α dPx dω dP
x = dPcosα = ghdωcosα = gh dωx B dP vì: dωcosα = dωx z dP d dω Và dP
z = dPcosβ = ghdωcosβ = gh dωz dP Hình 2-22 x dω x vì: dωcosβ = dω dω z z
Trong đó: α - góc giữa dP và trục Ox nằm ngang.
β - góc giữa dP và trục Oz thẳng đứng.
Xác định áp lực tổng hợp PX P dP hd h X X X CX X x x P h (2-33) X CX X
Trong đó: ωX - hình chiếu của mặt trụ ABCD lên mặt yOz,
ωX là diện tích hình chữ nhật MB có đáy nằm ngang, chiều rộng đáy bằng
chiều dài đờng sinh ℓ của hình trụ;
hcx- độ ngập sâu của trọng tâm diện tích ω X;
g - trọng lợng riêng của chất lỏng.
Xác định áp lực tổng hợp PZ P dP hd W Z Z Z ABCDEFGH ▼ z z P Z = gWABCDEFGH (2-34) θ P
Trong đó: WABCDEFGH - thể tích khối lăng trụ thẳng
đứng ABCDEFGH, hình này được gọi là vật áp lực. Vì
thế PZ bằng trọng lượng vật áp lực. Hình 2-23
Thể tích vật áp lực đuợc tính theo công thức: 38 WABCDEFGH = WABFE.ℓ (2-35)
Trong đó: WABFE - diện tích hình cong ABEF; ℓ - chiều dài đường sinh.
Có thể định nghĩa vật áp lực nh sau: Vật áp lực là một khối lăng trụ giới hạn bởi mặt
cong và hình chiếu thẳng đứng của nó lên mặt thoáng chất lỏng có áp suất bằng áp suất khí quyển (p0 = pa).
Áp lực thuỷ tĩnh P tác dụng lên mặt trụ phải hướng vào mặt trụ và vuông góc với tiếp
tuyến của mặt trụ tại điểm tiếp xúc. Áp lực này đi qua tâm của mặt trụ và lập với phương
ngang một góc θ (hình 2-23) sao cho: P tg θ = Z (2-36) PX
Trường hợp mặt cong là mặt cầu cũng có thể phân tích áp lực dư Pd ra ba thành phần là
các hình chiếu lên ba trục toạ độ, sau đó xác định áp lực dư theo công thức (2-31). Các áp
lực nguyên tố đều đồng quy tại một điểm là tâm của hình cầu, do đó áp lực tổng hợp sẽ đi qua tâm của hình cầu.
Khi giải bài toán có tính đến áp lực thuỷ tĩnh tác dụng lên mặt cong hình trụ tròn có
đường sinh ℓ, điều quan trọng là phải chọn hệ trục toạ độ sao cho có một trục song song với
đường sinh ℓ của mặt trụ để một hình chiếu của áp lực bằng không.
Khi tính thành phần PZ phải xác định được thể tích vật áp lực vì trị số của thành phần
PZ đúng bằng trọng lượng vật áp lực. Sau đây là các trường hợp xác định phương chiều vật áp lực (Hình 2-24). . ▼ ▼ ▼ ▼ ▼ PZ PZ P P P Z Z Z a. b. c. d. e. Hình 2-24
1. Trường hợp chất lỏng ở ngay trên mặt cong, có thể chất lỏng chiếm toàn bộ vật áp
lực hoặc chiếm một phần, còn phía kia của mặt cong tiếp xúc với không khí. Khi đó
thành phần PZ quay xuống dưới và mang dấu +
2. Trường hợp chất lỏng ở phía dưới mặt cong. Thành phần PZ hướng lên trên và mang dấu -
3. Khi mặt cong có hình dạng phức tạp, vật áp lực cũng có hình dạng phức tạp. Để xác định
dấu của vật áp lực và phương chiều của PZ, thường phải phân mặt cong phức tạp làm nhiều
phần đơn giản để đa về 2 trường hợp nêu trên 39 Ví dụ 2.7
Xác định áp lực thuỷ tĩnh dư tác dụng lên một cửa van hình trụ đặt nằm ngang ngập
sâu trong nước.. Biết độ sâu nước phía thượng lưu h1 = 6m; hình trụ có đường kính d = 5m
và đường sinh ℓ = 9m. Ở phía hạ lưu không có nước (hình 2-25). Giải
Chọn hệ trục toạ độ Oyxz có trục ▼
Oz thẳng đứng, trục Oy song song với
đường sinh ℓ của cửa van hình trụ, gốc hcx
toạ độ trùng với tâm mặt trụ O. P x
Khi đó các hình chiếu lên 3 trục toạ Z h1 θ O
độ của áp lực thuỷ tĩnh P d dư tác dụng lên P - cửa van trụ là: P X dư (PX, PY, PZ) P ωx Trong đó có thành phần P ▼ Y = 0. z
Như vậy, áp lực thuỷ tĩnh dư tác Hình 2-25
dụng lên cửa van được tính bằng công thức : 2 2 P P P du X Z
Thành phần P X nằm ngang được xác định như áp lực thuỷ tĩnh tác dụng lên hình chữ
nhật có đáy là ℓ và chiều cao là d
PX = θ.hcxωx = θ(h1 - d + d/2)dℓ =
= 9810 (6- 5 +2,5)59 = 1.545.075 N
Thành phần PZ thẳng đứng được xác định bằng trọng lượng vật áp lực.
Trong trường hợp này vật áp lực được xác định là dấu - hướng lên trên (hình 2-24), có
thể tích là một nửa hình trụ đường kính d và đường sinh ℓ. 2 2 P d 1 , 3 4 5 Z = 9 8 . 10 9 86 . 6 345 6 , 25 N 2 4 8
Như vậy áp lực thuỷ tĩnh dư tác dụng lên cửa van là: P 075 . 545 . 1 2 625 , 345 . 866 2 37 , 027 . 880 N du
Áp lực thuỷ tĩnh dư tác dụng lên cửa van là Pdư =880.027,37 N và hợp với phương nằm PZ 866 3 . 45 6 , 25
ngang một góc θ sao cho : tg θ = 5 , 0 6 P 5 . 1 45 0 . 75 X
Hay θ = arctg0,56 = 29014'55''.
Áp lực thuỷ tĩnh dư tác dụng lên cửa van hợp với phương nằm ngang một góc
θ = 29014'55'' và được thể hiện trong hình 2-25 40
Câu hỏi và bài tập chương 2 Câu hỏi
Câu 2.1. Định nghĩa về 2 tính chất cơ bản của áp suất thuỷ tĩnh.
Câu 2.2. Cách th nh lập phương trình vi phân cân bằng của chất lỏng v ý nghĩa của nó.
Câu 2.3. Thế nào là mặt tự do, mặt đẳng áp ?
Câu 2.4. Cách thành lập phương trình cơ bản của thuỷ tĩnh học và ý nghĩa của nó.
Câu 2.5. Phân biệt các loại áp suất thuỷ tĩnh.
Câu 2.6. Biểu đồ phân bố áp suất thuỷ tĩnh là gì ? cách xác định.
Câu 2.7. Cách xác định áp lực thuỷ tĩnh lên hình phẳng, hình cong? Bài tập Bài 2.1:
Tìm độ chênh mực nước trong ống đo áp , biết áp suất tuyệt đối trên mặt thoáng trong bình là p 1 = 1,06 at. Cho 3 9810N / m . Nếu cho h n
1 = 1,2 m tìm áp suất tại đáy bình (hình 2-26) pa p1 h A h M Hình 2-26 Bài 2.2:
Xác định chiều cao nước dâng lên trong ống chân không h, nếu như áp suất tuyệt đối
trong bình pB = 0,95 at, áp suất mặt thoáng phía ngoài ống là áp suất khí trời? Cho 3 9810N / m . Nếu p ) thì độ n
B = 0 at và chất lỏng là thuỷ ngân ( 3 Hg 132925N / m
cao hHg dâng lên trong ống đo áp là bao nhiêu mm? (Hình 2-27) pB pa A Hình 2-27 41 Bài 2.3:
Xác định áp suất dư tại điểm O, A, B trong ống dẫn bán kính R = 30cm nếu biết
chiều cao cột thuỷ ngân trong ống đo áp h1 = 25 cm. Khoảng cách từ tâm ống đến mặt phân
cách nước và thuỷ ngân là h2 = 40 cm. Cho trọng lượng riêng của thuỷ ngân và của nước trong điều kiện này là: 3 133416N / m ; 3
9810N / m . (Hình 2-28) Hg n
Xác định áp suất dư tại điểm D nếu h3 = 10 m ? áp suất này là loại áp suất gì? pa D h 3 h C E G 1 A h 2 O B n tn Hình 2-28 Bài 2.4:
Xác định áp suất dư của nước trong ống theo các số đọc của áp kế thuỷ ngân. Cao
trình mực thuỷ ngân trong trục ống z1 = 1,75 dm; z2 = 3 dm; z3 = 1,5 dm; z4 = 2,5 dm. Biết 3 133416N / m ; 3 9810N / m Hg n pa Z2 Z4 Z1 Z3 Z0 Hình 2-29 Bài 2.5:
Xác định độ cao của mực Hg tại A khi cho biết áp suất chỉ trong các áp kế là p1 =
0,9 at, p2 = 1,86 at và độ cao của các mức chất lỏng biểu diễn như hình vẽ. Không khí 120(cm) 112(cm) DÇu 2 H O 106(cm) C B A Hg Hình 2-30 42
Biết trọng lượng riêng của dầu và thuỷ ngân là 3 9025 N / m 132925 N m dau , 3 / Hg và 3
9810N / m . Cho g = 9,81 m/s2; áp suất trên mặt thoáng của ống là áp suất khí trời. n
Giải thích: Trên hình là kí hiệu cao trình của các mặt chất lỏng: là chiều cao của mặt chất
lỏng tính từ một mặt chuẩn cố định đến vị trí mặt chất lỏng đó. Bài 2.6:
Xác định áp suất tuyệt đối tại đầu pittông A khi cho độ cao các mực thuỷ ngân trong
ống đo áp chữ U biểu diễn như hình vẽ. Trọng lượng riêng của dầu và thuỷ ngân là 3 9025N / m
132925 N m .Cho g = 9,81 m/s2; áp suất trên mặt thoáng dau và 3 / Hg
của ống là áp suất khí trời. A DÇu 24 cm 3 cm Hg Hình 2-31 Bài 2.7:
Sơ đồ bên cho thấy điểm B cao hơn điểm A một đoạn z = 15cm. Chất lỏng ở trong
ống chữ U ngược là dầu hoả có 3 , xác định: dh 7456N / m
1/ Độ chênh áp suất: pA – pB khi h = 85 cm trong hai trường hợp:
a) Trong các bình chứa là dầu mỏ có 3 7848N / m dm
b) Trong các bình chứa nước có 3 9810N / m n
2/ Độ chênh áp suất là bao nhiêu khi z = 0, các bình chứa dầu mỏ và h = 85 cm. h z Hình 2-32 43 Bài 2.8:
Xác định áp suất của dòng khí trong ống A biết mực nước dâng lên trong ống đo áp là h = 50 cm. Cho 3
9810N / m , áp suất mặt thoáng là áp suất không khí. A h p a Hình 2-33
Bài 2.9: Một cửa van AB có bề rộng b = 7 m; Trọng lượng G
= 3000 N được nhúng chìm trong nước (Hình bên). Cửa van
quay quanh khớp bản lề tại B và tựa lên tường phẳng tại A.
Hãy xác định mực nước h để cửa van sẽ bắt đầu mở? Hình 2-34
Bài 2.10: Một đập nước l một phần tư mặt trụ bán kính R = 20 m (có kích thước như hình
vẽ), rộng 50 m. Xác định áp lực dư (trị số, phương, chiều,
điểm đặt) của nước lên đập? Hình 2-35
Bài 2.11: Van K sẽ đậy kín miệng ống dẫn nếu hệ thống
đòn bẩy a, b ở vị trí nằm ngang (Hình vẽ). Tính xem với
áp suất của nước trong ống dẫn bằng bao nhiêu thì van K
sẽ mở ra được? Biết rằng cánh tay đòn b = 5a, đường
kính ống d = 50 mm, đường kính phao cầu D = 200 mm.
Trọng lượng phao v hệ thống đòn bẩy không đáng kể. Hình 2-36 44 Bài 2.12:
Xác định lực Q để nâng tấm chắn nghiêng một
góc α, quay quanh trục O (Hình 2-37). Chiều rộng tấm
chắn b = 1,50 m, khoảng cách từ mặt nước đến trục O,
a = 20 cm. Góc α = 600, H = 1,50 m. Bỏ qua trọng
lượng tấm chắn và ma sát trên bản lề của trục O. Hình 2-37 Bài 2.13:
Vẽ biểu đồ áp suất lên mặt cong ngập trong chất lỏng cho các trường hợp dưới đây. A B C Hình 2-38 Bài 2.14:
Van hình trụ có thể quay xung quanh trục nằm ngang O (hình 2-39). Trọng tâm của
van nằm trên đường bán kính tạo thành góc o
45 theo phương ngang và cách trục quay O 1
một đoạn OA = r . Biết bán kính r = 40 cm, chiều dài L = 100 cm, mực nước trước cửa 5
van luôn cao hơn điểm C, áp suất trên mặt thoáng là áp suất khí trời, trọng lượng riêng của
nước 9810N/m3. Xác định trọng lượng của van để van ở vị trí cân bằng như hình vẽ. n pa 2r = D Hình 2-39 45 Chương 3
ĐỘNG LỰC HỌC CHẤT LƯU
Chương này chúng ta nghiên cứu những nét chính của chất lỏng chuyển động. Nhiều
hiện tượng thủy lực phức tạp, không thể nghiên cứu hoàn toàn bằng lý thuyết được mà phải
kết hợp với thực nghiệm.
Trong phạm vi thủy lực đại cương, thường sử dụng ba định lụât bảo toàn: Khối
lượng, Năng lượng và Động lượng. 3.1. KHÁI NIỆM CƠ BẢN
Động lực học chất lỏng nghiên cứu những quy luật chung về chuyển động của chất
lỏng có xét tới các lực tác dụng. Khi chất lỏng thực (có tính nhớt) chuyển động, xuất hiện
sức ma sát trong giữa các lớp của chất lỏng. Vì vậy những kết luận động lực học của chất
lỏng lý tưởng (chất lỏng bỏ qua tính nhớt) và chất lỏng thực là khác nhau.
Động học chất lỏng nghiên cứu chuyển động z
của chất lỏng mà không xét đến lực tác dụng.
Để nghiên cứu dòng chất lỏng ta cần phải uz
chọn được mô hình động học tương ứng. Ở đây uy
sẽ dùng phương pháp nghiên cứu dòng chất lỏng M ux của Ơle. O
Chọn hệ trục tọa độ Oxyz cố định. Một chất x x y
điểm M của chất lỏng chuyển động có tọa độ M'
(x,y,z) và vận tốc là u. Chiếu vận tốc u này lên Hình 3-1 y
các trục tọa độ ta có các thành phần vận tốc ux, uy, uz (Hình 3-1): ux = f1(x,y,z,t) uy = f2(x,y,z,t) (3-1) uz = f3(x,y,z,t)
Nếu biết được các giá trị của hàm số này đối với từng trường hợp cụ thể thì ta có thể xác
định được sự phân bố vận tốc và vị trí của điểm chất lỏng đó tại thời điểm bất kỳ.
Phân loại chuyển động của chất lỏng.
Tất cả các chuyển động của chất lỏng đều có thể phân thành 2 nhóm: chuyển động
không ổn định và chuyển động ổn định.
Ta gọi Chuyển động không ổn định là chuyển động mà các yếu tố của nó phụ thuộc vào
thời gian và không gian, tức là: u = u(x, y, z, t); p = p(x, y, z, t) v.v... Hay u p 0 0 t t
Ví dụ: Chuyển động của dòng chất lỏng trong trường hợp tháo cạn bình chứa là chuyển động không ổn định 46
Ta gọi Chuyển động ổn định là chuyển động mà các yếu tố của nó chỉ phụ thuộc vào tọa
độ không gian mà không phụ thuộc thời gian, tức là:
u = u(x, y, z); p = p(x, y, z) v.v... Hay u p 0 0 t t 3.2. CÁC ĐỊNH NGHĨA. 3.2.1. Quỹ đạo
Quỹ đạo là đường đi của một phần tử chất lỏng trong không gian chứa đầy chất lỏng
chuyển động. Phương trình vi phân của quỹ đạo là: u u x y uz dt (3-2) dx dy dz 3.2.2. Đường dòng
Đường dòng là đường cong tại u1
một thời điểm cho trước, đi qua các u2
phần tử chất lỏng có vectơ lưu tốc là u M 3
những tiếp tuyến của đường cong ấy. M2 3 M4 u Đường dòng M 4
Có thể vẽ đường dòng trong môi 1 Hình 3-2
trường chất lỏng chuyển động như
sau: tại một thời điểm t phần tử M có tốc độ u, cũng ở thời điểm đó, phần tử chất lỏng M1 ở
sát cạnh phần tử M và nằm trên véctơ u, có tốc độ u1, tương tự cũng ở thời điểm trên ta cũng
có M2 và u2 ... Mi và ui. Đường cong C đi qua các điểm M1, M2 ... Mi ... lấy tốc độ u1, u2 ...
ui ... làm tiếp tuyến chính là một đường dòng ở thời điểm t (Hình 3-2).
Theo định nghĩa về đường dòng thì hai đường dòng khác nhau không thể giao nhau hoặc tiếp xúc nhau.
Phương trình vi phân của đường dòng có dạng sau: u uy u x z (3-3) dx dy dz
Nếu chuyển động là không ổn định thì tại một điểm cố định hướng của vận tốc sẽ thay
đổi theo thời gian. Do đó, tại một điểm với thời gian khác nhau sẽ có các đường dòng khác nhau đi qua.
Trong chuyển động ổn định, tại mọi điểm trong dòng chảy, trị số và hướng của vận tốc
đều không phụ thuộc vào thời gian. Vì vậy đường dòng và quỹ đạo của phần tử chất lỏng chỉ là một.
3.2.3. Dòng nguyên tố và dòng chảy.
Trong không gian chứa đầy chất lỏng chuyển động, lấy một đường cong kín giới hạn
một vi phân diện tích vô cùng nhỏ d. Tất cả các đường dòng đi qua các điểm trên đường
cong kín đó tạo thành một mặt có dạng ống gọi là ống dòng (Hình 3-3). 47
Khối lượng chất lỏng chuyển động ở trong không gian giới hạn bởi ống dòng gọi là
dòng nguyên tố. Do tính chất không giao nhau của những đường dòng, chất lỏng không thể
xuyên qua ống dòng mà đi ra hoặc đi vào dòng nguyên tố được.
Trong không gian chứa đầy chất lỏng chuyển
động, lấy một đường cong kín giới hạn một diện tích
hữu hạn bao gồm vô số vi phân diện tích d vô
cùng nhỏ, tạo nên vô số dòng nguyên tố, trong đó:
Tập hợp những dòng nguyên tố này gọi là dòng
chảy. Môi trường chất lỏng chuyển động có thể coi
là môi trường liên tục bao gồm vô số dòng nguyên dω Hình 3-3
tố, môi trường đó gọi là một dòng chảy. ω
Khi nghiên cứu tính chất động học và động lực
học của chất lỏng chuyển động, có thể dùng hai mẫu dòng chảy sau:
1. Dòng chảy được coi như là tập hợp của vô số phần tử chất lỏng. Nghiên cứu mẫu
này, thường đi đến những phương trình vi phân, nhưng khó tích phân để thu được những
công thức tính toán cho dòng chảy thực tế, có kích thước cụ thể. Đó là bài toán ba chiều.
Phương pháp này có ý nghĩa rất lớn về mặt lý thuyết cũng như về phương pháp nghiên cứu.
2. Dòng chảy được coi là tập hợp bởi vô số dòng nguyên tố. Khi nghiên cứu theo mẫu
này, dễ dàng đi đến công thức tính toán cho dòng chảy có kích thước hữu hạn. Đó là bài
toán một thứ nguyên (còn gọi là bài toán một chiều) và cũng là phương pháp thường dùng
để suy ra những công thức tính toán.
Trong nội dung của chương này, mẫu dòng chảy thứ hai sẽ được sử dụng khi nghiên cứu.
3.2.4. Những yếu tố thuỷ lực của dòng chảy
a. Diện tích mặt cắt ướt: (m2)
Mặt cắt thẳng góc với tất cả các đường dòng gọi là mặt cắt ướt hay mặt ướt của dòng
chảy. Mặt cắt ướt có thể là phẳng khi các đường dòng là những đường thẳng song song, và
có thể cong khi các đường dòng
không song song. Diện tích của mặt A D
cắt ướt ký hiệu là , đơn vị là m2. d = 2r Với hình tròn: = d2/4 (Hình 3-4a) B C b. Chu vi ướt: (m) Hình 3-4a Hình 3-4b
Chu vi ướt là bề dài của phần tiếp xúc giữa chất lỏng và thành rắn của mặt cắt ướt. Thí dụ: Hình tròn = d (Hình 3-4a)
Hình thang cân = AB + BC + CD (Hình 3-4b)
c. Bán kính thủy lực: R (m)
Là tỉ số giữa diện tích mặt cắt ướt và chu vi ướt. 48 R (3-4)
Bán kính thủy lực của mặt cắt ướt hình tròn chứa đầy nước (hình 3-4a) là: 2 R = d d r 4 d 4 2
d. Lưu lượng: Q, dQ (m3/s)
Là thể tích chất lỏng đi qua một mặt cắt ướt nào đó trong một đơn vị thời gian.
Nếu mặt cắt ướt của một dòng nguyên tố có diện tích là d thì lưu lượng nguyên tố dQ
của dòng nguyên tố bằng: dQ = ud (3-5)
Lưu lượng của toàn dòng chảy là tổng số các lưu lượng nguyên tố trên mặt cắt ướt của toàn dòng: Q = dQ u d (3-6)
e. Lưu tốc trung bình mặt cắt của dòng chảy: v (m/s)
Lưu tốc trung bình mặt cắt của dòng
chảy là tỷ số của lưu lượng Q đối với diện
tích của mặt cắt ướt đó (Hình 3-5), ký Q
hiệu bằng v, đơn vị đo bằng m/s, cm/s : v u Q v (3-7)
Như vậy lưu lượng bằng thể tích hình Hình 3-5
trụ có đáy là mặt cắt ướt , có chiều cao
bằng lưu tốc trung bình mặt cắt ướt v.
3.2.5. Phân loại dòng chảy.
a. Dòng chảy không đều và đều
Dòng chảy không đều là dòng chảy có các đường dòng không phải là những đường
thẳng song song. Như vậy những dòng nguyên tố của dòng chảy không đều cũng không
phải là thẳng song song. Dọc theo dòng chảy không đều, mặt cắt ướt, lưu tốc điểm tương
ứng thay đổi. Thí dụ: Dòng chảy trong ống hình nón cụt, trong ống hình tròn tại chỗ uốn
cong, trong máng có bề rộng thay đổi v.v....
Dòng chảy đều là dòng chảy có các đường dòng là các đường thẳng song song; như vậy
những dòng nguyên tố của dòng chảy đều là thẳng song song. Trong dòng chảy đều hình
dạng, diện tích mặt cắt, sự phân bố lưu tốc điểm tương ứng như nhau, không đổi dọc theo
dòng chảy. Thí dụ: dòng chảy đầy ống trong những ống thẳng v.v....
b. Dòng chảy có áp, không áp và dòng tia
Dòng chảy có áp là dòng chảy mà chu vi của các mặt cắt ướt hoàn toàn là những thành
rắn cố định. Đặc điểm của dòng chảy có áp là chảy đầy ống, tại tất cả các điểm của mặt cắt 49
ướt, áp lực thủy động không bằng áp lực không khí. Thí dụ: chảy đầy ống dẫn nước là dòng chảy có áp.
Dòng chảy không áp là dòng chảy mà chu vi ướt của các mặt cắt ướt có bộ phận là
thành rắn cố định, có bộ phận là mặt tự do tiếp xúc với không khí. Thí dụ dòng chảy trong
sông, trong kênh, áp lực lên mặt nước bằng áp lực không khí.
Nếu toàn bộ chu vi ướt của mặt cắt ướt không tiếp xúc với thành rắn mà tiếp xúc với
không khí hoặc với chất lỏng khác thì gọi là dòng tia.
c. Dòng chảy đổi dần và đổi đột ngột
Dòng chảy đổi dần là dòng chảy có các đường dòng gần là những đường thẳng song
song, mặt cắt ướt coi là phẳng. Đặc điểm của mặt cắt có dòng chảy đổi dần là trên mặt cắt
lực quán tính coi như không có, do đó sự phân bố áp lực coi như theo quy luật thủy tĩnh.
Dòng chảy đổi đột ngột là dòng chảy mà các đường dòng không thể coi như những
đường thẳng song song. Đặc điểm của dòng chảy đổi đột ngột là trên mặt cắt có tác dụng
của lực quán tính, do đó sự phân bố áp lực không tuân theo quy luật thủy tĩnh.
Một dòng chảy có thể mang nhiều tính chất nói trên.
3.3. PHƯƠNG TRÌNH LIÊN TỤC CỦA DÒNG CHẢY ỔN ĐỊNH
Chất lỏng chuyển động một cách liên tục không hình thành những vùng không gian
trống. Tính chất liên tục đó có thể biểu thị bởi biểu thức toán học gọi là phương trình liên tục.
Trên một dòng nguyên tố xét hai mặt cắt AA và BB có diện tích tương ứng là d1 và
d2 với lưu tốc điểm tương ứng u1 và u2. (Hình 3-6)
Sau thời gian dt, khối chất lỏng ở trong B'
dòng nguyên tố giới hạn bởi hai mặt cắt AA B u2
và BB có vị trí mới được giới hạn bởi hai d 2 A'
mặt cắt A'A' và B'B'. Ngoài ra, trong chuyển A u B' 1
động ổn định, hình dạng của dòng nguyên tố d1 B u2 Δt
không thay đổi theo thời gian, đồng thời A A' u1Δt
chất lỏng không xuyên qua ống dòng mà đi
ra hay đi vào dòng nguyên tố. Theo tính Hình 3-6
chất liên tục của chất lỏng thì trong dòng
nguyên tố không có chỗ trống, đối với chất lỏng không nén được thì thể tích chất lỏng trong
đoạn dòng nguyên tố giới hạn bởi hai mặt cắt ướt AA và BB phải là một trị số không đổi, tức là:
W[AA,BB] = W[A’A’,B’B’]
Hay WAA’ = WBB' (vì đoạn giữa hai mặt cắt A’A’ và BB là chung)
Do đó: u1d1dt = u2d2dt Nên u1d1 = u2d2 (3-8)
Phương trình (3-8) là phương trình liên tục của dòng nguyên tố chảy ổn định. Theo (3-5)
thì biểu thức (3-8) viết thành: dQ1 =dQ2 hoặc dQ = const. (3-9) 50
Chú ý rằng trong phương trình (3-9) không có yếu tố lực nên nó đúng cho cả chất lỏng
lý tưởng lẫn chất lỏng thực.
Từ phương trình liên tục (3-9) của dòng nguyên tố ổn định, có thể suy ra phương trình
liên tục cho toàn dòng chảy ổn định. Tích phân phương trình (3-9) cho toàn mặt cắt ướt, ta được: u . d u . d (3-10) 1 1 2 2 1 2
Theo (3-7) có thể dựa vào lưu tốc trung bình mặt cắt v1 và v2 tại những mặt cắt ướt 1 và
2 tương ứng. Do đó phương trình (3-10) viết thành: v1 1 = v1 1 (3-11)
Phương trình (3-11) là phương trình liên tục của dòng chảy ổn định của chất lỏng không
nén được. Nó đúng cho cả chất lỏng lý tưởng và chất lỏng thực tế. Từ công thức (3-7) có thể biến đổi (3-11) thành: Q1 = Q2 hay Q = const (3-12) v Từ (3-11) sẽ có 1 2
tức là trong dòng chảy ổn định, lưu tốc trung bình mặt cắt v tỷ v 2 1
lệ nghịch với diện tích mặt cắt ướt .
3.4. PHƯƠNG TRÌNH BECNULI CỦA DÒNG NGUYÊN TỐ CHẢY ỔN ĐỊNH.
Định luật động năng được phát biểu như sau: "Sự biến thiên động năng của một khối
lượng nhất định khi nó di động trên một quãng đường, bằng công của các lực tác dụng lên
khối lượng đó, cũng trên quãng đường đó", tức là: 2 mu ( ) A Fl 2
3.4.1. Đối với chất lỏng lý tưởng
Trong dòng chảy ổn định của z
chất lỏng lý tưởng, xét một đoạn 1
dòng nguyên tố giới hạn bởi mặt cắt P1 a
1-1 và 2-2 có diện tích tương ứng là 1'
d1 và d2. Chọn mặt chuẩn nằm b
ngang Ox, như vậy mặt cắt 1-1 có 1 2 trọng tâm ở độ cao z d1 1 so với mặt s1 c
chuẩn, tại trọng tâm có áp suất thủy d2 1' 2'
động là p1, lưu tốc là u1. Mặt cắt 2-2 z1
có trọng tâm ở độ cao z P 2 đối với 2
mặt chuẩn, áp suất thủy động tại 2
trọng tâm là p2 và lưu tốc là u2. z s 2 2 2' (Hình 3-7).
Sau một thời gian vô cùng nhỏ x
t, các phần tử chất lỏng của mặt Hình 3-7 51
cắt ướt 1-1 đã di động được một quãng đường đến vị trí 1'-1', độ dài s1 của quãng đường đó bằng: s1 = u1t.
Cũng trong thời gian vô cùng nhỏ t, các phần tử chất lỏng của mặt cắt ướt 2-2 đã di
động đến vị trí 2'-2', độ dài s2 của quãng đường đó bằng: s2= u2t
Lưu lượng đi qua mặt cắt ướt 1-1 và 2-2 là: dQ = u1d1 = u2 d2.
Không gian giữa 2 mặt cắt 1-1 và 2'-2' có thể chia làm 3 khu vực: a, b, c
Trong thời gian t, sự biến thiên động năng (đn) của đoạn dòng nguyên tố chảy ổn
định đang xét bằng hiệu số động năng của khu c và a, vì động năng của khu b không đổi. 2 2 u 1 u 2 ) 2 2 u u (d ) n dQ ( t dQdt( 2 1 ) 2 g 2
Công của ngoại lực tác dụng lên đoạn dòng nguyên tố đang xét gồm có: Công của trọng
lực và áp lực thủy động.
Công sinh ra bởi trọng lực CTR-L của đoạn dòng nguyên tố đang xét bằng công của trọng
lực khối chất lỏng khu a di chuyển một độ cao là z1-z2 để đi tới khu c, được tính như sau:
CTR-L= d1 s1g(z1-z2) = dQt(z1-z2)
Áp lực thủy động tác dụng lên đoạn dòng nguyên tố đang xét gồm lực:
P 1= p1d1 thẳng góc và hướng vào mặt cắt ướt 1-1
P 2= p2d2 thẳng góc và hướng vào mặt cắt ướt 2-2
Còn các động áp lực bên hướng thẳng góc với phương chuyển động nên không sinh ra
công. Công sinh ra bởi áp lực P1 và P 2 bằng:
CA-L = P1.s1 - P2.s2 = p1d1s1 - p2d2s2
hay CA-L = p1d1u1t - p2d2u2t = dQ( p1 - p2 ) t
Tổng công của các nội áp lực được coi bằng không vì đang nghiên cứu chất lỏng lý
tưởng. (Giả thiết rằng đoạn dòng nguyên tố đang xét thuộc một dòng chảy đổi dần, do
không có ma sát nên mọi phần tử chất lỏng sẽ có cùng dịch chuyển).
Vì vậy, theo định luật động năng sẽ có: (đ.n) = CTR-L + CA-L 2 2 Tức là: u u ) dQ t ( 2 1 d Q t z ( 1 z 2 ) dQ p ( 1 p 2 ) t g 2
Chia cả 2 vế cho dQt, tức là viết phương trình động năng cho một đơn vị trọng lượng chất lỏng sẽ được: 2 2 u2 u1 p p (z z ) ( 1 2 ) 2g 2 1 2 g 52 2 2 Vậy: p u p u z 1 1 (3-13) 1 z 2 2 2 g 2 g 2
Vì các mặt cắt 1-1 và 2-2 của dòng nguyên tố là tùy ý chọn, nên phương trình (3-13) có 2 thể viết dưới dạng: p u z const (3-14) 2 g
Phương trình (3-13) và (3-14) gọi là phương trình BECNULI của dòng nguyên tố chất
lỏng lý tưởng chuyển động ổn định. Đây là một phương trình cơ bản và quan trọng của thủy lực.
3.4.2. Phương trình BECNULI của dòng nguyên tố chất lỏng thực chảy ổn định.
Chất lỏng thực có tính nhớt và khi nó chuyển động thì sinh ra sức ma sát trong, làm cản
trở chuyển động. Muốn khắc phục sức cản đó, chất lỏng phải tiêu hao một phần cơ năng
biến thành nhiệt năng, mất đi không lấy lại được.
Vì vậy cơ năng của chất lỏng thực giảm dần dọc theo dòng chảy: 2 p u z const g 2
Nếu chất lỏng chuyển động từ mặt cắt 1-1 đến 2-2 thì: p u2 p u2 z 1 1 z 2 2 1 2 2 g 2g
Ký hiệu h'W là phần năng lượng bị tiêu hao khi một đơn vị trọng lượng chất lỏng chuyển
động từ mặt cắt 1-1 đến 2-2 thì phương trình BECNULI của dòng nguyên tố chất lỏng thực
viết cho mặt cắt 1-1 và 2-2 sẽ là: 2 2 p u p u 1 1 2 2 z z h ' 1 2 2 g 2 w g (3-15)
Trong (3-15), h'W gọi là tổn thất năng lượng của một đơn vị trọng lượng của dòng
nguyên tố khi nó chuyển động từ mặt cắt (1-1) đến mặt cắt (2-2) hay còn gọi là tổn thất cột
nước của dòng nguyên tố.
3.4.3. Ý nghĩa của phương trình BECNULI viết cho dòng nguyên tố chảy ổn định.
a. Ý nghĩa năng lượng của ba số hạng trong phương trình BECNULI
Trong phương trình BECNULI các số hạng đều viết đối với một đơn vị trọng lượng chất
lỏng. Tương tự như trong phần thủy tĩnh học, ta đã biết ý nghĩa năng lượng của 2 số hạng z
và p là: z là vị năng đơn vị; p là áp năng đơn vị; (z + p ) biểu thị thế năng đơn vị. 2
Còn số hạng thứ ba u chính là động năng của một đơn vị trọng lượng chất lỏng gọi tắt 2 g
là động năng đơn vị. Tổng của ba số hạng trong phương trình BECNULI biểu thị tổng cơ
năng của một đơn vị trọng lượng chất lỏng, tức là tổng của thế năng đơn vị và động năng
đơn vị. Cơ năng đơn vị của dòng nguyên tố chất lỏng lý tưởng chảy ổn định là hằng số, còn 53
cơ năng đơn vị của dòng nguyên tố chất lỏng thực chảy ổn định giảm dần dọc theo dòng chảy.
b. Ý nghĩa thủy lực của ba số hạng trong phương trình BECNULI 2
Trong phương trình BECNULI, cả 3 số hạng z, p , u đều có thứ nguyên là chiều dài. g 2
Số hạng thứ nhất z được gọi là độ cao hình học hay cột nước vị trí biểu thị cho độ cao
của điểm đang xét trong mặt cắt ướt của dòng nguyên tố so với mặt chuẩn.
Số hạng thứ hai p đại biểu cho độ cao áp suất tại điểm đang xét của mặt cắt ướt dòng
nguyên tố hay cột nước áp suất. Có thể dùng độ cao cột nước để thể hiện áp suất tuyệt đối hay áp suất dư. 2
Số hạng thứ ba u gọi là cột nước lưu tốc. 2g 2 Độ cao p u H z
kể từ mặt chuẩn gọi là cột nước động lực của dòng nguyên tố g . 2
hoặc là tổng cột nước.
h'w gọi là tổn thất cột nước của đoạn dòng nguyên tố giới hạn từ mặt cắt 1-1 đến 2-2
Như vậy các số hạng của
phương trình BECNULI viết E' E' hw' cho dòng nguyên tố chất 2 u22 u Đường năng 1
lỏng lý tưởng hay chất lỏng 2 g 2g 2
thực chảy ổn định đều có thứ
Đường cột nước đo áp u2 p 2
nguyên là độ dài nên có thể
dùng hình vẽ để biểu diễn sự H1 p1 H2
biến thiên của các cột nước 1 2
dọc theo dòng chảy, vẽ theo u1 z2
tỷ lệ xích định trước. (Đối z1 1
với chất lỏng lý tưởng: Vì 2 p u tổng số O O H z tại Hình 3-8 2g
bất kỳ mặt cắt ướt nào trên cùng một dòng nguyên tố chảy ổn định đều là một hằng số, nên
biểu diễn cách mặt chuẩn một đoạn thẳng không đổi H. (Đường E' - E')
Đường đi qua đỉnh các đoạn Hi gọi là đường tổng cột nước, đường này biểu diễn sự
biến thiên của cơ năng đơn vị dọc theo dòng chảy nên còn gọi là đường năng. (Hình 3-8).
+ Với chất lỏng lý tưởng, do tổng cột nước H' của các mặt cắt ướt không đổi dọc theo
chiều dài của dòng nguyên tố chảy ổn định nên đường năng (E' - E') là đường thẳng nằm ngang.
+ Với chất lỏng thực, do cơ năng đơn vị của dòng nguyên tố chảy ổn định giảm đi theo
chiều chảy nên đường tổng cột nước không thể nằm ngang được mà sẽ thấp dần; nó có thể 54
là một đường thẳng hoặc cong vì trị số h'W có thể tăng đều hoặc không đều dọc theo chiều chảy.
Đường đi qua đỉnh các đoạn (z + p ) của các mặt cắt trên một dòng nguyên tố gọi là
đường cột nước đo áp hoặc là đường thế năng. (Hình 3-8)
Hình dạng của đường cột nước đo áp quyết định bởi hình dạng của dòng nguyên tố.
Tại những nơi dòng chảy mở rộng, lưu tốc giảm nên đường cột nước đo áp hướng lên trên;
tại nơi dòng chảy thu hẹp lại, lưu tốc tăng lên thì đường cột nước đo áp lại thấp xuống, do
đó đường cột nước đo áp có thể là nằm ngang, lên cao hoặc xuống thấp. Đường đo áp cong
hay thẳng tùy theo hình dạng của dòng nguyên tố.
3.4.4. Độ dốc thuỷ lực và độ dốc đo áp của dòng nguyên tố
a. Định nghĩa độ dốc thủy lực
Độ dốc thủy lực là tỷ số giữa độ hạ thấp của đường tổng cột nước (tức đường năng) đối
với độ dài của đoạn dòng nguyên tố trên đó thực hiện độ hạ thấp đó. Kí hiệu độ dốc thủy
lực của dòng nguyên tố là J'.
Trong trường hợp tổng quát, khi đường tổng cột nước là đường cong thì các độ dốc thủy
lực ở các mặt cắt ướt không bằng nhau, nên: dH d p u2 dh ' J'= (z w ) (3-16) dl dl 2 g dl
Trong đó: H là tổng cột nước, l là độ dài của đoạn dòng nguyên tố. Độ dốc thủy lực phải
là trị số dương nên đằng trước đạo hàm phải đặt dấu âm, vì dọc theo chiều dòng chảy số gia dH bao giờ cũng âm.
Khi dòng chảy đều đường tổng cột nước là một đường thẳng thì độ dốc thủy lực là: J'= dh' h' w w (3-17) dl l
b. Định nghĩa độ dốc đường đo áp
Độ dốc đường đo áp tức độ dốc đường thế năng là tỷ số giữa độ hạ thấp xuống hoặc lên
cao của đường đo áp đối với độ dài của dòng nguyên tố trên đó thực hiện độ hạ thấp hoặc
dâng cao đó. Kí hiệu độ dốc đo áp của dòng nguyên tố là Jp'. p d z J' (3-18) p dl
Dấu biểu thị cột nước đo áp dọc theo dòng chảy, có thể là dương, có thể âm. Trong
trường hợp đặc biệt, khi diện tích của mặt cắt ướt d = const, tức là lưu tốc u và cột nước 2
lưu tốc u không đổi dọc theo dòng chảy, độ dốc thủy lực và độ dốc đo áp bằng nhau: J' = 2g J'p. 55
3.5. PHƯƠNG TRÌNH BECNULI CỦA TOÀN DÒNG CHẤT LỎNG THỰC CHẢY ỔN ĐỊNH.
Để có được phương trình BECNULI cho toàn dòng chất lỏng thực chảy ổn định cần tích
phân phương trình (3-15) trên toàn mặt cắt ướt của dòng chảy. Trên cùng một mặt cắt
của dòng chảy, lưu tốc và áp suất thủy động p thường phân bố khác nhau ở các dòng nguyên
tố khác nhau, quy luật phân bố cũng không biết. Vì vậy, sự suy rộng để tìm ra phương trình
BECNULI cho toàn dòng chảy chỉ tiến hành được trong những điều kiện nhất định. Điều
kiện đó là dòng chảy phải đổi dần.
3.5.1. Dòng chảy đổi dần
Dòng chảy đổi dần là dòng chảy ổn định, có các đường dòng gần là các đường thẳng
song song (hình 3-9), nghĩa là bán kính cong r của đường dòng khá lớn.
Dòng chảy như vậy có đầy đủ điều kiện cho phép bỏ qua lực quán tính (sinh ra bởi độ
cong của đường dòng). Mặt cắt ướt của dòng chảy đổi dần được coi là phẳng, những đường
dòng được coi như vuông góc với mặt cắt ướt phẳng. Đồng thời những thành phần lưu tốc
và gia tốc nằm ngang trên mặt cắt ướt được coi như có thể bỏ qua (ux = u, uy= 0). Tại những
mặt cắt ướt, ở đó dòng chảy là đổi dần, lực quán tính không đáng kể mà chỉ có tác dụng của
trọng lực là lực khối duy nhất, áp lực thủy động không có thành phần tiếp tuyến. Sự phân
bố áp lực thủy động hoàn toàn giống như sự phân bố áp lực thủy tĩnh. Như vậy trên những
mặt cắt ướt đó, theo công thức cơ
bản của thủy tĩnh, sẽ có: 1 1' Mặt cắt z + p = const. ướt thực
Trong đó: z, p ứng với từng vị Mặt cắt u trí trên mặt cắt ướt ưtớ ínt h toán u ux
Ví dụ: Nếu a và b là hai điểm r 1 1' Hình 3-9
cùng nằm trên mặt cắt 1-1 thì: a) b) z p p p a+ a b 1 z b z 1
Nhưng cột nước đo áp ở những mặt cắt khác nhau (mặt cắt 1-1 và 2-2) có trị số khác nhau: z p p 1 2 1 + z2 Hình 3-10 56
3.5.2. Phương trình BECNULI của toàn dòng chất lỏng thực chảy ổn định.
Để có thể từ phương trình BECNULI của dòng nguyên tố suy diễn phương trình
BECNULI cho toàn dòng chảy cần dựa trên các giả thiết sau:
- Chất lỏng là không nén được ( = const).
- Không có sự thêm bớt lưu lượng dọc theo đoạn dòng chảy đang xét (Q = const).
- Tại những mặt cắt đã hw chọn (1-1 và 2-2) dòng v2 2 2
chảy phải là đổi dần 2 Đường năng v 1 1 2 g Xét một dòng chất 2g
Đường cột nước đo áp 2 p u 2
lỏng thực chảy ổn định, 2 dω
đổi dần bao gồm vô số các p1 dω 2
dòng nguyên tố. Trên đoạn 1 u1 2
dòng chảy đó lấy hai mặt 1 ω2 z
cắt 1-1 và 2-2, tại hai mặt 2 Toàn dòng chảy ω1
cắt này có diện tích lần 1 z 1 Dòng nguyên tố
lượt là 1 và 2. Lấy một dòng nguyên tố tùy ý. O O Theo phương trình (3-15), Hình 3-11
có thể viết phương trình
BECNULI cho đoạn dòng nguyên tố chất lỏng thực đó.
Gọi lưu lượng dòng nguyên tố là dQ, trọng lượng tương ứng là dQ. Để viết biểu thức
năng lượng của toàn dòng phải nhân các số hạng của phương trình BECNULI (3-15) với
dQ, sau đó tích phân trên toàn mặt cắt 1 và 2: 2 2 p u p u ( z 1)dQ dQ ( z )dQ dQ h ' .dQ 1 1 2 2 2 2 g 2 g w 2 2 2 1 1 (3-19)
Như vậy cần phải giải quyết ba dạng tích phân sau: u 2 a) ( p z ) b) dQ c) h ' dQ dQ w . 2 g
a) Xét tích phân thứ nhất: ( p z
)dQ biểu thị tổng thế năng của toàn dòng chảy tại mặt
cắt ướt. Từ giả thiết dòng chảy là đổi dần tại mặt cắt ướt đang xét nên: p p (z ) dQ ( z ) Q u2
b) Xét tích phân thứ hai: .dQ
biểu thị tổng động năng của toàn dòng chảy tại mặt cắt . 2 g
ướt. Ở đây phải dùng khái niệm về lưu tốc trung bình mặt cắt v để tính tích phân này. Biết
rằng: u = v u. Mà dQ = u.d, nên: 57 u2 3 3 dQ u d v( u) d v(3 v 3 2 u v 3 u2 ( u)3 ) d . 2 g 2g 2g 2g Vì (u 3) d
là một đại lượng vô cùng nhỏ bậc cao bên cạnh những đại lượng vô
cùng nhỏ bậc thấp hơn nên có thể bỏ đi không tính, còn số hạng . u d 0 . Thật vậy, theo (3-6):
Q = ud (v u d
) v d (u)d Q (u)d .
Rõ ràng là u.d 0 Vậy: 3v 2 ( u) d 3v 2 ( u ) d 2 u 2 3 2 3 v dQ v 3v ( u ) d v 1 Q 1 3 2 2g 2g 2 g v 2g v 2 3 ( ) u d Đặt 1 (3-20) 2 v 2 2 u v Sẽ có d Q v 3 Q 2 g 2g g 2 3 u d Hoặc = (3-21) v 3
Theo (3-21) thì là tỷ số giữa động năng thực của dòng chảy và động năng tính bằng lư
u tốc trung bình. Hệ số đặc trưng cho sự phân bố lưu tốc không đều trên mặt cắt ướt. Sự
không đều càng lớn thì trị số càng lớn. Từ (3-20) có thể thấy rằng hệ số bao giờ cũng
lớn hơn 1. Hệ số được gọi là hệ số sửa chữa động năng hoặc là hệ số Cơ-ri-ô-lit. Khi
nước chảy trong kênh, ống, máng v.v... thường có giá trị từ 1,05 đến 1,1.
c) Xét tích phân thứ ba h ' : Gọi h w dQ
W là tổn thất năng lượng trung bình của một đơn
vị trọng lượng chất lỏng từ mặt cắt (1-1) đến mặt cắt (2-2) hoặc nói gọn là tổn thất cột nước
trong đoạn dòng chảy, ta có: h' =Qh w dQ w
Căn cứ vào kết quả của ba tích phân trên, biểu thức (3-19) có thể viết dưới dạng sau: 2 2 p 1 1v1 p 2 v (z ) d Q d Q (z ) .dQ 2 2 d . Q h Q 1 2 w (3-22) 2g g 2
Viết phương trình cho một đơn vị trọng lượng chất lỏng, tức là chia các số hạng của (3- 22) cho Q, sẽ được: 58 p 1 1 v 2 1 p2 2 v 2 z z 2 h (3-23) 1 2 w g 2 g 2
Đây là phương trình BECNULI của toàn dòng chất lỏng thực chảy ổn định đổi dần. Nó
là một trong những phương trình cơ bản và quan trọng nhất của thủy lực học. Muốn vận
dụng đúng phương trình, cần những điểm sau:
1. Khi ứng dụng phương trình BECNULI của toàn dòng chất lỏng thực chảy ổn định đổi
dần cần thỏa mãn 5 điều kiện sau:
- Dòng chảy phải ổn định.
- Lực khối chỉ là trọng lực.
- Chất lỏng không nén được.
- Lưu lượng là một hằng số.
- Dòng chảy tại mặt cắt đã chọn phải đổi dần, còn dòng chảy giữa hai mặt cắt đó không
nhất thiết phải là chảy đổi dần. 2 2. Vì tổng số p v z
giống nhau cho mọi điểm trên cùng một mặt cắt ướt nên khi 2g
viết phương trình BECNULI có thể tùy ý chọn điểm nào trên mặt cắt ướt cũng được. Như
vậy, không yêu cầu hai điểm dùng để viết phương trình BECNULI ở hai mặt cắt phải cùng
ở trên một dòng nguyên tố. Khi chọn điểm, tất nhiên, nên chọn sao cho phương trình được đơn giản.
3. Áp suất p1 và p2 có thể là áp suất tuyệt đối hay áp suất dư nhưng phải cùng loại với nhau.
4. Trong tính toán thường lấy 1 2 1 , nhưng thực tế hai trị số này khác nhau.
5. Độ dốc thủy lực J và độ dốc đo áp Jp của toàn dòng chảy có ý nghĩa hoàn toàn giống
như của dòng nguyên tố chất lỏng thực. Độ dốc thủy lực: dH d p v2 dh J z w ( ) (3-24) dl dl 2 g dl h
Khi đường năng là đường thẳng thì: J = w (3-25) l d p Độ dốc đo áp: J (3-26) p z dl p p (z 1 ) z ( 2 ) 1 2
Khi đường cột nước đo áp là đường thẳng thì: J (3-27) p l 59
3.6. PHƯƠNG TRÌNH ĐỘNG LƯỢNG CỦA TOÀN DÒNG CHẢY ỔN ĐỊNH
Để xây dựng phương trình động lượng cho toàn dòng chảy ổn định thay đổi dần có thể
dựa vào định luật động lượng, như sau: "Hình chiếu lên trục X bất kỳ của độ biến thiên
động lượng của một vật thể chuyển động trong một đơn vị thời gian bằng tổng hình chiếu
lên trục X của xung lượng các ngoại lực tác dụng vào vật thể trong thời gian đó", tức là: KX = (XLNL) (3-28) X
trong đó: KX - hình chiếu lên trục X của độ biến thiên động lượng K X =mu2x-mu1x
(XLNL) - tổng hình chiếu lên trục X của xung lượng các ngoại lực X (XLNL) . X Fx dt
Như vậy, trong phương trình động lượng chỉ có ngoại lực mà không có nội lực, nên khi
vận dụng định luật động lượng cho chất lỏng chuyển động chỉ cần xem xét tình hình dòng
chảy ở mặt biên giới mà không đòi hỏi phải biết tình trạng nội bộ ở bên trong dòng chảy.
Khi nghiên cứu cần tách đoạn dòng chảy đang xét ra khỏi toàn dòng bằng một mặt kín giới
hạn đoạn dòng đó. Mặt kín này được gọi là mặt kiểm tra, thường lấy hai mặt cắt ướt giới
hạn đoạn dòng và mặt bên của đoạn dòng đó làm mặt kiểm tra.
Công thức biểu thị định luật động lượng trong toàn dòng chất lỏng thực chảy ổn định x 2 u2 2' Mặt kiểm tra ω2 2 1 1' v 1 2 2 2' u1 v c v Δt ω 2 1 1 b 2 a 1’ 1 1 Hình 3-12 v 1 Δt
đổi dần đựơc xác định như sau:
Xét đoạn dòng chảy ổn định được giới hạn bởi 2 mặt cắt (1-1) và (2-2). Tại mặt cắt 1-1
và 2-2 dòng chảy là đổi dần, diện tích của các mặt cắt này là 1 và 2, lưu tốc trung bình là
v1 và v2. Chọn trục X bất kỳ (Hình 3-12). Sau khoảng thời gian t đoạn dòng này chuyển
động đến vị trí mới được giới hạn bởi hai mặt cắt 1'-1' và 2'-2'. Có thể chia phần dòng chảy
giữa 1-1 và 2'-2' ra làm 3 khu vưc: a, b và c.
3.6.1. Tính độ biến thiên động lượng của đoạn dòng
Vì dòng chảy là ổn định nên:
K = ĐL(1'-2') - ĐL(1-2) = ĐL(c) - ĐL(a) (3-29)
Trong đó: K - độ biến thiên động lượng của đoạn dòng; ĐL(1'-2') - động lượng của
đoạn dòng từ 1'-1' đến 2'-2'; ĐL(1-2) - động lượng của đoạn dòng từ 1-1 đến 2-2; ĐL(c) -
động lượng của khu c; ĐL(a) - động lượng của khu a. 60
Như đã biết động lượng được tính theo công thức dK = u.dm
Trong đó: u - lưu tốc điểm; dm - khối lượng của chất điểm.
Vì chất lỏng được coi là tập hợp của một hệ thống chất điểm, chiếm toàn bộ phần không
gian chuyển động của dòng chảy, do đó có thể tính được động lượng của khu c như sau:
ĐL(c) = dK udm u d Q t 2 tu d (3-30) 2 2 2 2
Biết rằng u = v u, nên sẽ có: ĐL(c) = . t 2 u d t (v 2) u .d . t v 2v u ( ) u d 2 2 2 2 2 2 2 2
Trong Đ3.5 đã chứng minh được rằng ( ) u . d 0 , nên: ( 2 u ) d §L (c ) t 2 v 2 ( u) d . tv . 1 2 2 2 22 2 2 v 2 2 2 ( ) u . d Đặt 2 a
, vì mặt cắt 2-2 là chọn bất kỳ nên tổng quát có thể gọi: o2 1 2 v 2 2 ( u)2.d a 1 o 2 v . (3-31)
Do đó, động lượng của khu c sẽ là: ĐL(c) = 2 t v o 2 2 Q t o 2v2 2
Tương tự như vậy theo (3-30) sẽ có động lượng của khu a là: ĐL(a) = 2 tu d Q t v 1 o 1 1
Hình chiếu lên trục X bất kỳ của động lượng được tính như sau:
ĐL(c)X = ĐL(c).cos2 = Qt (3-32) o v cos Q t 2 2 2 o v 2 2 X ĐL(a)X = ĐL(a).cos1 = Q t cos (3-33) o1v1 1 Q t o1v1X
Trong đó: 1 và 2 - góc giữa 1 v và 2 v với trục X;
v1X - hình chiếu của lưu tốc trung bình 1 v lên trục X.
v2X - hình chiếu của lưu tốc trung bình v2 lên trục X.
Từ (3-29), (3-32) và (3-33) có thể tính được hình chiếu lên trục X của độ biến thiên
động lượng của đoạn dòng chảy đang xét là:
KX = ĐL(c)X - ĐL(a)X = Qt(o2v2X - o1v 1X) (3-34) 61
3.6.2. Tính xung lượng của các ngoại lực.
Theo công thức tính xung lượng của các ngoại lực: XLNL = F.t
Trong đó: F - ngoại lực; t - thời gian tác dụng.
Tổng hình chiếu lên trục X của xung lượng các ngoại lực tác dụng vào đoạn dòng sẽ là: (XLNL) = F X X.t (3-35)
Trong đó: F X - hình chiếu lên trục X của hợp lực các ngoại lực.
Thay (3-34) và (3-35) vào (3-28) sẽ có phương trình sau:
Qt[o2v 2X - o1 v1X] = FXt (3-36)
Chia cả hai vế của (3-36) cho t sẽ được phương trình viết cho một đơn vị thời gian.
FX = .Q.[o2.v2X - o1.v1X] (3-37)
Phương trình (3-37) chính là phương trình động lượng của toàn dòng chất lỏng thực
chảy ổn định đổi dần. Từ phương trình này có thể phát biểu như sau: "Hình chiếu lên một
trục bất kỳ của độ biến thiên động lượng của đoạn dòng chảy ổn định trong một đơn vị thời
gian bằng hình chiếu lên trục đó của hợp lực các ngoại lực tác dụng vào đoạn dòng trong đơn vị thời gian ấy".
3.6.3. Ý nghĩa vật lý của hệ số o.
Từ (3-30) và (3-31) sẽ có: tu2d Q t v 0 2 u 2 d (u ) d Nên suy ra 1 (3-38) o 2 v v 2
0 gọi là hệ số sửa chữa động lượng hoặc hệ số Businetscơ, nó là tỷ số giữa động lượng
thực của dòng chảy và động lượng của đoạn dòng đó tính theo lưu tốc trung bình.
Theo (3-38), thấy rằng: 0 > 1. Đối với dòng chảy trong sông, kênh 0= 1.02 1.05.
Trong thực tế tính toán thường chọn 1.
Khi áp dụng phương trình động lượng cần chú ý mấy điểm sau:
- Tại mặt cắt 1-1 và 2-2 dòng chảy được coi là chảy ổn định, đổi dần.
- Không có sự thêm, bớt lưu lượng vào đoạn dòng giữa 1-1 và 2-2.
- Chất lỏng là không nén được ( = const).
- Động lượng của khối chất lỏng trong một đơn vị thời gian sẽ mang dấu (+) nếu chất
lỏng đi ra khỏi mặt kiểm tra, mang dấu (-) nếu đi vào trong mặt kiểm tra.
- Dấu của cos tùy theo trị số góc lập nên bởi vectơ tốc độ v và chiều dương của trục tọa độ. 62
3.7. ỨNG DỤNG CỦA PHƯƠNG TRÌNH BECNULI. 3.7.1. Ống Pitot:
- Là một dụng cụ đo lưu tốc điểm. Gồm hai ống nhỏ
đường kính chừng vài mm: một ống thẳng (1) và một 0
ống đầu uốn cong 90 (2), hai miệng ống đặt sát nhau.
Sau khi ta đặt vào vị trí muốn đo lưu tốc, đọc độ
chênh mực nước, sẽ tính ra được lưu tốc điểm.
- Thật vậy, viết phương trình Becnuli cho hai mặt cắt
1-1 và 2-2, với mặt chuẩn qua điểm đo. Vì ống 1 có
vận tốc u chảy lướt trên miệng nên có cột nước lưu
tốc. Ống 2 hướng ngược dòng chảy nên không có cột nước lưu tốc. Hình 3-13. Ống Pitot 2 Ống đo áp có giá trị p u z và độ chênh H Vì vậy: u 2.g. H (3-39) g 2
Để tính đến ảnh hưởng của độ nhớt chất lỏng và sự phá hoại cấu tạo dòng chảy khi
đặt ống Pitot, cần thêm vào công thức trên hệ số sửa chữa φ xác định bằng thí nghiệm. Khi
đó lưu tốc được xác định theo: u . 2 g. H trong đó φ = 1-1,04 (3-40) 3.7.2. Ống Venturi
Là dụng cụ đo lưu lượng gồm hai đoạn ống ngắn có đường kính khác nhau, ở mỗi đoạn có lắp ống đo áp.
Viết phương trình Becnuli cho mặt cắt 1-1 và 2-2, mặt chuẩn trùng với trục ống. Nếu bỏ qua h , ta có W p 1 v2 1 1 p2 2v 22 (3-41) 2g 2g Lấy α1 = α2 = 1 ta có 2 2 v v p p 2 1 1 2 h . (3-42) 2g
Mặt khác theo phương trình liên tục ta có: v . v . 1 1 2 2 2 Vì vậy: D 1 v v .
v Thay vào phương trình (3-42) ta được 2 1 1 d 2 63 2 D 4 v 1 1 d 2 gh h hay v 2g 1 4 D 1 d Hình 3-14. Ống Venturi : 2 Lưu lượng D 2gh Q v . h (3-43) 1 1 4 D 4 1 d 2 Trong đó hệ số D 2g (3-44) 4 4 D 1 d Ví dụ 3.1.
Nước từ bể chứa hở, chảy qua đường ống có các đường kính d1 = 50 mm, d2 = 40
mm, d3 = 25 mm (Hình 3-15). Xác định cột nước cần thiết H để cólưu lượng Q = 10 m3/h.
Vẽ đường năng và đường đo áp. Bỏ qua tổn thất năng lượng. Giải:
Tính vận tốc trung bình của nước ra khỏi ống tại mặt cắt 3-3. Q Q 1 , 0 4 v 3 , 5 6 m 5 / s 3 d 2 3600 1 , 3 . 4 0 , 0 . 252 3 4
Cột nước cần thiết H, được xác định từ phương trình Becnuli, viết cho mặt cắt 0-0 và 3-3, lấy mặt chuẩn 0-0: 2 2 p .v p .v 0 0 0 3 3 3 z z h 0 3 w 0 3 2g 2g
Với 0 = 3=1 và p0 = pa với giả thiết không có tổn thất (hw0-3= 0) ta có 64 p0 p v2 H a 0 0 3 thay số vào H = 1,63 m 2 g Hình 3-15
Để vẽ được đường đo áp, cần phải xác định vận tốc trung bình và cột nước vận tốc tại đoạn ống 1 và 2. Q 1 , 0 4 v 1 , 1 4 m 2 / s 3600 1 , 3 . 4 0 , 0 . 52 1 Và Q 1 , 0 4 v , 1 4 m 2 / s 1 3600 1 , 3 . 4 0 , 0 . 52 1 Q 1 , 0 4 v 22 , 2 212 v và , 0 25m 2 , 2 2 m 1 / s 3600 1 , 3 . . 4 , 0 042 2 g 2 8 , 9 . 1 2
Vì bỏ qua tổn thất năng lượng nên đường năng là một đường thẳng nằm ngang đi qua 0-0.
Độ cao đo áp ở bất kỳ mặt cắt nào cũng được xác định bằng hiệu số giữa đường năng p v 2
và cột nước vận tốc ở mặt cắt đó: H 2
. Nối tất cả các độ cao đo áp ta được đường 0 2g đo áp cần vẽ Ví dụ 3-4.
Hãy xác định nước dâng lên ở độ cao nào trong ống, nếu một đầu của ống được nối
với mặt cắt thu hẹp của ống dẫn, còn đầu kia được thả vào nước. Lưu lượng ở trong ống Q =
0,025 m3/s; áp suất dư p1 = 49.103Pa, các đường kính d1 = 100 mm và d2 = 50 mm (Hình vẽ 3-16). Giải:
Viết phương trình Becnuli đối mặt cắt (1-1) và (2-2), mặt chuẩn đi qua trục ống (bỏ qua tổn
thất), lấy a1 = a 2 có dạng: p v 2 p v2 4Q 4Q 1 1 2 2 vì v và v sau khi biến đổi ta có 2 g 2g 1 2 4d 2 2 4d 1 2 65 Hình 3-16 p p 2 2 1 16 Q . 1 1 7 , 2 m 2g 2 d 4 1 d 42
Ta được chiều cao với dấu âm và chính là chiều cao chân không. Nước trong ống sẽ
dâng lên chiều cao hck = 2,7 m. Ví dụ 3-5.
Một đoạn ống cong nằm ngang chuyển chất lỏng với
lưu lượng Q = 20 l/s (Hình vẽ 3-17). Đường kính trong của
ống d = 100 mm. áp suất dư của chất lỏng trong ống bằng 2
at. Tính thành phần nằm ngang của lực do chất lỏng tác dụng lên ống cong. Giải Tính lực bề mặt ω Hình 3-17
1 = ω2 = 0,785.10-2 m2 = 78,5.10 -4 m2 p 1 1 p2 . 1 104 2 8 , 9 . 1.78 . 5 , 10 4 1540N 3
Tính xung lực thủy động 2 . 0 10 v và ρ = 10 3 Kg/m3 1 v2 p 4 2 2 , 2 2 m 5 / s 78 . 5 , 10
Vậy: ρ.Q.v1 = ρ.Q.v2 = 103.20.10-3.2,55 = 51 N
Chiếu lên trục ngang (theo phương chiều trên hình vẽ):
Fx = - ρ2ω2 – ρ2.Q.v2 = - (1540 + 51) = - 1591 N
Tính hợp lực trong mặt phẳng ngang: Vì lý do đối xứng nên F F 2 2250N
Chú ý: Nếu bỏ qua xung lực thuỷ động ρQv thì bài toán này có thể giải theo phương
pháp tính áp lực thuỷ tĩnh. 66
Câu hỏi và bài tập chương 3 Câu hỏi
Câu 3.1. Phân biệt các loại chuyển động trong chất lỏng.
Câu 3.2. Định nghĩa đường dòng, ống dòng, dòng nguyên tố. Đặc tính của dòng nguyên tố.
Câu 3.3. Các yếu tố thuỷ lực của dòng chảy – cách xác định.
Câu 3.4. Phương trình liên tục của dòng chảy.
Câu 3.5. Thành lập và phân biệt rõ giữa phương trình vi phân chuyển động của chất lỏng lý
tưởng và chất lỏng thực.
Câu 3.6. Phương trình Becnuli viết cho dòng chất lỏng lý tưởng và chất lỏng thực. ý nghĩa
hình học và năng lượng của nó.
Câu 3.7. Nêu một số ứng dụng cụ thể của Phương trình Becnuli.
Câu 3.8. Phương trình biến thiên động lượng và mô men động lượng trong chuyển động dừng. Bài tập Bài 3.1. (Hình 3-18) D 1 l
Để đo lưu lượng nước chuyển trong ống
(đường kính D), người ta lắp trên đó một thiết bị a d 2
đo áp được gọi là ống Venturi , tại chỗ thu hẹp
có đường kính d < D. Cho biết các đường kính 1
ống D = 200mm, d = 100mm, a=200, b=300, và b 2 h = 600mm.
1/ Bỏ qua tổn thất cột nước, thiết lập hệ thức : Q = f(h). h
2/ Tính lưu lượng Q cho hai trường hợp: Hg
a/ Khi bỏ qua tổn thất cột nước.
b/ Khi tính đến tổn thất cột nước với hệ số
lưu lượng của ống , 0 95 . Hình 3-18 Cho g = 9,81 m/s2 , N/m3 n 9810 và γHg =132890 N/m3 n Bài 3.2. (Hình 3-19) A
Nước chảy trong ống A và B có cùng đường kính
d1 = d2 = d = 100mm. Để đo độ chênh áp suất giữa hai B z
đường ống , người ta nối vào đó một ống đo áp . Xác A
định vận tốc và lưu lượng trong ống A nếu tỷ năng E ở
ống A và ống B bằng nhau. Biết z = 1cm; Q z B = 11,8l/s. h B
Cho hệ số 1, g = 9,81 m/s2 , 9810 N/m3 n tn Hình 3-19 67 Bài 3.3. (Hình 3-20)
Trên trục ống dẫn nước người ta đặt một ống
Pitô với vi áp kế thuỷ ngân. Xác định vận tốc nước
chảy trong ống umax nếu hiệu số mực thuỷ ngân trong áp kế h 18mm. Cho 9810N/m3; n 13 5 , N/m3. Hg h Bài 3.4. (Hình 3-21)
Xác định lưu lượng nước chảy trong ống Hình 3-20
Venturi nếu cho chỉ số áp kế thuỷ ngân hHg =
600mm, D = 200mm, d = 75mm. Khoảng cách giữa D 1 hai mặt cắt l l
1-2 = 400m, ống nghiêng một góc o
30 , hệ số lưu lượng , 0 95 . a d 2 Bài 3.5. (Hình 3-22) 1
Tia chất lỏng phun lên theo phương thẳng b 2
đứng từ ống có đường kính d0 với vận tốc v0 và gặp
phải vật cản trên đường đi có dạng hai nửa quả cầu
(Hình vẽ). Biết trọng lượng vật cản là G, trọng lượng
riêng chất lỏng g. Xác định độ cao z mà vật được h Hg
nâng lên so với miệng ống (theo vo). Hình 3-21 Hình 3-22 68 Chương 4.
TÍNH TOÁN, THIẾT KẾ HỆ THỐNG THỦY KHÍ
Trong chương này trình bày các cơ sở tính toán cho các kết cấu và hệ thống cụ thể
liên quan đến thủy khí. Đồng thời, trình bày phương pháp mô hình hóa, mô phỏng các hệ
thống điều khiển thủy khí đang sử dụng rổng ãi ngày nay.
4.1. TỔN THẤT CỘT NƯỚC
4.1.1. Các dạng tổn thất năng lượng.
Trong phương trình Becnuly viết cho toàn dòng chảy chất lỏng thực ổn định, đổi dần, số
hạng hw là tổn thất năng lượng của một đơn vị trọng lượng chất lỏng để khắc phục sức cản
của dòng chảy trong đoạn dòng đang xét. Có thể chia tổn thất làm hai dạng:
Tổn thất dọc đường sinh ra trên toàn bộ bề dài dòng chảy đều hoặc không đều đổi dần ký hiệu là hd.
Tổn thất cục bộ sinh ra tại những nơi cá biệt, ở đó dòng chảy bị biến dạng đột ngột ký
hiệu là hc. Thí dụ: tổn thất tại nơi ống uốn cong, ống mở rộng, nơi có đặt khóa v.v...
Nguyên nhân của tổn thất cột nước, dù dưới dạng nào, cũng do ma sát giữa các phần tử
chất lỏng và giữa chất lỏng với thành rắn tiếp xúc. Công tạo nên bởi lực ma sát này biến
thành nhiệt năng mất đi không thể lấy lại được.
Với giả thiết là các dạng tổn thất trên xảy ra độc lập đối với nhau, thì tổn thất năng
lượng hw của dòng chảy có thể viết: hw = hd + hc (4-1)
Trong đó: hd - tổng các tổn thất dọc đường của dòng chảy; hc - tổng các tổn thất cục bộ của dòng chảy.
4.1.2. Hai trạng thái chuyển động của chất lỏng. 1. Khái niệm.
Trong thực tế tồn tại hai trạng thái B
chảy khác nhau của chất lỏng nhớt. Tùy
theo trạng thái chảy mà cấu tạo của K 2
dòng chảy, sự phân bố lưu tốc, sự phân
bố ứng suất tiếp, tổn thất năng lượng K1
v.v... có những quy luật khác nhau.
Vào năm 1883, nhà bác học người
Anh Relnold là người đầu tiên phát
biểu rõ ràng về vấn đề này. a)
Trong thiết bị thí nghiệm của b)
Relnold có các bộ phận như sau:
Một bình chứa chất lỏng A được c)
nối với một ống thủy tinh T. Khi mở Hình 4-1
một phần khóa K1, nước từ bình A có 69
thể chảy vào ống T với các vận tốc khác nhau. Nước màu có màu nuóc đi từ lọ đựng màu B
qua ống dẫn vào ống thí nghiệm T. Dưới vận tốc nhỏ, dòng màu trong ống không bị hòa tan
với nước xung quanh và có dạng một đường chỉ thẳng- dòng chảy trong trường hợp này gọi
là chảy tầng. Trạng thái chảy trong đó các phần tử chất lỏng chuyển động theo những tầng
lớp không xáo lộn vào nhau gọi là trạng thái chảy tầng (Hình 4-1a).
Khi tăng vận tốc trong ống T, dòng nước màu lúc đầu có dạng sóng, sau đó hầu như
biến mất, hòa tan trên toàn bộ mặt cắt và nhuộm đều khắp chất lỏng xung quanh. Chuyển
động của chất lỏng trở nên hỗn loạn, các phần tử chất lỏng được nhuộm màu bay đi về mọi
phía, va chạm với các phần tử khác và với thành ống v.v...; chuyển động đó được gọi là
chuyển động rối. Đặc trưng cơ bản của dòng rối là tồn tại thành phần vận tốc ngang so với
phương chuyển động của dòng chảy. Trạng thái chảy trong đó các phần tử chất lỏng chuyển
động vô trật tự, xáo trộn vào nhau gọi là trạng thái chảy rối (Hình 4-1b).
Trạng thái chảy quá độ từ rối sang tầng hoặc từ tầng sang rối gọi là trạng thái chảy phân giới. (Hình 4-1b)
Làm thí nghiệm theo trình tự ngược lại, lúc đầu cho vận tốc dòng chảy trong ống lớn sau
đó nhỏ dần sẽ thấy lúc đầu là chảy rối sau đó là trạng thái phân giới và cuối cùng là chảy tầng.
Kết quả thí nghiệm của Rây nôn chứng tỏ rằng, quá độ từ tầng sang rối hay rối sang tầng
xảy ra dưới những trị số vận tốc nhất định.
Lưu tốc ứng với dòng chảy chuyển từ trạng thái tầng sang trạng thái rối gọi là lưu tốc
phân giới trên. Ký hiệu là vKT
Lưu tốc ứng với dòng chảy chuyển từ trạng thái rối sang trạng thái tầng gọi là lưu tốc
phân giới dưới. Ký hiệu là vKd
Qua thí nghiệm thấy: vKT > vKd
Lưu tốc phân giới không những phụ thuộc vào loại chất lỏng mà còn phụ thuộc vào
đường kính ống làm thí nghiệm.
2. Tiêu chuẩn phân biệt hai trạng thái chảy
Dựa vào kết quả nhiều thí nghiệm, Rây-nôn đã dùng một đại lượng không thứ nguyên
xét đến các yếu tố cơ bản của chuyển động: vận tốc trung bình v, đường kính d, mật độ của
chất lỏng và hệ số nhớt động lực , để đặc trưng cho trạng thái chảy, đó là số Rây-nôn. Re = v d . (4-1)
Trong đó: v - lưu tốc trung bình mặt cắt; - hệ số động học nhớt; d -đường kính ống.
Trị số Rây-nôn tương ứng với trạng thái phân giới từ chảy tầng sang chảy rối, hoặc
ngược lại từ chảy rối sang chảy tầng, gọi là trị số Rây-nôn phân giới ReK
Ứng với vK trên, sẽ có số Rây-nôn phân giới trên (ReKT). Ứng với vKduoi , ta có số Rây-nôn
phân giới dưới (ReKd). Trạng thái chảy ứng với số Rây-nôn Re < ReKd bao giờ cũng là chảy
tầng. Trạng thái chảy có Re > ReKT bao giờ cũng là chảy rối. Trạng thái chảy có ReKd <
Re < ReKT có thể là chảy tầng hoặc là chảy rối, nhưng thường là chảy rối. 70
Qua nhiều thí nghiệm thấy được rằng ReKT không có một trị số xác định, thường dao
động từ 12000 đến 50000. Trái lại, đối với ReKd của mọi loại chất lỏng và đối với các đường
kính ống khác nhau đều có một trị số không đổi và bằng 2320. Do đó ReKd được dùng làm
tiêu chuẩn để phân biệt trạng thái chảy. Vì vậy, đối với dòng chảy đều trong ống thì:
Khi Re < 2320 sẽ có trạng thái chảy tầng. Khi 2320 < Re < 4000 có trạng thái chảy quá
độ từ tầng sang rối. Khi Re > 4000 sẽ có trạng thái chảy rối.
Đối với kênh hở số Rây nôn tính như sau: Re v.R R =
; trong đó: R - bán kính thủy lực.
Khi ReR < 580 - có trạng thái chảy tầng; khi ReR > 580 - có trạng thái chảy rối.
3. Lớp mỏng chảy tầng; các thành nhám và trơn thuỷ lực.
Như đã biết, trạng thái chảy rối được đặc trưng bởi sự xáo trộn của các phần tử chất
lỏng. Số Rây-nôn càng lớn thì sự xáo trộn xảy ra càng mạnh, nhưng sự xáo trộn đó phân bố
không đều trên mặt cắt ngang của ống, sông hoặc kênh. Ở càng gần các thành rắn, những
chuyển động ngang của các phần tử càng vấp phải những ranh giới rắn nên gặp nhiều khó
khăn; vì thế càng gần thành rắn, dòng chảy
càng có xu thế chảy thành tầng lớp. Do đó,
ngay sát thành rắn hình thành dòng chảy tầng Chảy rối
trong một lớp rất mỏng gọi là lớp mỏng chảy Lớp mỏng chảy tầng có chiều dày t. dt D tầng
Mặt khác, một vật liệu bất kỳ không được
tinh chế cẩn thận luôn có bề mặt nhám. Các a)
mấu gồ ghề phân bố không đều hoặc ít, hoặc Chảy rối
nhiều, chiều cao trung bình của các mấu D
gọi là độ nhám tuyệt đối. d Lớp mỏng
+ Khi lớp mỏng chảy tầng che kín hoàn chảy tầng b)
toàn những chỗ lồi của các mấu gồ ghề (t > Hình 4-2
). Khi đó tổn thất cột nước dọc đường
không phụ thuộc độ nhám của thành. Trong trường hợp này thành rắn được gọi là thành
trơn thuỷ lực. (Hình 4-2a)
+ Nếu chiều dày lớp mỏng chảy tầng bé hơn độ nhám tuyệt đối ((t < ) và do đó những
mấu gồ ghề nhô ra dưới lớp mỏng chảy tầng thì thành rắn được gọi là thành nhám thuỷ lực. (Hình 4-2b)
+ Thí nghiệm đã chứng minh được rằng hd thành nhám thủy lực lớn hơn hd của thành trơn thủy lực.
4.1.3. Tổn thất cột nước dọc đường
1. Công thức tính tổn thất dọc đường.
a. Công thức tổng quát Đácxy tính tổn thất cột nước dọc đường hd trong dòng chảy đều.
Kết quả thí nghiệm chứng tỏ rằng, tổn thất cột nước dọc đường (h d) của dòng chảy
trong ống của chất lỏng trong ống phụ thuộc vào các yếu tố sau đây:
+ Đường kính ống d và chiều dài l của ống; 71
+ Các tính chất vật lý của chất lỏng (mật độ và độ nhớt );
+ Vận tốc trung bình của chất lỏng trong ống v;
+ Độ nhám tuyệt đối của thành rắn .
Công thức để xác định tổn thất cột nước dọc đường do Đácxy tìm ra từ thế kỷ thứ XIX
bằng thực nghiệm và gọi là công thức Đácxy : 2 h l v d = (4-2) d 2 g
Trong đó: - hệ số ma sát dọc đường không có thứ nguyên phụ thuộc vào trạng thái
chảy và tính chất của ống; g - gia tốc trọng trường.
Đối với mặt cắt ướt không phải là hình tròn, trong công thức Đácxy (4-2) sẽ thay
bán kính thủy lực cho đường kính theo công thức: d = 4R, tức là: 2 h l v d = (4-3) R 4 g 2
Hai công thức (4-2) và (4-3) là công thức tổng quát tính tổn thất cột nước dọc đường
cho dòng chảy đều, dùng cho cả dòng chảy tầng lẫn dòng chảy rối.
Hệ số ma sát đối với dòng chảy tầng chỉ phụ thuộc vào số Rây nôn.
Đối với dòng chảy rối, bằng lý thuyết và thực nghiệm đã chứng tỏ rằng: Ở khu thành
trơn chỉ phụ thuộc vào số Rây nôn; ở khu thành nhám phụ thuộc vào số Re và độ nhám
tương đối /d; còn ở khu sức cản bình phương hệ số chỉ phụ thuộc vào độ nhám của ống. b. Công thức Sedi
Trong dòng chảy đều, việc xác định lưu tốc trung bình mặt cắt v là rất cần thiết. 2 h Từ công thức Đacxy: h l v d d = với lưu ý J = R 4 2g l Sẽ được: v = C RJ (4-4) Trong đó: C – hệ số Sêdi, C = 8g
Công thức (4-4) gọi là công thức Sêdi, một công thức rất quan trọng trong thuỷ lực học.
Khác với hệ số ma sát , hệ số Sêdi có thứ nguyên, đơn vị đo là: m / s và được xác định
bằng các công thức thực nghiệm.
Biết lưu lượng Q = .v, có thể viết: Q = C RJ (4-5)
Công thức (4-4), (4-5) được sử dụng rộng rãi trong thuỷ lực đặc biệt cho dòng chảy đều trong kênh hở.
Có thể nhận thấy rằng hai công thức Đácxy và Sêdi có thể suy diễn ra nhau. Cả hai đều
biểu thị mối quan hệ giữa lưu tốc trung bình với tổn thất cột nước dọc đường do ma sát gây
ra. Muốn sử dụng những công thức đó, cần biết các giá trị của hệ số và C.
2. Những công thức xác định hệ số và C 72
a. Những công thức xác định hệ số Đácxy . * Trạng thái chảy tầng
Đối với trạng thái chảy tầng trong ống tròn có: = 64 (4-6) Re đối với kênh hở: = 24 với Re v.R Re R = R
*. Trạng thái chảy rối trong khu thành trơn thủy lực.
+ Khi Re 100.000 dùng công thức Bơladiut (1912). 3 , 0 16 (4-7) tron 1 4 Re
+ Khi Re 100.000 ( nhưng với điều kiện thành trơn), dùng công thức Cônacốp (1947) 1 (4-8) tron 2 8 , 1 ( lg Re ) 5 , 1 d
*. Trạng thái chảy rối trong khu quá độ từ thành trơn sang thành nhám
Có thể dùng công thức Antơsun (1952) 0,25 , 1 46 100 1 , 0 (4-9) d Re
*. Trạng thái chảy rối trong khu sức cản bình phương (SCBP):
Sử dụng công thức Pơrantơ - Nicuratsơ 1 d d 2 lg 1 , 1 4 2 lg( 7 , 3 1 ) (4-10) SCBP
b. Những công thức kinh nghiệm xác định hệ số Sedi C
Đối với dòng chảy rối ở khu sức cản bình phương, có thể sử dụng những công thức
sau để tính hệ số Sedi. Hệ số C có thứ nguyên là m / s; bán kính thủy lực R có thứ nguyên là mét. *. Công thức Maninh (1890) C = 1 1 6 .R (4-11) n
Trong đó: n- hệ số nhám, n <0,02; R - bán kính thủy lực, R < 0,5m
Công thức này cho kết quả tốt đối với ống và kênh hở.
*. Công thức Phoóc cơ rây me (1923) 1 C = 1 5 .R (4-12) n
Công thức này thích hợp với kênh đất trong trạng thái còn tốt, với n > 0,020
*. Công thức Pavơlôpski (1925) 73 C = 1 y .R (4-13) n
Trong đó: y - số mũ, phụ thuộc độ nhám và bán kính thủy lực. y = 2,5 n 1 , 0 3 7 , 0 5 R ( n ) 1 , 0
Công thức này dùng cho cả ống và kênh hở, với R < 3 5 m.
*. Công thức I.I. Agơrốtskin (1949) C = 17,72 (k + lgR) (4-14) Trong đó
k - thông số về độ nhám của kênh, k có quan hệ với n như sau: k = 1 1 , 7 72 n .
c. Tiêu chuẩn phân biệt các trạng thái chảy .
Một vấn đề rất quan trọng là phải tìm ra được tiêu chuẩn phân biệt các khu vực sức cản
để áp dụng các công thức tính một cách thích hợp. Trạng thái chảy tầng và chảy rối phân
biệt bằng số ReK = 2320 (đối với ống tròn) hay ReK = 580 (đối với kênh hở); trong trạng
thái chảy rối có thể phân biệt các khu sức cản bằng cách so sánh số Re với các số Rây nôn giới hạn (Regh).
Bảng 4-1: Tiêu chuẩn phân biệt các trạng thái chảy. Trạng thái chảy Số Re = vd Chảy tầng Re < 2320 Chảy quá độ 2320 Re < 4000 Thành trơn thủy lực 4000 Re Retron Chảy rối Thành nhám thủy lực Retron < Red < Renham Sức cản bình phương Re Renhám 87 Trong bảng trên: Re d Trơn = 27 (4-15) Re 191 d d nhám = 21 6 , C
4.1.4. Tổn thất cục bộ
Tổn thất cột nước rất lớn ở những nơi mà dòng chảy thay đổi đột ngột về phương
hướng, về dạng mặt cắt ướt, tức là tại những nơi mà đường dòng và mặt cắt ướt đều cong.
Thí dụ: tại những nơi ống uốn cong, mở rộng hoặc thu hẹp đột ngột, có chướng ngại
vật....Tổn thất cột nước tại những nơi này gọi là tổn thất cục bộ.
Để tiện tính toán, cần giả thiết rằng tổn thất cột nước cục bộ coi như xảy ra tập trung
vào một mặt cắt điển hình nhất. Để xác định tổn thất cục bộ có thể sử dụng công thức Vétsbatsơ: 74 2 h v c = . (4-16) c . 2 g
Trong đó: c - hệ số tổn thất cục bộ thường được xác định bằng thí nghiệm. Trong thực
tế, dòng chảy ở những chỗ cần tính tổn thất cục bộ là dòng chảy rối thuộc khu sức cản bình
phương, do đó hệ số tổn thất cục bộ không phụ thuộc Re mà chỉ phụ thuộc vào dạng hình
học của chỗ có tổn thất cục bộ.
v - lưu tốc trung bình mặt cắt, lấy ở mặt cắt trước hoặc sau nơi có tổn thất cục bộ, tùy
theo cách xác định c .
1. Tổn thất cục bộ khi ống đột ngột mở rộng. Công thức Boóc đa.
Khi dòng chảy từ đoạn ống nhỏ có diện tích
chuyển đột ngột sang đoạn ống to có diện tích
sẽ xảy ra tổn thất cột nước cục bộ (Hình 4-3). Tổn w
thất này được tính theo công thức Boóc đa. v 1 h ( 2 v 1 v ) 2 đm = . (4-17) v 2 g 2 2 2 hoặc: h v1 Hình 4-3 đm = 1 (4-18) 2g 2 2 h v2 đm = 1 (4-19) 2g
Trong đó: v1 - lưu tốc trung bình trong đoạn ống nhỏ; v2 - lưu tốc trung bình trong đoạn ống to.
2. Một số dạng tổn thất cục bộ khác
*. Tổn thất do co hẹp đột ngột (Hình 4-4) 2 h v2 c.h = (4-20) c h . 2g với v1 ch = 1 ( 5 , 0 ) ω Trong đó: v
c.h - hệ số tổn thất do co hẹp đột 2
ngột; v2 - lưu tốc trung bình trong đoạn ống nhỏ ở
sau nơi xảy ra co hẹp; - diện tích mặt cắt ướt của Hình 4-4
ống nhỏ; - diện tích mặt cắt ướt của ống to trước nơi có tổn thất.
*. Tổn thất khi chảy từ bể vào ống h
Khi dòng chảy từ bể chứa vào ống do sự co hẹp vào hra
đột ngột (hình 4-5) nên có tổn thất cục bộ, gọi là tổn
thất vào ống hvào. Vì diện tích của bể lớn gấp nhiều lần
diện tích của ống, nên. Hình 4-5 75 2 h v vào = (4-21) vµo 2g
Trong đó: vào = 0,5 là hệ số tổn thất khi cửa vào sắc mép; v - lưu tốc trung bình trong ống.
*. Tổn thất khi chảy ra khỏi ống đến bể chứa (hình 4-5).
Khi chảy ra khỏi ống, kí hiệu là hra, được tính theo công thức: 2 h v ra = (4-22) ra 2g
Trong đó: ra = 1,0 là hệ số tổn thất khi ra khỏi ống; v - lưu tốc trung bình trong ống.
Ngoài ra còn một số dạng tổn thất cục bộ khác nữa, có thể tra hệ số tổn thất C trong
bảng tính thủy lực và tính hc theo công thức (4-16) Ví dụ 4-1.
Bể kín A có áp suất dư trên mặt thoáng là p od
pod = 0,1at nối với bể hở B qua đường ống gồm 1 1
hai đoạn ống có chiều dài l H 1 = 30m và l2 = 40m 2 2
với đường kính ống lần lượt là d l2 ,d2 1 = 0,1m, d2 = l1,d1
0,2m. Độ nhám tuyệt đối của 2 đoạn ống là =
0,8mm, độ nhám n = 0,013, nhiệt độ của nước A B
là to = 20oC. Biết lưu lượng qua đường ống là Q = 19 l/s. (Hình 4-6 Hình 4-6
1. Xác định chế độ chảy trong 2 ống.
2. Xác định độ chênh mực nước giữa 2 bể.
3. Vẽ đường năng E-E, đường đo áp P-P. Giải:
1. Xác định chế độ chảy trong 2 ống.
Ống 1: Tính số Rây-nôn: Theo công thức (4-1) có: Re v d . d =
Với nước ở nhiệt độ to = 20oC tra bảng thủy lực, tìm được = 0,0101 (cm2/s) Q Q v 4 4 , 0 019 1 = , 2 42 m/s 2 d 1 14 , 3 1 , 0 2 1 Re d . v 242 10 d = 2.396.418 > 4000 , 0 0101
Dòng chảy trong ống là dòng chảy rối. Cần phải xác định chảy rối trong khu vực nào?
So sánh số Red với số Retron và Renhám : 8 8 7 7 Re d 100 tron = 27 =27 =6727 8 , 0 76 Re 191 d d nhám = 6 , 21 C
. Để biết được hệ số Sê di cần phải biết được trạng thái chảy
của ống. Giả thiết dòng chảy ở trong khu sức cản bình phương. 1 1
Xác định C theo công thức Maninh: C = 1 1 1 , 0 6 .R = 6 ( ) =41,59 ( m / s ) n , 0 013 4 Từ đó Re d 100 nhám = 21 6 , C 2 , 1 6 41 5 , 9 = 112.293 8 , 0
Vậy Red > Renhám . Dòng chảy ở khu sức cản bình phương. Giả thiết là đúng (nếu Red <
Renhám cần phải giả thiết lại trạng thái chảy)
* Tương tự, cũng tìm được trạng thái chảy trong đoạn ống thứ 2: v 4Q 2 = 6 , 0 05 m/s; Red2 = 1.198.020 2 d 2
Cũng giả thiết dòng chảy trong khu SCBP: C = 46,47 ( m / s ) d 100 Renhám = 6 , 21 C 6 , 21 59 , 41 = 252.123 8 , 0
Vậy dòng chảy trong khu SCBP. Giả thiết là đúng.
+ Xác định hệ số ma sát 1 và 2. Ta có: . 8 g 1 = = 0,0454; tương tự 2 = 0,036. 2 C
2. Xác định độ chênh lệch cột nước H.
Viết phương trình Bécnuly cho 2 mặt cắt 1-1 và 2-2, Lấy mặt cắt 2-2 làm mặt chuẩn: 2 2 p v p v z 1 1 1 1 z 2 2 2 2 h w 2g 2g
Trong đó: z1= H; p1d = pod = 0,2at = 0,2 98,1 = 19,62 KN/m2; 1 = 2 = 1,0; = 9,81KN/m3
z2= 0; p2d = 0; Do 2 bể A và B rất lớn nên v1 0; v2 0. Vậy H + p1 h (1) w 1 2 Với hw1-2 = h h = (h c d
vào + hdm + hra ) + (h d1 + hd2 ) 2 2 Trong đó: + h v1 v1 vào = 5 , 0 với v v
1 là vận tốc dòng chảy trong đoạn ống 1. g . 2 . 2 g 2 2 + h v v 2 2 ra = , 1 0 với v r
2 là vận tốc dòng chảy trong đoạn ống 2. . 2 g . 2 g 2 2 2 2 2 + h v2 2 2 v2 d2 2 v2 v2 dm = ( ) 1 ( ) 1 9 dm . 2 g . 2 g 1 d2 . 2 g . 2 g 1 77 2 2 2 + h l v 30 v v 1 1 1 1 d1 = 1 . =0,0454 =1 , 3 62 d 2g 1 , 0 2 g 2g 1 2 2 + h l 40 2 2 v2 v2 v2 d2 = 2. =0,036 = 2 , 7 d 2 2 , 0 2 2 2 g g g 2 2 Vậy h v1 v 2 w1-2 = 14 1 , 2 + 17 2 , 2 g 2 g 2 2 Mặt khác, lại có: d d 1 2 1v1 = 2v 2 hay suy ra v 1 v v 2 1 = 4v2. 4 4 2 h v2 w1-2 = 243 1 , 2 . Trong đó v2 = 0,605 m/s 2 g Vậy hw1-2 = 4,53m (2)
Thay (2) vào (1) có kết quả: H = 4,53 - 2 H = 2,53 m
3. Vẽ đường năng, đường đo áp. hvào p Ta có: od hd1 h E-E vào = 0,15m; hđm = 0,17m; P-P hđm hd2 h 2 1v1 /2g 2 d1 = 4,06m; hd2 = 0,13m; 2v2 /2g P-P hra hra = 0,02m Hình 4-7
4.2. HỆ THỐNG ĐIỀU KHIỂN THỦY KHÍ 4.2.1. Nguyên lý cơ bản
Điều khiển là quá trình của một hệ thống, trong đó dưới tác dụng của một hay nhiều
đại lượng vào, các đại lượng ra thay đổi theo một quy luật nhất định của hệ thống đó.
Một hệ thống điều khiển bao gồm: phần tử xử lý và Phần tử đưa tín hiệu Cơ cấu chấp hành điều khiển ví dụ : ví dụ : ví dụ : - công tắc , nút bấm - van đảo chiều - xilanh - công tắc hành trình - van chắn - động cơ thủy khí - cảm biến bằng tia - van tiết lưu
- bộ biến đổi áp lực - van áp suất - phần tử khuếch đại
Hình 4.8. Tổng quan hệ điều khiển 78
Hệ thống điện thủy khí được biểu diễn một cách tổng quát theo hình dưới đây. mạch
điều khiển thông thường là điện một chiều .
Mạch điện điều khiển cơ cấu chấp hành M ạng điện bộ phân phối điện u vào = 230 v / 50 hz i vào = 10 a u tip ra = 24 v dc ira = 5 a nút nhấn phần tử điều khiển rơle (van đảo chiều) nam châm điện
Hình 4.9. Hệ điều khiển Điện thủy khí
4.2.2. Các phần tử điện – thủy khí:
1) Van đảo chiều điều khiển bằng nam châm điện: Tên thiết bị Ký hiệu
Van đảo chiều điều khiển trực tiếp bằng nam châm điện và lò xo
Van đảo chiều điều khiển trực tiếp bằng
nam châm điện cả hai phía
Van đảo chiều điều khiển gián tiếp bằng
nam châm điện và khí nén
Van đảo chiều điều khiển gián tiếp bằng
nam châm điện cả hai phía
Van đảo chiều điều khiển gián tiếp bằng
nam châm điện và khí nén 2) Các phần tử điện: Tên thiết bị Ký hiệu Công tắc:
Trong điều khiển, công tắc, nút nhấn là 2 4 1 3
các phần tử đưa tín hiệu. phần này giới
thiệu 2 loại công tắc thông dụng là công tắc 1 2 4
đóng mở và công tắc chuyển mạch. công tắc đóng mở công tắc chuyển mạch 79 Tên thiết bị Ký hiệu Nút nhấn:
- Nút nhấn đóng mở: bình thường 3 và 4 1 3 2
không nối với nhau, khi nhấn nút, 3 nối với 4 4.
- Nút nhấn chuyển mạch: thường có 2 tiếp 1
điểm thường kín và thường hở. khi nhấn 2 4
nút, tiếp điểm thường kín sẽ hở ra và tiếp
điểm thường hở sẽ kín lại nút nhấn đóng nút nhấn chuyển mở mạch Rơle:
Rơle được sử dụng như phần tử xử lý tín
hiệu. có nhiều loại rơle khác nhau tùy theo công dụng. - Rơle đóng mạch:
Khi dòng điện vào cuộn dây cảm Tiếp điểm chính Tiếp điểm phụ
ứng, lực từ trường xuất hiện sẽ hút lõi sắt,
trên đó có lắp các tiếp điểm. các tiếp điểm 1 3 5 13 21 31 41
chính để đóng mở mạch chính, các tiếp
điểm phụ để đóng mở các mạch điều khiển. 2 4 6 14 22 32 42 - Rơle điều khiển: a1
Rơle điều khiển khác rơle đóng 3 1
mạch ở chỗ là rơle điều khiển đóng mở cho k
mạch công suất nhỏ và thời gian đóng mở rất nhỏ. a 4 2 2 -Rơle tác động muộn:
Khi cấp nguồn điện vào cuộn k, thì a 1 3 k
sau một khoảng thời gian t, các tiếp điểm
k1 mới được tác động. k 2 4 a
-Rơle thời gian nhả muộn: b k
Khi ngừng cấp điện cho cuộn hút k 1 3 b k
thì sau một thời gian t các tiếp điểm k1 k 1 k
mới trở lại vị trí ban đầu. 2 4 a2 80 Tên thiết bị Ký hiệu
công tắc hành trình điện - cơ: 2
Bình thường tiếp điểm 1 nối với 2, khi 4
con lăn chạm cữ hành trình, tiếp điểm 1 nối s với 4. 1 2 4 s 2 a. khi không tác động: 4 b. khi có sự tác động: s 1 a b 1
Công tắc hành trình nam châm: 4
Công tắc hành trình nam châm thuộc
lọai công tắc hành trình không tiếp xúc. b 1
Cảm biến cảm ứng từ:
Cảm biến cảm ứng từ hoạt động dựa trên
nguyên tắc cảm ứng điện từ. với sự thay
đổi khoảng cách giữa cảm biến và vật sẽ
làm độ rộng xung của tín hiệu tại ngõ ra thay đổi. Cảm biến điện dung:
Khi có vật cản sẽ làm điện dung của
cảm biến thay đổi dẫn đến tần số riêng của
bộ dao động bên trong cảm biến thay
đổi,làm cho tần số tín hiệu ngõ ra của cảm biến thay đổi. Cảm biến quang:
Cảm biến quang gồm 2 bộ phận: - Bộ phận phát quang - Bộ phận nhận quang
Do sự bố trí của 2 bộ phận này mà ta
có 2 dạng cảm biến quang: cảm biến quang
1 chiều và cảm biến quang phản hồi. bộ
phận nhận quang sẽ nhận tín hiệu quang từ
bộ phận phát gửi về điều khiển. 81
3) phần tử chuyển đổi tín hiệu:
Phần tử chuyển đổi tín hiệu p(bar) khí nén – điện: Nguyên lý họat động
của phần tử chuyển đổi tín hiệu 1 p
khí nén điện: áp suất p vào cửa đóng
z sẽ điều khiển đóng mở công p m b °
tắc để điều khiển tiếp điểm 1 z t ° nối với tiếp điểm 2. 1 2 0 tín hiệu điện
Trong điều khiển, tín hiệu
điều khiển (áp suất khí nén) có
thể tác động trực tiếp lên màng
để đóng mở tiếp điểm.
Tín hiệu khí nén x tác động x
lên màng làm thay đổi tiếp điểm.
Hay kết hợp với phần tử x
khuếch đại để thay đổi tiếp điểm. p
4) Phần tử chuyển đổi tín hiệu điện – khí nén:
Nguyên lý cơ bản của chuyển đổi tín hiệu điện khí nén là nam châm điện. khi cấp
điện cho cuộn dây nam châm, lõi từ dịch chuyển sẽ làm thay đổi vị trí của nòng van, thực
hiện chức năng điều khiển.
4.2.3. Ứng dụng PLC trong điều khiển 1. Giới thiệu:
Thành phần cơ bản của S7-200 là khối xử lý trung tâm CPU-12 hoặc CPU-14. Ở đây xin
chỉ đề cập đến CPU-14. 2. Mô tả:
- Có 14 ngõ vào: từ I0.0 đến I0.7 và từ I1.0 đến I1.5.
- Có 10 ngõ ra : từ Q0.0 đến Q0.7 và từ Q1.0 đến Q1.1.
- Có 14 led báo trạng thái các ngõ vào, 10 led báo trạng thái các ngõ ra.
- Có 03 led báo trạng thái của CPU:
- Led SF : Báo trạng thái CPU còn tốt hay bị hỏng.
- Led RUN: Báo trạng thái CPU đang hoạt động.
- Led STOP: Báo trạng thái CPU đang ngưng hoạt động.
Ngoài ra, khi có yêu cầu giao tiếp lớn, S7-200 cho phép ta kết nối thêm các modul mở rộng.
Số modul mở rộng tối đa là 7, tương ứng với số ngõ vào cực đại là 64, số ngõ ra cực đại là: 82
- Các ngõ vào, ra đều có mức điện áp tác động là 24VDC. Các cổng ra SF I0.0 I1.0 Q0.0 Q1.0 RUN I0.1 I1.1 Q0.1 Q1.1 STO I0.2 I1.2 Q0.2 I0.3 I1.3 Q0.3 I0.4 Q0.4 I1.4 SIMATIC I0.5 I1.5 Q0.5 S7-200 I0.6 Q0.6 I0.7 Q0.7 Các cổng vào Cổng truyền thông Hình 4.10. Kết cấu PLC
Tính năng của CPU-14 DC/DC/DC: - Nguồn nuôi: 24VDC.
- Mức logic ngõ vào : 24VDC = [1]. 0VDC = [0]. - Mức logic ngõ ra : 24VDC = [1]. 0VDC = [0].
Tải ngõ ra phải làm việc ở 24VDC và dòng tối đa là 50mA.
- Có 2048 từ nhớ chương trình chứa trong ROM.
- Có 2048 từ nhớ dữ liệu, trong đó 512 từ đầu tiên thuộc ROM.
- Có 128 timer, tùy theo độ phân giải mà chia làm 3 loại: + 04 timer 01ms. + 16 timer 10ms. + 108 timer 100ms.
- Có 128 bộ đếm – Counter, tùy vào cách đếm mà chia làm 2 loại: + Đếm lên : Count up.
+ Đếm lên xuống : Count up-down.
- Có 688 bit nhớ đặt biệt dùng để thông báo trạng thái và đặt chế độ làm việc.
- Các chế độ ngắt và xử lý ngắt gồm: + Ngắt truyền thông. + Ngắt sườn lên. + Ngắt sườn xuống. + Ngắt thời gian.
+ Ngắt của bộ đếm tốc độ cao. + Ngắt truyền xung.
- Có 03 bộ đếm tốc độ cao với tần số: 2KHz và 7KHz.
- Có 02 bộ phát xung kiểu POT hoặc kiểu PWM.
- Có 02 bộ điều chỉnh tương tự.
- Toàn bộ vùng nhớ không bị mất dữ liệu trong 190 giờ khi PLC bị mất nguồn nuôi. a) Cấu trúc bộ nhớ: 83
Bộ nhớ của S7-200 được chia làm 4 vùng: _ Vùng chương trình. _ Vùng tham số. _ Vùng dữ liệu.
Trong đó hai vùng nhớ dữ liệu và đối tượng có vai trò quan trọng trong việc thực hiện một chương trình. b) Vùng dữ liệu:
. V - Variable memory : Vùng nhớ biến.
. I - Input image register : Vùng đệm ngõ vào.
. Q - Output image register : Vùng đệm ngõ ra.
. M – Internal memory bits : Vùng nhớ trong.
. SM – Special memory bits : Vùng nhớ đặc biệt.
- Các vùng nhớ này đều có thể truy cập được theo bit, byte, word hay double word:
+ Truy suất theo bit: Một lần một bit.
Cú pháp: Tên vùng nhớ (+) địa chỉ byte (+) . (+) địa chỉ bit.
Ví dụ: I0.0 : chỉ bit 0 của byte 0 của vùng I.
+Truy suất theo byte: mỗi lần 1 byte.
Cú pháp: Tên vùng nhớ (+) B (+) địa chỉ byte.
Ví dụ: VB1 : chỉ byte 1 của vùng V. +Truy suất theo word:
Cú pháp: tên vùng nhớ (+) W (+) địa chỉ byte cao.
Ví dụ: VW100: chỉ word 100 gồm 2 byte 100 và 101 thuộc vùng V.
+Truy suất theo Double word:
Cú pháp: Tên vùng nhớ (+) D (+) địa chỉ byte cao.
Ví dụ: VD150 : chỉ double word gồm 4 byte: 150, 151, 152, 153. c) Vùng đối tượng:
Được phân chia như sau: -Timer: từ T0 đến T127.
-Bộ đếm: từ C0 đến C127.
-Bộ đệm cổng vào tương tự: từ AW0 đến AW30.
-Bộ đệm cổng ra tương tự: từ AQW0 đến AQW30.
-Thanh ghi Acumulator: từ AC0 đến AC3, trong đó thanh ghi AC) không có khả năng làm con trỏ.
-Bộ đếm tốc độ : từ HSC0 đến HSC2
d) Cách thực hiện một chương trình: 84
PLC làm việc theo nguyên tắc thực hiện các vòng lặp. Mỗi vòng lặp được gọi là
một vòng quét. Mỗi vòng quét hoàn chỉnh gồm các bước như sau: 4. Chuyển dữ 1. Nhập dữ liệu liệu từ bộ đệm từ ngoại vi vào ảo ra ngoại vi. bộ đệm ảo. 3. Truyền thông và 2. Thực hiện tự kiểm tra lỗi. chương trình.
Hình 4.11. Các bước thực hiện chương trình
Bước 1: Nhập dữ liệu từ thiết bị ngoại vi vào bộ đệm.
Bước 2: Thực hiện chương trình.
Bước 3: Truyền thông và tự kiểm tra lỗi.
Bước 4: Chuyển dữ liệu từ bộ đệm ảo ra ngoài.
e) Cấu trúc một chương trình:
- Một chương trình điều khiển có thể được viết trên phần mềm STEP7-
MICRO/Dos hay STEP7-MICRO/Win.
- Có thể nạp chương trình vào cho CPU nhờ máy tính cá nhân hoặc thiết bị lập trình bằng tay PG702.
- Một chương trình của S7-200 gồm các phần sau:
- Chương trình chính được kết thúc bằng lệnh MEND.
- Các chương trình con và chương trình xử lý ngắt phải được viết sau lệnh MEND.
- Một chương trình con được bắt đầu bằng lệnh SBR và kết thúc bằng lệnh RET.
- Một chương trình xử lý ngắt được bắt đầu bằng lệnh INT và kết thúc bằng lệnh RETI.
f) Các chế độ làm việc: STOP/TERN/RUN:
Ta chọn chế độ làm việc của PLC bằng cách tác động vào công tắc ba vị trí
Stop/Tern/Run. Khi nạp chương trình vào PLC phải để công tắc ở vị trí Stop.
g) Soạn thảo một chương trình trong S7-200: - Dạng LADer - Dạng STatement List
h) Qui trình thiết kế hệ điều khiển dùng PLC:
Để thiết kế một hệ điều khiển dùng PLC ta thực hiện các bước sau:
- Xác định yêu cầu điều khiển:
Nắm rõ cấu tạo và nguyên tắc hoạt động của thiết bị, yêu cầu điều khiển là gì. - Vẽ lưu đồ: 85
Bước vẽ lưu đồ giúp ta có thể nhìn một cách tổng quan về yêu cầu điều khiển và kết
nối giữa hệ thống với thiết bị. - Xác định I/O:
Ngõ vào thường là các tiếp điểm, rơle, … Ngõ ra thường là các cuộn dây, motor, contactor… - Viết chương trình:
Khi xây dựng lưu đồ đúng,ta sẽ chuyển được sang sơ đồ LAD một cách dễ dàng.
- Nạp chương trình vào PLC:
Để mô phỏng chương trình, cần thiết phải nạp vào PLC. - Kiểm tra:
Trong quá trính mô phỏng, nếu phát hiện sai sót, lỗi, ta sẽ thoát ra ngoài để sửa lại
chương trình. Nếu chương trình chạy tốt, ta kết nối PLC với các thiết bị.
- Kết thúc: Kết nối PLC với các thiết bị và chấm dứt. 4.3. MÔ HÌNH HÓA 4.3.1. Phần mềm FluidSIM
Bộ phần mềm này cho phép người sử dung xây dựng và mô phỏng một cơ cấu điện -
thủy lực – khí nén. Bộ phần mềm bao gồm cả phần hướng dẫn sử dụng và các chức năng
kèm theo. Địa chỉ website: www.fluidsim.com hoặc www.festo.com/didactic Các phần tử lựa chọn Khu vực làm việc (xậy dựng mô hình)
Hình 4.12. Giao diện chính của FluidSim
Các thao tác đóng mở và ghi file giống như các phần mềm thông dụng khác.
Ở cột các phần tử lựa chọn bao gồm nhiều phần tử định sẵn 1) Phần tử bơm (pump) 86
- Dùng mô tả một bơm đơn giản trong hệ thống đang dùng - Tham số lựa chọn
(1) Lưu lượng (Flow): từ 0 – 16 lít/phút)
(2) Áp suất làm việc: 0 đến 350 bar
2) Tổ hợp bơm (pump unit)
- Dùng mô tả một hệ bơm trong hệ thống đang dùng - Tham số lựa chọn
(1) Lưu lượng (Flow): từ 0 – 16 lít/phút)
(2) Áp suất làm việc: 0 đến 350 bar
Nó có van định lượng giới hạn 3) Thùng đựng (Tank)
- Dùng mô tả thùng đựng môi chất làm việc trong hệ thống
4) Đầu giắc nối (Hose with quick-action coupling)
- Dùng để nối các đường khối với nhau - Tham số điều chỉnh
Chiều dài có thể là từ 0-3000 (mm) bước nhảy 600 mm 5) Bộ lọc (filter)
- Mô tả kết cấu của bộ phận lọc trên hệ khí nén và thủy lực
6) Van dừng khẩn cấp (Shuttle Valve)
- Mô tả kết cấu của bộ phận lọc trên hệ khí nén và thủy lực
7) Cân bằng áp suất (Two Pressure) 87
- Mô tả kết cấu của bộ phận lọc trên hệ khí nén và thủy lực
8) Van hai ngả (2/n Way valve)
- Mô tả kết cấu của bộ phận lọc trên hệ khí nén và thủy lực
- Định nghĩa thân van và kiểu làm việc của nó
- Các lựa chọn về tham số điều khiển và những đặc tính liên
quan mà người dùng yêu cầu
- Các dạng điều khiển bằng tay
(manual); Cơ khí (Mechanical); Thủy
lực điện (Hydraulic Electrical)
- Cũng như thân van (Valve Body)
9) Van ba ngả (3/n Way valve)
- Mô tả kết cấu của bộ phận lọc trên hệ khí nén và thủy lực
- Định nghĩa thân van và kiểu làm việc của nó
- Các lựa chọn về tham số điều khiển và những đặc tính liên
quan mà người dùng yêu cầu
- Các dạng điều khiển bằng tay
(manual); Cơ khí (Mechanical); Thủy
lực điện (Hydraulic Electrical)
- Cũng như thân van (Valve Body)
10) Van bốn ngả (4/n Way valve)
- Mô tả kết cấu của bộ phận lọc trên hệ khí nén và thủy lực
- Định nghĩa thân van và kiểu làm việc của nó
- Các lựa chọn về tham số điều khiển và những đặc tính liên
quan mà người dùng yêu cầu 88
- Các dạng điều khiển bằng tay
(manual); Cơ khí (Mechanical); Thủy
lực điện (Hydraulic Electrical)
- Cũng như thân van (Valve Body)
11) Van năm ngả (5/n Way valve)
- Mô tả kết cấu của bộ phận lọc trên hệ khí nén và thủy lực
- Định nghĩa thân van và kiểu làm việc của nó
- Các lựa chọn về tham số điều khiển và những đặc tính liên
quan mà người dùng yêu cầu
- Các dạng điều khiển bằng tay
(manual); Cơ khí (Mechanical); Thủy
lực điện (Hydraulic Electrical)
- Cũng như thân van (Valve Body)
12) Pít tông – xy lanh (Double Acting cylinder): Loai 1
- Mô tả hệ xy lanh – pít tông điều khiển chuyển động bằng thanh truyền
- Các thông số điều khiển
- Lực (Force): -1000 đến 1000 (N)
- Hành trình cực đại (Max. stroke) : 10 đến 6000 mm (bước 200 mm)
- Vị trí pítông:….(Piston position)
- Hành trình cực đại (Max. stroke)
- Diện tích pít tông (Piston Area): 1- 805 cm2
- Diện tích xéc măng (Piston Ring Area): 0,5-425 cm2
13) Pít tông – xy lanh (Double acting cylinder with shock adsorber at stroke end): Loại 2 89
- Mô tả hệ xy lanh – pít tông điều khiển chuyển động bằng tải gân ra bởi áp lục
- Các thông số điều khiển
- Lực (Force): -1000 đến 1000 (N)
- Hành trình cực đại (Max. stroke) : 10 đến 6000 mm (bước 200 mm)
- Vị trí pítông:….(Piston position)
- Hành trình cực đại (Max. stroke)
- Diện tích pít tông (Piston Area): 1- 805 cm2
- Diện tích xéc măng (Piston Ring Area): 0,5-425 cm2
4.3.2. Phần mềm kết nối PLC thủy khí
Sau khi nắm được các kiến thức cơ bản về hệ thủy lực và khí nén, trong phần này
cung cấp cho người đọc cách sử dụng phần mềm để mô phỏng hệ điều khiển này
Phần mềm GWIN cho phép thực hiện việc mô phỏng và tính tóan một số hệ điều
khiển thủy lực cũng như việc kết nối với PLC điều khiển bên ngoài.
Hình 4.13. Giao diện chính của GWIN
Các phần tử được thiết kế sẵn với các công dữ liệu đầu vào
4.3.3. Các phần mềm khác
ENPANET là một phần mềm biểu diễn chu trình của nước và chất lượng nước bên
trong mạng đường ống có áp. Một mạng gồm có đường ống, nút (chỗ giao nhau của các
đường ống), máy bơm, van và bể chứa hoặc nguồn nước. ENPANET tính toán lưu lượng
trong mỗi ống, áp lực tại mỗi nút, chiều cao cột nước trong bể chứa và nồng độ hoá chất của
mạng trong suốt một chu trình của nhiều khoảng thời gian.
Chạy trong hệ điều hành Windows, EPANET cung cấp một môi ttrường tiện ích cho
việc chỉnh sửa các số liệu đầu vào, chạy mô phỏng các tuyến ống và chất lượng nước, xem 90
kết quả theo nhiều dạng: Sơ đồ mạng với các màu qui định cho các giá trị áp lực tại nút,
trình bày dữ liệu dạng bảng, biểu đồ chuỗi thời gian.
Hình 4.14. Giao diện của EPANET
Trình tự sử dụng ENPANET bao gồm:
1- Vẽ một sơ đồ hình học miêu tả hệ thống cấp nước, có các đối tượng: a. Nguồn nước b. Máy bơm c. Đường ống
d. Nút (Chỗ giao của các đường ống) e. Bể chứa
2- Chỉnh sửa các thuộc tính của đối tượng:
a. Thông số nguồn nước b. Thông số máy bơm
c. Chiều dài và đường kính ống
d. Cao độ, toạ độ của nút e. Thông số bể chứa
3- Mô tả sự hoạt động của hệ thống
a. Đường đặc trưng của máy bơm b. Thông số thời gian
c. Thông số điều khiển
4- Lựa chọn và đặt các phương pháp phân tích 5- Chạy phân tich 6- Xem kết quả 91
Ví dụ 4.2.Thiết kế mạch thuỷ lực và mạch điện điều khiển của một đầu khoan tự động.
Yêu cầu: Đưa chi tiết vào vị trí cần
khoan, khi đó ta ấn nút START, đầu khoan
tịnh tiến đến và khoan chi tiết. Đến khi đủ
chiều sâu cần thiết đầu khoan tự động quay
về. Trong quá trình gia công nếu xảy ra sự
cố ta ấn nút (S2), đầu khoan tự động lùi về.
- Sơ đồ mạch thuỷ lực như sau: Hình 4.15.. Máy khoan
Hình 4.16. Mạch điện điều khiển thi ết bị khoan
Hình 4.15 Sơ đồ mạch thuỷ lực của thiết bị khoan. Ví dụ 4.3.
Điều khiển xilanh tác dụng đơn (a) Mạch khí nén: Hình 4.17 (b) Mạch điện khí nén: 92 Hình 4.18
(c) Viết chương trình điều khiển bằng PLC
I0.0 : nút nhấn thường mở (PB1)
Q0.0: ngõ ra điều khiển DV1-SOL-A và đèn L1 Hình 4.19
1) Khi nhấn nút PB1 xi lanh sẽ chuyển động duỗi ra. Lúc đó có dòng điện chạy qua
SOL-A làm van tác động, dòng khí qua van lên xilanh làm xilanh duỗi ra.
2) Xilanh tác dụng đơn hoạt động theo nguyên tắc không khí được nén vào nòng
xilanh làm cho thanh piston duỗi ra. Khi không khí nén trong xilanh được xả ra
ngoài các lò xo sẽ đẩy piston trở về vị trí ban đầu.
3) Khi thả nút PB1 ra không có dòng điện qua SOL-A nữa, lúc đó van DV1 sẽ trở
về vị trí ban đầu( xả khí ra ngoài) xilanh sẽ chuyển động thụt lùi nhờ lò xo. 93 BÀI TẬP CHƯƠNG 4
Bài 4.1: Sử dụng phần mềm FluidSim để xây dựng và tính toán sơ đồ thủy khí điện của chu
trình liên tục của xi lanh tác động kép (hình 4-20) Hình 4-20
Bài 4.2: Thiết bị lắp ráp có độ dôi
Thiết kế mạch điều khiển thủy lực của cơ cấu dùng để lắp ráp có độ dôi, với yêu cầu kỹ thuật như sau:
Đưa chi tiết cần lắp vào vị trí lắp, ấn nút S1 cơ cấu tịnh tiến xuống lắp và ép chặt chi
tiết đến khi đủ áp suất 20 bar, đèn H sáng, thì cơ cấu tự quay về. Nếu trong quá trình gia
công xảy ra sự cố thì ấn nút S2 cơ cấu quay về vị trí ban đầu.
Bài 4.3: Cơ cấu cấp phôi theo kiện
Thiết kế mạch điều khiển thủy lực cấp phôi theo khối kiện nhiều sản phẩm, với yêu
cầu kỹ thuật sau: Nhấn nút 1S cơ cấu đẩy phôi hoạt động từ vị trí giới hạn S1 đến giới hạn
S2 để đẩy sản phẩm. Khi công tắc S2 tác động thì pittông đẩy trở về vị trí ban đầu và thực
hiện tiếp lần đẩy mới. Đẩy đúng 12 phôi thì ngừng ở vị trí ban đầu. Trong quá trình đẩy
phôi có vấn đề thì nhấn nút 2S và trở về vị trí ban đầu. Bài 4.4:
Thiết kế mạch tác động cân bằng dành cho (ưu tiên tắt ) trên hệ thống điều khiển ổn
định của xilanh tác động kép,không ổn định của nguồn –ra/vào-theo tuần tự (hình 4-21) Hình 4-21 94 TÀI LIIỆU THAM KHẢO
[1]. Lê Thượng Hiền, Bùi Văn Bình, Công nghệ thuỷ lực và khí nén .
Đại học Điện lực (2008).
[2]. Ngô Vi Châu, Nguyễn Phước Hoàng, Vũ Duy Quang, Đặng Huy Chi, Võ Sĩ
Huỳnh, Lê Danh Liên. Bài tập thuỷ lực và máy thuỷ lực, tập I, II,
Nxb Đại học và THCN, Hà Nội - 1979.
[3]. Nguyễn Ngọc Phương, Hệ thống điều khiển bằng khí nén, NXB Giáo dục, 1999
[4]. Hoàng Đức Liên, Kỹ thuật thủy khí. Đại học Nông nghiệp Hà nội 2007
[5]. Peter Croser; Frank Ebel, Pneumatic Theory Festo Didactic, 1989
[6]. M.Guillon, Hydraulic control systems London, Butterworths, 1969
[7]. G.Prede; D.Scholz, Electropneumatics Theory , Festo Didactic, 1989
[8 ]. The components of Hydraulics
Technic Documents of Festo Didactic, 1999 [9]. Pneumatics Exercise
KCCI, Korea Chamber of Commerce & Industry
[10]. Electropneumatics Exercise
KCCI, Korea Chamber of Commerce & Industry
[11]. Fluidsim- Guid book, Newyork 2009 [12]. www. epanet.de. [13]. www.Fluidsim.com
[14]. Schlichting H., Boundary – Layer Theory,
McGraw-Hill book company, New York –1979.
[15]. Suhas V. Patankar, Numerical Heat Transfer and Fluid flow,
Hemisphere publishing corporation, Washington - 1980. 95