
















































































Preview text:
1
ÑAÏI HOÏC QUOÁC GIA TP HOÀ CHÍ MINH
TRÖÔØNG ÑAÏI HOÏC BAÙCH KHOA Vuõ Duy Cöôøng GIAÙO TRÌNH CÔ LYÙ THUYEÁT
(Taùi baûn laàn thöù nhaát)
NHAØ XUAÁT BAÛN ÑAÏI HOÏC QUOÁC GIA
TP HOÀ CHÍ MINH - 2002 2 MỤC LỤC LÔØI NOÙI ÑAÀU 5
PHẦN I. TĨNH HỌC VẬT RẮN
Chöông 1. CAÙC KHAÙI NIEÄM CÔ BAÛN VAØ HEÄ TIEÂN ÑEÀ TÓNH HOÏC 8
1.1. Caùc khaùi nieäm cô baûn 8
1.2. Heä tieân ñeà tónh hoïc 10
1.3. Moät soá moâ hình phaûn löïc lieân keát thöôøng gaëp 11
Chöông 2. THU GOÏN HEÄ LÖÏC. PHÖÔNG TRÌNH CAÂN BAÈNG CUÛA HEÄ LÖÏC 16
2.1. Hai ñaïi löôïng ñaëc tröng cuûa heä löïc 16
2.2. Ñònh lyù töông ñöông cô baûn 17 2.3. Caùc heä quaû 19
2.4. Ñieàu kieän caân baèng cuûa heä löïc 22
2.5. Baøi toaùn caân baèng cuûa vaät raén 23 2.6. Caùc ví duï 25
2.7. Baøi toaùn caân baèng cuûa heä vaät raén 31
2.8. Caùc ví duï baøi toaùn caân baèng cuûa heä vaät raén 32
Chöông 3. CAÙC BAØI TOAÙN ÑAËC BIEÄT 39
3.1. Baøi toaùn ñoøn phaúng 39 3.2. Baøi toaùn giaøn 39 Chöông 4. MA SAÙT 48
4.1. Ma saùt, caùc löïc ma saùt vaø tính chaát cuûa chuùng 48
4.2. Baøi toaùn caân baèng cuûa vaät raén chæ keå ñeán ma saùt tröôït 50
4.3. Moâ hình baøi toaùn caân baèng coù keå ñeán ma saùt laên 56
Chöông 5. TROÏNG TAÂM 59 5.1. Caùc ñònh nghóa 59
5.2. Caùc phöông phaùp xaùc ñònh toïa ñoä troïng taâm cuûa caùc vaät 62
5.3. Troïng taâm cuûa moät soá vaät ñoàng chaát 65
PHAÀN II. ÑOÄNG HOÏC 68
Chöông 6. ÑOÄNG HOÏC ÑIEÅM 69
6.1. Khaûo saùt ñoäng hoïc ñieåm baèng phöông phaùp vector vaø toïa ñoä Decartes 69
6.2. Khaûo saùt chuyeån ñoäng ñieåm baèng toïa ñoä cöïc 70
6.3. Khaûo saùt chuyeån ñoäng ñieåm baèng toïa ñoä töï nhieân 71
6.4. Moät soá chuyeån ñoäng ñaëc bieät 72
Chöông 7. CHUYEÅN ÑOÄNG CÔ BAÛN CUÛA VAÄT RAÉN 76
7.1. Chuyeån ñoäng tònh tieán cuûa vaät raén 76
7.2. Chuyeån ñoäng quay quanh truïc coá ñònh cuûa vaät raén 77
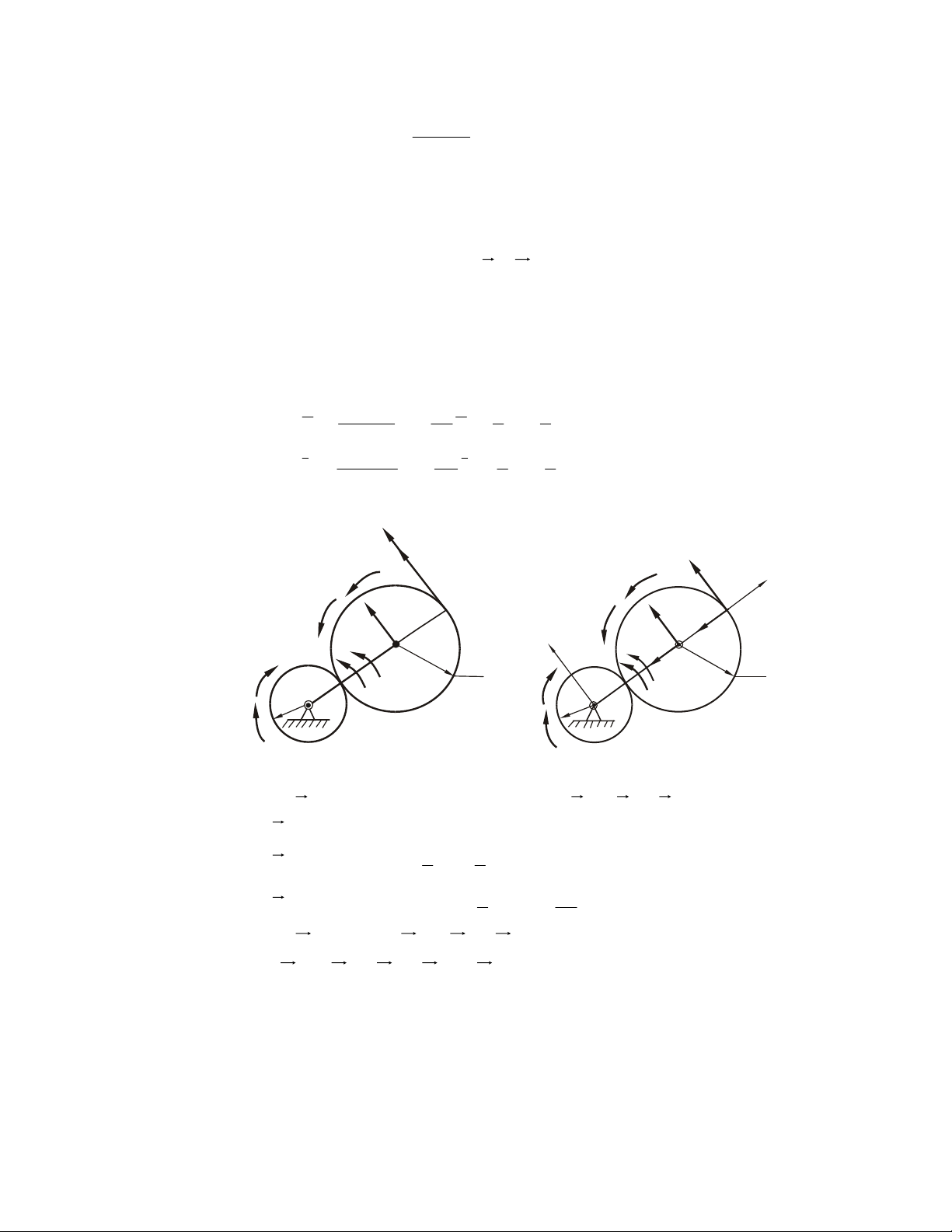
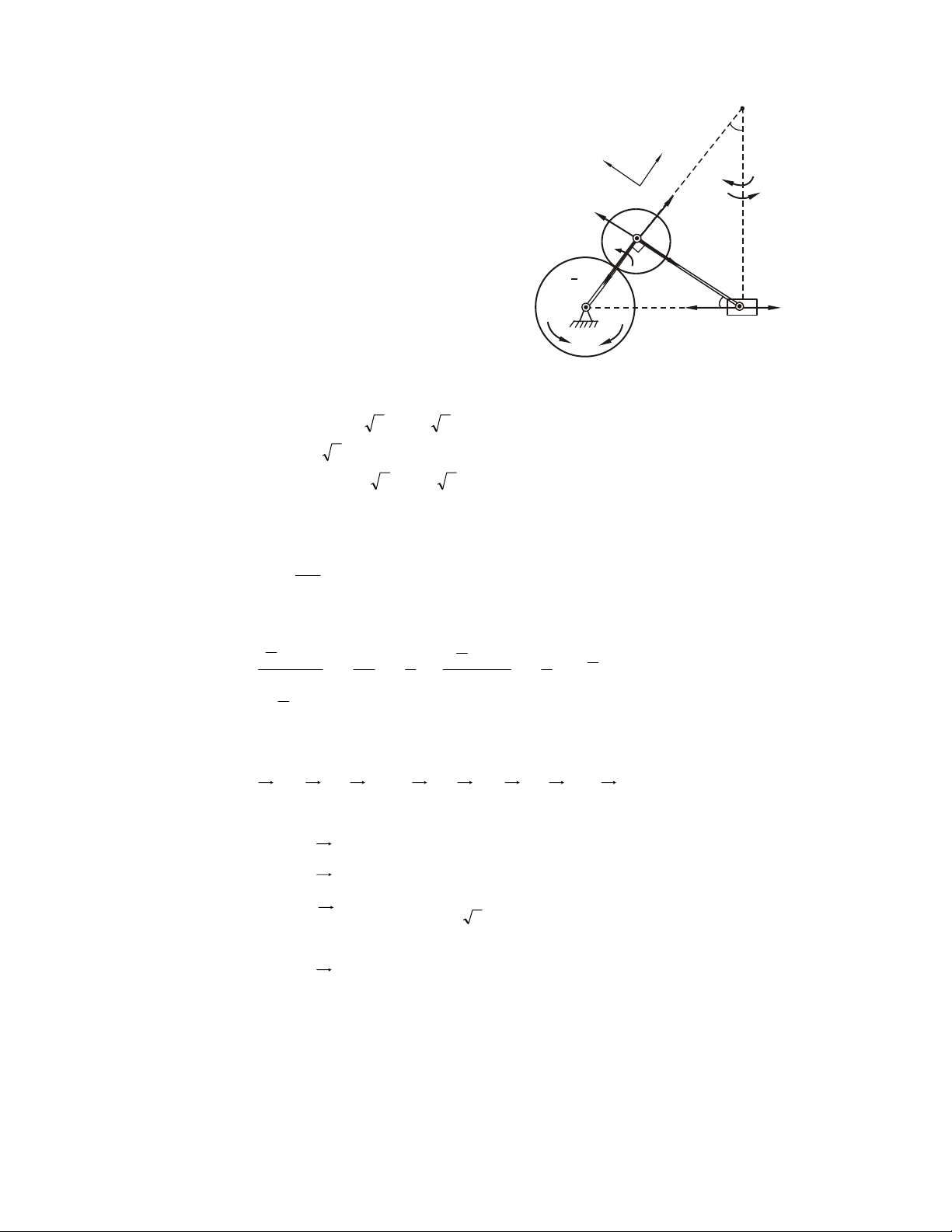
7.3. Caùc cô caáu truyeàn ñoäng cô baûn 79 7.4. Caùc ví duï 80
Chöông 8. CHUYEÅN ÑOÄNG PHÖÙC HÔÏP CUÛA ÑIEÅM 83
8.1. Moâ hình baøi toaùn vaø caùc ñònh nghóa 83
8.2. Caùc ñònh lyù hôïp vaän toác, gia toác 85
8.3. Phöông phaùp giaûi caùc baøi toaùn chuyeån ñoäng phöùc hôïp 86 3 8.4. Caùc ví duï 86
Chöông 9. CHUYEÅN ÑOÄNG SONG PHAÚNG CUÛA VAÄT RAÉN 95
9.1. Khaûo saùt chuyeån ñoäng caû vaät 95
9.2. Khaûo saùt chuyeån ñoäng cuûa ñieåm thuoäc vaät 96
9.3. Nhöõng chuyeån ñoäng song phaúng ñaëc bieät 101
9.4. Phöông phaùp giaûi baøi toaùn chuyeån ñoäng song phaúng 103 9.5. Caùc ví duï 104
PHAÀN III. ÑOÄNG LÖÏC HOÏC 120
Chöông 10. MÔÛ ÑAÀU ÑOÄNG LÖÏC HOÏC PHÖÔNG TRÌNH VI PHAÂN
CHUYEÅN ÑOÄNG CUÛA CHAÁT ÑIEÅM VAØ HEÄ CHAÁT ÑIEÅM 121
10.1. Caùc khaùi nieäm cuûa ñoäng löïc hoïc 121
10.2. Phöông trình vi phaân chuyeån ñoäng cuûa chaát ñieåm vaø heä chaát ñieåm 123
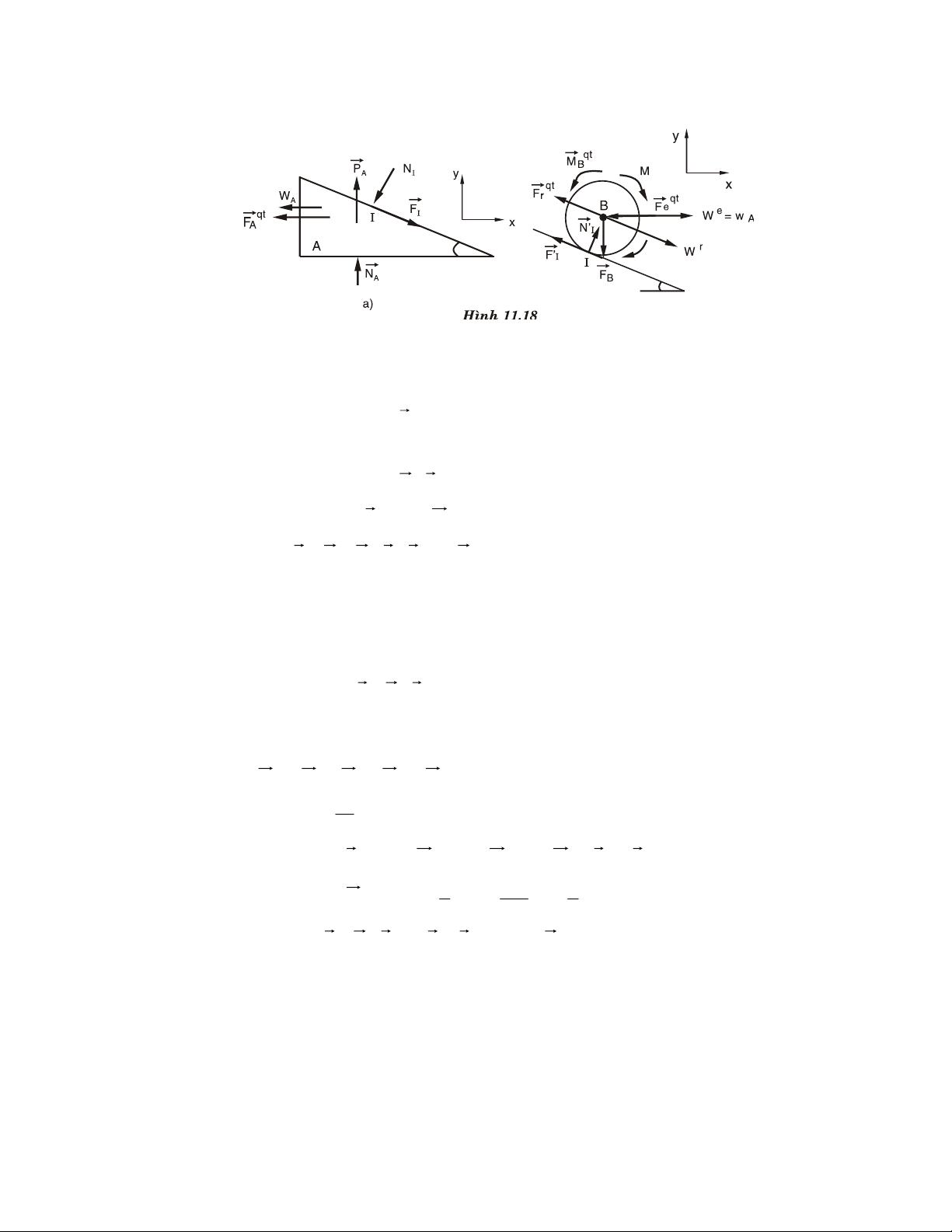
Chöông 11. NGUYEÂN LYÙ D’ ALEMBERT 129
11.1. Caùc ñaëc tröng hình hoïc khoái löôïng cuûa cô heä 129
11.2. Löïc quaùn tính, nguyeân lyù D’ Alembert 132
11.3. Thu goïn heä löïc quaùn tính 133
11.4. Phaûn löïc ñoäng löïc truïc quay 135
11.5. Noäi dung aùp duïng vaø caùc ví duï 136
Chöông 12. CAÙC ÑÒNH LYÙ TOÅNG QUAÙT ÑOÄNG LÖÏC HOÏC 147
12.1. Caùc ñònh lyù chuyeån ñoäng khoái taâm - ñoäng löôïng moâmen ñoäng löôïng 147
12.2. Ñònh lyù ñoäng naêng 155
Chöông 13. NGUYEÂN LYÙ DI CHUYEÅN KHAÛ DÓ 172
13.1. Moät soá khaùi nieäm cô baûn 172
13.2. Nguyeân lyù di chuyeån khaû dó 179
Chöông 14. PHÖÔNG TRÌNH TOÅNG QUAÙT ÑOÄNG LÖÏC HOÏC
VAØ PHÖÔNG TRÌNH LAGRANGE II 185
14.1. Phöông trình toång quaùt cuûa ñoäng löïc hoïc 185
14.2. Phöông trình Lagrange II 189
Chöông 15. LYÙ THUYEÁT VA CHAÏM 199
15.1. Ñònh nghóa, ñaëc ñieåm cuûa hieän töôïng va chaïm
vaø caùc giaû thieát cuûa lyù thuyeát va chaïm 199
15.2. Caùc ñònh lyù toång quaùt cuûa ñoäng löïc hoïc trong quaù trình va chaïm 201
15.3. Va chaïm thaúng xuyeân taâm cuûa hai vaät chuyeån ñoäng tònh tieán 204
15.4. Va chaïm cuûa vaät quay quanh moät truïc coá ñònh 209
PHAÀN IV. BAØI TOAÙN TÖÏ GIAÛI 212 A. PHAÀN TÓNH HOÏC 212 B. PHAÀN ÑOÄNG HOÏC 224
C. PHAÀN ÑOÄNG LÖÏC HOÏC 230 TAØI LIEÄU THAM KHAÛO 254 4
LÔØI NOÙI ÑAÀU
Giaùo trình naøy ñöôïc bieân soaïn nhaèm phuïc vuï sinh vieân ngaønh cô khí vaø xaây
döïng. Tuy nhieân, sinh vieân, kyõ sö caùc ngaønh khaùc muoán tìm hieåu nhöõng kieán thöùc
cô baûn cuûa cô hoïc coù theå duøng taøi lieäu naøy tham khaûo.
Ñeå ñaùp öùng yeâu caàu treân, taùc giaû ñaõ maïnh daïn ñöa ra moät soá thay ñoåi
trong phaàn trình baøy noäi dung vaø moät soá vaán ñeà ñaùng chuù yù sau: 1- Phaàn tónh hoïc
Lyù thuyeát ñöôïc xaây döïng laáy ñònh lyù töông ñöông cô baûn laøm trung taâm.
Caùc baøi toaùn caân baèng coù keå ñeán hai loaïi ma saùt (tröôït, laên) chæ coù theå
ñaùnh giaù chính xaùc ôû traïng thaùi caân baèng. Neáu vaät ñaõ khôûi ñoäng khoâng theå söû
duïng ñieàu kieän caân baèng tónh.
2- Ñoäng löïc hoïc Nguyeân lyù
D’ ALEMBERT ñöôïc trình baøy tröôùc ñeå coù theå giaûi quyeát ñaày ñuû
caùc yeâu caàu veà ñoäng löïc cuûa cô heä, xaùc ñònh ñöôïc mieàn giôùi haïn cuûa caùc tham soá
phuø hôïp vôùi traïng thaùi chuyeån ñoäng cuûa cô heä ngay töø ñaàu, traùnh söï ngoä nhaän
caùc keát quaû tính toaùn.
3- Ñeå taïo ñieàu kieän thuaän lôïi cho ngöôøi ñoïc, giaùo trình daønh khoaûng 60%
noäi dung cho caùc ví duï vaø baøi taäp töï laøm. Trong ñoù coù moät soá baøi taäp toång hôïp
xuyeân suoát noäi dung cuûa moân hoïc.
Ñeå hoaøn thaønh giaùo trình naøy, taùc giaû ñaõ nhaän ñöôïc söï hoã trôï nhieät tình
cuûa caùc ñoàng nghieäp Nguyeãn Quoác Vieät, Vuõ Coâng Hoøa, Nguyeãn Ñaéc Thieän trong
vieäc ñaùnh maùy baûn thaûo. Taùc giaû xin chaân thaønh caûm ôn söï giuùp ñôõ quyù baùu naøy.
Nhöõng suy nghó treân ñaây hoaøn toaøn döïa vaøo chuû quan cuûa taùc giaû neân
khoâng traùnh khoûi thieáu soùt. Taùc giaû mong nhaän ñöôïc söï ñoùng goùp cuûa caùc
ñoàng nghieäp vaø baïn ñoïc nhaèm giuùp taùc giaû xaây döïng giaùo trình ngaøy caøng hoaøn thieän.
Moïi yù kieán xin gôûi veà: Boä moân Cô Kyõ thuaät - Tröôøng Ñaïi hoïc Baùch khoa -
Ñaïi hoïc Quoác gia TP Hoà Chí Minh - 268 Lyù Thöôøng Kieät, F14, Q10. Taùc giaû
Thaïc só VUÕ DUY CÖÔØNG 5 PHAÀN I TÓNH HOÏC VAÄT RAÉN
Tónh hoïc laø phaàn ñaàu cuûa cô hoïc lyù thuyeát khaûo saùt söï caân baèng cuûa vaät
theå chòu taùc duïng cuûa löïc
Hai vaán ñeà chính ñöôïc giaûi quyeát trong tónh hoïc laø thu goïn heä löïc vaø ñieàu
kieän caân baèng cuûa heä löïc.
Nhôø phöông phaùp tröøu töôïng hoùa vaø moâ hình hoùa chuùng ta xaây döïng caùc
khaùi nieäm cô baûn vaø nhöõng tieân ñeà laøm cô sôû ñeå giaûi quyeát caùc vaán ñeà ñaët ra.
Nhöõng khaùi nieäm cô baûn neâu ra nhöõng moâ hình cô baûn nhaát cuûa caùc ñoái
töôïng khaûo saùt.
Nhöõng tieân ñeà neâu leân nhöõng chaân lyù khaùch quan deã nhaän thaáy, vaø nhöõng
quan heä ñaàu tieân giöõa caùc moâ hình cô baûn.
Taát caû caùc ñaùnh giaù, keát luaän coù ñöôïc sau naøy ñeàu phaûi ñöôïc chöùng minh
chaët cheõ töø heä tieân ñeà. 6 Chöông 1
CAÙC KHAÙI NIEÄM CÔ BAÛN VAØ
HEÄ TIEÂN ÑEÀ TÓNH HOÏC Noäi dung
- Caùc moâ hình cô baûn vaø heä tieân ñeà
- Khaùi nieäm veà lieân keát, phaûn löïc lieân keát
- Caùc moâ hình phaûn löïc lieân keát Yeâu caàu
- Hieåu vaø nhôù caùc khaùi nieäm cô baûn, heä tieân ñeà tónh hoïc
- Naém vöõng caùc moâ hình phaûn löïc lieân keát, nguyeân taéc chung ñeå bieåu
dieãn caùc phaûn löïc lieân keát.
1.1. CAÙC KHAÙI NIEÄM CÔ BAÛN 1. Vaät raén tuyeät ñoái
Vaät raén tuyeät ñoái laø vaät theå khoâng bò bieán daïng trong moïi tröôøng hôïp chòu löïc.
Vaät raén tuyeät ñoái chính laø vaät theå ñaøn hoài ñöôïc lyù töôûng hoùa boû qua bieán daïng.
Trong thöïc teá neáu bieán daïng cuûa vaät coù aûnh höôûng khoâng ñaùng keå trong
tính toaùn, vaät khaûo saùt ñöôïc xem laø vaät raén tuyeät ñoái.
Chaát ñieåm laø vaät raén tuyeät ñoái ñaëc bieät. Töø ñaây veà sau, neáu khoâng coù löu
yù gì, vaät khaûo saùt ñöôïc hieåu laø vaät raén tuyeät ñoái.
2. Traïng thaùi caân baèng
Vaät raén ñöôïc goïi laø caân baèng ñoái vôùi moät heä quy chieáu neáu noù ñöùng yeân
hay chuyeån ñoäng thaúng ñeàu ñoái vôùi heä quy chieáu ñoù.
Heä quy chieáu laø moät vaät raén ñöôïc choïn laøm chuaån ñeå quan saùt, ñaùnh giaù
vò trí cuûa vaät khaûo saùt. Trong giaùo trình naøy, heä quy chieáu ñöôïc choïn laø heä quy chieáu quaùn tính. 3. Löïc
Löïc laø ñaïi löôïng ñaëc tröng cho taùc duïng cô hoïc cuûa vaät theå naøy leân vaät theå khaùc.
Löïc ñöôïc bieåu dieãn baèng vector buoäc hoaëc c (A ) F où theå qua caùc hình chieáu: F = F ( , F , F ) x y z . 7
Löïc taäp trung laø löïc bieåu dieãn cho töông taùc cô hoïc thoâng qua moät vuøng
raát beù, xem nhö moät ñieåm (A). Ngöôøi ta noùi löïc F ñaët taïi A.
Löïc phaân boá bieåu dieãn cho taùc ñoäng cô hoïc thoâng qua moät mieàn.
4. Moät soá ñònh nghóa khaùc
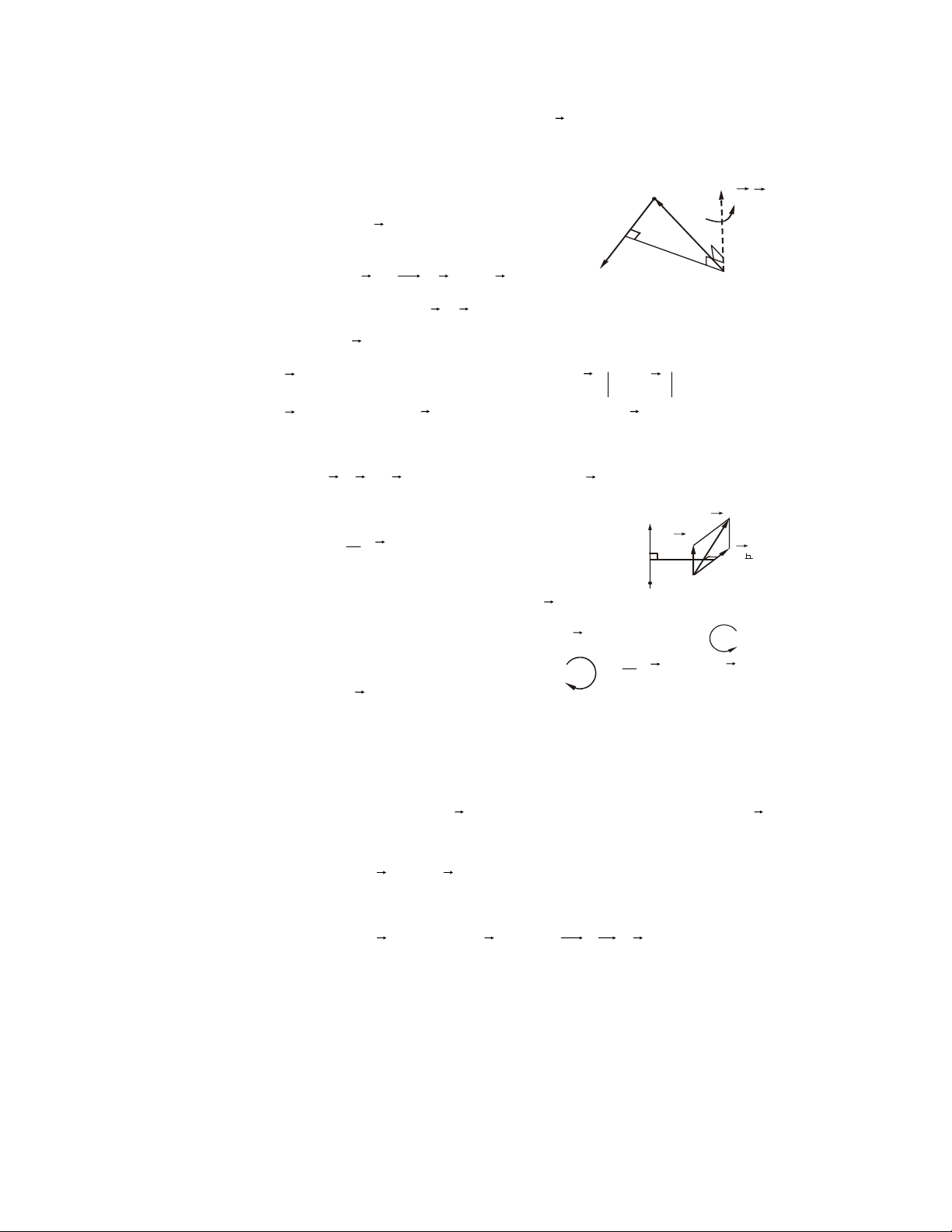
1- Moâmen cuûa löïc ñoái vôùi taâm A m(F) o
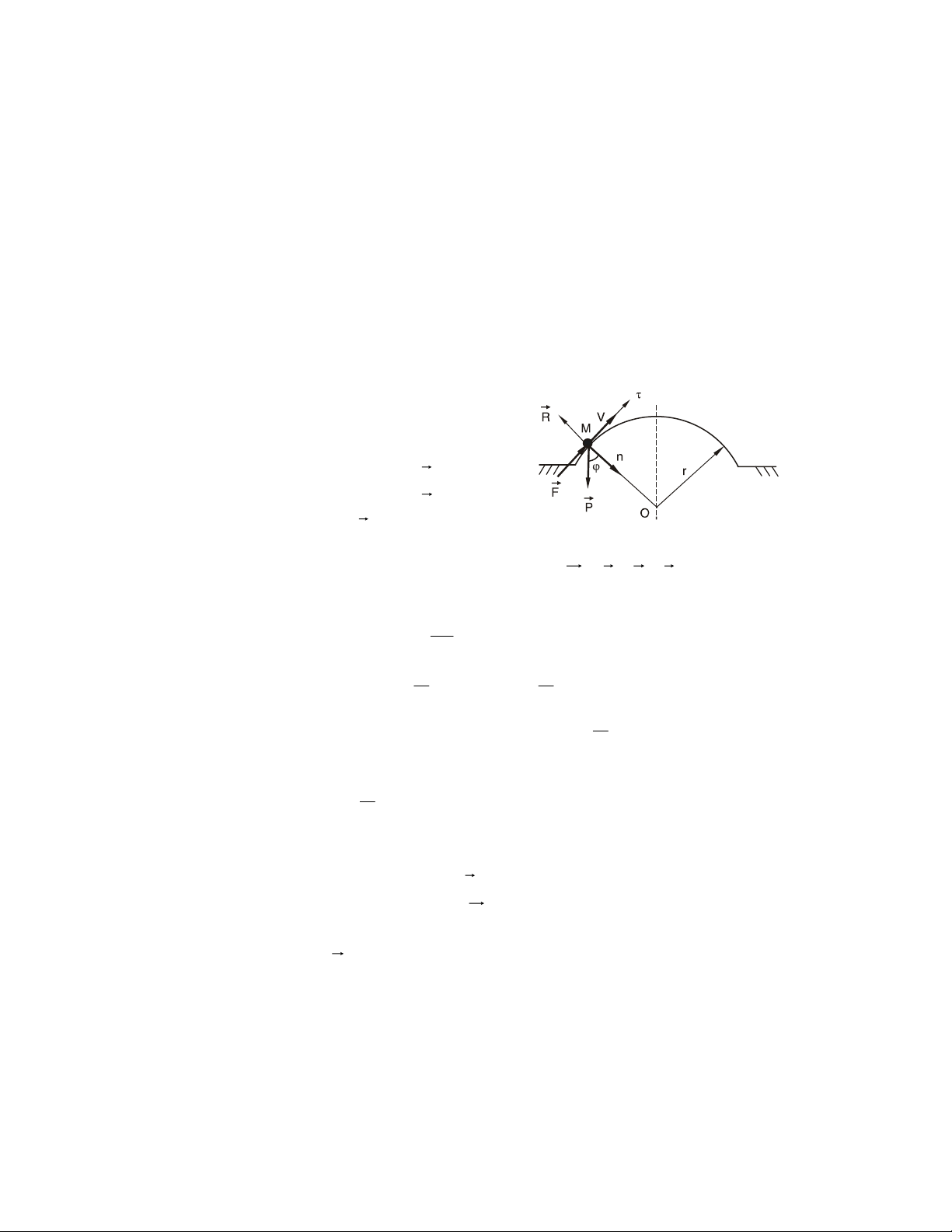
Moâmen cuûa löïc F ñaët taïi A ñoái vôùi taâm O laø r
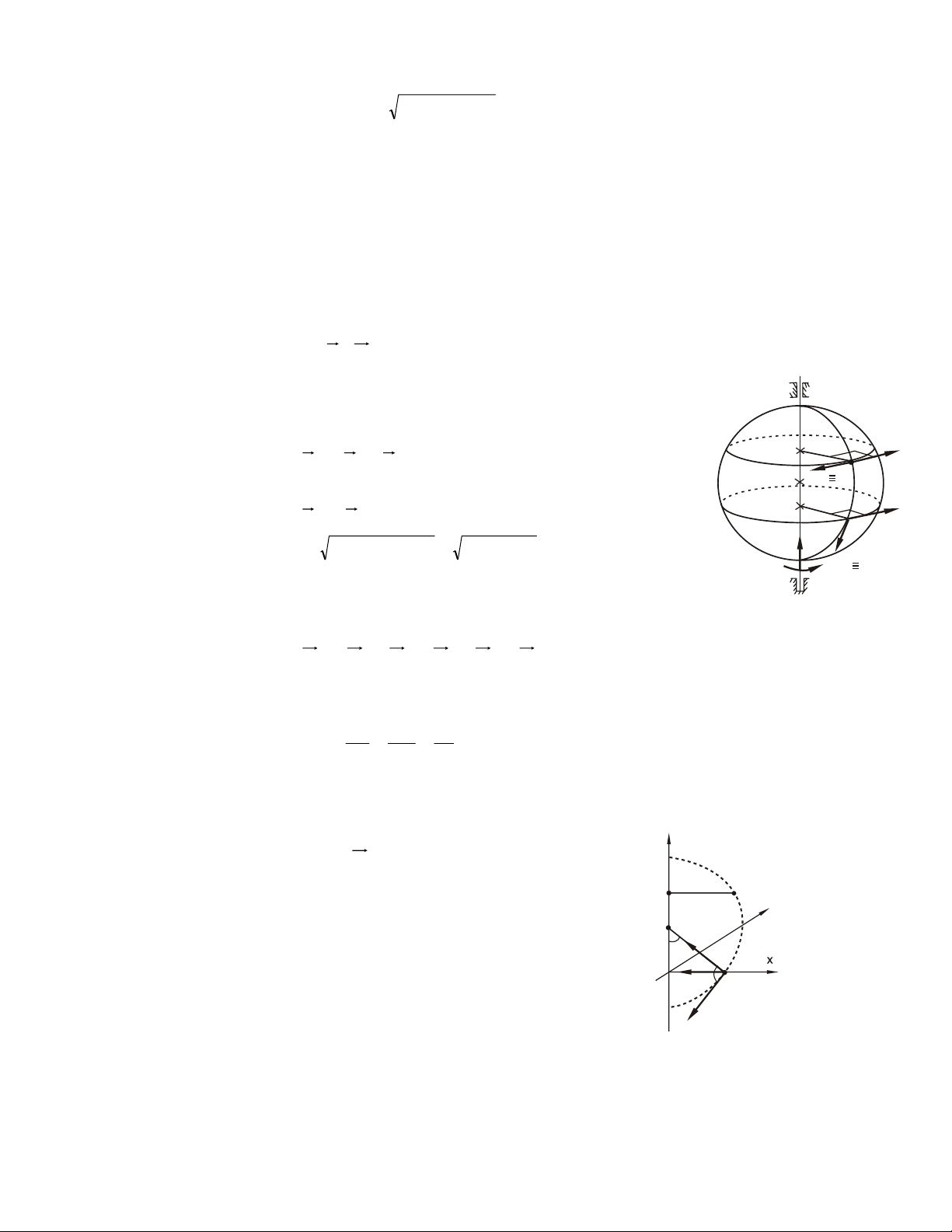
ñaïi löôïng vector ñaët taïi O: d mr ) F ( = OA × F = rr F O o × (1.1) Hình 1.1 Bieåu dieãn: cho rr r = , x ( r , y ) z ; F = ( F X, Y, ) Z (1.1) r r r r ⇔ m ) F ( = y . Z ( − Y ) z . i + (X z . − ) x . Z j + (Y x . − X y . k ) o (1.2) m r ) F ( r o
- vuoâng goùc vôùi maët phaúng chöùa O vaø F , m o ) F ( = d.F m r ) F ( o
= 0 khi giaù cuûa F qua O (vaø taát nhieân caû khi F = 0)
2- Moâmen cuûa löïc ñoái vôùi truïc ( Δ ) Phaân tích r F = F⊥ + F// ( ⊥
F vuoâng goùc truïc Δ, F// song song truïc Δ) r Moâmen cuûa
F ñoái vôùi truïc Δ laø löôïng ñaïi soá F (Δ) F// m ) F ( = ± ⊥ dF F Δ I d (1.3) A O Hình 1.2
d- laø khoaûng caùch töø truïc A ñeán giaù cuûa F⊥
- Laáy daáu coäng neáu nhìn töø ñænh truïc Δ thaáy F⊥ coù xu theá quay +
- Laáy daáu tröø neáu coù xu theá quay ngöôïc laïi _ m ) F ( = 0 Δ khi F song
song truïc Δ hay giaù F caét truïc Δ
Trong taøi lieäu naøy chuùng ta quy öôùc caùc ñaïi löôïng moâmen qua caùc chöõ M, M, m.
Ñònh lyù lieân heä
Hình chieáu moâmen cuûa löïc F ñoái vôùi taâm O ∈ ( Δ ) baèng moâmen cuûa F vôùi truïc ( Δ ): hc r (1.4) Δ [mo Δ ∈ ]) F ( = m ) F ( Δ
Chöùng minh. Theo H.1.2 ta coù: hc r r Δ [mo∈ Δ ) F ( ]= hcΔ[mo F ( ⊥ ∈ Δ )]= hc [ OI ( + IA)AF⊥ Δ ]
theo (1.3), ta coù ñieàu phaûi chöùng minh. 8 3- Heä löïc Heä löïc ϕ F ( k ) ≡ F
( 1, F2,....,Fn ) : laø caùc löïc cuøng taùc ñoäng vaøo moät vaät khaûo saùt.
Hai heä löïc töông ñöông: laø heä löïc ϕ F (
k ) töông ñöông vôùi Ψ( P ’e) (kyù hieäu ϕ F ( k ) ≡ ψ P
( e)) neáu chuùng coù cuøng taùc duïng cô hoïc.
Hôïp löïc cuûa heä löïc: laø hôïp löïc R cuûa heä löïc ϕ F (
k ) , laø moät löïc duy nhaát
töông ñöông vôùi heä löïc: R ≡ ϕ F ( k ) .
Heä löïc caân baèng: laø heä löïc ϕ F (
k ) caân baèng hay coøn goïi laø töông ñöông khoâng (ϕ F ( k ) ≡ )
0 neáu heä löïc taùc duïng vaøo vaät khoâng laøm thay ñoåi traïng thaùi chuyeån ñoäng cuûa vaät.
1.2. HEÄ TIEÂN ÑEÀ TÓNH HOÏC
1. Tieân ñeà 1 (caëp löïc caân baèng)
Heä hai löïc caân baèng khi vaø chæ khi chuùng cuøng ñöôøng taùc duïng, höôùng
ngöôïc chieàu nhau, cuøng cöôøng ñoä. F , F ( ' F ) ≡ 0 ⇔ F’ S F S F’ 2. Tieân ñeà 2 Hình 1.3
Theâm hay bôùt caëp löïc caân baèng , F ( '
F ) ≡ 0 khoâng laøm thay ñoåi taùc duïng cuûa heä löïc , ⎛ , F F , F ⎞ ⎜ 1, F2 F ,... n ⎟ ≡ ( F 1, F2,...,Fn ) ⎝ ⎠
3. Tieân ñeà hình bình haønh löïc
Hai löïc cuøng ñaët taïi moät ñieåm töông ñöông vôùi F R
moät löïc ñaët taïi ñieåm ñoù ñöôïc bieåu dieãn baèng vector
ñöôøng cheùo hình bình haønh coù hai caïnh laø hai löïc F’ thaønh phaàn. (F Hình 1.4 A , ' F A ) ≡ RA
4. Tieân ñeà löïc töông taùc
Löïc taùc duïng vaø phaûn taùc duïng giöõa hai vaät laø hai löïc laàn löôït ñaët leân moãi
vaät töông taùc chuùng cuøng ñöôøng taùc duïng, höôùng ngöôïc chieàu nhau, cuøng cöôøng ñoä.
5. Tieân ñeà hoùa raén
Vaät bieán daïng ñang caân baèng hoùa raén laïi vaãn caân baèng (ñieàu ngöôïc laïi khoâng ñuùng). 9
6. Tieân ñeà giaûi phoùng lieân keát, vaät gaây lieân keát, vaät chòu lieân keát
1- Vaät khoâng töï do, vaät töï do
- Vaät khoâng töï do laø vaät khoâng theå di chuyeån tuøy yù trong laân caän beù töø vò trí ñang xeùt.
- Vaät töï do laø vaät coù theå dòch chuyeån tuøy yù veà moïi höôùng trong laân caän beù töø vò trí ñang xeùt.
2- Vaät chòu lieân keát, vaät gaây lieân keát
Vaät khaûo saùt (S) ñöôïc quy öôùc laø vaät chòu lieân keát, caùc vaät theå khaùc töông
taùc cô hoïc vôùi S ñöôïc goïi laø caùc vaät gaây lieân keát, chuùng coù vai troø caûn trôû
chuyeån ñoäng hay xu höôùng chuyeån ñoäng cuûa S laø vaät khoâng töï do.
3- Tieân ñeà giaûi phoùng lieân keát
Vaät khoâng töï do coù theå xem laø töï do neáu ta thay theá caùc vaät gaây lieân keát
baèng caùc phaûn löïc lieân keát.
7. Moät soá heä quaû vaø moâ hình phaûn löïc lieân keát
Heä quaû tröôït löïc: Vôùi vaät raén tuyeät ñoái
löïc laø ñaïi löôïng vector tröôït S S , F Chöùng minh. Cho B F
( A ), taïi ñieåm B tuøy yù treân F B giaù cuûa F A
A chuùng ta ñaët heä löïc caân baèng F ( , F, B
B ) ≡ 0 coù tính chaát FB chính laø F A Hình 1.5 tröôït veà ñieåm B. v r r r F ( A ) = A F ( , B F , B F ) ≡ B
F : ñieàu phaûi chöùng minh. 4 1 4 23 r ≡0
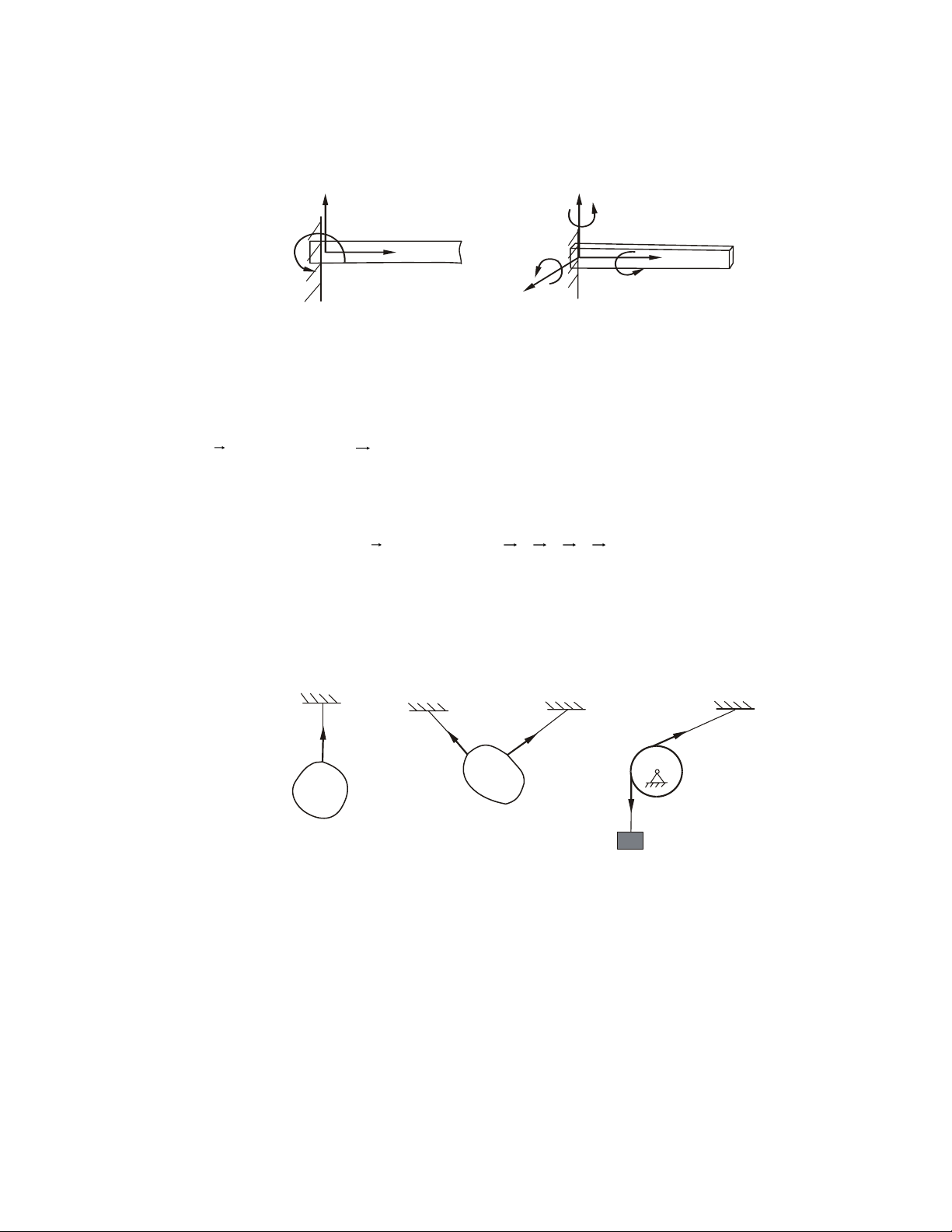
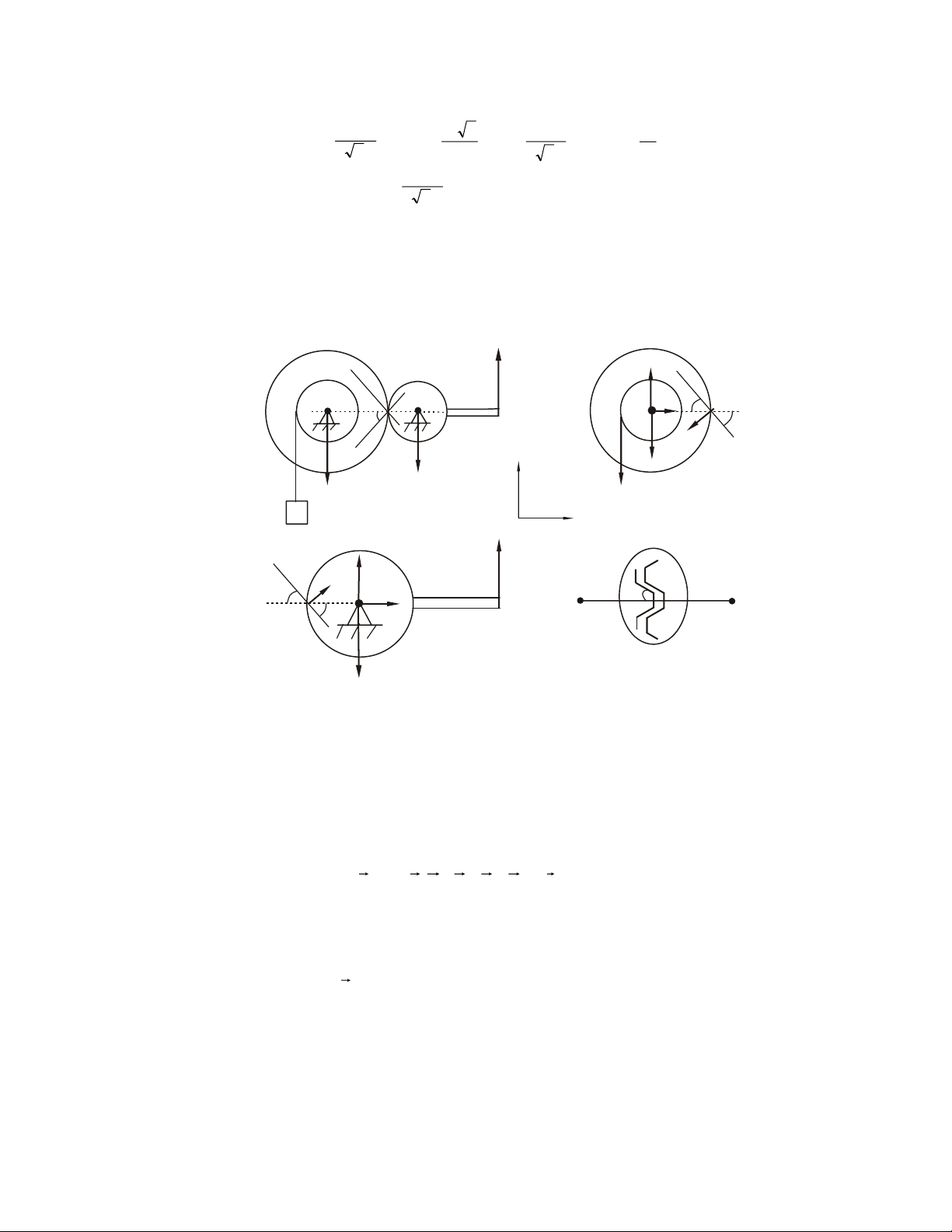
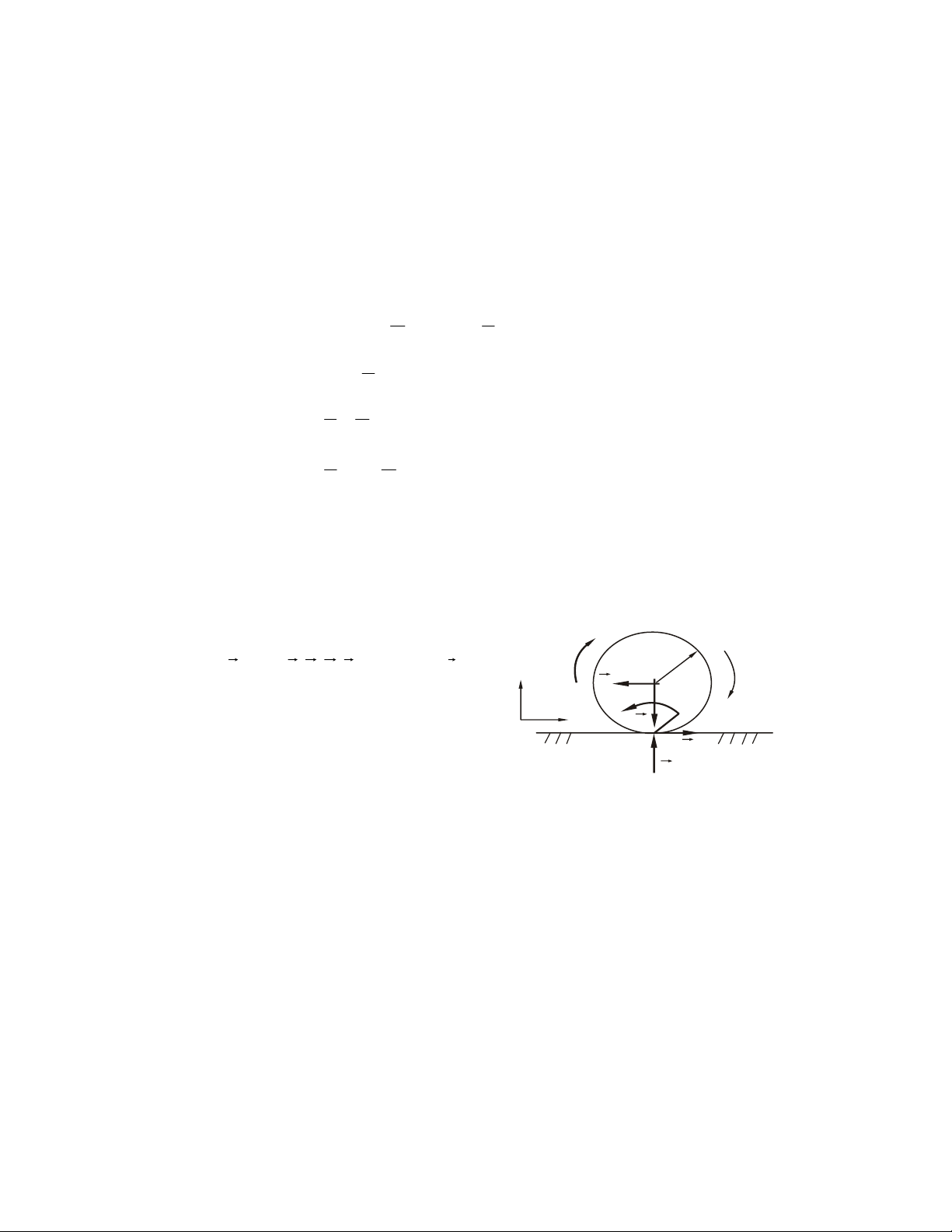
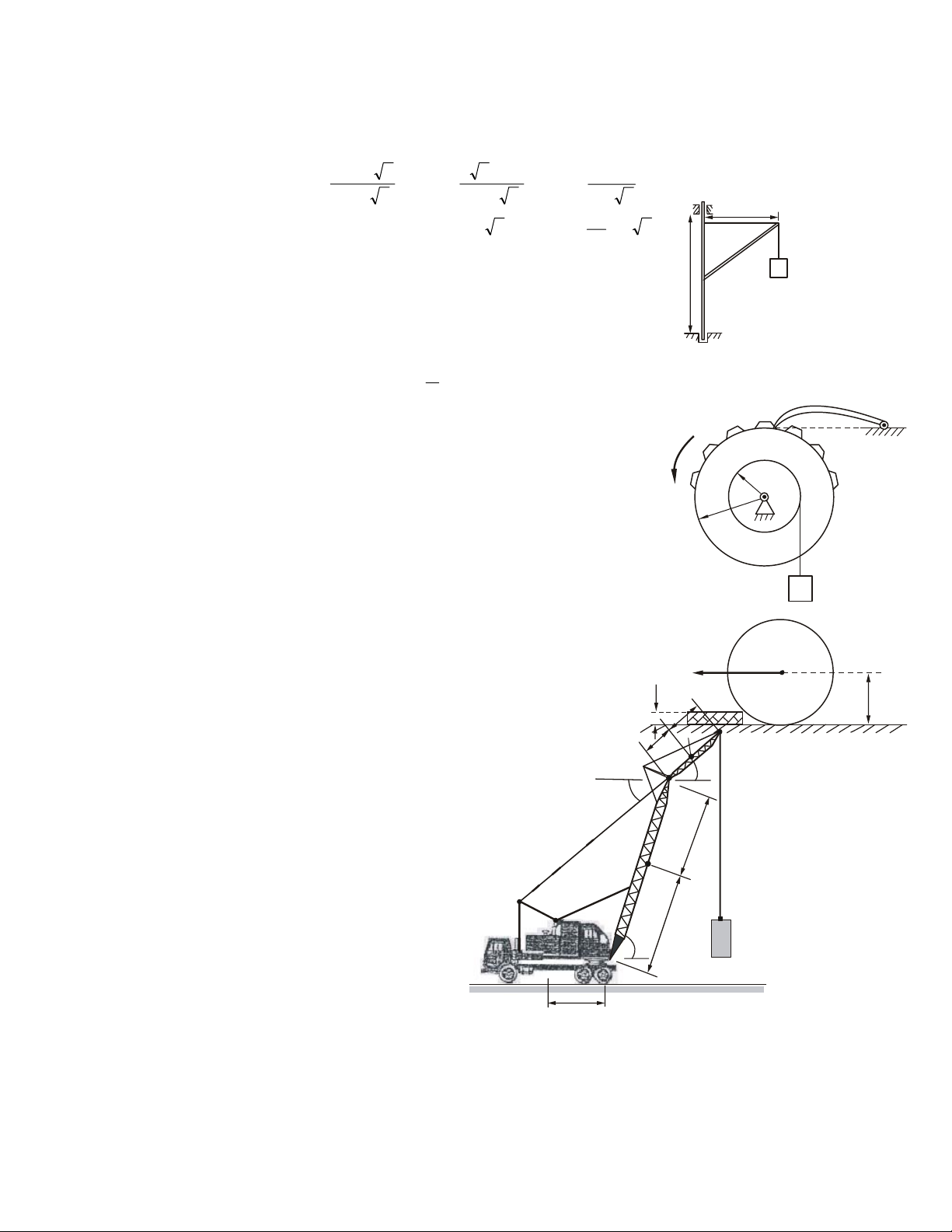
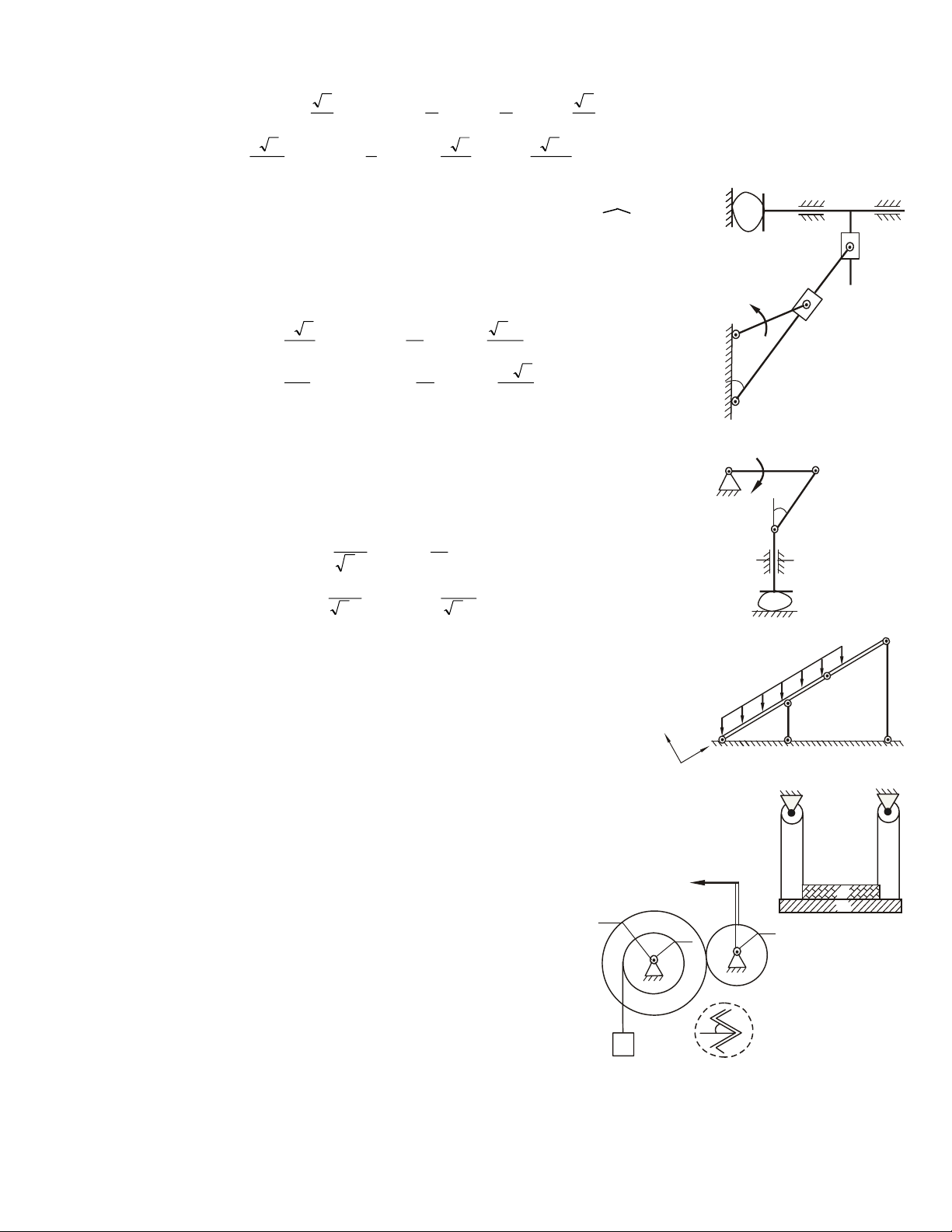
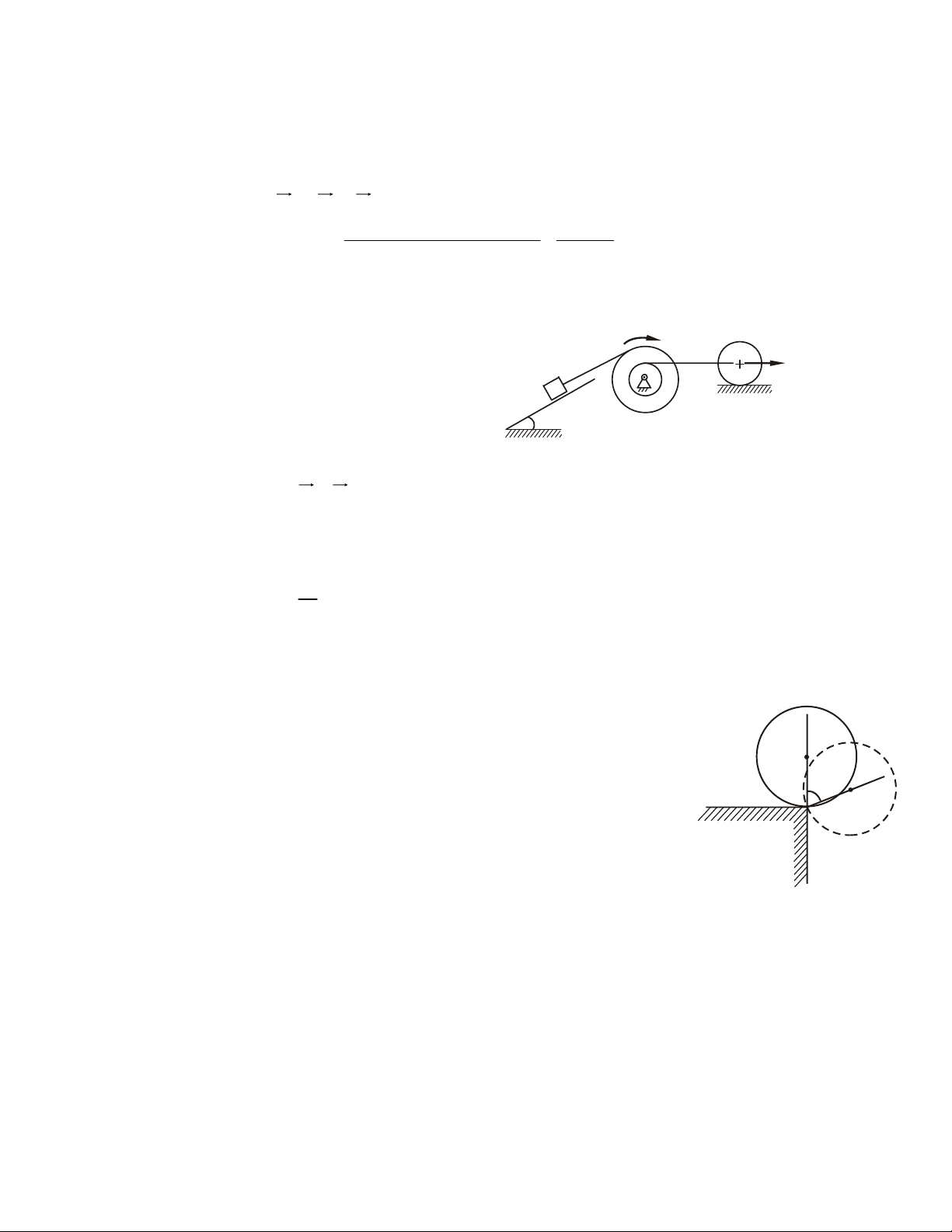
1.3. MOÄT SOÁ MOÂ HÌNH PHAÛN LÖÏC LIEÂN KEÁT THÖÔØNG GAËP
• Tính chaát cuûa phaûn löïc lieân keát
Theo tieân ñeà 6, phaûn löïc lieân keát phaûi thay theá ñöôïc vai troø caûn trôû
chuyeån ñoäng hay xu höôùng chuyeån ñoäng cuûa vaät gaây lieân keát ñaët vaøo vaät khaûo
saùt S, do ñoù chuùng phuï thuoäc hai yeáu toá:
- Khaû naêng chuyeån ñoäng cuûa vaät khaûo saùt (do löïc hoaït ñoäng taùc ñoäng vaøo
S) ñöôïc bieåu hieän qua cöôøng ñoä cuûa phaûn löïc (luoân luoân laø aån soá).
- Tính chaát caûn trôû chuyeån ñoäng hay xu höôùng chuyeån ñoäng cuûa vaät gaây
lieân keát (ñaët vaøo vaät khaûo saùt) ñöôïc bieåu hieän qua phöông (chieàu) cuûa phaûn löïc.
Döïa vaøo caùc ñaùnh giaù naøy chuùng ta seõ bieåu dieãn caùc thaønh phaàn phaûn löïc cuûa
moät soá moâ hình lieân keát thöôøng gaëp trong kyõ thuaät.
• Caùc moâ hình phaûn löïc lieân keát 10
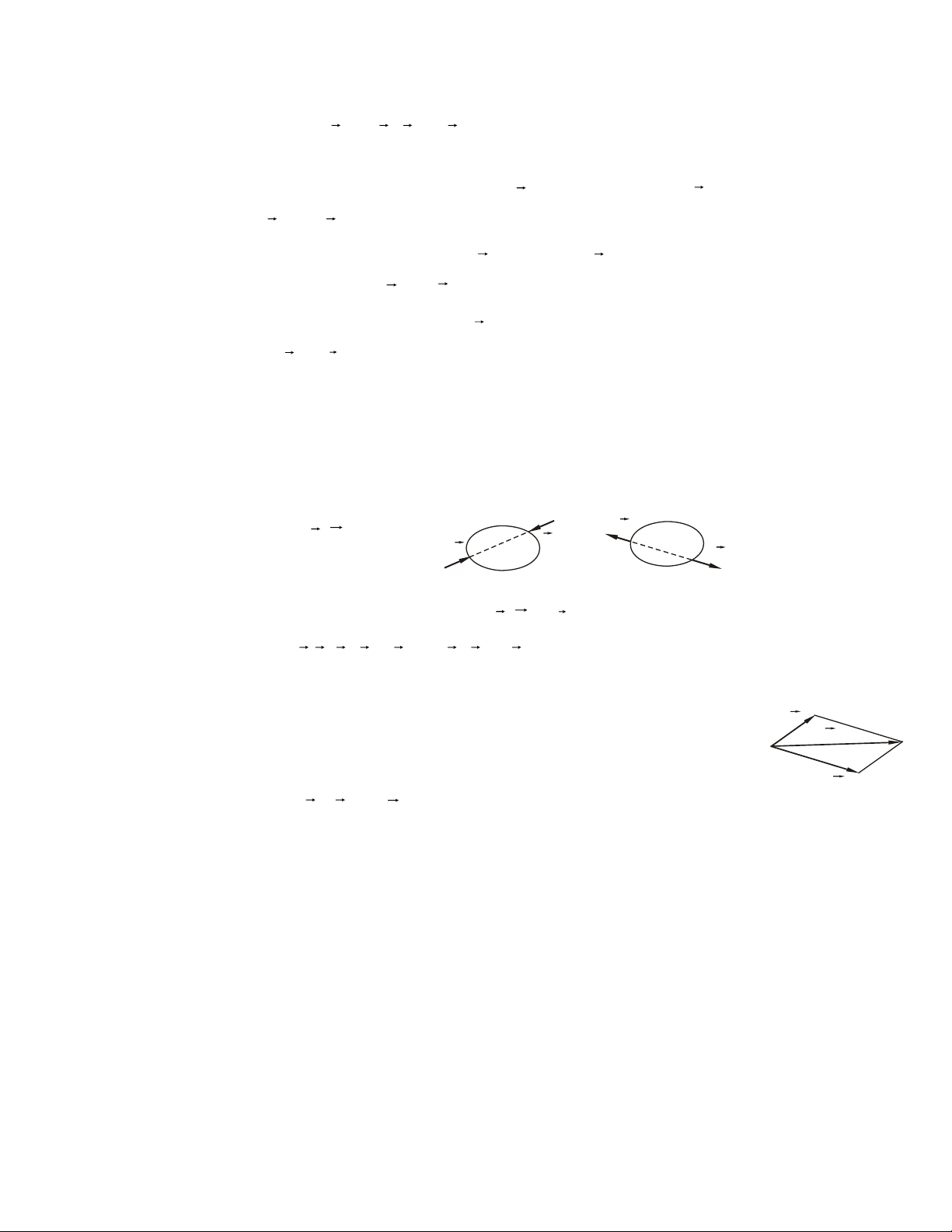
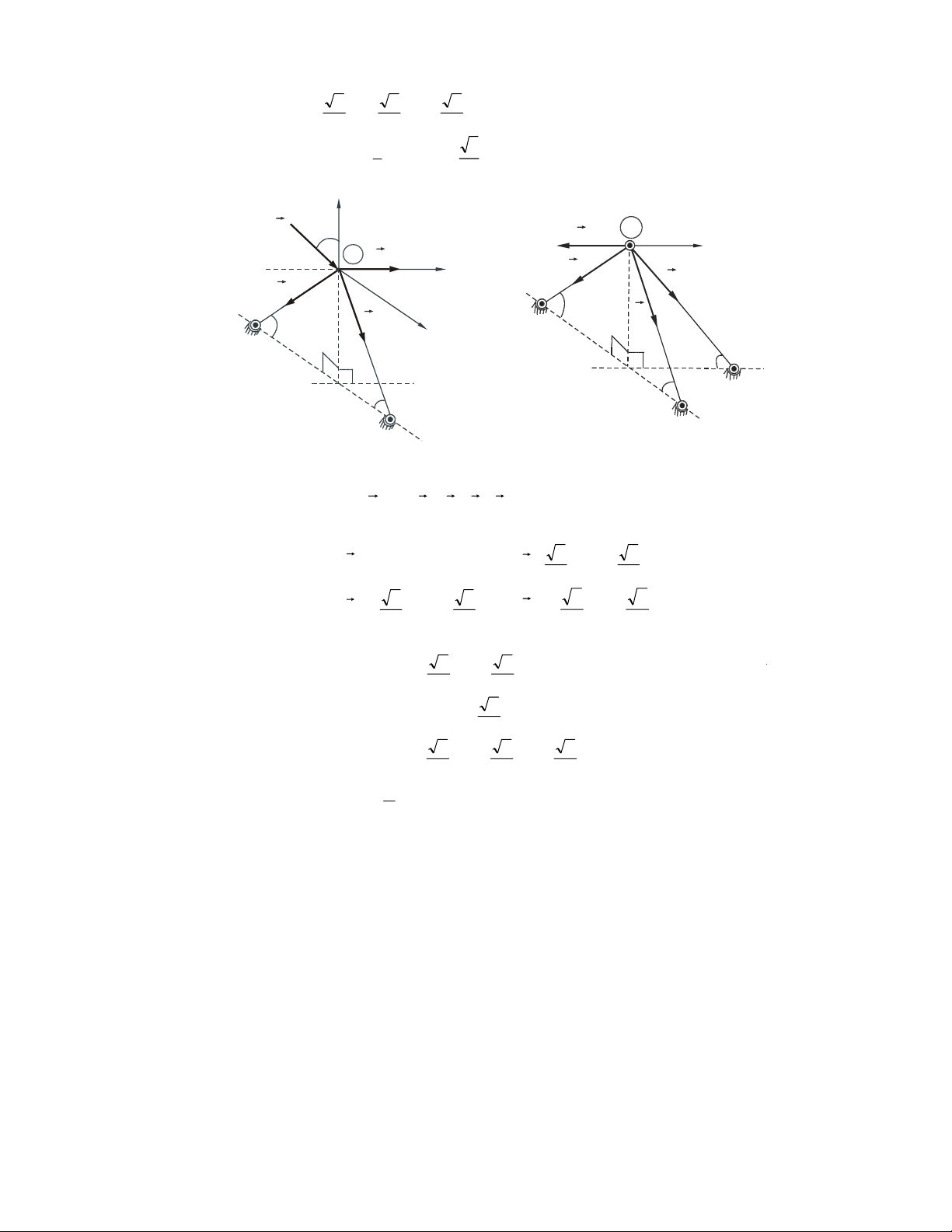
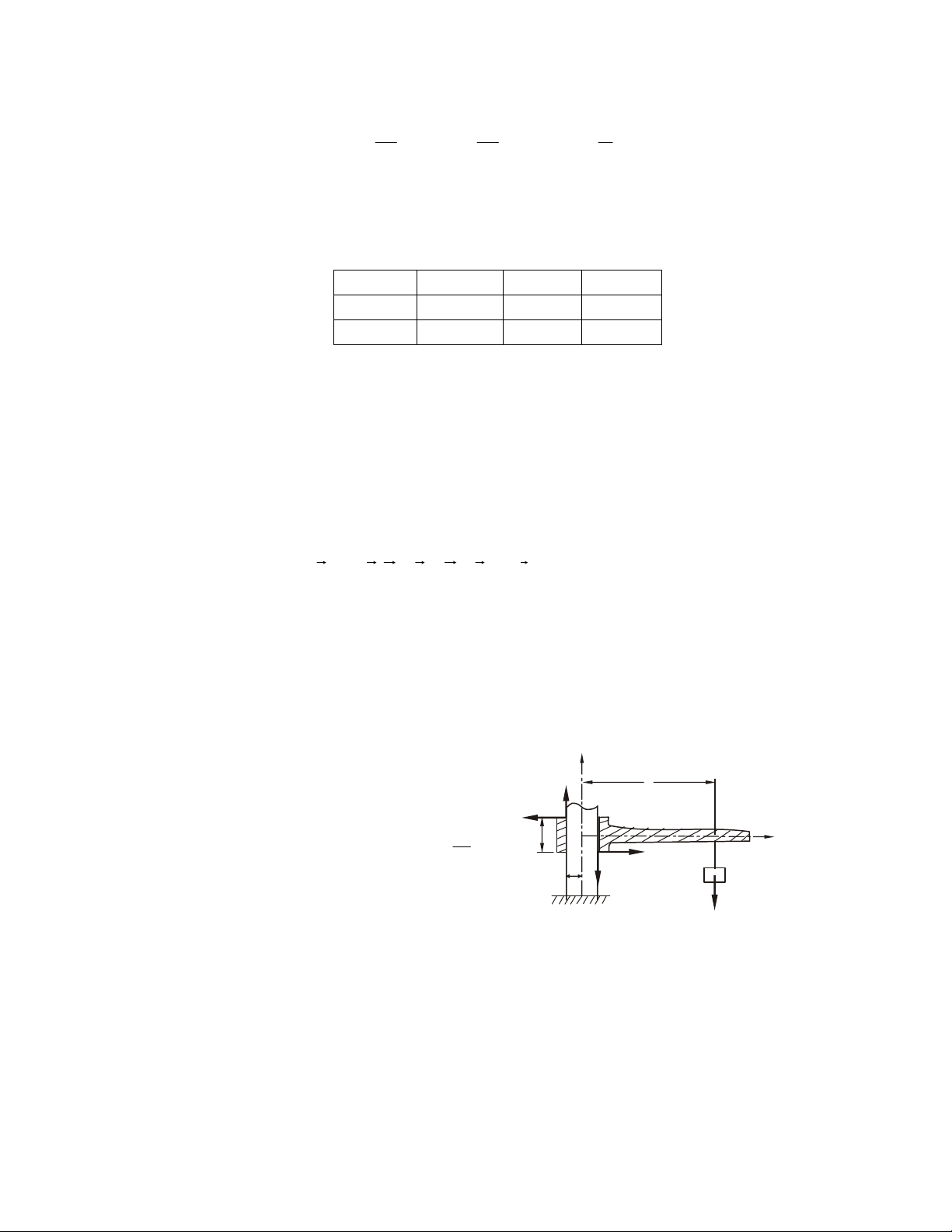
1- Phaûn löïc lieân keát töïa moät chieàu (khoâng ma saùt) S S A N A a) b) Hình 1.6
Vaät khaûo saùt töïa treân beà maët cuûa vaät gaây lieân keát, maët töïa chæ coù khaû
naêng caûn trôû chuyeån ñoäng vaø xu höôùng chuyeån ñoäng cuûa vaät khaûo saùt theo
phöông phaùp tuyeán chuùng taïi ñieåm tieáp xuùc. Phaûn löïc ñaët vaøo vaät taïi tieáp ñieåm
höôùng theo phaùp tuyeán ngoaøi cuûa maët töïa.
Ni - trong H.1.6a; NA - trong H.1.6b
- Phaûn löïc coù phöông chieàu xaùc ñònh, caàn tìm cöôøng ñoä.
- Moät soá moâ hình lieân keát töïa trong kyõ thuaät: NA N NB A NB C N S A B S A N B C A A a) b) c) Hình 1.7
2- Lieân keát baûn leà truï (khôùp baûn leà) Ry R Rx A ) b) Hình 1.8
Loaïi lieân keát goàm hai oáng truï loàng vaøo nhau, vaät khaûo saùt khoâng coù xu
höôùng quay quanh truïc vuoâng goùc vôùi truïc baûn leà. Ñeå ñôn giaûn, chuùng ta xem
moâ hình phaúng, hình troøn trong vaø voøng troøn ngoaøi töïa leân nhau, khoâng cho ñi ra
khoûi nhau. Phaûn löïc luoân luoân ñi qua taâm O (chung) naèm trong maët phaúng
vuoâng goùc vôùi truïc baûn leà, tröôït veà O, phaûn löïc ñöôïc bieåu dieãn qua hai thaønh phaàn vuoâng goùc ( R ,xRy)..
Chieàu cuûa chuùng ñöôïc choïn moät caùch chuû quan, coù theå khoâng ñuùng nhö thöïc teá. 11 - Moâ hình kyõ thuaät: S A S A S A • • • • • Hình 1.9
- Moâ hình kyõ thuaät keát hôïp: S A S S A A • • • • Hình 1.10
Phaûn löïc trong moâ hình thöù 3 cuûa H.1.10 laø loaïi töïa hai chieàu, chieàu phaûn
löïc chöa bieát cuï theå. Hai moâ hình ñaàu laø phaûn löïc töïa moät chieàu.
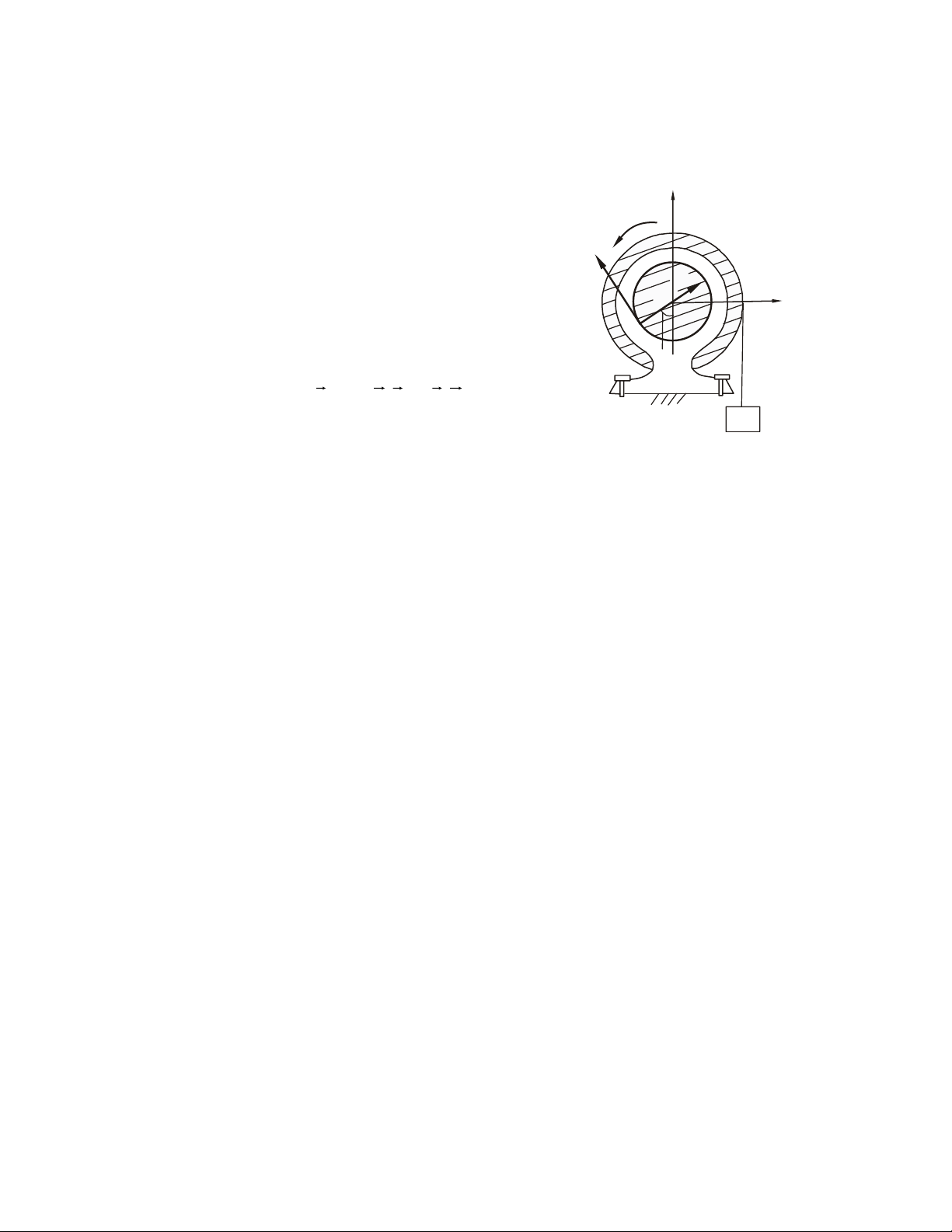
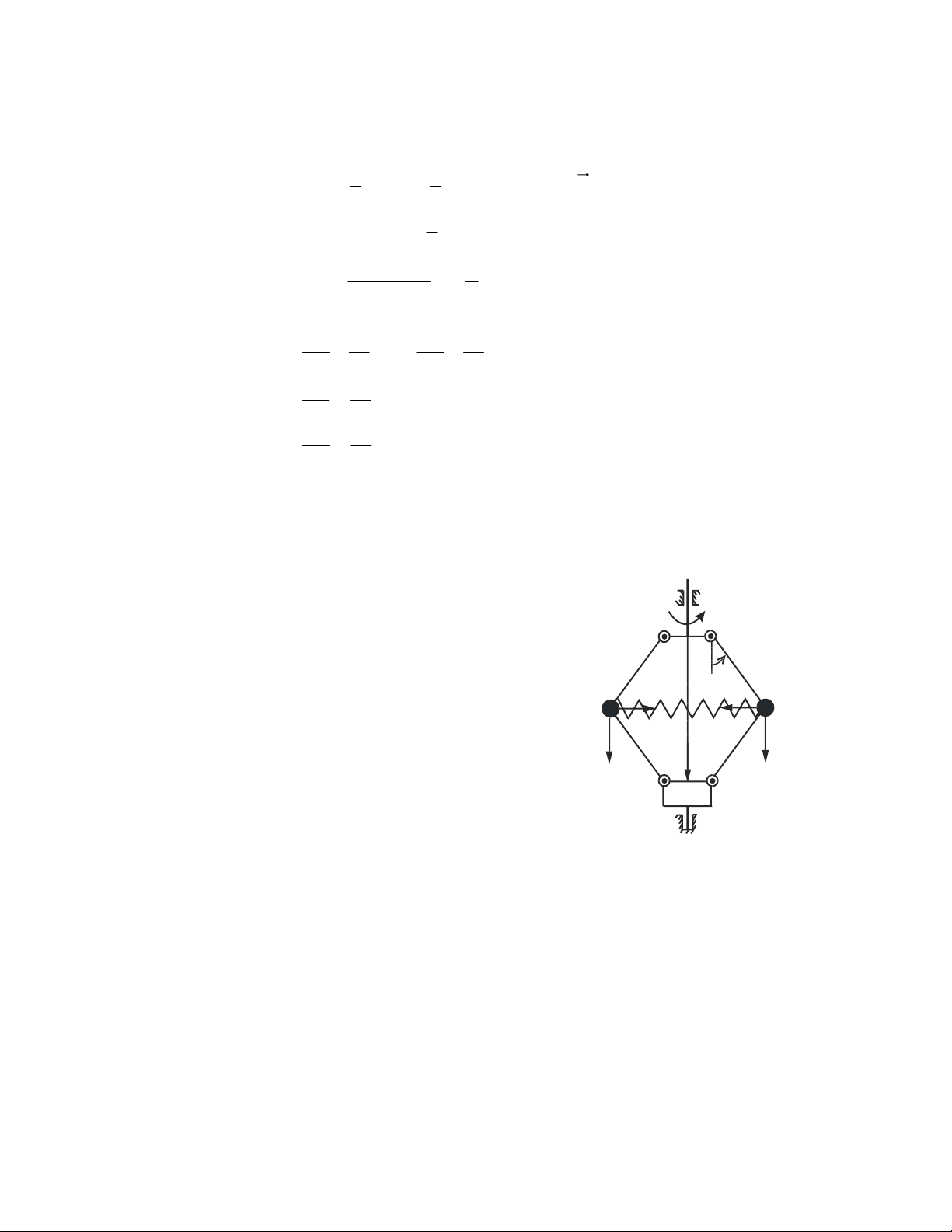
3- Lieân keát baûn leà caàu (khôùp caàu)
Hai quaû caàu loàng vaøo nhau, coù theå quay töông ñoái vôùi nhau nhöng hai taâm
luoân truøng nhau. Do khoâng caûn quay quanh baát cöù truïc naøo neân vector moâmen
phaûn löïc ñoái vôùi taâm O baèng khoâng, coøn vector chính phaûn löïc luoân ñi qua taâm
O ñöôïc phaân laøm ba thaønh phaàn vuoâng goùc R ( R R , R , ) x y z . Lieân keát ñöa vaøo baøi toaùn ba aån soá. A A R z z z R z R R y O y A A Ay Ay R R A x x x Ax a) b) a) b) Hình 1.11 Hình 1.12
Moâ hình trong kyõ thuaät (H.1.11b).
4- Lieân keát goái ñôõ
Ñaây laø lieân keát keát hôïp lieân keát töïa vaø baûn leà truï (H.1.12)
Phaûn löïc goàm ba thaønh phaàn Ax, Ay, Az (coù moät truïc laø truïc baûn leà truï).
Lieân keát ñöa vaøo baøi toaùn ba aån soá. 12
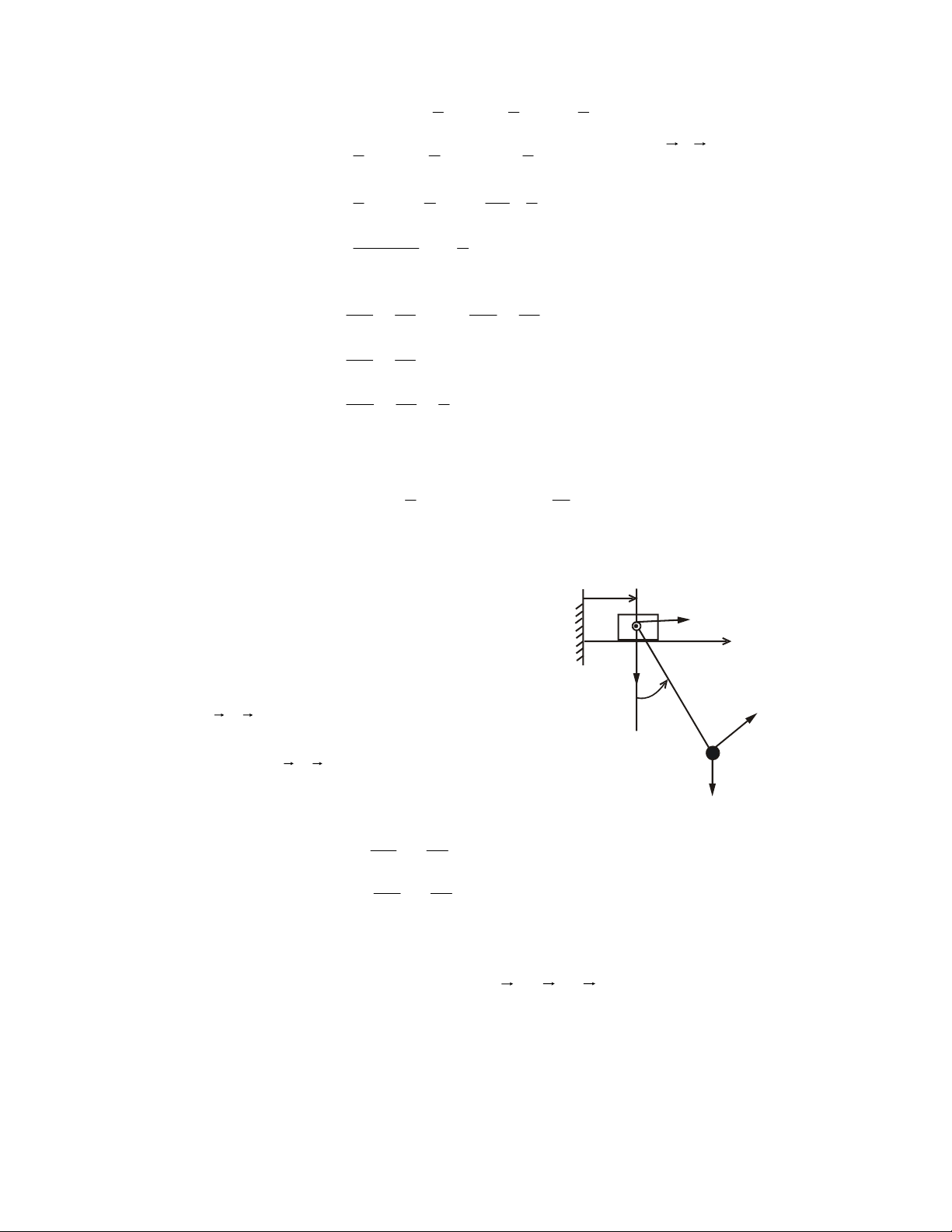
5- Lieân keát ngaøm
Vaät khaûo saùt chòu lieân keát ngaøm khi bò vaät gaây lieân keát giöõ chaët khoâng
cho thöïc hieän baát cöù chuyeån ñoäng naøo. Ví duï: coät truï choân chaët vaøo loøng ñaát,
ñaàu daàm caém chaët vaøo töôøng, hai phaàn cuûa moät vaät raén. A Ax y My A M x z M Ax A A A Mx A a) z b) Hình 1.13 - Ngaøm phaúng: (H.1.13a)
Tröôøng hôïp vaät khaûo saùt chæ coù xu theá chuyeån ñoäng trong maët phaúng
(Oxy). Caùc thaønh phaàn phaûn löïc lieân keát phaûi caûn trôû (dòch chuyeån theo hai
phöông x, y quay quanh truïc z). Phaûn löïc thu veà taâm A goàm 3 thaønh phaàn: RA (A ,A ) x
y , ngaãu M A ñeàu chöa xaùc ñònh chieàu cuï theå. Caùc xu höôùng chuyeån ñoäng ñoàng thôøi
- Ngaøm khoâng gian: (H.113b)
Vaät khaûo saùt coù xu theá chuyeån ñoäng trong khoâng gian, lyù luaän nhö treân
phaûn löïc thu veà A coù: RA(A ,A ,A ) x y z vaø MA (Mx M , y M
, z) goàm saùu thaønh phaàn
chöa coù chieàu cuï theå.
6- Lieân keát daây
Daây meàm, caêng neân chæ caûn trôû xu höôùng chuyeån ñoäng cuûa vaät doïc theo
daây (laøm daây ñöùt). Phaûn löïc ñaët taïi ñieåm daây baét ñaàu tieáp xuùc vôùi vaät khaûo saùt,
coù chieàu höôùng vaøo vaät gaây lieân keát. B T T TA T A B B S A A S T S Hình 1.14
7- Lieân keát thanh
Vaät khaûo saùt chæ coù hai lieân keát meàm (töïa, baûn leà), khoâng chòu löïc taùc
ñoäng vôùi giaù khoâng ñi qua hai ñieåm lieân keát naøy ñöôïc goïi laø lieân keát thanh.
Phaûn löïc lieân keát laø hai löïc cuøng cöôøng ñoä, ngöôïc chieàu ñaët taïi caùc ñieåm
lieân keát naèm treân giaù chöùa hai ñieåm lieân keát. 13
Caùc phaûn löïc lieân keát thanh: SA, SB, SC, SD F SA S B B C A S A C B SD D SA SB
8- Caùc lieân keát phöùc taïp Moâ hình phaúng Phaûn löïc Moâ hình khoâng gian Phaûn löïc S Mz N S Rz Mx R M R y y x S Mz Rz Mx R M x R My S S Ry R R M x x My Mz S S Ry R R x y R Mx 14 Chöông 2 THU GOÏN HEÄ LÖÏC
PHÖÔNG TRÌNH CAÂN BAÈNG CUÛA HEÄ LÖÏC Noäi dung
Chöông naøy ñöa ra caùc daïng thu goïn töông ñöông cuûa heä löïc, nhöõng ñieàu
kieän caân baèng cuûa heä löïc laøm cô sôû ñeå ñaùnh giaù taùc duïng cuûa chuùng vaø giaûi baøi
toaùn caân baèng cuûa vaät raén, heä vaät raén. Yeâu caàu
Naém vöõng ñieàu kieän töông ñöông cô baûn cuûa hai heä löïc, caùc ñieàu kieän
caân baèng cuûa heä löïc. Bieát caùch aùp duïng giaûi baøi toaùn caân baèng cuûa vaät raén, heä vaät raén.
2.1. HAI ÑAÏI LÖÔÏNG ÑAËC TRÖNG CUÛA HEÄ LÖÏC
1. Vector chính cuûa heä löïc
1- Ñònh nghóa: vector chính cuûa heä löïc laø vector töï do ( , R ) baèng toång caùc vector löïc thuoäc heä: , R = ΣFk (2.1) F1 F2
2- Phöông phaùp xaùc ñònh •'
Hình hoïc: vector ñoùng kín ña giaùc löïc. R R’ Fn Giaûi tích: R( ' ' ' X , Y , Z ) ' ⇔ X = Σ ' ' ky F ; Y = Σ ky F ; Z = Σ kz F (2.2)
2. Vector moâmen chính cuûa heä löïc ñoái vôùi moät taâm
1- Ñònh nghóa: vector moâmen chính cuûa heä löïc ñoái vôùi taâm O ( Mo ) cuûa heä löïc
baèng toång caùc vector moâmen cuûa löïc thuoäc heä laáy cuøng ñoái vôùi taâm ñoù:
2- Phöông phaùp xaùc ñònh
Duøng (1.2) chuùng ta nhaän ñöôïc: r r Mo = Σ Z
( y − Y z )i + Σ(X z − Z x ) j+ Σ(Y x − X y k ) k k k k k k k k k k k k (2.4) trong ñoù: löïc ( F Xk , k Y Z
, k ) - baùn kính ñieåm ñaët löïc thöù k laø k rr (xk, yk, zk)
3- Tính baát bieán cuûa ,
R vaø Mo qua caùc pheùp bieán ñoåi töông ñöông 15
Ñònh lyù 2.1. Hai ñaïi löôïng ,
R vaø Mo baát bieán qua caùc pheùp bieán ñoåi töông
ñöông (tieân ñeà 2 vaø 3).
Chöùng minh. Do caëp löïc caân baèng coù ,
R = 0 vaø Mo = 0 (taâm O tuøy yù), khi duøng tieân ñeà 2 coù ngay ,
R vaø Mo cuûa heä löïc khoâng ñoåi. Vôùi tieân ñeà 3:
- Xeùt hai löïc F1,F2 vaø hôïp löïc F12 nhö H.2.1 F1 + F2 = F12 ,
⇒ R = ΣFX = F1 + F2 + F3 + ... + Fn = F12 + F3 + ... + Fn ,
⇒ R baát bieán khi duøng tieân ñeà 3. - Ñaët
F12 (X, Y, Z) coøn Fi (X1, Y1, Z1), F12 (X2, Y2, Z2) Theo tieân ñeà 3: F
X = X1 + X2; Y = Y1 + Y2; Z = Z1 + Z2 F12 A Duøng coâng thöùc (1.2): ⇒ m r F ( r r 1) + o m F ( 2) o = m F ( 12) o F2 Chöùng toû: Hình 2.1 M r r r r o = m F ( 1) + o m F ( 2) o + m F ( 3) o + … + m F ( n) o = mr F ( r r 12) o + m F ( 3) o + … + m F ( n) o
⇒ Mo baát bieán trong pheùp bieán ñoåi tieân ñeà 3.
2.2. ÑÒNH LYÙ TÖÔNG ÑÖÔNG CÔ BAÛN ⎧ Ñònh lyù 2.2. R' = R' ϕ F ( ) ≡ ⎪ 1 2 1 P ( ) k ϕ2 i ⇔ ⎨⎪⎩M10 =M20
Chöùng minh. Tröôùc heát ta chöùng minh: ⎧ , , 1) ϕ ⎪R = R 1 2 1 F ( k ) ≡ ϕ P ( ) ⇒ 2 i ⎨ ⎪⎩M1 0 = M2 0
Chuùng ta thöøa nhaän hai heä löïc töông ñöông neáu coù theå bieán ñoåi qua nhau
baèng caùc pheùp bieán ñoåi töông ñöông (tieân ñeà 2, 3). Do: ϕ F ( ) ≡ 1 ϕ P ( 2
i ) neân ta coù theå bieán ñoåi chuùng qua nhau. Song , R vaø k
Mo baát bieán ñoái vôùi caùc pheùp bieán ñoåi, suy ra: ⎧ , , ⇒ ⎪R = R ⎨ 1 2 ⎪⎩M1 0 = M2 0 16 ⎧ , , 2) R = R ϕ ⎪ 1 2 1 F ( k ) ≡ ϕ2 P ( i ) ⇐ ⎨ ⎪⎩M1 0 = M2 0 Xeùt heä ϕ1 F ( vaø ϕ2 P
( i ) . Chuùng ta laáy ñieåm O vaø hai ñieåm A, B k )
(A, O, B khoâng thaúng haøng), phaân tích caùc löïc Fk ≡ F ( O
k , FkA , FkB) , caùc thaønh
phaàn töông ñöông ñi qua O, A, B. ⇒ heä ϕ F ( ) 1
≡ ba heä löïc ñoàng quy: F ( kO); ϕ F ( ϕ F ( kB) k 1 ϕ kA ); 2 3 Deã daøng nhaän ñöôïc: ϕ F ( kO) ; o F 1 ≡ ϕ F ( kA) FA; 2 ≡ ϕ F ( kB) ≡ B 3 F ⇒ ϕ F ( k) F ( O, FA, FB) 1 ≡
Goïi OE laø giao tuyeán cuûa hai maët phaúng , O ( F ** A ) vaø , O ( FB ) . Treân OE laáy FO FK
ñieåm I vaø phaân tích caùc löïc FA theo F * caùc phöông AO vaø AI, F O F O B theo caùc B
phöông BO vaø BI. Tieáp tuïc tröôït caùc löïc F
veà O vaø I roài laáy caùc hôïp löïc (tieân ñeà F B A 3). FI A * ⇒ ϕ FL E 1 F ( k ) ≡ F ( O , FA ,FB ) ≡ F ( O ,F1) L I töông töï ta coù: * ϕ P ( Hình 2.2 2 i ) ≡ P ( O ,PA ,PB ) ≡ P ( O ,FH )
(H thuoäc giao tuyeán OG, coù theå khaùc OE).
Cuoái cuøng, laáy ñieåm L thuoäc giao tuyeán cuûa hai maët phaúng , O ( FI) vaø , O ( PH ).
Phaân tích caùc löïc F1 vaø PH theo caùc phöông ñi qua L vaø O, tröôït caùc löïc
thaønh phaàn veà hai ñieåm O, L. Sau ñoù laáy hôïp löïc seõ ñöôïc ** FO vaø FL : ** ⇒ ϕ1 F ( k ) ≡ F ( O , FL ) töông töï ta coù: * * ϕ P ( 2 i ) ≡ P ( O ,PL ) Duøng caùc ñieàu kieän: - M r r O 1 = M O 2 ⇔ m F ( L) = m P ( L) ⇒ FL = P L O O - , ** * ** * R1 , = R2 * ⇔ FL + FO = PL + PO * ⇒ FO = PO ⇒ ϕ F ( ) 1 vaø ϕ P ( 2
1 ) ñöôïc bieán ñoåi töông ñöông sang heä löïc thöù ba k truøng nhau. Chöùng toû: ϕ1 F ( ≡ ϕ2 P ( 1) . k ) 2.3. CAÙC HEÄ QUAÛ 17
1. Vector moâmen ngaãu löïc
1- Xeùt heä hai löïc: ( , ,
F F ) cuøng phöông, ngöôïc chieàu, cuøng cöôøng ñoä nhöng
khaùc giaù taùc duïng. Do , R = 0, MO ≠ 0 , neân ( , ,
F F ) khoâng töông ñöông moät löïc,
ñaây laø moät heä löïc toái giaûn ñaëc bieät, ñöôïc goïi laø ngaãu.
Chuùng ta seõ chöùng toû moâmen chính cuûa ngaãu khoâng phuï thuoäc taâm laáy moâmen: F , M r r O = mO ) F ( + mO F ( ) d A , = OA × F + OB × F B α , , M = OA × F + OA × F + AB × F O , , , = OA × F
( + F ) + AB × F = AB × F (ñpcm) O • F’ 2- Hai ngaãu: ( , , F F ) vaø ( , F1,F1 ) coù vector Hình 2.3
moâmen chính baèng nhau seõ töông ñöông nhau (vì , R = ).
0 Chöùng toû vector moâmen chính cuûa ngaãu laø vector töï do, hoaøn toaøn ñaëc
tröng cho moät ngaãu, ñöôïc goïi ngaén goïn laø vector moâmen cuûa ngaãu. 2. Ñònh lyù thu goïn Heä löïc ϕ1 F (
, khi thu goïn veà moät taâm O, töông ñöông vôùi moät löïc baèng k )
vector chính cuûa heä löïc ,
R vaø moät ngaãu baèng vector moâmen chính cuûa heä laáy cuøng vôùi taâm O ñoù: , ϕ F ( ) ≡ (Ro,Mo ) k vôùi: , R r o = F Σ k vaø: Mo = Σm F ( K ) o
Chöùng minh. Vôùi O tuyø yù xaùc ñònh chuùng ta chæ caàn chöùng minh taïi ñoù heä löïc
goàm hai thaønh phaàn: löïc R baèng vector chính vaø moät ngaãu coù moâmen chính
baèng moâmen chính cuûa heä löïc ñoái vôùi cuøng taâm ñoù. Heä löïc naøy töông ñöông vôùi
heä löïc ban ñaàu do vector chính vaø vector moâmen chính ñoái vôùi taâm O cuûa chuùng baèng nhau.
3. Caùc tröôøng hôïp ñaëc bieät 1- r0 , ≠ R ⊥ MO ⇔ ϕ F ( k ) ≡ RΔ (hôïp löïc R r r Δ coù giaù Δ vôùi ,
RΔ = R vaø giaù Δ thoûa maõn m R ( Δ) = Σm F ( O O k ))
Chöùng minh. Choïn A r
∈ maët phaúng ⊥ MO vaø ñi qua O, , Δ // R 18 M Caùch O ñoaïn o d = , naèm veà höôùng cuûa , R quay 90o theo chieàu , R Mo laáy A ∈ Δ , , r r r r r ⇒ ϕ F ( k) ≡ R
( O, MO) ≡ RA m (R' ), M ) ≡ (R ) ≡ (RΔ) A o o A 1 4 4 2 4 4 3 r ≡O
Hôïp löïc cuûa nhöõng heä löïc ñaëc bieät
- Heä löïc song song: ( Fk // OZ ) Neáu , r
R ≠ 0 seõ coù hôïp löïc: ϕ F ( ) k ≡ R Δ
- Heä löïc phaúng: F ( k ∈ Oxy) Neáu , r R ≠ 0 ⇒ ϕ F
( k ) ≡ RΔ (coù hôïp löïc) do ta laáy ñieåm A ∈ Oxy laøm taâm thu goïn: ⇒ MA ⊥ Oxy ⇒ MA ⊥ R
- Hôïp löïc cuûa heä löïc phaúng song song
Cho heä löïc phaân boá nhö H.2.4. Xeùt phaân toá x
Δ k , heä löïc phaân boá treân ñoä
daøi naøy töông ñöông moät löïc Fk : r ' F F k = q(xk ). x Δ k - ñaët taïi ' x k R q(x) Δ F l k Hôïp löïc: R r Δ = F = F Σ k = q dx ) x ( ∫ o X Giaù
Δ ñöôïc xaùc ñònh töø ñieàu kieän: O d X’ k Δ Xk l M = Σm F ( Hình 2.4 k ) = Δ Δ q( x ). x . dx ∫ o O o l∫q( xdx ). x M R d = M → d = ΔO = o Δ Δ (2.5) O l RΔ ∫ q( dx ) x o
trong ñoù: ΔO - laø truïc qua O vaø vuoâng goùc maët phaúng löïc.
- Heä löïc phaân boá ñeàu (H.2.5) l2 qo Hôïp löïc: 2 l R1; R = qo.l; OI = = (2.6) qol 2
- Heä löïc phaân boá tuyeán tính (H.2.6) coù ngay: qo qo1 q( ) x 2 = x → R = ; OI = 1 (2.7) 1 1 2 3 19 R F I R qo I qo x O I l O I l l
Nhaän xeùt: Caùc hôïp löïc coù cöôøng ñoä baèng dieän tích phaân boá, ñi qua troïng taâm
cuûa bieåu ñoà dieän tích. 2- , , R = , 0 Mo ≠ 0 ⇔ ϕ F ( k) ≡ ngaãu toång hôïp Q , Q ( ) coù moâmen baèng
moâmen chính cuûa heä löïc ñoái vôùi taâm O. Chuù yù: Khi , R, = , 0 ϕ F ( k ) ≡ ngaãu Q , Q (
) neân moâmen chính cuûa heä
khoâng phuï thuoäc taâm laáy moâmen. 3- , R = , 0 Mo ≠ 0 ⇔ ϕ F ( k) ≡ 0 (2.8)
Chöùng minh. Do heä löïc caân baèng ( , , F F ) coù ,
R = 0 vaø moâmen chính ñoái vôùi taâm baát kyø O Mo = 0
4. Heä ba löïc caân baèng
Heä ba löïc caân baèng thì ñoàng phaúng. Neáu caùc löïc song song vôùi nhau thì coøn phaûi ñoàng quy.
Chöùng minh. Xeùt heä ba löïc F
( 1, F2, F3) ⇔ R = 0 vaø MA = 0 (taâm A tuøy yù).
Coù theå xaûy ra caùc tröôøng hôïp:
• F1 // F 2 : Töø: R = 0 ⇒ F ( 1 + F2 = F − 3) ≠ 0 ⎧ F ( phaúng maët ,F ) Chöùng toû: ∈ F ( ⎪ 1 2 1 , F 2 ) ≡ R12 ⎨ ⎪⎩// F1 ⇒ F ( 1, F2, F3) ≡ R ( 12, F3) ≡ 0 Chöùng toû
F3 cuøng giaù vôùi R12 ⇒ F3 // F2 // F1 vaø ñoàng phaúng.
• F1 khoâng song song vôùi F 2
Choïn ñieåm A tuøy yù coá ñònh thuoäc giaù cuûa F3 laøm taâm laáy moâmen chính: 20
Hai vector moâmen naøy ñaët taïi A maø coù toång baèng 0 ⇒ ít nhaát chuùng cuøng
phöông ⇔ hai maët phaúng F ( 1, A) vaø F ( 2, A) truøng nhau, töùc F ( 1,F2, A) ñoàng phaúng. Do A tuøy yù neân suy ra F
( 1, F2 , F3 ) phaûi thuoäc cuøng moät maët phaúng. Goïi
giao ñieåm cuûa F1,F2 laø I, ñeå chöùng minh ba löïc ñoàng quy chuùng ta söû duïng: M r r r r 1 = m F ( 1) + m F ( 2) 1 1 + m F ( 3) = 0 + 0 + m F ( 3) = 0 ⇒ F3 1 1 phaûi ñi qua I (do F3 ≠ ). 0 Vaäy F
( 1, F2, F3) ñoàng quy phaúng.
2.4. ÑIEÀU KIEÄN CAÂN BAÈNG CUÛA HEÄ LÖÏC
Töø (2.8) chuùng ta nhaän ñöôïc nhöõng ñieàu kieän caân baèng cuûa heä löïc:
1. Heä löïc toång quaùt (khoâng gian) ⎧ R, = ΣF = 0 ⎪ x kx , ⎪ R = Σ y F = k y 0 R, = ΣF = 0 0 ≡ ϕ F ( ⎪⎪ Z z k k ) ⇔ ⎨ (2.9) ⎪Mox = Σm F ( x k ) = 0 ⎪ ⎪M = Σ oy my F ( k) = 0 ⎪⎩Moz = Σmz F ( k) = 0
Vôùi caùc heä löïc ñaëc bieät moät soá phöông trình coù theå töï thoûa maõn neân soá ñieàu kieän giaûm ñi.
2. Heä löïc song song F ( k // ) OZ ⎧ ⎪ ΣF = 0 z k ⎪ 0 ≡ ϕ F ( k) ⇔ ⎨ m F ( k) = ∑ 0 (2.10) ⎪ x ⎪⎩ m F ( k) = ∑ 0 y
Do ba phöông trình coøn laïi töï thoûa maõn.
3. Heä löïc ñoàng quy ϕ F
( ok ), caùc löïc ñi qua O ⎧ ΣF = kx 0 ⎪ 0 ≡ ϕ F ( k) ⇔ ⎨ ΣF = 0 ky (2.11) ⎪ ⎩ ΣF = 0 kz Do: M r O = Σm F ( O k ) = 0 töï thoûa maõn z
4. Heä löïc phaúng ϕ F ( k ), F ∀ k ∈ Oxy MA
Vôùi ñieåm A tuøy yù thuoäc maët phaúng löïc Oxy m y A A F ( k) = m k ). F ( = ± d F k AZ k k dk Fk x Hình 2.7 21
Vector moâmen cuûa caùc löïc naøy ñeàu cuøng phöông neân ta coù theå quy öôùc thay theá mA F
( k ) bôûi giaù trò ñaïi soá: mA F ( k ) = mAZ F ( k) = ± d k k F (2.12)
Ta laáy daáu (+) hoaëc (-) theo quy taéc moâmen cuûa löïc ñoái vôùi truïc (H.2.7).
Ñieàu kieän caân baèng cuûa heä löïc phaúng coù ba daïng: ⎧ΣF = 0 k x Daïng 1: 0 ≡ ϕ F ( ⎪ k ) ⇔ ⎨ΣF = 0 ky (2.13) ⎪ ⎩Σm F ( A k ) = MA = 0
vôùi A tuøy yù thuoäc maët phaúng löïc. ⎧R 0
Ñieàu kieän naøy hieån nhieân do (2.12): ⎪ = ⇒ ⎨ ⎪⎩MA = 0 ⎧ΣF = k x 0 Daïng 2: 0 ≡ ϕ F ( ⎪ k ) ⇔ ⎨MA = Σm F ( A k ) = 0 (2.14) ⎪ ⎩MB = Σm F ( B k ) = 0 (vôùi AB OX)
Chöùng minh. Heä löïc ϕ F
( k ) töông ñöông ñoàng thôøi heä 1 vaø heä 2 (H.2.8) ⇒ heä 1 ≡ heä 2 Thu heä 1 veà B: R’k R’B A A , , ⇒ heä 1 ≡ R ( r B, mB R ( A) ≡ heä 2 , ⇒ m r Heä 1 Heä 2 B R ( A) = 0 Ñieàu naøy chöùng toû: Hình 2.8 - Hoaëc ' RA coù giaù ñi qua B: , ⇒ Rx = F Σ ≠ 0 k x
maâu thuaãn ñieàu kieän ñaàu tieân. - Hoaëc '
RA = 0 keát hôïp MA = 0 ta coù ñieàu phaûi chöùng minh. ⎧MA = Σm F ( k) = 0 A Daïng 3: ⎪ 0 ≡ ϕ F ( k ) ⇔ ⎨MB = ΣmB F ( k) = 0 (2.15) ⎪ ⎩MC = Σm F ( C k ) = 0
Söû duïng phöông phaùp chöùng minh treân: neáu ' RA ≠ 0 thì , R phaûi coù giaù
chöùa ñoaïn AB vaø AC, do A, B, C, khoâng thaúng haøng neân khoâng theå xaûy ra
tröôøng hôïp treân. Vaäy ,
R = 0 , ta coù ñieàu phaûi chöùng minh.
2.5. BAØI TOAÙN CAÂN BAÈNG CUÛA VAÄT RAÉN
1. Moâ hình baøi toaùn 22
Moät vaät raén khoâng töï do (chòu lieân keát) chòu taùc duïng cuûa löïc (löïc hoaït ñoäng) ñang caân baèng.
Nhöõng yeâu caàu ñöôïc ñaët ra laø:
- Xaùc ñònh caùc phaûn löïc lieân keát
- Tìm ñieàu kieän caân baèng
Töùc tìm caùc yeâu caàu cuûa löïc hoaït ñoäng vaø caùc yeáu toá hình hoïc ñeå vaät
khaûo saùt ñöôïc caân baèng. 2. Phöông phaùp giaûi
1- Choïn vaät khaûo saùt: xem xeùt kyõ moâ hình baøi toaùn (hình veõ), chuùng ta choïn vaät
raén naøo (coù theå laø chaát ñieåm) chòu taùc ñoäng cuûa taát caû caùc löïc hoaït ñoäng.
2- Ñaët löïc: löïc ôû ñaây bao goàm caùc löïc hoaït ñoäng vaø phaûn löïc lieân keát.
Xem xeùt kyõ moâ hình vaät khaûo saùt, xaùc ñònh ñaày ñuû caùc lieân keát, so saùnh
vôùi caùc moâ hình maãu ñeå thay theá heát caùc lieân keát baèng caùc phaûn löïc töông öùng.
3- Laäp phöông trình caân baèng
- Phaân tích caùc löïc ñaët vaøo vaät khaûo saùt (keå caû phaûn löïc) theo ba phöông cuûa truïc toaï ñoä.
- Laäp caùc phöông trình caân baèng töø ñieàu kieän caân baèng cuûa heä löïc (keå caû caùc phaûn löïc): ⎧ΣF = 0 ⎧Mox = mx F ( k) = ∑ 0 k x ⎪ ⎪⎪ ⎨ΣF = 0 k y vaø: ⎨Moy = m F ( y k ) = ∑ 0 ⎪ ⎪ ⎩ΣF = 0 z k ⎪⎩Moz = m F ( z k ) = ∑ 0
- Vôùi löu yù caùc ngaãu toàn taïi trong heä löïc ñaët vaøo vaät khoâng xuaát hieän
trong caùc phöông trình hình chieáu ñaûm baûo vector chính baèng khoâng.
Chuù yù: Neáu ⊥ F Δ ⇒ m ) F ( = ± Fd Δ
trong ñoù: d - laø ñoaïn vuoâng goùc chung giöõa Δ vaø F
Duøng (1.4) vaø (2.4) chuùng nhaän ñöôïc: Mox = Σ F ( y − F z ) = ; 0 kz k ky k Moy = Σ F ( z − F x = 0 kz k ky k
ÔÛ ñaây: (xk, yk, zk) - laø toaï ñoä ñieåm ñaët cuûa löïc Fk
- Tröôøng hôïp heä löïc phaúng F
( k ∈ Oxy) duøng (2.12) laäp phöông trình caân baèng ngaãu löïc.
3. Ñaùnh giaù baøi toaùn
1- Neáu soá phöông trình caân baèng ñoäc laäp ñöôïc (r) baèng aån soá (s) (soá thaønh
phaàn phaûn löïc), baøi toaùn coù nghieäm duy nhaát (ñöôïc goïi laø baøi toaùn tónh ñònh).
2- Neáu r > s coù khaû naêng xaûy ra: 23
- Seõ dö ra moät soá phöông trình (= r – s) khoâng chöùa aån soá (phaûn löïc). Ñaây
chính laø caùc ñieàu kieän raøng buoäc caùc löïc hoaït ñoäng vaø nhöõng ñaïi löôïng hình hoïc
trong baøi toaùn. Nhöõng ñieàu kieän naøy ñöôïc goïi laø ñieàu kieän caân baèng.
- Trong heä phöông trình laäp ñöôïc toàn taïi caùc phöông trình maâu thuaãn vôùi
nhau. Chuùng ta xem xeùt laïi moâ hình baøi toaùn:
+ Ñaët phaûn löïc ñuùng chöa?
+ Moâ hình baøi toaùn coù toàn taïi trong thöïc teá khoâng?
3- Neáu r < s: Baøi toaùn thuoäc loaïi sieâu tónh, chuùng seõ ñöôïc giaûi quyeát trong moân hoïc sau.
4. Giaûi phöông trình vaø bieän luaän Theo nguyeân taéc:
- Phaûn löïc töïa moät chieàu vaø söùc caêng daây luoân luoân döông.
- Caùc phaûn löïc khaùc coù chieàu ñuùng nhö ñaõ choïn neáu keát quaû döông.
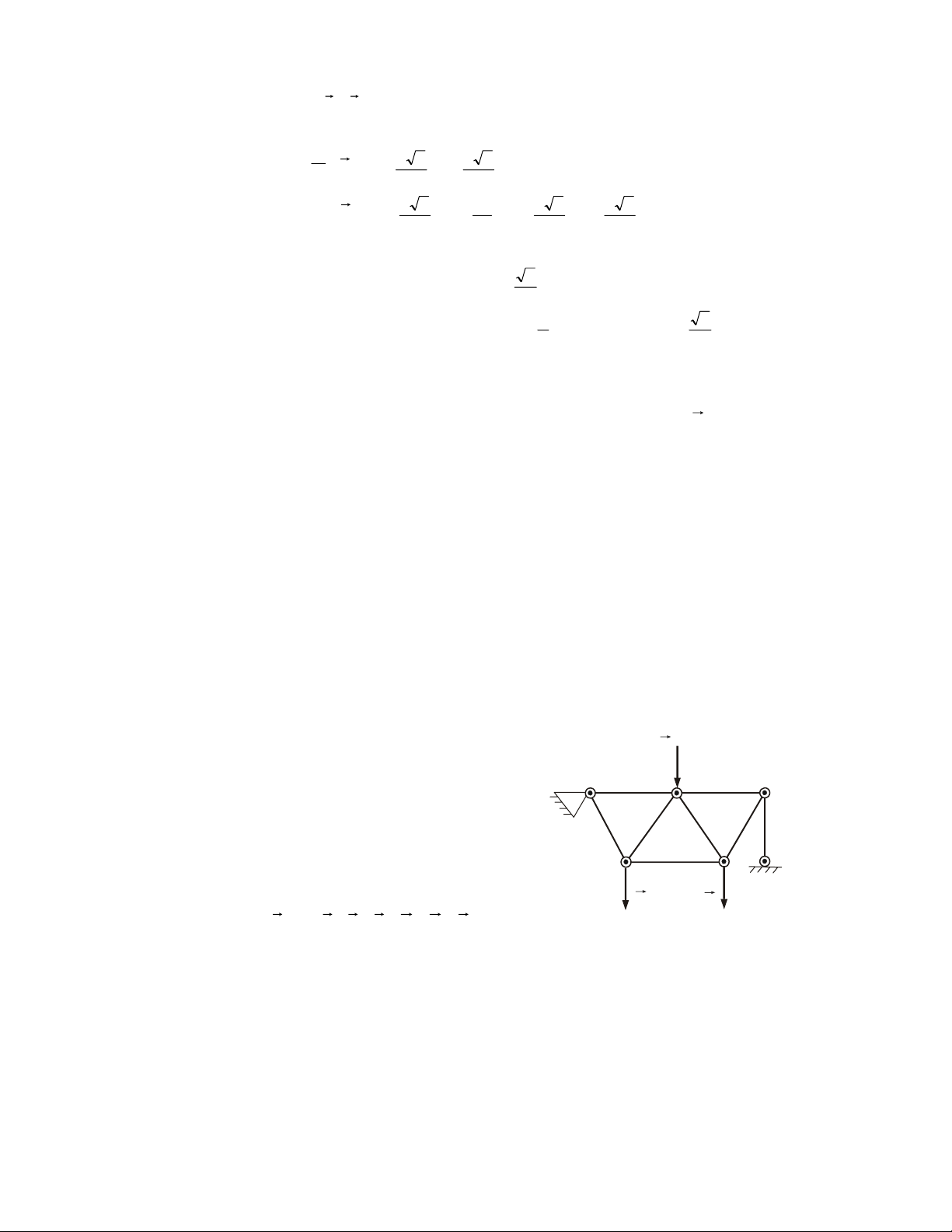
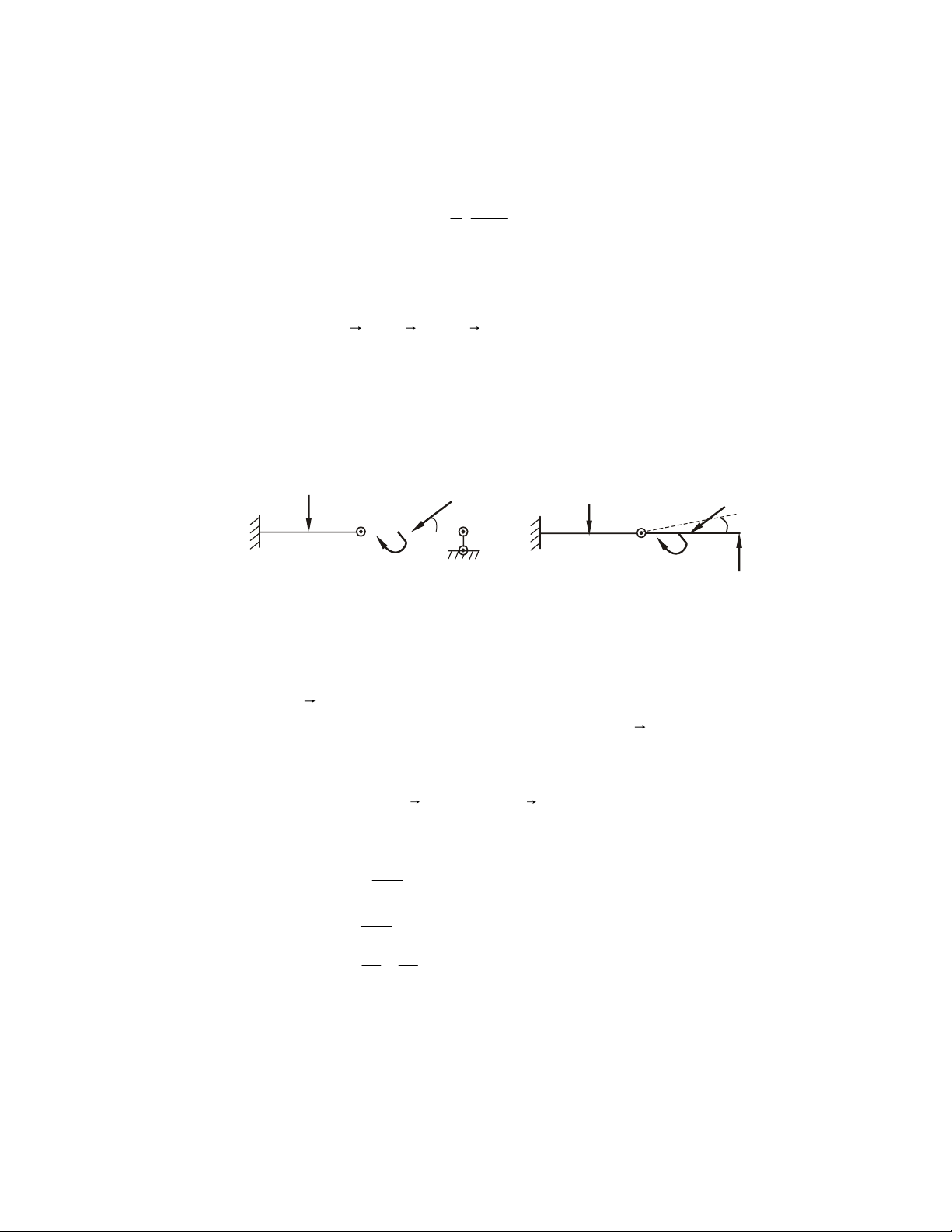
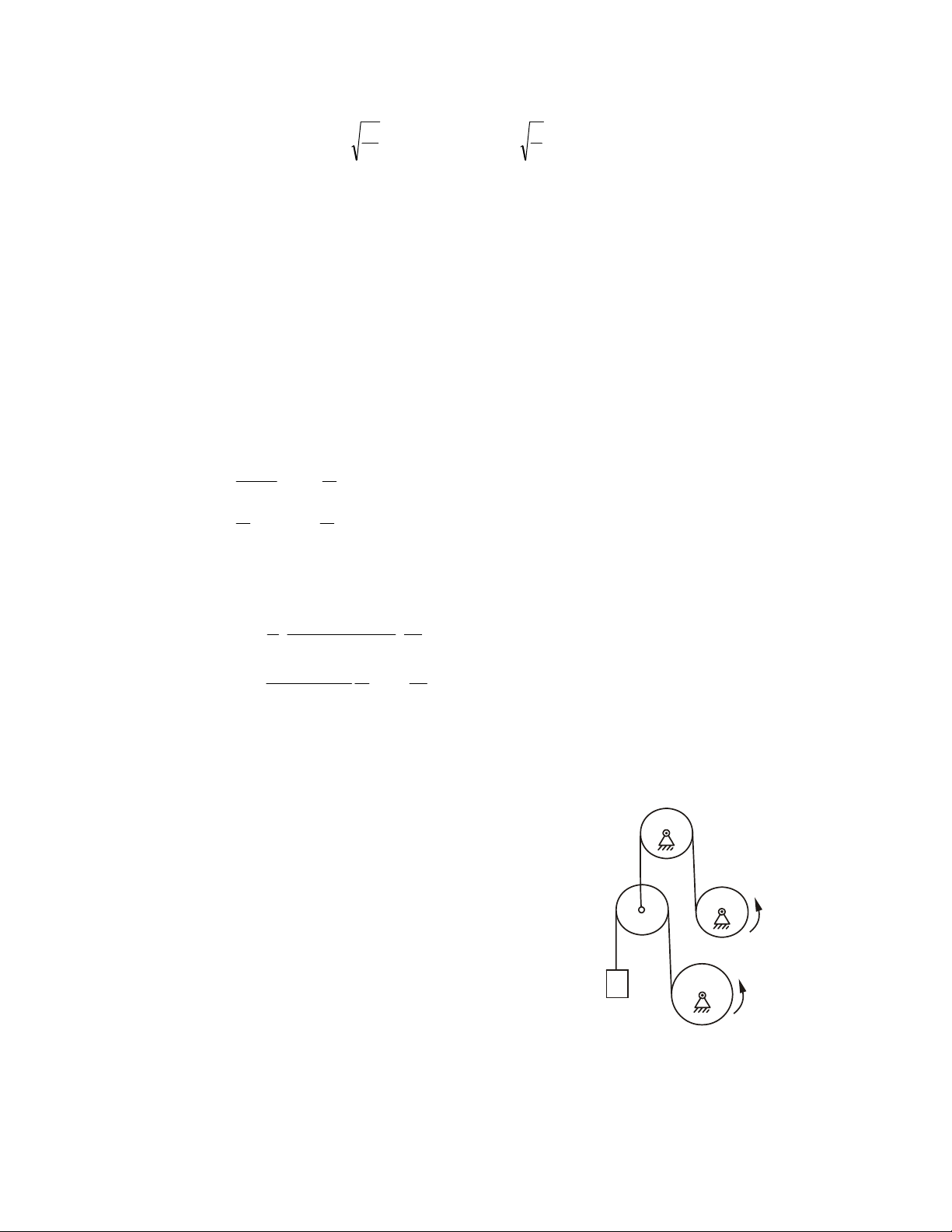
Ngöôïc chieàu ñaõ choïn neáu keát quaû aâm. 2.6. CAÙC VÍ DUÏ
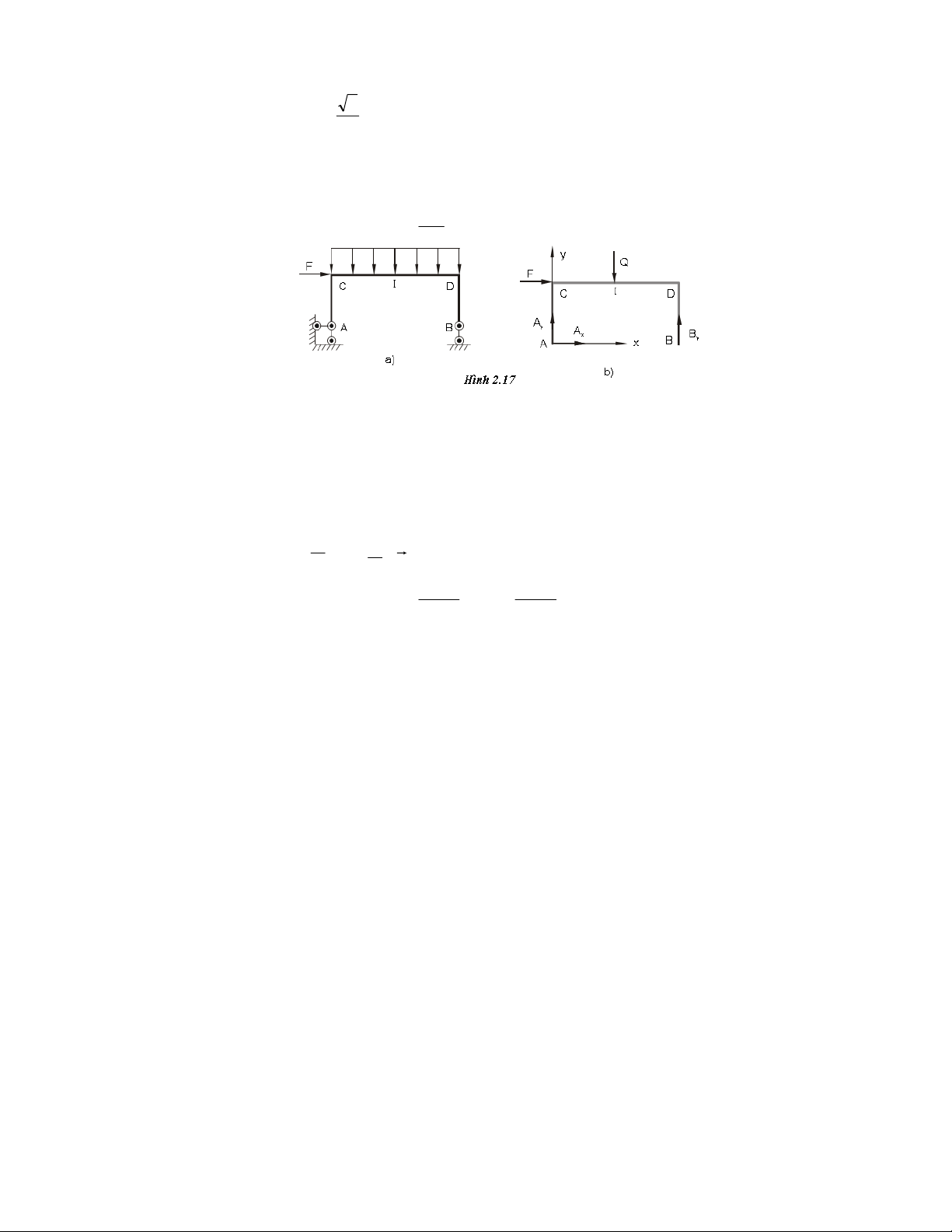
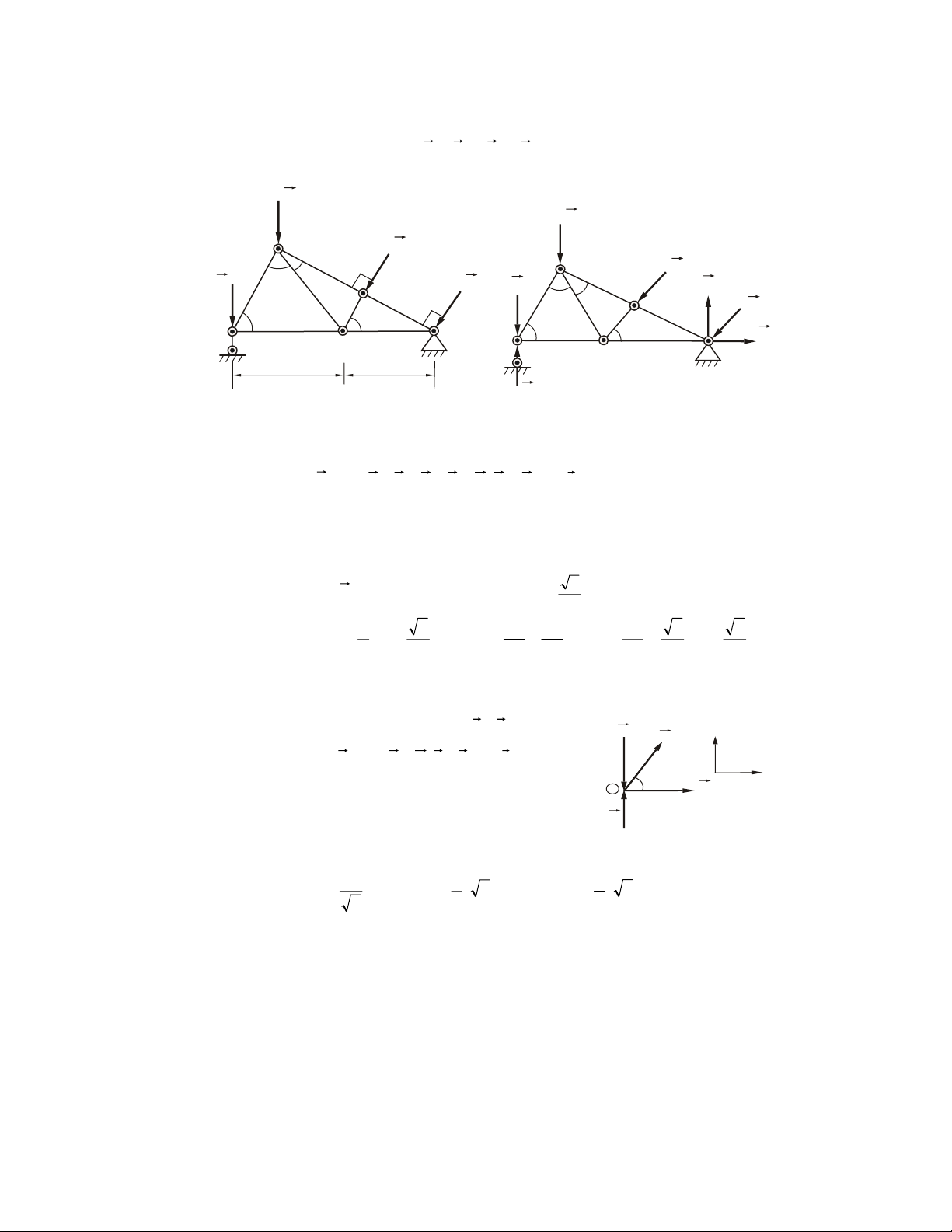
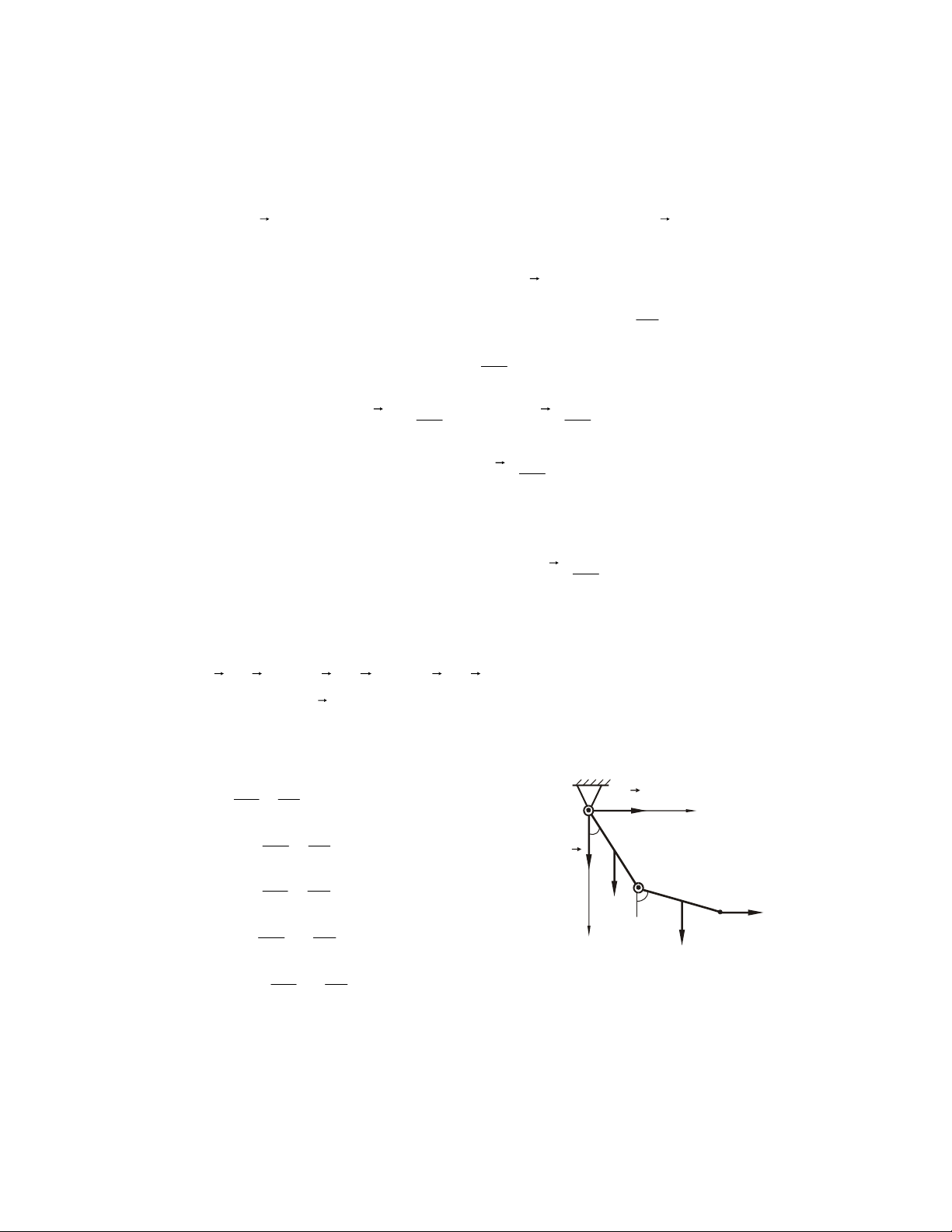
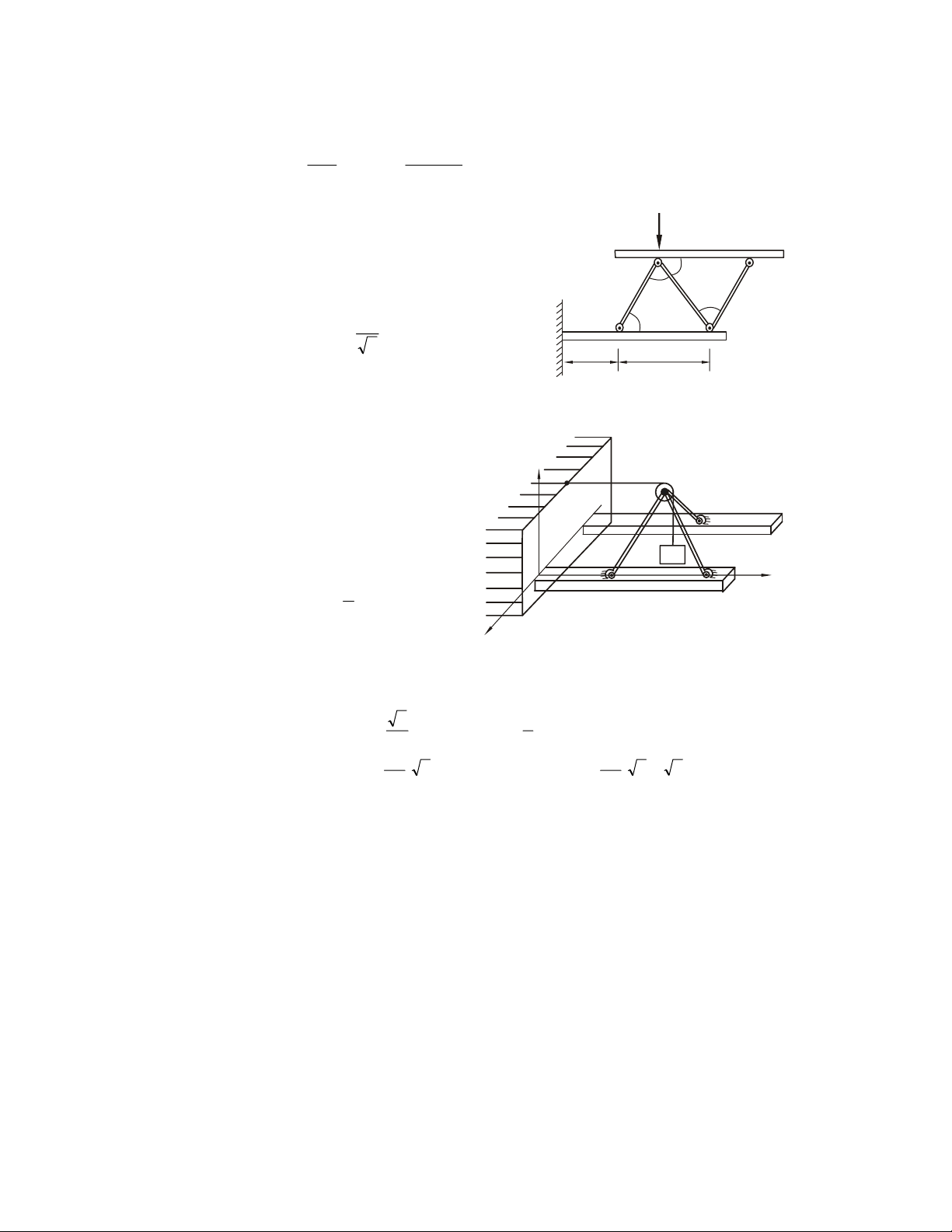
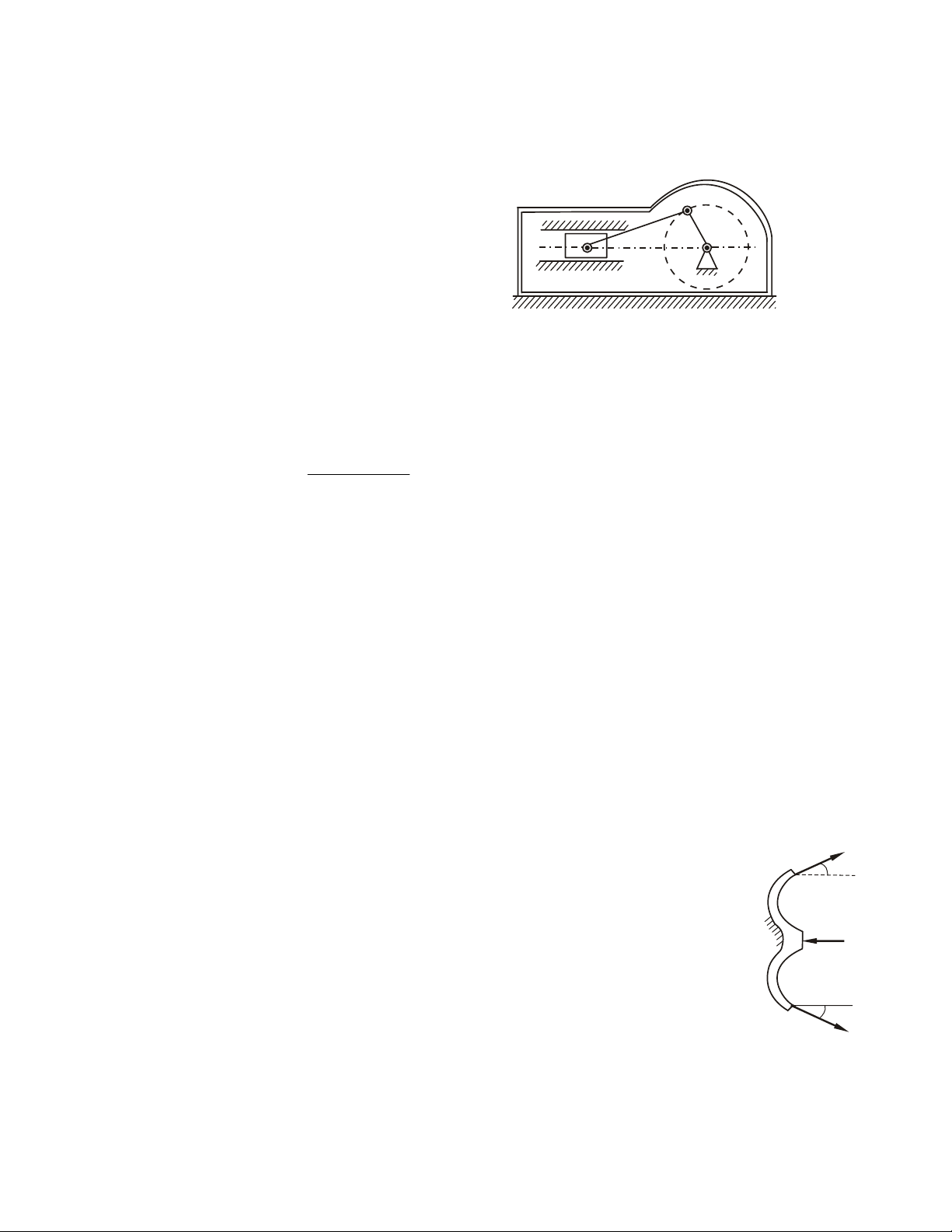
Ví duï 2.1. Giaûi phoùng lieân keát (vaät khaûo saùt S) S B A O F O F A B B S S (1) A O (2) (3) F S S B S A B A A B F F F (4) (5) (6) B M A S S F B Q A (8) (7) S A Q A B Daây S coù troïng löôïng Q Q (9) (10) Hình 2.9 24
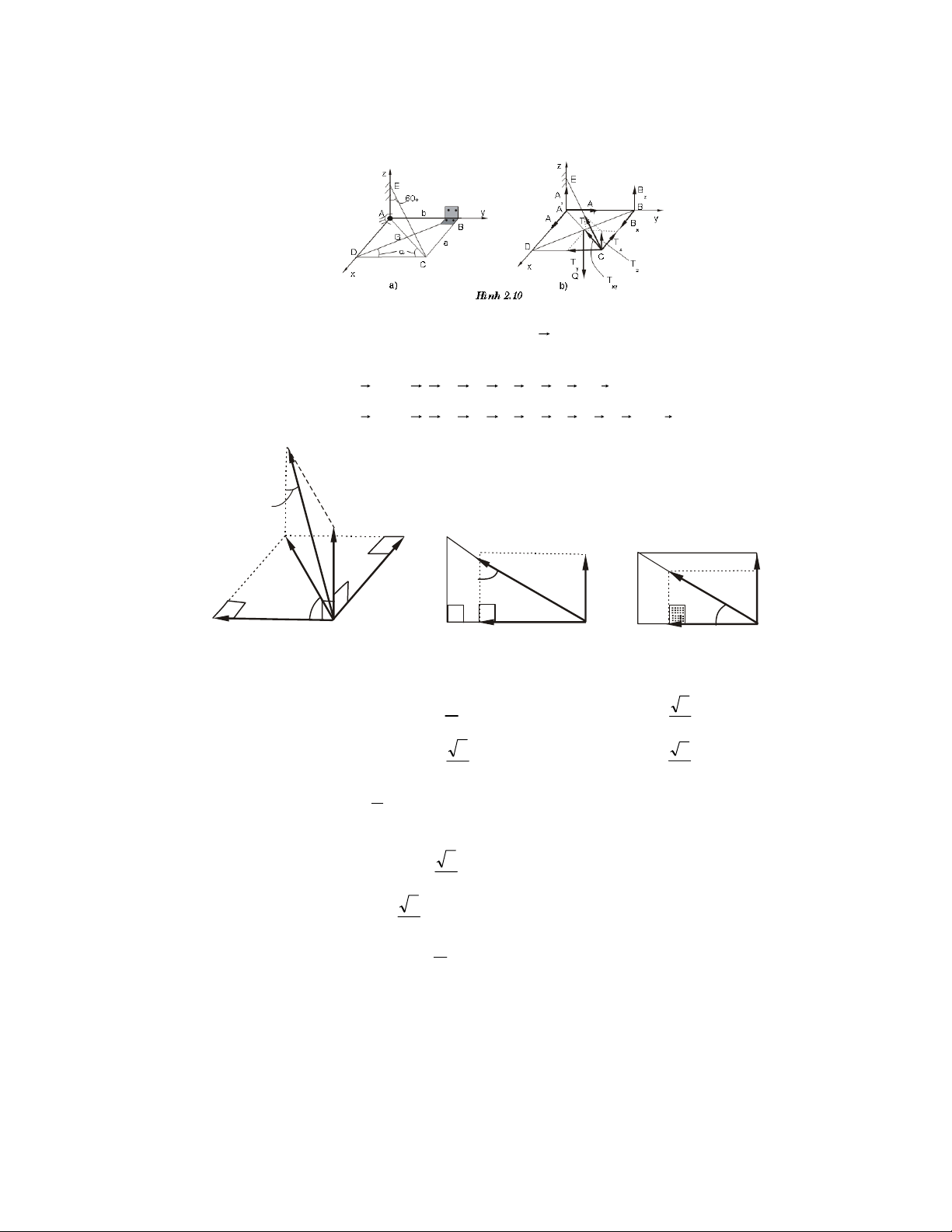
Ví duï 2.2. Taám chöõ nhaät ABCD vôùi: AB = b; BC = a, troïng löôïng Q, ñöôïc giöõ
naèm ngang nhôø daây CE vaø caùc lieân keát nhö hình veõ 2.10a. Xaùc ñònh phaûn löïc A, B vaø söùc caêng daây T?
Giaûi. • Choïn vaät khaûo saùt: taám ABCD
• Ñaët löïc: Caùc phaûn löïc vaø troïng löôïng Q ñöôïc bieåu dieãn nhö treân
H.2.10. Taám ABCD caân baèng döôùi taùc duïng cuûa heä löïc: ϕ F ( k ) ≡ , Q ( A x , A y , Az,Bx ,Bz, ) T ≡ 0 hay chi tieát hôn: ϕ F ( k ) ≡ , Q
( A x , A y , A z, Bx , Bz, Tx , Ty , Tz ) ≡ 0 T 60o E A … … … T …… z … A B … … Txy Tx Tz Tx Txy … 60o …… …… …… … … α … … …… ……… … ……… … … … … … … T … … … … … … …… … α T C y A T C D C xy Ty Hình 2.11 Trong H.2.11: o T T o 3 z = T cos 60 = ; T = T cos 30 T 2 xy = 2 3 T = 3 x Txy sin α = T sin α ; T = T cos α = T cos α 2 y xy 2 vôùi: tg a α = b
• Phöông trình caân baèng (heä löïc khoâng gian) 3 ΣF kx = A x + Bx − T sin α = 0 (1) 2 3 ΣF ky = A y − T cos α = 0 (2) 2 T F Σ = A + B + = Q = 0 z k z z (3) 2 25 b Mox = Σmx F ( k) = − Q + bBz + bTz = 0 2 b 1 ⇔ − Q + bBz + b T = 0 (4) 2 2 a Moy = Σm F ( y k ) = Q − aT = 0 2 z a a ⇔ Q − T = 0 (5) 2 2 Moz = Σm F ( k) = −bB = 0 z x (6) (do T caét truïc z ⇒ m ) T ( 0 z = )
• Giaûi saùu aån töø heä saùu phöông trình chuùng ta nhaän ñöôïc: B 3 3 Q x = 0; Bz = 0; T = Q; Ax = Q sin α ; A Q cos α ; A 2 y = 2 z = 2 Nhaän xeùt:
- Do caùc thaønh phaàn phaûn löïc taïi A tính ñöôïc ñeàu > 0 phaûn löïc taïi A coù
chieàu nhö hình veõ. Taïi B phaûn löïc = 0 ⇒ coù theå boû baûn leà B.
- Neáu taïi A laø lieân keát baûn leà truï (truïc baûn leà laø y) baøi toaùn chæ coù naêm aån.
Heä phöông trình caân baèng laäp ñöôïc chæ thay ñoåi ôû phöông trình 2: 3 ⇒ T cos α = 0 2
Suy ra T = 0 seõ maâu thuaãn vôùi caùc phöông trình coøn laïi. Sai laàm ôû choã
taám ABCD khoâng ñöùng yeân taïi vò trí ñoù maø seõ chuyeån ñoäng doïc theo truïc y sang beân traùi.
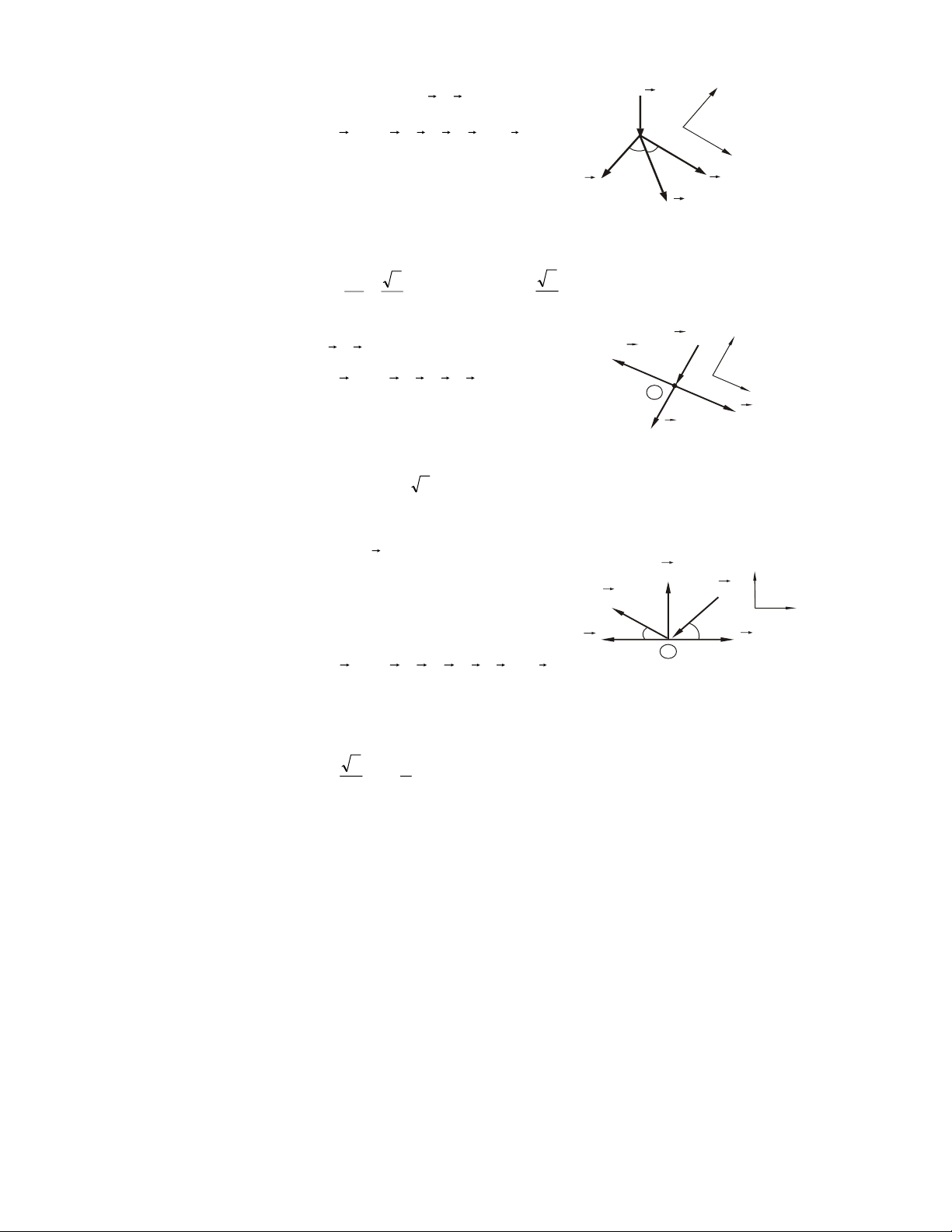
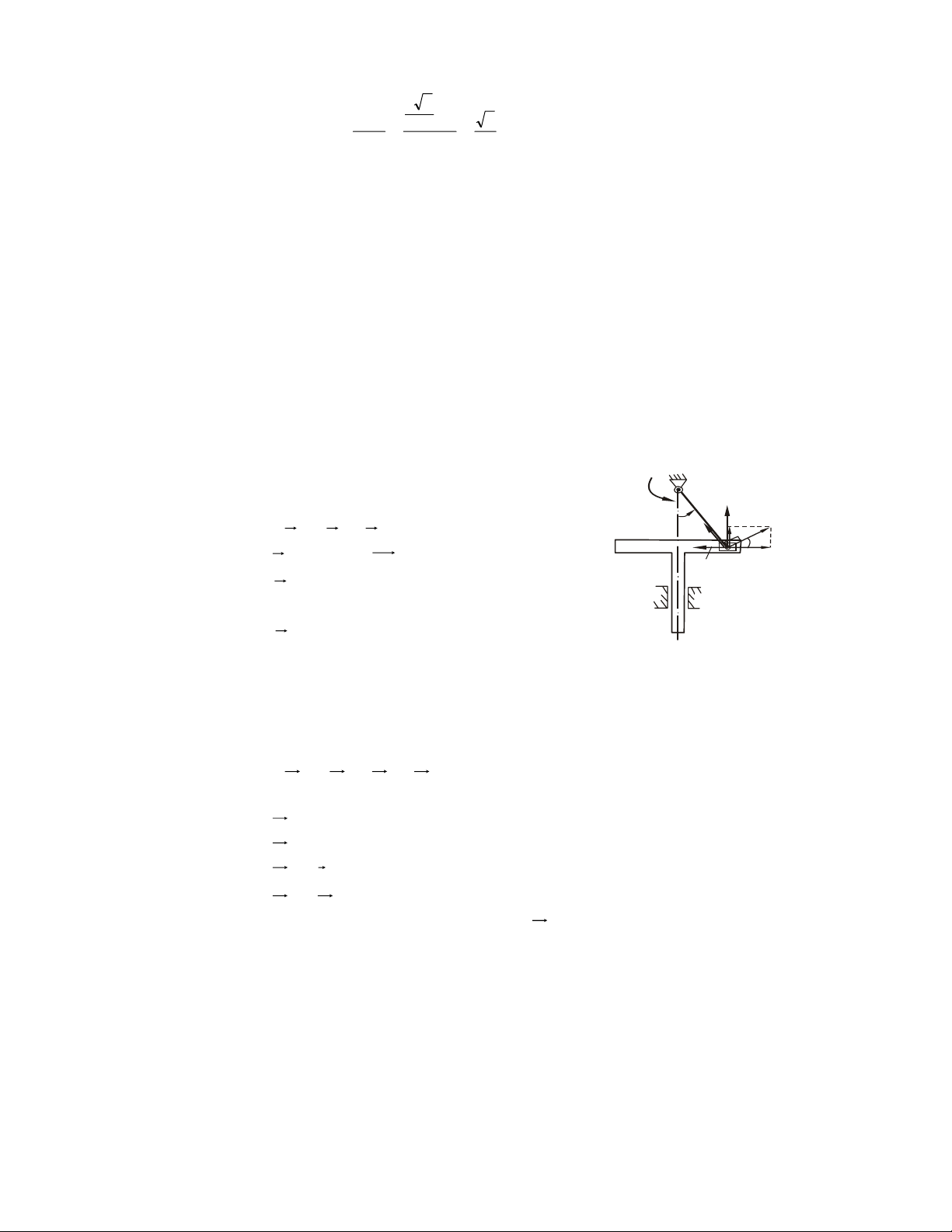
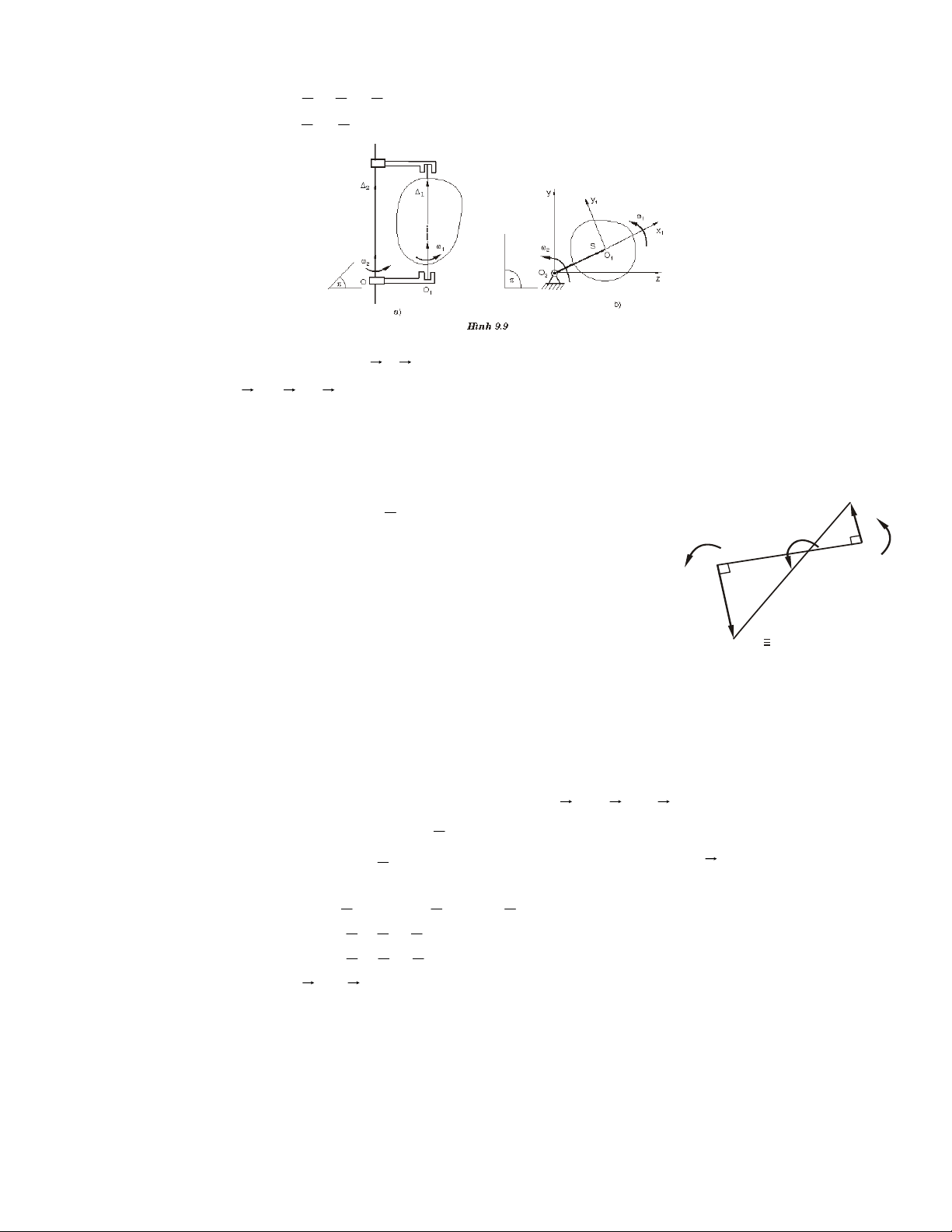
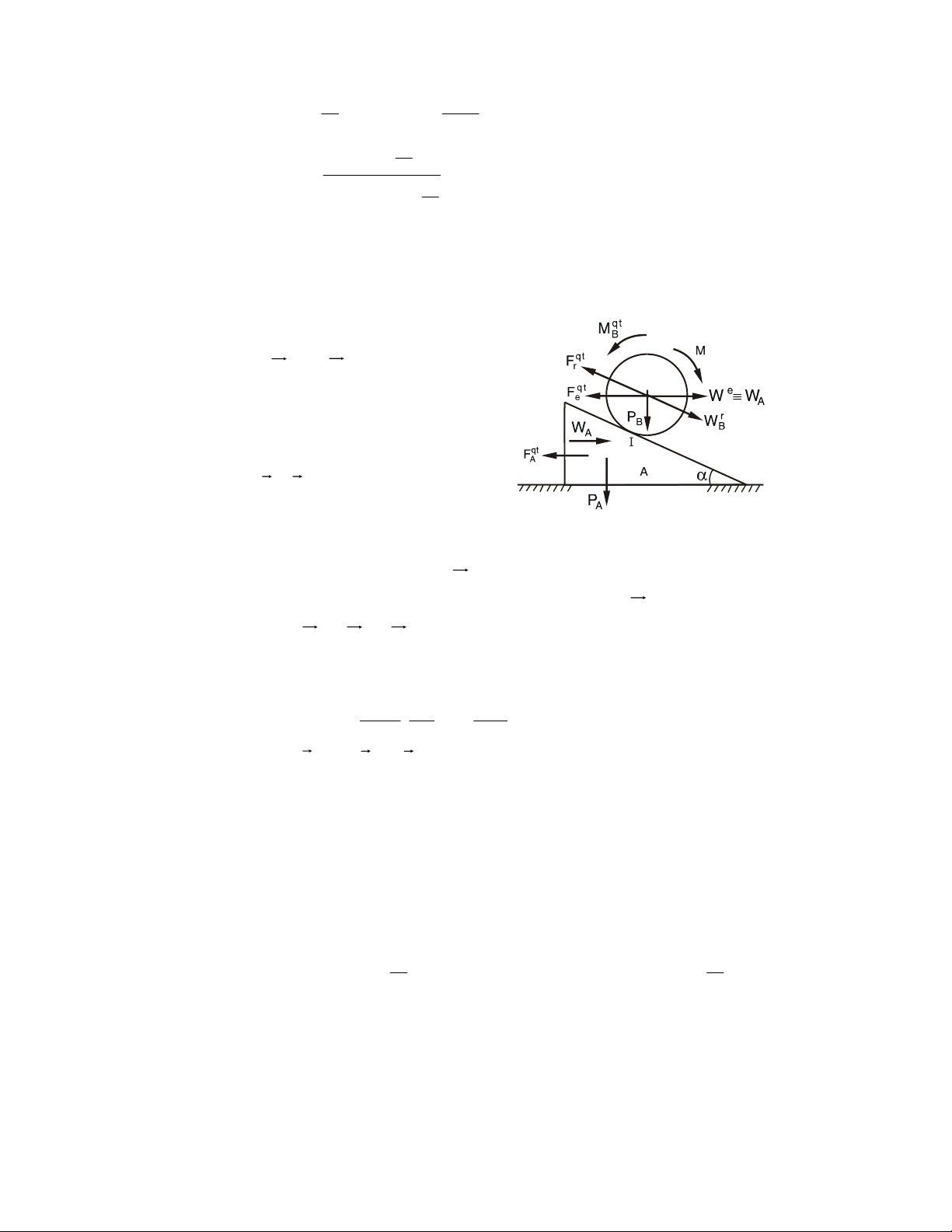
Ví duï 2.3. Xeùt baøi toaùn ôû moâ hình 8 (H.2.9). Truïc quay caân baèng nhö hình veõ,
baùn kính troáng lôùn laø R, truïc (nhoû) laø r, caùc khoaûng caùch caàn thieát cho nhö hình
veõ. Tìm ñieàu kieän cuûa moâmen M ñeå truïc caân baèng vaø tính phaûn löïc taïi A, B?
(boû qua troïng löôïng truïc).
Giaûi. • Vaät khaûo saùt: Truïc quay. z z a b M Az M Bz O x A y B Ax Bx Q x Q Hình 2.12
• Ñaët löïc: Taïi A, B ñeàu laø caùc baûn leà truï neân heä löïc ñaët vaøo vaät khaûo saùt bieåu dieãn nhö H.2.12: 26 ϕ F ( k ) ≡ , Q ( Az,Bx ,Bz, ) ngM ≡ 0
• Phöông trình caân baèng: x k F Σ = Ax + Bx = 0 (1) z k F Σ = A + B − Q z z = 0 (2) Σm F ( k x ) = − aQ + a ( + B ) b z = 0 (3) Σm F ( k) = Q R M y − = 0 (4) Σm F ( k z ) = − a ( + B ) b x = 0 (5)
( ΣFky = 0 töï thoûa maõn)
• Giaûi: Ñaây laø heä naêm phöông trình vôùi boán aån soá phaûn löïc. Phöông trình
khoâng chöùa phaûn löïc M = RQ chính laø ñieàu kieän caân baèng (neáu M ≠ RQ truïc seõ quay).
Vôùi M naøy ta giaûi ñöôïc: A b a x = Bx = 0; Az = Q; B Q a + b z = a + b
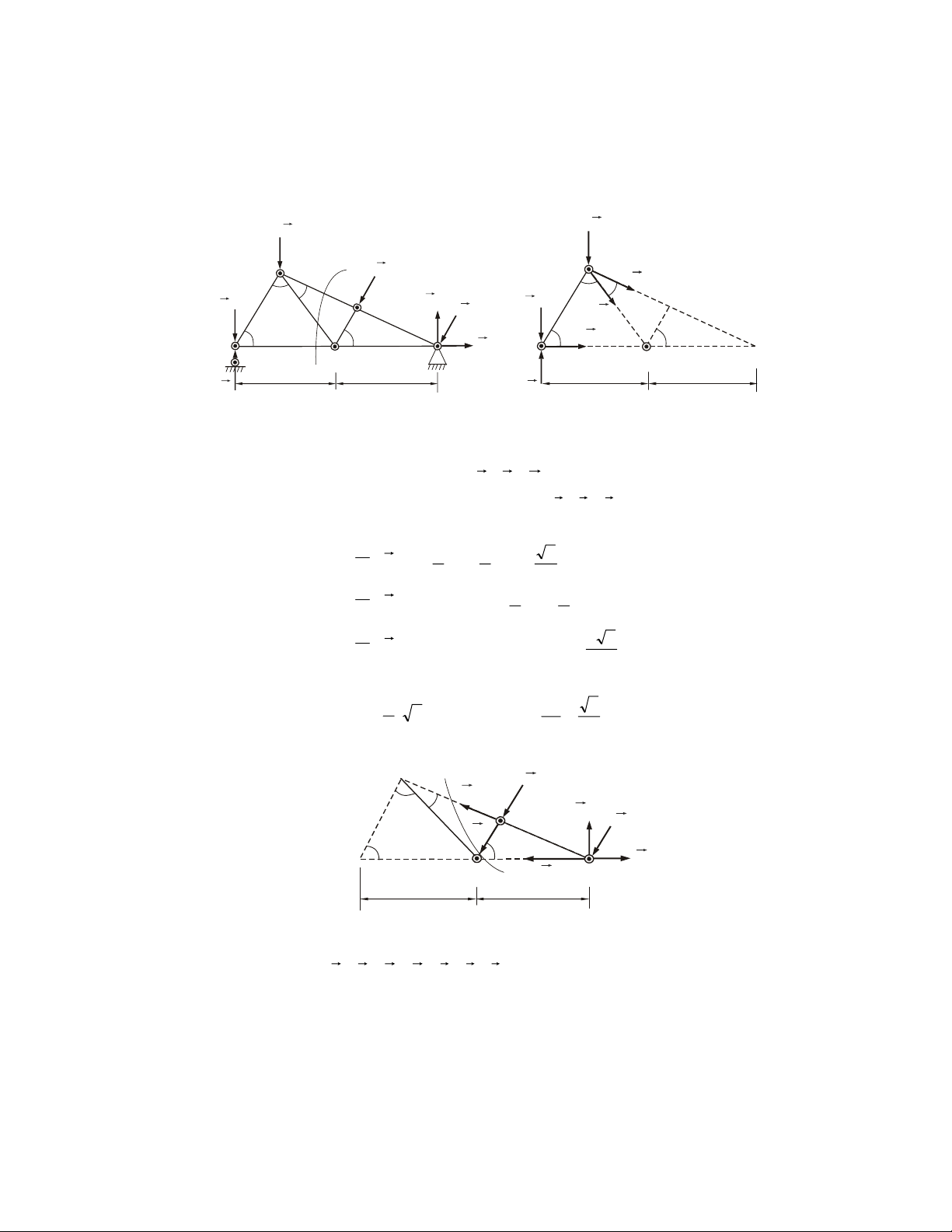
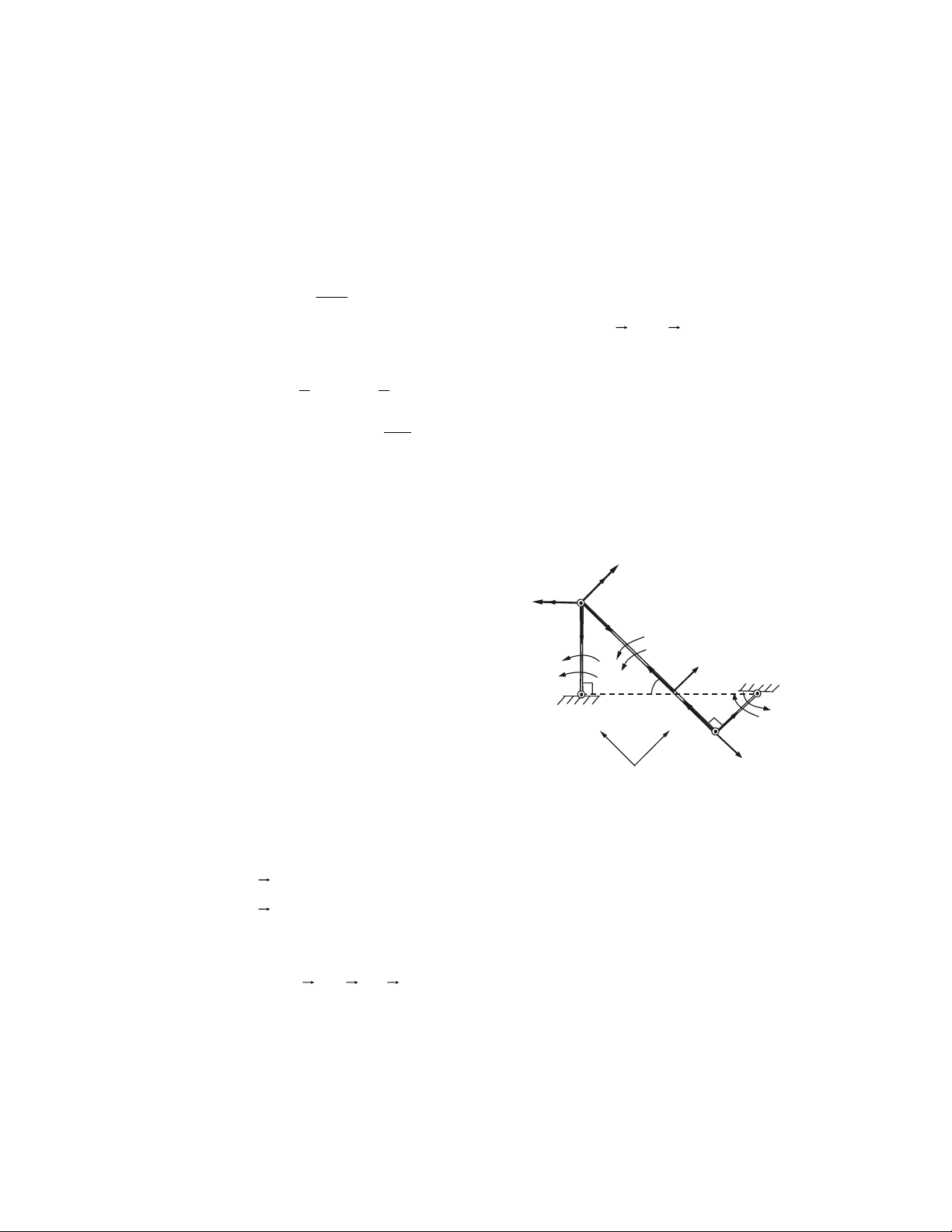
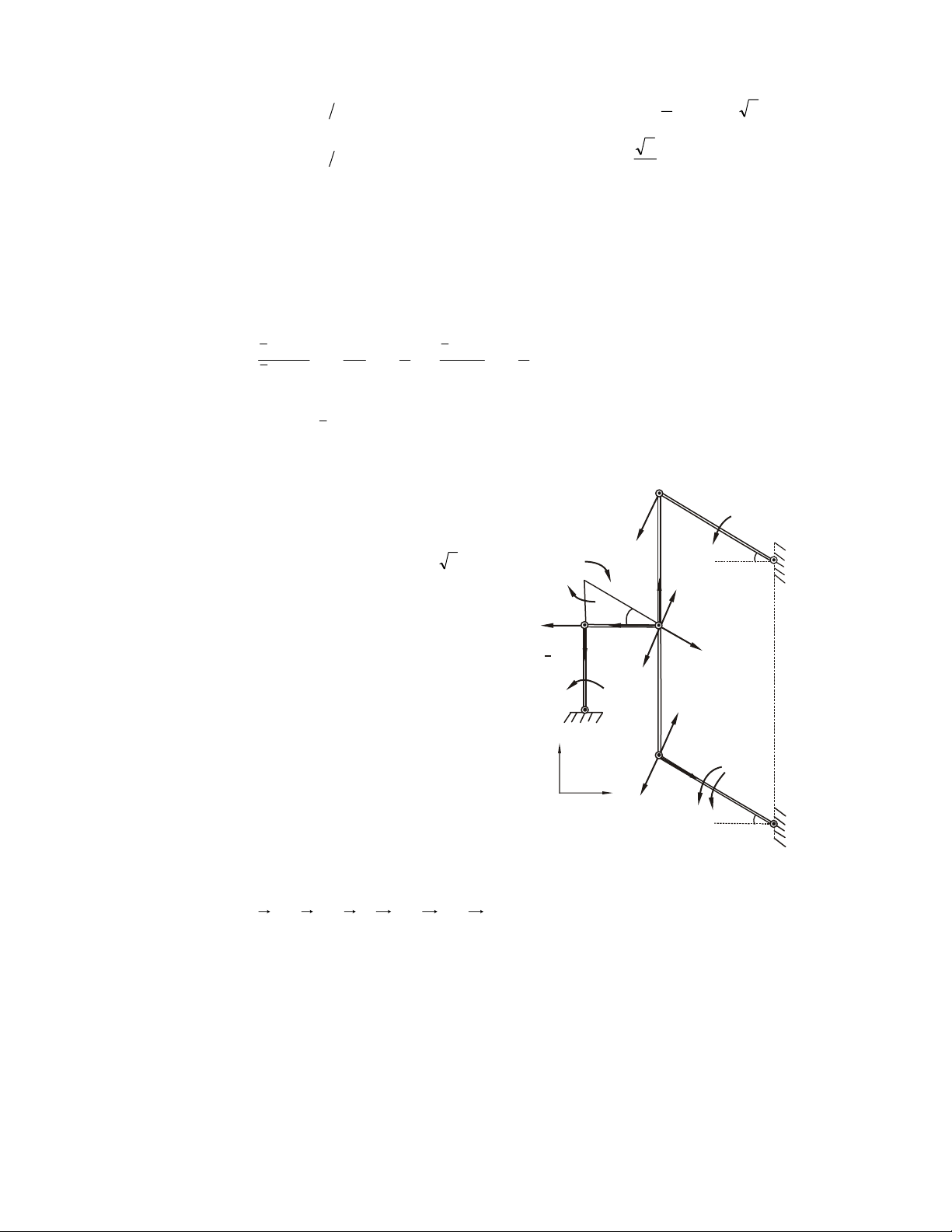
Ví duï 2.4. Thanh gaáp khuùc ABCD coù ABC thuoäc maët phaúng ngang, BCD thuoäc
maët phaúng ñöùng (H.2.13a). Khôùp caàu taïi D, oå quay taïi A (xem nhö baûn leà truï).
Chòu löïc nhö hình veõ. Cho AB = a, BC = b, CD = c. Tìm phaûn löïc taïi A, D khi z A Az m A 1 A m y 1 O m y 2 B C m2 B m C 3 x m3 a) D Dz Dy D b) Hình 2.13 Dx thanh caân baèng?
Giaûi. • Vaät khaûo saùt: Thanh gaáp khuùc ABCD
• Ñaët löïc: Caùc löïc hoaït ñoäng ngaãu m1, m2, m3 (bieåu dieãn töông öùng laø
vector moâmen naèm doïc theo caùc phöông nhö H.2.13b, ñöùng ôû ñænh caùc vector
thaáy caùc ngaãu quay theo chieàu ngöôïc chieàu kim ñoàng hoà), caùc phaûn löïc lieân keát A y , A z, Dx , Dy Dz . ⇒ heä löïc ϕ F ( r r r
k ) = ( A y , A z , D x , D y Dz , ngaãu m , m , m ) ≡ 0 1 2 3 27
• Phöông trình caân baèng: F Σ x k = Dx = 0 (1) Σ k F y = Ay + Dy = 0 (2) F Σ z k = Az + Dz = 0 (3) r Ox M = Σm F ( x k ) = m1 + bDz + cDy = 0 (4) M r Oy = Σm F ( k) y = − m2 − cDx − aDz = 0 (5) r Oz M = m Σ F ( k) z = m3 − bDx + aDy = 0 (6)
• Giaûi: Töø naêm phöông trình (1), (2), (3), (5), (6), chuùng ta ñöôïc: D m3 m2 m3 m2 x = 0; Dy = − ; D − A A a z = ; a y = ; a z = a
Theá caùc giaù trò vaøo phöông trình (4) coøn laïi seõ nhaän ñöôïc: m b c 1 = m2 + m3 a a z
khoâng chöùa aån (phaûn löïc), ñaáy chính laø ñieàu M kieän caân baèng. z y
Caùc thaønh phaàn Dy, Dz coù chieàu A
ngöôïc chieàu ñaõ choïn. My
- Tröôøng hôïp oå quay taïi A coù ñoä daøi
nhaát ñònh: phaûn löïc A coù theâm hai thaønh
phaàn caûn quay quanh truïc y vaø z laø x Hình 2.14 m r , m r . Ay
Az Baøi toaùn thuoäc loaïi sieâu tónh (coù baûy aån soá phaûn löïc).
Ví duï 2.5. Moät truï troøn troïng löôïng Q (baùn kính R) ñaët trong hoá moùng (ñoä roäng
l) ñöôïc bieåu dieãn moâ hình phaúng nhö H.2.15a. Xaùc ñònh phaûn löïc taïi A, B?
Giaûi. • Vaät khaûo saùt: Truï troøn taâm O
• Ñaët löïc: Taïi A vaø B laø caùc lieân keát töïa (moät chieàu), caùc phaûn löïc ñeàu ñi
qua taâm O vaø coù chieàu nhö H.2.15b. y y O x A O x α A NB Q B B l a) b) Hình 2.15 Heä löïc ϕ F ( k ) ≡ , Q
( NA , NB ) ≡ 0 ñoàng quy phaúng.
• Phöông trình caân baèng: (laäp ñöôïc hai phöông trình caân baèng): F Σ x k = NA − NB cos α = 0 ΣF = − Q + N sin α = 0 k y B 28
• Giaûi heä phöông trình: N = Q cot g ; Q A α N = B sin α Tính α ? Ta coù: l − R ⎛ l − R ⎞ cos α = ⇒ α = ar ⎜ cos ⎟ R ⎝ R ⎠
Chuù yù: Vôùi heä ba löïc phaúng ñoàng quy caân baèng ta coù theå duøng ñieàu kieän
ñoùng kín tam giaùc löïc.
Ví duï 2.6. Cho daàm AB coù lieân keát vaø chòu löïc nhö H.2.16a (ngaãu M vaø löïc F
ñeàu thuoäc maët phaúng xy). Bieát AI = a, BI = 2a. Xaùc ñònh phaûn löïc taïi A, B. y F F A B y Y 60o Ax 60o x B A A I I B M d M a) b) Hìn H h 2.16 ình 2.16
Giaûi. • Vaät khaûo saùt: Daàm AB
• Ñaët löïc: Taïi A lieân keát baûn leà truï, taïi B lieân keát töïa moät chieàu choáng luùn
xuoáng phía döôùi. Heä löïc nhaän ñöôïc: ϕ F ( k ) ≡ ,
F ngaãu M, A x , A y , By ) ≡ 0
• Phöông trình caân baèng: o F F Σ = A + F cos 60 = 0 ⇔ A x k x x = − (1) 2 o 3
ΣF ky = A y + F sin 60 + By = 0 ⇔ A y + By + F = 0 (2) 2 3 MA = Σm F ( A k ) = −M + aB 3 + dF = 0 ⇔ −M + aB 3 + a F = 0 y y (3) 2
• Giaûi: Heä ba phöông trình coù ba aån A F M 3 M 3 x = − ; B − F A − − 2 y = ; a 3 6 y = F a 3 3
• Nhaän xeùt: Ax < 0, Ay < 0 chuùng seõ coù chieàu ngöôïc laïi, coøn By ñaõ ñuùng chieàu neân: B M 3 3 y ≥ 0 ⇔ − F ≥ 0 ⇔ M ≥
aF - laø ñieàu kieän caân baèng a 3 6 2 29 - Neáu 3 M < aF ⇒ By < ,
0 töùc lieân keát taïi B caûn trôû ñaàu B ñi leân, song 2
lieân keát khoâng coù khaû naêng, töùc ñaàu B seõ ñi leân ⇔ daàm AB chuyeån ñoäng quay quanh A.
Ví duï 2.7. Cho khung ABCD coù lieân keát vaø chòu löïc nhö H.2.17a. Tính phaûn löïc
taïi A vaø B? Bieát AC = BD = CD = 1 m; F = 100 KN; q = 20 KN/m. 2
Giaûi. • Vaät khaûo saùt: Khung ABCD.
• Ñaët löïc: Taïi A töông öùng lieân keát baûn leà truï, taïi B töïa hai chieàu, heä löïc phaân boá ) q
(r ñöôïc thay töông ñöông bôûi Q = 2q = 40 KN ñaët taïi I nhö H.2.17b ⇒
• Phöông trình caân baèng: F Σ kx = Ax + F = 0 (1) ΣF = A − Q + B = 0 k y y y (2) MB = Σm F ( k) = Q − F − A 2 = 0 B y (3) • Giaûi: A Q − F Q + F x = –F; Ay = ; B 2 y = 2
Thay soá chuùng ta thaáy Ax, Ay ñeàu < 0, By > 0. Vaäy chieàu cuûa Ax, Ay phaûi
laáy ngöôïc laïi: Ax = 100 KN; Ay = 30 KN; By = 70 KN.
2.7. BAØI TOAÙN CAÂN BAÈNG CUÛA HEÄ VAÄT RAÉN
Chuùng ta coù theå laäp ñieàu kieän caân baèng cuûa heä vaät raén theo hai phöông phaùp:
Phöông phaùp taùch vaät: Thieát laäp ñieàu kieän caân baèng cuûa moãi vaät raén thuoäc heä.
Phöông phaùp hoùa raén: Thieát laäp ñieàu kieän caân baèng cuûa toaøn heä raén vaø
töøng phaàn cuûa heä hoùa raén (coù theå moät vaät, hai vaät,… ∈heä) sao cho soá phöông
trình laäp ñöôïc ñuû giaûi quyeát caùc yeâu caàu cuûa baøi toaùn.
Chuùng ta chöùng toû heä n vaät raén duø caân baèng duøng phöông phaùp naøo (cuõng
töông ñöông), ñieàu kieän caân baèng cuûa n heä löïc caân baèng töông öùng ñaët vaøo moãi vaät raén thuoäc heä.
Chöùng minh. Ta chæ caàn chöùng minh cho heä hai vaät S1, S2. Neáu nhieàu vaät raén
chæ caàn hoùa raén S1, S2 vaø ta chöùng minh töông töï. 30 Hoùa raén S ) 1 ( ( ) 2
1, S2 heä löïc taùc ñoäng vaøo caû hai vaät: ϕ F ( k ,Fk ) vôùi: ) 1 (
Fk - laø caùc löïc ngoaøi ñaët vaøo S1 (2)
Fk - laø caùc löïc ngoaøi ñaët vaøo S2 (loaïi löïc naøy thöôøng ñöôïc kí hieäu laø e Fk )
Ñeå ñôn giaûn ta giaû söû giöõa S1 vaø S2 coù moät lieân keát (neáu theâm lieân keát ta
ñaët theâm löïc töông taùc). Taùch rieâng S ) 1 (
1. Heä löïc taùc ñoäng vaøo S1 laø: 1 ϕ F ( k , F21)
trong ñoù: F21 - laø löïc töông taùc cuûa S2 taùc ñoäng vaøo S1 Taùch rieâng S ) 2 (
2. Heä löïc taùc ñoäng vaøo S2 laø: ϕ2 F ( k , F12)
trong ñoù: F12 - laø löïc töông taùc cuûa S1 taùc ñoäng vaøo S2, dó nhieân: F12 = - F21
(loaïi löïc naøy thöôøng ñöôïc goïi laø noäi löïc vaø thöôøng ñöôïc kí hieäu laø i Fk ) Vì vaäy: F12 + F21 = 0; m
r A (F12) + mrA (F21 ) = 0 vôùi A ∀ Ñieàu ñoù chöùng toû , ) 1 ( ( ) 2 R vaø MA cuûa heä ϕ F ( k ,Fk ) thoûa maõn: , , , R = R1 + R2; MA = M1A + M2A
coù nghóa laø chæ hai trong ba heä löïc treân caân baèng thì heä löïc coøn laïi buoäc phaûi caân baèng.
2.8. CAÙC VÍ DUÏ BAØI TOAÙN CAÂN BAÈNG CUÛA HEÄ LÖÏC VAÄT RAÉN
Ví duï 2.8. Hai baùnh xe hình noùn O vaø O’ aên khôùp raêng ôû C, chòu caùc ngaãu M, M’
nhö H.2.18a, baùn kính töông öùng cuûa caùc baùnh raêng laø r, r’. Baùnh xe O’ taùc ñoäng
vaøo baùnh xe O löïc R nghieâng vôùi phöông CO goùc α vaø maët phaúng chöùa ( R ,
CO ) nghieâng vôùi maët phaúng chöùa baùnh xe O (Cyz) goùc β . Cho O’A = a.
Xaùc ñònh lieân heä giöõa M, M’ ñeå cô heä caân baèng? Tìm phaûn löïc taïi A.
Giaûi. Ñaây laø cô heä hai vaät raén caân baèng chòu löïc taùc ñoäng cuûa heä löïc khoâng
gian, soá phöông trình caân baèng ñöôïc thieát laäp laø 12 = 6 × 2. Xem xeùt moâ hình
taïi caùc lieân keát B, C, D ñaõ coù saùu aån, coøn taïi A (ñoä daøi cuûa oáng truï phaûi ñuû lôùn) z z z 1 M Rcz z B M 2 D Bz R B C Dz x R O c O x D α 1 By B α Dy x Rcx x O’ y C O’ 1 M’ R C cxy R β cy M’ β Max2 y y A x x 2 A A Ay a) b) Hình 2 Hình 2.18 .18 y May2 2 31
chæ khoâng caûn trôû quay quanh truïc Z2 ⇒ A x, A y , Az, ngaãu MAx M , Ay (toång
coäng coù 11 aån phaûn löïc). Chuùng ta seõ tìm ñöôïc moät phöông trình laø ñieàu kieän
lieân heä giöõa M vaø M’.
Döôùi ñaây ta duøng phöông phaùp taùch vaät: Vaät I:
• Xeùt baùnh xe O caân baèng (keå caû truïc khoâng troïng löôïng BD).
• Ñaët löïc: xem H.2.18b, heä löïc taùc ñoäng: ϕ F ( 1 k ) ≡ , ngM ( Rc ,Bx ,By ,Bz,Dy ,Dz) ≡ O
Chuùng ta bieåu dieãn Rc qua ba hình chieáu (H.2.19): ⎧R = R cos α z c ⎪ ⇒ ⎨R = R sin α.sinβ x c ⎪ ⎩R = R sin α.cosβ y c
• Phöông trình caân baèng:
Neáu phaûi giaûi heát taát caû caùc aån, chuùng ta laäp ñaày
ñuû saùu phöông trình caân baèng (vôùi heä truïc B x1 y1 z1), nhöng do yeâu caàu cuûa baøi
toaùn khoâng caàn xaùc ñònh caùc phaûn löïc taïi B, D neân ta chæ caàn laäp moät phöông
trình moâmen ñoái vôùi truïc x1 ñeå traùnh naêm aån ôû B, D. Σm 1 x F
( k) = −M + Ry r. = 0 ⇔ −M + R sin . α cos β r . = 0 (do R M x // x B 1, Rz caét x B 1 ) ⇒ R = r sin α cos β Vaät II:
• Xeùt baùnh raêng O’ caân baèng (keå caû truïc).
• Ñaët löïc: Heä löïc bieåu dieãn treân H.2.20b) vôùi chuù yù ,
Rc laø phaûn löïc ñaët taïi
C cuûa baùnh raêng O’ ngöôïc chieàu vôùi Rc , ( , Rc = Rc ). , ⇒ ϕ F ( ' 2
k ) ≡ ( A x, A y , Az, Rc, ngM , MAx2, MAy2) ≡ 0
• Phöông trình caân baèng: kx F Σ ' = Ax + Rx = A − x R sin α sin β = 0 (1) kz F Σ ' = Az + Rz = A − z R cos α = 0 (3) Σm F ( k) = m R ( x2 x2 y ) + M = R'y a . + M = 0 Ax2 Ax2 ⇔ R . a sin . α cosβ + M = 0 Ax2 (4) Σm F ( y2 k ) = m R ( , y2 x) + m R ( , 2 y z) + M = 0 Ay2 ⇔ − a R . sin . α sin β + r'R cos α + M = 0 Ay2 (5) Σm F ( ) = M' k + m R ( 2 z 2 z y ) = 0 ⇔ M ' − r'R sin . α cos β = 0 (6)
• Giaûi heä naêm phöông trình ñaàu ta ñöôïc: 32 A M M M x = tg ; β A A cot g r y = ; r z = α r cosβ ' aM M = − ; aM r M Ax2 M = β tg − cot gα r Ay2 r r cos β ' Coøn phöông trình (6) ' r ⇒ M = M ⇔ rM' = r'M r
Ñaáy chính laø ñieàu kieän caân baèng.
Ví duï 2.9. Cô heä coù lieân keát vaø chòu löïc nhö H.2.20a. Bieát:
P1 = 10 KN; P2 = 20 KN; M = 35 KNm; q = 2 KN/m
AB = 2BC= 2CE = ED = 2m. Tính phaûn löïc taïi A, B, C. P2 P2 α = 30o Ay Q B B P y y 1 M q M A B B ’ x x x α = 30o A B C E A I B C E MA B ’y a) b) Hình 2.20
Giaûi. Cô heä hai vaät raén phaúng caân baèng. Chuùng ta duøng phöông phaùp taùch vaät. Vaät I:
• Khaûo saùt daàm AB caân baèng.
• Ñaët löïc: xem H.2.20b. Heä löïc: ϕ F ( r 1 k ) ≡ ), q (( Ax, Ay ngM , , B A x, By ) ≡ 0 ⇔ , Q ( A x A y ,Bx ,By ngM , ) ≡ Q ( 0 = AI , q 2 = ) m 1 A
• Phöông trình caân baèng: kx F Σ = Ax − Bx = 0 (1) Σ ky F = Ay − Q + By = 0 (2) Σm F ( k) B = M − A 2 + 1 Q . A y = 0 (3)
Trong heä ba phöông trình naøy coù naêm aån, chuùng ta phaûi laäp theâm phöông trình: Vaät II:
• Khaûo saùt daàm BCED caân baèng
• Ñaët löïc: xem H.2.20b. Heä löïc taùc ñoäng: , , ϕ2 F ( k ) ≡ ( Bx ,By ,P1, , C P2, ngM) ≡ 0 (chuù yù: , , Bx = −Bx ,By = −By ) .
• Phöông trình caân baèng: o kx F Σ = Bx − 1 P cos 30 − 2 P = 0 (4) Σ o ky F = B − − P sin 30 + C y 1 = 0 (5) 33 m r Σ F ( k) c = −M + 1 B . y + 2 2 P . = 0 (6)
Giaûi heä saùu phöông trình:
Ax = 20 + 5 3 ; Ay = 9; MA = 14
Bx = 20 + 5 3 ; By = -5; C = 0; (ñôn vò KN vaø KNm) Nhaän
xeùt: Taïi C khoâng coù phaûn löïc ⇒ coù theå boû goái C
Ví duï 2.10. Cho cô caáu 4 thanh ABCD (C, D coá ñònh), xaùc ñònh ñoä lôùn cuûa R ñeå
cô caáu caân baèng ôû vò trí ñang xeùt. Xaùc ñònh öùng löïc trong caùc thanh. Bieát Q = 10
KN, taïi A, B, C, D ñeàu laø caùc khôùp baûn leà. A B y y1 45o 30o S S ’ 2 2 B x1 A 60o 45o 30o 60o C C Q S D S1 3 R x D a) b) Hình 2.21
Giaûi. Ñaây laø loaïi cô caáu ñaëc bieät, caùc thanh ñeàu chòu lieân keát thanh (tröø CD)
neân coù ba öùng löïc trong ba thanh. Ta chæ caàn xeùt söï caân baèng cuûa hai nuùt A, B
seõ laäp ñöôïc boán phöông trình caân baèng töø hai heä löïc ñoàng quy ñeå giaûi ra ba öùng
löïc vaø moät ñieàu kieän caân baèng (H.2.21b)
• Xeùt nuùt A caân baèng coù heä löïc: ϕ1 F ( k ) ≡ , Q ( S1, S2) ≡ 0 Phöông trình caân baèng:
(ta giaû thieát caùc thanh ñeàu chòu keùo ⇒ caùc Si coù chieàu nhö H. 2.21b) 2 F Σ kx = Q + S2 = 0 (1) 2 2 F Σ ky = − S 1 + S2 = 0 (2) 2
Giaûi. S2 = – Q 2 = –10 2 ; S1 = – Q = –10.
• Xeùt nuùt B caân baèng, chòu taùc duïng heä löïc: , , ϕ F ( 2 k ) ≡ , R
( S3,S2 ), (chuù yù: S2 = − S 2)
Phöông trình caân baèng: (heä truïc Bx1y1). 3 F Σ 1 kx = − S 2 − R = 0 (3) 2 R F Σ = − S − = 0 1 ky 3 (4) 2 Giaûi. 2 2 2 R 2 = − S = Q 2 20 ; S3 = 10 − (ñôn vò KN, m). 3 2 = 3 3 3
Chuù yù: Neáu öùng löïc töông öùng döông ( > 0) thanh chòu keùo, öùng löïc töông
öùng aâm ( < 0) thanh chòu neùn (ñoåi chieàu). 34
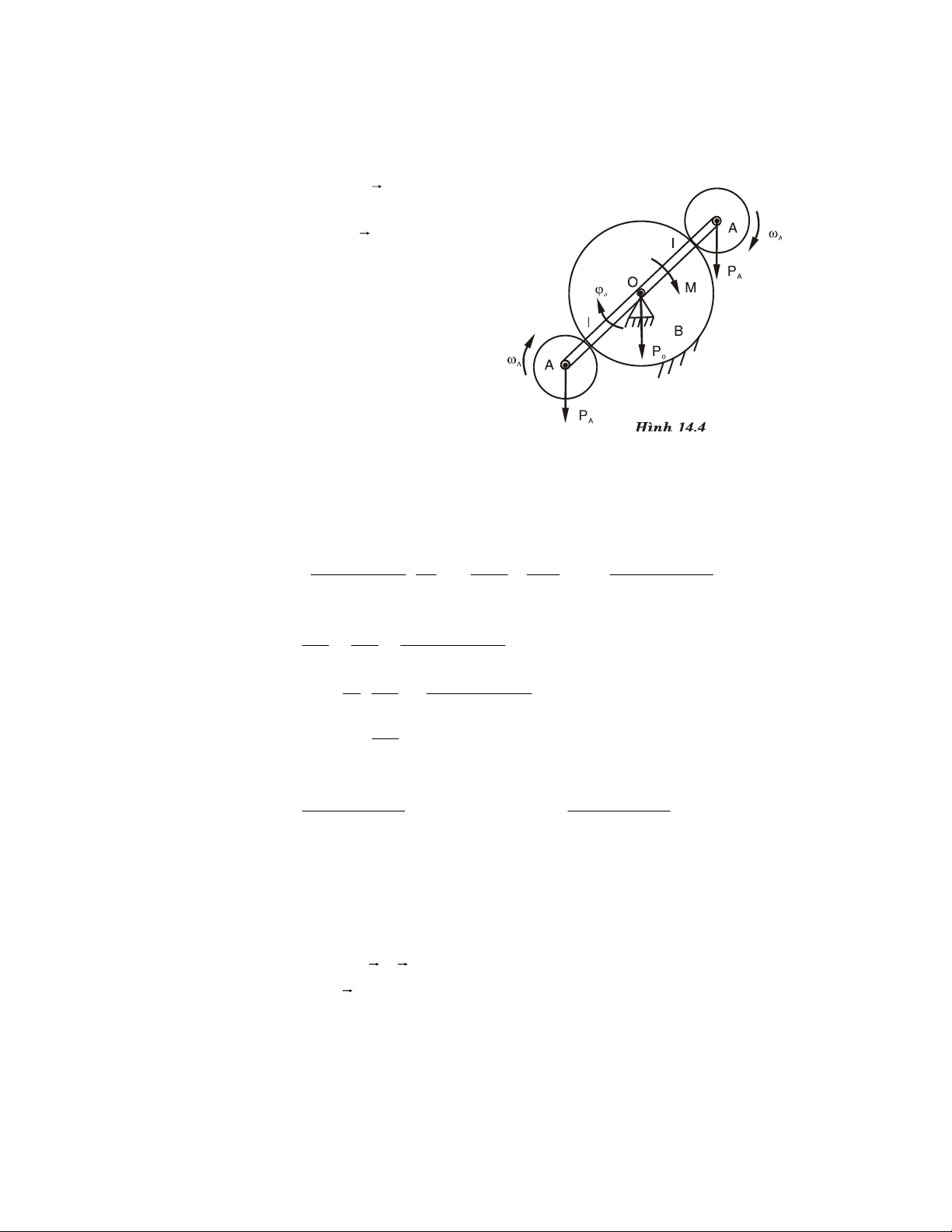
Ví duï 2.11. Ngaãu M ñaët vaøo tay quay OA quay ñöôïc quanh O, con chaïy A coù
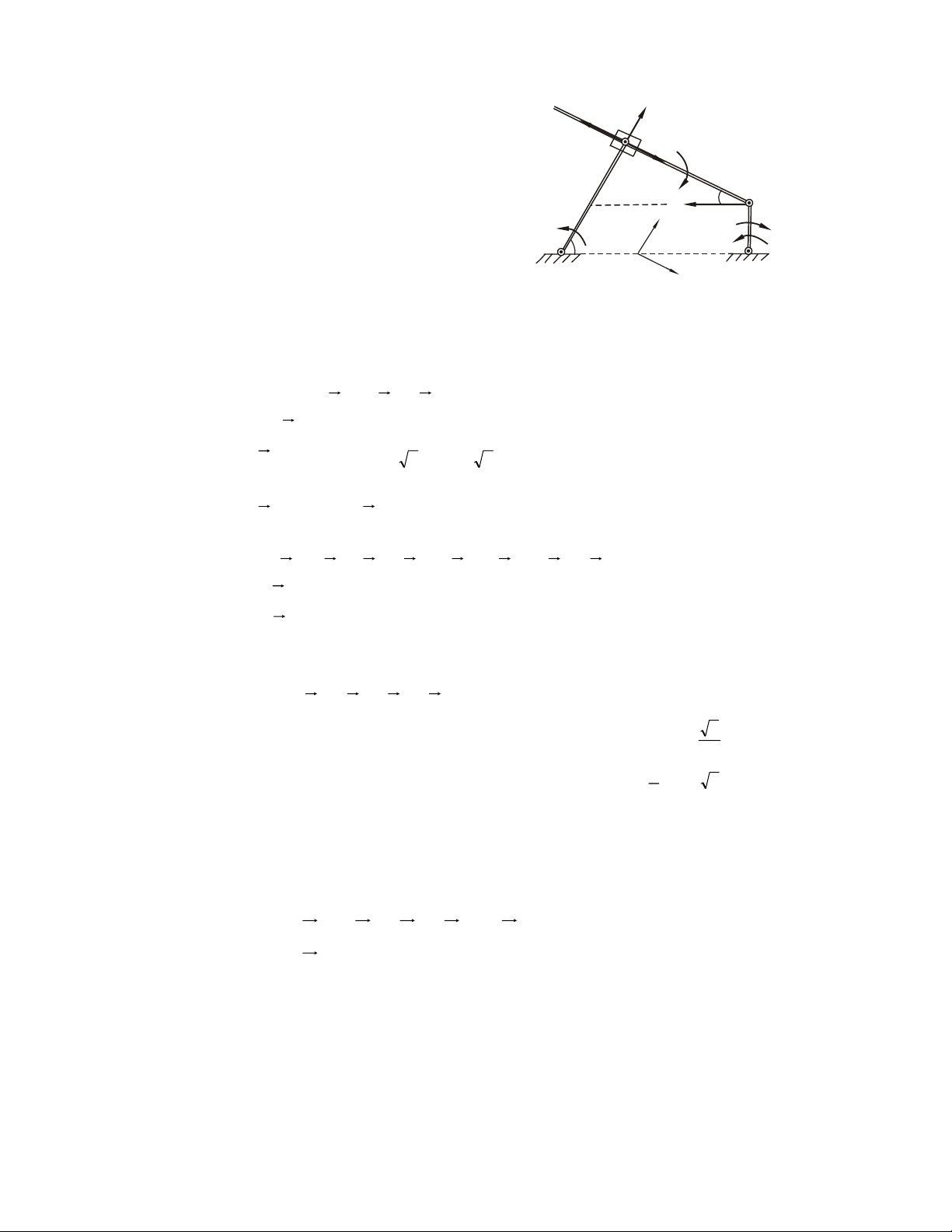
theå tröôït doïc CB. Cho bieát goùc )C = 30o; CB = 3R; OA = R, tìm Q ñeå cô caáu caân
baèng taïi vò trí ñang xeùt (H.2.22a). Xaùc ñònh phaûn löïc taïi O,C? x Q Q B B O M y M A O x A O A 30o Ox N C A 30o y 30o Cx a) b) Hình 2.22
Giaûi. Cô caáu goàm ba vaät raén: tay quay OA, con chaïy A, thanh CB.
Do khoâng caàn tính phaûn löïc giöõa choát baûn leà taïi A cuûa tay quay vaø con
chaïy chuùng ta hoùa raén, xeùt OA (bao goàm caû con chaïy) caân baèng. Vaät I:
• Xeùt hoùa raén OA vaø con chaïy A caân baèng
• Ñaët löïc: Khi boû lieân keát giöõa thanh CB vaø con chaïy A laø lieân keát töïa
(hai chieàu) chuùng ta ñöôïc heä löïc ϕ F ( 1 k ) ≡ , ngM ( Ox, Oy, NA) ≡ O N ( A ⊥ ) BC
• Phöông trình caân baèng: o 3 kx F Σ = Ox + NA cos 30 = Ox + NA = 0 (1) 2 1 Σ o ky
F = Oy − NA sin 30 = Oy − NA = 0 (2) 2 ΣmA F ( k) = M − O . R y = 0 (3) • Giaûi ñöôïc: M 3 M M 2 Ox = − ; O ; N R y = R A = R Vaät II:
• Töông töï xeùt thanh CB caân baèng. , ,
• Ñaët löïc: Heä löïc ⇒ ϕ2 F ( k ) ≡ , Q ( N A , Cx , Cy ) ≡ ( 0 NA = −NA )
• Phöông trình caân baèng o 3 kx F Σ
= Cx − NA cos 30 + Q = Cx − NA + Q = 0 (4) 2 1 Σ o ky F = Cy + NA sin 30 = Cy + NA = 0 (5) 2 Σm F ( C k ) = RN 2 − R 3 sin 60o Q . A = 0 (6) 35
• Giaûi heä ba phöông trình M 8 Q = ; M 3 M C M x = − Q = ; C = 3 R 3 R 3 3R y − R Nhaän xeùt: Khi M 8 Q =
cô caáu caân baèng, caùc thaønh phaàn phaûn löïc coù 3 R 3
giaù trò nhö ñaõ ñònh (vôùi Ox vaø Cy ñoåi chieàu).
Ví duï 2.12. Cho cô caáu chòu löïc vaø coù lieân keát nhö H.2.23a, caùc baùn kính töông
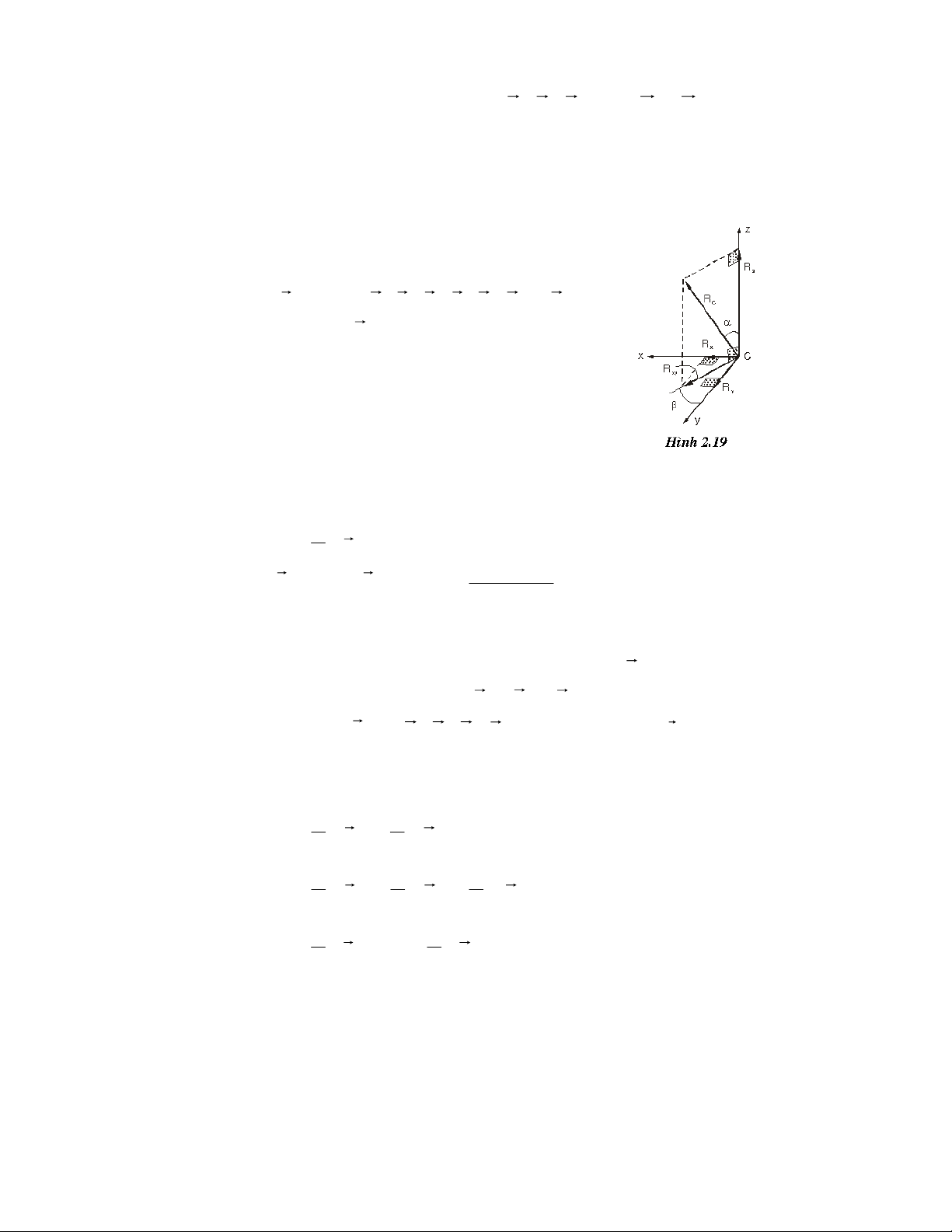
öùng R1 = 2.r1 = 2.R; OA = a = 1,5R. Hai baùnh raêng aên khôùp taïi I coù ñoä lôùn goùc raêng laø 2 ϕ .
Tìm ñieàu kieän cuûa P ñeå cô caáu caân baèng, xaùc ñònh phaûn löïc taïi O, O1 vaø löïc aên khôùp raêng. F O1y O O ϕ I 1 O ϕ 1 A O1x I N1 Q1 y Q P 1 P a) x c) F Oy Q N1 ϕ ϕ O A I Ox O1 O b) Q Hình 2.23 d) Hình 2.23
Giaûi. Cô caáu hai vaät raén caân baèng (taùch vaät). Vaät I:
• Xeùt baùnh raêng O caân baèng.
Do xu theá quay cuûa baùnh xe O vaø O1, phaûn löïc töïa taïi maët raêng I coù xu
theá caûn trôû söï quay cuûa caùc baùnh raêng ⇒ hai raêng tieáp xuùc ôû caùc maët phía treân
cuûa ñöôøng truïc OO1 (H.2.23 b,c, d). • Ñaët löïc: Heä löïc ⇒ ϕ F ( o k ) ≡ , F ( N1, Ox, Oy, ) Q ≡ 0
• Phöông trình caân baèng: kx F Σ = O + N sin ϕ x I = 0 Σ ky F = O + F − Q + N cos ϕ y I = 0 Σm r O F ( k) = aF − R cos ϕ 1 N . = 0 36 • Giaûi: O = − ϕ F 5 , 1 x Ftg 5 , 1 ; Oy =Q –2,5F; N = I cos ϕ Vaät II:
• Xeùt baùnh raêng O1 caân baèng. • Ñaët löïc: , 1 ϕ F ( k ) ≡ , P ( Q ,Q ,O 1 1x 1y , N1) ≡ 0
• Phöông trình caân baèng: kx F Σ = O − x 1 NI sin ϕ = 0 Σ ky F
= O1y − NI cos ϕ − Q1 = 0 Σm r 1O F ( k) = 1 r p − R1 cos ϕ N . I = 0
• Giaûi: O1x = 1,5 Ftg ϕ ; O1y = Q1 + 1,5F
vaø P = 3F ⇒ Ñaây chính laø ñieàu kieän caân baèng. 37 Chöông 3
CAÙC BAØI TOAÙN ÑAËC BIEÄT
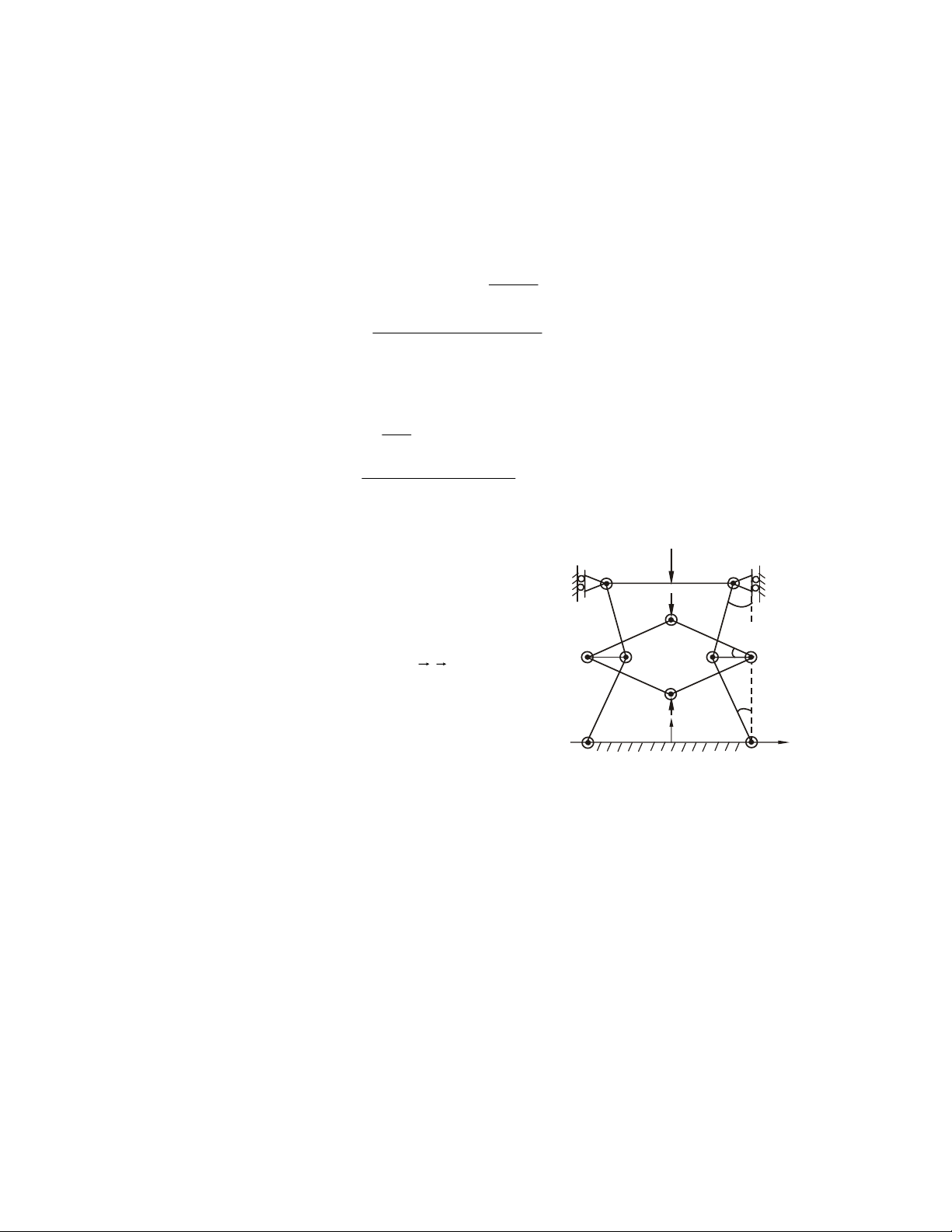
3.1. BAØI TOAÙN ÑOØN PHAÚNG
Trong caùc ví duï 2.11, 2.12 coù nhöõng vaät raén thuoäc cô caáu chæ coù theå quay
quanh moät truïc coá ñònh khi caùc löïc ngoaøi khoâng thoûa maõn moät yeâu caàu naøo ñoù.
Neáu chuù yù ñeán tính chaát naøy cuûa chuùng, ta coù theå tìm ñieàu kieän caân baèng moät caùch nhanh choùng hôn.
1. Ñònh nghóa ñoøn phaúng
Vaät raén coù theå quay quanh moät truïc coá ñònh qua O chòu taùc duïng cuûa heä
löïc naèm trong moät maët phaúng vuoâng goùc vôùi truïc quay ñöôïc goïi laø ñoøn phaúng:
ví duï caùc baùnh raêng O, O1 trong ví duï 5, thanh CB trong ví duï 4 laø nhöõng ñoøn phaúng.
2. Ñieàu kieän caân baèng cuûa ñoøn
Heä löïc taùc ñoäng vaøo ñoøn goàm caû phaûn löïc oå truïc. Phöông caân baèng khoâng
chöùa phaûn löïc oå truïc (Δo) chæ coù theå laø: ΣmΔ ) F ( = .
0 Ñaây chính laø ñieàu kieän caân o
baèng cuûa ñoøn phaúng (xem laïi ví duï 2.11 vaø 2.12). 3.2. BAØI TOAÙN GIAØN 1. Giaøn phaúng
1- Ñònh nghóa: Giaøn phaúng laø caáu truùc cöùng laøm baèng caùc thanh thaúng lieân keát
vôùi nhau baèng caùc khôùp baûn leà truï ôû hai ñaàu. Nhöõng thanh naøy ñeàu cuøng naèm
trong moät maët phaúng. Caùc ñieåm lieân keát cuûa giaøn ñöôïc goïi laø nuùt, taát caû taûi
troïng ngoaøi taùc ñoäng leân giaøn chæ ñaët taïi caùc nuùt.
2- Giaøn tónh ñònh: Do caùc thanh chæ lieân keát taïi hai ñaàu muùt, caùc thanh phaûi
ñöôïc lieân keát theo hình tam giaùc, khoâng coù thanh thöøa.
Goïi soá thanh cuûa giaøn laø k, soá nuùt laø n. Ba thanh ñaàu tieân seõ taïo thaønh
moät tam giaùc coù ba nuùt, muoán taïo theâm moät nuùt môùi caàn theâm hai thanh. Vaäy
moái lieân heä giöõa soá nuùt vaø soá thanh laø k = 2n – 3. Neáu soá thanh ít hôn, giaøn seõ
khoâng cöùng. Neáu soá thanh nhieàu hôn, giaøn seõ sieâu tónh.
3- Tính giaøn baèng phöông phaùp taùch nuùt
Tröôùc heát ta xeùt giaøn hoùa raén caân baèng ñeå xaùc ñònh caùc phaûn löïc goái, sau
ñoù xeùt caân baèng cuûa caùc nuùt. Do moãi nuùt cuûa giaøn chòu taùc duïng cuûa heä löïc ñoàng
quy phaúng, chæ coù hai phöông trình caân baèng ñoäc laäp, chuùng ta xuaát phaùt töø nuùt 38
coù hai öùng löïc aån vaø giaûi ñöôïc ngay caùc aån naøy. Sau ñoù cöù tieáp tuïc nhö vaäy cho
ñeán khi xaùc ñònh heát caùc öùng löïc aån trong giaøn.
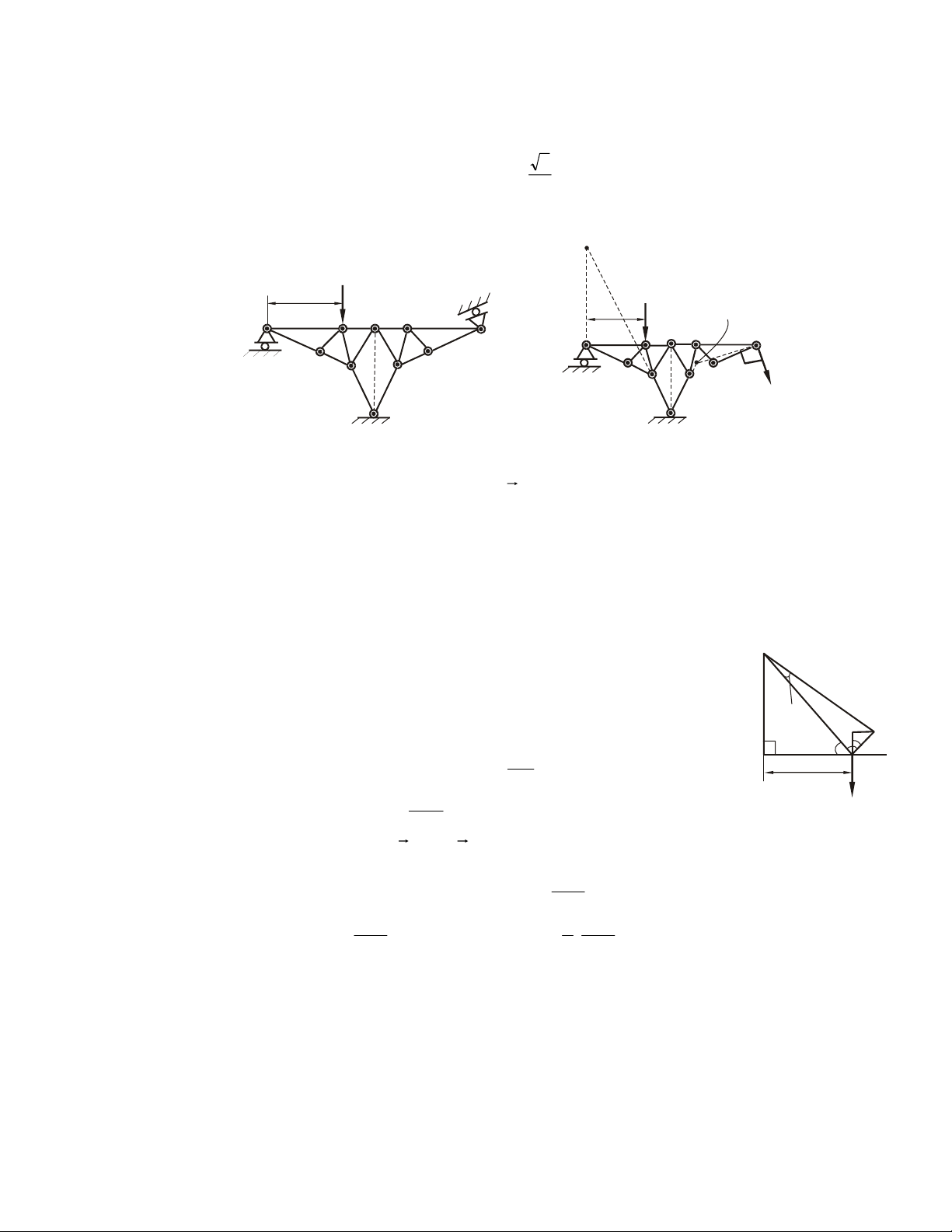
Ví duï 3.1. Cho giaøn chòu löïc ( F1, F2, F3, F4 ) nhö H.3.1.
Xaùc ñònh öùng löïc cuûa caùc thanh. F2 F2 C F3 4 C F3 30o F 5 60o 4 1 F4 F1 B D 3 D y 0 o 60o 6 3 5 F 7 6 0 o 6 3 4 6 0 o 7 1 2 60o A B 1 60o 2 A Bx E E B a a A Hình 3.1 Hình 3.2
Giaûi. • Xaùc ñònh phaûn löïc taïi goái A, B.
- Xeùt giaøn hoùa raén caân baèng, heä löïc taùc ñoäng nhö H.3.2: ϕ F ( k ) ≡ F
( 1, F2, F3, F4 , A, Bx, By ) ≡ 0 Phöông trình caân baèng: ΣF = F − cos 60o − F cos 60o + B = 0 kx 3 4 x
ΣF = A − F − F − F sin 60o − F sin 60o + B = 0 ky 1 2 3 4 y 3 m Σ r B F ( k) = − aA 2 + aF 2 1 + aF 5 , 1 2 + a F3 = 0 2 Giaûi ñöôïc: 3 3 F3 F F A 3 3 = 2 1 F + 2 F + 3 F ; B 4 = ; B = + F + F 4 4 x + 2 2 y 3 4 4 4 2
• Ñeå xaùc ñònh caùc öùng löïc thanh khi xaùt caùc nuùt vôùi öùng löïc chöa bieát ta
luoân giaû söû coù chieàu ñi ra khoûi nuùt (thanh chòu keùo).
- Xeùt nuùt A (H.3.3): Hai aån laø S1,S5 F1 S y 1 Heä löïc: ϕ F ( 1 k ) ≡ F ( 1, A, S1, S5) ≡ 0 x Phöông trình caân baèng 60o A S2 ΣF = S + S cos 60o = 0 kx 1 5 A Hình 3.3 ΣF = A − F + S sin 60o = 0 ky 1 5 Giaûi ñöôïc: 2 1 1 S = F ( − A) = − ( F 3 F ); 5 + S1 = ( F 3 2 + F3) 3 1 2 2 3 4 39 x
- Xeùt nuùt C (H.3.4): Hai aån laø S F2 4 , S6 Heä löïc: , ϕ C 2 F ( k ) ≡ F ( 2, S5, S4, S6) ≡ 0 60o o 30 y Phöông trình caân baèng: S S 5 4 ΣF
= F cos 60o + S + S cos 30o = 0 S kx 2 4 6 6 Hình 3.4 ΣFky = −S5 − F cos 30o 2 − S sin 30o 6 = 0 ⎛ ⎞ Giaûi ñöôïc: 2 F 3 3 S = ⎜− − ⎟ 4 = − − 3 F ; S 2 S F = F (thay S 2 2 6 5 2 3 ⎜ 2 ⎟ 5 keå caû daáu). ⎝ ⎠ - Xeùt nuùt D (H.3.5) F4 x Hai aån laø S S 3 , S7 4 Heä löïc: , ϕ y 3 F ( k ) ≡ F ( 3,S4 ,S3,S7 ) ≡ 0 D Phöông trình caân baèng: S3 F Σ S kx = S − 4 + S3 = 0 7 ΣF = −F − S = 0 ky 3 7 Hình 3.5 Giaûi ñöôïc: S = S = − ( 5 , 0 3F + F ) 3 4 3 2 S7 = − 3 F - Xeùt nuùt B (H.3.6)
Chæ coøn moät aån S2 (do chuùng ta ñaõ söû duïng By x
heä hoùa raén neân neáu xeùt taùch heát caùc vaät caân baèng F S 4 3
seõ toàn taïi caùc phöông trình phuï thuoäc. Coù theå söû y
duïng caùc phöông trình naøy ñeå kieåm tra keát quaû). 60 o S 30o 2 B x B Heä löïc: , ϕ F ( 4 k ) ≡ F ( 4 ,Bx ,By ,S3,S2) ≡ 0 Hình 3.6 Phöông trình caân baèng: ΣF
= B − F cos 60o − S cos 30o − S = 0 kx x 4 3 2 Giaûi ñöôïc: 3 5 S2 = 2 F + 3 F 4 4 Nhaän xeùt:
- Caùc thanh 1, 6, 2, coù öùng löïc > 0 ⇒ chòu keùo
- Caùc thanh 3, 4, 5, 7 coù öùng löïc < 0 ⇒ chòu neùn
4- Tính giaøn baèng phöông phaùp maët caét (Ritô)
Phöông phaùp naøy thöôøng duøng khi chæ caàn tính öùng löïc trong moät soá thanh caàn thieát.
Chuùng ta caét töôûng töôïng giaøn laøm hai phaàn sao cho laùt caét ñi qua caùc
thanh caàn tính öùng löïc (nhieàu nhaát laø ba thanh chöa bieát öùng löïc), sau ñoù xeùt caân 40
baèng cuûa moät phaàn thích hôïp. Laäp caùc phöông trình caân baèng thích hôïp nhaát ñeå
giaûi ra caùc öùng löïc caàn thieát.
Ví duï 3.2. Xeùt laïi ví duï tröôùc, ôû ñaây yeâu caàu: a) Tính S1, S6, S4. b) Tính S2, S7. F F2 2 m C F C 3 4 S4 60o D 60o 30o D F 5 30o By F 1 F 1 4 6 S 7 3 6 60o 60 o 1 60o 2 60o S A B A 1 B x E E a m a a a A A Hình 3.7 Hình 3.8
Giaûi. Tröôùc heát cuõng xaùc ñònh phaûn löïc caùc goái nhö ví duï treân: A, Bx, By.
a) Caét giaûn bôûi maët caét (m, m) nhö H.3.7. Xeùt phaàn traùi caân baèng H.3.8
- Heä löïc taùc duïng goàm caùc löïc F1,F2, A ñaõ bieát vaø ba öùng löïc thay theá
cho phaàn lieân keát beân phaûi cuûa giaøn ñaõ boû ñi laø S1, S4, S6.
- Phöông trình caân baèng: a a 3 Σm F ( C k ) = F − A + a S = 0 2 1 2 2 1 a a Σm F ( E k ) = aF − aA − S + F = 0 1 2 4 2 2 a 3 ΣmB F ( k) = aF 2 1 − aA 2 + aF 5 , 1 2 + S6 = 0 2
- Giaûi heä phöông trình naøy, trong moãi phöông trình chæ coù moät aån: 1 S = ( F 3 F ); F2 3 1 + S4 = − − F3; S = F 4 2 3 2 2 6 3
b) Caét töôûng töôïng giaøn bôûi maët caét n-n ñi qua ba thanh 4, 7, 2 (H.3.9). C n F3 S4 60o D 30o By F S 4 7 60o A Bx E n S2 B a a Hình 3.9
c) Xeùt phaàn beân phaûi caân baèng:
- Heä löïc: ( F3, F4, Bx, By , S4, S7, S2 ) ≡ 0 41 - Hai aån: S2,S7
- Phöông trình caân baèng: a 3 a 3 ΣmB F ( k) = − F3 − S7 = 0 2 2 a 3 a 3 a 3 a 3 m Σ r D F ( k) = − Bx + By − F4 − S2 = 0 4 4 2 4
- Giaûi töøng phöông trình: ⎛ 3 ⎞ ⎜EB = , a ⇒ BD = a ⎟ S ⎜ 2 ⎟ 7 = – F3; ⎜ o 3 o 3 ⎟ ⎜BH = .
BD cos 30 = a , DH = BD sin = a ⎟ ⎝ 4 4 ⎠
5- Phöông phaùp tónh ñoà (ñoà thò)
Giaøn phaúng caân baèng ⇔ caùc nuùt thuoäc giaøn caân baèng, heä löïc taùc duïng
vaøo töøng nuùt laø heä löïc ñoàng quy, heä löïc ñoàng quy caân baèng chæ caàn R = 0 ⇔ ña
giaùc löïc cuûa heä löïc ñoùng kín.
Phöông phaùp tónh ñoà ñöôïc thöïc hieän nhö sau:
Xeùt nuùt cuûa giaøn coù khoâng quaù hai öùng löïc aån (ñaõ bieát phöông). Choïn moät
ñieåm goác xaùc ñònh vaø ñaët lieân tieáp taát caû caùc löïc ñaõ bieát taùc duïng vaøo nuùt theo
quy taéc coäng vector. Töø ñieåm goác ta keû moät tia song song vôùi phöông cuûa moät
trong hai öùng löïc aån, töø ñieåm ngoïn cuûa vector löïc (ñaõ bieát) cuoái cuøng ta keû song
song vôùi öùng löïc aån coøn laïi, hai tia caét nhau taïo moät ña giaùc. Döïa treân ña giaùc
ñoù ta xaùc ñònh hai vector öùng löïc aån.
(Taát caû ñöôïc veõ theo moät tæ leä xích sao cho phuø hôïp, chaúng haïn 1 cm ⇔ 1 KN)
Ví duï 3.3. Cho giaøn phaúng nhö H.3.10. Xaùc ñònh öùng löïc caùc thanh.
Bieát: F1 = 10; F2 = F3 = 6 (KN); a = 2 m. F1
Giaûi. Ñeå toàn taïi nuùt chöùa hai aån, chuùng ta
xaùc ñònh phaûn löïc taïi caùc goái A, B baèng A a II a B 2
caùch xeùt giaøn hoùa raén caân baèng. Taïi A coù 6 a 3 a 7
hai thaønh phaàn phaûn löïc. Taïi B do thanh 1 a 5 a a
BC lieân keát thanh neân phaûn löïc taïi B chæ I 4 III
coù thaønh phaàn theo phöông BC. Heä löïc: C F2 F3 ϕ F ( k ) ≡ F ( 1,F2,F3, A x , A y , ) B ≡ 0 Hình 3.10 42
- Phöông trình caân baèng: A F B y 1 F Σ x k = A x = 0 Ax ΣF = −F − F − F + A + B = 0 a II a A B k y 1 2 3 y 2 6 m Σ r A = aF − 1 + aB 2 − F 5 , 1 3 − aF 5 , 0 2 = 0 a 3 a 7 1 a 5 a
- Giaûi heä phöông trình: a A I 4
x = 0; Ay = F1 + F2 + F3 – B = 11 III B = 0,5 (F F 1 + 0,5F2 + 1,5F3) = 11 2 F3
1- Xaùc ñònh hai öùng löïc S1, S2 taïi Hình 3.11
nuùt A: Taùch nuùt A nhö H.3.12a Ay
Hai thanh 1 vaø 2 chöa ñaët löïc, töø N
moät ñieåm M veõ löïc A y keû tia song song S A 1
vôùi thanh 1, töø ñieåm goùc keû tia song song y 2
vôùi thanh 2, chuùng caét nhau taïi L. Theo 60o A M L
quy taéc ñoùng kín ña giaùc löïc ta coù chieàu 60o S2 S 1 a) b)
1 vaø S 2 nhö hình veõ. Ño ñoä daøi NL ta tính ñöôïc S Hình 3.12
1 theo tæ leä xích, ño ñoä daøi LM ta tính ñöôïc S2.
Nhìn vaøo nuùt A ôû H.3.12a so vôùi H.12b: 3
S1 ñi ra : thanh 1 chòu keùo, L S 4 E
S2 ñi vaøo : thanh 2 chòu neùn. 60o S 60o S 1 3 2- Xeùt nuùt I (H. 3.13) 60o 4 I S 1 F Caùc löïc ñaõ bieát F 2 2 , S1 vaø hai aån S N 3 , S4 F2
- Veõ rieâng nuùt I xuaát phaùt töø ñieåm Hình 3.13
M döïng hai löïc ñaõ bieát F2, S1 noái tieáp
S3 = EM ñi vaøo nuùt I (neùn)
S4 = LE ñi ra nuùt I (keùo) 3- Xeùt nuùt II (H.3.14) F Q 1 M S S5 Coù ba löïc ñaõ bieát S II 6 1 F ,S2,S3 vaø hai 2 F P 1 aån S 6 5 , S6 . S S
- Veõ rieâng nuùt II xuaát phaùt töø M: 2 S 3 3 5 N L S5 = PQ (neùn) Hình 3.14 S6 = QM (neùn) 4- Tính
S7 , ta chæ caàn xeùt nuùt B (H3.15) Hai löïc ñaõ bieát S , B 6 vaø moät aån S7 43 LM = S 7 (keùo) B L
6. Phöông phaùp Maxoen - Cremona N
Chuùng ta coù theå tính giaøn baèng caùch 6 S o B
goäp taát caû bieåu ñoà caùc nuùt treân moät bieåu ñoà B
chung theo nguyeân taéc sau:
1- Xaùc ñònh phaûn löïc caùc goái (baèng 7 M Hình 3.15 caùch hoùa raén giaøn)
2- Bieåu dieãn taát caû caùc löïc ñaõ bieát ra phaàn bieân cuûa giaøn (tröôït löïc). Kí
hieäu caùc vuøng naèm giöõa caùc löïc giöõa caùc thanh giaøn baèng caùc chöõ in A, B, C ...
3- Döïng ña giaùc löïc (xuaát phaùt töø nuùt hai aån) cuûa caùc löïc ñaõ bieát theo thöù
töï chieàu quay cuûa kim ñoàng hoà (ña giaùc ñoùng kín) theo moät tæ leä xích ñaõ choïn,
nuùt A. Quy öôùc goác vaø ngoïn cuûa löïc treân ña giaùc laø caùc chöõ thöôøng töông öùng
naèm hai beân löïc ngoaøi bieân cuûa giaøn cuõng theo chieàu kim ñoàng hoà quay. Ta thu
ñöôïc ña giaùc abcdl vôùi ñöôøng ñaäm neùt.
4- Döïng theâm caùc ña giaùc löïc kín cho töøng nuùt giaøn. Baét ñaàu töø nuùt hai aån
kín xuaát phaùt töø löïc ñaõ bieát (cuõng theo thöù töï chieàu quay cuûa kim ñoàng hoà), goác
vaø ngoïn cuûa öùng löïc thanh töông öùng laø caùc chöõ caùi hai beân thanh theo quy öôùc
quay cuøng chieàu kim ñoàng hoà quanh nuùt ñoù.
Ví duï 3.4. Xeùt laïi ví duï 3.3 ôû treân.
- Xuaát phaùt töø löïc ñaõ bieát A ta veõ ñöôïc ña giaùc löïc ñoùng kín abcdea ñoùng
kín (ñoaïn thaúng) cuûa caùc löïc taùc duïng vaøo giaøn hoùa raén.
- Nuùt I: Döïng ña giaùc löïc cho nuùt I coù hai aån. Xuaát phaùt töø löïc ñaõ bieát A ⇔ ab
. Ña giaùc cuûa caùc löïc aån abg. Caùc ñænh cuõng ñaët theo quy taéc thöù töï cuøng
chieàu quay kim ñoàng hoà qua nuùt I. d A F1 B g b I B II C A III B 2 6 f e 1 G 3 H 7 5 D A F V 4 IV c h a F2 E F3 a) b) Hình 3.16 Nhö vaäy: S1 = ga S
, 2 = bg (goác vaø ngoïn vector laø hai chöõ thöôøng töông
öùng hai beân cuûa löïc theo thöù töï chieàu quay cuøng chieàu kim ñoàng hoà nuùt I).
- Nuùt V: Xuaát phaùt töø hai löïc ñaõ bieát F2 1 S ,
ta nhaän ñöôïc ñöôøng gaáp khuùc
eag (theo quy taéc laáy hai chöõ caùi hai beân löïc theo cuøng chieàu quay cuûa kim ñoàng 44
hoà quanh nuùt laø goác vaø ngoïn. Theo phöông phaùp quen thuoäc ta veõ ñöôïc ña giaùc eagfe: S3 = gf; S4 = fe
- Nuùt IV: Hai löïc ñaõ bieát F3 S
, 4 ñöôïc bieåu dieãn qua def töông töï ta nhaän
ñöôïc ña giaùc defhd: S5 = fh ; S7 = hd
- Coøn moãi aån S6. Nhìn leân H.3.16 theo quy taéc chung ñaáy laø ñoaïn ch neáu xeùt nuùt II. 2. Giaøn khoâng gian
Caùc thanh cuûa giaøn phaân boá trong khoâng gian. Ñeå xaùc ñònh öùng löïc trong
caùc thanh chuùng ta duøng phöông phaùp taùch nuùt.
Ví duï 3.5. Cho giaøn khoâng gian ñöôïc taïo bôûi naêm thanh nhö H.3.17. Taïi nuùt I
chòu taùc duïng cuûa löïc P naèm trong maët phaúng thaúng ñöùng (ñi qua hai thanh 3 vaø 6) vaø nghieâng 45o so z P vôùi phöông thaúng 45o ñöùng. Bieát caùc maët I 3 II phaúng chöùa caùc y thanh 1, 2 vaø caùc 1 4 x thanh 4, 5 cuøng thaúng 45o 45o 6 ñöùng, vaø cuøng vuoâng 2 5 goùc vôùi maët phaúng 45o chöùa caùc thanh 3, 6. 45o Tính öùng löïc caùc thanh. 45o Hình 3.17
Giaûi. Heä caân baèng laø
giaøn khoâng gian coù saùu aån öùng löïc.
Xeùt söï caân baèng cuûa hai nuùt I vaø II ñeå xaùc ñònh caùc öùng löïc. 1-
Xeùt nuùt I caân baèng (H.3.18): Ñaët löïc ϕ F ( r 1 k ) ≡ , p ( S1, S2, S3) ≡ 0
- Xaùc ñònh hình chieáu caùc löïc: r 2 2 , 0 ( p , p − ); p 2 2 S2( S2 0, , − S2) 2 2 2 2 2 2 S1(− S1 0, , − S1); S3 , 0 ( S3 ) 0 , 2 2
- Phöông trình caân baèng: 2 2 F Σ kx = 0 − S1 + S2 + 0 = 0 2 2 2 Σ ky F = p + 0 + 0 + S3 = 0 2 45 2 2 2 Σ kz F = − p − 1 S − S2 = 0 2 2 2 Giaûi ñöôïc: S p 2 1 = S2 = − ; S3 = − p 2 2 z P 45o II S3 y I S3 y S4 S S 6 1 45o S5 45o S2 x 45o 45o 45o Hình 3.19 Hình 3.18 2-
Xeùt nuùt II caân baèng (H.3.19). Ñaët löïc: ′ ϕ F ( 2 k ) ≡ S
( 3, S4, S5, S6) ≡ 0
- Xaùc ñònh hình chieáu caùc löïc: ′ S 2 2 3 , 0 ( − S ); 0 , 3 S5( S 0, , − S ) 2 5 2 5 2 2 2 2 S4 (− S4 0, , − S4); S6 , 0 ( S6 ,− S6) 2 2 2 2
- Phöông trình caân baèng: 2 2 Σ kx F = 0 − S4 + S5 = 0 2 2 2 Σ ky F = − S 3 + 0 + S6 = 0 2 2 2 2 Σ kz F = 0 − S4 − S5 − S6 = 0 2 2 2 Giaûi ñöôïc: S p 1 = S2 = + ; S 2 6 = – p
Nhaän xeùt: Caùc thanh 1, 2, 3, 6 chòu neùn, caùc thanh 4, 5 chòu keùo 46 Chöông 4 MA SAÙT Noäi dung
- Boå sung moâ hình phaûn löïc lieân keát cho phuø hôïp vôùi thöïc tieãn.
- Thieát laäp ñieàu kieän caân baèng cuûa vaät khaûo saùt khi coù keå ñeán ma saùt. Yeâu caàu
- Naém vöõng moâ hình phaûn löïc khi coù ma saùt.
- Thieát laäp ñöôïc ñieàu kieän caân baèng phuø hôïp vôùi khaû naêng chuyeån ñoäng
cuûa vaät khaûo saùt ñeå giaûi caùc baøi toaùn trong kyõ thuaät.
4.1. MA SAÙT, CAÙC LÖÏC MA SAÙT VAØ TÍNH CHAÁT CUÛA CHUÙNG 1. Ma saùt
1- Hieän töôïng hai vaät töïa leân nhau, caûn trôû chuyeån ñoäng hay xu höôùng
chuyeån ñoäng töông ñoái cuûa vaät naøy treân beà maët cuûa vaät kia ôû choã tieáp xuùc ñöôïc goïi laø ma saùt.
2- Nhöõng löïc xuaát hieän do ma saùt giöõa hai vaät ñöôïc goïi laø löïc ma saùt.
3- Tuøy theo tính chaát giöõa hai beà maët tieáp xuùc vaø traïng thaùi töông ñoái
giöõa hai vaät, ngöôøi ta chia ma saùt thaønh caùc loaïi:
- Ma saùt khoâ: beà maët giöõa hai vaät töông taùc tröïc tieáp vôùi nhau.
- Ma saùt nhôùt: giöõa hai beà maët töông taùc cuûa hai vaät coù moät lôùp moûng chaát boâi trôn.
- Ma saùt tónh: hai beà maët töông taùc ñöùng yeân töông ñoái vôùi nhau (vaät khaûo
saùt ñöùng yeân so vôùi maët töïa).
- Ma saùt ñoäng: hai beà maët töông taùc chuyeån ñoäng töông ñoái vôùi nhau (vaät
khaûo saùt chuyeån ñoäng treân maët töïa).
2. Caùc löïc ma saùt vaø tính chaát cuûa chuùng
1- Moâ hình phaûn löïc lieân keát coù keå ñeán ma saùt
Treân thöïc teá, vaät khaûo saùt tieáp xuùc vôùi maët töïa treân moät mieàn naøo ñoù (voâ
soá ñieåm). Taïi moät ñieåm töïa coù moät thaønh phaàn phaûn löïc. 47
Thay theá cho mieàn lieân keát töïa laø moät heä caùc phaûn löïc ϕ F ( k ). Duøng lyù
thuyeát thu goïn veà moät ñieåm A treân maët töïa: , ϕ F
( k ) ≡ (RA , MA ), (xem H.4.1b) Chuùng ta phaân tích ,
RA vaø MA theo caùc phöông thích hôïp ñeå lyù giaûi khaû
naêng caûn trôû chuyeån ñoäng cuûa noù (H.4.1.c): , (RA , MA ) ≡ ( , N Fm, Mx, Ml ) M M x A MA N S S R’ S A R’A mieàn töïa A ñieåm töïa A F π π m π M1 a) b) b) c)c) Hình 4.1 Hình 4.1
2- Caùc ñònh nghóa -
Mx cuøng phöông phaùp tuyeán chung goïi laø moâmen ma saùt xoay (caûn vaät xoay). -
Ml naèm trong maët phaúng tieáp tuyeán chung goïi laø ma saùt laên (caûn vaät laên). -
N theo phöông phaùp tuyeán chung laø thaønh phaàn phaùp tuyeán quen thuoäc. -
Fm naèm trong maët phaúng tieáp tuyeán chung goïi laø löïc ma saùt tröôït (caûn
vaät tröôït treân maët töïa).
3- Tính chaát cuûa löïc ma saùt, ñònh luaät Coulomb
- Caùc löïc ma saùt hoaøn toaøn tuaân theo caùc tính chaát cuûa phaûn löïc lieân keát.
- Thöïc nghieäm chöùng toû caùc löïc ma saùt coøn tuaân theo ñònh luaät sau ñaây: Ma saùt tónh Fm ≤ ; fN Mx ≤ k1 ; N M ≤ k (4.1) l 2N
trong ñoù: f, k1, k2 - laø caùc heä soá ma saùt tröôït, xoay vaø laên tónh.
ÔÛ traïng thaùi tôùi haïn saép xaûy ra chuyeån ñoäng, caùc quan heä treân trôû thaønh ñaúng thöùc. Ma saùt ñoäng ' F f N; ' M k N M = k' (4.2) m = ; x = N 1 l 2 trong ñoù: f, ' '
k1, k2 - laø caùc heä soá ma saùt tröôït, xoay vaø laên ñoäng.
Taát caû caùc heä soá naøy ñeàu ñöôïc tìm töø thöïc nghieäm, chuùng chæ phuï thuoäc
tính chaát cuûa beà maët tieáp xuùc, khoâng phuï thuoäc dieän tích tieáp xuùc. 48
Trong caùc baøi toaùn thöïc teá thöôøng xaûy ra, vaät khaûo saùt coù moät soá khaû
naêng chuyeån ñoäng chuû yeáu noåi baät hôn caùc khaû naêng khaùc, cho neân cuõng chæ coù
vaøi loaïi ma saùt ñoùng vai troø quan troïng trong töøng baøi toaùn cuï theå.
Sau ñaây ta xeùt moät soá baøi toaùn ñieån hình.
4.2. BAØI TOAÙN CAÂN BAÈNG CUÛA VAÄT RAÉN CHÆ KEÅ ÑEÁN MA SAÙT TRÖÔÏT
1. Moâ hình baøi toaùn F F k ms2 Vaät raén S caân baèng: N2
- Heä löïc caân baèng: ϕ F ( A k, Fmi, N ) 2 i N1
(bao goàm caû caùc thaønh phaàn ma saùt).
- Ñieàu kieän khoâng tröôït A F 1 ms1 F1 ≤ f iNI i( = ) 2 , 1 Xu höôùng tröôït Hình 4.2
2. Phöông phaùp giaûi
1- Söû duïng ñieàu kieän caân baèng giaûi tích
Duøng ñieàu kieän caân baèng cuûa heä löïc vaø ñieàu kieän khoâng tröôït, chuùng ta
thu ñöôïc moät heä hoãn hôïp goàm caùc phöông trình vaø baát phöông trình. Nghieäm thu
ñöôïc töø heä naøy seõ laø caùc baát ñaúng thöùc neân vaät khaûo saùt coù moät mieàn caân baèng
(khoâng phaûi moät vò trí nhö tröôùc).
Sau khi tìm ñöôïc mieàn caân baèng, chuùng ta môùi giaûi caùc phaûn löïc aån.
Trong nhieàu tröôøng hôïp, chuùng ta khaûo saùt vaät raén caân baèng ôû traïng thaùi
tôùi haïn (saép tröôït). Luùc naøy (Fi = fiNi) ñieàu kieän n
caân baèng cuûa vaät raén laø moät heä phöông trình. N
Nghieäm nhaän ñöôïc laø moät giaù trò bieân cuûa mieàn R
caân baèng, (chuùng ta) vaøo thöïc teá ñeå suy ra mieàn N * R * caân baèng.
2- Ñieàu kieän caân baèng hình hoïc α ϕ
Ñaët phaûn löïc töïa toång hôïp laø R ≡ F ( m, ) N
Goïi goùc nghieâng giöõa R vaø phaùp tuyeán nr laø α . Do: F A m ≤ fN
neân tg α taêng, khaû naêng tröôït F F F* m taêng → goùc α m m π taêng theo. Hình 4.3
ÔÛ traïng thaùi tôùi haïn, vector phaûn löïc toång * hôïp * R taïo vôùi nr goùc F
ϕ (phöông thay ñoåi trong khoâng gian) vaø: tg ϕ = m = f N*
Ñieàu kieän khoâng tröôït (caân baèng): α ≤ . ϕ 49
Hình noùn coù ñænh laø ñieåm töïa, truïc laø phaùp tuyeán nr (ra khoûi maët töïa), goùc
ôû ñænh 2 ϕ goïi laø noùn ma saùt.
Chuùng ta coù ñieàu kieän caân baèng:
- Phaûn löïc toaøn phaàn R naèm trong noùn ma saùt - Khi
R naèm treân bieân cuûa noùn ma saùt, vaät ôû traïng thaùi tôùi haïn 3. Caùc ví duï
Ví duï 4.1. Taûi A troïng löôïng Q ñaët treân N x
maët nghieâng nhö hình veõ. Bieát heä soá ma Fms
saùt tröôït giöõa A maët phaúng nghieâng laø f. A
Tìm ñieàu kieän cuûa goùc nghieâng α ñeå taûi Xu höôùng tröôït caân baèng. α Q
Giaûi. Giaû söû taûi A ñang caân baèng öùng
vôùi goùc nghieâng α nhö H4.4. Hình 4.4 Hình 4.4
- Heä löïc ñaët vaøo A: ϕ F ( k ) ≡ , Q ( NA , Fm ) ≡ 0
- Phöông trình caân baèng: F = F − Q sin α = 0 ∑ kx m (1) F = N − Q cos α = 0 ∑ ky A (2)
Ñieàu kieän khoâng tröôït: m F ≤ fN A (3)
- Giaûi heä phöông trình: Fm = Qsin ; α NA = Qcos α (3)
⇒ Q sinα ≤ f Q cosα ⇒ tgα ≤ f
Ñaët f = tg ϕ ⇒ ñieàu kieän caân baèng: t α g ≤ t ϕ g ⇔ α ≤ ϕ
Töø keát quaû treân, chuùng ta coù theå suy ra phöông phaùp xaùc ñònh heä soá ma
saùt tröôït baèng thöïc nghieäm: taêng goùc α töø töø khi A baét ñaàu chuyeån ñoäng, tang
cuûa goùc nghieâng taïi vò trí ñoù baèng heä soá ma saùt tröôït.
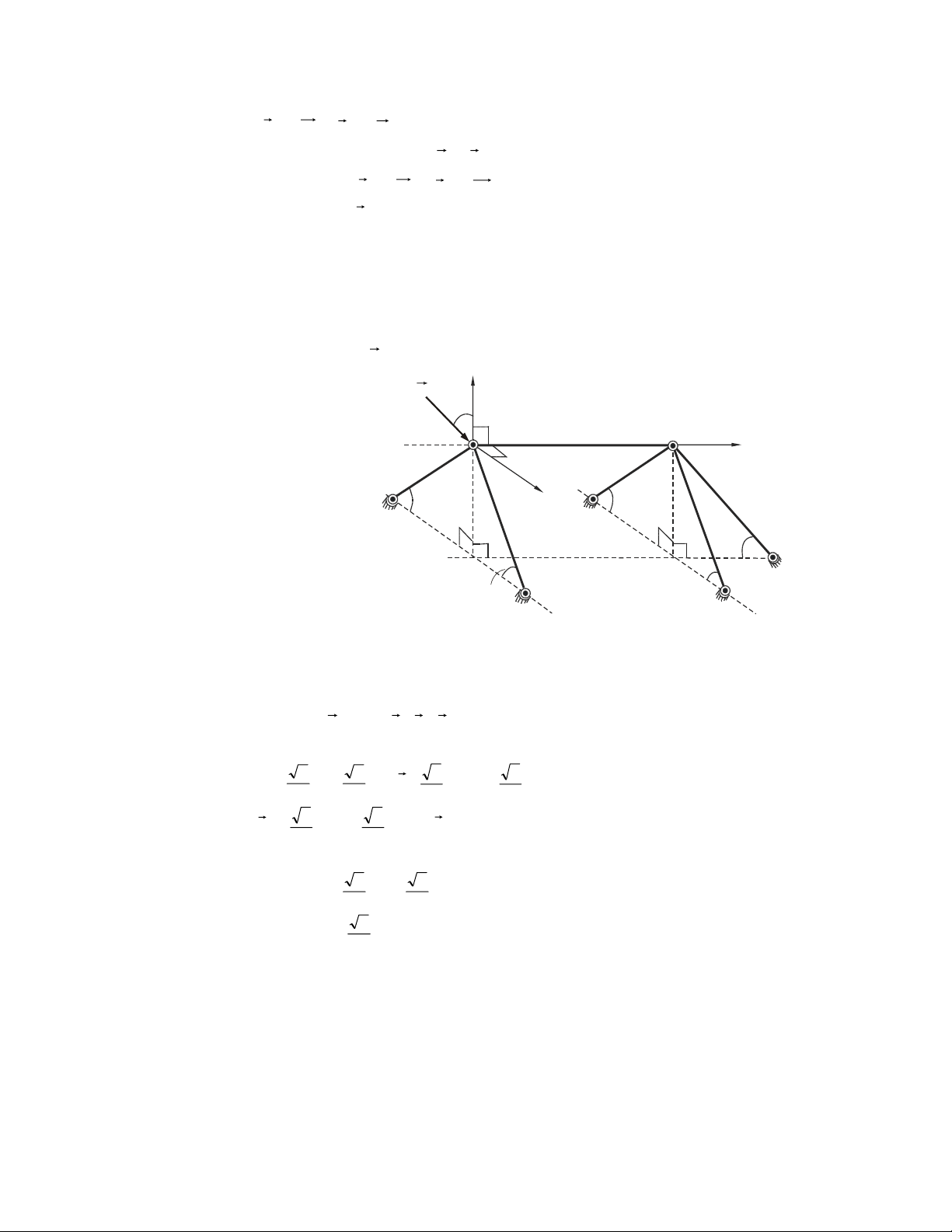
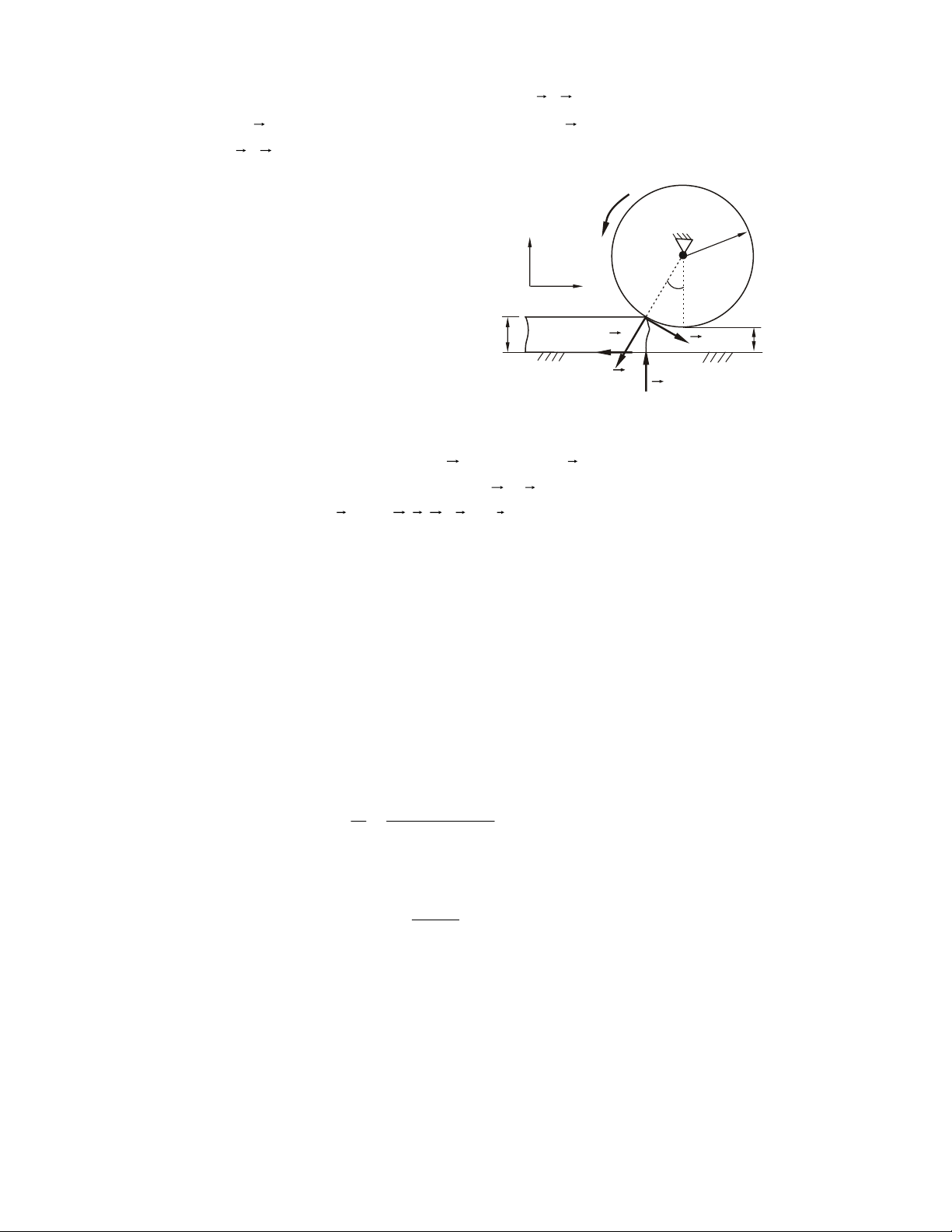
Ví duï 4.2. Boû qua troïng löôïng cuûa thang. Xaùc ñònh vôùi giaù trò naøo cuûa α, moät
ngöôøi coù theå treøo ñeán taän ñænh thang (H.4.5). Cho bieát goùc ma saùt tröôït giöõa
thang vôùi saøn vaø töôøng laø α . o
Giaûi. Xeùt thang caân baèng taïi vò trí giôùi haïn nhö H.4.5. Goïi troïng löôïng cuûa ngöôøi laø P. Chuù
yù: Vaät töïa taïi hai ñieåm A, B, traïng thaùi saép tröôït taïi caùc ñieåm coù theå
tôùi khoâng cuøng luùc, nhöng vaät saép tröôït hai ñieåm töïa ñeàu ôû traïng thaùi tôùi haïn.
Heä löïc taùc ñoäng (RA , RB,P) ≡ 0 ⇒ Heä löïc phaûi ñoàng quy taïi I.
Neáu ngöôøi dòch chuyeån xuoáng phía A, ñieåm ñoàng quy I seõ dòch chuyeån
theo chieàu döông truïc x, vector phaûn löïc toaøn phaàn taïi A ñi qua ñieåm ñoàng quy 50
seõ taïo vôùi phöông phaùp tuyeán goùc nhoû hôn goùc αo ⇒ baûo ñaûm khoâng tröôït taïi A.
Khi ngöôøi dòch chuyeån leân phía treân, ñieåm ñoàng quy I seõ dòch chuyeån
ngöôïc chieàu truïc x, phaûn löïc toaøn phaàn taïi A coù goùc nghieâng vôùi phöông phaùp
tuyeán taêng theo, ñaït cöïc trò khi ngöôøi ñöùng taïi B, luùc naøy ñieåm ñoàng quy seõ y y dθ/2 DN RB I dF dθ/2 ϕ T + dT x ο B A B dθ T α α θ ϕ ο RA O P Q P x A Hình 4 Hình 4.5 .5 Hình 4.6
truøng vôùi ñieåm B, phaûn löïc toaøn phaàn taïi A ñi qua B, goùc α = ϕ . o
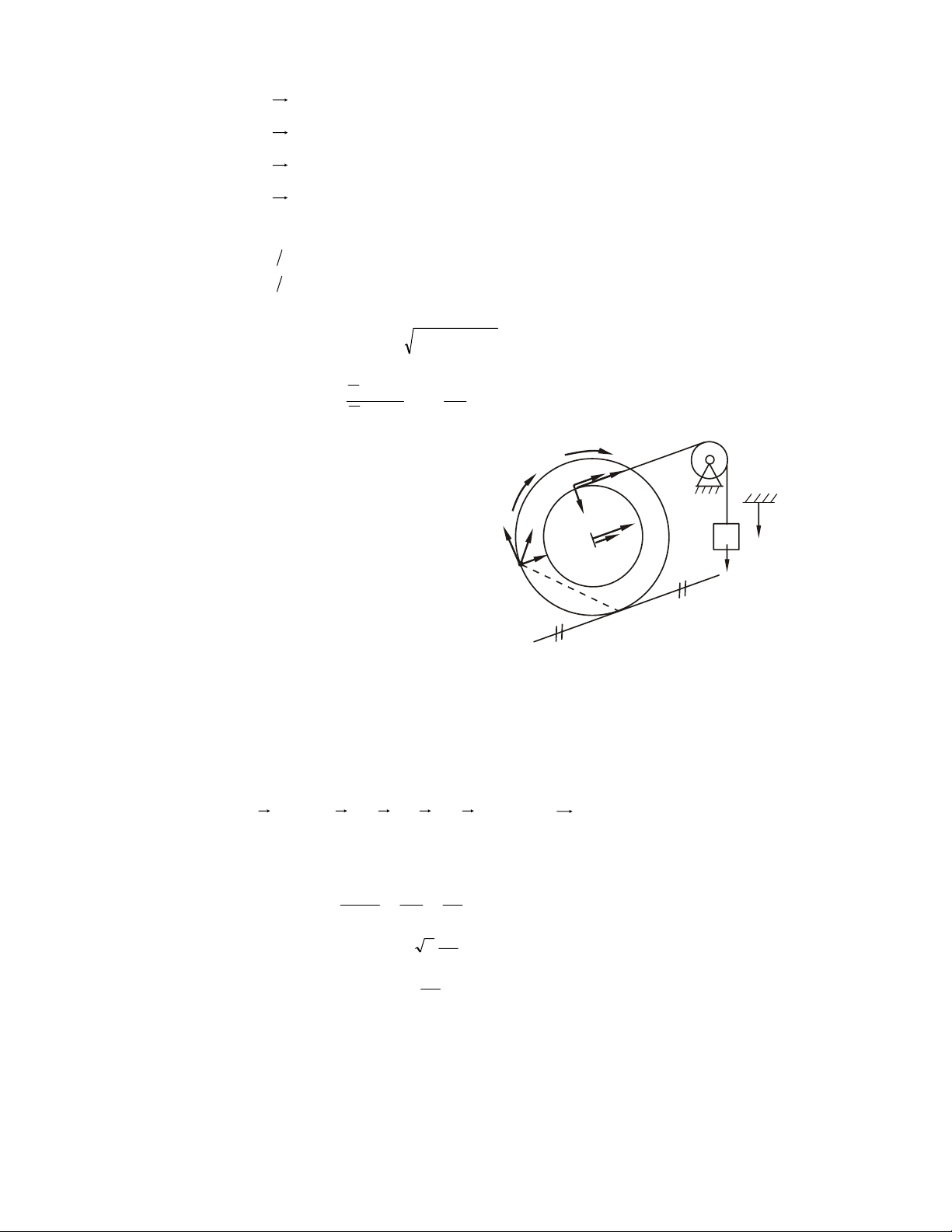
Ví duï 4.3. Daây meàm oâm truï troøn coá ñònh nhö H4.6. Löïc P ñaët vaøo moät ñaàu daây.
Bieát heä soá ma saùt tröôït giöõa daây vaø truïc laø f. Tìm löïc Q nhoû nhaát ñaët vaøo ñaàu
daây kia ñeå daây caân baèng (khoâng tröôït).
Giaûi. Giaû söû goùc oâm cuûa daây laø α vaø löïc Q toái thieåu seõ laøm daây caân baèng tôùi
haïn (saép tröôït theo chieàu löïc ). P
Caét töôûng töôïng moät phaân toá daây voâ cuøng beù AB (töông öùng vôùi goùc d ). θ
Heä löïc taùc ñoäng vaøo phaân toá AB laø: ϕ F ( k ) ≡ ( , T T + d , T d , N d ) F ≡ 0
{d N laø phaûn löïc phaùp, d F laø phaûn löïc tieáp}
- Phöông trình caân baèng: dθ dθ F = dF + T cos − (T + ) dT cos = 0 ∑ kx 2 2 dθ dθ F = dN − T sin − (T + ) dT sin = 0 ∑ ky 2 2
Boû qua voâ cuøng beù baäc hai, chuùng ta nhaän ñöôïc: dF = dT (1) dN = Td θ (2) 51
Ñieàu kieän saép tröôït: dF = fdN (3) P α
Töø heä phöông trình dT dT P ⇒ = θ fd ⇒ = θ fd ⇔ ln = fα T ∫ T ∫ Q Q 0 hay: Q = Pe–f α
Ñaây laø giaù trò nhoû nhaát cuûa Q ñeå daây khoâng bò löïc P keùo tröôït leân truïc.
Chuùng ta tính moät soá giaù trò cuï theå trong tröôøng hôïp daây gai vaø goã (f = 0,5). α Q/P α Q/P π 0,208 3π 0,009 π 2 0,043 4π 0,002
Qua baûng treân ta thaáy khi quaán daây hai voøng ( α = 4π ), neáu löïc P = 10000 N, chæ caàn Q = 20 N.
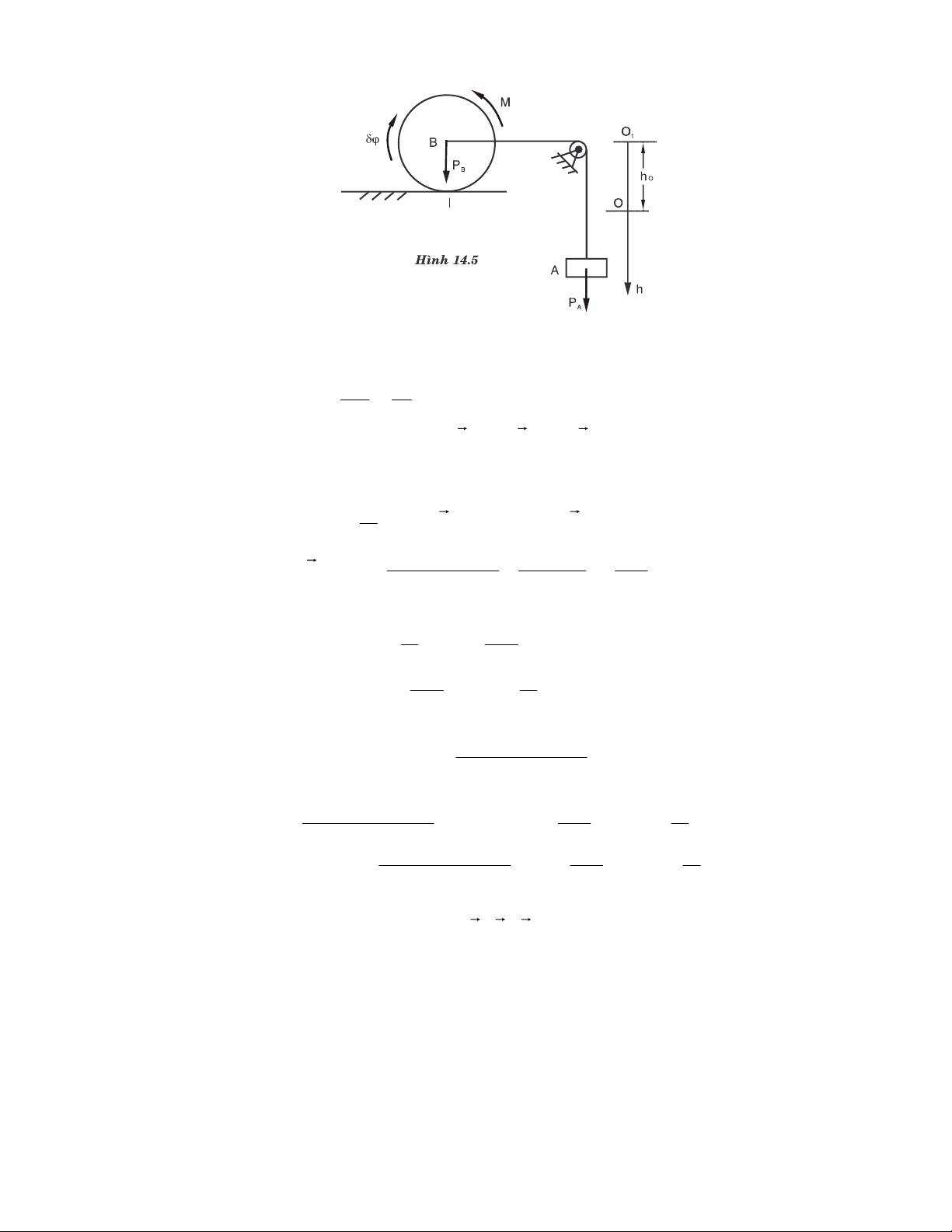
Ví duï 4.4. Giaù treo ma saùt nhö H.4.7. Tìm vò trí an toaøn cuûa taûi troïng khi treo
vaøo giaù ñeå giaù khoâng bò tröôït xuoáng. Bieát heä soá ma saùt tröôït giöõa giaù vaø truï laø f,
boû qua troïng löôïng cuûa giaù.
Giaûi. Xeùt giaù treo ôû traïng thaùi caân baèng tôùi haïn vôùi taûi troïng P ôû vò trí nhö H.4.7. - Ñaët löïc: ϕ F ( k ) ≡ , P ( NA ,FA , NB,FB ) ≡ 0
- Phöông trình caân baèng: F = N − N = 0 ∑ kx A B F = F + F − P = 0 ∑ ky B A m = hN ∑ r A − rF 2 B − x ( − P ) r = 0 A
Ñieàu kieän khoâng tröôït: FB = fNB; FA = fNA
- Giaûi heä naêm phöông trình ta y ñöôïc: F x A = FB = P/ 2 FB
Thay keát quaû vaøo phöông trình NB B RA x
moâmen, chuùng ta nhaän ñöôïc: x = h h O f 2 A NA r
Ñaây laø vò trí cuûa bieân mieàn caân FA
baèng. Keát hôïp thöïc teá, khi taûi treo coù toïa P
ñoä x > h/2f giaù seõ caân baèng. Hình 4.7
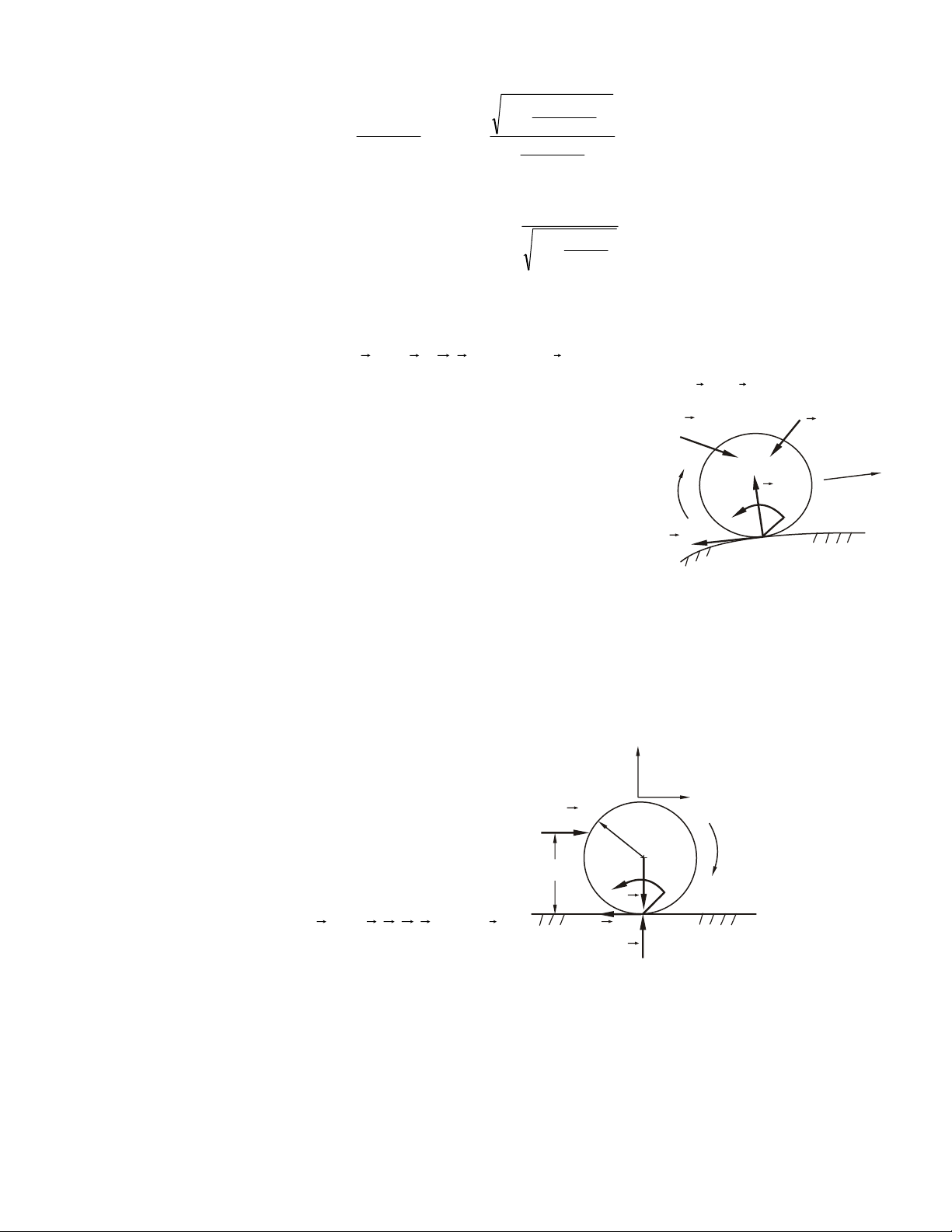
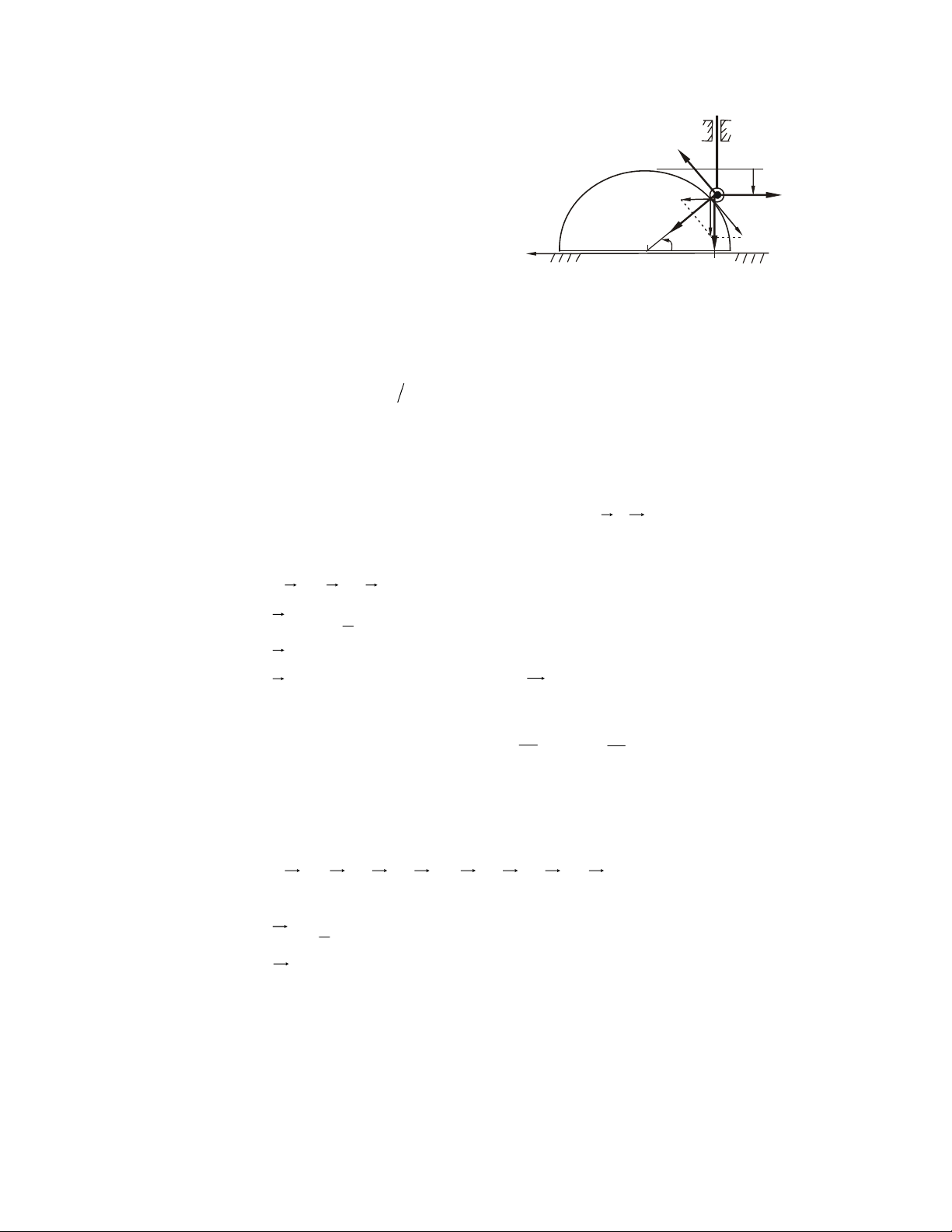
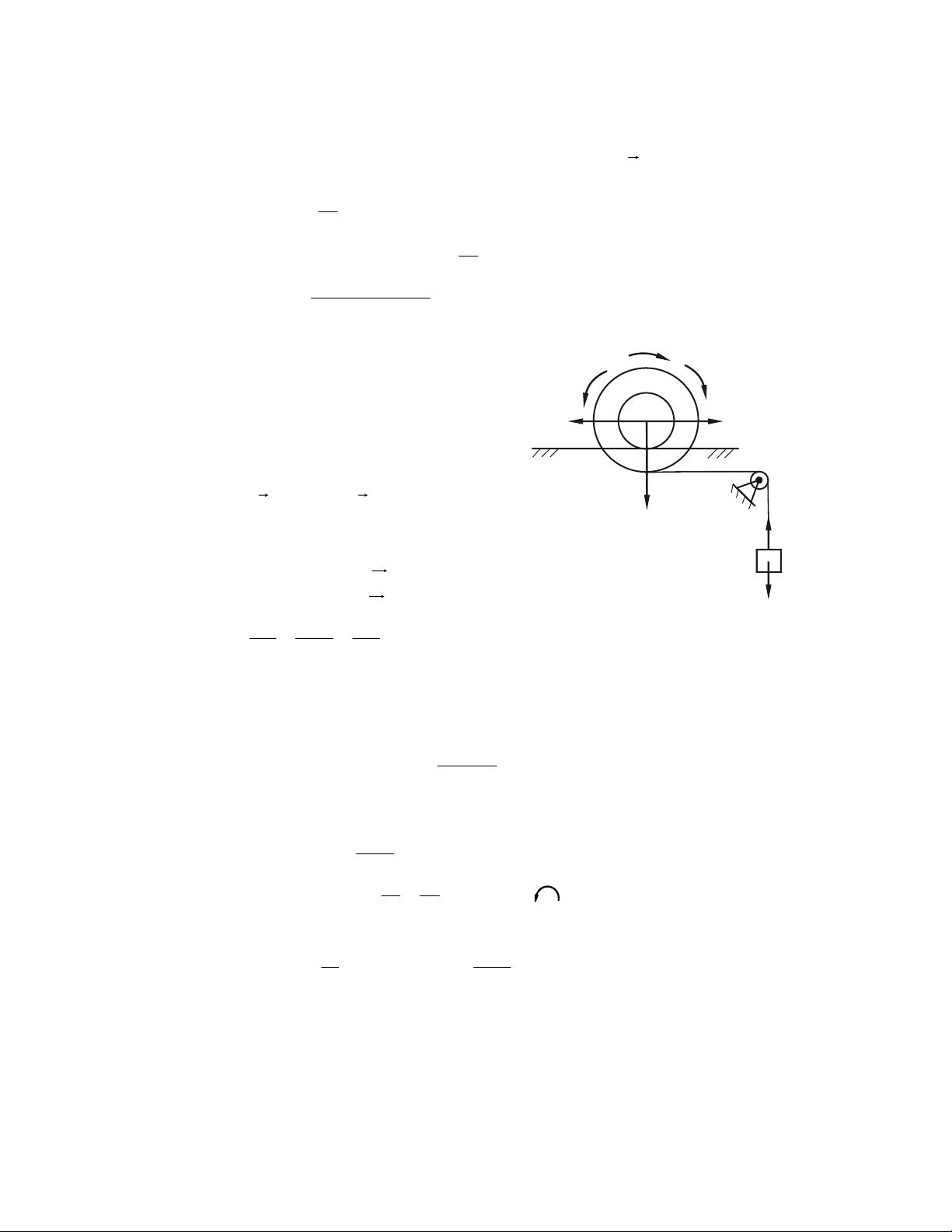
Ví duï 4.5. Cho truïc tôøi nhö H4.8.
Tìm ñieàu kieän cuûa ngaãu M ñeå tôøi caân baèng. Bieát heä soá ma saùt tröôït taïi oå truïc laø f. 52
Giaûi. Khaû naêng chuyeån ñoäng cuûa truïc tôøi coù theå theo hai chieàu:
- Neáu M ñuû lôùn, truïc tôøi quay ngöôïc chieàu kim ñoàng hoà;
- Neáu M ñuû nhoû, truïc tôøi seõ quay thuaän chieàu kim ñoàng hoà.
Xeùt truïc tôøi ôû traïng thaùi caân baèng tôùi haïn saép quay theo chieàu ngöôïc
chieàu kim ñoàng hoà. Ñieåm töïa cuûa truïc leân oå y
truïc khoâng theå ôû vò trí thaáp nhaát (taïi vò trí naøy M
khoâng coù thaønh phaàn löïc naøo ñeå caân baèng F
vôùi löïc ma saùt) maø phaûi dòch chuyeån veà phía Ν beân traùi I nhö H.4.8. O x
- Ñaët löïc: taûi troïng Q, troïng löïc P cuûa I
truïc tôøi, ngaãu M, löïc ma saùt F, phaûn löïc phaùp ϕ N. ϕ F ( k ) ≡ , Q ( , P , M , F ) N
Phöông trình caân baèng (baùn kính vaønh Q Hình 4.8
trong vaø ngoaøi cuûa truïc tôøi töông öùng laø r, R): F = N sin ϕ − F cos ϕ 0 ∑ kx =
F = N cos ϕ + F sin ϕ − P − Q 0 ∑ ky = m = M − rQ 2 − rF 0 ∑ r o =
Ñieàu kieän saép tröôït: F = fN
- Giaûi heä phöông trình, chuùng ta nhaän ñöôïc: tg
ϕ = f (töùc goùc ϕ laø goùc ma saùt) F = (P + Q) sin ϕ M = QR + (P + Q)rsin ϕ
Giaù trò M ôû treân laøm cho truïc caân baèng tôùi haïn saép quay theo chieàu ngöôïc
chieàu kim ñoàng hoà. Vôùi: M < QR + (Q + P)rsin ,
ϕ tôøi khoâng theå quay theo chieàu
ngöôïc chieàu kim ñoàng hoà.
- Töông töï, xeùt tröôøng hôïp tôøi saép quay theo chieàu kim ñoàng hoà. Vò trí tieáp
xuùc cuûa truïc vaø oå truïc taïi H, löïc ma saùt ñoåi chieàu. Chuùng ta seõ tìm ñöôïc ñieàu
kieän ñeå truïc tôøi khoâng quay theo chieàu kim ñoàng hoà laø: M > QR – (Q + P)rsin ϕ
Keát hôïp, chuùng ta coù ñieàu kieän caân baèng:
QR – (Q + P)rsin ϕ < M < QR + (Q + R)rsin ϕ
Chuù yù: Coù theå tìm ñieàu kieän caân baèng hình hoïc, sau ñoù suy ra ñieàu kieän cuûa M. 53
Taïi vò trí caân baèng tôùi haïn, heä löïc goàm , Q , P
ngaãu M vaø phaûn löïc toaøn
phaàn RI phaûi caân baèng. Ñieàu kieän caân baèng cuûa RI phaûi coù phöông thaúng ñöùng do Q , P
ñeàu thaúng ñöùng. Suy ra tg ϕ = f.
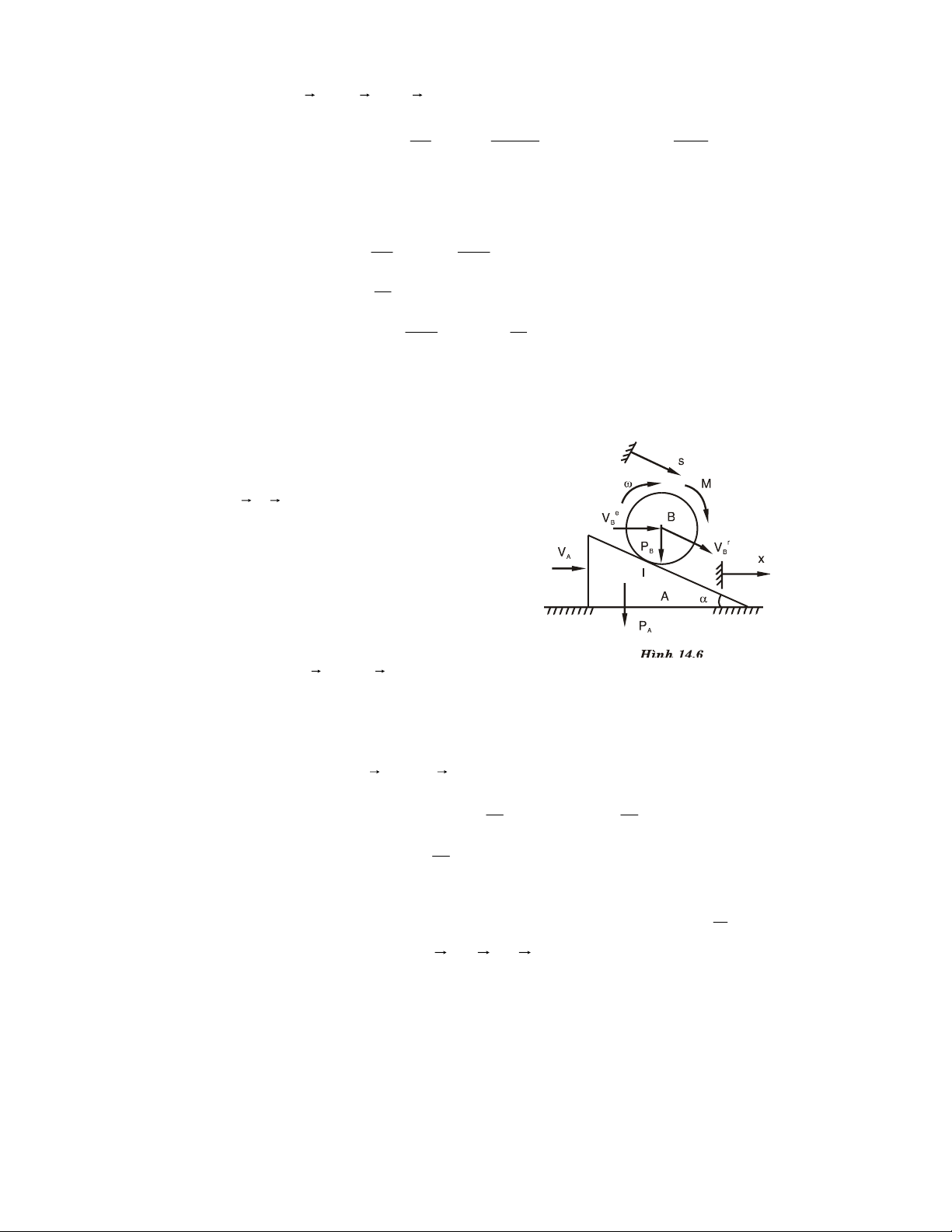
Ví duï 4.6. Truïc caùn nhö H.4.9. M
Heä soá ma saùt giöõa truïc vaø vaät
caùn laø f, giöõa vaät caùn vaø maët ngang R y laø f O 1.
Tìm ñoä daøy cuûa vaät caùn ñeå truïc x α
coù theå laøm vieäc ñöôïc (vaät caùn bò keùo I H theo cuøng truïc). d a
Giaûi. Ñeå truïc caùn laøm vieäc ñöôïc, vaät A F1 F
caùn baét ñaàu tieáp xuùc vôùi truïc caùn taïi I N
phaûi thoûa maõn khoâng tröôït taïi I, saép N1 Hình 4.9 tröôït treân neàn ngang. - Ñaët löïc:
Phaûn löïc taïi I: phaùp tuyeán N ; ma saùt tröôït F .
Töông töï, phaûn löïc taïi neàn goàm: N1 ; F1 (boû qua troïng löôïng vaät). ⇒ ϕ F ( k ) ≡ , N ( , F N1, F1) ≡ 0
- Phöông trình caân baèng:
F = −N sin α + F cos α − F = 0 ∑ kx 1 (1) F
= −N cos α − F sin α + N = 0 ∑ ky 1 (2)
Ñieàu kieän saép tröôït ôû neàn ngang: F1 = f1N1 (3)
Ñieàu kieän chöa tröôït taïi I : F ≤ fN (4)
- Giaûi heä phöông trình: (1) ⇒ F = F cos α − N sin α 1 (2) ⇒ N = 1 N cos α + F sin α Duøng (3) ⇒ F cos α − N sin α = f 1N cos α + f1F sin α ⇔ (cos F α − f1 sin ) α = f ( N 1 cos α + sin ) α F f cos α + sin 1 α ⇒ = ≤ f N cos α − f sin 1 α Duøng (4) ⇒ f cos α + sin α ≤ f cos α − ff sin α 1 1 ⇒ f ( f + ) 1 sin α ≤ f ( − f ) cos α 1 1 (ñieàu kieän: f > f1) f − f ⇒ tg 1 α ≤ (*) ff + 1 1
Goïi ñoä daøy cuûa taám laø d, khoaûng caùch töø taâm O ñeán saøn ngang laø R + a, ta tính ñöôïc: 54 ⎛ R + a − d 2 1 − ⎟⎞ ⎜ R + a − d ⎝ R cos α = ⇒ tg ⎠ α = R R + a − d R ⎛ ⎞ ⎜ ⎟
Duøng (*) ta nhaän ñöôïc: ⎜ 1 ⎟ d ≤ a + ⎜ R 1 − ⎟ . ⎛ f − f1 ⎞ ⎜⎜ 1 + ⎜ ⎟ ⎟⎟ ⎝ ⎝ ff + 1 1 ⎠ ⎠
4.3. MOÂ HÌNH BAØI TOAÙN CAÂN BAÈNG COÙ KEÅ ÑEÁN MA SAÙT LAÊN
1. Moâ hình baøi toaùn vaø phöông phaùp giaûi
1- Vaät raén S caân baèng chòu taùc duïng cuûa heä löïc: ϕ ) F ( ≡ F ( k , , N Fm, ngM ) ≡ 0 l
2- Phöông trình caân baèng: laäp caùc phöông trình caân baèng töø ( ϕ Fk ) ≡ 0
3- Caùc ñieàu kieän (ma saùt): Fn Fk
- Khoâng tröôït : Fm ≤ fN Xu hö ô n g t röôt - Khoâng laên : M ≤ kN Xu l höôùng N S
4- Bieän luaän caùc khaû naêng: M laên l
- Ñieàu kieän vaät khoâng laên vaø Fms khoâng tröôït Hình 4.10
- Ñieàu kieän vaät khôûi ñoäng laên khoâng tröôït
- Ñieàu kieän vaät khôûi ñoäng tröôït khoâng laên. 2. Caùc ví duï
Ví duï 4.7. Con laên ñoàng chaát baùn kính R, troïng löôïng P chòu taùc duïng cuûa löïc Q
nhö H.4.11. Bieát heä soá ma saùt tröôït vaø laên giöõa con laên vaø maët ñöôøng töông öùng
laø f, k. Tìm giaù trò cuûa Q ñeå con laên caân baèng.
Giaûi. Trong caùc baøi toaùn loaïi naøy, ta y
khoâng aùp duïng ñöôïc heä phöông trình caân
baèng tôùi haïn chung, bôûi vì caùc ñieàu kieän x
laên vaø tröôït laø ñoäc laäp, khoâng baét buoäc Q Xu
cuøng ñaït tôùi ñieàu kieän tôùi haïn. R höôùng O
- Vaät khaûo saùt: con laên. laên h M - Ñaët löïc: P ϕ F ( I k ) = , P ( , Q , N Fm , ) M ≡ 0 Fm N
- Phöông trình caân baèng: F = Q − F = 0 ∑ kx m Hình 4.11 55 F = N − P 0 ∑ ky = m = M − Qh = 0 ∑ r 1
Giaûi heä phöông trình: giaûi ba phöông trình ñaàu chuùng ta nhaän ñöôïc: N = P; Fm = Q; M = Qh
⇒ khoâng tröôït : Q ≤ fP ⇒ khoâng laên : Qh ≤ kP ⇔ Q ≤ Pk / h
- Ñeå con laên caân baèng (khoâng laên, khoâng tröôït): Q k ≤ f min( , ) P h
Chuù yù: Giaû söû k < f, chuùng ta coù caùc tröôøng hôïp: h k Q <
≤ f : vaät khôûi ñoäng laên khoâng tröôït h p k Q < f <
: vaät khôûi ñoäng vöøa tröôït vöøa laên. h p
Ví duï 4.8. Cuõng con laên treân nhöng chòu löïc Q ñaët ôû taâm O vaø ngaãu M nhö hình
veõ. Tìm ñieàu kieän ñeå con laên coù theå laên khoâng tröôït.
Giaûi. - Khaûo saùt con laên caân baèng ôû traïng thaùi saép laên theo chieàu cuûa ngaãu M.
- Ñaët löïc: do khaû naêng chuyeån ñoäng nhö treân ta xaùc ñònh heä löïc nhö H4.12 Choïn ϕ F ( M R k ) = , P ( , Q , N , F , ngM ) m ≡ 0 xu Q O y höôùng
- Phöông trình caân baèng: m laên F = F Q ∑ x P kx − = 0 I F F = N P ∑ ky − = 0 Hình 4.12 N m = m − M + RQ ∑ r = 0 I
- Ñieàu kieän khoâng tröôït : F ≤ fN
- Coù theå laên ñöôïc (saép laên: tôùi haïn) : m = kN - Giaûi heä hoãn hôïp : F = Q; N = P; m = M – RQ
Thay vaøo hai ñieàu kieän sau:
- Khoâng tröôït : Q ≤ fP (1)
- Saép laên (tôùi haïn) : M – RQ = kP ⇔ M = RQ + kP (2)
Keát hôïp (1) vaø (2) ta coù ñieàu kieän saép laên khoâng tröôït: 56 RQ + kP = M ≤ (Rf + k)P
Khi taêng M ñieàu kieän bò phaù vôõ ⇒ con laên seõ laên.
⇒ Ñieàu kieän ñeå con laên khôûi ñoäng laên ñöôïc theo chieàu khoâng tröôït laø: RQ + Kp < M Chuù
yù: Khi con laên ñaõ laên, ñieàu kieän caân baèng tónh khoâng coøn baûo ñaûm,
caùc phöông trình caân baèng khoâng duøng ñöôïc.
Neáu goïi k1 laø heä soá caûn laên ñoäng, ñieàu kieän laên khoâng tröôït laø: RQ + kP < M < 1 f R 3 ( P + k 2 P ) RQ 2 1 −
(tham khaûo keát quaû ví duï 12.14).
Tröôøng hôïp aûnh höôûng quay cuûa Q lôùn hôn cuûa M, xu höôùng laên cuûa con laên seõ theo chieàu
Heä löïc taùc ñoäng vaøo laên (töï do) chæ coù duy nhaát ngaãu ma saùt ñoåi chieàu.
Töông töï chuùng ta nhaän ñöôïc:
- Ñieàu kieän khoâng tröôït: Q ≤ f P - Ñieàu kieän saép laên: M = RQ – kP
Keát hôïp, chuùng ta ñöôïc ñieàu kieän laên khoâng tröôït theo chieàu M < RQ – kP (**)
Keát luaän: - Khi M thoûa (*), con laên khôûi ñoäng laên khoâng tröôït veà beân phaûi
- Khi M thoûa (**), con laên khôûi ñoäng laên khoâng tröôït veà beân traùi 57 Chöông 5 TROÏNG TAÂM 5.1. CAÙC ÑÒNH NGHÓA
1. Taâm cuûa caùc löïc song song A
Khaùi nieäm veà taâm cuûa caùc löïc z 2 C1
song song ñöôïc ñeà caäp ñeán khi giaûi moät F2
soá baøi toaùn cô hoïc, ñaëc bieät laø khi xaùc A F’ 1 2 C2
ñònh troïng taâm cuûa caùc vaät. F1 C F’
Xeùt heä löïc song song vaø cuøng 1 An z chieàu F c
1, F2, ... Fn taùc duïng leân vaät theå A3 F’ Fn taïi caùc ñieåm A n 1, A2, ..., An (H.5.1), ta O F3 x y
thaáy raèng heä löïc naøy coù hôïp löïc R cuøng F’ c 3 y R
chieàu vôùi caùc löïc thaønh phaàn vaø coù trò c x R’ soá: Hình 5.1 R = ∑ kF (5.1)
Neáu ta xoay taát caû caùc löïc cuûa heä cuøng moät goùc vaø theo moät chieàu thì ta
seõ ñöôïc nhöõng heä löïc môùi song song cuøng chieàu, coù cuøng trò soá vaø ñieåm ñaët,
nhöng khaùc chieàu so vôùi heä cuõ (ví duï caùc ñöôøng chaám chaám treân H.5.1). Hôïp
löïc cuûa töøng heä löïc song song naøy roõ raøng coù cuøng trò soá R, nhöng coù ñöôøng taùc
duïng khaùc. Muoán tìm ñöôøng taùc duïng naøy, moãi laàn ta phaûi xaùc ñònh ñieåm naøo ñoù
maø ñöôøng naøy ñi qua. Ta chöùng minh raèng, trong taát caû caùc laàn quay nhö theá,
ñöôøng taùc duïng cuûa hôïp löïc bao giôø cuõng ñi qua cuøng moät ñieåm C. Thöïc vaäy,
ñaàu tieân coäng caùc löïc F1 vaø F2, ta thaáy trong moïi caùch quay löïc, hôïp löïc R1 cuûa
chuùng (khoâng veõ treân hình) bao giôø cuõng ñi qua ñieåm C1 naèm treân ñöôøng thaúng
A1A2 vaø thoûa maõn ñaúng thöùc F1.A1C1 = F2.A2C1, vì khi quay löïc, caû vò trí cuûa
ñöôøng thaúng A1A2 laãn ñaúng thöùc naøy ñeàu khoâng ñoåi. Coäng löïc R1 vôùi F3 ta ñöôïc
hôïp löïc cuûa chuùng, ñoàng thôøi cuõng laø hôïp löïc cuûa caùc löïc F1, F2, F3, seõ bao giôø
cuõng ñi qua ñieåm C2 naèm treân ñöôøng thaúng C1A3.... Tieáp tuïc pheùp coäng ñoù cho 58
tôùi vector cuoái cuøng, ta thaáy hôïp löïc R cuûa heä löïc ñeàu ñi qua cuøng moät ñieåm C
coù vò trí khoâng ñoåi ñoái vôùi caùc ñieåm A1, A2, ..., An (töùc laø ñoái vôùi vaät raén).
Ñieåm C coá ñònh thuoäc ñöôøng taùc duïng cuûa hôïp löïc cuûa heä löïc song song,
khi quay taát caû caùc löïc thuoäc heä chung quanh ñieåm ñaët töông öùng cuøng moät
chieàu vôùi cuøng moät goùc quay, goïi laø taâm cuûa caùc löïc song song.
2. Xaùc ñònh taâm cuûa caùc löïc song song
Ta tìm toïa ñoä taâm cuûa caùc löïc song song. Xaây döïng Oxyz laø heä truïc toïa ñoä
Decaster (H.5.1), goïi toïa ñoä cuûa caùc ñieåm trong heä truïc ñoù laø A1(x1, y1, z1),
A2(x2, y2, z2), ..., C(xc, yc, zc). Bieát raèng vò trí cuûa ñieåm C khoâng phuï thuoäc vaøo
chieàu cuûa caùc löïc, neân ñaàu tieân ta xoay caùc löïc quanh ñieåm ñaët sao cho chuùng
song song vôùi truïc Oz roài aùp duïng ñònh lyù Varinhoâng ñoái vôùi caùc löïc ' ' ' 1 F , 2 F n F ..., ,
vöøa xoay. Vì R’ laø hôïp löïc cuûa heä löïc ñoù, ta ñöôïc: m (R') = m F ( ' ) y ∑ y k (5.2)
Nhöng töø (H.5.1), ta thaáy raèng my(R’) = Rxc, vì R’ = R
Cuõng töông töï nhö vaäy m ' y F ( '1) = F1x1, vì F F ... 1 = 1
Thay caùc ñaïi löôïng ñoù vaøo ñaúng thöùc (5.2), ta coù:
Rxc = F1x1 + F2x2 + ... + Fnxn töø ñaây suy ra: F x + F x + ... + F x F x ∑ x k k 1 1 2 2 n n c = = R R
Ñoái vôùi toïa ñoä yc ta cuõng coù coâng thöùc töông töï nhö vaäy (laáy moâmen ñoái
vôùi truïc Ox). Ñeå xaùc ñònh zc ta laïi xoay taát caû caùc löïc song song vôùi truïc Oy vaø
aùp duïng ñònh lyù Varinhoâng, laáy caùc moâmen ñoái vôùi truïc Ox cho caùc löïc (ñöôïc
bieåu dieãn baèng caùc ñöôøng chaám gaïch). ta ñöôïc:
– Rzc = – F1z1 + (–F2z2) + ... + (–Fnzn)
Töø ñaây ta seõ tìm ñöôïc zc.
Keát quaû laø ta seõ coù caùc coâng thöùc sau ñaây xaùc ñònh caùc toïa ñoä cuûa taâm heä löïc song song: F ∑ kx F ∑ ky F ∑ kz x k = ; c y k = ; z k = (5.3) R c R c R
trong ñoù: R - xaùc ñònh theo ñaúng thöùc (5.1).
Ta thaáy raèng caùc coâng thöùc (5.1) vaø (5.3) cuõng ñuùng cho taát caû caùc löïc
song song coù chieàu khaùc nhau, neáu xem Fx nhö caùc ñaïi löôïng ñaïi soá (theo chieàu
naøy ta laáy daáu döông, theo chieàu kia ta laáy daáu aâm) vaø neáu R ≠ 0.
3. Troïng taâm cuûa vaät raén
Caùc vaät ôû gaàn maët ñaát ñeàu chòu taùc duïng cuûa löïc höôùng thaúng töø treân
xuoáng döôùi goïi laø troïng löïc. 59
Ñoái vôùi caùc vaät coù kích thöôùc raát nhoû so vôùi baùn kính traùi ñaát, thì coù theå
xem caùc troïng löïc taùc duïng leân caùc phaân toá cuûa vaät nhö caùc löïc song song vaø coù
giaù trò khoâng ñoåi ñoái vôùi töøng phaân toá khi vaät xoay.
Hôïp löïc cuûa caùc troïng löïc p1, p2, ..., pn taùc duïng leân caùc phaân toá cuûa vaät
ñöôïc kyù hieäu laø P (H.5.2). Trò soá cuûa löïc naøy baèng troïng löôïng cuûa vaät vaø ñöôïc
xaùc ñònh theo ñaúng thöùc: P = ∑ k P
Duø vaät quay theá naøo, caùc löïc pk vaãn giöõ z
nguyeân caùc ñieåm ñaët treân vaät vaø song song vôùi
nhau, chæ coù chieàu cuûa chuùng thay ñoåi (so vôùi vaät).
Bôûi vaäy, nhö ñaõ chöùng minh trong muïc 1, hôïp löïc P C P1
cuûa caùc löïc pk ôû moïi vò trí cuûa vaät seõ ñi qua cuøng
moät ñieåm C coá ñònh cuûa vaät laø taâm cuûa caùc löïc song P1 P song p O 1
k. Ñieåm ñoù goïi laø troïng taâm cuûa vaät. Vaäy: y
troïng taâm cuûa vaät theå laø ñieåm coá ñònh cuûa vaät theå ñoù
maø ñöôøng taùc duïng cuûa hôïp löïc cuûa troïng löïc caùc P x Hình 5.2
phaân toá cuûa vaät phaûi ñi qua vôùi moïi vò trí cuûa vaät
trong khoâng gian. Söï toàn taïi cuûa ñieåm naøy ñaõ chöùng minh trong muïc 1.
Caùc toïa ñoä cuûa troïng taâm laø taâm caùc löïc song song, ñöôïc xaùc ñònh theo
caùc coâng thöùc (5.3) baèng: p x ∑ p y ∑ p z ∑ x k k k k c = ; y k c = ; z k = (5.5) P P c P
trong ñoù: xk, yk, zk - laø caùc toïa ñoä caùc ñieåm ñaët löïc troïng löïc pk cuûa caùc phaân toá vaät.
Cuoái cuøng ta thaáy raèng, theo ñònh nghóa, troïng taâm laø ñieåm hình hoïc.
Ñieåm naøy coù theå naèm caû ôû ngoaøi phaïm vi vaät khaûo saùt (ví duï nhö ñoái vôùi vaät hình vaønh khaên).
4. Toïa ñoä troïng taâm cuûa caùc vaät ñoàng chaát
Ñoái vôùi vaät ñoàng chaát, troïng löôïng pk cuûa baát keå phaàn naøo cuûa noù cuõng tyû
leä vôùi theå tích Vk cuûa phaàn ñoù: Pk = γVk, coøn troïng löôïng P cuûa caû vaät tyû leä vôùi
theå tích V cuûa noù, töùc laø P = γV, trong ñoù γ laø troïng löôïng cuûa moät ñôn vò theå
tích. Thay caùc giaù trò naøy cuûa P vaø pk vaøo caùc coâng thöùc (5.5), ta thaáy raèng thöøa
soá chung γ ôû töû soá ñöôïc ñöa ra ngoaøi ngoaëc ñôn coù theå giaûn öôùc cho thöøa soá
chung γ ôû maãu soá, neân töø caùc coâng thöùc (5.5), ta ñöôïc: v ∑ ky v ∑ ky v ∑ kz x k = ; c y k = ; z k = (5.6) V c V c V
Ta thaáy troïng taâm cuûa vaät ñoàng chaát chæ phuï thuoäc vaøo daïng hình hoïc cuûa
noù, khoâng phuï thuoäc vaøo ñaïi löôïng γ . Vì nguyeân nhaân ñoù maø ñieåm C vôùi caùc
toïa ñoä ñöôïc xaùc ñònh theo caùc coâng thöùc (5.6) ñöôïc goïi laø troïng taâm cuûa theå tích V. 60
Suy luaän töông töï nhö vaäy, ta thaáy neáu vaät laø moät baûn phaúng moûng vaø ñoàng chaát thì: s ∑ kx s ∑ ky x k = ; c y k = (5.7) S c S
trong ñoù: S - laø dieän tích cuûa caû baûn
sk - laø caùc dieän tích cuûa caùc phaàn cuûa baûn.
Ñieåm coù caùc toïa ñoä ñöôïc xaùc ñònh theo coâng thöùc (5.7) goïi laø troïng taâm
cuûa dieän tích S. Cuõng vaäy, ta coù caùc coâng thöùc xaùc ñònh toïa ñoä troïng taâm cuûa moät ñöôøng cong laø: l x ∑ l y ∑ l z ∑ x k k k k c = ; y k c = ; z k = (5.8) L L c L
trong ñoù: L - laø chieàu daøi cuûa caû ñöôøng cong
lx - laø caùc chieàu daøi cuûa caùc phaàn ñöôøng cong.
Theo caùc coâng thöùc (5.8), ta coù theå xaùc ñònh troïng taâm cuûa caùc vaät laøm
baèng moät daây maûnh tieát dieän khoâng ñoåi.
Nhö vaäy, troïng taâm cuûa moät vaät ñoàng chaát laø troïng taâm cuûa theå tích, dieän
tích hoaëc ñöôøng cong töông öùng.
5.2. CAÙC PHÖÔNG PHAÙP XAÙC ÑÒNH TOÏA ÑOÄ TROÏNG TAÂM CUÛA CAÙC VAÄT
Töø caùc coâng thöùc chung thu ñöôïc ôû treân, ta coù theå chæ ra nhöõng phöông
phaùp cuï theå xaùc ñònh toïa ñoä troïng taâm cuûa caùc vaät nhö sau:
1. Phöông phaùp ñoái xöùng
Neáu vaät ñoàng chaát coù maët phaúng, truïc hoaëc taâm ñoái xöùng, thì troïng taâm
cuûa vaät naèm töông öùng hoaëc treân maët phaúng ñoái xöùng, hoaëc truïc ñoái xöùng, hoaëc taâm ñoái xöùng.
Ví duï, giaû söû vaät ñoàng chaát coù maët phaúng ñoái xöùng. Khi ñoù vaät bò maët
phaúng naøy chia thaønh hai phaàn coù troïng löôïng p1 vaø p2 baèng nhau vaø coù caùc
troïng taâm ôû caùch ñeàu maët phaúng ñoái xöùng. Do ñoù troïng taâm cuûa vaät laø ñieåm maø
hôïp löïc cuûa hai löïc p1 vaø p2 song song vaø baèng nhau ñi qua, nhaát thieát phaûi naèm
treân maët phaúng ñoái xöùng. Khi vaät coù truïc hoaëc taâm ñoái xöùng ta cuõng coù keát quaû töông töï.
Töø tính chaát ñoái xöùng, ta suy ra laø troïng taâm cuûa vaønh troøn ñoàng chaát, cuûa
baûn troøn hoaëc chöõ nhaät, cuûa hình hoäp chöõ nhaät, cuûa khoái caàu vaø cuûa caùc vaät
ñoàng chaát khaùc coù taâm ñoái xöùng ñeàu phaûi naèm taïi taâm hình hoïc (taâm ñoái xöùng) cuûa chuùng.
2. Phöông phaùp phaân chia
Neáu coù theå chia caét vaät thaønh moät soá höõu haïn caùc phaàn maø vò trí troïng
taâm cuûa töøng phaàn ñaõ bieát roõ, thì coù theå tính tröïc tieáp toïa ñoä troïng taâm cuûa caû 61
vaät theo caùc coâng thöùc töø (5.5) ñeán (5.8). Khi ñoù soá haïng ôû töû soá seõ baèng soá caùc
phaàn maø vaät ñöôïc chia ra.
Ví duï 5.1. Haõy xaùc ñònh caùc toïa ñoä troïng taâm cuûa baûn ñoàng chaát treân H.5.3. Taát
caû caùc kích thöôùc ño baèng cm.
Giaûi. Döïng caùc truïc toïa ñoä vaø chia baûn thaønh ba hình chöõ nhaät (ñöôøng chia laø
caùc ñöôøng chaám chaám). Tính caùc toïa ñoä troïng taâm cuûa moãi hình chöõ nhaät vaø
dieän tích cuûa caû baûn (xem baûng). y 2 6 C3 1 2 3 2 xk -1 1 5 8 2 C2 yk 1 5 9 zk 4 20 12 2 C1 x Hình 5. Hình 5.3 3
Dieän tích cuûa caû baûn baèng: S = s1 + s2 + s3 = 3,6 cm2
Thay caùc giaù trò baèng soá ñaõ tính ñöôïc vaøo caùc coâng thöùc (5.7), ta ñöôïc: x s 1 1 + x2s2 + x s 3 − 4 + 20 + 60 1 x 3 c = = = 2 cm S 36 9 y s 1 1 + y2s2 + y s 3 4 + 100 + 108 8 y 3 c = = = 5 cm S 36 9
Vò trí cuûa troïng taâm C xaùc ñònh ñöôïc nhö ñaõ chæ treân H.5.3. Ñieåm C naèm ôû
ngoaøi dieän tích cuûa baûn. Qua ví duï naøy, moät laàn nöõa ta khaúng ñònh raèng troïng
taâm cuûa vaät laø moät ñieåm hình hoïc coù theå naèm beân ngoaøi chu tuyeán cuûa vaät.
3. Phöông phaùp buø tröø (phöông phaùp khoái löôïng aâm)
Phöông phaùp naøy laø moät tröôøng hôïp
rieâng cuûa phöông phaùp phaân chia ñöôïc söû duïng
ñoái vôùi caùc vaät coù loã khuyeát, khi ñaõ bieát troïng
taâm cuûa vaät khoâng coù loã khuyeát vaø troïng taâm R
cuûa baûn thaân loã khuyeát. C r C
Ví duï 5.2. Xaùc ñònh vò trí cuûa troïng taâm cuûa 1 C 2
baûn troøn baùn kính R coù moät loã khuyeát troøn baùn
kính r (H.5.4). Khoaûng caùch C1C2 = a.
Giaûi. Troïng taâm cuûa baûn naèm treân ñöôøng C1C2, Hình 5.4
vì laø truïc ñoái xöùng. Döïng caùc truïc toïa ñoä. Ñeå
xaùc ñònh caùc toïa ñoä xc, ta buø theâm dieän tích ñeå cho baûn troøn trôû thaønh kín (phaàn 62
I), sau ñoù laáy dieän tích naøy tröø ñi dieän tích cuûa maët troøn khuyeát (phaàn II). ÔÛ ñaây
dieän tích cuûa phaàn II laø phaàn khuyeát, neân phaûi ñeå daáu aâm. Khi ñoù: s1 = R2 π ; x1 = 0; s2 = − r2 π ; x2 = a S = s 2 2 1 = s2 = π(R − r )
thay caùc giaù trò vöøa tìm ñöôïc vaøo (5.7), ta ñöôïc: 2 1 x 1 s + x2 2 s ar xc = = − vaø: y 2 2 S R − r c = 0
Ta thaáy troïng taâm C tìm ñöôïc naèm beân traùi ñieåm C1
4. Phöông phaùp tích phaân
Neáu khoâng theå chia vaät ra thaønh moät soá phaàn höõu haïn vôùi caùc troïng taâm
ñaõ bieát, thì ñaàu tieân chia vaät thaønh caùc theå tích beù v
Δ k naøo ñoù. Ñoái vôùi caùc theå
tích naøy, caùc coâng thöùc (5.6) coù daïng: x ∑ k v Δ x k c = ... (5.9) V
trong ñoù: xk, yk, zk - laø caùc toïa ñoä cuûa moät ñieåm naøo ñoù naèm beân trong theå tích v Δ k .
Sau ñoù laáy giôùi haïn caùc ñaúng thöùc (5.9) khi cho v
Δ k tieán daàn tôùi khoâng,
töùc laø thu caùc theå tích ñoù veà ñieåm. Khi ñoù caùc toång ôû töû soá seõ bieán thaønh caùc tích
phaân treân toaøn theå tích cuûa vaät vaø do ñoù caùc coâng thöùc (5.9) ôû giôùi haïn cho ta: 1 x 1 1 c = ; xdv yc = ; ydv z = zdv (5.10) V ∫ V ∫ c V ∫ (V) (V) (V)
Ta cuõng laáy ñöôïc töông töï nhö vaäy ñoái vôùi caùc toïa ñoä troïng taâm cuûa dieän
tích vaø cuûa ñöôøng cong, baèng caùch laáy giôùi haïn caùc coâng thöùc (5.7) vaø (5.8): 1 x 1 1 c = ; xdl yc = ; ydl z = zdl (5.12) L ∫ L ∫ c L ∫ (L) (L) L ( )
5. PHÖÔNG PHAÙP THÖÏC NGHIEÄM
Coù theå xaùc ñònh troïng taâm cuûa caùc vaät khoâng ñoàng chaát coù hình daïng
phöùc taïp (nhö maùy bay, ñaàu taøu hoûa,...) baèng phöông phaùp thöïc nghieäm. Moät
trong nhöõng phöông phaùp thöïc nghieäm (phöông phaùp treo) ñoù laø: treo vaät treân
daây hoaëc daây caùp buoäc taïi moät soá ñieåm naøo ñoù. Phöông cuûa daây treo seõ cho ta
phöông cuûa troïng löïc. Giao ñieåm cuûa caùc phöông ñoù chính laø troïng taâm cuûa vaät.
Coøn phöông phaùp thöïc nghieäm khaùc ñeå xaùc ñònh troïng taâm laø phöông
phaùp caän. Noäi dung cuûa phöông phaùp naøy ñöôïc noùi roõ ôû ví duï döôùi ñaây.
Ví duï 5.3. Ta seõ chöùng minh laøm theá naøo coù theå xaùc ñònh baèng phöông phaùp
thöïc nghieäm vò trí troïng taâm cuûa maùy bay (khoaûng caùch a), neáu bieát khoaûng caùch AB = l (H.5.5). 63
Muoán vaäy, ñaët baùnh B leân baøn caân ñeå tìm aùp löïc cuûa baùnh leân baøn caân.
Baèng caùch ñoù xaùc ñònh ñöôïc giaù trò cuûa phaûn löïc N1, cuõng baèng caùch ñoù ta xaùc
ñònh ñöôïc phaûn löïc N2. Tính toång moâmen cuûa caùc löïc ñoái vôùi troïng taâm C cuûa
maùy bay vaø cho toång naøy baèng khoâng ta ñöôïc N2a – N1(1 – a) = 0. Töø ñaây suy ra: N11 a = N1 + N2
Roõ raøng laø N1 + N2 = P, trong ñoù P laø troïng löôïng cuûa maùy bay. Do ñoù,
neáu bieát tröôùc giaù trò cuûa P thì ñeå xaùc ñònh a ta chæ caàn caân moät laàn.
5.3. TROÏNG TAÂM CUÛA MOÄT SOÁ VAÄT ÑOÀNG CHAÁT 1. Troïng taâm cuûa cung
Xeùt cung AB baùn kính R coù goùc taâm AOB = 2α. Theo tính chaát ñoái xöùng,
troïng taâm cuûa cung naøy naèm treân truïc Ox (H.5.6). Ta haõy tìm toïa ñoä xc theo caùc
coâng thöùc (5.12). Muoán vaäy, giaû thöû MM’ laø moät phaân toá treân cung AB coù chieàu
daøi dl = Rdω, toïa ñoä x cuûa phaân toá MM’ seõ laø x = rcosω. Thay caùc giaù trò cuûa x
vaø dl vaøo coâng thöùc thöù nhaát cuûa (5.12) vaø chuù yù raèng tích phaân phaûi laáy treân
toaøn boä chieàu daøi cung, ta coù: B α 2 2 = 1 x = R xdl cos ϕ ϕ d = R 2 sin α c L ∫ L ∫ L A −α
trong ñoù: L - laø chieàu daøi cung AB vaø baèng R.2 α .
Töø ñaây ta suy ra: troïng taâm cuûa cung troøn naèm treân truïc ñoái xöùng caùch taâm O m y oä sin α x = B c R α M’ trong ñoù: goùc R dl α ño baèng radian. M
Ta cuõng coù theå coù keát quaû naøy maø khoâng caàn O ϕ dϕ C
duøng tôùi khaùi nieäm tích phaân. α x
Theo coâng thöùc (5.8), neáu goïi l Δ k laø chieàu daøi
cuûa phaân toá cung, ta coù: A 1 xc = ∑ xk l Δ k L Hình 5.6
vôùi: xk - laø toïa ñoä cuûa phaân toá l
Δ k , trong ñoù vôùi ñoä 64
chính xaùc tôùi giaù trò baäc cao xk = Rcos ϕk (ôû ñaây thay ϕ baèng ϕk ). Khi ñoù: xk l Δ k = R l Δ k cos ϕk = R y Δ , k töø ñoù suy ra: ∑x Δl = R Δ ∑ y = AB . R k k k
. Bôûi vaäy, neáu bieát raèng AB = 2R.sin α vaø L
= R.2 α ta ñi ñeán coâng thöùc (5.13).
2. Troïng taâm cuûa tam giaùc B
Ta döïng caùc ñöôøng thaúng song song vôùi
caïnh AD ñeå chia tam giaùc ABD thaønh n daûi heïp
(H.5.7). Troïng taâm cuûa moãi daûi roõ raøng seõ naèm
treân trung tuyeán BE cuûa tam giaùc. Do ñoù, troïng
taâm cuûa toaøn boä tam giaùc cuõng naèm treân trung C
tuyeán naøy. Ta cuõng coù keát quaû nhö vaäy ñoái vôùi D hai trung tuyeán khaùc. A E
Do ñoù, suy ra: troïng taâm cuûa baûn tam giaùc Hình 5.7
naèm treân giao ñieåm caùc ñöôøng trung tuyeán cuûa noù.
Bôûi vaäy, nhö ñaõ bieát: CE = 1 3BE
3. Troïng taâm cuûa hình quaït
Xeùt moät hình quaït OAB baùn kính R vôùi y B
goùc taâm baèng 2 α (H.5.8). Haõy töôûng töôïng raèng
caùc baùn kính keû töø taâm O chia dieän tích cuûa hình R
quaït OAB thaønh n hình quaït nhoû. Taïi giôùi haïn
khi taêng soá n leân voâ haïn, caùc hình quaït naøy coù O α C x
theå xem nhö laø caùc tam giaùc phaúng vôùi troïng α
taâm naèm treân cung DE baùn kính baèng 2R/3. Do 2 R 3
ñoù, troïng taâm cuûa hình quaït OAB seõ truøng vôùi
troïng taâm cuûa cung DE maø vò trí cuûa noù ñöôïc A Hình 5.8 Hình 5.8
xaùc ñònh theo coâng thöùc (5.13). Keát quaû laø:
Troïng taâm cuûa hình quaït naèm treân truïc ñoái xöùng caùch taâm O moät ñoaïn baèng: 2 sin α x = c R 3 α
4. Troïng taâm cuûa khoái choùp
Xeùt khoái choùp tam giaùc (khoái töù dieän) E
ABDC (H.5.9). Ñeå xaùc ñònh troïng taâm cuûa
khoái ñoù, ta döïng caùc maët phaúng song song
vôùi ñaùy ABD chia khoái thaønh n maët caét B
phaân toá. Khi taêng n leân voâ haïn thì ôû giôùi C
haïn ta coù theå xem n maët caét ñoù laø nhöõng C2
tam giaùc phaúng. Troïng taâm cuûa caùc tam A C1
giaùc naøy naèm treân ñöôøng thaúng EC1 noái K D Hình 5.9 65
ñænh E cuûa khoái choùp vôùi troïng taâm C1 cuûa ñaùy. Bôûi vaäy, troïng taâm cuûa toaøn
khoái choùp cuõng naèm treân ñöôøng thaúng EC1.
Cuõng vôùi nhöõng suy luaän nhö theá ta thaáy raèng troïng taâm cuûa khoái choùp
phaûi naèm treân ñöôøng thaúng BC2 noái ñænh B vôùi troïng taâm cuûa maët ADE. Bôûi
vaäy, troïng taâm caàn tìm naèm taïi ñieåm C laø giao ñieåm cuûa caùc ñöôøng thaúng EC1 vaø BC2.
Ta xaùc ñònh vò trí cuûa ñieåm C. Vì caùc ñöôøng thaúng C1C2 vaø BE chia caùc
caïnh cuûa goùc BKE thaønh caùc phaàn tyû leä nhau, neân chuùng song song nhau vaø C
Δ 1CC2 ~ Δ ECB. Ngoaøi ra, vì KC1 = KB/3 neân C1C2 = BE/3. Do ñoù, ta tìm ñöôïc: CC1 C1C2 1 = = CE CE 3 neân: 1 1 CC1 = CE = C1E (5.15) 3 4
Keát quaû naøy cuõng ñuùng ñoái vôùi moïi khoái choùp ña giaùc vaø ôû giôùi haïn cuõng
ñuùng ñoái vôùi caû khoái noùn. Vaäy:
Troïng taâm cuûa khoái choùp (hay khoái noùn) naèm treân ñoaïn thaúng noái ñænh
choùp (ñænh noùn) vôùi troïng taâm cuûa ñaùy vaø ôû caùch ñaùy moät ñoaïn baèng moät phaàn
tö chieàu daøi cuûa ñoaïn thaúng ñoù.
Coâng thöùc xaùc ñònh caùc toïa ñoä troïng taâm cuûa moät soá vaät ñoàng chaát khaùc
coù theå tìm thaáy trong caùc saùch tra cöùu kyõ thuaät. 66 PHAÀN II ÑOÄNG HOÏC
Ñoäng hoïc laø moät phaàn cuûa cô hoïc lyù thuyeát, nghieân cöùu caùc tính chaát
hình hoïc cuûa chuyeån ñoäng cuûa vaät theå. Ñoái töôïng khaûo saùt cuûa ñoäng hoïc laø vaät
raén vaø ñoäng ñieåm (ñieåm hình hoïc chuyeån ñoäng).
Ñoäng hoïc ngoaøi vieäc cung caáp kieán thöùc cho phaàn ñoäng löïc hoïc, coøn laø
cô sôû trong moân hoïc chuyeån ñoäng.
Ñoäng hoïc, ngoaøi vieäc cung caáp kieán thöùc cho
phaàn ñoäng löïc hoïc, coøn laø cô sôû trong caùc moân hoïc khaùc nhö: cô caáu maùy, ñoäng hoïc maùy,...
Chuyeån ñoäng cuûa vaät theå dieãn ra trong khoâng gian, troâi theo thôøi gian.
Khoâng gian ôû ñaây ñöôïc choïn laø khoâng gian Eclit, thôøi gian troâi ñeàu theo moät
chieàu taêng, luoân laáy thôøi ñieåm xuaát phaùt chuyeån ñoäng laøm goác (öùng vôùi t = 0).
Khi khaûo saùt chuyeån ñoäng bao giôø cuõng phaûi choïn moät vaät chuaån ñöôïc goïi
laø heä quy chieáu ñeå töø ñoù quan saùt vò trí cuûa vaät theå. Roõ raøng tính chaát chuyeån
ñoäng cuûa vaät theå phuï thuoäc vaøo vieäc choïn heä quy chieáu.
Ñeå thuaän lôïi trong tính toaùn, söû duïng ñöôïc caùc kieán thöùc toaùn hoïc, ngöôøi
ta gaén vaøo quy chieáu (vaät raén chuaån) moät heä toïa ñoä thích hôïp. Nhö vaäy khaûo
saùt chuyeån ñoäng cuûa vaät theå ñoái vôùi moät heä quy chieáu nghóa laø khaûo saùt
chuyeån ñoäng cuûa vaät theå trong heä toïa ñoä naøo ñoù.
Noäi dung khaûo saùt chuyeån ñoäng cuûa vaät theå bao goàm caùc vaán ñeà sau ñaây:
1- Laäp phöông trình chuyeån ñoäng: thieát laäp quan heä haøm soá giöõa caùc thoâng
soá ñònh vò vôùi thôøi gian ñeå chæ ra vò trí cuûa vaät theå moät caùch lieân tuïc. Ñoái vôùi
ñoäng ñieåm coøn coù theå chæ ra quyõ ñaïo.
2- Xaùc ñònh caùc ñaëc tröng cuûa chuyeån ñoäng, cuï theå laø vaän toác, gia toác. 68 Chöông 6 ÑOÄNG HOÏC ÑIEÅM Noäi dung
Khaûo saùt chuyeån ñoäng cuûa ñoái töôïng ñôn giaûn nhaát laø ñoäng ñieåm. Qua ñoù
trình baøy moät caùch cuï theå noäi dung vaø phöông phaùp nghieân cöùu trong ñoäng hoïc. Yeâu caàu
- Naém vöõng phöông phaùp thieát laäp phöông trình chuyeån ñoäng, caùc ñaïi
löôïng ñaëc tröng cuûa ñoäng hoïc (vaän toác, gia toác)
- Nhôù caùc coâng thöùc xaùc ñònh caùc ñaïi löôïng ñaëc tröng cuûa chuyeån ñoäng,
moái quan heä giöõa chuùng, ñeå aùp duïng khi giaûi caùc baøi toaùn thöïc teá.
Ñeå giaûi quyeát ñöôïc caùc yeâu caàu cuûa ñoäng hoïc ñieåm ñaët ra, chuùng ta coù
theå söû duïng nhieàu phöông phaùp moâ taû chuyeån ñoäng khaùc nhau tuøy thuoäc vaøo
tính chaát cuûa chuyeån ñoäng vaø muïc ñích chính caàn giaûi quyeát. Döôùi ñaây chuùng ta
ñöa ra boán phöông phaùp nghieân cöùu ñoäng hoïc ñieåm.
6.1. KHAÛO SAÙT ÑOÄNG HOÏC ÑIEÅM BAÈNG PHÖÔNG
PHAÙP VECTOR VAØ TOÏA ÑOÄ DECARTES
1. Phöông trình chuyeån ñoäng
Xeùt ñoäng ñieåm M chuyeån ñoäng trong khoâng gian. z M
Neáu choïn moät ñieåm tuøy yù xaùc ñònh O laøm goác thì vò trí M
hoaøn toaøn xaùc ñònh bôûi vector OM r = . r k Khi M chuyeån ñoäng: j i y O rr = rr ) t ( (6.1) x
Phöông trình (6.1) chính laø phöông trình chuyeån Hình 6.1 ñoäng cuûa M. 69
Taïi goác O, xaây döïng heä truïc Oxyz, vò trí cuûa M hoaøn toaøn xaùc ñònh bôûi: ⎧x = x(t) ⎪ ⎨y = y(t) ⎪ ⎩z = ( z t)
(6.2) chính laø phöông trình chuyeån ñoäng cuûa M trong heä toïa ñoä Decartes. 2. Vaän toác, gia toác
Caùc ñaïi löôïng vaän toác, gia toác raát quen thuoäc. ÔÛ ñaây chæ ñöa ra caùc bieåu
thöùc moâ taû chuùng trong caùc phöông phaùp nghieân cöùu töông öùng. 1 - Vaän toác
Vaän toác ñoäng ñieåm kyù hieäu laø: V Phöông phaùp vector: dr V = r&r = (6.3) dt
(Töø ñaây ñaïo haøm theo thôøi gian kí hieäu laø (.))
Phöông phaùp toaï ñoä Decartes: r r r V = Vxi + Vy j + Vzk ôû ñaây: dx V = = dy dz &; x x V = = y ; V = = z dt y dt & z dt & 2- Gia toác
Gia toác ñoäng kieåm kí hieäu laø wr 2r - Phöông phaùp vector: &r d r W = V = = r&r (6.4) dt2 r
- Phöông phaùp toïa ñoä Decartes: W = W &r &r x i + Wy j + Wzk ôû ñaây: Wx = ; x& W = ; y y & Wz = z&
3. Tính chaát chuyeån ñoäng bieåu thò qua V, W
1- Ñoäng ñieåm chuyeån ñoäng thaúng
V cuøng phöông vôùi W ⇔ V x W = 0 (6.5)
2- Ñoäng ñieåm chuyeån ñoäng cong
V khaùc phöông vôùi W ⇔ V x W ≠ 0 2
Xeùt söï bieán thieân cuûa chuyeån ñoäng qua: 2 2 V = V töø dV = V 2 W . (6.6) dt
3- Ñoäng ñieåm chuyeån ñoäng nhanh daàn
V taêng theo thôøi gian ⇔ V W . > 0
4- Ñoäng ñieåm chuyeån ñoäng ñeàu
V giaûm theo thôøi gian ⇔ V W . = 0
5- Ñoäng ñieåm chuyeån ñoäng chaäm daàn ⇔ V W . < 0 70
6.2. KHAÛO SAÙT CHUYEÅN ÑOÄNG ÑIEÅM BAÈNG TOÏA ÑOÄ CÖÏC
1. Phöông trình chuyeån ñoäng
Xeùt chuyeån ñoäng M treân maët phaúng Oxy, vò trí cuûa M hoaøn toaøn xaùc ñònh bôûi hai tham soá: - Ñoä daøi r = OM y M
- Goùc ñaïi soá giöõa Ox vaø OM : P r
Khi M chuyeån ñoäng, r vaø ϕ thay ñoåi theo j ro thôøi gian: ϕ Po x i ⎧r = r ) t ( Hình 6.2 ⎨ Hình 6.2 (6.7) ⎩ϕ = ϕ ) t (
(6.7) chính laø phöông trình chuyeån ñoäng. 2. Vaän toác, gia toác
Goïi Or laø truïc cöïc coù höôùng döông theo chieàu OM vôùi vector ñôn vò laø rr . π
o Quay OM theo chieàu ngöôïc kim ñoàng hoà moät goùc ta ñöôïc truïc OP coù 2
vector ñôn vò laø Po. Duøng quan heä chuyeån ñoåi truïc, ta coù: r r r r ⎧ r = i cos ϕr + j sin ϕr
⎧ r&r = −iϕ sin ϕ + ϕ cos ϕ = ϕ&r &r &r P . ⎪ ⎪ o o ⎨ o ⇒ ⎨ (6.8) ⎪ r r r r r r ⎩P &r r o = −i ϕ sin + j cos ϕ
⎪⎩P = −iϕ&r cos ϕ − jϕ sin ϕ = ϕ −&r &r o o r . 1- Vaän toác
Söû duïng (6.3) ta ñöôïc: d V = r&r = r r r &r o r . r ( ) = & o r . r + o r . r = r V o r + P V Po (6.9) dt trong ñoù: V = ; r &r r & V = ϕ p r
2- Gia toác 2 d W = r = r . r ( r &r ) = W rr + W P (6.10) 2 o r o p o dt trong ñoù: W = r − r 2 & & ; W r r 2 & r ϕ = ϕ p & + &ϕ
6.3. KHAÛO SAÙT CHUYEÅN ÑOÄNG ÑIEÅM BAÈNG TOÏA ÑOÄ TÖÏ NHIEÂN
1. PHÖÔNG TRÌNH CHUYEÅN ÑOÄNG
Nhöõng tröôøng hôïp ñaõ bieát quyõ ñaïo cuûa ñoäng ñieåm, chuùng ta thöôøng khaûo
saùt chuyeån ñoäng cuûa chuùng baèng toïa ñoä töï nhieân. b M τ + Γ O ν Hình 6.3 71
Giaû söû quyõ ñaïo cuûa ñoäng ñieåm laø ( Γ ), neáu laáy ñieåm tuøy yù xaùc ñònh O ∈ Γ
laøm goác vaø quy öôùc chieàu döông treân quyõ ñaïo, vò trí cuûa chuyeån ñoäng ñieåm M
hoaøn toaøn xaùc ñònh thoâng qua ñoä daøi ñaïi soá s = OM. Khi M chuyeån ñoäng: s = s ) t ( (6.11)
(6.11) laø phöông trình chuyeån ñoäng cuûa ñoäng ñieåm trong heä toïa ñoä töï nhieân.
2. Vaän toác, gia toác
1- Tam dieän ñoäng Frene
Vaän toác ñaëc tröng caû höôùng chuyeån ñoäng trong khoâng gian, toïa ñoä s
khoâng theå hieän ñöôïc vai troø naøy. Ñeå moâ taû ñöôïc höôùng chuyeån ñoäng cuûa ñoäng
ñieåm (treân quyõ ñaïo) chuùng ta xaây döïng tam dieän ñoäng Frene.
Xeùt tam dieän vuoâng Mτnb coù goác luoân truøng vôùi M, chuyeån ñoäng theo M -
τr laø vector ñôn vò tieáp tuyeán vôùi quyõ ñaïo taïi M theo chieàu döông. -
nr laø vector ñôn vò phaùp tuyeán chính vuoâng goùc vôùi τr , höôùng vaøo phía
loõm cuûa quyõ ñaïo, naèm trong maët phaúng giôùi haïn ñi qua ba ñieåm M vaø hai ñieåm
thuoäc quyõ ñaïo M1, M2 laân caän khi M1 vaø M2 tieán ñeán M (maät tieáp) r -
b laø vector ñôn vò truøng phaùp tuyeán coù phöông chieàu sao cho M τ nb laø
moät heä toïa ñoä vuoâng goùc thuaän. 2- Vaän toác
Töø ñònh nghóa, chuùng ta coù toác ñoä cuûa ñoäng ñieåm: V = s&
- Neáu chuyeån ñoäng theo chieàu döông quyõ ñaïo, töùc V cuøng chieàu τr , toïa
ñoä sr taêng theo thôøi gian ⇒ s& > 0
- Neáu chuyeån ñoäng ngöôïc chieàu döông, töùc V ngöôïc chieàu τr , toïa ñoä s giaûm theo thôøi gian ⇒ s& < 0
Keát hôïp, chuùng ta vieát ñöôïc: V = τr &s (6.12) 3- Gia toác r 2 & &r r & &r r dτ ds r s W = V =
s τ + s&rτ = s&τ + s& = s&τ + nr = W rτ + τ w r nn (6.13) ds dt ρ
(Chuù yù raèng τr ñoåi höôùng) trong ñoù: W = τ
s& - goïi laø gia toác tieáp (6.14) 2 2 & = s W = V n
- goïi laø gia toác phaùp (6.15) ρ ρ r ( dτ 1
= nr ñaõ ñöôïc chöùng minh ôû hình vi phaân vôùi ds
ρ laø baùn kính cong cuûa quyõ ρ ñaïo taïi M). 72
6.4. MOÄT SOÁ CHUYEÅN ÑOÄNG ÑAËC BIEÄT 1. Chuyeån ñoäng thaúng
Choïn phöông chuyeån ñoäng laøm truïc toïa ñoä (truïc x). Chuùng ta nhaän ñöôïc:
phöông trình chuyeån ñoäng: x = x(t) Vaän toác : V = x& Gia toác : W = x&
Ví duï 6.1. Xeùt chuyeån ñoäng cuûa vò trí hình chieáu leân moät ñöôøng thaúng cuûa moät
ñieåm thuoäc vaät quay quanh truïc coá ñònh vaän toác goác khoâng thay ñoåi ωo , caùch
truïc quay ñoaïn a (H.6.4). M
Giaûi. Giaû söû thôøi ñieåm ñaàu ñoäng ñieåm truøng vôùi
vò trí Mo, chuùng ta nhaän ñöôïc: Mo a ) t ( x = a cos(ϕ + ) α = a cos( o ω t + ) α ϕ
laø phöông trình chuyeån ñoäng. α Vaän toác: V = x& = a − ω sin(ω t + ) O x x o o α o x Hình 6.4 Gia toác : W = x Hình 6.4 & = −a 2 ω cos(ω t + α) 2 = ω − x o o o
2. Chuyeån ñoäng troøn V
Ví duï 6.2. Cho ñoäng ñieåm M chuyeån ñoäng treân ñöôøng troøn theo luaät OM M = s = at
2 . Töø phöông trình chuyeån
ñoäng daïng toïa ñoä töï nhieân ta coù: W + ithin W V = sτr & = a 2 τr 0 I 2 2 &r r V r a 4 W = V = s&τ + n = 0 + nr = W nr R R n
3. Chuyeån ñoäng Xycôloâít Hình 6.5
Ví duï 6.3. Xeùt chuyeån ñoäng cuûa ñieåm M treân bieân cuûa
ñöôøng troøn laên khoâng tröôït treân ñöôøng thaúng (H.6.6) coù vaän toác cuûa taâm laø V1 = const. Tìm quyõ ñaïo, V , W cuûa ñoäng ñieåm. Giaûi. y V W I M ϕ O A 2 R π x Hình 6.6 Hình 6.6
1- Phöông trình chuyeån ñoäng
Laáy heä truïc toïa ñoä Oxy coù O truøng vôùi vò trí cuûa M khi tieáp xuùc ñöôøng
thaúng coá ñònh. Taïi thôøi ñieåm baát kyø, vò trí M(x, y) ñöôïc xaùc ñònh: 73
⎧x = OA − R sin ϕ = AM − r sin ϕ ⎨ (6.17) ⎩y = R − R cos ϕ = R 1 ( − cos ϕ) ôû ñaây: V t V 1 ϕ = = ω ñaët ( t 1 ω =
, R - laø baùn kính cuûa ñöôøng troøn. R R x V t R sin t Thay vaøo (6.17): ⎧ = − ω ⎨ 1 (6.18) ⎩y = R − R cos ϕ = 1 ( R − cos ω ) t
Phöông trình (6.18) laø phöông trình chuyeån ñoäng daïng tham soá. Quyõ ñaïo
cuûa noù laø ñöôøng cong Xycôloâít (H.6.6). 2- Vaän toác
V(Vx, Vy ) : Vx = x& = V − Ι Rω cos t ω = VΙ 1 ( − cos ω ) t Vy = Rω sin t ω = VΙ sin t ω V = V2 + V2 V 2 . sin ω = t x y 1 2 xeùt: x V 1 − cos t ω t = tg ω = tg ϕ = y V sin t ω 2 2 Suy ra
V - coù phöông luoân ñi qua ñieåm cao nhaát cuûa ñöôøng troøn
3- Gia toác: W( x W , y
W ): W = V ω Ι sin t x ω ; Wy = V ω Ι cos ωt 2 2 2 V ⇒ W = W Ι x + Wy = V1ω = R xeùt: Wx = ω tg t = ϕ tg . Suy ra
W - coù phöông ñi qua taâm I. Wy
4- Tính baùn kính cong cuûa quyõ ñaïo (P) 2 dv d ω ω V W = = (V .2 sin ) t = V ω cos t Ι cos ω = t τ dt dt Ι 2 Ι 2 R 2 2 2 2 V W = W − W Ι sin ω = t n τ R 2 ω 2 4V2Ι sin2 t suy ra: V 2 ρ = = 4R sin ω = t Wn V2Ι ω 2 sin t R 2
Baùn kính cong taêng daàn töø chaân ñeán ñænh Xycôloâít.
4. Chuyeån ñoäng Parabol
Ví duï 6.4. Ñoäng ñieåm chuyeån ñoäng theo quy luaät: ⎧x = t 300 ⎪ ⎨ (m, s) ⎪ 2 ⎩y = t 400 − t 5 Tìm V, ,
W ñoä cao, taàm xa vaø baùn kính cong taïi ñoä cao cöïc ñaïi. Giaûi.
1- Vaän toác, gia toác 74 V(V , V ) x y : V = x 300 x = ; V = y& = 400 t 10 y − V(W , W ) : W = x& = 0 x y x ; W = y& = 10 y − 2- Ñoä cao h
Ñoäng ñieåm ñaït taïi ñoä cao h luùc: Vy = 0 ⇔ t = 40 s
Tính ñöôïc: hmax = y(40) = 8000 (m) 3- Taàm xa S y h M O S x Hình 6. Hình 6.7 7
Taàm xa S laø toïa ñoä x cuûa ñoäng ñieåm töông öùng thôøi ñieåm y = 0 ⇒ t = 80 (s), (t = 0 loaïi)
Tính ñöôïc : S = x(80) = 24.000 (m)
4- Baùn kính cong ρ (hmax )
Taïi vò trí khaûo saùt: V(40) = Vx (40) = 300 (m) Ñeå tìm Wn, ta tìm τ W vaø W. 2 2 2 2 V = x V + y V ⇒ V = 000 . 250 − t 8000 + t 100 t 200 − 8000 W = & τ V = 2 2 000 . 250 − t 8000 + t 100 2 2 300 ⇒ n W = W − W = τ 2 2500 − t 80 + t 2 Taïi t = 40 coù V ρ = = = ) m ( 9000 W t 40 n 75 Chöông 7
CHUYEÅN ÑOÄNG CÔ BAÛN CUÛA VAÄT RAÉN Noäi dung
Khaûo saùt hai chuyeån ñoäng cô baûn cuûa vaät raén laø chuyeån ñoäng tònh tieán vaø
quay quanh truïc coá ñònh, laøm cô sôû ñeå nghieân cöùu caùc chuyeån ñoäng phöùc taïp khaùc. Yeâu caàu
- Naém vöõng ñaëc ñieåm cuûa chuyeån ñoäng tònh tieán
- Naém vöõng caùc ñaëc tröng moâ taû vaät chuyeån ñoäng quay quanh truïc coá ñònh
vaø caùc coâng thöùc xaùc ñònh chuùng
- Naém vöõng caùc coâng thöùc lieân heä ñaëc tröng chuyeån ñoäng cuûa vaät vaø ñieåm thuoäc vaät
7.1. CHUYEÅN ÑOÄNG TÒNH TIEÁN CUÛA VAÄT RAÉN 1. Ñònh nghóa
Chuyeån ñoäng tònh tieán cuûa vaät raén laø chuyeån ñoäng maø moãi ñoaïn thaúng
thuoäc vaät coù phöông khoâng ñoåi trong suoát quaù trình chuyeån ñoäng. Ví duï:
- Thuøng xe chuyeån ñoäng treân ñöôøng thaúng
- Vaät raén AB trong cô caáu boán khaâu hình bình haønh (H.7.1) A B Hình Hình 7.7. 1 1
2. Ñaëc ñieåm cuûa chuyeån ñoäng tònh tieán
Ñònh lyù. Khi vaät raén chuyeån ñoäng tònh tieán, vaän toác, gia toác cuûa moïi ñieåm thuoäc
vaät töông öùng baèng nhau quyõ ñaïo cuûa chuùng gioáng nhau.
Chöùng minh. Xeùt hai chuyeån ñoäng tuøy yù A, B thuoäc vaät S chuyeån ñoäng tònh tieán (H.7.2), chuùng ta coù: rr = rr + AB ( B A 76 Vaän toác: V &r B = r &r &rB = rA = VA do ( AB = ) const (7.2) Gia toác: WB = &r &rB V = A V = WA (7.3)
- Quyõ ñaïo: giaû söû quyõ ñaïo cuûa A laø A Γ , töø z B
(7.1) ñieåm B coù quyõ ñaïo B Γ chính laø A Γ dòch r
chuyeån tònh tieán ñoä dôøi B A
AB , vaäy hai quyõ ñaïo phaûi gioáng nhau. rA Nhaän xeùt: O y x
- Töø ñaëc ñieåm cuûa chuyeån ñoäng tònh tieán, ñeå Hình 7.2
khaûo saùt chuyeån ñoäng cuûa caû vaät, chuùng ta chæ caàn
khaûo saùt chuyeån ñoäng cuûa moät ñieåm thuoäc vaät
- Chuùng ta noùi vaät raén chuyeån ñoäng tònh tieán thaúng, troøn... coù nghóa laø
ñieåm thuoäc vaät chuyeån ñoäng thaúng, troøn...
7.2. CHUYEÅN ÑOÄNG QUAY QUANH TRUÏC COÁ ÑÒNH CUÛA VAÄT RAÉN 1. Ñònh nghóa
Vaät raén chuyeån ñoäng coù hai ñieåm coá ñònh laø vaät raén quay quanh hai truïc
coá ñònh ñi qua hai ñieåm ñoù.
2. Khaûo saùt chuyeån ñoäng caû vaät
1- Phöông trình chuyeån ñoäng z
Xeùt maët phaúng P gaén chaët vaøo vaät vaø chöùa ϕ
truïc quay. Xaùc ñònh vò trí cuûa vaät töông ñöông xaùc ω
ñònh vò trí cuûa (P). Laäp maët phaúng chöùa truïc quay ε
( π ) coá ñònh, vò trí cuûa (P) hoaøn toaøn xaùc ñònh bôûi k P
goùc nhò dieän ϕ giöõa ( π ) vaø (P) (H.7.3). π
Khi vaät raén chuyeån ñoäng, ϕ laø haøm cuûa O y thôøi gian: x Hình 7.3 ϕ = ϕ ) t ( (7.4)
Phöông trình (7.4) chính laø phöông trình chuyeån ñoäng cuûa vaät raén.
Chuùng ta quy öôùc chieàu quay döông ( ϕ > 0 ) neáu nhö nhìn töø ñænh truïc
quay vaät quay theo chieàu ngöôïc chieàu kim ñoàng hoà, ( ϕ < 0 ) neáu quay ngöôïc laïi.
2- Vaän toác goùc
• Vaän toác goùc cuûa vaät raén quay quanh truïc coá ñònh
Vaän toác goùc cuûa vaät raén quay quanh truïc coá ñònh laø ñaïi löôïng ñaïi soá: ω = ϕ& (7.5)
- Vaät quay chieàu döông : ω > 0 77 - Vaät quay chieàu aâm : ω < 0 - Ñôn vò rad/s
Trong kyõ thuaät coøn duøng ñôn vò voøng/phuùt: n voøng/phuùt nπ ⇔ rad / s 30
• Vector vaän toác goùc
Ñeå theå hieän ñöôïc phöông cuûa truïc quay thoâng qua vector ñôn vò chæ
phöông ( k ), chuùng ta ñònh nghóa vector vaän toác goùc ωr laø vector naèm treân truïc
quay (bieåu dieãn theâm moät muõi teân voøng) (H.7.3): r &rω = &ϕ k (7.6)
Nhö vaäy, neáu bieát ωr chuùng ta bieát phöông truïc quay, chieàu quay vaø vaän toác quay.
3- Gia toác goùc
• Gia toác goùc vaät raén quay quanh truïc coá ñònh Laø ñaïi löôïng : ε = ω& = ϕ& (7.7)
• Vector gia toác εr Töông töï r r
ωr chuùng ta coù : rε = &ω k = &ϕ k
4- Tính chaát cuûa chuyeån ñoäng qua ωr ,εr
Töông töï aûnh höôûng cuûa V, W ñeán chuyeån ñoäng, chuùng ta xeùt bieán thieân cuûa 2 2 ωr = ω : r2 dω 2 ωr.εr. dt r. ω εr = 0 ⇔ vaät raén quay ñeàu r.
ω εr > 0 ( ωr, εr cuøng chieàu) ⇔ vaät raén quay nhanh daàn r.
ω εr < 0 ( ωr, εr ngöôïc chieàu) ⇔ vaät raén quay chaäm daàn
3. Khaûo saùt chuyeån ñoäng thuoäc ñieåm vaät
1- Phöông trình chuyeån ñoäng Δ
Xeùt M thuoäc vaät caùch truïc quay Δ ñoaïn IM = r
Khi vaät chuyeån ñoäng vaïch neân quyõ ñaïo troøn
trong maët phaúng vuoâng goùc truïc quay coù taâm I (H.7.4). ω
Choïn ñieåm O treân quyõ ñaïo truøng vôùi vò trí ñaàu r M
cuûa M laøm goác, ta nhaän ñöôïc phöông trình chuyeån I ϕ ñoäng: s = OM = . r ϕ ) t ( O 2- Vaän toác
• Phaân boá vaän toác treân tia baùn kính thuoäc maët Hình 7.4 phaúng quyõ ñaïo AÙp duïng: V = s&τ 78 trong ñoù: s = Ι ϕ . M &r & = rω ⇒ V = ω τr r Neáu choïn
τr cuøng chieàu quay: V = ωτr r
Döïa vaøo (7.10) treân moät tia baùn kính, vaän toác caùc ñieåm phaân boá tuyeán
tính theo luaät tam giaùc vuoâng (H.7.6) taêng theo r heä soá ω: V = r ω
• Bieåu dieãn vaän toác qua ωr
Chuùng ta deã daøng kieåm chöùng: V = ωr × OM = ωr × ρr (H.7.6)
ÔÛ ñaây O laø ñieåm thuoäc truïc quay. 3- Gia toác ε
• Bieåu dieãn treân maët phaúng quyõ ñaïo VM ω W Ι (H.7.5) ithin α r r W = W W τ + Wn M r r & Wτ = s τ = r ε τ Wτ Hình 7.5 2 V W r r n = n = rω n 2 r
Xeùt moät ñieåm thuoäc tia baùn kính coù: W tg τ ε α = =
- khoâng phuï thuoäc vaøo vò trí cuûa ñieåm 2 n W ω Coøn ñoä lôùn: 2 2 2 4 W = Wτ + n W = r ε + ω Δ
Tæ leä vôùi khoaûng caùch r heä soá 2 4 ε + ω
W phaân boá treân moät tia baùn kính theo quy I Wτ M W
luaät tuyeán tính tam giaùc nhoïn (H.7.5) n ω ρ
• Bieåu dieãn qua ωr, εr (H.7.6) ε dV d W = = (r ω × r) ρ O dt dt = εr × ρr + r ω × V = Wτ + Wn ôû ñaây: r r W r τ = ε × ρ ; Wn = ω × V Hình 7.6
7.3. CAÙC CÔ CAÁU TRUYEÀN ÑOÄNG CÔ BAÛN
1. Söï caàn thieát cuûa caùc boä truyeàn löïc
Trong moät maùy hoaëc heä thoáng maùy, ñoäng cô (khaâu ñaàu) chæ taïo ra chuyeån
ñoäng ñôn giaûn (thöôøng laø quay quanh truïc coá ñònh). Caùc nhaø thieát keá phaûi taïo ra
boä phaän trung gian (khaâu daãn) ñeå bieán ñoåi chuyeån ñoäng cuûa ñoäng cô thaønh
nhöõng chuyeån ñoäng theo yù muoán ôû khaâu coâng taùc. 79
2. Caùc boä truyeàn ñôn giaûn
1- Truyeàn chuyeån ñoäng quay quanh truïc coá ñònh thaønh chuyeån ñoäng quay
quanh truïc coá ñònh (thay theá cheá ñoä quay) song song vôùi nhau
Duøng daây ñai, xích, baùnh raêng... (H.7.7) R1 ω1 R1 R2 R2 O O O 1 2 2 O1 ω1 ω2 ω2 R R 1 1 R R 2 2 O O O 2 1 2 O1 ω1 ω2 ω2 ω1 Hình 7.7 ω ε 1 1 R2 ⎛ Z2 ⎞ = = ± ⎜= ± ⎟ ω ε 2 2 R1 ⎝ 1 Z ⎠
Z1, Z2 - laø soá raêng töông öùng cuûa caùc baùnh raêng 1 vaø 2
Trong coâng thöùc (7.11) hai baùnh raêng quay cuøng chieàu ta laáy daáu coäng,
ngöôïc chieàu laáy daáu (−).
2- Truyeàn ñoäng cô caáu cam V V 2 2 ω V1 O Tònh tieán tònh tieán Quay tònh tieán Hình 7.8 7.4. CAÙC VÍ DUÏ
Ví duï 7.1. Cho cô caáu truyeàn ñoäng nhö H.7.9, bieát goùc quay cuûa truï O laø 2 ϕ = a ( )
2 t coù chieàu nhö H.7.9. Xaùc ñònh ω, ε cuûa truï O 1cuõng nhö chuyeån ñoäng cuûa taûi A.
Giaûi. • Phaân tích chuyeån ñoäng
Cô caáu goàm ba vaät raén chuyeån ñoäng: 80
- Truï O vaø O1 quay quanh caùc truïc
coá ñònh töông öùng coù quan heä truyeàn R1 r1 R
ñoäng baùnh raêng tieáp xuùc ngoaøi.
- Taûi A chuyeån ñoäng tònh tieán O O1 thaúng ñöùng. I ω
• Vaän toác, gia toác: (choïn chieàu ε quay laø chieàu döông)
- Truï O: ω = ϕ& = at ; ε = ϕ& = a A
Truï quay nhanh daàn ñeàu theo Hình 7.9 chieàu hình veõ
- Truï O1 (laáy chieàu quay laøm chieàu döông) R R R R ω = ω at 1 = ; ε = ω& = ε = a R R 1 1 1 1 R R 1 1 Truï
O1 cuõng quay nhanh daàn ñeàu theo chieàu hình veõ
- Taûi A: quaõng ñöôøng cuûa taûi A vaø cuûa daây laø nhö nhau vaø cuõng baèng
quaõng ñöôøng cuûa ñieåm thuoäc truï o1 caùch truïc moät ñoaïn r1. ⎧ r R V = r ω = 1 at A 1 1 R ⎪⎪ ⇒ ⎨ 1 ⎪ r R W & A V 1 A a ( r ε 1 1) ⎪ = = = = ⎩ R1
Taûi A chuyeån ñoäng ñi leân nhanh daàn ñeàu.
Ví duï 7.2. Cho cô caáu truyeàn ñoäng giöõa hai truïc vuoâng goùc vôùi nhau nhö H.7.10.
Giaû thieát khoâng coù söï tröôït töông ñoái theo chieàu quay. Bieát truïc I dòch chuyeån
doïc truïc theo luaät x = 0,1 + 0,2t (m,s) ñoàng thôøi quay quanh truïc vôùi vaän toác goùc 120 voøng/ phuùt.
Tìm chuyeån ñoäng cuûa truïc II. x 0,4 I R = 0,4 1 R = x 2 ω1 OII E OI ε2 ω2 ω ε ω 2 2 1 Hình 7.11 Hình 7.10 II
Giaûi. Hai truïc quay tieáp xuùc taïi E. Töông töï caùc baùnh raêng tieáp xuùc ngoaøi, chæ
khaùc laø hai truïc vuoâng goùc (H.7.11). 81 R1 4 , 0 ⇒ 2 ω = 1 ω = 120 . (voøng/phuùt) x 1 , 0 + t 2 , 0 hay: 6 , 1 π 32 , 0 π 2 ω = rad ( / ) s ⇒ ε = ω& = − 1 , 0 + t 2 , 0 2 2 2 1 , 0 ( + ) t 2 , 0
Chöùng toû truïc II quay chaäm daàn.
Ví duï 7.3. Xaùc ñònh chuyeån ñoäng cuûa caàn cam AB
cuûa cô caáu cam (H.7.12). Ñóa troøn baùn kính R; OI V2 = ω
l ; quay ñeàu vaän toác goùc ωo A β Giaûi. R O α
• Phaân tích chuyeån ñoäng I ϕ
- Caàn cam AB tònh tieán thaúng ñöùng
- Cam quay ñeàu quanh truïc O
• Phöông trình chuyeån ñoäng Hình 7.12
Ñeå tìm chuyeån ñoäng cuûa caàn cam chuùng ta caàn tìm OA = x(t), choïn truïc x
höôùng leân treân. Giaû söû vò trí ban ñaàu cuûa caûm öùng ϕ 0 o = .
⇒ OA = x = R cos β − l cos ϕ AÙp duïng: l R R l sin = = → sin ϕ β = sin β sin α sin ϕ R l cos β = 2 R − 2 2 l sin ϕ R
⇒ phöông trình chuyeån ñoäng cuûa caàn AB:
x = l R2 − l2 sin2 ω t − l cos ω t o o • Vaän toác 2 l ω 2 sin ω t V = x& = l o ω sin o ω t o o − 2 R2 − l2 sin2 o ω t • Gia toác W = v& = x& = 2 2 2 2 2 2 2 2 2 161 o ω 2 sin o ω t R ( − 1 sin o ω ) t − 1 o ω sin 2 o ω t = 1 o ω cos o ω t − 2 2 2 3 / 2 R ( 16 − 1 sin o ω ) t 82 Chöông 8
CHUYEÅN ÑOÄNG PHÖÙC HÔÏP CUÛA ÑIEÅM
8.1. MOÂ HÌNH BAØI TOAÙN VAØ CAÙC ÑÒNH NGHÓA 1. Moâ hình baøi toaùn
Nhieàu tröôøng hôïp trong thöïc teá yeâu caàu
chuùng ta phaûi khaûo saùt ñoäng ñieåm trong
nhöõng heä quy chieáu khaùc nhau. Chaúng haïn
nhö con laéc dao ñoäng ñoái vôùi traàn xe ñang z1 j k
chaïy treân ñöôøng. Nhöõng baøi toaùn loaïi naøy i O
ñöôïc giaûi quyeát thoâng qua moâ hình toång quaùt k1 j X sau. i 1 1 y
Ñoäng ñieåm M chuyeån ñoäng trong heä O 1 1 Hình 8.1
quy chieáu Oxyz. Heä quy chieáu Oxyz laïi x1
chuyeån ñoäng ñoái vôùi heä quy chieáu O1x1y1z1 ñöôïc xem laø heä coá ñònh (H.8.1).
Vaán ñeà ñaët ra ôû ñaây laø khaûo saùt chuyeån ñoäng cuûa M trong töøng heä quy
chieáu vaø quan heä giöõa caùc chuyeån ñoäng naøy. 2. Caùc ñònh nghóa
1- Chuyeån ñoäng töông ñoái
Chuyeån ñoäng cuûa M(x,y,z) trong heä ñoäng Oxyz ñöôïc goïi laø chuyeån ñoäng
töông ñoái. Ñaây laø chuyeån ñoäng maø ngöôøi quan saùt caûm nhaän ñöôïc khi gaén chaët
mình vôùi heä ñoäng (Oxyz).
Vaän toác töông ñoái : V r (hoaëc r V )
Gia toác töông ñoái : Wr (hoaëc r V )
laø vaän toác vaø gia toác trong chuyeån ñoäng töông ñoái. Caùc ñaïi löôïng naøy ñöôïc xaùc
ñònh ñoái vôùi heä ñoäng (Oxyz). r r r
Chuù yù: Caùc vector ñôn vò chæ phöông cuûa heä ñoäng i ,j k , coá ñònh trong heä
ñoäng nhöng bieán thieân (quay) trong heä coá ñònh (O1 x1 y1 z1). Chuùng ta nhaän ñöôïc: 83 r r r r r r dOM d Vr = Oxyz= ( xi + yj + k z ) = x&i + y&j + &k z (8.1) dt dt Oxyz r r r r r r dVR d Wr = Oxyz= ( x&i + y&j + & k z ) = x&i + y&j + k z (8.2) dt dt & Oxyz
2- Chuyeån ñoäng tuyeät ñoái
Chuyeån ñoäng cuûa ñieåm M(x1, y1, z1) ñoái vôùi heä coá ñònh O1x1y1z1 ñöôïc goïi
laø chuyeån ñoäng tuyeät ñoái. a a
Vaän toác tuyeät ñoái Va (hoaëc V ), gia toác tuyeät ñoái Wa (hoaëc W ) laø vaän
toác, gia toác ñöôïc tính trong chuyeån ñoäng tuyeät ñoái. Chuù yù ñeán tính chaát caùc
vector ñôn vò cuûa töøng heä toïa ñoä. Chuùng ta nhaän ñöôïc: O d 1M d Va = O = + 1x1y1z O ( O 1 1 ) OM dt dt O1x1y1z1 (8.3) • r r r
= O O+ x&i + y&i + &k z + xi + yj + k z &r &r &r 1 dV W a a = dt 1 O 1 x y1 1 z • • &r &r &r r r r r r r = O1 O + xi + y j+ k z + ( 2 x&i + y&j + k
z& )+ x&i + y&j + + k z& (8.4)
3- Chuyeån ñoäng theo
Chuyeån ñoäng cuûa heä ñoäng ñoái vôùi heä coá ñònh ñöôïc goïi laø chuyeån ñoäng theo.
Ñeå ñoäng ñieåm M theå hieän ñöôïc chuyeån ñoäng theo chuùng ta ñöa ra khaùi
nieäm truøng ñieåm M* cuûa M laø ñieåm thuoäc heä ñoäng nhöng truøng vôùi ñoäng ñieåm M taïi vò trí ñang xeùt. e
Töông öùng chuùng ta coù vaän toác theo: * V = VM e Gia toác theo: * W = WM
Chuù yù: taïi thôøi ñieåm ñang xeùt: * * 1 O M ≡ 1 O O + OM * * r * r * r r r ⇔ O ⎛ ⎞ 1M ≡ O O 1 + ⎜x i + y j + z k⎟ = O O 1 + xi + yj + k z (do * M ≡ M ) ⎝ ⎠
Chuù yù: M* coá ñònh trong heä ñoäng Oxyz neân caùc toïa ñoä x, y, z cuûa M taïi vò
trí naøy ñöôïc xem laø caùc haèng soá. * • • e O d M ⇒ V 1 = = O O + xi + y j k z &r &r &r + (8.5) dt O x y z 1 1 1 1 1 84 e e • • dV W &r &r &r = O x y z = O1 O + xi + y j+ k z (8.6) dt 1 1 1 1
8.2. CAÙC ÑÒNH LYÙ HÔÏP VAÄN TOÁC, GIA TOÁC
1. Ñònh lyù hôïp vaän toác
Vaän toác tuyeät ñoái cuûa ñoäng ñieåm baèng toång hình hoïc vaän toác töông ñoái vaø vaän toác theo. V a = V r + V e (8.7)
Chöùng minh. Söû duïng (8.1), (8.3) vaø (8.5), chuùng ta coù ngay keát quaû.
2. Ñònh lyù hôïp gia toác
Gia toác tuyeät ñoái cuûa ñoäng ñieåm baèng toång hình hoïc gia toác töông ñoái, gia
toác theo vaø thôøi gia toác phuï coârioâlit WC . Wa = Wr + We + WC (8.8) trong ñoù: W r C = ( 2 e ω × Vr) (8.9)
Chöùng minh. Söû duïng (8.2), (8.4) vaø (8.6) chuùng ta coù keát quaû (8.8) trong ñoù ⎛ W &r &r &r c = 2 x & i + y&j + &k z ⎟⎞ ⎜ (8.10) ⎝ ⎠
1- Tröôøng hôïp heä ñoäng tònh tieán ( e ωr = 0 )
Chuùng ta coù ngay: i = j = k&r &r &r = 0 ⇒ Wc = 0
2- Tröôøng hôïp heä ñoäng quay quanh truïc coá ñònh (H.8.2) Caùc vector i , k , j &r &r &r
töông öùng laø vaän toác ñaàu muùt cuûa chuùng. Söû duïng (7.13): r r r Δ i&r r = &r r &r r e ω × ;i j = e ω × ;j k = e ω × ; k r r r (8.10) ⇒ W r C = 2 e
ω × (x&i + y&j + &k z ) (8.1) ⇒ W r C = 2 e ω × Vr
Ngay caû khi heä ñoäng chuyeån ñoäng toång quaùt coâng j k y
thöùc (8.9) vaãn ñuùng nhöng O e
ωr laø vaän toác goùc töùc thôøi doïc i
theo truïc quay töùc thôøi. Hình 8.2
3- Phöông phaùp thöïc haønh xaùc ñònh W x Hình 8.2 c
Töø coâng thöùc (8.1) chuùng ta deã daøng suy ra gia toác Wc Wc = ω 2 eV ⊥
r . Höôùng truøng höôùng cuûa Vr khi ñaõ quay theo chieàu ⊥ quay cuûa ωe goùc π 2 .
ÔÛ ñaây Vr laø hình chieáu cuûa
leân phöông vuoâng goùc vôùi vector ⊥ V r . e ωr
8.3. PHÖÔNG PHAÙP GIAÛI CAÙC BAØI TOAÙN CHUYEÅN ÑOÄNG PHÖÙC HÔÏP
Nhöõng baøi toaùn trong chöông naøy ñöôïc chia theo caùc daïng sau: 85
- Baøi toaùn tìm phöông trình chuyeån ñoäng: ví duï (8.1)
- Baøi toaùn toång hôïp: bieát caùc chuyeån ñoäng thaønh phaàn (töông ñoái, theo)
tìm chuyeån ñoäng tuyeät ñoái (caùc ví duï 8.2, 8.3, 8.4)
- Baøi toaùn phaân tích: bieát chuyeån ñoäng tuyeät ñoái tìm caùc chuyeån ñoäng
thaønh phaàn (caùc ví duï 8.5, 8.6, 8.7).
Tuy nhieân cuõng coù nhöõng baøi toaùn hoãn hôïp bao goàm töøng phaàn cuûa caùc loaïi baøi toaùn treân.
Ñeå giaûi ñöôïc caùc loaïi baøi toaùn naøy chuùng ta caàn phaûi:
1- Naém vöõng caùc ñònh nghóa veà chuyeån ñoäng
2- Choïn heä ñoäng phuø hôïp vôùi töøng baøi toaùn (thöôøng choïn vaät raén sao cho
caùc ñieåm chuùng ta caàn xaùc ñònh chuyeån ñoäng hay moâ taû chuyeån ñoäng lieân quan
tröïc tieáp ñeán vaät raén naøy).
3- Bao giôø cuõng giaûi caùc ñaïi löôïng thuoäc veà vaän toác tröôùc baèng caùch aùp duïng tröïc tieáp: V a = V e + V r
4. Sau khi giaûi ñöôïc caùc ñaïi löôïng vaän toác chuùng ta söû duïng phöông trình:
Vieát moät caùch toång quaùt: n τ n τ n W r a + Wa = We + We + Wr + ω 2 × e Vr⊥
Chieáu phöông trình vector naøy leân caùc truïc thích hôïp chuùng ta seõ giaûi
ñöôïc caùc ñaëc tröng gia toác. 8.4. CAÙC VÍ DUÏ
Ví duï 8.1. Baêng ñeå ghi dao ñoäng tònh tieán theo phöông Ox vaän toác 2 m/s. Ñaàu
buùt (gaén vaøo vaät dao ñoäng theo phöông Oy) veõ leân baêng ñöôøng hình sin vôùi bieân
ñoä AB = 2,5 cm; O1C = 8 cm. Tìm phöông trình dao ñoäng cuûa vaät neáu ñieåm O
öùng vôùi vò trí cuûa vaät luùc t = 0. y1 y V = 2 m/s B x x 1 O C 1 A O Hình 8.3
Giaûi. Chuùng ta caàn tìm dao ñoäng cuûa ñieåm ñaàu buùt, ñieåm naøy lieân heä tröïc tieáp
vôùi baêng giaáy. Choïn baêng giaáy laøm heä ñoäng, ñöôøng hình sin treân baêng chính laø
quyõ ñaïo töông ñoái cuûa ñieåm thuoäc vaät (vaät chuyeån ñoäng tònh tieán).
Xaây döïng heä Oxy coá ñònh, heä O1x1y1 gaén chaët vaøo baêng giaáy laøm heä
ñoäng, töø H.8.3 chuùng ta nhaän ñöôïc phöông trình chuyeån ñoäng töông ñoái cuûa
ñieåm thuoäc vaät (ñaàu buùt): 86 x = t 200 ⎧ ⎨ 1 (cm/s) ⎩y = 5 . 2 sin ω t 1 1 Taàn soá voøng 1
ω ñöôïc tính qua chu kyø T = 8/200 = 0,04 s π 2 ⇒ ω = = π 50 1 T
Duøng pheùp ñoåi toïa ñoä chuùng ta nhaän ñöôïc phöông trình dao ñoäng cuûa vaät:
Ví duï 8.2. Moät con thuyeàn bôi qua soâng coù vaän toác so vôùi maët nöôùc yeân laëng laø
u, doøng soâng chaûy vôùi toác ñoä v. Chieàu roäng cuûa soâng laø h. Tìm höôùng cuûa ur ñeå
con thuyeàn qua soâng nhanh nhaát ?
Giaûi. Giaû söû ngöôøi laùi thuyeàn cho thuyeàn chaïy theo höôùng ur nhö H.8.4. AÙp
duïng coâng thöùc hôïp vaän toác khi choïn maët nöôùc laøm heä ñoäng V r r a = u + v y
Chieáu phöông trình vector leân hai V = x& = u sin α + v truïc x, y: ⎧ ⇒ ax u ⎨ α V ⎩V = y& = u cos α A ay h M v
Laáy tích phaân theo t töø thôøi ñieåm x
(xuaát phaùt) ñeán thôøi ñieåm ñang xeùt chuùng ta O Hình 8.4 Hình 8.4 nhaän ñöôïc: ⎧x = u ( sin α + ) v . t ⇒ ⎨ ⎩y = u cos α t .. Khi caäp beán: y = h h ⇒ t =
laø thôøi ñieåm caäp beán u cos α
Quaõng ñöôøng thuyeàn troâi doïc theo bôø soâng luùc caäp beán laø: x = u sin α + h ) v = α + hv htg u cos α u cos α
Muoán qua soâng nhanh nhaát: h α = , 0 tmin = u
⇒ höôùng cho thuyeàn ñi vuoâng goùc vôùi bôø soâng.
Ví duï 8.3. Boä phaän ñieàu tieát ly taâm quay
quanh truïc thaúng ñöùng vôùi vaän toác goác khoâng ω W o C ñoåi V W e r x o ω = rad 6
/ s . Caùc quaû vaêng gaén vaøo ñaàu Wne
cuoái cuûa loø xo thöïc hieän dao ñoäng trong raõnh Vr O
sao cho khoaûng caùch töø troïng taâm I cuûa noù tôùi
truïc quay bieán thieân theo luaät: I Hình 8.5 87
OI = x = (0,1 + 0,05 sin8 π t) m, (t tính theo giaây). Haõy tính:
a) Vaän toác, gia toác ñieåm I taïi thôøi ñieåm gia toác coârioâlit cuûa noù ñaït giaù trò lôùn nhaát.
b) Gia toác coârioâlit khi quaû vaêng ôû vò trí xa nhaát.
Giaûi. Choïn ñóa quay laøm heä ñoäng (quay ñeàu quanh truïc coá ñònh). Xeùt chuyeån
ñoäng cuûa khoái taâm I cuûa quaû vaêng thöïc hieän chuyeån ñoäng hôïp:
- Chuyeån ñoäng töông ñoái: dao ñoäng thaúng doïc theo truïc ñoäng Ox (gaén
chaët vaøo ñóa) vôùi quy luaät ñaõ bieát OI = x = (0,1 + 0,05sin8 π t) (m)
- Chuyeån ñoäng theo: laø chuyeån ñoäng cuûa ñieåm thuoäc ñóa quay quanh truïc
O coá ñònh vaän toác goùc o ω (= ) const
• Vaän toác: (tính vaän toác taïi vò trí tuøy yù) AÙp duïng: V a = V e + V r V V I e : V (m/s) e = . OI ωo = 1 , 0 ( + 05 , 0 sin 8 t π ).ωo W W C1 I x ⊥OI thuaän chieàu quay ω Ve o 1 Vr1 I V O r : Vr = x& = 4 , 0 π cos 8 t π (m/s) W ne 1
doïc theo phöông truïc ñoäng Ox 0 ,15 • Gia toác
AÙp duïng: Wa = We + Wr + WC τ n W Hình 8.6 a = We + We .. n ⎧ = ω . OI 2 = ω x 2 = 1 , 0 ( + 05 , 0 sin π 8 ω ) t 2 trong ñoù: ⎪ W o o o e ⎨ ⎪⎩↑↑ OI τ ⎧= ω . OI = 0 ⎪ W o e ⎨
(do ñóa quay ñeàu, εo = 0 ) ⎪⎩⊥OI Wr : W = x& = − 2 , 3 2 r π sin 8 t
π , doïc theo phöông truïc x (H.8.5) WC = 2ωo × V r : W = 8 , 4 . π cos t C π ⊥Vr thuaän chieàu quay ω do ( V r ⊥ o ) o ω
a) Gia toác WC ñaït giaù trò lôùn nhaát khi: cos 8 t π 1 = 1 ⇔ sin 8 t π 1 = 0
Töông öùng: x1 = 0,1; Vr1 = 0,4 π ; Ve1 = 0,1 ωo = 0,6 Wn = 1 , 0 2 ω = ; 6 , 3 1 e o W 1r = 0 ; W = ω 1 C 8 , 0 π = π o 8 , 4
Töø H.8.6 chuùng ta nhaän ñöôïc: WI = V21e + V21r = 4 , 1 (m/s) 88 WI = W2CI + (Wn1e)2 = 5 , 15 (m/s2)
b) Khi quaû vaêng ôû vò trí xa nhaát ⇔ sin 8 t π 2 = 1 ⇒ cos 8 t π 2 = 0 ⇒ WC2 = 0
Chuù yù: ÔÛ ñaây chuùng ta giaû söû taïi thôøi ñieåm t1 ñóa ñang coù vò trí ôû treân
H.8.6 ⇔ tia OI xaùc ñònh.
Ví duï 8.4. Cho quaû caàu quay quanh truïc thaúng ñöùng vaän toác goùc khoâng ñoåi ωo .
Chaát ñieåm M chuyeån ñoäng ñeàu doïc theo ñöôøng kinh tuyeán, coøn N chuyeån ñoäng
ñeàu theo ñöôøng vó tuyeán vôùi vaän toác töông ñoái u, v khoâng ñoåi nhö H8.7. Xaùc ñònh Va, Wa cuûa M, N ?
Giaûi. Choïn quaû caàu laøm heä ñoäng. B • Vaän toác Ñieåm M: rN H AÙp duïng: V a = V e + V r Ve N trong ñoù: V M ; u M O V r v r = Ve = . IM ωo = M r .ωo M M I rM ôû ñaây: Vr ⊥ Ve (H.8.7) M Ve M M 2 M 2 2 2 2 ⇒ ωo a V = (Vr ) + ( e V ) = u + M r .ωo V r u Ñieåm N: A töông töï: V N ; v N r = Ve = . HN ωo = N r .ωo Hình 8.7 • Gia toác: (H.8.8) AÙp duïng: τ n τ n
Wa = Wr + Wr + We + We + WC (i) - Ñieåm M: coù: Wτ 0 r = (do Vr = u = const) 2 2 2 n V u u W = = ; r = (OM = R) ρ OM R Wτ 0 e = (do quaû caàu quay ñeàu) n 2 2 e W = M r .ωo = . IM ωo W = ω C 2 o u . cos β = ω 2 ou cos α z Phöông cuûa W B
C vuoâng goùc maët phaúng kinh tuyeán
qua M (tieáp tuyeán vó tuyeán). H N
Choïn heä truïc toïa ñoä Decartes coù truïc z theo truïc
quay, truïc x naèm trong maët phaúng kinh tuyeán nhö H.8.7. O y ωnr
Chieáu (i) leân ba truïc toïa ñoä: α I n β ωe M A V u r = Hình 8.8 89 ⎧ n n u2 ⎪W = − ax Wr sin α − W = − e sin α − r ω2 R M o ⎪⎪ ⎨W = ay W = − ω C 2 ou cos α ⎪ ⎪ u2 n ⎪W = W cos α = cos α ⎩ az r R Ñieåm N: coù: Wτ 0 r = (do Vr = v = const) 2 2 n v v r W = = HN N r Wτ 0 e = n 2 2 e W = . HN ωo = N r .ωo n C W = 2 o ω Vr = 2ωo , v chieàu ↑↓ We vaø: n Wr 2 v ⇒ coù ngay: n n 2 ax W = vaø C W − e W − r W = 2ωov − N r ωo − W = W = 0. ay az N r
Ví duï 8.5. Cho cô caáu caàn gaït nhö H.8.9. Tay quay OA quay ñeàu quanh O coá
ñònh vaän toác goùc ωo laøm cho thanh O1B laéc qua laïi quanh O1, con chaïy A tröôït
doïc O1B. Bieát OA = r, haõy xaùc ñònh 1
ω , ε1 cuûa O1B taïi vò trí nhö H.8.9.
Giaûi. Giöõa vaät ñaõ bieát chuyeån ñoäng laø thanh OA vaø vaät chöa bieát chuyeån ñoäng
laø thanh O1B coù ñieåm lieân heä duy nhaát laø A (ñaàu muùt thanh OA vaø tieáp xuùc vôùi O1B). Choïn
O1B laøm heä ñoäng vaø xeùt ñieåm A chuyeån ñoäng hôïp:
- Chuyeån ñoäng tuyeät ñoái cuûa A: thuoäc OA quay ñeàu quanh O
- Chuyeån ñoäng töông ñoái: tröôït thaúng doïc theo O1B (naèm doïc theo O1B
quan saùt chuyeån ñoäng cuûa A).
- Chuyeån ñoäng theo: O1B quay quanh O1 coá ñònh • Vaän toác
AÙp duïng: V a = V e + V r (*) + V V R a : V a = r.ωo a WC OA ⊥ thuaän chieàu ω Vr o ω V o e + V O e : V = O A.ω = r 2 ω ? (chöa bieát) e 1 1 1 n A W τ W = W a a e ⊥ O A thuaän chieàu 1 1 ω (chöa bieát). W n
Chuùng ta choïn moät chieàu giaû ñònh e ω1 + V r : V = ? (chöa bieát) ε r 1 cuøng phöông O1B ? (chöa bieát chieàu) 30o
Chuùng ta choïn moät chieàu giaû ñònh y Chieáu o rωo (*) x ⇒ − a V sin 30 = − e V ⇔ = e V O1 2 x Hình 8.9 90 Chieáu o 3 (*) y ⇒ a V cos 30 = Vr ⇔ rωo = Vr 2
Caùc keát quaû nhaän ñöôïc ñeàu lôùn hôn khoâng, chöùng toû chieàu cuûa V e, V r
ñöôïc choïn ñuùng, suy ra: Ve ωo 1 ω = = O A 4 1
(chuùng ta coù theå xaùc ñònh Ve, Vr theo quy taéc tam giaùc vector kín). • Gia toác
AÙp duïng: Wa = We + Wr + WC τ n τ n
⇔ Wa + Wa = We + We + Wr + WC (**) + τ Wa : τa W = rε 0 o = (do ε ) 0 o = + n Wa : n a W 2 = rωo ↑↑ AO + Wr : Wr = ? (chöa bieát) cuøng phöông O1B (chöa bieát chieàu).
Chuùng ta choïn chieàu giaû ñònh nhö hình veõ 2 ω . r 2 + n ω W n 2 o o e : W = O A.ω = . r 2 e 1 1 = 16 8 ↑↑ AO1 3 + WC : 2 C W = 2 1 ω V . r = r ωo 4 ⊥Vr thuaän chieàu quay 1 ω (do 1 ωv ⊥ r V ) Chieáu (**) / x n o ⇒ − τ a W cos 30 = e W + 0 + 0 − C W
Chieáu (**) / y ⇒ −Wn sin 30o = 0 − Wn + W + 0 a e r ⎧ r 3 r 3 − ω2 = τ W − ω2 o e o ⎪⎪ ⇔ ⎨ 2 4 ⎪ r 2 r 2 ⎪− ω = − ω + W ⎩ o o r 2 8
Giaûi heä phöông trình chuùng ta nhaän ñöôïc: r 3 2 τ r 3 r W = − ωo ; 2 W = − ω 8 e o 4
Keát quaû treân chöùng toû Wr vaø τe
W coù chieàu ngöôïc chieàu ñaõ choïn, coù ñoä lôùn
laø trò soá döông töông öùng. 91 r 3 2 τ ωo e W 4 3 2 ⇒ ε1 = = = ωo (cuøng chieàu O 1 ω ) 1A 2r 8
Thôøi ñieåm ñang xeùt thanh O1B quay nhanh daàn. Chuù
yù: Neáu khoâng caàn tính Wr chuùng ta boû phöông trình (**) / y.
Ví duï 8.6. Cô caáu Culít goàm tay quay OA = r quay ñeàu quanh truïc O coá ñònh vôùi
vaän toác goùc ωo, laøm cho Culít chuyeån ñoäng leân, xuoáng. Tìm vaän toác, gia toác cuûa
Culít theo goùc quay cuûa tay quay OA (H.8.10).
Giaûi. Cô caáu coù tay quay OA ñaõ bieát chuyeån ñoäng. Ñieåm A töïa vaøo Culít coù vai
troø truyeàn ñoäng. Choïn Culít laøm heä ñoäng, xeùt chuyeån ñoäng hôïp cuûa ñieåm A.
Chuyeån ñoäng tuyeät ñoái: A thuoäc OA quay ñeàu quanh O (ñaõ bieát)
Chuyeån ñoäng theo: Culít tònh tieán thaúng ñöùng
Chuyeån ñoäng töông ñoái: ñöùng treân Culít chuùng ta thaáy A chuyeån ñoäng
thaúng ngang ôû phaàn treân cuûa chöõ T. ω O
• Vaän toác (taïi vò trí töông öùng goùc ϕ ) o We ϕ AÙp duïng: V V W a a V a = V e + V r e ϕ + Va{= r ω ; A Vr
o ⊥ OA thuaän chieàu quay ωo } Wr +
V e{= ? (chöa bieát ñoä lôùn); phöông thaúng
ñöùng} (choïn chieàu giaû ñònh ñi leân) +
V r {= ? (chöa bieát ñoä lôùn); phöông naèm
ngang} (choïn chieàu nhö H.8.10). Hình 8.10
Nhìn töø H.8.10 chuùng ta giaûi ra ngay:
Ve = Va. sin ϕ = rωo sin ωot
(chính laø vaän toác cuûa Culít). • Gia toác
AÙp duïng: Wa = We + Wr + WC (**) ôû ñaây: +
We coù phöông thaúng ñöùng, choïn chieàu giaû ñònh ñi leân +
Wr coù phöông naèm ngang, choïn chieàu giaû ñònh sang traùi (H.8.10) +
WC = 0 (heä ñoäng tònh tieán) + n Wa = Wa (do OA quay ñeàu)
Chieáu (**) leân truïc thaúng ñöùng (chieàu We ): ⇒ W = W cos ϕ = r 2 ω cos ω t e a o o 92
(Chính laø gia toác cuûa Culít). Wτr
Ví duï 8.7. Caàn cam chuyeån ñoäng nhanh h
daàn ñeàu, sau 4 giaây tröôït töø vò trí cao A Ve W
nhaát xuoáng ñoaïn h = 4 cm laøm cho cam n V e W a r V
coù baùn kính R = 10 cm tröôït ngang. I ϕ W r x a O
Xaùc ñònh vaän toác, gia toác cuûa cam Hình 8.11 taïi vò trí treân.
Giaûi. Xeùt ñaàu caàn cam chuyeån ñoäng thaúng. Töø giaû thieát xaùc ñònh ñöôïc phöông
trình chuyeån ñoäng h' = t2 4 (cm). Xem ñaàu caàn thöïc hieän chuyeån ñoäng hôïp khi laáy cam laøm heä ñoäng.
- Chuyeån ñoäng tuyeät ñoái ñaõ bieát
- Chuyeån ñoäng töông ñoái: ñaàu cam tröôït treân ñöôøng chu tuyeán troøn cuûa cam.
- Chuyeån ñoäng theo: tònh tieán cuøang cam neân V e, We chính laø vaän toác, gia toác cuûa cam. • Vaän toác
AÙp duïng: V a = V e + V r (*) + V a { ' t =h = = ;
2 höôùng thaúng ñöùng ñi xuoáng} 2 +
V e{= ? (chöa bieát); phöông ngang, choïn chieàu giaû ñònh nhö hình veõ} +
V r {= ?; höôùng nghieâng xuoáng vaø ⊥ IA }
Chieáu (*) leân höôùng AI: 6 ⇒ V 8
a sin ϕ = Ve cos ϕ vôùi: sin ϕ = ; cos ϕ = 10 10 ⇒ e V = t 2 gϕ = 5 , 1 (cm/s)
Chieáu (*) leân phöông Vr: ⇒ a V cosϕ = − e V sinϕ + r V ⇒ V 5 , 2 r = (cm/ s). • Gia toác AÙp duïng: τ n
Wa = We + Wr + WC = We + Wr + Wr + Wc (**) ôû ñaây: + Wa{ 1
= , phöông thaúng ñöùng ñi xuoáng} 2 +
We{ = ? (chöa bieát), phöông naèm ngang, choïn chieàu giaû ñònh nhö hình veõ} 93 +
Wτr{ = ? (chöa bieát), phöông ⊥ AI , choïn chieàu giaû ñònh nhö hình veõ} 2 + n V W r r = = 625 , 0 (cm/ s2) IA +
WC = 0 (heä ñoäng tònh tieán). Chieáu (**) / AI: n ⇒ a W sin ϕ = − e W cos ϕ + r W n 1 W ⇒ W = − tg r (cm/s2) e ϕ + = 41 , 0 2 cos ϕ
Daáu coäng chöùng toû cam coù gia toác ñuùng chieàu ñaõ choïn.
Cam chuyeån ñoäng nhanh daàn taïi thôøi ñieåm t = 4s coù vaän toác V = 1,5 cm/s; gia toác W = 0,41 (cm/s2). 94 Chöông 9
CHUYEÅN ÑOÄNG SONG PHAÚNG CUÛA VAÄT RAÉN Noäi dung
Khaûo saùt moät daïng chuyeån ñoäng phöùc hôïp cuûa vaät raén thöôøng gaëp trong kyõ thuaät. Yeâu caàu
- Naém vöõng phöông phaùp phaân tích chuyeån ñoäng song phaúng thaønh
chuyeån ñoäng tònh tieán (theo) cuøng ñieåm cöïc vaø quay (töông ñoái) quanh cöïc
- Söû duïng thuaàn thuïc caùc coâng thöùc moâ taû quan heä vaän toác, gia toác hai
ñieåm ñeå giaûi caùc baøi toaùn thöïc teá
- Bieát caùch xaùc ñònh vaø söû duïng taâm vaän toác töùc thôøi ñeå giaûi caùc baøi toaùn veà vaän toác.
9.1. KHAÛO SAÙT CHUYEÅN ÑOÄNG CAÛ VAÄT 1. Ñònh nghóa
Chuyeån ñoäng song phaúng laø chuyeån ñoäng
cuûa vaät raén trong ñoù moãi ñieåm thuoäc vaät ñeàu P1
naèm trong moät maët phaúng song song vôùi moät A
maët phaúng quy chieáu coá ñònh.
2. Moâ hình chuyeån ñoäng phaúng P2
Xeùt ñoaïn AB ∈ vaät vaø vuoâng goùc vôùi B
maët phaúng quy chieáu. Do A, B chuyeån ñoäng
trong caùc maët phaúng song song vôùi nhau (A ∈ S
P1, B ∈ P2) ⇒ ñoaïn AB chuyeån ñoäng tònh tieán π (H.9.1).
Nhö vaäy, khaûo saùt chuyeån ñoäng cuûa vaät Hình 9.1
töông ñöông khaûo saùt chuyeån ñoäng cuûa taäp caùc ñöôøng thaúng vuoâng goùc maët
phaúng quy chieáu (ñeàu tònh tieán), töông ñöông khaûo saùt chuyeån ñoäng cuûa thieát
dieän S treân maët phaúng quy chieáu (S laø taäp hôïp nhöõng giao ñieåm cuûa caùc ñöôøng
thaúng thuoäc vaät vuoâng goùc vôùi maët phaúng quy chieáu).
3. Phöông trình chuyeån ñoäng 95
Vò trí cuûa thieát dieän S trong maët phaúng cuûa noù hoaøn toaøn xaùc ñònh bôûi vò
trí cuûa ñoaïn AM ∈ S (AM coá ñònh trong S). Ñeå xaùc ñònh AM chuùng ta chæ caàn
bieát vò trí cuûa A(x, y) vaø goùc ϕ giöõa truïc naèm y
ngang coá ñònh Ox vaø tia AM (H.9.2). S M
Töø ñoù ta coù phöông trình chuyeån ñoäng cuûa S: A ϕ ⎧x = A xA )t ( ⎪ ⎨y = y ) t ( A A (9.1) ϕ ⎪⎩ϕ = ϕ )t ( O x
4. Vaän toác cuûa vaät Hình 9.2
Vaän toác cuûa caû vaät cuõng ñöôïc moâ taû thoâng qua tröôøng vaän toác cuûa ñieåm A
(ñieåm cöïc) vaø tröôøng vaän toác goùc quay quanh A: V = x& ) t ( ⎧ VA V ( , V x x y ⎨ ) (9.2) ⎩V = y& ) t ( y ω = ϕ& 5. Gia toác
Töông töï chuùng ta coù: ⎧W = V& = x& ) t ( ⎪ WA(W , W x x x y ⎨ ) (9.3) ⎪⎩W = V& = y& )t ( y ε = ω& = ϕ&
9.2. KHAÛO SAÙT CHUYEÅN ÑOÄNG CUÛA ÑIEÅM THUOÄC VAÄT
1. Phöông trình chuyeån ñoäng
Xeùt ñieåm tuøy yù xaùc ñònh M(x, y) ∈ S (H.9.2) Chuùng ta coù: OM = OA + AM x x ) t ( A . M cos ) t ( Duøng (9.1) ⎧ = + ϕ ⇒ ⎨ A (9.4) ⎩y = y ) t ( + . AM sin ϕ ) t ( A 2. Vaän toác
Ñeå xaùc ñònh ñaëc tröng vaän toác vaø gia y1 V
toác chuùng ta xaây döïng heä ñoäng A MA V 1x1y1 tònh y M
tieán cuøng cöïc A (coù tính chaát Ax1 // Ox, Ay // Oy). M VA ϕ A Ñieåm M x
∈ S coù chuyeån ñoäng theo laø 1
tònh tieán cuøng cöïc A, chuyeån ñoäng töông ñoái O x
laø chuyeån ñoäng troøn quanh cöïc A cuøng thieát Hình 9.3 dieän S. 1- Vaän toác 96 V M = V e + V r (*)
- Moïi ñieåm ∈ heä ñoäng A1x1y1 coù cuøng vaän toác V A ⇒ V e = V M* = V A - Ñaët
V r = VMA laø vaän toác cuûa M quay quanh cöïc A. VMA (= MA.ω , ⊥ MA
thuaän chieàu quay cuûa S quanh cöïc A). ⇒ (*) ⇔ V M = V A + V MA (9.5)
Chuùng ta coøn coù theå bieåu dieãn (9.5) döôùi daïng V r M = V A + ω × AM (9.6) ÔÛ ñaây
ωv laø vaän toác goùc cuûa thieát dieän.
2- Ñònh lyù quan heä vaän toác giöõa hai ñieåm
Do vieäc choïn cöïc A laø tuøy yù neân (9.5) hoaëc (9.6) moâ taû moái quan heä vaän toác giöõa hai ñieåm.
Ñònh lyù. Vaän toác giöõa hai ñieåm M, N tuøy yù thuoäc thieát dieän S thoûa maõn quan heä: V M = V N + V (9.7) MN hay: V r M = VN + ω × NM (9.8)
Heä quaû. Hình chieáu vaän toác cuûa hai ñieåm leân phöông noái hai ñieåm ñoù baèng nhau.
Chöùng minh. Coù ngay keát quaû do V MN ⊥ MN
3- Xaùc ñònh vaän toác baèng phöông phaùp duøng taâm vaän toác töùc thôøi
Ñònh lyù. ÔÛ moãi thôøi ñieåm neáu thieát dieän S coù:
• ω ≠ 0 seõ toàn taïi duy nhaát ñieåm P ∈ S, VP = 0, P ñöôïc goïi laø taâm vaän toác
töùc thôøi (TVTTT) vaø vaän toác moïi ñieåm ∈ S ñöôïc phaân boá gioáng nhö S ñang
quay quanh taâm P. Chuùng ta noùi S quay töùc thôøi quanh TVTTT vôùi vaän toác goùc ω .
• ω = 0 vaän toác moïi ñieåm ∈ S ñeàu baèng nhau. Chuùng ta noùi S tònh tieán töùc thôøi. Chöùng minh
• Tröôùc heát chuùng ta chöùng minh ∃ P
Xeùt ñieåm M ∈ S, giaû söû coù V M ≠ 0 (neáu VM = 0 ⇒ P ≡ M). Döïng tia Md
⊥ V M ) (cuøng chieàu V M khi ñaõ quay 90o theo chieàu ω ). Treân tia vöøa döïng laáy ñieåm P sao cho = M V MP . ω M Tính: V V M p = V M + V = 0 PM Vì ω VPM(= . PM ω = M V , ↑↓ VM - Chöùng minh P duy nhaát VM P Giaû söû
∃ P1 coù Vp1 = 0 d Hình 9.4 97 Tính: V p = V + V ⇔ 0 = 0 + V 1 p 1 pp 1 pp ⇒ 0 = V = PP .ω ⇔ P ≡ P pp1 1 1 Vaäy P laø duy nhaát.
- Choïn P laøm ñieåm cöïc: VM = VMP
(laø vaän toác cuûa M quay quanh taâm P vôùi vaän toác goùc ω) • Khi ω = 0
Vôùi moïi M, N ∈ S chuùng ta coù ngay VM = VN khi duøng (9.6).
4- Quy taéc thöïc haønh tìm vaän toác töùc thôøi
• Bieát vaän toác moät ñieåm (M) vaø phöông vaän toác ñieåm khaùc (N) khoâng
song song vôùi nhau (H.9.5a), khi ñoù P laø giao ñieåm cuûa hai tia ñi qua M, N
vuoâng goùc töông öùng vôùi caùc vaän toác vaø VM ω = PM V M V M m M V M N M Phöông VN VT N ω P ω P ω P VN N a) b) c) M V O M V ω N N P d) e) Hình 9.5
• Bieát vaän toác hai ñieåm (M, N) song song vôùi nhau vaø vuoâng goùc vôùi MN
(H.9.5b,c). Taâm P ñöôïc xaùc ñònh nhö hình veõ vaø V V M − N ω = MN
• Vaän toác hai ñieåm (M, N) song song vôùi nhau vaø khoâng vuoâng goùc vôùi
MN (H.9.5d). Duøng ñònh lyù hình chieáu vaän toác ⇒ V M = V N .
Chöùng toû vaän toác moïi ñieåm baèng nhau taïi thôøi ñieåm naøy ⇒ thieát dieän S tònh tieán töùc thôøi. W A
• Hình phaúng laên khoâng tröôït treân y1
ñöôøng phaúng (H. 9.5e). Do khoâng coù söï y
tröôït neân ñieåm P ∈ S tieáp xuùc vôùi giaù coá n M W ñònh coù V MA ω τ p = 0 ⇒ P laø TVTTT. WMA
3. Gia toác cuûa ñieåm thuoäc hình phaúng S A x1 W
1- Bieåu thöùc gia toác cuûa ñieåm ∈ S M ε WMA O x Hình 9.6 98
Xeùt ñieåm M ∈ S chuyeån ñoäng phöùc hôïp, töông töï nhö vaän toác: WM = We + Wr + WC ôû ñaây: W = ; 0 We = WA ; Wr C = WMA
goïi laø gia toác cuûa M chaïy quanh cöïc A. τ n
WMA = WMA + WMA trong ñoù: τ WMA (= . MA ε
, ⊥MA höôùng thuaän chieàu ε ). n WMA (= MA. 2 ω , ↑↑ MA ⇒ WM = W A + WMA
2. Quan heä gia toác hai ñieåm cuûa hình phaúng S
Do cöïc A laø ñieåm tuøy yù xaùc ñònh, chuùng ta coù ngay quan heä gia toác giöõa
hai ñieåm tuøy yù M, N ∈ S: WM = WN + WMN (9.10)
Chuùng ta coù theå bieåu dieãn chi tieát hôn: τ n τ n τ n WM + WM = WN + WN + WMN + WMN (9.11)
(Ñieåm M, N neáu coù quyõ ñaïo thaúng, thaønh phaàn n W = 0 )
3- Taâm gia toác töùc thôøi Q
Ñònh lyù. ÔÛ moãi thôøi ñieåm ∃ duy nhaát ñieåm Q ∈ S coù M W W M α
Q = 0. Q ñöôïc goïi laø taâm gia toác töùc thôøi vaø gia toác
cuûa ñieåm ∈ S phaân boá gioáng nhö S ñang quay quanh Q ε vôùi ω ω, ε töông öùng. α Q Chöùng minh W QM d
• Chöùng toû ∃ Q (H.9.7): Hình 9.7 Xeùt M
∈ S coù WM ≠ 0 ⇒ M ≡ Q)
Döïng tia Md cuøng chieàu WM khi ñaõ quay quanh M theo chieàu ε goùc α vôùi tg ε α = . 2 ω
Treân tia Md laáy ñieåm Q sao cho: M W MQ = 2 4 ε + ω Tính: WQ = WM + WQM
Xem (H.9.7) chuùng ta nhaän thaáy: WQM (W = QM ( τQM W )2 + ( QM W )2 N = 99 2 4 = QM ε + ω = M
W höôùng ngöôïc höôùng WM ) ⇒ WQ = 0
• Chöùng toû Q duy nhaát: Giaû söû ∃ Q M WM 1 coù W ε α 1 Q = 0 Q
Xeùt quan heä gia toác giöõa Q vaø Q WN 1: WQ = WQ + W ⇔ = + 1 QQ 0 0 W 1 QQ1 N Hình 9.8 ⇒ QQ1. 2 4 ε + ω = 0 ⇒ QQ1 = 0 hay Q1 truøng vôùi Q.
• Neáu choïn Q laøm ñieåm cöïc chuùng ta coù ngay: τ N WM = WQM = WMQ + wMQ
Gia toác M ñöôïc xaùc ñònh gioáng nhö S ñang quay quanh Q vôùi cheá ñoä ω, ε töông öùng.
4- Phöông phaùp thöïc haønh xaùc ñònh Q - Bieát ω ε
. vaø gia toác moät ñieåm WM : chuùng ta xaùc ñònh Q gioáng nhö muïc 3 - Bieát ω ε
, vaø phöông gia toác hai ñieåm M, N Töø M, N ta keû hai tia taïo vôùi WM , W Chuù yù:
- Thoâng thöôøng ñeå giaûi baøi toaùn gia toác chuùng ta thöôøng duøng quan heä gia
toác hai ñieåm [bieåu thöùc (9.10) hoaëc (9.11)], ít duøng taâm Q. - Taâm Q
≠ taâm P, chuùng chæ truøng nhau khi S quay quanh ñieåm coá ñònh (P
≡ Q ≡ ñieåm coá ñònh).
- Chæ ñöôïc xem S quay quanh TVTTT P khi giaûi vaän toác, khoâng ñöôïc xaùc
ñònh gia toác gioáng nhö S quay quanh P.
Töông töï, chæ ñöôïc xaùc ñònh gia toác gioáng nhö S quay quanh Q.
9.3. NHÖÕNG CHUYEÅN ÑOÄNG SONG PHAÚNG ÑAËC BIEÄT
1. Chuyeån ñoäng quay ñoàng thôøi quanh hai truïc song song
Ñònh lyù. Cho vaät raén quay quanh truïc ñoäng Δ1 vôùi vaän toác goùc 1 ω (vaän toác goùc
töông ñoái). Truïc Δ1 laïi quay quanh truïc Δ2 ( Δ1 // Δ2 ) ñöôïc coi laø coá ñònh vôùi vaän toác goùc 2
ω (vaän toác goùc theo H.9.9a). Vaät raén seõ chuyeån ñoäng song phaúng
coù maët phaúng quy chieáu vuoâng goùc Δ2 vôùi vaän toác goùc: 100 ω = 1 ω + 2 ω (9.12) (tröôøng hôïp ω + ω = 0 1 2 vaät raén tònh tieán).
Chöùng minh. Chuùng ta deã daøng nhaän thaáy moãi ñieåm M thuoäc vaät thöïc hieän
chuyeån ñoäng hôïp, coù V e ,V r ñeàu vuoâng goùc vôùi truïc quay Δ ⇒ 2 vaän toác tuyeät
ñoái V a = V e + V r cuõng phaûi vuoâng goùc vôùi Δ2 , chöùng toû quyõ ñaïo cuûa M thuoäc
moät maët phaúng vuoâng goùc vôùi Δ2 .
Suy ra vaät chuyeån ñoäng song phaúng, vì vaäy chæ caàn khaûo saùt chuyeån ñoäng
cuûa vaät qua moâ hình phaúng (H.9.9b).
- Xaây döïng heä ñoäng O1x1y1 quay theo V O o1 1O2 vôùi vaän toác goùc 2 ω quanh O2 coá ñònh, O ω2 ω
1x1 luoân naèm doïc theo O2O1. Xeùt ñieåm O2 1 ω O1
∈ S chuyeån ñoäng hôïp (ñieåm ∈ S’ nhöng truøng O P 2
vôùi O2 taïi thôøi ñieåm ñang xeùt):
- Töông ñoái: quay xung quanh O1 vôùi vaän toác goùc 1 ω (H.9.10): V rO2 V ⇒ r V = 1 O O2. 1 ω - Theo: ñieåm ∈ heä ñoäng O Hình 9.10 1x1y1, song
ñaây laø ñieåm coá ñònh thuoäc heä ñoäng neân: Ve = 0 ⇒ O V = + = +
(chuùng ta bieåu dieãn ôû H.9.10 cho roõ raøng) 2 e V Vr 0 Vr
Vôùi ñieåm O1 ∈ S chuùng ta coù ngay: V = O O .ω , O
coù höôùng nhö H.9.10õ. 1 1 2 2
Söû duïng quan heä vaän toác hai ñieåm O1, O2: V = V + V (*) 1 O O2 1 O O2 Chuùng ta quy öôùc neáu 2
ω > 0 (ngöôïc chieàu kim ñoàng hoà) thì V 0 1 O >
(thuaän chieàu ω2 ). Goïi ω laø vaän toác goùc cuûa S. Chieáu (*) leân höôùng V chuùng 1 O ta nhaän ñöôïc: O O ω 1 2. = − 2 O O ω 1 2. + 1 O O ω 1 2. ⇒ ω = 1 ω + 2 ω Tröôøng hôïp ω = 1 ω + 2 ω = 0 : V M = V N ; ∀ N M, ∈ ⇒ S
vaät raén tònh tieán töùc thôøi 101
Chuù yù: Coâng thöùc (9.12) ñuùng vôùi moïi thôøi ñieåm neân chuùng ta coù ngay: ε = 1 ε + 2 ε (9.13) vaø: ϕ = 1 ϕ + 2 ϕ (9.14) 2. CÔ CAÁU VI SAI
Xeùt cô caáu goàm tay quay OA vaø baùnh xe II
quay ñoäc laäp vôùi nhau quanh truïc coá ñònh qua O. I ε ω o
Baùnh xe I quay quanh taâm A ñoàng thôøi laên khoâng o A O
tröôït töông ñoái treân vaønh cuûa baùnh xe II (H.9.11).
Cô caáu loaïi naøy ñöôïc goïi laø cô caáu vi sai. ω2 II
Taïi thôøi ñieåm ñang xeùt ñaõ bieán chuyeån ñoäng ε2
cuûa tay quay OA ( ωo, ε1) vaø cuûa baùnh xe II (ω2,ε2) Hình 9.11
- Ñeå giaûi baøi toaùn naøy chuùng ta thöôøng söû
duïng coâng thöùc Vilit: choïn OA laøm heä ñoäng vaø chieàu quay laøm chieàu döông: ω r1 ω a 1 − o ω R2 = = ± 2 ω r ω a 2 − o ω 1 R
(daáu (+) neáu tieáp xuùc trong nhö H.9.11, daáu (–) neáu tieáp xuùc ngoaøi).
töø ñoù chuùng ta coù keát luaän: R1 − R2 R2 1 ω ≡ ω a 1 = ωo + 2
ω (tieáp xuùc trong) (9.15) R1 R1 1 R + R2 R2 1 ω ≡ ω a 1 = o ω − 2 ω (tieáp xuùc ngoaøi) (9.16) 1 R 1 R
Chuù yù: ω > 1
0 ⇒ baùnh xe I quay cuøng chieàu OA ω < 1
0 ⇒ baùnh xe I quay ngöôïc chieàu OA
Caùc coâng thöùc (9.15), (9.16) ñuùng cho ∀t R − R R ⇒ 1 2 2 1 ε& = εo + 2 ε (tieáp xuùc trong) 1 R 1 R 1 R + R2 R2 1 ε = εo − 2 ε (tieáp xuùc ngoaøi) 1 R 1 R 3. Roøng roïc ñoäng
Xeùt moâ hình roøng roïc ñoäng nhö hình
9.12. Caùc nhaùnh daõy ñi qua I, H song song. VI Δ
Caùc baùn kính töông öùng R, r. + VH
Chuùng ta seõ tìm moái quan heä giöõa + V I O H
I , V H , W I , W H vaø ω, ε cuûa roøng roïc?
Quy öôùc höôùng döông vaø chieàu quay döông nhö hình veõ. Hình 9.12 102 AÙp duïng V H = V I + V HI (*) Trong ñoù V HI = IHω = (R + r) , ω höôùng döông.
Chieáu (*) leân truïc Δ ⇒ V = H V + I R ( + r)ω V − V H I ⇒ ω =
; neáu ω > 0 chieàu quay döông, ω < 0 chieàu quay aâm (R + r) W − W H I ⇒ ε = R + r
9.4. PHÖÔNG PHAÙP GIAÛI BAØI TOAÙN CHUYEÅN ÑOÄNG SONG PHAÚNG
Baøi toaùn toång quaùt ñöôïc yeâu caàu ôû ñaây laø xaùc ñònh hình phaúng chuyeån
ñoäng song phaúng. Töùc laø chuùng ta phaûi xaùc ñònh ñöôïc chuyeån ñoäng cuûa moät
ñieåm cöïc ∈ hình phaúng vaø chuyeån ñoäng quay quanh ñieåm cöïc ñoù ( ω, ε ).
Hình phaúng chuyeån ñoäng song phaúng thöôøng lieân keát ñoäng vôùi giaù coá ñònh
vaø caùc vaät raén chuyeån ñoäng khaùc (quay quanh truïc coá ñònh, tònh tieán). Chuù yù
ñeán ñaëc ñieåm naøy chuùng ta ñöa ra phöông phaùp giaûi nhö sau:
- Ñeå xaùc ñònh chuyeån ñoäng cuûa ñieåm cöïc chuùng ta xeùt nhöõng ñieåm ñaëc
bieät, thöôøng laø ñieåm lieân keát giöõa vaät raén ñaõ bieát chuyeån ñoäng vaø hình phaúng.
- Ñeå xaùc ñònh chuyeån ñoäng quay cuûa hình phaúng quanh cöïc chuùng ta thöôøng söû duïng:
1- Giaûi vaän toác
- Duøng taâm vaän toác töùc thôøi {caùc ví duï (9.1), (9.2), (9.3), (9.4), (9.7)}.
- Duøng quan heä vaän toác goùc (9.12) hay (9.15), (9.16) khi hình phaúng ñoàng
thôøi quay quanh caùc truïc song song {caùc ví duï (9.2), (9.7)}.
- Duøng ñònh lyù quan heä vaän toác hai ñieåm ∈ S. Trong ñoù moät ñieåm ñaõ bieát
(thöôøng laø ñieåm cöïc) vaø ñieåm thöù hai thöôøng laø bieát quyõ ñaïo do ∈ moät vaät raén
khaùc {caùc ví duï (9.5), (9.6), (9.7), (9.8)} hoaëc lieân quan tôùi chuyeån ñoäng cuûa vaät
raén khaùc {caùc ví duï (9.9), (9.10)}.
2- Giaûi gia toác
- Tính tröïc tieáp ε = ω& khi bieát ω laø haøm cuûa thôøi gian (tröôøng hôïp cô caáu
ñoái xöùng: truïc troøn laên khoâng tröôït, vi sai, haønh tinh) {caùc ví duï (9.2), (9.3), (9.4), (9.7)}.
- Duøng quan heä gia toác hai ñieåm ñaëc bieät (M, N): WM = WN + WMN n τ n τ n τ
⇔ WM + WM = WN + WN + WMN + WMN 103
Chieáu phöông trình leân hai truïc xaùc ñònh, chuùng ta nhaän ñöôïc hai phöông
trình ñaïi soá ñeå giaûi ra caùc aån caàn thieát {caùc ví duï (9.5), (9.6), (9.8)}.
Tröôøng hôïp soá aån trong phöông trình vector lôùn hôn 2 chuùng ta phaûi tìm
theâm tính chaát môùi cuûa caùc ñieåm ñaëc bieät ñeå xaây döïng theâm caùc phöông trình
sao cho toång soá aån baèng toång caùc phöông trình ñaïi soá nhaän ñöôïc {caùc ví duï (9.9), (9.10)}. 9.5. CAÙC VÍ DUÏ Ví duï 9.1.
Xeùt cô caáu haønh tinh nhö H.9.13. Bieát y V
ban ñaàu tay quay ôû vò trí naèm ngang beân A ε ω 2 2
phaûi vaø chuyeån ñoäng theo luaät: II A ϕ = ( ϕ t) = 3 t 2 2 + (rad) R ε 2 ϕ ϕ t - tính theo giaây o ω B 2r 0 M
• Laäp phöông trình chuyeån ñoäng cuûa O ϕ R baùnh xe II 1 A x C
• Xaùc ñònh vaän toác goùc 2 ω , gia toác I ε2. Hình 9.13
Giaûi: • Phaân tích chuyeån ñoäng:
Cô caáu goàm ba vaät raén:
- Tay quay OA quay quanh truïc O coá ñònh (bieát chuyeån ñoäng) - Baùnh xe I coá ñònh
- Baùnh xe II chuyeån ñoäng song phaúng laên khoâng tröôït leân baùnh xe I coá ñònh.
• Laäp phöông trình chuyeån ñoäng: ñeå xaùc ñònh chuyeån ñoäng cuûa baùnh xe
II chuùng ta choïn cöïc A (xA,yA) vaø tìm chuyeån ñoäng quay quanh cöïc A. Taïi thôøi
ñieåm (H.9.13) OA quay goùc ϕ , baùn kính AM gaén chaët vôùi baùnh xe II veõ töø vò trí
naèm ngang (AC) chuyeån tôùi AM nhö H.9.13. Do laên khoâng tröôït R ⇒ BM = BC ⇔ R 1 1 ϕ = R2 ϕ2r ⇒ ϕ = ϕ 2r R2
So vôùi höôùng cuõ, tia AM ñaõ quay goùc: R ϕ = ϕ + ϕ = ϕ + 1 ϕ 2 2r R2
Phöông trình chuyeån ñoäng: xA = (R1 + R2)cos ϕ yA = (R1 + R2)sin ϕ ⎛ R ⎞ ϕ = 1 + 1 ϕ 2 ⎜⎜ ⎟⎟ vôùi: ϕ = 3 + 2t2 ⎝ R2 ⎠
• Giaûi ω2 : xeùt tieáp ñieåm B chính laø taâm vaän toác töùc thôøi cuûa baùnh xe II VA R1 + R2 R1 + R2 ⇒ ω = = ϕ& = 4t 2 chieàu nhö hình veõ. R R R 2 2 2 104
• Giaûi ε2 : bieåu thöùc ω2 laø haøm cuûa t R R ⇒ 1 2 ε2 = & 2 ω 4 + = R2
Ví duï 9.2. Cho cô caáu vi sai: tay quay OA quay quanh truïc qua O coá ñònh, baùnh
xe I taâm A laên khoâng tröôït leân baùnh xe II cuõng quay ñöôïc quanh O (ñoäc laäp vôùi
OA). Taïi thôøi ñieåm ñang xeùt bieát ωo, εo cuûa tay quay vaø ω2, ε2 cuûa baùnh xe II (H.9.14), OA= 3R2 = 0,6 m. a) Tìm 1
ω , ε1 cuûa baùnh xe I vaø VM, WM ?
b) Tính vôùi caùc giaù trò: o ω = 2 ω = rad 2 / s 2 εo = 2ε2 = 4rad / s
Giaûi: a) Ñeå tính 1
ω , ε1 cuûa baùnh xe I chuùng ta duøng coâng thöùc vilit (9.16), (9.18): R2 + R1 R2 3 1 ω = ω − ω = ω + ω 0 1 > R o R 2 2 o 2 2 1 1 R + R R 2 1 2 3 1 ε1 = ε − ε2 = ε + ε > 0 R o R 2 o 2 2 1 1
Chöùng toû baùnh xe I coù 1
ω vaø ε1 cuøng chieàu vôùi ωo, εo cuûa tay quay OA. VM VMA WτMA ω ω 1 1 x τ ε V 1 A M ε W 1 A M A n y WMA εo ε A o R1 Wn R1 ω A 2 ω ω o 2 ωo O R I R I 2 2 II II ε2 ε2 Hình 9.14 Hình 9.15 Tính
V M : (H.9.14): duøng ñieåm A laøm cöïc: V M = V A + V MA + V A = 1 R ( + R2) o ω = R 3 2 o ω + V ⎛ 3 1 ⎞ MA = ω . AM = 1 R1⎜ ω + ω o 2 ⎟ ⎝ 2 2 ⎠ + ⎛ 3 ⎞ R V 1 M = A V + MA V = ⎜ R 3 2 + R1 o ω ⎟ + o ω ⎝ 2 ⎠ 2 Tính WM (H.9.15): WM = WA + WMA (*) n τ n τ ⇔ WM = WA + WA + WMA + WMA 105 + n WA = (R1 + R2) 2 ω o + τ WA = (R1 + R2) εo + n W 2 MA = R1 ω 1 + τ WMA = R1 ε1
Chieáu phöông trình (*) leân caùc truïc thích hôïp: n n 2 2 (*) x ⇒ Mx W = − A W + 0 − MA W
+ 0 = −(R1 + R2)ωo − R1ω1 (*) y ⇒ τ τ My W = 0 + A W + 0 + MA W = (R1 + R2)εo + R1ε1
b) Tính vôùi caùc giaù trò cuï theå: ω 4rad / ; s 1 = ε 7rad / s 1 = V 2 2 M = 2,8 m/s; 2 M W = Mx W + My W = m 22 , 10 / s
Chuù yù: Neáu caùc coâng thöùc (9.15) ñeán (9.18) khoù nhôù ta chæ caàn aùp duïng: 2 ω − ωo R1 = ± 1 ω − ωo R2 D
Ví duï 9.3. Con laên hai taàng baùn ε
kính töông öùng R = 2r = 0,4 m ωτBO V
ñöôïc keùo leân laên khoâng tröôït nhôø ω B
taûi A. Bieát A rôi xuoáng theo quy ωnBO VO VC S
luaät: s = 3 + 4t2 (m,s). Tìm ω, ε ωτco A O ω n O ωco
cuûa con laên, vaän toác, gia toác caùc C VA
ñieåm B, C, O cuûa con laên taïi thôøi ñieåm t = 2s (H.9.16). I
Giaûi. Yeâu caàu cuûa baøi toaùn thöïc ra
laø xaùc ñònh chuyeån ñoäng song Hình 9.16
phaúng cuûa con laên (laên khoâng
tröôït) thoâng qua chuyeån ñoäng ñaõ
bieát taûi A (tònh tieán). Töø VA = s& = t
8 (m/s), chuùng ta phaûi (tìm) ω, ε vaø vaän toác,
gia toác moät ñieåm cuûa con laên:
Neáu laáy ñoaïn daây nghieâng BD laøm heä ñoäng, con laên khoâng tröôït treân
nhaùnh daây naøy, ñöùng trong heä ñoäng quan saùt ñieåm B laø taâm vaän toác töùc thôøi: r r e e V e
B = 0 → V B = V B + V B = V B (phöông ox ) → B V = B V = s& = A V ⇒ VB = t 8 (m/s)
• Vaän toác: duøng taâm vaän toác töùc thôøi I VB t 8 40 ⇒ ω = = = t (rad/s) R + r 6 , 0 3 40 V = . IC ω 4 , 0 2 C = t (m/s) 3 40 V = . IO ω 4 , 0 O = t (m/s) 3 106
Taát caû coù höôùng nhö H.9.15 Taïi thôøi ñieåm t = 2s: 80 32 2 ω = = 7 , 26 (rad/s); VC = = 1 , 15 ; Vo = 7 , 10 (m/s) 3 3
• Gia toác: do ω laø haøm cuûa t ⇒ ε = ω& = 3 , 13 (rad/s2)
Coøn haøm O coù quyõ ñaïo thaúng ⇒ W = V& = 3 , 5 o o (m/s2)
Choïn ñieåm O laøm cöïc chuùng ta xaùc ñònh taïi t = 2: + n τ
WB = WO + WBO = WO + WBO + WBO (*) trong ñoù: Wn = r 2 ω = 7 , 26 . 2 , 0 2 2 , 142 BO = (m/s2) τ WBO = rε = 13,3 . 2 , 0 = 2,7 (m/s2)
Taát caû coù höôùng nhö H.9.16
Chieáu (*) leân caùc truïc x, y: (*) x ⇒ W = W + Wτ = ( 8 m / s2) Bx O BO (*) y ⇒ W = −Wn = − ( 2 , 142 m / s2) By BO ⇒ WB = W2Bx + W2By = 4 , 142 (m/s2) A WA + 1 VA n τ
WC = WO + WCO = WO + WCO + WCO (**) trong ñoù: Wn = R 2 ω 4 , 284 CO = (m/s2) Wτ = Rε 4 , 5 CO = (m/s2) 2 (**) x ⇒ W = W + Wn = 7 , 289 Cx O CO (m/s2) V V H 3 3 (**) y ⇒ W = Wτ = 4 , 5 (m/s2) H I Cy CO VL ω ⇒ W = W2 + W2 = 8 , 289 3 C Cx Cy (m/s2) ω4
Ví duï 9.4. Cô heä nhö H.9.17 V4 Bieát R E
1 = R4 = 2R2 = 0,1m, R3 = 0,05m. L 4 K
Giaû thieát caùc daây lieân keát caùc roøng roïc ñeàu
thaúng ñöùng (II). Tìm VA, WA khi cho VM = 0,4 V (m/s), W K M = 0,2 (m/s). VM WM Hình 9.17 107
Giaûi. Goïi taâm caùc roøng roïc töông öùng laø 1, 2, 3, 4 coù: V3 = V4 = VM
Caùc ñieåm I, H, K, L töông öùng thuoäc caùc roøng roïc. Do daây khoâng daõn neân ta coù ngay t ∀ : VH = VK; VL = VA (*) • Vaän toác
- Xeùt roøng roïc 3 laø chuyeån ñoäng laên khoâng tröôït treân nhaùnh daây beân phaûi
coá ñònh neân I laø taâm vaän toác töùc thôøi. ⇒ VH = V 2 3 = V 2 M = 8 , 0 (m/s) VH ω = 8 (rad/s) 3 = R 2 3
- Xeùt roøng roïc 4 laø chuyeån ñoäng song phaúng. Bieát V k vaø V 4 chuùng ta tìm
ngay ñöôïc taâm vaän toác töùc thôøi E vôùi: 2 4 EK = R4 EL , = R4 3 3 K V ⇒ L V = EL 4 ω = EL = K V 2 = 4 M V EK vaø: VA = 4 VM = 1,6 (m/s2) • Gia toác
Do tính ñoái xöùng cuûa cô caáu: chuùng ta coù caùc quan heä haøm ( ∀t ). → A W = 4 M W
Ví duï 9.5. Cô caáu boán khaâu OABO1 nhö VAB
H.9.18. Taïi thôøi ñieåm ñang xeùt: V Wτ OA ñaït vaän toác goùc A A ω = AB o 2 (rad/s) Wτ Wn Gia toác goùc ε = A n AB o 1 (rad/s2) WA cho: OA = a = 0,3 m ω εo Wn1A Wτ O 1A ω ε 1B = b = 0,2 m o O1 45o
Xaùc ñònh vaän toác goùc , ω 1 ω , gia I ω1 O ε1 toác goùc V ε ,ε B n
1 töông öùng cuûa thanh AB vaø y WB x O B
1B, cuõng nhö vaän toác, gia toác ñieåm I WτB ∈ AB taïi vò trí H.9.18. Hình 9.18
Giaûi. Cô caáu goàm thanh OA vaø O1B quay
quanh truïc coá ñònh, thanh AB chuyeån ñoäng song phaúng. Ñeå xaùc ñònh chuyeån
ñoäng cuûa AB chuùng ta xeùt hai ñieåm ñaëc bieät A vaø B. • Vaän toác VA { = OAω 6 , 0 m ( / ) s o = , höôùng nhö H.9.18} VB { = O1B 1 ω = 2 , 0 1
ω ? chöa bieát; phöông ⊥ O1B, choïn chieàu giaû ñònh nhö H.9.18}.
Khi xem A, B cuøng ∈ thanh AB: V A = V B + V AB (*) 108 VAB { = . AB ω = a ( 2 + ) b ω = 3 , 0 ( 2 + ) 2 ,
0 ω ? chöa bieát; phöông ⊥ AB,
choïn chieàu giaû ñònh nhö H.9.18}.
Chieáu (*) leân caùc truïc x, y: (*) x ⇒ −V cos 45o = 0 + V ⇔ − 3 , 0 2 = 3 , 0 ( 2 + ) 2 , 0 ω A AB o (*) y ⇒ −VA cos 45 = B V + 0 ⇒ 3 , 0 2 = 2 , 0 1 ω Giaûi ra: − 3 2 ω =
(rad/s–1) = –0,67 (rad/s–1) (laáy chieàu ngöôïc chieàu ñaõ choïn) 3 2 + 2 ω 5 , 1 2 1 =
(rad/s; chieàu nhö hình veõ ñöôïc xaùc ñònh nhö H.9.18
Chuù yù: Chuùng ta coù theå duøng TVTTTP laø giao cuûa ñöôøng OA vaø O1B. • Gia toác + n τ WA = WA + WA n trong ñoù: W 2 A { = OA.ω 2 , 1 o =
(m/s2), höôùng ñöôïc xaùc ñònh nhö H.9.18} τ WA { = . OA εo = 3 ,
0 (m/s2), höôùng ñöôïc xaùc ñònh nhö H.9.18} + n τ WB = WB + WB n trong ñoù: W 2 B { = O . B ω = 9 , 0 1 1
(m/s2), höôùng ñöôïc xaùc ñònh nhö H.9.18} τ WB { = O1 . B 1 ε = . 2 , 0 1
ε ? chöa bieát; phöông ⊥ O1B choïn chieàu giaû ñònh nhö H.9.18}.
AÙp duïng quan heä gia toác hai ñieåm: n τ n τ n τ
WA = WB + WAB ⇔ WA + WA = WB + WB + WAB + WAB (**) trong ñoù : n W 8 , 1 AB { = . AB 2 ω = = 28 , 0
(m/s2), höôùng nhö H.9.18} 3 2 + 2 τ WAB { = ε . AB = 3 , 0 2 + ε 2 , 0 = 624 , 0
ε chöa bieát; phöông ⊥ AB choïn
chieàu giaû ñònh nhö H.9.18}.
Chieáu (**) leân caùc truïc x, y: n o τ o n τ
(**) x ⇒ −W cos 45 − W cos 45 = W = 0 + 0 + A A B AB W ⇔ − 6 , 0 2 − 15 , 0 2 = 9 , 0 + 3 , 0 ( 2 + ε ) 2 , 0
(**) y ⇒ −Wn cos 45o + Wτ cos 45o = 0 − Wτ − Wn + 0 A A B AB 8 , 1 ⇔ − 6 , 0 2 − 15 , 0 2 = − 2 , 0 ε1 − 3 2 + 2
Giaûi heä hai phöông trình, chuùng ta nhaän ñöôïc: ε = – 3,16 ε1 = 3,9 Nhaän xeùt:
- Thanh AB coù cheá ñoä quay nhanh daàn vôùi ε = 2,77 (rad/s2) (chieàu H.9.18) 109 - Thanh
O1B quay quanh O, chaäm daàn.
Laáy ñieåm A laøm cöïc chuùng ta tính ñöôïc: n τ n τ
WI = WA + WIA ⇒ WI = WA + WA + WIA + WIA (***) trong ñoù: n WIA (= . AI 2 ω = a 2 2 ω = 108 , 0 , höôùng nhö H.9.18} τ WIA (= . AI ε = ; 32 , 1 höôùng nhö H.9.18)
Chieáu (***) leân caùc truïc x, y: (* * *) x ⇒ n o τ o Ix W τ
= −W cos 45 − W cos 45 + 0 + A A IA W = − 6 , 0 2 − 15 , 0 2 + 32 , 1 = 26 , 0 (m/s2) (* * *) y ⇒ n o τ o n Iy
W = −W cos 45 + W cos 45 + W + 0 A A IA = − 6 , 0 2 + 15 , 0 2 + 18 , 0 = − 45 , 0 (m/s2) ⇔ Iy W = 45 , 0
(m/s2) coù chieàu ngöôïc chieàu truïc y. ⇔ 2 2 1 W = WIx + WIy = 51 , 0 (m/s2)
Ví duï 9.6. Hai con chaïy A, B noái vôùi nhau bôûi thaønh y
cöùng ñoä daøi 2 m; A coù theå tröôït leân raõnh naèm ngang; V
B coù theå tröôït leân raõnh thaúng ñöùng. Bieát A chuyeån B ñoäng theo luaät: B x sin π =
t . Tìm ω, ε cuûa thanh AB 4 W taïi caùc thôøi ñieåm t B ε = 0 1 = 0, t2 = 2 (giaây). ω
Giaûi. Thanh AB chuyeån ñoäng song phaúng coù hai Wn ñieåm ñaëc bieät laø: AB Wτ VAB AB x
- A ñaõ bieát chuyeån ñoäng O A VA
- B ñaõ bieát quyõ ñaïo (thaúng) Hình 9.19
• Vaän toác: aùp duïng: V A = V B + V AB (*) trong ñoù: V π π A { = x & =
cos t cuøng phöông x, (x > 0) cuøng chieàu truïc x, x < 0 4 4 ngöôïc chieàu truïc x}
V B = ? chöa bieát; phöông truïc y, choïn chieàu giaû ñònh döông (cuøng chieàu truïc y). V AB = .
AB ω = 2ω ? chöa bieát, phöông ⊥ AB, choïn chieàu giaû ñònh H.9.19
a) Taïi thôøi ñieåm t = 0 ⇒ x = V , 0 π (H.9.19) A = 4 Chieáu (*) x ⇒ V = 0 − V π ⇔ = 2 π A AB − ω ⇒ ω = − 4 8 Vaäy π ω =
(rad/s) coù chieàu nhö hình veõ 8 110
b) Taïi thôøi ñieåm t = 2 (s) ⇒ x = 1, V y A = 0 (H.9.20) VB Chieáu (*) o ⇒ 0 = 0 + AB V cos 30 x B ⇒ V = 0 ⇔ ω 0 AB = ω = 0
{thanh AB tònh tieán (döøng) töùc thôøi, vaän toác ôû moãi W ε B 30o ñieåm ñeàu baèng VA = 0} W V n AB AB
Chuù yù: Chuùng ta coù theå söû duïng VTTT tröôøng x O hôïp a) chính laø B) W A A WτAB • Gia toác Hình 9.20 AÙp duïng: n τ
WA = WB + WAB ⇔ WA = WB + WAB + WAB (**) 2 ⋅⋅ W π π A { = x& = −
sin t cuøng höôùng truïc x khi x > 0, ngöôïc höôùng truïc x 16 4 khi x& < 0}.
WB = ? chöa bieát; phöông doïc truïc y, choïn chieàu giaû ñònh aâm 2 n W π AB { = . AB 2 ω =
, höôùng nhö H.9.19 (choïn giaû ñònh)} cho tröôøng hôïp 32
(a) vaø baèng 0 cho tröôøng hôïp (b) τ WAB {= .
AB ε = 2ε ? chöa bieát; höôùng choïn giaû ñònh nhö H.9.20 hoaëc H.9.19}
a) Taïi thôøi ñieåm t = 0 ⇒ x = 0, WA = 0 (H.9.19) Chieáu: τ (**) x ⇒ 0 = 0 + 0 + τ AB W ⇒ W = 0 ⇒ ε 0 AB = 2
b) Taïi thôøi ñieåm t = 2 (s) ⇒ x = 1, W π A (=
coù chieàu ngöôïc H.9.20) 16 Chieáu: C τ o τ o (**) x ⇒ A W = 0 + 0 − AB W sin 60 − AB W sin 60 − π 3 π ⇔ = −2ε ⇒ ε = 16 2 16 3
Vaäy thanh AB taïi thôøi ñieåm naøy coù gia toác goùc ε theo chieàu ngöôïc kim
ñoàng hoà vôùi ñoä lôùn baèng π (rad/s2) 16 3
Ví duï 9.7. Cô caáu nhö H.9.21. Thanh HB gaén chaët vaøo baùnh xe I, ñaàu B lieân keát
vôùi con chaïy tröôït ñöôïc treân ñöôøng naèm ngang. Baùnh xe I vaø II cuøng tay quay
OA lieân keát daïng vi sai. Bieát tay quay OA quay ñeàu vaän toác goùc ω 2 o = rad/s,
baùn kính caùc baùnh xe töông öùng R1 = 0,2 m, R2 = 0,4 m. Xaùc ñònh VB, WB, 1 ω , 1 ε . 111
Giaûi. Neáu ta chuù yù ñeán töøng caëp chuyeån P ñoäng (ñoäc laäp): 30o
- Tay quay OA vaø baùnh xe I: thanh y x ω1
HB chính laø cô caáu tay quay thanh truyeàn ε1 (OA vaø thanh AB). VA WτAB A
- Tay quay OA cuøng caùc baùnh xe I I ωo Wn
vaø II laø cô caáu vi sai. AB = n H W W A
Töø ñoù ta coù phöông phaùp giaûi A II O 30o WB • Vaän toác VB ω B 2 ε2
- Duøng taâm vaän toác töùc thôøi P laø giao
cuûa ñöôøng thaúng OA vaø ñöôøng vuoâng goùc Hình 9.21 vôùi OB.
coù: AB = (R1 + R2) 3 = 0,6 3 (m)
PA = AB 3 = 3 (R1 + R2) = 1,8 (m)
PB = 2(R1 + R2) 3 = 1,2 3 (m)
Töø: VA = OA. ωo = 0,6 . 2 = 1,2 (m/s)
Chuùng ta tính ñöôïc: (H.9.21): VA ⎫ ω = = 67 , 0 (rad / ) s 1 ⎪ PA ⎬ chieàu nhö 21 . H V = PBω = 37 , 1 (m / ) s ⎪ B 1 ⎭
Vaän toác goùc cuûa baùnh xe II ñöôïc tính töø coâng thöùc: 2 ω − o ω R1 1 2 ω − 2 1 = − = − ⇔ = − ⇔ 2ω − 4 = 67 , 0 + 2 − ω − ω R 2 − 67 , 0 − 2 2 2 1 o 2 ⇒ ω 34 , 3 2 =
(rad/s) cuøng chieàu tay quay • Gia toác
- Duøng quan heä gia toác hai ñieåm ñaëc bieät A, B τ n τ n
WA = WB + WAB ⇔ WA + WA = WB + WAB + WAB (*) trong ñoù : + Wτ 0 A = + n WA (= OA. 2 ω = 4 ,
2 (m/s2), chieàu nhö H.9.21). o +
WB = ? chöa bieát; phöông OB choïn chieàu giaû ñònh nhö H.9.21 τ + WAB { = . AB ε = 6 , 0 3 ε ? 1 1
chöa bieát; phöông ⊥ AB choïn chieàu giaû ñònh nhö H.9.21}. n + WAB { = . AB 2 ω 46 , 0 1 =
(m.s2), höôùng nhö H.9.21} 112 Chieáu: n o τ 1 (*) x ⇒ − A W = B W cos 60 + AB W + 0 ⇔ − 4 , 2 = B W + 6 , 0 3ε1 2 Chieáu: o n 3 (*) y ⇒ 0 = − W
B cos 30 + 0 − WAB ⇔ 0 = − WB − 46 , 0 2
Giaûi heä phöông trình chuùng ta nhaän ñöôïc:
WB = –0,54 (m/s2), chieàu WB ngöôïc chieàu ñaõ choïn vaø coù ñoä lôùn 0,54 (m/s2).
ε1 = –2,08 (rad/s2), chieàu nhö H.9.21 (laáy chieàu ngöôïc chieàu 1 ω ), ñoä lôùn 2,08 (rad/s2). Ñeå xaùc ñònh
ε2 chuùng ta söû duïng tieáp coâng thöùc Vilit: ε2 − εo R1 1 ε2 − 0 1 = − = − ⇔ = − (do ε 0 chuùng ta choïn chieàu ε − ε R 2 08 , 2 2 o = 1 o 2 ε1 laøm chieàu döông) Giaûi ra: ε = 04 , 1 2 −
{laáy chieàu nhö hình veõ (ngöôïc chieàu ε1 ñaõ choïn); ñoä lôùn 10,4 (rad/s2)}
Ví duï 9.8. Cho cô caáu nhö H.9.22, tay D
quay OA quay ñeàu vaän toác goùc ωo = 10 ω12 (rad/s) cho: VD OA = 20 cm; AB = 10 3 (cm); 30o ε P O τ 2 O W 1C = O2D = 40 cm BA τ ω WB Tính vaän toác goùc 12 ω cuûa thanh VA A 30o B O W n 1C vaø O2D. BA n Wn = B W A W
Giaûi. Cô caáu goàm caùc vaät raén chuyeån A VB ñoäng nhö sau: ωo O
- Thanh OA quay quanh truïc O coá W τC ñònh y
- Thanh AB chuyeån ñoäng song n C WC ω phaúng 12 x V ε12 C
- Thanh CD chuyeån ñoäng tònh tieán 30o - Thanh O O1 1C vaø O2D quay töông Hình 9.22
öùng quanh caùc truïc coá ñònh cuøng moät cheá ñoä.
Töø keát luaän treân suy ra: V B = V C = V D ,WB = WC = WD
Quyõ ñaïo cuûa ba ñieåm B, C, D laø caùc ñöôøng troøn baùn kính R = 40 (cm). • Vaän toác
Xaùc ñònh ngay TVTTTP nhö H.9.22 (cuûa AB). 113 1 AP = AB = 10 (cm); BP = 20 (cm) 3 do VA = . OA ωo = 200(cm/s) VA ⎫ ⇒ ω = ω = = 20 (rad / ) s AB ⎪ AP ⎬ chieàu nhö hình 22 . 9 . H ⇒ V ⎪ B = . BP ω = 400 ⎭ VC VB ω = =
10 (rad/s), chieàu nhö H.9.22 12 = O C O C 1 1 • Gia toác AÙp duïng: τ n τ n τ n
WB = WA + WBA ⇔ WB + WB = WA + WA + WBA + WBA (*) trong ñoù: τ τ WB = WC {= O .
C ε = 40ε ? chöa bieát; phöông 1 12 12 ⊥ O1C, chieàu giaû ñònh nhö H.9.22}. n n W 2 B = WC ( = O . C ω = 4000 1 12
(cm/s), höôùng nhö H.9.22) τ WA = 0 n WA { = . OA 2
ω = 2000 (cm/s2), höôùng nhö H.9.22} τ WBA { = .
BA ε = 10 3ε ? chöa bieát; phöông ⊥ AB, choïn chieàu giaû ñònh nhö H.9.22} n WBA { = . BA 2
ω = 4000 3 (cm/s2, höôùng nhö H.9.20} Chieáu o n o n (*) x ⇒ τ B W sin 30 + B W cos 30 = 0 + 0 + 0 − BA W ⇔ 20ε + 2000 3 = 4000 3 12 − Chieáu
(*) y ⇒ Wτ cos 30o − Wn sin 30o = 0 − Wn + Wτ + 0 B B A BA ⇔ 20 ε 3 − 2000 = −2000 + 10 ε 3 12
Giaûi hai phöông trình chuùng ta nhaän ñöôïc: ε = 300 3 12 −
[ laáy chieàu nhö H.9.22 (ngöôïc chieàu ñaõ choïn) coù ñoä lôùn 300 3 (rad/s2)] ε = 600 −
3 [ laáy chieàu nhö H.9.22 (ngöôïc chieàu ñaõ choïn) coù ñoä lôùn 600 3 (rad/s2)]
Chuù yù: Neáu khoâng caàn tính ε chuùng ta khoâng caàn phöông trình chieáu
(*)/y tuy nhieân vaãn phaûi giaûi ω 114
Ví duï 9.9. Cô caáu goàm tay quay OA gaén C V VA*B
baûn leà vôùi con chaïy A tröôït ñöôïc treân thanh A
BC, thanh BC gaén baûn leà vôùi thanh O A 1B. ω Cho O V
1B = 0,2 (m); OA = 0,4 (m). Bieát taïi r
vò trí ñang xeùt, tay quay OA quay ñeàu vôùi 30o B I y V ω B ω o = 2 (rad/s) vaø 1 ω = 1 (rad/s); ε1 = 2 o ε 60o ω 1 (rad/s2). Xaùc ñònh 1 ω, ε cuûa thanh BC. x O O 1 Giaûi. Hình 9.23 • Vaän toác
Thanh BC chuyeån ñoäng song phaúng
Xeùt hai ñieåm ñaëc bieät A*, B ñeàu thuoäc BC (A* ≡ A) AÙp duïng: V A* = V B + V A*B (*) trong ñoù: V B {= O . B ω = 2 ,
0 (m/s), höôùng nhö H.9.23}. 1 1 V A* {= A* B . B ω = AI 3ω = 4 , 0 ( 3 − )
1 ω ? chöa bieát; phöông ⊥ A*B, choïn
chieàu giaû ñònh nhö H.9.23 V * A ? Ñeå tìm *
V A chuùng ta xeùt ñieåm A chuyeån ñoäng hôïp khi laáy BC laøm heä ñoäng.
⇒ V A = V e + V r = V A* + V r ⇒ V A* = V A − V r + V A {= OA.ω = 8 ,
0 (m/s), höôùng nhö H.9.23} o +
V r = ? chöa bieát; phöông doïc theo BC choïn chieàu giaû ñònh nhö H.9.23
Chuùng ta bieåu dieãn laïi (*) (*) ⇔ V A − V r = V B + A* V B (**): chæ coù hai aån Chieáu (**)/x o 3
⇒ −V − V = −V cos 30 + 0 ⇔ − 8 , 0 − V = − 2 , 0 A r B r 2 Chieáu (**)/y o 1
⇒ −0 + 0 = −VB sin 30 + V * ⇔ 0 = − 2 , 0 + 4 , 0 ( 3 − ) 1 ω A B 2
Giaûi heä hai phöông trình ta ñöôïc:
Vr = – 0,63 (m/s) {chieàu ngöôïc chieàu hình veõ, ñoä lôùn 0,63 (m/s)} ω = 34 , 0 (rad/s)
• Gia toác: aùp duïng: τ n τ n WA* = WB + WB + WA*B + WA*B (3*) trong ñoù: τ WB {= O . B ε = 4 ,
0 (m/s2), höôùng nhö H.9.24 1 1 115 n WB {= O . B 2 ω = 2 , 0 (m/s2), höôùng 1 C W W nhö H.9.24} r C τ ε W A A*B = { ε . AB = ε 3 , 0 (m/s2), phöông Τ n ω W W A*B A*B
⊥ AB, choïn chieàu giaû ñònh nhö H.9.24 W n = τ A WA B W I 30o B n WA*B {= . AB 2 ω = 03 , 0 (m/s2), höôùng y ε ω 1 nhö H.9.24} ω 1 Wn o B *
V A ñöôïc tính theo phöông phaùp O x O1
chuyeån ñoäng hôïp cuûa ñieåm A (laáy BC ≡ Hình 9.24 heä ñoäng)
WA = We + Wr + WC = WA* + Wr + WC (4*) ⇒ W = WA − Wr − W * C A ôû ñaây: + WA = WnA {= OA. 2 ω = 6 ,
1 (m/s2), höôùng nhö H.9.24} +
Wr = ?; phöông doïc theo BC, choïn chieàu giaû ñònh nhö H.9.24 + WC {= 2ωV = 43 , 0 r
(m/s2), höôùng nhö H.9.24} Duøng
(3*) vaø (4*) nhaän ñöôïc: τ n τ n
WA − Wr + WC = WB + WB + WA*B + WA*B (5*) Chieáu τ o n o n *) 5 ( x ⇒ 0 − r W + 0 = B W cos 30 + B W sin 30 + 0 + W A*B 3 1 ⇔ −Wr = 4 , 0 + 2 , 0 + 03 , 0 2 2 Chieáu n τ o n o τ *) 5 (
y ⇒ −W − 0 + W = W sin 30 − W cos 30 + 0 − A C B B W A*B 1 3 ⇔ − 6 , 1 + 43 , 0 = 4 , 0 − 2 , 0 − ε 3 , 0 2 2
Giaûi heä hai phöông trình ñöôïc:
Wr = –0,47 (chieàu ngöôïc chieàu H.9.24, ñoä lôùn 0,48 (m/s2)
ε = 4 (rad/s2) chieàu nhö H.9.24.
Ví duï 9.10. Thanh AB luoân töïa leân ñænh O, ñaàu B tröôït leân maët ngang. Cho AI
= 1 m, IB = 2 m. Taïi thôøi ñieåm ñang xeùt bieát VB = 4 ms–1, WB = 2 ms–2 ?. Xaùc ñònh VA, WA .
Giaûi. Thanh AB chuyeån ñoäng phaúng, chuùng ta chuù yù ñeán hai ñieåm ñaëc bieät B vaø I thuoäc thanh AB. • Vaän toác Xeùt
VI. Ñöôïc xaùc ñònh qua chuyeån ñoäng hôïp khi laáy heä ñoäng Oxy (coù Ox // AB) quay cuøng AB. 116 ⇒ V I = V e + V r ( V e = ,
0 do truøng ñieåm laø ñieåm goùc coá ñònh cuûa heä ñoäng. +
V r = ? chöa bieát; phöông Ox (doïc theo AB do chuyeån ñoäng töông ñoái doïc theo Ox). V I = V r
Töø ñaây chuùng ta coù theå duøng phöông phaùp chieáu quen thuoäc ñeå giaûi ra VI,
ω hoaëc coù theå duøng nhieàu phöông phaùp khaùc.
Chaúng haïn duøng TVTTTP laø giao cuûa truïc Oy ( ⊥ V I ) vaø tia qua B vuoâng goùc vôùi V B . Coù: PB = 2IB = 4m V ⇒ B ω = = 1 (rad/s) PB ⇒ V = PA.ω = 13 6 , 3 A = (m/s), VI = . IP ω = 46 , 3 (m/s) = Vr • Gia toác AÙp duïng: τ n
WB = WI + WBI + WBI . ÔÛ ñaây xem I chuyeån ñoäng hôïp: ⇒ WI = We + Wr + WC trong ñoù: + We = ,
0 do truøng ñieåm laø ñieåm O coá ñònh + Wr = ?; phöông doïc AB WC {= 2 V ω = 2 V ω = 92 , 6
(m/s2); höôùng nhö H.9.26} r I P P y τ ε WAB y W ω C A A ω I n I V WAB A O V = O r VI x Wr WnBI W 30o V B B B B x Hình 9.25 Wτ Hình 9.26 BI Chuùng ta nhaän ñöôïc: τ n WB = Wr + WC + WBI + WBI (*) 117 +
WB {= 2 (m/s2); höôùng H.9.26} + τ WBI {= .
IB ε = 2ε ? chöa bieát choïn chieàu giaû ñònh nhö H.9.26} + n WBI {= . IB 2
ω = 2 (m/s2), höôùng nhö H.9.26} Chieáu
(*) y ⇒ W sin 30o = 0 + W − τ W + 0 ⇔ 1 = 92 , 6 − ε 2 B C BI
Giaûi phöông trình ñöôïc:
ε = 2,96 (rad/s2) chieàu nhö H.9.26
(*) x ⇒ Wr = 2 + 3 = 3,73 (m/s2) Tính: τ W A n = WB + WAB = WB + WAB + WAB τ AB W = . 3 ε = ; 9 , 8 Wn 3 AB = (m/s2) ⇒ o n Ax W = W cos 30 + W = 73 , 4 B AB o τ (m/s2) Ay W = W sin 30 + W = 9 , 9 B AB 118 PHAÀN III ÑOÄNG LÖÏC HOÏC
Ñoäng löïc hoïc laø moät phaàn cuûa cô hoïc lyù thuyeát nghieân cöùu caùc quy luaät
chuyeån ñoäng cuûa vaät theå döôùi taùc duïng cuûa löïc.
Noùi moät caùch roõ raøng hôn: ñoäng löïc hoïc nghieân cöùu quan heä töông taùc
qua laïi giöõa löïc laø nguyeân nhaân gaây ra chuyeån ñoäng vaø chuyeån ñoäng maø vaät theå
nhaän ñöôïc töø taùc ñoäng cuûa caùc löïc treân.
Vaät theå ôû ñaây ñöôïc hieåu laø chaát ñieåm, heä chaát ñieåm vaø vaät raén tuyeät ñoái
(vaät raén tuyeät ñoái laø moät heä chaát ñieåm ñaëc bieät).
Caùc keát quaû veà löïc trong tónh hoïc vaø chuyeån ñoäng trong ñoäng hoïc seõ ñöôïc
tieáp tuïc söû duïng ôû ñaây. 119
Chöông 10
MÔÛ ÑAÀU ÑOÄNG LÖÏC HOÏC
PHÖÔNG TRÌNH VI PHAÂN CHUYEÅN ÑOÄNG
CUÛA CHAÁT ÑIEÅM VAØ HEÄ CHAÁT ÑIEÅM Noäi dung
- Ñöa ra caùc khaùi nieäm cô baûn duøng trong ñoäng löïc hoïc
- Thieát laäp phöông trình vi phaân chuyeån ñoäng cuûa chaát ñieåm vaø cô heä Yeâu caàu
- Naém vöõng caùc khaùi nieäm neâu trong chöông naøy
- Thieát laäp ñöôïc phöông trình vi phaân chuyeån ñoäng cuûa chaát ñieåm vaø cô
heä. Bieát giaûi moät soá baøi toaùn thuaän vaø moät soá baøi toaùn nghòch cuûa chaát ñieåm vaø cô heä.
10.1. CAÙC KHAÙI NIEÄM CUÛA ÑOÄNG LÖÏC HOÏC 1. Chaát ñieåm
Chaát ñieåm laø ñieåm hình hoïc coù khoái löôïng.
Trong thöïc teá, nhöõng vaät raén maø kích thöôùc cuûa coù khoâng aûnh höôûng ñeán
quaù trình tính toaùn ñöôïc xem nhö chaát ñieåm. Ví duï nhö baøi toaùn xaùc ñònh quyõ
ñaïo cuûa teân löûa, chuyeån ñoäng cuûa vaät raén tònh tieán. 2. Cô heä
Cô heä laø taäp hôïp caùc chaát ñieåm maø chuyeån ñoäng cuûa chuùng phuï thuoäc laãn nhau.
- Cô heä töï do laø cô heä maø caùc chaát ñieåm cuûa chuùng töông taùc vôùi nhau vaø
vôùi giaù (vaät raén khoâng thuoäc cô heä) chæ qua löïc taùc duïng
Nhö vaäy caùc chaát ñieåm cuûa cô heä töï do coù theå dòch chuyeån tuøy yù trong
moät laân caän beù töø vò trí ñang xeùt, ví duï nhö heä maët trôøi.
- Cô heä khoâng töï do (cô heä chòu lieân keát) laø taäp hôïp caùc chaát ñieåm maø vò
trí vaø vaän toác cuûa chuùng ngoaøi vieäc chòu aûnh höôûng cuûa löïc coøn bò raøng buoäc bôûi
moät soá ñieàu kieän hình hoïc cho tröôùc (ñöôïc goïi laø caùc lieân keát), ví duï nhö cô caáu maùy.
3. Vaät raén tuyeät ñoái 120
Vaät raén tuyeät ñoái laø moät cô heä ñaëc bieät coù khoaûng caùch giöõa hai chaát
ñieåm baát kyø luoân coá ñònh.
- Vaät raén ñaøn hoài boû qua tính bieán daïng (bieán daïng beù) ñöôïc xem laø vaät raén tuyeät ñoái
- Chaát ñieåm laø moät vaät raén ñaëc bieät 4. Löïc
Khaùi nieäm löïc toång quaùt hôn trong tónh hoïc. Löïc laø ñaïi löôïng phuï thuoäc vò
trí rr , vaän toác V vaø thôøi gian t: F F(rr = , V, t).
Ví duï: - Löïc keùo cuûa ñoäng cô töø traïng thaùi khôûi ñoäng phuï thuoäc t
- Löïc caûn phuï thuoäc vaän toác V
- Löïc haáp daãn phuï thuoäc vò trí rr
5. Heä quy chieáu quaùn tính
Ñeå khaûo saùt chuyeån ñoäng cuûa ñoái töôïng, chuùng ta choïn moät vaät chuaån ñeå
ñaùnh giaù chuyeån ñoäng, ñöôïc goïi laø heä quy chieáu. Heä quy chieáu quaùn tính laø heä
quy chieáu maø trong ñoù heä tieân ñeà Newton ñöôïc nghieäm ñuùng, noùi caùch khaùc,
trong ñoù moät chaát ñieåm coâ laäp khoâng coù löïc taùc duïng seõ chuyeån ñoäng theo quaùn tính.
Ñeå bieåu dieãn caùc bieåu thöùc tính toaùn, ngöôøi ta gaén coá ñònh vaøo heä quy
chieáu nhöõng heä toïa ñoä thích hôïp. Töø ñaây veà sau, neáu khoâng coù löu yù gì ñaëc bieät
chuùng ta hieåu raèng caùc baøi toaùn ñöôïc khaûo saùt trong heä quy chieáu quaùn tính.
Quaû ñaát vaø caùc vaät raén chuyeån ñoäng thaúng ñeàu ñoái vôùi quaû ñaát thoâng
thöôøng ñöôïc choïn laøm heä quy chieáu quaùn tính trong kyõ thuaät.
6. Toùm taét heä tieân ñeà Newton-Galile
Chaát ñieåm chòu taùc duïng cuûa löïc seõ chuyeån ñoäng thoûa maõn quan heä: mW = F1 + F2 + ... + Fn
trong ñoù : W = W1 + W2 + ... + Wn ; vôùi: m Wk = Fk
Caùc tieân ñeà veà löïc töông taùc vaø giaûi phoùng lieân keát töông töï nhö trong tónh hoïc. 7. Heä ñôn vò
Theo heä SI (quoác teá) laáy caùc ñôn vò cô sôû: - Ñoä daøi : m - Khoái löôïng : kg - Thôøi gian : s
Caùc ñaïi löôïng cô hoïc khaùc ñeàu coù thöù nguyeân phuø hôïp vôùi caùc daãn xuaát cuûa noù.
10.2. PHÖÔNG TRÌNH VI PHAÂN CHUYEÅN ÑOÄNG CUÛA CHAÁT ÑIEÅM VAØ HEÄ CHAÁT ÑIEÅM
1. Phöông trình vi phaân chuyeån ñoäng cuûa chaát ñieåm 121
1- Daïng vector vaø toïa ñoä Decartes
Xeùt chaát ñieåm khoái löôïng m chòu taùc duïng cuûa löïc F . Goïi baùn kính vector
cuûa chaát ñieåm laø rr ta nhaän ñöôïc: m r&r = F (10.1)
Chieáu phöông trình vector (10.1) leân caùc truïc toïa ñoä Decartes: ⎧ x m & = x F z ⎪ ⎨ y m & = y F (10.2) ⎪ ⎩ z m & = M(m) z F r
Heä phöông trình (10.2) laø heä phöông trình vi
phaân chuyeån ñoäng trong heä toïa ñoä Decartes. y
2- Daïng toïa ñoä töï nhieân x
Chieáu phöông trình (10.1) leân caùc truïc cuûa Hình 10.1 M τ
nb, chuùng ta nhaän ñöôïc: ⎧ mW = ms& = F ⎪ τ τ 2 2 ⎪ v s& ⎨ mW = m = m = n n F (10.3) ⎪ ρ ρ ⎪ ⎪ 0 = F ⎩ b
Caùc phöông trình daïng naøy aùp duïng thuaän lôïi khi ñaõ bieát quyõ ñaïo chuyeån ñoäng cuûa chaát ñieåm.
2. Phöông trình vi phaân chuyeån ñoäng cuûa heä chaát ñieåm
Xeùt chaát ñieåm Mk cuûa heä N chaát ñieåm coù khoái löôïng töông öùng mk, gia toác
Wk . Tuøy theo tính chaát cuûa cô heä, chuùng ta coù theå phaân chia löïc taùc duïng vaøo chaát ñieåm M e
k theo löïc ngoaøi Fk , löïc trong i
Fk hay löïc hoaït ñoäng Fk vaø phaûn
löïc lieân keát Rk maø ta coù heä phöông trình vi phaân döôùi daïng: e i mk Wk = Fk + Fk (k = 1 ... n) (10.4) hoaëc: mk Wk = Fk + Rk (k = 1 ... n) (10.5)
3. Phöông phaùp aùp duïng
Ñeå thieát laäp ñöôïc phöông trình vi phaân chuyeån ñoäng cuûa chaát ñieåm vaø cô
heä, aùp duïng chuùng giaûi caùc baøi toaùn ñoäng löïc, chuùng ta tuaàn töï thöïc hieän caùc böôùc sau:
- Xaùc ñònh chaát ñieåm hoaëc heä chaát ñieåm, khaûo saùt taïi vò trí tuøy yù xaùc ñònh
(khoâng ñöôïc laáy vò trí ñaëc bieät)
- Xaùc ñònh caùc löïc ñaët leân chaát ñieåm (bao goàm caû phaûn löïc)
- Laäp phöông trình vector cuûa chuyeån ñoäng: mW = ΣFk
- Choïn heä truïc toïa ñoä thích hôïp: (10.2), (10.3)
- Laäp phöông trình vi phaân chuyeån ñoäng (caùc phöông trình hình chieáu leân caùc truïc toïa ñoä). 122
a- Neáu baøi toaùn cho quy luaät chuyeån ñoäng yeâu caàu xaùc ñònh löïc gaây ra
chuyeån ñoäng ñoù cuûa chaát ñieåm khaûo saùt, chuùng ta chæ caàn thöïc hieän caùc pheùp
tính vi phaân. Ñaây laø nhöõng baøi toaùn thuaän.
b- Neáu baøi toaùn cho löïc taùc duïng yeâu caàu xaùc ñònh chuyeån ñoäng xaûy ra,
chuùng ta phaûi thöïc hieän caùc pheùp tính tích phaân. Ñaây laø nhöõng baøi toaùn nghòch.
Vieäc tích phaân caùc phöông trình vi phaân, heä phöông trình vi phaân laø raát
khoù khaên, cho ñeán nay cuõng chæ giaûi ñöôïc moät soá daïng. Ñeå traùnh tình traïng naøy,
ngöôøi ta thöôøng giaûi baøi toaùn cô hoïc baèng moät phöông phaùp khaùc (seõ trình baøy ôû
caùc chöông sau) ñeå tìm ra caùc tính chaát quan troïng cuûa chuyeån ñoäng, ñuû duøng trong thöïc teá. 4. Caùc ví duï
Ví duï 10.1. Xeùt taûi khoái löôïng m chuyeån ñoäng ñeàu treân caàu cong baùn kính r vôùi
vaän toác V. Tìm aùp löïc cuûa xe leân caàu.
Giaûi. Xeùt xe nhö moät chaát ñieåm M taïi moät
vò trí tuøy yù xaùc ñònh (H.10.2)
- Caùc löïc taùc duïng vaøo xe taûi: Troïng löïc : P g mr =
Phaûn löïc phaùp tuyeán : R Löïc toång hôïp F taùc duïng leân xe theo Hình 10.2 phöông ngang
- Phöông trình chuyeån ñoäng daïng vector: mW = P + R + F (*)
- Duøng toïa ñoä töï nhieân (ñaõ bieát quyõ ñaïo cuûa chaát ñieåm) M τ nb: 2 (*) V ⇒ mW = m = P cos ϕ R n − r 2 2 Giaûi ra: V V R = P cos ϕ − m = m(g cos ϕ − ) r r 2
Ñeå toàn taïi aùp löïc leân caàu V ⇒ R > 0 ⇔ g cos ϕ − > 0 r
AÙp löïc nhoû nhaát taïi chaân caàu (ϕ ), max
aùp löïc lôùn nhaát taïi ñænh caàu ( ϕ = 0 ). 2 Neáu: V g cos ϕ − < ,
0 xe seõ bay khoûi maët ñöôøng. r
Ví duï 10.2. Khaûo saùt chuyeån ñoäng cuûa ñieåm naëng trong tröôøng troïng löïc.
Giaûi. - Xeùt chuyeån ñoäng cuûa ñieåm naëng
- Löïc taùc duïng duy nhaát : P g mr = - Phöông trình vector : mW g mr =
- Choïn heä truïc toïa ñoä Oxyz coù goác taïi vò trí ban ñaàu cuûa chaát ñieåm, vector
vaän toác ban ñaàu Vo ∈ Oyz (H.10.3) 123 ⎧ x m & = 0
Phöông trình hình chieáu: ⎪⎨ y m & = 0 ⎪⎩ z m & = −mg
Tích phaân ba phöông trình vi phaân treân vôùi ñieàu kieän ñaàu: x = x ; 0 & = 0 o o y = o y ; 0 & = o Vo cosα z z = o z ; 0 & = o Vo sin α V M Chuùng ta nhaän ñöôïc: o x = 0 α P y = (V O y o cos ) α t x 2 Hình 10.3 t z = (Vo sin α)t − g 2
Nhö vaäy ñieåm naëng chuyeån ñoäng trong maët phaúng thaúng ñöùng Oyz coù quyõ
ñaïo laø ñöôøng parabol: g z = − y2 + tgα y . 2V2 cos2 o α
Ví duï 10.3. Taûi troïng treo treân loø xo. Bieát khoái löôïng taûi laø m, ôû traïng thaùi caân
baèng tónh loø xo daõn ra moät ñoä daøi δ . Tìm chuyeån ñoäng cuûa taûi.
Giaûi. - Xeùt chuyeån ñoäng cuûa taûi - Löïc taùc ñoäng: Troïng löïc : P g mr =
Löïc caêng cuûa loø xo : F = c rr − δ
( rr laø vector dòch chuyeån cuûa ñaàu loø xo keå töø vò trí O F
khoâng co daõn vaø c laø heä soá cöùng cuûa loø xo). x
- Phöông trình chuyeån ñoäng daïng vector: x m W = P + F P
- Choïn truïc x thaúng ñöùng coù goác taïi O laø vò trí caân baèng Hình 10.4
tónh cuûa taûi, xeùt vò trí baát kyø cuûa taûi coù toïa ñoä x (H.10.4). Chieáu leân truïc x: x m & = mg − c (δ + ) x (*)
Thôøi ñieåm ñaàu, taûi troïng tónh (vaän toác, gia toác baèng khoâng) neân: 0 = mg − δ c ⇒ mg = δ c (*) c g ⇔ x& = − x ⇔ x& + x = 0 m δ
Phöông trình coù nghieäm: x = Asin(kt + α )
vôùi: k = g / δ ; coøn A vaø α tìm ñöôïc töø caùc ñieàu kieän ñaàu.
Giaû söû cho: y(0) = a; y& (0) = Vo Caân baèng tónh chuùng ta tính ñöôïc: 2 P 2 V A a = a o + , α = arctg(k ) δ k2 V o O x F x Hình 10.5 124
Chuù yù: Baøi toaùn töông töï: khoái truï ñaët trong chaát loûng coù troïng löôïng
rieâng γ . Neáu dieän tích ñaùy cuûa truïc laø S ta coù löïc ñaåy Achemet (H.10.5): F = . S γ.(δ + ) x
Chuùng ta cuõng coù phöông trình dao ñoäng nhö treân vôùi: Sγ g k = = m δ
Ví duï 10.4. Xeùt chuyeån ñoäng cuûa xe taûi treân ñöôøng. Thuøng xe khoái löôïng m1
dao ñoäng thaúng ñöùng ñoái vôùi truïc baùnh xe theo quy luaät: x = a1 sin( 1 ω t + α1)
Truïc baùnh xe laïi dao ñoäng thaúng ñöùng ñoái vôùi maët ñöôøng theo quy luaät:
Tìm aùp löïc treân maët ñöôøng.
Giaûi. Xeùt chuyeån ñoäng thaúng ñöùng cuûa xe nhö heä hai chaát ñieåm coù khoái löôïng öùng m1 vaø m2:
Moâ hình chuyeån ñoäng nhö H.10.6a P1 x m m 1 1 x = x + x 1 2 F x 12 m F21 m 2 2 x2 P x 2 2 R O O a) b) c) Hình 10.6
Xeùt chuyeån ñoäng cuûa taûi m1 coù moâ hình chuyeån ñoäng nhö H.10.6b.
ÔÛ ñaây: laáy truïc x thaúng höôùng leân, goác truøng vôùi maët ñöôøng.
Toïa ñoä cuûa taûi laø: x1 = x + x2. Löïc taùc ñoäng P r 1 = m g F , 21 1
- laø phaûn löïc cuûa taûi m2 taùc ñoäng leân taûi m1.
Phöông trình chuyeån ñoäng: 1 m W1 = P + F21 ⇔ m1x1 = 21 F − 1 P ⇔ −m [a 2 ω sin(ω t + α ) + a 2
ω sin(ω t + α )] = F − m g 1 1 1 1 1 2 2 2 2 21 1 ⇒ F = m [g − a 2 ω sin(ω t + α ) − a 2 ω sin(ω t + α )] 21 1 1 1 1 1 2 2 2 2
Xeùt chuyeån ñoäng cuûa taûi m2 nhö H.10.6c
Phöông trình chuyeån ñoäng: m W 2 2 = P2 + F21 + R ôû ñaây: P r 2 = m ; g 2
F12 = −F21 - laø phaûn löïc cuûa taûi m1 leân taûi m2
R - laø phaûn löïc cuûa maët ñöôøng. ⇒ m2x&2 = F − 12 − P2 + R 125 ⇔ R = m g + m g − m a 2 ω sin(ω t + α ) − (m + m )a 2 ω sin(ω t + α ) 2 1 1 1 1 1 1 1 2 2 2 2 2
R - laø ñaïi löôïng bieán thieân tuaàn hoaøn
Ví duï 10.5. Xeùt xe taûi nhö treân nhöng ôû ñaây cho bieát heä soá cöùng cuûa ñeäm meàm
naèm giöõa thuøng xe vaø truïc xe laø c1, giöõa truïc xe vaø maët ñöôøng laø c2.
Tìm chuyeån ñoäng thaúng ñöùng cuûa xe.
Giaûi. - Xem xe laø heä hai chaát ñieåm ⇔ taûi m1 vaø m2. Moâ hình chuyeån ñoäng nhö H.10.7 δ2 m O1 1 δ P 1 1 Caân baèng tónh Loø xo m1 x F khoâng taûi δ2 m 12 1 O2 2 F21 m2 x2 x1 P2 F x2 a) b) c) Hình 10.7
- Xeùt chuyeån ñoäng cuûa taûi m1 nhö H.10.7b
Phöông trình chuyeån ñoäng: r 1 m 1 W = m g + F21 1
ôû ñaây: F21 - laø phaûn löïc cuûa loø xo (1) taùc ñoäng leân taûi m1.
⇒ m1x&1 = m1g − c1(x1 + 1 δ − x2)
⇔ m1x&1 = − c1(x1 − x2)
Xeùt chuyeån ñoäng cuûa taûi m2 nhö H.10.7c
Phöông trình chuyeån ñoäng: m W r 2 2 = m g + F21 − F 2 (chuù yù: F12 = F21) ⇒ m r 2x2 = m2g + c1(x1 + 1 δ − x2) − c2(δ2 + x2) ⇒ m2x&2 = 1 c 1 x − 1 c ( + c2)x2
ôû ñaây: F - laø phaûn löïc cuûa loø xo döôùi (c2) taùc ñoäng leân taûi m2.
Keát hôïp ta nhaän ñöôïc heä: m x& = −c (x − x ) ⎧ ) 1 ( ⎨ 1 1 1 1 2 ⎩m x& = c x − c ( + c )x 2 2 1 1 1 2 2 ) 2 (
Chuùng ta coù theå giaûi heä (1) vaø (2) baèng caùch ñöa veà giaûi heä phöông trình
vi phaân caáp 4 tuyeán tính heä soá haèng bôûi heä phöông trình töông ñöông. 126 m x& = −c (x − x ) ⎧ ) 3 ( ⎨ 1 1 1 1 2 ⎩m m + x&& & [c m + c ( + c )m ]x& + c c x = 0 2 2 1 2 1 2 1 2 1 2 2 ) 4 (
Xeùt (4) coù phöông trình ñaëc tröng: m1m 4 2λ + [c1m2 + c ( 1 + c2 m ) ] 2 1 λ + c1c2 = 0 Vieát goïn theo daïng: A 4 λ + B 2 λ + C = 0
giaûi heä phöông trình truøng phöông treân (chuù yù: Δ > 0 vaø − B ± Δ < 0 ) ta coù: 1 λ = i 1 β ; λ2 = −i 1
β ; λ3 = iβ2; λ4 = −iβ2 ôû ñaây: B − Δ B + Δ 1 β = ; β = 2A 2 2A
Chuùng ta seõ nhaän ñöôïc nghieäm cuûa (4):
x2 = a1 cos β1t + a2 sin β1t + a3 cos β2t + a4 sin β2t
Theá keát quaû naøy vaøo phöông trình (3) chuùng ta giaûi ñöôïc x1 cuõng thuoäc
loaïi ñieàu hoøa. Caùc haèng soá ai ñöôïc xaùc ñònh töø boán ñieàu kieän ñaàu x1 vaø x2. 127 Chöông 11
NGUYEÂN LYÙ D’ALAMBERT Noäi dung
Söû duïng caùc phöông trình caân baèng tónh quen thuoäc ñeå giaûi caùc baøi toaùn ñoäng löïc. Yeâu caàu
- Naém vöõng ñònh nghóa löïc quaùn tính, caùc coâng thöùc thu goïn löïc quaùn tính.
- AÙp duïng thaønh thaïo nguyeân lyù giaûi caùc baøi toaùn ñoäng löïc.
11.1. CAÙC ÑAËC TRÖNG HÌNH HOÏC KHOÁI LÖÔÏNG CUÛA CÔ HEÄ
Khoái löôïng cuûa phaân toá vaø söï phaân boá cuûa noù trong cô heä aûnh höôûng tröïc
tieáp ñeán chuyeån ñoäng cuûa heä cô. Döôùi ñaây ta xem xeùt moät soá ñaëc tröng hình hoïc
khoái löôïng cuûa ñoäng cô.
1. Khoái taâm cuûa heä cô
Ñieåm C coù baùn kính vector: r ∑ m rr r = k k C ∑ (11.1) mk
Ñöôïc goïi laø khoái taâm cuûa cô heä, trong ñoù mk vaø kr laø khoái löôïng vaø baùn
kính vector cuûa chaát ñieåm thöù k. Ñeå ñôn giaûn ñaët M = ∑mk . ⎧ ∑m x ⎪ x = k k ⎪ C M ⎪ mky ⎪ ∑ ⇔ ) 1 . 11 ( k ⎨ y = C (11.2) ⎪ M ⎪ ∑mkz ⎪ z = k ⎪ C M ⎩
Neáu heä goàm nhieàu vaät raén coù theå xem mk, kr laø khoái löôïng vaø baùn kính
vector khoái taâm cuûa vaät thöù k töông öùng.
Deã daøng thaáy trong tröôøng troïng löïc khoái taâm C cuûa heä truøng vôùi troïng taâm cuûa heä.
2. Moâmen quaùn tính cuûa vaät raén
1- Moâ men quaùn tính ñoái vôùi truïc Δ cuûa vaät raén 128 J = 2 Δ' ∑mkhk (11.3)
trong ñoù: mk, hk - laø khoái löôïng vaø khoaûng caùch ñeán truïc Δ cuûa chaát ñieåm thöù k töông öùng. z
- Xeùt trong heä toïa ñoä Oxyz (H.11.1):
Chaát ñieåm mk coù toïa ñoä xk, yk, zk seõ coù: zk J = x ∑m (y2 + z2) k k k rk y J = k y O ∑m z(2 + x2) k k k (11.4) y J = x z k ∑mk(x2 + k y2k) Hình 11.1
2- Tích quaùn tính (moâmen quaùn tính ly x taâm)
Caùc ñaïi löôïng sau ñaây ñöôïc goïi laø caùc tích quaùn tính: J = xy ∑mkxkyk J = yz ∑mkykzk (11.5) J = zx ∑mkzkxk
3- Moâmen quaùn tính ñoái vôùi taâm (Jo ): J = O ∑ 2 mk k r (11.6)
ôû ñaây: kr - laø baùn kính vector cuûa chaát ñieåm thöù k coù goác ôû taâm O.
Trong heä toïa ñoä Oxyz (laáy O truøng vôùi goác toïa ñoä): 2 2 2 1 JO = m
∑ k(xk + yk + zk) = (Jx + Jy + Jz) (11.7) 2
4- Baùn kính quaùn tính
Vôùi töøng vaät raén cuï theå ngöôøi ta coøn ñöa ra ñònh nghóa baùn kính quaùn tính
ρ thoûa maõn ñieàu kieän: 2 J = Mρ Δ (11.8)
trong ñoù: M - laø khoái löôïng cuûa vaät.
3. Moâmen quaùn tính cuûa moät soá vaät ñoàng chaát
1- Thanh thaúng ñoàng chaát khoái löôïng M, ñoä daøi L mk (M) D C x A B (M) xk x Δxk L L A B a) b) Hình 11.2 Choïn truïc
Δ ñi qua ñaàu thanh vaø vuoâng goùc vôùi thanh nhö H.11.2. 129
Duøng tröïc tieáp ñònh nghóa, chia thanh thaønh caùc ñoaïn Δxk khoái löôïng M 2 m ML k = x
Δ k , chuùng ta tính ñöôïc: J = L Δ (11.9) 3
Coâng thöùc naøy vaãn ñuùng khi thay thanh baèng taám chöõ nhaät ABCD (H.11.2b).
2- Vaønh troøn, maët truï troøn ñoàng chaát khoái löôïng M, baùn kính R R O (M) O R mk (M) a) b) Hình 11.3 Truïc
Δ vuoâng goùc vôùi maët phaúng chöùa ñöôøng troøn, ñi qua taâm cuûa ñöôøng
troøn. Duøng ñònh nghóa chuùng ta coù ngay: 2 J = MR (11.10) Δ
3- Taám troøn, truï troøn ñoàng chaát khoái löôïng M, baùn kính R Δ Δ O R r O (M) R (M) a) b) Hình 11.4
Truïc Δ ñi qua taâm O vuoâng goùc vôùi maët troøn.
Chuùng ta chia taám troøn thaønh caùc vaønh moûng Δrk coù khoái löôïng töông öùng laø: M mk = 2 ( r π k. r Δ k) R2 π
vôùi vaønh moûng naøy ta coù: 2 M dJ = Δ mkrk = 2 ( r3 π k . r Δ k) R2 π R 3 3 Mr 2 r 2Mr 1 J = k k 2 Δ ∑dJΔ ∑ Δ = ⇒ J = Δ dr MR (11.11) 2 ∫ = 2 R R 2 Δr →0 Δr →0 k k 0
4- Caùc ñònh lyù lieân heä 130
Sau ñaây chuùng ta neâu leân moät soá ñònh lyù lieân heä moâmen quaùn tính giöõa caùc truïc.
Ñònh lyù 11.1. (Lieân heä giöõa caùc truïc song song) 2 J = J Δ Δc + Md (11.12)
ôû ñaây: ΔC - laø truïc song song vôùi Δ vaø ñi qua khoái taâm C, khoaûng caùch giöõa Δ vaø
ΔC laø d, khoái löôïng cuûa vaät raén laø M.
Ñònh lyù 11.2. (Lieân heä giöõa caùc truïc khoâng song song) 2 2 2
J = Jx cos α + Jy cos β + Jz cos γ − 2Jxy cos α cosβ Δ (11.13)
− 2Jyz cosβ cos γ − 2Jxz cos γ cosα
ôû ñaây: Δ - ñi qua goác O cuûa heä truïc Oxyz vaø coù caùc cosin chæ phöông laø α, β, γ.
5- Caùc ñònh nghóa veà truïc quaùn tính chính
Truïc quaùn tính chính: truïc z ñöôïc goïi laø truïc quaùn tính chính taïi ñieåm O
(thuoäc truïc z) neáu: Jyz = Jzx = 0
Truïc quaùn tính chính trung taâm: truïc ñang xeùt laø truïc quaùn tính chính taïi
moät ñieåm thuoäc truïc, neáu truïc naøy ñi qua khoái taâm C cuûa vaät thì seõ ñöôïc goïi laø
truïc quaùn tính chính trung taâm.
Truïc quaùn tính chính trung taâm laø truïc quaùn tính chính ñoái vôùi moïi ñieåm thuoäc vaät.
Ngöôøi ta chöùng minh ñöôïc taïi moät ñieåm tuøy yù luoân toàn taïi ba truïc quaùn
tính ñoái vôùi ñieåm ñoù vaø vuoâng goùc vôùi nhau töøng ñoâi moät.
11.2. LÖÏC QUAÙN TÍNH, NGUYEÂN LYÙ D’ALAMBERT
1. Ñoái vôùi chaát ñieåm
1- Löïc quaùn tính cuûa chaát ñieåm
Xeùt chaát ñieåm chuyeån ñoäng gia toác W , khoái löôïng m.
Löïc quaùn tính cuûa chaát ñieåm laø ñaïi löôïng: qt F = −mW (11.14)
2- Nguyeân lyù D’Alambert
Trong chuyeån ñoäng cuûa chaát ñieåm, löïc thöïc taùc ñoäng leân chaát ñieåm vaø löïc
quaùn tính cuûa noù laø heä löïc caân baèng. Töø phöông trình: qt mW = F ⇒ F − mW = 0 ⇔ F + F = 0 (11.15)
(11.15) laø bieåu thöùc moâ taû nguyeân lyù D’Alembert cho chaát ñieåm. 2. Ñoái vôùi heä cô
1- Löïc quaùn tính cuûa cô heä
Xeùt heä chaát ñieåm coù khoái löôïng mk vaø gia toác Wk . 131 Heä ( qt qt
Fk ) trong ñoù Fk = −mk Wk ñaët taïi chaát ñieåm thöù k laø heä löïc quaùn tính cuûa cô heä.
2- Nguyeân lyù D’Alembert cho cô heä
Xeùt chaát ñieåm thöù k chòu taùc duïng cuûa ngoaïi löïc e Fk vaø noäi löïc i Fk : e i qt ⇒ F ( k F , k F , k ) ≡ 0 ⎧ e i qt Rk Fk Fk Fk 0 ⎪ = + + = ⇒ ⎨ ⎪ e i qt r r r ⎩MkO = m F ( O k ) + m F ( O k ) + m F ( O k ) = 0 ⎧ e i qt R = R + R + R = 0 laáy toång theo k: ⎪ ⇒ ⎨ (11.16) ⎪ e i qt ⎩MO = MO + MO + MO = 0 trong ñoù: e e e e R = ∑F r k MO = ∑m F ( O k ) i i i i R = ∑F r k = 0 vaø: MO = ∑ m F ( O k ) = 0 qt qt qt qt R = ∑F r k MO = ∑m ( F ) O K ⎧ e qt R R 0 (11.16) ⎪ + = ⇔ ⎨ (11.17) ⎪ e qt ⎩MO + MO ) ≡ 0 e qt ⇔ F ( k F , k ) = 0 (k = 1..n) (11.18)
(11.18) moâ taû nguyeân lyù D’Alembert cho cô heä.
Trong chuyeån ñoäng cuûa cô heä, heä löïc goàm caùc löïc thöïc taùc ñoäng vaøo cô heä
vaø löïc quaùn tính cuûa cô heä laø heä löïc caân baèng.
11.3. THU GOÏN HEÄ LÖÏC QUAÙN TÍNH
Ñeå aùp duïng nguyeân lyù D’Alembert chuùng ta phaûi xaùc ñònh ñöôïc qt qt R M , O
(O laø ñieåm tuøy yù xaùc ñònh).
1. Vector chính quaùn tính qt qt
R = ∑Fk = −∑mk Wk = −MWC (11.19)
Vector chính quaùn tính cuûa cô heä baèng tích khoái löôïng vaø gia toác khoái taâm
cuûa cô heä, chieàu ngöôïc chieàu gia toác khoái taâm.
2. Vector moâmen chính quaùn tính ñoái vôùi moät taâm cuûa vaät raén
1- Vaät raén chuyeån ñoäng tònh tieán
Chuùng ta thu goïn heä löïc quaùn tính veà khoái taâm C. Tính: 132 N N N qt qt M r r r r C = ∑ mC F ( k ) = ∑ r − k ( x mk Wk) = WC x∑ m r = k k WC × r M = C 0 k−1 k=1 k=1 (do W r k = WC ( k ∀ vaø ) r = 0 C )
- Trong chuyeån ñoäng tònh tieán heä löïc quaùn tính coù hôïp löïc baèng vector
chính ñaët taïi khoái taâm C (H.11.5). z ε Mk qt k r − C R = C W M C O y C W • j x Hình 11.5 Hình 11.6
2- Vaät raén quay quanh truïc coá ñònh
Xeùt vaät raén quay quanh truïc Δ vôùi gia toác goùc εr . Chuùng ta thu goïn heä löïc
quaùn tính veà ñieåm O ∈ Δ (H.11.6). N N qt τ n M r r o = r x(-m W ∑ k k k ) = r x(-m W ∑ k k k - m W k k ) k 1 = k 1 = N N = − m r r x( εr r x r ) − m rr [ x ωr ( x ωr r x r )] ∑ k k k ∑ k k k k 1 = k 1 = N N
∑ m [−εx z i − εy z j + ε 2 ( x + ε 2 y )k] − k k k k k k k ∑ m [ω2y z i − ω2 k k k xkyk j] k =1 k =1 = ( J 2 ε xz − ω Jyz) i + ( J 2 ε yz + ω Jxz ) j - J ε z k (11.20) trong ñoù: rr r r k (x k y , k z , k ); ω , 0 , 0 ( ); ω ε , 0 , 0 ( ) ε
Chuùng ta bieåu dieãn cuï theå qt R = −MWC : qt r r r r r R = − {( M ε r x ) + ω ( x ω r x )} C C (11.21) = {( M y 2 ε + ω x ) i + ( 2 ω y − x ε ) j } C C C C
3- Hình phaúng chuyeån ñoäng song phaúng
Chuùng ta cuõng thu goïn veà khoái taâm.
Xaây döïng heä toa ñoä ñoäng Cxyz (H.11.7) coù Cxy ≡ maët phaúng quy chieáu
cuûa chuyeån ñoäng song phaúng, duøng coâng thöùc (11.20): 133 ⇒ M qt = − J (11.22) C ε z k .
Heä löïc quaùn tính thu goïn bieåu dieãn ôû H.11.8.
Coâng thöùc cuõng ñuùng cho VR coù maët phaúng ñoái xöùng chuyeån ñoäng phaúng trong maët phaúng ñoù.
11.4. PHAÛN LÖÏC ÑOÄNG LÖÏC TRUÏC QUAY
Xeùt vaät raén quay quanh truïc coá ñònh qua A, B vaän toác goùc ω, gia toác goùc ε, moâ taû ôû H.11.9. Heä löïc: qt q+ F ( k ,A x A , y A , z B , x B , y R , o M , o ) ≡ 0 Fk A B Az O A x Ay x Bx Y B y Hình 11.9
1. Phöông trình caân baèng (duøng 11.20 vaø 11.21) ⎧ Σ X = Σ k F + kx A + x B + ω ( M 2 x x + ε c yc ) = 0 ⎪ ⎪ Σ Y = ΣF + A + B + ω ( M 2y − εx ) = 0 ⎪ k ky y y c c Σ Z = Σ k F + kz Az ⎪⎪⎨ (11.23) 2 ⎪ Σ m = Σm F ( x x k ) + m (A ) + m B ( ) + εJ ω J = 0 x y x y xz yz ⎪ 2 ⎪ Σ m = Σm F ( y y k ) + m (A ) + m B ( ) + εJ + ω J = 0 y x y x yz xz ⎪ ⎪⎩ Σ m = Σm F ( z z k ) − εJ = 0 z
Naêm thaønh phaàn phaûn löïc taïi caùc oå truïc A, B xaùc ñònh töø naêm phöông
trình ñaàu cuûa heä phöông trình (11.23). Phöông trình cuoái: Jz ε ≡ Jz ϕ = Σmz F ( k ) (11.24)
laø phöông trình vi phaân chuyeån ñoäng cuûa vaät raén quay quanh truïc coá ñònh. Z ε C y R qt C W rk c M qtc Mk(mk) x Hình 11.7 Hình 11.8
2. Phaûn löïc ñoäng löïc truïc quay 134
Phaûn löïc ñoäng löïc ñöôïc xaùc ñònh töø (11.23) phuï thuoäc vaøo caû löïc ngoaøi (
Fk ) vaø caùc ñaëc tröng chuyeån ñoäng (ω, ε). Caùc thaønh phaàn chæ do chuyeån ñoäng
sinh ra (ω, ε) ñöôïc goïi laø phaûn löïc ñoäng löïc. Nhöõng thaønh phaàn naøy thöôøng bieán
thieân tuaàn hoaøn, laø nguyeân nhaân chính laøm hö hoûng oå truïc.
Deã daøng nhaän thaáy, ñeå caùc thaønh phaàn phaûn löïc ñoäng löïc ñeàu baèng
khoâng, ta caàn phaûi coù: ⎧ ω 2x + εy = 0 ⎪ C C ω 2y + ε C x = C 0 ⎪⎪ ⎨ (11.25) ⎪ ε J − ω2J = 0 zx yz ⎪ ⎪ 2 ⎩ ε J + ω J = 0 yz xz
Trong heä (11.25) xem ω2 vaø ε laø aån khoâng ñoàng thôøi baèng khoâng neân caùc
ñònh thöùc heä soá phaûi baèng khoâng: x2 ⇒ + y2 = J ; 0 2 + J2 = 0 C C zx zy x ⇒ y = J ; 0 = J = 0 C C zx zy
⇒ truïc quay laø truïc quaùn tính chính trung taâm
Keát luaän: Khi truïc quay laø truïc quaùn tính chính trung taâm, aùp löïc ñoäng cuûa
caùc oå truïc seõ gioáng nhö tröôøng hôïp vaät quay ñang ñöùng yeân (caân baèng tónh).
Ñaây laø cô sôû lyù thuyeát cuûa caân baèng ñoäng truïc quay.
11.5. NOÄI DUNG AÙP DUÏNG VAØ CAÙC VÍ DUÏ 1. Noäi dung aùp duïng
1- Nguyeân lyù D’Alembert thöôøng aùp duïng ñeå tìm:
- Ñieàu kieän caân baèng töông ñoái
- Caùc ñaëc tröng ñoäng hoïc
- Caùc phaûn löïc lieân keát trong cô heä, phaûn löïc ñoäng cuûa oå truïc.
2- Nguyeân lyù D’Alembert coøn giuùp chuùng ta thieát laäp:
- Phöông trình vi phaân chuyeån ñoäng cuûa vaät quay quanh truïc coá ñònh (11.24)
- Phöông trình vi phaân chuyeån ñoäng cuûa taám phaúng trong chuyeån ñoäng song phaúng.
Xuaát phaùt töø (11.19) vaø (11.22): ⎧ e ⎪ M x& = Σ C Fkx ⎪ ⎨ M y& = Σ C Feky (11.26) ⎪ ⎪ e ⎩ J ϕ& = Σ z mz F ( k ) c c
(xaùc ñònh ñöôïc quy luaät chuyeån ñoäng cuûa cöïc C vaø quay quanh truïc ñi qua C). 135 2. Caùc ví duï O
Ví duï 11.1. Toa xe chuyeån ñoäng x
thaúng ngang vôùi gia toác W . Taûi A T α
khoái löôïng m ñöôïc treo bôûi daây Fqt ... W .. . ... ... ..
meàm taïi O. Tìm goùc leäch .. . α vaø söùc ... .. ... ... m A
caêng daây T khi con laéc A caân baèng P ñoái vôùi toa xe. y
Giaûi. Xeùt con laéc khi ñaõ caân baèng
töông ñoái. Giaû söû coù goùc α nhö hình veõ. Heä löïc: qt F , T , P ( ) ≡ 0 Hình 11.10
Xaây döïng heä toïa ñoä ñoäng Oxy (H.11.10):
ΣX = Fqt − T sin α = 0 ⇔ mW = T sin α k ΣY = k
P − T cos α = 0 ⇔ P = T cos α W mg ⇒ α tg = T ; = g α cos
Ví duï 11.2. Ñoäng cô khoái löôïng m, boä phaän leäch taâm coù (theâm) khoái löôïng m1
xem nhö caùch truïc quay ñoaïn l (taâm sai). Ñoäng cô ñöôïc gaén chaët treân daàm ñaøn
hoài ñoä cöùng k nhö hình veõ. Laäp phöông trình chuyeån ñoäng cuûa ñoäng cô (boû qua
troïng löôïng daàm), bieát ñoäng cô quay ñeàu vôùi vaän toác goùc ωo. O I l A ϕ y Hình 11.11
Giaûi. Goïi vò trí truïc ñoäng cô laø ñieåm I. Choïn truïc z thaúng ñöùng höôùng xuoáng coù
goác O taïi vò trí caân baèng tónh cuûa I, luùc naøy ñoä voõng cuûa daàm laø a, ta coù ngay: (
Xeùt ñoäng cô taïi vò trí tuøy yù (I coù toïa ñoä z) töông öùng tay quay ñaït goùc ϕ (H.11.11). Caùc löïc thöïc: - Caùc troïng löïc: P r = P ; g m r 1 = m g 1
- Phaûn löïc ñaøn hoài cuûa daàm: Fñh = – k(a + z) 136
Caùc löïc quaùn tính:
Ñoäng cô chuyeån ñoäng tònh tieán, coù hôïp qt löïc quaùn tính laø: O F qt I FA I e qt A qt FI = − m WI ( WI = ) z& F P Ar
Taûi A chuyeån ñoäng hôïp, quay quanh taâm PI
I ñoàng thôøi I tònh tieán cuøng ñoäng cô. Tính: z e r r r F W ñh A = W + W = WI + Wn + Wτ trong ñoù: r = 2 r Hình 11.12 n W
lωo ; Wτ = lεo = l o ω& = 0 qt qt qt ⇒ F ≡ F ( I F , A ) vôùi: qt qt 2 qt I F = m & l Ar F ; z = 1 m o ω F ; = m z Ar 1 & heä löïc: qt qt qt , P
( P1, Fñh, FI , FAr , FAe) ≡ 0 ⇒ P + 2 1 P − k a ( + ) z − (m + m1 z
) & + m1l ω cos(ω t) = 0 o o k m1 ⇒ z& + z = l 2 ω cos t m + m o ωo 1 m + m1
Ñaây laø phöông trình vi phaân chuyeån ñoäng cuûa ñoäng cô. Ñoäng cô dao ñoäng
cöôõng böùc thaúng ñöùng tuaàn hoaøn cuøng taàn soá cuûa löïc kích ñoäng ωo.
Ví duï 11.3. Cho cô heä nhö H.11.13. Bieát truïc quay laø truï troøn ñoàng chaát troïng
löôïng Q, taûi A troïng löôïng P, ngaãu M haèng soá ñaët vaøo truïc quay. Boû qua ma saùt oå truïc.
Haõy xaùc ñònh WA, söùc caêng daây T, phaûn löïc oå truïc taïi O. M O R y T A W A A P F qt A Hình 11.13 Hình 11.14
Giaûi. Caùc phaûn löïc taïi O, söùc caêng daây T lieân quan ñeán hai vaät raén chuyeån ñoäng
laø truï O vaø taûi A. Chuùng ta xeùt chuyeån ñoäng cuûa töøng vaät raén taïi thôøi ñieåm xaùc
ñònh tuøy yù töông öùng A ñaït WA, truï A ñaït gia toác goùc ε.
Xeùt taûi A chuyeån ñoäng (H.11.14): 137 Heä löïc: ( qt F , T , P A ) ≡ 0 Phöông trình caân baèng: P ΣY = T − P − W 0 k = (1) g A
Phöông trình (1) khoâng giaûi ñöôïc hai aån T vaø WA.
Xeùt chuyeån ñoäng cuûa truïc O (H.11.15). Heä löïc: R , Q ( o ngaãu , T , M , M qt) ≡ 0 o .
ÔÛ ñaây truïc quay ñi qua O ≡ khoái taâm neân: qt R = . 0 vôùi: Mqt = J ε. o (ngöôïc chieàu ε); o z T’ = T vaø WA ε = R Phöông trình caân baèng: X Σ M k = Rox = 0 (2) Ro ΣY = −T − Q + R k oy = 0 (3) y M qt o Σm = M − Mqt − T . R = 0 ε o o (4) O
Giaûi heä boán phöông trình ta ñöôïc: x M − RP W = g 2 A P 2 ( + ) Q R T’ Q WA QR + M 2 T = P 1 ( + ) = P g P 2 ( + ) Q R Hình 11.15 Rox = 0 QR + M 2 Roy = Q + T = Q + P P 2 ( + ) Q R
Nhaän xeùt:
M – RP > O ⇒ taûi A ñi leân
M – RP = O ⇒ taûi A ñöùng yeân (ban ñaàu cô heä ñöùng yeân)
M – RP < O ⇒ taûi A ñi xuoáng
Ví duï 11.4. Baùnh xe chuû ñoäng cuûa oâtoâ y
baùn kính R khoái löôïng m, baùn kính quaùn
tính ñoái vôùi truïc quay laø ρ, chòu ngaãu M Ε
löïc chuû ñoäng M, aùp löïc thaúng ñöùng qua truïc (taûi troïng) laø P P1 1 = 4 mg.
Tìm ñieàu kieän cuûa ngaãu M ñeå R qt O WC x
baùnh xe laên khoâng tröôït vaø xaùc ñònh NI
phaûn löïc taïi I, bieát heä soá ma saùt tröôït qt P M
giöõa baùnh xe vaø maët ñöôøng laø f, boû qua C ma saùt laên. I F I Hình 11.16 138
Giaûi. Xeùt baùnh xe chuyeån ñoäng song phaúng. Caùc löïc taùc duïng: - Troïng löïc : P g mr = - Taûi troïng : P r 1 = g m 4
(aùp löïc cuûa truïc quay)
- Phaûn löïc phaùp tuyeán taïi I : NI
- Phaûn löïc ma saùt taïi I : FI - Ngaãu M
Caùc thaønh phaàn löïc quaùn tính thu goïn: qt R qt C ñaët taïi C: R = mW = ε mR C C qt M = J ε . = ρ2 m ε C C Phöông trình caân baèng: ⎧ ΣX = k F − I Rqt = F − ε I mR = 0 ⎪ ⎨ ΣY = N − P − P = 0 k I 1 ⎪ ⎩Σm = C Mqt − M + RF = ρ C I m 2ε − M + RF = I 0 Giaûi heä phöông trình: M MR ε = F ; = N ; = P + P = mg 5 m( 2 ρ + R ) I 2 2 ρ + R I 1 2
Ñeå caùc keát quaû treân chaáp nhaän ñöôïc phaûi coù ñieàu kieän laên khoâng tröôït: 2 2 m 5 (ρ + R )g FI ≤ f N . I ⇔ M ≤ f R
Ñaây chính laø ñieàu kieän cuûa M. M
Ví duï 11.5. Heä thoáng con laên vaø taûi A
lieân keát nhö hình veõ. Cho taûi A khoái B
löôïng m1, con laên khoái löôïng m2, caùc baùn
kính R = 2r vaø baùn kính quaùn tính ñoái vôùi I C truïc qua taâm laø ρ. H
Xaùc ñònh gia toác taûi A, gia toác goùc W
cuûa con laên, söùc caêng daây, phaûn löïc taïi I. A Hình 11.17
Xem con laên laên khoâng tröôït vaø boû qua A y M y T PB Rqt B W x A B W x A qt I FI P MB F qt A N A I VH T1 H a) b) Hình 11.17 139
khoái löôïng cuûa daây vaø ma saùt laên.
Giaûi. Xeùt chuyeån ñoäng cuûa taûi A: taïi thôøi ñieåm ñang xeùt ñaït WA (ñi leân), H.11.18a. Heä löïc: qt P ( A F , T , A ) ≡ 0 ΣY = T − P − Fqt = 0 k A A
⇔ T − m1g − m1WA = 0 (1)
Xeùt chuyeån ñoäng cuûa con laên B (H.11.18b).
- Quan heä ñoäng hoïc: con laên B chuyeån ñoäng song phaúng laên khoâng tröôït
coù I laø taâm vaän toác töùc thôøi vaø do daây khoâng d
Hình 11.18 aõn (VH = VA): VH VA VA ⇒ ωB = = = HI R − r r
Quan heä naøy ñuùng vôùi moïi t neân: WA εB = ω&B = r laáy chieàu nhö H.11.18b. suy ra: VB = rωB; B W = rεB = A W
- Laäp heä löïc caân baèng:
Thu goïn heä löïc quaùn tính cuûa con laên veà taâm B: Rqt = m W = m W B 2 B 2 A qt 2 2 W M = J ε = m A B B B ρ r coù chieàu nhö hình veõ.
Caùc löïc thöïc: - Ngaãu M; troïng löïc P r B = m 2g
- Söùc caêng daây T1 (chuù yù T1 = T do roøng roïc khoâng coù khoái löôïng) - Phaûn löïc NI F
, I (löïc ma saùt tröôït). qt ⇒ löïc Heä P (M, :
B , T1 , NI , FI , R B , Mqt ) ≡ 0 B
- Phöông trình caân baèng: ⎧
⎪ΣX = T + F − Rqt = T + F − m W = 0 ) 2 ( k I B I 2 A ⎪
⎨ΣY = N − P = N − m g = 0 k I B I 2 ) 3 ( ⎪ ⎪ qt qt 2 W Σm = M − M + R . r + T . r = m ρ A − M + rm W + rT = 0 ) 4 ( ⎩ I B B 2 r 2 A
- Giaûi heä boán phöông trình ta ñöôïc: 140 (M − rm g)r W 1 = A m r2 + m ( 2 ρ + r2 ) 1 2 Mm r + m m g( 2 ρ + r2 ) T 1 1 2 = m r2 + m ( 2 ρ + r2 ) 1 2 N = m F ; g = m W − T I 2 I 2 A Nhaän xeùt:
- Neáu: WA > 0 ⇔ M > rm1g : taûi A ñi leân
WA = 0 ⇔ M = rm1g : taûi A ñöùng yeân (cô heä caân baèng)
W A< 0 ⇔ M < rm1g : taûi A ñi xuoáng.
- Töø bieåu thöùc tính ñöôïc FI < 0. Vaäy löïc ma saùt taïi I coù chieàu ngöôïc laïi.
Caùc keát quaû chæ ñöôïc chaáp nhaän neáu: FI < fNI ⇔ FI < fm2g
vôùi: f - laø heä soá ma saùt tröôït.
- Cho cuï theå: m2 = 4m1; ρ = r
Tröôøng hôïp 1: khi M = 4m1rg 1 4 8 ⇒ WA = T ; g = m1 F ; g I = m1g < NI = 4m1 g 3 3 3 (coù theå chaáp nhaän) Tröôøng hôïp
2: khi M = 22m1rg 7 10 18 ⇒ WA = T ; g = m1 F ; g I = m1g > NI = 4m1 (loaïi) g 3 3 3
Ví duï 11.6. Cô heä hai baäc töï do nhö hình
veõ: con laên laø truï troøn ñoàng nhaát taâm B,
khoái löôïng m2, boû qua ma saùt giöõa A vaø
neàn ngang. Giaû söû con laên laên khoâng tröôït. Xaùc ñònh WA ,WB , phaûn löïc cuûa
neàn ngang vaø taùc duïng töông hoã taïi I khi
cho khoái löôïng cuûa laêng truï A laø m1. Hình 11.19 141
Giaûi. Cô heä coù hai vaät raén chuyeån ñoäng. Xeùt chuyeån ñoäng cuûa töøng vaät: Hình 11.20
Xeùt chuyeån ñoäng cuûa laêng truï A, taïi thôøi ñieåm ñang xeùt giaû söû ñaït gia toác WA (H.11.20a).
- Ñaët löïc: caùc löïc thöïc ñaët vaøo A Troïng löïc : P r A = m1g Phaûn löïc : NA
Phaûn löïc taïi I : NI, FI Löïc quaùn tính: qt FA = m1WA Heälöïc: qt P ( A , NA , NI, FI, FA ) ≡ 0
- Phöông trình caân baèng:
ΣX = −N sin α + F cos α − m W = 0 k I I 1 A ) 2 (
ΣY = −F sin α − N cos α + N − m g = ) 0 k I I A 1 ) 3 (
Xeùt chuyeån ñoäng cuûa con laên B cuõng taïi thôøi ñieåm ñoù (H.11.20b). Ñaët löïc: Caùc löïc thöïc: , , PB N , I F , I , ngaãu M.
Löïc quaùn tính: con laên chuyeån ñoäng song phaúng laên khoâng tröôït treân laêng
truï A, ñoàng thôøi laêng truï A tònh tieán ngang ⇒ taâm B chuyeån ñoäng hôïp: e r r WB = W + W = WA + W r gia toác goùc: W εB =
, chieàu giaû thieát nhö hình veõ. R Suy ra: qt r qt qt B F = − 2 m WB = − 2 m WA − 2 m W = e F + Fr r qt 1 2 B W 1 r MB = JBε = m2R = m2RW 2 R 2 Heä löïc: , , qt qt P ( B, NI, FI, , M Fe , Fr , Mqt ) ≡ 0 B
- Heä phöông trình caân baèng chung caû heä: 142 ⎧ ) 1 ( ⎪
− N sin α + F cos α − m W = 0 I I 1 A ⎪
− F sin α − N cos α + N − m g = 0 I I A 1 ) 2 ( ⎪⎪
⎨N sin α − F cos α − m W − m Wr cos α = 0 I I 2 A 2 ) 3 ( ⎪ ⎪ − m ) 4 (
2g + NI cos α + FI sin α + m W r 2 sin α = 0 ⎪ ⎪ r ) 5 ( ⎩ m 5 , 0 RW − M − F R = 0 2 I Giaûi heä phöông trình: 1 r M ) 5 ( ⇒ I F = m2 B W − 2 R 1 M 3 r ) 4 ( ⇒ NI = B P ( + sin α − m2 sinαW ) cos α R 2 ' M 3 r ) 2 ( ⇒ NA = m1g + B P + sin α − m2 sin αW R 2 M 1 r r − sin α + m2 sinα B W = m1g + B P − m2 sinαW R 2
Thay caùc giaù trò naøy vaøo (1) vaø (3) khöû WA chuùng ta nhaän ñöôïc: M ( 2 m + m )( + m g sin α) 1 2 2 r R W = m m 3 ( + m + m 2 sin2 α) 2 1 2 2 Theá r
W vaøo caùc bieåu thöùc treân ta tìm ra caùc aån soá töông öùng. Nhaän xeùt:
- Qua ví duï naøy chuùng ta thaáy raèng ñoái vôùi cô heä nhieàu baäc töï do neáu
duøng phöông phaùp naøy seõ phaûi giaûi moät heä ñoàng thôøi goàm nhieàu phöông trình raát phöùc taïp.
- Chuùng ta seõ duøng phöông phaùp khaùc, ôû chöông sau, ñeå giaûi ñaëc tröng
ñoäng hoïc tröôùc, laøm ñôn giaûn quaù trình tính toaùn.
Ví duï 11.7. Thanh gaáp khuùc vuoâng goùc ñoàng chaát AOB, tieát dieän khoâng ñoåi,
troïng löôïng P. Thanh coù theå quay quanh choát baûn leà O gaén chaët treân truïc quay
thaúng ñöùng DE. Khi truïc DE quay ñeàu vôùi vaän toác goùc ωo naøo ñoù thanh caân
baèng töông ñoái öùng vôùi goùc ϕ . Xaùc ñònh ωo vaø phaûn löïc oå truïc theo ϕ. 143 Hình 11.21 y D Dx i O x a b rk Hình 11.22 Mk A Ey B E Ex Hình 11.19 y Ro F qt qt k O O Fk O X qt C2 F1 I ϕ C qt 1 a H F2 A A B P1 P2 B a) b) c) Hình 11.19
Giaûi. Xeùt chuyeån ñoäng cuûa thanh AOB ôû traïng thaùi caân baèng öùng vôùi goùc ϕ xaùc
ñònh: caùc löïc thöïc taùc duïng:
- Troïng löïc P1 vaø P2 cuûa thanh OA vaø OB
- Phaûn löïc oå truïc Ro cuûa oå truïc O.
Thu goïn heä löïc quaùn tính:
Khi thanh AOB ñaõ oån ñònh, caùc ñoaïn OA, OB quay ñeàu quanh truïc DE.
Moät phaân toá thuoäc thanh seõ coù löïc quaùn tính ly taâm duy nhaát. qt Fk = − m k Wk = ± mkr 2 k ωo i
(laáy daáu (–) neáu phaân toá ∈ OA, laáy daáu (+) neáu phaân toá ∈ OB).
Treân moãi thanh löïc quaùn tính phaân boá theo luaät tuyeán tính tam giaùc song
song cuøng chieàu, heä löïc naøy coù hôïp löïc ñi qua taâm cuûa dieän tích heä löïc vaø baèng
vector chính cuûa heä löïc (löu yù: qt R = −MWC ). Chuùng ta nhaän ñöôïc: 144 qt P1 Pa a F = W 1 C = . sin . 2 ϕ ω g 1 a + b 2 o qt P2 Pb b F = W = . cos . 2 2 ϕ ω g C2 a + b 2 o 1 1 AI = BH ; a = b 3 3 Heä löïc: qt qt P ( 1, P2, Ro, F1 , F2 ) ≡ 0
Caùc phöông trình caân baèng:
Xaây döïng heä truïc ñoäng Oxy chöùa AOB quay cuøng AOB. ⎧ ) 1 ( ⎪ΣX = k R + ox Fqt − 2 Fqt = 1 0 ) 2 ( ⎪⎪⎨ΣY = k R − oy P − 1 P = 2 0 ⎪ ⎪ Pa2 2 Pb2 qt 2 qt ⎪Σm = sinϕ + bsinϕF . − cosϕ − a cosϕF . ⎩ o a ( 2 + ) b 3 2 a ( 2 + ) b 3 1 ) 3 (
Giaûi heä ba phöông trình cho ta: 2 2 2 a ( 3 sin ϕ − b cos ϕ ω = ) o a ( 3 − b3) sin ϕ 2 P 2 R o ω = a ( 2 sin ϕ − b2 cos ) ϕ ox a ( 2 + ) b R = P oy
Chuù yù: Ñeå xaùc ñònh phaûn löïc ñoäng taïi oå truïc D, E chuùng ta chæ laäp caùc
phöông trình caân baèng trong heä toïa ñoä ñoäng töø heä löïc: r D
( x, Ex, Ey,−Rox,−Roy) ≡ 0
maø khoâng caàn duøng heä (11.23).
Ví duï 11.8. Ñóa troøn ñoàng chaát cuûa tuabin hôi coù baùn kính R = 0,2 m, khoái löôïng
m = 3,27 kg gaén chaët vaøo truïc quay nheï AB ñi qua taâm O cuûa ñóa. Maët phaúng
cuûa ñóa nghieâng vôùi truïc AB moät goùc α = 0,02 rad. Truïc AB quay ñeàu 3000 voøng/phuùt.
Tính aùp löïc ñoäng löïc leân truïc oå ñôõ, bieát OA = 0,5 m; OB = 0,3 m. y a b y y A 1 y B D z α 1 D y α A B A α B z z O O ω A Bx x x C C , x a) Hình 11.20 b) Hình 11.23 145
Giaûi. Xeùt chuyeån ñoäng cuûa heä thoáng ñóa vaø truïc quay.
Choïn heä truïc ñoäng gaén vôùi truïc quay Oxyz coù Oy nghieâng vôùi ñóa goùc α
vaø vuoâng goùc vôùi truïc quay.
Heä phöông trình (11.23) thaønh: ⎧ Añl + Bñl + ω ( M 2x + εy ) = 0 ⎪ x x C C Añl + y Bñl + ω y ( M 2y − ε C xC) = 0 ⎪⎪ ⎨ ⎪m (Añl) + m B ( ñl) + εJ − ω2J = 0 x y x x xz yz ⎪ ⎪ ñl ñl 2 ⎩m (A ) + m B ( ) + εJ + ω J = 0 y x y x yz xz ôû ñaây: xC = yC = 0 Ñeå tính
Jxz, Jyz chuùng ta xaây döïng heä toïa ñoä ñoäng Ox1y1z1 coù Ox1 ≡ Ox.
Oy1z1 laø Oyz quay goùc α quanh truïc Ox.
J = Σm y z = Σm (y cos α + z sin α z )( cos α − y sin ) yz k k k k k 1 k 1 k 1 k 1 α
= Σm y z cos2 α + Σm z2 sin α cos k k 1 k 1 k k 1 α
− Σm y2 sin α cos α − Σm z y sin2 k k 1 k k 1 k 1 α = J cos2 α − J sin2 α + Σm z ( 2 + x2 ) sin α cos y α 1z1 y1z1 k k 1 k 1 − Σmk(y2k 1 + x2k 1 ) sin α cos α 1 2 1 2 1
= (Jy −J )sinα cosα = ( mR − mR )sin α cosα = − mR2 sin a 2 1 1 z 4 2 8
Chuù yù: Caùc ñaïi löôïng Jxz, J = 0 1 y 1 z
Thay vaøo heä phöông trình chuùng ta nhaän ñöôïc: ⎧ Añl + Bñl = 0 ⎪ x x Añl + Bñl = 0 y y ⎪⎪ ⎨ ñl ñl 2 1
⎪− aA + bB + ω . mR2 sin α 2 = 0 y y o ⎪ 8 ⎪⎩ aA ñl − x bBñl = x 0 Giaûi heä ta ñöôïc: Añl = x Bñl = x 0 ñl mR2 ñl sin α 2 A = − y B = ω2 = y o 74 , 2012 sin α a ( 8 + ) b 146 Chöông 13
NGUYEÂN LYÙ DI CHUYEÅN KHAÛ DÓ Noäi dung
Xaây döïng moät phöông phaùp ngaén goïn, tröïc tieáp xaùc ñònh:
- Ñieàu kieän caân baèng cuûa cô heä
- Caùc thaønh phaàn phaûn löïc ñaët vaøo cô heä.
Nguyeân lyù di chuyeån khaû dó (DCKD) coøn laøm cô sôû ñeå thieát laäp phöông
trình vi phaân chuyeån ñoäng toång quaùt cuûa cô heä khoâng töï do. Yeâu caàu
- Naém vöõng ñònh nghóa DCKD, bieát caùch xaùc ñònh toïa ñoä suy roäng, baäc töï do cuûa cô heä
- AÙp duïng nguyeân lyù DCKD giaûi ñöôïc caùc baøi toaùn caân baèng hay chuyeån ñoäng cuûa cô heä.
13.1. MOÄT SOÁ KHAÙI NIEÄM CÔ BAÛN
1. Phöông trình lieân keát
Xeùt cô heä khoâng töï do (muïc 10.1), vò trí vaø vaän toác cuûa caùc chaát ñieåm
thuoäc cô heä seõ thoûa maõn caùc moái quan heä naøo ñoù ñoäc laäp vôùi ñieàu kieän ñaàu vaø
caùc löïc hoaït ñoäng ñöôïc goïi laø caùc lieân keát. Tröôøng hôïp toång quaùt caùc lieân keát
ñöôïc moâ taû qua quan heä haøm soá: f (rr , rr , t) ≥ k , 0 = l, i , N = l, S i k k (13.1)
ñöôïc goïi laø caùc phöông trình lieân keát. trong ñoù: r r k r , k
r - laø vò trí vaø vaän toác chaát ñieåm thöù k
N - laø soá chaát ñieåm cuûa cô heä, s laø soá lieân keát.
- Trong chöông naøy chuùng ta haïn cheá xeùt loaïi cô heä chæ chòu caùc lieân keát coù daïng: f r 1 (rk ) = k ; 0 = 1, l ; N = 1, S (13.2)
laø loaïi lieân keát giöõ, döøng, hình hoïc.
2. Di chuyeån khaû dó - baäc töï do cuûa cô heä
1- Di chuyeån khaû dó
Di chuyeån khaû dó cuûa cô heä laø taäp di chuyeån voâ cuøng beù cuûa caùc chaát ñieåm
cuûa cô heä töø vò trí ñang xeùt sang vò trí laân caän maø vaãn thoûa maõn caùc lieân keát taïi vò trí ñang xeùt. 147
Ñeå phaân bieät vôùi di chuyeån thöïc voâ cuøng beù cuûa cô heä ñöôïc bieåu dieãn qua d { r r
k } chuùng ta moâ taû DCKD qua { r δ k } . trong ñoù: k
rr - laø baùn kính vector cuûa chaát ñieåm thöù k cuûa cô heä.
Xeùt cô heä chæ chòu caùc lieân keát (13.2) Cho cô heä moät DCKD { rr
δ k} taïi vò trí ñang xeùt, suy ra: f r r i r ( k + r δ k) = 0 (13.3)
Trong khi ñoù cuõng toàn taïi duy nhaát moät di chuyeån thöïc r d { rk } töø vò trí ñang
xeùt thoûa maõn caùc lieân keát: f r r i r ( k + r d k) = 0 (13.4) Neáu xem { rv δ r k } vaø r d
{ k } töông öùng laø caùc taäp nghieäm cuûa caùc phöông
trình (13.3), (13.4). Do (13.3) vaø 13.4) hoaøn toaøn gioáng nhau neân taäp nghieäm r d { r v
k } truøng vôùi taäp nghieäm { r δ k } .
Nhö vaäy di chuyeån thöïc phaûi thuoäc taäp caùc DCKD: r d { r v k } ∈ { r δ k }
Coù nghóa laø sau khoaûng thôøi gian dt toàn taïi duy nhaát moät di chuyeån thöïc r d { r v
k } thuoäc taäp caùc DCKD { r δ k }
Neáu caùc lieân keát phuï thuoäc thôøi gian t, taäp caùc DCKD {δrk } thoûa maõn
lieân keát taïi thôøi ñieåm t ñang xeùt: ⇔ f r r 1 r ( k + r δ k, t) = 0 (13.5)
Coøn taäp di chuyeån thöïc d
{ rk } thoûa maõn lieân keát taïi thôøi ñieåm (t + dt):
caùc phöông trình (13.5) vaø (13.6) khaùc nhau: ⇒ r d { r r k } ∉ { r δ k }
2- Baäc töï do cuûa cô heä
Taïi moãi vò trí cuûa cô heä coù voâ soá DCKD { rr
δ k } . Noùi chung caùc DCKD
khoâng ñoäc laäp tuyeán tính do phaûi thoûa maõn caùc phöông trình lieân keát. Chuùng ta
coù theå choïn trong taäp { rr
δ k } moät heä vector cô sôû caùc DCKD ñoäc laäp tuyeán tính,
moïi DCKD cuûa heä ñeàu bieåu dieãn ñöôïc qua moät toå hôïp tuyeán tính cuûa heä vector
cô sôû. Baäc töï do cuûa cô heä baèng soá vector cô sôû cuûa taäp DCKD { rr δ k } cuûa cô heä.
Ví duï 13.1. Vieân bi M ñöôïc xuyeân qua bôûi daây keõm cöùng coá ñònh (H.13.1), { rv δ }
k laø taäp caùc vector voâ cuøng beù naèm theo phöông tieáp tuyeán vôùi daây taïi M.
Choïn rδ = 1 (nhö hình veõ) laøm vector cô sôû: r r ⇒ δr = aδ M (13.7)
Baäc töï do cuûa cô heä naøy baèng moät. 148 M M δ δ 1 1 Π δ2 Hình 13.1 Hình 13.2
Ví duï 13.2. Xeùt vieân bi M luoân luoân töïa leân maët cong. Taäp
{δrk } laø vector voâ cuøng beù naèm treân maët phaúng Π tieáp tuyeán taïi M vôùi maët cong. Choïn
δ1 ,δ2 laø hai vector ñôn vò vuoâng goùc naèm treân Π coù goác taïi M: ⇒ δrM r = a1δ1 + a2δ2 (13.8)
Baäc töï do cuûa heä naøy baèng hai.
3. Toïa ñoä suy roäng
1- Caùc ñònh nghóa
Vò trí cuûa moät chaát ñieåm ñöôïc xaùc ñònh qua ba toïa ñoä (x, y, z). Cô heä N
chaát ñieåm ñöôïc xaùc ñònh qua 3N toïa ñoä {xi, yi, zi}, i = , 1 N .
Vôùi cô heä khoâng töï do caùc toïa ñoä cuûa chaát ñieåm phaûi thoûa maõn s phöông
trình lieân heä: f1(xk, yk, zk) = 0
Soá toïa ñoä ñoäc laäp cuûa cô heä chæ coøn laø: r = 3N – s
(Vôùi caùc cô heä ñöôïc xeùt ôû ñaây r baèng soá baäc töï do cuûa cô heä).
Töø ñoù chuùng ta nhaän thaáy: Neáu chuù yù ñeán nhöõng lieân keát ñaët vaøo cô heä, vò
trí cuûa noù coù theå ñöôïc xaùc ñònh moät caùch ñôn giaûn qua caùc thoâng soá ñöôïc choïn
thích hôïp, kyù hieäu laø: {q1, q, ..., qn}.
- Taäp caùc thoâng soá naøy ñöôïc goïi laø toïa ñoä suy roäng cuûa cô heä
- Taäp caùc toïa ñoä suy roäng ñoäc laäp tuyeán tính vöøa ñuû ñeå xaùc ñònh vò trí cô
heä ñöôïc goïi laø heä toïa ñoä ñuû, kyù hieäu {q1, q2, ..., qn}
(Caùc cô heä xeùt trong chöông naøy coù soá toïa ñoä ñuû baèng soá baäc töï do).
2- Phöông phaùp xaùc ñònh
Trong thöïc teá ñeå xaùc ñònh baäc töï do vaø toïa ñoä suy roäng cuûa cô heä caùc vaät
raén, chuùng ta phaân tích khaû naêng chuyeån ñoäng cuûa caùc vaät raén thuoäc cô heä. Chuù yù raèng:
- Vaät raén tònh tieán theo moät giaù xaùc ñònh, vaät raén quay quanh truïc coá ñònh,
vaät raén chuyeån ñoäng laên khoâng tröôït ñeàu coù moät baäc töï do
- Vaät raén chuyeån ñoäng phaúng coù moät ñieåm ñaõ xaùc ñònh quyõ ñaïo, vaät raén
vöøa quay quanh truïc coá ñònh vöøa tröôït treân truïc ñoù ñeàu coù hai baäc töï do
- Vaät raén chuyeån ñoäng phaúng, vaät raén quay quanh taâm coá ñònh ñeàu coù ba baäc töï do 149
Tröôùc heát chuùng ta coá ñònh moät vaät raén s1 coù baäc töï do thaáp nhaát thuoäc cô
heä, caùc tröôøng hôïp coù theå xaûy ra:
- Neáu cô heä coá ñònh thì soá baäc töï do cuûa cô heä baèng soá baäc töï do cuûa s1.
Toïa ñoä suy roäng ñöôïc choïn laø caùc thoâng soá xaùc ñònh vò trí cuûa s1.
- Cô heä toàn taïi moät soá vaät raén vaãn chuyeån ñoäng ñöôïc. Chuùng ta tieáp tuïc coá
ñònh vaät s2 coù baäc töï do thaáp nhaát trong chuyeån ñoäng khi ñaõ giöõ s1 ñöùng yeân,
tuaàn töï nhö vaäy cho ñeán luùc cô heä hoaøn toaøn ñöôïc coá ñònh. Baäc töï do cuûa cô heä
baèng toång laàn löôït baäc töï do cuûa caùc vaät s1, s2,... xeùt trong caùc chuyeån ñoäng töông öùng.
Ví duï 13.3. Cho cô heä nhö H.13.3. Giaû sD E
söû con laên D laên khoâng tröôït. Xaùc ñònh
baäc töï do vaø choïn heä toïa ñoä ñuû. D
Giaûi. Con laên D laên khoâng tröôït coù ϕc
moät baäc töï do (moät thoâng soá xaùc ñònh). α
Chuùng ta choïn laø ñoä dôøi taâm D C
theo maët nghieâng sD. Coá ñònh vaät D
(coá ñònh sD) roøng roïc E seõ ñöùng yeân A
song roøng roïc C vaãn quay ñöôïc quanh B
taâm C (coá ñònh) laøm cho A. B tònh tieán Hình 13.3
thaúng. Coá ñònh tieáp C (coá ñònh goùc
quay ϕC) cô heä hoaøn toaøn ñöùng yeân.
Cô heä coù hai baäc töï do, chuùng ta choïn heä toïa ñoä ñuû: q1 ≡ sD; q2 ≡ ϕC.
Ví duï 13.4. Cô heä goàm tay quay θ C
OA quay ñöôïc quanh truïc qua O,
tay quay AB quay ñöôïc quanh s B γ
truïc qua A, vaät E vöøa quay ñöôïc D
quanh AB vöøa tònh tieán doïc theo E Α
AB, tay quay CD quay ñöôïc Ψ
quanh truïc qua C. Tìm baäc töï do
cuûa cô heä, choïn heä toïa ñoä ñuû.
Giaûi. Theo phöông phaùp treân, khi O ϕ
coá ñònh goùc ϕ thanh AB vaãn quay Hình 13.4
ñöôïc quanh A (coá ñònh). Coá ñònh tieáp goùc quay ψ cuûa thanh AB, vaät E vaãn
chuyeån ñoäng ñöôïc treân AB (coá ñònh). Coá ñònh goùc quay θ cuûa E quanh AB, vaät
E vaãn coù theå tònh tieán doïc theo AB. Coá ñònh tieáp ñoä dôøi s cuûa E, thanh CD vaãn
coøn quay ñöôïc quanh C. Cuoái cuøng khi cho goùc quay γ coá ñònh, cô heä hoaøn toaøn ñöùng yeân. 150
Baäc töï do cuûa cô heä baèng toång caùc thoâng soá ñoäc laäp vöøa ñöôïc neâu treân.
Cô heä coù baäc töï do laø 5. Heä toïa ñoä ñöôïc choïn:
q1 ≡ ϕ; q2 ≡ ψ; q3 = θ; q4 = s; q5 = γ 4. Löïc suy roäng
1- Ñònh nghóa: Xeùt cô heä N chaát ñieåm chòu taùc duïng cuûa caùc löïc hoaït ñoäng ( a F r
k ). Cho cô heä thöïc hieän moät DCKD { r δ k } , caùc löïc ( a Fk ) seõ thöïc hieän
coâng treân ñoä dôøi ñoù: N N ∑ a δA = r k ∑Fk δ. kr (13.9) R =1 k =1
ñöôïc goïi laø coâng khaû dó. Choïn heä toïa ñoä suy roäng {qi}, i = , 1 n . n r r rr ⇒ δr = δ k k r q ( 1, q2,..., qn) ∑ δ = k δq ∂ i q i=1 i (13.10) N N n r n N r n a r a r ⇒ ∑ δAk ∑ Fk ∑ ∂ = k δqi ∑⎛⎜ ∂ = k F q Q q ∂q ⎜ ∑ ⎞ ⎟ k δ = ∂q ⎟ i ∑ δi i k =1 k =1 i=1 i i=1 ⎝ k =1 i ⎠ i=1 N r trong ñoù: a δ k r Qi = Fk ∑ (13.11) q ∂ k =1 i
ñöôïc goïi laø löïc suy roäng öùng vôùi toïa ñoä qi.
2- Phöông phaùp xaùc ñònh N r
a) AÙp duïng tröïc tieáp ñònh nghóa: a δ k r Qi = Fk ∑ q ∂ k =1 i
Ví duï 13.5. Con laéc keùp chòu löïc nhö H.13.5. Choïn q1 ≡ ϕ, q2 ≡ ψ. Tìm caùc löïc
suy roäng. Cho OA = 2a; AB = 2b; I, H laø caùc trung ñieåm.
Giaûi. Bieåu dieãn caùc vector lieân quan qua toïa ñoä Decartes vaø toïa ñoä suy roäng: F1 ≡ P , O ( P F ); 2 ≡ Q , O ( Q F ); 3 ≡ F , F ( O) r r r r ≡ r = a sinϕ i + a cos j 1 I ϕ r r r r r2 ≡ rH = a 2 ( sinϕ + bsin ) ψ i + a 2 ( cosϕ + b cos ) ψ j r r r r r ≡ r = a 2 ( sinϕ + b 2 sin ) ψ i + a 2 ( cosϕ + b 2 cos ) ψ j 3 B rr ∂ rs ∂ r r 1 1 ⇒ = = a cos . ϕ i − a sin . ϕ j i x q ∂ 1 ϕ ∂ O rr ∂ rr 1 ∂ 1 = = 0 ϕ q I ∂ 2 ψ ∂ j rr ∂ rr ∂ r r A 2 2 = = a 2 cos . ϕ i − a 2 sin ϕj H q ∂ 1 γϕ F Ψ r r y B r ∂ ∂ r r 2 r 2 = = b cos . ψ i − b sin . ψ j Q q ∂ 2 ψ ∂ r r r ∂ r ∂ r r 3 3 = = a 2 cos . ϕ i − a 2 sin . ϕ j Hình 13.5 q ∂ 1 ψ ∂ 151 r r r ∂ r ∂ r r 3 3 = = b 2 cos . ψ i − b 2 sin . ψ j q ∂ 2 ψ ∂ r 3 ∂r ⇒ Q ≡ Q = ∑ k 1 ϕ F . = k =1 k ϕ ∂ = [ a . 0 cos ϕ + − .( p a sin ϕ)] + [ a 2 . 0 cos ϕ + − .( Q a 2 sin ϕ)] + [ a 2 . F cos ϕ + − .( 0 a 2 sin ϕ)] = −ap sin ϕ − aQ 2 sin ϕ + aF 2 cos ϕ r 3 ∂r Q ≡ Q = ∑ k 2 Fk . = ψ k =1 ψ ∂ = [ 0 . 0 + ]0 . p + [ b . 0 cos ψ + .( Q −b sin ψ)] + [ b 2 . F cos ψ + .( 0 2 − b sin ψ)] = − Qb sin ψ + bF 2 cos . ψ
b) Tröôøng hôïp heä {qi} laø heä toïa ñoä ñuû,caùc qi ñoäc laäp tuyeán tính ⇒ caùc δqi
cuõng ñoäc laäp tuyeán tính Ñeå tính
Qi chuùng ta cho heä DCKD sao cho:
δqj ≠ 0 (δqj > 0) coøn: δqi = 0 ∀ i ≠ j N r ⇒ ∑δA = k ∑Q δq = Q δ i i j. q j k =1 i=1
Heä soá cuûa bieåu thöùc tính coâng chính laø löïc suy roäng töông öùng.
Ví duï 13.6. Laáy ví duï 13.3 vôùi caùc löïc tích cöïc: caùc troïng löïc PA,PB, PD vaø
ngaãu M nhö H.13.6. Tính caùc löïc suy roäng. Bieát caùc baùn kính töông öùng rC, rD, rE.
Giaûi. Heä toïa ñoä ñuû: q1 ≡ sD, q2 ≡ ϕC. Tính Q S 1 M D Cho cô heä DCKD: E
δq1 = δsD > 0, δq2 = δϕC = 0 (khoâng cho roøng roïc C quay). Deã daøng tính ñöôïc: PD ϕ c α
∑δA )1( = δA P(A) + δA P(B) + δA P(D) + δA(M) k C s δ D = A P s δ D + B P s δ D + . M − D P sin . α s δ D E r A M B = P ( + P + − P sin α). s A B D δ D rE PA M PB = P ( + P + − P sin α).δ 1 q A B r D Hình 13.6 E M ⇒ Q = P + P + − P sin α 1 A B r D E Tính Q2
Cho cô heä DCKD: δq1 = δqsD = 0; δq2 = δϕC > 0 (ñieåm C coá ñònh, roøng roïc C quay quanh taâm). 152
∑δA )2( = δA P(A) + δA P(B) + δA P(D) + δA(M) k = A P C r . δϕC − B P C r . .δϕC + 0 + 0 = A P ( − B P C r ). .δϕC = A P ( − B P C r ). . q δ 2 ⇒ Q2 = A P ( − B P r ). .C
c) Tröôøng hôïp caùc löïc hoaït ñoäng laø löïc theá ( Fk )
Trong phaàn tính coâng ôû chöông 13 chuùng ta ñaõ coù: π ∂ π ∂ π ∂ kx F = − ; F = − ky ; F = − x ∂ kz k y ∂ k z ∂ k
trong ñoù: π - laø haøm theá naêng. N N N Xeùt: ∑ δA = r k ∑ Fkδr = k ∑ F( δx + F δy + F ∂ kx k ky k kz zk ) k=1 k=1 k=1 N = −∑ ⎛ π ∂ π ∂ π ∂ ⎞ ⎜ δx + δy + δ k k k z ⎟ ∂x ∂y ∂z k =1 ⎝ k k k ⎠ N ⎛ π ∂ n ∂xk π ∂ n ∂yk π ∂ n ∂z ⎞ = −∑ ⎜ k ⎜ ∑ δq + i ∑ δq + i ∑ δq ⎟ i ⎟ ∂x ∂q ∂y ∂q ∂z ∂q k =1 ⎝ k i=1 i k i=1 i k i=1 i ⎠ n N n x y z = ∑ − ∑⎛ π∂ ∂ k π ∂ ∂ k π ∂ ∂ ⎞ ⎜ + + k δ ⎟ q = i ∑ π∂ − δqi x q y q z q q i 1 k 1 ⎝ ∂ ∂ ∂ ∂ ∂ ∂ k i k i k i ⎠ ∂ = = i =1 i ⇒ Q − π ∂ i = q ∂ i
Trong tröôøng hôïp caùc löïc hoaït ñoäng coù caû löïc theá vaø löïc khoâng theá chuùng ta coù theå tính: Q π ∂ i = −
+ Qi (löïc khoâng theá) q ∂ i
trong ñoù: π - laø haøm theá cuûa caùc löïc theá.
Ví duï 13.7. Xeùt laïi moâ hình cô heä ôû ví duï 13.5.
Giaûi. Caùc löïc tích cöïc coù theá: , P Q
; löïc khoâng theá: F . Choïn goác theá naêng laø O. ⇒
haøm π = A(P) + A(Q) = (− aP cos ) ϕ − a 2 ( cos ϕ + b cos ψ Q ) π ∂ ∗ t ⇒ − = −aP sin ϕ − aQ 2
sin ϕ = Q1(löïc theá) = Q1 ϕ ∂ π ∂ ∗ t −
= −bQ sin ψ = Q2(löïc theá) = Q2 ψ ∂
Vôùi löïc khoâng theá F duøng hai phöông phaùp treân ta deã daøng tính ñöôïc caùc
löïc suy roäng töông öùng (xem heä chæ coù löïc hoaït ñoäng F ): QF1 = aF 2 cos ϕ Q ; F 2 = 2bF cos
Chuùng ta nhaän ñöôïc caùc löïc suy roäng: Q ≡ Q = Qt + QF = −aP sin ϕ − aQ 2 sin ϕ + aF 2 cos ϕ 1 ϕ 1 1 Q ≡ Q = Qt
+ QF = −bQ sin ψ + 2bF cos ψ 2 ψ 2 2
5. Lieân keát lyù töôûng 153
Cô heä ñöôïc goïi laø chòu lieân keát lyù töôûng neáu toång coâng cuûa taát caû caùc
phaûn löïc lieân keát ( Rk ) ñaët vaøo cô heä treân moïi DCKD ñeàu baèng khoâng: N ∑ δA = r r r ∑ Rkδr = 0 ∀ δ k { k r } k=1
Trong thöïc teá caùc cô heä goàm vaät raén, daây meàm khoâng daõn, boû qua ma saùt
ñeàu laø cô heä chòu lieân keát lyù töôûng. Tröôøng hôïp toàn taïi thaønh phaàn phaûn löïc sinh
coâng treân DCKD, chuùng ta xem thaønh phaàn naøy thuoäc caùc löïc hoaït ñoäng, khi ñoù
cô heä ñöôïc khaûo saùt nhö chòu lieân keát lyù töôûng.
13.2. NGUYEÂN LYÙ DI CHUYEÅN KHAÛ DÓ
1. Phaùt bieåu nguyeân lyù DCKD
- Ñieàu kieän caàn vaø ñuû ñeå cô heä chòu lieân keát giöõ, döøng, hình hoïc vaø lyù
töôûng caân baèng ôû vò trí ñang xeùt laø: toång coâng cuûa taát caû caùc löïc hoaït ñoäng treân
moïi DCKD keå töø vò trí ñoù ñeàu baèng khoâng: N N ∑ a δ a A = r r k ∑ Fkδr = ∀ 0 δ k { k r } (13.13) k=1 k=1
- Bieåu dieãn nguyeân lyù DCKD trong heä toïa ñoä ñuû {qi}, i = , 1 r : N r a ⇒ F r k r δ = Q q δ = 0 { ∀ q δ } ∑ k ∑ i i i (13.14) k=1 i−1 Do caùc
δqi ñoäc laäp tuyeán tính, suy ra (13.14) töông ñöông: Q = i ; 0 1, r i =
2. Caùc loaïi baøi toaùn aùp duïng nguyeân lyù DCKD
Nguyeân lyù DCKD thöôøng ñöôïc aùp duïng Ñeå giaûi hai loaïi baøi toaùn sau:
- Tìm ñieàu kieän caân baèng cuûa cô heä
- Tìm caùc thaønh phaàn phaûn löïc tónh cuûa cô heä y B
Ví duï 13.8. Cô caáu hình bình haønh A G2
ABCD (H.13.7). Taïi A, B, C, D, O1, G O1 O 2
2 ñeàu laø caùc khôùp baûn leà (khoâng b I
ma saùt). Cô caáu phaân boá ñoái xöùng H a ñoái vôùi truïc O C 1O2. Hai taûi troïng G1, O G 2
2 coù troïng löôïng Q1, Q2 töông öùng. D
Tìm ñieàu kieän caân baèng cuûa heä. Hình 13.7
Giaûi. Cô heä thoûa maõn caùc ñieàu kieän cuûa nguyeân lyù DCKD. Caùc khung ADH vaø
BCI chæ coù theå chuyeån ñoäng tònh tieán. Cho cô heä moät DCKD coù δyB = –δyA
nhöng δyB = δy(G2), δyA = δy(G1) → δy(G2) = –δy(G1). 154
AÙp duïng nguyeân lyù DCKD: ñieàu kieän caân baèng cuûa cô heä: ∑ δAa = k Q δ 1 yG + 1 Q δ 2 yG = 2 0 ⇔ Q ( − 1 Q2)δyG = ∀ 1 , 0 δ { y(G1,2)} →ÑKCB: Q1 = Q2
khoâng phuï thuoäc (a,b)
Ví duï 13.9. Xeùt laïi moâ hình cô heä trong ví duï 13.6 (H.13.6). Tìm ñieàu kieän caân baèng cuûa cô heä.
Giaûi. Cô heä coù hai baäc töï do. AÙp duïng ñieàu kieän caân baèng trong heä toïa ñoä suy roäng ñuû: q ( ≡ s , q ≡ ϕ 2 ) 1 D C ⎧ M ⎪Q = 1 P + A P + − B PD sin α = 0 ÑKCB ⇔ ⎨ rE ⎪ ⎩Q = 2 P ( − A PB)r = C 0 M = r P ( sin α − P − P ) ⎧ ⇔ ⎨ E D A B ⎩P = A B P
Ví duï 13.10. Hoäp toác ñoä ñöôïc bieåu dieãn ôû H.13.8. Baùnh raêng 1 coá ñònh (gaén chaët
vaøo voû hoäp toác ñoä) baùn kính r1. Caëp baùnh raêng 2 - 3 gaén chaët vôùi nhau quay
quanh truïc ñoäng qua A naèm treân tay quay OA (caëp 2’ - 3’ cuøng kích thöôùc quay
quanh truïc A’ treân tay quay OA’) coù baùn kính töông öùng r2, r3, baùnh raêng 4 gaén
chaët vôùi truïc IV. Tìm ngaãu M2 ñaët treân truïc IV ñeå cô caáu caân baèng (hoaëc chuyeån
ñoäng döøng) neáu coù ngaãu M1 ñaët vaøo truïc I. δϕ δϕ 3 3 3 δϕ2 2 A 2 3 A A M ω ω 3 O 1 2 ω1 4 I 4 IV O ω 1 O 4 M M 1 2 1 δϕ1 A’ A 2’ 3’ A 2’ 3’ Hình 13.8 Hình 13.9 Hình 13.10
Giaûi. Deã daøng nhaän thaáy cô heä coù moät baäc töï do, choïn q1 ≡ ϕ1 (goùc quay cuûa truïc I cuøng chieàu M1).
Töø H.13.9 khi cho truïc I (tay quay AA’) quay goùc δϕ1 > 0 (δq1 > 0) ⇒ baùnh raêng hai quay goùc: 1 r + 2 r δϕ2 = . 1
δϕ ≡ δϕ3 laø goùc quay cuûa baùnh raêng 3 (H.13.10). 2 r 155
Ñeå xaùc ñònh moái quan heä giöõa δϕ3 vaø δϕ4 chuùng ta tìm lieân heä giöõa ω3 vaø ω4.
AÙp duïng coâng thöùc Vilit: ( 3 ω − 1 ω ) r . 3 = ( − 4 ω − 1 ω ) r . 4 ⇒ ω r . 3 3 − 1 ω (.r + r 3 4 ) = ω − r . 4 4 ⇒ 3 δϕ r . 3 − 1 δϕ (.r3 + r4) = 4 δϕ − r . 4 Bieåu dieãn δϕ3 qua δϕ1: ⎡ r + r ⎤ ⇒ 4 r δϕ4 = ⎢( 3 r + 4 r ) 1 2 − 2 r . ⎥ 1 δϕ ⎣ 3 r ⎦ [ 2 r ( 3 r + 4 r ) − 3 r ( 1 r + 2 r )] ⇒ δϕ4 = δϕ1 4 r 2 r
Ñieàu kieän caân baèng cuûa cô heä: Aa δ ∑ k = M1 1 δϕ − M2δϕ4 = 0 M ⇔ M 2 1 1 δϕ −
[r2(r3 + r4) − r3(r1 + r2)] 1 δϕ = 0 r r 4 2 4 r 2 r ⇒ M2 = 1
M coù chieàu nhö hình veõ 2 r ( 3 r + 4 r ) − 3 r ( 1 r + 2 r )
Ví duï 13.11. Tìm moái quan heä giöõa caùc löïc P vaø Q trong maùy eùp ñöôïc bieåu dieãn ôû H. 13.11.
Giaûi. Chuùng ta nhaän thaáy cô heä coù moät baäc Q
töï do, moïi vò trí cuûa cô heä ñeàu ñöôïc bieåu
dieãn qua moät thoâng soá naøo ñoù ñöôïc choïn P
laøm toïa ñoä suy roäng. Noùi caùch khaùc, toïa ñoä β D
caùc ñieåm thuoäc heä phaûi bieåu dieãn ñöôïc qua B α C
nhau. Caùc löïc hoaït ñoäng , Q P ñeàu theo E
phöông thaúng ñöùng cho neân chuùng ta chæ β P
quan taâm ñeán dòch chuyeån thaúng ñöùng cuûa y x caùc ñieåm (I, D, E). O
- Tung ñoä cuûa caùc ñieåm ñaëc bieät: Hình 13.11
ñaët: AB = a; CD = b; BC = e; AI = d yI = a 2 cos β ⎫ ⇒ y = a cos β + b sin ⎪ α ⎬ (*) D y = a cos β − b sin ⎪ E α ⎭ vaø lieân heä hình hoïc:
BC = e = bcosα – (d – asinβ)
⇔ bcosα + asinβ = d + e = const (**)
- Cho cô heä moät DCKD chuùng ta nhaän ñöôïc: 156 δy = − I a 2 sin β δβ . ⎫ (*) ⎪ ⇒ δy = −a sin β δβ . + b cos α δα . D ⎬ ⎪ δy = −a sin β δβ . − b cos α δα . E ⎭ (**) ⇒ bsin . α δα = a cos . β δ . β Bieåu dieãn δα qua δβ: a cosβ δα = . δβ b sin α y a sin . a cot g cos . δ = − β δβ + α β δβ ⇒ D δy = −a sin β αβ . − a cot gα cosβ δβ . E
- Ñieàu kieän caân baèng cuûa cô caáu: Aa δ ∑ k = A δ (Q) + A δ (PD) + A δ (PE) = 0 ⇔ − .( Q − a 2 sin . β )
δβ − Pa(− sin β + cot gα cos ) β δβ + Pa(-sinβ - cotgαcos ) β δβ = (2aQsinβ - 2Pacotgαcos ) β δβ = 0
⇔ aQsinβ - Pacotgαcosβ = 0 ⇔ Q = P.cotg .cotg α . β
Ví duï 13.12. Cô caáu goàm hai daàm lieân keát vaø chòu löïc nhö H.13.12a.
Bieát AI = IB = BH = HC = a. Xaùc ñònh phaûn löïc taïi A, C. F F 2 F F2 A B H o 30 A B δϕ C C I I H m m RC a) b) Hình 13.12
Giaûi. Baøi toaùn yeâu caàu tính thaønh phaàn phaûn löïc naøo chuùng ta thay theá lieân keát
töông öùng vôùi thaønh phaàn ñoù vaø söû duïng ñieàu kieän caân baèng cuûa nguyeân lyù DCKD. - Tính RC
Xeùt cô caáu caân baèng sau khi thay khôùp taïi C baèng RC . Cho cô caáu moät
DCKD töø vò trí caân baèng (daàm AB coá ñònh, daàm BC chæ coù theå quay quanh B)
BC quay moät goùc δϕ quanh B nhö H.13.12b. ⇒ Aa δ ∑ k = A δ (F1)+ A δ (m) + A δ (F2)+ A δ (RC) = 0 ⇔ Aa δ
∑ k = 0 − mδϕ − F sin30o 2 a . δϕ + RC. a 2 δϕ = 0 ⎛ F a . ⇔ − m 2 − + aR 2 ⎞ ⎜ C . ⎟ δϕ = 0 { ∀ } δϕ ⎝ 2 ⎠ F a . ⇒ −m 2 − + aR 2 = 0 C 2 m F ⇒ R 2 C = + a 2 4 -
Tính ngaãu phaûn löïc (MA) taïi A 157
Xeùt caân baèng cuûa cô caáu sau khi thay lieân keát ngaøm taïi A bôûi baûn leà vaø
ngaãu caûn MA. Cho cô caáu moät DCKD töø vò trí ñang xeùt nhö H.13.2c: AB quay goùc δψ. ⇒ ∑ Aa δ k = A δ (MA ) + A δ F ( 1) + A δ ( ) m + A δ F ( 2) = 0 ⇔ M .δψ − F a . δψ + . m δψ − F sin 30o a . .δψ = 0 A 1 2 a ⇔ (M − F a . + m − F . ).δψ = 0 { ∀ δψ} A 1 2 2 a a ⇔ M − a F . + m − F . = 0 ⇒ M = F 2 ( + F ) − m A 1 2 2 A 2 1 2 RAy F1 F F 2 1 M F2 A RAx I 30o A I B H C B H C M m A MA c) d) Hình 13.12 - Tính RAy
Xeùt caân baèng cuûa cô caáu sau khi thay theá ngaøm taïi A: ⇔ (M , R A Ax , R Ay )
Cho cô caáu moät DCKD töø vò trí caân baèng nhö H.13.12d. (BC coá ñònh, AB quay quanh B goùc δθ). ⇒ Aa δ ∑ k = A δ (MA ) + A δ (RA ) + A δ (R y A ) + A δ F ( 1) + A δ ) m ( + A δ F ( 2) = 0 x ⇔ M .δθ − R a 2 . δθ + 0 + F a . δθ + 0 + 0 = 0 A A y 1 ⇔ (MA − aR 2 A + aF y 1).δθ = 0 ⇒ MA − aR 2 A + aF y 1 = 0 F1 MA F2 m ⇒ RA = + = F y + − 2 a 2 1 4 a 2 - Tính RAx R
Cho cô caáu ôû H.13.12d, thöïc A F1 M F2
hieän DCKD töø vò trí caân baèng tònh tieán A RAx 30o δx
theo phöông ngang löôïng δx > 0 I B H C (H.13.12e). MA Hình 13.12e ⇒ ∑ Aa δ = A δ (M ) + A δ (R k A A ) + A δ (R + δ + δ + δ = x A ) A F ( 1) A F ( 2) A( ) m 0 y 158 ⇔ 0 + R . x δ + 0 + 0 − F . cos 30o. x δ + 0 = 0 Ax 2 ⇔ (R − F . cos 30o ). x δ = 0 { ∀ x} A δ x 2 o 3
⇒ RAx − F2. cos 30 = 0 ⇒ RAx = F2. 2
Ví duï 13.13. Heä hai giaøn I vaø II noái nhau baèng baûn leà D vaø coù lieân keát vôùi giaù
nhö H.13.13a. Tìm phaûn löïc töïa taïi B. C1 a P C K D a P 2 A B D A K B I E H II I E II H RB a) b) Hình 13.13
Giaûi. Thay theá goái B bôûi phaûn löïc töïa RB , caùc giaøn I vaø II chæ coù khaû naêng chuyeån ñoäng phaúng.
Cho cô heä DCKD: nuùt B dòch chuyeån theo chieàu (phaùp tuyeán maët töïa)
löôïng δsB, nuùt H chæ coù theå quay quanh C. Suy ra giaøn II thöïc hieän DCKD quay
töùc thôøi quanh taâm VTTT C2 goùc δϕ2 theo chieàu kim ñoàng hoà. Töông öùng giaøn I
quay töùc thôøi quanh taâm töùc thôøi C1 goùc δϕ1 theo chieàu ngöôïc chieàu kim ñoàng hoà (H.13.13b). Lieân heä giöõa δϕ1 vaø δϕ2 qua nuùt D. ⇒ DC2.δϕ2 = 1 DC .δ 1 ϕ
Tính dòch chuyeån thaúng ñöùng δ δϕ 1 cuûa ñieåm K trong 1 DCKD ôû treân H.13.13c: δ1 α α a A δ a K 1 = CK. 1 δϕ .cos α = CK. 1 δϕ . CK DC P 2 = a. 1 δϕ = a. .δϕ2 Hình 13.13c 1 DC AÙp duïng: Aa δ ∑ k = A δ ) P ( + A δ (RB) = 0 DC ⇔ − . P δ1 + RB C . 2 . B δϕ = 0 ⇔ (− a . P . 2 2 + RB C . 2 ). B δϕ2 = 0 { ∀ δϕ2} DC1 DC2 a DC ⇒ − . aP + R C . B = 0 ⇒ R = P . 2 C (ñaët B = ) b DC B 2 B b DC 2 1 1 159 Chöông 14
PHÖÔNG TRÌNH TOÅNG QUAÙT ÑOÄNG LÖÏC
HOÏC VAØ PHÖÔNG TRÌNH LAGRANGE II Noäi dung
Ñöa ra hai phöông phaùp thieát laäp phöông trình vi phaân chuyeån ñoäng cuûa
caùc cô heä khoâng töï do. Yeâu caàu
- Bieát caùch thieát laäp phöông trình vi phaân chuyeån ñoäng cuûa caùc cô heä
- Tích phaân hoaëc tìm ñöôïc moät soá tích phaân ñaàu cuûa caùc daïng phöông
trình vi phaân chuyeån ñoäng ñôn giaûn.
14.1. PHÖÔNG TRÌNH TOÅNG QUAÙT CUÛA ÑOÄNG LÖÏC HOÏC
1. Thieát laäp phöông trình toång quaùt cuûa ñoäng löïc hoïc
Xeùt chaát ñieåm Mk cuûa cô heä chòu lieân keát giöõ, döøng, hình hoïc vaø lyù töôûng,
caùc löïc thöïc taùc duïng leân Mk: - Löïc hoaït ñoäng Fk
- Phaûn löïc lieân keát Rk
Neáu chuùng ta theâm löïc quaùn tính: qt Fk = −mk Wk
ta seõ coù heä löïc caân baèng: F ( k, Rk, Fqt k ) ≡ 0 (D’Alembert)
⇔ Fk + Rk + Fqtk = 0 (14.1)
cho cô heä moät di chuyeån khaû dó tuøy yù { k rr
δ }, nhaân hai veá cuûa (14.1) vôùi k rr δ : qt ⇔ F r r r k r δ k + Rk r δ k + Fk r δ k = 0 Laáy toång theo k: N N N qt ⇒ ∑F r r r kδr + k ∑Rkδr + k ∑Fk δr = k 0 k=1 k=1 k=1 N qt ⇔ ∑⎛ ⎞ ⎜F r k + Fk ⎟δr = 0 (14.2) ⎝ ⎠ k k=1 N ( ∑ R r kδr = k
0 do lieân keát lyù töôûng) k=1 160 N ⇔ ∑ (F r k − mkWk) δ r = k 0 (14.3) k=1 N ⇔ ∑ ([F − xk mkx&k ) δ x + k (F − ky mkx& )δ y + & (14.4) k k (F − kz mkzk ) δ zk ] = 0 k=1
Phöông trình (14.3) hoaëc (14.4) ñöôïc goïi laø phöông trình toång quaùt cuûa ñoäng löïc hoïc.
Tröôøng hôïp cô heä bao goàm caùc vaät raén, chuùng ta thay heä löïc quaùn tính
cuûa caùc chaát ñieåm baèng keát quaû thu goïn cuûa chuùng treân töøng vaät raén. 2. AÙp duïng
Tröôùc heát bieåu dieãn caùc ñaïi löôïng gia toác caàn thieát treân hình veõ cuûa moâ
hình baøi toaùn, ñaët tröïc tieáp caùc löïc quaùn tính leân cô heä (neáu laø vaät raén thì ñaët löïc
quaùn tính thu goïn). Tieáp theo cho cô heä moät di chuyeån khaû dó ñeå laäp phöông
trình daïng (14.3) hay (14.4), töø ñoù giaûi ra caùc aån caàn thieát.
- Tröôøng hôïp cô heä moät baäc töï do moïi di chuyeån khaû dó cuûa caùc ñieåm ñaët
löïc (keå caû löïc quaùn tính) phaûi ñöôïc bieåu dieãn qua di chuyeån cuûa chæ moät tham
soá. Chuùng ta laäp ñöôïc moät phöông trình
- Tröôøng hôïp cô heä coù nhieàu baäc töï do (r baäc töï do), chuùng ta cho cô heä
thöïc hieän töông öùng (r) caùc di chuyeån khaû dó ñoäc laäp tuyeán tính ñeå laäp ñöôïc heä
(r) phöông trình, giaûi ra caùc aån cuûa baøi toaùn
Ví duï 14.1. Giaûi laïi baøi toaùn trong ví duï 12.15 chöông 12 baèng phöông trình toång quaùt ñoäng löïc hoïc.
Giaûi. Cô heä khaûo saùt goàm tay quay AOA vaø hai baùnh xe taâm A. Cô heä thoûa maõn
ñaày ñuû caùc ñieàu kieän ñeå aùp duïng phöông trình toång quaùt ñoäng löïc hoïc.
Giaû söû taïi thôøi ñieåm ñang xeùt tay quay AA coù vaän toác goùc ωo gia toác εo. τ n ⇒ coù A taâm : WA = WA + WA q t M qt R A vôùi: n 2 2 R Aτ qt An A W = (R + r)ωo = r 5 o ω τ A W = (R + r)εo = 5rεo A
Caùc thaønh phaàn löïc quaùn tính thu I M δϕ
goïn cuûa tay quay AA vaø caùc baùnh xe taâm A O ε o
A ñöôïc bieåu dieãn treân H.14.1. δϕo 2 B qt mr 25 I M qt 2 o = εo ; M = mρ ε qt 12 A A M δϕ o A Rqt = r 5 . m 2 ωo ; qt R = r 5 . m ε A An Aτ o qt
Cho cô heä moät di chuyeån khaû dó: tay qt R R Aτ An qt M Hình 14.1 quay AA quay goùc δϕ A o töông öùng caùc baùnh xe A seõ thöïc hieän: R + r δϕA = δβϕo = 5δϕo r vaø: s δ A = R ( + ) r δϕo = r
5 δϕo (laø di chuyeån cuûa A theo quyõ ñaïo). 161
Do toång coâng cuûa caùc troïng löïc vaø caùc qt R
ôû ñaây baèng khoâng treân moïi di An chuyeån: qt ⇒ A ⎛ ⎞ δ Σ k + A δ Σ k = δ ( A ) M + A δ ( qto M ) + 2 A δ ( qtA M ) qt + 2 A δ ⎜R τ ⎟ = 0 A ⎝ ⎠ ⎛ 25 2 2 ⇔ M − mr ⎞ ⎜ o ε − m 2 ρ 25 . o ε − r 5 . m 2 o ε r 5 . o δϕ ⎟ = 0 ⎝ 12 ⎠ 2 2 25 2 o ⇔ M − m 50 ρ o ε − mr 50 o ε − mr ε = 0 12 M 12 ⇔ o ε = ( 2 2 m r 625 + 600ρ )
Ví duï 14.2. Xem laïi moâ hình baøi toaùn ôû ví qt B M duï 12.12.
Giaûi: - Cô heä khaûo saùt goàm taûi A, con laên εB M
taâm B, daây meàm vaø roøng roïc C, thoûa maõn B qt
caùc ñieàu kieän cuûa phöông trình toång quaùt B W B R ñoäng löïc hoïc. I
- Caùc löïc hoaït ñoäng: C H P r r B P A = m P ; g B = m g 1 2 ; ngaãu M - Caùc löïc quaùn tính: qt RA
Giaû söû vaøo thôøi ñieåm ñang xeùt taûi A A
ñi xuoáng ñaït gia toác WA , con laên taâm B
laên khoâng tröôït ñaït A P WB , seõ coù lieân heä: Hình 14.2 B W A W A W εB = = = ⇒ A W = B W r R − r r
Caùc löïc quaùn tính thu goïn cuûa caùc vaät raén töông öùng: qt R = m W A 1 A qt R = m W = m W B 2 B 2 A 2 qt M = J m2ρ WA B BεB = H.14.2) (xem r
- Cho cô heä moät di chuyeån khaû dó: taûi A ñi xuoáng ñoä dôøi thaúng ñöùng δh,
töông öùng taâm B di chuyeån ngang sang traùi ñoä dôøi: R − r δ x = δ h = h δ r vaø quay moät goùc: x δ h δ δϕ = = theo chieàu r r ⇒ Σ A δ + Σ A qt χδ = P . h δ − Mδϕ − Rqt . h δ − Rqt . x δ − Mqt .δϕ = 0 k k A A B B 2 ⎛ M m ⇔ P − − m W − m W 2ρ − W ⎞ ⎜ ⎟ h δ 0 A = ⎝ r 1 A 2 A r2 A ⎠ 162 2 ⎛ M ⎞ ⎛ 2 m ρ ⎞ ⇔ ⎜ A P − ⎟ − ⎜ 1 m + 2 m + ⎟W = 0 2 A ⎝ r ⎠ ⎝ r ⎠ M 1 m g − r ⇔ A W = 2 ρ 1 m + 2 m + 2 m 2 r
Chuù yù: Caùc baøi toaùn coù con laên laên khoâng tröôït luoân toàn taïi löïc ma saùt taùc
ñoäng vaøo con laên taïi ñieåm tieáp xuùc, nhöng löïc ma saùt naøy khoâng sinh coâng treân
moïi di chuyeån khaû dó cuûa con laên (khoâng tröôït) neân lieân keát naøy thuoäc loaïi lieân keát lyù töôûng.
Ví duï 14.3. Xem laïi moâ hình baøi toaùn ôû
ví duï 11.6 (chöông 11). ÔÛ ñaây chæ yeâu caàu tìm WA vaø WB .
Giaûi. Heä coù hai baäc töï do thoûa maõn caùc
ñieàu kieän cuûa phöông trình toång quaùt ñoäng löïc hoïc.
- Caùc löïc hoaït ñoäng taùc duïng vaøo cô heä: PA P , B , ngaãu M
- Caùc löïc quaùn tính thu goïn: Hình 14.3
Giaû söû taïi thôøi ñieåm ñang xeùt chuùng ta coù:
+ Gia toác cuûa laêng truï A laø WA
+ Gia toác töông ñoái cuûa taâm B ñoái vôùi laêng truï A laø: r WB r WB = WA + WB
Caùc löïc quaùn tính thu goïn nhaän ñöôïc: qt F qt qt r = m W F ; = m W F ; = m W A 1 A e 2 A r 2 B 2 r qt M 2 m R B W 2 m R r = . = W B B 2 R 2 ôû ñaây: qt qt FB qt = Fe + Fr
Cho cô heä moät di chuyeån khaû dó ñaëc bieät: laêng truï A di chuyeån ngang δx,
truï taâm B coá ñònh töông ñoái treân A. ⇒ Σ A δ k + Σ Aqt δ = Fqt − . x δ − Fqt k A e . x δ − Fqt r . cos . α x δ = 0 ⇔ (m W + m W + m Wr cos 1 A 2 A 2 B α) x δ = 0 ⇔ (m + m 1 2 )w + m cos α W . r = 0 A 2 B (*)
Cho cô heä moät di chuyeån khaû dó ñaëc bieät khaùc: laêng truï A coá ñònh, truï taâm
B laên khoâng tröôït treân maët phaúng nghieâng ñoä dôøi δs. qt M qt qt qt s ⇒ A δ δ Σ k + A δ Σ k = s δ + PB sin . α s δ − Fe cos . α s δ − Fr . s δ − MB = 0 R R 163 M m 3 ⇔ + m2g sin α − m2 cos α W . 2 A − WrB = 0 (**) R 2 Giaûi heä (*), (**): ⎛ M ⎞ ⎛ M 2⎜ + m ⎞ 2g sin α⎟ cos α ( 2 m1 + m2)⎜ + m2g sin α⎟ ⎝ R ⎠ r ⎝ R ⎠ A W = − W ; = 2 B m 2 2 sin α + m2 + m 3 1 m2( 2 m 2 1 sin α + m2 + m 3 1) Nhaän xeùt:
- WA < 0: laêng truï A luoân chuyeån ñoäng theo chieàu ngöôïc laïi
- Sau khi giaûi ñöôïc caùc ñaëc tröng ñoäng hoïc, muoán xaùc ñònh caùc phaûn löïc
chuùng ta chæ caàn aùp duïng phöông phaùp tónh ñoäng löïc hình hoïc cho töøng vaät raén
chuyeån ñoäng (nguyeân lyù D’Alembert).
14.2. PHÖÔNG TRÌNH LAGRANGE II
1. Thieát laäp phöông trình Lagrange II
Xeùt cô heä thoûa maõn caùc ñieàu kieän cuûa muïc 14.1. Bieåu dieãn phöông trình
toång quaùt ñoäng löïc hoïc daïng (14.3) cuûa cô heä qua heä toïa ñoä suy roäng ñuû {qi}: N N ⇔ ∑ m r k Wk δδ . k r = ∑ F r k δ . k r k=1 k=1 N r ⇔ ∑ m r k Wk δ . k r = ∑ Q δ i. qi (14.5) k=1 i=1
vôùi: r - laø soá toïa ñoä suy roäng ñoäc laäp ñuû, chính baèng soá baäc töï do cuûa cô heä. N
Chuùng ta seõ bieåu dieãn ∑ m r k Wkδ k r qua toïa ñoä suy roäng: k=1 N N r r r N r r ∂ ⎛ ∂r ⎞ k r m k k Wkδ ∑ k r = m ∑ kWk q δ ∑ i = ∑ ⎜⎜ ∑ mk Wk δ . q (14.6) q ∂ ⎟⎟ ∂ i q k=1 k=1 i=1 i i=1 ⎝ k=1 i ⎠ N r N r tính: ∂ k r dVk ∂r mk Wk = k m = ∑ ∑ ∂ k q dt ∂q k=1 i k =1 i N r N d r ∑ ∂r d r = k mk Vk − ∑ ⎛ ∂ k ⎞ mk Vk ⎜ ⎟ (14.7) dt ∂q dt ∂q k =1 i k=1 ⎝ i ⎠ r r tính: ∂ k r d ⎛ ∂ k r ⎞ ; ⎜ ⎟ ∂qi dt ⎝ ∂qi ⎠ do: rkr r ≡ k r (t, q1, q2, …, qr) r r r r r d k r ∂ k r ∂ k r ∂ k r ∂V k ⇒ V k = = q ∑ & j + ⇒ = (14.8) dt q ∂ t ∂ q ∂ q ∂ j=1 j i & i r d ⎛ ∂ r k r ⎞ ∂ ⎛ k r d ⎞ ∂Vk ⎜ ⎟ = ⎜ ⎟ = (14.9) dt ⎝ q ∂ i ⎠ q ∂ i ⎝ dt ⎠ q ∂ i
Thay keát quaû ôû (14.8) vaøo (14.7) chuùng ta nhaän ñöôïc: 164 N r N 2 N 2 ∑ ∂ k r d m V m V m d T ∂ T ∂ k Wk = ∑ ∂ ⎛ ⎞ k k − k k ⎜⎜ ⎟⎟ ∑ ∂ ⎛ ⎞ ⎜⎜ ⎟⎟ = − (14.10) ∂q dt ∂q& 2 ∂q 2 dt q ∂& ∂ k=1 i k=1 i ⎝ ⎠ k=1 i ⎝ ⎠ i qi N ôû ñaây: 1 T = ∑ 2 mkVk 2 k =1
Söû duïng (14.6) sau ñoù thay vaøo (14.5): r r d T T ⇒ ∑⎛ ∂ ∂ ⎞ − δq = ⎜⎜ ⎟⎟ Q q (14.11) dt ∂q& ∂ i ∑ δi i q i=1 ⎝ i i ⎠ i=1 Do caùc
δqi ñoäc laäp tuyeán tính: d T ∂ T ) 11 . 14 ( ∂ ⇔ − = Qi ( i = r .. 1 ) (14.12) dt q ∂& i q ∂ i
Heä caùc phöông trình (14.12) ñöôïc goïi laø caùc phöông trình Lagrange II.
Tröôøng hôïp caùc löïc hoaït ñoäng laø löïc theá, goïi haøm theá laø: Π = Π(q1,q2, …, qr) d ⎛ T ∂ ⎞ T ⇒ ) 12 . 14 ( ∂ Π ∂ ⇔ − = − (i = 1..r) dt ⎜⎜ q ⎟⎟ ⎝ ∂& i q ∂ ⎠ i q ∂ i d ⎛ T ∂ Π ∂ ⎞ ⎛ T ∂ Π ∂ ⎞ ⇔ − − − = 0 dt ⎜⎜ q ∂& q ⎟⎟ ⎜⎜ ∂& q ∂ q ⎟⎟ ⎝ i i ⎠ ⎝ i ∂ i ⎠ d ⎛ L ∂ ⎞ ⎛ L ∂ ⎞ ⇔ − = 0 (i = 1..r) (14.13) dt ⎜⎜ q ⎟⎟ ⎜⎜ ∂& q ⎟⎟ ⎝ i ⎠ ⎝ ∂ i ⎠ do: Π ∂
= 0 ; haøm: L = T – Π - ñöôïc goïi laø haøm Lagrange. q ∂& i
2. Phöông phaùp aùp duïng
Caùc phöông trình Lagrange II coù theå aùp duïng ñeå khaûo saùt chuyeån ñoäng
cuûa moïi cô heä chòu lieân keát giöõ, döøng vaø hình hoïc.
Vaán ñeà chuû yeáu ôû ñaây laø phaûi thieát laäp ñöôïc phöông trình Lagrange II cho
cô heä, chuùng ta caàn thöïc hieän theo caùc böôùc sau ñaây:
1) Xaùc ñònh soá baäc töï do vaø heä toïa ñoä ñuû cuûa cô heä {qi}
2) Tröôøng hôïp chòu lieân keát lyù töôûng, haõy bieåu dieãn taát caû caùc löïc hoaït
ñoäng taùc duïng leân heä
Tröôøng hôïp toàn taïi caùc lieân keát khoâng lyù töôûng, chuùng ta vaãn xem heä
thuoäc loaïi lieân keát lyù töôûng neáu coi caùc thaønh phaàn phaûn löïc cuûa caùc lieân keát
khoâng lyù töôûng nhö nhöõng löïc hoaït ñoäng
3) Tính caùc löïc suy roäng Qi. Ñeå traùnh sai laàm chuùng ta neân cho cô heä thöïc
hieän di chuyeån khaû dó sao cho δqi > 0
4) Tính ñoäng naêng T cuûa cô heä trong chuyeån ñoäng thöïc cuûa noù vaø bieåu
dieãn qua caùc toïa ñoä suy roäng qi, q&i
5) Thay theá caùc ñaïi löôïng vöøa tính ñöôïc vaøo heä (14.12)
Tröôøng hôïp caùc löïc hoaït ñoäng coù theá, chuùng ta tính Qi qua haøm theá Π =
Π(q1, q2, …, qr) vaø aùp duïng caùc phöông trình daïng (14.13). 165
Ví duï 14.4. Xem laïi moâ hình baøi toaùn ôû ví duï 12.15 chöông 12.
Giaûi. 1) Cô heä coù moät baäc töï do, choïn toïa ñoä suy roäng q1 = ϕ1 (goùc quay cuûa tay quay AOA)
2) ÔÛ ñaây cô heä chòu lieân keát lyù töôûng, caùc löïc hoaït ñoäng ñaët vaøo cô heä:
- Caùc troïng löïc PA cuûa hai baùnh xe taâm A
- Troïng löïc Po cuûa tay quay AOA
- Ngaãu M ñaët vaøo tay quay
3) Tính löïc suy roäng: Q = Q 1 o ϕ
Cho cô heä moät di chuyeån khaû dó:
tay quay quay moät goùc δϕo theo chieàu döông (H.14.4). ⇒ A δ Σ k = Mδϕo
(do caùc troïng löïc coù toång coâng baèng
khoâng treân moïi di chuyeån khaû dó) ⇒ Q1 = M
4) Tính ñoäng naêng T qua ϕo, ωo:
Giaû söû taïi thôøi ñieåm ñang xeùt tay quay ñaït vaän toác ωo, chuùng ta coù ngay: 2 2 2 2 2 2 mo( R 2 + r 2 ) o ω ⎛ A mV mρ 2 ⎞ r 625 + 600ρ 2 ⇒ T = . + 2⎜⎜ + ωA = mϕ ⎟⎟ & o 12 2 ⎝ 2 2 ⎠ 24 Tính caùc ñaïo haøm: 2 2 T ∂ T ∂ r 625 + 600ρ = = mϕ&o q ∂&1 ϕ ∂& o 12 2 2 d ⎛ T ∂ ⎞ r 625 + 600 ρ ⇒ ⎜ ⎟ = mϕ&o dt ⎝ q ∂&1 ⎠ 12 T ∂ = 0 q ∂ 1
5) AÙp duïng phöông trình (14.12) laäp phöông trình Lagrange II: 2 2 r 625 + 600ρ M 12
mϕ&o = M ⇒ εo = ϕ&o = 2 2 12 r 625 + 600ρ
Ví duï 14.5. Xem laïi moâ hình baøi toaùn ôû ví duï 12.13 chöông 12.
Giaûi. 1) Cô heä moät baäc töï do, choïn heä toïa ñoä suy roäng q1 = h (laø ñoä dôøi thaúng
ñöùng höôùng xuoáng cuûa taûi A).
2) Cô heä chòu lieân keát lyù töôûng, caùc löïc hoaït ñoäng goàm coù: - Ngaãu M - Caùc troïng löïc PA, PB
- Troïng löïc P3 cuûa daây (khoâng bieåu dieãn treân H.14.5) 166 3) Tính
Q1: cho cô heä moät di chuyeån khaû dó töø moät vò trí tuøy yù xaùc ñònh
(luùc naøy A coù ñoä dôøi h): taûi A ñi xuoáng ñoä dôøi δh, con laên B quay moät goùc töông öùng: x δ B h δ δϕ = = R R ⇒ Σ A δ k = A δ (M) + A δ (P1) + A δ (P2 ) + A δ (P3)
Xem ví duï 12.13 chöông 12 vôùi chuù yù trong caùc bieåu thöùc tính coâng chuùng
ta thay theá h bôûi δh, ho bôûi ho + h. ⇒ A δ ( ) M M = − δ ; h A δ (P1 ) = m1gδ ; h A δ (P2 ) = 0 R 2 2 ⎧ + + δ + ⎫ A δ (P3) ([ho h) ] h (ho h) m3g = m g 3 ⎨ − ⎬ = (.h + h o ) h δ L 2 L 2 L ⎩ ⎭
ñaõ boû qua voâ cuøng beù baäc hai cuûa δh. ⎡ M m3g ⇒ Σ A δ = − + m g ⎤ k ⎢ 1 + (h + h o ) h δ ⎥ ⎣ R L ⎦ m g ⇒ Q = m g 3 1 1 + (ho + ) M h − L R 4) Tính ñoäng naêng T: m 2 1 + m 3 2 + m 2 3 2 T = + + = & A T B T daây T h 4
5) Laäp phöông trình Lagrange II: m 2 + m 3 + m 2 m g 1 2 3 h& = Q = m g 3 1 1 + (ho + ) M h − 4 L R giaûi ñöôïc: 2 ⎡ m3g W = h& = m g + A 1 (h + h o ) M⎤ ⎢ − ⎥ m 2 + 1 m 3 + 2 m 2 3 ⎣ L R ⎦
Chuù yù: Trong baøi naøy chuùng ta coù theå tính löïc suy roäng Q1 töø haøm theá
naêng cuûa caùc löïc theá. Caùc troïng löïc P1, P2, P3 ñaàu laø caùc löïc theá.
Laáy goác O1 cuûa truïc h laøm goác tính theá naêng: 167 Π = Π(P1 )+ Π(P2 )+ ΠP3 + = −P1(h + h) P + 0 3 o + (h + h o ) ho h = −m g 1 (h + h o ) m3g − (h + h o )2 L 2 L 2
Löïc suy roäng Q1 laø toång cuûa hai thaønh phaàn: löïc suy roäng Q1(Π) do caùc löïc
theá sinh ra vaø löïc suy roäng Q1(M) do löïc khoâng theá (ngaãu M) sinh ra. Deã daøng tính ñöôïc: Q Π ∂ 1 (Π) m g = − = m g 3 1 + (ho + h) h ∂ L Q2( ) M M = − R m g ⇒ Q = m g 3 1 1 + (ho + ) M h − L R
Ví duï 14.6. Xem laïi moâ hình baøi toaùn ôû ví duï 11.6 chöông 11.
Giaûi. 1) Cô heä coù hai baäc töï do, choïn heä toïa ñoä ñuû: -
q1 = x - ñoä dôøi cuûa laêng truï A theo höôùng ngang -
q2 = s - ñoä dôøi töông ñoái cuûa taâm
B ñoái vôùi laêng truï A
2) Caùc löïc hoaït ñoäng taùc duïng leân heä: PA, PB , ngaãu M
3) Tính caùc löïc suy roäng Q1, Q2
- Tính Q1: cho cô heä di chuyeån khaû dó ñaëc bieät: q δ 1 = x δ > ; 0 q δ 2 = s δ = 0
(B gaén chaët vaøo laêng truï A). ⇒ A δ Σ k = A δ (PA ) + A δ (PB ) + A
δ (M) = 0 + 0 + 0 = 0 ⇒ Q1 = 0
- Tính Q2: cho cô heä di chuyeån khaû dó ñaëc bieät: q δ 1 = x δ = ; 0 q δ 2 = s δ > 0
(laêng truï A coá ñònh, con laên B laên khoâng tröôït treân laêng truï A): ⇒ Σ A δ k = A δ (PA ) + A δ (PB) + A δ (M) = s ∂ ⎛ M = 0 + P ⎞ Bδ . s sin α + M = ⎜m2g sin α + ⎟ s δ R ⎝ R ⎠ M ⇒ Q 2 = m2g sin α + R
4) Tính ñoäng naêng T: giaû söû taïi thôøi ñieåm ñang xeùt laêng truï A ñaït vaän toác V s A = x
& . Con laên B chuyeån ñoäng song phaúng coù vaän toác goùc: ω = ϕ&B = R
taâm B chuyeån ñoäng hôïp coù: e r VB = VB + VB trong ñoù: V e = V ; V r = s B A B & 168 1 2 1 2 1
⇒ T = T + T = m V + J ω + m2V 2 A B 2 1 A 2 B 2 B 1 2 1 2 2 1 2 2 e r
= m V + m R ω + m ⎛⎜V e + V r + 2V ⎞ 1 A 2 2 B B B V . ⎟ 2 4 2 B ⎝ ⎠ 1 2 1 s2 2 & 1 = m1x& + m2R + m (x2 2 & + s2 & + 2& &. s . x cos α) 2 4 R2 2 m + m 1 2 2 3 = x& + m s2 & + m cos α & s . x . & 2 4 2 2 5) Tính caùc ñaïo haøm: T ∂ T ∂ T ∂ T = = ; 0 ∂ = = 0 q ∂ x ∂ q ∂ s 1 2 ∂ T ∂ T ∂ = = (m + m 1 2 )x & + m cos α s .& q ∂& x 2 1 ∂& T ∂ T ∂ 3 = = m s& + m cos α x .& q ∂& s ∂& 2 2 2 2
AÙp duïng phöông trình (14.12): ⎧ ( m + m 1 2 )x& + m cos α s .& = 0 2 ⎪ ⎨ 3 M ⎪ m cos α x
. & + m s& = m g sin α + ⎩ 2 2 2 2 R
Giaûi heä phöông trình hai aån x& vaø s&& chuùng ta nhaän ñöôïc keát quaû nhö cuõ.
Ví duï 14.7. Con laéc Eliptic coù con chaïy A khoái löôïng m1; taûi B khoái löôïng m2;
thanh AB daøi l boû qua troïng löôïng. y
Xem ma saùt laø khoâng ñaùng keå, haõy laäp VA
phöông trình chuyeån ñoäng cuûa con laéc. A y
Giaûi. 1) Cô heä laø con laéc coù hai baäc töï do,
choïn heä toïa ñoä ñuû q P 1 = y; q2 = ϕ (H.14.7) A
2) Caùc löïc hoaït ñoäng: caùc troïng löïc ϕ r P V r B A , PB VB
3) Tính caùc löïc suy roäng Q1, Q2 B Do P Hình 14.7
A , PB laø caùc löïc theá.
Choïn goác theá naêng laø troïng taâm cuûa A, PB
chuùng ta coù: Π = – lPBcosϕ ⇒ Q Π ∂ Π ∂ = − = − 0 1 = q ∂ 1 y ∂ Π ∂ Π ∂ Q = − = − = 2 –lP ∂q ϕ ∂ Bsinϕ 2
4) Tính ñoäng naêng : T = TA +TB
Caùc quan heä ñoäng hoïc : VA = y&
Quaû naëng B chuyeån ñoäng hôïp coù: e r V B = V B + V Bv 169 trong ñoù: e V r B = V = A & V ; y = ϕ . AB B & = l ϕ .& (xem H.14.7). 1 2 1 A T 2 = m1VA = m1y& 2 2 1 2 1 ⎛ 2 2 e e r r ⎞ B T = m V = 2 B m2⎜V + V + B B 2V B V . B ⎟ = 2 2 ⎝ ⎠ 1 = 2 m (& + 2 2 y
l2 &ϕ + 2y& .l &. y cos ) ϕ 2 2 m 1 + m 2 1 ⇒ T = + m 2 2 l2 y&
+ m y&. l ϕ&. cos ϕ 2 2 2 5) Tính caùc ñaïo haøm: T ∂ T ∂ = = 0 ; ∂T ∂ = T = −m l sin ϕ 2 & ϕ . y . & q ∂ 1 y ∂ ∂q ϕ ∂ 2 T ∂ T ∂ = = (m1 + m2)y& + m2l cos . ϕ &ϕ q ∂& y ∂ 1 & T ∂ T ∂ = = m l2 &ϕ + m l cos ϕ y .& q 2 2 ∂& 2 &ϕ ∂
Töø caùc heä thöùc treân thieát laäp ñöôïc heä phöông trình vi phaân chuyeån ñoäng: (m + m 1 2 )y& + m l cos . ϕ ϕ& − m l 2 ϕ& sin ϕ = 0 2 2 m l2ϕ& + m l cos ϕ y . & − m l sin ϕ ϕ .& y& + m l sin ϕ y .&ϕ& = −m gl sin ϕ 2 2 2 2 2 (⎪⎧m + 1 m2 )y& + m2l cos ϕ ϕ . & − m2l sin ϕ ϕ . 2 & = 0 ⇔ ⎨ ⎪⎩cos ϕ y . & + l ϕ ϕ & + g sin ϕ = 0 M
Ví duï 14.8. Heä ñieàu tieát ly taâm coù moâ hình nhö B A 1 H.14.8.
Hai quaû vaêng khoái löôïng m ϕ 1, taûi E khoái löôïng m F F 2 B B 1 AB = BC = 1; CC1 = AA1 = 2a
Ban ñaàu khi AB thaúng ñöùng, loø xo BB1 (coù P1
ñoä cöùng k) khoâng giaõn; truïc quay chòu taùc ñoäng P P 1 1 C1 E C
cuûa ngaãu M khoâng ñoåi; boû qua ma saùt ôû caùc oå
truïc. Laäp phöông trình chuyeån ñoäng cuûa cô heä. Hình 14.8
Giaûi. 1) Cô heä coù hai baäc töï do, choïn heä toïa ñoä suy roäng ñuû:
− q1 ≡ θ laø goùc quay cuûa truïc ñöùng laáy chieàu döông cuøng chieàu cuûa ngaãu M
− q2 ≡ ϕ laø goùc quay töông ñoái cuûa AB quanh truïc baûn leà ñoäng qua ñieåm A. 170
2) Caùc löïc hoaït ñoäng: − Ngaãu M − Caùc troïng löïc: P r r 1 = m ; g P 1 2 = m g 2
− Caùc löïc ñaøn hoài F cuûa loø xo ñaët vaøo caùc quaû vaêng B vaø B1 ñöôïc tính nhö sau:
Khi AB thaúng ñöùng, loø xo khoâng daõn. Taïi vò trí tuøy yù xaùc ñònh töông öùng
goùc quay ϕ, loø xo coù ñoä giaõn daøi Δ = 2lsinϕ ⇒ F = 2klsinϕ vaø phöông chieàu nhö hình veõ.
3) Tính caùc löïc suy roäng: trong caùc löïc hoaït ñoäng chæ coù ngaãu M laø loaïi
löïc khoâng coù theá, ta seõ tính caùc Qi baèng toång caùc Qi töông öùng bôûi löïc khoâng theá
Q 1i vaø caùc löïc coù theá Qi2 : ⇒ Qi = Q 1i + Qi2
Vôùi löïc khoâng theá, ngaãu M, khi cho cô heä thöïc hieän caùc di chuyeån khaû dó
ñaëc bieät (δθ > 0; δϕ = 0) vaø (δθ = 0; δ ϕ > 0) chuùng ta deã daøng tính ñöôïc: Q11 = M ; Q21 = 0 Vôùi caùc löïc theá ( 1 P 1 P , P , F , F ,
2 ) chuùng ta xaây döïng haøm theá Π (laáy goác
tính teá naêng töông öùng vò trí ban ñaàu cuûa cô heä khi thanh AB thaúng ñöùng):
Π = 2Π(P1) + Π(P2) + 2Π(F) 2 P 2 l 1 ( cos ) P l 2 . 1 ( cos ) k 2 (l sin ) const = − ϕ + − ϕ + ϕ + 1 2 = gl 2 (m + m )(l − cos ϕ) + 2 2 kl 2 sin ϕ 1 2 ⇒ Q Π ∂ Π ∂ 12 = − = − = 0 q ∂ 1 θ ∂ Q Π ∂ Π ∂ 2 22 = − = − = − m ( gl 2 + m ) sin ϕ − kl 2 sin ϕ 2 ∂q ϕ ∂ 1 2 2 ⇒ Q1 = M Q 2 2 = − kl 2 sin ϕ 2 − m ( gl 2 + m ) sin ϕ 1 2
4) Tính ñoäng naêng T: taïi vò trí tuøy yù 1 2 1 2 T = B T 2 + E T = . 2 m1 B V + m2 E V 2 2
Tính VB: do B chuyeån ñoäng hôïp neân e r V B V B
= V B (heä ñoäng laø khung quay ABB1A1). e
VB - laø vaän toác quay xung quanh truïc quay, höôùng vuoâng goùc maët phaúng
khung vaø coù ñoä lôùn: V e = a ( + l sin ϕ)θ& B 171 r
VB - laø vaän toác cuûa ñieåm B thuoäc thanh AB quay quanh truïc ñoäng qua A
coù höôùng vuoâng goùc thanh AB (töùc cuõng vuoâng goùc vôùi e VB ) vaø coù ñoä lôùn: V r = lϕ B & 2 e r 2 2 2 2 2 2 ⇒ V & B = V B = (V B + V B ) = a ( + lsin ) ϕ θ + l ϕ&
Tính VE: goïi toïa ñoä cuûa taûi E (theo phöông thaúng ñöùng vôùi chieàu döông
höôùng leân, goác truøng vôùi vò trí ban ñaàu) laø y. Chuùng ta coù ngay: y = l 2 − l 2 cos ϕ 2 2 2 2 ⇒ VE = y& = l 2 sin ϕ y .& ⇒ VE = 4l sin . ϕ ϕ& vaäy: T = m & 1 (a + l sin ϕ)2 2 2 2 2 2 2 θ + m1l ϕ& + m 2 2l sin . ϕ ϕ&
5) Tính caùc ñaïo haøm rieâng: Τ ∂ Τ ∂ = = 0 q ∂ 1 θ ∂ Τ ∂ Τ ∂ = = m 2 a ( + l sin ) ϕ l 2 cos .
ϕ ϕ& + 2m l2 sin ϕ 2 ∂q ϕ ∂ 1 2 2 Τ ∂ Τ ∂ = = m 2 a ( + l sin ϕ 2 ) θ& ∂q& ∂y 1 1 & Τ ∂ Τ ∂ = = m
2 1 l2 ϕ& + 4m l2 sin2 ϕ ϕ .& q ∂& 2 2 ϕ ∂&
Söû duïng caùc keát quaû nhaän ñöôïc ñöa vaøo phöông trình Lagrange II, ta coù: m 2 a ( l sin )l cos . 2 & m 2 l2 sin 2 . 2 − + ϕ ϕ θ − ϕ ϕ 1 2 & = − kl 2 2 sin ϕ 2 − m ( gl 2 + m ) sin ϕ 1 2
3. Caùc tích phaân ñaàu cuûa chuyeån ñoäng
Phöông trình Lagrange II cuûa cô heä thöôøng laø heä r phöông trình vi phaân
caáp hai phi tuyeán (r laø soá baäc töï do cuûa cô heä). Tích phaân heä naøy trong daïng kín
chæ ñaït ñöôïc moät soá ít caùc tröôøng hôïp. Tuy nhieân trong moät soá lôùp caùc cô heä
chuùng ta coù theå tìm thaáy caùc tích phaân ñaàu cuûa chuùng, töø ñoù phaùt hieän ra nhieàu
ñaëc tính quan troïng cuûa chuyeån ñoäng cuûa cô heä. Döôùi ñaây seõ trình baøy hai lôùp
cô heä laø caùc cô heä baûo toaøn chæ chòu taùc duïng cuûa caùc löïc hoaït ñoäng coù theá vaø
caùc cô heä coù toïa ñoä xycôlic.
1- Tích phaân naêng löôïng
Cô naêng E cuûa heä baûo toaøn. Do ñoäng naêng cuûa heä chæ laø haøm cuûa vaän toác,
phaûi laø ñaïo haøm baäc nhaát cuûa toïa ñoä suy roäng: T = T(qi, q&i ) 172
coøn theá naêng π chæ cuûa löïc theá laø haøm cuûa vò trí: π = π(qi)
⇒ E = π + T = const laø moät tích phaân ñaàu hay coøn goïi laø tích phaân naêng löôïng.
2- Tích phaân Xycôlic
Toïa ñoä Xycôlic: toïa ñoä qi ñöôïc goïi laø Xycôlic neáu: Τ ∂ = Q ; 0 = 0 (14.14) q i ∂ i
Chuùng ta nhaän thaáy phöông trình Lagrange II töông öùng toïa ñoä naøy coù daïng: d ⎛ Τ ∂ ⎞ = 0 Τ ∂ ⇒ = const (14.15) dt ⎜⎜ q ⎟⎟ ∂& q ⎝ i ∂ ⎠ & i
Ñaúng thöùc (14.15) laø moät tích phaân ñaàu cuûa heä, ñöôïc goïi laø tích phaân Xycôlic.
Cuõng ôû ví duï 14.7 chuùng ta coù q1 laø toïa ñoä Xycôlic, chuùng ta coù theâm moät tích phaân ñaàu Xycôlic: (m + m 1 2 )y& + m l cos . ϕ ϕ& = const 2 (14.16) 173 Chöông 15
LYÙ THUYEÁT VA CHAÏM Noäi dung
Xaây döïng phöông phaùp nghieân cöùu hieän töôïng ñoäng löïc ñaëc bieät (va chaïm). Yeâu caàu
- Naém vöõng caùc ñaëc ñieåm cuûa va chaïm, caùc ñònh lyù ñöôïc aùp duïng trong va chaïm.
- Giaûi ñöôïc caùc ñaïi löôïng ñoäng hoïc caàn thieát trong caùc tröôøng hôïp va chaïm ñaëc bieät.
15.1. ÑÒNH NGHÓA, ÑAËC ÑIEÅM CUÛA HIEÄN TÖÔÏNG VA CHAÏM VAØ CAÙC
GIAÛ THIEÁT CUÛA LYÙ THUYEÁT VA CHAÏM 1. Ñònh nghóa
Va chaïm laø moät tröôøng hôïp ñaëc bieät cuûa chuyeån ñoäng cô hoïc, trong ñoù
vaän toác cuûa caùc chaát ñieåm cuûa cô heä bieán ñoåi höõu haïn veà ñoä lôùn vaø veà höôùng
trong khoaûng thôøi gian raát beù khoaûng 10–2s, 10–3s,... khoaûng thôøi gian ñoù ñöôïc
goïi laø thôøi gian va chaïm vaø ñöôïc kyù hieäu bôûi τ.
Hieän töôïng va chaïm ñöôïc gaëp nhieàu laàn trong thöïc teá, nhö trong reøn, daäp,
ñoùng coïc, nghieàn vaät lieäu...
2. Caùc ñaëc ñieåm cuûa quaù trình va chaïm
1- Ñaëc ñieåm thöù nhaát
Quaù trình va chaïm xaûy ra trong khoaûng thôøi gian raát beù nhöng gaây ra söï
bieán ñoåi vaän toác höõu haïn, nghóa laø trong va chaïm vaän toác raát lôùn.
Nhö vaäy trong va chaïm xuaát hieän löïc raát lôùn, ñeå phaân bieät vôùi caùc löïc
thoâng thöôøng, ngöôøi ta goïi ñoù laø löïc va chaïm. Löïc va chaïm laø nhöõng löïc lieân keát
do keát quaû cuûa vieäc xuaát hieän hoaëc bieán maát ñoät ngoät cuûa caùc lieân keát. Löïc va
chaïm raát lôùn so vôùi caùc löïc thoâng thöôøng nhö troïng löïc, aùp löïc... Ñoù laø ñaëc ñieåm
thöù nhaát cuûa hieän töôïng va chaïm.
Löïc va chaïm raát lôùn gaây ra söï bieán ñoåi vaän toác caùc chaát ñieåm moät löôïng
höõu haïn, nghóa laø ñoäng löôïng cuûa caùc chaát ñieåm bieán ñoåi höõu haïn. Vì vaäy, trong
khi nghieân cöùu quaù trình va chaïm, ngöôøi ta khoâng döïa vaøo löïc va chaïm maø döïa vaøo xung löïc va chaïm. 174 τ S = ∫ dt N (15.1) o
trong ñoù: N - laø löïc va chaïm, τ laø thôøi gian va chaïm.
2- Ñaëc ñieåm thöù hai
Do hieän töôïng xaûy ra töùc thôøi neân trong khoaûng thôøi gian va chaïm raát beù,
caùc chaát ñieåm cuûa cô heä di chuyeån raát ít, coù theå chöùng minh ñoaïn di chuyeån cuûa
caùc chaát ñieåm trong quaù trình va chaïm laø nhöõng ñaïi löôïng beù cuøng baäc vôùi thôøi
gian va chaïm. Noùi khaùc ñi, trong quaù trình va chaïm caùc chaát ñieåm cuûa cô heä di
chuyeån khoâng ñaùng keå. Ñoù laø ñaëc ñieåm thöù hai cuûa hieän töôïng va chaïm.
3- Ñaëc ñieåm thöù ba
Quan saùt quaù trình va chaïm ngöôøi ta nhaän thaáy quaù trình va chaïm tieán
trieån theo hai giai ñoaïn: giai ñoaïn bieán daïng vaø giai ñoaïn khoâi phuïc. Giai ñoaïn
bieán daïng xaûy ra trong khoaûng thôøi gian τ1, baét ñaàu töø luùc hai vaät vöøa tieáp xuùc
vôùi nhau, do khaû naêng bieán daïng cuûa chuùng, choã tieáp xuùc hai vaät xaûy ra quaù
trình bieán daïng töø luùc hai vaät coù vaän toác khaùc nhau vaø keát thuùc khi hai vaät coù vaän toác baèng nhau.
Giai ñoaïn khoâi phuïc keùo daøi trong khoaûng thôøi gian τ2 baét ñaàu töø thôøi
ñieåm cuoái cuûa giai ñoaïn bieán daïng, luùc ñoù hai vaät coù vaän toác baèng nhau, do tính
chaát ñaøn hoài, caùc vaät coù theå laáy laïi hình daùng moät phaàn hay hoaëc hoaøn toaøn vaø
keát thuùc khi hai vaät coù vaän toác khaùc nhau, chuùng rôøi khoûi nhau.
Caên cöù vaøo möùc ñoä khoâi phuïc hình daïng cuõ cuûa caùc vaät va chaïm ngöôøi ta
phaân loaïi va chaïm thaønh va chaïm meàm vaø va chaïm ñaøn hoài.
- Va chaïm meàm laø quaù trình va chaïm trong ñoù khoâng coù giai ñoaïn khoâi
phuïc. Ñaëc ñieåm cuûa loaïi va chaïm naøy laø khi keát thuùc quaù trình va chaïm nhöõng
phaàn töû cuûa hai vaät ôû mieàn tieáp xuùc coù cuøng vaän toác phaùp tuyeán.
- Va chaïm ñaøn hoài laø quaù trình va chaïm trong ñoù coù giai ñoaïn khoâi phuïc,
caùc vaät va chaïm khoâi phuïc moät phaàn hay toaøn boä hình daùng tröôùc va chaïm cuûa noù.
- Neáu hình daùng cuûa caùc vaät ñöôïc khoâi phuïc hoaøn toaøn thì va chaïm ñöôïc
goïi laø hoaøn toaøn ñaøn hoài. Ñaëc ñieåm cuûa va chaïm ñaøn hoài laø khi keát thuùc va
chaïm, vaän toác phaùp tuyeán cuûa cuûa nhöõng phaàn töû thuoäc hai vaät taïi mieàn tieáp xuùc laø khaùc nhau.
3. Caùc giaû thieát cuûa lyù thuyeát va chaïm
Hieän töôïng va chaïm laø hieän töôïng raát phöùc taïp. Ñeå khaûo saùt coù keát quaû
baøi toaùn va chaïm caàn phaûi ñôn giaûn hoùa quaù trình thöïc, chæ giöõ laïi nhöõng tính
chaát cô baûn nhaát, nghóa laø phaûi xaây döïng moâ hình khaûo saùt baèng caùch ñöa ra
nhöõng giaû thieát veà va chaïm. Vieäc nghieân cöùu tæ mæ caùc ñaëc ñieåm ñaõ neâu cuûa
hieän töôïng va chaïm cho pheùp ñöa ra nhöõng giaû thieát sau:
1- Giaû thieát thöù nhaát 175
Vì trong va chaïm xuaát hieän löïc va chaïm raát lôùn, neân khi khaûo saùt quaù
trình va chaïm caàn boû qua caùc löïc thoâng thöôøng nhö troïng löïc, aùp löïc,... maø chæ keå ñeán löïc va chaïm.
2- Giaû thieát thöù hai
Trong quaù trình va chaïm do caùc chaát ñieåm di chuyeån ñoaïn raát beù neân
trong vieäc khaûo saùt quaù trình va chaïm coù theå boû qua di chuyeån cuûa caùc chaát
ñieåm trong va chaïm. Noùi khaùc ñi, giaû thieát raèng trong quaù trình va chaïm, caùc
chaát ñieåm cuûa cô heä khoâng di chuyeån vò trí, töùc ñöùng yeân.
3- Giaû thieát thöù ba
Quaù trình va chaïm tieán trieån theo hai giai ñoaïn: bieán daïng vaø khoâi phuïc.
Ñeå phaûn aûnh ñaëc ñieåm cuûa quaù trình va chaïm, ngöôøi ta so saùnh hai giai ñoaïn ñoù
qua xung löôïng cuûa löïc va chaïm trong töøng giai ñoaïn: τ τ 1 2 S1 = ∫ N1 S ; dt 2 = ∫ N2dt (15.2) o o
trong ñoù: N1 vaø N2 - laø löïc va chaïm trong giai ñoaïn bieán daïng vaø khoâi phuïc.
Töø ñoù ngöôøi ta ñöa ra khaùi nieäm veà heä soá khoâi phuïc k: S2 k = (15.3) S1
Heä soá khoâi phuïc k phuï thuoäc vaøo nhieàu yeáu toá phöùc taïp. Newton ñaõ ñöa
ra giaû thieát: heä soá khoâi phuïc k laø haèng soá trong quaù trình va chaïm. Ñoù laø giaû
thieát thöù ba trong quaù trình va chaïm.
Heä soá khoâi phuïc k chæ phuï thuoäc vaøo vaät lieäu cuûa caùc vaät va chaïm.
- Ñoái vôùi va chaïm meàm : k = 0
- Ñoái vôùi va chaïm hoaøn toaøn ñaøn hoài : k = 1
- Ñoái vôùi va chaïm ñaøn hoài noùi chung : 0 < k < 1.
4. Caùc vaán ñeà giaûi quyeát trong baøi toaùn va chaïm
Trong baøi toaùn va chaïm thoâng thöôøng caàn xaùc ñònh caùc ñaïi löôïng sau:
- Vaän toác cuûa cô heä sau va chaïm
- Xung löôïng caùc löïc trong caùc giai ñoaïn va chaïm
- Löôïng maát ñoäng naêng trong va chaïm
15.2. CAÙC ÑÒNH LYÙ TOÅNG QUAÙT CUÛA ÑOÄNG LÖÏC HOÏC TRONG QUAÙ TRÌNH VA CHAÏM
Do caùc giaû thieát veà va chaïm, caùc ñònh lyù toång quaùt cuûa ñoäng löïc hoïc ñoái
vôùi caùc cô heä va chaïm coù caùc ñaëc tính rieâng. Döôùi ñaây chuùng ta thieát laäp caùc
ñònh lyù toång quaùt cuûa ñoäng löïc hoïc cho cô heä va chaïm.
1. Ñònh lyù ñoäng löôïng
Ñònh lyù ñoäng löôïng cuûa cô heä, nhö ñaõ bieát coù daïng sau: e Q = Q = 1 o ∑ Sk 176 trong ñoù: ∑ e
Sk - laø toång xung löôïng caùc löïc ngoaøi.
Ñoái vôùi baøi toaùn va chaïm, do boû qua caùc löïc thoâng thöôøng neân ∑ e Sk chæ
laø toång xung löôïng caùc löïc va chaïm ngoaøi.
Ngoaøi ra cô heä va chaïm thöôøng laø vaät raén hoaëc heä vaät raén, neân ñoäng
löôïng cô heä thöôøng ñöôïc bieåu dieãn döôùi daïng: Q r r 1 = Mu c Q ; o = Mv c
trong ñoù: M - laø khoái löôïng cô heä ur r
c , vc - laø vaän toác khoái taâm cuûa cô heä sau vaø tröôùc va chaïm.
Do ñoù, ñònh lyù ñoäng löôïng ñoái vôùi cô heä chòu va chaïm ñöôïc phaùt bieåu nhö sau:
Ñònh lyù 15.1. Bieán thieân ñoäng löôïng cuûa heä trong va chaïm baèng toång xung
löôïng caùc löïc va chaïm ngoaøi. e Mur − v Mr = c c ∑ Sk (15.4)
2. Ñònh lyù moâmen ñoäng löôïng
Ñònh lyù moâmen ñoäng löôïng ñoái vôùi cô heä coù daïng: e dLo = ∑ r ⎛ ⎞ mo ⎜Fk ⎟ dt ⎝ ⎠
trong ñoù: Lo - laø moâmen ñoäng löôïng cuûa cô heä ñoái vôùi ñieåm coá ñònh O ∑ r ⎛ e ⎞ e m r o ⎜ F k ⎟ = ∑ k r Fk ⎝ ⎠
laø toång moâmen cuûa caùc ngoaïi löïc taùc duïng leân cô heä ñoái vôùi ñieåm O trong ñoù: k
rr - laø vector ñònh vò cuûa chaát ñieåm Mk ñoái vôùi goác O. ⎛ ⎞ do ñoù: e dLo = ⎜ r ⎟ ∑ rkFk dt ⎜ ⎟ ⎝ k ⎠
Tích phaân hai veá cuûa ñaúng thöùc treân trong khoaûng thôøi gian τ, ta coù: τ e ( ) 2 L r o − ) 1 ( Lo = ∑ ∫ ⎛ ⎞ ⎜r ∧ k Fk ⎟dt ⎝ ⎠ k o
Döïa vaøo giaû thieát cô heä khoâng thay ñoåi vò trí trong va chaïm, neân trong
khoaûng thôøi gian va chaïm τ, vector ñònh vò k
rr laø haèng vector, do ñoù: τ e e e ) 2 ( L r r r o − ) 1 ( Lo = ∑ r ∧ k ∫Fkdt = ∑r ∧ k Sk ∑ ⎛ = mo Sk ⎟⎞ ⎜ (15.5) ⎝ ⎠ k o k k trong ñoù: e
Sk - laø xung löôïng cuûa löïc va chaïm ngoaøi taùc duïng leân chaát ñieåm Mk.
Nhö vaäy ta coù ñònh lyù sau:
Ñònh lyù 15.2. Bieán thieân moâmen ñoäng löôïng cuûa cô heä ñoái vôùi moät ñieåm coá ñònh
trong khoaûng thôøi gian va chaïm baèng toång moâmen caùc xung löôïng cuûa caùc löïc
va chaïm ngoaøi ñoái vôùi cuøng ñieåm coá ñònh aáy. 177 e ( ) 2 L r o − ) 1 ( Lo = ∑ ⎛ ⎞ mo ⎜Sk ⎟ ⎝ ⎠
Töø ñoù ta deã daøng nhaän ñöôïc ñònh lyù sau:
Ñònh lyù 15.3. Bieán thieân moâmen ñoäng löôïng cuûa cô heä ñoái vôùi moät truïc coá ñònh
trong khoaûng thôøi gian va chaïm baèng toång moâmen xung löôïng cuûa caùc löïc va
chaïm ngoaøi ñoái vôùi truïc aáy. e ) 2 ( Lz − ) 1 ( Lz ∑ ⎛ = mz Sk ⎟⎞ ⎜ (15.6) ⎝ ⎠
Ñoái vôùi tröôøng hôïp cuûa vaät quay quanh moät truïc coá ñònh ta coù: e J ω − J ω = z 2 z 1 ∑ ⎛ ⎞ mz⎜Sk ⎟ (15.7) ⎝ ⎠ trong ñoù: 2 ω vaø 1
ω - laø vaän toác goùc cuûa vaät quay öùng vôùi thôøi ñieåm sau vaø tröôùc va chaïm
Jz - laø moâmen quaùn tính cuûa vaät ñoái vôùi truïc quay.
3. Ñònh lyù ñoäng naêng
Trong va chaïm coù moät löôïng ñoäng naêng cung caáp cho trong quaù trình bieán
daïng, nghóa laø cô naêng khoâng baûo toaøn. Vì vaäy thoâng thöôøng khoâng söû duïng
ñònh lyù ñoäng naêng ñeå khaûo saùt baøi toaùn va chaïm.
Söï maát ñoäng naêng trong va chaïm laø do hieän töôïng bieán daïng dö qua va
chaïm, keøm theo söï bieán ñoåi noäi naêng cuûa cô heä. Vì vaäy neáu muïc ñích laø gaây
bieán daïng, ví duï trong coâng vieäc reøn, daäp,... thì phaûi tìm caùch taêng löôïng maát
ñoäng naêng, vì löôïng maát ñoäng naêng naøy seõ chuyeån thaønh naêng löôïng gaây bieán
daïng. Ngöôïc laïi, khi söû duïng va chaïm cho muïc ñích laøm dòch chuyeån cô heä, nhö
ñoùng ñinh, ñoùng coïc, thì phaûi giaûm löôïng maát ñoäng naêng trong va chaïm ñeán
möùc nhoû nhaát, ñeå ñoäng naêng coøn laïi laø lôùn nhaát. Chính nhôø löôïng ñoäng naêng
coøn laïi sau va chaïm naøy seõ laøm cho cô heä di chuyeån sau va chaïm.
Vì vaäy ñeå giaûi quyeát baøi toaùn va chaïm thöôøng chæ söû duïng hai ñònh lyù:
ñònh lyù ñoäng löôïng vaø ñònh lyù moâmen ñoäng löôïng.
Döôùi ñaây ta seõ aùp duïng hai ñònh lyù ñoù ñeå khaûo saùt hai baøi toaùn quan troïng cuûa va chaïm.
15.3. VA CHAÏM THAÚNG XUYEÂN TAÂM CUÛA HAI VAÄT CHUYEÅN ÑOÄNG TÒNH TIEÁN Hình 15.1
Xeùt hai vaät chuyeån ñoäng tònh tieán va chaïm vaøo nhau taïi I.
Goïi vaän toác khoái taâm cuûa caùc vaät tröôùc va chaïm laàn löôït laø vr1 vaø vr . 2 178
Phaùp tuyeán chung cuûa hai maët tieáp xuùc cuûa hai vaät taïi I, ñöôøng n1In2 ñöôïc
goïi laø ñöôøng va chaïm.
Ñöôøng noái hai khoái taâm cuûa hai vaät C1C2 ñöôïc goïi laø ñöôøng xuyeân taâm (H.15.1a).
- Va chaïm thaúng laø va chaïm trong ñoù vr1 vaø vr2 ñeàu song song vôùi ñöôøng va chaïm n1In2 (H.15.1a).
- Va chaïm thaúng xuyeân taâm laø va chaïm maø ñöôøng va chaïm n1In2 truøng
vôùi ñöôøng xuyeân taâm C1C (H.15.1b), coøn caùc vaän toác vr1 vaø vr2 höôùng doïc theo
ñöôøng va chaïm vaø ñöôøng xuyeân taâm (H.15.1b).
Chuùng ta chæ khaûo saùt tröôøng hôïp tònh tieán thaúng xuyeân taâm cuûa hai vaät
trong ñieàu kieän boû qua ma saùt taïi choã tieáp xuùc. 1. Moâ hình baøi toaùn
Cho hai vaät khoái löôïng m1m2 chuyeån ñoäng tònh tieán vôùi vaän toác vr1 vaø vr2
(v1 > v2 cuøng höôùng theo ñöôøng va chaïm cuõng ñoàng thôøi laø ñöôøng xuyeân taâm C1IC2).
Haõy tìm vaän toác khoái taâm hai vaät sau va chaïm ur1 vaø ur2 ; xung löôïng caùc
löïc va chaïm trong töøng giai ñoaïn va chaïm vaø löôïng maát ñoäng naêng trong va
chaïm. Bieát heä soá khoâi phuïc laø k. 2. Giaûi baøi toaùn
1- Caùc giai ñoaïn va chaïm
Va chaïm ñaøn hoài vôùi heä soá khoâi phuïc k coù hai giai ñoaïn va chaïm:
- Giai ñoaïn bieán daïng xaûy ra trong khoaûng thôøi gian τ1 baét ñaàu töø luùc hai
vaät tieáp xuùc nhau coù vaän toác khaùc nhau vr1 vaø vr2 vaø keát thuùc khi chuùng coù vaän toác baèng nhau ur .
Goïi xung löïc va chaïm trong giai ñoaïn naøy laø S1 .
- Giai ñoaïn khoâi phuïc xaûy ra trong khoaûng thôøi gian τ2, baét ñaàu töø luùc hai
vaät coù vaän toác baèng nhau ur vaø keát thuùc luùc hai vaät rôøi nhau vaø coù vaän toác ur1 vaø ur2 .
Goïi xung löïc va chaïm trong giai ñoaïn naøy laø S2 . Caùc xung löïc sr r 1 s
, 2 höôùng theo ñöôøng va chaïm C1nC2.
2- Caùc phöông trình va chaïm
Döïa vaøo ñònh lyù ñoäng löôïng trong va chaïm, ta seõ vieát phöông trình va
chaïm cho töøng vaät trong caùc giai ñoaïn va chaïm.
Trong giai ñoaïn bieán daïng, phöông trình va chaïm cho vaät thöù nhaát laø: m1u – m1v1 = –S1 (15.8)
vaø ñoái vôùi vaät thöù hai seõ laø: m2u – m2v2 = –S2 (15.9) 179
Trong giai ñoaïn khoâi phuïc phöông trình va chaïm ñoái vôùi vaät thöù nhaát vaø
vaät thöù hai laàn löôït laø: m1u1 – m1u = –S2 (15.10) m2u2 – m2u = S1 (15.11)
Töø giaû thieát thöù ba veà va chaïm, ta coù: S2 = kS1 (15.12) 3. Keát quaû
Chuùng ta nhaän ñöôïc phöông trình chöùa naêm aån u, u1, u2, S1, S2.
Töø (15.8) vaø (15.9) ta nhaän ñöôïc: m1v1 + m2v2 m1u1 + m2u2 u = = (15.13) m1 + m2 m1 + m2
Thay bieåu thöùc (15.13) cuûa u vaøo (15.8) hoaëc (15.9) ta coù: m1m2 1 S = (v1 − v2) (15.14) m1 + m2
Töø (15.12) ta tính ñöôïc: m1m2 S2 = 1 kS = k (v1 − v2) (15.15) m1 + m2
Baây giôø thay (15.13), (15.15) vaø (15.10) vaø (15.11) ta nhaän ñöôïc: m u1 = v − (1 + k) 2 1 (v1 − v2) (15.16) m1 + m2 m u2 = v − (1 + k) 2 2 (v1 − v2) (15.17) m1 + m2
Töø (15.16) vaø (15.17) deã daøng ruùt ra: u2 − u1 ur k = = (15.18) v1 − v2 vr
trong ñoù: vr vaø ur - laø vaän toác töông ñoái cuûa vaät thöù hai ñoái vôùi vaät thöù nhaát sau vaø tröôùc va chaïm.
Keát quaû vöøa nhaän ñöôïc laø cô sôû cuûa moät phöông phaùp ñôn giaûn do heä soá
khoâi phuïc. Nhaèm muïc ñích naøy ta khaûo saùt baøi toaùn sau:
Thaû moät vieân bi rôi khoâng vaän toác ñaàu töø ñoä cao h C1
1 xuoáng maët phaúng ngang coá ñònh. Sau khi va •
chaïm vaøo maët phaúng ngang coá ñònh vieân bi naåy leân vôùi ñoä cao h2 (H.15.2). C • 2 h1
Ñeå tìm heä soá khoâi phuïc k theo coâng thöùc
(15.18) ta caàn tìm vaän toác v h
r, ur cuûa vieân bi tröôùc vaø 2
sau va chaïm. Vieân bi rôi töø ñoä cao h1 khoâng vaän toác
ñaàu neân khi chaïm vaøo maët phaúng ngang noù coù vaän Hình toác: v = gh 2 1 .
Ñoù chính laø vaän toác töông ñoái cuûa vieân bi ñoái vôùi maët phaúng ngang tröôùc va chaïm. 180
Ñeå tìm vaän toác töông ñoái ur cuûa vieân bi sau va chaïm ta nhaän xeùt raèng
chính nhôø vaän toác ur ñoù maø vieân bi naåy leân ñöôïc ñoä cao h2: vaäy: ur = gh 2 2 do ñoù: u gh 2 h k r 2 2 = = = < 1 (15.19) v gh 2 h r 1 1
Baây giôø ta tính löôïng maát ñoäng naêng trong va chaïm. Goïi T1 vaø T2 laàn löôït
laø ñoäng naêng cuûa cô heä tröôùc vaø sau va chaïm: 1 2 1 2 1 2 1 2 1 T = m1v1 + m2v2 2 T ; = m1u1 + m2u2 2 2 2 2
Do ñoù löôïng maát ñoäng naêng baèng: 1 1 T Δ = 1 T − 2 T = m1( 2 2 v1 − u1 ) + m2( 2 2 v2 − u2 ) (15.20) 2 2
Baây giôø ta bieåu dieãn löôïng maát ñoäng naêng naøy theo caùc thoâng soá ñoäng
hoïc cuûa cô heä tröôùc va chaïm. Muoán theá ta vieát löôïng maát ñoäng naêng trong daïng sau: 1 1 ΔΤ
= m1(v1 − u1 ) ( v1 + u1 ) + m2 (v2 − u2 ) ( v2 + u2 ) 2 2 vì: m v 2 1 − u1 = (1 + k) (v1 − v2 ) m1 + m2 m v 1 2 − u 2 = −(1 − k) (v1 − v2) m1 + m 2 neân: 1 m m ΔΤ 1 2 =
(1 + k) ( v1 − v2 ) ( v1 − v2 + u1 − u2 ) 2 m1 + m2
Chuù yù ñeán ñaúng thöùc: u1 – u2 = –k(v1 – v2) chuùng ta nhaän ñöôïc: 1 m1m2 ΔΤ =
(1 + k) ( v1 − v2 )[ v1 − v2 − k(v1 − v2 )] 2 m + m 1 2 (15.21) 1 m1m2 = ( 2 1 − k )( v1 − v )2 2 2 m1 + m2
Trong tröôøng hôïp va chaïm meàm, k = 0, ta coù: 1 m1m2 ΔΤ = (v1 − v )2 2 (15.22) 2 m1 + m2
Neáu va chaïm hoaøn toaøn ñaøn hoài, k = 1, thì: ΔΤ = 0 (15.23)
Nghóa laø trong va chaïm hoaøn toaøn ñaøn hoài, ñoäng naêng cuûa cô heä khoâng bò maát ñi.
Baây giôø ta xeùt tröôøng hôïp khi v2 = 0, töùc vaät thöù nhaát va chaïm vaøo vaät thöù
hai ban ñaàu ñöùng yeân, luùc ñoù: 181 1 m1m2 ΔΤ = ( 2 1 − k ) 2 m2 v1 = ( 2 1 − k ) o Τ (15.24) 2 m1 + m2 m1 + m2
trong ñoù: To - laø ñoäng naêng cuûa heä tröôùc va chaïm: 1 2 o Τ = m1v1 (15.25) 2
Ñeå bieát tyû leä giöõa löôïng ñoäng naêng bò maát ñi trong va chaïm so vôùi ñoäng
naêng cuûa toaøn cô heä tröôùc va chaïm ta thieát laäp tyû soá: ΔΤ m2 = ( 2 1 − k ) (15.26) o Τ m1 + m2
Trong reøn, daäp muïc ñích laø laøm cho vaät caøng bò bieán daïng nhieàu caøng toát,
neân löôïng maát ñoäng naêng caøng nhieàu caøng toát. Vì vaäy hieäu suaát cuûa quaù trình
reøn ñöôïc ñònh nghóa baèng tyû soá: ΔΤ m2 1 1 η = = ( 2 1 − k ) = ( 2 1 − k ) (15.27) Τ m + m m o 1 2 1 1 + m2
Ñeå nhaän ñöôïc hieäu suaát lôùn caàn phaûi coù: m1 << 1 m2
töùc m1 beù hôn m2 nhieàu laàn, nghóa laø ñe phaûi coù khoái löôïng lôùn hôn nhieàu laàn so
vôùi khoái löôïng cuûa buùa. Ñeå taêng khoái löôïng cuûa ñe ngöôøi ta gaén chaët ñe vaøo neàn.
Trong ñoùng coïc muïc ñích laø laøm cho coïc caøng luùn saâu caøng toát. Do ñoù
ñoäng naêng coøn laïi sau va chaïm caøng lôùn caøng toát, töùc laø ñoäng naêng tieâu hao
trong va chaïm caøng ít caøng toát.
Töø ñoù hieäu suaát cuûa ñoùng coïc seõ laø: o Τ − ΔΤ ΔΤ m1 1 η2 = = 1 − = ( 2 1 − k ) = ( 2 1 − k ) (15.28) Τ Τ m + m m o o 1 2 2 1 + m1
Ñeå coù hieäu suaát ñoùng coïc lôùn, caàn coù: m2 << 1 m1
töùc m1 lôùn hôn m2 nhieàu laàn, nghóa laø khoái löôïng cuûa buùa lôùn hôn nhieàu laàn khoái löôïng cuûa coïc.
Ví duï 15.1. Buùa coù khoái löôïng m1 rôi töï do töø ñoä cao h
so vôùi ñaàu coïc. Coïc coù khoái löôïng m2. Cöù sau moät laàn
chòu va ñaäp coïc ñi xuoáng moät ñoaïn d. Tìm löïc caûn
trung bình cuûa ñaát taùc duïng leân coïc. Giaû thieát va chaïm meàm (H.15.3).
Giaûi. Ñaây laø baøi toaùn va chaïm hai vaät chuyeån ñoäng
tònh tieán. Quaù trình va chaïm baét ñaàu töø luùc buùa ñaäp
vaøo ñaàu coïc vaø keát thuùc ngay sau ñoù. 182
Quaù trình buùa rôi töø ñoä cao h xuoáng ñeán ñaàu coïc vaø quaù trình buùa vaø coïc
sau va chaïm nhaän ñöôïc vaän toác u luùn saâu moät ñoaïn d roài döøng laïi laø caùc quaù trình khoâng va chaïm.
Quaù trình va chaïm baét ñaàu töø luùc buùa ñaäp vaøo ñaàu coïc vôùi vaän toác v1, coøn
coïc coù vaän toác v2 = 0 vaø keát thuùc khi buùa vaø coïc cuøng nhaän ñöôïc vaän toác u. Vì
va chaïm laø meàm neân chæ coù giai ñoaïn bieán daïng vaø heä soá khoâi phuïc k = 0.
Töø coâng thöùc (15.13) ta coù: m1v1 u1 = u2 = u = m1 + m2
Vaän toác v1 ñöôïc xaùc ñònh nhôø ñònh lyù ñoäng naêng daïng höõu haïn aùp duïng
cho quaù trình rôi töï do cuûa ñaàu buùa: 2 m1v1 − 0 = m1gh 2 töø ñoù: v1 = gh 2 vaäy: u m1 m = v 1 = gh 2 (a) m1 + m 1 2 m1 + m2
Sau khi buùa vaø coïc nhaän ñöôïc vaän toác u thì cuøng luùn xuoáng moät ñoaïn d
roài döøng laïi. AÙp duïng ñònh lyù ñoäng naêng daïng höõu haïn cho quaù trình sau va chaïm naøy, ta coù: 1 0 − (m1 + m ) u 2 2 = − Fds = −F ∫ tbd 2 o
trong ñoù: F - laø löïc caûn cuûa ñaát taùc duïng leân coïc
Ftb laø giaù trò trung bình cuûa noù.
Thay giaù trò tìm ñöôïc cuûa u töø (a) vaøo ñaúng thöùc treân vaø sau khi ruùt goïn, 2 ta ñöôïc: m1 h F = g tb m + m d 1 2
15.4. VA CHAÏM CUÛA VAÄT QUAY QUANH MOÄT TRUÏC COÁ ÑÒNH
Khaûo saùt moät taám phaúng quay quanh
moät truïc coá ñònh thaúng goùc vôùi maët phaúng y O
cuûa taám taïi O. Xung löïc va chaïm S taùc duïng SOy
trong maët phaúng cuûa taám, nghieâng vôùi S S
ñöôøng noái ñieåm O vaø khoái taâm C cuûa taám Ox
moät goùc α. Taïi thôøi ñieåm va chaïm, taám coù α vaän toác goùc ω I
o. Tìm vaän toác goùc ω cuûa taám
sau va chaïm vaø caùc xung löôïng cuûa caùc
phaûn löïc ôû truïc O. Cho bieát taïi thôøi ñieåm x
ñaàu OC truøng vôùi ñöôøng thaúng ñöùng (H.15.4). Hình 15.4
Khaûo saùt taám quay. Xung löïc va chaïm ngoaøi taùc duïng vaøo taám laø xung löïc
va chaïm S vaø xung löïc va chaïm cuûa phaûn löïc taïi O. 183
AÙp duïng ñònh lyù ñoäng löôïng vaø phöông trình vaät quay cho quaù trình va
chaïm (15.4) vaø (15.7) ta coù: u Mr r c − v M c = S + So (15.29) J ω − J ω = m o o o o (S) (15.30)
trong ñoù: M - khoái löôïng cuûa taám vr r c u
, c - vaän toác khoái taâm C cuûa taám tröôùc vaø sau va chaïm
So - xung löïc va chaïm cuûa phaûn löïc taïi O
Jo - moâmen quaùn tính cuûa taám ñoái vôùi truïc quay O o
ω , ω - vaän toác goùc cuûa taám tröôùc vaø sau va chaïm.
Chieáu hình (15.29) leân caùc truïc Ox vaø Oy, trong ñoù truïc Oy truøng vôùi ñöôøng OC, ta coù: Muc − Mvc = S sinα + Sox (15.31) 0 = S cos α + Soy (15.32)
coøn (15.30) ñöôïc vieát trong daïng sau: Jo (ω − o ω ) = S sin α OI . (15.33)
trong ñoù: I - giao ñieåm cuûa ñöôøng taùc duïng cuûa xung löïc va chaïm S vôùi ñöôøng OC.
ñaët OC = a, ta coù: uc = aω; vc = aωo
Phöông trình (15.31) baây giôø seõ laø: ( Ma ω − o ω ) = S sin α + Sox (15.34)
Töø (15.32), (15.33) vaø (15.34) chuùng ta deã daøng tìm ñöôïc caùc ñaïi löôïng ω, Sox, Soy.
Thöïc vaäy, töø (15.33) chuùng ta nhaän ñöôïc: ω = ω + S OI sin α o (15.35) Jo
töø (15.32), ta coù: Soy = –Scosα (15.36)
Khi thay (15.35) vaøo (15.34) ta tìm ñöôïc: ⎛ MaOI ⎞ S = S sin ox ⎜ α − 1⎟ (15.37) ⎝ Jo ⎠
Nhö vaäy döôùi taùc duïng cuûa xung löïc va chaïm S
, truïc O seõ chòu löïc va chaïm So ñöôïc tính theo caùc
coâng thöùc (15.36) vaø (15.37).
Va chaïm phaùt sinh taïi oå truïc quay seõ laøm hö
hoûng oå ñoù vaø ngoãng truïc. Do ñoù caàn tìm ñieàu kieän ñeå
taïi oå truïc khoâng xuaát hieän xung löïc va chaïm phaûn löïc,
khi taám chòu taùc duïng cuûa xung löïc va chaïm S coù giaù trò baát kyø.
Ñeå thöïc hieän ñieàu kieän naøy, caàn phaûi: 184 S = − S cos α 0 oy = (a) ⎛ MaOI S = S sin α − 1⎞ ⎜ ⎟ 0 ox = (b) ⎝ Jo ⎠ Töø (a) ta coù: cosα = töùc ; 0 π α = 2 vaø töø (b), ta ruùt ra: OI . Ma − 1 = 0 Jo vaäy: J OI o = (15.38) Ma
Do ñoù, ñeå taïi truïc O khoâng xuaát hieän xung löïc va chaïm cuûa phaûn löïc khi
taám chòu taùc duïng cuûa xung löïc va chaïm coù giaù trò baát kyø, thì xung löïc va chaïm
S phaûi taùc duïng vuoâng goùc vôùi ñöôøng thaúng OC vaø ñi qua ñieåm I naèm treân
ñöôøng OC thoûa maõn ñieàu kieän (15.38).
Ñieåm I ñöôïc goïi laø taâm va chaïm.
Ví duï 15.2. Xaùc ñònh taâm va chaïm cuûa moät thanh ñoàng chaát quay trong maët
phaúng quanh ñieåm coá ñònh O (H.15.5).
Giaûi. Giaû söû thanh coù chieàu daøi l. Truïc quay O caùch ñaàu muùt thanh moät ñoaïn
baèng x, goïi I laø taâm va chaïm vaø caùch ñaàu muùt kia cuûa thanh moät ñoaïn y.
Kyù hieäu OI = ρ; OC = a trong ñoù C laø troïng taâm cuûa thanh.
Theo coâng thöùc (15.38) ta coù: Jo ρ = Ma
Döïa vaøo coâng thöùc tính moâmen quaùn tính cuûa vaät raén ñoái vôùi caùc truïc
song song, ta coù: Jo = Jc +Ma2 vaäy: J ρ c = + a (15.39) Ma
Khi thay caùc ñaïi löôïng: 2 1 1 Ml ρ = a + − a ; y = − ; x Jc = 2 2 12
vaøo (15.39) vaø sau khi raát goïn ta nhaän ñöôïc: ⎛ 1 ⎞ ⎛ 1 ⎞ 2 12 ⎜ − y ⎟ ⎜ − x ⎟ = l (15.40) ⎝ 2 ⎠ ⎝ 2 ⎠ 185
Noù cho pheùp ta xaùc ñònh y khi bieát x hoaëc ngöôïc laïi. Roõ raøng y vaø x hoaùn
vò ñöôïc cho nhau. Ñieàu ñoù coù nghóa laø taâm va chaïm vaø truïc quay coù theå thay ñoåi vò trí cho nhau.
Khi y = 0 thì x = 1 / 3 , töùc khi taâm va chaïm naèm ngay taïi ñaàu muùt cuûa
thanh thì truïc quay phaûi naèm caùch ñaàu muùt kia moät ñoaïn baèng moät phaàn ba
chieàu daøi thanh, töùc caùch taâm va chaïm moät ñoaïn baèng hai phaàn ba chieàu daøi
thanh. Ñieàu ñoù ñöôïc xaùc ñònh trong caùc tröôøng hôïp: khi caàm buùa, caàm rìu, caàm
cuoác,... ñeå choã tay caàm khoâng bò va chaïm, tay naém phaûi caùch ñaàu cuoái, nôi coù
xung löïc va chaïm moät khoaûng baèng hai phaàn ba chieàu daøi cuûa caùn (H.15.6a).
Khi x = 0 thì y = 1 / 3 töùc laø khi truïc quay ôû moät ñaàu muùt cuûa thanh thì taâm
va chaïm caàn naèm caùch ñaàu muùt kia moät khoaûng baèng hai phaàn ba chieàu daøi cuûa
thanh (H.15.6b), ví duï tröôøng hôïp buùa quay nghieàn vaät lieäu ñeå truïc theo buùa, töùc
laø ôû ñaàu muùt cuûa buùa, khoâng chòu va chaïm thì caùc vaät lieäu nghieàn seõ va chaïm
vôùi buùa taïi ñieåm caùch truïc treo buùa moät khoaûng baèng hai phaàn ba chieàu daøi cuûa buùa. 186
PHAÀN IV. BAØI TAÄP TÖÏ GIAÛI A. PHAÀN TÓNH HOÏC
I. MOÄT VAÄT RAÉN CAÂN BAÈNG
1. Cho vaät raén S coù lieân keát vaø chòu löïc nhö hình veõ. Bieát: Q = 2 KN; q = 2
KN/m; M = 8 KNm; F = 1 KN; a = 1 m; b = 2 m; α = 60o; β = 30o.
(Moâ hình naøo khoâng coù caùc ñaïi löôïng töông öùng ñöôïc xem nhö chuùng baèng khoâng). α α B B α O S β O A S A O S Q Q B A β β Q b) a) c) M q B Q a A b α F q b M Q b M A F B B α β a β b a a b α F A d) e) g) Ñaùp soá: 2 2 T = ; N ; ; TA = ;1 B = T = 3 S ; = 1 T 3 3 A 3 B A B = Ñaùp soá: 34 3 5 S B = − N = − A = A 2 x + 3 2 4 SA B 27 9 3 x = − 2 B = B = 2 y 8 x 8 3 B 1 25 y = 3 − SA B = 2 NA = 8 y 8 q1 q2 α F A Q B cho: q b a M a b M 1 = 3 KN/m b F b q2 = 2 KN/m β B A Q h) i) 187 Ñaùp soá: 4 − 11 3 B 2 3 − 13 15 x = ; B = ; S = 2 + 2 3 y 2 + 2 3 A 1 + 3 B a B 23 x = 1 − ; B ; y = 5 , 4 − 3 M = − 3 3 B − 6 E
2. Giaù treo taûi E troïng löôïng P coù lieân keát oå ñôõ taïi A, baûn leà b
taïi B. Cho a = 1 m, b = 2 m, troïng löôïng cuûa giaù treo laø Q coù
ñöôøng taùc duïng caùch truïc AB ñoaïn l = 0,5 m. Xaùc ñònh phaûn löïc taïi A, B? A Ñaùp soá: A P X = –Bx = 0,25Q + ; A 2 y = P + Q.
3. Truïc tôøi coù moâ hình nhö hình veõ. Taûi E
A troïng löôïng P = 20 KN, taûi troïng cuûa
tôøi Q = 3 KN; R = 2r = 0,2 m.
a) Tìm giaù trò cuûa M ñeå heä caân baèng r O
b) Vôùi giaù trò M tìm ñöôïc xaùc ñònh phaûn R löïc taïi O, E.
Ñaùp soá: M ≤ 2 KNm, NE = 10 – 5 M,
OX = 10 – 5 M, Oy = 20 (KN). A
4. Quaû lu ñoàng chaát troïng löôïng Q = 2
KN, baùn kính R = 60 cm. Xaùc ñònh löïc
keùo ngang caàn thieát P ñeå keùo ñöôïc quaû
lu vöôït qua baäc ñaù cao 8 P A cm. 8cm 60cm Ñaùp soá: P ≥ 1,15 3m KN. G 3m 2 C
5. Xe caåu nhö hình veõ. Taûi 30o
troïng ñöôïc giöõ L(4 KN). 35o B
Thanh AB troïng löôïng 1,2 KN troïng taâm G1, thanh BC 8m
troïng löôïng 0,6 KN troïng G1 taâm G2. a) Xaùc ñònh söùc D
caêng daây caùp vaø phaûn löïc 8m taïi A 45o L A b) Xe coù theå giöõ taûi G3
L toái ña laø bao nhieâu ñeå baûo 2m 188
ñaûm khoâng laät, cho troïng löôïng cuûa xe (khoâng caàn truïc) Q = 20 KN ñaët taïi troïng taâm G3.
Ñaùp soá: TBD = 76,8; AX = 62,9; Ay = 65,6 (KN).
6. Ñeå giöõ chieác xuoàng ngöôøi ta duøng giaù treo nhö hình veõ. Xaùc ñònh phaûn löïc taïi
A, B vaø C bieát troïng löôïng cuûa xuoàng laø 8 KN. 1,2m D B 2m . A . C 80 o 3m
7. Ñeå giöõ ñöôïc thanh AB treo taûi troïng Q ngöôøi ta H
duøng hai daây BI, BH ñöôïc boá trí nhö hình veõ. Bieát 30 o K 30 o B
IBH thuoäc maët phaúng naèm ngang, ABK thuoäc maët
phaúng thaúng ñöùng. Xaùc ñònh caùc söùc caêng daây vaø I öùng löïc cuûa thanh AB. 45 o Q Ñaùp soá: Q S = − ; Q 2 T = T B I H = A 3
8. Taám hình vuoâng ABCD ñöôïc giöõ naèm ngang nhôø
saùu thanh nhö hình veõ taïo thaønh moät khoái laäp A D
phöông. Troïng löôïng cuûa taám laø P. Tìm öùng löïc cuûa caùc thanh. 1 2 B Ñaùp soá: S C 1 = S3 = S4 = S5 = 0 P S = S 6 2 = − 3 2 4 6
9. Moâ taû sô ñoà löïc taùc ñoäng leân caùc thanh gaáp khuùc 5
nhö hình veõ. ÔÛ ñaây daây BC naèm trong maët phaúng
vuoâng goùc vôùi EB, taïo vôùi maët phaúng AEB goùc 30o.
Cho AI = 2IB = 2BK = 2KC = 2 m; AE = EB = 1 m. Tính caùc phaûn löïc A C C 4 5 N m I B E 200 N K 30 o B 500 N 300 N 189 A
10. Thanh AB coù lieân keát vaø chòu löïc nhö hình veõ. 1,5m
Xaùc ñònh phaûn löïc taïi A vaø caùc söùc caêng daây.
Ñaùp soá: Ax = Ay = –200 N 1 C ,5 AZ = TE = TD = 200 N. m
11. Truïc quay AB coù lieân keát oå ñôõ taïi A, B nhö 2m
hình veõ. Bieát söùc caêng T 2m
1, T2 nghieâng vôùi phöông B
naèm ngang Ox goùc α = 30o. Cho a = 0,4 m; b = 0,6 E F = 200 N
m; baùn kính voâ laêng (lôùn) laø R = 0,4 M; truïc quaán
daây r = 0,2 m; Q = 10 KN; T1 = 6 KN. Xaùc ñònh söùc caêng T2 ñeå truïc quaán daây
caân baèng vaø tìm phaûn löïc caùc oå truïc. z a b a A B y x α T1 Q T1
12. Caùnh cöûa ñoàng chaát hình chöõ nhaät ABCD coù z D
troïng löôïng P. Cho AD = a 4 , AB = a. Ñeå giöõ caùnh 120o
cöûa caân baèng ngöôøi ta duøng daây CE.
Tìm söùc caêng vaø phaûn löïc taïi oå A, baûn leà D
neáu löïc taùc ñoäng F vaøo ñieåm B song song vôùi phöông naèm ngang nhö hình veõ. A y E Ñaùp soá: P 3 B T = F 6 ; X x F A = − + F (2 − 2) 4 2 3 F YA = P − Z ; A = P + F 3 12 2 P 3 X B = − − F ( 2 − ) P 3 1 ; YD = F − 4 2 12 4m K L
II. HEÄ VAÄT RAÉN CAÂN BAÈNG
13. Daàm hai ñoaïn AE, EB coù lieân keát nhö hình veõ. 1m 1m
Caàn truïc troïng löôïng Q = 5 KN coù
giaù naèm treân ñöôøng KE. Taûi P = 1 KN P
Xaùc ñònh caùc phaûn löïc taïi A, B. A B 4m E 8m 190
Ñaùp soá: YA = 5,375; xA = 0; MA = 20,5, NB = 0,625 (KN,m)
Ñaùp soá: XA = 0; YA = 53,75; MA = 205
NB = 6,25; XE = 0; YC = 43,75 (KN,m)
14. Cho cô caáu nhö hình veõ. Bieát: P1 α C
P1 = 10 KN; P2 = 12 KN; M = 25 KNm q = 2 KN/m; α = 60o. M
Xaùc ñònh caùc phaûn löïc taïi A. B, C. 4m q
Ñaùp soá: XA = -7,39; XB = -4,39; XC = 4,39 P2 α Y A A = 12,8; YB B = 7,86; YC = 4,14 3m 3m 2m 2m
15. Cho heä hai vaät raén caân baèng nhö hình
veõ (hình a) hoaëc (hình b). Bieát:
b = 2a = 2 m; q = 2 KN/m; qo = 0,75 KN; F = 3 KN; α = 60o.
Xaùc ñònh phaûn löïc taïi A, B, C trong caùc tröôøng hôïp sau: a) M = 1 KNm; b) M = 1,5 KNm; c) M = 3 KNm. D a q F A A b M C B M a a α qo α b B a F Hình a Hình b
16. Cô caáu goàm hai thanh AB vaø CD coù lieân keát vaø F Q chòu löïc nhö hình veõ. 30 o
Xaùc ñònh phaûn löïc taïi A, D, C. C B A
Bieát: AC = CI = ID = a; CB = 2a. I
17. Cô caáu tay quay caàn laéc (hình a) {tay quay thanh
truyeàn (hình b)} chòu löïc nhö hình veõ. Tìm quan heä P
giöõa F vaø M ñeå cô caáu caân baèng, töø ñoù xaùc ñònh D
phaûn löïc taïi O vaø phaûn löïc taïi baûn leà B. F A M a B r r M B O 45o F O 2r 30o Hình a Hình b O1 191 Ñaùp soá: 2 F F 2 M = O ; aF x = − O ; y = S ; B = F 2 2 2 2 3 3 9 3 3 3 3 r S = F; O = − ; F O = ; F M F B = 4 x 8 y 8 8
18. Cô caáu maùy eùp nhö hình veõ. E D Bieát: OA = OB = r; BA = AC; o OBC = 30 G
Tìm löïc eùp vaøo vaät G cuõng nhö caùc phaûn C
löïc oå truïc O, B vaø phaûn löïc töïa taïi caùc con chaïy A, C. Ñaùp soá: M A 2 3 M M 3 NA = O ; M y = − O ; = r 3 r x r 3 O M 2 M − 3 3 N 0o C = = NG B ; x = B ; y = M r 3 r 3 r 3 B
19. Maùy eùp ôû vò trí nhö hình veõ. O M
Cho OA = R, ñoä daøi BC = 2BD = 2d. A
Tìm öùng löïc trong tay bieân AB, löïc eùp taïi 30 o
C vaø phaûn löïc cuûa oáng maùng tröôït (thu veà D). B Ñaùp soá: M 2 M S = − N ; AB = 3R C R D M −Md Dx = M ; = R 3 D R 3 C
20. Caàu doác AB = 60 m; BC = 30 m nghieâng 30o nhôø hai coät choáng CC, DDC.
Ñoaøn taøu AE troïng löôïng 20 KN/m. E
Tìm phaûn löïc taïi A, öùng löïc caùc coät vaø löïc töông hoã taïi B. Boû qua B troïng
löôïng caàu, xem troïng löôïng taøu gaây aùp löïc vuoâng goùc treân caàu; AD = 40 m; AE D =70 m. A y D’ C’
Ñaùp soá: SC = –33,33; SD = –1044,34; Bx = 83,34 x
Ax = 135,55; Ay = 218,14; By = 57,72.
21. Khoái A taûi troïng 500 N, khoái B troïng löôïng 300
N ñöôïc giöõ baèng daây caùp nhö hình beân. Boû qua
khoái löôïng caùc roøng roïc.
Xaùc ñònh caùc söùc caêng daây vaø löïc töông A taùc giöõa hai taám. F A B Ñaùp soá: T = 200 N; N R1 A,B = 100 r R
22. Cho heä truïc tôøi coù hai baùnh raêng nhö hình veõ. 1 O O I
Caùc baùn kính töông öùng R1, r1, R, OA = a.
a) Tìm löïc F ñeå cô heä caân baèng α I Q 192
b) Tính phaûn löïc töông hoã ôû choã aên khôùp raêng vaø phaûn löïc taïi O. Ñaùp soá: r R r Q F = 1 N ; Q = 1 aR I 1 R1 cos α
23. Giaù ñôõ nhö hình veõ. P
Xaùc ñònh öùng löïc caùc thanh vaø phaûn löïc taïi ngaøm A. 60o 1 60o 2 3 Ñaùp soá: 60o P 60o S = S = − S ; = 0 1 2 3 3 l 2a A = ; 0 A = M ; P x y A = (l + a)P
24. Giaù ba chaân ABCD daïng choùp
ñeàu lieân keát goái caàu vôùi hai daàm z E
cong xon naèm ngang song song vôùi
nhau. Roøng roïc E gaén vaøo ñænh D choùp ñeàu. P
Xaùc ñònh phaûn löïc ngaøm O. A B y O Bieát AB = 2AO = a 2
(xem troïng löïc P ñi qua ñænh cuûa x hình choùp ABDE). Ñaùp soá: 2 2 Ox = −P O ; y = O ; P z = P 6 3 Pa Mox = − ( 6 − 2) Pa M ; = M ; 0 oy oz = − ( 3 − 2) 6 12
25. Hai truïc AB vaø CD song song naèm ngang, mang hai baùnh xe aên khôùp raêng
taïi I. Bieát AB = 1 m, R = R1 = 0,4 m; BO = CO1 = O1D = 0,5 m; r1 = 0,2
m. Phaùp tuyeán chung cuûa caùc maët raêng taïi I coù phöông In. Cho P = 1
KN, tìm M ñeå cô heä caân baèng, xaùc ñònh phaûn löïc taïi caùc oå truïc A, B, C, D vaø löïc töông hoã taïi I. 193 z n O α I D B o1 y m A C x P
III. BAØI TOAÙN CAÂN BAÈNG COÙ KEÅ MA SAÙT
26. Thanh ñoàng chaát AB coù troïng löôïng P ñöôïc töïa treân neàn C
ngang, heä soá ma saùt tröôït giöõa chuùng laø f. Thanh ñöôïc giöõ B ϕ
caân baèng ôû ñoä nghieâng 45o nhôø daây BC. Tính goùc nghieâng ϕ
cuûa daây khi thanh ôû traïng thaùi saép tröôït. Α 45o Ñaùp soá: P f 2 tg + ϕ = Pf
27. Maâm quay A duøng ñeå naâng ñaàu maùy xe A
löûa coù moâ hình nhö hình veõ. Caùc con laên hình
noùn B ñöôïc boá trí giöõa maâm A vaø neàn. Bieát heä B B 2α
soá ma saùt tröôït giöõa con laên vaø neàn laø f. Xaùc
ñònh goùc 2 α cuûa con laên ñeå chuùng caân baèng
(töï haõm) duø aùp löïc cuûa maâm raát lôùn.
Ñaùp soá: 2α ≤ ϕ = arctgf
28. Tìm goùc nghieâng cho pheùp cuûa raêng ñinh vít (ñoä 2α
nghieâng cuûa ren) ñeå ñinh vít khoâng tröôït duø löïc caøng
lôùn, cho goùc ma saùt taïi maët tieáp xuùc laø ϕ.
Ñaùp soá: α < ϕ.
29. Cho taûi A vaø B coù lieân keát nhö hình veõ. Heä soá ma
saùt tröôït giöõa A vaø B laø μ A 1 = 0,3 giöõa B vaø maët P B
nghieâng laø: μ2 = 0,4 cho mA = mB = 250 kg 30 o
a) Tìm löïc P toái thieåu ñeå B chuyeån ñoäng.
b) Xaùc ñònh söùc caêng trong hai tröôøng hôïp: - B saép chuyeån ñoäng
- B ñang trong mieàn caân baèng.
Ñaùp soá: a) P = 1863,4 N 194 b) T = 1110 N; T = 0
30. Cho truï ñaëc ñoàng chaát chòu löïc nhö hình veõ. Heä soá ma P
saùt tröôït μ = 0,3. Tìm ñoä cao x ñeå truï coù theå vöôït qua, 3m bieát P = 250 N. x
Ñaùp soá: x = 0,17 m.
31. Caùc truï troøn ñoàng chaát gioáng nhau cuøng khoái löôïng m
= 50 kg. Heä soá ma saùt giöõa caùc maët tieáp xuùc laø μ = F
0,2. Tìm löïc F ñeå heä caân baèng. 30o
32. Tìm caùc löïc F1, F2 ñaët vaøo cô caáu haõm F
ñeå truïc quay caân baèng. 1 F2
Bieát truïc quay chòu taùc ñoäng cuûa
ngaãu M = 16KN; baùn kính R = 0,2 m; heä 1m
soá ma saùt tröôït giöõa caùc caàn haõm vaø truïc B quay laø f = 0,2. Ñaùp soá: 0,4m F1 + F2 ≥ 160 KN
33. Maùy daùt kim loaïi goàm hai truïc caùn O,
O’ quay ngöôïc chieàu nhau. Vaät caùn ñöôïc O
ñaët treân heä thoáng con laên.
Bieát baùn kính moãi truïc laø r; 2a 2d
OO’ = 2 d; heä soá ma saùt tröôït giöõa vaät caùn vaø truïc caùc f = tgϕ. O’
Tìm ñoä daøy lôùn nhaát 2a cuûa vaät
caùn ñeå maùy coù theå laøm vieäc ñöôïc. Ñaùp soá: a = 2(d – rcosϕ) Q
34. Cho heä thoáng neâm nhö hình veõ.
Tìm löïc P toái thieåu ñaët vaøo neâm A B
ñeå neâm B ñöôïc naâng leân. Bieát goùc ma saùt α P A 195
giöõa caùc neâm laø ϕ1, giöõa neâm A vaø neàn ngang laø ϕ2.
Boû qua troïng löôïng cuûa caùc neâm vaø ma saùt taïi oå tröôït ñöùng. Cho α > ϕ2.
35. Hai vaät A, B troïng löôïng töông öùng 200 B
N vaø 300 N noái vôùi nhau baèng daây maûnh.
Bieát heä soá ma saùt tröôït vôùi maët nghieâng laø: A fA = 0,5; fB = 2/3.
Heä hai vaät coù caân baèng khoâng? 30O
Tìm söùc caêng daây vaø caùc löïc ma saùt.
Ñaùp soá: heä caân baèng; FA = 86,6 N; FB = 213,4 N; T = 13,4 N.
36. Taám moûng troïng löôïng P ñaët treân hai baùnh xe A vaø B ñoàng chaát cuøng baùn
kính R, troïng löôïng p. Bieát heä soá ma saùt tröôït, laên giöõa baùnh xe vôùi maët ñöôøng
vaø taám moûng ñeàu laø f vaø k. Troïng taâm taám laø G. Xaùc ñònh löïc keùo F ñeå heä ôû
traïng thaùi saép laên khoâng tröôït. a b G A B Ñaùp soá: k F = (P + p) ≤ fP . R
37. Cô heä coù lieân keát chòu löïc nhö
hình veõ. Bieát taûi A troïng löôïng Q; A
taûi B troïng löôïng P; heä soá ma saùt
tröôït giöõa A vaø neàn laø f. R r
Tìm ñieàu kieän cuûa heä ñeå M
caân baèng. Boû qua ma saùt oå truïc.
Ñaùp soá: rP < M < rP + Qf m
38. Cho cô heä goàm hai thanh ABC
vaø DH lieân keát, chòu löïc nhö hình
veõ. Daây meàm noái vaøo ñaàu H vaét qua B
roøng roïc khoâng troïng löôïng, khoâng ma saùt ôû oå truïc, taûi E coù troïng löôïng P. Bieát:
AB = DC = 2BC = 2HC = 2 m; P = 4 3 KN ; F = 6 KN M1 = 20 KNm; M 9 3 ; KNm 2 = q = 10 KN/m.
Giaû söû maët nghieâng trôn nhaün:
- Xaùc ñònh phaûn löïc taïi A, C theo goùc α 196
- Trong hai tröôøng hôïp α = 30o vaø α = 80o, giaù trò caùc phaûn löïc laø bao nhieâu ?
2) Cho heä soá ma saùt tröôït giöõa E vaø maët nghieâng laø: f = 1 3
- Tính laïi caùc phaûn löïc taïi A, C vôùi hai giaù trò goùc α = 60o vaø α = 20o.
Giaû thieát khi ñaët taûi E leân maët nghieâng daây chöa caêng. I 60o E H M2 α M C 1 q 30o A D B 30o F Ñaùp soá: 1) α = 30o ; A = 25 , 5 3 − ; 25 , 2 A = 25 , 16 − 25 , 2 3 x y M = 75 , 41 − 75 , 6 3 ; N A C = (5 , 4 3 − ) 1 α = 80o ; A = 3 ; 3 A = ; 23 M = ; 26 N = 0 x y A C 2) α = 20o ; A = 25 , 5 ; 3 A = ; 75 , 32 M = 5 , 39 − 25 , 2 ; 3 N = 5 , 4 3 x y A C α = 80o ; A = 75 , 3 ; 3 A = ; 25 , 25 M = 5 , 30 − 75 , 0 ; 3 N = 5 , 1 3 x y A C
39. Cho heä khung goàm hai daàm gaáp khuùc ñöôïc moâ taû qua caùc hình veõ döôùi ñaây.
Caùc soá lieäu cho ôû baûng: P P Q(KN/ Hình a b c d 1(KN 2(KN ) ) m) 1 8,6 11,4 1,4 200 80 32 9,4 12,4 0,7 46 84 34 2 6,4 2,8 7,2 4,2 82 12 5,8 3,6 5,4 4,6 28 13 3 6,8 7,4 5,2 0,8 21 14 7,8 6,6 5,4 1,1 36 12 197 4 6,2 4,6 4,8 5,2 44 12 5,8 8,2 6,4 4,6 38 11 5 3,6 4,4 6,2 9,2 84 14 3,6 4,2 5,8 9,6 88 22 6 6,4 7,4 1,2 86 26 4,2 8,8 10,2 0,9 42 124 3,6 a a a a a a P P C 1 2 c c d a P c c B 1 B b P1 b c d b A B A Hình 1 Hình 2 Hình 3 a a P a a 1 5q q C C C b d b B P B d d 1 d b c c A B Hình 4 Hình 5 Hình 6
40. Cho caùc daøn phaúng döôùi ñaây:
a) Xaùc ñònh öùng löïc trong caùc thanh baèng phöông phaùp taùch nuùt
b) Xaùc ñònh öùng löïc trong caùc thanh baèng phöông phaùp tónh ñoà 198
c) Xaùc ñònh öùng löïc trong caùc thanh 1, 2, 3 baèng phöông phaùp maët caét P2 1 B P 1 B 2 P1 P3 P 2 1 3 2 30o 2 45o 3 30o 30o A 3 A 30o a a a 3 P P P3 P 3 1 1 1 30o P2 30 2 o Hình 1 Hình 2 A 60o 3 A P A B B a 1 P2 P 1 P1 P 2 1 Hình 5 Hình 3 6 a 2 2 B 30o 3 A 45o 1 A a P P3 2 P3 Hình 3 Hình 4 B. PHAÀN ÑOÄNG HOÏC
I. CHUYEÅN ÑOÄNG CÔ BAÛN CUÛA VAÄT RAÉN
1. Cô caáu nhö hình veõ. Bieát ω = 2, ε = 1 A M B (rad,s). Tìm:
VM; WM taïi vò trí ñang xeùt. ω ε Cho OA = OB = a; O1O2 = AB O O 1 2 Ñaùp soá: I ωo O O z z 1 VM = VA = aω = ; a 2 WM = WA = aε = a Wn = Wn = a 2 ω = a 4 M A εo
2. Cô caáu truyeàn ñoäng baèng baùnh raêng daây ñai nhö hình veõ. II Bieát: O ω 2 o = 2; εo = 2(rad,s) Vaø: R1 R2 Ro = = = 1 r = 2 r 2 4 199 Tìm:
V A, WA - taïi thôøi ñieåm ñang xeùt Ñaùp soá: 1 r 1 r VA = ωo A W ; = εo 8 8
3. Cho truïc quay duøng ñeå thaû quaû A B 25 mm
caân M ñi xuoáng nhö hình veõ. Haõy ε = 2 rad/s o
xaùc ñònh vaän toác, gia toác cuûa quaû caân m m ω = 4 rad/s 75 o
M bieát tay quay coù ω = 4rad/s; εo = 2rad/s2. C Ñaùp soá: V = mm 100 / s ↓ ; W = 2 mm 50 / s ↑ C C
II. CHUYEÅN ÑOÄNG PHÖÙC HÔÏP M
4. Xe A chuyeån ñoäng treân ñöôøng ngang vôùi H
vaän toác V, gia toác W nhö hình veõ. Taûi B V
tröôït treân giaù nghieâng HK vôùi quy luaät S = B
2t2. Ban ñaàu B naèm taïi H. Xaùc ñònh W
V B, WB taïi caùc thôøi ñieåm t1 = 1s, t2 = 2s A α (HK ñuû daøi). K
Ñaùp soá: VB = V + Vr V ; ) 1 ( = V ; 4 ) 2 ( = 8 r r WB = W + Wr W ; ) 1 ( = W ( )2 = 4 r r
5. Cô caáu ñieàu tieát ly taâm: khung quay I H
quanh truïc thaúng ñöùng vaän toác goùc ω1 ω e e
o = 4, gia toác goùc εo = 2 taïi thôøi ñieåm ε α 1
ñang xeùt nhö hình veõ. Caàn IB quay quanh I
vôùi vaän toác goùc ω1 = 2, gia toác goùc ε1 = 1 B B
(rad,s). Cho e = 0,1 m; IB = 0,3 m. Xaùc ωo
ñònh VB, WB taïi thôøi ñieåm ñoù. εo
6. Cho cô caáu nhö hình veõ. Bieát ωo = 4; εo B ε B C o A ωo 30o C ωo εo 60o Hình a Hình a Hình b Hình b 200
= 1 (rad,s); OA = 1 m (hoaëc OB = 0,6 m). Tìm V, W cuûa thanh BC (hình a vaø b). 7. Cho ω B E o = 2, εo = 1 (rad,s). Tìm V, W cuûa thanh BE εo O A
Bieát OA = 1 (m); O1B = 3 (m). O1 60o
8. Tay quay OA quay ñeàu vaän toác goùc ωo B
= 5 rad/s. Tìm vaän toác vaø gia toác cuûa caàn BC
theo goùc θ. Caùc kích thöôùc treân hình veõ. C Ñaùp soá: V = 750cosθmm / s ↑ 150 mm A ω = 5 rad/s θ W = 3750sinθ 2 mm / s ↓ O
9. Thanh CED quay ñöôïc quanh truïc E trong d E
maët phaúng thaúng ñöùng. Caùc choát A. B tröôït
trong caùc raõnh cuûa thanh vöøa tröôït ñöôïc θ y
trong caùc giaù töông öùng thaúng ñöùng vaø naèm 90o h ngang. A B
Xaùc ñònh vaän toác goùc ω, gia toác goùc ε VA C x D cuûa thanh CEB theo y. A
10. Cô caáu goàm nöûa hình troøn taâm B baùn
kính R = 3 m chuyeån ñoäng theo quy luaät x
= 0,8sinπt (m,s) (hình beân). B1 α I x
Tìm quy luaät chuyeån ñoäng cuûa thanh O IA. Bieát IO = 1,5 m
III. CHUYEÅN ÑOÄNG SONG PHAÚNG R r
11. Cô caáu con laên hình truï hai taàng laên B
khoâng tröôït nhö hình veõ do chuyeån ñoäng cuûa C I A 201
taûi A. Cho R = 2r = 0,4 (m). Taûi A ñi xuoáng theo quy luaät x = 2t2. Tìm
VB, WB, ω, ε cuûa truï taïi thôøi ñieåm t1 = 2; t2 = 4 (s).
12. Cô caáu vi sai nhö hình veõ, cho R R 2 1 = = ). m ( 2 , 0
Taïi thôøi ñieåm ñang xeùt tay 2 R1 ωo quay OA coù: ω A o = 2; εo = 2 (rad,s). Tính ω R
1, ε1, ω2, ε2 cuûa caùc baùnh raêng 2 εo töông öùng.
13. Cô caáu nhö hình veõ, giaû söû con laên laên khoâng tröôït. Cho RB = RC = 2rc = 0,2 (m). Bieát:
VA = 2 (m/s); WA = 1 (m/s2); VB = 1 (m/s); WB = 1 (m/s2). Tính
ωB, εB, ωC, εC vaø VD, WD. VA A WA . B C . W . B V I B α D A ωo
14. Cho cô caáu boán khaâu nhö hình beân. Cho εo
AB = CD = 0,4 m; BC = AD = 0,2 m. Xaùc
ñònh ω, ε cuûa thanh BC bieát AB coù ω C o = 2; ε D o = 2 (rad,s). B A
15. Cô caáu tay quay thanh truyeàn nhö hình veõ. Bieát OA ñaït ω ω o = 3, εo = 1 (rad,s). o εo B Tìm V O
B , WB vaø vaän toác goùc ω 30 o 1, gia
toác goùc ε1 cuûa thanh AB khi OA = 0,4 (m). D
16. Cô caáu nhö hình beân vôùi chuù yù thanh ID A C
noái baûn leà vôùi thanh AB ñoàng thôøi tröôït
ñöôïc trong oå C. Taïi vò trí treân hình veõ bieát ε o ω I o B O 30 o 202
ωo = 3, εo = 1 (rad/s). Cho OA = 0,6 (m); AI = IB. Tính ω1, ε1 cuûa thanh ID.
17. Cô caáu nhö hình veõ (hình a, b). Con laên laên khoâng tröôït treân ñöôøng naèm ngang coù V 2
o = 6 (m/s) khoâng ñoåi. Cho OA = R = ) m ( 4 , 0 , tìm ω, ε cuûa thanh 3
AC taïi vò trí treân hình veõ (AC noái baûn leà taïi A). A A V C V C 30o o 30o o O O Hình a Hình b
18. Tay quay OA noái baûn leà vôùi thanh BC (hình
beân). Bieát taïi thôøi ñieåm ñang xeùt OA ñaït ωo = 2, ε C
o = 2 (rad,s). Cho BC = 1 m = 2OA. Xaùc ñònh VB, V , W C B, WC cuõng nhö ω, ε cuûa thanh BC. 30o Ñaùp soá: A
V = 3 → ; V = 1 ↓ ; W = 2 − 3 ← B C B εo ω 2 3 W = o C 1 + ↓ ; ω = 2 ε = 4 3 − 4 3 O B
19. Cô caáu nhö hình veõ. Cho AC = a, BC = b. Taïi
thôøi ñieåm ñang xeùt. Bieát VA, VB , tìm VC, WC . B C 4 4 Ñaùp soá: VA VB VC = ; 0 C W = + 2 2 a b VB A V A
20. Hình truï taâm O bò keïp giöõa hai thanh V1
raêng, cho bieát hai thanh raêng tònh tieán
coù vaän toác, gia toác töông öùng laø A W1 V1, W1, V2, W2 . O R Xaùc ñònh
Vo, Wo vaø ω, ε cuûa truï V B 2
(giaû thieát khoâng coù söï tröôït giöõa truïc O vaø caùc thanh raêng). W2 Ñaùp soá: V1 + V W − W V 2 o = ; W 1 2 = ; 2 o 2 203 V1 − V2 W1 + W ω 2 o = ; ε = R 2 o R 2
21. Coù heä goàm hai Puli I, II cuøng baùn kính
vaø thanh OA, daây ñai khoâng tröôït treân II R
Puli. Puli I coá ñònh, cho tay quay OA coù ε ωo o A ωo, εo (hình beân).
Xaùc ñònh chuyeån ñoäng cuûa Puli II. O
Ñaùp soá: ω = 0 ; ε = 0 I 2 2
22. Cho con laên hai taàng laên khoâng tröôït R
treân ñöôøng ngang nhö hình veõ. Bieát taâm O . r ñaït V V o = 4 (m/s); Wo = 2 (m/s2) O o . . R = 2r = 0,4 m wo Tìm V A, W A .
(xem daây treo thaúng ñöùng) A
23. Cô caáu truyeàn ñoäng nhö hình veõ. Tay ω = 4 rad/s BC
quay BC quay ñeàu quanh truïc B coá ñònh R vaän toác goùc ω D
o = 4 rad/s. Xaùc ñònh vaän toác A goùc ω B C
R, εR cuûa baùnh xe R khi baùnh xe D ωR coá ñònh. 150 mm 75 mm Ñaùp soá: ωR = 6rad/s; εR = 0 R
24. Cô caáu nhö hình veõ. Baùnh raêng coá ñònh
baùn kính 4 in naèm ôû trung taâm. Taám C P P
quay ñöôïc quanh truïc coá ñònh truøng vôùi S
taâm cuûa baùnh xe coá ñònh. Ba baùnh raêng 4 in C
ñoäng P gaén ñoái xöùng vaøo taám C baùn kính 2 ωc ω 2 in R = 5 rad/s in. Bieát ωR = 5 rad/s. P Tìm ωC?
Ñaùp soá: ωC = 4rad / s
25. Cho hoäp soá nhö hình veõ. Bieát soá raêng cuûa caùc baùnh raêng:
Hình a: Z1 = 80; Z2 = 20; Z3 = 40
Hình b: Z1 = 70; Z2 = 20; Z3 = 30 204
Tìm vaän toác goùc ωII cuûa truïc II. 2 2 3 3 ωI 1 ωI 4 4 II 1 I ω 2 1 2 3 3 Hình a ω 2 4 I 3 I II 2 3 1 Hình b
C. PHAÀN ÑOÄNG LÖÏC HOÏC
I. ÑOÄNG LÖÏC HOÏC ÑIEÅM
1. Baøn maùy baøo khoái löôïng m1 = 700 kg, vaät gia coâng khoái löôïng m2 = 300 kg.
Vaän toác oån ñònh trong haønh trình laø v = 0,5 m/s, thôøi gian laáy ñaø t = 0,5 s. Xaùc
ñònh löïc caàn thieát ñeå laáy ñaø (xem chuyeån ñoäng cuûa baøn trong khoaûng thôøi gian
naøy laø nhanh daàn ñeàu) vaø löïc ñeå duy trì baøn maùy chuyeån ñoäng ñeàu trong quaù
trình tieáp theo. Cho bieát heä soá ma saùt tröôït luùc laáy ñaø laø f1 = 0,14; luùc chuyeån
ñoäng ñeàu laø f2 = 0,07.
Ñaùp soá: P1 = 2374 N; P2 = 686,7 N.
2. Moät oâ toâ chôû haøng coù khoái löôïng 6 taán chaïy xuoáng moät chieác phaø vôùi toác ñoä
21,6 km/giôø, sau ñoù chuyeån ñoäng chaäm daàn ñeàu theâm 10 m thì döøng laïi. Tính
toång löïc caêng cuûa caùc daây caùp giöõ phaø (giaû thieát luoân luoân caêng). Ñaùp soá: 10791 N.
3. Moät saøng quaëng thöïc hieän dao ñoäng ñieàu hoøa thaúng ñöùng vôùi bieân ñoä
a = 5 cm. Xaùc ñònh taàn soá k nhoû nhaát cuûa saøng ñeå cho caùc haït quaëng nhaûy ñöôïc leân khoûi maët saøng.
Ñaùp soá: k = 14 rad/s 205
4. Moät vaät naëng rôi xuoáng gieáng moû khoâng vaän toác ban ñaàu, sau thôøi gian 6,5
giaây ngöôøi ta nghe thaáy tieáng va vaøo ñaùy gieáng. Cho bieát vaän toác cuûa tieáng
ñoäng laø 330 m/s. Tìm ñoä saâu cuûa gieáng. Ñaùp soá: 175 m.
5. Khi baùnh ñaø bò vôõ, maûnh vaêng xa nhaát ñi ñöôïc ñoaïn naèm ngang töø choã vôõ laø
280 m (cuøng ñoä cao). Boû qua söùc caûn khoâng khí. Tìm giaù trò nhoû nhaát cuûa vaän
toác goùc baùnh ñaø taïi thôøi ñieåm xaûy ra söï coá, bieát baùn kính baùnh ñaø laø R = 1,75 m.
Ñaùp soá: n = 286 voøng/phuùt.
6. Tìm vaän toác lôùn nhaát cuûa quaûù caàu coù khoái löôïng m = 10 kg, coù baùn kính
R = 8 cm, chuyeån ñoäng trong khoâng khí chòu löïc caûn laø R = kSv2 (trong ñoù S laø
dieän tích tieát dieän cuûa vaät theo phöông chuyeån ñoäng, v laø vaän toác, k laø heä soá
caûn). (ÔÛ ñaây laáy k = 0,2352 Ns2/m4).
Ñaùp soá: vmax = 144 m/s.
7. Moät chaát ñieåm khoái löôïng m chuyeån ñoäng thaúng döôùi taùc duïng cuûa löïc thay
ñoåi theo quy luaät F = Fo cosωt. Trong ñoù Fo haèng soá. Tìm phöông trình chuyeån
ñoäng cuûa chaát ñieåm, bieát vaän toác ban ñaàu cuûa noù laø Vo. Ñaùp soá: F x o = (t − cos t ω ) + vot m 2 ω
8. Moät oáng thaúng ñöùng ñaët taïi taâm cuûa beå troøn, ñaàu treân
haøn kín. Taïi ñoä cao 1m ngöôøi ta ñuïc caùc loã hoång ñeå nöôùc
tuoân ra vôùi vaän toác ban ñaàu 4g V = o m/s. ÔÛ ñaây ϕ 3cos 1m ϕ
laø goùc nghieâng baén ra cuûa tia nöôùc so vôùi phöông naèm 2R ngang ( π ϕ <
). Xaùc ñònh baùn kính R nhoû nhaát cuûa beå ñeå 2
nöôùc khoâng ñi ra ngoaøi thaønh beå vôùi baát kyø ñoä cao naøo cuûa thaønh beå.
Ñaùp soá: R = 2,83 m.
9. Söï leäch cuûa tia catoát trong töø tröôøng haït coù khoái löôïng
m mang ñieän tích aâm e ñi vaøo töø tröôøng thuaàn nhaát coù F
cöôøng ñoä H vôùi vaän toác v V
o tröïc giao vôùi höôùng cöôøng ñoä
töø tröôøng. Xaùc ñònh quyõ ñaïo tieáp theo cuûa haït, bieát raèng H m
löïc taùc duïng leân noù: F = − .( e v ∧ H) .
Ñaùp soá: ñöôøng troøn baùn kính mv R o = . eH 206
10. Quaû caân nhoû M buoäc vaøo ñaàu sôïi daây khoâng daõn O M
MOA. Giöõ A cho quaû caân quay 120 voøng/phuùt quanh truïc 1
oáng (OA) vôùi baùn kính R = MC. Keùo töø töø sôïi daây OA cho R OM ngaén daàn ñeán OM M
1. Khi ñoù quaû caân vaïch ñöôøng troøn 2 baùn kính R/2 = M A R
1C1. Quaû caân ñang quay quanh truïc OA bao nhieâu voøng/phuùt? C
Ñaùp soá: 480 voøng/phuùt.
11. Heä soá ma saùt giöõa baùnh xe oâ toâ vaø maët ñöôøng laø bao nhieâu ñeå xe döøng laïi
sau 6 giaây keå töø luùc haõm xe (xem baùnh xe khoâng quay keå töø luùc haõm). Bieát toác
ñoä luùc baét ñaàu haõm laø V = 72 km/h.
Ñaùp soá: μ = 0,34.
II. CAÙC ÑÒNH LYÙ TOÅNG QUAÙT CUÛA ÑOÄNG LÖÏC HOÏC
1. Ñònh lyù chuyeån ñoäng khoái taâm
12. Xaùc ñònh di chuyeån ngang cuûa con taøu B
mang caàn caåu khi caàn AB mang vaät naëng 30 o
coù khoái löôïng baèng 2 taán caát thaúng ñöùng
leân töø vò trí ban ñaàu nghieâng goùc 30o nhö A
hình veõ: khoái löôïng cuûa taøu vaø caàn caåu
baèng 20 taán, chieàu daøi AB baèng 8 m. Boû
qua söùc caûn cuûa nöôùc vaø khoái löôïng cuûa caàn AB.
13. Hai vaät naëng A vaø B coù khoái löôïng m1 vaø m B
2 ñöôïc noái vôùi nhau baèng moät sôïi daây E
meàm, nheï vaø khoâng daõn vaø ñöôïc ñaët leân K A
caùc maët KL vaø KE cuûa laêng truï DEKL.
Laêng truï coù khoái löôïng m ñöôïc ñaët treân D 60 o L
neàn ngang nhaün vaø cöùng. Tìm di chuyeån
cuûa laêng truï khi vaät naëng A tröôït xuoáng
theo maët nghieâng KL moät ñoaïn daøi S (hình
veõ). Ban ñaàu heä ñöùng yeân. o Ñaùp soá: (m cos 60 + m ) 1 2 Δ = S m + m + m y 1 2 3 B
14. Moät taám ñoàng chaát ABC coù hình daïng M
laø moät tam giaùc vuoâng caân, caïnh huyeàn AB C
daøi 12 cm ñöôïc ñaët thaúng ñöùng töïa ñænh A
treân maët phaúng ngang nhaün khoâng ma saùt.
Ngöôøi ta thaû cho taâm phaúng ñoå xuoáng döôùi x
taùc duïng cuûa troïng löïc. Haõy xaùc ñònh quyõ A 207
ñaïo cuûa ñieåm M naèm chính giöõa caïnh beân BC. Chuù yù: trong suoát thôøi gian
chuyeån ñoäng ñænh A luoân luoân naèm treân maët ngang (hình veõ).
Ñaùp soá: ñoaïn cung elip 9(x – 2)2 + y2 = 90.
15. Moät ñoäng cô hôi nöôùc ñaët naèm
ngang treân maët moùng nhaün trôn. Tay A
quay OA coù chieàu daøi laø r vaø quay ñeàu B O
vôùi vaän toác goùc laø ω. Thanh truyeàn coù
ñoä daøi baèng tay quay (OA = AB).
Coi khoái löôïng cuûa caùc boä phaän
chuyeån ñoäng ñöôïc thu goïn veà thaønh hai khoái löôïng m1 vaø m2 taäp trung ôû ñaàu tay
quay vaø ôû troïng taâm cuûa piston. Khoái löôïng cuûa voû ñoäng cô laø m3. Xaùc ñònh
chuyeån ñoäng ngang cuûa voû ñoäng cô. Cho bieát ban ñaàu piston ôû vò trí xa nhaát veà beân traùi.
Neáu ñoäng cô ñöôïc baét vít chaët xuoáng neàn, tìm aùp löïc cuûa ñoäng cô leân
neàn vaø caét ngang buloâng. Boû qua löïc caêng ban ñaàu cuûa buloâng (xem hình veõ). Ñaùp soá: (m + m 2 1 2 ) r x = (cosωt − ) 1 m1 + m2 + m3 N = (m1 + m2 + m3) 2 g − m1rω sin ω T = (m1 + m 2 ) r 2 2 ω cos t ω
2. Ñònh lyù ñoäng löôïng
16. Moät ñaàu ñaïn coù khoái löôïng m = 0,02 kg bay ra khoûi noøng suùng vôùi vaän toác v
= 650 m/s. Thôøi gian ñaàu ñaïn chaïy trong noøng suùng laø t = 0,000955 s. Tieát dieän
ngang cuûa noøng suùng laø σ = 1,5.10-4 m2. Tìm aùp suaát trung bình cuûa hôi noå trong
noøng suùng. Boû qua taùc duïng cuûa troïng löïc vaø cuûa aùp suaát khí quyeån.
Ñaùp soá: P = 91.106 N/m2
17. Noøng suùng ñaïi baùc ñaët naèm ngang troïng löôïng 110 KN. Troïng löôïng vieân
ñaïn baèng 540 N. Vaän toác vieân ñaïn luùc ra khoûi mieäng suùng vo = 900 m/s. Xaùc
ñònh vaän toác giaät luøi cuûa noøng suùng ôû thôøi ñieåm vieân ñaïn bay ra.
Ñaùp soá: vaän toác giaät luøi cuûa noøng suùng baèng 4,42 m/s vaø höôùng ngöôïc chieàu
chuyeån ñoäng cuûa vieân ñaïn. V 2
18. Xaùc ñònh thaønh phaàn aùp löïc cuûa nöôùc song song α
vôùi truïc ñoái xöùng cuûa caùnh coá ñònh cuûa roâto tuabin.
Cho bieát löu löôïng theå tích cuûa nöôùc laø Q vaø khoái
löôïng rieâng cuûa noù laø γ. Vaän toác cuûa nöôùc luùc va vaøo V 1
caùnh tuabin laø v1 höôùng song song vôùi truïc ñoái xöùng, α V 2 208
vaän toác luùc ra khoûi caùnh laø v2 hôïp vôùi maët phaúng ñoái xöùng goùc α (xem hình veõ).
Ñaùp soá: N = γQ(v1 + v2cosα)
3. Ñònh lyù moâmen ñoäng löôïng
19. Moät moâtô ñieän chòu taùc duïng cuûa moät ngaãu löïc toång hôïp (phaùt ñoäng vaø caûn)
coù moâmen quay laø M = a – bω, trong ñoù a, b laø caùc haèng soá döông coøn ω laø vaän
toác goùc moâtô. Moâmen quaùn tính cuûa roâto ñoái vôùi truïc quay hình hoïc laø J. Tìm
bieåu thöùc vaän toác goùc ω trong quaù trình môû maùy töø traïng thaùi ñöùng yeân.
20. Ñeå haõm nhanh moät voâ laêng lôùn ngöôøi ta duøng haõm ñieän. Khi voâ laêng chuyeån
ñoäng doøng ñieän caûm öùng gaây neân moät moâmen haõm taùc duïng vaøo voâ laêng vaø coù
giaù trò tyû leä vôùi vaän toác V treân vaønh voâ laêng M1 = kV, trong ñoù k laø heä soá tyû leä.
Moâmen caûn do ma saùt gaây ra ôû truïc voâ laêng baèng M2 coi nhö khoâng ñoåi. Voâ
laêng coù ñöôøng kính D, coù moâmen quaùn tính ñoái vôùi truïc quay laø J. Luùc baét ñaàu
haõm voâ laêng coù toác ñoä goùc ωo.
Hoûi sau bao laâu döøng haún chuyeån ñoäng, boû qua taùc duïng cuûa troïng löïc. Ñaùp soá: 2J ⎛ ω kD ⎞ T = o ⎜⎜ ln 1 + ⎟⎟ kD ⎝ M 2 2 ⎠
21. Moät vaät raén quay quanh truïc coá ñònh khôûi ñoäng töø traïng thaùi ñöùng yeân chòu
taùc duïng cuûa moâmen quay khoâng ñoåi M vaø cuûa moâmen caûn M1 =αω2, trong ñoù
α laø haèng soá vaø ω laø vaän toác goùc cuûa vaät. Moâmen quaùn tính cuûa vaät ñoái vôùi truïc
quay laø J. Tìm luaät bieán thieân cuûa vaän toác goùc theo thôøi gian vaø tìm giaù trò vaän
toác goùc giôùi haïn cuûa vaät. Ñaùp soá: M eβ − 1 t ω = , 2 ñoù trong :β = αM α eβ + 1 t J
22. Ñeå xaùc ñònh moâmen quaùn tính cuûa moät vaät
ñaõ cho ñoái vôùi moät truïc AB qua khoái taâm C cuûa D E
vaät, ngöôøi ta treo vaät baèng hai thanh AO vaø BE
gaén cöùng vaøo vaät, sao cho AB song song vôùi DE
vaø cuøng naèm ngang. Hai thanh AD vaø BE quay A B C
ñöôïc töï do quanh truïc DE coá ñònh (xem hình veõ).
Sau ñoù cho vaät dao ñoäng vaø ño nöûa chu kyø T cuûa dao ñoäng. Cho bieát troïng löôïng
cuûa vaät laø P vaø khoaûng caùch giöõa AB vaø DE baèng h. Boû qua troïng löôïng cuûa hai
thanh treo vaø boû qua ma saùt ôû caùc khôùp quay. Tính moâmen quaùn tính cuûa vaät ñoái
vôùi truïc AB (hình veõ). 209 ⎛ T2 h ⎞ Ñaùp soá: J = ⎜ hP − ⎟ ⎜ . 2 ⎟ ⎝ Π g ⎠
23. Ñeå xaùc ñònh moâmen J cuûa baùnh ñaø A baùn kính R =
50 cm ñoái vôùi truïc quay qua troïng taâm cuûa noù. Ngöôøi ta O
quaán vaøo baùnh ñaø sôïi daây meàm nheï ñaàu daây treo quaû caân A
B troïng löôïng P1 = 8 kg vaø quan saùt sau 16 giaây quaû caân haï
xuoáng ñoaïn h = 2 m. Ñeå loaïi ma saùt oå truïc ngöôøi ta thay
quaû caân thöù hai troïng löôïng P1 = 4 kg, thaáy thôøi gian ñi h
ñoaïn ñöôøng treân laø 25 giaây. Xem moâmen caûn khoâng ñoåi vaø
khoâng phuï thuoäc quaû caân. Haõy tính J. B 1 ( ⎛ ⎞ P − P − ⎜ − ⎟ 1 2 ) 1 P1 P2 2h g ⎜ 2 2 ⎟ Ñaùp soá: T 2 ⎝ 1 T J = R . 2 ⎠ = kgm 1061 2. 1 1 − T2 T2 1 2 (Ti laø thôøi gian).
4. Ñònh lyù ñoäng naêng
24. Moät vaät tröôït xuoáng khoâng vaän toác ñaàu theo maët phaúng nghieâng goùc 30o so
vôùi phöông naèm ngang, heä soá ma saùt baèng 0,1. Hoûi sau khi ñi ñöôïc 2 m vaät coù
vaän toác baèng bao nhieâu? Ñaùp soá: 4,02 m/s.
25. Ñaát ñöôïc neän baèng buùa coù troïng löôïng 600 N vaø thieát dieän ñaùy 12 dm2 rôi töø
ñoä cao h = 1 m, buùa luùn saâu vaøo ñaát 1 cm. Xem löïc caûn cuûa ñaát leân buùa khoâng
ñoåi. Hoûi ñaát chòu ñöôïc taûi cöïc ñaïi bao nhieâu ñeå khoâng bò luùn.
(Giaû thieát neàn ñaát khoâng bò luùn khi chòu taûi neáu taûi naøy khoâng vöôït qua löïc caûn
maø buùa gaëp phaûi khi luùn vaøo ñaát).
Ñaùp soá: 50,5 N/cm2.
26. Cho cô caáu haønh tinh nhö hình veõ. Caùc 3
baùnh 1, 2, 3 laø caùc ñóa troøn ñoàng chaát, cuøng 2
baùn kính r, cuøng khoái löôïng m. Tay quay OA
ñöôïc xem laø moät thanh ñoàng chaát coù khoái 1 O
löôïng m1. Tính ñoäng naêng cuûa cô caáu theo vaän
toác goùc tay quay (xem hình veõ). 2 2 Ñaùp soá: r T = m 33 ( m 8 ω + 1) . 3
27. Tính ñoäng naêng cuûa daây xích maùy keùo khi
maùy keùo chuyeån ñoäng vôùi vaän toác vo. Khoaûng
caùch giöõa hai truïc baùnh xe laø l, baùn kính baùnh V
xe laø r, troïng löôïng cuûa daây xích treân moät meùt O l daøi laø γ. 210 Ñaùp soá: γ 2 T = 2 (l + r π )vo . g
28. Tính ñoäng naêng cuûa cô heä tay quay raõnh tröôït nhö C
hình veõ theo vaän toác goùc ω cuûa tay quay vaø goùc quay A
ϕ. Cho tay quay OC daøi R khoái löôïng m1, con chaïy A
khoái löôïng m2, thanh AB khoái löôïng m3 vaø OK = l O ϕ K
(xem con chaïy nhö chaát ñieåm). 2 Ñaùp soá: T ω = [m R2 cos4 ϕ + 3 2l(m + m ) 1 2 3 ] 6 cos4 ϕ
29. Moät ñoäng cô ñieän keùo moät heä thoáng truyeàn ñoäng B
duøng xích nhö treân hình veõ. Heä thoáng ñoù laøm vieäc nhö sau: luùc môû maùy, xích baét
ñaàu chuyeån ñoäng vôùi gia toác W vaø khi ñaõ ñaït ñöôïc Wmax thì giöõ nguyeân toác ñoä
ñoù. Ñöôøng kính cuûa truïc chính gaén vôùi ñoäng cô O baèng 2r 3
1, ñöôøng kính cuûa hai roøng roïc khaùc laø 2r2
vaø 2r3. Ñoái vôùi truïc quay cuûa chuùng moâmen quaùn O
tính cuûa truïc quay chính laø J 1 1, moâmen quaùn tính O2
cuûa caùc roøng roïc laø J Q
2 vaø J3. Troïng löôïng cuûa hoøm 2
ñöôïc keùo leân laø Q1, cuûa hoøm ñöôïc thaû xuoáng laø
Q2. Moãi ñôn vò daøi cuûa daây xích naëng laø q vaø xích Q1
coù ñoä daøi l. Tính coâng suaát cuûa ñoäng cô trong quaù
trình môû maùy vaø trong quaù trình chaïy oån ñònh V = Vmax (xem hình). Ñaùp soá: ⎡⎛ Q + Q + ql J J J ⎞ ⎤ W 1 2 1 2 3 = ⎢ + + + W + (Q − Q ⎜⎜ 2 2 2 ⎟⎟ 1 2 )⎥V g ⎣⎝ r r r 1 2 3 ⎠ ⎦
30. Moät con laên ñoàng chaát hình truï troøn
xoay coù ñöôøng kính 60 cm vaø coù khoái A
löôïng 392 kg, chuyeån ñoäng laên khoâng 1,5
tröôït treân maët phaúng ngang do moät ngöôøi
ñaåy. Löïc ñaåy P coù phöông chieàu khoâng
ñoåi vaø theo höôùng thanh ñaåy AO. Thanh 1,2
AO daøi 1,5 m; ñoä cao cuûa A so vôùi neàn O
ngang laø 1,2 m. Boû qua ma saùt ôû oå truïc
vaø ma saùt laên cuûa maët neàn.
a) Xaùc ñònh P sao cho khi ngöôøi ñaåy ñi ñöôïc 2 m thì truïc con laên ñaït vaän toác 0,8 m/s.
b) Neáu keå ñeán ma saùt caûn laên cuûa neàn vôùi heä soá k = 0,5 cm thì löïc P
phaûi coù cöôøng ñoä baèng bao nhieâu, laáy g = 9,8 m/s2.
c) Sau khi ñaït vaän toác caàn thieát nhö treân, muoán giöõ chuyeån ñoäng ñeàu
cuûa truïc baùnh xe, caàn giaûm cöôøng ñoä cuûa löïc P ñi bao nhieâu?
Ñaùp soá: a) P1 = 117,6 N; b) P2 = 199,9 N; c) Giaûm P moät löôïng laø 118,9 N. 211
31. Moät ngaãu löïc coù moâmen quay M khoâng ñoåi taùc duïng leân tang cuûa moät truïc
tôøi coù baùn kính baèng R vaø coù troïng O löôïng laø P M
1: quaán vaøo tang tôøi moät sôïi
daây meàm nheï vaø khoâng daõn roài buoäc A
ñaàu muùt töï do cuûa daây vaät naëng A coù α
troïng löôïng P2 ñeå keùo noù leân theo maët
phaêûng nghieâng coù goùc nghieâng laø α so vôùi maët phaúng ngang.
Heä soá ma saùt tröôït ñoäng giöõa maët phaúng vaø maët phaúng nghieâng laø f.
Tang tôøi ñöôïc xem laø moät truïc troøn ñoàng chaát.
Tìm bieåu thöùc vaän toác goùc cuûa truïc tôøi theo goùc quay cuûa noù (xem hình). Ñaùp soá: 2 M − P R(sin α + f cos α) ω = g 2 . ϕ R P + P 2 1 2
32. Moät vaät naëng P ñöôïc treo vaøo ñaàu moät sôïi daây meàm khoâng daõn chieàu daøi l
vaø moãi ñôn vò daøi cuûa noù coù troïng löôïng P. Daây naøy ñöôïc quaán vaøo tang cuûa
moät truïc tôøi coù baùn kính baèng R vaø coù moâmen quaùn tính ñoái vôùi truïc quay baèng
J. Vaät naëng rôi xuoáng laøm quay truïc tôøi. Luùc ñaàu ñoaïn daây treo buoâng daøi moät
ñoaïn Xo vaø cô heä ñöùng yeân. Boû qua ma saùt cuûa caùc oå truïc quay vaø chieàu daøi cuûa
daây cuõng nhö söï thay ñoåi theá naêng cuûa phaàn daây quaán.
Xaùc ñònh vaän toác rôi cuûa vaät naëng theo ñoä daøi x cuûa ñoaïn daây treo. [ P 2 + P(x + x )(x − x ) o o ] Ñaùp soá: V = R g . gJ + P ( + ) pl R2
33. Truïc tôøi goàm hai truï gaén ñoàng truïc nhö hình M
veõ, moâmen quaùn tính töông öùng ñoái vôùi truïc cuûa O O2 1
chuùng laø J1, J2. Boû qua troïng löôïng cuûa roøng roïc
vaø daây. Tìm vaän toác goùc ω cuûa heä truïc tôøi theo
ñoä dôøi S (ñi leân) cuûa taûi D khi cho ngaãu M
(const) taùc duïng nhö hình veõ. Ñaùp soá: D 2M − P(r2 − r1) ω = 2 2gS (r − r 2 1 [ ) P(r − r )2 + 4g(J + J ) 2 1 1 2 ]
34. Con laên ñoàng chaát baùn kính r troïng löôïng P ñaët T
treân neàn nhaùm naèm ngang ñöôïc quaán daây nhö hình O
veõ. Moät ñaàu daây ñöôïc keùo vôùi söùc caêng T höôùng α 2a
khoâng ñoåi, baùn kính quaùn tính cuûa con laên ñoái vôùi
truïc cuûa noù laø ρ. Caùc kích thöôùc coøn laïi cho treân hình veõ. 212
Tìm quy luaät chuyeån ñoäng cuûa truïc con laên. Ñaùp soá: T rg(r cos α − a) 2 x = t (t tính theo giaây). 2 2 P ( 2 ρ + r )
35. Nhôø daây khoâng daõn, khoâng troïng löôïng vaét qua
roøng roïc D (boû qua troïng löôïng vaø ma saùt oå truïc) D
sau ñoù quaán vaøo tang quay B, do ñoù khi taûi A troïng B C
löôïng P haï xuoáng thì con laên keùp C laên khoâng tröôït A
treân ñöôøng naèm ngang. Tang quay B baùn kính r gaén
chaët vôùi con laên keùp C baùn kính R, toång troïng löôïng Q, baùn kính quaùn tính ñoái
vôùi truïc naèm ngang qua taâm laø ρ. Tìm WA? 2 Ñaùp soá: P(R + r) A W = g . 2 2 2 Q(ρ + R ) + P(R + r)
36. Ngöôøi ta quaán daây meàm quanh ñóa moûng hình truï A khoái
löôïng m. Ñaàu kia cuûa daây buoäc chaët, giöõ nhaùnh daây thaúng ñöùng
nhö hình veõ vaø thaû cho rôi khoâng vaän toác ban ñaàu. Xaùc ñònh vaän
toác V cuûa taâm A theo ñoä dôøi h vaø söùc caêng daây. Ñaùp soá: 2 1 V = gh 3 T , = . mg 3 3
37. Moät daây ñoàng chaát daøi laø L coù moät phaàn L - 1
naèm treân maët baøn ngang nhaün moät phaàn
buoâng töï do. Xaùc ñònh khoaûng thôøi gian T
ñeå daây rôøi khoûi maët baøn, bieát raèng taïi thôøi l
ñieåm ñaàu chieàu daøi cuûa phaàn daây thaû buoâng
daøi laø l vaø vaän toác ñaàu baèng khoâng (xem hình). ⎛ 2 2 ⎞ Ñaùp soá: L ⎜ L + L − l ⎟ T = ⎜ ln g l ⎟ ⎝ ⎠
38. Khaûo saùt chuyeån ñoäng cuûa cô caáu bieåu
dieãn treân hình veõ. Cô caáu chuyeån ñoäng M
trong maët phaúng ngang. Tay quay OA ñöôïc 1 O
xem laø moät thanh ñoàng chaát daøi l naëng P.
Hai roøng roïc ñoäng vaø coá ñònh coù cuøng baùn
kính r, cuøng troïng löôïng Q vaø ñöôïc xem laø nhöõng ñóa ñoàng chaát. Taùc duïng leân
tay quay moät ngaãu löïc coù moâmen khoâng ñoåi M.
Tìm gia toác goùc cuûa tay quay. Boû qua söï tröôït giöõa ñai truyeàn vaø hai roøng roïc. Ñaùp soá: gM 3 ε = 2 Q ( + ) P 3 l 213
39. Khaûo saùt chuyeån ñoäng cuûa hoäp toác ñoä bieåu dieãn treân hình veõ. Truïc daãn vaø
truïc bò daãn lieân heä vôùi nhau baèng caùc caëp baùnh raêng haønh tinh keùp. Truïc daãn I
mang tay quay AB, truïc bò daãn IV mang baùnh raêng 4, caùc oå truïc ñaët treân hai ñaàu
tay quay mang truïc caùc caëp baùnh raêng haønh tinh 2-3. 2 2 3 3 ωΙ 1 ωΙ 4 4 II 1 ω I Ι 2 2 3 3
Cho bieát caùc baùn kính r1, r2, r3, r4 cuûa caùc baùnh raêng, moâmen quaùn tính
cuûa truïc daãn vôùi caùc chi tieát gaén treân noù ñoái vôùi truïc quay hình hoïc cuûa noù baèng
J1. Caëp baùnh raêng haønh tinh 2-3 coù khoái löôïng m2 vaø coù troïng taâm naèm treân truïc
ñoái xöùng hình hoïc cuûa noù vaø coù moâmen quaùn tính ñoái vôùi truïc ñoù laø J2. Moâmen
quaùn tính ñoái vôùi truïc bò daãn vaø caùc chi tieát laép vôùi noù ñoái vôùi truïc quay hình
hoïc cuûa noù laø J4. Truïc daãn chòu taùc duïng cuûa ngaãu löïc caûn coù moâmen M1, truïc bò
daãn chòu taùc duïng ngaãu löïc caûn coù moâmen M4, giaû thieát M1 vaø M4 ñeàu khoâng
ñoåi, boû qua ma saùt. Tìm gia toác goùc cuûa truïc l (xem hình). 1 r 3 r 1 M − 4 M 1 ( − ) Ñaùp soá: 2 r 4 r 1 ε = 2 1 r 2 1 r 3 r 2 1 J + m 2 2 1r ( + 2 r ) + J 2 2 1 ( + ) + 1 J 1 ( − ) 2 r 2 r 4 r
40. Moät vaät A coù troïng löôïng P ñöôïc keùo leân töø traïng thaùi
ñöùng yeân nhôø tôøi B coù baùn kính R, troïng löôïng Q vaø chòu O
taùc duïng ngaãu löïc coù moâmen M = M M o – αω2 trong ñoù Mo B
vaø α laø caùc haèng soá, ω laø vaän toác cuûa goùc tôøi. Cho bieát baùn
kính cuûa tôøi ñoái vôùi truïc quay O baèng ρ. Tìm vaän toác goùc
giôùi haïn cuûa tôøi quay vaø vaän toác goùc cuûa quaù trình chuyeån
tieáp cuûa noù töø traïng thaùi yeân nghæ. ABt − ABt A Ñaùp soá: A e − e gh ω = ; ω = gh ω ABt − ABt B e + e M − PR trong ñoù: A = g B ; g α = 2 2 2 2 PR + Qp PR + Qp
III. NGUYEÂN LYÙ D’ALAMBERT 214
41. Toa xe troïng löôïng P laên theo ñöôøng ray A
AB sau ñoù theo ñöôøng troøn voøng laïi BCB, baùn C
kính a. Hoûi phaûi thaû xe khoâng vaän toác ban ñaàu M
töø ñoä cao h bao nhieâu ñeå xe ñi heát ñöôøng troøn? h
Xaùc ñònh aùp löïc N cuûa xe leân ñöôøng troøn taïi O ϕ ñieåm M. B Ñaùp soá: h 2 h ≥ N ; a 5 , 2 = P( − 2 + 3cos ) ϕ . a
42. Taûi Q = 2 KN ñöôïc thaû ñeàu vôùi toác ñoä v = 5 m/s thì ñoät
ngoät bò haõm. Boû qua troïng löôïng daây haõy xaùc ñònh söùc
caêng cöïc ñaïi khi taûi troïng dao ñoäng thaúng ñöùng tieáp theo,
bieát heä soá cöùng cuûa daây laø C = 4 KN/cm.
Ñaùp soá: T = 47,1 KN. Q
43. Ñaàu maùy xe löûa chuyeån ñoäng ñeàu
treân ñöôøng ray thaúng ngang vôùi vaän toác A
72 km/h. Xaùc ñònh aùp löïc phuï leân ray do B
taùc duïng quaùn tính cuûa thanh AB gaây ra. O1 O 1
Khoái löôïng cuûa AB laø m = 200 kg ñöôïc
phaân boá ñeàu. Tay quay coù ñoä daøi
O1A = 0,3 m, baùn kính baùnh xe laø R = 1
m, giaû thieát caùc baùnh xe laên khoâng tröôït (hình veõ). Ñaùp soá: N 10 . 03 , 24 3 . N max =
44. Cô heä nhö hình veõ, daây meàm khoâng
daõn, taûi A troïng löôïng P1, taûi B troïng
löôïng P2, boû qua caùc aûnh höôûng cuûa ma A
saùt vaø khoái löôïng khaùc. B
Tính aùp löïc toång hôïp leân moâ D cuûa D C α laêng truï C. Ñaùp soá: 1 P sin α − 2 P cos N α = 1 P 1 P + 2 P
45. Cô heä nhö hình veõ, boû qua khoái löôïng daây, khoái löôïng khaùc
vaø ma saùt caùc oå truïc. Xaùc ñònh: gia toác W cuûa taûi P theo Q;
Ñieàu kieän ñeå taûi P ñi xuoáng; Ñieàu kieän ñeå taûi P chuyeån ñoäng P ñeàu. Ñaùp soá: 4P − Q P 1 W = 4g ; = . P 16 + Q Q 4 Q 215
46. Hai taûi troïng M1, M2 coù troïng löôïng töông öùng P1, P2 buoäc
vaøo hai ñaàu cuûa sôïi daây meàm nheï nhö hình veõ. Boû khoái löôïng
cuûa roøng roïc. Tìm söùc caêng caùc nhaùnh daõy vaø gia toác caùc taûi troïng. M1 Ñaùp soá: P2 − P1 P 2 1P W = g ; T = T 2 = . P1 + P 1 2 2 P1 + P2 M2
47. Caùc giaû thieát vaø yeâu caàu nhö baøi treân (46) nhöng roøng roïc
ñöôïc xem laø vaønh troøn ñoàng chaát troïng löôïng P. P2 − P1 P1( P 2 2 + P) P2( P 2 1 + P) Ñaùp soá: W = g T ; = T ; = . P1 + P + P 1 2 P1 + P + P 2 2 P1 + P2 + P
48. Boä ñieàu chænh ly taâm quay ñeàu vaän toác goùc ωo. a
Tìm lieân heä goùc leäch α vaø vaän toác goùc ω C o neáu khoái C l
truï A troïng löôïng P1, caùc quaû caân B cuøng troïng α α löôïng P B B
2, loø xo coù ñoä cöùng k gaén chaët ñaàu treân vôùi
thanh CC. Caùc kích thöôùc cho treân hình veõ (boû qua α α
caùc troïng löôïng tay quay vaø loø xo). A ωo Ñaùp soá: 2 P1 + P2 + lk 2 1 ( − cos α) ω = g tg . α P2 a ( + l sin α)
49. Daàm AB troïng löôïng Q ñöôïc keùo
theo sau xe taûi nhôø daây meàm nheï BC, C B
bieát CD = h; AB = a; BC = l. Tìm gia h A
toác W toái thieåu cuûa xe ñeå ñaàu A coù theå D
rôøi khoûi maët ñöôøng. Tính söùc caêng daây
T trong tröôøng hôïp naøy (hình veõ). Ñaùp soá: g g 2 2 P P(l + a) W = = (l + a) − h ; T = = . tgα h sin α h
50. Cho cô heä nhö hình veõ, boû qua ma saùt ôû oå truïc O vaø M
taûi B. Cho caùc troïng löôïng töông öùng laø PA = 2PB vaø PC;
baùn kính quaùn tính cuûa truï C ñoái vôùi truïc quay O laø ρ vaø R = 2r. B 30o A Wa 216
a) Xaùc ñònh WA vaø söùc caêng cuûa caùc nhaùnh daây.
Vôùi nhöõng giaù trò naøo cuûa M thì keát quaû ñöôïc chaáp nhaän?
b) Vôùi caùc giaù trò cuï theå PB = 100 N; PC = 400 N; M = 21,2 Nm; ρ
= 0,08 m; r = 0,1 m; EO = 2 m; taïi thôøi ñieåm ban ñaàu EB = 0,6 m; laáy g = 10 m/s2.
Haõy xaùc ñònh phaûn löïc taïi ngaøm E. Ñaùp soá: a) 3 M + A P R − B P r 2 3 B P r A W = gR B T ; = B P + A W 2 2 2 P R + P r + P ρ 2 gR A B C qt 3 1 2 2 A T = A P − R ; A M ≤ PBr + P ( Br + PCρ ) 2 R b) W = ; 1 , 9 T = ; 1 , 132 T = ; 18 E = ; 8 , 22 E = ; 3 , 561 M = 8 , 451 A B A x y E (N,m).
51. Moät neâm nhaün troïng löôïng P goùc ôû ñænh P
laø 2α ñaåy taùch hai taám vaùn naèm treân neàn P P 1
ngang nhö hình veõ. Cho troïng löôïng moãi taám 1 vaùn laø P 2 α
1, boû qua caùc aûnh höôûng cuûa ma saùt,
haõy vieát phöông trình chuyeån ñoäng cuûa neâm vaø caùc taám vaùn. 2 Ñaùp soá: Wt Pcotgα S = ñoù trong W : = g neâm 2 α Pcotg + 2P α tg 1 2 W t 1 P S = ñoù trong W : = g . vaùn 2 1 P cot gα + P 2 tg 1 α
52. Thanh thaúng ñoàng chaát ñöôïc gaén baèng baûn leà
vaøo truïc quay thaúng ñöùng nhö hình veõ. Cho: ω A O
OA = a; OB = b. Truïc quay ñeàu vôùi vaän toác goùc ωo,
choát baûn leà naèm ngang, boû qua ma saùt. Tìm heä thöùc
giöõa ωo vaø goùc nghieâng ϕ khi thanh AB ñaõ oån O x
ñònh ñoái vôùi truïc quay. ϕ B Ñaùp soá: g 3 a − b cos ϕ = . . 2 2 ω a2 − ab b2 ω o + o E
53. Treân truïc quay ñoái xöùng ñoäng löïc AB thaúng ϕ
ñöùng, ngöôøi ta gaén thanh OD vuoâng goùc vôùi AB O
vaø OE, coøn thanh OE taïo vôùi AB goùc ϕ (hình y D A x 217
veõ). Cho OE = OD = l, AB = 2OA = 2OB = 2a. Taïi caùc ñaàu muùt E, D ngöôøi ta
gaén caùc taûi troïng ñeàu coù khoái löôïng m. Xaùc ñònh aùp löïc ñoäng löïc leân truïc quay
khi boû qua troïng löôïng caùc thanh vaø kích thöôùc cuûa taûi troïng. Ñaùp soá: ⎧ ω2 X = = ml A X ⎪⎪ B 2 ⎨ ⎪ ω ml 2 a ( − l cos ϕ) sin ϕ ω ml 2 a ( + l cos ϕ) sin ϕ ⎪Y = A ; Y = ⎩ a 2 B a 2
54. Taám hình chöõ nhaät ñoàng chaát troïng löôïng P quay
ñeàu trong truïc thaúng ñöùng vôùi vaän toác goùc ωo (cosnt). ω
Haõy xaùc ñònh löïc xeù taám laøm ñoâi theo ñöôøng ñi o a qua truïc quay. a 2 Ñaùp soá: Pa S ωo = a 4g
55. Truï ñaëc ñoàng chaát coù lieân keát vaø chòu löïc nhö hình
veõ. Tìm chu kyø dao ñoäng cuûa taâm truïc C vaøo söùc caêng
daây. Cho bieát ñoä cöùng loø xo laø K, daây meàm, nheï khoâng K daõn. Ñaùp soá: 8 mg 2 y& = − T ; ky = + . ky (Laáy goác y laø vò m 3 2 3 C y
trí caân baèng tónh cuûa taâm C). mg
56. Thanh ñoàng chaát AB ñöôïc ñaët leân hai truï O x
troøn cuøng baùn kính quay ngöôïc chieàu nhau nhö A C
hình veõ. Thanh AB chuyeån ñoäng ñöôïc nhôø löïc B
ma saùt giöõa truïc quay vaø thanh vôùi heä soá μ.
1/ Xaùc ñònh chuyeån ñoäng cuûa thanh khi noù
ñaët dòch khoûi vò trí ñoái xöùng moät ñoaïn x l l o vôùi vaän
toác ban ñaàu vo = 0; AB = 4l. 2/ Tìm
μ bieát chu kyø dao ñoäng T cuûa thanh baèng hai giaây. 2 ⎛ μ ⎞ Ñaùp soá: g 4 x = x cos⎜ t⎟ ; π l μ = . o ⎜ ⎝ l ⎟ gT2 ⎠
57. Ñeå xaùc ñònh ñoä nhôùt cuûa chaát loûng culong duøng
phöông phaùp sau. Cho baûn moûng treo vaøo loø xo thöïc hieän
dao ñoäng trong khoâng khí (boû qua söùc caûn) ño chu kyø dao
ñoäng T1, sau ñoù cho baûn A dao ñoäng trong chaát loûng vaø ño
chu kyø T2. Löïc ma saùt giöõa baûn A vaø chaát loûng laáy theo coâng thöùc: A F = 2Sηv 218
trong ñoù: S - laø dieän tích beà maët baûn A
η - laø heä soá nhôùt; v - laø vaän toác cuûa baûn
Haõy xaùc ñònh η khi bieát troïng löôïng baûn laø P. Ñaùp soá: P π η = T2 − T2 . gST1T 2 1 2
Chuù yù: Phöông trình dao ñoäng coù caûn: x& + 2 x δ& + x ω = 0 → taàn soá dao ñoäng 2 1 ω = ω − δ .
IV. PHÖÔNG TRÌNH TOÅNG QUAÙT ÑOÄNG LÖÏC HOÏC VAØ PHÖÔNG TRÌNH LAGRANGE II
58. Thanh DE coù troïng löôïng Q töïa treân ba con laên nhö nhau vaø coù cuøng troïng
löôïng P. Thanh chòu taùc duïng löïc ngang F höôùng veà beân phaûi. Coi nhö khoâng
xaûy ra hieän töôïng tröôït giöõa thanh vaø caùc con laên cuõng nhö giöõa caùc con laên vaø neàn ngang.
Tìm gia toác cuûa thanh DE. Coi caùc con laên nhö nhöõng khoái truï ñoàng chaát. D E F A B C
Boû qua ma saùt laên (xem hình). Ñaùp soá: gF 8 W = . Q 8 + P 9
59. Laäp phöông trình vi phaân chuyeån ñoäng cuûa con laéc toaùn hoïc khoái löôïng m
ñöôïc treo vaøo ñaàu töï do cuûa moät daây ñaøn hoài coù ñoä daøi khi caàn baèng l vaø coù ñoä cöùng ñaøn hoài laø c. ⎧ g 1 ( + ) z ϕ& + &ϕ z 2 & + sin ϕ = 0 Ñaùp soá: ⎪⎪ l ⎨ ⎪ 2 c g ⎪z& − 1 ( + ) z ϕ& + z + 1 ( − cos ϕ) = 0 ⎩ m l
trong ñoù: ϕ - laø goùc leäch cuûa daây treo ñoái vôùi phöông thaúng ñöùng z - laø
ñoä daõn töông ñoái cuûa daây so vôùi chieàu daøi khi caân baèng.
Trong ñieàu kieän dao ñoäng nhoû, phöông trình chuyeån ñoäng cuûa con laéc ñöôïc vieát nhö sau: 219 ⎛ c ⎞ ⎛ g ⎞ z = A ⎜ sin t + α⎟ ϕ ; = B ⎜ sin t + β⎟ ⎜ ⎟ ⎜ ⎟ ⎝ m ⎠ ⎝ l ⎠
vôùi A, B, α, β phuï thuoäc vaøo ñieàu kieän ñaàu cuûa chuyeån ñoäng.
60. Moät oáng truï troøn roãng, ñoàng chaát, coù troïng löôïng P, baùn kính ñaùy R vaø coù
theå quay quanh truïc thaúng ñöùng. Treân maët trong cuûa oáng truï coù xeû moät raõnh
ñinh oác, böôùc cuûa ñöôøng ñinh oác laø h. Moät vieân bi nhoû chaïy trong raõnh aáy döôùi
taùc duïng cuûa troïng löôïng baûn thaân. Boû qua ma saùt. Thaønh laäp phöông trình vi
phaân chuyeån ñoäng cuûa cô heä, cho bieát ban ñaàu heä ñöùng yeân. Tìm phöông trình
chuyeån ñoäng cuûa cô heä. Ñaùp soá:
Phöông trình vi phaân chuyeån ñoäng: Q + P 2 Q R θ& + R sin γ s .& = 0 q q Q Q R sin θ γ & + s& = P cos γ. q q
Phöông trình chuyeån ñoäng: g P sin 2γ t2 θ = . . 2 QR cos2 γ + PR 2 Q cos 2γ + P P t2 s = cos . γ Q cos2 γ + P Q 2 trong ñoù:
θ - laø goùc quay cuûa truï s - laø
quaõng ñöôøng ñi ñöôïc cuûa vieân bi theo raõnh.
61. Vaät A coù khoái löôïng m ñöôïc keùo leân nhôø caùc
truïc quay I vaø II coù cuøng baùn kính R vaø moâmen
quaùn tính cuûa chuùng ñoái vôùi truïc quay rieâng baèng J
J. Xaùc ñònh gia toác cuûa vaät A neáu caùc truïc quay I
chòu taùc duïng cuûa caùc ngaãu löïc coù moâmen laø M1 M1
vaø M2. Boû qua khoái löôïng cuûa caùc roøng roïc vaø J
ma saùt ôû caùc oå truïc. Coi caùc daây laø nheï, khoâng A II M 2 220
daõn vaø khoâng tröôït ñoái vôùi caùc roøng roïc (hình veõ). Ñaùp soá: M 2 1 + M2 − mgR 5 A W = 2 J + mR 5
62. Moät daàm coù tieát dieän vuoâng, khoái löôïng m
bò khoeùt moät loã hình truï baùn kính R ñöôïc noái
vôùi thaønh coá ñònh nhôø moät loø xo coù ñoä cöùng C C O O
vaø coù theå tröôït khoâng ma saùt doïc theo phöông 1 ϕ
ngang. Doïc theo beà maët cuûa loã laên khoâng tröôït
moät hình truï ñoàng chaát khoái löôïng m, baùn kính r (r < R), xem hình veõ.
Thaønh laäp phöông trình vi phaân chuyeån ñoäng cuûa heä. ⎧(M + )
m x& + m(R − r) cos ϕ ϕ
. & − m(R − r) sin ϕ ϕ . 2 & + x . c = 0 Ñaùp soá: ⎪⎨ 3 ⎪m(R − r) cos ϕ x
. & + m(R − r)2ϕ& + mg(R − r) sin ϕ = 0 ⎩ 2
trong ñoù: x - laø hoaønh ñoä troïng taâm cuûa daàm
ϕ - laø goùc giöõa ñoaïn thaúng noái taâm cuûa loã vaø taâm cuûa truï ñoái vôùi ñöôøng thaúng ñöùng.
63. Thaønh laäp phöông trình vi phaân
chuyeån ñoäng cuûa moät con laéc coù khoái C
löôïng m vaø ñoä daøi l, ñieåm treo cuûa noù m1
naèm taïi taâm cuûa ñóa baùn kính r vaø coù khoái löôïng m x
1. Ñóa coù theå laên khoâng
tröôït doïc truïc ngang Ox, taâm cuûa ñóa noái ϕ M
vôùi töôøng coá ñònh nhôø moät loø xo coù ñoä cöùng C (xem hình). ⎧ 2 Ñaùp soá: ⎪ m 3 ( + m 2 )x& + ml 2 cos ϕ ϕ . & − ml 2 sin ϕ ϕ .& + x . c 2 = 0 ⎨ 1 ⎪⎩cos ϕ x . & + ϕ .l & + g sin ϕ = 0
64. Treân hình veõ cho moät sô ñoà maùy ghi ñòa chaán. Gaén treân beä maùy moät cuoän töï
caûm coù n voøng daây vôùi baùn kính r vaø coù ñieän trôû OÂm toång coäng laø R, vaø heä soá töï
caûm L. Loõi saét töø laø moät hình truï ñoàng truïc vôùi cuoän töï caûm vaø gaây ra trong
khoaûng khoâng cuûa noù moät töø tröôøng phaúng vaø xuyeân taâm vôùi heä soá caûm öùng B.
Loõi saét coù khoái löôïng M vaø M
ñöôïc ñôõ baèng caùc loø xo coù heä soá cöùng
toång coäng laø C vaø coøn chòu taùc duïng cuûa c/2 c/2
löïc caûn nhôùt βx, trong ñoù x laø chuyeån rôøi
cuûa loõi saét töø tính töø vò trí caân baèng cuûa
noù. Neàn rung theo quy luaät ξ =
ξosinωt. Ñoùng kín maïch ñieän baèng caùch A
noái lieàn hai cöïc cuoän töï caûm baèng daây 221
daãn coù ñieän trôû nhoû khoâng ñaùng keå. Thaønh laäp phöông trình vi phaân chuyeån
ñoäng cuûa heä (xem hình). ⎧ 2
Ñaùp soá: ⎪Mx& + βx& + cx − π 2 q rnB& = Mξ ω sin ωt ⎨ o ⎪⎩Lq& + q R& + π 2 x rnB& = 0
65. Thaønh laäp phöông trình chuyeån ñoäng cuûa L
moät heä cô ñieän ñöôïc bieåu dieãn nhö treân hình
veõ. Chieàu daøi cuûa loø xo luùc khoâng bieán daïng C o
baèng 1, ñoä cöùng cuûa noù baèng C, khoái löôïng a + 1
cuûa vaät vôùi taám ñoäng baèng m. Khi loø xo m R e(t)
khoâng bò bieán daïng khoaûng caùch giöõa caùc P(t)
taám ñoäng vaø coá ñònh cuûa tuï baèng a, coøn ñieän ~ dung cuûa noù baèng C1. ⎧ q x m & + cx − = mg + P(t) aC Ñaùp soá: ⎪⎪⎨ 1 ⎪ q q Lq& + − a ( − x) + q R& = ( e t) ⎪⎩ C aC o 1
V. CAÙC BAØI TOAÙN ÑOÄNG LÖÏC HOÏC VAÄT RAÉN MOÄT VAØ HAI BAÄC TÖÏ
DO (BAØI TOAÙN TOÅNG HÔÏP)
66. Hai truïc chuyeàn ñoäng nhö hình veõ. Bieát tæ soá
truyeàn giöõa truïc I vaø truïc II laø 1/2, moâmen quaùn R
tính ñoái vôùi truïc quay (hình hoïc) cuûa moãi truïc laø 1 O O 1 2 J R 2
1, J2; baùn kính cuûa truïc I laø R1, goùc môû cuûa raêng
laø α. Xaùc ñònh vaän toác goùc, gia toác goùc cuûa truïc II
(vaø phaûn löïc aên khôùp raêng) trong caùc tröôøng hôïp: a) M = const.
b) M = Mo – aω1. Trong tröôøng hôïp naøy xaùc ñònh theâm vaän toác goùc giôùi haïn cuûa truïc quay II.
67. Cô heä nhö hình veõ, giaû thieát con laên B (laø R
truï troøn ñoàng chaát) laên khoâng tröôït treân maët r
phaúng nghieâng, truï keùp O coù moâmen quaùn tính O
ñoái vôùi truïc quay laø Jo. Xaùc ñònh WA, VA töø M
traïng thaùi ñöùng yeân khi cho: B a) P I A
A = 2 KN; PB = 1 KN; Po = 6 KN
M = 0,2 KNm; Jo = 25.10-5 kgm2 α
R = 2RB = 2r = 0,2 m; α = 30o.
b) Cuøng vôùi caùc giaù trò treân chæ thay ñoåi M = 2 KNm. Bieåu thöùc tính
VA, WA coù thay ñoåi khoâng? (höôùng daãn: chuù yù ñeán söùc caêng daây). 222
68. Cô heä goàm taûi A vaø con laên B noái vôùi
nhau baèng daây meàm nheï quaán qua roøng roïc
C nhö hình veõ. Khoái löôïng töông öùng cuûa caùc C
vaät raén laø mA, mB, mC, heä soá ma saùt tröôït tónh
vôùi maët töïa cuûa con laên B laø f A B 1, taûi A laø f2, heä
soá ma saùt tröôït ñoäng giöõa maët töïa vaø A laø f2’, α β R R B C = . 2
Boû qua caùc aûnh höôûng caûn trôû chuyeån ñoäng khaùc. Ñaët ngaãu MC (const) vaøo roøng roïc C.
a) Xaùc ñònh WB trong chuyeån ñoäng ñi leân töø traïng thaùi ñöùng yeân (coi laêng truï E coá ñònh).
b) Tính söùc caêng caùc nhaùnh daây, vaø phaûn löïc töïa taïi A theo caùc khaû
naêng xaûy ra. Töø ñoù ñaùnh giaù laïi keát quaû cuûa caâu a.
c) Xeùt tröôøng hôïp cuï theå:
mA = 10 kg; mB = 6 kg; MC = 40 Nm; RC = 0,2 m; f1 = f2 = 0,7; f2 = 0,4; α = 60o (laáy g = 10 m/s2).
69. Cô heä nhö hình veõ. Taûi A troïng
löôïng P, con laên B (laø truï troøn ñoàng M
chaát) troïng löôïng Q baùn kính R. Giaû B
thieát con laên laên khoâng tröôït (theo chieàu cuûa M). A I
Boû qua ngaãu caûn laên, haõy xaùc ñònh: a)
WA; εB; WB; ωB; VB cuûa taûi A vaø con laên khi boû qua ma saùt ôû roøng roïc.
b) Xaùc ñònh söùc caêng daây vaø phaûn löïc taïi I khi cho Q = 200 N;
P = 100 N; R = 0,2 m; heä soá ma saùt tröôït giöõa con laên vaø maët neàn laø f = 0,7.
Tìm nhöõng giaù trò cuûa M ñeå ñaûm baûo laên khoâng tröôït.
70. Con laên troïng löôïng Q coù baùn kính laø R M
quaán daây meàm khoâng daõn treo taûi troïng A B troïng löôïng P. Cho Q 2 JB = R vaø ngaãu M 12g
(haèng soá) ñaët vaøo con laên. Vôùi giaû thieát con I
laên laên khoâng tröôït haõy xaùc ñònh: a)
WA töø traïng thaùi ñöùng yeân.
Tìm ñieàu kieän ñeå taûi A ñi leân, ñi A α xuoáng. 223
b) Phaûn löïc taïi I laø bao nhieâu? Khi cho heä soá ma saùt tröôït giöõa con laên vaø
maët nghieâng laø f, tìm giaù trò cho pheùp cuûa M ñeå caùc keát quaû ñöôïc chaáp nhaän.
Tính caùc giaù trò khi laáy: R = 0,4 m; Q = 600 N; P = 100 N; f = 0,6; α = 30o
(hình veõ). Giaû thieát xem daây thaúng ñöùng. Ñaùp soá: e r e r WA = W + W ; W = W = B W M − P
( + P sin α + Q sin α)R M − 180 W = gR B = J g + PR2 B 1 ( + sin α) + QR2 38
FI = 1,97M – 5,26; NI = 0,22M + 5,6519
Khoâng tröôït: –166,09 < M < 187,15 (N,m,s)
71. Cô heä nhö hình veõ. Boû qua ma saùt M
ôû A vaø oå truïc O cuõng nhö ma saùt laên
cuûa lieân keát taïi I. Ngaãu Mo, löïc F laø B B
caùc haèng soá, troïng löôïng töông öùng A I
cuûa caùc vaät raén laø PA, PB, Po. Giaû thieát α
con laên B laên khoâng tröôït. Haõy xaùc ñònh: a)
WA , WB töø traïng thaùi ñöùng yeân.
b) Söùc caêng caùc nhaùnh daây vaø phaûn löïc taïi I.
c) Ñaùnh giaù caùc keát quaû khi cho:
Ro = 2ro = 2RB = 0,2 m; α = 30o; P P = P 2 o = = ; n 200 A B 4
Heä soá ma saùt tröôït taïi I laø f = 0,6. Giaù trò Mo vaø F ñöôïc cho nhö sau: - Mo = 30 Nm; F = 40 N. - Mo = 60 Nm; F = 10 N.
72. Khoái truï troøn ñoàng chaát ñöôïc ñaët treân
saøn ngang AB ôû gaàn meùp nhoïn saéc B cuûa
saøn sao cho meùp ñoù song song vôùi ñöôøng C
sinh cuûa hình truï, baùn kính khoái truï laø R. o
Truyeàn cho khoái truï vaän toác ban ñaàu raát nhoû α C
ñeå noù laên xuoáng khoâng tröôït quanh meùp B.
Giaû söû luùc maët phaúng chöùa meùp B vaø truïc
truï taïo vôùi maët phaúng thaúng ñöùng goùc α thì
khoái truï rôøi meùp B. Boû qua ma saùt laên vaø löïc caûn cuûa khoâng khí.
Tìm giaù trò cuûa α vaø vaän toác goùc cuûa khoái truï taïi thôøi ñieåm ñoù. Töø ñoù
suy ra vaän toác goùc cuûa khoái truï trong chuyeån ñoäng tieáp theo. 224 Ñaùp soá: 4 g α = ar cos ; ω = 2 7 R 2
73. Moät daàm ñoàng chaát daøi AB = 2l ñöôïc ñaët ôû vò trí
naèm ngang, ôû thôøi ñieåm naøo ñoù daây ôû B bò ñöùt vaø daàm A
baét ñaàu chuyeån ñoäng quay quanh truïc A. Taïi thôøi ñieåm B
daàm thaúng ñöùng ñaàu A bò maát lieân keát.
Xaùc ñònh quyõ ñaïo khoái taâm cuûa daàm vaø vaän ω
toác cuûa noù trong chuyeån ñoäng tieáp theo. Ñaùp soá: 2 2 g 3 y = lx 3 − l 3 , ω = . l 2
74. Taûi M naèm ôû ñænh cuûa voøm caàu nhaün baùn kính R A M nhaän ñöôïc vaän toác V ϕ
o. Tôùi vò trí naøo taûi M seõ rôøi khoûi
voøm caàu? Vôùi giaù trò naøo cuûa Vo taûi M seõ rôøi voøm caàu
ngay taïi thôøi ñieåm ban ñaàu? R O 2 Ñaùp soá: 2 V ϕ = ar cos( o + ) ; V gR 3 gR 3 o ≥
75. Hai truï troøn xoay ñoàng chaát A, B coù troïng R1
löôïng laàn löôït laø P1, P2 vaø baùn kính töông öùng R1, R O
2 ñöôïc quaán bôûi hai sôïi daây meàm, nheï phaân boá 1
ñoái xöùng vôùi maët phaúng vuoâng goùc vôùi truïc truï vaø
ñi qua taâm cuûa truïc truï. Khoái truï B rôi xuoáng
khoâng vaän toác ban ñaàu vöøa nhaû daây vöøa laøm quay R2
truï A quanh truïc coá ñònh. O2
Boû qua caùc aûnh höôûng cuûa löïc caûn, haõy xaùc ñònh:
- Vaän toác goùc cuûa moãi truï.
- Quy luaät chuyeån ñoäng cuûa taâm O2 vaø söùc caêng cuûa moãi nhaùnh daây. Ñaùp soá: 1 P 2gt 2 P 2gt ωA = ; ωB = 1 P 3 + 2 P 2 R1 1 P 3 + 2 P 2 R2 g P ( + P ) P + P S 1 2 = t2 T ; 1 2 = . O 2 P 3 + P 2 P 3 ( 2 + P 2 ) 1 2 1 2
76. Cho cô heä nhö hình veõ. Troïng löôïng töông
öùng cuûa caùc vaät laø PA, PB, PE. Boû qua taát caû
caùc troïng löôïng khaùc vaø ma saùt caùc oå truïc. A
a) Xaùc ñònh gia toác ñi xuoáng cuûa taûi E C
B töø traïng thaùi ñöùng yeân khi cho heä soá ma saùt
tröôït tónh ft vaø tröôït ñoäng fñ cuûa taûi A treân neàn ngang. B 225
Töø ñoù suy ra ñieàu kieän cuûa caùc troïng löïc ñeå B khôûi ñoäng ñi xuoáng?
b) Xeùt cuï theå caùc tröôøng hôïp:
+ PA = 160 N; 2PE = PB = 200 N; ft = 0,5; fñ = 0,3.
+ Nhö caâu a) chæ thay ñoåi ft = 0,7; fñ = 0,4.
77. Cô heä goàm taûi A vaø con laên B noái vôùi Mc
nhau baèng daây meàm nheï quaán qua roøng
roïc C nhö hình veõ. Caùc vaät raén khoái C
löôïng töông öùng laø mA, mB, mC; laêng truï B
E coù troïng löôïng Q; heä soá ma saùt tröôït E F
tónh vôùi maët töïa cuûa con laên B laø f α β 1, taûi A
laø f2, heä soá ma saùt tröôït ñoäng giöõa maët töïa vaø A laø f R 2’, R B C = . 2
Laêng truï E chòu taùc ñoäng cuûa löïc F naèm ngang, ngaãu MC (const) ñaët
vaøo roøng roïc C. Boû qua ma saùt giöõa E vaø neàn.
a) Laäp phöông trình vi phaân chuyeån ñoäng cuûa cô heä.
b) Tính söùc caêng cuûa nhaùnh daây vaø aùp löïc leân neàn ngang.
c) Xeùt tröôøng hôïp cuï theå:
RC = 0,2 m; MA = 10 kg; mB = 6 kg; Q = 200 N; F = 100 N
MC = 40 Nm; f1 = f2 = 0,7; f2 = 0,4; α = 60o (laáy g = 10 m/s2)
78. Cho cô heä nhö hình veõ, giaû söû con laên B laên khoâng tröôït, xem daây treo taûi A thaúng ñöùng. Bieát:
PA = 20 N; r = 0,1 m; PB = 100 N R = 0,2 m; PD = 100 N; ρ = 0,1 m
(ρ laø baùn kính quaùn tính cuûa con laên B ñoái vôùi truïc ñi qua taâm B vaø vuoâng goùc
vôùi maët phaúng chuyeån ñoäng).
I. Laêng truï D ñöôïc giöõ coá ñònh:
1/ Cho taûi A ñi xuoáng theo quy luaät s = 0,2 + 0,3t2 (m). Xaùc ñònh
V B, WB taïi thôøi ñieåm t = 1 giaây. Daây ñöôïc xem nhö khoâng daõn. 2/ Xem khoái löôïng cuûa
daây vaø roøng roïc khoâng ñaùng keå. M Haõy: a) Xaùc ñònh W R A ñi xuoáng r
töø traïng thaùi ñöùng yeân. B A
b) Tính söùc caêng caùc nhaùnh I
daây vaø phaûn löïc taïi tieáp ñieåm I, töø D 30o 226
ñoù xaùc ñònh nhöõng giaù trò cuûa ngaãu M ñeå ñaûm baûo keát quaû ôû caâu a) (con laên laên
khoâng tröôït vaø taûi A ñi xuoáng) khi cho heä soá ma saùt tröôït giöõa con laên vaø maët
nghieâng laø f = 0,5 vaø boû qua ma saùt laên.
II. Giaû söû laêng truï coù theå tröôït treân neàn ngang:
1/ Cho M = 3 Nm, xaùc ñònh heä soá ma saùt tröôït tónh lôùn nhaát giöõa laêng
truï D vaø neàn ngang ñeå D coù theå chuyeån ñoäng ñöôïc?
2/ Giaû söû ma saùt giöõa D vaø neàn ngang khoâng ñaùng keå, laäp phöông
trình vi phaân chuyeån ñoäng cuûa cô heä. VI. VA CHAÏM
79. Thieát bò duøng ñeå xaùc ñònh heä soá khoâi phuïc O
cuûa vaät lieäu baèng thuï nghieäm, goàm moät thanh
quay ñöôïc trong maët phaúng thaúng ñöùng quanh ϕ x
truïc naèm ngang qua O. Caùch O moät ñoaïn x naøo
ñoù ngöôøi ta gaén leân thanh maãu caàn thöû. Thaû cho
thanh rôi khoâng vaän toác töø ñaàu vò trí naèm ngang,
thanh quay quanh O vaø khi ñeán vò trí thaúng ñöùng
thì maãu thöû ñaäp vaøo maãu coá ñònh cuõng ñöôïc cheá
taïo baèng cuøng vaät lieäu nhö maãu noùi treân. Chieàu daøi cuûa thanh baèng l.
Xaùc ñònh heä soá khoâi phuïc k neáu sau va chaïm thanh bò baät laïi moät goùc ϕ so
vôùi vò trí thaúng ñöùng vaø tìm khoaûng caùch x ñaët maãu thöû so vôùi truïc quay O ñeå
khi va chaïm khoâng sinh ra phaûn löïc va chaïm taïi O (xem hình). Ñaùp soá: ϕ 2 k = 2 sin x ; = l. 2 3
80. Moät con laéc thöû ñaïn goàm coù truï AB ñöôïc
treo vaøo truïc O naèm ngang. Khoái truï chöùa O
ñaày caùt. Vieân ñaïn ñöôïc baén vaøo khoái truï,
xuyeân vaøo caùt laøm cho khoái truï quay quanh
truïc O moät goùc α naøo ñoù so vôùi ñöôøng thaúng h
ñöùng. Cho bieát khoái löôïng cuûa truï baèng M, a
khoaûng caùch töø ñöôøng va chaïm ñeán truïc
quay O baèng a. Giaû thieát raèng truïc O khoâng
chòu taùc duïng cuûa löïc va chaïm, nghóa laø ah = C
ρ2. Khoái löôïng vieân ñaïn baèng m (xem hình).
Tìm vaän toác cuûa vieân ñaïn theo goùc leäch α cuûa con laéc. Ñaùp soá: Mh ( 2 + ma) g v = sin α m a 2 227
81. Moät khoái hình hoäp AB ñöôïc ñaët
treân moät taám laên theo ñöôøng ray naèm
ngang vôùi vaän toác v. Nhôø moät maáu B C
treân taám, khoái hình hoäp khoâng bò tröôït h B V
ñoái vôùi taám nhöng coù theå quay quanh
maáu B. Cho h laø chieàu cao cuûa troïng
taâm cuûa khoái hình hoäp ñoái vôùi taám, ρ laø
baùn kính quaùn tính cuûa khoái hình hoäp ñoái vôùi maáu B.
a) Xaùc ñònh vaän toác goùc ω cuûa khoái hình hoäp quanh maáu B khi taám bò döøng töùc thôøi.
b) Xem khoái hình hoäp laø vaät ñoàng chaát coù chieàu cao h = 3 m, chieàu daøi
doïc taám baèng 4 m. Tìm vaän toác v cuûa taám ñeå khoái hình hoäp AB bò laät nhaøo quanh maáu B (xem hình). Ñaùp soá: h ω = V ; v = km 30 / . s 2 ρ
82. Khaûo saùt va chaïm heä goàm hai vaät A vaø B, trong ñoù vaät A coù theå chuyeån
ñoäng töï do theo höôùng ngang, coøn vaät B ñöôïc gaén vaøo loø xo coù heä soá cöùng C.
Giaû söû raèng tröôùc va chaïm vaät A coù vaän toác v10 > 0 coøn vaät B coù vaän toác v20 = 0. V1o B
Tìm vaän toác cuûa hai vaät sau va chaïm vaø thôøi ñieåm t1 hai vaät laïi va
chaïm vaøo nhau tieáp theo vaø chaïm laàn ñaàu. Cho bieát khoái löôïng caùc vaät töông
öùng baèng m1 vaø m2, heä soá khoâi phuïc baèng k (xem hình). Ñaùp soá: m1 − km2 m1 + m2k vA = v10 ; vB = v10 m1 + m2 m1 + m2
Vaø khoaûng thôøi gian t1 ñöôïc xaùc ñònh töø phöông trình sieâu vieät: sin vt1 m1 − km2 = vt1 m1 + m2 trong ñoù: c v = m2



