
































































































































































Preview text:
Trần Diên Hiển (Chủ biên) Nguyễn Thuỷ Chung CƠ SỞ TOÁN HỌC CỦA MÔN TOÁN TIỂU HỌC MỤC LỤC 1 Chương I
Những cơ sở ngôn ngữ toán học ở tiểu học I.
Mệnh đề và các phép logic I.1. Mệnh đề I.2. Các phép logic
II. Các bài toán về suy luận logic ở trường phổ thông
II.1. Phương pháp lập bảng
II.2. Phương pháp suy luận đơn giản
II.3. Phương pháp loại trừ
II.4. Phương pháp biểu đồ Ven III. Công thức
III.1. Khái niệm về công thức
III.2. Giá trị chân lí của công thức
III.3. Sự tương đương logic và đẳng thức
III.4. Phép biến đổi công thức
III.5. Mệnh đề liên hợp, điều kiện cần, điều kiện đủ, điều kiện cần và đủ IV. Quy tắc suy luận IV.1. Định nghĩa
IV.2. Các quy tắc suy luận thường gặp V.
Mệnh đề tổng quát và mệnh đề tồn tại
V.1. Khái niệm về hàm mệnh đề
V.2. Phép phủ định hàm mệnh đề V.3. Mệnh đề tổng quát V.4. Mệnh đề tồn tại
V.5. Phủ định mệnh đề tổng quát hoặc tồn tại VI. Suy luận và chứng minh VI.1. Suy luận là gì? VI.2. Suy luận diễn dịch VI.3. Suy luận nghe có lí
VII. Khái niệm và hệ thống khái niệm trong dạy học toán ở tiểu học
VII.1. Nội hàm và ngoại diên của khái niệm
VII.2. Quan hệ giữa các khái niệm
VII.3. Định nghĩa khái niệm
VII.4. Vấn đề hình thành khái niệm trong dạy học toán ở tiểu học VIII. Tập hợp
VIII.1. Khái niệm tập hợp
VIII.2. Cách xác định tập hợp
VIII.3. Tập con và quan hệ bao hàm
VIII.4. Các phép toán trên tập hợp
VIII.5. Tích Đề-các của các tập hợp
VIII.6. Mặt phẳng toạ độ Đề-các 2 Bài tập chương I Chương II
Phương pháp thống kê trong nghiên cứu khoa học giáo dục I.
Các khái niệm cơ bản về thống kê toán học
I.1. Đại cương về thống kê toán
I.2. Các phương pháp chọn mẫu I.3. Hàm phân phối mẫu
I.4. Đa giác tần suất và tổ chức đồ tần suất
I.5. Trung bình mẫu và phương sai mẫu I.6. Trung vị mẫu I.7. Mô men mẫu
I.8. Hệ số tương quan mẫu II. Ước lượng tham số
II.1. Ước lượng và khoảng tin cậy của số trung bình hay kì vọng a
II.2. Ước lượng và khoảng tin cậy của tỉ lệ hay xác suất p III.
Kiểm định giả thiết thống kê
III.1. Kiểm định giá trị trung bình a của tổng thể (so sánh số trung bình quan sát
với số trung bình lí thuyết)
III.2. Kiểm định giả thiết về tỉ lệ hay xác suất p (so sánh tần suất quan sát với
xác suất p của biến cố A theo lí thuyết)
III. 3. So sánh hai giá trị trung bình của hai mẫu quan sát
III.4. So sánh hai xác suất dựa trên tần suất thu được trên hai mẫu quan sát IV.
Yếu tố thống kê trong môn toán tiểu học Bài tập chương II Chương III
Cơ sở toán học của các yếu tố hình học trong môn toán tiểu học I.
Phương pháp tiên đề trong xây dựng lí thuyết môn hình học
I.1. Các khái niệm cơ bản
I.2. Hệ thống các tiên đề hình học
I.3. Hệ thống định nghĩa các khái niệm
I.4. Các định lí và tính chất hình học II.
Định nghĩa các khái niệm hình học
II.1. Định nghĩa các hình hình học
II.2. Định nghĩa các quan hệ hình hình học
II.3. Khái niệm về độ dài đoạn thẳng, chu vi, diện tích và thể tích các hình III.
Các bài toán về xác định hình hình học
III.1. Bài toán quỹ tích (tìm tập hợp điểm) III.2. Bài toán dựng hình
III.3. Dựng đoạn thẳng vô tỉ 3 IV.
Yếu tố hình học trong môn toán tiểu học
IV.1. Hình thành các khái niệm hình học cho học sinh tiểu học
IV.2. Xây dựng công thức tính chu vi, diện tích và thể tích các hình
IV.3. Giải toán có nội dung hình học Bài tập chương III Chương IV
Cơ sở toán học của các tập hợp số trong môn toán tiểu học I.
Cơ sở toán học của số học các số tự nhiên trong môn toán tiểu học
I.1. Xây dựng tập số tự nhiên I.1.1. Song ánh
I.1.2. Tập hợp tương đương
I.1.3. Tập hợp hữu hạn và vô hạn - Bản số tập hợp
I.1.4. Xây dựng tập số tự nhiên
I.1.5. Hình thành khái niệm số tự nhiên trong môn toán tiểu học
I.2. Cơ sở toán học của quan hệ thứ tự trong tập số tự nhiên ở tiểu học
I.2.1. Quan hệ thứ tự trong tập số tự nhiên
I.2.2. Số tự nhiên liền trước, liền sau và số tự nhiên liên tiếp
I.2.3. Quan hệ thứ tự trong tập số tự nhiên ở tiểu học
I.3. Cơ sở toán học của các phép toán trong tập số tự nhiên ở tiểu học
I.3.1. Phép cộng và phép nhân I.3.2. Phép trừ I.3.3. Phép chia
I.3.4. Các phép tính trong tập số tự nhiên ở tiểu học
I.4. Lí thuyết chia hết trong tập số tự nhiên và các bài toán về chia hết ở tiểu học
I.4.1. Ước chung lớn nhất
I.4.2. Bội chung nhỏ nhất I.4.3. Số nguyên tố
I.4.4. Hệ ghi số cơ số g và hệ thập phân ở tiểu học
I.4.5. Các dấu hiệu chia hết cho 2, 3, 4, 5, 9, 25 và 11
I.4.6. Các bài toán về chia hết ở tiểu học II.
Cơ sở toán học của số học các phân số trong môn toán tiểu học
II.1. Quan hệ tương đương và tập thương
V.1.1. Định nghĩa và tính chất của quan hệ tương đương
V.1.2. Định lí về tập thương
II.2. Xây dựng tập số hữu tỉ không âm
II.3. Quan hệ thứ tự trong tập số hữu tỉ không âm
II.4. Các phép toán trong tập số hữu tỉ không âm
II.4.1. Phép cộng và phép nhân II.4.2. Phép trừ II.4.3. Phép chia
II.5. Nội dung dạy học phân số ở tiểu học
II.5.1. Hình thành khái niệm phân số ở tiểu học 4
II.5.2. Quan hệ so sánh các phân số ở tiểu học
II.5.3. Xây dựng các phép toán trong tập phân số
II.5.4. Giải toán về phân số ở tiểu học III.
Cơ sở toán học của tập số thập phân ở tiểu học
III.1. Phân số thập phân
III.2. Số thập phân không âm
III.3. Quan hệ thứ tự trong tập số thập phân không âm
III.4. Số thập phân vô hạn tuần hoàn
III.5. Nội dung dạy học số thập phân ở tiểu học
III.5.1. Hình thành khái niệm phân số ở tiểu học
III.5.2. Quan hệ so sánh các phân số ở tiểu học
III.5.3. Xây dựng các phép toán trong tập số thập phân ở tiểu học
VI.5.4. Giải toán về số thập phân ở tiểu học Bài tập chương IV Chương V
Cơ sở toán học của các phương pháp giải toán tiểu học I.
Phương trình bậc nhất và các phương pháp giải toán: tính ngược từ cuối,
phương pháp ứng dụng đồ thị và phương pháp đại số
I.1. Biểu thức toán học I.2. Phương trình
I.3. Phương trình tương đương
I.4. Phương trình bậc nhất
I.5. Phương trình bậc nhất và phương pháp tính ngược từ cuối
I.6. Phương trình bậc nhất và phương pháp ứng dụng đề thị
I.7. Phương trình bậc nhất và phương pháp đại số
II. Hệ phương trình bậc nhất hai ẩn II.1. Định nghĩa
II.2. Phương pháp giải hệ phương trình bậc nhất x+y=t
II.3. Hệ phương trình bậc nhất dạng: x y h
và phương pháp giải toán về
tìm hai số biết tổng và hiệu của chúng x y=s
II.4. Hệ phương trình bậc nhất dạng: ax
by 0 và phương pháp chia tỉ lệ x y s
II.5. Hệ phương trình bậc nhất dạng: ax by c
và phương pháp giả thiết tạm
ax by m
II.6. Hệ phương trình bậc nhất dạng: cx
dy n và phương pháp khử 5
ax y c
II.7. Hệ phương trình bậc nhất dạng: y bx c
' và phương pháp giải toán về
tìm hai số biết hai hiệu số
II.8. Phép quy nạp hoàn toàn và phương pháp thử chọn
II.9. Yếu tố đại số trong môn toán tiểu học Bài tập chương V
TRẢ LỜI HOẶC HƯỚNG DẪN GIẢI BÀI TẬP Tài liệu tham khảo 6 CHƯƠNG I
NHỮNG CƠ SỞ CỦA NGÔN NGỮ TOÁN HỌC Ở TIỂU HỌC
I. Mệnh đề và các phép logic I.1. Mệnh đề
Trong môn tiếng Việt ở trường phổ thông, chúng ta đã làm quen với khái niệm về
câu. Các câu thường gặp có thể chia thành hai loại: loại thứ nhất gồm những câu phản
ánh tính đúng hoặc sai một thực tế khách quan. Mỗi câu như thế được hiểu là một mệnh
đề. Loại thứ hai gồm những câu không phản ánh tính đúng hoặc sai một thực tế khách quan nào.
Để kí hiệu các mệnh đề ta dùng các chữ cái a, b, c... Trong logic ta không quan
tâm đến cấu trúc ngữ pháp của các mệnh đề mà chỉ quan tâm đến tính “đúng” hoặc “sai” của chúng.
Nếu a là mệnh đề đúng thì ta nói nó có giá trị chân lí bằng 1, kí hiệu là G(a) = 1,
nếu a là mệnh đề sai thì ta nói nó có giá trị chân lí bằng 0, kí hiệu là G(a) = 0. Chẳng hạn, các câu
+ a = “Nước Việt Nam nằm ở châu Á” là mệnh đề đúng, G(a) = 1;
+ b = “Bắc Kinh là thủ đô của nước Pháp” là mệnh đề sai; G(b)= 0;
+ c = “Tháng Hai có 30 ngày” là mệnh đề sai, G(c) = 0;
+ d = “31 là số lẻ” là mệnh đề đúng, G(d) = 1;
+ e = “Số 13 chia hết cho 3” là mệnh đề sai, G(e) = 0;
+ x = “3 lớn hơn 7” là mệnh đề sai, G(x) = 0;
+ y = “Tứ giác có bốn cạnh bằng nhau là hình vuông” là mệnh đề sai, G(y) = 0; Các câu
+ “3 cộng với 2 bằng mấy?”
+ “Bạn tốt nghiệp phổ thông năm nào?”
+ “Giờ học hôm nay thú vị quá!”
+ “Tất cả hãy anh dũng tiến lên!”
đều không phải là mệnh đề. Nói chung, những câu nghi vấn, câu mệnh lệnh và câu cảm
thán đều không phải là mệnh đề. Chú ý
1. Trong thực tế ta gặp những câu mà tự nó chưa phản ánh tính đúng hoặc sai một
thực tế khách quan nào, nhưng khi gắn nó với một văn cảnh nhất đinh (thời gian, địa
điểm,...) thì nó trở thành một mệnh đề (đúng hoặc sai). Nó đúng ở thời gian, địa điểm này
nhưng lại sai ở thời gian, địa điểm khác. Song ở bất kì thời điểm nào, địa điểm nào nó 7
cũng luôn có giá trị chân lí đúng hoặc sai. Những mệnh đề như thế ta gọi là “mệnh đề mở”. Chẳng hạn:
+ Sinh viên năm thứ nhất đang học toán + Trời mưa
+ Điểm chuẩn vào khoa ta năm nay cao hơn năm ngoái
+ 9 giờ sáng hôm nay tôi đang ở Cần Thơ
đều là những mệnh đề mở.
2. Ta thừa nhận các luật sau đây của logic mệnh đề
a) Luật bài trung: Mỗi mệnh đề phải hoặc đúng hoặc sai, không có mệnh đề nào
không đúng cũng không sai.
b) Luật mâu thuẫn (hay còn gọi là luật phi mâu thuẫn): không có mệnh đề nào vừa đúng vừa sai. I.2. Các phép logic
Khi có hai số a và b, dùng các phép toán cộng, trừ, nhân, chia tác động vào hai số đó
ta sẽ có những số mới (gọi là tổng hiệu, tích, thương của hai số đó).
Khi có hai mệnh đề a và b, người ta cũng xây dựng các phép toán tác động vào hai
mệnh đề đó để nhận được những mệnh đề mới. Dưới đây ta lần lượt xây dựng các phép toán đó.
I.2.1 Phép phủ định
Phủ định của mệnh đề a là một mệnh đề, kí hiệu là a hoặc non a, đúng khi a sai
và sai khi a đúng. Bảng chân lí của phép phủ định được cho bởi bảng sau: a a 1 0 0 1 Ví dụ 1.1
a) Phủ định của mệnh đề a = “Mỗi tuần lễ có 7 ngày” là mệnh đề a = “Mỗi tuần
lễ không có 7 ngày” hoặc “Không phải mỗi tuần lễ có 7 ngày”.
Ở đây: G(a) = 1 và G( a) = 0.
b) Phủ định của mệnh đề b = “4 lớn hơn 8” là mệnh đề b =“4 không lớn hơn 8” hoặc “4 nhỏ hơn hoặc bằng 8”.
Ở đây: G(b) = 0 và G( b) = 1. Chú ý:
Phủ định của một mệnh đề có nhiều cách diễn đạt khác nhau, chẳng hạn:
“Vàng không phải là kim loại” 8
“Không phải vàng là kim loại”
“Vàng đâu có phải là kim loại”
“Nói vàng là kim loại không đúng” hoặc “15 không lớn hơn 7”
“15 nhỏ hơn hoặc bằng 7”
“Không phải 15 lớn hơn 7”
“15 đâu có lớn hơn 7”
“Nói 15 lớn hơn 7 là sai” ... I.2.2. Phép hội
Hội của hai mệnh đề a, b là một mệnh đề c, đọc là a và b, kí hiệu là c = a b, đúng
khi cả hai mệnh đề a, b cùng đúng và sai trong các trường hợp còn lại.
Giá trị chân lí của phép hội được xác định bởi bảng sau a b a b 1 1 1 1 0 0 0 1 0 0 0 0
Chú ý: Để thiết lập mệnh đề hội của hai mệnh đề a, b ta ghép hai mệnh đề đó bởi liên từ
“và” hay một liên từ khác cùng loại. Những liên từ đó là: mà, nhưng, song, song le, đồng
thời, vẫn, cùng... hoặc dùng dấu phẩy (,) thay cho liên từ “và” hoặc không dùng liên từ gì. Ví dụ 1.2
a) “Thành phố Hà Nội là thủ đô nhưng không phải là thành phố lớn nhất của cả
nước” là hội của hai mệnh đề a = “Thành phố Hà Nội là thủ đô của cả nước” và b =
“Thành phố Hà Nội không phải là thành phố lớn nhất cả nước”.
Rõ ràng G(a) = G(b) = 1 nên G (a b) = 1.
b) “Lúc 6 giờ sáng hôm qua tôi đang có mặt ở Hà Nội và Thành phố Hồ Chí
Minh” là hội của hai mệnh đề a = “Lúc 6 giờ sáng hôm qua tôi đang có mặt ở Hà Nội” và
b = “Lúc 6 giờ sáng hôm qua tôi đang có mặt ở Thành phố Hồ Chí Minh”.
Rõ ràng hai mệnh đề này không thể cùng đúng nên G (a b) = 0.
c) “100 là số tròn chục chia hết cho 3” là hội của hai mệnh đề a = “100 là số tròn
chục” và b = “100 chia hết cho 3”.
Ở đây G(a) = 1 và G(b) = 0 nên G (a b) = 0. 9
c) “Góc vuông có số đo lớn hơn góc nhọn nhưng nhỏ hơn góc tù” là hội của hai
mệnh đề a = “Góc vuông có số đo lớn hơn góc nhọn” và b = “Góc vuông có số đo nhỏ
hơn góc tù”. Ở đây G(a) = G(b) = 1 nên G (a b) = 1.
d) Cô Nga nói thạo tiếng Anh mà không biết tiếng Đức là hội của hai mệnh đề mở
a = “Cô Nga nói thạo tiếng Anh” và b = “Cô Nga không biết tiếng Đức”. Ví dụ 1.3
Minh vừa trẻ, đẹp trai, học giỏi mà lại có nhiều tài lẻ.
Chú ý: Đôi khi trong mệnh đề có liên từ “và” nhưng lại không có nghĩa của mệnh đề hội. Chẳng hạn:
“Tuần vừa qua, tổ Một đạt được 12 điểm 9 và 10”.
“Vườn nhà chú Tư có 300 cây cam và ổi”. I.2.3 Phép tuyển
Tuyển của hai mệnh đề a, b là một mệnh đề c, đọc là a hoặc b, kí hiệu c = a b, sai
khi cả hai mệnh đề a, b cùng sai và đúng trong các trường hợp còn lại.
Giá trị chân lí của phép tuyển được xác định bởi bảng sau: a b a b 1 1 1 1 0 1 0 1 1 0 0 0 Ví dụ 1.4
a) “Mỗi năm có bốn mùa hoặc 2 lần 5 bằng 10” là tuyển của hai mệnh đề a = “Mỗi
năm có bốn mùa” và b = “2 lần 5 bằng 10”.
Ở đây G(a) = G(b) = 1 nên G (a b) = 1.
b) “50 là số tròn chục hoặc là số nguyên tố” là tuyển của hai mệnh đề
a = “50 là số tròn chục” và b = “50 là số nguyên tố”.
Ở đây G(a) = 1 và G(b) = 0 nên G(a b) = 1.
c) “Tháng Năm có 28 ngày hoặc 3 + 3 = 10” là tuyển của hai mệnh đề
a = “Tháng Năm có 31 ngày” và b = “3 + 3 = 10”.
Ở đây G(a) = G(b) = 0 nên G(a b) = 0.
d) “Cô An chưa có gia đình hay cô đã tốt nghiệp đại học”. Chú ý: 10
1. Để thiết lập mệnh đề tuyển của hai mệnh đề a, b ta ghép hai mệnh đề đó bởi liên
từ “hoặc” (hay một liên từ khác cùng loại).
2. Khi thiết lập mệnh đề tuyển của nhiều mệnh đề, ta dùng dấu chấm phẩy thay cho liên từ “hoặc”. Chẳng hạn:
“Số có tận cùng bằng 0; 2; 4; 6 hoặc 8 thì chia hết cho 2”.
“Lớp ta hôm nay học Toán, Tiếng Việt, Tiếng Anh hoặc Thể dục”.
3. Liên từ “hoặc” trong thực tế thường được dùng với hai nghĩa: loại trừ và không loại trừ.
4. Phép tuyển “hoặc a hoặc b” là phép tuyển loại trừ để chỉ a hoặc b nhưng không thể cả a lẫn b.
Phép tuyển “a hoặc b” là phép tuyển không loại trừ để chỉ a hoặc b và có thể cả a lẫn b. Chẳng hạn:
“Hôm nay là hoặc Chủ nhật hoặc thứ Bảy” là phép tuyển loại trừ
“24 là số chẵn hoặc chia hết cho 3”
“Hôm nay là Chủ nhật hoặc ngày lễ”
là những phép tuyển không loại trừ.
Dưới đây, nếu không nói gì thêm, ta sẽ chỉ xét các phép tuyển không loại trừ. I.2.4. Phép kéo theo
Cho hai mệnh đề a và b. Mệnh đề a kéo theo b là một mệnh đề được tạo thành theo
mẫu “Nếu a thì b”, kí hiệu là a b, sai khi a đúng mà b sai và đúng trong các trường hợp còn lại.
Giá trị chân lí của mệnh đề a b được xác định bởi bảng sau: a b a b 1 1 1 1 0 0 0 1 1 0 0 1 Ví dụ 1.5
a) “Nếu 19 là số nguyên tố thì 2 lần 2 là 4” là mệnh đề đúng.
b) “Nếu mỗi tuần có 7 ngày thì một năm có 10 tháng” là mệnh đề sai.
c) “Nếu tổng các góc trong tam giác bằng 360 độ thì hình chữ nhật có hai đường
chéo bằng nhau” là mệnh đề đúng.
d) “Nếu 5 + 5 = 11 thì tháng Hai có 31 ngày” là mệnh đề đúng. Chú ý: 11
1. Mệnh đề “a kéo theo b” thường được diễn đạt dưới nhiều hình thức khác nhau, chẳng hạn: “nếu a thì b” “a suy ra b” “có a thì có b” ...
2. Trong logic, khi xét giá trị chân lí của mệnh đề a b người ta không quan tâm
đến mối quan hệ về nội dung của hai mệnh đề đó. Không phân biệt trường hợp a có phải
là nguyên nhân để có b hay không, mà chỉ quan tâm đến tính đúng, sai của chúng.
3. Trong văn học, mệnh đề kéo theo còn được diễn đạt bằng nhiều hình thức phong phú. Chẳng hạn:
“Bao giờ bánh đúc có xương
Bấy giờ dì ghẻ mới thương con chồng” hoặc
“Chuồn chuồn bay thấp thì mưa,
Bay cao thì nắng, bay vừa thì râm”
I.2.5. Phép tương đương
Cho hai mệnh đề a và b. Mệnh đề a tương đương b là một mệnh đề được tạo thành
theo mẫu “a khi và chỉ khi b”, kí hiệu là a b, đúng khi cả hai mệnh đề a, b cùng đúng
hoặc cùng sai và sai trong các trường hợp còn lại.
Giá trị chân lí của mệnh đề tương đương được xác định bởi bảng sau: a b a b 1 1 1 1 0 0 0 1 0 0 0 1 Chú ý:
1. Trong thực tế, mệnh đề “a tương đương b” còn được diễn đạt dưới nhiều hình
thức khác nhau. Chẳng hạn: “a khi và chỉ khi b”
“a nếu và chỉ nếu b” ...
2. Cũng như mệnh đề kéo theo, trong logic, khi xét giá trị chân lí của mệnh đề
a b người ta không quan tâm đến mối quan hệ về nội dung của hai mệnh đề đó. Không
phân biệt trường hợp a có phải là nguyên nhân để có b hay không hoặc ngược lại, mà chỉ
quan tâm đến tính đúng, sai của chúng. Ví dụ 1.6 12
a) “Tháng 12 có 31 ngày khi và chỉ khi Trái Đất quay xung quanh Mặt Trời” là mệnh đề đúng.
b) “ 3 < 7 khi và chỉ khi 70 chia hết cho 3” là mệnh đề sai.
c) “Tổng các góc trong một tam giác bằng 90 0nếu và chỉ nếu 13 là số nguyên tố” là mệnh đề sai.
d) “Tháng Hai có 31 ngày khi và chỉ khi 2 x 2 = 11” là mệnh đề đúng.
II. Các bài toán về suy luận logic ở phổ thông
Các bài toán về suy luận logic ở phổ thông thường là những bài toán về suy luận
đơn giản. Suy luận đơn giản là những phép suy luận không dùng những công cụ của logic
mệnh đề (phép phủ định, phép hội, phép tuyển...). Các bài toán về suy luận đơn giản là
những bài toán khi giải không đòi hỏi phải tính toán cồng kềnh mà chỉ cần vận dụng một
cách sáng tạo những hiểu biết thông thường về thiên nhiên, đời sống xã hội và thực tế lao
động sản xuất để dẫn dắt từ những điều kiện đã cho đến kết luận của bài toán.
Dưới đây ta lần lượt nghiên cứu các phương pháp thường sử dụng khi giải các bài toán dạng này.
II.1. Phương pháp lập bảng
Các bài toán giải bằng phương pháp lập bảng thường xuất hiện hai nhóm đối
tượng (chẳng hạn tên người và nghề nghiệp, hoặc vận động viên và giải thưởng, hoặc tên
sách và màu bìa...). Khi giải ta thiết lập một bảng gồm các hàng và các cột. Các cột ta liệt
kê các đối tượng thuộc nhóm thứ nhất, còn các hàng ta liệt kê các đối tượng nhóm thứ hai.
Dựa vào điều kiện trong đề bài, ta loại bỏ dần (ghi số 0) các ô (là giao của mỗi
hàng và mỗi cột). Những ô còn lại (không bị loại bỏ) là kết quả của bài toán. Ví dụ 2.1
Ba người thợ hàn, thợ tiện và thợ điện đang ngồi trò chuyện trong giờ nghỉ giải
lao. Người thợ hàn nhận xét:
- Ba chúng ta làm nghề trùng với tên của ba chúng ta, nhưng không ai làm nghề trùng với tên mình cả. Bác Điện hưởng ứng: - Bác nói đúng.
Bạn hãy cho biết tên và nghề nghiệp của mỗi người. Giải
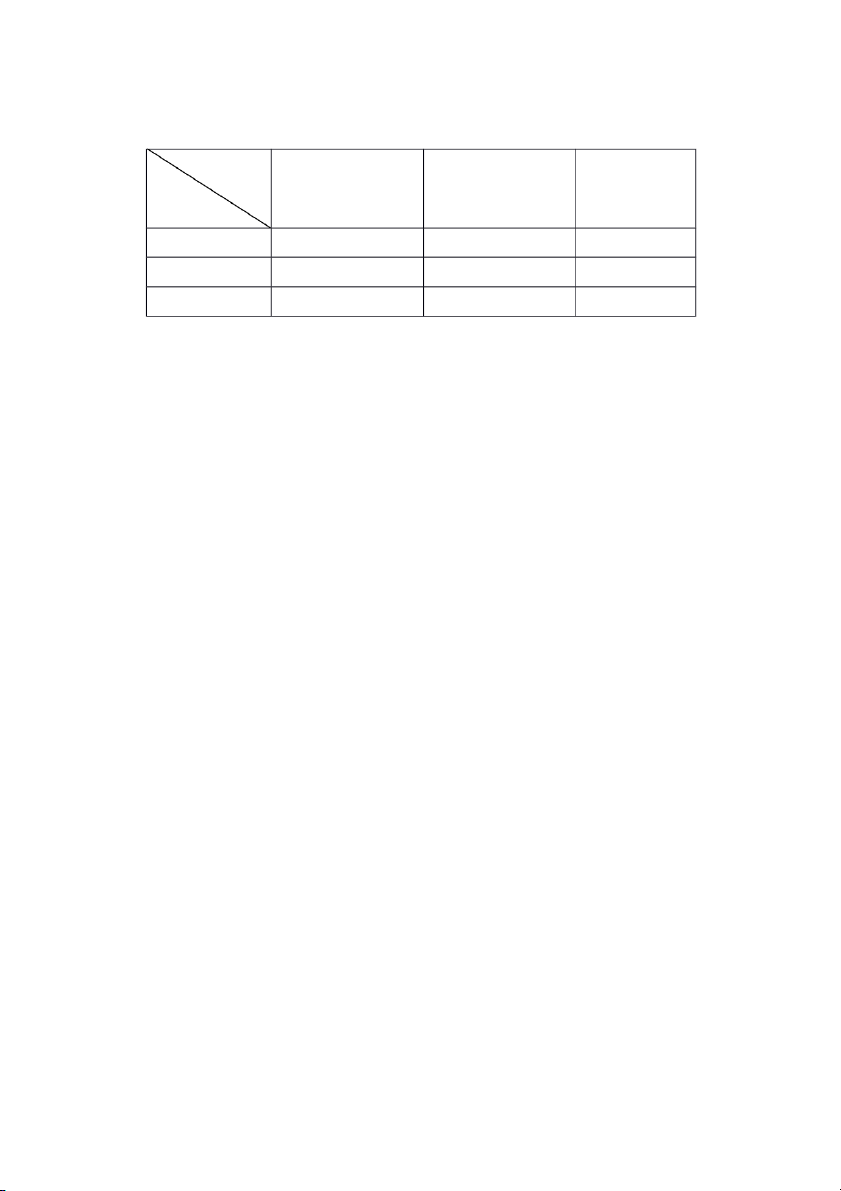
Ta thiết lập bảng sau: Nghề nghiệp hàn tiện điện Tên người Hàn 0 X 13 (1) (2) (3) X 0 Tiện (4) (5) (6) 0 X 0 Điện (7) (8) (9)
Theo đề bài, không ai có tên trùng với nghề của mình, cho nên ta ghi số 0 vào các
ô 1 ; 5 và 9. Bác Điện hưởng ứng nhận xét của bác thợ hàn nên bác Điện không làm nghề
hàn. Ta ghi số 0 vào ô số 7.
- Nhìn cột 2 ta thấy bác thợ hàn không tên là Hàn, không tên là Điện. Vậy bác thợ
hàn tên là Tiện. Ta đánh dấu X vào ô số 4.
- Nhìn hàng 4 ta thấy bác Điện không làm nghề hàn cũng không làm nghề điện.
Vậy bác làm nghề tiện. Ta đánh dấu X vào ô số 8.
- Nhìn hàng 2 và ô 8 ta thấy bác Hàn không làm nghề hàn, cũng không làm nghề
tiện. Vậy bác làm nghề điện. Đánh dấu X vào ô số 3.
Kết luận: Bác Hàn làm thợ điện. Bác Tiện là thợ hàn. Bác Điện làm thợ tiện. Ví dụ 2.2
Trên bàn là ba cuốn sách giáo khoa: Văn, Toán và Địa lí được bọc ba màu khác
nhau: xanh, đỏ, vàng. Cho biết cuốn bọc bìa màu đỏ đặt giữa hai cuốn Văn và Địa lí,
cuốn Địa lí và cuốn màu xanh mua cùng một ngày. Bạn hãy xác định mỗi cuốn sách đó bọc bìa màu gì.
Giải: Ta có bảng sau: Tên sách Văn Toán Địa lí Màu bìa X 0 xanh (1) (2) (3) 0 X 0 đỏ (4) (5) (6) X vàng (7) (8) (9)
Theo đề bài “cuốn bìa màu đỏ đặt giữa hai cuốn Văn và Địa lí”. Vậy cuốn sách
Văn và Địa lí đều không bọc màu đỏ cho nên cuốn Toán phải bọc màu đỏ. Ta ghi số 0 vào
ô 4 và 6, đánh dấu X vào ô 5.
Mặt khác, “cuốn Địa lí và cuốn bìa màu xanh mua cùng ngày”. Điều đó có nghĩa
là cuốn Địa lí không bọc màu xanh. Ta ghi số 0 vào ô 3. 14
- Nhìn cột thứ tư, ta thấy cuốn Địa lí không bọc màu xanh cũng không bọc màu
đỏ. Vậy cuốn Địa lí bọc màu vàng. Ta đánh dấu X vào ô 9.
- Nhìn vào cột 2 và ô 9 ta thấy cuốn Văn không bọc màu đỏ, cũng không bọc màu
vàng. Vậy cuốn Văn bọc màu xanh. Ta đánh dấu X vào ô 1.
Kết luận: Cuốn Văn bọc màu xanh, cuốn Toán bọc màu đỏ, cuốn Địa lí bọc màu vàng. Ví dụ 2.3
Trên bàn có bốn hộp kín được đánh số thứ tự 1; 2; 3 và 4. Trong mỗi hộp đựng
một trong bốn loại quả: đào, mận, bưởi hoặc cam. Ba bạn Lộc, Đạt và Thanh tham gia trò
chơi như sau: Mỗi bạn lần lượt đoán trong mỗi hộp đựng quả gì, nếu ai đoán đúng ít nhất
một hộp thì sẽ được phần thưởng. Lộc đoán trước:
- Hộp thứ nhất đựng cam, hộp thứ hai đựng mận, hộp thứ ba đựng bưởi và hộp thứ tư đựng đào. Đạt đoán tiếp:
- Hộp thứ nhất đựng đào, hộp thứ hai đựng bưởi, hộp thứ ba đựng cam và hộp thứ tư đựng mận. Cuối cùng Thanh đoán:
- Hộp thứ nhất đựng mận, hộp thứ hai đựng cam, hộp thứ ba đựng đào và hộp thứ tư đựng bưởi.
Kết thúc cuộc chơi, ban giám khảo công bố cả ba bạn đều không đạt phần thưởng.
Bạn hãy cho biết trong mỗi hộp đựng quả gì.
Giải: Ta thiết lập bảng và ghi vào bảng theo lập luận sau Theo đề bài ta có:
- Lộc không được phần thưởng. Vậy hộp thứ nhất không đựng cam, hộp thứ hai
không đựng mận, hộp thứ ba không đựng bưởi và hộp thứ tư không đựng đào. Ta ghi số 0 vào các ô 4; 6; 11 và 13.
- Đạt không được phần thưởng. Vậy hộp thứ nhất không đựng đào, hộp thứ hai
không đựng bưởi, hộp thứ ba không đựng cam và hộp thứ tư không đựng mận. Ta ghi tiếp
số 0 vào các ô 1; 7; 12 và 14.
- Thanh cũng không được phần thưởng, cũng lập luận như trên rồi ta ghi tiếp số 0 vào các ô 2; 8 ; 9 và 15. Quả đào mận bưởi cam Hộp 0 0 X 0 1 (1) (2) (3) (4) X 0 0 0 2 (5) (6) (7) (8) 15 0 X 0 0 3 (9) (10) (11) (12) 0 0 0 X 4 (13) (14) (15) (16)
Nhìn hàng thứ hai ta thấy hộp thứ nhất không đựng đào, không đựng mận, cũng
không đựng cam. Vậy nó đựng bưởi. Ta đánh dấu X vào ô 3.
Tương tự ta được: hộp thứ hai đựng dấu (đánh dấu X vào ô 5), hộp thứ ba đựng
mận (đánh dấu X vào ô 10) và hộp thứ tư đựng cam (đánh dấu X vào ô 16). Ví dụ 2.4
Giờ Văn cô giáo trả bài kiểm tra. Bốn bạn Tuấn, Hùng, Lan, Quân ngồi cùng bàn
đều đạt điểm 8 trở lên. Giờ ra chơi Phương hỏi điểm của bốn bạn.
- Tuấn trả lời: “Lan không đạt điểm 10, mình và Quân không đạt điểm 9 còn Hùng không đạt điểm 8”.
- Hùng thì nói: “Mình không đạt điểm 10, Lan không đạt điểm 9 còn Tuấn và
Quân đều không đạt điểm 8”.
Bạn hãy cho biết mỗi người đã đạt điểm mấy.
Giải: Ta lập bảng và ghi bảng theo lập luận ở dưới Tên Tuấn Hùng Lan Quân Điểm X 0 0 X 10 (1) (2) (3) (4) 0 X 0 0 9 (5) (6) (7) (8) 0 0 X 0 8 (9) (10) (11) (12)
Theo Tuấn ta ghi số 0 vào các ô 3 ; 5 ; 8 và 10.
Theo Hùng ta ghi số 0 vào các ô 2 ; 7 ; 9 và 12.
Vì bốn bạn đều đạt điểm 8 trở lên, nên nhìn vào cột 2, ta kết luận Tuấn đạt điểm
10. Tương tự với các cột 3; 4 và 5 ta kết luận Hùng đạt điểm 9, Lan đạt điểm 8 còn Quân đạt điểm 10. Ví dụ 2.5
Năm người thợ tên là Da, Điện, Hàn, Tiện và Sơn làm năm nghề khác nhau trùng
với tên của năm người đó, nhưng không ai có tên trùng với nghề của mình. Bác thợ da lấy
em gái của bác Da. Tên của bác thợ da trùng với nghề của anh vợ mình và vợ bác chỉ có 16
hai anh em. Bác Tiện không làm thợ sơn mà lại là em rể của bác thợ hàn. Bác thợ sơn và
bác Da là hai anh em cùng họ.
Bạn hãy cho biết bác Da và bác Tiện làm nghề gì. Giải Tên người Da Điện Hàn Tiện Sơn Nghề nghiệp 0 0 da (1) (2) (3) (4) (5) 0 0 X điện (6) (7) (8) (9) (10) X 0 0 hàn (11) (12) (13) (14) (15) 0 tiện (16) (17) (18) (19) (20) 0 0 0 sơn (21) (22) (23) (24) (25)
Vì không ai làm nghề trùng với tên của mình nên ta ghi số 0 vào các ô 1; 7; 13; 19 và 25.
Bác Tiện không làm thợ sơn nên ta ghi số 0 vào ô 24. Mặt khác bác Tiện là em rể
của bác thợ hàn nên bác Tiện không phải là thợ hàn. Ta ghi số 0 vào ô 14. Nhìn cột 5 ta
thấy bác Tiện chỉ có thể là thợ da hoặc thợ điện.
Nếu bác Tiện là thợ da thì theo đề bài, bác Da là thợ tiện. Như vậy bác Tiện vừa là
em rể của bác thợ tiện vừa là em rể của bác thợ hàn, mà vợ bác Tiện chỉ có hai anh em. Điều này vô lí.
Vậy bác Tiện là thợ điện. Ta ghi số 0 vào ô 4 và dấu X vào ô 9.
Bác Tiện là thợ điện nên bác Da không phải là thợ điện. Ta ghi số 0 vào ô 6. Bác
thợ sơn và bác Da là hai anh em cùng họ nên bác Da không là thợ sơn. Ta ghi số 0 vào ô 21.
Theo lập luận phần trên thì bác Da không phải là thợ tiện. Vậy bác Da là thợ hàn. Ta đánh dấu X vào ô 11.
II.2. Phương pháp suy luận đơn giản
Suy luận đơn giản là phép suy luận không dùng công cụ của logic mệnh đề. Dưới
đây ta xét một số ví dụ minh hoạ cho phương pháp giải này. Ví dụ 2.6 17
Một viên quan nước Lỗ đi sứ sang Tề, bị vua Tề xử phạt tội chết và bị hành quyết:
hoặc chém đầu hoặc treo cổ. Trước khi hành quyết nhà vua cho sứ giả được nói một câu
và giao hẹn nếu nói đúng thì chém đầu, nếu nói sai thì treo cổ. Sứ giả mỉm cười và nói
một câu mà nhờ đó đó thoát chết.
Bạn hãy cho biết câu nói đó của sử giả như thế nào.
Phân tích: Điều kiện của nhà vua đặt ra là nếu nói đúng thì chém đầu, nếu nói sai
thì treo cổ. Vì nhà vua cho rằng một câu nói chỉ có thể đúng hoặc sai, như thế vị sứ giả
chắc chắn sẽ bị chết. Nhưng nhà vua không tính đến khả năng vị sứ giả sẽ nghĩ ra câu nói
mà đem chém đầu thì sứ giả nói sai (cho nên sứ giả không bị chém đầu) còn nếu đem treo
cổ thì sứ giả nói đúng (nên không bị treo cổ). Câu nói đó là : “Tôi sẽ bị treo cổ”.
Giải: Câu nói của sứ giả là: “Tôi sẽ bị treo cổ”.
- Nếu nhà vua đem sứ giả đi chém đầu thì sứ giả nói sai. Mà nói sai thì phải xử
treo cổ chứ không thể chém đầu sứ giả.
- Nếu nhà vua đem treo cổ sứ giả thì sứ giả nói đúng. Mà nói đúng thì phải đem
chém đầu chứ không thể treo cổ.
Sứ giả không bị chém đầu, không bị treo cổ cho nên đã thoát chết. Ví dụ 2.7
Người ta đồn rằng ở một ngôi đền nọ rất thiêng do ba vị thần ngự trị: thần Thật
Thà (luôn luôn nói thật), thần Dối Trá (luôn luôn nói dối) và thần Khôn Ngoan (khi nói
thật, khi nói dối). Các vị thần đều ngự ở trên bệ thờ và sẵn sàng trả lời câu hỏi khi có
người thỉnh cầu. Nhưng vì hình dạng của ba vị thần giống hệt nhau nên người ta không
biết vị thần nào để tin hay không tin.
Một hôm, một học giả từ phương xa đến ngôi đền gặp các thần để xin lời thỉnh
cầu. Bước vào đền, học giả hỏi thần ngồi bên phải: - Ai ngồi cạnh ngài? - Đó là thần Dối Trá.
Tiếp đó hỏi thần ngồi giữa: - Ngài là thần gì? - Ta là thần Khôn Ngoan.
Cuối cùng ông ta quay sang hỏi thần ngồi bên trái: - Ai ngồi cạnh ngài? - Đó là thần Thật Thà.
Nghe xong học giả khẳng định được mỗi vị là thần gì. Bạn hãy cho biết học giả đó
đã suy luận như thế nào. Phân tích
Ta nhận xét, cả ba câu hỏi của vị học giả đều nhằm xác định một thông tin là thần
ngồi giữa là thần gì? Kết quả nhận được các câu trả lời như sau: 18
Thần bên phải: Đó là thần Dối Trá.
Thần ở giữa: Ta là thần Khôn Ngoan.
Thần bên trái: Đó là thần Thật Thà.
Dựa vào các câu trả lời, vị học giả trước hết đã suy luận để xác định ai là thần Thật
Thà. Tiếp theo dựa vào câu trả lời của vị thần Thật Thà thì xác định được vị thần thứ hai, rồi thứ ba.
Ngoài ra còn có thể giải bằng cách khác: Suy luận để xác định ai là thần Dối Trá
(hoặc Khôn Ngoan) trước, sau đó xác định hai vị thần còn lại. Giải
Cách 1: Ta nhận xét
- Thần ngồi bên trái không phải là thần Thật Thà, vì ngài nói thần ngồi giữa là thần Thật Thà.
- Thần ngồi giữa cũng không phải là thần Thật Thà, vì ngài nói: “Ta là thần Khôn Ngoan.”
Vậy thần ngồi bên phải là thần Thật Thà. Theo câu trả lời của ngài thì ngồi giữa là
thần Dối Trá. Cuối cùng, thần bên trái là thần Khôn Ngoan. Cách 2: Ta nhận xét
- Nếu thần ngồi bên trái là thần Dối Trá thì thần bên phải là thần Thật Thà hoặc
Khôn Ngoan. Nếu ngồi bên phải là thần Thật Thà thì ngồi giữa là thần Dối Trá. Điều này
vô lí, vì bên trái cũng là thần Dối Trá. Nên bên phải là thần Khôn Ngoan thì ngồi giữa là
thần Thật Thà. Điều này vô lí, vì ngài nói: “Tôi là thần Khôn Ngoan”.
Vậy bên trái không phải là thần Dối Trá.
- Nếu bên phải là thần Dối Trá thì ngồi giữa là thần Thật Thà hoặc Khôn Ngoan.
Nhưng ngài không phải là thần Thật Thà, vì ngài nói: “Tôi là thần Khôn Ngoan”. Nếu
ngồi giữa là thần Khôn Ngoan thì bên trái là thần Thật Thà. Điều này vô lí, vì ngài nói:
“Ngồi giữa là thần Thật Thà”.
Vậy bên phải cũng không phải là thần Dối Trá. Vậy, ta suy ra ngồi giữa là thần Dối
Trá. Như vậy bên trái không phải là thần Thật Thà, vì ngài nói: “Ngồi giữa là thần Thật
Thà”. Thế thì bên trái là thần Khôn Ngoan. Cuối cùng, bên phải là thần Thật Thà.
Cách 3: Tương tự, ta có thể suy luận để xác định ai là thần Khôn Ngoan trước. Sau đó
xác định hai vị thần còn lại. Ví dụ 2.8
Ở một xã X có hai làng: dân làng A chuyên nói thật, còn dân làng B chuyên nói
dối. Dân hai làng thường qua lại thăm nhau. Một chàng thanh niên nọ về thăm bạn ở làng
A. Vừa bước vào xã X, đang ngơ ngác chưa biết đây là làng nào, chàng thanh niên gặp
ngay một cô gái và anh ta hỏi người này một câu. Sau khi nghe trả lời chàng thanh niên
bèn quay ra (vì biết chắc mình đang ở làng B) và sang tìm bạn ở làng bên cạnh. 19
Bạn hãy cho biết câu hỏi đó thế nào và câu trả lời đó ra sao mà chàng thanh niên
lại khẳng định chắc chắn như vậy.
Phân tích: Để nghe xong câu trả lời người thanh niên đó có thể khẳng định được
mình đang đứng trong làng A hay làng B thì anh ta phải nghĩ ra một câu hỏi sao cho câu
trả lời của cô gái chỉ phụ thuộc vào họ đang đứng trong làng nào mà không phụ thuộc cô
gái ấy là người làng nào. Cụ thể hơn: Cần đặt câu hỏi để cô gái trả lời là “phải”, nếu họ
đang đứng trong làng A và “không phải”, nếu họ đang đứng trong làng B.
Giải: Câu hỏi của người thanh niên đó là: “Có phải chị là người làng này không?”
Trường hợp 1: Họ đang đứng trong làng A: Nếu cô gái là người làng A thì câu trả lời
là: “Phải”; nếu cô gái là người làng B thì câu trả lời cũng là “Phải” (vì dân làng B chuyên nói dối).
Trường hợp 2: Họ đang đứng ở trong làng B. Nếu cô gái là người làng A thì câu trả lời là:
“Không phải”; nếu cô gái là người làng B thì câu trả lời cũng là: “Không phải”.
Như vậy, nếu họ đang đứng trong làng A thì câu trả lời chỉ có thể là “Phải”, còn
nếu họ đang đứng trong làng B thì câu trả lời chỉ có thể là “Không phải”.
Người thanh niên quyết định quay ra, vì anh đó nghe câu trả lời là “Không phải”. Ví dụ 2.9
Một hôm anh Quang lấy quyển album ra giới thiệu với mọi người. Cường chỉ vào
người đàn ông trong ảnh và hỏi anh Quang: “Người đàn ông này có quan hệ thế nào với
anh?” Anh Quang bèn trả lời: “Bà nội của chị gái vợ anh ấy là chị gái của bà nội vợ tôi”.
Bạn hãy cho biết anh Quang và người đàn ông ấy quan hệ với nhau thế nào.
Giải: Bà nội của chị gái vợ anh ấy cũng chính là bà nội của vợ anh ấy. Bà nội của vợ anh
ấy là chị gái của bà nội vợ anh Quang. Vậy vợ anh ấy và vợ anh Quang là hai chị em con
dì con già. Suy ra anh Quang và người đàn ông ấy là hai anh em rể họ. Ví dụ 2.10
Trong giờ ngoại khoá, thầy giáo gọi 6 em nam và 6 em nữ ra sân trường và giao
cho lớp trưởng nhiệm vụ tập hợp các bạn đứng thành vòng tròn sao cho không có hai bạn
nữ nào đứng cạnh nhau và đối diện với một bạn nữ qua tâm vòng tròn là một bạn nam.
Suy nghĩ một lát, lớp trưởng trả lời: “Thưa thầy, không thể xếp được như vậy!”. Bạn lớp
phó học tập tiếp luôn: “Nhưng nếu bớt đi một bạn nam và một bạn nữ hoặc thêm một bạn
nam và một bạn nữ thì xếp được thưa thầy!”
Bạn hãy cho biết hai bạn nói đúng hay sai, giải thích tại sao.
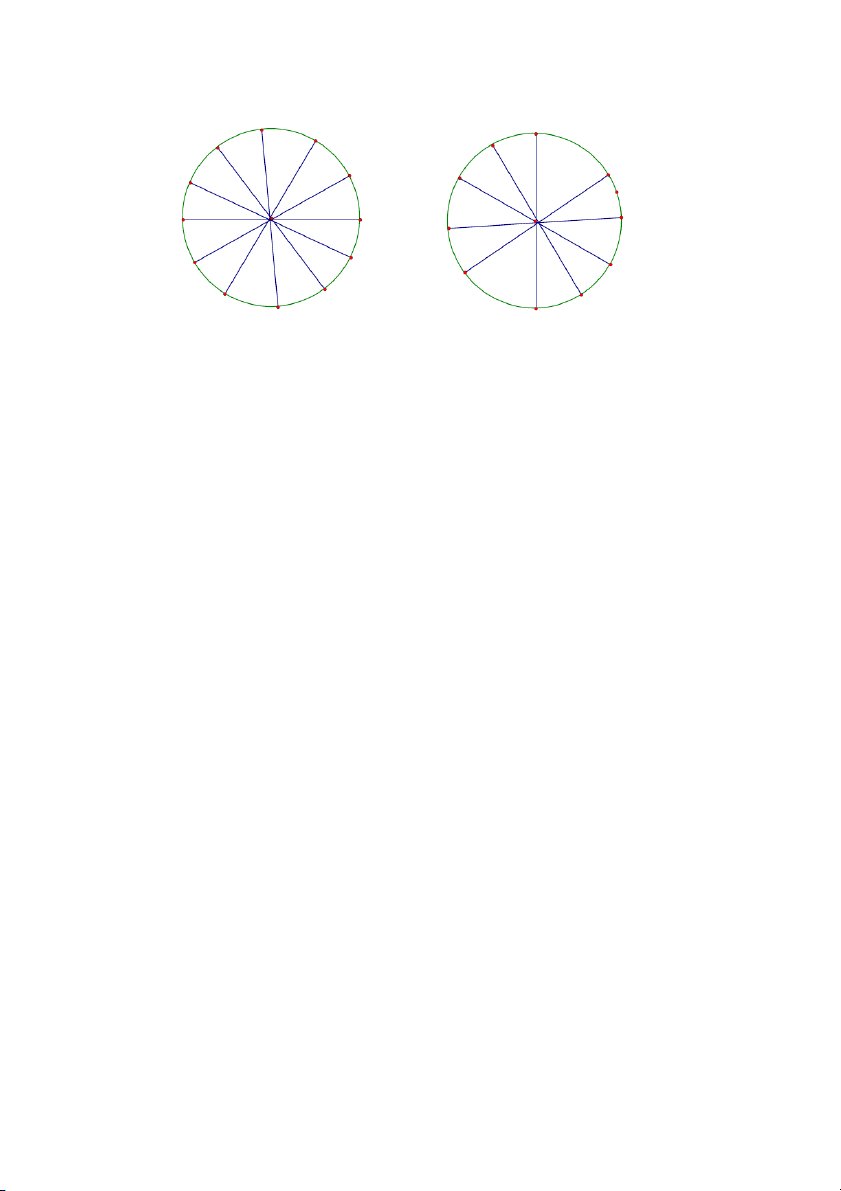
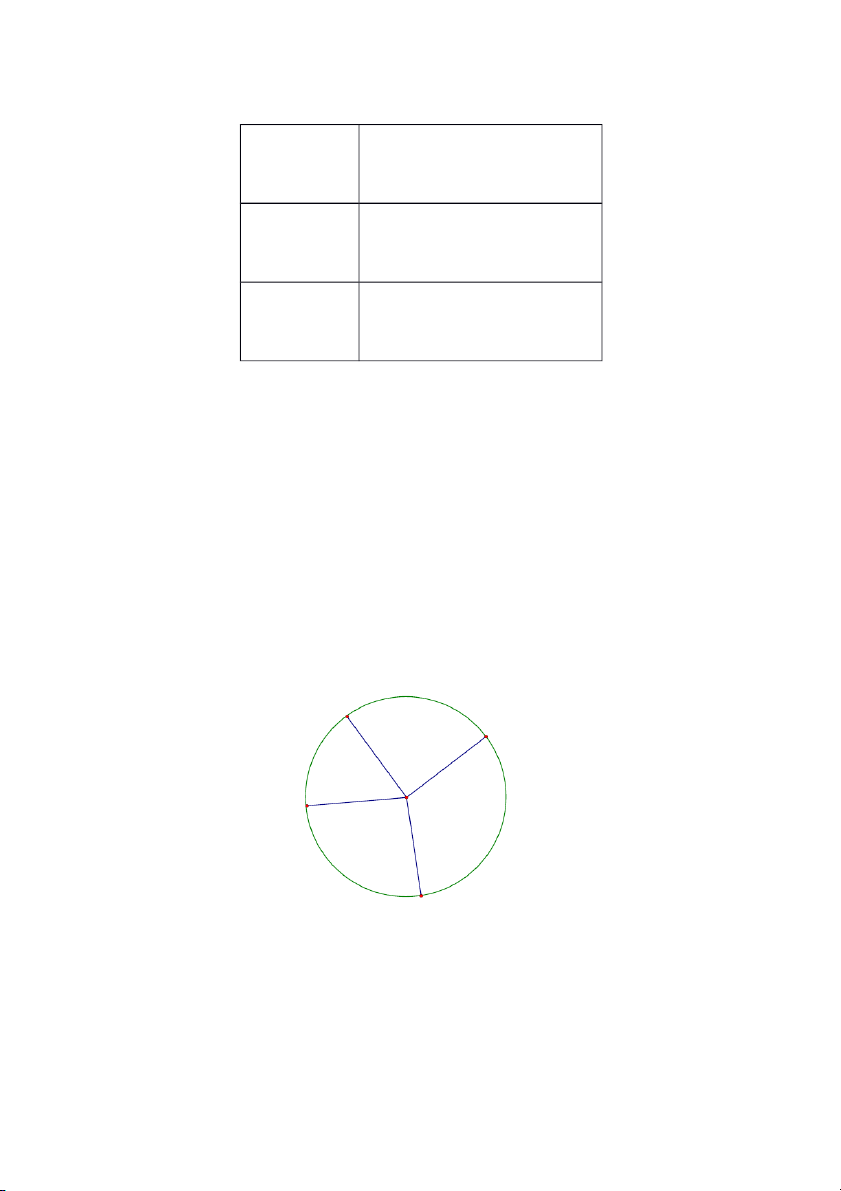
Giải: Ta chia đường tròn thành 12 phần đều nhau như hình vẽ. Ta đánh số các điểm chia
theo thứ tự từ 1 đến 12. 20 1 2 1 12 10 3 9 2 11 10 4 8 3 9 5 4 7 6 8 5 7 6
Để hai bạn nữ không đứng cạnh nhau thì ta phải xếp các bạn nữ vào đứng ở các
điểm ghi số lẻ, các bạn nam đứng ở các điểm ghi số chẵn (hoặc ngược lại).
Nhìn trên hình vẽ ta thấy đối diện với một bạn mang số lẻ qua tâm đường tròn
cũng là một bạn mang số lẻ và đối diện với một bạn mang số chẵn qua tâm đường tròn là
một bạn mang số chẵn. Như vậy đối diện với một bạn nữ qua tâm đường tròn là một bạn
nữ (chứ không thể là bạn nam).
Giả sử bớt đi một bạn nam và một bạn nữ:
Ta chia vòng tròn thành 10 phần bằng nhau như hình vẽ. Ta đánh số các điểm chia
theo thứ tự từ 1 đến 10. Ta xếp các bạn nữ vào các điểm chia mang số lẻ và các bạn nam
vào các điểm chia mang số chẵn (hoặc ngược lại). Nhìn trên hình vẽ ta thấy đối diện với
một bạn mang số lẻ trên đường tròn là một bạn mang số chẵn. Như vậy đối diện với một
bạn nữ qua tâm vòng tròn là một bạn nam và không có hai bạn nữ nào đứng cạnh nhau.
Tương tự trường hợp thêm một nam và một nữ.
Vậy hai bạn đó nói đúng. Ví dụ 2.11
Một đoàn du khách trên đường đi thăm rừng Cúc Phương. Đến một ngã ba đường
họ đang không biết rẽ lối nào thì nhìn thấy hai chú bé đang chăn trâu bên cạnh đường. Họ
được nghe mọi người lưu ý từ trước rằng, trong hai cậu có một cậu chuyên nói thật còn
cậu thứ hai chuyên nói dối. Khi được hỏi, các cậu chỉ trả lời: “Đúng” hoặc “Không”.
Nhưng mọi người không biết cậu nào nói thật còn cậu nào nói dối.
a) Một người lại gần và đặt hai câu hỏi cho một trong hai cậu bé. Sau khi nghe trả
lời ông ta xác định được đường nào đi rừng Cúc Phương.
b) Lát sau, một cô gái khác chỉ hỏi một trong hai cậu bé một câu. Sau khi nghe trả
lời cô cũng biết lối nào đi rừng Cúc Phương.
Bạn hãy cho biết các câu hỏi đó thế nào. Phân tích: 21
a) Để bằng hai câu hỏi cho một cậu bé người đó xác định được lối nào đi rừng Cúc
Phương thì người đó dùng câu hỏi thứ nhất để xác định em đó là nói thật hay nói dối.
Dựa vào đó dùng câu hỏi thứ hai để xác định lối nào đi rừng Cúc Phương.
b) Để bằng một câu hỏi cho một cậu bé, cô gái xác định được lối nào đi rừng Cúc
Phương thì câu hỏi về một trong hai con đường có đi rừng Cúc Phương hay không và câu
trả lời nhận được không phụ thuộc vào cậu bé đó nói thật hay nói dối. Giải
a) Trước hết người đó chỉ vào con trâu và hỏi một trong hai cậu bé: “Đây là con trâu có phải không?”
Trường hợp 1: Cậu bé trả lời “Đúng” thì cậu nói thật. Khi đó du khách chỉ vào một
trong hai con đường và hỏi tiếp:“Có phải lối này đi rừng Cúc Phương hay không?”. Nếu
cậu bé trả lời là “Đúng” thì lối đó đi rừng Cúc Phương, nếu cậu bé trả lời là “Không” thì
lối thứ hai đi rừng Cúc Phương.
Trường hợp 2: Cậu bé trả lời là “Không” thì cậu đó nói dối. Sau đó đặt tiếp câu
hỏi như trên. Trong trường hợp này, nếu cậu bé trả lời là “Đúng” thì lối thứ hai đi rừng
Cúc Phương và ngược lại.
b) Cô gái chỉ vào một con đường và hỏi một trong hai cậu bé: “Nếu tôi hỏi bạn cậu
lối này có đi rừng Cúc Phương không thì bạn cậu trả lời thế nào?”
Trường hợp 1: Lối đó đi rừng Cúc Phương. Nếu cậu bé được hỏi là người nói thật
(cậu thứ hai là người nói dối) thì câu trả lời là “Không”. Nếu cậu bé được hỏi là người
nói dối (cậu thứ hai là người nói thật) thì câu trả lời cũng là “Không”.
Trường hợp 2: Lối đó không đi rừng Cúc Phương. Lập luận như trong trường hợp
1 ta nhận được câu trả lời luôn là “Có” (cho dù cậu bé được hỏi là người nói thật hay nói dối).
Qua phân tích trên đây ta thấy: Nếu câu trả lời luôn là “Không” thì lối đó đi rừng
Cúc Phương. Ngược lại, nếu câu trả lời là “Có” thì lối đó không đi rừng Cúc Phương.
II.3. Phương pháp loại trừ Ví dụ 2.12
Tổ Toán của một trường trung học phổ thông có năm người: thầy Hùng, thầy
Quân, cô Vân, cô Hạnh và cô Cúc. Kì nghỉ hè cả tổ được hai phiếu đi nghỉ mát. Mọi
người đều nhường nhau, thầy hiệu trưởng đề nghị mỗi người đề xuất một ý kiến. Kết quả như sau:
1. Thầy Hùng và thầy Quân đi.
2. Thầy Hùng và cô Vân đi.
3. Thầy Quân và cô Hạnh đi.
4. Cô Cúc và cô Hạnh đi.
5. Thầy Hùng và cô Hạnh đi.
Cuối cùng thầy hiệu trưởng quyết định chọn đề nghị của cô Cúc, vì theo đề nghị đó thì
mỗi đề nghị đều thoả mãn một phần và bác bỏ một phần. 22
Bạn hãy cho biết ai đó đi nghỉ mát trong kì nghỉ hè đó.
Phân tích: Để chọn được đề nghị thoả mãn yêu cầu của đề bài ta lần lượt xét đề
nghị của từng người. Sẽ có hai khả năng xảy ra:
- Có một trong bốn đề nghị còn lại bác bỏ hoàn toàn. Trường hợp này ta loại bỏ đề nghị đó.
- Không có đề nghị nào trong bốn đề nghị còn lại bị bác bỏ hoàn toàn. Trường hợp
này ta chọn đề nghị đó. Giải: Ta nhận xét:
- Nếu chọn đề nghị thứ nhất thì đề nghị thứ tư bị bác bỏ hoàn toàn. Vậy không thể
chọn đề nghị thứ nhất và thứ tư.
- Nếu chọn đề nghị thứ hai thì đề nghị thứ ba bị bác bỏ hoàn toàn. Vậy không thể
chọn đề nghị thứ hai và thứ ba.
- Nếu chọn đề nghị thứ năm thì mỗi đề nghị trong bốn đề nghị còn lại đều thoả
mãn một phần và bác bỏ một phần.
Vậy kì nghỉ hè năm đó thầy Hùng và cô Hạnh đi nghỉ mát. Ví dụ 2.13
Sau giờ tập luyện buổi sáng đội tuyển thể thao rủ nhau vào quán ăn trưa. Thực đơn
của quán có tám món: gà luộc, nem rán, chim quay, đậu rán, bò xào, cá rán, ốc xào măng
và canh chua. Toàn đội thống nhất sẽ gọi ba món trong thực đơn cho bữa ăn. Nguyện
vọng của các cầu thủ chia ra thành năm nhóm như sau:
Nhóm 1: Gà luộc, nem rán và chim quay.
Nhóm 2: Đậu rán, bò xào và cá rán.
Nhóm 3: Bò xào, cá rán và ốc xào măng.
Nhóm 4: Nem rán, ốc xào măng và canh chua.
Nhóm 5: Gà luộc, bò xào và canh chua.
Cuối cùng toàn đội đồng ý với thực đơn của đội trưởng đã chọn, vì theo thực đơn đó mỗi
nhóm đều có ít nhất một món mà mình ưa thích.
Hỏi toàn đội hôm đó đó ăn những món gì? Giải: Ta nhận xét:
- Nếu chọn thực đơn của nhóm một thì cả nhóm hai và ba đều không có món nào
mà mình ưa thích. Vậy không thể chọn thực đơn của ba nhóm đầu.
- Nếu chọn thực đơn của nhóm bốn thì nhóm hai không có món nào mà mình ưa
thích. Vậy không thể chọn thực đơn của nhóm bốn.
- Nếu chọn thực đơn của nhóm năm thì mỗi nhóm trong bốn nhóm còn lại đều có
ít nhất một món mà mình ưa thích.
Vậy bữa trưa hôm đó toàn đội đã chọn thực đơn gồm ba món: gà luộc, bò xào và canh chua. 23 Ví dụ 2.14
Năm bạn Anh, Bình, Cúc, Doan, An quê ở năm tỉnh: Bắc Ninh, Hà Tây, Cần Thơ,
Nghệ An, Tiền Giang. Khi được hỏi quê ở tỉnh nào, các bạn trả lời như sau:
Anh: Tôi quê ở Bắc Ninh, còn Doan ở Nghệ An.
Bình: Tôi cũng quê ở Bắc Ninh, còn Cúc ở Tiền Giang.
Cúc: Tôi cũng quê ở Bắc Ninh, còn Doan ở Hà Tây.
Doan: Tôi quê ở Cần Thơ, còn Anh ở Hà Tây.
Nếu không bạn nào trả lời sai hoàn toàn thì quê của mỗi bạn ở tỉnh nào? Phân tích:
- Trước hết ta cần hiểu “không bạn nào trả lời sai hoàn toàn” nghĩa là gì?
Mỗi câu trả lời đều nói về quê quán của hai người. Nếu câu trả lời sai hoàn toàn thì
có nghĩa là quê của cả hai người đó đều không ở hai tỉnh đó. Vậy câu trả lời không sai
hoàn toàn có nghĩa là một trong hai người hoặc cả hai người có quê ở hai tỉnh đó.
Chẳng hạn, câu trả lời của Anh không sai hoàn toàn, có nghĩa là: hoặc Anh quê ở
Bắc Ninh còn quê của Doan không ở Nghệ An hoặc quê của Anh không ở Bắc Ninh còn
Doan quê ở Nghệ An hoặc Anh quê ở Bắc Ninh và Doan quê ở Nghệ An.
- Để xác định quê quán của mỗi bạn, ta lần lượt xét câu trả lời của mỗi người. Mỗi
câu trả lời nói về quê quán của hai người. Ta lần lượt xét các trường hợp sau:
+ Quê của người thứ nhất trong câu trả lời là đúng. Bằng suy luận ta xét các câu
trả lời của bốn người còn lại. Nếu không có câu nào sai hoàn toàn thì ta xác định được
quê của người đó. Tiếp đó ta xác định quê của bốn người còn lại. Nếu có một câu trả lời
(trong bốn câu còn lại) bị sai hoàn toàn thì quê của người thứ nhất trong câu trả lời không
ở tỉnh đó. Vậy quê của người thứ hai trong câu trả lời là đúng. Tiếp đó ta tìm quê của bốn người còn lại.
+ Quê của người thứ nhất trong câu trả lời là sai. Vậy quê của người thứ hai trong
câu trả lời là đúng. Ta xác định được quê của người này. Tiếp đó ta xác định quê của bốn người còn lại.
Giải: Giả sử Anh quê ở Bắc Ninh thế thì quê của Bình và Cúc đều không ở Bắc Ninh.
Vậy theo Bình thì Cúc quê ở Tiền Giang và theo Cúc thì Doan quê ở Hà Tây. Vì Anh quê
ở Bắc Ninh nên quê của Anh không ở Hà Tây. Vậy theo An thì An quê ở Cần Thơ. Cuối
cùng còn Bình quê ở Nghệ An (vì bốn bạn kia quê ở bốn tỉnh còn lại rồi). Ví dụ 2.15
Cúp Tiger 98 có 4 đội lọt vào vũng bán kết: Việt nam, Singapor, Thái Lan và
Inđônêxia. Trước khi vào đấu vòng bán kết ba bạn Dũng, Quang, Tuấn dự đoán như sau:
Dũng: Singapor nhì, còn Thái Lan ba.
Quang: Việt Nam nhì, còn Thái Lan thứ tư.
Tuấn: Singapor nhất và Inđônêxia nhì.
Kết quả mỗi bạn dự đoán đúng một đội và sai một đội. 24
Hỏi mỗi đội đã đạt giải mấy? Giải
- Nếu Singapor đạt giải nhì thì Singapor không đạt giải nhất. Vậy (theo Tuấn) thì
Inđônêxia đạt giải nhì. Điều này vô lí vì có hai đội đều đạt giải nhì.
- Nếu Singapor không đạt giải nhì thì theo Dũng, Thái Lan đạt giải ba. Như vậy,
Thái Lan không đạt giải tư. Theo Quang, Việt Nam đạt giải nhì. Thế thì Inđônêxia không
đạt giải nhì. Vậy theo Tuấn, Singapor đạt giải nhất, cuối cùng còn đội Inđônêxia đạt giải tư.
Kết luận: Thứ tự giải của các đội trong Cúp Tiger 98 là: Nhất: Singapor Nhì: Việt Nam Ba: Thái Lan Tư: Inđônêxia
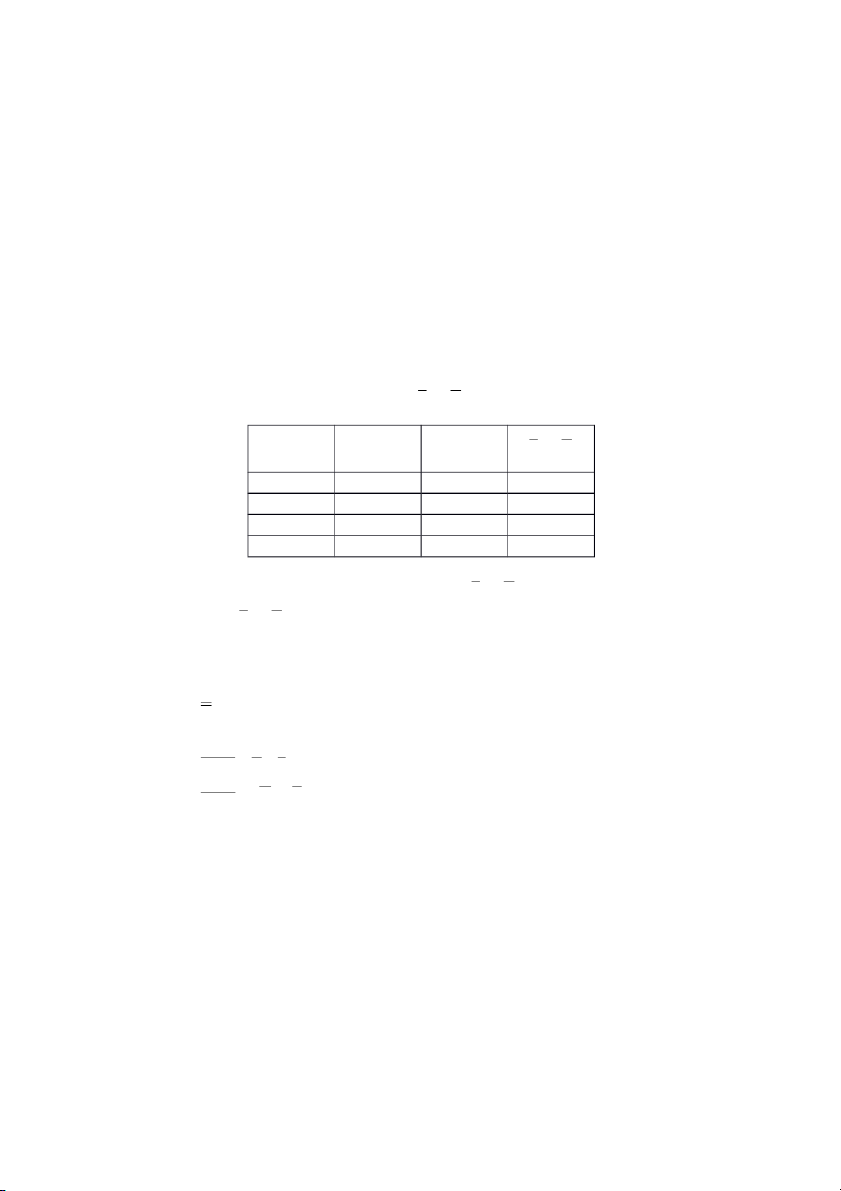
II.4. Phương pháp biểu đồ Ven
Trong khi giải một số bài toán, người ta thường dùng những đường cong kín để mô
tả mối quan hệ giữa các đại lượng trong bài toán. Nhờ sự mô tả này ta đi đến lời giải một
cách tường minh và thuận lợi. Những đường cong như thế ta sẽ gọi là biểu đồ Ven. Phương
pháp giải dùng biểu đồ Ven ta gọi là phương pháp biểu đồ Ven. Ví dụ 2.16
Để phục vụ cho hội nghị quốc tế, Ban tổ chức đã huy động 30 cán bộ phiên dịch
tiếng Anh và 25 cán bộ phiên dịch tiếng Pháp, trong đó có 12 cán bộ phiên dịch được cả
hai thứ tiếng Anh và Pháp. Hỏi:
a) Ban tổ chức đã huy động tất cả bao nhiêu cán bộ phiên dịch cho hội nghị đó?
b) Có bao nhiêu cán bộ chỉ dịch được tiếng Anh? Chỉ dịch được tiếng Pháp?
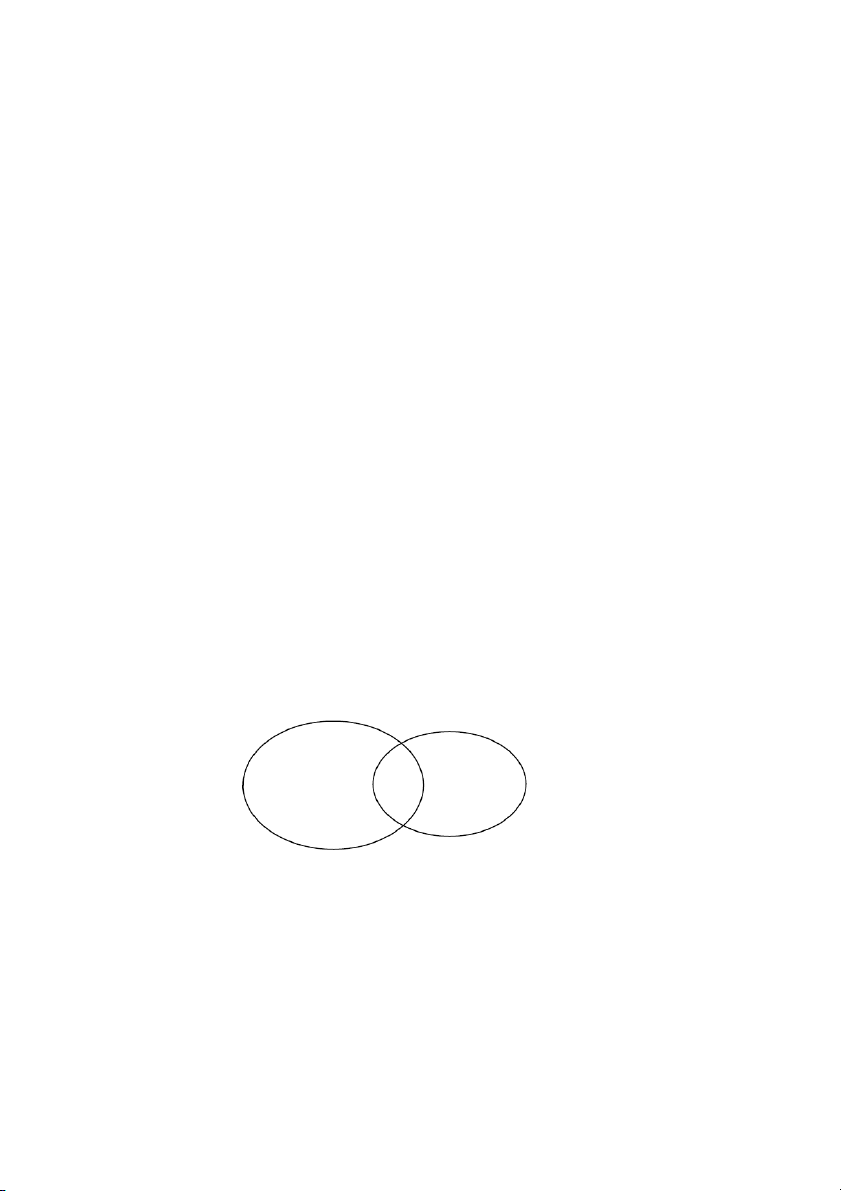
Giải: Số lượng cán bộ phiên dịch được Ban tổ chức huy động cho hội nghị có thể mô tả
bởi biểu đồ Ven ở hình 3. ? 12 ?
Tiếếng Anh: 30Tiếếng Pháp: 25 Tấết cả: ? Nhìn vào sơ đồ ta có:
Số cán bộ chỉ phiên dịch được tiếng Anh là: 25 30 - 12 = 18 (người).
Số cán bộ chỉ phiên dịch được tiếng Pháp là: 25 - 12 = 13 (người).
Số cán bộ phiên dịch được Ban tổ chức huy động cho hội nghị là: 30 + 13 = 43 (người).
Trả lời: Ban tổ chức đã huy động tất cả 43 cán bộ phiên dịch cho hội nghị, trong đó
có 18 người chỉ dịch được tiếng Anh và 13 người chỉ dịch được tiếng Pháp. Ví dụ 2.17
Có bao nhiêu số có ba chữ số là số lẻ hoặc chia hết cho 3?
Giải: Số các số lẻ có ba chữ số là:
(999 - 101) : 2 + 1 = 450 (số).
Các số chẵn có ba chữ số chia hết cho 3 lập thành dãy số cách đều: 102, 108, 114, ..., 996.
Số các số chẵn có ba chữ số chia hết cho 3 là:
(996 - 102) : 6 + 1 = 150 (số).
Bây giờ ta mô tả bài toán bằng biểu đồ Ven như hình 4.
Sốế l : 450Sốế chia hếết cho 3 ẻ 150 Tấết cả: ? Nhìn vào sơ đồ ta có:
Số các số có ba chữ số là số lẻ hoặc chia hết cho 3 là: 450 + 150 = 600 (số).
Trả lời: Có tất cả 600 số có ba chữ số là số lẻ hoặc chia hết cho 3. Ví dụ 2.18
Lớp 9A có 30 em tham gia dạ hội tiếng Anh và tiếng Trung, trong đó có 25 em nói
được tiếng Anh và 18 em nói được tiếng Trung. Hỏi có bao nhiêu em nói được cả hai thứ tiếng? 26
Giải: Các em học sinh lớp 9A tham gia dạ hội có thể được mô tả bằng biểu đồ Ven ở hình 5.
Tiếếng Anh: 25Tiếếng Trung: 18 ? Tấết c : 30 ả
Số học sinh chỉ nói được tiếng Trung là: 30 – 25 = 5 (em).
Số em nói được cả hai thứ tiếng là: 18 – 5 = 13 (em).
Trả lời: Có 13 em nói được cả tiếng Anh và tiếng Trung. Ví dụ 2.19.
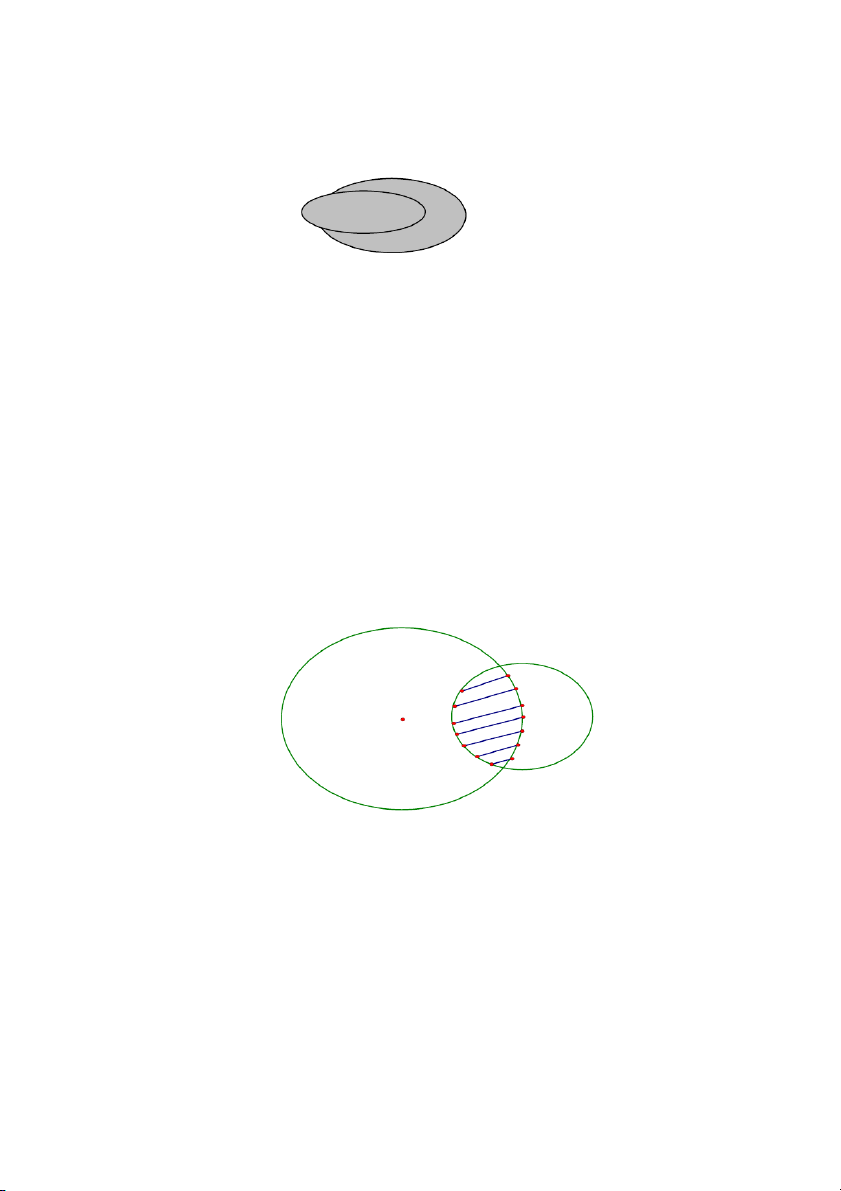
Trong hội khoẻ Phù Đổng có 100 vận động viên đăng kí dự thi. Mỗi vận động viên được
đăng kí dự thi một hoặc hai trong ba môn: ném tạ, bơi lội hoặc đấu cờ vua. Kết quả có 30
vận động viên chỉ thi đấu cờ vua, 53 người đăng kí thi ném tạ và 45 người đăng kí thi bơi.
Hỏi có bao nhiêu người đăng kí thi đấu cả hai môn ném tạ và bơi lội?
Giải: Các vận động viên đăng kí thi đấu có thể được mô tả bởi hình 6. Ném tạ: 53 Bơi: 18 ? Cờ vua: 30ch sốố ữ Tấết cả: 100 là sốố l ẻ h n di ơ n ệ
Số vận động viên đăng kí thi ném tạ hoặc bơi lội là: 琀 ch hình 100 - 30 = 70 (người). tròn. 27
Số vận động viên đăng kí cả hai môn ném tạ và bơi lội là:
(45 + 53) - 70 = 28 (người).
Trả lời: Có 28 vận động viên đăng kí thi đấu cả hai môn ném tạ và bơi lội. III. Công thức
III.1. Khái niệm về công thức
Trong toán học ta đã làm quen với biểu thức toán học (là dãy kí hiệu chỉ ra các
phép toán và thứ tự thực hiện các phép toán trên các số hoặc các chữ nhận giá trị từ một trường số).
Trong logic mệnh đề, người ta xây dựng khái niệm công thức tương tự biểu thức toán học trong toán học.
Trong mục I.1 ta đã làm quen với mệnh đề (xác định) và mệnh đề mở (chưa xác
định). Ta sẽ gọi chung là các biến mệnh đề.
Cho các biến mệnh đề p, q, r,... Khi dùng các phép logic tác động vào chúng, ta sẽ
nhận được các biến mệnh đề ngày càng phức tạp hơn. Mỗi mệnh đề như thế và cả những
mệnh đề xuất phát ta gọi là công thức. Hay nói cách khác:
a) Mỗi biến mệnh đề là một công thức.
b) Nếu P,Q là những công thức thì P , P Q, P Q, P Q, P Q cũng đều là công thức.
c) Mọi dãy kí hiệu không xác định theo các quy tắc trên đây đều không phải là công thức. Ví dụ 3.1
Từ các biến mệnh đề p, q, r ta thiết lập được công thức:
(p q) r
(p q) r
(p q) r
(p q) (q p) ....
III.2. Giá trị chân lí của công thức Cho công thức P " p q"
Ta gán cho các biến mệnh đề p, q những giá trị chân lí xác định, chẳng hạn:
- G(p) = 1 và G(q) = 0 thì p q là mệnh đề sai. Suy ra p q là mệnh đề đúng,
hay G( p q) 1 .
- G(p) = G(q) = 1 thì p q là mệnh đề đúng. Suy ra p q là mệnh đề sai, hay
G( p q) 0 . 28
Như vậy khi gán cho mỗi biến mệnh đề có mặt trong công thức P một giá trị chân
lí xác định thì công thức P sẽ trở thành một mệnh đề (đúng hoặc sai). Nếu P là mệnh đề
đúng (hoặc sai) thì ta nói công thức P có giá trị chân lí bằng 1 (hoặc 0) ứng với hệ chân lí
vừa gán cho các biến mệnh đề có mặt trong công thức đó. Ví dụ 3.2
p p là công thức luôn có giá trị chân lí bằng 0 với mọi biến mệnh đề p. Ví dụ 3.3
( p q) ( p q) là công thức luôn có giá trị chân lí bằng 1 với mọi biến mệnh đề p, q. Ví dụ 3.4
Lập bảng giá trị chân lí của công thức P "
( p q) ( p q) Giải p q q p p q P 1 1 1 0 1 1 0 0 0 0 0 1 0 0 0 0 0 0 1 1
Dựa vào bảng chân lí trên ta có thể khẳng định:
- Nếu p và q cùng đúng hoặc cùng sai thì P đúng.
- Nếu nếu p hoặc q đúng còn mệnh đề thứ hai sai thì P sai. Ví dụ 3.5
Lập bảng giá trị chân lí của công thức “(p q) r” = Q Giải p q r p q Q 1 1 1 1 1 1 1 0 1 0 1 0 0 1 0 1 0 1 1 1 0 1 1 1 1 0 1 0 1 0 0 0 1 0 0 0 0 0 0 0
III.3. Sự tương đương logic và đẳng thức 29
Cho P và Q là hai công thức. Ta nói rằng hai công thức P và Q tương đương logic
với nhau, kí hiệu là P Q, nếu với mọi hệ chân lí gán cho các biến mệnh đề có mặt trong
hai công thức đó thì chúng luôn nhận giá trị chân lí như nhau.
Đặc biệt, hai mệnh đề a, b gọi là tương đương logic với nhau, kí hiệu a b, nếu
chúng cùng đúng hoặc cùng sai. Chú ý:
1. Trong logic không có khái niệm hai mệnh đề bằng nhau mà chỉ có khái niệm hai
mệnh đề tương đương logic với nhau.
Hai mệnh đề tương đương logic có thể về nội dung chúng hoàn toàn không liên
quan với nhau. Chẳng hạn:
“Tháng Hai có 30 ngày 2 x 2 = 10”.
2. P Q ta gọi là một đẳng thức.
3. Để chứng minh hai công thức tương đương logic với nhau ta thường dùng
phương pháp lập bảng giá trị chân lí. Chẳng hạn:
Chứng minh đẳng thức sau: p q q p p q p q q p 1 1 1 1 1 0 0 0 0 1 1 1 0 0 1 1
Nhìn vào bảng trên ta thấy hai công thức p q và q p luôn cùng đúng hoặc cùng sai.
Vậy ta có p q q p
Dưới đây là một số phép tương đương logic thường gặp:
Phủ định của phủ định (1) p p
Luật Đờ-Moóc-Găng (2)
p q p q (3)
p q p q
Tính chất kết hợp của các phép logic (4)
(p q) r p (q r) (5)
(p q) r p (q r)
Tính chất giao hoán của các phép logic (6) p q q p (7)
p q q p (8)
p q q p
Tính chất phân phối 30 (9)
p (q r) (p q) (p r)
(10) p (q r) (p q) (p r) Tính lũy đẳng (11) p p p (12) p p p
Biểu diễn phép kéo theo qua các phép logic khác
(13) p q p q
(14) p q p q
(15) p q q p
Biểu diễn phép tương đương qua các phép logic khác
(16) p q (p q) (q p) p (17) p q q
Ta dùng kí hiệu 1 (hoặc 0) để chỉ biến mệnh đề luôn đúng (hoặc luôn sai). Ta có
các đẳng thức sau về 0 và 1 (18) p 0 0 (19) p 1 p (20) p 0 p (21) p 1 1 (22)
p p (luật bài trung) (23)
p p (luật mâu thuẫn)
III.4. Phép biến đổi công thức
Khái niệm công thức trong logic mệnh đề tương tự như khái niệm biểu thức toán
học trong toán học; khái niệm đẳng thức tương tự như khái niệm hằng đẳng thức trong toán học.
Dựa vào các đẳng thức, ta có thể thực hiện phép biến đổi đồng nhất để chứng minh
một đẳng thức hoặc đưa một công thức về dạng đơn giản hơn.
Để cho tiện, ta quy ước:
1. Các phép logic trong một công thức được thực hiện theo thứ tự ; ;
Với quy ước này, chẳng hạn ta sẽ viết:
p q r thay cho ( p q) r p v q ^ r u thay cho [p v (q ^ r)] u
2. Không viết dấu ngoặc ở ngoài đối với mỗi công thức.
Với quy ước này, chẳng hạn, ta sẽ viết: p ^ q r 31 Thay cho [(p ^ q) r]
3. Nếu có dấu phủ định trên một công thức nào đó thì ta bỏ dấu ngoặc ở hai đầu công thức đó. Chẳng hạn, ta sẽ viết p q ^ r Thay cho
( p q) r.
Ví dụ 3.6. Chứng minh rằng:
( p ^ q ^ r) v (p ^ q ^ r) v (q ^ r) (p q) ^ r.
Biến đổi lần lượt ta có:
( p ^ q ^ r) v ( p ^ q ^ r) v (q ^ r)
[(p ^ q) v ( p ^ q)] ^ r v (q ^ r) [ p ^ (q v q )] ^ r v (q ^ r) ( p ^ 1) ^ r v (q ^ r) ( p ^ r) v (q ^ r) ( p v q) ^ r) (p q) ^ r
Ví dụ 3.7. Rút gọn công thức:
( p q p q) q
(p q p q ) q [
p q (p q)] q Ta có: [
( p q) ( p q)] q ( p ) q q q
III.5. Mệnh đề liên hợp, điều kiện cần, điều kiện đủ, điều kiện cần và đủ
III.5.1. Mệnh đề liên hợp
Từ mệnh đề “Nếu một số chia hết cho 4 thì nó chia hết cho 2” (1) ta có thể thiết
lập được các mệnh đề
“Nếu một số chia hết cho 2 thì nó chia hết cho 4” (2)
“Nếu một số chia hết cho 4 thì nó không chia hết cho 2” (3)
“Nếu một số không chia hết cho 2 thì nó không chia hết cho 4” (4)
Các mệnh đề (1); (2); (3); (4) gọi là những mệnh đề liên hợp
Một cách tổng quát, ta định nghĩa
Nếu ta gọi p q (1) là mệnh đề thuận thì
q p (2) là mệnh đề đảo của (1)
p q (3) là mệnh đề phản của (1) 32
q p (4) là mệnh đề phản đảo của (1)
Các mệnh đề thuận, đảo, phản và phản đảo ta gọi là những mệnh đề liên hợp.
Áp dụng đẳng thức (15) ta có p q q p
q p p q Hay:
- Mệnh đề thuận tương đương logic với mệnh đề phản đảo;
- Mệnh đề phản tương đương logic vơi mệnh đề đảo. Ví dụ 3.8
Thiết lập các mệnh đề liên hợp với mệnh đề sau: “Nếu một số chia hết cho 6 thì nó chia hết cho 3”
Sau đó tìm giá trị chân lí của chúng
Các mệnh đề liên hợp của nó là
- Nếu một số chia hết cho 3 thì nó chia hết cho 6.
- Nếu một số không chia hết cho 6 thì nó không chia hết cho 3
- Nếu một số không chia hết cho 3 thì nó không chia hết cho 6
Dễ dàng thấy rằng mệnh đề thuận và phản đảo là các mệnh đề đúng còn mệnh đề
đảo và phản là các mệnh đề sai. Ví dụ 3.9
Thiết lập các mệnh đề liên hợp với mệnh đề sau:
“Nếu ABC vuông ở A thì BC2 = AB + 2 AC2
Sau đó tìm giá trị chân lí của chúng
Các mệnh đề liên hợp của nó là
- Nếu ABC thoả mãn hệ thức BC = 2
AB2 + AC 2thì nó vuông ở A.
- Nếu ABC không vuông ở A thì BC2 AB2 + AC 2
- Nếu ABC không thoả mãn hệ thức BC2 = AB + 2
AC2 thì nó không vuông ở A.
Từ môn hình ở trường phổ thông ta thấy cả bốn mệnh đề trên đều có giá trị chân lí bằng 1.
III.5.2. Điều kiện cần, điều kiện đủ, điều kiện cần và đủ
Trong toán học, nếu ta chứng minh được p q là mệnh đề đúng thì ta nói rằng
- p là điều kiện đủ để có q
- q là điều kiện cần để có p
Trong trường hợp này, mệnh đề p q có thể diễn đạt bằng nhiều cách khác nhau, chẳng hạn: - Nếu có p thì có q
- p là điều kiện đủ để có q
- q là điều kiện cần để có p - Có p ắt có q - Muốn có p phải có q - Có q khi có p ..... 33
Trong toán học, nếu ta chứng minh được đồng thời cả hai mệnh đề p q và q p
đều đúng thì ta nói rằng:
- p là điều kiện cần và đủ để có q
- q là điều kiện cần và đủ để có p
Theo phép tương đương (16) ta có
p q (p q) (q p)
Trong trường hợp này, mệnh đề p q có thể diễn đạt bằng nhiều cách khác nhau, chẳng hạn:
- Điều kiện cần và đủ để có p là q
- Để có p, điều kiện cần và đủ là q
- Điều kiện ắt có và đủ để có p là q
- Có p khi và chỉ khi có q ...
Trong toán học, mỗi định lí được phát biểu dưới dạng một mệnh đề đúng p q,
trong đó, p gọi là giả thiết, q gọi là kết luận của định lí.
Ta thiết lập mệnh đề đảo q p của định lí đó. Nếu q p cũng là mệnh đề đúng
thì ta nói định lí đã cho có định lí đảo. Ngược lại, ta nói định lí đã cho không có định lí đảo.
Trong trường hợp định lí có định lí đảo, ta thường phát biểu kết hợp cả định lí
thuận và đảo dưới dạng điều kiện cần và đủ p q. Ví dụ 3.10
Hãy xét xem định lí sau có định lí đảo hay không: “Nếu tứ giác ABCD có hai
đường chéo cắt nhau ở trung điểm của mỗi đường thì nó là hình bình hành”.
Nếu có, hãy phát biểu chúng dưới dạng điều kiện cần và đủ.
Mệnh đề đảo của định lí đó cho là: “Nếu tứ giác ABCD là hình bình hành thì hai
đường chéo của nó cắt nhau ở trung điểm của mỗi đường”.
Từ môn hình học ở trường phổ thông ta đã biết đây là mệnh đề đúng. Vậy định lí đó có định lí đảo.
Kết hợp giữa định lí thuận và đảo được phát biểu như sau: “Điều kiện cần và đủ để
tứ giác ABCD là hình bình là hai đường chéo của nó cắt nhau ở trung điểm của mỗi đường”. Ví dụ 3.11
Cũng hỏi như ví dụ 3.10 đối với định lí: “Nếu số tự nhiên a có chữ số hàng đơn vị
bằng 0 hoặc 5 thì nó chia hết cho 5”.
Mệnh đề đảo của định lí đó cho là: “Nếu số tự nhiên a chia hết cho 5 thì nó có chữ
số hàng đơn vị bằng 0 hoặc bằng 5”.
Từ trường phổ thông ta đã biết mệnh đề đảo là mệnh đề đúng. Vậy định lí trên có định lí đảo.
Kết hợp giữa định lí thuận và đảo ta có: 34
“Số tự nhiên a chia hết cho 5 khi và chỉ khi chữ số hàng đơn vị của nó bằng 0 hoặc
5” hoặc “Điều kiện ắt có và đủ để số tự nhiên a chia hết cho 5 là chữ số hàng đơn vị của nó bằng 0 hoặc 5”.
IV. Quy tắc suy luận
Phân tích mỗi chứng minh toán học ta thấy nó bao gồm một số hữu hạn bước suy
luận. Trong mỗi bước suy luận ta đã vận dụng những quy tắc nhất định để từ những mệnh
đề đã được thừa nhận là đúng có thể rút ra một mệnh đề mới.
Dưới đây ta trình bày những quy tắc thường dùng trong các bước suy luận như thế.
Định nghĩa: Cho A, B, C là những công thức. Nếu tất cả các hệ chân lí của các
biến mệnh đề có mặt trong các công thức đó làm cho A, B nhận giá trị chân lí bằng 1
cũng làm cho C nhận giá trị chân lí bằng 1 thì ta nói có một quy tắc suy luận từ các tiên
đề A, B dẫn tới hệ quả logic C của chúng. A, B Ta kí hiệu là C A,B
Từ định nghĩa ta dễ dàng thấy rằng để chứng minh C là một quy tắc suy luận ta
chỉ cần lập bảng giá trị chân lí đối với các công thức A, B, C. Trong đó chỉ ra rằng mỗi
khi A, B nhận giá trị chân lí bằng 1 thì C cũng nhận giá trị chân lí bằng 1 Ví dụ 4.1 p q,q r
Chứng minh rằng ta có quy tắc suy luận p r
Sau đó nêu ví dụ minh hoạ về vận dụng quy tắc đó trong dạy học toán. Ta có bảng chân lí p q r p q q r p r 1 1 1 1 1 1 1 1 0 1 0 0 1 0 1 0 1 1 1 0 0 0 1 0 0 1 1 1 1 1 0 1 0 1 0 1 0 0 1 1 1 1 0 0 0 1 1 1
Nhìn vào bảng trên ta thấy mỗi khi p q và q r nhận giá trị chân lí bằng 1 thì
p r cũng nhận giá trị chân lí bằng 1. p q,q r
Vậy ta có quy tắc suy luận p r
. Ta sẽ gọi là quy tắc suy luận bắc cầu. Chẳng hạn, ta chọn
“p q” là mệnh đề “Nếu a chia hết cho 6 thì nó chia hết cho 3”.
“q r” là mệnh đề “Nếu a chia hết cho 3 thì tổng các chữ số của nó chia hết cho 3”. 35
Áp dụng quy tắc suy luận bắc cầu ta có: “Nếu a chia hết cho 6 thì tổng các chữ số của nó chia hết cho 3”. Ví dụ 4.2
Chứng minh rằng ta có quy tắc suy luận sau: p q, q p
Cho ví dụ về vận dụng quy tắc suy luận đó trong dạy học toán.
Ta có bảng giá trị chân lí sau: p q q p q p 1 1 0 1 0 1 0 1 0 0 0 1 0 1 1 0 0 1 1 1
Từ bảng trên ta suy ra quy tắc suy luận p q, q p
Ta đã biết “nếu a chia hết cho 3 thì tổng các chữ số của nó chia hết cho 3”.
Số 146 có tổng các chữ số không chia hết cho 3 nên số 146 không chia hết cho 3.
Dưới đây là các quy tắc suy luận thường được vận dụng trong suy luận toán học: 1. p q, p
(Quy tắc suy luận Modus ponens) q p q,q 2. p
(Quy tắc kết luận ngược Modus Lollens) 3. p q, q r
(Quy tắc suy luận bắc cầu) p r p q,q r p q,q p 4. 5. p r p q p q, p p r, q r 7. 6. q p q r p q, r s 9. 8. p q, p r p r q s p q r p q, r s p q 10. p r q s
11. q p (Quy tắc phản đảo) p q p q ,
12. p q q p
p q, p q 13. p
(Quy tắc chứng minh phản chứng)
V. Mệnh đề tổng quát và mệnh đề tồn tại 36
V.1 Khái niệm về hàm mệnh đề Ta xét các ví dụ sau:
1. “Số tự nhiên n chia hết cho 3”:về phương diện ngôn ngữ thì đây là một câu.
Nhưng câu này chưa phản ánh tính đúng hoặc sai một thực tế khách quan nào, cho nên nó
chưa phải là mệnh đề. Song nếu ta thay n bởi một số tự nhiên cụ thể. Chẳng hạn
- Thay n = 45 ta được mệnh đề đúng: “45 chia hết cho 3”
- thay n = 103 ta được mệnh đề sai: “103 chia hết cho 3” 2. “2x + 3 > 17”
Tương tự, “2x + 3 > 17” chưa phải là mệnh đề, song nếu ta thay x bởi một số thực cụ thể, chẳng hạn
- Thay x = 10 ta có mệnh đề đúng “2 . 10 + 3 > 17”
- Thay x = 1 ta cú mệnh đề sai “2 . 1 + 3 > 17”
3. Câu “Ông A là nhà vật lí vĩ đại” cũng chưa phải là mệnh đề. Nếu ta chọn “Ông
A” là Niu-tơn ta được mệnh đề đúng “Niu tơn là nhà vật lí vĩ đại”. Nếu ta chọn Ông A” là
“Tố Hữu” ta được mệnh đề sai “Tố Hữu là nhà vật lí vĩ đại”
4. Câu “Tứ giác ABCD là hình chữ nhật” chưa phải là mệnh đề. Nếu ta chọn
ABCD là tứ giác trong hình (b) ta được mệnh đề sai, hình (a) ta được mệnh đề đúng A B A B D C D C Hình A Hình B
Từ các ví dụ trên ta đi đến định nghĩa sau:
Những câu có chứa các biến mà bản thân nó chưa phải là mệnh đề nhưng khi thay
các biến đó bởi những phần tử xác định thuộc tập X thì nó trở thành mệnh đề (đúng hoặc
sai) ta sẽ gọi là hàm mệnh đề
Tập X gọi là miền xác định; tập các phần tử thuộc X khi thay vào ta được mệnh đề
đúng gọi là miền đúng; thay vào ta được mệnh đề sai gọi là miền sai của hàm mệnh đó
Ta dùng kí hiệu T(n), F(x), G(y), .......... để chỉ các hàm mệnh đề. Chẳng hạn:
- Hàm mệnh đề T(n) = “Số tự nhiên n chia hết cho 3” có miền xác định là tập các số
tự nhiên. Tập các số tự nhiên chia hết cho 3 là miền đúng của T(n). Tập các số tự nhiên
không chia hết cho 3 là miền sai của T(n)
- Hàm mệnh đề “Tứ giác ABCD là hình chữ nhật” cú miền xác định là tập các hình
tứ giác, miền đúng là tập các hình chữ nhật
V.2 Phủ định một hàm mệnh đề
Cho F(x) là hàm mệnh đề xác định trên miền X. Ta gọi phủ định của hàm mệnh đề
F(x) là một hàm mệnh đề, kí hiệu là F(x), sao cho đối với mỗi a X, F(a) là mệnh đề
phủ định của mệnh đề F(a) Chẳng hạn:
- Phủ định của hàm mệnh đề T(n) = “số tự nhiờn n chia hết cho 3” là hàm mệnh đề 37
T (n) = “số tự nhiên n không chia hết cho 3”
- Phủ định của hàm mệnh đề F(x) = “2x + 3 > 17” là hàm mệnh đề F (x) = “2x + 3 17”
V.3. Mệnh đề tổng quát
Ta đặt vào trước hàm mệnh đề F(x) = “2x + 1 > 5” cụm từ
“với mọi x R ta có”, ta được mệnh đề sai:
“Với mọi x R ta có F(x)” hay “Với mọi x R ta có 2x + 1 > 5”
Một cách tổng quát, cho T(x) là hàm mệnh đề xác định trên miền X. Ta gọi mệnh
đề dạng:“Với mọi x X ta có T(x)” hoặc “Với mọi x X, T(x)” là mệnh đề tổng quát
(hoặc toàn thể, phổ biến, phổ cập, ....). Ký hiệu là T(x)
x X, T(x) hoặc ( x X) T(x) hoặc x X
Ký hiệu gọi là lượng từ tổng quát (hoặc toàn thể, phổ biến, phổ cập, ....) 38 Ví dụ 5.1
“ n N, n là số nguyên tố” là mệnh đề sai
“ n N, 2n là số chẵn” là mệnh đề đúng “ x R, x + 1 > 2 0” là mệnh đề đúng “ x R, x - 1 = 2 0” là mệnh đề sai Chú ý
Mệnh đề tổng quát trong thực tế được diễn đạt dưới nhiều hình thức khác nhau. Chẳng hạn
- Tất cả người Việt nam đều nói thạo tiếng Anh
- Mọi người Việt nam đều nói thạo tiếng Anh
- Người Việt nam nào chẳng nói thạo tiếng Anh
- Đã là người Việt nam thì ai chẳng nói thạo tiếng Anh ......
V.4. Mệnh đề tồn tại
Ta đặt trước hàm mệnh đề F(x) = “2x + 1 > 5” cụm từ
“Tồn tại x R sao cho” ta được mệnh đề đúng:
“Tồn tại x R sao cho F(x)” hay “Tồn tại x R sao cho 2x + 1 > 5”
Một cách tổng quát, cho T(x) là hàm mệnh đề xác định trên miền X. Ta gọi mệnh
đề dạng “Tồn tại x X sao cho T(x)” hoặc “Tồn tại x R: T(x)” là mệnh đề tồn tại. Ký hiệu là T (x)
x X : T(x) hoặc x X
Ký hiệu gọi là lượng từ tồn tại Ví dụ 5.2
- “Tồn tại số tự nhiên n sao cho n là số nguyên tố” là mệnh đề đúng
- “Tồn tại số thực x sao cho x2 - 1 = 0” là mệnh đề đúng
- “Tồn tại số thực x sao cho x2 + 1 = 0” là mệnh đề sai Chú ý
1.Trong thực tế, mệnh đề tồn tại còn được diễn đạt dưới những dạng khác nhau, chẳng hạn:
- Tồn tại ít nhất một người Việt nam nói thạo tiếng Anh
- Có một người Việt nam nói thạo tiếng Anh
- Ít ra cũng có một người Việt nam nói thạo tiếng Anh
- Có nhiều người Việt nam nói thạo tiếng Anh .....
2. Ta dựng kí hiệu “! x X : T(x)” với nghĩa tồn tại duy nhất một x X sao cho T(x)”
V.5. Phủ định của mệnh đề tồn tại và tổng quát
Phủ định các mệnh đề tổng quát và tồn tại được thiết lập theo quy tắc dưới đây: 39 x X ,T( ) x x
X :T (x) x
X :T (x) x
X ,T (X ) Ví dụ 5.3
- Mọi tam giác đều đều là tam giác cân Có một tam giác đều không phải là tam giác cân, là mệnh đề đúng.
- Người Việt nam nào chẳng nói thạo tiếng Anh Có ít nhất một người Việt nam nói
không thạo tiếng Anh, là mệnh đề đúng.
- Có một số tự nhiên chia hết cho 3 Mọi số tự nhiên đều chia hết cho 3, là mệnh đề sai.
- Có ít nhất một số thực x là nghiệm của phương trình x -
2 3x - 4 = 0 Mọi số thực x đều
không phải là nghiệm của phương trình x 2- 3x - 4 = 0 Phương trình x 2- 3x - 4 = 0
không có nghiệm thực, là mệnh đề sai.
VI. Suy luận và chứng minh VI.1. Suy luận là gì?
Suy luận là rút ra một mệnh đề mới từ một hay nhiều mệnh đề đó biết. Những
mệnh đề đã biết gọi là tiền đề, một mệnh đề mới được rút ra gọi là kết luận của suy luận.
Hai kiểu suy luận thường gặp là: suy luận diễn dịch (hay còn gọi là suy diễn) và
suy luận nghe có lí (hay suy luận có lí).
VI.2. Suy luận diễn dịch
VI.2.1 Suy luận diễn dịch là gì?
Suy luận diễn dịch (hay còn gọi là suy diễn) là suy luận theo những quy tắc suy
luật tổng quát (của logic mệnh đề). Trong suy luận diễn dịch, nếu các tiền đề đúng thì kết
luận rút ra cũng phải đúng.
Trong logic vị từ, ngoài những quy tắc suy luận của logic mệnh đề ta thường gặp và
vận dụng hai quy tắc suy luận dưới đây:
x X , P(x), a X (1) P (a ) x X
,P (x ) Q (x ),P (a ) (2) Q(a)
(1) có nghĩa là nếu P(x) đúng với mọi x X và a X thì P(a) là mệnh đề đúng.
(2) có nghĩa là: Nếu P(x) Q(x) đúng với mọi x X và P(a) đúng với a X thì
Q(a) cũng là mệnh đề đúng. Ví dụ 6.1
TĐ 1: Mọi số tự nhiên có tổng các chữ số chia hết cho 9 thì nó chia hết cho 9.
TĐ 2: Số 432135 có tổng các chữ số chia hết cho 9.
KL: Vậy 432135 chia hết cho 9. Ví dụ 6.2
TĐ 1: Nếu tứ giác là hình thoi thì hai đường chéo của nó vuông góc với nhau.
TĐ 2: Tứ giỏc ABCD là hình thoi. 40 Vậy AC BD. Ví dụ 6.3
- Với mọi x R, sin2x + cos x = 1. 2 - 14 R sin 2 o c s2 1 Vậy 14 14
Trong ba ví dụ nêu trên, các tiền đề đều đúng, ta đó vận dụng các quy tắc suy luận
(1) vừa nêu trên. Vì vậy các kết luận của chúng phải đúng. Ví dụ 6.4 TĐ 1: 672 chia hết cho 3. TĐ 2: 672 chia hết cho 4
KL: 672 chia hết cho 3 và 4.
Trong ví dụ này, các tiền đề đều đúng, ta đó vận dụng quy tắc suy luận: q , p p q Ví dụ 6.5 Từ các tiền đề
TĐ 1: Nếu a chia hết cho 6 thì nó chia hết cho 3.
TĐ 2: Nếu a chia hết cho 3 thì tổng các chữ số của nó chia hết cho 3.
KL: "Nếu a chia hết cho 6 thì tổng các chữ số của nó chia hết cho 3".
Ở đây các tiền đề đều là những định lí đó được chứng minh trong toán học. Ta đó
vận dụng quy tắc suy luận bắc cầu: p q , q r p r
VI.3.2. Suy luận diễn dịch trong dạy học toán ở tiểu học
Trong dạy học toán ở tiểu học, ta thường xuyên vận dụng phép suy luận diễn dịch.
Cụ thể là: mỗi khi cung cấp cho học sinh những kiến thức mới (có thể là một quy
tắc thực hành tính toán, một công thức tính chu vi hoặc diện tích các hình, phương pháp
giải một dạng toán, ….) Học sinh vận dụng để giải các bài tập thực hành. Trong mỗi hoạt
động thực hành này, ta đó vận dụng phép suy luận diễn dịch.
Ví dụ 6.6.
Sau khi học dấu hiệu chia hết cho 5, học sinh thực hành giải bài tập 1 SGK Toán 4, trang 96:
Trong các số 35; 8; 57 660; 4674; 3000; 945; 5553: a) Số nào chia hết cho 5?
b) Số nào không chia hết cho 5? Học sinh giải như sau: 41
a) Các số chia hết cho 5 là: 35; 57 660; 3000; 945 (vì chúng có tận cùng bằng 0 hoặc 5).
b) Các số không chia hết cho 5 là: 8; 4674; 5553 (vì chúng có tận cùng khác 0 và 5.
Ở đây chúng ta đã vận dụng phép suy luận diễn dịch:
TĐ 1: Là dấu hiệu chia hết cho 5 (Các số có chữ số tận cùng bằng 0 hoặc 5 thì chia
hết cho 5) hoặc dấu hiệu không chia hết cho 5 (các số không có tận cùng bằng 0
hoặc 5 thì không chia hết cho 5)
TĐ 2: Là các số đã cho trong đề bài (có hoặc không có tận cùng bằng 0 hoặc 5)
KL: là lời giải của bài toán nêu trên.
Ví dụ 6.7.
Sau khi học công thức tính diện tích hình thang, học sinh thực hành giải bài tập 2a
SGK Toán 5, trang 94: Tính diện tích hình thang sau: 4cm 5cm 9cm Học sinh giải như sau:
Diện tích hình thang đã cho là: (9 4) 5 1 2 3 2 ( cm ) 2 2
Ở đây chúng ta đó vận dụng phép suy luận diễn dịch:
TĐ 1: Là công thức tính diện tích hình thang.
TĐ 2: Là các số liệu đó cho trong bài toán: đáy lớn bằng 9cm; đáy nhỏ bằng 4cm và chiều cao bằng 5cm.
KL: là lời giải của bài toán nêu trên.
Ví dụ 6.8.
Sau khi học quy tắc tìm số trung bình cộng, học sinh thực hành giải bài tập 2 SGK Toán 4, trang 27:
Bốn em Mai, Hoa, Hưng, Thịnh lần lượt cân nặng là 36kg, 38kg, 40kg, 34kg. Hỏi
trung bình mỗi em cân nặng bao nhiêu ki-lô-gam? Học sinh giải như sau:
Trung bình mỗi em cân nặng là:
(36 + 38 + 40 + 34) : 4 = 37(kg) Đáp số: 37 kg 42
Ở đây chúng ta đó vận dụng phép suy luận diễn dịch:
TĐ 1: Là Quy tắc tìm số trung bình cộng (Muốn tìm số trung bình cộng của nhiều
số, ta tính tổng các số đó, rồi chia tổng đó cho số các số hạng)
TĐ 2: Là các số liệu đó cho trong đề bài.
KL: là lời giải của bài toán nêu trên.
VI.4. Suy luận nghe có lí
Suy luận nghe có lí (hay còn gọi là suy luận có lí) là suy luận không theo một quy
tắc suy luận tổng quát nào. Nó chỉ xuất phát từ những tiền đề đúng để rút ra một kết luận.
Kết luận này có thể đúng mà cũng có thể sai.
Mặc dù suy luận nghe có lí có hạn chế nêu trên nhưng nó có ý nghĩa rất quan trọng
trong khoa học và đời sống: giúp chúng ta từ những quan sát cụ thể có thể rút ra những giả
thuyết, phán đoán để rồi sau đó tìm cách chứng minh chặt chẽ giả thuyết đó. Nó đặt cơ sở
cho nhiều phát minh trong khoa học.
Trong toán học, hai kiểu suy luận nghe có lí thường sử dụng là: phép suy luận quy
nạp và phép suy luận tương tự.
VI.4.1. Suy luận quy nạp
Suy luận quy nạp là một kiểu suy luận nghe có lí. Trong đó tiền đề thường là một
số hiện tượng (có thể là những ví dụ minh hoạ) mà tính đúng đắn của nó được kiểm
chứng trực tiếp thông qua tính toán cụ thể để từ đó rút ra kết luận cần thiết (có thể là một
quy tắc, một công thức, một tính chất,…) cho các trường hợp chung, tổng quát. Ví dụ 6.9. Từ các tiền đề: - 4 + 3 = 3 + 4 - 15 + 48 = 48 + 15 - 243 + 358 = 358 + 243
Ta rút ra kết luận: Tổng của hai số tự nhiên không thay đổi khi ta thay đổi thứ tự
của các số hạng trong tổng đó.
Đây là phép suy luận quy nạp. Trong phép suy luận này, các tiền đề đúng và kết luận rút ra cũng đúng. Ví dụ 6.10:
Tìm quy luật của dãy số sau: 0; 1; 3; 16; 95; …. Giải: Ta nhận xét:
- Số hạng thứ ba là 3 = (0 + 1) x 3 ;
- Số hạng thứ tư là 16 = (1 + 3) x 4 ;
- Số hạng thứ năm là 95 = (3 + 16) x 5 ;
Vậy quy luật của dãy số đó cho là: Mỗi số hạng, kể từ số hạng thứ ba bằng tổng của
hai số hạng đứng liền trước nó nhân với thứ tự của số hạng đó hay: un = (un-1 + un-2 ) x n. 43
Ở đây ta đó vận dụng phép suy luận quy nạp:
TĐ 1: Là nhận xét thứ nhất
TĐ 2: Là nhận xét thứ hai
TĐ 3: Là nhận xét thứ ba
KL: Là quy luật của dãy số được rút ra. Ví dụ 6.11. Từ các tiền đề: - 42 chia hết cho 3 - 72 chia hết cho 3 - 132 chia hết cho 3
Ta rút ra kết luận: Những số có chữ số hàng đơn vị bằng 2 thì nó chia hết cho 3.
Đây là phép suy luận quy nạp. Trong phép suy luận này, xuất phát từ những tiền đề
đúng mà kết luận rút ra lại sai.
VI.4.2. Suy luận quy nạp trong dạy học toán ở tiểu học
Trong dạy học toán ở tiểu học, ta thường xuyên vận dụng phép suy luận quy nạp.
Cụ thể là: mỗi khi cần cung cấp cho học sinh những kiến thức mới (có thể là một
quy tắc thực hành tính toán, một công thức tính chu vi hoặc diện tích các hình, phương
pháp giải một dạng toán,...) Chúng ta thường nêu một số ví dụ minh hoạ tính đúng đắn
của quy tắc (hoặc công thức hoặc tính chất,…) cần rút ra để rồi từ đó nhận xét và rút ra
kiến thức mới cần cung cấp . Trong mỗi hoạt động “dạy bài mới” này, ta đã vận dụng phép suy luận quy nạp.
Ví dụ 6.12.
Khi dạy bài “Chu vi hình chữ nhật”, SGK Toỏn 3 trang 87 ta bắt đầu bằng bài
toán: Tính chu vi hình chữ nhật ABCD: A 4cm B 3cm 3cm D 4cm C
Giải: Chu vi hình chữ nhật ABCD là: (4 + 3 + 4 + 3) = 14(cm) Hoặc: (4 + 3) x 2 = 14(cm)
Từ đây ta rút ra quy tắc: Muốn tính chu vi hình chữ nhật ta lấy chiều dài cộng
với chiều rộng (cùng đơn vị đo) rồi nhân với 2.
Ở đây ta đó vận dụng phép suy luận quy nạp:
TĐ 1: Đề bài và lời giải của bài toán nêu trên.
KL: là quy tắc tính chu vi hình chữ nhật. 44
Ví dụ 6.13.
Khi dạy bài “Tìm hai số biết tổng và hiệu của hai số đó”, SGK Toán 4 trang 47 ta
bắt đầu bằng bài toán: Tổng của hai số bằng 70. Hiệu của chúng bằng 10. Tìm hai số đó.
Giải: Ta có sơ đồ sau: ? Số lớn: 10 70 ? Số bé:
Hai lần số bé là: 70 – 10 = 60 Số bé là: 60 : 2 = 30 Số lớn là: 30 + 10 = 40
Vậy hai số cần tìm là 30 và 40.
Từ đây ta rút ra công thức:
Số bé = (Tổng – Hiệu) : 2
Ở đây ta đã vận dụng phép suy luận quy nạp:
TĐ 1: Đề bài và lời giải của bài toán nêu trên.
KL: là công thức tìm số bé khi biết tổng và hiệu của hai số.
Ví dụ 6.14.
Khi dạy bài “Cộng hai số thập phân”, SGK Toán 5 trang 49 ta bắt đầu bằng bài
toán: Đường gấp khúc ABC có đoạn thẳng AB dài 1,84m và đoạn thẳng BC dài 2,45m.
Hỏi đường gấp khúc đó dài bao nhiêu mét?
Giải: Ta phải thực hiện phép cộng: 1,84 + 2,45 = ?(m) Ta có: 1,84m = 184cm 184 2,45m = 245cm + 245 429 429cm = 4,29m Vậy 1,84 + 2,45 = 4,29(m).
Thông thường ta đặt phép tính như sau: 1,84
Thực hiện phép cộng như cộng hai số tự nhiên + 2,45
Viết dấu phẩy ở tổng thẳng cột với dấu phẩy của cỏc 4,29 số hạng.
Từ đây ta rút ra quy tắc sộng hai số thập phân:
Muốn cộng hai số thập phân ta làm như sau:
- Viết số hạng này dưới số hạng kia sao cho dấu phảy đặt thẳng cột với nhau.
- Cộng như cộng hai số tự nhiên.
- Đặt dấu phảy ở tổng thẳng cột với dấu phảy của các số hạng.
Ở đây ta đó vận dụng phép suy luận quy nạp: 45
TĐ 1: Đề bài và lời giải của bài toán nêu trên.
KL: là quy tắc cộng hai số thập phân.
VI.4.3. Suy luận tương tự
Suy luận tương tự là một kiểu suy luận nghe có lí. Trong đó tiền đề thường là một
phép suy luận mà tính đúng đắn của nó được thiết lập để từ đó rút ra kết luận cần thiết (có
thể là một quy tắc, một công thức, một tính chất, …..) cho một phép suy luận khác có
những điều kiện tương tự gần giống với phép suy luận nêu trong tiền đề.
Kết luận được rút ra có thể đúng nhưng cũng có thể sai. Song kiểu suy luận tương
tự có ý nghĩa đặc biệt quan trọng trong nhiều phát minh khoa học. Chẳng hạn, từ một
định lí đã được chứng minh trong hình học phẳng, người ta đưa ra giả định một định lí
tương tự trong hình học không gian. Sau đó người ta tìm cách chứng minh điều giả định
đó. Nếu thành công ta được một định lí mới, nếu thất bại, người ta bác bỏ điều dự đoán đó. Ví dụ 6.15.
Từ định lí trong hình học phẳng "Nếu hai đường thẳng cùng song song với đường
thẳng thứ ba thì chúng song song với nhau".
Ta đưa ra một giả thuyết "Hai mặt phẳng cùng song song với một mặt phẳng thứ
ba thì chúng song song với nhau".
Đây là phép suy luận tương tự. Trong hình học không gian ta đã chứng minh giả
thuyết nêu ra ở đây là đúng. Nhờ vậy ta được một định lí trong hình học không gian!
Ví dụ 6.16.
Cũng từ định lí nêu trên trong ví dụ trên ta đưa ra giả thuyết "Hai mặt phẳng cùng
song song với đường thẳng thứ ba thì song song với nhau".
Đây là phép suy luận tương tự. Trong hình học không gian ta đã chỉ ra được giả
thuyết nêu ra ở đây là sai. Nhờ vậy ta bác bỏ giả thuyết nêu trên!
VI.4.4. Suy luận tương tự trong dạy học toán ở tiểu học
Trong dạy học toán ở tiểu học, ta thường xuyên vận dụng phép suy luận tương tự.
Cụ thể là: Từ một quy tắc thực hành tính toán đó được thiết lập trước đó (trong
vòng số nhỏ hơn, hoặc trong tập số tự nhiên), ta rút ra một quy tắc thực hành tính toán
tương tự (cho một vòng số lớn hơn hoặc trong tập phân số, số thập phân). Ví dụ 6.17.
- Từ quy tắc cộng các số có hai chữ số, ta rút ra quy tắc cộng các số có ba và nhiều chữ số;
- Từ các tính chất giao hoán, kết hợp và phân phối,…. của các phép toán
trong tập số tự nhiên ta rút ra tính chất tương tự của các phép toán trong tập
phân số và số thập phân. - ….
Ví dụ 6.18.
Cho tam giác ABC có diện tích 100cm .
2 Gọi M, N, P theo thứ tự là trung điểm của
các cạnh AB, AC, BC. Nối M, N, P. Tìm diện tích tam giác MNP. 46 Giải. A M N B P C Nối A với P. Ta có: 1 2 S 1 00 : 2 5 0(cm ) S 2 ABC ABP =
, vì hai tam giác chung đường cao hạ từ đỉnh
A và P là trung điểm của BC. 1 2 S S 5 0 : 2 2 5(cm ) PBM 2 PBA
, vì hai tam giác chung đường cao hạ từ đỉnh
P và M là trung điểm của AB. Tương tự ta cũng có: S 2 AMN = SCNP = 25cm .
SMNP =SABC – (SAMN + SBMP + SCNP) = 100 – (25+25+25) = 25(cm2)
Ở đây ta đó sử dụng phép suy luận tương tự: từ cách tính diện tích tam giác BMP
ta suy ra diện tích các tam giác AMN và CNP.
VII. Khái niệm và hệ thống khái niệm toán học ở tiểu học
VII.1. Nội hàm và ngoại diên của khái niệm
Khái niệm là một hình thức của tư duy trừu tượng, phản ánh những thuộc tính
chung, chủ yếu, bản chất của các sự vật và hiện tượng.
Mỗi khái niệm đều có nội hàm và ngoại diên:
- Nội hàm của một khái niệm là tập hợp các dấu hiệu chung, cơ bản được
phản ánh trong khái niệm.
- Ngoại diên của khái niệm là tập hợp những cá thể có chứa những dấu
hiệu chung, cơ bản được phản ánh trong khái niệm. Ví dụ 7.1. Khái niệm con người:
Nội hàm của khái niệm con người gồm những thuộc tính, chẳng hạn, động
vật có xương sống, có vú, biết lao động, có ngôn ngữ riêng,... Những dấu hiệu khác,
chẳng hạn, béo, gầy, tóc bạc, da trắng,… không phải con người nào cũng có.Vì vậy nó
không thuộc nội hàm của khái niệm con người.
Ngoại diên của khái niệm con người gồm những dấu hiệu, chẳng hạn,
người da trắng, da đen, da vàng , đàn ông, đàn bà, béo, gầy,… Ví dụ 7.2.
Khái niệm hình chữ nhật:
Nội hàm của nó là: hình tứ giác có bốn góc vuông, có hai đường chéo bằng
nhau, các cặp cạnh đối diện bằng nhau,… 47
Ngoại diên của nó, chẳng hạn, là các dấu hiệu chiều dài gấp đôi chiều rộng,
có chu vi bằng 120m, có diện tích 60 m2,…
Trong toán học,mỗi khái niệm có thể xác định bởi một hàm mệnh đề tương
ứng. Ngoại diên của khái niệm chính là miền đúng của hàm mệnh đề đó. Ví dụ 7.3.
a) Xét khái niệm số chẵn. Ta có thể thiết lập hàm mệnh đề ”số tự nhiên n là số
chẵn” Ngoại diên của số chẵn là tập hợp các số 0, 2, 4, 6,…
Các số 1,3,5,…không thuộc ngoại diên của số chẵn
b) Xét khái niệm phân số: Ta có thể thiết lập hàm mệnh đề” x là phân số” a
Ngoại diên của khái niệm phân số là tập hợp các số dạng b trong đó a là số tự 1 4 11 ; ; ;...
nhiên, b là số tự nhiên khác 0. Như vậy 2 7 5
thuộc ngoại diên của khái niện phân số.
Ví dụ 7.4.
Xét khái niệm thành phố. Ta thiết lập hàm mệnh đề” A là thành phố”
Như vậy, chẳng hạn, Hà Nội, Cần Thơ thuộc ngoại diên của khái niệm thành phố.
Ấp Bắc, Bản Tà Nựng không thuộc ngoại diên của khái niệm này.
Nội hàm và ngoại diên của một khái niệm có liên quan mật thiết với nhau và theo
tương quan “tỉ lệ nghịch”. Nghĩa là nội hàm càng sâu, càng rộng thì ngoại diên càng hẹp và ngược lại.
VII.2. Quan hệ giữa các khái niệm
Cho khái niệm A có ngoại diên là tập S được xác định bởi hàm mệnh đề A(x). Để
cho tiện, ta sẽ nói khái niệm A(x) có ngoại diên là S.
Giả sử A(x) và B(x) là hai khái niệm có ngoại diên là S và P tương ứng. Ta nói rằng:
(i) A(x) và B(x) là hai khái niệm đồng nhất, nếu S = P
(ii) A(x) là khái niệm rộng hơn B(x) (hay B(x) hẹp hơn A(x) ), nếu P là tập con thực sự của S;
Trong trường hợp này, ta nói A(x) là khái niệm chủng so với B(x) hay B(x) là khái niệm loại so với A(x). (iii)
A(x) và B(x) là hai khái niệm chèo nhau, nếu S P; P S;S P
Trong trường hợp này ta còn nói A(x) và B(x) là hai khái niệm giao nhau. (iv)
A(x) và B(x) là hai khái niệm tách rời, nếu S và P là hai tập rời nhau. (v)
A(x) và B(x) là hai khái niệm mâu thuẫn nếu chúng là hai khái niệm tách
rời và ngoại diên của chúng hợp lại thành ngoại diên của một khái niệm rộng hơn chúng.
Ví dụ 7.5.
a) Khái niệm hình tam giác có ba cạnh bằng nhau và hình tam giác có ba góc bằng
nhau là hai khái niệm đồng nhất. 48
b) Khái niệm hình tứ giác rộng hơn khái niệm hình chữ nhật, hay khái niệm hình
tứ giác là chủng, khái niệm hình chữ nhật là loại.
c) Số chẵn và khái niệm số nguyên tố là hai khái niệm chèo nhau.
d) Khái niệm số tự nhiên có hai chữ số và số tự nhiên có ba chữ số là hai khái niệm tách rời.
e) Khái niệm số chẵn và khái niệm số lẻ là hai khái niệm mâu thuẫn.
VII.3. Định nghĩa khái niệm
VII.3.1.Định nghĩa là gì?
Yêu cầu cơ bản của việc trình bày bất cứ một khoa học nào là phải
xác định một cách rõ ràng và chính xác tất cả các khái niệm gặp trong khoa
học ấy. Mỗi khi dùng một từ để diễn tả một khái niệm mới (mà chưa gặp
trước đó) ta cần phải làm rõ cho mọi người hiểu chính xác ý nghĩa của từ đó
thông qua những khái niệm đã biết ở phần trước (tức là làm rõ nội hàm của khái niệm đó).
Tương tự, khi dùng một kí hiệu mới phải quy định rõ ý nghĩa của kí hiệu này.
Công việc trên đây dẫn đến định nghĩa khái niệm. Hay nói cách khác:
Định nghĩa là tách một sự vật (cần định nghĩa) ra khỏi những sự vật
tiếp cận với nó và chỉ rõ bản chất thuộc tính (tức là nội hàm) của nó.
Trong toán học, định nghĩa thường được hiểu là sự giới hạn về nội
dung và phạm vi của một khái niệm (hay một thuật ngữ, một kí hiệu) thông
qua các khái niệm đã biết trước đó. Ví dụ 7.6.
Muốn định nghĩa hình vuông, ta phải làm hai việc:
a) Phân biệt nó với các hình mà ta có thể lẫn lộn như hình chữ nhật,
hình thoi, hình bình hành,… (đều là những tứ giác lồi).
b) Chỉ rõ thuộc tính bản chất của nó: hình vuông có đầy đủ các tính
chất của hình bình hành, hình chữ nhật, hình thoi.
Như vậy ta có thể định nghĩa hình vuông theo nhiều cách:
Hình vuông là một hình bình hành có các cạnh bằng nhau và các góc bằng nhau
Hình vuông là hình chữ nhật có các cạnh bằng nhau
Hình vuông là hình thoi có các góc bằng nhau
Hình vuông là tứ giác có 4 góc vuông và 4 cạnh bằng nhau
VII.3.2.Cấu trúc logic của một định nghĩa
Mỗi định nghĩa thường có hai phần: khái niệm được định nghĩa và khái niệm
để định nghĩa, hai phần này được nối với nhau bởi từ “là“ (hoặc một cụm từ khác tương đương).
Ta có thể tóm tắt bởi sơ đồ sau: A là B
Khái niệm được định nghĩa
Khái niệm để định nghĩa 49
Chú ý. 1.Từ “là” trong định nghĩa đôi khi còn được thay bằng các cách diễn
đạt khác, chẳng hạn, “nếu” hoặc “khi và chỉ khi” hoặc dùng kí hiệu A =def B hoặc A =đn B.
2. Trong cấu trúc trên, phần được định nghĩa là khái niệm mới, cần được làm
sáng tỏ. Phần để định nghĩa là những khái niệm đã biết. Dùng khái niệm đã biết này
để hình thành các dấu hiệu nhằm phân biệt khái niệm mới với các khái niệm khác
(gần gũi với nó) đó được biết trước đó.
3. Đôi khi phần để định nghĩa được đặt trước phần được định nghĩa. Trong
trường hợp này, từ “là” thay bằng “được gọi là”.
Trong trường hợp này, định nghĩa có cấu trúc là : B được gọi là A Để định nghĩa được định nghĩa
Ví dụ 7.7. Định nghĩa hình vuông:
Cách 1. “Hình vuông là hình chữ nhật có các cạnh bằng nhau”
Cách 2. “Hình chữ nhật có các cạnh bằng nhau được gọi là hình vuông” Ví dụ 7.8.
Định nghĩa hai đường thẳng song song:
Cách 1. Hai đường thẳng song song là hai đường thẳng cùng nằm trong một
mặt phẳng và không có điểm chung;
Cách 2. Hai đường thẳng song song, nếu chúng cùng nằm trong một mặt
phẳng và không có điểm chung;
Cách 3. Hai đường thẳng song song khi và chỉ khi chúng cùng nằm trong
mặt phẳng và không có điểm chung;
Cách 4. Hai đường thẳng cùng nằm trong mặt phẳng và không có điểm
chung được gọi là hai đường thẳng song song. Ví dụ 7.9.
Định nghĩa ước của số nguyên: Cho a và b là hai số nguyên;
Cách 1. Số nguyên b gọi là ước của số nguyên a nếu tồn tại số nguyên q sao cho a = bq.
Cách 2. Nếu tồn tại số nguyên q sao cho a = bq thì ta nói b là ước của a.
Ví dụ 7.10. Định nghĩa hàng hóa:
Cách 1. Hàng hóa là sản phẩm do lao động làm ra, dùng để trao đổi trên thị trường.
Cách 2. Sản phẩm do con người làm ra dùng để trao đổi trên thị trường được gọi là hàng hóa.
Cách 3. Sản phẩm do lao động làm ra được gọi là hàng hóa nếu nó được
dùng để trao đổi trên thị trường.
VII.3.3.Các quy tắc của định nghĩa
Quy tắc 1.Những khái niệm dùng để định nghĩa phải là những khái niệm đã
biết, đã định nghĩa trước đó. 50
Vi phạm quy tắc này sẽ dẫn đến định nghĩa vòng quanh hoặc luẩn quẩn. Chẳng hạn:
Định nghĩa số chẵn: Số chẵn là số chia hết cho 2.
Định nghĩa số chia hết cho 2: số chia hết cho 2 là số chẵn. Hoặc :
Góc vuông là góc bằng 90o.
Độ là góc có số đo bằng 1/90 góc vuông . Hoặc :
Tội phạm là kẻ phạm tội.
Chú ý.Theo quy tắc 1 thì để định nghĩa một khái niệm ta phải dựa vào
những khái niệm đã biết trước đó. Để định nghĩa khái niệm đã biết trước đó ta lại
phải dựa vào dựa vào một khái niệm đã biết trước đó nữa,… Rõ ràng là ta không
thể kéo dài mãi yêu cầu này. Chính vì vậy ta phải chọn một số khái niệm xuất phát
không được định nghĩa mà gọi là những khái niệm cơ bản hay khái niệm nguyên thuỷ.
Người ta xác định khái niệm nguyên thuỷ bằng cách mô tả nó thông qua các
ví dụ hoặc các biểu tượng.
Chẳng hạn, trong hình học: các khái niệm điểm, đường thẳng, mặt phẳng là các khái niệm cơ bản;
Trong lí thuyết tập hợp thì khái niệm tập hợp là khái niệm cơ bản, trong
logic thì khái niệm mệnh đề là khái niệm cơ bản, …
Quy tắc 2. Ngoại diên của khái niệm được định nghĩa và khái niệm dùng
để định nghĩa phải bằng nhau.
Vi phạm quy tắc này sẽ dẫn đến định nghĩa quá rộng hoặc quá hẹp. Chẳng hạn:
Hình chữ nhật là tứ giác có hai góc vuông là định nghĩa quá rộng
Hình chữ nhật là tứ giác có bốn góc vuông và bồn cạnh bằng nhau là định nghĩa quá hẹp.
Quy tắc 3. Các dấu hiệu dùng để định nghĩa cần ngắn gọn, không chứa đựng
những dấu hiệu có thể suy ra từ những dấu hiệu khác đã nêu trong định nghĩa. Chẳng hạn:
Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau.
Hình chữ nhật là hình bình hành có bốn góc vuông.
Là những định nghĩa chưa ngắn gọn.
VII.3.4.Phân loại định nghĩa
Trong toán học, ta thường gặp hai loại định nghĩa là: định nghĩa đặt tên (hay
gọi tên) và định nghĩa kiến thiết.
Trong định nghĩa đặt tên, người ta đưa ra tên gọi hoặc một kí hiệu ngắn gọn
thay cho một biểu thức hay một mệnh đề phức tạp. Ví dụ 7.11.
a) Gọi a là đoạn thẳng nối hai điểm A,B cho trước;
b) Ta kí hiệu T là tích của các số nguyên tố nhỏ hơn 100;
c) Ta kí hiệu f(x) là hàm số xác định bởi quy tắc: 51
f(x) = esin x + ecos x – 2 x3
d) Số tự nhiên p gọi là số nguyên tố nếu không tồn tại các số tự nhiên a,b khác 1 và p sao cho p = ab.
Khác với định nghĩa đặt tên, định nghĩa kiến thiết thường có hai phần: phần
kiến thiết và phần đặt tên. Ví dụ 7.12.
a) Tồn tại duy nhất một số thực là nghiệm của phương trình: 10x = 2.
Ta gọi số đó là lô-ga-rít cơ số 10 của 2, kí hiệu là lg 2.
b) Tồn tại giới hạn hữu hạn: 1 n lim(n )
n , khi n dần tới vô cùng.
Ta gọi giới hạn đó là số e.
c) Với mọi số nguyên a và b, trong đó b khác 0, luôn tồn tại duy nhất một
cặp số nguyên q và r sao cho:
a = bq + r, trong đó 0 r b .
Trong trường hợp này, ta sẽ gọi a là số bị chia, b là số chia, q là thương gần đúng và
r là số dư trong phép chia a cho b. Ta kí hiệu là: a : b = q (dư r) Ví dụ 7.13.
Một dạng định nghĩa kiến thiết thường gặp là định nghĩa truy chứng. Chẳng
hạn: a) Định nghĩa lũy thừa bậc n: (i) Đặt ao = 1
(ii) Với n = 1,2,3,…Ta đặt a = a n .a n – 1
b) Định nghĩa đạo hàm bậc n của hàm số:
(i)Trước hết ta định nghĩa đạo hàm bậc nhất của hàm số f(x) tại , điểm x f (x ) o: o
(ii) với n = 2, 3, 4… ta gọi đạo hàm bậc n của f(x) tại xo là đạo
hàm của đạo hàm bậc n – 1 của hàm số f(x) tại x : o f(n)(x ` o) = (f(n – 1)(x )) o
VII.4. Vấn đề hình thành các khái niệm toán học ở tiểu học
Hình thành các khái niệm toán học cho học sinh tiểu học là nhiệm vụ quan trọng
trong quá trình dạy và học toán ở tiểu học. Các khái niệm toán học trong môn toán tiểu
học có thể phân chia thành 7 nhóm:
Nhóm thứ nhất: Gồm những khái niệm về số và cấu tạo số tự nhiên, phân số và số thập phân.
Nhóm thứ hai: Gồm những khái niệm về so sánh số tự nhiên, phân số và số thập phân.
Nhóm thứ ba: Gồm những khái niệm về các phép tính với số tự nhiên, phân số và số thập phân. 52
Nhóm thứ tư: Gồm các khái niệm về đại lượng
Nhóm thứ năm: Gồm những khái niệm về hình học.
Nhóm thứ sáu: Gồm những khái niệm về thống kê.
Nhóm thứ bảy: Gồm những khái niệm về giải toán có lời văn.
Trong các sách giáo khoa phổ thông nói chung, sách giáo khoa toán tiểu học nói
riêng, do những hạn chế về trình độ của học sinh, những yêu cầu về sư phạm người ta
chưa thể đưa ra những định nghĩa chính xác, hiện đại về nhiều khái niệm toán học. Thay
vào đó, người ta hình thành các khái niệm vừa đảm bảo tính khoa học, vừa đảm bảo tính
sư phạm phù hợp với đặc điểm tâm, sinh lí của lứa tuổi học sinh. Đồng thời đáp ứng yêu
cầu phát triển của môn học.
Ở tiểu học, do đặc điểm tâm sinh lí và trình độ nhận thức của học sinh, các khái
niệm toán học được hình thành thông qua các biểu tượng hoặc bằng cách mô tả trực quan
từ đó nêu dấu hiệu nhận biết mỗi khái niệm thông qua một số đặc điểm của khái niệm đó.
Ví dụ 7.14.
Khái niệm phân số: *
Trong Lí thuyết số ta định nghĩa “Mỗi cặp sắp thứ tự (a;b) N N , trong đó N là a
tập số tự nhiên, *
N là tập số tự nhiên khác 0, ta gọi là một phân số. Ta dùng kí hiệu b để
chỉ phân số (a;b), trong đó a gọi là tử số và b là mẫu số”.
Ở tiểu học (SGK Toán 4) thông qua các hình ảnh trực quan (biểu diễn số phần
được tô màu trên băng giấy hoặc biểu diễn kết quả bài toán chia 4 quả cam cho 3 người, a
…) ta hình thành khái niệm “Phân số b , trong đó mẫu số b chỉ số phần đơn vị được chia a
ra và tử số a chỉ số phần được lấy đi. Phân số b còn được hiểu là thương của phép chia
số tự nhiên a cho số tự nhiên khác không b”.
Ví dụ 7.15.
Khái niệm so sánh các số tự nhiên:
Trong Lí thuyết số ta định nghĩa:
“Cho a và b là hai số tự nhiên. Ta nói rằng số tự nhiên a nhỏ hơn hoặc bằng số tự
nhiên b, kí hiệu là a b
, nếu tồn tại hai tập hữu hạn A, B sao cho a A ;b B vaA B.
Ở tiểu học, các khái niệm so sánh các số tự nhiên được hình thành qua nhiều công đoạn:
- So sánh các số trong phạm vi 10:
“Ngày đầu tiên đến trường, học sinh đó được làm quen với thuật ngữ: nhiều hơn, ít hơn.
Tiếp đó, học sinh được làm quen với dấu” <” và “>”.
Bằng trực quan hình ảnh, chẳng hạn: 53 Từ bức tranh:
Ta hình thành quan hệ 3 > 2.
Bằng cách đó, ta hình thành cho học sinh quan hệ so sánh các số trong phạm vi 10.
- So sánh các số có nhiều chữ số:
“Bằng việc trang bị quy tắc so sánh các số có nhiều chữ số (đưa về số sánh số
chữ số hoặc so sánh các chữ số cùng hàng), học sinh có kiến thức hoàn chỉnh về quan hệ
thứ tự trong tập số tự nhiên”
Ví dụ 7.16. Khái niệm phép cộng:
Trong Lí thuyết số ta định nghĩa:
“Cho a và b là hai số tự nhiên. Tồn tại hai tập hữu hạn A và B sao cho
a A ;b B, A B . Ta gọi tổng của hai số tự nhiên a và b là số tự nhiên c AB ,
kí hiệu là c = a + b.
Quy tắc cho tương ứng mỗi cặp số tự nhiên a, b với một số tự nhiên c nói trên ta
gọi là phép cộng các số tự nhiên”.
Sau đó, bằng công cụ của bản số tập hợp, ta chứng minh sự tồn tại và tính duy
nhất của phép cộng hai số tự nhiên, hay nói cách khác ta khẳng định: phép công các số tự
nhiên luôn thực hiện được.
Ở tiểu học phép cộng các số tự nhiên được hình thành qua nhiều công đoạn:
- Hình thành bảng cộng trong phạm vi 10 (SGK Toán 1):
“Bằng trực quan hình ảnh, chẳng hạn: Từ bức tranh:
Ba con vit Hai con vit
Ta hình thành phép toán 3 + 2 = 5.
Bằng cách đó, ta hình thành cho học sinh các phép cộng trong phạm vi 10 (cộng trong bảng). 54
- Phép cộng trong phạm vi 100 ( SGK Toán 1 và Toán 2):
“Sau khi hình thành các phép cộng có tổng bằng 10, bằng kĩ thuật tách một
phép cộng qua 10 thành phép cộng có tổng bằng 10 cộng với phần còn lại, ta hình thành
bảng cộng trong phạm vi 20.
Bằng cách đưa về phép cộng theo cột dọc và kỹ thuật cộng các chữ số
cùng hàng, ta hình thành phép cộng các số trong phạm vi 100.
- Phép cộng các số có nhiều chữ số (SGK Toán 2, Toán 3, Toán 4):
Bằng kĩ thuật cộng các chữ số cùng hàng, ta hình thành phép cộng các số có nhiều chữ số”.
Ví dụ 7.17. Khái niệm hình tròn:
Trong môn toán ở trường phổ thông, ta định nghĩa:
“Hình tròn tâm O, bán kính R là tập hợp các điểm trong mặt phẳng sao cho
khoảng cách từ nó tới điểm O cố định cho trước không vượt quá R.
Đường tròn tâm O, bán kính R là tập hợp các điểm trong mặt phẳng sao cho
khoảng cách từ nó tới điểm O cố định cho trước luôn bằng R”.
Ở tiểu học, khái niệm hình tròn và đường tròn được hình thành qua nhiều công đoạn:
- Hình thành khái niệm hình tròn thông qua các biểu tượng:
“Ngay từ tiết học đầu tiên ở lớp 1, học sinh đã làm quen với hình tròn thông qua
các biểu tượng:cái đĩa, cái bánh xe đạp”.
Giới thiệu các yếu tố của một hình tròn: “Bằng hình vẽ: M A B O
Giới thiệu cho học sinh:
+ Hình tròn tâm O, bán kính OM và đường kính AB.
+ Tâm O là trung điểm của đường kính AB.
+ Độ dài đường kính gấp hai lần độ dài bán kính.
- Giới thiệu đường tròn và các dấu hiệu của hình tròn:
“Dùng com pa vẽ hình tròn tâm O, bán kính R thì đầu chì của com pa vạch trên tờ
giấy một đường tròn.
Nối tâm O với một điểm M trên đường tròn ta được đoạn thẳng OM là bán kính của hình tròn. 55
Tất cả các bán kính của hình tròn đều bằng nhau OA = OB = OM.
Đoạn thẳng nối hai điểm M, N trên đường tròn và đi qua tâm O là đường kính của hình tròn.
Trong một hình tròn, đường kính gấp 2 lần bán kính”. Ví dụ 7. 18.
Khái niệm về toán có lời văn: Các bài toán có lời văn ở tiểu học có thể phân chia thành 4 nhóm:
Nhóm thứ nhất: Gồm các bài toán đơn: Toán về thêm, bớt một số đơn vị; toán về
gấp (hoặc giảm) một số lên (hoặc đi) một số lần và toán về so sánh số này gấp hoặc kém mấy lần số kia.
Nhóm thứ hai: Gồm các bài toán hợp, chẳng hạn, toán hợp với hai phép tính là
cộng hoặc trừ; toán hợp trong đó ít nhất một phép tính là nhân hoặc chia.
Nhóm thứ ba: Gồm 8 dạng toán có văn điển hình:
- Tìm hai số biết tổng và hiệu của hai số đó.
- Toán về số trung bình cộng.
- Tìm hai số biết hiệu và tỉ số của hai số đó.
- Tìm hai số biết tổng và tỉ số của hai số đó.
- Toán về đại lượng tỉ lệ thuận.
- Toán về đại lượng tỉ lệ nghịch.
- Toán về tỉ số phần trăm.
- Toán về chuyển động đều.
Nhóm thứ tư: Gồm một số bài toán khác, chẳng hạn, toán về tìm phân số của một
số; toán về tỉ lệ bản đồ.
Đối với mỗi dạng toán, thông qua một bài toán mẫu, giáo viên dẫn dắt học sinh
nhận biết cấu trúc của bài toán: cái đã cho, cái phải tìm là gì. Để từ đó nhận dạng dạng
toán đó. Đồng thời hướng dẫn học sinh các bước giải sau khi đã nhận dạng bài toán đó. VIII. Tập hợp
VIII.1. Khái niệm tập hợp
Tập hợp là khái niệm không định nghĩa. Để hiểu khái niệm tập hợp, ta có thể mô
tả nó thông qua một số ví dụ, chẳng hạn:
- Tập hợp các số tự nhiên.
- Tập hợp sinh viên năm thứ nhất của khoa Giáo dục tiểu học.
- Tập hợp các dân tộc đang sống trên đất nước Việt Nam.
- Tập hợp các điểm trong mặt phẳng.
Các đối tượng cấu thành tập hợp được gọi là các phần tử của tập hợp đó. Ta
dùng các chữ cái in hoa A, B, C, X, Y, Z,… để kí hiệu các tập hợp; các chữ cái a, b, c, x,
y, z,… để kí hiệu phần tử của tập hợp.
Nếu a là phần tử của tập A thì ta viết a A (đọc là a thuộc tập A); nếu a không
phải là phần tử của tập A thì ta viết a A (đọc là a không thuộc tập A). 56
VIII.2. Cách xác định một tập hợp
Để xác định một tập hợp người ta thường dùng các cách sau:
Liệt kê tất cả các phần tử của tập đó trong một dấu ngoặc. Chẳng
hạn, tập hợp C các chữ số chẵn 0, 2, 4, 6, 8 ta viết: C 0; 2;4;6; 8
Tập hợp X gồm ba phần tử x, y, z ta viết: X
x; y; z
Chỉ rõ tính chất đặc trưng của các phần tử thuộc tập hợp đó,
chẳng hạn, tập hợp D các dân tộc đang sinh sống trên đất nước Việt Nam ta viết:
D = {x: x là một dân tộc đang sinh sống trên đất nước Việt Nam}
Tập hợp P các số nguyên tố ta viết:
P = {p: p là số nguyên tố}
Người ta còn dùng một đường cong kín để biểu thị một tập hợp (gọi
là biểu đồ Ven). Chẳng hạn, ta biểu thị tập hợp C: n p a c b c d e m 1 C
Hình bên cho ta biết: các phần tử a, b, c, d, e thuộc tập C và các phần tử m, n, p không thuộc tập C.
Tập hợp không có phần tử nào ta gọi là tập rỗng và kí hiệu là: . Chẳng hạn, tập
các số nguyên tố lớn hơn 2 là tập rỗng, tập các số thực là nghiệm của phương trình: x2 + x + 1 = 0 là tập rỗng.
Tập chỉ có một phân tử ta gọi là tập hợp đơn tử. Nếu tập M chỉ có một phần tử là x, ta viết: M = {x}
VIII.3. Tập con và quan hệ bao hàm
VIII.3.1. Định nghĩa.
Cho A và B là hai tập hợp. Ta nói rằng tập A là tập con của tập B, kí hiệu là A B
, nếu mọi phần tử của tập A đều thuộc tập B
Hay nói cách khác, A B , nếu x
, x A x B 57 B A
Nếu A là tập con của tập B thì ta còn nói A là bộ phận của tập B hay tập B chứa
tập A, kí hiệu là B A .
Ta gọi quan hệ hoặc là quan hệ bao hàm.
Các hệ thức A B, B A ta gọi là các bao hàm thức.
Nếu A là tập con của B và có một phần tử của tập B không thuộc tập A thì ta nói A
là tập con thực sự của tập B.
Ta nói tập A bằng tập B, kí hiệu là A B , nếu mỗi phần tử của tập A đều thuộc tập B và ngược lại.
Ta dựng kí hiệu P(X) để chỉ tập tất cả các tập con của tập hợp X. Ví dụ 8.1.
a) Tập các số tự nhiên chẵn C chẵn là tập con của tập các số tự nhiên N.
b) Tập các hình chữ nhật là tập con của tập các hình tứ giác.
c) Trong khoa Giáo dục tiểu học: tập các sinh viên năm thứ nhất là tập con của tập
tất cả sinh viên của khoa.
d) Tập các hình chữ nhật và tập các hình bình hành có hai đường chéo bằng nhau là hai tập bằng nhau.
VIII.3.2. Tính chất của quan hệ bao hàm
Định lí 1.1. (về tính chất của quan hệ bao hàm)
a) Với mọi tập A, ta luôn có: . A
b) Mọi tập A đều là tập con của chính nó.
c) Nếu A B và B A thì A = B.
d) Nếu A B và B C thì A C .
Chứng minh. Đơn giản.
VIII.4. Các phép toán trên tập hợp VIII.4.1. Phép hợp
Định nghĩa. Cho A và B là hai tập hợp. Ta gọi hợp của hai tập A và B là tập hợp H,
kí hiệu là H A B, gồm cỏc phần tử thuộc tập A hoặc thuộc tập B. A B
x : x Ahoacx Hay: B . Ta quy ước:
A B C (
A B) C . 58
Bằng phương pháp quy nạp, ta định nghĩa:
A A A .
.. A A (
A A A .
.. A ) A 1 2 3 n 1 n 1 2 3 n 1 n A B A B Ví dụ 8.2. A B a, , b , c d, , e , h , m , n x
a) A = {a, b, c, d, e, h} và B = {d, h, m, n, x} thì
b) C là tập các số tự nhiên chẵn và L là tập các số tự nhiên lẻ thì C L là tập N tất cả các số tự nhiên.
c) Gọi X là tập tất cả các hình chữ nhật và V là tập tất cả các hình vuông thì
X V X VIII.4.2. Phép giao
Định nghĩa. Cho A và B là hai tập hợp. Ta gọi giao của hai tập A và B là tập hợp
G, kí hiệu là G A B , gồm các phần tử đồng thời thuộc cả tập A và tập B. Hay: A B
x : x Avàx B . Ta quy ước:
A B C (
A B) C
Bằng phương pháp quy nạp, ta định nghĩa:
A A A ... A A A A A A A n n ( ... n ) 1 2 3 1 1 2 3 1 n A B A B Ví dụ 8.3.
a) A = {a, b, c, d, e, h} và B = {d, h, m, n, x} thì A B d, h .
C P 2
b) C là tập các số tự nhiên chẵn và P là tập các số nguyên tố thì .
c) Gọi X là tập tất cả các hình chữ nhật và V là tập tất cả các hình vuông thì X V V 59
VIII.4.3. Hiệu hai tập hợp
Định nghĩa. Cho A và B là hai tập hợp. Ta gọi hiệu của hai tập A và B là tập
hợp D, kí hiệu là G A B, gồm các phần tử thuộc cả tập A mà không thuộc tập B. A B
x : x Avàx Hay: B . A B A B
Nếu A là tập con của tập X thì hiệu X – A gọi là phần bù của tập A trong tập X, kí hiệu là C X (A). Ta gọi tập hợp: ( , A ) B (
A B) (B ) A
Là hiệu đối xứng của hai tập A và B. Ví dụ 8.4.
a) A = {a, b, c, d, e, h} và B = {d, h, m, n, x} thì: A B
a ,b,c, e ; B A
m,n, x ; ( , A ) B , a , b , c , e , m , n x .
b) Gọi X là tập tất cả các hình chữ nhật và V là tập tất cả các hình vuông thì C (V ) X
là tập các hình chữ nhật không phải là hình vuông.
VIII.4.4. Tính chất của các phép toán trên tập hợp
Định lí 8.2. (Về tính chất của phép hợp và phép giao các tập hợp)
a) Tính chất giao hoán: Với mọi tập A, B ta luôn có:
A B B A ; A B B . A
b) Tính chất kết hợp: Với mọi tập A, B, C ta luôn có:
(A B) C A (B C);
(A B) C A (B C ).
c) Tính chất lũy đẳng: Với mọi tập hợp A ta luôn có: A A ; A
A A A A ; A A . A
d) Luật Đờ Moóc-găng: Cho A và B là các tập con của tập X, ta có:
X (A B )(X A) (X B );
X (A B )(X A) (X B ). Chứng minh. a), b), c) đơn giản.
d) Giả sử x X (A B) x X và x A B 60
x X và x không thuộc cả hai tập A và B
x (X )
A và x X B x(X )
A (X B)
Tương tự ta chứng minh đẳng thức còn lại.
VIII.4. Tích Đề-các của các tập hợp
VIII.4.1. Cặp sắp thứ tự
Định nghĩa. Cho a và b là hai phần tử tùy ý. Từ hai phần tử a, b ta thiết lập một
phần tử mới, gọi là cặp sắp thứ tự a, b và kí hiệu là (a;b)
Hai cặp sắp thứ tự (a;b) và (c;d) gọi là bằng nhau, kí hiệu là (a;b) = (c;d), nếu a = c và b = d.
Trường hợp đặc biệt, với hai phần tử khác nhau a và b thì (a;b) và (b;a) là hai cặp khác nhau.
Chẳng hạn, với hai số tự nhiên 2 và 3 ta thiết lập được hai cặp sắp thứ tự khác nhau (2;3) và (3;2).
Tương tự tư định nghĩa bộ sắp thứ tự (a1;a2;…;a ) với n phần tử bất kì cho tr n ước.
VIII.4.2. Tích Đề-các
Định nghĩa. Cho A và B là hai tập hợp. Ta gọi tích Đề-các của hai tập A và B là
tập hợp T, kí hiệu là T A B
, gồm các cặp sắp thứ tự (a;b) sao cho a thuộc tập A và b thuộc tập B. A B ( ; a )
b : a Avàb B Hay: .
Tương tự, ta định nghĩa: A A . .. A
(a ;a ;...;a ) :a A ;i 1 , 2,...,n 1 2 n 1 2 n i i Ta quy ước: A x A = A ; 2
Ký hiệu A để chỉ tích Đề các củ n
a n tập hợp đều bằng A.
Ví dụ 8.5.
Cho X = {x; y; z} và Y = {1; 2} ta có: X Y
(x;1);(y;1);(z;1);( ; x 2 Y X (1; ) x ;(1; ) y ;(1; ) z ;(2; ) x ;(2; ) y ;(2; z ) Rõ ràng là X Y Y X .
Nói chung, phép lấy tích Đề-các không có tính chất giao hoán.
VIII.4.3. Mặt phẳng toạ độ Đề-các
Ở trường phổ thông ta đó biết mặt phẳng toạ độ x0y.
Ta xét tích Đề-các A x A trường hợp tập A là tập các số thực R, ta được tích Đề-
các R2. Ta sẽ đồng nhất tập R2 với mặt phẳng toạ độ x0y: y 61 b M 0 a c x d N
Mỗi cặp sắp thứ tự (a;b) R2 ta cho tương ứng với một điểm M = [a;b] trong mặt
phẳng toạ độ x0y (có hoành độ bằng a và tung độ bằng b).
Đảo lại, mỗi điểm N = [c;d] trong mặt phẳng toạ độ x0y cho tương ứng với một cặp (c;d) R2.
Bằng cách trên đây, ta đó đồng nhất tập R2 với mặt phẳng toạ độ x0y và sẽ gọi là
mặt phẳng toạ độ Đề-các.
Tương tự ta đồng nhất tích Đề-các R3 với không gian 0xyz và gọi là không gian toạ độ Đề-các. CHƯƠNG II
Phương pháp thống kê trong nghiên cứu khoa học giáo dục
I. Các khái niệm cơ bản về thống kê toán học
I.1. Đại cương về thống kê toán
Cho X là tập hợp (hữu hạn hoặc vô hạn) các đối tượng nào đó. Giả sử ta cần khảo
sát một tính chất đặc trưng nào đó của các đối tượng trong tập hợp X (có thể là một đặc
tính sinh học, một số đo, một chỉ số,…).
Có hai cách giải quyết yêu cầu nói trên: -
Cách thứ nhất: khảo sát lần lượt từng đối tượng của tập X về tính chất đặc
trưng mà ta quan tâm để từ đó rút ra kết luận; -
Cách thứ hai: chọn ngẫu nhiên một số đối tượng đại diện theo một tiêu chí nào
đó của tập X để kháo sát. Từ đó ta rút ra kết luận cần thiết.
Trong thực tế, làm theo cách thứ nhất thường gặp nhiều khó khăn: tốn kém về thời
gian và vật chất, trong trường hợp các đối tượng được khảo sát bị hỏng sau mỗi lần khảo
sát thí kết quả khảo sát sẽ không còn ý nghĩa. Vì vậy người ta thường phải chọn cách làm thứ hai. 62
Trong trường hợp này, ta gọi tập các đối tượng được chọn ra để khảo sát là tập
mẫu, số phần tử của tập mẫu gọi là kích thước mẫu. Việc chọn từ tập hợp X ra các phần
tử để khảo sát ta gọi là phép lấy mẫu. Dãy kết quả thu được trong khảo sát gọi là dãy số
liệu quan sát. Tập X gọi là tập tổng quát.
Ví dụ 1.1.
Ta cần xác định trong lượng của các gói bánh xuất xưởng của một phân xưởng sản
xuất bánh kẹo. Người ta lấy ngẫu nhiên 50 gói bánh từ lô hàng xuất xưởng của phân
xưởng đó. Lần lượt cân từng gói. Kết quả ta thu được 50 số liệu về trọng lượng của các gói bánh này.
Ở đây: tập tất cả các gói bánh trong lô hàng xuất xưởng của phân xưởng đó là tập
tổng quát; 50 gói bánh được chọn ra để khảo sát là tập mẫu; số 50 là kích thước mẫu và
50 số liệu về trọng lượng của các gói bánh là dãy số liệu quan sát.
I.2. Phương pháp chọn mẫu
Trong thực tế ta thường gặp hai cách chọn mẫu dưới đây :
a) Chọn ngẫu nhiên có hoàn lại: Theo cách lấy mẫu này thì sau khi lấy ngẫu nhiên
một phần tử từ tập hợp tổng quát và khảo sát, ta trả lại phần tử đó vào tập hợp tổng quát
trước khi chọn tiếp phần tử thứ hai (không loại trừ khả năng lần sau chọn lại phần tử đã chọn trước đó).
b) Chọn ngẫu nhiên không hoàn lại: Trong cách lấy mẫu này, ta không trả lại phần
tử đã lấy ra vào tập tổng quát trước khi lấy tiếp phần tử khác.
Chú ý.1. Vì ta căn cứ vào kết quả khảo sát trên tập mẫu để rút ra kết luận cần thiết
cho toàn bộ tập tổng quát về tính chất đặc trưng cần khảo sát nên các phần tử của tập mẫu
phải đại diện một cách đúng đắn cho tập tổng quát.
2. Khi số phần tử của tập tổng quát đủ lớn thì sự sai khác trong kết quả
khảo sát giữa hai cách chọn mẫu là không đáng kể.
I.3. Hàm phân phối mẫu
Định nghĩa 1.1.Giả sử từ tập tổng quát X ta chọn tập mẫu có kích thước n.
Khảo sát lần lượt từng phần tử của tập mẫu, ta nhận được dãy số liệu: x1 , x , … , x 2 n .
Ta gọi dãy này là dãy các số liệu thống kê. Không làm mất tính tổng quát,
ta có thể giả sử dãy đó sắp xếp theo giá trị tăng dần hay dãy không giảm (nếu không, ta
sắp xếp lại thứ tự). Với mỗi số thực x, gọi n xlà số các số liệu trong dãy số liệu thống kê nói trên nhỏ hơn x.
Ta gọi hàm số F (x) xác định bởi quy tắc: n 63 n F (x x ) n
n , với mỗi số thực x
là hàm phân phối mẫu (hay hàm phân phối thực nghiệm). Ví dụ 1.2.
Để xác đinh chiều cao trung bình của các cây bạch đàn trong một khu rừng
bạch đàn, người ta chọn ngẫu nhiên 40 trong khu rừng đó. Đo chiều cao từng cây và nhận
được kết quả trong bảng sau: Chiều cao 8m 8,5m 9m 11m Số cây 5 12 15 8
Vậy bảng trên là dãy số liệu thống kê nhận được từ quan sát trên tập mẫu gồm
40 cây bạch đàn chọn ngẫu nhiên trong khu rừng bạch đàn đó.
Hàm phân phối mẫu được xác định bởi quy tắc sau : , 0 nê ..... u x 8 5 nêu.. 8 . x 5 , 8 40 17 ( F ) x ,nêu 5 , 8 .... x 9 40 32 ,nêu. 9 ... x 11 40
,1nêu....x 11
I.4. Đa giác tần suất và tổ chức đồ tần suất
Giả sử trong dãy n số liệu thống kê có k giá trị đôi một khác nhau:
x , x ,..., x 1 2 k x
Trong đó j xuất hiện trong dãy với tần số kj sao cho : k1 + k2 + … + k = n k k j ta gọi k n j là tần số và Wj =
là tần suất của xj trong quan sát nói trên.
Định nghĩa 1.2.Ta gọi đường gấp khúc nối các điểm [x1;W ] 1 ; [x2;W ] 2 ; …. ; [x ;W k
k] trong mặt phẳng toạ độ (x0y) là đa giác tần suất của mẫu trên. Ví dụ 1.2.
Đa giác tần suất của mẫu quan sát trong ví dụ 1.2 là đường gấp khúc nối các điểm:
[8;1/8] ; [8,5;3/10] ; [9;3/8] và [11;1/5] 64
Đồ thị đó là hình dưới đây: W 1 8 8,5 9 10 11 x
Ta chia đoạn [x1;x ] thành m phần bằng nhau, mỗi ph k ần có độ dài: xk - x1 h = m
Gọi Wi là tần số các quan sát nằm trong khoảng thứ i, với i = 1, 2,…, m. Tức là:
Số quan sát trong khoảng (xi;xi+1] Ti = n
Định nghĩa 1.3. Tổ chức đồ tần suất là một đa giác hình bậc thang lập nên bởi các Ti
hình chữ nhật có đáy bằng khoảng chia thứ i trên trục hoành, chiều cao bằng tỉ số h , với i = 1 , 2 , … , m. Ví dụ 1.3.
Hãy thiết lập tổ chức đồ tần suất của quan sát trong ví dụ 3.1 với m = 4. Ta có: 11 8 h , 0 75 4 ... sô x , 8 ; 8 ( ] 75 T i , 0 ; 425 1 40 sô ...x i , 9 ; 75 , 8 ( ] 5 T 0 ; 375 , 2 40 sô...x , 10 ; 5 , 9 ( ] 25 T i ; 0 3 40 s ...xi , 10 ( ] 11 ; 25 T , 0 2 4 40 65 T , 0 425 T 0 375 , 1 0 ; 57 , 2 ; 5 , 0 0 75 , 0 75 , 0 75 , 0 75 , T T 3 ; 0 4 , 0 4. 0 75 , 0 75 ,
Tổ chức đồ tần suất là hình dưới đây : 0,57 0,5 0,4 8 8,75 9,5 10,25 11
I.5.Trung bình mẫu và phương sai mẫu
Định nghĩa 1.4. Giả sử x , x 1 , … , x 2
là dãy số liệu thống kê thu được từ n
một quan sát trên tập mẫu có kích thước n. Ta gọi số:
x1 x2 ... x X n n a) n
là trung bình (hay kì vọng) mẫu trong quan sát nói trên. n 1 S 2 (x X 2 ) n k n b) n k1 là phương sai mẫu. n 1 x( X 2 n ) k a) S n k 1 n =
là độ lệch chuẩn mẫu. n x Xn k E k 1 d) n n
là độ lệch tuyệt đối mẫu.
Chú ý.Nếu dãy số liệu thống kê nhận k giá trị khác nhau x1 , x 2, …,xk với tần số n , n 1 , … , n 2
k tương ứng thì kì vọng và phương sai mẫu được xác định bởi công thức: 66
x n x n ... x n X 1 1 2 2 n k k n k 1 S2 (x X 2 ) n n n i i n i1
Ví dụ 1.4. Trung bình mẫu trong ví dụ 1.2 được xác định bởi công thức: 8 5 5 , 8 12 9 15 11 8 X 40 125 , 9 40
Phương sai mẫu được xác định bởi công thức: 8 ( 1 , 9 2 ) 5 2 2 5 5 , 8 ( 1 , 9 2 ) 5 2 12 (9 1 , 9 2 ) 5 2 15 1 ( 1 1 , 9 2 ) 5 2 8 S 40 9 , 0 8 40 I.6.Trung vị mẫu
Định nghĩa 1.5. Trung vị mẫu là số liệu nằm chính giữa dãy số liệu thống kê
(sau khi đã sắp xếp cãc số liệu từ nhỏ đến lớn hoặc ngược lại) nếu kích thước mẫu n là số lẻ;
Nếu n là số chẵn, n = 2m , thì trung vị mẫu là số trung bình cộng của xm và xm+1.
Mốt mẫu là giá trị trong dãy số liệu có tần số xuất hiện lớn nhất trong dãy số liệu đó.
Ví dụ 1.5. Mẫu trong ví dụ 1.2 có trung vị bằng 9 (vì kích thước mẫu n = 40 và các giá trị
thứ 20 và 21 đều bằng 9); có mod cũng bằng 9 (vì tần số xuất hiện của 9 trong dãy là lớn nhất (bằng 15). I.7. Mô men mẫu Định nghĩa 3.6. Ta gọi số : n 1 Mk k xi a) n i1
là mô men gốc mẫu bậc k ; n 1 C (x X ) k k n i b) n i1
là mô men trung tâm mẫu bậc k.
I.8. Hệ số tương quan mẫu
Định nghĩa 3.7.Giả sử x1 , x2 , … , x và y n , y 1 , … , y 2 n là hai dãy số liệu
thống kê thu được từ kết quả quan sát trên hai tập mẫu đều có kích thước n. Ta gọi số: n n n n x y ( x )( y )
k k k k k 1 k 1 k 1 r n n n n [ 2 nx x n y y k ( k )2 ][ 2 k ( k )2 ] k 1 k 1 k 1 k 1 67
là hệ số tương quan mẫu.
Chú ý. Đôi khi ta tính hệ số tương quan mẫu bằng công thức sau: n
( x X n)( y Yn) k k k r 1 n n [ x ( X 2 2 n ) ][ (y Y ) ] k n k k 1 k 1
Ví dụ 1.6. Trong một thí nghiệm trên bảy con chuột bạch để kháo sát sự tương quan giữa
thời gian sống sót y của chuột và liều độc x, ta được các số liệu trong bảng sau: X 0 1 2 3 4 5 6 Y 4,25 3 3 1,75 1,5 0,5 0,25
Hãy tính hệ số tương quan r giữa x và y.
Bằng tính toán trực tiếp ta được: x 2 ; 1 k y 1 4 2 , ; 5 X 7 ; 3 Y 7 0 , 2 3 ; 5 k
(xk X )(yk Y ) 18 ;5
, (xk X )2 2 ;8 (yk Y )2 1 2 6 , 76. 7 7 7 7 18 5 , r 9 , 0 8 28 1 , 2 676
II. Ước lượng tham số
Trong nghiên cứu khoa học, trong y tế, trong lao động sản xuất,…, ta thường
gặp và phải xử lí các bài toán dưới đây: (i)
Xác định khoảng ước lượng số trung bình a của các phần tử thuộc
một tập tổng quát X cho trước dựa trên kết quả các số liệu quan sát trên một tập mẫu (có
kích thước n) lấy ra từ tập X. (ii)
Xác định khoảng ước lượng tần số xuất hiện của biến cố A trong tập
tổng quát X cho trước dựa trên kết quả các số liệu quan sát trên tập mẫu (có kích thước n) lấy ra từ tập X.
Trong lí thuyết thống kê toán, người ta đã tìm ra những công cụ để xử lí các
bài toán nêu trên kèm theo độ tin cậy nhất định.
Trong mục này ta giới thiệu các công cụ này và thực hành vận dụng để xử lí
những bài toán nêu trên gặp trong thực tế.
III.1. Ước lượng và khoảng tin cậy của số trung bình hay kỳ vọng a
Để xử lí những bài toán dạng này, ta sử dụng kết quả dưới đây (đã được chứng
minh bằng lí thuyết thống kê toán):
Nếu nếu kết quả quan sát trên một tập mẫu có kích thước n lấy từ một tổng
thể có phân phối chuẩn có phương sai 2
chưa biết, ta nhận được dãy các số liệu X , X 1 2, X
3, …, Xn thỡ số trung bình a của tổng thể có khoảng ước lượng (với mức ý nghĩa hoặc
độ tin cậy 1 ) là : 68 S * S * X t
n a X t n n n n n
Trong đó hệ số t : (t ) 1
- Đựơc tra trong bảng phân phối chuẩn sao cho
2 , nếu n 30
- Được tra trong bảng phân phối Student với n – 1 bậc tự do, nếu n < 30. 2 *
Sn là phương sai suy rộng được xác định bởi công thức : m *2 1 2 n S (X X ) n n k 1 k1
Chú ý. Trong phần dưới đây, nếu không nói gì thêm thì các tập tổng quát mà ta
xét đều có phân phối chuẩn. Ví dụ 1.7.
Để xác định chiều cao trung bình của các cây bạch đàn trong một khu rừng bạch
đàn, người ta chọn ngẫu nhiên 50 cây trong khu rừng đó rồi đo chiều cao từng cây. Kết
quả nhận được bảng số liệu sau: Chiều cao 8 m 9 m 11 m 12 m Số cây 6 15 9 20
Biết rằng chiều cao các cây bạch đàn có phân phối chuẩn, tìm khoảng ước lượng
chiều cao trung bình a của các cây bạch đàn trong khu rừng đó với độ tin cậy 99%.
Sau đó nêu ý nghĩa thực tiễn của các số liệu tìm được. Giải:
Tra bảng phân phối chuẩn ta được t0,01 = 2,576. Ta có : 1 X 8 ( 6 9 15 11 9 12 ) 20 , 10 44 50 50 2 * 1 S [(8 10 4 , 4)2 6 (9 10 4 , 4)2 1 5 1 ( 1 10 4 , 4)2 9 1 ( 2 10 4 , 4)2 2 0] 50 49 3 , 2 9
Áp dụng công thức ta được khoảng ước lượng của chiều cao trung bình a các cây
bạch đàn trong khu rừng đó với độ tin cậy 99% là: 3 , 2 9 3 , 2 9 1 , 0 44 5 , 2 76 a 1 , 0 44 5 , 2 76 50 50 9 8 , 8 a 1 . 1 ..ha . y ...a 8 , 9 ( 8m1 ; 1 ) m
Ý nghĩa thực tiễn của các số liệu tìm được là: Không dưới 99% số cây bạch đàn
trong khu rừng đó có chiều cao nằm trong khoảng 9,88m đến 11m, hay nói cách khác, số 69
cây có chiều cao nhỏ hơn hoặc bằng 9,88m hay lớn hơn hoặc bằng 11m chiếm không quá 1%. Ví dụ 1.8.
Để xác định trọng lượng trung bình của các gói kẹo xuất xưởng, người ta chọn
ngẫu nhiên 28 gói trong lô hàng xuất xưởng, cân từng gói và kết quả nhận được bảng số liệu sau: 285 g 290 g 295 g 300 g 310 Trọng lượng 2 5 13 3 5 Số gói
Biết rằng trọng lượng của các gói kẹo có phân phối chuẩn , tìm khoảng ước
lượng trọng lượng trung bình a các gói kẹo xuất xưởng của phân xưởng đó với độ tin cậy 90%.
Sau đó nêu ý nghĩa thực tiễn của các số liệu vừa tìm được.
Giải:Tra bảng phân phối Student ta được t = 1,71.T 0,90 a có: 1 X (285 2 290 5 295 1 3 300 3 310 ) 5 29 , 6 61 28 28 1 *2 2 2 2 2 2 S [(285 296,61) 2 (290 296,61) 5 (295 296,61) 1 3 (300 296,61) 3 (310 296,61) 5 ] 5 3,80 28 27
Áp dụng công thức ta được khoảng ước lượng trọng lượng trung bình a các gói kẹo xuất
xưởng của phân xưởng đó với độ tin cậy 90% là : 53 8 , 53 8 , 296 6 , 1 , 1 71 a 296 6 , 1 , 1 71 28 28 29 , 4 24 a 298 9
, 8...hay ....a (29 , 4 24g ;298 9 , 8g )
Ý nghĩa thực tiễn của các số liệu tìm được là: Không dưới 90% số số gói kẹo xuất
xưởng có trọng lượng nằm trong khoảng từ 294,24g đến 298,98g, hay nói cách khác, số
gói kẹo có trọng lượng nhỏ hơn hoặc bằng 294,24g hay lớn hơn hoặc bằng 298,98g chiếm không quá 10%.
III.2. Ước lượng và khoảng tin cậy của tỉ lệ hay xác suất p
Bài toán này thường gặp trong nhiều lĩnh vực khác nhau: chẳng hạn ước
lượng tỷ lệ phế phẩm trong lô hàng xuất xưởng của một cỏ sở sản xuất nào đó, tỷ lệ học
sinh nắm được luật về an toàn giao thông, tỷ lệ người mù chữ ở một địa phương nào đó,
tỷ lệ người khỏi bệnh khi dùng một loại thuốc nào đó,…
Nói chung, ở đây ta lấy mẫu từ tổng thể có phân phối nhị thức có xác suất
chưa biết p (chỉ xác suất hỏng của một sản phẩm, chỉ xác suất nắm được luật giao thông
khi kiểm tra ngẫu nhiên một học sinh nào đó, chỉ xác suất khỏi bệnh khi sử dụng loại
thuốc,…). Trong phần này, ta tìm khoảng ước lượng của xác suất hay tỉ lệ p nói trên. 70
Để xử lí những bài toán dạng này, ta sử dụng kết quả dưới đây (đã được chứng
minh bằng lí thuyết thống kê toán):
Nếu W là tần suất của biến cố A quan sát được trên một tập mẫu có kích m
thước n (W = n , với m là số lần xuất hiện biến cố A trong n phép thử) thì tỷ lệ hay xác
suất p chưa biết của biến cố A trong tổng thể có khoảng ước lượng (với mức ý nghĩa
hoặc độ tin cậy 1 ) là : 1 ( W ) W 1 ( W ) W t p W t n n (t ) 1 Trong đó hệ số t
được tra trong bảng phân phối chuẩn sao cho 2 .
Ví dụ 1.9. Để xác định tỷ lệ công nhân mắc bệnh nghề nghiệp trong một khu công
nghiệp khai thác mỏ, người ta kiểm tra sức khoẻ cho 120 công nhân chọn ngẫu nhiên
trong khu mỏ đó. Kết quả có 48 người mắc bệnh nghề nghiệp. Tìm khoảng ước lượng của
tỷ lệ người mắc bệnh nghề nghiệp trong khu mỏ đó, với độ tin cậy 95%.
Sau đó nêu ý nghĩa thực tiễn của các số liệu vừa tìm được. Giải: 48 W , 0 , 40 t 96 , 1 . Ta có : 120 0,05
Áp dụng công thức ta có khoảng ước lượng của p với độ tin cậy 95% là : , 0 40 1 ( , 0 40) , 0 40 1 ( , 0 40) , 0 40 9 , 1 6 p , 0 40 9 , 1 6 120 120 3 , 0 123 p , 0 4877 Hay p (31,23%; 48,77%).
Ý nghĩa thực tiễn của của số liệu trên đây là: không dưới 95% số lần thử có tỷ
lệ người mắc bệnh nằm trong khoảng từ 31,23% đến 48,77% hay số lần thử có tỷ lệ
người mắc bệnh nằm ngoài khoảng trên chiếm không quá 5%. Ví dụ 1.10.
Để xác định tỷ lệ học sinh yêu thích môn toán trong một trường tiểu học, người ta
phát phiếu điều tra cho 160 học sinh của trường đó. Kết quả có 104 em trả lời thích học
toán và 56 em trả lời không thích học toán ví toán khó.
a) Với độ tin cậy 99% hãy cho biết ít nhất có bao nhiêu phần trăm học sinh của
trường đó thích học toán?
b) Với độ tin cậy 85% hãy cho biết tối đa có bao nhiêu phần trăm học sinh của
trường đó không thích học toán?
Sau đó nêu ý nghĩa thực tiễn của các số liệu vừa tìm được. Giải: 106 W , 0 ; 65 W 1 W , 0 ; 35 t 5 , 2 ; 76 t , 1 . 44 Ta có: 160 0,01 0 1 , 5 71
a)Áp dụng công thức ta có khoảng ước lượng của p với độ tin cậy 99% là : , 0 65 1 ( 6 , 0 5) , 0 65 1 ( 6 , 0 5) 0 6 , 5 5 , 2 76 p 6 , 0 5 5 , 2 76 160 160 0 5 , 529 p 7 , 0 471 Hay p (55,29%; 74,71%).
Vậy với độ tin cậy 99% ta có thể khẳng định ít nhất có 55,29% số học sinh của
trường đó thích học toán.
Ý nghĩa thực tiễn của các số liệu trên đây là: không dưới 99% lần khảo sát sẽ
có kết quả tỉ lệ học sinh thích học toán tối thiểu 55,29%.
b)Áp dụng công thức ta có khoảng ước lượng của p với độ tin cậy 85% là : 3 , 0 5 1 ( 3 , 0 ) 5 3 , 0 5 1 ( 3 , 0 5) 3 , 0 5 , 1 44 p 5 , 0 , 1 44 160 160 , 0 2957 p , 0 4043 Hay p (29,57%; 40,43%).
Vậy với độ tin cậy 85% ta có thể khẳng định tối đa có 40,43% số học sinh của
trường đó không thích học toán.
Ý nghĩa thực tiễn của các số liệu trên đây là: không quá 85% lần khảo sát sẽ
có kết quả tỉ lệ học sinh không thích học toán tối đa là 40,43%.
Chú ý.Khi sử lí những bài toán mà kích thước mẫu quan sát quá bé (n 10) và
những bài toán tần suất quá nhỏ (W 0,1) hoặc quá lớn (W 0,9 ) ta có thể sử dụng
những kết quả đã cho trong bảng 6 và bảng 7 việc tính toán sẽ đơn giản hơn. Ví dụ 1.11.
Điều trị cho 8 bệnh nhân bằng một loại thuốc A, kết quả cú 5 người khỏi bệnh.
Với độ tin cậy 95% hãy cho ước lượng về tỷ lệ bệnh nhân khỏi bệnh khi được điều trị bằng loại thuốc A. Giải:
Tra trong bảng 6 ứng với cột x = 3 và n = 8 ta được giới hạn dưới p 1= 24,5% và giới hạn trên p2 = 91,5%.
Vậy tỷ lệ người khỏi bệnh khi điều trị bằng loại thuốc A nằm trong khoảng từ 24,5 đến 91,5%. Ví dụ 1.12.
Để xác định tỷ lệ người mù chữ ở một tỉnh X, người ta kiểm tra ngẫu nhiên 12
000 người trong độ tuổi đi học, kết quả có 36 người không biết chữ. Tìm khoảng ước
lượng của tỷ lệ người không biết chữ ở tỉnh X với độ tin cậy 95%. Giải:
Gọi p là tỷ lệ người không biết chữ ở tỉnh X. Ta ước lượng p bằng tuần suất 36 W , 0 003 12000 . Ta tra bảng 7:
Nhìn vào dòng 30, cột 6 trong bảng ta được hai số liệu : 25,2 và 49,8.
Cận dưới p1 và cận trên p của khoảng ước lượng được 2 xác định như sau :
np1 = 25,2 . Suy ra p1 = 25,2 : 12 000 = 0,0021
np2 = 49,8. Suy ra p2 = 49,8 : 12 000 = 0,0042. 72
Vậy với độ tin cậy 95% ta có thể khẳng định tỷ lệ người không biết chữ trong tỉnh
X trong khoảng từ 0,21 đến 0,42%.
III.Kiểm định giả thiết thống kê
Trong phần này ta giải quyết các bài toán:
- So sánh số trung bình của mẫu quan sát với số trung bình theo lí thuyết để rút ra
kết luận: độ sai lệch là đáng kể hay không?
- So sánh tần suất của biến cố A trong mẫu quan sát với xác suất của biến cố A
theo lí thuyết để rút ra kết luận: độ sai lệch là đáng kể hay không?
- So sánh hai số trung bình trên hai mẫu quan sát để rút ra kết luận: hai số trung
bình theo lí thuyết sai lệch là đáng kể hay không? Số nào lớn hơn?
- So sánh hai tần suất của biến cố A trong hai mẫu quan sát để rút ra kết luận: hai
xác suất của biến cố A theo lí thuyết sai lệch có đáng kể hay không? Số nào lớn hơn? ...............
Thông tin duy nhất ta có ở đây là các số liệu quan sát trên tập mẫu. Để giải quyết
các bài toán dạng này, ta đưa ra: Trường hợp 1:
Giả thiết H: a = a0 Số trung bình mẫu và số trung bình theo lí thuyết có độ sai
lệch không đáng kể (chấp nhận giả thiết H). Hay:
Đối thiết K: a a0 Số trung bình mẫu và số trung bình theo lí thuyết có độ sai
lệch đáng kể (bác bỏ giả thiết H và chấp nhận đối thiết K). Trường hợp 2:
Giả thiết H: p = p0: Tần suất của biến cố A trong quan sát trên tập mẫu và xác
suất của biến cố A theo lí thuyết có độ sai lệch không đáng kể (chấp nhận giả thiết H).
Đối thiết K: p p0: Tần suất của biến cố A trong quan sót trên tập mẫu và xác
suất của biến cố A theo lí thuyết có độ sai lệch đáng kể (bác bỏ giả thiết H và chấp nhận đối thiết K).
Khi bác bỏ hay chấp nhận giả thiết H ta có thể mắc phải hai loại sai lầm dưới đây
- Sai lầm loại I: Ta bác bỏ giả thiết H trong khi H đúng
- Sai lầm loại II: Ta chấp nhận giả thiết H trong khi H sai
Ta cố gắng hạn chế tới mức tối thiểu cả hai loại sai lầm này. Nhưng khi kích thước
mẫu cố định thì điều này khó khả thi. Do vậy người ta thường cho phép được mắc sai lầm
loại I với xác suất (thường gọi là mức ý nghĩa hay độ tin cậy 1- ). Sau đó hạn chế
đến mức tối thiểu việc mắc sai lầm loại II.
III.1. Kiểm định giá trị trung bình a của tổng thể (so sánh số trung bình quan sát
với số trung bình lí thuyết)
a) Kiểm định hai phía 73
Trong thực tế ta thường gặp vấn đề sau đây: qua quan sát trên một tập mẫu có kích
thước n (lấy từ tổng thể X nào đó) ta nhận được số trung bình mẫu X . Mặt khác, ta đó
biết số trung bình của các phần tử trong tập tổng quát theo lí thuyết là a. Từ đây nảy sinh
câu hỏi: sự sai lệch giữa trung bình mẫu X và trung bình theo lí thuyết a là đáng kể hay không?
Để xử lí những bài toán dạng này, ta sử dụng kết quả sau đây:
Giả sử kết quả quan sát trên tập mẫu có kích thước n với phương sai chưa biết ta
nhận được dãy số liệu X1, X2,..., Xn.
Ta kiểm định giả thiết H: a = a 0với đối thiết K: a a0 và mức ý nghĩa (hay độ
tin cậy 1-).
Trước hết ta tính: Xn a - n 0 M * S X * S n
, trong đó n là trung bình mẫu, n là độ lệch chuẩn của mẫu,
xác định bởi công thức: n *2 1 Sn 2 ( X k - X ) 1 - n k 1 M - Nếu
< t thì ta chấp nhận giả thiết H: a = a với mức ý nghĩa 0 (độ tin cậy 1 - ). M - Nếu
t thì ta bác bỏ giả thiết H hay chấp nhận đối thiết K: a a0 . Ơ đây: (t ) 1 - Nếu n 30 thì t
tra trong bảng phân phối chuẩn sao cho 2
- Nếu n < 30 thì t tra trong bảng phân phối Studen với n - 1 bậc tự do.
Ví dụ 1.13.
Trọng lượng tiêu chuẩn của một gói kẹo xuất xưởng là 300g. Người ta chọn ngẫu
nhiên 61 gói kẹo trong lô hàng xuất xưởng đem cân và nhận được trọng lượng trung bình *
của 61 gói đó là 299,3g và độ lệch chuẩn S61 = 7,2. Hỏi với mức ý nghĩa = 0,05 trọng
lượng của các gói kẹo xuất xưởng có đạt tiêu chuẩn hay không?. Giải:
Ở đây ta có giả thiết: a = 300 và đối thiết: a 300.
Vì n > 30 nên tra bảng phân phối chuẩn ta được t0,05 = 1,96.
Áp dụng công thức ta có: 74 299,3 3 - 00 61 M 7,2 0,76.
Vì 0,76 < 1,96 nên ta chấp nhận giả thiết H tức là trọng lượng trung bình của các
gói kẹo xuất xưởng bằng 300g với độ tin cậy 95%.
Ý nghĩa thực tiễn của các số liệu trên đây là: số gói kẹo có trọng lượng khác 300g
trong lô hàng xuất xưởng chiếm không quá 5%.
Ví dụ 1.14.
Nuôi 15 con gà theo chế độ ăn riêng, sau ba tháng mức tăng trọng lần lượt của 15 con đó như sau:
3kg; 2,8kg; 3kg; 4kg; 2,5kg; 4kg; 3,5kg;
3kg; 4kg; 2kg; 3kg;4kg; 3,2kg; 3,5kg; 4kg .
Biết mức tăng trọng trung bình của gà theo chế độ ăn bình thường là 2,8 kg. Hỏi
với độ tin cậy 95% thì gà cho ăn theo chế độ riêng mức tăng trọng trung bình có thay đổi hay không?.
Giải: Ta có giả thiết H : a = 2,8 và đối thiết K : a 2,8.
Ơ đây ta có n = 15 < 30, tra bảng phân phối Student ta được t = 2,145 0,05 Ta có:
X15 = ( 3x4 + 2,8 + 4x5 + 2,5 +3,5x2 +2 +3,2 ) : 15 = 3,3 2 * S [ 3 ( ) 3 , 3 2 4 ( 8 , 2 , 3 ) 3 2 (4 ) 3 , 3 2 5 ( 5 , 2 ) 3 , 3 2 5 , 3 ( ) 3 , 3 2 2 15 (2 ) 3 , 3 2 ( , 3 2 ) 3 , 3 2] :14 0 6 , 2
Áp dụng công thức ta có : , 3 3 8 , 2 15 M , 2 459 145 , 2 , 0 62
Vậy ta bác bỏ giả thiết H mà chấp nhận đối thiết K: với chế độ ăn riêng, mức tăng
trọng trung bình của gà khác 2,8 kg với độ tin cậy 95%.
b) Kiểm định một phía khi phương sai chưa biết Nếu X a n
o thì ta kiểm định một phía theo công thức dưới đây:
Giả sử kết quả quan sát trên tập mẫu có kích thước n với phương sai chưa biết ta
nhận được dãy số liệu X1, X2,..., Xn.
Ta kiểm định giả thiết H: a = a0 với đối thiết K: a > a 0và mức ý nghĩa (hay độ
tin cậy 1-).
Trước hết ta tính: 75 X ( - a ) n n o M * S X * S n
, trong đó n là trung bình mẫu, n là độ lệch chuẩn của
mẫu, xác định bởi công thức: n *2 S 1 X n 2 ( - X ) n 1 - k k 1
- Nếu M < t thì ta chấp nhận giả thiết H: a = a0 với mức ý nghĩa (độ tin cậy 1-).
- Nếu M > t thì ta bác bỏ giả thiết H hay chấp nhận đối thiết K: a > a0 . Ơ đây: (t ) 1
- Nếu n 30 thì t tra trong bảng phân phối chuẩn sao cho 2
- Nếu n < 30 thì t tra trong bảng phân phối Studen với n - 1 bậc tự do.
Chú ý. Nếu X a n
o thì ta kiểm định một phía theo công thức dưới đây:
Kiểm định giả thiết H: a = ao với đối thiết K: a < a , ta tính o (a X ) n o n M * Sn .
- Nếu M < t thì ta chấp nhận giả thiết H: a = a với mức ý nghĩa 0 (độ tin cậy 1 - ).
- Nếu M > t thì ta bác bỏ giả thiết H hay chấp nhận đối thiết K: a < a0 . Ơ đây: (t ) 1 - Nếu n 3
0 thì t tra trong bảng phân phối chuẩn sao cho 2
- Nếu n < 30 thì t tra trong bảng phân phối Student với n - 1 bậc tự do.
Ví dụ 1.15.
Trọng lượng tiêu chuẩn của một gói kẹo xuất xưởng là 300g. Người ta chọn ngẫu
nhiên 61 gói kẹo trong lô hàng xuất xưởng đem cân và nhận được trọng lượng trung bình *
của 61 gói đó là 288g và độ lệch chuẩn S60 = 7,2. Hỏi với mức ý nghĩa = 0,05 trọng
lượng của các gói kẹo xuất xưởng có nhẹ hơn trong lượng tiêu chuẩn hay không?. Giải:
Ở đây ta kiểm định giả thiết : a = 300 và đối thiết : a 300.
Vì n > 30 nên tra bảng phân phối chuẩn ta được t0,05 = 1,96. Ap dụng công thức ta có: 76 (300-288) 61 M 7,2 13,02
Vì 13,02 > 1,96 nên ta bác bỏ giả thiết H và chấp nhận đối thiết K: a < ao tức là
trọng lượng trung bình của các gói kẹo xuất xưởng nhẹ hơn trọng lượng tiêu chuẩn với độ tin cậy 95%.
Ví dụ 1.16.
Nuôi 15 con gà theo chế độ ăn riêng, sau ba tháng mức tăng trọng lần lượt của 15 con đó như sau:
3kg; 2,8kg; 3kg; 4kg; 2,5kg; 4kg; 3,5kg;
3kg; 4kg; 2kg; 3kg; 4kg; 3,2kg; 3,5kg; 4kg .
Biết mức tăng trọng trung bình của gà theo chế độ ăn bình thường là 2,8 kg. Hỏi
với độ tin cậy 95% thì gà cho ăn theo chế độ riêng mức tăng trọng trung bình có cao hơn trước hay không?.
Giải: Ta có giả thiết H : a = 2,8 và đối thiết K : a > 2,8.
Ơ đây ta có n = 15 < 30, tra bảng phân phối Student ta được t = 2,145 0,05 Ta có:
X15 = ( 3x4 + 2,8 + 4x5 + 2,5 +3,5x2 +2 +3,2 ) : 15 = 3,3 *2 S [ (3 ) 3 , 3 2 4 ( 8 , 2 , 3 ) 3 2 (4 ) 3 , 3 2 5 ( 5 , 2 ) 3 , 3 2 ( 5 , 3 ) 3 , 3 2 2 15 (2 ) 3 , 3 2 , 3 ( 2 ) 3 , 3 2 ] :14 0 6 , 2
Áp dụng công thức ta có: 3 , 3 ( ) 8 , 2 15 M , 2 459 2 1 , 45 0 6 , 2
Vậy ta bác bỏ giả thiết H mà chấp nhận đối thiết K: với chế độ ăn riêng, mức tăng
trọng trung bình của gà cao hơn 2,8 kg.
III.2. Kiểm định giả thiết về tỷ lệ hay xác suất p (so sánh tần suất thu được từ quan
sát với xác suất của biến cố A theo lí thuyết)
III.3.2.1. Kiểm định hai phía:
Giả sử kết quả quan sát trên tập mẫu có kích thước n 30 ta thấy có k lần xuất hiện biến cố A.
Ta kiểm định tỷ lệ hay xác suất p của biến cố A với giả thiết H: p = p0 và đối thiết
K: p p0 và mức ý nghĩa (hay độ tin cậy 1 - )
Trước hết ta tính: W p - n o k V p ( 1- p = ) 0 0
, trong đó W = n là tần suất của biến cố A trong quan sát. 77 - Nếu V t
< thì ta chấp nhận giả thiết H với mức ý nghĩa (hay độ tin cậy 1 - ) - Nếu V t
thì ta bác bỏ giả thiết H hay chấp nhận đối thiết K với mức ý nghĩa
(hay độ tin cậy 1 - ) ở đây t (t
tra trong bảng 1 sao cho ) = 1 - 2
Ví dụ 1.17.
Ở một địa phương tỷ lệ mắc bệnh A đã được xác định nhiều lần là 34%. Sau một
đợt điều trị bằng một loại thuốc, người ta kiểm tra lại 120 người thấy 24 còn người mắc bệnh A.
Hỏi với độ tin cậy 95% tỷ lệ người mắc bệnh A ở địa phương đó sau khi được điều
trị bằng loại thuốc nêu trên có thay đổi không? Giải: 24
Ơ đây ta có n = 120; W = 120 = 0,2; = 0,05.
Tra bảng ta được: t = 1,96; Giả thiết H: p = 0,34 với 0,05 đối thiết K: P 0,34. , 0 0 - 2 ,34 120 V 0,34 0,05 = 0,66 . 3,23.
Vì 3,23 > 1,96 nên ta bác bỏ giả thiết p = 0,34. Vậy tỷ lệ người mắc bệnh A ở địa phương có thay đổi.
III.3.2.2. Kiểm định một phía
Trong công thức trên:
a) Nếu W > p thì ta kiểm định giả thiết H: p = p o
o với đối thiết K: p > p như sau: o (W p - ) n 0 p ( 1 p - ) + Nếu V = 0 0
> t thì ta bác bỏ giả thiết H: p = po mà chấp nhận
nhận đối thiết K: p > p0. (W p - ) n 0 p ( 1 p - ) + Nếu V = 0 0
< t thì ta chấp nhận giả thiết H: p = po
b)Nếu W < po thì ta kiểm định giả thiết H: p = po với đối thiết K: p < po như sau: ( p W ) n o + Nếu V = p p - (1 ) 0 0
> t thì ta bác bỏ giả thiết H: p = po mà chấp nhận đối thiết K: p < p .0 78 (p W ) n o + Nếu V = p ( 1 - p ) 0 0
< t thì ta chấp nhận giả thiết H: p = po Trong ví dụ trên ta có: 0,34 ( - 0,2) 120 0,34 0,34) - (1 3,23 >1,96
Vậy ta kết luận tỷ lệ người mắc bệnh ở địa phương đó sau một đợt điều trị giảm đi.
III.3. So sánh hai giá trị trung bình của hai mẫu quan sát khi
Trong thực tế ta thường phải so sánh hiệu quả của hai phương pháp dạy học tác
động tới kết quả học tập của học sinh; hiệu quả của hai phương pháp điều trị trong y học
tác động tới hiệu quả khỏi bệnh của bệnh nhân, tác dụng của hai loại phân tới năng suất của cây trồng,…
Dưới đây ta giải quyết các bài toán dạng này:
III.3.1. Trường hợp tổng kích thước hai mẫu lớn hơn 60
Để giải quyết các bài toán dạng này, ta sử dụng kết quả dưới đây:
Để so sánh hai số trung bình của hai tổng thể có phân phối chuẩn có cùng phương sai 2
dựa vào hai trung bình mẫu X , X A
B thu được trên hai mẫu quan sát có kích
thước nA và nB ( trong đó nA + nB > 60 ), ta kiểm định giả thiết H: a1 = a với đối 2
thiết K: a1 a2 với ý nghĩa (hay độ tin cậy 1 - )
Trước hết ta tính: X - X A B u 2 2 S S A B n n A
B , trong đó SA và SB theo thứ tự là độ lệch chuẩn mẫu quan sát
trên các mẫu A và B.
- Nếu u < t ; thì ta chấp nhận giả thiết H: a1 = a với mức ý nghĩa 2 (hay độ
tin cậy 1 - ).
- Nếu u t thì ta bác bỏ giả thiết H mà chấp nhận đối thiết K: a 1 a .2 (t ) 1
Ở đây t tra trong bảng phân phối chuẩn sao cho 2 79
Ví dụ 1.18.
Để so sánh trọng lượng trẻ sơ sinh là con so so với con dạ ở một bệnh viện phụ
sản, người ta tiến hành một quan sát như sau:
- Theo dõi trọng lượng của 95 trẻ sơ sinh là con so, nhận được trọng lượng trung 2
bình của 95 cháu này bằng 2798g và độ lệch chuẩn bình phương SA = 190000.
- Theo dõi trọng lượng của 105 trẻ sơ sinh là con dạ, nhận được trọng lượng trung 2
bình của 105 cháu này bằng 3166g và độ lệch chuẩn bình phương SB= 200704.
Với độ tin cậy 95%, hãy cho biết trọng lượng trung bình của trẻ sơ sinh là con so
và trẻ sơ sinh là con dạ ở bệnh viện đó có khác nhau không? Giải: 2 Ở đây ta có X S
A = 2798; nA = 95 và A = 190000. X 2 S
B = 3166; nB = 105 và B = 200704, = 0,05.
Tra bảng ta được t0,05 = 1,96. Ta có : X X - A B 2798 3 - 166 2 2 S S A B 190000 200704 n u= A nB = 95 105 5,88 > 1,96.
Vậy ta kết luận: trọng lượng trung bình của trẻ sơ sinh là con so và con dạ ở bệnh
viện phụ sản đó khác nhau.
III.3.2. Trường hợp phương sai chưa biết và tổng kích thước hai mẫu nhỏ hơn 60
Để so sánh hai số trung bình của hai tổng thể cú phân phối chuẩn có cùng phương sai 2
dựa vào hai trung bình mẫu X , X A
B thu được trên hai mẫu quan sát có
kích thước nA và nB ( trong đó nA + nB < 60) ta lập tỷ số: X X A B u 1 1 S A,B n n A B Trong đó: 80 n n A B ( x X )2 ( x X )2 A A B B 2 1 1 S A,B n n A B 2 hoac : ( x )2 ( x )2 2 A 2 x x A B B 2 n n SA B A B , n n 2 A B
Ta kiểm định giả thiết H: a a a
1 = a2 , đối thiết K: 1
2 , với mức ý nghĩa (hay độ tin cậy 1 - ).
- Nếu u t thì ta chấp nhận giả thiết H và kết luận hai số trung bình khác nhau không có ý nghĩa; - Nếu u t
thì ta bác bỏ giả thiết H và chấp nhận đối thiết K.
ở đây t được tra trong bảng phân phối Student với nA + n B – 2 bậc tự do.
Ví dụ 1.19.
Để so sánh mức tăng trọng của hai giống gà, người ta chăm sóc chúng với cùng
một chế độ thức ăn. Sau một thời gian, người ta chọn ngẫu nhiên 12 con từ đàn thứ nhất
và 15 con từ đàn thứ hai, cân từng con và nhận được bảng số liệu sau : Đàn thứ nhất: Trọng 2,5 3 3,2 3,5 4 lượng (kg) Số lượng 1 3 4 2 2 (con) Đàn thứ hai: Trọng 2 2,8 3,5 4,2 lượng (kg) Số lượng 2 2 6 5 (con) 2 2
Giả sử các quan sát trên độc lập và có phân phối chuẩn N(a , ) N (a , 1 và ) 2
.Với mức ý nghĩa 0,1 hãy so sánh mức tăng trọng của hai giống gà nói trên. Giải: Ta có : n1 + n – 2
2 = 12 + 15 – 2 = 25.Tra bảng phân phối Student với 25 bậc tự do ta được t = 1,71 0,1 1. 81 X A ( 5 , 2 3 3 , 3 2 4 5 , 3 2 4 ) 2 :12 , 3 275 X B ( 2 2 8 , 2 2 5 , 3 6 , 4 2 ) 5 :15 , 3 44 (x A X A)2 ( 5 , 2 , 3 27 ) 5 2 (3 , 3 27 ) 5 2 3 , 3 ( 2 2 , 3 7 ) 5 2 4 5 , 3 ( , 3 27 ) 5 2 2 (4 , 3 27 ) 5 2 2 2 (x X )2 ( 2 , 3 44) 2 2 ( 8 , 2 , 3 44) 2 2 5 , 3 ( , 3 44) 2 6 ( , 4 2 , 3 44) 2 5 7 8 , 76 B B 2 2 7 8 , 76 S A B S , 3 , 0 9 ; 5 A,B , 0 63 12 15 2 , 3 275 , 3 44 u 6 , 0 76 , 1 711 1 1 , 0 63 12 15
Vậy với mức ý nghĩa 10% ta chấp nhận giả thiết H: a1 = a2 hay mức tăng trọng của
hai giống gà nói trên khác nhau không đáng kể.
III.3.3. Kiểm định một phía khi phương sai chưa biết 2 2
Kiểm định một phía khi phương sai chưa biết (ta giả sử 2 1 )
a)Nếu X X B A
và nA + nB > 60 thì ta kiểm định giả thiết H : o a 1 = a2 với đối
thiết K: a1 < a như sau: 2 (X B X ) u A t 1 1 S A,B + Nếu n n A B
thì ta bác bỏ giả thiết H mà chấp nhận đối thiết K: a t
1 < a , trong đó hệ số 2 tra tương tự mục trên. (X B X ) u A t 1 1 S A,B + Nếu nA nB
thì ta chấp nhận giả thiết H.
b)Nếu X X B A
và nA + nB < 60 thì ta kiểm định giả thiết H: a1 = a2 vơi
đối thiết K: a < a 1 2 như sau: (X B X ) u A t 1 1 S , A B + Nếu n n A B
thì ta bác bỏ giả thiết H mà chấp nhận đối thiết K: a t 1 < a 2 , trong đó hệ số
tra trong bảng phân phối Student với nB + nA – 2 bậc tự do. (X B X ) u A t 1 1 S A,B + Nếu n n A B
thì ta chấp nhận giả thiết H. 82
III.4. So sánh hai xác suất theo lí thuyết dựa trên tần suất thu được từ mẫu quan sát
Giả sử kết quả quan sát trên hai phép thử Bécnuli ta nhận được dãy số liệu sau:
- Số phép thử trong dãy thứ nhất là n1, số lần xuất hiện biến cố A là k 1và xác suất
của biến cố A trong mỗi phép thử là p1.
- Số phép thử trong dãy thứ hai là n2, số lần xuất hiện biến cố A là k 2và xác suất
của biến cố A trong mỗi phép thử là p2.
Ta kiểm định giả thiết H: p1 = p2 với đối thiết K :p1 p 2ở mức ý nghĩa (hay độ tin cậy 1 - ) Trước hết ta tính: k k 1 2 - n n 1 2 1 1 k k k k 1 2 1 2 - 1 n n n n n n 1 2 1 2 1 d = 2
- Nếu d < t ; thì chấp nhận giả thiết H: p1 = p2
- Nếu d t , thì bác bỏ giả thiết H hay chấp nhận đối thiết K: p1 p2. (t ) 1
Ơ đây hệ số t tra trong bảng phân phối chuẩn sao cho 2 . Ví dụ 1.20.
Cùng một loại hạt giống lấy từ trong kho người ta đem gieo trên hai vườn ươm
khác nhau: trong vườn thứ nhất người ta gieo 100 hạt có 80 hạt nảy mầm; trong vườn thứ
hai người ta gieo 125 hạt có 90 hạt nảy mầm.
Hãy so sánh tỷ lệ hạt giống nói trên nảy mầm khi đem gieo trong hai vườn ươm đó với mức ý nghĩa 5%.
Giải: ở đây n = 100, k 1
1 = 80; n2 = 125, k2 = 90 và = 5%. t
Tra bảng ta được 2 ; = 1,96. Ta có : 80 90 - d 100 125 1 1 8 0 9 0 8 0 9 0 1 - 100 12 5 10 0 1 2 5 10 0 1 2 5
Vậy tỷ lệ hạt giống nảy mầm khi gieo trên hai vườn ươm trên được coi là như nhau . 83 k k 1 2 Chú ý. Nếu n n 1
2 thì ta đưa về bài toán kiểm định giả thiết : H
o : p1 = p với đối thiết K : p 2
1 < p2 với mức ý nghĩa .
Tiêu chuẩn kiểm định giả thiết H ở đây là : o
c) Giả thiết H bị bác bỏ ở mức o , nếu : k k 2 1 n n 2 1 Z t 1 1 k k k k 1 2 1 1 ( )( )(1 ) n n n n n n 1 2 1 2 1 2
Và chấp nhận giả thiết H t o, nếu Z . k k 1 2
Tương tự đối với trường hợp n n 1 2 .
IV.Yếu tố thống kê trong môn toán tiểu học
Yếu tố thống kê là một trong năm mạch kiến thức của môn Toán ở Tiểu học. Nó gồm các nội dung sau :
a) Dãy số liệu thống kê;
b) Bảng số liệu thống kê; c) Biểu đồ;
d) Số trung bình của dãy số liệu;
e) Giải toán về thống kê.
1.Dãy số liệu thống kê
Giới thiệu cho học sinh :
a) Các khái niệm cơ bản của dãy số liệu: số số hạng của dãy số liệu, thứ tự của số
hạng; số số hạng của dãy số liệu,…
b) Cách đọc và phân tích các số liệu của dãy;
c) Biết xử lí số liệu của dãy ở mức độ đơn giản;
d) Thực hành lập dãy số liệu từ một quan sát cụ thể.
2.Bảng số liệu thống kê
Giới thiệu cho học sinh:
a) Cấu tạo của bảng số liệu thống kê: hàng và cột, bảng đơn, bảng kép;
b) Cách đọc và phân tích số liệu trong bảng;
c) Biết cách xử lí số liệu trong bảng;
d) Thực hành lập bảng số liệu từ một quan sát cụ thể. 3.Biếu đồ
Giới thiệu cho học sinh: 84
a) Cấu tạo của ba loại biểu đồ: biểu đồ tranh, biểu đồ cột và biểu đồ hình quạt;
b) Biết cách đọc và phân tích số liệu trong mỗi loại biểu đồ;
c) Thực hành lập biểu đồ từ một quan sát cụ thể.
4.Giá trị trung bình của các số liệu thống kê
Giới thiệu cho học sinh:
a) Khái niệm về số trung bình cộng;
b) Quy tắc tìm số trung bình cộng của hai hay nhiều số;
c) Thực hành tìm số trung bình cộng của các số liệu quan sát.
5.Giải toán về thống kê số liệu:
Các bài toán về thống kê số liệu ở tiểu học có thể phân ra thành các dạng cơ bản
a) Thực hành đọc và phân tích các số liệu thống kê;
b) Thực hành xử lí các số liệu thống kê;
c) Thực hành lập dãy số liệu, bảng số liệu và biểu đồ từ một quan sát cụ thể;
d) Thực hành giải toán với các số liệu trê biểu đồ.
Ví dụ 1.22. (xem [3],trang 24,bài 1)
Biểu đồ dưới đây nói về số cây khối lớp Bốn và khối lớp Năm đã trồng 50 45 40 35 30 25 45 20 40 35 15 28 10 22 5 0 4A 4B 4C 5A 5B
Nhìn vào biểu đồ trên hãy trả lời các câu hỏi sau :
a) Những lớp nào đã tham gia trồng cây?
b) Lớp 4A trồng được bao nhiêu cây? Lớp 5B trồng được bao nhiêu cây? Lớp 5C
trồng được bao nhiêu cây?
c) Khối lớp Năm có mấy lớp tham gia trồng cây? Là những lớp nào?
d) Lớp nào trồng được nhiều cây nhất? Trong bài tập này : -
Các câu a, b củng cố cho học sinh kỹ năng đọc số liệu trên biểu đồ cột; -
Các câu c, d củng cố cho học sinh kỹ năng phân tích số liệu trên biểu đồ cột
Ví dụ 1.23. (xem [3], trang 33, bài 2]
Biểu đồ dưới đây nói về số thóc gia đình bác Hà đã thu hoạch được trong ba năm 2000, 2001, 2002 : 85 Năm 2000 vẽ 3 bịch thóc Năm 2001 vẽ 3 bịch thóc Năm 2002 vẽ 5 bịch thóc
Chú ý : Mỗi …..(vẽ 1 bịch thóc) chỉ 10 tạ thóc.
Dựa vào biểu đồ trên, hãy trả lời các câu hỏi dưới đây :
a) Năm 2002 gia đình bác Hà thu hoạch được mấy tấn thóc?
b) Năm 2002 gia đình bác Hà thu hoạch nhiều hơn năm 2000 bao nhiêu tạ thóc?
c) Cả ba năm gia đình bác Hà thu hoạch được tấn thóc? Năm nào thu hoạch
được nhiều thóc nhất? Năm nào thu hoạch được ít thóc nhất?
Các câu trong bài tập này rèn cho học sinh kỹ năng đọc và phân tích số liệu trong
biểu đồ tranh.Thực hành xử lí số liệu trên biểu đồ tranh. Đồng thời, tích hợp kiến thức
giữa biểu đồ tranh với các mạch kiến thức khác : đo lường và giải toán.
Ví dụ 1.24. (xem [4] , trang 9, bài 2)
Kết quả điều tra về ý thích ăn hoa quả của 120 bạn học sinh mô tả trên biểu đồ hình quạt dưới đây: Cam: 20% Mít:15% Na: 40% Xoài: 25%
Nhìn vào biểu đồ trên em hãy cho biết :
a) Có bao nhiêu bạn thích ăn na?
b) Số bạn thích ăn na gấp bao nhiêu lần số bạn thích ăn cam? 86
Trong bài tập này : học sinh được củng cố kỹ năng đọc và xử lí số liệu trên biểu đồ
quạt.Thông qua đó, giúp học sinh củng cố kỹ năng tính toán về tỉ số phần trăm.
Ví dụ 1.25. (xem [3], bài 3, tiết 34)
Tàu Thắng Lợi trong ba tháng đầu năm đã đánh bắt được số cá như sau:
Tháng 1: 5 tấn; Tháng 2: 2 tấn; Tháng 3: 6 tấn.
Hãy vẽ tiếp biểu đồ dưới đây : 87 Tấn 7 6 5 4 3 2 1 0 Th.1 Th.2 Th.3 (Tháng)
Bài toán trên bước đầu hình thành cho học sinh kỹ năng vẽ biểu đồ ở mức độ đơn giản.
Ví dụ 1.6. ( xem [2], bài 2 ,trang 138)
Dưới đây là bảng thống kê số cây bản Na trồng được trong 4 năm : Năm 2000 2001 2002 2003 Loại cây Thông 1875 cây 2167 cây 1980 cây 2540 cây Bạch 1745 cây 2040 cây 2165 cây 2515 cây đàn
Dựa vào bảng trên hãy trả lời các câu hỏi dưới đây :
a) Năm 2002 bản Na trồng được nhiều hơn năm 2000 bao nhiêu cây bạch đàn?
b) Năm 2003 trồng được tất cả bao nhiêu cây thông và cây bạch đàn?
Bài toán trên giúp học sinh rèn kỹ năng đọc, phân tích và xử lí số liệu
của bảng số liệu thống kê. Thông qua đó, bài toán tích hợp giữa mạch kiến thức
thống kê với giải toán có lời văn và giáo dục môi trường.
Ví dụ 1.27.(xem [2], bài 4, trang 139)
Trong cuộc thi chào mừng ngày Nhà giáo Việt Nam, các bạn khối Ba đã đạt được các giải sao đây:
Văn nghệ : 3 giải nhất và 2 giải ba;
Kể chuyện : 2 giải nhất, 1 giải nhì và 4 giải ba
Cờ vua : 1 giải nhất và 2 giải nhì. 88
Hãy viết số thích hợp vào bảng thống kê các giải của khối Ba đạt được (theo mẫu): Môn Văn nghệ Kể chuyện Cờ vua Giải Nhất 3 Nhì 0 Ba 2
Thông qua ví dụ này, bước đầu học sinh thực hành lập bảng số liệu thống kê.
Ví dụ 1.28. ( xem [2], bài 1, trang 135)
Bốn bạn Dũng, Hà, Hưng, Quân có chiều cao theo thứ tự là:
129 cm, 132 cm , 125 cm , 135 cm.
Dựa vào dãy số liệu trên hãy trả lời các câu hỏi sau:
a) Hùng cao bao nhiêu xăng-ti-mét?
Dũng cao bao nhiêu xăng-ti-mét?
Hà cao bao nhiêu xăng-ti-mét?
Quân cao bao nhiêu xăng-ti-mét?
b) Dũng cao hơn Hùng bao nhiêu xăng-ti-mét?
Hà thấp hơn Quân bao nhiêu xăng-ti-mét?
Bài tập trên rèn cho học sinh kỹ năng đọc và phân tích số liệu của dãy số liệu thống kê. Bài tập chương II
Bài 1.Trong kết quả của CHƯƠNG III
Cơ sở toán học của các yếu tố hình học ở tiểu học
I. Phương pháp tiên đề trong xây dựng lí thuyết môn hình học
Môn hình học được xây dựng trên cơ sở 4 thành tố cơ bản sau: Các khái niệm cơ bản
Hệ thống các tiên đề hình học
Hệ thống các định nghĩa hình học
Hệ thống các định lí, tính chất của các hình hình học
1. Các khái niệm hình học cơ bản:
Trong hình học, cũng như các ngành khoa học khác, mỗi khi đưa ra một khái niệm
mới (có thể là một thuật ngữ hay một kí hiệu) người ta phải định nghĩa nó thông qua
những khái niệm đã biết trước đó. Khi đưa ra khái niệm trước đó người ta lại phải 89
định nghĩa nó thông qua các khái niệm trước đó nữa,… Cứ như thế, rõ ràng là không
thể định nghĩa được mãi cho tất cả các khái niệm hình học. Vì vậy người ta phải đưa
ra một số khái niệm cơ bản ban đầu không định nghĩa.
Khái niệm cơ bản là những khái niệm không được định nghĩa. Để hiểu các khái
niệm này, người ta mô tả nó thông qua các hình ảnh, biểu tượng. Hệ thống các khái
niệm cơ bản trong hình học bao gồm: Điểm Đường thẳng Mặt phẳng
Quan hệ liên thuộc (điểm thuộc đường thẳng, điểm thuộc mặt phẳng)
Điểm nằm giữa hai điểm kia Quan hệ toàn đẳng
2. Hệ thống các tiên đề:
Tiên đề là những mệnh đề toán học mà tính đúng đắn của nó được mặc nhiên thừa
nhận mà không cần chững minh. Dưới đây là hệ thống một số các tiên đề trong hình học:
Tiên đề 1: Qua hai điểm khác nhau trong mặt phẳng, xác định được một và chỉ
một đường thẳng qua hai điểm đó.
Tiên đề 2. Qua ba điểm không thẳng hàng xác định được một và chỉ một mặt phẳng qua ba điểm đó
Tiên đề 3. Nếu hai điểm A, B đều thuộc đường thẳng a thì đường thẳng qua hai
điểm A, B trùng với đường thẳng a.
Tiên đề 4. Qua 1 điểm ở ngoài một đường thẳng ta dựng được một và chỉ một
đường thẳng song song với đường thẳng đã cho.
Tiên đề 5. Trong ba điểm phân biệt thuộc một đường thẳng có duy nhất 1 điểm nằm giữa hai điểm kia.
Tiên đề 6. Nếu 2 mặt phẳng có chung một điểm thì chúng có chung một điểm khác nữa.
3. Hệ thống định nghĩa các khái niệm hình học
Từ các khái niệm cơ bản, người ta định nghĩa những khái niệm mới và như vậy: hệ
thống khái niệm hình học ngày càng phong phú hơn.
4. Các định lí và tính chất hình học
Từ các định nghĩa, tiên đề hình học, vận dụng các suy luận logic, người ta chứng
minh để rút ra các định lí và tính chất hình học.
Từ các định nghĩa, tiên đề, định lí và tính chất đã được chứng minh ta tiếp tục định
nghĩa các khái niệm mới, chứng minh các tính chất mới,... làm cho nội dung môn hình
học ngày một phong phú hơn.
II. Định nghĩa các khái niệm hình học
Các khái niệm hình học có thể phân chia thành bốn nhóm: -
Các khái niệm cơ bản (khái niệm không định nghĩa); -
Các khái niệm về các hình hình học; -
Các khái niệm về quan hệ giữa các hình hình học; 90 -
Các khái niệm về chu vi, diện tích và thể tích các hình.
II.1. Định nghĩa các hình hình học
II.1.1. Định nghĩa hình hình học
Mỗi tập hợp H gồm các điểm trong mặt phẳng hoặc trong không gian, ta gọi là
một hình hình học. Nếu H là tập các điểm trong mặt phẳng thì ta gọi H là hình phẳng, nếu
H là tập hợp các điểm trong không gian thì ta gọi H là hình không gian. Nếu H là tập
rỗng thì ta gọi H là hình rỗng.
Dưới đây ta hệ thống các định nghĩa về các hình hình học đã được học trong
chương trình môn toán ở trường phổ thông:
II.1.2. Định nghĩa các hình phẳng
1. Định nghĩa đoạn thẳng: Đoạn thẳng AB là hình gồm điểm A, điểm B và tất cả
các điểm nằm giữa A và B.
Đoạn thẳng AB còn gọi là đoạn thẳng BA. Hai điểm A và B gọi là các đầu mút của đoạn thẳng AB. A B
2. Định nghĩa tia: Cho đường thẳng xy và một điểm O trên đường thẳng đó. Hình
gồm điểm O và một phần đường thẳng xy bị chia ra bởi điểm O được gọi là một tia gốc
O (hay còn gọi là một nửa đường thẳng gốc O). y O x
Trong hình trên ta có tia Ox và tia Oy cùng chung gốc O.
Ta gọi Ox và Oy là hai tia đối nhau (hay nói cách khác, hai tia đối nhau là hai tia
cùng chung một gốc và chúng tạo thành một đường thẳng.
3. Định nghĩa đường gấp khúc (đơn, tự cắt, khép kín)
Cho một dãy n điểm phân biệt {A1; A2; A3; …; An}. Hình tạo bởi dãy các
đoạn thẳng {A1A2; A2A3; A3A4; …; An-1An } sao cho không có hai đoạn thẳng liên tiếp
nhau nào cùng nằm trên một đường thẳng ta sẽ gọi là một đường gấp khúc, kí hiệu là A1A A 2
3…An với điểm đầu là A1 và điểm cuối là An.
Các điểm Ai gọi là các đỉnh và các đoạn AiAi+1 với i = 1, 2, …, n-1 gọi là các
cạnh (hay đốt) của đường gấp khúc đó.
Nếu đường gấp khúc có điểm đầu trùng với điểm cuối ( A A n 1 ) thì ta gọi là
đường gấp khúc khép kín.
Nếu hai cạnh bất kì của đường gấp khúc có nhiều nhất một điểm chung (nếu có
một điểm chung thì điểm chung đó phải là đỉnh của đường gấp khúc) thì ta gọi là
đường gấp khúc đơn, ngược lại ta gọi là đường gấp khúc tự cắt. 91 D D D B B B C E E A C A C A E I
Đường gấp khúc: đơn đơn khép kín tự cắt khép kín
4. Định nghĩa góc: Góc là một hình gồm hai tia có chung gốc. Gốc chung của hai
tia gọi là đỉnh, hai tia gọi là các cạnh của góc đó. y y B O x O A x Hình A Hình B
Trên hình A: Điểm O gọi là đỉnh, hai tia Ox và Oy gọi là cạnh của góc xOy.
Ta viết: góc xOy hoặc góc yOx hoặc góc O và dùng các kí hiệu tương ứng là ……………
Góc xOy trong hình B còn gọi là góc AOB hoặc góc BOA.
Góc có hai cạnh là hai tia đối nhau gọi là góc bẹt. y O x
5. Định nghĩa tam giác: Tam giác ABC là hình gồm ba đoạn thẳng AB, BC và CA
sao cho ba điểm A, B, C không thẳng hàng ký hiệu là A
BC , trong đó A, B, C gọi là các
đỉnh; AB, BC, CA gọi là các cạnh và các góc BAC, góc ABC, góc ACB gọi là các góc
của tam giác đó. A M B C N P 92 Tam giác ABC Tam giác MNP
6. Định nghĩa tứ giác, hình chữ nhật, vuông, bình hành, hình thoi, hình thang:
Tứ giác ABCD là một hình gồm bốn đoạn AB, BC, CD và DA, trong đó bất kì hai
đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
Các điểm A, B, C, D gọi là các đỉnh, các đoạn thẳng AB, BC, CD và DA gọi là các
cạnh của tứ giác đó. A A B D D B C C
Hình chữ nhật là hình tứ giác có bốn góc vuông A B D C
Hình chữ nhật ABCD có các góc A, góc B, góc C và góc D đều vuông; hai cạnh
AB và CD gọi là chiều dài, AD và BC gọi là chiều rộng của hình chữ nhật đó.
Hình vuông là hình tứ giác có bốn góc vuông và bốn cạnh bằng nhau. A B D C
Hình vuông ABCD có các góc A, góc B, góc C và góc D đều vuông; các cạnh AB,
BC, CD và AD đều bằng nhau.
Hình thoi là hình tứ giác có bốn cạnh bằng nhau A D B C
Hình thoi ABCD có bốn cạnh AB, BC, CD và AD đều bằng nhau
Hình bình hành là hình tứ giác có các cặp cạnh đối song song A B D C
Tứ giác ABCD trong hình dưới đây có AB song song với CD được gọi là hình thang.
Cạnh AB gọi là đáy nhỏ, cạnh CD gọi là đáy lớn và các cạnh AD, BC gọi là cạnh bên của hình thang đó. A B D C
Hình thang là hình tứ giác có hai cạnh đối song song
7. Định nghĩa đa giác, đa giác lồi, lõm;
Hình đa giác n cạnh (hay còn gọi là n-
giác) là hình tạo bởi một đường gấp khúc khép kín có n đoạn.
Trong phần dưới đây ta chỉ xét các đa giác tạo thành từ các đường gấp khúc đơn.
Khi n = 3 ta gọi là hình tam giác
Khi n = 4 ta gọi là hình tứ giác
Khi n = 5 ta gọi là hình ngũ giác
Khi n = 6 ta gọi là hình lục giác
Khi n = 8 ta gọi là hình bát giác …….
8. Định nghĩa hình lồi, hình lõm:
Cho H là một hình hình học. Ta gọi hình H là hình lồi nếu
với 2 điểm A, B bất kì
thuộc hình H thì đoạn thẳng nối hai điểm A, B luôn nằm trọn trong hình H. Nếu H
không phải là hình lồi thì ta gọi H là hình lõm. hình lõm hình lôi 94
9. Định nghĩa miền trong, miền ngoài của đa giác
Cho D Là một hình đa giác trong mặt phẳng P. Tập hợp P – D được chia thành hai
phần rời nhau: một trong hai phần đó có thể chứa chọn vẹn một đường thẳng, ta gọi là
miền ngoài của đa giác D; phần còn lại (không thể chứa bất kì một đường thẳng nào) ta
gọi là miền trong của đa giác đó B A A E C D
Phần gạch chéo là miền trong, phần còn lại là miền ngoài của ngũ giác ABCDE.
Hình đa giác có miền trong tạo thành một hình lồi được gọi là đa giác lồi.
Ta sẽ chỉ xét các hình đa giác đơn lồi.
10. Định nghĩa đường tròn, hình tròn:
Cho R là số thực dương và O là điểm cố định trong mặt phẳng P.
a) Tập hợp C các điểm M trong mặt phẳng P sao cho khoảng cách từ M tới O luôn
không đổi và bằng R ta gọi là đường tròn tâm O bán kính R và kí hiệu là C(O;R).
b) Tập hợp K các điểm M trong mặt phẳng P sao cho khoảng cách từ M tới O
không vượt quá R ta gọi là hình tròn tâm O bán kính R và kí hiệu là K (O;R). M R O
II.1.3. Định nghĩa các hình không gian
3.1. Định nghĩa mặt cầu và hình cầu: tâm và bán kính
Cho R là số thực dương và O là điểm cố định trong không gian.
a) Tập hợp C các điểm M trong không gian sao cho khoảng cách từ M tới O luôn
không đổi và bằng R ta gọi là mặt cầu tâm O bán kính R và kí hiệu là C(O;R).
b) Tập hợp K các điểm M trong không gian sao cho khoảng cách từ M tới O không
vượt quá R ta gọi là hình cầu tâm O bán kính R và kí hiệu là K(O;R). 95
3.2. Định nghĩa mặt trụ và hình trụ
Cho R là số thực dương, d là đường thẳng cố định trong không gian.
a) Tập hợp T các điểm M trong không gian sao cho khoảng cách từ M tới d luôn
không đổi và bằng R ta gọi là mặt trụ, đường
thẳng d gọi là trục, R gọi là bán kính của mặt trụ đó.
b) Tập hợp Tr các điểm M trong không gian sao cho khoảng cách từ M tới d không
vượt quá R ta gọi là khối trụ, đường thẳng d gọi là trục, R
gọi là bán kính của khối trụ đó.
c) Hình H trong không gian được gọi là hình đa diện nếu nó được tạo thành từ
một số hữu hạn miền đa giác sao cho mỗi điểm của H thuộc chỉ một trong các khả năng sau:
(i) Là điểm trong của đúng một trong các đa giác tạo thành;
(ii) Là điểm nằm trên cạnh của đúng hai đa giác liền kề; (iii)
Là đỉnh chung của một số các đa giác tạo thành.
Mỗi miền đa giác đã cho gọi là một mặt, mỗi cạnh chung của hai đa giác gọi là
một cạnh và mỗi đỉnh chung gọi là một đỉnh của hình đa diện đã cho.
d) Mỗi hình đa diện chia không gian thành hai tập: một trong hai tập đó có thể chứa
trọn vẹn một đường thẳng, ta gọi là miền ngoài, tập thứ hai gọi là miền trong của hình đa diện đó.
e) Hình tạo bởi hình đa diện cùng với miền trong của nó được gọi là khối đa diện.
II.2. Định nghĩa quan hệ giữa các hình hình học
II.2.1.Quan hệ bằng nhau
Phép biến đổi đẳng cự là quy tắc cho tương ứng mỗi điểm từ mặt phẳng R2 vào
chính nó (hoặc từ không gian R 3vào chính nó) sao cho khoảng cách giữa hai điểm
qua phép biến đổi đó không thay đổi.
Các phép tịnh tiến, phép đối xứng trục, đối xứng tâm, phép quay đều là phép biến đổi đẳng cự.
Hai hình H và H’ gọi là bằng nhau, nếu tồn tại một phép đẳng cự biến hình này về hình kia.
II.2 .2. Quan hệ vuông góc
Hai đường thẳng xy và x’y’ cắt nhau và trong các góc tạo thành có một góc
là góc vuông được gọi là hai đường thẳng vuông góc và kí hiệu là xy x ' y '. y’ x O y x’
Hai đường thẳng xy và x’y’ là hai đưởng thẳng vuông góc và cắt nhau tại
O, ta còn nói đường thẳng xy vuông góc với đường thẳng x’y’ tại O. 96
II.2.3.Quan hệ song song
Hai đường thẳng song song là hai đường thẳng không có điểm chung. a b
Đường thẳng a song song với đường thẳng b và kí hiệu là a . b
Hai đường thẳng phân biệt nếu không cắt nhau thì song song với nhau.
II.2.4.Quan hệ đồng dạng
Định nghĩa hai tam giác đồng dạng: Tam giác ABC gọi là đồng dạng với tam A' B' B 'C ' A'C '
giác A’B’C’, kí hiệu là A
BC ….. nếu AB BC
AC và góc A = góc A’; góc B = góc B’; góc C = góc C’. A' B ' B 'C ' A'C ' k Ta gọi tỉ số AB BC AC
là tỉ số đồng dạng của hai tam giác đó. A A' C' B' B C
Tam giác ABC đồng dạng với tam giác A’B’C’.
II.2.5.Hình đẳng hợp
Định nghĩa hai hình đẳng hợp Hai đa giác D và D’ gọi là đẳng hợp với nhau,
nếu tồng tại các hình F , F 1 , …., F 2 n sao cho: (i)
các hình đó đôi một không có điểm trong chung; n n F F k k (ii) D = k 1 và D’ = k 1
Ví dụ hình H đẳng hợp với hình H’: 97 H H’
II.3. Khái niệm về độ dài đoạn thẳng, chu vi, diện tích và thể tích các hình
a) Độ dài của đoạn thẳng là quy tắc cho tương ứng mỗi đoạn thẳng AB với một số thực dương sao cho: (i)
Hai đoạn thẳng bằng nhau thì độ dài của chúng cũng bằng nhau. (ii)
Nếu C là điểm nằm giữa A và C thì độ dài đoạn thẳng AB bằng tổng độ dài hai đoạn thẳng AC và CB.
Độ dài của đoạn thẳng AB ta cũng kí hiệu là AB và còn gọi là khoảng cách giữa hai điểm A và B.
b) Diện tích hình đa giác là quy tắc cho tương ứng mỗi hình đa giác D với một số
thực s(D) thỏa mãn các tính chất sau: (i) s(D) > 0; (ii)
Nếu đa giác D được hợp thành từ hai hình đa giác không giao nhau D1 và D2 thì s(D) = s(D1) + s(D2) (iii)
Nếu đa giác D1 nằm trọn trong đa giác D2 thì s(D1) < s(D2); (iv)
Nếu hình vuông V có cạnh bằng 1 đơn vị độ dài thì sV) = 1 đơn vị diện tích. c)
Thể tích khối đa diện là quy tắc cho tương ứng mỗi khối đa diện D với
một số thực v(D) thỏa mãn các tính chất sau: (i) v(D) > 0; (ii)
Nếu khối đa diện D được hợp thành từ hai khối đa diện không giao
nhau D1 và D2 thì v(D) = s(D1) + s(D2) (iii)
Nếu khối đa diện D1 nằm trọn trong khối đa diện D2 thì v(D1) < v(D2); (iv)
Nếu khối lập phương L có cạnh bằng 1 đơn vị độ dài thì v(L) = 1 đơn vị thể tích.
III. Các bài toán về xác định hình hình học
III.1.Bài toán quỹ tích (tìm tập hợp điểm)
a) Định nghĩa. Bài toán về xác định tập hợp các điểm của một hình H, khi biết các
điểm thuộc hình đó cùng có một tính chất T được gọi là bài toán quỹ tích, hay
còn gọi là bài toán về tìm tập hợp điểm.
b) Các bước giải bài toán quỹ tích. Khi giải bài toán quỹ tích ta thường tiến hành
theo các bước dưới đây: 98
Bước 1. Dự đoán quỹ tích. Trong bước này, ta xét một vài trường hợp đặc
biệt để dự đoán những điểm có tính chất T sẽ nằm trong một hình H nào đó.
Bước 2. Phần thuận. Ta chỉ ra rằng những điểm có tính chất T phải nằm trong hình H nói trên.
Bước 3. Phần đảo. Ta chứng minh rằng mỗi điểm nằm trong hình H đều có tính chất T.
Từ các kết quả trên ta đi đến kết luận tập hợp các điểm (trong mặt phẳng
hoặc trong không gian) có tính chất T nằm trong hình H.
c)Các bài toán quỹ tích cơ bản đã thiết lập trong môn toán phổ thông
Trong chương trình hình học ở trường phổ thông, chúng ta đã được học hệ thống
các bài toán cơ bản về quỹ tích. Chẳng hạn:
1) Bài toán quỹ tích về đường trung trực của đoạn thẳng.
2) Bài toán quỹ tích về đường phân giác của một góc
3) Bài toán quỹ tích về các điểm cách đều một đường thẳng a cho trước một đoạn không đổi bằng h
4) Bài toán quỹ tích về các điểm cách đều hai đường thẳng song song cho trước.
5) Bài toán quỹ tích về cung chứa góc
6) Bài toán quỹ tích dạng: MA2 + MB2 = a2
7) Bài toán quỹ tích dạng: MA – MB 2 = k 2 2
8) Bài toán quỹ tích về đường tròn. …….
Sử dụng các bài toán quỹ tích cơ bản đã được thiết lập trong sách khoa, người ta giải
các bài toán quỹ tích trong môn hình học.
Ví dụ 3.1. Cho đường tròn tâm O, bán kính R và một điểm A ở ngoài hình tròn đó. Tìm
quỹ tích các điểm M là trung điểm các dây cung của đường tròn đó và đi qua A.
Giải. 1) Phần thuận. Giả sử M là trung điểm của dây cung BC đi qua A. Nối O với
M. Theo tính chất của dây cung ta suy ra OM BC . Vậy điểm M luôn nhìn đoạn thẳng
cố định AC dưới góc không đổi (bằng 1v).
Suy ra điểm M phải nằm trên cung tròn IOH đường kính AO ở trong hình tròn tâm O, bán kính R. I C M B R A O n D N H E 99
2) Phần đảo. Lấy điểm N thuộc cung tròn IOH. Nối A với N cắt đường tròn tâm O,
bán kính R tại D và E. Ta chứng minh ND = NE. Thật vậy, nối O với N. Góc ANO = 1v
(vì chắn nửa đường tròn). Suy ra N là trung điểm của dây cung DE hay ND = NE.
Từ các kết quả trên ta đi đến kết luận: quỹ tích các điểm M là trung điểm các dây
cung đi qua A của đường tròn tâm O, bán kính R là một cung tròn đường kính AO và nằm trong hình tròn tâm O.
III.2.Bài toán dựng hình a) Định nghĩa. Bài
toán về xác định một hình H (có thể là một một đoạn thẳng,
một tam giác hay một đa giác,… ) khi biết một số yếu tố của hình đó (có thể là góc, cạnh,
…) được gọi là bài toán dựng hình.
Các bài toán dựng hình ở trường phổ thông được chia thành hai loại: dựng hình
bằng thước và compa và dựng hình bằng phương pháp đại số.
b) Các bước giải bài toán dựng hình bằng thước và compa. Khi giải bài toán dựng
hình ta thường tiến hành theo các bước dưới đây:
Bước 1.Phân tích. Trong bước này, ta giả sử hình H đã dựng được. Căn cứ
vào các tính chất hình đó phải thỏa mãn, ta chỉ ra một dãy các bước phải dựng để nhận được hình H.
Bước 2. Dựng hình. Ta chỉ ra thứ tự các bước cần dựng để nhận được hình H.
Bước 3. Chứng minh. Ta chứng minh rằng mỗi điểm nằm trong hình H đều có tính chất T. Bước 4. Biện luận.
Từ các kết quả trên ta đi đến kết luận tập hợp các điểm (trong mặt phẳng
hoặc trong không gian) có tính chất T nằm trong hình H.
c) Các bài toán dựng hình cơ bản đã thiết lập trong môn toán phổ thông
1) Dựng đoạn thẳng bằng a cho trước
2) Dựng đường phân giác của một góc
3) Dựng đường trung trực cuả một đoạn thẳng
4) Dựng đường thẳng qua A và vuông góc với đường thẳng a cho trước
5) Dựng đường thẳng qua A và song song với đường thẳng a cho trước
6) Chia đôi, chia ba một đoạn thẳng
7) Dựng góc bằng cho trước
8) Dựng tam giác biết các cạnh a, b, c.
9) Dựng tam giác biết các cạnh a, b, và góc xen giữa
10) Dựng tam giác biết các cạnh a và hai góc kề
11) Dựng tam giác vuông biết các cạnh huyền và 1 góc nhọn.
12) Dựng tam giác vuông biết các cạnh huyền và một cạnh góc vuông.
Sử dụng các bài toán dựng hình cơ bản và các bài toán quỹ tích cơ bản đã được thiết
lập trong sách khoa, người ta giải các bài toán hình học trong môn hình học. Ví dụ 3.2.
Dựng tam giác ABC, biết cạnh BC = a, góc B = và đường cao AH = h. 100
Giải. Phân tích. Giả sử tam giác ABC đã dựng được có cạnh BC = a, góc B =
và đường cao AH = h. Ta thấy đỉnh A cách đường thẳng AB một đoạn bằng h. suy ra A
là giao của cạnh Bx của góc xBC và đường song song với BC, cách BC một đoạn bằng h.
Dựng hình. Dựng đoạn thẳng BC = a. Dựng góc xBC = . Dựng đường thẳng
song song với BC và cách BC một đoạn bằng h, cắt Bx tại A. Nối A với C.
Ta được tam giác ABC cần dựng. x A h H C B
Chứng minh. Rõ ràng là tam giác ABC có BC = a; góc B = . Ta phải chứng
minh đường cao AH = h. Thật vậy, ví A nằm trên đường song song với BC và cách Bc
một đoạn bằng h và AH vuông góc với BC nên AH = h.
Biện luận. Vì đường song song với Bc luôn cắt Bx tại duy nhất 1 điểm nên bài
toán có duy nhất một nghiệm hình.
III.3. Dựng đoạn thẳng vô tỉ
Đôi khi ta gặp những bài toán phải dựng đoạn thẳng có độ dài là số vô tỉ.
Chẳng hạn a 2;b 5;...
Đối với những bài toán dạng này, ta dùng phương pháp đại số. Ví dụ 3.3.
Cho đoạn thẳng a. Hãy dựng đoạn thẳng x a 3. 2 2 2 2 Giải. Ta có x a
3 4a a (2a) a
Theo Pi-ta-go ta có x sẽ là cạnh của tam giác vuông có cạnh huyền bằng 2a
và cạnh góc vuông bằng a. Từ đó suy ra cách dựng như sau: 2a x=a 3 a
Ví dụ 3.4. Cho đoạn thẳng a. Hãy dựng đoạn thẳng x a 7. 101 2 2 2 2 Giải. Ta có x a
7 9a 2a (3a) (a 2)
Theo Pi-ta-go ta có x sẽ là cạnh của tam giác vuông có cạnh huyền bằng 3a
và cạnh góc vuông bằng a 2 (là đường chéo của hình vuông có cạnh bằng a). Từ đó suy ra cách dựng như sau: a x=a 7 a 2 3a
IV. Yếu tố hình học trong môn toán tiểu học
Yếu tố hình học là một trong năm mạch kiến thức trong môn toán tiểu học. Nội
dung mạch yếu tố hình học có thể phân chia thành các mảng kiến thức: hình thành các
khái niệm hình học cho học sinh tiểu học; xây dựng các công thức tính chu vi, diện
tích và thể tích của các hình và giải toán có nội dung hình học.
IV.1. Hình thành các khái niệm hình học cho học sinh tiểu học
Các khái niệm hình học ở tiểu học có thể phân chia thành ba nhóm: -
Các khái niệm về các hình hình học; -
Các khái niệm về quan hệ giữa các hình hình học; -
Các khái niệm về chu vi, diện tích và thể tích các hình.
IV.1.1. Hình thành khái niệm các hình hình học cho học sinh tiểu học
Trong môn toán tiểu học, người ta hình thành cho học sinh khái niệm về các hình
hình học sau: điểm, đoạn thẳng, đường gấp khúc, góc (góc nhọn, góc vuông, góc tù và
góc bẹt), tam giác, hình tứ giác, hình chữ nhất, hình vuông, hình bình hành, hình thoi,
hình thang, hình trong, khối hộp chữ nhật, khối lập phương, hình trụ và hình cầu.
Đối với mỗi hình hình học thường được hình thành qua hai công đoạn: giới thiệu
biểu tượng về hình đó và giới thiệu các dấu hiệu nhận biết đối với hình đó. Chẳng hạn:
Ví dụ 3.5.
Hình thành khái niệm hình chữ nhật: -
Giới thiệu khái niệm hình chữ nhật thông qua các biểu tượng về hình
chữ nhật: bìa sách, mặt bảng, mặt bàn học,...;
- Giới thiệu các dấu hiệu nhận biết hình chữ nhật: A B D C
+ Hình chữ nhật ABCD có 4 đỉnh là đỉnh A, đỉnh B, đỉnh C, đỉnh D; 102
+ Có 4 cạnh là AB = CD, gọi là cạnh dài; AD = BC, gọi là cạnh
rộng. Độ dài của cạnh dài gọi là chiều dài và độ dài của cạnh rộng gọi là chiều rộng;
+ Có 4 góc vuông là góc A, góc B, góc C và góc D;
+ Có các cặp cạnh đối song song với nhau là AB song song với CD và AD song song với BC. + Hai đường chéo AC = BD.
Ví dụ 3.6.
Hình thành khái niệm hình hộp chữ nhật -
Giới thiệu khái niệm hình hộp chữ nhật thông qua các biểu tượng về
hình hộp chữ nhật: viên gạch, hộp phấn, bao diêm,…;
- Giới thiệu các dấu hiệu nhận biết về hình hộp chữ nhật: A B D B’ D’ ’
+ Hình hộp chữ nhật ABCDA’B’C’D’ có 8 đỉnh là đỉnh A, đỉnh B,
đỉnh C, đỉnh D, đỉnh A’, đỉnh B’, đỉnh C’, đỉnh D’;
+ Có 12 cạnh là AB = CD = A’B’ = C’D’, gọi là cạnh dài; AD = BC
= A’D’ = B’C’, gọi là cạnh rộng, AA’ = BB’ = CC’ = DD’, gọi là chiều cao. Độ dài
của cạnh dài gọi là chiều dài và độ dài của cạnh rộng gọi là chiều rộng;
+ Có 6 mặt đều là hình chữ nhật: ABCD và A’B’C’D’ gọi là mặt
đáy, ABB’A’, ADA’D’, DCD’C’, BCB’C’ gọi là các mặt bên;
IV.1.2. Hình thành khái niệm về quan hệ giữa các hình hình học
Ở tiểu học, hình thành các mối qua hệ sau giữa các hình hình học: quan hệ bằng
nhau của hai đoạn thẳng; quan hệ lớn hơn và bé hơn giữa các nhọn, góc vuông và góc tù;
quan hệ song song và vuông góc giữa hai đường thẳng.
a) Hai đoạn thẳng bằng nhau là hai đoạn thẳng có số đo bằng nhau.
b) Góc vuông lớn hơn góc nhọn và nhỏ hơn góc tù.
c) Kéo dài hai cạnh AD và DC của hình chữ nhật ta được hai đường thẳng AD vuông góc với BC: A B C D d)
Kéo dài hai cạnh AB và CD của hình chữ nhật ta được hai đường thẳng AB song song với CD: 103 A B C D
IV.1.3. Khái niệm về chu vi, diện tích và thể tích các hình
a) Chu vi của hình tam giác ( hoặc tứ giác) là tổng độ dài các cạnh của hình ấy.
b) Khái niệm diện tích và thể tích được hình thành dựa trên các tiên đề về diện
tích và thể tích các hình đã nêu ở phần trên. Chẳng hạn:
Ví dụ 3.7.
Hình thành khái niệm diện tích (SGK Toán 3):
a) Hình chữ nhật nằm hoàn toàn trong hình tròn. Ta nói: diện tích hình chữ nhật bé
hơn diện tích hình tròn. A B
b) Hình A gồm 5 ô vuông như nhau và hình B cũng gồm 5 ô vuông như thế. Ta nói: Diện
tích hình A bằng diện tích hình B. P M N
c) Hình P gồm 10 ô vuông như nhau được tách thành hai hình M và N.
Ta nói: Diện tích hình P bằng tổng diện tích hai hình M và N. 104
IV.2. Xây dựng công thức tính chu vi, diện tích và thể tích các hình
Do đặc điểm về tư duy, trình độ nhận thức và đặc điểm tâm sinh lí của học sinh tiểu
học, sách giáo khoa chọn phương pháp quy nạp không hoàn toàn để xây dựng các quy
tắc, công thức tính diện tích và thể tích của các hình.
Cụ thể là: để xây dựng công thức tính diện tích hoặc thể tích một loại hình nào đó,
người ta đưa ra bài toán về tính diện tích (hoặc thể tích) của hình đó. Bằng thao tác phù
hợp (chia ô hoặc cắt ghép,…) người ta rút ra cách tính diện tích (hoặc thể tích) hình này.
Từ đó rút ra quy tắc và công thức tổng quát cần thiết. Chẳng hạn:
Ví dụ 3.8.
Xây dựng công thức tính diện tích hình chữ nhật:
Ta bắt đầu bằng bài toán: Tính diện tích hình chữ nhật ABCD có chiều dài 4cm và chiều rộng 3cm.
Ta chia hình chữ nhật ABCD thảnh 12 ô vuông bằng nhau (có cạnh 1cm) như hình vẽ: B A D C
Dễ ràng nhận thấy diện tích 1 hình vuông bằng 1cm2. Vậy diện tích hình chữ nhật ABCD bằng 12cm2. Ta thấy: 12 = 4 x 3.
Từ đó ta rút ra quy tắc: Muốn tính diện tích hình chữ nhật, ta lấy chiều dài nhân với
chiều rộng (cùng đơn vị đo). S = a x b,
Trong đó a là chiều dài, b là chiều rộng.
Ví dụ 3.9. Xây dựng công thức tính diện tích hình thang.
Ta bắt đầu bằng bài toán: Tính diện tích hình thang ABCD có đáy lớn bằng a, đáy
nhỏ bằng b và đường cao bằng h.
Ta dùng một mảnh bìa hình thang có đáy lớn bằng a, đáy nhỏ bằng b và đường cao
bằng h. Ta cắt mảnh bìa hình thang rồi ghép lại để được một hình tam giác như hình vẽ: B A b (1) h M (1) o D H a C B N Theo cách cắt ghép ta có: 105 DN A H
(DC CN ) A H
(DC AB ) A H S 2 2 2 ABCD = SADN = Thay vào ta được: (a b ) h s ABCD 2
Muốn tính diện tích hình thang, ta lấy đáy lớn cộng đáy nhỏ nhân với chiều cao
(cùng đơn vị đo) rồi chia cho 2. 106 Chương IV
Cơ sở toán học của các tập hợp số trong môn Toán tiểu học
I. Cơ sở toán học của số học các số tự nhiên ở Tiểu học
I.1. Xây dựng tập số tự nhiên I.1.1. Song ánh
Định nghĩa. Cho X và Y là hai tập hợp. Quy tắc cho tương ứng mỗi phần tử x thuộc
tập X với một phần tử duy nhất y = f(x) thuộc tập Y gọi là ánh xạ từ tập X vào tập Y và kí hiệu là:
f : X Y
x y f ( ) x
Tập X gọi là miền xác định (hay tập nguồn), tập Y gọi là tập đích của ánh xạ f.
Với mỗi x X ta gọi f(x) là ảnh của phần tử x, x là tạo ảnh của f(x) qua ánh xạ f.
Nếu A là tập con của X thì ta gọi tập: f ( )
A f (x) : x A
là ảnh của tập A qua ánh xạ f.
Trường hợp đặc biệt, f(X) gọi là tập ảnh của ánh xạ f.
Định nghĩa. Cho f là ánh xạ từ tập X vào tập Y. Ta gọi:
a) f là đơn ánh, nếu với mỗi x , x X , x x f (x ) f (x ). 1 2 1 2 1 2 Hay với hai tạo ảnh
khác nhau cho ta hai ảnh khác nhau.
b) f là toàn ánh, nếu với mỗi y Y x
X : f (x) .
y Hay f(X) = Y. Trong trường
hợp này ta nói f là ánh xạ từ tập X lên tập Y.
c) f là song ánh, nếu f vừa là đơn ánh vừa là toàn ánh.
Ví dụ 4.1. X , a , b ,
c d, e ;Y 1, 2,3, 4,5 Cho . Ta định nghĩa:
f : X Y
xác định bởi quy tắc: f(a) = f(e) = 1; f(b) = 2; f(c) = 3 và f(d) = 4. Khi đó f là một ánh xạ
từ X vào Y, f không phải là đơn ánh và cũng không phải là toàn ánh.
Ví dụ 4.2.
Mỗi hàm số ta đã gặp trong trường phổ thông xác định một ánh xạ với miền xác định
là tập xác định của hàm số đó vào tập số thực R.
Chẳng hạn, hàm số y = 2 x– 1 xác định một ánh xạ từ R vào R với quy tắc xác định là
quy tắc xác định của hàm số đó.
Ánh xạ trên là đơn ánh nhưng không phải là toàn ánh.
Hàm số y = x + 1 cũng xác định một song ánh: 3 107 : R R 3
x (x) x 1 từ tập R lên chính nó.
Ví dụ 4.3.
Cho X là tập các điểm trên đoạn thẳng AB và Y là tập các điểm trên đoạn thẳng CD. Ta định nghĩa: O M B A g : X Y M C N D
g(M ) N
trong đó M và N được xác định như hình vẽ. Khi đó g là song ánh từ tập X lên tập Y.
Ví dụ 4.4.
Gọi A là tập con người đang sống trên Trái Đất và B là tập các tên gọi của những
người đó. Nếu ta định nghĩa: với mỗi a thuộc tập A cho ứng với một phần tử b = f(a) là
tên của người đó thì ta được một toàn ánh từ A lên B nhưng không phải là đơn ánh (ta giả
thiết là mỗi người chỉ có một tên gọi).
Định nghĩa. Cho f là song ánh từ tập X lên tập Y. Ta gọi ánh xạ: 1 f :Y X 1
y f ( y) x 1
là ánh xạ ngược của f, nếu với mọi x X ta luôn có f ( f (x)) x , hay với mọi 1
y Y : f ( f (y)) . y
Ví dụ 4.5. 1 1
Ánh xạ ngược của ánh xạ trong ví dụ 4.1 xác định bởi quy tắc 3
( y) y 1 với mỗi số thực y.
Ví dụ 4.6.
Ánh xạ g trong ví dụ 4.2 có ánh xạ ngược g-1 xác định bởi quy tắc g-1(N) = M. Định nghĩa. Cho:
f : X Y
g : Y Z Ta gọi ánh xạ: h: X Z x z ( h )
x g( f ( ) x )
là ánh xạ hợp (hay tích) của hai ánh xạ f và g. 108
Ví dụ 4.7.
Khái niệm hàm hợp là trường hợp đặc biệt của ánh xạ hợp.
Ví dụ 4.9.
Cho X và Y là hai tập hợp trong ví dụ 4.1 và Z
An,Cuc, Ng
a . Ta định nghĩa: f là
ánh xạ trong ví dụ 4.1 và g là ánh xạ từ Y vào Z: g(1) = An, g(2) = g(5) = Cúc và g(3) =
g(4) = Nga. Khi đó ánh xạ tích: h : X Z xác định bởi quy tắc: h(a) =An; h(b) = Cúc; h(c) = h(d) = Nga và h(e) = An.
Định lí 4.1. Tính chất của các phép toán trên ánh xạ: (i)
Tích của hai đơn ánh là một đơn ánh. (ii)
Tích của hai toàn ánh là một toàn ánh. (iii)
Tích của hai song ánh là một song ánh. Chứng minh. (i)
Giả sử f là đơn ánh từ X vào Y, g là đơn ánh từ Y vào Z; x ,1 x2 là hai phần
tử khác nhau thuộc X. Vì f là đơn ánh nên f (x ) f (x ) 1 2
. Vì g cũng là đơn ánh nên
g( f (x )) g( f (x )) h(x ) h (x ). 1 2 hay 1 2 (ii) và (iii)Tương tự (i).
I.1.2. Tập hợp tương đương
Định nghĩa. Cho X và Y là hai tập hợp. Ta nói rằng tập X tương đương với tập Y, kí hiệu là X Y
, nếu tồn tại song ánh f từ X lên Y.
Ví dụ 4.10.
Tập X và tập Y trong ví dụ 4.1 tương đương với nhau.
Ví dụ 4.11.
Theo ví dụ 4.2 ta có tập các điểm thuộc đoạn thẳng AB tương đương với tập các
điểm thuộc đoạn thẳng CD.
Ví dụ 4.12.
Tập I gồm các số thực nằm giữa 0 và 1 (I = (0;1)) tương đương với tập các số thực dương R.
Thật vậy, song ánh f xác định bởi quy tắc: 1
f (x) x
Ví dụ 4.13.
Tập (a; b) các số thực nằm giữa a và b và tập (c; d) các số thực nằm giữa c và d tương đương với nhau.
Định lí 4.2. (Tính chất của quan hệ tương đương giữa các tập hợp)
Quan hệ tương đương giữa các tập hợp thỏa mãn các tính chất sau đây:
(i) Tính phản xạ: Mọi tập A đều tương đương với chính nó.
(ii) Đối xứng: Nếu A tương đương với B thì B cũng tương đương với A.
(iii) Bắc cầu: Nếu A tương đương với B và B tương đương với C thì A tương đương với C.
Chứng minh. Đơn giản.
I.1.3. Tập hợp hữu hạn và vô hạn - Bản số tập hợp 109
Định nghĩa. Cho A là một tập hợp. Ta nói rằng:
a) A là tập vô hạn nếu A tương đương với một tập con thực sự của nó.
b) A là tập hữu hạn nếu A không phải là tập vô hạn, hay A không tương đương với
mọi tập con thực sự của nó.
Ví dụ 4.14.
Các tập X, Y trong ví dụ 4.1 là hữu hạn
Ví dụ 4.15.
Tập các điểm thuộc một đoạn thẳng là tập vô hạn;
Tập các số nằm giữa hai số a và b là tập vô hạn.
Định lí 4.3. (Tính chất của tập hữu hạn) (i)
Mọi tập con của tập hữu hạn là tập hữu hạn. (ii)
Hợp của hai tập hữu hạn là một tập hữu hạn. (iii)
Tích Đề-các của hai tập hữu hạn là một tập hữu hạn.
Chứng minh. (i) Giả sử A là tập hữu hạn và B là tập con của A. Giả sử B là tập vô
hạn. Khi đó tồn tại tập con thực sự B ' B và tương đương với B. Theo định nghĩa, tồn tại song ánh:
f : B B ' Đặt A' (
A \ B) B '. Ta dễ dàng chỉ ra rằng A’ là tập con thực sự của A và tương
đương với A. Suy ra A là tập vô hạn. Điều này trái với giả thiết. Ta có đpcm. (ii)
Giả sử A và B là hai tập hữu hạn. Ta chứng minh A B cũng là tập hữu
hạn. Trước hết ta xét trường hợp A và B là hai tập rời nhau.
Giả sử A B là tập vô hạn. Khi đó tồn tại một đơn ánh f từ A B vào chính nó
nhưng không phải là toàn ánh, tức là a
A B x
A B : f (x) a
. Ta có thể giả thiết a . A
Đặt A f ( )
A ; B f (B)
A A , B B , A B . 1 1 khi đó 1 1 1 1
Đặt A A B
A B \ B ; B 2 1 thì 2 1 2
Bằng phương pháp quy nạp ta dễ dàng suy ra: hợp của một họ hữu hạn các tập hữu hạn là tập hữu hạn. (iii)
Giả sử A và B là hai tập hữu hạn. Ta chứng minh A x B cũng là tập hữu hạn.
Ta xét các tường hợp sau:
a) B là tập rỗng. Hiển nhiên A x B là tập hữu hạn. b) B b thì A B A
b . Từ đây dễ dàng chỉ ra A x B là tập hữu hạn. n A B A ; A A
b i n i i i , 1 . B
b ; b ;...; b 1 2 n c) thì i 1 Từ đây suy ra đpcm.
Định nghĩa. Hai tập A và B tương đương với nhau ta nói chúng có cùng bản số. Ta
dùng kí hiệu CardA, hoặc A , để chỉ bản số của tập A.
Vậy nếu A = B thì Card A = Card B.
Ví dụ 4.16. 110 a C rd Card
x , với x là phần tử bất kì;
Hai tập X và Y trong ví dụ 4.1 có cùng bản số;
Tập các điểm thuộc hai đoạn thẳng bất kì có cùng bản số;
Tập các số nằm giữa hai số a, b và tập các số nằm giữa hai số c, d có cùng bản số.
Ví dụ 4.17.
Tập các điểm thuộc nửa đường tròn đường kính AB có cùng bản số với tập các
điểm thuộc đường kính của đường tròn đó.
Thật vậy, mỗi điểm M thuộc đoạn thẳng AB ta cho tương ứng với một điểm N thuộc nửa
đường tròn theo hình vẽ dưới đây: N A M B
I.1.4. Xây dựng tập số tự nhiên
Định nghĩa. Bản số của một tập hữu hạn gọi là một số tự nhiên. Ta dùng các chữ
cái a, b, c,… để kí hiệu các số tự nhiên. Hay nói một cách khác, nếu A là tập hữu hạn thì
bản số của tập A xác định một số tự nhiên và kí hiệu là a = Card A.
Tập tất cả các số tự nhiên ta kí hiệu là N.
Ví dụ 4.18.
Card là một số tự nhiên. Kí hiệu là 0.
Card là một số tự nhiên. Kí hiệu là 1. , Card
là một số tự nhiên. Kí hiệu là 2. …
I.1.5. Hình thành khái niệm số tự nhiên trong môn Toán tiểu học
Trong chương trình môn Toán tiểu học, các khái niệm về số tự nhiên được trình
bày trong môn Toán từ lớp 1 đến hết học kì I của lớp 4. Nó bao gồm các nội dung sau:
- Giới thiệu 10 chữ số cơ bản từ 0 đến 9;
- Hình thành khái niệm các số tự nhiên có 1, 2 và nhiều chữ số: hàng và lớp của một số tự nhiên.
- Giới thiệu cách đọc, viết và phân tích theo cấu tạo của một số tự nhiên.
- Giới thiệu khái niệm số chẵn, số lẻ, số tròn chục và số tròn trăm,…
- Giới thiệu khái niệm số liền trước, liền sau của một số tự nhiên và hai số tự nhiên liên tiếp.
Mười chữ số cơ bản từ 0 đến 9 được hình thành dựa trên công cụ bản số tập hợp. Nó
được trình bày bằng ngôn ngữ đơn giản nhất phù hợp với học sinh tiểu học. Chẳng hạn,
trong sách giáo khoa Toán 1:
- Từ biểu tượng hai con mèo, hai học sinh, hai chấm tròn,… dẫn đến số 2. 111
- Từ biểu tượng năm cái máy bay, năm cái kéo, năm chấm tròn,… dẫn đến số 5.
- Từ biểu tượng trong chậu có ba con cá: dùng vợt lần đầu vớt 1 con trong chậu
còn 2 con, lần thứ hai vớt 1 con nữa còn 1 con và lần thứ ba vớt 1 con nữa thì trong chậu
không còn con nào. Từ đó dẫn đến số 0.
Các số tự nhiên có 2, 3 và nhiều chữ số được hình thành dựa trên công cụ là các que tính
hoặc ô vuông,… phù hợp với học sinh của lớp đó. Chẳng hạn:
- Trong sách giáo khoa Toán 1: Từ biểu tượng một bó 10 que tính đặt cạnh 6 que
tính dẫn đến số 16;
- Trong sách giáo khoa Toán 2: Từ biểu tượng một bảng có 100 ô vuông đặt cạnh
bảng có 20 ô vuông và 5 ô vuông dẫn đến số 125;
- Trong sách giáo khoa Toán 3: Nhìn vào bảng ở cột nghìn ghi
số 8, cột trăm ghi
số 5, cột chục ghi số 6 và cột đơn vị ghi số 3 dẫn đến số 85634, đọc là tám nghìn năm trăm sáu mươi ba; - …
Khái niệm số tròn chục, tròn trăm thông qua những số tự nhiên cụ thể, học sinh
hiểu số tròn chục là những số có hàng đơn vị bằng 0. Số tròn trăm là những số có hàng
đơn vị và hàng chục bằng 0.
Khái niệm số liền trước, số liền sau được hình thành bằng hình ảnh trực quan trên tia số (SGK Toán 1).
Khái niệm số chẵn, số lẻ được hình thành dựa trên dấu hiệu chia hết cho 2 (SGK
Toán 4): số chia hết cho 2 là số chẵn, số không chia hết cho 2 là số lẻ.
I.2. Cơ sở toán học của quan hệ thứ tự trong tập số tự nhiên ở tiểu học
I.2.1. Quan hệ thứ tự trong tập số tự nhiên
Định nghĩa. Cho a và b là hai số tự nhiên, trong đó a = Card A và b = Card B. Ta nói rằng:
a) Số tự nhiên a nhỏ hơn hoặc bằng số tự nhiên b, kí hiệu là a b , nếu A tương
đương với một tập con của B.
b) a nhỏ hơn b, kí hiệu là a < b, nếu a b và a . b
c) a lớn hơn hoặc bằng b, kí hiệu là a , b nếu b .a
d) a lớn hơn b, kí hiệu là a > b, nếu b < a. Các hệ thức a b & a b
ta gọi là các bất đẳng thức, các hệ thức a < b và a > b gọi
là các bất đẳng thức nghiêm ngặt.
Ta thừa nhận mà không chứng minh bổ đề Căng-to dưới đây:
Bổ đề Căng-to. Với hai tập A và B bất kì luôn xảy ra một trong hai khả năng dưới đây: (i)
A tương đương với một tập con của B; (ii)
B tương đương với một tập con của A.
Nếu đồng thời xảy ra cả hai khả năng trên thì A tương đương với B.
Định lí 4.3. (Tính chất của quan hệ thứ tự trong tập số tự nhiên)
Quan hệ thứ tự trong tập hợp N các số tự nhiên thỏa mãn các tính chất sau đây: (i)
Tính phản xạ: a N : a a ; 112 (ii)
Phản đối xứng: Nếu a b và b a thì a = b. (iii)
Bắc cầu: Nếu a ; b b c thì a c . (iv)
Không tồn tại số tự nhiên a nhỏ hơn số 0, hay 0 là số tự nhiên nhỏ nhất. (v)
Không tồn tại số tự nhiên lớn nhất, hay mọi số tự nhiên a đều tồn tại một số
tự nhiên b lớn hơn nó. Chứng minh.
(i) Suy ra từ định lí 4.2 (i)
(ii) (iii) Suy ra từ định nghĩa và bổ đề Căng-to
(iv) Giả sử tồn tại số tự nhiên a = Card A và a < 0 = Card . Như vậy A tương
đương với tập con thực sự của . Điều này vô lí.
(v) Giả sử a là số tự nhiên tuỳ ý. Rõ ràng là b = a
C rdA > a.
Hệ quả. Tập số tự nhiên là vô hạn.
Chứng minh. Suy ra trực tiếp từ (v).
I.2.2. Số tự nhiên liền trước, liền sau và số tự nhiên liên tiếp
Định nghĩa. Cho a là số tự nhiên, a = Card A và x là phần tử không thuộc tập A.
Ta gọi số tự nhiên b = Card A x là số liền sau của a và kí hiệu là a’ = b.
Nếu b là số liền sau của a thì ta gọi a là số liền trước của b và kí hiệu là ,b . a
Hai số tự nhiên a và b nêu trên gọi là hai số tự nhiên liên tiếp.
Định lí 4.4. (Tính chất của số liền sau)
(i) Mỗi số tự nhiên a luôn có duy nhất một số liền sau;
(ii) Số 0 không có số liền trước;
(iii) Nếu a và b là hai số tự nhiên sao cho a < b thì a’ . b Chứng minh.
(i) Sự tồn tại: Giả sử a là số tự nhiên, a = Card A. Theo định nghĩa: số liền sau a’ = A A Card
x với x .A Rõ ràng là Card
x cũng là số tự nhiên.
Tính duy nhất: Giả sử b và c là hai số liền sau của a, trong đó b = CardA x , c C
ardA y với x và y đều không thuộc A. Rõ ràng là A
x A y . Từ đó suy ra b = c.
(ii) Suy ra từ định lí 4.3.
(iii) Giả sử a và b là hai số tự nhiên, trong đó a < b và a = Card A và b = Card B sao cho A .
B Vì a < b nên tồn tại x B \ .
A Đặt B ' A x . Ta có
a’ = Card B’ và A B ' B nên a ' . b
Hệ quả. Giữa hai số tự nhiên a và số liền sau a’ của nó không tồn tại một số tự nhiên nào khác.
Thật vậy, giả sử tồn tại số tự nhiên b sao cho a < b < a’. Từ đó suy ra a ' b a '.
Điều này vô lí. Ta có đpcm.
Ta gọi tính chất trên đây là tính rời rạc của tập số tự nhiên. 113 0 a
C rd;1 C ard Chú ý. Đặt ; 2 1 ';3 2 '; 4 3
';.... Cứ tiếp tục như trên ta
nhận được dãy các số tự nhiên:
1; 2; 3; 4; ….; 10; 11; …; 100; 101;
Định nghĩa. Cho A là tập con của tập số tự nhiên N. Ta nói rằng:
a) A là tập bị chặn trên (hay chặn dưới) nếu tồn tại số tự nhiên M (hay m) sao cho:
a M (a m ), a A
Nếu tập A đồng thời bị chặn trên và chăn dưới thì ta gọi A là tập bị chặn.
b) Số tự nhiên M (hay m) gọi là số lớn nhất (hay nhỏ nhất) của tập A, nếu M ( A m ) A và a M (a m ) a . A
Ta thừa nhận tính chất sau đây của tập số tự nhiên:
Mọi tập con khác rỗng bị chặn trên của tập số tự nhiên đều có số lớn nhất.
Mọi tập con khác rỗng của tập số tự nhiên đều có số nhỏ nhất.
I.2.3. Quan hệ thứ tự trong tập số tự nhiên ở Tiểu học
Trong chương trình môn Toán tiểu học, quan hệ so sánh giữa các số tự nhiên được
trình bày trong môn Toán từ lớp 1 đến hết học kì I của lớp 4 theo các giai đoạn:
- Từ các biểu tượng dẫn đến khái niệm so sánh giữa hai đối tượng;
- Hình thành các kĩ năng so sánh các số tự nhiên;
- Xây dựng các quy tắc so sánh giữa các số tự nhiên;
- Tổng kết các tính chất của dãy số tự nhiên; - …
Bằng các biểu tượng, ngay từ tiết học đầu tiên sách giáo khoa Toán 1 hình thành
cho học sinh khái niệm nhiều hơn, ít hơn.
Bằng công cụ bản số, hình thành cho học sinh khái niệm về quan hệ so sánh giữa
các số tự nhiên. Chẳng hạn:
- Từ bức tranh 5 quả bóng và 3 quả bóng dẫn học sinh đến quan hệ so sánh 3 < 5 và 5 > 3 (SGK Toán 1),…
- Từ biểu tượng mô tả số 234 và biểu tượng mô tả số 235 dẫn đến quan hệ so sánh
234 < 235 và 235 > 234 (SGK Toán 2),…
Từ các hiện tượng tích lũy qua các số đến 10, đến 100, đến 1000, đến 10 000, sách
giáo khoa Toán 3 rút ra cho học sinh quy tắc: 1) Trong hai số:
- Số nào có ít chữ số hơn thì bé hơn;
- Số nào có nhiều chữ số hơn thì lớn hơn. 2)
Nếu hai số có số bằng nhau thì so sánh từng cặp chữ số ở cùng một
hàng, kể từ trái sang phải. 3)
Nếu hai số có cùng số chữ số và từng cặp chữ số ở cùng một hàng
đều giống nhau thì hai số đó bằng nhau. 4)
Dần hình thành cho học sinh kĩ năng xác định số lớn nhất, số bé
nhất trong một nhóm các số tự nhiên cho trước và sắp xếp chúng theo thứ tự tăng dần hoặc giảm dần.
Từ kiến thức về số tự nhiên đã học, sách giáo khoa Toán 4 chốt lại cho học sinh: 114
a) Các số 0; 1; 2; 3; …; 9;10;…;100; …; 1000; … là các số tự nhiên;
b) Các số tự nhiên xếp theo thứ tự từ bé đến lớn tạo thành dãy số tự nhiên:
0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10;11; ….
c) Có thể biểu diễn số tự nhiên trên tia số: 0 1 2 3 4 5 6 7 8 9 10
d) Thêm 1 vào bất kì một số tự nhiên nào cũng được số tự nhiên liền sau nó.
Vì vậy không có số tự nhiên lớn nhất và dãy số tự nhiên có thể kéo dài mãi.
e) Bớt 1 ở bất kì số tự nhiên nào khác 0 ta cũng được số tự nhiên liền trước
nó. Không có số tự nhiên nào liền trước số 0 nên số 0 là số tự nhiên bé nhất.
g) Trong dãy số tự nhiên: hai số liên tiếp thì hơn hoặc kém nhau 1 đơn vị.
I.3. Cơ sở toán học của các phép toán trong tập số tự nhiên ở tiểu học
I.3.1. Phép cộng và phép nhân
I.3.1.1. Định nghĩa và tính chất
Bổ đề 1. Với hai số tự nhiên a và b luôn tồn tại hai tập hữu hạn rời nhau A và B
sao cho a = Card A và b = Card B.
Chứng minh. Giả sử a và b là hai số tự nhiên, trong đó a = Card A và b = Card B
với A và B là các tập hữu hạn.
Nếu A B thì ta có đpcm.
Chọn hai phần tử tùy ý x y , ta đặt A' A
x ; B ' B
y thì A’ và B’ đều là tập
hữu hạn và A' ;
A B ' B nên a = Card A’ và b = Card B’. Như vậy hai tập A’ và B’ thỏa mãn yêu cầu.
Bổ đề 2. Giả sử A, B, A’ và B’ là các tập hữu hạn sao cho
A A', B B '; A B A' B,. Khi đó:
(i )A B A 'B '; (ii )A B A ' B '.
Chứng minh. Đơn giản.
Định nghĩa. Cho a và b là hai số tự nhiên, trong đó a = Card A và b = Card B với
A và B là hai tập hữu hạn rời nhau. Ta gọi:
a) Tổng của hai số tự nhiên a và b là một số tự nhiên c, kí hiệu là c = a + b, trong đó c = Card A . B
Quy tắc cho tương ứng mỗi cặp số tự nhiên a, b với một số tự nhiên c nói trên ta
gọi là phép cộng các số tự nhiên, trong đó a và b gọi là các số hạng, s gọi là tổng và a + b cũng gọi là tổng.
b) Tích của hai số tự nhiên a và b là một số tự nhiên p, kí hiệu là p = a x b (hoặc
a.b hoặc ab), trong đó p = Card A . B
Quy tắc cho tương ứng mỗi cặp số tự nhiên a, b với một số tự nhiên p nói trên ta
gọi là phép nhân các số tự nhiên, trong đó a, b gọi là các thừa số, p gọi là tích và a.b cũng gọi là tích.
Nhận xét. Từ định nghĩa, định lí 4.3 và các bổ đề 1, 2 ta dễ dàng suy ra: 115
a) Với mỗi cặp số tự nhiên a, b luôn tồn tại duy nhất một số tự nhiên c là tổng của chúng.
b) Với mỗi cặp số tự nhiên a, b luôn tồn tại duy nhất một số tự nhiên b là tích của chúng.
Định lí 4.5. (Tính chất của phép cộng và nhân)
(i) Tính giao hoán: Với mọi số tự nhiên a và b ta luôn có: a + b = b + a; a.b = b.a
(ii) Tính kết hợp: Với mọi số tự nhiên a, b, c ta luôn có:
a + (b + c) = (a + b) + c; a.(b.c) = (a.b).c
(iii) Tính phân phối: Với mọi số tự nhiên a, b, c ta luôn có: a.(b + c) = a.b + a.c
(iv) Phần tử trung lập: Với mọi số tự nhiên a ta luôn có:
a + 0 = 0 + a = a; a.1 = 1.a = a
(v) Tính chất của số kề sau: Với mọi số tự nhiên a ta luôn có: Số kề sau a’ = a + 1.
Chứng minh: (i); (ii) và (iii) suy ra trực tiếp từ định nghĩa phép cộng, phép nhân và
các tính chất giao hoán, kết hợp, phân phối của các phép toán trên tập hợp. (iv)
Rõ ràng là: A ; A A
x A . Từ đây suy ra đpcm. a C rdA (v)
Theo định nghĩa số kế sau a’ = x a C rdA mà CardA x a
C rdA Card x a 1.
Chú ý. Để cho đơn giản, ta quy ước:
a) Viết a + b + c thay cho a + (b + c) hoặc (a + b) + c;
b) Viết a.b.c thay cho a.(b.c) hoặc (a.b).c.
I.3.1.2. Tính đơn điệu của phép cộng và phép nhân
Định lí 4.6. (Tính đơn điệu của phép cộng và phép nhân)
Với mọi số tự nhiên a, b, c ta luôn có: (i)a b a c b c; . a c . b ; c
(ii)a c b
c a b
:luật giản ước của phép cộng. . a c . b ; c c 0 a b
:luật giản ước của phép nhân.
(iii )a c b c a b . a c . b c a . b Chứng minh.
(i) Giả sử a = Card A; b = Card B; c = Card C, trong đó A C B C . Nếu a
= b thì rõ ràng a + c = b + c.
Nếu a < b, ta có thể coi A B, A B . Khi đó AC B C, A C B C . Từ đây suy ra a + c < b + c.
Tương tự đối với phép nhân.
(ii) Giả sử a + c = b + c và a < b. Theo chứng minh trên suy ra a + c < b + c. Điều
này trái với giả thiết. Suy ra đpcm.
Tương tự đối với phép nhân. (iii) Suy ra từ (i). 116
Nhận xét. Từ định nghĩa ta suy ra phép cộng và phép nhân các số tự nhiên luôn thực hiện được. I.3.2. Phép trừ
Định lí 4.7. (Về sự tồn tại, tính duy nhất của hiệu hai số tự nhiên)
Giả sử a và b là hai số tự nhiên, b a
. Khi đó tồn tại duy nhất một số tự nhiên c sao cho b + c = a. Chứng minh. Giả sử a C ard ; A b a
C rdB; B .
A Đặt C = A\B và c Card C. Rõ ràng là A B
C; B C và a = b + c.
Định nghĩa. Cho a và b là hai số tự nhiên, trong đó b .
a Ta gọi số tự nhiên c
trong định lí 4.7 là hiệu của a và b, kí hiệu là c = a – b .
Quy tắc cho tương ứng mỗi cặp số tự nhiên a, b với một số tự nhiên c nêu trên ta
gọi là phép trừ các số tự nhiên.
Định lí 4.8 (Về tính chất của phép trừ)
Với mọi số tự nhiên a, b, c ta luôn có: a.(b – c) = a.b – a.c
nếu một trong hai vế có nghĩa. Chứng minh.
Giả sử b – c = d. Suy ra b = c + d. Ta có: a.b = a.(c + d) = a.c + a.d.
Từ đây suy ra a.(b – c) = a.d = a.b – a.c.
Nhận xét. Từ định nghĩa ta suy ra phép trừ các số tự nhiên không phải luôn thực hiện được.
I.3.3. Phép chia
I.3.3.1. Quan hệ chia hết và phép chia hết trong tập số tự nhiên
Định nghĩa. Cho a và b là hai số tự nhiên, trong đó b khác 0. Ta nói rằng a chia
hết cho b, kí hiệu là a b
(hay b chia hết a, kí hiệu là b a ) nếu tồn tại số tự nhiên q sao cho: a = bq.
Trong trường hợp này ta sẽ gọi a là số bị chia, b là số chia và q là thương của
phép chia a cho b và viết là: a q a : b = q hay b .
Quy tắc cho tương ứng mỗi cặp số tự nhiên a, b với một số tự nhiên q nói trên ta
gọi là phép chia các số tự nhiên.
Ví dụ 4.19.
15 chia hết cho 3 (hay 3 chia hết 15), vì 15 = 3.5. Ta viết: 15 : 3 = 5
132 chia hết cho 12 (hay 12 chia hết 132), vì 132 = 12 . 11. Ta viết: 132 : 12 = 11.
Định lí 4.9. (Tính chất của quan hệ chia hết)
(i) Với mọi số tự nhiên a khác 0 ta luôn có a a ; (ii) Nếu a b và b a thì a = b; 117 (iii) Nếu a b và b c thì a . c
(iv) Số 0 chia hết cho mọi số tự nhiên khác 0;
(v) Mọi số tự nhiên đều chia hết cho 1. Chứng minh.
(i) Rõ ràng, vì a = a.1. (ii) Giả sử a b và b a
. Suy ta tồn tai q,q ' N sao cho a = b.q và b = a.q’. Thay
vào ta được a = a.q.q’. Suy ra q.q’ = 1 hay q = q’ = 1. Thay vào ta được a = b. (iii) Giả sử a b và b c
. Suy ta tồn tai q,q ' N sao cho a = b.q và b = c.q’. Thay
vào ta được a = c.q.q’. Suy ra đpcm. (iv) Rõ ràng là 0 = b.0. (v) Rõ ràng là a = 1.a.
Nhận xét. Mỗi phép chia hai số tự nhiên có không quá một thương.
Thật vậy, giả sử a và b là hai số tự nhiên và a : b = q, a : b = q’. Theo định nghĩa ta
có : a = b.q và a = b .q’. Suy ra b.q = b.q’. Vì b khác 0 nên q = q’.
I.3.3.2. Phép chia có dư
Định lí 4.10. (Về phép chia có dư trong tập số tự nhiên)
Giả sử a và b là hai số tự nhiên, trong đó b 0 . Khi đó tồn tại duy nhất một cặp số
tự nhiên q và r sao cho: a b
q r;0 r b Chứng minh.
a) Sự tồn tại: Giả sử a và b là hai số tự nhiên, b 0 . A
m :bm Đặt a
Rõ ràng là tập A khác rỗng và bị chặn trên nên nó có phần tử lớn nhất. Ta gọi phần
tử lớn nhất là q và đặt r = a – bq. Rõ ràng là: a b
q r;0 r b
b) Tính duy nhất: Giả sử tồn tại q ,q , r ,r N : a bq r bq r ,0 r ,r . b 1 2 1 2 1 1 2 2 1 2 Giả sử q q . 1
2 Khi đó tồn tại số tự nhiên m sao cho q2 = q1 + m. Ta có: bq2 + r2 = b(q + m) + r 1 = bq 2 + bm + r 1 2 = bq + r 1 . 1
Suy ra bm + r2 = r1. Vì r1 < b nên điều này xảy ra khi và chỉ khi m = 0 Vậy q1 = q2 và r1 = r . 2 Ta có đpcm.
Định nghĩa. Cho a và b là hai số tự nhiên, trong đó b khác 0, q và r là hai số nêu
trong định lí trên đây. Ta sẽ gọi q là thương gần đúng (hay thương hụt) và r là số dư trong phép chia a cho b.
Quy tắc cho tương ứng mỗi cặp số tự nhiên a, b với một cặp số tự nhiên q và r nói
trên ta gọi là phép chia có dư trong tập số tự nhiên.
Chú ý. Từ định nghĩa ta thấy rằng phép chia hết là trường hợp đặc biệt của phép
chia có dư (khi số dư bằng 0).
Ví dụ 4.20. 17 : 5 = 3 (dư 2)
67 : 4 = 16 (dư 3); 131 : 12 = 11 (dư 11).
I.3.4. Các phép tính trong tập số tự nhiên ở Tiểu học
I.3.4.1. Phép cộng và phép trừ trong tập số tự nhiên ở Tiểu học 118
Trong chương trình tiểu học, phép cộng và trừ các số tự nhiên được trình bày trong
môn Toán từ lớp 1 đến hết kì I của lớp 4 theo bốn giai đoạn:
- Dùng các biểu tượng dẫn đến ý nghĩa của phép cộng và ý nghĩa của phép trừ;
- Xây dựng các bảng cộng, trừ làm cơ sở để mở rộng các phép tính đó trong các vòng số lớn hơn;
- Xây dựng các quy tắc thực hành pháp cộng và phép trừ;
- Mở rộng khái niệm mỗi phép tính để được khái niệm dãy tính, biểu thức.
Phép cộng và trừ các số trong phạm vi 10 (hay còn gọi là cộng trừ trong bảng)
được hình thành dựa trên công cụ bản số tập hợp. Nó được trình bày bằng ngôn ngữ đơn
giản nhất phù hợp với học sinh tiểu học. Chẳng hạn, trong sách giáo khoa Toán 1:
- Từ biểu tượng hai ô tô và một ô tô hoặc một con rùa và hai con rùa,… dẫn đến
phép cộng 2 + 1 = 3 hoặc 1 + 2 = 3.
- Từ biểu tượng bốn con cá và một con cá dẫn đến phép cộng 4 + 1 = 5 hoặc từ
biểu tượng ba con vịt và hai con vịt dẫn đến phép cộng 3 + 2 = 5,...
- Từ biểu tượng hai con ong đang đậu trên cành hoa và một con bay đi dẫn đến
phép trừ 3 – 1 = 2 và 3 – 2 = 1;
- Từ biểu tượng có bảy chấm tròn lấy đi 3 chấm tròn còn lại bốn chấm tròn dẫn
đến phép trừ 7 – 3 = 4 và 7 – 4 = 3,…
Trong sách giáo khoa Toán 2 và Toán 3 dần hình thành cho học sinh quy tắc thực
hành phép cộng hoặc phép trừ các số có 2, 3 chữ số dựa trên công cụ là các que tính hoặc
ô vuông, … phù hợp với học sinh của lớp đó. Chẳng hạn:
- Trong sách giáo khoa Toán 2: Từ biểu tượng bốn bó que tính đặt cạnh 7 que tính
và 2 bó que tính đặt cạnh 5 que tính dẫn đến phép cộng 47 + 25 = 72 và qua đó hình
thành quy tắc cộng các số có hai chữ số;
- Trong sách giáo khoa Toán 2: Từ biểu tượng 54 que tính, gồm 5 bó que tính đặt
cạnh 4 que tính và hai bó que tính đặt cạnh ba que tính dẫn đến phép trừ 57 – 23 = 34 và
qua đó hình thành quy tắc trừ các số có hai chữ số;
- Trong sách giáo khoa Toán 4: dựa vào quy tắc thực hành phép cộng và trừ đó học
trong các vòng số trước giới thiệu cho học sinh quy tắc thực hành phép cộng và trừ các số có nhiều chữ số. - …
I.3.4.2. Phép nhân và phép chia trong tập số tự nhiên ở Tiểu học
Trong chương trình tiểu học, phép nhân và chia số tự nhiên được trình bày trong
môn Toán từ lớp 2 đến hết học kì I của lớp 4 theo bốn giai đoạn: a) Phép nhân:
- Dùng các biểu tượng kết hợp với phép cộng dẫn đến ý nghĩa của phép nhân;
- Xây dựng các bảng nhân làm cơ sở để mở rộng phép nhân trong các vòng số lớn hơn;
- Xây dựng các quy tắc thực hành phép nhân;
- Mở rộng khái niệm phép nhân để được khái niệm dãy tính, biểu thức.
Trong sách giáo khoa Toán 2: Từ biểu tượng năm cặp chấm tròn gắn với dãy tính
cộng: 2 + 2 + 2 + 2 + 2 = 10 ta dẫn đến phép nhân 2 x 5 = 10. Từ đó hình thành ý nghĩa của phép nhân. 119
Bảng nhân 2 được hình thành dựa trên các biểu tượng kết hợp với ý nghĩa của phép nhân. Chẳng hạn:
- Trong sách giáo khoa Toán 2: Từ biểu tượng các tấm bìa có hai chấm tròn ta xây dựng bảng nhân 2;
- Trong sách giáo khoa Toán 3: Từ biểu tượng các tấm bìa có chín chấm tròn ta xây dựng bảng nhân 9;
Trong sách giáo khoa Toán 3 và Toán 4 dần hình thành cho học sinh quy tắc thực
hành phép nhân các số có 2, 3 chữ số dựa trên các bảng nhân đã có.
Lần lượt từ phép nhân (ngoài bảng) với số có 1 chữ số đến phép nhân với số có 2, 3 và nhiều chữ số. b) Phép chia:
- Dùng các biểu tượng kết hợp với phép nhân dẫn đến ý nghĩa của phép chia;
- Xây dựng các bảng chia làm cơ sở để mở rộng phép chia trong các vòng số lớn hơn;
- Xây dựng các quy tắc thực hành phép chia;
- Mở rộng khái niệm phép chia để được khái niệm dãy tính, biểu thức.
Trong sách giáo khoa Toán 2: Từ biểu tượng 6 ô vuông chia thành 2 phần bằng
nhau ta dẫn đến phép chia: 6 : 2 = 3 ; để tìm số ô trong mỗi phần và dẫn đến phép chia:
6 : 3 = 2 để tìm số phần khi biết mỗi phần có 3 ô.
Bảng chia được hình thành dựa trên các biểu tượng kết hợp với phép nhân. Chẳng hạn:
- Trong sách giáo khoa Toán 2: Từ biểu tượng các tấm bìa có hai chấm tròn và
phép nhân ta xây dựng bảng chia 2;
- Trong sách giáo khoa Toán 3: Từ biểu tượng các tấm bìa có chín chấm tròn và
phép nhân ta xây dựng bảng chia 9;
Trong sách giáo khoa Toán 3 và Toán 4 dần hình thành cho học sinh quy tắc thực
hành phép chia cho số có 2, 3 chữ số dựa trên các bảng nhân và bảng chia đã có.
Lần lượt từ phép chia (ngoài bảng) cho số có 1 chữ số đến phép chia cho số có 2, 3 và nhiều chữ số.
I.3.4.3. Giới thiệu thành phần các phép tính
Trong chương trình môn Toán lớp 2, ta lần lượt giới thiệu các thành phần của mỗi
phép tính cộng, trừ, nhân, chia: 35 + 24 = 59 35 Số hạng + 24 Số hạng 59 Tổng Số hạng Số hạng Tổng
Chú ý. 35 + 24 cũng gọi là tổng 59 – 35 = 24 59 Số bị trừ – 35 Số trừ 59 Hiệu Số bị trừ Số trừ Hiệu 120
Chú ý. 59 – 35 cũng gọi là hiệu 2 x 5 = 10 Thừa số Thừa số Tích
Chú ý. 2 5 cũng gọi là tích x 6 : 2 = 3 Số bị chia Số chia Thương
Chú ý. 6 : 2 cũng gọi là thương
I.3.4.4. Tính chất của các phép tính trong tập số tự nhiên
Trong chương trình môn Toán tiểu học, từ lớp 1, khi dạy mỗi phép tính ta chú ý
giới thiệu các tính chất của phép tính đó (giao hoán, kết hợp, tính chất của số 0, tính chất
của số 1,…) như những hiện tượng riêng lẻ, để đến lớp 4 sách giáo khoa tổng kết mỗi
tính chất đó thành các quy tắc: tính chất giao hoán, tính chất kết hợp, quy tắc nhân một
số với một tổng hoặc một hiệu, quy tắc chia một tổng (hoặc một hiệu hoặc một tích hoặc
một thương) cho một số, tính chất của số 0, số 1, … Chẳng hạn:
- Khi dạy phép cộng trong bảng cho học sinh nhận xét:
2 + 3 = 3 + 2 (= 5); 3 + 6 = 6 + 3 (= 9)
- Khi dạy phép cộng các số có 2, 3 và nhiều chữ số cho học sinh nhận xét: a 20 350 1208 b 30 250 2764 a + b 20 + 30 = 50 350 + 250 = 600 1208 + 2764 = 3972 b + a 30 + 20 = 50 250 + 350 = 600 2764 + 1208 = 3972
Từ đó rút ra tính chất giao hoán của phép cộng: Khi đổi chỗ các số hạng trong
một tổng thì tổng không thay đổi.
Cũng tương tự ta giới thiệu tính chất giao hoán của phép nhân bằng cách cho học nhận xét: a b c (a + b) + c a + (b + c) 5 4 6 (5 + 4) + 6 = 15 5 + ( 4 + 6) = 15 35 15 20 (35 + 15) + 20 = 70 35 + (15 + 20) = 70 28 49 51 (28 + 49) + 51 = 128 28 + (49 + 51) = 128
Từ đó rút ra tính chất kết hợp của phép cộng: Khi cộng một tổng với một số ta có
thể cộng số thứ nhất với tổng của hai số còn lại. 121
Tương tự ta giới thiệu tính chất kết hợp của phép nhân.
- Trong sách giáo khoa Toán 2, từ các hiện tượng: 1 x 2 = 1 + 1 = 2 1 x 3 = 1 + 1 + 1 = 3 1 x 4 = 1 + 1 + 1 + 1 = 4
Ta rút ra tính chất: 1 nhân với số nào cũng bằng chính nó.
Tương tự ta giới thiệu các tính chất còn lại của số 1 và số 0.
- Trong sách giáo khoa Toán 4, từ nhận xét: 4 x (3 + 5) = 4 x 8 = 32 4 x 3 + 4 x 5 = 12 + 20 = 32
Ta rút ra quy tắc: Khi nhân một số với một tổng, ta có thể nhân số đó với từng số
hạng của tổng rồi cộng các kết quả lại.
Tương tự ta giới thiệu các tính chất còn lại.
I.4. Lí thuyết chia hết trong tập số tự nhiên và các bài toán về chia hết trong tập số
tự nhiên ở Tiểu học
I.4.1. Ước chung lớn nhất
I.4.1.1. Định nghĩa.
Cho a và b là các số tự nhiên, trong đó b khác 0. Ta nói rằng:
a) b là ước của a nếu a chia hết cho b.
Nếu b là ước của a thì ta còn nói a là bội của b.
b) Số tự nhiên d là ước chung của a và b, nếu d đồng thời là ước của a và của b.
Từ định nghĩa ta dễ dàng suy ra:
a) Tập U(a) các ước của a luôn khác rỗng và bị chặn bởi a, vì rõ ràng là 1U(a).
b) Tập UC(a;b) = U(a) U( )
b các ước chung của a và b luôn khác rỗng và bị chặn trên.
Ví dụ 4.21. 1;2;3;4;6;1 U(12) = 2 UC(12;18) 1; 2;3; 6
Định nghĩa. Cho a và b là hai số tự nhiên, trong đó ít nhất một số khác 0. Ta gọi
số d lớn nhất trong số các ước chung của hai số a, b là ước chung lớn nhất của chúng. Ta
kí hiệu là d = (a; b) (hay d = UCLN (a; b)).
Nhận xét. Rõ ràng là: với hai số tự nhiên không cùng bằng 0 luôn tồn tại duy nhất
một ước chung lớn nhất.
Ví dụ 4.22. (12; 18) = 6; (15; 60) = 15; ( 8; 15) = 1.
Chú ý. Tương tự ta định nghĩa: Ước chung lớn nhất của n số tự nhiên không cùng
bằng 0 là số lớn nhất trong số các ước chung của n số đó.
Ví dụ 4.23. (12; 18; 42) = 6; (8; 24; 72) = 8; (18; 12; 25) = 1
I.4.1.2. Tính chất của ước chung lớn nhất.
Định lí 4.11. (Về tính chất của ước chung lớn nhất) 122
(i) Nếu a chia hết cho b thì (a; b) = b;
(ii) Nếu a : b = q (dư r) thì (a; b) = (b; r). Chứng minh. (i) Đơn giản.
(ii) Ta chứng minh UC(a; b) = UC(b; r).
Thật vậy, nếu m là ước chung của a và b thì m cũng là ước của r = a – bq. Suy ra
m là ước chung của b và r.
Đảo lại, giả sử m là ước chung của b và r. Vậy m cũng là ước của a = bq + r
Suy ra m là ước chung của a và b. Ta có đpcm.
Định lí 4.12. (Về thuật toán Ơ-cơ-lit)
Muốn tìm ước chung lớn nhất của hai số tự nhiên ta làm như sau:
a) Lấy số lớn chia cho số nhỏ. Nếu phép chia không dư thì số nhỏ sẽ là ước chung
lớn nhất của hai số đã cho;
b) Nếu phép chia còn dư thì ta lại lấy số nhỏ chia cho số dư thứ nhất và cứ tiếp tục
như thế cho đến khi phép chia không dư thì dừng lại. Số chia cuối cùng trong phép chia
không dư đó sẽ là ước chung lớn nhất của hai số đã cho. Chứng minh.
Giả sử a và b là hai số tự nhiên. Nếu a chia hết cho b thì theo định lí 4.11: b = (a; b).
Giả sử a = bq1 + r1. Ta thực hiện liên tiếp các phép chia: b = r1q2 + r2 r1 = r2q3 + r3 …
Sau một số bước (nhiều nhất là b bước) thì phép chia sẽ không còn dư: rn-1 = rnqn+1. Vì r > r 1
2 > r3 > … > rn-1 > rn.
Theo định lí 4.11 thì (a; b) = (b; r1) = (r ; r 1 2) = … (rn-1; rn) = r . n
Ví dụ 4.24.
Dùng thuật toán Ơ-cơ-lit tìm ước chung lớn nhất của 21 và 77.
Ta thực hiện liên tiếp các phép chia: 77 : 21 = 3 (dư 14); 21 : 14 = 1 (dư 7); 14 : 7 = 2. Vậy (21; 77) = 7.
Định lí 4.13. (Tính chất của ước chung lớn nhất)
(i) Để d = (a; b), điều kiện cần và đủ là d là ước chung của a, b và d chia hết cho
mọi ước chung của a, b;
(ii) (ma; mb) = m(a; b), với mọi số tự nhiên m khác 0; a b 1 ( ; ) (a;b) (iii) m m m
, với mọi số tự nhiên m là ước chung của a và b. Chứng minh.
(i) Điều kiện đủ: Rõ ràng.
Điều kiện cần: Suy ra từ chứng minh thuật toán Ơ-cơ-lit. 123
(ii) Nhân cả hai vế của mỗi đẳng thức trong chứng minh thuật toán Ơ-cơ-lit ta
được thuật toán Ơ-cơ-lit đối với ma và mb. Vậy (ma; mb) = mr = m(a; b). n 1 1 1 1 (m a;m b) ( m ; a ) b (iii) Ta có (a; b) = m m m m . Từ đây suy ra đpcm.
I.4.2. Bội chung nhỏ nhất
I.4.2.1. Định nghĩa.
Cho a và b là các số tự nhiên, trong đó b khác 0. Ta nói rằng số tự nhiên m là bội
chung của a và b nếu m đồng thời là bội của a và của b.
Từ định nghĩa ta dễ dàng suy ra:
a) Tập B(a) các bội của a gồm các số tự nhiên dạng na, với n là số tự nhiên. b) Tập BC(a;b) = B( ) a B( )
b các bội chung của a và b là một tập vô hạn, vì nó
chứa các số dạng nab, với n là số tự nhiên.
Ví dụ 4.25. 0;12;24;36;48;.. B(12) = . BC(12;8) 0; 24; 48;...
Định nghĩa. Cho a và b là hai số tự nhiên đều khác 0. Ta gọi số c nhỏ nhất khác 0
trong số các bội chung của hai số a, b là bội chung nhỏ nhất của chúng. Ta kí hiệu là
c = [a; b] (hay c =BCNN (a; b)).
Nhận xét. Rõ ràng là: với hai số tự nhiên đều khác 0 luôn tồn tại duy nhất một bội chung nhỏ nhất. Ví dụ 4.25.
[12; 8] = 24; [15; 60] = 60; [8; 15] = 120
Chú ý. Tương tự ta định nghĩa: Bội chung nhỏ nhất của n số tự nhiên đều khác 0
là số nhỏ nhất khác 0 trong số các bội chung của n số đó.
Ví dụ 4.26.
[12; 8; 20] = 120; ( 8; 24; 72) = 72; [18; 12; 25] = 900
Nhận xét. Từ định nghĩa ta dễ dàng suy ra: Nếu a > 0 và a chia hết cho b thì [a; b] = a.
I.4.3. Số nguyên tố
I.4.3.1. Định nghĩa.
Cho p là số tự nhiên lớn hơn 1. Ta gọi p là số nguyên tố, nếu p chỉ chia hết cho 1 và chính nó.
Tập tất cả các số nguyên tố ta kí hiệu là P.
Số tự nhiên a lớn hơn 1 không phải là số nguyên tố ta gọi là hợp số.
Tất tất cả các hợp số ta lí hiệu là H. Như vây: N P
H 0, 1 .
Chẳng hạn, 3, 5, 7, 11, 17, … là các số nguyên tố và 4, 12, 15, 28,… là các hợp số.
Hai số 0 và 1 không phải là số nguyên tố và cũng không phải là hợp số.
I.4.3.2. Tính chất của số nguyên tố Định lí 4.14.
(i) Ước nhỏ nhất khác 1 của một số tự nhiên lớn hơn 1 là một số nguyên tố. 124
(ii) Tập P tất các số nguyên tố là vô hạn.
(iii) Giả sử a là số tự nhiên. Nếu mọi ước khác 1 của a đều lớn hơn a thì a là số
nguyên tố, hay nói cách khác: nếu a là hợp số thì nó có một ước khác 1 và không vượt quá a . Chứng minh.
(i) Giả sử p là ước nhỏ nhất khác 1 của a nhưng p là hợp số. Theo định nghĩa sẽ
tồn tại q, s sao cho p = qs, trong đó 1 < q < p. Vì a chia hết cho p và p chia hết cho q nên
a chia hết cho q. Vậy q là ước khác 1 của a. Điều này vô lí, vì p là ước nhỏ nhất khác 1 của a.
(ii) Giả sử tập P hữu hạn, P
p ; p ;...; pn . 1 2
Đặt p = p1. p2…pn + 1. Nếu p là hợp
số thì p có một ước nguyên tố q (là ước nhỏ nhất khác 1 của p). Vì tập P hữu hạn nên q = p i n i, với 1
. Suy ra q chia hết p – p1.p …p 2
n = 1. Điều nay vô lí. Vậy p là số nguyên tố mà p .
P Suy ra tập P là vô hạn.
(iii) Giả sử a là hợp số lớn hơn 1. Vậy ước nhỏ nhất khác 1 của a là số nguyên tố, 2
ta kí hiệu là p. Ta có a = p.q. Vì p là ước nhỏ nhất của a nên p q
hay p pq a hay
p a. Ta có đpcm.
Chú ý. Tính chất (iii) trong định lí trên cho ta thuật toán để kiểm tra một số tự
nhiên a có phải là số nguyên tố hay không:
a) Tìm các số nguyên tố không vượt quá a.
b) Lần lượt kiểm tra mỗi sô nguyên tố đó có phải là ước của a hay không, nếu tất
cả các số nguyên tố đó đều không phải là ước của a thì a là số nguyên tố.
Vận dụng thuật toán trên đây ta thiết lập bảng các số nguyên tố nhỏ hơn một số tự nhiên n cho trước.
Chẳng hạn, lập bảng các số nguyên tố không vượt quá 100: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 Cách làm như sau:
1) Các số nguyên tố nhỏ hơn 100 là 2, 3, 5, 7.
2) Lần lượt gạch bỏ các số trong bảng là bội của 2, 3, 5, 7.
3) Các số còn lại không bị gạch sẽ là các số nguyên tố nhỏ hơn 100! 125
Bảng số nguyên tố trên đây ta gọi là sàng Ơ-ra-to-sơ-ten.
I.4.3.3. Số nguyên tố cùng nhau và số nguyên tố sánh đôi
Định nghĩa. Cho a và b là hai số tự nhiên. Ta nói rằng a và b là hai số nguyên tố
cùng nhau nếu (a; b) = 1.
Ta nói a1, a2, …, a là các số n
nguyên tố sánh đôi nếu chúng đôi một nguyên tố cùng nhau.
Ví dụ 4.27.
8 và 15 là hai số nguyên tố cùng nhau; 24 và 35 là hai số nguyên tố cùng nhau.
12, 65, 77, 437 là các số nguyên tố sánh đôi.
I.4.3.4. Tính chất của ước chung lớn nhất và bội chung nhỏ nhất
Định lí 4. 15. (Về tính chất của ước chung lớn nhất)
(i) Nếu a và c nguyên tố cùng nhau thì (ab; c) = (b; c).
(ii) Nếu ab chia hết cho c, trong đó a và c là hai số nguyên tố cùng nhau thì b chia hết cho c.
(iii) Nếu a đồng thời chia hết cho b và c, trong đó b và c là hai số nguyên tố cùng
nhau thì a chia hết cho tích của b và c.
(iv) Giả sử ước chung lớn nhất của a và b bằng d. Khi đó tồn tại cặp số tự nhiên m
và n sao cho a = dm; b = dn, trong đó m và n là hai số nguyên tố cùng nhau. Chứng minh.
(i) Giả sử d = (ab; c) và d’ = (b; c). Ta có:
- d là ước chung của ab và c nên d cũng là ước chung của ab và bc. Suy ra d là
ước của (ab; bc) = b(a; c) = b. Vậy d là ước chung của b và c. Suy ra d là ước của (b; c) = d’ (1).
- d’ là ước chung của b và c nên d’ cũng là ước chung của ab và c nên d’ là ước của (ab; c) = d (2)
Từ (1) và (2) suy ra d = d’. (iii)
Giả sử ab chia hết cho c. Suy ra (ab; c) = c. Mặt khác, theo (i) ta có (b; c) =
(ab; c) = c. Suy ra b chia hết cho c. Ta có đpcm. (iv)
Giả sử (a; b) = d. Suy ra tồn tại số tự nhiên m, n sao cho a = dm, b = dn.
Nếu m và n không nguyên tố cùng nhau thì tồn tại d’ khác 1 sao cho m = d’p và n = d’q.
Thay vào ta được a = dd’p và b = dd’q. Điều này trái với giả thiết d là ước chung lớn nhất của a và b.
Ví dụ 4.28.
Chứng minh rằng tích của ba số tự nhiên liên tiếp sẽ chia hết cho 6.
Giải: Giả sử a là một số tự nhiên. Đặt T = a(a + 1)(a + 2). Ta chứng minh T chia hết cho 6.
Thật vậy, rõ ràng là T chia hết cho 2, vì trong 2 số tự nhiên liên tiếp phải có một số chẵn (1).
- Nếu a chia hết cho 3 thì T chia hết cho 3;
- Nếu a chia cho 3 dư 1 thì a + 2 chia hết cho 3 nên T chia hết cho 3;
- Nếu a chia cho 3 dư 2 thì a + 1 chia hết cho 3 nên T chia hết cho 3.
Từ các kết quả trên ta suy ra T chia hết cho 3 (2). 126
Vì 2 và 3 là hai số nguyên tố cùng nhau nên từ (1) và (2) ta suy ra T chia hết cho 2.3 = 6. Ta có đpcm.
Ví dụ 4.29.
Tìm nghiệm nguyên dương của hệ phương trình sau: x y 1 20(1) ( ;x y) 1 5(2)
Giải: Từ (2) ta có (x; y) = 15. Theo tính chất (iv) suy ra tồn tại hai số tự nhiên m, n
sao cho a = 15m và b = 15n, trong đó (m; n) = 1. Thay vào phương trình (1) ta được: 15m + 15n = 120 hay m + n = 8.
Số 8 có thể phân tích thành tổng của 0 và 8; 1 và 7; 2 và 6; 3 và 5; 4 và 4.
Vì (m; n) = 1 nên m và n chỉ có thể là 1 và 7 hoặc 3 và 5.
Thay vào ta được nghiệm của hệ đã cho là: x 1 5 x 1 05 x 4 5 x 7 5 1 2 3 4 ; ; và y 1 05 y 1 5 y 7 5 y 4 5 1 2 3 4
Định lí 4. 16. (Về tính chất của bội chung nhỏ nhất)
(i) Với mọi số tự nhiên a, b đều khác 0 ta luôn có: ab [a;b] . (a;b)
(ii) Nếu a và b là hai số nguyên tố cùng nhau thì [a; b] = ab.
(iii) Với mọi số tự nhiên m khác 0 ta luôn có [am; bm] = m[a; b]. Chứng minh.
(i) Giả sử d = (a; b). Theo định lí 4.15 tồn tại cặp số tự nhiên m, n sao cho a = dm, ab u
b = dn, trong đó (m; n) = 1. Đặt
d . Ta chứng minh u = [a; b]. dm.dn u
dmn anb . m Thật vậy, ta có d
Vậy u là bội chung của a và b.
Đảo lại, giả sử v là bội chung của a và b vậy v = ak và ak chia hết cho b. Suy ra ak b mk n d d
. Vì (m; n) = 1 nên k chia hết cho n hay k = nq. Thay vào ta được v = anq =
uq. Vậy v là bội của u. Ta có đpcm. (ii) Suy ra từ (i) m .a mb m . a mb ab [m ; a mb] . m [ m a;b]. (iii) Ta cú (m ; a m ) b ( m ; a ) b ( ; a ) b
Chú ý. Từ định lí trên đây ta dễ dàng suy ra: “Để m = [a; b], điều kiện cần và đủ là
m là bội chung của a và b và m chia hết mọi bội chung của hai số đó.
Ta thừa nhận mà không chứng minh định lí sau đây:
Giả sử a, b, c là ba số tự nhiên, trong đó: 127 1 2
a p . p .... n p ; 1 2 n 1 2
b p . p .... n p ; 1 2 n 1 2
c p . p .... n pn , 1 2 Trong đó p ; p i ; j ; k 1
2; …; pn là các số nguyên tố đôi một khác nhau, là các số tự nhiên. Khi đó: 1 m 2 )( a ; a ; b ) m n m c 1 p . 2 p .... n p ; 1 k 2 ) b [ ; a ; b ] k k n c 1 p . 2 p .... n p . m m
in ; ; ; k a M x ; ; i i i i j j j j Trong đó với i, j = 1, 2, …, n.
Định lí trên có thể phát biểu thành lời dưới dạng một quy tắc như sau:
Muốn tìm ƯCLN hoặc BCNN của hai hay nhiều số tự nhiên ta làm như sau:
a) Phân tích chúng thành tích của các thừa số nguyên tố đôi một khác nhau;
b) Ước chung lớn nhất của các số đó cho bằng tích của các thừa số chung
với số mũ nhỏ nhất;
c) Bội chung nhỏ nhất của các số đó cho bằng tích của các thừa số chung
và riêng với số mũ lớn nhất. Ví dụ 4.30.
Ước chung lớn nhất của hai số tự nhiên bằng 7, bội chung nhỏ nhất của chúng
bằng 105. Tìm hai số đó.
Giải: Gọi hai số cần tìm là a và b. Theo đề bài ta có (a; b) = 7 và [a; b] = 105. Vì
(a; b) = 7 theo định lí 4.15 tồn tại các số tự nhiên m, n sao cho a = 7m và b = 7n, trong đó
m và n là hai số nguyên tố cùng nhau. Theo định lí 4.16 ta có: . a b [ ; a ] b . (a;b) 7 . m 7n 105 . m n 1 5 Thay vào ta được: 7 .
Số 15 có thể phân tích thành tích của 1.15 hoặc 3.5.
Thay vào ta được các cặp số cần tìm là: 7 và 105 hoặc 21 và 35.
Ví dụ 4.31.
Cho a = 240; b = 8820 và c = 7425. Tìm ước chung lớn nhất và bội chung nhỏ nhất của ba số đó. Giải: Ta có:
240 = 24. 3. 5; 8820 = 2 .2 3 .2 5. 72 và 7425 = 33. 52. 11. Áp dụng quy tắc trên ta được: (240; 8820; 7425) = 3. 5 = 15; [240; 8820; 7425] = 2 . 3 4 3. 5 . 7 2 2.11 = 5 821 200.
I.4.4. Hệ ghi số cơ số g và hệ thập phân ở Tiểu học
I.4.4.1. Định nghĩa hệ ghi số cơ số g
Định lí 4.17. Cho a là số tự nhiên lớn hơn 0 và g là số tự nhiên lớn hơn 1. Khi đó
tồn tại các số tự nhiên c0, c , c 1 , …, c 2 sao cho: n 128 n n 1 n 2
a c g c g c g
.... c g c n n 1 n 2 1 0 (*) trong đó 0 c
g i n c i 1; 0,1,..., ; n 0.
Dạng biểu diễn trên đây là duy nhất đối với mỗi cặp số tự nhiên a, g. Chứng minh.
Thực hiện liên tiếp các phép chia cho g, gọi số dư trong mỗi bước chia đó theo thứ
tự là c0, c1, c2, …, cn ta có: a = gq0 + c0 q0 = gq1 + c1 q1 = gq2 + c2 ………….. qn-2 = gqn-1 + cn-1 qn-1 = g.0 + cn trong đó 0 c
g 1;c 0. i n
Lần lượt thay các đẳng thức trên (từ dưới lên) ta được: n n 1 n 2
a c g c g c g
.... c g c n n 1 n 2 1 0
Ta sẽ chứng minh dạng biểu diễn trên đây là duy nhất. Thật vậy, giả sử: n n 1 n 2
a c g c g c g
.... c g c n n 1 n 2 1 0 n n 1 n 2 và
a b g b g b g
.... b g b n n 1 n 2 1 0
vì c 0và b0 đều là số dư trong phép chia a cho g nên c0 = b . Lập 0
luận tương tự ta được các
hệ số ci = bi với i = 1, 2, …, n. Ta có đpcm.
Định nghĩa. Giả sử a và g là hai số tự nhiên được biểu diễn bởi đẳng thức (*)
trong định lí 4.17. Trong trường hợp này ta viết: a c c c c c n n n .... 1 2 1 0g
và gọi là dạng biểu diễn của số tự nhiên a trong hệ ghi số cơ số g hay còn gọi là hệ g- phân.
Ví dụ 4.32. 13 = 1.23 +1. 2 + 1 = 1.2 2 3 + 1.2 + 0.2 + 1. 2 Vậy 8 1 101 . 2
54 = 1.72 +5 = 1.72 + 0.7 + 5. Vậy 54 1 05 . 7 54 = 4.11 + 10. Đặt 1 0 ta có 54 411
503 = 3.122 + 5.12 + 11. Đặt 11 ta có 5033512 Chú ý.
1) Để biểu diễn một số tự nhiên a trong hệ g-phân ta phải dùng các chữ số từ 0 đến
g – 1. 2) Khi cơ số g lớn hơn 10 thì 10 chữ số cơ bản từ 0 đến 9 không đủ để biểu diễn,
vì vậy ta phải bổ sung thêm các kí tự mới (ngoài 10 chữ số cơ bản) đó là: 1 0; 1 1; 1 2;... 129
3) Để biểu diễn số tự nhiên a trong hệ g-phân ta thực hiện liên tiếp các phép chia
cho g cho đến khi được thương bằng 0 thì dừng lại. Số dư trong các phép chia đó sẽ là
các chữ số biểu diễn a trong hệ g-phân.
I.4.4.2. So sánh các số trong hệ ghi số cơ số g
Khi thực hành so sánh các số trong hệ g-phân, ta vận dụng quy tắc dưới đây: a c c c ....c c
b b b b ....b b Giả sử n n 1 n 2 1 0 g và m m1 m 2 1 0 g .
a) Nếu n < m thì a < b;
b) Nếu n = m thì a và b có cùng số chữ số. Trong trường hợp này ta lần lượt so
sánh các chữ số cùng hàng từ trái sang phải. Số nào có chữ số đầu tiên lớn hơn thì số đó lớn hơn.
Ví dụ 4.33. 792 1032 2411 414 8 8 ; 5 5 2108 2703 31105 31015 9 9 ; 6 6
I.4.4.3. Các phép toán trong hệ ghi số cơ số g a) Phép cộng và trừ
Ví dụ 4.34.
Hãy lập bảng cộng trong hệ cơ số g = 7. + 0 1 2 3 4 5 6 0 0 1 2 3 4 5 6 1 1 2 3 4 5 6 10 2 2 3 4 5 6 10 11 3 3 4 5 6 10 11 12 4 4 5 6 10 11 12 13 5 5 6 10 11 12 13 14 6 6 10 11 12 13 14 15
Cách điền như sau: chẳng hạn:
- Ta muốn điền vào ô có hàng bằng 2, cột bằng 3: ta lấy 2 + 3 = 5 < 7. Vậy ta điền 5 vào ô đó;
- Ta muốn điền vào ô có hàng bằng 6, cột bằng 5: ta lấy 6 + 5 = 11 > 7. Ta lấy 11
chia cho 7 được thương bằng 1 dư 4. Kết quả sẽ là 14. Vậy ta điền 14 vào ô đó. Ta có quy tắc sau:
Muốn điền vào một ô bất kì trong bảng cộng của hệ g-phân, ta lấy số chỉ hàng
cộng với số chỉ cột của ô đó: nếu kết quả nhỏ hơn cơ số thì viết luôn, nếu kết quả từ cơ số
trở lên, ta chia cho cơ số rồi đọc từ thương đến số dư
Ví dụ 4.35. Tính: 5476 4725 8 8
Trước hết ta viết lại phép tính theo cột dọc: 130 5476 (8) + 4725 12423 Vậy: 5476 4725 1 2423 8 8 8 . Cách làm như sau:
- Cộng lần lượt từ phải sang trái;
- 6 + 5 = 11. Lấy 11 chia cho 8 được thương bằng 1, dư 3. Ta viết 3 nhớ 1.
- 7 + 2 = 9, nhớ 1 bằng 10. Lấy 10 chia cho 8 được thương bằng 1 dư 2. Ta viết 2 nhớ 1
- Cứ tiếp tục như thế…
Ví dụ 4.36. Tính: 2031 745 9 9
Trước hết ta viết lại phép tính theo cột dọc: 2031 (9) - 745 1175 Vậy: 2031 745 1 175 9 9 9 . Cách làm như sau:
- Trừ lần lượt từ phải sang trái;
- 1 không trừ được 5, mượn 1 (lấy 1 + 9 = 10) rồi lấy 10 trừ 5 bằng 5, viết 5 nhớ 1.
- 4 nhớ 1 bằng 5; 3 không trừ được 5, mượn 1 (3 + 9 = 12) rồi lấy 12 trừ 5 bằng 7, viết 7 nhớ 1.
- Cứ tiếp tục như thế… b) Phép nhân và chia Ví dụ 4.37.
Hãy lập bảng nhân trong hệ cơ số g = 6. x 1 2 3 4 5 1 1 2 3 4 5 2 2 4 10 12 14 3 3 10 13 20 23 4 4 12 20 24 32 5 5 14 23 32 41
Cách điền như sau: chẳng hạn:
- Ta muốn điền vào ô có hàng bằng 3, cột bằng 1: ta lấy 3 x 1 = 3 < 6. Vậy ta điền 3 vào ô đó;
- Ta muốn điền vào ô có hàng bằng 5, cột bằng 4: ta lấy 5 x 4 = 20 > 6. Ta lấy 20
chia cho 6 được thương bằng 3 dư 2. Kết quả sẽ là 32. Vậy ta điền 32 vào ô đó. 131 Ta có quy tắc sau:
Muốn điền vào một ô bất kì trong bảng nhân của hệ g-phân, ta lấy số chỉ hàng
nhân với số chỉ cột của ô đó: nếu kết quả nhỏ hơn cơ số thì viết luôn, nếu kết quả từ cơ
số trở lên, ta chia cho cơ số rồi đọc từ thương đến số dư.
Ví dụ 4.35. Tính: 435 5 4 6 6
Trước hết ta viết lại phép tính theo cột dọc: 432 (6) x 54 3012 3502 42032 Vậy: 435 5 4 4 2032 6 6 6 . Cách làm như sau:
- Nhân lần lượt từ phải sang trái;
- Ở tích riêng thứ nhất: 4 x 2 = 8. Lấy 8 chia cho 6 được thương bằng 1, dư 2. Ta viết 2 nhớ 1.
- 4 x 3 = 12, nhớ 1 bằng 13. Lấy 13 chia cho 6 được thương bằng 2 dư 1. Ta viết 1 nhớ 2.
- Cứ tiếp tục như thế…
Ví dụ 4.36. Tính: 14443 : 32 5 5
Trước hết ta viết lại phép tính theo cột dọc: 144’4’3’ 32 (5) 114 243 304 233 213 201 12 Vậy: 14443 :32 2 43 (d 1 u 2 ) 5 5 5 5 . Cách làm như sau: 132
- Chia lần lượt từ trái sang phải;
- Ở lần chia thứ nhất: 144 : 32 được thương bằng 2. Lấy 2 3 2 1 14 5 5 5 . Lấy 144 114 3 0 5 5 5 .
- Hạ tiếp 4 ta được 3045 rồi tiếp tục chia như trên.
- Cứ tiếp tục như thế…
I.4.4.4. Các phép toán trong hệ ghi số cơ số g
- Trong môn Toán ở trường tiểu học, học sinh chủ yếu được thực hành (đếm, so
sánh, tính toán, …) trong hệ cơ số g = 10 hay còn gọi là hệ thập phân. Trong hệ thập
phân: cứ 10 đơn vị của hàng sau có giá trị bằng 1 đơn vị ở hàng liền trước nó.
- Ngoài hệ thập phân, học sinh cũng được làm quen với một số hệ cơ số khác, chẳng hạn:
+ Hệ cơ số g = 2 hay còn gọi là hệ nhị phân, ở Tiểu học thường gọi là cặp.
Trong hệ nhị phân: cứ 2 đơn vị của hàng sau có giá trị bằng 1 đơn vị ở hàng liền trước nó.
+ Hệ cơ số g = 12 hay còn gọi là hệ thập nhị phân, ở Tiểu học thường gọi
là tá. Trong hệ thập nhị phân: cứ 12 đơn vị của hàng sau có giá trị bằng 1 đơn vị ở hàng liền trước nó.
+ Hệ cơ số g = 60 hay còn gọi là hệ thập lục phân. Phép đếm này ta gặp
trong phép đo thời gian: 1 giờ = 60 phút; 1 phút = 60 giây. Trong hệ thập lục phân: cứ 60
đơn vị của hàng sau có giá trị bằng 1 đơn vị ở hàng liền trước nó. …
- Khi biểu diễn các số tự nhiên trong hệ thập phân ta cần lưu ý:
+ Ta sẽ viết 2047; 672 thay cho 2047 ;672 10 10 ;
+ Khi biểu diễn một số tự nhiên có ít nhất 1 chữ số chưa xác định ta phải
dùng dấu gạch ngang trên số đó. Trong trường hợp này, ta quy ước: mỗi kí tự viết dưới
dấu gạch ngang biểu diễn 1 chữ số từ 0 đến 9. Chữ số đầu tiên kể từ bên trái phải khác 0.
Chẳng hạn: abcd;2a4 ; b 16a;...
+ Khi đặt phép tính theo cột dọc thì không cần dùng dấu gạch ngang, chẳng hạn: abcde + ba6m
I.4.5. Các dấu hiệu chia hết cho 2, 3, 4, 5, 9, 25 và 11
Định lí 4.18. Số tự nhiên a chia hết cho 2 khi và chỉ khi chữ số hàng đơn vị của nó bằng 0, 2, 4, 6 hoặc 8. Chứng minh. Giả sử a c c c c n n ... 1 1 0 . Ta có: n n 1 n 1 n 2
a c 10 c 10 ... c10 c (
c 10 c 10
... c ).10 c n n 1 1 0 n n 1 1 0
Từ đây suy ra a chia hết cho 2 khi và chỉ khi c 0chia hết cho 2 hay c0 = 0, 2, 4, 6 hoặc 8. Ta có đpcm. 133
Định lí 4.19. Số tự nhiên a chia hết cho 5 khi và chỉ khi chữ số hàng đơn vị của nó bằng 0 hoặc 5.
Chứng minh. Tương tự định lí 4.18.
Định lí 4.20. Số tự nhiên a chia hết cho 3 (hoặc 9) khi và chỉ khi tổng các chữ số
của nó chia hết cho 3 (hoặc 9). Chứng minh. Giả sử a c c ...c c n n 1 1 0 . Ta có: n n 1
a c 10 c 10
... c10 c n n 1 1 0 n n 1 c (9 1) c (9 1 )
... c (9 1) c n n 1 1 0 . ...... T 9 (c c ... c c ) n n n 1 1 0
Từ đây suy ra a chia hết cho 3 (hoặc 9) khi và chỉ khi c n+ cn-1 + … + c + 1 c0 chia hết cho
3 (hoặc 9) hay tổng các chữ số của a chia hết cho 3 (hoặc 9). Ta có đpcm.
Định lí 4.22. Số tự nhiên a chia hết cho 4 (hoặc 25) khi và chỉ khi số tạo bởi hai
chữ số tận cùng của nó chia hết cho 4 (hoặc 25). Chứng minh. Giả sử a c c ...c c n n 1 1 0 . Ta có: n n1
a c 10 c 10
... c10 c n n 1 1 0 n 2 n 3 ( c 10 c 10 ...
c ).100 c c n n 1 2 1 0
Từ đây suy ra a chia hết cho 4 (hoặc 25) khi và chỉ khi c c 1 0 chia hết cho 4 (hoặc
25) hay số tạo bởi hai chữ số tận cùng của a chia hết cho 4 (hoặc 25). Ta có đpcm.
Định lí 4.23. Số tự nhiên a chia hết cho 11 khi và chỉ khi hiệu giữa tổng các chữ số
hàng chẵn và tổng các chữ số hàng lẻ của nó chia hết cho 11. Chứng minh. Giả sử a c c c c n n ... 1 1 0 . Ta có: n n 1 a n c 10 n c 110 ... 1 c10 0 c n n 1 c
(11 1) c (11 1)
... c (11 1) c n n 1 1 0 n n 1 11
T ( 1) c 11
T ( 1) c ... 11
T c c n n n 1 n 1 1 1 0 11
(T T ... T ) (c c c ...
c ) (c c ... c ) n n 1 1 0 2 4 2 k 1 3 2 k 1
Từ đây suy ra a chia hết cho 11 khi và chỉ khi hiệu giữa tổng các chữ số hàng chẵn
và tổng các chữ số hàng lẻ chia hết cho 11. Ta có đpcm.
Ví dụ 4.37.
Tìm một số tự nhiên n nằm giữa 5000 và 6000 sao cho số đó chia hết cho 6, 9 và 25. Giải: 134
Vì n nằm giữa 5000 và 6000 nên nó có dạng n 5
abc . Vì n chia hết cho 25 nên bc
chia hết cho 25, mặt khác n chia hết cho 6 nên nó phải là số chẵn. Suy ra n 5 a00 hoặc n 5 a50.
a) Xét trường hợp n 5
a50 : vì n chia hết cho 9 nên 5 + a + 5 + 0 = a + 10 chia hết
cho 9. Suy ra a = 4. Thay vào ta được n = 5400.
b) Xét trường hợp n 5
a00 : vì n chia hết cho 9 nên 5 + a + 0 + 0 = a + 5 chia hết
cho 9. Suy ra a = 8. Thay vào ta được n = 5850.
Ví dụ 4.38.
Cho số tự nhiên a. Viết các chữ số của a theo thứ tự ngược lại ta được số tự nhiên
b lớn gấp 3 lần a. Chứng minh rằng b chia hết cho 9. Giải. Giả sử a c c ...c . 1 2
k Viết các chữ số của a theo thứ tự ngược lại ta được số tự nhiên
b c c ...c c 3 a k k 1 2 1 (1).
Từ đây suy ra b chia hết cho 3. Theo dấu hiệu chia hết cho 3 ta suy ra: s = ck + ck-1
+ … + c 2+ c1 chia hết cho 3. Như vậy, a cũng có tổng các chữ số chia hết cho 3 nên a
chia hết cho 3, thành thử a = 3q.
Thay vào (1) ta được b = 9q. Như vậy b chia hết cho 9. Suy ra tổng s các chữ số
của b chia hết cho 9. Tổng các chữ số của a cũng chia hết cho 9.
Suy ra a chia hết cho 9. Ta có đpcm.
Ví dụ 5.39.
Tìm số chẵn có ba chữ số sao cho số đó chia hết cho 5, 9 và 11. Giải:
Gọi số cần tìm là n a
bc . Vì n là số chẵn chia hết cho 5 nên c = 0. Thay vào ta được n a
b0 . Vì n chia hết cho 11 nên a – b chia hết cho 11. Suy ra a = b.
Mặt khác n chia hết cho 9 nên a + b + 0 = a + b chia hết cho 9. Suy ra a + b chỉ có thể bằng 0, 9 hoặc 18.
Từ các kết quả trên đây suy ra a = b = 9. Thay vào ta được n = 990.
Ví dụ 4.40.
Chứng minh rằng trong 11 số tự nhiên bất kì luôn tồn tại hai số mà hiệu của chúng chia hết cho 2 và 5. Giải:
Với 11 số tự nhiên ta có 11 chữ số hàng đơn vị ứng với các số đó. Vì chỉ có 10 chữ
số hàng đơn vị khác nhau (là 0, 1, 2, …, 9) nên ắt phải có 2 trong 11 số đó có cùng chữ số
hàng đơn vị. Hiệu của hai số này sẽ là số tròn chục nên nó chia hết cho cả 2 và 5.
I.4.6. Các bài toán về chia hết ở tiểu học
Sách giáo khoa Toán 4 giới thiệu cho học sinh các dấu hiệu chia hết cho 2, 3, 5 và 9. Cụ thể là:
a) Dấu hiệu chia hết cho 2:
- Các số có chữ số tận cùng bằng 0, 2, 4, 6 hoặc 8 thì chia hết cho 2.
- Các số có chữ số tận cùng bằng 1, 3, 5, 7 hoặc 9 thì không chia hết cho 2. 135
b) Dấu hiệu chia hết cho 5:
- Các số có chữ số tận cùng bằng 0 hoặc 5 thì chia hết cho 5.
- Các số không có chữ số tận cùng bằng 0 và 5 thì không chia hết cho 5.
c) Dấu hiệu chia hết cho 9:
- Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9.
- Các số có tổng các chữ số không chia hết cho 9 thì không chia hết cho 9.
d) Dấu hiệu chia hết cho 3:
- Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.
- Các số có tổng các chữ số không chia hết cho 3 thì không chia hết cho 3.
Ngoài các dấu hiệu nêu trên, để giải các bài toán nâng cao về chia hết ở Tiểu học,
ta cần bổ sung một số tính chất. Chẳng hạn:
1) Một số khi chia cho 2 dư 1 thì chữ số hàng đơn vị của nó bằng 1, 3, 5, 7 hoặc 9.
2) Một số khi chia cho 5 dư 1 thì chữ số hàng đơn vị của nó bằng 1 hoặc 6; dư 2 thì
chữ số hàng đơn vị của nó bằng 2 hoặc 7; dư 3 – bằng 3 hoặc 8; dư 4 – bằng 4 hoặc 9.
3) Số tự nhiên a và tổng các chữ số của nó luôn có cùng số dư khi chia cho 3 (hoặc 9).
4) Hiệu của hai số có cùng số dư khi chia cho k là một số chia hết cho k.
Dưới đây ta minh hoạ một số ví dụ:
Ví dụ 4.41.
Cho sáu chữ số 0, 1, 2, 3, 4, 5. Từ sáu chữ số đó cho có thể viết được bao nhiêu:
a) Số chẵn có bốn chữ số khác nhau?
b) Số có bốn chữ số khác nhau chia hết cho 5?
c) Số có bốn chữ số khác nhau khi chia cho 5 dư 3?
d) Số lẻ có bốn chữ số chia hết cho 5? Giải:
a) Mỗi số cần tìm có dạng abc0 hoặc abc2;abc4 .
Ta xét các số thuộc nhóm 1: - Có 5 cách chọn a; - Có 4 cách chọn b; - Có 3 cách chọn c.
Vậy số các số viết được thuộc nhóm 1 là: 5 x 4 x 3 = 60 (số).
Bây giờ ta xét các số thuộc nhóm 2 và nhóm 3: - Có 4 cách chọn a; - Có 4 cách chọn b; - Có 3 cách chọn c.
Vậy số các số viết được thuộc nhóm 2 và nhóm 3 là: 4 x 4 x 3 x 2 = 96 (số)
Số các số chẵn có bốn chữ số khác nhau viết được từ sáu chữ số đó cho là: 60 + 96 = 156 (số)
b) Mỗi số cần tìm có dạng abc0 hoặc abc5 . Ta xét các số thuộc nhóm 1: - Có 5 cách chọn a; 136 - Có 4 cách chọn b; - Có 3 cách chọn c.
Vậy số các số viết được thuộc nhóm 1 là: 5 x 4 x 3 = 60 (số).
Bây giờ ta xét các số thuộc nhóm 2: - Có 4 cách chọn a; - Có 4 cách chọn b; - Có 3 cách chọn c.
Vậy số các số viết được thuộc nhóm 2 là: 4 x 4 x 3 = 48 (số)
Số các số có bốn chữ số khác nhau chia hết cho 5 viết được từ sáu chữ số đó cho là: 60 + 48 = 108 (số)
c) Mỗi số cần tìm có dạng abc3 . Ta thấy: - Có 4 cách chọn a; - Có 4 cách chọn b; - Có 3 cách chọn c.
Vậy số các số có bốn chữ số khác nhau khi chia cho 5 dư 3 viết được từ sáu chữ số
đó cho là: 4 x 4 x 3 = 48 (số).
d) Mỗi số cần tìm có dạng abc5. Ta thấy: - Có 4 cách chọn a; - Có 5 cách chọn b; - Có 5 cách chọn c.
Vậy số các số lẻ có bốn chữ số chia hết cho 5 viết được từ sáu chữ số đó cho là: 4 x 5 x 5 = 100 (số).
Ví dụ 4.42.
Thay a và b bởi chữ số thích hợp để được số tự nhiên n a
54b là số nhỏ nhất có
bốn chữ số khác nhau chia hết cho 3 và 5. Giải:
Vì n chia hết cho 5 nên c = 0 hoặc 5. Vì n có bốn chữ số khác nhau nên c = 0.
Thay vào ta được n a540. Vì n chia hết cho 3 nên a + 5 + 4 + 0 = a + 9 chia hết cho 3. Suy ra
a = 0, 3, 6 hoặc 9. Số nhỏ nhất cần tìm là 3540.
Ví dụ 4.43.
Hãy viết thêm vào bên trái số 302 một chữ số và bên phải hai chữ số để nhận được
số nhỏ nhất có sáu chữ số khác nhau chia hết cho 5 và 9. Giải:
Gọi chữ số viết thêm vào bên trái là a, hai chữ số viết thêm vào bên phải là b, c. Số
cần tìm có dạng n 3
a 02bc . Vì n chia hết cho 5 nên c = 0 hoặc 5. Mặt khác, vì n có sáu
chữ số khác nhau nên c = 5. Thay vào ta được n a 302 5 b .
Vì n chia hết cho 9 nên a + 3 + 0 + 2 + b + 5 = a + b + 10 chia hết cho 9. Suy ra a + b = 8 hoặc 17. 137
a) Nếu a + b = 17 thì a = 8; b = 9 hoặc a = 9; b = 8. Thay vào ta được các số 830295 và 930285.
b) Nếu a + b = 9. Số 9 có thể biểu diễn thành tổng của các cặp số sau: 0 và 9 (loại);
1 và 8 (chọn); 2 và 7 (loại); 3 và 6 (loại); 4 và 5 (loại). Thay vào ta được các số 130285 và 830215.
Số nhỏ nhất cần tìm là 130 285.
Ví dụ 4.44.
Cho 5 chữ số 0, 5, 6, 7, 8. Từ năm chữ số đó cho có thể viết được bao nhiên số:
a) Có ba chữ số khi chia cho 5 dư 3?
b) Có ba chữ số khác nhau khi chia cho 5 dư 2?
c) Có ba chữ số khác nhau khi chia cho 5 dư 1 và cho 9 dư 5? Giải:
a) Số cần tìm có dạng n a 8 b . Ta thấy: - Có 4 cách chọn a; - Có 5 cách chọn b.
Vậy số các số có ba chữ số khi chia cho 5 dư 3 viết được từ năm chữ số đó cho là: 4 x 5 = 20 (số).
b) Số cần tìm có dạng n a b7 . Ta thấy: - Có 3 cách chọn a; - Có 3 cách chọn b.
Vậy số các số có ba chữ số khác nhau khi chia cho 5 dư 3 viết được từ năm chữ số
đã cho là: 3 x 3 = 9 (số). c)
Số cần tìm có dạng n a
b6 . Vì n chia cho 9 dư 5 nên a + b + 6 chia cho 9
dư 5. Suy ra a + b = 8 hoặc 17.
- Xét trường hợp a + b = 8. Trong năm số đó cho, số 8 có thể phân tích thành tổng của 0 vơi 8.
Vậy số có ba chữ số khi chia cho 5 dư 1, cho 9 dư 5 viết được từ năm chữ số đó cho là 806.
Ví dụ 4.45.
Thay a và b bởi chữ số thích hợp để được số tự nhiên n a
37b là số chẵn lớn nhất
có bốn chữ số khi chia cho 3 dư 2, cho 5 dư 3. Giải:
Số cần tìm có dạng n a37b . Vì n chia cho 5 dư 3 nên c = 3 hoặc 8. Mặt khác n là
số chẵn nên c = 8. Thay vào ta được n a378 .
Vì n chia cho 3 dư 2 nên a + 3 + 7 + 8 = a + 18 chia cho 3 dư 2. Suy ra a = 2, 5, 8.
Thay vào ta được các số 2378; 5378; 8378.
Số lớn nhất cần tìm là 8378.
II. Cơ sở toán học của tập phân số ở Tiểu học
II.1. Quan hệ tương đương và tập thương
II.1.1. Định nghĩa và tính chất của quan hệ tương đương 138
Định nghĩa. Cho X là một tập hợp. Mỗi tập con R của tích Đề-các X x X ta gọi là
một quan hệ hai ngôi trên tập X.
Ta nói rằng hai phần tử a, b của tập X có quan hệ hai ngôi R hay còn nói a quan hệ
R với b, kí hiệu là a R b, nếu (a;b) . R
Định nghĩa. Cho R là quan hệ hai ngôi trên tập X. Ta nói rằng quan hệ hai ngôi R có tính chất: a)
nếu a R a với mọi phần tử a thuộc t Phản xạ, ập X;
b) Đối xứng, nếu: a
,b X ,aRb bRa ;
c) Bắc cầu, nếu: a , ,
b c X ,aRb & bRc aR . c
Quan hệ hai ngôi R gọi là quan hệ tương đương nếu R có tính chất phản xạ, đối
xứng và bắc cầu.
Nếu R là quan hệ tương đương, ta sẽ viết a e b hoặc a b thay cho a R b.
Ví dụ 4.46.
Nếu trên tập các số tự nhiên N ta định nghĩa: hai số tự nhiên a và b có quan hệ e
khi và chỉ khi chúng có cùng chữ số tận cùng.
Ta dễ dàng chỉ ra rằng e là một quan hệ tương đương xác định trên tập N.
Ví dụ 4.47.
Gọi A là tập tất cả học sinh của lớp 5A. Trong tập A ta định nghĩa: hai học sinh
a b nếu chúng ngồi cùng bàn.
Ta dễ dàng chỉ ra rằng là một quan hệ tương đương xác định trên tập A.
Ví dụ 4.49.
Quan hệ đồng dạng hoặc quan hệ bằng nhau giữa các hình tam giác là những quan
hệ tương đương trên tập tất cả các tam giác trên mặt phẳng. Ví dụ 4.50. -
Quan hệ vuông góc và quan hệ song song giữa các đường thẳng
trong mặt phẳng đều không phải là quan hệ tương đương. -
Quan hệ chia hết giữa các số tự nhiên không phải là quan hệ tương
đương trong tập số tự nhiên N. -
Quan hệ “là bạn” trong một tập thể người cũng không phải là quan hệ tương đương.
II.1.2. Định lí về tập thương
Định nghĩa. Cho là quan hệ tương đương xác định trong tập X và a X . Ta gọi tập: C(a)
x X : x a
là lớp tương đương của phần tử a. Phần tử a gọi là phần tử đại diện của lớp C(a).
Ta gọi tập tất cả các lớp tương đương:
C(x) : x X X
là tập thương của tập X chia theo quan hệ tương đương . Kí hiệu là Ví dụ 4.51.
Tìm tập thương của tập các số tự nhiên N chia theo quan hệ tương đương e “có
cùng chữ số tận cùng” trong ví dụ 4.46. 139 Giải:
Ta phải làm hai việc: Chứng minh e là quan hệ tương đương (xem ví dụ 4.46) và
xác định tập thương N e .
Với mỗi số tự nhiên a thì C(a) là tập các số tự nhiên có cùng chữ số tận cùng với
a. Nếu ta kí hiệu C(i) là tập các số tự nhiên có chữ số tận cùng bằng i với i = 0, 1, 2, …, 9 thì: N
C(0); C(1);C(2);...; C(9 ) e
Ví dụ 4.52.
Tìm tập thương của tập A các em học sinh của lớp 5A chia theo quan hệ tương
đương “ngồi cùng bàn” trong ví dụ 4.47. Giải:
Ta phải làm hai việc: Chứng minh là quan hệ tương đương (xem ví dụ 4.47) và
xác định tập thương A .
Với mỗi học sinh a của lớp 5A thì C(a) là tập các học sinh ngồi cùng bàn với a. Vì A
vậy mỗi phần tử của tập thương là một bàn có học sinh ngồi trong lớp đó.
Định lí 4. 24. (Về tính chất của tập thương)
Giả sử e là quan hệ tương đương xác định trên tập X và a, b, c X . Khi đó: (i )Ca ) ;
(ii )C (a ) C (b ) a b ;
(iii )C (a ) C
(b ) C (a )C (b ) . Chứng minh.
(i) Rõ ràng là aC(a) . Từ đó suy ra đpcm.
(ii) Điều kiện cần: Hiển nhiên.
Điều kiện đủ: Giả sử a b
và x C(a) x a x b
x C(b) C(a) C (b).
(iii) Điều kiện cần: hiển nhiên. ( C ) a ( C ) b x C( ) a ( C ) b x ; a x b
Điều kiện đủ: Giả sử a b
C(a) C (b).
Chú ý. Định lí 4.24 cho ta biết: Nếu trong tập X xác định một quan hệ tương
đương thì ta có thể phân chia tập X thành các tập con khác rỗng, đôi một không giao nhau
sao cho hợp các tập con đó cho ta cả tập X.
Phép phân chia này trở thành cơ sở của việc mở rộng các tập hợp số trong toán học.
II.2. Xây dựng tập số hữu tỉ không âm
II.2.1. Sự cần thiết phải xây dựng tập số hữu tỉ không âm
Nếu dừng lại ở tập số tự nhiên thì nhiều phép chia không thực hiện được, chẳng
hạn 3 : 7, 25 : 8, 1 : 6,… 140
Nếu dừng lại ở tập số tự nhiên thì nhiều số đo của các phép đo đại lượng không
thực hiện được, chẳng hạn, không thể biểu diễn số đo 12cm; 2m 4dm bằng đơn vị là mét;
không thể biểu diễn 100g; 3006g; 4kg 25g bằng đơn vị là ki-lô-gam, …
Trong môn Toán ở trường phổ thông, nhiều tính chất của các phép toán về phân số
(tính chất giao hoán, tính chất kết hợp, tính chất phân phối của phép cộng và phép nhân,
…) không chứng minh được chặt chẽ mà phải thừa nhận (thông qua một số ví dụ minh
hoạ). Trong thực tế cuộc sống lao động và sản xuất, do yêu cầu phát triển của các ngành
khoa học và kĩ thuật luôn đặt ra yêu cầu giải quyết những tồn tại nêu trên.
Vì vậy, trong phần này ta mở rộng tập số tự nhiên thêm các số mới để trong tập
hợp số mới đó khắc phục những hạn chế nêu trên
II.2.2. Xây dựng tập số hữu tỉ không âm
Mỗi cặp sắp thứ tự (a; b), trong đó a là số tự nhiên, b là số tự nhiên khác 0 ta sẽ
gọi là một phân số không âm (hay để cho gọn, ta sẽ gọi là phân số). Tập tất cả các phân
số ta kí hiệu là P. Như vậy
P = N x N*, trong đó N* là tập các số tự nhiên khác 0. a
Để chỉ phân số, ta dùng kí hiệu b thay cho (a; b). Trên tập P ta định nghĩa quan hệ hai ngôi " " như sau: a c a c ;
Hai phân số b d gọi là tương đương, kí hệu là b d , nếu ad = cd. 1 4 3 9 ; ;... 2 8 4 12 1 2 3 Chẳng hạn,
. 2 không tương đương với 5 ; 4 không tương 4 ;... đương với 3
Ta dễ dàng chỉ ra rằng " "
là quan hệ tương đương xác định trên tập các phân số
P. Theo định lí 4.24 ta có thể phân chia tập P thành các lớp tương đương và nhận được a a P C ( ) : P tập thương b b . a ( C ) Mỗi lớp tương đương
b là một tập hợp các phân số bằng nhau (bằng phân số a ). b Chẳng hạn: 1 1 2 3 45 120 ( C ) ; ; ;...; ;...; ;... 2 2 4 6 90 240 3 3 6 9 45 75 ( C ) ; ; ;...; ;...; ;... 4 4 8 12 60 100 141 a ( C ) Mỗi lớp tương đương
b ta sẽ gọi là một số hữu tỉ không âm (để cho gọn ta gọi a r C ( ).
là số hữu tỉ), kí hiệu là
b Tập tất cả các số hữu tỉ không âm ta kí hiệu là Q . Như vậy Q P . Chú ý. a a r C ( ) .
1. Mỗi số hữu tỉ không âm
b là một tập hợp các phân số bằng phân số b a a r ( C ).
Để cho gọn, ta sẽ dùng kí hiệu b để chỉ số hữu tỉ
b Chẳng hạn: ta dựng kí hiệu 1 1 9 9 r C ( ) r ( C );... 2 để chỉ số hữu tỉ 2 ; 5 để chỉ phân số 5
2. Mỗi số hữu tỉ không âm r chỉ có duy nhất một đại diện là phân số tối giản. p p ' à v
Thật vậy, giả sử q
q' là hai phân số tối giản cùng là đại diện của số hữu tỉ r. p p'
Theo định nghĩa lớp tương đương ta có q
q ' . Suy ra pq’ = p’q. Vì ƯCLN(p; q) =
ƯCLN(p’; q’) = 1 nên p = p’ và q = q’. Suy ra đpcm.
Ta quy ước: khi nói đến phân số đại diện của số hữu tỉ r ta hiểu là phân số tối p giản q đó. a .
3. Mỗi số tự nhiên a có thể biểu diễn dưới dạng một phân số là 1 Vì vậy mối số a
tự nhiên a cũng xác định duy nhất một số hữu tỉ r có phân số đại diện là 1 . Thành thử tập
số tự nhiên N có thể coi là bộ phận của tập số hữu tỉ Q+. 0 1 ( C ) C( )
4. Ta quy ước số hữu tỉ xác định bởi
1 là 0 và số hữu tỉ xác định bởi 1 là 1.
II.3. Quan hệ thứ tự trong tập số hữu tỉ không âm
Ở phổ thông ta đã biết: 3 5 3 5 r C ( ) s C ( )
- 7 7 . Vậy ta có thể so sánh hai số hữu tỉ 7 và 7 được hay không? 2 3 2 3 r C ( ) s C ( )
- 7 5 . Vậy ta có thể so sánh hai số hữu tỉ 7 và 5 được hay không? 142
Một cách tổng quát: hãy đưa ra một quy tắc để có thể so sánh hai số hữu tỉ bất kì a c r C ( ) s C( ) b và
d ! Đáp ứng yêu cầu này bằng định nghĩa dưới đây: a c r ( C ) s C( )
Định nghĩa. Cho hai số hữu tỉ b và d . Ta nói rằng:
a) Số hữu tỉ r nhỏ hơn hoặc bằng số hữu tỉ s, kí hiệu là r s , nếu ad b c.
b) Số hữu tỉ r nhỏ hơn số hữu tỉ s, kí hiệu là r < s, nếu r s & r s ;
c) Số hữu tỉ r lớn hơn hoặc bằng số hữu tỉ s, kí hiệu là r s nếu s r ;
d) Số hữu tỉ r lớn hơn số hữu tỉ s, kí hiệu là r > s, nếu s r. Các hệ thức r s & r s
ta gọi là các bất đẳng thức, các
hệ thức r < s và r > s gọi
là các bất đẳng thức nghiêm ngặt.
Nhận xét. Bằng định nghĩa trên đây, ta đã đưa việc so sánh các số hữu tỉ về so sánh các số tự nhiên. Ví dụ 4.53. 3 5 ( C ) C( ) 7 7 vì 3.7 < 5.7; 5 3 ( C ) C ) 9 11 vì 5.11 > 9.3; 2 6 ( C ) ( C ) – 5 15 vì 2.15 = 5.6.
Định lí 4. 25. (Về tính chất của quan hệ thứ tự trong tập Q+)
(i) Việc so sánh hai số hữu tỉ không phụ thuộc vào sự lựa chọn các phân số đại diện của chúng;
(ii) Quan hệ thứ tự có tính chất phản xạ: Với mọi số hữu tỉ r ta luôn có r r ;
(iii) Quan hệ thứ tự có tính chất phản đối xứng: Với mọi số hữu tỉ r, s ta luôn có:
(r s & s r ) r s ;
(iv) Quan hệ thứ tự có tính chất bắc cầu: Với mọi số hữu tỉ r, s, t ta luôn có:
(r s & s t ) r t ; Chứng minh. a a ' c c ' , ,
(i) Giả sử b b ' là hai phân số đại diện của số hữu tỉ r và d d ' là hai phân số đại
diện của số hữu tỉ s, trong đó ad b .
c Ta sẽ chứng minh a 'd ' b 'c '.
Thật vậy, theo giả thiết: ab ' a ' ; b cd ' c
'd. Giả sử a’d’ > c’b’. Áp dụng tính chất
của tập số tự nhiên ta có:
a’bcd’ = ab’c’d và adc’b’ < bca’d’.
điều này vô lí. Ta có đpcm. (iii) và (iii) Rõ ràng. a c m
r ; s ; t (iv) Giả sử b d n , trong đó r s , s t ad b ; c cn m d adcn b cmd an m b r t . 143 Định lí 4.26.
(i) Tính trù mật của tập số hữu tỉ: Xen giữa hai số hữu tỉ khác nhau tồn tại vô số
các số hữu tỉ khác chúng;
(ii) Tiên đề Ác-si-mét: mọi số hữu tỉ đều bị chặn trên bởi một số tự nhiên, hay nói
cách khác, với mọi số hữu tỉ r luôn tồn tại số tự nhiên n sao cho r < n. Chứng minh. a c r , s (i) Giả sử b
d là hai số hữu tỉ, trong đó r > s. Suy ra ad < bc. Đặt ad bc t . 2bd Ta có: c 2bc ad bc 2ad a d 2bd 2bd 2bd b
Từ đây suy ra r > t > s. Ta có đpcm. a r . (ii) Giả sử
b Theo nguyên lí Ác-si-mét, trong tập số tự nhiên tồn tại số tự
nhiên n sao cho nb > a. Suy ra n > r.
II.4. Các phép toán trong tập số hữu tỉ không âm
II.4.1. Phép cộng và phép nhân
II.4.1.1.Định nghĩa và ví dụ a c r C ( );s C ( ).
Định nghĩa. Cho r và s là hai số hữu tỉ không âm, trong đó b d Ta gọi:
a) Tổng của hai số hữu tỉ r và s là một số hữu tỉ t, kí hiệu là t = r + s, trong đó ad bc t C( ) bd
. Quy tắc cho tương ứng mỗi cặp số hữu tỉ r, s với một số hữu tỉ t nói trên ta
gọi là phép cộng các số hữu tỉ, trong đó r và s gọi là các số hạng, t là tổng và r + s cũng gọi là tổng.
b) Tích của hai số hữu tỉ r và s là một số hữu tỉ p, kí hiệu là p r s (hoặc r.s hoặc ac p C ( ) rs), trong đó
bd . Quy tắc cho tương ứng mỗi cặp số hữu tỉ r, s với một số hữu tỉ p
nói trên ta gọi là phép nhân các số hữu tỉ, trong đó r và s gọi là các thừa số, p
gọi là tích
và s.r cũng gọi là tích.
Ví dụ 4.54. 4 7
Cho r và s là hai số hữu tỉ có phân số đại diện tương ứng là 9 và 12 . Ta có: 4.12 9.7 37
r s C( ) ( C ). 9.12 36 4.7 7 .r s ( C ) ( C ). 9.12 27 144
Chú ý. Từ định nghĩa ta chứng minh tổng và tích của hai số hữu tỉ không phụ
thuộc vào việc lựa chọn các phân số đại diện của chúng.
Hay nói cách khác: Với hai số hữu tỉ bất kì r và s luôn tồn tại duy nhất một số hữu
tỉ t là tổng và một số hữu tỉ p là tích của chúng. a a ' c c' , ,
Giả sử b b ' là hai phân số đại diện của số hữu tỉ r và d d ' là hai phân số đại ad bc
a 'd ' b 'c ' ( C ) ( C )
diện của số hữu tỉ s, trong đó . Ta sẽ chứng minh bd b 'd '
Thật vậy, theo giả thiết: ab ' a ' ; b cd ' c
'd. Áp dụng tính chất của tập số tự nhiên ta cú:
ab’dd’ = a’bdd’ và cd’bb’ = c’dbb’ hay (ad + bc)b’d’ = (a’d’ + b’c’)bd
Từ đây suy ra tổng của hai số hữu tỉ không phụ thuộc vào việc lựa chọn các phân số đại diện của chúng.
Tương tự ta chứng minh được tính duy nhất của tích hai số hữu tỉ.
II.4.1.2.Tính chất của phép cộng và phép nhân
Định lí 4.27. (Tính chất của phép cộng và phép nhân các số hữu tỉ)
Giả sử r, s, t là ba số hữu tỉ bất kì. Khi đó:
(i) Tính chất giao hoán: r + s = s + r và r.s = s. r
(ii) Tính chất kết hợp:
(r + s) + t = r + (s + t) và (r.s).t = r.(s.t)
(iii) Tính chất của số 0 và số 1:
r + 0 = 0 + r = r và r.1 = 1.r = r
(iv) Tính chất phân phối:
r.(s + t) = r.s + r.t và (s + t).r = s.r + t.r
(v) Luật giản ước:
r + t = s + t suy ra r = s và r.t = s.t , với t 0 suy ra r = s.
(vi) Phần tử nghịch đảo:Với mọi số hữu tỉ r 0
luôn tồn tại duy nhất số nghịch đảo 1 r của r sao cho 1 r.r 1 .
(vii) Tích của hai số hữu tỉ bằng 0 khi và chỉ khi ít nhất một trong hai số đó bằng 0. Chứng minh.
(i), (ii), (iii), (iv) đơn giản: suy ra trực tiếp từ tính chất của các phép toán trong tập số tự nhiên. a c m , ,
(v) Giả sử b d n theo thứ tự là các phân số đại diện của các số hữu tỉ r, s, t. Theo định nghĩa ta có: an bm cn dm
r t C(
); s t C( ) bn dn . Vỡ r + t = s + t nên:
(an bm)dn b (
n cn dm) hay andn + bmdn = bncn + bndm. Suy ra ad = bc. 145 Từ đây suy ra đpcm.
Tương tự ta chứng minh luật giản ước đối với phép nhân. a b r ( C ) 0 a 0. 1 r C ( ) (vi) Giả sử b Đặt
a sẽ là số nghịch đảo của r. a c ac r C ( ), s C ( ) 0 (vii) Giả sử b
d thỏa món r.s = 0. Theo định nghĩa ta có bd .
Suy ra ac = 0. Theo tính chất của phép nhân các số tự nhiên ta có a = 0 hoặc b = 0. Từ
đây suy ra r = 0 hoặc s = 0.
Định lí 4.28. (Tính đơn điệu của phép cộng và phép nhân các số hữu tỉ)
Giả sử r, s và t là ba số hữu tỉ bất kì. Ta có:
Nếu r s thì r t s t và rt st.
Đặc biệt, nếu r < s và t > 0 thì rt < st. Chứng minh. a c m , ,
Giả sử b d n theo thứ tự là các phân số đại diện của các số hữu tỉ r, s, t. Theo định nghĩa ta có: an bm cn dm
r t C(
); s t C( ) bn dn . Vì r s nên: ad bc.
Lần lượt biến đổi ta được:
andn + bmdn cnbn + dmbn hay (an + bm)dn (cn + dm)bn Từ đây suy ra đpcm.
Tương tự ta chứng minh tính đơn điệu của phép nhân.
II.4.2. Phép trừ a c r C ( );s C ( ).
Định nghĩa. Cho r và s là hai số hữu tỉ không âm, trong đó b d Ta
gọi hiệu của hai số hữu tỉ r và s là một số hữu tỉ u, kí hiệu là u = r – s, trong đó ad bc u ( C ) bd
, nếu ad – bc là số tự nhiên. Quy tắc cho tương ứng mỗi cặp số hữu tỉ r, s
với một số hữu tỉ u nói trên ta gọi là phép trừ các số hữu tỉ, trong đó r là số bị trừ, s là số
trừ và u là hiệu và r – s cũng gọi là hiệu.
Ví dụ 4.55. 8 7
Cho r và s là hai số hữu tỉ có phân số đại diện tương ứng là 9 và 12 . Ta có: 8.12 9.7 11
r s C( ) C( ). 9.12 36
Định lí 4.29. (Tính chất của phép trừ các số hữu tỉ)
Giả sử r, s, t là ba số hữu tỉ bất kì. Khi đó:
(i) r – s = u khi và chỉ khi u + s = r
(ii) r(s – t) = rs – rt, nếu một trong hai vế có nghĩa. Chứng minh. 146 a c m , ,
(i) Giả sử b d n theo thứ tự là các phân số đại diện của các số hữu tỉ r, s, u. Theo ad bc m r s ( C ) ( C ) u định nghĩa ta có bd n khi và chỉ khi: a dm cn
and – bcn = bdm hay and = bdm + bcn. Suy ra b dn Từ đây suy ra đpcm.
(ii) Đặt u = s – t , từ (i) ta suy ra s = u + t. Ta có:
rs = r(u + t) = ru + rt = r(s – t) + rt. Từ đây ta suy ra đpcm. II.4.3. Phép chia Định lí 4.30.
Giả sử r và s là hai số hữu tỉ, trong đó s khác 0. Khi đó tồn tại duy nhất một số hữu tỉ q sao cho qs = r. Chứng minh. Vì s 0
nên theo định lí 4.27 tồn tại số hữu tỉ nghịch đảo s-1. Đặt q = rs-1 Rõ ràng là qs = rs-1s = r.
Định nghĩa. Ta gọi số hữu tỉ q trong định lí 4.30 là thương của hai số hữu tỉ r và s, kí hiệu là q = r : s.
Quy tắc cho tương ứng mỗi cặp số hữu tỉ r, s với một số hữu tỉ q nói trên ta gọi là
phép chia các số hữu tỉ, trong đó r là số bị chia, s là số chia và q là thương, r : s cũng gọi là thương.
Ví dụ 4.56. 8 7
Cho r và s là hai số hữu tỉ có phân số đại diện tương ứng là 9 và 12 . Ta có: 8.12 32 r: s ( C ) ( C ). 9.7 21
Nhận xét. Từ các kết quả trên ta thấy:
1. Phép cộng và phép nhân các số hữu tỉ (không âm) luôn thực hiện được.
2. Phép trừ các số hữu tỉ không phải bao giờ cũng thực hiện được.
3. Phép chia một số hữu tỉ bất kì cho một số hữu tỉ khác 0 luôn thực hiện được.
II.5. Nội dung dạy học phân số ở Tiểu học
Trong chương trình môn Toán tiểu học, nội dung về phân số được trình bày trong
môn toán lớp 4 và 5. Nó bao gồm các nội dung sau:
- Hình thành khái niệm phân số;
- So sánh các số phân số;
- Các phép tính về phân số; - Hỗn số;
- Giải toán về phân số.
II.5.1. Hình thành khái niệm phân số ở Tiểu học 147
Khái niệm về phân số được trình bày trong môn Toán lớp 4 và 5. Nó bao gồm các nội dung sau: -
Thông qua các biểu tượng hình thành khái niệm phân số (nhỏ hơn 1); -
Từ phép chia có dư dẫn đến khái niệm phân số; -
Giới thiệu cách đọc, viết và nhận biết cấu tạo của một phân số; -
Giới thiệu khái niệm hỗn số. Chẳng hạn:
- Từ biểu tượng một hình (hình tròn, hình vuông, băng giấy, …) được chia
thành các phần bằng nhau, trong đó có một số phần được tô màu ta hình thành khái niệm phân số nhỏ hơn 1.
- Thông qua một số bài toán về phép chia có dư (chẳng hạn, chia 3 cái bánh cho 4 3 5 ; ;...
người, chia 5 quả cam cho 4 người, … ta dẫn đến các phân số 4 4 ) để hình
thành khái niệm phân số (nhỏ hơn hoặc lớn hơn 1).
Từ các khái niệm trên, ta chốt lại cho học sinh:
1. Cấu tạo của một phân số gồm: tử số là số tự nhiên viết trên gạch ngang; mẫu số
là số tự nhiên khác 0 viết dưới gạch ngang.
2. Thương của phép chia một số tự nhiên cho một số tự nhiên khác 0 có thể viết
thành một phân số, tử số là số bị chia và mẫu số là số chia.
3. Mỗi số tự nhiên có thể viết thành một phân số có tử số là số tự nhiên đó và mẫu số bằng 1. 3
- Từ nhu cầu biểu diễn 2 cái bánh và 4 cái bánh ta hình thành cho học sinh khái 3 2 . niệm hỗn số 4
II.5.2. Quan hệ so sánh các phân số ở Tiểu học
Trong chương trình môn Toán tiểu học, quan hệ so sánh giữa các phân số được
trình bày trong môn Toán lớp 4. Gồm các nội dung sau:
- Giới thiệu khái niệm phân số bằng nhau (chính là khái niệm phân số tương
đương ta đó xây dựng ở phần trên).
- Hình thành khái niệm và củng cố các kĩ năng rút gọn phân số;
- Hình thành khái niệm và xây dựng quy tắc quy đồng mẫu số các phân số;
- Xây dựng các quy tắc so sánh hai phân số (có cùng mẫu số và không cùng mẫu số). Chẳng hạn:
- Từ biểu tượng một băng giấy ta hình thành cho học sinh khái niệm hai phân số bằng nhau;
- Trên cơ sở khái niệm hai phân số bằng nhau, ta hình thành khái niệm và quy tắc
rút gọn phân số, khái niệm và quy tắc quy đồng mẫu số các phân số;
- Bằng các hình ảnh trực quan, hình thành cho học sinh quy tắc so sánh hai phân
số (có cùng hoặc không cùng mẫu số). 148
II.5.3.Xây dựng các phép toán trong tập phân số
Các phép trong tập phân số được hình thành cho học sinh lớp 4 theo bốn bước: 1
Từ các bài toán thực tế kết hợp với các biểu tượng, hình thành ý nghĩa của mỗi phép toán; 2
Hình thành quy tắc thực hành mỗi phép toán (cộng, trừ, nhân và chia các phân số); 3
Giới thiệu tính chất của các phép tính về phân số. 4
Rèn kĩ năng thực hành các phép tính. Cụ thể là:
- Dùng biểu tượng bằng giấy được chia thành các phần bằng nhau sách giáo khoa
(SGK) hình thành ý nghĩa và quy tắc thực hành phép cộng (hoặc phép trừ) hai phân số có cùng mẫu số.
- Vận dụng phương pháp quy đồng mẫu số, SGK hình thành ý nghĩa và quy tắc
thực hành phép cộng (hoặc phép trừ) hai phân số không cùng mẫu số.
- Từ một bài toán thực tế về tính diện tích hình chữ nhật kết hợp với biểu tượng về
mảnh bìa được chia thành các phần bằng nhau, SGK hình thành ý nghĩa và quy tắc thực
hành phép nhân hai phân số.
- Từ một bài toán thực tế về tính chiều dài hình chữ nhật khi biết diện tích và chiều
rộng của hình đó, SGK hình thành ý nghĩa và quy tắc thực hành phép chia hai phân số.
- Các tính chất (giao hoán, kết hợp, phân phối, nhân một số với một tổng, …) của
các phép toán về phân số được suy ra trực tiếp từ các tính chất tương ứng của các phép
toán trên tập số tự nhiên thông qua phép suy luận tương tự (trong các tiết luyện tập).
II.5.4. Giải toán về phân số ở Tiểu học
Các bài toán về phân số ở Tiểu học có thể phân chia thành bốn dạng:
Dạng 1. Toán về cấu tạo phân số;
Dạng 2. Toán về so sánh phân số;
Dạng 3. Toán về các phép toán trên phân số;
Dạng 4. Toán có văn điển hình trên tập phân số;
Dưới đây ta minh hoạ ví dụ cho từng dạng toán.
Dạng 1. Toán về cấu tạo phân số;
Ví dụ 4.57. Viết các phân số:
a) Có tổng của tử số và mẫu số bằng 8;
b) Lớn hơn 1 và có tích của tử số và mẫu số bằng 12. Giải:
a) Số 8 có thể phân tích thành tổng của các cặp số sau: 0 và 8; 1 và 7; 2 và 6; 3 và
5; 4 và 4. Các phân số có tổng của tử số và mẫu số bằng 8 là: 0 1 7 2 6 3 5 4 ; ; ; ; ; ; ; . 8 7 1 6 2 5 3 4
b) Số 12 có thể phân tích thành tích của các cặp số sau: 1 và 12; 2 và 6; 3 và 4.
Các phân số lớn hơn 1 có tích của tử số và mẫu số bằng 12 là: 12 6 4 ; ; . 1 2 3 149 Ví dụ 4.58.
Tích của tử số và mẫu số của một phân số nhỏ hơn 1 bằng 315, khi chia cả tử và
mẫu của phân số đó cho 3 ta được phân số tối giản. Tìm phân số đó. Giải:
Số 315 có thể phân tích thành tích của các cặp số sau: 1 và 315; 3 và 105; 5 và 63; 7 và 45; 9 và 35; 15 và 21.
Các phân số lớn hơn 1 có tích của tử số và mẫu số bằng 315 là: 1 3 5 7 9 15 ; ; ; ; ; 315 105 63 45 35 21 3 15 ; .
Bằng phương pháp thử chọn ta nhận được phân số cần tìm là: 105 21
Ví dụ 4.59. Rút gọn phân số sau: 232323 132132 ) a ; ) b . 414141 231231 Giải: Ta có: 232323 232323:10101 23 ) a . 414141 414141:10101 41
132132 132132 :1001 132 132 : 33 4 ) b . 231231 231231:1001 231 321: 33 7
Dạng 2. Toán về so sánh phân số
Ví dụ 4.60.
Sắp xếp các phân số sau: 5 3 5 ) a ; ;
7 4 8 theo thứ tự từ lớn đến bé; 4 2 8 ) b ; ;
7 5 11 theo thứ tự từ bé đến lớn. Giải:
a) Quy đồng mẫu số các phân số đã cho ta được: 5 40 3 42 5 35 42 40 35 ; ; . 7 56 4 56 8
56 Vì 56 56 56 nên các phân số đã cho xếp theo 3 5 5 ; ; .
thứ tự từ lớn đến bé là: 4 7 8
b) Quy đồng tử số các phân số đã cho ta được: 4 8 2 8 8 8 8 ; . 7 14 5
20 Vì 20 14 11 nên các phân số đã cho xếp theo thứ tự từ 2 4 8 ; ; . bé đến lớn là: 5 7 11
Ví dụ 4.61. 150
Không quy đồng mẫu số, hãy viết các phân số sau theo thứ tự từ bé đến lớn: 45 35 17 ; ; . 7 9 4 Giải: Ta có: 45 3 35 8 17 1 6 ; 3 ; 4 . 7 7 9 9 4
4 Vì 3 < 4 < 6 nên các phân số đã cho xếp theo thứ tự từ 35 17 45 ; ; . bé đến lớn là: 9 4 7
Dạng 3. Toán về các phép toán trên phân số
Ví dụ 4.62.
Tính giá trị của biểu thức: 1414 1313 ) a ; 2121 1414 135135 112112 ) b . 189189 224224 Giải: 1414 1313 14 13 2 13 4 13 17 ) a . 2121 1414 21 14 7 14 14 14 135135 112112 135 112 5 1 10 7 3 ) b . 189189 224224 189 224 7 2 14 14
Ví dụ 4.63. Tính: 9 5 6 17 ) a ; 14 8 7 24 2013 2008 2015 2011 1006 ) b . 2015 2011 2012 2013 1004 Giải:
Áp dụng tính chất giao hoán và tính chất kết hợp của phép cộng và phép nhân ta có: 9 5 6 17 9 6 5 17 ) a ( ) ( ) 14 8 7 24 14 7 8 24 912 15 17 21 32 3 4 9 8 17 . 14 24 14 24 2 3 6 6 2013 2008 2015 2011 1006 2013 2015 2008 2011 1006 ) b ( ) ( ) 2015 2011 2012 2013 1004 2015 2012 2011 2013 1004 2013 2008 1006 2008 1006 1004 2 1006 1. 2012 2013 1004 2012 1004 1006 2 1004
Dạng 4. Toán có văn điển hình trên tập phân số 151
Ví dụ 4.64. 2
Hai bà đi chợ bán trứng, sau khi nhẩm tính, một bà bảo: “ 5 số trứng của tôi gấp 4 2 4
1,5 lần 7 số trứng của bà và 5 số trứng của tôi nhiều hơn 7 số trứng của bà là 40 quả”.
Hỏi mỗi bà đã mang bao nhiêu trứng ra chợ bán? Giải: 3
Vì 1,5 = 2 nên theo đề bài ta có sơ đồ sau: ?quả 2
5 số trứng của bà thứ nhất: ?quả 40 quả 4
7 số trứng của bà thứ hai: 2
5 số trứng của bà thứ nhất là: 40 x 3 = 120 (quả)
Số trứng của bà thứ nhất mang ra chợ bán là: 120 : 2 x 5 = 300 (quả) 4
7 số trứng của bà thứ hai là: 40 x 2 = 80 (quả)
Số trứng của bà thứ hai mang ra chợ bán là: 80 : 4 x 7 = 140 (quả)
Đáp số: 300 quả và 140 quả.
Ví dụ 4.65.
Hai đội vần tải được giao vận chuyển một lô hàng: sau khi Đội I vận chuyển được 3 3
5 số hàng được giao và Đội II vận chuyển được 8 số hàng được giao thì số hàng còn lại 3
của cả hai đội là 560 tấn, trong đó số hàng còn lại của Đội I bằng 4 số hàng của Đội II.
Hỏi lúc đầu mỗi đội được giao vận chuyển bao nhiên tấn hàng?
Giải: Theo đề bài ta có sơ đồ sau: ?tấn
Số hàng còn lại của Đội I: ?tấn 560 tấn
Số hàng còn lại của đội II:
Số hàng còn lại của Đội I là: 560 : (3 + 4) x 3 = 240 (tấn) 152
Số hàng còn lại của Đội II là: 560 – 240 = 320 (tấn)
Số hàng của Đội I được giao vận chuyển lúc đầu là: 240 tấn ? tấn 240 : 2 x 5 = 600 (tấn)
Số hàng của Đội II được giao vận chuyển lúc đầu là: 320 tấn ? tấn 320 : 5 x 8 = 512 (tấn)
Đáp số: Đội I: 600 tấn hàng Đội II: 512 tấn hàng
III. Cơ sở toán học của tập số thập phân ở Tiểu học
III.1. Phân số thập phân 3 116 35 12 ; ; ; ;... Các phân số 10 100 1000 1
đều có mẫu số là lũy thừa của 10 với số mũ tự
nhiên. Các phân số dạng này ta thường gặp trong các phép đo đại lượng, chẳng hạn: 25 1m ; m
- Chiều dài cạnh bàn là 1m25cm hay 100 365 kg;
- Gói hàng cân nặng 365g hay 1000 - … a
Định nghĩa. Phân số b gọi là phân số thập phân, nếu mẫu số b của nó là lũy thừa n
của 10 với số mũ tự nhiên (b 1
0 ,n N ). 3 116 35 12 ; ; ; ;...
Chẳng hạn các phân số 10 100 1000 1
là những phân số thập phân. 3 3
Phân số 4 không phải là phân số thập phân, nhưng 4 lại bằng phân số thập phân 75
100 . Từ đây ta đi đến a
Định nghĩa. Phân số b gọi là biểu diễn được dưới dạng thập phân nếu nó bằng
một phân số thập phân nào đấy. 153 1 24 15 ; ; ;...
Chẳng hạn, các phân số 2 25 8
là những phân số biểu diễn được dưới dạng 2 9 35 ; ; ;...
thập phân; các phân số 3 14 24
không biểu diễn được dưới dạng thập phân.
Dưới đây ta đưa ra một dấu hiệu để nhận biết một phân số có biểu diễn được dưới
dạng thập phân hay không:
Định lí 4.31. (Điều kiện để phân số biểu diễn được dưới dạng thập phân) p
Để phân số tối giản q biểu diễn được dưới dạng thập phân, điều kiện cần và đủ là
mẫu số q của nó không chứa ước nguyên tố nào khác ngoài 2 và 5. Chứng minh. n m
Điều kiện đủ. Giả sử q chỉ có ước nguyên tố là 2 và 5. Vậy q 2
5 . Giả sử n m . p p
p .2m n
p .2m n p . n m m m m Ta có q 2 5 2 5 10
Vậy phân số q biểu diễn được dưới dạng thập phân. p a
Điều kiện cần. Giả sử phân số tối giản q 10n . Suy ra a.q = p.10 .n
Giả sử k là một ước nguyên tố khác 2 và 5 của q. Suy ra k là ước của p. Vậy k = p
UC(p; q). Vì phân số q tối giản nên k = 1. Ta có đpcm. Ví dụ 4.66. 127 13 31 ; ;
- Các phân số 40 16 125 đều tối giản và mẫu số của chúng chỉ có ước nguyên tố
là 2 hoặc 5 nên chúng biểu diễn được dưới dạng thập phân. 7 13 31 ; ;
- Các phân số 9 14 120 đều tối giản và mẫu số của mỗi phân số đó có ước
nguyên tố khác 2 và 5 nên chúng không biểu diễn được dưới dạng thập phân. 21 3 13 1 ;
- Phân số 14 2 65 5 đều biểu diễn được dưới dạng thập phân.
III.2. Số thập phân không âm
Để tiện lợi trong tính toán và sử dụng, người ta đưa ra một cách biểu diễn riêng
cho các phân số thập phân.
Định nghĩa. Số hữu tỉ r gọi là số thập phân không âm (để cho gọn, ta gọi là số
thập phân), nếu nó có một đại diện là phân số thập phân hay nói cách khác: phân số đại
diện của nó biểu diễn được dưới dạng thập phân.
Tập tất cả các số thập phán (không âm) ta kí hiệu là Q . 10 Ví dụ 4.67. 154 123 9 8 13 47 ; ; ; ; Q ; 10 10 16 100 40 10000 9 17 17 ; ; Q . 10 7 12 30
Như chúng ta đã biết, mỗi số thập phân có một cách biểu diễn là phân số thập
phân. Cách biểu diễn này có nhược điểm là cồng kềnh, không tiện lợi trong thực hành
tính toán. Vì vậy, ta thường biểu diễn các số thập phân dưới dạng thu gọn, chẳng hạn: 123 1 2,3 + 10
và đọc là mười hai đơn vị nguyên và ba phần mười của đơn vị hoặc
để cho gọn, ta đọc: mười hai phẩy ba. 71 0 ,71 + 100
và đọc là: không đơn vị nguyên và bảy mươi một phần một trăm của
đơn vị hoặc để cho gọn ta đọc: không phẩy bảy mươi mốt. 43 0 ,0043 + 10000
và đọc là không đơn vị nguyên và bốn mươi ba phần mười
nghìn của đơn vị hoặc để cho gọn ta đọc: không phẩy không không bốn ba.
Vậy dạng thu gọn của số thập phân là dạng viết không có mẫu số của phân số
thập phân theo quy tắc dưới đây: -
Bỏ mẫu số, đồng thời dùng dấu phẩy phân chia các chữ số của tử số
thành hai nhóm: nhóm thứ nhất đứng bên phải dấu phẩy có số chữ số bằng số chữ số 0 ở
mẫu số; nhóm thứ hai đứng bên trái dấu phẩy gồm các chữ số còn lại của tử số. -
Nếu số chữ số của tử số ít hơn hay bằng số chữ số 0 ở mẫu số thì ta
viết thêm những chữ số 0 vào trước tử số trước khi dùng dấu phẩy phân chia.
Số đứng bên trái dấu phẩy gọi là phần nguyên, nhóm các chữ số đứng bên phải
dấu phẩy gọi là phần thập phân của số đó.
Chẳng hạn, số thập phân 32,0013 có phần nguyên là 32 và phần thập phân là nhóm các chữ số 0013.
Như vậy mỗi số thập phân có hai cách biểu diễn: dạng phân số và dạng thu gọn.
III.3. Quan hệ thứ tự trong tập số thập phân không âm
Vì Q Q 1 0
nên việc so sánh hai số thập phân ta đưa về so sánh hai số hữu tỉ tương ứng. Cụ thể là:
Định nghĩa. Cho r và s là hai số thập phân. Ta nói rằng số thập phân r nhỏ hơn
hoặc bằng số thập phân s, kí hiệu là r s, nếu số hữu tỉ r nhỏ hơn hoặc bằng số hữu tỉ s.
Ví dụ 4.68.
Hãy so sánh hai số thập phân r = 9,63 và s = 12,1. 963 121 9,63 1 2,1. Ta có 100 10
Xây dựng quan hệ thứ tự trong tập số thập phân như trên có ưu điểm về phương
diện lí thuyết, nhưng có nhược điểm là cồng kềnh trong thực hành so sánh (phải đưa về
so sánh các phân số). Vì vậy khi so sánh các số thập phân ta thường sử dạng một trong hai quy tắc dưới đây: 155
Quy tắc 1. Muốn so sánh một số thập phân với một số thập phân ta làm như sau:
1) Làm cho số chữ số ở phần thập phân của chúng bằng nhau (bằng cách viết thêm
chữ số 0 vào những hàng còn thiếu);
2) Bỏ dấu phẩy, ta nhận được hai số tự nhiên;
3) So sánh hai số tự nhiên vừa nhận được, số nào lớn hơn thì số thập phân tương
ứng với nó sẽ lớn hơn. Nếu hai số tự nhiên bằng nhau thì hai số thập phân tương ứng cũng bằng nhau.
Quy tắc 2. Muốn so sánh một số thập phân với một số thập phân ta làm như sau: 1
So sánh phần nguyên với phần nguyên, số nào có phần nguyên lớn hơn sẽ lớn hơn; 2
Nếu phần nguyên của chúng bằng nhau thì ta so sánh chữ số phần mười, số nào
có chữ số phần mười lớn hơn sẽ lớn hơn; 3
Nếu chữ số phần mười của chúng cũng bằng nhau thì ta so sánh chữ số phần trăm
và cứ tiếp tục như thế cho đến khi gặp hàng lớn hơn. 4
Nếu phần nguyên và các chữ số ở phần thập phân của chúng đều bằng nhau thì hai số đó bằng nhau. Ví dụ 4.69
Hãy so sánh hai số thập phân r = 9,63 và s = 12,1.
Cách 1.Ta có 12,1 = 12,10. Vì 963 < 1210 nên 9,63 < 12,1.
Cách 2. vì 9 < 12 nên 9,63 < 12,1.
III.4. Số thập phân vô hạn tuần hoàn
Trong tập số tự nhiên N ta đã chỉ ra rằng giữa hai số tự nhiên a và số liền sau của
nó là một khoảng trống. Trong tập số hữu tỷ Q ta đó chỉ ra rằng giữa hai số hữu tỉ bất kì
luôn tồn tại vô số các số hữu tỉ khác chúng.
Định lí dưới đây khẳng định tính chất tương tự của tập số thập phân Q 10 như trong tập số hữu tỉ:
Định lí 4.32. (Về tính trù mật của tập số thập phân)
Với mọi số hữu tỉ r, với mọi số tự nhiên k tồn tại một số thập phân t sao cho: 1 1 r t r 10 k 10 k
Hay nói cách khác: mỗi số hữu tỉ r đều có thể xấp xỉ bới một số thập phân t với sai số nhỏ tùy ý. Chứng minh.
Giả sử r Q ;k N.
Theo tiên đề Ác-si-mét tồn tại số tự nhiên n sao cho r < n. Ta đặt: : 1 0k X a N a
.r . Rõ ràng là X N, X và bị chặn trên. Từ đây suy ta X M M 1 r .
có phần tử lớn nhất, kí hiệu là M. Thế thì 1 0k M
.r M 1 hay 10k 10k 10k M t Đặt 10k ta được đpcm. 156
Chú ý. Định lí 4.32 khẳng định về mặt lí thuyết sự tồn tại của số thập phân t nhưng
chưa đưa ra thuật toán để tìm số thập phân này.
Trong thực hành tính toán ta tìm t như sau: Giả sử ta phải tìm số thập phân xấp xỉ a r số hữu tỉ
b với sai số nhỏ hơn 10-k. M t
Gọi M là thương gần đúng của phép chia a.10k chia cho b. Khi đó 10k là số thập phân cần tìm.
Ví dụ 4.70. 7 r
1) Hãy xấp xỉ số hữu tỉ
11 bởi một số thập phân với sai số nhỏ hơn 10-5 .
Giải: Ta chia 7.10 5cho 11 được thương là 63636 (dư 4). Vậy số thập phân cần tìm là 0,63636. 43 r
2) Hãy xấp xỉ số hữu tỉ
22 bởi một số thập phân với sai số nhỏ hơn 10-3.
Giải: Ta chia 43.10 3cho 22 được thương là 1954 (dư 12). Vậy số thập phân cần tìm là 1,954. a r
Trong các tiết trước, ta đó biết rằng mỗi số phân số tối giản b có hai khả năng:
- Nếu mẫu số b không chứa ước nguyên tố nào khác 2 và 5 thì r là một số thập phân;
- Nếu mẫu số b có chứa ước nguyên tố khác cả 2 và 5 thì r không phải là số thập
phân. Trong trường hợp này, theo định lí 4.32 thì r có thể xấp xỉ bởi một số thập phân với sai số nhỏ tùy ý.
Trong tiết này, chúng ta chỉ ra rằng những số hữu tỉ như thế có thể biểu diễn bởi
một số “thập phân” theo nghĩa rộng. 13 r
Trước hết ta bắt đầu bằng một bài toán cụ thể: Hãy xấp xỉ phân số 11 bởi các
số thập phân với những sai số khác nhau. Vận dụng phương pháp tiến hành ở phần trên ta được các kết quả sau: 1
- Nếu sai số không vượt quá 100 thì ta được số 1,18; 1
- Nếu sai số không vượt quá 10000 thì ta được số 1,1818;
- Nếu sai số không vượt quá 6
10 thì ta được số 1,181818; - …
Cứ tiếp tục quá trình trên đây ta đi đến kết quả sau: 13.
- Không bao giờ nhận được một số thập phân bằng 11 157
- Cứ tiếp tục mãi quá trình trên đây ta nhận được số “thập phân” có vô số chữ số ở phần thập phân.
- Các chữ số ở phần thập phân sẽ lặp lại một cách tuần hoàn có chu kì bằng 18. Trong
trường hợp này ta viết: 13 13 1 ,181818... 1 ,(18) 11 hay 11
và gọi là số thập phân vô hạn tuần hoàn” với chu kì bằng 18. 855 r .
Tiếp theo ta xét bài toán tương tự đối với phân số
22 Lập luận tương tự như
trên ta nhận được kết quả sau:
- Nếu sai số không vượt quá 10-3 ta được số thập phân 38,863;
- Nếu sai số không vượt quá 10-5 ta được số thập phân 38,86363;
- Nếu sai số không vượt quá 10-7 ta được số thập phân 38,8636363. 855 3 8,8636363... Vậy 22
Ta nhận được số thập phân vô hạn tuần hoàn nhưng chu kì (là 63) không bắt đầu ngay sau
dấu phẩy mà bắt đầu từ chữ số thập phân thứ hai. Những số như thế, ta gọi là số thập
phân vô hạn tuần hoàn tạp. Trong trường hợp này ta viết: r = 38,9(63) a
Một cách tổng quát: giả sử phân số b không phải là số thập phân. Ta thực hiện
liên tiếp các phép chia a cho b (bằng cách thêm chữ số 0 vào bên phải số dư sau mỗi bước
chia và tiếp tục chia) ta sẽ gặp lại số dư r nào đó mà đã gặp trong bước chia trước đó. Khi
đó quá trình sẽ lặp lại vì vậy các chữ số ở thương cũng sẽ lặp lại một cách tuần hoàn. Số
thập phân nhận được có vô số chữ số ở phần thập phân, trong đó có một nhóm chữ số lặp
đi lặp lại một cách tuần hoàn. Nhóm chữ số lặp lại đó là thương bộ phận giữa hai số dư
bằng nhau gọi là chu kì của số thập phân vô hạn tuần hoàn đó. Nếu chu kì bắt đầu ngay
sau dấu phẩy thì gọi là số thập phân vô hạn tuần hoàn đơn, ngược lại, gọi là số thập
phân vô hạn tuần hoàn tạp.
III.5. Nội dung dạy học số thập phân ở Tiểu học
Trong chương trình môn Toán tiểu học, nội dung về số thập phân được trình bày
trong môn toán lớp 5. Nó bao gồm các nội dung sau:
- Hình thành khái niệm số thập phân;
- So sánh các số thập phân;
- Các phép tính về số thập phân;
- Giải toán về số thập phân.
III.5.1. Hình thành khái niệm số thập phân ở Tiểu học
Khái niệm về số thập phân trong môn toán lớp 5 bao gồm các nội dung sau: -
Hình thành khái niệm số thập phân; -
Giới thiệu cách đọc, viết và nhận biết cấu tạo của một số thập phân; -
Giới thiệu các hàng của một số thập phân; -
Dùng số thập phân để biểu diễn các số đo đại lượng. 158
Chẳng hạn: thông qua các thao tác cụ thể, khái niệm “số thập phân” được hình
thành cho học sinh theo hai con đường:
- Số thập phân là cách viết không có mẫu số của phân số thập phân, chẳng hạn: 1 8 1024 0 ,1; 0 ,08; 1 ,024;... 10 100 1000
- Số thập phân là cách biểu diễn các số đo đại lượng (từ nhiều đơn vị đo về một
đơn vị đo hoặc từ đơn vị đo nhỏ hơn về đơn vị đo lớn hơn), chẳng hạn:
3m 7dm = 3,7m; 12m = 0,012km; 3kg 50g = 3,050kg;
2 tấn 35kg = 2,035 tấn; 458cm = 0,0458m 2 2 ;…
Từ các khái niệm trên, ta chốt lại cho học sinh:
- Cấu tạo của một số số thập phân gồm: phần nguyên là số tự nhiên đứng bên trái
dấu phẩy và phần thập phân là nhóm các chữ số đứng bên phải dấu phẩy. Giữa phần
nguyên và phần thập phân được phân cách nhau bởi dấu phẩy. Chẳng hạn số 12,045 có
phần nguyên là 12, phần thập phân là 045 và đọc là mười hai phẩy không bốn năm.
- Từ cấu tạo của số thập phân, ta hình thành khái niệm các hàng phần mười, phần
trăm, phần nghìn của số thập phân. Chẳng hạn, số thập phân 12,045 có chữ số hàng phần
mười là 0, hàng phần trăm là 4 và hàng phần nghìn là 5.
III.5.2. Quan hệ so sánh các số thập phân ở Tiểu học
Tương tự như đối với phân số, khi so sánh hai số thập phân ta hướng tới hai tình huống:
- Số này lớn hơn hoặc bé hơn số kia;
- Rút ra kết luận hai số đó bằng nhau.
Thông qua phép đo đại lượng (độ dài) ta đưa việc so sánh các số thập phân về so
sánh các số tự nhiên (mà học sinh đó thành thạo trước đó). Cụ thể là: từ bài toán “So sánh
35,7m và 35,698m” ta lần lượt đưa ra nhận xét:
- Phần nguyên của chúng bằng nhau (đều bằng 35m); 7 m 7 00mm
- Phần thập phân của 35,7m là 10
; phần thập phân của 35,698m là 698 7 698 m 6 98mm m m 100 . Vì 700mm > 698mm nên 10 1000 . Do đó 35,7m > 35,698m.
Từ đây ta rút ra quy tắc: Muốn so sánh hai số thập phân ta làm như sau:
a) So sánh phần nguyên của hai số đó. Số nào có phần nguyên lớn hơn sẽ lớn hơn;
b) Nếu phần nguyên của chúng bằng nhau thì so sánh phần thập phân, lần lượt từ
hàng phần mười, phần trăm, phần nghìn,…, đến cùng một hàng nào đó, số thập phân
nào có chữ số ở hàng tương ứng lớn hơn sẽ lớn hơn.
c) Nếu phần nguyên và các chữ số ở phần thập phân của hai số đó bằng nhau thì
hai số đó bằng nhau.
Đồng thời, sách giáo khoa cũng rút ra quy tắc: Nếu viết thêm (hoặc xóa đi) chữ số
0 ở cuối phần thập phân của một số thập phân thì ta được một số thập phân bằng nó. 159
III.5.3. Xây dựng các phép toán trong tập số thập phân ở Tiểu học
Các phép trong tập số thập phân được trình bày trong môn Toán lớp 5 theo năm bước:
1) Từ các bài toán thực tế hình thành ý nghĩa của mỗi phép toán;
2) Hình thành quy tắc thực hành mỗi phép toán (cộng, trừ, nhân và chia các số thập phân);
3) Giới thiệu tính chất của các phép tính về số thập phân;
4) Giới thiệu các quy tắc tính nhẩm: nhân, chia nhẩm với 10; 100; 1000; …
5) Rèn kĩ năng thực hành các phép tính. Cụ thể là:
- Từ bài toán về cộng độ dài hai đoạn thẳng, SGK hình thành ý nghĩa và quy tắc
thực hành phép cộng hai số thập phân;
- Cũng tương tự như vậy đối với phép trừ;
- Từ một bài toán thực tế về tính chu vi một hình tam giác có ba cạnh bằng nhau,
SGK hình thành ý nghĩa và quy tắc thực hành phép nhân các số thập;
- Phép chia các số thập phân được giới thiệu qua các bước:
+ Chia một số thập phân cho một số tự nhiên;
+ Chia một số tự nhiên cho một số tự nhiên có thương là số thập phân;
+ Chia một số tự nhiên cho một số thập phân;
+ Chia một số thập phân cho một số thập phân.
Ở mỗi bước đều xuất phát từ một bài toán thực tế về số đo đại lượng đọ dài.
- Các tính chất (giao hoán, kết hợp, phân phối, nhân một số với một tổng, …) của
các phép toán về số thập phân được suy ra trực tiếp từ các tính chất tương ứng của các
phép toán trên tập số tự nhiên thông qua phép suy luận tương tự (trong các tiết luyện tập).
III.5.4. Giải toán về số thập phân ở Tiểu học
Các bài toán về số thập phân ở Tiểu học có thể phân chia thành bốn dạng:
Dạng 1. Toán về cấu tạo số thập phân;
Dạng 2. Toán về so sánh số thập phân;
Dạng 3. Toán về các phép toán trên số thập phân;
Dạng 4. Toán về tỉ số phần trăm;
Dưới đây ta minh hoạ ví dụ cho từng dạng toán.
Dạng 1. Toán về cấu tạo số thập phân
Ví dụ 4.71.
Viết các số sau đây dưới dạng số thập phân: 7 123 ) a ; ) b ; 100 10 9 ) c . 40 Giải: 160 7 ) a 0 ,07; 100 123 ) b 1 2,3; 10 9 225 ) c 0 ,225. 40 1000 Ví dụ 4.72.
Viết các số đo dưới đây dưới dạng số thập phân:
a) 25dm 5cm với đơn vị là mét;
b) 70g với đơn vị là ki-lô-gam;
c) 5dm2 8cm2 với đơn vị là mét vuông;
d) 2m2 5cm2 với đơn vị là đề-xi-mét vuông. Giải: 255 ) a 25d 5 m cm cm 2 ,55m 100 70 ) b 70 g kg 0 ,070 k ; g 1000 508 2 2 2 2 )
c 5dm 8cm m 0,0508m ; 10000 20005 2 2 2
d)2 m 5 cm 2 ,0005m . 10000
Ví dụ 4.73.
Cho ba chữ số 0, 1, 2. Hãy viết tất cả các số thập phân có ba chữ số ở cả phần
nguyên và phần thập phân nhỏ hơn 20 sao cho mỗi chữ số đã cho xuất hiện trong cách viết đúng 1 lần. Giải:
Các số thập phân cần tìm là: 0,12 0,21; 1,02; 1,20; 2,01; 10, 2; 2,10; 12,0.
Ví dụ 4.74.
Các chữ số phần mười và phần trăm của một số thập phân có hai chữ số ở phần
thập phân là hai số chẵn liên tiếp viết theo thứ tự tăng dần. Tích các chữ số ở phần thập
phân bằng phần nguyên của số đó. Các chữ số ở cả phần nguyên và phần thập phân đều
khác nhau. Tìm số thập phân đó.
Giải: Phần thập phân của số thập phân cần tìm có thể là: 02; 24; 46; 68. Ta có bảng sau: 161 Phần thập phân Phần nguyên Số thập phân Kết luận 02 0 0,02 Loại 24 8 8,24 Chọn 26 24 24,64 Loại 68 48 48,68 Loại
Số thập phân cần tìm là 8,24.
Dạng 2. Toán về so sánh số thập phân
Ví dụ 4.75.
Viết các số thập phân sau:
a) 5,90; 8,293; 9,029; 4,94 theo thứ tự từ bé đến lớn;
b) 72,037; 72,730; 72, 703; 72,307 theo thứ tự từ lớn đến bé. Giải:
a) Các số đã cho viết theo thứ tự từ bé đến lớn là: 4,94; 5,90; 8,293; 9,029.
b) Các số đã cho viết theo thứ tự từ lớn đến bé là:
72,730; 72,703; 72,307; 72,037.
Ví dụ 4.76.
Viết 5 số thập phân nằm giữa hai số 2,5 và 2,6. Giải:
Các số thập phân cần tìm là: 2,51; 2,52; 2,53; 2,54; 2,55.
Ví dụ 4.77. Thay a bởi chữ số thích hợp để: 0,46 < 0.4a6 < 0,485 Giải:
- Để 0,46 < 0,4a6 thì a = 6, 7, 8 hoặc 9;
- Để 0,4a6 < 0,485 thì a = 1, 2, 3, 4, 5, 6 hoặc 7;
- Từ đó suy ra để 0,46 < 0,4a6 < 0,485 thì a = 6 hoặc 7.
Dạng 3. Toán về các phép toán trên số thập phân
Ví dụ 4.78. Tìm y: a) 51,42 – y = 3,45 : 0,12 b) 8,064 x y = 2,4 : 0,25 c) y : 5,6 = 0,8 x 2,25 d) 2,85 : y = 1,4 – 0,65 Giải:
a) 51,42 – y = 3,45 : 0,12 = 28,75 y = 51,42 – 28,75 = 22,67. b) 8.064 x y = 2,4 : 0,25 = 9,6 y = 8,064 : 9,6 = 0,84 c) y : 5,6 = 0,8 x 2,25 = 1,8 y = 1,8 x 5,6 = 10,08 162 d) 2,85 : y = 1,4 – 0,65 = 0,75 y = 2,85 : 0,75 = 3,8.
Ví dụ 4.79. Cho: (x 4, 25) : 0,5 A (5,25 4,75) 2 ,5 a) Tìm A, khi x = 5; b) Tìm x để A = 12.
Giải: a) Thay x = 5 ta có: (5 4,25) : 0,5 9,25 : 0,5 18,5 A 1 4,8. (5, 25 4,75) 2 ,5 0,5 2 ,5 1, 25 b) Khi A = 12 ta có (x 4, 25) : 0,5 12 (5, 25 4,75) 2 ,5 (x 4, 25) : 0,5 12 0,5 2, 5 (x 4,75) : 0,5 12 1, 25 (x 4,75) : 0,5 12 1 , 25 (x 4,75) : 0,5 15 x 4,75 15 0, 5 x 4,75 7, 5 x 7,5 4,75 x 2,75.
Ví dụ 4.80.
Tính giá trị biểu thức sau bằng cách hợp lí nhất: 0, 2 213 7 0,14 2460 54,1 14 ) a ;
1 4 7 ... 64 365 (213, 78 43,75 0, 37) ( 49,6 : 0, 25 24,8 8 ) ) b . 5,13 2, 45 12,48 : 0,75 Giải: a) Ta có:
0,2 x 213 x 7 + 0,14 x 2460 + 54,1 x 14
= 1,4 x 213 + 1,4 x 246 + 541 x 1,4
= 1,4 x (213 + 246 + 541) = 1,4 x 1000 = 1400.
Tiếp theo ta tính giá trị của biểu thức ở mẫu: 1 + 4 + 7 + … + 64 là tổng các số
hạng của dãy số cách đều có số hạng đầu bằng 1, số hạng cuối bằng 64, khoảng cách
bằng 3 và số số hạng của dãy số đó là:
(64 – 1) : 3 + 1 = 22 (số hạng) 163
Giá trị của biểu thức ở mẫu là:
(1 + 64) x 22 : 2 – 365 = 350.
Giá trị của biểu thức đã cho là: 1400 4. 350 b) Ta nhận xét:
49,6 : 0,25 – 24,8 x 8 = 49,6 x 4 – 49,6 x 4 = 0.
Vậy giá trị cuả biểu thức đã cho bằng 0.
Ví dụ 4.81.
Tìm một số thập phân, biết rằng khi chia số đó cho 2 rồi trừ đi 1,8 sau đó nhân với
2,5 ta được kết quả bằng 37,5. Giải:
Số trước khi nhân với 2,5 là: 37,5 : 2,5 = 15
Số trước khi bớt đi 1,8 là: 15 + 1,8 = 16,8 Số cần tìm là: 16,8 x 2 = 33,6.
Ví dụ 4.82.
Thay mỗi chữ trong phép tính sau bởi chữ số thích hợp để được phép tính đúng: ) a 8 , a ba 1 c , 4 d 4 d ,1 ; c )
b 13, ab: 2,6 , a . b Giải:
a) Ta viết lại phép tính như sau: 8 a , b a + c 1 , 4 d d 4, 1 c
Theo kết quả phép tính thì phép cộng chữ số hàng chục không nhớ, suy ra phép
cộng chữ số hàng chục chỉ có thể là: 8 + 1 = 9. Vậy c = 1 và d = 9.
Thay vào phép tính ta sẽ tìm được a = 2 và b = 6.
Thay vào ta được phép tính cần tìm là: 82,62 11, 49 9 4,11.
b) Ta viết lại phép tính như sau: 13,ab = a,b x 2,6 hay 13 + 0,ab = 0,ab x 26 0,ab x 26 – 0,ab = 13 0,ab x (26 – 1) = 13 0,ab x 25 = 13
0,ab = 13 : 25 = 0,52 suy ra a = 5 và b = 2.
Thay vào ta được phép tính cần tìm là: 13,52 : 2,6 = 5,2 164
Dạng 4. Toán về tỉ số phần trăm Ví dụ 4.83.
Lớp 5A có 40 học sinh, trong đó có 22 học sinh nữ. Hỏi số học sinh nữ chiếm bao
nhiêu phần trăm của cả lớp? Giải:
Tỉ số phần trăm học sinh nữ của lớp 5A là: 22 : 40 = 0,55 0,55 = 55% Đáp số: 55%
Ví dụ 4.84.
Lãi suất tiết kiệm 0,65%/tháng. Cô Thu gửi tiết kiệm 80 000 000 đồng. Hỏi sau
một tháng cô được bao nhiêu tiền lãi? Giải:
Số tiền lãi của cô Thu sau một tháng là:
80000000 : 100 x 0,65 = 520 000 (đồng) Đáp số: 520 000 đồng
Ví dụ 4.85.
Trong kho có 60 tấn gạo nếp. Số gạo nếp chiếm 15% tổng số gạo trong kho. Hỏi
trong kho có tất cả bao nhiêu tấn gạo? Giải:
Tổng số gạo trong kho là: 60 : 15 x 100 = 400 (tấn) Đáp số: 400 tấn gạo
Ví dụ 4.86.
Một người bán chiếc quạt với giá 200 000 đồng thì được lãi 10% trong giá bán.
Hỏi để lãi 15% giá gốc thì người đó phải bán chiếc quạt với giá bao nhiêu tiền? Giải:
Lãi 10% trong giá bán có nghĩa là: Nếu ta coi giá bán là 100% thì tiền lãi chiếm 10%, tiền gốc chiếm 90%.
Giá gốc của chiếc quạt đó là:
200000 : 100 x 90 = 180000 (đồng)
Lãi 15% giá gốc có nghĩa là: Nếu ta coi giá gốc là 100% thì tiền lãi bằng 15% và giá bán bằng 115%.
Để lãi 15% giá gốc thì người đó phải bán chiếc quạt với giá là:
180000 : 100 x 115 = 207000 (đồng) Đáp số: 207 000 đồng
Ví dụ 4.87.
Khi tăng bán kính của một hình tròn thêm 10% thì diện tích hình đó sẽ tăng thêm bao nhiêu phần trăm? Giải: Theo đề bài ta có: 165 110 11 R R cu cu ; 100 10 11 11 S R R 3 ,14 R R 3 ,14 moi moi moi 10 cu 10 cu 121 R R S cu cu 3,14 121% cu. R 100 mới = 110% Rcũ =
Diện tích hình tròn đó sẽ tăng: 121% - 100% = 21% Đáp số: 21% BÀI TẬP CHƯƠNG 4 166 Chương V
Cơ sở toán học của các phương pháp giải toán ở Tiểu học
I. Phương trình bậc nhất và các phương pháp giải toán: tính ngược từ cuối, phương
pháp ứng dụng đồ thị và phương pháp đại số
I.1. Biểu thức toán học
Biểu thức toán học là một cách kí hiệu chỉ rõ các phép toán và thứ tự thực hiện các
phép toán đó trên các số hoặc các chữ nhận giá trị từ một tập hợp số T cho trước. Các số
hoặc các chữ nhận giá trị xác định gọi là hằng số, các chữ nhận giá trị biến đổi (thuộc tập T) gọi là biến số.
Tập các giá trị của biến số thuộc tập T, khi thay vào làm cho biểu thức toán học có
nghĩa ta gọi là miền xác định của biểu thức đó.
Căn cứ vào các phép toán xuất hiện trong biểu thức, người ta phân chia biểu thức
toán học thành: biểu thức nguyên (đa thức), phân thức, biểu thức đại số, biểu thức vô tỉ,
biểu thức mũ, biểu thức lô-ga-rit, biểu thức lượng giác. Chẳng hạn: F(x) = 4x5 + 2x4 – 5x + x 3 – 12x + 1 2 là đa thức bậc 5; 3 2 x x 2 G(x) = 2 x 1 là phân thức đại số; H(x) = x 1 x2 2 3 2 là biểu thức mũ; ……… I.2. Phương trình
Cho f(x) và g(x) là hai biểu thức toán học với miền xác định là Df và D gtương ứng. Ta gọi quan hệ: f(x) = g(x) (1)
là một phương trình với miền xác định là D D D f g .
Trong đó f(x) gọi là vế trái và g(x) gọi là vế phải của phương trình (1).
Mỗi giá trị a D khi thay vào ta được giá trị của hai vế của phương trình bằng nhau: f(a) = g(a)
Tập tất cả các nghiệm của phương trình (1) ta kí hiệu là S.
Công việc đi tìm tập S gọi là giải phương trình.
Nếu tập S chỉ có một phần tử thì ta nói phương trình (1) có duy nhất một nghiệm,
nếu tập S có k phần tử thì ta nói phương trình (1) có k nghiệm phân biệt; nếu S là tập vô
hạn thì ta nói phương trình (1) có vô số nghiệm; nếu S là tập rỗng thì ta nói phương trình (1) vô nghiệm.
I.3. Phương trình tương đương 167 Cho f1(x) = g1(x) (1) và f2(x) = g2(x) (2)
là hai phương trình với tập hợp nghiệm là S1 và S tương ứng. 2
Ta nói rằng phương trình (1) tương đương với phương trình (2), kí hiệu là (1) (2), nếu S1 = S2.
Hay nói cách khác: hai phương trình gọi là tương đương nếu nó có cùng tập nghiệm.
Khi giải phương trình, người ta bắt đầu từ những phương trình đơn giản. Sau đó
khi gặp những phương trình mới phức tạp hơn người ta sẽ biến đổi để đưa về những
phương trình đã biết cách giải trước đó.
Một câu hỏi đặt ra là: Liệu trong quá trình biến đổi như thế có làm thay đổi tập
nghiệm (làm mất nghiệm hoặc sinh thêm nghiệm mới) của phương trình đã cho? Hay nói
cách khác: Những phép biến đổi như thế nào sẽ không làm thay đổi tập hợp nghiệm (ta
gọi là phép biến đổi tương đương các phương trình)?
Các định lí dưới đây giúp ta trả lời câu hỏi đó.
Định lí 5.1. Cho f(x) = g(x) (1)
là một phương trình với miền xác định D và h(x) là một biểu thức xác định trên miền D.
Khi đó, phương trình (1) tương đương với phương trình: f(x) + h(x) = g(x) + h(x) (1 ) h
Hay nói cách khác: Nếu ta cộng hoặc trừ cả hai vế của một phương trình với cùng
biểu thức xác định trên miền xác định của phương trình đã cho thì ta nhận được một
phương trình mới tương đương với phương trình đã cho.
Chứng minh. Đơn giản. Ví dụ 5.1. Phương trình: x2 – 5x + 4 = 0
tương đương với phương trình:
2x2 – 4x + 1 = x2 – x – 3
Định lí 5.2. Cho f(x) = g(x) (1)
là một phương trình với miền xác định D và k(x) là một biểu thức xác định trên miền D. Khi đó:
Phương trình (1) tương đương với phương trình: f(x)k(x) = g(x)k(x) (1k)
Hay nói cách khác: Nếu ta nhân hoặc chia cả hai vế của một phương trình với
cùng biểu thức xác định và khác không trên miền xác định của phương trình đã cho thì ta
nhận được một phương trình mới tương đương với phương trình đã cho.
Chứng minh. Đơn giản.
Ví dụ 5.2. Phương trình: x2 – 5x + 4 = 0 168
tương đương với phương trình: x4 – 5x3 + 5x – 5x + 4 = 0 2 Thật vậy, vì x – 5x 4
3 + 5x2 – 5x + 4 = ( x2 – 5x + 4)(x + 1). 2
I.4. Phương trình bậc nhất
Phương trình bậc nhất là một phương trình sau một số phép biến đổi tương đương ta đưa được về dạng:
ax + b = 0, trong đó a 0 . (1)
Phương trình bậc nhất (1) có duy nhất một nghiệm là: b x a Chẳng hạn, phương trình 3x – 2 = x + 4 Có nghiệm là: x = 3
Từ cách giải phương trình bậc nhất ta hình thành một số phương pháp giải toán ở Tiểu học:
I.5. Phương trình bậc nhất và phương pháp tính ngược từ cuối
Ví dụ 5.3.
Tìm một số, biết rằng khi bớt số đó đi 3 sau đó chia cho 2 rồi cộng với 1,5, cuối
cùng nhân với 4 được kết quả bằng 40.
Dùng kiến thức về giải phương trình bậc nhất, ta giải bài toán như sau: Gọi số cần tìm là x;
Khi bớt số đó đi 3 ta có: x – 3;
Khi chia cho 2 ta được: (x-3) : 2
Khi cộng với 1,5 ta được: (x – 3) : 2 + 1,5;
Khi nhân với 4 ta được: [(x – 3) : 2 + 1,5] x 4;
Theo đề bài ta có phương trình: [(x – 3) : 2 + 1,5] x 4 = 40 Giải ra ta được x = 20.
Ở Tiểu học, chưa có khái niệm về phương trình và giải phương trình, vận dụng các
quy tắc về tìm thành phần chưa biết của phép tính, ta giải bài toán như sau:
Số trước khi nhân với 4 là: 40 : 4 = 10
Số trước khi cộng với 1,5 là: 10 – 1,5 = 8,5
Số trước khi chia cho 2 là: 8,5 x 2 = 17 Số cần tìm là: 17 + 3 = 20
Cách giải trên đây ta gọi là phương pháp tính ngược từ cuối.
Chú ý. 1. Cơ sở toán học của phương pháp tính ngược từ cuối là các quy tắc tìm
thành phần chưa biết của phép tính. 169
2. Các bài toán về tính ngược từ cuối có thể ra cho học sinh từ lớp 2. Ở mỗi lớp
cần phù hợp với vòng số và kĩ năng tính toán của lớp đó.
3. Phương pháp tính ngược từ cuối không chỉ dùng để giải toán số học mà còn
dùng để giải các bài toán có lời văn. Ví dụ 5.4.
Dì út đi chợ bán trứng. Lần thứ nhất bán một nửa số trứng thêm nửa quả, lần thứ
hai bán một nửa số trứng còn lại thêm nửa quả thì còn lại hai chục trứng. Hỏi dì Út đã
mang bao nhiêu trứng ra chợ bán? Giải:
Số trứng còn lại sau lần bán thứ nhất là:
2 chục trứng = 20 quả trứng ½ quả 20 quả ? quả 1 (20 ) 2 41 2 (quả)
Số trứng lúc đầu dì Út mang ra chợ bán là: ½ quả 41 quả ? quả 1 (41 ) 2 8 3 2 (quả) Đáp số: 83 quả trứng
I.6. Phương trình bậc nhất và phương pháp ứng dụng đồ thị
Ví dụ 5.3 có thể giải cho học sinh tiểu học bằng cách khác như sau:
Theo đề bài ta có sơ đồ: - 3 : 2 + 1,5 x 4 ? 40
Dựa vào sơ đồ ta có số cần tìm là: (40 : 4 – 1,5) x 2 + 3 = 20
Cách giải như trên ta gọi là phương pháp ứng dụng đồ thị. Hình vẽ trên ta gọi là
đồ thị của bài toán.
I.7. Phương trình bậc nhất và phương pháp đại số
Ví dụ 5.3 còn có thể giải bằng cách sau: 170 Gọi số cần tìm là x; Theo đề bài ta có: ((x – 3) : 2 + 1,5) x 4 = 40
(x – 3) : 2 + 1,5 = 40 : 4 (tìm thừa số trong phép nhân) 10
(x – 3) : 2 = 10 – 1,5 (tìm số hạng trong phép cộng) 8,5
x – 3 = 8,5 x 2 (tìm số bị chia) 17
x = 17 + 3 (tìm số bị trừ) x = 20
Cách giải như trên ta gọi là Phương pháp đại số hay còn gọi là phương pháp dùng chữ thay số.
Chú ý. Ở Ttiểu học, nói chung người ta hạn chế dùng phương pháp đại số.
II. Hệ phương trình bậc nhất hai ẩn II.1. Định nghĩa.
Hệ phương trình bậc nhất hai ẩn là một hệ phương trình sau một số phép biến đổi
tương đương ta đưa được về dạng: ax + by = c a’x + b’y = c’
trong đó các hệ số a, a’, b, b’ không đồng thời bằng 0.
II.2. Phương pháp giải hệ phương trình bậc nhất
a) Phương pháp khử:
Ví dụ 5.5. Giải hệ phương trình: 3x – 5y = 4 (1) 4x + 3y = 15 (2) Giải:
Nhân cả 2 vế của phương trình (1) với 4 và phương trình (2) với 3 ta được: 12x – 20y = 16 (3) 12x + 9y = 45 (4)
Trừ vế với vế của phương trình (4) cho phương trình (3) ta được: 29y = 29 y = 1.
Thay vào phương trình (1) ta được x = 3. b) Phương pháp thế
Từ phương trình (1) ta tính được: 5y 4 x (3) 3
Thay vào (3) phương trình (2) ta được: 5y 4 4 3y 1 5 3 20y + 16 +9y = 45 171 y = 1
Thay vào (3) ta được x = 3.
c) Phương pháp định thức Ta có: 3; 5 D 3.3 4.( 5)29; 4;3 4; 5 D 4. 3 15.( 5) 87; x 15;3 3;4 D 3. 15 4.4 29. y 4;15 Từ đây ta được: D D x x 3; y y 1 . D D
Từ cách giải hệ phương trình bậc nhất ta hình thành một số phương pháp giải toán ở Tiểu học: x+y=t
II.3. Hệ phương trình bậc nhất dạng: x y h
và phương pháp giải toán về tìm hai
số biết tổng và hiệu của chúng
Ví dụ 5.6.
Tổng của hai số bằng 60, hiệu của chúng bằng 10. Tìm hai số đó.
Trước hết ta dùng phương pháp toán sơ cấp giải bài toán trên:
Gọi số thứ nhất là x, số thứ hai là y. Theo đề bài ta có hệ phương trình: x + y = 60 (1) x – y = 10 (2) Cách 1.
Cộng vế với vế của (1) và (2) ta được: 2x = 70 x = 70 : 2 x = 35
Thay vào (1) ta được: y = 60 – 35 y = 25.
Vậy hai số cần tìm là 35 và 25. Cách 2.
Trừ vế với vế của (1) và (2) ta được: 2y = 50 y = 50 : 2 y = 25
Thay vào (1) ta được: x = 60 – 25 x = 35.
Vậy hai số cần tìm là 35 và 25. 172
Từ hai cách giải trên, ta diễn giải thành phương pháp giải cho học sinh tiểu học như sau: Cách 1.
Theo đề bài ta có sơ đồ: ? Số thứ nhất: Số thứ hai: 60 ? 10
Giả sử số thứ hai tăng thêm 10 đơn vị, như vậy ta được hai số bằng nhau và bằng số lớn.
Hai lần số lớn là: 60 + 10 = 70 Số lớn là: 70 : 2 = 35 Số bé là: 60 – 35 = 25
Trả lời: Hai số cần tìm là: 35 và 25.
Từ đây ta rút ra công thức:
Số lớn = (Tổng + Hiệu) : 2 Cách 2.
Theo đề bài ta có sơ đồ: ? Số thứ nhất: 60 Số thứ hai: 10 ?
Giả sử số thứ nhất giảm bớt 10 đơn vị, như vậy ta được hai số bằng nhau và bằng số bé.
Hai lần số bé là: 60 – 10 = 50 Số bé là: 50 : 2 = 25 Số lớn là: 60 – 25 = 35
Trả lời: Hai số cần tìm là: 35 và 25.
Từ đây ta rút ra công thức:
Số bé = (Tổng – Hiệu) : 2
Ở Tiểu học, hai cách giải trên đây ta gọi là phương pháp thế để giải bài toán về
tìm hai số khi biết tổng và hiệu của chúng. Ví dụ 5.6a.
Chú Tư thu hoạch trên hai thửa ruộng được 18 tạ thóc, trong đó thửa thứ nhất thu
hoạch được nhiều hơn thửa thứ hai 4 tạ. Hỏi chú thu hoạch trên mỗi thửa ruộng được bao nhiêu tạ thóc?
Trước hết ta dùng phương pháp toán sơ cấp giải bài toán trên: 173
Gọi số thóc thu hoạch được trên thửa ruộng thứ nhất là x và thửa ruộng thứ hai là
y. Theo đề bài ta có hệ phương trình: x + y = 18 (1) x – y = 4 (2) Cách 1.
Cộng vế với vế của (1) và (2) ta được: 2x = 22 x = 22 : 2 x = 11 Thay vào (1) ta được: y = 18 – 11 y = 7
Trả lời: Chú Tư thu hoạch trên thửa thứ nhất được 11 tạ thóc và trên thửa thứ hai được 7 tạ thóc. Cách 2.
Trừ vế với vế của (1) và (2) ta được: 2y = 14 y = 14 : 2 y = 7 Thay vào (1) ta được: x = 18 – 7 x = 11
Trả lời: Chú Tư thu hoạch trên thửa thứ nhất được 11 tạ thóc và trên thửa thứ hai được 7 tạ thóc.
Từ hai cách giải trên, ta diễn giải thành phương pháp giải cho học sinh tiểu học như sau:Cách 1:
Số thóc thu hoạch trên thửa ruộng thứ nhất là: (18 + 4) : 2 = 11(tạ)
Số thóc thu hoạch trên thửa ruộng thứ hai là: 18 – 11 = 7(tạ)
Đáp số: Thửa thứ nhất: 11 tạ; Thửa thứ hai: 7 tạ Cách 2:
Số thóc thu hoạch trên thửa ruộng thứ hai là: (18 – 4) : 2 = 7(tạ)
Số thóc thu hoạch trên thửa ruộng thứ hai là: 18 – 7 = 11(tạ)
Đáp số: Thửa thứ nhất: 11 tạ; Thửa thứ hai: 7 tạ
Ở Tiểu học, hai cách giải trên đây ta gọi là phương pháp thế để giải bài toán về
tìm hai số khi biết tổng và hiệu của chúng. 174 x y =s
II.4. Hệ phương trình bậc nhất dạng: ax by 0
và phương pháp chia tỉ lệ
Ví dụ 5.7. 2
Tổng của hai số bằng 84, trong đó số thứ nhất bằng 5 số thứ hai. Tìm hai số đó.
Trước hết ta dùng phương pháp toán sơ cấp giải bài toán trên:
Gọi số thứ nhất là x, số thứ hai là y. Theo đề bài ta có hệ phương trình: x + y = 84 (1) 2 y x = 5 (2) Thay (2) vào (1) ta được: 2y + 5y = 84 . 5 7y = (84 : 7) . 5 y = 60
Thay vào (1) ta được: x = 84 – 60 x = 24.
Vậy hai số cần tìm là 24 và 60.
Từ cách giải trên, ta diễn giải thành phương pháp giải cho học sinh tiểu học như sau:
Theo đề bài ta có sơ đồ: ? Số thứ nhất: 84 Số thứ hai: ?
Tổng số phần bằng nhau là: 2 + 5 = 7 (phần)
Giá trị của một phần là: 84 : 7 = 12
Số thứ hai là: 12 x 5 = 60
Số thứ nhất là: 12 x 2 = 24
Trả lời: Hai số cần tìm là: 24 và 60.
Ở Tiểu học, cách giải trên đây ta gọi là phương pháp chia tỉ lệ để giải bài toán về
tìm hai số khi biết tổng và tỉ số của chúng.
Ví dụ 5.7a. 175
Hai đội vận tải được giao vận chuyển 480 tấn hàng. Số hàng của đội Hai vận 5
chuyển được bằng 3 số hàng của đội Một. Hỏi mỗi đội đã vận chuyển được bao nhiêu tấn hàng?
Trước hết ta dùng phương pháp toán sơ cấp giải bài toán trên:
Gọi số hàng của đội Một vân chuyển được là x và đội Hai là y. Theo đề bài ta có hệ phương trình: x + y = 480 (1) 5 x y = 3 (2)
Thay (2) vào (1) ta được: 3x + 5x = 480 . 3 8x = 480 . 3 x = (480 : 8) . 3 x = 180 thay vào (1) ta được: y = 480 – 180 y = 300
Trả lời: Đội thứ nhất vận chuyển được 180 tấn hàng, đội thứ Hai vận chuyển được 300 tấn hàng.
Từ cách giải trên, ta diễn giải thành phương pháp giải cho học sinh tiểu học như sau:
Theo đề bài ta có sơ đồ: ? tấn Đội 1: 480 tấốn Đội 2: ? tấốn
Tổng số phần bằng nhau là: 3 + 5 = 8 (phần)
Giá trị của một phần bằng nhau là: 480 : 8 = 60 (tấn)
Số hàng của đội Một vận chuyển được là: 60 x 3 = 180 (tấn)
Số hàng của đội Hai vận chuyển được là: 480 – 180 = 300 (tấn)
Đáp số: Đội Một: 180 tấn hàng; Đội Hai: 300 tấn hàng
Ở Tiểu học, cách giải trên đây ta gọi là phương pháp chia tỉ lệ để giải bài toán về
tìm hai số khi biết tổng và tỉ số của chúng. Ví dụ 5.8.
Tìm hai số, biết rằng số thứ nhất gấp 4 số thứ hai và hơn số thứ hai 36 đơn vị.
Trước hết ta dùng phương pháp toán sơ cấp giải bài toán trên:
Gọi số thứ nhất là x, số thứ hai là y. Theo đề bài ta có hệ phương trình: x – y = 36 (1) x = 4y (2) Thay (2) vào (1) ta được: 176 4y – y = 36 3y = 36 y = 36 : 3 y = 12.
Thay vào (1) ta được: x = 12 + 36 x = 48.
Vậy hai số cần tìm là 48 và 12.
Từ cách giải trên, ta diễn giải thành phương pháp giải cho học sinh tiểu học như sau:
Theo đề bài ta có sơ đồ: ? Số thứ nhất: Số thứ hai: 36 ?
Hiệu số phần bằng nhau là: 4 – 1 = 3 (phần)
Số thứ hai là: 36 : 3 = 12
Số thứ nhất là: 12 + 36 = 48
Trả lời: Hai số cần tìm là: 48 và 12.
Ở Tiểu học, cách giải trên đây ta gọi là phương pháp chia tỉ lệ để giải bài toán về
tìm hai số khi biết hiệu và tỉ số của chúng. Ví dụ 5.8a.
Khối Năm và khối Bốn của Trường Tiểu học Kim Liên tham gia Tết trồng cây. Số 3
cây của khối Bốn trồng được bằng 5 số cây của khối Năm và kém khối Năm 218 cây.
Hỏi mỗi khối trồng được bao nhiêu cây?
Trước hết ta dùng phương pháp toán sơ cấp giải bài toán trên:
Gọi số cây khối Bốn trồng được là x và số cây khối Năm trồng được là y. Theo đề
bài ta có hệ phương trình: y – x = 218 (1) 3 y x = 5 (2) Thay (2) vào (1) ta được: 5y – 3y = 218 . 5 2y = 218 . 5 y = (218 : 2) . 5 y = 545 thay vào (1) ta được: x = 545 – 218 x = 327 177
Trả lời: Khối Bốn trồng được 327 cây và khối Năm trồng được 545 cây.
Từ cách giải trên, ta diễn giải thành phương pháp giải cho học sinh tiểu học như sau:
Theo đề bài ta có sơ đồ: ? cấy 218 cấy Khối 4: Khối 5: ? cấy
Hiệu số phần bằng nhau là: 5 – 3 = 2 (phần)
Giá trị của một phần bằng nhau là: 218 : 2 = 109 (cây)
Số cây của khối Năm trông được là: 109 x 5 =545 (cây)
Số cây của khối Bốn trồng được là: 545 – 218 = 327 (cây)
Đáp số: Khối Bốn: 327 cây; Khối Năm: 545 cây
Ở Tiểu học, cách giải trên đây ta gọi là phương pháp chia tỉ lệ để giải bài toán về
tìm hai số khi biết hiệu và tỉ số của chúng. x+y=m
II.5. Hệ phương trình bậc nhất dạng: ax+by n
và phương pháp giả thiết tạm
Ví dụ 5.9. Vừa gà, vừa chó Bó lại cho tròn Có mười sáu con Bốn mươi chân chẵn.
Hỏi có bao nhiêu con gà? Bao nhiêu con chó?
Trước hết ta dùng phương pháp toán sơ cấp giải bài toán trên:
Gọi số gà là x, số chó là y. Theo đề bài ta có hệ phương trình: x + y = 16 (1) 2x + 4y = 40 (2)
Nhân cả hai vế của (1) với 2 ta được: 2x + 2y = 32 (1’) 2x + 4y = 40 (2’)
Trừ vế với vế của (2’) cho (1’) ta được: 2y = 8 y = 4
Thay vào (1) ta được: x = 16 – 4 x = 12.
Trả lời: có 12 con gà và 4 con chó.
Từ cách giải trên, ta diễn giải thành phương pháp giải cho học sinh tiểu học như sau: 178
Giả sử tất cả 16 con đều là gà.
Tổng số chân là: 16 x 2 = 32 (chân)
Số chân hụt đi là: 40 – 32 = 8 (chân)
Mỗi con chó hơn một con gà số chân là: 4 – 2 = 2 (chân)
Vì mỗi con chó bớt đi 2 chân nên tất cả hụt đi 8 chân. Số chó là: 8 : 2 = 4 (con)
Số gà là: 16 – 4 = 12 (con)
Đáp số: 12 con gà và 4 con chó.
Ở Tiểu học, cách giải trên đây ta gọi là phương pháp giả thiết tạm.
Tương tự, nếu ta giả sử tất cả đều là chó ta sẽ được cách giải thứ hai.
Chú ý. Ngoài cách giải trên, bài toán này còn có cách giải “mẹo” như sau:
Giả sử mỗi con chó có 2 chân, mỗi con gà có 1 chân.
Số chân đếm được là: 40 : 2 = 20 (chân)
Giả sử mỗi con chó có thêm 1 chân nữa. Số chân đếm được là 16 chân.
Số chó là: 20 – 16 = 4 (con)
Số gà là: 16 – 4 = 12 (con)
Ví dụ 5.9a.
Một tốp thợ dùng 13 đoạn ống nước gồm hai loại dài 8m và dài 5m để lắp đặt một
đoạn đường ống dài 77m. Hỏi tốp thợ phải dùng mỗi loại bao nhiêu ống để khi lắp đặt
không phải cắt một ống nào?
Trước hết ta dùng phương pháp toán sơ cấp giải bài toán trên:
Gọi số ống loại 8m là x và số ống loại 5m là y. Theo đề bài ta có hệ phương trình: x + y = 13 (1) 8x + 5y = 77 (2)
Nhân cả hai vế của (1) với 8 ta được: thay vào (1) ta được: 8x + 8y = 104 (1’) 8x + 5y = 77 (2’)
Trừ vế với vế của (1’) cho (2’) ta được: 3y = 27 y = 9
Thay vào (1) ta tính được x =4
Trả lời: Tốp thợ dùng 4 ống loại 8m và 9 ống loại 5m.
Từ cách giải trên, ta diễn giải thành phương pháp giải cho học sinh tiểu học như sau:
Giả sử dùng tất cả 13 ống loại 8m.
Chiều dài đường ống lắp được là: 13 x 8 = 104 (m)
Chiếu dài đường ống tăng thêm là: 104 – 77 = 27 (m)
Mỗi ống loại 8m dài hơn một ống loại 5m là: 8 – 5 = 3 (m) Số ống loại 5m là: 27 : 3 = 9 (ống) 179 Số ống loại 8m là: 13 – 9 = 4 (ống)
Đáp số: 4 ống loại 8m và 9 ống loại 5m. ax+by=c
II.6. Hệ phương trình bậc nhất dạng: a'x+b ' y c '
và phương pháp khử
Ví dụ 5.10.
Mẹ mua 5kg gạo tẻ và 3 kg gạo nếp hết 114 000 đồng. Một lần khác, mẹ mua 7kg
gạo tẻ và 4kg gạo nếp cùng loại hết 156 000 đồng. Tính giá tiền 1kg gạo mỗi loại.
Trước hết ta dùng phương pháp toán sơ cấp giải bài toán trên:
Gọi giá tiền 1kg gạo tẻ là x, giá tiền 1kg gạo nếp là y. Theo đề bài ta có hệ phương trình: 5x + 3y = 114 000 (1) 7x + 4y = 156 000 (2)
Nhân cả hai vế của (1) với 4, của (2) với (3) ta được: 20x + 12y = 456 000 (1’) 21x + 12y = 468 000 (2’)
Trừ vế với vế của (2’) cho (1’) ta được: x = 12 000
Thay vào (1) ta được: y = 18 000
Trả lời: Giá tiền 1kg gạo tẻ là 12 000 đồng và 1 kg gạo nếp là 18 000 đồng.
Từ cách giải trên, ta diễn giải thành phương pháp giải cho học sinh tiểu học như sau:
Giả sử số gạo mỗi loại lần 1 mua tăng gấp 4 lần, lần 2 mua tăng gấp 3 lần. Vậy ta có:
20kg gạo tẻ và 12kg gạo nếp giá 456 000 đồng
21kg gạo tẻ và 12kg gạo nếp giá 468 000 đồng.
Số gạo tẻ lần 2 mua nhiều hơn lần 1 là: 21 – 20 = 1 (kg)
Số tiền lần 2 mua nhiều hơn lần 1 là: 468 000 – 456 000 = 12 000 (đồng)
Số gạo nếp hai lần mua là như nhau, vậy 12 000 đồng là giá tiền của 1kg gạo tẻ.
Giá tiền 1 kg gạo nếp là: (114 000 – 12 000 x 5) : 3 = 18 000 (đồng)
Đáp số: 12 000 đồng 1kg gạo tẻ;
18 000 đồng 1kg gạo nếp
Ở tiểu học, cách giải trên đây ta gọi là phương pháp khử. a x - y =c
II.7. Hệ phương trình bậc nhất dạng: y - bx c '
và giải toán về tìm hai số biết hai hiệu số
Ví dụ 5.11.
Một tốp thợ được giao lắp đặt một đoạn đường ống nước. Trong kho có hai loại
ống: dài 7m và dài 9m, số lượng bằng nhau. Chú thợ cả tính rằng: nếu dùng loại ống 7m 180
thì thiếu 11m, nếu dùng loại ống 9m thì thừa 17m. Hỏi trong kho có bao nhiêu ống mỗi
loại và chiều dài đường ống cần lắp đặt là bao nhiêu mét?
Trước hết ta dùng phương pháp toán sơ cấp giải bài toán trên:
Gọi số ống mỗi loại là x, chiều dài đường ống cần láp đặt là y. Theo đề bài ta có hệ phương trình: 9x – y = 17 (1) y – 7x = 11 (2)
Cộng vế với vế của (1) và (2) ta được: 2x = 28 x = 14 Thay vào (2) ta được: y = 109
Trả lời: Chiều dài đường ống cần lắp đặt là 109m và trong kho có 14 ống mỗi loại.
Từ cách giải trên, ta diễn giải thành phương pháp giải cho học sinh tiểu học như sau:
Mỗi ống loại 9m dài hơn một ống loại 7m là: 9 – 7 = 2 (m)
Chiều dài đường ống lắp bằng loại ống 9m dài hơn chiều dài đường ống lắp đặt bằng loại ống 7m là: 11 + 17 = 28 (m) Số ống mỗi loại là: 28 : 2 = 14 (ống)
Chiều dài đường ống là: 7 x 14 + 11 = 109 (m) Đáp số: 109m; 14 ống
Ở Tiểu học, cách giải trên đây ta gọi là phương pháp giải toán về tìm hai số biết hai hiệu số. Ví dụ 5.12.
Đầu năm học, cô giáo chủ nhiệm lớp 4C xếp chỗ ngồi cho các bạn. Cô nhẩm tính:
nếu xếp mỗi bàn 3 học sinh thì 4 học sinh không có chỗ ngồi; nếu xếp mỗi bàn 4 học sinh
thì thừa 2 bàn không có học sinh ngồi. Hỏi lớp 4C có bao nhiêu học sinh và bao nhiêu bàn?
Trước hết ta dùng phương pháp toán sơ cấp giải bài toán trên:
Gọi số bàn là x, số học sinh của lớp 4C là y. Theo đề bài ta có hệ phương trình: 4x – y = 4.2 (1) y – 3x = 4 (2)
Cộng vế với vế của (1) và (2) ta được: x = 12 Thay vào (2) ta được: y = 40
Trả lời: Lớp đó có 40 học sinh và 12 bàn.
Từ cách giải trên, ta diễn giải thành phương pháp giải cho học sinh tiểu học như sau: 181
Mỗi bàn ngồi 4 học sinh hơn một bàn ngồi ba học sinh là: 4 – 3 = 1 (HS)
Tổng số học sinh ngồi mỗi bàn 4 học sinh hơn tổng số học sinh ngồi mỗi bàn 3 học sinh là: 4 + 4 x 2 = 12 (HS) Số bàn là: 12 : 1 = 12 (bàn) Số học sinh là: 3 x 12 + 4 = 40 (HS) Đáp số: 40 học sinh; 12 bàn
II.8. Phép quy nạp hoàn toàn và phương pháp thử chọn
Trong chương I chúng ta đã làm quen với phép quy nạp hoàn toàn. Ở Tiểu học,
người ta vận dụng phép suy luận này trong giải nhiều bài toán cho học sinh tiểu học.
Dưới đây chúng ta minh hoạ một số ví dụ.
Ví dụ 5.13.
Tích của tử số và mẫu số của một phân số lớn hơn 1 bằng 315, khi chia cả tử và
mẫu của phân số đó cho 3 ta được một phân số tối giản. Tìm phân số đó. Giải:
Số 315 có thể phân tích thành tích của các cặp số sau: 1 và 315; 3 và 105; 5 và 63; 7 và 45; 9 và 35; 15 và 21.
Các phân số cần tìm có thể là: 315 105 63 45 35 21 ; ; ; ; ; . 1 3 5 7 9 15 Ta có bảng sau: a : 3 a b :3 phân số tối Kết luận b giản? 315 315: 3 Loại 1 1:3 105 105: 3 35 Chọn 3 3: 3 1 63 63:3 Loại 5 5: 3 45 45 :3 Loại 7 7 : 3 35 35 :3 Loại 9 9 :3 21 21:3 7 Chọn 15 15: 3 5 182 105 21 à v .
Vậy các phân số cần tìm là: 3 15
Cách giải như trên, ta gọi là phương pháp thử chọn.
Ví dụ 5.14. 3
Một khu đất hình chữ nhật có diện tích 735m2, chiều rộng bằng 5 chiều dài. Hỏi
cần bao nhiêu chiếc cọc để rào xung quanh khu đất đó? Biết rằng khoảng cách giữa hai
cọc bằng 0,5m và ở một góc người ta để lối ra vào rộng 3m. Giải:
Số 735 có thể là tích của các cặp số tự nhiên sau: 1 và 735; 3 và 245; 5 và 147; 7 và 105; 21 và 35.
Bằng phương pháp thử chọn ta tìm được chiều rộng của khu đất là 21m, chiều dài là 35m.
Chu vi khu đất là: (21 + 35) x 2 = 112 (m)
Số cọc cần dùng là: (112 – 3) : 0,5 + 1 = 219 (cọc) Đáp số: 219 cọc
Ví dụ 5.15. Bài 5.9 có thể giải bằng phương pháp thử chọn như sau: Ta có bảng sau: Số con chó Số con gà Tổng số chân Kết luận 1 15 4 x 1 + 15 x 2 = 34 < 40 Loại 2 14 4 x 2 + 14 x 2 = 36 < 40 Loại 3 13 4 x 3 + 13 x 2 = 38 < 40 Loại 4 12 4 x 4 + 12 x 2 = 40 = 40 Chọn
Mỗi khi tăng 1 con chó và giảm 1 con gà thì tổng số chân tăng thêm 2.
Nếu số chó lớn hơn 4 thì số chân lớn hơn 40.
Vậy có 12 con gà và 4 con chó.
II.9. Yếu tố đại số trong môn Toán tiểu học
Trong chương trình môn Toán tiểu học, nội dung về các yếu tố đại số được trình
bày trong môn toán lớp 4 và 5. Nó bao gồm các nội dung:
- Khái niệm về biểu thức số và giá trị của biểu thức số; -
Khái niệm về biểu thức chứa chữ và giá trị số của biểu thức chứa chữ; -
Ứng dụng biểu thức chứa chữ đề phát biểu các tính chất của các
phép toán và quy tắc thực hành tính toán; -
Ứng dụng biểu thức chưa chữ để xây dựng công thức tính chu vi,
diện tích và thể tích các hình; -
Ứng dụng của yếu tố đại số để hình thành các phương pháp giải toán cho học sinh tiểu học. 183 184 TÀI LIỆU THAM KHẢO
[1] Trần Diên Hiển – Nguyễn Xuân Liêm: Giáo trình Cơ sở lí thuyết tập hợp và logic
toán - NXB Giáo dục, Hà Nội 2006.
[2] Trần Diên Hiển – Nguyễn Văn Ngọc: Giáo trình Toán cao cấp 1 - NXB Đại học Sư phạm, Hà Nội 2008.
[3] Trần Diên Hiển – Bùi Huy Hiền: Giáo trình các tâ «p hợp số – NXB Giáo dục 2012
[4] Trần Diên Hiển – Nguyễn Tiến Tài – Nguyễn văn Ngọc: Giáo trình lý thuyết số –
NXB Đại học sư phạm, 2103
[5] Vũ Tuấn – Nguyễn Văn Đoành: Giáo trình Toán sơ cấp – NXB Đại học sư phạm, 2013
[6] Trần Diên Hiển – Vũ Viết Yên: Giáo trình Toán cao cấp 2 - NXB Đại học Sư phạm, Hà Nội 2006.
[7] Trần Diên Hiển: Các bài toán về suy luận logic - NXB Giáo dục, Hà Nội 2002.
[8] Trần Diên Hiển: Thực hành giải toán tiểu học - NXB Đại học sư phạm 2013.
[9] Đỗ Đình Hoan và tập thể: Toán 1, 2, 3, 4, 5. NXB Giáo dục - Hà Nội 2013.
[10] Phan Đức Chính và tâ ’p thể: Toán 6, 7, 8, 9. NXB Giáo dục - 2015 185