Góc giữa hai mặt phẳng: Định nghĩa, cách xác định và Bài tập
Môn toán học đặc biệt là phần hình học, được coi là một trong những môn khó, bởi vì nó liên quan
đến các khái niệm về góc và các thông tin tương ứng. Vậy góc giữa hai mặt phẳng: Định nghĩa, cách
xác định và Bài tập vận dụng như thế nào? Hãy cùng Luật Minh Khuê tìm hiểu qua bài viết dưới đây.
1. Góc giữa hai mặt phẳng được hiểu như thế nào?
- Khái niệm: Góc giữa hai mặt phẳng là góc được hình thành bởi hai đường thẳng lần lượt vuông góc
với hai mặt phẳng đó.
Trong không gian ba chiều, góc giữa hai mặt phẳng còn được gọi là "góc khối", là phần không gian bị
chặn giữa hai mặt phẳng. Góc giữa hai mặt phẳng được đo bằng góc giữa hai đường thẳng trên mặt
hai mặt phẳng đó, có cùng phương vuông góc với giao tuyến của hai mặt phẳng.
- Tính chất: Từ định nghĩa trên, ta có các tính chất sau:
• Góc giữa hai mặt phẳng song song bằng 0 độ.
• Góc giữa hai mặt phẳng trùng nhau bằng 0 độ.
2. Cách xác định góc giữa 2 mặt phẳng
Để xác định chính xác góc giữa hai mặt phẳng, bạn có thể áp dụng những cách sau đây:
Đặt P là mặt phẳng thứ nhất và Q là mặt phẳng thứ hai.
Trường hợp 1: Hai mặt phẳng (P) và (Q) song song hoặc trùng nhau, trong trường hợp này góc giữa
hai mặt phẳng được xem là bằng 0.
Trường hợp 2: Hai mặt phẳng (P) và (Q) không song song hoặc trùng nhau.
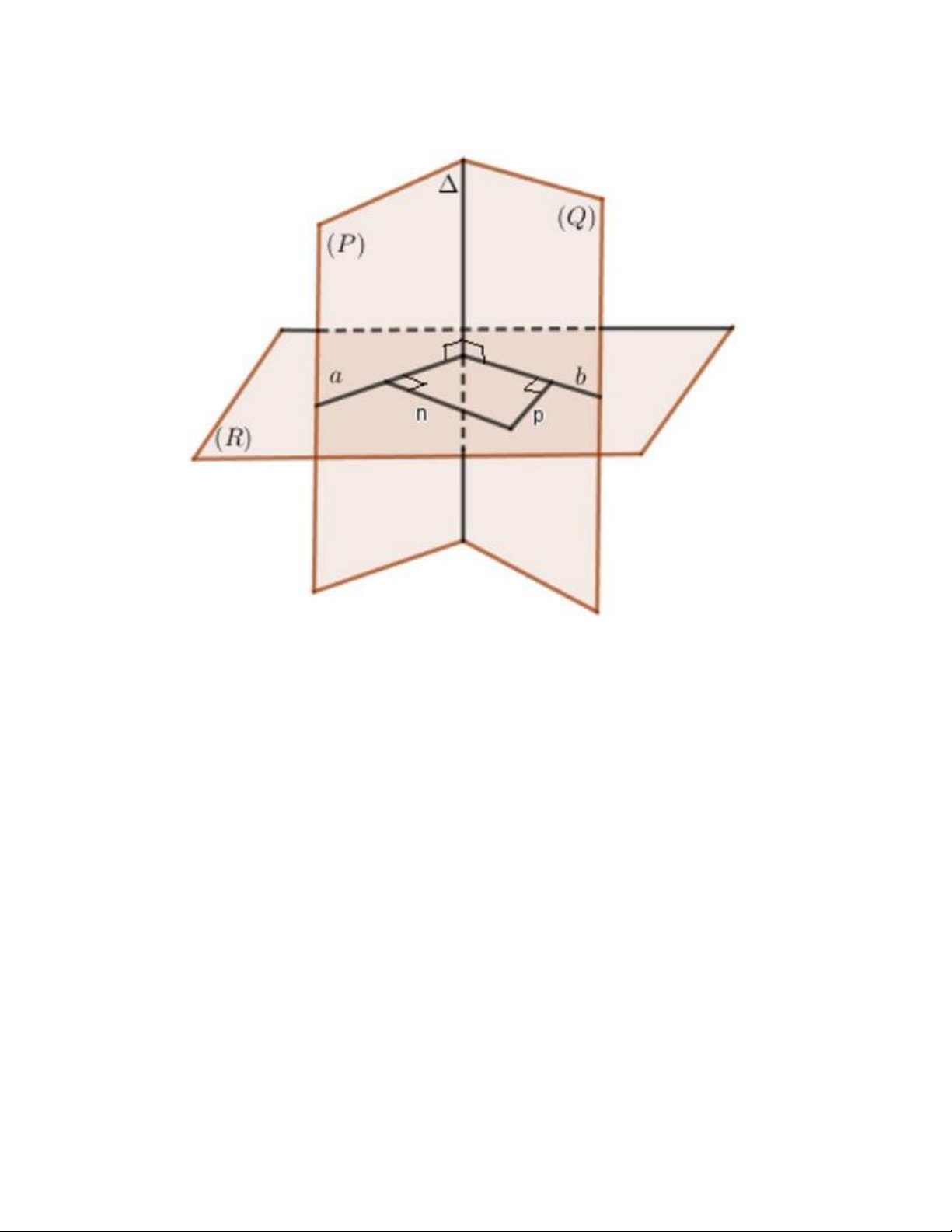
Cách thứ nhất để xác định góc giữa hai mặt phẳng (P) và (Q) là dựng hai đường thẳng n và p, lần lượt
vuông góc với hai mặt phẳng đó. Khi đó, góc giữa hai mặt phẳng (P) và (Q) sẽ bằng góc giữa hai đường thẳng n và p.
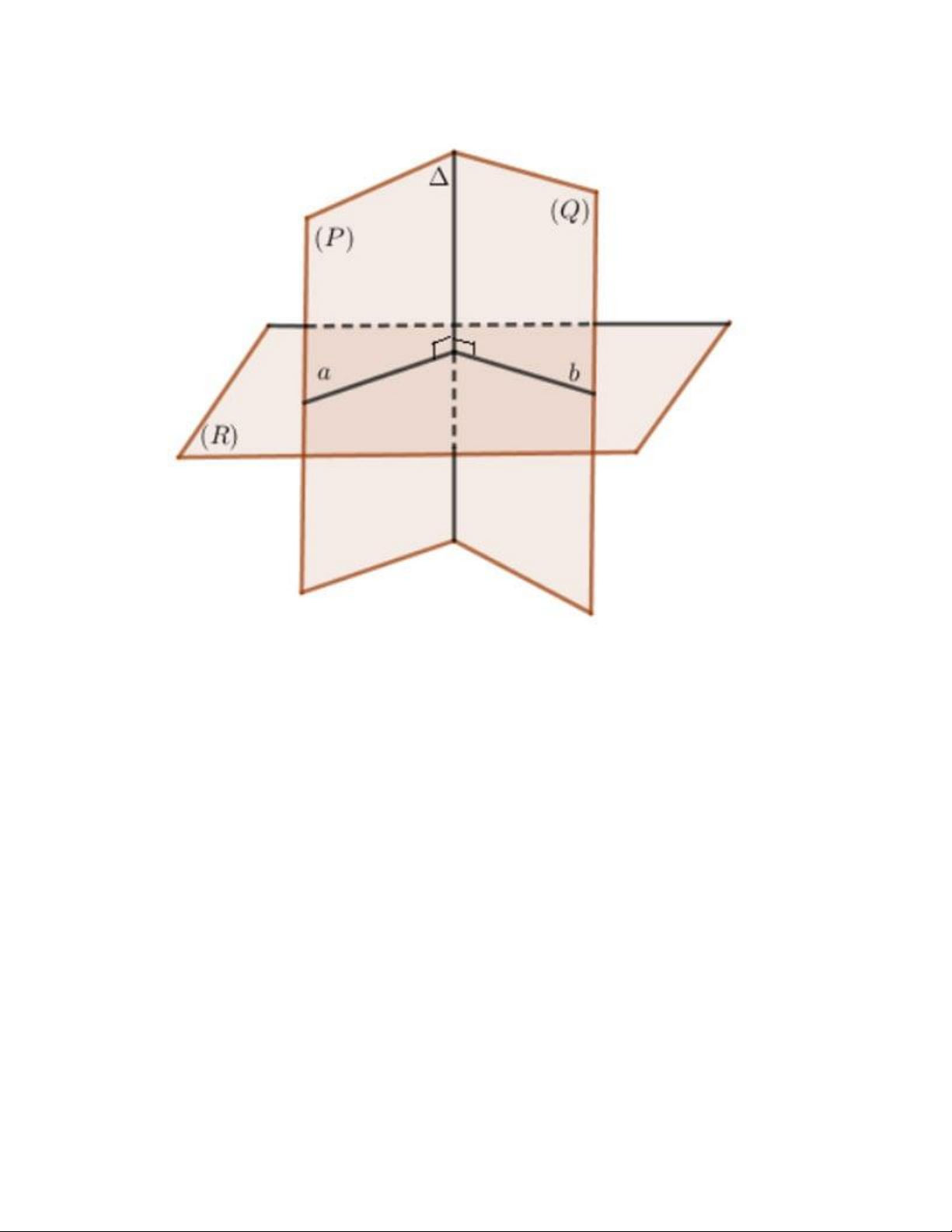
Cách thứ hai để xác định góc giữa hai mặt phẳng là bước đầu tiên, xác định giao tuyến Δ của hai mặt
phẳng (P) và (Q). Sau đó, tìm một mặt phẳng (R) vuông góc với giao tuyến Δ của hai mặt phẳng (P) và
(Q), và giao mặt phẳng (R) với hai mặt phẳng tại các đường giao a và b.
⇒ Góc giữa hai mặt phẳng (P) và (Q) sẽ là góc giữa hai đường a và b.
3. Bài tập áp dụng
Câu 1: Cho tam giác ABC vuông tại A. Cạnh AB = a nằm trong mặt phẳng(P), cạnh AC = a√2 , AC tạo với
(P) một góc 60°. Chọn khẳng định đúng trong các khẳng định sau?
A. (ABC) tạo với (P) góc 45°
B. BC tạo với (P) góc 30°
C. BC tạo với (P) góc 45°
D. BC tạo với (P) góc 60°
Câu 2: Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai ?
A. Góc giữa hai mặt phẳng (ACD) và (BCD) là góc ∠AIB B. (BCD) ⊥ (AIB)
C. Góc giữa hai mặt phẳng (ABC) và (ABD) là góc ∠CBD D. (ACD) ⊥ (AIB)
Câu 3: Cho hình chóp S. ABC có SA ⊥ (ABC) và AB ⊥ BC , gọi I là trung điểm BC. Góc giữa hai mặt phẳng
(SBC) và (ABC) là góc nào sau đây? A. Góc SBA. B. Góc SCA. C. Góc SCB. D. Góc SIA.
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA ⊥ (ABCD), gọi O là tâm hình vuông
ABCD. Khẳng định nào sau đây sai?
A. Góc giữa hai mặt phẳng (SBC) và (ABCD) là góc ∠ABS
B. Góc giữa hai mặt phẳng (SBD) và (ABCD) là góc ∠SOA
C. Góc giữa hai mặt phẳng (SAD) và (ABCD) là góc ∠SDA D. (SAC) ⊥ (SBD)
Câu 5: Cho hình lập phương ABCD.A1B1C1D1 . Gọi α là góc giữa hai mặt phẳng (A1D1CB) và (ABCD).
Chọn khẳng định đúng trong các khẳng định sau? A. α = 45° B. α = 30° C. α = 60° D. α = 90°
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình vuông có tâm O và SA ⊥ (ABCD). Khẳng định nào sau đây sai ?
A. Góc giữa hai mặt phẳng (SBC) và (ABCD) là góc ∠ABS B. (SAC) ⊥ (SBD)
C. Góc giữa hai mặt phẳng (SBD) và (ABCD) là góc ∠SOA
D. Góc giữa hai mặt phẳng (SAD) và (ABCD) là góc ∠SDA
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc ∠ABC = 60°. Các cạnh SA ; SB ; SC
đều bằng a(√3/2) . Gọi φ là góc của hai mặt phẳng (SAC) và (ABCD) . Giá trị tanφ bằng bao nhiêu? A. 2√5 B. 3√5 C. 5√3 D. Đáp án khác
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D. AB = 2a; AD = DC = a. Cạnh
bên SA vuông góc với đáy và SA = a√2. Chọn khẳng định sai trong các khẳng định sau? A. (SBC) ⊥ (SAC)
B. Giao tuyến của (SAB) và (SCD) song song với AB
C. (SDC) tạo với (BCD) một góc 60°
D. (SBC) tạo với đáy một góc 45°
Câu 9: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = AA’ = a; AD = 2a. Gọi α là góc giữa đường chéo
A’C và đáy ABCD. Tính α . A. α ≈ 20°45' B. α ≈ 24°5' C. α ≈ 30°18' D. α ≈ 25°48'
Câu 10: Cho hình lập phương ABCD.A'B'C'D'. Xét mặt phẳng (A’BD). Trong các mệnh đề sau mệnh đề nào đúng?
A. Góc giữa mặt phẳng ( A’BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng α mà tanα = 1/√2 .
B. Góc giữa mặt phẳng (A’BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng α mà tanα = 1/√3
C. Góc giữa mặt phẳng (A’BD) và các mặt phẳng chứa các cạnh của hình lập phương phụ thuộc vào
kích thước của hình lập phương.
D. Góc giữa mặt phẳng ( A’BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng nhau.
Câu 11: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số
đo góc hợp bởi cạnh bên và mặt đáy. A. 30° B. 45° C. 60° D. 75°
Câu 12. Cho hình chóp tứ giác đều có cạnh đáy bằng a√2 và chiều cao bằng a√2/2 . Tính số đo của góc
giữa mặt bên và mặt đáy. A. 30° B. 45° C. 60° D. 75°
Câu 12: Cho hình chóp S.ABCD có đáyABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy và SA
= a. Góc giữa hai mặt phẳng (SBC) và (SCD) bằng bao nhiêu? A. 30° B. 45° C. 90° D. 60°
Câu 13: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA ⊥ (ABCD); SA = x. Xác định x để
hai mặt phẳng (SBC) và (SCD) tạo với nhau góc 60°. A. x = 3a/2 B. x = a/2 C. x = a D. x = 2a
Câu 14: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA ⊥ (ABC). Gọi E; F lần lượt là trung
điểm của các cạnh AB và AC . Góc giữa hai mặt phẳng (SEF) và (SBC) là : A. ∠CSF B. ∠BSF C. ∠BSE D. ∠CSE
Câu 15: Cho tam giác đều ABC có cạnh bằng a và nằm trong mặt phẳng (P). Trên các đường thẳng
vuông góc với (P) tại B và C lần lượt lấy D; E nằm trên cùng một phía đối với (P) sao cho BD = a(√3/2),
CE = a√3 . Góc giữa (P) và (ADE) bằng bao nhiêu? A. 30° B. 60° C. 90° D. 45°
Câu 16. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
B. Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Các mặt phẳng cùng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước thì luôn
đi qua một đường thẳng cố định.
D. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.
Câu 17. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
B. Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Các mặt phẳng cùng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước thì luôn
đi qua một đường thẳng cố định.
D. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.
Câu 18: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu hình hộp có bốn mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
B. Nếu hình hộp có ba mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
C. Nếu hình hộp có hai mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
D. Nếu hình hộp có năm mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
Câu 19. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu hình hộp có bốn mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
B. Nếu hình hộp có ba mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
C. Nếu hình hộp có hai mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
D. Nếu hình hộp có năm mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
Câu 20. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.
B. Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với hai mặt
phẳng cắt nhau cho trước.
D. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
Để tìm hiểu thêm thông tin liên quan, mời quý bạn đọc tham khảo bài viết: Góc là gì? Cách nhận biết
góc vuông, góc nhọn, góc tù, góc bẹt?
Trên đây là toàn bộ nội dung bài viết của Luật Minh Khuê liên quan đến vấn đề: Góc giữa hai mặt
phẳng: Định nghĩa, cách xác định và Bài tập. Mọi thắc mắc chưa rõ hay có nhu cầu hỗ trợ vấn đề pháp
lý khác, quý khách hàng vui lòng liên hệ với bộ phận tư vấn pháp luật trực tuyến qua số
hotline: 1900.6162 hoặc gửi yêu cầu tư vấn qua email: lienhe@luatminhkhue.vn để được hỗ trợ và
giải đáp kịp thời. Xin trân trọng cảm ơn quý khách hàng đã quan tâm theo dõi bài viết của Luật Minh Khuê.