Hướng dẫn giải bài tập chương 11. Phương trình tiếp diện , phương trình pháp tuyến

Hướng dẫn giải bài tập Chương 11
Giảng viên: Nguyễn Minh Hải
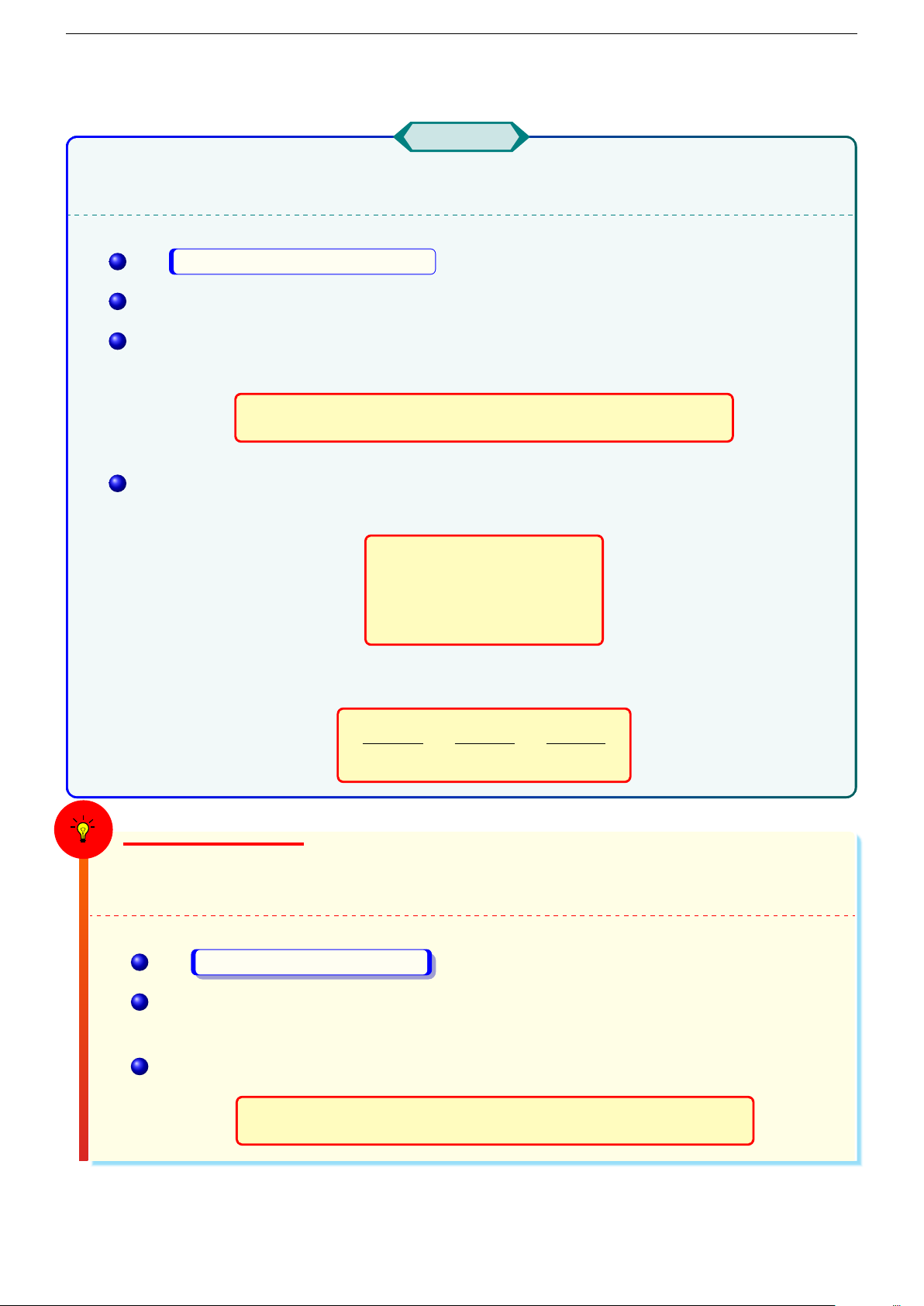
PHƯƠNG TRÌNH TIẾP DIỆN, PHƯƠNG TRÌNH PHÁP TUYẾN Bài toán
Cho mặt (S) : G(x, y, z) = C và P (x0, y0, z0) ∈ (S). Viết phương trình tiếp diện, phương
trình pháp tuyến của (S) tại P . 1 Đặt
F (x, y, z) = G(x, y, z) − C . 2
Tìm ∇F (x0, y0, z0) = ⟨Fx(P0); Fy(P0); Fz(P0)⟩. 3
Tiếp diện của (S) tại P (x0, y0, z0) là mặt phẳng qua P (x0, y0, z0) và nhận
∇F (x0, y0, z0) là vec tơ pháp tuyến
Fx(P0)(x − x0) + Fy(y − y0) + Fz(P0)(z − z0) = 0 4
Pháp tuyến của (S) tại P0 là đường thẳng qua P0 và nhận ∇F (x0, y0, z0) làm vec tơ
chỉ phương, có phương trình tham số là: x = x  0 + Fx(P0)t  y = y0 + Fy(P0)t  z = z0 + Fz(P0)t
hoặc phương trình dạng chính tắc: x − x0 y − y0 z − z0 = = Fx(P0) Fy(P0) Fz(P0)
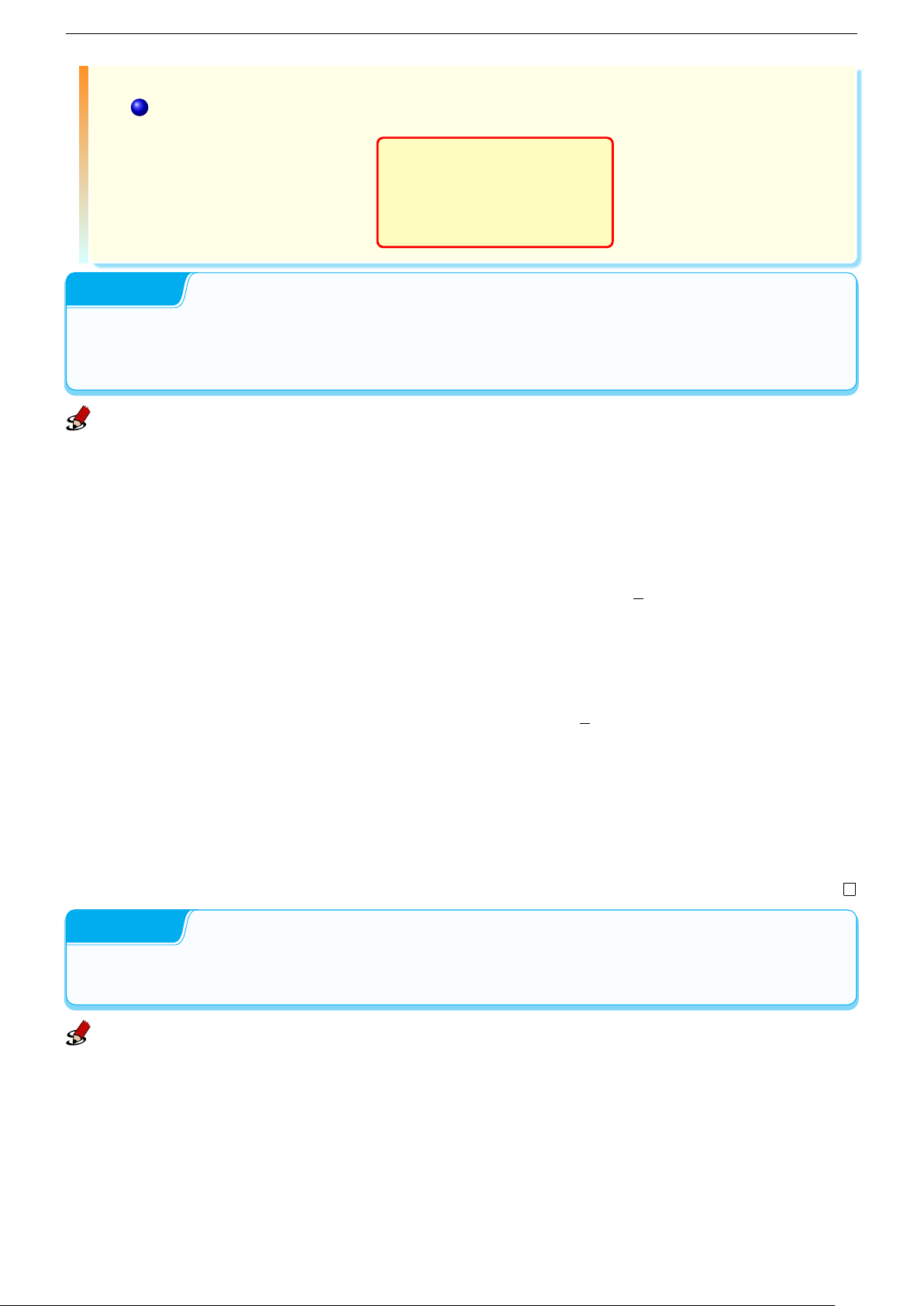
Trường hợp đặc biệt
Cho (S) : z = f (x, y) và P0(x0; y0; z0) ∈ (S). Viết phương trình tiếp diện và phương
trình pháp tuyến của (S) tại P0(x0; y0; z0). 1 Đặt F (x, y, z) = f (x, y) − z . 2 Tính
∇F (P0) = ⟨fx(P0); fy(P0); −1⟩ 3
Phương trình tiếp diện của (S) tại P0.
fx(P0)(x − x0) + fy(P0)(y − y0) + (−1)(z − x0) = 0 1
Hướng dẫn giải bài tập Chương 11
Giảng viên: Nguyễn Minh Hải 4
Phương trình pháp tuyến của (S) tại P0 x = x  0 + fx(P0)t  y = y0 + fy(P0)t  z = z0 − t Ví dụ 0.1
Tìm phương trình tiếp diện (mặt phẳng tiếp xúc) và pháp tuyến của (S) : x3y − y2 + z2 = 7 tại P (1, 2, 3).
Lời giải. Đặt F (x, y, z) = x3y − y2 + z2 − 7. Ta có   F F  x = 3x2y  x(1; 2; 3) = 6   F ⇒ y = x3 − 2y Fy(1; 2; 3) = −3   F  z = 2z Fz(1; 2; 3) = 6
Vậy ∇F (1, 2, 3) = ⟨6, −3, 6⟩. 1
Tiếp diện của (S) tại P (1, 2, 3) là mặt phẳng qua P và nhận N =
∇F (1, 2, 3) = ⟨2, −1, 2⟩ 3
là vec tơ pháp tuyến, có dạng
2(x − 1) − (y − 2) + 2(z − 3) = 0 ⇔ 2x − y + 2z − 6 = 0 1
Pháp tuyến của (S) tại P là đường thẳng qua P và nhận N =
∇F (1, 2, 3) = ⟨2, −1, 2⟩ là vec 3
tơ chỉ phương nên phương trình có dạng x = 1 + 2t   y = 2 − t  z = 3 + 2t Ví dụ 0.2
Tìm phương trình tiếp diện và pháp tuyến của (S) : z = 4x2 + y2 + 2 tại x = 1 và y = 1.
Lời giải. Đặt F (x, y, z) = 4x2 + y2 + 2 − z. Khi đó
∇F (x, y, z) = ⟨8x, 2y, −1⟩ ⇒ ∇F (1, 1, 7) = ⟨8, 2, −1⟩ Vậy
• Tiếp diện của (S) tại P (1, 1, 7) là
8(x − 1) + 2(y − 1) − (z − 7) = 0 ⇒ 8x + 2y − z = 3 2
Hướng dẫn giải bài tập Chương 11
Giảng viên: Nguyễn Minh Hải
• Pháp tuyến của (S) tại P (1, 1, 7) là x = 1 + 8t   y = 1 + 2t  z = 7 − t 3