Câu 3.a. Bài tập Điện học (cơ bản) Câu 3.a.1. Q 5  Q  3 Hai điện tích điểm 1 nC và 2
nC nằm cách nhau một khoảng r 35  cm.
a) Tính thế năng tương tác tĩnh điện giữa 2 điện tích điểm này. Ý nghĩa của dấu của kết quả?
b) Tính điện thế tại điểm nằm chính giữa 2 điện tích điểm. Đáp án:
Thế năng tương tác tĩnh điện giữa hai điện tích: 1 Q 2 Q 7 U   3.852 1  0 4 r 0 (J) (5 điểm)
Dấu trừ của thế năng tương tác thể hiện hai điện tích hút nhau.
Điện thế tại điểm nằm chính giữa hai điện tích: 1 Q Q2 V V  V    102.71  1 2 4 r 2 4 r 2 0   0   (V). (5 điểm) 1 Câu 3.a.2.
Hai hạt nhỏ mang điện tích 3
 q và q được gắn chặt vào một
thanh cách điện và cách nhau một khoảng d . Một hạt mang
điện thứ 3 có thể trượt tự do dọc theo thanh. Xác định vị trí cân
bằng của hạt thứ 3 này. Cân bằng đó có bền không? Đáp án:
Gọi khoảng cách từ hạt thứ 3 (mang điện tích q ) đến hạt mang điện tích 3
 q là x . Ở vị trí cân bằng,
lực tác dụng từ hạt mang điện tích 3
 q bằng và ngược hướng với hạt mang điện tích q : 3  qq qq  2 40x 4  0 d x 2 (5 điểm Từ đó: d  x 1 d   x  x 3 1  1 3 (5 điểm
Giả sử hạt thứ 3 mang điện tích dương q dịch chuyển khỏi vị trí cân bằng về bên trái, khi đó lực đẩy từ điện tích 3
 q tăng do khoảng cách x giảm, còn lực đẩy từ điện tích q giảm do d  x tăng. Vì vậy
lực tổng hợp tác dụng lên điện tích q có hướng từ 3
 q về phía q và kéo điện tích q về vị trí cân
bằng. Lập luận tương tự khi điện tích q dịch chuyển khỏi vị trí cân bằng về bên phải, cũng như khi
điện tích q là âm. Kết luận: cân bằng là bền. 2 Câu 3.a.3. Bốn mặt kín từ S S  
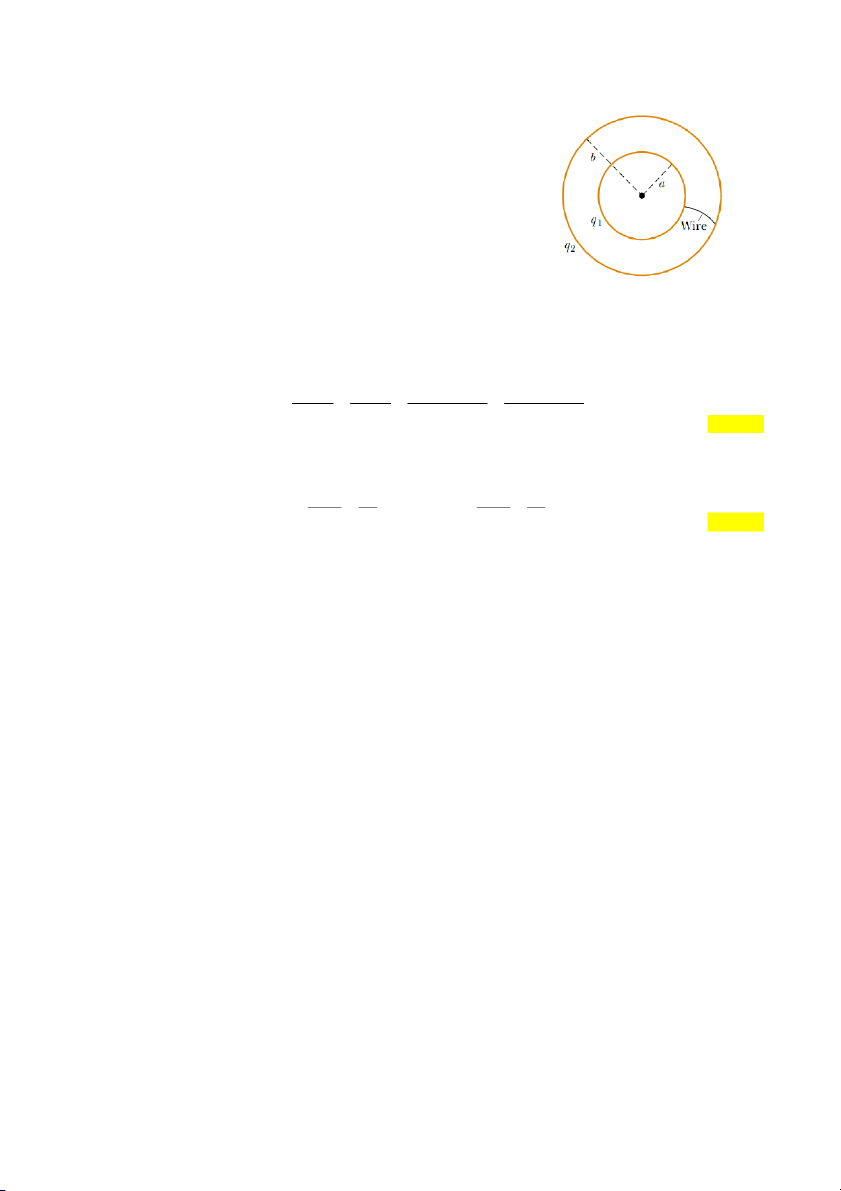
1 đến 4 cùng các điện tích 2Q , Q , và Q
được cho trong hình vẽ. Hãy tìm điện thông qua từng mặt kín đó. Đáp án:
Điện thông qua mặt S1 :
   2Q  Q S  QS 1   1 1 (2,5 điểm) Điện thông qua mặt 2 S :
   Q  Q S 0  2   2 (2,5 điểm)
Điện thông qua mặt S3 :
   2Q  Q   Q S 2  QS 3    3 3 (2,5 điểm) Điện thông qua mặt 4 S :  0  4
, do không có điện tích nào bên trong mặt 4 S (2,5 điểm) 3 Câu 3.a.4.
Một quả cầu đặc bán kính R 4
 0 cm mang điện tích Q 26
 µC phân bố đều trong toàn bộ thể tích
của nó. Tính giá trị của điện trường tại điểm cách tâm cầu (a) 0 cm, (b) 10 cm, (c) 40 cm, và (d) 60 cm. Đáp án:
Chọn mặt Gauss là mặt cầu bán kính r . Với r  R , điện tích nằm bên trong mặt cầu đó là: 3 4 3 . r q  r  Q 3 3 R (2,5 điểm) Áp dụng định lý O-G:   2 .  .4 q E dS E r     r R r R  0 Q  E  r r R 3 4 R 0 (2,5 điểm)
Với r R , điện tích nằm bên trong mặt cầu đó là Q . Áp dụng định lý O-G: 2   .4 Q E r r R 0 Q  E  r R  2 4 0r (2,5 điểm)
Thay các dữ liệu của đề bài thu được: E 0  E 3  65119 E 1  460477 E 6  49101 0 cm ; 10 cm V/m, 40 cm V/m, 60 cm V/m. (2,5 điểm) 4 Câu 3.a.5.
Trong phân hạch hạt nhân, một hạt nhân nguyên tử Uranium-238 gồm 92 proton phân rã thành 2 hạt –15
nhân nhỏ hơn (hình cầu) gồm 46 proton và có bán kính R 5  .9 1
 0 m. Tính lực đẩy tĩnh điện giữa
hai hạt nhân nhỏ này ngay sau khi phân rã, tức khi hai quả cầu hạt nhân nhỏ nằm sát nhau. Đáp án:
Giả sử ở trạng thái ban đầu, hai hạt nhân nhỏ hình cầu nằm sát nhau, khoảng cách giữa tâm của chúng
là 2R . Lực đẩy tĩnh điện giữa chúng là: 2 2 Z e F  d 4  2R2 0 , với Z 46  (5 điểm)
Thay dữ liệu vào thu được F 3  506 d N. (5 điểm) 5 Câu 3.a.6.
a) Tính vận tốc của proton được gia tốc từ trạng thái nghỉ bởi hiệu điện thế U 120  V.
b) Tính vận tốc của electron được gia tốc từ trạng thái nghỉ bởi hiệu điện thế U 120  V.  27 m 1  .6726219×10  31
Cho khối lượng của proton là m  9.1×10 p
kg, khối lượng electron là e kg.  19 q 1  .6×10  19
Điện tích của proton là q  1.6×10 p
C, điện tích của electron là e C. Đáp án:
a) Động năng của proton thu được sau khi gia tốc: 1 2q U 2 p W  m v q  U  v  1  51518.87 d, p 2 p p p p m p (m/s) (5 điểm)
b) Động năng của proton thu được sau khi gia tốc: 1 2 q U 2 e W
 m v q U  v  6  495983.54 d, e 2 e e e e me (m/s) (5 điểm) 6 Câu 3.a.7.
Hai vỏ cầu vật dẫn đồng tâm có bán kính là a 0.4  m và b 0.5 
m, được nối với nhau bởi một dây dẫn. Nếu đặt lên hệ
một điện tích Q 10 
µC thì điện tích được phân bố trên mỗi vỏ cầu là bao nhiêu? Đáp án:
Gọi điện tích trên mỗi vỏ cầu là 1
q và 2q. Do hai vỏ cầu được nối với nhau bằng dây dẫn nên điện thế
trên 2 vỏ cầu bằng nhau:  1 q 2 q 1 q 2 q Q V     4 a 4 b 4 a b 4  0 0 0   0  a b  (5 điểm)
Vậy điện tích trên từng quả cầu là: a 40 b 50 q Q   q Q   1 2 a  b 9 µC và a  b 9 µC (5 điểm) 7 Câu 3.a.8.
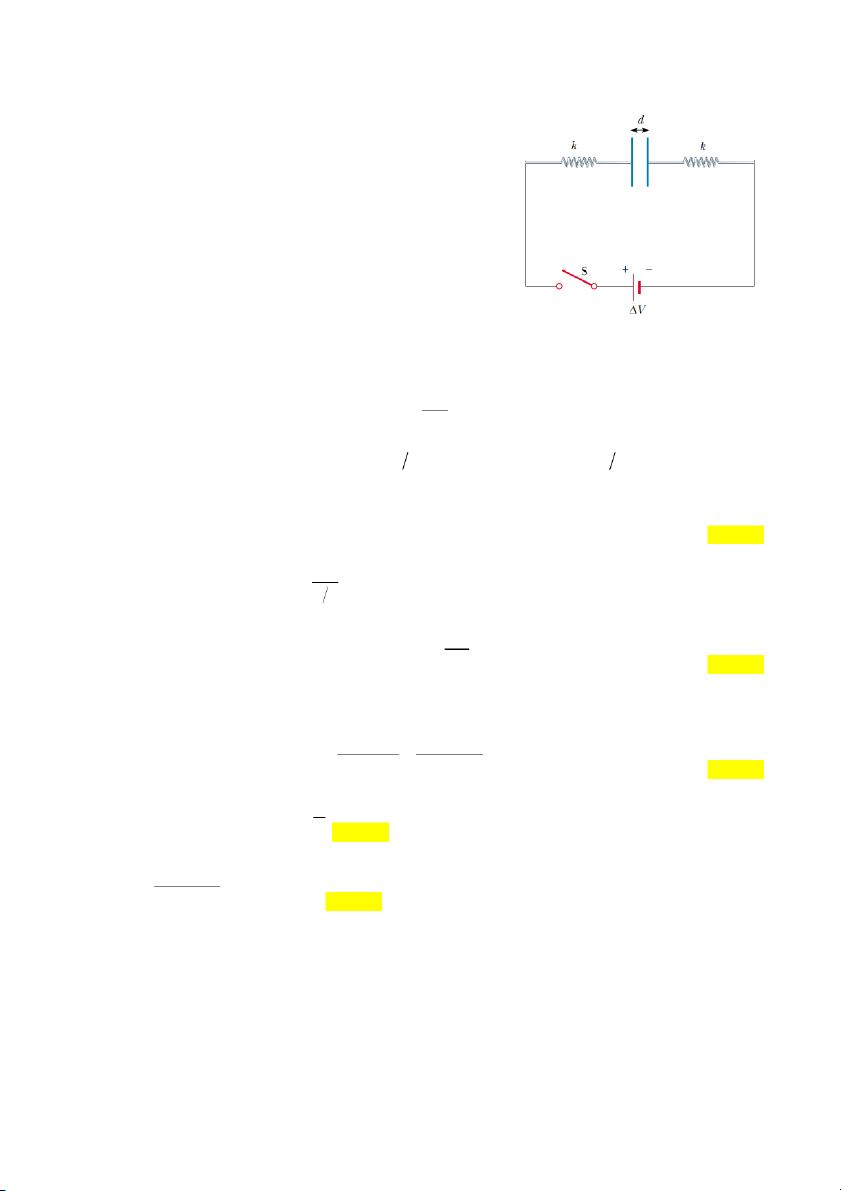
Hai bản kim loại giống nhau được nối với hai lò xo kim loại có
độ cứng k và nối với nguồn V  100  V. Khi khóa S mở, hai
bản không tích điện, khoảng cách giữa hai bản là d 8  mm và
tạo thành tụ điện có điện dung C 2  µF. Khi đóng khóa S,
khoảng cách giữa hai bản giảm đi còn một nửa.
a) Tính điện tích trên mỗi bản kim loại.
b) Độ cứng của mỗi lò xo là bao nhiêu? Đáp án:
Gọi A là diện tích của một bản kim loại. Hai bản kim loại tạo thành một tụ điện phẳng với điện dung:  A 0 C  d
Khi đóng khóa S, khoảng cách giữa hai bản là d 2 , mỗi lò xo giãn một đoạn d 4 , điện dung của tụ là C  2
 C . Điện tích trên tụ là: q C  V 400 µC (2 điểm) V E  2E
Điện trường giữa hai bản tụ là d 2
, với E là điện trường do một bản kim loại gây ra: V E   d (2 điểm)
Lực hút giữa hai bản kim loại là: C   V   2 C  V   2 2 F qE     d d d (2 điểm) d F F k 
Ở trạng thái cân bằng: d dh 4 (2 điểm) 8  C V 2 k  2500 Từ đó: 2 d (N/m). (2 điểm) 8 Câu 3.a.9.
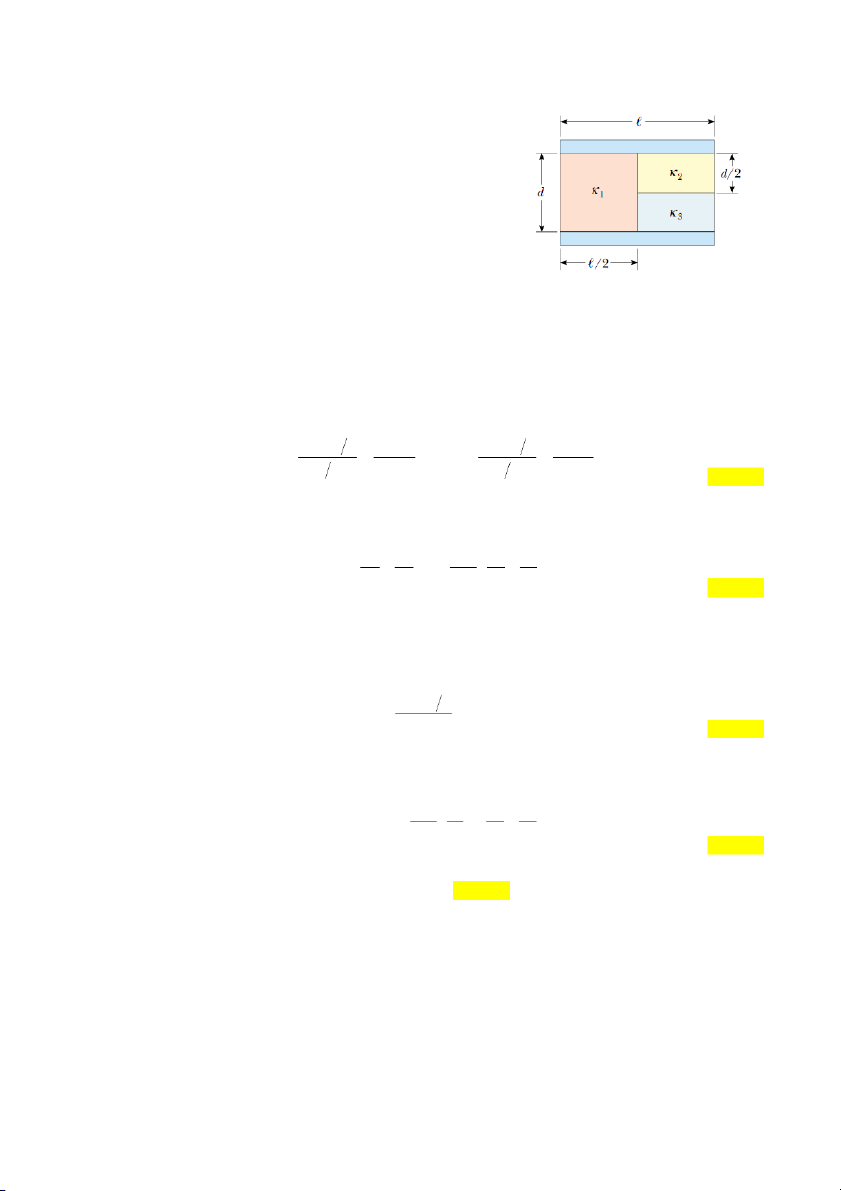
Một tụ điện phẳng sử dụng 3 chất điện môi với các hằng số   
điện môi 1 , 2 và 3 . Coi l d  .
a) Xây dựng công thức điện dung của tụ theo diện tích bản
tụ A , khoảng cách giữa 2 bản tụ d , và các hằng số điện    môi 1 , 2 và 3 .  4.9
b) Tính kết quả với A 1  cm ,2 d 2  mm, 1 ,  5  .6  2  .1 2 , và 3 . Đáp án:  
Giả sử đặt một lá kim loại mỏng có độ dày không đáng kể vào giữa hai chất điện môi 2 và 3 . Khi đó
lá kim loại này sẽ đóng vai trò là điện cực trung gian và tạo thành 2 tụ điện mắc nối tiếp với điện dung tương ứng là:   A 2     A 2   0 2 0 2A   0 3 0 3 A   2 C 3 C d 2 d và d 2 d (2 điểm)
Điện dung tương đương là: 1 1  1 1   A 1 1  0 C       23     2 C 3 C d   2 3  (2 điểm) 
Tụ điện tương đương C C
23 tiếp tục mắc song song với tụ điện 1 có điện môi 1 do cùng tiếp xúc với
hai bản cực của tụ điện chính. Điện dung của tụ 1 C :   A 2 0 1 C  1 d (2 điểm)
Vậy điện dung của tụ điện chính là:  1  A  1 1    0 1 C         1 C 23 C  d  2     2 3    (2 điểm)  12
Thay dữ liệu vào thu được: C 1  .76 1  0 F 1  .76 pF. (2 điểm) 9 Câu 3.a.10.
Tính công suất nhiệt tỏa ra trên từng điện trở trong mạch trên hình vẽ. Đáp án:
Hai điện trở 4 Ω mắc song song nên tương đương 1 điện trở 2 Ω.
Gọi dòng điện chạy qua nguồn 50 V và điện trở R 2   I 1
là 1 , chạy qua nguồn 20 V và điện trở R 2   2
là I2 (quy ước chạy từ cực dương của các nguồn), dòng điện chạy qua điện trở tương đương
2 Ω là I3 (quy ước chạy từ trên xuống dưới). Chiều dương của các ô mạng theo chiều kim đồng hồ. (2 điểm)
Các phương trình định luật Kirchhoff:
I  I  I 0  1 2 3 
2I 2I  50 0  1 3
2I  2I  20 0   2 3 (2 điểm)
Giải hệ phương trình trên thu được: I 2  0 A 1  I 1  5 A 2 I 5  A  3 (2 điểm)
Công suất tỏa nhiệt trên từng điện trở: 2 P R  I 8  00 W 1 1 1  2 P R  I 450 W 2 2 2  2 P R  I 5  0 W 3 3 3  (2 điểm)
Công suất tỏa nhiệt trên từng điện trở 4 Ω là P P P 2 2  5 W 31 32 3 . (2 điểm) 10