KHÁI NIỆM HÀM SỐ VÀ ĐỒ THỊ KHÁI NIỆM HÀM SỐ
Khái niệm hàm số và đồ thị hàm số. Tài liệu được sưu tầm. Mời các bạn tham khảo
Chủ đề: Chương 6: Hàm số, đồ thị và ứng dụng (KNTT) 61 tài liệu
Môn: Toán 10 3.2 K tài liệu
Tác giả:
Preview text:
KHÁI NIỆM HÀM SỐ VÀ ĐỒ THỊ KHÁI NIỆM HÀM SỐ
- Kiến thức cần nhớ
- Hàm số
- Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.
- Cho hàm số y = f(x), nếu ứng với x = a ta có y = f(a) thì f(a) được gọi là giá trị của hàm số.
- Tọa độ một điểm:
Trên mặt phẳng, ta vẽ hai trục số Ox và Oy vuông góc với nhau tại gốc O của mỗi trục, khi đó ta có hệ trục tọa độ Oxy.
Các trục Ox, Oy gọi là các trục tọa độ.
Ox gọi là trục hoành và thường được vẽ nằm ngang, Oy gọi là trục tung và thường được vẽ thẳng đứng.
Giao điểm O được gọi là gốc tọa độ.
Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy.
Hai trục Ox, Oy chia mặt phẳng tọa độ thành bốn góc: góc phần tư thứ I, II, III, IV
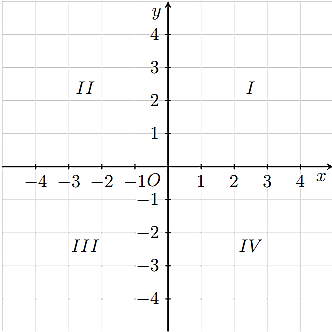
- Tọa độ của một điểm trên mặt phẳng tọa độ
Ta xác định vị trí một điểm P trong mặt phẳng tọa độ Oxy bằng cách dùng hai số thực như sau:
Từ P vẽ các đường vuông góc với các trục tọa độ cắt trục hoành tại điểm a và trục tung tại điểm b.
Khi đó cặp số (a; b) gọi là tọa độ của điểm P và kí hiệu là P(a; b). Số a gọi là hoành độ và số b gọi là tung độ của điểm P.
Gốc tọa độ O có tọa độ là (0; 0).
- Xác định một điểm trên mặt phẳng tọa độ khi biết tọa độ của nó
Để xác định một điểm P có tọa độ là (a; b), ta thực hiện các bước sau:
+ Tìm trên trục hoành điểm a và vẽ đường thẳng vuông góc với trục này tại điểm a.
+ Tìm trên trục tung điểm b và vẽ đường thẳng vuông góc với trục này tại điểm b.
+ Giao điểm của hai đường thẳng vừa vẽ cho ta điểm P cần tìm
- Đồ thị của hàm số: Đồ thị của hàm số y = f(x) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm M(x; f(x)).
- Các dạng bài tập
- Hàm số, bảng giá trị của hàm số
Bài 1: Các giá trị tương ứng của hai đại lượng x và y được cho bởi các bảng sau. Đại lượng y có phải là một hàm số của đại lượng x không?
Bài 2: Cho hàm số y = f(x) = 3x+2. Lập bảng các giá trị tương ứng của y khi x nhận các giá trị lần lượt là −2; −1; 0; 1; 2.
Bài 3: Cho hàm số y = f(x) = −2x + 1.
a) Tính f(10); f(−10).
b) Lập bảng giá trị của hàm số với x lần lượt bằng −2; −1; 0; 1; 2.
Bài 4:
- Tính giá của hàm số
tại x = 1; x = −1.
- Cho hàm số y = f(x) = mx + m − 1, biết f(3) = 8. Tính f(3).
Bài 5: Nhà bác học Galileo Galilei (1564 − 1642) là người đầu tiên phát hiện ra quan hệ giữa quãng đường chuyển động y (m) và thời gian chuyển động x (giây) của một vật được biểu diễn gần đúng bởi hàm số y = 
Bài 6: Số tiền điện phải trả trong tháng khi lượng điện sử dụng x (kWh) trong khoảng từ 51 kWh đến 100 kWh được cho bởi công thức sau
T(x) = 1734x − 2800 (đồng).
a) Tính số tiền điện phải trả khi lượng điện tiêu thụ trong tháng là 90 kWh.
b) Nếu số tiền điện phải trả trong tháng là 144 590 đồng thì gia đình đó đã sử dụng bao nhiêu kWh điện?
Bài 7: Giá cước taxi của một hãng xe taxi khi quãng đường di chuyển x km trong khoảng từ 1 km đến 30 km được cho bởi công thức sau:
T(x) = 10000 + 13600 · (x − 1) (đồng).
- Tính số tiền phải trả khi xe di chuyển 20 km.
- b) Nếu một hành khách phải trả 200 400 đồng thì hành khách đó đã di chuyển bao nhiêu kilômét?
Bài 8: Vẽ một hệ trục tọa độ Oxy và đánh dấu các điểm A(−1; 2) và B(3; 4).
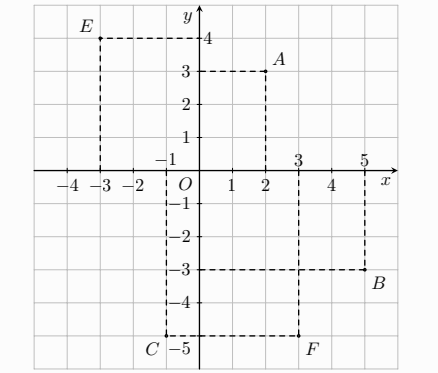
Bài 9 : Tìm tọa độ của các điểm A, B, C trong hình sau:
Bài 10: Vẽ đồ thị của hàm số y = f(x) cho bằng bảng sau:
Bài 11:
Bài 12: Biểu diễn hai điểm A (2; 1) và B(4; 5) trên cùng một mặt phẳng tọa độ. Tính khoảng cách giữa hai điểm đó.
Bài 13: Cho tam giác ABC có A(1; 1); B(3; 3) và C(5; 1).
a) Tính chu vi tam giác ABC;
b) Chứng minh rằng tam giác ABC vuông cân.
Bài 14: Cho các điểm A(2; 4), B(−1; 0) và C(0; 4).
a) Biểu diễn trên các điểm A, B, C trên mặt phẳng tọa độ.
b) Tính chu vi và diện tích của tam giác ABC.
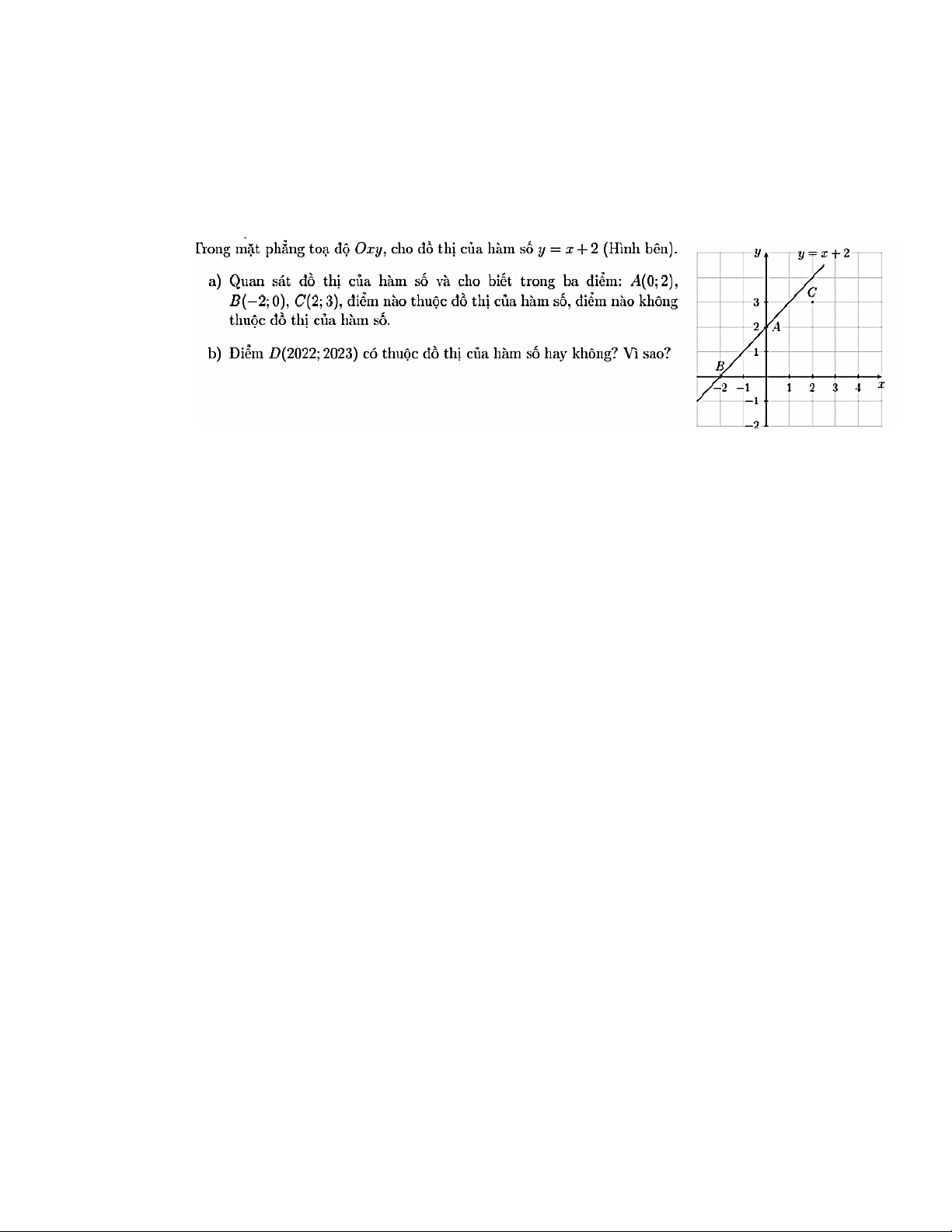
Bài 15: Cho hàm số y = f(x) = √ x. Trong các điểm A(9; 3), B(4; −2), M(−1; 1) điểm nào thuộc đồ thị (G) của hàm số cho?
