




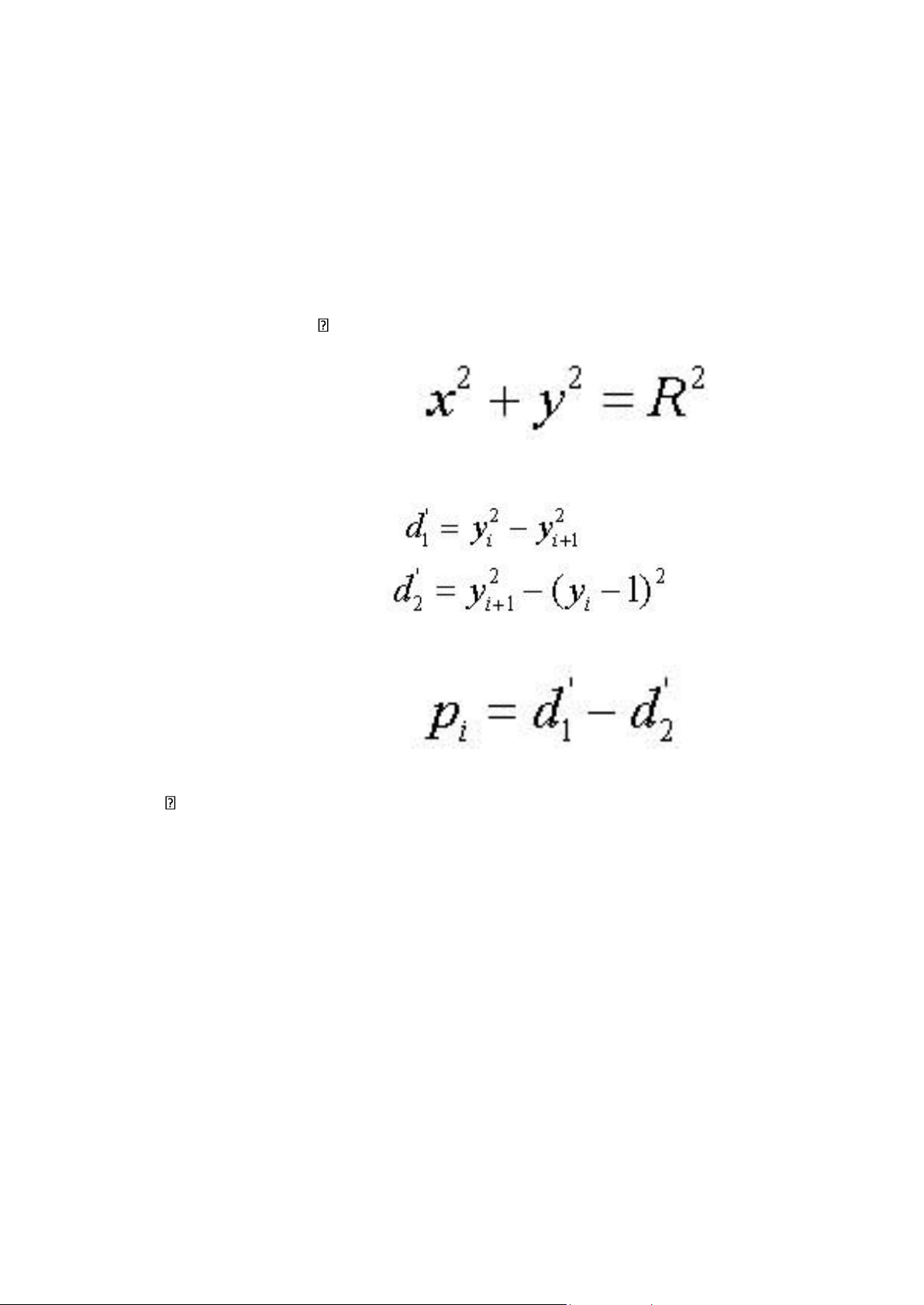






Preview text:
lOMoAR cPSD| 60729183 1.1. 1.2. 1.3.
1.4. Các khái niệm cơ bản về đồ họa máy tính
1.4.1. Đồ họa máy tính
Đồ họa máy tính là một ngành khoa học Tin học chuyên nghiên cứu về các phương
pháp và kỹ thuật để có thể mô tả và thao tác trên các đối tượng của thế giới thực bằng máy tính.
Về bản chất: đó là một quá trình xây dựng và phát triển các công cụ trên cả hai lĩnh
vực phần cứng và phần mềm hổ trợ cho các lập trình viên thiết kế các chương trình có khả năng đồ họa cao.
Với việc mô tả dữ liệu thông qua các hình ảnh và màu sắc đa dạng của nó, các
chương trình đồ họa thường thu hút người sử dụng bởi tính thân thiện, dể dùng,... kích
thích khả năng sáng tạo và nâng cao năng suất làm việc. 1.4.2. Các kỹ thuật đồ họa máy tính
a), Kỹ thuật đồ họa điểm
Các mô hình, hình ảnh của các đối tượng được hiển thị thông qua từng pixel (từng mẫu rời rạc) [1] Đặc điểm:
• Có thể thay đổi thuộc tính
• Xoá đi từng pixel của mô hình và hình ảnh các đối tượng.
• Các mô hình hình ảnh được hiển thị như một lưới điểm (grid) các pixel rời rạc
• Từng pixel đều có vị trí xác định, được hiển thị với một giá trị rời rạc (số
nguyên) các thông số hiển thị (màu sắc hoặc độ sáng)
• Tập hợp tất cả các pixel của grid cho chúng ta mô hình, hình ảnh đối tượng
mà chúng ta muốn hiển thị.
Phương pháp để tạo ra các pixel:
• Phương pháp dùng phần mềm để vẽ trực tiếp từng pixel một.
• Dựa trên các lý thuyết mô phỏng (lý thuyết Fractal, v.v) để xây dựng nên
hình ảnh mô phỏng của sự vật.
• Phương pháp rời rạc hoá (số hoá) hình ảnh thực của đối tượng.
• Có thể sửa đổi (image editing) hoặc xử lý (image processing) mảng các lOMoAR cPSD| 60729183
pixel thu được theo những phương pháp khác nhau để thu được hình ảnh đặc trưng của đối tượng
b), Kỹ thuật đồ họa Vector
Xây dựng mô hình hình học cho hình ảnh đối tượng, xác định các thuộc tính
của mô hình hình học, sau đó dựa trên mô hình này để thực hiện quá trình tô trát để hiển
thị từng điểm của mô hình, hình ảnh của đối tượng. [1]
Kỹ thuật này chỉ lưu trữ mô hình toán học của các thành phần trong mô hình
hình học cùng với các thuộc tính tương ứng mà không cần lưu lại toàn bộ tất cả các pixel
của hình ảnh đối tượng. [1]
So sánh giữa Đồ họa điểm và Đồ họa Vector: [1] Đồ họa điểm Đồ họa vector
Hình ảnh và mô hình của các vật thể được
biểu diễn dưới dạng tập hợp các điểm của
Không thay đổi thuộc tính của từng điểm trực lưới tiếp
Xử lý với từng thành phần hình học cơ sở
Thay đổi thuộc tính của các pixel dẫn đến
của nó và thực hiện quá trình tô trát và hiển
thay đổi từng phần và từng vùng của hình ảnh thị lại.
Quan sát hình ảnh và mô hình của hình ảnh và
Copy được các pixel từ một hình ảnh này
sự vật ở nhiều góc độ khác nhau bằng cách sang hình ảnh khác
thay đổi điểm nhìn và góc nhìn
Bảng 1.1.2.1. Bảng so sánh giữa Đồ họa điểm và Đồ họa Vector
c), Kỹ thuật đồ họa 3D
Đồ họa 3D là kỹ thuật đồ họa đang được tập trung phát triển nhất trong thời điểm
hiện tại, với sự quan tâm và tiềm năng của các ứng dụng như không gian ảo hay hình chiếu
ba chiều. Nhà thiết kế đồ họa phải thực hiện rất nhiều bước khác nhau và áp dụng nhiều
kỹ thuật tạo dựng hình ảnh phức tạp để có được một đôí tượng hình ảnh 3D đúng nghĩa.
Trước hết, khung cơ bản (wire-frame) của vật thể phải được dựng trong một phần
mềm đồ họa máy tính, sau đó các phần của vật thể sẽ được thêm vào và nối với nhau
(rigged) để tạo sự liên kết chân thực, đặc biệt là với các vật thể có khả năng chuyển động.
Sau đó vật thể phải được render.
Đây là bước mất thời gian và phức tạp nhất vì một vật thể 3D có nhiều bề mặt khác
nhau với các chất liệu khác nhau, độ trong suốt hay mờ đục, màu sắc, mức độ bắt sáng hay
phản sáng khác nhau. Để tạo được một vật thể 3D thật nhất có thể, nhiều kỹ thuật toán học lOMoAR cPSD| 60729183
được áp dụng để tính toán và mô phỏng cách ánh sáng chiếu và phản chiếu vào các loại
mặt phẳng khác nhau như ray tracing hay radiosity,… 1.4.3. Các lĩnh vực đồ họa máy tính a), Kiến tạo đồ họa
Các hệ CAD/CAM(Computer Aided Design/Computer Aided Manufacture
System): kỹ thuật đồ hoạ tập hợp các công cụ, các kỹ thuật trợ giúp cho thiết kế các chi
tiết và các hệ thống khác nhau: hệ thống cơ, hệ thống điện, hệ thống điện tử….
Đồ hoạ minh hoạ (Presentation Graphics): gồm các công cụ giúp hiển thị các số liệu
thí nghiệm một cách trực quan, dựa trên các mẫu đồ thị hoặc các thuật toán có sẵn.
Đồ hoạ hoạt hình và nghệ thuật: bao gồm các công cụ giúp cho các hoạ sĩ, các nhà
thiết kế phim hoạt hình chuyên nghiệp làm các kỹ xảo hoạt hình, vẽ tranh... Ví dụ: phần
mềm 3D Studio, 3D Animation, 3D Studio Max. [1] b), Xử lý đồ họa
Kỹ thuật xử lý ảnh (Computer Imaging): sau quá trình xử lý ảnh cho ta ảnh sốcủa
đối tượng. Trong quá trình xử lý ảnh sử dụng rất nhiều các kỹ thuật phức tạp: kỹ thuật khôi
phục ảnh, kỹ thuật làm nổi ảnh, kỹ thuật xác định biên ảnh.
Kỹ thuật nhận dạng (Pattern Recognition): từ những ảnh mẫu có sẵn ta phân loại
theo cấu trúc, hoặc theo các tiêu trí được xác định từ trước và bằng các thuật toán chọn lọc
để có thể phân tích hay tổng hợp ảnh đã cho thành một tập hợp các ảnh gốc, các ảnh gốc
này được lưu trong một thư viện và căn cứ vào thư viện này ta xây dựng được các thuật
giải phân tích và tổ hợp ảnh. [1]
Kỹ thuật tổng hợp ảnh (Image Synthesis): là lĩnh vực xây dựng mô hình và hình ảnh
của các vật thể dựa trên các đối tượng và mối quan hệ giữa chúng. [1]
1.5. Các giải thuật đồ họa cơ bản
1.5.1. Thuật toán Bresenham
a), Thuật toán Bresenham vẽ đường thẳng
Ý tưởng thuật toán:
• Thay thế các phép toán trên số thực bằng các phép toán trên số nguyên.
• Giảm thời gian của thuật toán hơn so với DDA.
• Hạn chế phép toán được thực hiện để giảm tải thời gian. Đặt vấn đề:
• Cho 2 điểm A(x1,y1) và B(x2,y2) . Vẽ đường thẳng đi qua A,B . Giải thuật:
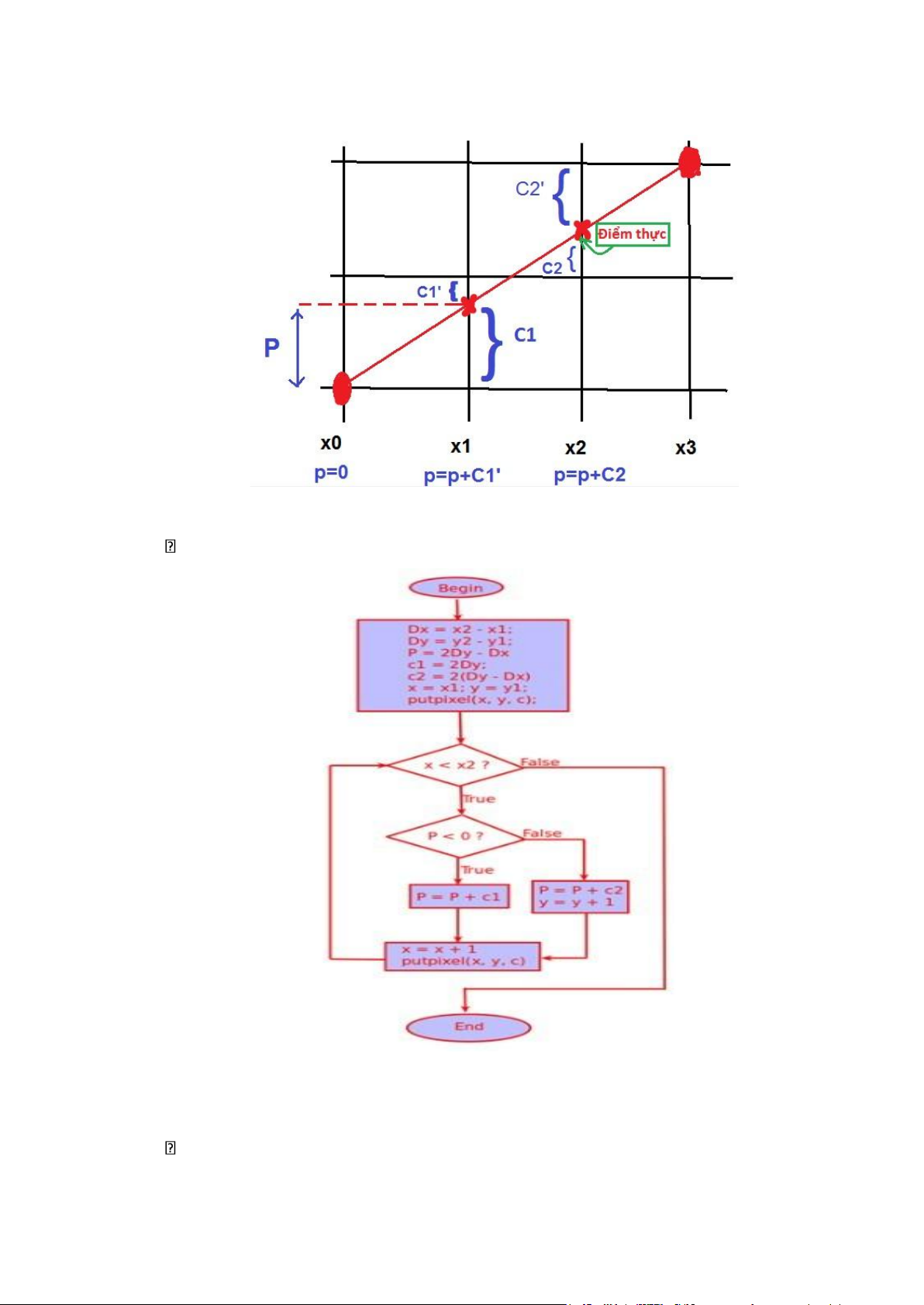
• Thuật toán Bresenham đưa ra cách chọn yi+1 là yi hay yi+1 theo một hướng
khác . Đó là so sánh khoảng cách giữa điểm thực y với 2 điểm gần kề nó nhất. Nếu điểm
nào nằm gần điểm thực hơn thì sẽ được chọn làm điểm vẽ tiếp theo. [2] lOMoAR cPSD| 60729183
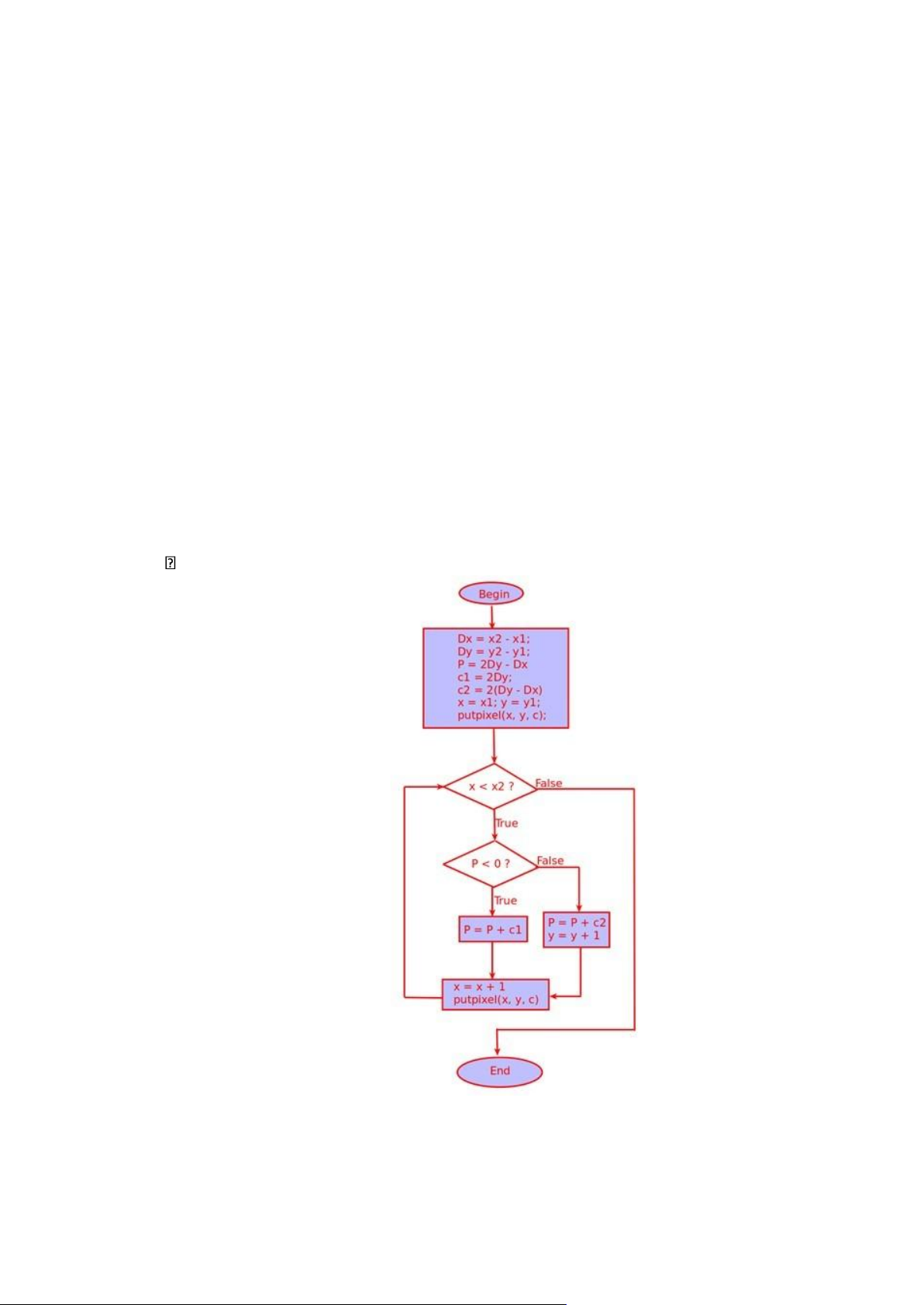
Hình 1.2.1.1. Mô tả giải thuật Bresenham vẽ đường thẳng
Xét trường hơp 0• Gọi y là giá trị thực (giá trị chính xác) của đường thẳng tại x ở bước thứ i+1. • y = m(xi + 1)+b.
• Gọi d1 là khoảng cách từ y đến yi .
• Gọi d2 là khoảng cách từ y đến yi+1 . Ta có:
Dễ thấy d1- d2 tồn tại phép toán với số thực m = dy/dx .Và để tuân thủ theo đúng ý
tưởng thuật toán chỉ thực hiện các phép toán trên số nguyên, ta khử phân số ( triệt tiêu mẫu
số) bằng cách nhân 2 vế với dx: [2] lOMoAR cPSD| 60729183
Sau khi đi phân tích một hồi như ở trên, nhiều bạn sẽ có thắc mắc là “Sao lại đặt
Pi= dx(d1- d2) , rồi tại sao lại đi tìm Pi+1 theo Pi ? lOMoAR cPSD| 60729183
Đầu tiên , hãy nhìn hình dưới đây:
Hình 1.2.1.2. Giải thích “Điểm thực” của giải thuật Bresenham vẽ đường thẳng Lưu đồ thuật toán:
Hình 1.2.1.3. Lưu đồ thuật toán Bresenham vẽ đường thẳng
b), Thuật toán Bresenham vẽ đường tròn Ý tưởng: lOMoAR cPSD| 60729183
• Giả sử tại bước thứ i ta đã xác định được (xi, yi)
• Tại bước thứ i + 1 o Ta có xi + 1 = xi + 1 o Gọi yi +1 là giá trị chính xác
của tung độ tương ứng với điểm có hoành độ là (xi +1)
o d1 là khoảng cách giữa yi và yi + 1 o
d2 là khoảng cách giữa yi +1 và (yi -1) o Khi
đó nếu d1 < d2 thì yi +1 = yi o Ngược lại yi +1
= yi – 1. [3] Phương trình đường tròn:
• Phương trình đường tròn có hàm mũ tại y nên nếu tính d1, d2 theo y thì sẽ
có hàm căn làm chậm thuật toán, do vậy ta đặt: [3] • Đặt: • Tính pi+1 theo pi Lưu đồ thuật toán lOMoAR cPSD| 60729183
Hình 1.2.1.4. Lưu đồ thuật toán Bresenham vẽ đường tròn
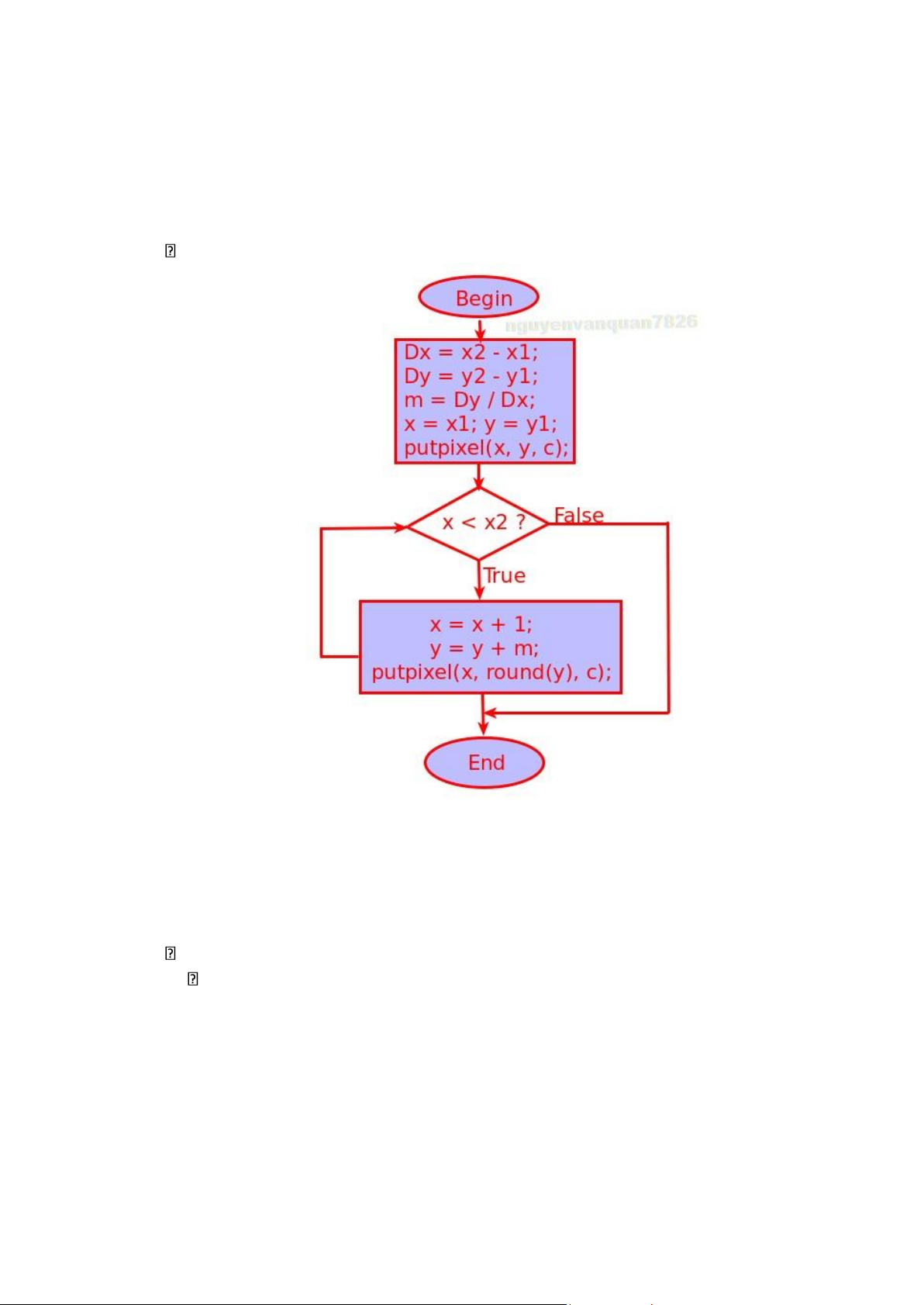
1.5.2. Thuật toán DDA Đặt vấn đề:
• Cho 2 điểm A(x1 , y1 ) và B(x2 , y2 ). Hãy vẽ đường thẳng đi qua 2 điểm đó.
Xây dựng thuật toán: Với kiến thực được học hồi nhỏ (cấp 2), phương trình đường
thẳng có thể phát biểu dưới dạng: • (d) y=m.x +b • m=( y2- y1)/( x2- x1) • b= y1-mx1
• Trong đó: m là hệ số góc
Giả sử vẽ được (xi, yi). Tiếp theo, chọn yi+1 là y
i hay yi+1 dựa vào phương trình của đường thẳng d. [4]
Hình 1.2.2.1. Mô tả thuật toán DDA lOMoAR cPSD| 60729183
Thay xi+1 vào phương trình đường thẳng d: • Yi+1=m(xi +1) + b • Yi+1 =mxi +b+m • Yi+1 =yi +m Lưu đồ thuật toán:
Hình 1.2.2.2. Lưu đồ thuật toán DDA
1.5.3. Thuật toán Mid-point
a), Thuật toán Mid-point vẽ đường thẳng
Đặt vấn đề: Cho 2 điểm A(x1,y1) và B(x2,y2). Vẽ đường thẳng đi qua 2 điểm A,B Giải thuật: Xét 0 lOMoAR cPSD| 60729183
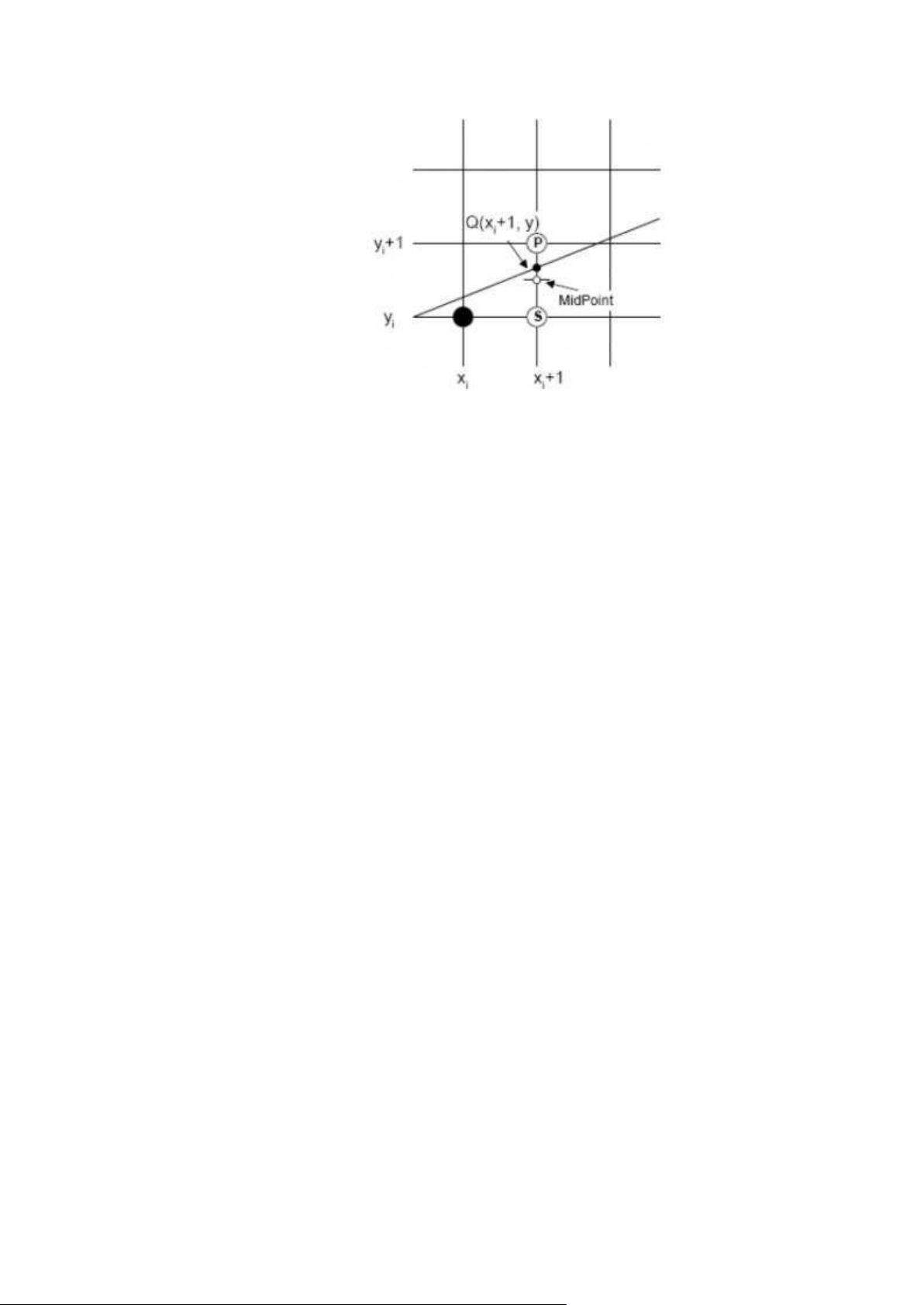
Hình 1.2.3.1. Mô tả thuật toán Mid-point vẽ đường thẳng
Thuật toán Midpoint đưa ra cách chọn điểm yi+1 là yi hay yi+1 bằng cách so sánh điểm
thực Q(xi+1 , y) với điểm Midpoint là trung điểm của S và P.
Nếu điểm Q nằm dưới điểm Midpoint thì ta chọn điểm S là điểm vẽ tiếp theo. Ngược
lại , nếu điểm Q nằm trên điểm Midpoint thì ta chọn P.
Ta có dạng tổng quát của PT đường thẳng : • Ax + By +C=0 •
Với A= yo – y1 ; B= -(x2 –x1) ; C=x2y1 –x1y2 • Đặt F(x,y)= Ax+ By +C
Ta có nhận xét vị trí tương đối của điểm Midpoint (x,y) với đường thẳng: •
F(x,y) < 0 nếu (x,y) nằm phía trên đường thẳng •
F(x,y) = 0 nếu (x,y) thuộc về đường thẳng •
F(x,y) > 0 nếu (x,y) nằm phía dưới đường thẳng
Lúc này việc chọn các điểm S, P ở trên được đưa về việc xét dấu của: pi =
2F(Midpoint) = 2F(xi +1 , yi +1/2) •
Nếu pi < 0 ⇒ Midpoint nằm phía trên đường thẳng ⇒Lúc này điểm thực Q
nằm phía dưới điểm Midpoint ⇒ Chọn S(xi +1, yi). •
Nếu pi >= 0 ⇒ Midpoint nằm phía dưới đường thẳng ⇒ Lúc này điểm
thực Q nằm trên điểm Midpoint ⇒ Chọn P(xi +1, yi +1). Mặt khác:
pi+1 –pi = 2F(xi+1 +1 , yi+1 +1/2) – 2F(xi +1 , yi +1/2)
⇒ pi+1 –pi =2[A(xi+1 +1) + B(yi+1 +1/2) +C] – 2[A(xi +1) + B(yi+1/2) +C] lOMoAR cPSD| 60729183
⇒ pi+1 –pi = 2A + 2B(yi+1 – yi) ⇒
pi+1 –pi = 2Dy – 2Dx(yi+1 – yi) Vậy: •
pi+1 =pi + 2Dy nếu pi <0 do ta chọn yi+1 =yi •
pi+1 =pi + 2Dy – 2Dx nếu pi >=0 do ta chọn yi+1 =yi +1
Ta tính giá trị p1 ứng với điểm ban đầu (x1, y1) với nhận xét rằng điểm (x1, y1) là
điểm thuộc đường thẳng, tức là có Ax1 + By1 + C =0.
p1 = 2F(x1 +1, y1 +1/2) = 2[A(x1 +1) +B(y1 +1/2) +C]
⇒ p1 = 2(Ax1 + By1 +C) +2A +B ⇒ p1 = 2A + B ⇒ p1 = 2Dy-Dx
Ta thấy kết quả của thuật toán Midpoint tương tự thuật toán Bresenham như đã nói ở trên. [5] Lưu đồ thuật toán:
Hình 1.2.3.2. Lưu đồ thuật toán Mid-point vẽ đường thẳng lOMoAR cPSD| 60729183
b), Thuật toán Mid-point vẽ đường Elipse Đặt vấn đề:
Vẽ elip bằng thuật toán Midpoint. Giải thuật:
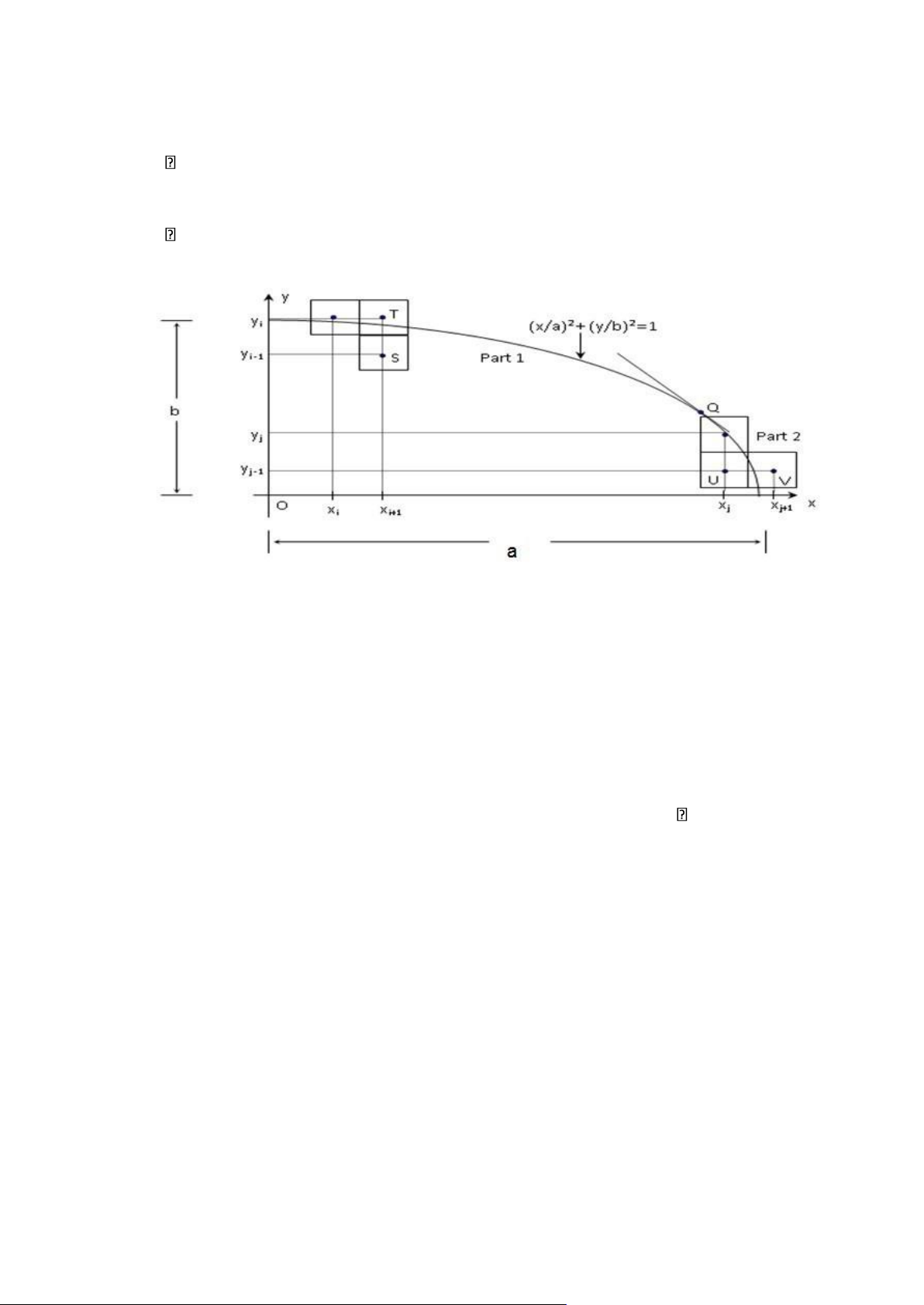
Hình 1.2.3.3. Giải thuật Mid-point vẽ đường Elipse Để
đơn giản, chúng ta sẽ chọn vẽ hình Elip có tâm ở gốc tọa độ.
Phương trình của đường Elip: •
f(x,y) = b2x2 + a2y2 – a2b2 o < 0 nếu (x,y) nằm bên trong elip.
o = 0 nếu (x,y) nằm trên elip.
o 0 nếu (x,y) nằm bên ngoài elip. Ý
tưởng và phân tích giải thuật:
Chia Elip làm 2 phần tại điểm Q nơi có hệ số góc của tiếp tuyến với Elip bằng -1
(véc tơ gradient bằng 1) ( lý do tại sao lại phải chia làm 2 phần thì bài 6 mình đã giải thích
rồi nhé). Tại vùng thứ nhất, x biến thiên nhanh hơn y và tại vùng thứ hai , y biến thiên
nhanh hơn x. Nhớ lại công thức hệ số góc của đường cong : •
dx/dy = fx/fy = (2b2x) /( 2a2y) •
Trong đó: fx và fy là đạo hàm riêng phần của f(x,y) theo x, theo y. Trong phần thứ nhất:
Giả sử đã vẽ được điểm (xi,yi) , điểm tiếp theo trên elip được chọn trong bước nhảy
i+1 là T hoặc S. Trung điểm I của TS sẽ quyết định điểm nào được chọn. Giá trị của f(x,y) tại điểm I: lOMoAR cPSD| 60729183 •
di = f(xi + 1, yi – ½) = b2(xi + 1)2 + a2(yi – ½)2 – a2b2
Nếu di ≥ 0 thì trung điểm I nằm ngoài đường elip => điểm được chọn là S.
Nếu di < 0 thì trung điểm I nằm trong đường elip => điểm được chọn là T. Ta lại có: •
di+1 = f(xi+1 + 1, yi+1 – ½) = b2(xi+1 +1)2 + a2(yi+1 – ½)2 – a2b2 Suy ra: •
di+1 – di = b2[(xi+1 +1)2 – (xi +1)2] +a2[(yi+1 – ½)2 – (yi – ½)2] Vì xi+1 = xi+1 nên: •
di+1 – di = 2b2xi+1 + b2 + a2[(yi+1 – ½)2 – (yi – ½)2] Nếu điểm được chọn
là T (di < 0) thì yi+1 = yi . Ta có : •
di+1 = di + 2b2xi+1 + b2 (= di + fx + b2) • = di + 2b2 (xi + 1) + b2 • = di + b2 (2xi + 3)
Nếu điểm được chọn là S (di ≥ 0) thì yi+1 = yi – 1 Ta có: •
di+1 = di + 2b2xi+1 + b2 – 2a2yi+1 (= di + fx + b2 – fy) •
= di + 2b2 (xi + 1) + b2 – 2a2 (yi – 1) •
= di + b2 (2xi + 3) + a2 (-2yi + 2) Với điểm đầu tiên (0,b) ta có: •
d1 = f(0,b) = b2 + a2(b – ½)2 – a2b2 = b2 ─ a2b + a2/4
Trong phần thứ hai: Chúng ta tính toán như phần 1. Giả sử ta phải xác định điểm
(xj+1,yj+1) tiếp theo trên elip trong bước j+1. Điểm được chọn là U hoặc V. Trung điểm K
của UV sẽ quyết định việc chọn điểm U hay điểm V. Giá trị của f(x,y) tại điểm K: •
ej = f(xj + ½, yj – 1) = b2(xj + ½)2 + a2(yj – 1)2 – a2b2 Nếu ej ≥ 0 điểm
được chọn là U. Nếu ej < 0 điểm được chọn là V. Ta lại có: •
ej+1 = f(xj+1 + ½, yj+1 – 1) = b2(xj+1 + ½)2 + a2(yj+1 – 1)2 – a2b2 Suy ra: •
ej+1 – ej = b2[(xj+1 + ½)2 – (xj + ½)2] + a2[(yj+1 – 1)2 – (yj – 1)2] •
= b2[(xj+1 + ½)2 – (xj + ½)2] – 2a2yj+1 + a2 Nếu điểm được chọn là U
(tức ej ≥ 0) thì xj+1 = xj Ta có: •
ej+1 = ej – 2a2yj+1 + a2 (= ej – fy + a2) lOMoAR cPSD| 60729183 • = ej – 2a2(yj -1) + a2 • = ej – a2(3 – 2yj)
Nếu điểm được chọn là V (tức ej < 0 )thì xj+1 = xj+1 Ta có: •
ej+1 = ej + 2b2xj+1 – 2a2yj+1 + a2 (= ej + fx – fy + a2) •
= ej + 2b2(xj + 1)– 2a2(yj -1) + a2 •
= ej + b2(2xj + 2)+ a2(3 -2yj )
Giá trị khởi tạo ban đầu trong phần 2 phụ thuộc vào vị trí cuối cùng của phần 1 , giả sử là (xk,yk). Khi đó: •
e1 = f(xk + ½, yk – 1) = b2(xk + ½) + a2(yk – 1)2 – a2b2 Lưu đồ thuật toán:
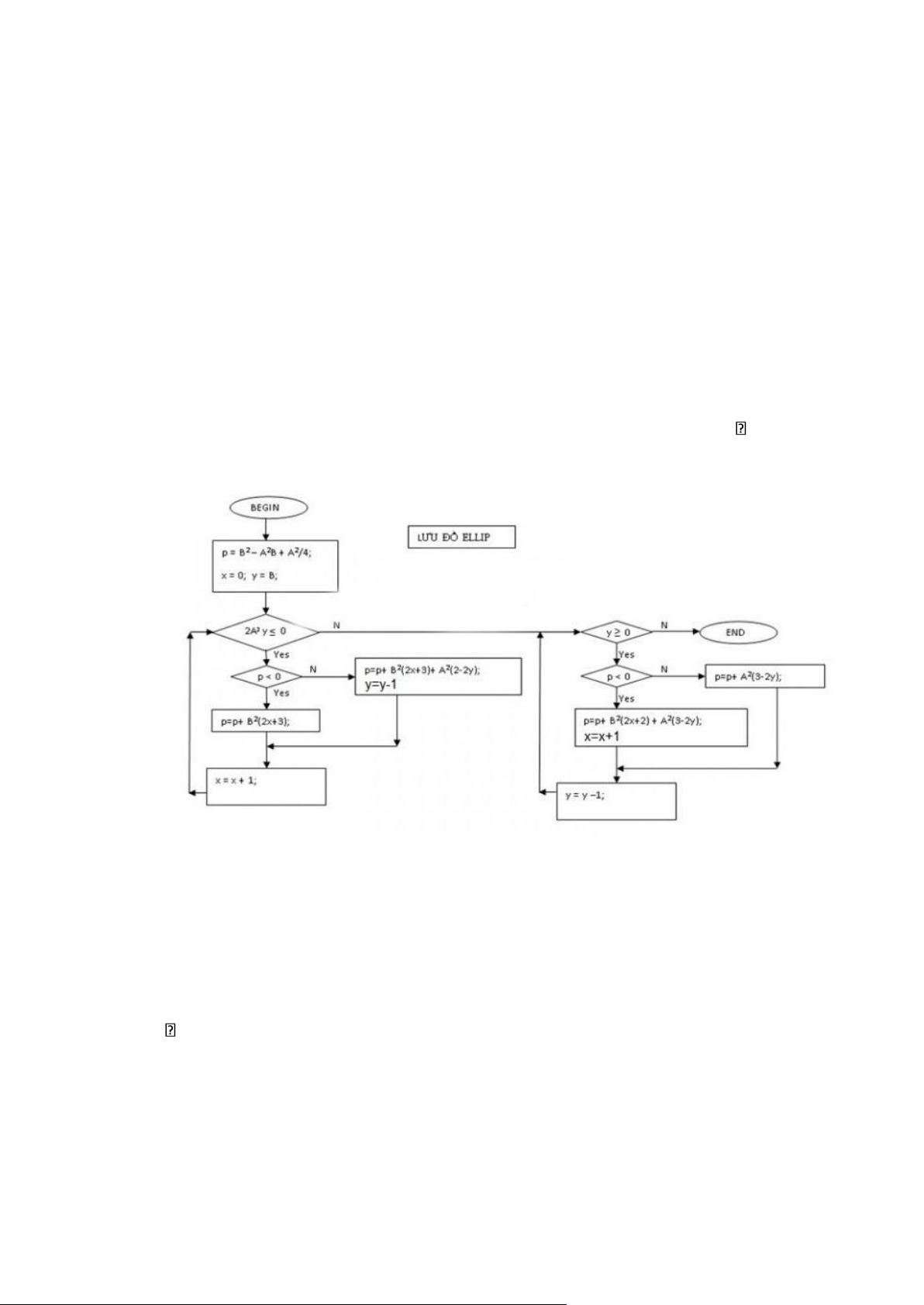
Hình 1.2.3.4. Lưu đồ thuật toán Mid-point vẽ đường Elipse
1.6. Ứng dụng của đồ họa máy tính
Công nghệ và công cụ đồ họa máy tính đã phát triển đáng kể trong các lĩnh vực đồ
họa 2D và 3D, mang lại nhiều ứng dụng đa dạng. Dưới đây là một số công nghệ và công
cụ phổ biến trong mỗi lĩnh vực và các ứng dụng của chúng: Đồ họa 2D: •
Vector Graphics (Đồ họa Vector): Sử dụng đối tượng hình học (như đường
thẳng, hình tròn, hình vuông) để tạo ra hình ảnh. Công cụ phổ biến: Adobe Illustrator,
CorelDRAW. o Ứng dụng: Thiết kế logo, biểu đồ, minh họa sách, vv. lOMoAR cPSD| 60729183 •
Raster Graphics (Đồ họa Raster): Sử dụng các pixel để tạo ra hình ảnh.
Công cụ phổ biến: Adobe Photoshop, GIMP. o Ứng dụng: Chỉnh sửa ảnh, thiết
kế đồ họa cho web, in ấn. •
Motion Graphics (Đồ họa chuyển động): Tạo ra các hình ảnh động, video
ngắn. Công cụ phổ biến: Adobe After Effects, Blender. o Ứng dụng: Quảng
cáo, video giới thiệu, đồ họa trực tuyến. Đồ họa 3D: •
Modeling (Mô hình hóa): Tạo ra các đối tượng 3D từ các hình
học cơ bản. Công cụ phổ biến: Autodesk Maya, Blender, Cinema 4D. o Ứng
dụng: Phim hoạt hình, trò chơi video, kiến trúc, thiết kế sản phẩm. •
Rendering (Kỹ thuật Rendering): Chuyển đổi mô hình 3D thành hình ảnh
hoặc video cuối cùng. Công cụ phổ biến: Autodesk 3ds Max, V-Ray, Arnold. o
Ứng dụng: Phim ảnh, quảng cáo, phát triển sản phẩm. •
Animation (Hoạt hình): Tạo ra các chuyển động cho các đối tượng 3D.
Công cụ phổ biến: Autodesk Maya, Blender, Cinema 4D. o Ứng dụng:
Phim hoạt hình, trò chơi video, giáo dục.
Ứng dụng của Công nghệ Đồ họa Máy tính: •
Giáo dục và Đào tạo: Sử dụng trong việc tạo ra các tài liệu giáo trình, video
học hoặc phần mềm giả lập để hỗ trợ quá trình học tập. •
Giải trí: Tạo ra phim hoạt hình, trò chơi video và trải nghiệm thực tế ảo để
giải trí và giáo dục người dùng. •
Thiết kế sản phẩm: Sử dụng để tạo mô hình 3D của các sản phẩm mới, từ
thiết kế ý tưởng ban đầu đến sản phẩm thực tế. •
Kiến trúc và Xây dựng: Dùng để tạo ra mô phỏng 3D của các dự án xây
dựng, giúp kỹ sư và kiến trúc sư hiểu rõ hơn về cách các công trình sẽ trông như trước khi được xây dựng. •
Quảng cáo và Tiếp thị: Sử dụng trong việc tạo ra hình ảnh và video độc đáo lOMoAR cPSD| 60729183
để quảng cáo sản phẩm và dịch vụ, thu hút sự chú ý của khách hàng. lOMoAR cPSD| 60729183
CHƯƠNG 2. THIẾT KẾ SẢN PHẨM ĐỒ HỌA 3D VỚI OPENGL
2.1. Xây dựng ý tưởng thiết kế
"Thiết kế dãy phố" là một ý tưởng thú vị cho một dự án thiết kế bằng OpenGL. Đây
có thể là một mô hình 3D của một phố nhỏ, có các công trình kiến trúc như tòa nhà cao
tầng, nhà ở, cây xanh, và đường phố.
Dưới đây là các bước lên ý tưởng của nhóm để bắt đầu:
Xác định kiến trúc chung: Đầu tiên, nhóm sẽ quyết định về loại kiến trúc và phong
cách mà muốn áp dụng cho dãy phố của mình. Có thể là một phố cổ điển với những căn
nhà hoặc một phố hiện đại với các tòa nhà cao tầng và biển báo giao thông.
Thiết kế các tòa nhà: Sử dụng OpenGL để tạo ra các mô hình 3D của các tòa nhà
trên phố. Tạo ra các hình hộp đơn giản để biểu diễn các tòa nhà hoặc thậm chí tạo ra các
mô hình chi tiết hơn với cửa sổ, cửa, và các chi tiết kiến trúc khác.
Tạo ra đường phố và vỉa hè: Sử dụng các đa giác và hình học khác để tạo ra các
đường phố và vỉa hè. Điều này có thể bao gồm việc vẽ các hình chữ nhật để biểu diễn
đường và các hình thoi hoặc hình tròn để biểu diễn các vườn hoa hoặc cây xanh.
Thêm các chi tiết như cây cỏ: Để làm cho phố trở nên sống động hơn, thêm vào các
chi tiết như cây cỏ, hoa, cây cối. Điều này có thể được thực hiện bằng cách sử dụng các
mô hình 3D có sẵn hoặc tạo ra chúng từ các hình hộp và đa giác đơn giản.
Tạo ánh sáng: Sử dụng kỹ thuật chiếu sáng trong OpenGL để tạo ra hiệu ứng ánh
sáng tự nhiên. Trong dự án này nhóm sử dụng các nguồn sáng sau
Nguồn sáng môi trường – Nguồn sáng GL_LIGHT0 o
GLfloat ambientLight[] = { 10.2f, 10.2f, 10.2f, 1.0f }; o
GLfloat diffuseLight[] = { 10.8f, 10.8f, 10.8f, 10.0f }; o
GLfloat specularLight[] = { 10.0f, 10.0f, 0.0f, 10.0f }; o
GLfloat position[] = { 10.0f, 20.0f, 2.0f, 1.0f };
Tương tác với người dùng: Tạo ra các tính năng tương tác với người dùng bằng cách
cho phép di chuyển xung quanh trong "dãy phố" bằng cách sử dụng các phím điều hướng
hoặc chuột. Thêm các tính năng như zoom và xoay để người dùng có thể khám phá phố từ
nhiều góc độ khác nhau.
Nhóm đã vẽ ra một sơ đồ mô phỏng “Dãy phố” với góc nhìn từ trên xuống dưới để dễ hình dung như sau: lOMoAR cPSD| 60729183
Hình 2.1.1. Mô phỏng lên ý tưởng thiết kế “Dãy phố” từ góc nhìn trên xuống
2.2. Vẽ các đối tượng 3D Vẽ cây: • Ảnh thiết kế:
Hình 2.2.1. Ảnh thiết kế đối tượng cây • Vị trí đặt: o glTranslatef(x, y + 23, z); o glTranslatef(x, y, z); lOMoAR cPSD| 60729183 Màu sắc:
o glColor3f(0.3, 0.015, 0.13); o glColor3f(0.015, 0.3, 0.13); Kích thước:
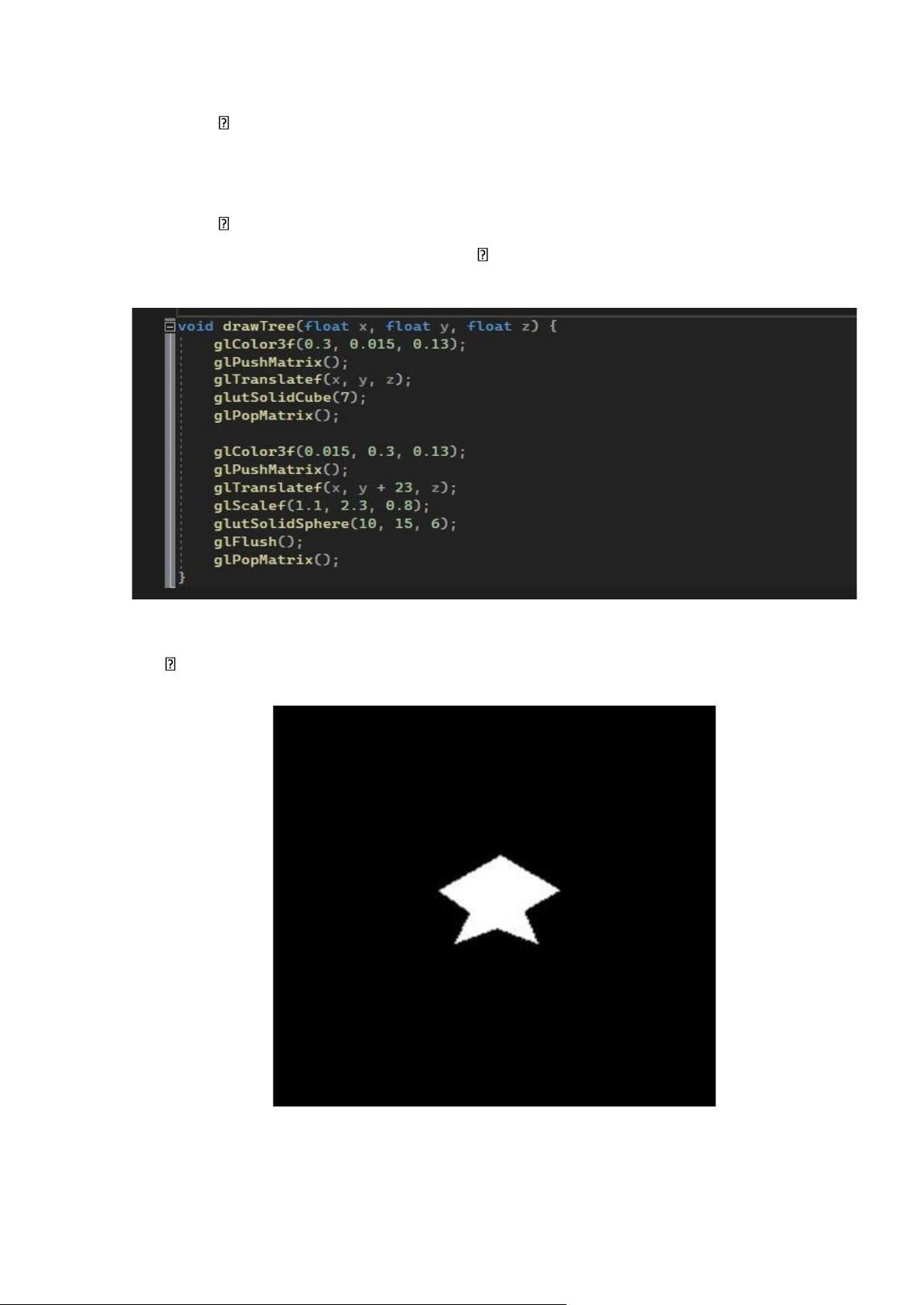
o glScalef(1.1, 2.3, 0.8); Code sinh đối tượng:
Hình 2.2.2. Hàm sinh đối tượng cây Vẽ ngôi sao:
• Ảnh thiết kế đối tượng:
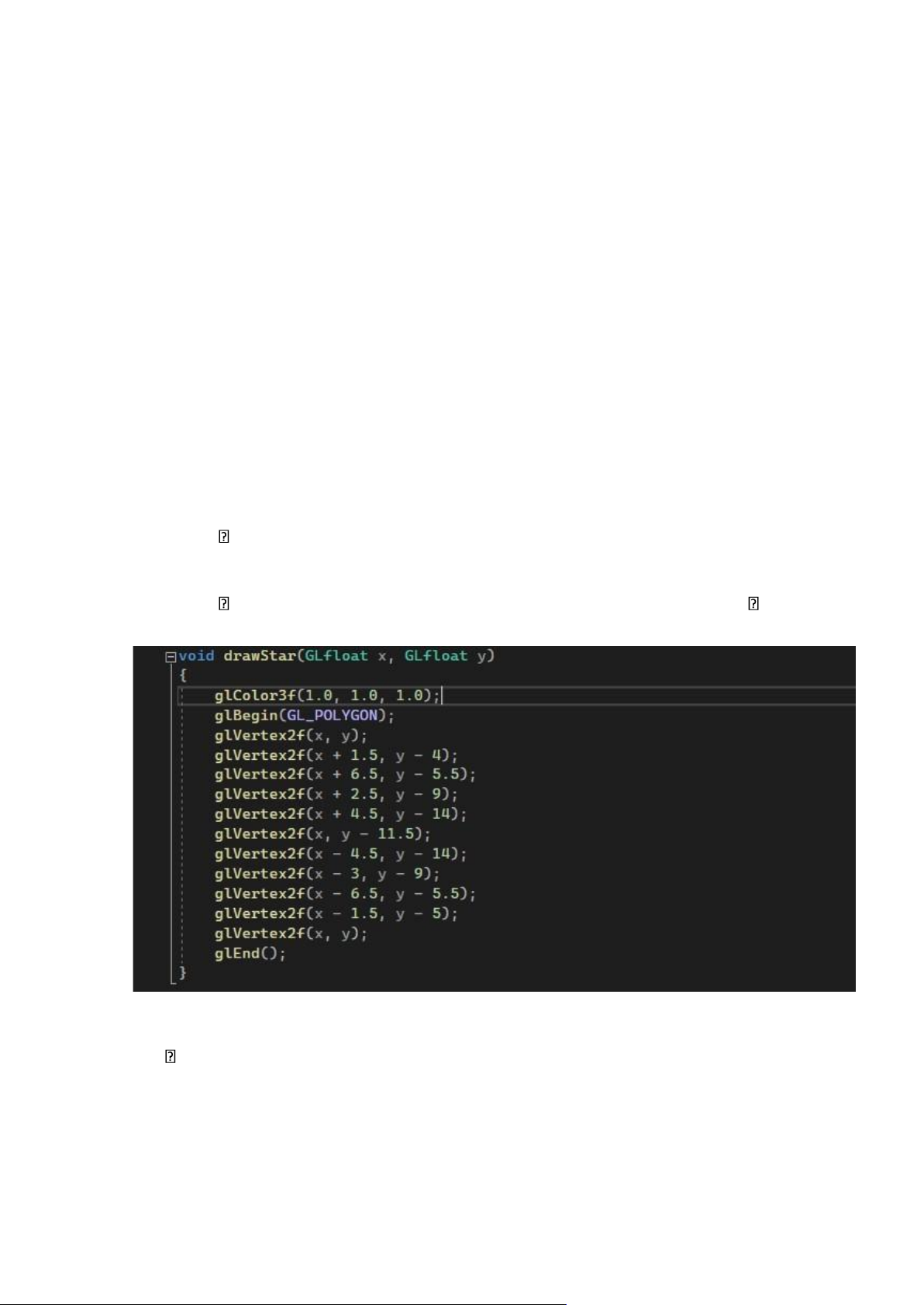
Hình 2.2.3. Ảnh thiết kế đối tượng ngôi sao lOMoAR cPSD| 60729183
• Vị trí đặt đối tượng: o glVertex2f(x, y); o glVertex2f(x + 1.5, y - 4); o
glVertex2f(x + 6.5, y - 5.5); o glVertex2f(x + 2.5, y - 9); o
glVertex2f(x + 4.5, y - 14); o glVertex2f(x, y - 11.5); o
glVertex2f(x - 4.5, y - 14); o glVertex2f(x - 3, y - 9); o
glVertex2f(x - 6.5, y - 5.5); o glVertex2f(x - 1.5, y - 5); o glVertex2f(x, y); Màu sắc: o glColor3f(1.0, 1.0, 1.0);
Kích thước: Phụ thuộc tham số truyền vào cho hàm glVertex3f Code sinh đối tượng:
Hình 2.2.4. Hàm sinh đối tượng ngôi sao Vẽ tòa nhà cao tầng
• Ảnh thiết kế đối tượng:



