lOMoAR cPSD| 36844358
Câu 1: Kiểm định xem tỷ lệ thiếu máu ở trẻ em ở nghiên cứu này có khác với tỷ
lệ thiếu máu ở trẻ em tại Thành phố A là 20% hay không với độ tin cậy 95%?
So sánh một tỷ lệ nghiên cứu với một tỷ lệ cho trước ta sử dụng Chi Square Test
Gọi p là tỉ lệ thiếu máu ở trẻ em trong nghiên cứu; p0 là tỉ lệ thiếu máu ở thành phố A Ta có p0=0.2
H0: p=0.2 Tỉ lệ thiếu máu ở trẻ em trong nghiên cứu là 20%
H1: p ≠ 0.2 Tỉ lệ thiếu máu ở trẻ em trong nghiên cứu khác 20%
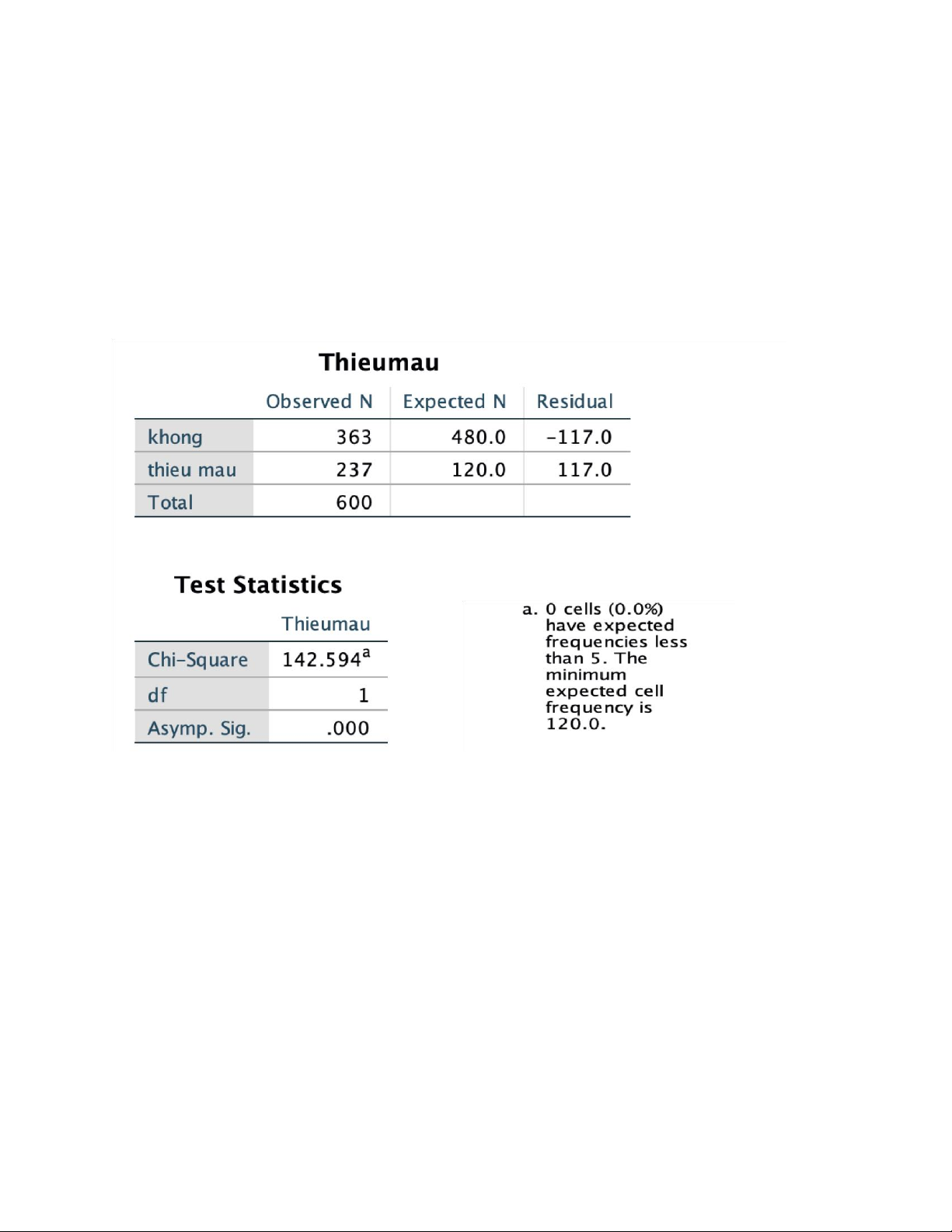
Nếu p<0.05 (mức ý nghĩa) thì ta bác bỏ H0 nhận H1 và ngược lại Thu được bảng như sau:
Kết luận: χ2=142.594; Asymp. Sig. p<0,001 với tỉ lệ số kỳ vọng <5 là 0% nên ta bác bỏ giả
thuyết H0 và nhận giả thuyết H1. Từ đó, tỉ lệ thiếu máu của trẻ trong nghiên cứu không tương
đương với tỉ lệ trong thành phố A là 20% với độ tin cậy là 95%.
Câu 2: Tình trạng thiếu máu có liên quan đến nhóm cân nặng lúc sinh (< 2.500
gram và ≥ 2.500 gram) hay không với độ tin cậy 95%.
Gọi p1 và p2 lần lượt là tỷ lệ thiếu máu ở hai nhóm cân nặng lúc sinh H0: p1=p2. H1: p1≠p2
Nếu p<0.05 (mức ý nghĩa) thì ta bác bỏ H0 nhận H1 và ngược lại
Mã hoá biến cân nặng thành biến “nhomcnls” để chia thành hai nhóm dưới và trên 2500 gram
bằng lệnh Recode into different variables
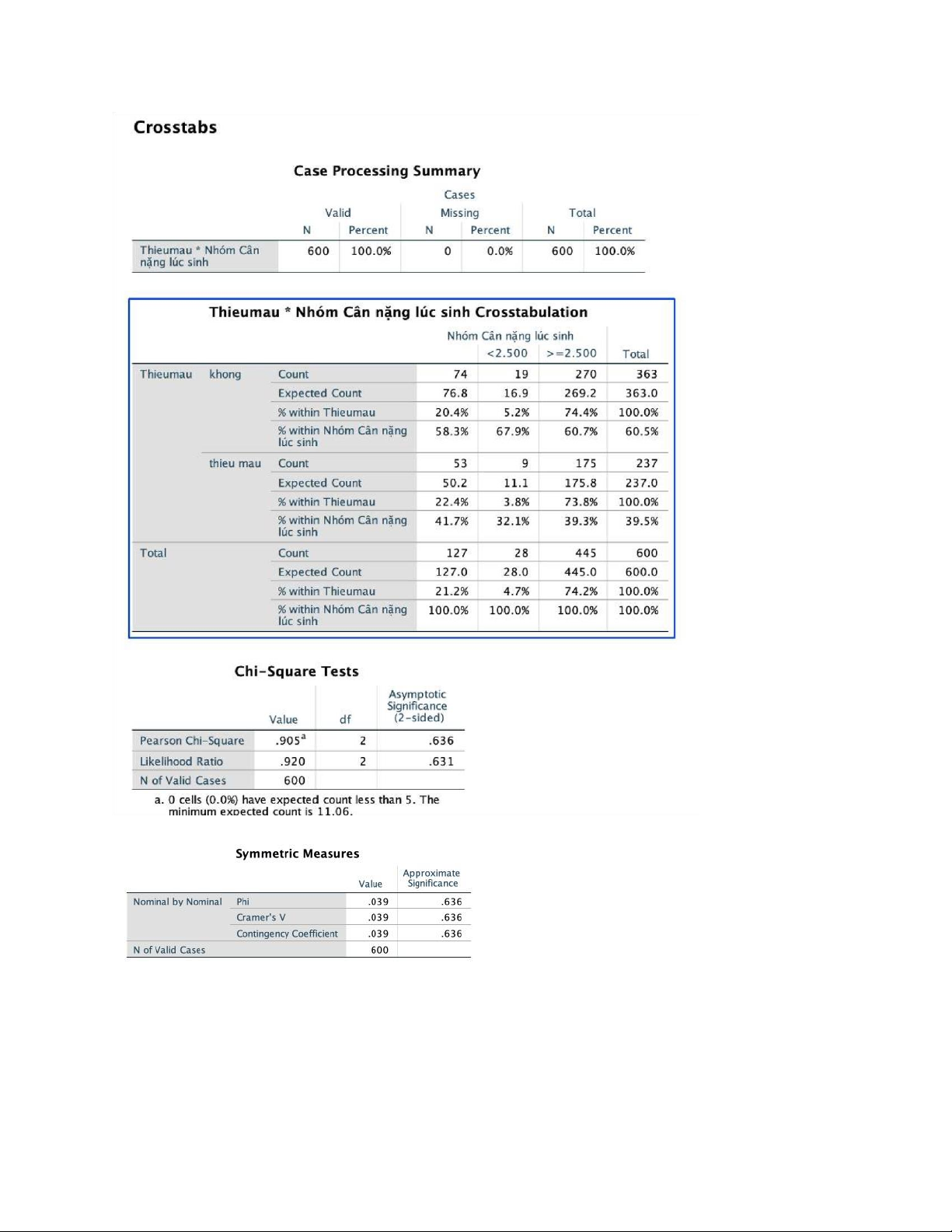
Kiểm định 2 tỷ lệ ở hai nhóm độc lập ta thực hiện lệnh Crosstabs và thu được bảng sau: lOMoAR cPSD| 36844358
Kết luận: χ2=0.905, df=2, p=0.636>0.05 với tỉ lệ số kỳ vọng <5 là 0% nên ta bác bỏ giả thuyết
H1 và nhận giả thuyết H0. Vậy tỉ lệ thiếu máu ở hai nhóm cân nặng là tương đương nhau nên cân
nặng lúc sinh không liên quan đến mức độ thiếu máu ở trẻ.
Câu 3: Trình độ học vấn của mẹ có liên quan đến nhóm cân nặng lúc sinh của
trẻ hay không với độ tin cậy 95%?
Gọi p1, p2, p3 lần lượt là tỷ lệ nhẹ cân phân theo trình độ học vấn mẹ
H0: p1=p2=p3 tỉ lệ nhẹ cân không liên quan đến trình độ học vấn mẹ
H1: p1≠p2≠p3 tỉ lệ nhẹ cân liên quan đến trình độ học vấn mẹ lOMoAR cPSD| 36844358
Nếu p<0.05 (mức ý nghĩa) thì ta bác bỏ H0 nhận H1 và ngược lại
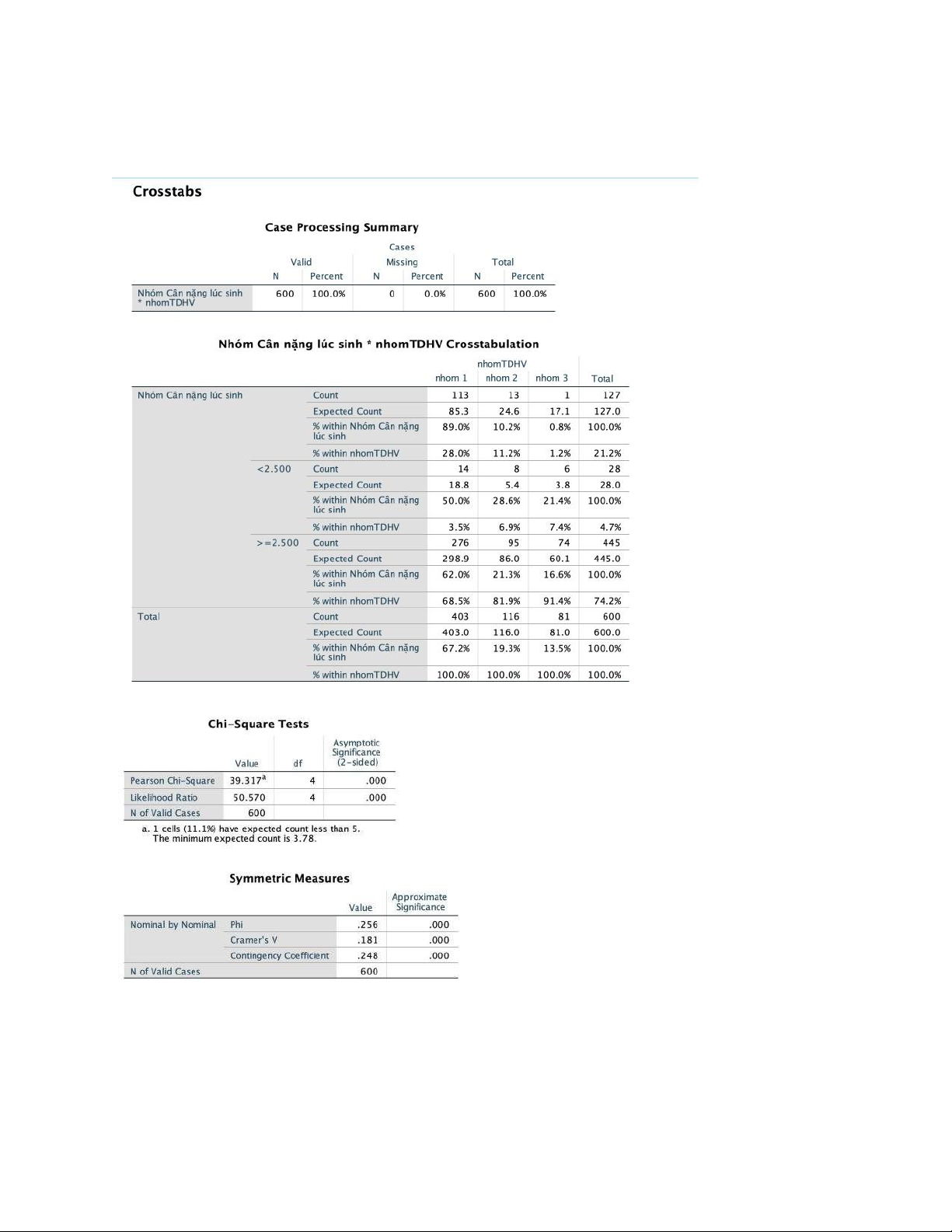
Kiểm định 3 tỷ lệ độc lập ta thực hiện lệnh Crosstabs và thu được bảng sau
Vì bảng tiếp liên lớn (df=4), tất cả các ô có giá trị mong đợi và =<20% số ô có giá trị mong đợi
<5 nên ta chấp nhận kết quả của Chi-square Test
Kết luận: χ2=39.317, df=4, p<0.001 nên ta bác bỏ giả thuyết H0 và nhận H1. Vậy trình độ học
vấn của mẹ có ảnh hưởng đến tình trạng nhẹ cân ở trẻ.
Câu 4: Tình trạng thiếu máu có liên quan đến trình độ học vấn của mẹ hay
không với độ tin cậy 95%.
Gọi p1, p2, p3 lần lượt là tỷ lệ thiếu máu phân theo trình độ học vấn mẹ lOMoAR cPSD| 36844358
H0: p1=p2=p3 tỉ lệ thiếu máu không liên quan đến trình độ học vấn mẹ
H1: p1≠p2≠p3 tỉ lệ thiếu máu liên quan đến trình độ học vấn mẹ
Nếu p<0.05 (mức ý nghĩa) thì ta bác bỏ H0¬ nhận H1 và ngược lại
Kiểm định 3 tỷ lệ độc lập ta thực hiện lệnh Crosstabs và thu được bảng sau:
Kết luận: χ2=1.515, df=2, p=0.469>0.05 nên ta bác bỏ giả thuyết H1 và nhận H0. Vậy trình độ
học vấn của mẹ không ảnh hưởng đến tình trạng thiếu máu ở trẻ.
Câu 5: Phương pháp sinh có liên quan đến đến nhóm cân nặng lúc sinh của trẻ
(<2500 g và >=2500g) hay không với độ tin cậy 95%?
Gọi p1, p2, p3 lần lượt là tỷ lệ nhẹ cân phân theo phương pháp sinh
H0: p1=p2=p3 tỉ lệ nhẹ cân không liên quan đến phương pháp sinh
H1: p1≠p2≠p3 tỉ lệ nhẹ cân liên quan đến phương pháp sinh
Nếu p<0.05 (mức ý nghĩa) thì ta bác bỏ H0 nhận H1 và ngược lại
Kiểm định 3 tỷ lệ độc lập ta thực hiện lệnh Crosstabs và thu được bảng sau lOMoAR cPSD| 36844358
Ta có tỉ lệ số ô có giá trị kỳ vọng <5 trên 20% nên bác bỏ kiểm định Chi-square
Chạy lại lệnh Crosstabs với Fisher’s Exact Test lOMoAR cPSD| 36844358
Kết luận: Lúc này p = 0.295 > 0.05 nên ta bác bỏ giả thuyết H1 nhận giả thuyết H0. Vậy phương
pháp sinh không liên quan đến cân nặng của trẻ.
Bài 2.1: Kiểm định xem chiều cao của các trẻ > 10 tuổi có khác biệt với
chiều cao 140 cm với độ tin cậy 95%?
H0: có khác biệt với chiều cao 140 cm
H1: không có khác biệt với chiều cao 140 cm
Nếu p<0.05 (mức ý nghĩa) thì ta bác bỏ H0 nhận H1 và ngược lại
Dùng lệnh Select Cases để thống kê trên trẻ >10 tuổi
So sánh trung bình của một mẫu với giá trị cho trước ta dùng One-sample T-test
Kết luận: p=0.471 > 0.05 nên ta chấp nhận giả thuyết H0 và bác bỏ giả thuyết H1. chiều cao của
các trẻ > 10 tuổi không khác biệt với chiều cao 140 cm với độ tin cậy 95%
Bài 2.2: Cho biết số lượng và tỷ lệ các trẻ nhẹ cân (cân nặng lúc sinh <
2500g) và không nhẹ cân (≥ 2.500g). Kiểm định xem trung bình chu vi
vòng cánh tay của trẻ > 10 tuổi có khác nhau giữa tình trạng lúc sinh
nhẹ cân và không nhẹ cân với độ tin cậy 95%? lOMoAR cPSD| 36844358
H0: trung bình chu vi vòng cánh tay của trẻ không có khác biệt với tình trạng cân nặng lúc sinh
H1: trung bình chu vi vòng cánh tay của trẻ có khác biệt với tình trạng cân nặng lúc sinh
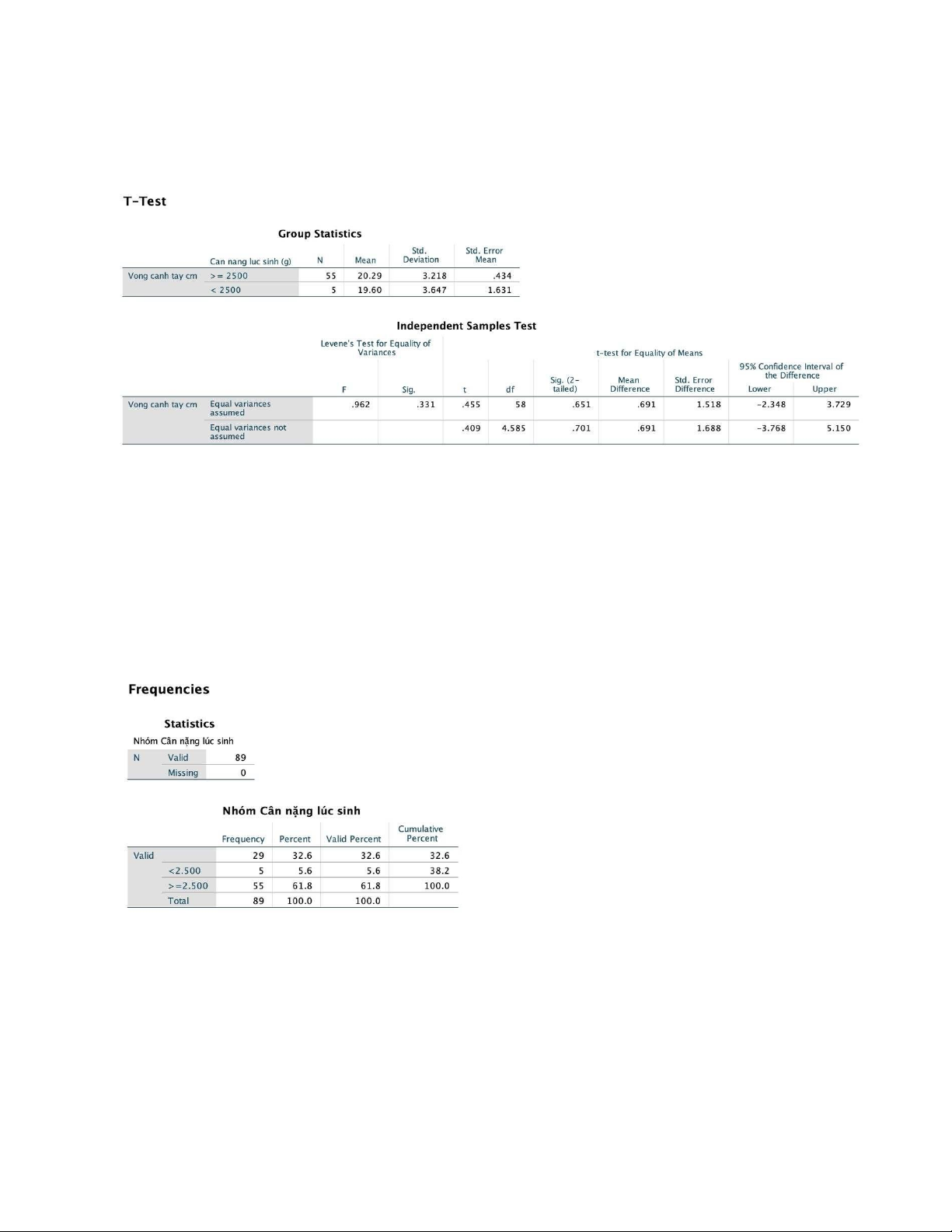
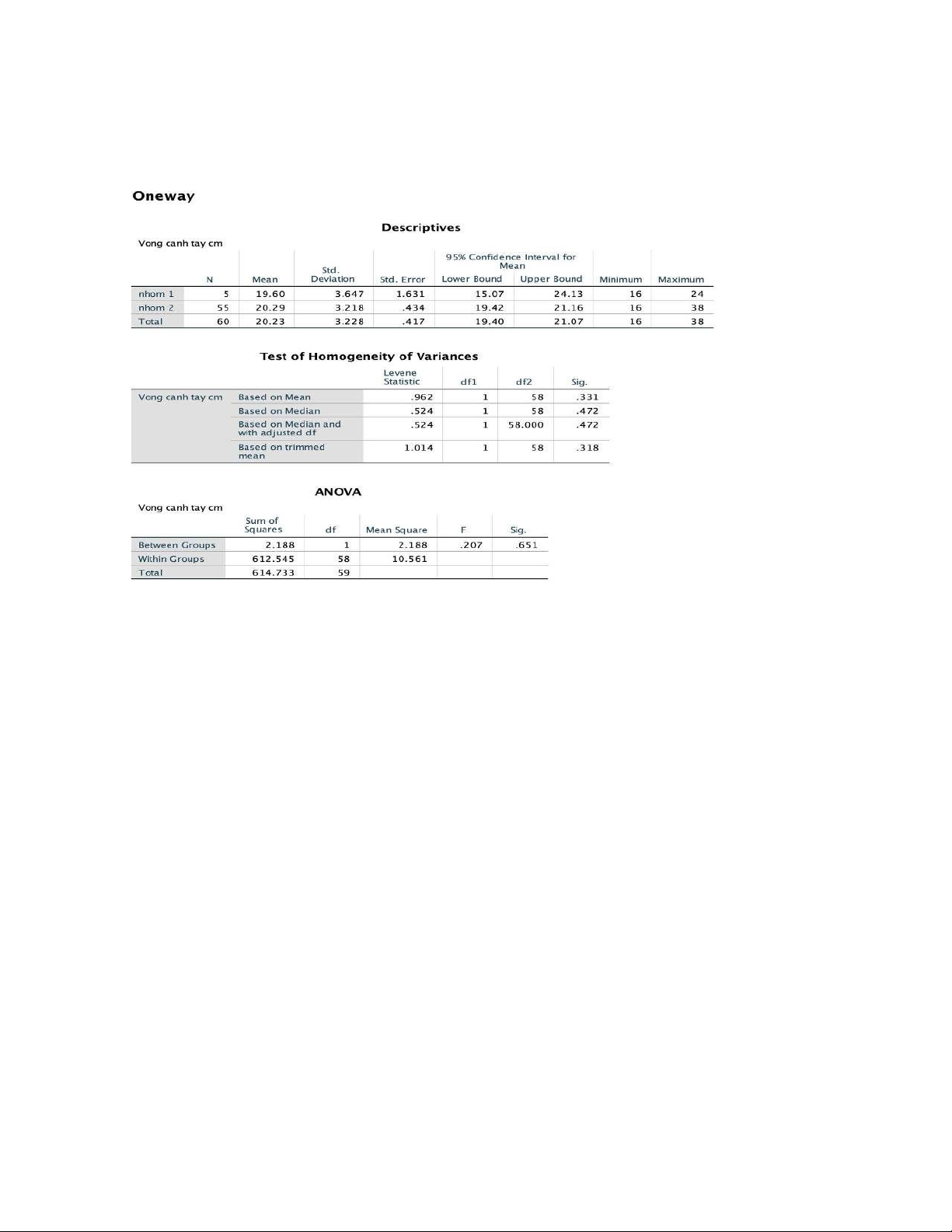
So sánh hai trung bình của hai mẫu độc lập ta dùng Independent Samples T-test
Kết luận: p=0.331 > 0.05 nên 2 phương sai tương đương, độ tin cậy 95%
=> đọc kết quả ở dòng 1 p=0.651>0.05 nên
ta chấp nhận H0 bác bỏ H1.
Vậy trung bình chu vi vòng cánh tay của trẻ > 10 tuổi không khác nhau giữa tình trạng lúc sinh
nhẹ cân và không nhẹ cân với độ tin cậy 95%.
Số lượng và tỷ lệ trẻ nhẹ cân ta sử dụng lệnh Frequencies:
Kết luận: Trong nhóm trẻ >10 tuổi, có 29 trẻ nhẹ cân chiếm 32.6% tổng số trẻ, có 55 trẻ cân
nặng bình thường chiếm 61.8% trong tổng số trẻ
2.3 Phân nhóm cân nặng lúc sinh của trẻ làm 3 nhóm: nhóm 1: <
2.500g; nhóm 2: 2.500 - 4.000g; nhóm 3: > 4.000g. Cho biết số
lượng và tỷ lệ các nhóm cân nặng lúc sinh. Kiểm định xem trung
bình chu vi vòng cánh tay của trẻ > 10 tuổi có khác nhau giữa
các nhóm cân nặng lúc sinh với độ tin cậy 95%?
H0: trung bình chu vi vòng cánh tay của trẻ > 10 tuổi tương đương nhau
giữa các nhóm cân nặng lúc sinh lOMoAR cPSD| 36844358
H1: trung bình chu vi vòng cánh tay của trẻ > 10 tuổi khác nhau
giữa các nhóm cân nặng lúc sinh
Nếu p<0.05 (mức ý nghĩa) thì ta bác bỏ H0 nhận H1 và ngược lại
Kết luận: p=0.651>0.05 nên chấp nhận H0
Vậy trung bình chu vi vòng tay của trẻ >10 tuổi có cân nặng lúc sinh khác nhau là tương đương nhau.