
















Preview text:
Kinh-tế-lượng - kinh tế
Kinh tế Lượng (Trường Đại học Luật Thành phố Hồ Chí Minh)
KINH TẾ LƯỢNG Ưu điểm Nhược điểm • Miễn phí • Thuật ngữ khó hiểu
• Chạy trên nhiều nền tảng • Dùng lệnh
• Rất nhiều phương pháp phân tích • Khó hiểu
• Nhiều phương pháp “advanced” không
có trong các chương trình khác
• Biểu đồ tuyệt vời
• Nhiều packages cho chuyên dụng • Open source Curve: duong cong Abs: gia tri tuyet doi Factorial: giai thua Exp: e mu
Dnorm: chuan hóa (phân phối chuẩn) Gan: x<-
Log cơ số 7 của 2: log(2,7): cơ số nằm sau
1. Hãy viết hàm hồi quy tổng thể
Mô hình hồi quy tổng thể dạng tuyến tính mô tả quan hệ giữa GDP và vốn đầu tư tương ứng được viết theo công thức sau: GDP = β0 + β1*ic + u Trong đó:
• GDP là biến phụ thuộc (dependent variable), là giá trị GDP ước lượng.
• ic là biến độc lập (independent variable), là giá trị vốn đầu tư tương ứng.
• β0 là hệ số chặn (intercept), là giá trị GDP ước lượng khi ic = 0.
• β1 là hệ số hồi quy (regression coefÏcient), thể hiện mức độ thay đổi của GDP khi ic thay đổi.
• u là sai số ngẫu nhiên (error term), đại diện cho các yếu tố khác có thể ảnh hưởng đến GDP
ngoài vốn đầu tư tương ứng.
2. Hãy viết mô hình hồi quy tổng thể dạng tuyến tính mô tả quan hệ giữa GDP và vốn đầu tư tương ứng
GDP^ (GDP.hat) = 35.92960 + 0.97729*ic Trong đó:
Hệ số chặn ^B 0 là 35.92960, có nghĩa là khi giá trị của vốn đầu tư bằng 0 thì giá trị GDP được ước lượng là 35.92960.
Hệ số hồi quy ^B 1 cho biết mức độ tác động của vốn đầu tư tương ứng đến GDP. Ở đây, hệ số hồi quy
là 0.97729, có nghĩa là khi giá trị của vốn đầu tư tương ứng tăng lên 1 tỷ đồng thì giá trị GDP được
ước lượng tăng lên 0.97729 tỷ đồng. Chương 2
Case 2.1 trong trang excel đầu - IQ Max: 145 IQ min: 72 - Thu nhập Min: 2137 Max: 471 Định nghĩa
Phương sai: là trung bình (có trọng số) của bình phương của bình phương các sai lệch.
VDu: điểm môn học tối đa 5 điểm
Trung bình điểm môn học KTL 4 điểm => 1 bạn 9 điểm => sai lệch 5 điểm; 1 bạn 3 điểm sai lệch -1 điểm Qua phần mềm R
Tính median: trung vị, có 50% người có IQ cao hơn 120 or có 50% người có IQ thấp hơn 120 Tính summary
Có 25% người trong mẫu nghiên cứu có điểm IQ từ 92 trở xuống
25% người trong mẫu nghiên cứu có điểm IQ 112 điểm trở lên?? Sumary tiền
Ng có thu nhập trong tháng thấp nhất là 115 đô
PT hồi quy ước lượng được biểu diễn dạng thông thường estimated equation Y=Bo + P1x Trọng tâm buổi 3:
giải thích cơ chế cách thức xây dựng pt hồi quy ước lượng
giải thích được hàm số case 2.2: C5. (i)
Mô hình hàm ý hệ số co giãn cố định giữa rd và sales
Ptrinh hồi quy ước lượng dưới dạng thông thường
Log(rd) = Bo + B1Log(sales) + u
Khi sales tăng 1% thì rd thay đổi B1%
⇨ Hệ số co giãn ước lượng của rd theo sales: B1 = 1.076
⇨ Khi sales tăng 1% thì rd sẽ tăng lên 1.076% (ii) Dùng R VD thêm:
Sales theo rd: Log(sales) = 4.1177 + 0.8458log(rd)
Mục tiêu: có khả năng đọc hiểu, kế thừa các nghiên cứu quốc tế
Definition of the simple linear regression model
Explains variable Y in terms of variable X Intercept par Case Study 2.3 Bài C6 _ trang 74
- Mục tiêu nghiên cứu: tim ra nhân tố ảnh hưởng đến tỷ lệ đến lớp của sinh viên - Phạm vi nghiên cứu:
o Về không gian: chỉ nghiên cứu trong 1 môn học (32 buổi)
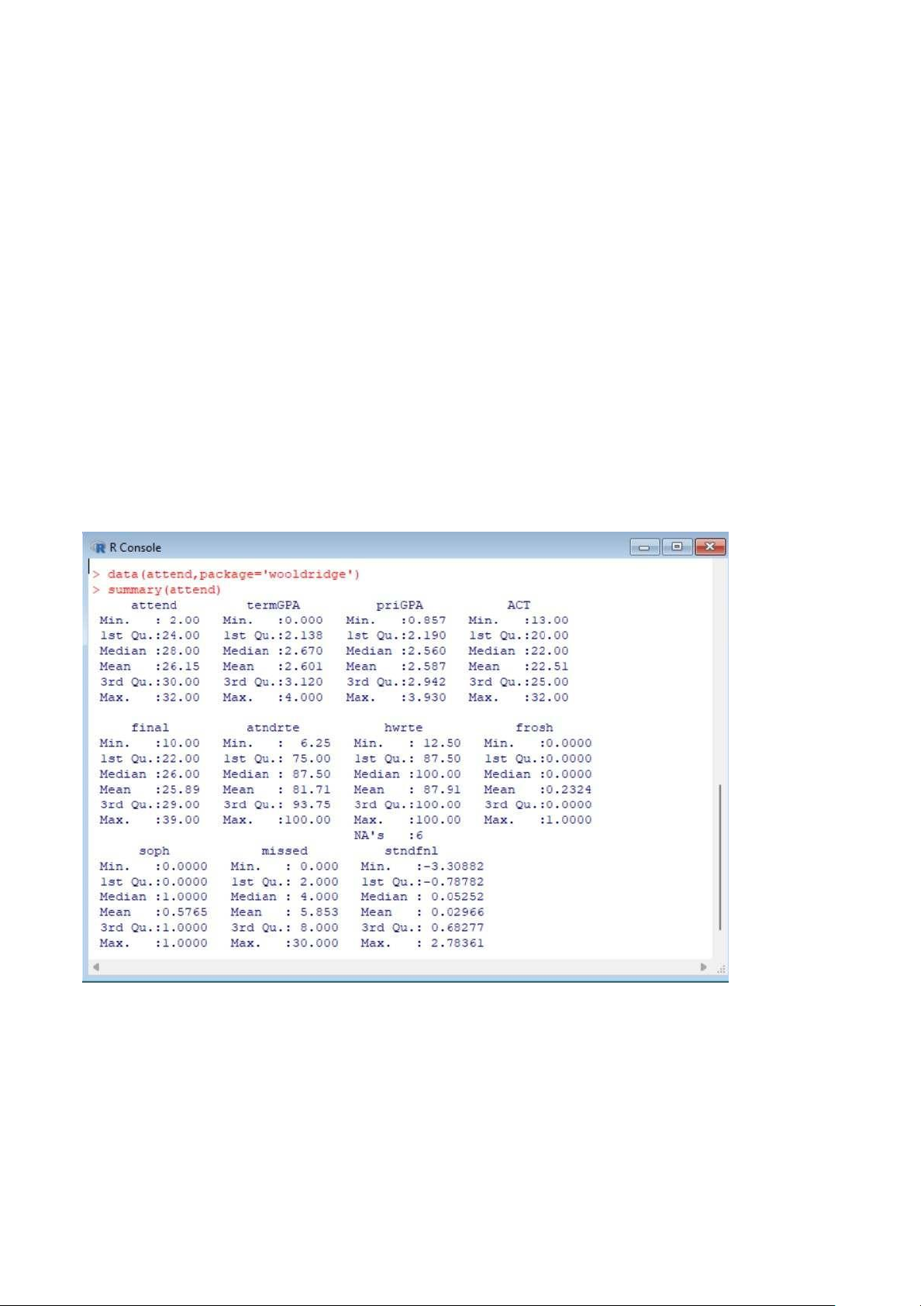
o Về thời gian: 1 học kỳ Biến ACT:
- Min 13: SV có số điểm thấp nhất trong mẫu nghiên cứu là 13 điểm
- Max 32: SV có số điểm cao nhất trong mẫu nghiên cứu là 32 điểm
- Median: 50% SV trong mẫu có điểm cao hơn 22 điểm
- Mean: điểm số trung bình của tất cả sv trong mẫu là 21,55
- 1st Qu : 25% sinh viên trong mẫu nghiên cứu có điểm thấp hơn 20 điểm
- 3rd Qu : 25% SV trong mẫu nghiên cứu có điểm cao hơn 25 điểm Gọn hơn viết:
Biến ACT có giá trị biến động từ 13 đến 32 điểm, với giá trị trung bình là 22,51 điểm. Có 50%
SV trong mẫu nghiên cứu có điểm ACT cao hơn 22 điểm. Trong khi, tỉ lệ SV có điểm ACT hơn
cao 25 điểm là 25% thì tỉ lệ SV có số điểm thấp hơn 20 điểm là 25% Mô hình tổng thể Atndrte = Bo + B1*ACT + u
Giải thích: Khi ACT tăng 1 điểm thì atndrte sẽ thay đổi B1
Dấu kì vọng để xem là dương hay âm, có tác động hay không. (i )
Phương trình hồi quy ước lượng:
Atndrte = 98,9008 – 0.7637*ACT (iii) R2 = 0,02446
⇨ ACT giải thích chưa đến 2,5% sự khác biệt trong tỷ lệ đến lớp dự kiến của SV (iv)
Nhiều nhân tố ảnh hưởng chứ ko chỉ mỗi ACT ảnh hưởng. ngoài ra chỉ 2 quan sát ko thể kết luận vội vàng.
Kết luận: Chênh lệch giữa tỉ lệ đến lớp dự đoán (atndrte) của 2 sinh viên có điểm ACT chênh
lệch 10điểm: 10*|-0,7376| = 7,376 (v).
Atndrte (giá trị ước lượng atndrte) có giá trị lớn nhất là
= 98,9008 – 0,7637*ACTmin = 98,9008 – 0,7637*13 = 88,9799 (%)
Atndrte có giá trị nhỏ nhất là: 98,908 – 0,7637*ACTmin = 74,4696 (%)
**Như vậy, dữ liệu của yêu cầu là không có cơ sở: atndrte Tổng hợp:
Model là mô hình: y ko mũ và có u
Estimated equation là PT hồi quy ước lượng: y có mũ và ko có u
Logarit tự nhiên khác gì logarit bán tự nhiên
Log(atndrte) = 98,9008 – 0.7637*ACT
Case 3.1 (trang 87 đến trang 102)
• Mục tiêu nghiên cứu: đánh giá tác động của các nhân tố ảnh hưởng đến kết quả học tập của HS
• Đối tượng nghiên cứu: 408 trường THPT
• Phạm vi nghiên cứu: bang Mechegan, lớp 10
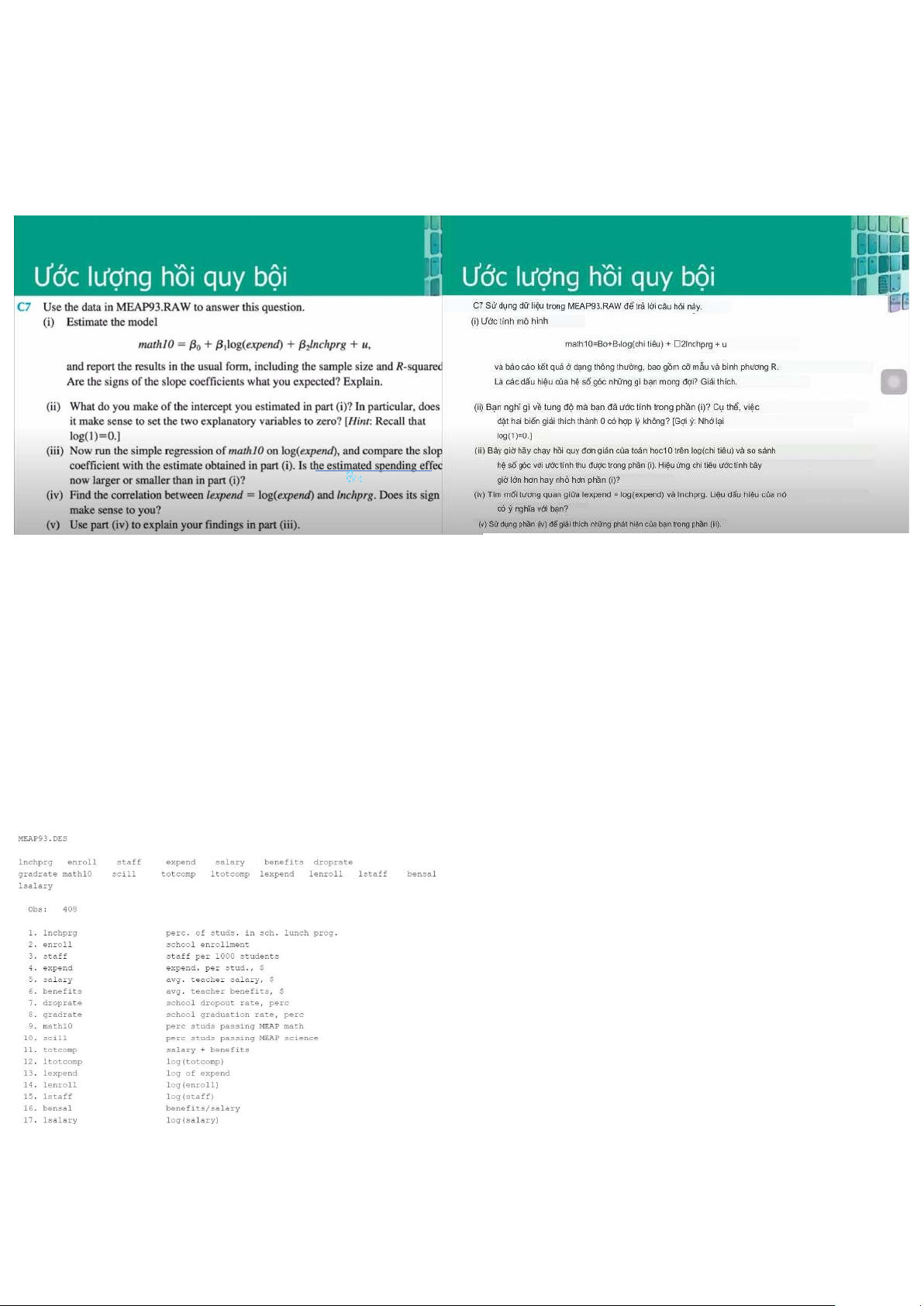
1. Phần trăm tỉ lệ sinh viên tham gia
tỉ lệ bữa ăn học đường 2/ Nhập học
Math^ = -20,36 + 6,23log(expend) - 0.305lnchprg N = 408, R2 = 0,18 *giải thích:
- B1^ = 6,23 có ý nghĩa khi chi phí đào tạo cho
mỗi học sinh tăng 1% thì ước lượng tỉ lệ học
sinh đậu kỳ thi toán (Math10^) tăng 6,23% , với
điều kiện biến độc lập khác (lchprg) ko đổi
(bản thân 6,23% đã tác động thuần đến kết quả
học tập (tác động riêng lẻ), còn có thể hiểu 6,23
ko nắm vai trò quyết định math10^ mà còn rất
nhiều biến khác tác động đến).
Biến độc lập khác : “Partialling out” nghĩa là
“thuần” (pure) => sách trang 86 dịch là riêng
phần, còn có thể dung với nghĩa riêng có, thuần (pure)
- B2^ = -0,305 có ý nghĩa là khi tỷ lệ học sinh cần
bữa ăn học đường của chính phủ tang lên 1% thì math10^ giảm 0,305%
Math^ = -68,34 + 11,16log(expend) N = 408, R2 = 0,03
Dưới hồi quy bội trên hồi quy đơn
Dưới tác động nhiều hơn vì đơn có hệ số 11.16 còn bội 6.23
Cùng nghiên cứu nhưng 2 hệ số khác nhau sẽ có 1 PT sai. PT hồi quy đơn sai vì bỏ mất biến
quan trọng là lunch program Case 3.2
Kiểm tra chất lượng nghiên cứu: SJR - Scimago Journal & Country Rank. - Mục tiêu nghiên cứu:
Công bố khoa học này kiểm định sự khác biệt về giá được áp đặt bởi các
cửa hàng thức ăn nhanh cho các khu vực với các khách hàng có sự khác biệt về
chủng tộc và khác biệt nhiều về thu nhập
- Phạm vi nghiên cứu: trên 400 cửa hàng tại 2 bang NJ và Pennsylvania
Trong trường hợp case 3.2 nó rơi vào tình huống underestimated.
Chệch do bỏ sót biến quan trọng
Vì sao chệch nhiều hay ít, do ở 2 biến B2^ và Ơ1~
Vì Ơ1~ âm, vì người da màu thường có thu nhập thấp (hoặc hệ số
tương quan giữa người da màu và thu nhập nghịch nhau (người da
màu nhiều thì thu nhập thấp)) B2^ dương
Cả 2 nhân nhau ra âm nên underestimated
Tại sao đã có phương sai vẫn cần tìm độ lệch chuẩn?
Phương sai là độ đo của sự phân tán của dữ liệu trong một tập hợp,
trong khi độ lệch chuẩn là căn bậc hai của phương sai.
Mặc dù phương sai và độ lệch chuẩn đều cung cấp thông tin về độ
biến động của dữ liệu, tuy nhiên, việc sử dụng độ lệch chuẩn có một
số lợi ích so với phương sai trong một số trường hợp cụ thể.
Đầu tiên, độ lệch chuẩn có thể được sử dụng để tính toán khoảng tin
cậy cho các giá trị dự báo hoặc ước lượng. Nó cũng được sử dụng để
xác định xem liệu các giá trị nằm ngoài phạm vi kỳ vọng hay không.
Thứ hai, độ lệch chuẩn có thể giúp đánh giá sự khác biệt giữa các
phân phối dữ liệu khác nhau. Nếu hai tập hợp dữ liệu có cùng
phương sai nhưng có độ lệch chuẩn khác nhau, thì tập hợp dữ liệu có
độ lệch chuẩn lớn hơn có sự biến động lớn hơn.
Cuối cùng, độ lệch chuẩn cũng được sử dụng trong việc xác định các
điểm ngoại lai hoặc các giá trị bất thường trong tập dữ liệu. Nếu một
giá trị nằm rất xa so với giá trị trung bình, nó có thể được xem là
một điểm ngoại lai. Trong trường hợp này, việc sử dụng độ lệch
chuẩn có thể giúp xác định các giá trị này một cách chính xác hơn.
Tóm lại, phương sai và độ lệch chuẩn đều là các độ đo quan trọng
của độ biến động dữ liệu. Trong một số trường hợp, độ lệch chuẩn có
thể được ưu tiên sử dụng để đánh giá và phân tích dữ liệu.
Phương sai khác gì hệ số tương quan?
Phương sai cho ta biết độ lệch của các giá trị dữ liệu so với
trung bình và giúp ta đánh giá được mức độ phân tán của dữ liệu trong một tập hợp.
Phương sai là một đại lượng đo lường mức độ phân tán của một
tập hợp dữ liệu. Trong khi đó, hệ số tương quan là một đại lượng đo
lường mức độ tương quan giữa hai biến ngẫu nhiên. Mặc dù phương
sai và hệ số tương quan đều liên quan đến đo lường mức độ tương
quan giữa các biến, nhưng chúng có ý nghĩa và ứng dụng khác nhau.
Khi ta đã biết giá trị phương sai của hai biến, ta có thể xác định được
mức độ phân tán của chúng đối với nhau, nhưng ta không thể biết
được mức độ tương quan giữa chúng. Hệ số tương quan giúp ta đo
lường mức độ tương quan giữa hai biến và cho phép ta đưa ra các
kết luận về mối quan hệ giữa chúng. Nó có giá trị từ -1 đến 1, trong
đó giá trị 0 cho thấy không có mối quan hệ tuyến tính giữa hai biến,
giá trị gần 1 cho thấy một mối quan hệ tuyến tính mạnh giữa chúng,
và giá trị gần -1 cho thấy một mối quan hệ tuyến tính âm mạnh giữa chúng.
Vì vậy, dù đã biết giá trị phương sai của hai biến, ta vẫn cần
tìm hệ số tương quan để hiểu rõ hơn về mối quan hệ giữa chúng.
Vì sao phải đánh giá tác động riêng phần? không đánh giá
tác động riêng phần được không?
Phải đánh giá tác động riêng phần vì đánh giá tác động riêng
phần là rất quan trọng vì nó giúp cho các nhà kinh tế hiểu rõ hơn về
tác động của các yếu tố khác nhau đến kết quả. Ngoài ra, đánh giá
tác động riêng phần cũng giúp các nhà nghiên cứu hiểu được rõ hơn
về tác động của các biến độc lập đến các biến phụ thuộc, và giúp họ
có thể dự đoán kết quả của các hành động.
Việc không đánh giá tác động riêng phần có thể dẫn đến các kết
luận sai lầm hoặc không chính xác trong phân tích kinh tế. Nếu chỉ
đánh giá tác động tổng thể của một yếu tố đến kết quả, chúng ta sẽ
không biết được tác động riêng phần (riêng lẻ) của các yếu tố khác
lên kết quả đó. Điều này có thể dẫn đến các kết luận sai lầm về tác
động của các yếu tố trong một mô hình kinh tế phức tạp.
Case 4.1 (Câu C8 - Trang 184): Hồi quy bội: suy diễn
=> Tại sao lại có k trong lệnh > data(k401ksubs..) trong khi tên tệp dữ liệu là 401ksubs? Kết quả
Lệnh xem số quan sát có fsize <= 1 (iii)
Hệ số góc ước lượng của age (b2^) có nghĩa: khi giữ inc cố định. Nếu
một người tăng thêm 1 tuổi thì giá trị dự đoán của nettfa của người
này tăng thêm khoảng 843 đô la
Đối với inc vì đơn vị đo là 1 đô nên nettfa cũng có đơn vị theo 1 đô (cent) (iv)
Giả thuyết đối (null hypothesis) là giả định rằng sự chênh lệch giữa
hai tập dữ liệu là do sự ngẫu nhiên, không có sự khác biệt có ý nghĩa
giữa chúng. Điều này được đưa ra như một giả định ban đầu và cần
được kiểm tra để xác định liệu nó có thể bị bác bỏ hay không.
Giả thuyết thay thế (alternative hypothesis) là giả định rằng sự
chênh lệch giữa hai tập dữ liệu là do sự khác biệt có ý nghĩa giữa
chúng. Điều này được đưa ra như một giả định thay thế cho giả
thuyết đối và được chấp nhận khi ta bác bỏ giả thuyết đối.
Bác bỏ giả thuyết đối có thể được thực hiện bằng cách so sánh giá
trị p (p-value) của thống kê t (t-statistic) hoặc F-statistic với mức ý
nghĩa (significance level) đã được chọn trước. Nếu giá trị p nhỏ hơn
mức ý nghĩa, chúng ta sẽ bác bỏ giả thuyết đối và chấp nhận giả thuyết thay thế.
Mức ý nghĩa là một giá trị được chọn trước để xác định mức độ chấp
nhận được của lỗi bác bỏ giả thuyết đối. Thông thường, mức ý nghĩa
được chọn là 0,05 hoặc 0,01, nghĩa là nếu giá trị p nhỏ hơn mức ý
nghĩa này, chúng ta sẽ bác bỏ giả thuyết đối.
Khi giả thuyết đối được bác bỏ, ta kết luận rằng sự khác biệt giữa hai
tập dữ liệu là có ý nghĩa thống kê. Khi giả thuyết đối không được bác
bỏ, ta kết luận rằng không có sự khác biệt có ý nghĩa thống kê giữa hai tập dữ liệu. Bước 1:
Phát triển giả thuyết H0: B0 = 0 và H1: B0 khác 0
Nghĩa là với giả thuyết H0 ở mẫu B0 tuy có giá trị nhưng đối với tổng
thể thì không có giá trị vì bằng 0
Bước 2: xác định mức ý nghĩa alpha = 5%
Bước 3: thu nhập dữ liệu mẫu (2017)
Tính giá trị thống kê kiểm định (t-statistic)
Đối với giả thuyết H0: B0 = 0 và H1: B0 khác 0
Nếu chưa biết độ lệch chuẩn của tổng thể thì dùng t. t = (-43.04 – 0)/4.08 = -10.54
Trong đó 4.08 là sai số chuẩn của intercept
Bước 4: tính p-value; với cỡ mẫu lớn trên 100 thì phân phối t tiệm
cận với phân phối chuẩn hóa (chuẩn hóa thì giá trị trung bình về 0
(=0), độ lệch chuẩn = 1), tính được p-value xấp xỉ = 0
Bước 4. So p-value với alpha: 0 < 5%. Bác bỏ p-value => p-value = 0.044
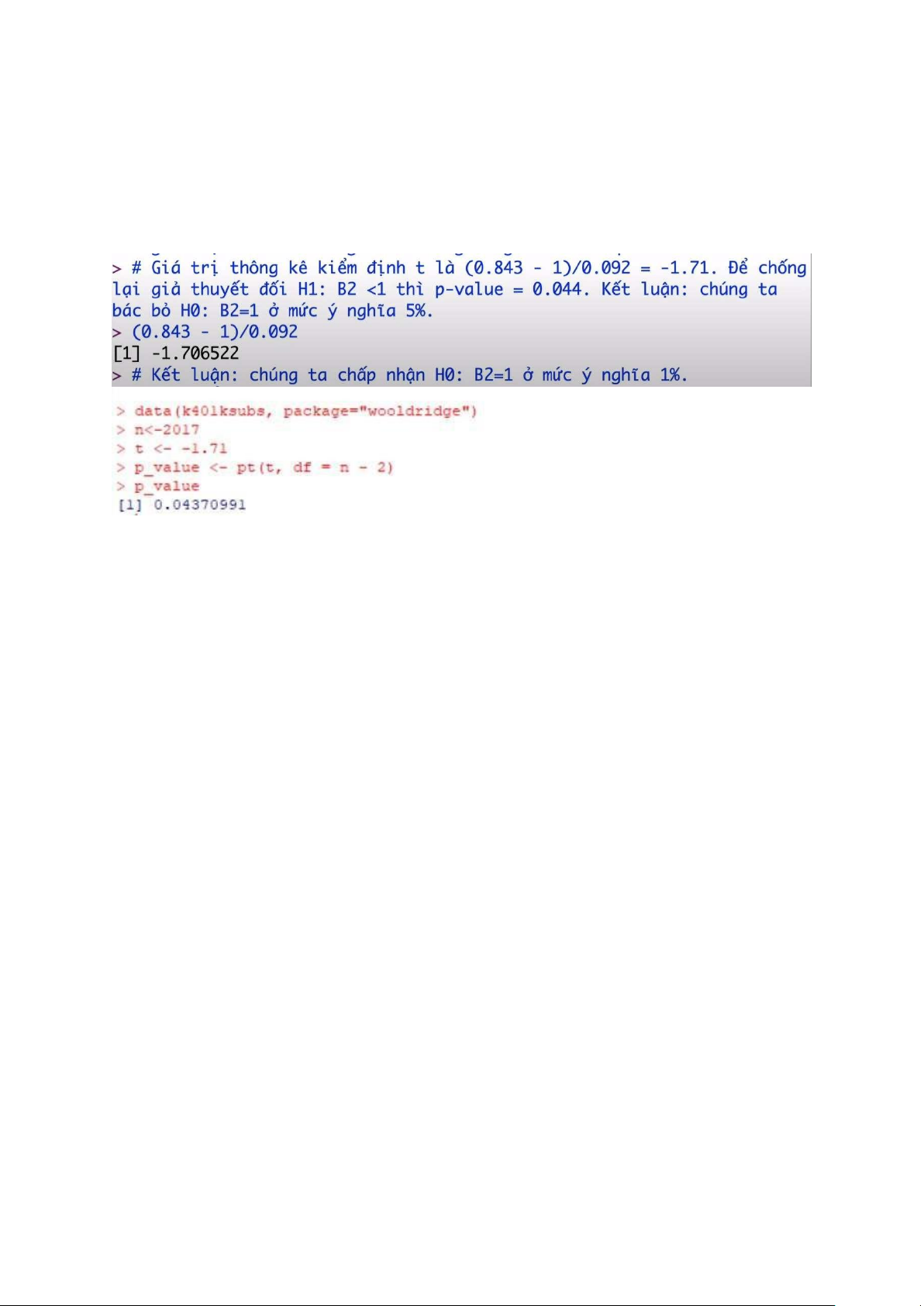
Khi xây dựng giả thuyết rỗng H0: B2=1 và mức ý nghĩa alpha=0.05,
ta quyết định bác bỏ H0 nếu giá trị p-value nhỏ hơn alpha. Vì trong
trường hợp này, p-value=0.044 < alpha = 0.05, nên ta sẽ bác bỏ giả
thuyết rỗng H0: B2=1 tại mức ý nghĩa 5%. Nghĩa là, kết quả cho
thấy B2 khác với giá trị dự kiến 1 với mức độ tin cậy 95%.
Nếu muốn giảm sai sót xuống mức thấp hơn, ta có thể lựa chọn mức
ý nghĩa 1% (hay 0.01). Khi đó, ta chấp nhận H0: B2 = 1 nếu p-
value > 0.01, (p-value trong TH này = 0.044). Hay còn có thể hiểu,
khi p-value <= 0.01, ta sẽ bác bỏ H0: B2 = 1.
Nếu p-value nhỏ hơn alpha, ta sẽ bác bỏ giả thuyết H0 và chấp nhận
giả thuyết H1. Nếu p-value lớn hơn hoặc bằng alpha, ta không thể bác bỏ giả thuyết H0.
Biến inc có ý nghĩa thống kê.
Đ sẽ có dạng: tìm khoảng tin cậy 95% cho hệ số góc của 1 biến bất kỳ Ơ1~ = CASE 4.2
Use the data in DISCRIM.RAW to answer this question. (i) Use OLS to estimate the model
log(psoda) = B0 + B1prpblck + B2log(income) + B3prppov + u,
and report the results in the usual form. Is statistically different from zero at the 5% level against a
two-sided alternative? What about at the 1 % level? (ii)
What is the correlation between log(income) and prppov? Is each variable statistically
significant in any case? Report the two-sided p-values. (iii)
To the regression in part (i), add the variable log(hseval). Interpret its coefÏcient and
report the two-sided p-value for Ho:log(hseval)= 0. (iv)
In the regression in part (iii), what happens to the individual statistical significance of
log(income) and prppov? Are these variables jointly significant? (Compute a p-value.)
What do you make of your answers? (v)
Given the results of the previous regressions, which one would you report as most
reliable in determining whether the racial makeup of a zip code influences local fast- food prices?" trans
(i) Để ước lượng mô hình bằng OLS, bạn cần chạy phương trình hồi quy sau:
log(psoda) = B0 + B1prpblck + B2log(income) + B3prppov + u,
và báo cáo kết quả dưới dạng thông thường. Liệu có khác biệt đáng kể so với 0 ở mức ý nghĩa 5% với
giả thuyết hai chiều? Còn ở mức 1% thì sao?
(ii) Tính tương quan giữa log(income) và prppov. Mỗi biến có ý nghĩa thống kê không? Báo cáo giá trị p hai chiều.
(iii) Thêm biến log(hseval) vào mô hình hồi quy của câu (i). Diễn giải hệ số và báo cáo giá trị p hai
chiều cho giả thuyết H0: log(hseval) = 0.
(iv) Trong mô hình hồi quy của câu (iii), ý nghĩa thống kê của log(income) và prppov như thế nào? Hai
biến có ý nghĩa thống kê đồng thời không? (Tính giá trị p.) Bạn suy nghĩ gì về kết quả của mình?
(v) Dựa trên kết quả của các mô hình hồi quy trước đó, bạn sẽ báo cáo mô hình nào là đáng tin cậy
nhất trong việc xác định liệu sự đa dạng chủng tộc của một mã vùng có ảnh hưởng đến giá thức ăn
nhanh địa phương hay không? (i)
Giả thuyết đối hai phía (two-tailed hypothesis)
Giả thuyết đối hai phía được sử dụng trong các tình huống khi chúng
ta muốn kiểm tra xem một tham số của quần thể có khác với giá trị
dự đoán hay không, mà không quan tâm đến hướng khác biệt. Ví dụ,
giả sử có một mẫu dữ liệu và muốn kiểm tra xem trung bình của
biến trong mẫu có khác với giá trị trung bình dự đoán không.
Khi sử dụng giả thuyết đối hai phía, ta đưa ra hai giả thuyết như sau:
• Giả thuyết H0: Trung bình của biến trong quần thể bằng với giá
trị dự đoán (trung bình = giá trị dự đoán).
• Giả thuyết H1: Trung bình của biến trong quần thể khác với giá
trị dự đoán (trung bình ≠ giá trị dự đoán).
Giá trị p-value là xác suất để chúng ta quan sát được kết quả kiểm
định mẫu như thế nào nếu giả thuyết H0 là đúng. Khi kiểm định giả
thuyết đối hai phía, giá trị p-value được tính bằng phần diện tích của
phân phối xác suất tương ứng với cả hai bên của giả thuyết H1. Nếu
giá trị p-value nhỏ hơn mức ý nghĩa alpha, chúng ta có thể kết luận
rằng có bằng chứng để bác bỏ giả thuyết H0 và chấp nhận giả
thuyết H1, tức là trung bình của biến trong quần thể khác với giá trị
dự đoán. Nếu giá trị p-value lớn hơn mức ý nghĩa alpha, chúng ta
không có đủ bằng chứng để bác bỏ giả thuyết H0 và không có cơ sở
để kết luận rằng trung bình của biến trong quần thể khác với giá trị dự đoán.
log(psoda)^ = -1.463 + 0.073prpblck + 0.137log(income) + 0.38prppov (0.29) (0.03) (0.03) (0.13)
Để kiểm tra xem hệ số B1^ có ý nghĩa thống kê tại mức ý nghĩa 5%
với giả thuyết đối hai phía hay không, ta thực hiện các bước sau:
Bước 1: Xác định giả thuyết:
• H0: B1 = 0 (hệ số tương ứng với prpblck không có ảnh hưởng đến psoda)
• H1: B1 ≠ 0 (hệ số tương ứng với prpblck có ảnh hưởng đến psoda)
Giả thuyết đối hai phía được sử dụng ở đây vì chúng ta quan tâm
đến sự khác biệt của hệ số so với giá trị không, không phải chỉ quan
tâm đến hướng tăng hoặc giảm của hệ số.
Bước 2: Xác định mức ý nghĩa (alpha) và độ tin cậy (confidence level)
• Mức ý nghĩa: 5% = 0.05
• Độ tin cậy: 95% = 0.95 (tương ứng với giả thuyết đối hai phía)
Bước 3: Tính toán giá trị t-statistic
• t = (B1 - 0) / SE(B1) = (0.073 – 0)/(0.03) = 2.433
• Trong đó, B1 là giá trị ước lượng của hệ số prpblck, SE(B1^) là
sai số chuẩn tương ứng.
Bước 4: Tính toán giá trị p-value
• p-value là xác suất tìm thấy t-statistic lớn hơn giá trị tương ứng
trong phân phối t với n-2 độ tự do (n là kích thước mẫu) nếu giả thuyết H0 là đúng.
• p-value được tính bằng cách sử dụng phần mềm thống kê hoặc bảng phân phối t. P-value = 0.0181
Bước 5: Đưa ra kết luận
• Nếu p-value < alpha (0.05), ta có thể bác bỏ giả thuyết H0 và
kết luận rằng hệ số prpblck có ảnh hưởng đến psoda.
• Nếu p-value > alpha (0.05), ta không thể bác bỏ giả thuyết H0
và kết luận rằng không có đủ bằng chứng để cho rằng hệ số prpblck khác 0. ***: p-value < 0.001
**: 0.001 ≤ p-value < 0.01 *: 0.01 ≤ p-value < 0.05 .: 0.05 ≤ p-value < 0.1 : p-value ≥ 0.1
• Vì giá trị này nhỏ hơn mức ý nghĩa α=0.05, nên ta có thể bác
bỏ giả thuyết H0 và kết luận rằng hệ số B1^ khác 0 có ý nghĩa
thống kê tại mức ý nghĩa 5%, hay hệ số prpblck có ảnh hưởng đến psoda.
• Tuy nhiên, đối với mức ý nghĩa α=0.01 (1%). P-value> α
(0.0181>0.01); ta không thể bác bỏ giả thuyết H0 và kết luận
rằng không có đủ bằng chứng để cho rằng hệ số prpblck khác 0. (ii)
Hệ số tương quan giữa hai biến là một đại lượng cho biết mức độ
tương quan giữa các giá trị của hai biến. Hệ số tương quan được
đánh giá từ -1 đến 1, trong đó 1 là tương quan hoàn hảo và -1 là
tương quan hoàn toàn nghịch đảo giữa hai biến. Nếu hệ số tương
quan gần 0, thì hai biến không có mối quan hệ tuyến tính.
Trong trường hợp này, hệ số tương quan giữa log(income) và prppov
là -0.7249, có giá trị âm, cho thấy mối tương quan nghịch giữa hai
biến. Điều này có thể được giải thích rằng khi thu nhập tăng lên, tỷ
lệ người nghèo trong một khu vực giảm, do đó, prppov giảm.
Is each variable statistically significant in any case? Report the two-sided p-values.
log(psoda)^ = -1.463 + 0.073prpblck + 0.137log(income) + 0.38prppov (0.29) (0.03) (0.03) (0.13)
Để kiểm tra xem hệ số B2 có ý nghĩa thống kê tại mức ý nghĩa 5%
với giả thuyết đối hai phía hay không, làm tương tự câu (i)
• H0: B1 = 0 (hệ số tương ứng với log(income) không có ảnh hưởng đến psoda)
• H1: B1 ≠ 0 (hệ số tương ứng với log(income) có ảnh hưởng đến psoda)
• Mức ý nghĩa: 5% = 0.05
• t = (B2 - 0) / SE(B2) = (0.137 – 0)/(0.03) = 4.5667
p-value = 4.8x10^-7 ~~ 0 ; ***: p-value < 0.001
P-value < alpha (0.001 < 0.05), ta có thể bác bỏ giả thuyết H0 và
kết luận rằng log(income) có ảnh hưởng đến psoda.
=> biến log(income) có tính chính xác thống kê ở mức ý nghĩa 5% (iii)
Thêm biến log(hseval) vào mô hình hồi quy của câu (i). Diễn giải hệ số và báo cáo giá trị p
hai chiều cho giả thuyết H0: log(hseval) = 0.
