lOMoARcPSD|50713028 KHÓA LĐ LIVESTREAM
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2023 ĐỀ THI THỬ SỐ 4 Bài thi: TOÁN (Đề thi có 06 trang)
Thời gian làm bài: 90 phút, không kể thời gian phát ề
Họ, tên thí sinh:………………………………………….............
Số báo danh:……………………………………………………..
Câu 1: Số iểm cực trị của ồ thị hàm số y x4 4x2 1 là A.4. B.3. C.2. D.1.
Câu 2: Với a, b là các số thực dương tùy ý và a 1, loga3 b bằng A. 3 loga b . B. 3loga b. C. loga b . D. loga b.
Câu 3: Tính nguyên hàm của hàm số y sin x 1 A. sin x 1 dx cos x 1 C B. sin x 1 dx x 1 cos x 1 C C. sin x 1 dx cos x 1 C D. sin x 1 dx 1 x cos x 1 C
Câu 4: Cho số phức z 2i 8. Số phức liên hợp của z là A. z 2i 8 B. z 2i 8 C. z 2i 8 D. z 2i 8
Câu 5: Khối bát diện ều là khối a diện ều loại A. 3;4 . B. 4;3 . C. 5;3 . D. 3;5 .
Câu 6: Trong không gian Oxyz, tọa ộ của vector a i 2 j 3k là A. 1; 2; 3 . B. 3; 2; 1 . C. 2; 1; 3 . D. 2; 3; 1 .
Câu 7: Khẳng ịnh nào sau ây úng? n! k! n! k! A. C k k k D. C k n
B. Cn C. Cn n k ! n k ! k n k! ! n n n k! !
Câu 8: Số phức z 2 1i i có mô un bằng A.2 2 B. 2 C. 4 2 D. 2 3 3 3
Câu 9: Cho f x dx 2 và g x dx 3. Tính giá trị của ˆch phân L 2 f x g x dx 0 0 0 A. L 4 B. L 4 C. L 1 D. L 1
Câu 10: Hàm số y 3x 1 có ạo hàm là A. y' 3x 1ln3. B. y' 3x ln3. C. y' 3x 1. D. y' 3 .x Trang 1/6 lOMoARcPSD|50713028
Câu 11: Cho hàm số a thức bậc ba y f x có ồ thị như hình vẽ:
Mệnh ề nào sau ây là mệnh ề úng?
A. Hàm số f x ồng biến trên 1; .
B. Hàm số f x nghịch biến trên ; 2 .
C. Hàm số f x ồng biến trên 0; .
D. Hàm số f x nghịch biến trên 2;1 .
Câu 12: Cho hàm số y f x liên tục trên và có bảng xét dấu ạo hàm như hình vẽ
Hàm số y f x có bao nhiêu iểm cực trị? A. 1 B. 2 C. 4 D. 3
Câu 13: Mệnh ề nào sau ây là sai? A. log a logb ab 0 B. ln x 0 x 1 C. ln x 1 0 x 1 D. loga logb 0a b e dx Câu 14: Tích phân 1 bằng x A.e. B.1. C.e 1. D. 1.
Câu 15: Cho số phức z 4 3i có iểm biểu diễn trên mặt phẳng tọa ộ Oxy là M . Tính ộ dài OM A. 7 B. 5 C. 25 D. 4
Câu 16: Bán kính áy của khối trụ tròn xoay có thể ˆch bằng V và chiều cao bằng h là A. r 2V B. r 3V C. r V D. r V h h 2 h h
Câu 17: Trong không gian Oxyz , cho hai iểm A 3;1; 2 và B 1;3;2 . Trung iểm oạn AB có tọa ộ là A. 2; 1; 2 B. 1;2;0 C. 2;4;0 D. 4; 2; 4
Câu 18: Trong không gian Oxyz , mặt phẳng Oxy có phương trình là A. y 0 B. x 0 C. x y z 0 D. z 0
Câu 19: Cho một cấp số cộng u 1 n có u1 , u8 26. Tìm công sai d 3 A. d B. d C. d D. d
Câu 20: Cho hình chóp S ABC. có SA vuông góc với áy, SA AB a. Tính góc giữa ường thẳng SB và mặt phẳng ABC . A.75o B. 45o C. 30o D. 60o
Câu 21: Nghiệm của phương trình 5x 3 51 x là Trang 2/6 lOMoARcPSD|50713028 A. x 1 B. x 2 C. x 1 D. x 2
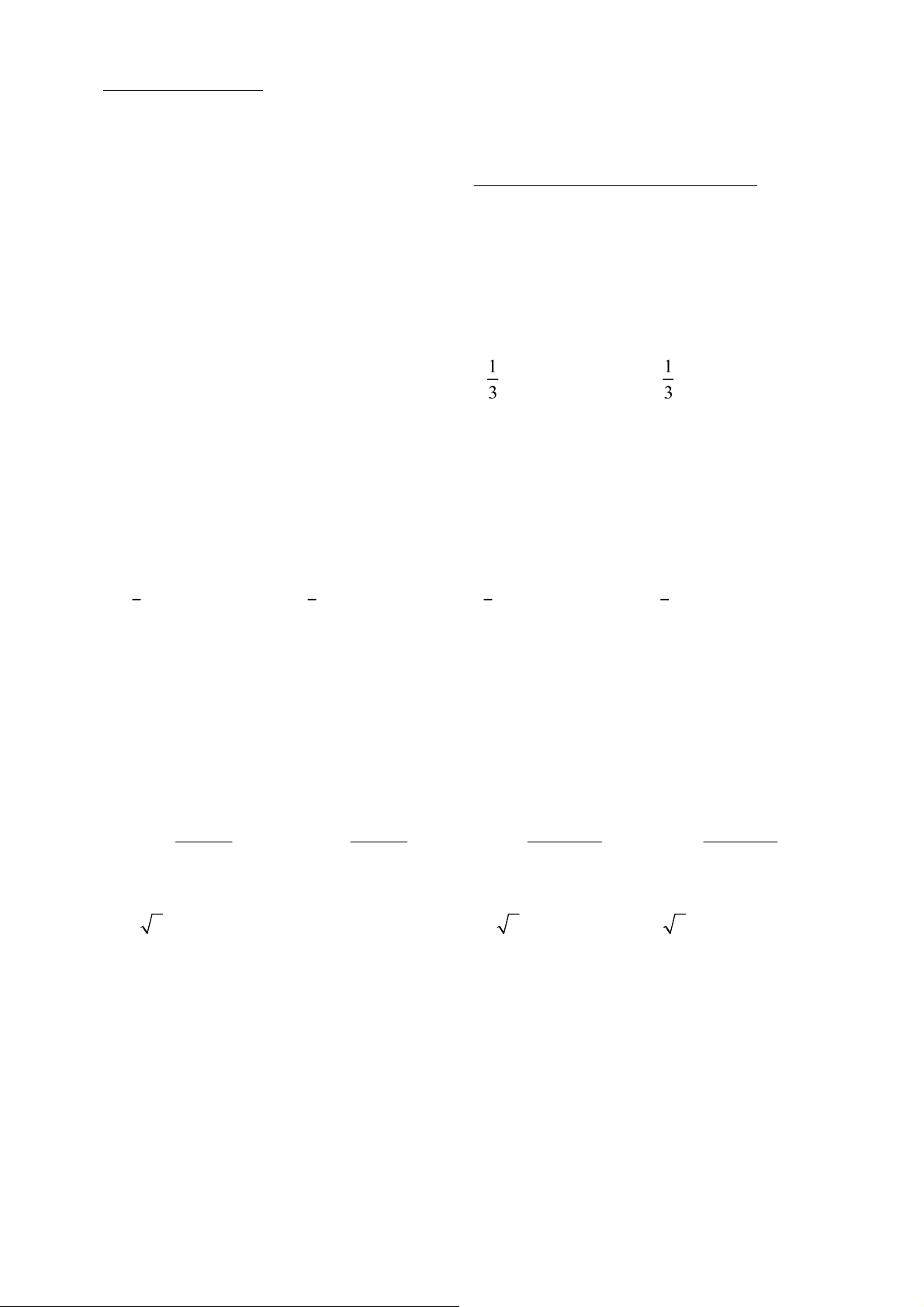
Câu 22: Cho hàm số y f x có bảng biến thiên như hình vẽ:
Tiệm cận ứng và –ệm cận ngang của ồ thị hàm số ã cho lần lượt có phương trình là A. x 1, y 2 . B. x 2, y 1. C. x 2, y 2 . D. x 1, y 1.
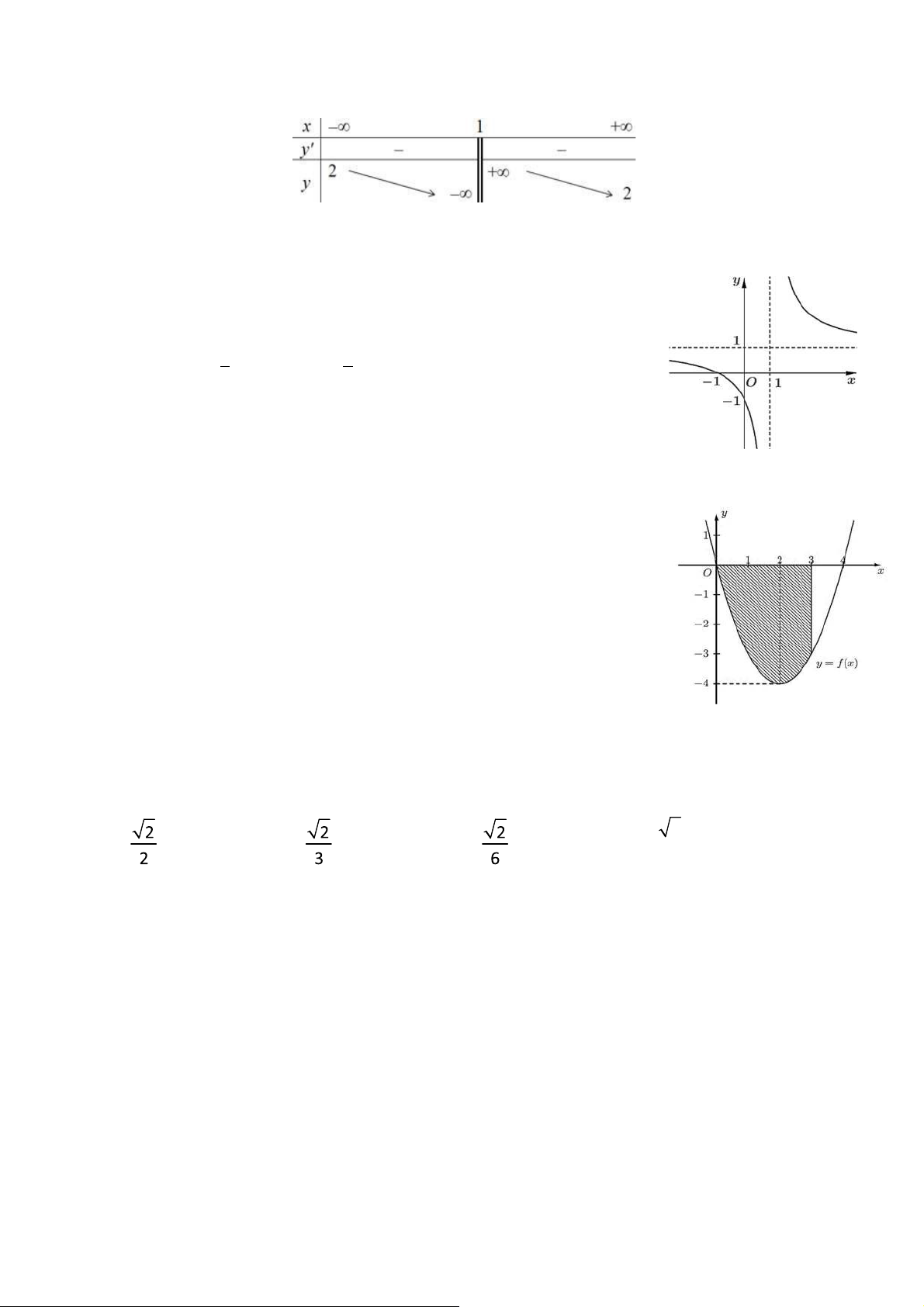
Câu 23: Đường cong trong hình vẽ là ồ thị của hàm số nào sau ây? A. y x 1 . B. y x 1 . x 1 x 1 C. y x3 3x 2. D. y x4 2x2 1.
Câu 24: Giá trị lớn nhất của hàm số y x3 3x2 9x 3 trên oạn 1;3 bằng A.14. B. 2. C.40. D.30.
Câu 25: Cho hàm số y f x có ồ thị như hình vẽ:
Diện ˆch S của miền ược tô ậm ược ˆnh theo công thức nào sau ây? 3 4 A. S f x dx . B. S f x dx . 0 0 3 4 C. S f x dx . D. S f x dx . 0 0
Câu 26: Thể ˆch của khối chóp ều S ABCD.
có tất cả các cạnh bằng a là A. a3. B. a3. C. a3. D. 2a3.
Câu 27: Trong không gian Oxyz , phương trình của ường thẳng d i qua iểm A 1;2; 5 và vuông góc với
mặt phẳng P :2x 3y 4z 5 0 là x 1 2t x 2 t x 1 2t x 2 t A. y 2 3t B. y 3 2t C. y 2 3t D. y 3 2t z 5 4t z 4 5t z 5 4t z 4 5t
Câu 28: Cho hình chóp S ABCD. có SA ABCD , áy ABCD là hình chữ nhật. Biết AD 2a , SA a. Khoảng cách từ A ến SCD bằng Trang 3/6 lOMoARcPSD|50713028 3a 3a 2 2a 2a 3 A. . B. . C. . D. . 7 2 5 3
Câu 29: Gọi z1 là nghiệm phức có phần ảo dương của phương trình 2z2 2z 5 0. 1 2020 Mô un của i z1 bằng z 10 B. C. 13 D. 130
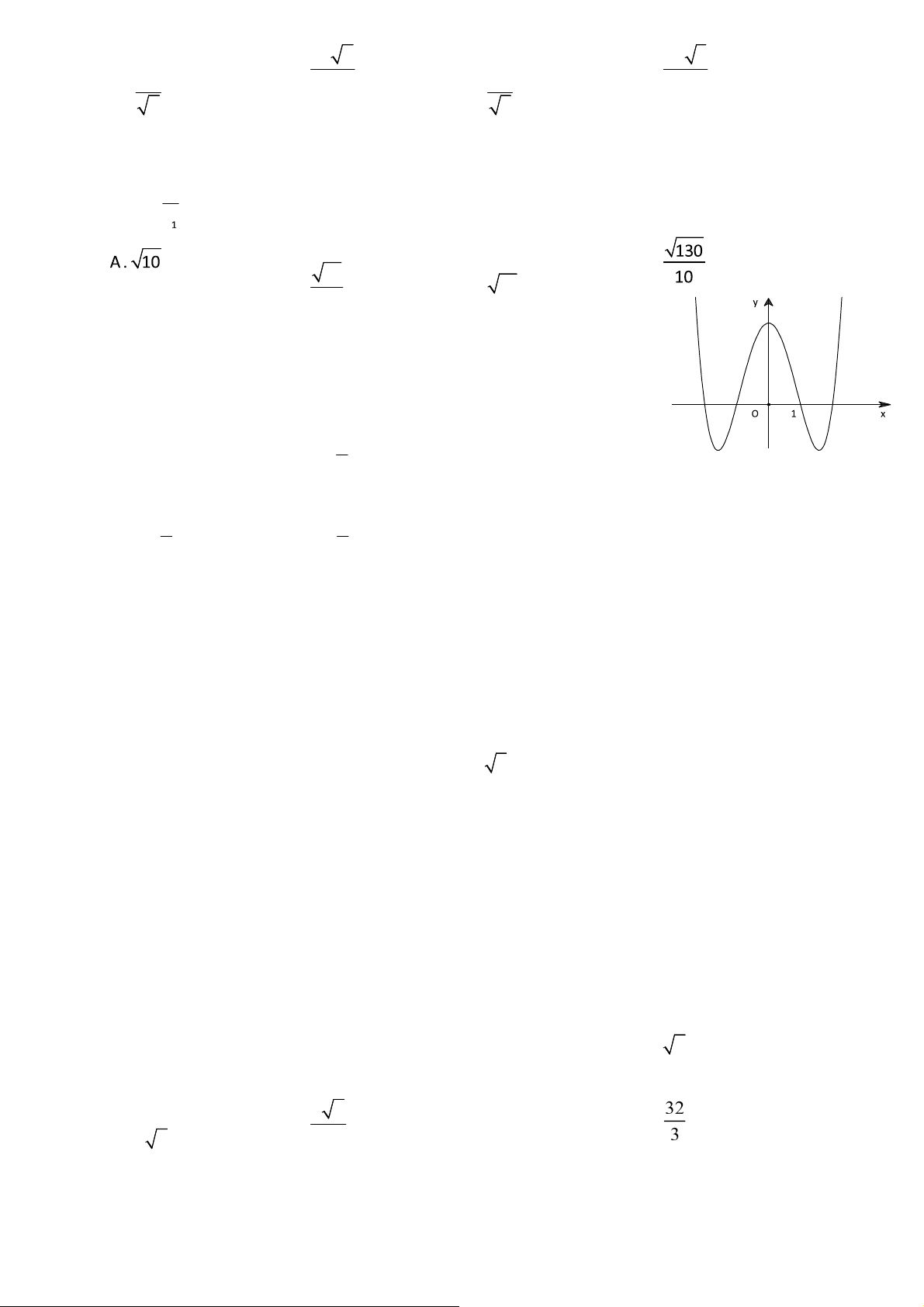
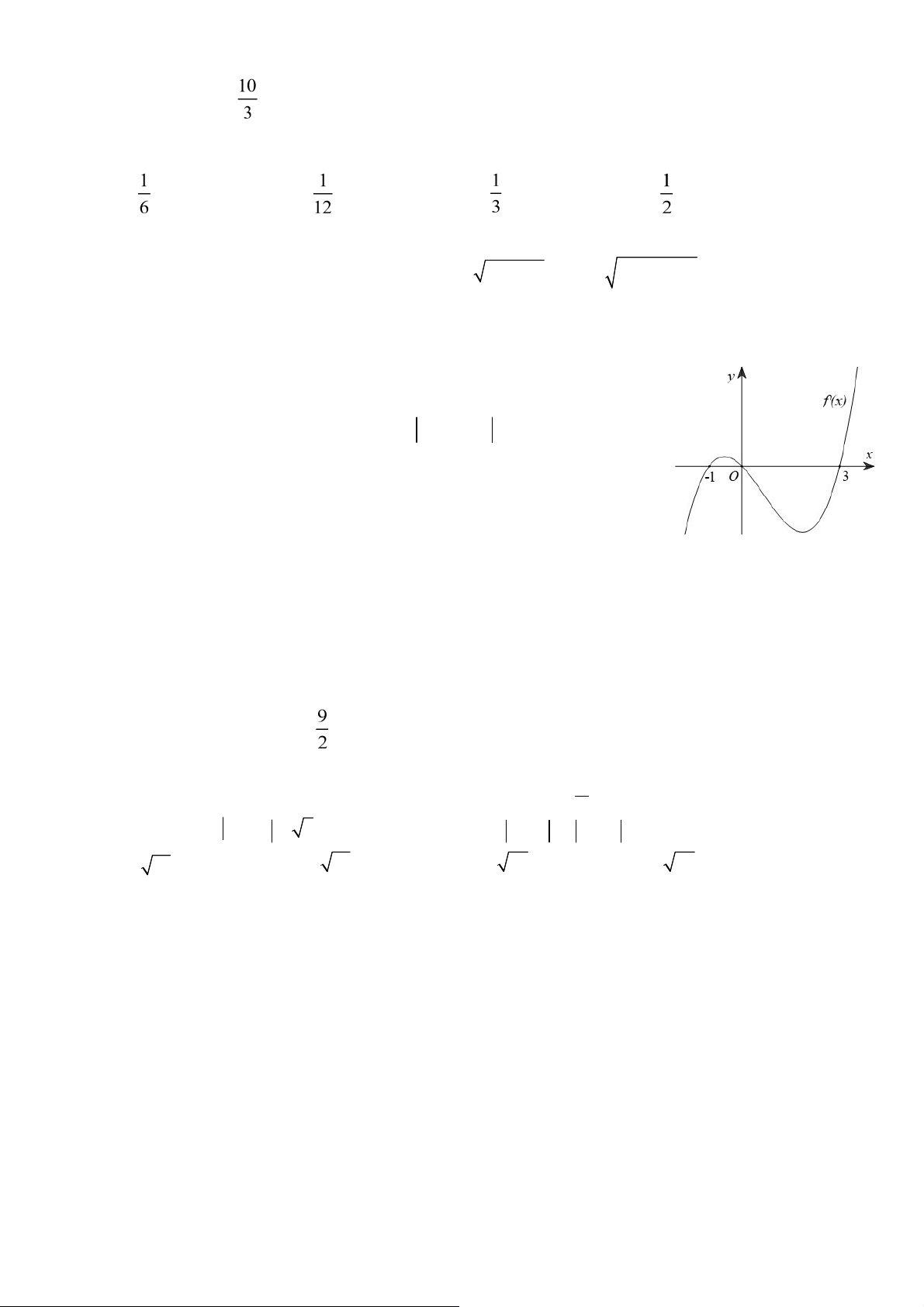
Câu 30: Cho hàm số y f x ax3 bx2 cx d, a 0 có ồ thị như hình vẽ
bên. Mệnh ề nào dưới ây úng? A. f ' 12 0. B. f ' 12 0. C. f ' 12 0. D. f ' 12 0.
Câu 31: Cho bất phương trình log22 2x 4log2 x 4 0. Khi ặt t log2 x thì bất phương trình ã cho trở
thành bất phương trình nào sau ây? A.t2 4t 3 0. B.t2 2t 3 0. C.t2 0. D.t2 4t 4 0.
Câu 32: Cho hình chóp tam giác ều có cạnh áy bằng
6 và chiều cao h 1. Tính diện ˆch mặt cầu
ngoại –ếp hình chóp ã cho A. S 27 B. S 6 C. S 5 D. S 9 x t
Câu 33: Trong không gian Oxyz , cho ường thẳng d : y 1 t t
. Mặt phẳng i qua O và chứa d z 2 có phương trình là A. 2x 2y z 0. B. 2x 2y z 0 . C. x 2y z 0 . D. x 2y z 0 .
Câu 34: Cho khối hộp chữ nhật ABCD A B C D. có áy là hình vuông, AC 2 2a , góc giữa hai mặt phẳng C BD
và ABCD bằng 45 . Thể ˆch của khối hộp chữ nhật ã cho bằng 3 4 2 3 33 A. 4 2a . B. a . C. 32a . D. a . 3 Trang 4/6 lOMoARcPSD|50713028
Câu 35: Nếu 1 f 3 1x dx 10 thì 4 f x 4x dx bằng 0 1 A. 20. B. 4. C. . D. 0.
Câu 36: Trong khuôn viên một trường ại học có 5000 sinh viên, một sinh viên vừa trở về sau kì nghỉ và bị
nhiễm virus cúm truyền nhiễm kéo dài. Sau ó lây lan cho các sinh viên của trường và sự lây lan này ược
mô hình hóa bởi công thức y 1 49995000e 0,8t , t
0 . Trong ó y là tổng số học sinh
bị nhiễm sau t ngày. Các trường ại học sẽ cho các lớp học nghỉ khi có nhiều hơn hoặc bằng 40% số sinh viên bị lây
nhiễm. Sau ít nhất bao nhiêu ngày thì trường cho các lớp nghỉ học? A. 11. B. 12. C. 10. D. 13.
Câu 37: Trong không gian với hệ tọa ộ Oxyz , cho iểm I 3;0;1 . Mặt cầu S có tâm I và cắt mặt phẳng
P : x 2y 2z 1 0 theo một thiết diện là một hình tròn. Diện ˆch của hình tròn này bằng .
Phương trình mặt cầu S là A. x 3 2 y2 z 1 2 2 B. x 3 2y2 z 1 2 25 C. x 3 2y2 z1 2 5 D. x 3 2y2 z 1 2 4
Câu 38: Chọn ngẫu nhiên lần lượt hai số nguyên dương bé hơn 100. Tính xác suất ể hiệu hai số vừa ược chọn là một số lẻ. A. . B. . C. . D. .
Câu 39: Cho hàm số f x có ạo hàm liên tục trên 0; 2
, thỏa mãn 02 f x cos xdx2 2 và f 0 1. 2 Khi ó f x sin2xdx bằng 0 A. 3. B. 5. C. 3. D. 2.
Câu 40: Có bao nhiêu giá trị nguyên của tham số m ể phương trình 4x m.2x 1 3m 6 0 có hai nghiệm trái dấu? A. 3. B. 5. C. 4. D. 2. Trang 5/6 lOMoARcPSD|50713028
Câu 41: Tất cả giá trị thực của tham số m ể ồ thị hàm số y x4 3m 4 x2 m2 cắt trục hoành tại bốn iểm phân biệt là A. m ; 4 54;0 0; . B. m 34;0 0; . C. m 4;0 0; . D. m \ 0 . 5
Câu 42: Trong mặt phẳng tọa ộ Oxy, xét hai iểm A B,
lần lượt là các iểm biểu diễn các số phức z và
1 2i z . Biết rằng diện ˆch của tam giác OAB bằng 8, mô un của số phức z bằng A. 2. B. . C. 2 2. D. 4 2. 2
Câu 43: Trong không gian Oxyz, cho ường thẳng x 1 : y 1 z và hai mặt phẳng 1 1 2
P : x 2y 3z 0, Q : x 2y 3z 4 0. Mặt cầu có tâm thuộc ường thẳng và –ếp xúc với cả hai mặt
phẳng P và Q có bán kính bằng 12 2 A. . B. . C. . D. . 7 7 7 7
Câu 44: Hình nón N có ỉnh S , tâm ường tròn áy là O, góc ở ỉnh bằng 120 . Một mặt phẳng qua
S cắt hình nón N theo thiết diện là tam giác vuông SAB . Biết rằng khoảng cách giữa hai ường thẳng AB và SO bằng 3. Tính diện ˆch xung Cho hàm số y f quanh S xq x của hình nón N Số giá trị nguyên của
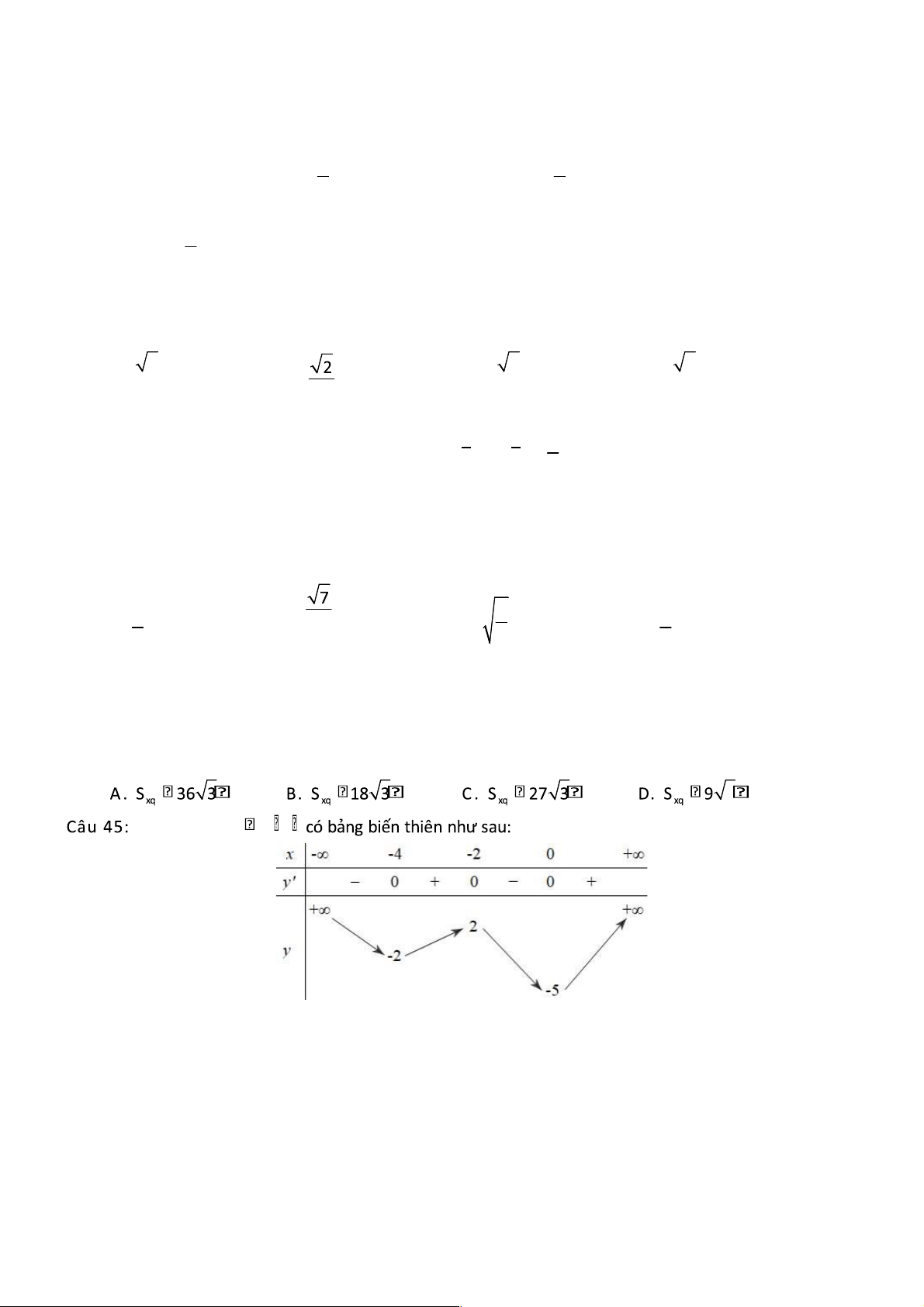
tham số m ể phương trình 3f x 2 4x m 5 có ít nhất 5 nghiệm thực phân biệt thuộc khoảng 0; là A.12. B.14. C.13. D.11. Trang 6/6 lOMoARcPSD|50713028
Câu 46: Biết hàm số f x ax3 bx2 3x 1 a b, ,a 0 ạt cực trị tại hai iểm x1 , x2 thỏa mãn x1 x2 4 và f x 1 f x 2
. Gọi y g x là hàm số bậc nhất có ồ thị i qua hai iểm cực trị của ồ thị hàm
số y f x . Diện ˆch hình phẳng giới hạn bởi hai ường y f x và y g x bằng A. B. C. D.
Câu 47: Có bao nhiêu số nguyên dương a thỏa mãn 1 ln2 a lna 1 a 3 2 a3 1? A.2. B.1. C.3. D.4.
Câu 48: Cho hàm số a thức y f x có f 0 1 và ồ thị hàm số f x
như hình vẽ. Số iểm cực trị của hàm số y f f x 3 là A. 9 B. 8 C. 7 D. 10
Câu 49: Trong không gian Oxyz , cho hai iểm A 10;6; 2 , B 5;10; 9 và mặt phẳng :2x 2y z 12 0. Điểm M di ộng trên
sao cho MA MB, luôn tạo với
các góc bằng nhau. Biết rằng M luôn thuộc một ường tròn
cố ịnh. Hoành ộ của tâm ường tròn bằng A. 10 B. C. 2 D. 4
Câu 50: Gọi S là tập hợp tất cả các số phức z sao cho số phức w z 2 là số thuần ảo. Xét các số phức z
2i z1, z2 S thỏa mãn z1 z2 3 , giá trị lớn nhất của P z1 6 2 z2 62 bằng A.2 15 B. 4 15 C. 2 78 D. 78
---------------HẾT--------------- Trang 7/6