lOMoARcPSD|50713028 KHÓA LĐ LIVESTREAM
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2023 Bài thi: TOÁN ĐỀ THI THỬ SỐ 6
Thời gian làm bài: 90 phút, không kể thời gian phát ề (Đề thi có 05 trang)
Họ, tên thí sinh:………………………………………….............
Số báo danh:……………………………………………………..
Câu 1: Nghiệm của phương trình log2 2x 6 3 là: A. x 6 B. x 9 C. x 8 D. x 7
Câu 2: Tập xác ịnh của hàm số y 7x là A. 0; B. C. 0; D. \ 0
Câu 3: Họ nguyên hàm của hàm số f x cos x là A. cos x C B. cos x C C.sin x C D. sin x C
Câu 4: Gọi S là diện ych của hình phẳng giới hạn bởi các ường y 3x, y 0,x 0, x 2. Mệnh ề nào dưới ây úng? 2 2 2 2 A. S 3xdx B. S 32xdx C. S 3xdx D. S 32xdx 0 0 0 0
Câu 5: Cho z 4 5i . Số phức ối của z là: A. 4 5i B. 4 5i C. 5 4i D. 4 5i
Câu 6: Cho lăng trụ ứng ABC A B C. '
' ' có áy ABC là tam giác vuông tại C CA CB a, và AA' 6a .
Thể ych khối lăng trụ ABC A B C. ' ' ' bằng A.2a3 B.3a3 C.a3 D.6a3
Câu 7: Một hình trụ có bán kính áy r 5cm , chiều cao h 7cm. Thể ych của khối trụ ó bằng A.175 cm3 B. cm3 C.70 cm3 D.35 cm3
Câu 8: Trong không gianOxyz , cho 2 vectơ u 5;4;2 và v 1;2;4 . Tích có hướng u v, là? A. 12;18; 6 B. 12; 18; 6 C. 12;18;6 D. 12; 18; 6
Câu 9: Trong không gian Oxyz, cho mặt phẳng P :4x 3y z 1 0. Điểm nào dưới ây thuộc P A. M 0;2; 1 B. N 1;1; 6 C. P 1; 6; 1 D.Q 0;2;1
Câu 10: Có bao nhiêu cách xếp 4 học sinh nam và 5 học sinh nữ thành 1 hàng dọc? A.9! B.9 C.20 D. 4!.5! Trang 1/5 lOMoARcPSD|50713028
Câu 11: Dãy số nào sau ây KHÔNG phải là cấp số nhân? A.1;2;4;8;16 B.1;2;3;4;5 C.1; 1;1; 1; 1 D.1; 2;4; 8; 16
Câu 12: Cho số phức z thỏa mãn z 3 i 0. Mô un của z bằng A. 4. B. 10 . C. 3 . D. 10 . 3
Câu 13: Biết F x x3 C là nguyên hàm của hàm số f x trên tập số thực; Tính I f x dx 1 A. 23 B. 20 C. 26 D.17
Câu 14: Biểu thức P 3 x.4 x, x 0 viết dưới dạng lũy thừa với số mũ hữu tỷ là: A. P x B. P x C. P x D. P x
Câu 15: Cho hàm số f x liên tục trên \ 1 và có bảng xét dấu của f ' x như sau:
Số iểm cực trị của hàm số ã cho là A.1 B.3 C.4 D.2 Câu 16: Trên khoảng 0;
, ạo hàm của hàm số y x là 1 A. y x B. y x 3 C. y x D. y x
Câu 17: Giá trị nhỏ nhất của hàm số f x x4 24x2 4 trên 0;19 bằng: A. 150 B. 148 C. 149 D. 144
Câu 18: Đồ thị hàm số y x3 7x 8 cắt trục hoành tại bao nhiêu iểm có hoành ộ âm A. 0 B.1 C.2 D.3
Câu 19: Trong không gian Oxyz, cho các iểm M 1;2; 3 , N 3;2;4 . Độ dài oạn thẳng MN bằng A. 53 B.2 13 C.2 53 D.3 6 x m
cận ứng nằm bên trái trục tung là: A. 4046 B. 4044 C. 2022 D. 2023
Câu 21: Cho z1 3 2i z, 2 4 5i . Tính z1 z2 A. z1 z2 1 7i B. z1 z2 12 10i C. z1 D. z1 z2 7 3i z2 7 7i Câu 22: Hàm số y x4
2x2 1ồng biến trên khoảng nào dưới ây? A. 0; B. ;1 C. 1; D. ;0
Câu 23: Đồ thị hàm số nào dưới ây có šệm cận ứng Trang 2/5 lOMoARcPSD|50713028 1 x2 x Câu 20: D. y 2 3x S 2 ố các giá A. y x3 3x2 x 1 B. y 2 1 C. y log2 x x 1 trị nguyên x của tham
Câu 24: Thể ych khối cầu nội šếp hình lập phương có cạnh bằng 2 là số m
thuộc 2023;2023 ể ồ thị hàm số y 2x 4 có šệm A. 4 B.8 C. D.
Câu 25: Trong không gian cho hệ trục Oxyz, cho A 1;1;2 , B 4;0;11 , C 0; 21;0 . Tìm tọa ộ iểm D
sao cho ABCD là hình bình hành A. 5; 20;9 B. 5;20; 9 C. 5; 20;9 D. 5; 20; 9
Câu 26: Cho hình chóp S ABCD.
có áy ABCD là hình chữ nhật tâm I, cạnh bên SA vuông góc với áy.
Khẳng ịnh nào sau ây úng? A. SCD SAD B. SBC SIA C. SDC SAI D. SBD SAC
Câu 27: Trong không gian Oxyz, cho hai mặt phẳng P : x 2y2z 1 0 và Q : 2x 2y z 3 0.
Gọi là góc giữa hai mặt phẳng P và Q . Tính cos . A. . B. . C. . D. .
Câu 28: Cho tam giác ABC vuông cân tại A, có cạnh AB a. Gọi H là trung iểm của BC . Thể ych của khối
nón tạo thành khi quay hình tam giác ABC xung quanh trục AH là: 3 a3 a3 2 a3 2 a3 A. B. C. D. 12 12 6 12
Câu 29: Trong không gian với hệ trục Oxyz cho ba iểm A 1;2;3 , B 1;0;2 , C x y ; ; 2 thẳng hàng. Khi ó x y bằng Trang 3/5 lOMoARcPSD|50713028 A. x y B. x y 1 C. x y D. x y 17
Câu 30: Cho hàm số f x xác ịnh trên \ 1 thoả mãn f ' x 1 , f 0 2022 , f 2 2023. x 1 Tính S f 3 f 1 A. S 0 B.S ln 4045 C.S 1 D.S ln 2
Câu 31: Một người gửi 50 triệu ồng vào một ngân hàng với lãi suất 6% /năm. Biết rằng nếu không rút
šền ra khỏi ngân hàng thì cứ sau mỗi năm số šền lãi sẽ ược nhập vào gốc ể ynh lãi cho năm šếp theo.
Hỏi sau ít nhất bao nhiêu năm người ó nhận ược số šền hơn 100 triệu ồng bao gồm cả gốc và lãi? Giả
ịnh trong suốt thời gian gửi, lãi suất không ổi và người ó không rút šền ra. A.13năm B.12năm C.14năm D.11 năm
Câu 32: Một ô tô ang chạy thì người lái ạp phanh. Từ thời iểm ó, ô tô chuyển ộng chậm dần ều với vận tốc v t 12t
24 m s/ trong ó t là khoảng thời gian ynh bằng giây, kể từ lúc bắt ầu ạp
phanh. Hỏi từ lúc ạp phanh ến ến khi dừng hẳn, ô tô di chuyển bao nhiêu mét? A.15m B.24m C.20m D.18m
Câu 33: Có bao nhiêu giá trị của m ể hàm số y x3 2m 3 x2
m2 2m x 2 ạt cực ại tại x 0? A.1 B. Vô số C.0 D.2
Câu 34: Cho hàm số f x ex.2021 .x2 Chọn khẳng ịnh úng trong các khẳng ịnh sau. A. f x 1 x 2xln2021 0. B. f x 1 x2 ln2021 0. C. f x 1 x x2 ln2021 0 D. f x 1 1 x2 ln2021 0
Câu 35: Cho hình chóp S ABCD. có áy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với áy và SA
a 3 . Khoảng cách từ D ến mặt phẳng SBC bằng 2 5aa a 3 A. . B. a 3 . C. . D. . 52 2
Câu 36: Có bao nhiêu giá trị nguyên của m ể bất phương trình log 2
3 x m log3 x m nghiệm úng với mọi giá trị của x 0; . A. 7 B. 6 C.4 D.5 Câu 37: Biết 2 x 3 x 3 01 x 2 2 2 x 1 dx a lnb với a b,
là các số nguyên dương. Tính P a 2 b2 A.13 B.5 C.4 D.10
Câu 38: Tập hợp các iểm biểu diễn số phức z thỏa mãn z 4 z 4 8 trên mặt phẳng phức là : A. Đoạn thẳng B. Đường Elip C. Tập rỗng D. Đường thẳng
Câu 39: Trong không gian với hệ toạ ộ Oxyz , cho mặt phẳng P : x y z 1 0 và hai iểm Trang 4/5 lOMoARcPSD|50713028
A 1; 1;2 , B 2;1;1 . Mặt phẳng Q :ax by z c 0chứa A B, và vuông góc với mặt phẳng P ,
khi ó biểu thức T a b cbằng A.-1 B.-2 C.2 D.1
Câu 40: Cho hình chóp S ABC.
có SA ABC , SA a, ABC ều cạnh a. Tính tang góc giữa ường thẳng SC và mặt phẳng SAB 31 A. B. C. D. 2 52 Câu 41: Cho z 1 1. Tính P z 1 2023 2023 zz A. P 1 B. P 1 C. P 2 D. P 0
Câu 42: Cho khối chóp S ABCD. có áy là hình bình hành. Gọi M N,
là hai iểm nằm trên hai cạnh SC SD,
sao cho SM 1 , SN 2, biết G là trọng tâm tam giác SAB. Tính tỉ số thể ych VG MND. SC 2 ND VS ABCD. A. B. C. D.
Câu 43: Từ hộp chứa 12 quả cầu gồm 3 quả cầu ỏ,4 quả cầu xanh và 5 quả cầu vàng, lấy ngẫu nhiên ồng
thời 5 quả. Xác suất ể số quả cầu còn lại trong hộp có ủ 3 màu là A. . B. . C. . D. .
Câu 44: Có bao nhiêu số nguyên m 2023;2023 ể ồ thị hàm số y x3 mx2 m 2m 1 x m2 có
hai iểm cực trị nằm về hai phía của trục hoành ? A. 4044 B. 4046 C. 4047 D. 4045
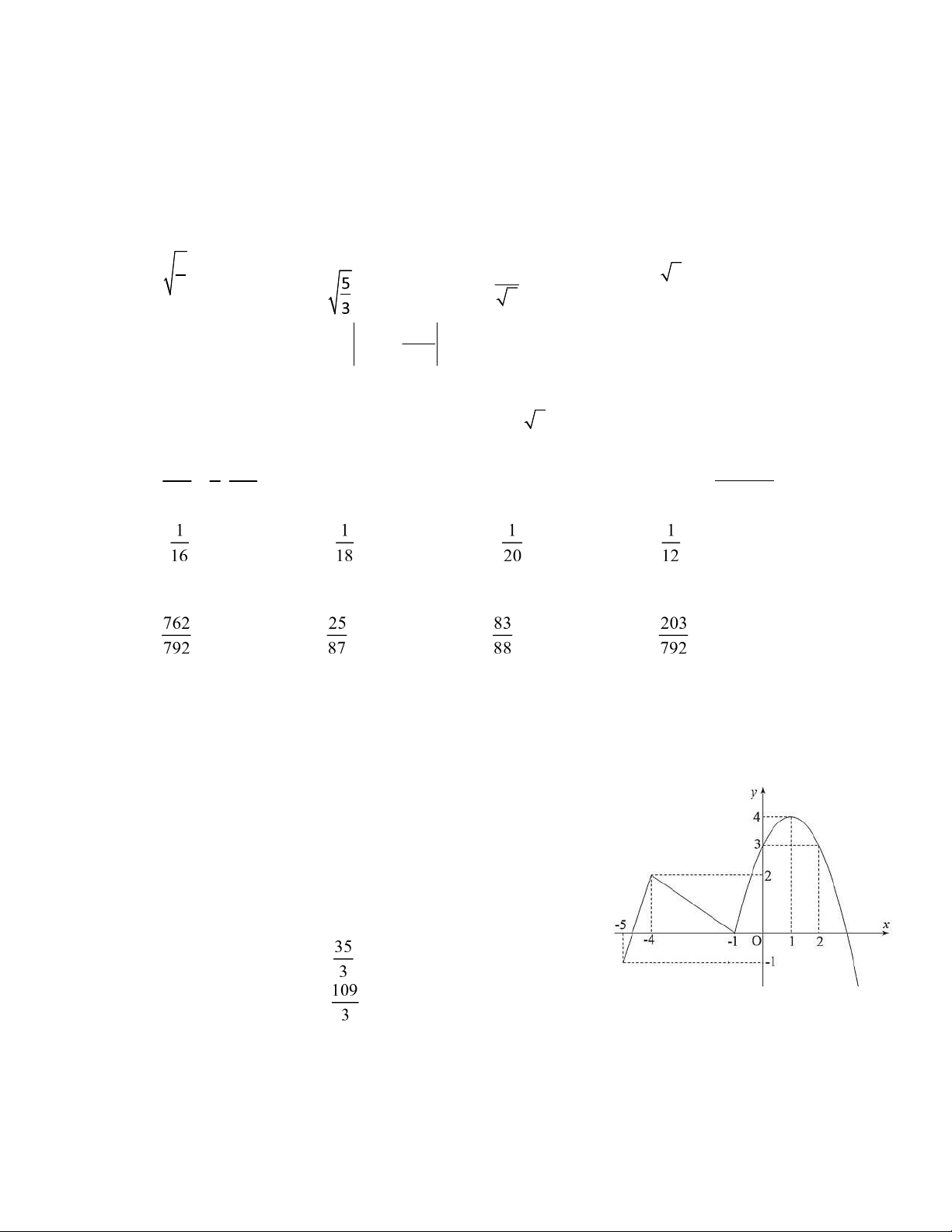
Câu 45: Cho hàm số y f x . Đồ thị của hàm số y f ' x trên
5;3 như hình vẽ (phần cong của ồ thị là một phần của parabol
y ax2 bx c). Biết f 0 0, giá trị của 2 f 5 3 f 2 bằng A.33 B. C.11 D. Trang 5/5 lOMoARcPSD|50713028
Câu 46: Cho hàm số y f x có ạo hàm f ' x x 1 x 1 2 x 2 . Giá trị nhỏ nhất của hàm số y f 2x 1 83 x3 4x2 53,x 1; 12 bằng A. f 0 1 B. f 1 C. f 1 D. f 2
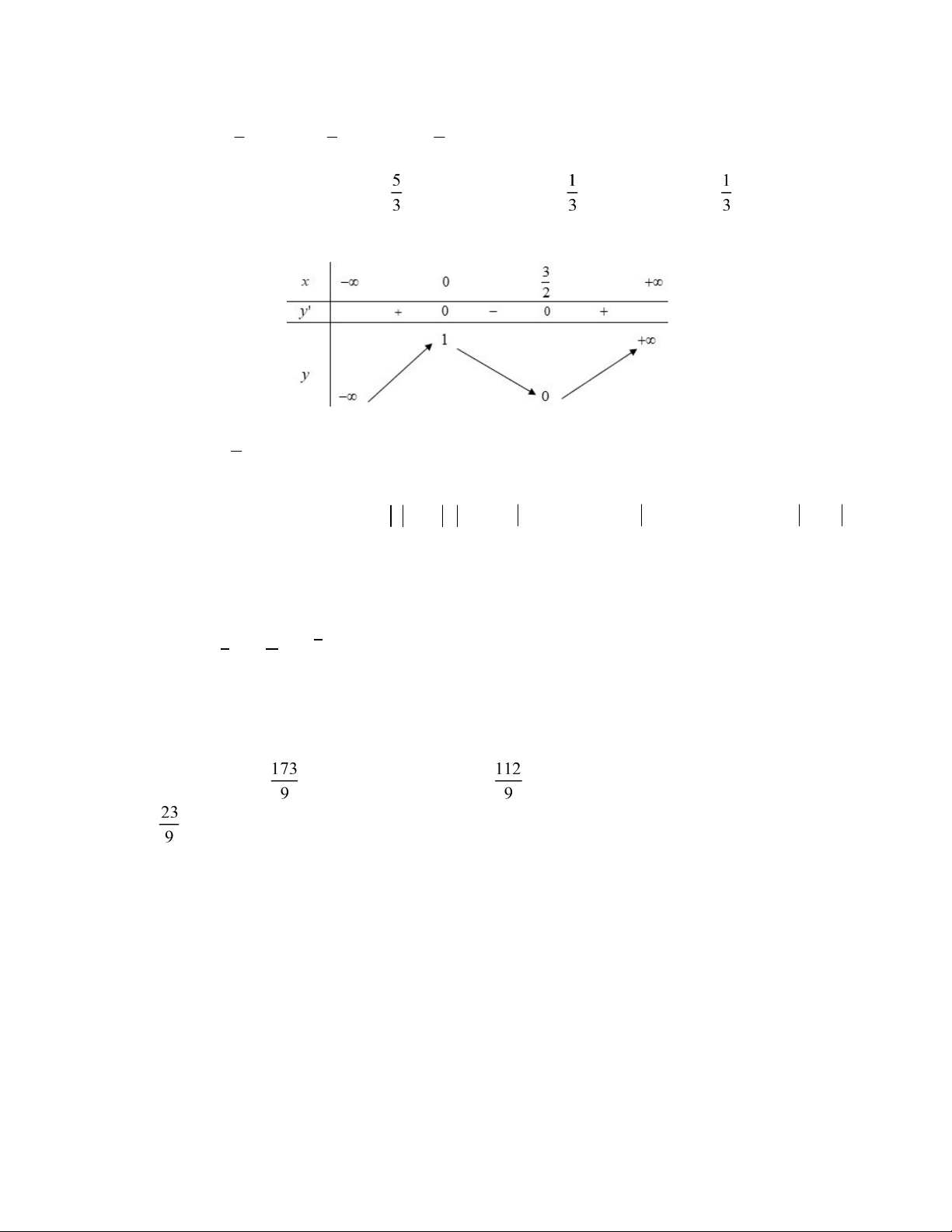
Câu 47: Cho hàm số f x bậc 3 có bảng biến thiên như sau: Đặt g x f 12 f 2 x f x
. Phương trình g ' x 0 có bao nhiêu nghiệm phân biệt ? A. 7 B.8 C. 6 D.9
Câu 48: Xét các số phức z w, thỏa mãn z 1, w 2. Khi z w 3
4i ạt giá trị lớn nhất thì 2z w bằng A. 8 . B. 2. C. 4. D. 3 .
Câu 49: Trong không gian với hệ tọa ộ Oxyz , cho mặt cầu ( ):S x2 y2 z2 2x 4y 6z 13 0 và
ường thẳng d : x 1 y 2 z 1 . ĐiểmM a b c ; ; a 0 nằm trên ường thẳng d sao cho từ M kẻ 1 1 1
ược ba šếp tuyến MAMBMC, , ến mặt cầu S ( ABC, , là các šếp iểm) và AMB 60 , BMC 90 , CMA 120 . Tính a3 b3 c3 . A. a3 b3 c3 . B. a3 b3 c3 . C. a3 b3 c3 8. D. a3 b3 c3 .
Câu 50: Gọi S là tập hợp tất cả các giá trị thực của m ể tồn tại duy nhất cặp số x y; thoả mãn logx y2 2 2
4x 4y m2 6m 3 1và x2 y2 2x 4y 1 0 . Tổng các giá trị của các phần tử thuộc tập S bằng A.12 B.0 C.6 D.8 ------------HẾT------------ Trang 6/5