lOMoARcPSD|50713028 KHÓA LĐ LIVESTREAM
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2023 Bài thi: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian phát ề ĐỀ THI THỬ SỐ 9 (Đề thi có 06 trang)
Họ, tên thí sinh:………………………………………….............
Số báo danh:……………………………………………………..
Câu 1: Tập xác ịnh D của hàm số y x 1 là: A. D \ 1 . B. D . C. D 1; . D. D 1; .
Câu 2: Khẳng ịnh nào sau ây úng ? A. cos1 1 2 xdx tan x C . B. 2 dx tan x C . cos x C. cos12 xdx cot x C . 1 1 D. 2 dx cot x C .
Câu 3: Kết quả của uch phân I 2x 1 dx là cos x 0 A. 2. B.1. C.3. D. 4.
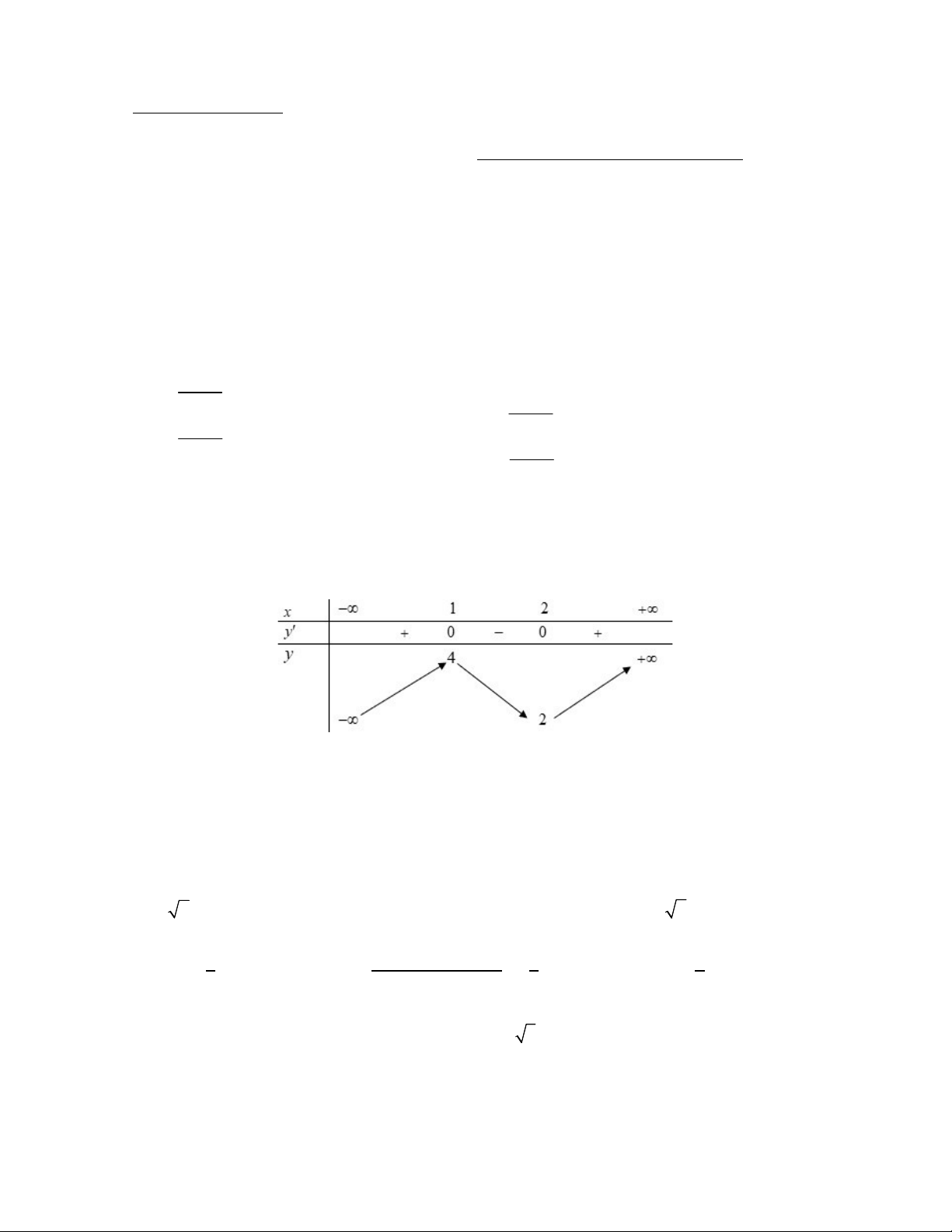
Câu 4: Cho hàm số y f x có bảng biến thiên như sau :
Khẳng ịnh nào sau ây là sai ?
A. Hàm số ồng biến trên ;4
B. Hàm số ồng biến trên 5;2023
C. Hàm số ồng biến trên 2;
D. Hàm số nghịch biến trên 1;2
Câu 5: Trong không gian Oxyz, cho vectơ a 1;2; 1 . Độ dài của vectơ a bằng A. 2. B. 2. C. 6. D. 6.
Câu 6: Khối cầu có ường kính 8a . Thể uch khối cầu ó là : 2048 a3 2048 256 a3 256 A. B. C. D. 3 3 3 3
Câu 7: Cho khối lập phương có ộ dài ường chéo bằng 3 3. Thể uch khối lập phương ã cho bằng A.9. B.12. C. 27. D.18.
Câu 8: Trên mặt phẳng tọa ộ, cho M 2;3 là iểm biểu diễn của số phức z. Phần thực của z bằng Trang 1/6 lOMoARcPSD|50713028 A. 3 B.3 C. 2 D. 2
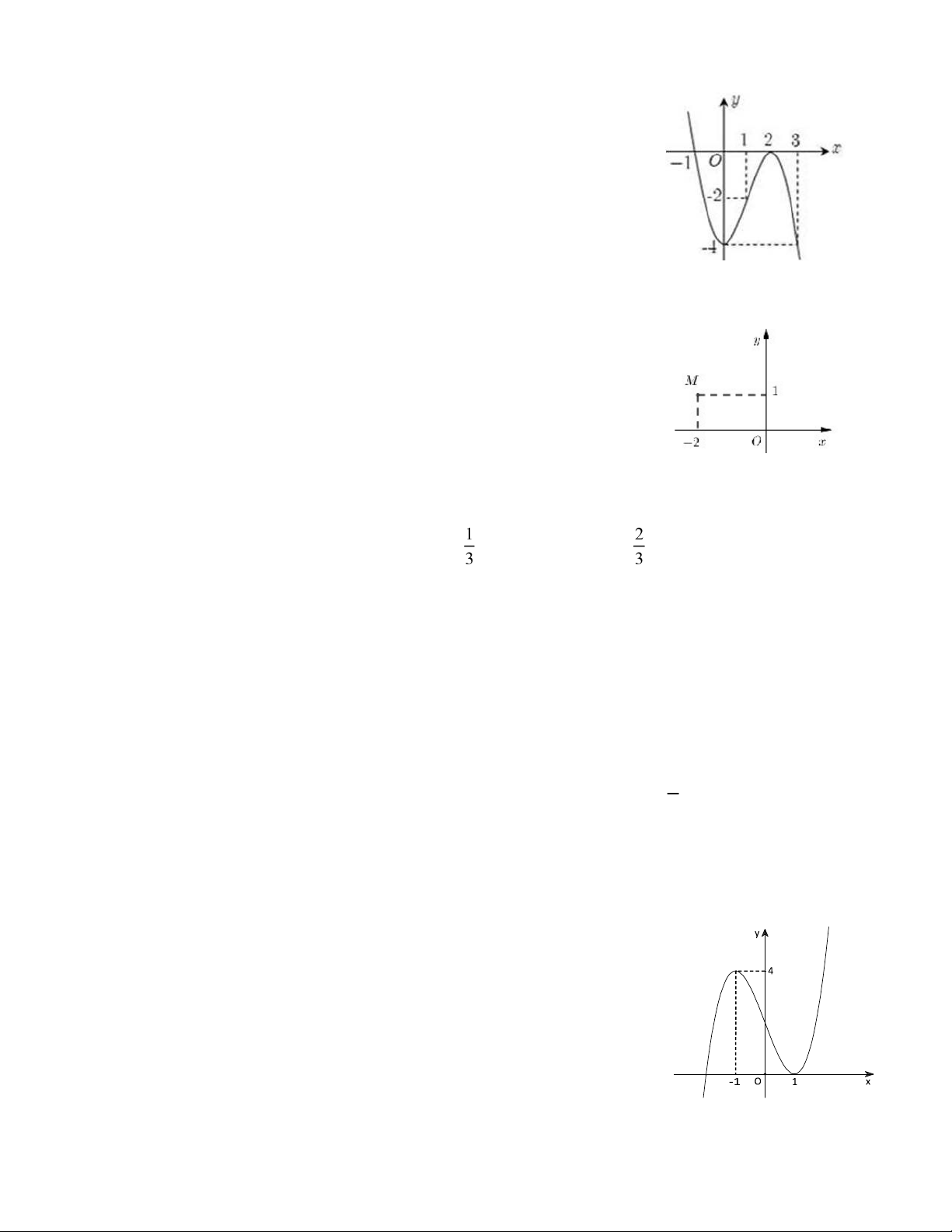
Câu 9: Cho hàm số y f x xác ịnh trên và có ồ thị hàm số y f ' x là
ường cong trong hình vẽ, hàm số y f x ã cho
ồng biến trên khoảng nào dưới ây? A. 4;0 B. ;1 C. 2; D. 0;2
Câu 10: Điểm M trong hình vẽ bên là iểm biểu diễn số phức nào? A. z 1 2i B. z 2 i C. z 2 i D. z 1 2i Câu 11: Cho
x2 1 dx F x C . Khẳng ịnh nào dưới ây úng? A. F ' x x2 1 B. F ' x x2 C. F ' x x3 x D. F ' x x2 1
Câu 12: Tập nghiệm của bất phương trình 32x 4 là A. ;2 B. 2; C. ;log 23 D. ;log 43
Câu 13: Cho hai số thực a b, tùy ý khác 0 thỏa mãn 3a 4 .b Giá trị của a bằng b A.ln0,75 B.log 43 C.log 34 D.ln12
Câu 14: Số giao iểm của ồ thị hàm số y x 4 2x2 với trục hoành là A.1 B.2 C.3 D.4
Câu 15: Cho hàm số y ax3 bx2 cx d a b c d , , ,
có ồ thị như hình vẽ.
Giá trị cực –ểu của hàm số ã cho bằng A. 0. B. 1. C. 4. D. 1. Trang 2/6 lOMoARcPSD|50713028
Câu 16: Tính ạo hàm của hàm số f x e2 3x A. f ' x 2e2 3x B. f ' x 2e2 3x C. f ' x 2ex 3 D. f ' x e2 3x
Câu 17: Số phức liên hợp của số phức z 2 5i là A. z 5 2i B. z 2 5i C. z 5i D. z 5i
Câu 18: Thể uch khối hộp chữ nhật có ộ dài các cạnh là a a a,3 ,5 bằng A.15a B.15a2 C.15 D.15a3
Câu 19: Trong không gian Oxyz, góc giữa hai mặt phẳng P : x y z 11 0 và Q : 2x 2y 2z 7 0 bằng A.0 .0 B.90 .0 C.180 .0 D.45 .0
Câu 20: Cho mặt cầu S : x2 y2 z2 2x 4y 2z 3 0. Tính bán kính R của mặt cầu S A. R 9 B. R 3 C. R 3 D. R 3 3
Câu 21: Cho số phức z 5 2i , phần ảo của số phức z2 2z bằng A.13 B. 6 C. 16 D.11
Câu 22: Cho hình phẳng H giới hạn bởi ồ thị của hàm số y 2x2 x 1 và trục hoành. Thể uch của vật
tròn xoay khi quay H quanh trục hoành bằng 9 81 9 81 A. B. C. D. 8 80 8 80
Câu 23: Cho các số thực dương a b; thỏa mãn log2 a x ,log2b y . Giá trị biểu thức P log2 a b2 3 theo x y; bằng A.2x 3y B. x 3y C.3x 2y D.2x 3y Câu 24: Cho hàm số y
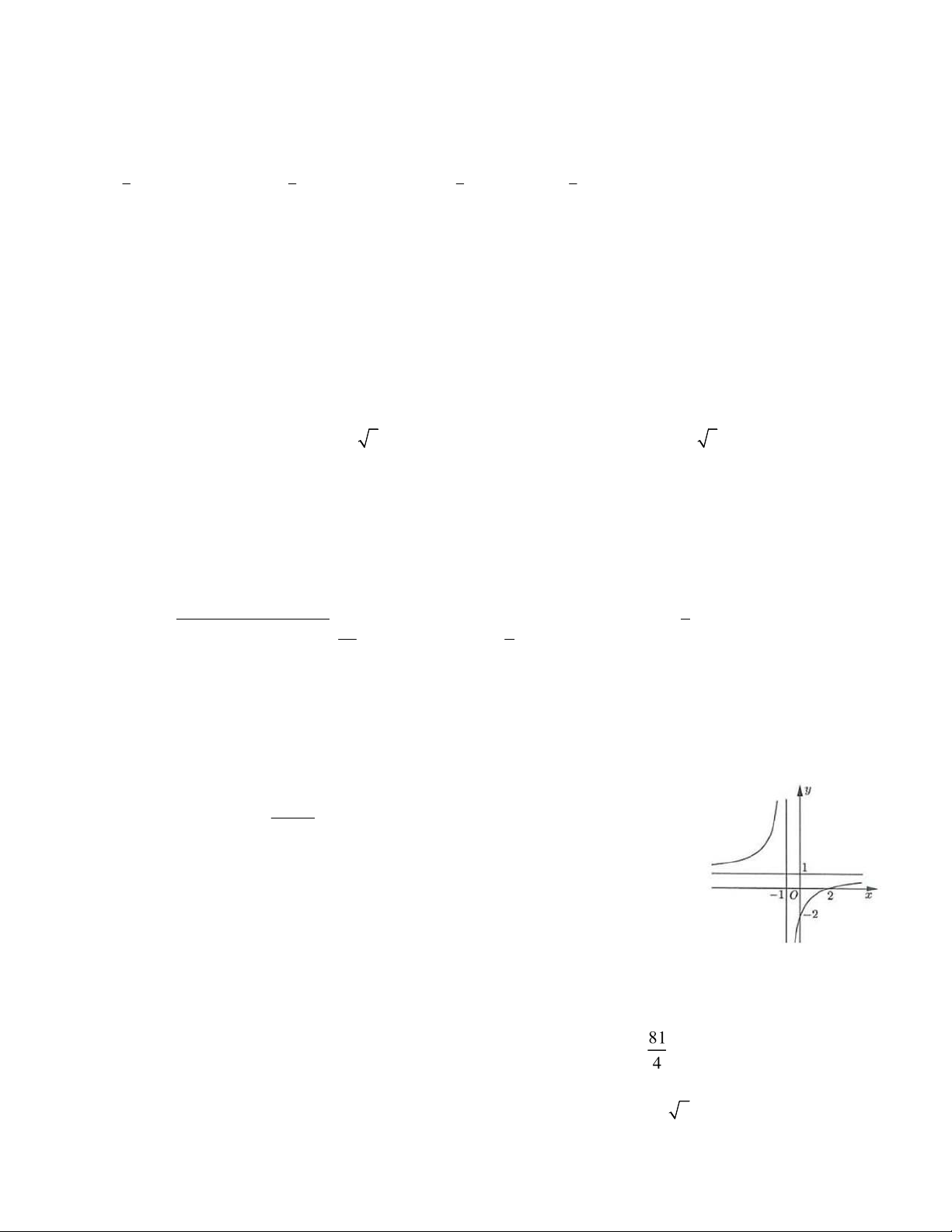
ax b có ồ thị là ường cong trong hình bên. cx d
Tọa ộ giao iểm của ồ thị hàm số ã cho và trục tung là A. 0; 2 . B. 2;0 . C. 2;0 . D. 0;2 .
Câu 25: Cho phương trình 4x 2x 1 3
0. Khi ặt t 2x ta ược phương trình nào sau ây? A.t2 2t 3 0 B.2t2 3t 0 C.t2 t 3 0 D. 4t 3 0
Câu 26: Cho khối lăng trụ tam giác ều có cạnh áy bằng 3cmvà thể uch bằng cm3. Khi ó ộ dài cạnh bên
của khối lăng trụ ã cho bằng A.3cm B.3 3cm C. 4cm D.3 2cm Trang 3/6 lOMoARcPSD|50713028
Câu 27: Trong không gian Oxyz, cho hai vectơ a 1; 2; 1 và b 2;1;1 . Giá trị cos a b, bằng A. . B. 6 . C. . D. . 12 12
Câu 28: Cho cấp số nhân un với số hạng ầu u1 1và công bội q 2. Hỏi số 1024là số hạng thứ mấy? A.10 B.9 C.8 D.11
Câu 29: Cho hình chóp S ABC. có SA vuông góc với mặt phẳng ABC , biết SA a 3 và tam giác 2 ABC
ều cạnh a. Góc tạo bởi hai mặt phẳng SBC và ABC bằng A.450 B.900 C.600 D.300
Câu 30: Cho hình trụ có diện uch xung quanh bằng 18 a2 và ộ dài ường cao bằng a . Tính bán kính R của
ường tròn áy của hình trụ ã cho theo a A. R 3a B. R 9a C. R 6a D. R 18a
Câu 31: Trong không gian với hệ toạ ộ Oxyz , cho ường thẳng d : x 1 y z 5 và mặt phẳng 1 3 1 P :3x 3y 2z 6
0. Khẳng ịnh nào dưới ây úng? A.d nằm trong P B.d song song với P C.d vuông góc với P
D.d cắt và không vuông góc với P
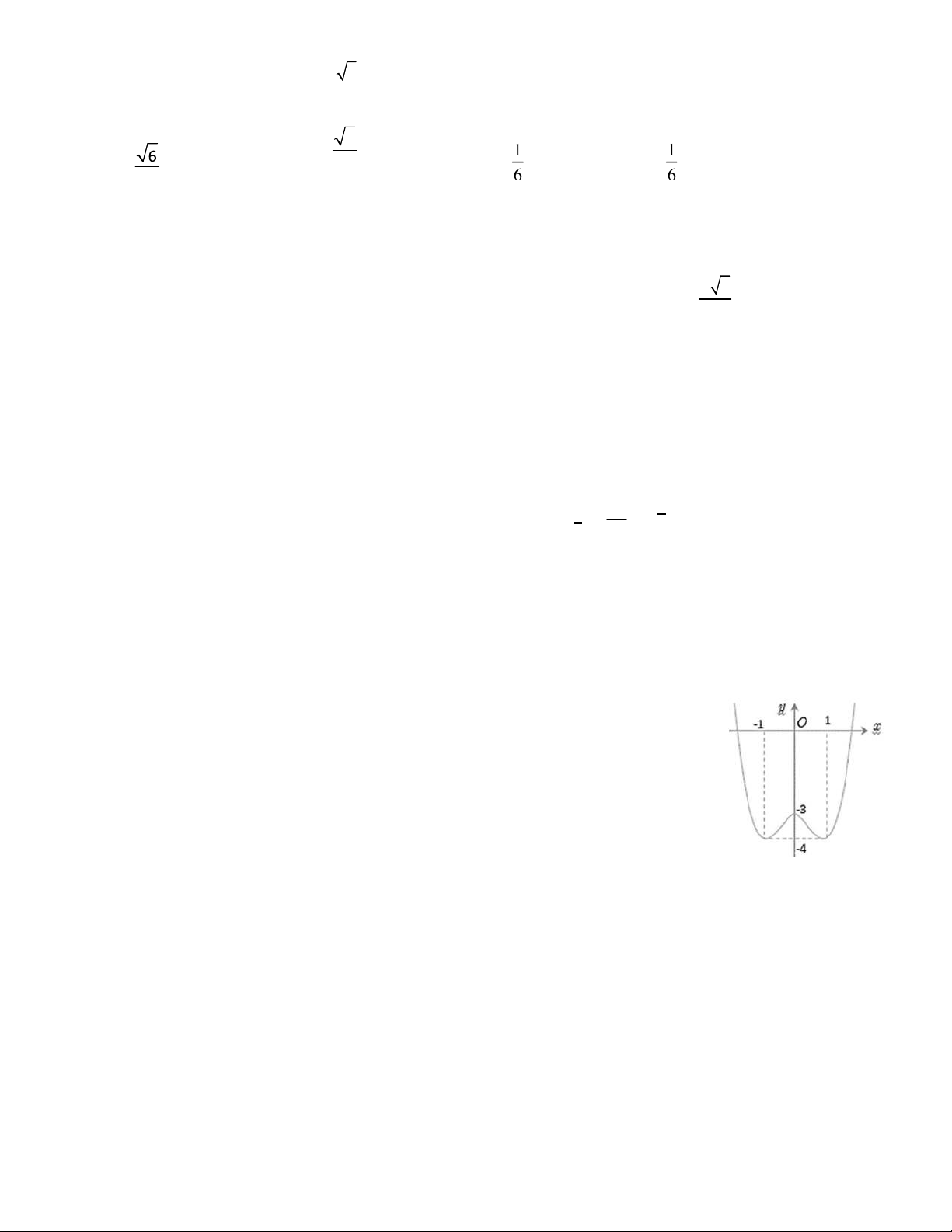
Câu 32: Cho hàm số f x ax4 bx2 c có ồ thị là ường cong trong hình bên.
Có bao nhiêu giá trị nguyên thuộc oạn 2;5 của tham số m ể phương trình f x
m có úng hai nghiệm thực phân biệt? A. 6 B. 7 C.8 D.9
Câu 33: Cho iểm A 1;2; 1 và mặt phẳng P : x 2y z 3 0. Phương trình mặt
phẳng Q i qua iểm A và song song với mặt phẳng P là A. x 2yz 40. B. x 2y z 2 0. C. x 2y z 4 0. D. x 2y z 4 0.
Câu 34: Cho khối lăng trụ ều ABC A B C. ' '
' có cạnh áy bằng 2 .a Biết khoảng cách từ A' ến mặt phẳng AB C'
' bằng a. Thể uch khối lăng trụ ã cho bằng Trang 4/6 lOMoARcPSD|50713028
3 2a3 3 2a3 3 2a3 2a3 A. B. C. D. 4 8 2 2
Câu 35: Trong không gian với hệ trục tọa ộ Oxyz, cho ường thẳng d : x 1 y 2 z và mặt phẳng 2 1 3 P : x 6y 4z 27
0. Gọi M a b c ;; là giao iểm của d và P . Tính S 2a b c A. S 10 B.S 13 C.S 11 D.S 12
Câu 36: Có bao nhiêu giá trị nguyên của tham số m ể hàm số y x5 4x3 mx 2024 có bốn iểm cực trị? A.36 B.34 C.37 D.35
Câu 37:Cho hàm số y ax3 bx2 cx d a b c d, , , có ồ thị
là ường cong trong hình bên. Mệnh ề nào dưới ây úng? A. a 0;b 0;c 0 . B. a 0;b 0;c 0. C. a 0;b 0;c 0. D. a 0;b 0;c 0.
Câu 38: Cho hình chóp S ABCD.
có áy là hình vuông, cạnh a. Tam giác SAB là tam giác ều và
nằm trong mặt phẳng vuông góc với áy. Khoảng cách giữa 2 ường thẳng AB và SC bằng a 3 a 21 a 2 A. B.a C. D. 7 7 2 Câu 39: Cho hàm số f x 3axx 1 khi x 2 2ab khi x
2. Biết 20 f x 2 1 xdx 5 . Tính giá trị biểu thức T 2a b2 1 A.77 B.79 C.78 D.80
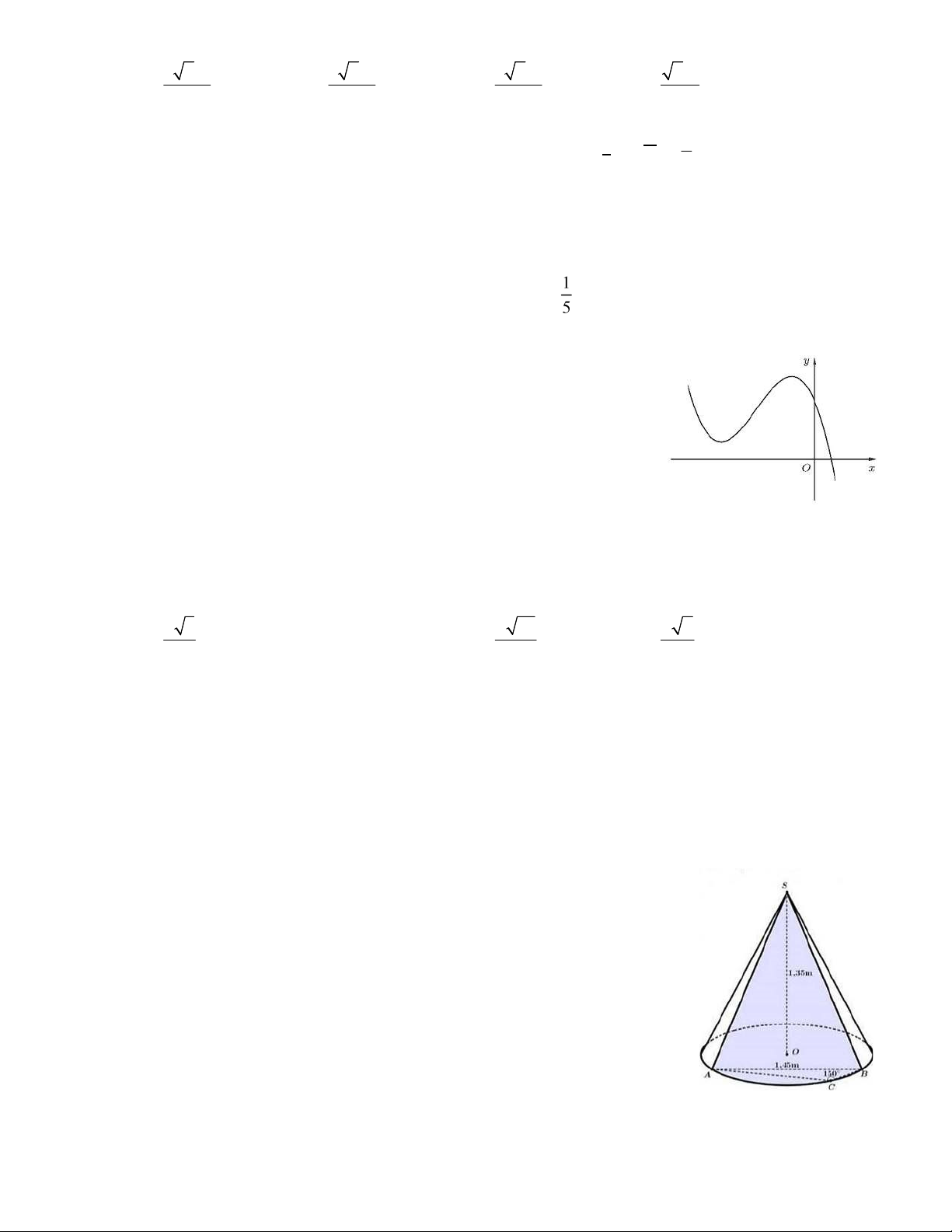
Câu 40: Cửa hàng A có ặt trước sảnh một cái nón lớn với chiều cao 1,35m và sơn
cách iệu hoa văn trang trí một phần mặt ngoài của hình nón ứng với cung nhỏ
AB như hình vẽ. Biết AB 1,45m , ACB 150ovà giá triền trang trí là 2.000.000
ồng mỗi mét vuông. Hỏi số –ền mà cửa hàng Acần dùng ể trang trí là bao nhiêu? A.4.215.000 ồng B.4.510.000 ồng C.3.021.000 ồng D.3.008.000 ồng Trang 5/6 lOMoARcPSD|50713028
Câu 41: Gọi A là tập hợp các số tự nhiên có 4 chữ số khác nhau ược tạo ra từ các chữ số 0 ,1, 2 ,3, 4 ,5, 6 . Lấy
ngẫu nhiên một số từ tập hợp A . Xác suất ể số lấy ược là số tự nhiên không lớn hơn 2503 là A. . B. . C. . D. .
Câu 42: Trong không gian với hệ tọa ộ Oxyz cho iểm A 2; 1; 2 và ường thẳng d có phương trình
d : x 1 y 1 z 1. Gọi P là mặt phẳng i qua iểm A, song song với ường thẳng d và 1 1 1
khoảng cách từ d tới mặt phẳng P là lớn nhất. Khi ó mặt phẳng P vuông góc với mặt phẳng nào sau ây? A. x 3y2z 100 B.3x z 2 0 C. x 2y3z 10 D. x y 6 0
Câu 43: Tập nghiệm của bất phương trình log 3 x2 x 4 1 2log5 x2 x 5 3 là a b; . Khi ó tổng a 2b bằng A.1. B.3. C. 4. D. 2.
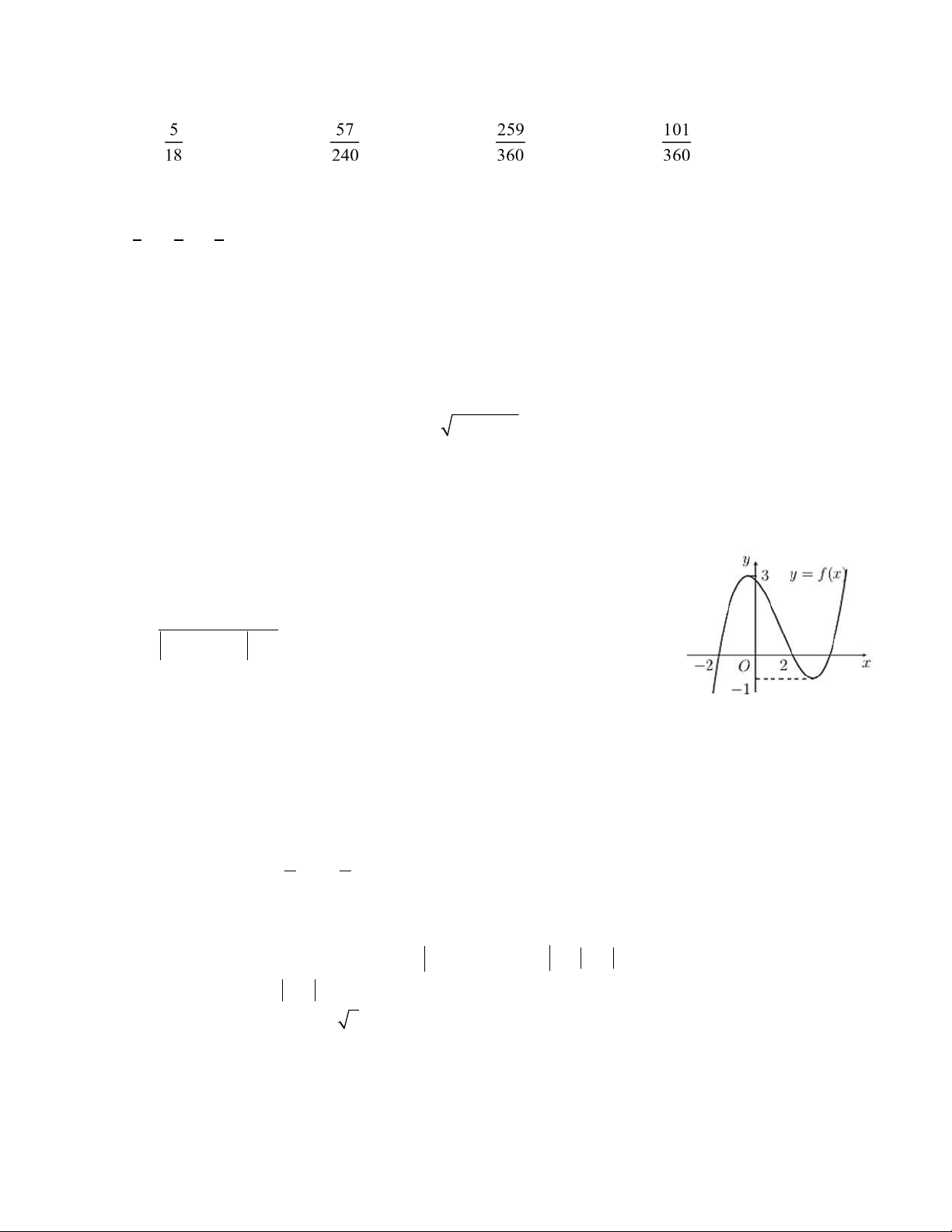
Câu 44: Cho hàm số bậc ba y f x có ồ thị như hình vẽ.
Có tất cả bao nhiêu giá trị nguyên của tham số m ể ồ thị hàm số g x 3 1 có 8 –ệm cận ứng? 3f x 3x m A.3 B. 6 C. 4 D.5
Câu 45: Cho hàm số y f x liên tục và có ạo hàm trên thỏa mãn 5 f x 7 f 1 x 3 x2 2x , x . Biết rằng a
10 x f.' x dx b , với ab là phân số tối giản. Giá trị của 8a 3b là A. 16 B.1 C.16 D. 0
Câu 46: Xét các số phức z thỏa mãn iều kiện z2 2z 4 4i 2 z 1 . Gọi M và m lần lượt là giá trị lớn
nhất và nhỏ nhất của z 1 . Giá trị của M m bằng Trang 6/6 lOMoARcPSD|50713028 A. 2 B.2 6 C.14
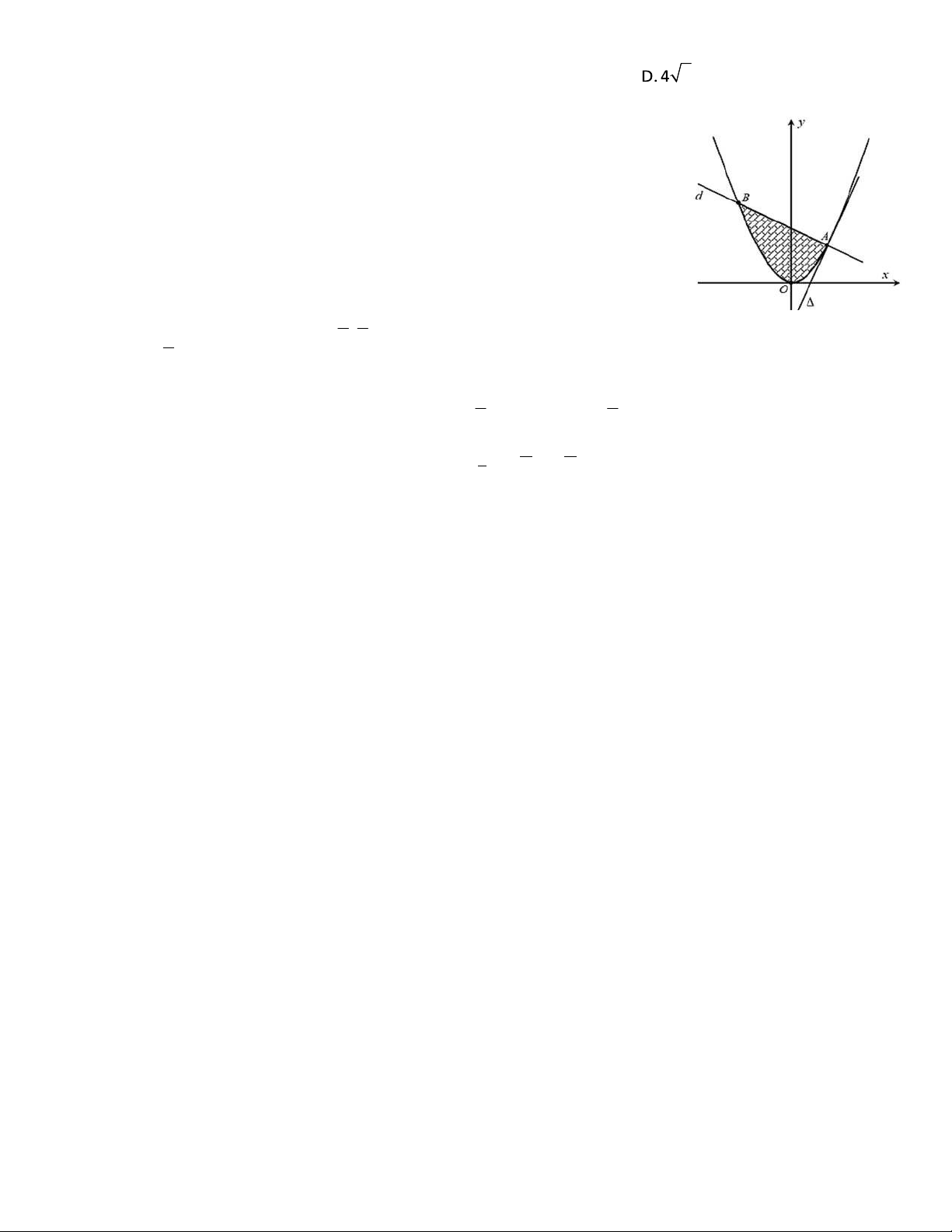
Câu 47: Trong mặt phẳng Oxy, cho parabol P : y x2 và một iểm A a
a ; 2 với a 0 nằm trên P . Gọi là –ếp tuyến của P tại A d, là
ường thẳng i qua A và vuông góc với . Biết diện uch của hình phẳng giới hạn bởi P và
d (phần gạch sọc) ạt giá trị nhỏ 2
1 2 nhất. Khi ó a thuộc khoảng nào sau ây? C. 3;1 D. 4 3; A. 1; 32 B. 0; 14
Câu 48: Trong không gian Oxyz, cho ường thẳng d : x 1 y 2 z 2 và mặt phẳng P : x y 2z 8 0. 1 2 1
Tam giác ABC có A 1;2; 2 và trọng tâm G nằm trên d. Khi các ỉnh B C, di ộng trên P sao cho khoảng cách
từ A tới ường thẳng BC ạt giá trị lớn nhất, một vectơ chỉ phương của ường thẳng BC là A. 16; 10;3 . B. 3; 1;4 . C. 4; 2;1 . D. 1;2;0 .
Câu 49: Có tất cả bao nhiêu cặp số nguyên x y; thoả mãn bất phương trình
x 2y . log 2 x2 y2 log2 x 2y 2y x 6x y 12 5y ? A.61 B.62 C.64 D.65
Câu 50: Cho các hàm số f x x2 4x m và g x x2 1
x2 2 2023. Số các giá trị nguyên của
tham số m 2023;2023 ể hàm số y g f x
có ồng biến trên khoảng 3; là A. 2019 B. 2021 C. 2022 D. 2020
-------------HẾT------------- Trang 7/6