


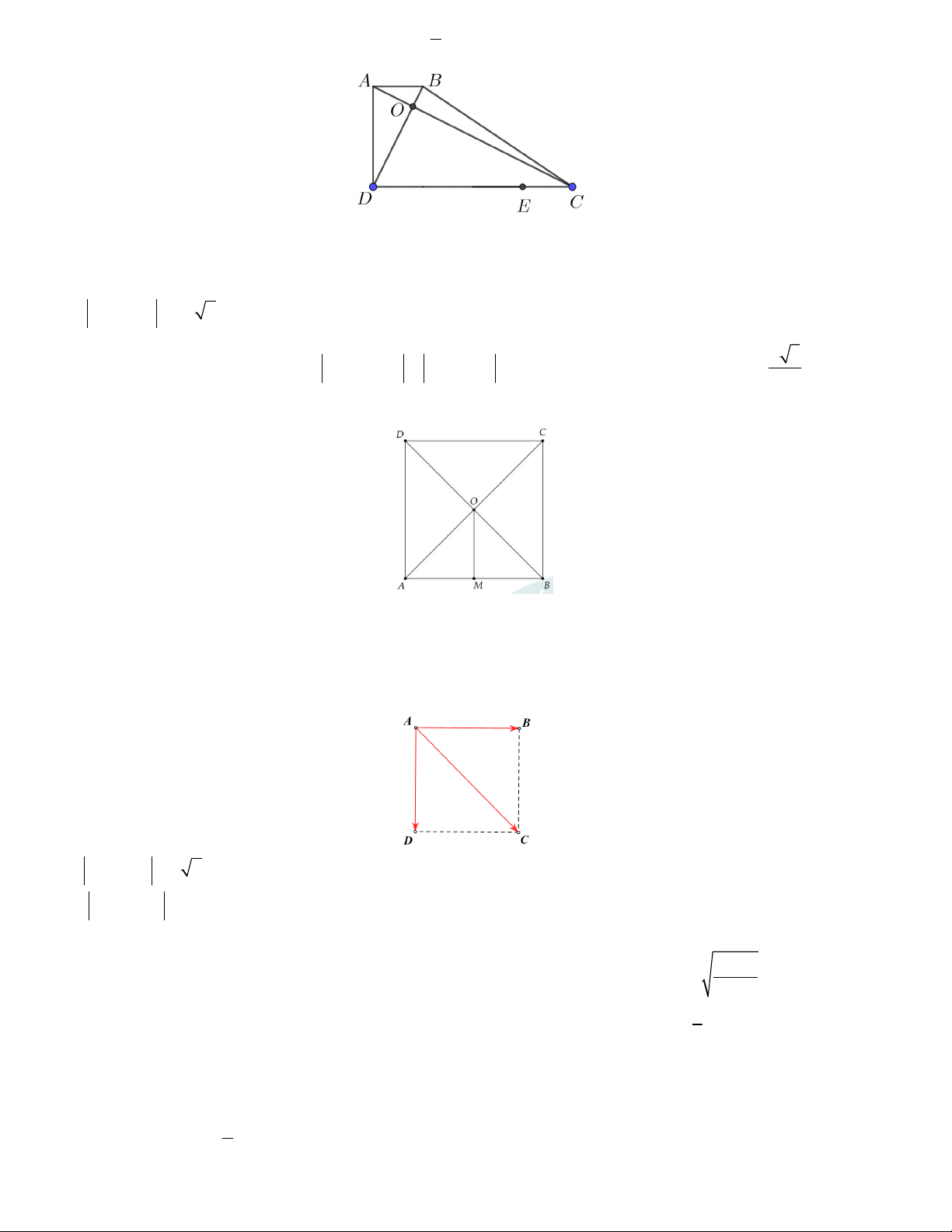
Preview text:
TÀI LIỆU THAM KHẢO TOÁN HỌC PHỔ THÔNG
______________________________________________________________ A . B AC A .
B AC cos A
-------------------------------------------------------------------------------------------- TOÁN 10 THPT
TRẮC NGHIỆM ĐÚNG, SAI VECTOR TRONG MẶT PHẲNG
(KẾT HỢP 3 BỘ SÁCH GIÁO KHOA)
THÂN TẶNG TOÀN THỂ QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TRÊN TOÀN QUỐC
CREATED BY GIANG SƠN (FACEBOOK)
ĐÁP ÁN CHI TIẾT PDF BẠN ĐỌC VUI LÒNG LIÊN HỆ TÁC GIẢ:
GACMA1431988@GMAIL.COM (GMAIL); TEL 0398021920
THÀNH PHỐ THÁI BÌNH – THÁNG 11/2024 1 TOÁN 10 THPT
TRẮC NGHIỆM ĐÚNG, SAI VECTOR TRONG MẶT PHẲNG
__________________________________________ DUNG NỘI DUNG BÀI TẬP LƯỢNG 5 FILE
TRẮC NGHIỆM ĐÚNG, SAI VECTOR TRONG MẶT PHẲNG 1 file 4 trang 2
VECTOR TRONG MẶT PHẲNG LỚP 10 THPT
(LỚP BÀI TOÁN TRẮC NGHIỆM ĐÚNG, SAI P1)
_________________________________________________
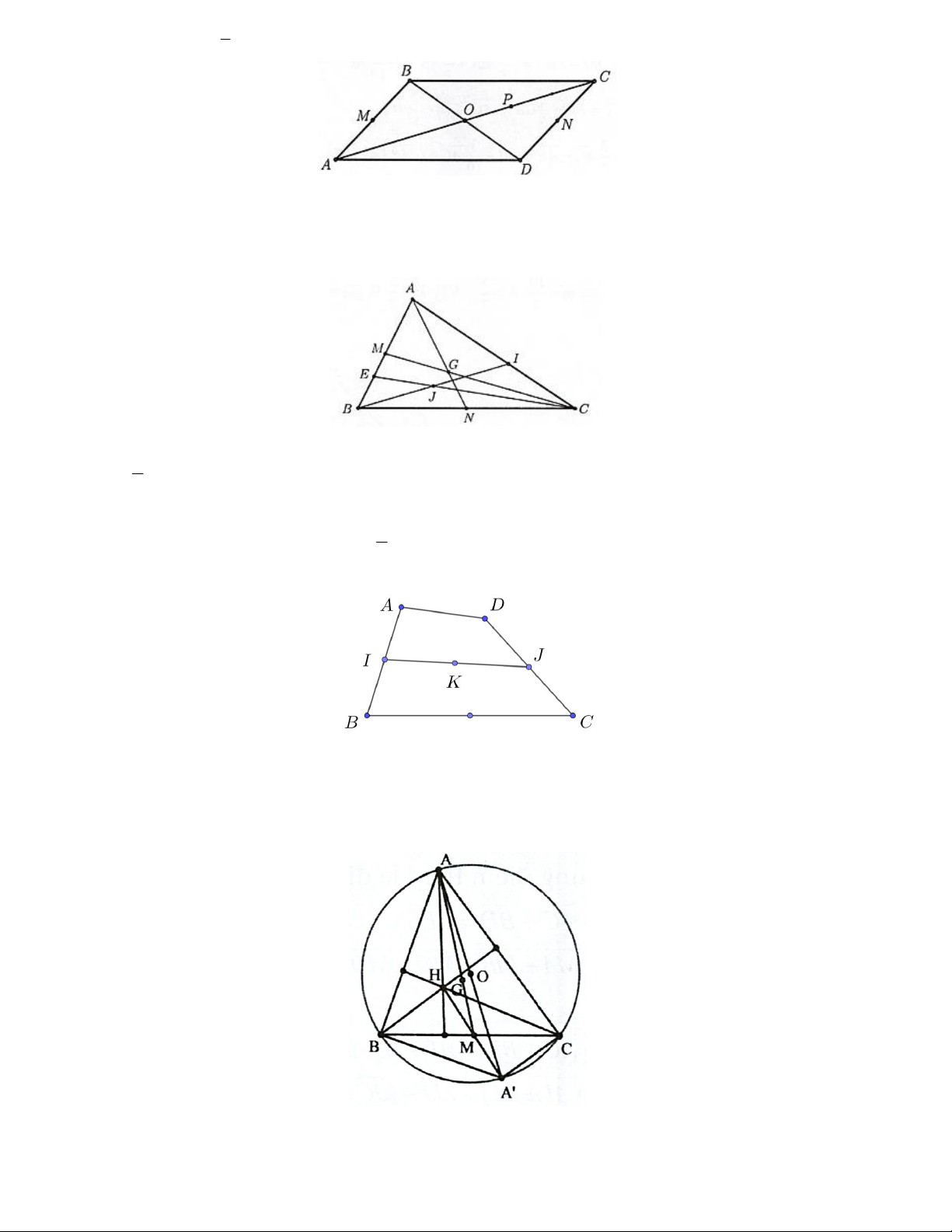
Câu 1. Cho hình thang ABCD với hai đáy là AB và CD; M , N là trung điểm của AD, BC . Khi đó: a) MN / /CD
b) Có 4 vectơ (khác 0 ) cùng phương AB mà giá không trùng với đường thẳng AB
c) Có 3 vectơ (khác 0 ) cùng hướng AB mà giá không trùng với đường thẳng AB
d) Có 5 vectơ (khác 0 ) cùng phương AB mà giá không trùng với đường thẳng AB
Câu 2. Cho hình thang ABCD với hai đáy là AB và CD . Biết rằng nếu | AC | |
BD | thì | BC | | AD | . Khi đó:
a) Hai đường chéo AC và BD có độ dài bằng nhau
b) Hình thang ABCD là hình thang cân
c) Hai cạnh bên AD và BC có độ dài không bằng nhau d) Nếu | BC | |
AD | thì | AC | | BD |
Câu 3. Cho ngũ giác ABCDE . Khi đó:
a) Có 10 vectơ (khác 0 ) được lập ra từ các cạnh ngũ giác
b) Có 5 vectơ (khác 0 ) được lập ra từ các đường chéo của ngũ giác
c) Có 3 vectơ (khác 0 ) được lập ra từ các cạnh của tam giác ABC
d) Có 4 vectơ (khác 0 ) được lập ra từ các đường chéo của tứ giác ABCD
Câu 4. Trên đường thẳng d lấy bốn điểm ,
A B, C, D phân biệt. Lấy một điểm P không thuộc d . Khi đó:
a) Có 4 vectơ gốc A
b) Có 10 vectơ (khác 0 ) được lập ra từ các điểm ,
A B, C, D, P .
c) Có 10 vectơ tạo thành từ 4 điểm ,
A B, C, D .
d) Có 11 vectơ (khác AB ) mà cùng phương với AB trong các vectơ tạo thành từ 4 điểm ,
A B, C, D
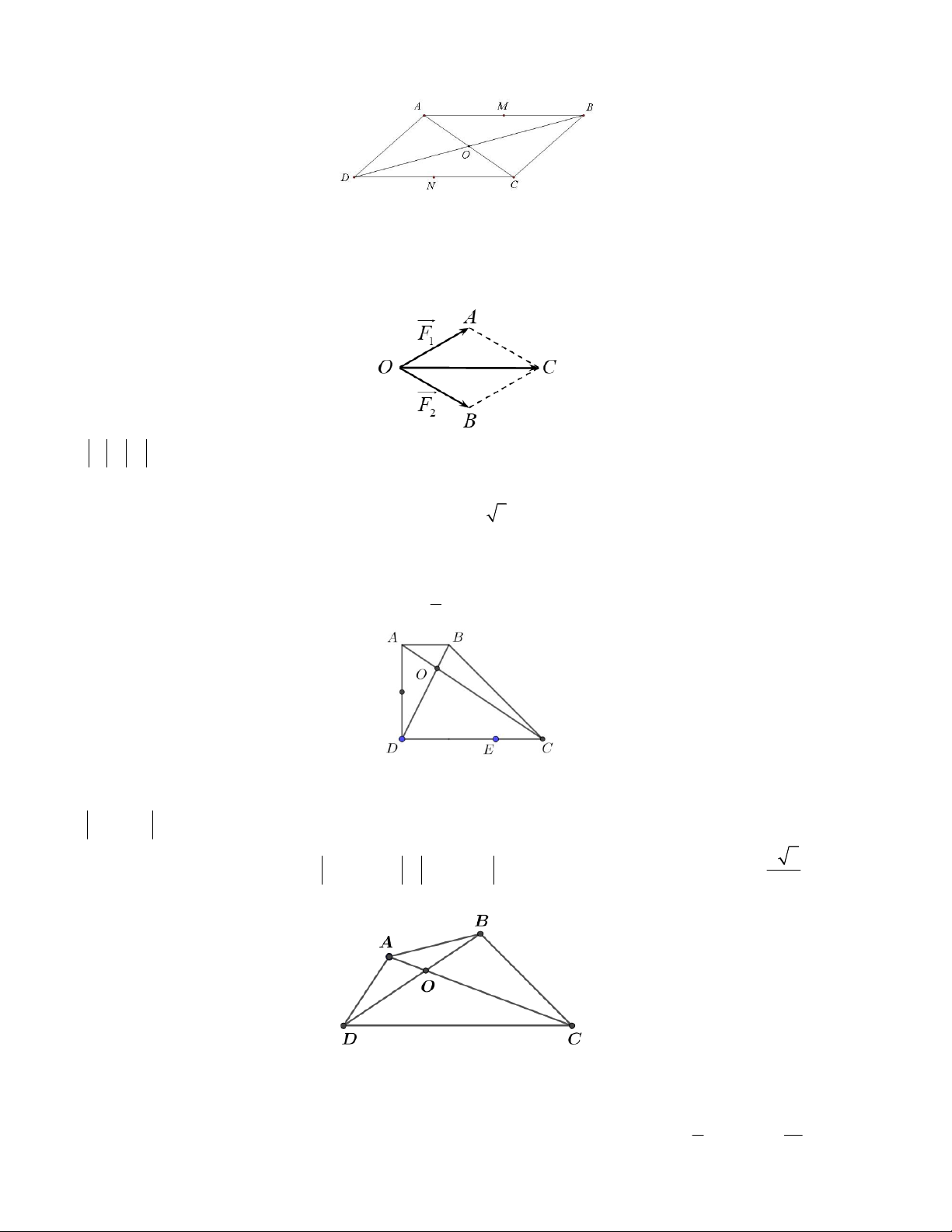
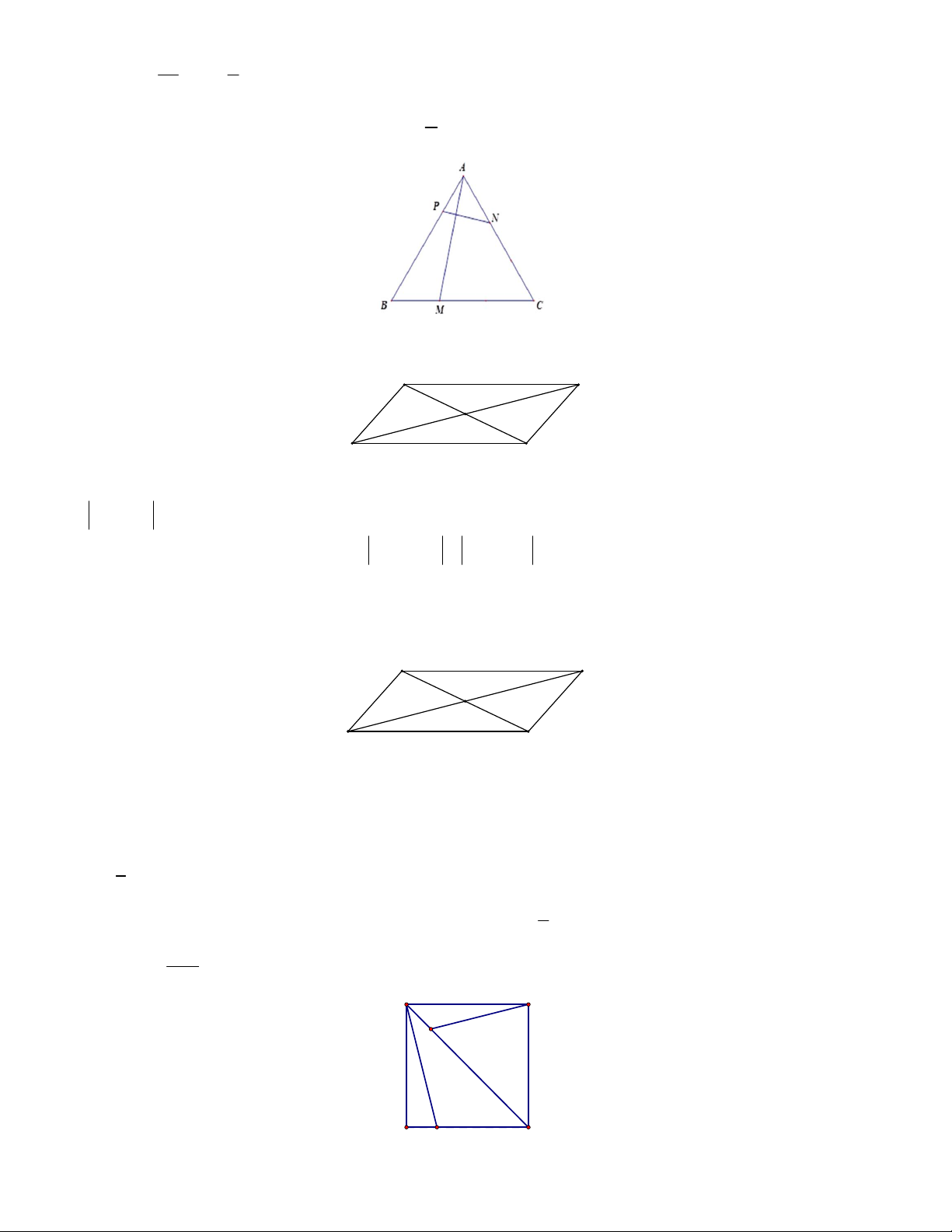
Câu 5. Cho tam giác ABC có M và N lần lượt là trung điểm của AB và AC . Lấy điểm P đối xứng với điểm
M qua N . Khi đó: a) MN BC b) | MP | | BC |
c) MN và BC ngược hướng d) MP BC .
Câu 6. Cho tam giác ABC có G là trọng tâm. Gọi D là điểm đối xứng của B qua ,
G M là trung điểm của BC . Khi đó:
1
a) MD MG GD
b) AG 2AB AC 3
1 5 1
c) CD AB AC BN d) MD AB AC. 3 6 6
Câu 7. Cho ABC , gọi M , N , P lần lượt là trung điểm của BC, C , A AB . Khi đó:
a) vectơ AB cùng phương với vectơ MN
b) Có 6 vectơ khác vectơ không và cùng phương với AB có điểm đầu, điểm cuối lấy từ các điểm đã cho. 3
c) vectơ AP ngược hướng vectơ PB
d) Có 3 vectơ khác vectơ không và cùng hướng với AB có điểm đầu và điểm cuối lấy từ các điểm đã cho.
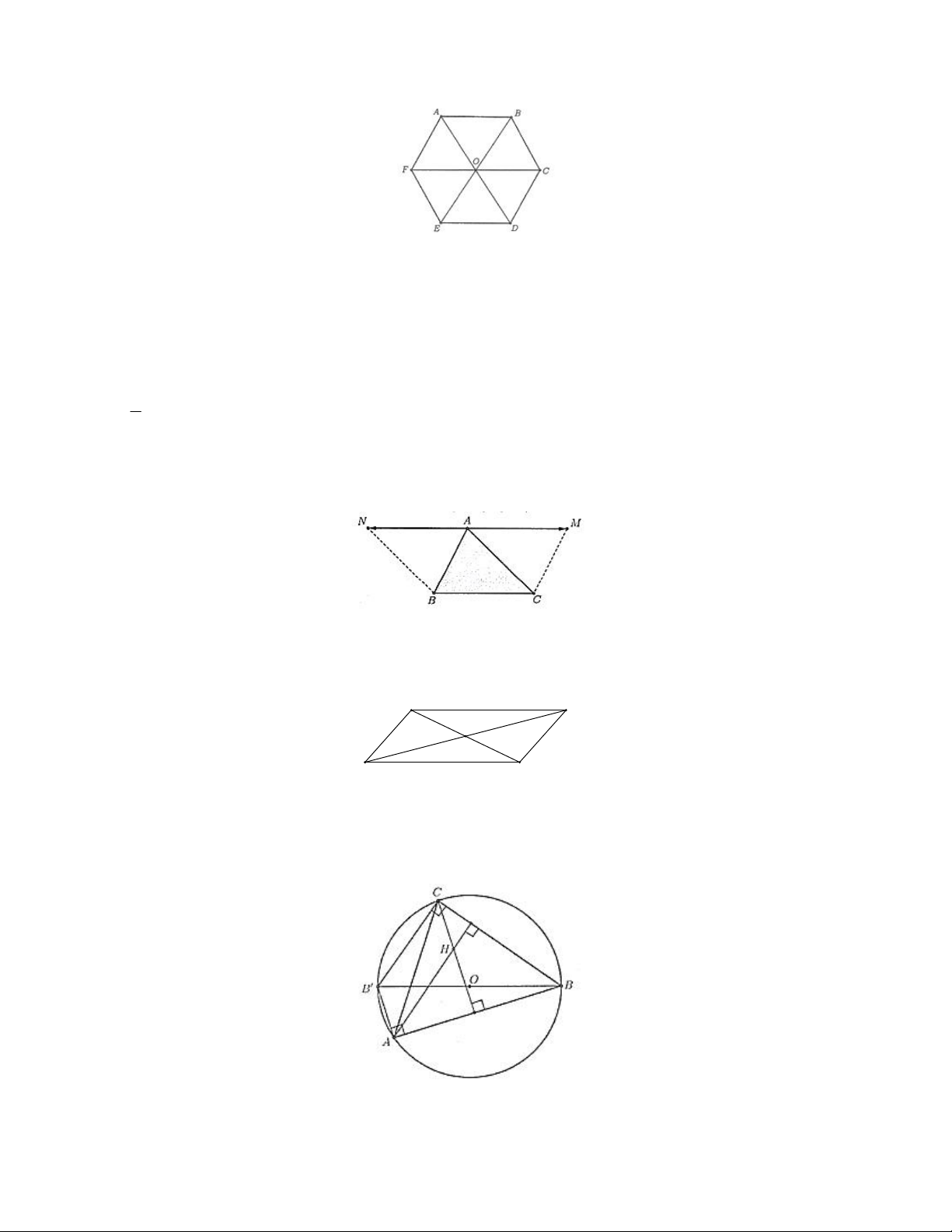
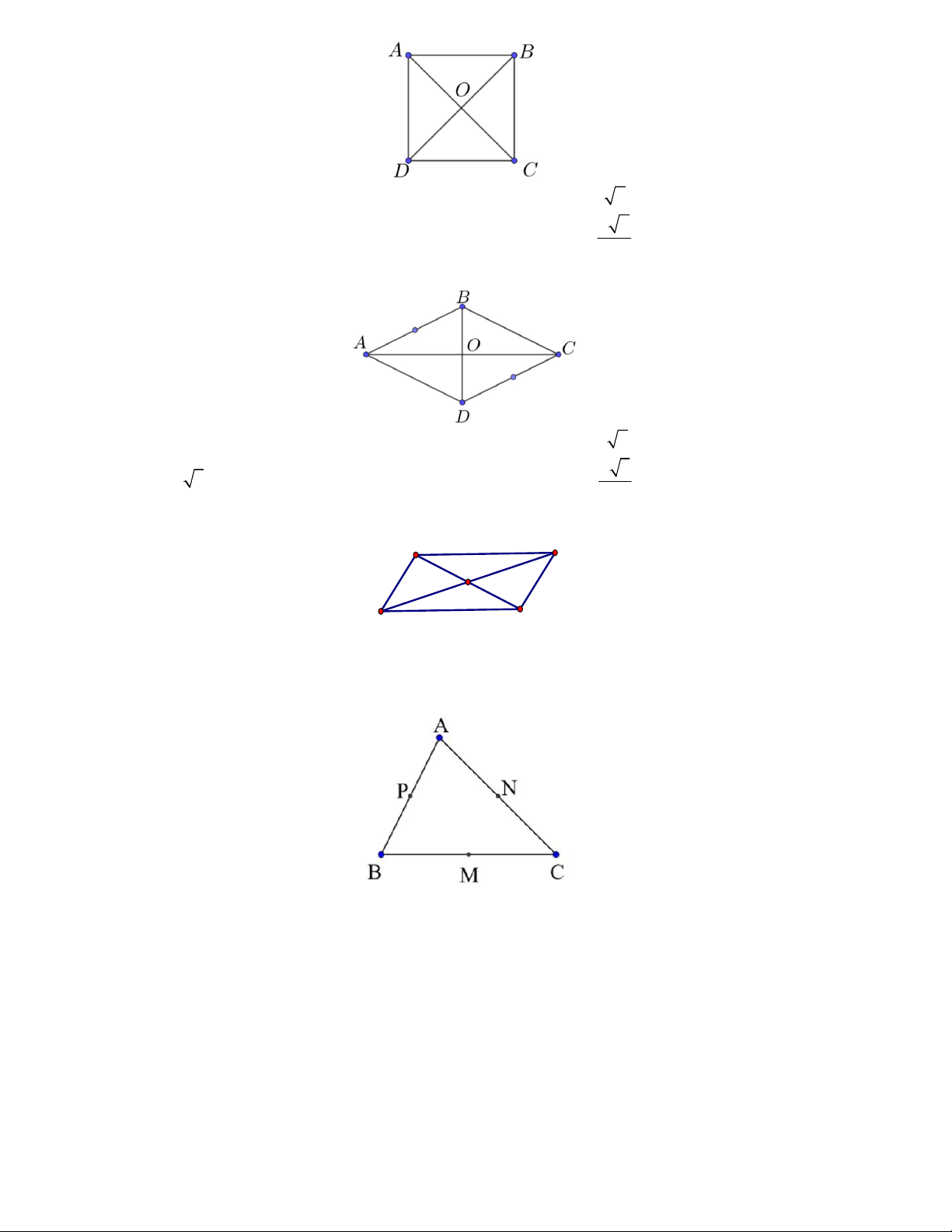
Câu 8. Cho lục giác đều ABCDEF có tâm O . Khi đó:
a) vectơ OA cùng phương với OD
b) Có 9 vectơ khác vectơ không và cùng phương với vectơ OA .
c) vectơ AB ngược hướng OC
d) Có 3 vectơ khác vectơ không và cùng hướng với vectơ AB .
Câu 9. Cho tứ giác ABCD . Gọi M , N , P, Q lần lượt là trung điểm AB, BC , CD, DA . Khi đó:
a) MN là đường trung bình của tam giác ACD 1 b) PQ AC 2
c) Tứ giác MNPQ là hình thang d) MN QP
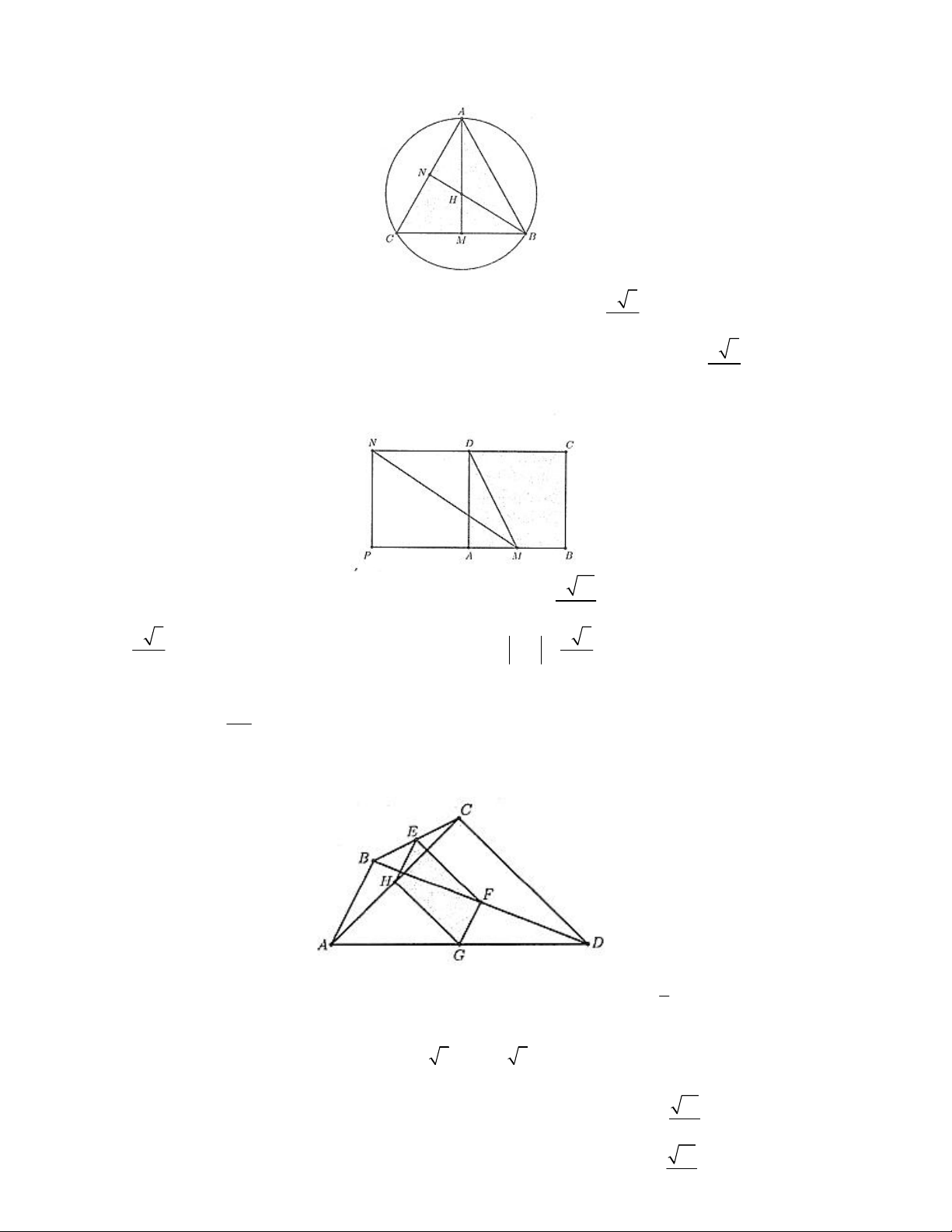
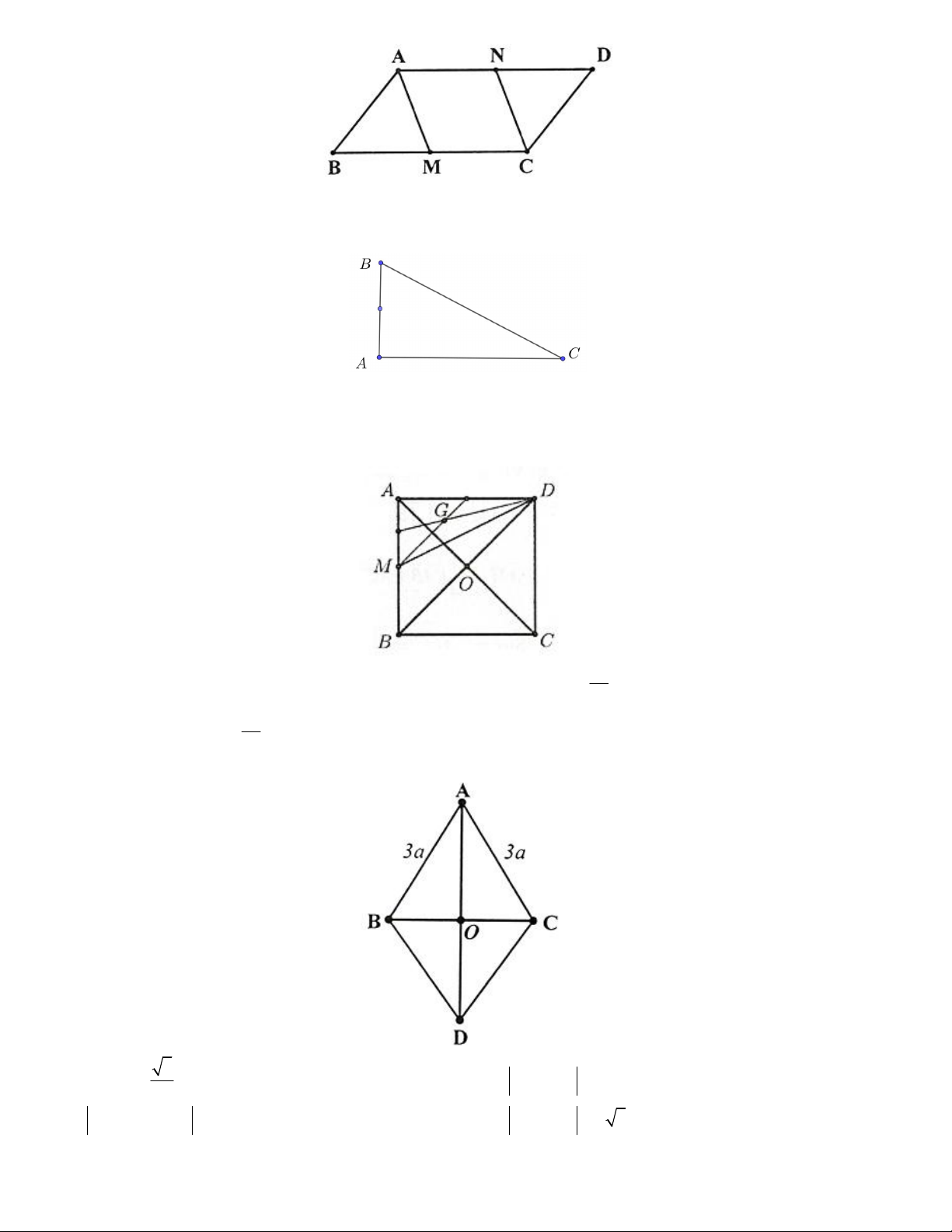
Câu 10. Cho tam giác ABC . Hãy dựng các điểm M , N sao cho AM BC , AN CB . Khi đó:
a) AM ngược hướng với BC
b) ABCM là hình bình hành
c) ACBN là hình bình hành
d) AM , AN là hai vectơ đối nhau
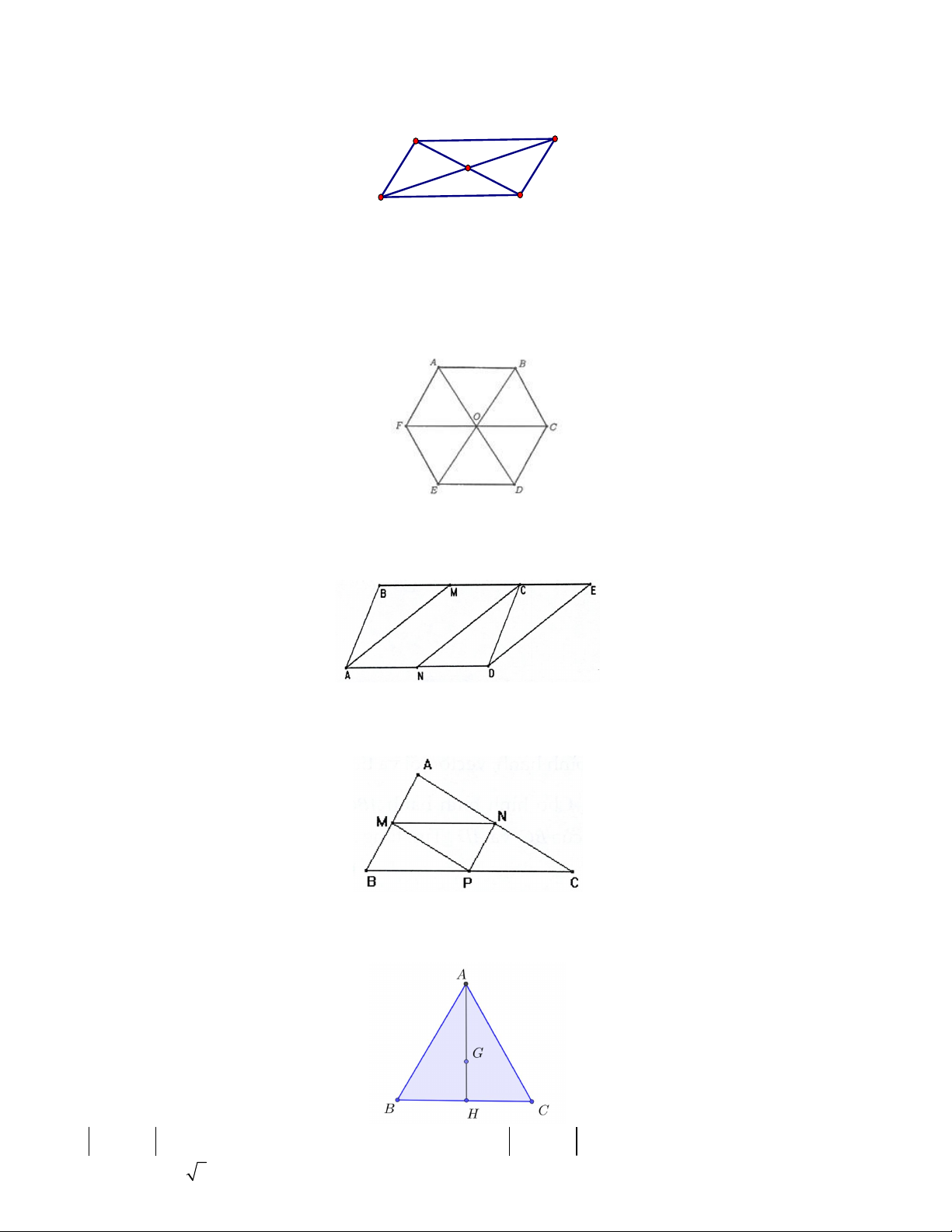
Câu 11. Cho hình bình hành ABCD . Gọi O là giao điểm của AC và BD (Hình bên). A B O D C
a) OA và OC là hai vectơ đối nhau.
b) OB và DO là hai vectơ đối nhau.
c) AB và CD là hai vectơ đối nhau.
d) OB và AB là hai vectơ đối nhau.
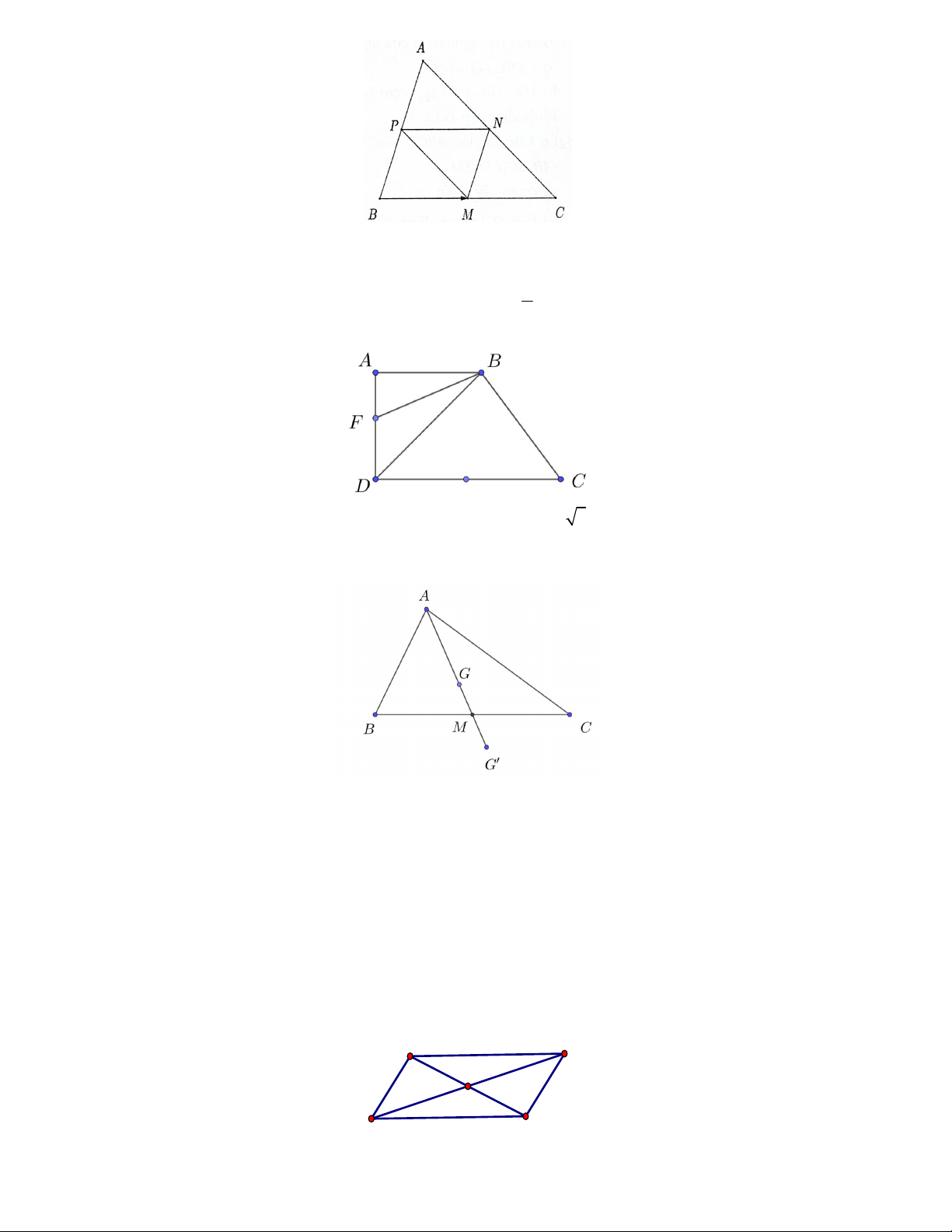
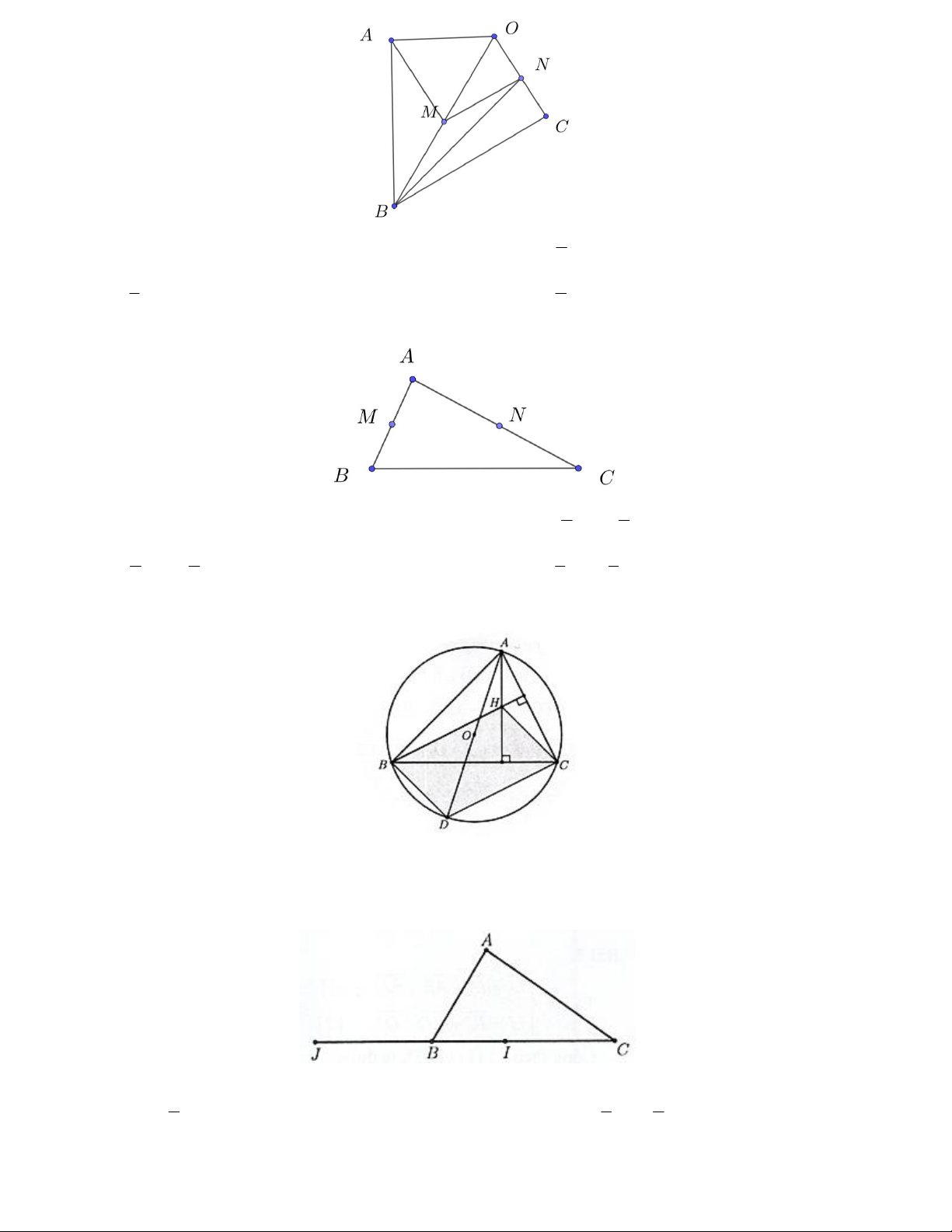
Câu 12. Cho ABC có trực tâm H và O là tâm đường tròn ngoại tiếp tam giác. Gọi
B là điểm đối xứng của
B qua O . Khi đó:
a) BC BC
b) BC / / AB
c) tứ giác
AB CH là hình bình hành. d) AH B C; AB HC
Câu 13. Cho tứ giác ABCD . Khi đó:
a) Có 5 vectơ liên quan đến điểm A
b) Có 4 vectơ liên quan đến điểm B mà không liên quan đến A 4
c) Có 2 vectơ liên quan đến hai điểm C, D
d) Có 10 vectơ (khác 0) có điểm đầu và điểm cuối là các điểm ,
A B, C, D ?
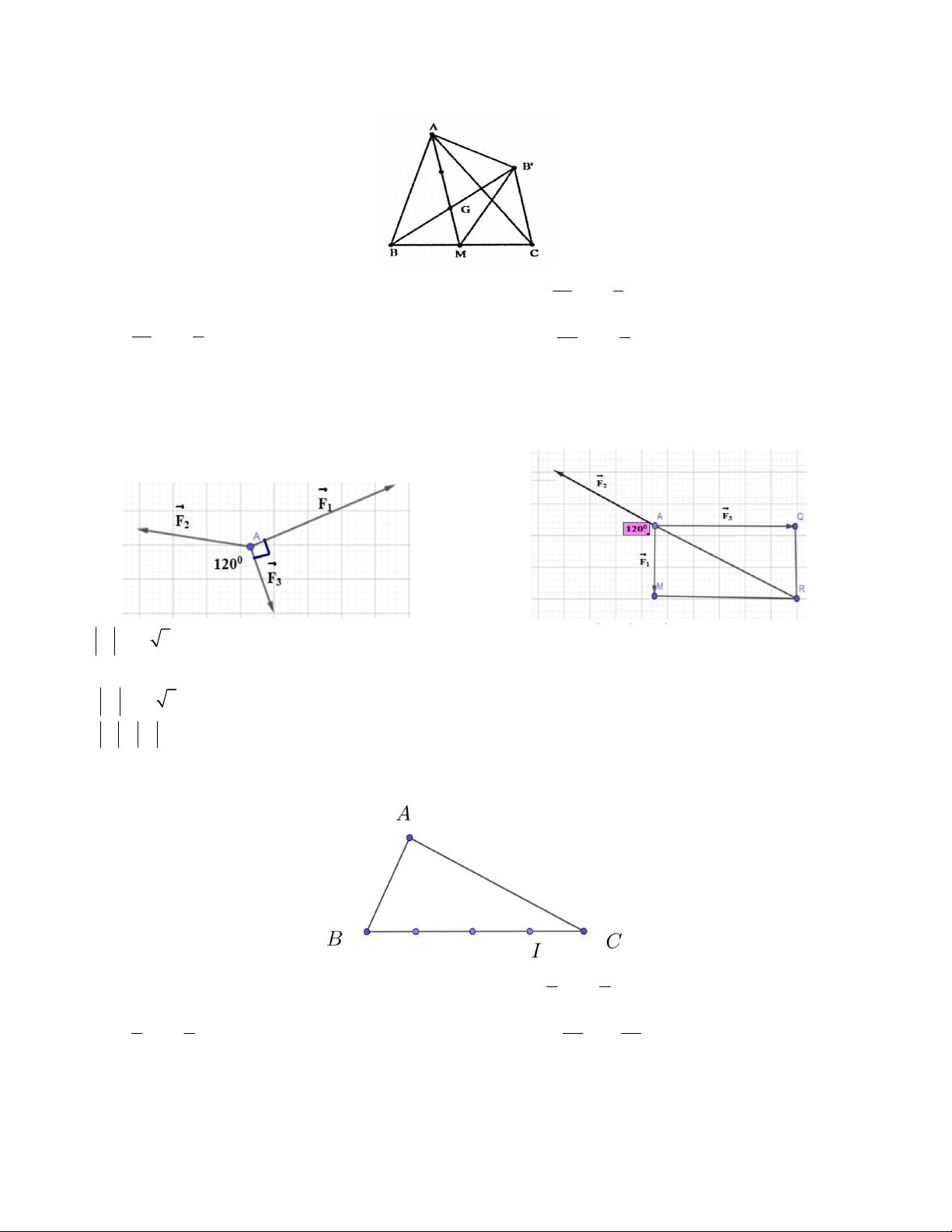
Câu 14. Cho ABC đều cạnh a , trực tâm H . Khi đó: a 3 a) AH BC b) AH 2
a 3
c) HA HB HC d) | HA | | HB | | HC | . 3
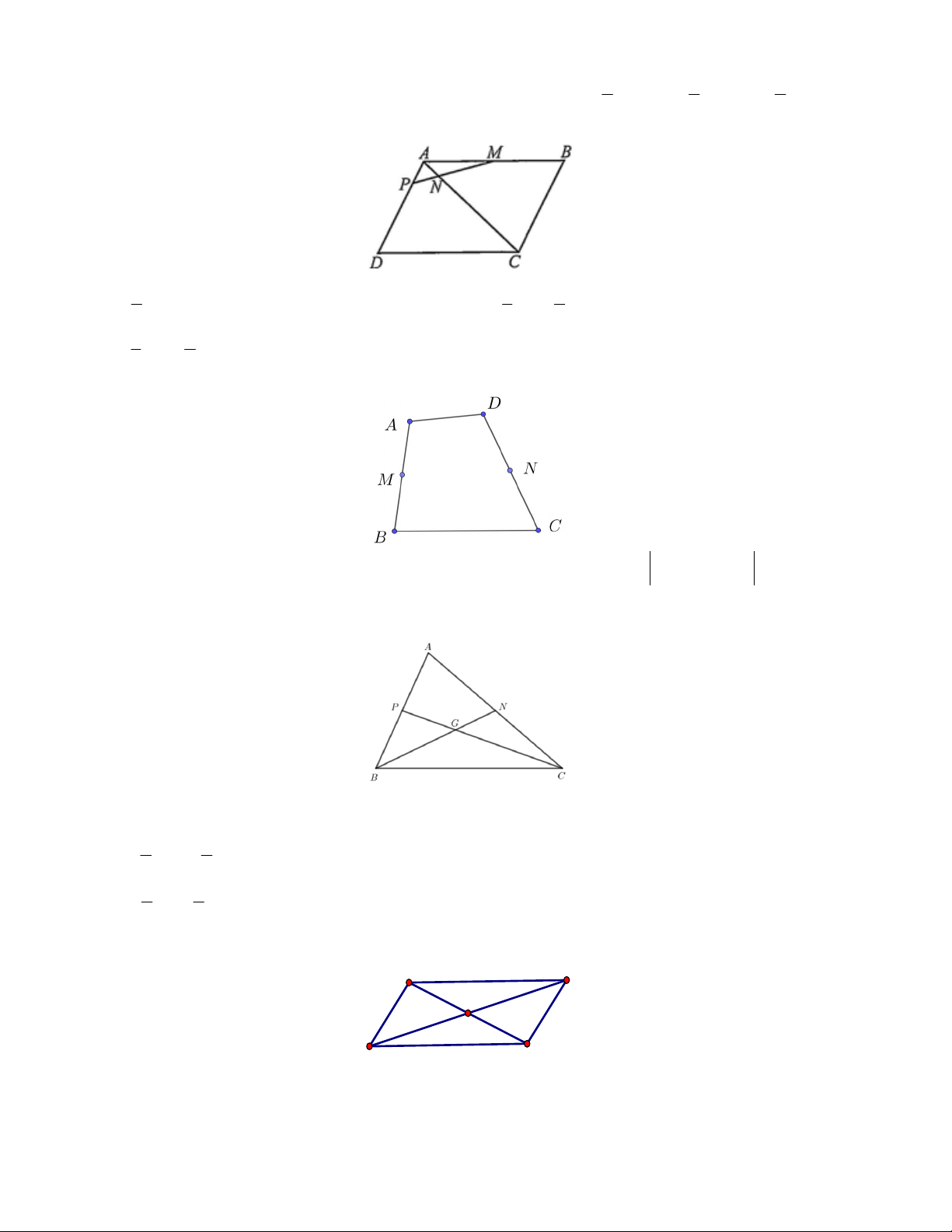
Câu 15. Cho hình vuông ABCD cạnh a . Gọi M là trung điểm AB, N là điểm đối xứng với C qua D . Khi đó: a 13 a) 2 2 2 MD AD AM b) MN . 2 a 3 a 3 c) MD d) MN 2 12
Câu 16. Cho ABC có , ,
A B C lần lượt là các trung điểm của các cạnh BC, C , A AB . Khi đó:
AB
a) BC C A A B .
b) Hai vectơ BC, AB ngược hướng 2
c)
BC C A A B . d) BC CA .
Câu 17. Cho tứ giác ABCD . Gọi E, F , G, H theo thứ tự là trung điểm của BC, BD , AD, AC . Khi đó: 1
a) EF lần lượt là đường trung bình của các tam giác BCD b) GH CD 3
c) EFGH là hình bình hành d) HG FE
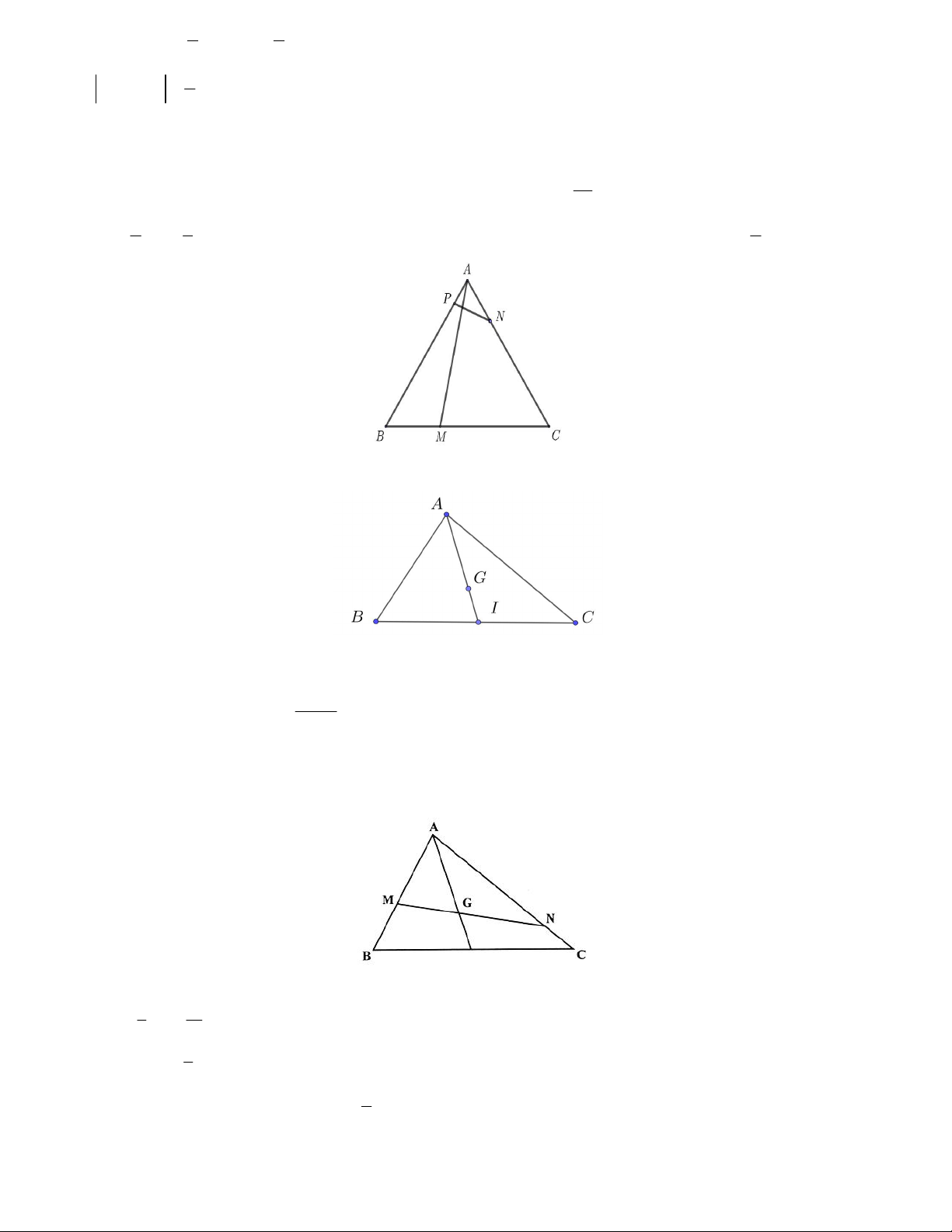
Câu 18. Cho tam giác ABC vuông tại A có AB 3, AC 2 3. Gọi M là trung điểm BC và H là hình chiếu
vuông góc của A lên BC . Khi đó: 15 a) 2 2 2
BC AB AC b) | AM | 4 15
c) AB AC AH BC d) | AH | 5 5
Câu 19. Cho tam giác ABC . Gọi M , N , P lần lượt là trung điểm của các cạnh BC, CA và AB . Khi đó:
a) PN là đường trung bình của tam giác ABC
b) PN , MC cùng hướng với vectơ BM
c) BM NP
d) BM có các vectơ đối là NP, CM , MB . 1
Câu 20. Cho hình thang ABCD vuông tại A và có AB AD
DC a . Gọi BF là đường phân giác trong 2
của tam giác ABD(F AD) . Khi đó: a) 2 2 2
CA DA DC
b) | CA | a 3 c) ABF 45
d) | BF | 2.08a
Câu 21. Cho tam giác ABC có G là trọng tâm. Gọi
G là điểm đối xứng với G qua trung điểm M của BC .
Khi đó: a) Vectơ G , A G G cùng hướng b) GA 3GM
c) GA G G b) BG G C, BG GC, BM MC, GM MG , AG GG
Câu 22. Cho tứ giác ABCD . Gọi P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DA . Gọi O là giao
điểm của PQ, SR và M , N lần lượt là trung điểm của AC, BD . Khi đó:
a) PQ là đường trung bình của tam giác ABC
b) PQRS là hình bình hành
c) PMRN là hình bình hành.
d) OM , ON là hai vectơ bằng nhau.
Câu 23. Cho hình bình hành ABCD . Khi đó: A B O D C
a) CB CD CA
b) AC DA CD
c) BA BC AC
d) BA BC AD CD 6
VECTOR TRONG MẶT PHẲNG LỚP 10 THPT
(LỚP BÀI TOÁN TRẮC NGHIỆM ĐÚNG, SAI P2)
_________________________________________________
Câu 1. Cho hình bình hành ABCD tâm O . Gọi M , N lần lượt là trung điểm của các cạnh AB, CD .
a) DA DB 2DM .
b) DA DB DC 2DO .
2 2 2
c) OM ON AD .
d) DB DA DC 2 . DA DC cos ADC .
Câu 2. Có hai lực F , F cùng tác động vào một vật đứng tại điểm O , biết hai lực F , F đều có cường độ là 1 2 1 2
50 N và chúng hợp với nhau một góc 60 .
a) F F 50N. 1 2 b) F F 1 2
c) Vật đó phải chịu một lực tổng hợp có cường độ bằng 50 3 N.
d) Lực tổng hợp tạo với lực F một góc 60 . 1
Câu 3. Cho hình thang ABCD vuông tại A và D , AB a, AD 2a, DC 3AB . Gọi O là giao điểm của AC 2
và BD , E là điểm thuộc cạnh DC sao cho DE DC . 3
a) DC 3BA .
b) AB AC AE .
c) BA BD 2a . a 2
d) Tập hợp các điểm M thỏa mãn MC 3MA MB MC là đường tròn tâm O bán kính bằng . 2
Câu 4. Cho tứ giác ABCD có O là giao điểm hai đường chéo. Xét tính đúng, sai của các khẳng định
a) OA OC AC . b) . DA DB D . A DB 1 .
c) AB AD CD CB .
d) AB CD AD CB .
2 4
Câu 5. Cho tam giác đều ABC và các điểm M , N, P thỏa mãn BM k BC , CN CA , AP AB . 3 15
Xét tính đúng, sai của các khẳng định
a) AP AN AM . 7
b) AM (1 k ) AB k AC . 4 1 c) PN AB AC . 15 3 1
d) Giá trị k để AM vuông góc với PN để k . 6
Câu 6. Cho hình bình hành ABCD có AB 6 . Gọi O là giao điểm của AC và BD (Hình bên). A B O D C
a) AB AD D B .
b) BA BC 2BO .
c) Tập hợp các điểm M thỏa mãn M thỏa MB MC MB MA là đường tròn có bán kính bằng 2.
d) AB D A CB CD
Câu 7. Cho hình bình hành ABCD có AB a , giao điểm của hai đường chéo là O . Trên đường thẳng chứa
cạnh BC của tam giác ABC lấy một điểm M sao cho 2MB 3MC . A B O D C
Xét tính đúng, sai của các khẳng định
a) DA DB OD OC .
b) DA DB DC 0 .
c) CO OB BA . d) AM 2
AB 3AC .
Câu 8. Cho hình vuông ABCD cạnh a . Gọi M , N lần lượt thuộc các đoạn thẳng BC và AC sao cho 1 BM
MC , CN k AN . 3
1
a) AB AD AC . b) AM AB BC . 4 1 c) DN DA
AB AD.
d)Giá trị k thỏa mãn AM DN thì k 5; 3 . 1 k A D N B M C
Câu 9. Cho hình thang ABCD vuông tại A và D , AB a, AD 2a, DC 4AB . Gọi O là giao điểm của AC 8 3
và BD , E là điểm thuộc cạnh DC sao cho DE
DC . Xét tính đúng, sai của các khẳng định 4 a) DE 3AB .
b) AB AC AE .
c) AD AC 4a 2 . a 5
d) Tập hợp các điểm M thỏa mãn MD 4MB MA MC là đường tròn tâm O bán kính bằng . 5
Câu 10. Cho hình vuông ABCD có tâm O . Các khẳng định sau đúng hay sai
a) AB CD .
b) AB AD 2AC. c) 2 A . D OC a .
d) OA mOB OC là véctơ đối của BD khi m 2 .
Câu 11. Cho hình vuông ABCD cạnh a . Xét tính đúng, sai của các khẳng định
a) AB AD a 2
b) AB 2CD a c) 2 A . B AC 4a .
2 k a
d) Tập hợp điểm M sao cho M . A MC M .
B MD k là đường tròn có bán kính bằng R . 2 1 Câu 12. Cho ABC
có trọng tâm G , H là chân đường cao kẻ từ A sao cho BH
HC . Điểm M di động 3
trên BC sao cho BM xBC . Gọi I là trung điểm cạnh BC . Xét tính đúng, sai của các khẳng định
a) AB AC 2AI .
2
b) MA GC MC IA . 3 9
5 2 c) MA GC x BC HA . 6 3 2 d) MA GC HA . 3
Câu 13. Cho tam giác đều ABC cạnh bằng 3 . Lấy các điểm M , N , P lần lượt trên các cạnh BC, C , A AB sao
cho BM 1, CN 2, PA x 0 x 3 . Xét tính đúng, sai của các khẳng định 2 a a) AB AC b) A . B AC . 3 2 1 1 c) AM AB AC
d) Giá trị của x để AM PN là x . 3 3 2
Câu 14. Cho tam giác ABC có góc A nhọn và 2 2
AB AC 4 , BC a , trọng tâm G , gọi I là trung điểm BC .
Xét tính đúng, sai của các khẳng định
a) AG BG CG 0 .
b) AB AC 4AG . 2
c 6 c) A .
B BC BC.CA . CA AB . 2 d) A .
B AC có giá trị lớn nhất bằng 2.
Câu 15. Cho tam giác ABC . Trên cạnh AB lấy điểm M sao cho 2BA 5BM . Gọi G là trọng tâm tam giác
ABC . Gọi N là điểm trên AC sao cho AN xAC . Xét tính đúng, sai của các khẳng định
a) AB AC 2AG .
1 4 b) MG AC AB . 3 15 3
c) MN x AC AB . 5 3
d) Ba điểm M , N , G thẳng hàng khi x . 4 10
VECTOR TRONG MẶT PHẲNG LỚP 10 THPT
(LỚP BÀI TOÁN TRẮC NGHIỆM ĐÚNG, SAI P3)
_________________________________________________ 1 1 1
Câu 1. Cho hình bình hành ABCD và các điểm M , N, P thoả mãn AM AB, AN AC, AP AD . Khi 2 6 4 đó: 1 1 1 a) AN ( AB AD) b) MN AB . AD 6 3 6
1 1 c) MP AD AB
d) Ba điểm M , N, P thẳng hàng. 3 2
Câu 2. Tứ giác ABCD có M , N là trung điểm của AB, CD . Gọi G là trọng tâm tam giác ABC . Khi đó:
a) MA MB 0
b) Có vô số điểm T thỏa mãn TA TB TC 3 .
c) MN MA AC
d) 2MN AC BD.
Câu 3. Cho tam giác ABC có hai đường trung tuyến BN,CP . Khi đó:
a) G là trọng tâm của tam giác ABC , ta có : GA GB GC 0
b) BA BC 3BN 2 2 c) AB BN CP 3 3 2 2
d) BC CP BN. 3 3
Câu 4. Cho hình bình hành ABCD có tâm ,
O M là một điểm bất kỳ. Khi đó: A B O D C
a) AB AD AC
b) AB 5AC AD 6AC
c) MA MB MC MD MO
d) MA MB MC MD 4MO
Câu 5. Cho tứ giác OABC . Gọi M , N lần lượt là trung điểm của OB và OC . Khi đó: 11
1
a) AM AO AB b) AM OB OA ; 2
1 1 c) BN OC OB ; d) MN (OC OB) . 3 2
Câu 6. Cho ABC . Gọi M , N lần lượt là trung điểm của A , B AC . Khi đó:
2 4
a) 2CM CB CA
b) AB CM BN 3 3 4 2
1 1 c) AC CM BN d) MN BN CM . 3 3 3 3
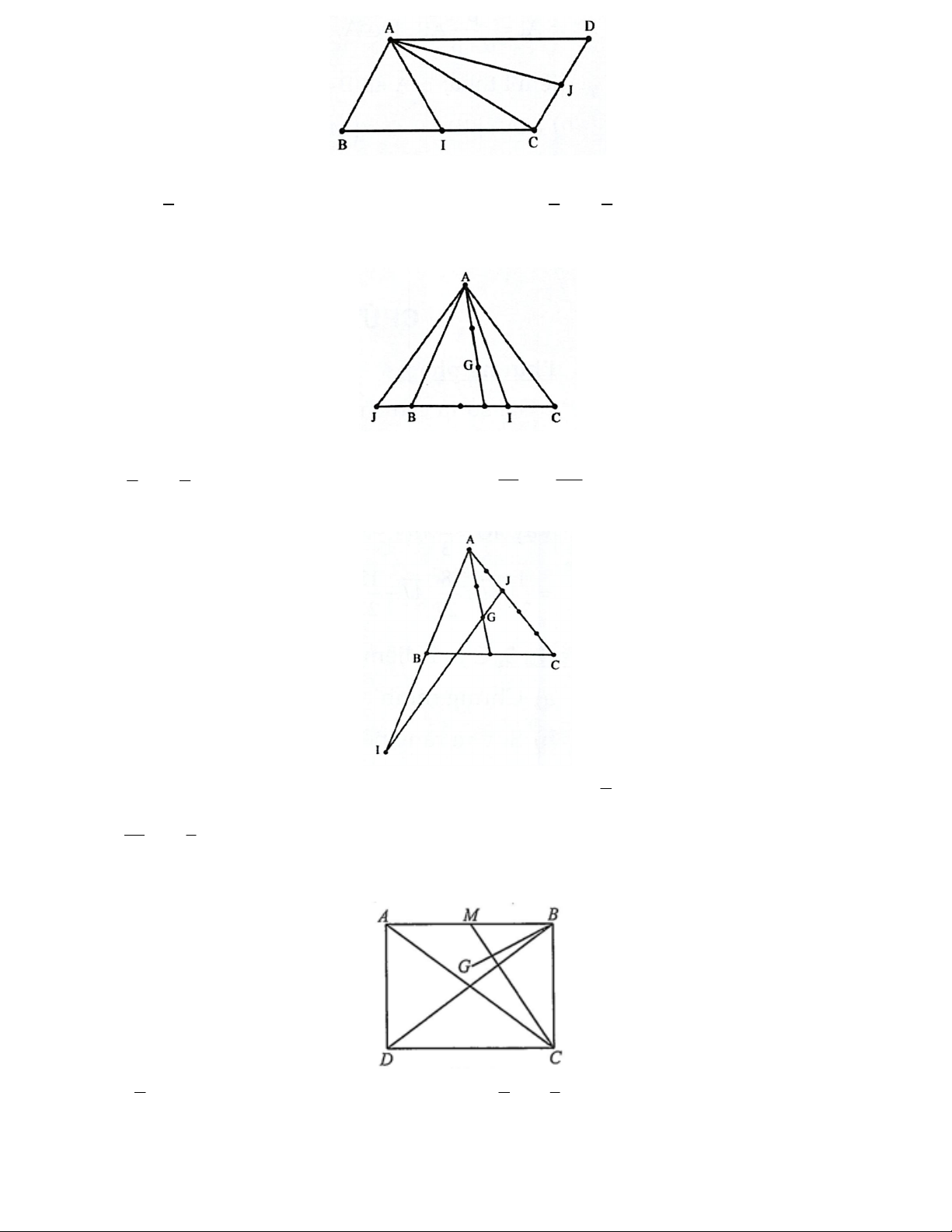
Câu 7. Cho ABC nội tiếp đường tròn tâm ,
O H là trực tâm tam giác, D là điểm đối xứng của A qua O . Khi đó: a) BD / /CH b) CD / / BH
c) HA HB HC 3HO ;
d) OA OB OC 3OH
Câu 8. Cho tam giác ABC. Gọi I là điểm trên cạnh BC sao cho 2CI 3BI và J là điểm trên BC kéo dài sao
cho 5JB 2JC . Phân tích các vectơ AI , AJ theo cặp vectơ AB, AC . Xét tính đúng, sai của các khẳng định a) 2IC 3 IB b) 5JB 3JC 2
5 2
c) AI 2AB AC d) AJ AB AC 5 3 3
Câu 9. Cho hình bình hành ABCD , tâm O . Gọi M , N theo thứ tự là trung điểm của A ,
B CD và P là điểm thỏa 12 1
mãn hệ thức: OP OA . Khi đó: 3
a) OA 3OP 0
b) 3AP 3AC 0
c) Ba điểm B, P, N không thẳng hàng
d) Ba đường thẳng AC, B , D MN đồng quy
Câu 10. Cho tam giác ABC có G là trọng tâm. Gọi M , N lần lượt là trung điểm của A ,
B BC . Lấy hai điểm
I, J sao cho: 2IA 3IC 0 và 2JA 5JB 3JC 0 . Khi đó:
a) M , N, J thẳng hàng. 3 b) JM JN 2
c) J là trung điểm của BI . 5
d) Gọi E là điểm thuộc AB sao cho AE
AB thì C, E, J thẳng hàng. 7
Câu 11. Cho tứ giác ABCD . Gọi I , J lần lượt là trung điểm AB và C ,
D K là trung điểm IJ , M là điểm bất kì. Khi đó:
a) AC BD 2IJ
b) AD BC 2IJ
c) MI MJ MK
d) MA MB MC MD 4MK
Câu 12. Cho tam giác ABC có M là trung điểm BC . Gọi G là trọng tâm, H là trực tâm, O là tâm đường tròn
ngoại tiếp tam giác ABC ,
AA là đường kính của ( ) O . Khi đó: a) BH A C b) AH 2OM
c) HA HB HC 3HO
d) OA OB OC 3OH
Câu 13. Cho hình bình hành ABCD . Gọi I , J lần lượt là trung điểm BC và CD . Khi đó: 13
a) AC AB AD
b) AI AC AB
3
1 1 c) AI AB AD d) AJ AB . AD 2 2 2
Câu 14. Cho tam giác ABC có trọng tâm G. Gọi I là điểm trên cạnh BC sao cho 2CI BI . Điểm J là điểm trên
cạnh BC kéo dài sao cho 5JB JC . Khi đó: a) BI 2CI
b) AI AB 3AC
5 3
14 172 c) AJ AB AC d) AG AI AJ 4 4 27 27
Câu 15. Cho ABC có trọng tâm G . Gọi I , J là 2 điểm định bởi IA 2IB , 3JA 2JC 0 .Khi đó: 2 a) AI 3AB b) IJ 2 AB AC 5 5 1 c) IG AB AC
d) 3 điểm I , J ,G thẳng hàng. 3 3
Câu 16. Cho hình chữ nhật ABCD, AB 4a, AD 3a . Gọi M là trung điểm của A ,
B G là trọng tâm tam giác ACM (Hình). 1 3 1 a) CM BA 3BC b) BG BA BC. 2 2 3
c) BC BA 0 b) 2
BG CM a . 14
VECTOR TRONG MẶT PHẲNG LỚP 10 THPT
(LỚP BÀI TOÁN TRẮC NGHIỆM ĐÚNG, SAI P4)
_________________________________________________
Câu 1. Cho bốn điểm ,
A B, C, D . Khi đó:
a) AB BC CA
b) AD DA 0
c) AB CD AD CB ;
d) AB CD AC DB
Câu 2. Cho hình bình hành ABCD tâm O . Khi đó: A B O D C
a) BA AB 0
b) OA AC OC
c) OA OB DC CB
d) OB OA CA DC
Câu 3. Cho tam giác ABC . Bên ngoài của tam giác vẽ các hình bình hành ABIJ, BCP , Q CAR . S Khi đó:
a) RJ RA AJ
b) IQ IB QB
c) PS PC SC
d) RJ IQ PS 0
Câu 4. Cho ngũ giác ABCDE . Các điểm M , N, , P , Q ,
R S theo thứ tự là trung điểm của các đoạn E , A A , B BC,C , D M , P NQ . Khi đó:
1 1 a) RS (MN PQ) b) RS E . D 2 3 1 c) RS cắt ED d) RS ED 4
Câu 5. Cho hình vuông ABCD có cạnh bằng a . Khi đó:
a) AD AB AC
b) Gọi E là điểm đối xứng với B qua C . Khi đó ADEC là hình thang.
c) | AD AB | a 2
d) | AD AC | a 3 .
Câu 6. Cho tam giác ABC đều cạnh a , có trọng tâm G . H là trung điểm cạnh BC. Khi đó:
a) AB BC AC
b) | AB CB | 2a ; a 3
c) | AB AC | a 3 ;
d) | BG BC | . 2 15
Câu 7. Cho sáu điểm ,
A B, C, D, E, F . Khi đó:
a) AB CD EF CB ED FA .
b) AB AF CD CB EF DE .
c) AB CD AD CB .
d) AC BD EF AF BC ED .
Câu 8. Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Khi đó: A B O D C
a) AB AC AD
b) AC BA AD
c) | AB AD | AC
d) Nếu | AB AD | |
CB CD | thì ABCD là hình thoi.
Câu 9. Cho lục giác đều ABCDEF tâm O . Khi đó:
a) AB CD
b) AB OD AC
c) AB OC FC
d) AB AE FD AF
Câu 10. Cho hình bình hành ABCD . Hai điểm M và N lần lượt là trung điểm của BC và AD . Khi đó:
a) MC AN
b) NC MC AN
c) AM CD BM
d) AM AN AB AD
Câu 11. Cho tam giác ABC . Các điểm M , N , P lần lượt là trung điểm của AB, AC, BC . Khi đó:
a) AM AN NM
b) MN NC MP
c) MN PN MP
d) BP CP PC
Câu 12. Cho tam giác ABC đều cạnh a . H là trung điểm của cạnh BC. G là trọng tâm tam giác. Khi đó:
a) AB AC AH .
b) AB AC BC .
c) | AB AC | a 3
d) | AB AC | a 16
Câu 13. Cho hình vuông ABCD cạnh a , có O là giao điểm hai đường chéo . Khi đó:
a) O là trung điểm của AC, BD
b) | OA CB | a 2 a 2
c) | AB DC | a
d) | CD DA | 2
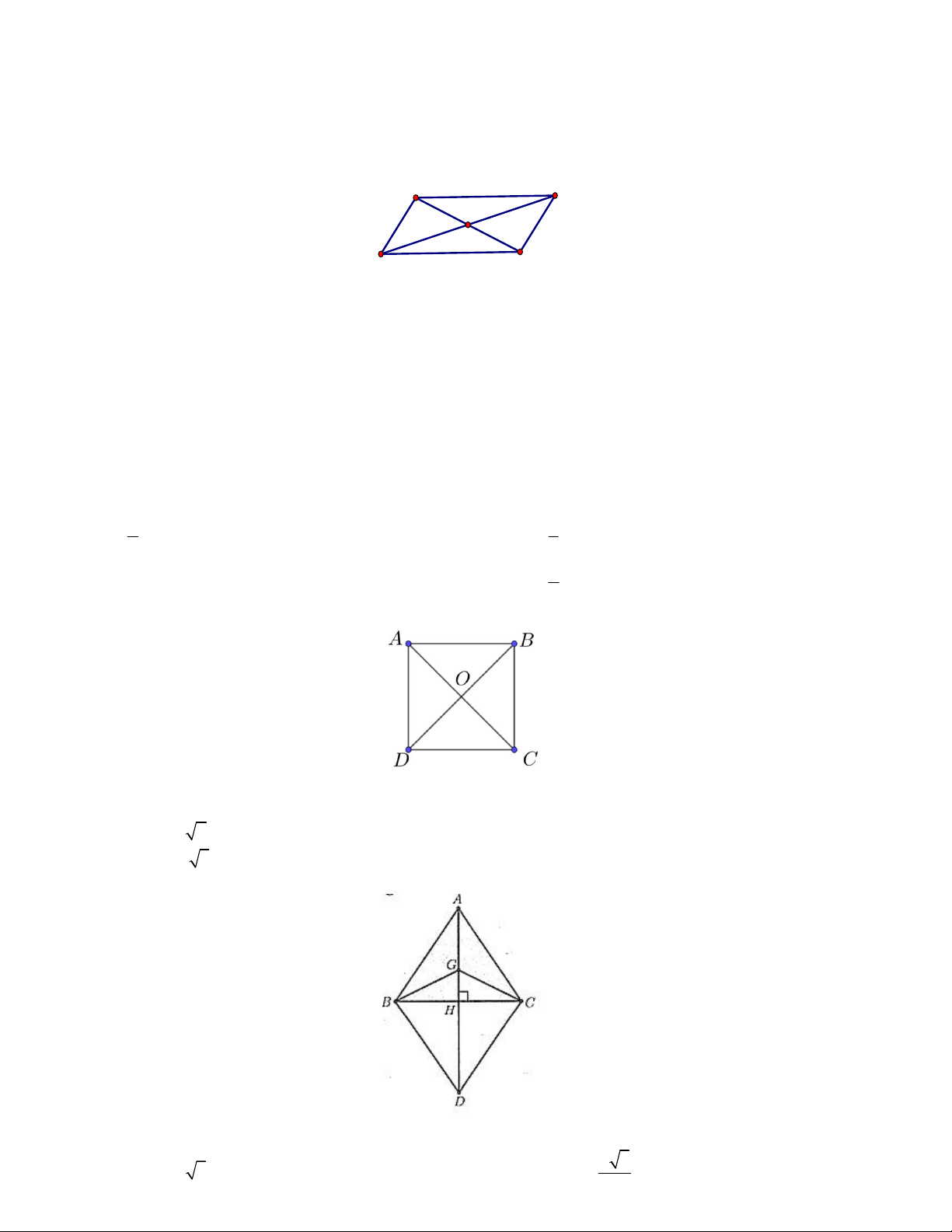
Câu 14. Cho hình thoi ABCD cạnh a , có BAD 60
. Gọi O là giao điểm hai đường chéo. Khi đó:
a) BAD, BCD đều cạnh a .
b) | AB AD | a 2 a 3
c) | BA BC | a 3
d) | OB DC | 2
Câu 15. Gọi O là tâm hình bình hành ABCD . Khi đó: A B O D C
a) OA OB CD .
b) OB OC OD OA
c) AB AD DB .
d) BC BA DC DA
Câu 16. Cho tam giác ABC . Gọi M , N , P lần lượt là trung điểm của BC, CA , AB . Khi đó:
a) Tứ giác BMNP và APMN là hình bình hành
b) BM CN AP 0 .
c) AP AN AC BM .
d) OA OB OC OM ON OP với O là điểm bất kì.
Câu 17. Cho 5 điểm ,
A B, C, D, E . Khi đó:
a) AB BC CA
b) AB BC CD DE CE AE
c) AC BD AD
d) AB CD AC BD
Câu 18. Cho 6 điểm ,
A B, C, D, E, F phân biệt. Khi đó:
a) AB BD AC
b) AB DF BD FA 0
c) BE CE CF BF 0
d) AD BE CF AE BF CD 17
Câu 19. Cho hình bình hành ABCD với M và N lần lượt là trung điểm của BC và AD . Khi đó:
a) DA DC DB
b) CM CN AB CD
c) MA MC 0
d) AM CD BM
Câu 20. Cho tam giác ABC vuông tại A có AB ,
a BC 2a . Khi đó: a) ACB 60 b) 2
BA BC a
c) 2
BC CA 3a . b) 2
AB BC BC CA CA AB 4 a
Câu 21. Cho hình vuông ABCD tâm O, có cạnh a . Biết M là trung điểm của AB,G là trọng tâm tam giác ADM . Khi đó: 2 a a) 2
AB CA a b) AM AC 3 2
a
c) AD BD OM AC d) 2
( AB AD)(BD BC ) a 2
Câu 22. Cho tam giác ABC đều có cạnh bằng 3a . Khi đó: 3 a) AO 3a
b) AB AC 2a 2
c) AB CB AC 0
d) AB AC a 3 18
VECTOR TRONG MẶT PHẲNG LỚP 10 THPT
(LỚP BÀI TOÁN TRẮC NGHIỆM ĐÚNG, SAI P5)
_________________________________________________
Câu 1. Cho ABC có trọng tâm G . Gọi M là trung điểm BC ,
B là điểm đối xứng của B qua G . Khi đó: 1 1 a) Tứ giác
AGCB là hình bình hành b) CB AB AC 3 3
1 2 5 1 c) AB AB AC. d) MB AB AC 3 3 6 6
Câu 2. Chất điểm A đang chuyển động, khi tác động vật lí bằng 3 lực 1
F , F2, F3 như hình bên thì vật đó đứng
yên. Coi ma sát không đáng kể và lực ngoại cảnh không ảnh hưởng gì đến chất điểm A . Biết F 3 có độ lớn
bằng 30 N , Xét tính đúng, sai của các khẳng định tính độ lớn các lực F , F 1 2 a) F 10 3. 1
b) F F F 1 2 3 c) F 10 3. 2 d) F F . 1 2
Câu 3. Cho ABC . Gọi I là điểm nằm trên cạnh BC sao cho IB 3IC . Gọi J và K lần lượt là các điểm thuộc
cạnh AC, AB sao cho JA 2JC , KB 3KA . Khi đó: 3 3
a) IB và IC ngược hướng b) AI AB AC 4 4
1 2 20 48 c) JK AB AC d) BC AI JK 4 3 17 17
Câu 4. Cho tam giác ABC . Hai điểm M , N được xác định bởi các hệ thức: BC MA 0, AB NA 3AC 0 . Khi đó: a) MN 3AC
b) Hai vectơ MN , AC cùng phương
c) M thuộc đường thẳng AC
d) Hai đường thẳng MN và AC song song.
Câu 5. Cho hai vectơ a, b thoả mãn | a | 3,| b | 4, (a, b ) 150 . Khi đó: 19 a) a b 6 3
b) (a b) (a b) 7.
c) (3a b) (a 2b) 5 30 3
d) (3a b) (a 2b) 5 30 3 3
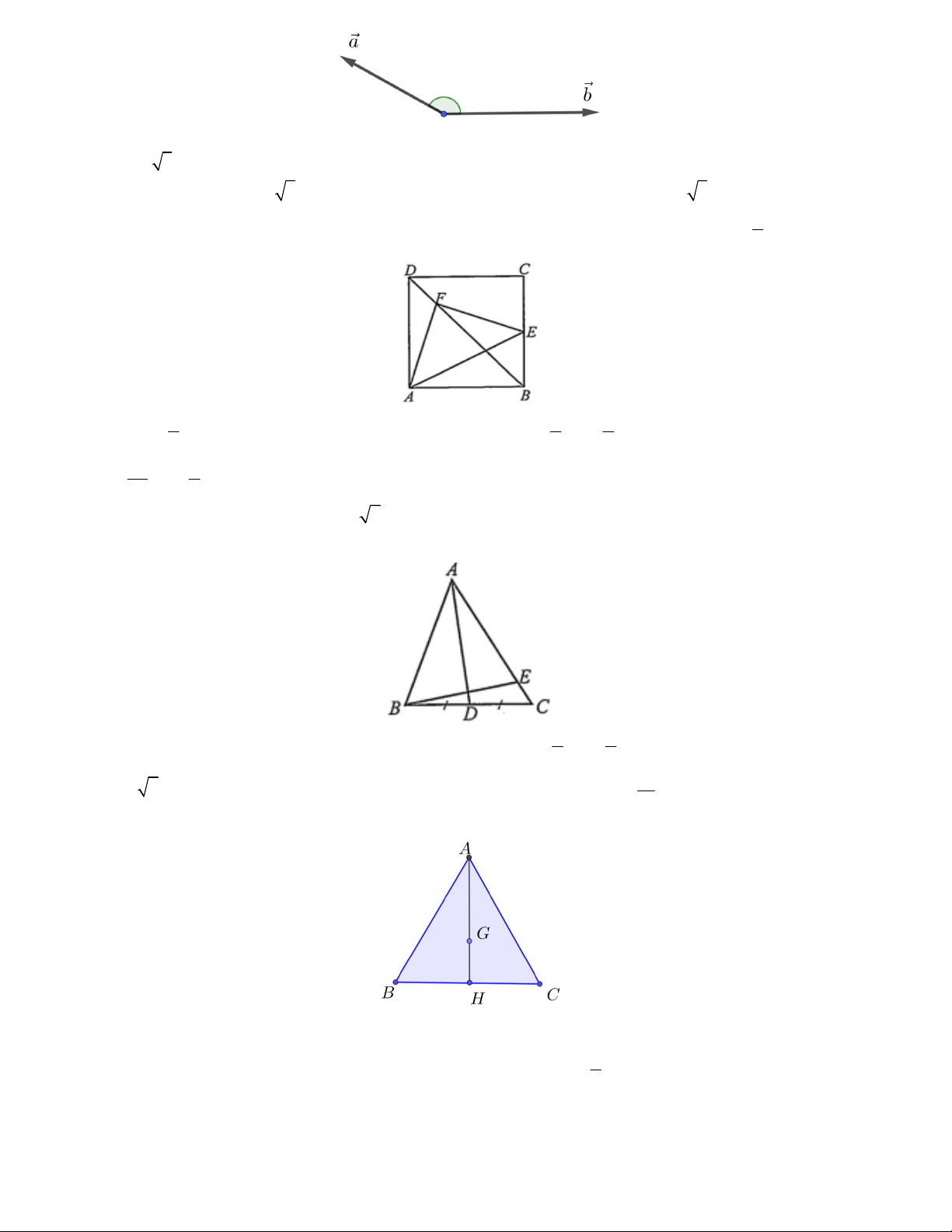
Câu 6. Cho hình vuông ABCD cạnh a . Lấy E là trung điểm của BC , điểm F thoả mãn BF BD Khi đó: 4
1 1 5 a) AE AB AD b) AF AB AD. 2 4 4 3 1 c) EF AB AD.
d) Tam giác AEF vuông cân. 4 4
Câu 7. Cho tam giác ABC có có AB 4 2, AC 6, BAC 45
. Gọi D là trung điểm của đoạn thẳng BC .
Điểm E thoả mãn AE k AC(k ) (Hình). Khi đó: 1 1
a) AB AC 20 b) AD AB AC 2 2 14 c) BC 3 5
d) AD BE khi k . 15
Câu 8. Cho tam giác ABC đều có AB a , đường cao AH . Khi đó:
a) ( AB, AC ) 30 b) ( AH , CB) 90 3 c) (C , A BC ) 120 d) 2 AH.BA a . 4
Câu 9. Cho hình thoi ABCD có cạnh bằng 2 và góc B bằng 60 . Khi đó: 20




