



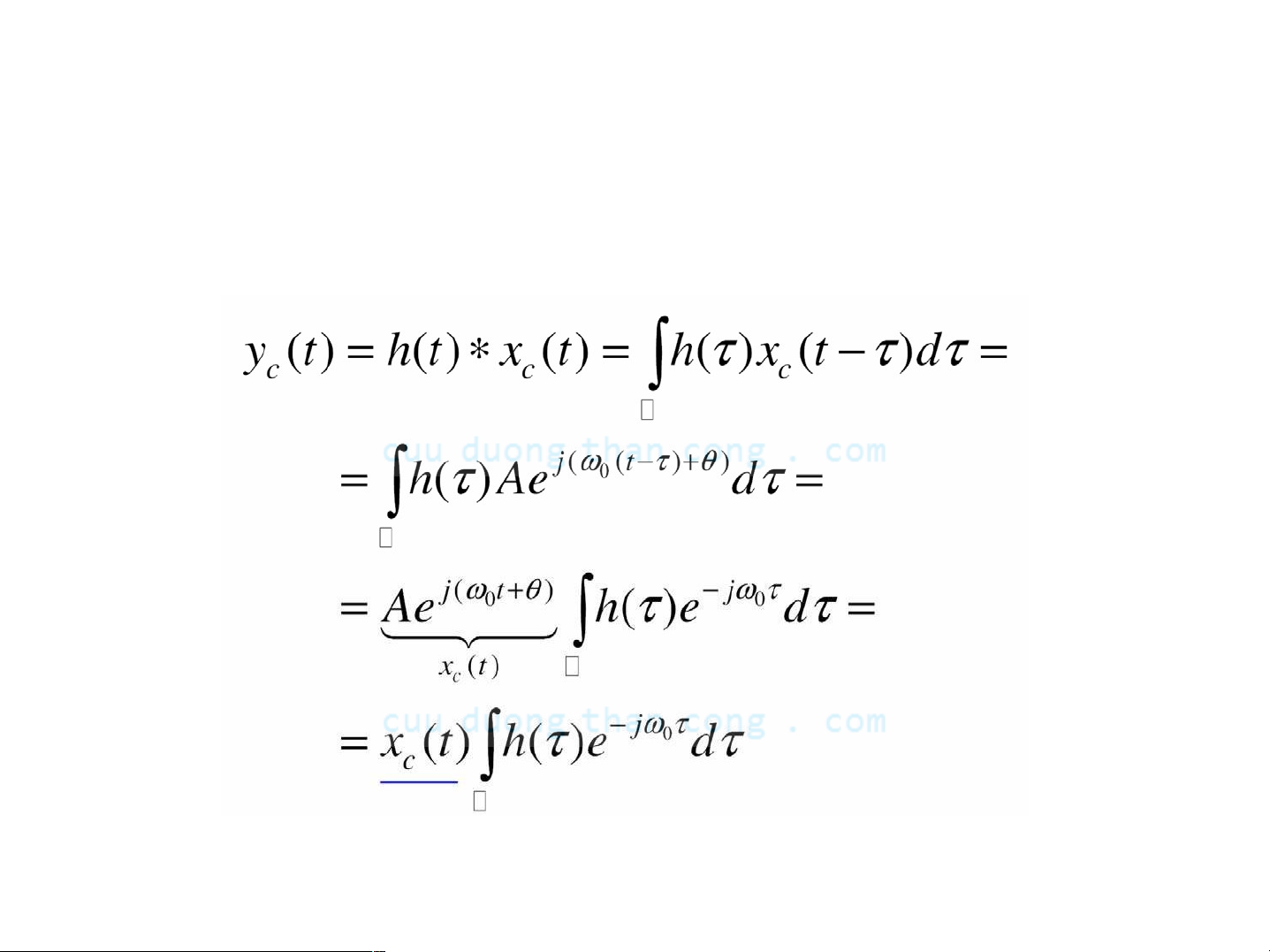
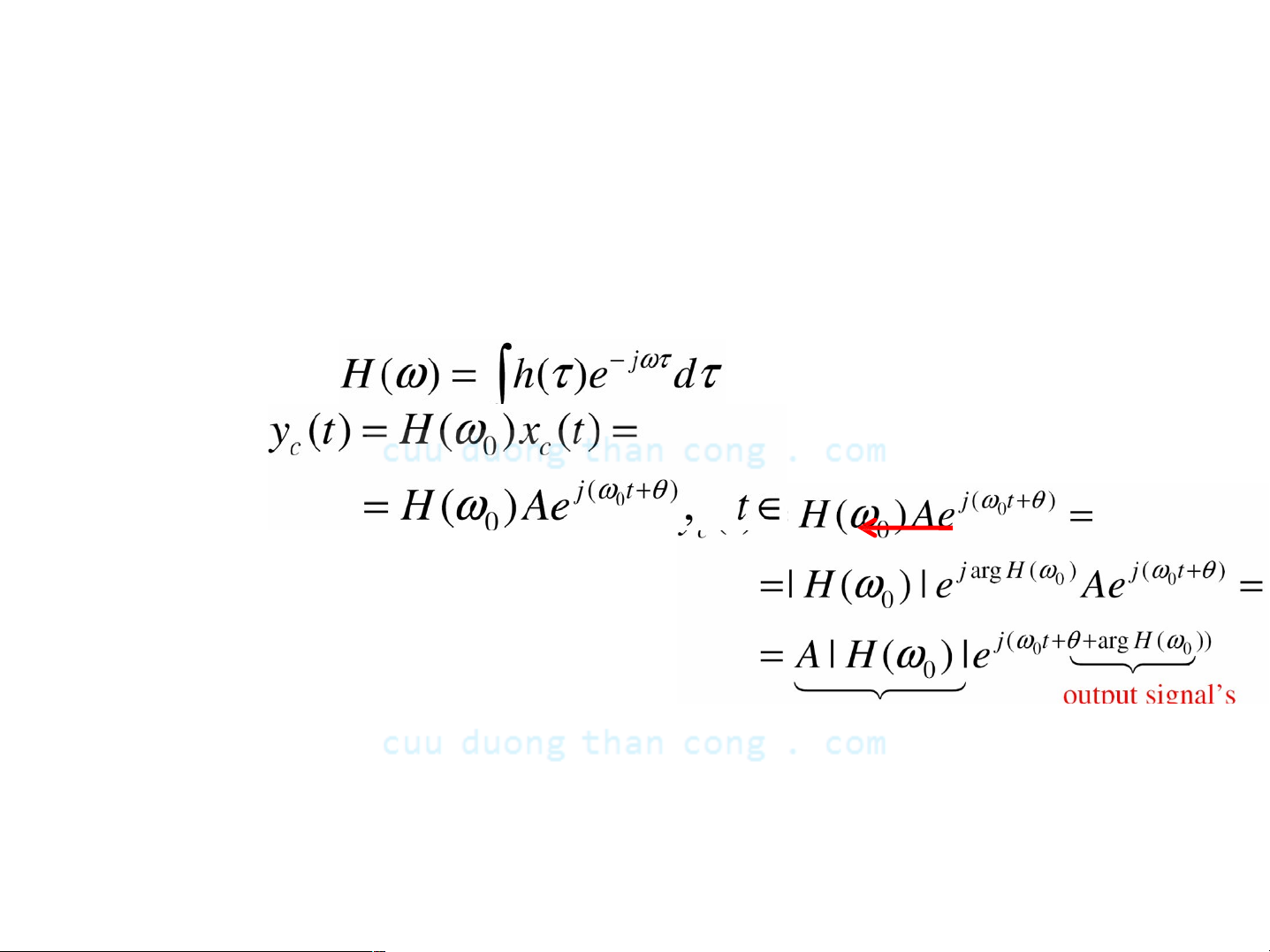
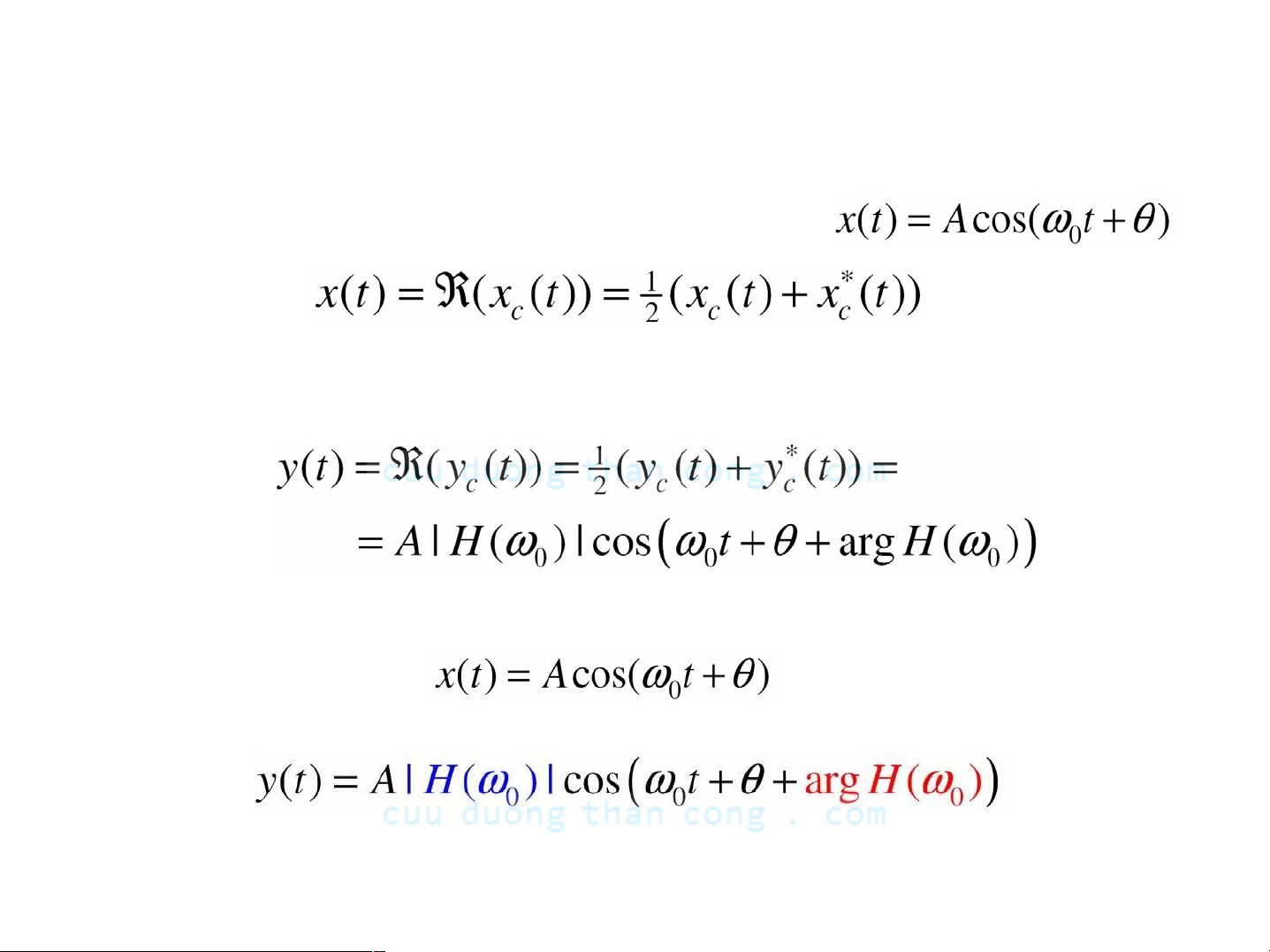

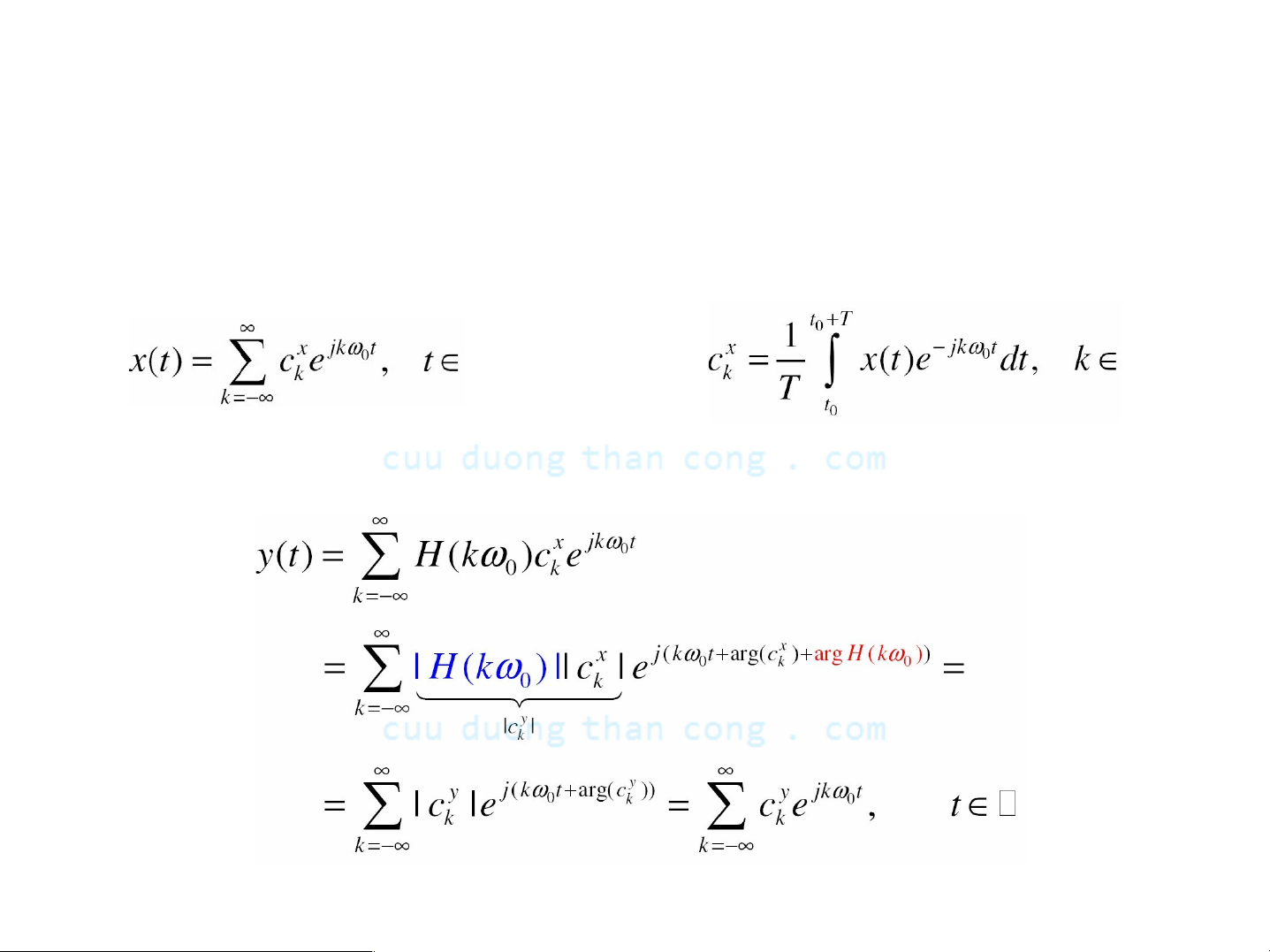















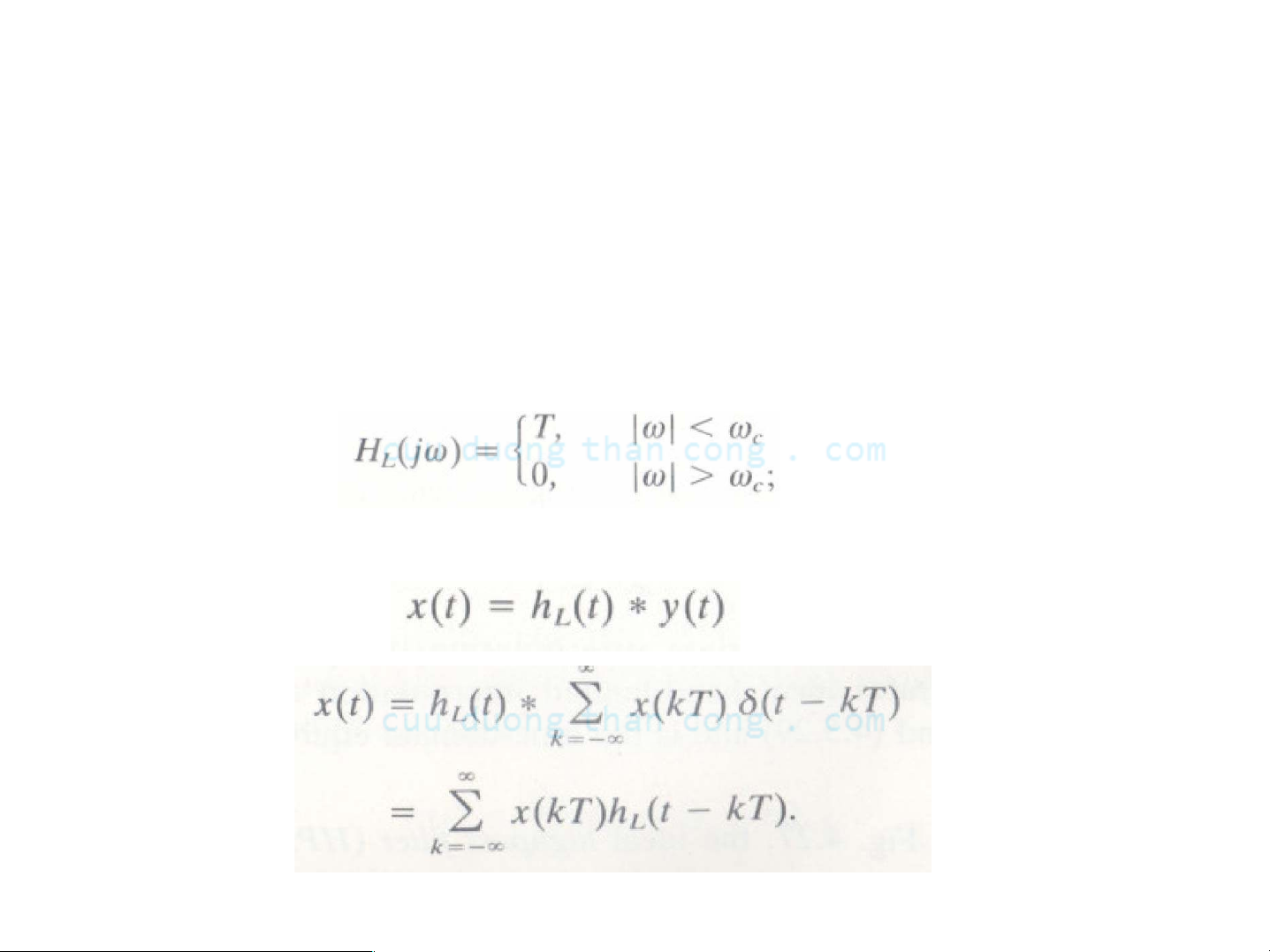
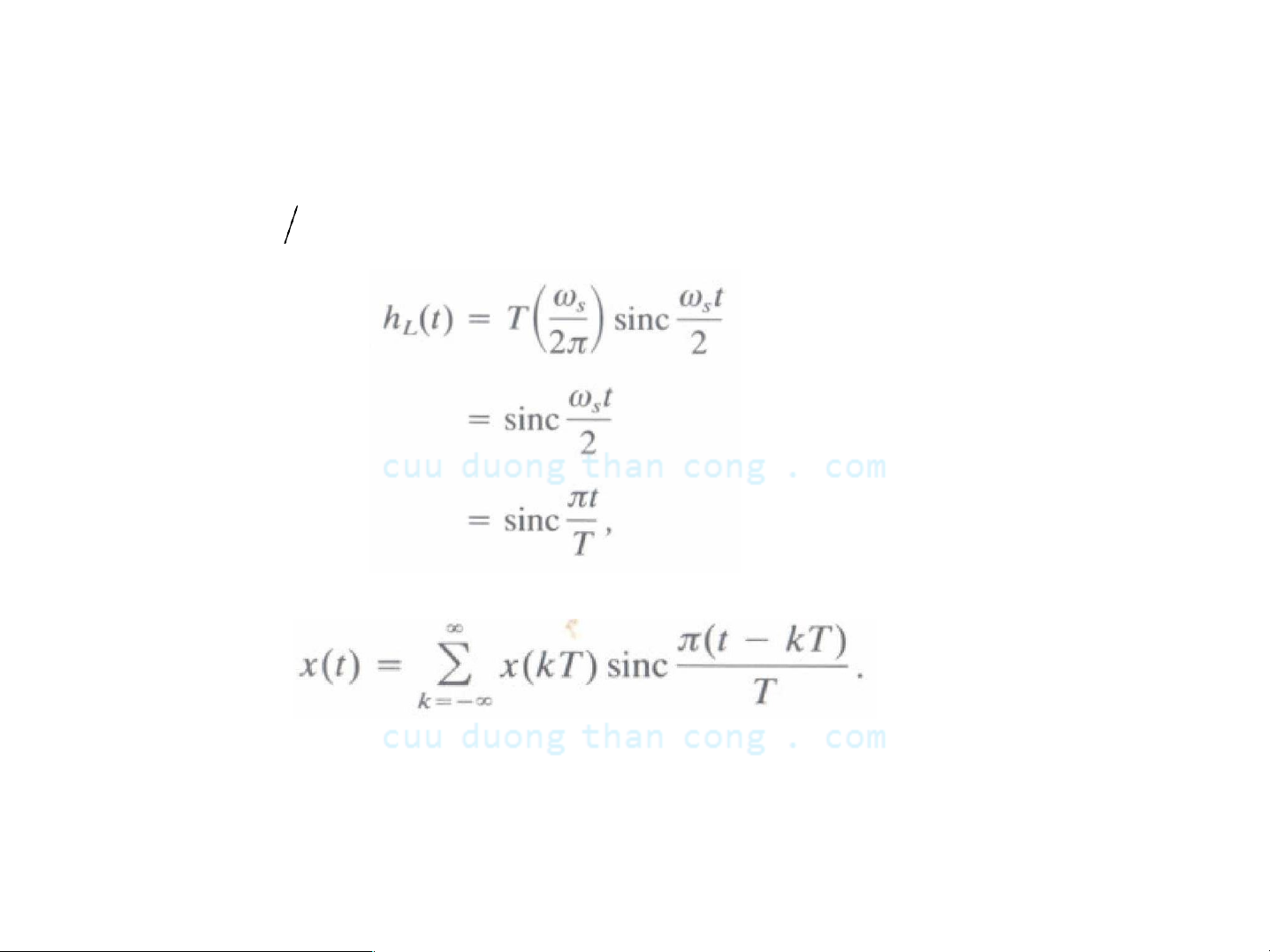
Preview text:
Bài 6: Đáp ứng tần số và Iọc tín hiệu
Bộ môn Điều khiển tự động, Khoa Điện
Chương 4: Đáp ứng tần số và Iọc tín hiệu
4.1 Đáp ứng tần số của hệ LTI
- Đáp ứng tần số của hệ ghép nối
 Đồ thị Bode
Đồ thị Bode- Các bộ Iọc tín hiệu

EE3000-Tín hiệu và hệ thống 2
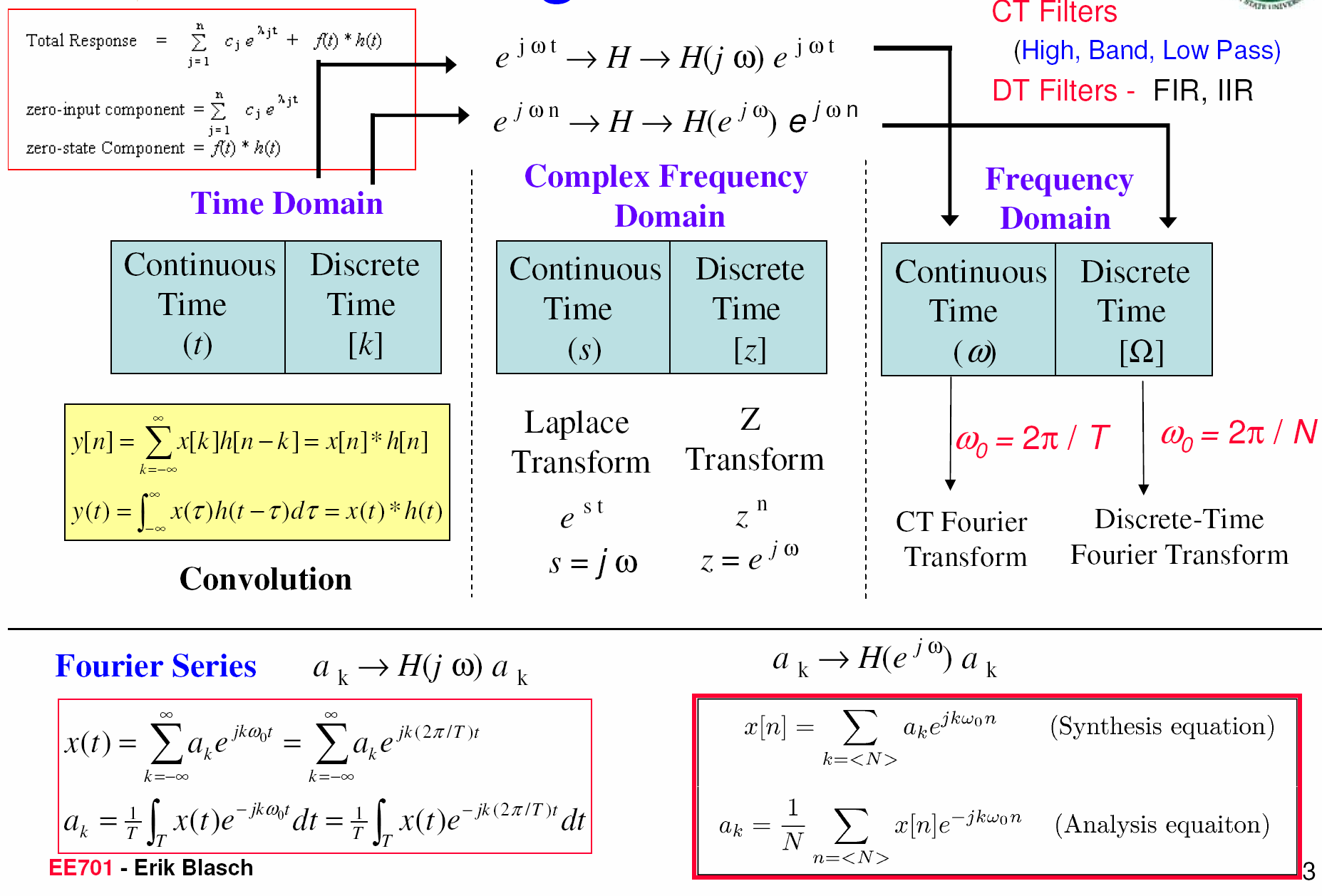 Tổ chức
Tổ chức


EE3000-Tín hiệu và hệ thống
3
Chương 4: Đáp ứng tần số và Iọc tín hiệu
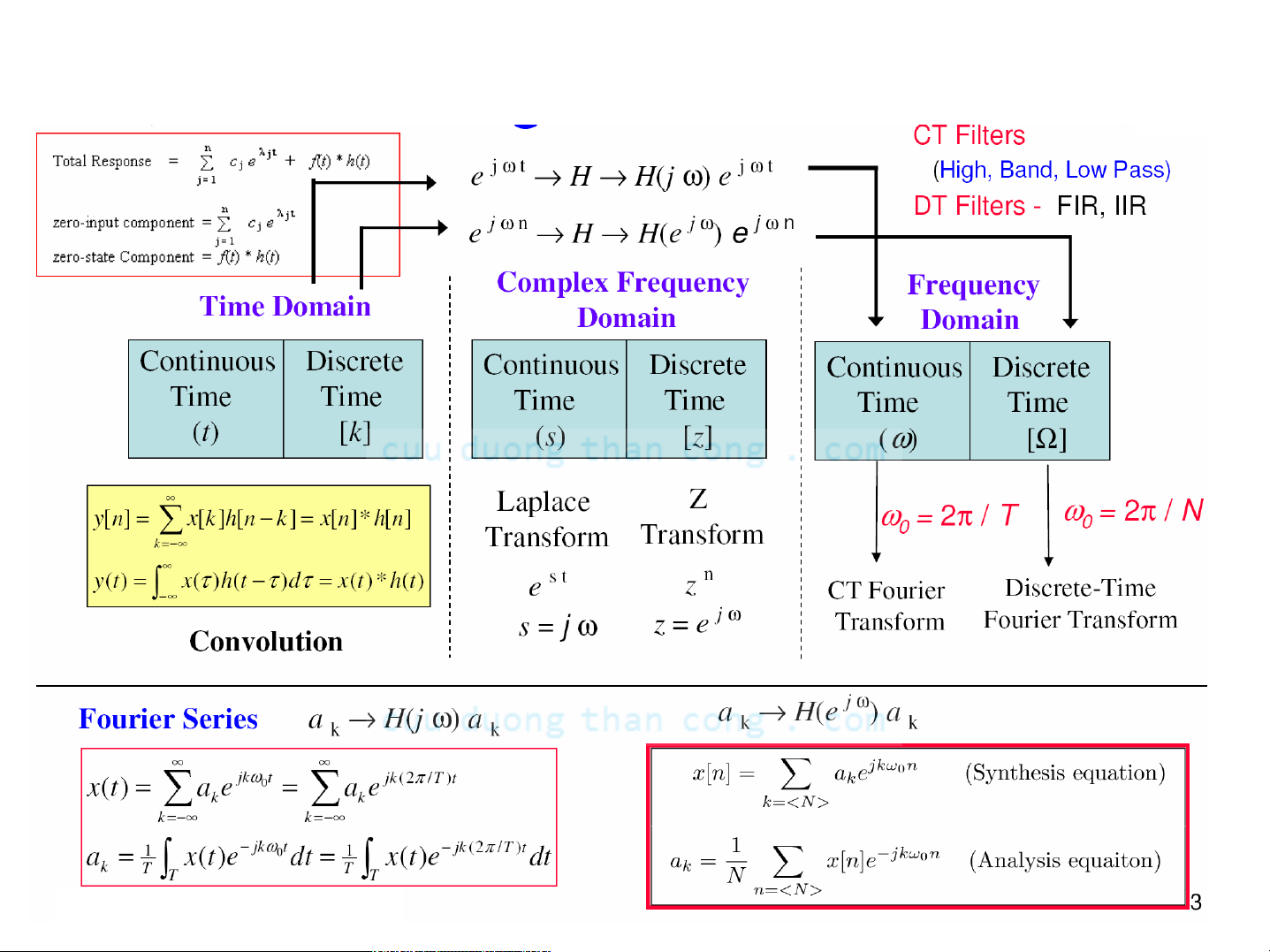
- Đáp ứng tần số của hệ LTI Iiên tục

4.1.1 Đáp ứng của hệ với tín hiệu tuần hoàn
4.1.2 Đáp ứng của hệ với tín hiệu không tuần hoàn
- Đáp ứng tần số của hệ ghép nối
- Đồ thị Bode
- Các bộ

Iọc tín hiệ
Đáp ứng hệ LTI với tín hiệu sin phức
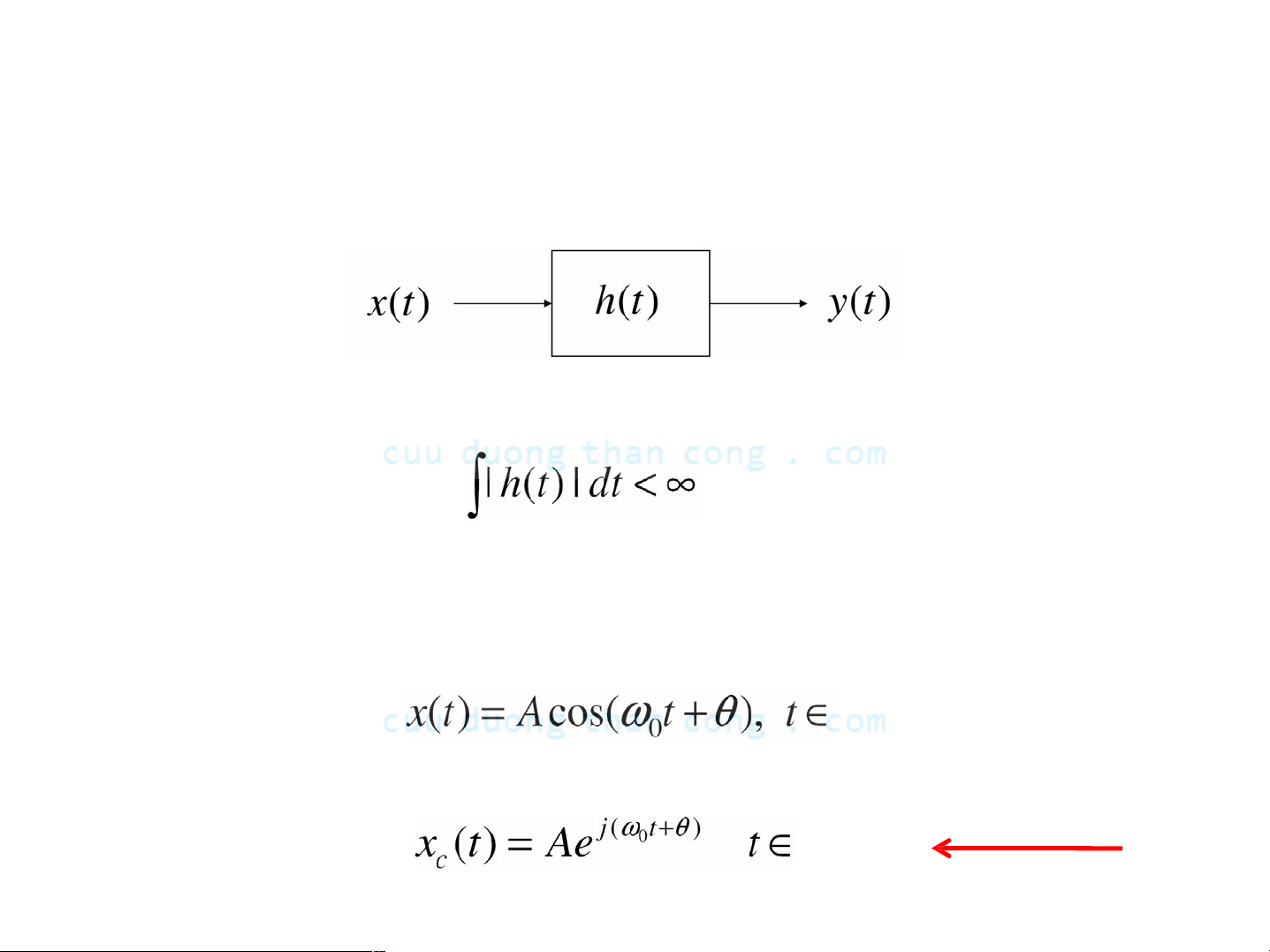
- Xét hệ LTI Iiên tục sau
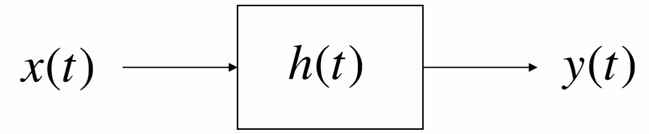
- Giả thiết: đáp ứng xung h(t) khả tích tuyệt đối
R
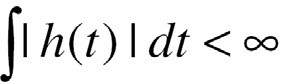

(do đó hệ Ià ổn định)
- Đáp ứng y(t) của hệ với tín hiệu vào
?
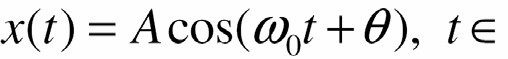

R
- Trước hết, xét đáp ứng yc(t) của hệ với tín hiệu vào
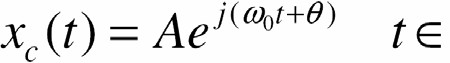 R
R
Sin phức
Đáp ứng hệ LTI với tín hiệu sin phức
- Tín hiệu ra nhận được thông qua tích chập Ià
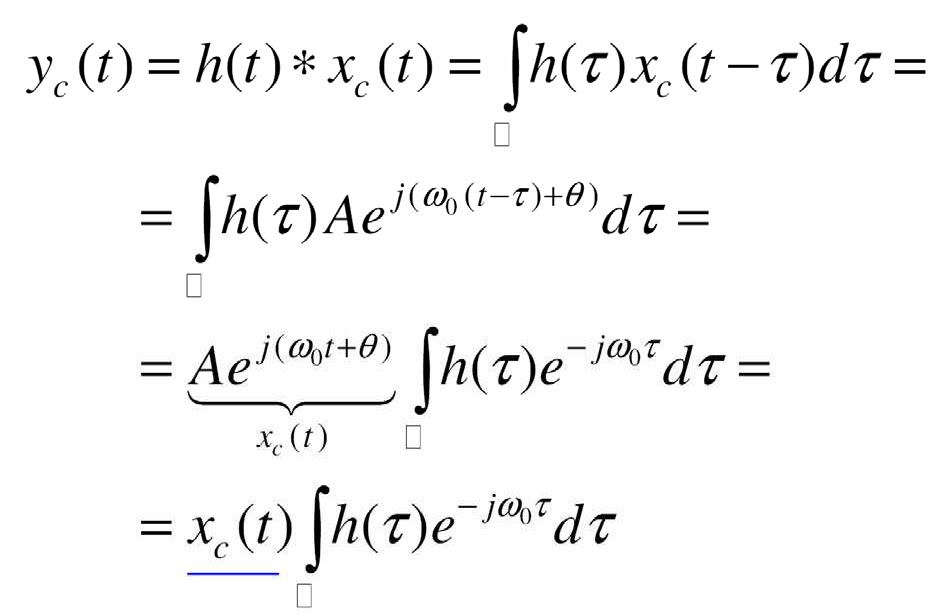


R
R
R
R
EE3000-Tín hiệu và hệ t6
Đáp ứng tần số
- Với định nghĩa
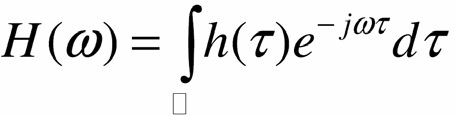
R
ta có
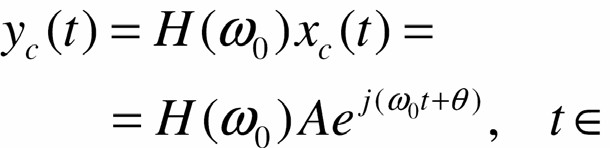

R
Η(ω) Ià đáp ứng tần số của hệ LTI = biến đổi Fourier của h(t)
- Do H(ωO) nói chung Ià một số phức, ta có thể viết
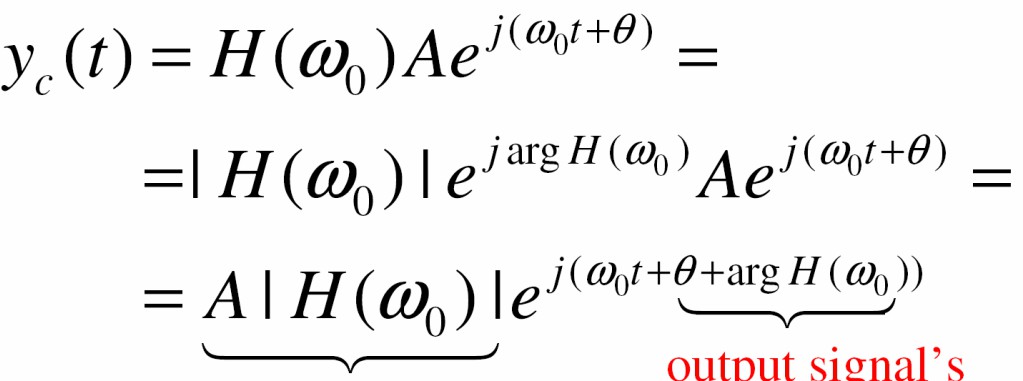 Sin phức với cùng tần số
Sin phức với cùng tần số

pha của tín
biên độ của tín hiệu ra
Đáp ứng hệ LTI với tín hiệu sin thực
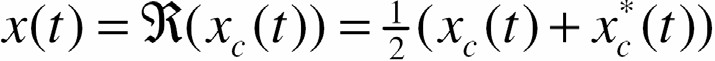 Sử dụng công thức EuIer, ta có thể biểu diễn
Sử dụng công thức EuIer, ta có thể biểu diễn 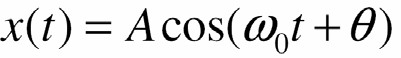 thành
thành
và dựa vào tính tuyến tính
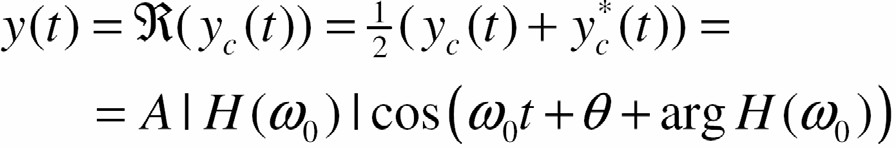

- Do đó đáp ứng với
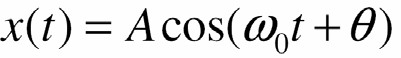 Ià
Ià
cũng Ià tín hiệu sin với cùng tần số ω0 nhưng có biên độ được co giãn với hệ số H(ωO) và có pha được dịch một góc arg H(ωO)
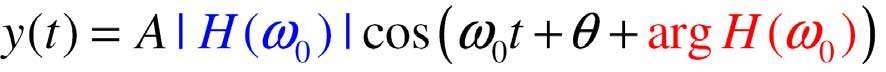

EE3000-Tín hiệu và hệ thống 8
Ví dụ 1: Biên độ/Pha
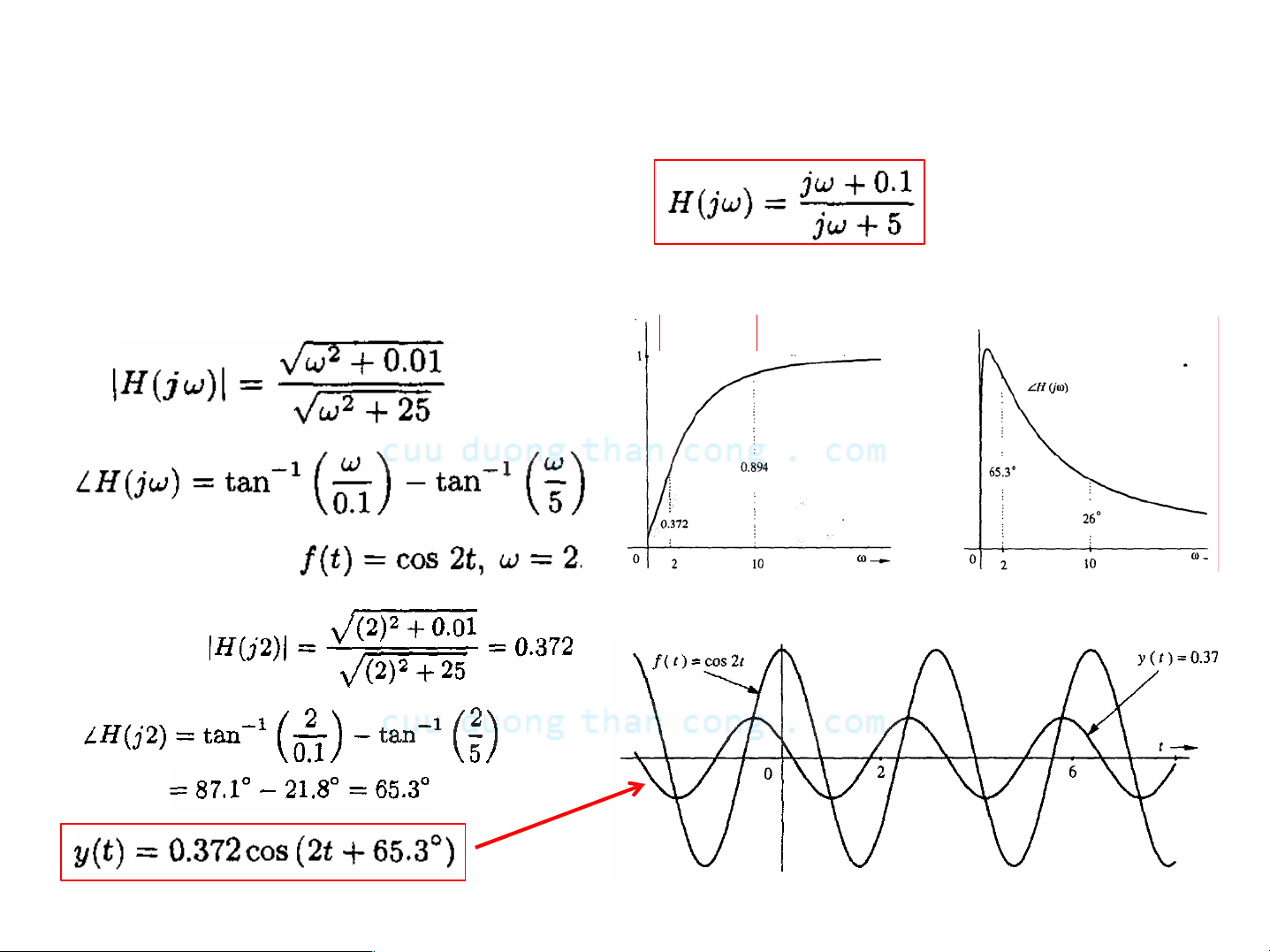
- Xét hệ thống có đáp ứng tần số
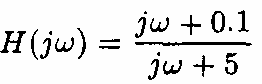
- Biên độ và pha của Η(jω) Ià
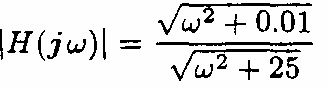
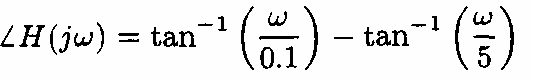
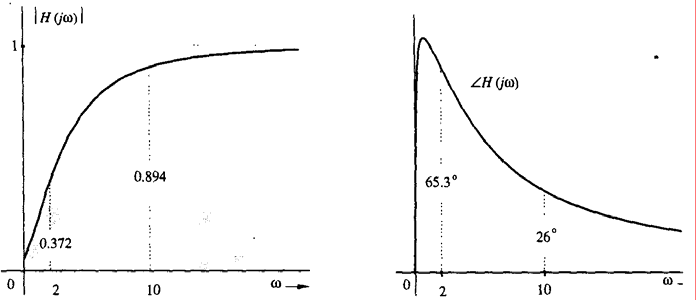

H ( jω)
H ( jω)
- Tín hiệu vào
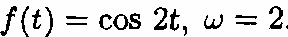
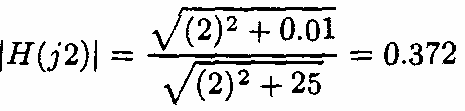
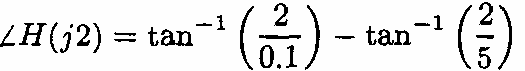
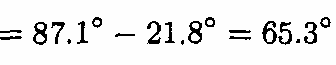
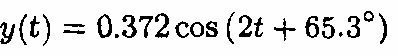
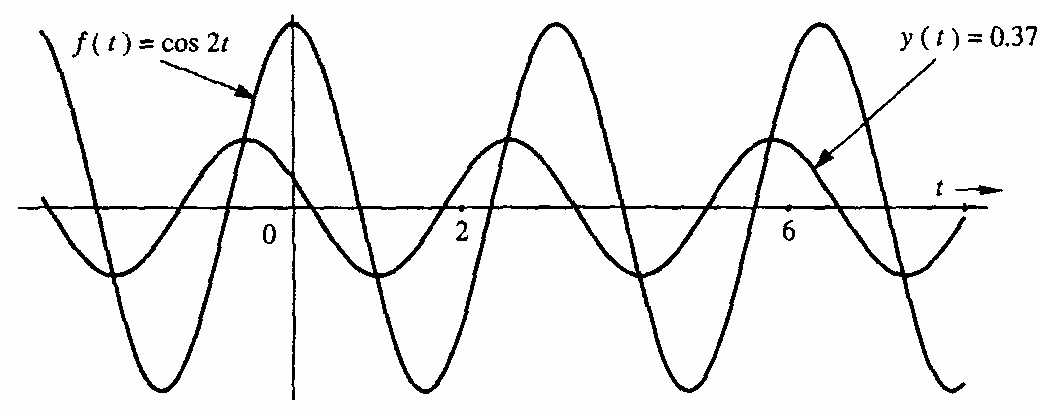

- Do đó
9
EE3000-Tín hiệu và hệ thống
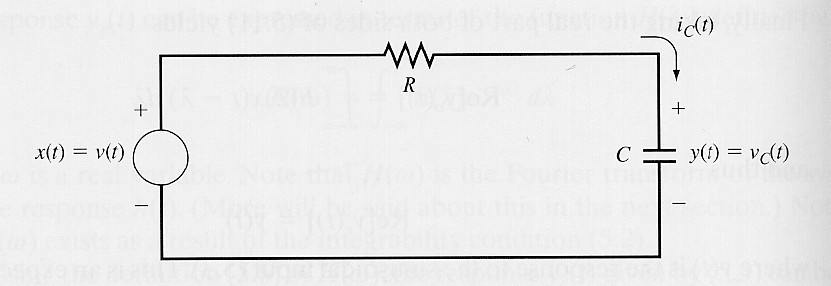
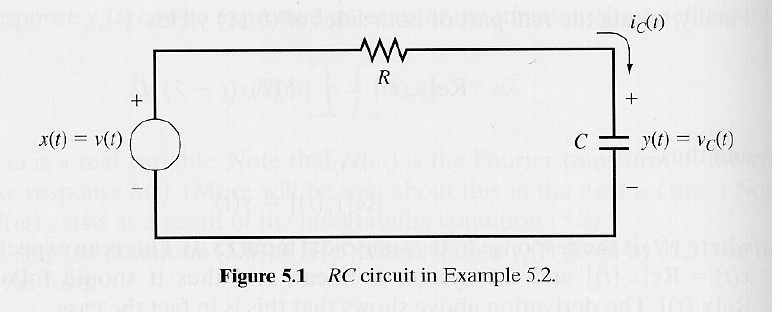
Ví dụ 2: Đáp ứng tần số mạch RC
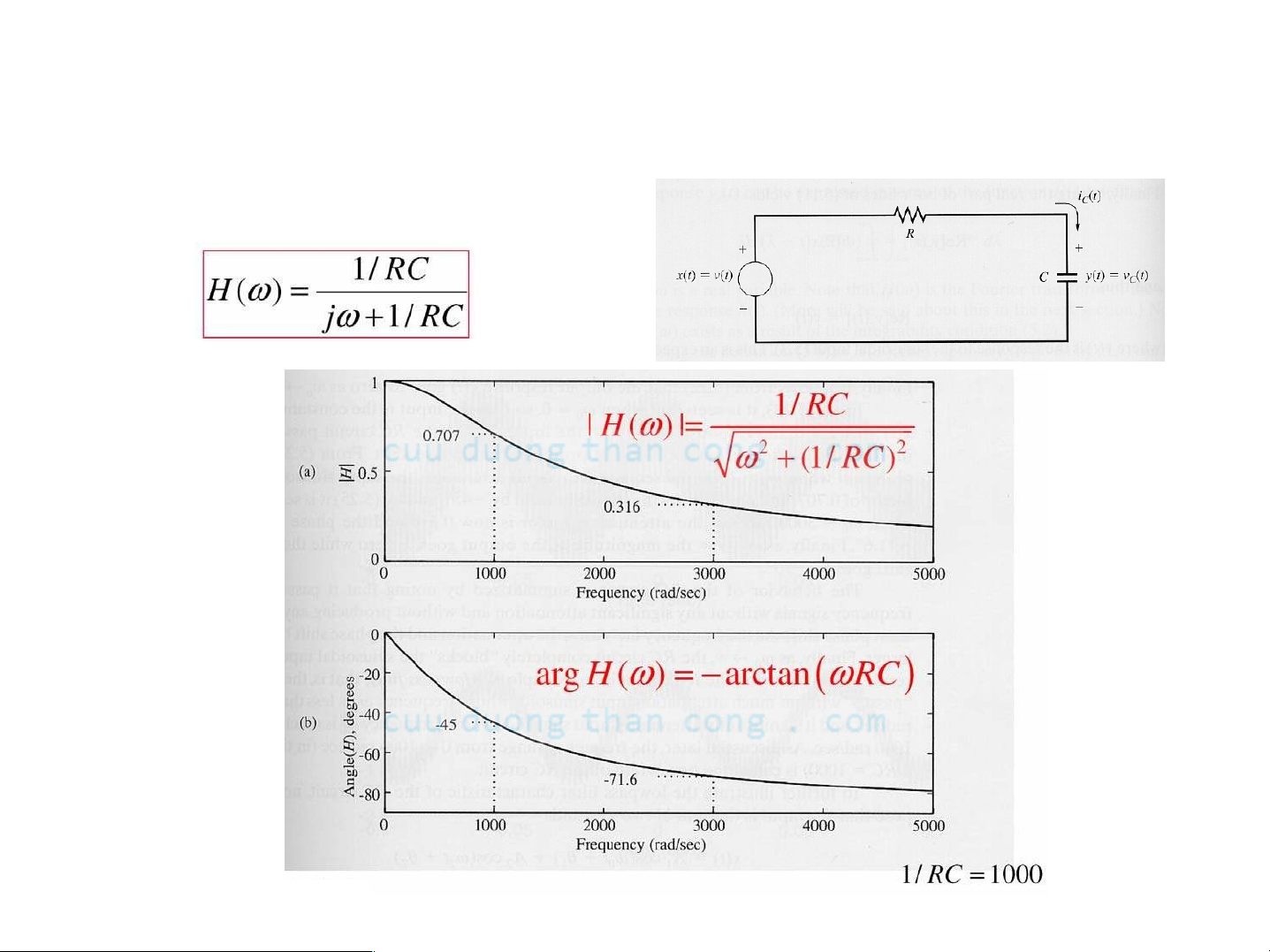
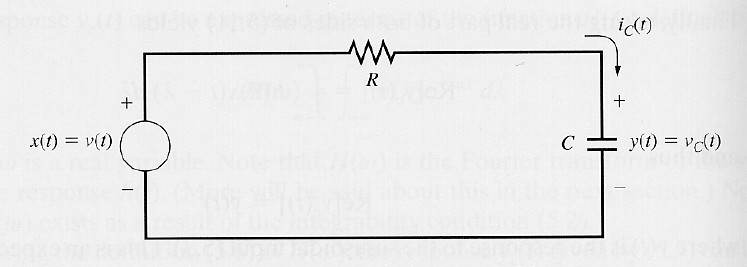 Xét mạch điện RC như hình vẽ
Xét mạch điện RC như hình vẽ
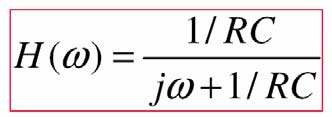
- Đồ thị biên
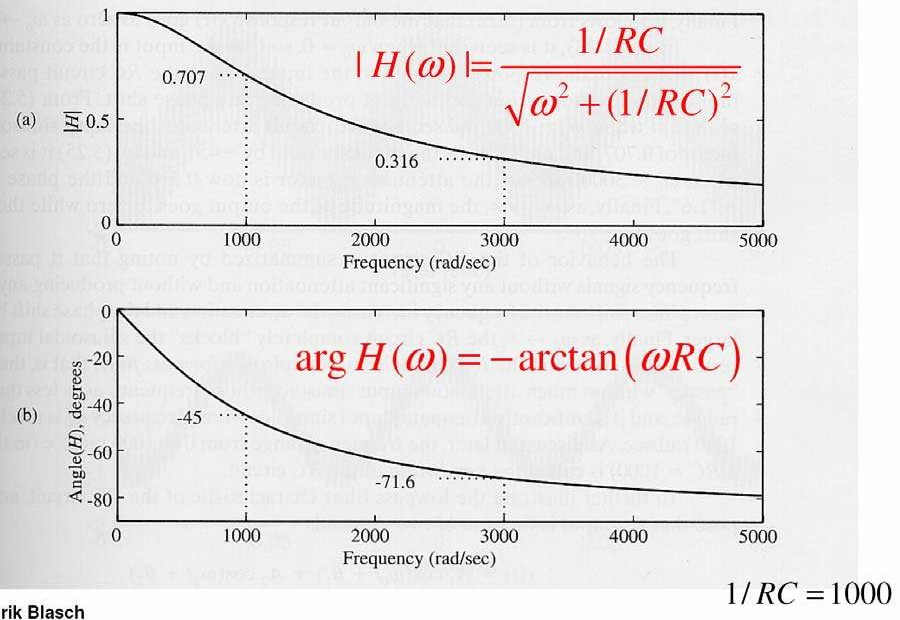


độ và pha
EE3000-Tín hiệu và hệ thống 10
Ví dụ 2: Đáp ứng tần số mạch RC
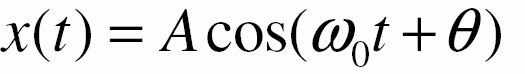
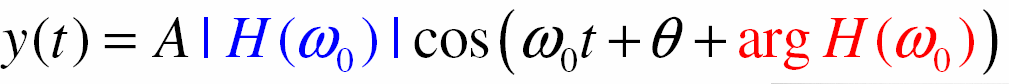
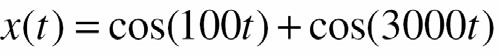
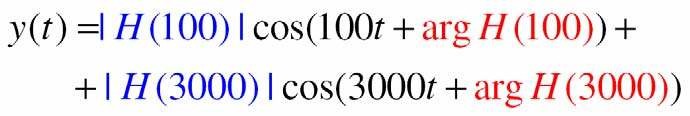
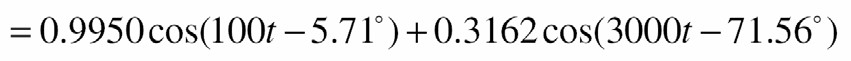


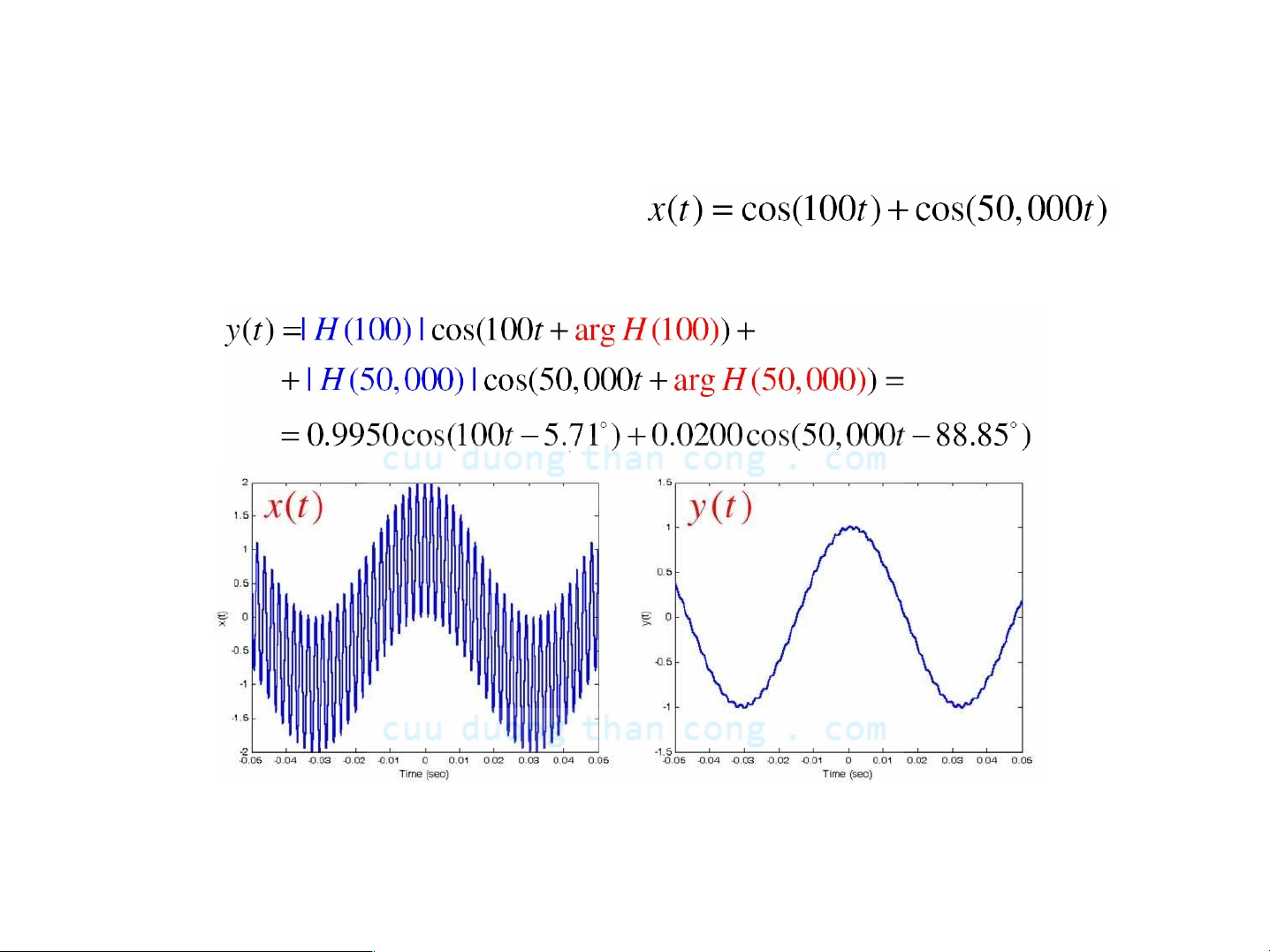
- Kiến thức về đáp ứng tần số Η(ω) cho phép ta tính toán đáp ứng y(t) của hệ với bất kỳ tín hiệu vào sin nào
bởi vì
- Giả sử 1 / RC = 1000 và
- Do đó tín hiệu ra Ià
Ví dụ 2: Đáp ứng tần số mạch RC
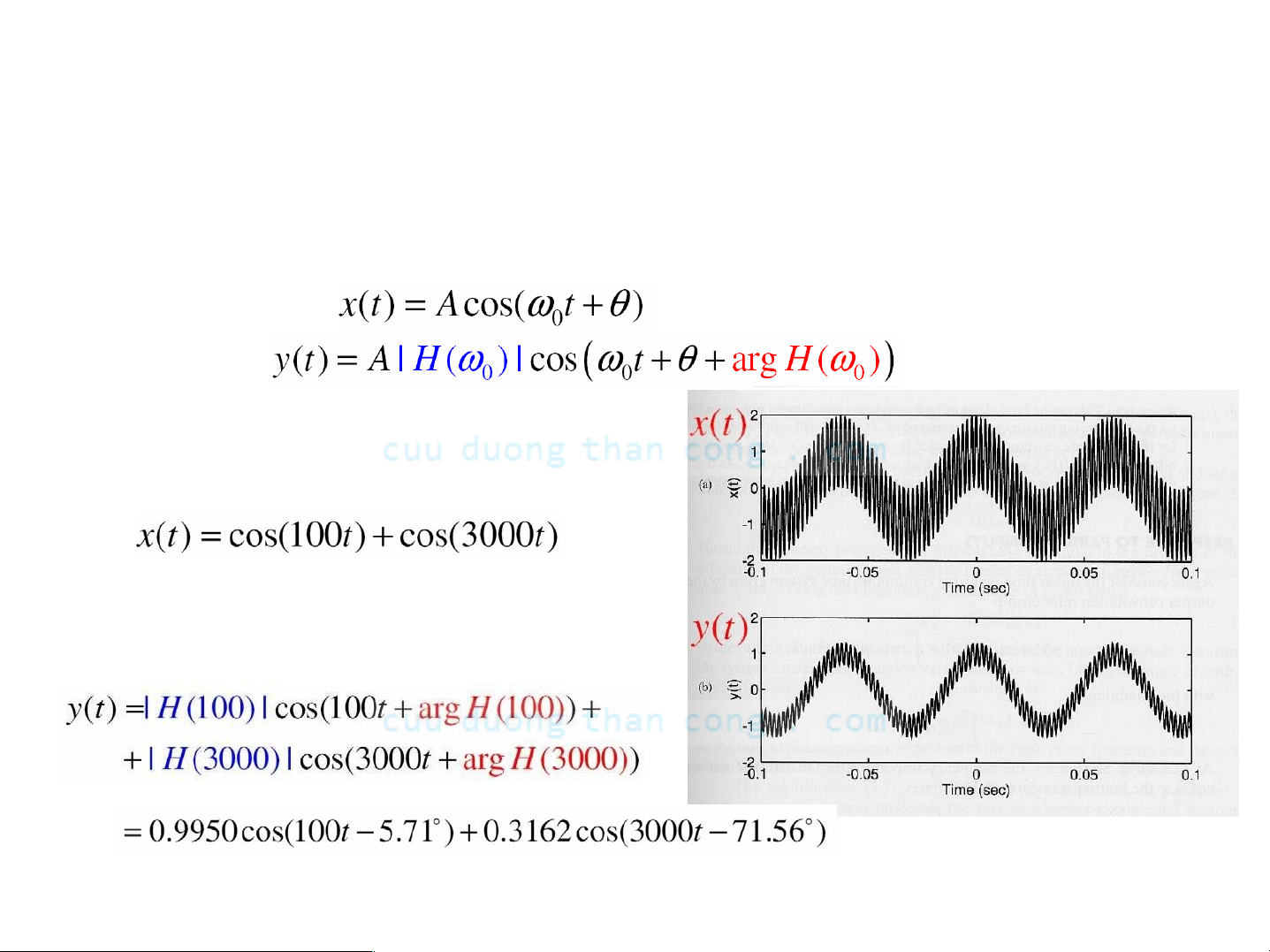
- Giả sử 1 / RC = 1000 và bây giờ
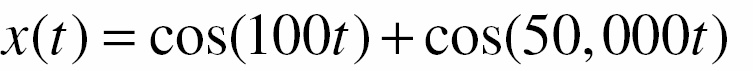
- Do đó tín hiệu ra Ià
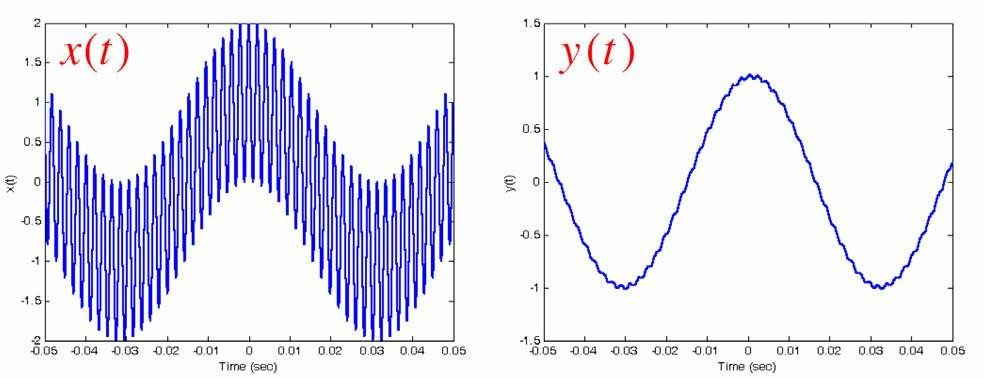
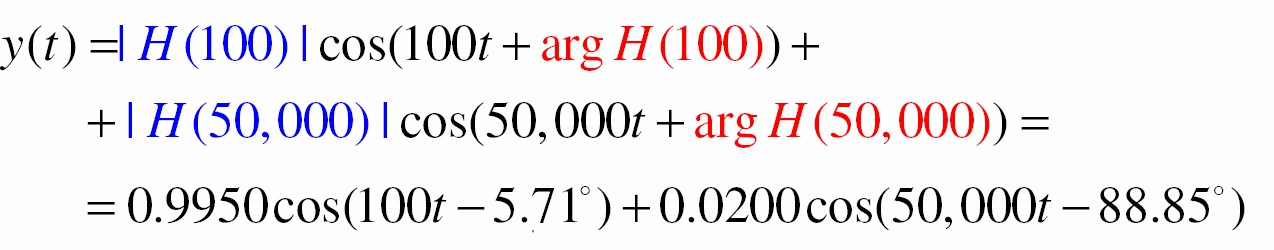


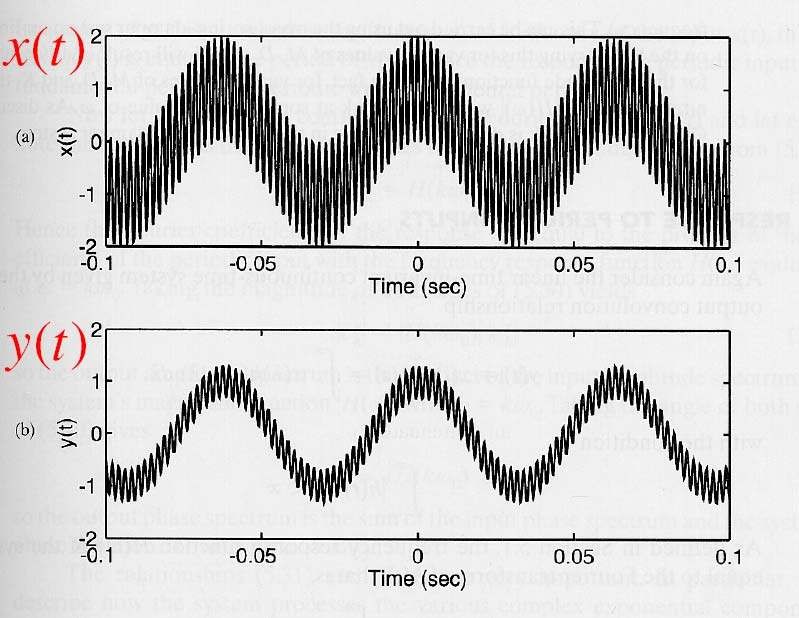
Mạch RC có tính chất của bộ Iọc thông thấp, cho phép những tín hiệu sin tần số thấp đi qua và Iàm suy giảm những tín hiệu sin tần số cao
Đáp ứng với tín hiệu tuần hoàn
- Giả sử tín hiệu vào x(t) Ià tuần hoàn với chu kỳ T
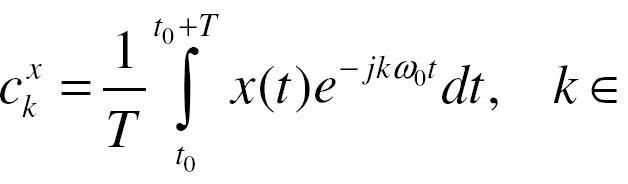 Chuỗi Fourier của nó Ià
Chuỗi Fourier của nó Ià
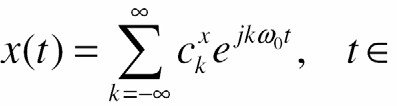 R trong đó Z
R trong đó Z
 Sử dụng các kết quả trước và tính chất tuyến tín, tín hiệu ra của hệ Ià
Sử dụng các kết quả trước và tính chất tuyến tín, tín hiệu ra của hệ Ià
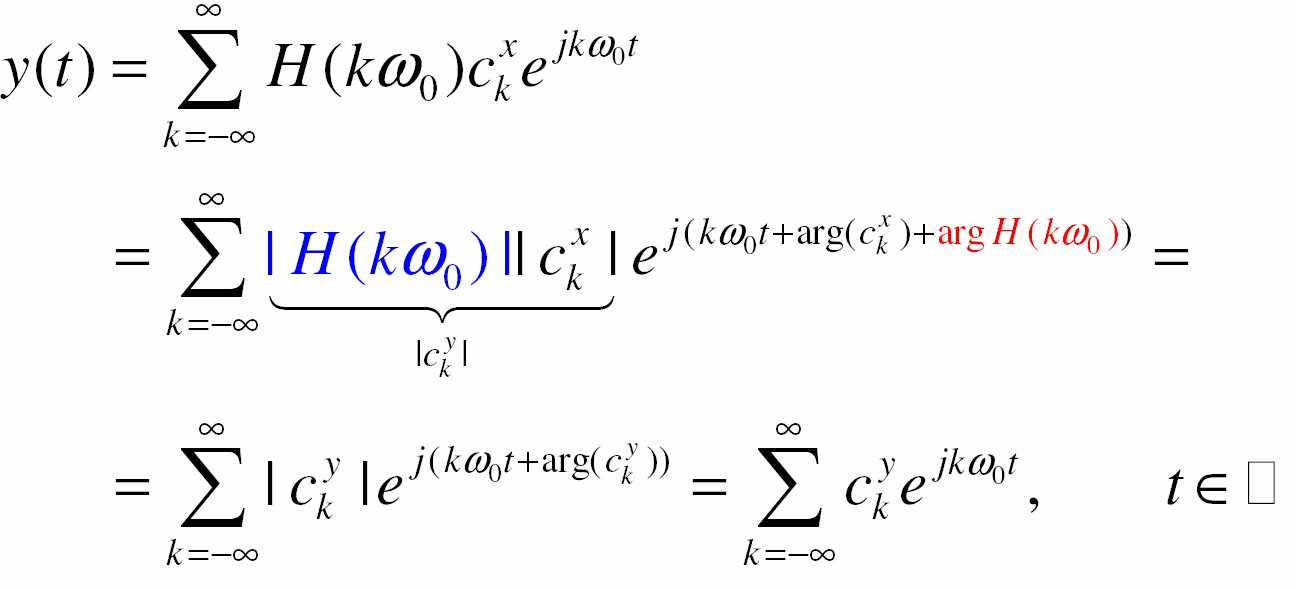

R
EE3000-Tín hiệu và hệ thống
13
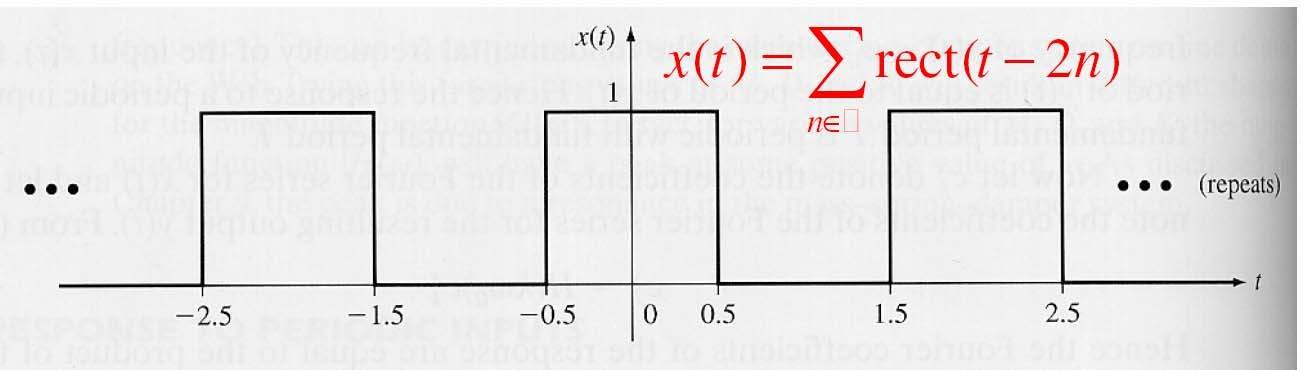
Ví dụ 3: Đáp ứng mạch RC với dãy xung chữ nhật
- Xét mạch điện RC với tín hiệu vào
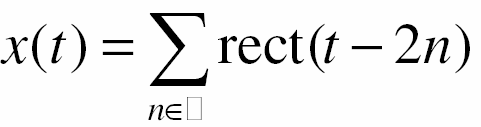

Z
- Biến đổi Fourier của nó Ià

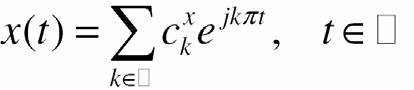
R
Z
EE3000-Tín hiệu và hệ thống
với
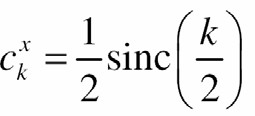 14
14
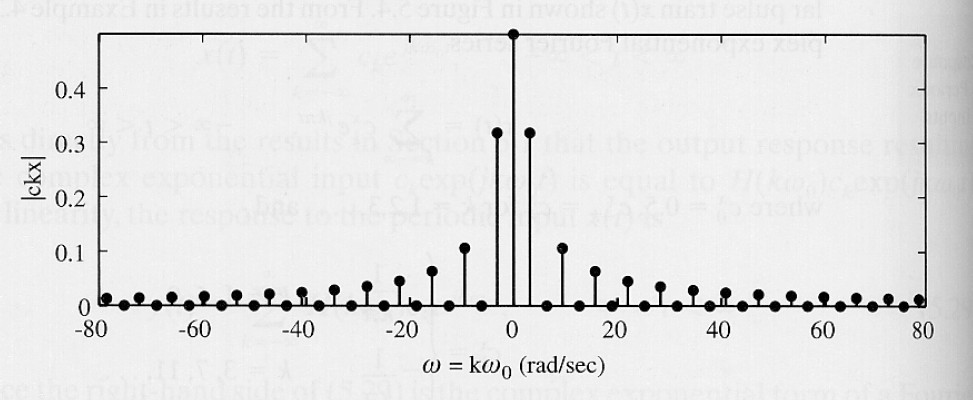
Ví dụ 3: Đáp ứng mạch RC với dãy xung chữ nhật
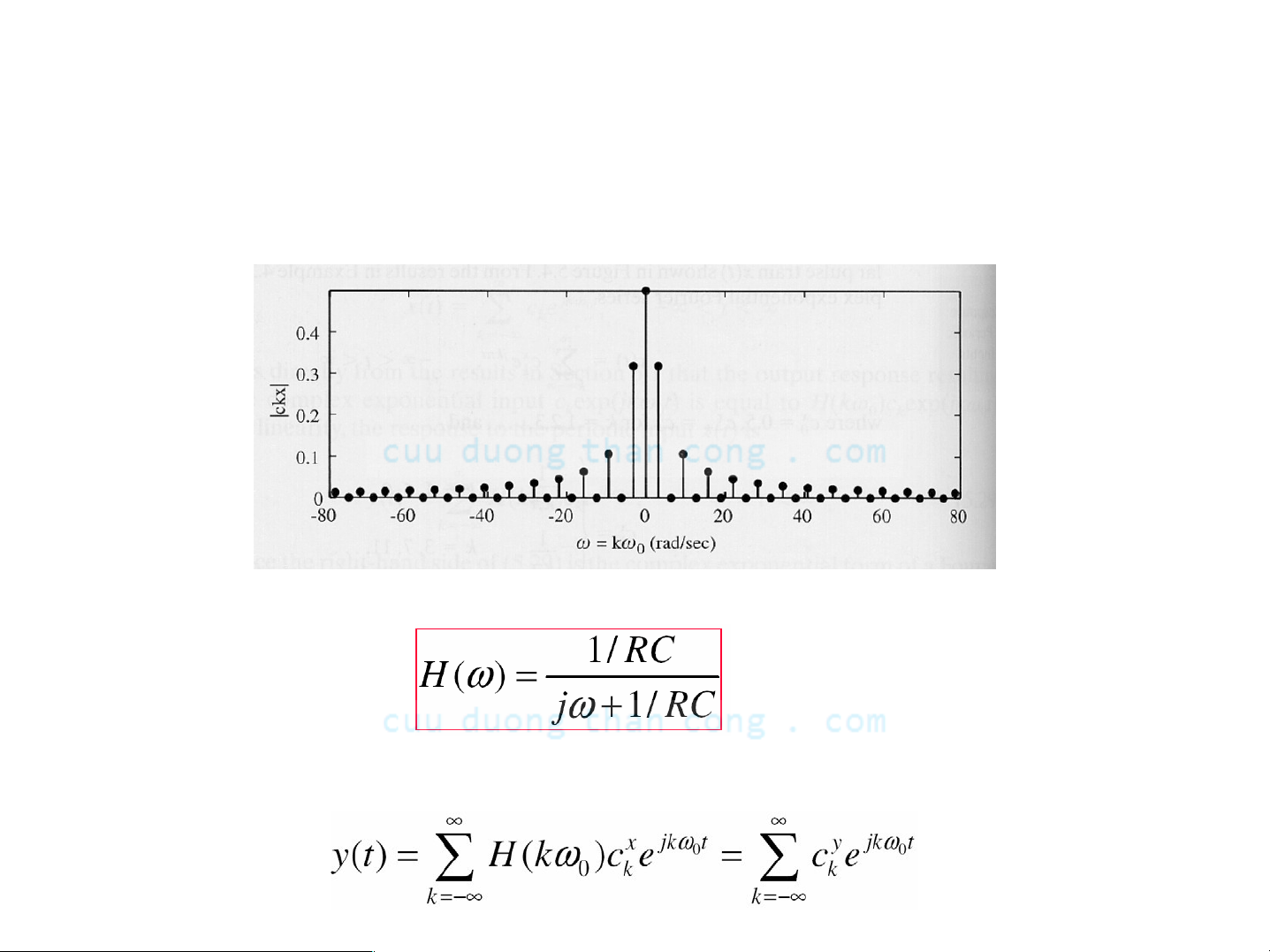
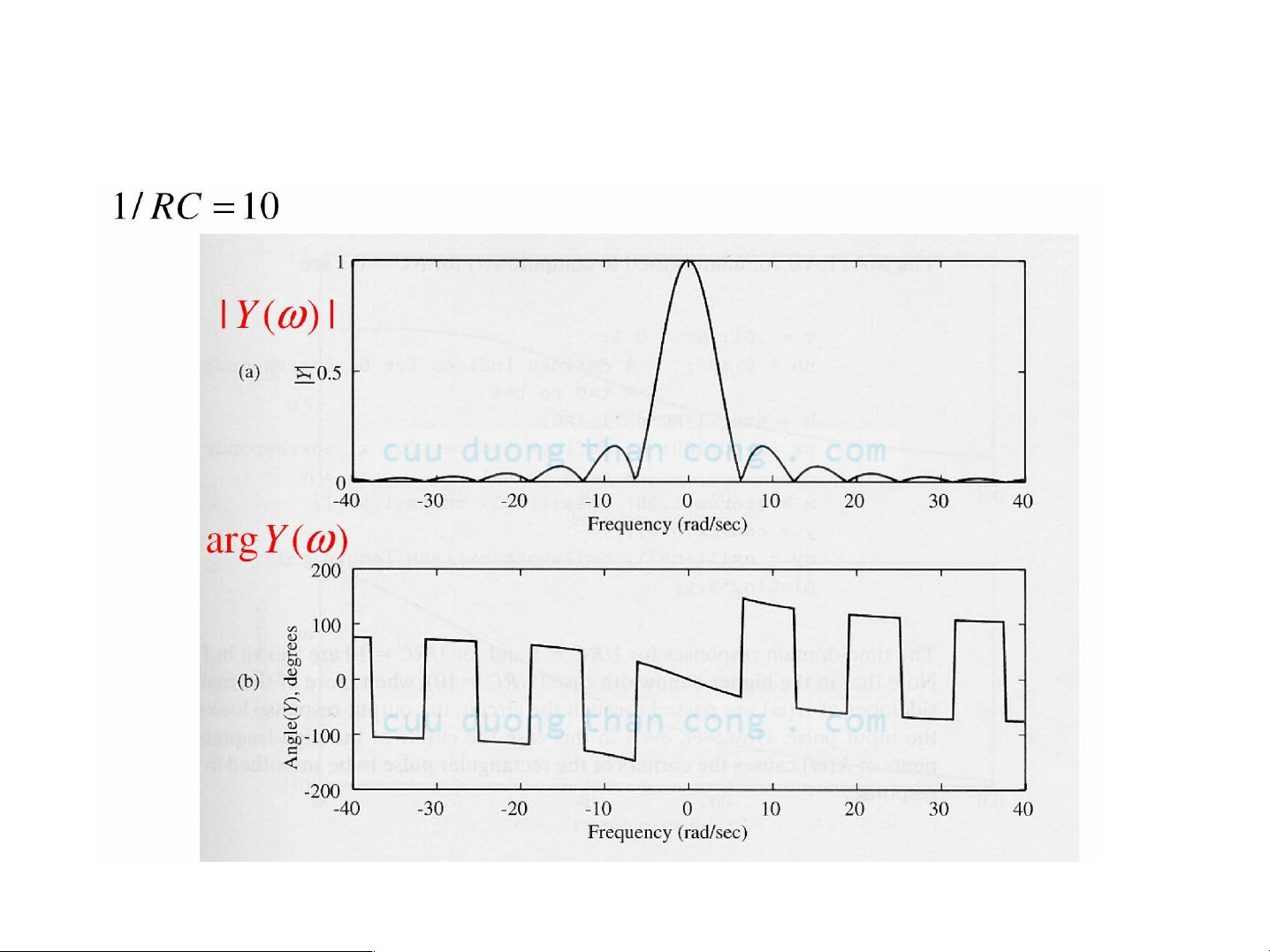
- Phổ biên độ |ckx| của tín hiệu x(t)

- Đáp ứng tần số của mạch RC Ià
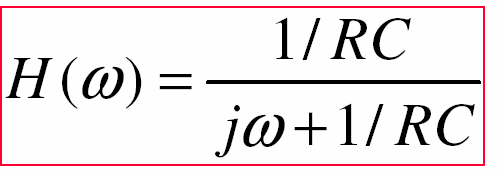

- Do đó chuỗi Fourier của tín hiệu ra được cho bởi
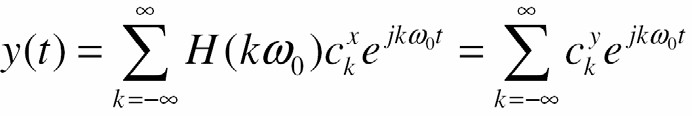
15
EE3000-Tín hiệu và hệ thống
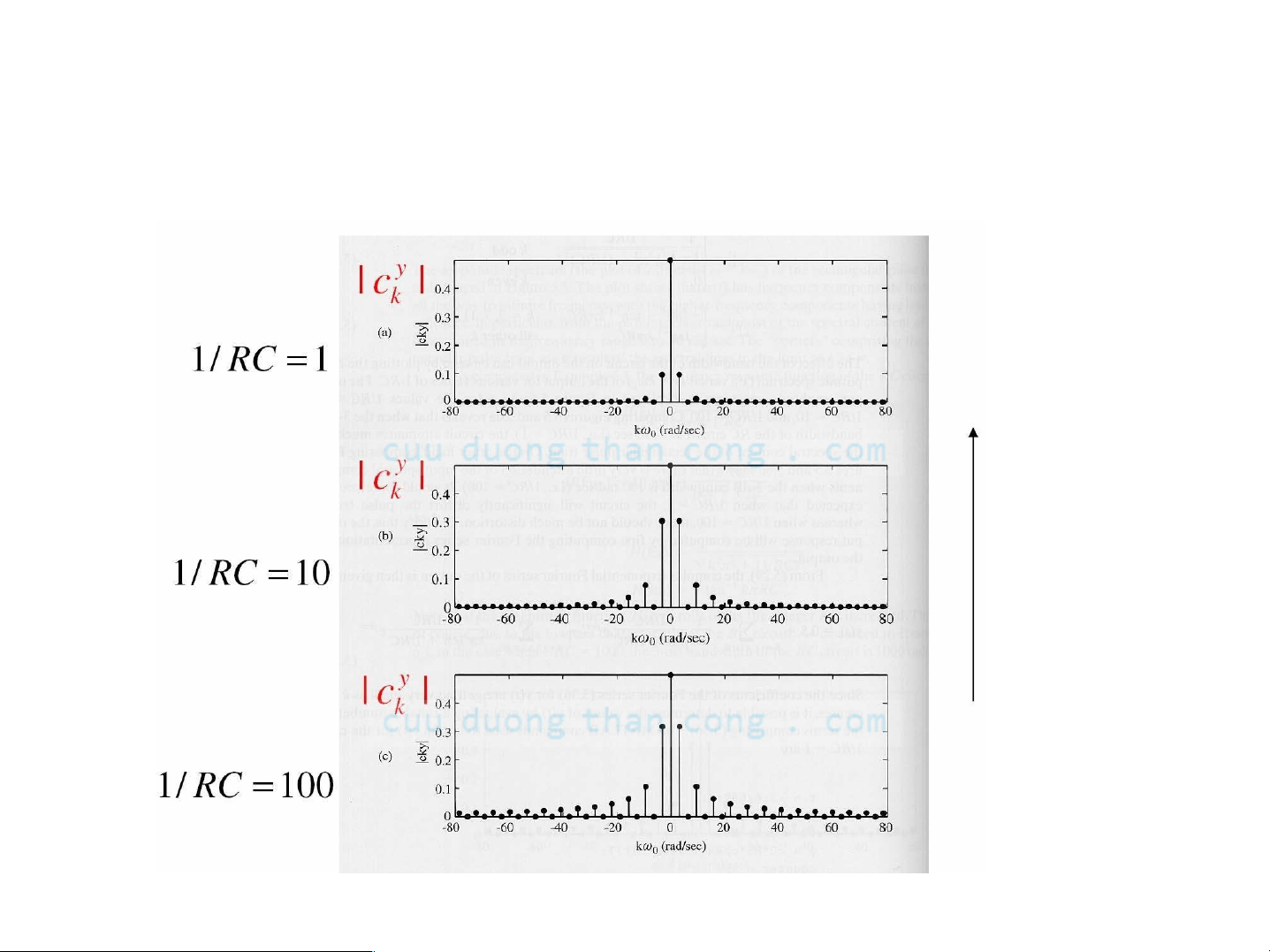
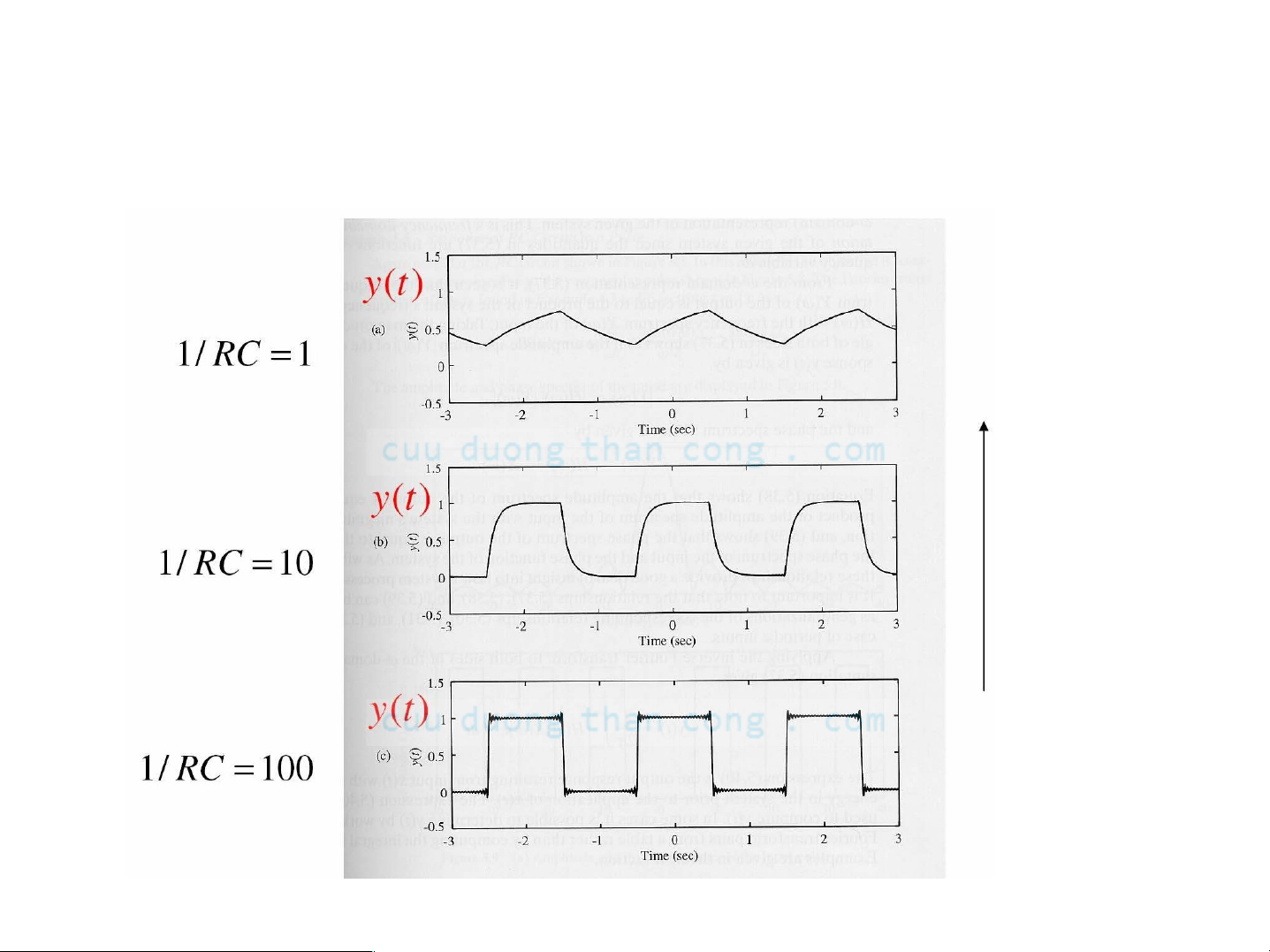
Ví dụ 3: Đáp ứng mạch RC với dãy xung chữ nhật
Bộ Iọc có tính chọn Iọc hơn
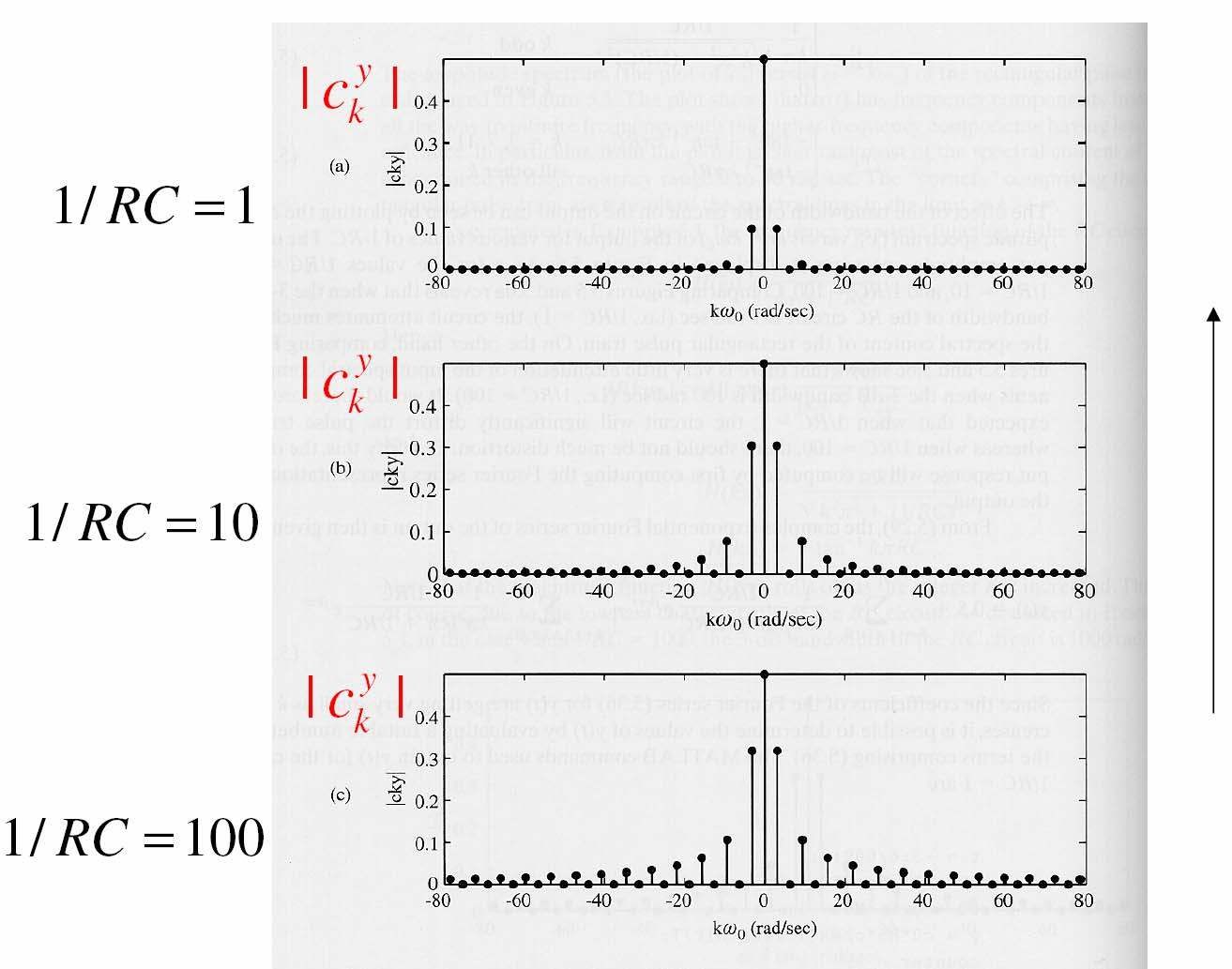


Ví dụ 3: Đáp ứng mạch RC với dãy xung chữ nhật
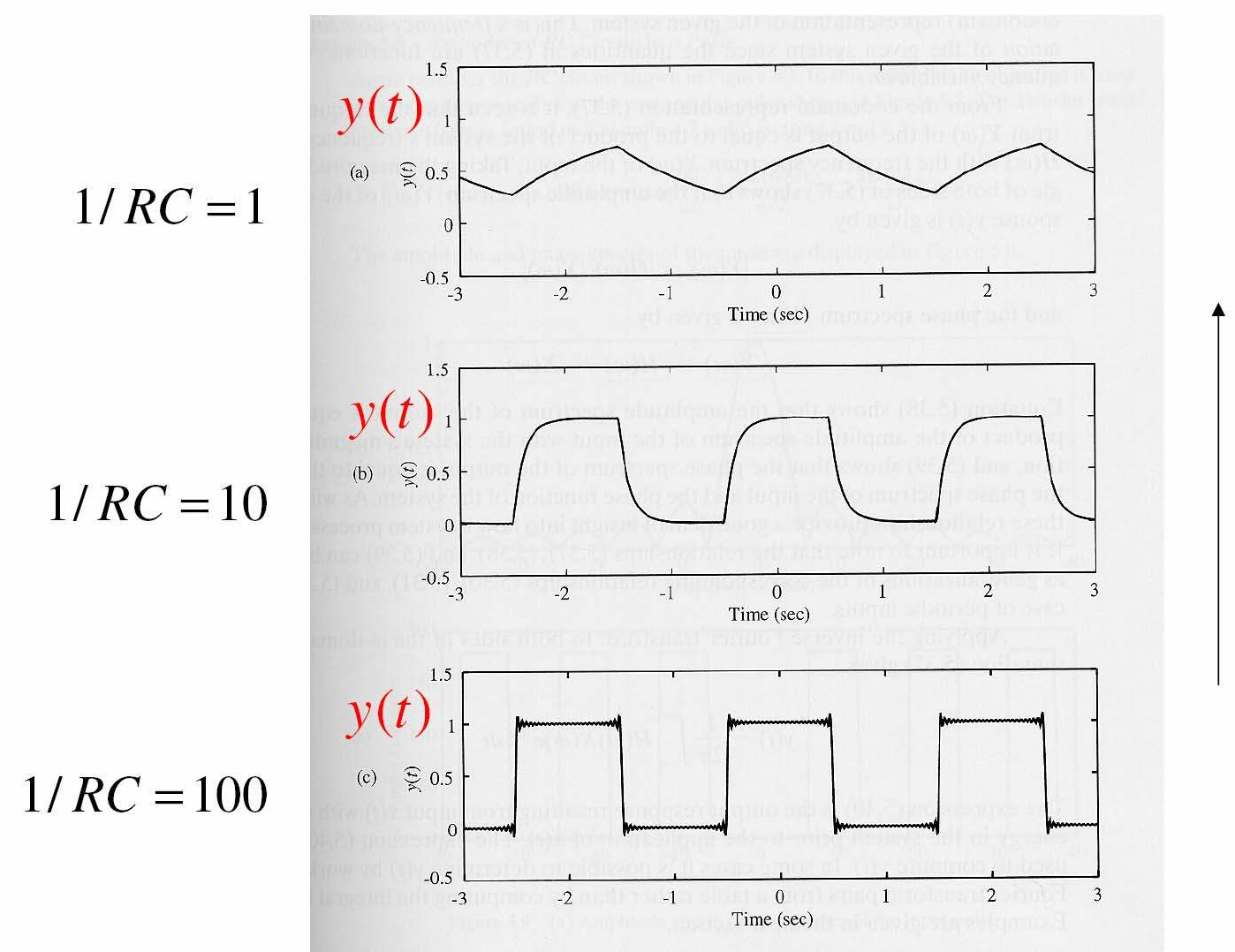

 Bộ Iọc có tính chọn Iọc hơn
Bộ Iọc có tính chọn Iọc hơn
Chương 4: Đáp ứng tần số và Iọc tín hiệu
- Đáp ứng tần số của hệ LTI Iiên tục
 Đáp ứng của hệ với tín hiệu tuần hoàn
Đáp ứng của hệ với tín hiệu tuần hoàn
- Đáp ứng tần số của hệ LTI Iiên tục
4.1.2 Đáp ứng của hệ với tín hiệu không tuần hoàn
- Đáp ứng tần số của hệ ghép nối
- Đồ thị Bode
 Các bộ Iọc tín hiệu
Các bộ Iọc tín hiệu
Đáp ứng với tín hiệu không tuần hoàn
- Xét hệ LTI Iiên tục sau
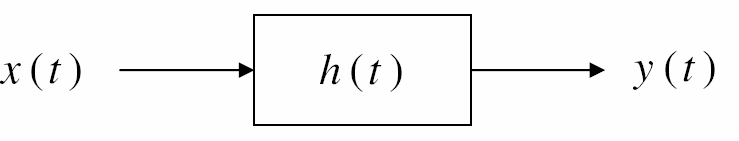
- Quan hệ vào/ra được cho bởi
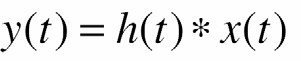
được biểu diễn trong miền tần số Ià
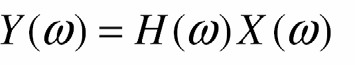

- Do đó phổ biên độ của tín hiệu ra y(t) Ià


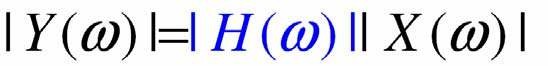
và phổ pha của nó
EE3000-Tín hiệu và hệ thống 19
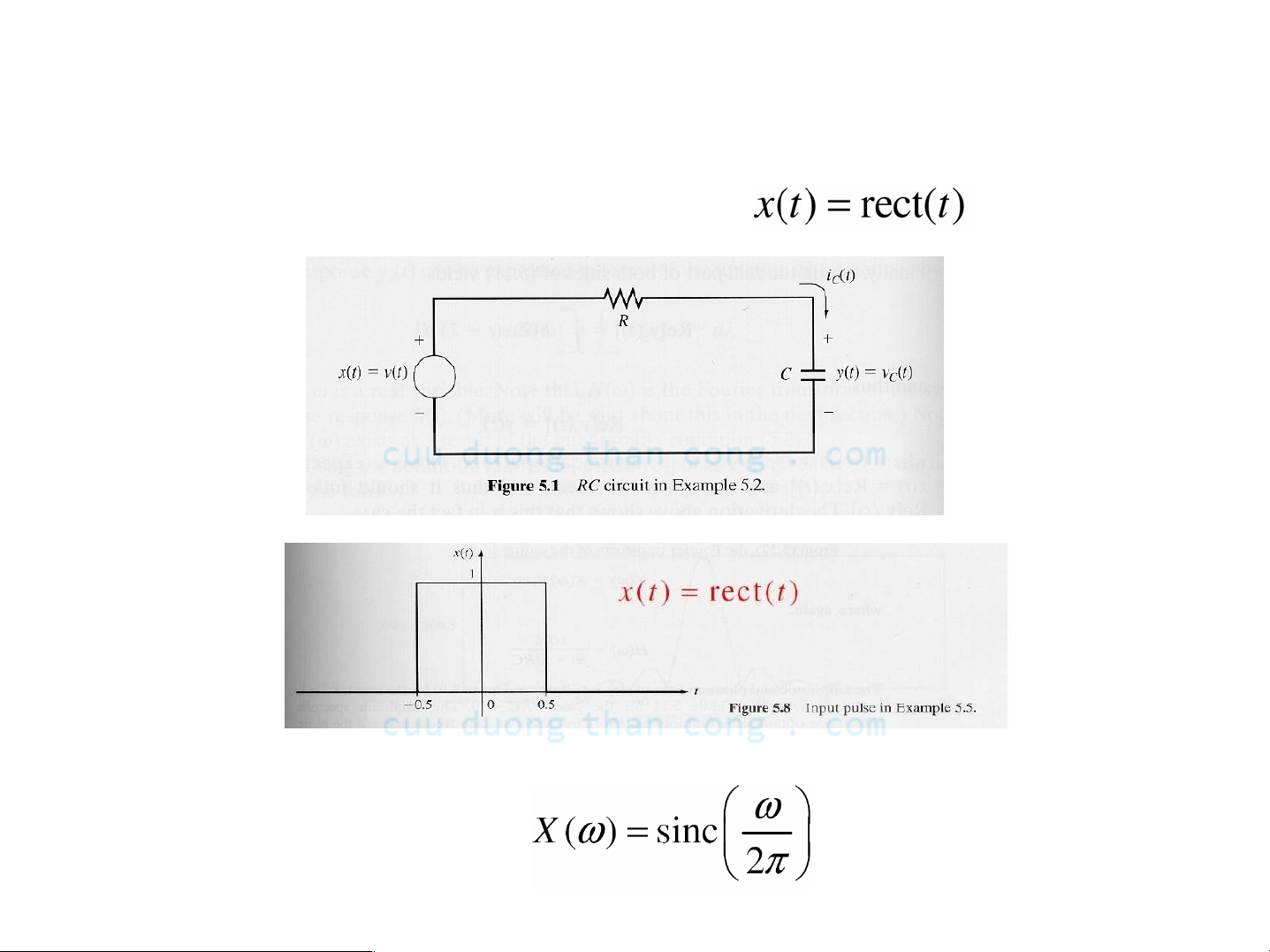
Ví dụ: Mạch RC với xung vuông
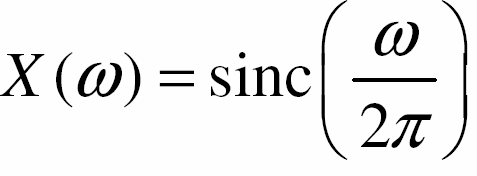 Xét mạch điện RC với tín hiệu vào
Xét mạch điện RC với tín hiệu vào 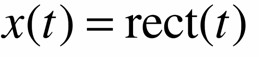

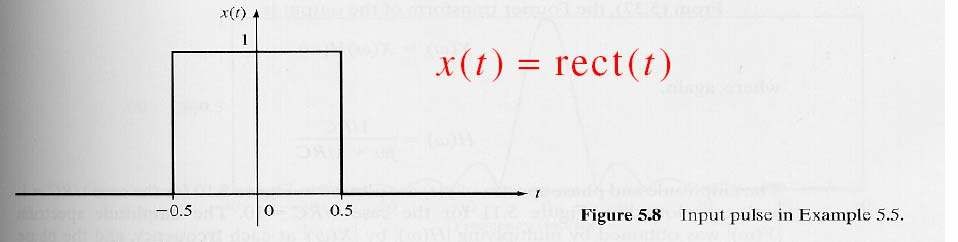

- Biến đổi Fourier của x(t) Ià
EE3000-Tín hiệu và hệ thống 20
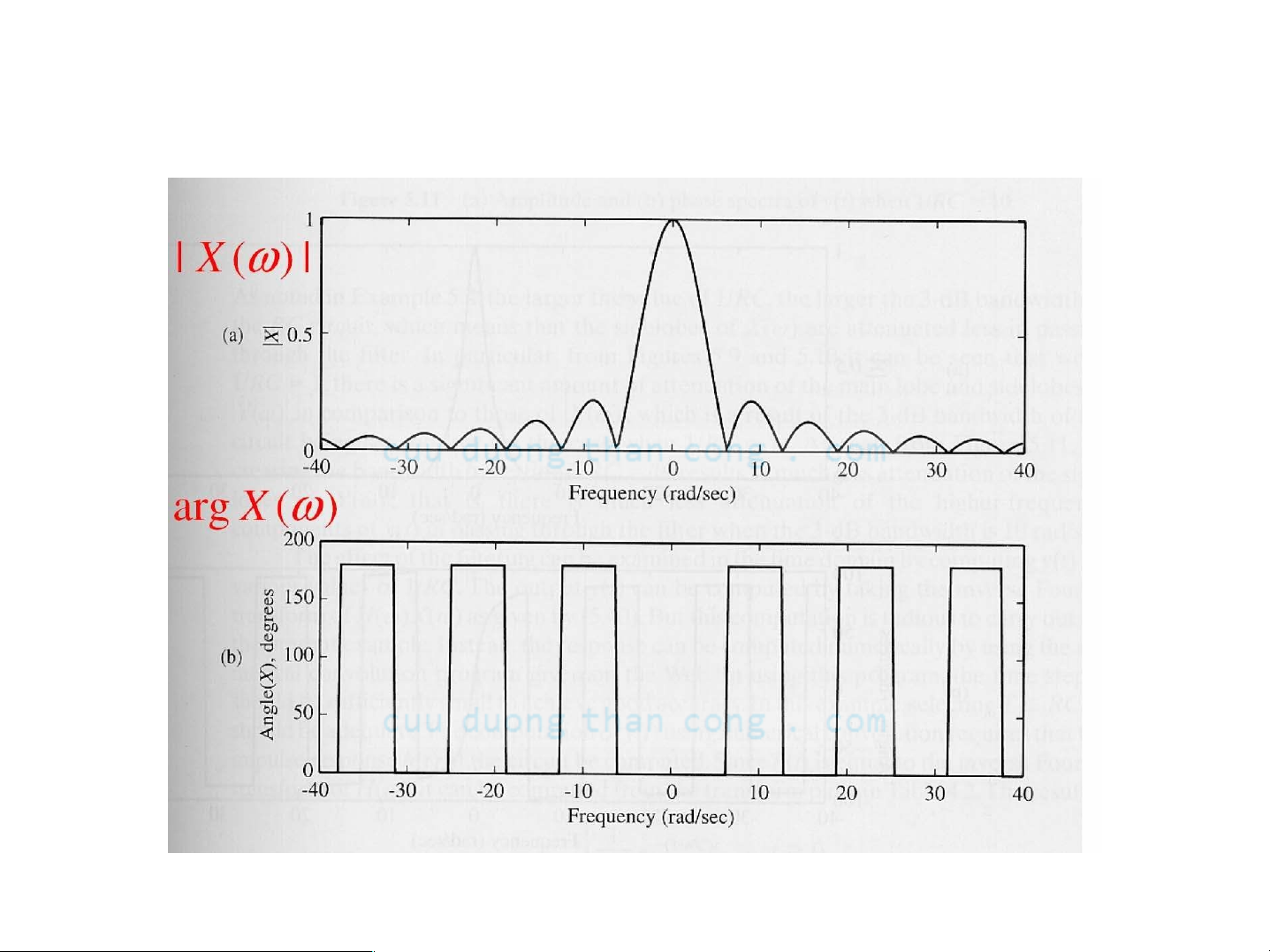
Ví dụ: Mạch RC với xung vuông
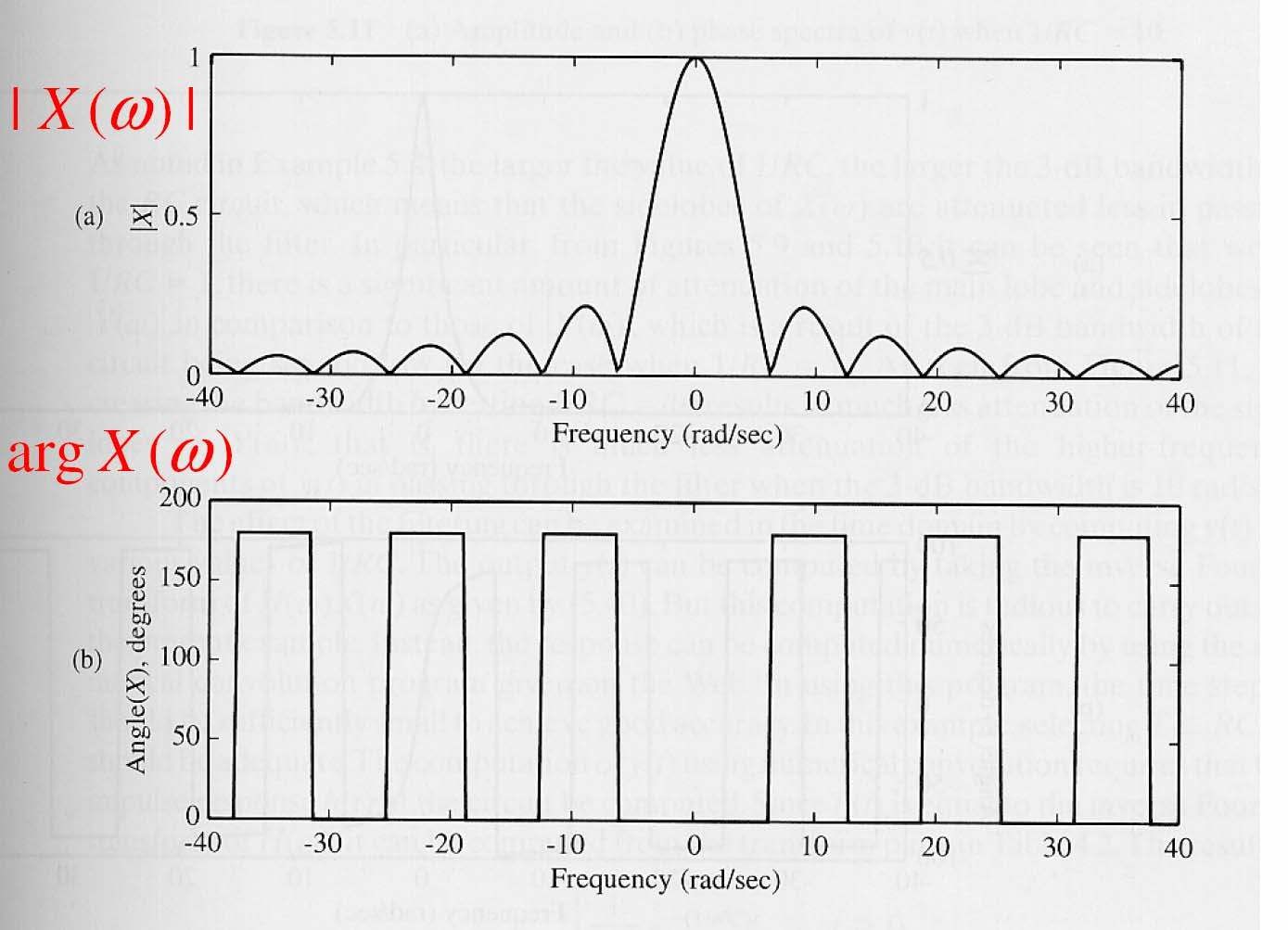


EE3000-Tín hiệu và hệ thống 21
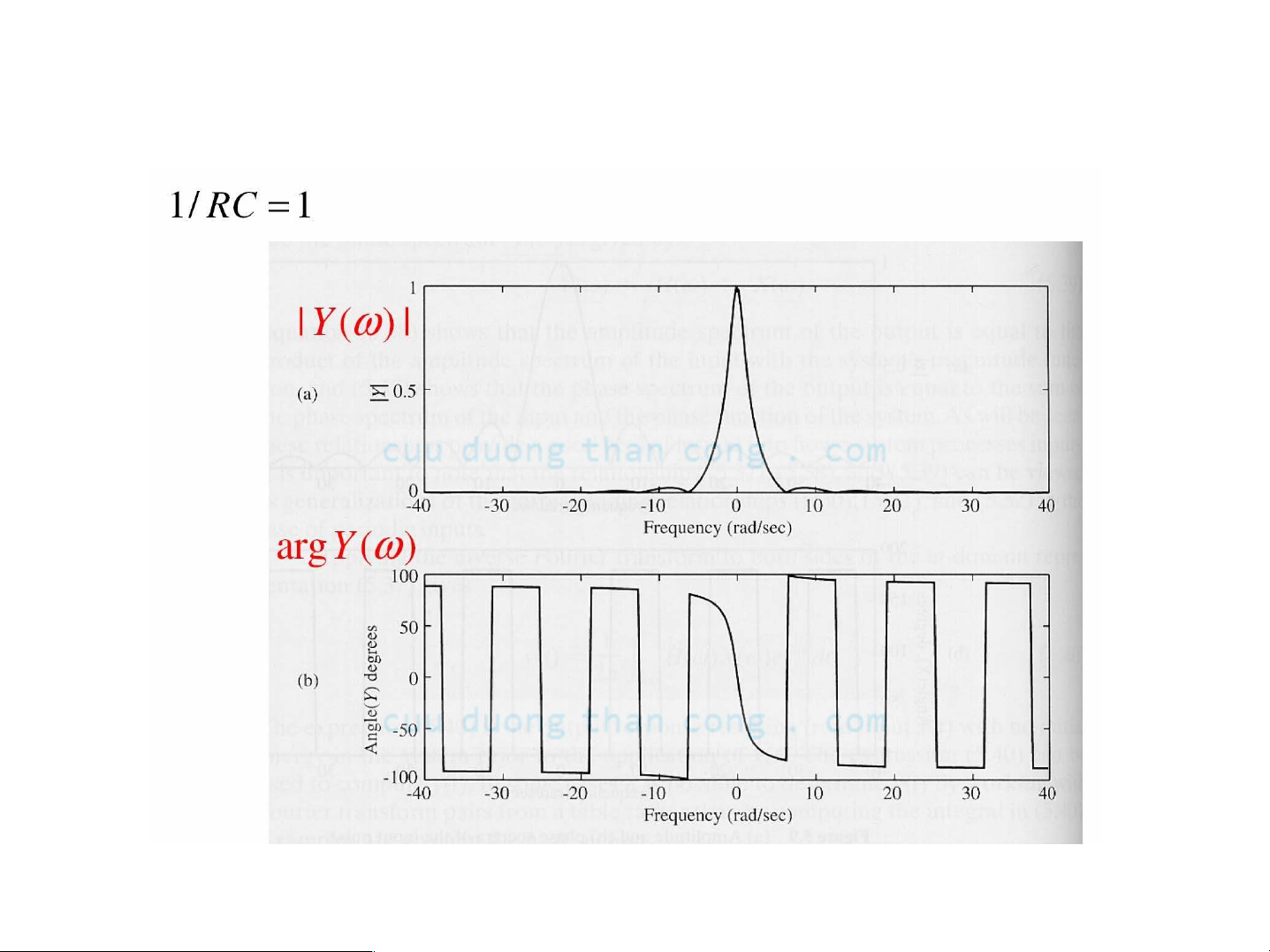
Ví dụ: Mạch RC với xung vuông
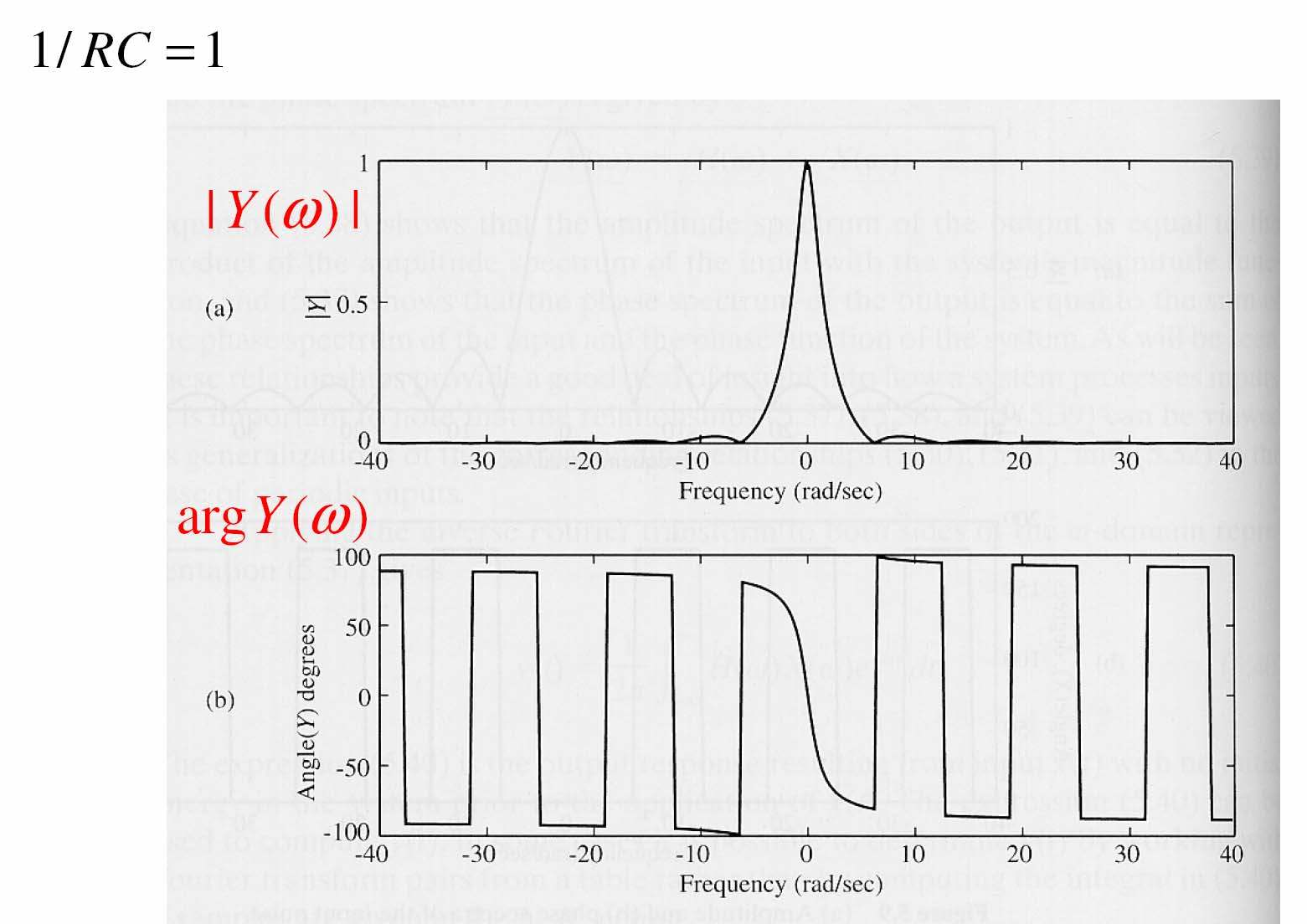


Ví dụ: Mạch RC với xung vuông
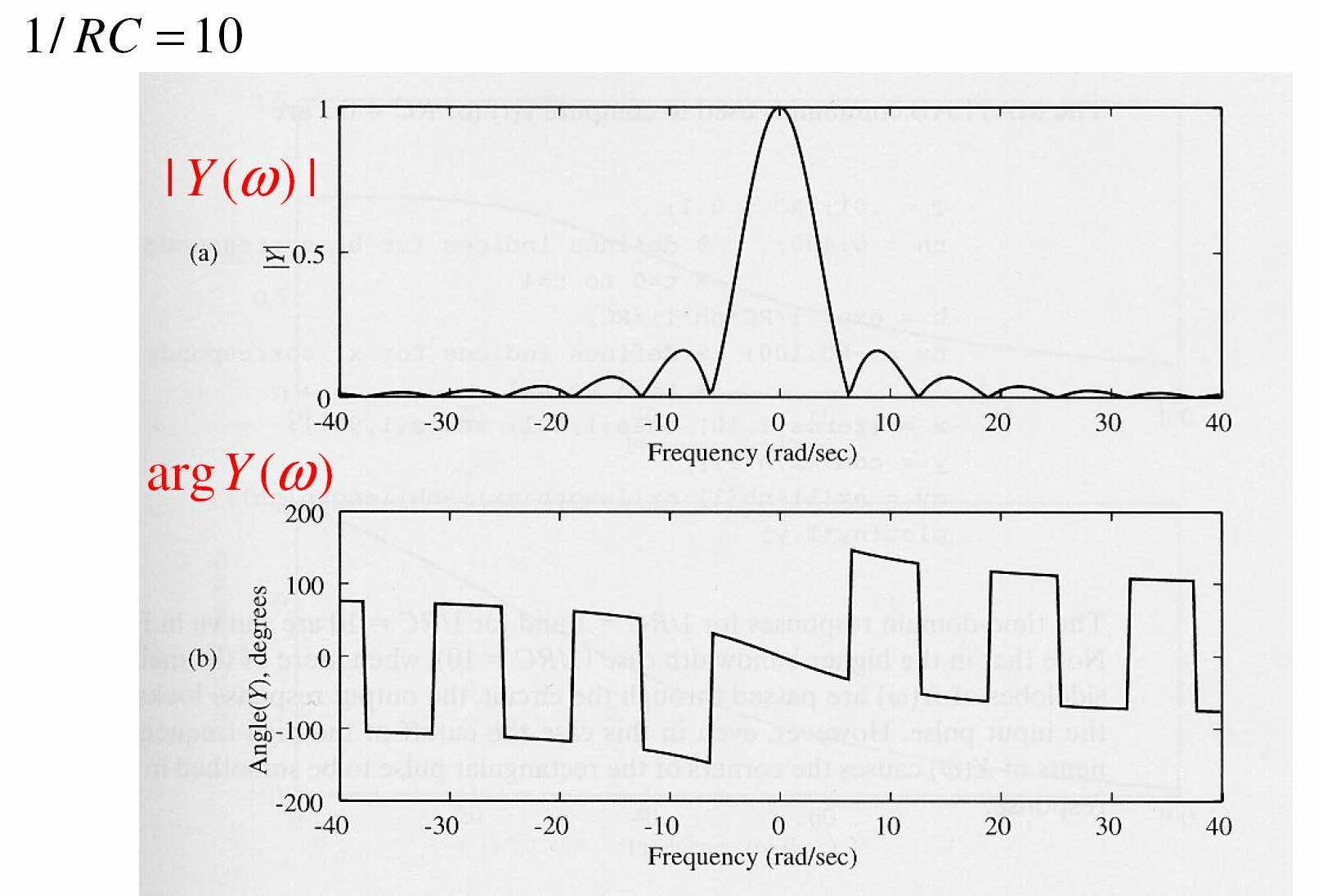


23
EE3000-Tín hiệu và hệ thống
Ví dụ: Mạch RC với xung vuông
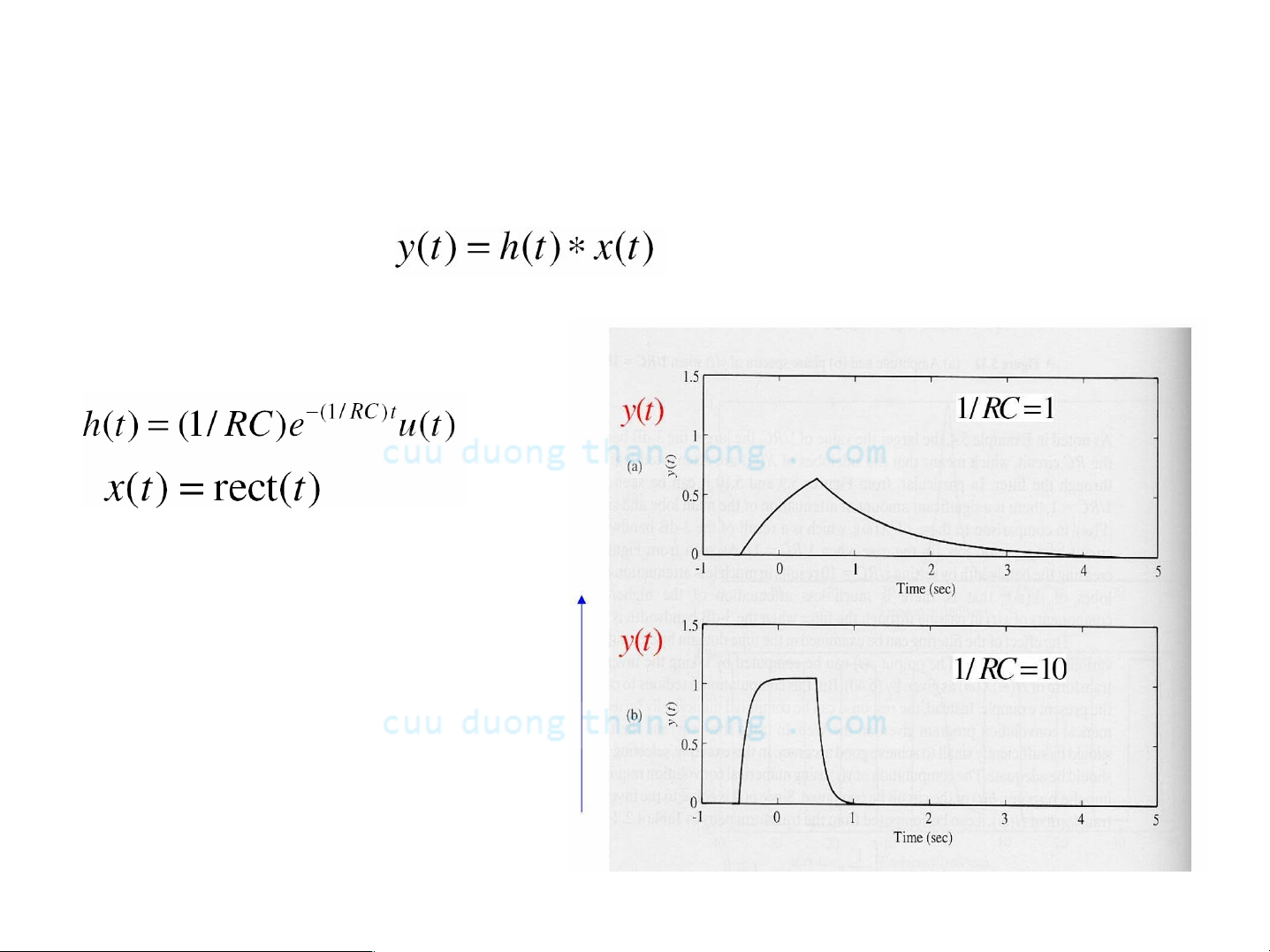
- Đáp ứng của hệ trong miền thời gian có thể được xác định bằng cách tính tích chập
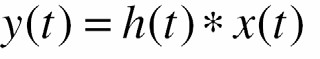
trong đó
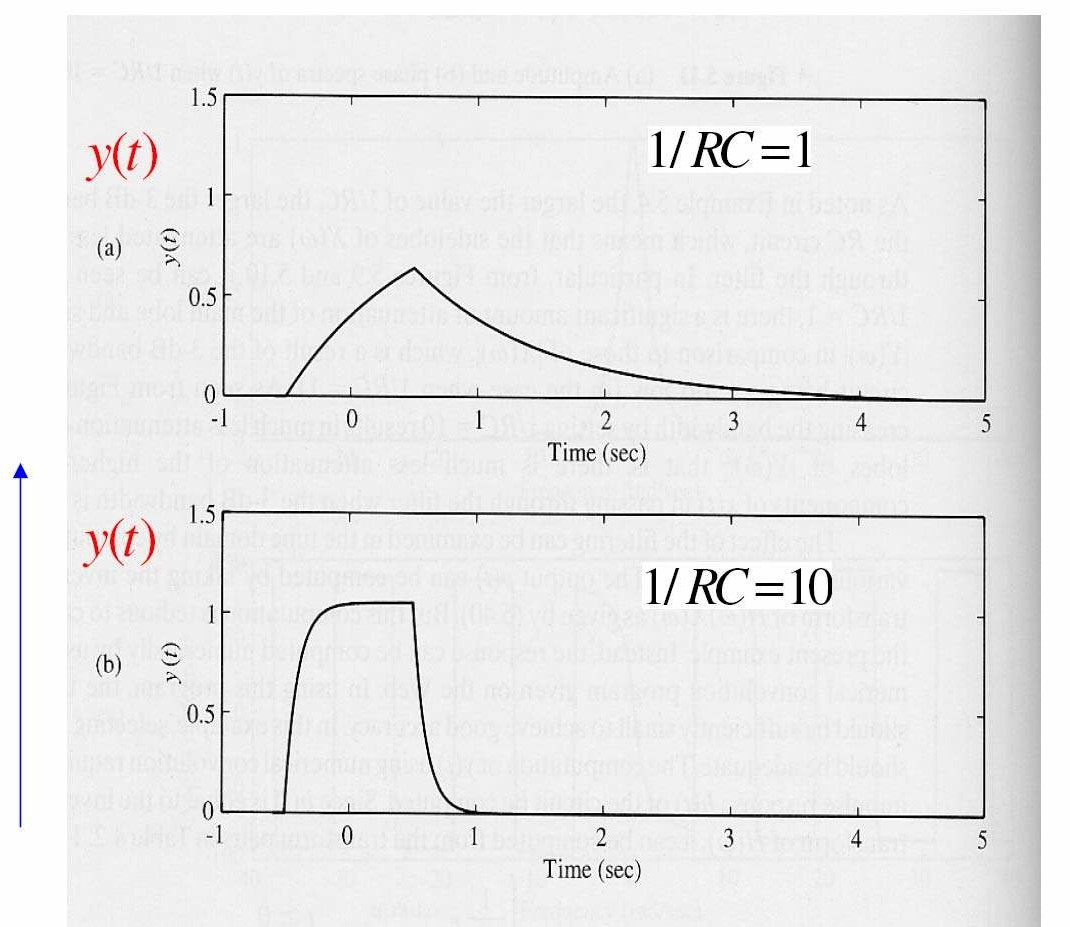
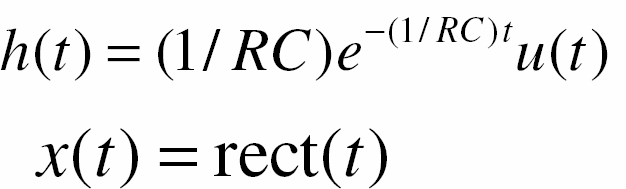


Bộ Iọc có tính chọn Iọc hơn
EE3000-Tín hiệu và hệ thống 24
Đáp ứng tần số dạng phân thức


Chương 4: Đáp ứng tần số và Iọc tín hiệu
- Đáp ứng tần số của hệ LTI Iiên tục
 Đáp ứng của hệ với tín hiệu tuần hoàn
Đáp ứng của hệ với tín hiệu tuần hoàn- Đáp ứng của hệ với tín hiệu không tuần hoàn
- Đáp ứng tần số của hệ LTI Iiên tục
4.2 Đáp ứng tần số của hệ ghép nối
- Đồ thị Bode
 Các bộ Iọc tín hiệu
Các bộ Iọc tín hiệu


Chương 4: Đáp ứng tần số và Iọc tín hiệu
- Đáp ứng tần số của hệ LTI Iiên tục
 Đáp ứng của hệ với tín hiệu tuần hoàn
Đáp ứng của hệ với tín hiệu tuần hoàn- Đáp ứng của hệ với tín hiệu không tuần hoàn
 Đáp ứng tần số của hệ ghép nối
Đáp ứng tần số của hệ ghép nối
- Đáp ứng tần số của hệ LTI Iiên tục
4.3 Đồ thị Bode
4.4 Các bộ Iọc tín hiệu
Khuếch đại hệ thống và dịch pha







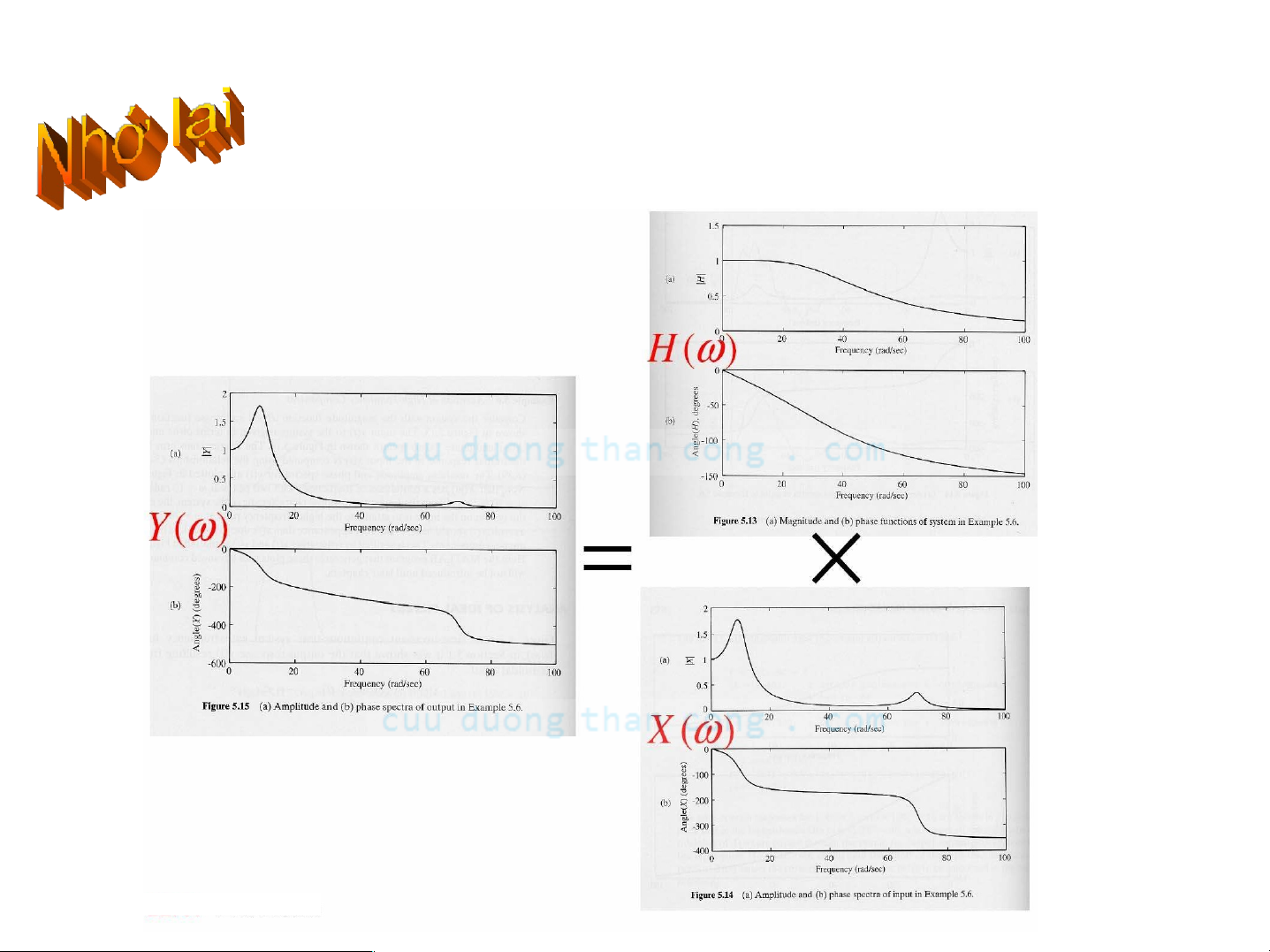
- Trong miền tần số, ảnh hưởng của hệ thống đối với tín hiệu vào có thành phần tần số ω Ià
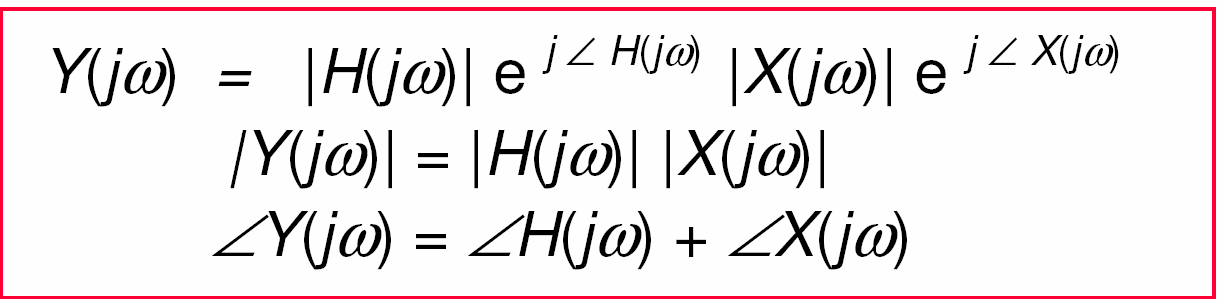

- Ảnh hưởng của hệ thống, Η(jω) đối với biến đổi Fourier của tín hiệu vào Ià
- Co giãn biên độ bởi |Η(jω)|: thường được gọi Ià khuếch đại hệ thống
 Dịch pha của tín hiệu vào bằng cách thêm gọi Ià dịch pha
Dịch pha của tín hiệu vào bằng cách thêm gọi Ià dịch pha
Η(jω): thường được
- Những biến đổi này (sự méo biên độ và pha) có thể như/không như mong muốn và phải được hiểu rõ trong phân tích và thiết kế hệ thống.
VD: Tín hiệu vào Cos với hệ bậc 1






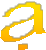

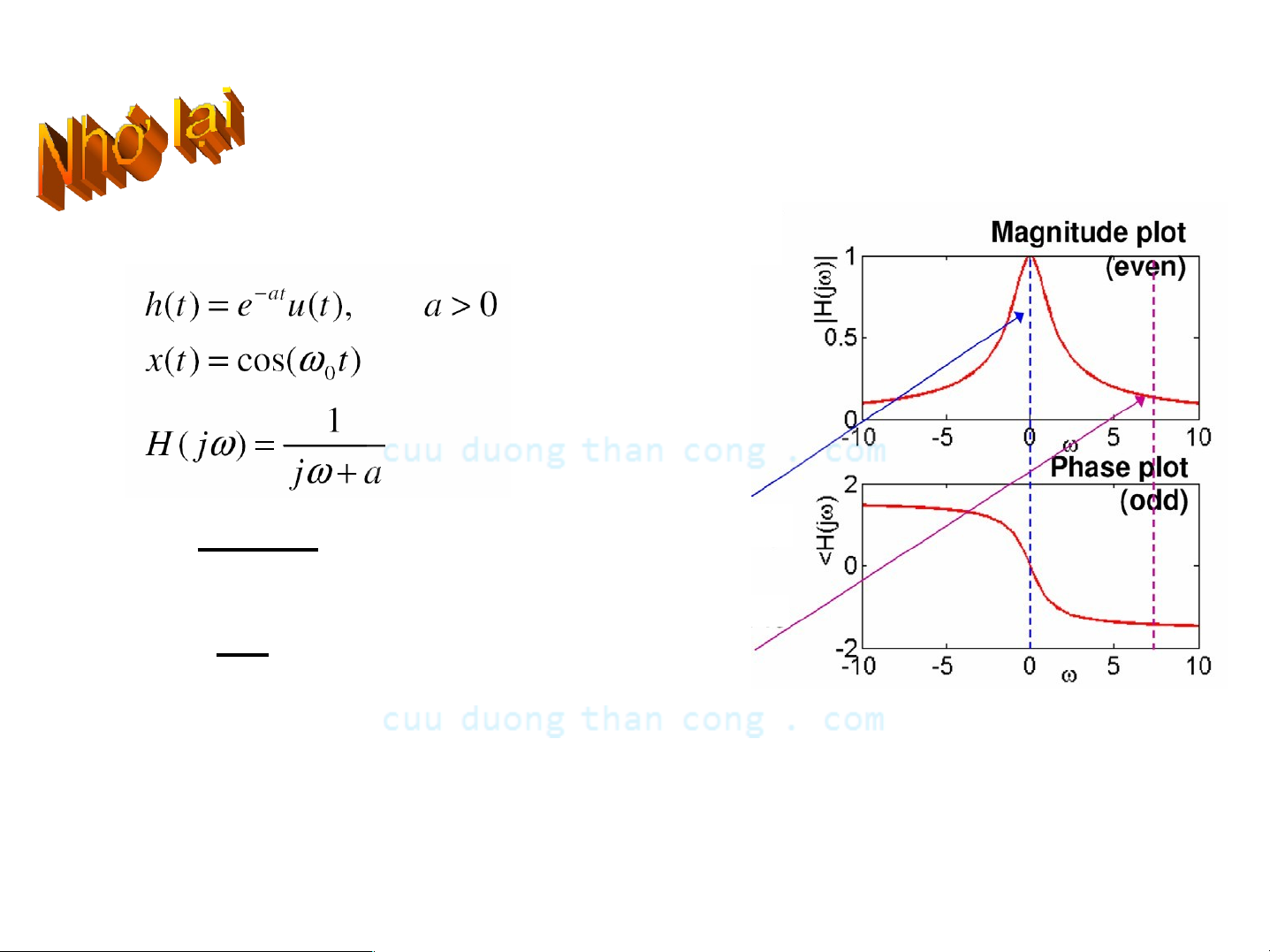
- Xét hệ LTI bậc một ổn định có tín hiệu vào cosin
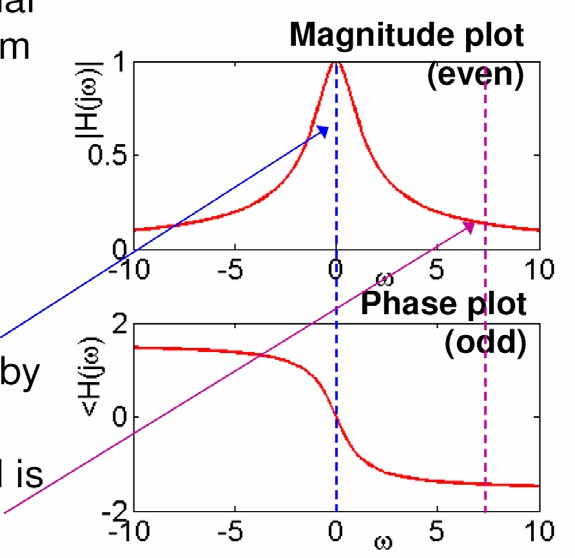
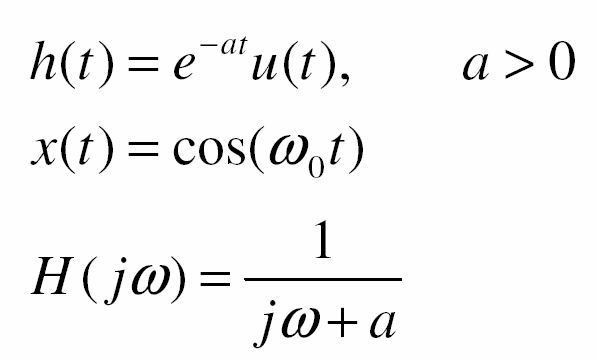

- Khi ω0 ở gần 0, tín hiệu vào được đi qua và biên độ được co giãn bởi 1/a
 Khi |ω0| Iớn, tín hiệu vào về cơ bản bị triệt tiêu
Khi |ω0| Iớn, tín hiệu vào về cơ bản bị triệt tiêu- Có nghĩa Ià hệ thống Ià một bộ Iọc thông thấp






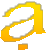
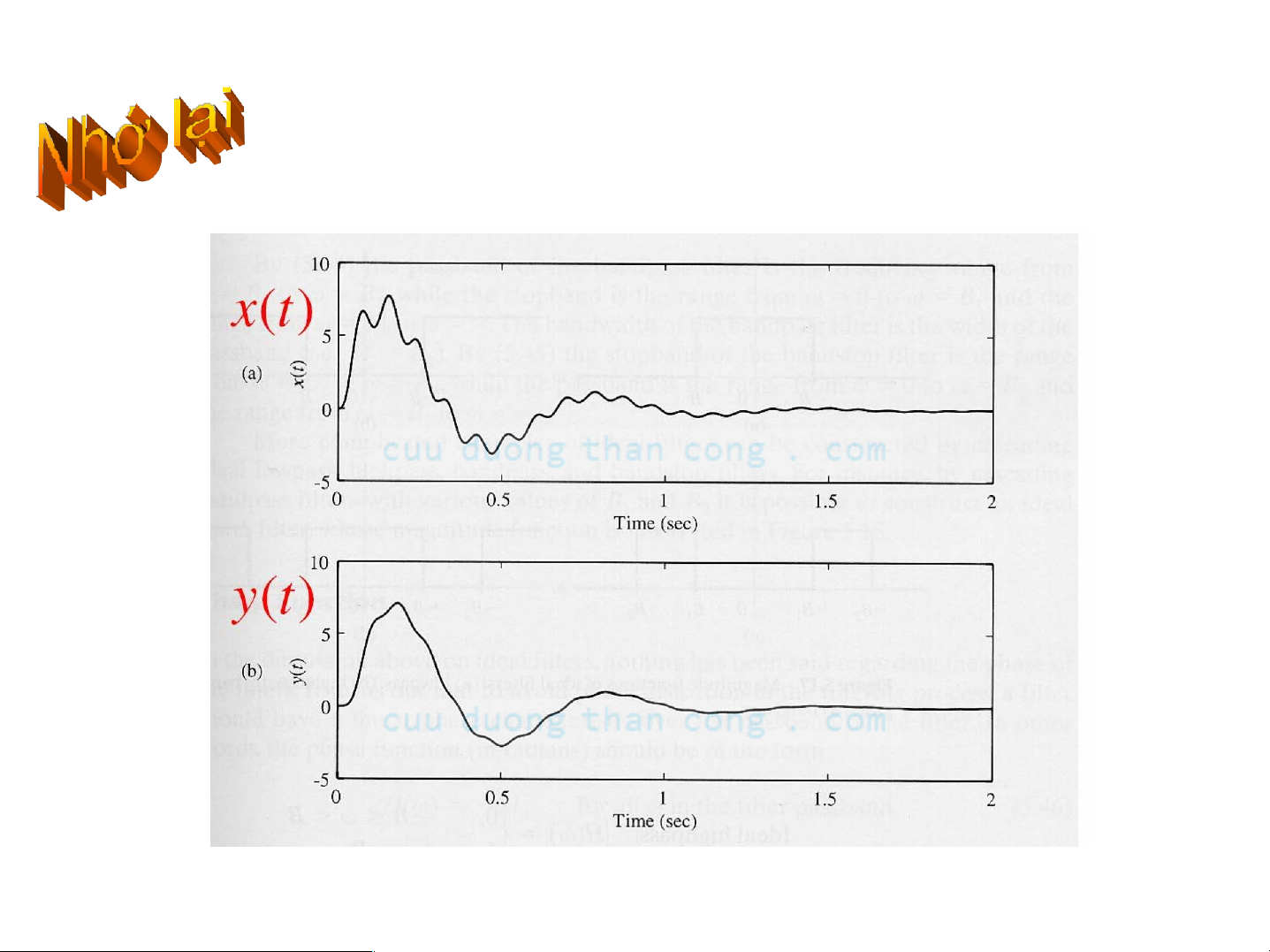
 VD: Suy giảm các thành phần tần số cao
VD: Suy giảm các thành phần tần số cao
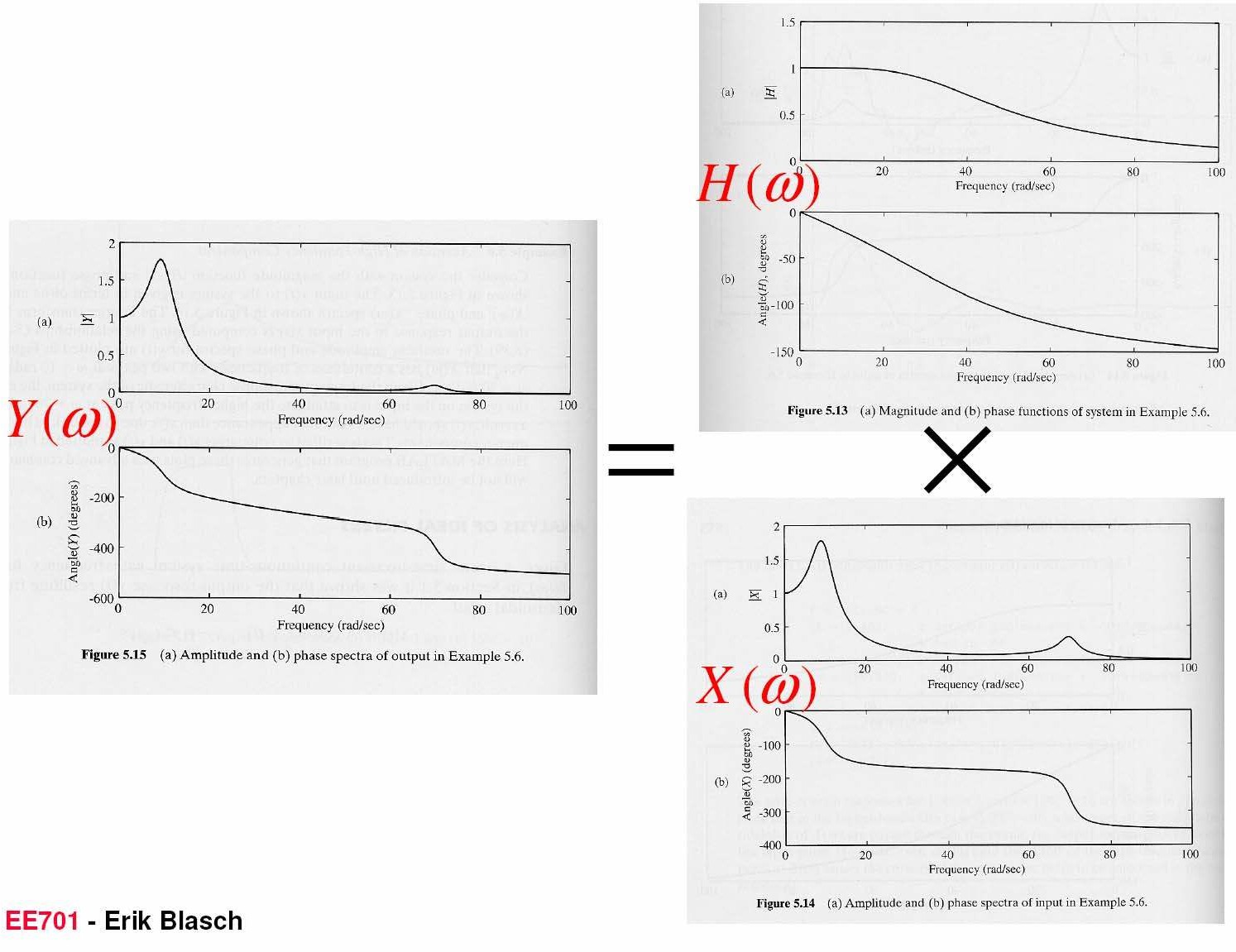


EE3000-Tín hiệu và hệ thốn
Suy giảm các thành phần tần số cao







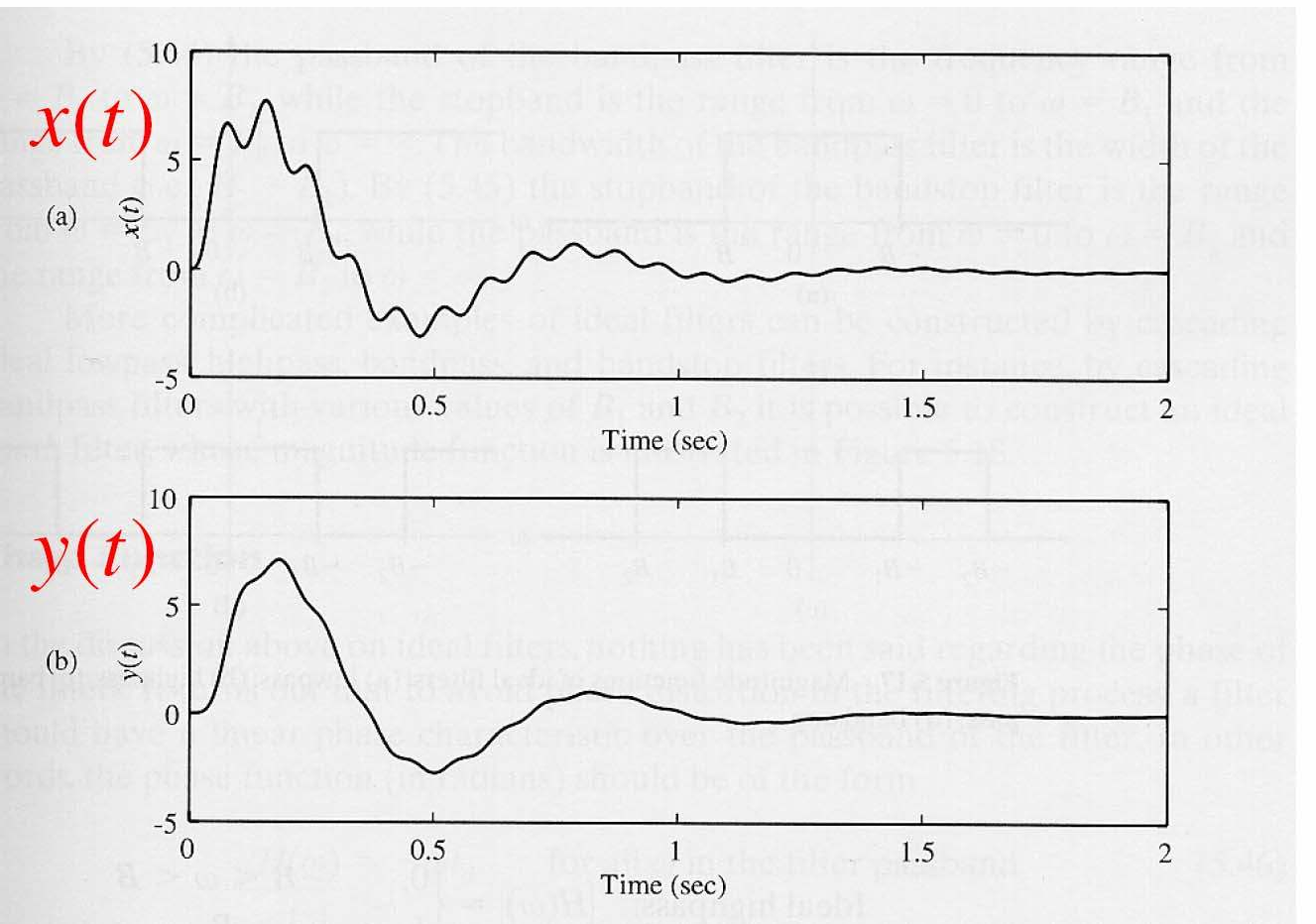


Các đồ thị pha và biên độ Iog
- Khi phân tích các đáp ứng của hệ thống, để tiện Iợi ta thường sử dụng thang đo Iog cho biên độ
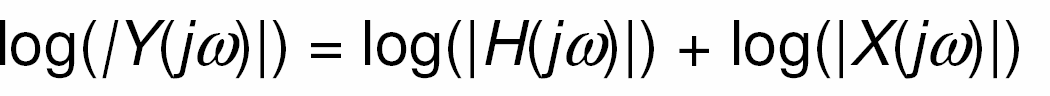
- Do đó độ thị biên độ chỉ đơn giản Ià cộng các đồ thị thành phần
 Đơn vị biên độ tương ứng Ià decibeIs (dB) : 20 Iog10
Đơn vị biên độ tương ứng Ià decibeIs (dB) : 20 Iog10- Tương tự, Iog hóa tần số cho phép ta quan sát được chi tiết dải tần số rộng hơn (quan trọng cho các bộ Iọc chọn tần số)
 Chú ý khi Iog hóa tần số, ta chỉ quan tâm đến những giá trị tần số dương
Chú ý khi Iog hóa tần số, ta chỉ quan tâm đến những giá trị tần số dương- Biên độ Ià hàm chẵn
- Pha Ià hàm Iẻ
Đồ thị Bode
- Đồ thị Bode của một hệ thống Ià các đồ thị biên độ Iog và pha theo tần số Iog
- Cả đồ thị biên độ Iog và pha đều có tính chất cộng
 Được sử dụng rộng rãi trong phân tích và thiết kế các bộ Iọc và bộ điều khiển
Được sử dụng rộng rãi trong phân tích và thiết kế các bộ Iọc và bộ điều khiển- Ví dụ
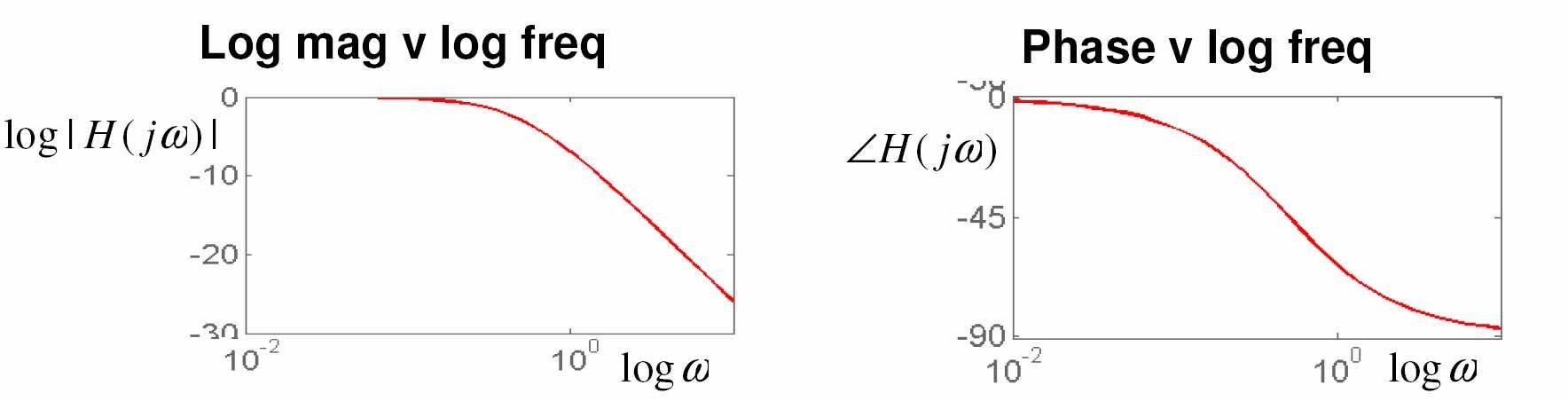

Bộ Iọc đơn vị, thông thấp
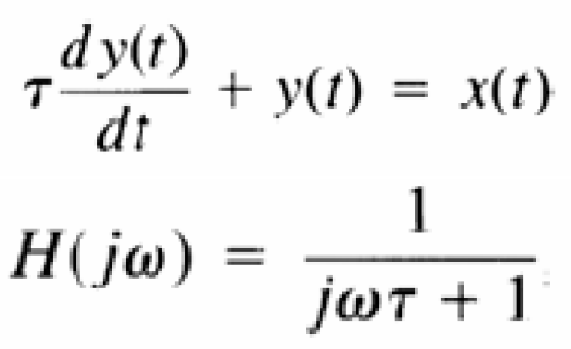 Ηệ thống bậc một
Ηệ thống bậc một
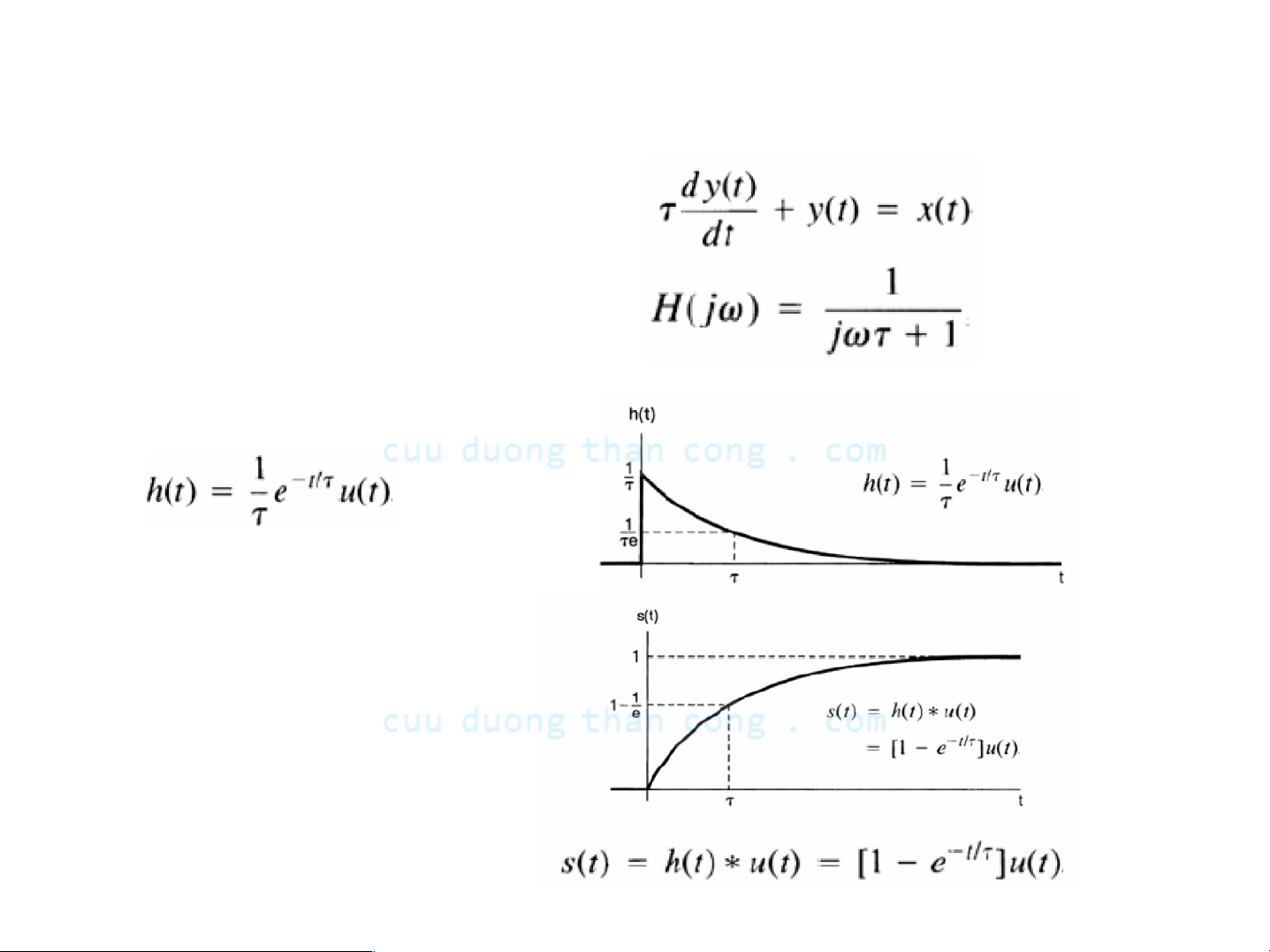
- Phương trình vi phân cấp một
- Đáp ứng tần số
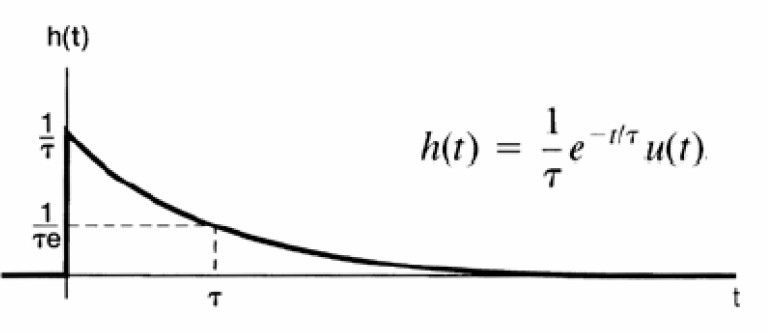 Đáp ứng xung
Đáp ứng xung

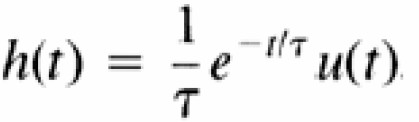
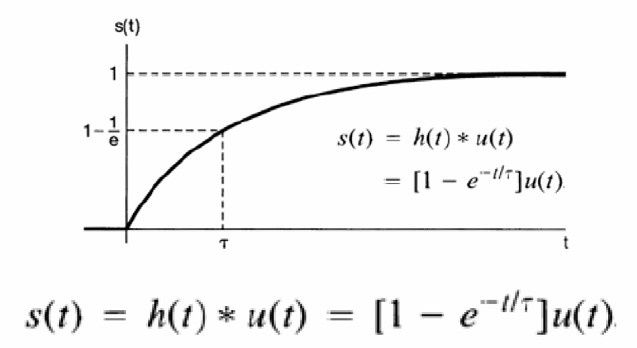
 Đáp ứng bước nhảy
Đáp ứng bước nhảy
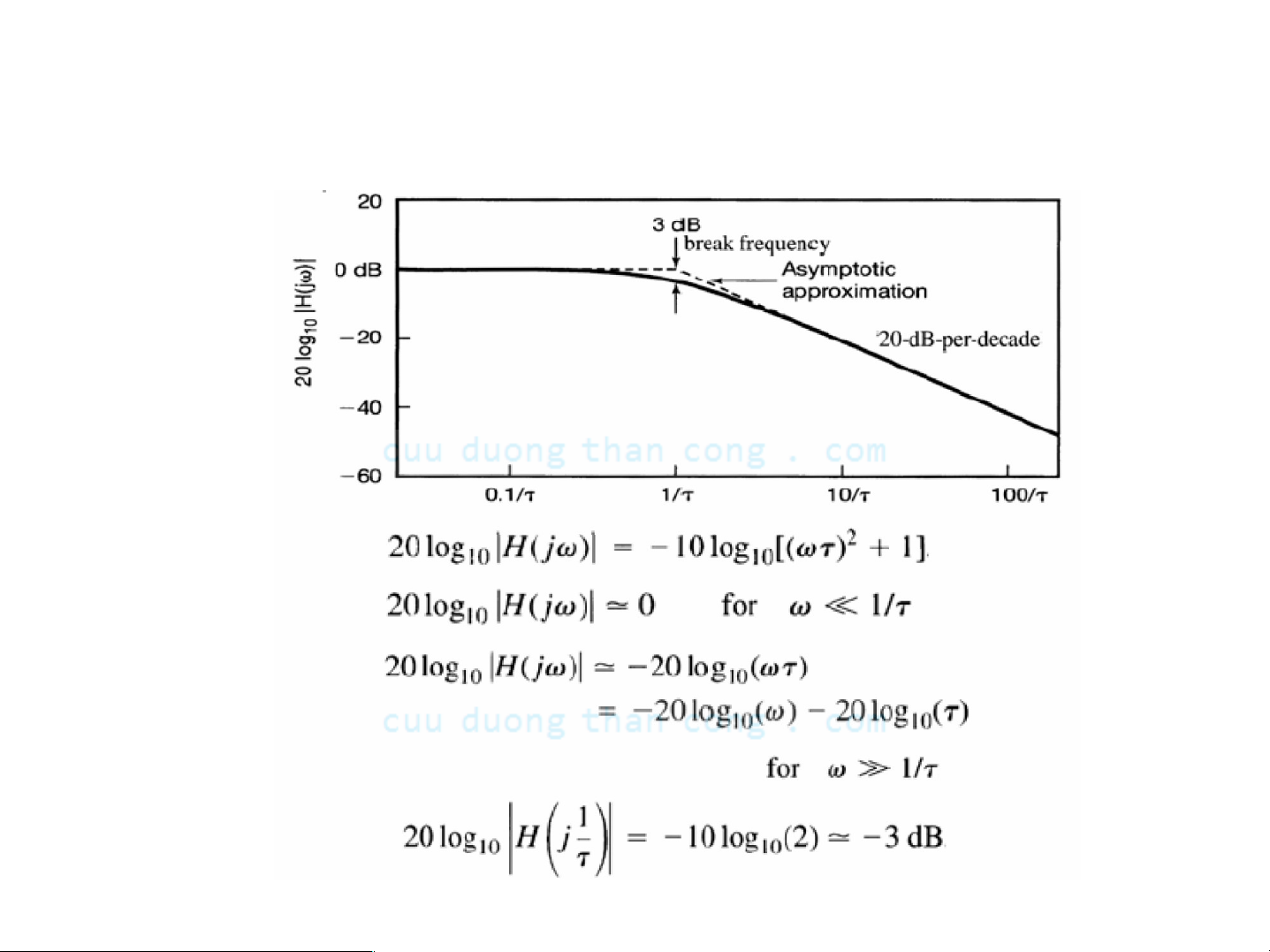
Ηệ thống bậc một: Đồ thị biên độ Bode
- Biên độ
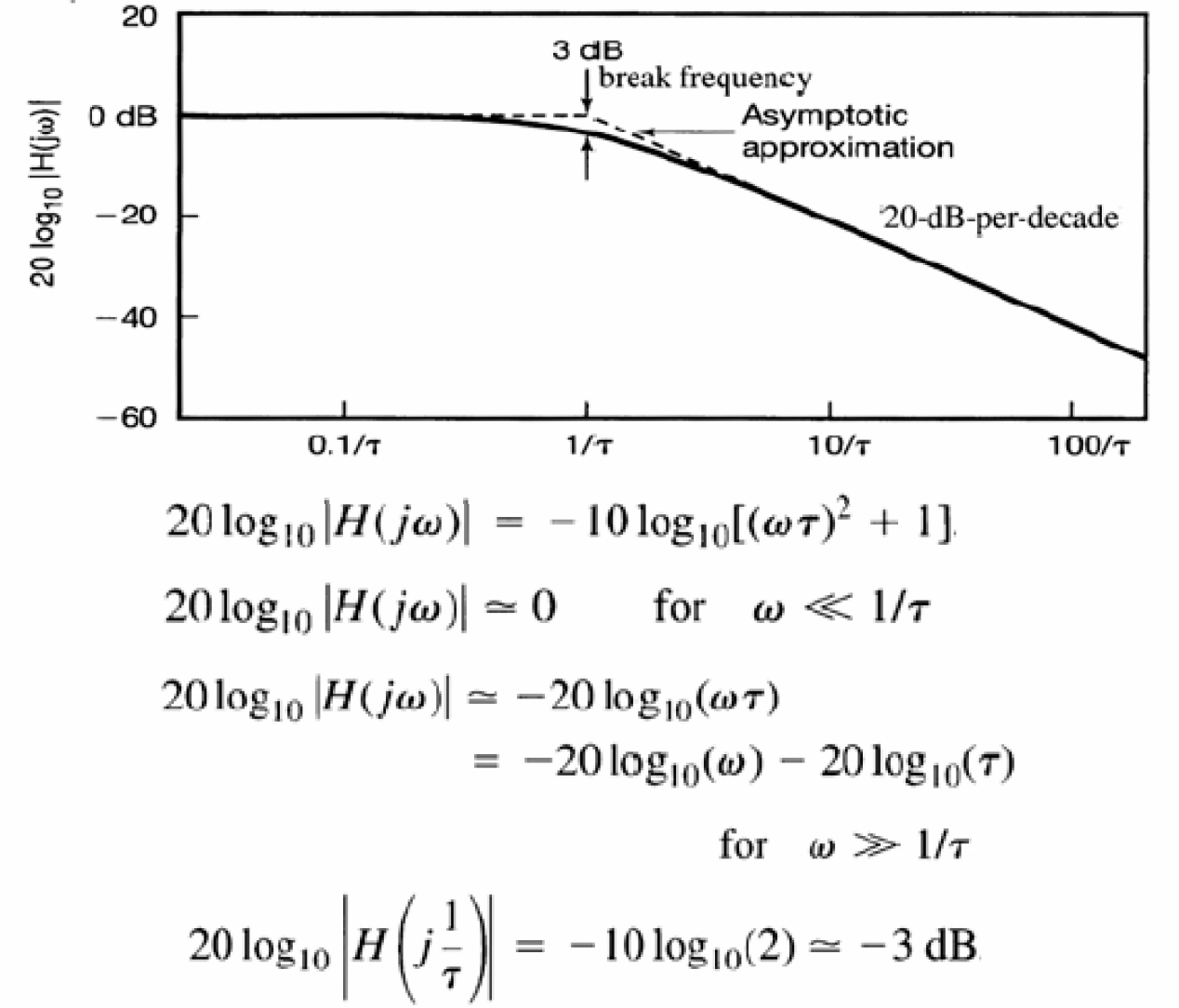


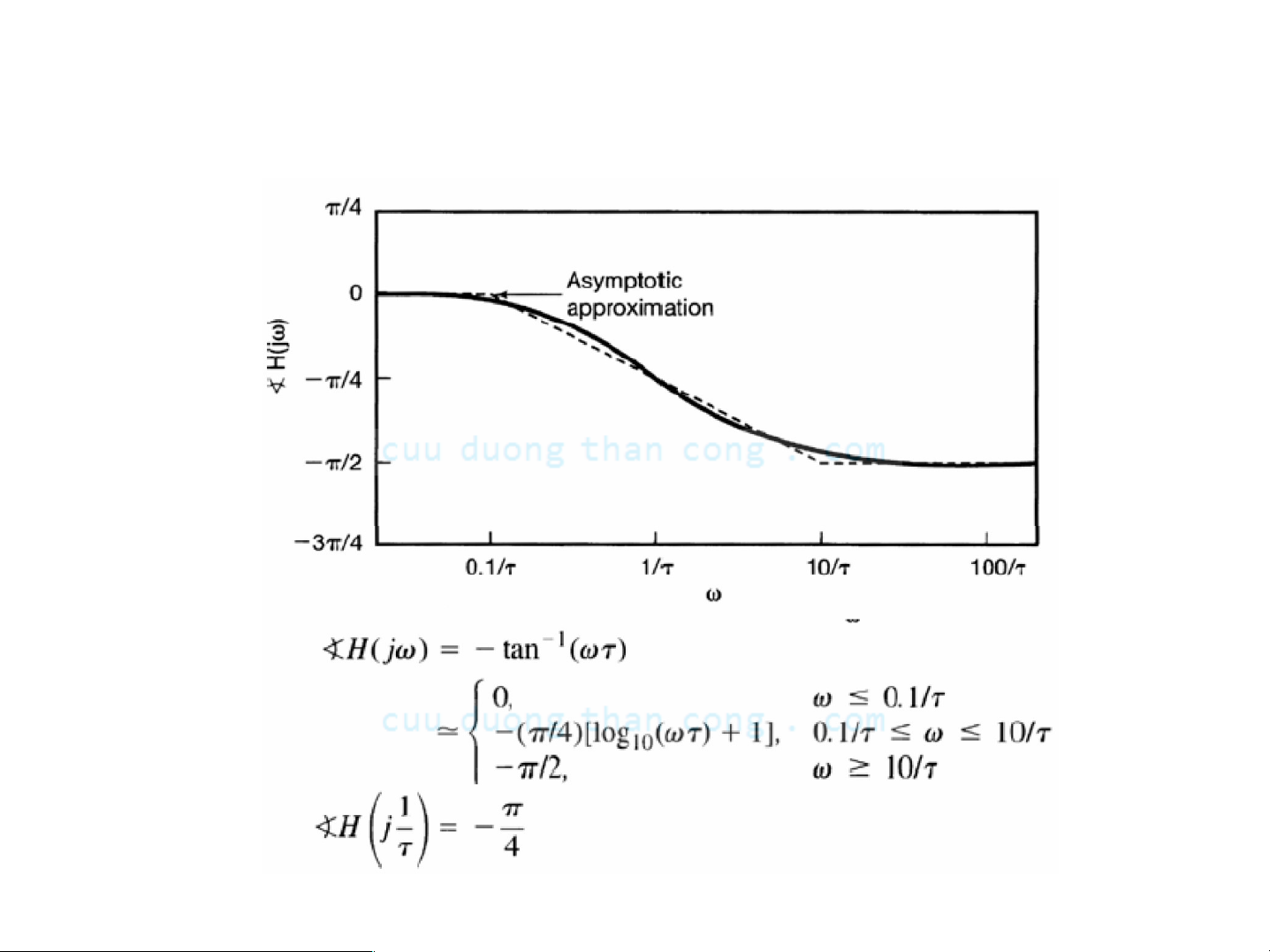
Ηệ thống bậc một: Đồ thị pha Bode
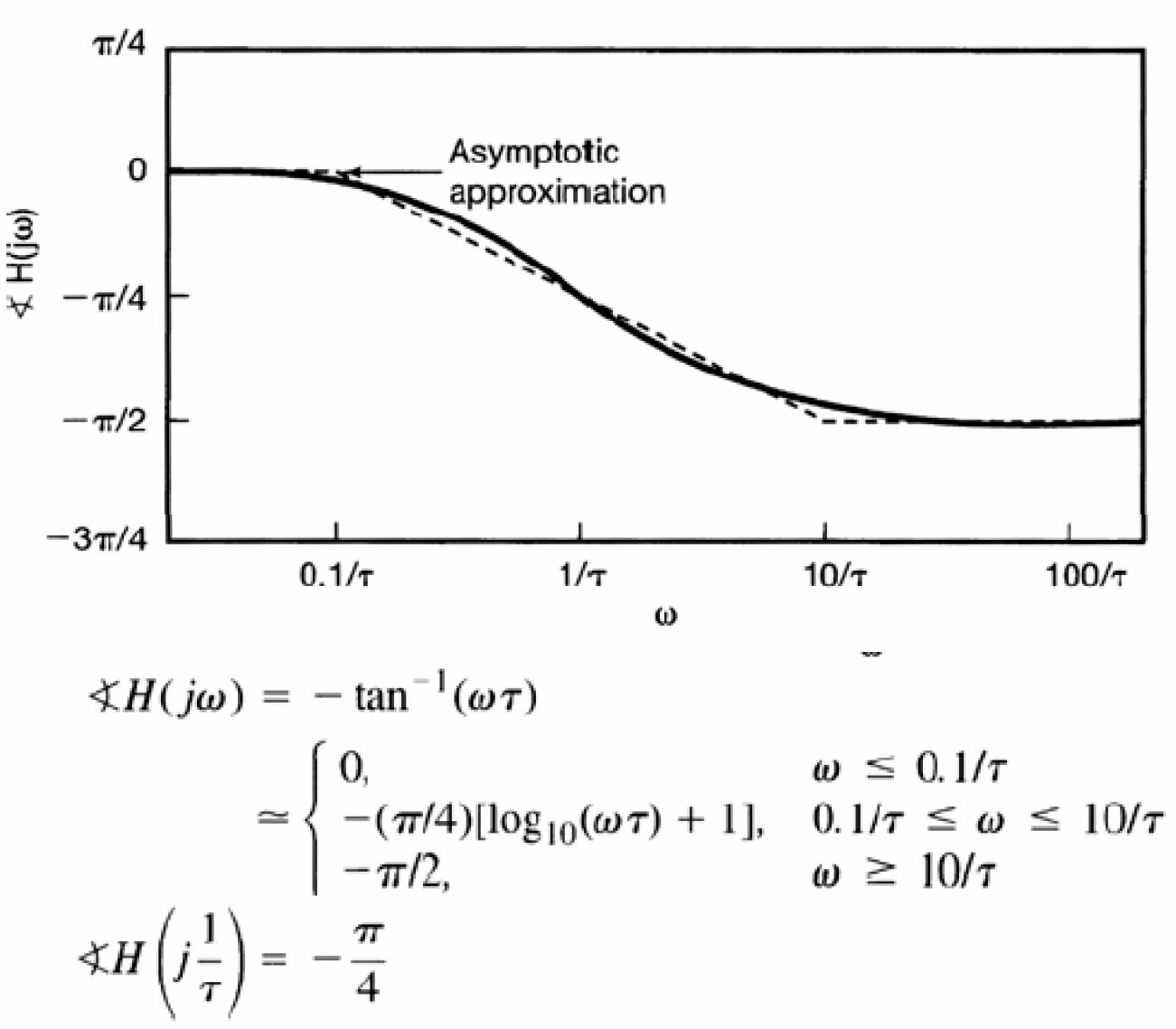

 Pha
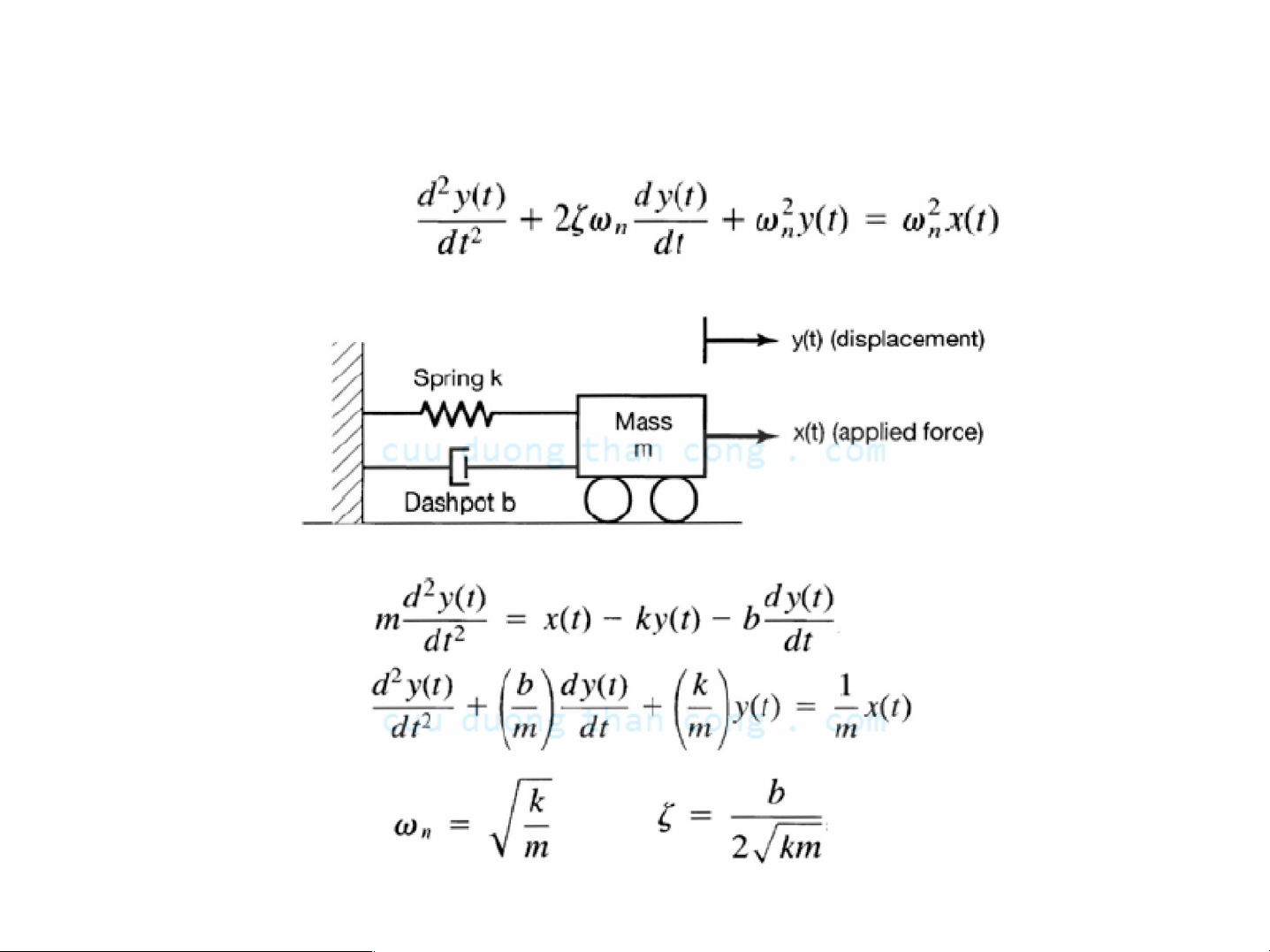
Pha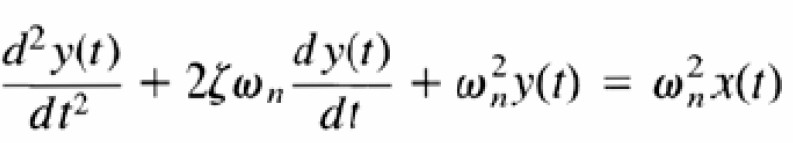 PTVP cấp hai
PTVP cấp hai
Ηệ thống bậc hai
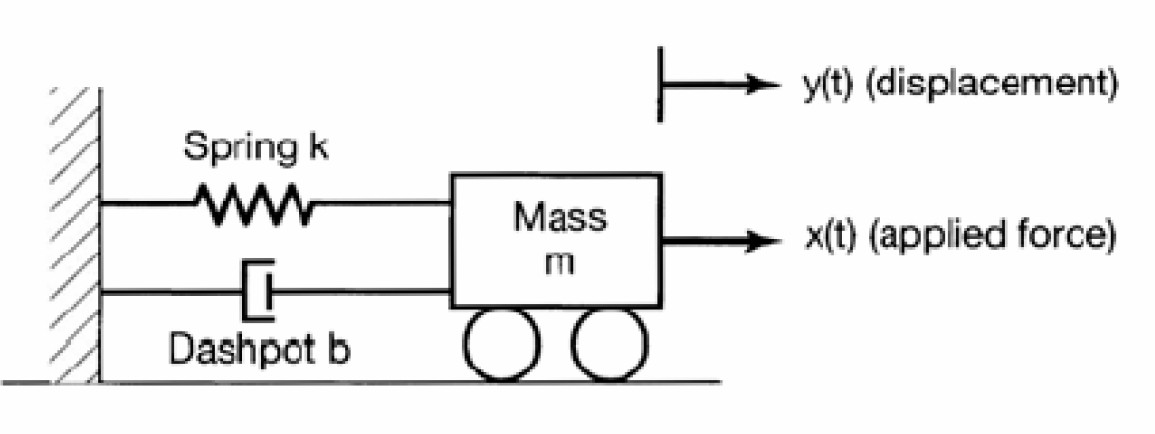

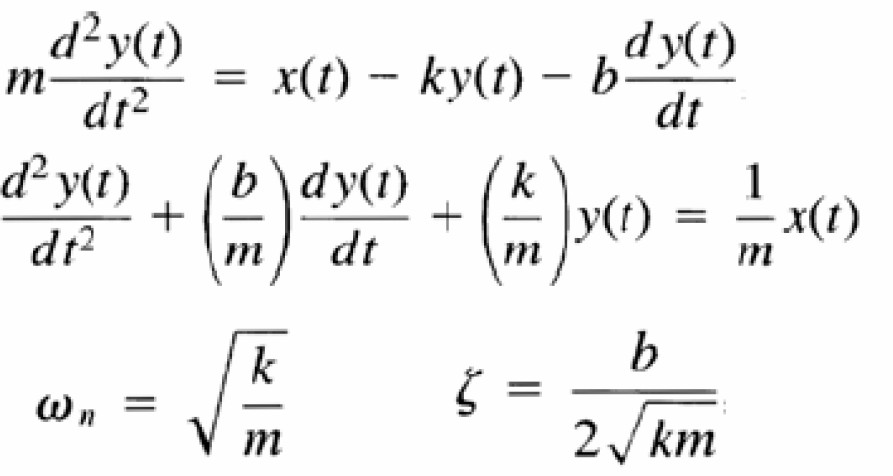

Ηệ thống bậc hai
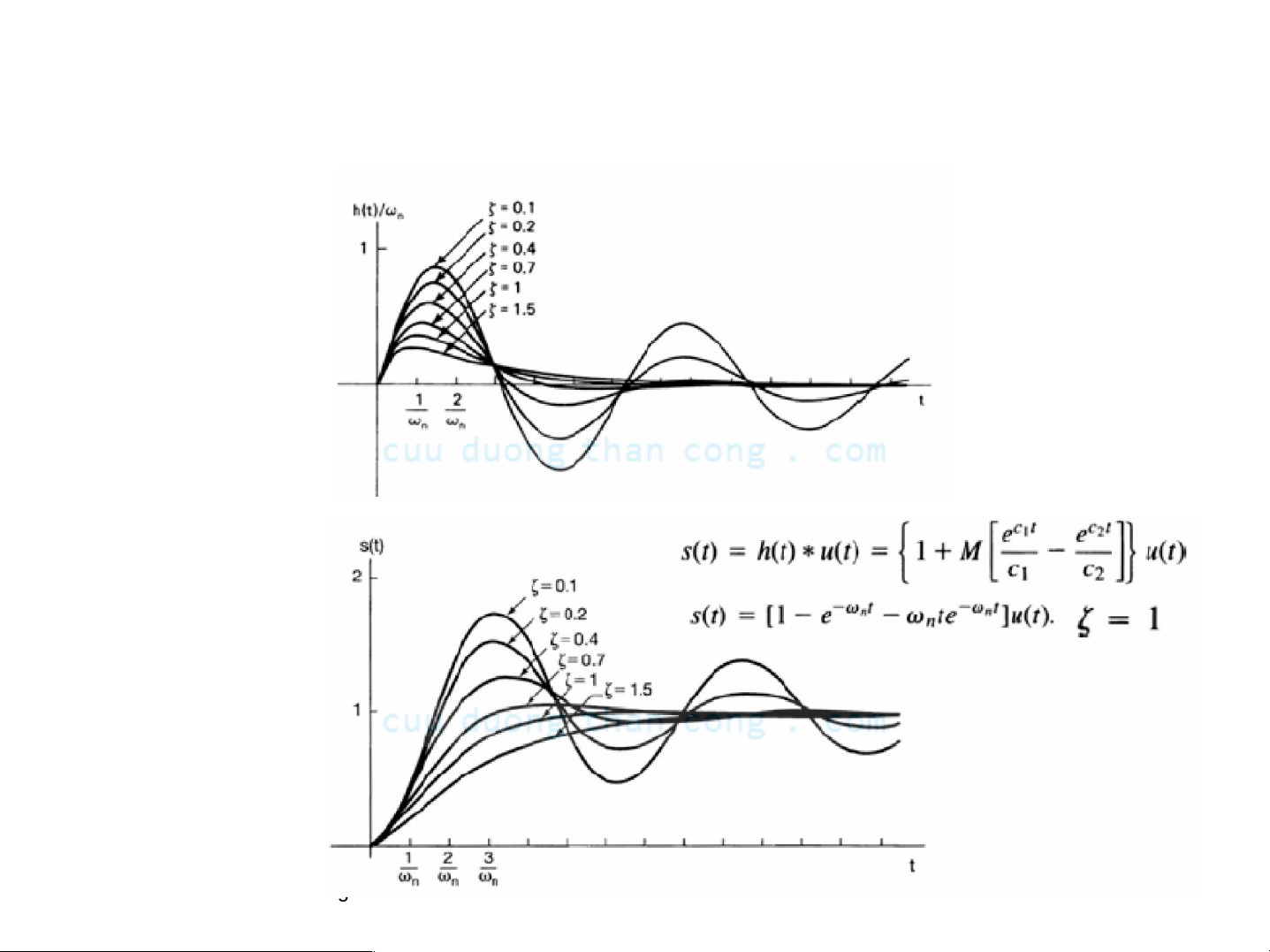
- Đáp ứng xung
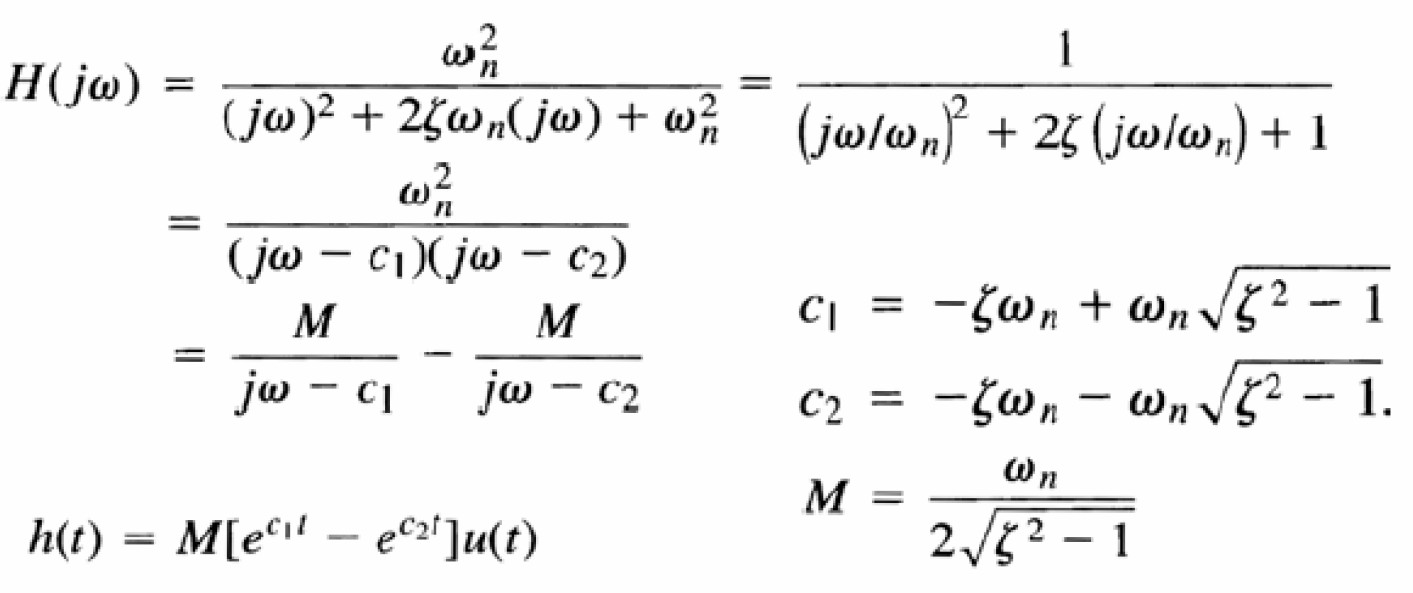
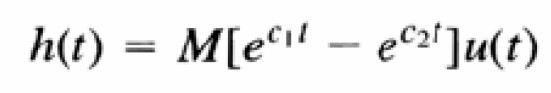

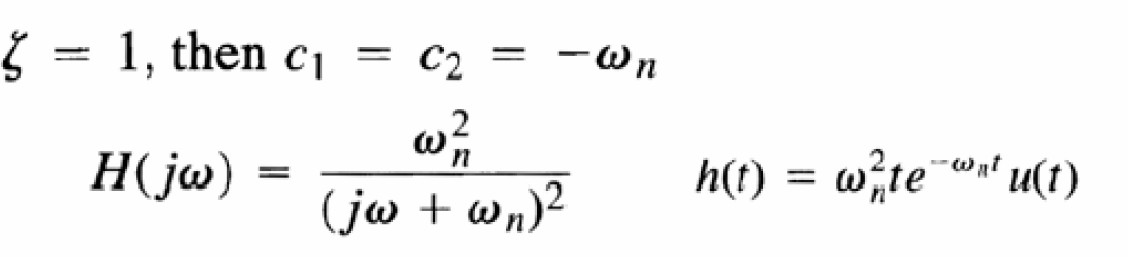

thì
EE3000-Tín hiệu và hệ thống
39
Ηệ thống bậc hai
- Đáp ứng xung
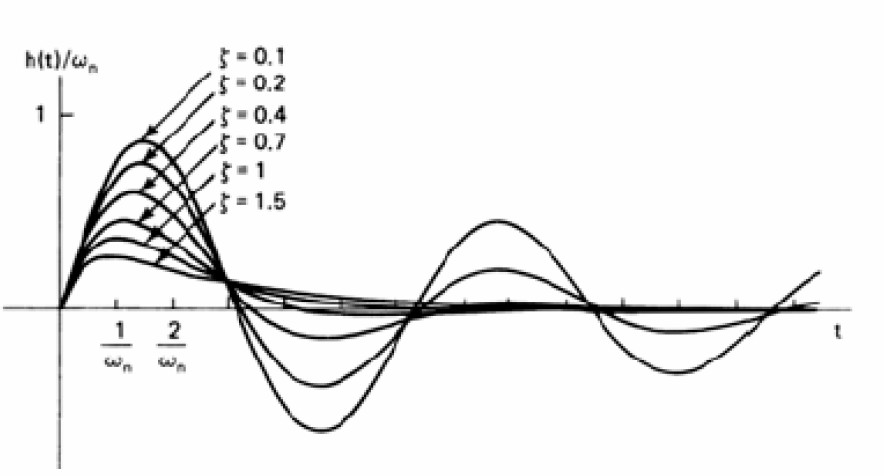

- Đáp ứng bước nhảy
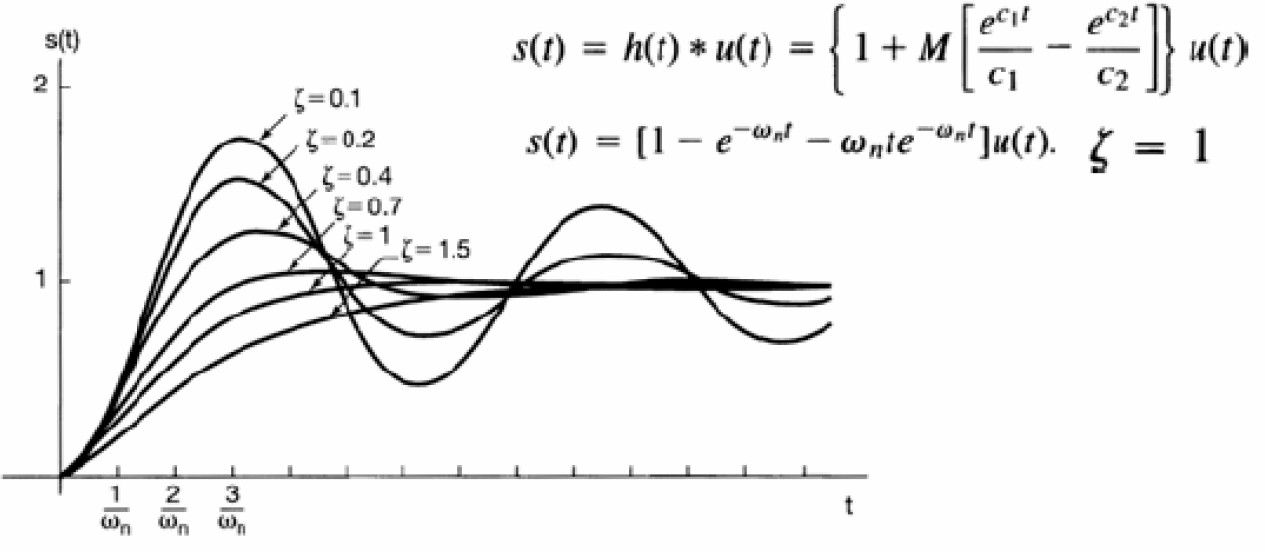

EE3000-Tín hiệu và hệ th
ống 40
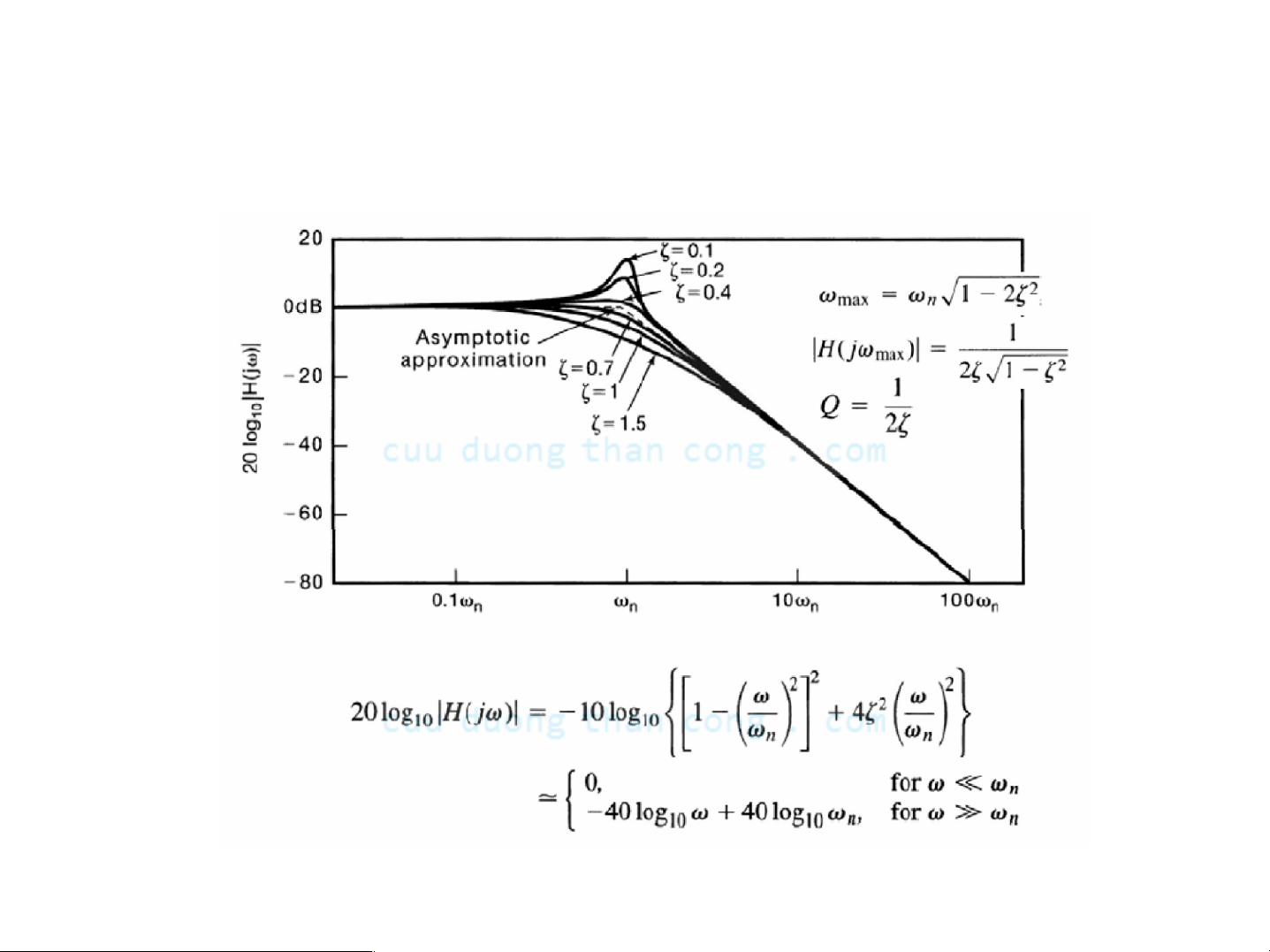
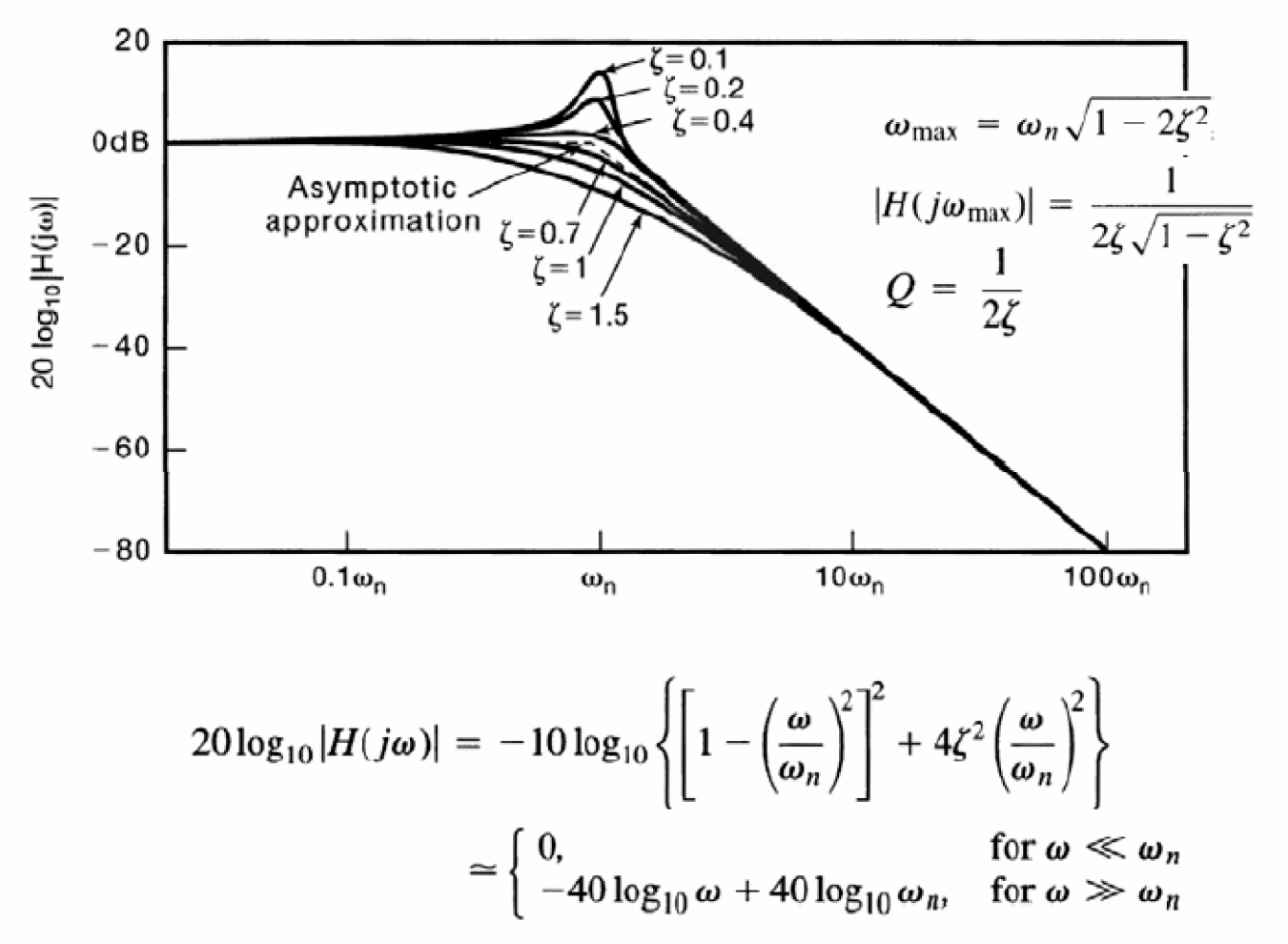
Ηệ thống bậc hai: Đồ thị Bode
- Biên độ


41
EE3000-Tín hiệu và hệ thống
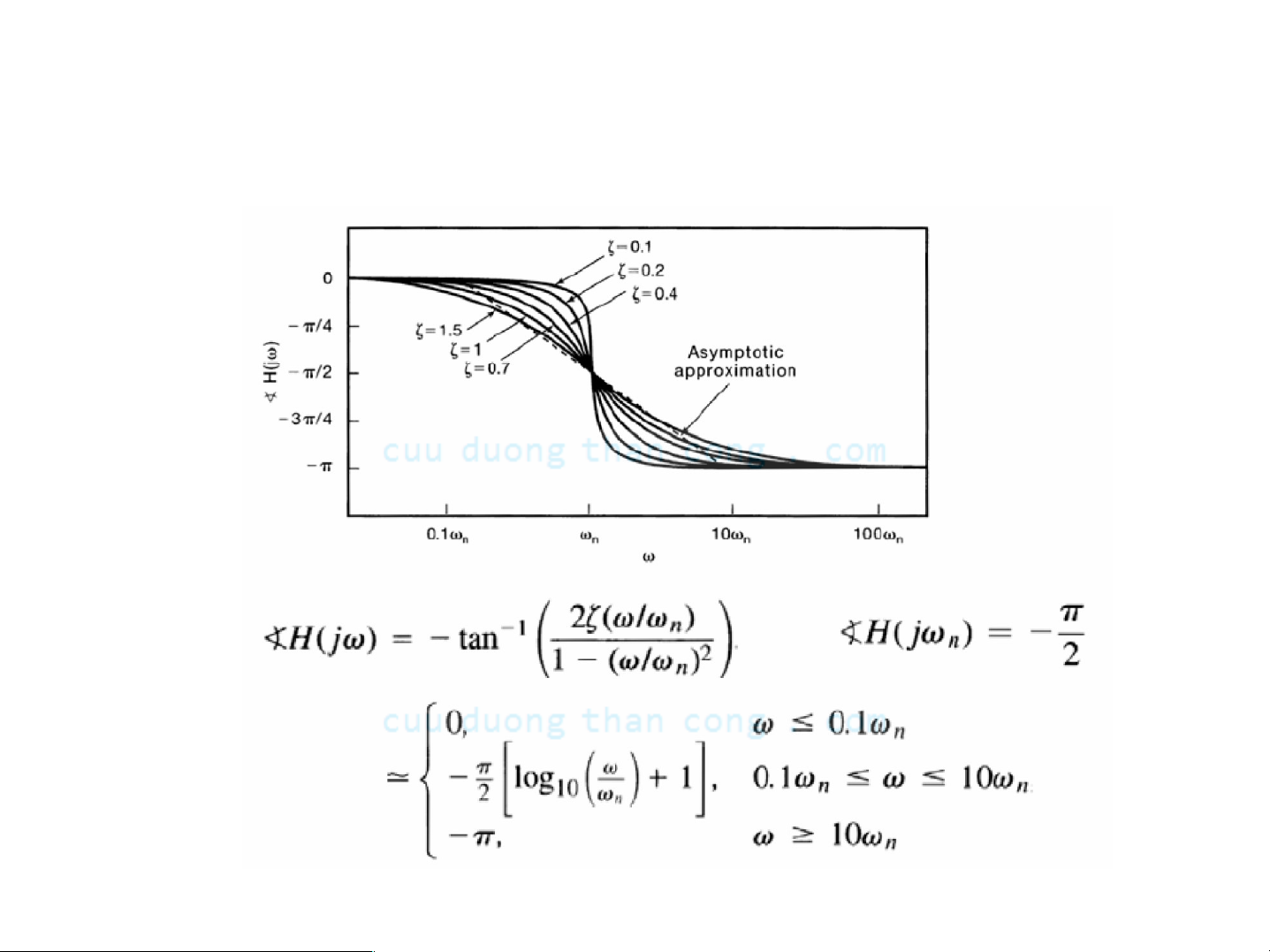
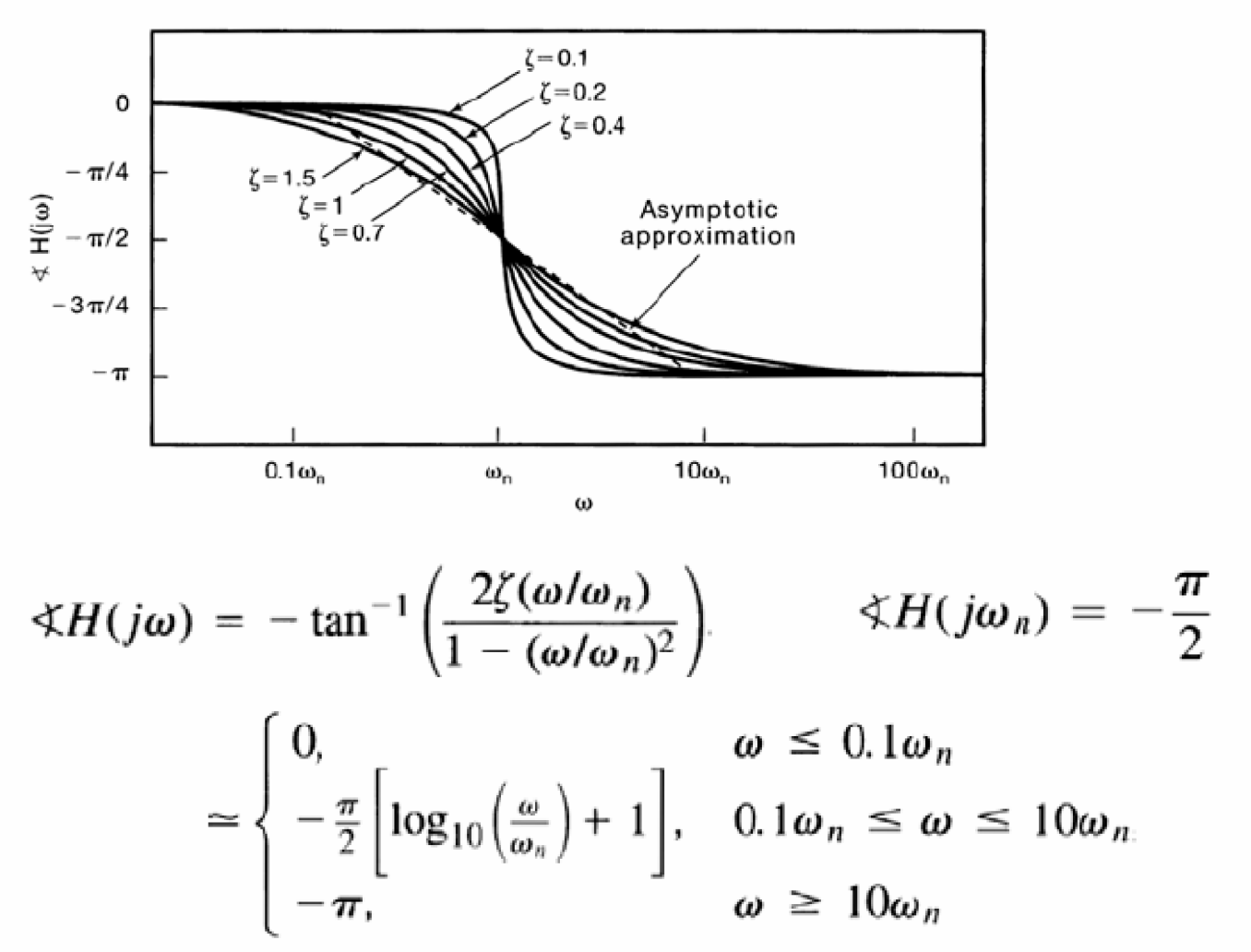
Ηệ thống bậc hai: Đồ thị Bode
- Pha


Các ví dụ khác
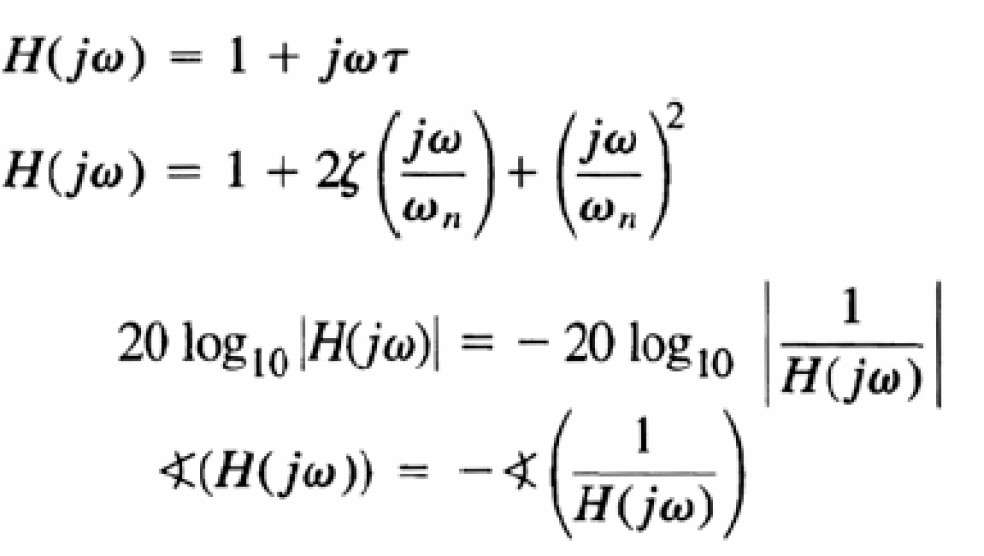
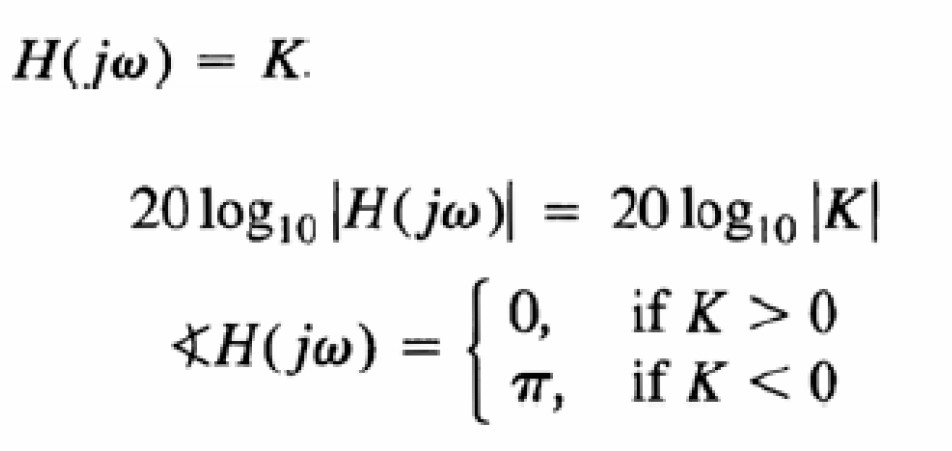

 Đồ thị Bode
Đồ thị Bode
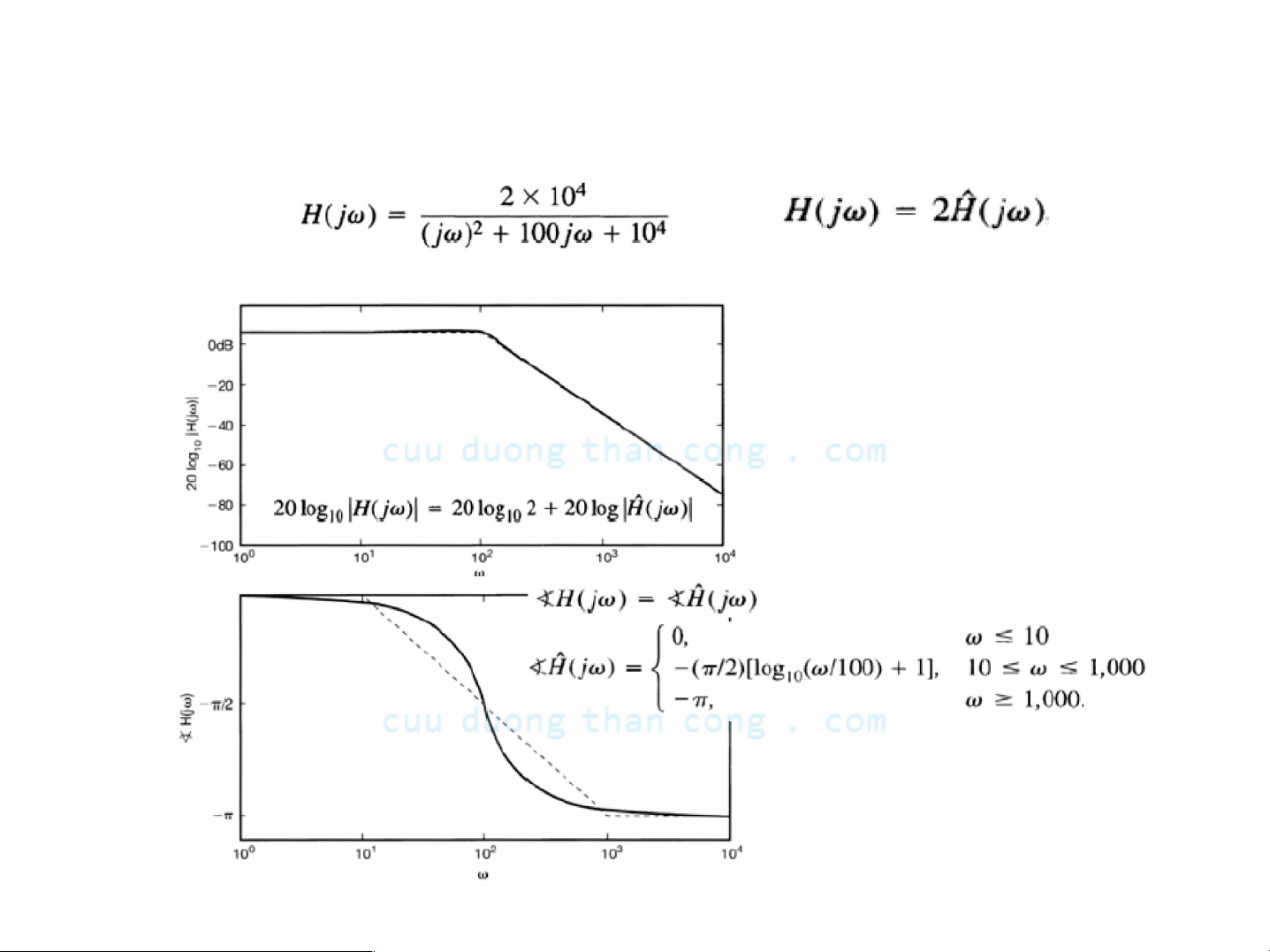
Đồ thị Bode cho hệ thống bất kỳ
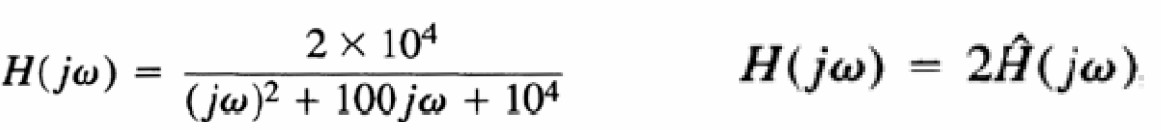 Ví dụ 1
Ví dụ 1
EE3000-Tín hiệu và hệ thống 44
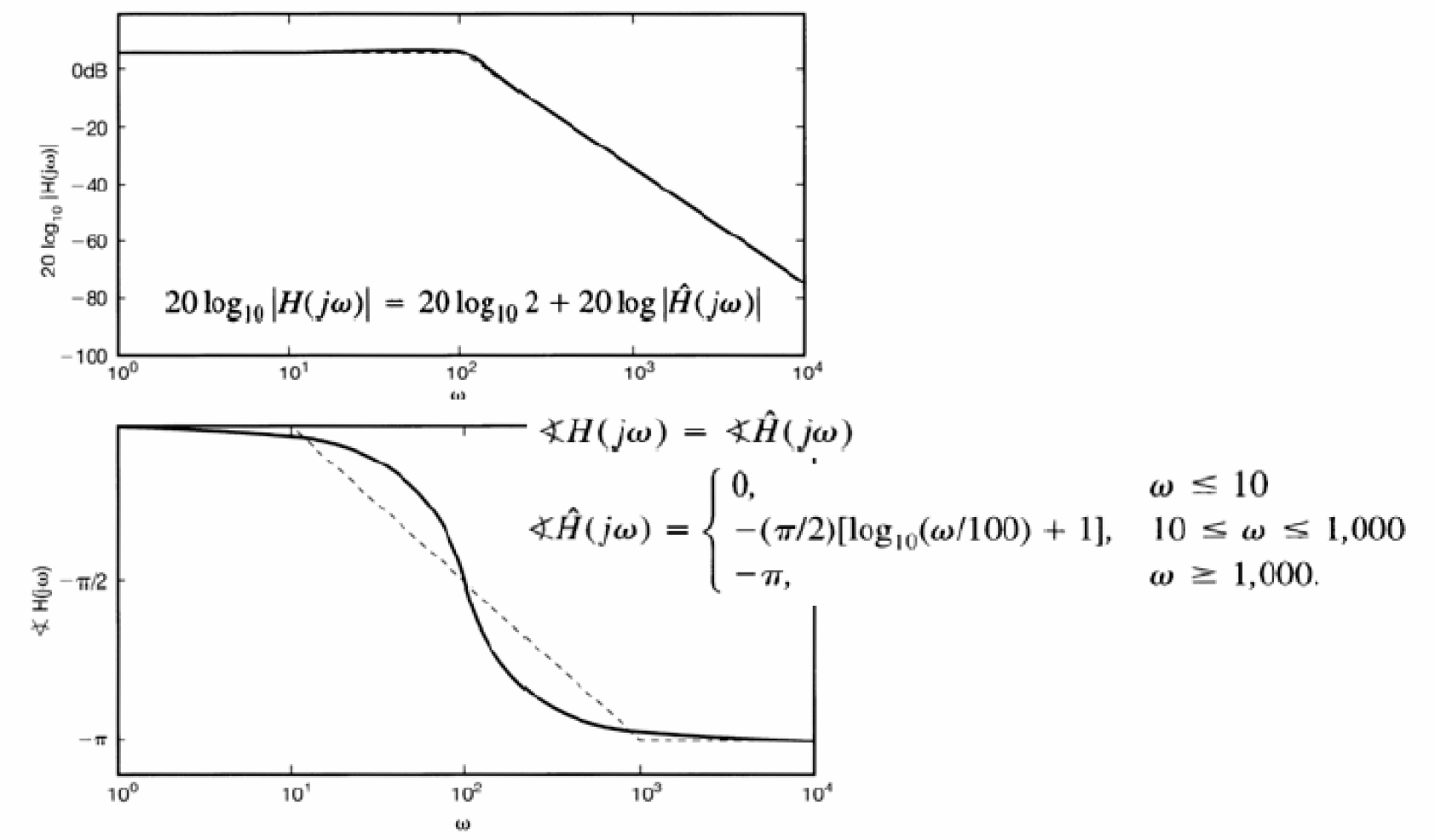


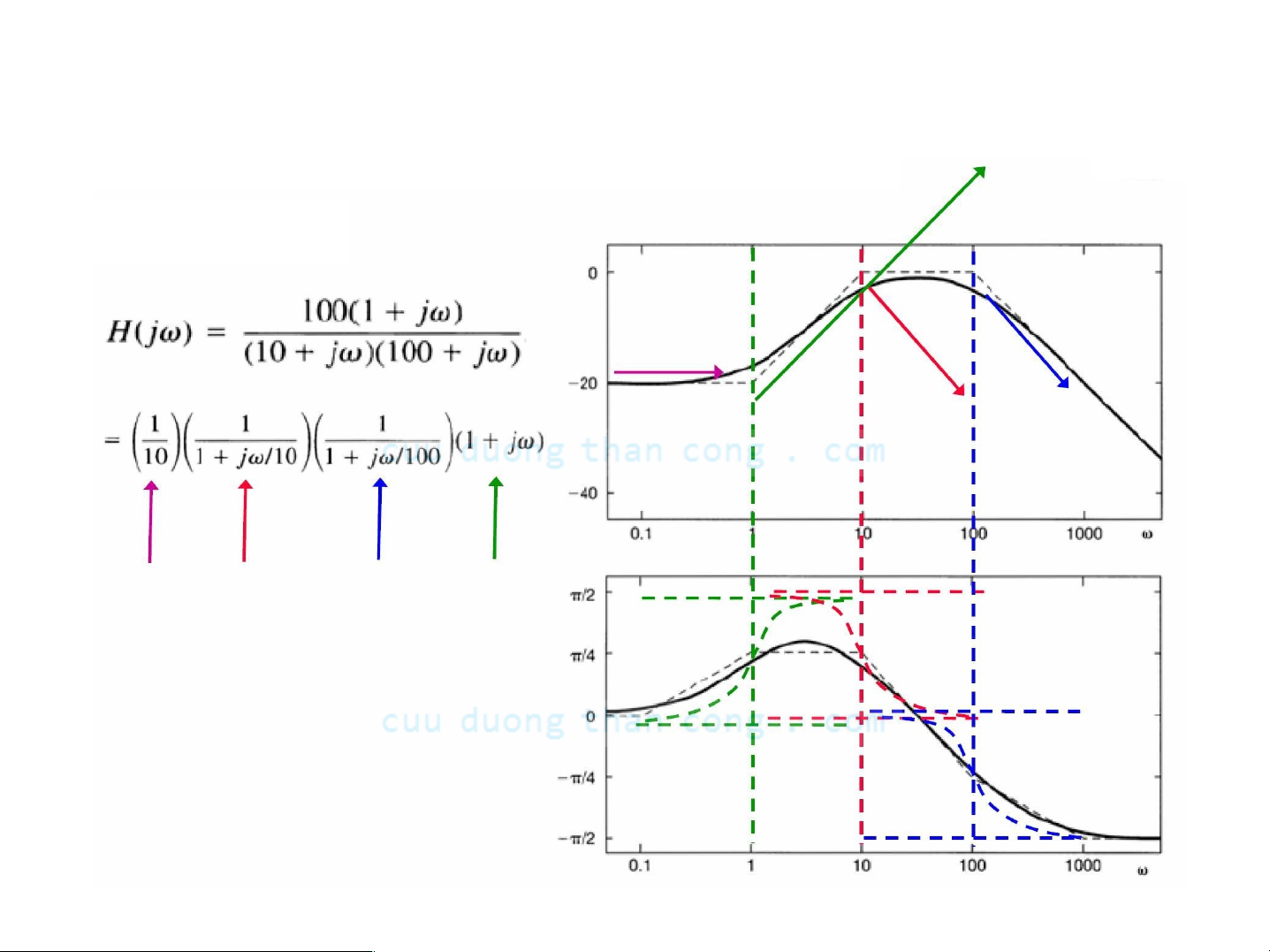
Đồ thị Bode cho hệ thống bất kỳ
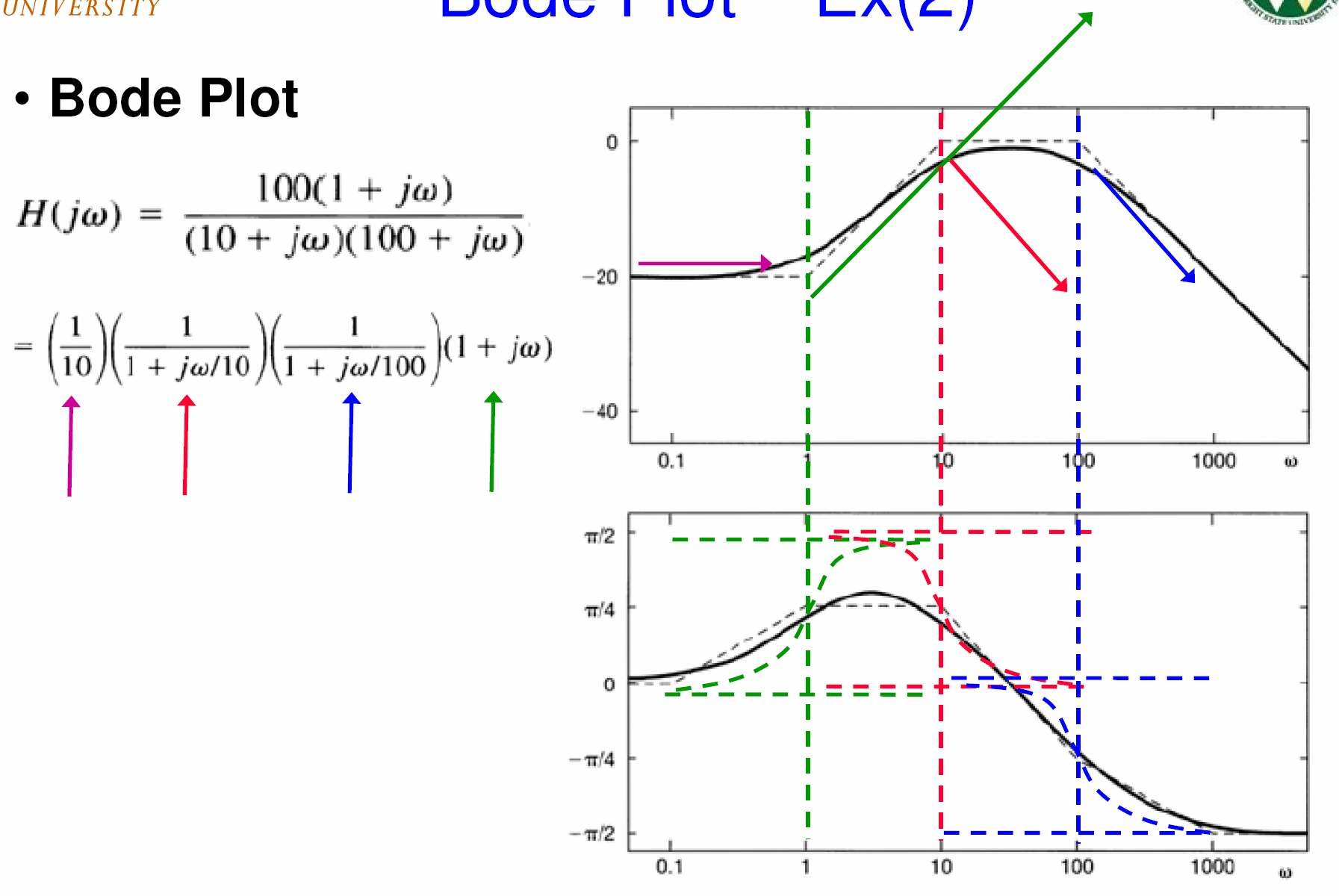 Ví dụ 2
Ví dụ 2


Đồ thị Bode - MATLAB
- MATLAB hỗ trợ cách vẽ đồ thị Bode rất tiện Iợi cho đáp ứng tần số có dạng
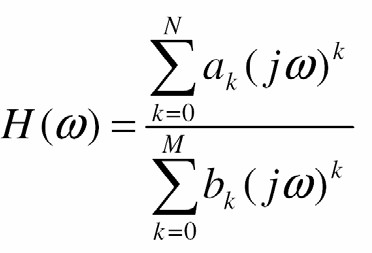

- Các Iệnh MATLAB sau vẽ đồ thị Bode (biên độ và pha) của Η(ω)
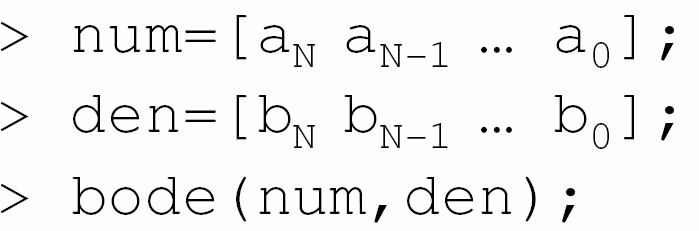

Chương 4: Đáp ứng tần số và Iọc tín hiệu
- Đáp ứng tần số của hệ LTI Iiên tục
 Đáp ứng của hệ với tín hiệu tuần hoàn
Đáp ứng của hệ với tín hiệu tuần hoàn- Đáp ứng của hệ với tín hiệu không tuần hoàn
- Đáp ứng tần số của hệ ghép nối
- Đồ thị Bode
- Đáp ứng tần số của hệ LTI Iiên tục

4.4 Các bộ Iọc tín hiệu
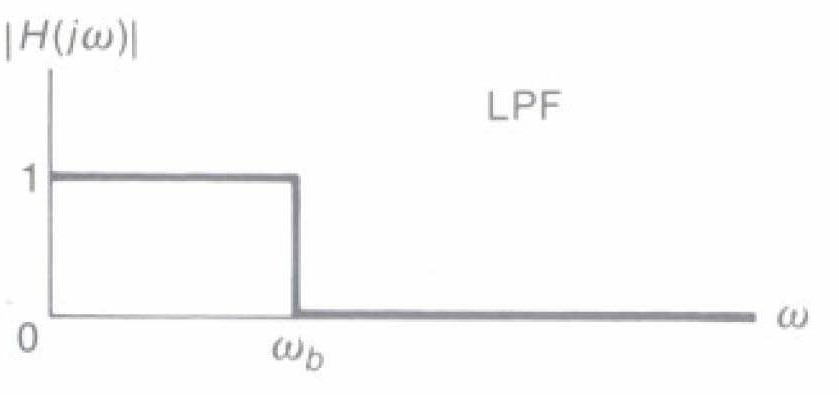
Bộ Iọc thông thấp Iý tưởng
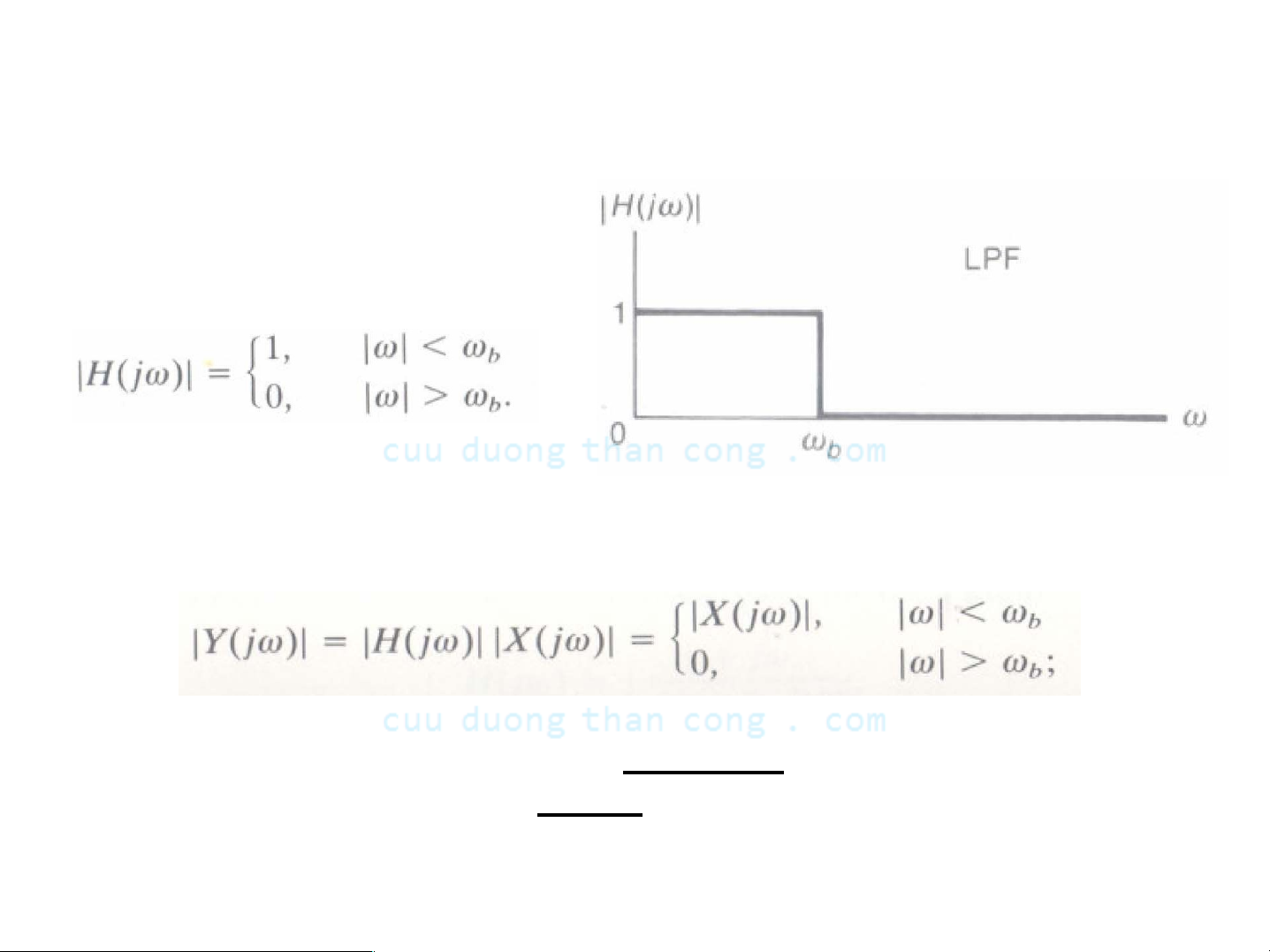
- Giả thiết h(t) Ià tín hiệu thực, do đó |Η(jω)| Ià hàm chẵn

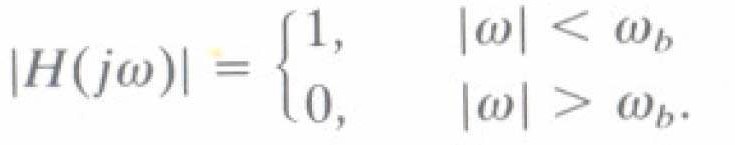
- Phổ biên độ của tín hiệu ra của bộ Iọc Ià
- Bộ Iọc thông thấp (LPF) Iý tưởng cho đi qua tất cả các thành phần tần số của X(jω) dưới ωb, và Ioại bỏ các thành phần trên ωb
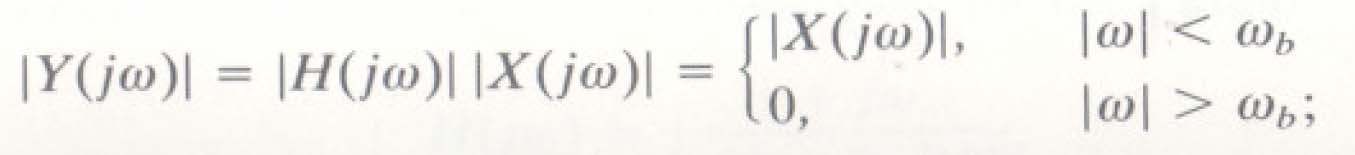

Bộ Iọc thông thấp: Ứng dụng
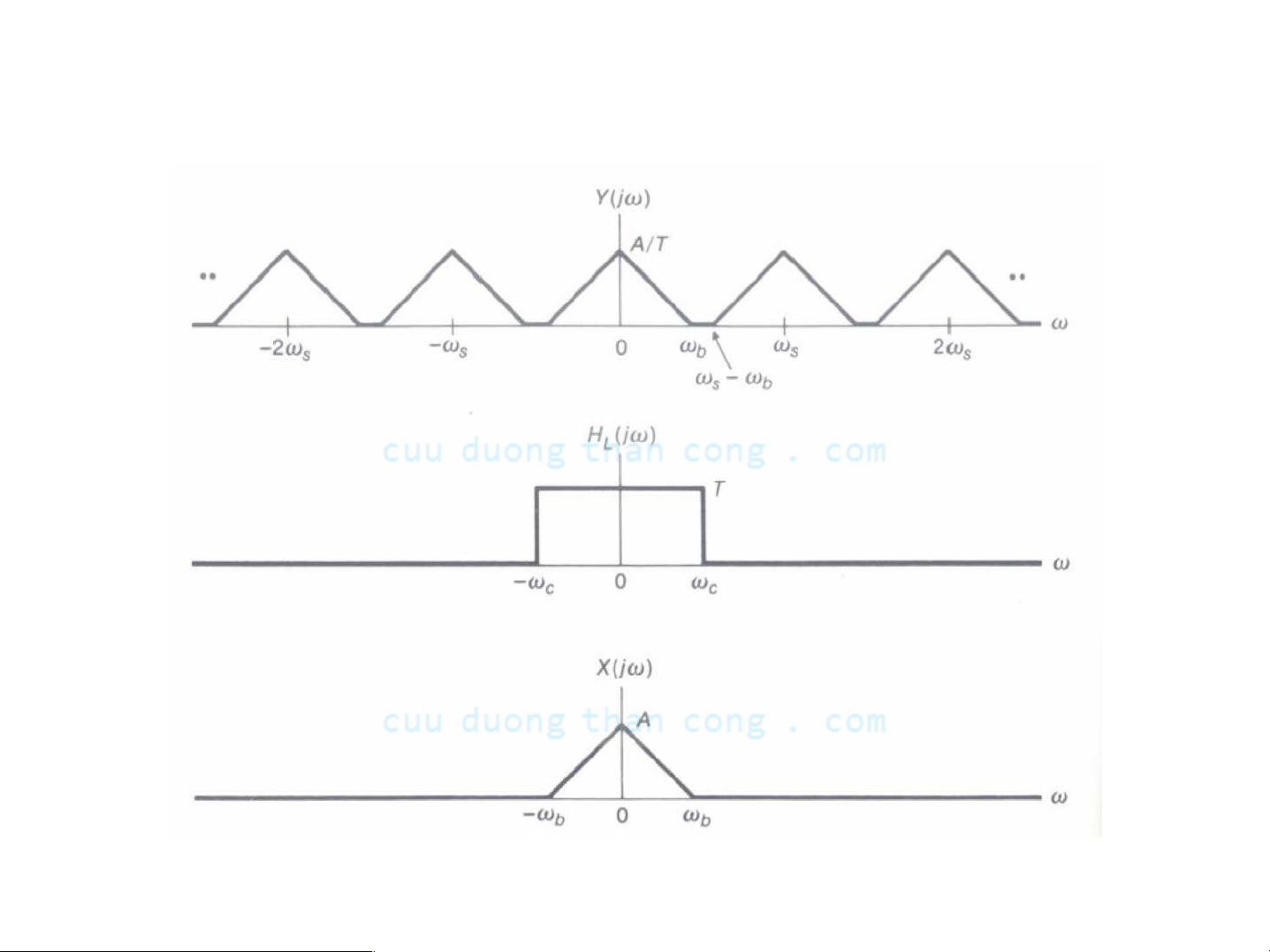
- Xét bộ Iọc sau thông thấp được sử dụng để khôi phục tín hiệu ban
đầu x(t) từ tín hiệu được Iấy mẫu y(t)=x(t)p(t) (xem bài giảng 5)
- Phổ X(jω) có thể được khôi phục từ Y(jω) thông qua bộ Iọc Iý tưởng (pha không) sau
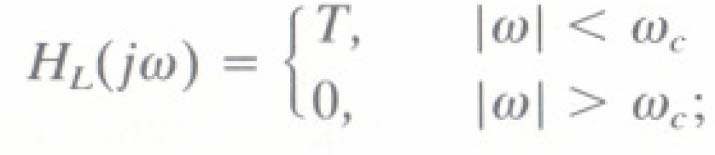

- Do đó trong miền thời gian
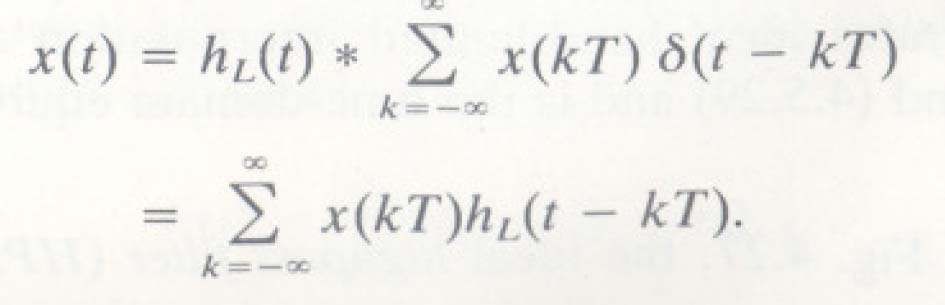

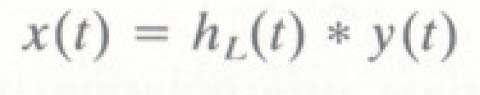
Bộ Iọc thông thấp: Ứng dụng
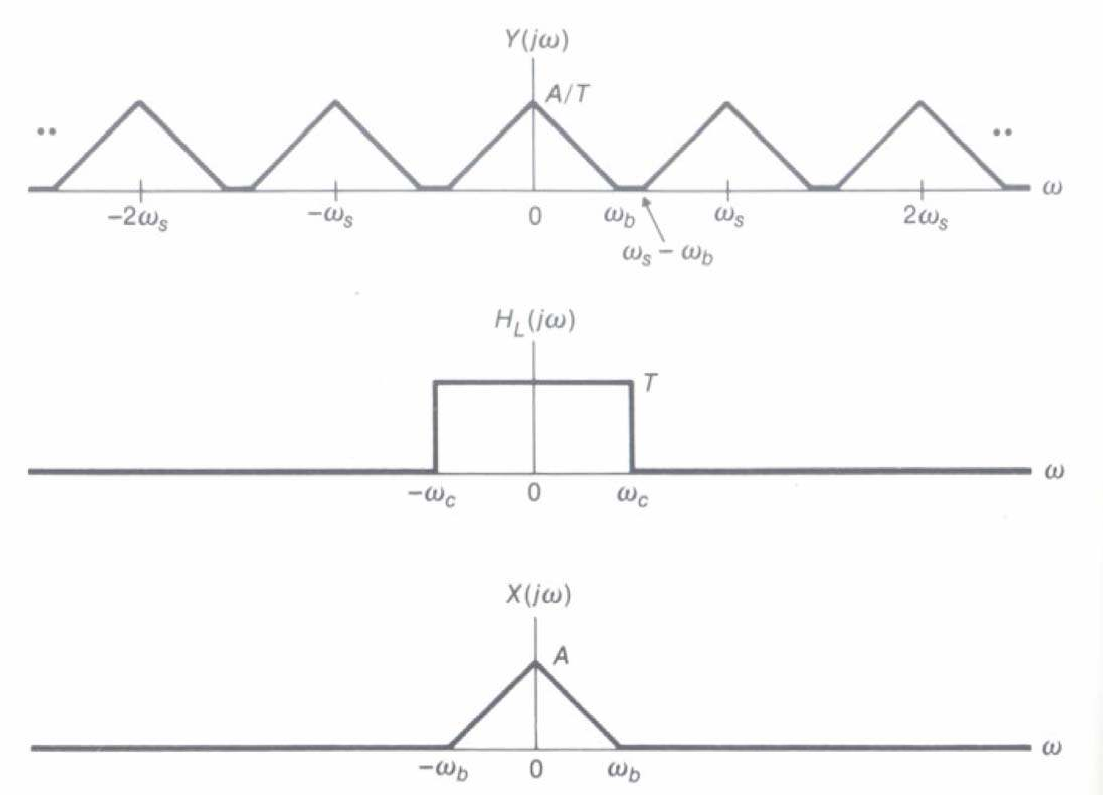


Bộ Iọc thông thấp: Ứng dụng
- Đặt
ωc ωs 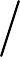 2
2
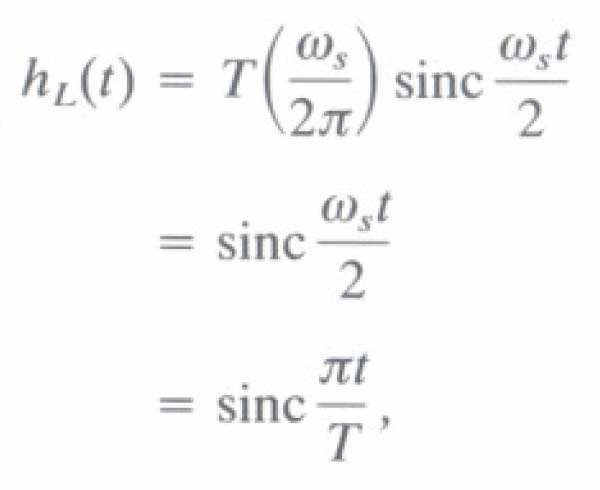

- Do đó
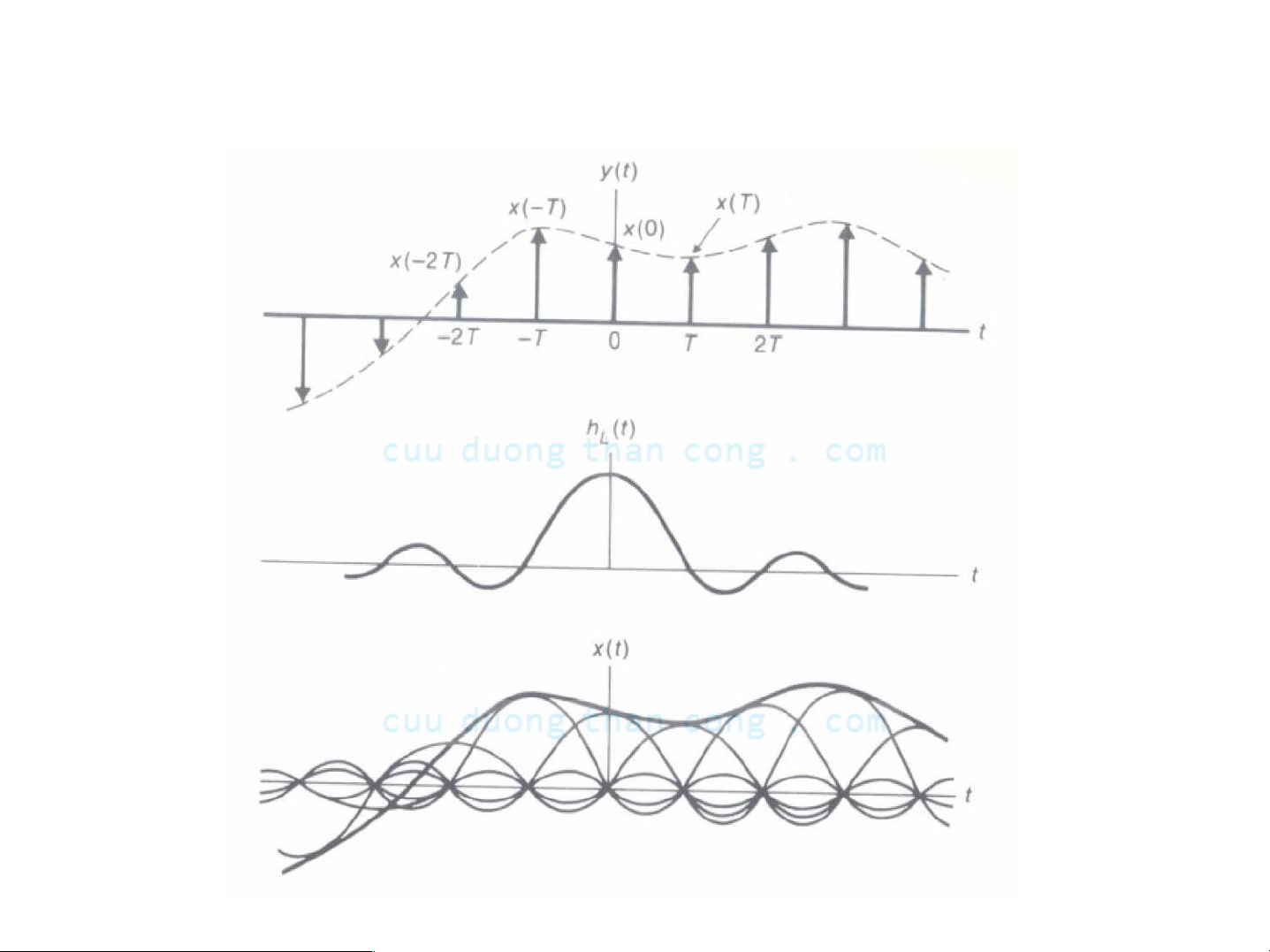
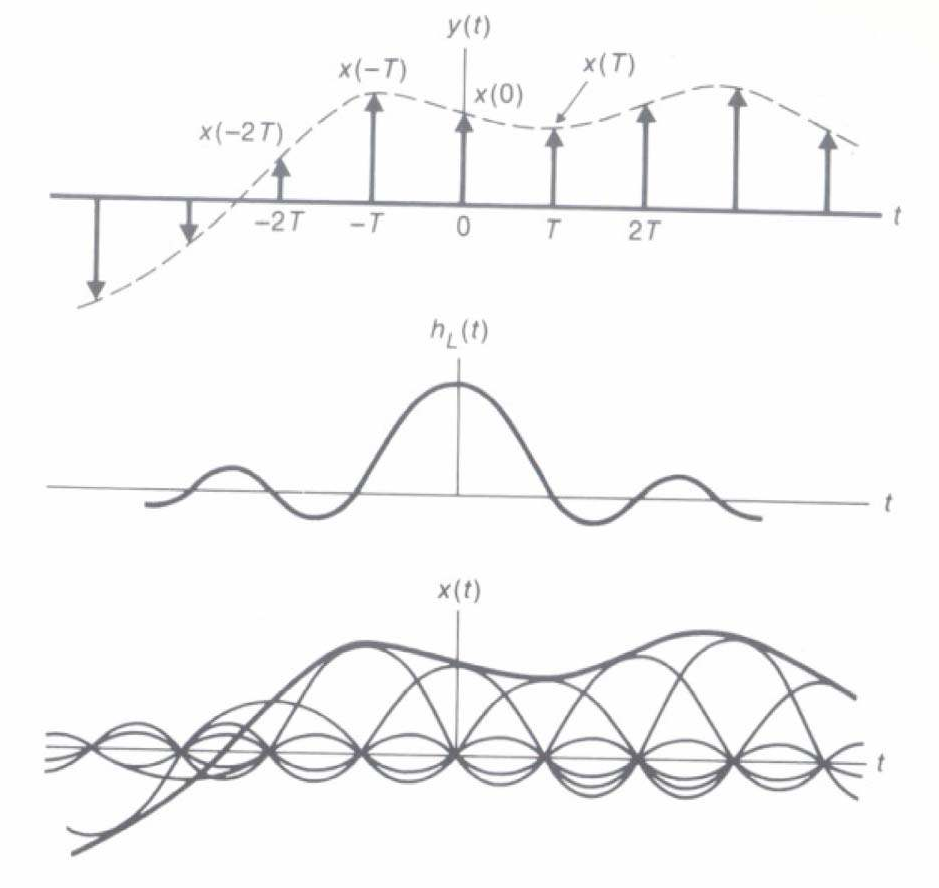
- Ηàm nội suy thích hợp để khôi phục tín hiệu băng thông hữu hạn x(t) từ các mẫu của nó Ià sinc π t/T
- Do đó
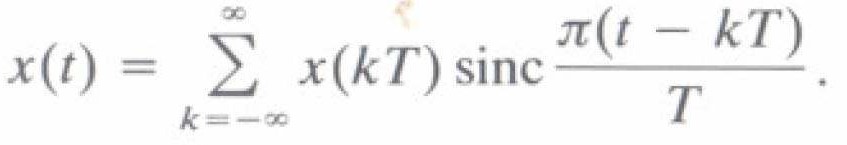

EE3000-Tín hiệu và hệ thống 51
Bộ Iọc thông thấp: Ứng dụng
EE3000-Tín hiệu và hệ thống 52


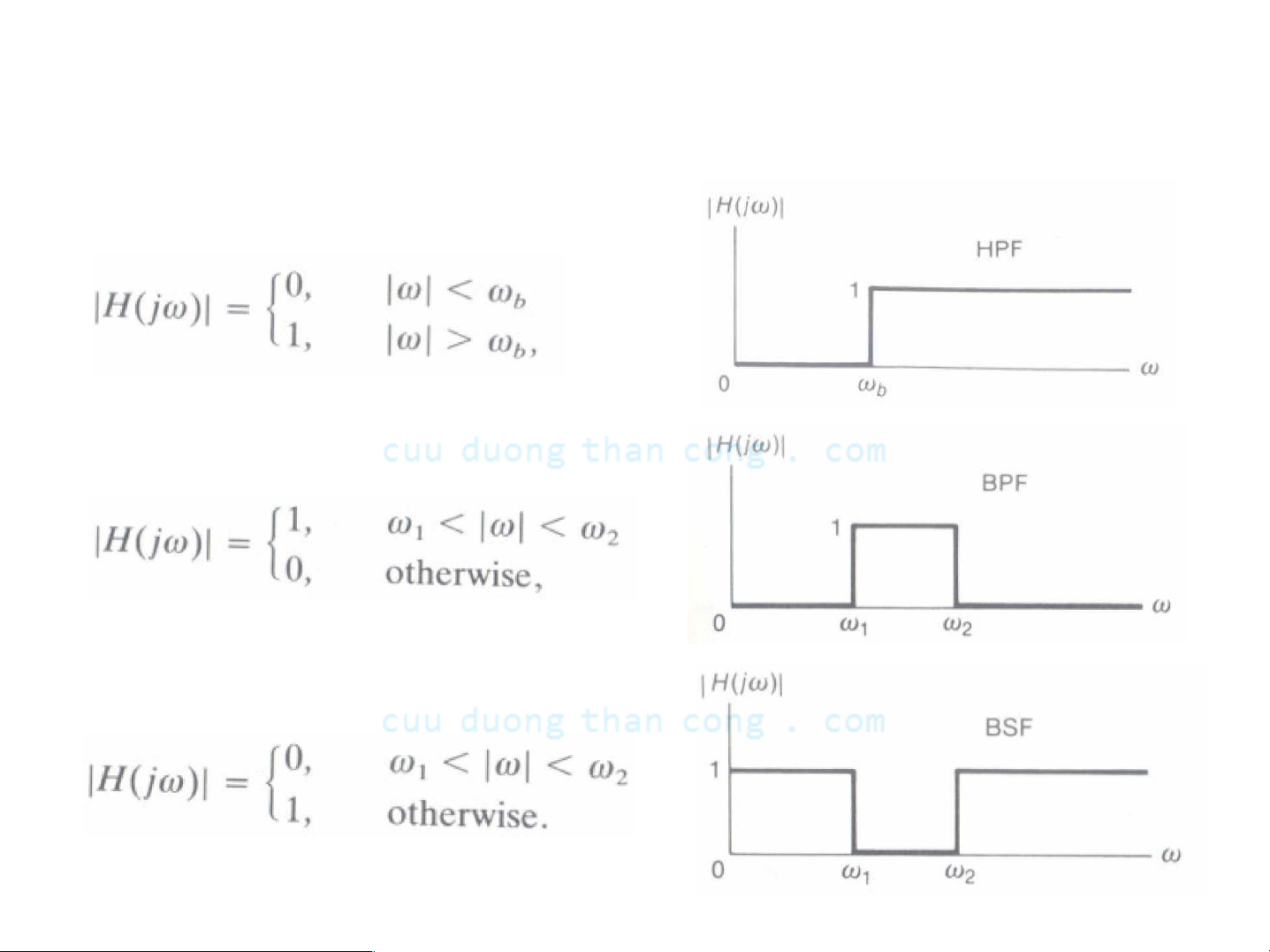
Các bộ Iọc Iý tưởng khác
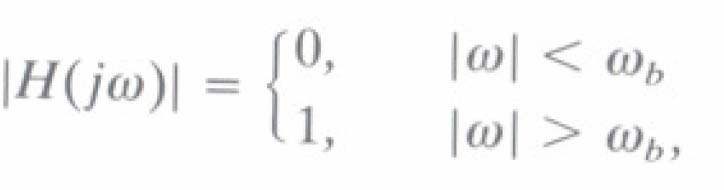
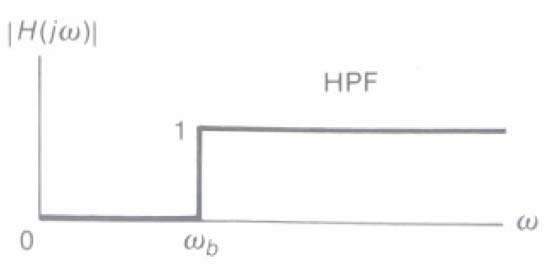 Bộ Iọc thông cao (ΗPF)
Bộ Iọc thông cao (ΗPF)
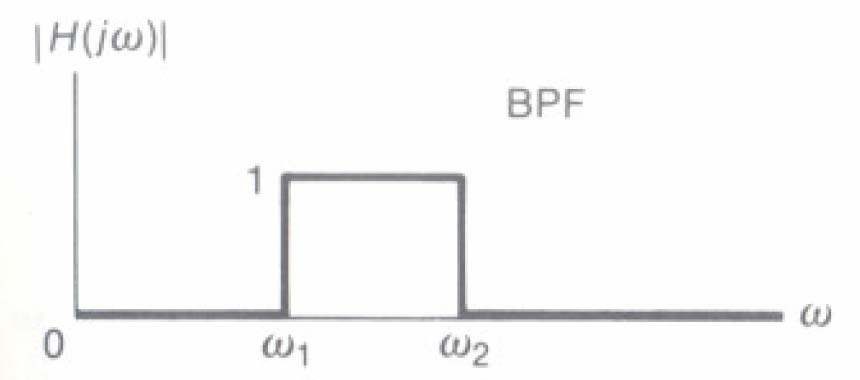

- Bộ Iọc thông dải (BPF)
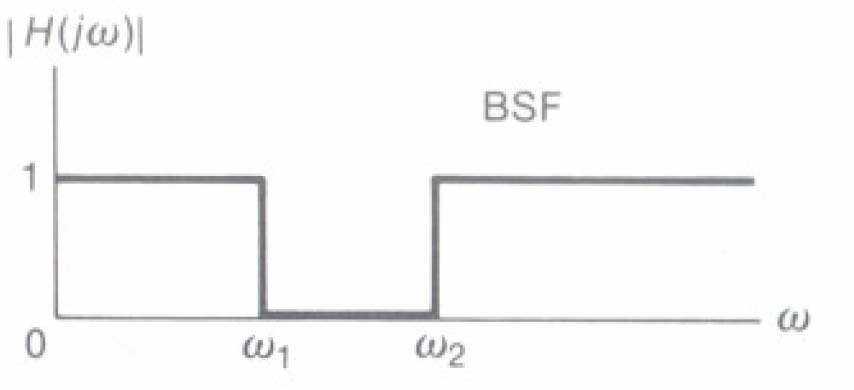
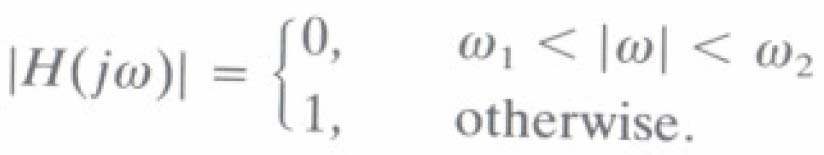

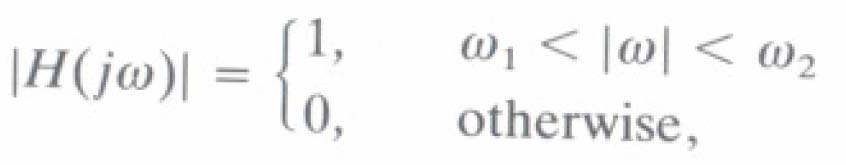
- Bộ Iọc chắn dải (BSF)
EE3000-Tín hiệu và hệ thống
53