
















Preview text:
CHƯƠNG III PHÁN ĐOÁN ***
I. Khái quát về phán đoán:
1. Định nghĩa: Phán đoán là một điều khẳng định hay phủ định, đúng hoặc sai VD:
- Hạnh phúc là đấu tranh
- Nguyễn Trãi không phải tác giả của Bình Ngô Đại Cáo
- Quảng cáo là sức mạnh của cạnh tranh - Dây cao su dẫn điện
- Số 1 không là số nguyên tố - Ông An là Luật sư
2. Phán đoán và câu:
=> Kết luận: Câu là lớp vỏ ngôn ngữ của phán đoán
Phán đoán là nội dung logic của câu
*Lưu ý: - Tôi đang nói dối
không phải phán đoán vì nó mang tính qua lại (tức là nói dối, nối thật,...)
- Ớt nào là ớt chẳng cay? Không phải phán đoán
- Chúng ta có nên hút thuốc lá không?
Không phải phán đoán vì câu hỏi này mang tính chất bên trong trả lời
- Câu này sai. Không phải phán đoán vì mang tính sau đúng, đúng sai.
* Bài tập ví dụ: Các câu sau đây có phải phán đoán không ? - Bông hoa này màu đỏ Phán đoán
- Ly hôn là chấm dứt quan hệ hôn nhân của vợ chồng Phán đoán
- Khoa học pháp lý là khoa học XH – NV Phán đoán.
- Tại sao phải học môn này? Không, vì mang tính chất nghi vấn, tự bản thân hỏi.
- Tôi biết anh ta giỏi- Phán đoán.
3. Phân loại phán đoán:
II. Phán đoán thuộc tính đơn:
1. Định nghĩa: - Là phán đoán đơn
- Khẳng định hay phủ định một tính chất nào đó của đối tượng 2. Cấu trúc:
- Chủ từ S: Nêu lên loại đối tượng mà phán đoán nói về
- Thuộc từ P: Nêu tính chất mà phán đoán khẳng định hay phủ định về đối tượng
*Tính chất P: Khẳng định hay phủ định toàn bộ đối tượng trong S thì với mọi; Còn nếu khẳng
định hay phủ định một số đối tượng trong S thì tồn tại.
- Hệ từ: Từ hoặc cấu trúc câu nêu sự khẳng định hay phủ định tính chất hay MQH của phán đoán
- Lượng từ: Từ hoặc cấu trúc câu nêu lên đặc trưng về lượng của phán đoán.
Bài tập: Phân tích các câu sau thành cấu trúc của phán đoán đơn: a. An là sinh viên.
b. Rắn là loài bò sát.
c. Mọi số chẵn đều chia hết cho 2.
d. Một số kim loại không dẫn điện.
e. Một số sinh viên không là sinh viên đại học Luật TP.HCM.
f. Người Việt Nam không thích chiến tranh
g. Đa số người dân không quan tâm đến chính trị
h. Không phải sinh viên nào cũng giỏi tiếng anh. i. Tôi biết anh ta giỏi
k. Không ai muốn bất hạnh
l. Nước nở ra khi đóng băng m. Mai rất yêu Bình Câ
Phân tích câu S P Hệ từ Lượng u a An Sinh viên Là Với mọi b Rắn Bò sát Là Với mọi c Sỗ chẵn Chia hết cho 2 Là Với mọi d e Sinh viên
Sinh viên đại học Không là Một số luật TP. HCM f - Người Việt Nam không
là người thích chiến tranh.
- Người Việt Nam là người không thích chiến tranh. g
- Đa số người dân không là người quan tâm chính trị
- Đa số người dân là người
không quan tâm đến chính trị. h
- Một số sinh viên không
là người giỏi tiếng anh.
- Một số sinh viên giỏi tiếng anh. i k - Mọi người không là muốn bất hạnh.
- Mọi người đều là người không muốn bất hạnh l m
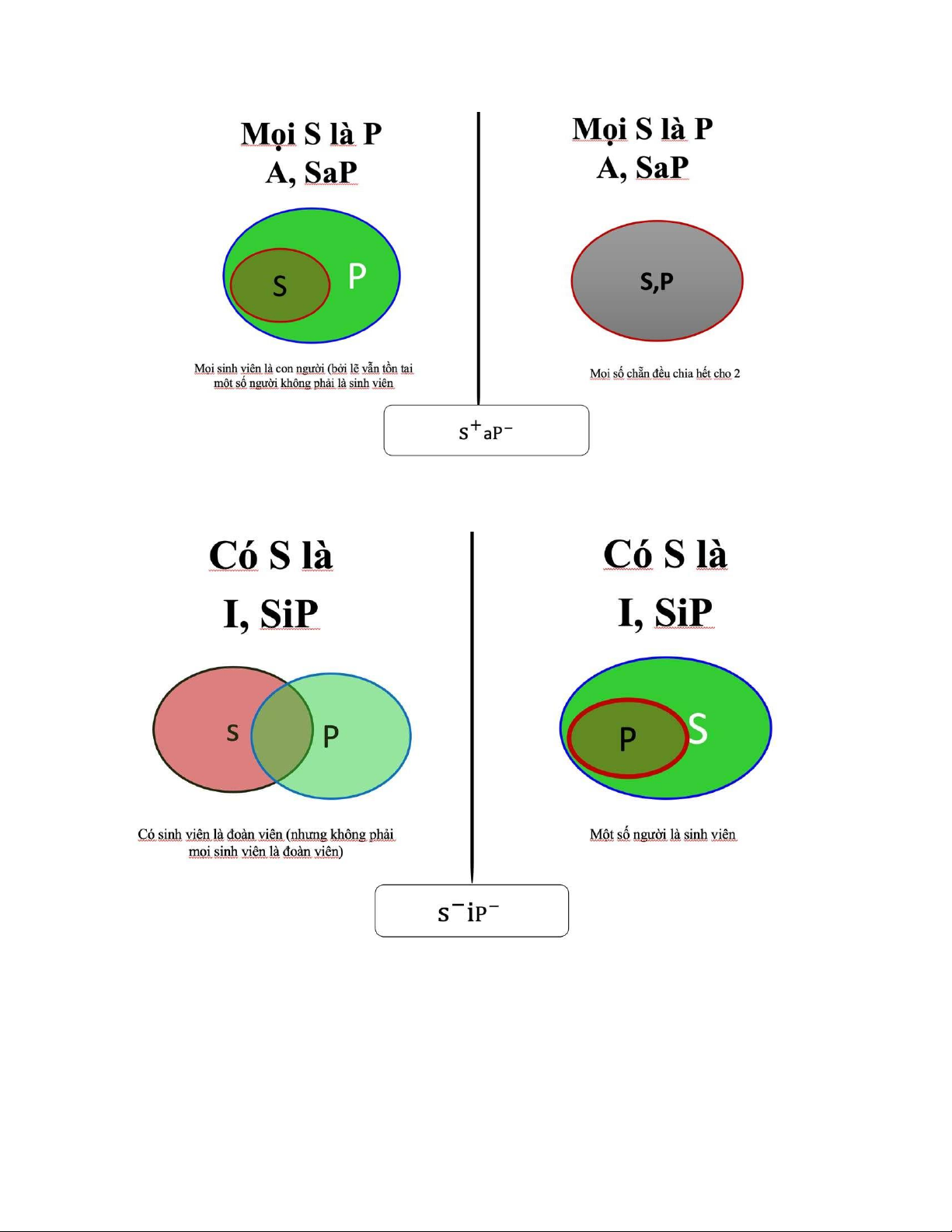
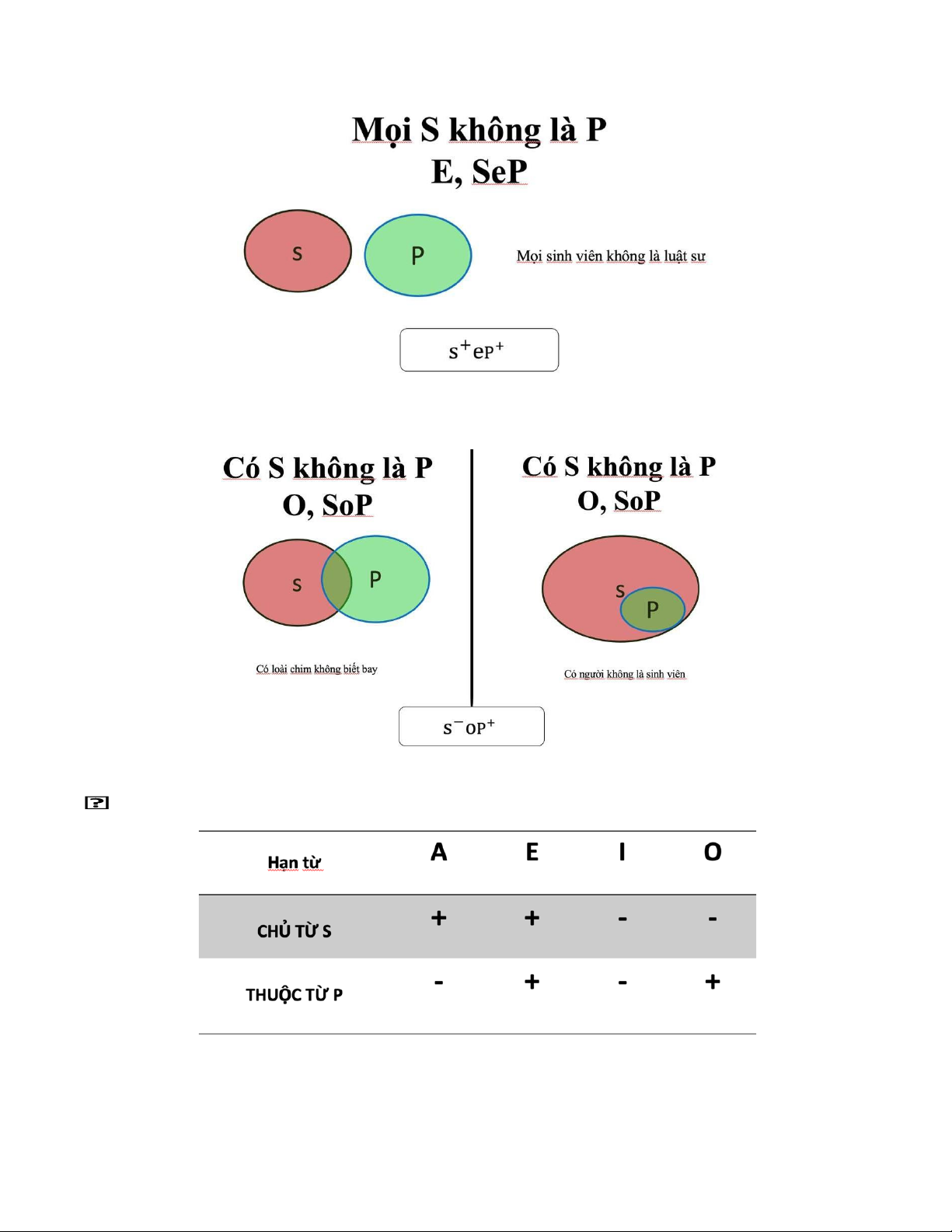
3. Các loại phán đoán thuộc tính đơn:
a. Khẳng định toàn thể: ***
b. Khẳng định bộ phận:
c. Phủ định toàn thể:
d. Phủ định bộ phận: Kết luận:
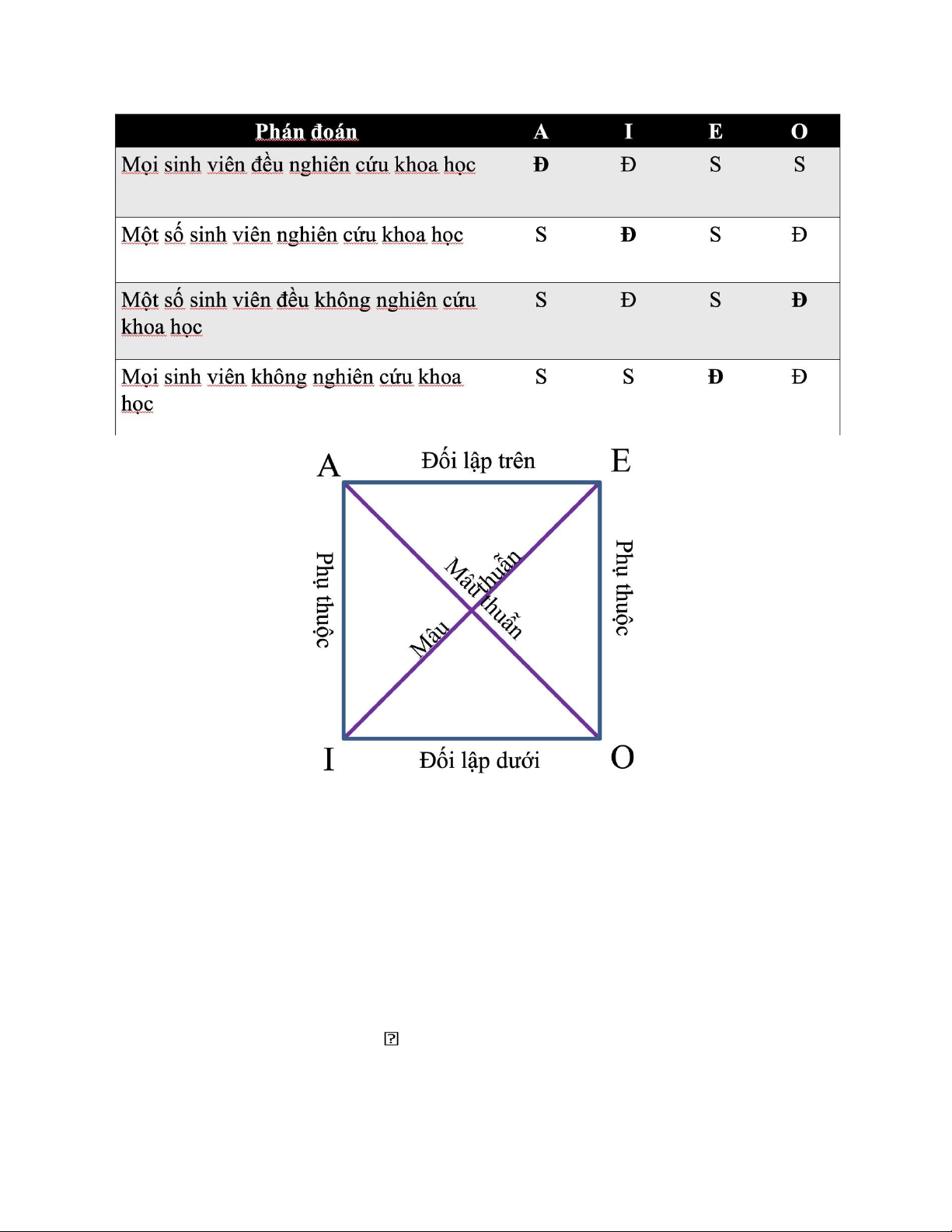
Mối liên hệ giữa các phán đoán:
III. Phán đoán phức:
1. Khái niệm: Phán đoán phức là phán đoán được liên kết bởi nhiều phán đoán đơn. VD:
• Nếu là chim tôi sẽ là loài bồ câu trắng.
• Người nào vô ý làm chết người thì bị phạt tù từ 6 tháng đến 5 năm.
• Sinh viên có thể học tiếng Anh hoặc học tiếng Pháp.
• Anh ta vừa vui vừa hồi hộp Anh ta vui – Anh ta hồi hộp.
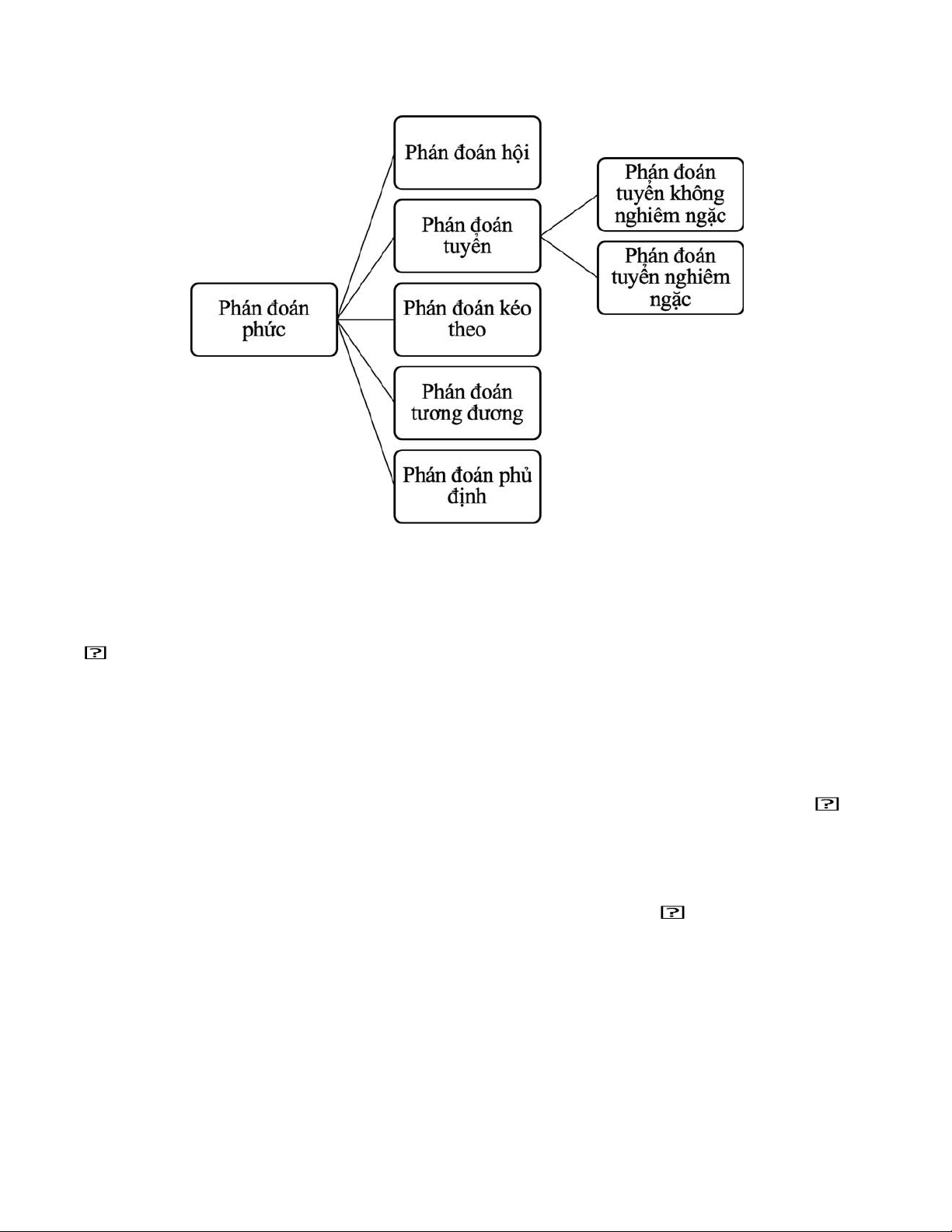
2. Các loại phán đoán:
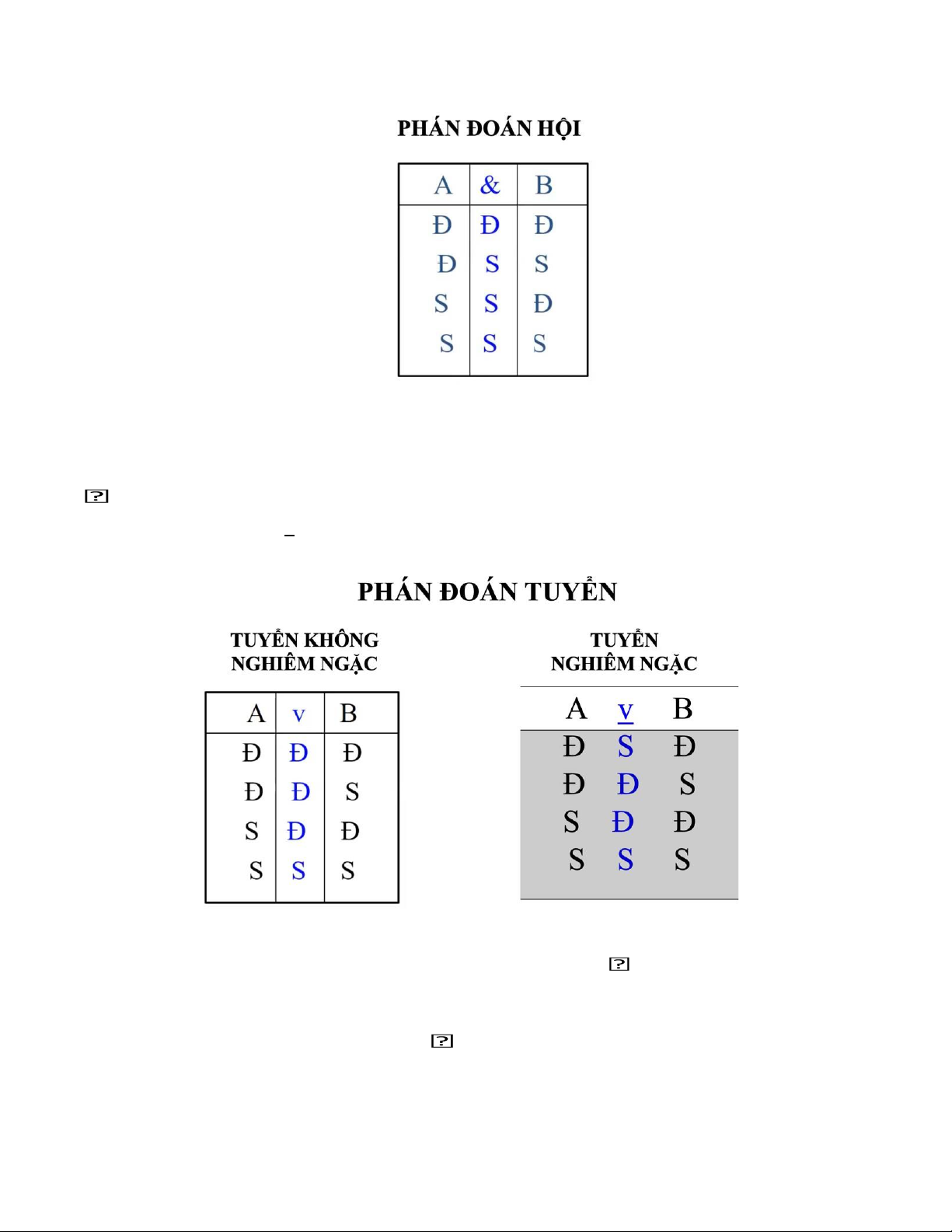
a. Phán đoán hội:
- Là phán đoán được tạo thành bằng cách liên kết hai hay nhiều phán đoán bất kỳ bằng phép hội.
- Liên từ: dấu phẩy, và, đồng thời, song, vẫn, còn, nhưng, mà, và Kí hiệu: A & B VD:
• Nam đọc báo còn Ngọc xem tivi
• Mai vừa vui vừa bất ngờ
• Công nhân khi về hưu, bệnh tật hoặc mất sức lao động thì được hưởng BHXH Công
nhân khi về hưu thì được hưởng BHXH và Công nhân bệnh tật thì được hưởng BHXH và
Công nhân mất sức lao động thì được hưởng BHXH.
• Nhà nước nghiêm cấm và trừng trị mọi hành động phản quốc Nhà nước nghiêm cấm
mọi hành động phản quốc và Nhà nước trừng trị mọi hành động phản quốc.
b. Phán đoán tuyển:
- Là phán đoán được tạo thành từ các phán đoán bất kỳ và liên kết với nhau bằng phép tuyển
- Liên từ: hay là, hoặc là Bao gồm:
+ Tuyển nghiêm ngặt: A v B
+ Tuyển không nghiêm ngặt: A v B
* Phán đoán tuyển không nghiêm ngặc:
• Cần bảo hành xe sau 2 tháng hoặc/và khi đã đi 2000km
Có nghĩa xe đi tháng vẫn được
bảo hành/ Xe đi được 2000km vẫn được bảo hành.
• Anh đi đón em hoặc chị đi đón em
Tức là Anh đi đón em thì em được về nhà. Nếu a n h
không đi đón thì chị đi đón thì em vẫn được về nhà. Có nghĩa đường nào thì em cũng về được nhà.
* Phán đoán tuyển nghiêm ngặc:
• Hôm nay là thứ bảy hoặc chủ nhật.
• Cây hoa sống hoặc đã chết.
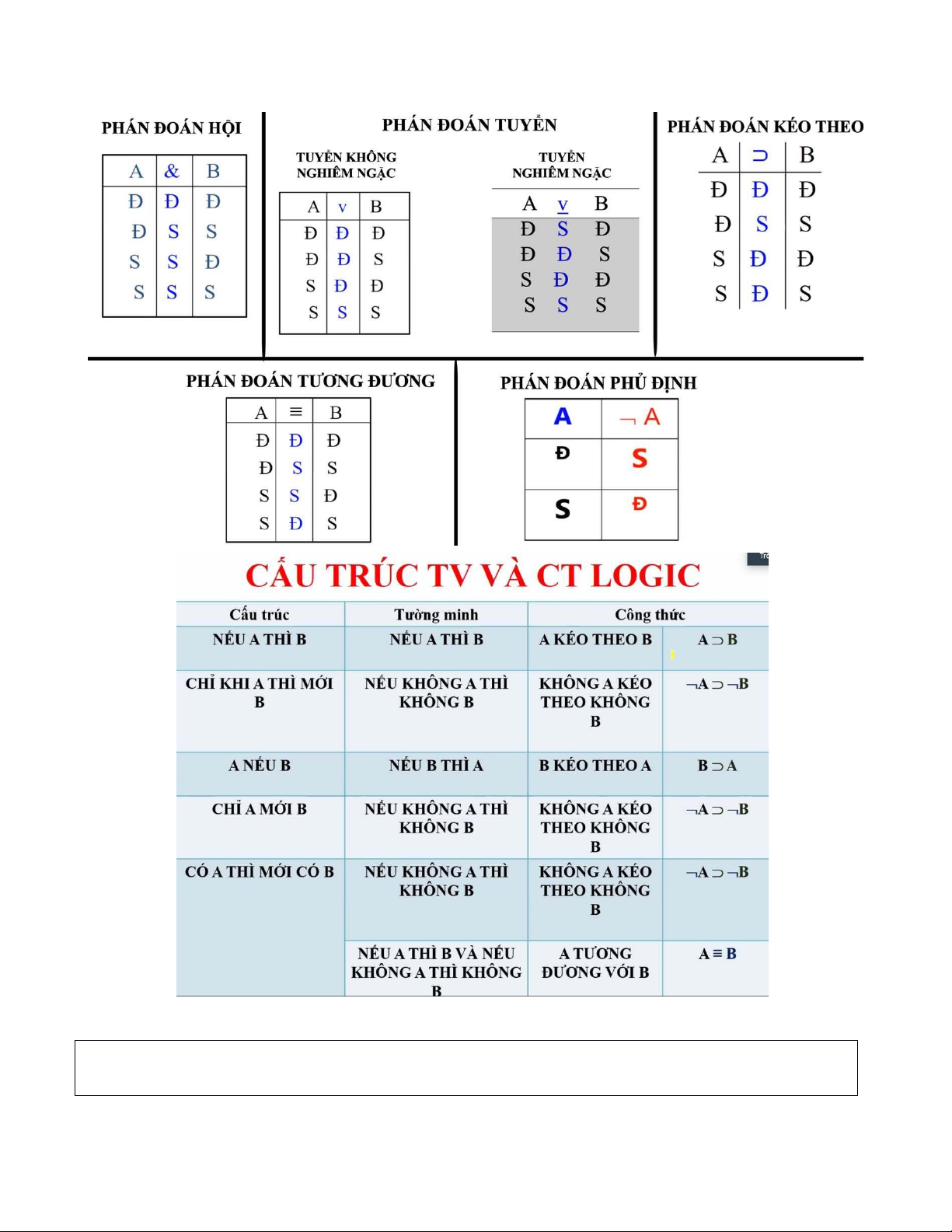
c. Phán đoán kéo theo:
- Là phán đoán được tạo thành từ các phán đoán đơn và liên kết với nhau bằng phép kéo theo.
- Liên thì: Nếu…thì, vậy,…, thì…, nên, suy ra… Dạng: A ⊃ B VD:
• Nếu trời mưa thì đường ướt.
• Một dân tộc đoàn kết thì có thể vượt qua mọi khó khăn.
• Nếu anh tìm được lá diêu bông, em sẽ lấy anh làm chồng.
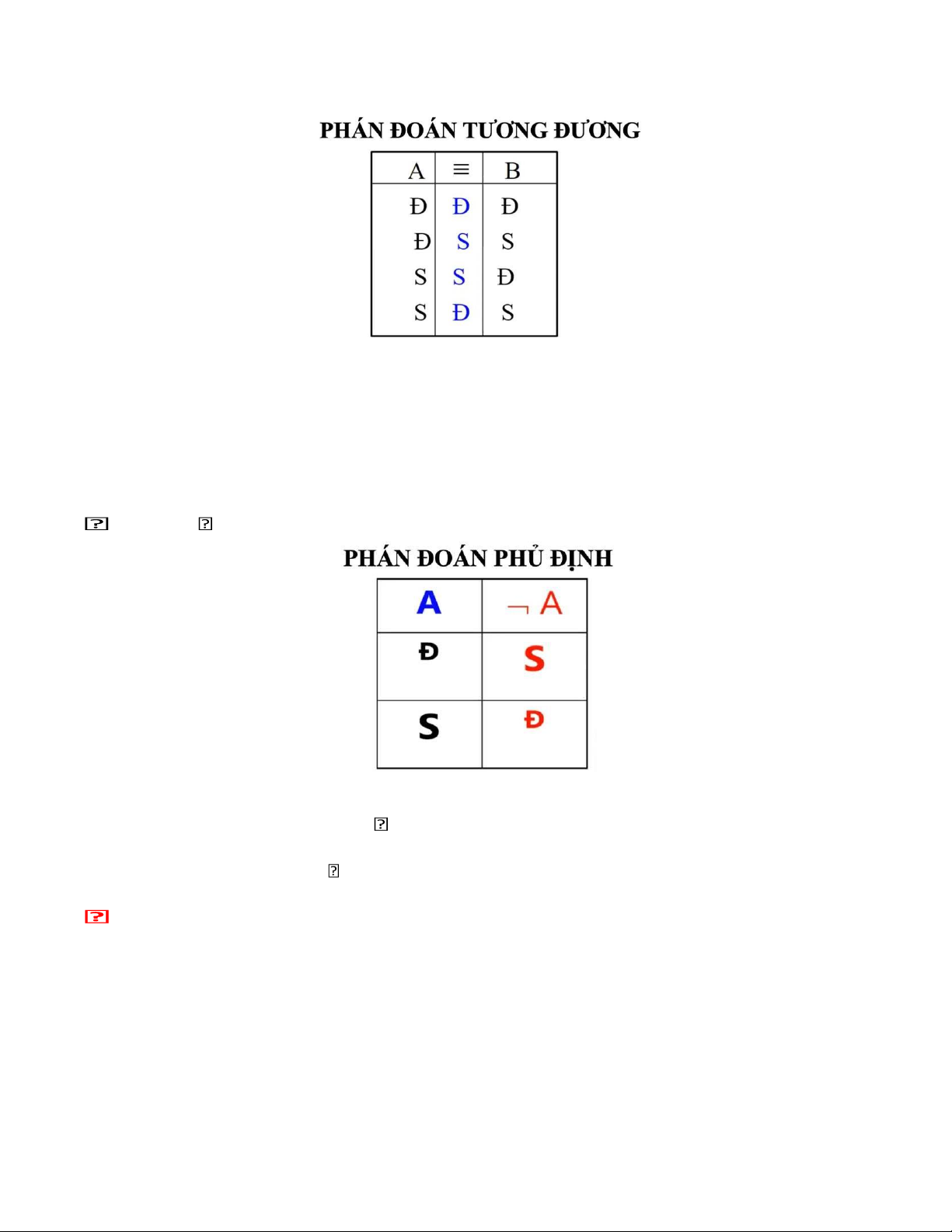
d. Phán đoán tương đương:
- Là phán đoán được tạo thành từ các phán đoán đơn và liên kết với nhau bằng phép tương đương.
- Biểu thị: Tương đương, điều kiện cần và đủ,khi và chỉ khi, chỉ khi… Dạng: A ≡ B.
VD: Tứ giác ABCD là hình chữ nhật khi và chỉ khi tứ giác ABCD là hình bình hành có hai đường chéo bằng nhau.
e. Phán đoán phủ định:
- Phán đoán phủ định khác với các phán đoán phức khác, nó được tạo thành từ một phán đoán và
một phép toán phủ định. Ký hiệu: , ~ VD:
• Số 9 không phải là số chẵn Tức là số 9 phủ định của nó là số chẵn
• Nam không phạm tội Tức là khẳng định của nó là Nam phạm tội. KẾT LUẬN: BTVN:
1. Có tự do thì có hạnh phúc 2. An 20 hay 21 tuổi
3. Nếu Nam học bài sẽ thi đậu. Nam thi đậu, vậy Nam đã học bài.
4. Triết học, pháp luật có tính giai cấp.
5. Đèn bàn làm việc không sáng, khi và chỉ khi, điện bị ngắt nguồn hoặc bóng đèn bị hỏng.
6. Chăm chỉ và có phương pháp học tập đúng bạn sẽ có kết quả học tập tốt.
7. Nói rằng người Việt Nam vừa yêu hòa bình vừa thích chiến tranh là không đúng.
8. Chừng nào (chỉ khi) giặc Tây nhổ hết cỏ nước Nam thì mới hết người Nam đánh Tây.
9. Cố ý phạm tội là phạm tội trong trường hợp là nhận thức rõ hành vi của mình có tính chất
gây nguy hiểm cho xã hội, thấy trước hậu quả của hành vi đó và mong muốn hoặc có ý thức
để mặc hậu quả xảy ra.
10. Chắc chắn rằng cả Nam và Minh đều không đi học, bởi hoặc Nam hoặc Minh đi học thì
nhóm của họ đã được tranh luận. Thế nhưng thực tế nhóm của họ không được tranh luận.
11. Ăn nhiều mà ít tập thể dục sẽ bị béo phì. Béo phì dễ bệnh tim mạch, như vậy anh ấy không tập thể dục.
3. Quy luật và mâu thuẫn logic:
- Quy luật logic: Là phán đoán đúng trong mọi trường hợp.
VD: Trời mưa hoặc trời không mưa A v ¬A
- Mâu thuẫn logic: Là phán đoán sai trong mọi trường hợp.
VD: Trời mưa và trời không mưa A & ¬A
4. Các phương pháp xác định quy luật và mâu thuẫn logic:
CÁCH 1: LẬP BẢNG CHÂN TRỊ:
- Bước 1: Lập bảng chân trị. Kẻ bảng có dòng.
Trong đó: n là số lượng phán đoán đơn trong phán đoán phức.
- Bước 2: Gán giá trị theo nguyên tắc chia đôi.
- Bước 3: Tính giá trị
• Trong ngoặc đơn trước ngoài ngoặc sau
• Thứ tự ưu tiên: ¬, &, V, ⊃ ,≡
• Cùng dấu làm từ phải sang trái Kết luận
- CT ĐÚNG HẾT: CT LÀ QL LOGIC
- CT SAI HẾT: CT LÀ MÂU THUẪN
- CT VỪA ĐÚNG VỪA SAI: CT KHÔNG LÀ QL LOGIC
*? BTVD: ((p
r ) & q) ((r p) Q (r q)) BTVN: 1. p⊃(q⊃¬p)
2. ((p& ¬r) ⊃q) ⊃ (r ⊃(¬pvq))
3. (¬r&(p⊃q)) ⊃((r ⊃p)vq)
4. (pv(q&r)) ⊃((pvq)&(pvr))
CÁCH 2: LẬP BẢNG NGỮ NGHĨA:
* Ý tưởng bảng ngữ nghĩa: Đi tìm dòng sai mà không cần bảng chân trị ?
- Bảng chân trị của công thức A
- Có dòng sai A không là quy luật logic
- Không có dòng sai A là quy luật logic - Lập bảng phát hiện dòng sai
Kết luận: Bảng ngữ nghĩa hay bảng chân lý rút gọn là phương pháp xác định xem công thức
nào đó có phải là quy luật logic hay không bằng cách tìm xem trong bảng chân lý có dòng
sai hay không. Nếu không có dòng sai nào thì công thức đã cho là quy luật logic.
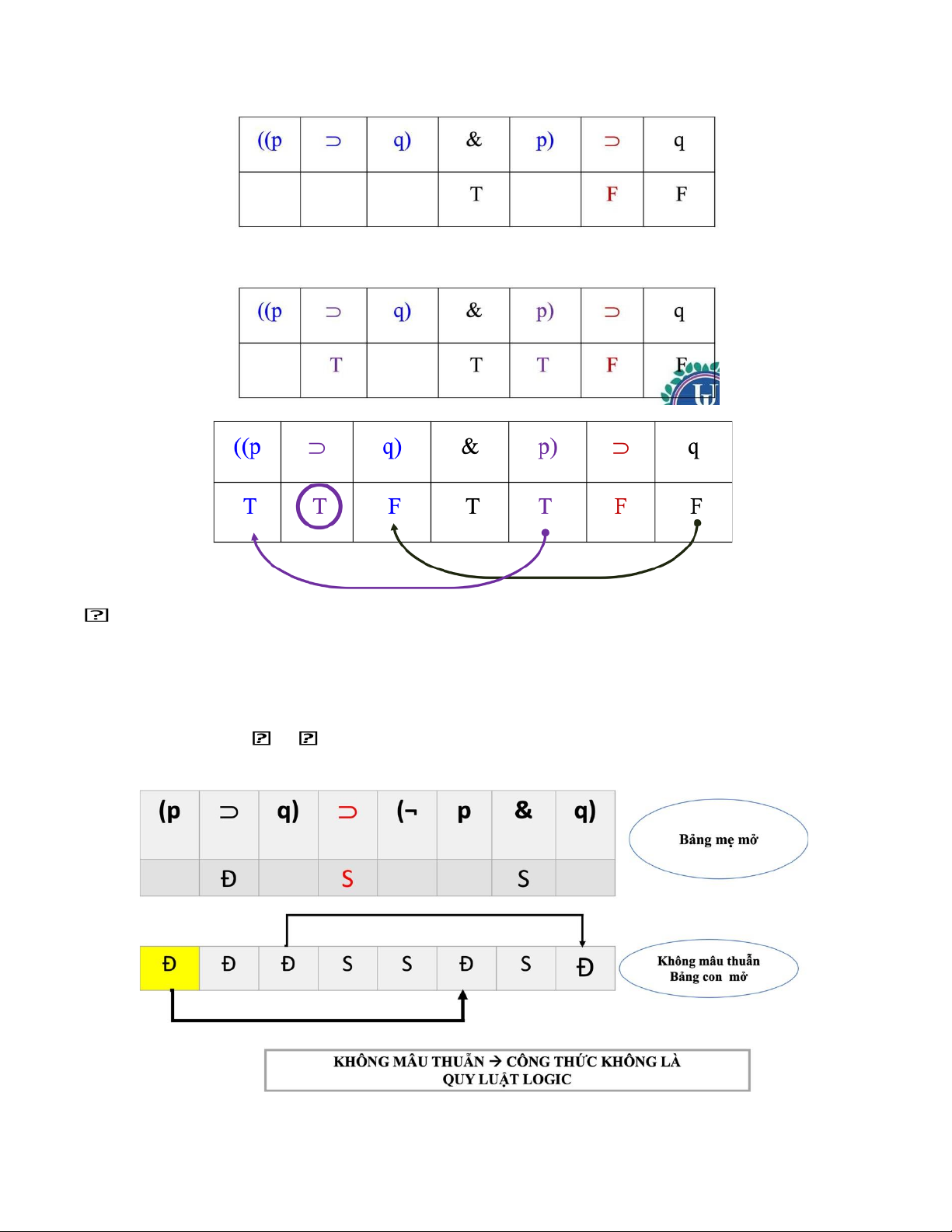
* Các bước để lập bảng ngữ nghĩa:
- Bước 1: Kẻ bảng gồm 2 dòng, ghi công thức vào dòng 1
- Bước 2: Ghi S vào dòng 2, ở ngay phép toán chính
- Bước 3: Căn cứ vào giá trị đã có, xác định các giá trị còn lại
• Nếu gặp MÂU THUẪN CÓ DÒNG SAI
• Nếu KHÔNG gặp MÂU THUẪN KHÔNG CÓ DÒNG SAI
* Bài làm ví dụ: ((p q) & p) q
Ta xét xem các cột trong giá trị có mâu thuẫn hay không, nếu có nghịch lý thì ta có thể kết
luận giả định ban đầu của ta công thức đã cho công thức không phải là quy luật logic là một
giả định sai lầm, vậy công thức đã cho là quy luật logic.
* Bài làm ví dụ: (p q) (¬p & q)
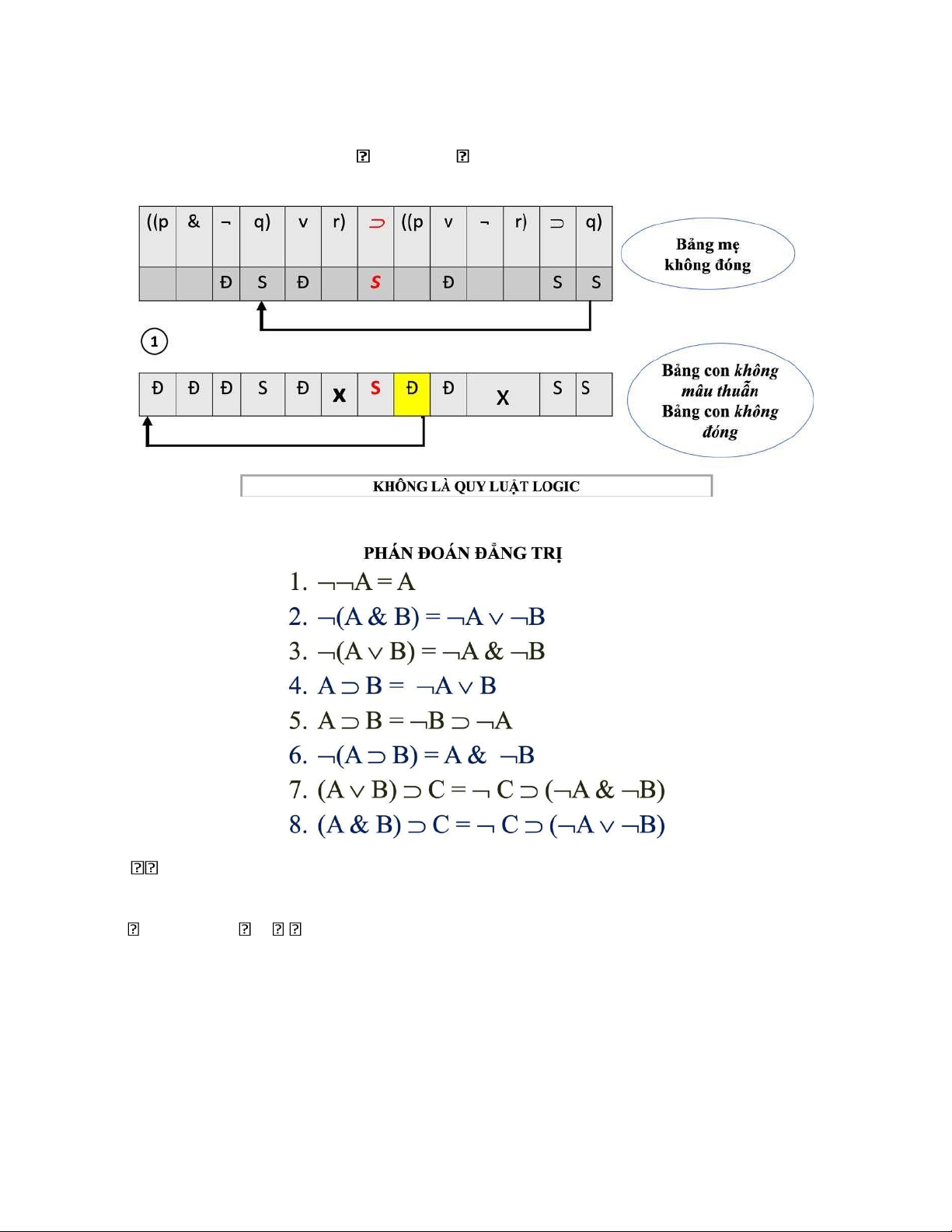
* Bài làm ví dụ: ((p & ¬q) v r) ((p v ¬r) q)
III. Phán đoán đẳng trị: VD: A = A
“Không phải tôi không muốn đi chơi với em” tương đương với “Tôi muốn đi chơi với em” VD: (A & B) = A B
“Không phải An vừa biết tiếng Anh hay vừa biết tiếng Pháp đâu” tương đương với “Hoặc
An không biết tiếng Anh, hoặc An không biết tiếng Pháp”. BÀI TẬP:
Câu 1: Xác định quy luật logic hay mâu thuẫn logic: a. p (q ¬p) b. ((p v q) r)) ((¬p & q) ¬r) c. ((p v q) & (p r)) ((q r) r)
d. (¬p (¬q& ¬r)) ((q r) v p)
e. ((qv¬p )&(p& ¬r)) (¬p (qvr)) f. (p q) (¬p & q)
g. ((p & ¬q) v r) ((p v ¬r) q) h. p⊃(q⊃ ¬p)
i . ((p & ¬r) ⊃q) ⊃(r ⊃(¬p v q))
k. (¬r & (p⊃q)) ⊃((r ⊃p)vq)
l. (p v (q&r)) ⊃ ((pvq) & (pvr))
Câu 2: “Nếu có tiền thì Minh mua laptop. Minh có tiền, vậy Minh mua laptop”. Suy luận sau có đúng không?
Câu 3: Ông chủ nói: “Nếu anh không làm việc này hoặc làm không tốt sẽ bị đuổi việc. Anh đã
làm tốt việc này, vì vậy anh ấy nghĩ anh ấy sẽ không bị đuổi việc”. Hỏi anh ta suy luận đúng hay sai?
Câu 4: “Nếu sách của ngài đúng với kinh Koran thì sách ngài thừa. Nếu sách của ngài không
đúng với kinh Koran thì sách ngài có hại. Sách thừa hay sách có hại cần phải đốt”. Hỏi suy luận đúng hay sai?
Câu 5: Tìm phán đoán tương đương với các phán đoán sau (gợi ý: Áp dụng công thức phán
đoán đẳng trị):
a. Nếu khiêm tốn thì được mọi người yêu mến.
b. Nếu học chăm chỉ và đúng phương pháp thì sẽ vượt qua kì thi này.
c. Không phải cô ấy vừa hát hay vừa xinh đẹp. CHƯƠNG IV
SUY LUẬN TRỰC TIẾP VỚI TIỀN ĐỀ LÀ PHÁN ĐOÁN THUỘC TÍNH ĐƠN ***
I. Khái luận chung vấn đề: 1. Suy luận:
a. Khái niệm: Suy luận (suy diễn logic) là hình thức của tư duy, trong đó từ một số tri thức đã có rút ra tri thức mới.
b. Cấu trúc suy luận:
- Tiền đề: là những tri thức đã biết, hoặc được thừa nhận, làm cơ sở cho suy luận. Có thể được
tạo thành từ nhiều tri thức, sự kiện khác nhau
Mỗi sự kiện hay tri thức trong phần tiền đề
cũng được gọi là các tiền đề.
- Kết luận: Là tri thức được rút ra. Có thể có gồm nhiều tư tưởng, tri thức khác nhau Mỗi tri
thức hay tư tưởng trong phần kết luận được gọi là các kết luận.
c. Phân loại suy luận:
2. Suy luận diễn dịch trực tiếp với tiền đề là phán đoán đơn:
a. Định nghĩa: Suy luận trực tiếp là loại suy luận diễn dịch bao gồm 1 tiền đề và 1 kết luận
Không thể thu được kết luận nhiều thông tin hơn tiền đề.
b. Các loại suy luận diễn dịch trực tiếp:
II. Phân tích các loại suy luận trực tiếp với tiền đề là phán đoán thuộc tính đơn:
1. Đảo ngược phán đoán (đổi chỗ phán đoán): Đổi chỗ chủ từ và vị từ của phán đoán ban đầu,
giữ nguyên chất phán đoán. Bài tập Đáp án
Mọi văn bản pháp luật đều tuân theo hiến pháp
Có sinh viên là đoàn viên
Có đoàn viên là sinh viên
Phụ nữ có thai không chịu án tử hình
Người chịu án tử hình lkhông là phụ nữ có thai Một số hoa có màu đỏ
Một số vật màu đỏ là hoa.
Mọi sinh viên đều học Logic
Một số người học logic đều là sinh viên.
Hiến pháp đầu tiên nước Việt Nam là Hiến
Hiến pháp 1946 là Hiến pháp đầu tiên của Việt pháp 1946 Nam.
Một số người là sinh viên
Mọi sinh viên đều là người.
Một số sinh viên là đoàn viên
Một số đoàn viên là sinh viên.
Trẻ em không là đại biểu Quốc hội
Đại biểu Quốc hội không là trẻ em.
2. Đổi chất phán đoán: Là biến đổi phán đoán từ khẳng định thành phủ định và ngược lại. Đề Đáp án
Mọi công dân đều tuân thủ pháp luật
Mọi công dân đều không vi phạm pháp luật.
Mọi sinh viên đều không muốn thi rớt
Mọi sinh viên đều muốn thi đậu.
Một số kẻ thích chiến tranh
Một số kẻ không thích hòa bình.
Một số người không chân thực
Một số người giả dối
Mọi tử tù là kẻ có tội
Mọi tử tù không là kẻ vô tội
Mọi văn bản pháp luật đều tuân theo Hiến Mọi văn bản pháp luật đều không vi Hiến pháp
Một số sinh viên không siêng năng
Một số sinh viên lười biếng
Một số phụ nữ thích độc thân
Một số phụ nữ không thích lập gia đình.
Mọi bệnh do Virus gây ra đều là bệnh không Mọi bệnh do Virus gây ralà bệnh đều không là
thể điều trị bằng kháng sinh.
điều trị bằng kháng sinh.
Một số thông tin trên mạng xã hội giả dối
Một số thông tin trên mạng xã hội không phải là sự thật An là đoàn viên
An không là không đoàn viên.
Anh Huy là người môi giới chứng khoán
Anh Huy không là người không môi giới chứng khoán
Những người học luật sư đều am hiểu logic
Mọi người làm luật sư đều không là không am hiểu logic.
3. Đặt đối lập vị từ: Là dạng suy luận thu được bằng cách thực hiện lần lượt hai thao tác đổi
chất và đảo ngược phán đoán (đổi chất + đổi chỗ (đảo ngược)). Đề Đáp án
Mọi kẻ buôn bán túy đều không tuân thủ pháp Một số kẻ vi phạm pháp luật là đối tượng luật. buôn bán ma tuý.
Người Việt Nam yêu hòa bình
Một số phụ nữ không thích lập gia đình
Một số phụ nữ thích độc thân
Có sinh viên không học tập tốt
Một số sinh viên lười biếng trong học tập
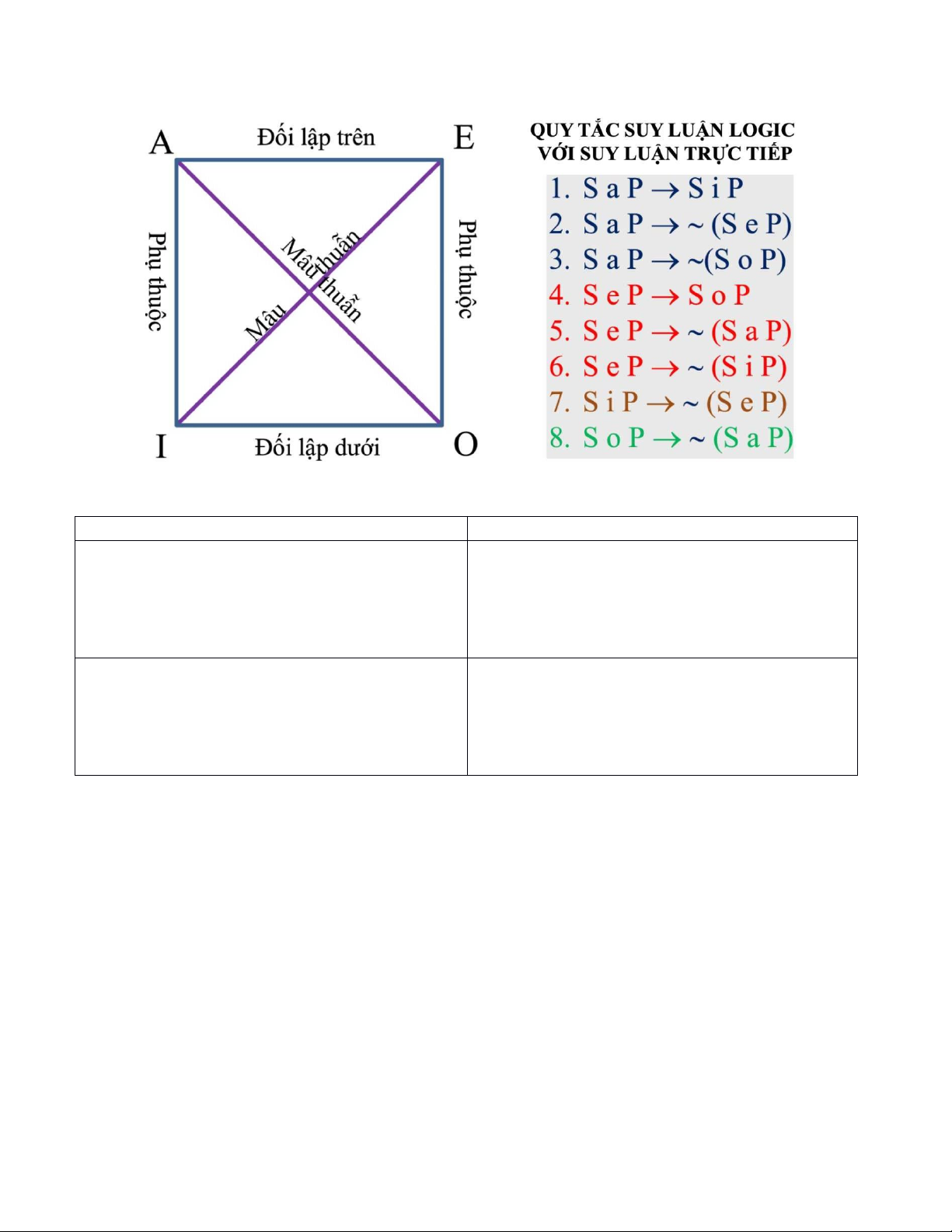
4. Suy luận theo hình vuông logic: Đề Đáp án
Người Việt Nam yêu hòa bình
Một số loài thú không sống dưới nước
CHƯƠNG V: TAM ĐOẠN LUẬN NHẤT QUYẾT ĐƠN
I. Định nghĩa và cấu trúc:
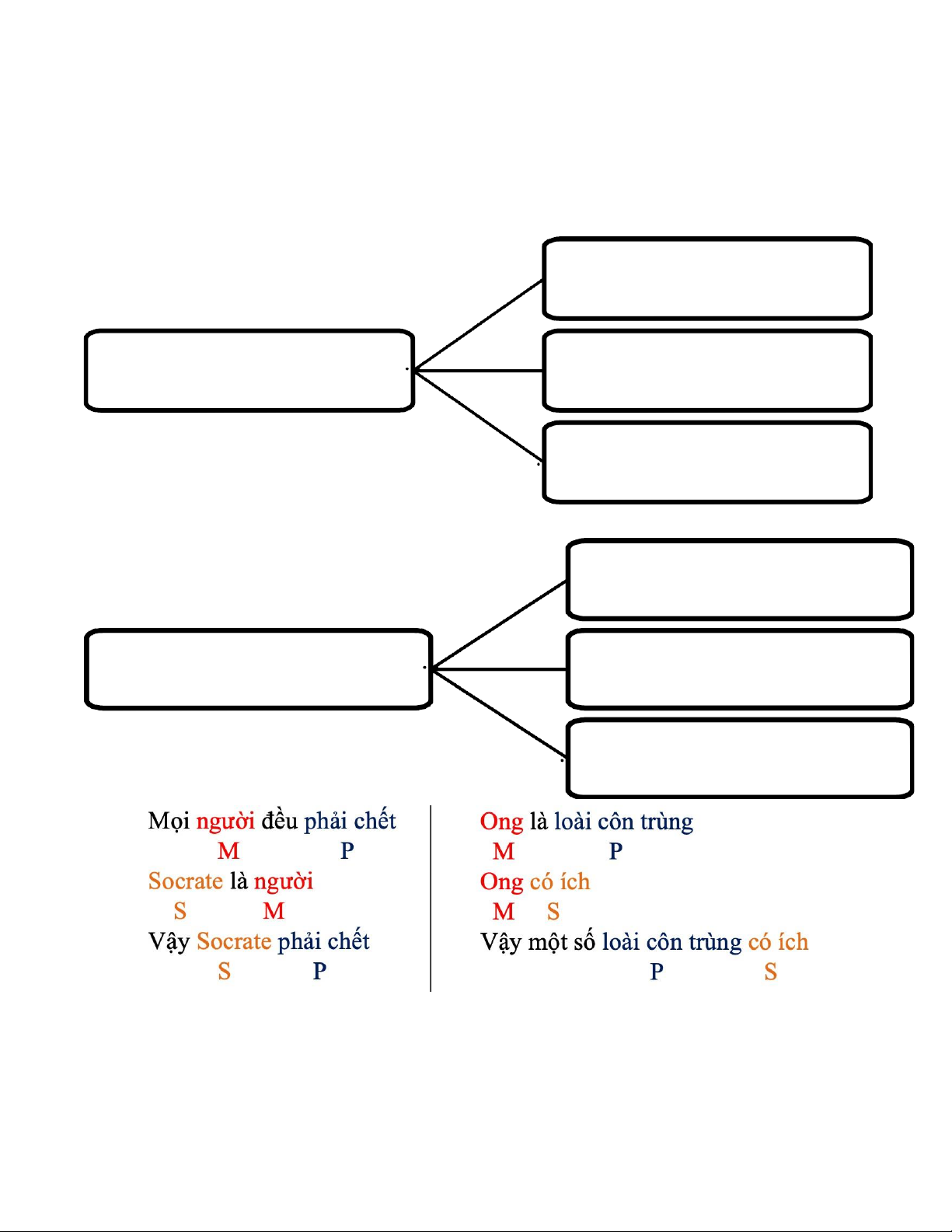
1. Định nghĩa: Tam đoạn luận đơn là suy luận diễn dịch gồm có hai tiền đề và kết luận đều là
các phán đoán thuộc tính đơn, với đúng ba thuật ngữ (hạn từ, từ) khác nhau. 2. Cấu trúc:
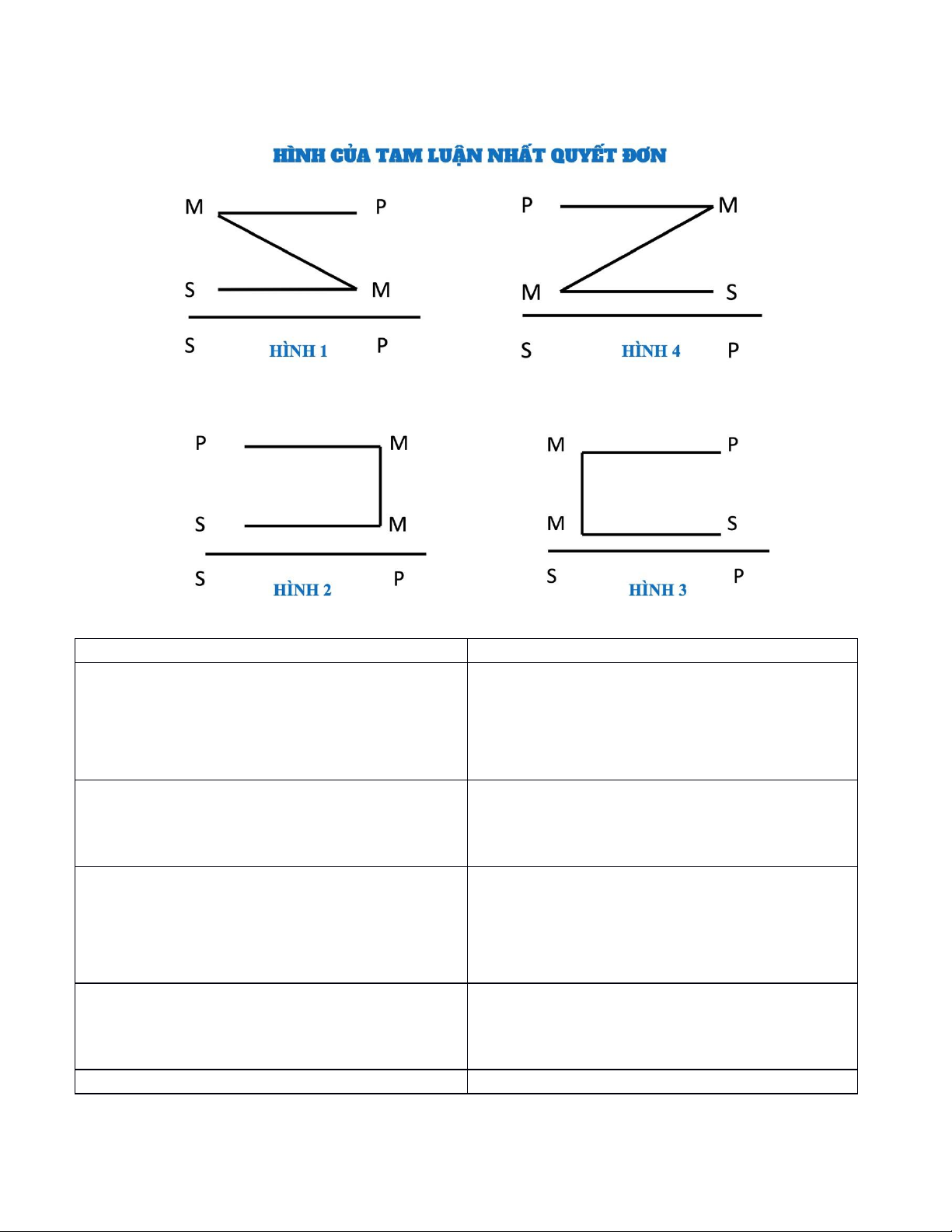
II. Hình của tam đoạn luận nhất quyết đơn:
Bài tập: Xác định hình tam đoạn luận nhất quyết đơn sau: Bài tập Đáp án
Người da đỏ sống trong rừng.
Người da đỏ không chặt phá rừng.
Vậy bộ tộc sống trong rừng không chặt phá rừng
Mọi người đều có quyền sống. Tử tội là người.
Vậy tử tội có quyền sống.
Người hay giúp đỡ người khác thường hay
được mọi người yêu mến.
Người tốt hay giúp đỡ người khác.
Vậy, người tốt được mọi người yêu mến.
Mọi sinh viên đều học môn Logic Nam là sinh viên Vậy Nam học môn Logic Nước mưa thì mặn, Ly nước này không mặn.
Vậy ly nước này không phải nước mưa.
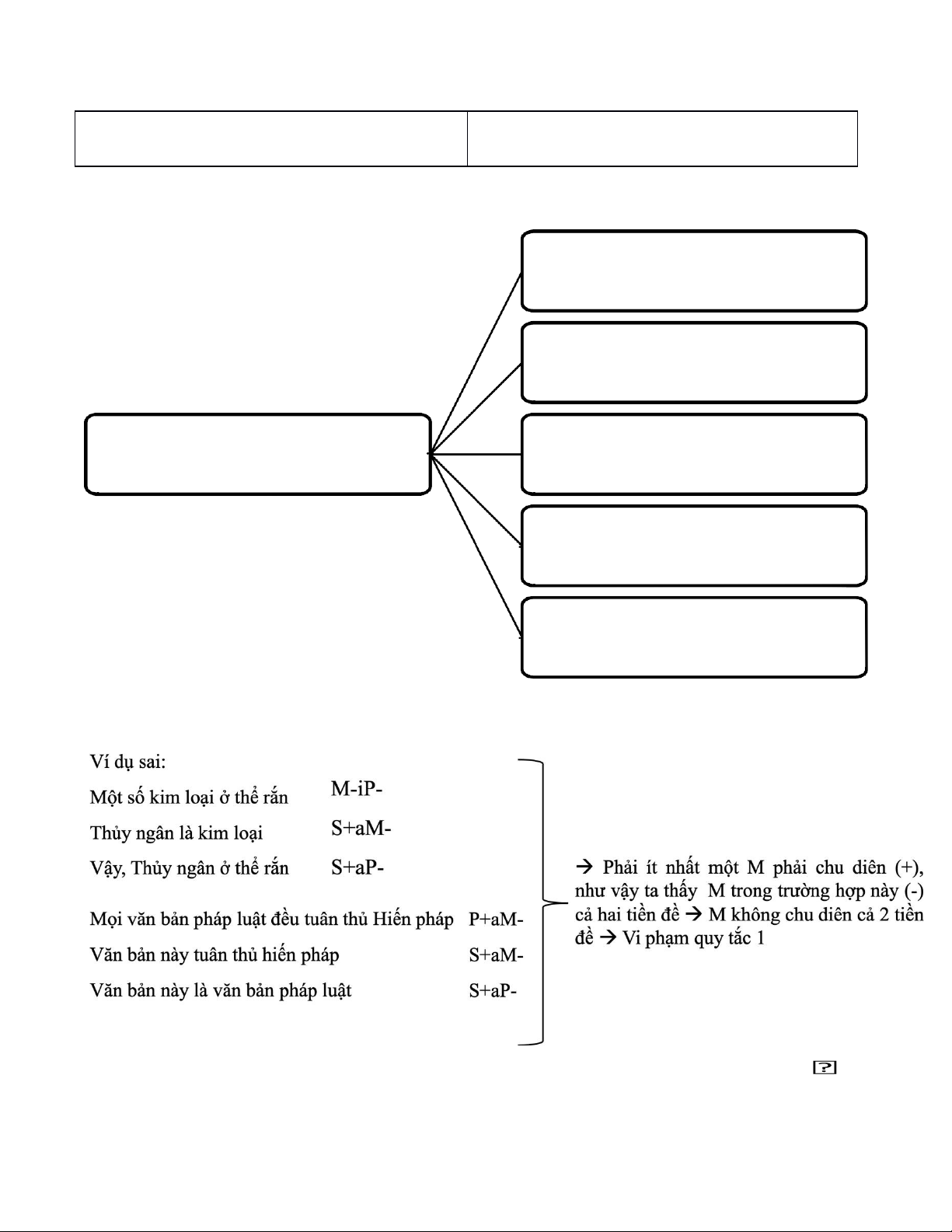
III. Các quy tắc chung của tam đoạn luận đơn:
* Quy tắc 1: Trung từ M phải chu diên (+) ít nhất là ở một tiền đề.
* Quy tắc 2: Một từ không chu diên trong tiền đề thì không thể chu diên trong kết luận Trên
trừ dười cộng là vi phạm.
Bài tập vận dụng:
Mọi người phạm tội đều có hành vi nguy hiểm cho xã hội
Anh A không là người phạm tội
Vậy, anh A không có hành vi nguy hiểm cho xã hội
* Quy tắc 3: Phải có tiền đề khẳng định
Phải có ít nhất dạng A hoặc I mới thoả m ã n. Ví dụ vi phạm:
New York không phải là Thủ đô Mỹ (E)
Thành Phố X không phải là New York (E) Vi phạm quy tắc 3
* Quy tắc 4: Nếu có tiền đề phủ định thì kết luận phải phủ định Ví dụ vi phạm:
Mọi kẻ phạm tội đều không tránh khỏi bị trừng trị E
Kẻ buôn bán ma túy là kẻ phạm tội A
Kẻ buôn bán ma túy đều tránh khỏi bị trừng trị A
Vi phạm nguyên tắc 4 vì tiền đề 1 đã phủ định mà kết luận lại khẳng định
Bài tập vận dụng:
Vi phạm pháp luật là hành vi có lỗi.
Hành vi có lỗi không là hành vi của người tâm thần.
Vậy, hành vi của người tâm thần là hành vi vi phạm pháp luật
* Quy tắc 5: Nếu hai tiền đề đều khẳng định thì kết luận phải khẳng định. Ví dụ vi phạm:
Mọi khoa học đều có phương pháp nghiên cứu riêng A Logic học là khoa học A
Vậy, Logic học không có phương pháp nghiên cứu riêng
Vi phạm quy tắc 5 vì cả hai tiền đề đèu khẳng định mà kết luận lại phủ định.
Bài tập vận dụng:
Mọi luật sư đều tốt nghiệp đại học ngành Luật
Anh Nam tốt nghiệp đại học ngành Luật
Vậy, Anh Nam không là luật sư
Lưu ý: các trường hợp không xem là tam đoạn luận (xét các ví dụ sau):
Vật chất tồn tại vĩnh viễn Con ruồi là vật chất
Vậy con ruồi tồn tại vĩnh viễn
Con ruồi, vật chất, vĩnh viễn & vật chất.
Bởi lẽ, vật chất ở tiền đề đầu tiên là dạng tồn tại con ruồi, vật chất ở tiền đề thứ hai là vật chất trong triết học
Nhiều hơn 3 loại từ nên không xem là tam đoạn luận
KẾT LUẬN: ĐÂY KHÔNG LÀ TAM ĐOẠN LUẬN, BỞI NÓ CÓ NHIỀU HƠN 3 HẠNG TỪ
IV. Tam đoạn luận giản lược:
1. Khái niệm: Tam đoạn luận đơn giản lược là tam đoạn luận mà một tiền đề (tiểu tiền đề hoặc
đại tiền đề) hoặc một kết luận đã bị lược bỏ
Lược bỏ tiểu tiền đề, đại tiền đề hay kết luận.
VD: Mọi sinh viên đều học môn Logic,Nam là sinh viên.
Mọi sinh viên đều học môn Logic. Vậy, Nam học Logic
Nam là sinh viên. Vậy Nam học môn Logic.
2. Phục hồi tiền đề:
- Căn cứ vào quy tắc chung để phục hồi tiền đề.
- Nếu vi phạm quy tắc chung thì không phục hồi được tiền đề.
- Tiền đề được phục hồi có thể có nhiều kết quả.
Bài tập ví dụ: Phục hồi tiền đề bị lược bỏ của tam đoạn luận MaP, SaP ?
1. Tiền đề bị lược bỏ là tiểu tiền đề. S—M; M – S
2. Căn cứ vào quy tắc 4 “Nếu có tiền đề phủ định thì kết luận phải phủ định” S+aM-; M+aS- ; S-iM-; M-iS-
3. Căn cứ vào quy tắc 2 “Một từ không chu diên trong tiền đề thì không thể chu diên trong kết luận” S+aM-
Bài tập ví dụ: Phục hồi tiền đề bị lược bỏ của tam đoạn luận SoM, SaP ?
Quy tắc 4: Nếu có tiền đề phủ định thì kết luận phải phủ định Không phục hồi được
BÀI TẬP VẬN DỤNG:
Câu 1 (TL): Xác định các quy tắc trong câu sau có vi phạm hay không ? Câu hỏi Bài giải
Người da đỏ sống trong rừng.
Người da đỏ không chặt phá rừng.
Vậy bộ tộc sống trong rừng không chặt phá rừng
Mọi người đều có quyền sống. Tử tội là người.
Vậy tử tội có quyền sống.
Người hay giúp đỡ người khác thường hay
được mọi người yêu mến.
Người tốt hay giúp đỡ người khác.
Vậy, người tốt được mọi người yêu mến.
Truy tố là nhằm đưa bị can ra xét xử
Truy tố là hoạt động tố tụng
Vậy, một số hoạt động tố tụng là nhằm đưa bị can ra xét xử
Câu 2 (TN): Xét các cặp tiền đề được liệt kê trong các đáp án dưới đây, hãy chọn đáp án
không chứa cặp tiền đề vi phạm các quy tắc chung của tam đoạn luận nhất quyết đơn.
A. AA, AE, AI, EA, EO, IA, IE, OA.
B. AA, AE, AI, AO, EA, IA, IE, OA, II.
C. AA. AE, AI, AO, EA, IA, IE, AO.
D. AA, EE, AE, AI, AO, EA, IA, IE, OA.
Câu 3 (TN): Xét xem tam đoạn luận đơn sau đây đúng hay sai, vì sao? “Ai học giỏi cũng có
nhiều khả năng tìm được việc làm tốt sau khi tốt nghiệp. Sau khi tốt nghiệp Minh có nhiều
khả năng tìm được việc làm tốt. Vậy Minh học giỏi”.
A. Sai, vì trung từ không chu diên trong cả hai tiền đề;
B. Đúng, vì tuân thủ tất cả các quy tắc của tam đoạn luận đơn;
C. Sai, vì cả hai tiền đề đều là phán đoán bộ phận;
D. Sai, vì trên thực tế không phải ai học giỏi cũng có nhiều khả năng tìm được việc là sau khi tốt nghiệp.
Câu 4 (TN): Cho tam đoạn luận đơn: “Loài chim khỏe bay rất cao. Đại bàng bay rất cao. Vậy
đại bàng là loài chim khỏe” Suy luận đã cho hợp logic hay không, vì sao?
A. Sai. Vì trung từ có ngoại diên không đầy đủ trong cả hai tiền đề;
B. Sai, vì cả hai tiền đề là phán đoán khẳng định;
C. Đúng, vì tuân thủ tất cả các quy tắc chung của tam đoạn luận đơn;
D. Sai, vì đại từ chu diên trong đại tiền đề mà không chu diên trong kết luận.
Câu 5 (TL): Phục hồi tiền đề bị lược bỏ của những tam đoạn luận sau: a. MaP, SaP b. SeM, SeP c. PoM, SoP d. SoM, SaP
Câu 6 (TL): Xác định các quy tắc trong câu sau có vi phạm hay không: a. AEE - 1 b. AEE - 2 c. AII - 3 d. AEI – CHƯƠNG VI
SUY LUẬN VỚI TIỀN ĐỀ LÀ PHÁN ĐOÁN PHỨC ***
I. Định nghĩa, đặc điểm, xác định tính đúng sai và phương pháp kiểm tra tính hợp logic
của suy luận với tiền đề phức:
1. Định nghĩa: Suy luận với tiền đề là phán đoán phức (suy luận với tiền đề phức) là suy luận có
một tiền đề là phán đoán phức hoặc tất cả tiền đề là phán đoán phức.
2. Đặc điểm:
- Suy luận với tiền đề phức không sử dụng thông tin chứa trong cấu trúc S – P của phán đoán
thuộc tính đơn có trong tiền đề mà chỉ quan tâm thông tin chứa trong liên từ logic kết nối phán
đoán đơn thành phán đoán phức.
- Suy luận với tiền đề phức Suy luận diễn dịch
Suy luận hợp Logic – tức là đúng - khi và chỉ khi kết luận của nó đúng trong mọi trường hợ p
mà tất cả các tiền đề của nó đều đúng.
Suy luận với tiền đề phức đúng (hợp logic) khi và chỉ khi kết luận của nó đúng trong mọi
trường hợp mà tất cả các tiền đề nó cùng đúng
4. Phương pháp kiểm tra tính hợp logic:
- Viết tiền đề và kết luận dưới dạng công thức.
- Nối các tiền đề bằng các liên từ logic thích hợp
+ Dấu hội (&) nối ở giữa các phần tiền đề.
+ Dấu kéo theo (⊃) nối ở giữa phần tiền đề và kết luận.
- Xét công thức biểu thị suy luận có đúng (hợp logic hay không)
Sử dụng bảng ngữ nghĩa
hoặc bảng chân trị để xác định tính đúng sai.
II. Một số dạng thức suy luận tự nhiên với tiền đề phức:
1. Modus ponens (dạng thức khẳng định):
2. Modus tollens (dạng thức phủ định):
3. Phản đảo (Reverse):
4. Tam đoạn luận điều kiện (Hypothetical Syllogism): Tuy hình thức của nó là tam đoạn luận
điều kiện, hình thức suy luận đúng nhưng do một trong những tiền đề sai nên dẫn đến kết luận sai:
5. Tam đoạn luận lựa chọn:
6. Song quan luận:
7. Modus Tollend – De Morgan:
III. Phương pháp sử dụng giả định trong suy luận:
Gỉa định sử dụng khi không đủ thông tin để suy diễn.
Ta chứng minh công thức logic sau đúng bằng cách đặt giả định như sau: Có nghịch lý giả định ban đầu SAI
Mệnh đề mâu thuẫn với giả định đúng C ô n g
thức trên là quy luật Logic.
IV. Ví dụ ứng dụng
- Ví dụ 1: Nếu anh bắn vào quá khứ bằng súng lục thì tương lai sẽ bắn anh bằng đại bác. Anh đã
bắn vào quá khứ bằng súng lục. Vậy, tương lai sẽ bắn anh bằng đại bác.
- Ví dụ 2: Nếu người Ai Cập cổ đại không có nền văn minh phát triển cao thì họ không thể xây
dựng các công trình vĩ đại như kim tự tháp. Người Ai Cập cổ đại đã xây dựng được các công
trình vĩ đại như kim tự tháp. Vậy họ đã có nền văn minh phát triển cao.
- Ví dụ 3:
Anh : Tôi quê ở Bắc Ninh, còn Doan ở Nghệ An.
Bình : Tôi quê ở Bắc ninh, còn Cúc ở Tiền Giang.
Cúc : Tôi cũng quê ở Bắc Ninh, còn Doan ở Hà Tây.
Doan : Tôi quê ở Nghệ An, còn Em ở Cần Thơ.
Không có câu trả lời nào sai cả hai phần. Không có hai người nào cùng quê.
- Ví dụ 4:
Hỏi thần bên phải: Ai ngồi cạnh ngài?
Trả lời: Đó là thần Nói Dối.
Hỏi thần ngồi giữa: - Thần là Thần gì?
Trả lời: Ta là Thần Khôn Ngoan!
Hỏi thần bên trái: - Ai ngồi cạnh ngài? Trả lời : Đó là thần Thật Thà.
Nhà thông thái khẳng định được mỗi vị thần là thần gì. Hãy cho biết nhà thông thái đã suy luận như thế nào?
- Ví dụ 5:
Hai người bạn gặp nhau. A nói với B: Anh là nhà tóan học, vậy hãy đoán xem các con tôi bao nhiêu tuổi.
Hãy cho tôi thông tin! B đáp.
A: Tôi có 3 con, tích các tuổi của chúng là 36. B: Hãy cho thêm thông tin.
A: Tổng tuổi của chúng bằng số cửa sổ căn nhà đối diện.
B: Nhìn, nghĩ rồi nói: Hãy cho thêm thông tin!
A: Mắt của đứa lớn nhất màu xanh. Hỏi tuổi của chúng ?




