
















Preview text:
TR7ÍNG DẠI HỌC VĂN LANG
KHOA KHOA HỌC CO BẢN - BỘ MȎN KHOA HỌC TỤ NHIȆN * TÀI LINU XÁC SUẤT THỐNG KÊ Ngày 16 tháng 8 năm 2019
Downloaded by VietJack TV Of icial (vietjackvideos@gmail.com) Mṇc lṇc
1 GIẢI TÍCH TỔ HÑP 6
1.1 Nguyȇn lý c®ng. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.2 Nguyȇn lý nhȃn. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.3 Chỉnh hợp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7
1.4 Hoán vị. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.5 Tỗ hợp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .8
2 BIẾN CỐ VÀ XÁC SUẤT CỦA BIẾN CỐ 10
2.1 M®t số khái ni»m cơ bản. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10
2.1.1 Dối tmợng nghiȇn cáu. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.1.2 Phép thả, khȏng gian mấu và biến cố. . . . . . . . . . . . . . . . . . . . . . . . . 10
2.1.3 Mối quan h» giǎa các biến cố. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
2.1.4 Các tính chất. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
2.2 Dịnh nghǐa xác suất. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .12
2.2.1 Dịnh nghǐa xác suất theo cỗ diễn. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
2.2.2 Dịnh nghǐa xác suất theo thống kȇ. . . . . . . . . . . . . . . . . . . . . . . . . . . 13
2.2.3 Dịnh nghǐa xác suất theo tiȇn dề Komogorov. . . . . . . . . . . . . . . . . . .14
2.3 Các cȏng thác xác suất. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.3.1 Cȏng thác c®ng. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.3.2 Cȏng thác xác suất có diều ki»n. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .17
2.3.3 Cȏng thác xác suất nhȃn. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
2.3.4 Cȏng thác xác suất dầy dủ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .20
2.3.5 Cȏng thác xác suất Bayes. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.3.6 Cȏng thác Bernoul i. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22 3 BIẾN NGẪU NHIÊN 24
3.1 Dịnh nghǐa. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 2
Downloaded by VietJack TV Of icial (vietjackvideos@gmail.com) Ths. Lê Thị Hồng Thuy Học kỳ 2/2018-2019 3
3.2 Biễu diến biến ngấu nhiȇn . . . . . . . . . . . . . . . . . . . . . . . . . . 25
3.2.1 Biến ngấu nhiȇn rời rạc . . . . . . . . . . . . . . . . . . . . . . . 25 3.2.2
Biến ngấu nhiȇn liȇn tục . . . . . . . . . . . . . . . . . . . . . . . 28
3.3 Hàm phȃn phối . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
3.3.1 Biến ngấu nhiȇn rời rạc . . . . . . . . . . . . . . . . . . . . . . . 29 3.3.2
Biến ngấu nhiȇn liȇn tục . . . . . . . . . . . . . . . . . . . . . . . 30
3.4 Hai biến ngấu nhiȇn rời rạc d®c lªp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .31
3.5 Hàm của biến ngấu nhiȇn. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
3.6 Các d°c trmng số. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
3.6.1 Kỳ vọng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 3.6.2
Giá trị tin chắc nhất . . . . . . . . . . . . . . . . . . . . . . . . . 36
3.6.3 Trung vị (Median) . . . . . . . . . . . . . . . . . . . . . . . . . . 36
3.6.4 Phmơng sai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
3.6.5 D® l»ch chuẫn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
3.7 Vectơ ngấu nhiȇn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39 3.7.1
Vectơ ngấu nhiȇn rời rạc . . . . . . . . . . . . . . . . . . . . . . . 40 3.7.2
Vectơ ngấu nhiȇn liȇn tục . . . . . . . . . . . . . . . . . . . . . . 42
3.8 Hi»p phmơng sai. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
3.9 H» số tmơng quan. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
3.10 Hàm tuyến tính của biến ngấu nhiȇn. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
3.11 Tỗ hợp tuyến tính của các biến ngấu nhiȇn. . . . . . . . . . . . . . . . . . . . . . . . . . 44
4 CÁC PHÂN PHỐI XÁC SUẤT THÔNG DỤNG 45
4.1 Quy luªt phȃn phối siȇu b®i. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
4.2 Quy luªt phȃn phối nhị thác. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
4.3 Quy luªt phȃn phối Poisson. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
4.4 Phȃn phối chuẫn tắc. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
4.5 Quy luªt phȃn phối chuẫn. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .53
4.6 Các cȏng thác xấp xỉ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
4.6.1 Xấp xỉ phȃn phối siȇu b®i. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .56
4.6.2 Xấp xỉ phȃn phối nhị thác. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
4.7 Phȃn phối Chi bình phmơng. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
4.8 Phȃn phối Student. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60 5 LÝ THUYẾT MẪU 62 K22T, K23NL Ths. Lê Thị Hồng Thuy Học kỳ 2/2018-2019 4
5.1 Thống kȇ là gì?. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
5.2 Các khái ni»m cơ bản. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
5.2.1 Tỗng thễ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
5.2.2 Mấu. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .63
5.2.3 Cách mȏ tả m®t mấu cụ thễ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
5.3 Các d°c trmng cơ bản của tỗng thễ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
5.4 Các d°c trmng cơ bản của mấu. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
5.5 Phȃn phối mấu. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
5.5.1 Phȃn phối của trung bình mấu. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
5.5.2 Phȃn phối của t l» mấu. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
6 7ÎC L7ÑNG CÁC THAM SỐ THỐNG KÊ 69
6.1 7ớc lmợng diễm. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
6.2 7ớc lmợng khoảng (trmờng hợp m®t mấu). . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
6.2.1 7ớc lmợng trung bình tỗng thễ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
6.2.2 7ớc lmợng t l» tỗng thễ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .76
6.2.3 Các chỉ tiȇu chính của bài toán mớc lmợng. . . . . . . . . . . . . . . . . . . . . 78
6.2.4 7ớc lmợng phmơng sai tỗng thễ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
7 KIỂM D±NH GIẢ THUYẾT THỐNG KÊ 82
7.1 Khái ni»m . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
7.2 Giả thuyết H0 và dối thuyết H1 . . . . . . . . . . . . . . . . . . . . . . . 82
7.2.1 Giả thuyết H0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
7.2.2 Dối thuyết H1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
7.2.3 Sai lầm loại I và sai lầm loại II . . . . . . . . . . . . . . . . . . . 83
7.3 Kiễm dịnh giả thuyết về kỳ vọng tỗng thễ (µ) . . . . . . . . . . . . . . . 84
7.3.1 So sánh kỳ vọng với m®t số (khi biết phmơng sai) . . . . . . . . 84
7.3.2 So sánh kỳ vọng với m®t số (khi chma biết phmơng sai) . . . . . 86
7.4 Kiễm dịnh giả thuyết về t l» tỗng thễ . . . . . . . . . . . . . . . . . . . 93
7.5 Kiễm dịnh giả thuyết về phmơng sai tỗng thễ . . . . . . . . . . . . . . . 94
7.6 So sánh hai kỳ vọng của hai tỗng thễ . . . . . . . . . . . . . . . . . . . . 96
7.7 So sánh hai t l» của hai tỗng thễ . . . . . . . . . . . . . . . . . . . . . . 100
7.8 Kiễm dịnh phi tham số (So sánh các b® số li»u) . . . . . . . . . . . . . 103
7.8.1 Kiễm dịnh giả thuyết về luªt phȃn phối . . . . . . . . . . . . . . 103
7.8.2 Kiễm dịnh giả thuyết về sự d®c lªp . . . . . . . . . . . . . . . . . 104 K22T, K23NL Ths. Lê Thị Hồng Thuy Học kỳ 2/2018-2019 5
8 MÔ HÌNH HỒI QUY HAI BIẾN 109
8.1 Nhǎng khái ni»m cơ bản. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
8.2 H» số tmơng quan mấu. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
8.3 Mȏ hình hồi quy hai biến. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .110
8.3.1 Hàm hồi quy tỗng thễ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110
8.4 7ớc lmợng và kiễm dịnh giả thuyết. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112
8.4.1 Hàm hồi quy mấu. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .112
8.4.2 Phmơng pháp bình phmơng bé nhất (OLS - Ordinary Least Square)113 K22T, K23NL ChG6ng 1 GIẢI TÍCH TỔ HÑP 1.1 Nguyên lj cộng
Giả sả m®t cȏng vi»c có thễ thực hi»n bằng m®t trong k phmơng pháp, trong dó
• Phmơng pháp 1 có n1 cách thực hi»n,
• Phmơng pháp 2 có n2 cách thực hi»n, . . . ,
• Phmơng pháp k có nk cách thực hi»n,
và hai phmơng pháp khác nhau khȏng có cách thực hi»n chung.
Khi dó, ta có n1 + n2 + · · · + nk cách thực hi»n cȏng vi»c.
Ví dṇ 1. Có 10 cái áo thun ngắn tay và 5 cái áo thun dài tay. Hỏi có bao nhiȇu cách chọn m®t cái áo thun ?
HGďng dẫn. Ta thấy có 2 phmơng án chọn áo thun.
Phmơng án 1: chọn áo thun ngắn tay; phmơng án này có 10 cách chọn.
Phmơng án 2: chọn áo thun dài tay; phmơng án này có 5 cách chọn.
Vªy, theo nguyȇn lý c®ng, ta có tất cả 10 + 5 = 15 cách chọn 1 cái thun. 1.2 Nguyên lj nhân
Ví dṇ 2. M®t ngmời có 12 cái áo và 5 cái quần. Hỏi có bao nhiȇu cách chọn dmợc m®t b® quần áo ?
HGďng dẫn. Ta thấy cȏng vi»c chọn m®t b® quần áo dmợc thực hi»n qua 2 giai doạn.
* Giai doạn 1: chọn áo, có 12 cách chọn.
* Giai doạn 2: chọn quần, có 5 cách chọn. 6 Ths. Lê Thị Hồng Thuy Học kỳ 2/2018-2019 7
Úng với mối cách chọn áo ở giai doạn 1, ta có 5 cách chọn quần ở giai doạn 2 dễ lªp
ra m®t b® quần áo. Vªy ta có tất cả 12 × 5 = 60 cách chọn. Tỗng quát, ta có
Giả sả m®t cȏng vi»c dmợc thực hi»n tuần tự theo k bmớc, trong dó
• Bmớc 1 có n1 cách thực hi»n,
• Bmớc 2 có n2 cách thực hi»n, . . . ,
• Bmớc k có nk cách thực hi»n,
Khi dó, ta có n1 × n2 × · · · × nk cách thực hi»n cȏng vi»c. 1.3 Chỉnh hỢp
Ví dṇ 3. Có 5 bác tranh và 7 cái móc treo trȇn tmờng. Có bao nhiȇu cách treo 5 bác
tranh này ? Biết rằng mối móc chỉ treo m®t bác tranh.
HGďng dẫn Cȏng vi»c treo tranh có 5 giai doạn sau:
+ Eiai doạn 1: Treo bác tranh thá nhất. Ta chọn ra m®t móc treo tà 7 cái móc
treo, có 7 cách chọn (còn lại 6 móc treo).
+ Eiai doạn 2: Treo bác tranh thá hai, có 6 cách chọn (còn lại 5 móc treo).
+ Eiai doạn 3: Treo bác tranh thá ba, có 5 cách chọn (còn lại 4 móc treo).
+ Eiai doạn 4: Treo bác tranh thá tm, có 4 cách chọn (còn lại 3 móc treo).
+ Eiai doạn 5: Treo bác tranh thá tm, có 3 cách chọn.
Vªy, theo nguyȇn lý nhȃn, ta có: 7 × 6 × 5 × 4 × 3 = 2520 cách treo.
Dịnh nghĩa 1.3.1. M®t chỉnh hợp n chªp k là m®t cách lấy k phần tả khác nhau
(có dễ ý dến thá tự, trªt tự sắp xếp) tà n phần tả khác nhau.
Với tªp hợp A gồm n phần tả, số chỉnh hợp n chªp k dmợc ký hi»u Aknvà xác dịnh bởi cȏng thác Ak n!
n = (n — k)!
trong dó n! = 1.2. .n, với quy mớc: 0! = 1.
Ví dṇ 4. Theo ví dụ trȇn, ta có: M®t cách treo 5 bác tranh là m®t cách chọn ra 5
móc treo khác nhau tà 7 móc treo (có dễ ý dến vị trí của chúng) → Mối cách treo là
m®t chỉnh hợp 7 chªp 5. Vªy có A5 = 7! 7! =
= 7.6.5.4.3 = 2520 7 (7 — 5)! 2! cách treo. K22T, K23NL Ths. Lê Thị Hồng Thuy Học kỳ 2/2018-2019 8
Nhªn xét 1. Mối cách treo 5 bác tranh là m®t cách lấy 5 cái móc treo tà 7 cái móc
treo. Dȃy là cách lấy có thá tự, bởi vì trªt tự lấy các móc khác nhau sě cho ta các
cách treo khác nhau. Vªy số cách lấy có thá tự 5 phần tả tà 7 phần tả dmợc tính nhm thế nào?
+ Mối phần tả lấy ra tà n phần tả tạo thành m®t nhóm. + Các nhóm khác nhau do:
* Các phần tả trong nhóm khác nhau. Chẫng hạn, 1 2 3 4 khác 3 4 5 6.
* Thá tự, trªt tự sắp xếp của các phần tả trong nhóm khác nhau. Chẫng hạn, 1 2 3 4 khác 3 4 2 1. 1.4 Hoán vị
Dịnh nghĩa 1.4.1. Có n phần tả khác nhau. M®t hoán v$ của n phần tả này là m®t
cách sắp xếp n phần tả này theo m®t thá tự xác dịnh.
Ví dṇ 5. Có 4 ngmời. Hỏi có bao nhiȇu cách xếp 4 ngmời này:
1. Ngồi thành m®t hàng dài.
2. Ngồi thành m®t vòng tròn.
3. Ngồi thành m®t vòng tròn có dánh số. HGďng dẫn.
1. Ngồi thành m®t hàng dài. A B C D 1 2 3 4
Mối cách xếp 4 ngmời này là m®t hoán vị của 4 ngmời này. Vªy có 4! cách.
2. Ngồi thành m®t vòng tròn. Chọn ra 1 ngmời làm mốc, ta thấy vị trí ban dầu của
ngmời này khȏng quan trọng (chẫng hạn: A làm mốc, A ở vị trí 1 cǔng nhm vị trí
2) ⇒ Chỉ xếp 3 ngmời còn lại: có 3! cách.
3. Ngồi thành m®t vòng tròn có dánh số: 4! cách. 1.5 Tổ hỢp
Dịnh nghĩa 1.5.1. M®t tỗ hợp n chªp k là m®t cách lấy k phần tả khác nhau (khȏng
dễ ý dến thá tự sắp xếp) tà n phần tả khác nhau. Số tỗ hợp n chªp k dmợc ký hi»u
là Ckn và dmợc tính theo cȏng thác: n! Ck .
n = k!(n — k)! K22T, K23NL Ths. Lê Thị Hồng Thuy Học kỳ 2/2018-2019 9
Ví dṇ 6. M®t phòng làm vi»c của m®t cȏng ty có 30 nhȃn viȇn.
1. Có bao nhiȇu cách Giám dốc chọn ra m®t Ban lǎnh dạo phòng gồm 3 ngmời?
2. Ban lǎnh dạo phòng gồm: Trmởng phòng, Phó phòng, Thm ký. Hỏi có bao nhiȇu
cách chọn ra Ban lǎnh dạo phòng? HGďng dẫn.
1. M®t Ban lǎnh dạo phòng là m®t cách chọn 3 ngmời tà 30 ngmời (chọn tùy ý, khȏng
quan tȃm dến thá tự sắp xếp).
⇒ Mối cách chọn là m®t tỗ hợp 30 chªp 3. ⇒ Số cách chọn là 3 C 03.
2. Cách 1: Vì 3 ngmời trong Ban lǎnh dạo có chác vụ rǒ ràng Trmởng phòng, Phó
phòng, Thm ký ⇒ Có dễ ý dến thá tự sắp xếp ⇒ Số cách chọn là A 330.
Cách 2: Cȏng vi»c chọn ra Ban lǎnh dạo phòng có 3 giai doạn:
+ Giai doạn 1: Chọn Trmởng phòng, có 30 cách.
+ Giai doạn 2: Chọn Phó phòng, có 29 cách.
+ Giai doạn 3: Chọn Thm ký, có 28 cách.
Vªy, ta có: 30.29.28 cách chọn.
Cách 3: Cȏng vi»c chọn ra Ban lǎnh dạo phòng có 2 giai doạn:
+ Giai doạn 1: Chọn 3 ngmời tùy ý trong 30 ngmời, có C330 cách.
+ Giai doạn 2: Úng với 3 ngmời dmợc chọn, chỉ dịnh 1 ngmời làm Trmởng phòng,
1 ngmời làm Phó phòng, 1 ngmời làm Thm ký có 3! cách. Vªy, ta có: 3
C30.3! cách chọn. Nhªn xét 2.
Akn = Ckn× k!.
Ví dṇ 7. Có 10 ngmời dịnh cm vào 3 nmớc: Anh, Pháp, My. Nmớc Anh nhªn 3 ngmời. Nmớc Pháp nhªn 3 ngmời. Nmớc My nhªn 4 ngmời.
Hỏi có bao nhiȇu cách sắp xếp?
HGďng dẫn. Dùng nguyȇn lý nhȃn
Ta khȏng chú ý dến thá tự sắp xếp vào 3 nmớc: Nmớc Anh: 1C30 Nmớc Pháp: C37 Nmớc My: C44
Vªy, ta có: C3 .C3.C4 cách. 10 7 4 K22T, K23NL ChG6ng 2
BIẾN CỐ VÀ XÁC SUẤT CỦA BIẾN CỐ
2.1 Một số khái ni»m c6 bản
2.1.1 Dối tGỢng nghiên cfíu
Trong cu®c sống, ta g°p rất nhiều hi»n tmợng mà kết quả của nó ta khȏng biết
chắc chắn dmợc. Chẫng hạn, khi gieo dồng xu, có thễ xuất hi»n m°t số cǔng có thễ
xuất hi»n m°t hình. Khi gieo m®t con xúc xắc, có thễ xuất hi»n m°t 6 chấm nhmng
có thễ xuất hi»n m°t 2 chấm . . . Các hi»n tmợng nhm thế dmợc gọi là hi»n tmợng ngấu nhiȇn.
Hi»n tuợng ngẫu nhiên là hi»n tmợng mà dù thực hi»n trong cùng m®t diều ki»n
nhmng vấn cho các kết quả khác nhau. Hi»n tmợng ngấu nhiȇn là dối tmợng nghiȇn
cáu của lý thuyết xác suất. Lý thuyết xác suất nghiȇn cáu tính quy luªt của hi»n tmợng ngấu nhiȇn.
2.1.2 Phép thfi, không gian mẫu và biến cố
Phép thủ là m®t khái ni»m cơ bản của lý thuyết xác suất nhmng khȏng có dịnh
nghǐa chính xác, tmơng tự khái ni»m diễm, dmờng thẫng . . . trong hình học phỗ thȏng.
Ta có thễ hiễu phép thả là m®t thí nghi»m hay m®t quan sát dmợc thực hi»n trong
m®t diều ki»n xác dịnh. Chẫng hạn nhm
- Tung m®t con xúc xắc, coi nhm là ta dǎ thực hi»n m®t phép thả.
- Kiễm tra bài m®t học sinh, coi nhm là ta dǎ thực hi»n m®t phép thả.
Tªp hợp tất cả các kết quả có thễ xảy ra của phép thả dmợc gọi là không gian mẫu
của phép thả dó, ký hi»u là Ω. Mối kết quả của phép thả dmợc gọi là m®t biến cố sơ
cấp, ký hi»u là ω. Mối tªp con của khȏng gian mấu dmợc gọi là biến cố.
M®t biến cố A dmợc gọi là xảy ra nếu có ít nhất m®t kết quả trong nó xảy ra.
M®t biến cố dmợc gọi là biến cố ngẫu nhiên nếu nó có thễ xảy ho°c khȏng xảy ra
sau khi thực hi»n phép thả. Ta thmờng dùng các chǎ in hoa, chẫng hạn A, B, C . . .,
A1, A2, A3 . . ., B1, B2, B3, . . . dễ ký hi»u biến cố ngấu nhiȇn. 10 Ths. Lê Thị Hồng Thuy Học kỳ 2/2018-2019 11
Ngoài các biến cố ngấu nhiȇn, ta còn có hai loại biến cố d°c bi»t:
• Biến cố chắc chắn là biến cố nhất dịnh xảy ra khi thực hi»n phép thả, ký hi»u: Ω.
• Biến cố không thể là biến cố khȏng bao giờ xảy ra khi thực hi»n phép thả, ký hi»u: ∅.
Ví dṇ 8. Tung m®t con xúc xắc cȃn dối dồng chất
+ Biến cố “xuất hi»n m°t có 7 chấm” là biến cố khȏng thễ.
+ Biến cố “xuất hi»n m°t có 6 chấm” là biến cố ngấu nhiȇn.
+ Biến cố “xuất hi»n m°t có số nút bé hơn hay bằng 6” là biến cố chắc chắn.
Ví dṇ 9. Xét m®t gia dình có 3 con. D°t
A = “gia dình có 2 con”,
B = “gia dình có 3 con”,
C = “gia dình có 2 con gái”
D = “gia dình có 1 trai, 1 gái”.
Biến cố nào là biến cố chắc chắn, biến cố khȏng thễ, biến cố ngấu nhiȇn?
Ví dṇ 10. H®p có 8 bi gồm: 6 bi trắng, 2 bi xanh. Lấy ra 3 bi xem màu. D°t
A = “lấy dmợc 1 bi trắng”,
B = “lấy dmợc 3 bi xanh”,
C = “lấy dmợc 3 bi”,
Biến cố nào là biến cố chắc chắn, biến cố khȏng thễ, biến cố ngấu nhiȇn?
2.1.3 Mối quan h» gifia các biến cố
Biến cố A dmợc gọi là kéo theo biến cố B nếu biến cố A xảy ra thì biến cố B xảy
ra. Ký hi»u: A ⊂ B.
Biến cố A và B dmợc gọi là hai biến cố tuơng duơng nếu biến cố A xảy ra thì biến
cố B xảy ra và ngmợc lại. Ký hi»u: A = B.
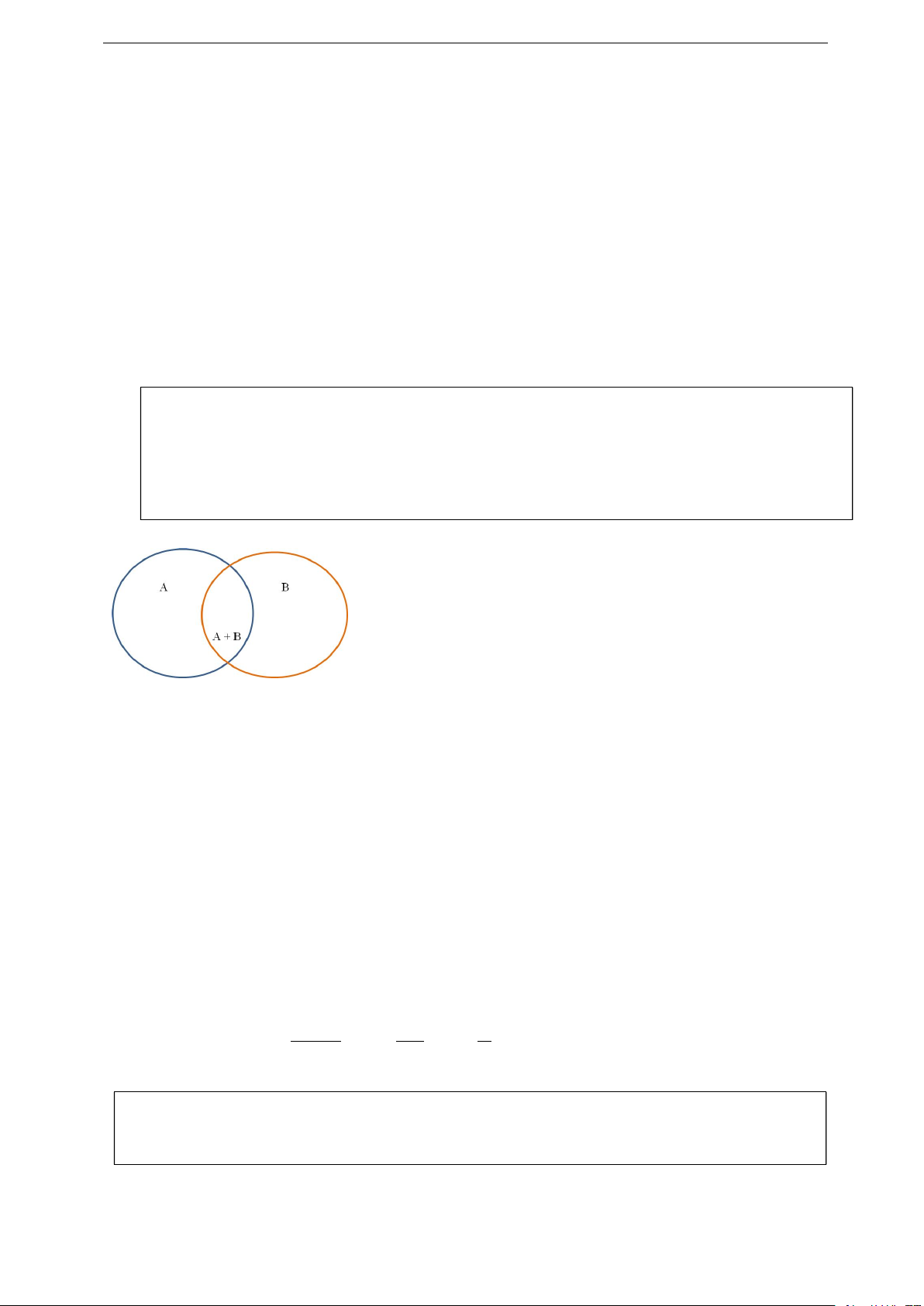
Hợp của hai biến cố A và B là biến cố C mà biến cố này xảy ra khi ít nhất m®t
trong hai biến cố A và B xảy ra. Kí hi»u: C = A ∪ B ho°c C = A + B. Nói cách khác,
nếu C = A ∪ B thì C xảy ra trong các trmờng hợp sau: A xảy ra, B khȏng xảy ra; B
xảy ra, A khȏng xảy ra; cả A và B cùng xảy ra.
Ta có thễ mở r®ng khái ni»m trȇn nhm sau: Hợp của n biến cố A1, A2, . ., An là
m®t biến cố A mà biến cố này xảy ra khi ít nhất m®t trong các biến cố A1, A2, . ., An
xảy ra. Lúc này, ta ký hi»u: A = A1 ∪ A2 ∪ . . ∪ An ho°c A = A1 + A2 + . . + An.
Eiao của hai biến cố A và B là m®t biến cố C mà biến cố này xảy ra khi A và B
dồng thời xảy ra khi thực hi»n phép thả. Lúc này, ta viết C = A ∩ B ho°c C = A.B ho°c C = AB. K22T, K23NL Ths. Lê Thị Hồng Thuy Học kỳ 2/2018-2019 12
Ta có thễ mở r®ng khái ni»m cho biến cố giao nhm sau: Eiao của n biến cố A1, A2,
. ., An là m®t biến cố A mà biến cố này xảy ra khi tất cả các biến cố A1, A2, . ., An
cùng xảy ra khi thực hi»n phép thả. Lúc này, ta ký hi»u: A = A1 ∩ A2 ∩ . . ∩ An ho°c
A = A1A2. .An. Nhªn xét 3. Ta có
- Mọi biến cố ngấu nhiȇn A dmợc biễu diến dmới dạng hợp của các biến cố sơ cấp.
Trong trmờng hợp này, mối biến cố sơ cấp dmợc gọi là m®t kết quả thu¾n lợi cho A.
- Biến cố chắc chắn là hợp của mọi biến cố sơ cấp có thễ có, nȇn còn gọi là “không
gian các biến cố sơ cấp”.
- Biến cố khȏng bao hàm biến cố nào là biến cố rỗng.
Hai biến cố A và B dmợc gọi là xung khắc nếu AB = ∅. Nói khác di, A và B xung
khắc khi A, B khȏng dồng thời xảy ra trong m®t phép thả.
Các biến cố A1, A2, . . . , An dmợc gọi là xung khắc tùng dôi nếu bất kỳ hai trong n
biến cố này xung khắc với nhau.
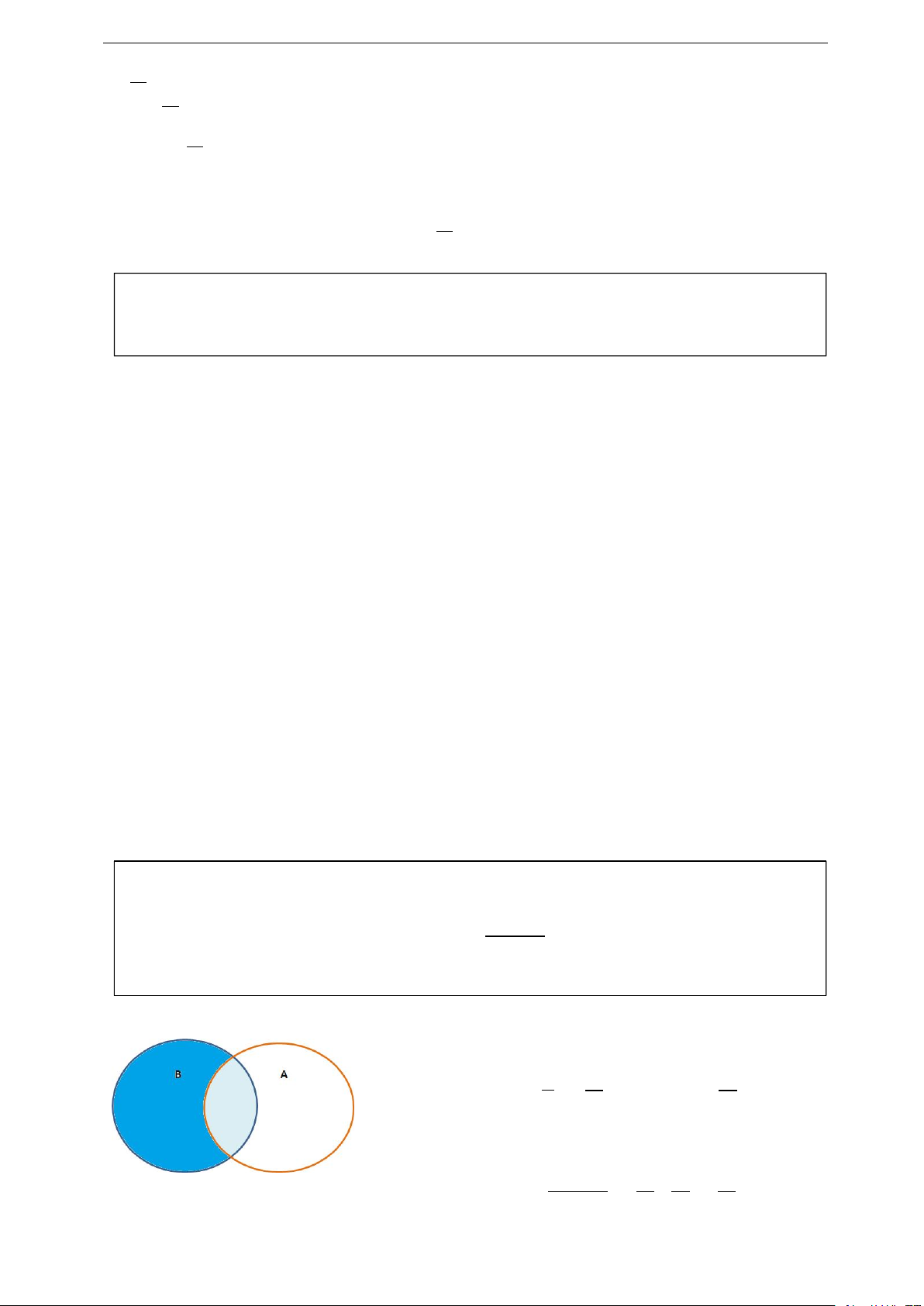
Biến cố dối l¾p của A, ký hi»u là A ho°c Ac ho°c A', là m®t biến cố mà biến cố
này xảy ra khi và chỉ khi biến cố A khȏng xảy ra trong cùng m®t phép thả. 2.1.4 Các tính chất
1. A = A, A + Ω = A, A + ∅ = A 1. A.∅ = ∅
2. A + A = A 2. A.A = A
3. A + B = B + A 3. A.B = B.A
4. A.(B + C) = (A.B) + (A.C)
4. A + (B.C) = (A + B).(A + C)
5. A + B = A.B
5. A.B = A + B
6. A + B + C = A.B.C
6. A.B.C = A + B + C
2.2 Dịnh nghĩa xác suất
2.2.1 Dịnh nghĩa xác suất theo cổ diển
Trong m®t phép thả, giả sả có tất cả n biến cố sơ cấp dồng khả năng có thễ xảy
ra, trong dó có mA biến cố sơ cấp thuªn lợi cho biến cố A. Khi dó, t số mAndmợc gọi
là xác suất của biến cố A, ký hi»u là P (A). m
Số biến cố sơ cấp thuªn lợi cho A P (A) = A |A| (2.1) n = = .
Tỗng số biến cố sơ cấp có thễ xảy ra |Ω|
Ví dṇ 11. Gieo m®t con xúc xắc cȃn dối, dồng chất. Tính xác suất xuất hi»n m°t lẻ. K22T, K23NL Ths. Lê Thị Hồng Thuy Học kỳ 2/2018-2019 13
HGďng dẫn. Phép thả này có 6 biến cố sơ cấp có khả năng xảy ra là A1, A2, . ., A6
với Ai là biến cố “xuất hi»n m°t có i chấm”, i = 1, . . . , 6.
Gọi A là biến cố xuất hi»n m°t lẻ, A = A1 + A3 + A5, tác có 3 biến cố sơ cấp dồng
khả năng thuªn lợi cho A. Theo dịnh nghǐa, ta có: 3
P (A) = = 0, 5. 6
Ví dṇ 12. M®t h®p có 8 sản phẫm, trong dó có 5 sản phẫm tốt và 3 sản phẫm xấu.
Lấy ngấu nhiȇn khȏng hoàn lại tà h®p dó ra 3 sản phẫm. Tính xác suất lấy dmợc 2 sản phẫm tốt.
HGďng dẫn. Gọi A là biến cố lấy dmợc 2 sản phẫm tốt. Mối kết quả của phép
thả tmơng áng với vi»c chọn 3 sản phẫm tà tªp hợp 8 sản phẫm, tác là m®t tỗ hợp
chªp 3 của 8 sản phẫm. Do dó, số kết quả của phép thả là 8C3.
Biến cố A xảy ra khi trong 3 sản phẫm dmợc chọn có 2 chính phẫm và 1 phế phẫm.
Do dó, số trmờng hợp thuªn lợi cho A là C2.C1. Vªy xác suất lấy dmợc 3 sản phẫm 5 3 tốt là: C2.C1
P (A) = 5 3 . C38
Nhªn xét 4. Cȏng thác xác suất cỗ diễn có nhǎng mu diễm và nhmợc diễm sau:
* Uu diểm: Tính dmợc chính xác các giá trị xác suất của biến cố mà khȏng cần
phải tiến hành phép thả. * Nhuợc diểm:
+ Chỉ áp dụng dmợc với phép thả có hǎu hạn các biến cố sơ cấp.
+ Khȏng phải lúc nào tất cả các biến cố sơ cấp cǔng xảy ra dồng khả năng.
+ Trong m®t số trmờng hợp thực tế, ta khȏng tính dmợc số phần tả của A.
Ví dṇ 13. M®t lȏ hàng có N sản phẫm. Lấy ngấu nhiȇn n (n < N) sản phẫm của lȏ
hàng. Tính xác suất lấy dmợc m sản phẫm xấu trong n sản phẫm lấy ra.
HGďng dẫn. D°t A là biến cố có m phế phẫm trong n sản phẫm lấy ra (m ≤ n).
Muốn tính P (A), ta phải biết số sản phẫm xấu của lȏ hàng là bao nhiȇu. Giả sả
rằng, ta biết dmợc số sản phẫm xấu của lȏ hàng là M thì xác suất CmCn−m
P (A) = M N−M . CnN
Tuy nhiȇn, trong thực tế ta khȏng thễ biết dmợc chính xác M vì ta khȏng thễ kiễm
tra (mở nắp) hết tất cả các sản phẫm trong lȏ hàng.
Ví dṇ 14. Quan sát số ngmời dến siȇu thị trong m®t ngày nào dó. Gọi A là biến cố
quan sát dmợc ngmời dến siȇu thị là nǎ. Ta có thễ xác dịnh dmợc số phần tả của A và Ω khȏng?
2.2.2 Dịnh nghĩa xác suất theo thống kê
Dịnh nghĩa 2.2.1. Giả sả khi tiến hành n phép thả d®c lªp trong nhǎng diều ki»n
nhm nhau, biến cố A xuất hi»n mA lần. Khi dó, t số mAn dmợc gọi là tần suất xuất K22T, K23NL Ths. Lê Thị Hồng Thuy Học kỳ 2/2018-2019 14
hi»n của biến cố A. Thực nghi»m thống kȇ cháng minh rằng, khi số phép thả n khá
lớn, tần suất của biến cố A luȏn dao d®ng quanh m®t giá trị khȏng dỗi p, (0 ≤ p ≤ 1).
Giá trị p dó dmợc gọi là xác suất của biến cố A. Nhm vªy, mA P (A) = lim . n→∞ n
Trong thực tế, khi số phép thả n dủ lớn, ta lấy tần suất làm xấp xỉ cho xác suất của biến cố A, P (A) mA ≈ . (2.2) n
Ví dṇ 15. Dễ nghiȇn cáu khả năng xuất hi»n m°t số khi tung dồng tiền xu, ngmời ta
tiến hành tung dồng tiền xu nhiều lần, khi số phép thả tăng lȇn, tần suất xuất hi»n
m°t số tiến dần dến 0, 5. Khi dó, ta xem xác suất xuất hi»n m°t số là 0, 5.
Bằng thực nghi»m, m®t số nhà khoa học dǎ thảy dồng tiền xu nhiều lần và nhªn dmợc các kết quả sau:
Ngmời thực hi»n Số lần thảy Số lần m°t hình Tần suất Buffon 4040 2048 0, 5069 Pearson 12000 6019 0, 5016 Pearson 24000 12012 0, 5005
và khi dó, ta nói xác suất nhªn dmợc m°t hình gần bằng 0, 5.
Ví dṇ 16. Khi m®t xạ thủ nào dó bắn 1000 viȇn dạn thì có khoảng 800 viȇn trúng
bia, khi dó ta nói xác suất dễ xạ thủ bắn trúng bia là 80%.
Nhªn xét 5. + Chỉ có thễ áp dụng cho các phép thả ngấu nhiȇn có thễ l°p lại nhiều
lần m®t cách d®c lªp trong các diều ki»n giống h»t nhau.
+ Dễ cho kết quả chính xác thì số lần thực hi»n phép thả n phải dủ lớn. Diều này
thực tế khȏng phải lúc nào cǔng làm dmợc.
2.2.3 Dịnh nghĩa xác suất theo tiên dề Komogorov
Xét phép thả ngấu nhiȇn với khȏng gian mấu là Ω. Gọi P(Ω) là tªp hợp tất cả
các tªp con của Ω. Theo tiȇn dề Komogorov, xác suất là m®t ánh xạ nhªn các giá trị
thực và xác dịnh trȇn P(Ω), P : P(Ω) → R
A '→ P(A) thỏa các tính chất sau: 1. P (Ω) = 1,
2. P(A) ≥ 0, ∀A ∈ P(Ω),
3. P(A1 ∪ A2 ∪ · · · ∪ An) = P(A1) + P(A2) + · · · + P(An), K22T, K23NL Ths. Lê Thị Hồng Thuy Học kỳ 2/2018-2019 15
với mọi dǎy hǎu hạn các biến cố A1, A2, . . . , An xung khắc tùng dôi, nghǐa là Ai∩Aj = ∅
với mọi i /= j.
Tà dịnh nghǐa, ta dế dàng suy ra thȇm dmợc các tính chất sau: 4. P(∅) = 0,
5. 0 ≤ P(A) ≤ 1, ∀A ∈ P(Ω).
2.3 Các công thfíc xác suất
2.3.1 Công thfíc cộng
Cho hai biến cố A, B bất kỳ. Khi dó,
P (A + B) = P (A) + P (B) — P (AB) . (2.3)
Fúc là, xác suất của tổng hai biến cố bằng tổng hai xác suất của tùng biến cố trù
di xác suất của tích hai biến cố dó.
Ví dṇ 17. Lớp có 50 sinh viȇn, trong dó có 20 sinh
viȇn giỏi tiếng Anh, 15 sinh viȇn giỏi tiếng Pháp, 7
sinh viȇn giỏi cả hai ngoại ngǎ. Chọn ngấu nhiȇn 1
sinh viȇn trong lớp. Tính xác suất:
1. Chọn dmợc 1 sinh viȇn giỏi ít nhất 1 ngoại ngǎ.
2. Chọn dmợc 1 sinh viȇn khȏng giỏi ngoại ngǎ nào hết.
HGďng dẫn. D°t các biến cố
1. A = “Sinh viȇn này giỏi tiếng Anh”
B = “Sinh viȇn này giỏi tiếng Pháp”
C = “Sinh viȇn này giỏi ít nhất m®t ngoại ngǎ”
Khi dó, C = A + B. Hơn nǎa, ta thấy A và B là hai biến cố khȏng xung khắc vì
có sinh viȇn giỏi cả hai ngoại ngǎ. Do vªy
P (C) = P (A + B) = P (A) + P (B) — P(AB) = 20/50 + 15/50 — 7/50 = 28/50.
2. D = “Sinh viȇn này khȏng giỏi ngoại ngǎ nào hết”
P(D) = P A + B = P(AB) = P (C) = 1 — P(C) = 1 — 28/50 = 22/50.
Với trmờng hợp ba biến cố A, B, C bất kỳ, ta có kết quả:
P (A + B + C) = P (A) + P (B) + P (C) — P (AB) — P (BC) — P (AC) + P(ABC). (2.4)
Nhớ lại rằng, hai biến cố A và B dmợc gọi là xung khắc nếu chúng khȏng dồng
thời xảy ra trong m®t phép thả, hay AB = ∅. Ta có kết quả K22T, K23NL Ths. Lê Thị Hồng Thuy Học kỳ 2/2018-2019 16
H» quả 2.3.1. Cho hai biến cố A, B xung khắc. Khi dó,
P (A + B) = P (A) + P (B) . (2.5)
Fúc là, nếu hai biến cố xung khắc thì xác suất của tổng hai biến cố bằng tổng hai
xác suất của tùng biến cố.
Ví dṇ 18. M®t h®p dựng 5 bi màu dỏ, 10 bi màu xanh, 15 bi màu trắng giống h»t
nhau. Lấy ngấu nhiȇn 1 bi và khȏng nhìn vào h®p. Hǎy tìm xác suất dễ lấy dmợc bi dỏ ho°c bi xanh. HGďng dẫn.
D°t A = “lấy dmợc bi màu dỏ”,
B = “lấy dmợc bi màu xanh”. Ta có 5 1 10 1 P (A) = = , P (B) = = . 30 6 30 3
Ta thấy A + B = “lấy dmợc bi màu dỏ ho°c màu xanh”. Do A, B là hai biến cố xung khắc nȇn 1 1 1
P (A + B) = P (A) + P (B) = + = . 3 6 2
Ví dṇ 19. Trong bình dễ 10 viȇn bi trong dó có 4 viȇn bi dỏ. Lấy ngấu nhiȇn 3 viȇn
bi. Tính xác suất dễ có 1 ho°c 2 viȇn bi dỏ. HGďng dẫn.
D°t A1 là biến cố 3 viȇn bi lấy ra có dúng 1 viȇn bi dỏ,
A2 là biến cố 3 viȇn bi lấy ra có dúng 2 viȇn bi dỏ
Gọi A là biến cố có 1 ho°c 2 viȇn bi dỏ. Ta sě tính P (A).
Ta thấy A1, A2 là hai biến cố xung khắc vì dǎ có 1 viȇn bi dỏ thì khȏng thễ có 2
viȇn bi dỏ và ngmợc lại. Do dó
P (A) = P (A1 + A2) = P (A1) + P (A2) C1.C2 C2.C1 4 4 6 = + 4 6 C3 C3 = . 5 10 10
H» quả 2.3.2. Với A là biến cố bất kỳ của phép thả, ta có
P (A) = 1 — P (A). (2.6)
Ví dṇ 20. Trong m®t vùng dȃn cm t l» ngmời mắc b»nh tim là 9%, mắc b»nh huyết
áp là 12% và mắc cả hai b»nh là 7%. Chọn ngấu nhiȇn m®t ngmời trong vùng dó. Tính
xác suất dễ ngmời dó khȏng mắc cả b»nh tim và b»nh huyết áp. HGďng dẫn
Gọi A = “Ngmời dó mắc b»nh tim”, B = “Ngmời dó mắc b»nh huyết áp” Ta có:
P(A) = 0, 09; P(B) = 0, 12; P (AB) = 0, 07
Gọi H = “Ngmời dó khȏng mắc b»nh tim và b»nh huyết áp” K22T, K23NL Ths. Lê Thị Hồng Thuy Học kỳ 2/2018-2019 17
H = “Ngmời dó mắc b»nh tim ho°c b»nh huyết áp”
Ta có: H = A + B, áp dụng cȏng thác (2.3) ta dmợc
P (H) = P (A + B) = P (A) + P (B) — P (AB) = 0, 09 + 0, 12 — 0, 07 = 0, 14.
Áp dụng cȏng thác (2.6), ta có
P (H) = 1 — P (H) = 1 — 0, 14 = 0, 86.
Mď rộng 2.3.1. Cho A1, A2, . . An là dǎy gồm n biến cố xung khắc tàng dȏi. Khi dó,
P (A1 + A2 + . . . + An) = P (A1) + P (A2) + . . . + P (An) . (2.7)
2.3.2 Công thfíc xác suất có diều ki»n
Trong nhiều trmờng hợp, m®t vấn dề dmợc d°t ra là: ta có thễ nói gì về xác suất
của biến cố A nếu có thȏng tin biến cố B nào dó (liȇn quan tới A) dǎ xảy ra? Trong
nhǎng trmờng hợp dơn giản nhất, cȃu trả lời khá dế dàng. Chẫng hạn, nếu A và B
xung khắc thì A khȏng thễ xảy ra, vì vªy xác suất dễ A xảy ra bằng 0. Trmờng hợp
khác, nếu B ⊂ A thì A chắc chắn xảy ra nȇn xác suất dễ A xảy ra bằng 1. Vấn dề còn
lại, nếu B dǎ xảy ra chỉ cho ta m®t phần thȏng tin về phép thả (tác cho A) thì khi
dó P (A) dmợc xác dịnh thế nào. Khái ni»m xác suất diều ki»n sě dmợc sả dụng cho trmờng hợp này.
Chẫng hạn, với phép thả rút ngấu nhiȇn m®t lá bài tà m®t b® bài 52 lá, ta cần
xác dịnh xem xác suất rút dmợc lá ách cơ là bao nhiȇu nếu biết rằng lá bài lấy ra là
lá dỏ. Trong tình huống này, d°t A = “Rút dmợc lá ách cơ”, B = “Rút dmợc lá dỏ”.
Ta cần tính xác suất dễ A xảy ra khi biết B dǎ xảy ra. M®t lªp luªn tự nhiȇn nhm
sau: Khi biết B dǎ xảy ra, nghǐa là ta dǎ biết lá bài lấy ra là lá dỏ, thì ta chỉ tªp
trung vào các lá bài dỏ trong b® bài. Vì b® bài có 26 lá dỏ và có duy nhất m®t lá ách
cơ nȇn xác suất dễ rút ra lá ách cơ là 1/26.
Sau dȃy là dịnh nghǐa của xác suất có diều ki»n:
Dịnh nghĩa 2.3.1. Cho A và B là hai biến cố của m®t phép thả, với P (B) > 0. Dại lmợng P (AB) P (A|B) = (2.8) P (B)
dmợc gọi là xác suất có diều ki»n của A khi biết B dã xảy ra.
Áp dụng cȏng thác (2.8), ta có thễ giải lại ví dụ trȇn nhm sau: Ta có C1 26 1 P (B) = 26 = , P (AB) = . C152 52 52 Do vªy P (AB) 1 52 1
P (A|B) = P (B) = 52 · 26 = 26. K22T, K23NL Ths. Lê Thị Hồng Thuy Học kỳ 2/2018-2019 18
Ví dṇ 21. H®p có 5 bi dỏ, 7 bi trắng. Lấy lần lmợt khȏng hoàn lại 2 bi. Biết rằng lần
m®t lấy dmợc bi T, tính xác suất lần 2 lấy dmợc bi T?
Giải. D°t A = “lấy dmợc bi T lần 1”, B = “lấy dmợc bi T lần 2”. Ta có 7 C2 7 P (A) = , P (AB) = 7 = C2 . 22 12 12 Do dó 7 22 6
P(B|A) = P(AB) = = . P (A) 712 11
Dịnh nghĩa 2.3.2. Nếu P (A|B) = P (A), nghǐa là sự xuất hi»n của biến cố B khȏng
ảnh hmởng dến xác suất của biến cố A, thì ta nói A d®c l¾p với B.
2.3.3 Công thfíc xác suất nhân
Với A và B là hai biến cố bất kì, ta có:
P (AB) = P (A).P (B|A) = P (B).P (A|B). (2.9)
Ví dṇ 22. Cho m®t h®p bi dựng 5 bi trắng, 4 bi den. Rút ngấu nhiȇn khȏng hoàn
lại lần lmợt 2 bi. Hǎy tìm xác suất dễ rút dmợc bi trắng trmớc bi den sau.
Giải. A = “Rút dmợc bi trắng”, B = “Rút dmợc bi den”. Khi dó, AB = “Rút dmợc
bi trắng trmớc và bi den sau”. Áp dụng cȏng thác xác suất nhȃn,
P (AB) = P (A).P (B|A). Ta có
P(A) = |A| = 5, P (B|A) = 4 = 1. |Ω| 9 8 2 Vªy 5 1 5
P (AB) = P (A).P (B|A) = 9 2 = 18.
Mď rộng 2.3.2. Gọi A, B, C, D, Ai, i = 1, . . . , n là các biến cố bất kỳ, ta có:
P (ABC) = P (A).P (B|A).P (C|AB), (2.10)
P (ABCD) = P (A).P (B|A).P (C|AB).P (D|ABC), (2.11)
P (A1A2 . . . An) = P (A1).P (A2|A1).P (A3|A1A2) . . . P (An|A1 . . . An−1).(2.12)
H» quả 2.3.3. Nếu A và B là hai biến cố d®c lªp thì
P (AB) = P (A).P (B). (2.13) K22T, K23NL Ths. Lê Thị Hồng Thuy Học kỳ 2/2018-2019 19
Chú j 2.3.1. Nếu hai biến cố A và B là d®c lªp, thì A cǔng d®c lªp với B.
Chfíng minh. Giả sả A, B là d®c lªp. Vì A = AB + AB, và AB và AB xung khắc, nȇn ta có
P (A) = P (AB) + P (AB)
= P (A)P(B) + P (AB) (vì A, B d®c lªp) Do dó, P AB
= P (A) (1 — P(B))
= P (A)P (B).
Dịnh nghĩa 2.3.3. Ba biến cố A, B, C dmợc gọi là d®c l¾p nếu
P (ABC) = P (A).P (B).P (C)
P (AB) = P (A).P (B)
P (AC) = P (A).P (C)
P (BC) = P (B).P (C)
Tỗng quát, n biến cố A1, A2, . . . , An dmợc gọi là d®c l¾p nếu bất kỳ k biến cố
A1′, A2′, . . . , Ar′, r ≤ n
P(A1′A2′ · · · Ar′) = P(A1′).P(A2′) · · · P(Ar′)
Chú ý rằng, nếu tà n biến cố d®c lªp A1, A2, . . . , An, i = 1, 2, . . . , n, ta thành lªp
n biến cố B1, B2, . . . , Bn, i = 1, 2, . . . , n, với Bi = Ai hay Bi = Ai, thì các biến cố
B1, B2, . . . , Bn, i = 1, 2, . . . , n, cǔng d®c lªp.
Ví dṇ 23. Cho m®t h®p bi dựng 5 bi trắng, 4 bi den. Rút ngấu nhiȇn lần lmợt tàng
bi ra 2 bi (rút có hoàn lại). Hǎy tìm xác suất dễ rút dmợc bi trắng trmớc bi den sau.
Giải. A = “Rút dmợc bi trắng”, B = “Rút dmợc bi den”, suy ra AB = “Rút dmợc
bi trắng trmớc và bi den sau”.
Do rút có hoàn lại nȇn hai biến cố A, B d®c lªp nhau. Vì vªy
P (AB) = P (A).P (B). Ta có
P (A) = |A| = 5, P (B) = |B| = 4. |Ω| 9 |Ω| 9 Vªy 5 4 20
P (AB) = P (A).P (B) = . = . 9 9 81
Ví dṇ 24. Ba xạ thủ A, B và C d®c lªp với nhau cùng nỗ súng vào m®t mục tiȇu.
Xác suất trúng của xạ thủ A, B và C tmơng áng là 0, 4; 0, 5 và 0, 7.
a. Tính xác suất dễ chỉ có duy nhất m®t xạ thủ bắn trúng.
b. Tính xác suất dễ có ít nhất m®t xạ thủ bắn trúng. K22T, K23NL Ths. Lê Thị Hồng Thuy Học kỳ 2/2018-2019 20 HGďng dẫn
Gọi A = “Xạ thủ A bắn trúng”, P(A) = 0, 4;
B = “Xạ thủ B bắn trúng”, P (B) = 0, 5;
C = “Xạ thủ C bắn trúng”, P(C) = 0, 7.
a. D°t H = “Chỉ có duy nhất m®t xạ thủ bắn trúng”
H = ABC + ABC + ABC
Sả dụng cȏng thác (2.3) và (2.9) (chú ý A, B và C d®c lªp), ta có
P (H) = P (A)P (B)P (C) + P (A)P (B)P (C) + P (A)P (B)P (C)
= (0, 4)(0, 5)(0, 3) + (0, 6)(0, 5)(0, 7) + (0, 6)(0, 5)(0, 3) = 0, 36.
b. D°t G = “Có ít nhất m®t xạ thủ bắn trúng”
G = A + B + C
P (D) = P (A) + P(B) + P(C) — P(A)P(B) — P(A)P(C) — P(B)P(C) + P(A)P(B)P(C)
= 0, 4 + 0, 5 + 0, 7 — 0, 2 — 0, 35 — 0, 28 + 0, 14 = 0, 91.
Ta có thễ tính P (D) bằng cách dùng cȏng thác (2.6). D = AB C Vªy,
P (D) = P (A)P (B)P ( C)
= (0, 6)(0, 5)(0, 3) = 0, 09.
Tà dó P (D) = 1 — P (D) = 0, 91.
2.3.4 Công thfíc xác suất dầy dủ
Cho m®t họ các biến cố A1, A2, . . . , An trong m®t phép thả ngấu nhiȇn. Họ A1, A2, . . . , An
dmợc gọi là dầy dủ nếu có duy nhất m®t biến cố trong họ xảy ra khi thực hi»n phép thả.
Nói khác di, họ A1, A2, . . . , An dầy dủ nếu
( A1 + A2 + ... + An = Ω,
AiAj = ∅, ∀i /= j.
Ví dṇ 25. Khi gieo dồng xu, thì biến cố A = “xuất hi»n m°t số” và biến cố B = “xuất
hi»n m°t hình” tạo thành h» dầy dủ.
Ví dṇ 26. Quan sát bài thi của m®t sinh viȇn. Gọi A0, A1, . . . , A10 tmơng áng là biến
cố bài thi dmợc 0, 1, . . . , 10 diễm, thì các biến cố A0, A1, . . . , A10 tạo thành h» dầy dủ. K22T, K23NL





