lOMoARcPSD| 36006477 lOMoAR cPSD| 36006477 PHẦN I XÁC SUẤT Chương I
BIẾN CỐ NGẪU NHIÊN
VÀ XÁC SUẤT CỦA BIẾN CỐ Nội dung của chương  Biến cố ngẫu nhiên
 Không gian mẫu, biến cố sơ cấp, phân loại các biến cố
 Xác suất của một biến cố
 Định nghĩa xác suất theo lối cổ điển
 Định nghĩa xác suất theo lối thống kê
 Các công thức tính xác suất lOMoARcPSD| 36006477
 Cộng, xác suất có điều kiện, nhân, xác suất đầy đủ, công
thức Bayes, công thức Bernoulli lOMoAR cPSD| 36006477
Biến cố ngẫu nhiên và xác suất
của biến cố ngẫu nhiên © 2003 Prentice-Hall, Inc. lOMoARcPSD| 36006477
1.1 Phép thử và biến cố  Phép thử
 Là việc thực hiện một nhóm điều kiện xác định nào đó để
quan sát một hiện tuợng có xảy ra hay không
 Phép thử phải có ít nhất 2 kết cục có thể xảy ra  Biến cố ngẫu nhiên
 Là kết quả xảy ra hay không xảy ra của việc thực hiện phép thử lOMoARcPSD| 36006477
 VD. Gieo một con xúc xắc là một phép thử
- Xuất hiện mặt một chấm là biến cố ngẫu nhiên
- Xuất hiện mặt chẵn là biến cố ngẫu nhiên
 VD. Lấy một lá bài trong tất cả 52 lá của một bộ bài tây là phép thử
 VD. Ném hòn đá xuống nước, xem xét hòn đá nổi hay chìm lOMoARcPSD| 36006477 1.2 Các loại biến cố
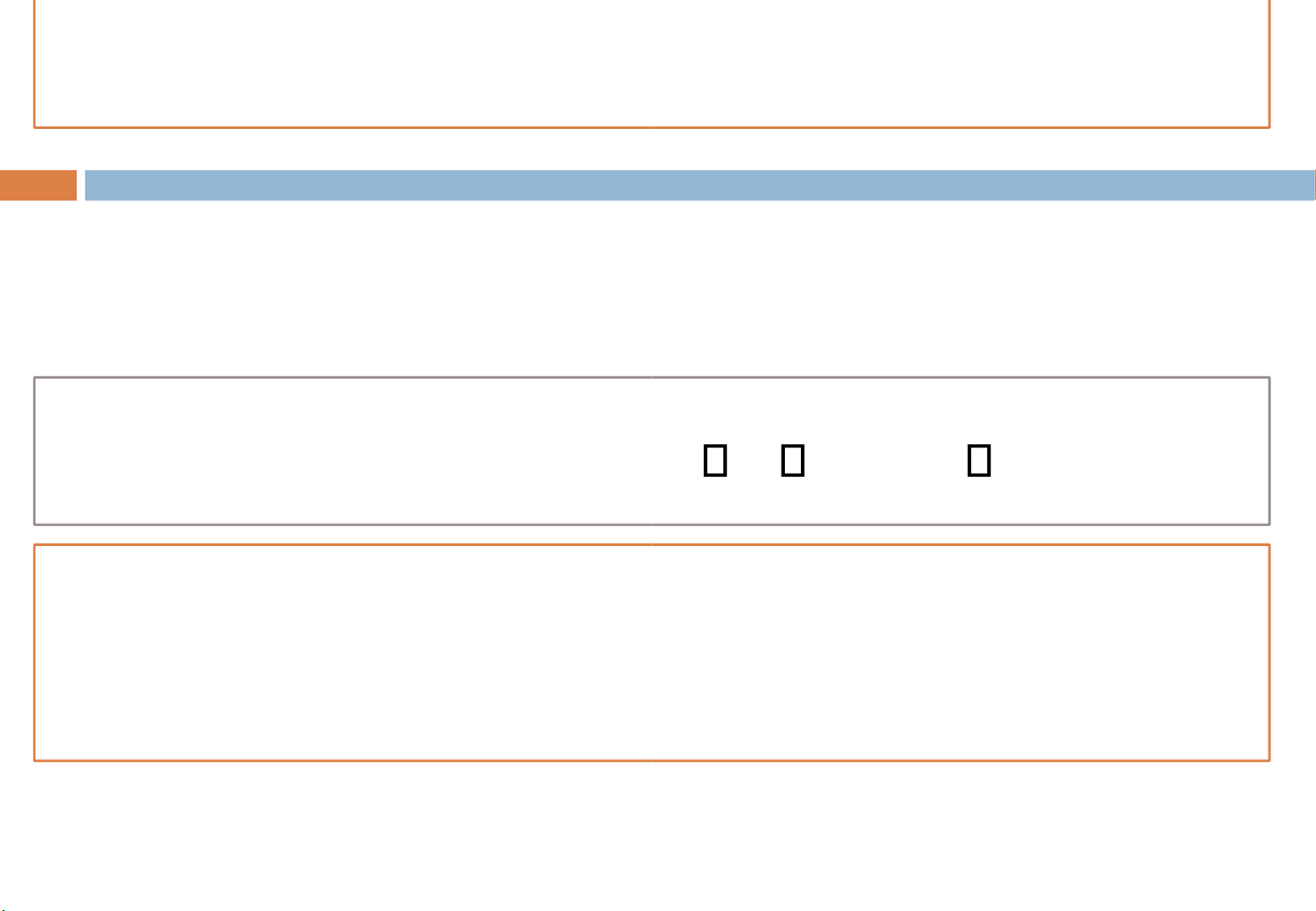
 Biến cố chắc chắn ( ) là biến cố nhất định xảy ra.
 Biến cố không thể ( ) là biến cố nhất định không xảy ra
 VD:Gieo một con xúc xắc:
- Biến cố xuất hiện mặt có số chấm nhỏ hơn 7 là biến cố chắc chắn.
- Biến cố xuất hiện mặt có 7 chấm là biến cố không thể. lOMoARcPSD| 36006477 Ví dụ
Xétmộtgiađìnhcó2 ngườicon
A = “giađìnhcó1 con traivàcon gái”
B = “giađìnhcó2 ngườicon”
C = “giađìnhcó3 con trai”
BiếncốnàolàBCNN. Bccc. Bckt
Một hộp có 8 sản phẩm trong đó có 2 sản phẩm xấu và 6 sản phẩm
tốt. Lấy ngẫu nhiên 3 sản phẩm từ hộp
A = “Lấy được 3 sp xấu”
B = “Lấy được 3 sản phẩm”
C = “Lấy được 1 sản phẩm tốt và 2 sản phẩm xấu” 1.3. lOMoARcPSD| 36006477 Các phép toán trên BCNN Biến cố kéo theo
Biến cố A kéo theo biến cố B (A B) nghĩa là nếu biến cố A
xảy ra thì biến cố B xảy ra Ví dụ Gia đình có 2 người con
A = “gia đình có 2 con gái”
B = “Gia đình có con gái ”
Một thí sinh thi đại học
A = “Thí sinh thi đậu đại học” lOMoARcPSD| 36006477
B = “Thí sinh được điểm 10 môn Toán”
1.3. Các phép toán trên BCNN
Biến cố bằng nhau (tương đương)
Biến cố A bằng biến cố B (A = B) A B và B A
Ví dụ Tung một con xúc xắc đồng chất
A = “Mặt chẵn xuất hiện”
B = “Xuất hiện mặt 2, 4, 6 chấm”
C = “Xuất hiện mặt 2, 4 chấm” 1.3. lOMoARcPSD| 36006477 Các phép toán trên BCNN
Một hộp có 4 bi trắng, 2 bi xanh và 2 bi vàng. Lấy ngẫu nhiên 2 bi để xem màu.
A = “lấy được 1 bi trắng”, B = “lấy được 1 bi xanh” Biến cố tổng
Biến cố tổng của A và B (A+B ) ít nhất một trong hai biến cố xảy ra
Ví dụ Tung một con xúc xắc đồng chất. Mặt nào có khả năng xuất hiện
A = “Mặt chẵn xuất hiện” lOMoARcPSD| 36006477
B = “Xuất hiện mặt lẻ ”
C = “Xuất hiện mặt chia hết cho 3”. Tìm A+B, A+C; B+C 1.3. lOMoARcPSD| 36006477 Các phép toán trên BCNN Biến cố tích
Biến cố tích của A và B (A.B ) đồng thời cả hai biến cố xảy ra
Ví dụ Tung một con xúc xắc đồng chất. Mặt nào có khả năng xuất hiện
A = “Mặt chẵn xuất hiện”
B = “Xuất hiện mặt lẻ ”
C = “Xuất hiện mặt chia hết cho 3”. Tìm A.B, A.C; B.C Biến cố xung khắc 1.3. lOMoARcPSD| 36006477 Các phép toán trên BCNN
Biến cố A và B được gọi là xung khắc nếu A, B không đồng thời xảy ra
Ví dụ Tung một con xúc xắc đồng chất. Mặt nào có khả năng xuất hiện
A = “Mặt chẵn xuất hiện”
B = “Xuất hiện mặt lẻ ”
C = “Xuất hiện mặt chia hết cho 3”. Biến cố đối lập
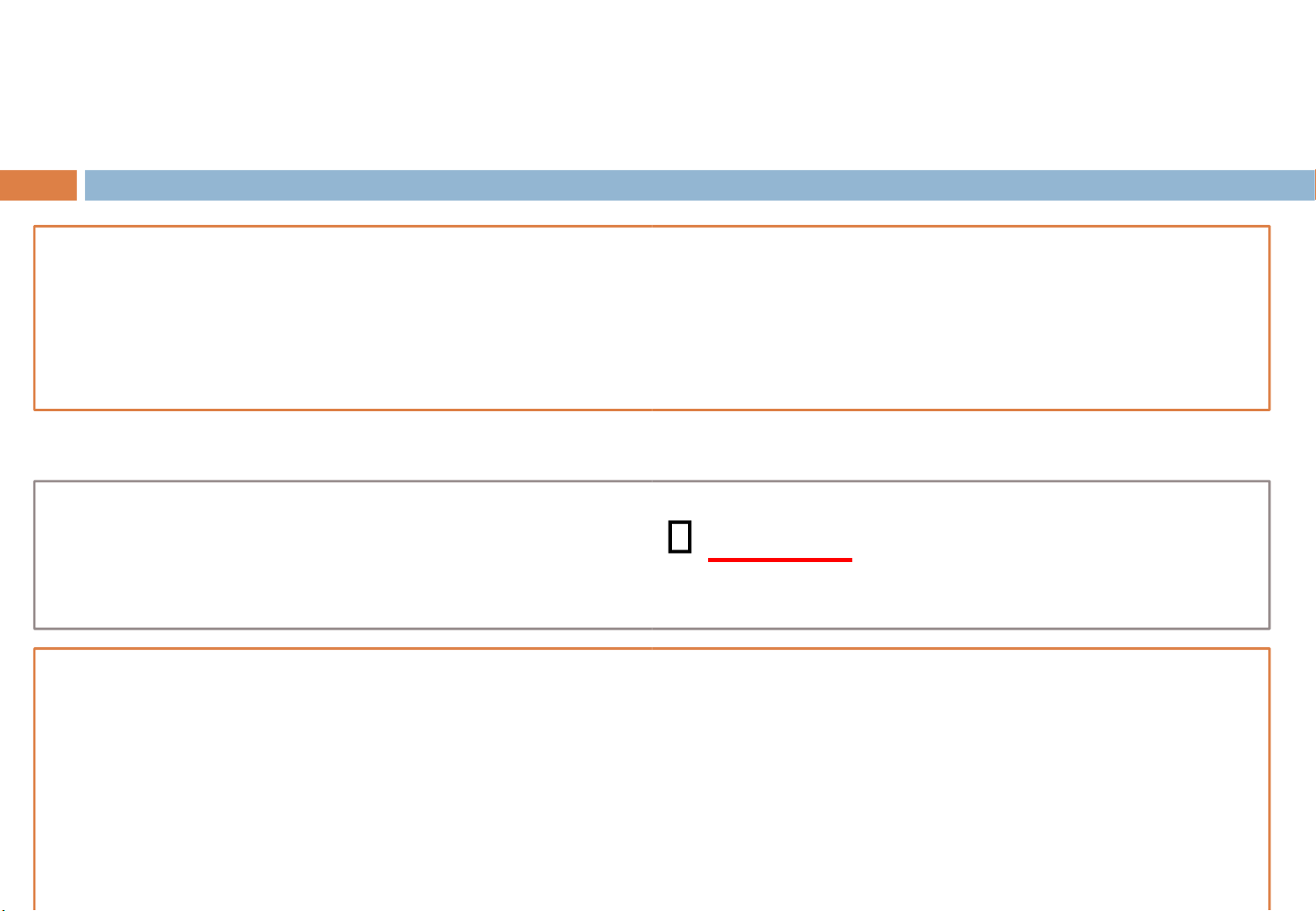
Biến cố đối lập của A A không xảy ra. Ký hiệu A 1.3. lOMoARcPSD| 36006477 Các phép toán trên BCNN
Ví dụ Tung một con xúc xắc đồng chất.
A = “Mặt chẵn xuất hiện”
B = “Xuất hiện mặt lẻ ”
C = “Xuất hiện mặt chia hết cho 2 hoặc 4”.
A, B có đối lập, B, C có đối lập
Ví dụ. Nhận xét sau đúng hay sai:
A, B xung khắc thì A, B đối lập Biến cố sơ cấp 1.3. lOMoARcPSD| 36006477 Các phép toán trên BCNN
Biến cố sơ cấp là biến cố không thể biểu diễn thành tổng của các biến cố khác.
Tập hợp tất cả các biến cố sơ cấp được gọi là kg mẫu
Ví dụ 1. Tung một con xúc xắc đồng chất.
Ai = “mặt có i chấm xuất hiện”, i = 1,2…, 6
B = “xuất hiện mặt lẻ” Biến cố sơ cấp
Ví dụ 2. Xét gia đình có 2 người con. Tìm tất cả các biến cố sơ cấp và không gian mẫu 1.3. lOMoARcPSD| 36006477 Các phép toán trên BCNN
Ví dụ 3. Tung một đồng xu 2 lần. Hãy xác định các biến cố sơ cấp và không gian mẫu.
Ví dụ 4. Tung một xúc xắc 2 lần. Biến cố nào là biến cố sơ cấp
A = “xuất hiện 2 mặt 4 chấm”
B = “xuất hiện một mắt 4 chấm, một mặt 6 chấm”
C = “tổng số chấm là 8” lOMoARcPSD| 36006477 Ví dụ
Có ba hộp sản phẩm, mỗi hộp có 10 sản phẩm trong đó có 3
sản phẩm xấu. Lấy mỗi hộp 1 sản phẩm.
Gọi Ai = “lấy được sản phẩm tốt ở hộp thứ i”, i = 1,2, 3.
Hãy biểu diễn qua Ai các biến cố sau: a)
A = “lấy được ba sản phẩm tốt” b)
B = “lấy được một sản phẩm tốt” c)
C = “lấy được sản phẩm tốt” d)
D = “không có sản phẩm nào tốt” lOMoARcPSD| 36006477 Ví dụ
Có 3 máy hoạt động độc lập. Gọi Ai = “máy thứ i bị hỏng.”,
i = 1,2, 3. Hãy biểu diễn qua Ai các biến cố sau: a)
A = “chỉ có máy 1 hỏng” b)
B = “Máy 1, 2 hỏng nhưng máy 3 không hỏng” c)
Ci = “Có i máy hỏng”, i = 1, 2, 3 d)
D = “Có nhiều nhất 2 máy hỏng” e)
E=“ Có ít nhất 2 máy hỏng” © 2003 Prentice-Hall, Inc. lOMoARcPSD| 36006477 Ví dụ © 2003 Prentice-Hall, Inc.
Một hộp có 4 bi trắng và 3 bi xanh. Lấy từ hộp ra 2 bi
để xem màu theo ba cách: Cách 1. Lấy ngẫu nhiên 2
bi Cách 2. Lấy lần lượt 2 bi.
Cách 3. Lấy có hoàn lại 2 bi
Tính xác suất lấy được 2 bi trắng lOMoARcPSD| 36006477
2. Xác suất của một biến cố
2.1. Định nghĩa xác suất cổ điển
Nếu trong một phép thử có n biến cố sơ cấp đồng khả năng
xuất hiện trong đó có m BCSC kéo theo biến cố A thì xác suất của A là m P A( ) n 2. 2.Tính chất - P( ) = 0 - P( ) = 1
- 0 P(A) 1 - A B thì P(A) P(B) lOMoARcPSD| 36006477
2.3. Ý nghĩa của xác suất
- Xác suất là số đo mức độ lOMoARcPSD| 36006477
1 xuất hiện của một biến cố sẽ xảy ra Chắc
trong một phép thử nhiều hay ít chắn
- Nếu p ~ 0 thì biến cố A gần như không xảy ra 0.5
- Nếu p ~ 1 thì biến cố A gần như chắc chắn xẩy ra 0
VD. Gieo hai con xúc xắc. Tính xác suất để
xuất hiện mặt bốn chấm và mặt sáu chấm Không thể lOMoARcPSD| 36006477 lOMoARcPSD| 36006477
2.4. Định nghĩa xác suất theo thống kê
Tần suất: Nếu thực hiện n lần phép thử, trong đó có m lần
xuất hiện biến cố A thì tần suất của A trong dãy n phép thử là tỷ số m/n. lOMoARcPSD| 36006477 fn( )A m n
Xác suất của biến cố A (ký hiệu là P(A)) được xác định:
P A( ) lim fn( )A n
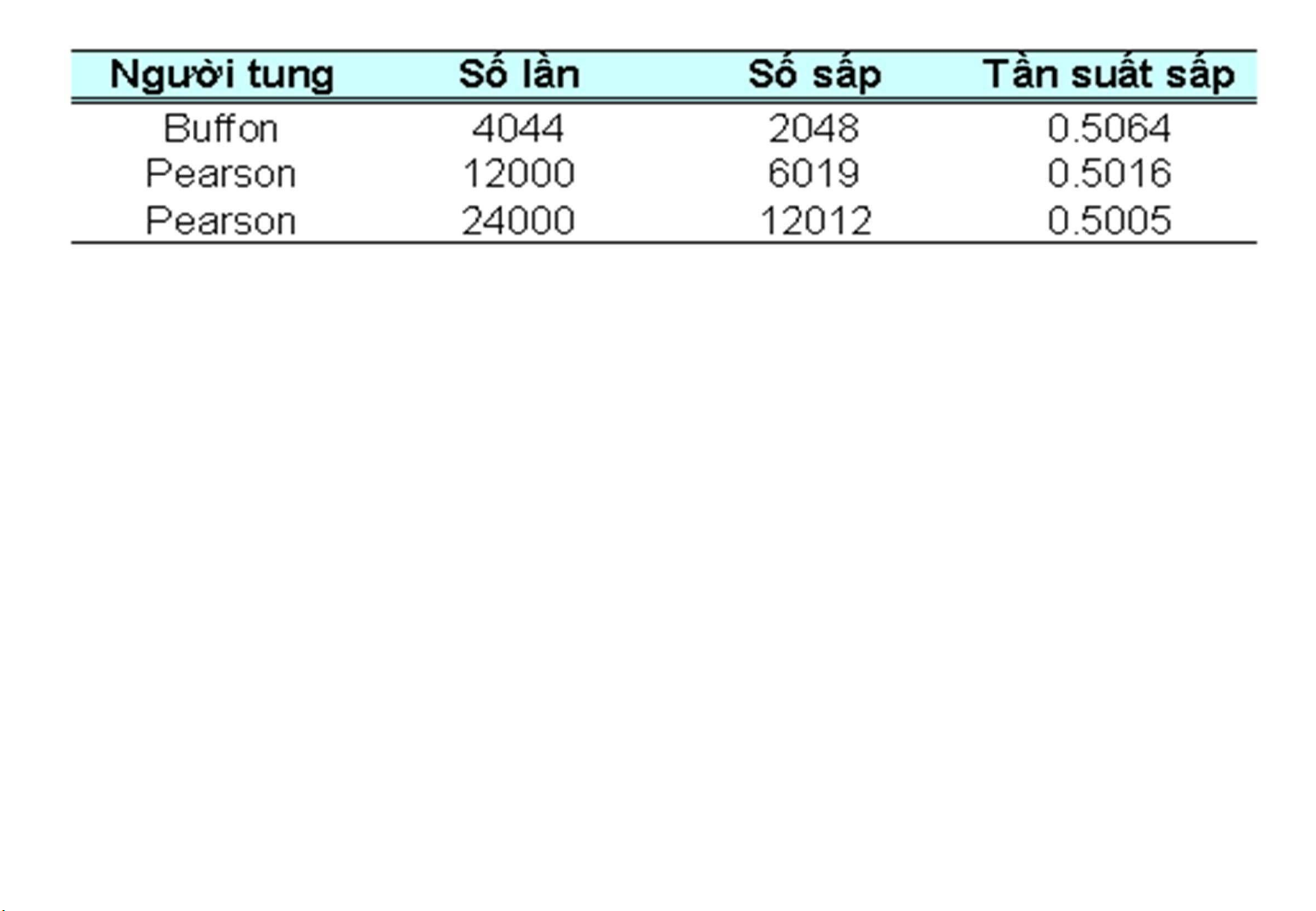
Ví dụ: Tung một đồng xu. Đếm số lần xuất hiện mặt sấp lOMoARcPSD| 36006477
Vậy xác suất xuất hiện mặt sấp là 0,5
2.5. Định nghĩa xác suất hình học, định nghĩa tổng quát
2.6. Nguyên lý xác suất lớn, xác suất nhỏ lOMoARcPSD| 36006477 Ví dụ
Một khách sạn có 6 phòng đơn. Có 6 khách nam và 4
khách nữ đến thuê phòng. Người quản lý khách sạn chọn
ngẫu nhiên 6 người để cho thuê. Tính xác suất để: a)
6 nam được thuê phòng (A) b)
2 nữ được thuê phòng (B) c)
Ít nhất 2 nữ được thuê phòng (C ) lOMoARcPSD| 36006477 Ví dụ
Ba khách hàng đi vào 6 quầy phục vụ của một ngân hàng. Tính xác suất để: a)
Cả 3 khách cùng đến một quầy (A) b)
Mỗi người đến một quầy khác nhau (B) c)
Hai trong 3 người đến một quầy (C) d)
Chỉ có một khách đến quầy số 1 (D) lOMoARcPSD| 36006477 Ví dụ Ví dụ
Có 30 tấm thẻ được đánh số từ 1 đến 30. Chọn ngẫu nhiên
10 tấm thẻ. Tính xác suất để: a)
Tất cả 10 thẻ đều là số chẵn b)
Có đúng 5 thẻ chia hết cho 3 lOMoARcPSD| 36006477 c)
Có 5 thẻ mang số lẻ, 5 thẻ mang số chẵn trong đó có 1 thẻ chia hết cho 10
Có 2 hộp đựng sản phẩm:
Hộp 1: 12 sản phẩm trong đó có 4 phế phẩm
Hộp 2: 10 sản phẩm trong đó có 3 phế phẩm. Chọn
ngẫu nhiên mỗi hộp một sản phẩm. Tính xác suất: a.
Lấy được 1 phế phẩm b. Lấy được 2 phế phẩm c.
Lấy được ít nhất một phế phẩm lOMoARcPSD| 36006477 Ví dụ
Một lớp học có 30 sinh viên trong đó có 20 SV biết
tiếng Anh, 15 SV biết vi tính, 12 biết tiếng Pháp. 10
biết TA và Vi tính, 6 SV biết Tiếng Anh và Tiếng
pháp, 5 SV biết Tiếng pháp và vi tính, 2 người biết
cả 3 loại. Chọn ngẫu nhiên một người. Tính xác suất a)
Biết ít nhất một loại kỹ năng lOMoARcPSD| 36006477 Ví dụ b) Chỉ biết một loại c) Biết 2 loại
Người ta thống kê được rằng trong 3 tháng cuối năm
có 6 trận mưa lớn. Tính tỷ lệ những ngày không
có mưa lớn quá một lần trong thời gian đó lOMoARcPSD| 36006477 Ví dụ
Có 5 bi bỏ ngẫu nhiên từng bi vào 6 hộp. Tính xác suất để: a. Có hộp có 5 bi b.
Mỗi hộp có không quá 1 bi c. Có hộp có 3 bi lOMoARcPSD| 36006477
Chọn ngẫu nhiên 2 sản phẩm từ hộp có 6 chính
phẩm và 4 phế phẩm. Tính xs lấy được 2 chính phẩm là: A. 1/2 B. 1/3 C. 1/6 D. 2/3
Chọn ngẫu nhiên lần lượt từng sản không hoàn
lại ra 3 sản phẩm từ hộp có 6 chính phẩm và 2
phế phẩm. Tính xs lấy được 2 chính phẩm là:
Downloaded by nguyen mo mo nguyen (ntm081102@gmail.com) lOMoARcPSD| 36006477 A. 5/56 B. 15/56 C. 15/14 D. 15/28